北京市东城区普通高中示范校高三年级综合能力测试
北京市东城区2023-2024学年高三下学期综合练习(一)试题

北京市东城区2023-2024学年度第二学期高三综合练习(一)生 物 2024.4 本试卷共10页,共100分。
考试时长90分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共30分)本部分共15题,每题2分,共30分。
在每题列出的四个选项中,选出最符合题目要求的一项。
1. 支原体是一类可用人工培养基培养的微小生物,会引发支原体肺炎等疾病。
如图为支原体的结构模式图。
下列关于支原体的叙述错误..的是A. 遗传物质是DNA和RNAB. 能完成蛋白质合成等生命活动C. 与细菌的区别之一是没有细胞壁D. 与动物细胞的主要区别是没有核膜2. 研究人员在适宜光强和黑暗条件下分别测定发菜放氧和耗氧速率随温度的变化,绘制曲线如图所示。
下列叙述错误..的是A.发菜生长的最适温度是25℃左右B.30℃时净光合速率是150μmol/(mg·h)C.35℃时光合作用速率等于呼吸作用速率D.在放氧和耗氧的过程中都有ATP的产生3. 下图是显微镜下观察到的洋葱(2n=16)根尖细胞分裂的部分图像,相关叙述正确的是a b c dA. 实验中制片的流程为:解离→染色→漂洗→制片B. a时期细胞中发生同源染色体两两配对的现象C. b时期细胞中的染色体数目与c时期相同D. d时期细胞中央出现细胞板逐渐扩展形成细胞壁4. 新型抗虫棉T与传统抗虫棉R19、sGK均将抗虫基因整合在染色体上,但具有不同的抗虫机制。
对三者进行遗传分析,杂交组合及结果如下表所示。
以下说法错误..的是 杂交组合 F1F2① T×R19 全部为抗虫株 全部为抗虫株② T×sGK 全部为抗虫株 抗虫株∶感虫株=15∶1A. T与R19的抗虫基因可能位于一对同源染色体上B. T与sGK的抗虫基因插入位点在非同源染色体上C. 杂交组合②的F2抗虫株中抗虫基因数量不一定相同D. R19与sGK杂交得到的F2中性状分离比为3:15. 16SrRNA 是原核生物核糖体RNA 的一种,在物种间有较大差异。
2022-2023学年北京市东城区高三下学期综合练习(一)数学试卷(PDF版)

北京市东城区2022-2023学年度第二学期高三综合练习(一)数 学 2023.3本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合22{|}0A x x -=<,且a A ∈,则a 可以为(A )2- (B )1-(C )32(D (2)在复平面内,复数iz对应的点的坐标是(3,1)-,则z = (A )13i + (B )3i + (C )3i -+ (D )13i -- (3)抛物线24x y =的准线方程为(A )1x = (B )1x =- (C )1y = (D )1y =- (4)已知0x >,则44x x-+的最小值为 (A )2- (B )0(C )1 (D )(5)在△ABC 中,a =2b c =,1cos 4A =-,则ABC S =△(A )(B )4(C ) (D )(6)设,m n 是两条不同的直线,αβ,是两个不同的平面,且m α⊂,αβ ,则“m n ⊥”是“n β⊥”的(A )充分而不必要条件 (B )必要而不充分条件(C )充分必要条件 (D )既不充分也不必要条件 (7)过坐标原点作曲线2e1x y -=+的切线,则切线方程为(A )y x = (B )2y x = (C )21e y x = (D )e y x =(8)已知正方形ABCD 的边长为 2,P 为正方形ABCD 内部(不含边界)的动点,且满足0PA PB ⋅=,则CP D P ⋅的取值范围是(A )(0,8] (B )[0,8) (C )(0,4] (D )[0,4)(9)已知1a ,2a ,3a ,4a ,5a 成等比数列,且1和4为其中的两项,则5a 的最小值为(A )64- (B )8- (C )164 (D )18(10)恩格斯曾经把对数的发明、解析几何的创始和微积分的建立称为十七世纪数学的三大成就.其中对数的发明,曾被十八世纪法国大数学家拉普拉斯评价为“用缩短计算时间延长了天文学家的寿命”.已知正整数N 的70次方是一个83位数,由下面表格中部分对数的近似值(精确到0.001),可得N 的值为(A )13 (B )14 (C )15 (D )16第二部分(非选择题 共110分)二、填空题 共5小题,每小题5分,共25分。
2024年北京市东城区高三下学期高考二模考试生物试卷含答案

北京市东城区2023-2024学年度第二学期高三综合练习(二)生物2024.5本试卷共10页,共100分。
考试时长90分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共30分)本部分共15题,每题2分,共30分。
在每题列出的四个选项中,选出最符合题目要求的一项。
1.生物膜的出现保证了细胞生命活动高效、有序进行。
下列结构具有生物膜的是A.溶酶体B.中心体C.染色体D.核糖体2.如图表示H+和蔗糖进出植物细胞的方式。
据图分析,下列实验处理中,可使蔗糖进入细胞速率加快的是A.降低细胞外蔗糖浓度B.降低细胞质H+浓度C.降低ATP合成酶活性D.降低膜上协同转运蛋白数量3.如图所示,细胞周期包括分裂间期(分为G1期、S期和G2期)和分裂期(M期),S期进行DNA复制。
对某动物(2n=12)的肠上皮细胞用含放射性的胸苷(DNA复制原料之一)短期培养15 min后,洗去游离的放射性胸苷,换用无放射性的新鲜培养液培养,并定期检测。
下列叙述错误的是A.d→a→b→c→d可表示一个细胞周期B.显微镜下观察,间期细胞数目多于M期C.M期细胞中染色体数目变化为12→24→12D.更换培养液后约10.1h开始出现被标记的M期细胞4.烟草花叶病毒(TMV)由蛋白质和RNA组成,用其RNA侵染正常烟草叶,叶片中可检测到TMV。
TMV侵染会引发烟草细胞中基因N表达上调,介导烟草的抗病毒反应,在侵染位点处形成坏死斑。
以下说法错误的是A.TMV的遗传物质是RNAB.可用烟草研磨液培养TMVC.敲除基因N会降低烟草抗TMV能力D.坏死斑能限制TMV的进一步扩散5.雌性小鼠在精子入卵后,被激活的卵子会完成减数分裂Ⅱ排出第二极体,如图所示,第二极体仅与受精卵分裂形成的2个子细胞之一接触。
在甲时期去除第二极体会导致胚胎明显缩小,不能正常存活,这一异常可通过向细胞1中注射第二极体的细胞提取液加以改善。
2024届北京市东城区高三下学期综合练习(一)(一模)英语试题(5)

2024届北京市东城区高三下学期综合练习(一)(一模)英语试题(5)一、听力选择题1. Where does the conversation probably take place?A.In a shop.B.In the man’s office.C.At the woman’s home.2. Who will go to a Christmas party ?A.Dorothy.B.Steven.C.Steven and his family3. What’s the girl doing?A.Reading a newspaper.B.Writing a story.C.Watching the news.4. What did Johnson do at the weekend?A.He attended a competition.B.He prepared for a speech.C.He played football with friends.5.A.She has lost a lot of weight.B.She lost some money last year.C.She spent a lot on cosmetic surgery.D.She is having health problems.二、听力选择题6. 听下面一段较长对话,回答以下小题。
1. What is playing on the radio station now?A.Commercials.B.A talk show.C.A music program.2. What do we know about the man?A.He hates to spend much time on news.B.He prefers detailed news stories.C.He often listens to news broadcasts.7. 听下面一段较长对话,回答以下小题。
北京市东城区2024届高三下学期综合练习(一)(一模)数学试题(含答案与解析)_4942

北京市东城区2023~2024学年度第二学期高三综合练习(一)数学本试卷共6页,150分.考试时长120分钟.注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 如图所示,U 是全集,,A B 是U 的子集,则阴影部分所表示的集合是( )A. A B ⋂B. A B ⋃C. ()U A B ⋂ðD. ()U A B ⋃ð2. 已知,R,0a b ab ∈≠,且a b <,则( ) A.11a b> B. 2ab b < C. 33a b <D. lg lg a b <3. 已知双曲线221x my -=的离心率为2,则m =( ) A 3B.13C. 3-D. 13-4. 设函数()11ln f x x=+,则( ) A. ()12f x f x ⎛⎫+=⎪⎝⎭ B. ()12f x f x ⎛⎫-=⎪⎝⎭C. ()12f x f x ⎛⎫= ⎪⎝⎭D. ()12f x f x ⎛⎫= ⎪⎝⎭.5. 已知函数()sin cos (0,0)f x t x x t ωωω=+>>的最小正周期为π,则函数()f x 的图象( )A. 关于直线π4x =-对称B. 关于点π,04⎛⎫-⎪⎝⎭对称 C. 关于直线π8x =对称 D. 关于点π,08⎛⎫⎪⎝⎭对称 6. 已知443243210()x m a x a x a x a x a +=++++,若0123481++++=a a a a a ,则m 的取值可以为( ) A. 2B. 1C. 1-D. 2-7. 《天工开物》是我国明代科学家宋应星所著的一部综合性科学技术著作,书中记载了一种制造瓦片的方法.某校高一年级计划实践这种方法,为同学们准备了制瓦用的粘土和圆柱形的木质圆桶,圆桶底面外圆的直径为20cm ,高为20cm .首先,在圆桶的外侧面均匀包上一层厚度为2cm 的粘土,然后,沿圆桶母线方向将粘土层分割成四等份(如图),等粘土干后,即可得到大小相同的四片瓦.每位同学制作四片瓦,全年级共500人,需要准备的粘土量(不计损耗)与下列哪个数字最接近.(参考数据:π 3.14≈)( )A 30.8mB. 31.4mC. 31.8mD. 32.2m8. 设等差数列{}n a 公差为d ,则“10a d <<”是“{}na n为递增数列”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件D. 既不充分也不必要条件9. 如图1,正三角形ABD 与以BD 为直径的半圆拼在一起,C 是弧BD的中点,O 为ABD △的中心.现将ABD △沿BD 翻折为1A BD ,记1A BD 的中心为1O ,如图2.设直线1CO 与平面BCD所成的角为.的θ,则sin θ的最大值为( )A.13B.12C.D.10. 已知()f x 是定义在R 上的函数,其图象是一条连续不断的曲线,设函数()()()()a f x f a g x a x a-=∈-R ,下列说法正确的是()A. 若()f x 在R 上单调递增,则存在实数a ,使得()a g x 在(),a ∞+上单调递增B. 对于任意实数a ,若()a g x 在(),a ∞+上单调递增,则()f x 在R 上单调递增C. 对于任意实数a ,若存在实数10M >,使得()1f x M <,则存在实数20M >,使得()2a g x M <D. 若函数()a g x 满足:当(),x a ∞∈+时,()0a g x ≥,当(),x a ∞∈-时,()0a g x ≤,则()f a 为()f x 的最小值第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11. 若复数1i iz +=,则z =_________.12. 设向量()()1,,3,4a m b ==- ,且a b a b ⋅=,则m =______. 13. 已知角,αβ的终边关于直线y x =对称,且()1sin 2αβ-=,则,αβ的一组取值可以是α=______,β=______.14. 已知抛物线21:4C y x =的焦点为1F ,则1F 的坐标为______;抛物线22:8C y x =的焦点为2F ,若直线()0y m m =≠分别与12,C C 交于,P Q 两点;且121PF QF -=,则PQ =______.15. 已知数列{}n a 的各项均为正数,满足21n n n a ca a +=+,其中常数c ∈R .给出下列四个判断:①若11,0a c =<,则()121n a n n <≥+; ②若1c =-,则()121n a n n <≥+; ③若()1,2n c a n n =>≥,则11a >; ④11a =,存实数c ,使得()2n a n n >≥. 其中所有正确判断的序号是______.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16. 在ABC中,cos cos cos a C c A B +=. (1)求B ∠;(2)若12,a D =为BC 边的中点,且3AD =,求b 的值.17. 某中学为了解本校高二年级学生阅读水平现状,从该年级学生中随机抽取100人进行一般现代文阅读速度的测试,以每位学生平均每分钟阅读的字数作为该学生的阅读速度,将测试结果整理得到如下频率分布直方图:(1)若该校高二年级有1500人,试估计阅读速度达到620字/分钟及以上的人数;(2)用频率估计概率,从该校高二学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为X ,求X 的分布列与数学期望()E X ;(3)若某班有10名学生参加测试,他们的阅读速度如下:506,516,553,592,617,632,667,693,723,776,从这10名学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为Y ,试在判断数学期望()E Y 与(2)中的()E X 的大小.(结论不要求证明) 18. 如图,在五面体ABCDEF 中,底面ABCD 为正方形,4,1AB EF ==.(1)求证://AB EF ;(2)若H 为CD 的中点,M 为BH的中点,,EM BH EM ⊥=,再从条件①、条件②这两个条件中选择一个作为已知,求直线CF 与平面ADE 所成角的正弦值. 条件①:ED EA =; 条件②:5AE =.注:如果选择条件①和条件②分别解答,按第一个解答计分 19. 已知函数()()ln 1f x x x =-.(1)求曲线()y f x =在2x =处的切线方程; (2)设()()g x f x '=,求函数()g x 的最小值;(3)若()2f x x a>-,求实数a 的值. 20. 已知椭圆2222:1(0)x y C a b a b +=>>短轴长为e =(1)求椭圆C 的方程;(2)设O 为坐标原点,直线l 是圆221x y +=的一条切线,且直线l 与椭圆C 交于,M N 两点,若平行四边形OMPN 的顶点P 恰好在椭圆C 上,求平行四边形OMPN 的面积.21. 有穷数列12,,,(2)n a a a n > 中,令()()*1,1,,p p q S p q a a a p q n p q +=+++≤≤≤∈N ,(1)已知数列3213,,,--,写出所有的有序数对(),p q ,且p q <,使得(),0S p q >;(2)已知整数列12,,,,n a a a n 为偶数,若(),11,2,,2n S i n i i ⎛⎫-+= ⎪⎝⎭,满足:当i 为奇数时,的(),10S i n i -+>;当i 为偶数时,(),10S i n i -+<.求12n a a a +++ 的最小值;(3)已知数列12,,,n a a a 满足()1,0S n >,定义集合(){}1,0,1,2,,1A i S i n i n =+>=- .若{}()*12,,,k A i i i k =∈N 且为非空集合,求证:()121,k i i i S n a a a >+++ .参考答案一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 如图所示,U 是全集,,A B 是U 的子集,则阴影部分所表示的集合是( )A. A B ⋂B. A B ⋃C. ()U A B ⋂ðD. ()U A B ⋃ð【答案】D 【解析】【分析】由给定的韦恩图分析出阴影部分所表示的集合中元素满足的条件,再根据集合运算的定义即可得解.【详解】由韦恩图可知阴影部分所表示的集合是()U A B ð. 故选:D.2. 已知,R,0a b ab ∈≠,且a b <,则( ) A.11a b> B. 2ab b < C. 33a b <D. lg lg a b <【答案】C 【解析】【分析】举出反例即可判断ABD ,利用作差法即可判断C. 【详解】当2,1a b =-=时,11,lg >lg a b a b<,故AD 错误; 当2,1a b =-=-时,221ab b =>=,故B 错误;对于C ,因a b <,所以0a b -<,因为0ab ≠,所以0a ≠且0b ≠,为则()()()3322213024a b a b a ab ba b a b b ⎡⎤⎛⎫-=-++=-++< ⎪⎢⎥⎝⎭⎣⎦, 所以33a b <,故C 正确. 故选:C.3. 已知双曲线221x my -=的离心率为2,则m =( ) A. 3 B.13C. 3-D. 13-【答案】B 【解析】【详解】由双曲线221x my -=可得:2211,a b m==,2c e a ====,所以13m =,故选:B . 4. 设函数()11ln f x x=+,则( ) A. ()12f x f x ⎛⎫+=⎪⎝⎭ B. ()12f x f x ⎛⎫-=⎪⎝⎭ C. ()12f x f x ⎛⎫= ⎪⎝⎭D. ()12f x f x ⎛⎫=⎪⎝⎭【答案】A 【解析】【分析】根据函数解析式,分别计算即可得解.【详解】函数()11ln f x x=+的定义域为()()0,11,+∞ , 对于A ,()1111111221ln ln ln lnf x f x x x x x⎛⎫+=+++=++= ⎪-⎝⎭,故A 正确; 对于B ,()111112111ln ln ln ln lnf x f x x x x x x⎛⎫-=+--=--=⎪-⎝⎭,故B 错误; 对于CD ,当e x =时,()11112,1011f x f x ⎛⎫=+==+= ⎪-⎝⎭,故CD 错误. 故选:A.5. 已知函数()sin cos (0,0)f x t x x t ωωω=+>>的最小正周期为π,则函数()f x 的图象( )A. 关于直线π4x =-对称B. 关于点π,04⎛⎫-⎪⎝⎭对称 C. 关于直线π8x =对称 D. 关于点π,08⎛⎫⎪⎝⎭对称 【答案】C 【解析】【分析】先利用辅助角公式化一,再根据周期性求出ω,根据最值求出t ,再根据正弦函数的对称性逐一判断即可.【详解】()()sin cos f x t x x x ωωωϕ=+=+,其中1tan tϕ=,因为函数的最小正周期为π, 所以2ππω=,解得2ω=,,=1t =(1t =-舍去),所以()πsin 2cos 224x x x f x ⎛⎫=+=+ ⎪⎝⎭,因为ππ144f ⎛⎫⎛⎫-=-=- ⎪ ⎪⎝⎭⎝⎭, 所以函数图象不关于直线π4x =-对称,也不关于点π,04⎛⎫- ⎪⎝⎭对称,故AB 错误;因为ππ82f ⎛⎫== ⎪⎝⎭,所以函数图象关于直线π8x =对称,不关于点π,08⎛⎫⎪⎝⎭对称,故C 正确,D 错误.故选:C .6. 已知443243210()x m a x a x a x a x a +=++++,若0123481++++=a a a a a ,则m 取值可以为( ) A. 2 B. 1 C. 1- D. 2-【答案】A 【解析】【分析】借助赋值法计算即可得.【详解】令1x =,有()443210118m a a a a a ++++==+, 即2m =或4m =-. 故选:A.7. 《天工开物》是我国明代科学家宋应星所著的一部综合性科学技术著作,书中记载了一种制造瓦片的方法.某校高一年级计划实践这种方法,为同学们准备了制瓦用的粘土和圆柱形的木质圆桶,圆桶底面外圆的直径为20cm ,高为20cm .首先,在圆桶的外侧面均匀包上一层厚度为2cm 的粘土,然后,沿圆桶母线方向将粘土层分割成四等份(如图),等粘土干后,即可得到大小相同的四片瓦.每位同学制作四片瓦,全年级共500人,需要准备的粘土量(不计损耗)与下列哪个数字最接近.(参考数据:π 3.14≈)( )A. 30.8mB. 31.4mC. 31.8mD. 32.2m【答案】B 【解析】【分析】结合圆柱体积公式求出四片瓦体积,再求需准备的粘土量.【详解】由条件可得四片瓦的体积22π1220π1020880πV =⨯⨯-⨯⨯=(3cm ) 所以500名学生,每人制作4片瓦共需粘土的体积为500880π440000π⨯=(3cm ), 又π 3.14≈,的的所以共需粘土的体积为约为31.3816m , 故选:B.8. 设等差数列{}n a 的公差为d ,则“10a d <<”是“{}na n为递增数列”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件【答案】A 【解析】【分析】利用等差数列通项公式求出na n,再利用单调数列的定义,结合充分条件、必要条件的意义判断即得.【详解】由等差数列{}n a 的公差为d ,得1n a a d nd =-+,则1n a a d d n n-=+, 当10a d <<时,10a d -<,而111n n >+,则111a d a d n n --<+,因此11n n a a n n +<+,{}n a n为递增数列;当{}n a n为递增数列时,则11n n a a n n +<+,即有111a d a dn n --<+,整理得1a d <,不能推出10a d <<,所以“10a d <<”是“{}n an为递增数列”的充分不必要条件.故选:A9. 如图1,正三角形ABD 与以BD 为直径的半圆拼在一起,C 是弧BD的中点,O 为ABD △的中心.现将ABD △沿BD 翻折为1A BD ,记1A BD 的中心为1O ,如图2.设直线1CO 与平面BCD 所成的角为θ,则sin θ的最大值为( )A.13B.12C.D.【答案】C 【解析】【分析】结合题意,可得1EO EC =1CO 在平面BCD 的投影为直线CE,借助正弦定理计算可得tan θ=tan θ的最大值即可得sin θ的最大值.【详解】取BD 中点E ,连接CE ,1A E ,由三角形ABD 为正三角形,故1O 在线段1A E 上,且1113EO A E BD ===,即1EO EC =, 由题意可得BD EC ⊥,1BD A E ⊥,1A E 、EC ⊂平面1ECO ,1A E EC E = , 故BD ⊥平面1ECO ,又1CO ⊂平面1ECO ,故直线1CO 在平面BCD 的投影为直线CE , 即1ECO θ=∠,则有()111sin sin sin sin πEO EC CO E O EC θθθ===∠--∠,整理可得tan θ=()10,πO EC ∠∈,令()()0,πf x x =∈,()f x ==',故当cos x ⎛∈- ⎝时,()0fx '<,当cos x ⎫∈⎪⎪⎭时,()0f x '>,令()00,πx ∈,且0cos x =,则0sin x ==, 则()f x 在()00,x 上单调递增,在()0,πx 上单调递减,即()f x 有最大值()0f x ===即tan θ,则sin θ=故选:C.【点睛】关键点点睛:本题关键点在于借助正弦定理表示出θ与1O EC ∠的关系,通过导数计算出tan θ的最大值从而得到sin θ的最大值.10. 已知()f x 是定义在R 上的函数,其图象是一条连续不断的曲线,设函数()()()()a f x f a g x a x a-=∈-R ,下列说法正确的是()A. 若()f x 在R 上单调递增,则存在实数a ,使得()a g x 在(),a ∞+上单调递增B. 对于任意实数a ,若()a g x 在(),a ∞+上单调递增,则()f x 在R 上单调递增C. 对于任意实数a ,若存在实数10M >,使得()1f x M <,则存在实数20M >,使得()2a g x M <D. 若函数()a g x 满足:当(),x a ∞∈+时,()0a g x ≥,当(),x a ∞∈-时,()0a g x ≤,则()f a 为()f x 的最小值【答案】D 【解析】【分析】首先理解函数()a g x 表达的是函数()f x 图像上两点割线的斜率,当x a →时,表示的为切线斜率,然后举反例设()f x x =可判断A 错误;设()2f x x =可得B 错误;设()sin f x x =可得C 错误;由函数单调性的定义可以判断D 正确. 【详解】函数()()()()a f x f a g x a x a-=∈-R 表达的是函数()f x 图象上两点割线的斜率,当x a →时,表示的为切线斜率;所以对于A :因为()f x 是定义在R 上的函数,其图象是一条连续不断的曲线,且()f x 在R 上单调递增, 所以设()f x x =,则()f a a =,此时()()()()1a f x f a x ag x a x ax a--===∈--R 为常数,即任意两点的割线的斜率为常数,故A 错误; 对于B :设()2f x x =,由图象可知,当x ∈R 时,随x 增大,点()(),x f x 与点()(),a f a 连线的割线斜率越来越大,即单调递增,但()f x 在R 不是单调函数,故B 错误;对于C :因为对于任意实数a 存在实数10M >,使得()1f x M <,说明()f x 为有界函数,所以设()sin f x x =,但割线的斜率不一定有界,如图当0x +→时,割线的斜率趋于正无穷,故C 错误;对于D :因为函数()a g x 满足:当(),x a ∞∈+时,()0a g x ≥, 即()()()()()()()00,a f x f a g x f x f a x a x a x a-⎡⎤=≥⇒--≥≠⎣⎦-,因为x a >,0x a ->,所以()()f x f a ≥; 同理,当(),x a ∞∈-时,()0a g x ≤, 即()()()()()()()00,a f x f a g x f x f a x a x a x a-⎡⎤=≤⇒--≤≠⎣⎦-,因为x a <,0x a -<,所以()()f x f a ≥; 所以()f a 为()f x 的最小值,故D 正确;故选:D.【点睛】关键点点睛:本题关键在于理解函数()a g x 表达的是函数()f x 图像上两点割线的斜率,当x a →时,表示的为切线斜率,然后通过熟悉的函数可逐项判断.第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11. 若复数1i iz +=,则z =_________.【解析】 【分析】利用复数的除法法则将复数表示为一般形式,然后利用复数的模长公式可计算出z 的值.【详解】()()21111i i i z i i i i i++===-+=- ,因此,z ==..【点睛】本题考查复数模的计算,同时也考查了复数的除法运算,考查计算能力,属于基础题.12. 设向量()()1,,3,4a m b ==- ,且a b a b ⋅=,则m =______.【答案】43-##113- 【解析】【分析】根据数量积的定义,向量共线的坐标表示,结合已知条件,求解即可. 【详解】设,a b的夹角为θ,cos a b a b a b θ⋅== ,故cos 1θ=,又[]0,πθ∈,故0θ=,,a b方向相同, 又()()1,,3,4a m b ==- ,则43m -=,解得43m =-,满足题意.故答案为:43-.13. 已知角,αβ的终边关于直线y x =对称,且()1sin 2αβ-=,则,αβ的一组取值可以是α=______,β=______.【答案】 ①.π3(答案不唯一,符合题意即可) ②. π6(答案不唯一,符合题意即可) 【解析】【分析】由角,αβ的终边关于直线y x =对称,可得π2π2k αβ+=+,再由()1sin 2αβ-=可得ππ6k β=+或ππ6k β=-+,即可求出答案. 【详解】因为角,αβ的终边关于直线y x =对称, 则π2π2k αβ+=+,Z k ∈,则π2π2k αβ=-+, 因为()1sin 2αβ-=,所以ππ1sin 2πsin 22πcos 2222k k ββββ⎛⎫⎛⎫-+-=-+== ⎪ ⎪⎝⎭⎝⎭,所有π22π3k β=+或π22π3k β=-+,Z k ∈, 解得:ππ6k β=+或ππ6k β=-+,Z k ∈,取0k =,β的一个值可以为π6,α的一个值可以为π3.故答案为:π3(答案不唯一,符合题意即可);π6(答案不唯一,符合题意即可).14. 已知抛物线21:4C y x =的焦点为1F ,则1F 的坐标为______;抛物线22:8C y x =的焦点为2F ,若直线()0y m m =≠分别与12,C C 交于,P Q 两点;且121PF QF -=,则PQ =______.【答案】 ①. ()1,0 ②. 2【解析】【分析】根据抛物线的方程即可得出焦点坐标,根据抛物线的定义求出12,PF QF ,进而可得出PQ . 【详解】由抛物线21:4C y x =,可得()11,0F ,设()()1122,,,P x y Q x y , 则11221,2PF x QF x =+=+,故121211PF QF x x -=--=,所以122x x -=, 所以122PQ x x =-=.故答案为:()1,0;2.15. 已知数列{}n a 的各项均为正数,满足21n n n a ca a +=+,其中常数c ∈R .给出下列四个判断:①若11,0a c =<,则()121n a n n <≥+; ②若1c =-,则()121n a n n <≥+; ③若()1,2n c a n n =>≥,则11a >; ④11a =,存在实数c ,使得()2n a n n >≥. 其中所有正确判断的序号是______. 【答案】②③④ 【解析】【分析】①直接取13c =-找矛盾;②通过21111111n n nn n n a a a a a a ++⇒=--=>-+,利用累加法求n a 的范围;③假设11a ≤找矛盾;④取2c =,根据函数单调性来确定其成立.【详解】对于①:若11,0a c =<,则21211ca c a a =+=+,当13c =-时,223a =,与213a <矛盾,①错误;对于②:若1c =-,则210n n n a a a +=-+>,所以01n a <<,又2112a a a =-+,若12113a a <-+,该不等式恒成立,即2013a <<, 由()2111111*********n n n n n n n nn n n n a a a a a a a a a a a a ++++⇒=⇒=+⇒-=--=--+由于01n a <<,所以111na >-, 所以1111n n a a +->,所以3n ≥时,11232111111111nn n n a a a a a a ---⎧->⎪⎪⎪->⎪⎨⎪⎪⎪->⎪⎩ ,累加得2112n n a a ->-, 所以2112231n n n n a a >-+>-+=+,所以()131n a n n <≥+, 综合得()121n a n n <≥+,②正确; 对于③:若()1,2n c a n n =>≥,21n n n a a a +=+,假设11a ≤,则21122a a a =+≤,与22a >矛盾,故11a >,③正确;对于④:当11a =时,若2c =,则212n n n a a a +=+,此时2121232a a a =+=>,根据二次函数22y x x =+可得其在()0,∞+上单调递增,并增加得越来越快,但是函数y x =在()0,∞+上单调递增,但增加速度恒定,故在22a >的情况下,n a n >必成立,即存在实数c ,使得()2n a n n >≥,④正确,故答案为:②③④.【点睛】方法点睛:对于数列判断题,我们可以通过赋值,举例的方法对选项进行确认和排除.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16. 在ABC中,cos cos cos a C c A B +=. (1)求B ∠;(2)若12,a D =为BC 边的中点,且3AD =,求b 的值. 【答案】(1)π6; (2)【解析】【分析】(1)由正弦定理可得sin()cos A C B B +=,结合三角和为π及诱导公式可得cos B =,即可得答案;(2)在ABD △中,由正弦定理可求得π2BAD ∠=,从而可得AB =ABC 中,利用余弦定理求解即可. 【小问1详解】解:因为cos cos cos a C c A B +=,由正弦定理可得sin cos sin cos cos A C C A B B +=,即sin()cos A C B B +=,sin(π)sin cos B B B B -==, 又因为sin 0B ≠,所以1B =,解得cos B =,又因为(0,π)B ∈, 所以π6B =; 【小问2详解】解:因为D 为BC 边的中点,12a =, 所以6BD CD ==, 设BAD θ∠=,在ABD △中,由正弦定理可得sin sin BD ADBθ=, 即6361sin 2θ==,解得sin 1θ=, 又因为(0,π)θ∈,所以π2θ=,在Rt △ABD 中,AB ===在ABC 中,π12,6AB BC B ===,由余弦定理可得:2222cos 1442721263AC AB BC AB AC B =+-⋅⋅=+-⨯⨯=,所以AC =即b =17. 某中学为了解本校高二年级学生阅读水平现状,从该年级学生中随机抽取100人进行一般现代文阅读速度的测试,以每位学生平均每分钟阅读的字数作为该学生的阅读速度,将测试结果整理得到如下频率分布直方图:(1)若该校高二年级有1500人,试估计阅读速度达到620字/分钟及以上的人数;(2)用频率估计概率,从该校高二学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为X ,求X 的分布列与数学期望()E X ;(3)若某班有10名学生参加测试,他们的阅读速度如下:506,516,553,592,617,632,667,693,723,776,从这10名学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为Y ,试判断数学期望()E Y 与(2)中的()E X 的大小.(结论不要求证明) 【答案】(1)600(2)分布列见解析,() 2.4E X =(3)()()E X E Y =【解析】【分析】(1)借助频率分布直方图计算即可得;(2)借助频率分布直方图可得阅读速度达到540字/分钟及以上的概率,得到X 的可能取值及其对应概率即可得,再计算期望即可; (3)借助期望计算公式计算即可得. 【小问1详解】()15000.003750.0010.0002580600⨯++⨯=,故可估计阅读速度达到620字/分钟及以上的人数为600人; 【小问2详解】从中任取一人,其阅读速度达到540字/分钟及以上的概率为:()0.0050.003750.0010.00025800.8+++⨯=,X 的可能取值为0、1、2、3,()0330C 0.20.008P X ==⨯=, ()1231C 0.80.20.096P X ==⨯⨯=, ()2232C 0.80.20.384P X ==⨯⨯=, ()0333C 0.80.512P X ==⨯=,则其分布列为:X12 3P0.008 0.0960.384 0.512其期望为:()30.8 2.4E X =⨯=; 【小问3详解】()()E X E Y =,理由如下:这10名学生中,阅读速度达到540字/分钟及以上的人数为8人,Y 的可能取值为1、2、3,()1282310C C 811C 12015P Y ====,()2182310C C 5672C 12015P X ====,()3082310C C 5673C 12015P X ====,则()177123 2.4151515E Y =⨯+⨯+⨯=, 故()()E X E Y =.18. 如图,在五面体ABCDEF 中,底面ABCD 为正方形,4,1AB EF ==.(1)求证://AB EF ;(2)若H 为CD 的中点,M 为BH的中点,,EM BH EM ⊥=,再从条件①、条件②这两个条件中选择一个作为已知,求直线CF 与平面ADE 所成角的正弦值. 条件①:ED EA =; 条件②:5AE =.注:如果选择条件①和条件②分别解答,按第一个解答计分 【答案】(1)证明见解析(2【解析】【分析】(1)先证明//AB 平面EFCD ,再利用线面平行的性质证明//AB EF ;(2)选①②:证明 EM ⊥平面ABCD ,建立以M 为原点的空间坐标系,求出平面ADE 的法向量,利用线面角公式求解 【小问1详解】证明:底面ABCD 为正方形,则//AB CD ,又AB ⊄平面EFCD ,CD ⊂平面EFCD , 则//AB 平面EFCD ,又平面EFCD 平面EFBA EF =,AB ⊂平面EFBA ,故//AB EF . 【小问2详解】选①,取AD 中点G ,连接,EG MG ,因为ED EA =,所以EG AD ⊥, 易知GM 为梯形ABHD 的中位线,则MG AD ⊥,又,,MG EG G MG EG ⋂=⊂平面EGM ,故AD ⊥平面EGM ,EM ⊂平面EGM ,则,,AD EM EM BH ⊥⊥,AD BH ⊂平面ABCD ,且,AD BH 必相交,故EM ⊥平面ABCD , 延长GM 交BC 于P ,则P 为中点,易得//,EF MP EF MP =,故EFPM 为矩形.以M 为原点,EM 所在直线为z 轴,MG 所在直线为x 轴,过M 作CB 平行线为y 轴,建立空间直角坐标系如图:则()()()((3,2,0,3,2,0,1,2,0,0,0,0,1,A D C E F ----,,则()0,4,0AD =-,(3,2,AE =--,(1,1,CF = ,设平面ADE 的法向量为(),,m x y z =,则00m AD m AE ⎧⋅=⎪⎨⋅=⎪⎩,即40320y x y -=⎧⎪⎨--+=⎪⎩,令x =()m = , 设直线CF 与平面ADE所成角为,sin cos ,m CF θθ===选②:取AD 中点G , 连接GM ,易知GM 为梯形ABHD 的中位线,3GM =,则AM =5AE =,EM =,则222AE EM AM =+,故,EM AM ⊥ 又,,,EM BH AM BH M AM BH ⊥⋂=⊂平面ABCD ,故EM ⊥平面ABCD , 延长GM 交BC 于P ,则P 为中点,易得//,EF MP EF MP =,故EFPM 为矩形.以M 为原点,EM 所在直线为z 轴,MG 所在直线为x 轴,过M 作CB 平行线为y 轴,建立空间直角坐标系如图:则()()()((3,2,0,3,2,0,1,2,0,0,0,0,1,A D C E F ----,,则()0,4,0AD =-,(3,2,AE =--,(1,1,CF = ,设平面ADE 的法向量为(),,m x y z =,则00m AD m AE ⎧⋅=⎪⎨⋅=⎪⎩,即40320y x y -=⎧⎪⎨--+=⎪⎩,令x =()m = , 设直线CF 与平面ADE所成角为,sin cos ,m CF θθ===19. 已知函数()()ln 1f x x x =-.(1)求曲线()y f x =在2x =处的切线方程; (2)设()()g x f x '=,求函数()g x 的最小值;(3)若()2f x x a>-,求实数a 的值. 【答案】(1)24y x =-(2)2(3)2a = 【解析】【分析】(1)求导,再根据导数的几何意义即可得解;(2)利用导数求出函数()g x 的单调区间,进而可求出最小值;(3)分1a ≤和1a >两种情况讨论,在1a >时,再分x a >和1x a <<两种情况讨论,分离参数,构造函数并求出其最值,即可得解. 【小问1详解】()()()ln 111xf x x x x '=-+>-, 则()()22,20f f '==,所以曲线()y f x =在2x =处的切线方程为()22y x =-,即24y x =-; 【小问2详解】()()()()ln 111xg x f x x x x '==-+>-, ()()()22112111x x x g x x x x ---'=+=---, 当12x <<时,()0g x '<,当2x >时,()0g x '>,所以函数()g x ()1,2上单调递减,在()2,+∞上单调递增, 所以()()min 22g x g ==; 【小问3详解】函数()f x 的定义域为()1,+∞, 当1a ≤时,0x a ->, 则()2f x x a>-,即()()2f x x a >-, 即()22a f x x -<-, 由(2)得()2f x '≥,令()()2h x f x x =-,则()()()201h x f x x ''=-≥>, 所以()h x 在()1,+∞上单调递增, 又当1x →时,()h x →-∞, 因为1a ≤,所以22a -≥-,此时()22a f x x -<-不恒成立,故1a ≤不符题意; 当1a >时,若x a >,则0x a ->, 则()2f x x a>-,即()()2f x x a >-,即()22a f x x -<-, 由上可知函数()()2h x f x x =-在(),a +∞上单调递增, 所以()()()()ln 12h x h a a a a x a >=-->,在所以()2ln 12a a a a -≤--,解得2a ≥①,若1x a <<,则()2f x x a>-,即()()2f x x a <-,即()22a f x x ->-, 由上可知函数()()2h x f x x =-在()1,a 上单调递增, 所以()()()()ln 1211h x h a a a a a <=--<<, 所以()2ln 12a a a a -≥--,解得2a ≤②, 由①②可得2a =, 综上所述,2a =.【点睛】方法点睛:对于利用导数研究不等式的恒成立与有解问题的求解策略:(1)通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围; (2)利用可分离变量,构造新函数,直接把问题转化为函数的最值问题.(3)根据恒成立或有解求解参数的取值时,一般涉及分离参数法,但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况,进行求解,若参变分离不易求解问题,就要考虑利用分类讨论法和放缩法,注意恒成立与存在性问题的区别.20. 已知椭圆2222:1(0)x y C a b a b +=>>的短轴长为e =(1)求椭圆C 的方程;(2)设O 为坐标原点,直线l 是圆221x y +=的一条切线,且直线l 与椭圆C 交于,M N 两点,若平行四边形OMPN 的顶点P 恰好在椭圆C 上,求平行四边形OMPN 的面积.【答案】(1)22163x y +=(2 【解析】【分析】(1)根据题意求出,a b ,即可得解;(2)分切线斜率是否存在两种情况讨论,当切线的斜率存在时,设切线方程为y kx m =+,先求出,k m 的关系,设()()1122,,,M x y N x y ,联立直线与椭圆的方程,利用韦达定理求出1212,x x x x +,进而可求得线段MN 的中点坐标,从而可求得点P 的坐标,再根据点P 在椭圆上,即可求得,k m ,再利用弦长公式求出MN ,即可得解.【小问1详解】由题意可得2222b ca ab c⎧=⎪⎪=⎨⎪=+⎪⎩,解得222633a b c ⎧=⎪=⎨⎪=⎩,所以椭圆C 的方程为22163x y +=; 【小问2详解】当圆的切线斜率不存在时,切线方程为1x =±, 当切线方程为1x =时,由椭圆的对称性可得()2,0P , 因为4021633+=<,所以点()2,0P 不在椭圆上,不符题意, 当切线方程为=1x -时,由椭圆的对称性可得()2,0P -, 因为4021633+=<,所以点()2,0P -不在椭圆上,不符题意, 所以切线的斜率存在,设切线方程为y kx m =+,1=,所以221m k =+①,联立22163y kx m x y =+⎧⎪⎨+=⎪⎩,整理得()222214260k x kmx m +++-=,则()()()()()22222222Δ16421261614212160k m k m k kk k ⎡⎤=-+-=+-++->⎣⎦,解得R k ∈,设()()1122,,,M x y N x y ,则2121222426,2121km m x x x x k k -+=-=++, 故()()221212222221422212121m k k m m y y k x x m k k k ++=++=-+=+++,所以线段MN 的中点坐标为222,2121km m k k ⎛⎫-⎪++⎝⎭, 因为四边形OMPN 为平行四边形,所以2242,2121km m P k k ⎛⎫- ⎪++⎝⎭, 又因为点P 在椭圆C 上, 所以()()22222221641621321k m m k k +=++②,将①代入②得()()()()222222281411321321k k kk k+++=++,解得k =,所以m =所以MN =====,所以12212OMPN OMN S S ==⨯=. 【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下:(1)设直线方程,设交点坐标为()11,x y 、()22,x y ;(2)联立直线与圆锥曲线的方程,得到关于x (或y )的一元二次方程,必要时计算∆; (3)列出韦达定理;(4)将所求问题或题中的关系转化为12x x +、12x x (或12y y +、12y y )的形式; (5)代入韦达定理求解.21. 有穷数列12,,,(2)n a a a n > 中,令()()*1,1,,p p q S p q a a a p q n p q +=+++≤≤≤∈N ,(1)已知数列3213,,,--,写出所有的有序数对(),p q ,且p q <,使得(),0S p q >; (2)已知整数列12,,,,n a a a n 为偶数,若(),11,2,,2n S i n i i ⎛⎫-+= ⎪⎝⎭,满足:当i 为奇数时,(),10S i n i -+>;当i 为偶数时,(),10S i n i -+<.求12n a a a +++ 的最小值;(3)已知数列12,,,n a a a 满足()1,0S n >,定义集合(){}1,0,1,2,,1A i S i n i n =+>=- .若{}()*12,,,k A i i i k =∈N 且为非空集合,求证:()121,k i i i S n a a a >+++ .【答案】(1)()1,4、()2,3、()2,4、()3,4(2)n 1-(3)证明见解析 【解析】【分析】(1)结合题意,逐个计算即可得;(2)由题意可得()1,0S n >,()2,10S n -<,可得当2n i ≠时,有12i n i a a -++≥,当2ni =时,1221n na a ++≥,结合11i n i i n i a a a a -+-++≥+,即可得解;(3)将()()121,k i i i S n a a a -+++ 展开,从而得到证明m i a 与1m i a +之间的项之和,1121i a a a -+++ ,112k k i i n a a a -+++++ 都为正数,即可得证.【小问1详解】(),p q ()1,4时,()(),321310S p q =-++-+=>, (),p q 为()2,3时,()(),2110S p q =+-=>, (),p q 为()2,4时,()(),21340S p q =+-+=>, (),p q 为()3,4时,()(),1320S p q =-+=>,故p q <,且使得(),0S p q >的有序数对有()1,4、()2,3、()2,4、()3,4; 【小问2详解】由题意可得()1,0S n >,()2,10S n -<,为又n a 为整数,故()1,1S n ≥,()2,11S n -≤-, 则()()11,2,12n S n S n a a --=+≥,同理可得()()212,13,22n S n S n a a ----=+≤-, 即有212n a a -+≥, 同理可得,当2ni ≠时,有12i n i a a -++≥, 即当2ni ≠时,有112i n i i n i a a a a -+-++≥+≥, 当2n i =时,122,1122n n n n S a a +⎛⎫+=+≥ ⎪⎝⎭,故()()12121122n n n n na a a a a a a a a -+⎛⎫+++=++++++ ⎪ ⎪⎝⎭()()121122n n n na a a a a a -+⎛⎫++++++ ⎪ ⎪⎝⎭≥ 22112n n -⎛⎫=+=- ⎪⎝⎭;【小问3详解】{}()*12,,,k A i i i k =∈N 时,当11i ≠时,()()()()2112111211211,k i i i i i i i S n a a a a a a a a a -++--+++=+++++++()()()22111312112112k k k k k i i i i i i i i n a a a a a a a a a ---++-++-+++++++++++++++ ,令m i A ∈且1m i A -∉,则有()1,0m S i n +>,(),0m S i n ≤, 又()1,0S n >,故()()1211,,0m m i S n S i n a a a --=+++> , 即有11210i a a a -+++> ,1120k k i i n a a a -+++++> ,令1m i A +∈且11m i A +-∉,则有()11,0m S i n ++>,()1,0m S i n +≤, 则()()111211,,0m m m i m m i i S i n S i n a a a ++++-+-=+++> ,即有()()()112212311211211210k k k i i i i i i i i i a a a a a a a a a --++-++-++-++++++++++++> ,故()()121,0k i i i S n a a a -+++> ,即()121,k i i i S n a a a >+++ , 当11i =时,()()()121211211,k i i i i i i S n a a a a a a ++--+++=+++()()()322111*********k k k k k i i i i i i i i n a a a a a a a a a ---++-++-+++++++++++++++> ,即()121,k i i i S n a a a >+++ 亦成立,即得证.【点睛】关键点点睛:本题最后一小问关键点在于将()()121,k i i i S n a a a -+++ 展开,从而得到证明m i a 与1m i a +之间的项之和,1121i a a a -+++ ,112k k i i n a a a -+++++ 都为正数,即可得证.。
北京市东城区普通高中示范校2020┄2021届高三3月联考综合练习二

东城区普通高中示范校高三综合练习(二)高三化学03命题学校:第109中学(物理)、第166中学(化学)、东直门中学(生物)学校:班级:姓名:成绩:可能用到的相对原子质量:H 1 C 12 O 16 Fe 56第I卷(选择题,共120分)6. 化学与生活密切相关。
下列有关的说法中不正确的是...A.光导纤维遇强碱会“断路”B.福岛核电站泄露的放射性物质l31I和127I互为同位素,化学性质几乎相同C.以NO和NO2为主的氮氧化物是形成光化学烟雾和酸雨的一个重要原因D.氢氧化铁溶胶、甘油与乙醇的混合液、含PM2.5的大气均具有丁达尔效应7. 普通水泥在固化过程中自由水分子减少并产生Ca(OH)2使溶液呈碱性。
根据这一物理化学特点,科学家发明了电动势法测水泥初凝时间。
此方法的原理如图所示,反应的总方程式为:2Cu+Ag2O = 2CuO+2Ag,下列有关说法正确的是A.电池工作时,OH—向正极移动B.测量原理示意图中,Ag2O为负极C.电流方向是从Ag2O/ Ag电极到Cu电极D.正极的电极反应为:2Cu+2OH——2e—= Cu2O+H2O8间,再向冷却后的混合液中滴加硝酸银溶液9.常温下,将amol/L 的MOH(可溶性弱碱)与bmol/L盐酸等体积混合,已知相同条件的是MOH的电离程度大于M+的水解程度,则下列有关推论不正确...A.若混合后溶液pH=7,则c(M+)=c(Cl-)B.若a=2b,则c(M+)>c(Cl-)>c(MOH) >c(OH-)>c(H+)C.若b=2a,则c(Cl-)>c(M+)>c(H+)>c(OH-)D.若混合后溶液满足c(H+)=c(OH-)+c(MOH),则可推出a=b10. 海洋中有丰富的食品、矿产、能源、药物和水产资源等(如下图所示):下列有关说法正确的是A.第①步中除去粗盐中的SO42-、Ca2+、Mg2+、Fe3+等杂质,加入药品的顺序为Na2CO3、NaOH、BaCl2和盐酸B.第②步中结晶出的MgCl2·6H2O可在空气中受热分解制无水MgCl2C.在第③④⑤步中溴元素均被氧化D.由海水提取的金属镁能与金属铝、氢氧化钠溶液在一定条件下形成原电池,金属镁作该原电池正极11.25℃、101kPa下:①2NaOH(s)+CO2(g)= Na2CO3(s)+H2O(l)△H=a kJ/mol②NaOH(s)+CO2(g) = NaHCO3(s)△H= b kJ/mol下列说法正确的是A.25℃、101kPa下:2NaHCO3(s)= Na2CO3(s)+ H2O(l)+CO2(g)△H= (2b-a) kJ/molB.相同温度下,同物质的量浓度的碳酸钠和碳酸氢钠溶液中的离子种类相同C.相同温度、压强条件下,向等体积等物质的量浓度的碳酸钠和碳酸氢钠中加入足量的盐酸,产生的二氧化碳不相等D .碳酸钠固体和碳酸氢钠固体中阴阳离子个数比相同12.下列说法正确的是A .相同条件下,同浓度的NaClO 溶液和Na 2CO 3溶液的碱性,前者更强B .Na 2CO 3溶液中通少量SO 2:2CO 32-+SO 2+H 2O = 2HCO 3-+SO 32-C .NaHCO 3溶液中通少量SO 2:2HCO 3-+SO 2 = CO 2+SO 32-+H 2OD .向氯水中分别加入等浓度的NaHCO 3和NaHSO 3溶液,均可提高氯水中HClO 的浓度25. (14分) U 、V 、W 、Y 、Z 是原子序数依次增大的短周 期主族元素,U 、Y 在周期表中的相对位置如右表;U 元素与氧元素能形成两种无色气体;W 是地壳中含量最多的 金属元素。
东城区普通高中示范校高三综合练习(二)

东城区普通高中示范校高三综合练习(二)高三数学 (理科) 2012.3学校_____________班级_______________姓名______________考号___________本试卷分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)一、本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.设全集2,{|30},{|1}U A x x x B x x ==-->=<-R ,则图中阴影部分表示的集合为 ( )A.}0|{>x xB.}13|{-<<-x xC.}03|{<<-x xD.}1|{-<x x2.已知直线l 过定点(-1,1),则“直线l 的斜率为0”是“直线l 与圆122=+y x 相切”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3. 已知直线m ,n 与平面α,β,下列命题正确的是 ( ) A .βα//,//n m 且βα//,则n m // B .βα//,n m ⊥且β⊥α,则n m ⊥ C .,βm n m =⊥ α且βα⊥,则α⊥n D .βα⊥⊥n m ,且βα⊥,则n m ⊥4.甲从正四面体的四个顶点中任意选择两个顶点连成直线,乙从该正四面体四个顶点中任意选择两个顶点连成直线,则所得的两条直线相互垂直的概率是 ( ) A.61 B. 92 C. 185 D. 315. 执行如图所示的程序框图,若输出的结果是8,则判断框内m 的取值范围是 ( ) A.(30,42]B.(42,56]C.(56,72]D.(30,72)6.一个几何体的三视图如图所示,则此几何体的体积是 ( ) A .112 B.80 C.72 D.64(第5题图)7. 已知约束条件340,210,380,x y x y x y -+≥⎧⎪+-≥⎨⎪+-≤⎩若目标函数)0(>+=a ay x z 恰好在点(2,2)处取得最大值,则a 的取值范围为 ( )A. 310<<aB.31≥a C . 31>a D . 210<<a8.如图,半径为2的⊙O 与直线MN 相切于点P ,射线PK 从PN 出发绕点P 逆 时针方向旋转到PM ,旋转过程中,PK 交⊙O 于点Q ,设POQ ∠为x ,弓 形PmQ 的面积为()S f x =,那么()f x 的图象大致是( )A B C D第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分。
2023-2024学年北京市东城区高三综合练习数学质量检测模拟试题(含答案)

2023-2024学年北京市东城区高三综合练习数学模拟试题一、单选题1.已知集合(){}lg 2M x y x ==-,{}e 1x N y y ==+,则M N ⋃=()A .(),-∞+∞B .()1,+∞C .[)1,2D .()2,+∞【正确答案】B 【分析】根据给定条件,求出函数的定义域、值域,再利用并集的定义求解作答.【详解】集合(){}{}{}lg 222M x y x x x x x ==-=-=,即(2,)M =+∞,e 11x +>,则(1,)N =+∞,所以()1,M N =+∞U .故选:B 2.已知向量()()1,3,2a m b ==- ,,且()a b b +⊥ ,则m =A .−8B .−6C .6D .8【正确答案】D【分析】由已知向量的坐标求出a b + 的坐标,再由向量垂直的坐标运算得答案.【详解】∵(1,),(3,2),(4,2)a m b a b m ==-∴+=- ,又()a b b +⊥ ,∴3×4+(﹣2)×(m ﹣2)=0,解得m =8.故选D .本题考查平面向量的坐标运算,考查向量垂直的坐标运算,属于基础题.3.下列函数中,是奇函数且在定义域内单调递减的是()A .()sin f x x=B .()2x f x =C .()3f x x x =+D .()()1e e 2x x f x -=-【正确答案】D【分析】根据函数的奇偶性,基本初等函数的单调性,逐项判断即可.【详解】对于A ,函数()sin f x x =为奇函数,但在定义域R 上函数不单调,故A 不符合;对于B ,()2x f x =的定义域为R ,()()22x x f x f x --===,则()2x f x =为偶函数,故B 不符合;对于C ,()3f x x x =+的定义域为R ,()()3f x x x f x -=--=-,则()3f x x x =+为奇函数,又函数3,y x y x ==在R 上均为增函数,故()3f x x x =+在R 上为增函数,故C 不符合;对于D ,()()1e e 2x x f x -=-的定义域为R ,()()()1e e 2x x f x f x --=-=-,则()()1e e 2x x f x -=-为奇函数,又函数e x y -=在R 上为减函数,e x y =在R 上为增函数,故()()1e e 2x x f x -=-在R 上为减函数,故D 符合.故选:D.4.若实数a 、b 满足220a b >>,则下列不等式中成立的是()A .a b >B .22a b>C .a b >D .2222log log a b >【正确答案】D【分析】对于D ,结合对数函数的单调性即可判断;对于ABC ,取2a =-,1b =-即可判断.【详解】由题意,220a b >>,所以2222log log a b >,故D 正确;当2a =-,1b =-时,220a b >>,但a b <,22a b <,a b <,故A ,B ,C 错误.故选:D.5.已知322()nx x +的展开式中各项系数和为243,则展开式中常数项为()A .60B .80C .100D .120【正确答案】B【分析】根据各项系数和求出n ,再由二项展开式通项公式求解即可.【详解】当1x =时,3243n =,解得5n =,则322()n x x +的展开式第1r +项351532155152552C ()()C 2C 2r r rr r r r r r r r T x x x x x ----+===,令1550r -=,解得3r =,所以335C 210880=⨯=,故选:B6.过抛物线24y x =的焦点F 的直线交抛物线于A B 、两点,若F 是线段AB 的中点,则AB =()A .1B .2C .3D .4【正确答案】D【分析】依据题意可知线段AB 为抛物线的通径可得结果.【详解】由题可知:线段AB 为抛物线的通径所以AB 4=故选:D7.已知{}n a 为等比数列,n S 为其前n 项和,若213S a =,223a a =,则4S =()A .7B .8C .15D .31【正确答案】C 【分析】设等比数列{}n a 的公比为q ,根据已知条件求出1a 、q 的值,再利用等比数列的求和公式可求得4S 的值.【详解】设等比数列{}n a 的公比为q ,则21213S a a a =+=,则212a a =,所以,212a q a ==,因为223a a =,即()21124a a =,10a ≠ ,解得11a =,因此,()441411215112a q S q --===--.故选:C.8.已知非零向量a ,b ,则“a 与b 共线”是“||a b a b -≤- ”的()A .充分不必要条件B .必要不充分条件C .充要条件D .即不充分也不必要条件【正确答案】B 【分析】取,a b 为方向相反的单位向量,得到不充分,根据()()22a b a b -≤- 得到0θ=,得到必要性,得到答案.【详解】若a 与b 共线,取,a b 为方向相反的单位向量,则||2a b -= ,0a b -= ,a b a b ->- ,不充分;若||a b a b -≤- ,则()()22a b a b -≤- ,整理得到a b a b ⋅≤⋅ ,若0a ≠ 且0b ≠r r ,设,a b 夹角为θ,则[]0,πθ∈,即cos a b a b θ⋅≤⋅ ,即1cos θ≤,即0θ=,故a与b 共线,必要性成立.综上所述:“a 与b 共线”是“||a b a b -≤- ”的必要不充分条件.故选:B9.血药浓度(Plasma Concentration )是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:根据图中提供的信息,下列关于成人使用该药物的说法中:①首次服用该药物1单位约10分钟后,药物发挥治疗作用;②每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒;③每向隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用;④首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒.其中正确说法的个数是()A .1B .2C .3D .4【正确答案】C【分析】根据图象,结合题意,逐个判断即可.【详解】①根据图象可知,首次服用该药物1单位约10分钟后,血液浓度达到最低有效浓度,药物发挥治疗作用,故正确;②根据图象可知,首次服用该药物1单位约1小时后血液浓度达到最大值,由图象可知两次服药间隔小于2小时,一定会产生药物中毒,故正确;③根据图象可知,每间隔5.5小时服用该药物1单位,可使血药浓度大于最低有效浓度,药物持续发挥治疗作用,故正确;④根据图象可知,首次服用该药物1单位3小时后,再次服用该药物1单位,会发生药物中毒,故错误.故选:C .10.已知M 是圆22:1C x y +=上一个动点,且直线1:30l mx ny m n --+=与直线222:30(,R,0)l nx my m n m n m n +--=∈+≠相交于点P ,则PM 的取值范围是()A .1]-B .1]-C .1]-+D .1]【正确答案】B 【分析】根据给定条件确定出点P 的轨迹,再借助圆与圆的位置关系及圆的几何性质计算作答.【详解】依题意,直线1:(3)(1)0l m x n y ---=恒过定点(3,1)A ,直线2:(1)(3)0l n x m y -+-=恒过定点()1,3B ,显然直线12l l ⊥,因此,直线1l 与2l 交点P 的轨迹是以线段AB 为直径的圆,其方程为:22(2)(2)2x y -+-=,圆心(2,2)N ,半径2r =C 的圆心(0,0)C ,半径11r =,如图:12||NC r r =+,两圆外离,由圆的几何性质得:min 12||||1PM NC r r =---,max 12||||1PM NC r r =++=,所以PM 的取值范围是.1]+故选:B思路点睛:判断两圆的位置关系常用几何法,即用两圆圆心距与两圆半径和与差之间的关系,一般不采用代数法.二、填空题11.已知a ,b 均为实数.若()i i i b a +=+,则ab =_____________.【正确答案】1-【分析】直接由复数的乘法及复数相等求解即可.【详解】()i i i i 1b a a ==++-,故1,1a b ==-,1ab =-.故答案为.1-三、双空题12.已知1F 、2F 分别是双曲线()222:109x y C a a -=≠的左、右焦点,P 是C 上的一点,且12216PF PF ==,则12PF F △的周长是___________,双曲线的离心率是___________.【正确答案】3454【分析】利用双曲线的定义求出a 的值,可求得c 的值,进而可求得12PF F △的周长以及该双曲线的离心率的值.【详解】因为12216PF PF ==,则28PF =,由双曲线的定义可得1221688a PF PF =-=-=,则4a =,则5c ===,所以,12210F F c ==,故12PF F △的周长为12121681034PF PF F F ++=++=,该双曲线的离心率为54c e a ==.故34;54.四、填空题13.在ABC 中,a =2b c =,1cos4A =-,则ABC S = ______.【分析】由余弦定理求解,b c ,由同角函数基本关系求出sin A ,代入面积公式求解即可.【详解】由余弦定理2222cos a b c bc A =+-可得222212444()64c c c c =+-⨯-=,解得2c =,则24b c ==,又sin A =所以411sin 222ABC S bc A ==⨯⨯=五、双空题14.若函数sin (0,0)y A x A ωω=>>在[0,1]上取到最大值A ,则ω的最小值为___________.若函数sin (0,0)y A x A ωω=>>的图象与直线y A =-在[0,1]上至少有1个交点,则ω的最小值为__________.【正确答案】2π32π【分析】利用正弦函数的图象和周期即可求解.【详解】要使sin (0)y A x ωω=>在区间[]0,1上取到最大值A ,则12ωπ≤,2πω≥,则ω的最小值为π2;又函数sin (0,0)y A x A ωω=>>与y A =-在[]0,1上至少有1个交点,即函数sin (0)y A x ωω=>在区间[]0,1上至少出现1次最小值,332144T ωπ∴=⋅≤,解得:32ω≥π,则ω的最小值是32π.故2π;32π.六、填空题15.在数列{}n a 中,对任意的*n ∈N 都有0n a >,且211n n n a a a ++-=,给出下列四个结论:①对于任意的3n ≥,都有2n a ≥;②对于任意10a >,数列{}n a 不可能为常数列;③若102a <<,则数列{}n a 为递增数列;④若12a >,则当2n ≥时,12n a a <<.其中所有正确结论的序号为_____________.【正确答案】③④【分析】对数列递推关系变形得到()()211112122n n n n n a a a a a ++++-=--=-+,得到2n a -与12n a +-同号,当102a <<时,02n a <<,①错误;当12a =时,推导出此时{}n a 为常数列,②错误;作差法结合102a <<时,102n a +<<,求出数列{}n a 为递增数列,③正确;由2n a -与12n a +-同号,得到当12a >,有2n a >,结合作差法得到{}n a 为递减数列,④正确.【详解】因为211n n n a a a ++-=,所以()()211112122n n n n n a a a a a ++++-=--=-+,因为任意的N n *∈都有0n a >,所以110n a ++>,所以2n a -与12n a +-同号,当102a <<,则3n ≥时,都有02n a <<,①错误;当12a =时,1222201a a a -=+=-,所以22a =,同理得:()23n a n =≥,此时{}n a 为常数列,②错误;()221111211n n n n n a a a a a ++++-=--=++-,由A 选项知:若102a <<,则102n a +<<,所以()221111211110n n n n n a a a a a +++++=---+>-+-==,则数列{}n a 为递增数列,③正确;由2n a -与12n a +-同号,当12a >,则2n ≥时,都有2n a >,且此时()221111211110n n n n n a a a a a +++++=---+<-+-==,所以数列{}n a 为递减数列,综上:若12a >,则当2,n ≥时,12n a a <<,④正确.故③④七、解答题16.已知函数()()2cos 2sin 102f x x x x ωωωω=-+<<.在下面两个条件中选择其中一个,完成下面两个问题:条件①:在()f x 图象上相邻的两个对称中心的距离为π2;条件②:()f x 的一条对称轴为π6x =.(1)求ω;(2)将()f x 的图象向右平移π3个单位(纵坐标不变),得到函数()g x 的图象,求函数()g x 在ππ,33⎡⎤-⎢⎥⎣⎦上的值域.【正确答案】(1)1ω=(2)[]2,1-【分析】(1)由三角函数的恒等变换对()f x 进行化简,再分别由条件①②求ω的值.(2)由三角函数的平移变换得()g x 的解析式,再由函数的定义域求值域即可.【详解】(1)()2cos 2sin 1f x x x x ωωω=-+2cos 2x xωω+π2sin(26x ω=+选①:()f x 图象上相邻两个对称中心的距离为π2,则2ππ2T ω==,则1ω=,选②:()f x 的一条对称轴为π6x =,则πππ2πZ 662k k ω⋅+=+∈,,31k ω∴=+,又02ω<<,则1ω=,于是()2sin 26f x x π⎛⎫=+ ⎪⎝⎭(2)将()2sin(2)6f x x π=+的图象向右移π3个单位长度(纵坐标不变),得到函数πππ()2sin[2(2sin(2)2cos 2362g x x x x =-+=-=-的图象 ππ[,]33x ∈-,∴2π2π2[,]33x ∈-,∴cos 2[,1]12x ∈-,()g x ∴的值域为[]2,1-.17.在四棱锥P -ABCD 中,底面ABCD 为直角梯形,BC AD ∥,90ADC ∠=︒,112BC CD AD ===,E 为线段AD 的中点.PE ⊥底面ABCD ,点F 是棱PC 的中点,平面BEF 与棱PD 相交于点G .(1)求证:BE FG ∥;(2)若PC 与AB 所成的角为π4,求直线PB 与平面BEF 所成角的正弦值.【正确答案】(1)证明见解析(2)3【分析】(1)利用平行四边形的判定定理和性质,结合线面平行的判定定理和性质定理进行证明即可;(2)建立空间直角坐标系,利用空间向量夹角公式进行求解即可.【详解】(1)证明:因为E为AD中点,所以112DE AD==.又因为BC=1,所以DE=BC.在梯形ABCD中,DE//BC,所以四边形BCDE为平行四边形.所以BE//CD.又因为BE⊄平面PCD,且CD⊂平面PCD,所以BE//平面PCD.因为BE⊂平面BEF,平面BEF∩平面PCD=FG,所以BE//FG..(2)因为PE⊥平面ABCD,且AE,BE⊂平面ABCD,所以PE⊥AE,且PE⊥BE.因为四边形BCDE为平行四边形,∠ADC=90°,所以AE⊥BE.以E为坐标原点,如图建立空间直角坐标系E﹣xyz.则()()()()()0,0,0,1,0,0,0,1,0,1,1,0,1,0,0E A B C D --.设()()0,0,0P m m >,所以()1,1,CP m =- ,()1,1,0AB =-uu u r .因为PC 与AB 所成角为π4,所以πcos ,cos 42CP AB CP AB CP AB ⋅===⋅ .所以m =则(P,11,222F ⎛⎫- ⎪ ⎪⎝⎭.所以()0,1,0EB =,11,22EF ⎛=- ⎝⎭,(0,1,PB = .设平面BEF 的法向量为(),,n x y z = ,则00n EB n EF ⎧⋅=⎪⎨⋅=⎪⎩,即0110.22y x y z =⎧⎪⎨-+=⎪⎩令x =,则1z =,所以)n = .所以cos ,3PB n PB n PB n⋅==⋅ .所以直线PB 与平面BEF的所成角的正弦值为3.18.某电视台举行文艺比赛,并通过网络对比赛进行直播.比赛现场有5名专家评委给每位参赛选手评分,场外观众可以通过网络给每位参赛选手评分.每位选手的最终得分由专家评分和观众评分确定.某选手参与比赛后,现场专家评分情况如表;场外有数万名观众参与评分,将评分按照[7,8),[8,9),[9,10]分组,绘成频率分布直方图如图:专家A B C D E 评分9.69.59.68.99.7(1)求a 的值,并用频率估计概率,估计某场外观众评分不小于9的概率;(2)从5名专家中随机选取3人,X 表示评分不小于9分的人数;从场外观众中随机选取3人,用频率估计概率,Y 表示评分不小于9分的人数;试求E (X )与E (Y )的值;(3)考虑以下两种方案来确定该选手的最终方案一:用所有专家与观众的评分的平均数x 作为该选手的最终得分,方案二:分别计算专家评分的平均数1x 和观众评分的平均数2x ,用122x x +作为该选手最终得分.请直接写出x 与122x x +的大小关系.【正确答案】(1)10.3,2;(2)见解析;(3)122x x x +<.【分析】(1)由频率和为1可得a 的值,用某场外观众评分不小于9的频率可估计概率;(2)计算概率可得分布列和期望.(3)由两组数据的比重可直接作出判断..【详解】(1)由图知10.20.50.3a =--=,某场外观众评分不小于9的概率是12.(2)X 的可能取值为2,3.P (X =2)=21413535C C C =;P (X =3)=343525C C =.所以X 的分布列为X23P 3525所以E (X )=2×32123555+⨯=.由题意可知,132Y B ⎛⎫ ⎪⎝⎭~,,所以E (Y )=np =32.(3)122x x x +<.本题考查了离散型随机变量的期望考查了超几何分布和二项分布,属中档题.19.已知函数()(1)ln (1)f x x x a x =+--.(I )当4a =时,求曲线()y f x =在()1,(1)f 处的切线方程;(Ⅱ)若当()1,x ∈+∞时,()0f x >,求a 的取值范围.【正确答案】(1)220.x y +-=(2)(],2.-∞【详解】试题分析:(Ⅰ)先求()f x 的定义域,再求()f x ',(1)f ',(1)f ,由直线方程的点斜式可求曲线()y f x =在(1,(1))f 处的切线方程为220.x y +-=(Ⅱ)构造新函数(1)()ln 1a x g x x x -=-+,对实数a 分类讨论,用导数法求解.试题解析:(I )()f x 的定义域为(0,)+∞.当4a =时,1()(1)ln 4(1),()ln 3f x x x x f x x x=+--=+-',(1)2,(1)0.f f =-='曲线()y f x =在(1,(1))f 处的切线方程为220.x y +-=(II )当(1,)x ∈+∞时,()0f x >等价于(1)ln 0.1a x x x -->+设(1)()ln 1a x g x x x -=-+,则222122(1)1(),(1)0(1)(1)a x a x g x g x x x x +-+=++'=-=,(i )当2a ≤,(1,)x ∈+∞时,222(1)1210x a x x x +-+≥-+>,故()0,()g x g x >'在(1,)+∞上单调递增,因此()0g x >;(ii )当2a >时,令()0g x '=得1211x a x a =-=-+由21x >和121=x x 得11x <,故当2(1,)x x ∈时,()0g x '<,()g x 在2(1,)x 单调递减,因此()0g x <.综上,a 的取值范围是(],2.-∞导数的几何意义,利用导数判断函数的单调性【名师点睛】求函数的单调区间的方法:(1)确定函数y =f (x )的定义域;(2)求导数y′=f′(x );(3)解不等式f′(x )>0,解集在定义域内的部分为单调递增区间;(4)解不等式f′(x )<0,解集在定义域内的部分为单调递减区间.20.已知椭圆2222:1(0)x y C a b a b +=>>的左、右顶点分别为A B ,,||4AB =,离心率为2.(1)求椭圆C 的方程;(2)设点D 为线段AB 上的动点,过D 作线段AB 的垂线交椭圆C 于不同的两点E 和F ,N 为线段AE 上一点(异于端点).当NDE DBF ∠=∠时,求||||AN AE 的值.【正确答案】(1)22142x y +=(2)23【分析】(1)根据题意,可得2a =,再由离心率可得c =再由椭圆中,,a b c 的关系即可得到b ,从而得到椭圆的方程;(2)根据题意,设出点,E F 的坐标,然后表示出点N 的坐标,再由tan tan NDE DBF ∠=∠列出方程,即可得到结果.【详解】(1)由已知||4AB =,可得24a =,则2a =,因为2c e a ==,所以c =且222422b a c =-=-=,所以椭圆的方程为22142x y +=.(2)设||||AN AE λ=,则()01AN AE λλ=<< ,由已知可得()()2,0,2,0A B -,设(),E m n ,则(),F m n -,(),N N N x y ,则()()2,,2,N N AN x y AE m n =+=+ ,所以22N x m λλ=+-,N y n λ=,即()22,N m n λλλ+-,又因为90NDE DBF ∠=∠≠︒,所以tan tan NDE DBF ∠=∠,所以222m m n n mλλλ--+=-,即122m n n m λλ-⋅+=⋅-,化简可得2214n m λλ-=-,又因为22142m n +=,所以2242m n -=,所以112λλ-=,解得23λ=或2λ=(舍),所以||2||3AN AE =.关键点睛:本题主要考查了椭圆的性质以及直线与椭圆的位置关系,难度较难,解答本题的关键是利用好ND 与BF 之间的关系,然后由tan tan NDE DBF ∠=∠列出方程,再通过计算,即可求解.21.对非空数集A ,B ,定义{},A B x y x A y B -=-∈∈,记有限集T 的元素个数为T .(1)若{}13,5A =,,{}1,2,4B =,求A A -,B B -,A B -;(2)若4A =,*A ⊆N ,{}1,2,3,4B =,当A B -最大时,求A 中最大元素的最小值;(3)若5A B ==,21A A B B -=-=,求A B -的最小值.【正确答案】(1)5,7,7A A B B A B -=-=-=;(2)13;(3)15(1)根据新定义求出,,A A B B A B ---,进而可得答案;(2)设{},,,A a b c d N *=⊆,a b c d <<<,当A 中元素与B 中元素的差均不相同时,A B -可取到最大值,进而可求出最大值,再通过4,4,4b a c b d c -≥-≥-≥得到12d a -≥,可得A 中最大元素的最小值;(3)对非空数集T ,定义运算{}|,,T x y x y T x y *=-∈≠,首先确定A 中不同的元素的差均不相同,B 中不同的元素的差均不相同,由12A B A B A B **-≥-可得A B -的最小值,然后验证最小值可以取到即可.【详解】解:(1){}13,5A = ,,{}1,2,4B =,{}{}{}4,2,0,2,4,3,2,1,0,1,2,3,3,1,0,1,2,3,4A A B B A B ∴-=---=----=--,5,7,7A A B B A B ∴-=-=-=;(2)设{},,,A a b c d N *=⊆,a b c d <<<,①4A B == ,2416A B ∴-≤=,当A 中元素与B 中元素的差均不相同时等号成立,所以A B -最大值为16;②当16A B -=时,A 中元素与B 中元素的差均不相同,()(){}0A A B B ∴--= ,又因为{}3,2,1,0,1,2,3B B -=---,4,4,4b a c b d c ∴-≥-≥-≥,12d a ∴-≥,则13d ≥,综上,A B -最大值为16,A 中最大元素的最小值为13;(3)对非空数集T ,定义运算{}|,,T x y x y T x y *=-∈≠,①5A =,()551121A A ∴-≤⨯-+=,当且仅当()55120A *=⨯-=时取等号,又因为21A A -=,所以A 中不同的元素的差均不相同,同理,B 中不同的元素的差均不相同,若,,,a a A b b B''∈∈因为a b a b a a b b a a b b ''''''-=-⇔-=-⇔-=-,1155201522A B A B A B **∴-≥-≥⨯-⨯= ,②令{}1,2,4,8,16A =,{}1,2,4,8,16B =-----,所以5A B ==,A 中不同元素的差均不相同,B 中不同元素的差均不相同,所以21A A B B -=-=,经检验,15A B -=符合题意,综上A B -的最小值为15.本题考查集合的新定义问题,正确理解题意是解题的关键,考查学生分析问题解决问题的能力,是一道难度较大的题目.。
北京市东城区普通高中示范校高三综合练习(二)(理综答案)
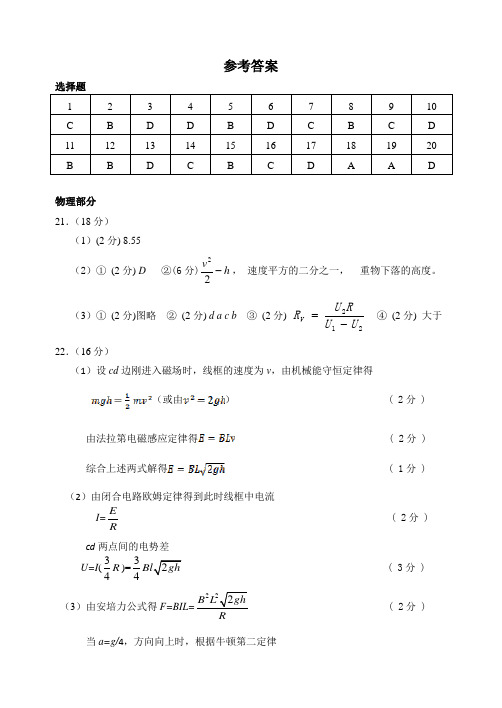
参考答案选择题物理部分 21.(18分) (1)(2分) 8.55 (2)①(2分) D ②(6分)h v-22, 速度平方的二分之一, 重物下落的高度。
(3)①(2分)图略 ②(2分) d a c b ③(2分) 212UU R U R V -=④(2分) 大于22.(16分)(1)设cd 边刚进入磁场时,线框的速度为v ,由机械能守恒定律得(或由) ( 2分 ) 由法拉第电磁感应定律得 ( 2分 ) 综合上述两式解得( 1分 )(2)由闭合电路欧姆定律得到此时线框中电流I=E R( 2分 )cd 两点间的电势差U=I (34R )=34( 3分 )(3)由安培力公式得 ( 2分 )当a=g/4,方向向上时,根据牛顿第二定律 F-mg=ma ,( 2分 )解得下落高度满足 h '= ( 2分 )23.(18分)解析(1)物块能通过轨道最高点的条件是(2分)v =2m/s (1分)(2分)解得s =1.25m (1分)(2)物块到P 点时(2分)v p =2m/s (1分)(2分)F N =4.8N (1分)(3)能达到。
因为洛仑兹力不做功,到达最高点速度仍为v =2m/s ,所受洛伦磁力背离圆 心,轨道对小物块会产生向下的支持力,所以能到达最高点L 。
(3分)落回到MN 水平面时,重力作功为0,洛伦磁力作功为0,所以速度的大小v t 等于 第一次经过N 点时的速度大小。
212N E qs m gs m v μ=+(2分)v t =N v =/s (1分)24.(20分)解析(1)将甲、乙及细线看成一个整体,根据牛顿第二定律,有:a m m E q E q B A B A )(+=-代入数据可得2/02.0s m a =(4分)(2)当B 发生的位移最大时,B 的电势能增量最大。
细线断裂前,A 、B 发生的位移均为m ats 09.0212==(1分)此时A 、B 的速度均为s m at v /06.00==(1分)细线断后,B 的加速度为2/06.0s m m E q a BB B -=-=(1分)当B 的速度为零时,B 发生的位移为m a v s BB 03.02020=-=(1分)整个运动过程中B 发生的最大位移为m s s s B Bm 12.0=+=(1分) 此时B 的电势能增量为J Es q Ep Bm B 7102.7-⨯==∆(2分)(3)当B 返回原点时,其电势能的增量为零。
北京市东城区2023届高三综合练习数学试题(含解析)

A. a b
B. 2a 2b
C. a b
D. log2 a2 log2 b2
5.已知
(x3
2 x2
)n
的展开式中各项系数和为
243,则展开式中常数项为(
)
A.60
B.80
C.
D.
6.过抛物线 y2 4x 的焦点 F 的直线交抛物线于 A、B 两点,若 F 是线段 AB 的中点,则
AB ( )
C.1, 2
2.已知向量
a
1,
m,b
3,
2
,且
(a
b)
b
,则
m=
D. 2,
A.−8
B.−6
C.6
D.8
3.下列函数中,是奇函数且在定义域内单调递减的是( )
A. f x sin x
B. f x 2 x
C. f x x3 x
D. f x 1 ex ex 2
4.若实数 a 、 b 满足 a2 b2 0 ,则下列不等式中成立的是( )
评分 9.6 9.5 9.6 8.9 9.7
(1)求 a 的值,并用频率估计概率,估计某场外观众评
分不小于 9 的概率; (2)从 5 名专家中随机选取 3 人,X 表示评分不小于 9 分的人数;从场外观众中随机 选取 3 人,用频率估计概率,Y 表示评分不小于 9 分的人数;试求 E(X)与 E(Y)的 值; (3)考虑以下两种方案来确定该选手的最终得分:方案一:用所有专家与观众的评分
六、填空题
15.在数列an 中,对任意的 n N*
都有 an
0
,且
an
2 1
an1
an
,给出下列四个结论:
①对于任意的 n 3 ,都有 an 2 ;
东城区普通高中示范校高三综合练习答案

东城区普通高中示范校高三综合练习一答案:9.12. -2 13.①②16 11.—3 14.卄2兀(315.解:(1) f (x) = sin ( x) cos2x4 2^cos(- 2x) 3cos2x2 2din 2x - —3 cos2x2 2_1=2 最小正周期兀sin (2x )3 T h.JI单调递增区间[…才二12八 1(2)向左平移一个单位;向下平移个单位6 2 9分13分16.解(1) n =1,a^ 2n _2 启=S - S =2 na n= 2n(n N )2 nb 3b2 3 b3 + +3 b n = a n , n ND 3b2 32b s+ +3f 厂时,n 一2,两式作差:3n^b n= a n- a n 4 =22b n =尹(n 一2),又d =233310分1 2(仁(R n )T n = 1 二31 - 3 313分17•解:(1)幕E , O 分别是SC,AC 的中点.OE // SA又:0E 二平面SABOE //平面 SAB(2)在 SAC 中, OE //AS ,. ASC=90 OE _ SC平面 SAC _ 平面 ABC , BCA 二 90 BC _ 平面 ASC ,OE 二平面ASC BC _ OE.OE _ 平面 BSC SF 二平面BSC OE _ SF所以无论F 在BC 的何处,都有 OE _ SF ⑶ 由(2) BC —平面ASC二 BC 丄 AS又 ASC =90AS _ SCAS _平面BCS AS _ SB-BSC 是二面角B - AS - C 的平面角 6 在 Rt BCS 中 cos BSC =所以二面角B - AS -C 的平面角的余弦值为.6 14分(2)法3314分n = (-2,1,-1)|n | | BC |所以二面角B - AS -C 的平面角的余弦值为2 2x y18.解:(1)设椭圆T 的方程为—2=1,a bO 是 AC.SO _ 平面 ABC同理可得BC _平面ASC 在平面ABC 内,过O 做OM _ AC以O 为原点,OM ,OC,OS 所在直线为x, y,z 轴,建立空间直角坐标系,如图所示,则O(0,0,0) A(0,-1,0),B(1,1,0), C(0,1,0),S(0,0,1),AS = (0,1,1),AB =(1,2,0),F BC ,设 F(x,1,0),一 1 1 。
北京市东城区示范校2020┄2021届高三上学期综合能力测试化学试卷Word版 含答案

北京市东城区普通高中示范校2021年上学期高三年级综合能力测试化学试卷本试卷分为第一部分(选择题)和第二部分(非选择题)。
试卷满分100分,考试时长:100分钟。
可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 S32 Fe 56 Cu 64 Ba 137第一部分(选择题 共42分)本部分共14小题,每小题3分,共42分。
在每小题列出的四个选项中,选出最符合题 目要求的一项。
1.化学与生产、生活密切相关。
下列叙述错误的是 ( ) A .光导纤维遇强碱会“断路”B .从海带中提取碘的过程涉及氧化还原反应C .钠可把钛、锆、铌、钽等金属从其熔融卤化物里还原出来D .绿色化学的核心是应用化学原理对环境污染进行治理 2.有关化学用语表达正确的是 ( )A. 聚苯乙烯的结构简式:B. -2S 的结构示意图:C. U 23592和U 23892互为同位素D. 过氧化氢电子式:+-+⎥⎦⎤⎢⎣⎡H O O H 2........::: 3. 2NaNO 是一种食品添加剂,它与酸性4KMnO 溶液可发生反应O H NO Mn X NO MnO 23224++→++-+--(未酸平)。
下列叙述中正确的是( )A. 生成31molNaNO 需消耗44.0molKMnO B. 反应过程中溶液的pH 减小 C. 该反应中-2NO 被还原 D. X 可以是盐酸4. 向2MnCl 溶液中加入过量难溶电解质MnS ,可使溶液中含有的+2Cu 、+2Pb 、+2Cd 等金属离子转化为硫化物沉淀,从而得到纯净的2MnCl 。
下列分析正确的是( )A. MnS 具有吸附性B. MnS 有还原性,将+++222Cd Pb Cu 、、还原后除去 C. MnS 溶液度大于CuS 、PbS 、CdSD. MnS 与+2Cu 反应的离子方程式是↓=+-+CuS S Cu 22 5. 下列溶液中微粒的浓度关于不正确的是( )A. NaClO 溶液中:()()()-++=ClO c HClO c NacB. 等体积、等物质的量浓度的NaX 和弱酸HX 混合,所得溶液中:()()()()-+-+>>>OH c H c X c Na cC. 将L mol mL /2.025的盐酸与L mol mL /1.0100的氨水混合,所得溶液中:()()()()()+--+>>⋅>>H c OH c O H NH c Cl c NH c 234D. 将L mol /1.0的S Na 2溶液与L mol /1.0的NaHS 溶液等体积混合,所得溶液中:()()()()()---++++=+OH c HS c S c H c Na c 226. 在温度1t 和2t 下,卤素单质()g X 2和2H 反应生成HX 的化学平衡常数如下表所示,仅根据下表数据不能判断的是( )22H F +HF 2 36108.1⨯ 32109.1⨯ 22H Cl +HCl 212107.9⨯ 11102.4⨯ 22H Br +HBr 2 7106.5⨯6103.9⨯22H I +HI 24334A. 已知12t t >,HX 的生成反应为放热反应 B. 在相同条件下,2X 平衡转化率22:Cl F >α C. 2X 与2H 反应的剧烈程度随着原子序数递增逐渐减弱 D. HX 的稳定性:HI HBr >7. 下图是某校实验小组设计的一套原电池装置,下列有关描述不正确的是( )A. 此装置能将化学能转变为电能B. 石墨的电极反应:--=++OH e O H O 44222 C. 电子由Cu 电极经导线流向石墨电极D. 电池总反应:O H CuCl HCl O Cu 2222242+=++ 8. 有关物质用途,用离子方程式解释不正确的是( )A. 氢氟酸刻蚀玻璃:O H SiF HF SiO 24224+↑=+ B. 明矾用于净水:()+++=+H OH Al O H Al33323C. 纯碱去除油污:OH CO 223+---+OH HCO 3D. 氯气制备“84”消毒液:O H ClO Cl OH Cl 222++=+---9. 下列装置或操作能达到实验目的的是( )10. 下图为元素周期表中部分短周期元素,其中Y 原子最外层电子数是其电子层数的2倍。
北京市东城区示范校2022届高三上学期综合能力测试数学(文)试题

北京市东城区示范校2022届高三上学期综合能力测试数学(文)试题数学试卷(文科)本试卷分第I卷和第II卷两部分,共150分。
考试时长120分钟。
第I卷(选择题共40分)一、选择题。
(本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项)1.已知集合A某R|2某2,B某R|某4某30,则AB()2A.(2,1]B.2,1C.2,2D.,2[3,)2.已知复数z1a2i,z212i,若A.2B.1C.2z1是纯虚数,则实数a的值为()z2D.43.“某3”是“co某”成立的()2B.必要不充分条件D.既不充分也不必要条件A.充分不必要条件C.充要条件4.下图是一算法的程序框图,若此程序运行结果为55,则在判断框中应填入关于k的判断条件是()A.k11B.k10C.k9D.k85.已知一个棱锥的三视图如下,根据图中标出的尺寸(单位:cm),可得这个棱锥的侧面积是()A.4cm2|某|B.12cm22C.842cm2D.44223cm26.已知f某2某a有唯一的零点,则实数a的值为()A.-3B.-222C.-1D.027.如图,直线y某2与圆某y4某30及抛物线y8某依次交于A、B、C、D四点,则|AB||CD|()A.13B.14C.15D.162某4某3,某0,8.已知f某不等式f某af2a某在a,a1上恒成2某2某3,某0,立,则实数a的取值范围是()第II卷(非选择题共110分)二、填空题。
(本大题共6小题,每小题5分,共30分)A.,2B.,0C.0,2D.2,0某y10,9.不等式组某y1,表示的平面区域的面积为__________。
某110.设平面向量a1,2,b2,y,若ab,则|2ab|=__________。
11.在等差数列an中,a13,a42,则a4a7...a3n1__________。
12.直线某3y40被圆某2y24截得的弦长为__________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
市东城区普通高中示校高三年级综合能力测试2015第一部分:听力理解(共三节, 30分)第一节(共5小题;每小题1.5分, 共7.5分)听下面5段对话或独白。
每段对话或独白后有一道小题, 从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话或独白后, 你将有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话或独白你将听一遍。
例:What is the man going to read?A. A newspaper.B. A magazine.C. A book.答案是A。
1. How much will the man pay for the flowers?A. $12.B. $20.C. $30.2. What did the woman do on Sunday morning?A. She went hiking.B. She saw a movie.C. She visited a relative.3. What will the man do immediately?A. Change the room for the woman.B. Help the woman with her luggage.C. Make a reservation for the woman.4. What’s the man doing?A. Complaining.B. Giving an excuse.C. Making an apology.5. Why is the announcement made?A. To report the weather.B. To cancel some activities.C. To announce school is over.第二节(共10小题;每小题1.5分, 共15分)听下面4段对话或独白。
每段对话或独白后有几道小题, 从每题所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前, 你将有5秒钟的时间阅读每小题。
听完后, 每小题将给出5秒钟的作答时间。
每段对话或独白你将听两遍。
听第6段材料, 回答第6至7题。
6. Where are the two speakers?A. At a party.B. On a plane.C. In a restaurant.7. What will the woman bring the man?A. A blanket.B. Food.C. Wine.听第7段材料, 回答第8至9题。
8. How will the woman get to Daniels Company?A. By bus.B. By subway.C. By car.9. When will the woman leave?A. At 8:30.B. At 8:50.C. At 9:30.听第8段材料, 回答第10至12题。
10. Why is the man going to Miami?A. To have lessons.B. To attend a wedding.C. To do some business.11. What does the man invite the woman to do?A. Have dinner.B. Do some sports.C. Go to a coffee shop.12. Who is on a tennis team?A. Kate.B. Mike.C. Jenny.听第9段材料, 回答第13至15题。
13. What’s the speaker mainly talking about?A. Driving safety.B. Travel arrangement.C. Suggestions on holidays.14. What does the speaker suggest?A. Stopping to have a rest from time to time.B. Relaxing by listening to the radio sometimes.C. Drinking coffee when you are tired during the journey.15. What does the speaker do?A. A tour guide.B. A police officer.C. A radio announcer.第三节(共5小题;每小题1.5分, 共7.5分)听下面一段独白, 完成第16至20五道小题, 每小题仅填写一个词。
听独白前, 你将有20秒钟的时间阅读试题, 听完后你将有60秒钟的作答时间。
这段独白你将听两遍。
第一节单项填空(共15小题;每小题1分, 共15分)从每题所给的A、B、C、D四个选项中, 选出可以填入空白处的最佳选项。
例:It’s so nice to hear from her again. __________, we last met more than thirty years ago.A. What’s moreB. That’s to sayC. In other word sD. Believe it or not答案是D。
21. What’s up, Bill? You __________upset.A. lookB. lookedC. have lookedD. had looked22. __________patient when you argue with someone who is not so reasonable.A. BeB. BeingC. To beD. Having been23. It is more important than ever to develop one’s maths, science and computer skills __________technological change is accelerating.A. thoughB. unlessC. untilD. because24. While looking for some personal documents, I happened to see an album __________some old photographs.A. containedB. to containC. containingD. being contained25. —Oh, I __________my passport!—Don’t worry. We have time to go back home and get it.A. forgetB. forgotC. will forgetD. had forgot26. His study was a mess with lots of books and magazines __________up everywhere.A. to pileB. having piledC. piledD. to be piled27. An advantage of being the youngest child in his family is __________he gets a lot of attention.A. thatB. whetherC. whyD. when28. Hotels fill up fast during the busy tourist season, __________it is necessary for tourists to make reservations in advance.A. orB. soC. forD. but29. He failed the driving test though he __________for a long time.A. practisesB. has practisedC. was practisingD. had been practising30. —Why won’t you go to Jim’s birthday party with us?—Well, I d on’t like him, if you __________know.A. canB. mayC. mustD. should31. Due to the light pollution, stars are too faint __________with naked eyes in the urban area.A. observingB. being observedC. to be observedD. to be observing32. The professor can answer almost any question __________we have about any history topic.A. asB. thatC. whyD. where33. —I think we are lost. I’ve no idea where we are. —I wish we __________the map with us.A. bringB. would bringC. have broughtD. had brought34. The books sold __________millions in one day, and the publisher had to print another ten thousand copies.A. withB. inC. forD. at35. The researchers have discovered __________they believe to be a new species.A. whichB. whoC. whereD. what第二节完形填空(共20小题;每小题1.5分, 共30分)阅读下面短文, 掌握其大意, 从每题所给的A、B、C、D四个选项中, 选出最佳选项。
The 100th Running Shoe KeychainWhen I was in Grade 6, I joined the cross country running club. I hated running but___36___ because my friends were in the club. I worked hard but no matter how hard I trained, I ___37___ came in the last. After yet another meet where I came in last, I told my coach that I was going to ___38___. 1 couldn’t run. I hated running and all I was doing was pulling the ___39___ down. I don’t remember his words, but I do remember he ___40___to let me quit. I remember feeling that he believed in me even though I didn’t believe in myself. I kept ___41___and participating in the meets. He never gave up on me. Instead, he always encouraged me to keep going, and told me that I could do it.Then the final meet came, a huge ___42___ with less than two hundred students running. We learned that not only the first 20 students ___43___ the line would win an award, but also the first 100 would be given a running shoe keychain as encouragement. We set off and I quickly ___44___behind. I didn’t stop and kept running. My friends who___45___me encouraged me to keep running. When I passed the ___46___, finally, and received the 100th keychain, there were still students behind me. For the first time, I was not the ___47___one! I remember how excited I felt and how my friends felt happy for me.The following week there was a school gathering. We were all called up in front of the school. The coach shared that we were high ___48___at the meet, and almost everyone on the team came home with ___49___. I felt ashamed, for I was the one who didn’t win an award. I only came in the 100th pl ace and didn’t ___50___ his praise. Then he came behind me, put his hands on my shoulders and told the school he was ___51___of me because I never gave up and because of that, Ipulled from last ___52___to the middle of the race—which was an unbelievable personal ___53___. He spoke on how we all ___54___one another and how well we worked together, ___55___we all were racing alone.I still keep that keychain, which tells me never to give up and always work with others. It doesn’t matter if you are the f irst;what matters is doing your best.36. A. obeyed B. joined C. agreed D. practised37. A. constantly B. approximately C. personally D. absolutely38. A. fall B. lose C. rest D. quit39. A. score B. coach C. team D. record40. A. regretted B. forbade C. refused D. hesitated41. A. begging B. applying C. failing D. training42. A. affair B. success C. amount D. honour43. A. to B. beyond C. over D. across44. A. followed B. fell C. left D. kept45. A. helped B. inspired C. passed D. supported46. A. field B. line C. test D. match47. A. least B. last C. quickest D. farthest48. A. spots B. speeds C. quality D. chance49. A. presents B. keychains C. wishes D. awards50. A. believe B. value C. deserve D. request51. A. aware B. proud C. capable D. sure52. A. place B. number C. race D. minute53. A. matter B. ambition C. victory D. opinion54. A. encouraged B. introduced C. proved D. attracted55. A. as if B. in case C. as long as D. even though第三部分:阅读理解(共两节, 40分)第一节(共15小题;每小题2分, 共30分)阅读下列短文, 从每题所给的A、B、C、D四个选项中, 选出最佳选项。
