病态矩阵
矿区坐标转换中病态矩阵与坐标粗差的处理算法

矿区坐标转换中病态矩阵与坐标粗差的处理算法矿区坐标转换是在矿区测量和地图制图过程中常见的一项工作。
它的目的是将矿区内的局部坐标系转换为全球坐标系(如UTM坐标系),以便将测量数据与地理信息系统(GIS)数据进行集成和分析。
在实际中,由于各种误差和扰动的存在,矿区坐标转换可能会产生病态矩阵问题,导致转换结果与真实坐标之间存在较大的差异。
解决病态矩阵问题以及处理坐标粗差是矿区坐标转换中必不可少的一项工作。
病态矩阵是指在矩阵计算中,由于矩阵的条件数较大,导致计算结果对输入误差高度敏感的情况。
在矿区坐标转换中,病态矩阵通常是由于矿区局部坐标系与全球坐标系之间的转换关系非常复杂造成的。
为了解决病态矩阵问题,可以采用以下方法:1. 数据预处理:在进行坐标转换之前,对采集到的局部坐标数据进行预处理。
包括数据的滤波、平差和精度分析等步骤,以提高数据的质量和可靠性。
2. 改进模型:病态矩阵问题通常是由于模型中存在的不稳定性引起的。
可以通过改进模型,如引入更多的控制点、加入附加方程等方法,来提高模型的稳定性和鲁棒性。
3. 数据加权:在进行坐标转换时,可以对数据进行加权处理。
通过为不同的数据点分配不同的权重,可以降低数据中误差较大的点对结果的影响,从而减小病态矩阵的影响。
坐标粗差是指由于错误的测量或错误的数据处理产生的偏离真实值较大的坐标点。
坐标粗差是矿区坐标转换中常见的问题,导致转换结果与真实坐标之间存在较大的差异。
为了处理坐标粗差,可以采用以下方法:2. 多样性数据分析:通过对不同类型的数据进行分析和比较,可以识别出可能存在的坐标粗差点。
使用不同的测量方法、不同的设备或多次测量等方式来获得更多的数据,以便对比和验证数据的一致性。
3. 自动检测和修复算法:可以使用自动检测和修复算法来处理坐标粗差问题。
这些算法可以根据一定的规则或经验知识,自动识别和修复异常点,以提高数据的精度和可靠性。
矿区坐标转换中的病态矩阵和坐标粗差问题是影响坐标转换结果准确性和可靠性的关键因素。
(完整word版)几何角度解释矩阵出现病态

矩阵的范数范数的定义若X是数域K上的线性空间,泛函║·║: X->R 满足:1. 正定性:║x║≥0,且║x║=0 <=> x=0;2. 正齐次性:║AB║│≤│A║B║;3. 次可加性(三角不等式):║A+B║≤║A║+║B║。
那么║·║称为X上的一个范数。
(注意到║x+y║≤║x║+║y║中如令y=-x,再利用║-x║=║x║可以得到║x║≥0,即║x║≥0在定义中不是必要的。
)在AX=B式中,当A、B有微小扰动时,参数估值X也有扰动:(A+ΔA)(X+ΔX)=B+ΔB (1)AΔX=ΔA(X+ΔX)+ΔBΔX=-A-1ΔA(X+ΔX)+A-1ΔB将上式两端取范数,并应用向量范数的三角不等式║AB║│≤│A║B║;║A+B║≤║A║+║B║。
||ΔX||≤||A-1||||ΔA||(||X|| +||ΔX||)+||A-1| ||ΔB|| 把含有ΔX的项移到式子的左边有:(1-||A-1||||ΔA||)||ΔX||≤||A-1||||ΔA|| ||X||+||A-1| ||ΔB||由于有||X||≤||A||/||B||将上式两端同时乘以||X||得:(1-||A-1||||ΔA||)||ΔX||/||X||≤||A-1||||ΔA|| +||A-1||||ΔB||A||/||B||;设K=||A||||A-||将上式整理的:(1-K||ΔA||/||A||)||ΔX||/||X||≤K(||ΔA||/||A||+||ΔB||/||B||);即有:||ΔX||/||X||≤k/(1-K||ΔA||/||A||)(||ΔA||/||A||+||ΔB||/||B||); 问题与实验1:试从几何的角度解释矩阵出现病态的原因,并用‘有说服力’的例子来支持你的观点;线性方程组解的敏感性的几何解释(2x2矩阵)线性方程组求解:两直线求交点下面两图分别反映了良态问题和病态问题两种情况。
病态矩阵 预处理 matlab

病态矩阵在数学和计算机科学中是一个重要的概念,它在多种领域都有着广泛的应用。
本文将结合 matlab 中的预处理方法,对病态矩阵进行深入探讨和分析,希望能够为相关领域的研究和实践提供一定的参考价值。
一、病态矩阵的定义和特性1. 病态矩阵的定义病态矩阵是指条件数(矩阵的最大奇异值与最小奇异值的比值)非常大的矩阵,这意味着它对输入数据的微小扰动非常敏感。
具体来说,当一个矩阵的条件数远大于1时,就可以认为它是病态矩阵。
2. 病态矩阵的特性病态矩阵在数学和计算机科学中有着重要的地位,它的特性主要包括:(1)对输入数据敏感:病态矩阵对输入数据的微小扰动非常敏感,可能导致计算结果的误差被放大。
(2)计算困难:病态矩阵在求逆、求解线性方程组等计算过程中可能会出现数值不稳定的情况,导致计算困难和误差的积累。
二、病态矩阵的预处理方法1. 规范化规范化是一种常用的病态矩阵预处理方法,它通过将矩阵的每一行除以该行的范数,使得矩阵的每一行都具有单位范数。
这样可以有效地减小矩阵的条件数,提高计算的稳定性和准确性。
2. 正交化正交化是另一种常用的病态矩阵预处理方法,它通过将矩阵进行正交变换,使得矩阵的列向量之间相互正交。
这样可以提高矩阵的条件数,改善计算的稳定性和精度。
3. 奇异值分解奇异值分解是一种更为复杂但有效的病态矩阵预处理方法,它通过将矩阵分解为奇异值矩阵、左奇异向量和右奇异向量,从而减小矩阵的条件数,提高计算的准确性。
三、matlab 中的病态矩阵预处理实现matlab 是一种强大的科学计算软件,它提供了丰富的病态矩阵预处理工具和函数,可以方便地进行病态矩阵的处理和分析。
下面我们主要介绍 matlab 中常用的病态矩阵预处理函数和实现方法。
1. cond 函数matlab 中的 cond 函数可以用来计算矩阵的条件数,从而帮助用户评估矩阵的病态程度。
通过 cond 函数,用户可以及时发现矩阵的病态特性,为后续的预处理和计算提供参考。
几何的角度解释矩阵出现病态

矩阵的范数范数的定义若X是数域K上的线性空间,泛函║·║: X->R 满足:1. 正定性:║x║≥0,且║x║=0 <=> x=0;2. 正齐次性:║AB║│≤│A║B║;3. 次可加性(三角不等式):║A+B║≤║A║+║B║ 。
那么║·║称为X上的一个范数。
(注意到║x+y║≤║x║+║y║中如令y=-x,再利用║-x║=║x║可以得到║x║≥0,即║x║≥0在定义中不是必要的。
)在AX=B式中,当A、B有微小扰动时,参数估值X也有扰动:(A+ΔA)(X+ΔX)=B+ΔB (1)AΔX=ΔA(X+ΔX)+ΔBΔX=-A-1ΔA(X+ΔX)+A-1ΔB将上式两端取范数,并应用向量范数的三角不等式║AB║│≤│A║B║;║A+B║≤║A║+║B║ 。
||ΔX||≤||A-1||||ΔA||(||X|| +||ΔX||)+||A-1| ||ΔB|| 把含有ΔX的项移到式子的左边有:(1-||A-1||||ΔA||)||ΔX||≤||A-1||||ΔA|| ||X||+||A-1| ||ΔB||由于有1/||X||≤||A||/||B||将上式两端同时乘以1/||X||得:(1-||A-1||||ΔA||)||ΔX||/||X||≤||A-1||||ΔA|| +||A-1||||ΔB||A||/||B||;设K=||A||||A-||将上式整理的:(1-K||ΔA||/||A||)||ΔX||/||X||≤K(||ΔA||/||A||+||ΔB||/||B||);即有:||ΔX||/||X||≤k/(1-K||ΔA||/||A||)(||ΔA||/||A||+||ΔB||/||B||);问题与实验1:试从几何的角度解释矩阵出现病态的原因,并用‘有说服力’的例子来支持你的观点;线性方程组解的敏感性的几何解释(2x2矩阵)线性方程组求解:两直线求交点下面两图分别反映了良态问题和病态问题两种情况。
《病态矩阵的例子》课件

了解病态矩阵的定义、性质以及其在各个领域中的应用。探索病态矩阵会导 致问题的原因,并探讨解决方法和数值稳定性。
什么是病态矩阵
病态矩阵是指在运算过程中非常敏感而导致精度损失的矩阵。了解病态矩阵的定义和基本特征。
矩阵的定义和性质
探索矩阵的基本定义和性质,包括矩阵的形式、操作和运算规则。理解矩阵在数学中的重要性。
病态矩阵的特点
了解病态矩阵的特点,例如条件数的增加,偏差的敏感性以及导致数值不稳定的原因。
为什么病态矩阵会导致问题
探讨病态矩阵会导致计算问矩阵的计算方法
介绍解决病态矩阵问题的计算方法,包括预处理技术和数值稳定的算法。
病态矩阵的影响因素
探讨病态矩阵的影响因素,包括矩阵的条件数、数据误差以及算法选择。
病态矩阵的应用领域
探索病态矩阵在物理学、经济学、生物学、工程学和机器学习等领域中的具 体应用案例。
badly conditioned matrix 解决方法

badly conditioned matrix 解决方法关于"badly conditioned matrix"(病态矩阵)的解决方法引言:在数值分析中,病态矩阵是一个特殊的矩阵,其条件数非常高,这意味着即使输入的数据有微小的误差,也会导致解的误差巨大。
病态矩阵是一种常见的问题,可能会对数值计算产生重大影响。
然而,幸运的是,我们可以采取一些措施来应对病态矩阵的挑战,并确保获得准确和稳定的解。
在本文中,将提供一些解决病态矩阵问题的方法,以便我们能够更好地理解和处理这一问题。
第一步:输入数据的预处理病态矩阵的条件数取决于输入数据的精确性。
因此,第一步是对输入数据进行预处理和修正以提高其准确性。
一种常用的方法是使用数值分析中的数值稳定性技术,如舍入误差分析和数值稳定算法。
通过这些技巧,我们可以识别并修复导致矩阵病态性的问题,从而减少条件数。
第二步:使用正则化技术正则化是通过添加一个正则化项来修改矩阵问题的数学表达式,以提高解的稳定性。
正则化技术广泛应用于矩阵和线性方程组的求解中,并可以有效地应对病态矩阵的挑战。
其中,Tikhonov正则化和岭回归是常见的正则化方法,它们在解决过拟合和病态矩阵问题方面具有良好的效第三步:使用迭代方法另一种应对病态矩阵的方法是使用迭代方法解决线性方程组。
迭代方法通过通过多次迭代逼近解来解决线性方程组,从而减少计算过程中的矩阵病态性对结果的影响。
常见的迭代方法包括雅可比迭代法、高斯-赛德尔迭代法和共轭梯度法。
这些方法通过在每次迭代中逐渐优化解的近似值,从而得到更准确和稳定的解。
第四步:使用奇异值分解奇异值分解(SVD)是解决病态矩阵问题的一种常用方法。
SVD是一种矩阵分解技术,可以将一个矩阵分解为三个矩阵的乘积:原始矩阵等于左奇异向量矩阵乘以奇异值矩阵再乘以右奇异向量矩阵的转置。
通过使用SVD,我们可以降低病态矩阵的条件数,并获得更准确和稳定的解。
第五步:使用正交变换正交变换是通过改变矩阵的基或坐标系来减少矩阵的病态性。
病态矩阵预处理方法

病态矩阵预处理方法矩阵在数学和工程领域中有着广泛的应用,而病态矩阵是指其条件数较大的矩阵。
病态矩阵的存在会给数值计算带来困扰,因为它们对计算的精确性和稳定性造成了挑战。
为了解决这个问题,病态矩阵预处理方法被提出。
病态矩阵的条件数是衡量矩阵病态程度的重要指标。
条件数越大,矩阵就越病态。
当条件数接近无穷大时,矩阵变得非常难以求逆和求解线性方程组。
在实际问题中,我们经常会遇到病态矩阵,因此需要采取一些预处理方法来改善计算的精确性和稳定性。
病态矩阵预处理方法的基本思想是通过对矩阵进行一系列操作,使其变得更加接近于非病态矩阵。
这些操作可以包括矩阵的估计、变换、缩放和正交化等。
下面将介绍几种常见的病态矩阵预处理方法。
1. 矩阵的估计通过对矩阵进行估计,可以得到一个近似的非病态矩阵。
常见的估计方法包括最小二乘法、正交多项式逼近和奇异值分解等。
这些方法可以有效地降低矩阵的条件数,提高求解的精确性和稳定性。
2. 矩阵的变换通过对矩阵进行变换,可以改变矩阵的结构和性质,从而降低其条件数。
常见的变换方法包括矩阵的对角化、特征值分解和Schur分解等。
这些变换可以将矩阵转化为更加简单和易于处理的形式,从而提高求解的效率和准确性。
3. 矩阵的缩放通过对矩阵进行缩放,可以将矩阵的元素大小调整到一个合适的范围内,从而降低矩阵的条件数。
常见的缩放方法包括列缩放和行缩放等。
这些方法可以使矩阵的元素大小均衡分布,减少条件数的差异性,提高计算的稳定性。
4. 矩阵的正交化通过对矩阵进行正交化,可以将矩阵的列向量变得正交或近似正交,从而降低矩阵的条件数。
常见的正交化方法包括Gram-Schmidt正交化和Householder正交化等。
这些方法可以使矩阵的列向量之间的关联性减弱,从而提高求解的准确性和稳定性。
病态矩阵预处理方法在数值计算中具有重要的意义。
通过对矩阵进行预处理,可以降低矩阵的条件数,提高求解线性方程组和求逆矩阵的准确性和稳定性。
(完整word版)几何角度解释矩阵出现病态

矩阵的范数范数的定义若X是数域K上的线性空间,泛函║·║: X->R 满足:1. 正定性:║x║≥0,且║x║=0 <=> x=0;2. 正齐次性:║AB║│≤│A║B║;3. 次可加性(三角不等式):║A+B║≤║A║+║B║ 。
那么║·║称为X上的一个范数。
(注意到║x+y║≤║x║+║y║中如令y=-x,再利用║-x║=║x║可以得到║x║≥0,即║x║≥0在定义中不是必要的。
)在AX=B式中,当A、B有微小扰动时,参数估值X也有扰动:(A+ΔA)(X+ΔX)=B+ΔB (1)AΔX=ΔA(X+ΔX)+ΔBΔX=-A-1ΔA(X+ΔX)+A-1ΔB将上式两端取范数,并应用向量范数的三角不等式║AB║│≤│A║B║;║A+B║≤║A║+║B║ 。
||ΔX||≤||A-1||||ΔA||(||X|| +||ΔX||)+||A-1| ||ΔB|| 把含有ΔX的项移到式子的左边有:(1-||A-1||||ΔA||)||ΔX||≤||A-1||||ΔA|| ||X||+||A-1| ||ΔB||由于有1/||X||≤||A||/||B||将上式两端同时乘以1/||X||得:(1-||A-1||||ΔA||)||ΔX||/||X||≤||A-1||||ΔA|| +||A-1||||ΔB||A||/||B||;设K=||A||||A-||将上式整理的:(1-K||ΔA||/||A||)||ΔX||/||X||≤K(||ΔA||/||A||+||ΔB||/||B||);即有:||ΔX||/||X||≤k/(1-K||ΔA||/||A||)(||ΔA||/||A||+||ΔB||/||B||); 问题与实验1:试从几何的角度解释矩阵出现病态的原因,并用‘有说服力’的例子来支持你的观点;线性方程组解的敏感性的几何解释(2x2矩阵)线性方程组求解:两直线求交点下面两图分别反映了良态问题和病态问题两种情况。
希尔伯特矩阵的病态性问题

希尔伯特矩阵的病态性问题(学号:200921100102 姓 名:陈丹丹 )一、问题叙述希尔伯特矩阵是著名的病态矩阵。
n 阶Hilbert 矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−++=)12/(1)1/(1/1)1/(13/12/1/12/11n n n n n H n L L L L L L L 其条件数 Cond(H n ) 如下表所示n2 3 4 5 6 Cond(H n )1.9281e+001 5.2406e+002 1.5514e+004 4.7661e+005 1.4951e+007随着n 的增大,矩阵条件数迅速增加。
猜测:希尔伯特矩阵条件数以指数规律增长。
即,设矩阵阶数为n ,有Cond(H n ) ≈ exp( a n + b )对表中的条件数做对数变换,问题转化为线性拟合问题ln[Cond(H n )] = a n + b ,( n = 2,3,4,5,6)线性函数的两个系数分别为a = 3.3935,b = – 3.8811故指数拟合函数为:Cond(H n ) ≈ exp(3.3935 n –3.8811 )拟合函数的残差向量为r 2 r 3 r 4 r 5 r 69.9860e-001 -2.0231e+001 -6.8994e+002 -5.7825e+003 5.9012e+005 我们讨论以下三个问题:(1)由于线性拟合所得残差向量较大,下面用实验确定:选择用几次多项式拟合较好(2)设D 是由H n 的对角线元素开方构成的对角矩阵,令11ˆ−−=D H D H nn ,不难看出该矩阵仍然是对称正定矩阵,而且其对角元素全为1。
将H n 变换为n H ˆ的技术称为预处理(Preconditioning )。
试分析函数)](/)ˆ(ln[nn H Cond H Cond 随n 变化的规律,绘制该函数的曲线。
(3)如果只用左预处理,即D 取希尔伯特矩阵对角元构成对角矩阵,用D 的逆阵左乘H 后条件数如何。
判断与处理病态问题的方法

判断与处理病态问题的方法病态问题是指在数值计算中出现的一些特殊情况,比如矩阵条件数非常大或非常小、线性方程组解出现明显的误差等。
这些问题可能会导致计算结果的不稳定性和不准确性,因此在数值计算中需要判断和处理病态问题。
本文将介绍判断与处理病态问题的方法。
一、判断病态问题1. 计算条件数条件数是衡量矩阵是否病态的一个重要指标。
当条件数很大时,说明矩阵非常接近奇异(singular)状态,此时求解线性方程组可能会产生误差。
因此,我们可以通过计算条件数来判断一个矩阵是否病态。
2. 检查残量在求解线性方程组时,我们可以通过计算残量来检查解的准确性。
如果残量很小,则说明解比较准确;如果残量很大,则说明解可能存在误差。
3. 分析特征值分布对于一个对称正定矩阵,它的特征值分布应该是均匀的,并且所有特征值都应该大于零。
如果特征值分布不均匀或有负特征值,则说明该矩阵可能是病态的。
二、处理病态问题1. 矩阵重构当发现一个矩阵是病态的时候,我们可以尝试对其进行重构,使其变得更加稳定。
比如,可以对矩阵进行平移、缩放或旋转等操作,使其条件数减小。
2. 正则化正则化是一种常用的处理病态问题的方法。
它通过在原始问题中添加一些额外的约束条件来限制解的范围,从而避免出现不稳定解。
常见的正则化方法包括Tikhonov正则化、L1正则化和L2正则化等。
3. 改变求解方法当一个线性方程组存在多个解时,我们可以通过改变求解方法来获取其中一个稳定且准确的解。
比如,可以使用QR分解、LU分解或Cholesky分解等方法来求解线性方程组。
4. 增加精度当计算结果存在误差时,我们可以通过增加计算精度来提高结果的准确性。
比如,在浮点数运算中使用double类型或long double类型来代替float类型。
结论:综上所述,判断和处理病态问题是数值计算中非常重要的一部分。
在实际应用中,我们需要根据具体情况选择合适的方法来判断和处理病态问题,以获得稳定且准确的计算结果。
病态矩阵的例子

>> norm(x'-ones(8,1))
ans =
9.3866e-007
>> norm(A*x'-b)
ans =
7.0278e-008
1.0000
1.0000
就是说,对于系数矩阵为 8 阶的 Hilbert 矩阵,用 Matlab 中 的”inv”语句,大致能达到 6-7 位有效数字,这时条件数为 10 的 10 次方量级。
Results may be inaccurate. RCOND = 2.632091e-017. >> rank(A) ans =
11
>> A=hilb(100); >> rank(A) ans =
18 >> A=hilb(1000); >> rank(A) ans =
24
>> rank(hilb(2000)) ans =
病态矩阵的例子
>> Eigenvalue=eig(A) Eigenvalue =
0.0000 0.0003 0.0114 0.2085 1.5671 >> cond(A) ans = 4.7661t;> x=inv(A)*b; >> x solution =x
0.0000
0.0000
0.0000
0.0262 0.2981 1.6959
>> cond(A)
ans =
1.5258e+010
0.0001
0.0015
>> b=A*ones(8,1);
>> x=(inv(A)*b)'
几何的角度解释矩阵出现病态

矩阵的范数范数的定义若X是数域K上的线性空间,泛函║·║: X->R 满足:1. 正定性:║x║≥0,且║x║=0 <=> x=0;2. 正齐次性:║AB║│≤│A║B║;3. 次可加性(三角不等式):║A+B║≤║A║+║B║ 。
那么║·║称为X上的一个范数。
(注意到║x+y║≤║x║+║y║中如令y=-x,再利用║-x║=║x║可以得到║x║≥0,即║x║≥0在定义中不是必要的。
)在AX=B式中,当A、B有微小扰动时,参数估值X也有扰动:(A+ΔA)(X+ΔX)=B+ΔB (1)AΔX=ΔA(X+ΔX)+ΔBΔX=-A-1ΔA(X+ΔX)+A-1ΔB将上式两端取范数,并应用向量范数的三角不等式║AB║│≤│A║B║;║A+B║≤║A║+║B║ 。
||ΔX||≤||A-1||||ΔA||(||X|| +||ΔX||)+||A-1| ||ΔB|| 把含有ΔX的项移到式子的左边有:(1-||A-1||||ΔA||)||ΔX||≤||A-1||||ΔA|| ||X||+||A-1| ||ΔB||由于有1/||X||≤||A||/||B||将上式两端同时乘以1/||X||得:(1-||A-1||||ΔA||)||ΔX||/||X||≤||A-1||||ΔA|| +||A-1||||ΔB||A||/||B||;设K=||A||||A-||将上式整理的:(1-K||ΔA||/||A||)||ΔX||/||X||≤K(||ΔA||/||A||+||ΔB||/||B||);即有:||ΔX||/||X||≤k/(1-K||ΔA||/||A||)(||ΔA||/||A||+||ΔB||/||B||);问题与实验1:试从几何的角度解释矩阵出现病态的原因,并用‘有说服力’的例子来支持你的观点;线性方程组解的敏感性的几何解释(2x2矩阵)线性方程组求解:两直线求交点下面两图分别反映了良态问题和病态问题两种情况。
《病态矩阵的例子》课件

03
CHAPTER
病态矩阵的影响
对计算结果的影响
不正确的解
病态矩阵可能导致数值计算的解完全 错误,即使算法本身是正确的。
解的不稳定性
即使使用相同的算法和相同的数据, 由于舍入误差,不同的计算可能会得 到不同的解。
对算法稳定性的影响
病态矩阵可能导致算法不稳定
在迭代算法中,病态矩阵可能导致算法发散或收敛到错误的 解。
21, 22, 23, 24, 25]
数值例子
``` 计算其条件数为inf,说明这是一个病态矩阵。
数值例子2:给定一个3x3的矩阵B,其元素如下
数值例子
``` [1000, 0.0001, 0.000001; 0.0001, 1000, 0.0001;
数值例子
• 0.000001, 0.0001, 1000]
迭代收敛性检查
在迭代过程中,检查算法 的收敛性,如果发现不收 敛的情况,则采取相应的 措施进行修正。
误差估计
在迭代过程中,估计误差 的大小,并根据误差的大 小调整算法的参数,以提 高数值精度。
病态矩阵的避免方法
避免零元素的出现
在构建矩阵时,尽量避免出现零元素,因为零元素可能会导致算 法的不稳定。
选择合适的数值方法
病态矩阵的识别
高条件数
可以通过计算矩阵的条件数来判断一个矩阵是否为病态矩 阵。如果条件数很大,则该矩阵可能是病态的。
接近奇异或退化
通过检查矩阵的特征值和奇异值,可以判断一个矩阵是否 接近奇异或退化。如果特征值或奇异值很小,则该矩阵可 能是病态的。
元素变化对结果影响
可以通过比较不同初始条件下计算结果的差异来判断一个 矩阵是否为病态矩阵。如果不同初始条件下的结果差异很 大,则该矩阵可能是病态的。
矩阵病态线性代数方程组的求解
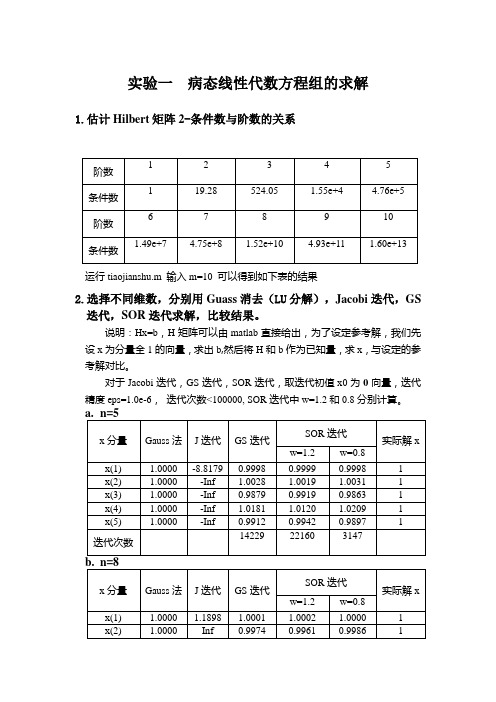
实验一病态线性代数方程组的求解1.估计Hilbert矩阵2-条件数与阶数的关系运行tiaojianshu.m输入m=10 可以得到如下表的结果2.选择不同维数,分别用Guass消去(LU分解),Jacobi迭代,GS 迭代,SOR迭代求解,比较结果。
说明:Hx=b,H矩阵可以由matlab直接给出,为了设定参考解,我们先设x为分量全1的向量,求出b,然后将H和b作为已知量,求x,与设定的参考解对比。
对于Jacobi迭代,GS迭代,SOR迭代,取迭代初值x0为0向量,迭代精度eps=1.0e-6,迭代次数<100000, SOR迭代中w=1.2和0.8分别计算。
取不同的n值,得到如下结果:对于Guass法,可以看出来,随着n的增大,求解结果误差变大,这是因为随着n增大,系数矩阵的条件数变大,微小的扰动就容易造成很大的误差。
最后得不到精确解。
对于Jacobi迭代,计算结果为Inf,说明是发散的。
对于GS迭代和SOR迭代,结果是收敛的,但是可以看出迭代次数比较多,并且对于不同维数GS和SOR收敛速度不一样,有时候GS快,有时SOR快。
对SOR取不同的w迭代速度也不一样,存在一个最优的松弛因子w。
并且可以知道,迭代次数多少跟初值x0也有关系。
3.讨论病态问题求解的算法。
通过上面的实验分析,可以看出,求解病态矩阵的时候要小心,否则可能得不到所要求的精确度。
可以采用高精度运算,用双倍多倍字长,使得由于误差放大而损失若干有效数字位之后,还能保留一些有效位。
另外可以通过对原方程作某些预处理,降低系数矩阵的条件数,因为cond(aA)=cond(A),所以不能通过将每一个方程乘上相同的常数来达到这个目标,可考虑将矩阵的每一行和每一列分别乘上不同的常数,亦即找到可逆的对角阵D1和D2将方程组化为D1AD2y=D1b,x=D2y这称为矩阵的平衡问题,但是这样计算量比原问题本身要多。
或者通过变分原理将求解线性方程组的问题转化为等价的求解无约束函数最优化问题的极小值等等,可以参考[1]郑洲顺,黄光辉,杨晓辉求解病态线性方程组的混合算法实验一所编程序如下:1.求条件数tiaojianshu.mm=input ('input m:=') ;N=[1:m];for i=1:mn=N(i);H=hilb(n);k=cond(H);disp('矩阵的阶数')disp(n)disp('矩阵')disp(H)disp('矩阵的条件数')disp(k)end2.Guass法①Guass.mfunction guass(n)n=input('请输入系数矩阵的维数n=');H=hilb(n);x_exact=ones(n,1);b=H*x_exact;x=Doolittle(H,b)a=input('是否继续,继续请按1,结束请按0:');if a==1guass(n);else end②Doolittle.mfunction x=Doolittle(A,b)% LU分解求Ax=b 的解N=size(A);n=N(1);L=eye(n,n);%L的对角元素为1U=zeros(n,n); %U为零矩阵U(1,1:n)=A(1,1:n)%U第一行L(1:n,1)=A(1:n,1)/U(1,1)%L第一列for k=2:nfor i=k:nU(k,i)=A(k,i)-L(k,1:(k-1))*U(1:(k-1),i)endfor j=(k+1):nL(j,k)=(A(j,k)-L(j,1:(k-1))*U(1:(k-1),k))/U(k,k) endendy=solveDownTriangle(L,b);%调用下三角系数矩阵求解函数x=solveUpTriangle(U,y);%调用上三角系数矩阵求解函数③solveDownTriangle.mfunction x=solveDownTriangle(A,b)%求下三角系数矩阵的线性方程组Ax=bN=size(A);n=N(1);for i=1:nif (i>1)s=A(i,1:(i-1))*x(1:(i-1),1);elses=0;endx(i,1)=(b(i)-s)/A(i,i);end④solveUpTriangle.mfunction x=solveUpTriangle(A,b)% 求上三角系数矩阵的线性方程组Ax=bN=size(A);n=N(1);for i=n:-1:1if (i<n)s=A(i,(i+1):n)*x((i+1):n,1);elses=0;endx(i,1)=(b(i)-s)/A(i,i);end3.Jacobi法function [x,n]=jacobi(a,x0)a=input('请输入系数矩阵的维数n=');x0=input('请输入迭代初始向量x0');eps=1.0e-6;%解的精度控制m=10000;%迭代步数控制H=hilb(a);%生成h矩阵x_exact=ones(a,1);%求出x精确值b=H*x_exact;D=diag(diag(H));L=-tril(H,-1);U=-triu(H,1);B=D\(L+U);f=D\b;x=x0;n=0;tol=1;while tol>=epsx=B*x0+f;n=n+1;tol=norm(x-x0);x0=x;if (n>=m)disp('迭代次数太多,可能不收敛');return;endenddisp(x)disp(n)4.GS法function [x,n]=gauseidel(a,x0)a=input('请输入系数矩阵的维数n=');x0=input('请输入迭代初始向量x0');eps=1.0e-6;%解的精度控制m=100000;%迭代步数控制H=hilb(a);%生成h矩阵x_exact=ones(a,1);%求出x精确值b=H*x_exact;D=diag(diag(H));L=-tril(H,-1);U=-triu(H,1);G=(D-L)\U;f=(D-L)\b;x=x0;n=0;tol=1;while tol>=epsx=G*x0+f;n=n+1;tol=norm(x-x0);x0=x;if (n>=m)disp('迭代次数太多,可能不收敛');return;endenddisp(x)disp(n)5.SOR法function [x,n]=SOR(a,x0,w)a=input('请输入系数矩阵的维数n=');x0=input('请输入迭代初始向量x0=');w=input('请输入w=');eps=1.0e-6;%解的精度控制m=100000;%迭代步数控制H=hilb(a);%生成h矩阵x_exact=ones(a,1);%求出x精确值b=H*x_exact;if (w<=0||w>=2)error;return;endD=diag(diag(H));L=-tril(H,-1);U=-triu(H,1);B=inv(D-L*w)*((1-w)*D+w*U);f=w*inv((D-L*w))*b;x=x0;n=0;tol=1;while tol>=epsx=B*x0+f;n=n+1;tol=norm(x-x0);x0=x;if (n>=m)disp('迭代次数太多,可能不收敛');return;endenddisp(x)disp(n)。
Hilbert矩阵病态性分析

Hilbert矩阵病态性分析200820303013 王刚一、问题叙述Hilbert矩阵是著名的病态矩阵,用迭代法解矩阵方程时,如果系数矩阵是Hilbert矩阵,则求解结果误差较大。
本文就研究Hilbert矩阵的病态性,和Hilbert 矩阵的阶数与迭代求解误差大小的关系。
二、问题分析MATLAB中有专门的Hilbert矩阵及其准确逆矩阵的生成函数,从而可以通过MATLAB求解出系数矩阵是Hilbert矩阵的矩阵方程比较准确的解,再根据条件数估计求解误差的大小。
三、实验程序及注释m=input('input m:='); %输入矩阵的阶数N=[m];for k=1:length(N)n=N(k); %矩阵的阶H=hilb(n); %产生n阶Hilbert矩阵disp(H) %输出n阶Hilbert矩阵Hi=invhilb(n); %产生完全准确的n阶逆Hilbert矩阵b=ones(n,1); %生成n阶全1向量x_approx=H\b; %利用左除H求近似解x_exact=Hi*b; %利用准确逆Hilbert矩阵求准确解ndb=norm(H*x_approx-b);nb=norm(b);ndx=norm(x_approx - x_exact);nx=norm(x_approx);er_actual(k)=ndx/nx; %实际相对误差K=cond(H); %计算Hilbert矩阵的条件数er_approx(k)=K*eps; %最大可能的近似相对误差er_max(k)=K*ndb/nb; %最大可能的相对误差enddisp('Hilbert矩阵阶数'),disp(N)format short edisp('实际误差 er_actual'),disp(er_actual),disp('')disp('近似的最大可能差 er_approx'),disp(er_approx),disp('') disp('最大可能误差 er_max'),disp(er_max),disp('')四、实验数据结果及分析程序运行后,输入矩阵阶数4时的输出为:input m:=41.0000 0.5000 0.3333 0.25000.5000 0.3333 0.2500 0.20000.3333 0.2500 0.2000 0.16670.2500 0.2000 0.1667 0.1429Hilbert矩阵阶数4实际误差er_actual1.0284e-013近似的最大可能误差er_approx3.4447e-012最大可能误差er_max4.7732e-011当输入不同的矩阵阶数时,误差大小如表1所示。
病态矩阵的特征值

病态矩阵的特征值嘿,朋友们!今天咱来聊聊病态矩阵的特征值这个神奇的玩意儿。
你说这病态矩阵啊,就好像是一个有点“脾气古怪”的家伙。
咱正常的矩阵就像是个乖巧听话的孩子,啥都好商量,可病态矩阵呢,就有那么些让人捉摸不透的地方。
咱想想啊,特征值这东西就像是矩阵的“性格特点”。
对于一般的矩阵,它的特征值都挺正常,能让咱清楚地了解它。
可病态矩阵的特征值啊,就有点像那调皮捣蛋的小孩子,时不时就给你闹出点幺蛾子来。
比如说吧,正常矩阵的特征值计算起来顺顺利利的,结果也很明确。
但病态矩阵的特征值呢,可能就会变得特别奇怪,让你算半天都摸不着头脑。
这就好比你要找个东西,在正常地方一下子就找到了,可在病态矩阵这里啊,就好像那东西藏得特别深,让你一顿好找。
你说这病态矩阵的特征值为啥就这么特殊呢?这就好像有些人的性格就是很特别一样,没办法呀!它就是这么与众不同。
有时候你想用常规方法去理解它,嘿,它还就不按套路出牌。
咱再打个比方,正常矩阵就像是一条笔直的大路,你顺着走就行。
可病态矩阵呢,就像是一条弯弯曲曲的小道,你得小心翼翼地走,不然一不小心就会迷路。
那遇到病态矩阵的特征值咱咋办呢?这可得有点耐心和技巧了。
不能着急,得慢慢琢磨,就像解开一个复杂的谜题一样。
而且啊,还得多尝试几种方法,可不能在一棵树上吊死。
你想想看,如果一直被病态矩阵的特征值给难住了,那多憋屈啊!咱可不能轻易被它打败,得想办法搞定它。
这就跟咱生活中遇到困难一样,不能退缩,得迎头而上。
反正啊,病态矩阵的特征值虽然有点麻烦,但咱也不能怕它。
咱要勇敢地去面对,去探索,去找到解决问题的办法。
咱可不能被它这点小古怪给吓住了,对吧?总之,病态矩阵的特征值虽然有点让人头疼,但也是个很有意思的东西。
它让我们知道,数学的世界里可不是只有那些规规矩矩的东西,还有很多奇怪又有趣的现象等着我们去发现呢!所以,大胆地去和病态矩阵的特征值过过招吧!。
矿区坐标转换中病态矩阵与坐标粗差的处理算法

矿区坐标转换中病态矩阵与坐标粗差的处理算法矿区坐标转换是指将采矿现场的实际坐标转换成地理坐标的过程。
在矿区坐标转换过程中,由于各种原因,可能会出现病态矩阵和坐标粗差的情况。
本文将介绍病态矩阵和坐标粗差的处理算法。
1. 病态矩阵的处理算法病态矩阵是指矩阵的条件数非常大,即矩阵的行列式很接近于零的情况。
在矿区坐标转换过程中,病态矩阵的存在会导致计算结果非常不稳定,甚至可能无法得到准确的解。
病态矩阵的处理算法一般有以下几种方法:(1)数据平差法:利用最小二乘法对数据进行平差处理,通过求解最优解来降低矩阵的条件数。
(2)奇异值分解法:将矩阵分解为奇异值矩阵的乘积形式,通过对奇异值进行处理来减小矩阵的条件数。
(3)正则化方法:在目标函数中引入正则化项,通过调整正则化参数来平衡模型的复杂度和数据的拟合程度,从而降低矩阵的条件数。
2. 坐标粗差的处理算法坐标粗差是指由于观测误差或其他原因导致的坐标值明显偏离真实值的情况。
在矿区坐标转换过程中,坐标粗差的存在会对计算结果产生较大的影响,因此需要采取适当的处理方法。
(1)3σ原则:根据正态分布的性质,坐标观测值的误差在三个标准差范围内的概率约为99.7%,所以可以将超出三个标准差范围的观测值认为是坐标粗差,并进行剔除或修正。
(2)最小二乘法:通过采用最小二乘法进行平差处理,可以将坐标粗差的影响最小化,并得到尽可能准确的结果。
(3)加权最小二乘法:根据坐标观测值的精度估计,为每个观测值赋予不同的权重,通过加权最小二乘法进行计算,可以有效降低坐标粗差的影响。
病态矩阵和坐标粗差是矿区坐标转换中常见的问题,需要通过合适的处理算法来解决。
根据具体情况选择适用的方法,可以提高坐标转换的准确性和稳定性。
矿区坐标转换中病态矩阵与坐标粗差的处理算法

矿区坐标转换中病态矩阵与坐标粗差的处理算法矿区坐标转换是矿务工程设计与管理中的一项重要工作,它是将不同坐标系下的点进行转换,以方便进行统一的分析和计算。
但在实际的转换过程中,由于数据的误差和精度等因素的影响,存在一定的病态矩阵以及坐标转换的粗差问题。
针对这些问题,本文提出了相应的处理算法。
一、病态矩阵问题在矿区坐标转换的过程中,经常会遇到病态矩阵的问题,这是由于输入数据的误差或者计算方法的不当导致的。
病态矩阵会使得计算结果出现异常或不稳定,因此需要对其进行处理。
处理方法如下:1、数据清洗在进行数据转换前,需要对输入数据进行清洗,去掉异常数据、重复数据等,并且需要对数据进行精度控制,保证输入数据的精度和准确度。
2、采用合适的计算方法在进行矩阵运算时,需要采用合适的计算方法,如求逆矩阵时采用高斯约旦消元法,避免使用高斯消元法,从而减少误差的传递。
3、采用加权计算在计算过程中,可以采用加权计算方法,给予重要点更大的权值,从而降低误差的传递,提高计算的精度。
二、坐标粗差问题在进行矿区坐标转换时,由于坐标系统的差异以及测量误差等因素,常常会出现坐标粗差的问题。
这会导致数据不准确,对后续的计算和分析产生不利的影响。
1、差分方法在进行坐标转换时,可以采用差分方法,即先确定一个基准点,然后将待转换的点与基准点进行差分计算,从而避免坐标系统的误差。
2、数据平滑在进行坐标转换前,可以对原始数据进行平滑处理,去掉离群点、毛刺等,从而降低数据的误差。
3、多重质量控制在进行矿区坐标转换时,可以采用多重质量控制方法,对数据进行反复检查和确认,以确保数据的准确性和精度。
总之,矿区坐标转换是一项复杂的任务,在实际中需要面对各种各样的问题。
只有通过合理的数据处理和计算方法,才能够保证数据的精度和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
病态矩阵
病态矩阵的最根本的特征:病态矩阵的条件数(||A||*||A^(-1)||定义为A 的条件数,||A||为A的范数,MATLAB中范数的求法c = cond(A,p),p为几范数,默认情况下为二范数)很大(可以用机器精度的一半来衡量,比如双精度浮点数的精度大约是10^(-16),那么条件数大于10^8就算比较坏了.),即最大特征值与最小特征值的比值很大。
病态矩阵对扰动特别敏感。
病态矩阵矩阵不能求逆。
例如,有一个变量是其他三个变量之和,这个变量也存在于模型中,这个矩阵就是病态矩阵。
解决方法:
1.利用正则化方法可以解决这一问题
最经典的正则化方法就是Tikhonov正则化,另外一种方法就是Total Variation
2.奇异值分解
将病态矩阵分解为A=SVD
3.模拟退火算法
/view/3a75ad82bceb19e8b8f6baad.html#opennewwindow
4./link?url=ripw0P7tMkcEl2x5zmkOJ-_iDFdfOLQ0Ox9ao cKY3sAJMFXEBQa__Yq6OVb3R41__nvgiWEQhA0bxXWzZzpQiFH7_IlNWlvqyrkKjLqvQ qC。
