实验78 基于MATLAB的数字滤波器设计
使用MATLAB进行数字滤波器设计的步骤与方法

使用MATLAB进行数字滤波器设计的步骤与方法数字滤波器是用于信号处理的重要工具,它可以对信号进行去噪、频率调整等操作。
而MATLAB作为一种强大的数学计算软件,提供了丰富的数字信号处理工具箱,可以方便地进行数字滤波器的设计与仿真。
本文将介绍使用MATLAB进行数字滤波器设计的步骤与方法。
1. 了解数字滤波器的基本原理在进行数字滤波器设计之前,首先需要了解数字滤波器的基本原理。
数字滤波器根据其频率响应特性可以分为低通、高通、带通和带阻滤波器等。
此外,数字滤波器的设计还需要考虑滤波器的阶数、截止频率以及滤波器类型等因素。
在设计中,我们可以选择滤波器的类型和相应的参考模型,然后利用MATLAB工具箱提供的函数进行设计。
2. 导入MATLAB中的数字信号处理工具箱使用MATLAB进行数字滤波器设计需要先导入数字信号处理工具箱。
通过在MATLAB命令窗口输入`>> toolbox`即可打开工具箱窗口,并可以选择数字信号处理工具箱进行加载。
加载完成后,就可以调用其中的函数进行数字滤波器设计。
3. 设计数字滤波器在MATLAB中,常用的数字滤波器设计函数有`fir1`、`fir2`、`iirnotch`等。
这些函数可以根据系统特性需求设计相应的数字滤波器。
以FIR滤波器为例,可以使用`fir1`函数进行设计。
该函数需要输入滤波器的阶数和截止频率等参数,输出设计好的滤波器系数。
4. 评估滤波器性能设计好数字滤波器后,需要进行性能评估。
可以使用MATLAB提供的`fvtool`函数绘制滤波器的幅频响应、相频响应和群延迟等。
通过观察滤波器在频域的性能表现,可以判断设计的滤波器是否满足要求。
5. 对滤波器进行仿真在对滤波器性能进行评估之后,还可以使用MATLAB进行滤波器的仿真。
通过将需要滤波的信号输入设计好的滤波器中,观察输出信号的变化,可以验证滤波器的去噪效果和频率调整能力。
MATLAB提供了函数`filter`用于对信号进行滤波处理。
基于matlab的数字滤波器设计

基于matlab的数字滤波器设计一.概述本文重点介绍MATLAB 中用于数字滤波器设计的函数组。
MATLAB具备设计高性能滤波器的众多工具(toolbox),包括数字滤波器设计工具箱(Digital Filter Design T oolbox)、滤波系统仿真工具箱(Filter Design and Analysis Toolbox )以及信号处理工具箱(Signal Processing Toolbox),可以设计数字滤波器的结构和参数,并实现Advanced Digital Filter Design。
二.数字滤波器介绍数字滤波器,也称计算滤波器,是指利用现代计算机中的数字回授技术来进行信号处理的方法,是对计算机处理信号的一种技术。
数字滤波器是模拟滤波器组成的数字信号处理系统,是将模拟的通全在一个硬件上实现的数字信号处理系统,它的功能比模拟滤波器更加强大。
目前它们已经应用于通信、声音、镜头、图像处理、仪器仪表、数据采集等领域。
三.MATLAB 中的滤波器设计(1)首先,MATLAB中提供了丰富的函数来实现滤波器设计工作。
其中最常用的函数有:a. firpm:有限冲激响应滤波器设计,支持线性和非线性过滤器设计。
b. butter:Butterworth低通和高通滤波器设计。
c. fir1:有限冲激响应低通和高通滤波器设计。
d. cheby1:Chebyshev第一类低通和高通滤波器设计。
(2) MATLAB还可以实现进阶的数字滤波器设计,用户可以用以下函数实现自动设计是否优化的滤波器:a. fda:设计优化低通滤波器b. fda2:设计优化定带滤波器c. fda3:设计优化双带和多带滤波器d. gfd:设计优化频谱均衡滤波器四.总结数字滤波器是一种应用广泛的信号处理技术,对于一些信号处理应用有着至关重要的作用。
MATLAB 可以简便的实现滤波器设计,并可以同时考虑多个优化目标,这些特性使其成为进行数字滤波器设计的理想工具。
实验报告基于MATLAB的数字滤波器设计

实验7\8基于MATLAB勺数字滤波器设计实验目的:加深对数字滤波器的常用指标和设计过程的理解。
实验原理:低通滤波器的常用指标:1 一6P 兰G(e^) ≤ 1 + 6P , for 国≤ ωPG(J") ≤ 6s, for 国s ≤ ⑷≤ ∏通带边缘频率:'P ,阻带边缘频率:'s,通带起伏:J P,通带峰值起伏:C(P= —20 IOg io (^-OP )【d B 】阻带起伏.冠SPaSSband StOPbandTran Siti onband Fig 7.1 TyPiCaI magn itude SPeCifiCati On for a digital LPF:S = -20 log ιo(r)[dB 】O数字滤波器有IIR和FlR两种类型,它们的特点和设计方法不同。
在MATLAB^,可以用[b , a]=butter ( N,Wr)等函数辅助设计IIR数字滤波器,也可以用b=fir1(N,Wn, 'type ')等函数辅助设计FIR数字滤波器。
实验内容:利用MATLAB编程设计一个数字带通滤波器,指标要求如下:通带边缘频率:∙∙P1=0.45^,∙∙ P2=0∙65 二,通带峰值起伏:[dB】O阻带边缘频率:'s10.3…,'s2 0.75…,最小阻带衰减:-S 4°[dB] O分别用IIR和FlR两种数字滤波器类型进行设计。
实验要求:给出IIR数字滤波器参数和FIR数字滤波器的冲激响应,绘出它们的幅度和相位频响曲线,讨论它们各自的实现形式和特点。
实验内容:IRR代码:wp=[0.45*pi,0.65*pi];ws=[0.3*pi,0.75*pi];Ap=1;A S=40;[N,Wc]=buttord(wp∕pi,ws∕pi,Ap,As);[b,a]=butter(N,Wc)%[b,a] = butter( n, Wn,'ftype')最小阻带衰减:I -W llrreqz(b-a=SUbP-Of(211=FnagHabS(H)-P-Of(WHLmag)-x ωb e 一(->5(W))y ωb e一(-≡M 一 HamW)口≡e (--R 一 HamW)一) grid On-SUbPOf(212=PhaSeHang-e(H=P -OfWPLPhaSe=x ωb e 一(->5(W))y ωb e -(- W⅛) ≡e (-一R盘a ≡m sB )≡-x ⅛x -幅度IHaOMI≡相拉SS 5 CUS S S 0⅛口 g >酉tt 2 =R ⅛⅛⅛J ≡B ⅛O S F NJ £Q 4S S U7 CJCD S >⅛⅛≡F-RV VWPl HO∙4*prWP2H0∙6*prV V WSl H 0∙3*prws2 H0∙7*prVV =Γl w i d f h Hmin((wprwsu(ws2lwp2))>> tr_width =0.3142>> M = ceil(6.2*pi/tr_width) + 1>> M = 63>> n=[0:1:M-1];>> wc1 = (ws1+wp1)/2; wc2 = (wp2+ws2)/2; >> wc=[wc1/pi,wc2/pi];>> window= hanning(M);>> [h1,w]=freqz(window,1);>> figure(1);>> subplot(2,1,1)>> stem(window);>> axis([0 60 0 1.2]);>> grid;>> xlabel('n');>> title('Hanning 窗函数');>> subplot(2,1,2)>> plot(w/pi,20*log(abs(h1)/abs(h1(1)))); >> axis([0 1 -350 0]);>> grid;>> xlabel('w/\pi');>> ylabel('幅度(dB)');>> title('Hanning 窗函数的频谱');>> hn = fir1(M-1,wc, hanning (M));>> [h2,w]=freqz(hn,1,512);>> figure(2);>> subplot(2,1,1)>> stem(n,hn);>> axis([0 60 -0.25 0.25]);>> grid;>> xlabel('n');>> ylabel('h(n)');>> title('Hanning 窗函数的单位脉冲响应'); >> subplot(2,1,2)>> plot(w/pi,20*log(abs(h2)/abs(h2(1)))); >> grid;>> xlabel('w/\pi');>> ylabel(' 幅度(dB)');>> figure(3);>> phase=angle(h1);>> plot(phase);>> axis([1 pi -1 0]);>> xlabel('w/\pi');>> ylabel(' 线性相位');>> title('Hanning 窗函数相位特性曲线')回FiIe Edit VieW InSert TOOlS DeSktOP WindOW HeIP◎ A 聾紳⑥毘謠▼层□ Ξ∣ ■ 0M FigUre 1 Hanning 窗函数OC S I I * iHanning®函数的频谱-100-200 -300 00.1 0.2 0.3 0.40.5 0.6 0.7 08 0.9 1w/x(8P)置Q FigUre 2 口 回 耳iHanni叩窗函数相位特性曲线O I I I I I I I。
基于MATLAB的数字滤波器设计

编号淮安信息职业技术学院毕业论文学生姓名。
学号。
系部。
专业。
班级。
指导教师。
顾问教师。
摘要本论文介绍了FIR数字滤波器的设计方法,即窗函数法。
在此基础上,用MATLAB实现IIR数字滤波器。
介绍了IIR数字滤波器的传统设计思想与步骤,及其计算机辅助设计方法。
以一数字带通滤波器为例,着重说明了基于MATLAB的三种滤波器的实现手段:模拟低通原型、合适模拟带通及直接原型,为数字滤波器设计带来全新的实现手段。
关键词:滤波 IIR滤波器 FIR滤波器MATLAB淮安信息职业技术学院目录第一章前言1.1 MATLAB 软件简介 (4)1.2数字滤波器技术的发展状况 (5)第二章数字滤波器的基本概念2.1数字滤波器的概况 (6)2.2 FIR 数字滤波器的基本概念 (6)2.2.1 FIR 数字滤波器的窗函数设计法 (7)2.2.2 窗函数设计法的步骤 (7)2.3 MATLAB环境下的实例 (9)2.3.1高通滤波器的设计 (9)2.3.2低通滤波器的设计 (10)第三章 IIR数字滤波器的设计过程及方法3.1 IIR滤波器的基本特点 (13)3.2 IIR滤波器的设计思路与步骤 (14)3.3 IIR 滤波器的设计 (14)3.4 IIR滤波器设计方法MATLAB的实现 (15)3.4.1 基于模拟低通原型的MATLAB实现 (15)3.4.2基于合适类型模拟滤波器的MATLAB实现 (16)3.4.3 基于直接原型变换法的MATLAB实现 (18)总结 (19)参考文献 (20)第一章前言1.1. MATLAB简介MATLAB (Matrix Laboratory)为美国Mathworks公司1983年首次推出的一套高性能的数值分析和计算软件,其功能不断扩充,版本不断升级,1992年推出划时代的4.0版,1993年推出了可以配合Microsoft Windous使用的微机版,95年4.2版,97年5.0版,99年5.3版,5.X版无论是界面还是内容都有长足的进展,其帮助信息采用超文本格式和PDF格式,可以方便的浏览。
实验报告基于MATLAB的数字滤波器设计

实验7\8 基于MATLAB 的数字滤波器设计实验目的:加深对数字滤波器的常用指标和设计过程的理解。
实验原理:低通滤波器的常用指标:PP j P for e G ωωδδω≤+≤≤-,1)(1πωωδω≤≤≤S S j for e G ,)(通带边缘频率:P ω,阻带边缘频率:S ω ,通带起伏:P δ,通带峰值起伏:])[1(log 2010dB p p δα--=,阻带起伏:s δ,最小阻带衰减:])[(log 2010dB s S δα-=。
数字滤波器有IIR 和FIR 两种类型,它们的特点和设计方法不同。
在MATLAB 中,可以用[b ,a]=butter (N,Wn )等函数辅助设计IIR 数字滤波器, 也可以用b=fir1(N,Wn,’ftype ’) 等函数辅助设计FIR 数字滤波器。
实验内容: 利用MATLAB 编程设计一个数字带通滤波器,指标要求如下:通带边缘频率:πω45.01=P ,πω65.02=P ,通带峰值起伏:][1dB p≤α。
阻带边缘频率:πω3.01=S ,πω75.02=S ,最小阻带衰减: ][40dB S ≥α。
分别用IIR 和FIR 两种数字滤波器类型进行设计。
实验要求:给出IIR 数字滤波器参数和FIR 数字滤波器的冲激响应,绘出它们的幅度和相位频响曲线,讨论它们各自的实现形式和特点。
实验内容: IRR 代码:wp=[0.45*pi,0.65*pi]; ws=[0.3*pi,0.75*pi]; Ap=1; As=40;[N,Wc]=buttord(wp/pi,ws/pi,Ap,As) ;[b,a]=butter(N,Wc)%[b,a] = butter(n,Wn,'ftype')S -PP SPassband StopbandTransition bandFig 7.1 Typical magnitudespecification for a digital LPF[H,w]=freqz(b,a);subplot(211);mag=abs(H);plot(w/pi,mag);xlabel('角频率(w)');ylabel('幅度|Ha(j\w)|');title('IIR|Ha(j\w)|');grid on;subplot(212);phase=angle(H);plot(w/pi,phase);xlabel('角频率(w)');ylabel('相位');title('IIR相位响应曲线');grid on;图像:FIR代码:>> wp1 = 0.4*pi; wp2 = 0.6*pi;>> ws1 = 0.3*pi; ws2 = 0.7*pi;>> tr_width = min((wp1-ws1),(ws2-wp2))>> tr_width =0.3142>> M = ceil(6.2*pi/tr_width) + 1>> M = 63>> n=[0:1:M-1];>> wc1 = (ws1+wp1)/2; wc2 = (wp2+ws2)/2; >> wc=[wc1/pi,wc2/pi];>> window= hanning(M);>> [h1,w]=freqz(window,1);>> figure(1);>> subplot(2,1,1)>> stem(window);>> axis([0 60 0 1.2]);>> grid;>> xlabel('n');>> title('Hanning窗函数');>> subplot(2,1,2)>> plot(w/pi,20*log(abs(h1)/abs(h1(1)))); >> axis([0 1 -350 0]);>> grid;>> xlabel('w/\pi');>> ylabel('幅度(dB)');>> title('Hanning窗函数的频谱');>> hn = fir1(M-1,wc, hanning (M));>> [h2,w]=freqz(hn,1,512);>> figure(2);>> subplot(2,1,1)>> stem(n,hn);>> axis([0 60 -0.25 0.25]);>> grid;>> xlabel('n');>> ylabel('h(n)');>> title('Hanning窗函数的单位脉冲响应'); >> subplot(2,1,2)>> plot(w/pi,20*log(abs(h2)/abs(h2(1)))); >> grid;>> xlabel('w/\pi');>> ylabel('幅度(dB)');>> figure(3);>> phase=angle(h1);>> plot(phase);>> axis([1 pi -1 0]);>> xlabel('w/\pi');>> ylabel('线性相位');>> title('Hanning窗函数相位特性曲线')。
基于MATLAB的数字滤波器的设计

基于MATLAB 的数字滤波器的设计1 引言数字滤波器是指完成信号滤波处理功能的,用有限精度算法实现的离散线性非时变系统,其输入是一组(由模拟信号取样和量化的)数字量,其输出是经过变换或说处理的另一组数字量。
数字滤波器具有稳定性高、精度高、灵活性大等突出优点。
这里所说的数字滤波器是指理想带通,低通等的频率选择数字滤波器。
数字滤波器设计的一个重要步骤是确定一个可实现的传输函数H(z),这个确定传输函数H(z)的过程称为数字滤波器设计。
数字滤波器的一般设计过程为:(1)按照实际需要,确定滤波器的性能要求(通常在频域内给定数字滤波的性能要求)。
(2)寻找一满足预定性能要求的离散时间线性系统。
(3)用有限精度的运算实现所设计的系统。
(4)通过模拟,验证所设计的系统是否符合给定性能要求。
2 数字滤波器的设计滤波器分为两种,分别为模拟滤波器和数字滤波器。
数字滤波器可以理解为是一个计算程序或算法,将代表输入信号的数字时间序列转化为代表输出信号的数字时间序列,并在转化的过程中,使信号按预定的形式变化。
数字滤波器有多种分类,从数字滤波器功能上分可分为低通、高通、带阻、带通滤波器,根据数字滤波器冲激响应的时域特征,可将数字滤波器分为两种,即无限长冲激响应滤波器(IIR )和有限长冲激响应滤波器(FIR )。
数字滤波器指标:一般来说,滤波器的幅频特性是分段常数的,以低通为例,在通带内逼近于1,阻带内逼近与0,实际设计的滤波器并非是锐截止的通带和阻带两个范围,两者之间总有一个过渡带。
在设计滤波器时事先给定幅频特性允许误差,在通带范围内幅度响应以误差1σ逼近于1,在阻带内幅度响应以误差2σ逼近于0。
πσσ≤≤≤≤≤≤-w w e H w w e H r jwc jw ,2|)(|,1|)(|11 (1)式中wc 和wr 分别为通带边界频率和阻带边界频率,wr-wc 为过渡带。
在具体的技术指标中往往用通带波动σ来表示1σ,用最小阻带衰减At 来表示2σ,其具体的对应公式这里就不详述了。
基于MATLAB的数字滤波器的设计摘要

本设计要研究的是基于MATLAB的数字滤波器的设计。则是应用计算机软件进行编程。首先了解滤波器的基本工作原理,针对不同数字滤波器所采用最合适的设计方法,设计FIR和IIR数字滤波器,以达到效果最佳。FIR一般要求信号具有线性相位,而FIR数字滤波器则可实现严格的线性相位,同时由于脉冲响应为有限长,因此还具有永远稳定的特性,鉴于此FIR主要解决了线性相位和稳定性的问题,否则多用IIR数字滤波器来实现。根据这个特点设计FIR和IIR滤波器,利用窗函数来设计FIR数字滤波器;利用模拟滤波器来设计IIR数字滤波器。
本设计主要给出了FIR数字滤波器与IIR数字滤波器的设计方法和原理。
关键词数字滤波器MATLAB FIR IIR
滤波是信号处理中最基本又极为重要的技术,利用滤波器技术可以从复杂的信号中提取出所需要的信号,抑制不需要的信号。绝大多数传感器输出的信号,在使用过程中,都必须进行滤波。所以滤波器是具有一定传输选择特性的、对信号进行加工处理的装置、它允许输入信号中的一些成分通过,抑制或衰减另一些成分。其功能是将输入信号变换为人们所需要的输入信号。
基于MATLAB的数字滤波器设计!!!

一、 实验目地(1)掌握双线性变换法及脉冲相应不变法设计IIR 数字滤波器地具体设计方法; (2) 熟悉用双线性变换法及脉冲响应不变法设计低通、高通和带通IIR 数字滤波器地计算机编程.二、 实验原理在MA TLAB 中,可以用下列函数辅助设计IIR 数字滤波器:1)利用buttord 和cheb1ord 可以确定低通原型巴特沃斯和切比雪夫滤波器地阶数和截止频率;2)[num,den]=butter (N,Wn )(巴特沃斯)和[num,den]=cheby1(N,Wn ),[num,den]=cheby2(N,Wn )(切比雪夫1型和2型)可以进行滤波器地设计;3)lp2hp,lp2bp,lp2bs 可以完成低通滤波器到高通、带通、带阻滤波器地转换;4)使用bilinear 可以对模拟滤波器进行双线性变换,求得数字滤波器地传输函数系数;5)利用impinvar 可以完成脉冲响应不变法地模拟滤波器到数字滤波器地转换. 三、 预习要求(1)在MATLAB 中,熟悉函数butter 、cheby1、cheby2地使用,其中:[num,den]=butter (N,Wn )巴特沃斯滤波器设计;[num,den]=cheby1(N,Wn )切比雪夫1型滤波器设计;[num,den]=cheby2(N,Wn )切比雪夫2型滤波器设计.(2)阅读附录中地实例,学习在MA TLAB 中进行数字滤波器地设计;(3)给出IIR 数字滤波器参数和滤波器地冲激响应,绘出它们地幅度和相位频响曲线,讨论它们各自地实现形式和特点.四、 实验内容利用MATLAB 编程,用脉冲响应不变法和双线性变换法设计一个数字带通滤波器,指标要求如下:通带边缘频率:π45.01=ΩP ,π65.02=ΩP ,通带峰值起伏:][1dB p ≤α.阻带边缘频率:π3.01=ΩS ,π8.02=ΩS ,最小阻带衰减: ][40dB S ≥α. 附录:例1 设采样周期T=250μs (采样频率fs =4kHz ),用脉冲响应不变法和双线性变换法设计一个三阶巴特沃兹滤波器,其3dB 边界频率为fc =1kHz.[B,A]=butter(3,2*pi*1000,'s');[num1,den1]=impinvar(B,A,4000);[h1,w]=freqz(num1,den1);[B,A]=butter(3,2/0.00025,'s');[num2,den2]=bilinear(B,A,4000);[h2,w]=freqz(num2,den2);f=w/pi*2000;plot(f,abs(h1),'-.',f,abs(h2),'-');grid;xlabel('频率/Hz ')ylabel('幅值/dB')程序中第一个butter地边界频率2π×1000,为脉冲响应不变法原型低通滤波器地边界频率;第二个butter地边界频率2/T=2/0.00025,为双线性变换法原型低通滤波器地边界频率.图1给出了这两种设计方法所得到地频响,虚线为脉冲响应不变法地结果;实线为双线性变换法地结果.脉冲响应不变法由于混叠效应,使得过渡带和阻带地衰减特性变差,并且不存在传输零点.同时,也看到双线性变换法,在z=-1即Ω=π或f=2000Hz处有一个三阶传输零点,这个三阶零点正是模拟滤波器在ω=∞处地三阶传输零点通过映射形成地.例2 设计一数字高通滤波器,它地通带为400~500Hz,通带内容许有0.5dB地波动,阻带内衰减在小于317Hz地频带内至少为19dB,采样频率为1,000Hz.正确wc=2*1000*tan(2*pi*400/(2*1000));wt=2*1000*tan(2*pi*317/(2*1000));[N,wn]=cheb1ord(wc,wt,0.5,19,'s');[B,A]=cheby1(N,0.5,wn,'high','s');[num,den]=bilinear(B,A,1000);[h,w]=freqz(num,den);f=w/pi*500;plot(f,20*log10(abs(h)));axis([0,500,-80,10]);grid;xlabel('')ylabel('幅度/dB')例3 设计一巴特沃兹带通滤波器,其3dB边界频率分别为f2=110kHz和f1=90kHz,在阻带f3 = 120kHz处地最小衰减大于10dB,采样频率fs=400kHz.w1=2*400*tan(2*pi*90/(2*400));w2=2*400*tan(2*pi*110/(2*400));wr=2*400*tan(2*pi*120/(2*400));[N,wn]=buttord([w1 w2],[0 wr],3,10,'s');[B,A]=butter(N,wn,'s');[num,den]=bilinear(B,A,400);[h,w]=freqz(num,den);f=w/pi*200;plot(f,20*log10(abs(h)));axis([40,160,-30,10]);grid;xlabel('频率/kHz')ylabel('幅度/dB')例4 一数字滤波器采样频率fs = 1kHz,要求滤除100Hz地干扰,其3dB地边界频率为95Hz 和105Hz,原型归一化低通滤波器为w1=95/500;w2=105/500;[B,A]=butter(1,[w1, w2],'stop');[h,w]=freqz(B,A);f=w/pi*500;plot(f,20*log10(abs(h))); axis([50,150,-30,10]); grid;xlabel('频率/Hz') ylabel('幅度/dB')。
基于MATLAB的数字滤波器设计

使用 算法设计滤波 器的时候,需根据要求确定 滤波 器 阶数 。
4 结 束语
本 文 重 点 在 于 充 分 利 用 与 发 挥 语 言 的 编
利 用 MA T L AB提 供 的 数 据 函 数 实 现 我 们 要 求 的算 法 , 设计 滤波 器 逼近 频 率 响 应 。 所 得 到 的 最佳 一致 滤 波 器 的频 率 响应 具 有 波 纹特 性 。 在
比如,带通 滤波器用作频谱分析仪中的选频装 置:低通滤波器用作数字信号分析系统中抗混 乱滤波 器;高通滤 波器用于检测仪中剔除低频 干扰 噪声;带阻滤波器用作 电涡流测振仪中的 陷波 器,等等。在 数字信 号处理过程中,滤波 器 占有 重 要 的 位 置 。 尤 其 在 图 像 处 理 与 输 出、
了巨大的进 展并且得到广泛的应用 。与模拟滤 波器 相 比 , 数 字 滤 波 器 具 有 很 多 突 出的 优 点 , 因为滤波 器各种特征都有 严格要求 , 缺一不可,
器 中, 把通过的频率范围的频率,叫做通频 带:
反之 ,信 号受到阻碍 的频 率范围称 为阻带;通 而这种设计方法恰恰能满足这种 它可 以自动 带和 阻带之 间的分 界频率称 为截止 频率 ;理想 加浅显 易懂 ,使数 字滤波器 的应用更 为广泛 , 避 免电压浮动变化 和噪声造成的影响。在设计 滤波器在通带 内的电压增 益为常数 ,在 阻带内 使用更加快捷 , 在仿真上我们也可 以轻 易完成 , 上,我们采用的是数学逼近理论 ,来实现逼近 的电压增益为零 ;实际滤波 器的通 带和 阻带之 对滤波器稳定性与严格线性相位 的仿真后的计 理论思想,满足给定频率特征,通常叫这种滤 间存 在 一 定 频 率 范 围 的过 渡 带 。 算 应 用 奠 定 更 好 的 基 础 。 文 章 通 过 分 析 滤 波 器 波器叫频率选择滤波器。 为确保计算 的准确性 , 设 计 方 式 , 简 要 阐 述 了用 MA T L AB来 完 成 数 . 1理 想滤波 器的频率特性 需 要 先 对 算 法 仿 真 计 算 ,尤 其 是 成 熟 、可 靠 性 2
基于matlab_数字滤波器的设计

引言:与模拟滤波器相对应,在离散系统中广泛应用数字滤波器。
它的作用是利用离散时间系统的特性对输入信号波形或频率进行加工处理。
或者说,把输入信号变成一定的输出信号,从而达到改变信号频谱的目的。
数字滤波器一般可以用两种方法来实现:一种方法是用数字硬件装配成一台专门的设备,这种设备称为数字信号处理机;另一种方法就是直接利用通用计算机,将所需要的运算编成程序让通用计算机来完成,即利用计算机软件来实现。
模拟滤波器在测试系统或专用仪器仪表中是一种常用的变换装置。
例如:带通滤波器用作频谱分析仪中的选频装置;低通滤波器用作数字信号分析系统中的抗频混滤波;高通滤波器被用于声发射检测仪中剔除低频干扰噪声;带阻滤波器用作电涡流测振仪中的陷波器,等等。
MATLAB是由美国Mathworks公司推出的用于数值计算和图形处理的科学计算系统环境。
MATLAB是英文MATrix LABoratory(矩形实验室)的缩写。
在MATLAB环境下,用户可以集成地进行程序设计,数值计算,图形绘制,输入输出,文件管理等各项操作。
除此之外,MATLAB还具有很强的功能扩展能力,与它的主系统一起,可以配备各种各样的工具箱,以完成一些特定的任务。
目前,Mathworks公司推出了18种工具箱。
用户可以根据自己的工作任务,开发自己的工具箱。
2滤波器简介2.1滤波器的概念滤波器是一种用来消除干扰杂讯的器件,将输入或输出经过过滤而得到纯净的交流电。
您可以通过基本的滤波器积木块----二阶通用滤波器传递函数,推导出最通用的滤波器类型:低通、带通、高通、帯阻和椭圆型滤波器。
传递函数的参数——f0、d、hHP、hBP和hLP,可用来构造所有类型的滤波器。
转降频率f0为s项开始占支配作用时的频率。
设计者将低于此值的频率看作是低频,而将高于此值的频率看作是高频,并将在此值附近的频率看作是带内频率。
阻尼d用于测量滤波器如何从低频率转变至高频率,它是滤波器趋向振荡的一个指标。
基于MATLAB的数字滤波器设计

基于MATLAB的数字滤波器设计学号:姓名:班级:1摘要数字滤波是数字信号处理中一个非常重要且应用普遍的技术。
FIR数字滤波器因其严格的线性相位等优点得到了广泛应用。
MATLAB是国际控制界的标准计算软件。
本文根据FIR数字滤波器设计的基本原理,介绍了窗函数,分析了数字滤波器的设计方法,对基于窗函数设计的FIR滤波器的特性进行了分析。
分别采用Hanning 窗、Hamming窗、Blackman窗和boxcar窗,利用MATLAB语言设计数字低通滤波器并给出了实验结果,达到了性能指标要求,引入了MATLAB工具软件进行设计。
关键词: FIR滤波器;窗函数法;低通2目录第1章绪论1 (4)1.1数字滤波器的研究背景和意义 (4)1.2数字滤波器的应用及现状 (4)1.3数字滤波器的设计方法 (5)第2章FIR滤波器 (5)2.1 FIR滤波器的基本概念 (5)2.2 FIR滤波器的特点 (6)2.3 FIR滤波器的种类 (6)第3章FIR数字滤波器的原理与设计 (8)3.1 FIR数字滤波器的结构特点 (8)3.2 FIR的线性相位特性 (9)3.3 FIR数字滤波器设计的基本步骤 (9)3.4 FIR数字滤波器的设计方法 (10)3.4.1 频率取样法 (10)3.4.2 FIR滤波器的最优化方法 (11)3.4.3 窗函数法 (14)3.3.4 三种设计方法的比较 (16)第4章FIR数字滤波器设计实例 (16)4.1用窗函数法设计FIR数字滤波器 (16)4.2用海明窗设计数字低通滤波器 (24)第5章总结 (26)3第1章绪论1.1数字滤波器的研究背景和意义当今,数字信号处理技术正飞速发展,它不但自成一门学科,更是以不同形式影响和渗透到其他学科;它与国民经济息息相关,与国防建设紧密相连;它影响或改变着我们的生产、生活方式,因此受到人们普遍的关注。
数字化、智能化和网络化是当代信息技术发展的大趋势,而数字化是智能化和网络化的基础,实际生活中遇到的信号多种多样,例如广播信号、电视信号、雷达信号、通信信号、导航信号等等。
基于MATLAB环境的数字滤波器的设计与仿真

基于MATLAB环境的数字滤波器的设计与仿真摘要:数字滤波器是数字信号处理中最重要的工具之一。
在许多科学技术领域中广泛采用数字滤波器进行信号处理。
数字滤波器分为两类,即有限脉冲响应滤波器(FIR)和无限脉冲响应滤波器(IIR)。
数字滤波器是由数字乘法器、加法器和延时单元组成的一种装置。
其功能是对输入离散信号的数字代码进行运算处理,以达到改变信号频谱的目的。
由于电子计算机技术和大规模集成电路的发展,数字滤波器已可用计算机软件实现,也可用大规模集成数字硬件实时实现。
本文针对在实际设计中要大量应用数字滤波器这一现实,对数字滤波器的基本理论、性能特点、设计方法进行了全面的分析,特别是对有限冲击响应数字滤波器(FIR)的设计进行了深入的探讨。
文章运用了MA TLAB仿真手段对数字滤波器的设计理论和设计方法方法进行了研究。
论文主要包括数字滤波器以及MATLAB在信号处理方面的概述,FIR数字滤波器设计方法的介绍,MATLAB语言仿真,以及最终结论。
本论文所采用的研究方法是仿真比较,介绍了常用滤波器的设计方法,通过MATLAB软件对各种方法分别实现仿真,然后对仿真结果进行比较。
通过对数字滤波器的理论研究为今后的实践奠定理论基础。
关键词:数字滤波器;FIR滤波器;MATLAB;仿真Design and Simulation of Digital FilterBased On MATLABAbstract: Digital filter is one of the most important parts of digital signal processing. In many fields of science and technology, it is widely used for digital signal processing. Digital filter includes finite impulse response filter(FIR) and infinite impulse response filter(IIR).Digital wave filter is a kind of installation that forms by digital multiplier, adder and the unit of delay time. Its function is to carry out operational handling for inputting the digital code of dispersed signal in order to reach the purpose that changes signal frequency spectra. Because of the development of the computer technical circuit of large scale integration digital wave filter can already realize with computer software, can also realize with the digital hardware real time of large scale integration. Digital wave filter is a dispersed time system. As digital filters, in particular FIR filters, are widely used in modern designs, this dissertation comprehensively anglicized fir’s basic theory, characters and design methodologies.In this paper, MATLAB simulation is employed to study the design theory and methods of digital filter. The summary of digital filter and MATLAB language are introduced. Method of FIR filter design, results of MATLAB simulation are described in detail as well. The common design methods of digital filter are simulated with MATLAB to find the result that I need before. It is hope that it can provide a reference for future appliance.Key Words: digital filter;FIR filter;MATLAB;simulation第一章绪论1.1 数字滤波器的现状及发展数字滤波器按单位脉冲响应的性质可分为无限长单位脉冲响应滤波器IIR和有限长单位脉冲响应滤波器FIR两种。
基于matlab的数字滤波器设计及仿真

滤波器的指标
■ 滤波器的指标常在频域给出 ■ 数字滤波器的频率响应特性曲线:
H(ejw)= |H(ejw)|ej (w) |H(ejw)|为幅频特性函数,表示信号通过该 滤波器后各频率的衰减情况。
(w)为相频特性函数,表示信号通过滤波器 后在时间上的延时情况。
二、MATLAB环境下IIR数字滤波器的设计
四、两个有趣的实验
1、利用MATLAB进行声音滤波: 利用MATLAB读取wav格式的声音文件,对
信号进行离散傅里叶变换,得到其频谱图,给 信号加杂音,然后设计一个数字滤波器将杂音 滤除,得到原音,最后比较滤波器的滤波效果。
语音读取和加噪
■ clear;close all; ■ [Y,Fs,NBITS]=WAVREAD("WindowsXP.wav"); ■ n=length(Y); ■ f=0:Fs/n:Fs*(n-1)/n; ■ K=0:1/(n-1):1; ■ subplot(2,3,1);plot(K,Y);title("语音信号的时域波形"); ■ Y1=fft(Y,n); ■ subplot(2,3,3);plot(f,abs(Y1));title("语音信号的频谱"); ■ noise=0.02*sin(2*pi*4000*K); ■ subplot(2,3,2);plot(K(1:50),noise(1:50));title("噪声的时域波形"); ■ s=length(noise); ■ noise1=fft(noise,s); ■ subplot(2,3,5);plot(f,abs(noise1));title("噪声的频谱"); ■ A=Y"+noise; ■ subplot(2,3,4);plot(K,A);title("含噪语音的时域波形"); ■ A1=fft(A,s); ■ subplot(2,3,6);plot(f,abs(A1));title("含噪语音的频谱");
基于MATLAB的滤波器设计

基于MATLAB的滤波器设计滤波是信号处理中非常重要的一项技术。
它可以去除噪声、提取有用的信号信息以及改善信号质量。
MATLAB是一种强大的数学计算工具,它提供了许多滤波器设计的功能,可以用来设计和实现各种滤波器。
在MATLAB中,有两种常见的滤波器设计方法:频域设计和时域设计。
频域设计方法基于傅里叶变换理论,将信号从时域转换到频域进行滤波,然后再进行反傅里叶变换将滤波后的信号转回时域。
时域设计方法则是直接对时域信号进行滤波,其中最常用的方法是卷积。
为了设计一个有效的滤波器,需要首先确定滤波器的类型和规格。
常见的滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
滤波器的规格包括截止频率和滤波器的阶数。
在MATLAB中,可以使用函数如butter、cheby1、cheby2、ellip和fir1等来设计不同类型的滤波器。
这些函数以不同的方式实现了频域设计和时域设计方法,可以根据需要选择适合的函数。
以设计一个低通滤波器为例,可以使用butter函数进行频域设计。
该函数的语法如下:[b, a] = butter(n, Wn, 'low')其中,n是滤波器的阶数,Wn是截止频率。
该函数返回滤波器的系数b和a,可以使用函数freqz来绘制滤波器的频率响应曲线。
另外,MATLAB还提供了Filter Design and Analysis Tool(FDA工具箱),它是一个交互式的图形界面工具,可以更方便地设计和分析滤波器。
通过该工具箱,用户可以自定义滤波器的类型、规格和参数,并可以可视化地观察滤波器的性能。
滤波器设计是一项非常复杂的任务,需要考虑许多因素,例如滤波器的性能、计算复杂度、阶数和实现方式等。
MATLAB提供了丰富的函数和工具,可以帮助用户快速、方便地进行滤波器设计,并可以根据需要进行优化和改进。
在设计滤波器时,需要仔细理解信号和滤波器的特性,选择合适的设计方法和参数,并进行实验和验证。
基于MATLAB的数字滤波器设计

唐山学院数字信号处理课程设计题目基于MATLAB的数字滤波器设计系 (部) 信息工程系班级 10通信本2姓名学号指导教师2013 年 1 月 7 日至 1 月 11 日共 1 周数字信号处理课程设计任务书课程设计成绩评定表目录1 绪论 (1)2数字滤波器的设计 (2)2.1数字滤波器的基本概念 (2)2.2利用双线性变换法设计IIR数字滤波器 (2)3课程设计的具体实现 (3)3.1对语音信号进行滤波的滤波器设计 (3)3.1.1 IIR数字滤波器的流程图 (3)3.1.2IIR低通滤波器设计 (3)3.1.3 IIR高通滤波器设计 (5)3.1.4IIR带通滤波器设计 (7)3.2对合成信号进行滤波的滤波器设计 (8)3.2.1设计目的和要求 (8)3.2.2合成信号的程序设计 (8)3.2.3合成信号的频谱程序设计 (9)3.2.4低通滤波器设计 (10)3.2.5 IIR带通滤波器设计 (11)3.2.6IIR高通滤波器滤波 (13)4软件简介 (15)4.1系统界面设计工具—GUI概述 (15)4.2界面设计及使用说明 (15)5结论 (17)6 致谢 (18)参考文献 (19)附录 (20)1 绪论与模拟滤波器相对应,在离散系统中广泛应用数字滤波器。
它的作用是利用离散时间系统的特性对输入信号波形或频率进行加工处理。
或者说,把输入信号变成一定的输出信号,从而达到改变信号频谱的目的。
数字滤波器一般可以用两种方法来实现:一种方法是用数字硬件装配成一台专门的设备,这种设备称为数字信号处理机;另一种方法就是直接利用通用计算机,将所需要的运算编成程序让通用计算机来完成,即利用计算机软件来实现。
模拟滤波器在测试系统或专用仪器仪表中是一种常用的变换装置。
例如:带通滤波器用作频谱分析仪中的选频装置;低通滤波器用作数字信号分析系统中的抗频混滤波;高通滤波器被用于声发射检测仪中剔除低频干扰噪声;带阻滤波器用作电涡流测振仪中的陷波器,等等。
基于matlab的滤波器设计

光电图像课程设计报告书课题名称基于matlab的滤波器设计图像复原的MATLAB实现1课程设计目的〔1〕了解基于matlab的滤波器处理及其根本操作;〔2〕学习MATLAB在滤波器中的使用;〔3〕提高学习与解决问题的能力。
2课程设计根本内容2.1滤波器的根本原理设计数字滤波器的任务就是寻求一个因果稳定的线性时不变系统,并使系统函数H〔z〕具有指定的频率特性。
数字滤波器从实现的网络构造或者从单位冲激响应分类,可以分成无限单位冲激响应〔IIR〕数字滤波器和有限长单位冲激响应〔FIR〕数字滤波器。
数字滤波器频率响应的三个要素:(1)幅度平方响应(2)相位响应(3)群时延响应IIR数字滤波器:IIR数字滤波器的系统函数为有理分数,即IIR数字滤波器的逼近问题就是求解滤波器的系数和,使得在规定的物理意义上逼近所要求的特性的问题。
如果是在s平面上逼近,就得到模拟滤波器,如果是在z平面上逼近,则得到数字滤波器。
FIR数字滤波器:设FIR的单位脉冲响应h〔n〕为实数,长度为N,则其z变换和频率响应分别为按频域采样定理FIR数字滤波器的传输函数H(z)和单位脉冲响应h〔z〕可由它的N歌频域采值H(k)唯一确定。
MATLAB中提供了几个函数,分别用于实现IIR滤波器和FIR滤波器。
(1)卷积函数conv,调用格式为,c=conv〔a,b〕该格式可以计算两向量a和b的卷积,可以直接用于对有限长信号采用FIR滤波器的滤波。
(2)函数filter的调用格式为,y=filter〔b,a,*〕该格式采用数字滤波器对数据进展滤波,既可以用于IIR滤波器,也可以用于FIR滤波器。
其中向量b和a分别表示系统函数的分子,分母多项式的系数,假设a=1,此时表示FIR滤波器,否则就是IIR滤波器。
该函数就是利用给出的向量b和a,对*中的数据进展滤波,结果放入向量y。
(3)函数fftfilt的调用格式为,y=fftfilt〔b,*〕该格式是利用基于FFT的重叠相加法对数据进展滤波,这种频域滤波技术只对FIR滤波器有效。
基于MATLAB工具箱的数字滤波器设计

基于MATLAB信号处理工具箱的数字滤波器设计摘要:传统数字滤波器工作起来,需要计算量很大,对于设计要求来说,又比较复杂,需要调整滤波特性,有很大的难度,并且影响它本身的应用以及功能。
本文中,主要介绍了利用MATLAB信号处理工具箱的功能,设计常规数字滤波器,设计过程中使用一些常用的专用软件。
对于,使用MATLAB语言程序设计以及信号处理工具箱的FDATool工具,各种界面的详细步骤都有详细的介绍。
对于MATLAB设计滤波器,为了减轻庞大的工作量,也为了简便直观,我们对比设计要求,以及滤波器特性的参数,这样才能更有利于,优化滤波器本身。
在本文中,主要解读了仿真软件Simulink对设计出来的滤波器仿真,设计过程中利用工具MATLAB。
我们验证结果的准确性,是通过软件仿真实验,从而达到对滤波器的设计。
关键词:MATLAB;模拟滤波器;数字滤波器目录1 引言 (1)2 模拟滤波器的设计 (1)2.1 几种常用的模拟滤波器 (2)2.2 巴特沃斯低通滤波器设计 (3)3 数字滤波器的设计 (5)4 结束语 (10)参考文献 (10)1引言基于对正弦基波,以及整词谐波的分析,可以得知系统电压,电流信号中,成分比较复杂,因此,在电力系统中,最关键的部件还是滤波器。
MATLAB和Mathematica、Maple共同称为三大数学软件。
MATLAB在数学类科技应用软件中,在数值计算方面地位不可代替。
MATLAB可以进行矩阵运算,绘制函数和数据,实现算法,创建用户界面,连接其他编程语言的程序等功能,它的应用方面主要在于,工程计算;控制设计;信号处理与通讯;图像处理信号检测;金融建模设计与分析等领域。
MATLAB的基本数据单位是矩阵,它的指令表达式与工程中常用的形式十分相似,故用MATLAB来解算问题要比其他语言完成事情简捷,因此可以直接使用,我们可以把自己的程序导入进MATLAB函数库中,方便以后的使用。
因此我们设计滤波时,根据指标,直接使用CAD程序,就可以得到高通、带通和带阻滤波器系统函数。
matlab数字滤波器的设计
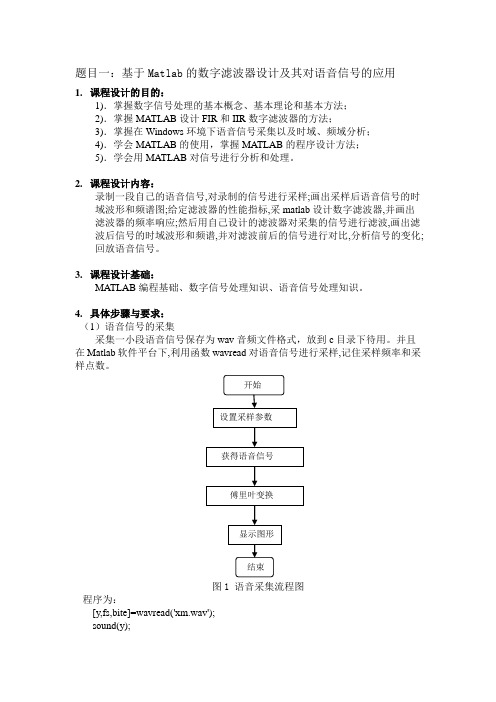
题目一:基于Matlab的数字滤波器设计及其对语音信号的应用1.课程设计的目的:1).掌握数字信号处理的基本概念、基本理论和基本方法;2).掌握MATLAB设计FIR和IIR数字滤波器的方法;3).掌握在Windows环境下语音信号采集以及时域、频域分析;4).学会MATLAB的使用,掌握MATLAB的程序设计方法;5).学会用MATLAB对信号进行分析和处理。
2.课程设计内容:录制一段自己的语音信号,对录制的信号进行采样;画出采样后语音信号的时域波形和频谱图;给定滤波器的性能指标,采matlab设计数字滤波器,并画出滤波器的频率响应;然后用自己设计的滤波器对采集的信号进行滤波,画出滤波后信号的时域波形和频谱,并对滤波前后的信号进行对比,分析信号的变化;回放语音信号。
3.课程设计基础:MATLAB编程基础、数字信号处理知识、语音信号处理知识。
4.具体步骤与要求:(1)语音信号的采集采集一小段语音信号保存为wav音频文件格式,放到c目录下待用。
并且在Matlab软件平台下,利用函数wavread对语音信号进行采样,记住采样频率和采样点数。
图1 语音采集流程图程序为:[y,fs,bite]=wavread('xm.wav');sound(y);wavrecord(2*fs,fs);fft(y);Y=fft(y);fp=1000;fr=1200;as=40;ap=1;[N, Wn] = BUTTORD(2*fp/fs, 2*fr/fs, ap, as);[B,A] = BUTTER(N,Wn);(2)语音信号的频谱分析要求画出语音信号的时域波形;然后对语音号进行快速傅里叶变换,得到信号的频谱特性。
程序为:[y,fs,bite]=wavread('xm.wav');sound(y);Y=fft(y);mag=abs(Y);phase=angle(Y);phase=phase*180/pi;dB=20*log10(abs(Y)+eps);t=(0:length(y)-1)/fs;figure(1)subplot(221);plot(t,y);title('波形图');xlabel('时间(s)');ylabel('幅度');f=(1:length(Y))*fs/length(Y);subplot(222);plot(f,mag);title('幅度谱');xlabel('频率(Hz)');ylabel('频谱幅度');subplot(223);plot(f,phase);title('相位谱');xlabel('频率(Hz)');ylabel('频谱相位');subplot(224);plot(f,dB);title('对数幅度谱');xlabel('频率(Hz)');ylabel('频谱幅度(dB)');显示为:图2 波形图(a) 幅度谱(b) 相位谱(c) 对数幅度谱(d)(3)设计数字滤波器,画出其频率响应曲线各滤波器的性能指标:1).低通滤波器性能指标fp=1000Hz, fs=1200Hz, As=40dB, Ap=1dB2).高通滤波器性能指标fs=4000Hz, fp=4300Hz, As=40dB, Ap=1dB3).带通滤波器性能指标fp1=1200 Hz, fp2=3 000 Hz, fs1=1000 Hz, fs2=3200Hz, As=40dB, Ap=1dB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验7\8 基于MATLAB 的数字滤波器设计
实验目的:加深对数字滤波器的常用指标和设计过程的理解。
实验原理:低通滤波器的常用指标:
P
P j P for e G ωωδδω
≤+≤≤-,1)(1
π
ωωδω≤≤≤S S j for e G ,)(
通带边缘频率:P ω,阻带边缘频率:S ω
,
通带起伏:P δ,通带峰值起伏:
]
)[1(log 2010dB p p δα--=,阻带起伏:s δ,
最小阻带衰减:
])[(log 2010dB s S δα-=。
数字滤波器有IIR 和FIR 两种类型,它们的特点和设计方法不同。
在MATLAB 中,可以用[b ,a]=butter (N,Wn )等函数辅助设计IIR 数字滤波器, 也可以用b=fir1(N,Wn,’ftype ’) 等函数辅助设计FIR 数字滤波器。
实验内容: 利用MATLAB 编程设计一个数字带通滤波器,指标要求如下:
通带边缘频率:πω45.01=P ,πω65.02=P ,通带峰值起伏:]
[1dB p
≤α。
阻带边缘频率:
π
ω3.01=S ,
πω75.02=S ,最小阻带衰减: ][40dB S ≥α。
分别用IIR 和FIR 两种数字滤波器类型进行设计。
实验要求:给出IIR 数字滤波器参数和FIR 数字滤波器的冲激响应,绘出它们的幅度和相位
频响曲线,讨论它们各自的实现形式和特点。
实验内容: IRR 代码:
wp=[0.45*pi,0.65*pi]; ws=[0.3*pi,0.75*pi]; Ap=1; As=40;
[N,Wc]=buttord(wp/pi,ws/pi,Ap,As) ;
[b,a]=butter(N,Wc)%[b,a] = butter(n,Wn,'ftype')
S ω-P
-P S
ωPassband Stopband
Transition band
Fig 7.1 Typical magnitude
specification for a digital LPF
[H,w]=freqz(b,a);
subplot(211);
mag=abs(H);
plot(w/pi,mag);
xlabel('角频率(w)');
ylabel('幅度|Ha(j\w)|');
title('IIR|Ha(j\w)|');
grid on;
subplot(212);
phase=angle(H);
plot(w/pi,phase);
xlabel('角频率(w)');
ylabel('相位');
title('IIR相位响应曲线');
grid on;
图像:
FIR代码:
>> wp1 = 0.4*pi; wp2 = 0.6*pi;
>> ws1 = 0.3*pi; ws2 = 0.7*pi;
>> tr_width = min((wp1-ws1),(ws2-wp2))
>> tr_width =0.3142
>> M = ceil(6.2*pi/tr_width) + 1
>> M = 63
>> n=[0:1:M-1];
>> wc1 = (ws1+wp1)/2; wc2 = (wp2+ws2)/2; >> wc=[wc1/pi,wc2/pi];
>> window= hanning(M);
>> [h1,w]=freqz(window,1);
>> figure(1);
>> subplot(2,1,1)
>> stem(window);
>> axis([0 60 0 1.2]);
>> grid;
>> xlabel('n');
>> title('Hanning窗函数');
>> subplot(2,1,2)
>> plot(w/pi,20*log(abs(h1)/abs(h1(1)))); >> axis([0 1 -350 0]);
>> grid;
>> xlabel('w/\pi');
>> ylabel('幅度(dB)');
>> title('Hanning窗函数的频谱');
>> hn = fir1(M-1,wc, hanning (M));
>> [h2,w]=freqz(hn,1,512);
>> figure(2);
>> subplot(2,1,1)
>> stem(n,hn);
>> axis([0 60 -0.25 0.25]);
>> grid;
>> xlabel('n');
>> ylabel('h(n)');
>> title('Hanning窗函数的单位脉冲响应'); >> subplot(2,1,2)
>> plot(w/pi,20*log(abs(h2)/abs(h2(1)))); >> grid;
>> xlabel('w/\pi');
>> ylabel('幅度(dB)');
>> figure(3);
>> phase=angle(h1);
>> plot(phase);
>> axis([1 pi -1 0]);
>> xlabel('w/\pi');
>> ylabel('线性相位');
>> title('Hanning窗函数相位特性曲线')。
