四川大学物理学院理论力学第五章课件 2
合集下载
四川大学理论力学第5章第一课时概要

同理有
dr va dt
i y j z k v r dr / dt x ~2 ~ 2 i j k ar d r / dt dv / dt x y z
3.动点的牵连速度和牵连加速度
(1)牵连运动:动系相对于定系的运动。 (2)牵连点的概念 定义:任一瞬时,动系上 与动点重合的点即为此瞬时动 点的牵连点。 (3)牵连速度 定义:某瞬时牵连点的速 度称为动点的牵连速度。用ve 表示。 (4)牵连加速度
系的 相 要 。运 对 建 本 动不立章 之同同的 间参一任 的考物务 关系体是
×
5.1 绝对运动 ·相对运动 ·牵连运动
一、动点——研究对象 动点是指相对于定系和动系均有运动的点。 二、两个坐标系 1 .固定坐标系 建立在固定参考物上的坐标系,简称定系。一般将 定系固结在地面上。 2.动坐标系 动坐标系指建立在相对于定系运动着的物体上的坐标系, 简称动系。有时可称为载体系。
M
例2. 动点: 小虫M , 定系: 地面 , 动系: 园柱 .
M
绝对运动: 螺旋线运动
相对运动: 直线运动
牵连运动: 定轴转动
例3.
动点: 套筒M , 定系: 地面 , 动系: CD . 绝对运动: 直线运动
A
M C
B
相对运动: 直线运动 牵连运动 : D 平动
例4.
动点: 滑块上的M , 定系: 地面 , 动系: AB .
三、三种运动——绝对运动、相对运动和牵连运动 1 .绝对运动:动点相对于定系的运动。 2 .相对运动:动点相对于动系的运动。 3 .牵连运动:动系相对于定系的运动。
例1.
动点: 车轮上的M , 定系: 地面 , 动系: 车箱 。 绝对运动: 旋轮线(摆线)运动 相对运动: 园周运动 牵连运动: 平动
dr va dt
i y j z k v r dr / dt x ~2 ~ 2 i j k ar d r / dt dv / dt x y z
3.动点的牵连速度和牵连加速度
(1)牵连运动:动系相对于定系的运动。 (2)牵连点的概念 定义:任一瞬时,动系上 与动点重合的点即为此瞬时动 点的牵连点。 (3)牵连速度 定义:某瞬时牵连点的速 度称为动点的牵连速度。用ve 表示。 (4)牵连加速度
系的 相 要 。运 对 建 本 动不立章 之同同的 间参一任 的考物务 关系体是
×
5.1 绝对运动 ·相对运动 ·牵连运动
一、动点——研究对象 动点是指相对于定系和动系均有运动的点。 二、两个坐标系 1 .固定坐标系 建立在固定参考物上的坐标系,简称定系。一般将 定系固结在地面上。 2.动坐标系 动坐标系指建立在相对于定系运动着的物体上的坐标系, 简称动系。有时可称为载体系。
M
例2. 动点: 小虫M , 定系: 地面 , 动系: 园柱 .
M
绝对运动: 螺旋线运动
相对运动: 直线运动
牵连运动: 定轴转动
例3.
动点: 套筒M , 定系: 地面 , 动系: CD . 绝对运动: 直线运动
A
M C
B
相对运动: 直线运动 牵连运动 : D 平动
例4.
动点: 滑块上的M , 定系: 地面 , 动系: AB .
三、三种运动——绝对运动、相对运动和牵连运动 1 .绝对运动:动点相对于定系的运动。 2 .相对运动:动点相对于动系的运动。 3 .牵连运动:动系相对于定系的运动。
例1.
动点: 车轮上的M , 定系: 地面 , 动系: 车箱 。 绝对运动: 旋轮线(摆线)运动 相对运动: 园周运动 牵连运动: 平动
大学物理第5章 刚体力学基础ppt课件

转轴的力臂。
z
or
d
F
P
Mz的方向平行于转轴,由右手螺旋定则确定。
2、F不在转轴平面内 把F分解为三个分量 Fz, Fr, Ft, Fr的力矩为零, Fz的力矩不为零, 但不影响刚体的定轴转动, Ft的力矩沿轴向, 它对角动量有贡献。
z
Fz
F
r
o
P Fr
Ft
3、多个力作用于刚体 各外力作用点各不相同,外力对转轴
1、转动定律适用条件:刚体定轴转动。 2、M 一定:作用不同刚体上,J 大时,β 小, 转速不宜
改变,转动惯性大。反之,J 小,转动惯性小。 — 转动惯量是物体转动惯性大小的量度。
M J 类比 F ma
3、刚体转动定律是解决刚体转动问题的重要定律。 应用时应注意以下问题: ① 力矩和转动惯量必须对同一转轴而言。
M
r
m1
对重物应用牛顿第二定律,得
T f m 2 g si n m 2 a
N
T
对滑轮应用转动定律,得
f
• o
T
MTrJ
m2g
关联方程为: a r
J
1 2
m1r 2
TT fN m 2gco s
联立得:
Mm2grsinm2gcos
1 2m1r2m2r2
由于 为常量,故滑轮作匀变速转动.则
2 2
an
l2
9gcos
4
例题5-10 一恒力矩M作用于斜面顶点的滑轮上,滑轮的半径为r,
质量为m1,质量为m2的重物通过一不可伸长的轻绳固定在轮的边
缘,重物沿倾角为α的斜面上升.重物与斜面间的摩擦系数为μ。
求:轮子由静止开始转过角 后获得多大的角速度?
z
or
d
F
P
Mz的方向平行于转轴,由右手螺旋定则确定。
2、F不在转轴平面内 把F分解为三个分量 Fz, Fr, Ft, Fr的力矩为零, Fz的力矩不为零, 但不影响刚体的定轴转动, Ft的力矩沿轴向, 它对角动量有贡献。
z
Fz
F
r
o
P Fr
Ft
3、多个力作用于刚体 各外力作用点各不相同,外力对转轴
1、转动定律适用条件:刚体定轴转动。 2、M 一定:作用不同刚体上,J 大时,β 小, 转速不宜
改变,转动惯性大。反之,J 小,转动惯性小。 — 转动惯量是物体转动惯性大小的量度。
M J 类比 F ma
3、刚体转动定律是解决刚体转动问题的重要定律。 应用时应注意以下问题: ① 力矩和转动惯量必须对同一转轴而言。
M
r
m1
对重物应用牛顿第二定律,得
T f m 2 g si n m 2 a
N
T
对滑轮应用转动定律,得
f
• o
T
MTrJ
m2g
关联方程为: a r
J
1 2
m1r 2
TT fN m 2gco s
联立得:
Mm2grsinm2gcos
1 2m1r2m2r2
由于 为常量,故滑轮作匀变速转动.则
2 2
an
l2
9gcos
4
例题5-10 一恒力矩M作用于斜面顶点的滑轮上,滑轮的半径为r,
质量为m1,质量为m2的重物通过一不可伸长的轻绳固定在轮的边
缘,重物沿倾角为α的斜面上升.重物与斜面间的摩擦系数为μ。
求:轮子由静止开始转过角 后获得多大的角速度?
四川大学理论力学时PPT课件

面内落下。点C的初始高度为h。开始时杆系静
止,求铰链C与地面相碰时的速度v。
A
解:取杆AC,当铰链 C 与地面相碰时,速度 瞬心 D 与 A 重合。根据对称性,由动能定理得
2TAC
0
2mg
h 2
2
1
1
ml2
vC
2
mgh
2 3 l
1 k
m2 g2 2kmgh
由于弹簧的变形量是正值,因此取正号,即
δmax
mg k
1 k
m2 g2 2kmgh
第33页/共52页
例2、链条长l,质量m,展开放在光滑的桌面 上,如图所示。开始时链条静止,并有长度为a的 一段下垂。求链条离开桌面时的速度。
解:将链条分为两段考虑,下垂段重力作功为
桌面段重力作功为 由动能定理得
W12 (mzC1 mzC2 )g mg(zC1 zC2 )
即质点系重力的功等于质点系的总重量与其重心 高度差之乘积,重心降低为正,重心升高为负。
重力的功与路径无关,仅取决于重心的始末位置。
第6页/共52页
(2)弹性力的功
设弹簧刚性系数为k,弹簧变形为,则弹力为
弹性力的功为
F k
W
动惯量为2mr2/5 )。
C
JO
1 3
ml2
2 5
mr2
m(l
r)2
m 20l 2 21r2 30lr 15
T
1 2
J
O
2
m 30
20l 2 21r 2 30lr
2
第24页/共52页
例4. 己知长l的杆和半径为r的均质圆盘质量均为m, 均质圆盘沿水平面纯滚,质心速度为u,试求图示位 置时系统的动能。
理论力学第五章

30o
第一种情况: 第一种情况:
摩擦力阻止其向下运动
∑F
x
=0
Q min cos α + Fm − G sin α = 0
− Q min sin α + N − G cos α = 0
∑F
利用
y
=0
Fm = f s N
Q min sin α − f s cos α =G = 135.31 N cos α + f s sin α
[例4] 例
宽a,高b的矩形柜放置 , 的矩形柜放置 a 在水平面上,柜重 ,重心C 在水平面上,柜重P,重心 在其几何中心,柜与地面间 在其几何中心, F h P C 的静摩擦因数是 fs,在柜的 b 侧面施加水平向右的力F, 侧面施加水平向右的力 , 求柜发生运动时所需推力F 求柜发生运动时所需推力 的最小值。 的最小值。
再以整体为对象, 再以整体为对象,有平衡方程 整体为对象
∑X = 0
FAx − FBx = 0
FAx = FBx = 72.17 N
下面判断系统是否处于静平衡 脚端A 极限静摩擦力分别为 脚端 与B 的极限静摩擦力分别为 :
r y
C
Fm A = f s A FAy = 75 N
r G
Fm B = f s B FBy = 75 N
解:
取矩形柜为研究对象,受力分析如图。 1 .假设不翻倒但即将滑动,考虑临界平衡。
y
列平衡方程
∑F = 0,
x
F − FA − FB = 0
F P
C
∑F
FB
x
y
= 0,
FNA + FNB − P = 0
FB = fs × FNB
第一种情况: 第一种情况:
摩擦力阻止其向下运动
∑F
x
=0
Q min cos α + Fm − G sin α = 0
− Q min sin α + N − G cos α = 0
∑F
利用
y
=0
Fm = f s N
Q min sin α − f s cos α =G = 135.31 N cos α + f s sin α
[例4] 例
宽a,高b的矩形柜放置 , 的矩形柜放置 a 在水平面上,柜重 ,重心C 在水平面上,柜重P,重心 在其几何中心,柜与地面间 在其几何中心, F h P C 的静摩擦因数是 fs,在柜的 b 侧面施加水平向右的力F, 侧面施加水平向右的力 , 求柜发生运动时所需推力F 求柜发生运动时所需推力 的最小值。 的最小值。
再以整体为对象, 再以整体为对象,有平衡方程 整体为对象
∑X = 0
FAx − FBx = 0
FAx = FBx = 72.17 N
下面判断系统是否处于静平衡 脚端A 极限静摩擦力分别为 脚端 与B 的极限静摩擦力分别为 :
r y
C
Fm A = f s A FAy = 75 N
r G
Fm B = f s B FBy = 75 N
解:
取矩形柜为研究对象,受力分析如图。 1 .假设不翻倒但即将滑动,考虑临界平衡。
y
列平衡方程
∑F = 0,
x
F − FA − FB = 0
F P
C
∑F
FB
x
y
= 0,
FNA + FNB − P = 0
FB = fs × FNB
四川大学物理学院理论力学第五章课件 4
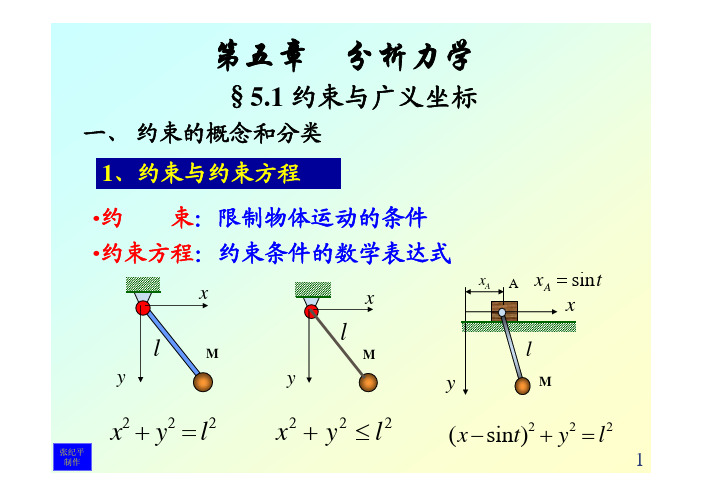
实位移
z
t + dt
dr M ′
u δr M δr t
y
x
O 虚位移
质系虚位移的发生与时间t的变化无关 (δ t ≡ 0),
因此它就是约束被“冻结”后,质系在此瞬时为约束 所允许的任意无限小位移。
张纪平 制作
9
dr ≠ δr
真实位移不仅与约束有关,还与运动、受力有关
张纪平 制作
10
讨论: – 虚位移只满足约束方程,实位移除满足约束方程
∑ ∑ ∑ ∑ ∑ δW
=
n i =1
Fi ⋅δ ri
n
=
i =1
Fi
⋅
s
(
α =1
∂ri ∂qα
s⎛
δ
qα
)
=
α
=1
⎜ ⎝
n i =1
Fi
⋅ ∂ri ∂qα
⎞ ⎟
δ
qα
⎠
=0
∑ Qα
=
n i =1
⎛ ⎜ ⎝
Fi
⋅
∂ri ∂qα
⎞ ⎟ ⎠
Qα 称为对应广义坐标qα的广义力
n
s
s
则
∑ ∑ ∑ δW = Fi ⋅δ ri = Qαδ qα = 0 δW = Qαδ qα = 0
1、达朗伯-拉格朗日方程
设受完整约束的力学体系有n个质点,设第i个质点受主动
力 Fi,受约束反力 R i ,则
V 分析力学 a 将约束看作是强制性的。 a 先找到约束允许的可能运动,再按照一定的 规则从所有可能的运动中得到真实的运动。 a 约束与力都是改变运动的原因。
张纪平 制作
3
二、广义坐标
1、自由度 独立坐标的个数
理论力学课件第五章

n ( Fi mi ri ) ri Ri ri 0 n i 1 i 1
( 3)
在理想约束下有:
( Fi m i ri ) ri 0
n i 1
(4)
称(4)式为达朗伯——拉格朗日方程,也常称 达朗伯原理。 下面我们在广义坐标下表示(4)式 ri ri (q1 , q2 ,qs , t ) 或
a i
——约束方程
2.约束的分类 根据约束方程中是否显含时间t,我们把约束方程分 为稳定约束和不稳定约束.
稳定约束:fa (ri ) fa ( xi , yi , zi ) 0 fa (ri , t ) fa ( xi , yi , zi , t ) 0 不稳定约束:
稳如:x 2 y 2 z 2 l 2
故
(q , q , t ) r r i
的偏导数,有 对(10)求 q ri ri (11) q q ri 求 对t的微商有 q
r d i dt q s 2 ri 2 ri q q q tq q 1 s r r i q i 1 q t
本课程中只研究完整力学系统。
二、广义坐标 若n个质点组成的力学系统受到k个完整约束,则系 统的独立数为3n-k=s个。因此用s个独立坐标就可描述 系统的位形。 对完整系统:定义描述系统位形的独立坐标数s=3n-k 为系统的自由度. 由于3n个坐标中独立的只有s个,因此可选取适当 的S个独立参量 q1,q2 ,, qs及t把那3n个不独立的坐标 表示出来。 (i 1,2n; s 3n) 即: ri ri (q1 , q2 ,qs , t )
理论力学课件 d-ch5A

m3 g
W 0
FIBrB
FIC2
r C2
cos 600
M
0
m3aB L m2aC2 cos600 L M 0
(m3
3 2 L2
3
m2
3 2L2 M ) 0
6
0
2020/11/28
39
理论力学
§5-1 动力学普遍方程
思考题:两个质量相同的均质圆盘和均质杆用铰链连接并由 绳索AB悬挂于天花板,在图示位置平衡,已知圆盘半径为R
理论力学
作业:5-1、5-2、5-3
本学期讲授的主要内容
•第五章 Lagrange方程 •第六章 刚体的定点运动与一般运动 •第七章 机械振动基础
课件下载信箱: bhlllx07@ , 密码:bhlllx 每周四交作业,每周四下午4:00-6:00答疑,地点:主337
2020/11/28
1697年,J、伯努利提出了著名的最速落线问题
o
x
v ds
dt ds
dt
v
g v 2gy
y
P(x0 , y0 )
ds 1 y'2dx
问题:在铅垂面内,质点沿什么曲线, 由O点下落到P点, 所用的时间最短?
(不计空气阻力和摩擦力,)
x0 1 y'2
t
dx 2gy
0
曲线方程为:
2020/11/28
x c( sin ) y c(1 cos )
25
理论力学
第五章 Lagrange方程
最速下降线:旋轮线
2020/11/28
26
理论力学
第五章 Lagrange方程
天坛祈年殿:建于1420年
2020/11/28
大学物理第五章刚体力学

v0
3
4J
4Ml
mv
例3 、如图所示,将单摆和一等长的匀质直杆悬挂在 同一点,杆的质量m与单摆的摆锤相等。开始时直杆
自然下垂,将单摆的摆锤拉到高度h0,令它自静止状
态下垂,于铅垂位置和直杆作弹性碰撞。求碰撞后直杆
下端达到的高度h。
l l
m
ho
h’
a
解:碰撞前单摆摆锤的速度为
c hc
h=3h0/2
b
L
mv
v o m o• L
(A) 2v 3L
(B) 4v 5L
(C) 6v 7L
8v (D) 9L
以顺时针为转动正方向
两小球与细杆组成的系统 对竖直固定轴角动量守恒
L
mv
v o m o• L
由 Lmv+Lmv=2mL2+J
及 J= mL2/3
可知正确答案为 [ C ]
6.如图所示,一均匀 细杆长为 l ,质量为 m,平放在摩擦系数
速度。
用功能定理重解该题
取起始位置为零势能参考点 O
0 mgl sin / 2 1 J2
2
A mg
3g sin
l
?棒端A的速度 vA 3gl sin
例2.已知:均匀直杆m,长为l,初始水平静止,
轴光滑,AO4l 。 求:杆下摆角后,角速度 ?
解:杆+地球系统, ∵只有重力作功,∴ E守恒。
1 (1 ml 2 ) 2 1 mgl(1 cos )
23
2
3
arccos23
例4、一飞轮以角速度0绕轴旋转,飞轮对轴的
转动惯量为J1,另一静止飞轮突然被啮合到同一 个轴上,该飞轮对轴的转动惯量为前者的两倍。 啮合后整个系统的角速度 (1/3)0 .
《理论力学五章》课件

力的分解
一个力可以分解为两个或 多个力,这些分力共同作 用产生与原力相同的效果 。
力的矩
力矩是力与力臂的乘积, 表示力对物体转动效果的 量度。
04
第四章 动量与动量守恒定律
动量与动量守恒定律的基本概念
动量
表示物体运动状态的物理 量,等于物体的质量与速 度的乘积。
动量守恒定律
在不受外力作用或所受外 力之和为零的系统中,系 统总动量保持不变。
动能与势能的转换关系
重力势能与动能转换
当物体在重力的作用下运动时,重力势能会转换为动能,反之亦然。
弹性势能与动能转换
当物体在弹力的作用下运动时,弹性势能会转换为动能,反之亦然。
动能与势能的应用实例
机械能守恒
在无外力作用的封闭系统中,动能和势能的总和保持不变 。
摆动
单摆或双摆的运动过程中,动能和重力势能之间相互转换 。
动力学的基本原理
牛顿第一定律
任何物体都保持静止或匀速直线运动的状态,除 非受到外力的作用。
牛顿第二定律
物体的加速度与作用在物体上的力成正比,与物 体的质量成反比。
牛顿第三定律
作用力和反作用力总是大小相等、方向相反、作 用在同一条直线上。
动力的合成与分解
01
02
03
力的合成
两个力等效于一个力,这 个力称为两个力的合力。
分解定理
速度和加速度可以进行任意方式的分解,但必须符合物理实际。例 如,对于定轴转动,通常采用切向和法向分解。
03
第三章 动力学基础
动力学的基本概念
力的概念ቤተ መጻሕፍቲ ባይዱ
力是物体之间的相互作用,是改变物体运动状态的原 因。
动量的概念
物体的动量等于其质量与其速度的乘积,表示物体运 动的剧烈程度。
《理论力学》课件 第5章

因而 dBA/dt 0 ,于是得
vA vB
将上式再求一次导数,则得
aA aB
例5-1
如图5-4所示的曲柄滑道机构,当曲柄 OA 在平面上绕定轴 O 转动 时,通过滑槽连杆中的滑块 A 的带动,可使连杆在水平槽中沿直
线往复滑动。若曲柄 OA 的长为 r ,曲柄与 x 轴的夹角为 t,
其中 是常数,求此连杆在任一瞬时的速度及加速度。
根据上述结论,可作出截面上各点的加速度的分布图,在通过轴心的 直线上,各点的加速度按线性分布,将加速度矢的端点连成直线,此 直线通过轴心,如图5-10(b)所示。
(a)
图5-10
(b)
例5-3
如图5-11所示,一半径 R 0.2 m 的圆轮绕定轴O 的转动方程
为 t2 4t , 单位为rad, t单位为s。求 t 1 s 时,轮
*
t
当 t 趋近于零时,刚体转动的瞬时角加速度为
lim * lim d
t 0
t0 t dt
刚体绕定轴转动的角加速度等于角速度对于时间的一阶导数,
或等于转角对于时间的二阶导数。
角加速度与角速度一样都是代数量,它的单位是 rad/s2
若 与 的符号相同,则角速度的绝对值随时间而增加,这 时称为加速转动;反之,若 与 的符号相反,则角速度
例
设有平动的刚体,在刚体上任取两点 A 和 B ,并连成一直线如
图5-3所示。运动开始时 AB 线在 A0B0 的位置;经过极短时间间 隔 t 之后,移至 A1B1 ;依次再继续移至 A2B2 , ,AnBn 等。
首先证明这两个任意点的轨迹形状是完全 相同的,根据刚体的定义得知 A,B 两点间 的距离保持不变。 因此 AB A0B0 A1B1 A2B2 AnBn
理论力学PPT课件第5章 动量定理、质点系动量定理、质点系动量矩定理

a cx 0 v cx 0
rc 常矢
xc 常量
2020/11/24
.
17
2020/11/24
.
18
思考:若 xc 常量 m i xi则 0对吗?
答: 对! mcx m ixi
经Δt
mc' x mixi'
m xc m ixi
当xc 0时
miΔxi 0.
应用见教材问题5.8(a)(P199)
2020/11/24
.
23
2020/11/24
.
?直升飞
机如果没有 尾翼将发生 什么现象
24
2020/11/24
.
?为什么 二者转动 方向相反
25
2020/11/24
.
?航天器是 怎样实现姿 态控制的
26
2020/11/24
.
?谁最先到
达顶点
27
2020/11/24
.
?跳远运
动员怎样 使身体在 空中不发 生转动
t2 t1
Fydt
I z
t2 t1
Fzdt
2020/11/24
.
6
二、动量定理与质心运动定理
1、动量定理
矢量微分形式: 投影微分形式:
dp dt
F
e R
dpx dt
F
e Rx
dpy dt
F
e Ry
dpz dt
F
e Rz
2020/11/24
.
7
矢量积分形式(又叫冲量定理):
p2 p1 IRe
2020/11/24
.
13
思考: F
F F
1.三个圆盘的运动是否一样? 2.三个圆盘的质心的运动是否一样?
大学物理课件 第五章-2

障碍后的波线
. . . . . . . . .
障碍物
平面波波面
声
3、用惠更斯原理解释
波
波的散射、反射、折射现象 的
(自学)
衍 射
障碍物
12
§5-6 波的叠加和干涉
一、波的叠加
两水波的叠加
S 1
S 2
13
1.波的独立传播原理:
几列同时在媒质中传播的波,它们的传播特性
(波长、频率、波速、波形)不会因其它波的存在 而发生变化。
解: 声波的平均能量密度
1 A2 2
2
1 2
1.29 (106 )2
(2
500)2
6.37 106
J
m3
声强 : I u 6.37 106 340 2.17 103 W m2
9
§5-5 惠更斯原理
一、原理
波动所到达的媒质中各点均可 作为发射子波的波源,其后任一 时刻这些子波的包迹就是新的波 阵面。
(2) OB长度
Y(cm)
10 •
u
解:O B
(O
) B 2
t 0时:yB 0,vB 0
B
2
-5 •
oB
C
20
-5
•
•
(o) (B)
x(cm)
则:O B (2 ) 40 3.3(3 cm) 3 2 2
x 2
3
*波动的特征:
(1)各质元只是在各自平衡位置附近振动.
(2)同一时刻,沿波线各质元振动状态不同,各质元相位依次落后
2 x
*u
=
T
= n
u由介质的性质决定.
T T振
n n振
由振源决定.
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N ri N ri 0
ri
(2)圆柱(刚体)在粗糙面上做无滑滚动
vP 0
张纪平 制作
rP 0 N rP f rP 0
f
P
N
15
(3)光滑铰链(门上的合页)
N1 r1 N 2 r2 N1 r12 相对虚位移
n
平衡状态
Fi ri Ri ri 0
n F r R r i i i i0
i 1 i 1
Fi Ri 0 (i 1,2, , n)
Ri ri 0
n i 1
(i 1,2, , n)
不可积的微分约束 不可积的运动约束
张纪平 制作
可解约束
不完整约束
完整约束
完整系
3
3、约束对运动的影响
牛顿力学 将约束看作是有未知力作用在质点上,使其 运动受限制。 约束都可以用未知力代替。 约束都可以用未知力代替 改变运动的原因都归结为力。 分析力学 将约束看作是强制性的。 先找到约束允许的可能运动,再按照一定的 规则从所有可能的运动中得到真实的运动。 约束与力都是改变运动的原因。
理想约束
受理想约束的力系平衡的 平衡条件 W Fi ri 0 充要条件
n i 1
W ( Fix xi Fiy y i Fiz z i ) 0
i 1
张纪平 制作
n
适用条件: 惯性系、理想不可解约束 18
二、广义平衡方程
ri q ri 1 q
可积 积
张纪平 制作
几何约束
2
竖直圆盘在无滑动 的平面xy上的滚动
a
sin sin a x
cos cos a y
d x a sin d 0 d y a cos d 0
d x cos d y sin 0
解:细杆的位置由杆的两端的坐标
杆的自由度为
s 62 4
? ? ?
不可以 可以 最佳
如果选择 xA , y A , , 为广义坐标
x A , y A , z A , xB
x A , y A , xB , y B
张纪平 制作
x A , y A , ,
x A , y A , z B , xB
s
n
广义坐标:q1 , q2 , , qs
ri ri (q1 , q2 , , qs , t )
q 1, 1 2, 2 , s 广义虚位移
s n s ri ri q ) Fi W Fi ri Fi ( q 0 q 1 i 1 i 1 1 q i 1 n ri Q Fi Q 称为对应广义坐标 q 的广义力 q i 1 n s s 则 W Fi ri Q q 0 W Q q 0
i 1
P
理想约束的例子 光滑面 光滑曲线 光滑 理想约束的例子:光滑面、光滑曲线、光滑 铰链、刚性杆、不可伸长的绳、纯滚动。
张纪平 制作
14
理想约束
Ri ri 0
n i 1
N
(1)光滑的线、面 ri N
ri
线、面静止, N i 0 dr 线、面运动, N dri 0
N
张纪平 制作
真实位移必须满足运动微分方程(牛顿定律)
7
2、虚位移
在给定瞬时 瞬时 质系为约束所允许的 瞬时,质系为约束所允许的 约束所允许的 可能发生 约束所允许的、可能发生 的无限小位移。用r表示。 N f i f i (r1 , r2 , rn , t ) 0 f i rj 0 j rj f i (r1 r1 , rn rn , t ) 0
n
i 1
1
1
Q1 Q 2 Q s 0
张纪平 制作
完整理想约束的质点系,平衡的充要条件是: 完整理想约束的质点系 平衡的充要条件是 所有的广义力都等于零 19
若作用在质点系上的主动力均为有势力,即
Vi Vi Vi F yi Fxi Fzi yi xi zi n n n ri Vi xi Vi yi Vi zi Vi Q Fi ) ( q yi q zi q i 1 i 1 xi q i 1 q
1
2、约束的分类
x 刚性杆
l
M
xA
A
xA sint
x
x
l
M
R
纯滚动
o
y
2
y
x y l
2 2 2
y
x y l
2 2
M
s
R ( x sint)2 y2 l 2 s
s R
•不可解约束: 约束方程为等式的约束 •可解约束:约束方程为不等式的约束 可解约束 约束方程为不等式的约束 f ( x, y, z ) 0 •稳定约束:约束方程中不显含时间t 的约束 •不稳定约束: 约束方程中显含时间t 的约束 •几何约束(完整约束):约束方程中不含速度项的约束 •运动约束(微分约束): f ( x, y , z; x , y , z ; t ) 0
x
张纪平 制作
x y l 0
2 2 2
l
刚性杆
等时变分
y
A
2 x x 2 y y 0
13
二、理想约束
1. 虚功
W F r 主动力 F i
n
M
r
F
或
W F cos r R 约束力 Ri
r
2 理想约束 2.
Ri ri 0
f r 0
M
f r
M1 12
张纪平 制作
f=0
等时变分
f i (r1 , r2 , rn , t ) 0
fi fi drj dt 0 t j rj
N
f i rj 0 j r j
N
等时变分运算与微分运算类似 但t = 0。 等时变分运算与微分运算类似,但 0 将矢径进行等时变分就是虚位移,将几何约束方程 进行等时变分就可以得到虚位移之间的关系。 进行等时变分就可以得到虚位移之间的关系
ri ri (q1 , q2 , , qs , t ) i 1,2, , n; s 3n
x
q1 , q 2 , , q s
张纪平 制作
y
l
M
x y l
2 2
2
s 1
广义坐标
5
例题
长为l的细杆AB 的一端被约束在水平桌面上, 确定其自由度.
(xA , yA , zA)和(xB , yB ,zB) 确定, 因 存在着2个约束方程:
N 虚位移的发生 fi fi fi fi x j y j z j 0 不需要时间! y j z j j x j
r
r
r
虚位移有无穷多个!
8
张纪平 制作
r
稳定约束情况
实位移
f i drj 0 j r j
f i (r1 , r2 , rn , t ) 0 f i (r1 dr1 , rn drn , t dt ) 0
f i fi df i drj dt 0 t j rj
N
dr
对稳定约束
fi dfi drj 0 j rj
?
不可以
6
§5.2 虚功原理
一、实位移与虚位移 实位移与虚位移 1. 实位移
质系实际发生的位移。同时满足动力学方程、初始 质系实际发生的位移 同时满足动力学方程 初始 条件和约束条件。 1,2, , k f ( x1 , y1 , z1 ,, x n , y n , z n ; t ) 0
N1
0
N2
(4)质量可忽略的刚性轻杆所连接的两个质点 FR1 FR 2 F R1 1 r12 FR 2 W FR1 r1 FR 2 r2 r1 FR1 r12 FR1 r12 e12 r2
2
0
张纪平 制作
O
16
(5)两个质点以柔软不可伸长的轻绳相连
W FT 1 r1 FT 2 r2
0 0 FT 1 r1 r2
FT 1
FT 2
m2
0
绳子不可伸长 0 m1
张纪平 制作
17
三、虚功原理
1、虚功原理 不可解约束(即双面约束) 任一质点 任 质点i
Fi iVi
V Vi
i 1
n
体系总的势能
V 对应于某一广义坐标的广义力,等于总 Q 势能对该广义坐标的偏导数冠以负号。 广义 标的偏导数冠以负号 q 势能对
保守系统的 平衡条件
s
张纪平 制作
V q 0 1 q
V 0 q
( 1, , 2 , , s )
第五章 分析力学
§5.1 约束与广义坐标
一、 约束的概念和分类 1、约束与约束方程 •约 束:限制物体运动的条件 •约束方程:约束条件的数学表达式 约束方程 约束条件的数学表达式
