2020年中考数学经典题型汇编 相似三角形(pdf,含解析)
2020年中考数学必考考点压轴题 专题24 相似三角形判定与性质(含答案)

专题24相似三角形判定与性质1.相似三角形:对应角相等,对应边成比例的两个三角形叫做相似三角形。
相似多边形对应边的比叫做相似比。
2.三角形相似的判定方法:(1)定义法:对应角相等,对应边成比例的两个三角形相似。
(2)平行法:平行于三角形一边的直线和其他两边(或两边延长线)相交,构成的三角形与原三角形相似。
(3)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,可简述为两角对应相等,两三角形相似。
(4)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应相等,并且夹角相等,那么这两个三角形相似,可简述为两边对应成比例且夹角相等,两三角形相似。
(5)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简述为三边对应成比例,两三角形相似。
3.直角三角形相似判定定理:①以上各种判定方法均适用②定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
③垂直法:直角三角形被斜边上的高分成的两个直角三角形与原三角形相似。
4.相似三角形的性质:(1)相似三角形的对应角相等,对应边成比例(2)相似三角形对应高的比、对应中线的比与对应角平分线的比都等于相似比(3)相似三角形周长的比等于相似比(4)相似三角形面积的比等于相似比的平方。
【例题1】(2019•海南省)如图,在Rt△ABC中,∠C=90°,AB=5,BC=4.点P是边AC上一动点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,当BD平分∠ABC时,AP的长度为()B.C.D.A.【答案】B.【解析】本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.根据勾股定理求出AC,根据角平分线的定义、平行线的性质得到∠QBD=∠BDQ,得到QB=QD,根据相似三角形的性质列出比例式,计算即可.∵∠C=90°,AB=5,BC=4,∴AC==3,∵PQ∥AB,∴∠ABD=∠BDQ,又∠ABD=∠QBD,∴∠QBD=∠BDQ,∴QB=QD,∴QP=2QB,∵PQ∥AB,∴△CPQ∽△CAB,∴==,即==,解得,CP=,∴AP=CA﹣CP=【例题2】(2019•四川省凉山州)在▱ABCD中,E是AD上一点,且点E将AD分为2:3的两部分,连接BE、AC相交于F,则S△AEF:S△CBF是.【答案】4:25或9:25.【解析】本题考查的是相似三角形的判定和性质、平行四边形的性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.分AE:ED=2:3、AE:ED=3:2两种情况,根据相似三角形的性质计算即可.①当AE:ED=2:3时,∵四边形ABCD是平行四边形,∴AD∥BC,AE:BC=2:5,∴△AEF∽△CBF,:S△CBF=()2=4:25;∴S△AEF②当AE:ED=3:2时,:S△CBF=()2=9:25。
2020年中考数学试题分类汇编之10 相似三角形(试题+详细答案)

2020年中考数学试题分类汇编之10相似三角形一、选择题1.(2020成都)(3分)如图,直线123////l l l ,直线AC 和DF 被1l ,2l ,3l 所截,5AB =,6BC =,4EF =,则DE 的长为( )A .2B .3C .4D .1032.(2020哈尔滨)(3分)如图,在ABC ∆中,点D 在BC 边上,连接AD ,点E 在AC 边上,过点E 作//EF BC ,交AD 于点F ,过点E 作//EG AB ,交BC 于点G ,则下列式子一定正确的是( )A .AE EFEC CD= B .EF EGCD AB= C .AF BGFD GC= D .CG AFBC AD= 3.(2020河北)在如图所示的网格中,以点O 为位似中心,四边形ABCD 的位似图形是( )A. 四边形NPMQB. 四边形NPMRC. 四边形NHMQD. 四边形NHMR4.(2020四川绵阳)如图,在四边形ABCD 中,AD ∥BC ,∠ABC =90°,AB =2,AD=2,将△ABC 绕点C 顺时针方向旋转后得△A ′B ′C ,当A ′B ′恰好经过点D 时,△B ′CD 为等腰三角形,若BB ′=2,则AA ′=( )A .B .2C .D .5.(2020无锡)如图,等边ABC ∆的边长为3,点D 在边AC 上,12AD =,线段PQ 在边BA 上运动,12PQ =,有下列结论:①CP 与QD 可能相等;②ΔAQD 与BCP ∆可能相似;③四边形PCDQ 面积的最大值为;④四边形PCDQ 周长的最小值为3+.其中,正确结论的序号为( )A. ①④B. ②④C. ①③D. ②③6.(2020重庆A 卷)如图,在平面直角坐标系中,ABC 的顶点坐标分别是(1,2)A ,(1,1)B ,(3,1)C ,以原点为位似中心,在原点的同侧画DEF ,使DEF 与ABC 成位似图形,且相似比为2:1,则线段DF 的长度为( )B. 2C. 4D.7.(2020重庆B 卷)如图,△ABC 与△DEF 位似,点O 为位似中心.已知OA ∶OD=1∶2, 则△ABC 与△DEF 的面积比为( ) A. 1∶2 B. 1∶3 C. 1∶4 D.1∶58.(2020甘肃定西)生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a 与全身b 的高度比值接近0.618,可以增加视觉美感.若图中b 为2米,则a 约为( )A.1.24米B.1.38米C.1.42米D.1.62米9.(2020四川遂宁)(4分)如图,在平行四边形ABCD 中,∠ABC 的平分线交AC 于点E ,交AD 于点F ,交CD 的延长线于点G ,若AF =2FD ,则BE EG的值为( )A .12B .13C .23D .3410.(2020广西南宁)(3分)如图,在△ABC 中,BC =120,高AD =60,正方形EFGH 一边在BC 上,点E ,F 分别在AB ,AC 上,AD 交EF 于点N ,则AN 的长为( )A .15B .20C .25D .3011.(2020广西玉林)(3分)(2020•玉林)一个三角形木架三边长分别是75cm ,100cm ,120cm ,现要再做一个与其相似的三角形木架,而只有长为60cm 和120cm 的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( ) A .一种B .两种C .三种D .四种12.(2020贵州遵义)(4分)如图,△ABO 的顶点A 在函数y =k x(x >0)的图象上,∠ABO =90°,过AO 边的三等分点M 、N 分别作x 轴的平行线交AB 于点P 、Q .若四边形MNQP 的面积为3,则k 的值为( )A .9B .12C .15D .1813.(3分)(2020•荆门)△ABC 中,AB =AC ,∠BAC =120°,BC =2√3,D 为BC 的中点,AE =14AB ,则△EBD 的面积为( )A .3√34B .3√38C .√34D .√3814.(2020山西)(3分)泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度,金字塔的影长,推算出金字塔的高度,这种测量原理,就是我们所学的( )A .图形的平移B .图形的旋转C .图形的轴对称D .图形的相似15.(2020浙江温州)(4分)如图,在Rt △ABC 中,∠ACB =90°,以其三边为边向外作正方形,过点C 作CR ⊥FG 于点R ,再过点C 作PQ ⊥CR 分别交边DE ,BH 于点P ,Q .若QH =2PE ,PQ =15,则CR 的长为( )A .14B .15C .8√3D .6√516.(2020海南)(3分)如图,在矩形ABCD 中,AB =6,BC =10,点E 、F 在AD 边上,BF 和CE 交于点G ,若EF =AD ,则图中阴影部分的面积为( )A .25B .30C .35D .40二、填空题17.(2020广州)如图7,正方形ABCD 中,△ABC 绕点A 逆时针旋转到△AB C '',AB ',AC '分别交对角线BD 于点E ,F ,若4AE =,则EF ED ⋅的值为 * .图7FB'E C'DCBA18.(2020河南)如图,在边长为的正方形ABCD 中,点,E F 分别是边,AB BC 的中点,连接,,EC FD 点,G H 分别是,EC FD 的中点,连接GH ,则GH 的长度为__________.19.(2020苏州).如图,在平面直角坐标系中,点A 、B 的坐标分别为()4,0-、()0,4,点()3,C n 在第一象限内,连接AC 、BC .已知2BCA CAO ∠=∠,则n =_________.20.(2020乐山)把两个含30角的直角三角板按如图所示拼接在一起,点E 为AD 的中点,连结BE 交AC 于点F .则AFAC=_________.21.(2020无锡)如图,在Rt ABC ∆中,90ACB ∠=︒,4AB =,点D ,E 分别在边AB ,AC 上,且2DB AD =,3AE EC =连接BE ,CD ,相交于点O ,则ABO ∆面积最大值为__________.22.(2020上海)(4分)《九章算术》中记载了一种测量井深的方法.如图所示,在井口B 处立一根垂直于井口的木杆BD ,从木杆的顶端D 观察井水水岸C ,视线DC 与井口的直径AB 交于点E ,如果测得AB =1.6米,BD =1米,BE =0.2米,那么井深AC 为 7 米.23.(2020吉林)(3分)如图,AB ∥CD ∥EF .若=,BD =5,则DF = 10 .24.(2020吉林)(3分)如图,在△ABC 中,D ,E 分别是边AB ,AC 的中点.若△ADE的面积为,则四边形DBCE 的面积为.25.(2020黑龙江牡丹江)(3分)如图,在Rt ABC ∆中,90C ∠=︒,点E 在AC 边上.将A ∠沿直线BE 翻折,点A 落在点A '处,连接A B ',交AC 于点F .若A E AE '⊥,4cos 5A =,则A F BF '= 13.26.(2020黑龙江牡丹江)(3分)如图,在Rt ABC ∆中,CA CB =,M 是AB 的中点,点D 在BM 上,AE CD ⊥,BF CD ⊥,垂足分别为E ,F ,连接EM .则下列结论中:①BF CE =; ②AEM DEM ∠=∠;③AE CE -=; ④2222DE DF DM +=;⑤若AE 平分BAC ∠,则:EF BF ; ⑥CF DM BM DE =,正确的有 ①②③④⑤⑥ .(只填序号)27.(2020山西)(3分)如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =4,CD ⊥AB ,垂足为D ,E 为BC 的中点,AE 与CD 交于点F ,则DF 的长为.解:如图,过点F 作FH ⊥AC 于H .28.(2020四川眉山)(4分)如图,等腰△ABC 中,AB =AC =10,边AC 的垂直平分线交BC 于点D ,交AC 于点E .若△ABD 的周长为26,则DE 的长为.29.(2020浙江温州)(5分)如图,在河对岸有一矩形场地ABCD ,为了估测场地大小,在笔直的河岸l 上依次取点E ,F ,N ,使AE ⊥l ,BF ⊥l ,点N ,A ,B 在同一直线上.在F 点观测A 点后,沿FN 方向走到M 点,观测C 点发现∠1=∠2.测得EF =15米,FM =2米,MN =8米,∠ANE =45°,则场地的边AB 为 15√2 米,BC 为 20√2 米.三、解答题30.(2020杭州)(8分)如图,在△ABC 中,点D ,E ,F 分别在AB ,BC ,AC 边上,DE ∥AC ,EF ∥AB .(1)求证:△BDE ∽△EFC . (2)设AF FC=12,①若BC =12,求线段BE 的长;②若△EFC 的面积是20,求△ABC 的面积.31.(2020安徽)(14分)如图1,已知四边形ABCD是矩形,点E在BA的延长线上,=.EC与BD相交于点G,与AD相交于点F,AF ABAE AD=.⊥;(1)求证:BD EC(2)若1AB=,求AE的长;(3)如图2,连接AG,求证:EG DG-=.32.(2020成都)(4分)如图,在矩形ABCD中,4BC=,E,F分别为AB,AB=,3CD边的中点.动点P从点E出发沿EA向点A运动,同时,动点Q从点F出发沿FC向点C⊥于点H,连接DH.若点P的速度是点Q的速度的2运动,连接PQ,过点B作BH PQ倍,在点P从点E运动至点A的过程中,线段PQ长度的最大值为线段DH长度的最小值为.33.(2020福建)如图,C 为线段AB 外一点.(1)求作四边形ABCD ,使得//CD AB ,且2CD AB =;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的四边形ABCD 中,AC ,BD 相交于点P ,AB ,CD 的中点分别为,M N ,求证:,,M P N 三点在同一条直线上.34.(2020河北)如图1和图2,在ABC ∆中,AB AC =,8BC =,3tan 4C =.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且2AM CN ==.点P 从点M 出发沿折线MB BN -匀速移动,到达点N 时停止;而点Q 在AC 边上随P 移动,且始终保持APQ B ∠=∠.(1)当点P 在BC 上时,求点P 与点A 的最短距离;(2)若点P 在MB 上,且PQ 将ABC ∆面积分成上下4:5两部分时,求MP 的长; (3)设点P 移动的路程为x ,当03x ≤≤及39x ≤≤时,分别求点P 到直线AC 的距离(用含x 的式子表示);(4)在点P 处设计并安装一扫描器,按定角APQ ∠扫描APQ ∆区域(含边界),扫描器随点P 从M 到B 再到N 共用时36秒.若94AK =,请直接..写出点K 被扫描到的总时长.35.(2020江西) 某数学课外活动小组在学习了勾股定理之后,针对图1中所示的“由直角三角形三边向外侧作多边形,它们的面积1S ,2S ,3S 之间的关系问题”进行了以下探究:类比探究(1)如图2,在Rt ABC ∆中,BC 为斜边,分别以,,AB AC BC 为斜边向外侧作Rt ABD ∆,Rt ACE ∆,Rt BCF ∆,若123∠=∠=∠,则面积1S ,2S ,3S 之间的关系式为 ;推广验证(2)如图3,在Rt ABC ∆中,BC 为斜边,分别以,,AB AC BC 为边向外侧作任意ABD ∆,ACE ∆,BCF ∆,满足123∠=∠=∠,D E F ∠=∠=∠,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;拓展应用(3)如图4,在五边形ABCDE 中,105A E C ∠=∠=∠=,90ABC ∠=,AB =2DE =,点P 在AE 上,30ABP ∠=,PE =,求五边形ABCDE 的面积.36.(2020苏州).如图,在矩形ABCD 中,E 是BC 的中点,DF AE ⊥,垂足为F .(1)求证:ABE DFA ∆∆∽;(2)若6AB =,4BC =,求DF 的长.37.(2020南京)(9分)如图,在ABC ∆和△A B C '''中,D 、D '分别是AB 、A B ''上一点,AD A D AB A B ''=''.(1)当CD AC AB C D A C A B ==''''''时,求证ABC ∆∽△A B C ''. 证明的途径可以用下面的框图表示,请填写其中的空格.(2)当CD AC BC C D A C B C ==''''''时,判断ABC ∆与△A B C '''是否相似,并说明理由.38(2020湖北武汉).问题背景:如图(1),已知A ABC DE ∽△△,求证:ABD ACE ∽; 尝试应用:如图(2),在ABC 和ADE 中,90BAC DAE ︒∠=∠=,30ABC ADE ︒∠=∠=,AC 与DE 相交于点F .点D 在BC 边上,AD BD =求DF CF的值;拓展创新:如图(3),D 是ABC 内一点,30BAD CBD ︒∠=∠=,90BDC ︒∠=,4AB =,AC =AD 的长.39.(2020宁夏)(6分)在平面直角坐标系中,△ABC 的三个顶点的坐标分别是A (1,3),B (4,1),C (1,1).(1)画出△ABC 关于x 轴成轴对称的△A 1B 1C 1;(2)画出△ABC 以点O 为位似中心,位似比为1:2的△A 2B 2C 2.40.(2020四川眉山)(10分)如图,△ABC和△CDE都是等边三角形,点B、C、E三点在同一直线上,连接BD,AD,BD交AC于点F.(1)若AD2=DF•DB,求证:AD=BF;(2)若∠BAD=90°,BE=6.①求tan∠DBE的值;②求DF的长.41.(2020山东泰安)(12分)小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形,∠ACB与∠ECD恰好为对顶角,∠ABC=∠CDE=90°,连接BD,AB=BD,点F是线段CE上一点.探究发现:(1)当点F为线段CE的中点时,连接DF(如图(2)),小明经过探究,得到结论:BD⊥DF.你认为此结论是否成立?是.(填“是”或“否”)拓展延伸:(2)将(1)中的条件与结论互换,即:BD⊥DF,则点F为线段CE的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.问题解决:(3)若AB=6,CE=9,求AD的长.42.(2020浙江宁波)(12分)【基础巩固】(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD•AB.【尝试应用】(2)如图2,在▱ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.【拓展提高】(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,∠EDF=12∠BAD,AE=2,DF=5,求菱形ABCD的边长.43.(2020浙江温州)(14分)如图,在四边形ABCD中,∠A=∠C=90°,DE,BF分别平分∠ADC,∠ABC,并交线段AB,CD于点E,F(点E,B不重合).在线段BF 上取点M,N(点M在BN之间),使BM=2FN.当点P从点D匀速运动到点E时,点Q恰好从点M匀速运动到点N.记QN=x,PD=y,已知y=−65x+12,当Q为BF中点时,y=24 5.(1)判断DE与BF的位置关系,并说明理由.(2)求DE,BF的长.(3)若AD=6.①当DP =DF 时,通过计算比较BE 与BQ 的大小关系.②连结PQ ,当PQ 所在直线经过四边形ABCD 的一个顶点时,求所有满足条件的x 的值.2020年中考数学试题分类汇编之10相似三角形四、选择题1.(2020成都)(3分)如图,直线123////l l l ,直线AC 和DF 被1l ,2l ,3l 所截,5AB =,6BC =,4EF =,则DE 的长为( )A .2B .3C .4D .103 解:直线123////l l l ,∴AB DE BC EF=, 5AB =,6BC =,4EF =,∴564DE =, 103DE ∴=, 选:D .2.(2020哈尔滨)(3分)如图,在中,点在边上,连接,点在边上,过点作,交于点,过点作,交于点,则下列式子一定正确的是ABC ∆D BC AD E AC E //EF BC AD F E //EG AB BC G ()A. B . C . D . 解:,, ,, , 故选:.3.(2020河北)在如图所示的网格中,以点O 为位似中心,四边形ABCD 的位似图形是( )A. 四边形NPMQB. 四边形NPMRC. 四边形NHMQD. 四边形NHMR解:如图所示,四边形ABCD 的位似图形是四边形NPMQ .故选:A4.(2020四川绵阳)如图,在四边形ABCD 中,AD ∥BC ,∠ABC =90°,AB =2,AD =2,将△ABC 绕点C 顺时针方向旋转后得△A ′B ′C ,当A ′B ′恰好经过点D 时,△B ′CD 为等腰三角形,若BB ′=2,则AA ′=( )AE EF EC CD =EF EG CD AB =AF BG FD GC =CG AF BC AD =//EF BC ∴AF AE FD EC =//EG AB ∴AE BG EC GC =∴AF BG FD GC=CA.B.2C.D.解:过D作DE⊥BC于E,则∠DEC=∠DEB=90°,∵AD∥BC,∠ABC=90°,∴∠DAB=∠ABC=90°,∴四边形ABED是矩形,∴BE=AD=2,DE=AB=2,∵将△ABC绕点C顺时针方向旋转后得△A′B′C,∴∠DB′C=∠ABC=90°,B′C=BC,A′C=AC,∠A′CA=∠B′CB,∴△A′CA∽△B′CB,∴=,∵△B′CD为等腰三角形,∴△B′CD为等腰直角三角形,∴CD=B′C,设B′C=BC=x,则CD=x,CE=x﹣2,∵CD2=CE2+DE2,∴(x)2=(x﹣2)2+(2)2,∴x=4(负值舍去),∴BC=4,∴AC==2,∴=,∴A′A=,故选:A.5.(2020无锡)如图,等边ABC ∆的边长为3,点D 在边AC 上,12AD =,线段PQ 在边BA 上运动,12PQ =,有下列结论:①CP 与QD 可能相等;②ΔAQD 与BCP ∆可能相似;③四边形PCDQ面积的最大值为16;④四边形PCDQ周长的最小值为32+.其中,正确结论的序号为( ) A. ①④ B. ②④ C. ①③ D. ②③ 解:①∵线段PQ 在边BA 上运动,12PQ =, ∴QD P AP C ≤<,∴CP 与QD 不可能相等,则①错误;②设AQ x =, ∵12PQ =,3AB =, ∴13-=2.52AQ ≤≤0,即 2.5x ≤≤0, 假设ΔAQD 与BCP ∆相似,∵∠A=∠B=60°, ∴AD AQ BP BC =,即121332x x =--, 从而得到22530x x -+=,解得1x =或 1.5x =(经检验是原方程的根),又 2.5x ≤≤0,∴解得的1x =或 1.5x =符合题意,即ΔAQD 与BCP ∆可能相似,则②正确;③如图,过P 作PE ⊥BC 于E ,过F 作DF ⊥AB 于F ,设AQ x =, 由12PQ =,3AB =,得13-=2.52AQ ≤≤0,即 2.5x ≤≤0, ∴132PB x =--,∵∠B=60°,∴132P x E --=⎫⎪⎝⎭,∵12AD =,∠A =60°,∴1224DF =⨯=,则1115332222PBCSBC PE x x ⎫⎫=⨯=⨯--=-⎪⎪⎝⎭⎝⎭,1122DAQSAQ DF x x =⨯=⨯=, ∴四边形PCDQ 面积为:15322ABC PBC DAQSS Sx x x ⎫--=⨯-=⎪⎝⎭, 又∵ 2.5x ≤≤0,∴当 2.5x =时,四边形PCDQ ,即四边形PCDQ , 则③正确;④如图,作点D 关于直线AB 的对称点D 1,连接D D 1,与AB 相交于点Q ,再将D 1Q 沿着AB 向B 端平移PQ 个单位长度,即平移12个单位长度,得到D 2P ,与AB 相交于点P ,连接PC ,∴D 1Q=DQ=D 2P ,11212AD D D AD ===,且∠AD 1D 2=120°,此时四边形PCDQ 的周长为:2CP DQ CD PQ CD CD PQ +++=++,其值最小,∴∠D 1AD 2=30°,∠D 2A D=90°,22AD =,∴根据股股定理可得,22CD =,∴四边形PCDQ 的周长为:2113322CP DQ CD PQ CD CD PQ ⎛⎫+++=++=-+= ⎪⎝⎭则④错误,所以可得②③正确,故选:D .6.(2020重庆A 卷)如图,在平面直角坐标系中,ABC 的顶点坐标分别是(1,2)A ,(1,1)B ,(3,1)C ,以原点为位似中心,在原点的同侧画DEF ,使DEF 与ABC 成位似图形,且相似比为2:1,则线段DF 的长度为( )B. 2C. 4D. 解:∵以原点为位似中心,在原点的同侧画△DEF ,使△DEF 与△ABC 成位似图形,且相似比为2:1,而A (1,2),C (3,1), ∴D (2,4),F (6,2),OFE DCBA∴DF故选:D .7.(2020重庆B 卷)如图,△ABC 与△DEF 位似,点O 为位似中心.已知OA ∶OD=1∶2,则△ABC 与△DEF 的面积比为( ) A. 1∶2 B. 1∶3 C. 1∶4 D.1∶5 .答案C.8.(2020甘肃定西)生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下与全身的高度比值接近0.618,可以增加视觉美感.若图中为2米,则约为( )A.1.24米B.1.38米C.1.42米D.1.62米答案:A9.(2020四川遂宁)(4分)如图,在平行四边形ABCD 中,∠ABC 的平分线交AC 于点E ,交AD 于点F ,交CD 的延长线于点G ,若AF =2FD ,则BE EG的值为( )A .12B .13C .23D .34解:由AF =2DF ,可以假设DF =k ,则AF =2k ,AD =3k , ∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB ∥CD ,AB =CD , ∴∠AFB =∠FBC =∠DFG ,∠ABF =∠G , ∵BE 平分∠ABC ,∴∠ABF =∠CBG , ∴∠ABF =∠AFB =∠DFG=∠G ,a b b a∴AB =CD =2k ,DF =DG =k ,∴CG =CD +DG =3k , ∵AB ∥DG ,∴△ABE ∽△CGE , ∴BE EG=AB CG=2k 3k=23,故选:C .10.(2020广西南宁)(3分)如图,在△ABC 中,BC =120,高AD =60,正方形EFGH 一边在BC 上,点E ,F 分别在AB ,AC 上,AD 交EF 于点N ,则AN 的长为( )A .15B .20C .25D .30解:设正方形EFGH 的边长EF =EH =x ,∵四边EFGH 是正方形,∴∠HEF =∠EHG =90°,EF ∥BC , ∴△AEF ∽△ABC ,∵AD 是△ABC 的高,∴∠HDN =90°, ∴四边形EHDN 是矩形,∴DN =EH =x , ∵△AEF ∽△ABC ,∴=(相似三角形对应边上的高的比等于相似比),∵BC =120,AD =60,∴AN =60﹣x , ∴=,解得:x =40,∴AN =60﹣x =60﹣40=20. 故选:B .11.(2020广西玉林)(3分)(2020•玉林)一个三角形木架三边长分别是75cm ,100cm ,120cm ,现要再做一个与其相似的三角形木架,而只有长为60cm 和120cm 的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( ) A .一种B .两种C .三种D .四种解:长120cm 的木条与三角形木架的最长边相等,则长120cm 的木条不能作为一边, 设从120cm 的木条上截下两段长分别为xcm ,ycm (x +y ≤120), 由于长60cm 的木条不能与75cm 的一边对应,否则x 、y 有大于120cm ,当长60cm的木条与100cm的一边对应,则x75=y120=60100,解得:x=45,y=72;当长60cm的木条与120cm的一边对应,则x75=y100=60120,解得:x=37.5,y=50.答:有两种不同的截法:把120cm的木条截成45cm、72cm两段或把120cm的木条截成37.5cm、50cm两段.故选:B.12.(2020贵州遵义)(4分)如图,△ABO的顶点A在函数y=k x(x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若四边形MNQP的面积为3,则k的值为()A.9B.12C.15D.18解:∵NQ∥MP∥OB,∴△ANQ∽△AMP∽△AOB,∵M、N是OA的三等分点,∴ANAM =12,ANAO=13,∴S△ANQS△AMP =14,∵四边形MNQP的面积为3,∴S△ANQ3+S△ANQ =14,∴S△ANQ=1,∵1S△AOB =(ANAO)2=19,∴S△AOB=9,∴k=2S△AOB=18,故选:D.13.(3分)(2020•荆门)△ABC中,AB=AC,∠BAC=120°,BC=2√3,D为BC的中点,AE=14AB,则△EBD的面积为()A .3√34B .3√38C .√34D .√38解:连接AD ,作EF ⊥BC 于F ,∵AB =AC ,∠BAC =120°,D 为BC 的中点, ∴AD ⊥BC ,AD 平分∠BAC ,∠B =∠C =30° 在Rt △ABD 中,BD =12BC =√3,∠B =30°,∴AB =BDcos30°=√3√32=2,∴AD =12AB =1,∵AE =14AB ,∴BE AB=34,∵EF ⊥BC ,AD ⊥BC ,∴EF ∥AD , ∴△BEF ∽△BAD ,∴EF AD=BE AB,∴EF 1=34∴EF =34, ∴S △BDE =12×BD ×EF =12×√3×34=3√38,选:B .14.(2020山西)(3分)泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度,金字塔的影长,推算出金字塔的高度,这种测量原理,就是我们所学的( )A .图形的平移B .图形的旋转C .图形的轴对称D .图形的相似选:D .15.(2020浙江温州)(4分)如图,在Rt △ABC 中,∠ACB =90°,以其三边为边向外作正方形,过点C 作CR ⊥FG 于点R ,再过点C 作PQ ⊥CR 分别交边DE ,BH 于点P ,Q .若QH =2PE ,PQ =15,则CR 的长为( )A .14B .15C .8√3D .6√5解:如图,连接EC ,CH .设AB 交CR 于J .∵四边形ACDE ,四边形BCJHD 都是正方形, ∴∠ACE =∠BCH =45°, ∵∠ACB =90°,∠BCI =90°,∴∠ACE +∠ACB +∠BCH =180°,∠ACB +∠BCI =90° ∴B ,C ,H 共线,A ,C ,I 共线, ∵DE ∥AI ∥BH ,∴∠CEP =∠CHQ , ∵∠ECP =∠QCH ,∴△ECP ∽△HCQ , ∴PC CQ=CE CH=EP HQ=12,∵PQ =15,∴PC =5,CQ =10, ∵EC :CH =1:2,∴AC :BC =1:2,设AC =a ,BC =2a , ∵PQ ⊥CRCR ⊥AB ,∴CQ ∥AB , ∵AC ∥BQ ,CQ ∥AB ,∴四边形ABQC 是平行四边形,∴AB =CQ =10, ∵AC 2+BC 2=AB 2,∴5a 2=100, ∴a =2√2(负根已经舍弃), ∴AC =2√5,BC =4√5,∵12•AC •BC =12•AB •CJ , ∴CJ =2√5×4√510=4,∵JR =AF =AB =10,∴CR =CJ +JR =14, 故选:A .16.(2020海南)(3分)如图,在矩形ABCD 中,AB =6,BC =10,点E 、F 在AD 边上,BF 和CE 交于点G ,若EF =AD ,则图中阴影部分的面积为( )A .25B .30C .35D .40解:过点G 作GN ⊥AD 于N ,延长NG 交BC 于M , ∵四边形ABCD 是矩形, ∴AD =BC ,AD ∥BC , ∵EF =AD ,∴EF =BC , ∵AD ∥BC ,NG ⊥AD , ∴△EFG ∽△CBG ,GM ⊥BC , ∴GN :GM =EF :BC =1:2, 又∵MN =BC =6, ∴GN =2,GM =4, ∴S △BCG =×10×4=20,∴S △EFG =×5×2=5,S 矩形ABCD =6×10=60, ∴S 阴影=60﹣20﹣5=35. 故选:C .五、填空题17.(2020广州)如图7,正方形ABCD 中,△ABC 绕点A 逆时针旋转到△AB C '',AB ',AC '分别交对角线BD 于点E ,F ,若4AE =,则EF ED ⋅的值为 * .【答案】16. 提示:由△EAF ∽△EDA,得到:EF EAEA ED=,所以:2EA EF ED =,∴EF ED ⋅=1618.(2020河南)如图,在边长为的正方形ABCD 中,点,E F 分别是边,AB BC 的中点,连接,,EC FD 点,G H 分别是,EC FD 的中点,连接GH ,则GH 的长度为__________.【答案】1【详解】过E 作EP DC ⊥,过G 作GQ DC ⊥,过H 作HR BC ⊥,垂足分别为P ,R ,R ,HR 与GQ 相交于I ,如图,∵四边形ABCD 是正方形,∴AB AD DC BC ====图7FB'E C'DCBA90A ADC ∴∠=∠=︒,∴四边形AEPD 是矩形,∴EP AD == ∵点E ,F 分别是AB ,BC 边的中点,∴12PC DC ==12FC BC == EP DC ⊥,GQ DC ⊥,GQ EP ∴//∵点G 是EC 的中点,GQ ∴是EPC ∆的中位线,12GQ EP ∴==,同理可求:HR =,由作图可知四边形HIQP 是矩形, 又HP=12FC ,HI=12HR=12PC , 而FC=PC , ∴ HI HP =,∴四边形HIQP 是正方形,∴2IQ HP ==,∴22GI GQ IQ HI =-=== HIG ∴∆是等腰直角三角形,1GH ∴==故答案为:1.19.(2020苏州).如图,在平面直角坐标系中,点A 、B 的坐标分别为()4,0-、()0,4,点()3,C n 在第一象限内,连接AC 、BC .已知2BCA CAO ∠=∠,则n =_________.【答案】14 5解:如图,过点C作CD⊥y轴,交y轴于点D,则CD∥AO,∴∠DCE=∠CAO,∵∠BCA=2∠CAO,∴∠BCA=2∠DCE,∴∠DCE=∠DCB,∵CD⊥y轴,∴∠CDE=∠CDB=90°,又∵CD=CD,∴△CDE≌△CDB(ASA),∴DE=DB,∵B(0,4),C(3,n),∴CD=3,OD=n,OB=4,∴DE=DB=OB-OD=4-n,∴OE=OD-DE=n-(4-n)=2n-4,∵A(-4,0),∴AO=4,∵CD∥AO,∴AOE∽CDE,∴AO OECD DE=,∴424 34nn-=-,解得:145n=,故答案:145.20.(2020乐山)把两个含30角的直角三角板按如图所示拼接在一起,点E为AD的中点,连结BE 交AC 于点F .则AF AC=_________.解:连接CE ,设CD=2x ,在RtΔACD 和RtΔABC 中,∠BAC=∠CAD=30º,∴∠D=60º,AD=4x ,=, BC=12AC,3=x , ∵点E 为AD 的中点, ∴CE=AE=DE=12AD =2x , ∴ΔCED 为等边三角形,∴∠CED=60º,∵∠BAD=∠BAE+∠CAD=30º+30º=60º,∴∠CED=∠BAD ,∴AB ∥CE ,∴AF BF CF EF=, 在ΔBAE 中,∵∠BAE=∠CAD=30º ∴AF 平分∠BAE ,∴3322AB BF x AE EF x ===, ∴32AF BF CF EF ==, ∴35AF AC =, 故答案为:35.21.(2020无锡)如图,在中,,,点,分别在边,上,且,连接,,相交于点,则面积最大值Rt ABC ∆90ACB ∠=︒4AB =D E AB AC 2DB AD =3AE EC =BE CD O ABO ∆为__________.解:如图1,作DG ∥AC ,交BE 于点G ,∴,∵ , ∴ ∵ ∴∴ ∵AB=4 ∴ ∴若面积最大,则面积最大, 如图2,当点△ABC 为等腰直角三角形时,面积最大,为,∴ 面积最大值为+故答案为:22.(2020上海)(4分)《九章算术》中记载了一种测量井深的方法.如图所示,在井口,BDG BAE ODG OCE △∽△△∽△2,3DG BD AE AB ==∴13CE AE =221DG CE ==ODG OCE △∽△=2DG OD CE OC =23OD CD =23ABO ABC S S =△△ABO ABC ABC 142=42⨯⨯ABO 284=33⨯83B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为7米.解:∵BD⊥AB,AC⊥AB,∴BD∥AC,∴△ACE∽△DBE,∴ACBD =AEBE,∴AC1=1.40.2,∴AC=7(米),答:井深AC为7米.23.(2020吉林)(3分)如图,AB∥CD∥EF.若=,BD=5,则DF=10.解:∵AB∥CD∥EF,∴==,∴DF=2BD=2×5=10.故答案为10.24.(2020吉林)(3分)如图,在△ABC中,D,E分别是边AB,AC的中点.若△ADE 的面积为,则四边形DBCE的面积为.解:∵D,E分别是△ABC的边AB,AC的中点,∴DE是△ABC的中位线,∴DE ∥BC ,DE =BC , ∴△ADE ∽△ABC ,∴=()2=()2=,∵△ADE 的面积为, ∴△ABC 的面积为2,∴四边形DBCE 的面积=2﹣=, 故答案为:.25.(2020黑龙江牡丹江)(3分)如图,在Rt ABC ∆中,90C ∠=︒,点E 在AC 边上.将A ∠沿直线BE 翻折,点A 落在点A '处,连接AB ',交AC 于点F .若A E AE '⊥,4cos 5A =,则A F BF '= 13.【解答】解:90C ∠=︒,4cos 5A =, ∴45AC AB =,设4AC x =,5AB x =,则3BC x =, AE AE ⊥',90AEA ∴∠'=︒,//A E BC ',由于折叠,(36090)2135A EB AEB ∴∠'=∠=-÷=︒,且△A EF BCF '∆∽,45BEC ∴∠=︒,即BCE ∆为等腰直角三角形,3EC x ∴=,AE AC EC x A E ∴=-==', ∴133A E A F x BC BF x ''===, 故答案为:13. 26.(2020黑龙江牡丹江)(3分)如图,在Rt ABC ∆中,CA CB =,M 是AB 的中点,点D 在BM 上,AE CD ⊥,BF CD ⊥,垂足分别为E ,F ,连接EM .则下列结论中: ①BF CE =;②AEM DEM ∠=∠;③AE CE -=;④2222DE DF DM +=;⑤若AE 平分BAC ∠,则:EF BF ;⑥CF DM BM DE =,正确的有 ①②③④⑤⑥ .(只填序号)解:90ACB ∠=︒,90BCF ACE ∴∠+∠=︒,90BCF CBF ∠+∠=︒,ACE CBF ∴∠=∠,又90BFD AEC ∠=︒=∠,AC BC =,()BCF CAE AAS ∴∆≅∆,BF CE ∴=,故①正确;由全等可得:AE CF =,BF CE =,AE CE CF CE EF ∴-===,连接FM ,CM ,点M 是AB 中点,12CM AB BM AM ∴===,CM AB ⊥, 在BDF ∆和CDM ∆中,BFD CMD ∠=∠,BDF CDM ∠=∠,DBF DCM ∴∠=∠,又BM CM =,BF CE =,()BFM CEM SAS ∴∆≅∆,FM EM ∴=,BMF CME ∠=∠,90BMC ∠=︒,90EMF ∴∠=︒,即EMF ∆为等腰直角三角形,EF AE CE ∴=-,故③正确,45MEF MFE ∠=∠=︒,90AEC ∠=︒,45MEF AEM ∴∠=∠=︒,故②正确,设AE 与CM 交于点N ,连接DN ,DMF NME ∠=∠,FM EM =,45DFM DEM AEM ∠=∠=∠=︒,()DFM NEM ASA ∴∆≅∆,DF EN ∴=,DM MN =,DMN ∴∆为等腰直角三角形,2DN DM∴=,而90DEA∠=︒,22222DE DF DN DM∴+==,故④正确;AC BC=,90ACB∠=︒,45CAB∴∠=︒,AE平分BAC∠,22.5DAE CAE∴∠=∠=︒,67.5ADE∠=︒,45DEM∠=︒,67.5EMD∴∠=︒,即DE EM=,AE AE=,AED AEC∠=∠,DAE CAE∠=∠,()ADE ACE ASA∴∆≅∆,DE CE∴=,MEF∆为等腰直角三角形,2EF EM∴=,∴22EF EF EF EMBF CE DE====,故⑤正确;CDM ADE∠=∠,90CMD AED∠=∠=︒,CDM ADE∴∆∽,∴CD CM DMAD AE DE==,BM CM=,AE CF=,∴,,故⑥正确;故答案为:①②③④⑤⑥.27.(2020山西)(3分)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为.解:如图,过点F作FH⊥AC于H.在Rt△ABC中,∵∠ACB=90°,AC=3,BC=4,∴AB===5,BM DMCF DE=CF DM BM DE∴=∵CD⊥AB,∴S△ABC=•AC•BC=•AB•CD,∴CD=,AD===,∵FH∥EC,∴=,∵EC=EB=2,∴=,设FH=2k,AH=3k,CH=3﹣3k,∵tan∠FCH==,∴=,∴k=,∴FH=,CH=3﹣=,∴CF===,∴DF=﹣=,故答案为.28.(2020四川眉山)(4分)如图,等腰△ABC中,AB=AC=10,边AC的垂直平分线交BC于点D,交AC于点E.若△ABD的周长为26,则DE的长为.解:∵边AC的垂直平分线交BC于点D,交AC于点E,∴∠AED=90°,AE=CE=AC==5,AD=CD,∴∠DAC=∠C,∵△ABD的周长为26,∴AB+BD+AD=AB+BD+CD=AB+BC=26,∵AB=AC=10,∴BC=16,∠B=∠C,∴∠B=∠DAC,∴△ABC∽△DAC,∴=,作AM⊥BC于M,∵AB=AC,∴BM=BC=8,∴AM===6,∴=,∴DE=,29.(2020浙江温州)(5分)如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2.测得EF=15米,FM =2米,MN=8米,∠ANE=45°,则场地的边AB为15√2米,BC为20√2米.【解答】解:∵AE⊥l,BF⊥l,∵∠ANE=45°,∴△ANE和△BNF是等腰直角三角形,∴AE=EN,BF=FN,∴EF=15米,FM=2米,MN=8米,∴AE=EN=15+2+8=25(米),BF=FN=2+8=10(米),∴AN=25√2,BN=10√2,∴AB=AN﹣BN=15√2(米);过C作CH⊥l于H,过B作PQ∥l交AE于P,交CH于Q,∴AE∥CH,∴四边形PEHQ和四边形PEFB是矩形,∴PE=BF=QH=10,PB=EF=15,BQ=FH,∵∠1=∠2,∠AEF=∠CHM=90°,∴△AEF ∽△CHM ,∴CH HM =AE EF =2515=53, ∴设MH =3x ,CH =5x ,∴CQ =5x ﹣10,BQ =FH =3x +2,∵∠APB =∠ABC =∠CQB =90°,∴∠ABP +∠PAB =∠ABP +∠CBQ =90°,∴∠PAB =∠CBQ ,∴△APB ∽△BQC ,∴AP BQ =PB CQ , ∴153x+2=155x−10,∴x =6,∴BQ =CQ =20,∴BC =20√2,故答案为:15√2,20√2.六、解答题30.(2020杭州)(8分)如图,在△ABC 中,点D ,E ,F 分别在AB ,BC ,AC 边上,DE ∥AC ,EF ∥AB .(1)求证:△BDE ∽△EFC .(2)设AF FC =12, ①若BC =12,求线段BE 的长;②若△EFC 的面积是20,求△ABC 的面积.【解答】(1)证明:∵DE ∥AC ,∴∠DEB =∠FCE ,∵EF ∥AB ,∴∠DBE =∠FEC ,∴△BDE ∽△EFC ;(2)解:①∵EF ∥AB ,∴BE EC =AF FC =12,∵EC =BC ﹣BE =12﹣BE ,∴BE 12−BE=12,解得:BE =4; ②∵AF FC =12,∴FC AC =23, ∵EF ∥AB ,∴△EFC ∽△BAC ,∴S △EFCS △ABC =(FC AC )2=(23)2=49, ∴S △ABC =94S △EFC =94×20=45. 31.(2020安徽)(14分)如图1,已知四边形是矩形,点在的延长线上,.与相交于点,与相交于点,.(1)求证:;(2)若,求的长;(3)如图2,连接,求证:.(1)证明:四边形是矩形,点在的延长线上,,又,,,,,即,故,(2)解:四边形是矩形,,,,,ABCD E BA AE AD =EC BD G AD F AF AB =BD EC ⊥1AB =AEAG EG DG -=ABCD E BA 90EAF DAB ∴∠=∠=︒AE AD =AF AB =()AEF ADB SAS ∴∆≅∆AEF ADB ∴∠=∠90GEB GBE ADB ABD ∴∠+∠=∠+∠=︒90EGB ∠=︒BD EC ⊥ABCD //AE CD ∴AEF DCF ∴∠=∠EAF CDF ∠=∠AEF DCF ∴∆∆∽, 即,设,则有,化简得,解得(舍去), . (3)如图,在线段上取点,使得,在与中,,,,,,,,为等腰直角三角形,.32.(2020成都)(4分)如图,在矩形中,,,,分别为,边的中点.动点从点出发沿向点运动,同时,动点从点出发沿向点运动,连接,过点作于点,连接.若点的速度是点的速度的2倍,在点从点运动至点的过程中,线段长度的最大值为 ,线段长度的最小值为 .解:连接交于,连接,取的中点,连接,,过点作于.∴AE AF DC DF=AE DF AF DC =(0)AE AD a a ==>(1)1a a -=210a a --=a =AE ∴EG P EP DG =AEP ∆ADG ∆AE AD =AEP ADG ∠=∠EP DG =()AEP ADG SAS ∴∆≅∆AP AG ∴=EAP DAG ∠=∠90PAG PAD DAG PAD EAP DAE ∴∠=∠+∠=∠+∠=∠=︒PAG ∴∆EG DG EG EP PG ∴-=-=ABCD 4AB =3BC =E F AB CD P E EA A Q F FC C PQ B BH PQ ⊥H DH P Q P E A PQ DH EF PQ M BM BM O OH OD O ON CD ⊥N四边形是矩形,,,四边形是矩形,,,,, , ,,,当点与重合时,的值最大,此时,,,,,,,,,,,,,故答案为.33.(2020福建)如图,C为线段AB 外一点.ABCD DF CF =AE EB =∴ADFE 3EF AD ∴==//FQ PE MFQ MEP ∴∆∆∽∴MF FQ ME PE=2PE FQ =2EM MF ∴=2EM ∴=1FM =P A PQ PM ==MQ PQ ∴=////MF ON BC MO OB =1FN CN ∴==3DN DF FN =+=1()22ON FM BC =+=OD ∴==BH PQ ⊥90BHM ∴∠=︒OM OB =1122OH BM ∴==DH OD OH -132DH ∴-DH ∴(1)求作四边形ABCD ,使得//CD AB ,且2CD AB =;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的四边形ABCD 中,AC ,BD 相交于点P ,AB ,CD 的中点分别为,M N ,求证:,,M P N 三点在同一条直线上.解:(1)则四边形ABCD 就是所求作的四边形.(2)∵AB CD ∥,∴ABP CDP ∠=∠,BAP DCP ∠=∠,∴ABP CDP ∆∆∽,∴AB AP CD CP. ∵,M N 分别为AB ,CD 的中点,∴2AB AM =,2CD CN =,∴=AM AP CN CP. 连接MP ,NP ,又∵BAP DCP ∠=∠,∴∽∆∆APM CPN ,∴∠=∠APM CPN ,∵点P 在AC 上∴180∠+∠=︒APM CPM ,∴180∠+∠=︒CPN CPM ,∴,,M P N 三点在同一条直线上.34.(2020河北)如图1和图2,在ABC ∆中,AB AC =,8BC =,3tan 4C =.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且2AM CN ==.点P 从点M 出发沿折线MB BN -匀速移动,到达点N 时停止;而点Q 在AC 边上随P 移动,且始终保持APQ B ∠=∠.(1)当点P 在BC 上时,求点P 与点A 的最短距离;(2)若点P 在MB 上,且PQ 将ABC ∆面积分成上下4:5两部分时,求MP 的长; (3)设点P 移动的路程为x ,当03x ≤≤及39x ≤≤时,分别求点P 到直线AC 的距离(用含x 的式子表示);(4)在点P 处设计并安装一扫描器,按定角APQ ∠扫描APQ ∆区域(含边界),扫描器随点P 从M 到B 再到N 共用时36秒.若94AK =,请直接..写出点K 被扫描到的总时长. (1)当点P 在BC 上时,PA ⊥BC 时PA 最小,∵AB=AC ,△ABC 为等腰三角形,∴PA min =tanC·2BC =34×4=3; (2)过A 点向BC 边作垂线,交BC 于点E ,S 上=S △APQ ,S 下=S 四边形BPQC ,∵APQ B ∠=∠,∴PQ ∥BC ,∴△APQ ∽△ABC , ∴AP AD PQ AB AC BC==,的∴2APQABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭, 当S S 上下=45时,24=9APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭, ∴23AP AB =, AE=2BC ·tan 3C =, 根据勾股定理可得AB=5, ∴2253AP MP AB +==, 解得MP=43; (3)当0≤x≤3时,P 在BM 上运动,P 到AC 的距离:d=PQ·sinC ,由(2)可知sinC=35, ∴d=35PQ , ∵AP=x+2, ∴25AP x PQ AB BC+==, ∴PQ=285x +⨯, ∴d=23855x +⨯⨯=24482525x +, 当3≤x≤9时,P 在BN 上运动,BP=x-3,CP=8-(x-3)=11-x ,d=CP·sinC=35(11-x )=-35x+335, 综上()()24480325253333955x x d x x ⎧+≤≤⎪⎪=⎨⎪-+≤≤⎪⎩;(4)AM=2<AQ=94, 移动的速度=936=14, ①从Q 平移到K ,耗时:92414-=1秒, ②P 在BC 上时,K 与Q 重合时 CQ=CK=5-94=114, ∵∠APQ+∠QPC=∠B+∠BAP ,APQ B ∠=∠∴∠QPC=∠BAP ,又∵∠B=∠C ,∴△ABP ∽△PCQ ,设BP=y ,CP=8-y ,AB BP PC CQ =,即51184y y =-, 整理得y 2-8y=554-, (y-4)2=94, 解得y 1=52,y 2=112, 52÷14=10秒, 112÷14=22秒, ∴点K 被扫描到的总时长36-(22-10)-1=23秒.35.(2020江西) 某数学课外活动小组在学习了勾股定理之后,针对图1中所示的“由直角三角形三边向外侧作多边形,它们的面积,,之间的关系问题”进行了以下探究: 1S 2S 3S类比探究(1)如图2,在中,为斜边,分别以为斜边向外侧作,,,若,则面积,,之间的关系式为 ;推广验证(2)如图3,在中,为斜边,分别以为边向外侧作任意,,,满足,,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;拓展应用(3)如图4,在五边形中,,,,点在上,,,求五边形的面积.【解析】(1) (2)成立;∵∠1=∠2=∠3,∠D=∠E=∠F ,∴△ABD ∽△CAE ∽△BCF. ∴∴∵△ABC 为直角三角形 ∴.∴,∴,∴成立. Rt ABC ∆BC ,,AB AC BC Rt ABD ∆Rt ACE ∆Rt BCF ∆123∠=∠=∠1S 2S 3S Rt ABC ∆BC ,,AB AC BC ABD ∆ACE ∆BCF ∆123∠=∠=∠D E F ∠=∠=∠ABCDE 105A E C ∠=∠=∠=90ABC ∠=AB =2DE =P AE 30ABP ∠=PE =ABCDE 123;S S S +=22122233,.S S AB AC S BC S BC ==221223.S S AB AC S BC ++=222AB AC BC +=1231S S S +=123S S S +=(3)过点A 作⊥BP 于点H.∵∠ABH=30°,AB=∴.∵∠BAP=105°,∴∠HAP=45°.∴∴,BP=BH+PH=∴.连接PD.∵,∴. ∴又∵∠E=∠BAP=105°,△ABP∽△EDP.∴∠EPD=∠APB=45°,.∴∠BPD=90°,∴连接BD.∴.∵tan ∠PBD=,∴∠PBD=30°.∵∠ABC=90°,∠ABC=30°,∴∠DBC=30°∵∠C=105°,∴△ABP ∽△EDP ∽△CBD.∴S △BCD =S △ABP +S△EDP =.∴S 五边形ABCDE =S △ABP +S △EDP +S △BCD +S △BPD36.(2020苏州).如图,在矩形ABCD中,E 是BC 的中点,DFAE ⊥,垂足为F.AH 3,60AH BH BAH ==∠=︒AP =3(33222ABP BP AH S ∆⋅+===2PE ED ==PE ED AP AB ====.PEEDAP AB =BDPEBP AP ==1PD =213BPD ABP S S ∆∆=⋅==32BPD PB PDS ∆⋅===PD BP =31222+=2)3)7++=(1)求证:ABE DFA ∆∆∽;(2)若6AB =,4BC =,求DF 的长.证明:(1)∵四边形ABCD 是矩形,∴90B ∠=︒,AD BC ∥.∴AEB DAF ∠=∠,∵DF AE ⊥,∴90DFA ∠=︒.∴B DFA ∠=∠,∴ABE DFA ∆∆∽.解:(2)∵ABE DFA ∆∆∽, ∴AB AE DF AD=. ∵4BC =,E 是BC 的中点, ∴114222BE BC ==⨯=. ∴在Rt ABE ∆中,AE == 又∵4AD BC ==,∴6DF =∴DF =37.(2020南京)(9分)如图,在和△中,、分别是、上一点,.ABC ∆A B C '''D D 'AB A B ''AD A D AB A B ''=''。
2020年中考数学专题 相似三角形综合练习(含答案)

2020年中考数学专题 相似三角形综合(含答案)一、单选题(共有10道小题)1.如图,在△ABC 中,∠ACB= 90,CD ⊥AB ,垂足为D ,点E 是AB 的中点,CD=DE=a ,则AB 的长为( )A .2aB .a 22C .3aD . 2.根据下列条件,△ABC 和△111C B A 不相似的是()A.∠A=68°,∠B=40°,∠A 1=68°,∠B 1=72°B.∠B=∠B 1,BC=2,BC:A 1 B 1= A B: B 1C 1C.AB=1,BC=2, CA=1.5,A 1 B 1=4, B 1 C 1 =8,D.AB=12,BC=15,CA=24,A 1 B 1=24,A 1 B 1=20,B 1 C 1 =25,A 1 C 1=32 3.用作位似图形的方法,可以将一个图形放大或缩小,位似中心( ) A.只能选在原图形的外部B.只能选在原图形的内部C.只能选在原形的边上D.可以选择任意位置4.如图,AB ,CD 都是BD 的垂线,AB=4,CD=6,BD=14。
P 是BD 上一点,连接AP ,CP ,所得两个三角形相似,则BP 的长是( )A.2B.5.6C.12D.上述都有可能5.如图,是一束平行的光线从教室窗户射入教室的示意图,测得光线与地面所成的角∠AMC=30°,窗户的高在教室地面上的影长MN=32m ,窗户的下沿到教室地面的距离BC=1m (点M ,N ,CC 在同一直线上),则窗户的高CAA B CD a 3346.如图,在□ABCD 中,EF ∥AB 交AD 于点E ,交BD 于点F ,DE:EA=3:4,EF=3,则CD 的长为( )A.4B.7C.3D.127.如图1,已知在△ABC 中,点D 、E 、F 分别是边AB 、AC 、BC 上的点,DE ∥BC ,EF ∥AB ,且AD:DB = 3:5,那么CF ∶CB 等于( ) A. 5:8 B. 3:8 C. 3:5 D.8.如图,如果点C 是线段AB 的黄金分割点(AC>BC ),则下列比例式正确的是( )A.AB ACAC BC= B.AB BC BC AC = C. AC BC BC AB = D. AC ABAB BC=9.如图,P 为平行四边形ABCD 的边AD 上的一点,E 、F 分别为PB ,PC 的中点,△PEF ,△PDC ,△PAB 的面积分别为12,,S S S ,若3S =,则12S S +的值为()A.24B.12C.6D.3 10.如图,在□ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则EF:FC 等于( ) A.3:2 B.3:1 C.1:1 D.1:2 二、填空题(共有8道小题)11.如图,梯形ABCD 的对角线相交于O ,G 是BD 的中点.若AD = 3,BC = 9,则GOBG=A B C DE F A B C P A BCDE F E F A B CD12.如图,平行四边形中,是边上的点,交于点,如果, 那么 .13.如图,正五边形ABCDE 与五边形A ’B ’C ’D ’E ’是位似图形,且相似比为21。
初三数学13 相似三角形-2024年中考数学真题分项汇编(全国通用)(解析版)

专题13 相似三角形一.选择题1.(2022·黑龙江哈尔滨)如图,,,AB CD AC BD ∥相交于点E ,1,2,3AE EC DE ===,则BD 的长为( )A .32B .4C .92D .6【答案】C【分析】根据相似三角形对应边长成比例可求得BE 的长,即可求得BD 的长.【详解】∵//AB CD ∴ABE CDE ∽ ∴AE BE EC DE= ∵1,2,3AE EC DE ===,∴32BE =∵BD BE ED =+ ∴92BD = 故选:C .【点睛】本题考查了相似三角形的对应边长成比例,解题的关键在于找到对应边长.2.(2022·广西贺州)如图,在ABC 中,25DE BC DE BC ==∥,,,则:ADE ABC S S 的值是( )A .325B .425C .25D .35【答案】B【分析】根据相似三角形的判定定理得到ADE ABC ,根据相似三角形的面积比等于相似比的平方计算,得到答案.【详解】解:25DE BC DE BC ==∥,,∴ADE ABC ,∴2224525ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ,故选:B .【点睛】此题考查相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.3.(2022·广西梧州)如图,以点O 为位似中心,作四边形ABCD 的位似图形''''A B C D ﹐已知'13OA OA =,若四边形ABCD 的面积是2,则四边形''''A B C D 的面积是( )A .4B .6C .16D .18【答案】D 【分析】两图形位似必相似,再由相似的图形面积比等于相似比的平方即可求解.【详解】解:由题意可知,四边形ABCD 与四边形''''A B C D 相似,由两图形相似面积比等于相似比的平方可知:''''22'1139ABCD A B C D S OA S OA ⎛⎫⎛⎫= ⎪= ⎪= ⎪ ⎪⎝⎭⎝⎭,又四边形ABCD 的面积是2,∴四边形''''A B C D 的面积为18,故选:D .【点睛】本题考察相似多边形的性质,属于基础题,熟练掌握相似图形的性质是解决本题的关键.4.(2022·四川雅安)如图,在△ABC 中,D ,E 分别是AB 和AC 上的点,DE ∥BC ,若AD BD =21,那么DE BC =( )A .49B .12C .13D .23【答案】D【分析】先求解2,3AD AB =再证明,ADE ABC ∽可得2.3DE AD BC AB ==【详解】解: AD BD =21,2,3AD AB ∴= DE ∥BC ,,ADE ABC ∴ ∽ 2,3DE AD BC AB ∴== 故选D 【点睛】本题考查的是相似三角形的判定与性质,证明ADE ABC △△∽是解本题的关键.5.(2022·内蒙古包头)如图,在边长为1的小正方形组成的网格中,A ,B ,C ,D 四个点均在格点上,AC 与BD 相交于点E ,连接,AB CD ,则ABE △与CDE △的周长比为( )A .1:4B .4:1C .1:2D .2:1【答案】D 【分析】运用网格图中隐藏的条件证明四边形DCBM 为平行四边形,接着证明ABE CDE ∽,最后利相似三角形周长的比等于相似比即可求出.【详解】如图:由题意可知,3DM =,3BC =, ∴DM BC =,而DM BC ∥,∴四边形DCBM 为平行四边形,∴AB DC ∥,∴BAE DCE ∠=∠,ABE CDE ∠=∠,∴ABE CDE ∽,∴21ABE CDE C AB C CD ===△△.故选:D .【点睛】本题考查了平行四边形的判定与性质、相似三角形的判定与性质及勾股定理,熟练掌握相关知识并正确计算是解题关键.6.(2022·黑龙江绥化)如图,在矩形ABCD 中,P 是边AD 上的一个动点,连接BP ,CP ,过点B 作射线,交线段CP 的延长线于点E ,交边AD 于点M ,且使得ABE CBP =∠∠,如果2AB =,5BC =,AP x =,PM y =,其中25x < .则下列结论中,正确的个数为( )(1)y 与x 的关系式为4y x x =-;(2)当4AP =时,ABP DPC ∽;(3)当4AP =时,3tan 5EBP ∠=.A .0个B .1个C .2个D .3个【答案】C 【分析】(1)证明ABM APB ∽,得AB AM AP AB=,将2AB =,AP x =,PM y =代入,即可得y 与x 的关系式;(2)利用两组对应边成比例且夹角相等,判定ABP DPC ∽;(3)过点M 作MF BP ⊥垂足为F ,在Rt APB △中,由勾股定理得BP 的长,证明FPM APB ∽,求出MF ,PF ,BF 的长,在Rt BMF △中,求出tan EBP ∠的值即可.【详解】解:(1)∵在矩形ABCD 中,∴AD BC ∥,90A D ∠=∠=︒,5BC AD ==,2AB DC ==,∴APB CBP ∠=∠,∵ABE CBP =∠∠,∴ABE APB ∠=∠,∴ABM APB ∽,∴AB AM AP AB=,∵2AB =,AP x =,PM y =,∴22x y x -=,解得:4y x x=-,故(1)正确;(2)当4AP =时,541DP AD AP =-=-=,∴12DC DP AP AB ==,又∵90A D ∠=∠=︒,∴ABP DPC ∽,故(2)正确;(3)过点M 作MF BP ⊥垂足为F ,∴90A MFP MFB ∠=∠=∠=︒,∵当4AP =时,此时4x =,4413y x x =-=-=,∴3PM =,在Rt APB 中,由勾股定理得:222BP AP AB =+,∴BP ===,∵FPM APB ∠=∠,∴FPM APB ∽,∴MF PF PM AB AP PB ==,∴24MF PF ==∴MF =PF =∴BF BP PF =-=∴3tan 4MF EBP BF ∠===故(3)不正确;故选:C .【点睛】本题主要考查相似三角形的判定和性质,勾股定理的应用,矩形的性质,正确找出相似三角形是解答本题的关键.7.(2022·湖北鄂州)如图,定直线MN ∥PQ ,点B 、C 分别为MN 、PQ 上的动点,且BC =12,BC 在两直线间运动过程中始终有∠BCQ =60°.点A 是MN 上方一定点,点D 是PQ 下方一定点,且AE ∥BC ∥DF ,AE =4,DF =8,ADBC 在平移过程中,AB +CD 的最小值为()A .B .C .D .【答案】C 【分析】如图所示,过点F 作FH CD ∥交BC 于H ,连接EH ,可证明四边形CDFH 是平行四边形,得到CH =DF =8,CD =FH ,则BH =4,从而可证四边形ABHE 是平行四边形,得到AB =HE ,即可推出当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF ,延长AE 交PQ 于G ,过点E 作ET ⊥PQ 于T ,过点A 作AL ⊥PQ 于L ,过点D 作DK ⊥PQ 于K ,证明四边形BEGC 是平行四边形,∠EGT =∠BCQ =60°,得到EG =BC =12,然后通过勾股定理和解直角三角形求出ET 和TF 的长即可得到答案.【详解】解:如图所示,过点F 作FH CD ∥交BC 于H ,连接EH ,∵BC DF FH CD ∥∥,,∴四边形CDFH 是平行四边形,∴CH =DF =8,CD =FH ,∴BH =4,∴BH =AE =4,又∵AE BC ∥,∴四边形ABHE 是平行四边形,∴AB =HE ,∵EH FH EF +≥,∴当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF ,延长AE 交PQ 于G ,过点E 作ET ⊥PQ 于T ,过点A 作AL ⊥PQ 于L ,过点D 作DK ⊥PQ 于K ,∵MN PQ BC AE ∥∥,,∴四边形BEGC 是平行四边形,∠EGT =∠BCQ =60°,∴EG =BC =12,∴=cos =6=sin GT GE EGT ET GE EGT ⋅⋅∠,∠,同理可求得8GL AL ==,,4KF DK ==,,∴2TL =,∵AL ⊥PQ ,DK ⊥PQ ,∴AL DK ∥,∴△ALO ∽△DKO ,∴2AL AO DK DO==,∴2133AO AD DO AD ====∴24OL OK ===,,∴42TF TL OL OK KF =+++=,∴EF ==故选C .【点睛】本题主要考查了平行四边形的性质与判定,相似三角形的性质与判定,勾股定理,解直角三角形,正确作出辅助线推出当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF 是解题的关键.8.(2022·广西贵港)如图,在边长为1的菱形ABCD 中,60ABC ∠=︒,动点E 在AB 边上(与点A 、B 均不重合),点F 在对角线AC 上,CE 与BF 相交于点G ,连接,AG DF ,若AF BE =,则下列结论错误的是( )A .DF CE =B .120BGC ∠=︒C .2AF EG EC =⋅D .AG【答案】D【分析】先证明△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,得DF =CE ,判断A 项答案正确,由∠GCB +∠GBC =60゜,得∠BGC =120゜,判断B 项答案正确,证△BEG ∽△CEB 得BE CE GE BE= ,即可判断C 项答案正确,由120BGC ∠=︒,BC =1,得点G 在以线段BC 为弦的弧BC 上,易得当点G 在等边△ABC 的内心处时,AG 取最小值,由勾股定理求得AG D 项错误.【详解】解:∵四边形ABCD 是菱形,60ABC ∠=︒,∴AB =AD =BC =CD ,∠BAC =∠DAC =12∠BAD =12(180)ABC ⨯︒-∠=60ABC ︒=∠,∴△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,∴DF =CE ,故A 项答案正确,∠ABF =∠BCE ,∵∠ABC =∠ABF +∠CBF =60゜,∴∠GCB +∠GBC =60゜,∴∠BGC =180゜-60゜=180゜-(∠GCB +∠GBC )=120゜,故B 项答案正确,∵∠ABF =∠BCE ,∠BEG =∠CEB ,∴△BEG ∽△CEB ,∴BE CE GE BE = ,∴2BE GE CE = ,∵AF BE =,∴2AF GE CE = ,故C 项答案正确,∵120BGC ∠=︒,BC =1,点G 在以线段BC 为弦的弧BC 上,∴当点G 在等边△ABC 的内心处时,AG 取最小值,如下图,∵△ABC 是等边三角形,BC =1,∴BF AC ⊥,AF =12AC =12,∠GAF =30゜,∴AG =2GF ,AG 2=GF 2+AF 2,∴2221122AG AG ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭, 解得AG D 项错误,故应选:D【点睛】本题主要考查了菱形的基本性质、等边三角形的判定及性质、圆周角定理,熟练掌握菱形的性质是解题的关键.9.(2022·贵州贵阳)如图,在ABC 中,D 是AB 边上的点,B ACD ∠=∠,:1:2AC AB =,则ADC 与ACB △的周长比是( )A .B .1:2C .1:3D .1:4【答案】B 【分析】先证明△ACD ∽△ABC ,即有12AC AD CD AB AC BC ===,则可得12AC AD CD AB AC BC ++=++,问题得解.【详解】∵∠B =∠ACD ,∠A =∠A ,∴△ACD ∽△ABC ,∴AC AD CD AB AC BC ==,∵12AC AB =,∴12AC AD CD AB AC BC ===,∴12AC AD CD AC AD CD AB AC BC AB AC BC ++====++,∴△ADC 与△ACB 的周长比1:2,故选:B .【点睛】本题主要考查了相似三角形的判定与性质,证明△ACD ∽△ABC 是解答本题的关键.10.(2022·广西)已知△ABC 与△A 1B 1C 1是位似图形,位似比是1:3,则△ABC 与△A 1B 1C 1的面积比( )A .1 :3B .1:6C .1:9D .3:1【答案】C【分析】根据位似图形的面积比等于位似比的平方,即可得到答案.【详解】∵△ABC 与△A 1B 1C 1是位似图形,位似比是1:3,∴△ABC 与△A 1B 1C 1的面积比为1:9,故选:C .【点睛】本题考查位似图形的性质,熟练掌握位似图形的面积比等于位似比的平方是解题的关键.11.(2022·山东临沂)如图,在ABC 中,∥DE BC ,23AD DB =,若6AC =,则EC =( )A .65B .125C .185D .245【答案】C【分析】由∥DE BC ,23AD DB =,可得2,3AD AE DB EC ==再建立方程即可.【详解】解: ∥DE BC ,23AD DB =,2,3AD AE DB EC ∴== 6AC =,62,3CE CE -∴= 解得:18.5CE =经检验符合题意故选C 【点睛】本题考查的是平行线分线段成比例,证明“23AD AE DB EC ==”是解本题的关键.12.(2022·山东威海)由12个有公共顶点O 的直角三角形拼成如图所示的图形,∠AOB =∠BOC =∠COD =…=∠LOM =30°.若S △AOB =1,则图中与△AOB 位似的三角形的面积为( )A .(43)3B .(43)7C .(43)6D .(34)6【答案】C【分析】根据题意得出A 、O 、G 在同一直线上,B 、O 、H 在同一直线上,确定与△AOB 位似的三角形为△GOH ,利用锐角三角函数找出相应规律得出OG=6x ,再由相似三角形的性质求解即可.【详解】解:∵∠AOB =∠BOC =∠COD =…=∠LOM =30°∴∠AOG =180°,∠BOH =180°,∴A 、O 、G 在同一直线上,B 、O 、H 在同一直线上,∴与△AOB 位似的三角形为△GOH ,设OA =x ,则OB=1cos30OA x ==︒,∴OC=24cos303OB x x ==︒,∴OD=3cos30OC x ==︒,…∴OG=6x ,∴6OG OA =,∴12643GOH AOB S S ⎛⎫== ⎪⎝⎭ ,∵1AOB S = ,∴643GOH S ⎛⎫= ⎪⎝⎭ ,故选:C .【点睛】题目主要考查利用锐角三角函数解三角形,找规律问题,相似三角形的性质等,理解题意,找出相应边的比值规律是解题关键.二.填空题13.(2022·贵州黔东南)如图,折叠边长为4cm 的正方形纸片ABCD ,折痕是DM ,点C 落在点E 处,分别延长ME 、DE 交AB 于点F 、G ,若点M 是BC 边的中点,则FG =______cm.【答案】53【分析】根据折叠的性质可得DE =DC =4,EM =CM =2,连接DF ,设FE =x ,由勾股定理得BF ,DF ,从而求出x 的值,得出FB ,再证明FEG FBM ∆∆ ,利用相似三角形对应边成比例可求出FG .【详解】解:连接,DF 如图,∵四边形ABCD 是正方形,∴4,90.AB BC CD DA A B C CDA ︒====∠=∠=∠=∠=∵点M 为BC 的中点,∴114222BM CM BC ===⨯=由折叠得,2,4,ME CM DE DC ====∠90,DEM C ︒=∠=∴∠90DEF ︒=,90,FEG ∠=︒设,FE x =则有222DF DE EF =+∴2224DF x =+又在Rt FMB ∆中,2,2FM x BM =+=,∵222FM FB BM =+∴FB ==∴4AF AB FB =-=在Rt DAF ∆中,222,DA AF DF +=∴2224(44,x +=+解得,124,83x x ==-(舍去)∴4,3FE =∴410233FM FE ME =+=+=∴83FB ==∵∠90DEM ︒=∴∠90FEG ︒=∴∠,FEG B =∠又∠.GFE MFB =∠∴△FEG FBM∆ ∴,FG FE FM FB=即4310833FG =∴5,3FG =故答案为:53【点睛】本题主要考查了正方形的性质,折叠的性质,勾股定理,相似三角形的判定与性质,正确作出辅助线是解答本题的关键.14.(2022·上海)如图,在△ABC 中,∠A =30°,∠B =90°,D 为AB 中点,E 在线段AC 上,AD DE AB BC=,则AE AC =_____.【答案】12或14【分析】由题意可求出12DE BC =,取AC 中点E 1,连接DE 1,则DE 1是△ABC 的中位线,满足112DE BC =,进而可求此时112AE AC =,然后在AC 上取一点E 2,使得DE 1=DE 2,则212DE BC =,证明△DE1E2是等边三角形,求出E1E2=14AC ,即可得到214AE AC =,问题得解.【详解】解:∵D 为AB中点,∴12AD DE AB BC ==,即12DE BC =,取AC 中点E 1,连接DE 1,则DE 1是△ABC 的中位线,此时DE 1∥BC ,112DE BC =,∴112AE AD AC AB ==,在AC 上取一点E 2,使得DE 1=DE 2,则212DE BC =,∵∠A =30°,∠B =90°,∴∠C =60°,BC =12AC ,∵DE 1∥BC ,∴∠DE1E2=60°,∴△DE1E2是等边三角形,∴DE 1=DE 2=E1E2=12BC ,∴E1E2=14AC ,∵112AE AC =,∴214AE AC =,即214AE AC =,综上,AE AC 的值为:12或14,故答案为:12或14.【点睛】本题考查了三角形中位线的性质,平行线分线段成比例,等边三角形的判定和性质以及含30°角的直角三角形的性质等,根据12DE BC =进行分情况求解是解题的关键.15.(2022·北京)如图,在矩形ABCD 中,若13,5,4AF AB AC FC ===,则AE 的长为_______.【答案】1【分析】根据勾股定理求出BC ,以及平行线分线段成比例进行解答即可.【详解】解:在矩形ABCD 中:AD BC ∥,90ABC ∠=︒,∴14AE AF BC FC ==,4BC =,∴144AE =,∴1AE =,故答案为:1.【点睛】此题考查了勾股定理以及平行线分线段成比例,掌握平行线分线段成比例是解题的关键.16.(2022·江苏常州)如图,在Rt ABC △中,90C ∠=︒,9AC =,12BC =.在Rt DEF 中,90F ∠=︒,3DF =,4EF =.用一条始终绷直的弹性染色线连接CF ,Rt DEF 从起始位置(点D 与点B 重合)平移至终止位置(点E 与点A 重合),且斜边DE 始终在线段AB 上,则Rt ABC △的外部被染色的区域面积是______.【答案】28【分析】过点F 作AB 的垂线交于G ,同时在图上标出,,M N F '如图,需要知道的是Rt ABC 的被染色的区域面积是MNF F S '梯形,所以需要利用勾股定理,相似三角形、平行四边形的判定及性质,求出相应边长,即可求解.【详解】解:过点F 作AB 的垂线交于G ,同时在图上标出,,M N F '如下图:90C ∠=︒ ,9AC =,12BC =,15AB ∴==,在Rt DEF 中,90F ∠=︒,3DF =,4EF =.5DE ∴==,15510AE AB DE =-=-= ,//,EF AF EF AF ''= ,∴四边形AEFF '为平行四边形,10AE FF '∴==,11622DEF S DF EF DE GF =⋅=⋅= ,解得:125GF =, //DF AC ,,DFM ACM FDM CAM ∴∠=∠∠=∠,DFM ACM ∴ ∽,13DM DF AM AC ∴==,1115344DM AM AB ∴===,//BC AF ' ,同理可证:ANF DNC ' ∽,13AF AN BC DN '∴==,345344DN AN AB ∴===,451530444MN DN DM ∴=-=-=,Rt ABC 的外部被染色的区域面积为130121028245MNF F S '⎛⎫=⨯+⨯= ⎪⎝⎭梯形,故答案为:28.【点睛】本题考查了直角三角形,相似三角形的判定及性质、勾股定理、平行四边形的判定及性质,解题的关键是把问题转化为求梯形的面积.17.(2022·广西)数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为______米.【答案】12【分析】根据同时、同地物高和影长的比不变,构造相似三角形,然后根据相似三角形的性质解答.【详解】解:设旗杆为AB ,如图所示:根据题意得:ABC DEF ∆∆ ,∴DE EF AB BC= ∵2DE =米, 1.2EF =米,7.2BC =米,∴2 1.2=7.2AB 解得:AB =12米.故答案为:12.【点睛】本题考查了中心投影、相似三角形性质的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.18.(2022·广东深圳)已知ABC 是直角三角形,90,3,5,B AB BC AE ∠=︒===连接CE 以CE 为底作直角三角形CDE 且,CD DE =F 是AE 边上的一点,连接BD 和,BF BD 且45,FBD ∠=︒则AF 长为______.【分析】将线段BD 绕点D 顺时针旋转90︒,得到线段HD ,连接BH ,HE ,利用SAS 证明EDH CDB ∆≅∆,得5EH CB ==,90HED BCD ∠=∠=︒,从而得出////HE DC AB ,则ABF EHF ∆∆∽,即可解决问题.【详解】解:将线段BD 绕点D 顺时针旋转90︒,得到线段HD ,连接BH ,HE ,BDH ∴∆是等腰直角三角形,又EDC ∆ 是等腰直角三角形,HD BD ∴=,EDH CDB ∠=∠,ED CD =,()EDH CDB SAS ∴∆≅∆,5EH CB ∴==,90HED BCD ∠=∠=︒,90EDC ∠=︒ ,90ABC ∠=︒,////HE DC AB ∴,,ABF EHF BAF HEF ∴∠=∠∠=∠,ABF EHF ∴∆∆∽,∴==-AB AF AF EH EF AE AF ,AE =∴35=AF ∴=,【点睛】本题主要考查了等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质等知识,解题的关键是作辅助线构造全等三角形.19.(2022·广西河池)如图,把边长为1:2的矩形ABCD 沿长边BC ,AD 的中点E ,F 对折,得到四边形ABEF ,点G ,H 分别在BE ,EF 上,且BG =EH =25BE =2,AG 与BH 交于点O ,N 为AF 的中点,连接ON ,作OM ⊥ON 交AB 于点M ,连接MN ,则tan ∠AMN =_____.【答案】58##0.625【分析】先判断出四边形ABEF 是正方形,进而判断出△ABG ≌△BEH ,得出∠BAG =∠EBH ,进而求出∠AOB =90°,再判断出△AOB ~△ABG ,求出OA OB ==△OBM ~△OAN ,求出BM =1,即可求出答案.【详解】解:∵点E ,F 分别是BC ,AD 的中点,∴11,22AF AD BE BC ==,∵四边形ABCD 是矩形,∴∠A =90°,AD ∥BC ,AD =BC ,∴12AF BE AD ==,∴四边形ABEF 是矩形,由题意知,AD =2AB ,∴AF =AB ,∴矩形ABEF 是正方形,∴AB =BE ,∠ABE =∠BEF =90°,∵BG =EH ,∴△ABG≌△BEH(SAS),∴∠BAG=∠EBH,∴∠BAG+∠ABO=∠EBH+∠ABO=∠ABG=90°,∴∠AOB=90°,∵BG=EH=25BE=2,∴BE=5,∴AF=5,∴AG==∵∠OAB=∠BAG,∠AOB=∠ABG,∴△AOB∽△ABG,∴OA OB ABAB BG AG==,即52OA OB==∴OA OB==∵OM⊥ON,∴∠MON=90°=∠AOB,∴∠BOM=∠AON,∵∠BAG+∠FAG=90°,∠ABO+∠EBH=90°,∠BAG=∠EBH,∴∠OBM=∠OAN,∴△OBM~△OAN,∴OB BM OA AN=,∵点N是AF的中点,∴1522AN AF==,52BM=,解得:BM=1,∴AM=AB-BM=4,∴552tan48ANAMNAM∠===.故答案为:5 8【点睛】此题主要考查了矩形性质,正方形性质和判定,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,求出BM 是解本题的关键.20.(2022·内蒙古赤峰)如图,为了测量校园内旗杆AB 的高度,九年级数学应用实践小组,根据光的反射定律,利用镜子、皮尺和测角仪等工具,按以下方式进行测量:把镜子放在点O 处,然后观测者沿着水平直线BO 后退到点D ,这时恰好能在镜子里看到旗杆顶点A ,此时测得观测者观看镜子的俯角α=60°,观测者眼睛与地面距离CD =1.7m ,BD =11m ,则旗杆AB 的高度约为_________m . 1.7≈)【答案】17【分析】如图容易知道CD ⊥BD ,AB ⊥BD ,即∠CDO =∠ABO =90°.由光的反射原理可知∠COD =∠AOB =60°,这样可以得到△COD ∽△AOB ,然后利用对应边成比例就可以求出AB .【详解】解:由题意知∠COD =∠AOB =60°,∠CDE =∠ABE =90°,∵CD =1.7m ,∴OD =60CD tan =︒≈1(m),∴OB =11-1=10(m),∴△COD ∽△AOB .∴CD OD AB OB =,即1.7110AB =,∴AB =17(m),答:旗杆AB 的高度约为17m .故答案为:17.【点睛】本题考查了解直角三角形的应用,相似三角形的应用,本题只要是把实际问题抽象到相似三角形中,利用相似三角形的性质就可以求出结果.21.(2022·湖北鄂州)如图,在边长为6的等边△ABC 中,D 、E 分别为边BC 、AC 上的点,AD 与BE 相交于点P ,若BD =CE =2,则△ABP 的周长为 _____.【答案】6+【分析】如图所示,过点E 作EF ⊥AB 于F ,先解直角三角形求出AF ,EF ,从而求出BF ,利用勾股定理求出BE 的长,证明△ABD ≌△BCE 得到∠BAD =∠CBE ,AD =BE ,再证明△BDP ∽△ADB ,得到62BP PD==,即可求出BP ,PD ,从而求出AP ,由此即可得到答案.【详解】解:如图所示,过点E 作EF ⊥AB 于F ,∵△ABC 是等边三角形,∴AB =BC ,∠ABD =∠BAC =∠BCE =60°,∵CE =BD =2,AB =AC =6,∴AE =4,∴cos 2sin AF AE EAF EF AE EAF =⋅∠==⋅∠=,,∴BF =4,∴BE =又∵BD =CE ,∴△ABD ≌△BCE (SAS ),∴∠BAD =∠CBE ,AD =BE ,又∵∠BDP =∠ADB ,∴△BDP ∽△ADB ,∴BD BP DP AD AB BD==,62BP PD==,∴BP PD =∴AP AD AP =-=,∴△ABP 的周长=6AB BP AP ++=故答案为:6+【点睛】本题主要考查了等边三角形的性质,解直角三角形,勾股定理,相似三角形的性质与判定,全等三角形的性质与判定,正确作出辅助线是解题的关键.22.(2022·山东潍坊)《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD 的面积为4,以它的对角线的交点为位似中心,作它的位似图形A B C D '''',若:2:1A B AB ='',则四边形A B C D ''''的外接圆的周长为___________.【答案】【分析】根据正方形ABCD 的面积为4,求出2AB =,根据位似比求出4A B ''=,周长即可得出;【详解】解: 正方形ABCD 的面积为4,∴2AB =,:2:1A B AB ''=,∴4A B ''=,∴A C ''==所求周长=;故答案为:.【点睛】本题考查位似图形,涉及知识点:正方形的面积,正方形的对角线,圆的周长,解题关键求出正方形ABCD 的边长.23.(2022·内蒙古包头)如图,在Rt ABC 中,90ACB ∠=︒,3AC BC ==,D 为AB 边上一点,且BD BC =,连接CD ,以点D 为圆心,DC 的长为半径作弧,交BC 于点E (异于点C ),连接DE ,则BE的长为___________.【答案】3##3-+【分析】过点D 作DF ⊥BC 于点F ,根据题意得出DC DE =,根据等腰三角形性质得出CF EF =,根据90ACB ∠=︒,3AC BC ==,得出AB =CF x =,则3BF x =-,证明DF AC ,得出BF BDCF AD=,列出关于x 的方程,解方程得出x 的值,即可得出3BE =.【详解】解:过点D 作DF ⊥BC 于点F ,如图所示:根据作图可知,DC DE =,∵DF ⊥BC ,∴CF EF =,∵90ACB ∠=︒,3AC BC ==,∴AB ===∵3BD BC ==,∴3AD =,设CF x =,则3BF x =-,∵90ACB ∠=︒,∴AC BC ⊥,∵DF BC ⊥,∴DF AC ,∴BF BDCF AD =,即3x x -=,解得:x =,∴226CE x ===-,∴3363BE CE =-=-+=.故答案为:3.【点睛】本题主要考查了等腰三角形的性质和判定,勾股定理,平行线分线段成比例定理,平行线的判定,作出辅助线,根据题意求出CF 的长,是解题的关键.24.(2022·江苏泰州)如图上,Δ,90,8,6,ABC C AC BC ∠=== 中O 为内心,过点O 的直线分别与AC 、AB 相交于D 、E ,若DE=CD+BE ,则线段CD 的长为__________.【答案】2或12##12或2【分析】分析判断出符合题意的DE 的情况,并求解即可;【详解】解:①如图,作//DE BC ,OF BC OG AB ⊥⊥,,连接OB ,则OD ⊥AC ,∵//DE BC ,∴OBF BOE ∠=∠∵O 为ABC ∆的内心,∴OBF OBE ∠=∠,∴BOE OBE ∠=∠∴BE OE =,同理,CD OD =,∴DE=CD+BE ,10AB ===∵O 为ABC ∆的内心,∴OF OD OG CD ===,∴BF BG AD AG==,∴6810AB BG AG BC CD AC CD CD CD =+=-+-=-+-=∴2CD =②如图,作DE AB ⊥,由①知,4BE =,6AE =,∵ACB AED CAB EAD ∠=∠∠=∠,∴ABC ADE ∆∆ ∴AB ADAC AE=∴1061582AB AE AD AC ⋅⨯===∴151822CD AC AD =-=-=∵92DE ===∴19422DE BE CD =+=+=∴12CD =故答案为:2或12.【点睛】本题主要考查三角形内心的性质、勾股定理、三角形的相似,根据题意正确分析出符合题意的情况并应用性质定理进行求解是解题的关键.25.(2022·黑龙江绥化)如图,60AOB ∠=︒,点1P 在射线OA 上,且11OP =,过点1P 作11PK OA ⊥交射线OB 于1K ,在射线OA 上截取12PP ,使1211PPPK =;过点2P 作22P K OA ⊥交射线OB 于2K ,在射线OA 上截取23P P ,使2322P P P K =.按照此规律,线段20232023P K 的长为________.20221【分析】解直角三角形分别求得11PK ,22P K ,33P K ,……,探究出规律,利用规律即可解决问题.【详解】解:11PK OA ⊥ ,11OPK ∴△是直角三角形,在11Rt OPK 中,60AOB ∠=︒,11OP =,12111tan 60PP PK OP ∴==⋅︒=11PK OA ⊥ ,22P K OA ⊥,1122PK P K ∴∥,2211OP K OPK ∴△∽△,222111P K OP PK OP ∴=,=221P K ∴,同理可得:2331P K =+,3441P K =,……,11n n n P K -∴=,2022202320231P K ∴=,20221.【点睛】本题考查了图形的规律,解直角三角形,平行线的判定,相似三角形的判定与性质,解题的关键是学会探究规律的方法.26.(2022·黑龙江)如图,在平面直角坐标系中,点1A ,2A ,3A ,4A ……在x 轴上且11OA =,212OA OA =,322OA OA =,432OA OA =……按此规律,过点1A ,2A ,3A ,4A ……作x轴的垂线分别与直线y =交于点1B ,2B ,3B ,4B ……记11OA B ,22OA B △,33 OA B ,44 OA B ……的面积分别为1S ,2S ,3S ,4S ……,则2022S =______.【答案】2【分析】先求出11A B =,可得11OA B S =112233n n A B A B A B A B ⋯⋯∥∥∥∥,从而得到11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △,再利用相似三角形的性质,可得11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231:2:2:2::2n ,即可求解.【详解】解:当x =1时,y =,∴点(1B ,∴11A B =∴11112OA B S =⨯= ,∵根据题意得:112233n n A B A B A B A B ⋯⋯∥∥∥∥,∴11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △,∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S :……∶n n OA B S = OA 12∶OA 22∶OA 32∶……∶OAn 2,∵11OA =,212OA OA =,322OA OA =,432OA OA =,……,∴22OA =,2342OA ==,3482OA ==,……,12n n OA -=,∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231246221:2:2:2::21:2:2:2::2n n --= ,∴11222n n n OA B OA B S S -= ,∴220222202222S ⨯-==故答案为:2【点睛】本题主要考查了图形与坐标的规律题,相似三角形的判定和性质,明确题意,准确得到规律,是解题的关键.27.(2022·广西)如图,在正方形ABCD 中,AB =,对角线,AC BD 相交于点O .点E 是对角线AC 上一点,连接BE ,过点E 作EF BE ⊥,分别交,CD BD 于点F 、G ,连接BF ,交AC 于点H ,将EFH △沿EF 翻折,点H 的对应点H '恰好落在BD 上,得到EFH '△若点F 为CD 的中点,则EGH '△的周长是_________.【答案】5+【分析】过点E 作PQ //AD 交AB 于点P ,交DC 于点Q ,得到BP =CQ ,从而证得BPE ≌EQF △,得到BE =EF ,再利用BC =F 为中点,求得BF ==BE EF ===,再求出2EO ==,再利用AB //FC ,求出ABH CFH △∽△21AH CH ==,求得216833AH =⨯=,18833CH =⨯=,从而得到EH =AH -AE =1610233-=,再求得EOB GOE △∽△得到21242OG ===,求得EG OG =1, 过点F 作FM ⊥AC 于点M ,作FN ⊥OD 于点N ,求得FM =2,MH =23,FN =2,证得Rt FH N '△≌Rt FMH 得到23H N MH '==,从而得到ON =2,NG =1,25133GH '=+=,从而得到答案.【详解】解:过点E 作PQ //AD 交AB 于点P ,交DC 于点Q ,∵AD //PQ ,∴AP =DQ ,BPQ CQE ∠=∠,∴BP =CQ ,∵45ACD ∠=︒,∴BP =CQ =EQ ,∵EF ⊥BE ,∴90PEB FEQ ∠+∠=︒∵90PBE PEB ∠+∠=︒∴PBE FEQ ∠=∠,在BPE 与EQF △中BPQ FQE PB EQPBE FEQ ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BPE ≌EQF △,∴BE =EF ,又∵BC AB ==F 为中点,∴CF =∴BF ==∴BE EF ===,又∵4BO ==,∴2EO ==,∴AE =AO -EO =4-2=2,∵AB //FC ,∴ABH CFH △∽△,∴AB AH CF CH=,21AH CH ==,∵8AC ==, ∴216833AH =⨯=,18833CH =⨯=,∴EH =AH -AE =1610233-=,∵90BEO FEO ∠+∠=︒,+90BEO EBO ∠∠=︒,∴FEO EBO ∠=∠,又∵90EOB EOG ∠=∠=︒,∴EOB GOE△∽△∴EG OG OE BE OE OB==,21242OG ===,∴EG OG =1,过点F 作FM ⊥AC 于点M ,∴FM=MC 2=,∴MH =CH -MC =82233-=, 作FN ⊥OD 于点N ,2,FN ==,在Rt FH N '△与Rt FMH 中FH FH FN FM'=⎧⎨=⎩∴Rt FH N '△≌Rt FHM∴23H N MH '==,∴ON =2,NG =1,∴25133GH '=+=,∴10533EGH C EH EG GH EH EG GH '''=++=++=△,故答案为:【点睛】本题考查了正方形的性质应用,重点是与三角形相似和三角形全等的结合,熟练掌握做辅助线是解题的关键.28.(2022·辽宁)如图,在正方形ABCD 中,E 为AD 的中点,连接BE 交AC 于点F .若6AB =,则AEF 的面积为___________.【答案】3【分析】由正方形的性质可知1113222AE AD AB BC ====,//AD BC ,则有AEF CBF ∽△△,然后可得12EF AE BF BC ==,进而问题可求解.【详解】解:∵四边形ABCD 是正方形,6AB =,∴6AD BC AB ===,//AD BC ,∴AEF CBF ∽△△,∴EF AE BF BC=,∵E 为AD 的中点,∴1113222AE AD AB BC ====,∴12EF AE BF BC ==,192ABE S AE AB =⋅= ,∴13EF BE =,∴133AEF ABE S S == ;故答案为3.【点睛】本题主要考查正方形的性质及相似三角形的性质与判定,熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键.29.(2022·贵州贵阳)如图,在四边形ABCD 中,对角线AC ,BD 相交于点E ,6cm AC BC ==,90ACB ADB ∠=∠=︒.若2BE AD =,则ABE △的面积是_______2cm ,AEB ∠=_______度.【答案】 36-36- 112.5【分析】通过证明ADE BCE ,利用相似三角形的性质求出23m AE =,263m CE =-,再利用勾股定理求出其长度,即可求三角形ABE 的面积,过点E 作EF ⊥AB ,垂足为F ,证明AEF 是等腰直角三角形,再求出AE CE =,继而证明()Rt BCE Rt BFE HL ≅ ,可知122.52EBF EBC ABC ∠=∠=∠=︒,利用外角的性质即可求解.【详解】90,ACB ADB AED BEC ∠=∠=︒∠=∠ ,ADE BCE ∴ ,AD AE BC BE∴=,6,2BC AC BE AD === ,设,2AD m BE m ==,62m AE m∴=,23m AE ∴=,263m CE ∴=-,在Rt BCE 中,由勾股定理得222BC CE BE +=,22226(6)(2)2m m ∴+-=,解得236m =-或236m =+ 对角线AC ,BD 相交于点E ,236m ∴=-,12AE ∴=-,6CE ∴=,∴(2111263622ABE S AE BC =⋅⋅=⨯-⨯=- ,过点E 作EF ⊥AB ,垂足为F ,90,ACB AC BC ∠=︒= ,45BAC ABC AEF ∴∠=∠=︒=∠,6AE AF AE CE ∴====,BE BE = ,()Rt BCE Rt BFE HL ∴≅ ,122.52EBF EBC ABC ∴∠=∠=∠=︒,112.5AEB ACB EBC ∴∠=∠+∠=︒,故答案为:36-,112.5.【点睛】本题考查了相似三角形的判定和性质,勾股定理,等腰直角三角形的判定和性质,全等三角形的判定和性质及三角形外角的性质,熟练掌握知识点是解题的关键.三.解答题30.(2022·河北)如图,某水渠的横断面是以AB 为直径的半圆O ,其中水面截线MN AB ∥.嘉琪在A 处测得垂直站立于B 处的爸爸头顶C 的仰角为14°,点M 的俯角为7°.已知爸爸的身高为1.7m .(1)求∠C 的大小及AB 的长;(2)请在图中画出线段DH ,用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).(参考数据:tan 76︒取4 4.1)【答案】(1)=76C ∠︒, 6.8(m)AB =(2)见详解,约6.0米【分析】(1)由水面截线MN AB ∥可得BC AB ⊥,从而可求得76C ∠=︒,利用锐角三角形的正切值即可求解.(2)过点O 作O H M N ⊥,交MN 于D 点,交半圆于H 点,连接OM ,过点M 作MG ⊥OB 于G ,水面截线MN AB ∥,即可得DH 即为所求,由圆周角定理可得14BOM ∠=︒,进而可得ABC OGM ,利用相似三角形的性质可得4OG GM =,利用勾股定理即可求得GM 的值,从而可求解.(1)解:∵水面截线MN AB∥BC AB ∴⊥,90ABC ∴∠=︒,90=76C CAB ∴∠=︒-∠︒,在t R ABC 中,90ABC ∠=︒, 1.7BC =,tan 76 1.7AB AB BC ∴︒==,解得 6.8(m)AB ≈.(2)过点O 作O H M N ⊥,交MN 于D 点,交半圆于H 点,连接OM ,过点M 作MG ⊥OB 于G ,如图所示:水面截线MN AB ∥,OH AB ⊥,DH MN ∴⊥,GM OD =,DH ∴为最大水深,7BAM ∠=︒ ,214BOM BAM ∴∠=∠=︒,90ABC OGM ∠=∠=︒ ,且14BAC ∠=︒,ABC OGM ∴ ,OG MG AB CB ∴=,即6.8 1.7OG MG =,即4OG GM =,在Rt OGM △中,90OGM ∠=︒, 3.42AB OM =≈,222OG GM OM ∴+=,即2224(3.4)GM GM +=(),解得0.8GM ≈,= 6.80.86DH OH OD ∴-=-≈,∴最大水深约为6.0米.【点睛】本题考查了解直角三角形,主要考查了锐角三角函数的正切值、圆周角定理、相似三角形的判定及性质、平行线的性质和勾股定理,熟练掌握解直角三角形的相关知识是解题的关键.31.(2022·吉林)下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线12l l ∥,ABC 与DBC △的面积相等吗?为什么?解:相等.理由如下:设1l 与2l 之间的距离为h ,则12ABC S BC h =⋅ ,12DBC S BC h =⋅△.∴ABC DBC S S = .【探究】(1)如图②,当点D 在1l ,2l 之间时,设点A ,D 到直线2l 的距离分别为h ,h ',则ABC DBC S h S h ='△△.证明:∵ABC S(2)如图③,当点D 在1l ,2l 之间时,连接AD 并延长交2l 于点M ,则ABC DBC S AM S DM =△△.证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒,∴AE ∥ .∴AEM △∽ .∴AE AM DF DM =.由【探究】(1)可知ABC DBC S S =△△ ,∴ABC DBC S AM S DM =△△.(3)如图④,当点D 在2l 下方时,连接AD 交2l 于点E .若点A ,E ,D 所对应的刻度值分别为5,1.5,0,ABC DBC S S △△的值为 .【答案】(1)证明见解析(2)证明见解析(3)73【分析】(1)根据三角形的面积公式可得11,22ABC DBC S S BC h BC h '=⋅=⋅ ,由此即可得证;(2)过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,先根据平行线的判定可得AE DF ,再根据相似三角形的判定可证AEM DFM ~ ,根据相似三角形的性质可得AE AM DF DM=,然后结合【探究】(1)的结论即可得证;(3)过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,先根据相似三角形的判定证出AME DNE ~ ,再根据相似三角形的性质可得73AM AE DN DE ==,然后根据三角形的面积公式可得12ABC S BC AM =⋅ ,12DBC S BC DN =⋅ ,由此即可得出答案.(1)证明:12ABC S BC h =⋅ ,12DBC BC h S '=⋅ ,ABC DBC S h S h ∴='.(2)证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒,AE DF ∴∥.AEM DFM ~∴ .AE AM DF DM∴=.由【探究】(1)可知ABC DBC S AE S DF= ,ABC DBC S AM S DM ∴= .(3)解:过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,则90AME DNE ∠=∠=︒,AM DN ∴ ,AME DNE ∴~ ,AM AE DN DE∴=, 点,,A E D 所对应的刻度值分别为5,1.5,0,5 1.5 3.5AE ∴=-=, 1.5DE =,3.571.53AM DN ∴==,又12ABC S BC AM =⋅ ,12DBC S BC DN =⋅ ,73ABCDBC S AM S DN =∴= ,故答案为:73.【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点,熟练掌握相似三角形的判定与性质是解题关键.32.(2022·山东青岛)如图,在Rt ABC △中,90,5cm,3cm ACB AB BC ∠=︒==,将ABC 绕点A 按逆时针方向旋转90︒得到ADE ,连接CD .点P 从点B 出发,沿BA 方向匀速运动,速度为1cm/s ;同时,点Q 从点A 出发,沿AD 方向匀速运动,速度为1cm/s .PQ 交AC 于点F ,连接,CP EQ .设运动时间为(s)(05)t t <<.解答下列问题:(1)当EQ AD ⊥时,求t 的值;(2)设四边形PCDQ 的面积为()2cm S ,求S 与t 之间的函数关系式;(3)是否存在某一时刻t ,使PQ CD ∥?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)16s 5(2)213714210S t t =-+(3)存在,65s 29t =【分析】(1)利用AQE AED △∽△得AQ AE AE AD =,即445t =,进而求解;(2)分别过点C ,P 作,CM AD PN BC ⊥⊥,垂足分别为M ,N ,证ABC CAM △∽△得,AB BC AC CA AM CM ==,求得121655AM CM ==,再证BPN BAC △∽△得BP PN BA AC=,得出45PN t =,根据ABC ACD APQ BPC PCDQ S S S S S S ==+-- 四边形即可求出表达式;(3)当PQ CD ∥时AQP ADC ∠=∠,易证APQ MCD △∽△,得出AP AQ MC MD =,则5161355t t -=,进而求出t 值.(1)解:在Rt ABC △中,由勾股定理得,4AC ===∵ABC 绕点A 按逆时针方向旋转90︒得到ADE。
2020年中考数学-相似三角形综合训练30题含解析
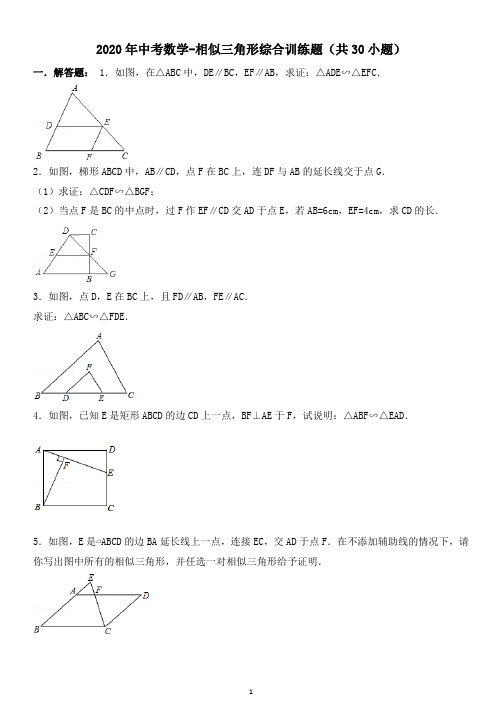
2020年中考数学-相似三角形综合训练题(共30小题)一.解答题:1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.5.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.6.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.7.如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC= _________ °,BC= _________ ;(2)判断△ABC与△DEC是否相似,并证明你的结论.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.9.如图,在四边形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.11.如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC 于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1cm/s的速度,沿C⇒D⇒A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.17、已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:_________ ;(2)请在下图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.24.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m。
2020年九年级数学中考三轮压轴专题:《二次函数与三角形相似》(解析版)

三轮压轴专题:《二次函数与三角形相似》1.如图,在平面直角坐标系中,直线y=﹣x+n与x轴,y轴分别交于点B,点C,抛物线y=ax2+bx+(a≠0)过B,C两点,且交x轴于另一点A(﹣2,0),连接AC.(1)求抛物线的表达式;(2)已知点P为第一象限内抛物线上一点,且点P的横坐标为m,请用含m的代数式表示点P到直线BC的距离;(3)抛物线上是否存在一点Q(点C除外),使以点Q,A,B为顶点的三角形与△ABC 相似?若存在,直接写出点Q的坐标;若不存在,请说明理由.解:(1)点C(0,),则直线y=﹣x+n=﹣x+,则点B(3,0),则抛物线的表达式为:y=a(x﹣3)(x+2)=a(x2﹣x﹣6),故﹣6a=,解得:a=﹣,故抛物线的表达式为:y=﹣x2+x+…①;(2)过点P作y轴的平行线交BC于点G,作PH⊥BC于点H,则∠HPG=∠CBA=α,tan∠CBA===tanα,则cosα=,设点P(m,﹣m2+m+),则点G(m,﹣m+),则PH=PG cosα=(﹣m2+m++m﹣)=﹣m2+m;(3)①当点Q在x轴上方时,则点Q,A,B为顶点的三角形与△ABC全等,此时点Q与点C关于函数对称轴对称,则点Q(1,);②当点Q在x轴下方时,(Ⅰ)当∠BAQ=∠CAB时,△QAB∽△BAC,则=,由勾股定理得:AC=,AQ===10,过点Q作QH⊥x轴于点H,由△HAQ∽△OAC得:==,∵OC=,AQ=10,∴QH=6,则AH=8,OH=8﹣2=6,∴Q(6,﹣6);该点在抛物线上;根据点的对称性,当点Q在第三象限时,符合条件的点Q(﹣5,﹣6);故点Q的坐标为:(6,﹣6)或(﹣5,﹣6);(Ⅱ)当∠BAQ=∠CBA时,则直线AQ∥BC,直线BC表达式中的k为:﹣,则直线AQ的表达式为:y=﹣x﹣1…②,联立①②并解得:x=5或﹣2(舍去﹣2),故点Q(5,﹣),=,而=,故≠,即Q,A,B为顶点的三角形与△ABC不相似,故舍去,Q的对称点(﹣4,﹣)同样也舍去,即点Q的为:(﹣4,﹣)、(5,﹣)均不符合题意,都舍去;综上,点Q的坐标为:(1,)或(6,﹣6)或(﹣5,﹣6).2.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c 经过点A,B.(1)求点B的坐标和抛物线的解析式;(2)设点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.①求PN的最大值;②若以B,P,N为顶点的三角形与△APM相似,请直接写出点M的坐标.解:(1)直线y=﹣x+c交于点A(3,0),与y轴交于点B,∴0=﹣2+c,解得c=2,∴B(0,2),∵抛物线y=﹣x2+bx+c经过点A,B,将点A、B的坐标代入抛物线表达式并解得:y=﹣x2+x+2;(2)①M(m,0),则P(m,),N(m,﹣m2+m+2),∴PN=﹣m2+m+2﹣=﹣m2+4m(0≤m≤3);当m=时,线段PN有最大值为3;②由(1)可知直线解析式为y=﹣x+2,∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,∴P(m,﹣m+2),N(m,﹣m2+m+2),∴PM=﹣m+2,AM=3﹣m,PN=﹣m2+m+2﹣(﹣m+2)=﹣m2+4m,∵△BPN和△APM相似,且∠BPN=∠APM,∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,当∠BNP=90°时,则有BN⊥MN,∴N点的纵坐标为2,∴﹣m2+m+2=2,解得m=0(舍去)或m=,∴M(,0);当∠NBP=90°时,过点N作NC⊥y轴于点C,则∠NBC+∠BNC=90°,NC=m,BC=﹣m2+m+2﹣2=﹣m2+m,∵∠NBP=90°,∴∠NBC+∠ABO=90°,∴∠ABO=∠BNC,∴Rt△NCB∽Rt△BOA,,∴=,解得m=0(舍去)或m=,∴M(,0);综上可知当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(,0)或(,0).3.已知抛物线y=x2+ax+b与x轴交于A(1,0),B(3,0)两点,与y轴交于点C.(1)填空:a=﹣4 b= 3 ;(2)如图1,已知E(,0),过点E的直线与抛物线交于点M、N,且点M、N关于点E对称,求直线MN的解析式;(3)如图2,已知D(0,1),P是第一象限内抛物线上一点,作PH⊥y轴于点H,若△PHD与△BDO相似,请求出点P的横坐标.解:(1)抛物线的表达式为:y=(x﹣1)(x﹣3)=x2﹣4x+3…①,故答案为:﹣4,3;(2)设点M、N的横坐标为m,n,直线MN的表达式为:y=k(x﹣)…②,联立①②并整理得:x2﹣(4+k)x+(3﹣k),则m+n=4+k,点M、N关于点E对称,则y M+y N=km﹣k+kn﹣k=k(m+n)﹣5k=0,即(4+k)k﹣5k=0,解得:k=0(舍去)或1,故直线MN的表达式为:y=x﹣;(3)设点P(m,m2﹣4m+3),则PH=m,HD=|m2﹣4m+3﹣1|,而OB=3,OD=1,则tan∠DOB=,若△PHD与△BDO相似,则tan∠HPD=或4,即=或4,即=或4,解得:m=或或.4.如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.(1)求抛物线的函数表达式;(2)如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;(3)如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.解:(1)将点A(0,1)和点B(3,﹣2)代入抛物物线y=﹣x2+bx+c中得,解得∴y=﹣x2+2x+1(2)如图1所示:过点D作DM∥y轴交AB于点M,设D(a,﹣a2+2a+1),则M(a,﹣a+1).∴DM=﹣a2+2a+1﹣(﹣a+1)=﹣a2+3a∴∵有最大值,当时,此时图1(3)∵OA=OC,如图2,CF∥y轴,∴∠ACE=∠ACO=45°,∴△BCD中必有一个内角为45°,由题意可知,∠BCD不可能为45°,①若∠CBD=45°,则BD∥x轴,∴点D与点B于抛物线的対称轴直线x=1対称,设BD与直线=1交于点H,则H(1,﹣2)B(3,﹣2),D(﹣1,﹣2)此时△BCD是等腰直角三角形,因此△ACE也是等腰直角三角形,(i)当∠AEC=90°时,得到AE=CE=1,∴E(1.1),得到t=1(ii)当∠CAE=90时,得到:AC=AE=,∴CE=2,∴E(1.2),得到t=2图2②若∠CDB=45°,如图3,①中的情况是其中一种,答案同上以点H为圆心,HB为半径作圆,则点B、C、D都在圆H上,设圆H与对称左侧的物线交于另一点D1,则∠CD1B=∠CDB=45°(同弧所对的圆周角相等),即D1也符合题意设由HD1=DH=2解得n1=﹣1(含去),n2=3(舍去),(舍去),∴,则,(i)若△ACE∽△CD1B,则,即,解得(舍去)(ii)△ACE∽△BD1C则,即,解得(舍去)综上所述:所有满足条件的t的值为t=1或t=2或或图35.如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).(1)求抛物线的解析式;(2)如图2,点P为直线BD上方抛物线上一点,若S△PBD=3,请求出点P的坐标.(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.解:(1)设抛物线的解析式为y=a(x﹣1)2+4,将点B(3,0)代入得,(3﹣1)2×a+4=0.解得:a=﹣1.∴抛物线的解析式为:y=﹣(x﹣1)2+4=﹣x2+2x+3.(2)过点P作PQ∥y轴交DB于点Q,∵抛物线的解析式为y=﹣x2+2x+3∴D(0,3).设直线BD的解析式为y=kx+b,∴,解得:,∴直线BD的解析式为y=﹣x+3.设P(m,﹣m2+2m+3),则Q(m,﹣m+3),∴PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.∵S△PBD=S△PQD+S△PQB,∴S△PBD=(3﹣m)=PQ=﹣m,∵S△PBD=3,∴﹣m=3.解得:m1=1,m2=2.∴点P的坐标为(1,4)或(2,3).(3)∵B(3,0),D(0,3),∴BD==3,设M(a,0),∵MN∥BD,∴△AMN∽△ABD,∴,即.∴MN=(1+a),DM==,∵△DNM∽△BMD,∴,∴DM2=BD•MN.∴9+a2=3(1+a).解得:a=或a=3(舍去).∴点M的坐标为(,0).6.如图,抛物线y=ax2+bx+c与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C (0,3),抛物线的对称轴与直线BC交于点D.(1)求抛物线的表达式;(2)在抛物线的对称轴上找一点M,使|BM﹣CM|的值最大,求出点M的坐标;(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,直接写出点E的坐标.解:(1)∵抛物线y=ax2+bx+c经过点A(1,0)、B(3,0)、C(0,3),∴,解得,∴抛物线的表达式为y=x2﹣4x+3;(2)∵抛物线对称轴是线段AB的垂直平分线,∴AM=BM,由三角形的三边关系,|BM﹣CM|=|AM﹣CM|<AC,∴点A、C、M三点共线时,|BM﹣CM|最大,设直线AC的解析式为y=mx+n,则,解得,∴直线AC的解析式为y=﹣3x+3,又∵抛物线对称轴为直线x=﹣=2,∴x=2时,y=﹣3×2+3=﹣3,故,点M的坐标为(2,﹣3);(3))∵OB=OC=3,OB⊥OC,∴△BOC是等腰直角三角形,∵EF∥y轴,直线BC的解析式为y=﹣x+3,∴△DEF只要是直角三角形即可与△BOC相似,∵D(2,1),A(1,0),B(3,0),∴点D垂直平分AB且到点AB的距离等于AB,∴△ABD是等腰直角三角形,∴∠ADB=90°,如图,①点F是直角顶点时,点F的纵坐标与点D的纵坐标相同,是1,∴x2﹣4x+3=1,整理得x2﹣4x+2=0,解得x=2±,当x=2﹣时,y=﹣(2﹣)+3=1+,当x=2+时,y=﹣(2+)+3=1﹣,∴点E1(2﹣,1+)E2(2+,1﹣),②点D是直角顶点时,易求直线AD的解析式为y=x﹣1,联立,解得,,当x=1时,y=﹣1+3=2,当x=4时,y=﹣4+3=﹣1,∴点E3(1,2),E4(4,﹣1),综上所述,存在点E1(2﹣,1+)或E2(2+,1﹣)或E3(1,2)或E4(4,﹣1),使以D、E、F为顶点的三角形与△BCO相似.7.如图,抛物线y=﹣x2+x+2与x轴交于点A,点B,与y轴交于点C,点D与点C 关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线1交抛物线于点Q.(1)求点A、点B、点C的坐标;(2)当点P在线段OB上运动时,直线1交直线BD于点M,试探究m为何值时,四边形CQMD是平行四边形;(3)点P在线段AB上运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.解:(1)抛物线y=﹣x2+x+2,当x=0时,y=2,因此点C(0,2),当y=0时,即:﹣x2+x+2=0,解得x1=4,x2=﹣1,因此点A(﹣1,0),B (4,0),故:A(﹣1,0),B(4,0),C(0,2);(2)∵点D与点C关于x轴对称,∴点D(0,﹣2),CD=4,设直线BD的关系式为y=kx+b,把D(0,﹣2),B(4,0)代入得,,解得,k=,b=﹣2,∴直线BD的关系式为y=x﹣2,设M(m,m﹣2),Q(m,﹣m2+m+2),∴QM=﹣m2+m+2﹣m+2=﹣m2+m+4,当QM=CD时,四边形CQMD是平行四边形;∴﹣m2+m+4=4,解得m1=0(舍去),m2=2,答:m=2时,四边形CQMD是平行四边形;(3)在Rt△BOD中,OD=2,OB=4,因此OB=2OD,①若∠MBQ=90°时,如图1所示,当△QBM∽△BOD时,QP=2PB,设点P的横坐标为x,则QP=﹣x2+x+2,PB=4﹣x,于是﹣x2+x+2=2(4﹣x),解得,x1=3,x2=4(舍去),当x=3时,PB=4﹣3=1,∴PQ=2PB=2,∴点Q的坐标为(3,2);②若∠MQB=90°时,如图2所示,此时点P、Q与点A重合,∴Q(﹣1,0);③由于点M在直线BD上,因此∠QMB≠90°,这种情况不存在△QBM∽△BOD.综上所述,点P在线段AB上运动过程中,存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似,点Q(3,2)或(﹣1,0).8.如图,在平面直角坐标系中,直线y=﹣x+4分别与x轴、y轴相交于点B、C,经过点B、C的抛物线y=﹣+bx+c与x轴的另一个交点为A.(1)求出抛物线表达式,并求出点A坐标.(2)已知点D在抛物线上,且横坐标为3,求出△BCD的面积;(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于x轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.解:(1)由已知可求B(6,0),C(0,4),将点B(6,0),C(0,4)代入y=﹣+bx+c,则有,解得,∴y=﹣x2+x+4,令y=0,则﹣x2+x+4=0,解得x=﹣1或x=6,∴A(﹣1,0);(2)∵点D在抛物线上,且横坐标为3,∴D(3,8),过点D作y轴的垂线交于点E,过点B作BF⊥DE交ED的延长线于点F;∴E(0,8),F(6,8),∴S△BCD=S梯形ECBF﹣S△CDE﹣S△BFD=(EC+BF)×OB﹣×EC×ED﹣×DF×BF =×(4+8)×6﹣×4×3﹣×3×8=36﹣6﹣12=18;(3)设P(m,﹣m2+m+4),∵PQ垂直于x轴,∴Q(m,0),且∠PQO=90°,∵∠COB=90°,∴点A、P、Q为顶点的三角形与△BOC相似有两种情况:①△PAQ∽△CBO时,==,∴=,解得m=5或m=﹣1,∵点P是直线BC上方的抛物线上,∴0≤m≤6,∴m=5,∴P(5,4);②△PAQ∽△BCO时,==,∴=,解得m=﹣1或m=,∵点P是直线BC上方的抛物线上,∴0≤m≤6,∴m=,∴P(,);综上所述:P(5,4)或P(,)时,点A、P、Q为顶点的三角形与△BOC相似.9.如图,抛物线y=﹣+bx+c过点A(3,0)和B(0,2),点M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.(1)求此抛物线的解析式;(2)若点P是MN的中点,则求点P的坐标;(3)若以点B、N、P为顶点的三角形与△AMP相似,请直接写出点P的坐标.解:(1)抛物线经过点A(3,0),B(0,2),∴,解得,∴抛物线的解析式为:;(2)∵B(0,2),∴可设直线AB的解析式为y=kx+2,将点A(3,0)代入y=kx+2,得,3k+2=0,∴k=﹣,∴直线AB的解析式为,由M(m,0),设,,则,,点P是MN的中点,即NP=PM,∴,解得(舍),∴;(3)∵∠APM=∠NPB,∴若以点B、N、P为顶点的三角形与△AMP相似,则存在△AMP∽△NBP和△AMP∽△BNP两种情况,如图,过点P作PH∥x轴交y轴于H,则△BHP∽△BOA,∴=,∵OA=3,PH=m,BA==,∴BP=m,∴AP=AB﹣BP=﹣m=,①当△AMP∽△NBP时,=,∴=,解得,m1=3(舍去),m2=,∴P1(,);②当△AMP∽△BNP时,=,∴=,解得,m1=3(舍去),m2=,∴P2(,);∴点P的坐标为(,)或(,).10.如图,抛物线y=x2+mx+n与直线y=﹣x+3交于A、B两点,交x轴于D、C 两点,连接AC、BC,已知A(0,3),C(3,0).(1)抛物线的函数关系式为y=x2﹣x+3 ,tan∠BAC=;(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位的速度运动到E点,再沿线段EA以每秒个单位的速度运动到点A 后停止,当点E的坐标是多少时,点M在整个运动过程中用时最少?(3)P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使以A、P、Q为顶点的三角形与△ABC相似?若存在,求出所有符合条件的P点坐标,若不存在,请说明理由.解:(1)将A(0,3),C(3,0)代入y=x2+mx+n,得,解得,∴抛物线的解析式为y=x2﹣x+3;联立,解得或,∴点B的坐标为(4,1),如图1,过点B作BH⊥x轴于H,∵C(3,0),B(4,1),∴BH=1,OC=3,CH=4﹣3=1,∴BH=CH=1,∵∠BHC=90°,∴∠BCH=45°,BC=,同理,∠ACO=45°,AC=3,∴∠ACB=180°﹣45°﹣45°=90°,∴tan∠BAC===,故答案为:y=x2﹣x+3,;(2)如图2,过A作射线AF∥x轴,过D作射线DF∥y轴,DF与AC交于点E,∵A(0,3),C(3,0),∴可设直线AC的解析式为y=kx+3,将点C(3,0)代入y=kx+3,得3k+3=0,∴k=﹣1,∴直线AC的解析式为y=﹣x+3,∵OA=OC,∠AOC=90°,∴∠ACO=45°,∵AF∥OC,∴∠FAE=45°,∴EF=AE•sin45°=AE,∴当且仅当AF⊥DF时,DE+EF取最小值,点M在整个运动中用时最少,为:t=+=DE+AE=DE+EF,∵在y=x2﹣x+3中,当y=0时,x1=3,x2=2,∴D(2,0),则E点横坐标为2,将x=2代入直线y=﹣x+3,得,y=1,∴E(2,1);(3)存在点P,使得以A、P、Q为顶点的三角形与△ABC相似,过点P作PG⊥y轴于G,则∠PGA=90°,设点P的横坐标为x,由P在y轴右侧可得x>0,则PG=x,∵PQ⊥PA,∠ACB=90°,∴∠APQ=∠ACB=90°,若点G在点A的下方,①如图3﹣1,当∠PAQ=∠CAB时,则△PAQ∽△CAB,∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,∴△PGA∽△BCA,∴==,∴AG=3PG=3x,则P(x,3﹣3x),把P(x,3﹣3x)代入y=x2﹣x+3,得x2﹣x+3=3﹣3x,解得,x1=0(舍去),x2=﹣1(舍去);②如图3﹣2,当∠PAQ=∠CBA时,则△PAQ∽△CBA,同理可得,AG=PG=x,则P(x,3﹣x),把P(x,3﹣x)代入y=x2﹣x+3,得x2﹣x+3=3﹣x,解得,x1=0(舍去),x2=,∴P(,);若点G在点A的上方,①如图3﹣3,当∠PAQ=∠CBA时,则△PAQ∽△CBA,同理可得,AG=PG=x,则P(x,3+x),把P(x,3+x)代入y=x2﹣x+3,得x2﹣x+3=3+x,解得,x1=0(舍去),x2=,∴P(,);②如图3﹣4,当∠PAQ=∠CAB时,则△PAQ∽△CAB,同理可得,AG=3PG=3x,则P(x,3+3x),把P(x,3+3x)代入y=x2﹣x+3,得x2﹣x+3=3+3x,解得,x1=0(舍去),x2=11,∴P(11,36),综上所述,满足条件的点P的坐标为(,),(,),(11,36).11.如图已知直线y=x+与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣),交x轴正半轴于D点,抛物线的顶点为M.(1)求抛物线的解析式;(2)设点P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求△PAB的面积及点P的坐标;(3)若点Q为x轴上一动点,点N在抛物线上且位于其对称轴右侧,当△QMN与△MAD相似时,求N点的坐标.解:(1)将点B(4,m)代入y=x+,∴m=,将点A(﹣1,0),B(4,),C(0,﹣)代入y=ax2+bx+c,解得a=,b=﹣1,c=﹣,∴函数解析式为y=x2﹣x﹣;(2)设P(n,n2﹣n﹣),则经过点P且与直线y=x+垂直的直线解析式为y=﹣2x+n2+n﹣,直线y=x+与其垂线的交点G(n2+n﹣,n2+n+),∴GP=(﹣n2+3n+4),当n=时,GP最大,此时△PAB的面积最大,∴P(,),∵AB=,PG=,∴△PAB的面积=××=;(3)∵M(1,﹣2),A(﹣1,0),D(3,0),∴AM=2,AB=4,MD=2,∴△MAD是等腰直角三角形,∵△QMN与△MAD相似,∴△QMN是等腰直角三角形,设N(t,t2﹣t﹣)①如图1,当MQ⊥QN时,N(3,0);②如图2,当QN⊥MN时,过点N作NR⊥x轴,过点M作MS⊥RN交于点S,∵QN=MN,∠QNM=90°,∴△MNS≌△NMS(AAS)∴t﹣1=﹣t2+t+,∴t=±,∴t>1,∴t=,∴N(,1﹣);③如图3,当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点N作NR ∥x轴,与过M点的垂线分别交于点S、R;∵QN=MQ,∠MQN=90°,∴△MQR≌△QNS(AAS),∴SQ=QR=2,∴t+2=1+t2﹣t﹣,∴t=5,∴N(5,6);④如图4,当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,过点N作x轴的平行线,与两垂线交于点R、S;∵QN=MN,∠MNQ=90°,∴△MNR≌△NQS(AAS),∴SQ=RN,∴t2﹣t﹣=t﹣1,∴t=2±,∵t>1,∴t=2+,∴N(2+,1+);综上所述:N(3,0)或N(2+,1+)或N(5,6)或N(,1﹣).12.如图,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为D,对称轴交x轴于点Q.(1)求抛物线对应的二次函数的表达式;(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD 相切,求点P的坐标;(3)在抛物线的对称轴上是否存在一点M,使得△DCM与△BQC相似?如果存在,求出点M的坐标;如果不存在,请说明理由.解:(1)∵A(﹣1,0),B(3,0).代入y=﹣x2+bx+c,得,解得b=2,c=3.∴抛物线对应二次函数的表达式为:y=﹣x2+2x+3;(2)如图1,设直线CD切⊙P于点E.连结PE、PA,作CF⊥DQ于点F.∴PE⊥CD,PE=PA.由y=﹣x2+2x+3,得对称轴为直线x=1,C(0,3)、D(1,4).∴DF=4﹣3=1,CF=1,∴DF=CF,∴△DCF为等腰直角三角形.∴∠CDF=45°,∴∠EDP=∠EPD=45°,∴DE=EP,∴△DEP为等腰三角形.设P(1,m),∴EP2=(4﹣m)2.在△APQ中,∠PQA=90°,∴AP2=AQ2+PQ2=[1﹣(﹣1)]2+m2∴(4﹣m)2=[1﹣(﹣1)]2+m2.整理,得m2+8m﹣8=0解得,m=﹣4±2.∴点P的坐标为(1,﹣4+2)或(1,﹣4﹣2).(3)存在点M,使得△DCM∽△BQC.如图2,连结CQ、CB、CM,∵C(0,3),OB=3,∠COB=90°,∴△COB为等腰直角三角形,∴∠CBQ=45°,BC=3.由(2)可知,∠CDM=45°,CD=,∴∠CBQ=∠CDM.∴△DCM与△BQC相似有两种情况.当时,∴,解得DM=.∴QM=DQ﹣DM=4﹣=.∴M1(1,).当时,∴,解得DM=3,∴QM=DQ﹣DM=4﹣3=1.∴M2(1,1).综上,点M的坐标为或(1,1).13.已知抛物线y=ax2+bx+3与x轴分别交于点A(﹣3,0),B(1,0),交y轴于点C,抛物线的顶点为点D.(1)抛物线的表达式及顶点D的坐标.(2)若点F是线段AD上一个动点,①如图1,当FC+FO的值最小时,求点F的坐标;②如图2,以点A,F,O为顶点的三角形能否与△ABC相似?若能,求出点F的坐标;若不能,请说明理由.解:(1)抛物线的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),故﹣3a=3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2﹣2x+3…①,函数的对称轴为:x=﹣1,故顶点D的坐标为:(﹣1,4);(2)①点D的坐标为:(﹣1,4),点A(﹣3,0),点C(0,3),作点O关于直线AD的对称轴R,连接CR交AD于点F,则点F为所求点,FC+FO=FC+RF=CR为最小,连接AR,设直线OR交AD于点H,由点A、D的坐标得,直线AD的表达式为:y=2x+6,则tan∠DAO=2=tanα,设∠HOA=∠β,则tanβ=,则cosβ=,sinβ=,OH=AO•cosβ=,OR=2OH=,y R=OR sinβ=,同理x R=﹣,故点R(﹣,),由点R、C的坐标得,直线RC的表达式为:y=x+3…②,联立①②并解得:x=﹣,y=,则点F(﹣,);②在Rt△ACD中,tan∠CAD===,在Rt△OBC中,tan∠OCB==,∴∠ACD=∠OCB,∵OA=OC,∴∠OAC=∠OCA=45°,∴∠FAO=∠ACB,若以A,F,O为顶点的三角形与△ABC相似,则可分两种情况考虑:当∠AOF=∠ABC时,△AOF∽△CBA,∴OF∥BC,设直线BC的解析式为y=kx+b,将点B、C的坐标代入上式并解得:直线BC的解析式为y=﹣3x+3,∴直线OF的解析式为y=﹣3x,直线AD的解析式为y=2x+6,联立直线OF、AD的表达式并解得:x=﹣,故点F(﹣,);当∠AOF=∠CAB=45°时,△AOF∽△CAB,∵∠CAB=45°,∴OF⊥AC,∴直线OF的解析式为y=﹣x,将上式与y=2x+6联立并解得:x=﹣2,故点F(﹣2,2);综合以上可得F点的坐标为(﹣,)或(﹣2,2).14.如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴对折,点A 落到点C处,过点A、B的抛物线y=﹣x2+bx+c与直线BC交于点B、D.(1)求直线BD和抛物线的解析式;(2)在直线BD上方的抛物线上求一点E,使△BDE面积最大,求出点E坐标;(3)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为顶点的三角形与△BOC相似?若存在,求出点M的坐标:若不存在,请说明理由.解:(1)令y=0,则x=﹣1,令x=0,则y=2,∴点A、B的坐标分别是:A(﹣1,0),B(0,2),根据对折的性质:点C的坐标是:(1,0),设直线BD解析式为y=kx+b,把B(0,2),C(1,0)代入y=kx+b,得,解得:k=﹣2,b=2,∴直线BD解析式为y=﹣2x+2,把A(﹣1,0),B(0,2)代入y=﹣x2+bx+c得,解得:b=1,c=2,∴抛物线的解析式为y=﹣x2+x+2;(2)解方程组得:和,∴点D坐标为(3,﹣4),作EF∥y轴交直线BD于F设E(x,﹣x2+x+2),F(x,﹣2x+2)∴EF=(﹣x2+x+2)﹣(﹣2x+2)=﹣x2+3x,△BDE面积S=×EF×x D=×(﹣x2+3x)=﹣(x﹣)2+,当x=时,三角形面积最大,此时,点E的坐标为:;(3)存在.∵点B、C的坐标分别是B(0,2)、C(1,0),∴BO=2,CO=1,①如图1所示,当△MON∽△BCO时,∴,即,∴MN=2ON,设ON=a,则M(a,2a),将M(a,2a)代入抛物线的解析式y=﹣x2+x+2得:﹣a2+a+2=2a,解得:a1=﹣2(不合题意,舍去),a2=1,∴点M的坐标为(1,2);②当△MON∽△CBO时,同理可得:,即,∴MN=ON,设ON=b,则M(b,b),将M(b,b)代入抛物线的解析式y=﹣x2+x+2得:∴,解得:(不合题意,舍去),,∴点M的坐标为(,),∴存在这样的点M(1,2)或.15.如图,抛物线y=ax2+2x+c经过A(﹣1,0),B两点,且与y轴交于点C(0,3),抛物线与直线y=﹣x﹣1交于A,E两点.(1)求抛物线的解析式;(2)坐标轴上是否存在一点Q,使得△AQE是以AE为底边的等腰三角形?若存在,请直接写出点Q的坐标;若不存在,说明理由.(3)P点在x轴上且位于点B的左侧,若以P,B,C为顶点的三角形与△ABE相似,求点P的坐标.解:(1)将A(﹣1,0),C(0,3)代入y=ax2+2x+c,得,解得,,∴抛物线的解析式为:y=﹣x2+2x+3;(2)联立,解得,或,∴E(4,﹣5),如图1,当点Q在x轴上时,设Q(m,0),∵AE为底边,∴QA=QE,∴QA2=QE2,即(m+1)2=52+(m﹣4)2,解得,m=4,∴Q1(4,0);当点Q在y轴上时,设Q(0,n),∵AE为底边,∴QA=QE,∴QA2=QE2,即n2+12=42+(n+5)2,解得,n=﹣4,∴Q2(0,﹣4);综上所述,Q1(4,0),Q2(0,﹣4);(3)如图2,过点E作EH⊥x轴于点H,∵A(﹣1,0),E(4,﹣5),∴AH=EH=5,AE==5,∠BAE=45°,又OB=OC=3,∴∠ABC=45°,AB=4,BC==3,设P(t,0),则BP=3﹣t,∵∠BAE=∠ABC=45°,∴只可能存在△PBC∽△BAE和△PBC∽△EAB两种情况,当△PBC∽△BAE时,,∴=,∴t=,∴P1(,0);当△PBC∽△EAB时,,∴=,∴t=﹣,∴P2(﹣,0),综上所述,点P的坐标为(,0)或(﹣,0).。
《相似三角形》中考试题选编(含答案)

4、(2008年杭州市)(本小题满分10分)
如图:在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F.
(1)证明:∠CAE=∠CBF;
(2)证明:AE=BF;
(3)以线段AE,BF和AB为边构成一个新的三角形ABG(点E与点F重合于点G),记△ABC和△ABG的面积分别为S△ABC和S△ABG,如果存在点P,能使得S△ABC=S△ABG,求∠C的取之范围。
°°°°
2、(2008湘潭市) 如图,已知D、E分别是 的AB、AC边上的点, 且 那么 等于( )
A.1:9B.1:3
C.1:8D.1:2
3、(2008 台湾)如图G是ABC的重心,直线L过A点与BC平行。若直线CG分别与AB、L交于D、E两点,直线BG与AC交于F点,则AED的面积:四边形ADGF的面积=?( )
A. B. C. D.
18、(2008 江苏 常州)如图,在△ABC中,若DE∥BC, = ,DE=4cm,则BC的长为( )
A.8cmB.12cmC.11cmD.10cm
19、(2008 江西南昌)下列四个三角形,与左图中的三角形相似的是()
20、(2008 重庆)若△ABC∽△DEF,△ABC与△DEF的相似比为2︰3,则S△ABC︰S△DEF为()
相似三角形中考真题试题汇编
二、填空题
6、(2008年江苏省南通市)已知∠A=40°,则∠A的余角等于=________度.
8、(2008年荆州)两个相似三角形周长的比为2:3,则其对应的面积比为___________.
9、(2008年庆阳市)两个相似三角形的面积比S1:S2与它们对应高之比h1:h2之间的关系为.
专题一 相似角三角形测量高度在实际问题应用 2020年中考数学冲刺几何题型 专项突破 相似三角形应用(解析版)

2020年中考数学冲刺几何题型专项突破相似三角形应用专题一相似角三角形测量高度在实际问题应用1、学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的垂直距离CD为()A.0.2 mB.0.3 m答案C解析∵AB⊥BD,CD⊥BD,∴∠ABO=∠CDO=90°.又∵∠AOB=∠COD,∴△ABO∽△CDO.则,∵AO=4 m,AB=1.6 m,CO=1 m,∴.解得CD=0.4,故选C.2、如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,AB:AC=1:9,则建筑物CD的高是()A.96m B.10.8m C.12m D.14m【解答】解:∵EB∥CD,∴△ABE∽△ACD,∴,即,解得:CD=10.8m,故选:B.3、如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为()A.4.8 m B.6.4 m C.8 m D.10 m【解答】解:由题意可得,=,即树高==8m,故选:C.4、如图,某班上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子DA恰好与甲影子CA在同一条直线上,已知甲身高1.8米,乙身高1.5米,甲的影长是6米,则甲、乙两同学相距()米.A.1 B.2 C.3 D.5【解答】解:设两个同学相距x米,∵△ADE∽△ACB,∴,∴,解得:x=1.故选:A.5、《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为()A.五丈B.四丈五尺C.一丈D.五尺【解答】解:设竹竿的长度为x尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,∴,解得x=45(尺).故选:B.6、如图,小颖为测量学校旗杆AB的高度,她想到了物理学中平面镜成像的原理,她在与旗杆底部A同一水平线上的E处放置一块镜子,然后推到C处站立,使得刚好可以从镜子E看到旗杆的顶部B.已知小颖的眼睛D离地面的高度CD=1.6m,她离镜子的水平距离CE=1.2m,镜子E离旗杆的底部A处的距离AE=3.6m,且A、C、E三点在同一水平直线你上,则旗杆AB的高度为()A.2.7m B.3.6m C.4.8m D.6.4m【解答】解:由题意可得:AE=1.5m,CE=1.2m,DC=1.6m,∵△ABC∽△EDC,∴,即,解得:AB=4.8m,故选:C.7、如图,身高为1.5米的某学生想测量一棵大树AB的高度,他沿着树影CB由C向B走,当走到点D时,他的影子顶端正好与树的影子顶端重合,此时,AEC三点恰好在一条直线上,经测得CD=1米,BD=3米,则树的高度AB为()A.3米B.4米C.4.5米D.6米【解答】解:根据题意,可知:△ABC∽△EDC,∴=,即=,∴AB=6.故选:D.8、某数学课外活动小组想利用树影测量树高,他们在同一时刻测得一身高为1.5m的同学的影长为1.35m,由于大树靠近一幢建筑物,因此树影的一部分落在建筑物上,如图,他们测得地面部分的影长为3.6m,建筑物上的影长为1.8m,则树的高度为()A.5.4 m B.5.8 m C.5.22 m D.6.4 m【解答】解:如图,BD=3.6米,CD=1.8米,∵同一时刻测得一身高为1.5米的同学的影长为1.35米,∴CD:DE=1.5:1.35,即1.8:DE=1.5:1.35,∴DE=1.62,∵CD∥AB,∴CD:AB=DE:BE,即1.8:AB=1.62:(1.62+3.6),∴AB=5.8(米).故选:B.9、如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.6米,求A、B、C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=12米,然后沿直线CG后退到点E 处,这时恰好在镜子里看到凉亭的顶端A,测得GE=2米,小明身高EF=1.6米,则凉亭的高度AB约为()A.9米B.9.6米C.10米D.10.2米【解答】解:由题意∠AGC=∠FGE,∵∠ACG=∠FEG=90°,∴△ACG∽△FEG,∴AC:EF=CG:GE,∴=,∴AC=9.6米,∴AB=AC+BC=9.6+0.6=10.2米.故选:D.10、如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE =30cm,EF=15cm,测得边DF离地面的高度AC=1.5m,CD=7m,则树高AB=()m.A.3.5 B.4 C.4.5 D.5【解答】解:∵∠DEF =∠BCD =90°,∠D =∠D , ∴△DEF ∽△DCB , ∴BC :EF =DC :DE ,∵DE =30cm =0.3m ,EF =15cm =1.5m ,AC =1.5m ,CD =7m , ∴,∴BC =3.5米,∴AB =AC +BC =1.5+3.5=5m , 故选:D .11、如图,某一时刻一根2m 长的竹竿EF 的影长GE 为1.2m ,此时,小红测得一棵被风吹斜的柏树与地面成30°角,树顶端B 在地面上的影子点D 与B 到垂直地面的落点C 的距离是3.6m ,求树AB 的长.【分析】先利用△BDC ∽△FGE 得到BC 3.6=21.2,可计算出BC =6m ,然后在Rt △ABC 中利用含30度的直角三角形三边的关系即可得到AB 的长.【解答】解:如图,CD =3.6m ,∵△BDC ∽△FGE ,∴BC CD =EF GE ,即BC 3.6=21.2,∴BC =6m.在Rt △ABC 中,∵∠A =30°,∴AB =2BC =12m ,即树长AB 是12m.12、红用下面的方法来测量学校教学大楼AB 的高度.如图,在水平地面点E 处放一面平面镜,镜子与教学大楼的距离AE =20m.当她与镜子的距离CE =2.5m 时,她刚好能从镜子中看到教学大楼的顶端B .已知她的眼睛距地面高度DC =1.6m ,请你帮助小红测量出大楼AB 的高度(注:入射角=反射角).13、如图,某一时刻,旗杆AB影子的一部分在地面上,另一部分在建筑物的墙面上.小明测得旗杆AB在地面上的影长BC为9.6m,在墙面上的影长CD为2m.同一时刻,小明又测得竖立于地面长1m的标杆的影长为1.2m.请帮助小明求出旗杆的高度.14、星期天,小丽和同学们在碧沙岗公园游玩,他们来到1928年冯玉祥将军为纪念北伐军阵亡将士所立的纪念碑前,小丽问:“这个纪念碑有多高呢?”请你利用初中数学知识,设计一种方案测量纪念碑的高度(画出示意图),并说明理由.【分析】设计相似三角形,利用相似三角形的性质求解即可.在距离纪念碑AB 的地面上平放一面镜子E ,人退后到D 处,在镜子里恰好看见纪念碑顶A .若人眼距地面距离为CD ,测量出CD 、DE 、BE 的长,就可算出纪念碑AB 的高.【解答】解:设计方案例子:如图,在距离纪念碑AB 的地面上平放一面镜子E ,人退后到D 处,在镜子里恰好看见纪念碑顶A .若人眼距地面距离为CD ,测量出CD 、DE 、BE 的长,就可算出纪念碑AB 的高.理由:测量出CD 、DE 、BE 的长,因为∠CED =∠AEB ,∠D =∠B =90°,易得△ABE ∽△CDE .根据CDAB =DEBE ,即可算出AB 的高.15、如图,在相对的两栋楼中间有一堵墙,甲、乙两人分别在这两栋楼内观察这堵墙,视线如图1所示.根据实际情况画出平面图形如图2(CD ⊥DF ,AB ⊥DF ,EF ⊥DF ),甲从点C 可以看到点G 处,乙从点E 可以看到点D 处,点B 是DF 的中点,墙AB 高5.5米,DF =100米,BG =10.5米,求甲、乙两人的观测点到地面的距离之差(结果精确到0.1米)【解答】解:由题意可知∠ABG=∠CDG=90°.又∵∠AGD为公共角,∴△ABG∽△CDG.∴=.∵DF=100米,点B是DF的中点,∴BD=BF=50米,∵AB=5.5米,BG=10.5米,∴=,∴CD≈31.69(米).又∵∠ABD=∠EFD=90°,∠EDF为公共角,∴△ADB∽△EDF,∴==,∴EF=2AB=11(米)∴CD﹣EF≈20.7(米)答:甲、乙两人的观测点到地面的距离之差约为20.7米.16、为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离B(树底)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,求树AB的高度.【解答】解:过点E作EF⊥BD于点E,则∠1=∠2,∵∠DEF=∠BEF=90°,∴∠DEC=∠AEB,∵CD⊥BD,AB⊥BD,∴∠CDE=∠ABE=90°,∴△CDE∽△ABE,∴=,∵DE=3.2米,CD=1.6米,EB=8.4米,∴=,解得AB=4.2(米).答:树AB的高度为4.2米.17、如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米.(1)求路灯A的高度;(2)当王华再向前走2米,到达F处时,他的影长是多少?【解答】解:(1)设BC=x米,AB=y米,由题意得,CD=1米,CE=3米,EF=2米,身高MC=NE=1.5米,∵△ABD∽△MCD,△ABF∽△NEF,∴,,,,解得,∴路灯A的高度为6米.(2)如图,连接AG交BF延长线于点H,∵△ABH∽△GFH,GF=1.5米,BH=3+3+2+FH=8+FH,∴,,解得(米).答:当王华再向前走2米,到达F处时,他的影长是米.18、某学校的学生为了对小雁塔有基本的认识,在老师的带领下对小雁塔进行了测量.测量方法如下:如图,间接测得小雁塔地部点D到地面上一点E的距离为115.2米,小雁塔的顶端为点B,且BD⊥DE,在点E处竖直放一个木棒,其顶端为C,CE=1.72米,在DE的延长线上找一点A,使A、C、B三点在同一直线上,测得AE=4.8米.求小雁塔的高度.【解答】解:由题意可得:△AEC∽△ADB,则=,故=,解得:DB=43,答:小雁塔的高度为43m.。
2024年中考数学复习(全国版)重难点09 相似三角形8种模型(解析版)

∴△ 퐶퐴 ∽△ 퐶 ,
∴ ∠퐶퐴 = ∠퐶 ,
∵ ∠퐶퐴 = ∠퐶퐵 ,
∴ ∠퐶 퐵 = ∠퐶퐵 ,
∴ 퐵퐶 = 퐶,
∴ 퐶 = 퐶퐵, ∴ ∠퐵 퐶 = ∠퐵퐴 ,
∴ 퐶//퐴 ,
∴
푃퐶 퐶
=
푃 퐴
=
2� �
=
2,
∴ 푃퐶 = 2퐶 = 4 2,
∵ ∠푃퐶퐵 = ∠푃퐴 ,∠퐶푃퐵 = ∠퐴푃 ,
.
【答案】2 【分析】过 D 作 垂直퐴퐶于 H 点,过 D 作 ∥퐴 交 BC 于 G 点,先利用解直角三角形求出퐶 的长, 其次利用△ 퐶 ∽△ 퐶퐵 ,求出퐶 的长,得出퐵 的长,最后利用△ 퐵 ∽△ 퐵퐴 ,求出퐵 的长, 最后得出答案. 【详解】解:如图:过 D 作 垂直퐴퐶于 H 点,过 D 作 ∥퐴 交퐵퐶于 G 点,
∴퐴
= 퐴�,即
퐴 �+
�
=
� 퐴
∴2
2+
�
=
� 2
解得 � = 5 − 1 或 � =− 5 − 1 < 0(不符题意,舍去)
则퐵 = � = 5 − 1
故答案为:2, 5 − 1. 【点睛】本题考查了矩形的性质、折叠的性质、三角形全等的判定定理与性质、相似三角形的判定与性质 等知识点,根据矩形与折叠的性质,正确找出两个相似三角形是解题关键. 3.(2020·山东济宁·中考真题)如图,在四边形 ABCD 中,以 AB 为直径的半圆 O 经过点 C,D.AC 与 BD 相
BC=DC,证明
OC∥AD,利用平行线分线段成比例定理得到퐶푃퐶
=
푃 퐴
=
2,则푃퐶
=
2퐶
= 4 2,然后证
初三数学相似三角形典型例题(附含答案解析)

2初三数学相似三角形(一)相似三角形是初中几何的一个重点,同时也是一个难点,本节复习的目标是:1. 理解线段的比、成比例线段的概念,会根据比例线段的有关概念和性质求线段的长或两线段的比,了解黄金分割。
2. 会用平行线分线段成比例定理进行有关的计算、证明,会分线段成已知比。
3. 能熟练应用相似三角形的判定和性质解答有关的计算与证明题。
4.能熟练运用相似三角形的有关概念解决实际问题本节的重点内容是相似三角形的判定定理和性质定理以及平行线分线段成比例定理。
本节的难点内容是利用判定定理证明两个三角形相似以及相似三角形性质的应用。
相似三角形是平面几何的主要内容之一, 在中考试题中时常与四边形、 圆的知识相结合 构成高分值的综合题,题型常以填空、选择、简答或综合出现,分值一般在 10%左右,有时也单独成题,形成创新与探索型试题;有利于培养学生的综合素质。
(二)重要知识点介绍: 1.比例线段的有关概念:在比例式 ab c (a : bc :d )中, a 、 d 叫外项,db 、c 叫内项, a 、c 叫前项, b 、d 叫后项, d 叫第四比例项,如果 b=c ,那么 b 叫做 a 、 d 的比例中项。
把线段 AB 分成两条线段 AC 和 BC ,使 AC=AB BC ,叫做把线段 AB 黄金分割, C 叫做线段 AB 的黄金分割点。
2. 比例性质:①基本性质: ac b d②合比性质:acb dad bca b c d bd③等比性质:a c⋯b dm (b d ⋯ nn ≠ 0) a c ⋯ m ab d ⋯ nb3.平行线分线段成比例定理:①定理:三条平行线截两条直线,所得的对应线段成比例,如图:l 1∥ l 2∥ l 3 。
AB 则BCDE , ABEF AC DE , BCDF AC EF ,⋯DF②推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。
③定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
2020中考数学试题分类汇编考点36相似三角形含解析-精装版

教学资料范本2020中考数学试题分类汇编考点36相似三角形含解析-精装版编辑:__________________时间:__________________【精选】20xx最新20xx中考数学试题分类汇编考点36相似三角形含解析一.选择题(共28小题)1.(20xx•重庆)制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是()A.360元B.720元C.1080元 D.2160元【分析】根据题意求出长方形广告牌每平方米的成本,根据相似多边形的性质求出扩大后长方形广告牌的面积,计算即可.【解答】解:3m×2m=6m2,∴长方形广告牌的成本是120÷6=20元/m2,将此广告牌的四边都扩大为原来的3倍,则面积扩大为原来的9倍,∴扩大后长方形广告牌的面积=9×6=54m2,∴扩大后长方形广告牌的成本是54×20=1080m2,故选:C.2.(20xx•玉林)两三角形的相似比是2:3,则其面积之比是()A.:B.2:3 C.4:9 D.8:27【分析】根据相似三角形的面积比等于相似比的平方计算即可.【解答】解:∵两三角形的相似比是2:3,∴其面积之比是4:9,故选:C.3.(20xx•重庆)要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边为()A.3cm B.4cm C.4.5cm D.5cm【分析】根据相似三角形的对应边成比例求解可得.【解答】解:设另一个三角形的最长边长为xcm,根据题意,得: =,解得:x=4.5,即另一个三角形的最长边长为4.5cm,故选:C.4.(20xx•内江)已知△ABC与△A1B1C1相似,且相似比为1:3,则△ABC与△A1B1C1的面积比为()A.1:1 B.1:3 C.1:6 D.1:9【分析】利用相似三角形面积之比等于相似比的平方,求出即可.【解答】解:已知△ABC与△A1B1C1相似,且相似比为1:3,则△ABC与△A1B1C1的面积比为1:9,故选:D.5.(20xx•××市)已知△ABC∽△DEF,相似比为2,且△ABC的面积为16,则△DEF的面积为()A.32 B.8 C.4 D.16【分析】由△ABC∽△DEF,相似比为2,根据相似三角形的面积的比等于相似比的平方,即可得△ABC与△DEF的面积比为4,又由△ABC的面积为16,即可求得△DEF的面积.【解答】解:∵△ABC∽△DEF,相似比为2,∴△ABC与△DEF的面积比为4,∵△ABC的面积为16,∴△DEF的面积为:16×=4.故选:C.6.(20xx•重庆)已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为()A.1:4 B.4:1 C.1:2 D.2:1【分析】利用相似三角形面积之比等于相似比的平方计算即可.【解答】解:∵△ABC∽△DEF,且相似比为1:2,∴△ABC与△DEF的面积比为1:4,故选:A.7.(20xx•临安区)如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是()A.B.C.D.【分析】根据正方形的性质求出∠ACB,根据相似三角形的判定定理判断即可.【解答】解:由正方形的性质可知,∠ACB=180°﹣45°=135°,A、C、D图形中的钝角都不等于135°,由勾股定理得,BC=,AC=2,对应的图形B中的边长分别为1和,∵=,∴图B中的三角形(阴影部分)与△ABC相似,故选:B.8.(20xx•广东)在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC 的面积之比为()A.B.C.D.【分析】由点D、E分别为边AB、AC的中点,可得出DE为△ABC的中位线,进而可得出DE∥BC及△ADE∽△ABC,再利用相似三角形的性质即可求出△ADE与△ABC 的面积之比.【解答】解:∵点D、E分别为边AB、AC的中点,∴DE为△ABC的中位线,∴DE∥BC,∴△ADE∽△ABC,∴=()2=.故选:C.9.(20xx•自贡)如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为()A.8 B.12 C.14 D.16【分析】直接利用三角形中位线定理得出DE∥BC,DE=BC,再利用相似三角形的判定与性质得出答案.【解答】解:∵在△ABC中,点D、E分别是AB、AC的中点,∴DE∥BC,DE=BC,∴△ADE∽△ABC,∵=,∴=,∵△ADE的面积为4,∴△ABC的面积为:16,故选:D.10.(20xx•××县一模)如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为()A.3:4 B.9:16 C.9:1 D.3:1【分析】可证明△DFE∽△BFA,根据相似三角形的面积之比等于相似比的平方即可得出答案.【解答】解:∵四边形ABCD为平行四边形,∴DC∥AB,∴△DFE∽△BFA,∵DE:EC=3:1,∴DE:DC=3:4,∴DE:AB=3:4,∴S△DFE:S△BFA=9:16.故选:B.11.(20xx•随州)如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为()A.1 B.C. 1 D.【分析】由DE∥BC可得出△ADE∽△ABC,利用相似三角形的性质结合S△ADE=S 四边形BCED,可得出=,结合BD=AB﹣AD即可求出的值,此题得解.【解答】解:∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,∴△ADE∽△ABC,∴()2=.∵S△ADE=S四边形BCED,∴=,∴===﹣1.故选:C.12.(20xx•哈尔滨)如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是()A. = B. = C. = D. =【分析】由GE∥BD、GF∥AC可得出△AEG∽△ABD、△DFG∽△DC A,根据相似三角形的性质即可找出==,此题得解.【解答】解:∵GE∥BD,GF∥AC,∴△AEG∽△ABD,△DFG∽△DCA,∴=, =,∴==.故选:D.13.(20xx•遵义)如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为()A.5 B.4 C.3 D.2【分析】先求出AC,进而判断出△ADF∽△CAB,即可设DF=x,AD=x,利用勾股定理求出BD,再判断出△DEF∽△DBA,得出比例式建立方程即可得出结论.【解答】解:如图,在Rt△ABC中,AB=5,BC=10,∴AC=5过点D作DF⊥AC于F,∴∠AFD=∠CBA,∵AD∥BC,∴∠DAF=∠ACB,∴△ADF∽△CAB,∴,∴,设DF=x,则AD=x,在Rt△ABD中,BD==,∵∠DEF=∠DBA,∠DFE=∠DAB=90°,∴△DEF∽△DBA,∴,∴,∴x=2,∴AD=x=2,故选:D.14.(20xx•扬州)如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE、AE分别交于点P,M.对于下列结论:①△BAE∽△CAD;②MP•MD=MA•ME;③2CB2=CP•CM.其中正确的是()A.①②③B.①C.①②D.②③【分析】(1)由等腰Rt△ABC和等腰Rt△ADE三边份数关系可证;(2)通过等积式倒推可知,证明△PAM∽△EMD即可;(3)2CB2转化为AC2,证明△ACP∽△MCA,问题可证.【解答】解:由已知:AC=AB,AD=AE∴∵∠BAC=∠EAD∴∠BAE=∠CAD∴△BAE∽△CAD所以①正确∵△BAE∽△CAD∴∠BEA=∠CDA∵∠PME=∠AMD∴△PME∽△AMD∴∴MP•MD=MA•ME所以②正确∵∠BEA=∠CDA∠PME=∠AMD∴P、E、D、A四点共圆∴∠APD=∠EAD=90°∵∠CAE=180°﹣∠BAC﹣∠EAD=90°∴△CAP∽△CMA∴AC2=CP•CM∵AC=AB∴2CB2=CP•CM所以③正确故选:A.15.(20xx•贵港)如图,在△ABC中,EF∥BC,AB=3AE,若S四边形BCFE=16,则S△ABC=()A.16 B.18 C.20 D.24【分析】由EF∥BC,可证明△AEF∽△ABC,利用相似三角形的性质即可求出则S△ABC的值.【解答】解:∵EF∥BC,∴△AEF∽△ABC,∵AB=3AE,∴AE:AB=1:3,∴S△AEF:S△ABC=1:9,设S△AEF=x,∵S四边形BCFE=16,∴=,解得:x=2,∴S△ABC=18,故选:B.16.(20xx•孝感)如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE⊥BD于点E,连CD分别交AE,AB于点F,G,过点A作AH⊥CD交BD于点H.则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△AFG∽△CBG;⑤AF=(﹣1)EF.其中正确结论的个数为()A.5 B.4 C.3 D.2【分析】①由等边三角形与等腰直角三角形知△CAD是等腰三角形且顶角∠CAD=150°,据此可判断;②求出∠AFP和∠FAG度数,从而得出∠AGF度数,据此可判断;③证△ADF≌△BAH即可判断;④由∠AFG=∠CBG=60°、∠AGF=∠CGB即可得证;⑤设PF=x,则AF=2x、AP==x,设EF=a,由△ADF≌△BAH 知BH=AF=2x,根据△ABE是等腰直角三角形之BE=AE=a+2x,据此得出EH=a,证△PAF∽△EAH得=,从而得出a与x的关系即可判断.【解答】解:∵△ABC为等边三角形,△ABD为等腰直角三角形,∴∠BAC=60°、∠BAD=90°、AC=AB=AD,∠ADB=∠ABD=45°,∴△CAD是等腰三角形,且顶角∠CAD=150°,∴∠ADC=15°,故①正确;∵AE⊥BD,即∠AED=90°,∴∠DAE=45°,∴∠AFG=∠ADC+∠DAE=60°,∠FAG=45°,∴∠AGF=75°,由∠AFG≠∠AGF知AF≠AG,故②错误;记AH与CD的交点为P,由AH⊥CD且∠AFG=60°知∠FAP=30°,则∠BAH=∠ADC=15°,在△ADF和△BAH中,∵,∴△ADF≌△BAH(ASA),∴DF=AH,故③正确;∵∠AFG=∠CBG=60°,∠AGF=∠CGB,∴△AFG∽△CBG,故④正确;在Rt△APF中,设PF=x,则AF=2x、AP==x,设EF=a,∵△ADF≌△BAH,∴BH=AF=2x,△ABE中,∵∠AEB=90°、∠ABE=45°,∴BE=AE=AF+EF=a+2x,∴EH=BE﹣BH=a+2x﹣2x=a,∵∠APF=∠AEH=90°,∠FAP=∠HAE,∴△PAF∽△EAH,∴=,即=,整理,得:2x2=(﹣1)ax,由x≠0得2x=(﹣1)a,即AF=(﹣1)EF,故⑤正确;故选:B.17.(20xx•泸州)如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则的值是()A.B.C.D.【分析】如图作,FN∥AD,交AB于N,交BE于M.设DE=a,则AE=3a,利用平行线分线段成比例定理解决问题即可;【解答】解:如图作,FN∥AD,交AB于N,交BE于M.∵四边形ABCD是正方形,∴AB∥CD,∵FN∥AD,∴四边形ANFD是平行四边形,∵∠D=90°,∴四边形ANFD是解析式,∵AE=3DE,设DE=a,则AE=3a,AD=AB=CD=FN=4a,AN=DF=2a,∵AN=BN,MN∥AE,∴BM=ME,∴MN=a,∴FM=a,∵AE∥FM,∴===,故选:C.18.(20xx•临安区)如图,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,若AD=4,DB=2,则DE:BC的值为()A.B.C.D.【分析】根据平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似,再根据相似三角形的对应边成比例解则可.【解答】解:∵DE∥BC,∴△ADE∽△ABC,∴===.故选:A.19.(20xx•恩施州)如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为()A.6 B.8 C.10 D.12【分析】根据正方形的性质可得出AB∥CD,进而可得出△ABF∽△GDF,根据相似三角形的性质可得出==2,结合FG=2可求出AF、AG的长度,由CG∥AB、AB=2CG可得出CG为△EAB的中位线,再利用三角形中位线的性质可求出AE的长度,此题得解.【解答】解:∵四边形ABCD为正方形,∴AB=CD,AB∥CD,∴∠ABF=∠GDF,∠BAF=∠DGF,∴△ABF∽△GDF,∴==2,∴AF=2GF=4,∴AG=6.∵CG∥AB,AB=2CG,∴CG为△EAB的中位线,∴AE=2AG=12.故选:D.20.(20xx•杭州)如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE.记△ADE,△BCE的面积分别为S1,S2()A.若2AD>AB,则3S1>2S2 B.若2AD>AB,则3S1<2S2C.若2AD<AB,则3S1>2S2 D.若2AD<AB,则3S1<2S2【分析】根据题意判定△ADE∽△ABC,由相似三角形的面积之比等于相似比的平方解答.【解答】解:∵如图,在△ABC中,DE∥BC,∴△ADE∽△ABC,∴=()2,∴若2AD>AB,即>时,>,此时3S1>S2+S△BDE,而S2+S△BDE<2S2.但是不能确定3S1与2S2的大小,故选项A不符合题意,选项B不符合题意.若2AD<AB,即<时,<,此时3S1<S2+S△BDE<2S2,故选项C不符合题意,选项D符合题意.故选:D.21.(20xx•永州)如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为()A.2 B.4 C.6 D.8【分析】只要证明△ADC∽△ACB,可得=,即AC2=AD•AB,由此即可解决问题;【解答】解:∵∠A=∠A,∠ADC=∠ACB,∴△ADC∽△ACB,∴=,∴AC2=AD•AB=2×8=16,∵AC>0,∴AC=4,故选:B.22.(20xx•××区)如图,点D、E、F分别是△ABC的边AB、AC、BC上的点,若DE∥BC,EF∥AB,则下列比例式一定成立的是()A. = B. = C. = D. =【分析】用平行线分线段成比例定理和相似三角形的判定即可得出结论.【解答】解:∵DE∥BC,∴,∵DE∥BC,∴△ADE∽△ABC,∴,∵EF∥AB,∴,∵EF∥AB,∴△CEF∽△CAB,∴,∵DE∥BC,EF∥AB,∴四边形BDEF是平行四边形,∴DE=BF,EF=BD,∴,,,,∴正确,故选:C.23.(20xx•荆门)如图,四边形ABCD为平行四边形,E、F为CD边的两个三等分点,连接AF、BE交于点G,则S△EFG:S△ABG=()A.1:3 B.3:1 C.1:9 D.9:1【分析】利用相似三角形的性质面积比等于相似比的平方即可解决问题;【解答】解:∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB,∵DE=EF=FC,∴EF:AB=1:3,∴△EFG∽△BAG,∴=()2=,故选:C.24.(20xx•达州)如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则的值为()A.B.C.D.1【分析】首先证明AG:AB=CH:BC=1:3,推出GH∥AC,推出△BGH∽△BAC,可得==()2=()2=, =,由此即可解决问题.【解答】解:∵四边形ABCD是平行四边形∴AD=BC,DC=AB,∵AC=CA,∴△ADC≌△CBA,∴S△ADC=S△ABC,∵AE=CF=AC,AG∥CD,CH∥AD,∴AG:DC=AE:CE=1:3,CH:AD=CF:AF=1:3,∴AG:AB=CH:BC=1:3,∴GH∥AC,∴△BGH∽△BAC,∴==()2=()2=,∵=,∴=×=,故选:C.25.(20xx•南充)如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF.下列结论正确的是()A.CE= B.EF= C.cos∠CEP=D.HF2=EF•CF【分析】首先证明BH=AH,推出EG=BG,推出CE=CB,再证明△CEH≌△CBH,Rt△HFE≌Rt△HFA,利用全等三角形的性质即可一一判断.【解答】解:连接EH.∵四边形ABCD是正方形,∴CD=AB═BC=AD=2,CD∥AB,∵BE⊥AP,CH⊥BE,∴CH∥PA,∴四边形CPAH是平行四边形,∴CP=AH,∵CP=PD=1,∴AH=PC=1,∴AH=BH,在Rt△ABE中,∵AH=HB,∴EH=HB,∵HC⊥BE,∴BG=EG,∴CB=CE=2,故选项A错误,∵CH=CH,CB=CE,HB=HE,∴△ABC≌△CEH,∴∠CBH=∠CEH=90°,∵HF=HF,HE=HA,∴Rt△HFE≌Rt△HFA,∴AF=EF,设EF=AF=x,在Rt△CDF中,有22+(2﹣x)2=(2+x)2,∴x=,∴EF=,故B错误,∵PA∥CH,∴∠CEP=∠ECH=∠BCH,∴cos∠CEP=cos∠BCH==,故C错误.∵HF=,EF=,FC=∴HF2=EF•FC,故D正确,故选:D.26.(20xx•临沂)如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是()A.9.3m B.10.5m C.12.4m D.14m【分析】先证明∴△ABE∽△ACD,则利用相似三角形的性质得=,然后利用比例性质求出CD即可.【解答】解:∵EB∥CD,∴△ABE∽△ACD,∴=,即=,∴CD=10.5(米).故选:B.27.(20xx•长春)《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为()A.五丈B.四丈五尺C.一丈D.五尺【分析】根据同一时刻物高与影长成正比可得出结论.【解答】解:设竹竿的长度为x尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,∴,解得x=45(尺).故选:B.28.(20xx•绍兴)学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为()A.0.2m B.0.3m C.0.4m D.0.5m【分析】由∠ABO=∠CDO=90°、∠AOB=∠COD知△ABO∽△CDO,据此得=,将已知数据代入即可得.【解答】解:∵AB⊥BD,CD⊥BD,∴∠ABO=∠CDO=90°,又∵∠AOB=∠COD,∴△ABO∽△CDO,则=,∵AO=4m,AB=1.6m,CO=1m,∴=,解得:CD=0.4,故选:C.二.填空题(共7小题)29.(20xx•邵阳)如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形:△ADF∽△ECF.【分析】利用平行四边形的性质得到AD∥CE,则根据相似三角形的判定方法可判断△ADF∽△ECF.【解答】解:∵四边形ABCD为平行四边形,∴AD∥CE,∴△ADF∽△ECF.故答案为△ADF∽△ECF.30.(20xx•北京)如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,若AB=4,AD=3,则CF的长为.【分析】根据矩形的性质可得出AB∥CD,进而可得出∠FAE=∠FCD,结合∠AFE=∠CFD(对顶角相等)可得出△AFE∽△CFD,利用相似三角形的性质可得出==2,利用勾股定理可求出AC的长度,再结合CF=•AC,即可求出CF的长.【解答】解:∵四边形ABCD为矩形,∴AB=CD,AD=BC,AB∥CD,∴∠FAE=∠FCD,又∵∠AFE=∠CFD,∴△AFE∽△CFD,∴==2.∵AC==5,∴CF=•AC=×5=.故答案为:.31.(20xx•包头)如图,在▱ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相交于点F,3AE=2EB,连接DF.若S△AEF=1,则S△ADF的值为.【分析】由3AE=2EB可设AE=2a、BE=3a,根据EF∥BC得=()2=,结合S△AEF=1知S△ADC=S△ABC=,再由==知=,继而根据S△ADF=S△ADC可得答案.【解答】解:∵3AE=2EB,∴可设AE=2a、BE=3a,∵EF∥BC,∴△AEF∽△ABC,∴=()2=()2=,∵S△AEF=1,∴S△ABC=,∵四边形ABCD是平行四边形,∴S△ADC=S△ABC=,∵EF∥BC,∴===,∴==,∴S△ADF=S△ADC=×=,故答案为:.32.(20xx•资阳)已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为9 .【分析】设四边形BCED的面积为x,则S△ADE=12﹣x,由题意知DE∥BC且DE=BC,从而得=()2,据此建立关于x的方程,解之可得.【解答】解:设四边形BCED的面积为x,则S△ADE=12﹣x,∵点D、E分别是边AB、AC的中点,∴DE是△ABC的中位线,∴DE∥BC,且DE=BC,∴△ADE∽△ABC,则=()2,即=,解得:x=9,即四边形BCED的面积为9,故答案为:9.33.(20xx•泰安)《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步面见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC 上)?请你计算KC的长为步.【分析】证明△CDK∽△DAH,利用相似三角形的性质得=,然后利用比例性质可求出CK的长.【解答】解:DH=100,DK=100,AH=15,∵AH∥DK,∴∠CDK=∠A,而∠CKD=∠AHD,∴△CDK∽△DAH,∴=,即=,∴CK=.答:KC的长为步.故答案为.。
2020中考数学 相似三角形专项精练(含答案)

2020中考数学相似三角形专项精练(含答案)基础题一、选择题1.如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是( )A.4B.4.5C.5D.5.52.在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的面积之比为( )A. B.C. D.3.如图,下列条件不能判定△ADB∽△ABC的是( )A.∠ABD=∠ACBB.∠ADB=∠ABCC.AB2=AD·ACD.=4.如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△ACD 的面积为( )A.15B.10C.D.55.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )A. B. C. D.6.如图,AD是△ABC的角平分线,则AB∶AC等于( )A.BD∶CDB.AD∶CDC.BC∶ADD.BC∶AC二、填空题7.如图,把△ABC沿AB边平移到△A'B'C'的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB=,则此三角形移动的距离AA'是.三、解答题8.如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.(1)证明:∠BDC=∠PDC;(2)若AC与BD相交于点E,AB=1,CE∶CP=2∶3,求AE的长.提升题一、选择题1.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①=;②△=;△③=;=.④△△其中,正确的有( )A.1个B.2个C.3个D.4个2.如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-、y=的图象交于B、A两点,则∠OAB的大小的变化趋势为( )A.逐渐变小B.逐渐变大C.时大时小D.保持不变二、填空题3.如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=EH,那么EH的长为.三、解答题4.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.(1)求证:AC·CD=CP·BP;(2)若AB=10,BC=12,当PD∥AB时,求BP的长.答案基础题一、选择题1.B2.C3.D A.∵∠ABD=∠ACB,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;B.∵∠ADB=∠ABC,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;C.∵AB2=AD·AC,∴=,∠A=∠A,△ABC∽△ADB,故此选项不合题意;D.=不能判定△ADB∽△ABC,故此选项符合题意.故选D.4.D ∵∠DAC=∠B,∠C=∠C,∴△ACD∽△BCA.∵AB=4,AD=2,∴△ACD的面积∶△ABC的面积为1∶4,∴△ACD的面积∶△ABD的面积为1∶3.∵△ABD的面积为15,∴△ACD的面积为5.故选D.5.C 延长FE交AB于点D,作EG⊥BC,EH⊥AC,则ED=EG=EH=-=-=2.设EF=FC=x.∵△ADF∽△ABC,∴=,∴=-.即x=.故选C.6.A 如图,过点B作BE∥AC交AD延长线于点E, ∵BE∥AC,∴∠DBE=∠C,∠E=∠CAD,∴△BDE∽△CDA,∴=,又∵AD是角平分线,∴∠E=∠DAC=∠BAD,∴BE=AB,∴=,∴AB∶AC=BD∶CD.二、填空题7.答案-1解析设BC与A'C'交于点E,由平移的性质知,AC∥A'C',∴△BEA'∽△BCA,∴S△BEA'∶S△BCA=A'B2∶AB2=1∶2.∴A'B=1,∴AA'=AB-A'B=-1.三、解答题8.解析(1)证明:∵AB=AD,AC平分∠BAD,∴AC⊥BD,∴∠ACD+∠BDC=90°.∵AC=AD,∴∠ACD=∠ADC.∵∠ADC+∠PDC=90°,∴∠BDC=∠PDC.(2)过点C作CM⊥PD于点M.∵∠BDC=∠PDC,∴CE=CM.∵∠CMP=∠ADP=90°,∠P=∠P,∴△CPM∽△APD,∴=.设CM=CE=x.∵CE∶CP=2∶3,∴PC=x.∵AB=AD=AC=1,∴=,解得x=,故AE=1-=.B组提升题组1.B ∵CD,BE是△ABC的中线,即D,E分别是AB、AC的中点,∴DE是△ABC的中位线,∴DE=BC,DE∥BC,∴=,∴△DOE∽△COB,则△△===,===,故①正确,②错误,③正确. 设△ABC的BC边上的高为AF,则S△ABC=BC·AF,S△ACD=S△ABC=BC·AF.∵在△ODE中,DE=BC,DE边上的高是×AF=AF,∴S△ODE=×BC×AF=BC·AF,∴△△=··=,故④错误.2.D 如图,分别过点A、B作AN⊥x轴、BM⊥x轴.∵∠AOB=90°,∴∠BOM+∠AON=∠AON+∠OAN=90°,∴∠BOM=∠OAN,∵∠BMO=∠ANO=90°,∴△BOM∽△OAN,∴=.设B-,,A,,则BM=,AN=,OM=m,ON=n,∴mn=,mn=.∵∠AOB=90°,∴tan∠OAB=①.∵△BOM∽△OAN,∴===②,由①②知tan∠OAB=为定值,∴∠OAB的大小不变.二、填空题3.答案解析∵四边形EFGH是矩形,∴EH∥BC,∴△AEH∽△ABC,设AD与EH交于点M, ∵AM⊥EH,AD⊥BC,∴=,设EH=3x,则有EF=2x,AM=AD-EF=2-2x, ∴-=,解得x=,则EH=.三、解答题4.解析(1)证明:∵AB=AC,∴∠B=∠C.∵∠APD=∠B,∴∠APD=∠B=∠C.∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,∴∠BAP=∠DPC,∴△ABP∽△PCD,∴=,即AB·CD=CP·BP.又∵AB=AC,∴AC·CD=CP·BP.(2)∵PD∥AB,∴∠APD=∠BAP.∵∠APD=∠C,∴∠BAP=∠C.又∵∠B=∠B,∴△BAP∽△BCA,∴=.∵AB=10,BC=12,∴=,∴BP=.。
2020年九年级数学中考专题复习训练-相似三角形的应用(解析版 ).pdf

处通过平面镜看到树的顶端 .如图,然后他量得 B、P 间的距离是 56 米,C、P 间距离是 12 米,他的身高是 1.7 米. 1 他这种测量的方法应用了物理学科的什么知识?请 简要说明; 2 请你帮他计算出树 AB 的高度.
2020 年九年级数学中考专题复习训练-相似三角形的应用
班级:___________姓名:___________ 得分:___________
一、选择题
1. 某小区门口的栏杆如图所示,栏杆从水平位置 BD 绕 O 点旋转到 AC 位置,已知 t, t t,垂足分别为 B、D, t h , h 1.晦 , t h 1 ,则栏
14. 10
解:如图所示:
第 1 页,共 20页
由题意得:㌳E上上 ,
㌳E∽
,
㌳E h E,
即0.ሴ h
,
.2 ͷ10ͷ20
解得 h 10.
所以 x 的最小值为 10.
15. h.1
解:利用 ㌳∽ t㌳,对应线段成比例解题, 因为 AB,CD 均垂直于地面,所以 上上 t, 则有 ㌳∽ t㌳,
㌳∽ t㌳,
2 当 x 为何值时,矩形 PQMN 的面积最大?最大值是多少?
23. 如图,小明家窗外有一堵围墙 AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最
高点 C 射进房间的地板 F 处,中午太阳光恰好能从窗户的最低点 D 射进房间的地 板 E 处,小明测得窗子距地面的高度 tt h 0.ሴ ,窗高 t h 1.2 ,并测得 t㌳ h 0.ሴ ,tE h ,且 O,D,C 三点在同一条直线上,求围墙 AB 的高度.
t
h
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年中考相似三角形经典题型汇编中考复习战略汇集相似三角形一、选择题1.已知a2=b3(a≠0,b≠0),下列变形错误的是()A.ab=23B.2a=3bC.ba=32D.3a=2b2.如图,DE∥FG∥BC.若DB=4FB,则EG与GC的关系是()A.EG=4GCB.EG=3GCC.EG=52GC D.EG=2GC第2题第3题3.如图,在▱ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F,则下列选项中的结论错误的是()A.F A∶FB=1∶2B.AE∶BC=1∶2C.BE∶CF=1∶2D.S△ABE∶S△FBC=1∶44.如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB 于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是()A.ABAE=AGADB.DFCF=DGADC.FGAC=EGBDD.AEBE=CFDF第4题第5题5.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?”意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影子长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为()A.五丈B.四丈五尺C.一丈D.五尺6.学校门口的栏杆如图所示,栏杆从水平位置BD绕点O旋转到AC位置.已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆D端下降的垂直距离CD为()A.0.2mB.0.3mC.0.4mD.0.5m第6题第7题7.如图,利用标杆BE测量建筑物CD的高度.已知标杆BE高1.2m,测得AB=1.6m,BC =12.4m,则建筑物CD的高是()A.9.3mB.10.5mC.12.4mD.14m8.如图,在△ABC中,D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为()A.2B.4C.6D.8第8题第9题9如图,在正方形ABCD中,G为CD边的中点,连接AG并延长交BC边的延长线于点E,对角线BD交AG于点F.已知FG=2,则线段AE的长度为()A.6B.8C.10D.1210.制作一块3m×2m矩形广告牌的成本是120元.在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,则扩大后矩形广告牌的成本是()A.360元B.720元C.1080元D.2160元11.两三角形的相似比是2∶3,则其面积比是()A.2∶3B.2∶3C.4∶9D.8∶2712.已知△ABC∽△DEF,相似比为2,且△ABC的面积为16,则△DEF的面积为()A.32B.8C.4D.1613.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边长为()A.3cmB.4cmC.4.5cmD.5cm14.如图,在△ABC中,D,E分别是AB,AC的中点.若△ADE的面积为4,则△ABC的面积为()A.8B.12C.14D.16第14题第15题15.如图,在△ABC中,D,E分别是边AC,AB的中点,BD与CE交于点O,连接DE.下列结论:①OEOB=ODOC;②DEBC=12;③S△DOES△BOC=12;④S△DOES△DBE=13.其中正确的有()A.1个B.2个C.3个D.4个16.如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则BDAD的值为()A.1B.22C.2-1D.2+1第16题第17题17.如图,在△ABC中,EF∥BC,AB=3AE.若S四边形BCFE=16,则S△ABC的值为()A.16B.18C.20D.2418.如图,在△ABC,△FGH中,D,E两点分别在AB,AC上,点F在DE上,G,H两点在BC上,且DE∥BC,FG∥AB,FH∥AC.若BG∶GH∶HC=4∶6∶5,则△ADE与△FGH 的面积比为()A.2∶1B.3∶2C.5∶2D.9∶4第18题第19题19.如图,在▱ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为()A.13B.14C.15D.1620.如图,四边形ABCD为平行四边形,E,F为CD边的两个三等分点,连接AF,BE交于点G,则S△EFG∶S△ABG等于()A.1∶3B.3∶1C.1∶9D.9∶1第20题第21题21如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为()A.32B.43C.53D.8522.如图,在正方形ABCD中,点E,F分别在边AD,CD上,AF,BE相交于点G.若AE=3ED,DF=CF,则AGGF的值是()A.43B.54C.65D.76第22题第23题23如图,AG∶GD=4∶1,BD∶DC=2∶3,则AE∶EC等于()A.3∶2B.4∶3C.6∶5D.8∶524.如图,E,F是▱ABCD对角线AC上两点,AE=CF=14AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则S△ADGS△BGH的值为()A.12B.23C.34D.1第24题第25题25.(2018·杭州)如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连接BE.记△ADE,△BCE的面积分别为S1,S2,下列结论正确的是()A.若2AD>AB,则3S1>2S2B.若2AD>AB,则3S1<2S2C.若2AD<AB,则3S1>2S2D.若2AD<AB,则3S1<2S226.如图,在矩形ABCD中,∠ADC的平分线与AB交于点E,点F在DE的延长线上,∠BFE=90°,连接AF,CF,CF与AB交于点G.有以下结论:①AE=BC;②AF=CF;③BF2=FG·FC;④EG·AE=BG·AB.其中正确的个数是()A.1B.2C.3D.4第26题第27题27.如图,点A在线段BD上,在BD的同侧作等腰直角三角形ABC和等腰直角三角形ADE,CD与BE,AE分别交于点P,M.下列结论:①△BAE∽△CAD;②MP·MD=MA·ME;③2CB2=CP·CM.其中正确的是()A.①②③B.①C.①②D.②③二、填空题28.已知ab=23,则a-2ba+2b的值为________.29.已知a6=b5=c4,且a+b-2c=6,则a的值为________.30.(2018·嘉兴)如图,直线l1∥l2∥l3,直线AC交l1,l2,l3于点A,B,C;直线DF交l1,l2,l3于点D,E,F.已知ABAC=13,则EFDE的值为________.第30题第31题31.如图,E是▱ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形:________________.32.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC =60m,EC=50m,则河宽AB=________m.第32题第33题33.如图,在矩形ABCD中,E为AD的中点,BD和CE相交于点F.如果DF=2,那么线段BF的长为________.34.如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F.若AB=4,AD=3,则CF的长为________.第34题第35题35.如图,△ABC的面积为12,D,E分别是边AB,AC的中点,则四边形BCED的面积为________.36.)如图,在▱ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相交=1,则S△ADF的值为________.于点F,3AE=2EB,连接DF.若S△AEF第36题第37题37.如图,在△ABC中,DE∥BC,BF平分∠ABC,交DE的延长线于点F.若AD=1,BD=2,BC=4,则EF的长为________.38.如图,点P1,P2,P3,P4均在坐标轴上,且P1P2⊥P2P3,P2P3⊥P3P4.若点P1,P2的坐标分别为(0,-1),(-2,0),则点P4的坐标为________.第38题第39题39.如图,正方形DEFG的顶点D,E在△ABC的边BC上,顶点G,F分别在边AB,AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长为________.40.如图,P是▱ABCD的边AD上一点,E,F分别是PB,PC的中点.若▱ABCD的面积为16 cm2,则△PEF的面积(阴影部分)是________cm2.第40题第41题41.如图,点A的坐标为(0,1),B是x轴正半轴上的一动点,以AB为边作Rt△ABC,使∠BAC =90°,∠ACB=30°.设点B的横坐标为x,点C的纵坐标为y,则y与x的函数解析式为____________.42.《九章算术》是中国传统数学最重要的著作之一,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步面见木?”用今天的话说,大意是,如图,四边形DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,问出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为________步.第42题第44题43.《九章算术》是我国古代数学名著,书中有下面的问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形的边长最大是多少步?”该问题的答案是________步.第46题44.如图,在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD =6,CD=4,则△ABC的面积为________.45△AOC在平面直角坐标系中的位置如图所示,OA=4,将△AOC绕点O逆时针旋转90°得到△A1OC1,A1C1交y轴于点B(0,2).若△C1OB∽△C1A1O,则点C1的坐标为________.第45题46如图,C为Rt△ACB与Rt△DCE的公共点,∠ACB=∠DCE=90°,连接AD,BE,过点C作CF⊥AD于点F,延长FC交BE于点G.若AC=BC=25,CE=15,DC=20,则EGBG的值为________.第46题第47题47如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=62,D,E分别是边BC,AC上的动点,则DA+DE的最小值为________.48如图,在矩形ABCD中,AB=2,BC=4,点E,F分别在BC,CD上.若AE=5,∠EAF =45°,则AF的长为________.第48题第49题49如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板.如果有4种不同的剪法,那么AP长的取值范围是__________.三、解答题50如图,在正方形ABCD中,M是BC边上一定点,连接AM.请用尺规作图法,在AM上作一点P,使△DPA∽△ABM.(不写作法,保留作图痕迹)51.如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.第55题52如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.(1)求证:△BDE∽△CAD;(2)若AB=13,BC=10,求DE的长.第52题53如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.求:(1)∠BDF的大小;(2)CG的长.第53题54求证:相似三角形对应边上的中线之比等于相似比.要求:①根据给出的△ABC及线段A′B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A′B′C′,使得△A′B′C′∽△ABC,不写作法,保留作图痕迹;②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.第54题55已知在△ABC中,AB=AC,∠BAC=90°,D,E分别是AB,AC的中点,将△ADE绕点A按顺时针方向旋转一个角度α(0°<α<90°)得到△AD′E′,连接BD′,CE′,如图①.(1)求证:BD′=CE′;(2)如图②,当α=60°时,设AB与D′E′交于点F,求BFFA的值.第55题56.若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足条件的AC的长.(2)如图①,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC.求证:△ABC是比例三角形.(3)如图②,在(2)的条件下,当∠ADC=90°时,求BDAC的值.第56题57如图,在菱形ABCD 中,AC 与BD 交于点O ,E 是BD 上一点,EF ∥AB ,∠EAB =∠EBA ,过点B 作DA 的垂线,交DA 的延长线于点G .(1)∠DEF 和∠AEF 是否相等?若相等,请证明;若不相等,请说明理由.(2)找出图中与△AGB 相似的三角形,并证明.(3)BF 的延长线交CD 的延长线于点H ,交AC 于点M .求证:BM 2=MF ·MH .第57题58如图①,在矩形ABCD 中,P 为CD 边上一点(DP <CP),∠APB =90°.将△ADP 沿AP 翻折得到△AD ′P ,PD ′的延长线交边AB 于点M ,过点B 作BN ∥MP 交DC 于点N .(1)求证:AD 2=DP ·PC .(2)请判断四边形PMBN 的形状,并说明理由.(3)如图②,连接AC ,分别交PM ,PB 于点E ,F .若DP AD =12,求EF AE 的值.第58题59如图①,在△ABC 中,矩形EFGH 的一边EF 在AB 上,顶点G ,H 分别在BC ,AC 上,CD 是边AB 上的高,CD 交GH 于点I.若CI =4,HI =3,AD =92,矩形DFGI 恰好为正方形.(1)求正方形DFGI 的边长.(2)如图②,延长AB 至点P ,使得AC =CP.将矩形EFGH 沿BP 的方向向右平移,当点G 刚好落在CP 上时,试判断移动后的矩形与△CBP 重叠部分的形状是三角形还是四边形,为什么?(3)如图③,连接DG,将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′,正方形DF′G′I′分别与线段DG,DB相交于点M,N,连接MN,求△MNG′的周长.第59题60在△ABC 中,E ,F 分别为线段AB ,AC 上的点(不与点A ,B ,C 重合).(1)如图①,若EF ∥BC ,求证:S△AEF S △ABC=AE·AF AB·AC.(2)如图②,若EF 不与BC 平行,(1)中的结论是否仍然成立?请说明理由.(3)如图③,若EF 上一点G 恰为△ABC 的重心,AE AB =34,求S△AEF S △ABC的值.第60题。
