2017.12.14三角形的面积
三角形面积所有公式

三角形面积所有公式三角形是几何学中最基本的形状之一。
它由三条线段组成,被称为三边。
本文将为您介绍三角形的面积公式。
第一种常用的三角形面积公式是“底乘高除以2”。
也就是说,如果我们知道三角形的底边的长度和该底边上的高度,那么我们可以通过将底边长度乘以高度,再除以2来计算三角形的面积。
这个公式也被称为“底高公式”。
另一种常用的计算三角形面积的公式是海伦公式。
海伦公式利用了三角形的三条边的长度来计算面积。
设三角形的三边长分别为a、b、c,s为半周长,即s=(a+b+c)/2。
那么根据海伦公式,三角形的面积S可以通过以下公式计算:S=sqrt(s(s-a)(s-b)(s-c))。
除了这两种常用的计算三角形面积的公式外,还有其他一些特殊情况下的公式。
当我们只知道三角形的两个边长a和b,以及它们之间的夹角C时,可以使用正弦公式来计算面积。
正弦公式可以表示为S=1/2ab*sinC,其中S表示三角形的面积。
当我们只知道三角形的两个边长a和b,以及它们之间的夹角A时,可以使用余弦公式来计算面积。
余弦公式可以表示为S=1/2ab*cosA,其中S表示三角形的面积。
如果我们只知道三角形的一个角度和两个边长,可以使用正弦公式或余弦公式来计算面积。
但如果我们知道三个角度,则需要使用角度和边长之间的关系来计算面积。
另外,如果我们知道三角形的一个角度和两个边的长度,还可以使用正切公式来计算面积。
正切公式可以表示为S=1/2ab*tanA,其中S表示三角形的面积。
除了这些常用的三角形面积公式,还有其他一些特殊情况下的公式,例如当我们知道三角形的高和边长时,可以使用S=1/2bh来计算面积。
还有,对于特殊形状的三角形,如等边三角形、直角三角形等,也有相应的面积公式。
总结起来,三角形的面积公式有:底乘高除以2、海伦公式、正弦公式、余弦公式、正切公式等。
选择合适的公式取决于我们所掌握的三角形信息。
希望本文的介绍对您在计算三角形面积时有所帮助。
三角形面积的面积公式

三角形面积的面积公式
三角形的面积可以使用以下公式来计算:
1. 通过底边和高:
三角形的面积 = 底边长度× 高÷ 2。
2. 通过三边长度:
根据海伦公式,可以计算出半周长 s:
s = (a + b + c) ÷ 2。
其中,a、b、c 分别是三角形的三边长度。
然后,利用海伦公式计算面积:
三角形的面积= √(s × (s a) × (s b) × (s c))。
3. 通过两边长度和夹角:
三角形的面积= 0.5 × 边1长度× 边2长度× sin(夹角)。
需要注意的是,以上公式适用于各种类型的三角形,包括等边三角形、等腰三角形和一般三角形。
在计算时,确保使用正确的边长和角度值。
此外,还可以使用向量法、行列式法等方法来计算三角形的面积,但这些方法相对复杂,一般不在初等数学中使用。
总结起来,计算三角形面积的公式有多种,可以根据已知条件选择适合的公式进行计算。
三角形面积公式的十五种形式

三角形面积公式的十五种形式三角形是一个常见的几何形状,它有许多有用的性质和公式。
其中最基本的公式是三角形的面积公式。
根据给定的边长和角度不同,三角形的面积公式有多种形式。
在本文中,我们将介绍三角形面积公式的十五种形式。
1.基本面积公式:三角形的面积等于底边乘以高的一半。
公式:A=(1/2)*b*h其中,A表示三角形的面积,b表示底边的长度,h表示高的长度。
2.海伦公式:根据三角形的三边长度来计算面积。
公式:A=√(s*(s-a)*(s-b)*(s-c))其中,A表示三角形的面积,a、b、c表示三个边的长度,s表示半周长(s=(a+b+c)/2)。
3.高脚公式:根据两条边和这两条边之间的夹角来计算面积。
公式:A = (1/2) * a * b * sin(C)其中,A表示三角形的面积,a、b表示两条边的长度,C表示这两条边之间的夹角。
4.底边和两边夹角公式:根据底边和两条边之间的夹角来计算面积。
公式:A = (1/2) * b * c * sin(A)其中,A表示三角形的面积,b、c表示两条边的长度,A表示底边和两条边之间的夹角。
5.两边和高公式:根据两条边和它们之间的高来计算面积。
公式:A=(1/2)*a*h其中,A表示三角形的面积,a表示其中一条边的长度,h表示这条边的高。
6.三边公式:根据三个边的长度来计算面积。
公式:A=(1/4)*√((a+b+c)*(-a+b+c)*(a-b+c)*(a+b-c))其中,A表示三角形的面积,a、b、c表示三个边的长度。
7.三边和角公式:根据三个边的长度和它们之间的角度来计算面积。
公式:A = (1/2) * a * b * sin(C)其中,A表示三角形的面积,a、b表示两条边的长度,C表示这两条边之间的夹角。
8.两边和一角公式:根据两条边的长度和它们之间的夹角,以及与一边相对的角度来计算面积。
公式:A = (1/2) * a * b * sin(C) * sin(D) / sin(B)其中,A表示三角形的面积,a、b表示两条边的长度,C表示这两条边之间的夹角,D表示与一边相对的角度,B表示另一条边与这两条边之间的夹角。
三角形的面积公式是什么该怎么计算

三角形的面积公式是什么该怎么计算在解决数学问题时,如果能够熟练掌握公式,那么对于解题事半功倍。
下面是由编辑为大家整理的“三角形的面积公式是什么该怎么计算”,仅供参考,欢迎大家阅读本文。
三角形的面积公式1.三角形面积=1/2×底×高;或者说,三角形面积=(底×高)÷2;2.已知三角形三边a,b,c,则(海伦公式)(S=(a+b+c)/2)。
三角形的性质角形任意两边之和大于第三边,任意两边之差小于第三边。
三角形两边的差小于第三边1、在平面上三角形的内角和等于180°(内角和定理)。
2、在平面上三角形的外角和等于360° (外角和定理)。
3、在平面上三角形的外角等于与其不相邻的两个内角之和。
4、一个三角形的三个内角中最少有两个锐角。
5、在三角形中至少有一个角大于等于60度,也至少有一个角小于等于60度。
6、在一个直角三角形中,若一个角等于30度,则30度角所对的直角边是斜边的一半。
7、三角形任意两边之和大于第三边,任意两边之差小于第三边。
三角形两边的差小于第三边拓展阅读:证明全等三角形的条件1.两个三角形对应的三条边相等,两个三角形全等,简称“边边边”或“SSS"。
2.两个三角形对应的两边及其夹角相等,两个三角形全等,简称“边角边”或“SAS”。
3.两个三角形对应的两角及其夹边相等,两个三角形全等,简称“角边角”或“ASA”。
4.两个三角形对应的两角及其一角的对边相等,两个三角形全等,简称“角角边”或“AAS”。
5.两个直角三角形对应的一条斜边和一条直角边相等,两个直角三角形全等,简称“直角边、斜边”或“HL”。
三角形的面积知识点总结

三角形的面积知识点总结在数学的广袤天地中,三角形是一个基础且重要的图形,而三角形的面积计算则是我们需要重点掌握的知识之一。
下面就让我们一起来详细梳理一下三角形面积的相关知识点。
一、三角形面积的定义三角形的面积是指三角形所占平面的大小。
通俗来讲,就是三角形在平面上所覆盖区域的度量。
二、三角形面积的计算公式1、最常见的公式是:面积=底×高÷2,通常用字母表示为 S =1/2 × a × h,其中 S 表示面积,a 表示三角形的底,h 表示这条底边对应的高。
这个公式的推导其实很直观。
我们可以把三角形补成一个平行四边形,因为平行四边形的面积是底乘高,而三角形的面积恰好是平行四边形面积的一半,所以就得到了这个公式。
2、已知三角形的两边及其夹角,可以使用正弦定理来计算面积。
公式为:S = 1/2 × a × b × sinC,其中 a、b 是两条边,C 是它们的夹角。
这个公式的原理是利用三角函数的关系,通过两边和夹角来计算三角形的面积。
三、三角形面积公式的应用1、已知底和高求面积这是最直接的应用。
比如一个三角形的底是 6 厘米,高是 4 厘米,那么它的面积就是 1/2 × 6 × 4 = 12 平方厘米。
2、已知两边及其夹角求面积例如,一个三角形的两条边分别是5 厘米和8 厘米,夹角是60 度,那么面积就是 1/2 × 5 × 8 × sin60°=10√3 平方厘米。
3、求与三角形面积相关的几何问题比如在一个组合图形中,需要通过计算三角形的面积来求出整个图形的面积。
四、三角形面积计算中的注意事项1、底和高要对应在使用“底×高÷2”这个公式时,底和高必须是相互对应的。
也就是说,从底边作的垂线的长度才是这条底边对应的高。
2、单位要统一计算面积时,底和高的长度单位要统一,如果不统一,需要先进行单位换算。
三角型面积公式大全

三角型面积公式大全三角形是平面几何中最基本的图形之一,它由三条边和三个内角组成。
计算三角形的面积是几何学中的一个重要问题,有多种不同的公式和方法可以用来计算三角形的面积。
在本文中,我们将介绍一些常见的三角形面积公式,并提供详细的解释和推导。
1.一般三角形的面积公式对于一般的三角形ABC,其面积可以通过以下公式计算:面积=1/2*底边长*高其中,底边长是任意两点之间的距离,高是从底边到对边的垂直距离。
2.海伦公式如果我们已知三角形的三条边的长度分别为a、b和c,那么可以通过海伦公式计算三角形的面积:面积 = sqrt(s * (s - a) * (s - b) * (s - c))其中,s是半周长,定义为s=(a+b+c)/2这个公式是由古希腊数学家海伦提出的,它不需要知道三角形的高度,只需要知道三条边的长度即可。
3.边长和重心法计算三角形面积如果我们已知三个顶点的坐标,可以通过边长和重心法计算三角形的面积。
这个方法涉及到计算三角形的边长和重心坐标,进而计算面积。
步骤:a)计算三角形的边长:根据三个顶点的坐标计算三条边的长度,分别记为a、b和c。
b)计算三角形的重心坐标:三角形的重心坐标可以通过三个顶点的坐标的平均值得到,即(x,y)=[(x1+x2+x3)/3,(y1+y2+y3)/3]。
c) 计算三角形的面积:使用重心坐标来计算三角形的面积,面积 = sqrt((s - a) * (s - b) * (s - c)),其中s = (a + b + c) / 24.阴影三角形法对于一些特殊的三角形,可以通过将其分割为更简单的几何形状来计算其面积。
例如,对于梯形形状的三角形,可以通过将其分割为两个直角三角形和一个矩形来计算其面积。
同样地,对于菱形形状的三角形,可以通过将其分割为两个直角三角形来计算其面积。
5. Heron公式Heron公式是由公元一世纪的古希腊数学家Hero of Alexandria提出的,用来计算三角形的面积,其公式如下:面积 = sqrt(s * (s - a) * (s - b) * (s - c))其中s=(a+b+c)/2,a、b和c分别是三角形的三条边的长度。
三角形面积计算公式大全

三角形面积计算公式大全三角形是几何中最简单的形状之一,其面积由底边长度和高度决定。
本文将详细介绍三角形的不同类型和计算面积的公式,包括直角三角形、等边三角形、等腰三角形和任意三角形。
同时,还将提供一些常见的解题技巧和实例。
1. 直角三角形(Right Triangle):直角三角形具有一个角度为90度的直角。
其面积公式为:S=1/2*底边长度*高度。
假设直角三角形的底边长度为a,高度为h,则面积公式可以简化为S=1/2*a*h。
2.等边三角形(Equilateral Triangle):等边三角形所有的边长相等,且所有的角度都为60度。
其面积公式为:S=(√3/4)*边长的平方。
假设等边三角形的边长为s,则面积公式可以简化为S=(√3/4)*s^23.等腰三角形(Isosceles Triangle):等腰三角形具有两个边长相等的边。
其面积公式为:S=1/2*底边长度*高度。
假设等腰三角形的底边长度为a,高度为h,则面积公式可以简化为S=1/2*a*h。
4. 任意三角形(Arbitrary Triangle):任意三角形的面积公式可以通过海伦公式(Heron's formula)计算。
海伦公式包含了三角形的三条边长。
假设三角形的三条边分别为a、b、c,其中s=(a+b+c)/2为半周长(semiperimeter),则面积公式为:S=√(s*(s-a)*(s-b)*(s-c))。
下面通过一些例题来演示如何使用这些公式:例题1:已知一个直角三角形的底边长度为5cm,高度为8cm,求其面积。
解答:直角三角形的面积公式为S = 1/2 * a * h,所以S = 1/2 * 5 * 8= 20cm²。
例题2:已知一个等边三角形的边长为6cm,求其面积。
解答:等边三角形的面积公式为S = (√3/4) * s^2,所以S = (√3/4) *6^2 = 9√3 cm²。
例题3:已知一个等腰三角形的底边长度为10cm,高度为12cm,求其面积。
三角形的面积公式,

三角形的面积公式,咱们在数学的世界里,三角形可是个常见的“小伙伴”。
要说三角形里一个很重要的知识,那就是三角形的面积公式啦!记得有一次,我带着孩子去公园玩耍。
看到公园的草坪被分成了一个个不同形状的区域,其中就有三角形的。
孩子好奇地问我:“爸爸,这个三角形的草坪有多大呀?”我就趁机跟他讲起了三角形的面积公式。
咱们先来说说三角形的面积公式到底是啥。
它就是:面积 = 底×高÷2。
你看,这公式简单又实用。
那这个公式是咋来的呢?咱们可以想象一下,把两个完全一样的三角形拼在一起,是不是就能拼成一个平行四边形啦?这个平行四边形的底就是三角形的底,高就是三角形的高。
而平行四边形的面积咱们会算呀,就是底乘高。
那一个三角形的面积不就是平行四边形面积的一半嘛,所以就有了底×高÷2 这个公式。
咱们来举个例子哈。
比如说有一个三角形,底是 6 厘米,高是 4 厘米。
那按照公式来算,面积就是 6×4÷2 = 12 平方厘米。
在实际生活中,这个公式用处可大了。
像盖房子的时候,工人师傅要算三角形的房梁面积;做衣服的时候,设计师要算三角形的布料面积。
再说说我家装修的时候,我想在客厅的墙上做一个三角形的装饰架。
量了量底是 80 厘米,高是 60 厘米。
我马上就用三角形面积公式算出了它的面积,好去买合适大小的板子。
还有一次,我在路边看到工人在铺一块三角形的地砖。
他们就是先量好底和高,然后用面积公式算出需要多少块地砖,这样就不会浪费材料啦。
咱们学习三角形面积公式,可不能光是死记硬背,得理解它,会用它解决实际问题。
总之,三角形的面积公式虽然简单,但作用可不小。
学会了它,咱们就能在生活中解决好多和三角形面积有关的问题啦!就像我和孩子在公园看到的那块三角形草坪,知道了面积公式,咱们就能算出它大概能容纳多少人在上面玩耍呢。
所以,同学们一定要好好掌握这个公式哟!。
三角形的面积如何计算

三角形的面积如何计算在我们的数学学习中,三角形是一种非常基础且重要的几何图形。
而要了解三角形的许多性质和应用,首先就得掌握如何计算它的面积。
三角形的面积计算方法有多种,这取决于我们所掌握的关于三角形的信息。
最常见也是最基础的方法是使用三角形的底和高来计算。
假设我们有一个三角形,我们把其中一条边作为底边,从这条底边相对的顶点向底边作垂线,这条垂线的长度就是三角形的高。
三角形的面积就等于底乘以高再除以 2。
用公式表示就是:面积 S =(底×高)÷ 2 。
比如说,有一个三角形,它的底边长度是 6 厘米,对应的高是 4 厘米。
那么它的面积就是:(6×4)÷2 = 12 平方厘米。
那为什么要除以 2 呢?我们可以这样来理解。
想象一下,我们有两个完全一样的这样的三角形,把它们拼在一起,是不是就拼成了一个平行四边形?这个平行四边形的底就是三角形的底,高就是三角形的高。
而平行四边形的面积是底乘以高,那一个三角形的面积就是平行四边形面积的一半,所以要除以 2 。
如果只知道三角形的三条边长,也能计算出它的面积。
这就要用到海伦公式。
海伦公式是这样的:假设三角形的三条边分别为 a、b、c,半周长 p =(a + b + c)÷ 2 ,那么三角形的面积 S =√p×(p a)×(p b)×(p c) 。
这个公式看起来有点复杂,但其实理解起来也不难。
它的原理是通过边长之间的关系来计算面积。
举个例子,如果一个三角形的三条边分别是 3 厘米、4 厘米、5 厘米。
首先计算半周长 p =(3 + 4 + 5)÷ 2 = 6 厘米。
然后代入海伦公式计算面积:S =√6×(6 3)×(6 4)×(6 5) =√6×3×2×1 =√36 =6 平方厘米。
除了上面两种常见的方法,在一些特殊的三角形中,还有更简便的计算方法。
三角形的面积计算学习如何计算三角形的面积

三角形的面积计算学习如何计算三角形的面积三角形是几何学中最基本的图形之一,计算其面积是我们学习数学的基础内容。
本文将介绍三角形的面积计算公式以及几种常见的计算方法。
一、三角形的面积计算公式在学习如何计算三角形的面积前,我们先了解一下三角形的面积计算公式。
对于已知底边长为a、高为h的三角形,其面积S可以通过以下公式计算得出:S = (1/2) * a * h这个公式是由底边与高的关系推导而来。
根据几何学原理,当三角形的高度与底边垂直时,可以得到一个矩形,该矩形的宽度为底边a,高度为h。
而三角形的面积正好是该矩形面积的一半。
二、计算方法一:已知底和高当我们已知三角形的底边长a和高h时,可以直接利用上述公式计算出三角形的面积。
举个例子,假设底边长度为5cm,高度为3cm的三角形,我们可以按照如下步骤计算其面积:1. 将底边长度和高度代入面积计算公式:S = (1/2) * 5 * 3,得到S = 7.5。
2. 因此,该三角形的面积为7.5平方厘米。
三、计算方法二:已知三边长度当我们已知三角形的三条边的长度a、b、c时,可以通过海伦公式计算出三角形的面积。
海伦公式的形式如下:S = √[s(s-a)(s-b)(s-c)]其中,s为三边长度之和的一半,即半周长。
将其带入公式后计算即可得到三角形的面积。
举个例子,假设已知一个三角形的三边长度分别为3cm、4cm、5cm,我们可以按照如下步骤计算其面积:1. 计算半周长s:s = (3 + 4 + 5) / 2 = 6。
2. 将s和三边长度代入海伦公式:S = √[6(6-3)(6-4)(6-5)],得到S = 6。
3. 因此,该三角形的面积为6平方厘米。
四、计算方法三:已知两边长度和夹角当我们已知三角形的两边长度a、b和它们之间的夹角α时,可以利用以下公式计算三角形的面积:S = (1/2) * a * b * sin(α)其中,sin(α)表示夹角α的正弦值。
三角形的面积与周长

三角形的面积与周长三角形是初中数学中最基本的几何图形之一,它具有独特的属性与特点。
其中,面积与周长是最为重要的两个属性,它们在解决实际问题与数学推导中都有着重要的应用。
一、三角形的面积三角形的面积是指由三角形所围成的区域的大小。
计算三角形的面积可以利用多种方法,其中最常见的是通过底边和高来计算。
对于任意三角形,其面积S可以通过以下公式计算:S = 1/2 * 底边 * 高其中,1/2 * 底边 * 高表示矩形的面积公式,而三角形是矩形的一半,所以要除以2。
三角形的底边可以是任意一条边,而高则需要垂直于这条边。
此外,还可以利用海伦公式来计算三角形的面积,该公式适用于已知三边长度的情况。
根据海伦公式,三角形的面积S可以通过以下公式计算:S = √[p * (p - a) * (p - b) * (p - c)]其中,p为三角形的半周长,也即是周长的一半。
而a、b、c则分别为三角形的三条边的长度。
二、三角形的周长三角形的周长是指三条边的长度之和。
计算三角形的周长很简单,只需要将三条边的长度相加即可。
周长 = 边1 + 边2 + 边3三、面积与周长的关系面积与周长是三角形的两个重要属性,它们之间存在一定的联系与关系。
一般来说,面积与周长并没有直接的数学公式关系,即不能通过面积直接求得周长,也不能通过周长直接求得面积。
然而,可以通过简单的推论发现,其他条件相同的情况下,面积越大,周长一般也会越大。
这是因为面积的增加通常会伴随着三角形的某一边增加,而其他两边也会相应增加,进而导致周长的增加。
四、应用举例1. 假设有一个三角形的底边长度为6cm,高为4cm,我们可以利用上述的面积公式计算出该三角形的面积为12平方厘米。
而周长则需要知道另外两条边的长度。
2. 如果已知一个三角形的三边长度分别为3cm、4cm、5cm,利用海伦公式可以计算出该三角形的面积为6平方厘米。
而周长则可以直接计算为12cm。
3. 在实际问题中,面积与周长往往同时出现。
三角形的面积

三角形的面积=底×高÷2。
公式S= a×h÷2正方形的面积=边长×边长公式S= a×a长方形的面积=长×宽公式S= a×b平行四边形的面积=底×高公式S= a×h梯形的面积=(上底+下底)×高÷2 公式S=(a+b)h÷2内角和:三角形的内角和=180度。
长方体的体积=长×宽×高公式:V=abh长方体(或正方体)的体积=底面积×高公式:V=abh正方体的体积=棱长×棱长×棱长公式:V=aaa圆的周长=直径×π 公式:L=πd=2πr圆的面积=半径×半径×π 公式:S=πr2圆柱的表(侧)面积:圆柱的表(侧)面积等于底面的周长乘高。
公式:S=ch=πdh=2πrh 圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。
公式:S=ch+2s=ch+2πr2圆柱的体积:圆柱的体积等于底面积乘高。
公式:V=Sh圆锥的体积=1/3底面×积高。
公式:V=1/3Sh分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变。
异分母的分数相加减,先通分,然后再加减。
分数的乘法则:用分子的积做分子,用分母的积做分母。
分数的除法则:除以一个数等于乘以这个数的倒数。
读懂理解会应用以下定义定理性质公式一、算术方面1、加法交换律:两数相加交换加数的位置,和不变。
2、加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,再同第三个数相加,和不变。
3、乘法交换律:两数相乘,交换因数的位置,积不变。
4、乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变。
5、乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变。
三角形的面积

三角形的面积=底×高÷2。
公式 S= a×h÷2正方形的面积=边长×边长公式 S= a2长方形的面积=长×宽公式 S= a×b平行四边形的面积=底×高公式 S= a×h梯形的面积=(上底+下底)×高÷2 公式 S=(a+b)h÷2内角和:三角形的内角和=180度。
长方体的表面积=(长×宽+长×高+宽×高 ) ×2 公式:S=(a×b+a×c+b×c)×2正方体的表面积=棱长×棱长×6 公式: S=6a2长方体的体积=长×宽×高公式:V = abh长方体(或正方体)的体积=底面积×高公式:V = abh正方体的体积=棱长×棱长×棱长公式:V = a3圆的周长=直径×π公式:L=πd=2πr圆的面积=半径×半径×π公式:S=πr2圆柱的表(侧)面积:圆柱的表(侧)面积等于底面的周长乘高。
公式:S=ch=πdh=2πrh圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。
公式:S=ch+2s=ch+2πr2圆柱的体积:圆柱的体积等于底面积乘高。
公式:V=Sh圆锥的体积=1/3底面×积高。
公式:V=1/3Sh算术1、加法交换律:两数相加交换加数的位置,和不变。
2、加法结合律:a + b = b + a3、乘法交换律:a × b = b × a4、乘法结合律:a × b × c = a ×(b × c)5、乘法分配律:a × b + a × c = a × b + c6、除法的性质:a ÷ b ÷ c = a ÷(b × c)7、除法的性质:在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变。
三角形的面积公式怎么算

三角形的面积公式怎么算
三角形的面积计算公式为:三角形底乘以高除以2。
三角形面积公式是指使用算式计算出三角形的面积,同一平面内,且不在同一直线的三条线段首尾顺次相接所组成的封闭图形叫做三角形。
常见的三角形有直角三角形、锐角三角形、钝角三角形等。
1
1、在平面上三角形的内角和等于180°(内角和定理)。
2、在平面上三角形的外角和等于360°(外角和定理)。
3、在平面上三角形的外角等于与其不相邻的两个内角之和。
推论:三角形的一个外角大于任何一个和它不相邻的内角。
4、一个三角形的三个内角中最少有两个锐角。
5、在三角形中至少有一个角大于等于60度,也至少有一个角小于等于60度。
6、三角形任意两边之和大于第三边,任意两边之差小于第三边。
三角形面积公式是什么

三角形面积公式是什么在数学解题中,公式通常是非常重要的一部分。
记住公式可以很方便的解题,大大减少工作量和工作时间。
一个公式可以解决一类问题。
那么,三角形的面积公式是什么呢?面积公式1.三角形面积=1/2×底×高;或者说,三角形面积=(底×高)÷22.已知三角形三边a,b,c,则(海伦公式)(s=(a+b+c)/2)s=sqrt[p(p-a)(p-b)(p-c)]=sqrt[(1/16)(a+b+c)(a+b-c)(a+c-b)(b+c-a)]=1/4sqrt[(a+b+c)(a+b-c)(a+c-b)(b+c-a)]判定方法若一个三角形的三边a,b,c(a<b<c)满足a^2+b^2>c^2,则这个三角形是锐角三角形;a^2+b^2=c^2,则这个三角形是直角三角形;a^2+b^2<c^2,则这个三角形是钝角三角形。
相关定理中位线定理三角形的中线平行于第三条边,等于第三条边的一半。
推论:通过三角形一边中点并与另一边平行的直线,必平分第三边。
中线定理三角形中线对边的平方和等于底边平方的一半和该边中线平方和的两倍。
三边关系定理三角形的任意两条边之和大于第三条边,任意两条边之差小于第三条边。
勾股定理勾股定理(Pythagoras定理)指出,在任何直角三角形中,两条直角边的长平方之和必须等于斜边长度的平方。
几何语言:若△abc满足∠abc=90°,则ab^2+bc^2=ac^2;勾股定理的逆定理也成立,即两条边的平方和等于第三条边的平方,那么这个三角形就是直角三角形。
几何语言:在△abc中∵ab²+bc²=ca²∴∠abc=90°。
三角形的面积

三角形的面积=底×高÷2。
公式S= a×h÷2 正方形的面积=边长×边长公式S= a×a 长方形的面积=长×宽公式S= a×b 平行四边形的面积=底×高公式S= a×h 梯形的面积=(上底+下底)×高÷2 公式S=(a+b)h÷2 内角和:三角形的内角和=180度。
长方体的体积=长×宽×高公式:V=abh 长方体(或正方体)的体积=底面积×高公式:V=abh 正方体的体积=棱长×棱长×棱长公式:V=aaa 圆的周长=直径×π 公式:L=πd=2πr 圆的面积=半径×半径×π 公式:S=πr2 圆柱的表(侧)面积:圆柱的表(侧)面积等于底面的周长乘高。
公式:S=ch=πdh=2πrh 圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。
公式:S=ch+2s=ch+2πr2 圆柱的体积:圆柱的体积等于底面积乘高。
公式:V=Sh 圆锥的体积=1/3底面×积高。
公式:V=1/3Sh 分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变。
异分母的分数相加减,先通分,然后再加减。
分数的乘法则:用分子的积做分子,用分母的积做分母。
分数的除法则:除以一个数等于乘以这个数的倒数。
读懂理解会应用以下定义定理性质公式一、算术方面1、加法交换律:两数相加交换加数的位置,和不变。
2、加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,再同第三个数相加,和不变。
3、乘法交换律:两数相乘,交换因数的位置,积不变。
4、乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变。
5、乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变。
三角形面积的万能公式
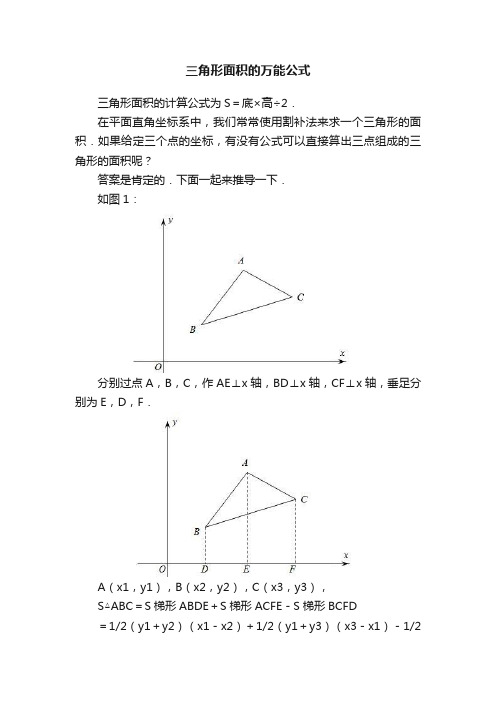
三角形面积的万能公式三角形面积的计算公式为S=底×高÷2.在平面直角坐标系中,我们常常使用割补法来求一个三角形的面积.如果给定三个点的坐标,有没有公式可以直接算出三点组成的三角形的面积呢?答案是肯定的.下面一起来推导一下.如图1:分别过点A,B,C,作AE⊥x轴,BD⊥x轴,CF⊥x轴,垂足分别为E,D,F.A(x1,y1),B(x2,y2),C(x3,y3),S△ABC=S梯形ABDE+S梯形ACFE-S梯形BCFD=1/2(y1+y2)(x1-x2)+1/2(y1+y3)(x3-x1)-1/2(y2+y3)(x3-x2)=1/2(x1y2+x2y3+x3y1-x1y3-x2y1-x3y2).如图2:分别过点A,B,C,作AE⊥x轴,BD⊥x轴,CF⊥x轴,垂足分别为E,D,F.A(x1,y1),B(x2,y2),C(x3,y3),S△ABC=S梯形BCFD-S梯形ABDE-S梯形ACFE=1/2(y2+y3)(x3-x2)-1/2(y1+y2)(x1-x2)-1/2(y1+y3)(x3-x1)=1/2(x1y3+x2y1+x3y2-x1y2-x2y3-x3y1).综上所述,在平面直角坐标系中,若A(x1,y1),B(x2,y2),C(x3,y3),则△ABC的面积为1/2|x1y2+x2y3+x3y1-x1y3-x2y1-x3y2|.这个公式这么复杂,应该如何记忆呢?第一步:按A(x1,y1),B(x2,y2),C(x3,y3)顺序排列,计算x1y2,x2y3,x3y1;第二步:按C(x3,y3),B(x2,y2),A(x1,y1)(与A,B,C排列相反)顺序排列,计算x3y2,x2y1,x1y3;第三步:计算1/2|x1y2+x2y3+x3y1-x1y3-x2y1-x3y2|.我爱压轴题中考数学压轴题全解析¥37.4 京东购买。
三角形的面积

三角形的面积三角形是几何学中最基本的形状之一,它由三条线段组成。
计算三角形的面积是几何学中的一个重要问题,本文将介绍三角形的面积计算方法以及相关的数学定理和公式。
一、基本概念和性质在介绍三角形的面积计算方法之前,我们先来了解一些与三角形相关的基本概念和性质。
1. 底和高:在任意一个三角形中,我们可以选取一条线段作为底,而且可以作它对应的垂线,这条垂线就是所选取的底所对应的高。
2. 三角形面积公式:根据三角形的性质,我们可以得到三角形的面积公式。
对于一个底为b,高为h的三角形,它的面积可以表示为S=1/2 * b * h。
二、三角形面积的计算方法1. 根据底和高计算:根据上述的三角形面积公式,如果我们已知一个三角形的底和高,那么我们可以直接计算出它的面积。
只需要将底和高的数值代入公式中进行计算即可。
2. 根据边长计算:除了通过底和高进行计算外,我们还可以根据三角形的边长计算它的面积。
我们可以使用海伦公式或者正弦定理来求解。
a. 海伦公式:对于一个已知三边长度为a、b、c的三角形,可以使用海伦公式来计算其面积。
公式为S=sqrt(s(s-a)(s-b)(s-c)),其中s为半周长,即s=(a+b+c)/2。
b. 正弦定理:对于一个已知三边长度为a、b、c,对应的夹角为A、B、C的三角形,可以使用正弦定理来计算其面积。
公式为S=1/2 *a *b * sin(C),其中C为夹角C的正弦值。
三、应用举例1. 例1:已知一个底为8cm,高为5cm的三角形,计算其面积。
解:根据三角形面积公式,代入底和高的数值,可以得到S=1/2 * 8 * 5=20cm²。
因此,该三角形的面积为20平方厘米。
2. 例2:已知一个三角形的三边长度分别为7cm、9cm、12cm,计算其面积。
解:根据海伦公式,首先计算半周长s=(7+9+12)/2=14cm。
然后代入公式进行计算,可以得到S=sqrt(14(14-7)(14-9)(14-12))=sqrt(14*7*5*2)=sqrt(980)=31.3cm²。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2
)。
面积相等的两个三角形能拼 成一个平行四边形。 ( )
1.看图求三角形的面积
2.5 4.8 1.5 8
15 22
2.看图求三角形斜边上的高
5cm 2.5cm ?
4cm
看图求直角三角形斜边上的高
6厘米
10厘米
8厘米
.
三角形的176平方米,求高
?米
22米
三角形中的等面积问题
复习等底等高的三角形面积相等
原来平行四边形的底
原 来( 平长 行方 四形 边的 形宽 的) 高 (长方形的长)
人教版五年级数学上册第五单元
一、用数方格的方法算三角形面积。
(不满一格的,都按半格计算)
1平方厘米
小结:不准确,又比较麻烦。
转化的思想
锐角三角形
锐角三角形
锐角三角形
高
两个完全一样的锐角三 角形,可以拼成一个平 行四边形。
S=ah÷2 =6× 4÷ 2 = 24 ÷ 2 = 12 (平方厘米)
两个完全一样的三角形都可以拼成一个平四边形。
( 原平 来行 三四 角边 形形 的的 高高 )
原来三角形的底
(平行四边形的底)
高
底
平行四边形的面积=底x高
每个三角形的面积等于拼成的平行四边面积的一半
三角形的面积=底x高÷ 2
S = a h÷2
A:2个
B:3个
C:4个
已知:平行四边形的面积相等, 红色的三角形面积相等吗?为什么?
把三角形分成面积相等的两部分
中点
把三角形分成面积相等的两部分
中点
把三角形分成面积相等的两部分
中点
把三角形分成面积相等的两部分
中点
中点
中点
把三角形分成面积相等的3部分
4部分? 5部分?6部分…
下图中每个平行四边形的面积都是50平方厘米, 涂色的三角形面积各是多少?为什么?
这个平行四边形的高等于 三 角 形 的 高
。
因为每个三角形的面积等于拼成的平行四边面积的
一半 。
所以
2 三角形的面积=底x高÷
S = a h÷2
红领巾底是100cm,高33 cm, 它的面积是多少平方厘米?
S=ah÷2
=100×33÷2 =1650(cm2)
答:它的面积是1650平方厘米。
S=ah÷2
请同学们比较一下,这两个三角形能 不能拼成一个平行四边形?为什么?
请同学们比较一下,这两个三角形能 不能拼成一个平行四边形?为什么?
请同学们比较一下,这两个三角形能 不能拼成一个平行四边形?为什么?
请同学们比较一下,这两个三角形能 不能拼成一个平行四边形?为什么?
请同学们比较一下,这两个三角形能 不能拼成一个平行四边形?为什么?
制作一个这样的警示牌,需要多少铁皮?
S =ah÷2
=7.8×9÷2
7.8dm
=35.1(d㎡)
9dm
努 力 吧 !
一种零件有一面是三角形, 三角形的底是5.6厘米,高是4 厘米。这个三角形的面积是 多少平方厘米?
5.6
4
指出下面三角形的底和高,并口算出它们的面积。 ( 单位:厘米)
4
2.5
2 三角形的面积=底x高÷
S = a h÷2
一种零件有一面是三角形, 三角形的底是5.6厘米,高是4 厘米。这个三角形的面积是 多少平方厘米?
5.6
4
用两种方法计算三角形的面积(单位:厘米)。
4.8
6 5 4
S=ah÷2 =4.8× 5÷ 2 = 24 ÷ 2 = 12 (平方厘米)
S=ah÷2 =6× 4÷ 2 = 24 ÷ 2 = 12 (平方厘米)
通过以上实验 可以看出: 这个平行四边形的底等于 三 角 形 的 底 。
这个平行四边形的高等于 三 角 形 的 高
。
因为每个三角形的面积等于拼成的平行四边面积的
一半 。
所以
2 三角形的面积=底x高÷
S = a h÷2
三角形的面积练习课
复习导入
(1)三角形的面积计算公式是什么? 三角形面积公式:S=ah÷2 (2)谁能说说三角形的面积公式和平行四边形的面积公式的 相同点和不同点? 三角形的面积公式为什么公式中有一个“÷2”? (3)一个三角形与一个平行四边形等底等高, 平行四边形的底是3米,高是2米。 三角形的面积是(
练习
1、计算三角形的面积。
4cm
5cm
在计算三角形的面积时,底和高应该注意什么? 注意:底和高应该是相对应的。
指出下面三角形的底和高,并口算出它们的面积。 ( 单位:厘米)
4
2.5
4
3
1.5
3
单位:厘米
7
8
8
这两个三角形的面积虽然相等,但形状不 同。所以,不能拼成平行四边形。
(2)比一比
6厘米
4
3
1.5
3
A
D
B
上图是一个平行四边形,看图填空:
E
C
平行四边形的面积是12平方厘米,三角形 ABC的面积是(
6 )平方厘米。
选择:下面图中面积计算是4 × 3 ÷ 2 的有(
①②
)。
3 4 ①
4
3
4
3
4 3 3.5 ④
②
③
用两种方法计算三角形的面积(单位:厘米)。
4.8
6 5 4
S=ah÷2 =4.8× 5÷ 2 = 24 ÷ 2 = 12 (平方厘米)
底
高
底
钝角三角形
钝角三角形
钝角三角形
高
两个完全一样的钝角三 角形,可以拼成一个平 行四边形。
底
高
底
直角三角形
直角三角形
直角三角形
两个完全一样的直角三角形, 可以拼成一个平行四边形。
高
底
直角三角形
两个完全一样的直角三角形, 可以拼成一个平行四边形。
高
底
高
底
请同学们比较一下,这两个三角形能 不能拼成一个平行四边形?为什么?
大正方形边长8cm, 小正方形边长6cm。 求阴 影面积。 8cm 6cm
S=ah÷2
=16×9.5÷2 =152÷2 =76(平方米) 12×76 =912(元) 答:种这片草坪需要912元。
三角形面积解决问题
注意:单位陷阱
小明买了一块长1.5 m, 高60d m的三角形毛玻璃, 每平方米毛玻璃价格是32元, 共花了多少钱?
一块长方形红布长30米,宽1.5米, 如果用它做底和高都是5分米的三角形小旗。 可以做多少面?
有一块三角形草地, 底长24m,高是底的一半。 如果每平方米的草可供4只羊吃一天, 这块草地可供多少只羊吃一天?
3
)平方米,
平行四边形的面积是(
6
)平方米。
用两个完全一样的三角形来拼,会怎么样?
通过以上实验 可以看出: 两个完全一样的三角形都可以拼成一个平四边形。 这个平行四边形的底等于 三 角 形 的 底 。
这个平行四边形的高等于 三 角 形 的 高
。
因为每个三角形的面积等于拼成的平行四边面积的
一半 。
所以
• 准备题:
底 高 面积
平行四 边形
3
5 10
4
5 4 5 10
12
25 20 20
三角形
8
10
50
h=2S÷a
=2×176÷22
=352÷22 =16(米) 答:高是16米。
下图中两个三角形面积相等吗?
为什么?每个三角形的面积是多少?
高8cm 底12cm
结论:三角形的面积与它的底和高有
关,与它的形状无关。
=12.5×7.2÷2 =90÷2 =45(cm2)
答:它的面积是45平方厘米。
大约在2000年前,我国数学名著 《九章算术》中的“方田章”就论述了 平面图形面积的算法。书中说:“方田 术曰,广从(zhòng)步数相乘得积步。” 其中“方田 ” 是指长方形田地, “广”和“从” 是指长和宽,也就是说:长方 形面积=长×宽。还说:“圭田术 曰,半广以乘正从。”就是说: 三角形面积=底×高÷2。
•如何把大三角形 •分成4个面积相等的小三角形? •有几种分法?
②也可把原三角形先二等分, 再把每一份分别二等分。
③还可以把原三角形每一条边等分, 再把三条边的中点相连。
A
B
C
平行四边形和三角形 面积相等,
高和底有什么关系?
如果一个三角形和一个平行四边 形面积相等。 三角形的底是平行四边形的二分 之一。 那么三角形的高是平行四边形高 的( 4 )倍。
A
8厘米
B
8厘米
C
8厘米
( A ) 的面积最大 ( B )和( C ) 的面积相等
练一练
1.完成下表。
底/cm
高/cm
三角形面积
5
7
17.5
2.4
8
10
65 13
9.6
/cm2
小结:
• 三角形的面积:S=ah÷2
• 根据三角形的面积计算公式可以推导出:
• 三角形的高:h=2S÷a
• 三角形的底:a=2S÷h
15
两个三角形是等底等高,
所以两个三角形的面积相等。
平行四边形与三角形
之间的联系
把一个平行四边形, 沿对角线分成两个完全相等的三角形,
底 )相当于三角形的( 底 平行四边形的(
), )相等。
高 平行四边形的(高 )和三角形的(
三角形面积是平行四边形( 2倍 ),
两个完全一样的三角形都可以拼成一个平四边形。
原来三角形的底
