初中数学七年级上册《3.6 整式的加减》学案
苏科版版数学七年级上册教学设计《3-6 整式的加减》

苏科版版数学七年级上册教学设计《3-6 整式的加减》一. 教材分析《苏科版数学七年级上册》第三单元第六节“整式的加减”是学生在掌握了整式的概念和运算法则之后进行的学习内容。
这部分内容主要让学生掌握整式加减的运算方法,并能够灵活运用到实际问题中。
教材通过例题和练习题的形式,帮助学生理解和掌握整式加减的运算规律。
二. 学情分析七年级的学生已经具备了一定的数学基础,对整式的概念和运算法则有一定的了解。
但是,学生在进行整式加减运算时,可能会对括号的作用、合并同类项的规则等知识点产生困惑。
因此,在教学过程中,需要针对这些知识点进行详细的讲解和练习。
三. 教学目标1.让学生掌握整式加减的运算方法。
2.培养学生解决实际问题的能力。
3.提高学生的数学思维能力。
四. 教学重难点1.整式加减的运算方法。
2.合并同类项的规则。
五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。
通过设置问题,引导学生思考和探索;通过案例分析,让学生理解和掌握整式加减的运算方法;通过小组合作学习,培养学生的团队协作能力。
六. 教学准备1.准备相关案例和练习题。
2.准备多媒体教学设备。
七. 教学过程1.导入(5分钟)通过一个实际问题,引导学生思考如何进行整式的加减运算。
例如:已知直线y=2x+3与直线y=x+1相交于点A,求点A的坐标。
2.呈现(15分钟)展示案例,让学生观察和分析两条直线的方程,找出它们的交点。
引导学生理解整式加减的运算方法,并解释为什么两条直线的交点就是它们的方程的解。
3.操练(15分钟)让学生分组进行练习,互相讨论和解决问题。
教师巡回指导,解答学生的疑问。
练习题包括:(1)求解方程组:[(2)已知直线y=3x+4与直线y=2x-1相交于点B,求点B的坐标。
4.巩固(10分钟)让学生总结整式加减的运算方法,以及如何解决实际问题。
教师点评学生的总结,并进行补充讲解。
5.拓展(5分钟)引导学生思考:如何判断两条直线是否相交?相交的条件是什么?教师给出答案,并解释相关知识点。
苏科版七年级数学上册3.6整式的加减教案
1.课本P70页练习1、2、3题。
【要点归纳】:
1.整式的加减实际上就是去括号、合并同类项这两个知识的综合。
2.整式的加减的一般步骤:
①如果有括号,那么先算括号。②如果有同类项,则合并同类项。
3.求多项式的值,一般先将多项式化简再代入求值,这样使计算简便。
【总结反思】:
板书设计
(用案人完成)
当堂作业
课外作业
教学札记
主备人
用案人
授课时间
月日
总第32课时
课题
课型
新授课
教学目标
1、在具体情境中认识整式的加减
2、能熟练地进行整式加减运算。
重点
能熟练地进行整式加运算。
难点
能熟练地进行整式加减运算。
教法及教具
先学后教,当堂训练
教
学
过
程
教学内容
个案调整
教师主导活动
学生主体活动
【导学指导】
一、情境引入
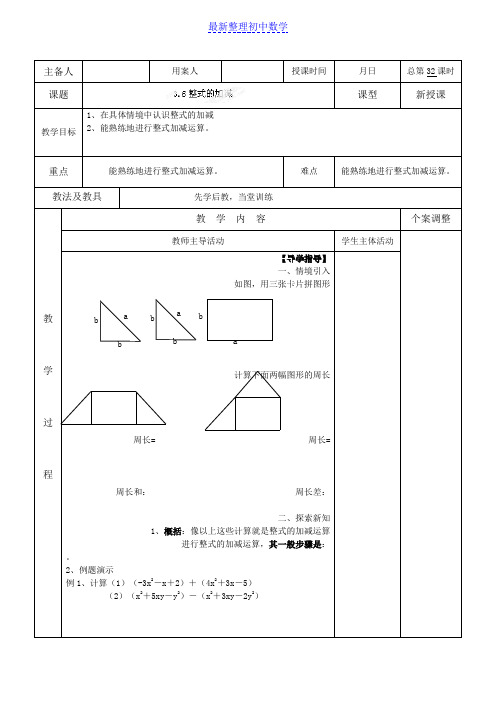
如图,用三张卡片拼图形
计算下面两幅图形的周长
周长=周长=
周长和:周长差:
二、探索新知
1、概括:像以上这些计算就是整式的加减运算
进行整式的加减运算,其一般步骤是:
。
2、例题演示
例1、计算(1)(-3x2-x+2)+(4x2+3x-5)
(2)(x2+5xy-y2)-(x2+3xy-2y2)
教
学
过
程
教学内容
个案调整
教师主导活动
学生主体活动
例2、(1)某个多项式与多项式2a2+a-1的和是4a2-3a-4,求这个多项式。
例3、(1)已知,a+b=4,ab=-2,求代数式(4a-3b-2ab)-(a-6b+ab)的值。
2019-2020学年七年级数学上册《3.6 整式的加减》教学案 (新版)苏科版.doc

2019-2020学年七年级数学上册《3.6 整式的加减》教学案 (新版)苏科版自我诊断题:1. 填空:(1)计算:x -(3x -2)+(2x -3) =___________;(3a 2+a -5) -(4-a +7a 2) =___________.(2) 单项式-3x 2y 减去单项式-7x 2y 的差为___________.(3) 已知多项式A 与4x 2-5xy -7y 2的和是x 2-2xy -y 2,则多项式A 为_____________.2. 选择:(1)计算(3a 2+2a +1) -(2a 2+3a -5)的结果为 ( )A .a 2-5a +6B .a 2-5a -4C .a 2-a -4D .a 2-a +6(2)已知A =3x 2+5y 2+6z 2,B =2x 2-2y 2-8z 2 ,C =2z 2-5x 2-3y 2 ,则A +B +C 的值为 ( ) A .3x -2y B .3x +2y C .-3x -2y D . -3x +2y3.化简:4.化简求值:(1)3x 3-[2x -(5x -x 3) ] ,其中x =12 (2)2x 2-y 2+(2y 2-x 2) -(x 2+2y 2),其中x =13,y =3.5.已知A =2x 2+xy +3y 2,B =x 2-xy +2y 2,求(1)A -3B ;(2)2A +B .6.一个多项式减去3a 2-9a +5得-7a 2+10a -5,求这个多项式.7.已知a +b =-2,ab =-3,求代数式2(4a -3b -2ab ) -3(2a -83b +ab )的值.备助学习单:一、温故知新:1.用简便方法计算:(1)574x +29x +71x ; (2)544y -27y -73y .3.已知A =1-x 2 ,B =x 2-4x -3,C =5x 2+4,求A -3B +C 的值.5.把多项式x 5-3x 3y 2-3y 2+3x 2-y 5写成两个整式的和,使其中一个只含5次项.二、备助方略:1.用代数式表示:(1)一件夹克进价为50元,标价为a 元,则这件夹克的利润为___________元.(2)小明拿100元钱去买单价为4.5元的钢笔n 支,则剩下的钱为_________元,小明最多能买这种钢笔_________支.(3)设n 为自然数,用n 表示三个连续的奇数__________________;三个连续的偶数_____________;三个连续的整数__________________________.(4)一个三位数个位数为x ,十位数比个位数大2,百位数是个位数的2倍,这个三位数是__________.(5)某商品原售价为a 元,先提价10%后又降价10%出售,则现在的售价为 ______ 元.2.下列代数式:①8a 7,②78a ,③a 2,④x 2+3x -12,⑤ y 2+3y -3y ,⑥5s -1,⑦6m 25-t,⑧6s , ⑨25(x +y ) ,⑩x +y π中,属于单项式的是________________;属于多项式的是_________________;属于整式的是__________________.(填序号)3.单项式5.2×105a 3bc 4的次数是__________,单项式-23πa 2b 的系数是_________. 4.若23a mb 3和-3a 2b n -1是同类项,则m = ,n = . 5.已知m 是绝对值最小的有理数,且-2am +2b y 与3a x b 2的差仍是单项式,试求代数式2x 2-3xy +6y 2-3mx 2+mxy -9my 2的值.。
七年级数学上册 3.6 整式的加减导学案(无答案)(新版)苏科版

学习
目标
1.会进行整式的加、减运算;
2.能说明整式加、减中每一步运算的算理.
重点难
点预测
重点
会进行整式的加、减运算。
难点
会进行整式的加、 减运算。
学生活动过程
教师导学过程
.一、自主学习(独学)
任务1:1、a+(—b+c)=a -(-b+c )=
2、下列去括号正确吗?如有错误,请改正.
(1) (2)
(1)4a+(- -1)-(3a+2 )(2)-x-3(x-y)+4(x-2y)
(3)2a-3b-[4a-(3a-b)]
2.求下列各式的值:
反思:
1.我学到的知识及思想方法:
2.改进:
已知有理数a,b,c在数轴上的位置如图,试化简代数式:
|a|-|a+b|+|c-a|+|b-c|.
b
a
0
c
四、当堂检测
1、下列 各式 中,去括号正确的是()
A.3(x+y)=3x+y B.-(m-2)=-m+2 C. 2(-a+ )=-2a+ D.-2(x-1)=-2x-1
2、去括号,再合并同 类项:
反馈练习:1 . 计算(1)2x-3y+7与6x-5y-2的和;
(2)(-3x2-x+2)+(4x2+3x-5);
(3)(x2+5xy-y2)-(x2+3xy-2y2);(4)2(1-a+a2)-3(2-a-a2).
2.求3y2-x2+(2x-y)-(x2+3y2)的值,其中x=1、y=-2.
பைடு நூலகம்三、拓展提升
(3)
(4)
任务2 :先去括号再合并同类项:
中学七年级数学上册《3.6 整式的加减》学案(无答案) (新版)苏科版

《3.6 整式的加减》学案学习目标:1.从实际背景中去体会进行整式的加减的必要性2.灵活运用整式的加减的步骤进行运算。
学习重点:整式加减的运算学习难点: 正确地去括号、合并同类项,及符号的正确处理课前导学 自主学习1、多项式中具有什么特点的项可以合并,怎样合并? (二次备课)2、如何去括号,它的依据是什么?3、下列各式,是同类项的一组是( )(A )y x 222与231yx (B )n m 22与22m n (C )ab 32与abc 4、写出下列式子是哪两个整式的和或差(1)()()b a b a 223+++ (2)()b a b a 23+++ (3)()()b a b a 223+-+(4)()b a b a 23--- (5)()()b a b a 22+-+(6)()b a b a 23+++-5、去括号后合并同类项:(1)()()b a b a 223+++ (2)()()b a b a 223+-+(3)()()b a b a 22+-+ (4)()b a b a 23---6、进行整式的加减运算时,如果 , 。
课堂活动 自主学习一、 探索: (二次备课)1、数学游戏: 任意写出一个两位数②交换这两位数的十位数字和个位数字,得到一个新两位数③求这两个两位数的和 观察计算结果,你会发现什么结论?这个结论对任意的两位数都成立吗?为什么?设这个数的十位数字是a ,个位数字是b ,则这个两位数可表示为 ,交换位置后所得的新两位数可表示为 ,它们的和可表示为 。
2、一种笔记本的单价是x (元),圆珠笔的单价是y (元),小红买这种笔记本3本,买圆珠笔2枝;小明买这种笔记本4个,买圆珠笔3枝,买这些笔记本和圆珠笔。
(1)小红和小明共花费多少钱?(2)小明比小红多花费多少钱?3、做大小两个长方体纸盒,尺寸如下(单位:厘米).(1)做这两个纸盒共用料多少平方厘米?(2)做大纸盒比小纸盒多用料多少平方厘米?议一议:在上面的问题中,分别涉及到了整式的什么运算?说说你是如何运算的?总结:整式的加减运算实质就是 自主学习 运算的结果是一个多项式或单项式。
3.6整式的加减(1)导学案

柞村中学
( )个棋子,n 个三角形需 2、计算: (1) (3k 2 7k ) (4k 2 3k 1) (2) (3 x 2 2 xy
1 x) (2 x 2 xy x) 2
个棋子
(3) 3a 5a (a 2) 4 1 3、 (1)求 x 2 7 x 2 与 2 x 2 4 x 1 的和 (2)求 4k 2 7k 与 k 2 3k 1的差 1、先化简,再求值: 5x 2 3x 2(2x 3) 4x 2
四、提高练习 继续加深学生对知识 的理解
知识梳理 学生对去括号法则运用不熟练 收获反思
2x 2 y 2、单项式 的系数是 3
、次数是 次 项式,其中二次项
复习旧知,为学习新知 做准备
3、多项式 3m3 2m 5 m 2 是 系数是 ab 与 abc 3
二、根据现实情景,讲 授新课 进行整式加减运算时, 如 果遇到括号先去括 号,再合并同类项。
4、下列各式,是同类项的一组是(
1 (A) 2 2 x 2 y 与 yx 2 3
(B) 2m 2 n 与 2m n2
5、去括号后合并同类项: (3a b) (5a 2b) (7a 4b)
二、探索练习: 1、如果用 a 、b 分别表示一个两位数的十位数字和个位数字,那么 这个两位数可以表示为 交换这个两位数的十位数 字和个位数字后得到的两位数为 这两个两位数的和为 2、如果用 a 、b、c 分别表示一个三位数的百位数字、十位数字和个 位数字, 那么这个三位数可以表示为 交换这个三位 数的百位数字和个位数字后得到的三位数为 这两个三位数的差为 ●议一议:在上面的两个问题中,分别涉及到了整式的什么运算? 说说你是如何运算的? ▲整式的加减运算实质就是 运算的结果是一个多项式或单项式。 三、小组合作,探究 三、巩固练习: 新知 1、填空: (1) 2a b 与 a b 的差是 通过巩固练习,学生 根据小组合作的结 (2) 、单项式 5 x 2 y 、 2 x 2 y 、 2 xy 2 、 4 x 2 y 的 果,理解整式的加减 和为 实际就是合并同类项 (3)如图所示,下面为由棋子所组成的三角形, 一个三角形需六个棋子,三个三角形需
2019-2020学年七年级数学上册《3.6整式的加减》学案 苏科版.doc

2019-2020学年七年级数学上册《3.6整式的加减》学案苏科版【学习目标】会进行简单的整式加,减运算.【学习重点】进行简单的整式加,减运算.【学习难点】在活动中发展学生的合作精神及探索问题的能力.【学习过程】『问题情境』动手操作准备三张如课本P80所示的卡片.用它们拼成各种形状不同的四边形,并计算它们的周长.(鼓励学生把长方形和等腰三角形拼成各种图形,分别计算出它们的周长和面积)这2个四边形周长的和是:(4a+2b)+(2a+4b)=4a+2b+2a+4b=6a+6b这2个四边形周长的差是:(4a+2b)-(2a+4b)=4a+2b-2a-4b=2a-2b『问题探讨』以上这些工作实际上是在进行整式的加减运算,揭示如何进行整式的加减运算进行整式的加减运算时,如果有括号先去括号,再合并同类项『例题讲评』例1、求2a2-4a+1与-3a2+2a-5的差.强调:要把两个代数式看成整体,列式时应加上括号巩固练习:(1)(-3a2-3a-1)-(5a2+6a-8) (2)(8mn-3m2)-5mn-2(3mn-2m2)例2、先化简再求值:5(3a2b-ab2)-4(-ab2+3a2b),其中a=-2,b=3小结一般步骤:1、去括号;2、合并同类项;3、代入求值。
巩固练习:先化简再求值:3y2-x2+(2x-y)-(x2+3y2),其中x=1,y=-23.6 整式的加减——随堂练习评价_______________ 1.减去2x等于x2-3x-6的多项式是 ( )A .x 2-5x -6B .x 2+5x -6C .x 2-x -6D .x 2+5x -6 2.长方形一边长为4m+n ,另一边比它小m -n ,则这个长方形的周长为 ( )A .4m+nB .8m+2nC .14m+6nD .12m+8n3.多项式y 3-5y 2-2y+1与多项式-y 3+5y 2+4y 的和一定是 ( )A .奇数B .偶数C .整数D .无法确定4.(1)多项式3a 2-b 2-2ab 与-b 2-4ab -3a 2的差是____________.(2)比2m 2-3m -4的2倍多m 2+2m 的多项式是_______________.5.若m -n=-3,mn=2,则(-5m+2)-5(2mn -n )=____________.6.已知A=5a 2-2ab+6,B=7ab -8a 2-7,则A -2B= .7.(1)2(__________)-x 2+2=3x 2-6;(2) 5m 2-3m+1=(m 2+m -2)+(___________).8.计算:(1) 5(x+y)-4(3x -2y)+3(2x -3y) (2) 4a 2b -[3ab 2-2(3a 2b+ab 2)]+ab 29. 化简求值:2xy -21(4xy -8x 2y 2)+2(3xy -5x 2y 2),其中x=21,y=-32.10.已知A=a 2+b 2-c 2,B=-4a 2+2b 2+3c 2,若A+B+C=0,求C .。
《3.6整式的加减》教学案

数学试卷2018-2019学年度第一学期七年级数学教学案(30)3.6 整式的加减【教学目标】1.会进行简单的整式加、减运算.2.能说明整式加、减中每一步运算的算理,逐步发展有条理的思考和表述的能力.【重、难点】会进行简单的整式加、减运算.【教学过程】一、情境创设1.操作:(1)准备三张如下图所示的卡片(2)思考:用它们拼成各种形状不同的四边形,并计算拼成的四边形的周长.二、探索活动活动一:1.整式的加减运算要进行哪些步骤?进行整式的加减运算时,三、例题教学例1.(1)求1422+-aa与5232-+-aa的差;(2)求多项式2x-3y+7与6x-5y-2的和.例2 求)3(4)3(52222baababba+---的值,其中3,2=-=ba.四、反馈练习1.课本 P87 练一练2.计算:(1)aba6)5(++(2))54()72(---xx(3))865()133(22-+---aaaa(4))23(25)38(22mmnmnmmn----3.求)3()2(32222yxyxxy+---+-的值,其中x =1、 y =-2.★4.化简求值:()()222222222yxxyxyx+--++-,其中3,31==yx.五、课堂小结六、课后作业课本习题 P87 1 21.(1) (2) (3) (4)2.(1) (2)abb。
苏科版-数学-七年级上册-导学案:3.6整式的加减

滨海县第一初级中学 初一数学 学科导学案编号 (29)学习目标:1.从实际背景中去体会进行整式的加减的必要性2.灵活运用整式的加减的步骤进行运算。
学习重点:整式加减的运算学习难点: 正确地去括号、合并同类项,及符号的正确处理课前导学自主学习 1、多项式中具有什么特点的项可以合并,怎样合并?(二次备课)2、如何去括号,它的依据是什么?3、下列各式,是同类项的一组是( )(A )y x 222与231yx (B )n m 22与22mn (C )ab 32与abc4、写出下列式子是哪两个整式的和或差(1)()()b a b a 223+++ (2)()b a b a 23+++ (3)()()b a b a 223+-+(4)()b a b a 23--- (5)()()b a b a 22+-+(6)()b a b a 23+++-5、去括号后合并同类项:(1)()()b a b a 223+++ (2)()()b a b a 223+-+(3)()()b a b a 22+-+ (4)()b a b a 23---6、进行整式的加减运算时,如果 , 。
课堂活动自主学习一、探索:(二次备课)1、数学游戏: 任意写出一个两位数②交换这两位数的十位数字和个位数字,得到一个新两位数③求这两个两位数的和观察计算结果,你会发现什么结论?这个结论对任意的两位数都成立吗?为什么?设这个数的十位数字是a,个位数字是b,则这个两位数可表示为,交换位置后所得的新两位数可表示为,它们的和可表示为。
2、一种笔记本的单价是x(元),圆珠笔的单价是y(元),小红买这种笔记本3本,买圆珠笔2枝;小明买这种笔记本4个,买圆珠笔3枝,买这些笔记本和圆珠笔。
(1)小红和小明共花费多少钱?(2)小明比小红多花费多少钱?3、做大小两个长方体纸盒,尺寸如下(单位:厘米).(1)做这两个纸盒共用料多少平方厘米?(2)做大纸盒比小纸盒多用料多少平方厘米?长宽高小纸盒 a b c 大纸盒 1.5a 2b 2c议一议:在上面的问题中,分别涉及到了整式的什么运算?说说你是如何运算的?总结:整式的加减运算实质就是 自主学习 运算的结果是一个多项式或单项式。
苏教科版初中数学七年级上册 3.6 整式的加减导学案

情境引入
b
b ab
准备三张如图所示的卡片
b
b
a
用它们拼成各种形状不同的四边形,并 计算它们的周长。
进行整式加 减运算时,如果有括号先去括 号,再合并同类项。 例 1:已知(x+3)2+|x+y+5|=0,求 3x2y -[-2xy+(x2y-4x2y)]-xy 的值。
TB:小初高题库
Байду номын сангаас
苏科版初中数学
相信自己,就能走向成功的第一步 教师不光要传授知识,还要告诉学生学会生活。数学思维
可以让他们更理性地看待人生
TB:小初高题库
苏科版初中数学
苏教科版初中数学
重点知识精选
掌握知识点,多做练习题,基础知识很重要! 苏科版初中数学 和你一起共同进步学业有成!
TB:小初高题库
3.6 整式的加减
苏科版初中数学
姓名________学号_________
班级_________
一、【学习目标】
1.会进行整式的加、减运算
2.能说明整式加、减中每一步运算的算理,逐步发展有条理思考和表述
的能力。
二、【学习重难点】
去括号和合并同类项的法则,进行整式的加减运算 三、【自主学习】 1、自学课本 P86 到 P87,完成练一练。 2、2a-(a-b)= 3、(a-b )+(-c-d)= 4、a-b 的相反数是 5、一个长方形的周长是 6a+8b,一边长为 2a+3b,求另一边的长。
四、【合作探究】
苏科版-数学-七年级上册-苏科版七上3.6整式的加减 精品教学案

初中-数学-打印版初中-数学-打印版2014-2015学年度第一学期七年级数学教学案(30)3.6 整式的加减【教学目标】1.会进行简单的整式加、减运算.2.能说明整式加、减中每一步运算的算理,逐步发展有条理的思考和表述的能力. 【重、难点】会进行简单的整式加、减运算. 【教学过程】 一、情境创设 1.操作:(1)准备三张如下图所示的卡片(2)思考:用它们拼成各种形状不同的四边形,并计算拼成的四边形的周长.二、探索活动活动一:1.整式的加减运算要进行哪些步骤?进行整式的加减运算时, 三、例题教学例1.(1)求1422+-a a 与5232-+-a a 的差;(2)求多项式2x -3y +7与6x -5y -2的和.例2 求)3(4)3(52222b a ab ab b a +---的值,其中3,2=-=b a .四、反馈练习1.课本 P 87 练一练2.计算:(1)a b a 6)5(++ (2))54()72(---x x(3))865()133(22-+---a a a a (4))23(25)38(22m mn mn m mn ----3.求)3()2(32222y x y x x y +---+-的值,其中x =1、 y =-2.★4.化简求值:()()222222222y xx y x y x +--++-,其中3,31==y x .五、课堂小结六、课后作业 课本习题 P 87 1 21.(1) (2) (3) (4)2.(1) (2)ab bb bb。
七年级上册数学《3.6 整式的加减》教案 (5)【精品】

整式的加减
教学目标:
1、在具体情境中认识整式的加减
2、能熟练地进行整式加减运算。
教学重点:
会进行整式的加减运算
教学难点:
能掌握整式加减的依据
课时:1
第1课时
教学过程:
一、情境引入
如图,用三张卡片拼图形
计算下面两幅图形的周长
周长= 周长=
周长和: 周长差:
二、探索新知
1、概括:像以上这些计算就是整式的加减运算
进行整式的加减运算,其一般步骤是: 。
例题讲解:
1、例1:求2a 2-4a+1与-3a 2+2a-5的差
2、计算(1)2x -3y +7与6x -5y -2的和;(2)(-3x 2-x +2)+(4x 2
+3x -5); b b b b b a a a
(3)(4a2-3a)+(2a2+a-1);(4)(x2+5xy-y2)-(x2+3xy-2y2);(5)2(1-a+a2)-3(2-a-a2).
例2:求5(3a2b-ab2)-4(-ab2+3a2b)的值,其中a=-2,b=3.
3.补充练习:
求3y2-x2+(2x-y)-(x2+3y2)的值,其中x=1、y=-2.
课内练习:数P87练一练1、2
教学反思:。
苏科版-数学-七年级上册-七年级数学上 3.6 整式的加减 备用学案

学习内容
学习目标
1.在具体的问题中体会去括号的必要性,能初步利用运算律去括号.
2.在现实问题中理解、总结去括号法则,并能利用法则解决简单的问题.培养学生代数推理能力.
订正栏
一、课前预习
1.当 时 hslx3y3h -2xy+(x2y-4x2hslx3y3h-xy}的值.
例4当 时,代数式 的值为2008,
4.先化简,后求值.
(1)化简:
(2)当 时,求上式的值.
【能力提升】
5.多项式 减去一个多项式A的差是 ,求这个多项式A.
6、某同学在做整式加减运算时,粗心大意,当将某整式减去xy-2yz+3xz时,误认为加上此式,所得答案为2yz-3xz+2xy,那么你能帮助他修改一下吗?
求:当 时,代数式 的值.
三、达标检测
【基础演练】
1.已知 ,那么代数式 的值为( )A.8B.10C Nhomakorabea12D.35
2.当x=3时,代数式px3+qx+1的值为2002,则当x=-3时,代数式px3+qx+1的值为( )
A.2000B.-2002C.-2000D.2001
3.若 ,则
等于( )
A. B. C. D.
3.6整式的加减-苏科版七年级数学上册教案

3.6 整式的加减-苏科版七年级数学上册教案一、知识点概述在学习代数式的基础上,本节课将进一步介绍整式的概念及加减法运算。
整式是由项代数式相加或相减,其中每一项都是常数或者变量或者它们的某一次方的积,这门知识是数学代数学中的重点。
二、教学目标1.掌握整式的定义。
2.熟练进行整式的加减运算,理解其运算规律。
3.通过练习,进一步提升对代数式的认识及能力。
三、教学重点1.整式的定义。
2.整式加减法运算的审题及运算规律。
四、教学难点1.把握整式加减法运算的特性,并且正确灵活应用。
2.掌握代数式加减运算的操作方法。
五、教学方法1.课前预习及自学。
2.教师讲解及板书演示。
3.学生课堂练习。
4.课后作业巩固。
1. 教师引入整式是数学中的重点,其定义对于整个数学代数学习的重要性不可忽略。
在本节课中,我们将会深入了解整式的定义及其加减法的运算规律。
通过训练,相信大家可以更好地理解和应用。
2. 整式的定义整式是由项代数式相加或相减的式子,这些项可以是常数或者变量或者它们的某一次方的积。
比如:2x2−3xy+6y−5这个式子中,2x2,−3xy,6y,−5都是项。
3. 整式的加减运算在进行整式的加减运算时,需要把同类项合并,即把具有相同字母和次数的项合并。
例如:2x2+5y2−3x2+4y2=(2−3)x2+(5+4)y2=−x2+9y2在计算的过程中,需要注意以下几点:1.消去同类项时,只是将它们的系数相加。
2.消去同类项时,变量的字母和次数必须相同。
3.最后的结果形式应按照字母表顺序进行排序。
4. 课堂练习请同学们结合书本P28-P32页上的例题进行课堂练习,并做好笔记和记录。
5. 课后作业1.完成书本P28-P32页上的练习题。
2.针对性做练习题巩固对整式的理解和运算。
本节课中,教师对整式的定义及加减运算的原理和步骤进行了讲解,通过数学具体的例子,使学生们更好地理解了整式加减的规律和方法。
针对书本课后练习,我们也要着手开展更为多样化的教学练习模式,引导学生充分掌握知识点并能够熟练应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学七年级上册
《3.6 整式的加减》学案
一、学习目标
1.能熟练运用合并同类项、去括号法则进行整式加减运算;
2.能利用整式的运算化简多项式并求值.
二、重点难点
重点:整式加减运算.
难点:整式加减运算.
三、导学问题
模块一 预习反馈
学习准备:
1、先去括号,再合并同类项:(1)(x+y)—(2x -3y) (2)()222223(2)a b
a b --+
2.整式加减的一般步骤为:__________________________________________________.
3、阅读教材:第95——96页。
教材精读
4、理解整式的加减的含义
按照下面的步骤做一做:(1)任意写一个两位数;
(2)交换这个两位数的十位数字和个位数字,又得到一个数;
(3)求这两个数的和。
再写几个两位数重复上面的过程。
这些和有什么规律?这个规律对任意一个两位数都成立? 提示:设a 表示十位数字,b 表示个位数字,那么这个两位数可以表示为:10a+b;交换位置后的两位数为: 。
再做一做:(1)任意写一个三位数;
(2)交换这个三位数的百位数字和个位数字,又得到一个数;
(3)两个数相减。
两个数相减后的结果有什么规律?这个规律对任意一个三位数都成立吗?
归结:要把上面式子进一步化简,实际上是要进行整式的加减运算.
整式加减的一般步骤:有括号要先去括号,再合并同类项。
实践练习:求整式x 2―7x―2与―2x 2+4x―1的差。
教材拓展
例1 已知A=2x 2+3ax-2x-1,B= -x 2+ax-1,且3A+6B 的值不含x 项,求a 的值。
解:3A+6B=3(2x 2+3ax-2x-1)+6(-x 2+ax-1)
=
因为不含x 项,所以x 项的系数为0.
实践练习:一本铁丝正好可以围成一个长是23a b +。
宽是a b +的长方形框,把它减去可围成一个长是a ,宽是b 的长方形(不计接缝)的一段铁丝,剩下部分铁丝长是多少?
模块二 合作探究
例2、 化简求值:(2x 3―xyz)―2(x 3―y 3+xyz)+(xyz―2y 3),其中x=1,y=2,z=―3。
提示:先去括号。
注意括号前的符号和系数。
实践练习:1、求整式3x 2―7x―12与―2x 2+7x―5的差。
2、化简:―2y 3+(3xy 2―x 2y)―2(xy 2―y 3)。
模块三 形成提升
1、若M 、N 都是七次多项式,则M-N 是( )
A 、常数
B 、次数不高于7的多项式
C 、7次多项式
D 、次数高于7次的多项式
2、计算:
(1)()()323232342y x y x y x ---+ (2)()()22232538x xy xy y
xy ----
(3)32232113()(6422a a b ab a a b --+
-+-23)ab
3、化简求值:
(1)()()222222222y
x x y y x +--+-,其中3,3
1==y x ;
(2)()()y x xy xy y x 2222335---,其中1,21-==
y x
(3)22223[22(2)]a b ab a b ab --+,其中1,2a b ==-
模块四 小结评价
1、进行整式加减的一般步骤: 。
2、去括号。
注意括号前的符号和系数
四、参考资料
1.新课程互动学习中“助你学习”。
