2012年潍坊第一次高考数学(理)模拟试题
山东省潍坊市2012年高考仿真试题(一)文科数学试题.pdf

第12讲┃ 简单机械 B 第12讲┃ 简单机械 50 第12讲┃ 简单机械 斜面 大 30 右 第12讲┃ 简单机械 1.5 330 第12讲┃ 简单机械 图略 第12讲┃ 简单机械 第12讲┃ 简单机械 第12讲┃ 简单机械 第12讲┃ 简单机械 右满足平衡条件 方便测量出两个力臂 第12讲┃ 简单机械 (3)改变钩码数量与位置,获取三组测量数据(如下表所示),可以减少实验的________,根据表中的数据你得出杠杆的平衡条件是:________________________,并完成下表中的空格。
实验 次序 动力 F1/N 动力臂 l1/cm 阻力 F2/N 阻力臂 l2/cm 1 2.0 5.00 1.0 10.00 2 2.0 10.00 2.0 10.00 3 2.0 10.00 4.0 ______ 误差 F1l1=F2l2 5.00 第12讲┃ 简单机械 400 N 560 N 图略 第12讲┃ 简单机械图略 第12讲┃ 简单机械 甲种方式更轻便、更合理。
两种方式的动力臂大致相同,阻力相等,根据杠杆平衡条件,甲方式的阻力臂小,所以手施加的动力小,感觉更轻便、更合理。
第12讲 简单机械 第12讲┃ 简单机械 考点38 探究:杠杆平衡条件 ┃考点自主梳理与热身反馈┃ 力 固定点 支点 力的作用线 第12讲┃ 简单机械 静止 匀速平衡螺母 水平位置 杠杆自重 右调 左调 水平 力臂 动力×动力臂=阻力×阻力臂 F1l1=F2l2 第12讲┃ 简单机械考点 39 杠杆分类与力臂作图 杠杆类别 力臂关系 力的关系 特点 生活举例 省力 杠杆 l1____l2 F1____F2 省力、费______ 撬棒、羊角锤、抽水机压柄、铡刀、独轮车 费力 杠杆 l1____l2 F1____F2 费力、省________ 镊子、筷子、钓鱼竿、理发剪刀 等臂 杠杆 l1____l2 F1____F2 不省力、不费距离 天平、跷跷板 2.杠杆力臂作图作图步骤:(1)找支点;(2)画力的作用线(用虚线);(3)画力臂(用虚线,过支点向力的作用线画垂线);(4)标力臂(大括号或背向箭头)。
山东省各地市2012年高考数学最新联考试题分类大汇编(11)排列组合

一、选择题:
6.(山东省济南市2012年2月高三定时练习理科)三位老师和三位学生站成一排,要求任何两位学生都不相邻,则不同的排法总数为 ( B )
A.720
B. 144
C.36
D.12
10.(山东省烟台市2012年高三诊断性检测理)用0,1,2,3,4排成无重复数字的五位数,要求偶数字相邻,奇数字也相邻,则这样的五位数的个数是( D )
A.36 B.32 C.24 D.20
二、填空题:
15.(山东省潍坊市2012年3月高三一轮模拟理科)某工厂将甲、乙等五名新招聘员工分配到三个不同的车间.每个车间至少分配一名员工,凰甲、乙两名员工必须分到同一个车间,则不同分法的种数为36 。
三、解答题:
- 1 -。
2012年高考数学模拟试题

A向 平 詈 单 长 -左 移 个 位 度
B向 平 詈 单 长 .右 移 个 位 度
A P真 q . 假 C“ .P或 q 为假 ”
A. 一 2
)
C. 一4 D. 4
B.2
5若 z . 为一条直线 , , 7为三个互不重合 的平 面 , 出 O , t 给
下面三个命题 :
( )t , - 1 O上7 卢j j 1 3 /;
点 , 0< 。则 。的值为 ( 且 x< , ) A.恒为正值 C .恒为负值 l. 0 给出下列命题
三、 解答题 : 本大题共 6小题 , 满分 7 4分. 解答 须写 出文
字说 明、 证明过程和演算步骤. 1. 本小题满分 1 7( 2分 ) 已知 向量 m =( c b , Ⅱ+ ,) n=( n—cb ) 且 m ・ 0 , 一0 , n= ,
)
其 中 A、 C是 AA C的 内角 , , , 别是 角 A, c的对 B、 B 0 6 c分 日,
q ( R, >O 的最小 - ) )
.
A .充分而不必要条 件 C .充要条件
正周期为 , 为了得 到函数 g )= OO ( CS X的图象 , ) 只要将 y= / ( 的 图象 ( ) )
3 已知命题 P 在 AA C中, C>/B是 s C>s B的 . : B i n i n
C .2个 D .3个 角为 3 。 0:
②a・ > 是 a b的夹角 为锐角 的充要条件 ; b 0, 、
6 已知 等差数列 { 的前 2 和为 10 那么 a a . a} 0项 0, ・ , 的最大值是 (
2012潍坊理数学一模0308

2012年高考模拟考试数学(理工农医类) 2012.3本试卷共4页.分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间l20分钟.第Ⅰ卷(选择题共60分)注意事项:1·答第1卷前,考生务必将自己的姓名、准考证号.考斌科目用铅笔涂写在答题卡上.2·每题选出答案后,用2B铅笔把答题卡对应题目的答案标号涂黑.如需改动.用橡皮擦干净后,再改涂其它答案标号一、选择题:本大题共l2小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合,集合N=A.(0.+∞) B.(1,+∞)C.(0,1) D.(0,1)∪(i,+∞)2.复数A.一i B.i C.5i D.4/5+i3.不等式的解集为4.命题为真命题的一个充分不必要条件是A.α≥4 8.α≤4 C.α≥5 D.α≤55.将函数y=cos2x的图象向右平移π/4个单位,得到函数的图象,则f(x)的表达式可以是6.运行右图所示的程序框图,若输出结果为13/7,则判断框中应该壤的条件是A.k>5 B.k>6C.k>7 D.k>87.已知向量α=(cosx,sinx),b=8.已知函数f(x)=,则函数y=f(x+1)的大数图象为9.在空间中.l、m、n是三条不同的直线,α、β、γ是三个不同的平面,则下列结论错误的是A.若α∥β,α∥γ,则β∥γB.若l∥α,l∥β,α∩β=m,则l∥mC.α⊥β,α⊥γ,β∩γ=l,则l⊥αD.若α∩β=m,β∩γ=l,γ∩α=n,l⊥m,l⊥n,则m⊥n10.直线4h一4y—k=0与抛物线y2=x交于A、B两点,若,则弦AB的中点到直线x+1/2=0的距离等于A.7/4 B.2 C.9/4 D.411.已知矩形ABCD的面积为8,当矩形周长最小时,沿对角线AC把△ACD折起,则三棱锥D—ABC的外接球的表面积等于A.4πB.8πC.16πD.24π12.若直角坐标平面内的两点P、Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称.则称点对[P,Q]是函数Y= f(x)的一对“友好点对”(点对[P,Q]与[Q,P]看作同一对“友好点对”).已知函数,f(x)=,则此函数的“友好点对”有A.0对B.1对C.2对D.3对第Ⅱ (非选择题 90分)注意事项:-1.将第Ⅱ卷答案用0.5mm的黑色签字笔答在答题纸的相应位置上。
【备战2012】高考数学 最新模拟专题06 不等式理

最新模拟专题【2012某某省某某市质检理】设102m <<,若1212km m +≥-恒成立,则k 的最大值为;【答案】8【解析】由题可知k 的最大值即为1212m m +-的最小值。
又1212m m +-22122()[2(12)]22()2212212m m m m m m m m -=++-=+++--8≥,取等号的条( )A .ab <b2<1B .21log b <21log a <0 C .2b <2a <2 D .a2<ab <1 【答案】C【解析】因为b <a <1,所以2b <2a <1,故选C.【某某省日照市2012届高三12月月考理】(11)如果不等式组⎪⎩⎪⎨⎧≥+-≥≥01,2,0y kx x y x 表示的平面区域是一个直角三角形,则该三角形的面积为(A )5121或(B )3121或(C )4151或(D )2141或【答案】:C 解析:有两种情形:(1)直角由x y 2=与01=+-y kx 形成,则21-=k ,三角形的三个顶点为(0,0),(0,1),(54,52),面积为51;(2)直角由0=x 与01=+-y kx 形成,则0=k ,三角形的三个顶点为(0,0),(0,1),(1,21),面积为41。
【某某实验中学2012届高三第四次诊断性考试理】10. 设x 、y 满足约束条件,若目标函数(其中0,0a b >>)的最大值为3,则的最小值为()[Zxxk.](A) . 3 (B) . 1 (C) .2 (D) . 4【某某省潍坊市三县2012届高三联考理】【2012某某市高三模拟统一考试理】已知变量x,y满足约束条件10,310,10,y xy xy x+-≤⎧⎪--≤⎨⎪-+≥⎩则2z x y=+的最大值为。
【答案】 2【解析】本题主要考查线性规划的最优解. 属于基础知识、基本运算的考查.实数x,y满足不等式组10,310,10,y xy xy x+-≤⎧⎪--≤⎨⎪-+≥⎩则可行域如图,作出2y x=-,平移,当直线通过A(1,0)时,2z x y=+的最小值是⒉. 【2012年某某市高三年级第三次质检理】在平面直角坐标系xOy上的区域D由不等式组给定.若M(x ,y)为D上的动点,点N 的坐标为(,1),则的最大值为._______【答案】4【解析】本题主要线性规划可行域的概念、平面向量的数量积. 属于基础知识、基本运算的考查.2z OM ON x y=⋅=+如图,作出变量,x y满足约束条件02x y x ⎧≤≤⎪≤⎨⎪≤⎩,可行域是图中的阴影部分;,2),作出直线y =,z y y z =+⇒=+,直线y z =+在y 轴上截距最大时,z 最大。
2012年高考数学模拟试题

图12012年高考模拟试题数 学(理科第Ⅱ卷)一.选择题(每题5分,共12小题,满分60分,每小题只有一个选项正确。
)1.设集合[)(]}1,0,log |{},,0,)21(|{2∈==+∞∈==x x y y N x y y M x,则集合N M 是A .[)+∞-∞,1)0,(B .[)+∞,0C .(]1,∞-D .)1,0()0,( -∞2.若()R b a bi a i i ∈+=+-,213,则=ab( )A .1-B .710C .7-D .73.⎰=+202)cos (sin πdx x a x ,则实数a 等于A .1-B .1C .3D .3-4.抛物线28y x =的焦点到双曲线221124x y -=的渐近线的距离为 A .1BCD5.执行图1所示的程序,输出的结果为20,则判断框中应填入的条件为 A .5a ≥ B .4a ≥ C .3a ≥ D .2a ≥6.函数xxx f +-=11ln)(的图象只可能是A B C D7.已知2a —b =(1-,3),c =(1,3),且a •c =3,| b |=4,则b 与c 的夹角为A .6π B .3π C .65π D .32π8.下列四个命题中真命题的个数是 ①若[]1,0,∈b a ,则不等式422<+b a 成立的概率是4π;②命题“∈∃x R ,02>-x x ”的否定是“∈∀x R ,02≤-x x ”; ③“若22bm am <,则b a <”的逆命题为真 ④命题[]1,0:∈∀x p ,1≥x e ,命题∈∃x q :R ,012<++x x ,则q p ∨为真A .0B .1C .2D .3 9.将圆⎩⎨⎧+==θθsin 1cos y x 的中心到直线y =kx 的距离记为d =f (k )给出下列判断①数列{nf (n )}是递增数列②数列})(1{2n f 的前n 项和是6)732(2++n n n ③1])(1)1(1[lim 1=-+-∞→n f n f n ④2)1()()1()(211++<++--n f n f n f n f 其中正确的结论是 A .①①②③④ B .①②③C .①③D .①10.现有4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两块不能用同一种颜色,则不同的着色方法共有A .24种B .30种C .36种D .48种11.设O 为坐标原点,点M 坐标为)2,3(,若点(,)N x y 满足不等式组:⎪⎪⎩⎪⎪⎨⎧≤+≤+≥≥420x y s y x y x ,当3≤s ≤5时,则ON OM ⋅的最大值的变化范围是A .[7,8]B .[7,9]C .[6,8]D .[7,15]12.若AB 是过椭圆)0(12222>>=+b a by a x 中心的一条弦,M 是椭圆上任意一点,且AM ,BM 与坐标轴不平行,AM k ,BM k 分别表示直线AM ,BM 的斜率,则AMk =BM kA .22a c -B .22a b -C .22b c -D .22ba -二.填空题(本大题共4小题,每小题5分,共20分) 13.若n m x x x f )31()21()(+++=(m , n 为正整数)的展开式中x 的系数为13,则2x 的系数是 。
2012年高考数学模拟试题

N I l F +2 I N I=2 = Fl 2 I a
。 . .
1 NI =。一c. Ⅳ点是椭 圆的右顶点 , C 轴 , ,. . 又 N上
C点轨迹为直线. 1. 案 : 0答 D 解析 ) n =l x+2 + +1 ( , 。) 在 0 +。 内单调递增 ,
每点切线斜率 的取值范 围.
1. 本 小 题 满 分 1 ) 8( 2分
体育课进行篮球 投篮达 标测试 , 定 : 规 每位 同学有 5次
投篮机会 , 若投 中 3次则 “ 达标 ” 为节 省测 试时 间 , ; 同时 规 定: 若投篮不 到 5次 已达标 , 则停 止投篮 ; 即使后 面投篮全 若
更 一 般 的结 论 , 加 以 证 明 . 并
4 , 。= 解得I I ÷ , I7P . 故I = I I
参 考答 案
一
7 .答 案 : C
、
选 择 题
2 .B
1 . 0 D
解析 : 对于选项 A, 结论有可能是 n在 内; 于选项 B 对 、
3B . 4 D . 5C . 6 A .
一 } _l = =一 = + ( l (i。1 ) l ) m枷 十 ) .
’ .
.
‘ .
.
I + l l I F1 PF1 I P = P l+ l M l+ l Ⅳ l I Ⅳ l+ I P = F1
故选 B . 3答案 :. . B
1 1,
P= = ) ()了 (3 ( ÷ = ) + 1
P= =() )c ) )万 (4 ÷‘ ( 1 ) 丁 +( ÷ = 2 0 P= :()2 = (5 ÷ ) ) ‘ 8 了
的分布列
山东省潍坊市2012届高三一轮模拟考试数学(理)试题

保密★启用前试卷类型:A2012年高考模拟考试数学(理工农医类) 2012.3本试卷共4页.分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间l20分钟.第Ⅰ卷(选择题共60分)注意事项:1·答第1卷前,考生务必将自己的姓名、准考证号.考斌科目用铅笔涂写在答题卡上.2·每题选出答案后,用2B铅笔把答题卡对应题目的答案标号涂黑.如需改动.用橡皮擦干净后,再改涂其它答案标号一、选择题:本大题共l2小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合,集合N=A.(0.+∞) B.(1,+∞)C.(0,1) D.(0,1)∪(i,+∞)2.复数A.一i B.i C.5i D.4/5+i3.不等式的解集为4.命题为真命题的一个充分不必要条件是A.α≥4 8.α≤4 C.α≥5 D.α≤55.将函数y=cos2x的图象向右平移π/4个单位,得到函数的图象,则f(x)的表达式可以是6.运行右图所示的程序框图,若输出结果为13/7,则判断框中应该壤的条件是A.k>5 B.k>6C.k>7 D.k>87.已知向量α=(cosx,sinx),b=8.已知函数f(x)=,则函数y=f(x+1)的大数图象为9.在空间中.l、m、n是三条不同的直线,α、β、γ是三个不同的平面,则下列结论错误的是A.若α∥β,α∥γ,则β∥γB.若l∥α,l∥β,α∩β=m,则l∥mC.α⊥β,α⊥γ,β∩γ=l,则l⊥αD.若α∩β=m,β∩γ=l,γ∩α=n,l⊥m,l⊥n,则m⊥n10.直线4h一4y—k=0与抛物线y2=x交于A、B两点,若,则弦AB的中点到直线x+1/2=0的距离等于A.7/4 B.2 C.9/4 D.411.已知矩形ABCD的面积为8,当矩形周长最小时,沿对角线AC把△ACD折起,则三棱锥D—ABC的外接球的表面积等于A.4πB.8πC.16πD.24π12.若直角坐标平面内的两点P、Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称.则称点对[P,Q]是函数Y= f(x)的一对“友好点对”(点对[P,Q]与[Q,P]看作同一对“友好点对”).已知函数,f(x)=,则此函数的“友好点对”有A.0对B.1对C.2对D.3对第Ⅱ (非选择题 90分)注意事项:-1.将第Ⅱ卷答案用0.5mm的黑色签字笔答在答题纸的相应位置上。
山东省潍坊市2012届高三第一次高考模拟

山东省潍坊市2012届高三第一次高考模拟英语第Ⅰ卷(共105分)第一部分:略第二部分:英语知识运用(共两节,满分35分)第一节:语法和词汇知识(共15小题;每小题1分,满分15分)从每题所给的A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21. 2011 tour was success for the two Irish players.A.The;aB.A;aC.The;不填D.不填;the22.—I want to go camping,just for a change.—OK,A.who cares?B.whatever you say.C.what’s up?D.it’s nice of you.23. you disagree with her,she’s worth listening to.A.Even ifB.In caseC.Only ifD.Ever since24.If the wound become woollen,do not hesitate to call me.A.shallB.mustC.shouldD.would25.The sale of the company’s new product is good.It has two million dollars so far.A.carried onB.kept upC.brought inD.consisted of26.What we’ll do is leave a note for Mum to tell her we back till late.A.have not beenB.are notC.won’t beD.were not27.My recent trip to Europe has left a impression on me.A.finalstingC.foreverD.long28.Our computer all the records of births and deaths in Britain since 1950.A.setsB.remainsC.standsD.holds29.This restaurant, by an old couple,has an inviting,homelike atmosphere that many restaurants lack.A.owningB.to ownC.having ownedD.owned30.The police arrived, the situation became calmer.A.after whichB.before whichC.in whichD.from which31.What seems to be a good thing to one person may be a bad thing to .A.otherB.anotherC.the otherD.the others32.If I buy more than one,will you give me a ?A.discountB.changeC.bargainpromise33.James Cameron is considered one of the greatest directors in the world his influence in film industry.A.in exchange forB.in spite ofC.on behalf ofD.in terms of34.The strange thing about Nicholas is he taught himself to read before he could speak.A.whatB.thatC.whetherD.if35.—Sweetheart.You will never believe this.I just won a car!—!I don’t believe it!A.Cheer upB.Good workC.Good heavensD.That’s awful第二节:完形填空(共20小题;每小题1分,满分20分)阅读下面短文,掌握其大意,从每题所给的A、B、C、D四个选项中,选出最佳选项,并在答题卡上将该项涂黑。
山东省潍坊市2012届高三模拟训练数学(理)试题.pdf

山东省潍坊市2012年高三模拟训练 的虚部为 A.一1 B.一 C. D.一i 2.函数y=lg(l-x)的定义域为A,函数y=()x的值域为B,则AB=A.(0,1)B.(,1) C. D.R 3.等比数列{}中,a3=6,前三项和S3=,则公比q的值为 A.l B.一 C.1或一D.一1或一 4.右图是函数y=Asin(x+)(x∈R)在区间[一] 上的图象.为了得到这个函数的图象,只要将y=sinx(x ∈R)的图象上所有的点 A.向左平移个单位长度,再把所得各点的横坐标缩 短到原来的倍,纵坐标不变 B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变 D.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 5.某程序框图如图所示,该程序运行后输出的S的值是 A.2 B.一 C.—3 D.— 6.已知抛物线=2px(p>0)焦点F恰好是双曲线=1(a>o,b>o)的右焦点,且双曲线过点(,譬),则该双曲 线的渐近线方程为 A.y=±2x B.y=±x C.y=±x D.y=±x 7.一个简单组合体的三视图及尺寸如右图所示(单位:mm),则该组 合体的体积为 A.32 B.48 C.56 D.64 8.若数列{}满足a1=2为数列an+an+1=2n+2n-1,Sn为数列{} 的前n项和,则log2(S2012 +2=A.2013 B.2012 C.2011 D.2010=(m,n) 与向量=(1,0)的夹角记为a,则a∈(0,)的概率为 A. B. C. D. 10.二次函数f(x)=ax2+2x+c(x∈R)的值域为[0,+),则a的最小值为 A.2 B.2+ C.4 D.2十2 11.盒中装有6个零件,其中4个是使用过的,另外2个未经使用,从中任取3个,若至少有一个是未经使用的不同取法种数是k,那么二项式(l+kx2)6的展开式中x4的系数为 A.3600 B.3840 C.5400 D.6000 一log2x,实数a、b、c满足f(a)f(b)f(c)<0,且0b C.xc 第Ⅱ卷(非选择题 共90分) 注意事项: 1.将第Ⅱ卷答案用0.5mm的黑色签字笔答在答题纸的相应位置上。
山东省潍坊市2012届高三下学期考前仿真模拟(五)数学(理)试题.pdf

2012年普通高考理科数学仿真试题(五) 本试卷分第I卷和第Ⅱ卷两部分,共5页.满分150分.考试用时120分钟.考试结束后,将本试卷和答题卡一并交回. 注意事项: 1.答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上. 2.第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.答案不能答在试卷上. 3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效. 4.填空题请直接填写答案,解答题应写出文字说明、演算步骤或推证过程. 第I卷(共60分) 一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合,则下列关系式正确的是 A.B.C.D. 2.设i是虚数单位,则是 A.B.C.1+ID. 3.下列命题中,真命题的个数有 ①;②;③函数是单调递减函数.A.0个B.1个C.2个D.3个 4.如右图,一个简单空间几何体的三视图,其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是 A.B. C.D. 5.已知椭机变量X服从正态分布N(4,1),且,则A.0.0912B.0.3413C.0.3174D.0.1587 6.若则A.112B.28C.D. 7.函数的图象可以是 8.把函数的图象上所有的点向左平移个单位长度,再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象所表示的函数为 A.B. C.D. 9.如果执行如图所示的程序框图,输入,那么输出等于 A.720 B.120 C.240 D.360 10.已知点F,A分别是椭圆的左焦点、右顶点,B(0,b)满足,则椭圆的离心率等于A.B. C.D. 11. 甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和方差如下表所示: 从这四个人中选择一人参加奥运会射击项目比赛,最佳人选是A.甲B.乙C.丙D.丁 12.对于函数,若存在区间(其中a<b),使得,则称区间M为函数的一个“稳定区间”.给出下列4个函数:①;②;③;④.其中存在“稳定区间”的函数有A.①③B.①②③C.①②③④D. 第II卷(非选择题 共90分) 二、填空题:本大题共4小题,每小题4分,共16分. 13.已知二次函数,点是区域内的随机点,则函数在区间上是增函数的概率为_______. 14.设F1、F2分别为双曲线的左、右焦点,若在双曲线右支上存在点P,满足,且F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的渐近线方程为________. 15.商家通常依据“乐观系数准则”确定商品销售价格,即根据商品的最低销售限价a,最高销售限价b(b>a)以及实数确定实际销售价格.这里,被称为乐观系数.经验表明,最佳乐观系数恰好使得是和的等比中项,据此可得,最佳乐观系数的值等于_____. 16.给出的下列四个命题中: ①命题“”的否定是“”; ②“”是“直线与直线相互垂直”的充分不必要条件; ③设圆与坐标轴有4个交点,分别为,则; ④关于x的不等式的解集为R,则 其中所有真命题的序号是________. 三、解答题:本大题共6小题,共74分. 17.(本小题满分12分)已知向量,函数 (1)求函数的最小正周期T; (II)已知a、b、c分别为△ABC内角A、B、C的对边,其中A为锐角,且,求A,b和△ABC的面积S. 18.(本小题满分12分)为加强大学生实践、创新能力和团队精神的培养,促进高等教育教学改革,教育部门主办了全国大学生智能汽车竞赛.该竞赛分为预赛和决赛两个阶段,参加决赛的队伍按照抽签方式决定出场顺序,通过预赛,选拔出甲、乙等五支队伍参加决赛. (I)求决赛中甲、乙两支队伍恰好排在前两位的概率; (II)若决赛中甲队和乙队之间间隔的队伍数记为X,求X的分布列和数学期望. 19.(本小题满分12分)在三棱锥P-ABC中,△PAC和△PBC是边长为的等边三角形,AB=2,O是AB中点. (I)在棱PA上求一点M,使得OM//平面PBC; (II)求证:平面PAB⊥平面ABC; (III)求二面角P-BC-A的余弦值. 20.(本小题满分12分)已知数列中,,且 (1)设,求数列成等比数列,求m的值及的前n项和. 21.(本小题满分12分)已知椭圆中心在坐标原点焦点在x轴上,离心率为,它的一个顶点为抛物线的焦点. (I)求椭圆方程; (II)若直线与抛物线相切于点A,求以A为圆心且与抛物线的准线相切的圆的方程; (III)若斜率为1的直线交椭圆于M、N两点,求△OMN面积的最大值(O为坐标原点). 22.(本小题满分14分)函数 (I)若在处取得极值,求的值; (II)若在其定义域内为单调函数求的取值范围; (III)若在[1,e]上至少存在一点,使得成立,求的取值范围.2012年普通高考理科数学仿真试题(五)答案。
【压轴题】高考数学第一次模拟试题带答案

【压轴题】高考数学第一次模拟试题带答案一、选择题1.设1i2i 1iz -=++,则||z = A .0B .12C .1D .22.如图所示的圆锥的俯视图为( )A .B .C .D .3.()22x xe ef x x x --=+-的部分图象大致是( )A .B .C .D .4.设5sin7a π=,2cos 7b π=,2tan 7c π=,则( ) A .a b c <<B .a c b <<C .b c a <<D .b a c <<5.在某种信息传输过程中,用4个数字的一个排列(数字允许重复)表示一个信息,不同排列表示不同信息,若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为 A .10B .11C .12D .156.设ω>0,函数y=sin(ωx+3π)+2的图象向右平移43π个单位后与原图象重合,则ω的最小值是A .23B .43C .32D .37.甲、乙、丙三人到三个不同的景点旅游,每人只去一个景点,设事件A 为“三个人去的景点各不相同”,事件B 为“甲独自去一个景点,乙、丙去剩下的景点”,则(A |B)P 等于( )A .49B .29C .12D .138.若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是 ( )A .2B .3C .4D .59.已知函数()(3)(2ln 1)xf x x e a x x =-+-+在(1,)+∞上有两个极值点,且()f x 在(1,2)上单调递增,则实数a 的取值范围是( )A .(,)e +∞B .2(,2)e eC .2(2,)e +∞D .22(,2)(2,)e e e +∞10.若干年前,某教师刚退休的月退休金为6000元,月退休金各种用途占比统计图如下面的条形图.该教师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元,则目前该教师的月退休金为( ).A .6500元B .7000元C .7500元D .8000元11.一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X 是一个随机变量,其分布列为P (X ),则P (X =4)的值为 A .1220B .2755C .2125D .2722012.已知a R ∈,则“0a =”是“2()f x x ax =+是偶函数”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件二、填空题13.i 是虚数单位,若复数()()12i a i -+是纯虚数,则实数a 的值为 .14.若过点()2,0M 3的直线与抛物线()2:0C y ax a =>的准线l 相交于点B ,与C 的一个交点为A ,若BM MA =,则a =____.15.若函数3211()232f x x x ax =-++ 在2,3⎡⎫+∞⎪⎢⎣⎭上存在单调增区间,则实数a 的取值范围是_______.16.已知复数z=(1+i )(1+2i ),其中i 是虚数单位,则z 的模是__________17.双曲线22221x y a b-=(0a >,0b >)的渐近线为正方形OABC 的边OA ,OC 所在的直线,点B 为该双曲线的焦点.若正方形OABC 的边长为2,则a=_______________. 18.设a R ∈,直线20ax y -+=和圆22cos ,12sin x y θθ=+⎧⎨=+⎩(θ为参数)相切,则a 的值为____.19.已知点()0,1A ,抛物线()2:0C y ax a =>的焦点为F ,连接FA ,与抛物线C 相交于点M ,延长FA ,与抛物线C 的准线相交于点N ,若:1:3FM MN =,则实数a 的值为__________.20.从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有_____________种.(用数字填写答案)三、解答题21.如图,四面体ABCD 中,O 、E 分别是BD 、BC 的中点,2AB AD ==,2CA CB CD BD ====. (1)求证:AO ⊥平面BCD ;(2)求异面直线AB 与CD 所成角的余弦值; (3)求点E 到平面ACD 的距离.22.某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4,现从这10人中随机选出2人作为该组代表参加座谈会.()1设A 为事件“选出的2人参加义工活动次数之和为4”,求事件A 发生的概率; ()2设X 为选出的2人参加义工活动次数之差的绝对值,求随机变量X 的分布列和数学期望.23.已知函数()3f x ax bx c =++在点2x =处取得极值16c -.(1)求,a b 的值;(2)若()f x 有极大值28,求()f x 在[]3,3-上的最小值.24.如图,矩形ABCD 和菱形ABEF 所在的平面相互垂直,ABE 60∠=︒,G 为BE 的中点.(Ⅰ)求证:AG ⊥平面ADF ;(Ⅱ) 求AB 3=,BC 1=,求二面角D CA G --的余弦值. 25.(选修4-4:坐标系与参数方程)在平面直角坐标系xOy ,已知曲线3cos :sin x aC y a⎧=⎪⎨=⎪⎩(a 为参数),在以O 原点为极点,x 轴的非负半轴为极轴建立的极坐标系中,直线l 的极坐标方程为2cos()124πρθ+=-. (1)求曲线C 的普通方程和直线l 的直角坐标方程;(2)过点()1,0M -且与直线l 平行的直线1l 交C 于A ,B 两点,求点M 到A ,B 的距离之积.26.某农场有一块农田,如图所示,它的边界由圆O 的一段圆弧MPN (P 为此圆弧的中点)和线段MN 构成.已知圆O 的半径为40米,点P 到MN 的距离为50米.现规划在此农田上修建两个温室大棚,大棚I 内的地块形状为矩形ABCD ,大棚II 内的地块形状为CDP ,要求,A B 均在线段MN 上,,C D 均在圆弧上.设OC 与MN 所成的角为θ.(1)用θ分别表示矩形ABCD 和CDP 的面积,并确定sin θ的取值范围;(2)若大棚I 内种植甲种蔬菜,大棚II 内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】分析:利用复数的除法运算法则:分子、分母同乘以分母的共轭复数,化简复数z ,然后求解复数的模. 详解:()()()()1i 1i 1i2i 2i 1i 1i 1i z ---=+=++-+ i 2i i =-+=,则1z =,故选c.点睛:复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数、共轭复数这些重要概念,复数的运算主要考查除法运算,通过分母实数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分.2.C解析:C 【解析】 【分析】找到从上往下看所得到的图形即可. 【详解】由圆锥的放置位置,知其俯视图为三角形.故选C. 【点睛】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图,本题容易误选B ,属于基础题.3.A解析:A 【解析】 【分析】根据函数的奇偶性,排除D ;根据函数解析式可知定义域为{}1x x ≠±,所以y 轴右侧虚线部分为x=1,利用特殊值x=0.01和x=1.001代入即可排除错误选项. 【详解】由函数解析式()22x x e e f x x x --=+-,易知()22x xe ef x x x ---=+-=() f x - 所以函数()22x xe ef x x x --=+-为奇函数,排除D 选项根据解析式分母不为0可知,定义域为{}1x x ≠±,所以y 轴右侧虚线部分为x=1,当x=0.01时,代入()f x 可得()0f x <,排除C 选项 当x=1.001时,代入()f x 可得()0f x >,排除B 选项 所以选A 【点睛】本题考查了根据函数解析式判断函数的图象,依据主要是奇偶性、单调性、特殊值等,注意图中坐标的位置及特殊直线,属于中档题.4.D解析:D 【解析】 【分析】 【详解】 因为,,所以,,且,所以,,所以,故选D.5.B解析:B 【解析】 【分析】 【详解】由题意知与信息0110至多有两个对应位置上的数字相同的信息包括三类: 第一类:与信息0110有两个对应位置上的数字相同有246C =个;第二类:与信息0110有一个对应位置上的数字相同有14C 4=个;第三类:与信息0110没有位置上的数字相同有04C 1=个,由分类计数原理与信息0110至多有两个数字对应位置相同的共有64111++=个, 故选B .6.C解析:C 【解析】函数sin 23y x πω⎛⎫=++ ⎪⎝⎭的图象向右平移43π个单位后44sin 2sin 23333w y w x wx ππππ⎡⎤⎛⎫⎛⎫=-++=+-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦所以有43332013222w kk k w w k w ππ=∴=>∴≥∴=≥ 故选C7.C解析:C 【解析】 【分析】这是求甲独自去一个景点的前提下,三个人去的景点不同的概率,求出相应的基本事件的个数,即可得出结果. 【详解】甲独自去一个景点,则有3个景点可选,乙、丙只能在剩下的两个景点选择,根据分步乘法计数原理可得,对应的基本事件有32212⨯⨯=种;另外,三个人去不同景点对应的基本事件有3216⨯⨯=种,所以61(/)122P A B ==,故选C. 【点睛】本题主要考查条件概率,确定相应的基本事件个数是解决本题的关键.8.D解析:D 【解析】试题分析:根据题意可知34xi y i -=+,所以有3{4y x =-=,故所给的复数的模该为5,故选D.考点:复数相等,复数的模.9.C解析:C 【解析】 【分析】求得函数的导数()(2)()x xe af x x x-'=-⋅,根据函数()f x 在(1,)+∞上有两个极值点,转化为0x xe a -=在(1,)+∞上有不等于2的解,令()xg x xe =,利用奥数求得函数的单调性,得到()1a g e >=且()222a g e ≠=,又由()f x 在(1,2)上单调递增,得到()0f x '≥在(1,2)上恒成立,进而得到x a xe ≥在(1,2)上恒成立,借助函数()x g x xe =在(1,)+∞为单调递增函数,求得2(2)2a g e >=,即可得到答案.【详解】由题意,函数()(3)(2ln 1)xf x x e a x x =-+-+,可得2()(3)(1)(2)()(2)()x xxxa xe a f x e x e a x e x x x x-'=+-+-=--=-⋅,又由函数()f x 在(1,)+∞上有两个极值点,则()0f x '=,即(2)()0x xe ax x--⋅=在(1,)+∞上有两解,即0x xe a -=在在(1,)+∞上有不等于2的解,令()xg x xe =,则()(1)0,(1)x g x x e x '=+>>,所以函数()xg x xe =在(1,)+∞为单调递增函数,所以()1a g e >=且()222a g e ≠=,又由()f x 在(1,2)上单调递增,则()0f x '≥在(1,2)上恒成立,即(2)()0x xe ax x--⋅≥在(1,2)上恒成立,即0x xe a -≤在(1,2)上恒成立,即x a xe ≥在(1,2)上恒成立,又由函数()xg x xe =在(1,)+∞为单调递增函数,所以2(2)2a g e >=,综上所述,可得实数a 的取值范围是22a e >,即2(2,)a e ∈+∞,故选C.【点睛】本题主要考查导数在函数中的综合应用,着重考查了转化与化归思想、逻辑推理能力与计算能力,对导数的应用的考查主要从以下几个角度进行:(1)考查导数的几何意义,求解曲线在某点处的切线方程;(2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数;(3)利用导数求函数的最值(极值),解决函数的恒成立与有解问题,同时注意数形结合思想的应用.10.D解析:D 【解析】 【分析】设目前该教师的退休金为x 元,利用条形图和折线图列出方程,求出结果即可. 【详解】设目前该教师的退休金为x 元,则由题意得:6000×15%﹣x×10%=100.解得x =8000. 故选D . 【点睛】本题考查由条形图和折线图等基础知识解决实际问题,属于基础题.11.D解析:D 【解析】 【分析】旧球个数x=4即取出一个新球,两个旧球,代入公式即可求解. 【详解】因为从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数为x=4,即旧球增加一个,所以取出的三个球中必有一个新球,两个旧球,所以129331227(4)220C C P X C ===,故选D . 【点睛】本题考查离散型随机变量的分布列,需认真分析P(X=4)的意义,属基础题.12.C解析:C 【解析】因为()2f x x ax =+是偶函数,所以22()()20f x x ax f x x ax ax -=-==+∴=所以0a =.所以“0a =”是“()2f x x ax =+是偶函数”的充要条件.故选C.二、填空题13.【解析】试题分析:由复数的运算可知是纯虚数则其实部必为零即所以考点:复数的运算 解析:2-【解析】试题分析:由复数的运算可知,()()12i a i -+是纯虚数,则其实部必为零,即,所以.考点:复数的运算.14.【解析】【分析】由直线方程为与准线得出点坐标再由可得点为线段的中点由此求出点A 的坐标代入抛物线方程得出的值【详解】解:抛物线的准线方程为过点且斜率为的直线方程为联立方程组解得交点坐标为设A 点坐标为因 解析:8【解析】 【分析】由直线方程为3(2)y x =-与准线:al x 4=-得出点B 坐标,再由BM MA =可得,点M 为线段AB 的中点,由此求出点A 的坐标,代入抛物线方程得出a 的值.【详解】解:抛物线()2:0C y ax a =>的准线方程为:a l x 4=-过点()2,0M 33(2)y x =-,联立方程组3(2)4y x a x ⎧=-⎪⎨=-⎪⎩,解得,交点B坐标为(a 4-, 设A 点坐标为00(,)x y , 因为BM MA =,所以点M 为线段AB 的中点,所以00()442402a x y ⎧+-⎪=⎪⎪⎨⎪+⎪=⎪⎩,解得(a A 44+,将)()a a 8A 444++代入抛物线方程,即))()2a 8aa 444+=+, 因为0a >, 解得8a =. 【点睛】本题考查了抛物线的性质、向量相等等知识,解决几何问题时,往往可以转化为代数问题来进行研究,考查了数形结合的思想.15.【解析】【分析】【详解】试题分析:当时的最大值为令解得所以a 的取值范围是考点:利用导数判断函数的单调性解析:1(,)9-+∞【解析】 【分析】 【详解】试题分析:2211()2224f x x x a x a ⎛⎫=-++=--++ ⎪⎝⎭'.当23x ⎡⎫∈+∞⎪⎢⎣⎭,时,()f x '的最大值为22239f a ⎛⎫=+ ⎪⎝⎭',令2209a +>,解得19a >-,所以a 的取值范围是1,9⎛⎫-+∞ ⎪⎝⎭.考点:利用导数判断函数的单调性.16.【解析】【分析】利用复数的运算法则模的计算公式即可得出【详解】解:复数z =(1+i )(1+2i )=1﹣2+3i =﹣1+3i∴|z|故答案为【点睛】对于复数的四则运算要切实掌握其运算技巧和常规思路如其【分析】利用复数的运算法则、模的计算公式即可得出. 【详解】解:复数z =(1+i )(1+2i )=1﹣2+3i =﹣1+3i , ∴|z |22(1)310=-+=. 故答案为10. 【点睛】对于复数的四则运算,要切实掌握其运算技巧和常规思路,如()()a bi c di ++=()()(,,,)ac bd ad bc i a b c d R -++∈.其次要熟悉复数相关概念,如复数(,)a bi a b R +∈的实部为a 、虚部为b 、模为22a b +、对应点为(,)a b 、共轭复数为a bi -.17.2【解析】试题分析:因为四边形是正方形所以所以直线的方程为此为双曲线的渐近线因此又由题意知所以故答案为2【考点】双曲线的性质【名师点睛】在双曲线的几何性质中渐近线是其独特的一种性质也是考查的重点内容解析:2 【解析】试题分析:因为四边形OABC 是正方形,所以45AOB ∠=︒,所以直线OA 的方程为y x =,此为双曲线的渐近线,因此a b =,又由题意知22OB =,所以22222(22)a b a a +=+=,2a =.故答案为2.【考点】双曲线的性质【名师点睛】在双曲线的几何性质中,渐近线是其独特的一种性质,也是考查的重点内容.对渐近线:(1)掌握方程;(2)掌握其倾斜角、斜率的求法;(3)会利用渐近线方程求双曲线方程的待定系数.求双曲线方程的方法以及双曲线定义和双曲线标准方程的应用都和与椭圆有关的问题相类似.因此,双曲线与椭圆的标准方程可统一为的形式,当,,时为椭圆,当时为双曲线.18.【解析】【分析】根据圆的参数方程确定圆的半径和圆心坐标再根据直线与圆相切的条件得出满足的方程解之解得【详解】圆化为普通方程为圆心坐标为圆的半径为由直线与圆相切则有解得【点睛】直线与圆的位置关系可以使解析:34【解析】 【分析】根据圆的参数方程确定圆的半径和圆心坐标,再根据直线与圆相切的条件得出a 满足的方程,解之解得。
2012年潍坊一模理综试卷

2012年高考模拟考试理科综合2012 3 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共12页,满分240分,考试用时150分钟。
考试结束后,将本试卷、答题卡和答题纸一并交回。
答卷前,考生务必将自己的姓名、准考证号、考试科目填涂在试卷、答题卡和答题纸规定的地方。
第Ⅰ卷(必做,共87分)注意事项:1.每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑。
如需改动,用橡皮擦干净以后,再涂写其他答案标号。
不涂答题卡,只答在试卷上不得分。
2.第Ⅰ卷共20小题,1-13题每小题4分,14-20题每小题5分,共87分。
以下数据可供答题时参考:相对原子质量:H 1 C 12N 14O 16Na 23S 32Cl 35 5Fe 56Cu 64Zn 65一、选择题(本题包括13小题,每小题只有一个选项符合题意)1.下列有关实验的描述不科学的是A.低温和秋水仙素诱导多倍体形成的原理是相同的B.提取绿叶中的色素时碳酸钙的作用是防止色素被破坏C.视野中观察到处于质壁分离状态的细胞,不能据此判断该细胞正在失水D.还原糖和蛋白质的检测实验中均需水浴加热2.右图表示某雄性动物中一个正在分裂的体细胞,下列相关描述错误的是A.若A和a所在的染色单体不分离,则产生的子细胞中染色体数目全部异常B.该细胞发生的变异可能是由于碱基对的替换引起的C.该细胞分裂到后期时细胞内有2对同源染色体,2个染色体组D.该细胞分裂所形成子细胞的基因型是BbX A Y和BbX a Y3.某植物群体中基因型AA、aa的个体分别占30%和20%,比较该群体自交与个体间自由交配得到的两个子代群体A.杂合子比例不同B.纯合子比例相同C.基因频率不同D.基因型频率相同4.下列实例与植物激素作用无关的是A.苹果果实自然发育成熟B.豆角茎的缠绕生长C.牵牛花早晨和中午呈现不同颜色D.秋天植物落叶5.采用一定手段破坏细胞中的高尔基体,下列各项受影响最小的是A.浆细胞合成并分泌抗体B.植物细胞进行有丝分裂C.呼吸酶的合成D.兴奋在突触处的传递6.若右图中的各部分彻底水解,得到产物种类最多的是A.①B.②C.③D.④7.2011年为国际化学年,主题为“化学—我们的生活,我们的未来”。
2012年高考数学经典模拟题含答案1

2012年高考模拟试题数 学(理科)考试说明:本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
(1)答题前,考生先将自己的姓名、准考证号码填写清楚。
(2)请按照题号顺序在各题目的答题区内作答,在草稿纸和试卷上答题视为无效。
(3)保持卡面清洁,不得折叠、不要弄皱,不准使用涂改液和刮纸刀等用具。
第Ⅰ卷(选择题 共60分)一.选择题(每题5分,共12小题,满分60分,每小题只有一个选项正确。
) 1. 若集合}22{+=+=x x x A ,},02{2>+=x x B 则=⋂B AA .)0,2(-B .)0,2[-C . ),0(+∞D .),0[+∞ 2. 复数ii-12的共轭复数是A .i -1B .i +1C .i +-1D .i --13.已知43)4sin(-=+πx ,则x 2sin 的值是A .81-B .81 C .42 D .42-4. 抛物线x y122-=的准线与双曲线13922=-y x 的两条渐近线所围成的三角形面积是A .3B .32C .2D .335. A 、B 两名同学在4次数学考试中的成绩统计如下面的茎叶图所示,若A 、B 的平均成绩分别是AX、B X ,则下列结论正确的是A .AX >BX ,B 比A 的成绩稳定 B .A X <BX ,B 比A 的成绩稳定 C .A X >BX ,A 比B 的成绩稳定 D .A X <BX, A 比B 的成绩稳定6. 双曲线)0,0(12222>>=-b a y x 的左、右焦点分别为1F 、2F ,离心率为e ,过的直线与双曲线的右支交与A 、B 两点,若AB F 1△是以A 为直角顶点的等腰直角三角形,则=2e A .323- B .323+ C .225+ D .225- 7. 函数)(x f y =在定义域)3,23(-内可导,其图像如图所示,记)(x f y =的导函数为)(x f y '=,则不等式0)(≤'x f 的解集为 A .]3,2[]1,31[⋃-B .]38,34[]31,1[⋃-C .]2,1[]21,23[⋃-D .),3[]2,1[]21,23[+∞⋃⋃-8.执行下面的程序框图,若9=P ,则输出的=SA .187B .98C .52D .13109. 已知某个几何体的三视图如图(正视图中的弧线是半圆),根据图中标出的尺寸,可得这个几何体的表面积是(单位:2cm )A .π24+B .π34+C .π26+D .π36+10.现将一个边不等的凸五边形的各边进行染色,每条边可以染红、黄、蓝三种颜色中的一种,但是不允许相邻的边有相同的颜色,则共有( )种染色方法A .30B .36C .48D .50 11.下列命题中正确的一项是 A .“21=m ”是“直线013)2(=+++my x m 与直线03)2()2(=-++-y m x m 相互平行”的充分不必要条件B .“直线l 垂直平面α内无数条直线”是“直线l 垂直于平面α”的充分条件D .R x p ∈∃:,0222≤++x x 。
高考数学理科模拟试题(附答案)

高三年级第一次模拟考试数 学 试 题(理)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,共150分,考试时间120分钟。
第Ⅰ卷(选择题,共40分)一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,将答案涂在答题卡上.........。
1.复数23()1i i +-= ( )A .-3-4iB .-3+4iC .3-4iD .3+4i2.已知条件:|1|2,:,p x q x a +>>⌝⌝条件且p 是q 的充分不必要条件,则实数a 的取值范围是( ) A .1a ≥ B .1a ≤ C .1a ≥- D .3a ≤-3.函数()|2|ln f x x x =--在定义域内零点可能落在下列哪个区间内( )A .(0,1)B .(2,3)C .(3,4)D .(4,5) 4.如右图,是一程序框图,则输出结果为( )A .49B .511 C .712 D .613 5.已知n S 为等差数列{}n a 的前n 项和,若641241,4,S S S S S ==则 的值为( )A .94B .32C .54D .46.要得到函数()sin(2)3f x x π=+的导函数'()f x 的图象,只需将()f x 的图象( )A .向左平移2π个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)B .向左平移2π个单位,再把各点的纵坐标缩短到原来的12倍(横坐标不变)C .向右平移4π个单位,再把各点的纵坐标伸长到原来的12倍(横坐标不变)D .向右平移4π个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) 7.过双曲线22221(0,0)x y a b a b-=>>的一个焦点F 引它的渐近线的垂线,垂足为M ,延长FM 交y 轴于E ,若|FM|=2|ME|,则该双曲线的离心率为( )A .3B .2C .3D .28.如图所示的每个开关都有闭合与不闭合两种可能,因此5个开关共有25种可能,在这25种可能中电路从P 到Q 接通的情况有( )A .30种B .10种C .24种D .16种第Ⅱ卷(非选择题,共110分)二、填空题:本大题共6小题,每小题5分,共30分,将答案填写在答题纸上。
高考数学-热点专题专练-专题六-算法、统计、概率、复数测试题-理精品
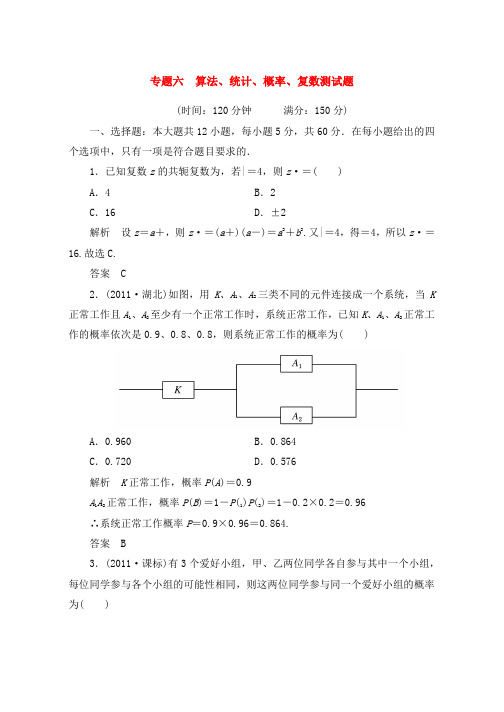
专题六算法、统计、概率、复数测试题(时间:120分钟满分:150分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z的共轭复数为,若|=4,则z·=( )A.4 B.2C.16 D.±2解析设z=a+,则z·=(a+)(a-)=a2+b2.又|=4,得=4,所以z·=16.故选C.答案C2.(2011·湖北)如图,用K、A1、A2三类不同的元件连接成一个系统,当K 正常工作且A1、A2至少有一个正常工作时,系统正常工作,已知K、A1、A2正常工作的概率依次是0.9、0.8、0.8,则系统正常工作的概率为( )A.0.960 B.0.864C.0.720 D.0.576解析K正常工作,概率P(A)=0.9A1A2正常工作,概率P(B)=1-P(1)P(2)=1-0.2×0.2=0.96∴系统正常工作概率P=0.9×0.96=0.864.答案B3.(2011·课标)有3个爱好小组,甲、乙两位同学各自参与其中一个小组,每位同学参与各个小组的可能性相同,则这两位同学参与同一个爱好小组的概率为( )解析古典概型,总的状况共3×3=9种,满意题意的有3种,故所求概率为P==.答案A4.对变量x,y有观测数据(,)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(,)(i=1,2,…,10),得散点图2.由这两个散点图可以推断( )A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C.变量x与y负相关,u与v正相关D.变量x与y负相关,u与v负相关解析夹在带状区域内的点,总体呈上升趋势的属于正相关;反之,总体呈下降趋势的属于负相关.明显选C.答案C5.某个容量为100的样本的频率分布直方图如图所示,则在区间[4,5)上的数据的频数为( )A.15 B.20C.25 D.30解析在区间[4,5)的频率/组距的数值为0.3,而样本容量为100,所以频数为30.故选D.答案D6.(2011·辽宁丹东模拟)甲、乙两名同学在五次测试中的成果用茎叶图表示如图,若甲、乙两人的平均成果分别是x甲、x乙,则下列结论正确的是( )A.x甲>x乙;乙比甲成果稳定B.x甲>x乙;甲比乙成果稳定C.x甲<x乙;甲比乙成果稳定D.x甲<x乙;乙比甲成果稳定解析由题意得,x甲=×(68+69+70+71+72)=×350=70,x乙=×(63+68+69+69+71)=×340=68,所以x甲>x乙.又=×(22+12+02+12+22)=×10=2,=×(52+02+12+12+32)=×36=7.2,所以甲比乙成果稳定.故选B.答案B7.(2012·福建)如图所示,在边长为1的正方形中任取一点P,则点P恰好取自阴影部分的概率是( )解析由图示可得,图中阴影部分的面积S=(-x)=错误!错误!=错误!-错误!=,由此可得点P恰好取自阴影部分的概率P==.答案C8.如图所示的流程图,最终输出的n的值是( )A.3 B.4C.5 D.6解析当n=2时,22>22不成立;当n=3时,23>32不成立;当n=4时,24>42不成立;当n=5时,25>52成立.所以n=5.故选C.答案C9.正四面体的四个表面上分别写有数字1,2,3,4,将3个这样的四面体同时投掷于桌面上,与桌面接触的三个面上的数字的乘积能被3整除的概率为( )解析将正四面体投掷于桌面上时,与桌面接触的面上的数字是1,2,3,4的概率是相等的,都等于.若与桌面接触的三个面上的数字的乘积能被3整除,则三个数字中至少应有一个为3,其对立事务为“与桌面接触的三个面上的数字都不是3”,其概率是3=,故所求概率为1-=.答案C10.用系统抽样法从160名学生中抽取容量为20的样本,将160名学生随机地从1~160编号,按编号依次平均分成20组(1~8号,9~16号,…,153~160号),若第16组抽出的号码为126,则第1组中用抽签的方法确定的号码是( ) A.5 B.6C.7 D.8解析设第1组抽出的号码为x,则第16组应抽出的号码是8×15+x=126,∴x=6.故选B.答案B11.(2011·杭州市第一次教学质量检测)体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则始终发到3次为止.设学生一次发球成功的概率为p(p≠0),发球次数为X,若X的数学期望E(X)>1.75,则p的取值范围是( )解析发球次数X的分布列如下表,所以期望解得p>(舍去)或p<,又p>0,故选C . 答案 C12.(2012·济宁一中高三模拟)某计算机程序每运行一次都随机出现一个五位的二进制数A =,其中A 的各位数中,a 1=1,(k 可取2,3,4,5)出现0的概率为,出现1的概率为.记ξ=a 1+a 2+a 3+a 4+a 5,当程序运行一次时,ξ的数学期望E(ξ)=( )解析 ξ=1,P 1=40=, ξ=2时,P 2=3·=, ξ=3时,P 3=·2·2=, ξ=4时,P 4=·3=, ξ=5时,P 5=4=,E(ξ)=1×+2×+3×+4×+5×=. 答案 C二、填空题:本大题共4小题,每小题4分,共16分,将答案填在题中的横线上.13.(2012·广东湛江十中模拟)在可行域内任取一点,规则如流程图所示,则能输出数对(x ,y)的概率为.解析如图所示,给出的可行域即为正方形与其内部.而所求事务所在区域为一个圆,两面积相比即得概率为.答案14.(2012·山东潍坊模拟)给出下列命题:(1)若z∈C,则z2≥0;(2)若a,b∈R,且a>b,则a+i>b+i;(3)若a∈R,则(a+1)i是纯虚数;(4)若z=,则z3+1对应的点在复平面内的第一象限.其中正确的命题是.解析由复数的概念与性质知,(1)错误;(2)错误;(3)错误,若a=-1,(a+1)i=0;(4)正确,z3+1=(-i)3+1=i+1.答案(4)15.(2011·上海)随机抽取的9位同学中,至少有2位同学在同一月份诞生的概率为.(默认每个月的天数相同,结果精确到0.001)解析P=1-≈0.985.答案0.98516.若某程序框图如图所示,则该程序运行后输出的y等于.解析由图中程序框图可知,所求的y是一个“累加的运算”,即第一步是3;其次步是7;第三步是15;第四步是31;第五步是63.答案63三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)某班主任对全班50名学生学习主动性和对待班级工作的看法进行了调查,统计数据如下表所示:是多少?抽到不太主动参与班级工作且学习主动性一般的学生的概率是多少?(2)试运用独立性检验的思想方法分析:学生的学习主动性与对待班级工作的看法是否有关系?并说明理由.(参考下表)主动参与班级工作且学习主动性一般的学生有19人,概率为.(2)K2==≈11.5,∵K2>10.828,∴有99.9%的把握说学生的学习主动性与对待班级工作的看法有关系.18.(本小题满分12分)在1996年美国亚特兰大奥运会上,中国香港风帆选手李丽珊以惊人的耐力和斗志,勇夺金牌,为香港体育史揭开了“突破零”的新一页.在风帆竞赛中,成果以低分为优胜.竞赛共11场,并以最佳的9场成果计算最终的名次.前7场竞赛结束后,排名前5位的选手积分如表一所示:表一此时让你预料谁将获得最终的成功,你会怎么看?解由表一,我们可以分别计算5位选手前7场竞赛积分的平均数和标准差,分别作为衡量各选手竞赛的成果与稳定状况,如表二所示.表二就是说,在前7场竞赛过程中,她的成果最为优异,而且表现也最为稳定.尽管此时还有4场竞赛没有进行,但这里我们可以假定每位运动员在各自的11场竞赛中发挥的水平大致相同(实际状况也的确如此),因此可以把前7场竞赛的成果看做是总体的一个样本,并由此估计每位运动员最终的竞赛的成果.从已经结束的7场竞赛的积分来看,李丽珊的成果最为优异,而且表现最为稳定,因此在后面的4场竞赛中,我们有足够的理由信任她会接着保持优异而稳定的成果,获得最终的冠军.19.(本小题满分12分)(2012·苏州五中模拟)设不等式组错误!表示的区域为A,不等式组错误!表示的区域为B,在区域A中随意取一点P(x,y).(1)求点P落在区域B中的概率;(2)若x、y分别表示甲、乙两人各掷一次正方体骰子所得的点数,求点P落在区域B中的概率.解(1)设区域A中随意一点P(x,y)∈B为事务M.因为区域A的面积为S1=36,区域B在区域A中的面积为S2=18.故P(M)==.(2)设点P(x,y)落在区域B中为事务N,甲、乙两人各掷一次骰子所得的点P(x,y)的个数为36,其中在区域B中的点P(x,y)有21个.故P(N)==.20.(本小题满分12分)某中学部分学生参与全国中学数学竞赛,取得了优异成果,指导老师统计了全部参赛同学的成果(成果都为整数,试题满分120分),并且绘制了“频率分布直方图”(如图),请回答:(1)该中学参与本次数学竞赛的有多少人?(2)假如90分以上(含90分)获奖,则获奖率是多少?(3)这次竞赛成果的中位数落在哪段内?(4)上图还供应了其他信息,请再写出两条.解(1)由直方图(如图)可知:4+6+8+7+5+2=32(人);(2)90分以上的人数为7+5+2=14(人),∴×100%=43.75%.(3)参赛同学共有32人,按成果排序后,第16个、第17个是最中间两个,而第16个和第17个都落在80~90之间.∴这次竞赛成果的中位数落在80~90之间.(4)①落在80~90段内的人数最多,有8人;②参赛同学的成果均不低于60分.21.(本小题满分12分)(2012·天津)现有4个人去参与某消遣活动,该活动有甲、乙两个嬉戏可供参与者选择.为增加趣味性,约定:每个人通过掷一枚质地匀称的骰子确定自己去参与哪个嬉戏,掷出点数为1或2的人去参与甲嬉戏,掷出点数大于2的人去参与乙嬉戏.(1)求这4个人中恰有2人去参与甲嬉戏的概率;(2)求这4个人中去参与甲嬉戏的人数大于去参与乙嬉戏的人数的概率;(3)用X,Y分别表示这4个人中去参与甲、乙嬉戏的人数,记ξ=-,求随机变量ξ的分布列与数学期望Eξ.解依题意,这4个人中,每个人去参与甲嬉戏的概率为,去参与乙嬉戏的概率为.设“这4个人中恰有i人去参与甲嬉戏\”为事务(i=0,1,2,3,4),则P()=4-i.(1)设4个人中恰有2人去参与甲嬉戏的概率为P(A2)P(A2)=22=.(2)设“这4个人中去参与甲嬉戏的人数大于去参与乙嬉戏的人数”为事务B,则B=A3∪A4,由于A3和A4互斥,故P(B)=P(A3)+P(A4)=3+4=.所以,这4个人中去参与甲嬉戏的人数大于去参与乙嬉戏的人数的概率为.(3)ξ的全部可能取值为0,2,4.由于A1与A3互斥,A0和A4互斥,故P(ξ=0)=P(A2)=,P(ξ=2)=P(A1)+P(A3)=,P(ξ=4)=P(A0)+P(A4)=.所以ξ的分布列是随机变量ξ22.(本小题满分14分)(2012·福建)受轿车在保修期内修理费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保障期内的概率;(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列;(3)该厂预料今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.解(1)设“甲品牌轿车首次出现故障发生在保修期内”为事务A.则P(A)==.(2)依题意得,X1的分布列为X2的分布列为(3)由(2)得,E(X1)=1×+2×+3×==2.86(万元),E(X2)=1.8×+2.9×=2.79(万元).因为E(X1)>E(X2),所以应生产甲品牌轿车.。
山东省潍坊市2012年高考仿真试题(一)理科数学试题.pdf

第11讲┃ 浮力 增大 第11讲┃ 浮力 第11讲┃ 浮力 1.2×10-4 m3 2 N 1.2 N 第11讲┃ 浮力 第11讲┃ 浮力D 第11讲┃ 浮力 第11讲┃ 浮力 第11讲┃ 浮力 2.5×103 1.5 1.0×10-4 第11讲 浮力 第11讲┃ 浮力 考点34 浮力及其计算 ┃考点自主梳理与热身反馈┃ 竖直向上 ρ液gV排 第11讲┃ 浮力 考点 35 物体的浮沉条件 第11讲┃ 浮力 第11讲┃ 浮力 考点 36 浮力的应用 漂浮 等于 不变 大于 上浮 自身重力 小于 浮力 第11讲┃ 浮力 考点 37 压强、浮力的综合计算 相等 越大 第11讲┃ 浮力 第11讲┃ 浮力 1.下列有关浮力的说法正确的是( ) A.物体的密度越大,受到的浮力越大 B.物体的体积越大,受到的浮力越大 C.物体浸入水中越深,受到的浮力越大 D.浸没在水中的物体,可能不受浮力 D 第11讲┃ 浮力 2.【2013·宜昌】两手分别拿着一个小木块和一个大石块浸没在水中,同时松手,小木块上浮,大石块下沉。
比较松手时两者所受的浮力( ) A.木块受的浮力大 B.石块受的浮力大 C.两者受的浮力一样大 D.条件不足,无法比较 B 第11讲┃ 浮力 D 第11讲┃ 浮力 5 3 600 第11讲┃ 浮力 ┃考向互动探究与方法归纳┃ 750 不变 [解析] 第11讲┃ 浮力 第11讲┃ 浮力 第11讲┃ 浮力 第11讲┃ 浮力 5×103 0.4 103 无关 第11讲┃ 浮力 第11讲┃ 浮力 第11讲┃ 浮力分析该类图象时要抓住关键点:深度为0时,弹簧测力计的示数为物体的重力;深度为10 cm时,物体刚好全部浸没;深度为10 cm以后,弹簧测力计示数不变,浮力大小与物体所处深度无关。
第11讲┃ 浮力 ┃考题自主训练与名师预测┃A 2.【2013·泉州】把密度为0.6×103 kg/m3、重为12 N的木块放入水中,当它静止时所处的状态及受到的浮力大小分别是( ) A.漂浮,F浮>12 N B.漂浮,F浮=12 N C.沉底,F浮<12 N D.沉底,F浮=12 N 第11讲┃ 浮力 B 3.2013年5月31日,南宁首艘千吨级维权执法专用海监船“中国海监1118号”在梧州顺利下水,这将增强海监队伍在北部湾海域的执法能力。
高考数学仿真试题(一) 理

2012年普通高考理科数学仿真试题(一)本试卷分第I 卷和第II 卷两部分,共4页,满分150分,考试用时120分钟,考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上。
2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上。
3.第II 卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
4.填空题请直接填写答案,解答题应写出文字说明、演算步骤或推证过程。
第I 卷(共60分) 一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数i z 2321-=,z 是z 的共轭复数,则2z = A. zB.z +21C. z1-D.z1 2.已知集合⎭⎬⎫⎩⎨⎧-<=11|x x A ,B={}01|<<-x x ,则 A. A ⊂≠B B. B ⊂≠A C.A=B D.=⋂B A3.曲线nx x y 1=在点(e , e )处的切线与直线1=+ay x 垂直,则实数a 的值为 A.2B.-2C.21D.-21 4.已知函数⎪⎩⎪⎨⎧<-≥-=-),0(12),0(21)(x x x f x x则该函数是A.偶函数,且单调递增B.偶函数,且单调递减C.奇函数,则单调递增D.奇函数,且单调递减 5.“cosx=1”是“sinx=0”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件 6.已知-9,a 1,a 2,a 3,-1五个实数成等差数列,-9,b 1,b 2,b 3,-1五个实数成等比数列,则231b a a -等于A. 34±B. 32±C. 34-D. 347.一个几何体的三视图如图所示,则该几何体的体积为A. 23aB. 63aC. 123aD. 183a8.圆心在曲线)0(412<=x x y 上,并且与直线y=-1及y 轴都相切的圆的方程是A. 2)1()2(22=-++y xB. 4)2()1(22=-+-y xC. 4)1()2(22=-+-y xD. 4)1()2(22=-++y x9.函数x x x f ππcos sin )(+=对任意的R x ∈都有)()()(21x f x f x f ≤≤成立,则12x x -的最小值为A.21 B.1 C.2 D.410.已知直线m ,l ,平面α,β,且α⊥m ,β⊂l ,给出下列命题:①若βα//,则l m ⊥;②若βα⊥,则l m //;③若l m ⊥,则βα//;④若l m //,则βα⊥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
保密★启用前 试卷类型:A
2012年潍坊第一次高考模拟考试
数 学(理工农医类)
2012.3
本试卷共4页,分第1卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.
考试时间120分钟.
第1卷(选择题共60分)
注意事项:
1.答第1卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上. 2.每题选出答案后,用2 B 铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再改涂其它答案标号.
一、选择题:本大题共l2小题。
每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.集合M={|
01
x x x >-},集合N={1
2|y y x =},则M ∩N=
A . (0,+∞)
B . (1,+∞)
C . (0,1)
D . (0,1)∪(1,+∞) 2.复数
122i i
+-=
A .-i
B .i
C .5 i
D .45i +
3.不等式| x -2| -| x -l | >0的解集为 A .(-∞,32
) B .(-∞,-32
)
C .(
32
,+∞) D .(-32
,+∞)
4.命题“∀x ∈[1,2],x 2-a ≤0”为真命题的一个充分不必要条件是
A .a ≥4
B .a ≤4
C .a ≥5
D .a ≤5
5.将函数y =cos2x 的图象向右平移4
π
个单位,得到函数y =f (x )·sin x 的图象,则f (x )的表达
式可以是
A .f (x )=-2cosx
B .f (x )=2cosx
C .f (x )=
2
sin2x D .f (x )=
2
(sin2x+cos2x)
6.运行右图所示的程序框图,若输出结果为137
,则判断
框中应该填的条件是 A .k>5 B .k>6 C .k>7 D .k>8
7.已知向量a =(cosx ,sinx),b =(,a ·b =85
,且
4
2
x π
π
<<
,则cos(4
x π
+
)的值
为 A .
45
B .
35
C .-45
D .-
35
8.已知函数f (x )= |ln |1||x e x x
--
,则函数y=f (x +1)的大致图象为
9.在空间中,l 、m 、n 是三条不同的直线,,,αβγ是三个不同的平面,则下列结论 错误的是
A. 若//,//αβαγ,则//βγ
B .若//,//,l l m αβαβ⋂=,则//l m
C .若,,l αβαγβγ⊥⊥⋂=,则l α⊥
D .若,,,,m l n l m l n αββγαγ⋂=⋂=⋂=⊥⊥,则m n ⊥
10.直线4kx-4y-k=0与抛物线y 2
=x 交于A 、B 两点,若|AB|=4,则弦AB 的中点到直线x+12
=0
的距离等于
A .
74
B .2 c .
94
D .4
11.已知矩形ABCD 的面积为8,当矩形周长最小时,沿对角线AC 把△ACD 折起,则三棱锥D —ABC 的外接球的表面积等于
A .4π
B .8π
C .1 6π
D .24π
1 2.若直角坐标平面内的两点P 、Q 满足条件:
①P 、Q 都在函数y=f (x )的图象上;②P 、Q 关于原点对称.
则称点对[P ,Q]是函数y=f (x )的一对“友好点对”(点对[P ,Q]与[Q ,P]看作同一对“友好点对"). 已知函数f (x )=22
log (0)4(0)
x x x x
x >⎧⎨
--≤⎩,则此函数的“友好点对”有
A .0对
B .1对
C .2对
D .3对
第Ⅱ卷 (非选择题共90分)
注意事项:
1.将第Ⅱ卷答案用0.5mm 的黑色签字笔答在答题纸的相应位置上。
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共4小题,每小题4分,共l 6分. 1 3.双曲线
22
2
1(0)x y a a
-=>的离心率为2,则该双曲线的渐近线方程为_________.
1 4.如图,长方形的四个顶点为O(0,0),A(1,0),B(1,2),C(0,2),曲线2y ax =经过点B .现将一质点随机投人长方形OABC 中,则质点落在图中阴影区域的概率是_______.
1 5.某工厂将甲、乙等五名新招聘员工分配到三个不同的车间,每个车间至少分配一名员工,且甲、乙两名员工必须分到同一个车间,则不同分法的种数为________.
1 6.已知定义在R 上的偶函数满足:f (x +4) =f (x )+f (2),且当x ∈[0,2]时,y= f (x )单调递减,给出以下四个命题: ①f (2)=0;
②x=-4为函数y=f (x )图象的一条对称轴;
③函数y=f (x )在[8,10]单调递增;
④若方程f (x )=m 在[-6,-2]上的两根为x 1,x 2,则x 1+x 2=-8. 以上命题中所有正确命题的序号为_________.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 1 7.(本小题满分1 2分)
设函数f (x )=2sin()2cos 1(0)6
2
x x πω
ωω--+>.直线与函数y=f (x )图象相邻两
交点的距离为π.
(I)求ω的值;
(Ⅱ)在△ABC 中,角A 、B 、C 所对的边分别是a 、b 、c ,若点(2
B ,0)是函数y=f (x )图
象的一个对称中心,且b=3,求△ABC 外接圆的面积.
1 8.(本小题满分l 2分)
在等比数列{a n }中,a n >0(n ∈N*),公比q ∈(0,1),且a 3a 5+2a 4a 6+a 3a 9=100,又4是a 4与a 6的等比中项.
(I)求数列{a n }的通项公式;
(Ⅱ)设b n =log 2a n ,求数列{|b n |}的前n 项和S n .
1 9.(本小题满分1 2分)
如图,正三棱柱ABC —A 1 B 1C l 中,AB=2,AA 1=3,D 为C1B 的中点,P 为AB 边上的动点.
(I)若P 为AB 中点,求证DP ∥平面ACC l A 1; (Ⅱ)若DP ⊥AB ,求二面角D —CP —B 的余弦值.
20.(本小题满分1 2分)
某学校为调查了解学生体能状况,决定对高三学生进行一次体育达标测试,具体测试项目有100米跑、立定跳远、掷实心球.测试规定如下:
①三个测试项目中有两项测试成绩合格即可认定为体育达标;
②测试时要求考生先从三个项目中随机抽取两个进行测试,若抽取的两个项目测试都合格或都不合格时,不再参加第三个项目的测试;若抽取的两个项目只有一项合格,则必须参加第三项测试.
已知甲同学跑、跳、掷三个项目测试合格的概率分别是
123
,,234
,各项测试时间间隔恰当,每次测试互不影响.
(I)求甲同学恰好先抽取跳、掷两个项目进行测试的概率; (Ⅱ)求甲同学经过两个项目测试就能达标的概率;
(Ⅲ)若甲按规定完成测试,参加测试项目个数为X ,求X 的分布列和期望.
2 1.(本小题满分1 2分)
已知直线l :y x =+
O :x 2
+y 2
=5,椭圆E :
222
2
1(0)y x a b a
b
-
=>>的离
心率3
e =
l 被圆O 截得的弦长与椭圆的短轴长相等.
(I)求椭圆E 的方程;
(Ⅱ)过圆O 上任意一点P 作椭圆E 的两条切线,若切线都存在斜率,求证两切线斜率之积为定值.
22.(本小题满分14分)
已知函数f (x )=2
(33),[2,](2)x
x x e x t t -+∈->-. (I)当t<1时,求函数y=f (x )的单调区间; (Ⅱ) 设m = f (-2),n = f (t ),求证m<n ;
(Ⅲ)设g(x)=f (x )+(2)x
x e -,判断并证明是否存在区间[a ,b ](a >1)使函数y=g(x)在[a ,b ]上的值域也是[a ,b ].。
