列联表
高级社会统计学第九部分 列联表

86.22 9.49 以认为子辈职业与父辈职业是有关系的
第九部分 列联表
四、列联强度 (一)变量间的相关 2 上节谈到通过统计量 值检验列联表变量间是否 存在关系.在确定了存在关系之后,进一步要问的问题将 是关系的程度如何.相关程度的度量方法根据变量层次 不同而有所不同.具体来说,由于列联表研究对象仅是定 类变量,因此列联表中的频次分布情况,不仅是检验是否 存在关系的依据,同时也是度量变量间关系强弱的依据. 相关程度越高,说明变量间的关系越密切.
四、列联表的检验 (一)列联表检验的原假设
H 0 : pij pi p j , 其中i 1,2, c; j 1,2, r 由于pi和p j 是总体的边缘分布, 一般都是未知的,因此可以用 样本中的边缘频率分布作为它的点估计值 : ni ˆ pi Pi , i 1,2, c n n j ˆ p j P j , j 1,2, r n ˆ、 P ˆ 表示样本的频率分布 P i j
第九部分 列联表
二、列联表中变量的分布
(二)边缘分布 同理, 关于x的边缘分布是把联合分布中的概率按列加总起来, 就得到关于x的 边缘分布 : p ( x x1 ) p11 p12 p1r p1 p ( x x2 ) p21 p22 p2 r p2 p ( x xc ) pc1 pc 2 pcr pc
四、列联强度
例, 对下表求系数和Q系数
未感冒 患感冒
解 :
新药 50 0
安慰药 28 22
50 22 0.53 (50 28)(0 22)(50 0)( 28 22)
22 50 0 Q 1 22 50 0 由于我们更关注新药对预防感冒是否有效,因此从 列联表上的频次看, Q系数应更有效.
列联表公式

列联表公式摘要:1.列联表公式的定义与概念2.列联表公式的分类与应用3.列联表公式的计算方法与示例4.列联表公式的优缺点分析5.列联表公式在实际问题中的应用案例正文:一、列联表公式的定义与概念列联表公式,是一种用于解决计数问题中列联表的统计分析方法,它是由英国数学家皮尔逊(Karl Pearson)发明的,被称为皮尔逊相关系数公式,也称为皮尔逊积矩相关系数。
它是一种用于衡量两个分类变量之间相关性的统计方法,其主要用于分析两组数据之间的相关程度。
二、列联表公式的分类与应用列联表公式主要分为两大类,一类是四格表,主要用于分析两组分类变量之间的关系;另一类是n 格表,主要用于分析多组分类变量之间的关系。
在实际应用中,列联表公式被广泛应用于社会科学、生物统计学、医学研究等领域。
三、列联表公式的计算方法与示例列联表公式的计算方法是通过公式来计算相关系数,其公式为:r = (n(ad - bc)) / sqrt(n(ad - bc) + (a + b)(c + d)(a + c)(b + d))。
其中,a、b、c、d分别代表四格表中四个格子的频数,n 代表样本容量。
以一个例子来说明,假设有两个变量A 和B,其中A 有两种可能的取值(A1 和A2),B 也有两种可能的取值(B1 和B2)。
如果我们有如下的频数:A1B1=40,A1B2=20,A2B1=10,A2B2=30。
则,a=60,b=60,c=30,d=50,n=150。
代入公式,可以得到相关系数r 的值。
四、列联表公式的优缺点分析列联表公式的优点在于其能够直观地反映出两组分类变量之间的相关程度,且计算简便,易于理解。
然而,其缺点在于,它只能反映出两组变量之间的相关程度,对于多组变量之间的相关性分析,需要使用其他的统计方法。
列联分析

列联分析一、列联表的构造列链表是由两个以上的变量进行交叉分类的频数分布表。
例如表1:表1(列)的划分类别视为C,则可以把每一个具体的列联表称为R×C列联表。
二、列联表的分布在表1中,最右边显示了态度变量的总数,如赞成改革方案的共有279人,反对改革方案的共有141人,对此称为行的边缘分布。
同理,100、120、90、110称为列边缘分布。
这样列联表所表现的就是在变量X条件下变量Y的分布,或者是在变量Y的条件下变量X的分布,因此又把列联表中的观察值分布称为条件分布,每个具体的观察值就是条件频数。
例如,一个公司赞成改革方案的职工有68人就是一个条件频数。
为了能在相同的基数上比较,使列联表中的数据提以对变量的联合分布的关系看得更清楚一些。
为了更深入的分析,需引入期望分布的概念。
期望值分布表。
如表3所示。
在全部420个样本中,赞成改革方案的有279人,占总数的66.4%,那么对第一分公司来说,赞成该方案的人数应当为0.664×100=66人,66人即为期望值。
将观察值和期望值频数结合在一起,就可以得到观察值和期望值对比分布表,如表4所示。
就应该有664.04321====ππππ(i π为第i 个分公司赞成改革方案的百分比),对于需要验证这一假设,可以采用2χ分布进行检验。
三、2χ统计量2χ可以用于变量间拟合优度检验和独立性检验,可以利用测定两个分类变量之间的相关程度。
若用0f 表示观察值频数,用e f 表示期望值频数,则2χ统计量为:()∑-=ee f f f 202χ计算2χ统计量的步骤(可见表5): 步骤一:用观察值0f 减去期望值e f 。
步骤二:将()e f f -0之差平方。
步骤三:将平方20)(e f f -结果除以e f 。
步骤四:将步骤三的结果加总。
表5 2χ计算表0f e f ()e f f -020)(e f f - 20)(e f f -/e f 6866 2 4 0.060606 75 80 -5 25 0.3125 57 60 -3 9 0.15 79 73 6 36 0.493151 32 34 -2 4 0.117647 45 40 5 25 0.625 33 30 3 9 0.3 31 37 -6 36 0.9729733.031877()∑-=ee f f f 202χ=3.03192χ统计量有这样几个特征:首相2χ≥0,因为它是对平方值结果的汇总。
列联表公式

列联表公式
【最新版】
目录
1.列联表的定义与作用
2.列联表的构成
3.列联表的计算公式
4.列联表的应用示例
正文
一、列联表的定义与作用
列联表,又称交叉频数表,是一种用于展示两组或多组数据之间关系的统计工具。
通过列联表,我们可以清晰地看到各组数据的频数分布情况,从而分析它们之间的联系和规律。
二、列联表的构成
列联表通常由四个部分组成,分别是:行标题、列标题、交叉频数和合计。
其中,行标题和列标题表示数据的分类项目,交叉频数是指在两个分类项目中同时出现的数据个数,合计则是指某一行或某一列的频数之和。
三、列联表的计算公式
列联表的计算公式主要包括以下两个方面:
1.交叉频数的计算公式:交叉频数 = 行频数×列频数 / 总频数
2.合计的计算公式:合计 = 行频数 + 列频数 - 交叉频数
四、列联表的应用示例
假设有一组关于某商场顾客购买行为的数据,我们可以通过列联表来分析顾客的购物习惯。
例如,我们可以将数据按照顾客的性别和购买的商品类别进行分类,然后计算各种情况下的交叉频数和合计。
通过分析列联
表,我们可以得出如下结论:
1.男性和女性顾客在购买商品类别上的差异;
2.不同商品类别的销售情况;
3.顾客的购物偏好等。
第9章 列联表

系数
系数
以值为基础的相关测量
系数
C系数 V 系数
相关系数
1.
2. 3.
测度 22列联表中数据相关程度的一个量 对于22 列联表, 系数的值在0~1之间 相关系数计算公式为 2
n
2 (nij eij) r c 2 式中: i 1 j 1 e ij n为实际频数的总个数,即样本容量
3.
2
i 1 j 1
r
c
(nij eij ) 2 eij
其自由度为(r 1)(c 1) 式中:nij
— 列联表中第i行第j列类别的实际频数 eij — 列联表中第i行第j列类别的期望频数
检验
P279: 例2
使用 统计量检验列联表时, 需要注意的问题?
1. 对于2×2列联表,需要用修正的公式:
10/40 20/40 10/40
2/57 35/57 20/57
60/124
32/124 1
合计
1
1
1
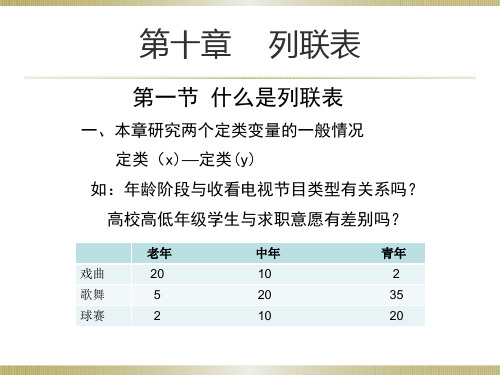
一般只研究控制自变量x之后,因变量y的条件分布。
列联表中变量的相互独立性
列联表中变量的相互独立性
关于y的条件分布
老年
戏曲
y边缘分布
计算结果见表10-15(P275)
中年
青年Βιβλιοθήκη 合计32/12420/27
第三节 列联表中的相关测量
列联强度
列联表中的相关测量
1.
统计量检验只检验了列联表变量间是否存在 关系,而没有测量关系的强度 列联表中的相关测量就是检验变量间关系的强度 列联表相关测量的指标主要有
2. 3.
以值为基础的相关测量
第十章列联表
Eij npij npi p* j nin j
n
(二)以减少误差比例为基础的相关性测试
我们知道社会现象的研究,旨在探索现象与现象之间的联系。 而现象间关系的研究,可以帮助我们从一个现象预测另一现 象。其中关系密切者,在预测中通过某一现象预测另一现象 时,其盲目性必较关系不密切者为少。 因此,变量间的相关程度,可以通过在不知y与x有关系时, 预测y时的全部误差与知道y与x有关系时,用x去预测y的误 差的相对误差的大小度量之。又称减少误差比例法(PRE)
现在来比较表10-17和表10-18,可以想象,如果总体中H0为 真的话,那么实测频次列联表的格值和期望频次列联表中的
格值相差不多的可能性较大。反之,如果两表的格值差距很
大,则原假设H0很可能不反映真实情况。
SPSS软件实现分析
输入数据
操作步骤:1.加权(date-weightcases-把频数选入 weight case by frequency variable) 2.选descriptive statitics-crosstable,把父辈职业、子 辈职业选入Row(s)和column(s) 3.点statitics选Chi square 继续 4.点cell 选cunt下的abserved 和Expected 最后点ok
为研究y的分类是否与x之分类有关,将数据先按x分作c类, 再分别统计x分类情况下y的分类。这样就得到了数据按两个 定类变量进行交叉分类的频次分配表,即二维列联表。
列联表的一般形式
y x x1
y1
N11
y2
N12
.
.
.
.
.
.
x2 . . . xc
N21 . . . Nc1
列联表与独立性检验

题型二 用等高堆积条形图分析两变量间的关系 [学透用活]
在等高堆积条形图中展示列联表数据的频率特征,比较图中两个深色条的 高可以发现两者频率不一样而得出结论,这种直观判断的不足之处在于不能给 出推断“两个分类变量有关系”犯错误的概率.
[典例2] 为了解铅中毒病人与尿棕色素为阳性是否有关系,分别对病人组 和对照组的尿液作尿棕色素定性检查,结果如下:
[微思考] 有人说:“根据小概率值α=0.01的独立性检验认为吸烟和患肺癌有 关”,是指“每100个吸烟者中就会有1个患肺癌.”你认为这种观点正确吗? 为什么?
提示:观点不正确.“根据小概率值α=0.01”说明的是吸烟与患肺癌有关程度 的概率值,不是患肺癌的百分数.
(二)基本知能小试
1.判断正误
[对点练清]
假设有两个分类变量 X 与 Y,它们的可能取值分别为 X=0, 1
和 Y=01, ,
其
2×2 列联表为:
X
X=0 X=1 合计
Y
Y=0 Y=1
10 18
m
26
10+m 44
合计
28 m+26 m+54
则当m取下面何值时,X与Y之间没有影响
A.8
B.9
C.14
D.19
()
解析:若 X 与 Y 之间没有影响,则有1288=262+6 m,解得 m≈14.4,所以当 m=14 时,X 与 Y 之间没有影响即 X 与 Y 的关系最弱. 答案:C
a
21
73
女生(X=1)
8
25
33
合计
b
则表中a,b处的值分别为________.
46
106
解析:∵a+21=73,∴a=52.b=a+8=52+8=60.
列联表

购买 意愿 To tal
愿意购买 不愿意购买
结果分析:
由于最低期望频数大于5,所以卡方值应选 2.761,相应P--值为0.430。 结论: 不能拒绝原假设,可认为购买意愿与地 区独立。 Chi-Squa re Tests
Pe arson Chi-S quare Likelihood Ratio Linea r-by-Linear Associati on N of Vali d Cases Va lue 2.761 a 2.784 .479 420 df 3 3 1 Asymp. S ig. (2-sided) .430 .426 .489
Chi-Square T ests Value 6.122a 6.178 5.872 150 df 2 2 1 Asy mp. Sig. (2-sided) .047 .046 .015
Pearso n Chi-S quare Lik elihood Ratio Lin ear-by -Linear Associatio n N of Valid C ases
愿意 购买
68
75
57
79
期望频数
实际频数 期望频数
66
32 34
80
45 40
60
33 30
73
31 37
不愿意 购买
如果原假设成立,则观测频数与期望频 数整体而言较接近。 统计量就是用来描述“整体而言较接 近”的指标,并且服从卡方分布。
统计量
1.
计算公式为:
2
i 1 j 1 r c
百分比分布
行百分比
愿意购买
列百分比
总百分比
东部地区 西部地区 南部地区 北部地区
列联表

列联表中的卡方检验法列联分析中的卡方检验法变量分为定距变量、定序变量与定类变量。
对于定类变量,即分类数据的描述与分析,通常采用列联表的形式,列联表常用来对品质数据之间的相关程度进行测量。
卡方检验法以卡方统计量为基础,常用来对变量之间是否存在相关关系、相关关系的程度以及实验前后的拟合程度进行分析。
卡方分析法作为一种重要的假设检验方法,对于指导实际工作具有重要的意义,被广泛用于调查科研及公司决策方面。
列联表与卡方分析方法的结合,使得问题分析更加简明、透彻。
卡方检验法常应用于拟合优度检验、独立性检验等,卡方统计量也常用来刻画列联相关系数,描述变量之间的相关程度。
一、关于卡方检验法的基本知识卡方检验法依靠的是卡方统计量,卡方统计量的选择与计算则显得尤为重要。
一般情况下,对于r*s 列联表来说,x 2=()∑∑==-r i sj eeijfff112^ 。
此时的卡方统计量常用于列联表中,f ij为所得样本的实际观测值,f e为期望值(即两个变量在互不相关的情况下的分布),nff f ji e ..*=。
f i .为f ij所对应的第i 行的观测值总和,f j .为f ij所对应的第j 列的观测值总和,n 为样本容量。
由于是用连续性的卡方分布来检验离散型的点计数据,所以期望值允许出现小数。
值得一提的是,在进行卡方检验时,有p 值检验法与临界值检验法两种。
P 值检验法多用在spss 软件分析中。
P 值即是所得的卡方统计量对应的右侧概率,以p 值与所给定的显著性水平ɑ相比较,若p>ɑ,卡方统计量落在了接受域内,即接受原假设,拒绝备择假设,反之则拒绝原假设。
临界值检验法是excel 分析中常用的方法,它在计算出了卡方统计量之后,利用所给定的显著性水平ɑ计算出其所对应的临界值,若x 2>x a 2,则拒绝原假设,反之则接受原假设。
二、拟合优度检验拟合优度检验是检验来自总体中的一类数据其分布是否与某种理论分布相一致的统计方法,常用检验多个比例是否相等,又称比例检验法、配合检验法。
列联表

.784
1
.376
N of Valid Cases
300
a. 0 cells (.0%) have expected count less than 5. The minimum expected count is 13.33.
结
束
Value 20.124b 18.652 20.953
20.033
df 1 1 1
1
Asy mp. Sig. (2-sided) .000 .000 .000
.000
Exact Sig. (2-sided)
.000
Exact Sig. (1-sided)
.000
N of Valid Cases
221
• 变量 X 条件下变量 Y 的分布,或在 变量 Y 条件下变量 X 的分布
• 每个具体的观察值称为条件频数
百分比分布
1. 条件频数反映了数据的分布,但不适合 进行对比
2. 为在相同的基数上进行比较,可以计算 相应的百分比,称为百分比分布。
行百分比分布
东部地区 西部地区 南部地区 北部地区 合计 愿意购买 24.4% 26.9% 20.4% 28.3% 100% 不愿意购买 22.7% 31.9% 23.4% 22.0% 100%
列百分比分布
东部地区 西部地区 南部地区 北部地区
愿意购买 68.0% 62.5% 63.35 71.8% 不愿意购买 32.0% 37.5% 36.7% 28.2%
合计 100% 100% 100% 100%
总百分比分布
东部地区 西部地区 南部地区 北部地区 合计 愿意购买 16.2% 17.8% 13.6% 18.8% 66.4% 不愿意购买 7.6% 10.7% 7.9% 7.4% 33.6%
列联表名词解释

列联表名词解释
列联表(contingency table),又称交叉表或分组表,是一种将两个或多个变量的频数或百分比分组展示的统计表格形式。
列联表通常用于分析和展示两个或多个变量之间的关系和相互作用。
列联表的行和列分别代表不同的变量,表格中的每一个单元格记录了对应行和列的交叉组合的频数或百分比。
通过分析列联表,可以直观地比较不同组合的频数或百分比,从而了解不同变量的关联程度。
列联表在统计学和市场研究中被广泛使用,常用于探索和分析两个或多个变量之间的关系,例如性别和购买行为之间的关系、年龄和健康状况之间的关系等。
通过列联表的分析,可以帮助研究人员发现变量之间的相互作用,提供有针对性的信息,支持决策和推断。
总之,列联表是一种用于展示和分析两个或多个变量之间关系的统计表格形式,通过比较不同组合的频数或百分比,可以揭示变量之间的关联程度。
列联分析

列联分析一、列联表的构造列链表是由两个以上的变量进行交叉分类的频数分布表。
例如表1:表1(列)的划分类别视为C,则可以把每一个具体的列联表称为R×C列联表。
二、列联表的分布在表1中,最右边显示了态度变量的总数,如赞成改革方案的共有279人,反对改革方案的共有141人,对此称为行的边缘分布。
同理,100、120、90、110称为列边缘分布。
这样列联表所表现的就是在变量X条件下变量Y的分布,或者是在变量Y的条件下变量X的分布,因此又把列联表中的观察值分布称为条件分布,每个具体的观察值就是条件频数。
例如,一个公司赞成改革方案的职工有68人就是一个条件频数。
为了能在相同的基数上比较,使列联表中的数据提以对变量的联合分布的关系看得更清楚一些。
为了更深入的分析,需引入期望分布的概念。
期望值分布表。
如表3所示。
在全部420个样本中,赞成改革方案的有279人,占总数的66.4%,那么对第一分公司来说,赞成该方案的人数应当为0.664×100=66人,66人即为期望值。
将观察值和期望值频数结合在一起,就可以得到观察值和期望值对比分布表,如表4所示。
就应该有664.04321====ππππ(i π为第i 个分公司赞成改革方案的百分比),对于需要验证这一假设,可以采用2χ分布进行检验。
三、2χ统计量2χ可以用于变量间拟合优度检验和独立性检验,可以利用测定两个分类变量之间的相关程度。
若用0f 表示观察值频数,用e f 表示期望值频数,则2χ统计量为:()∑-=ee f f f 202χ计算2χ统计量的步骤(可见表5): 步骤一:用观察值0f 减去期望值e f 。
步骤二:将()e f f -0之差平方。
步骤三:将平方20)(e f f -结果除以e f 。
步骤四:将步骤三的结果加总。
表5 2χ计算表0fe f()e f f -020)(e f f - 20)(e f f -/e f68 66 24 0.060606 75 80 -5 25 0.3125 57 60 -3 9 0.15 79 736 36 0.493151 32 34 -2 4 0.117647 45 40 5 25 0.625 33 30 3 9 0.3 31 37 -6 36 0.9729733.031877()∑-=ee f f f 202χ=3.03192χ统计量有这样几个特征:首相2χ≥0,因为它是对平方值结果的汇总。
列联表

列联表定义敏感性:在金标准判断有病(阳性)人群中,检测出阳性的几率。
真阳性。
(检测出确实有病的能力)特异性:在金标准判断无病(阴性)人群中,检测出阴性的几率。
真阴性。
(检测出确实没病的能力)假阳性率:得到了阳性结果,但这个阳性结果是假的。
即在金标准判断无病(阴性)人群中,检测出为阳性的几率。
(没病,但却检测结果说有病),为误诊率。
假阴性率:得到了阴性结果,但这个阴性结果是假的。
即在金标准判断有病(阳性)人群中,检测出为阴性的几率。
(有病,但却检测结果说没病),为漏诊率。
计算方法Sensitivity and specificity:完整定义1.True Positive (真正, TP)被模型预测为正的正样本;可以称作判断为真的正确率;2.True Negative(真负, TN)被模型预测为负的负样本;可以称作判断为假的正确率;3.False Positive (假正, FP)被模型预测为正的负样本;可以称作误报率;4.False Negative(假负, FN)被模型预测为负的正样本;可以称作漏报率;5.True Positive Rate(真正率, TPR)或灵敏度(sensitivity)TPR = TP/(TP + FN)正样本预测结果数/正样本实际数;6.True Negative Rate(真负率, TNR)或特指度(specificity)TNR = TN/(TN + FP)负样本预测结果数/负样本实际数;7.False Positive Rate (假正率, FPR)FPR = FP/(FP + TN)被预测为正的负样本结果数/负样本实际数;8.False Negative Rate(假负率, FNR)FNR = FN/(TP + FN)被预测为负的正样本结果数/正样本实际数假阳性率=假阳性人数÷金标准阴性人数即:假阳性率=b÷(b+d)公式为:假阳性率=b/(b+d)×100%(b:筛选为阳性,而标准分类为阴性的例数;d:阴性一致例数)假阴性率=假阴性人数÷金标准阳性人数即:β=c÷(a+c)。
分类变量与列联表

张的学生中女生的频率比考前心情不紧张的学生中女生的频
率高,可以认为考前心情与性别有关联.
[课堂评价]
1.下列变量中,不属于分类变量的是
A.性别
B.吸烟
C.学历
(
)
D.国籍
解析:“吸烟”不是分类变量,“是否吸烟”才是分类变量.
答案:B
2.下面的 2×2 列联表中,a,b 的值分别为
38
35
73
试绘制出列联表对应的等高堆积条形图,分析铅中毒病
人组和对照组的尿棕色素为阳性数有无差别,铅中毒病人与
尿棕色素为阳性是否有关联.
解:铅中毒病人组中尿棕色素为阳性和阴性的频率分别为
29
7
≈0.805 6 和 ≈0.194 4.
36
36
9
37
对照组中尿棕色素为阳性和阴性的频率分别为 ≈0.243 2 和
X
Y
)
合计
Y=y1
Y=y2
X=x1
c
a
e
X=x2
23
d
48
合计
b
78
121
A.54,43 B.53,43
(
C.53,42
D.54,42
解析:由 2×2 列联表可知,d=48-23=25,b=121-78=43,所以
a=78-d=78-25=53.故选 B.
答案:B
3.观察下列各图,其中两个分类变量 X,Y 之间关联性最
成对
数据
的统计分析
8.3
8.3.1
[学习目标]
列联表与独立性检验
分类变量与列联表
1.理解分类变量与列联表的含义.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
‥ ‥ nba ‥ ‥ n.a
概率分布表
特征A 合计 A1 B1 特 征 : B Bb 合计 B2 p11 p21 : pb1 p.1 A2 p12 p22 : pb2 p.2 ‥ ‥ Aj ‥ ‥ p1j ‥ ‥ p2j : : ‥ ‥ Aa ‥ ‥ p1a ‥ ‥ p2a : : p1. p2. : pb. 1
逻辑分类的原则
从方法的角度看,逻辑分类法所规定的 逻辑原则是进行分类的基础。进行分类,应 遵循以下逻辑原则:
⒈每个层次的分类必须按同一标准或准则进行。 ⒉必须按照事物的属种包含关系分层次进行。 ⒊分类得到的种与种之间必须是不相容的,即相互 独立的。 ⒋分类所产生的种的概念外延之和必须等于概念的 外延。
二维列联表分析
设特性A可以分为a类, 特性B可分为b类。随机观 察n个个体,把那些个体的属性A处于类型i,属性B 处于类型j的个体数在表中记为nij 。并且,
n. j = ∑ nij
i =1
a
ni. = ∑ nij
j =1
b
分别是属性A 处于类型j的个体数(列)和属性B处于 类型i的个体数(行)。 pij记为属性A、B分别处于类 型i、j的概率数,现作原假设H0:A、B两特性独立。 如果为真,则 H0: pij = pi. p. j (i=1,2,……,a; j=1,2,……,b) p 其中, i.为属性A处于类型i的概率,p. j 为属性B处于 类型j的概率。
第二章 信息分类分析
第一节 列联表
逻辑分类法
在分解方法中,分类方法是使用很早, 应用很广的一种方法。分类方法的基本思路 是:按照事物属性的异同将事物区别、划分 为不同的种类,因此,类是具有某种共同属 性的集合。 分类作为一种认识事物、区别事物的方 法已有几千年的历史了。一般来说,实用的 分类方法都是将事物区别为具有一定从属关 系的不同层次的大小类别,形成概念系统, 反映客观事物的联系和区别。
一维多项分类分析
将总体按照某种特性分为A1,A2,……Ak, 计k个类型,每一个体仅属于其中一个类型, 总体中属于k个类型的比例P1,P2,……Pk。 现从总体中随机抽查n个样本单位,其中属 于类Ai有ni个,i=1,2,…k。现作原假设: P1 = P2 =……= Pk 。
一维多项分类分析
2 k [ni − E (ni )] [ni − npi ] 2 χ =∑ =∑ E (ni ) npi i =1 i =1
合计
69 78 147
126 99 225
16 27 43
211 204 415
首先,应该考虑设定假设: H0:居民对地板的喜好与地区无关 H1:居民对地板的喜好与地区有关
如果H0成立,说明居民对地板的喜好与地区无 关,即居民对地板是否喜好与地区独立. 记:A={居民来自地区1}, B={居民喜好地板},则 P(A∩B)=p11,如果H0成立,则A与B独立,于是 P(A∩B)=P(A) ·P(B),而P(A) =p.1, P(B)=p1. ,从 而H0成立,必须有p11 = p1. · p.1 同理p12 = p1. · p.2 , p21 = p2. · p.1 故H0可表达成: H0: p ij = pi. · p.j H1:上述等式至少有一个不成立
一维多项分布的性质
多项分布是二项分布的扩展,可以看成是多项试验得到 的分布。有若干性质: 多项试验由n个相同的试验组成 每个试验的结果都落在k组中的某一组内 某个试验的结果落在某一特定组的概率在试验之间保持 k 不变。且有 ∑ pi = 1 i =1 试验是独立的 试验者关心的n1,n2,…nk,这里ni等于试验落在组i的数目。 注意,n1+n2+…+nk=n
列联表原理
在利用列联表进行分析时,首先表示出列 联表,列联表实际上是一个交叉的频数表, 利用所给频数构造一个卡方统计量,根据 样本数据计算得来的卡方值与一定自由度 下卡方临界值进行对比,从而判断是否接 受原假设。 实质上是品质相关的问题
列联表分析在处理两个或几个定性变量间 是否有真正意义上的独立问题是独具魅力。 其原因有三: 1、不必假定所感兴趣的总体服从何种分布; 2、列联分析适合于处理分类型变量间的关 系而且简单直观; 3、社会调查等大样本正好与列联分析的要 求相吻合. 主要介绍二维列联表分析
定义统计量
k
2
当n 充分大时,统计量服从自 E 由度为k-1的的χ2分布。式中,(ni ) 为属于类的期望频数,pi为属于Ai 类的样本频率。
一维多项分类分析
2 χ 2 > χ a (k − 1) , 给定显著性水平a,如果
则拒绝H0 ,即k个类型之间有显著差异 (或者说至少有一个类型与其他类型不 2 χ 2 ≤ χ a (k − 1) 同);如果 , 则 接 受 H0 , 即k个类型之间没有显著差异。
也算得上很大。故在0.05显著水平上否定H0, 即认为四个商场的服务质量的评价是显著不 一样的。 EXCEL软件实现过程 SPSS软件实现过程
操作过程如下: 操作过程如下: 选择Data→Weight Cases,进入Weight Cases对话框。 把“频数[f]”放入Frequency栏中,单击OK按钮。 从Analyze→Descriptive→Crosstabs,进入 ,进入Crosstabs 对话框。 对话框。把“商场”放入Row(s)栏:把“经营情况”放入 Column(s)栏。 单击Statistics按钮,进入 按钮, 对话框。选择Chi单击 按钮 进入Statistics对话框 对话框 square,单击continue按钮,返回Crosstabs主对话框。 单击Cell按钮,进入 按钮, 单击 按钮 进入Cell Display(格子显示)对话框。 (格子显示)对话框。 选择Observe、Expected、Row、Column,单击 Continue按钮,返回Crosstabs主对话框。 在主对话框中,单击OK按钮,提交运行Crosstabs过程。
按两个及以上特性(标志)对同一事物进 行分类,每一特性将事物分为若干个组, 利用这样的数据分析特性之间有无关系, 称为多维多项分析,由于它常借助于列联 表进行,所以又称为列联表分析。 列联表主要用于判断定性变量之间是否存 在相关关系。
举例
不同文化程度的人对某一些政策的态度? 不同地区的人与不同的工作作风的态度? 不同培训方法与培训后的业绩增长是否相干? 不同经历的人与他们对事物的看法是否一致? 不同民族与某种习惯是否相关? 不同层面的客户偏好与产品不同包装是否相关? 不同收入阶层对猪肉涨价的态度?
二维列联表分析
由于
pi. 、p. j 未知,常用估计值 ˆ ˆ p. j = n. j n 代替,则理论期望 pi. = ni. n
。
ˆ E (nij ) = ni. ⋅ n. j n 频数为
给定显著性水平a, 2 当 χ 2 > χ α [(a − 1)(b − 1)] 时,拒绝H0 ,属性Α、 Β不独立,存在相关关系; 2 χ 2 ≤ χ α [(a − 1)(b − 1)] 时,接受H0 ,属性Α、 当 Β相独立,不存在相关.
列联表
特征A 合计 A1 B1 特 征 : B Bb 合计 B2 n11 n21 : nb1 n.1 A2 n12 n22 : nb2 n.2 ‥ ‥ Aj ‥ ‥ n1j ‥ ‥ n2j : : ‥ ‥ Aa ‥ ‥ n1a ‥ ‥ n2a : : n1. n2. : nb. n
‥ ‥ nbj ‥ ‥ n.j
二维列联表分析
[例2.4] 在一次社会调查中,以问 在一次社会调查中, 卷方式调查了901 901人的年收入以及对 卷方式调查了901人的年收入以及对 工作的满意程度。其中, 工作的满意程度。其中,年收入分 为小于9000 9000元 9000元至24000元 元至24000 为小于9000元、9000元至24000元、 24000元至36000元以及超过36000元 元至36000元以及超过36000 24000元至36000元以及超过36000元 四档;对工作的满意程度B 四档;对工作的满意程度B分为很不 满意、较不满意、 满意、较不满意、基本满意和很满 意4档。调查结果可以用4×4列联表 调查结果可以用4 表示如下: 表示如下:
[例2.3]某市商业系统为提高商业服 务质量,对本市的四大商场进行调 查,收回有效问卷443张。每张问卷 对各商场按照优中差三种服务质量 评价,其结果用3×4列联表表示出 来,如表所示。试分析四个商场的 服务质量评价是否一致?
二维列联表分析
商场 绩效 优 中 差 合计 A 81 38 25 144 B 46 33 7 86 C 49 39 20 108 D 67 26 12 105 合计 243 136 64 443
二维列联表分析
[例2.2]一个建筑装饰公司对一个城市 三个地区的乔迁居民喜好地板的比例 感兴趣,目的是为了决定对这些地区应 采用何种营销策略.这个公司的调研部 门进行了一项调查,结果见下表,试证 明该城市不同地区的居民对地板的喜 好比例是否独立.
地 1 地 地 板 板 面 其 料 他 合计 2
区 3
‥ ‥ pbj ‥ ‥ p.j
‥ ‥ pba ‥ ‥ p.a
二维列联表分析
统计上已经证明,在n很大并且 E (nij ) i =1 j =1
a
b
[n
ij
− E (nij ) E (nij )
]
2
~ χ 2 [(a − 1)(b − 1)]
式中,期望频数 E (nij ) = npij , 且 H0 成 立 时 。 E (nij ) = npij = npi. p. j
二维列联表分析
期望频数估计表 绩效 优 中 差 合计 A 79 44.2 20.8 144 B 47.2 26.4 12.4 86 C 59.2 33.2 15.6 108 D 57.6 33.2 15.2 105 合计 243 136 64 443
