On colorings of squares of outerplanar graphs
感受数学之美的给孩子看的英文书

感受数学之美的给孩子看的英文书全文共3篇示例,供读者参考篇1Title: Exploring the Beauty of MathematicsIntroductionMathematics is more than just numbers and equations, it is a fascinating and intricate puzzle that challenges our minds and shapes the world around us. In this book, we will delve into the beauty of mathematics and explore its endless possibilities. Through engaging stories, colorful illustrations, and interactive activities, children will discover the magic of numbers and the wonders of geometry, algebra, and more.Chapter 1: The Power of PatternsFrom the mesmerizing spiral of a seashell to the symmetrical petals of a flower, patterns are everywhere in nature. In this chapter, children will learn how to recognize and create patterns using basic shapes and colors. Through hands-on activities such as drawing and coloring, they will develop a keen eye for symmetry and repetition.Chapter 2: The Joy of GeometryGeometry is the study of shapes and their properties, and it is the foundation of many mathematical concepts. In this chapter, children will explore the world of polygons, circles, and angles. They will learn how to measure and calculate areas and perimeters, and discover the beauty of tessellations and fractals.Chapter 3: The Wonder of NumbersNumbers are the building blocks of mathematics, and they hold endless mysteries waiting to be uncovered. In this chapter, children will learn about the history of numbers, from the ancient civilizations to modern mathematicians. They will explore the concepts of prime numbers, fractions, and decimals, and engage in fun games and puzzles to sharpen their numerical skills.Chapter 4: The Magic of AlgebraAlgebra is the language of equations and variables, and it is crucial for solving complex problems. In this chapter, children will embark on a journey through algebraic expressions, equations, and inequalities. They will learn how to simplify expressions, solve equations, and graph functions, giving them the tools to tackle real-world challenges with confidence.Chapter 5: The Beauty of CalculusCalculus is the study of change and motion, and it is a powerful tool for understanding the world around us. In this chapter, children will be introduced to the concepts of derivatives, integrals, and limits. They will explore the connection between calculus and physics, biology, and other sciences, and witness the beauty of mathematical modeling in action.ConclusionMathematics is a treasure trove of beauty and wonder, waiting to be explored by curious minds. By diving into the world of patterns, geometry, numbers, algebra, and calculus, children can unlock the secrets of the universe and unleash their creativity and problem-solving skills. This book is just the beginning of their mathematical journey, and I hope it inspires them to continue exploring the infinite possibilities of this fascinating field.篇2Title: Exploring the Beauty of Mathematics: A Book for ChildrenIntroductionMathematics is a beautiful and fascinating subject that is often misunderstood and feared by many children. However, it isessential to teach children about the beauty and wonders of mathematics from a young age to foster a love and appreciation for the subject. This book aims to introduce children to the beauty of mathematics in a fun and engaging way, helping them see the world through the lens of mathematics.Chapter 1: The Magic of NumbersIn this chapter, children will learn about the magic of numbers and how they are used in everyday life. From counting to discovering patterns and sequences, numbers are all around us. Children will explore the concept of symmetry, prime numbers, and the Fibonacci sequence, opening their minds to the beauty of mathematics.Chapter 2: The Language of ShapesShapes are everywhere, from the geometry of buildings to the symmetry of nature. In this chapter, children will learn about different geometric shapes, such as circles, squares, triangles, and polygons. They will discover the beauty of symmetry and tessellations, as well as the concept of fractals and the golden ratio.Chapter 3: The Art of Problem SolvingMathematics is not just about numbers and shapes but also about problem-solving. In this chapter, children will learn about different problem-solving strategies, such as breaking down a problem, looking for patterns, and using logical reasoning. They will explore puzzles, riddles, and games that challenge their minds and nurture their problem-solving skills.Chapter 4: The Power of PatternsPatterns are an essential part of mathematics, helping us make sense of the world around us. In this chapter, children will learn about different types of patterns, such as number patterns, shape patterns, and symmetry. They will discover how patterns are used in mathematics, art, music, and nature, showing them the interconnectedness of the world.Chapter 5: The Beauty of InfinityThe concept of infinity is both mind-boggling and beautiful. In this chapter, children will learn about different types of infinity, such as countable and uncountable infinity. They will explore the concept of limits, sequences, and series, as well as the infinite nature of fractals and the Mandelbrot set. Children will be amazed by the endless possibilities of infinity and its presence in mathematics and beyond.ConclusionMathematics is a subject full of wonder, beauty, and creativity. By introducing children to the beauty of mathematics at a young age, we can help them develop a love and appreciation for the subject. This book aims to inspire children to see the world through the lens of mathematics, encouraging them to explore, discover, and create with confidence and curiosity. Let's unlock the beauty of mathematics together and open the doors to endless possibilities.篇3Title: Discovering the Beauty of Mathematics: A Children's BookIntroduction:Mathematics is often seen as a difficult and intimidating subject, but in reality, it is a beautiful and fascinating field of study. Through this children's book, we aim to help young readers discover the beauty of mathematics and develop a deeper appreciation for the subject.Chapter 1: Introduction to MathematicsIn this chapter, we introduce the basic concepts of mathematics, such as numbers, shapes, and patterns. We explain how mathematics is all around us, from the natural world to the technology we use every day.Chapter 2: The Beauty of SymmetrySymmetry is a key concept in mathematics and can be found in nature, art, and architecture. In this chapter, we explore different types of symmetry and how they can be used to create beautiful designs.Chapter 3: Exploring PatternsMathematics is all about finding and understanding patterns. In this chapter, we look at different types of patterns, such as geometric patterns, number patterns, and fractals. We show how patterns can be both simple and complex, and how they can be found in nature and art.Chapter 4: The Magic of NumbersNumbers are the building blocks of mathematics, and they have many fascinating properties. In this chapter, we explore the beauty of numbers, from prime numbers to Fibonacci sequences. We also look at how numbers are used in everyday life, from telling time to measuring distances.Chapter 5: The Language of MathematicsMathematics has its own language, with symbols and equations that help us solve problems and communicate ideas. In this chapter, we introduce young readers to some basic mathematical symbols and show how they are used in equations.Chapter 6: The World of ShapesGeometry is a branch of mathematics that studies shapes and their properties. In this chapter, we explore different types of shapes, such as polygons, circles, and solids. We also look at how shapes are used in art and design.Conclusion:By the end of this book, we hope that young readers will have a better understanding of the beauty of mathematics and be inspired to explore the subject further. Mathematics is not just about solving equations - it is a way of thinking and seeing the world in a new light. We encourage children to embrace the beauty of mathematics and enjoy the journey of discovery that it offers.。
新视角研究生英语读说写2二单元课后练习答案省名师优质课赛课获奖课件市赛课一等奖课件

Unit 2: Reading comprehension
5. In paragraph 15, Mead speaks of “the need to define who you are by the place in which you live.” What does she mean?
Reference
Unit 2: Structure of the text
Text Outline
2. Body (Paras. 3–18)
1) The author’s detailed description oft_h_e_d_i_f_fe_r_e_n_t_h_o_m__e_s _s_h_e_h_a_d__li_v_e_d_i_n_w__h_e_n_s_h_e__w_a_s__a_c_h_i_ld__, especially the one at Hammonton. (Paras. 3–14)
Text Outline
1. Introduction (Paras. 1–2)
For many people, moving and traveling are v_e_r_y__d_if_fe_r_e_n_t_. But for the author, moving and staying at home, traveling and arriving are _a_ll_t_h_e_s_a_m__e_.
Reference
To illustrate that for many people, leaving home shouldn’t be anything sad because home is a place to which you come back again and again. But for the fishermen in these islands, it is a different story because they have to face the dangers when they are out to sea. They never know whether they will be able to return to their homes again. Their fate is hard to predict.
小学上册第十五次英语第5单元测验试卷

小学上册英语第5单元测验试卷英语试题一、综合题(本题有100小题,每小题1分,共100分.每小题不选、错误,均不给分)1.I like to build tall structures with my ________ (玩具名称).2. Depression began in the year ________. The Grea3.Plants can provide shelter for ______ (小动物).4. A tortoise can live for over ______ (一百年).5.The __________ can change due to human intervention.6.Which of these is a mode of communication?A. TelepathyB. PhoneC. DanceD. Art7.The basic unit of a carbohydrate is a ________.8.Which of these is a natural disaster?A. EarthquakeB. FestivalC. BirthdayD. Concert9.My aunt loves __________ (读书).10.My hamster loves to run on its _________ (轮子).11.What is the term for the fear of heights?A. ClaustrophobiaB. AcrophobiaC. AgoraphobiaD. NyctophobiaB12.The rabbit is hiding in the _______ (兔子藏在_______里).13.I love to ______ (尝试) new recipes.14.The teacher is ______ (kind) to all students.15.How many players are on a dodgeball team?A. 5B. 6C. 7D. 816.What do you call a book that tells about someone's life?A. FictionB. BiographyC. NovelD. AutobiographyB17.Which bird is known for its colorful feathers?A. SparrowB. PeacockC. PenguinD. CrowB18.Which of these is a popular sport?A. ChessB. FencingC. FootballD. Knitting19.What do you use to write on paper?A. BrushB. PencilC. KnifeD. SpoonB20.I enjoy making ______ with friends.21.My _____ (奶奶) tells me stories about her childhood. 奶奶给我讲她童年的故事。
tpo32三篇托福阅读TOEFL原文译文题目答案译文背景知识

tpo32三篇托福阅读TOEFL原文译文题目答案译文背景知识阅读-1 (2)原文 (2)译文 (5)题目 (7)答案 (16)背景知识 (16)阅读-2 (25)原文 (25)译文 (28)题目 (31)答案 (40)背景知识 (41)阅读-3 (49)原文 (49)译文 (53)题目 (55)答案 (63)背景知识 (64)阅读-1原文Plant Colonization①Colonization is one way in which plants can change the ecology of a site.Colonization is a process with two components:invasion and survival.The rate at which a site is colonized by plants depends on both the rate at which individual organisms(seeds,spores,immature or mature individuals)arrive at the site and their success at becoming established and surviving.Success in colonization depends to a great extent on there being a site available for colonization–a safe site where disturbance by fire or by cutting down of trees has either removed competing species or reduced levels of competition and other negative interactions to a level at which the invading species can become established.For a given rate of invasion,colonization of a moist,fertile site is likely to be much more rapid than that of a dry, infertile site because of poor survival on the latter.A fertile,plowed field is rapidly invaded by a large variety of weeds,whereas a neighboring construction site from which the soil has been compacted or removed to expose a coarse,infertile parent material may remain virtually free of vegetation for many months or even years despite receiving the same input of seeds as the plowed field.②Both the rate of invasion and the rate of extinction vary greatly among different plant species.Pioneer species-those that occur only in the earliest stages of colonization-tend to have high rates of invasion because they produce very large numbers of reproductive propagules(seeds,spores,and so on)and because they have an efficient means of dispersal(normally,wind).③If colonizers produce short-lived reproductive propagules,they must produce very large numbers unless they have an efficient means of dispersal to suitable new habitats.Many plants depend on wind for dispersal and produce abundant quantities of small,relatively short-lived seeds to compensate for the fact that wind is not always a reliable means If reaching the appropriate type of habitat.Alternative strategies have evolved in some plants,such as those that produce fewer but larger seeds that are dispersed to suitable sites by birds or small mammals or those that produce long-lived seeds.Many forest plants seem to exhibit the latter adaptation,and viable seeds of pioneer species can be found in large numbers on some forest floors. For example,as many as1,125viable seeds per square meter were found in a100-year-old Douglas fir/western hemlock forest in coastal British Columbia.Nearly all the seeds that had germinated from this seed bank were from pioneer species.The rapid colonization of such sites after disturbance is undoubtedly in part a reflection of the largeseed band on the forest floor.④An adaptation that is well developed in colonizing species is a high degree of variation in germination(the beginning of a seed’s growth). Seeds of a given species exhibit a wide range of germination dates, increasing the probability that at least some of the seeds will germinate during a period of favorable environmental conditions.This is particularly important for species that colonize an environment where there is no existing vegetation to ameliorate climatic extremes and in which there may be great climatic diversity.⑤Species succession in plant communities,i.e.,the temporal sequence of appearance and disappearance of species is dependent on events occurring at different stages in the life history of a species. Variation in rates of invasion and growth plays an important role in determining patterns of succession,especially secondary succession. The species that are first to colonize a site are those that produce abundant seed that is distributed successfully to new sites.Such species generally grow rapidly and quickly dominate new sites, excluding other species with lower invasion and growth rates.The first community that occupies a disturbed area therefore may be composed of specie with the highest rate of invasion,whereas the community of the subsequent stage may consist of plants with similar survival ratesbut lower invasion rates.译文植物定居①定居是植物改变一个地点生态环境的一种方式。
2023年高考英语外刊时文精读专题14气候变化与珊瑚礁

2023年高考英语外刊时文精读精练 (14)Climate change and coral reefs气候变化与珊瑚礁主题语境:人与自然主题语境内容:自然生态【外刊原文】(斜体单词为超纲词汇,认识即可;下划线单词为课标词汇,需熟记。
)Human beings have been altering habitats—sometimes deliberately andsometimes accidentall y—at least since the end of the last Ice Age. Now, though, that change is happening on a grand scale. Global warming is a growing factor. Fortunately, the human wisdom that is destroying nature can also be brought to bear on trying to save it.Some interventions to save ecosystems are hard to imagine andsucceed. Consider a project to reintroducesomething similar to a mammoth(猛犸象)to Siberiaby gene-editing Asian elephants. Their feeding habits could restore the grassland habitat that was around before mammoths died out, increasing the sunlight reflected into space and helping keep carbon compounds(碳化合物)trapped in the soil. But other projects have a bigger chance of making an impact quickly. As we report, one example involves coral reefs.These are the rainforests of the ocean. They exist on vast scales: half a trillion corals line the Pacific from Indonesia to French Polynesia, roughly the same as the number of trees that fill the Amazon. They are equally important harbor of biodiversity. Rainforests cover18% of the land’s s urface and offer a home to more than half its vertebrate(脊椎动物的)species. Reefs occupy0.1% of the oceans and host a quarter of marine(海洋的)species.And corals are useful to people, too. Without the protection which reefs afford from crashing waves, low-lying islands such as the Maldives would have flooded long ago, and a billion people would lose food or income. One team of economists has estimated that coral’s global ecosystem services are worth up to $10trn a year. reefs are, however, under threat from rising sea temperatures. Heat causes the algae(海藻) with which corals co-exist, and on which they depend for food and colour, to generate toxins(毒素)that lead to those algae’s expulsion(排出). This is known as “bleaching(白化)”, and can cause a coral’s death.As temperatures continue to rise, research groups around the world are coming up with plansof action. Their ideas include identifying naturally heat-resistant(耐热的)corals and moving themaround the world; crossbreeding(杂交)such corals to create strains that are yet-more heat-resistant; employing genetic editing to add heat resistance artificially; transplantingheat-resistant symbiotic(共生的)algae; and even repairing with the bacteria and other micro-organismswith which corals co-exist—to see if that will help.The assisted evolution of corals does not meet with universal enthusiasm. Without carbon reduction and decline in coral-killing pollution, even resistant corals will not survive the century. Some doubt whetherhumans will get its act together in time to make much difference. Few of these techniques are ready for action in the wild. Some, such as gene editing, are so controversial that it is doubtful they will be approved any time soon. scale is also an issue.But there are grounds for optimism. Carbon targets are being set and ocean pollution is being dealt with. Countries that share responsibilities for reefs are starting to act together. Scientific methods can also be found. Natural currents can be used to facilitate mass breeding. Sites of the greatest ecological and economical importance can be identified to maximise benefits.This mix of natural activity and human intervention could serve as a blueprint (蓝图)for other ecosystems. Those who think that all habitats should be kept original may not approve. But when entire ecosystems are facing destruction, the cost of doing nothing is too great to bear. For coral reefs, at least, if any are to survive at all, it will be those that humans have re-engineered to handle the future.【课标词汇精讲】1.alter (通常指轻微地)改动,修改;改变,(使)变化We've had to alter some of our plans.我们不得不对一些计划作出改动。
我小时候的梦想是当一名科学家的英语作文

我小时候的梦想是当一名科学家的英语作文全文共3篇示例,供读者参考篇1My Childhood Dream of Becoming a ScientistEver since I was a little kid, I've been fascinated by science and how it can explain the world around us. My dream has always been to become a scientist when I grow up. I want to make amazing discoveries and inventions that could help make the world a better place.I can still vividly remember the first time my love for science blossomed. It was during a family trip to the science museum when I was around 6 years old. The museum was filled with all sorts of cool interactive exhibits on different scientific topics like planets, dinosaurs, electricity, and more. I was completely mesmerized!One exhibit that really stuck with me was the one on dinosaurs. Seeing the gigantic fossil skeletons and learning about how these magnificent creatures roamed the Earth millions of years ago absolutely blew my mind. From that day on,I became obsessed with paleontology and dreamed of one day digging up dinosaur bones myself.As I got a little older, my interests in science expanded even further. In 2nd grade, we learned about the human body and I thought it was so incredible how all the different organs and systems worked together to keep us alive and healthy. I started wanting to be a doctor or surgeon.Then in 3rd grade, we studied astronomy and I became enamored with the vast mysteries of outer space. All the planets, stars, galaxies, black holes...it was just so mind-boggling to think about the endless wonders of the universe out there. For a while, I really wanted to be an astronaut or astrophysicist.Around this time, I also discovered my love for chemistry after my parents bought me a beginner's chemistry set for my birthday one year. I spent hours upon hours mixing different chemicals together and being amazed by the reactions I could create. Like tiny scientific magic tricks! Making a model volcano erupt or creating a snaky corkscrew out of a reaction were some of my favorites.In 4th grade, we learned about environmental science and going green. This sparked my interest in developing new renewable energy sources and technologies to combat climatechange and pollution. I started having dreams of being an environmental engineer who would help invent things like better solar panels or even nuclear fusion reactors.Now in 5th grade, I've recently become really interested in computer science and coding after my teacher started incorporating it into our lessons. It's been so fun and rewarding creating simple games and programs from scratch using code. Being able to build things from the ground up with just lines of text is like a superpower! Maybe I'll end up being a software engineer or leading a big tech company someday.The possibilities really do seem endless when it comes to science. And that's exactly why I'm so drawn to it – because it allows you to constantly make new discoveries, solve problems, and push the boundaries of what's possible. Scientists get to search for answers to some of life's biggest mysteries using experimentation and cutting-edge technology. How incredibly amazing is that?!Of course, I know being a scientist isn't all fun and games. It takes a ton of hard work, perseverance, and brainpower. All the studying, research, math, and obstacle after obstacle before finally making a breakthrough discovery. It's an incredibly difficult career path. But that's what makes the rewards sogratifying in the end when you DO make those game-changing findings or innovations after years of tireless effort.I'm sure my specific dream job will probably change and evolve over the years as I experience new things and develop different interests. But no matter what, I know without a doubt that I want to have a career in some field of science. Helping expand human knowledge and using my mind to make the world better just seems like the most incredible way to spend my life.Who knows, maybe I'll be the one who finally figures out how to resurrect woolly mammoths from extinction using DNA technology. Or invents a new form of safe, limitless energy that can power the entire planet. Or develops a futuristic biomedical device that can rewrite someone's genes to cure any disease or disability. Or leads the first human mission to Mars and beyond. The possibilities are endless for those who dare to dream big!I've still got a long road ahead of me before I can make my wildest scientific dreams a reality. Lots and lots of years of schooling, first here in Buffalo getting good grades, then onto a top university for undergrad, grad school after that, and who knows how many decades of research before any major breakthroughs. It'll be incredibly difficult, I'm sure. But I'm ready to put in the hard work!Science is so amazing and important – it quite literally helps shape the course of human civilization and life as we know it with each new finding or invention. That's why having a job where I get to be on the forefront of篇2My Dream of Becoming a ScientistEver since I was a tiny kid, I've wanted to be a scientist when I grow up. I'm not sure exactly when the idea first popped into my head, but I know it has been my biggest dream for as long as I can remember.Maybe it started from watching all those educational TV shows for kids like Sid the Science Kid and the Magic School Bus.I was always glued to the screen, totally captivated whenever they would explain cool science concepts in a fun,easy-to-understand way. Whether it was teaching about how butterflies go through metamorphosis or why the sky looks blue, I just couldn't get enough!Or maybe it was because my parents bought me tons of science kits and experiment books as gifts for my birthdays and holidays. You know, those kits where you can grow colourful crystals, build a little robot that moves around, or make avolcanic eruption in your own kitchen? I absolutely loved doing all those hands-on activities and feeling like a real scientist myself. It was the best when the experiments actually worked and didn't just totally flop.Whatever first sparked my interest, my dream of becoming a scientist is something that has stuck with me for my whole childhood so far. When I'm asked "What do you want to be when you grow up?", my answer hasn't changed – a scientist is 100% what I want to do, no questions asked.To me, being a scientist seems like the coolest job in the whole world. Scientists are like the ultimate explorers and adventurers, but instead of discovering new lands or sailing uncharted waters, they get to discover how the entire universe works and uncover the secrets of everything around us. They're dive into the deepest mysteries of life itself through their experiments and research.Whether it's peering through powerful telescopes to study distant galaxies and black holes, analyzing fossilized remains to understand ancient life on Earth millions of years ago, or using microscopes to observe teensy cells and microorganisms we can't even see with our naked eyes, scientists get to make sense of so many amazing and mind-blowing things.And they don't just sit around looking through lenses all day. The scientists I admire most are the ones who come up with creative ideas and inventions that make the world a better place. Like the scientists who figured out how to generate renewable energy from the sun's rays, or the brave scientists who developed life-saving medicines to cure diseases. Or the brilliant scientists who engineered ways for us to explore other planets through robots and spacecraft. So many incredible breakthroughs that have improved human life came from the tireless work and problem-solving skills of scientists.To me, being a scientist means getting to be curious, ask questions, and never stop learning and discovering new things. A scientist's job is all about solving mysteries, breaking barriers, and expanding the frontiers of human knowledge. How amazing is that?That sense of curiosity, wonder and drive to keep learning is exactly what motivates my passion for science. I'm the kind of kid who is constantly asking "Why?" about everything. Why is the sky blue? Why do birds have feathers? Why do planets orbit around the sun? I want to know the explanations behind how things work and the reasons why things happen in certain ways.I'm also super fascinated by the natural world around us –the plants, animals, ecosystems, atmosphere, and all the other parts of our environment. Whenever we go on hikes or nature walks, I'm the one running ahead on the trails, inspecting every wildflower, leaf, rock, or bug I come across. I could spend hours just flipping over logs and stones to see what kinds of critters might be hiding underneath. To me, the outdoor world is like an endless showcase of science in action.At home, I'm constantly doing little experiments and observations by mixing things together in the kitchen, building contraptions out of household items, or recording the weather patterns outside each day. I tried growing beans in plastic baggies on the windowsill and was amazed to watch the roots and sprouts emerge from the tiny seeds. And I'll never forget the time I made a lava lamp by mixing oil, food coloring and some other household ingredients – it looked just like the real thing! Hands-on experiments, no matter how small, ignite my curiosity and make me feel like a real scientist figuring out the secrets of the universe.If I become a scientist when I'm older, I think I'd love to work as a zoologist and study all kinds of amazing animals and their behaviors. Or maybe a botanist who researches plants andflowers and finds new ways for them to adapt and thrive. An astronomer could be cool too – I'd get to gaze at the stars and planets all night long. It's just so hard to choose one path when every branch of science has so many fascinating parts to explore.But no matter what specific type of scientist I become, I know it will be a job where I'll get to travel to new places, work with cutting-edge technologies, make groundbreaking discoveries, and always be learning new things every single day. To me, that sounds like the absolute best way to spend my life and career.Sure, being a scientist probably requires a whole lot of difficult studying, training, and many years of school to get there. And from what I've heard, doing science experiments and research can involve a ton of patience, perseverance and accidental failures before finally getting positive results. There are probably plenty of challenges and obstacles that real scientists have to overcome.But that's exactly what makes the idea of being a scientist so exciting – it will be tough, but I'll get to work hard at something I'm deeply passionate about. Nothing amazing was ever accomplished without hard work and dedication. And anythingthat's truly worth doing in life usually requires venturing through a few difficulties and detours to get there.So for now, even though I'm still just a kid, I'll keep nurturing my dream of one day growing up to wear that white lab coat as a scientist. I'll keep reading books about science concepts, watching videos about the latest discoveries, and practicing with those experiment kits as much as I can. I'll pay extra close attention during science class at school and study really hard so I can take advanced science courses as I get older.I know that staying focused and working towards my goal of becoming a scientist might not always be easy. There will probably be times when I feel frustrated, discouraged or maybe even start doubting if I can really make it happen. That's when I'll remember that curious,wide-eyed kid I once was who was first captivated by the wonders of science. I'll keep that passion alive by continuing to ask questions, seek out new knowledge, and never lose my sense of awe about the incredible world around me.Because to me, being a scientist wouldn't just be a career – it would be the ultimate way to keep exploring, learning and experiencing the magic of science every single day. I can't think of anything cooler than getting to unravel and understand thedeep mysteries of how our universe works. A life of science is a life of constant fascination and discovery.And that's a dream worth pursing for as long as it takes. I may be small now, but one day I'll get to grow up and wear that lab coat with pride as I work to make new scientific breakthroughs. Just call me a scientist-in-the-making ready to uncover the secrets of the cosmos!篇3My Dream of Becoming a Scientist When I Was LittleEver since I was a tiny kid, I dreamed of being a scientist when I grew up. I was always so curious about how things worked and why things happened the way they did. I wanted to know the answers to all the questions in the whole universe!I remember being really little, maybe 4 or 5 years old, and asking my mom a million "Why?" questions every single day. Why is the sky blue? Why can birds fly but we can't? Why does rain fall from the clouds? Why do I have to eat vegetables? My poor mom must have gotten so tired of me constantly asking "Why? Why? Why?" about absolutely everything!But I just couldn't help it. I had this burning desire to understand everything around me. The world was so fascinatingand magical, with all its strange rules and mysteries. I was determined to figure it all out when I became a grown-up scientist.One of my favorite things as a kid was doing little experiments and projects. My parents got me all kinds of science kits and activity books full of fun hands-on activities to learn about science concepts. I loved mixing up concoctions with my kiddie chemistry set, even if I did make a huge mess sometimes. I grew plants from seeds and learned about photosynthesis. I built a baking soda and vinegar volcano that actually erupted! It was so cool.I also spent hours outside observing things in nature. I would lie on my belly in the grass, using a magnifying glass to examine tiny bugs crawling on leaves and blades of grass. I dug in the dirt to find worms and rolly pollies. I watched clouds drifting across the sky and tried to identify their shapes. I collected rocks, leaves, feathers, and seed pods to study and sort into my own little nature museum at home.In school, science was easily my favorite subject. I remember in 2nd grade, we learned about the life cycle of butterflies. We even got to watch the whole process unfold right in our classroom, from crinkly little caterpillars munching on leaves totheir transformation into chrysalises to finally emerging as beautiful butterflies! Seeing that up close was pure magic to me. From then on, I was hooked on science.When I got a little older, I became obsessed with outer space.I stayed up late to watch meteor showers streak across the night sky. I read every single book about planets, stars, and galaxies that I could get my hands on. I desperately wanted to be an astronaut when I grew up so I could travel to different planets and walk on the moon. A nice astronomer who studies space from here on Earth would have been an okay back-up plan too though!I also went through phases of wanting to be a paleontologist to dig up dinosaur bones, a marine biologist swimming with whales and dolphins, or a scientist racing to find cures for diseases. There were just so many fascinating branches of science to explore!Of course, being a kid, my dream career changed approximately 947 times between the ages of 5 and 10. Some days I wanted to be a firefighter, a professional soccer player, or an ice cream taste tester instead. But the desire to be a scientist always lingered in the backof my mind.Whenever I heard about a new amazing scientific discovery or invention on the news or saw it in a book, I thought, "Wow! A scientist came up with that! I want to do things like that someday." The idea of using my brain to uncover secrets of the universe, invent incredible new technologies, or make the world a better place was endlessly exciting to me.I just knew that when I grew up, I would emerge from my cocoon of childhood as a beautiful, brave scientist in a white lab coat. I imagined myself peering through a powerful microscope, mixing up chemical formulas, or analyzing data on a chalkboard covered in complex equations. Maybe I would even journey to the depths of the rainforest, the peaks of the tallest mountains, or the inky blackness of space itself to investigate unexplored frontiers!Whenever there was a career day or chance to dress up as our dream jobs at school, you can bet I rocked that lab coat and safety goggles with pride. Sure, the other kids' costumes were frillier or had more pizazz. But I knew my scientist getup was a symbol of curiosity, intelligence, and world-changing potential. Being a scientist was going to be way cooler than being a dinosaur, princess, or superhero when I actually grew up.As I got older, of course, I started to better understand the hard work, dedication, and perseverance it actually takes to have a career in science. I learned that scientists don't just make one lightning bolt "Eureka!" discovery and call it a day. It takes years and years of patience, running experiments, recording data, facing failures and setbacks, revising hypotheses, and trying again.I knew it wouldn't be easy, but I was determined to put in that effort. The pursuit of knowledge was my calling in life! I was going to change the world through science, damn it! Or at the very least, I would spend my days playing a small but important role in expanding human understanding and helping to solve some of our most complex problems and mysteries.Well, here I am now, just a fresh-faced 11-year-old kid. My grown-up scientific career is still a little ways off. I've got middle school, high school, college, and probably tons of extra schooling after that still ahead of me before I can achieve my dream.But my sense of wonder about the world around me, my millions of curious questions, and my passion for discovering answers through science burn just as brightly today as they did when I was a little tyke. I can't wait to one day trade in my child'slab coat for a real one as a full-fledged scientist. Maybe I'll even get to put on one of those super awesome puffy white space suits and boundaway towards Mars!Who knows what incredible new realms I'll get to explore or what mind-blowing breakthroughs I might help uncover? There's a big, wide, endlessly fascinating universe out there just waiting for me and my fellow scientists to figure it all out. I've got my magnifying glass and notebook ready. Let's go!。
法语大学英语二考试B

三 峡 大 学 试 卷 班 级 学 号 姓 名密 封 线2010年春季学期2009级法语专业 《大学英语》(二)课程考试试卷( B 卷)注意:1、本试卷共5 页,含答题纸1页; 2、考试时间: 120 分钟 3、姓名、班号、考号必须写在指定地方注意事项:1、请同学们在试卷及答题纸规定的地方填写班级,序号,学号、姓名等信息。
2、此次期末考试试卷,所有答案一律写在答题纸上的密封线内,否则无效。
3、 打铃交卷时,请将试卷与答题纸分开放置,待老师清点无误后方可离开教室。
一、 从以下每题四个答案中选出最合适的一个选项或与下划线单词意思最接近的选项。
(每小题 1 分,共 10 分)1. I strongly _____of anyone who goes out at night and leaves his or her children alone. A. disapprove B. disprove C. object D. oppose2. They sent out more than 30 invitations to the seminar, but only 20 people showed up. A. turned up B. took part in C. attended D. accepted3. Nobody ventured to speak to the angry King.A. attemptedB. volunteeredC. daredD. wanted 4. The children ____ in line, then walked quietly into the schoolA. gatheredB. stoodC. formedD. performed5. She showed the caring side of her nature when she opened a hostel for homeless people.A. concerningB. sensitiveC. generousD. loving 6.Do not let yourself be persuaded into buying things that you do not really want. A. cheated into B. talked into C. made into D. misled into 7. Scientists in California believe they may have discovered a way to delay the aging process..A. prolongB. stopC. postponeD. quicken8. Soccer hooligans just laughed at the sort of sentence that the court gave themA. smiled atB. made fun ofC. acceptedD. obediently9. He tried to steer the conversation away from such dangerous topics A. change B. pick C. select D. elect10.The man who installed our washing machine advised me not to use the hottest wash. A. checked B. set up C. repaired D. disassembled二.为下列空白选出最合适的一个词并将代码填入空白处。
2023年高考英语话题通关精准练词汇+阅读+写作11太空宇宙探索(含答案)
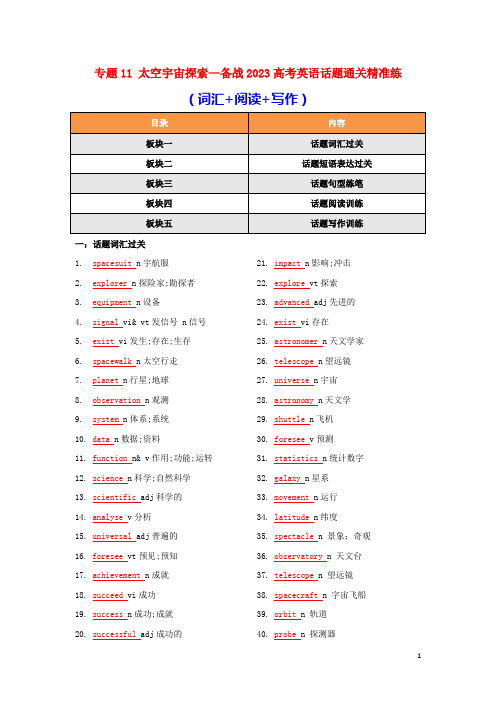
专题11 太空宇宙探索—备战2023高考英语话题通关精准练(词汇+阅读+写作)一:话题词汇过关1.spacesuit n宇航服2.explorer n探险家;勘探者3.equipment n设备4.signal vi& vt发信号 n信号5.exist vi发生;存在;生存6.spacewalk n太空行走7.planet n行星;地球8.observation n观测9.system n体系;系统10.data n数据;资料11.function n& v作用;功能;运转12.science n科学;自然科学13.scientific adj科学的14.analyse v分析15.universal adj普遍的16.foresee vt预见;预知17.achievement n成就18.succeed vi成功19.success n成功;成就20.successful adj成功的21.impact n影响;冲击22.explore vt探索23.advanced adj先进的24.exist vi存在25.astronomer n天文学家26.telescope n望远镜27.universe n宇宙28.astronomy n天文学29.shuttle n飞机30.foresee v预测31.statistics n统计数字32.galaxy n星系33.movement n运行titude n纬度35.spectacle n 景象;奇观36.observatory n 天文台37.telescope n 望远镜38.spacecraft n 字宙飞船39.orbit n 轨道40.probe n 探测器41.polar adj 两极的42.flyby n 飞越43.collision n 碰撞44.fossil n 化石45.sample n 样品;样本position n 合成物47.dimension n 范围;维度pound n 复合物49.spectrum n 光谱;系列50.discernible adj 可辨别的51.invasion n 入侵52.invisible adj 看不见的53.sunset n 日落54.enormity n 巨大55.tidal adj 潮汐的56.longitude n经度nd vt登陆;降落58.equator n赤道59.indicate v表明60.prove v 证实61.rocket 火箭unch pad 发射台63.booster 助推器64.mission 任务65.countdown 倒计时nd 登陆67.manned 载人的68.incredible adj难以置信的69.mystery n谜plex adj复杂的71.mysterious adj神秘的72.remain v仍然是73.unsolved adj未解决的74.disappearance n消失75.strange adj奇怪的76.curiosity n 好奇心二:话题短语表达过关would-be astronauts准宇航员1.sleep in private quarters睡在私人的房间里2.conduct scientific research进行科学研究3.in other research fields在其他研究领域nd on the Moon登上月球5.make major contributions作出了重大贡献6.have access to space travel能到太空旅游7.enhance the quality of humans’ lives提高人类的生活质量8.with the development of science and technology随着科技的发展9.do/work wonders创造奇迹10.have a negative effect有负面影响11.test new equipment检测新设备12.be curious about对……好奇13.be related to和……有关14.pay special attention to对……特别注意15.learn more about space多了解太空16.manned spaceship/spacecraft载人飞船17.realise one’s dream实现梦想18.send people into space把人送入太空19.one giant leap for mankind人类的一大步20.a space station太空站21.the outer space外太空22.make great progress取得巨大进步23.make measurements and observations做测量和观察24.solar system太阳系;类太阳系25.space exploration太空探索26.make a discovery做出发现27.the unknown不为人知的地方;人类尚未到达的地方28.amazing natural features神奇的自然特征29.supernatural powers超自然的力量30.the unexplained phenomenon无法解释的现象31.scientific explanation科学解释32.find out 找出,查明33.look into调查34.work out找到(解决办法)35.concrete evidence证据确凿三:话题句型练笔1:As well as doing these biological experiments,we carry out experiments in other research fields除了做这些生物实验,我们还在其他研究领域进行实验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Engineering Research Institute, University of Iceland, Hjarðarhagi 2-6, IS-107 Reykjavík, Iceland
On Colorings of Squares of Outerplanar Graphs∗
Geir Agnarsson
The results or opinions presented in this report are the responsibility of the authors. They should not be interpreted as representing the Research Institute or the University of Iceland. © Engineering Research Institute, University of Iceland, and the authors
†
Magn´ us M. Halld´ orsson
‡
Abstract We study vertex colorings of the square G2 of an outerplanar graph G. We find the optimal bound of the inductiveness, chromatic number and the clique number of G2 as a function of the maximum degree ∆ of G for all ∆ ∈ N. As a bonus, we obtain the optimal bound of the choosability (or the list-chromatic number) of G2 when ∆ ≥ 7. In the case of chordal outerplanar graphs, we classify exactly which graphs have parameters exceeding the absolute minimum. 2000 MSC: 05C05, 05C12, 05C15. Keywords: outerplanar, chordal, weak dual, power of a graph, greedy coloring, chromatic number, clique number, inductiveness.
An earlier version of this current paper appeared in SODA 2004 [2]. Department of Mathematical Sciences, George Mason University, MS 3F2, 4400 University Drive, Fairfax, VA 22030, geir@ ‡ Department of Computer Science, University of Iceland, Reykjav´ ık, Iceland. mmh@hi.is
Geir Agnarsson, Magnús M. Halldórsson. On Coloring Squares of Outerplanar Graphs, Engineering Research Institute, University of Iceland, Technical report VHI-04-2005, December 2005
On Coloring Squares of Outerplanar Graphs
Geir Agnarsson Magnús M. Halldórsson
December 2005
ii
On Coloring Squares of Outerplanar Graphs
Report nr. VHI-04-2005, Reykjavík 2005
† ∗
1
in the size of the graph [7]. The algorithm has also the special advantage that it requires only the square graph G2 and does not require information about the underlying graph G. The purpose of this article is to further contribute to the study of various vertex colorings of squares of planar graphs, by examining an important subclass of them, the class of outerplanar graphs. Observe that the neighborhood of a vertex with ∆ neighbors induces a clique in the square graph. Thus, the chromatic number, and in fact the clique number, of any graph of maximum degree ∆ is necessarily a function of ∆ and always at least ∆ + 1. Our results. We derive tight bounds on chromatic number, as well as the inductiveness and the clique number of the square of an outerplanar graph G as a function of the maximum degree ∆ of G. One of the main results, given in Section 3, is that when ∆ ≥ 7, the inductiveness of G 2 is exactly ∆. It follows that the clique and chromatic numbers are exactly ∆ + 1 and that Greedy yields an optimal coloring. As a bonus we obtain in this case that the choosability (see Definition 3.11) is the optimal ∆ + 1. We can then treat the low-degree cases separately to derive a linear-time algorithm independent of ∆. We examine in detail the low-degree cases, ∆ < 7, and derive best possible upper bounds on the maximum clique and chromatic numbers, as well as inductiveness of squares of outerplanar graphs. These bounds are illustrated in Table 1. We treat the special case of chordal outerplanar graphs separately, and further classify all chordal outerplanar graphs G for which the inductiveness of G2 exceeds ∆ or the clique or chromatic number of G 2 exceed ∆ + 1. ∆ 2 3 4 5 6 7+ ω ∆+1 ∆+1 ∆+2 ∆+1 ∆+1 ∆+1 Chordal ind ∆ ∆ ∆+1 ∆+1 ∆+1 ∆ χ ∆+1 ∆+1 ∆+2 ∆+1 ∆+1 ∆+1 ω ∆+3 ∆+2 ∆+2 ∆+1 ∆+1 ∆+1 General ind ∆+2 ∆+1 ∆+2 ∆+1 ∆+1 ∆ χ ∆+3 ∆+2 ∆+2 ∆+2 ∆+1 ∆+1
1
Introduction
The square of a graph G is the graph G2 on the same vertex set with edges between pair of vertices of distance one or two in G. Coloring squares of graphs has been studied, e.g., in relation to frequency allocation. This models the case when nodes represent both senders and receivers, and two senders with a common neighbor will interfere if using the same frequency. The problem of coloring squares of graphs has particularly seen much attention on planar graphs. A conjecture of Wegner [12] dating from 1977 (see [8]), states that the square of every planar graph G of maximum degree ∆ ≥ 8 has a chromatic number which does not exceed 3∆/2 + 1. The conjecture matches the maximum clique number of these graphs. Currently the best upper bound known is 1.66∆ + 78 by Molloy and Salavatipour [11]. An earlier paper of the current authors [1] gave a bound of 1.8∆ for the chromatic number of squares of planar graph with large maximum degree ∆ ≥ 749. This is based on bounding the inductiveness of the graph, which is the maximum over all subgraphs H of the minimum degree of H . It was also shown there that this was the best possible bound on the inductiveness. Borodin et al [4] showed that this bound holds for all ∆ ≥ 48. Inductiveness has the additional advantage of also bounding the list-chromatic number. Inductiveness leads to a natural greedy algorithm (henceforth called Greedy): Select vertex u ∈ V (G) of minimum degree, sometimes called a simplicial vertex of G, recursively color G \ u, and finally color u with the smallest available color. Alternatively, k -inductiveness leads to an inductive ordering u1 , u2 , . . . , un of the vertices such that any vertex u i has at most k neighbors among {ui+1 , . . . , un }. Then, if we color the vertices first-fit in the reverse order u n , un−1 , . . . , u1 (i.e. assigning each vertex the smallest color not used among its previously colored neighbors), the number of colors used is at most k + 1. Implemented efficiently, the algorithm runs in time linear
