浙江省东阳市南马高中2010届高三上学期期中考试(数学理)
浙江省东阳中学高三上学期期中考试(数学理).doc

浙江省东阳中学高三上学期期中考试(数学理)一、选择题:本大题共10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合}32|{<<-=x x M ,}1|{>=x x N ,则)(N M C R ⋂= ( )A .}31|{≥-≤x x x 或B .}31|{<<x xC .}31|{≥≤x x x 或D .∅ 2. 设向量a 和b 的长度分别为4和3,夹角为60°,则|a +b |的值为 ( ) A. 37 B. 13 C. 5D. 13.若22)sin(2cos -=-παα,则ααcos sin +的值为 ( ) A .- B . 12- C . 12 D 4.在各项都为正数的等比数列}{n a 中,首项31=a ,前三项和为21,则=++543a a a ( )A .33B .84C .90D .1895.已知双曲线22221x y a b-=(0a >,0b >)的一条渐近线的斜率为12,则该双曲线离心率是 ( )A.C.D.26. 若l 为一直线,γβα,,为三个互不重合的平面,给出三命题: ① βαγβγα⊥⇒⊥⊥, ② βγα,⊥∥βαγ⊥⇒③ l ∥βαβα⊥⇒⊥l , . 其中正确的命题有( ) A .0个 B .1个 C .2个 D .3个7.“18a =”是“对任意的正数x ,21ax x+≥”的 ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件8.函数()10<<=a xxa y x的图象的大致形状是( )9.设函数52 , -2x 0()()log (2x f x g x x ⎧≤<=⎨-+≤⎩,若()f x 是奇函数,则当x (0,2]∈时,()g x 的最大值是 ( ) A .14 B .34- C .34D .14-俯视图侧视图主视图10.设1a >,定义()111122f n n n n=+++++,如果对2n ∀≥,不等式 ()127log a f n b +>17log 7a b ++恒成立,则实数b 的取值范围是 ( )A.292,17⎛⎫ ⎪⎝⎭B. ()0,1C. ()0,4D. ()1,+∞二、填空题(本大题共7小题,每小题4分,共28分) 11.设向量(12)(23)==,,,a b ,若向量λ+a b 与向量(47)=--,c 共线,则=λ . 12.抛物线x y 162=上一点P 到x 轴的距离为12,则点P 与焦点F 间的距离|PF|=_______ 13. 将函数cos()3y x π=-的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再 向左平移6π个单位,所得函数的解析式为_________________________ 14.如上右图一个空间几何体的主视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为15.已知圆O :225x y +=和点A (1,2),过点A 且与圆O 相切的直线与两坐标轴围成的三角形的面积为 16.已知n S 是数列}{n a 的前n 项和,若nn n n n a 212)2)(1(1-+++=,则n S =__________17.设,x y 满足约束条件360200,0x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩,若目标函数(0,0)z ax by a b =+>>的最大值为12,则23a b +的最小值为______________三解答题(本大题共5小题,共72分)18. }{n a 是首项为4,公差0≠d 的等差数列,记前n 项和为n S ,若331S 和441S 的等比中项为551S . (1)求}{n a 的通项公式n a ; (2)求使0>n S 的最大n 值.19.已知向量.3sin 2)(),3sin ,3(cos ),1,3(x x f x x n m n m ⋅=-==记 (1)若)(],,0[x f x 求函数π∈的值域;(2)在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若A ac b C f sin ,,1)(2求且==的值。
浙江省东阳市南马高级中学高三上学期期中考试(物理).doc

2010年下学期南马高中期中考试试卷高三物理(理科)一、选择题(本题共12小题,每小题4分,共48分,1—6小题为单项选择题,7—12小题为不定项选择题。
)1.在某校举行的校运会上,某同学以s 8.11的成绩获得男子100米冠军,如果测得他起跑 后s 3时的瞬时速度为s m /6.7,跑到m 50处的瞬时速度为s m /5.8,根据以上条件,可 求出该同学在比赛中的A .起跑加速过程中的加速度B .跑完m 50所用的时间C .跑完全程的平均速度D .冲刺过终点时的瞬时速度 2.如图,质量为m 的物体悬挂在轻质的支架上,斜梁OB 与竖直 方向的夹角为θ,设水平横梁OA 和斜梁OB 作用于O 点的弹 力分别为1F 和2F 。
以下结果正确的是A .θsin 1mg F =B .θsin 1mgF =C .θcos 2mg F =D .θcos 2mgF =3.质点以初速度0v 做竖直上抛运动,下列对该质点落地前的运动判断正确的是 A .竖直上抛运动是竖直向上的匀减速运动和自由落体运动的合运动B .当2021gt t v <时,物体一定向下运动 C .当2021gt t v >时,物体一定向上运动D .当2021gt t v =时,物体上升到最高点4.如图,质量为1m 的木块受到向右的拉力F 的作用,在质量为2m 的长木板上向右滑行, 长木板保持静止状态。
已知木块与木板之间的动摩擦因数为1μ,木板与地面之间的动摩 擦因数为2μ,则A .木板受到地面的摩擦力大小一定为g m 11μB .木板受到地面的摩擦力大小一定为)(212g m g m +μC .若改变F 大小,且满足)(212g m g m F +>μ时,木板便会开始运动1m02I 0It It It2I 0I 0ID .以上说法均不正确5.如图所示,一个小球在竖直环内至少能做(1+n )次完整的 圆周运动,当它第(1-n )次经过环的最低点时的速度大小 为s m /7,第n 次经过环的最低点时速度大小为s m /5,则小 球第(1+n )次经过环的最低点时的速度v 的大小一定满足 A .等于s m /3 B .小于s m /1 C .等于s m /1 D .大于s m /16.压敏电阻是一种力传感器,其阻值会随所受压力的增大而减小,某 位同学利用压敏电阻设计了判断电梯运动状态的装置,其将压敏电 阻平放在电梯内,受压面朝上,在上面放一物体m ,电梯静止时电 流表示数为0I ,电梯在不同的运动过程中,电流表的示数分别如图 甲、乙、丙、丁所示,下列判断中错误的是甲 乙 丙 丁A .甲图表示电梯可能做匀速直线运动B .乙图表示电梯可能做变加速上升运动C .丙图表示电梯可能做匀加速上升运动D .丁图表示电梯一定做变加速下降运动 7.如图所示,放置在水平地面上的支架质量为M ,支架 顶端用细线拴着的摆球质量为m ,现将摆球拉至水平位置,而后释放,摆球运动过程中,支架始终不动。
2010高三数学理期中考试试卷及答案

福州三中2010—2011学年度高三上学期期中考试数学(理)试题本试卷分第I卷(选择题)和第II卷(非选择题)两部分共150分,考试时间120分钟。
注意事项:1•答第I卷前,考生务必将自己的姓名、考生号码(31103XXXX XXXX为班级+ 座号)、考试科目用铅笔涂写在答题卡上。
2•每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上。
3•考试结束,监考人将答题卡收回。
第I卷(选择题共50分)选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的•1(211 .设集合A= Q X -一£ X £2、B=(X X <1 ,I 2 JA . :x1< x<2;C .「XX:::2 /64cos71的2 .已sin ,值为2577A B.-25253 .等比数列a』中,4 =4 ,则a日6等于A.4B. 8A. x R,lg x =0B. x R,tanx =1则A U B=( )1 1B—<x G\I 2 JD.l x-1Exc2}( ) 44C— D. ——55( ) C.16D.32( ) C.Vx ER, X3A0D.時R,2X>04 .下列命题中的假命题.是:•_:,:•_ ,: = m,贝 U m _ ?&某种商品一年内每件出厂价在7千元的基础上,按月呈f(X )二"A >0>0|申|£上i 的模型波动(x 为月份),已知3月份达到最高价 9千元, \ 2)份价格最低为5千元,根据以上条件可确定 f (X)的解析式为9•如图,圆o 的内接 五角星”与圆o 交与A (i =1,234,5,)点,记弧AA41在圆0中所对的圆心角为a/i =1,2,3,4,),弧愿A 所对.啲圆心角为a 5 ,则c o3as c oas t a 5) —s i 3a 2 s i 2a 4 =― 3 5 .已知 ot € (—,兀),sin ot =—,贝V tan ( G + )等于254 11A .B . 7C.——7 7B . 7 D .— 76. m 、n 表示直线,:-J :-,表示平面,给出下列四个命题,其中真命题为(1) 匚 -m, n 二 x , n _ m,贝卜 l : (2) :-二 m,: 二 n,贝Un _ m (3) (4)m _ : , n 」i ,m _ n,贝U:--:A . (1 )、(2)B . ( 3)、(4)C. (2)、 (3)D . (2)、 (4)7.将函数y=3sin(x-v)的图象F 按向量(—,3)平移得到图象3F'若F 的一条对称轴是直线TtX ,则B 的一个可能取值是45 A. ■:12 5 B .12 11 C. 11D.-■:Asin(「) BA . nn*f (x) = 2sin( x )7 (1 乞 x 乞 12,x N )44JIJIB . C.f (x) =9sin( [X -[) (1 _ x _12,x N ) f(x)=2、-2s in — x 7(仁 x^12,x N )43171D . f(x)=2sin(;x — ;) 7(仁x ^12,x N )-20 A .B .C .D .10•已知函数y = f(x)和y =g(x)在[-2,2]的图象如下所示 y=f(x)四个命题:(1 )方程f[g(x)]=0有且仅有6个根;ee dLkx = -2 x12.已知向量 a = (3,1),b =(1,3),c =(k,2),若(a_c)丄 b ,则实数 k =13.已知极坐标系的极点在直角坐标系的原点 O 处,极轴与x 轴的正半轴重合.直线l 的极2x = 2cos -坐标方程为「si n (八)二 ,圆C 的参数方程为(参数y =g(x)给出下列(2 )方程g[ f (x)] 二0有且仅有3个根;(3)方程f[ f (x)H 0有且仅有5个根; (4)方程g[g(x)] 二0有且仅有4个根•其中正确的命题个数A . 1B . 2第II 卷 (非选择题共100 分)填空题:本大题共 5小题,每小题4分,共20分,把答案填在答题卡的相应位置.11 .C.-2 04 2 ly = 2si n 日+2日乏b,2让)),则圆心C到直线l的距离等于_________________2 214. 过双曲线 冷-爲=1的左焦点F 且垂直于x 轴的直线与双曲线相交于 M , N 两点,且a b双曲线的右顶点 A 满足MA _ NA ,则双曲线的离心率等于 _________________ .15. 符号X 1表示不超过x 的最大整数,如口!二丨-3丄1.081 - -2 ,定义函数{x } = X - IXI .那么下列命题中正确的序号是 _____________ .①函数{x }的定义域为R ,值域为0,1】. ② 方程 有无数多个解.③函数{x }是周期函数. ④函数{x }是增2函数.三、解答题:本大题共 6小题,共80分,解答应写出文字说明、证明过程或演算步骤.16. 本题(1 )、(2)两个必答题,每小题 7分,满分14分.(1)(本小题满分7分)已知x,y, z 为正实数,且1 1,求x 4y 9z 的最小值及取得最小值时 x, y, z 的x y z值.(2)(本小题满分7分)已知矩阵A = "333 ,若矩阵A 属于特征值6的一个特征 ^cd d17.(本小题满分 13分)已知f (x )二3sin2x ' 2 ■ 2cos 2 x . (1 )求f (x )的最小正周期与单调递减区间; (2 )在 ABC 中,a 、b 、c 分别是角 A 、B 、C 的对边,若向量为玄=",属于特征值1的一个特征向量为d 丿a 2勺[求矩阵A . 1一2丿能使整个矩形广告面积最小.19.(本小题满分13分)盒内有大小相同的 9个球,其中2个红色球,3个白色球, 4个黑色球.规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得-1分•现f (A) =4, b =1, .'ABC 的面积为 ,求a 的值.218.(本小题满分13分)迎世博,要设计如图的一张矩形广告,该广告含有大小相等的左中2右三个矩形栏目, 这三栏的面积之和为 60000cm ,四周空白的宽度为10cm , 之间的中缝空白的宽度为 5cm ,怎样确定广告矩形栏目高与宽的尺寸(单位: 栏与栏cm ),(单位:出的3个球中白色球的个数,求的分布列和数学期望.从盒内一次性取3个球.(1)求取出的3个球得分之和恰为1分的概率;(2)设•为取2 220.(本小题满分13 分)设椭圆C:笃爲=1 (a,b 0)的左、右焦点分别为F I,F2 ,若Pa bT T 1是椭圆上的一点,PR十PF? =4,离心率e=—. (1)求椭圆C的方程;(2)若P是第25一象限内该椭圆上的一点,PF1PF2,求点P的坐标;(3)设过定点P(0,2)的直线4与椭圆交于不同的两点代B,且/ AOB为锐角(其中O为坐标原点),求直线丨的斜率k的取值范围.1 2 121.(本小题满分14分)已知函数f(x)=lnx, g(x) ax bx. (1 )当a = b 时,求2 2函数h(x) = f (x)- g(x)的单调区间;(2)若b = 2且h(x) =f (x) £(x) 存在单调递减区间,求a的取值范围;(3)当a=0时,设函数f(x)的图象C与函数g x的图象C2 交于点P、Q,过线段PQ的中点R作x轴的垂线分别交G、C于点M、N,则是否存在点R,使G在点M处的切线与C2在点N处的切线平行?如果存在,请求出R的横坐标,如果不存在,请说明理由.【校本試卷】2010/11/04福建省福州三中2010届高三上学期半期考数学理科参考答案第I 卷(选择趣共50分)选tffi : 10^8. B 4^8 5 ft.共50 ft.在毎小U 给出的POf 选敗中.只有一取是符合邕口要来的. 【解析】D 【解析】B 【解析】C 【解析】C 【解析】 【解析】 【解析】 【解析】 【解析】【解析】当11仅当x = 2y = 3z 时等号成立.此时x=6,y = 3,z = 2 所以当x = 6j ,= 3,z = 2时.x + 4y + 9z 取得最小值36…(2)解:(1)依题意得c +d = 6 所以l3c-2"-2解得17. 解:<1) f (x) .................................................................... sin2x+2 + 2co^ x =>|'3siri2x+cos2x+3=2sin(2x - —) + 3 ............................................................../. T == n ...... 4 分21. 2. 3. 4. 5. 6. 7. &9.10.A B A D D C二、填空套: |】・ 12. 【解析】 【解13. 【解析】 第II 卷(非选择题共100分)每爪前4价.共20什,把苔果瞋在告总的fflBER.本大8H5^8.l-ln2 0 722 214・15. 三、解§«:本大&共6"、总・ 16. (1) *?:由柯西不等式得“ 4y + 9z =[(以)2 + (2&)2 +(3血)2 ]. [(±)2 +(金)2 +(十)2 ]2(侬•厶+ 2“・厶+ 3血•車)2 =36Vx yjy \!z【解析】 【解析】②®共80仔.解答应写出文字说明.演茸步iL —• —< Aa } = 6q 彳幻=“2,即令j < 2x + 2kn + ^-(keZ)< x <^ + ?^(k€ Z)rr 7/. f(x)的单调区间为[k7t + —,k7r +kez ................................. 6 分6・ 3*⑵由/(,4) = 4得心) = 2sin(2卄兰) + 3 = 4 ・・・sin(2/+夕)=£ ...... 7分6 6 * 2乂•: A 为 的内角.\-<24 + -<— :.2A^^ = — :\A = - ..................................... 9 分666663':S^ftc =^~、b = \ :. —/>csin A -:.c = 2 .............. 11 分2 2 2/. a 2 =62 +c 2 - 26c cos J = 4 + l-2x2xlx 丄=3/. a = V3 ................ 12 分 2200001&繇:设矩形栏目的髙为acm.宽为bcm.则a6 = 20000. .-.6 = ^^a广吿的高为a+20,宽为36 + 30(其中Q >0』>0) 广告的面积S = (fl + 20)(36 + 30)= 30(0 + 26) + 60600 = 30(a +毁也)+ 60600>30x 2」a x 毁型 + 60600 = 12000 + 60600 = 72600肖且仅当Q =型巴,即Q = 2(M)时,取等号,此时b = 100・故当广告的高为200am 宽为100cm 时.可使广告的面积最小.19.(I 〉解:记“取出1个红色球,2个白色球”为爭件“取出2个红色球.1个黑色球"为爭件B. 则取出3个球得分之和恰为1分为事件A+B. 则 P(/f + B) = P(£ + P(B) = ^~+^_ = ^ (2)解:歹可能的取值为0,1,23. 佗=0)=£|=丄, w CJ 21C 2C l 320•解:(I) —+ /=14 (2) •解:易知a=2上== J5所以片(一巧.0)迅(VLO). 05 则w > C ; 14 q 28 = 3) = g =丄.Cl 8410分 •绅数学期望#。
浙江省东阳市南马高中2010届高三上学期期中考试(生物)

浙江省东阳市南马高中2010届高三上学期期中考试生物一、单项选择题(每小题只有一个选项最符合题目要求。
每小题1分,共20分)1.蛋白质是细胞内最重要的生命物质之一,具有多样性和特异性,其结构与功能是相适应的。
下列有关蛋白质类物质与其功能对应正确的是A.胰岛素与调节 B.干扰素与催化C.DNA连接酶与DNA复制 D.载体与免疫2.下列关于念珠藻的说法正确的是A.线粒体是念珠藻进行有氧呼吸的主要场所B.念珠藻的遗传物质主要是DNA,其次是RNAC.核糖体是念珠藻细胞内蛋白质的“装配机器”D.叶绿体是念珠藻进行光合作用的场所3.在下列四个试管中分别加入一些物质,甲试管:新鲜乳酸奶;乙试管:甘氨酸溶液;丙试管:豆浆和蛋白酶;丁试管:鸡血液中的红细胞和蒸馏水。
上述四个试管中加入双缩脲试剂振荡后,有紫色反应的是A.甲、丁 B.甲、乙、丁 C.甲、乙、丙 D.甲、丙、丁4.右图为人体内能源物质代谢的部分过程图解,下列有关叙述正确的是A.处于饥饿状态时,血液中的葡萄糖可来自于肝糖元和肌糖元的分解B.d过程是氨基转换作用C.葡萄糖是细胞呼吸最常利用的物质,故图中的[H]只来自于葡萄糖的氧化分解D.人体所需的葡萄糖最终来源于绿色植物的光合作用,故人的同化作用类型为异养型5.下列有关细胞的叙述合理的是A.流感病原体、结核病病原体、人肿瘤细胞具有类似的细胞结构,都可以成为抗原B.效应T细胞合成抗体时有细胞核、核糖体、内质网、高尔基体等结构参与C.细胞全能性就是指一个细胞内所有基因同时得以表达D.细胞分裂存在于个体发育整个生命过程中,细胞分化在胚胎发育阶段达到最大6.呼吸作用是一切活细胞共有的生命活动,下列说法正确的是A.植物细胞受伤后呼吸速率明显减缓B.植物受涝冬季比夏季危害更大C.种子与果蔬的贮藏要求条件一致D.上一营养级生物呼吸消耗的能量不能传递到下一营养级7.右图是某些生物体内氢随化合物在体内的转移过程,下面对其分析错误的是A.[H]经①→②转移到葡萄糖时的过程为光合作用过程,此时A为NADPHB.[H]经②→①转移到水时的过程需要氧气参与,其发生一定要有线粒体C.[H]经②→④过程一般在缺氧条件下才能进行D.对人体而言,③过程不可能发生在肌肉细胞,⑤过程是错误的8.下图是某同学为了研究酵母菌的无氧呼吸所制作的一个实验装置。
浙江省东阳市南马高级中学高三上学期期中考试(历史).doc

下学期南马高中期中考试试卷高三历史(本试题卷分选择题和非选择题两部分,共6页。
时量90分钟,满分100分。
)一、选择题(本题共30小题,每小题2分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.李大钊在《史学要论》中指出,“一时代有一时代比较进步的历史观,一时代有一时代比较进步的知识;史观与知识的不断进步,人们对历史事实的解喻自然要不断的变动。
”他在这里强调历史研究要A.与时代同行 B.有历史观引导 C.为现实服务 D.充分掌握史实2.在印度尼西亚的三宝垅市有这样一幅题联“继张(骞)班(超)立功导域,开哥(伦布)麦(哲伦)探险先河”。
此联称颂的是A.玄奘 B.郑和 C.马可波罗 D.迪亚土3.“国家本置中书,门下以相检察,中书诏敕或有差失,则门下当行驳正。
”此制度始于A.秦汉时 B.隋 C.唐 D.北宋4.“元起朔方,固已崇尚释教(佛教),及得西域,世祖以地广而险远,……思有以因其俗而柔其人,乃郡县土番之地,设官分职,而领之于帝师。
”这里的“官”隶属于A.宣政院 B.中书省 C.理藩院 D.行中书省5.古代雅典城邦平民能在反对贵族的斗争中取得胜利,最重要的社会因素是A.平民开展暴力斗争 B.代表平民利益的领袖不断改革C.平民中不再有债奴 D.平民中新兴工商业者力量壮大6.“法律条文没有作出规定的,法官就不能受理。
譬如有公民的奴隶被人拐走或偷跑掉,此公民要求法律受理就要找法官,向他申明:根据某某法律,我认为此奴隶应归我所有。
法官确认后才能受理。
”这一描述主要说明罗马法A.重视法律程序 B.保留习惯旧俗 C.强调法官至上 D.体现人人平等7.有人形象地说南京既是中国近代史的起点,也是中国近代史的终点。
下列能够反映这种说法的两个历史片断是①洪秀全在天京颁布《天朝田亩制度》②在南京下关江面的英舰上签订中英《南京条约》③侵华日军代表在南京向中国代表递交投降书④人民解放军占领南京国民政府“总统府”A.②③ B.③④ C.①④ D.②④8.电视剧《亮剑》成功塑造了八路军独立团团长李云龙和国民党晋绥军某部团长楚云飞的形象。
浙江省东阳中学高三上学期期中考试(数学文).doc

浙江省东阳中学高三上学期期中考试(数学文)一、选择题1.设====A C B B A U U 则},4,3,2{},5,2,1{},5,4,3,2,1{ ( ) A. Φ B. }2{ C. }4,3{ D. }5,4,3,1{ 2.的是且"3""21">+>>y x y x ( ) A.充分不必要条件 B.必要不充分条件 C. 充要条件 D. 即不充分也不必要条件 3.由1,2,3三个数字组成的无重复数字的两位数字中,任取一个数,则恰为 奇数的概率是 ( ) A.61 B. 31 C. 21 D. 324.若复数21221)()1(1,54Z Z i i Z i Z -+=-=,则为虚数单位其中 在复平面上对应的点位于 ( ) A.第一象限 B.第二象限 C. 第三象限 D. 第四象限 5.函数52)(-+=x e x f x的零点个数是 ( ) A. 0 B. 1 C. 2 D.3 6.若yx xy y x 112,0,0+=>>,则的最小值是 ( ) A.2 B.23C.2D. 22 7.若双曲线)0,0(12222>>=-b a b y a x 的一个焦点到一条渐近线的距离等于焦距的41,则双曲线的渐近线方程是 ( ) A. 02=±y x B. 02=±y x C. 03=±y x D.03=±y x8.设n m ,是两条不同的直线,βα,是两个不同的平面,下列命题正确的是( )A. βαβα//,//,,则若n m n m ⊥⊥B. n m n m //,//,//,//则若βαβαC. n m n m ⊥⊥则若,//,//,αββαD. βαβα//,//,//,//则若n m n m 9.已知, 为两个非零向量,则下列命题不正确的是 ( )A.若b t a t 00,=∃=⋅使得实数则B.,00bt a t ==∃使得实数若C. t t 00,=∃+=+使得实数则D. t t +=+=∃使得实数若,,0010.已知数列32}{-=n a a n n 的通项公式为,将数列中的各项进行分组如下:第1组:1a ;第二组:32,a a ;第三组:654,,a a a ;如此继续,如果第k 组的最后一个数字为m a ;那么第1+k 组的1+k 个数依次排列为:⋅⋅⋅++,,21m m a a .则第10组的第一个数是 ( )A.91B.89C. 17D. 15 一、填空题11.某高中共有1000名学生,采用分层抽样的方法, 分别在三个年级的学生中抽取容量为100的一个样本, 其中在高一、高二年级中分别抽取30,35名学生,则该校高三年级有 名学生. 12.已知m 为非零实数.若函数)11ln(--=x my 的图像关于原点成中心对称,则m= 。
浙江省东阳南马高中高三数学上学期期中考试 理 新人教A版

南马高中2011年下学期高三数学(理)期中试卷一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.已知22)4sin()2cos(-=--πααπ,则cos sin αα+等于A..12 D .12-2.设偶函数)(x f 在(0,+∞)上为增函数,且0)1(=f ,则不等式()()0f x f x x+-<的解集为 A .(-1,0)∪(1,+∞) B .(-∞,-1)∪(0,1) C .(-∞,-1)∪(1,+∞) D .(-1,0)∪(0,1)3.一个几何体的三视图如图1所示,已知这个几何体的体积为h =AC ..4.设{}n a 是公差为正数的等差数列,若12318a a a ++=,123120a a a =,则111213a a a ++=A .46B .92C .138D .1325.设 l 、m 、n 为不同的直线,α、β为不同的平面,则正确的命题是 A .若 α⊥β,l ⊥α,则 l ∥β B .若 α⊥β,l α⊂,则 l ⊥β C .若 l ⊥m ,m ⊥n ,则 l ∥nD .若m ⊥α,n ∥β且α∥β,则 m ⊥n6.设函数ax x x f m+=)(的导函数是12)(+='x x f ,则数列})(1{n f )(*N n ∈的前n 项 和为 A .21++n n B .1+n n C .12++n n D .nn 1+7.已知x ,y 均为正数,且x≠y,则下列四个数中最大的一个是A .12(1x +1y )B .1x+yC .1xyD .12(x 2+y 2)8.已知各项均不为零的数列{}n a ,定义向量()1,+n n n a a c ,()1,+=n n d n ,n ∈*N . 下列命 题中真命题是俯视图A .若n ∀∈*N 总有n n d c ⊥成立,则数列{}n a 是等差数列B .若n ∀∈*N 总有n n d c ⊥成立,则数列{}n a 是等比数列C .若n ∀∈*N 总有n n d c //成立,则数列{}n a 是等差数列D .若n ∀∈*N 总有n n d c //成立,则数列{}n a 是等比数列9.定义方程()()f x f x '=的实数根x 0叫做函数()f x 的“新驻点”,如果函数()g x x =,()ln(1)h x x =+,()cos x x ϕ=(()x π∈π2,)的“新驻点”分别为α,β,γ,那么α, β,γ的大小关系是A .γβα<<B .βγα<<C .βαγ<<D .γαβ<<10.如图123,,l l l 是同一平面内的三条平行直线,1l 与2l 间的距离是2,2l 与3l 间的距离是4。
2010届高三数学上册期中考试试题4

2010届高三数学上册期中考试试题数学文科 2009.10本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分。
考试时间120分钟。
第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分。
在每个小题列出的四个先期中,选出符合题目要求的一项。
1.双曲线15422=-y x 的焦点坐标为( )A .(– 1,0),(1,0)B .(– 3,0),(3,0)C .(0,– 1),(0,1)D .(0,– 3),(0,3)2.函数y = log2x x -+32的定域为( )A .{x|–3<x <2}B .{x|–2<x <3}C .{x | x >3或x <– 2}D .{x | x <– 3或x >2}3.设a =3-π,b = lg4π, c =π1lg,则( )A .c <a <bB .c <b <aC .b <c <aD .b <a <c4.函数y = log2 ( x2 – 5x – 6 )单调递减区间是( )A .⎪⎭⎫ ⎝⎛∞-25, B .⎪⎭⎫⎝⎛+∞,25C .()1,-∞-D .(+∞,6)5.4.设m 、n 是两条不同的直线,α、β是两相没的平面,则下列命题中的真命题是( )A .若m ∥α, n ∥β,α∥β,则m ∥nB .若βα⊂⊂n m ,,m ∥n 则α∥βC .若m ⊥β,m ∥α,则α⊥βD .若β⊂m ,α⊥β,则m ⊥α6.若圆x2 + y2 – 2x + 4y = 0与直线x – 2y + a = 0相离,则实数a 的取值范围是( )A .– 2<a <8a >8或a <– 2B .a >0或a <– 10C .– 10<a <0D .a >8或a <– 2 7.已知向量= ( 1 , 3 ),= ( 3 , n )若2–与共线,则实数n 的值是( )A .323+B .323-C .6D .98.编号为1,2,3,4,5的5人入座编号也为1,2,3,4,5的5个座位,至多有两人对 号入座的不同坐法有( ) A .109种 B .110种 C .108种 D .111种第Ⅱ卷(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分。
浙江省东阳南马高中高三上学期期中考试(数学理).pdf

——梁启超 七年级历史下第23 课 大连市第四十五中学 艾宛虹 原因? 表现? 影响? 二、闭关政策闭关,并非完全断绝往来,而主要表现在对贸易进行严格的限制。
原因? 表现? 影响? 二、闭关政策 闭关,并非完全断绝往来,而主要表现在对贸易进行严格的限制。
原 因 清朝统治者坚持“以农为本,重农抑商”的政策。
当时中国占统治地位的仍然是自给自足的封建经济,资本主义萌芽虽然已有缓慢发展,但是不需要大宗的外国商品。
封建的自然经济使清朝统治者固步自封、虚骄自大,闭关自守。
乾隆帝曾说:“天朝物产丰盈,无所不有,原不籍外夷货物以通有无,特因天朝所产茶叶、瓷器、丝巾为西洋各国及尔国必需之物,是以加恩体恤。
” 2.天朝大国的浅见陋识 清军入关后,一些抗清力量转入南洋一带,清政府担心这些人重新打回来。
而这时西方殖民者在东南沿海经常进行海盗活动,这更使清政府忐忑不安,担心中国人民跟外界接触后会“滋扰生事”。
1、经济上没有迫切需要 3、为维护巩固清王朝的统治 原因 这位商人的苦衷是什么? 清王朝对外交往中的国策是什么?清王朝严格限制和禁止对外交往和贸易的政策。
表现 限制通商口岸 对进出口货物限制 提高关税抑制进口 实行商行制度,垄断对外贸易,监视外国商人 看 世 界 唇枪舌剑辩一辩 防御侵略 限制发展 阻碍交流 正 方:闭关锁国利大 VS 反 方:闭关锁国弊大 影 响: 弊却是 将来的 长远的 利只是 眼前的 暂时的 利弊 > 到1840年鸦片战争爆发时为止, 中国人均粮食仅有200公斤左右, 美国已接近1000公斤; 中国年产铁约二万吨,不及法国的1/10,不及英国的1/40。
中国的造船和航海业…… 中国的科学技术…… 影 响 防御侵略 阻碍交流 限制发展 七年级历史下第23课 大连市第四十五中学 艾宛虹 盘 点 收 获 巩 固 升 华 对 外 关 系 目的条件 经过 影响 郑和下西洋 闭关锁国 明 清 原因 表现 影响 含义 开放政策 闭关政策 板 书 设 计 课 堂小 结 七年级历史下第23课 大连市第四十五中学 艾宛虹 扬 帆 启 游戏规则: 请在扬帆起航四个字中选一个字,每组选派两位同学上前合作完成。
浙江省东阳南马高中高三上学期期中考试(数学文).pdf

法律 宪法 狭义的法律 法规 全国人民代表大会及其常务委员会制定 国务院和地方国家权力机关制定 Why? 法律是一种 特殊的行为规范? 法律是一种特殊的行为规范 1.在影剧院,看电影不能大声喧哗。
2.在学校里,上自习课必须保持安静,否则要扣除班级分。
3.在法院旁听审判必须保持安静。
同样是保持安静,但他们却各有不同。
请你猜一猜, 哪一种行为是法律? 法律和其他规则的区别有哪些? 法律是一种特殊的行为规范 1、国家制定或认可2、局部适用3、舆论、习惯、信念4、自然形成5、行政力量6、全国适用7、行政机关制定8、普遍适用9、国家强制力 产 生 调整范围 实现手段 社会 道德 纪律 规章 国家 法律 自然形成 行政机关 国家制定或认可 普遍适用 全国适用 局部适用 国家强制力 行政力量 舆论、习惯、信念 法律是由并依靠 保证实施的一种 的行为规范。
国家制定或认可 国家强制力 特殊 法律的特殊性 从制定上看: 从保障机制上看: 从适用范围上看: 由国家制定或认可,并要经过一定的法律程序。
法律依靠国家强制力保证实施。
法律在全国范围内对全体社会成员具有普遍约束力。
法律的本质: 法律是掌握国家政权的统治阶级意志的体现。
我国法律的本质: 我国法律体现人民的利益和意志。
法律的作用 法律维护社会秩序 法律促进社会进步 法律维护人们的合法权益 我国法律集中反映了人民的利益和意志,是一切公民行为的出发点和根本准则。
是我国现代化建设的重要目标。
建设社会主义法制国家 意义: 谢谢! 1、上课保持安静 2、积极主动的学习 3、把书上内容与现实生活相结合 4、个人探究与小组合作探究相结合 5、鼓励创新 推开法律之门 规矩成方圆 特殊的行为规范 生活离不开法 树立宪法意识 至高无上的地位 人民权利的保证书 崇尚宪法 依法治理国家 治国有方略 治国铸基石 学会监督依法行使权利 《思想品德》八年级(下册) 第1课 推开法律之门第一单元: 法律在我们身边 重点: 1、生活离不开法 2、法律的特殊性及法律的本质 难点: 法律的特殊性及法律的本质 设问: 这样的比赛成绩能不能算? 假如体育比赛当中都是这种场景, 那会是一种什么样子? 创设情境、导入课题 第2届奥运会的撑竿跳高比赛时,一位日本运动员拿着长杆,跑到横杆前,突然将长杆插在地上,并两手抓住杆子爬了上去,到了横杆高度时跳了过去,全场都一下子目瞪口呆,因为在当时的撑杆跳比赛规则中,没有规定是否允许爬杆,只是说用杆。
浙江省东阳中学高三上学期期中考试(数学理).pdf

东阳中学2011年下学期期中考试卷 (高三数学理) 一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知全集,集合,,则等于 A.或 B. C. D. 2.设是单位向量,则“”是“”的A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D. 既不充分也不必要条件 3.已知等差数列的公差为2,若成等比数列,则A.B.C. D. 4.若某多面体的三视图(单位: cm) 如图所示, 则此多面体是 A.cm B. cm C.cm D.cm3 5.设偶函数(的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则的值为A. B.C. D. 6.ABC的三边分别为a,b,c,其中c为斜边,直线ax+by+c=0与圆,(为常数, )交于两点,则 ( ) A.sinθ B.2sinθ C.tanθ D.2tanθ 7.设、是两条不同的直线,、是两个不同的平面. 考察下列命题,其中真命题是A. B.∥,∥ C.∥ D. 8.设双曲线C:(a>0,b>0)的右焦点为F,左,右顶点分别为A1,A2.过F且与双曲线C的一条渐近线平行的直线l与另一条渐近线相交于P,若P恰好在以A1A2为直径的圆上,则双曲线C的离心率为A. B.2 C.D.39.设平面向量=(x1,y1)=(x2,y2) ,定义运算⊙:⊙=x1y2-y1x2 .已知平面向量,,则下列说法错误的是A.(⊙)+(⊙)=0 B.存在非零向量,同时满足⊙=0且?=0 C.(+)⊙c=(⊙)+( ⊙) D.|⊙|2=||2||2||2 10.已知函数,则方程(为正实数)的根的个数不可能为( ) A.3个B.4个C.5个D.6个 二、填空题: 本大题共7小题,每小题4分,共28分. 11.已知复数( i为虚数单位),则= . 12.已知,,, ▲ .13.AB=2,BB1=4,则BB1与平面ACD1所成角的余弦值为 ▲ . 14.函数),若对所有的实数,都有成立,则= ▲ .] 15.已知上有两个不同的零点,则m的取值范围为16.已知,则的最大值与最小值的差为17.设和是抛物线上的两个动点,且在和处的抛物线切线相互垂直, 已知由及抛物线的顶点所成的三角形重心的轨迹也是一抛物线, 记为.对重复以上过程又得一抛物线,类推.设如此得到抛物线的序列为,若抛物线的方程为,经专家计算得,, , , , . 则=] 三. 解答题(本大题共5小题,满分72分.解题应写出文字说明,证明过程或演算步骤.) 18.(本小题满分14分) 在中,角所对的边分别为,且成等差数列. (Ⅰ)求角的大小;(Ⅱ)若,求边上中线长的最小值.是首项的等比数列,其前项和中,,成等差数列, (1)求数列的通项公式; (2)设,若,求证:. 20.(本小题满分15分) 如图,已知平行四边形ABCD中,,垂足为E,沿直线AE将△BAE翻折成△B’AE使得平面B’AE ⊥平面.连接’D,是’D上的点. (Ⅰ)当’P=PD时,求证CP⊥平面’D; (Ⅱ)当’P=2PD时,求二面角的余弦值. 21.(本小题满分15分) 如图,已知过点作抛物线的切线,切点在第二象限. (Ⅰ)求切点的纵坐标; (Ⅱ)若离心率为的椭圆恰好经过切点,设切线交椭圆的另一点为,记切线的斜率分别为,若,求椭圆方程. 22.(本小题满分14分) 已知函数. 的单调性; (II)设 .当时,若对任意,存在,(),使,求实数的最小值.高三数学理科期中答案 (18)(本小题满分14分) 解:()由题意得:, , .…………………………6分 (Ⅱ)设边上的中点为,由余弦定理得: , …………………………10分 ,当时取到”=” 所以边上中线长的最小值为.…………………………14分 另解:设边上的中点为,, ,以下同上面解答方式. (19)(本小题满分14分),则显然,,不构成等差数列. ∴, 当时,由,,成等差数列得 ∴ , ∵ ∴ ∴ (2)∵ ∴ ∴= = ,是递增数列. . (20)(本小题满分14分) ,平面平面,∴. 如图建立空间直角坐标系, …2分 则,,, ,,. ,,. …4分 ∵,,∴,. …6分 又,∴平面. …7分 (Ⅱ)设,则,, 由得:,解得,,, ∴,,. …10分 设面的法向量为,则. 取,,则, …12分 又平面的法向量为, 设二面角的大小为,则. …14分 (21)解:(Ⅰ)设切点,且,由切线的斜率为,得的方程为,又点在上, ,即点的纵坐标.…………5分 (Ⅱ)由(Ⅰ) 得,切线斜率, 设,切线方程为,由,得,…………7分 所以椭圆方程为,且过,…………9分 由, ,…………………11分 将,代入得:,所以, 椭圆方程为.………………15分 的定义域为, (1)若,从而当时,;当时, 此时函数的单调递增区间为,单调递减区间为 (2分) (2)若,则 ①当时,,从而当或时,, 当 时, 此时函数的单调递增区间为和,单调递减区间为; ②当时,, 此时函数的单调递增区间为,单调递减区间为 综上所述,当时,函数的单调递增区间为,单调递减区间为 ;当时,函数的单调递增区间为和,单调递减区间为. (7分) (II)由(I)可得当时,在区间上单调递增,在上单调递减, 所以在区间上, 由题意,对任意,存在(),使 从而存在()使, 即只需函数在区间()上的最大值大于-2, 又当时,,不符, 所以在区间()上. 解得,所以实数的最小值为. (14分) (第21题图) (第20题) (第5题图) 第4题。
数学(文)卷·浙江省东阳市南马高中2010届高三上学期期中试卷
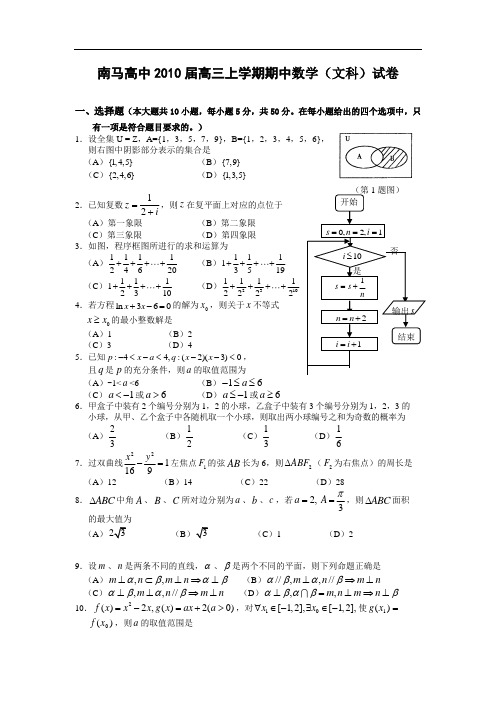
n an
,求数列{bn }的前 n
项和为Tn .
20.(本题满分 14 分)
下图是几何体 ABC A1B1C1 的三视图和直观图. M 是 CC1上的动点, N, E 分别是
AM , A1B1 的中点.
(Ⅰ)求证: NE // 平面 BB1C1C ;
2
2
(Ⅱ)当 M 在 CC1 的什么位置时, B1M 与平面 AA1C1C 所成的 角是 30 。
(Ⅲ)若函数 f (x) 与 g(x) 的图象有三个不同的交点,求实数 a 的取值范围。
南马高中高三数学(文科)期中答案 2009.10
1—10.CDABB BDBBA
11. x2 y2 1 98
12.4
13. 1 6
14. 9 4
15. 1 2
16.1
17. (, 2) (4, )
f (0) b 2 3
(I)求 p 的值; (Ⅱ)探究:当 k 变化时,点 Q 是否为定点?
22.(本题满分 15 分)
已知函数 f (x) 1 x3 a x2, g(x) 1 x2 ax a2 。
32
2
2
(I)当 a 2 时,求曲线 y f (x) 在点 P(3, f (3)) 处的切线方程;
(Ⅱ)当函数 y f (x) 在区间[0,1] 上的最小值为 1 时,求实数 a 的值; 3
N
F
B
B1
∴ B1MF 30
A
B1F 2, B1M 2 2 , C1M 2,
E A1
∴当 M 在 CC1 的中点时, B1M 与平面 AA1C1C 所成的角是 30 . ……14 分
21.(I)当 y 1时, x 1 , 2p
| AP | 1 p p ,得 p 1 2p 2
浙江省东阳中学高三数学上学期期中试题 理 新人教A版

浙江省东阳中学2014届高三数学上学期期中试题 理 新人教A 版一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中只有一项是符合题目要求的.1.已知集合22{|log 0},{|20}A x x B x x x =∈>=∈--<R R ,则A B =I ( )A. (1,2)-B. (1,)-+∞C. (1,1)-D. (1,2)2.已知复数()i i 1i a b +=-(其中,a b ∈R ,i 是虚数单位),则a b +的值为 ( ) A .2- B .1- C . 0 D .23.已知空间两条不同的直线,m n 和两个不同的平面,αβ,则下列命题中正确的是 ( ) A.若//,//,//,//m n m n αβαβ则 B.若//,,,//m n m n αβαβ⊥⊥则 C.若,//,,m n m n αβαβ⊥⊥⊥则 D.若,,m n αβαβ⊥⊥⊥则m n ⊥4.已知等差数列{}n a 的前n 项和为n S ,若22013,OA a OB a OC =⋅+⋅u u u r u u u r u u u r 且A,B,C 三点共线(该直线不过点O ),则2014S 等于 ( ) A.2014 B.2012 C.1012 D.1007 5.在△ABC中,“sin A >3πA >”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.已知,1,=>ab b a 则ba b a -+22的最小值是 ( )A .22B .2C .2D .17.已知等比数列{}n a 中,各项都是正数,且2312,21,a a a 成等差数列,则8967a a a a ++等于( )A .21+ B. 21- C. 223+ D. 223-8.已知两点(1,0),A B O 为坐标原点,点C 在第二象限,且ο120=∠AOC ,设2,(),OC OA OB λλλ=-+∈R u u u r u u u r u u u r则等于 ( ) A .1- B .2 C .2- D .19.已知2a b >≥.现有下列不等式:①23b b a >-;②4221ab a b+<+;③ab a b >+;④log 3log 3a b >.其中正确的是 ( )A. ①② B. ①③C. ②④ D. ③④10.已知函数),0[,)9()(2+∞∈-=x x x x f 存在区间[,][0,)a b ⊆+∞,使得函数()f x 在区间[,]a b 上的值域为[,]ka kb ,则最小的k 值为 ( ) A .36 B . 9 C .4 D . 1二、填空题:本大题共7小题,每小题4分,共28分.11.三视图如右的几何体的体积为12.已知数列{}n a 是正项等比数列,若132a =,44a =,则数列2{log }n a 的前n 项和n S 的最大值为 .13.在面积为2的正ABC ∆中,E,F 分别是AB ,AC 的中点,点P 在直线EF 上,则2+⋅的最小值是___________。
数学(理)卷·浙江省东阳市南马高中2010届高三上学期期中试卷

南马高中2010届高三上学期期中数学(理科)试卷一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.若集合{}0P y y =≥,P Q Q =I ,则集合Q 不可能...是 (A ){}2y y x = (B ){}2x y y = (C ){}lg y y x = (D )∅2.在821)x 的展开式中,常数项为 (A )-28 (B )-70 (C )70 (D )28 3.已知两条不同的直线m ,l 与三个不同的平面α,β,γ,满足l βγ=I , //l α,m α⊂,m γ⊥,那么必有(A )αγ⊥,m l ⊥ (B )αγ⊥,//m β (C )//m β,m l ⊥ (D )//αβ,αγ⊥4.在等比数列{}n a 中,0n a >,211a a =-,439a a =-,则45a a += (A )16 (B )27 (C )36 (D )815.已知a b c ,,均为实数,则“240b ac -≤”是“关于x 一元二次不等式c bx ax ++20>的解集为∅”的(A )充分不必要条件 (B )必要不充分条件(C )充分必要条件 (D )既不充分也不必要条件6.已知钝角三角形ABC 的最大边长为2,其余两边长为,x y ,则以(,)x y 为坐标的点 所表示平面区域的面积是(A )π (B )2π- (C )4π (D )42π-7.等比数列{}n a 中,11317,,2a q ==-记12(),n f n a a a =⋅…则当()f n 最大时,n 的 值为(A )7 (B )8 (C )9 (D )108.已知2,0()2,0xx f x x x ⎧≥⎪=⎨⎪<⎩,则[()]1f f x ≥的解集是(A)(,-∞ (B))+∞(C)(,1])-∞-+∞U (D)(,[4,)-∞+∞U9.双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为1F 、2F ,离心率为e ,过2F 的直线与双曲线的右支交于,A B 两点,若1F AB ∆是以A 为直角顶点的等腰直角三角形,则2e =(A)1+ (B)3+ (C)4- (D)5-10.若函数(),xf x x e =-⋅则下列命题正确的是(A )1(,),,()a x R f x a e ∀∈-∞∃∈> (B )1(,),,()a x R f x a e∀∈+∞∃∈> (C )1,(,),()x R a f x a e ∀∈∃∈-∞> (D )1,(,),()x R a f x a e∀∈∃∈+∞>二、填空题(本大题共7小题,每题4分,共28分。
浙江省东阳市南马高中高三物理上学期期中考试

浙江省东阳市南马高中2010届高三上学期期中考试物理一、选择题(本题13小题,每小题3分,共39分,每小题有一个或几个正确选项, 选全对得3分,选不全得2分,有选错的得0分,将答案填在答题卷内。
)1.17世纪意大利科学家伽利略在研究运动和力的关系时,提出了著名的斜面实验,其中 应用的物理思想方法属于( )A .等效替代B .实验归纳C .理想实验D .控制变量2.假设汽车紧急刹车制动后所受阻力的大小与汽车所受重力的大小差不多,当汽车以 20m/s 的速度行驶时,突然制动。
它还能继续滑行的距离约为( ) A .40m B .20m C .10m D .5m 3.一质点沿直线运动时的速度—时间图线如图所示,则以下说法中正确的是( )A .第1s 末质点的位移和速度都改变方向B .第2s 末质点的位移改变方向C .第4s 末质点的位移为零D .第3s 末和第5s 末质点的位置相同4.在机场和海港,常用输送带运送旅客和行李、货物,如图所示,a 为水平输送带,b 为倾斜输送带。
当行李箱随输送带一起匀速运动时, 下列几种判断中正确的是 ( )A .a 、b 两种情形中的行李箱都受到两个力作用B .a 、b 两种情形中的行李箱都受到三个力作用C .情形a 中的行李箱受到两个力作用,情形b 中的行李箱受到三个力作用D .情形a 中的行李箱受到三个力作用,情形b 中的行李箱受到四个力作用5.举重是中国代表团在奥运会上重要的夺金项目。
在举重比赛中,运动员举起杠铃时必 须使杠铃平衡一定时间,才能被裁判视为挺(或抓)举成功。
运动员可通过改变两手 握杆的距离来调节举起时双臂的夹角。
若双臂夹角变大,则下面关于运动员保持杠铃 平衡时手臂用力大小变化的说法正确的是 ( )A .不变B .减小C .增大D .不能确定6.在以加速度a =13g 匀加速上升的电梯里,有一质量为m 的人,上升了h 米,下列说 法正确的是( )A .人与电梯的总机械能守恒B .人的重力势能增加mghC .人对电梯的压力为23mgD .人对电梯的压力为43mg7.我国发射的神州五号载人宇宙飞船的周期约为90min ,如果把它绕地球的运动看作是 匀速圆周运动,飞船的运动和人造地球同步卫星的运动相比,下列判断中正确的是 A .飞船的轨道半径大于同步卫星的轨道半径 B .飞船的运行速度大于同步卫星的运行速度C .飞船运动的向心加速度大于同步卫星运动的向心加速度D .飞船运动的角速度小于同步卫星的角速度8.如图所示,质量为m 的质点静止地放在半径为R 的半球体上,质点与半球体间的动 摩擦因数为μ,质点与球心的连线与水平地面的夹角为θ,则下列说法正确的是( ) A .地面对半球体的摩擦力为零B .质点对半球体的压力大小为mgsin θC .质点所受摩擦力大小为mgsin θD .质点所受摩擦力大小为mgcos θ 9.如图所示,带箭头的直线表示某电场的电场线,虚线表示等势线,一个带负电的粒子 以一定初速度进入电场,由A 运动到B (轨迹为图中AB 实曲线所示).则(不计粒子 重力)( )A .A 点的电势较高B .带电粒子通过A 点时的加速度较大C .带电粒子通过B 点时动能较大D .带电微粒在B 点时的电势能较大10.如图,P 是位于粗糙水平桌面上的物块。
2010年东阳市高考模似数学理科参考答案

一、选择题:本大题共10小题, 每小题5分, 共50分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的 . 题号1 2 3 4 5 6 7 8 9 10 答案 D A D C C B C AD二、填空题:本大题有4小题, 每小题7分, 共28分. 请将答案填写在答题卷中的横线上. 11.669 12. 13. 100 14.15415. 3 16.436n C + 17.2 三、解答题:本大题有5小题, 共72分. 解答应写出文字说明, 证明过程或演算步骤.18.(本小题满分14分)解:(1)由正弦定理得:sin sin 45sin sin 60BC B AC A ⋅===. (2) ABC ∆的内角和A B C π++= ,3A π=203B π∴<< B B ABC AC sin 4sin sin == 3)62sin(32)32sin(sin 34sin 21+-=-=⋅=∴ππB B B C BC AC S π320<<B , 67626πππ<-<-∴B 当262ππ=-B 即6π=B 时,S取得最大值 19.(本小题满分14分)解:(1)三次内取完球的概率为P ,10334513224532=⨯⨯⨯⨯⨯+⨯⨯=p (2)ξ的分布列为:3431101010E ξ=++=. B 1(参考答案)()东阳市2010 年高考模拟考试试卷数学理科20.(本小题满分14分)解:(1)PAB ∆ 是正三角形,O 是AB 的中点∴PO AB ⊥ 又PO CD ⊥∴PO ABCD ⊥面(2)以O 为原点,AB 为x 轴,OP 为z 轴,如图建立空间直角坐标系(1,0,0),(1,0,0),(1,2,0),(1,4,0),A B C D P --(2,4,0)BD =- ,设面PCD 的一个法向量为m = 由2200200x y m PC x y m CD ⎧-+=⎧=⎪⎪⎨⎨+-=⎪=⎪⎩⎩ 得 从而得m =设BD 与面PCD 所成的角为θ,则1sin 5θ== 即BD 与面PCD 所成的角的正弦为15(3)法一://BM CN∴,,,B M C N 四点共面又BC//AD,即有BC//面P AD,∴//BC MN 且AD//MN∴四边形BCNM 是平行四边形,12BC MN AD ==∴MN 是PAD ∆的中位线∴M,N 分别是P A,PD 的中点法二,设,AM AP DN DP λβ==则(),(1,44)M N λββ--- ∴(),(2,24)BM CN λββ=-=--∵//BM CN∴CN BM γ=即2(2)240βγλβγ⎧-=-⎪-=⎨= 从而1212βγ⎧=⎪⎪⎨⎪=⎪⎩ 即M 、N 是P A 、PD 的中点.21.(本小题满分14分)解:(1)设p(x,y)由已知2224(2)y x y +=+-化简:24y x =这就是P 的轨迹方程 (2)设221212(,),(,(,1)44x x E x Q x M t - ME,MQ 的斜率分别为1,22- 211221142142x x t x x t ⎧+⎪=-⎪-⎪∴⎨⎪+⎪=⎪-⎩即2112222(1)21(2)82x t x x t x ⎧=++⎪⎪⎨⎪=-+-⎪⎩ 由(1)得21133(1)222t x =++≥由(2)得22133(4)822t x =--+≤ 123,1,42t x x ∴==-= 即13(1,(4,4),(,1)42E Q M --31224MQ ME =-==+=11125222416MEQ S MQ ME ∆∴==⨯⨯=22.(本小题满分16分)解:(1) '()ln 12ln 1f x x x =+-=-令'()0f x =得x e =.将',(),()x f x f x 变化情况列下表: x(0,)e e (,)e +∞ '()f x -0 + ()f x↘ 极值 ↗ 即(0,)e 是()f x 的递减区间,(,)e +∞是()f x 的递增区间,()f x 在x e =处有极小值.e -(2)[()()][ln ln ]f x f y x y y x ---ln 2ln 2ln ln ln ln 2()x x x y y y x y y xx x x y x y y y =--+-+=+--[ln ln 2(1)]x x x x y y y y y=+-- (*) 设1,()ln ln 2(1)x t Q t t t t t y=>=+-- 11'()ln 12ln 1Q t t t t t=++-=+- 设1()ln 1M t t t =+-,则22111'()0t M t t t t-=-=>.()M t ∴是递增函数. ()(1)0M t M 即'()0Q t <.()Q t ∴是递减函数.()(1)0Q t Q ∴<=即(*)()()ln ln .f x f y x y y x ∴<=0<∴--<。
浙江省东阳市南马高级中学2018-2019学年上学期高三期中数学模拟题
浙江省东阳市南马高级中学2018-2019学年上学期高三期中数学模拟题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1. 设函数()y f x =对一切实数x 都满足(3)(3)f x f x +=-,且方程()0f x =恰有6个不同的实根,则这6个实根的和为( )A.18B.12C.9D.0【命题意图】本题考查抽象函数的对称性与函数和方程等基础知识,意在考查运算求解能力.2. 已知点P 是双曲线C :22221(0,0)x y a b a b-=>>左支上一点,1F ,2F 是双曲线的左、右两个焦点,且12PF PF ⊥,2PF 与两条渐近线相交于M ,N 两点(如图),点N 恰好平分线段2PF ,则双曲线的离心率是( )A.5B.2 D.2【命题意图】本题考查双曲线的标准方程及其性质等基础知识知识,意在考查运算求解能力. 3. 执行如图所示的程序框图,输出的s 值为( )。
A-3BC D24. 已知向量(1,2)a =,(1,0)b =,(3,4)c =,若λ为实数,()//a b c λ+,则λ=( ) A .14 B .12C .1D .2 5. 某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m n +的值是( )A .10B .11C .12D .13【命题意图】本题考查样本平均数、中位数、茎叶图等基础知识,意在考查识图能力和计算能力. 6. 下列命题正确的是( )A .已知实数,a b ,则“a b >”是“22a b >”的必要不充分条件B .“存在0x R ∈,使得2010x -<”的否定是“对任意x R ∈,均有210x ->”C .函数131()()2xf x x =-的零点在区间11(,)32内D .设,m n 是两条直线,,αβ是空间中两个平面,若,m n αβ⊂⊂,m n ⊥则αβ⊥ 7. 设函数的集合,平面上点的集合,则在同一直角坐标系中,P 中函数的图象恰好经过Q 中两个点的函数的个数是 A4 B6 C8 D108. 已知全集为R ,且集合}2)1(log |{2<+=x x A ,}012|{≥--=x x x B ,则)(B C A R 等于( )A .)1,1(-B .]1,1(-C .)2,1[D .]2,1[【命题意图】本题考查集合的交集、补集运算,同时也考查了简单对数不等式、分式不等式的解法及数形结合的思想方法,属于容易题. 9. 设为全集,是集合,则“存在集合使得是“”的( )A 充分而不必要条件B 必要而不充分条件C 充要条件D 既不充分也不必要条件10.过抛物线22(0)y px p =>焦点F 的直线与双曲线2218-=y x 的一条渐近线平行,并交其抛物线于A 、 B 两点,若>AF BF ,且||3AF =,则抛物线方程为( )A .2y x =B .22y x =C .24y x =D .23y x =【命题意图】本题考查抛物线方程、抛物线定义、双曲线标准方程和简单几何性质等基础知识,意在考查方程思想和运算能力.11.设a ,b 为正实数,11a b+≤23()4()a b ab -=,则log a b =( )A.0B.1-C.1 D .1-或0【命题意图】本题考查基本不等式与对数的运算性质等基础知识,意在考查代数变形能与运算求解能力.12.设f (x )=(e -x -e x )(12x +1-12),则不等式f (x )<f (1+x )的解集为( )A .(0,+∞)B .(-∞,-12)C .(-12,+∞)D .(-12,0)二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.(﹣2)7的展开式中,x 2的系数是 .14.如图,在三棱锥P ABC -中,PA PB PC ==,PA PB ⊥,PA PC ⊥,PBC △为等边三角形,则PC 与平面ABC 所成角的正弦值为______________.【命题意图】本题考查空间直线与平面所成角的概念与计算方法,意在考查学生空间想象能力和计算能力. 15.如图,P 是直线x +y -5=0上的动点,过P 作圆C :x 2+y 2-2x +4y -4=0的两切线、切点分别为A 、B ,当四边形P ACB 的周长最小时,△ABC 的面积为________.16.已知平面向量a ,b 的夹角为3π,6=-b a,向量c a -,c b -的夹角为23π,23c a -=,则a 与c的夹角为__________,a c ⋅的最大值为 .【命题意图】本题考查平面向量数量积综合运用等基础知识,意在考查数形结合的数学思想与运算求解能力.三、解答题(本大共6小题,共70分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 2
(D) ( , 2] [4, )
9.双曲线
x y 2 1(a 0, b 0) 的左、右焦点分别为 F1 、 F2 ,离心率为 e ,过 F2 的直线与双曲线的 2 a b 2 右支交于 A, B 两点,若 F1 AB 是以 A 为直角顶点的等腰直角三角形,则 e
是 。
三、解答题(本大题共 5 小题,共 72 分。 )
18. (本题满分 14 分) 已知 f ( x) 2sin x (I)求 tan 的值;
2 2 x tan cos , 且 f ( ) 3 2 。 6 2 2 (Ⅱ)当 x , 时,求函数 f ( x) 的值域。 2
4.在等比数列 an 中, an 0 , a2 1 a1 , a4 9 a3 ,则 a4 a5 (A)16 (B)27
2
l // , m , m
(C)36
(D)81
2
5.已知 a,, b c 均为实数,则“ b 4ac 0 ”是“关于 x 一元二次不等式 ax bx c 0 的解集为 ”的 (A)充分不必要条件 (B)必要不充分条件 (C)充分必要条件 (D)既不充分也不必要条件 6.已知钝角三角形 ABC 的最大边长为 2,其余两边长为 x, y ,则以 ( x, y ) 为坐标的点 所表示平面区域的面积是 (A) (B) 2 (C) 4 (D) 4 2 7.等比数列 {an } 中, a1 317, q 值为 (A)7 (B)8
1 e
(B) a ( , ), x R, f ( x) a (D) x R, a ( , ), f ( x) a
1 e
1 e
1 e
二、填空题(本大题共 7 小题,每题 4 分,共 28 分。 )
1
11.若复数
1 2i (a R, i 为虚数单位)是纯虚数,则实数 a 的值为 a 1
(B) 3 2 2
x
(A) 1 2 2
(C) 4 2 2
(D) 5 2 2
10.若函数 f ( x) x e , 则下列命题正确的是 (A) a ( , ), x R, f ( x) a (C) x R, a ( , ), f ( x) a
e 2.71828 . (Ⅰ)若 p 0 ,求证: f x 1 x ;
p p e 2 2e ln x , g x ln x 1 ,其中无理数 x x p2
(Ⅱ)若 f x 在其定义域内是单调函数,求 p 的取值范围; (Ⅲ)对于区间(1,2)中的任意常数 p ,是否存在 x0 0 使 f x0 g x0 成立? 若存在,求出符合条件的一个 x0 ;否则,说明理由.
浙江省东阳市南马高中 2010 届高三上学期期中考试(数学理)
一、选择题(本大题共 10 小题,每小题 5 分,共 50 分。在每小题给出的四个选项中,只有一项是符
1.若集合 P y y 0 , P Q Q ,则集合 Q 不可能是 (A) y y x 2 2.在 ( 3 x 2 合题目要求的。 )
19. (本题满分 14 分) 如图,在 ABC 中, BD 为 AC 边上的高, BD 1, BC AD 2 ,沿 BD 将 ABD 翻折,使得 ADC 30 , 得几何体 B ACD (I)求证: AC 平面BCD ; (Ⅱ)求二面角 D AB C 的大小的余弦值。
AB (1, 3,1), DB (0, 0,1), AC (1, 0, 0), 设平面 ABD 的法向量为 n1 ( x, y, z ) , 则 n1 AB 0, n1 DB 0
所以
则 n1 ( 3, 3, 0)
x 3y z 0 ,取 x 3, y 3, z 0 , z 0
(11 分)
4
又设平面 ABC 的法向量为 n 2 ( x, y, z ) , 则 n 2 AB 0.n 2 AC 0
x 3y z 0 ,取 x 0, y 3, z 3 ,则 n 2 (0, 3,3) (13 分) x 0 n1 n 2 3 1 所以, cos n1 , n 2 | n1 | | n 2 | 2 3 2 3 4 1 因此,所求二面角 D AB C 的大小余弦值为 。 4
14.已知 a, b 均为单位向量,且它们的夹角为 60°, 当 | a b | ( R ) 取最小值时,
。
15.若 f x 是定义在 R 上的奇函数,且当 0 x 1 时, f x 2 1 .则函数 y f x x 的零点有 2
由
y kx m 由 x2 y 2 ,消去 y 得: (3 4k 2 ) x 2 8kmx 4m 2 12 0 1 3 4 8km 4m 2 12 则 x1 x2 .…………………9 分 , x x 1 2 3 4k 2 3 4k 2 3m 2 12k 2 . y1 y2 (kx1 m)(kx2 m) k 2 x1 x2 km( x1 x2 ) m 2 3 4k 2 由 OA OB ,知 x1 x2 y1 y2 0 .
1 , 记 f (n) a1 a2 … an , 则当 f (n) 最大时, n 的 2
(C)9 (D)10
x ,x 0 8.已知 f ( x) 2 ,则 f [ f ( x)] 1 的解集是 2 x , x 0 (A) ( , 2] (B) [4 2, )
21. (本小题满分 15 分) 1 x2 y 2 已知椭圆 C : 2 2 1 (a b 0) 的离心率为 ,椭圆上的点到焦点的最小距离为 1. 2 a b (Ⅰ)求椭圆 C 的方程; (Ⅱ)若直线 l 与椭圆 C 交于 A, B 两点,且 OA OB ( O 为坐标原点) , OH AB 于 H 点.试求点 H 的轨迹方程. 22. (本小题满分 15 分) 已知函数 f x px
19. (I)因为 BD AD, BD CD, AD CD D ,所以 BD 平面 ACD 。 (3 分) 又因为 AC 平面 ACD, 所以 AC BD
2 2 2
①(5 分)
在 ACD 中, ADC 30 , AD 2, CD
(Ⅱ)方法一; 在 BCD 中,过 D 作 DO BC 于 O ,则 AC DO ,所以 DO 平面 ABC 在 ABC 中,过 O 作 OE AB 于 E ,连 DE ,则 AB 平面 ODE , 所以 DEO 为二面角 D AB C 的平面角 (11 分) 在 RtΔABD 中,求得 AB 在 RtBCD 中,求得 DO
20. (本题满分 14 分) 已知 a 为实数, f ( x) ( x 4)( x a ).
2
2
(1)若 f ( 1) 0 , 求 f ( x) 在[—4,4]上的最大值和最小值;
(2)若 f ( x) 在 ,2 和 2, 上都是递增的,求 a 的取值范围。
(B) y y 2 x
(C) y y lg x
(D)
1 8 ) 的展开式中,常数项为 x2 (A)-28 (B)-70 (C)70 (D)28 3.已知两条不同的直线 m , l 与三个不同的平面 , , ,满足 l , ,那么必有 (A) , m l (B) , m // (C) m // , m l (D) // ,
参考答案
一、选择题(本大题共 10 小题,每小题 5 分,共 50 分。 )
3
题号 答案
1 C
2 D
3 A
4 B
5 B
6 B
7 C
8 D
9 D
10 A
11.2
12.45
13.
18. (Ⅰ)因为 f ( ) 2sin(
3 2 a 2
14.
2 所以 tan 2
1 ) tan 2 cos 2 3 tan 2 3 2 (4 分) 2 6 4 2
3 ,由余弦定理, 得 AC AD CD 2 AD CD cos ADC 1 2 2 2 因为 AD CD AC ,所以 ACD 90 ,即 AC CD 。② (7 分) 由①,②及 BD CD D ,可得 AC 平面 BCD (8 分)
5, DE
(1)若 l x 轴,可设 H x0 ,0 ,因 OA OB ,则 A x0 , x0 .
12 x0 2 x0 2 12 2 ,即 H 1 ,得 x0 7 ,0 . 7 4 3 12 若 l y 轴,可设 H 0, y0 ,同理可得 H 0, .………7 分 7 (2)当直线 l 的斜率存在且不为 0 时,设 l : y kx m ,
20. (1)最大值为 42,最小值为—54. (2) 2 a 2 。 21. (Ⅰ)解:由题意知: e
c 1 , a c 1 , a 2 b 2 c 2 ,解得 a 2, b 2 3 . a 2 x2 y 2 故椭圆的方程为 1 .…………………………5 分 4 3 (Ⅱ)解:设 A x1 , y1 , B x2 , y2 ,
。 。
12.设等差数列 {an } 的前 n 项和为 S n ,且 a3 a5 a7 15 ,则 S9 13.如图,测量河对岸的旗杆高 AB 时,选与旗杆底 B 在 同一水平面内的两个测点 C 与 D ,测得 BCD 75 ,
