非线性光学作业(1-2章)答案
2.1 非线性光学-耦合波方程.

第二章 耦合波方程及二次谐波的产生§2.1 引言第一章我们讨论了光波在介质中传播时的响应过程,给出了光电场在介质中产生的极化强度及介质非线性极化率张量的表达式,并详细讨论了它们的性质。
由于介质的极化强度随时间变化,它们作为场源产生辐射场,这些辐射场就是在介质中发生各种光学现象的光电场。
这一章主要内容:(1)由非线性介质中的波动方程导出稳态和瞬态耦合波方程,以及曼利——罗宾关系;(2)二次谐波(倍频)的小信号解及有泵浦损耗的条件下的解;(3)讨论满足二次谐波产生的相位匹配条件,包括角度相位匹配、温度相位匹配和准相位匹配;(4)二次谐波的有效非线性系数及高斯光束的二次谐波。
§2.2 耦合波方程2.2.1 非线性波动方程用麦克斯韦方程(Maxwell)组描述介质中的线性和非线性光学性质都是有效的。
国际单位制的麦克斯韦方程组如下:BE t∂∇⨯=-∂ (2.2.1-1) DH j t∂∇⨯=+∂ (2.2.1-2) D ρ∇⋅= (2.2.1-3)0B ∇⋅= (2.2.1-4)描写电磁场对介质作用的本构方程:0D E P ε=+ (2.2.1-5)()0B H M μ=+ (2.2.1-6) j E σ= (2.2.1-7)介质中无自由电荷和电流,则00ρ==j分别在用∇⨯运算作用于BE t∂∇⨯=-∂式左右两边得到: 00μμ⎛⎫∂∂∂∇⨯∇⨯=-∇⨯=- ⎪∂∂∂⎝⎭D E H t t t (2.2.1-8)由()2E E E ∇⨯∇⨯=∇∇•-∇及近似认为0E ∇•=;()()()0100101εεεχεχε=+=+⋅+=+⋅+=⋅+NLNLNLD E PE E P E PE P(2.2.1-9)从而得到波动方程为:()222εμμ∂⋅∂∇=+∂∂NLE PE t t (2.2.1-10) 小结:非线性波动方程右边多了一个非线性极化项22NLPt ∂∂,此非线性项可以看作一个波源,各种非线性光学现象的产生均是由此项引起的。
(非线性光学课件)第二章 非线性光学极化强度和极化率的经典

P(1) (t) 0R(1) ( ) E(t )d
E(t) E()eitd
()
P(1) (t)
R(1)
0
(
)
[
E()eiteid]d
0[
R(1) ( )eid ] E()eitd
0 (1) () E()eitd
P(1) ()eitd
() R(1) ( )ei d
R(1)
0
(
)
E(t
)d
0
E(r, t) 1 n [E()eit E*()eit ] 1 n E()eit
2 1
2 n
E() E0 (r) exp{i[k r (r)]} E(r) exp(ik r)
数学上引入负频率
E* ( )可写成E( )
P(1) (t)
R(1)
0
(
)
E(t
0 d1 d2[(2) (3;1,2 ) : E(1)E(2 ) ei3td3 (3 1 2 )]
0
d1
d2[(2)
(3;1,
2
)
:
E(1)E(2
)
(3
1
2
)]
ei3t
d3
P(2) (3) d1 d2[(2) (3;1,2 ) : E(1)E(2) (3 1 2 )]
R (1)
0
(t,
t1 )
E(t1 )dt1
因此有:
dP(1) (t T ) 0R(1) (t, t1) E(t1 T )dt1
P(1) (t T )
R(1)
0
(t,
t1)
E(t1
T
)dt1
R(1)
0
电子线路非线性部分课后答案
1-2 一功率管,它的最大输出功率是否仅受其极限参数限制?为什么?解:否。
还受功率管工作状态的影响,在极限参数中,P CM 还受功率管所处环境温度、散热条件等影响。
1-3 一功率放大器要求输出功率P 。
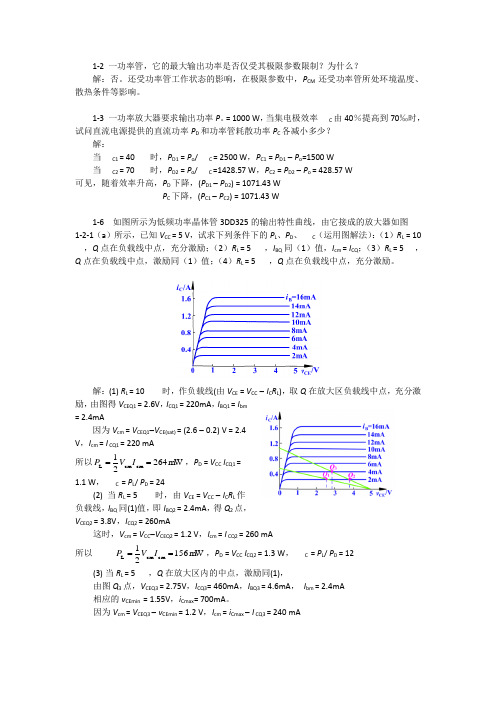
= 1000 W ,当集电极效率C 由40%提高到70‰时,试问直流电源提供的直流功率P D 和功率管耗散功率P C 各减小多少?解:当C1 = 40 时,P D1 = P o / C = 2500 W ,P C1 = P D1 - P o =1500 W当C2 = 70 时,P D2 = P o / C =1428.57 W ,P C2 = P D2 - P o = 428.57 W 可见,随着效率升高,P D 下降,(P D1 - P D2) = 1071.43 WP C 下降,(P C1 - P C2) = 1071.43 W 1-6 如图所示为低频功率晶体管3DD325的输出特性曲线,由它接成的放大器如图1-2-1(a )所示,已知V CC = 5 V ,试求下列条件下的P L 、P D 、C (运用图解法):(1)R L = 10,Q 点在负载线中点,充分激励;(2)R L = 5 ,I BQ 同(1)值,I cm = I CQ ;(3)R L = 5,Q 点在负载线中点,激励同(1)值;(4)R L = 5 ,Q 点在负载线中点,充分激励。
解:(1) R L = 10 时,作负载线(由V CE = V CC - I C R L ),取Q 在放大区负载线中点,充分激励,由图得V CEQ1 = 2.6V ,I CQ1 = 220mA ,I BQ1 = I bm = 2.4mA因为V cm = V CEQ1-V CE(sat) = (2.6 - 0.2) V = 2.4 V ,I cm = I CQ1 = 220 mA所以m W 26421cm cm L ==I V P ,P D = V CC I CQ1 =1.1 W , C = P L / P D = 24(2) 当 R L = 5 时,由V CE = V CC - I C R L 作负载线,I BQ 同(1)值,即I BQ2 = 2.4mA ,得Q 2点,V CEQ2 = 3.8V ,I CQ2 = 260mA这时,V cm = V CC -V CEQ2 = 1.2 V ,I cm = I CQ2 = 260 mA所以 m W 15621cm cm L ==I V P ,P D = V CC I CQ2 = 1.3 W , C = P L / P D = 12(3) 当 R L = 5 ,Q 在放大区内的中点,激励同(1),由图Q 3点,V CEQ3 = 2.75V ,I CQ3= 460mA ,I BQ3 = 4.6mA , I bm = 2.4mA 相应的v CEmin = 1.55V ,i Cmax = 700mA 。
非线性光纤光学第三版课后题答案

非线性光纤光学第三版课后题答案1、3.有的力可能只有受力物体,没有施力物体.[判断题] *对错(正确答案)2、探究物体所受滑动摩擦力大小与物体对接触面的压力的关系时,物体所受重力大小是需要控制的变量[判断题] *对错(正确答案)答案解析:需要控制接触面的粗糙程度相同3、36.关于热现象和热学规律﹐下列说法正确的是()*A.布朗运动表明,构成悬浮微粒的分子在做无规则运动B.两个分子的间距从极近逐渐增大到10ro的过程中,分子间的引力和斥力都在减小(正确答案)C.热量可以从低温物体传递到高温物体(正确答案)D.物体的摄氏温度变化了1℃,其热力学温度变化了273KE:两个分子的间距从极近逐渐增大到10ro的过程中,它们的分子势能先减小后增大。
4、下列事例中,利用热传递改变物体内能的是()[单选题]A.流星坠入大气层与空气摩擦生热B.用锯条锯木头,锯条发热C.人站在阳光下暴晒,感到很热(正确答案)D.古时候,人们利用钻木取火5、35.已知甲液体的密度ρ甲=5g/cm3,乙液体的密度ρ乙=2g/cm3,现在取一定量的甲乙液体混合,混合液体的密度为3g/cm3,液体混合前后总体积保持不变,则所取甲乙体积比V甲:V乙=()[单选题] *A.5:2B.2:5C.1:2(正确答案)D.2:16、32.下列涉及的物态变化现象解释正确的是()[单选题] *A.清晨河面上出现的薄雾是汽化形成的B.冰冻的衣服变干是熔化现象C.烧水时,壶嘴附近出现的“白气”是液化形成的(正确答案)D.浓雾逐渐散去是升华现象7、当绝缘棒接触验电器的金属球时箔片张开,说明绝缘棒带正电[判断题] *对错(正确答案)答案解析:金属箔片张开是由于箔片带同种电荷,无法确定具体带正电还是负电8、3.击剑比赛、体操比赛中运动员可视为质点.[判断题] *对错(正确答案)9、验电器是实验室里常常用验电器来检验物体是否带电。
用带正电的玻璃棒接触验电器的金属球,可以发现验电器原来闭合的两片金属箔张开一定的角度,如图61所示。
非线性光学第二次作业

受激布里渊散射受激布里渊散射(SBS )是强激光场与介质中的声波相耦合时产生的散射现象。
当强激光ω通过介质时,会在介质内产生频率为ωs 的相干声波,同时产生频率为ω-ωs 的散射光波。
声波和散射光波沿着特定的方向传播,并且具有域值性。
在SBS 过程中,可以理解成介质中的声波激发了散射。
因而,非线性介质的密度等声学特性与SBS 直接相关。
声波的激发与介质的电致伸缩或吸收效应相关。
电致伸缩效应是指介质在外加电场的作用下,能量分布发生变化使得介质发生形变,导致密度增大或者减小。
以下是受激布里渊散射的基本方程推导(主要摘自石顺祥《非线性光学》),以及它的相关应用等。
1.声波的运动方程设u(x,t)是介质内x 处的质点偏离平衡位置的位移,介质密度为ρm ,弹性系数为α。
介质在受到外加电场的作用时,作用在介质单位面积上的力除了弹性力外,还有阻尼力,以及电场作用下的离子极化以及位移所产生的应力(使介质发生形变,即电致伸缩效应)。
假定介质内电场E 由两束平面光波组成的,它们相对于声波的运动方向是任意的。
光波和声波的表示:cc e r E t E c c e r E t E cc e r E t E v k t w i s s v k t w i v k t w i s s .)(),r (.)(),r (.)(),r ()(1)(222)(1112211+=+=+=------ (1) 频率和相位匹配关系:→→→=-=-s sk k k 1212ωωω声波在介质中运动方程推导比较复杂,这里直接写出结论:2222*2211()2()()()()2s s s s s s s s s s s s m mdu r i i k ik v k v u r E r E r dr ηωγωρρ-+--= (2) 其中, ρm 表示介质密度,υs 声波速度,γ电致伸缩系数,ε介电常数,η声波耗散系数。
2.光波电场方程2*10112112*20221222222s s s s k dE E E dr k k dE E E dr k ωγμβμωγμβμ=--=-- (3)β是唯象引入的光波耗散系数。
(非线性光学课件)第二章 非线性光学极化强度和极化率的经典

(t
T
,
t1
)
E(t1
)dt1
R(1) (t, t1 T ) R(1) (t T , t1)
因果关系
t+T
t2 t1-T t1 R(1) (t, t1 T ) R(1) (t T , t1)
t 时间
响应函数和绝对时间t,t1无关,只和时间差t-t1有 关
R(1) (t, t1) R(1) (t t1)
4
2.1 非线性电极化率 2.1.1 极化强度的时域表达式
☆
2.1.2极化强度的频域表达式 2.1.3 电极化率的对称性 2.1.4 简并因子 2.2 Kramers-Kronig色散关系 2.2.1 电极化率实部与虚部的关系 2.2.2 电极化率实部和虚部的物理意义 2.2.3 非线性折射率与非线性吸收系数间的关系 2.3 非线性介质的波方程 2.3.1 非线性介质的麦克斯韦方程 2.3.2 各向异性非线性介质的时域波方程 2.3.3 各向异性非线性介质的频域波方程 2.3.4 各向同性非线性介质频域波方程 2.3.5 各向同性非线性介质时域波方程
t
t2
)
:
E(t1)E(t2
)dt1
类似地,t1、t2、t3时刻的电场对t时刻媒质的极化 强度也有贡献,这种贡献可以写成:
dP(3)
(t
)
R (3)
0
(t
t1,
t
t2
,
t
t3
)
E(t1)E(t2 )E(t3)dt1dt2dt3
P(3) (t)
dt3
dt2
R(3)
0
(t
t1,t t2,t
对于各向异性介质,极化强度P与电场强度E的方向不再相同, 电极化率是一个张量。
非线性光学习题解答终极版

非线性光学习题解答[李春蕾(2011111772)]第一章 晶体光学简介 电光效应1.解答:由于矢量运算不受坐标系的影响,只是表示形式不同而已,不妨在直角坐标系下建立方程,设x x y y z z k k e k e k e =++ ,x y z r xe ye ze =++,x y z e e e x y z∂∂∂∇=++∂∂∂ 则exp[i()]x y z fk x k y k z =++ 于是i i i i x y z x x y y z zf f f fe e e fk e fk e fk e fk x y z∂∂∂∇=++=++=∂∂∂,问题得证。
对于平面波,设0000exp[i()]()exp[i()]x x y y z z EE t k r E e E e E e t k r ωω=−⋅=++−⋅其中,0exp[i()]x x E E t k r ω=−⋅,0exp[i()]y y E E t k r ω=−⋅ ,0exp[i()]z z E E t k r ω=−⋅()()()(i i )(i i )(i i )i x y zy y x xz z x y z x y z x y z z y y z x x z z x y y x E e e e E E E E E E e e e x y z y z z x x y E E E e k E k E e k E k E e k E k E k E∇×∂∂∂∂∂∂∂∂∂==−+−+−∂∂∂∂∂∂∂∂∂=−++−++−+=×同理,i H k H ∇×=×.2.证明:在选定主轴坐标系的情况下,物质方程可以写成0i i i D E εε=,1,2,3i =同时,将晶体光学第一基本方程写成分量形式,20[()]ii i D n E k k E ε=−⋅,1,2,3i =联立两式,整理得到02()11ii i k k E D nεε⋅=− 对于对应同一个k 的两个电位移矢量D ′ 、D ′′,建立它们的标量积2222312022222211223322210221()()111111111111()()()()()()()()()()()1D D k k k k E k E n n n n n n k n n k E k E n n εεεεεεεεε′′′⋅ ′′′=⋅⋅++−−−−−−′′′′′′′′′′′′′′′=⋅⋅′′′− 22222331222222221223311111111111()()()()()()k k k k k n n n n n n εεεεε −+−+−−−−−−− ′′′′′′′′′由23122011i i ik n n ==−∑,得到大括号中的第一、三、五项之和为零,第二、四、六项之和为零,所以0D D ′′′⋅=即对应同一个k 的两个电位移矢量D ′ 、D ′′相互垂直.3.解答:22011i i k nε=−∑是方程20[()]i ii i E n E k k E εε=−⋅的本征值方程,设其本征值为m n ,相应的本征解为()m E ,则可以得到,()2()()0[()]m m m mEn E k k E ε⋅=−⋅ε晶体中可以有两个本征解,设另一个为()n E ,用其点乘上式得到()()()()()201[()]n m m n m mEE k k E E E n ε⋅−⋅=⋅⋅ε 交换指标m 和n 后可以得到()()()()()201[()]m n n m n nEE k k E E E n ε⋅−⋅=⋅⋅ε 上两式相减,考虑到介电常数张量ε为对称张量,则可以得到()()2201110m n n m E E n n ε −⋅⋅=ε 如果m n n n ≠,则有()()0m n EE ⋅⋅=ε 如果m n n n =,显然方程成立。
非线性光学试题答案

非线性光学试题1、简要说明线性光学与非线性光学的不同之处。
线性光学:光的独立传播定理;光的传播方向、空间分布在传播过程中可以发生变化,但光频率不发生变化;介质的主要光学参数只是入射光频率与偏振方向的函数,与光的强度无关。
非线性光学:光的独立传播定理不成立;光在传播过程中频率可能发生变化;介质的折射率与入射光的强度有关2、证明具有反演对称中心的晶类,其偶数阶非线性极化率为零。
证明:设A 为某对称操作,对于二阶非线性极化率(2)χ有(2)(2)'ijk ia jb kc ijkA A A χχ=,类似地,对于n 阶非线性极化率()n χ有()(2)......'...n ijk l ia jb kc lf ijk l A A A A χχ= 对于极化率张量(2)χ,实施对称操作后应保持不变,即(2)(2)'ijk ijk χχ= 所以(2)3(2)(1)ijk ijkχχ=-; 同理()(1)()......(1)n n n ijk l ijk l χχ+=-,当n 为偶数时,()...n ijk l χ为零3、 KDP 晶体是负单轴晶体,考虑I 类位相匹配。
(1) 设光波矢均沿(θ,ϕ)方向,求出此时有效非线性系数eff d 的表达式注:已知KDP 晶体的非线性系数矩阵为141436000000000000000d d d ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭(2)若要得到最佳倍频输出,问光波矢的方向(θ,ϕ)应取何值。
解:(1) 负单轴I 类:(2)eff jk i ijk j k d b d a a δ=-,其中,sin cos 0j a ϕϕ⎛⎫ ⎪=- ⎪ ⎪⎝⎭,cos cos sin cos sin j b ϕθϕθθ-⎛⎫⎪=- ⎪ ⎪⎝⎭所以,36362sin sin (cos )sin sin 2eff d d d θϕϕθϕ=-=-(2)222221/22222))arcsin[()]))((((eo o mooen n n n n n ωωωωωωθ-=- ,得到41o m θ=;将m θ代入上面的eff d 表达式,易得45o ϕ=因此,要得到最佳倍频输出,光波矢方向为(41,45)o o3 B 、考虑BBO 晶体中的II 型(o e e +→)相位匹配下的共线传播倍频过程2ωωω+→;(1)设光波矢均沿(θ,ϕ)方向,求出此时有效非线性系数eff d 的表达式。
非线性光学第二章第5-6节(打印PDF版)

第二 章
§2.5 非线性极化率张量元的基本特性(二阶为例)
§2.6 二阶非线性极化率张量的简化形式
§2.5 非线性极化率张量元的基本特性(以二阶为例) 一, 研究极化率张量元基本特性的必要性
非线性极化率是一个张量。一个 n 阶非线性极化率张量具有3(n+1)。研究张量元基本特性,如
对称特性,便可以大大简化张元数目。 完整地描述物质的非线性特性,必须了解不同频率的各外场通过介质所发生的相互作用对极化场
(ω1
+ω2
,
ω1
,
ω2
)E2
(ω1
)E1
(ω2
)
---(2.5-12)
+
χ (2) 122
(ω1
+ω2
,
ω1
,
ω2
)E2
(ω1
)E2
(ω2
)
+
χ (2) 123
(ω1
+ω2
,
ω1
,
ω2
)E2
(ω1
)E3
(ω2
)
+
χ (2) 131
光学第二章习题解答

λf ′ y= ∆ϕ 2πb
−4 ′ λf 4.8 × 10 × 600 π y= ∆ϕ = ⋅ = 0.18mm 2π b 2π × 0.4 2
λf′ 4.8 ×10−4 × 600 π y′ = ∆ϕ ′ = ⋅ = 0.06mm 2π b 2π × 0.4 6
y b sin θ ≈ btgθ = b = kλ f′ f′ 1000 y1 = λ = × 5.461× 10−4 = 0.5461mm b 1 f′ y3 = 3 λ = 1.638mm b
(2) 由单缝衍射次最大值的位置公式 由单缝衍射次最大
y 1 b sin θ k0 ≈ b ≈ ( k 0 + )λ f′ 2 3 f′ y10 = × λ 2 b 3 1000 −4 = × × 5.461× 10 = 0.819mm 2 1
2.1 单色平面光照射到一小圆孔上,将其波面 单色平面光照射到一小圆孔上, 分成波带,求第k个带的半径 个带的半径。 分成波带,求第 个带的半径。若圆孔中心到观察 点的距离r 点的距离 0为1m,单色光波长为 ,单色光波长为450nm,求此时 , 第一半波带的半径。 第一半波带的半径。 解:(1) :( )
ρ k = kr0 λ
k =1
D1 = 2 ρ1 = 2 r0 λ = 0.2828cm
2.3 波长为 波长为500nm的单色光源离光阑1m,光阑 的单色光源离光阑1 的单色光源离光阑 上有一半径分别为0.5mm和1mm的透光圆环,接 的透光圆环, 上有一半径分别为 和 的透光圆环 收点P离光阑 , 离光阑1 收点 离光阑1m,求P点的光强与没有光阑时的光 点的光强与没有光阑时的光 强度之比。 强度之比。 解:(1) :( )
非线性光学作业

受激布里渊散射(SBS )布里渊散射是指入射到介质的光波与介质内的弹性声波发生相互作用而产生的光散射现象。
由于光学介质内大量质点的热统计运动会产生弹性声波,引起介质密度随时间和空间的周期性变化,从而使介质折射率随时间和空间周期性的发生变化,因此声波振动介质可以被看作一个运动的光栅。
这样,一束频率为ω的光波通过光学介质时,会受到光栅的“衍射”作用,产生频率为(ω-ωs )的散射,这里的ωs 是弹性声波的频率。
可见,布里渊散射中声波的作用类似于拉曼散射中分子振动的作用。
频率为ω的强激光束通过某种介质(气体、液体和固体)时,会在介质内产生频率为ωs 的相干声波,同时产生频率为(ω-ωs )的散射光波。
声波和散射光波沿着特定的方向传播,并且只有入射光强度超过一定值时才能发生上述现象。
这种具有受激发射特性的布里渊散射,称为受激布里渊散射。
上述介质中产生的相干声波是介质在强入射激光作用下产生电致伸缩效应的结果。
1、声波运动方程的推导首先推导介质受到弹性力、阻尼力和电致伸缩力时,介质中声波的波动方程。
外界电场作用引起介质的应变会导致其介电常数改变,从而使静电储能目的发生相应的改变,即:1(())2E D δωδ=⋅ (1) 则介质总的电能改变为 21122W E DdV E dV E DdV δδδεδ=⋅=-+⋅⎰⎰⎰ (2) 所以 21()2W D E dV dV t t tεϕ∂∂∂=--∇⋅∂∂∂⎰⎰ (3) 式中,E ϕ=-∇。
因为()()sD dV DdV DdV D ndS ϕδϕδϕδϕδ∇⋅=∇⋅+∇⋅=⋅⎰⎰⎰⎰Ñ (4)并且,若取上述面积分的积分限远离介质,即r 趋于∞时,由于D ϕδ按r -3变化,所以面积分为零。
根据麦克斯韦方程D ρ∇⋅=,有()D D δδδρ∇⋅=∇⋅= (5) 将(5)式代入(3)式后,给出212W E dV dV t t tερϕ∂∂∂=-+∂∂∂⎰⎰ (6) 根据功能原理,上述静电储能的改变意味着存在一个作用力F ,改作用力所作的功率的负值等于静电储能的变化率,即有,W F vdV t∂=-⋅∂⎰ (7) 式中,v 是介质中质点的速度。
非线性光学作业(1-2章)答案

第一章作业1、用微扰方法求解一维振子的非线性响应。
提示:1)对于方程(1.2-11),将r进行微扰展开(1.2-13);2)对不同微扰阶次整理得到(1.2- 14 ~16)3)从低到高依次得到不同阶次方程的解(1.2- 17 ~19),求高阶解释,较低解可以当成不变量。
解:一维非简谐振子的运动方程为:d2r dt2+2hdrdt+ω02r−Ar2−Br3=−emE用微扰理论求解,将r展成幂级数:r=∑r kk其中r k~r k 这里取r=r1+r2+r3,且r1≫r2≫r3(1)对于与r同阶,保留r1项:⇒d 2r1dt2+2h dr1dt+ω02r−Ar12−Br13−emE….①(2)对于与r2同阶,保留r1,r2,r12:⇒d2(r1+r2)dt2+2hd(r1+r2)dt+ω02(r1+r2)−A(r1+r2)2−B(r1+r2)3=−emE⇒d 2r2dt2+2h dr2dt+ω02r2=Ar12……②(3)对于与r3同阶,保留r1,r2,r3,r1r2,r12项:⇒d2(r1+r2+r3)dt2+2hd(r1+r2+r3)dt+ω02(r1+r2+r3)−A(r1+r2+r3)2−B(r1+r2+r3)3=−emE⇒d 2r3dt2+2h dr3dt+ω02r3=2Ar1r2+Br13……③E(t)=E(ω)e−iωt+E∗(ω)e iωt=E(ω)e−iωt+c.c.r(t)=r(ω)e−iωt+r∗(ω)e iωt=r(ω)e−iωt+c.c.代入①得−ω2r1(ω)−2ihω+ω02r1(ω)=−e m E(ω)⇒r1(ω)=−em E(ω)1ω02−ω2−2ihω=−emE(ω)F(ω)⇒r1(t)=−em E(ω)F(ω)e−iωt−emE∗(ω)F(−ω)e iωt=−emE(ω)F(ω)e−iωt+c.c.r12(t)=(−emE(ω)F(ω)e−iωt−emE∗(ω)F(−ω)e iωt)2=e2m2E2(ω)F2(ω)e−2iωt+e2m2E(ω)E∗(ω)F(ω)F(−ω)+c.c…….(*)将上式(*)第一项代入②d2r2′dt2+2hdr2′dt+ω02r2′=Ae2m2E2(ω)F2(ω)e−2iωt相当于使振子作频率为2ω的强迫振动⇒r2′(t)=r2′(2ω)e−i2ωt−4ω2r2′(2ω)−4ihω+ω02r2′(2ω)= A e2m2E2(ω)F2(ω)r2′(2ω)= A e2m2E2(ω)F2(ω)F(2ω)r2′(t)=r2′(2ω)e−i2ωt= A e2m2E2(ω)F2(ω)F(2ω)e−i2ωt对于(*)式第二项与时间t无关:d2r2,, dt2+2hdr2,,dtω02r2,,=Ae2m2E(ω)E∗(ω)F(ω)F(−ω) r2,,(t)= Ae2m2E(ω)E∗(ω)F(ω)F(−ω)F(0)r2(t)=r2′(t)+r2,,(t)= A e2m2E2(ω)F2(ω)F(2ω)e−i2ωt+A e2m2E(ω)E∗(ω)F(ω)F(−ω)F(0)+c.c.同理推出r3(t)=−e 3m3E3(ω)[2A2F(2ω)+B]F(3ω)F3(ω)e−i3ωt−e3m3E2(ω)E∗(ω)[2A2F(2ω)+4A2ω02+3B]F(−ω)F3(ω)e−iωt+c.c.2、利用二阶非线性极化的一般表达式(2)()P t (1.2-26),可以得到双频分量光电场下二阶非线性极化表达式(1.2-38)。
非线性光学考试答案

闭卷题1.什么是非线性效应?答:非线性光学效应的唯象描述为⋅⋅⋅⋅⋅⋅+⋅+⋅=E E E p)2()1(χχ标量形式为⋅⋅⋅⋅⋅⋅+++=32E E E p γβα2.非线性效应的应用价值。
(1) 利用非线性光学效应能够改变或控制激光器的参数通过谐波、混频、参量振荡和放大及喇曼散射过程,可以做成各种变频器,即可将一种频率的激光辐射转换为另一种波段的相干辐射,而且这种转换效率可以做得很高。
这对扩展相干辐射的波段具有相当重要的意义。
利用非线性光学效应还可以改变或控制激光器输出的其它特性,如:脉宽、功率、频率稳定性等。
(2)利用非线性光学效应研究介质本身的原子或分子的微观性质由于可调谐激光器的发展,为利用共振增强的非线性光学效应研究原子或分子的高激发态及至自电离态提供了可能性。
(3)某些非线性效应也制约了强激光在介质中的传输3.波动方程组推导。
答:麦克斯韦方程H D J tDH tBE =⋅∇=⋅∇+∂∂=⨯∇∂∂-=⨯∇ρ 物质方程P E D 0+=ε H B 0μ= E J σ=()E B t∂∇⨯∇⨯=-∇⨯∂ 000B H D J t μμμ∂∇⨯=∇⨯=+∂()NL 00022E E P E t t tμεμμσ∂∂∂∇⨯∇⨯=-⋅--∂∂∂根据矢量关系:()2E E E ∇⨯∇⨯=∇∇⋅-∇由()NL D E P 0ε∇⋅=∇⋅⋅+=得出E 0∇⋅=(ε和NL P 都不是空间坐标函数)()NL200022E E E P t t tμσμεμ∂∂∂∇=+⋅+∂∂∂为非线性介质中的波动方程。
这就是所要求的电场源P 产生的光波电场E 随时间、空间变化的波动方程。
形式上类似于经典的强迫振动方程,式中右边第一项是阻尼项,第三项是激励项,即电极化强度P 作为场的激励源。
由它激发电磁场。
知道P 可以求场E 。
4.耦合方程组的推导。
答:(),E E r t =是空间坐标和时间t 的函数,通常是不同频率分量之和()(),,n nE r t E r t =∑同样非线性电极化强度也写成多个频率分量之和()(),,NLNLnnPr t P r t =∑每一个频率分量用复振幅表示,并沿空间z 方向传播()(),.n n ik z i n n E z t E z e c c ω-=+ ()(),..nnNLik z i t nn P z t E z e c c ω-=+对每一个频率分量都满足波动方程,并假设介质无损耗()0σ=()()()22200222,,,NLn n n E z t E z t P z t z tt μεμ∂∂∂⎡⎤=+⎣⎦∂∂∂ 方程左边:()()()()()()222222n n n n n n n n n n n n ik z i t ik z i t n n n n ik z i t ik z i t ik z i t n n nE z E z e ik E z e z z z E z E z e ik e k E z e z zωωωωω-----⎡⎤∂∂∂=+⎢⎥∂∂∂⎢⎥⎣⎦∂∂=+-∂∂方程右边 ()()'200222200,n n n n NLn n NLik z i t ik z i tn n n n P E z t t t E z e P e ωωμεμμωεμω--∂∂⎡⎤⋅+⎣⎦∂∂=--方程左右两边消掉n i teω-项,并令'n n n k k k ∆=-()()()22220022n NLn n i k z n n n n n n E z E z ik k E E P z e z zμωεμω-∆∂∂+-=-⋅-∂∂ 线性响应条件且介质无损耗条件下,0NLnP=,()()22,,0;0n n E z t E z t z z∂∂==∂∂()()220n n n n k E z E z μωε=⋅在非线性响应条件下,0NLn P ≠()()()2022n NL n n i k z n n n E z E z ik P z e z zμω-∆∂∂+=-∂∂ 在慢变化振幅近似下,即()()22n n nE z E z k z z∂∂∂∂ 振幅空间慢变化近似的物理意义:在空间约化波长2λπ的范围内,振幅变化很小,可以忽略。
非线性光学a(1---3.4)

(2)几种不同频率的光同时入射到介质中时,彼此间不 )几种不同频率的光同时入射到介质中时, 发生耦合作用,也不会产生新的频率, 发生耦合作用,也不会产生新的频率,并满足叠加 原理,互不干扰。 原理,互不干扰。
二、非线性极化
在强光场作用下,介质的电极化强度矢量 与外界电场强度 在强光场作用下,介质的电极化强度矢量P与外界电场强度 E成非线性关系: 成非线性关系: 成非线性关系
非线性光学的发展经历了三个阶段
二十世纪六十年代主要进行了二次谐波产生、和频、差频、 二十世纪六十年代主要进行了二次谐波产生、和频、差频、 双光子吸收、受激喇曼散射、受激布里渊散射、光参量振荡、 双光子吸收、受激喇曼散射、受激布里渊散射、光参量振荡、自 聚焦、光子回波、自感应透明等非线性光学现象的观察和研究; 聚焦、光子回波、自感应透明等非线性光学现象的观察和研究; 二十世纪七十年代人们更深入地研究了上述现象, 二十世纪七十年代人们更深入地研究了上述现象,并进行 了自旋反转受激喇曼散射、光学悬浮、消多普勒加宽、 了自旋反转受激喇曼散射、光学悬浮、消多普勒加宽、双光子 吸收光谱技术、相干反斯托克斯喇曼光谱学、 吸收光谱技术、相干反斯托克斯喇曼光谱学、非线性光学相位 共轭技术、光学双稳效应等非线性光学现象的研究; 共轭技术、光学双稳效应等非线性光学现象的研究; 二十世纪八十年代, 二十世纪八十年代,倍受人们注意的非线性光学新研究课 题是光学分叉和混沌、光的压缩态、多光子原子电离现象等。 题是光学分叉和混沌、光的压缩态、多光子原子电离现象等。 目前非线性光学逐渐由基础研究阶段进入应用基础研究和应用 研究阶段。 研究阶段。
讨论: ) 讨论:(1)从(2.1-3)式中可以看出,电极化强度 P(2) 中含有频率为 2 )式中可以看出, ω
非线性光学考试答案

闭卷题1.什么是非线性效应?答:非线性光学效应的唯象描述为⋅⋅⋅⋅⋅⋅+⋅+⋅=E E E p)2()1(χχ标量形式为⋅⋅⋅⋅⋅⋅+++=32E E E p γβα2.非线性效应的应用价值。
(1) 利用非线性光学效应能够改变或控制激光器的参数通过谐波、混频、参量振荡和放大及喇曼散射过程,可以做成各种变频器,即可将一种频率的激光辐射转换为另一种波段的相干辐射,而且这种转换效率可以做得很高。
这对扩展相干辐射的波段具有相当重要的意义。
利用非线性光学效应还可以改变或控制激光器输出的其它特性,如:脉宽、功率、频率稳定性等。
(2)利用非线性光学效应研究介质本身的原子或分子的微观性质由于可调谐激光器的发展,为利用共振增强的非线性光学效应研究原子或分子的高激发态及至自电离态提供了可能性。
(3)某些非线性效应也制约了强激光在介质中的传输3.波动方程组推导。
答:麦克斯韦方程J tH tB=⋅∇=⋅∇+∂∂=⨯∇∂∂-=⨯∇ρ 物质方程0+=ε 0μ= σ=()E B t∂∇⨯∇⨯=-∇⨯∂000B H D J tμμμ∂∇⨯=∇⨯=+∂()NL 00022E E P E t t tμεμμσ∂∂∂∇⨯∇⨯=-⋅--∂∂∂根据矢量关系:()2E E E ∇⨯∇⨯=∇∇⋅-∇由()NL D E P 0ε∇⋅=∇⋅⋅+= 得出E 0∇⋅= (ε 和NL P都不是空间坐标函数)()NL 200022E E E P t t tμσμεμ∂∂∂∇=+⋅+∂∂∂为非线性介质中的波动方程。
这就是所要求的电场源P 产生的光波电场E随时间、空间变化的波动方程。
形式上类似于经典的强迫振动方程,式中右边第一项是阻尼项,第三项是激励项,即电极化强度P 作为场的激励源。
由它激发电磁场。
知道P 可以求场E 。
4.耦合方程组的推导。
答:(),E E r t =是空间坐标和时间t 的函数,通常是不同频率分量之和()(),,n nE r t E r t =∑同样非线性电极化强度也写成多个频率分量之和()(),,NL NL n nP r t P r t =∑每一个频率分量用复振幅表示,并沿空间z 方向传播()(),.n n ik z i n n E z t E z e c c ω-=+()(),..n n NL ik z i t n n P z t E z e c c ω-=+对每一个频率分量都满足波动方程,并假设介质无损耗()0σ=()()()22200222,,,NL n n n E z t E z t P z t z ttμεμ∂∂∂⎡⎤=+⎣⎦∂∂∂方程左边:()()()()()()222222n n n n n n n n n n n n ik z i t ik z i tn n n n ik z i t ik z i t ik z i t n n nE z E z e ik E z e z z z E z E z e ik e k E z e z zωωωωω-----⎡⎤∂∂∂=+⎢⎥∂∂∂⎢⎥⎣⎦∂∂=+-∂∂方程右边 ()()'200222200,n n nn NLnn NL ik z i t ik z i tn n n n P E z t t t E z e P e ωωμεμμωεμω--∂∂⎡⎤⋅+⎣⎦∂∂=-- 方程左右两边消掉n i teω-项,并令'n n n k k k ∆=-()()()22220022n NLn n i k z n n n n n n E z E z ik k E E P z e z zμωεμω-∆∂∂+-=-⋅-∂∂线性响应条件且介质无损耗条件下,0NL n P = ,()()22,,0;0n n E z t E z t z z∂∂==∂∂()()220n n n n k E z E z μωε=⋅在非线性响应条件下,0NLn P ≠()()()2022n NLn n i k z n n n E z E z ik P z e z zμω-∆∂∂+=-∂∂在慢变化振幅近似下,即 ()()22n n n E z E z k z z∂∂∂∂ 振幅空间慢变化近似的物理意义:在空间约化波长2λπ的范围内,振幅变化很小,可以忽略。
非线性习题答案

练习题:1. 见p22(第2题图)------------------------------------------------------------------------------------2. 见p22—在μ<0时有一个稳定的不动点x=0; μ<0时有一个不稳定的不动点x=0两个稳定的不动点x =; (μκ=)(看图说话) 或者用数学说话(一个点)或者0x andx ==(三个点)-----------------------------------------------------------------------------------离,偏离量为0x x ξ=-;0x x ξ⇒=+代入方程x x ξ⇒=+---------------------------------------------------------------------------------3. (照猫画虎;照虎画猫?)2) 类似p39的做法令cos sin x y ρϕρϕ=⎧⎨=⎩【(2)式不易或不能分离变量 积分;极坐标化】则sin cos dy d d dt dt dtρϕϕρϕ=+ (3) 把x 、y 的极坐标表达式代入(2)式的最右边;给出对比(3)式和(4),令相应的系数相等,给出2()1d dtd dt ρρμρϕ⎫=-⎪⎪⎬⎪=⎪⎭【课本上的(1-5-10)式子和这个式子相同,只是漏掉了一个乘项,把它加上。
接下来对两个式子分别进行分离变量积分:2()d dtρρμρ=-2()d dt ρρμρ⇒=-2()d dt ρρρμ⇒=--21[]()d dtρρρμ⇒=--211[]()d dtρρρμρμ⇒-=--(0μ≠;0μ=的情况需另算)2[]()d d dt ρρρμρμρ⇒⇒-=--2[]()d d dt ρρρμρμρ⇒-=--22[ln ]2()d d dt ρρμρμ⇒-=--22()[ln ]2()d d dt ρμρμρμ-⇒-=--2ln()[ln ]2d d dt ρμρμ-⇒-=- ,每一项都可积分了!2ln()ln 2t Cρμρμ-⇒-=-+22ln()ln 22t C ρμρμ⇒--=-+22ln[()/]2t C ρμρμ⇒-=-+(已经令C=2C )222()/t C e μρμρ-+⇒=-221/t Ce μμρ-⇒=-(已经令C C e ⇒=)22/1tCeμμρ-⇒=-22/(1)tCeμμρ-⇒-=21/2[/(1)]t Ce μρμ-⇒=-当0μ=,则原式3d dt ρρ=-3d dt ρρ⇒=-3d dt ρρ-⇒=-22d dt ρ-⇒=--22dt C ρ-⇒=+22dt C ρ-⇒=+212dt C ρ⇒=+1/2[1/(2)]dt C ρ⇒=+另:1d dtϕ=d dtϕ⇒=d dt ϕ⇒=⎰⎰d dtϕ⇒=⎰⎰0t t ϕ⇒=-最后的积分结果:000t t ρμρμϕ⎧=≠⎪⎪==⎨⎪=-⎪⎩讨论:1. μ <0,距离ρ 随时间而缩短,当时间t →∞时ρ→0。
高等光学答案最终PDF版
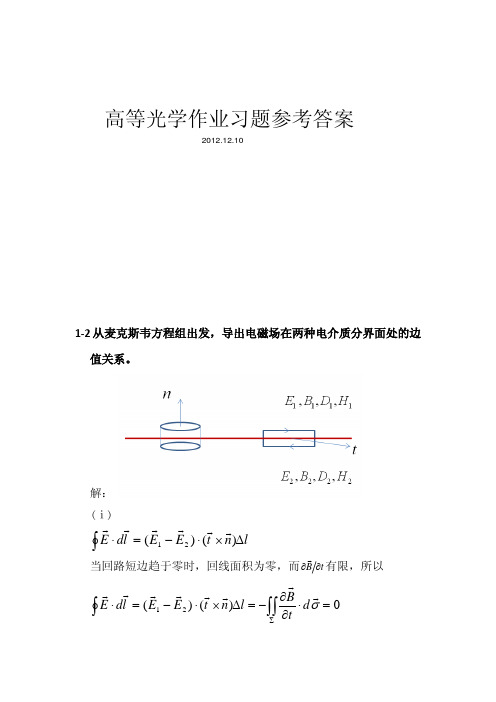
1-2 从麦克斯韦方程组出发,导出电磁场在两种电介质分界面处的边值关系。
解:(ⅰ)ln t E E l d E ∆×⋅−=⋅∫)()(21当回路短边趋于零时,回线面积为零,而t B ∂∂有限,所以0)()(21=⋅∂∂−=∆×⋅−=⋅∫∫∫Σσd t B l n t E E l d E高等光学作业习题参考答案2012.12.10即l E E n t ∆−⋅×)()(21l E E n t ∆−×⋅=))((210=得0)(21=−×E E n,即t t E E 21=(ⅱ)l t d t DJ l n t H H l d H ∆⋅=⋅∂∂+=∆×⋅−=⋅∫∫∫Σασ)()()(21t H H n t n t H H⋅=−×⋅=×⋅−α))(()()(2121当没有电流分布时0=α,得,0)(21=−×H H n即t t H H 21=(ⅲ)s n D D ds n D d D ∆⋅−=⋅=⋅∫∫)(21σ当不存在自由电荷时,0=sρ,积分0=∫∫∫Ωdv s ρ,所以0)(21=∆⋅−s n D D,即n n D D 21=(ⅳ)0)(21=∆⋅−=⋅=⋅∫∫s n B B ds n B d Bσ即n n B B 21=1-5 已知电场E 和磁场H 在直角坐标中的分量分别为:)cos(t kz A E x ω−=;);sin(wt kz B E y −=0=z E )sin(t kz B H x ωε−−=;)cos(t kz A H y ωε−=;0=z H试求电磁场的能量密度w 和玻印亭矢量S 。
解:HB E D µε==,电磁场能量密度)(21B H D E w ⋅+⋅=)(2122H E µε+= )]()([21222222z y x z y x H H H E E E +++++=µε )](sin )(cos [2)1(2222t kz B t kz A ωωµε−+−+=玻印亭矢量H E S ×=zyxz y xH H H E E E z y x =z H E H E y H E H E x H E H E x y y x z x x z y z z y)()()(−+−+−=z H E H E x y y x)(−=z t kz B t kz A))]((sin ))((cos [2222ωεωε−+−=1-6 设某一无限大介质中,,0,0==σρε、µ只是空间坐标的函数,试从麦克斯韦方程和物质方程出发证明:{}0)](ln [)()(ln 22=∇⋅∇+×∇×∇++∇εµεµωE E E E证明:)(),(r rµµεε==H B E Dµε==,E E E D⋅∇+⋅∇=⋅∇=⋅∇εεε由麦克斯韦方程 0=⋅∇D得 (ln )EE E εεε∇⋅∇⋅=−=−∇⋅取麦克斯韦方程组微分式第一式的旋度,)()(B tE ×∇∂∂−=×∇×∇其中,E E E 2)()(∇−⋅∇∇=×∇×∇2[(ln )]E E ε=−∇∇⋅−∇)()(H tB t µ×∇∂∂−=×∇∂∂− )(H H t×∇+×∇∂∂−=µµ)(µµµB t Dt×∇+∂∂∂∂= t B tE ∂∂×∇+∂∂= )(ln 22µεµ)()(ln 22E t E×∇×∇−∂∂=µεµ)()(B tE ×∇∂∂−=×∇×∇即222(ln )()[(ln )]0E E E E t εµµε∂∇−+∇×∇×+∇∇⋅=∂若ti e E E ω0 =,则22(ln )()[(ln )]0E E E E εµωµε∇++∇×∇×+∇∇⋅=1-7 从麦克斯韦方程组出发导出电磁场在有色散的非均匀介质中所满足的亥姆霍兹方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
������������������ ������������������ ������������������ = 1χ′ ������������������ = χ������������������ ������������������ ������������������ ������������������ = 1χ′ ������������������ = χ������������������
同理:χ������������������ = χ������������������ = χ������������������ = χ������������������ = χ������������������ = 0 对于2������ : ������������������ ������������������ ������������������ = (−1)3
4、KDP 晶体属于 42m 点群,具有 S4(z),C2(x), C2(y), 以及过 z 轴平分 x-y 的镜 面 m1、m2,试化简 Tijk。已知 0 1 0 1 0 0 1 4 : 1 0 0 2x : 0 1 0 2 y : 0 0 0 1 0 0 1 0 1 0 0 0 1 0 0 2 z : 0 1 0 m1 : 1 0 0 m2 : 1 0 0 1 0 0 1 0 0 0 1 0 0 1 1 0 0 0 0 1
e m
E(ω)
r1 (ω) = − E(ω)
m e m
e
1
2 ω2 0 −ω −2ihω
= − E(ω)F(ω)
m e m
e
r1 (t) = − E(ω)F(ω)e−iωt − =−
E ∗ (ω)F(−ω)eiωt
e E(ω)F(ω)e−iωt + c. c. m 2 e e 2( ) r1 t = (− E(ω)F(ω)e−iωt − E ∗ (ω)F(−ω)eiωt ) m m =
P
(2) (
2ε0 χ(2) (ω1 , ω2 )E(ω1 )E(ω2 )e−i(ω1+ω2 )t t) = }和频 +2ε0 χ(2) (−ω1 , −ω2 )E ∗ (ω1 )E ∗ (ω2 )ei(ω1 +ω2 )t
=
2ε0 χ(2) (ω1 , −ω2 )E(ω1 )E ∗ (ω2 )e−i(ω1−ω2 )t }差频 2ε0 χ(2) (−ω1 , ω2 )E ∗ (ω1 )E(ω2 )e−i(−ω1 +ω2 )t
d2 r2 dt2
+ 2h
dr2 dt
2 + ω2 0 r2 = Ar1 ……②
(3)对于与r 3 同阶,保留r1 ,r2 ,r3 ,r1 r2 ,r1 2 项: d2 (r1 + r2 + r3 ) d(r1 + r2 + r3 ) + 2h + ω2 0 (r1 + r2 + r3 ) 2 dt dt e − A(r1 + r2 + r3 )2 − B(r1 + r2 + r3 )3 = − E m
′( ) ′( r2 t = r2 2ω)e−i2ωt ′( −4ω2 r2 2ω)
− 4ihω +
′ ω2 0 r2 (2ω)
e2 2 = A 2 E (ω)F 2 (ω) m
′( r2 2ω)
e2 2 = A 2 E (ω)F 2 (ω)F(2ω) m
′( r2 2ω)e−i2ωt
′( ) r2 t
ε0 χ(2) (ω1 , ω1 )E(ω1 )E(ω1 )e−i2ω1t ε0 χ(2) (ω2 , ω2 )E(ω2 )E(ω2 )e−i2ω2t = 倍频 ε0 χ(2) (−ω1 , −ω1 )E ∗ (ω1 )E ∗ (ω1 )ei2ω1 t ε0 χ(2) (−ω2 , −ω2 )E ∗ (ω2 )E ∗ (ω2 )ei2ω2t } 2ε0 χ(2) (ω1 , −ω1 )E(ω1 )E ∗ (ω1 ) = } 零频 2ε0 χ(2) (ω2 , −ω2 )E(ω2 )E ∗ (ω2 )
′( ) r2 t
r2 (t) =
+
,, ( t) r2
e2 2 = A 2 E (ω)F 2 (ω)F(2ω)e−i2ωt + m
e2 A 2 E(ω)E ∗ (ω)F(ω)F(−ω)F(0) + c. c. m
同理推出r3 (t) = −
e3 m3
E 3 (ω)[2A2 F(2ω) + B]F(3ω)F 3 (ω)e−i3ωt
4A2 ω2 0
−
e3 m
E 2 (ω)E ∗ (ω) [2A2 F(2ω) + 3
+ 3B] F(−ω)F 3 (ω)e−iωt +c.c.
2、利用二阶非线性极化的一般表达式 P (2) (t ) (1.2-26) ,可以得到双频分量光电 场下二阶非线性极化表达式(1.2-38)。该式共有 16 项,请分析各项对应的二阶 非线性光学过程(和频、倍频、差频、光学整流) 。提示:考虑真实性条件(实 数条件)和本征对易对称性,每个非线性光学过程可能对应几项。
χ′ ������������������ = −χ������������������ χ������������������ = 0 χ′ ������������������ = −χ������������������ χ������������������ = 0
对于2������ : ����������������� ������������������ ������������������ = (−1)3
������������������ ������������������ ������������������ = (−1)3 χ′ ������������������ = −χ������������������ χ������������������ = 0
同理:χ������������������ = χ������������������ = χ������������������ = χ������������������ = χ������������������ = 0 对于2������ : ������������������ ������������������ ������������������ = (−1)3
χ′ ������������������ = −χ������������������ χ������������������ = 0
同理:χ������������������ = χ������������������ = χ������������������ = χ������������������ = χ������������������ = 0 对于������1 : ������������������ ������������������ ������������������ = 1χ′ ������������������ = χ������������������
=
e2 2 = A 2 E (ω)F 2 (ω)F(2ω)e−i2ωt m
对于(*)式第二项与时间 t 无关:
,, ,, d2 r2 dr2 e2 2 ,, + 2h + ω0 r2 = A 2 E(ω)E ∗ (ω)F(ω)F(−ω) 2 dt dt m ,, (t) r2
e2 = A 2 E(ω)E ∗ (ω)F(ω)F(−ω)F(0) m
d2 r3 dt2
+ 2h
dr3 dt
3 + ω2 0 r3 = 2Ar1 r2 + Br1 ……③
E(t) = E(ω)e−iωt + E ∗ (ω)eiωt = E(ω)e−iωt + c. c.
r(t) = r(ω)e−iωt + r ∗ (ω)eiωt = r(ω)e−iωt + c. c. 代入①得−ω2 r1 (ω) − 2ihω + ω2 0 r1 (ω) = −
非线性光学作业
第一章
材料科学与光电技术学院 1216 班 陈志琼
第一章作业 1、用微扰方法求解一维振子的非线性响应。 提示:1)对于方程(1.2-11),将 r 进行微扰展开(1.2-13); 2)对不同微扰阶次整理得到(1.2- 14 ~16) 3)从低到高依次得到不同阶次方程的解(1.2- 17 ~19) ,求高阶解 释,较低解可以当成不变量。 解:一维非简谐振子的运动方程为:
′ ′ ′ ⃑ ̂′ (1)A′ ̂i ∙ e ̂′ ̂j ∙ e ̂′ i = Ai δii = Ai e i =A∙e i = Aj e i = αij Aj
(2) αij e ̂′ ̂′ ̂je ̂′ ̂ j δii = e ̂j i =e i ∙e i =e (3) αij αij = e ̂′ ̂je ̂′ ̂k = e ̂′ ̂′ ̂j ∙ e ̂ k = δii δjk = δjk i∙e i ∙e i∙e ie
' ' ˆ j , A Ae ˆ' ˆ ˆ ˆ ˆ 3、 A A j e i i , ei e j ij , ij ei e j
ˆ j ij e ˆi' ; 求证: (1) Ai' ij Aj ; (2) e (3) ijik jk 。
解:
解:考虑到光电场真实性:ω−n = −ωn ; E(ω−n ) = E(−ωn ) = E ∗ (ωn )
二阶非线性极化的一般表达式:
P (2) (t) = ε0 ∑ χ(2) (ωm , ωn )E(ωm )E(ωn )e−i(ωm+ωn )t
