计算复习
计算方法复习题

《计算方法》复习题一 选 择(每题3分,合计42分)1. x* = 1.732050808,取x =1。
7320,则x 具有 位有效数字。
A 、3 B 、4 C 、5 D 、62. 取73.13≈(三位有效数字),则≤-73.13 。
A 、30.510-⨯B 、20.510-⨯C 、10.510-⨯D 、0。
5 3. 下面 不是数值计算应注意的问题。
A 、注意简化计算步骤,减少运算次数B 、要避免相近两数相减C 、要防止大数吃掉小数D 、要尽量消灭误差 4. 对任意初始向量)0(x 及常向量g ,迭代过程g x B xk k+=+)()1(收敛的充分必要条件是 。
A 、11<B B 、1<∞BC 、1)(<B ρD 、21B <5. 用列主元消去法解线性方程组,消元的第k 步,选列主元)1(-k rka ,使得)1(-k rk a = 。
A 、 )1(1max -≤≤k ikni a B 、 )1(max -≤≤k ikni k a C 、 )1(max -≤≤k kjnj k a D 、 )1(1max -≤≤k kjnj a6. 设ƒ(x)= 5x 3-3x 2+x +6,取x 1=0,x 2=0。
3,x 3=0。
6,x 4=0.8,在这些点上关于ƒ(x )的插值多项式为3()P x ,则ƒ(0.9)—3(0.9)P =__________。
A 、0 B 、0.001 C 、0。
002 D 、0.0037. 用简单迭代法求方程f (x )=0的实根,把方程f (x )=0转化为x =ϕ(x ),则f (x )=0的根是: .A 、y =x 与y =ϕ(x )的交点B 、 y =x 与y =ϕ(x )交点的横坐标C 、y =x 与x 轴的交点的横坐标D 、 y =ϕ(x )与x 轴交点的横坐标8. 已知x 0=2,f (x 0)=46,x 1=4,f (x 1)=88,则一阶差商f [x 0, x 1]为 。
人教五年级下册数学期末计算题综合复习(含答案)

人教五年级下册数学期末计算题综合复习(含答案)1.口算。
1588+= 3142-= 337-= 21213434+-+= 23÷= 20.65+= 20.3= 23155-+= 2.直接写出得数。
318-= 13÷= 1123+= 20.6= 2439-= 14355-+= 3.直接写出得数。
5548-= 559+= 7263+= 41255--= 1123-= 30.45+= 124-= 154565++= 4.直接写得数。
321010+= 1145+= 7293-= 5117-= 10.42÷= 1.6×5= 1158-= 0.75-0.14= 560÷80= 12.56÷4= 5.细心计算。
931010-= 1588+= 5164-= 45199-+= 417-=10.754+=0.52= 1-1÷4= 6.递等式计算,怎样算简便就怎样算。
731846-+ 1342995⎛⎫-+ ⎪⎝⎭ 3583118118+++ 7.下面各题,能简便计算的用简便方法计算。
2433510+- 53449797+++ 20411191515-- 8.计算下面各题。
能简算的要简算。
74535995+++ 51731111-- 111124816+++9.计算下面各题,能简算的要简算。
7338810⎛⎫-+ ⎪⎝⎭ 3514123⎛⎫-- ⎪⎝⎭ 2433510+- 13546767-+- 10.计算下面各题,能简算的要简算。
①513668⎛⎫++ ⎪⎝⎭ ②1343677-- ③31117218218+++ ④2.487.8 2.48 1.2 2.48⨯+⨯+ 11.解方程。
4x÷3=2.4 5.4x -4.6x =7.2 18×2+3x =6012.解方程。
1647x -= 0.2 1.448x x += 220.915.8x +⨯= 13.解方程。
五上期末复习(计算)

1.直接写得数。
0.2×0.14﹦ 3.4+1.6﹦ 0.73-0.3﹦ 7.1+1.09=3.5×20﹦ 30÷0.6﹦ 20-19.3= 0.36÷1.2=2.用竖式计算。
0.48×1.5 8.84÷1.7 5.98÷2.3=0.125×1.4≈ 14×0.16= 4.8×0.25=(保留两位小数)3.用递等式计算。
(能简算的要用简便方法计算)13.8÷(1.38×0.02) 3.9+0.56+6.1+0.44 3.74×9.6+0.4×3.74 (9.17+9.17+9.17+9.17)×2.51、直接写出得数。
0.66-0.6= 3.7+0.3= 5+0.5= 0.92=1.4×100=2.8÷0.1= 1.2×0.5= 6.4÷0.02=2、用竖式计算。
3.1-0.68 0.26×3.2 32÷0.640.04×0.12= 3.84×2.6≈ 5.76×3=(保留一位小数)3、计算下面各题,能简便的要用简便方法计算。
〔0.5+(2-0.75)〕×1.6 10.73-4.76-5.24 7.4×2.43-1.43×7.4 39.86-(22.9+9.86 )1、直接写出得数。
0.2×0.4= 2.8÷0.7= 7²= 4x+5x= 9a-8a= 0.307×100= 0.37+0.3= 5.6÷10=2、列竖式计算,并保留两位小数。
9.75×1.5= 2.58+3.4= 6-4.95=8.64÷8= 5.98÷2.3= 25.8÷0.63、怎样算简便就怎样算。
金融学计算题复习

金融学计算题复习计算题一:1.某人3年后需一笔93170元的货币,银行存款的年利率为10%,他应该筹集多少本金存入银行,才能在3年后得到这一数量的货币?求解:由题意所述本利和(s)=93170,r=10%,n=3由:s=p/(1+rn)。
则:p=s/(1+rn)=93170/(1+10%?3)=71670元。
即为必须筹措71670元,就可以在3年后获得93170元的货币。
(见到教材p76页公式。
)2.银行发放一笔金额为30000元,期限为3年,年利率为10%的贷款,规定每半年复利一次,试计算3年后本利和是多少?求解:年利率为10%,半年利率为10%÷2=5%则:s=p(1+r)n=30000*(1+5%)3*2=40203元。
即为三年后的本利和为40203元。
3.设某一时期的名义利率为2%,当物价上涨率为4%时,要保持实际利率不变,怎么办?解:当名义利率为2%,物价上涨4%时,实际利率为:2%-4%=-2%即实际利率下跌了2%。
如果名义利率提高到4%,实际利率则为:4%-4%=0即实际利率不变。
所以,要保持实际利率不变,需把名义利率提高到6%。
4.某国2021年一季度的名义利率为10%,通货膨胀率为4%,请分别以粗略的方法和精确的方法求实际利率。
求解:粗略方法:rb=rb?rf=10%?4%=6%准确的方法:rb=-----=------=9.52%5.某人有存款50万元、负债15万元和货币值随物价变动的资产30万元,当通货膨胀率为100%时,其总名义资产的净值是多少?求解:1.名义资产净值=50万+60万?15万=95万元5.某人在银行存人3年期存款100万元,若3年期定期存款年利率为4%,请利用单利法和复利法分别计算在利息所得税率为20%时,此人存满3年的实得利息额。
解:(1)单利计算法:i=p*r*n=100*4%*3=12万元实际利息额=12*(1-20%)=9.6万元(2)复利计算法:i=p*(1+r)n-p=100*(1+4%)3-100=12.49万元实际利息额=12.49*(1-20%)=9.992万元排序题型二:1.某企业将一张票面金额为10000元、3个月后到期的商业票据,提交银行请求贴现。
《会计基础》计算题复习重点

《会计基础》计算题复习重点1、有关资产负债及所有者权益的计算考点:资产=负债+所有者权益注意必须是同一时点【例题】某公司期初资产总额为300000元,当期期末负债总额比期初减少20000元,期末所有者权益比期初增加80000元,则该企业期末权益总额为多少元?【解析】设期初负债为某,期初所有者权益为y则某+y=300000期末的负债为某-20000,期末的所有者权益为y+80000“期末的权益”=“期末的负债”+“期末的所有者权益”=某-20000+y+80000=某+y+60000=360000【例题】某企业资产总额为150万元,当发生下列三笔经济业务后:(1)从银行取得借款30万元存入银行;(2)用银行存款偿还债务15万元;(3)收回应收账款4万元存入银行,其资产总额为()万元。
【解析】要准确判断三项业务的性质,(1)是资产和负债同时增加30万,(2)是资产和负债同时减少15万,(3)是资产内部的银行存款增加4万,应收账款减少4万,总资产不变。
因此答案为150+30-15=165【例题】某公司8月末负债总额100万元,9月份收回外单位所欠货款15万元,用银行存款归还借款10万元,用银行存款预付购货款5万元,则9月末负债总额为()。
【解析】“9月份收回外单位所欠货款15万元”属于资产内部一增一减;“用银行存款归还借款10万元”属于资产和负债同时减少;“用银行存款预付购货款5万元”属于一项资产增加另一项资产减少。
答案为100-10=90。
假设在上述业务基础上,又发生:发行债券100万,购买某上市公司债券50万,向投资者分配股票股利5万(已办妥相关手续),决定向投资者分配现金股利3万。
则:负债余额为:90+100+32、权责发生制下的收入、费用计算【例题】某企业1月计提并支付工紫80000元,其中厂部管理人员工资30000元,生产人员工资40000元,车间管理人员工资10000元,预支厂部上半年书报费2400,预付上半年生产车间保险费6000元,计提本月固定资产折旧20000元,其中生产用固定资产的折旧为15000元,发生固定资产维修费为10000元,其中生产用固定资产的维修费为6000元,为财务人员小王报销差旅费500元。
计算题复习ppt

p =
P(1 - P) n
p =
P(1 - P) n 1 - n N
6.2区间估计公式
抽样极限误差
x = t x
p = t p
平均数区间估计
(x - x ) X (x + x )
成数区间估计
(p- p ) P (p + p )
6.3简单随机抽样的必要样本容量的计算公式:
4、间隔不等的间断时点数列
a0 + a1 an-1 + an a1 + a2 f1 + f 2 + ......+ fn 2 2 a= 2 n fi
i =1
相邻两次登记的 时间间隔
4.3 相对数和平均数序时平均数的计算
相对数或平均数数列中的各项数值(以c表示)是 根据两个有联系的总量数据(分别用a和b表示) 对比而求得,用符号表示即c=a/b。 由于相对数或平均数是不能直接相加的,因此简 单地将C平均是不正确的! 相对数或平均数的序时平均数只能根据它们本 身的公式进行计算,即
r=
x - xy - y f x - x f y - y
2
2
f
(加权式)
7.3 简单直线回归方程的配合方法
• 回归方程式,其一般形式为:
yc = a + bx
• 应用最小平方法原理有:
y = na + b x
b=
b =
n xy - x y n x 2 - ( x) 2
上限公式和下限公式的累积方 向不一样,推荐下限公式
算术平均数与众数、中位数之间的关系
• 在对称分布(即正态)时x = M e = M o
• 在右偏时 • 在左偏时 • 适度偏态时
财务管理计算题复习

二、重点计算公式:1.复利终值的计算(已知现值P 求终值F ): 2.复利现值的计算(已知终值F 计算复利现值P ): P= F ×(P/F ,I ,n)1.普通年金终值的计算(已知年金 A ,求年金终值F )公式: F=A ( F / A ,i ,n) 2.普通年金现值的计算(已知年金A ,求年金现值 P )公式: P = A (P / A ,i ,n )3.即付年金终值的计算(已知即付年金A ,求年金终值F ):4.即付年金现值的计算(已知即付年金A ,求年金现值P ): 5、银行借款资金成本计算:K =借款额×利率×(1-所得税率)/借款额-筹资费用×100%6、普通股资本成本的计算:当条件为发行价时,普通股资本成本当条件为股市的股价时,普通股成本7、财务杠杆系数的计算:因为:息税前利润(简称EBIT)的计算公式为:即:息税前利润(简称EBIT) = (销售收入-变动成本-固定成本)÷(销售收入-变动成本-固定成本)-利息费用8、项目投资决策方法的计算公式:(1)计算项目的计算期=建设期+生产经营期(2)计算固定资产折旧额=(固定资产投资额-固定资产残值)÷设备使用年限 (3)所得税=净利润*税率=(营业收入-营业成本-折旧额)税率 (4)税后利润=营业收入-营业成本-折旧额-所得税 (5)计算初始现金流量 = 固定资产投资+垫支流动资金 (6)计算营业现金净流量=该年税后利润+该年折旧额(7)计算终结现金净流量 = 固定资产残值收入+ 回收垫支流动资金量9、折现评价指标:指在计算过程中充分考虑和利用资金时间价值因素的指标,又称为动态评价指标,包括:净现值、净现值率、现值指数和内含报酬率等指标。
它们的计算公式是:(1)净现值(NPV):净现值(NPV)=∑(项目投产后各年的现金净流量×复利现值系数)-初始投资额)n ,i ,P /F (P F =1]-1)n I,[(F/A,A F +⨯=1],-1)n I,[(P/A,A P +⨯=股利固定增长率-筹资费率)(股市现在的股价股利固定增长率刚支付的股利+⨯+=%1001)1(k 股利固定增长率-筹资费率)普通股总额(第一年预期股利+=%1001K 股利固定增长率-筹资费率)发行价(第一年预期股利+=%1001K 利息费用固定成本变动成本销售收入固定成本变动成本销售收入财务杠杆系数-----=∆∆=EBIT/EBIT EPS /EPS )DFL (aM a x )b p (a bx px EBIT -=--=--=(2)(3)或:现值指数(PI )=l +净现值率(NPVR )1、 复利现值的计算:【例1】:某人想在5年后从银行取出10000元,若按5%的复利率计算,现在应一次存入的金额多少?( 查复利现值系数表如:[F/p,5%,5]=0.7835) 解P=F[P/P ,ⅰ,n]= 1000×[F/p,5%,5]=10000×0.7835=7835(元)2、P19普通年金终值的计算:【例1-3】张先生每年年末存入银行1000元,连续存5年,银行年利率10%,则5年后张先生可以一次性从银行取出多少钱?[F/A ,10%,5]=6.1051 解: F = A [F/A ,ⅰ,n]= 1000[F/A ,106%,5]= 1000*6.1051=6105.1元3、P94银行借款成本的计算:【例3-8】某企业取得银行借款500万元, 筹措借款的费用率为0.2%, 年利率10%, 期限5年, 每年付息一次, 到期一次还本, 企业所得税率为25%, 计算这笔借款的资金成本。
2-6年级数学计算题复习

二年级数学计算题班级姓名一、我能默写乘法口诀1×1=1二、我能计算正确。
4500-500= 3600+240= 18÷9= 52-8-24= ()÷6=9 97-43= 2300+4000= 27÷9= 2000+900= 12÷4×5= 24÷6= 90+10= ()+9=81 21÷7= 3600+4000= 2×4×6= 76+14= 1200+800= 54÷6= 3200-3000= 64+25= 5千克=()克 50+700= 40+(17-8)= 570-380= 37+54= 900-400= 480-260= 48-29= 32÷8= 36-8+50= 1200-700= 4×()=28 76+14= 4×2÷8= 20÷5= 56÷8÷7= 570-300= 7×6= 63÷7= 7×()=56 2500-2000= 9×()=36 500+700= 三、我会估。
482+146≈ 758+106≈ 928-392≈ 486-176≈210+390≈ 487-135≈ 925-178≈ 589+394≈620-147≈ 409+211≈ 986-312≈ 726-289≈四、递等式计算(脱式计算)。
14-5×2 5×(6+2) 41-30+70 (15+15)÷6= = = == = = =五、用竖式计算(笔算)。
1、让我来做一做。
620 630 380 730 +270 -350 +470 -3302、列竖式计算下列各题。
24+35= 87-35= 48+37=360+230= 93-65= 460-340=280+450= 8200-800= 1000-680=六、拓展提高。
最新人教版小学数学四年级下册计算题归类复习题最新

计算题归类复习1.直接写得数。
35×11= 0.17×100= 0.7-0.47= 0÷23=2.8+1.06= 8-0.76= 0.5×10÷100= 55-40-8=4-2.9= 0.75+0.25= 0.45×100 60÷1000= 7-5.23= 2.4+1.6= 102×6= 0.8÷100×10=0.68-0.06= 1.2一0.5= 11.7+2= 5.9+1.6=125×8= 14÷5= 25×4= 25×8= 0.4+8.7= 4.5+3.6= 0.28+0.12= 1.4-0.9= 7.4+6= 5-1.4-0.6= 35÷100= 25×3×4=10-0.09= 0.29×10= 150×6= 84+16×5=0.15+0.4= 0.09×100= 4×0.25= 4×6×25= 12.9-2.9= 5.42-1.72-2.28= 3.69×0= 38.7÷100=12.8-9.8= 100×0.1= 20-2.7-7.3= 6-1.6=125-27×0= 0.3+0.06= 50-50÷5= 3400÷25÷4= 6-2.2= 2.7+6.3= 0.25×1000= 1-0.08= 630÷70= 14÷100= 5+15×6= 28×0÷56=1.8-0.7=2.4+0.8= 7×99+7= 24-19+24+19=7.5-2.8= 4-2.1= 5×(33-25)= 300-84-16= 5.5-3.2= 0.6-0.37= 25 ×(4+8)= 100÷5÷4=0.25×100= 360÷18= 1-0.01= 0÷21×7=24-8×2= 35-8+10= 2.5+7.5= 299+63=125×8= 910÷7= 300-82= 41.5-41.5= 1.56-0.35= 100÷25= 0.39+0.61= 4.9-2.8=0.67×100= 35+24-16= 48÷8×9= 125×8=1.2+0.15= 8-4.6= 0÷0.98×1= 25×4=2. 计算下面各题,能简算的要简算。
经济学计算题复习

1、已知某一时期内某商品的需求函数为Q D =50-5P,供给函数为Qs = -10+5p。
(1)求均衡价格和均衡数量(2)计算均衡时的需求弹性?(3)计算当价格为3时,供给价格弹性是多少?2、某消费者的需求价格弹性e d=1.3,在其他条件不变的情况下,商品价格下降2%,对需求数量有什么影响?3、某消费者的需求的收入弹性e y=2.2,在其他条件不变的情况下,消费者收入提高5%,对需求数量有什么影响?4、在某需求曲线上存在3点A、B、C、A点对应价格为8,对应需求量为10;B点对应价格为6,对应需求量为20;C点对应价格为4,对应需求量为30,计算在B点到C点的需求价格弧弹性。
5、假设一国人口为2000万,就业人数为900万,失业人数为100万。
这个国家中的失业率为多少?6、假定某企业全部成本函数为Tc=30000+5Q—Q2,Q为产出数量。
那么总变动成本TVC、不变成本、平均可变成本、平均不变成本、边际成本分别为多少?7、假定某商品的价格从6美元降到5美元,需求量将从9单位增加到11单位,则该商品卖者的总收益如何?8、某厂商生产5件衣服的总成本为1500元,其中厂房和机器折旧为500元,工人工资及原材料费用为1000元,那么平均可变成本为多少?9、根据以下数据,乘数最大的是()A 边际消费倾向为0.6B 边际消费倾向为0.4C 边际消费倾向为0.75D 边际消费倾向为0.910、当某消费者的收入上升20%,其对某商品的需求量上升5%,则商品的需求收入弹性为多少?11、在两部门的经济中,消费函数为C=100+0.8y,投资为I=50.试计算:(1)均衡的国民收入和消费水平;(2)该经济的投资乘数。
12、根据简单国民收入决定理论,如果投资增加150亿元,边际消费倾向为0.8,则收入水平将增加14、当法定准备率为20%,商业银行最初所吸收的存款为1000亿元时,银行体系将会使存款总额扩大到多少?15、如果美元对马克的汇率1美元兑换2马克,那么马克对美元的汇率是1马克兑换几美元?16)如下(1)求该商品的均衡价格和均衡数量。
计算专项复习

四年级下册数学计算专项练习1、怎样算简便就怎样算。
(80+8)×12577×101-77201×45125×32×25 360÷8÷5 87×99+87125×88 270÷45351+69+49+31756-(156+58) 35×9976×18+25×18-182、、运算(1)、直接写得数5.46÷10= 2-0.6= 5.8×100= 4.8+7.5+5.2= 594-137= 0.6÷100= 90+0.9= 3.54+10.46= 9.6-3.8-1.2= 485-298=(2)怎样简便就怎样算。
332×4+68×4 1.35-0.87+0.65-0.13 64×2519.92+14.4-9.92 78×101 6.9+0.1-6.9+0.1(3)、列式计算。
①、4.5与2.5的和乘5的积是多少?②6.7与3.8的差与和各是多少3、(1)1、直接写得数。
6-5.12= 14.4-2.4= 25×8= 0.052×100= 2.5+3.8= 4.1+5.09=1-0.7= 25×9×4= 36÷100= 4.8+5.2= 81÷3= 50+125×8=(2).用竖式计算并验算。
19.08+5.83= 20-3.18=(3)计算,能简算的要简算。
125×17×8 35×102 56×67+32×56+5612.7+0.98+3.02+3.3 5.6-1.71-0.29 24.52-(7.5+4.52)4、计算,用简便方法618-(352-282) 12.36-5.64-4.36 125×(80+8) 73×101-73625÷125÷8 15×32+25×8 6.55+7.37+2.63+0.455、(1)直接写得数。
初中数学中考计算题复习(最全)-含答案

by by
4, 2
的解为
x
y
2, 1,
,则
2a-3b
的值为多少?
参考答案与试题解析
一.解答题(共 30 小题)
第 11 题 图
米的扇花台,那
a2 b2
.
2x y 5
3、已知 x 2 y 6 那么 x-y 的值是(
)
A. 1
B. ―1
C. 0
D. 2
4、若不等式组
x b
a2 2x 0
的解集是
1
x
1
,求
a
b
2010
的值
(1)23((xy12))5xy18
(5)
y 1 4
x
3
2
2x 3y 1
÷
+ ,其中 x=2 +1.
26.(1)计算:
;
(2)解方程:
.
27.计算:
.
28.计算:
.
29.计算:(1+ )2013﹣2(1+ )2012﹣4(1+ )2011.
30.计算:
.
1.化简求值:
,选择一个你喜欢且有意义的数代入求值.
2.先化简,再求值
,然后选取一个使原式有意义的 x 值代入求值.
一.解答题(共 30 小题)
1.计算题:
①
;
②解方程:
.
2.计算:
+(π﹣2013)0.
3.计算:|1﹣ |﹣2cos30°+(﹣ )0×(﹣1)2013.
4.计算:﹣
.
5.计算:
.
6.
.
7.计算:
.
8.计算: 9.计算:
软考计算复习资料
列式:
(3-1)+
|(-925.93+428.67+396.92) | = 2.27
367.51
0 -925.93
1
2
3
2.27
第4页/共26页
选C
PERT(计划评审技术)计算
μ
第5页/共26页
PERT(计划评审技术)计算
第6页/共26页
PERT(计划评审技术)计算
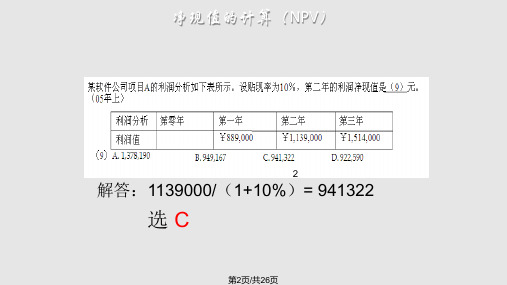
例1:公司的某项目即将开始,项目经理估计该项目10天即可完 成,如果出现问题耽搁了也不会超过20天完成,最快6天即可完 成。根据项目历时估计中的三点估算法,你认为该项目的历时为 (37)该项目历时的估算标准差为(38) 。 (37)A.10天 B.11天 C.12天 D.13天 (38)A.2.1天 B.2.2天 C.2.3天 D.2.4天
第23页/共26页
决策树分析
80x65%+(-30)x35%
第24页/共26页
70x65%+10x35%
谢谢!再见! 祝大家取得好成绩!
第25页/共26页
感谢您的观看!
第26页/共26页
—CV、SV、EAC、ETC —CPI、SPI
公式:CV=EV‐AC, SV=EV‐PV CPI=EV/AC(支出), SPI=EV/PV(进度)
型偏差
预测技术: ETC=(BAC‐EV) 当前偏差被看做是非典型的 ETC=(BAC‐EV)/CPI 当前偏差被看做是代表未来的典型偏差 EAC=AC+ETC ‐‐‐‐衍化为下面两个公式 EAC=AC+BAC‐EV 当前偏差被看做是非典型的 EAC=AC+(BAC‐EV)/CPI 当前偏差被看做是代表未来的典
计算方法复习题

计算⽅法复习题第⼀章误差1 问3.142,3.141,722分别作为π的近似值各具有⼏位有效数字?分析利⽤有效数字的概念可直接得出。
解π=3.141 592 65…记x 1=3.142,x 2=3.141,x 3=722.由π- x 1=3.141 59…-3.142=-0.000 40…知3411110||1022x π--?<-≤? 因⽽x 1具有4位有效数字。
由π- x 2=3.141 59…-3.141=-0.000 59…知2231021||1021--?≤-因⽽x 2具有3位有效数字。
由π-722=3.141 59 …-3.142 85…=-0.001 26…知231021|722|1021--?≤-因⽽x 3具有3位有效数字。
2 已知近似数x*有两位有效数字,试求其相对误差限。
分析本题显然应利⽤有效数字与相对误差的关系。
解利⽤有效数字与相对误差的关系。
这⾥n=2,a 1是1到9之间的数字。
%5101211021|*||*||)(|1211*=??≤?≤-=+-+-n ra x x x x ε 3 已知近似数的相对误差限为0.3%,问x*⾄少有⼏位有效数字?分析本题利⽤有效数字与相对误差的关系。
解 a 1是1到9间的数字。
1112*10)1(2110)19(21102110003%3.0)(--?+≤?+?=?<=a x r ε设x*具有n 位有效数字,令-n+1=-1,则n=2,从⽽x*⾄少具有2位有效数字。
4 计算sin1.2,问要取⼏位有效数字才能保证相对误差限不⼤于0.01%。
分析本题应利⽤有效数字与相对误差的关系。
解设取n 位有效数字,由sin1.2=0.93…,故a 1=9。
411*10%01.01021|*||*||)(-+-=≤?≤-=n r a x x x x ε解不等式411101021-+-≤?n a 知取n=4即可满⾜要求。
5 为了使计算32)1(6)1(41310---+-+=x x x y的乘除法运算次数尽量地少,应将表达式改写为怎样的形式?解设.))64(3(10,11t t t y x t -++=-=在数值计算中,应注意简化运算步骤,减少运算次数,使计算量尽可能⼩。
三年级数学下册计算部分复习题1

计算部分复习题1、直接写出得数。
(略)2、列竖式计算,除法的要验算。
76×34= 18×45= 94×26= 62×91= 38×26=75×28= 543÷3= 804÷4= 756÷8= 545÷5=567÷8= 819÷8= 324÷3= 985÷7= 720÷3=704÷5= 8016÷4= 362÷3= 10-3.5= 3.75+5.25=7.6-3.57= 6.7+2.4= 9.80+7.5= 30.2-24.8=3、脱式计算。
24×5+700 81÷3÷9 40+60÷5 500-300÷4700-600÷5 50+50×22 346÷2+506 17 ×34-27837+16×28 65+11×12 56+37×21 61+12×2343+21×23 45+32×55 38+25×31 48+52×21 87+35×4999+46×97 44+81×33 31+98×7638+53×47 67+81×90 99+54×5656+56×76 190+18×11 41+51×8796+72×44 98+55×67 37+43×7732+58×86 25+67×22 44+88×2299+65×34 89+78×46 48+63×9156+89×77 35+49×82 47+99×8958+85×33 49+65×33 79+92×93125+82×37 152+58×33 117+58×77 196+55×31 198+12×89 137+22×88 132+12×37 250+23×38 440+13×36 199+25×89 819+49×90 418+57×67 516+27×36 315+57×34 147+28×36 518+18×47 419+29×54 128+28×19 319+32×56 189+42×37 818+41×53 32+65×37 850+27×38 269+85×39 215+35×47 652+78×36 107+29×64 307+77×83 635+57×86 556+38×87 671+92×23 493+18×67 465+85×34 378+54×27 498+56×26 807+51×46 909+37×35 414+58×47 731+59×67 308+47×87 167+81×90 299+33×77 506+21×49 190+76×34 41+47×36 245+53×69 752+53×87 817+56×89 837+68×36 865+98×49 356+76×58 561+57×92 43+59×38 458+86×36 538+27×38 548+52×59 87+29×78 299+39×48 544+56×21 531+51×88 38+23×38 67+59×57 99+35×36265+54×66 552+53×46 417+88×62 237+26×48 665+39×45 256+15×64 761+63×25 643+31×63 645+42×83 338+19×62 648+33×59 587+19×83 999+26×63 644+42×39 431+24×66 38+72×26 567+35×61 699+53×16 506+56×56 19+23×93 99+53×33 125+16×55 352+28×32 217+29×37 307+46×52 265+23×53 556+73×26 631+52×33 243+21×23 345+21×37 378+49×77 478+56×65 787+53×53 399+42×66 544+35×27 731+35×46 438+55×69 67+51×38 899+35×51 506+32×64 177+58×35 741+34×57 689+22×89 872+23×52 412+26×62 541+20×87 49+52×15 396+41×35 11+83×59 258+45×67 743+76×38 529+25×62 248+31×53 487+28×65 38+35×46 344+25×75 831+56×65 51+16×62 267+35×59 846+28×73 125+35×82 127+28×39 59+26×3871+21×63 581+51×52 753+53×82 317+46×36 713+53×83 26+85×37 305+44×53 548+38×94 793+59×36 389+52×34 544+37×92 131+28×56 238+33×87 67+58×98 100+29×32 26+68×61 85+57×96 52+69×67 103+13×81 552+71×38 817+26×73 745+35×91 565+37×93 856+17×83 286+26×82 78+87×36 23+52×87 90+56×38 999+27×37 888+28×38 199+28×36 777+29×73 766+38×83 666+27×72 767+81×90 399+29×92 656+38×96 222+39×96 898+37×61 212+30×76 252+32×83 717+28×73 939+72×29 565+36×83 656+88×35 828+35×63 121+63×16 555+86×37 777+26×42 323+43×67 111+29×37 565+38×67 789+66×39 373+69×73 646+85×69 167+26×83 399+78×39 293+31×68 717+32×97 828+37×86 73+15×46 90+76×19 52+16×3850+93×13 23+40×91 80+73×26 12+57×34 863+26×26 353+55×63 105+53×63 555+28×72 373+68×19 55+16×62 66+38×67 121+49×82 666+37×68 535+56×37 81+30×59 33+26×14 51+18×67 19+84×19 87+26×88 95+31×72 59+77×81 91+72×53 93+29×93 75+37×75 88+85×38 68+62×26 37+33×43 59+56×95 24+82×23 36+68×36 78+73×87 57+85×95 99+59×59 58+53×77 190+88×31 61+52×57 31+35×53 69+83×38 69+65×96 85+58×99 83+69×86 96+88×69 75+55×68 29+73×67 89+92×28 66+76×77 93+33×63 82+66×82 99+59×71 82+87×73 51+22×37 75+53×35 86+36×39 85+29×26 63+28×27 29+37×38 82+66×73 23+87×79 28+36×67 87+18×76 100+32×25 79+64×68 56+37×5793+18×36 92+27×38 256+57×69123+13×26 93+23×36 71+89×16236+12×76 525+26×39 999+59×67302+38×67 36+27×38 82+36×274、列式计算(注意:列式计算只能用综合式,不能用分步式)(1)38个27是多少?(2)两个因数都是18,它们的积是多少?(3)两个因数的积是315,一个因数是5,求另一个因数是多少?(4)最小的两位数与最大的两位数的积食多少?(5)一个数是56.39,另一个数是13.68,它们的和、差各是多少?(6)一个数除以15商是35,余数是7,这个数是多少?(7)13乘以一个数是351,这个数是多少?(8)23与16的积加上215,和是多少?(9)69与57的差再乘以16,积是多少?(10)25的18倍是多少?(11)比13的24倍多67的数是多少?(12)14的27倍再除以4,商是多少?。
初中数学中考计算题复习最全)-含答案

一.解答题(共30小题)1.计算题:①;②解方程:.2.计算:+(π﹣2013)0.3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013.4.计算:﹣.5.计算:.6..7.计算:.8.计算:.9.计算:.10.计算:.11.计算:.12..13.计算:.14.计算:﹣(π﹣3.14)0+|﹣3|+(﹣1)2013+tan45°.15.计算:.16.计算或化简:(1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|.(2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2)17.计算:(1)(﹣1)2013﹣|﹣7|+×0+()﹣1;(2).18.计算:.(1)19.(2)解方程:.20.计算:(1)tan45°+sin230°﹣cos30°•tan60°+cos245°;(2).21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60°(1)计算:.22.(2)求不等式组的整数解.(1)计算:23.(2)先化简,再求值:(﹣)÷,其中x=+1.24.(1)计算:tan30°25.计算:(1)(2)先化简,再求值:÷+,其中x=2+1.26.(1)计算:;(2)解方程:.27.计算:.28.计算:.29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011.30.计算:.1.化简求值:,选择一个你喜欢且有意义的数代入求值.2.先化简,再求值,然后选取一个使原式有意义的x值代入求值.3.先化简再求值:选一个使原代数式有意义的数代入中求值.4.先化简,再求值:,请选择一个你喜欢的数代入求值.5.(2010•红河州)先化简再求值:.选一个使原代数式有意义的数代入求值.6.先化简,再求值:(1﹣)÷,选择一个你喜欢的数代入求值.7.先化简,再求值:(﹣1)÷,选择自己喜欢的一个x求值.8.先化简再求值:化简,然后在0,1,2,3中选一个你认为合适的值,代入求值.9.化简求值(1)先化简,再求值,选择你喜欢的一个数代入求值.10.化简求值题:(1)先化简,再求值:,其中x=3.(2)先化简,再求值:,请选一个你喜欢且使式子有意义的数字代入求值.(3)先化简,再求值:,其中x=2.(4)先化简,再求值:,其中x=﹣1.11.(2006•巴中)化简求值:,其中a=.12.(2010•临沂)先化简,再求值:()÷,其中a=2.13.先化简:,再选一个恰当的x值代入求值.14.化简求值:(﹣1)÷,其中x=2.15.(2010•綦江县)先化简,再求值,,其中x=+1.16.(2009•随州)先化简,再求值:,其中x=+1.17.先化简,再求值:÷,其中x=tan45°.18.(2002•曲靖)化简,求值:(x+2)÷(x﹣),其中x=﹣1.19.先化简,再求值:(1+)÷,其中x=﹣3.20.先化简,再求值:,其中a=2.21.先化简,再求值÷(x﹣),其中x=2.22.先化简,再求值:,其中.23.先化简,再求值:(﹣1)÷,其中x—.25.(2011•新疆)先化简,再求值:(+1)÷,其中x=2.26.先化简,再求值:,其中x=2.27.(2011•南充)先化简,再求值:(﹣2),其中x=2.28.先化简,再求值:,其中a=﹣2.29.(2011•武汉)先化简,再求值:÷(x ﹣),其中x=3. 30.化简并求值:•,其中x=21.. 2。
大学计算方法复习题

大学计算方法复习题一、选择题1. 在数值分析中,下列哪个算法是用于求解线性方程组的?A. 欧几里得算法B. 高斯消元法C. 快速傅里叶变换D. 牛顿迭代法2. 插值法中,拉格朗日插值法与牛顿插值法的主要区别是什么?A. 计算复杂度B. 误差大小C. 插值点的选取D. 适用的函数类型3. 下列哪个不是数值积分的方法?A. 辛普森法则B. 梯形法则C. 牛顿法D. 复合梯形法则4. 求解常微分方程的数值方法中,欧拉法和改进欧拉法的主要区别是什么?A. 计算精度B. 计算速度C. 稳定性D. 适用的方程类型5. 在数值优化问题中,梯度下降法和牛顿法的主要区别是什么?A. 收敛速度B. 计算复杂度C. 需要的初始点D. 适用的问题类型二、简答题1. 简述数值稳定性和数值误差的概念,并举例说明它们在数值计算中的重要性。
2. 解释什么是病态问题,并举例说明在实际问题求解中如何避免或减少病态问题的影响。
3. 描述牛顿-拉弗森方法(Newton-Raphson method)的基本思想,并简述其优缺点。
三、计算题1. 给定线性方程组:\[\begin{align*}3x + 2y &= 5 \\6x - y &= 8\end{align*}\]使用高斯消元法求解该方程组,并给出解。
2. 假设有一组数据点:(1, 2), (2, 3), (3, 5),使用拉格朗日插值法求一个三次多项式 \( P(x) \),使其通过这些点,并计算\( P(2.5) \) 的值。
3. 给定函数 \( f(x) = x^2 \),使用复合梯形法则计算在区间 [0, 1] 上的积分近似值,取子区间数 \( n = 4 \)。
四、论述题1. 论述数值分析在现代科学技术中的重要性,并举例说明其在不同领域的应用。
2. 讨论数值方法在解决实际问题时可能遇到的困难和挑战,并提出可能的解决方案。
五、附加题1. 给定一个函数 \( f(x) \),讨论如何选择合适的数值方法来求解其零点,并比较不同方法的优缺点。
小升初计算题专题复习(四则运算+小数加减法+量的计算)

之
一 定义
1.什么是四则运算? 加法运算、减法运算、乘法运算、除法运算
2.第一级运算和第二级运算各指什么? 第一级:加、减法 第二级:乘、除法
二 运算顺序:
1、在有括号的算式里要先算括号里面的。
2、在只有加减法或只有乘除法的算式里要 按从左往右的顺序计算。
3、在既有有加减法又有乘除法的算式里要 先算乘除法再算加减法。
3.用简便方法计算
①283 × 5 + 17 × 5 ②73+3.4+27+5.6 ③25×64×125 ④2×570-80×57
4.计算下列各式,能简便的要简便
①(16+16+16+16 )×25 ②16.7-5.4-4.6 ③51+49
1.
我看了一本300页的故事书,看了 5天后,还剩180页没看。
她平均每天看多少页?
2.
三(1)班同学把卖废品所得的钱全部捐给了希望工程, 具体情况如下:
名称
废纸
易拉罐
塑料瓶
收入(元) 47.75
25.2
68.4
(1)三(1)卖废纸所得的钱比卖塑料瓶的钱少多少元?
(2)三(1)卖废纸和易拉罐的总钱数比卖塑料瓶的钱 多多少元?
• 工作总量÷工作时间=工作效率
常用的数量关系式
• 4、加数+加数=和 和-一个加数 =另一个加数
• 5、被减数-减数=差 被减数-差 =减数 差+减数=被减数
• 6、因数×因数=积 积÷一个因数 =另一个因数
• 6、被除数÷除数=商 被除数÷商 =除数 商×除数=被除数
• 在有余数的除法中: (被除数-余数)÷ 除数=商
5.用竖式计算,并验算。
