讲义1
讲义:第1章 第2讲

考点一 匀变速直线运动规律及应用1.基本规律(1)速度公式:v =v 0+at . (2)位移公式:x =v 0t +12at 2.(3)位移速度关系式:v 2-v 20=2ax .这三个基本公式,是解决匀变速直线运动的基石.均为矢量式,应用时应规定正方向. 2.两个重要推论(1)物体在一段时间内的平均速度等于这段时间中间时刻的瞬时速度,还等于初、末时刻速度矢量和的一半,即:v =v t =v 0+v2. (2)任意两个连续相等的时间间隔T 内的位移之差为一恒量,即:Δx =x 2-x 1=x 3-x 2=…=x n -x n -1=aT 2.3.v 0=0的四个重要推论(1)1T 末、2T 末、3T 末、……瞬时速度的比为: v 1∶v 2∶v 3∶…∶v n =1∶2∶3∶…∶n . (2)1T 内、2T 内、3T 内……位移的比为: x 1∶x 2∶x 3∶…∶x n =12∶22∶32∶…∶n 2.(3)第一个T 内、第二个T 内、第三个T 内……位移的比为:x Ⅰ∶x Ⅱ∶x Ⅲ∶…∶x n =1∶3∶5∶…∶(2n -1).(4)从静止开始通过连续相等的位移所用时间的比为:t 1∶t 2∶t 3∶…∶t n [思维深化]飞机着陆后以6 m /s 2的加速度做匀减速直线运动,若其着陆速度为60 m/s ,则它着陆后12 s内滑行的距离是多少? 某位同学的解法如下:由位移公式x =v 0t +12at 2,代入已知量求得滑行距离x =288 m ,请分析以上解析是否正确,若不正确,请写出正确的解析. 答案 不正确.解析如下:先求出飞机着陆后到停止所用时间t .由v =v 0+at ,得t =v -v 0a =0-60-6 s =-10 s ,由此可知飞机在12 s 内不是始终做匀减速运动,它在最后2 s 内是静止的.故它着陆后12 s 内滑行的距离为x =v 0t +at 22=60×10 m +(-6)×1022m =300 m.1.[基本规律的应用]一个做匀变速直线运动的质点,初速度为0.5 m/s ,第9 s 内的位移比第5 s 内的位移多4 m ,则该质点的加速度、9 s 末的速度和质点在9 s 内通过的位移分别是( ) A .a =1 m /s 2,v 9=9 m/s ,x 9=40.5 m B .a =1 m /s 2,v 9=9 m/s ,x 9=45 m C .a =1 m /s 2,v 9=9.5 m/s ,x 9=45 m D .a =0.8 m /s 2,v 9=7.7 m/s ,x 9=36.9 m 答案 C解析 根据匀变速直线运动的规律,质点在t =8.5 s 时刻的速度比在t =4.5 s 时刻的速度大4 m/s ,所以加速度a =Δv Δt =4 m/s 4 s =1 m /s 2,v 9=v 0+at =9.5 m/s ,x 9=12(v 0+v 9)t =45 m ,选项C 正确.2.[刹车问题]汽车以20 m /s 的速度做匀速直线运动,见前方有障碍物立即刹车,刹车后加速度大小为5 m/s 2,则汽车刹车后第2 s 内的位移和刹车后5 s 内的位移为( ) A .30 m,40 m B .30 m,37.5 m C .12.5 m,40 m D .12.5 m,37.5 m答案 C解析 由v =v 0+at ,可求得汽车刹车后运动时间t =4 s ,刹车后第2 s 内位移x 2=20×2-12×5×22-20×1+12×5×12 m =12.5 m .刹车后5 s 内位移即为4 s 内的位移,看成反向初速度为0的匀加速直线运动,x 5=12at 2=12×5×42 m =40 m.3.[两个重要推论的应用]一列火车做匀变速直线运动驶来,一人在轨道旁边观察火车运动,发现在相邻的两个10 s 内,火车从他跟前分别驶过8节车厢和6节车厢,每节车厢长8 m(连接处长度不计).求: (1)火车的加速度的大小; (2)人开始观察时火车速度的大小. 答案 (1)0.16 m /s 2 (2)7.2 m/s解析 (1)由题意知,火车做匀减速直线运动,设火车加速度大小为a ,人开始观察时火车速度大小为v 0,L =8 m Δx =aT 2,8L -6L =a ×102 a =2L 100=2×8100m /s 2=0.16 m/s 2 (2)v t =v 平=8L +6L 2T =14×820 m /s =5.6 m/s2v t =v 0-aT ,解得v 0=7.2 m/s4.[v 0=0重要推论的应用]一列车由等长的车厢连接而成.车厢之间的间隙忽略不计,一人站在站台上与第一节车厢的最前端相齐.当列车由静止开始做匀加速直线运动时开始计时,测量第一节车厢通过他的时间为2 s ,则从第5节至第16节车厢通过他的时间为多少? 答案 4 s解析 取车为参考系,把车的运动转化为人做匀加速直线运动. 据通过连续相等的位移所用时间之比为t 1∶t 2∶t 3∶…∶t n =1∶(2-1)∶(3-2)∶…∶(n -n -1)得 2Δt =1(16-15)+(15-14)+…+(5-4)=116-4=12. 所以Δt =4 s.记住两个推论,活用一种思维1.两个重要推论公式 (1)v t =2v t =v 0+v t 2(2)Δx =aT 22.用逆向思维法解决刹车问题(1)逆向思维法:匀减速到速度为零的直线运动一般看成逆向的初速度为零的匀加速直线运动.(2)对于刹车类问题,实质是汽车在单方向上的匀减速直线运动问题.速度减为零后,加速度消失,汽车停止不动,不再返回,若初速度为v 0,加速度为a ,汽车运动时间满足t ≤v 0a,发生的位移满足x ≤v 202a.考点二 常用的几种物理思想方法1.一般公式法一般公式指速度公式v =v 0+at ,位移公式x =v 0t +12at 2及推论式2ax =v 2-v 20,它们均是矢量式,使用时要注意方向性,一般以v 0方向为正方向,已知量与正方向相同者取正,与正方向相反者取负.未知量按正值代入,其方向由计算结果决定. 2.平均速度法定义式v =x t 对任何性质的运动都适用,而v =12(v 0+v )只适用于匀变速直线运动.3.中间时刻速度法利用“任一时间t 中间时刻的瞬时速度等于这段时间t 内的平均速度”,即2v t =v =12(v 0+v ),适用于匀变速直线运动. 4.推论法对一般的匀变速直线运动问题,若出现相等的时间间隔问题,应优先考虑用Δx =aT 2求解. 5.逆向思维法把运动过程的“末态”作为“初态”的反向研究问题的方法,一般用于末态已知的情况. 6.图象法应用v -t 图象,可以把较复杂的问题转变为较简单的数字问题来解决. [思维深化]做匀变速直线运动的物体,在t s 内通过的位移为x ,则中间时刻的速度2v t 和位移中点的速度2v x 谁大呢?答案 方法一:图象法由图知v x >v t .方法二:数学求差法2v t =v 0+v t2 2v x =v 20+v 2t22v x 2-2v t 2>0所以2v x >2v t5.[比例法的应用]做匀减速直线运动的物体经4 s 停止,若在第1 s 内的位移是14 m ,则最后1 s 内的位移是( )A .3.5 mB .2 mC .1 mD .0 答案 B解析 利用“逆向思维法”,把物体的运动看成逆向的初速度为零的匀加速直线运动,则匀减速直线运动的物体在相等时间内的位移之比为7∶5∶3∶1,所以71=14 m x 1,x 1=2 m .故选B.6.[中间位置速度公式的应用]滑板爱好者由静止开始沿一斜坡匀加速下滑,经过斜坡中点时的速度为v ,则到达斜坡底端时的速度为( ) A.2v B.3v C .2v D.5v 答案 A解析 由匀变速直线运动的中点位置的速度公式2v x =v 20+v22,有v = 0+v 2底2,得v 底=2v ,所以只有A 项正确.7.[平均速度公式的应用]质点由A 点出发沿直线AB 运动,行程的第一部分是加速度大小为a 1的匀加速运动,接着做加速度大小为a 2的匀减速运动,到达B 点时恰好速度减为零.若AB 间总长度为s ,则质点从A 到B 所用时间t 为( ) A.s (a 1+a 2)a 1a 2B.2s (a 1+a 2)a 1a 2 C.2s (a 1+a 2)a 1a 2D.a 1a 22s (a 1+a 2)答案 B解析 设第一阶段的末速度为v , 则由题意可知:v 22a 1+v 22a 2=s ,解得:v =2a 1a 2sa 1+a 2;而s =0+v 2t 1+v +02t 2=v 2t ,由此解得:t =2(a 1+a 2)sa 1a 2,所以选B. 8.[物理思想方法的综合应用]物体以一定的初速度从斜面底端A 点冲上固定的光滑斜面,斜面总长度为l ,到达斜面最高点C 时速度恰好为零,如图1,已知物体运动到距斜面底端34l 处的B 点时,所用时间为t ,求物体从B 滑到C 所用的时间.图1答案 t解析 方法一:逆向思维法物体向上匀减速冲上斜面,其逆过程为由静止开始向下匀加速滑下斜面.设物体从B 到C 所用的时间为t BC .由运动学公式得x BC =at 2BC 2,x AC =a (t +t BC )22,又x BC =x AC4,由以上三式解得t BC =t . 方法二:基本公式法因为物体沿斜面向上做匀减速运动,设初速度为v 0,物体从B 滑到C 所用的时间为t BC ,由匀变速直线运动的规律可得v 20=2ax AC ①v 2B =v 20-2ax AB ② x AB =34x AC ③由①②③解得 v B =v 02④又v B =v 0-at ⑤ v B =at BC ⑥由④⑤⑥解得t BC =t . 方法三:比例法对于初速度为零的匀加速直线运动,在连续相等的时间内通过的位移之比为x 1∶x 2∶x 3∶…∶x n =1∶3∶5∶…∶(2n -1).因为x CB ∶x BA =x AC 4∶3x AC4=1∶3,而通过x BA 的时间为t ,所以通过x BC 的时间t BC =t .方法四:中间时刻速度法利用推论:匀变速直线运动中中间时刻的瞬时速度等于这段位移的平均速度,vAC =v 0+02=v 02.又v 20=2ax AC ,v 2B =2ax BC ,x BC =x AC 4.由以上三式解得v B =v 02.可以看成v B 正好等于AC 段的平均速度,因此B 点是这段位移的中间时刻,因此有t BC =t . 方法五:图象法根据匀变速直线运动的规律,画出v -t 图象.如图所示.利用相似三角形的规律,面积之比等于对应边的平方比,得S △AOC S △BDC =CO 2CD 2,且S △AOC S △BDC =41,OD =t ,OC =t +t BC .所以41=(t +t BC )2t 2,解得t BC =t .匀变速直线运动规律中应用的两个技巧1.匀减速直线运动减速到0时,通常看成反向的初速度为0的匀加速直线运动. 2.若告诉匀变速直线运动的时间和位移,通常要考虑应用平均速度公式,求出中间时刻的瞬时速度.考点三 自由落体和竖直上抛运动1.特点和规律 (1)自由落体运动的特点 ①从静止开始,即初速度为零. ②只受重力作用的匀加速直线运动. ③公式:v =gt ,h =12gt 2,v 2=2gh .(2)竖直上抛运动的特点 ①初速度竖直向上.②只受重力作用的匀变速直线运动. ③若以初速度方向为正方向,则a =-g . 2.处理竖直上抛运动的方法 (1)分段处理①上升阶段做匀减速直线运动,下降阶段做自由落体运动. ②几个特征物理量上升的最大高度H =v 202g ,上升到最高点所用的时间T =v 0g ,回到抛出点所用的时间t =2v 0g,回到抛出点时的速度v =-v 0. (2)全程处理①初速度为v 0(设为正方向),加速度为a =-g 的匀变速直线运动. ②v >0时,物体上升. v <0时,物体下降.③h >0时,物体在抛出点上方. h <0时,物体在抛出点下方. [思维深化]如图2所示,物体以初速度v 0竖直上抛,A 、B 为途中的任意两点,C 为最高点.请分析以下问题:图2(1)物体从A →C 的时间t AC 与从C →A 的时间t CA 有什么关系? (2)物体在上升和下降过程经过A 点的速度有什么关系? (3)从A →B 和从B →A 的重力势能变化量有什么关系?答案 (1)时间对称性:物体上升过程中从A →C 所用时间t AC 和下降过程中从C →A 所用时间t CA 相等.(2)速度对称性:物体上升过程经过A 点的速度与下降过程经过A 点的速度大小相等、方向相反.(3)能量对称性:物体从A →B 和从B →A 重力势能变化量的大小相等,均等于mgh AB .9.[自由落体运动规律的应用]一小石块从空中a 点自由落下,先后经过b 点和c 点,不计空气阻力.经过b 点时速度为v ,经过c 点时速度为3v ,则ab 段与ac 段位移之比为( ) A .1∶3 B .1∶5 C .1∶8 D .1∶9 答案 D解析 物体做自由落体运动, 2gh ab =v 2① 2gh ac =(3v )2②由①②得h ab h ac =19,故D 正确.10.[竖直上抛运动规律的应用]气球下挂一重物,以v 0=10 m /s 的速度匀速上升,当到达离地高度h =175 m 处时,悬挂重物的绳子突然断裂,那么重物经多长时间落到地面?落地时的速度多大?空气阻力不计,g 取10 m/s 2. 答案 见解析解析 解法一:分成上升阶段和下落阶段两个过程处理. 绳子断裂后重物要继续上升的时间t 1和上升的高度h 1分别为 t 1=v 0g=1 sh 1=v 202g=5 m故重物离地面的最大高度为H =h 1+h =180 m 重物从最高处自由下落,落地时间和落地速度分别为 t 2=2Hg=6 s v =gt 2=60 m/s所以从绳子突然断裂到重物落地共需时间为t =t 1+t 2=7 s.解法二:取全过程作为一个整体考虑,从绳子断裂开始计时,经时间t 后重物落到地面,规定初速度方向为正方向,则重物在时间t 内的位移h ′=-175 m ,由位移公式有: h ′=v 0t -12gt 2即-175=10t -12×10t 2=10t -5t 2t 2-2t -35=0解得t 1=7 s ,t 2=-5 s(舍去) 所以重物落地速度为:v =v 0-gt =10 m /s -10×7 m/s =-60 m/s 其中负号表示方向向下,与初速度方向相反.抓住两种运动的实质,选用不同的解题技巧1.根据定义,全盘接收对自由落体运动,v 0=0,a =g ,将匀变速运动的所有公式和推论全部接收过来.2.机智灵活,思维发散(1)对竖直上抛运动,既能分段处理又可全程处理.(2)全程处理时,要注意速度、加速度、位移等的方向,方程以匀减速体现,初速度方向与重力加速度方向必相反.如 速度公式:v =v 0-gt 或v =-v 0+gt 位移公式:h =v 0t -12gt 2或h =-v 0t +12gt 2(3)理解运算结果中的负号.考点四 多过程组合问题多过程问题解题思路如果一个物体的运动包含几个阶段,就要分段分析,各段交接处的速度往往是联系各段的纽带.可按下列步骤解题:(1)画:分清各阶段运动过程,画出草图; (2)列:列出各运动阶段的运动方程;(3)找:找出交接处的速度与各段间的位移-时间关系; (4)解:联立求解,算出结果.11.[匀加速与匀速运动组合](2014·海南·13)短跑运动员完成100 m 赛跑的过程可简化为匀加速运动和匀速运动两个阶段.一次比赛中,某运动员用11.00 s 跑完全程.已知运动员在加速阶段的第2 s 内通过的距离为7.5 m ,求该运动员的加速度及在加速阶段通过的距离. 答案 5 m/s 2 10 m解析 设运动员在匀加速阶段的加速度为a ,在第1 s 和第2 s 内通过的位移分别为x 1和x 2. 在第1 s 和第2 s 内运动员都做匀加速运动,由运动学规律得 x 1=12at 20①x 1+x 2=12a (2t 0)2②式中t 0=1 s.联立①②两式并代入已知条件,得a =5 m/s 2.③设运动员做匀加速运动的时间为t 1,匀速运动的时间为t 2,匀速运动的速度为v ;跑完全程的时间为t ,全程的距离为x . 依题意及运动学规律,得t =t 1+t 2④v =at 1⑤ x =12at 21+v t 2⑥ 设匀加速阶段通过的距离为x ′,则x ′=12at 21⑦联立③④⑤⑥⑦式,并代入数据得x ′=10 m.12.[匀减速与匀加速的组合]已知一足够长的粗糙斜面,倾角为θ,一滑块以初速度v 1=16 m /s 从底端A 点滑上斜面,经2 s 滑至B 点后又返回A 点.其运动过程的v -t 图象如图3所示.已知上滑的加速度大小是下滑的4倍.求:(已知sin 37°=0.6,cos 37°=0.8,重力加速度g =10 m/s 2)图3(1)AB 之间的距离;(2)滑块再次回到A 点时的速度及滑块在整个运动过程中所用的时间. 答案 (1)16 m (2)8 m/s 6 s解析 (1)由v -t 图象知AB 之间的距离为x AB =16×22m =16 m. (2)设滑块从A 点滑到B 点过程的加速度大小为a 1,从B 点返回A 点过程的加速度大小为a 2,由题意知a 1=4a 2.根据a 1t 21=a 2t 22=2x AB ,得t 2=a 1t 21a 2=4 s 因为v 12t 1=v 22t 2,则滑块返回A 点时的速度为v 2=8 m/s则滑块在整个运动过程中所用的时间为t =t 1+t 2=6 s.多过程组合问题的“三个”处理技巧1.用图象分析运动学问题能很好地反映出物体的运动规律,且直观、形象,这是图象法的优势,一些物理量的关系能通过图象很明显地反映出来.2.将末速度为零的匀减速直线运动通过逆向思维转化为初速度为零的匀加速直线运动. 3.多运动过程的转折点的速度是联系两个运动过程的纽带,因此,转折点速度的求解往往是解题的关键.1.质点做直线运动的位移x 与时间t 的关系为 x =5t +t 2(各物理量均采用国际单位制单位),则该质点( )A .第1 s 内的位移是5 mB .前2 s 内的平均速度是6 m/sC .任意相邻的1 s 内位移差都是1 mD .任意1 s 内的速度增量都是2 m/s 答案 D解析 由匀变速直线运动的位移公式x =v 0t +12at 2,对比题给关系式可得v 0=5 m /s ,a =2m/s 2,则第1 s 内的位移是6 m ,A 错;前2 s 内的平均速度是v =x 2t =5×2+222 m /s =7 m/s ,B 错;Δx =aT 2=2 m ,C 错;任意1 s 内的速度增量Δv =a Δt =2 m/s ,D 对.2.做匀加速直线运动的物体途中依次经过A 、B 、C 三点,已知AB =BC =l2,AB 段和BC段的平均速度分别为v 1=3 m /s 、v 2=6 m/s ,则: (1)物体经过B 点时的瞬时速度v B 为多大?(2)若物体运动的加速度a =2 m/s 2,试求AC 的距离l . 答案 (1)5 m/s (2)12 m解析 (1)设物体运动的加速度大小为a ,经A 、C 点的速度大小分别为v A 、v C .由匀加速直线运动规律可得:v 2B -v 2A =2a ×l 2① v 2C -v 2B =2a ×l 2② v 1=v A +v B 2③v 2=v B +v C 2④解①②③④式得:v B =5 m/s (2)解①②③④式得: v A =1 m /s ,v C =7 m/s由v 2C -v 2A =2al 得:l =12 m.3.(2014·山东·23)研究表明,一般人的刹车反应时间(即图4甲中“反应过程”所用时间)t 0=0.4 s ,但饮酒会导致反应时间延长.在某次试验中,志愿者少量饮酒后驾车以v 0=72 km /h 的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L =39 m .减速过程中汽车位移x 与速度v 的关系曲线如图乙所示,此过程可视为匀变速直线运动.重力加速度的大小g 取10 m/s 2.求:甲乙 图4(1)减速过程汽车加速度的大小及所用时间; (2)饮酒使志愿者的反应时间比一般人增加了多少;(3)减速过程汽车对志愿者作用力的大小与志愿者重力大小的比值. 答案 (1)8 m/s 2 2.5 s (2)0.3 s (3)415解析 (1)设减速过程中汽车加速度的大小为a ,所用时间为t ,由题可得初速度v 0=20 m/s ,末速度v t =0,位移x =25 m ,由运动学公式得v 20=2ax ①t =v 0a② 联立①②式,代入数据得 a =8 m/s 2③ t =2.5 s ④(2)设志愿者反应时间为t ′,反应时间的增加量为Δt ,由运动学公式得 L =v 0t ′+x ⑤ Δt =t ′-t 0⑥联立⑤⑥式,代入数据得 Δt =0.3 s ⑦(3)设志愿者所受合外力的大小为F ,汽车对志愿者作用力的大小为F 0,志愿者质量为m ,由牛顿第二定律得 F =ma ⑧由平行四边形定则得F 20=F 2+(mg )2⑨联立③⑧⑨式,代入数据得 F 0mg =415. 练出高分基础巩固1.假设某无人机靶机以300 m /s 的速度匀速向某个目标飞来,在无人机离目标尚有一段距离时发射导弹,导弹以80 m/s 2的加速度做匀加速直线运动,以1 200 m/s 的速度在目标位置击中该无人机,则导弹发射后击中无人机所需的时间为( ) A .3.75 s B .15 s C .30 s D .45 s 答案 B解析 导弹由静止做匀加速直线运动,即v 0=0,a =80 m/s 2 ,据公式v =v 0+at ,有t =v a =1 20080s =15 s ,即导弹发射后经15 s 击中无人机,选项B 正确. 2.一辆汽车在平直公路上做刹车实验,若从0时刻起汽车在运动过程中的位移与速度的关系式为x =(10-0.1v 2) m ,则下列分析正确的是( ) A .上述过程的加速度大小为10 m/s 2 B .刹车过程持续的时间为5 s C .0时刻的初速度为10 m/s D .刹车过程的位移为5 m 答案 C解析 由v 2-v 20=2ax 可得x =12a v 2-12a v 20,对照x =(10-0.1v 2) m ,可知a =-5 m /s 2,v 0=10 m/s ,选项A 错误,C 正确;由v =v 0+at 可得刹车过程持续的时间为t =2 s ,由v 2-v 20=2ax 可得刹车过程的位移x =10 m ,选项B 、D 错误.3.某同学在实验室做了如图1所示的实验,铁质小球被电磁铁吸附,断开电磁铁的电源,小球自由下落,已知小球的直径为0.5 cm ,该同学从计时器上读出小球通过光电门的时间为1.00×10-3 s ,g 取10 m/s 2,则小球开始下落的位置距光电门的距离为( )图1A .1 mB .1.25 mC .0.4 mD .1.5 m 答案 B解析 本题主要考查瞬时速度的含义.小球通过光电门的时间很短,这段时间内的平均速度可看成瞬时速度,v =xt =5 m/s ,由自由落体运动规律可知h =v 22g =1.25 m ,B 正确.4.(多选)做匀减速直线运动的质点,它的加速度大小为a ,初速度大小为v 0,经过时间t 速度减小到零,则它在这段时间内的位移大小可用下列哪些式子表示( ) A .v 0t -12at 2B .v 0t C.v 0t 2 D.12at 2 答案 ACD5.(多选)给滑块一初速度v 0使它沿光滑斜面向上做匀减速运动,加速度大小为g2,当滑块速度大小减为v 02时,所用时间可能是( )A.v 02gB.v 0gC.3v 0gD.3v 02g 答案 BC解析 当滑块速度大小减为v 02时,其方向可能与初速度方向相同,也可能与初速度方向相反,因此要考虑两种情况,即v =v 02或v =-v 02,代入公式t =v 0-v a 得t =v 0g 或t =3v 0g ,故B 、C正确.6.(多选)在一次救灾活动中,一辆救灾汽车由静止开始做匀加速直线运动,刚运动了8 s ,由于前方突然有巨石滚下,堵在路中央,所以又紧急刹车,匀减速运动经4 s 停在巨石前.则关于汽车的运动情况,下列说法正确的是( ) A .加速、减速中的加速度大小之比为a 1∶a 2等于2∶1 B .加速、减速中的平均速度大小之比v 1∶v 2等于1∶1 C .加速、减速中的位移大小之比x 1∶x 2等于2∶1 D .加速、减速中的加速度大小之比a 1∶a 2不等于1∶2 答案 BC解析 汽车由静止运动8 s ,又经4 s 停止,加速阶段的末速度与减速阶段的初速度相等,由v =at ,知a 1t 1=a 2t 2,a 1a 2=12,A 、D 错;又由v 2=2ax 知a 1x 1=a 2x 2,x 1x 2=a 2a 1=21,C 对;由v=v2知,v 1 ∶v 2=1∶1,B 对. 7.(多选)物体做匀加速直线运动,在时间T 内通过位移x 1到达A 点,接着在时间T 内又通过位移x 2到达B 点,则物体( ) A .在A 点的速度大小为x 1+x 22TB .在B 点的速度大小为3x 2-x 12TC .运动的加速度为2x 1T 2D .运动的加速度为x 1+x 2T 2答案 AB解析 匀变速直线运动全程的平均速度等于中间时刻的瞬时速度,则v A =v =x 1+x 22T ,A 正确.设物体的加速度为a ,则x 2-x 1=aT 2,所以a =x 2-x 1T 2,C 、D 均错误.物体在B 点的速度大小为v B =v A +aT ,代入数据得v B =3x 2-x 12T,B 正确.综合应用8.A 、B 两小球从不同高度自由下落,同时落地,A 球下落的时间为t ,B 球下落的时间为t2,当B 球开始下落的瞬间,A 、B 两球的高度差为( ) A .gt 2 B.38gt 2 C.34gt 2 D.14gt 2答案 D9.一个从地面竖直上抛的物体,它两次经过一个较低的点a 的时间间隔是T a ,两次经过一个较高点b 的时间间隔是T b ,则a 、b 之间的距离为( ) A.18g (T 2a -T 2b ) B.14g (T 2a -T 2b ) C.12g (T 2a -T 2b ) D.12g (T a -T b ) 答案 A解析 根据时间的对称性,物体从a 点到最高点的时间为T a 2,从b 点到最高点的时间为T b2,所以a 点到最高点的距离h a =12g (T a 2)2=gT 2a 8,b 点到最高点的距离h b =12g (T b 2)2=gT 2b 8,故a 、b 之间的距离为h a -h b =18g (T 2a -T 2b ),故选A. 10.(多选)一物体以初速度v 0做匀减速运动,第1 s 内通过的位移为x 1=3 m ,第2 s 内通过的位移为x 2=2 m ,又经过位移x 3物体的速度减小为0,则下列说法中正确的是( ) A .初速度v 0的大小为2.5 m/s B .加速度a 的大小为1 m/s 2C .位移x 3的大小为1.125 mD .位移x 3内的平均速度大小为0.75 m/s 答案 BCD解析 第1 s 末的速度v 1=x 1+x 22T =2.5 m /s ,则A 错误;由Δx =aT 2可得加速度的大小a =1 m/s 2,则B 正确;物体的速度由2.5 m/s 减小到0所需时间t =Δv-a=2.5 s ,经过位移x 3的时间t ′为1.5 s ,故x 3=12at ′2=1.125 m ,C 正确;位移x 3内的平均速度v =x 3t ′=0.75 m/s ,则D正确.11.如图2所示是在2014年韩国仁川亚运会上,我国某优秀跳水运动员在跳台上腾空而起的英姿,运动员从离水面10 m 高的平台上向上跃起,举起双臂直体离开台面,此时其重心位于从手到脚全长的中点,跃起后重心升高0.45 m 达到最高点,落水时身体竖直,手先入水(在此过程中运动员水平方向的运动忽略不计),求:(计算时,可以把运动员看作全部质量集中在重心的一个质点,g 取10 m/s 2)图2(1)运动员起跳时的速度v 0.(2)从离开跳台到手接触水面的过程中所经历的时间t (结果保留3位有效数字). 答案 (1)3 m/s (2)1.75 s解析 (1)上升阶段:-v 20=-2gh 解得v 0=2gh =3 m/s (2)上升阶段:0=v 0-gt 1 解得:t 1=v 0g =310 s =0.3 s自由落体过程:H =12gt 22解得t 2=2H g = 2×10.4510s ≈1.45 s 故t =t 1+t 2=0.3 s +1.45 s =1.75 s12.(2014·新课标Ⅰ·24)公路上行驶的两汽车之间应保持一定的安全距离.当前车突然停止时,后车司机可以采取刹车措施,使汽车在安全距离内停下而不会与前车相碰.通常情况下,人的反应时间和汽车系统的反应时间之和为1 s ,当汽车在晴天干燥沥青路面上以108 km/h 的速度匀速行驶时,安全距离为120 m .设雨天时汽车轮胎与沥青路面间的加速度为晴天时的25,若要求安全距离仍为120 m ,求汽车在雨天安全行驶的最大速度. 答案 20 m /s(72 km/h)解析 设路面干燥时,刹车时汽车的加速度大小为a 0,安全距离为s ,反应时间为t 0,由运动学公式得s =v 0t 0+v 202a 0①式中,v 0为汽车刹车前的速度.设在雨天行驶时,汽车的加速度为a ,依题意有 a =25a 0② 设在雨天行驶时汽车,安全行驶的最大速度为v ,由运动学公式得 s =v t 0+v 22a③联立①②③式并代入题给数据得 v =20 m /s(72 km/h)13.珠海航展现场“空军八一飞行表演队”两架“歼-10”飞机表演剪刀对冲的精彩空中秀.质量为m 的“歼-10”飞机表演后返回某机场,降落在跑道上的减速过程简化为两个匀减速直线运动过程.飞机以速度v 0着陆后立即打开减速阻力伞,加速度大小为a 1,运动时间为t 1;随后在无阻力伞情况下匀减速直至停下.在平直跑道上减速滑行总路程为x .求第二个减速阶段飞机运动的加速度大小和时间.答案 (v 0-a 1t 1)22x +a 1t 21-2v 0t 1 2x +a 1t 21-2v 0t 1v 0-a 1t 1解析 如图,A 为飞机着陆点,AB 、BC 分别对应两个匀减速直线运动过程,C 点停下.A 到B 过程,依据运动学规律有: x 1=v 0t 1-12a 1t 21,v B =v 0-a 1t 1B 到C 过程,依据运动学规律有: x 2=v B t 2-12a 2t 22,0=v B -a 2t 2 A 到C 过程,有x =x 1+x 2 联立解得a 2=(v 0-a 1t 1)22x +a 1t 21-2v 0t 1t 2=2x +a 1t 21-2v 0t 1v 0-a 1t 1。
数据库系统讲义(1)

《数据库系统讲义》第1章绪论第一节数据库系统概述1.1.1 数据、数据库、数据库管理系统、数据库系统数据、数据库、数据库管理系统和数据库系统是与数据库技术密切相关的四个基本概念。
一、数据(DATA)数据是数据库中存储的基本对象。
数据在大多数人头脑中的第一个反应就是数字。
其实数字只是最简单的一种数据,是数据的一种传统和狭义的理解。
广义的理解,数据的种类很多,文字、图形、图像、声音、学生的档案记录、货物的运输情况等,这些都是数据。
可以对数据做如下定义:描述事物的符号记录称为数据。
描述事物的符号可以是数字,也可以是文字、图形、图像、声音、语言等,数据有多种表现形式,它们都可以经过数字化后存入计算机。
为了了解世界,交流信息,人们需要描述这些事物。
在日常生活中直接用自然语言(如汉语)描述。
在计算机中,为了存储和处理这些事物,就要抽出对这些事物感兴趣的特征组成一个记录来描述。
例如:在学生档案中,如果人们最感兴趣的是学生的姓名、性别、年龄、出生年月、籍贯、所在系别、入学时间,那么可以这样描述:(李明,男,21,1972,江苏,计算机系,1990)因此这里的学生记录就是数据。
对于上面这条学生记录,了解其含义的人会得到如下信息:李明是个大学生,1972年出生,男,江苏人,1990年考入计算机系;而不了解其语义的人则无法理解其含义。
可见,数据的形式还不能完全表达其内容,需要经过解释。
所以数据和关于数据的解释是不可分的,数据的解释是指对数据含义的说明,数据的含义称为数据的语义,数据与其语义是不可分的。
二、数据库(DataBase,简称DB)数据库,顾名思义,是存放数据的仓库。
只不过这个仓库是在计算机存储设备上,而且数据是按一定的格式存放的。
人们收集并抽取出一个应用所需要的大量数据之后,应将其保存起来以供进一步加工处理,进一步抽取有用信息。
在科学技术飞速发展的今天,人们的视野越来越广,数据量急剧增加。
过去人们把数据存放在文件柜里,现在人们借助计算机和数据库技术科学地保存和管理大量的复杂的数据,以便能方便而充分地利用这些宝贵的信息资源。
《变态心理学》讲义(1)

《变态心理学》《变态心理学》《变态心理学》第一章概述一、变态心理学的含义与研究内容。
(一)、含义:1、佩奇:是心理学的分支,它主要研究变态的精神行为过程。
2、科里曼:是心理学的特殊领域,主要通过发展和综合的心理学原则来分析变态行为。
3、基斯卡:是特定研究人格障碍和行为障碍的学科。
4、罗森、福克斯、戈里高里:试图了解和解释在常态和普通人格结构中的变态行为。
总结:变态心理学是研究人的心理和行为异常的规律及其矫治的学科。
对定义的理解:1、是一门特殊学科;2、都强调研究行为和心理两个方面;3、在研究变态的时候需要参照常态;4、既是理论研究,又是应用研究,理论研究更注重理论、原则,应用研究更注重预防、治疗的技术和方法;既研究主观世界(主观的心理和行为),又研究客观的环境。
(二)、研究内容。
以上方面出现问题时,就是变态心理学研究的内容。
二、变态心理学研究范畴。
1、发展历史、研究方法;2、划分变态和正常心理的标准;3、介绍心理和行为异常的原因(病因学)。
4、症状和综合征;5、预防和治疗。
三、变态心理学的发展简史。
(一)、历史回顾。
1、早期阶段(迷信时期,奴隶制之前)。
(1)、考古学的发现;(2)、四大文明古国(古希腊、古印度、中国、古巴比伦)认为精神病的病因是魔鬼附体,治疗者是神父或者巫师,治疗方法:烧屎尿、鞭打、饥饿等,治疗原则:对身体的侮辱,使善良的精灵不忍呆在这儿,使恶鬼不愿呆在这儿。
2、中世纪前的光明时期(自然主义时代,奴隶制的鼎盛时期)。
(1)、古希腊、古罗马的贡献希波克里特(气质体液说:黄黑、胆汁、血液、黏液),古希腊医学之父。
①朴素唯物主义:首次提出病理学和医学的研究模式,用大脑疾病解释大脑的变态疾病。
②对病因的解释:遗传、情感、环境、肌肉和神经紧张;③病因分类:a、躁狂症;b、抑郁症;c、谵妄症。
(谵妄:由高热、中毒以及其他疾病而引起意识模糊、短时间内精神错乱的症状。
如说胡话,不认识熟人等)总结:他是病理学和人道主义的丰碑。
研究生统计学讲义第1讲第一章绪论-PPT文档资料

意义
1.利用概率论与数理统计进行统计设计,搜集和整理 资料,对分析结果进行恰当的解释,作出科学结论。 2.保证分组具有可比性,保证有合适的样本容量. 3.控制实验误差,是否在科学上具有可重复性. 4.在撰写论文或报告时,将大量原始数据归纳整理为 正确的统计指标,按照规范列出统计表(图). 5.能够读懂国内外医学文献中的统计资料,判断其 可靠程度和局限性,吸收和借鉴.
3.概率与频率 概率(probability)和频率(frequency) 都是反映某一随机事件发生可能性大小的度量。 若随机事件A在n次独立重复试验中发生了m次,则称 m为频数(counts)。称比值m/ n为事件A在n次试验中出 现的频率或相对频数(relative frequency) ,0≤m/ n≤1, 即事件A发生的频率为m/ n。 试 验 者 De Morgan Buffon Pearson Pearson 掷币数n 2048 4040 12000 24000 正面数m 1061 2048 6019 12019 正频率fn 0.5181 0.5069 0.5016 0.5005
2.总体、个体与样本 研究对象的全体称为总体 (population)。构成总体的每个成员称为个体,亦称 样品或观察单位。总体是根据研究目的所确定的性 质相同的所有个体的研究指标值的集合。 个体(individual)即观察单位(study unit)。总 体的性质特征由其各个个体的性质而定,要研究总 体的性质或特征,须对它的个体进行观测。 从总体中随机抽取部分个体的过程称为抽样 (sampling),从总体中随机抽取的代表总体的部分个 体的观察值集合称为样本(sample)。样本中所包含的 个体数目,即样本例数,称为样本含量(sample size) 。总体中有很多个体,究竟哪些个体在抽样中被抽 到,要依机会而定。因此,样本是随机变量;
同济大学的高等数学讲义 (1)

1 xn − 1 < 4 10 只要n>10000即可.即从第10001项开始的以后所有项都
满足这一要求. 一般:要使
1 xn − 1 < k 10 只要n>10k 即可.即从第(10k+1)项开始的以后所有项都
满足这一要求.
对上面例的分析,可以看到,无论一个正数取得多么 小,总可以找到自然数n,在这项以后的所有项与1的距 离都可以小于该数.数学上用ε 来表示一个任意小的正 数.由此得到极限的精确定义:
我们知道:两个数a 和b 的接近程度可用两数差的绝 对值来刻画.
(−1)n+1 x − 1 = 1 对数列 xn = 1 + ,n ,故只要n充分大, n n xn − 1 就充分小.例如要使
xn − 1 < 1 10 2
只要n>100即可.即从第101项开始的以后所有项都满足 这一要求;
再如,要使
3.极限的定义 定义 设数列 ( x n )n =1 ,如果存在常数a,使得对任意给
∞
定的正数ε (不论它多么小),总存在自然数N,只要N>n, 不等式
xn − a < ε
都成立,那么称常数a 是数列 ( x n )n =1 的极限,,或则
∞
称数列 ( x n )n =1 收敛于a,记为
∞
lim xn = a,
∴ ∀ε > 0, 取δ = ε , 当 0 < x − (− 1 ) < δ , 有
从而当n>N时,有
xn = ( xn − a ) + a ≤ xn − a + a ≤ 1 + a ,
取
M = max{ x1 , x2 ,
xN ,1 + a },
道德经叶曼讲义第1章

“道”生万物,它自己再进入万物之中,不但成为万物,并且成为万物运动变化的规律、是生命新陈代谢、循环不息的根本。这么说来,它不仅是原因,同时也是结果。比如花开了,花是它;花谢之后结了果子,果子也是它;果子又要生长繁殖,长出新的树,这树还是它。花是果的因,果是树的因,树又是花的因。在互为因果的生命循环中,道自然地体现在其中。讲到这里,诸位有没有产生一个问题:既然道不可知,老子怎么知道有“道”的存在呢?大家知道,求知是一个渐进的过程,我们认知的事物首先是通过眼睛看到的,耳朵听到的,肌肤触摸到的,比如电灯亮了,我们知道有电,可是在十八世纪的时候人们还不知道闪电是怎么回事。富兰克林看到天上的闪电,就产生了要去研究它的想法。等到阴天打雷的时候,他在风筝上绑了一把金属钥匙,把风筝放到天上去,就这样把天上的闪电带下来了,通过实验他发现天上的闪电跟我们日常生活中各种电的现象是一样的。我们今天对电的认识已经很深,可以用水力发电,用煤发电,用核子发电。可是电在哪里呢?你拿一个电给我看,拿不出来吧?它是看不见,摸不着的。但它表现为某种形态,电灯发出来的光、扩音机发出的声音,甚至我们穿纤维衣服的时候摩擦到身体会哗哗响,有时还冒火光,那都是电。假如没有这些东西的话,我们不知道电的存在。同样,道假如不能够化生万物,我们也就不知道道的存在,它化生万物,我们能从万物的运动变化中去体认它。
新高二暑假讲义 第1讲 空间向量及其运算(解析版)

第1讲空间向量及其运算新课标要求1.经历由平面向量推广到空间向量的过程,了解空间向量的概念。
2.经历由平面向量的运算及其法则推广到空间向量的过程。
3.掌握空间向量的线性运算。
4.掌握空间向量的数量积。
知识梳理1.空间向量的概念与平面向量一样,在空间,我们把具有大小和方向的量叫做空间向量,空间向量的大小叫做空间向量的长度或模,空间向量用字母a,b,c ...表示.2.几个常见的向量零向量长度为0的向量叫做零向量单位向量模为1的向量叫做单位向量相反向量与向量a 长度相等而方向相反的向量,叫做a 的相反向量,记做-a 共线向量如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量。
我们规定:零向量与任意向量平行.相等向量方向相同且模相等的向量叫做相等向量3.向量的线性运算交换律:+=+a b b a ;结合律:()();()()λμλμ+=+=a b +c a +b c a a ;分配律:();()λμλμλλλ+=++=+a a a a b a b .4.共面向量平行于同一平面的向量,叫做共面向量.5.空间向量的数量积||||cos ,⋅=<>a b a b a b 零向量与任意向量的数量积为0.名师导学知识点1空间向量的有关概念【例1-1】(咸阳期末)已知是空间的一个单位向量,则的相反向量的模为A.1B.2C.3D.4【分析】本题考查了向量的基础知识,根据向量模的概念求解即可;【解答】解:因为是空间的一个单位向量,所以的相反向量的模,故选A.【变式训练1-1】(龙岩期末)在平行六面体中,与向量相等的向量共有A.1个B.2个C.3个D.4个【分析】本题考查了相等向量及其平行六面体的性质,考查了推理能力与计算能力,属于基础题.利用相等向量及其平行六面体的性质即可得出.【解答】解:如图所示,与向量的相等的向量有以下3个:故选C.知识点2空间向量的线性运算【例2-1】(泰安期末)如图所示,在长方体中,O为AC的中点.化简:________;用,,表示,则________.【分析】本题考查空间向量的线性运算,属于基础题.利用化简即可;将分解为,继而进行正交分解即可.【解答】解:..【例2-2】(河西区期末)在三棱锥中,,,,D为BC的中点,则A. B.C. D.【分析】本题考查空间向量的加减运算,属于基础题.若D为BC的中点,则,根据向量的减法法则即可得到答案.【解答】解:依题意得,故选A.【变式训练2-1】(东湖区校级一模)在空间四边形ABCD中,M,G分别是BC,CD的中点,则A. B. C. D.【分析】本题考查了空间向量的加减运算及数乘运算,属于基础题.根据题意,将进行转化,即可得解.【解答】解:.【变式训练2-2】(随州期末)如图,已知长方体,化简下列向量表达式,并在图中标出化简结果的向量.;.【解析】解:..向量,如图所示.知识点3共面向量【例3-1】(珠海期末)已知A,B,C三点不共线,点M满足.,,三个向量是否共面点M是否在平面ABC内【解析】解,,,向量,,共面.由知向量,,共面,又它们有共同的起点M,且A,B,C三点不共线,,A,B,C四点共面,即点M在平面ABC内.【变式训练3-1】(日照期末)如图所示,已知矩形ABCD和矩形ADEF所在的平面互相垂直,点M,N分别在对角线BD,AE上,且,.求证:向量,,共面.【解析】证明:因为M在BD上,且,所以.同理.所以.又与不共线,根据向量共面的充要条件可知,,共面.知识点4空间向量的数量积【例4-1】(溧阳市期末)已知长方体中,,,E为侧面的中心,F为的中点试计算:.【解析】解:如图,设,,,则,,....【变式训练4-1】(兴庆区校级期末)如图所示,在棱长为1的正四面体ABCD中,E,F分别是AB,AD的中点,求:.【解析】解,..,.,,.名师导练A组-[应知应会]1.(台江区校级期末)长方体中,若,,,则等于A. B.C. D.【分析】本题考查空间向量的运算,属基础题.根据空间向量的运算法则求解即可.【解答】解:,故选C.2.(秦皇岛期末)若空间四边形OABC的四个面均为等边三角形,则的值为A. B. C. D.0【分析】本题主要考查了空间向量的运算、向量的数量积、向量垂直的判定,属于中档题.先求出向量的数量积,由它们的数量积为0判断,所以向量的夹角为,由此得出结论.【解答】解:,空间四边形OABC的四个面为等边三角形,,,,,,故选D.3.(定远县期末)给出下列几个命题:向量,,共面,则它们所在的直线共面;零向量的方向是任意的;若,则存在唯一的实数,使.其中真命题的个数为A.0B.1C.2D.3【分析】本题主要考查命题的真假判断与应用,比较基础.利用向量共面的条件判断.利用零向量的性质判断.利用向量共线的定理进行判断.【解答】解:假命题.三个向量共面时,它们所在的直线或者在平面内或者与平面平行;真命题.这是关于零向量的方向的规定;假命题.当,则有无数多个使之成立.故选B .4.(葫芦岛期末)在下列条件中,使M 与A 、B 、C 一定共面的是A.;B.;C.D.【分析】本题考查空间向量基本定理,考查学生分析解决问题的能力,属于基础题.利用空间向量基本定理,进行验证,对于C ,可得,,为共面向量,从而可得M 、A 、B 、C四点共面.【解答】解:对于A ,,无法判断M 、A 、B 、C 四点共面;对于B ,,、A 、B 、C 四点不共面;C 中,由,得,则,,为共面向量,即M 、A 、B 、C 四点共面;对于D ,,,系数和不为1,、A 、B 、C四点不共面.故选C .5.(多选)(点军区校级月考)已知1111ABCD A B C D -为正方体,下列说法中正确的是()A .221111111()3()A A A D AB A B ++= B .1111()0A C AB A A -=C .向量1AD 与向量1A B的夹角是60︒D .正方体1111ABCD A B C D -的体积为1||AB AA AD【分析】本题考查的是用向量的知识和方法研究正方体中的线线位置关系及夹角与体积.用到向量的加法、减法、夹角及向量的数量积,研究了正方体中的线线平行、垂直,异面直线的夹角及正方体的对角线的计算、体积的计算.【解答】解:由向量的加法得到:111111A A A D A B A C ++= , 221113AC A B =,∴22111()3()AC A B = ,所以A 正确;1111A B A A AB -= ,11AB A C ⊥,∴110A C AB =,故B 正确;1ACD ∆ 是等边三角形,160AD C ∴∠=︒,又11//A B D C ,∴异面直线1AD 与1A B 所成的夹角为60︒,但是向量1AD 与向量1A B的夹角是120︒,故C 不正确;1AB AA ⊥ ,∴10AB AA = ,故1||0AB AA AD =,因此D 不正确.故选:AB .6.(都匀市校级期中)空间的任意三个向量,,,它们一定是________向量填“共面”或“不共面”.【分析】正确理解共面向量定理是解题的关键.由于可用向量,线性表示,即可判断出空间中的三个向量,,是否是共面向量.【解答】解:可用向量,线性表示,由空间中共面向量定理可知,空间中的三个向量,,一定是共面向量.7.(池州模拟)给出以下结论:两个空间向量相等,则它们的起点和终点分别相同;若空间向量,,满足,则;在正方体中,必有;若空间向量,,满足,,则.其中不正确的命题的序号为________.【分析】本题考查的知识点是空间相等的定义,难度不大,属于基础题.根据相向相等的定义,逐一分析四个结论的真假,可得答案.【解答】解:若两个空间向量相等,则它们方向相同,长度相等,但起点不一定相同,终点也不一定相同,故错误;若空间向量,,满足,但方向不相同,则,故错误;在正方体中,与方向相同,长度相等,故,故正确;若空间向量,,满足,,则,故正确;故答案为.8.(未央区校级期末)O为空间中任意一点,A,B,C三点不共线,且3148OP OA OB tOC=++,若P,A,B,C四点共面,则实数t=.【分析】利用空间向量基本定理,及向量共面的条件,即可得到结论.【解答】解:由题意得,3148OP OA OB tOC=++,且P,A,B,C四点共面,∴31148t++=18t∴=,故答案为:18.9.(天津期末)在正四面体P ABC-中,棱长为2,且E是棱AB中点,则PE BC的值为.【分析】如图所示,由正四面体的性质可得:PA BC⊥,可得:0PA BC=.由E是棱AB中点,可得1()2PE PA PB=+,代入PE BC,利用数量积运算性质即可得出.【解答】解:如图所示,由正四面体的性质可得:PA BC⊥,可得:0PA BC=.E是棱AB中点,∴1()2PE PA PB=+,∴1111()22cos12012222PE BC PA PB BC PA BC PB BC=+=+=⨯⨯⨯︒=-.故答案为:1-.10.(三明期中)如图所示,在正六棱柱中化简,并在图中标出表示化简结果的向量化简,并在图中标出表示化简结果的向量.【解析】解:.,在图中表示如下:.在图中表示如下:11.(都匀市校级期中)如图所示,在四棱锥中,底面ABCD为平行四边形,,,底面求证:.【解析】证明:由底面ABCD为平行四边形,,,知,则.由底面ABCD ,知,则.又,所以,即.12.(西夏区校级月考)如图所示,平行六面体1111ABCD A B C D -中,E 、F 分别在1B B 和1D D 上,且11||||3BE BB =,12||||3DF DD =(1)求证:A 、E 、1C 、F 四点共面;(2)若1EF xAB y AD z AA =++ ,求x y z ++的值.【分析】(1)利用向量三角形法则、向量共线定理、共面向量基本定理即可得出.(2)利用向量三角形法则、向量共线定理、共面向量基本定理即可得出.【解答】(1)证明: 1111111212()()3333AC AB AD AA AB AD AA AA AB AA AD AA AB BE AD DF AE AF =++=+++=+++=+++=+.A ∴、E 、1C 、F 四点共面.(2)解: 111211()333EF AF AE AD DF AB BE AD DD AB BB AB AD AA =-=+-+=+--=-++ ,1x ∴=-,1y =,13z =,13x y z ∴++=.B 组-[素养提升]1.(多选)(三明期中)定义空间两个向量的一种运算||||sin a b a b a =<⊗ ,b > ,则关于空间向量上述运算的以下结论中恒成立的有()A .a b b a=⊗⊗ B .()()a b a b λλ=⊗⊗ C .()()()a b c a c b c +=+⊗⊗⊗ D .若1(a x = ,1)y ,2(b x = ,2)y ,则1221||a b x y x y =-⊗【分析】A 和B 需要根据定义列出左边和右边的式子,再验证两边是否恒成立;C 由定义验证若a b λ= ,且0λ>,结论成立,从而得到原结论不成立;D 根据数量积求出cos a < ,b > ,再由平方关系求出sin a < ,b > 的值,代入定义进行化简验证即可.【解答】解:对于A ,||||sin a b a b a =<⊗ ,b > ,||||sin b a b a b ==<⊗ ,a > ,故a b b a =⊗⊗ 恒成立;对于:()(||||sin B a b a b a λλ=<⊗ ,)b > ,()||||||sin a b a b a λλλ=<⊗ ,b > ,故()()a b a b λλ=⊗⊗ 不会恒成立;对于C ,若a b λ= ,且0λ>,()(1)||||sin a b c b c b λ+=+<⊗ ,c > ,()()||||sin a c b c b c b λ+=<⊗⊗ ,||||sin c b c b >+< ,(1)||||sin c b c b λ>=+< ,c > ,显然()()()a b c a c b c +=+⊗⊗⊗ 不会恒成立;对于D ,cos a < ,1212||||x x y y b a b +>= ,sin a < ,b >= ,即有||||||a b a b a ==⊗=1221||x y x y ===-.则1221||a b x y x y =-⊗ 恒成立.故选:AD .。
李俊慧经济学讲义【1】

经济学讲义-第一讲:入门序言(作者:本博客管理员)(2011-11-04 21:27:39)说明:1、这系列文章是本博客管理员(不是张五常教授!)根据给本科一年级的经济学专业学生讲授“微观经济学”、“宏观经济学”的授课内容而整理出来的讲义。
使用的主干教材是张五常教授的老师赫舒拉发所编写的《价格理论及其应用》,并在授课过程中将张五常教授的旧版《经济解释》三卷本有机地结合进来,是本博客管理员在实际的经济学教学之中探索将张五常经济学透过主流教科书传授给经济学学生的成果。
2、本系列不定期更新,甚至可能写着写着会因兴趣缺缺而中止,本博客管理员对此不作任何担保!3、如有愚蠢无知、明显缺乏科学逻辑的评论,一律不予回答,只作删除处理。
另外,不看完这个系列最新更新之前的以往所有文章就急于提问,提问内容其实早在前面的文章中给出了回答的,也是一删了之!)第一讲:入门序言今天我们开始学习经济学。
但是在正式地开始学习之前,我要先跟大家打一支预防针。
这支预防针就是:不要相信教科书!以前你们在中学读书,都会把教科书上写的东西奉为金科玉律,认为一定是没错的。
但我告诉你们,现在你们上来大学读书了,首先就要明白大学与中学的学习有很多根本性的不同,其中一点,就是你们现在学习的专业知识是学科前沿,不再是中学的基础教育学习的是已经早有定论的东西。
在大学里,尤其是在学习经济学的时候,教科书只是一本参考书,里面其实充满了错误!但大家不要以为这是因为这本书不好,这本书已经够好了!不是这本书充满了错误,而是目前所有的经济学教科书都充满了错误!为什么会这样?这是因为经济学这门学科还太年轻了!让我先跟大家介绍一下经济学的发展历史吧。
大家知道美国是哪一年独立的?对,是1776年。
在同一年,英国有一位叫亚当·斯密的人出版了一本书,这本书的名字很长,所以它的中译名一般我们是使用其简称《国富论》。
这本书的出版,就标志着经济学成为了一门学科。
也就是说,亚当·斯密是经济学的开山鼻祖,相当于是武侠小说里的那个武当派的张三丰一样。
结构化面试理论课讲义-1-基本理论介绍

结构化面试理论课讲义第一节理论介绍一、结构化面试:通过面对面交流选拔人才(以德为先、德才兼备)交流感很重要!二、考试题型:1. 综合分析题——综合分析能力(第一印象,易造成差异化,至关重要)(1)社会现象(2)政策行为(3)名言警句(=习语)(4)漫画(社会现象、态度观点)(5)反驳(6)串词(7)演讲2. 自我认知题——岗位匹配程度(目前基本不考)3. 人际关系题——人际沟通能力(基础、常规、必学)认识、领导、同时、你、群众之间的关系可能放在情景模拟中考察4. 组织管理题——组织协调能力做事——效果最重要中规终局——有创意、套路+细节5. 应急应变题——应急应变能力各种让你措手不及的事情(来及实际工作中)不确定性、无规律6. 实务处理题——实务处理能力7. 其他——思维与表达能力目的:让考官认可你。
一般有七位考官,有1~2位女考官。
1. 主客观并存科学——来自于多年的工作经验外在+内容并重(有些时候,外在甚至大于内容)2. 任他“嬉笑怒骂”,做好自己一般15~20 min,但10:30(或16:00)以后进去的,13 min就结束3. 交流感:语言、表情(微表情)、眼神一般女生面试成绩高于男生4. 考官也是人:当作一位自己尊敬的领导或老师面试的目的:让考官认可我四、认识对手1. 大神对手(形式+内容)2. 小白对手(一般无纯小白)3. 面试基本都参较培训,要形成差异化啊4. 考生之间的差距有些是考试之前形成的5. 考生之间的差距有些是考场之上形成的6. 既要高看对手,又要轻视对手7. 努力就好,大家都是同路人。
五、认识考场1. 特点:高压、规范培训——建立自信2. 如何应对?(1)做到心中有数:扎实学习理论知识,反复开口答题(2)做好随机应变:心理素质+学以致用1. 考试流程:到场→抽签→候考→考试→离场候考——聊天时要注意技巧有耐心。
抽签——1号要稳(1~3号不会直接打分);最后的号要简洁、干练考试——有引导员带入,敲门之后进去,站椅子旁,问好(各位考官,上午好!我是X号考生),考官会说请坐下,然后坐下、坐直、手放桌子上,先看着考官,考官会说导语,然后就可以开始看题,一般3~4道题(可以思考一道达一道,也可以一次性完成),结束后起立鞠躬、说谢谢各位考官,然后走人。
离港系统培训讲义(1)
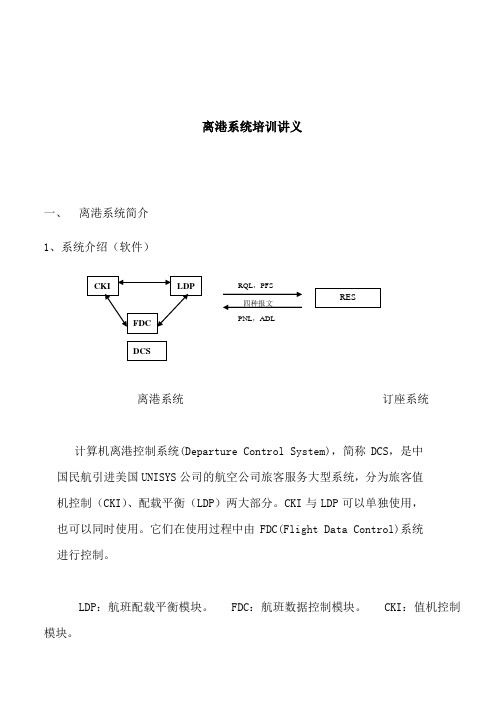
离港系统培训讲义一、离港系统简介1、系统介绍(软件)离港系统订座系统计算机离港控制系统(Departure Control System),简称DCS,是中国民航引进美国UNISYS公司的航空公司旅客服务大型系统,分为旅客值机控制(CKI)、配载平衡(LDP)两大部分。
CKI与LDP可以单独使用,也可以同时使用。
它们在使用过程中由FDC(Flight Data Control)系统进行控制。
LDP:航班配载平衡模块。
FDC:航班数据控制模块。
CKI:值机控制模块。
CHECK-IN(CKI)是一套自动控制和记录旅客登机活动过程的系统。
USAS CKI记录旅客所乘坐的航班、航程、座位证实情况,记录附加旅客数据(如行李重量、中转航站等),记录接收旅客情况或将旅客列为候补情况。
USAS CKI可以顺序接收旅客、候补旅客,也可以选择接收;旅客也可以一次办理多个航班的登机手续。
LOAD PLANNING (LDP)主要完成航班配载平衡,打印舱单功能。
FLIGHT DATA CONTROL (FDC)完成航班数据控制。
2、操作终端与主机的连接(硬件)DCS 主机--------通讯设备(路由器,DCP)-------- 终端(仿真终端)离港系统的主机在北京,各地机场用户使用的终端通过通讯设备与主机联系。
用户在终端上所作指令都要传到主机进行处理,然后将反馈信息传回用户终端。
3、系统键盘使用基础知识目前系统中使用的终端主要有科比亚、昌霖、实达几种,有些机场使用微机仿真终端。
终端的键盘设置基本一致,常用的键名称及其功能如下:XMIT 传送指令输入MSG WAIT 释放MESSAGESOE 指令起始符DELETE IN LINE 删除单个字符INSERT IN LINE 增加单个字符FCTN + P 清除屏幕显示FCTN + 1 (2、3、4……) F1 (F2、F3、F4……)功能键微机上的功能键可以根据用户的需要自己定义。
心理学讲义

心理学讲义《心理学》讲义1第一章为绪论第一节心理学的研究对象一、什么是心理学心理学是一门研究人的心理现象及其发生,发展规律的科学。
它的发展,既离不开现代生理学和生物学,也离不开辨证唯物主义哲学和其它社会科学,因比,心理学是一门自然科学和社会科学交叉的边缘学科。
二、心理学研究对象——心理现象(一)心理过程1。
认知过程(知识):人在认识客观世界的活动中所表现出的各种心理现象。
包括:感觉、知觉、记忆、思维、想象。
2.情绪过程:人认识客观事物时产生的各种内心体验过程。
3、意志过程(意):人们努力克服困难,完成任务以实现他们的目标。
意志过程中产生的行为就是意志行为。
4、知、情、意、行的关系:知识是情感和意义的基础;行动是在知识的基础上产生的,由情感驱动。
它能提高认知能力,增强情绪,磨练意志;意图控制和调节情绪,提高知识水平。
(2)人格心理学1。
个性倾向:个体活动的基本倾向和动力。
包括:动机、需要、兴趣、信念、理想、世界观等。
2、个性心理特征:通常表现出稳定的个体的心理特征。
包括:气质、性格和能力。
心理过程与个性心理的关系:心理过程与个性心理是个体心理现象的两个方面,都是心理学研究的具体内容。
心理过程从心理现象的组成部分研究个体心理现象的共性,这是人格形成的基础;人格心理学从个体心理现象的表现来分析个体心理的差异。
心理过程和人格心理学是在社会实践中发展和形成的。
一方面,人格心理学是在心理过程的基础上形成的。
没有对客观世界的理解,就不可能产生情感;没有积极的意志和行动,就不可能形成一个人的性格、气质、能力、理想、信念和世界观。
另一方面,形成的人格心理可以调节心理过程,并在心理过程中表现出来。
第二节心理学的任务和意义一、心理学的基本任务是研究心理现象的本质和发展的一般规律。
(二)、心理学的特殊任务就是把心理活动的一般规律应用于各种不同的实践领域,揭示人们在各种特殊活动条件下的心理现象和规律。
二、学习心理学的意义(一)理论意义1、心理学的研究为马克思主义哲学的基本原理提供了科学的论据,学习心理学有助于树立辨证唯物主义世界观。
《逻辑与思维方法》讲义(1)

起首语1.主要的生活有三种选择:第一种是享乐生活,第二种是政治生活,第三种则是思辨的、静观的生活。
2. 最好先讨论普遍的善,看看争议到底在哪里。
尽管这种争议有点使人为难,因为理念学说是我们所敬爱的人提出来的。
不过作为一个爱智慧的人,较好的选择应该是维护真理而牺牲个人的友情。
两者都是我们所珍爱的,但人的责任却要我们更尊重真理。
——[古希腊] 亚里士多德《尼各马可伦理学》2主要参考教材1.《逻辑学导论》,[美]Irving M. Copi, Carl Cohen,中国人民大学出版社,2007。
2.《简明逻辑学导论》,[美]Patrick Hurley,世界图书出版社,2010。
3.《逻辑学导论》,陈波,中国人民大学出版社,2003。
4.《普通逻辑》(增订本),《普通逻辑》编写组,上海人民出版社,1993。
5.《逻辑基础》,王路,人民出版社,2004。
1.关于宽容的经典故事:美国著名战斗机试飞员鲍伯·胡佛经验丰富,技术高超。
在长年的试飞生涯中,顺利地试飞了许多机型。
有一次,他接受命令参加飞行表演,完成任务后飞回洛杉矶。
途中飞机突发故障,两个引擎同时失灵。
他临危不惧,果断沉着地采取了措施,奇迹般地将飞机落在了机场。
他和安全人员检查飞机情况,发现造成事故的原因是用油不对。
他驾驶的是螺旋式飞机,用的却是喷汽式机油。
负责加油的机械师吓得面如土色,见了胡佛便痛哭不已,因为他一时的疏忽可以造成飞机失事和三个人的死亡。
但是胡佛并没有大发雷霆,而是向前轻轻抱住他,真诚地对他说:“为了证明你干得好,我想请你明天干飞机维修工作。
”这位机械工后来一直跟着胡佛,负责他的飞机维修,没有发现任何差错。
请思考:你认为是否可以原谅机械师?62.某岛上男性公民分为骑士和无赖。
骑士只讲真话,无赖只讲假话。
甲和乙是该岛上的土著居民,关于他俩,甲说了以下这句话:“或者我是无赖,或者乙是骑士”根据上述条件,可推出以下哪项结论?A.甲和乙都是骑士。
中国文学批评理论讲义(1)概述

概说中国文学有着悠久的历史,中国文学理论批评的历史也是相当悠久的。
它可分为古代文学理论批评、近代文学理论批评和现代文学理论批评三个阶段。
古代文学理论批评理论批评的萌芽中国古代文学理论批评萌芽很早。
在《周易·艮六五》中就曾提到“言有序”的问题,在《尚书·尧典》中则有“诗言志,歌永言,声依永,律和声,八音克谐,无相夺伦,神人以和”的说法。
《尧典》虽系后人伪托,但仍反映了先秦时期人们对于诗歌音乐的认识。
在《吕氏春秋·仲夏纪·古乐》篇中,保留着许多原始艺术产生于模仿自然的宝贵史料,而且在《国语·郑语》中所记载的公元前8世纪史伯和郑桓公的对话中,就用朴素的原始的五行学说来解释艺术。
史伯认为世界上的万事万物是由土、金、木、水、火5种原素和合而成的,音乐也是“和六律”而成,即音乐是由各种高度不同的音阶协调而成的,单一的声音不会有音乐,单一的事物不会有文采:“声一无听,物一无文,味一无果,物一不讲。
”这无疑是一个光辉的思想。
在《左传·昭公二十年》晏婴和齐侯的对话中,更进一步认为政治和音乐不能只求单一的“同”,而应追求对立诸因素和谐统一的“和”,对音乐来说,应该是“清浊、大小、短长、疾徐、哀乐、刚柔、迟速、高下、出入、周疏,以相济也”。
即各种对立因素要相反相成,相互为用。
他们所提出的艺术辩证法思想、关于“和乐”的中和之美的思想,对中国的美学思想、艺术创作及文艺理论批评,曾发生过深远的影响。
公元前7世纪时《左传》提出了“九功之德,皆可歌也”,“无礼不乐,所由叛也”(《左传·文公七年》),强调诗乐要歌颂“德礼”;公元前6世纪伶州鸠又从原始的阴阳学说解释音乐的形成,认为音乐只有按照自然的阴阳之气的规律和特点制作,并保持和谐,才能“以遂八风”,使阴阳和顺谐调,“风雨时至,嘉生繁祉”,并提出了“政象乐”(《国语·周语下》)的观点,以及医和所提出的对音乐“节”制(《左传·昭公元年》)的思想,都曾为后世继承和发挥。
WeleUnit教材词汇讲义(1)高一英语人教版

必修一Wele Unit教材词汇Listening and Speakingexchange①[C]&[U]交换;沟通I'm an exchange student from the UK.我是一名来自英国的交换生。
Would you like my old TV in exchange for this camera?用我的旧电视机换这部照相机,你情愿吗? We must promote an exchange of ideas and information.我们必需促进思想和信息的沟通。
②[C](商品的)调换The store’s policy is not to allow returns or exchanges.这家商店的规定是商品概不退换。
③[U](货币的)兑换foreign exchange an exchange rate汇率④交易所①交换;沟通exchange views/ideas交换意见/沟通思想Before graduation,students exchange presents with each other. 毕业前,同学们互赠礼物。
②更换;兑换I'dlike to exchange this dress for one ofa larger。
You can exchange your currency for dollars in the hotel你可以在旅馆把钱兑换成美元。
lecture1.n[C]①(尤指高校中的)讲座;讲课,演讲attend/go to a lectur e 听讲座give/deliver alecture on history作历史讲座②教训;训斥IknowIshouldstop drinking—don’t give me a lecture about it. 我知道我该戒酒,别教训我了。
①vi讲课;作讲座;演讲He lectures on。
左维老师群论讲义 1

fi = φ ( gi ) f j = φ (g j ) g k = gi g j , f k = fi f j φ ( g k ) = f k
同构映射Φ将G中的单位元素映射为群F中的单位元素, 将群G中的互逆 元映射为F中的相应的互逆元. φ ( g 0 g i ) = φ ( g i g 0 ) = φ ( g i ) = φ ( g 0 )φ ( g i ) = φ ( g i )φ ( g 0 )
n
Cn = {e, a, a 2 , …, a n 1} 构成一个群, 称为n阶循环群. 空间反演群是一个2阶循环群.
4) 平面正三角形对称群D3 . 保持平面正三角形空间 3 位置不变的所有转动变换
A 2
O
e : 不转 f : 绕 z 轴转4π/3 b : 绕 2 轴转π
d : 绕 z 轴转2π/3 a : 绕 1 轴转π c : 绕 3 轴转π
f , g ∈ G fg = h ∈ G
f , g , h ∈ G ( fg )h = f ( gh) ef = fe = f 1 f ∈ G , 存在逆元素 f ∈ G , 使 f 1 f = ff 1 = e
f ∈G
,有
c) 单位元素. 集合G中存在一个单位元素e, 对任意元素 d) 可逆性. 对任意元素
则称集合G为一个群.
● 有限群: 由有限个元素构成的群. 群元的个数定义为群的阶. 有限群: 例子: 1) 由 {-1,0,1} 三个数组成的集合, 定义数的加法为群的乘法运算, 构成一个三阶有限群, 单位元素为0. 2) 空间反演群: 三维实空间中的恒等变换 E ( E r = r )和反演变换 I ( I r = r ). 如果定义群的乘法为从左向右依次施行变换, 则E 和I 构 成一个二阶有限群, 称为空间反演群. 3) n阶循环群 Cn . 由一个元素 a 的幂构成的有限群. 设 a = e , 则
健康管理师基础知识讲义(1-4章)

健康管理师基础知识讲义第一章健康管理概论第一节概述健康管理:以现在健康概念和中医治未病的思想为指导,运用医学、管理学等相关学科的理论、技术和方法,对个体或群体健康状况及影响健康的危险因素进行全面连续的检测、评估和干预,实现以促进人人健康为目标的新型医学过程。
健康管理的宗旨:是有效地利用有限的资源来达到最大的健康效果,主体是经过系统医学教育或培训并取得相应资质的医务工作者。
客体是健康人群、亚健康人群(亚临床人群)、以及慢性非传染性疾病早期或扛复期人群。
健康管理的具体做法:是提供有针对性的科学健康信息,创造条件采取行动来改善健康,重点是慢性非传染性疾病的预防和风险因素控制。
健康管理服务的两大支撑点是信息技术和金融保险。
健康管理的公众理念:是“病前主动防,病后科学管,跟踪服务不间断”健康管理的任务:是防大病、管慢病、促健康。
健康管理目标:1.完善健康和福利;2.减少健康危险因素;3.预防高危人群患病;4.易化疾病早期诊断;5.增加临床效用效益。
6.避免可预防的疾病相关并发症的发病;7.消除和减少无效或不必要的医疗服务;8.对疾病结局做出度量并提供持续的评估和改进。
管理的目的:是使有限的资源得到最大化的利用,即以最小的投入获得最大效用。
健康服务领域中的管理可看作是以改善个人和人群健康以达到最大健康效益的过程。
二、健康管理的目标与特点健康管理的特点:标准化、足量化、个体化和系统化健康管理的具体服务内容和工作流程:必须依据循证医学和循证公共卫生的标准和学术界已经公认的预防和控制指南及规范。
健康评估和风险干预的结果既要针对个体和群体的特征和健康需求,又要注重服务的可重复性和有效性,强调多平台合作提供服务。
三、健康管理的理论与实践溯源治未病思想:源自距今已有两千余年历史的中医学典籍《黄帝内经》,这种“上医治未病”的思想可谓古人对健康管理最精辟和朴素的概括,被认为是健康管理的理论与实践溯源头。
治未病思想作为祖国医学传统文化的重要组成部分,一直传承到今天。
NDT讲义(1)

神经发育疗法Neurodevelopment Treatment ( NDT)第一节核心概念神经发育疗法是由英国物理治疗师Berta Bobath和她的丈夫Karel Bobath 根据“运动发育控制理论”,经过多年的实践经验确立的治疗方法。
20世纪,这一方法曾是用于中枢神经系统疾患最普遍的康复治疗方法。
它主要采用抑制异常姿势,促进正常姿势的方法治疗中枢神经损伤的患者,如偏瘫、脑瘫,因此该方法又被称为通过反射抑制和促通而实现治疗目的的神经发育治疗法。
它的核心概念包括:1、反射性抑制,利用与痉挛模式相反的活动和姿势来抑制异常姿势和活动。
如:角弓反张、头前屈、脊柱弯曲、上、下肢屈曲/伸展模式RIP vs TIP2、关键点控制,指治疗师在患者身上的特定部位进行调节,使痉挛减轻,同时促进姿势和运动。
3、促进姿势反应,不需患者过度用力来引导形成功能活动的运动姿势,并学习体验这些功能活动的运动姿势以达到治疗目的。
值得提出的是,对原始反射性姿势的“正确”利用是NDT方法近年来更为积极的发展。
4、感觉刺激,如通过叩击提高患者一定部位肌肉的肌紧张,在四肢躯干上有规律地叩击后出现肌紧张,保持患者正常姿势。
5、整体治疗,将患者看作一个有机的整体,而不只是治疗患病部位。
需要通过全身活动、躯干运动提高患者的整体功能。
Bobath夫妇最早提出这种治疗方法是在20世纪40年代。
B.Bobath早年在德国接受体操和运动疗法的专门训练,后来到英国开始对神经科患者进行治疗。
在对成年偏瘫患者治疗的过程中,她注意到有些患者患侧肢体痉挛,而且不能计划和执行正常的运动模式。
在训练的过程中,B.Bobath努力帮助这些患者以及其他类似的患者,使他们的患侧肢体重新获得协调的运动模式。
经过反复的试验,她发明了一些能改变脑卒中患者异常肌张力以及可以教会患者患侧重新学会比较正常的运动模式的方法。
她的这种对成年脑卒中患者进行治疗性运动的方法是建立在她对日常生活中重要的运动成分分析的基础之上的。
清华大学高等代数讲义-1

f : Mn(R) −→ R A −→ detA
f : GLn(R) −→ GLn(R) A −→ A−1
Example 11 设 [a, b] 上全体可微函数的集合为 A,[a, b] 上全体函数的集合 为 B, 令
D : A −→ B
f −→ f
即 ∀f ∈ A, 有 D(f ) = f .
Lesson 1
A=
10 01
,B =
10 00
,C =
00 00
则 SM2(R)/ ∼= = {[A], [B], [C]}
Lesson 1
4
若按相似关系 (∼) 进行分类,其代表元记作:
D=
λ1 0 0 λ2
, λ1 ≥ λ2, λ1, λ2 ∈ R
则 SM2(R)/ ∼ = {[D]}
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本课程内容(0) ∙第1章信息资源管理基本概念∙第2章信息资源管理基本理论∙第3章信息系统资源管理∙第4章网站信息资源管理∙附录本课程内容(1) ∙第1章信息资源管理基本概念∙ 1.1 信息概述∙ 1.1.1 信息的含义∙ 1.1.2 信息的分类∙ 1.1.3 信息的特性∙ 1.1.4 信息的功能本课程内容(2) ∙第1章信息资源管理基本概念∙ 1.2 知识概述∙ 1.2.1 知识的含义∙ 1.2.2 知识的分类∙ 1.2.3 知识对经济的作用本课程内容(3) ∙第1章信息资源管理基本概念∙ 1.3 信息资源∙ 1.3.1 资源概述∙ 1.3.2 信息资源概述∙ 1.3.3 信息资源的类型∙ 1.3.4 信息资源的度量本课程内容(4) ∙第1章信息资源管理基本概念∙ 1.4 信息化∙ 1.4.1 信息化的含义∙ 1.4.2 信息化水平的测度方法∙ 1.4.3 国家信息化指标构成方案本课程内容(5) ∙第1章信息资源管理基本概念∙ 1.5 信息产业∙ 1.5.1 产业与产业结构的概念∙ 1.5.2 信息产业的含义和特征∙ 1.5.3 信息产业的分类本课程内容(6) ∙第1章信息资源管理基本概念∙ 1.6 知识经济∙ 1.6.1 知识经济的由来∙ 1.6.2 知识经济的内涵∙ 1.6.3 知识经济的特征∙ 1.6.4 知识经济的意义本课程内容(7) ∙第1章信息资源管理基本概念∙ 1.7 知识管理∙ 1.7.1 知识管理概述∙ 1.7.2 企业知识管理本课程内容(8) ∙第2章信息资源管理基本理论∙ 2.1 信息资源管理理论的主要内容∙ 2.1.1 信息资源管理的含义∙ 2.1.2 信息资源管理的产生与发展∙ 2.1.3 信息资源管理的理论基础∙ 2.1.4 信息资源管理学的理论框架∙ 2.1.5 信息资源管理的组织与人员∙ 2.1.6 信息资源管理的标准化本课程内容(9)∙第2章信息资源管理基本理论∙ 2.2 狭义信息资源管理过程∙ 2.2.1 信息需求分析∙ 2.2.2 信息源分析∙ 2.2.3 信息资源采集∙ 2.2.4 信息资源加工∙ 2.2.5 信息资源存储∙ 2.2.6 信息资源检索∙ 2.2.7 信息资源开发∙ 2.2.8 信息资源利用∙ 2.2.9 信息资源传递∙ 2.2.10 信息资源反馈本课程内容(10) ∙第3章信息系统资源管理∙ 3.1 信息系统资源管理概述∙ 3.1.1 信息系统概念∙ 3.1.2 信息系统建设中的文档管理∙ 3.1.3 信息系统的运行维护管理∙ 3.1.4 信息系统的审计与评价本课程内容(11) ∙第3章信息系统资源管理∙ 3.2 信息系统建设项目管理∙ 3.2.1 信息系统与项目管理∙ 3.2.2 信息系统项目的计划管理∙ 3.2.3 信息系统项目的进度管理∙ 3.2.4 信息系统项目的人员管理本课程内容(12) ∙第3章信息系统资源管理∙ 3.3 信息系统质量管理∙ 3.3.1 质量与质量管理概述∙ 3.3.2 全面质量管理∙ 3.3.3 ISO 9000族标准∙ 3.3.4 信息系统的质量管理本课程内容(13) ∙第3章信息系统资源管理∙ 3.4 信息系统安全管理∙ 3.4.1 信息系统安全概述∙ 3.4.2 信息系统面临的威胁和攻击∙ 3.4.3 信息系统的安全技术本课程内容(14) ∙第4章网站信息资源管理∙ 4.1网站信息资源管理概述∙ 4.1.1 网站概述∙ 4.1.2 网站的项目管理本课程内容(15) ∙第4章网站信息资源管理∙ 4.2 网站建设项目的规划设计∙ 4.2.1 网站建设项目的环境分析1∙ 4.2.2 网站建设项目的系统规划∙ 4.2.3 网站建设项目的系统设计∙ 4.2.4 网站建设项目的软硬件选择∙ 4.2.5 网站建设项目规划书的写作本课程内容(16)∙第4章网站信息资源管理∙ 4.3 网站建设项目的具体实现∙ 4.3.1 网页设计的原则与策略∙ 4.3.2 网站建设的主要技术本课程内容(17)∙第4章网站信息资源管理∙ 4.4 网站建设项目的运行维护∙ 4.4.1 网站的评测∙ 4.4.2 网站的推广∙ 4.4.3 网站的网络管理∙ 4.4.4 网站的安全管理本课程内容(18)∙附录∙“信息资源管理概论”考试大纲∙"信息资源管理概论"自测试卷(一)∙"信息资源管理概论"自测试卷(二)本课程成绩计分说明(kjcj-0)∙考试成绩计分办法∙平时成绩构成说明考试成绩计分办法 (kjcj-1)∙考试成绩=平时成绩(60%)+期末考试成绩(40%)平时成绩构成说明 (kjcj-2)∙平时成绩=名词解释成绩(10%)+案例编写成绩(10%)+试卷编写成绩(10%)+个人讲课成绩(10%) +小组项目成绩(20%)+其他加分成绩名词解释成绩计算说明 (kjcj-3)∙数量:≥ 5个;∙分值:10分;∙范围:各小组所选择的章节;∙要求:不能与别人完全相同,否则不能得分;格式规范;字迹清楚;给出自评得分。
∙格式及样例:∙名词解释成绩计分细节:案例编写成绩计算说明 (kjcj-4)∙数量:≥1个;∙分值:10分;∙范围:各小组所选择的章节;∙要求:不能与别人完全相同,否则不能得分;格式规范;字迹清楚;给出自评得分。
∙格式及样例:∙案例编写成绩计分细节:试卷编写成绩计算说明 (kjcj-5)∙数量:1个;∙分值:10分;∙范围:各小组所选择的章节;∙要求:不能与别人完全相同,否则不能得分;格式规范;字迹清楚;给出标准答案;给出自评得分。
∙格式及样例:∙试卷编写成绩计分细节:个人讲课成绩计算说明 (kjcj-6)∙数量:1次;∙分值:10分;∙时间:15-20分钟;∙范围:各小组所选择的章节;∙要求:最大限度地表现出自己的口头表达能力;最大限度地展现自己的聪明才智;给出自评得分。
∙样例:略∙个人讲课成绩计分细节:每次讲课分别由任课老师(6)、课代表(2)、讲课者本人(2)三方分别给出成绩,再按三方不同权值计算得出最终的得分。
小组项目成绩计算说明 (kjcj-7)∙数量:1个;∙分值:10分;∙范围:各小组所选择的章节;∙要求:不能与别人完全相同,否则不能得分;最大限度地展现自己的聪明才智;格式规范;字迹清楚;给出自评得分。
∙格式及样例:∙小组项目成绩计分细节:小组项目成绩计算说明 (kjcj-7) 小组项目参考选题:∙本教材书评(参考范例:《中国图书评论》、《光明日报》等);∙第1章:∙有文可考的信息定义已不下一百个(P3);∙中外名著所占的存储空间估算值(P33);∙某省市信息化指数测度;∙著名企业知识管理案例。
∙第2章:∙ Delphi方法的具体应用(P184);∙头脑风暴法的具体应用。
小组项目成绩计算说明 (kjcj-7) 小组项目参考选题:∙第3章:∙运用项目管理方法设计教学评价系统;∙运用项目管理方法设计学生成绩管理系统;∙运用项目管理方法设计自动出卷系统。
∙第4章:∙规划设计“信息资源管理”课程教学网站;∙撰写一份电子商务类网站商业计划书。
∙(参考:商业计划书编写指南。
电子工业出版社2002年4月)小组项目成绩计算说明 (kjcj-7) 小组项目补充说明:∙每个项目小组选出组长一名,具体职责是:按项目管理思想进行任务划分;组织本组成员按预定进度保质保量地完成本小组项目各项任务;∙各项目小组不承担具体任务。
如果本小组成功完成任务,则得满分;否则,扣除一定的分数。
其他加分成绩计算说明 (kjcj-8)∙数量:不限;∙范围:不限;∙分值:10分;2∙要求:最大限度地展现自己的聪明才智;∙格式及样例:无∙其他加分成绩计分细节:一概述周光召在浙江大学演讲•消耗物质•生活质量•消耗信息苹果公司乔布斯的故事•1 1983年,28岁的史蒂文·乔布斯在一次陷入僵局的会议上,命名“苹果”电脑• 2 三要素:技术、能说会道、未来意识• 3 孔子:“道不远人,远人非道”一什么是信息• 1 事物不确定性的度量•揭示信息的日常职能:了解外部环境。
• 2 控制系统调节活动时,与外界相互交换相互作用的内容•信息的社会、政治职能:规范和协调社会秩序。
二什么是传播•国内观点:•1信息在时间或空间的移动和变化•2社会信息的传递•3人们交流的活动•4信息的双向流通过程二什么是传播•国外观点:•1努力同别人建立共同的东西。
•2变独有为共有。
•3我们了解别人并进而使自己被别人了解的过程。
•4人际关系成立的基础。
是精神现象转换成符号,并在一定的距离空间得到搬运,经过一定时间得到保存的手段。
二什么是传播•国外观点:•5通过讯息进行社会相互作用•6传播是互动•7用言语交流思想•8运用符号—词语、图片、数字等传递信息、思想、感情等。
•9传递刺激以影响另一些人行为的过程。
三传播类型概述• 1 内部传播• 2 同亲近的人• 3 工作单位• 4 维持型交流• 5 同业务上和社会上只有一面之交的人交流• 6 通过书籍和大众媒介•7 日常暗示•即:内向、人际、组织、大众传播四种类型四第四媒体•1报纸、广播、电视后出现的网络•2标志性事件:斯塔尔报告•31998年9月12日,克林顿性丑闻•4两天共2000万人•5美国标准:媒体使用占总人口20%•6互联网称为工作场合的第一媒体五第五媒体•手机• 1 “写手”• 2 春节100亿条• 3 零点预定准时发送20万(搜狐)• 4 日本人开发手机键盘• 5 无线上网六传播学的体系•北京广播学院胡正荣《传播学总论》第一章传播学论•1传播学的兴起•2研究对象•3研究方法第二章传播论•1传播的含义、类型•2人类传播演进的过程第三章传播材料论•1信息的实质•2特征•3社会信息化•4符号、符号类型、符号系统•5语言、文字第四章传播类型论•1内向传播:形式、核心•2人际传播:符号互动与人际传播、人际传播的基础、动机•3组织传播:形式、方向和功能•4大众传播:界定、特征、功能第五章传播过程论•1传播模式•2线性传播过程•3控制论传播过程•4系统论传播过程第六章传播者论•1制度环境•2传播者与把关人第七章传播内容论•1传播内容的生产与流动•2传播内容分析第八章传播媒介论•1媒介分析•2传播途径的比较分析•3媒介价值与媒介文化第九章受众论•1受众界定与类型•2受众行为的动机与目的•3传受关系•4受众权力•5受众价值开发3第十章传播效果论•1传播效果的不同时期理解•2传播效果的普遍取向第十一章传播实践论•1广播电视传播实践•2广告媒介传播战略研究•3整合营销传播研究•4西方宣传研究•5跨文化传播研究七北京大学传播学体系一概论•1传播学的由来•2传播学的先驱二传播学基本问题•1定义:共享说、劝服说、过程说•2功能:社会雷达、管理、指导、娱乐•3形式•4模式三符号、意义与言语传播•1传播符号•2语义•3语言的作用•4影响语义的因素•5提高语言传播功能四非言语传播•1性质•2类型•3暗示作用•4提高非言语传播的能力五内向传播•1认识自我•2自我观念的形成•3马斯洛需求层次论•4内向传播•5影响内向传播的变量•6防卫机制六人际传播与人际关系•1定义与特点•2相关理论:功能理论、关系理论、一以协调理论•3影响人际关系的变量:社会渗透、自我展露、信任、反馈与前反馈•4人际关系发展的阶段•5处理人际矛盾第七章小群体传播•1群体传播的特点•2小群体中的传播行为:群体规范、功能角色、互动发展•3领导行为与领导者:产生、风格、技巧•4影响小群体传播的变量:人格、内聚力、矛盾冲突、群体压力第八章组织传播•1功能:告知、管理、说服、一体化•2传播方向:•3传播网络第九章大众传播研究的控制分析•1比较媒介制度•2媒介的内部控制第十章大众传播的内容分析•1内容影响受众•2传播方法的一般通则•3媒介的编辑方法第十一章受众分析•1特征与一般理论•2反馈与取得反馈的方法第十二章大众传播研究的早期和中期的效果分析•1枪弹论与战争宣传•2有限效果论:两极传播论、舆论领袖、中介因素论第十三章大众传播效果研究的晚期发展•1选择性过程的深入研究•2适当效果论•3强效果论•4传播效果的制约因素和增强效果的原则第十四章说服与传播•1说服模式•2劝服设计第十五章传播与社会发展•1发展传播学的兴起•2大众传播在国家发展中的功能与作用•3大众传播与国家发展的若干问题第十六章大众传播学研究方法•1实地调查•2内容分析•3控制试验八信息传播学的综合体系•Who(谁)——Says What(说什么)——in What Channel(通过什么渠道)——to Whom(对谁)——with What Effects(取得什么效果)4。
