平行四边形判定练习题3
《平行四边形》习题精选及参考答案

《平行四边形》习题精选及参考答案一、填空题1.过□ABCD的顶点A、C分别作对角线BD的垂直线,垂足为E、F,则四边形AECF是 .2.延长△ABC的中线AD到E,使DE=AD 则四边形ABEC是四边形.3.在四边形ABCD中∠A=50°欲使四边形为平行四边形,则∠B= ,∠C=,∠D= .4.在四边形中,任意相邻两个内角互补,则这个四边形是四边形.5.如图12-1-29,在□ABCD中,E、F为AB、CD的中点,连结DE、EF、BF则图中共有个平行四边形.6.在□ABCD中连结BD作AE⊥BD,CF⊥BD,垂足分别为E、F,连结CE、AF,点P、Q在线段BD上,且BP=DQ,连结AP、CP、AQ、CQ,MN分别交AB、CD于M、N连结AM、CM、NA、NC,那么图中平行四边形(除□ABCD外)有个,它们是 .二、判断题1.平行四边形的对边分别相等()2.平行四边形的对角线相等()3.平行四边形的邻角互补()4.平行四边形的对角相等()5.平行四边形的对角线互相平分一组对角()6.对角线平分平行四边形的四个三角形的面积相等()三、选择题1.能判断四边形是平行四边形的条件是()A.一组对边平行,另一组对边相等B.一组对边平行,一组对角相等C.一组对边平行,一组邻角互补D.一组对边相等,一组邻角相等2.能确定平行四边形的大小和形状的条件是()A.已知平行四边形的两邻边B.已知平行四边形的两邻角C.已知平形四边形的两对角线D.已知平行四边形的两边及夹角3.平行四边形一边为32,则它的两条对角线长不可能为()A.20和18 B.40和50C.60和30 D.32和504.如图12-1-30所示,已知□ABCD的对角线的交点是O,直线EF过O点且平行于BC,直线GH过O且平行AB,则图中有()个平行四边形.A.5个B.6个C.7个D.10个5.能判定四边形为平行四边形的是()A.一组对角相等B.两条对角线互相垂直C.两条对角线互相平分 D.一对邻角互补6.以下结论正确的是()A.对角线相等,且一组对角也相等的四边形是平行四边形.B.一边长为5,两条对角线分别是4和6的四边形是平行四边形.C.一组对边平行,且一组对角相等的四边形是平行四边形.D.对角线相等的四边形是平行四边形.7.在□ABCD中,点E、F分别在边BC、AD上,如果点E,F分别由下列各种情况得到的,那么四边形AECF不一定是平行四边形的是()A.AE、CF分别平分∠DAB、∠BCDB.AE,CF使∠BEA=∠CFDC.E、F分别是BC、AD的中点D.BE=BC,AF=AD8.□ABCD对角线交点为O,△OBC的周长为59cm,且AD=28cm,两对角线之差为14cm,则对角线长为()A.12cm和9cm B.24cm 和38cmC.8.5cm和22.5cm D.15.5cm 和29.5cm四、解答题1.如图12-1-31所示,在□ABCD中,AE平分∠BAD,CF平分∠BCD,四边形AECF是平行四边形吗?2.如图12-1-32所示,四边形ABCD中∠B=∠D,∠1=∠2,则四边形ABCD是平行四边形吗?为什么?3.如图12-1-33所示,四边形ABCD的对角线AC、BD相交于点O,E、F分别是OD、OB上一点,若∠ECD=∠FAB,EC=AF,则四边形AECF是平行四边形吗?为什么?4.如图12-1-34所示,四边形ABCD中AB=CD,∠DBC=90°,FD⊥AD于D,求证四边形ABCD 是平行四边形.5.如图12-1-35所示,△ABC中DE在BC边上,N、M在AB、AC上,且EN与DM互相平分,MD ∥AB,NE∥AC求证:BD=DE=CE五、证明题1.已知:如图12-1-18,在□ABCD中,E、F是对角线BD上的两点,且BE=DF.求证:(1)AE=CF(2)AE∥CF2.已知:如图12-1-19,四边形ABCD为平行四边形,E、F是直线BD延长线上的两点,且DE =BF,求证AE=CF参考答案一、填空题1.平行四边形点拨:由一组对边平行且相等,即可判断2.平行四边形3.130°,50°,130°4.平行四边形点拨:由题意可得两组对边分别平行5.4个点拨:□ABCD,□ADFE,□EFCB,□EDFB6.3个□AECF,□APCQ,□AMCN二、判断题1.√ 2.×点拨:对角线不一定相等,但互相平分3.√ 4.√5.×点拨:对角线不平分一组对角,只是自己互相平分 6.√三、选择题1.B 2.D 3.A 4.D 5.C 6.C 7.B 8.B四、解答题1.解:四边形AECF是平行四边形点拨:由□ABCD知∠BCD=∠BAD,又AE平分∠BAD,CF平分∠BCD,故∠EAF=∠ECF,又∠AF ∥EC,故∠AEC+∠EAF=18O°,即∠AEC+∠ECF=18O°,所以AE∥CF,故四边形AECF是平行四边形.2.解:四边形ABCD是平行四边形由∠1=∠2得DC∥AB,所以∠D+∠DAB=18O°,又∠B=∠D,所以∠DAB+∠B=180°,所以AD∥BC,即四边形ABCD为平行四边形.3.解:是平行四边形点拨:AB∥CD,故∠ACD=∠CAB,又∠ECD=∠FAB,故∠ACD-∠ECD=∠CAB-∠FAB,即∠ACE =∠CAF,所以CE=AF,CE=AF,故AFCE是平行四边形.4.证明:∵BD⊥AD ∴∠BDA=90°∵∠DBC=90°,DC=AB,DB=DB∴△ADB≌△CBD ∴AD=BC∴四边形ABCD是平行四边形5.证明:∵NE,MD互相平分∴四边形MNDE为平行四边形∴MN DE又∵MD∥AB,NE∥AC ∴四边形MNBD、MNEC为平行四边形∵MN=BD,MN=CE ∴BD=DE=CE五、证明题1.证明:∵四边形ABCD为平行四边形∴AB DC ∴∠ABE=∠CDF在△ABE和△CDF中∴△ABE≌△CDF(SAS)∴AE=CF ∴∠AEB=∠CFD∴∠AED=∠BFC(等角的补角相等)∴AE∥CF2.证明:如图(3)所示∵四边形ABCD是平行四边形∴AD∥BC,AD=BC ∴∠1=∠2∵BD是直线∴∠1+∠3=180°,∠2+∠4=180°∴∠3=∠4∴△ADE≌△CBF ∴AE=CF。
平行四边形的判定(3)练习

平行四边形的判定(3)练习目标导航两组对边分别平行的四边形是平行四边形两组对边分别相等的四边形是平行四边形两条对角线互相平分的四边形是平行四边形两组对角分别相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形基础过关1.不能判定四边形是平行四边形的题设为( )A.AB ∥CD ,AD ∥BCB.AB=CD ,AD=BCC.AD ∥BC ,AB=CDD.AB ∥CD ,AB=CD2.判定四边形是平行四边形的条件是( )A.对角线相等B.对角线互相垂直C.对角线互相垂直且相等D.对角线互相平分3.如图,在□ABCD 中,EF ∥AB ,GH ∥AD ,EF 交GH 于点O ,则该图中平行四边形的个数共有( )A .7个B .8个C .9个D .11个4.如图,在□ABCD 中,E 、F 分别为AB 、DC 的中点,连结DE 、DB 、EF 、FB ,则图中共有________个平行四边形.能力提高5.如果一个四边形以其对角线交点为中心,在平面内旋转180°,与原四边形重合,则这个四边形是__________.6.如图,DE ∥BC ,AE=EC ,延长DE 到F ,使EF=DE ,连结AF 、FC 、CD ,则图中的四边形ADCF 是__________,四边形BCFD 是__________.7.一个四边形的四条边长依次为a 、b 、c 、d ,且满足a 2+b 2+c 2+d 2=2ac+2bd ,那么这个四边形一定是_________.8.把边长为3cm ,4cm ,6cm 的两个全等三角形拼成四边形,一共能拼成______种不同的四边形,其中有____个平行四边形.9.下列条件能组成一个平行四边形的是( )A.相邻的两边分别是5 cm 和7 cm ,一条对角线长是13 cm(4题图) D F E A B C (3题图) OA B DC EF H GB.两组对边分别是3 cm 和4 cmC.一条边长是7 cm ,两条对角线长分别是3 cm 和4 cmD.一组对角都是135° ,另一组对角都是40°10.下列命题中正确命题的个数有( )①一组邻角互补的四边形是平行四边形 ②邻角都互补的四边形是平行四边形③两组对角分别相等的四边形是平行四边形 ④一组对角相等的四边形是平行四边形A.4B.3C.2D.1 11.以不在同一直线上的三个点为顶点作平行四边形,最多能作( ) A.4个 B.3个 C.2个D.1个 12.已知:如图,E 、F 是四边形ABCD 的对角线AC 上的两点,AF =CE ,DF =BE ,DF ∥BE. 求证:(1)△AFD ≌△CEB ; (2)四边形ABCD 是平行四边形.13.在四边形ABCD 中,AE ⊥BD 于E ,CF ⊥BD 于F ,AE=CF ,∠BAC=∠DCA ,求证:四边形ABCD 是平行四边形.14.如图,在ABCD 对角线AC 上分别取E 、F ,使AE=CF ,求证:四边形BFDE 是平行四边形.15.如图,在△ABC 中,BD 平分∠ABC ,DE ∥BC ,EF ∥AC ,求证:BE=CF. O EFBC AD16.如图,已知□ABCD 中,AC 的平行线MN 分别交DA 、DC 的延长线于M 、N ,交AB ,BC 于P ,Q ,求证:QM=NP .17.如图,在△ABC 中,AB=AC=8cm ,D 为BC 上任意一点,DE ∥AB ,DF ∥AC ,F 、E 分别在AB 、AC 上,求四边形AFDE 的周长.18.如图,梯形ABCD 中,AB ∥CD ,E 是BC 的中点,AE 、DC 的延长线相交于点F ,连结AC 、BF.(1)求证:AB=CF ;(2)四边形ABFC 是什么四边形,并说明理由.B N QD C A PMD FECAB F E DBC A聚沙成塔19.如图,等边△ABC ,D 、E 分别是BC 、AC 上两点,且BD=CE ,以AD 为边在AC 一侧作等边△ADF.求证:四边形BDFE 是平行四边形.FE ABC D E D FB AC。
18.1.2平行四边形的判定(3)

学习目标
1.掌握并识记三角形的中位线定义及中 位线定理; 2.会证明三角形的中位线定理与应用中 位线定理进行计算和证明
自学指导
1.阅读课本P47练习下的内容,识记并掌握三 角形的中位线的定义;
2.思考P48“思考云图”中的问题;
3.思考P48的探究,解决探究中的问题,并证明 三角形的中位线定理; 4.请用文字及符号语言叙述三角形的中位线 定理(注意P48的黄色书签). 9分钟时间内看哪些同学能快速完成并熟背 定理
选做题:
3.已知:如图,E、F、G、H分别是AB、BC、CD、 DA的中点.求证:四边形EFGH是平行四边形.
当堂检测
请在6分钟内完成教材第49页的练习题1、3两 题,看哪一组完成的又快又好。
必做题:
当堂训练
第 3题 C
1.△ABC中,D、E分别是AB、AC的中点,∠A=50°, ∠B=70°,则∠AED=_____ ;BC=10cm,则 A DE=______.
D E
B
第 1题
2.求证顺次连结任意四边形各边中点所得的四边 形是平行四边形。
初中数学 第19章 平行四边形综合检测题(三)及答案

第19章 平行四边形综合检测题(三)一、选择题(每题3分,共30分)1、一块均匀的不等边三角形的铁板,它的重心在( )A.三角形的三条角平分线的交点B.三角形的三条高线的交点C.三角形的三条中线的交点D.三角形的三条边的垂直平分线的交点 2、如图1,如果□ABCD 的对角线AC 、BD 相交于点O ,那么图中的全等三角形共有( )A.1对B.2对C.3对D.4对3、平行四边形的一边长是10cm ,那么这个平行四边形的两条对角线的长可以是( )A.4cm 和6cmB.6cm 和8cmC.8cm 和10cmD.10cm 和12cm4、在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是( )A.AC =BD ,AB =CD ,AB ∥CDB.AD //BC ,∠A =∠CC.AO =BO =CO =DO ,AC ⊥BDD.AO =CO ,BO =DO ,AB =BC5、如图2,过矩形ABCD 的四个顶点作对角线AC 、BD 的平行线,分别相交于E 、F 、G 、H 四点,则四边形EFGH 为( )A.平行四边形 B 、矩形 C 、菱形 D. 正方形6、如图3,大正方形中有2个小正方形,如果它们的面积分别是S 1、S 2,那么S 1、S 2的大小关系是( )A.S 1 > S 2B.S 1 = S 2C.S 1<S 2D.S 1、S 2 的大小关系不确定 7、矩形一个角的平分线分矩形一边为1cm 和3cm 两部分,则这个矩形的面积为( )A.3cm 2B. 4cm 2C. 12cm 2D. 4cm 2或12cm 28、如图4,菱形花坛 ABCD 的边长为 6m ,∠B =60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为( ) A.123m B.20m C.22m D.24m图3A DCBHEFG图2OABD C图19、如图5,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C 点与A 点重合,则折痕EF 的长是( ) A .3B .23C .5D .2510、如图6,是由两个正方形组成的长方形花坛ABCD ,小明从顶点A 沿着花坛间小路直到走到长边中点O ,再从中点O 走到正方形OCDF 的中心O 1,再从中心O 1走到正方形O 1GFH 的中心O 2,又从中心O 2走到正方形O 2IHJ 的中心O 3,再从中心O 3走2走到正方形O 3KJP 的中心O 4,一共走了31 2 m ,则长方形花坛ABCD 的周长是( ) A.36 m B.48 mC.96 mD.60 m二、填空题(每题3分,共30分)11、如图7, 若将四根木条钉成的矩形木框变形为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于___.12、如图8,过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ ,那么图中矩形AMKP 的面积S 1与矩形QCNK 的面积S 2的大小关系是S 1 S 2(填“>”或“<”或“=”).13、如图9,四边形ABCD 是正方形,P 在CD 上,△ADP 旋转后能够与△ABP ′重合,若AB =3,DP =1,则PP ′=___.14、已知菱形有一个锐角为60°,一条对角线长为6cm ,则其面积为___cm 2.图6图4FEDCBA图5D CBA 图7图9图8 KNM Q CB15、如图10,在梯形ABCD 中,已知AB ∥CD ,点E 为BC 的中点, 设△DEA 的面积为S 1,梯形ABCD 的面积为S 2,则S 1与S 2的关系为___.16、如图11,四边形ABCD 的两条对角线AC 、BD 互相垂直,A 1B 1C 1D 1四边形ABCD 的中点四边形.如果AC =8,BD =10,那么四边形A 1B 1C 1D 1的面积为___.17、如图12,□ABCD 中,点E 在边AD 上,以BE 为折痕,将△ABE 向上翻折,点A 正好落在CD 上的点F ,若△FDE 的周长为8,△FCB 的周长为22,则FC 的长为___. 18、将一张长方形的纸对折,如图13所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 条折痕,如果对折n 次,可以得到 条折痕.三、解答题(共40分)19、如图14,等腰梯形ABCD 中,AD ∥BC ,∠DBC =45°,翻折梯形ABCD ,使点B 重合于D ,折痕分别交边AB 、BC 于点F 、E ,若AD =2,BC =8.求BE 的长.……第一次对折第二次对折第三次对折图13图11A 1B 1C 1D 1D ABC D ABCEF图12FE DCBA 图14图10ED CB A20、在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD 分割成四个部分,使含有一组对顶角的两个图形全等;(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有___组;(2)请在图15的三个平行四边形中画出满足小强分割方法的直线; (3)由上述实验操作过程,你发现所画的饿两条直线有什么规律?21、如图16,已知四边形ABCD 是平行四边形,∠BCD 的平分线CF 交边AB 于F ,∠ADC 的平分线DG 交边AB 于G . (1)线段AF 与GB 相等吗?(2)请你在已知条件的基础上再添加一个条件,使得△EFG 为等腰直角三角形,并说明理由.ABCDABCDDCBA图15图1622、如图17,已知□ABCD 中,E 为AD 的中点,CE 的延长线交BA 的延长线于点E .(1)试说明线段CD 与F A 相等的理由;(2)若使∠F =∠BCF ,□ABCD 的边长之间还需再添加一个什么条件?请你补上这个条件,并说明你的理由(不要再增添辅助线).23、如图,已知平行四边形ABCD 中,对角线AC BD ,交于点O ,E 是BD 延长线上的点,且ACE △是等边三角形. (1)求证:四边形ABCD 是菱形;(2)若2AED EAD ∠=∠,求证:四边形ABCD 是正方形.ECDBAOABCDE F图1724、已知:如图19,四边形ABCD 是菱形,E 是BD 延长线上一点,F 是DB 延长线上一点,且DE =BF .请你以F 为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可). (1)连结____________;(2)猜想:______=______; (3)证明:25、如图20,已知正方形ABCD 的对角线AC 、BD 相交于点O ,E 是AC 上一点,连结EB ,过点A 作AM ⊥BE ,垂足为M ,AM 交BD 于点F .(1)试说明OE =OF ;(2)如图21,若点E 在AC 的延长线上,AM ⊥BE 于点M ,交DB 的延长线于点F ,其它条件不变,则结论“OE =OF ”还成立吗?如果成立,请给出说明理由;如果不成立,请说明理由.O C图19DABEF图20EM F CO DBA图21EFOCMDAB参考答案一、1,C ;2,D ;3,D ;4,C ;5,C ;6,A ;7,D ;8,B ;9,D ;10,C .二、11,30°;12,=;13,14,;15,1212S S =;16,20;17,7;18,15、2n -1.三、21,由题意得△BEF ≌△DFE,∴DE=BE,∵在△BDE 中,DE=BE,∠DBE=45°,∴∠BD E=∠DBE=45°,∴∠DEB=90°,∴DE ⊥BC.∴EC=12(BC -AD)= 12(8-2)=3.∴BE=5;22,(1)无数;(2)只要两条直线都过对角线的交点即可;(3)这两条直线过平行四边形的对称中心(或对角线的交点); 23,:(1)四边形ABCD 是平行四边形,AO CO ∴=.又ACE △是等边三角形,EO AC ∴⊥,即DB AC ⊥.∴平行四边形ABCD 是菱形;(2)ACE △是等边三角形,60AEC ∴∠=.EO AC ⊥,1302AEO AEC ∴∠=∠=.2AED EAD ∠=∠,15EAD ∴∠=.45ADO EAD AED ∴∠=∠+∠=.四边形ABCD 是菱形,290ADC ADO ∴∠=∠=.∴四边形ABCD 是正方形.24,(1)说明△CED ≌△CEA 即可,(2)BC =2AB ,理由略;25,(1)四边形ABCD 是矩形.连结OE .∵四边形ABCD 是平行四边形,∴DO =OB ,∵四边形DEBF 是菱形,∴DE =BE ,∴EO ⊥BD ,∴∠DOE = 90°,即∠DAE = 90°,又四边形ABCD 是平行四边形,∴四边形ABCD 是矩形.(2)解:∵四边形DEBF 是菱形,∴∠FDB =∠EDB ,又由题意知∠EDB =∠EDA ,由(1)知四边形ABCD 是矩形,∴∠ADF =90°即∠FDB +∠EDB +∠ADE =90°,则∠ADB = 60°,∴在Rt △ADB 中,有AD ∶AB =1:3,即3=BCAB;26,(1)连结AF ;(2)猜想AF =AE ;(3)连结AC ,交BD 于O ,因为四边形ABCD 是菱形,所以AC ⊥BD 于O ,DO =BO ,因为DE =BF ,所以EO =BO 所以AC 垂直平分EF ,所以AF =AE ;27,(1)因为四边形ABCD 是正方形,所以∠BOE =∠AOF =90°,OB =OA ,又因为AM ⊥BE ,所以∠MEA +∠MAE =90°=∠AFO +∠MAE ,所以∠MEA =∠AFO ,所以Rt △BOE 可以看成是绕点O 旋转90°后与Rt △AOF 重合,所以OE =OF ;(2)OE =OF 成立.证明:因为四边形ABCD是正方形,所以∠BOE=∠AOF=90°,OB=OA又因为AM BE,所以∠F+∠MBF=90°=∠B+∠OBE,又因为∠MBF=∠OBE,所以∠F=∠E,所以Rt△BOE可以看成是由Rt△AOF绕点O旋转90°以后得到的,所以OE=OF;。
第20章《平行四边形的判定》测试题3

第20章《平行四边形的判定》测试题3一、填空题1、顺次连接一个任意四边形四边的中点,得到一个四边形。
2.命题“平行四边形的对角线互相平分”的逆命题是 .3.矩形的对角线相交成的角中,有一个角是60°,这个角所对的边长为20cm ,则其对角线长为_______,矩形的面积为________.4.一个菱形的两条对角线长分别为6cm ,8cm ,这个菱形的边长为_______,•面积S=______.5.如图,□ABCD 中,AE 、CF 分别是∠BAD 和∠BCD 的角平分线,根据现有的图形,请添加一个条件,使四边形AECF 为菱形,则添加的一个条件可以是 (只需写出一个即可,图中不能再添加别的“点”和“线”).6、如图,在平行四边形ABCD 中,E 、F 是对角线BD 上的两点,要使△ADF ≌△CBE ,还需添加一个什么条件? 。
(只需添加一个条件)三、证明题1、在平行四边形ABCD 中,E 、F 为对角线BD 上的三等分点。
求证:四边形AFCE 是平行四边形。
2、在如图菱形ABCD 中,对角线AC 、BD 相交于O ,E 、F 分别是AB 、BC 的中点。
求证:OE=OF 。
A B C DE F (第15题)B D A CF E3、已知:如图,已知:D 是△ABC 的边AB 上一点,CN ∥AB ,DN 交AC 于, 若MA=MC ,求证:四边形ADCN 是平行四边形4.已知:如图,D 是△ABC 的BC 边上的中点,DE ⊥AC ,DF ⊥AB ,垂足分别是E 、F ,且BF=CE.求证:(1)△ABC 是等腰三角形;(2)当∠A=90°时,试判断四边形AFDE 是怎样的四边形,证明你的结论.4、已知:如图7,在梯形ABCD 中A D ∥BC ,AB=DC 。
点E 、F 、G 分别在边AB 、BC 、CD 上,AE=GF=GC 。
(1) 求证:四边形AEFG 是平行四边形;(2) 当∠FGC=2∠EFB 时,求证:四边形AEFG 是矩形。
数学四年级上册《平行四边形的认识》练习题(含答案)

第五单元《平行四边形和梯形》第2课时《平行四边形的认识》一.选择题1.(2018秋•黄埔区期末)只有一组对边平行的四边形是()A.长方形B.平行四边形C.梯形2.(2016春•宝安区校级月考)两组对边分别平行的四边形是()A.梯形B.平行四边形C.长方形D.正方形3.(2014秋•凤阳县期末)平行四边形有()条高.A.1 B.2 C.无数条4.(2018秋•昆明期末)从平行四边形的一条边上的一点到对边可以引()垂线.A.一条B.两条C.无数条5.(2015•谢家集区模拟)平行四边形四个角的和是()A.180度B.360度C.540度二.填空题6.平行四边形的周长是38厘米,其中一条边长是10厘米,与它相邻的一条边长是厘米.7.(2019秋•孝昌县期末)平行四边形的互相平行;对角.8.(2018•吉水县)平行四边形的对边,对角.9.平行四边形四个内角和为,对角.三.判断题10.(2018秋•玉泉区期末)平行四边形的所有高都相等..(判断对错)11.(2016秋•仙桃期末)平行四边形四条边的长度确定了,它的形状就确定了..(判断对错)12.平行四边形中不可能有直角.(判断对错)13.(2018秋•长阳县期末)长方形和正方形也具有不稳定性..(判断对错)四.操作题14.(2012•永春县校级自主招生)(1)以如图线段AB为底,虚线线段CD为高,画一个平行四边形.(2)如果A、B、C看作三个点,那么A点在C点的方向上;C点在B点的方向上.15.在右边画一个同样的平行四边形.16.在如图中画出一个平行四边形:17.(2011秋•路南区期末)请将下面的图形改成平行四边形.18.量出平行四边形四条边的长度,并填在横线上.AB=,BC=,CD=,DA=.通过测量边长可以知道:.19.画一个一组邻边分别是3厘米和2厘米、两边夹角是60度的平行四边形.20.画一画,利用下面三角形画一个平行四边形21.(2015秋•遵义期末)画一个高为3厘米的平行四边形,并标出高.五.解答题22.(2017•云阳县)做一做.(请你在方格图上画一个平行四边形)23.(2014秋•历城区校级期末)画一个底边是4厘米的平行四边形.24.(2013秋•万安县期末)在下面的平行四边形中,已知∠B=55°,请写出其他三个角的度数.∠A=;∠C=;∠D=.25.(2015秋•仪陇县月考)一个平行四边形的一条边长12厘米,比邻边少2厘米,这个平行四边形的周长是多少厘米?26.小明用一根50厘米长的铁丝围出了一个平行四边形,其中一条边长18厘米,另外三条边长分别是多少厘米?27.平行四边形的周长是56厘米,其中一条边长是10厘米.平行四边形另外三条边分别是多少厘米?28.(2012秋•赣州期末)在右边画出一个同样的平行四边形.29.(2009秋•富宁县期末)在下面的方格纸上画一个平行四边形.你画的平行四边形的边长分别是、、、;周长是.参考答案第五单元《平行四边形和梯形》第2课时《平行四边形的认识》一.选择题1.(2018秋•黄埔区期末)只有一组对边平行的四边形是()A.长方形B.平行四边形C.梯形[解答]解:只有一组对边平行的四边形是梯形;故选:C.2.(2016春•宝安区校级月考)两组对边分别平行的四边形是()A.梯形B.平行四边形C.长方形D.正方形[解答]解:两组对边分别平行的四边形是平行四边形;故选:B.3.(2014秋•凤阳县期末)平行四边形有()条高.A.1 B.2 C.无数条[解答]解:由分析可知,平行四边形有无数条高,故选:C.4.(2018秋•昆明期末)从平行四边形的一条边上的一点到对边可以引()垂线.A.一条B.两条C.无数条[解答]解:由分析得出:从平行四边形的一条边上的一点到对边可以引一条垂线.故选:A.5.(2015•谢家集区模拟)平行四边形四个角的和是()A.180度B.360度C.540度[解答]解:连接平行四边形的一条对角线,把这个平行四边形分成了两个相等的三角形,则平行四边形的四个内角的度数之和,正好等于这两个三角形的内角和之和,因为三角形的内角和是180度,180°×2=360°.所以平行四边形的内角和是360度.故选:B.二.填空题6.平行四边形的周长是38厘米,其中一条边长是10厘米,与它相邻的一条边长是9厘米.[解答]解:38÷2﹣10=19﹣10=9(厘米)答:与它相邻的一条边长是9厘米.故答案为:9.7.(2019秋•孝昌县期末)平行四边形的对边互相平行;对角相等.[解答]解:由分析可知:平行四边形的对边互相平行;对角相等.故答案为:对边、相等.8.(2018•吉水县)平行四边形的对边相等,对角相等.[解答]解:平行四边形的对边相等,对角相等.故答案为:相等,相等.9.平行四边形四个内角和为360°,对角相等.[解答]解:平行四边形四个内角和为360°,对角相等.故答案为:360°,相等.三.判断题10.(2018秋•玉泉区期末)平行四边形的所有高都相等.×.(判断对错)[解答]解:平行四边形的高为两组,所以平行四边形有两组高,每组的高都相等且有无数条,但每个平行四边形的所有高的长度都相等,说法是错误的;故答案为:×.11.(2016秋•仙桃期末)平行四边形四条边的长度确定了,它的形状就确定了.×.(判断对错)[解答]解:因为平行四边形具有不稳定性,所以所以即使平行四边形四条边的长度确定了,它的形状依然不能确定.所以原题的说法错误.故答案为:×.12.平行四边形中不可能有直角.×(判断对错)[解答]解:长方形、正方形是特殊的平行四边形,四个角都是直角.所以平行四边形中不可能有直角说法错误.故答案为:×.13.(2018秋•长阳县期末)长方形和正方形也具有不稳定性.√.(判断对错)[解答]解:长方形和正方形也具有不稳定性;故答案为:√.四.操作题14.(2012•永春县校级自主招生)(1)以如图线段AB为底,虚线线段CD为高,画一个平行四边形.(2)如果A、B、C看作三个点,那么A点在C点的西南方向上;C点在B点的西北方向上.[解答]解:(1)画图如下:(2)那么A点在C点的西南方向上;C点在B点的西北方向上;故答案为:西南,西北.15.在右边画一个同样的平行四边形.[解答]解:如图:16.在如图中画出一个平行四边形:[解答]解:根据平行四边形的定义,可以画出图形如下:17.(2011秋•路南区期末)请将下面的图形改成平行四边形.[解答]解:作图如下:18.量出平行四边形四条边的长度,并填在横线上.AB= 2.1cm,BC= 4.3cm,CD= 2.1cm,DA= 4.3cm.通过测量边长可以知道:平行四边形的对边相等.[解答]解:量出平行四边形四条边的长度如下:AB=2.1cm,BC=4.3cm,CD=2.1cm,DA=4.3cm通过测量边长可以知道:平行四边形的对边相等.故答案为:2.1cm,4.3cm,2.1cm,4.3cm;平行四边形的对边相等.19.画一个一组邻边分别是3厘米和2厘米、两边夹角是60度的平行四边形.[解答]解:20.画一画,利用下面三角形画一个平行四边形[解答]解:21.(2015秋•遵义期末)画一个高为3厘米的平行四边形,并标出高.[解答]解:作平行四边形及高如下,该平行四边形即高为3厘米的平行四边形:五.解答题22.(2017•云阳县)做一做.(请你在方格图上画一个平行四边形)[解答]解:画图如下:23.(2014秋•历城区校级期末)画一个底边是4厘米的平行四边形.[解答]解:作图如下:24.(2013秋•万安县期末)在下面的平行四边形中,已知∠B=55°,请写出其他三个角的度数.∠A=125°;∠C=125°;∠D=55°.[解答]解:因为平行四边形ABCD中,∠B=55°,则∠A=∠C=180°﹣55°=125°,∠B与∠D为平行四边形的对角,所以∠B=∠D,即∠D=55°.故答案为:125°、125°、55°.25.(2015秋•仪陇县月考)一个平行四边形的一条边长12厘米,比邻边少2厘米,这个平行四边形的周长是多少厘米?[解答]解:12+2=14(厘米)(12+14)×2=26×2=52(厘米)答:这个平行四边形的周长是52厘米.26.小明用一根50厘米长的铁丝围出了一个平行四边形,其中一条边长18厘米,另外三条边长分别是多少厘米?[解答]解:AB+AD=50÷2=25厘米假设AB=18厘米,所以AD=25﹣18=7(厘米)由于平行四边形的对边相等则所以CD=AB=18厘米,BC=AD=7厘米.答:平行四边形另外三条边分别是18厘米、7厘米、7厘米.27.平行四边形的周长是56厘米,其中一条边长是10厘米.平行四边形另外三条边分别是多少厘米?[解答]解:AB+AD=56÷2=28厘米,假设AB=10厘米,所以AD=28﹣10=18厘米,由于平行四边形的对边相等则,所以CD=AB=10厘米,BC=AD=18厘米.答:平行四边形另外三条边分别是10厘米、18厘米、18厘米.28.(2012秋•赣州期末)在右边画出一个同样的平行四边形.[解答]解:平行四边形的底是3.3厘米,高是2厘米,则:29.(2009秋•富宁县期末)在下面的方格纸上画一个平行四边形.你画的平行四边形的边长分别是6厘米、5厘米、6厘米、5厘米;周长是22厘米.[解答]解:(1)如图所示:;画的平行四边形的边长分别是6厘米、5厘米、6厘米、5厘米;(2)周长是:6+5+6+5=22(厘米).答:周长是22厘米.故答案为:6厘米、5厘米、6厘米、5厘米;22厘米.。
初中-数学-人教版-第18章平行四边形单元测试(三)

第18章平行四边形单元测试(三)一、单选题(每小题3分,共30分)1、在△ABC 中,若AB =8,BC =15,AC =17,则AC 边上的中线BD 的长为( )A. 8B. 8.5C. 9D. 9.52、下列命题中正确的是( )A. 有一组邻边相等的四边形是菱形B. 有一个角是直角的平行四边形是矩形C. 对角线垂直的平行四边形是正方形D. 一组对边平行的四边形是平行四边形3、如图,在平行四边形ABCD 中,A 40∠=︒,则B ∠大小为( )A. 40︒B. 45︒C. 60︒D. 140︒ 4、如图,平行四边形ABCD 的对角线交于点O ,且AB =6,△OCD 的周长为16,则AC 与BD 的和是( )A. 22B. 20C. 16D. 105、如图,在四边形ABCD 中,对角线AC 、BD 相交于点O ,下列条件不能判定四边形ABCD 为平行四边形的是( )A. AB △CD ,AD △BCB. OA =OC ,OB =ODC. AD =BC ,AB △CDD. AB =CD ,AD =BC6、如图,在▱ABCD 中,已知AD =5cm ,AB =3cm ,AE 平分∠BAD 交BC 边于点E ,则EC 等于( )A. 1cmB. 2cmC. 3cmD. 4cm7、如图,将长方形ABCD 沿线段OG 折叠到''OB C G 的位置,'OGC ∠等于100°,则'DGC ∠的度数为( )A. 20°B. 30°C. 40°D. 50°8、如图,在菱形ABCD 中,AE BC ⊥于E ,BE EC =,AC 2=,则菱形ABCD 的周长是()A. 5B. 10C. 8D. 129、如图,菱形ABCD 中,过顶点C 作CE BC ⊥交对角线BD 于E 点,已知134A ∠=︒,则BEC ∠的大小为( )A. 23︒B. 28︒C. 62︒D. 67︒10、如图,正方形ABCD 内有两条相交线段MN ,EF ,M ,N ,E ,F 分别在边AB ,CD ,AD ,BC 上.小明认为:若MN =EF ,则MN ⊥EF ;小亮认为:若MN ⊥EF ,则MN =EF ,你认为( )A. 仅小明对B. 仅小亮对C. 两人都对D. 两人都不对二、填空题(每小题4分,共28分)11、已知平行四边形ABCD 中,△B =5△A ,则△D =______.12、一个矩形的两条对角线的一个夹角等于60°,对角线长为8,则矩形的较长边等于______.13、已知一个菱形的边长为5,其中一条对角线长为8,则这个菱形的面积为______. 14、将一张长方形纸片按如图所示的方式折叠,BD 、BE 为折痕,若30ABE ∠=︒,则DBC ∠为______度.15、如图,在菱形ABCD 中,对角线,AC BD 交于点O ,过点A 作AH BC ⊥于点H ,已知BO =4,S 菱形ABCD =24,则AH =______.16、如图,四边形ABCD 和四边形CEFG 都是正方形,且B ,C ,E 三点都在同一条直线上,连接BD ,DF ,BF ,当BC =6时,△DBF 的面积为______.17、如图,△A 1B 1C 1中,A 1B 1=4,A 1C 1=5,B 1C 1=7.点A 2,B 2,C 2分别是边B 1C 1,A 1C 1,A 1B 1的中点;点A 3,B 3,C 3分别是边B 2C 2,A 2C 2,A 2B 2的中点;…;以此类推,则第2019个三角形的周长是______.三、解答题一(每小题6分,共18分)18、如图,请在下列四个论断中选出两个作为条件,推出四边形ABCD 是平行四边形,并予以证明(写出一种即可).△AD △BC ;△AB =CD ;△△A =△C ;△△B +△C =180°.已知:在四边形ABCD 中,______.求证:四边形ABCD 是平行四边形.19、如图,在△ABC 中,AB =AC ,AD 平分△BAC 交BC 于点D ,分别过点A 、D 作AE △BC 、DE △AB ,AE 与DE 相交于点E ,连结CE. 求证:四边形ADCE 是矩形.20、如图,矩形ABCD 的对角线AC ,BD 交于点O ,且DE AC ,CE BD .求证:四边形OCED 是菱形.四、解答题二(每小题8分,共24分)21、如图,在正方形ABCD 中,点E 是BC 的中点,连接DE ,过点A 作AG ED ⊥交DE 于点F ,交CD 于点G .(1)证明:ADG DCE ∆∆≌;(2)连接BF ,证明:AB FB =.22、如图,在四边形ABCD 中,AD △BC ,AB =BC ,对角线AC 、BD 交于点O ,BD 平分△ABC ,过点D 作DE △BC ,交BC 的延长线于点E ,连接OE.(1)求证:四边形ABCD 是菱形;(2)若DC =AC =4,求OE 的长.23、在Rt ABC 中,9030C A D E F ∠︒∠︒=,=,,,分别是AC AB BC ,,的中点,连接ED EF ,.()1求证:四边形DEFC 是矩形;()2请用无刻度的直尺在图中作出ABC ∠的平分线(保留作图痕迹,不写作法).五、解答题三(每小题10分,共20分)24、如图1,O 为正方形ABCD 的中心,分别延长OA 、OD 到点F 、E ,使OF =2OA ,OE =2OD ,连接EF .将△EOF 绕点O 逆时针旋转a 角得到△E 1OF 1(如图2).(1)探究AE 1与BF 1的数量关系,并给予证明;(2)当a =30°时,求证:△AOE 1为直角三角形.25、在△ABCD 中,△BAD 的平分线交直线BC 于点E ,交直线DC 于点F .(1)在图1中证明CE =CF ;(2)若△ABC =90°,G 是EF 的中点(如图2),直接写出△BDG 的度数;(3)若△ABC =120°,FG △CE ,FG =CE ,分别连接DB 、DG (如图3),求△BDG 的度数.参考答案1、【答案】B【分析】首先判定△ABC是直角三角形,再根据在直角三角形中,斜边上的中线等于斜边的一半可得答案.【解答】△82+152=289=172,△AB2+BC2=AC2,△△ABC是直角三角形,△ABC=90°,△BD是AC边上的中线,△BD=12AC=8.5,选B.2、【答案】B【分析】利用特殊四边形的判定定理对个选项逐一判断后即可得到正确的选项.【解答】A、一组邻边相等的平行四边形是菱形,选项错误;B、正确;C、对角线垂直的平行四边形是菱形,选项错误;D、两组对边平行的四边形才是平行四边形,选项错误.3、【答案】D【分析】由平行四边形的性质得出邻角互补,即可得出结果.【解答】解:△四边形ABCD是平行四边形,△AD△CD,△△A+△B=180°,△△B=180°-△A=140°;选:D.4、【答案】B【分析】本题考查了平行四边形的性质.【解答】△四边形ABCD是平行四边形,△AB=CD=6,△△OCD的周长为16,△OD+OC=16−6=10,△BD=2DO,AC=2OC,△平行四边形ABCD的两条对角线的和=BD+AC=2(DO+OC)=20,选B.答案第1页,共15页5、【答案】C【分析】根据平行四边形的判定定理分别进行分析即可.【解答】A、根据两组对边分别平行的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题意;B、根据对角线互相平分的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题意;C、不能判定四边形ABCD是平行四边形,故此选项符合题意;D、根据两组对边分别相等的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题意;选:C.6、【答案】B【分析】本题考查了平行四边形的性质.【解答】解:如图,∵AE平分∠BAD交BC边于点E,∴∠BAE=∠EAD,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=5,∴∠DAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE=3,∴EC=BC-BE=5-3=2.选B.7、【答案】A【分析】本题考查了矩形的性质.【解答】由折叠的可知∠OGC=∠OGC′=100°,∴∠OGD=180°-∠OGC=80°,∴∠DGC′=∠OGC′-∠OGD=100°-80°=20°,选A.8、【答案】C【分析】连接AC,根据线段垂直平分线的性质可得AB=AC=2,然后利用周长公式进行答案第3页,共15页计算即可得答案.【解答】如图连接AC ,BE EC =,AE BC ⊥,AB AC 2∴==,∴菱形ABCD 的周长428=⨯=,选C .9、【答案】D【分析】先说明ABD =∠ADC =∠CBD ,然后再利用三角形内角和180°求出即可∠CBD 度数,最后再用直角三角形的内角和定理解答即可.【解答】解:∵菱形ABCD∴AB =AD∴∠ABD =∠ADC∴∠ABD =∠CBD又∵134A ∠=︒∴∠CBD =∠BDC =∠ABD =∠ADC =12(180°-134°)=23° ∴BEC ∠=90°-23°=67°故答案为D .10、【答案】C【分析】分别过点E 作EG ⊥BC 于点G ,过点M 作MP ⊥CD 于点P ,设EF 与MN 相交于点O ,MP 与EF 相交于点Q ,根据正方形的性质可得EG =MP ;对于小明的说法,先利用“HL ”证明Rt △EFG ≌Rt △MNP ,根据全等三角形对应角相等可得∠MNP =∠EFG ,再根据角的关系推出∠EQM =∠MNP ,然后根据∠MNP +∠NMP =90°得到∠NMP +∠EQM =90°,从而得到∠MOQ =90°,根据垂直的定义即可证得MN ⊥EF ;对于小亮的说法,先推出∠EQM =∠EFG ,∠EQM =∠MNP ,然后得到∠EFG =∠MNP ,然后利用“角角边”证明△EFG ≌△MNP ,根据全等三角形对应边相等可得EF =MN .【解答】如图,过点E 作EG ⊥BC 于点G ,过点M 作MP ⊥CD 于点P ,设EF 与MN 相交于点O ,MP 与EF 相交于点Q ,∵四边形ABCD 是正方形,∴EG =MP ,对于小明的说法:在Rt △EFG 和Rt △MNP 中,MN EF EG MP ⎧⎨⎩==, ∴Rt △EFG ≌Rt △MNP (HL ),∴∠MNP =∠EFG ,∵MP ⊥CD ,∠C =90°,∴MP ∥BC ,∴∠EQM =∠EFG =∠MNP ,又∵∠MNP +∠NMP =90°,∴∠EQM +∠NMP =90°,在△MOQ 中,∠MOQ =180°-(∠EQM +∠NMP )=180°-90°=90°, ∴MN ⊥EF ,故甲正确.对小亮的说法:∵MP ⊥CD ,∠C =90°,∴MP ∥BC ,∴∠EQM =∠EFG ,∵MN ⊥EF ,∴∠NMP +∠EQM =90°,又∵MP ⊥CD ,∴∠NMP +∠MNP =90°,∴∠EQM =∠MNP ,∴∠EFG =∠MNP ,在△EFG 和△MNP 中,答案第5页,共15页90EFG MNP EGF MPN EG MP ∠∠⎧⎪∠∠︒⎨⎪⎩====,∴△EFG ≌△MNP (AAS ),∴MN =EF ,故小亮的说法正确,综上所述,两个人的说法都正确.选C .11、【答案】150°【分析】本题考查了平行四边形的性质.【解答】如图所示:△四边形ABCD 是平行四边形,△AD △BC ,△△A +△B =180°,△D =△B ,△△B =5△A ,△6△A =180°,解得△A =30°,△△D =△B =30°×5=150°.12、【答案】【分析】由矩形的对角线相等且平分可求得较短边与对角线的一半所构成的三角形为等边三角形,则可求得答案.【解答】解:如图,在矩形ABCD 中,AC =BD =8,△AOB =60°,则OA =OB =12×8=4, △△AOB 为等边三角形,△AB =4,在Rt △ABC 中,由勾股定理得:BC,故答案为:13、【答案】24【分析】本题考查了菱形的性质.【解答】如图,△菱形ABCD 中,BD =8,AB =5,△AC △BD ,OB =12BD =4,△OA ,△AC =2OA =6,△这个菱形的面积为:12AC •BD =12×6×8=24. 14、【答案】60【分析】根据翻折的性质可知,△ABE =△A ′BE ,△DBC =△DBC ′,又△△ABE +△A ′BE +△DBC +△DBC ′=180°,△ABE =30°,继而即可求出答案.【解答】根据翻折的性质可知,△ABE =△A ′BE ,△DBC =△DBC ′,又△△ABE +△A ′BE +△DBC +△DBC ′=180°,△△ABE +△DBC =90°,又△△ABE =30°,△△DBC =60°.故答案为:60.15、【答案】245【分析】根据菱形面积=对角线积的一半可求AC ,再根据勾股定理求出BC ,然后由菱形的面积即可得出结果.【解答】△四边形ABCD 是菱形,∴4,BO DO AO CO ===,AC BD ⊥,∴8BD =, ∵1242ABCD S AC BD =⨯=菱形, ∴6AC =, ∴132OC AC ==,∴5BC ==,答案第7页,共15页∵24ABCD S BC AH =⨯=菱形, ∴245AH =; 故答案为:245. 16、【答案】18【分析】设正方形CEFG 的边长为a ,根据正方形的性质、三角形的面积公式、梯形的面积公式即可求出答案.【解答】设正方形CEFG 的边长为a6BC =,四边形ABCD 是正方形6,90CD BC BCD ∴==∠=︒四边形CEFG 是正方形90,,6E DCE EF CE a BE BC CE a ∴∠=∠=︒===+=+DBF BCD BEF DCEF S S S S ∆∆∆∴=+-梯形11166(6)(6)222a a a a =⨯⨯++⋅-⋅+ 18=故答案为:18.17、【答案】201412【分析】由三角形的中位线定理得:B 2C 2,A 2C 2,A 2B 2分别等于A 1B 1、B 1C 1、C 1A 1的12,△△A 2B 2C 2的周长等于△A 1B 1C 1的周长的一半,以此类推可求出结论.【解答】△△A 1B 1C 1中,A 1B 1=4,A 1C 1=5,B 1C 1=7,△△A 1B 1C 1的周长是16,△A 2,B 2,C 2分别是边B 1C 1,A 1C 1,A 1B 1的中点,△B 2C 2,A 2C 2,A 2B 2分别等于A 1B 1、B 1C 1、C 1A 1的12, …,以此类推,则△A 4B 4C 4的周长是312×16=2; △△A n B n △n 的周长是4122n -, △第2019个三角形的周长是4201822=201412,故答案为:201412.18、【答案】已知:△△(或△△或△△或△△),证明见解答.【分析】根据平行四边形的判定方法就可以组合出不同的结论,然后即可证明.【解答】其中解法一是证明两组对角相等的四边形是平行四边形;解法二是证明两组对边平行的四边形是平行四边形;解法三是证明一组对边平行且相等的四边形是平行四边形;解法四是证明两组对角相等的四边形是平行四边形.已知:△△,△△,△△,△△均可,其余均不可以.解法一:已知:在四边形ABCD 中,△AD △BC ,△△A =△C ,求证:四边形ABCD 是平行四边形.证明:△AD △BC ,△△A +△B =180°,△C +△D =180°.△△A =△C ,△△B =△D .△四边形ABCD 是平行四边形.解法二:已知:在四边形ABCD 中,△AD △BC ,△△B +△C =180°,求证:四边形ABCD 是平行四边形.证明:△△B +△C =180°,△AB △CD ,又△AD △BC ,△四边形ABCD 是平行四边形;解法三:已知:在四边形ABCD 中,△AB =CD ,△△B +△C =180°,求证:四边形ABCD 是平行四边形.证明:△△B +△C =180°,△AB △CD ,又△AB =CD ,△四边形ABCD 是平行四边形;解法四:已知:在四边形ABCD 中,△△A =△C ,△△B +△C =180°,答案第9页,共15页求证:四边形ABCD 是平行四边形.证明:△△B +△C =180°,△AB △CD ,△△A +△D =180°,又△△A =△C ,△△B =△D ,△四边形ABCD 是平行四边形.19、【答案】见解答【分析】先证明四边形ABDE 是平行四边形,得出AE =BD ,由等腰三角形的性质得出BD =CD ,AD △BC ,得出AE =CD ,△ADC =90°,证出四边形ADCE 是平行四边形.即可得出结论.【解答】证明△AE △BC 、DE △AB ,△四边形ABDE 是平行四边形.△AE =BD ,△AB =AC ,AD 平分△BAC ,△BD =CD ,AD △BC ,△AE =CD ,△ADC =90°,又△AE △BC ,△四边形ADCE 是平行四边形.△四边形ADCE 是矩形.20、【答案】见解答【分析】首先根据两对边互相平行的四边形是平行四边形证明四边形OCED 是平行四边形,再根据矩形的性质可得OC =OD ,即可利用一组邻边相等的平行四边形是菱形判定出结论.【解答】证明:△DE AC ,CE BD ,△四边形OCED 是平行四边形,△四边形ABCD 是矩形,∴AC BD =,OA OC =,OB OD =,∴OC OD =,△四边形OCED 是菱形.21、【答案】(1)见解答;(2)见解答.【分析】(1)依据正方形的性质以及垂线的定义,即可得到△ADG =△C =90°,AD =DC ,△DAG =△CDE ,即可得出△ADG △△DCE ;(2)延长DE 交AB 的延长线于H ,根据△DCE △△HBE ,即可得出B 是AH 的中点,进而得到AB =FB .【解答】证明:(1)四边形ABCD 是正方形,90ADG C AD DC ︒∴∠∠==,=,又AG DE ⊥,90DAG ADF CDE ADF ︒∴∠+∠∠+∠==,DAG CDE ∴∠∠=,ADG DCE ASA ∴∆∆≌()(2)如图所示,延长DE 交AB 的延长线于H ,E 是BC 的中点,BE CE ∴=,又90C HBE DEC HEB ︒∠∠∠∠==,=,DCE HBE ASA ∴∆∆≌(), BH DC AB ∴==,即B 是AH 的中点,又90AFH ︒∠=,Rt AFH ∴∆中,12BF AH AB ==. 22、【答案】(1)证明见解答;(2)4.【分析】(1)由AD △BC ,BD 平分△ABC ,可得AD =AB ,结合AD △BC ,可得四边形ABCD 是平行四边形,进而,可证明四边形ABCD 是菱形,(2)由四边形ABCD 是菱形,可得OC =12AC =2,在Rt △OCD 中,由勾股定理得:OD =4,根据“在直角三角形中,斜边上的中线等于斜边的一半”,即可求解.【解答】(1)证明:△AD △BC ,答案第11页,共15页△△ADB =△CBD ,△BD 平分△ABC ,△△ABD =△CBD ,△△ADB =△ABD ,△AD =AB ,△AB =BC ,△AD =BC ,△AD △BC ,△四边形ABCD 是平行四边形,又△AB =BC ,△四边形ABCD 是菱形;(2)解:△四边形ABCD 是菱形,△AC △BD ,OB =OD ,OA =OC =12AC =2, 在Rt △OCD 中,由勾股定理得:OD4,△BD =2OD =8,△DE △BC ,△△DEB =90°,△OB =OD ,△OE =12BD =4. 23、【答案】(1)证明见解答;(2)作图见解答.【分析】(1)首先证明四边形DEFC 是平行四边形,再根据有一个角是直角的平行四边形是矩形即可判断.(2)连接EC DF ,交于点O ,作射线BO 即可.【解答】(1)证明:D E F ,,分别是AC AB BC ,,的中点,////DE FC EF CD ∴,,∴四边形DEFC 是平行四边形,90DCF ∠︒=,∴四边形DEFC 是矩形(2)连接EC DF ,交于点O ,作射线BO ,射线BO 即为所求.24、【答案】(1)AE 1=BF 1;证明见解答(2)见解答【分析】(1)利用旋转不变量找到相等的角和线段,证得11E AO F BO ≅后即可证得结论;(2)利用已知角,得出1130GAE GE A ∠=∠=︒,从而证明直角三角形.【解答】(1)11AE BF =,证明如下. 证明:O 为正方形ABCD 的中心,∴OA OD =,2OF OA =,2OE OD =,∴OE OF =,将EOF △绕点O 逆时针旋转α角得到11E OF ,∴11OE OF =,11F OB E OA ∠=∠,OA OB =,∴11E AO F BO ≅,∴11AE BF =;(2)证明:取1OE 中点G ,连接AG ,90AOD ∠=︒,30α=︒,∴19060E OA α∠=︒-=︒,12OE OA =,∴OA OG =,答案第13页,共15页∴160E OA AGO OAG ∠=∠=∠=︒,∴1AG GE =,∴1130GAE GE A ∠=∠=︒,∴190E AO ∠=︒,∴1AOE 为直角三角形.25、【答案】(1)见解答;(2)45°;(3)见解答.【分析】(1)根据AF 平分△BAD ,可得△BAF =△DAF ,利用四边形ABCD 是平行四边形,求证△CEF =△F 即可;(2)根据△ABC =90°,G 是EF 的中点可直接求得;(3)分别连接GB 、GC ,求证四边形CEGF 是平行四边形,再求证△ECG 是等边三角形,由AD △BC 及AF 平分△BAD 可得△BAE =△AEB ,求证△BEG △△DCG ,然后即可求得答案.【解答】(1)证明:如图1,△AF 平分△BAD ,△△BAF =△DAF ,△四边形ABCD 是平行四边形,△AD △BC ,AB △CD ,△△DAF =△CEF ,△BAF =△F ,△△CEF =△F .△CE =CF .(2)解:连接GC 、BG ,△四边形ABCD 为平行四边形,△ABC =90°,△四边形ABCD 为矩形,△AF 平分△BAD ,△△DAF=△BAF=45°,△△DCB=90°,DF△AB,△△DF A=45°,△ECF=90°△△ECF为等腰直角三角形,△G为EF中点,△EG=CG=FG,CG△EF,△△ABE为等腰直角三角形,AB=DC,△BE=DC,△△CEF=△GCF=45°,△△BEG=△DCG=135°在△BEG与△DCG中,∵EG CGBEG DCG BE DC=⎧⎪∠=∠⎨⎪=⎩,△△BEG△△DCG,△BG=DG,△CG△EF,△△DGC+△DGA=90°,又△△DGC=△BGA,△△BGA+△DGA=90°,△△DGB为等腰直角三角形,△△BDG=45°.(3)解:延长AB、FG交于H,连接HD.△AD△GF,AB△DF,△四边形AHFD为平行四边形△△ABC=120°,AF平分△BAD△△DAF=30°,△ADC=120°,△DF A=30°△△DAF为等腰三角形△AD=DF,△CE=CF,△平行四边形AHFD为菱形△△ADH,△DHF为全等的等边三角形△DH=DF,△BHD=△GFD=60°△FG=CE,CE=CF,CF=BH,∴BH=GF在△BHD与△GFD中,∵DH DFBHD GFD BH GF=⎧⎪∠=∠⎨⎪=⎩,∴△BHD≌△GFD,∴∠BDH=∠GDF∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°.答案第15页,共15页。
平行四边形的判定3

3、△ABC中,D是AB中点,E是AC上的
定 理 应 用:
⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2 倍或 1/2提供了一个新的途径
注意:
在处理问题时,要求同时出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线
E
C
2
F
B
C
A
D E
证明:如 图,延 长DE 到 F,使
EF=DE ,连 结CF. ∵DE=EF 、∠AED=∠CEF 、AE=EC
F ∴△ADE ≌△CFE
∴AD=FC 、∠A=∠ECF ∴AB∥FC 又AD=DB ∴BD∥ CF且 BD =CF 所以 ,四边形BCFD是平行四边形
B
C
∴DE ∥ BC 且 DE=1/2BC
平行四边形判定(3)
A
D
E
B
C
回顾与联想:
(1)AB∥CD, BC∥AD
(2) AB=CD,BC=AD (3) AB∥CD,AB=CD (4) ∠A= ∠C , ∠ B=∠ D (5) AO=OC, BO=OD
□ ABCD
B
A O C
D
引例:如图,点D、E分别是△ABC的边AB、 1 A AC的中点,求证DE∥BC且DE= BC
已知如图1,BD、CE分别是 △ABC的外角 平分线,过点A作AF⊥BD,AG ⊥CE,垂足 分别是F、G,连结FG,延长AF、AG,与直 线BC相交,求证: FG=1/2(AB+BC+AC)
∟
D F
A E G B C
H H
K
平行四边形性质和判定习题(答案详细)

平行四边形性质和判定习题(答案详细)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(平行四边形性质和判定习题(答案详细))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为平行四边形性质和判定习题(答案详细)的全部内容。
平行四边形性质和判定习题1.如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.(1)求证:BE=DF;(2)若 M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形状(不必说明理由).2.如图所示,▱AECF的对角线相交于点O,DB经过点O,分别与AE,CF交于B,D.求证:四边形ABCD是平行四边形.3.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.4.已知:如图,在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF、AD.求证:EF=AD.5.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.6.如图,已知,▱ABCD中,AE=CF,M、N分别是DE、BF的中点.求证:四边形MFNE是平行四边形.7.如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.8.在▱ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.9.如图所示,DB∥AC,且DB=AC,E是AC的中点,求证:BC=DE.10.已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?11.如图:已知D、E、F分别是△ABC各边的中点,求证:AE与DF互相平分.12.已知:如图,在▱ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE、四边形DCOE都是平行四边形.13.如图,已知四边形ABCD中,点E,F,G,H分别是AB、CD、AC、BD的中点,并且点E、F、G、H有在同一条直线上.求证:EF和GH互相平分.14.如图:▱ABCD中,MN∥AC,试说明MQ=NP.15.已知:如图所示,平行四边形ABCD的对角线AC,BD相交于点O,EF经过点O并且分别和AB,CD相交于点E,F,点G,H分别为OA,OC的中点.求证:四边形EHFG是平行四边形.16.如图,已知在▱ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.(1)求证:四边形GEHF是平行四边形;(2)若点G、H分别在线段BA和DC上,其余条件不变,则(1)中的结论是否成立?(不用说明理由)17.如图,在△ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.(1)求证:AF=CE;(2)如果AC=EF,且∠ACB=135°,试判断四边形AFCE是什么样的四边形,并证明你的结论.18.如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2(1)求证:D是EC中点;(2)求FC的长.19.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.(1)求证:四边形EFCD是平行四边形;(2)若BF=EF,求证:AE=AD.20.如图,四边形ABCD,E、F、G、H分别是AB、BC、CD、DA的中点.(1)请判断四边形EFGH的形状?并说明为什么;(2)若使四边形EFGH为正方形,那么四边形ABCD的对角线应具有怎样的性质?21.如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.(1)当AB≠AC时,证明:四边形ADFE为平行四边形;(2)当AB=AC时,顺次连接A、D、F、E四点所构成的图形有哪几类?直接写出构成图形的类型和相应的条件.22.如图,以△ABC的三边为边,在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF,那么,四边形AFED是否为平行四边形?如果是,请证明之,如果不是,请说明理由.23.在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.若点P在BC边上(如图1),此时PD=0,可得结论:PD+PE+PF=AB.请直接应用上述信息解决下列问题:当点P分别在△ABC内(如图2),△ABC外(如图3)时,上述结论是否成立?若成立,请给予证明;若不成立,PD,PE,PF与AB之间又有怎样的数量关系,请写出你的猜想,不需要证明.24.如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连续PM并延长到点E,使ME=PM,连接DE.探究:(1)请猜想与线段DE有关的三个结论;(2)请你利用图2,图3选择不同位置的点P按上述方法操作;(3)经历(2)之后,如果你认为你写的结论是正确的,请加以证明;如果你认为你写的结论是错误的,请用图2或图3加以说明;(注意:错误的结论,只要你用反例给予说明也得分)(4)若将“Rt△ABC"改为“任意△ABC”,其他条件不变,利用图4操作,并写出与线段DE有关的结论(直接写答案).25.在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD分割成四个部分,使含有一组对顶角的两个图形全等;(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有_________组;(2)请在图中的三个平行四边形中画出满足小强分割方法的直线;(3)由上述实验操作过程,你发现所画的两条直线有什么规律?26.如图,在直角梯形ABCD中,AB∥CD,∠BCD=Rt∠,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC 方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.(1)求CD的长;(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.27.已知平行四边形的三个顶点的坐标分别为O(0,0)、A(2,0)、B(1,1),则第四个顶点C的坐标是多少?28.已知平行四边形ABCD的周长为36cm,过D作AB,BC边上的高DE、DF,且cm,,求平行四边形ABCD的面积.29.如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(﹣3,),B(﹣2,3),C(2,3),点D在第一象限.(1)求D点的坐标;(2)将平行四边形ABCD先向右平移个单位长度,再向下平移个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少?(3)求平行四边形ABCD与四边形A1B1C1D1重叠部分的面积?30.如图所示.▱ABCD中,AF平分∠BAD交BC于F,DE⊥AF交CB于E.求证:BE=CF.答案与评分标准1.如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.(1)求证:BE=DF;(2)若 M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形状(不必说明理由).考点:平行四边形的判定与性质;全等三角形的判定与性质。
专题训练(3) 平行四边形的性质与判定的四种运用

专题训练(三) 平行四边形的性质与判定的四种运用► 类型一 平行四边形与全等三角形1.用两个全等三角形最多能拼成________个不同的平行四边形.2.如图3-ZT -1,在平行四边形ABCD 中,分别以BC ,AD 为边作等边三角形BCM 和等边三角形AND ,MN 与AC 交于点O .求证:OM =ON .图3-ZT -13.如图3-ZT -2,△ABC 中,分别以AB ,AC 为边向三角形外作△ABD 和△ACE ,使AD =AB ,AE =AC ,∠BAD =∠CAE =90°.AH ⊥BC ,H 为垂足,点F 在HA 的延长线上,且AF =BC .求证:四边形AEFD 是平行四边形.图3-ZT -2► 类型二 平行四边形与等腰三角形4.如图3-ZT -3所示,在▱ABCD 中,AC 的垂直平分线交AD 于点E ,且△CDE 的周长为8,则▱ABCD 的周长是( )A .10B .12C .14D .16图3-ZT -35.如图3-ZT -4,在平行四边形ABCD 中,AB >AD ,按以下步骤作图:以点A 为圆心,小于AD 的长为半径画弧,与AB ,AD 分别交于点E ,F ,再分别以点E ,F 为圆心,大于12EF 的长为半径画弧,两弧交于点G ;作射线AG 交CD 于点H ,则下列结论中不能由条件推理得出的是( )A .AG 平分∠DAB B .AD =DHC .DH =BCD .CH =DH图3-ZT-46.如图3-ZT-5,平行四边形ABCD和平行四边形DCFE的周长相等,∠B+∠F=220°,则∠DAE的度数为________.图3-ZT-57.在▱ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为________.8.如图3-ZT-6所示,如果▱ABCD的一内角∠BAD的平分线交BC于点E,且AE =BE,求▱ABCD各内角的度数.图3-ZT-69.如图3-ZT-7,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC.(1)求证:BE=AF;(2)若∠ABC=60°,BD=6,求四边形ADEF的面积.图3-ZT-7►类型三平行四边形中的中点问题10.如图3-ZT-8所示,在平行四边形ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交于点O,则OA长的取值范围是()图3-ZT-8A.2 cm<OA<5 cmB.2 cm<OA<8 cmC.1 cm<OA<4 cmD.3 cm<OA<8 cm11.已知:如图3-ZT-9,四边形ABCD中,AC=7,BD=8,E,F,G,H分别是边AB,BC,CD,DA的中点,则四边形EFGH的周长是________.图3-ZT-912.如图3-ZT-10所示,▱ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BC=5,则对角线BD=__________.图3-ZT-1013.如图3-ZT-11,AC,BD是四边形ABCD的对角线,E,F分别是AD,BC的中点,M,N分别是BD,CA的中点,求证:EF,MN互相平分.图3-ZT-1114.如图3-ZT-12所示,在▱ABCD中,M是BC的中点,且AM=9,BD=12,AD =10,求▱ABCD的面积.图3-ZT-12►类型四平行四边形中数学思想的运用15.整体思想如图3-ZT-13,在平行四边形ABCD中,对角线AC与BD交于点O,△AOB与△AOD的周长之和为11.4 cm,两对角线的长度之和为7 cm,则这个平行四边形的周长为________cm.图3-ZT-1316.转化思想——分散向集中转化如图3-ZT-14,等边三角形ABC的边长为7 cm,M为△ABC内任一点,MD∥AC,ME∥AB,MF∥BC,则MD+ME+MF=________.图3-ZT-1417.分类讨论思想如图3-ZT-15,直线a和b平行,直线a上有一个定点M和一个动点P,点P从点M开始以2 cm/s的速度向点A的方向运动;直线b上有两个定点E和N,EN=12 cm,动点Q以4 cm/s的速度从点E向点N的方向运动,则经过几秒后,以点P,Q,M,N为顶点的四边形是平行四边形?图3-ZT-15详解详析1.[答案] 32.证明:在平行四边形ABCD 中,AD ∥BC ,AD =BC , ∴∠OAD =∠OCB .∵在等边三角形BCM 和等边三角形AND 中, ∠NAD =∠MCB =60°,AN =AD ,BC =MC , ∴∠NAO =∠MCO ,AN =MC . 又∵∠AON =∠COM , ∴△AON ≌△COM ,∴OM =ON .3.证明:∵∠BAD =90°,点F 在HA 的延长线上, ∴∠DAF +∠BAH =90°.∵AH ⊥BC ,∴∠ABC +∠BAH =90°, ∴∠DAF =∠ABC .又∵AD =BA ,AF =BC , ∴△DAF ≌△ABC (SAS), ∴DF =AC ,∠ADF =∠BAC . ∵AE =AC ,∴AE =DF .∵∠DAE +∠BAC =180°, ∴∠DAE +∠ADF =180°, ∴AE ∥DF ,∴四边形AEFD 是平行四边形. 4.[答案] D5.[解析] D 根据作图可知,AG 平分∠DAB ,故A 正确;再由平行线的性质知∠BAH =∠DHA ,故∠DAH =∠DHA ,所以AD =DH ,再由AD =BC ,得DH =BC .所以应选D.6.[答案] 20° 7.[答案] 3或5[解析] 易知BE =AB =DC =FC .(1)如图①,当AE ,DF 在▱ABCD 内部没有交点时,AB =12×(AD -EF )=3;(2)如图②,当AE ,DF 在▱ABCD 内部相交时,AB =12×(AD +EF )=5.8.解:∵四边形ABCD 是平行四边形, ∴∠BAD =∠C ,∠B =∠D ,AD ∥BC , ∴∠BAD +∠B =180°,∠DAE =∠BEA . 又∵AE 平分∠BAD ,∴∠BAE =∠DAE , ∴∠BAE =∠BEA ,∴AB =BE .又∵AE =BE ,∴AB =BE =AE ,∴∠B =60°, ∴∠D =60°,∠BAD =∠C =120°.[点评] 当平行四边形中有角平分线、线段垂直平分线或特殊角(30°,60°角等)时,通常可以得到等腰三角形,反之亦然.9.解:(1)证明:∵DE ∥AB ,EF ∥AC ,∴∠ABD =∠BDE ,四边形ADEF 是平行四边形,∴AF =DE .∵BD 是△ABC 的角平分线, ∴∠ABD =∠DBE ,∴∠DBE =∠BDE ,∴BE =DE ,∴BE =AF .(2)如图,过点D 作DG ⊥AB 于点G ,过点E 作EH ⊥BD 于点H . ∵∠ABC =60°,BD 是∠ABC 的平分线, ∴∠ABD =∠EBD =30°, ∴DG =12BD =12×6=3.∵BE =DE ,∴BH =DH =12BD =3,∴EH =3,DE =2 3,∴四边形ADEF 的面积=DE ·DG =6 3.10.[答案] C 11.[答案] 15[解析] ∵EF 是△ABC 的中位线,∴EF 平行且等于12AC ,同理,HG 平行且等于12AC ,∴EF 平行且等于HG ,∴四边形EFGH 是平行四边形, ∴四边形EFGH 的周长=2(EF +FG )=2×(12×7+12×8)=15.12.[答案] 2 213.证明:如图,连接EM ,MF ∵FN 是△ABC 的中位线, ∴FN 平行且等于12AB ,同理,EM 平行且等于12AB ,∴FN 平行且等于EM ,∴四边形EMFN 是平行四边形, ∴EF ,MN 互相平分.14.解:如图,延长BC 至点E ,使CE =CM ,连接DE . ∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AD =BC ,∴AD ∥ME .又∵M 是BC 的中点,∴BC =2CM =2CE =2BM , ∴AD =ME =10,BE =15,∴四边形AMED 是平行四边形,∴DE =AM =9.∵BD 2+DE 2=122+92=225=152=BE 2,∴BD ⊥DE ,∴▱ABCD 的面积=2(△BDE 的面积-△DCE 的面积)=2×(12×9×12-12×9×12×13)=72.[点评] 在平行四边形的对角线互相平分这一性质中,体现出了线段中点的特点,有中点时就有可能有三角形的中线、中位线、线段垂直平分线等,需灵活处理,积累经验.15.[答案] 8.8[解析] △AOB 的周长等于AO +BO +AB ,而△AOD 的周长等于AO +DO +AD ,即两个三角形的周长之和为AB +AD +AC +BD .因为AC 与BD 的长度之和等于7 cm ,所以AB 与AD 的长度之和等于4.4 cm ,因此平行四边形的周长为8.8 cm.16.[答案] 7 cm[解析] 过点D 作DQ ∥MF ,延长FM 交AB 于点P ,易证△ADQ 和△DPM 为等边三角形, 故MD =PD ,MF =DQ =AD ,ME =BP ,所以MD +ME +MF 可转化为边AB 的长,等于7 cm. 17.解:设运动时间为t s ,则MP =2t cm ,QN =(12-4t )cm(t <3)或QN =(4t -12)cm(t >3). 当t <3时,如图①,因为MP ∥QN ,所以当MP =QN 时,四边形PQNM 为平行四边形, 即2t =12-4t ,解得t =2;当t >3时,如图②,因为MP ∥QN ,所以当MP =QN 时,四边形PNQM 为平行四边形, 即2t =4t -12,解得t =6.所以经过2 s或6 s后,以点P,Q,M,N为顶点的四边形为平行四边形.。
平行四边形知识点及同步练习、含答案3

平行四边形的特征【学习目标】1.探索并掌握平行四边形的特征.2.灵活运用平行四边形的特征解决问题.3.平行四边形一般转化成三角形的问题来解决.【基础知识概述】 1.平行四边形:(1)平行四边形的定义:两组对边分别平行的四边形是平行四边形. (2)平行四边形的表示:平行四边形用符号“”表示. 平行四边形ABCD 记作,读作平行四边形ABCD . (3)平行四边形定义的作用:①由定义知平行四边形的两组对边分别平行.②由定义可以得出只要四边形中两组对边分别平行,那么这个四边形是平行四边形. 2.平行四边形的特征:(1)平行四边形的邻角互补,对角相等. (2)平行四边形的对边平行且相等. (3)平行四边形的对角线互相平分.(4)平行四边形是中心对称图形,对角线的交点为对称中心.(5)若一条直线过平行四边形两对角线的交点,则这直线被一组对边截下的线段以对角线的交点为中点,且这条直线二等分平行四边形的面积.注意:①特征:都是通过连对角线把四边形问题转化成三角形问题来处理的,即通过平移或旋转,利用重合来证明的.②夹在两条平行线间的平行线段是指端点分别在两条平行线上的平行线段. ③互相平分指两条线段有公共的中点. 3.平行四边形特征的作用:可以用来证明线段相等、角相等及两直线平行等.如图12-1-1,有如下结论:⎪⎪⎩⎪⎪⎨⎧==∠=∠∠=∠==(对角线互相平分),(对角相等),(对边相等),(对边平行),是平行四边形,则如果四边形DO BO CO AO D B C A ADBC CD AB AD//BC CD //AB ABCD 4.两条平行线间的距离:(1)定义:两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线间的距离.(2)两平行线间的距离处处相等.注意:距离是指垂线段的长度,是大于0的.①平行线的位置确定后,它们的距离是定值,不随垂线段的位置改变.②平行线间的距离处处相等,因此在作平行四边形的高时,可根据需要灵活选择位置.5.平行四边形的面积:(1)如图12-1-2①,.也就是(a是平行四边形任何一边长,h必须是a边与其对边的距离).(2)同底(等底)同高(等高)的平行四边形面积相等.如图12-1-2②,有公共边BC,则.注意:这里的底是相对而言的,也就是高所在的边,平行四边形任意一边都可以作底,底确定后,高也就确定了.【例题精讲】例1如图12-1-3,已知的对角线相交于点O,过O作直线交AB于E,交CD 于F,可得OE=OF.为什么?分析:要得到OE=OF,可先证得它们所在△AEO与△CFO(△BEO与△DFO)重合.解:在中,∵AB∥CD,OD=OB,∴∠1=∠2,∠3=∠4,∴将△BOE绕点O旋转180度后与△DOF重合.∴OE=OF.注意:把线段与角归结为平行四边形的边,对角线或对角,利用平行四边形的特征证明.例2(1)在中,∠A︰∠B=2︰3,求各角的度数.(2)已知的周长为28cm,AB︰BC=3︰4,求它的各边的长.分析:(1)在平行四边形中,邻角是互补的,而对角是相等的,所以∠A与∠B必是邻角,其和为180°,可据此列式求出角度.(2)平行四边形的对边相等,所以周长为邻边之和的2倍,可以据此列式求出各边长.解:(1)由于∠A、∠B是平行四边形的两个邻角,所以∠A+∠B=180°.又因为∠A︰∠B=2︰3,不妨可设∠A=2k,∠B=3k,那么2k+3k=180°,可以解得k=36°,则∠A=∠C=72°,∠B=∠D=108°.(2)由于在中,AB=CD,BC=AD.所以AB+BC+CD+AD=28,即AB+BC =14.由题意得AB︰BC=3︰4,因此可设AB=3k,BC=4k,那么有3k+4k=14,解得k =2,则AB=CD=6cm,BC=AD=8cm.例3如图12-1-4,已知的周长为60 cm,对角线AC、BD相交于点O,△AOB 的周长比△BOC的周长长8cm,求这个四边形各边长.分析:由平行四边形对边相等知AB+BC=平行四边形周长的一半=30cm,又由△AOB 的周长比△BOC的周长长8 cm知AB—BC=8cm,由此两式,可得各边长.解:∵四边形ABCD为平行四边形,∴AB=CD,AD=CB,AO=CO.∵AB+CD+AD+CB=60,AO+AB+OB-(OB+BC+OC)=8,∴AB十BC=30,AB-BC=8,∴AB=CD=19,BC=AD=11.答:这个四边形各边长分别为19 cm,11 cm,19 cm,11 cm.注意:①平行四边形的邻边之和等于平行四边形周长的一半.②平行四边形被对角线分成四个小三角形,相邻两个三角形周长之差等于邻边之差.思考:如图12-1-4,如果△AOB与△AOD的周长之差为8,而AB∶AD=3∶2,那么的周长为多少?提示:周长为80.设AB=3x,则AD=2x,依题意有3x-2x=8,∴x=8,∴AB=3x=3×8=24,AD=2x=2×8=16.∴周长=2(24+16)=80.例4 如图12-1-5,在中,∠B=120°,DE⊥AB,垂足为E,DF⊥BC,垂足为F.求∠ADE,∠EDF,∠FDC的度数.分析:由平行四边形对角相等、邻角互补得∠A=∠C,∠A+∠B=180°,再由垂直得到角为90°即可.解:在中,∵∠A=∠C,AD∥BC,∴∠A+∠B=180°.∴∠A=180°-∠B=60°.∴∠C=60°.∵DE⊥AB,DF⊥BC,∴∠ADE=∠FDC=90°-∠A=90°-60°=30°.注意:在平行四边形中求角的度数时,一般运用平行四边形的特征,即对角相等、邻角互补来进行求解.【中考考点】会利用平行四边形证明角相等,线段相等及直线平行.【命题方向】多以中档题型出现,填空、选择、计算、证明等各种形式都会涉及.【常见错误分析】例7如图12-1-7,中,AC和BD交于O,OE⊥AD于E,OF⊥BC于F,则OE=OF.为什么?错解:∵,∴OA=OC,∵OE⊥AD,OF⊥BC,∴∠AOE=∠COF.又∠1=∠2,∴△AOE旋转180°后与△COF重合,∴OE=OF.误区分析:错误出于∠AOE=∠COF这一步骤,原因在于默认了E,O,F三点共线,而已知条件中并没有这个结论,其实E,O,F三点共线在证题过程中应该加以证明,否则就犯了推理没有根据,理由不充足的逻辑错误.正解:解法一:∵,∴AD∥BC,∴∠3=∠4.又OA=OC,∠AEO=∠CFO=90°,∴△AOE旋转180°后与△COF重合,∴OE=OF.解法二:∵AD∥BC,OE⊥AD∴OE⊥BC.又OF⊥BC,∴直线OE与OF重合,即E,O,F三点共线,∴∠1=∠2.又∵OA=OC,∠AEO=∠CFO=90°,∴△AOE旋转180°后与△COF重合,∴OE=OF.此命题可推广如下:已知中,AC 和BD 交于O ,过点O 作直线EF 交AD 于F ,交BC 于F ,则OE =OF .求解(略).这个推广后的命题,是平行四边形中一个十分重要的基本命题,利用它的结果可以证明很多问题成立.【学习方法指导】1.学习平行四边形的特征时,按照对角、对边、对角线的顺序去理解,便于记忆和应用.2.本节主要内容是平行四边形的定义及特征,并且要重点理解两条平行线间的距离的概念.【同步达纲练习】 一、填空题1.若一个平行四边形相邻的两内角之比为2︰3,则此平行四边形四个内角的度数分别为____________.2.在中,周长为28,两邻边之比为3︰4,则各边长为____________. 3.在中,∠A =30°,AB =7 cm ,AD =6 cm ,则=____________. 4.一个平行四边形的一边长是8,一条对角线长是6,则它的另一条对角线x 的取值范围为____________.5.中,周长为20cm ,对角线AC 交BD 于点O ,△OAB 比△OBC 的周长多4,则边AB =____________,BC =____________.6.平行四边形的边长等于5和7,这个平行四边形锐角的平分线把长边分成两条线段长各是____________.7.已知等腰△ABC 的一腰AB =9 cm ,过底边上任一点P 作两腰平行线分别交AB 于M ,交AC 于N ,则AN 十PN =____________.8.平行四边形两邻边分别是4和6,其中一边上的高是3,则平行四边形的面积是____________.9.平行四边形邻边长是 4 cm 和8cm ,一边上的高是 5 cm ,则另一边上的高是____________.10.如图12-1-8,中,E 是AD 的中点,BD 与EC 相交于F ,若2S EFD =∆,则BFC S ∆=____________.11.已知P 为内一点,,则PCD PAB S S ∆∆+=____________.12.已知的对角线相交于点O ,它的周长为10 cm ,△BCO 的周长比△AOB 的周长多2cm ,则AB =____________.二、解答题13.已知,如图12-1-9,在△ABC中,BD是∠ABC的平分线,DE∥BC交AB于E,EF ∥AC交BC于F,则BE=FC,为什么?14.如图12-1-10,中,E,F是对角线BD上两点,且BE=FD,连结AE,FC,则AE=FC,试说明理由.15.如图12-1-11,中,对角线AC长为10 cm,∠CAB=30°,AB长为6 cm,求的面积.16.如图12-1-12,在等边△ABC中,P为△ABC内一点,PD∥AB,PE∥BC,PF∥AC,D,E,F分别在AC,AB和BC上,试说明PD+PF+PE=AB.17.从平行四边形的一个锐角顶点作两条高,如果这两条高的夹角是135°,求此平行四边形的各角的度数.三、思考题18.如图12-1-13,EF 过对角线的交点O ,交AD 于E ,交BC 于F ,若AB =4,BC =5,OE =1.5,求四边形EFCD 的周长.19.以平行四边形ABCD 两邻边BC 、CD 为边向外作正△BCP 和正△CDQ ,则△APQ 为正三角形,请说明理由.参考答案【同步达纲练习】 一、1.72°,108°,72°,108° 2.6,8,6,83.2cm 21 4.10<x<22 5.7cm ,3 cm 6.5,2 7.9 cm 8.12或189.cm 2510.8 11.50 12.1.5cm 二、13.提示:由△BED 是等腰三角形得到BE =ED ,由四边形DEFC 是平行四边形得到ED =FC 即可.14.提示:通过△ABE 与△DCF 重合可以得出.15.2cm 30.16.延长FP 交AB 于G ,延长DP 交BC 于H ,四边形AGPD ,EBHD 为平行四边形,PD =AG ,PH =BE ,△GEP ,△PHF 为等边三角形,PE =EG ,PH =PF =BE ,PD +PF +PE =AG +GE +EB =AB .17.45°,135°,45°,135°. 三、18.OE =OF =1.5,AE =CF ,DE =BF ,ED +CF =BF +FC =5,CD =AB =4,四边形EFCD 的周长为2×1.5+5+4=12.19.提示:证明△ABP 、△QDA 、△QCP 三个三角形重合,可得出AP =AQ =PQ 即可.。
平行四边形的判定3 习题集

课题:19.1.2平行四边形的判定(3)主备:班级:姓名:学习时间:学习目标:1、掌握三角形中位线的概念,掌握三角形中位线定理2、能熟练运用三角形中位线性质进行有关证明和计算3、理解两条平行线间的距离。
学习重点:掌握和运用三角形中位线的性质学习难点:三角形中位线性质的证明(辅助线的添加方法)学习过程:一、学前准备:平行四边形的判定:1、定义:_____________________________________.2、判定定理(1)_____________________________________(2)_____________________________________(3)_____________________________________(4)_____________________________________ 二、探究新知:探究一:3、(例题):如图,点D,E分别是△ABC的边AB、AC的中点,求证:DE∥BC,且DE=12BC.归纳总结:4、三角形中位线的概念:连接三角形______的_______的线段叫做三角形的中位线5、(1)三角形有_____条中位线(2)三角形的中位线与中线有什么区别?三角形的中位线的两端点都是三角形边的________,而三角形的中线只有一个端点是边的_________,另一个端点是三角形的一个顶点。
6、三角形中位线定理:三角形的中位线_________于第三边,并且__________第三边的_______。
几何语言:∵DE是△ABC的中位线.∴DE____BC, DE= ______ BC三、针对练习:7、如图1:在△ABC中,DE是中位线(1)若∠ADE=60°,则∠B= 度,理由是____________________(2)若BC=8cm,则DE= cm,理由是_____________________8、如图2:在△ABC中,D、E、F分别是各边中点,AB=6cm,AC=8cm ,BC=10cm,则△DEF的周长= cm探究二:(预习课本89页)9、两点之间的距离:______________________________10、点到直线的距离:________________________________11、两条平行线间的距离:________________________________BA CDEF543AED FB C第1页第2页第3页 第4页APE FMNCB12、(例题)a,b 是两条平行线。
平行四边形判定练习题

平行四边形的判定练习题1、两组对角____的四边形是平行四边形;2、两组对边____或____的四边形是平行四边形;3、对角线___的四边形是平行四边形.4、一组对边____的四边形是平行四边形.5、下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是()A.1:2:3:4B.2:2:3:3C.2:3:2:3D.2:3:3:26、下面给出的条件中,能判定一个四边形是平行四边形的是()A.一组对边平行,另一组对边相等B.一组对边平行,一组对角互补C.一组对角相等,一组邻角互补D.一组对角相等,另一组对角互补7、在下面给出的条件中,能判定四边形ABCD是平行四边形的是()A.AB=BC,AD=CDB.AB∥CD,AD=BCC.AB∥CD,∠B=∠DD.∠A=∠B,∠C=∠D8、用两个全等的三角形按不同的方法拼成四边形,在这些拼出的四边形中,平行四边形最多有()A.1个B.2个C.3个D.4个9、在下列条件中,能判定四边形ABCD为平行四边形的是()A.AB=AD,CB=CDB.AB∥CD,AD=BCC.AB=CD,AD=BCD.∠A=∠B,∠C=∠D10、判断:一组对边平行,一组对边相等的四边形是平行四边形。
()11、判断:一组对边平行且相等的四边形是平行四边形.()12、判断:两组邻角相等的四边形是平行四边形.()13、判断:两组邻角互补的四边形是平行四边形.()14、判断:对角线互相垂直的四边形是平行四边形()15、判断:一组邻边相等且一条对角线平分另一条对角线的四边形是平行四边形。
()16、判断:平行四边形一组对边中点的连线与另一组对边平行且相等.()17、判断:对角线互相垂直且相等的四边形是平行四边形.()解答题:18、已知:如图,在平行四边形ABCD中,E,F分别是AB,DC上的两点,且AE=CF.求证:BD,EF互相平分19、已知:如图,在平行四边形ABCD中,点M,N在对角线AC上,且AM=CN. 求证:四边形BMDN是平行四边形.20、已知:如图,在平行四边形ABCD中,E,F分别是AB,CD上的两点,且AE=CF,AF,DE相交于点M,BF,CE相交于点N.求证:四边形EMFN是平行四边形.(要求不用三角形全等来证)21、已知:如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E,F在AC上,且AE=CF.求证:四边形EGFH是平四边形.22、已知:如图,在平行四边形ABCD中,AB=2BC,E,F在直线BC上,且BE=BC =CF.求证:AF⊥DE.BGE B C 友情提示:本资料代表个人观点,如有帮助请下载,谢谢您的浏览!。
平行四边形判定专项练习30题

平行四边形的判定专项练习30题(有答案)1.如图,四边形ABCD中,AD∥BC,ED∥BF,AF=CE,求证:ABCD是平行四边形.2.如图,四边形ABCD中,∠BAC=90°,AB=11﹣x,BC=5,CD=x﹣5,AD=x﹣3,AC=4.求证:四边形ABCD为平行四边形.3.已知四边形ABCD的对角线AC与BD交于点O,现给出四个条件:①OA=OC;②AB=CD;③∠BAD=∠DCB;④AD∥BC.请你从中选择两个,推出四边形ABCD为平行四边形,并写出你的推理过程.(1)从以上4个条件中任意选取2个条件,能推出四边形ABCD是平行四边形的有(用序号表示)_________ .(2)从(1)中选出一种情况,写出你的推理过程.4.如图,已知:点B、E、F、D在一条直线上,DF=BE,AE=CF.请从下列三个条件中选择一个合适的条件,添加到已知条件中,使四边形ABCD是平行四边形,并说明理由,供选择的三个条件(请从其中选择一个):①AB=DC;②BC=AD;③∠AED=∠CFB.5.如图,在▱ABCD中,AC交BD于点O,点E,点F分别是OA,OC的中点,请判断线段BE,DF的位置关系和数量关系,并说明你的结论.6.如图所示,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF,猜想:四边形ADEF 是什么四边形,试证明你的结论.7.如图,已知BE⊥AD,CF⊥AD,且BE=CF.求证:(1)AD是△ABC的中线;(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.8.如图,矩形ABCD的两条对角线AC和BD相交于点O,E、F是BD上的两点,且∠AEB=∠CFD.求证:四边形AECF 是平行四边形.9.如图:在四边形ABCD中,AD∥BC,AB=CD,E是BC上一点,DE=AB.求证:四边形ABED是平行四边形.10.如图,已知 AB∥DC,E是BC的中点,AE,DC的延长线交于点F;(1)求证:△ABE≌△FCE;(2)连接AC,BF.则四边形ABFC是什么特殊的四边形?请说明理由.11.等边△ABC中,点D在BC上,点E在AB上,且CD=BE,以AD为边作等边△ADF,如图.求证:四边形CDFE是平行四边形.12.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.若∠BAC=30°,EF⊥AB,垂足为F,连结DF.求证:(1)△ABC≌△EAF;(2)四边形ADFE是平行四边形.13.已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.求证:四边形DFGE是平行四边形.14.如图所示:在四边形ABCD中,AD∥BC、BC=18cm,CD=15cm,AD=10cm,AB=12cm,动点P、Q分别从A、C同时出发,点P以2cm/秒的速度由A向D运动,点Q以3cm/秒的速度由C向B运动.(1)几秒钟后,四边形ABQP为平行四边形?并求出此时四边形ABQP的周长(2)几秒钟后,四边形PDCQ为平行四边形?并求出此时四边形PDCQ的周长.15.求证:顺次连接四边形各边中点所得的四边形是平行四边形.16.△ABC中,中线BE、CF相交于O,M是BO的中点,N是CO的中点,求证:四边形MNEF是平行四边形.17.如图,AD=DB,AE=EC,FG∥AB,AG∥BC.(1)证明:△AGE≌△CFE;(2)说明四边形ABFG是平行四边形;(3)研究图中的线段DE,BF,FC之间有怎样的位置关系和数量关系.18.如图,△ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连接EF、EB.(1)求证:△ABE≌△ACD;(2)求证:四边形EFCD是平行四边形.19.已知在△ABC中,D、E分别是AB、AC的中点,点F在DE的延长线上,且EF=DE,图中有几个平行四边形?请说明你的理由.20.如图,在△ABC中,AD是中线,点E是AD的中点,过A点作BC的平行线交CE的延长线于点F,连接BF.求证:四边形AFBD是平行四边形.21.如图:在四边形ABCD中,AD∥BC,E是BC的中点,BC=2AD.找出图中所有的平行四边形,并选择一个说明它是平行四边形的理由.22.求证:两组对角分别相等的四边形是平行四边形.23.已知:如图,A、B、C、D在同一条直线上,且AB=CD,AE∥DF,AE=DF.求证:四边形EBFC是平行四边形.24.如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.图中的四边形BFCE 是平行四边形吗?为什么?25.已知点E、F、G、H分别为四边形ABCD四边的中点,试问四边形EFGH的形状并说明理由.26.如图,已知四边形ABCD中AD=BC,点A、B、E在同一条直线上,且∠B=∠EAD,试说明四边形ABCD是平行四边形.27.如图,AD∥BC,ED∥BF,且AE=CF,求证:四边形ABCD是平行四边形.28.已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证:四边形DEFG是平行四边形.29.如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.当AB≠AC时,求证:四边形ADFE为平行四边形.30.已知:在四边形ABCD中,AD∥BC,且AB=DC=5,AC=4,BC=3.求证:四边形ABCD为平行四边形.平行四边形的判定30题参考答案:1.∵AD∥BC,∴∠DAE=∠BCF,∵ED∥BF,∴∠DEF=∠BFE,∴∠AED=∠CFB,又∵AF=CE,∴AE=CF,在△ADE和△CBF中:∵∠DAE=∠BCF,∠AED=∠CFB,AE=CF,∴△ADE≌△CBF(AAS),∴AD=CB,即:AD∥CB,AD=CB,∴四边形ABCD是平行四边形,2.∵∠BAC=90°,AB=11﹣x,BC=5,AC=4.∴(11﹣x)2+42=52,解得:x1=8,x2=14>11(舍去),当x=8时,BC=AD=5,AB=CD=3,∴四边形ABCD为平行四边形.3.(1)解:能推出四边形ABCD是平行四边形的有①④、③④;故答案是:①④、③④;(2)以①④为例进行证明.如图,在四边形ABCD中,OA=OC,AD∥BC.证明:∵AD∥BC,∴∠DAO=∠BCO.∴在△AOD与△COB中,,∴△AOD≌△COB(ASA),∴AD=BC,∴在四边形ABCD中,AD BC,∴四边形ABCD为平行四边形.4.选择①,∵DF=BE,AE=CF,AB=CD,∴△ABE≌△CDF(sss),∴∠ABE=∠CDF,∴四边形ABCD是平行四边形.5. BE=DF,BE∥DF因为ABCD是平行四边形,所以OA=OC,OB=OD,因为E,F分别是OA,OC的中点,所以OE=OF,所以BFDE是平行四边形,所以BE=DF,BE∥DF 6.四边形ADEF是平行四边形.连接ED、EF,∵△ABD、△BCE、△ACF分别是等边三角形,∴AB=BD,BC=BE,∠DBA=∠EBC=60°.∴∠DBE=∠ABC.∴△ABC≌△DBE.同理可证△ABC≌△FEC,∴AB=EF,AC=DE.∵AB=AD,AC=AF,∴AD=EF,DE=AF.∴四边形ADEF是平行四边形7.(1)∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD.∵∠BDE=∠CDF,BE=CF,∴△BED≌△CFD.∴BD=CD.∴AD是△ABC的中线.(2)四边形BECF是平行四边形,由(1)得:BD=CD,ED=FD.∴四边形BECF是平行四边形8.∵四边形ABCD是矩形∴AB∥CD,AB=CD,∴∠ABE=∠CDF,又∵∠AEB=∠CFD,∴△ABE≌△CDF,∴BE=DF,又∵四边形ABCD是矩形,∴OA=OC,OB=OD,∴OB﹣BE=OD﹣DF,∴OE=OF,∴四边形AECF是平行四边形9.∵AD∥BC,AB=CD,∴四边形ABCD是等腰梯形,∴∠B=∠C,∵DE=AB,∴∠DEC=∠B,∴AB∥DE,∴四边形ABED是平行四边形.10.(1)证明:∵AB∥DC,∴∠1=∠2,∠FCE=∠EBA,∵E为BC中点,∴CE=BE,∵在△ABE和△FCE中,∠1=∠2,∠FCE=∠EBA,CE=BE,∴△ABE≌△FCE;(2)四边形ABFC是平行四边形;理由:由(1)知:△ABE≌△FCE,∴EF=AE,∵CE=BE,∴四边形ABFC是平行四边形11.连接BF,∵△ADF和△ABC是等边三角形,∴AF=AD=DF,AB=AC=BC,∠ABC=∠ACD=∠CAB=∠FAD=60°,∴∠FAD﹣∠EAD=∠CAB﹣∠EAD,∴∠FAB=∠CAD,在△FAB和△DAC中,∴△FAB≌△DAC(SAS),∴BF=DC,∠ABF=∠ACD=60°,∵BE=CD,∴BF=BE,∴△BFE是等边三角形,∴EF=BE=CD,在△ACD和△CBE中∵,∴△ACD≌△CBE(SAS),∴AD=CE=DF,∵EF=CD,∴四边形CDFE是平行四边形.12.(1)∵△ABE为等边三角形,EF⊥AB,∴EF为∠BEA的平分线,∠AEB=60°,AE=AB,在△ABC和△EAF中,,∴△ABC≌△EAF(AAS);(2)∵∠BAC=30°,∠DAC=60°,∴∠DAB=90°,即DA⊥AB,∵EF⊥AB,∴AD∥EF,∵△ABC≌△EAF,∴EF=AC=AD,∴四边形ADFE是平行四边形13.在△ABC中,∵AD=BD,AE=CE,∴DE∥BC且DE=BC.在△OBC中,∵OF=FB,OG=GC,∴FG∥BC且FG=BC.∴DE∥FG,DE=FG.∴四边形DFGE为平行四边形14.(1)x秒后,四边形ABQP为平行四边形.则2x=18﹣3x,解得x=3.6.3.6秒钟后,四边形ABQP为平行四边形,此时四边形ABQP的周长是3.6×2×2+12×2=38.4cm.(2)y秒后,四边形PDCQ为平行四边形.10﹣2y=3y,解得y=2.2秒钟后,四边形PDCQ为平行四边形,此时四边形PDCQ的周长是3.6×2×2+15×2=43.2cm.15.:连接BD,∵E、F为AD,AB中点,∴FE BD.又∵G、H为BC,CD中点,∴GH BD,故GH FE.同理可证,EH FG.∴四边形FGHE是平行四边形16.∵BE,CF是△ABC的中线,∴EF∥BC且EF=BC,∵M是BO的中点,N是CO的中点,∴EF∥MN且EF=MN,∴四边形MNEF是平行四边形.17.(1)证明:∵AG∥BC(已知)∴∠G=∠EFC(两直线平行,内错角相等)∵∠AEG=∠FEC(对顶角相等),又AE=EC(已知)∴△AGE≌△CFE(AAS);(2)说明:∵FG∥AB,AG∥BC(已知)∴四边形ABFG是平行四边形(平行四边形的定义);(3)解:线段DE,BF,FC之间的位置关系是DE∥BF,DE∥FC,数量关系是DE=BF=FC,理由:由(1)可知△AGE≌△CFE∴AG=FC,FE=EG(全等三角形的对应边相等),∴E是FG的中点,又∵AD=DB(已知)∴DE为三角形ABC的中位线,∴DE=BC,DE∥BC,即DE∥BF,DE∥FC,由(2)可知四边形ABFG是平行四边形∴AG=BF,∴BF=FC=BC,∴DE=BF=FC,即线段DE,BF,FC之间的位置关系是DE∥BF,DE∥FC,数量关系是DE=BF=FC.18.(1)∵△ABC和△ADE都是等边三角形,∴AE=AD,AB=AC,∠EAD=∠BAC=60°,∴∠EAD﹣∠BAD=∠BAC﹣∠BAD,即:∠EAB=∠DAC,∴△ABE≌△ACD(SAS);(2)证明:∵△ABE≌△ACD,∴BE=DC,∠EBA=∠DCA,又∵BF=DC,∴BE=BF.∵△ABC是等边三角形,∴∠DCA=60°,∴△BEF为等边三角形.∴∠EFB=60°,EF=BF∵△ABC是等边三角形,∴∠ABC=60°,∴∠ABC=∠EFB,∴EF∥BC,即EF∥DC,∴四边形EFCD是平行四边形19.平行四边形ADCF和平行四边形DBCF.理由:(1)∵D、E分别是AB、AC边的中点,∴DE∥BC ,.又∵EF=DE,∴DF=BC,∴四边形DBCF是平行四边形;(2)在四边形ADCF中,∵EF=DE,又∵E是AC边的中点,∴EA=EC,∴四边形ADCF是平行四边形20.∵E为AD中点,∴AE=DE,∵AF∥BC,∴∠AFE=∠DCE,在△AEF和△CED中∵,∴△AEF≌△CED(AAS),∴AF=DC,∵AD是△ABC的中线,∴BD=DC,∴AF=BD,即AF∥BD,AF=BD,故四边形AFBD是平行四边形21.图中有两个平行四边形:▱ABED、▱AECD.∵,∴AD=BE,∵AD∥BC,∴四边形ABED是平行四边形.22.已知:四边形ABCD,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形,证明:∵∠A=∠C,∠B=∠D,∠A+∠B+∠C+∠D=360°,∴2∠A+2∠B=360°,∴∠A+∠B=180°,∴AD∥BC,同理AB∥CD,∴四边形ABCD是平行四边形.在△ABE和△DCF中∴△ABE≌△DCF(SAS),∴EB=FC,∠ABE=∠DCF,∵∠ABE+∠EBC=180°,∠DCF+∠FCB=180°,∴∠EBC=∠FCB,∴BE∥FC,∵BE=FC,∴四边形EBFC是平行四边形24.∵CE∥BF,BD=CD,∴△BDF≌△CDE,∴BF=CE,∴四边形BFCE是平行四边形.25.四边形EFGH是平行四边形证明:连接AC、BD∵E、F、G、H分别为四边形ABCD四边的中点∴EH=BD,FG=BD,HG=AC,EF=AC∴EH=FG,EF=HG∴四边形EFGH是平行四边形.26.∵∠B=∠EAD,∴AD∥BC,∵AD=BC,∴四边形ABCD是平行四边形.27.∵AD∥BC,∴∠EAD=∠FCB,又ED∥BF,∴∠FED=∠EFB,∠AED=180°﹣∠FED,∠CFB=180°﹣∠EFB,∴∠AED=∠CFB,又已知AE=CF,∴△AED≌△CFB,∴AD=BC,∴四边形ABCD是平行四边形.28.∵AD∥BC,∴∠EAD=∠FCB,又ED∥BF,∴∠FED=∠EFB,∠AED=180°﹣∠FED,∠CFB=180°﹣∠EFB,∴∠AED=∠CFB,又已知AE=CF,∴△AED≌△CFB,∴AD=BC,∴四边形ABCD是平行四边形.29.∵△ABE、△BCF为等边三角形,∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°.∴∠FBE=∠CBA,在△FBE和△CBA中,,∴△FBE≌△CBA(SAS).∴EF=AC.又∵△ADC为等边三角形,∴CD=AD=AC.∴EF=AD.同理可得AE=DF.∴四边形AEFD是平行四边形30.∵AB=5,AC=4,BC=3∴AB2=AC2+BC2∴∠BCA=90°∵AD∥BC∴∠DAC=∠BCA=90°∵DC=5,AC=4,∴AD2=DC2﹣AC2=9∴AD=BC=3∴四边形ABCD为平行四边形.。
平行四边形判定(3)

平行四边形Hale Waihona Puke 2 平行四边形的判定(三)
复习引入:
问题一:
1.平行四边形的定义是什么?它有什么作用? 2.平行四边形有那些性质? 3.判定四边形是平行四边形的方法有哪些?
复习引入:
问题二: 在笔直的铁轨上,夹在铁轨之间的平行枕
木是否一样长?你能说明理由吗?与同伴交流.
问题数学化:
已知,直线a//b,过直线a上任两点A,B分别 向直线b作垂线,交直线b于点C,点D,如图, ① 线段AC,BD所在直线有什么样的位置关系? ② 比较线段AC,BD的长。
上海 2006 高考 理科 状元-武亦 文
武亦文 格致中学理科班学生 班级职务:学习委员 高考志愿:复旦经济 高考成绩:语文127分 数学142分 英语144分 物理145分 综合27分 总分585分
“一分也不能少”
“我坚持做好每天的预习、复习,每 天放学回家看半小时报纸,晚上10: 30休息,感觉很轻松地度过了三年 高中学习。”当得知自己的高考成 绩后,格致中学的武亦文遗憾地说 道,“平时模拟考试时,自己总有 一门满分,这次高考却没有出现, 有些遗憾。”
班主任: 我觉得何旋今天取得这样的成绩, 我觉得,很重要的是,何旋是土生土长的北京 二中的学生,二中的教育理念是综合培养学生 的素质和能力。我觉得何旋,她取得今天这么 好的成绩,一个来源于她的扎实的学习上的基 础,还有一个非常重要的,我觉得特别想提的, 何旋是一个特别充满自信,充满阳光的这样一 个女孩子。在我印象当中,何旋是一个最爱笑 的,而且她的笑特别感染人的。所以我觉得她 很阳光,而且充满自信,这是她突出的这样一 个特点。所以我觉得,这是她今天取得好成绩 当中,心理素质非常好,是非常重要的。
平行四边形的性质和判定提高训练 (3)

如图,在平面直角坐标系中,▱OABC的顶点A、C的坐标分别
为A(2,0)、C(-1,2),反比例函数 y k (k≠0)的图象
x
经过点B. (1)求k的值. (2)将▱OABC沿x轴翻折,点C落在点C′处,判断点C′是 否在反比例函数
y k x
(k≠0)的图象上,请通过计算说明理
由.
如图①,已知正比例函数和反比例函数的图象都经过点M(- 2,-1),且P(-1,-2)是双曲线上的一点,Q为坐标平面 上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B. (3) (2) 当点 如图②,当点 Q在直线MO Q在第一象限中的双曲线上运动时,作以 上运动时,直线MO上是否存在这样的点Q, (1) 写出正比例函数和反比例函数的关系式; OP、OQ 为邻边的平行四边形 OPCQ,求平行四边形OPCQ周 使得△ OBQ 与△OAP面积相等?如果存在,请求点的坐标; 如果不存在,请说明理由; 长的最小值.
(常考题)人教版初中数学八年级数学下册第三单元《平行四边形》测试题(含答案解析)(4)

一、选择题1.如图,ABC 中,//DE BC ,//EF AB ,要判定四边形DBFE 是菱形,可添加的条件是( )A .BD EF =B .AD BD =C .BE AC ⊥D .BE 平分ABC ∠ 2.如图为某城市部分街道示意图,四边形ABCD 为正方形,点G 在对角线BD 上,GE CD ⊥,GF BC ⊥,1500m AD =,小敏行走的路线为B AG E →→→,小聪行走的路线为B A D E F →→→→.若小敏行走的路程为3100m ,则小聪行走的路程为( )A .3100mB .4600mC .5500mD .6100m 3.如图,Rt ABC ∆中,90BAC AB AC AD BC ︒∠==⊥,,于点D ABC ∠,的平分线分别交AC AD 、于EF 、两点,M 为EF 的中点,AM 的延长线交BC 于点N ,连DM ,下列结论:①DF DN =; ②DMN ∆为等腰三角形;③DM 平分BMN ∠;④AE NC =,其中正确结论的个数是( )A .1个B .2个C .3个D .4个4.在平面直角坐标系中,长方形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,OA =3,OB =4,D 为边OB 的中点,若E 为x 轴上的一个动点,当△CDE 的周长最小时,求点E 的坐标( )A .(一3,0)B .(3,0)C .(0,0)D .(1,0) 5.下列说法正确的是( )A .有一个角是直角的平行四边形是正方形B .对角线互相垂直的矩形是正方形C .有一组邻边相等的菱形是正方形D .各边都相等的四边形是正方形 6.如图,把长方形纸片ABCD 沿对角线折叠,设重叠部分为EBD △.下列说法错误的是( )A .AE CE =B .12AE BE =C .EBD EDB ∠=∠ D .△ABE ≌△CDE 7.四边形ABCD 中,对角线AC BD 、交于点O .给出下列四组条件:①AB ∥CD ,AD ∥BC ;②AB CD =,AD BC =;③AO CO =,BO DO =;④AB ∥CD ,AD BC =.其中一定能判定这个四边形是平行四边形的条件共有( )A .1组;B .2组;C .3组;D .4组. 8.如图,点D 和点E 分别是BC 和BA 的中点,已知AC =4,则DE 为( )A .1B .2C .4D .89.如图,在123A A A △中,160A ∠=︒,230A ∠=︒,131A A =,3+n A 是1(1,2,3)n n A A n +=⋅⋅⋅的中点,则202120222023A A A △中最短边的长为( )A .100912B .101012 C .101112 D .10211210.如图,在Rt ABC 中,90C =∠,30A ∠=,D 是 AC 边的中点,DE AC ⊥于点D ,交AB 于点E ,若83AC =,则DE 的长是( )A .8B .6C .4D .211.如图,将长方形ABCD 沿对角线BD 折叠,使点C 落在点C ′处,BC ′交AD 于E ,AD =8,AB =4,则重叠部分(即BDE )的面积为( )A .6B .7.5C .10D .2012.如图所示,已知Rt ABC 中,90B ︒∠=,3AB =,4BC =,D F 、分别为AB AC 、的中点,E 是BC 上动点,则DEF 周长的最小值为( )A .240+B .213+C 13D .6二、填空题13.如图,四边形ABCD 为菱形,以AD 为斜边的Rt AED △的面积为3,2DE =,点E ,C 在BD 的同侧,点P 是BD 上的一动点,则PE PC +的最小值是_____________.14.如图,在矩形ABCD 中,连接AC ,按以下步骤作图:分别以点A ,C 为圆心,以大于12AC 的长为半径作弧,两弧分别相交于点M ,N ,作直线MN 交BC 于点E ,连接AE .若AB =1,BC =2,则BE =_____.15.在四边形ABCD 中,AD ∥BC ,要使四边形ABCD 是平行四边形,还需添加一个条件,这个条件可以是__________.(只要填写一种情况)16.如图,,E F 分别是ABCD 的边,AD BC 上的点.8,60,EF DEF =∠=︒将EFCD 四边形沿EF 翻折,得到四边形',EFCD ED '交BC 于点,G 则GEF △的周长为________.17.菱形有一个内角为120︒,较长的对角线长为63,则它的面积为__________. 18.如图,在ABC 中,45BAC ∠=︒,4AB AC ==,点D 是AB 上一动点,以AC 为对角线的所有平行四边形ADCE 中,DE 的最小值是________.19.如图,点E 是矩形ABCD 的边AD 上的一点,且12DE AE =,连接BE 并延长交CD 的延长线于点F ,若4AB =,6BC =,则EDF 的周长为__________.20.在△ABC中,AD是BC边上的高线,CE是AB边上的中线,CD=AE,且CE<AC.若AD=6,AB=10,则CE=___________三、解答题21.如图,将长方形ABCD边AD沿折痕AE折叠,使点D落在BC上的点F处,已知AB=6,△ABF的面积是24,求DE的长.22.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且=.∠=∠,BE CFAC BD=,EBC FCB求证:四边形AFDE是平行四边形;23.如图,CD是线段AB的垂直平分线,M是AC延长线上一点.(1)在图中补充完整以下作图,保留作图痕迹:作∠BCM 的角平分线CN ,过点B 作CN 的垂线,垂足为E ;(2)求证:四边形BECD 是矩形;(3)AB 与AC 满足怎样的数量关系时,四边形BECD 是正方形?证明你的结论. 24.如图,菱形ABCD 的边长为2.2BD =,E ,F 分别是边AD ,CD 上的两个动点,且满足2AE CF +=.(1)求证:BDE BCF △≌△;(2)判断BEF 的形状,并说明理由.25.如图,在中,,D 为的中点,,,连接交于点O .(1)证明:四边形为菱形; (2)若,,求菱形的高.26.如图1,正方形ABCD ,E 为平面内一点,且90BEC ∠=︒,把BCE 绕点B 逆时针旋转90︒得BAG ,直线AG 和直线CE 交于点F .(1)证明:四边形BEFG 是正方形;(2)若135AGD ∠=︒,猜测CE 和CF 的数量关系,并说明理由;(3)如图2,连接DF ,若13AB =,17CF =,求DF 的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】当BE 平分∠ABC 时,四边形DBFE 是菱形,可知先证明四边形BDEF 是平行四边形,再证明BD=DE 即可解决问题.【详解】解:当BE 平分∠ABC 时,四边形DBFE 是菱形,理由:∵DE ∥BC ,∴∠DEB=∠EBC ,∵∠EBC=∠EBD ,∴∠EBD=∠DEB ,∴BD=DE ,∵DE ∥BC ,EF ∥AB ,∴四边形DBFE 是平行四边形,∵BD=DE ,∴四边形DBFE 是菱形.其余选项均无法判断四边形DBFE 是菱形,故选:D .【点睛】本题考查菱形的判定、平行四边形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题.2.B解析:B【分析】连接CG ,由正方形的对称性,易知AG=CG ,由正方形的对角线互相平分一组对角,GE ⊥DC ,易得DE=GE .在矩形GECF 中,EF=CG .要计算小聪走的路程,只要得到小聪比小敏多走了多少就行.【详解】解:连接GC ,∵四边形ABCD 为正方形,所以AD=DC ,∠ADB=∠CDB=45°,∵∠CDB=45°,GE ⊥DC ,∴△DEG 是等腰直角三角形,∴DE=GE .在△AGD 和△GDC 中,AD CD ADG CDG DG DG ⎧⎪∠∠⎨⎪⎩===,∴△AGD ≌△GDC (SAS )∴AG=CG ,在矩形GECF 中,EF=CG ,∴EF=AG .∵BA+AD+DE+EF-BA-AG-GE ,=AD=1500m .∵小敏共走了3100m ,∴小聪行走的路程为3100+1500=4600(m ),故选:B .【点睛】本题考查了正方形的性质、全等三角形的性质和判定、矩形的性质及等腰三角形的性质.解决本题的关键是证明AG=EF ,DE=GE .3.D解析:D【分析】求出BD AD =,DBF DAN ∠=∠,BDF ADN ∠=∠,证明()FBD NAD ASA ≅即可判断①,证明()AFB CNA ASA ≅,推出CN AF AE ==即可判断④,证明()ABM NBM ASA ≅,得AM MN =,由直角三角形斜边的中线的性质推出AM DM MN ==,ADM ABM ∠=∠,即可判断③,根据三角形外角性质求出DNM ∠,证明MDN DNM ∠=∠,即可判断②.【详解】解:∵90BAC ∠=︒,AB AC =,AD BC ⊥,∴45ABC C ∠=∠=︒,AD BD CD ==,90ADN ADB ∠=∠=︒,∴45BAD CAD ∠=︒=∠,∵BE 平分ABC ∠, ∴122.52ABE CBE ABC ∠=∠=∠=︒, ∴9022.567.5BFD AEB ∠=∠=︒-︒=︒,∴67.5AFE BFD AEB ∠=∠=∠=︒,∴AF AE =,AM BE ⊥,∴90AMF AME ∠=∠=︒,∴9067.522.5DAN MBN ∠=︒-︒=︒=∠,在FBD 和NAD 中,FBD DAN BD ADBDF ADN ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴()FBD NAD ASA ≅,∴DF DN =,故①正确;在AFB △和CNA 中,4522.5BAF C AB ACABF CAN ∠=∠=︒⎧⎪=⎨⎪∠=∠=︒⎩, ∴()AFB CNA ASA ≅,∴AF CN =,∵AF AE =,∴AE CN =,故④正确;在ABM 和NBM 中,90ABM NBM BM BMAMB NMB ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩,∴()ABM NBM ASA ≅,∴AM MN =,在Rt ADN △中,AM DM MN ==,∴22.5DAN ADM ABM ∠=∠=︒=∠,∴22.522.545DMN DAN ADM ∠=∠+∠=︒+︒=︒,∴DM 平分BMN ∠,故③正确;∵4522.567.5DNA C CAN ∠=∠+∠=︒+︒=︒,∴1804567.567.5MDN DNM ∠=︒-︒-︒=︒=∠,∴DM MN =,∴DMN 是等腰三角形,故②正确.故选:D .【点睛】 本题考查了全等三角形的性质与判断,三角形外角性质,三角形内角和定理,直角三角形斜边上中线的性质,等腰三角形的性质和判定,解题的关键是熟练掌握这些性质定理进行证明求解.4.D解析:D【分析】由于C 、D 是定点,则CD 是定值,如果△CDE 的周长最小,即DE +CE 有最小值.为此,作点D 关于x 轴的对称点D′,当点E 在线段CD′上时,△CDE 的周长最小.【详解】如图,作点D 关于x 轴的对称点D′,连接CD′与x 轴交于点E ,连接DE .若在边OA 上任取点E′与点E 不重合,连接CE′、DE′、D′E′由DE′+CE′=D′E′+CE′>CD′=D′E +CE =DE +CE ,∴△CDE 的周长最小.∵OB =4,D 为边OB 的中点,∴OD =2,∴D (0,2),∵在长方形OACB 中,OA =3,OB =4,D 为OB 的中点,∴BC =3,D′O =DO =2,D′B =6,∵OE ∥BC ,∴Rt △D′OE ∽Rt △D′BC , ∴OE D O BC D B='', 即:623OE =,即:OE =1, ∴点E 的坐标为(1,0)故选:D .【点睛】此题主要考查轴对称−−最短路线问题,解决此类问题,一般都是运用轴对称的性质,将求折线问题转化为求线段问题,其说明最短的依据是:两点之间线段最短.5.B解析:B【分析】根据正方形的判定:①先判定四边形是矩形,再判定这个矩形有一组邻边相等;②先判定四边形是菱形,再判定这个矩形有一个角为直角进行分析即可.【详解】解:A.有一个角是直角的平行四边形是正方形,说法错误,应是矩形,不符合题意;B.对角线互相垂直的矩形是正方形,说法正确,符合题意;C.一组邻边相等的矩形是正方形,说法错误,不合题意;D.各边都相等的四边形是菱形,不是正方形,不合题意.故选B.【点睛】本题主要考查了正方形的判定,关键是掌握正方形的判定方法.6.B解析:B【分析】由折叠的性质和平行线的性质可得∠ADB=∠CBD,可得BE=DE,可证AE=CE,由“SAS”可证△ABE≌△CDE,即可求解.【详解】解:如图,∵把矩形纸片ABC'D沿对角线折叠,∴∠CBD=∠DBC',CD=C'D=AB ,AD=BC=BC',∵AD ∥BC',∴∠EDB=∠DBC',∴∠EDB=∠EBD ,故选项C 正确;∴BE=DE ,∵AD=BC ,∴AE=CE ,故选项A 正确;在△ABE 和△CDE 中,AB CD A C AE CE =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△CDE (SAS ),故选项D 正确; 没有条件能够证明12AE BE =, 故选:B .【点睛】本题考查了翻折变换,全等三角形的判定和性质,矩形的性质,掌握折叠的性质是本题的关键. 7.C解析:C【分析】根据平行四边形的判定方法对①②③④分别作出判断即可求解.【详解】解:①AB ∥CD ,AD ∥BC ,根据两组对边分别平行的四边形是平行四边形即可得到四边形是平行四边形;②AB CD =,AD BC =,根据两组对边分别相等的四边形是平行四边形即可得到四边形是平行四边形;;③AO CO =,BO DO =,根据对角线互相平分的四边形是平行四边形即可得到四边形是平行四边形;④AB ∥CD ,AD BC =,无法判定四边形是平行四边形.故选:C【点睛】本题考查了平行四边形的判定,熟练掌握平行四边形的定义和判定定理是解题关键. 8.B解析:B【分析】根据三角形中位线定理解答即可.【详解】解:∵点D 和点E 分别是BC 和BA 的中点,∴DE 是△ABC 的中位线,∴DE =12AC =12⨯4=2, 故选:B .【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.9.B解析:B【分析】根据已知条件和图形的变化可得前几个图形的最短边的长度,进而可得结论.【详解】解:在△A 1A 2A 3中,∠A 1A 3A 2=90°,∠A 2=30°,A 1A 3=1,A n+3是A n A n+1(n=1、2、3…)的中点,可知:A 4A 5//A 1A 3,A 3A 4=A 2A 4,∴∠A 3A 5A 4=90°,∠A 4A 3A 2=∠A 2=30°,∴△A 1A 2A 3是含30°角的直角三角形,同理可证△A n A n+1A n+2是含30°角的直角三角形.△A 1A 2A 3中最短边的长度为A 1A 3=1=012, △A 3A 4A 5中最短边的长度为A 4A 5=12=112, △A 5A 6A 7中最短边的长度为A 5A 7=21142=, …, 所以△A n A n+1A n+2中最短边的长度为1212n -,则△A 2019A 2020A 2021中最短边的长度为120211221122n --==101012. 故选:B .【点睛】 本题考查了规律型:图形的变化类,解决本题的关键是观察图形的变化寻找规律.也考查了直角三角形斜边的中线,三角形的中位线,平行线的性质,含30°角的直角三角形的性质,以及等腰三角形的性质等知识.10.C解析:C【分析】根据直角三角形的性质得到AB=2BC ,利用勾股定理求出BC ,再根据三角形中位线定理求出DE .【详解】解:∵在Rt △ABC 中,∠C=90°,∠A=30°,∴AB=2BC ,设BC=x ,则AB=2x ,∴(2224x x =+, 解得:x=8或-8(舍),∴BC=8,∵D 是 AC 边的中点,DE AC ⊥,∴DE=12BC=4, 故选C .【点睛】本题考查了含30°角的直角三角形的性质,三角形的中位线的性质,熟练掌握直角三角形的性质是解题的关键.11.C解析:C【分析】由折叠结合矩形的性质先证明,BE DE =设,BE DE x == 则8,AE x =- 再利用勾股定理求解,x 从而可得BDE 的面积.【详解】 解: 长方形ABCD ,8,4,AD AB ==//,AD BC ∴,ADB CBD ∴∠=∠由对折可得:,CBD C BD '∠=∠,ADB C BD '∴∠=∠,BE DE ∴=设,BE DE x == 则8,AE x =-由222,BE AB AE =+ ()22248,x x ∴=+-1680,x ∴=5,x ∴= 5,DE BE ∴==115410.22BDE S DE AB ∴==⨯⨯=故选:.C【点睛】本题考查的是矩形与折叠问题,勾股定理的应用,矩形的性质,掌握以上知识是解题的关键.12.B解析:B【分析】先根据三角形的中位线定理可求得DF 的长为2,然后作出点F 关于BC 的对称点F′,连接DF′交BC 于点E ,此时DEF 周长的最小,由轴对称图形的性质可知EF=EF′,从而可得到ED+EF=DF′,再证明四边形DBMF 为矩形,得出FF′=3,然后在Rt △DFF′中,由勾股定理可求得DF′的长度,从而可求得三角形DEF 周长的最小值.【详解】解:如图,作点F 关于BC 的对称点F′,连接DF′交BC 于点E .此时DE+EF 最小∵点D 、F 分别是AB 和AC 的中点,BC=4,3AB =,∴DF=12BC=2,DF//BC ,BD=1.5, ∵点F 与点F′关于BC 对称,∴EF=EF′,FF′⊥BC ,FM= F′M , ∴DE+EF 最小值为DE+ EF′=DF′,90DFF ∠'=︒,∵DF//BC ,90B ∠=︒,∴90B BDF FMB ∠=∠=∠=︒,∴四边形DBMF 为矩形,∴BD=FM=1.5,∴FF′=3,在Rt △DFF′中,2'2222313DF DF FF +=+='∴△DEF 周长的最小值=DF+D 13故选:B【点睛】本题主要考查的是轴对称路径最短问题,以及勾股定理,矩形的判定,作出点F 关于BC 的对称点,将DE+EF 转化为DF′的长是解题的关键.二、填空题13.3【分析】根据菱形的轴对称性可得AC 关于BD 对称当APE 三点共线时的值最小为AE 再根据三角形的面积即可得出答案【详解】解:∵四边形菱形∴AC 关于BD 对称∵点EC 在BD 的同侧∴当APE 三点共线时的值最 解析:3【分析】根据菱形的轴对称性可得A 、C 关于BD 对称,当A 、P 、E 三点共线时,PE PC +的值最小为AE ,再根据三角形的面积即可得出答案.【详解】解:∵四边形ABCD 菱形,∴A 、C 关于BD 对称,∵点E ,C 在BD 的同侧,∴当A 、P 、E 三点共线时,PE PC +的值最小,且最小值为AE ;∵以AD 为斜边的Rt AED △的面积为3, 2DE =, ∴112322⨯=⨯=AE DE AE , ∴AE=3, ∴PE PC +的最小值是3故答案为:3.【点睛】本题考查了菱形的性质、最短问题、面积法等知识,解题的关键是利用轴对称解决最值问题,是中考常考题型.14.【分析】根据作图过程可得MN 是AC 的垂直平分线可得EA=EC 再根据矩形性质和勾股定理即可得到结论【详解】解:在矩形ABCD 中∠B=90°根据作图过程可知:MN 是AC 的垂直平分线∴EA=EC ∴EA=C 解析:34【分析】根据作图过程可得MN 是AC 的垂直平分线,可得EA=EC ,再根据矩形性质和勾股定理即可得到结论.【详解】解:在矩形ABCD 中,∠B=90°,根据作图过程可知:MN 是AC 的垂直平分线,∴EA=EC ,∴EA=CE=BC-BE=2-BE ,在Rt △ABE 中,根据勾股定理,得222EA AB BE =+,∴22221BE BE -=+(),解得BE=34, 故答案为34. 【点睛】本题考查了作图-基本作图,线段垂直平分线的性质,矩形的性质,解决本题的关键是掌握基本作图方法.15.(答案不唯一)【分析】根据平行四边形的判定定理有一组对边平行且相等的四边形是平行四边形即可填写【详解】解:∵AD ∥BCAD=BC ∴四边形ABCD 是平行四边形故答案为:AD=BC (答案不唯一)【点睛】解析:AD BC =(答案不唯一)【分析】根据平行四边形的判定定理“有一组对边平行且相等的四边形是平行四边形”即可填写.【详解】解:∵AD ∥BC ,AD=BC ,∴四边形ABCD 是平行四边形.故答案为:AD=BC (答案不唯一)【点睛】本题考查了平行四边形的判定,熟知平行四边形的判定定理是解题的关键,本题有多种答案,如可以根据平行四边形的定义填写AB ∥CD 等.16.24【分析】根据平行四边形的性质得到AD ∥BC 由平行线的性质得到∠AEG=∠EGF 根据折叠的性质得到推出△GEF 是等边三角形于是得到结论【详解】解:∵四边形ABCD 是平行四边形∴AD ∥BC ∴∠AEG解析:24【分析】根据平行四边形的性质得到AD ∥BC ,由平行线的性质得到∠AEG=∠EGF ,根据折叠的性质得到60GEF DEF ∠=∠=︒,推出△GEF 是等边三角形,于是得到结论.【详解】解:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠AEG=∠EGF ,∵将四边形EFCD 沿EF 翻折,得到EFC D '',∴60GEF DEF ∠=∠=︒,∴∠AEG=60°,∴∠EGF=60°,∴△EGF 是等边三角形,∵EF=8,∴△GEF 的周长=24,故答案为:24.【点睛】此题考查平行四边形的性质,折叠的性质,等边三角形的判定及性质,熟练掌握基本性质是解题关键.17.【分析】由题意画出菱形根据菱形的对角线性质得继而解出由含30°角的直角三角形性质解得在中利用勾股定理解得进一步得到最后由菱形的面积公式解题即可【详解】解:如图菱形中在中设则解得菱形的面积故答案为:【 解析:183 【分析】 由题意画出菱形ABCD ,根据菱形的对角线性质得160,2BAC BAD AC BD ∠=∠=︒⊥,继而解出30ABO ∠=︒,由含30°角的直角三角形性质解得33BO =,在Rt ABO 中,利用勾股定理解得3AO =,进一步得到6AC =,最后由菱形的面积公式解题即可.【详解】解:如图,菱形ABCD 中,120BAD ∠=︒,160,2BAC BAD AC BD ∴∠=∠=︒⊥ 30ABO ∴∠=︒63BD =33BO ∴=在Rt ABO 中,设AO x =,则2AB x =,222(33)(2)x x ∴+=22274x x +=解得3x =3AO ∴=6AC ∴=∴菱形的面积6362183S =÷=故答案为:183.【点睛】本题考查菱形的性质、菱形的面积、含30°角的直角三角形、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.18.2【分析】平行四边形ADCE的对角线的交点是AC的中点O当OD⊥AB时OD最小即DE最小根据直角三角形勾股定理即可求解【详解】解:如图∵平行四边形ADCE的对角线的交点是AC的中点O又AB=AC=4解析:22【分析】平行四边形ADCE的对角线的交点是AC的中点O,当OD⊥AB时,OD最小,即DE最小,根据直角三角形勾股定理即可求解.【详解】解:如图∵平行四边形ADCE的对角线的交点是AC的中点O,又AB=AC=4∴OC=OA=12AC=2当OD⊥AB时,OD最小,即DE最小.∵OD⊥BA,∠BAC=45°,∴∠AOD=45°∴△ADO为等腰直角三角形在Rt△ADO由勾股定理可知OD=222∴2故答案为:2【点睛】本题考查了勾股定理,平行四边形的性质,即平行四边形对角线互相平分,正确理解DE 最小值的条件是关键.19.【分析】由矩形ABCD证明求解再证明证明再利用勾股定理求解从而可得答案【详解】解:矩形ABCD故答案为:【点睛】本题考查的是勾股定理的应用等腰三角形的判定与性质矩形的性质掌握以上知识是解题的关键解析:【分析】由矩形ABCD ,4AB =,6BC =,12DE AE =,证明6,AD BC == 90,A ADC ∠=∠=︒求解4AB AE ==,再证明45FED AEB ∠=∠=︒,证明2DE DF ==, 再利用勾股定理求解,EF 从而可得答案.【详解】 解: 矩形ABCD ,4AB =,6BC =6,AD BC ∴== 90,A ADC ∠=∠=︒ 12DE AE =,,AE DE AD += 42AE DE ∴==,,4AB AE ∴==,45,AEB ∴∠=︒45,FED ∴∠=︒90ADC ∠=︒,90EDF ,∴∠=︒ 45DEF DFE ∴∠=∠=︒,2DE DF ∴==,EF ∴===224DEF C ∴=++=+故答案为:4+【点睛】本题考查的是勾股定理的应用,等腰三角形的判定与性质,矩形的性质,掌握以上知识是解题的关键.20.【分析】先根据勾股定理求得AB 再做△ABD 的中位线EF 可得EF=3BF=DF=4从而可得CF=1再次利用勾股定理即可求得CE 【详解】解:∵AD 是BC 边上的高线AD=6AB=10∴∠D=90°∵CE 是【分析】先根据勾股定理求得AB ,再做△ABD 的中位线EF ,可得EF=3,BF=DF=4,从而可得CF=1,再次利用勾股定理即可求得CE .【详解】解:∵AD 是BC 边上的高线,AD =6,AB =10,∴∠D=90°,BD 8==,∵CE 是AB 边上的中线,CD =AE ,∴152CD AE BE AB ====, 取BD 的中点F,连接CF ,∴EF 为△ABD 的中位线,∴132EF AD ==,EF//AD , ∴∠EFB=∠D=90°, 在Rt △BEF 中,根据勾股定理,2222534BF BE EF =-=-=,∴DF=BD-BF=8-4=4,∴CF=CD-DF=5-4=1,在Rt △CEF 中,根据勾股定理,22221310CE CF EF +=+=10【点睛】本题考查三角形中位线的定理,勾股定理.能正确作出辅助线,构造直角三角形是解题关键.三、解答题21.103【分析】先根据三角形的面积公式求得BF 的长,然后根据勾股定理可求得AF=10,由翻折的性质和矩形的性质可知BC=10,故此FC=2,最后在△EFC 中,由勾股定理列方程求解即可.【详解】解:∵S △ABF =24,∴12AB•BF =24,即12×6×BF =24. 解得:BF=8.在Rt △ABF 中由勾股定理得:22AB BF +=10.由翻折的性质可知:BC=AD=AF=10,ED=FE .∴FC=10-8=2.设DE=x ,则EC=6-x .在Rt △EFC 中,由勾股定理得:EF 2=FC 2+EC 2,x 2=4+(6-x )2.解得:x=103, ∴DE=103. 【点睛】本题主要考查的是矩形与折叠、三角形的面积公式、勾股定理的应用,根据勾股定理列出关于x 的方程是解题的关键.22.见解析【分析】证明△ABE ≌△DCF ,得到AE=DF ,∠EAB=∠FDC ,推出AE ∥DF ,即可证明结论.【详解】解:∵AC=BD ,即AB+BC=CD+CB ,∴AB=CD ,∵∠EBC=∠FCB ,∴∠ABE=∠DCF ,在△ABE 和△DCF 中,AB CD ABE DCF BE CF =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△DCF (SAS ),∴AE=DF ,∠EAB=∠FDC ,∴AE ∥DF ,∴四边形AFDE 是平行四边形.【点睛】本题考查了全等三角形的判定和性质,平行四边形的判定,解题的关键是根据全等得到对应角和对应边相等.23.(1)如图所示,见解析;(2)见解析;(3)当ABAC 时,矩形BECD 是正方形,证明见解析.【分析】(1)根据角平分线及垂线的作图方法依次作图;(2)根据CD 是AB 的垂直平分线,推出∠CDB =90°,AC =BC ,利用CN 平分∠BCM 求出∠DCN =∠DCB +∠BCN =90°,由BE ⊥CN 求得∠BEC =90°,即可得到结论;(3)当AB时,矩形BECD 是正方形,由AD =BD ,ABAC ,求得BDAC ,根据AD ⊥CD ,∠CDB =90°,推出BD =CD ,由此得到矩形BECD 是正方形.【详解】(1)解:如图所示,(2)证明:∵ CD 是AB 的垂直平分线,∴ CD ⊥BD ,AD =BD ,∴ ∠CDB =90°,AC =BC ,∴ ∠DCB =12∠ACB , ∵ CN 平分∠BCM , ∴∠BCN =12∠BCM , ∵∠ACB +∠BCM =180°, ∴∠DCN =∠DCB +∠BCN =12(∠ACB +∠BCM )=90°, ∵ BE ⊥CN ,∴ ∠BEC =90°,∴ 四边形BECD 是矩形;(3)当AB 2时,矩形BECD 是正方形∵ AD =BD ,AB 2AC ,∴ BD 2, ∵ AD ⊥CD ,∠CDB =90°,∴ BD =CD ,∴ 矩形BECD 是正方形.【点睛】此题考查作图—角平分线、垂线,矩形的判定定理,正方形的判定定理,正确作图及熟练掌握矩形和正方形的判定定理是解题的关键.24.(1)见解析;(2)等边三角形,理由见解析【分析】(1)由菱形ABCD 边长与对角线都是2,知ABD △和BCD △都是等边三角形.可得60BDE BCF ∠=∠=︒,BD BC =,可证BDE BCF △≌△;(2)由BDE BCF △≌△,得DBE CBF ∠=∠,BE BF =,利用=60DBF DBE DBF CBF ∠+∠=∠+∠︒.可证BEF 为等边三角形.【详解】(1)证明:∵菱形ABCD 的边长为2,2BD =,∴ABD △和BCD △都是等边三角形.∴60BDE BCF ∠=∠=︒,BD BC =,∵2AE DE AD +==,而2AE CF +=,∴DE CF =,∴BDE BCF △≌△;(2)解:BEF 为等边三角形.理由如下:∵BDE BCF △≌△,∴DBE CBF ∠=∠,BE BF =,∵60DBC DBF CBF ∠=∠+∠=︒°,∴60DBF DBE ∠+∠=︒.即60EBF ∠=︒.∴BEF 为等边三角形.【点睛】 本题考查菱形的性质,等边三角形的判定与性质,三角形全等判定与性质,掌握菱形的性质,等边三角形的判定与性质,三角形全等判定与性质是解题解题关键.25.(1)见解析;(2)【分析】(1)先证明四边形ADCE 是平行四边形,再由直角三角形斜边上的中线性质得出CD=AB=AD ,即可得出四边形ADCE 为菱形;(2)过点D 作DF ⊥CE ,垂足为点F ;先证明△BCD 是等边三角形,得出∠BDC=∠BCD=60°,CD=BC=6,再由平行线的性质得出∠DCE=∠BDC=60°,在Rt △CDF 中,求出DF 即可.【详解】解:(1)证明:∵AE ∥CD ,CE ∥AB ,∴四边形ADCE 是平行四边形,∵∠ACB=90°,D 为AB 的中点,∴CD=AB=AD ,∴四边形ADCE 为菱形;(2)过点D 作DF ⊥CE ,垂足为点F ,如图所示:DF 即为菱形ADCE 的高,∵∠B=60°,CD=BD ,∴△BCD 是等边三角形,∴∠BDC=∠BCD=60°,CD=BC=6,∵CE ∥AB ,∴∠DCE=∠BDC=60°,∴∠CDF=30°,又∵CD=BC=6,∴CF=3,∴在Rt △CDF 中,DF==.【点睛】本题考查了平行四边形的判定、菱形的判定、等边三角形的判定与性质、平行线的性质,熟练掌握直角三角形的性质,并能进行推理论证与计算是解决问题的关键.26.(1)见解析;(2)CE=CF ,理由见解析;(3)522【分析】(1)根据正方形的判定定理进行证明即可;(2)证明Rt ADH ≌Rt BAG 得DH AG =,AH=BG ,再证明△DHG 是等腰直角三角形,可得DH=BH=AG ,最后由BEFG 是正方形可得结论;(3)分点F 在AB 右侧和左侧两种情况求解即可.【详解】解:(1)证明:90BEC =︒∠,把BCE 绕点B 逆时针旋转90︒得BAG , BE BG ∴=,90EBG ∠=︒,90BGA ∠=︒,则90BGF ∠=︒,90BEC EBG BGF ∴∠=∠=∠=︒,∴四边形BEFG 是正方形;(2)CE CF =,理由如下:过D 点作DH AF ⊥,垂足为H ,如图,四边形ABCD 是正方形,90BAD ∴∠=︒,AB AD =,90BGA ∠=︒,90DAH BAG ∴∠+∠=︒,90BAG ABG ∠+∠=︒,DAH ABG ∴∠=∠,在Rt ADH 和Rt BAG 中,90,DAH ABG BGA AHD AD AB ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩Rt ADH ∴≌()Rt BAG AAS ,DH AG ∴=,∵∠DGH =180°-∠AGD =45°∴在Rt △DHG 中,∠GDH =45°∴DH =GH =AG ∴1122AG GH AH BG === 又AG CE =,EF BG =,2EF CE ∴=,CE CF ∴=;(3)①点F 在AB 右侧时,如图,过D 作DK ⊥AG ,交其延长线于K .设正方形BEFG 的边长为x ,则BE x =,17CE x =-,在Rt BEC △中,13BC =,根据勾股定理可得,222BE CE BC +=,即222(17)13x x +-=,解得112x =,25(x =不符合条件,舍去),即12BG BE ==,17125AG CE ==-=,∵四边形BEFG 是正方形,∴∠BAD =90°.∵DK ⊥AG ,∴∠K =90°.∵∠BAG +∠KAD =180°—∠BAD =90°∠ADK +∠KAD =90°∴∠BAG =∠ADK在Rt △ABG 和Rt △DAK 中,90G K AB ADBAG ADK ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩所以Rt △ADK ≌Rt BAG ,则AK =BG =12,DK =AG =5,∵AF +FK =AK =BG=GF=AG +AF∴FK =AG =5在R t △DFK 中,根据勾股定理可得,DF 2252DK FK +=②点F在AB左侧时,如图,过D作DK⊥AG,交其延长线于K.方法同①,可得FK=AG=12,在R t△DFK中,根据勾股定理可得,DF22122+=DK FK综上所述,DF的长为522【点睛】此题是几何变换综合题,主要考查了旋转的性质,全等三角形的判定和性质,正方形的性质,勾股定理,熟练掌握相关性质和定理是解本题的关键.。
青岛版2020八年级数学下册第六章平行四边形单元基础达标练习题3(附答案)
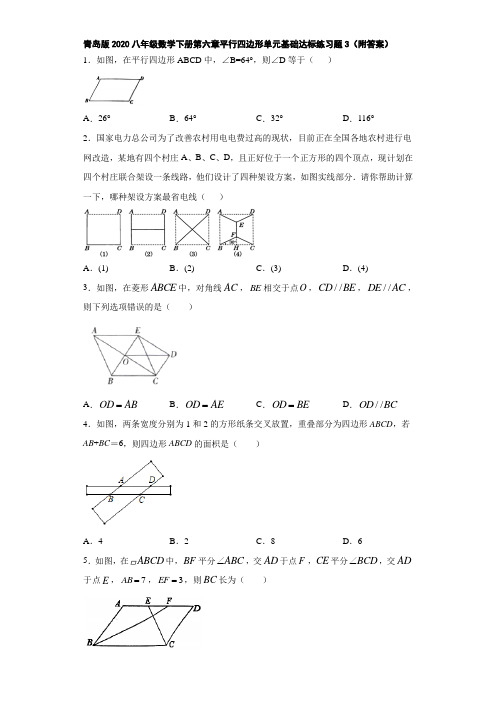
12.从 A,B 两题中任选一题作答:
A.如图,在 ΔABC 中,分别以点 A,B 为圆心,大于 1 AB 的长为半径画弧,两弧交与 2
点 M,N,作直线 MN 交 AB 于点 E,交 BC 于点 F,连接 AF。若 AF=6,FC=4,连 接点 E 和 AC 的中点 G,则 EG 的长为__.
B.如图,在 ΔABC 中,AB=2,∠BAC=60°,点 D 是边 BC 的中点,点 E 在边 AC 上 运动,当 DE 平分 ΔABC 的周长时,DE 的长为__.
19.如图,△ ABC 中,D、E 分别是 BC、AC 的中点,BF 平分∠ABC,交 DE 于点 F, 若 AB=12,BC=9,则 EF 的长是_____.
20.如图,在直角坐标系中,A、B 两点的坐标分别为(0,8)和(6,0),将一根橡皮筋两 端固定在 A、B 两点处,然后用手勾住橡皮筋向右上方拉升,使橡皮筋与坐标轴围成一 个矩形 AOBC,则橡皮筋被拉长了_____个单位长度.
菱形的两对角线长分别为 6、4,则该菱形的面积为 6×4× =12.
故选:C. 【点睛】 考查菱形的面积公式:对角线的积的一半,还考查了学生的读图能力. 8.A 【解析】 【分析】 根据真命题的概念逐个判断即可. 【详解】 根据真命题的概念可得,根据条件可以推出结论,就说明此命题为真命题. A 对角线互相平分的四边形是平行四边形是真命题. B 对角线相等的四边形是矩形是假命题,因为等腰梯形的对角线也相等. C 对角线互相垂直的四边形的菱形是假命题,梯形的对角线也可能垂直.
21.如图,在四边形 ABCD 中,E、F 分别是 AD、BC 的中点,G、H 分别是 BD、AC 的中点且 AB=CD,则 EF 与 GH 有怎样的关系?请说明你的理由.
平行四边形练习题(3套)附答案

卷1一、选择题(3′×10=30′)1.下列性质中,平行四边形具有而非平行四边形不具有的是().A.内角和为360° B.外角和为360° C.不确定性 D.对角相等2.ABCD中,∠A=55°,则∠B、∠C的度数分别是().A.135°,55° B.55°,135° C.125°,55° D.55°,125°3.下列正确结论的个数是().①平行四边形内角和为360°;②平行四边形对角线相等;③平行四边形对角线互相平分;④平行四边形邻角互补.A.1 B.2 C.3 D.44.平行四边形中一边的长为10cm,那么它的两条对角线的长度可能是().A.4cm和6cm B.20cm和30cm C.6cm和8cm D.8cm和12cm5.在ABCD中,AB+BC=11cm,∠B=30°,S ABCD=15cm2,则AB与BC的值可能是(). A.5cm和6cm B.4cm和7cm C.3cm和8cm D.2cm和9cm6.在下列定理中,没有逆定理的是().A.有斜边和一直角边对应相等的两个直角三角形全等;B.直角三角形两个锐角互余;C.全等三角形对应角相等;D.角平分线上的点到这个角两边的距离相等.7.下列说法中正确的是().A.每个命题都有逆命题 B.每个定理都有逆定理C.真命题的逆命题是真命题 D.假命题的逆命题是假命题8.一个三角形三个内角之比为1:2:1,其相对应三边之比为().A.1:2:1 B.12:1 C.1:4:1 D.12:1:29.一个三角形的三条中位线把这个三角形分成面积相等的三角形有()个.A.2 B.3 C.4 D.510.如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=•14,•AC=19,则MN的长为().A.2 B.2.5 C.3 D.3.5二、填空题(3′×10=30′)11.用14cm长的一根铁丝围成一个平行四边形,短边与长边的比为3:4,短边的比为________,长边的比为________.12.已知平行四边形的周长为20cm,一条对角线把它分成两个三角形,•周长都是18cm,则这条对角线长是_________cm.13.在ABCD中,AB的垂直平分线EF经过点D,在AB上的垂足为E,•若ABCD•的周长为38cm,△ABD的周长比ABCD的周长少10cm,则ABCD的一组邻边长分别为______.14.在ABCD中,E是BC边上一点,且AB=BE,又AE的延长线交DC的延长线于点F.若∠F=65°,则ABCD的各内角度数分别为_________.15.平行四边形两邻边的长分别为20cm,16cm,两条长边的距离是8cm,•则两条短边的距离是_____cm.16.如果一个命题的题设和结论分别是另一个命题的______和_______,•那么这两个命题是互为逆命题.17.命题“两直线平行,同旁内角互补”的逆命题是_________.18.在直角三角形中,已知两边的长分别是4和3,则第三边的长是________.19.直角三角形两直角边的长分别为8和10,则斜边上的高为________,斜边被高分成两部分的长分别是__________.20.△ABC的两边分别为5,12,另一边c为奇数,且a+b+•c•是3•的倍数,•则c•应为________,此三角形为________三角形.三、解答题(6′×10=60′)21.如右图所示,在ABCD中,BF⊥AD于F,BE⊥CD于E,若∠A=60°,AF=3cm,CE=2cm,求ABCD的周长.22.如图所示,在ABCD中,E、F是对角线BD上的两点,且BE=DF.求证:(1)AE=CF;(2)AE∥CF.F C DAEB23.如图所示,ABCD的周长是103+62,AB的长是53,DE⊥AB于E,DF⊥CB交CB•的延长线于点F,DE的长是3,求(1)∠C的大小;(2)DF的长.24.如图所示,ABCD中,AQ、BN、CN、DQ分别是∠DAB、∠ABC、∠BCD、•∠CDA的平分线,AQ与BN交于P,CN与DQ交于M,在不添加其它条件的情况下,试写出一个由上述条件推出的结论,并给出证明过程(要求:•推理过程中要用到“平行四边形”和“角平分线”这两个条件).25.已知△ABC的三边分别为a,b,c,a=n2-16,b=8n,c=n2+16(n>4).求证:∠C=90°.26.如图所示,在△ABC中,AC=8,BC=6,在△ABE中,DE⊥AB于D,DE=12,S△ABE=60,•求∠C的度数.27.已知三角形三条中位线的比为3:5:6,三角形的周长是112cm,•求三条中位线的长.28.如图所示,已知AB=CD,AN=ND,BM=CM,求证:∠1=∠2.29.如图所示,△ABC的顶点A在直线MN上,△ABC绕点A旋转,BE⊥MN于E,•CD•⊥MN 于D,F为BC中点,当MN经过△ABC的内部时,求证:(1)FE=FD;(2)当△ABC继续旋转,•使MN不经过△ABC内部时,其他条件不变,上述结论是否成立呢?30.如图所示,E是ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF =S△EFC.答案:一、1.D 2.C 3.C 4.B 5.A 6.C 7.A 8.B 9.C 10.C二、11.3cm 4cm 12.8 13.9cm和10cm 14.50°,130°,50°,130° • • 15.10 16.结论题设 17.同旁内角互补,两直线平行18.5.13 直角三、21.ABCD的周长为20cm 22.略23.(1)∠C=45°(2) 24.略25.•略 26.∠C=90° 27.三条中位线的长为:12cm;20cm;24cm28.提示:连结BD,取BD•的中点G,连结MG,NG29.(1)略(2)结论仍成立.提示:过F作FG⊥MN于G 30.略卷二一、填空题(每空2分,共28分)1.已知在 中,AB =14cm ,BC =16cm ,则此平行四边形的周长为 cm .2.要说明一个四边形是菱形,可以先说明这个四边形是 形,再说明 (只需填写一种方法)3.如图,正方形ABCD 的对线AC 、BD 相交于点O .那么图中共有 个等腰直角三角形.4.把“直角三角形、等腰三角形、等腰直角三角形”填入下列相应的空格上.(1)正方形可以由两个能够完全重合的 拼合而成; (第3题)(2)菱形可以由两个能够完全重合的 拼合而成;(3)矩形可以由两个能够完全重合的 拼合而成. 5.矩形的两条对角线的夹角为 60,较短的边长为12cm ,则对角线长为 cm .6.若直角梯形被一条对角线分成两个等腰直角三角形,那么这个梯形中除两个直角外,其余两个内角的度数分别为 和 .7.平行四边形的周长为24cm ,相邻两边长的比为3:1,那么这个平行四边形较短的边长为 cm .8.根据图中所给的尺寸和比例,可知这个“十”字标志的周长为 m .(第8题) (第10题) 9.已知平行四边形的两条对角线互相垂直且长分别为12cm 和6cm ,那么这个平行四边形 的面积为 2cm .10.如图,l 是四边形ABCD 的对称轴,如果AD ∥BC ,有下列结论: (1)AB ∥CD ;(2)AB=CD ;(3)AB ⊥BC ;(4)AO=OC .其中正确的结论是 .(把你认为正确的结论的序号都填上)二、选择题(每题3分,共24分)11. 如果一个多边形的内角和等于一个三角形的外角和,那么这个多边形是( )A 、三角形B 、四边形C 、五边形D 、六边形12.下列说法中,错误的是 ( )A.平行四边形的对角线互相平分B.对角线互相平分的四边形是平行四边形C. 平行四边形的对角相等D.对角线互相垂直的四边形是平行四边形13.给出四个特征(1)两条对角线相等;(2)任一组对角互补;(3)任一组邻角互补;(4)是轴对称图形但不是中心对称图形,其中属于矩形和等腰梯形共同具有的特征的共有 ( )A.1个B.2个C.3个D.4个14. 四边形ABCD 中,AD//BC ,那么 的值可能是( )A 、3:5:6:4B 、3:4:5:6C 、4:5:6:3D 、6:5:3:415.如图,直线a ∥b ,A 是直线a 上的一个定点,线段BC 在直线b 上移动,那么在移动过程中ABC ∆的面积 ( )A.变大B.变小C.不变D.无法确定 AB C D EF 1m 1m A B C a b ABCD A B CD O A B CD O l(第15题) (第16题) (第17题)16.如图,矩形ABCD 沿着AE 折叠,使D 点落在BC 边上的F 点处,如果 60=∠BAF ,则DAE ∠ 等于 ( )A. 15B. 30C. 45D. 6017.如图,在ABC ∆中,AB=AC =5,D 是BC 上的点,DE ∥AB 交AC 于点E ,DF ∥AC 交AB 于点F , 那么四边形AFDE 的周长是 ( )A.5B.10C.15D.2018.已知四边形ABCD 中,AC 交BD 于点O ,如果只给条件“AB ∥CD ”,那么还不能判定四形 ABCD 为平行四边形,给出以下四种说法:(1)如果再加上条件“BC=AD ”,那么四边形ABCD 一定是平行四边形;(2)如果再加上条件“BCD BAD ∠=∠”,那么四边形ABCD 一定是平行四边形;(3)如果再加上条件“AO=OC ”,那么四边形ABCD 一定是平行四边形;(4)如果再加上条件“CAB DBA ∠=∠”,那么四边形ABCD 一定是平行四边形其中正确的说法是( )A.(1)(2)B.(1)(3)(4)C.(2)(3)D.(2)(3)(4)三、解答题(第19题8分,第20~23题每题10分,共48分)19.如图, 中,DB=CD , 70=∠C ,AE ⊥BD 于E .试求DAE ∠的度数. (第19题)20.如图,中,G 是CD 上一点,BG 交AD 延长线于E ,AF=CG , 100=∠DGE . (1)试说明DF=BG ; (2)试求AFD ∠的度数.(第20题)21.工人师傅做铝合金窗框分下面三个步骤进行:(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH ;(2)摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ;(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: .A BC D EABCD A B C D F E GABCD(图①) (图②) (图③) (图④)(第21题)22.李大伯家有一口如图所示的四边形的池塘,在它的四个角上均有一棵大柳树,李大伯开挖池塘,使池塘面积扩大一倍,又想保持柳树不动,如果要求新池塘成平行四边形的形状.请问李大伯愿望能否实现?若能,请画出你的设计;若不能,请说明理由.(第22题)ADBC答案1.60.2.平行四边形;有一组邻边相等.3.8. 提示:它们是.,,,,,,,ACDBCDABCABDAODCODBOCAOB∆∆∆∆∆∆∆∆4.(1)等腰直角三角形; (2)等腰三角形; (3)直角三角形.7.3.8.4. 提示:如图所示,将“十”字标志的某些边进行平移后可得到一个边长为1m的正方形,所以它的周长为4m.8题)9. 36. 提示:菱形的面积等于菱形两条对角线乘积的一半.10. (1)(2)(4). 提示:四边形ABCD是菱形.11.B. 12.D.13.C. 14.C.15.C. 提示:因为ABC∆的底边BC的长不变,BC边上的高等于直线ba,之间的距离也不变,所以ABC∆的面积不变.16.A. 提示:由于()BAFDAEFAEDAEFAE∠-=∠=∠∠∠9021,所以通过折叠后得到的是由. 17.B. 提示:先说明DF=BF,DE=CE,所以四边形AFDE的周长=AF+DF+DE+AE=AF+BF+CE+AE=AB+AC.18.C.19.因为BD=CD,所以,CDBC∠=∠又因为四边形ABCD是平行四边形,所以AD∥BC,所以,DBCD∠=∠因为20709090,,=-=∠-=∠∆⊥DDAEAEDBDAE中所以在直角.20.(1)因为四边形ABCD是平行四边形,所以AB=DC,又AF=CG,所以AB-AF=DC-CG,即GD=BF,又DG∥BF,所以四边形DFBG是平行四边形,所以DF=BG;(2)因为四边形DFBG是平行四边形,所以DF∥GB,所以AFDGBF∠=∠,同理可得DGEGBF∠=∠,所以100=∠=∠DGEAFD.21.(1)平行四边,两组对边分别相等的四边形是平行四边形;(2)矩,有一个是直角的平行四边形是矩形.22.如图所示,连结对角线AC、BD,过A、B、C、D分别作BD、AC、BD、AC的平行线,且这些平行线两两相交于E、F、G、H,四边形EFGH即为符合条件的平行四边形.ABCDEFGH练习31、把正方形ABCD 绕着点A ,按顺时针方向旋转得到正方形AEFG ,边FG 与BC 交于点H (如图).试问线段HG 与线段HB 相等吗?请先观察猜想,然后再证明你的猜想.2、四边形ABCD 、DEFG 都是正方形,连接AE 、CG .(1)求证:AE =CG ;(2)观察图形,猜想AE 与CG 之间的位置关系,并证明你的猜想.3、将平行四边形纸片ABCD 按如图方式折叠,使点C 与A 重合,点D 落到D ′ 处,折痕为EF .(1)求证:△ABE ≌△AD ′F ;(2)连接CF ,判断四边形AECF 是什么特殊四边形?证明你的结论.挑战自我:1、 (2010年眉山市).如图,每个小正方形的边长为1,A 、B 、C 是小正方形的顶点,则∠ABC 的度数为( )A .90°B .60°C .45°D .30°2、(2010福建龙岩中考)下列图形中,单独选用一种图形不能进行平面镶嵌的图形是( )A. 正三角形B. 正方形C. 正五边形D. 正六边形3.(2010年北京顺义)若一个正多边形的一个内角是120°,则这个正多边形的边数是( )A .9B .8C .6D .4A B C D E F D ′ DC A B G H F E4、(2010年福建福州中考)如图4,在□ABCD 中,对角线AC 、BD 相交于点O ,若AC=14,BD=8,AB=10,则△OAB 的周长为 。
3平行四边形的判定作业

第三章平行四边形的判定(课后作业)1.如图,四边形ABCD中,下列条件不能判定四边形ABCD是平行四边形的是()A.AB∥CD,AD∥BC B.AB∥CD,AB=CD C.AB=CD,AD=BC D.AD∥BC,AB=CD2.如果四边形ABCD的对角线相交于点O,且AO=CO,那么下列条件中不能判断四边形ABCD为平行四边形的是()A.OB=OD B.AB∥CD C.AB=CD D.∠ADB=∠DBC3.如图,在四边形ABCD中,若已知AB∥CD,再添加下列条件之一,能使四边形ABCD成为平行四边形的条件是()A.∠DAC=∠BCA B.∠DCB+∠ABC=180°C.∠ABD=∠BDC D.∠BAC=∠ACD(第1题图)(第3题图)4.四边形ABCD中,AD∥BC.要判别四边形ABCD是平行四边形,还需满足条件()A.∠A+∠C=180°B.∠B+∠D=180°C.∠B+∠A=180°D.∠A+∠D=180°5.若以A(﹣1,0),B(2,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在()A.第一象限B.第二象限C.第三象限D.第四象限6.一个四边形的三个相邻内角度数依次如下,那么其中是平行四边形的是()A.88°,108°,88°B.88°,104°,108°C.88°,92°,92°D.88°,92°,88°7.已知凸四边形ABCD中,AB=6cm,BC=5cm,CD=6cm,当AD=__________cm时,四边形ABCD为平行四边形.8.在如图所示的四边形ABCD中,已知AB∥CD,要使它为平行四边形,在不添加任何辅助线的前提下,还需添加一个条件,这个条件是__________.9.如图所示,在平行四边形ABCD中,E、F分别为AD、BC边上的一点,若添加一个条件__________,则四边形EBFD为平行四边形(只填一个条件即可).(第9题图)(第10题图)10.点A、B、C是平面内不在同一条直线上的三点,点D是此平面内任意一点,若A、B、C、D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有__________个.11.已知:如图,在四边形ABCD中,E是边BC的中点,连接DE并延长,交AB的延长线于点F,且AB=BF,∠F=∠CDE.求证:四边形ABCD是平行四边形.12.如图,在△ABC中,D是AC的中点,E是BC延长线上一点,过A作AF∥BE,连接ED并延长交AF于点F,连接AE、CF.求证:四边形AFCE是平行四边形.13.如图,O为四边形ABCD的对角线BD的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF,AE∥CF,AE=CF.求证:四边形ABCD是平行四边形.14.四边形ABCD在坐标系中的坐标为A(8,0),B(6,4),C(0,4),O(0,0),P点在CB上从C点向B点运动,运动速度为每秒2个单位;Q点在AO上从A点向O点运动,运动速度为每秒3个单位,P点和Q点同时运动,其中一点达到终点另一点随即停止运动,设运动时间为t秒,那么当t为何值时四边形ABPQ为平行四边形?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形的判定练习题(解答题专项练习)
1、已知:如图,在平行四边形ABCD 中, E, F 分别是AB, DC 上的两点, 且AE = CF. 求 证:BD,EF 互相平分
2、已知:如图,在平行四边形ABCD 中,点M,N 在对角线AC 上,且AM=CN. 求证:四边形BMDN 是平行四边形.
3、已知:如图,在平行四边形ABCD 中, E, F 分别是AB, CD 上的两点,且AE = CF, AF,DE 相交于点M ,BF,CE 相交于点N.
求证:四边形EMFN 是平行四边形.(要求不用三角形全等来证)
4、已知:如图,在平行四边形ABCD 中,点G,H 分别是AB,CD 的中点,点E,F 在A C 上,且 AE = CF. 求证:四边形EGF H 是平四边形.
5、已知:如图,△ABC 中, D 是AB 的中点, E 是AC 上的一点,
(1)猜想:DF 与AE 间的关系是 ___________ .
⑵证明你的猜想.
C
EF//AB, DF//BE.
6.如图,已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF求
证:四边形BFDE是平行四边形
7.如图,平行四边形ABCD中,AF= CH DE= BG
求证:EG和HF互相平分。
图20.1.3-1
8.如图所示,在四边形ABCD中, M是BC中点,AM BD互相平分于点0,那么请说明AM=DC且AM/ DC
9、如图所示,已知□ ABCD中, AE CF分别是/ DAB / BCD的平分线,求证:四边形AFCE是平行四边形。
10.如图,在△ ABC 中, BD 平分/ ABC DE// BC 交 AB 于点 E , EF// AC 交 BC 于点 F , 已知,如图4,^ABC 是等边三角形,过 AC 边上的点D 作DG// BC ,
交AB 于点
G
(2)过点E 作EF// DB 交BC 于点F ,连结AF,求/ AFE 的度数。
12.已知如图所示,点O 为平行四边形ABCD 勺对角线BD 的中点,直线EF 经过点0, 分别交BA DC 的延长线于E 、F 两点,求证:AE=CF
13.已知:如图所示,平行四边形 ABCD 勺对角线AC BD 湘交于点0, EF 经过点0 并且分别和AB CD 相交于点E 、F ,又知G H 分别为0A 0C 的中点.
14 已知:如图口ABCD 勺对角线AC BD 交于点0, E 、F 是AC 上的两点,并且
AE=CF
在GD 和延长线上取点E ,使DE= DC 连接AE BD (1)求证:△ AGE^A
DAB 11. E
图
求证:四边形BFDE是平行四边形.
变式(1)若上题中的其它条件都不变,E 、F 是平行四边形ABCD 寸角线AC 延长线 上的两点,那么结论是否成立?
/ CAB=/ A ',/
BCA=/ C
; 变式(2):若E 、F 是平行四边形 ABCD 寸角线AC 上的两点,且E 、F 是0A 0C 的 变式(3):若E 、F 是平行四边形 ABCD 寸角线AC 上的两点,且 BE1 OA.DFI0C., 结论是否成立
?
15. 已知:如图,A B'// BA
B' C’// CB C ‘ A’// AC C
B 中点,结论是否成立?
A ______________ D
求证:⑴ / ABC=/ B ', A 各边的中点.
16、已知:如图,AB=DC=EF AD=BC DE=C|B图中有哪些互相平行的线段?
D
E
17、小明用手中六个全等的正三角形做拼图游戏时,拼成一个六边形.你能在图中 找出所有的平行四边形吗?请用符号表示出来.
18、已知:如图, ABCD 中,点E 、F 分别在CD AB 上, DF// BE, EF 交BD 于点O.
求证:EO=OF
第18题图
19、已知:如图所示,在口 ABCD 中,E 、
F 分别为AB CD 的中点, 求证:四边形AECF 是平行四边形.
第19题图
E。
