《平行四边形的判定》典型例题

合集下载

平行四边形的判定含答案

平行四边形的判定一．选择题（共15小题）1．如图，▱ABCD的对角线AC，BD交于点O，若AC＝6，BD＝8，则AB的长可能是（）A．10B．8C．7D．62．如图，平行四边形ABCD的对角线AC，BD相交于点O，下列结论错误的是（）A．OA＝OC B．AB＝CD C．AD＝BC D．∠ABD＝∠CBD 3．如图，平行四边形OABC的顶点A，B坐标分别为（﹣6，0），（﹣8，2），则点C的坐标是（）A．（1，2）B．（﹣1，2）C．（2，2）D．（﹣2，2）4．如图，在平行四边形ABCD中，AC、BD相交于点O，AB⊥AC，若AB＝4，AC＝6，则△COD的周长是（）A．8B．10C．12D．165．如图，四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）A．AB∥DC，AD∥BC B．AB＝DC，AD＝BCC．AO＝CO，BO＝DO D．AB＝DC，AD∥BC6．如图，在四边形ABCD中，对角线AC和BD相交于点O，下列条件不能判断四边形ABCD 是平行四边形的是（）A．AB∥DC，AD∥BC B．AB＝DC，AD＝BCC．AB∥DC，AD＝BC D．OA＝OC，OB＝OD7．如图，四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（）A．∠ABD＝∠BDC，OA＝OC B．∠ABC＝∠ADC，AB＝CDC．∠ABC＝∠ADC，AD∥BC D．∠ABD＝∠BDC，∠BAD＝∠DCB 8．满足下列条件的四边形，不一定是平行四边形的是（）A．两组对边分别平行B．两组对边分别相等C．一组对边平行且相等D．一组对边平行，另一组对边相等9．下列四个选项中，能判断四边形ABCD是平行四边形的是（）A．AB＝CD，AC＝BD B．∠A＝∠B，∠B＝∠CC．AB＝CD，AD∥BC D．AB∥CD，∠A＝∠C10．从①AB∥CD；②AB＝CD；③BC∥AD；④BC＝AD，这四个条件中选取两个，使四边形ABCD成为平行四边形，下面不能说明是平行四边形的是（）A．①②B．①③C．②④D．①④11．在下列条件中，能判定四边形为平行四边形的是（）A．两组邻边相等B．一组对边平行且另一组对边相等C．两组对边分别平行D．对角线互相垂直12．不能判定四边形ABCD为平行四边形的条件是（）A．AB∥CD，AD＝BC B．AB∥CD，∠A＝∠CC．AD∥BC，AD＝BC D．∠A＝∠C，∠B＝∠D13．如图，在四边形ABCD中，AB∥CD，要使四边形ABCD是平行四边形，下列可添加的条件不正确的是（）A．AD＝BC B．AB＝CD C．AD∥BC D．∠A＝∠C 14．下列给出的条件中，能判断四边形ABCD是平行四边形的是（）A．AB∥CD，AD＝BC B．∠B＝∠C；∠A＝∠DC．AB＝CD，CB＝AD D．AB＝AD，CD＝BC15．下列条件中，能判定四边形ABCD为平行四边形的个数是（）①AB∥CD，AD＝BC；②AB＝CD，AD＝BC；③∠A＝∠B，∠C＝∠D；④AB＝AD，CB＝CDA．1个B．2个C．3个D．4个二．解答题（共15小题）16．如图，点B，E，C，F在一条直线上，AB＝DE，AC＝DF，BE＝CF．（1）求证：△ABC≌△DEF；（2）连接AD，求证：四边形ABED是平行四边形．17．如图，在四边形ABCD中，AB＝CD，DE⊥AC于点E，BF⊥AC于点F，且DE＝BF．求证：四边形ABCD是平行四边形．18．已知：如图，在四边形ABCD中，∠BAC＝∠ACD＝90°，AB＝CD，点E是CD的中点．（1）求证：四边形ABCE是平行四边形；（2）若AC＝4，AD＝4，求四边形ABCE的面积．19．如图，四边形ABCD的对角线AC、BD相交于点O，BO＝DO，点E、F分别在AO，CO上，且BE∥DF，AE＝CF．求证：四边形ABCD为平行四边形．20．如图：已知∠B＝∠E＝90°，点B、C、F、E在一条直线上AC＝DF，BF＝EC．求证四边形ACDF是平行四边形．21．如图，在四边形ABCD中，AD∥BC且AD＝9cm，BC＝6cm，点P、Q分别从点A、C 同时出发，点P以1cm/s的速度由A向D运动，点Q以2cm/s的速度由C向B运动．问几秒后直线PQ将四边形ABCD截出一个平行四边形？22．已知：如图，A，B，C，D在同一直线上，且AB＝CD，AE＝DF，AE∥DF．求证：四边形EBFC是平行四边形．23．如图，已知△ABC是等边三角形，E为AC上一点，连接BE．将AC绕点E旋转，使点C落在BC上的点D处，点A落在BC上方的点F处，连接AF．求证：四边形ABDF是平行四边形．24．如图，已知，AE⊥BD于E点，CF⊥BD于F点，∠1＝∠2，BE＝DF，连接AB，CD．求证：四边形ABCD是平行四边形．25．如图，点B、E、C、F在一条直线上，AB＝DF，AC＝DE，BE＝FC．连接AF、BD，求证：四边形ABDF是平行四边形．26．如图，AD是△ABC边BC上的中线，AE∥BC，BE交AD于点F，F是BE的中点，连结CE．求证：四边形ADCE是平行四边形．27．如图，D是△ABC的边AB上一点，CE∥AB，DE交AC于点F，若F A＝FC．求证：四边形ADCE是平行四边形；28．如图，在四边形ABCD中，AB＝CD，DE⊥AC，BF⊥AC，垂足分别为E，F，且DE ＝BF．求证：（1）AE＝CF；（2）四边形ABCD是平行四边形．29．如图，已知△ABC是等边三角形，点D在BC边上，△ADF是以AD为边的等边三角形，过点F作BC的平行线交线段AC于点E，连接BF．求证：（1）△AFB≌△ADC；（2）四边形BCEF是平行四边形．30．如图，点B、E、C、F在一条直线上，AB∥DF，AC∥DE，BE＝FC，连接BD、AF．求证：四边形ABDF是平行四边形．平行四边形的判定参考答案与试题解析一．选择题（共15小题）1．如图，▱ABCD的对角线AC，BD交于点O，若AC＝6，BD＝8，则AB的长可能是（）A．10B．8C．7D．6解：∵四边形ABCD是平行四边形，∴OA＝AC＝3，OB＝BD＝4，在△AOB中：4﹣3＜AB＜4+3，即1＜AB＜7，∴AB的长可能为6．故选：D．2．如图，平行四边形ABCD的对角线AC，BD相交于点O，下列结论错误的是（）A．OA＝OC B．AB＝CD C．AD＝BC D．∠ABD＝∠CBD 解：A、∵平行四边形ABCD的对角线AC、BD相交于点O，∴OA＝OC，故此选项不符合题意；B、∵四边形ABCD是平行四边形，∴AB＝CD，故此选项不符合题意；C、∵四边形ABCD是平行四边形，∴AD＝BC，故此选项不符合题意；D、当四边形ABCD是菱形时，∠ABD＝∠CBD，故此选项符合题意；故选：D．3．如图，平行四边形OABC的顶点A，B坐标分别为（﹣6，0），（﹣8，2），则点C的坐标是（）A．（1，2）B．（﹣1，2）C．（2，2）D．（﹣2，2）解：∵A（﹣6，0），∴OA＝6，∵四边形OABC是平行四边形，∴BC∥OA，BC＝OA＝6，∵B（﹣8，2），∴C（﹣2，2），故选：D．4．如图，在平行四边形ABCD中，AC、BD相交于点O，AB⊥AC，若AB＝4，AC＝6，则△COD的周长是（）A．8B．10C．12D．16解：∵在平行四边形ABCD中，AC、BD相交于点O，AB⊥AC，若AB＝4，AC＝6，∴BO＝，∴BD＝10，∴△COD的周长＝OD+OC+CD＝5+3+4＝12，故选：C．5．如图，四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）A．AB∥DC，AD∥BC B．AB＝DC，AD＝BCC．AO＝CO，BO＝DO D．AB＝DC，AD∥BC解：A、∵AB∥CD，AD∥BC，∴四边形ABCD是平行四边形，故此选项不符合题意；B、∵AB＝DC，AD＝BC，∴四边形ABCD是平行四边形，故此选项不符合题意；C、∵AO＝CO，BO＝DO，∴四边形ABCD是平行四边形，故此选项不符合题意；D、AB＝DC，AD∥BC无法得出四边形ABCD是平行四边形，故此选项符合题意；故选：D．6．如图，在四边形ABCD中，对角线AC和BD相交于点O，下列条件不能判断四边形ABCD 是平行四边形的是（）A．AB∥DC，AD∥BC B．AB＝DC，AD＝BCC．AB∥DC，AD＝BC D．OA＝OC，OB＝OD解：∵AB∥DC，AD∥BC，∴四边形ABCD是平行四边形，故选项A中条件可以判定四边形ABCD是平行四边形；∵AB＝DC，AD＝BC，∴四边形ABCD是平行四边形，故选项B中条件可以判定四边形ABCD是平行四边形；∵AB∥DC，AD＝BC，则无法判断四边形ABCD是平行四边形，故选项C中的条件，不能判断四边形ABCD是平行四边形；∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形，故选项D中条件可以判定四边形ABCD是平行四边形；故选：C．7．如图，四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（）A．∠ABD＝∠BDC，OA＝OC B．∠ABC＝∠ADC，AB＝CDC．∠ABC＝∠ADC，AD∥BC D．∠ABD＝∠BDC，∠BAD＝∠DCB 解：A、∵∠ABD＝∠BDC，OA＝OC，又∠AOB＝∠COD，∴△AOB≌△COD，∴DO＝BO，∴四边形ABCD是平行四边形，故此选项不合题意；B、∠ABC＝∠ADC，AB＝CD不能判断四边形ABCD是平行四边形，故此选项符合题意；C、∵AD∥BC，∴∠ABC+∠BAD＝180°，∵∠ABC＝∠ADC，∴∠ADC+∠BAD＝180°，∴AB∥CD，∴四边形ABCD是平行四边形，故此选项不合题意；D、∵∠ABD＝∠BDC，∠BAD＝∠DCB，∴∠ADB＝∠CBD，∴AD∥CB，∵∠ABD＝∠BDC，∴AD∥CB，∴四边形ABCD是平行四边形，故此选项不合题意；故选：B．8．满足下列条件的四边形，不一定是平行四边形的是（）A．两组对边分别平行B．两组对边分别相等C．一组对边平行且相等D．一组对边平行，另一组对边相等解：A、∵两组对边分别平行的四边形是平行四边形，∴选项A不符合题意；B、∵两组对边分别相等的四边形是平行四边形，∴选项B不符合题意；C、∵一组对边平行且相等的四边形是平行四边形，∴选项C不符合题意；D、∵一组对边平行，另一组对边相等的四边形可能是等腰梯形或平行四边形，∴选项D符合题意；故选：D．9．下列四个选项中，能判断四边形ABCD是平行四边形的是（）A．AB＝CD，AC＝BD B．∠A＝∠B，∠B＝∠CC．AB＝CD，AD∥BC D．AB∥CD，∠A＝∠C解：A、AB＝CD，AC＝BD不能判定四边形ABCD是平行四边形，故此选项错误；B、∠A＝∠B，∠B＝∠C不能判定四边形ABCD是平行四边形，故此选项错误；C、AB＝CD，AD∥BC不能判定四边形ABCD是平行四边形，故此选项错误；D、∵AB∥CD，∴∠A+∠D＝∠B+∠C＝180°，∵∠A＝∠C，∴∠B＝∠D，∴四边形ABCD是平行四边形，故此选项正确；故选：D．10．从①AB∥CD；②AB＝CD；③BC∥AD；④BC＝AD，这四个条件中选取两个，使四边形ABCD成为平行四边形，下面不能说明是平行四边形的是（）A．①②B．①③C．②④D．①④解：根据平行四边形的判定，符合条件的有4种，分别是：①②、③④、①③、②④．故选：D．11．在下列条件中，能判定四边形为平行四边形的是（）A．两组邻边相等B．一组对边平行且另一组对边相等C．两组对边分别平行D．对角线互相垂直解：A、两组邻边相等的四边形是筝形，故本选项不符合题意；B、一组对边平行且另一组对边相等的四边形可能是等腰梯形或平行四边形，故本选项不符合题意；C、两组对边分别平行的四边形是平行四边形，故本选项符合题意；D、对角线互相平分的四边形才是平行四边形，故本选项不符合题意；故选：C．12．不能判定四边形ABCD为平行四边形的条件是（）A．AB∥CD，AD＝BC B．AB∥CD，∠A＝∠CC．AD∥BC，AD＝BC D．∠A＝∠C，∠B＝∠D解：A、AB∥CD，AD＝BC，不能判定四边形ABCD为平行四边形，错误；B、∵AB∥CD，∴∠A+∠D＝180°，∵∠A＝∠C，∴∠C+∠D＝180°，∴AD∥BC，∴四边形ABCD为平行四边形，正确；C、∵AD∥BC，AD＝BC，∴四边形ABCD为平行四边形，正确；D、∵∠A＝∠C，∠B＝∠D，∴∠A+∠D＝∠C+∠D＝180°，∴AD∥BC，AB∥CD，∴四边形ABCD为平行四边形，正确；故选：A．13．如图，在四边形ABCD中，AB∥CD，要使四边形ABCD是平行四边形，下列可添加的条件不正确的是（）A．AD＝BC B．AB＝CD C．AD∥BC D．∠A＝∠C解：D、当AB∥CD，AD＝BC时，四边形ABCD可能为等腰梯形，所以不能证明四边形ABCD为平行四边形；B、AB∥CD，AB＝DC，一组对边分别平行且相等，可证明四边形ABCD为平行四边形；C、AB∥CD，AD∥BC，两组对边分别平行，可证明四边形ABCD为平行四边形；D、∵AB∥CD，∴∠A+∠D＝180°，∵∠A＝∠C，∴∠C+∠D＝180°，∴AD∥BC，∴四边形ABCD为平行四边形；故选：A．14．下列给出的条件中，能判断四边形ABCD是平行四边形的是（）A．AB∥CD，AD＝BC B．∠B＝∠C；∠A＝∠DC．AB＝CD，CB＝AD D．AB＝AD，CD＝BC解：A、根据AD∥CD，AD＝BC不能判断四边形ABCD是平行四边形，故本选项错误；B、根据∠B＝∠C，∠A＝∠D不能判断四边形ABCD是平行四边形，故本选项错误；C、根据AB＝CD，AD＝BC，得出四边形ABCD是平行四边形，故本选项正确；D、根据AB＝AD，BC＝CD，不能判断四边形ABCD是平行四边形，故本选项错误；故选：C．15．下列条件中，能判定四边形ABCD为平行四边形的个数是（）①AB∥CD，AD＝BC；②AB＝CD，AD＝BC；③∠A＝∠B，∠C＝∠D；④AB＝AD，CB＝CDA．1个B．2个C．3个D．4个解：①AB∥CD，AD＝BC，不能判定四边形ABCD为平行四边形；②AB＝CD，AD＝BC；能判定四边形ABCD为平行四边形；③∠A＝∠B，∠C＝∠D；不能判定四边形ABCD为平行四边形；④AB＝AD，CB＝CD；不能判定四边形ABCD为平行四边形；能判定四边形ABCD为平行四边形的个数有1个，故选：A．二．解答题（共15小题）16．如图，点B，E，C，F在一条直线上，AB＝DE，AC＝DF，BE＝CF．（1）求证：△ABC≌△DEF；（2）连接AD，求证：四边形ABED是平行四边形．（1）证明：∵BE＝CF，∴BE+EC＝CF+EC，∴BC＝EF，在△ABC和△DEF中，，∴△ABC≌△DEF（SSS）；（2）证明：由（1）得：△ABC≌△DEF，∴∠B＝∠DEF，∴AB∥DE，又∵AB＝DE，∴四边形ABED是平行四边形．17．如图，在四边形ABCD中，AB＝CD，DE⊥AC于点E，BF⊥AC于点F，且DE＝BF．求证：四边形ABCD是平行四边形．证明：∵DE⊥AC于点E，BF⊥AC于点F，∴∠DEC＝∠BF A＝90°，在Rt△ABF和Rt△CDE中，∴Rt△ABF≌Rt△CDE（HL），∴∠DCE＝∠BAF，∴AB∥CD，又∵AB＝CD，∴四边形ABCD是平行四边形．18．已知：如图，在四边形ABCD中，∠BAC＝∠ACD＝90°，AB＝CD，点E是CD的中点．（1）求证：四边形ABCE是平行四边形；（2）若AC＝4，AD＝4，求四边形ABCE的面积．（1）证明：∵∠BAC＝∠ACD＝90°，∴AB∥EC，∵点E是CD的中点，∴，∵，∴AB＝EC，∴四边形ABCE是平行四边形；（2）解：∵∠ACD＝90°，AC＝4，，∴，∵，∴AB＝2，∴S平行四边形ABCE＝AB•AC＝2×4＝8．19．如图，四边形ABCD的对角线AC、BD相交于点O，BO＝DO，点E、F分别在AO，CO上，且BE∥DF，AE＝CF．求证：四边形ABCD为平行四边形．证明：∵BE∥DF，∴∠BEO＝∠DFO，在△BEO与△DFO中，，∴△BEO≌△DFO（ASA），∴EO＝FO，∵AE＝CF，∴AE+EO＝CF+FO，即AO＝CO，∵BO＝DO，∴四边形ABCD为平行四边形．20．如图：已知∠B＝∠E＝90°，点B、C、F、E在一条直线上AC＝DF，BF＝EC．求证四边形ACDF是平行四边形．证明：∵BF＝EC，∴BF﹣CF＝EC﹣CF，即BC＝EF，在Rt△ABC和Rt△DEF中，，∴Rt△ABC≌Rt△DEF（HL），∴∠ACB＝∠DFE，∴∠ACF＝∠DFC，∴AC∥DF，又∵AC＝DF，∴四边形ACDF是平行四边形．21．如图，在四边形ABCD中，AD∥BC且AD＝9cm，BC＝6cm，点P、Q分别从点A、C 同时出发，点P以1cm/s的速度由A向D运动，点Q以2cm/s的速度由C向B运动．问几秒后直线PQ将四边形ABCD截出一个平行四边形？解：设点P，Q运动的时间为ts．依题意得：CQ＝2t，BQ＝6﹣2t，AP＝t，PD＝9﹣t．①当BQ＝AP时，四边形APQB是平行四边形．即6﹣2t＝t，解得t＝2．②当CQ＝PD时，四边形CQPD是平行四边形，即2t＝9﹣t，解得：t＝3．所以经过2或3秒后，直线PQ将四边形ABCD截出一个平行四边形．22．已知：如图，A，B，C，D在同一直线上，且AB＝CD，AE＝DF，AE∥DF．求证：四边形EBFC是平行四边形．证明：连接AF，ED，EF，EF交AD于O．∵AE＝DF，AE∥DF．∴四边形AEDF为平行四边形，∴EO＝FO，AO＝DO，又∵AB＝CD，∴AO﹣AB＝DO﹣CD，∴BO＝CO，又∵EO＝FO，∴四边形EBFC是平行四边形．23．如图，已知△ABC是等边三角形，E为AC上一点，连接BE．将AC绕点E旋转，使点C落在BC上的点D处，点A落在BC上方的点F处，连接AF．求证：四边形ABDF是平行四边形．证明：∵△ABC是等边三角形，∴AC＝BC＝AB，∠ACB＝60°；∵将AC绕点E旋转∴ED＝CE，EF＝AE∴△EDC是等边三角形，∴DE＝CD＝CE，∠DCE＝∠EDC＝60°，∴FD＝AC＝BC，∴△ABC、△AEF、△DCE均为等边三角形，∴∠CDE＝∠ABC＝∠EF A＝60°，∴AB∥FD，BD∥AF，∴四边形ABDF是平行四边形．24．如图，已知，AE⊥BD于E点，CF⊥BD于F点，∠1＝∠2，BE＝DF，连接AB，CD．求证：四边形ABCD是平行四边形．证明：∵AE⊥BD于E点，CF⊥BD于F点，∴∠AED＝∠BFC＝90°，∵BE＝DF，∴BE+EF＝DF+EF，即：BF＝DE又∵∠1＝∠2，∴△ADE≌△CBF（ASA），∴AD＝BC，又∵∠1＝∠2，∴AD∥BC，∴四边形ABCD是平行四边形．25．如图，点B、E、C、F在一条直线上，AB＝DF，AC＝DE，BE＝FC．连接AF、BD，求证：四边形ABDF是平行四边形．解：∵BE＝FC，∴BE+EC＝FC+EC，∴BC＝FE，在△ABC和△DFE中，，∴△ABC≌△DFE（SSS），∴∠ABC＝∠DFE，∴AB∥DF，又∵AB＝DF，∴四边形ABDF是平行四边形．26．如图，AD是△ABC边BC上的中线，AE∥BC，BE交AD于点F，F是BE的中点，连结CE．求证：四边形ADCE是平行四边形．证明：∵AD是△ABC边BC上的中线，F是BE的中点，∴BF＝EF，BD＝CD，∴DF∥CE，∴AD∥CE，∵AE∥BC，∴四边形ADCE是平行四边形．27．如图，D是△ABC的边AB上一点，CE∥AB，DE交AC于点F，若F A＝FC．求证：四边形ADCE是平行四边形；证明：∵CE∥AB，∴∠BAC＝∠ECA，在△DAF和△ECF中，∴△DAF≌△ECF（ASA），∴CE＝AD，∴四边形ADCE是平行四边形；28．如图，在四边形ABCD中，AB＝CD，DE⊥AC，BF⊥AC，垂足分别为E，F，且DE ＝BF．求证：（1）AE＝CF；（2）四边形ABCD是平行四边形．证明：（1）∵DE⊥AC，BF⊥AC，∴∠DEC＝∠BFC＝90°，在Rt△DEC和Rt△BFC中，，∴Rt△DEC≌Rt△BFC（HL），∴EC＝AF，∴EC﹣EF＝AF﹣EF即AE＝FC；（2）∵Rt△DEC≌Rt△BFC，∴∠DCE＝∠BAF，∴AB∥DC，又∵AB＝DC，∴四边形ABCD是平行四边形．29．如图，已知△ABC是等边三角形，点D在BC边上，△ADF是以AD为边的等边三角形，过点F作BC的平行线交线段AC于点E，连接BF．求证：（1）△AFB≌△ADC；（2）四边形BCEF是平行四边形．证明：（1）∵△ABC和△ADF都是等边三角形，∴AF＝AD，AB＝AC，∠F AD＝∠BAC＝60°，又∵∠F AB＝∠F AD﹣∠BAD，∠DAC＝∠BAC﹣∠BAD，∴∠F AB＝∠DAC，且AF＝AD，AB＝AC∴△AFB≌△ADC（SAS）；（2）∵△AFB≌△ADC，∴∠ABF＝∠C＝60°．又∵∠BAC＝∠C＝60°，∴∠ABF＝∠BAC，∴FB∥AC，又∵BC∥EF，∴四边形BCEF是平行四边形；30．如图，点B、E、C、F在一条直线上，AB∥DF，AC∥DE，BE＝FC，连接BD、AF．求证：四边形ABDF是平行四边形．证明：∵BE＝FC，∴BE+CE＝FC+CE，即BC＝FE，∵AB∥DF，AC∥DE，∴∠ABC＝∠DFE，∠ACB＝∠DEF，在△ABC和△DFE中，，∴△ABC≌△DFE（ASA），∴AB＝DF，∵AB∥DF，∴四边形ABDF是平行四边形．。

平行四边形判定,题型归纳

对角线取值范围问题（同三角形第三边中线取值范围）平行四边形一边长为10, —条对角线长为6,则它的另一条对角线长a的取值范围为（）A. 4<a<16 B . 14<a<26 C . 12<a<20 D . 8<a<32平行四边形的判定：1:定义法：两组对边分别平行的四边形是平行四边形2: 一组对边平行且相等的四边形是平行四边形3:两组对边分别相等的四边形是平行四边形4:对角线相互平分的四边形是平行四边形14.平行四边形的判定（一）定义法：两组对边分别平行的四边形是平行四边形例题1:如图，四边形ABCD是平行四边形，连接AC.过点A作AEL BC于点E;过点C作CF// AE交AD于点F;求证：四边形AECF为平行四边形练习：1、已知：如图，△ ABC是等边三角形，D E分别是BA、CA的延长线上的点，且AD=AE连接ED并延长到F,使得EF=EC,连接AF、CF、BE.（1）求证：四边形BCFD是平行四边形;证明：（1 △ ABC为等边三角形，且AE=AD,•••由题可知 / AED=Z ADE=Z EAD=60°••• EF/ BC,又••• EC=EF,•△ ECF为等边三角形,即/ EFC=Z EDB=60°,•CF// BD•••四边形BCFD为平行四边形.2、如图：平行四边形ABCD中, M N分别是AB CD的中点，AN与DM相交于点P, BN与CM相交于点Q试说明PQ与MN互相平分。

3、如图，在四边形ABCD中，AH、CG BE、FD分别是/ A、/ C、/ B、/ D的角平分线，且BE// FD, AH// CG证明四边形ABCD为平行四边形.15.平行四边形的判定（二）：一组对边平行且相等的四边形是平行四边形例题1:如图，在ABCD中，延长CD到E,使DB CC,连接BE交AD于点F,交AC于点G求证：AF= DF【答案】解：（1）证明：如图1,连接BD AE,•••四边形ABCD是平行四边形，••• AB// CD AB= CD•/ DE= CD • AB// DE AB= DE=•四边形ABDE是平行四边形。

(完整版)平行四边形的性质判定练习题

第一部分平行四边形的性质练习题例题1、平行四边形得周长为50cm ，两邻边之差为5cm,求各边长。

变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2：3，则AB=_______,BC=________. 变题2.四边形ABCD 是平行四边形，∠BAC=90°,AB=3,AC=4,求AD 的长。

例题2.平行四边形ABCD 中，∠A-∠B=20°,求平行四边形各内角的度数。

变题3.平行四边形ABCD 中，AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________. 变题4.如图，在平行四边形ABCD 中，∠BAC=34°, ∠ACB=26°，求∠DAC 与∠D 的度数。

例题3.如图，在平行四边形ABCD 中，CE ⊥AD,CF ⊥BA 交BA 的延长线于F ，∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。

变题5.如图，平行四边形ABCD 的周长为50，其中AB=15，∠ABC=60°，求平行四边形面积。

1、如图，四边形ABCD 是平行四边形，AB=6cm,BC=8cm ，∠B=70°,则AD=________,CD=______,∠D=_______,∠A=______,∠C=_______.2、平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2：3，则AB=_______,BC=________.3、平行四边形得周长为50cm ，两邻边之差为5cm,则长边是________ ，短边是__________.4、平行四边形ABCD 中，∠A-∠B=20°, 则∠A=_______ ∠B=________5、.平行四边形ABCD 中，AE 平分∠DAB, ∠DEA=20°,则∠C=____,∠B_____.6、平行四边形 ABCD 中，∠A+∠C=200°.则：∠A= _______，∠B= _________ .7、如图，平行四边形ABCD 的周长为50，其中AB=15，∠ABC=60°，求平行四边形面积。

平行四边形的判定常考题(含详细解析)

一、选择题<共14小题）1、<2003•广西）如图所示，在△ABC中，AB=AC=5，D是BC上的点，DE∥AB交AC于点E，DF∥AC交AB于点F，那么四边形AFDE的周长是< ）A、5B、10C、15D、202、在四边形ABCD中，AB∥CD，若ABCD不是梯形，则∠A：∠B：∠C：∠D可能为< ）A、2：3：6：7B、3：4：5：6C、3：5：7：9D、4：5：4：53、<2006•佛山）如图，平面上两颗不同高度、笔直的小树，同一时刻在太阳光线照射下形成的影子分别是AB、DC，则< ）b5E2RGbCAPA、四边形ABCD是平行四边形B、四边形ABCD是梯形C、线段AB与线段CD相交D、以上三个选项均有可能4、<2005•柳州）不能判断四边形ABCD是平行四边形的是< ）A、AB=CD，AD=BCB、AB=CD，AB∥CDC、AB=CD，AD∥BCD、AB∥CD，AD∥BC5、<2004•聊城）如图，有两块全等的含30°角的三角板拼成形状不同的平行四边形，最多可以拼成< ）p1EanqFDPwA、1个B、2个C、3个D、4个6、<2002•山西）A，B，C，D在同一平面内，从①AB∥CD，②AB=CD，③BC∥AD，④BC=AD这四个中任选两个作为条件，能使四边形ABCD为平行四边形的选法有< ）DXDiTa9E3dA、6种B、5种C、4种D、3种7、<1998•内江）能判定四边形是平行四边形的条件是< ）A、一组对边平行，另一组对边相等B、一组对边相等，一组邻角相等C、一组对边平行，一组邻角相等D、一组对边平行，一组对角相等8、已知四边形ABCD，AC与BD相交于点O，如果给出条件AB∥CD，那么还不能判定四边形ABCD为平行四边形，以下四种说法正确的是< ）RTCrpUDGiT①如果再加上条件BC=AD，那么四边形ABCD一定是平行四边形；②如果再加上条件∠BAD=∠BCD，那么四边形ABCD一定是平行四边形；③如果再加上条件AO=CO，那么四边形ABCD一定是平行四边形；④如果再加上条件∠DBA=∠CAB，那么四边形ABCD一定是平行四边形．A、①②B、①③④C、②③D、②③④9、已知四边形ABCD的对角线相交于O，给出下列5个条件①AB∥CD；②AD∥BC；③AB=CD；④∠BAD=∠DCB．从以上4个条件中任选2个条件为一组，能推出四边形ABCD为平行四边形的有< ）5PCzVD7HxAA、6组B、5组C、4组D、3组10、在四边形ABCD中，从①AB∥CD；②AB=CD；③BC∥AD；④BC=AD中任选两个使四边形ABCD为平行四边形的选法有jLBHrnAILg< ）A、3B、4C、5D、611、四边形ABCD中，AD∥BC，当满足下列< ）条件时，四边形ABCD是平行四边形．A、∠A+∠C=180°B、∠B+∠D=180°C、∠A+∠B=180°D、∠A+∠D=180°12、以不在同一直线上的三个点为顶点作平行四边形，最多能作< ）A、4个B、3个C、2个D、1个13、在下列给出的条件中，能判定四边形ABCD为平行四边形的是< ）A、AB=BC，CD=DAB、AB∥CD，AD=BCC、AB∥CD，∠A=∠CD、∠A=∠B，∠C=∠D14、下列哪组条件能判别四边形ABCD是平行四边形< ）A、AB∥CD，AD=BCB、AB=CD，AD=BCC、∠A=∠B，∠C=∠DD、AB=AD，CB=CD二、填空题<共4小题）15、<2018•常德）如图，四边形ABCD中，AB∥CD，要使四边形ABCD为平行四边形，则应添加的条件是_________．<添加一个条件即可，不添加其它的点和线）．xHAQX74J0X16、<2009•郴州）如图，在四边形ABCD中，已知AB=CD，再添加一个条件_________ <写出一个即可），则四边形ABCD是平行四边形．<图形中不再添加辅助线）LDAYtRyKfE17、如图，△ABC、△ACE、△ECD都是等边三角形，则图中的平行四边形有哪些_________ _________ ．Zzz6ZB2Ltk18、把边长为3，5，7的两个全等三角形拼成四边形，一共能拼成_________ 种不同的四边形，其中有_________ 个平行四边形．dvzfvkwMI1三、解答题<共8小题）19、<2018•贵阳）如图，E，F是四边形ABCD的对角线AC上两点，AF=CE，DF=BE，DF∥BE．rqyn14ZNXI求证：<1）△AFD≌△CEB；<2）四边形ABCD是平行四边形．20、<2018•本溪）我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形．请解答下列问题：EmxvxOtOco<1）写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称；<2）探究：当等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和与其中一条对角线的大小关系，并证明你的结论．SixE2yXPq521、<2006•镇江）已知：如图，在四边形ABCD中，AC与BD相交于点O，AB∥CD，AO=CO．6ewMyirQFL求证：四边形ABCD是平行四边形．22、<2004•万州区）已知：如图，已知：D是△ABC的边AB上一点，CN∥AB，DN交AC于，若MA=MC，求证：CD=AN．kavU42VRUs23、如图，在△ABC中，D是BC边的中点，F、E分别是AD及其延长线上的点，CF∥BE．<1）求证：△BDE≌△CDF；<2）请连接BF，CE，试判断四边形BECF是何种特殊四边形，并说明理由．24、如图，F、C是线段AD上的两点，AB∥DE，BC∥EF，AF=DC，连接AE、BD，求证：四边形ABDE是平行四边形．y6v3ALoS8925、<2006•泰安）已知：如图，以△ABC的边AB为直径的⊙O交边AC于点D，且过点D的切线DE平分边BC．M2ub6vSTnP<1）BC与⊙O是否相切？请说明理由；<2）当△ABC满足什么条件时，以点O，B，E，D为顶点的四边形是平行四边形？并说明理由．26、<2007•南宁）如图，在△ABC中，点D，E分别是AB，AC边的中点，若把△ADE绕着点E顺时针旋转180°得到△CFE．0YujCfmUCw<1）请指出图中哪些线段与线段CF相等；<2）试判断四边形DBCF是怎样的四边形，证明你的结论．答案与评分标准一、选择题<共14小题）1、<2003•广西）如图所示，在△ABC中，AB=AC=5，D是BC上的点，DE∥AB交AC于点E，DF∥AC交AB于点F，那么四边形AFDE的周长是< ）eUts8ZQVRdA、5B、10C、15D、20考点：平行四边形的性质；等腰三角形的性质；平行四边形的判定。

(完整版)平行四边形性质和判定习题(答案详细)(可编辑修改word版)

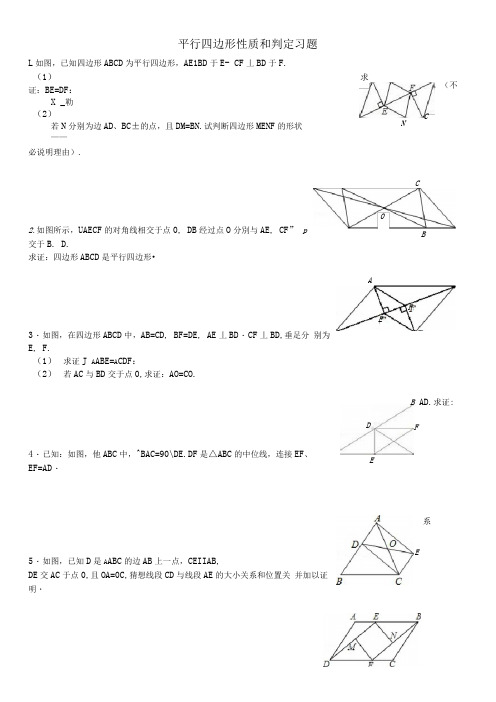
平行四边形性质和判定习题L如图，已知四边形ABCD为平行四边形，AE1BD于E- CF丄BD于F.（1）求证：BE=DF：X _勒（2）若N分别为边AD、BC±的点，且DM=BN.试判断四边形MENF的形状——必说明理由）.2.如图所示，UAECF的对角线相交于点0, DB经过点O分別与AE, CF” p交于B. D.求证：四边形ABCD是平行四边形•3・如图，在四边形ABCD中，AB=CD, BF=DE, AE丄BD・CF丄BD,垂足分别为E, F.（1）求证J A ABE=A CDF：（2）若AC与BD交于点0,求证：AO=CO.4・已知：如图，他ABC中，^BAC=90\DE.DF是△ABC的中位线，连接EF、EF=AD・5・如图，已知D是A ABC的边AB上一点，CEIIAB,DE交AC于点0,且OA=0C,猜想线段CD与线段AE的大小关系和位置关并加以证明・B AD.求证:。

（不CNCBAFED FE系E6・如图，已知，UABCD中，AE=CF, M、N分别是DE、BF的中点.求证：四边形MFNE是平行四边形•7・如图，平行四边形ABCD, E 、F 两点在对角线BD 上，且BE=DF,连接AE. EG CF, FA ・求证：四边形AECF 是平行四边形•& 在UABCD 中，分别以AD 、BC 为边向内作等边△ADE 和等边△BCF,连接BE. DF ・求证：四边形BEDF 是平行四边形・DBIIAC,且DB 丄AC. E 是AC 的中点，求证：BC=DE ・2如图，在梯形ABCD 中，ADIIBC, AD=24cm. BC=30cm,点P 自点A 向D 以IcmZs 的速度运动，到D 点Q 自点C 向B 以2cm/s 的速度运动，到B点即停止，直线PQ 截梯形为两个四边形•问当P. Q同时10. 已知脣点即停止. 出发，几秒后其中一个四边形为平行四边形？IL 如图：已知D 、E 、F 分别是A ABC 各边的中点, 求证：AE 仃DF 互相平分.如图所示, 9・ED13.如图，已知四边形ABCD中，点E, F. G, H分别是AB、CD、AC. BD的中点，并且点E、F、G、H有在同一条直线上.求证：EF和GH互相平分・14.如图J oABCD 中，MNIIAC.试说明MQ=NP.15.已知：如图所示「平行四边形ABCD的对角线AC, BD柑交于点6 EF经过点0并且分别和AB. CD相交于点E, F,点G, H分别为OA, 0C的中点.求证：四边形EHFG是平行四边形.-46 如制已知的ABCD中,E、F是对角线BD上的两点，BE=DF,点G、H分别在BA和DC的延长线上，且AG=CH. 连接GE、EH、HF、FG.（1）求证：四边形GEHF是平行四边形；（2）若点G、H分别在线段BA和DC上，尖余条件不变，则（1）中的结论是否成立？（不用说明理由）17.如图，在A ABC中，D是AC的中点，E是线段BC延长线一点，过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.（1）求证J AF=CE：（2）如果AC=EF,且ZACB=135\试判断四边形AFCE是什么样的四边形，并证明你的结论・18,如图平行四边形ABCD 中.mBC=6（几点E 、F 分別在CD.BC 的延长线上，AE||BD ・ EEhBB 垂足为点F, DF=2 （1）求证：D 是EC 中点；（2）求FC 的长.19.如图，已知A ABC 是等边三角形，点D 、F 分别在线段BC 、AB 匕厶EFB=60。

平行四边形例题

平行四边形例题
例题：在平行四边形ABCD中，AB = 5，BC = 3，求平行四边形ABCD的周长。

题目解析：
1. 首先明确平行四边形的性质，平行四边形的对边相等。

- 在平行四边形ABCD中，AB与CD是一组对边，BC与AD是另一组对边。

- 已知AB = 5，根据对边相等可知CD = 5；已知BC = 3，根据对边相等可知AD = 3。

2. 然后求平行四边形的周长。

- 平行四边形的周长等于四条边的长度之和，即C = AB+BC + CD+AD。

- 把AB = 5，BC = 3，CD = 5，AD = 3代入可得：C=5 + 3+5+3 = 16。

再看一道例题：
例题：平行四边形ABCD中，∠A比∠B大30°，求平行四边形ABCD各个内角的度数。

题目解析：
1. 利用平行四边形邻角互补的性质。

- 在平行四边形ABCD中，∠A与∠B是邻角，所以∠ A+∠ B = 180^∘。

2. 又因为∠A比∠B大30°，即∠ A=∠ B + 30^∘。

- 把∠ A=∠ B + 30^∘代入∠ A+∠ B = 180^∘中，得到(∠ B + 30^∘)+∠ B=180^∘。

- 化简可得2∠ B+30^∘=180^∘，移项得到2∠ B = 180^∘-30^∘=150^∘，解得∠ B = 75^∘。

- 因为∠ A=∠ B + 30^∘，所以∠ A=75^∘+30^∘=105^∘。

- 根据平行四边形的对角相等，可知∠ C=∠ A = 105^∘，∠ D=∠ B = 75^∘。

《平行四边形的判定》典型例题

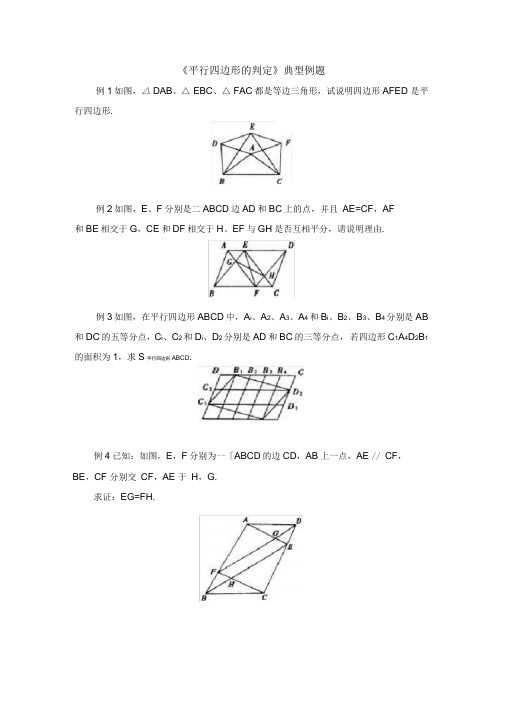
《平行四边形的判定》典型例题例1如图，△ DAB、△ EBC、△ FAC都是等边三角形，试说明四边形AFED 是平行四边形.例2如图，E、F分别是二ABCD边AD和BC上的点，并且AE=CF，AF和BE相交于G，CE和DF相交于H、EF与GH是否互相平分，请说明理由.例3如图，在平行四边形ABCD中，A i、A2、A3、A4和B i、B2、B3、B4 分别是AB 和DC的五等分点，C i、C2和D i、D2分别是AD和BC的三等分点，若四边形C1A4D2B1的面积为1，求S平行四边形ABCD.例4已知：如图，E，F分别为一「ABCD的边CD，AB上一点，AE // CF，BE，CF 分别交CF，AE 于H，G.求证：EG=FH.例5如图，已知：四边形ABCD中，AE丄BD , CF丄BD , E, F为垂足, 且AE=CF，/ BAC=DCA.求证：四边形ABCD是平行四边形.又、;AE^P"：参考答案例1分析要证四边形AFED是平行四边形，应观察：两组对边是否相等、两组对角是否相等，或一组对边是否平行且相等、对角线是否相互平分.但在本题中没有对角线，也没有明显的对角之间的关系，因此可以先考虑去证明四边形AFED的对边是否相等.事实上，AD=AB=BD，EF是否能等于这三条边中的一条呢？可以看到丄二二三丄EF=AB=BD .同理DE=AC=AF，因此，所要证的四边形AFED 是平行四边形.证明■:= = ，且召U 二丑匚二FC.•.込C 三随EC AS二EF.又丄二丄.丄厶「，同理J7 = Z'S .. AFED是平行四边形.例2分析若EF、GH互相平分，那么四边形EGFH应是平行四边形.观察已知条件，可以证明四边形EGFH是平行四边形.证明•…口二是平行四边形，.AE= FC, AH “ FG且ED 壮辄ED=BF..四边形AECF是平行四边形，•••又四边形EDFB是平行四边形，•壬三''■巴二，• ?s ' ■在四边形GEHF 中, ，•四边形GEHF是平行四边形，• EF和GH互相平分.说明：本题中多次使用了平行四边形的性质：对边平行且相等以及平行四边形的判断方法：对边平行且相等的四边形是平行四边形. 通过解题应熟悉平行四边形的性质及判别.例3 分析平行四边形ABCD被■- - 宀和一】分别成15个相等的小平行四边形。

平行四边形判定经典题型

平行四边形判定经典题型平行四边形是初中数学中的一个经典题型，通常出现在几何学习中的平行线与四边形的章节中。

判定一个四边形为平行四边形，需要根据题目给出的条件进行分析和推理。

下面是几个常见的判定平行四边形的题型及其解题思路。

1. 已知四边形的对角线互相平分题目描述：已知ABCD是一个四边形，AC和BD两条对角线相交于点O，且满足AO=OC和BO=OD。

判断ABCD是否为平行四边形。

解题思路：由于AO=OC和BO=OD，可以得出AO和OC是两相等的向量，BO和OD是两相等的向量。

可以利用向量运算加法和减法判断AO和BO以及OC和OD是否平行，如果平行，则可以判定四边形ABCD为平行四边形。

2. 已知四边形的两对边互相平行题目描述：已知ABCD是一个四边形，且满足AB∥CD以及AD∥BC。

判断ABCD是否为平行四边形。

解题思路：根据题目所给条件，AB∥CD和AD∥BC，可以利用平行线的性质，推导出角A=角C和角B=角D。

如果角A=角C和角B=角D成立，则可以判定四边形ABCD为平行四边形。

3. 已知四边形的两组对边比例相等题目描述：已知四边形ABCD，满足AB/CD = AD/BC。

判断ABCD是否为平行四边形。

解题思路：根据题目所给条件，AB/CD = AD/BC，可以利用四边形的相似比例性质，如果AB/CD = AD/BC成立，则可以判定四边形ABCD为平行四边形。

4. 已知四边形的对边互相平等题目描述：已知ABCD是一个四边形，满足AB = CD以及AD = BC。

判断ABCD是否为平行四边形。

解题思路：根据题目所给条件，AB = CD和AD = BC，可以利用四边形的性质，如果AB = CD和AD = BC成立，则可以判定四边形ABCD为平行四边形。

5. 已知四边形的一个内角和一个对角线题目描述：已知ABCD是一个四边形，且角A和角C满足A+C=180°，对角线BD相交于点O。

判断ABCD是否为平行四边形。

八年级数学下册《平行四边形的判定》单元测试卷(附带答案)

八年级数学下册《平行四边形的判定》单元测试卷(附带答案)一．选择题1．四边形ABCD中，AD∥BC．要判别四边形ABCD是平行四边形，还需满足条件（）A．∠A+∠C＝180°B．∠B+∠A＝180°C．∠A＝∠D D．∠B＝∠D2．四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）A．AB∥DC，AD∥BC B．AB＝DC，AD＝BCC．AO＝CO，BO＝DO D．AB＝DC，AD∥BC3．如图，四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（）A．∠ABC＝∠ADC，AD∥BC B．∠ABD＝∠BDC，∠BAD＝∠DCBC．∠ABD＝∠BDC，OA＝OC D．∠ABC＝∠ADC，AB＝CD4．下列说法不正确的是（）A．两组对边分别平行的四边形是平行四边形B．一组对边平行，另一组对边相等的四边形是平行四边形C．一组对边平行且相等的四边形是平行四边形D．一组对边平行，一组对角相等的四边形是平行四边形5．如图，在▱ABCD中，AB＝6，BC＝8，∠C的平分线交AD于E，交BA的延长线于F，则AE+AF的值等于（）A．2B．3C．4D．66．如图，将▱ABCD沿对角线AC折叠，使点B落在B′处，若∠1＝∠2＝44°，则∠B为（）A．66°B．104°C．114°D．124°7．已知四边形ABCD的对角线AC、BD相交于点O，给出下列5个条件：①AB∥CD；②OA＝OC；③AB ＝CD；④∠BAD＝∠DCB；⑤AD∥BC，从以上5个条件中任选2个条件为一组，能判定四边形ABCD 是平行四边形的有（）组．A．4B．5C．6D．78．如图，在平行四边形ABCD中，E，F是对角线BD上不同的两点，连接AE，CE，AF，CF．下列条件中，不能得出四边形AECF一定是平行四边形的为（）A．BE＝DF B．AE＝CF C．AF∥CE D．∠BAE＝∠DCF9．如图，在▱ABCD中，点E，F分别在边BC，AD上，有下列条件：①BE＝DF；②AE∥CF；③AE＝CF；④∠BAE＝∠DCF．其中，能使四边形AECF是平行四边形的条件有（）A．1个B．2个C．3个D．4个10．如图，在▱ABCD中，∠ABC＝45°，BC＝4，点F是CD上一个动点，以F A、FB为邻边作另一个▱AEBF，当F点由D点向C点运动时，下列说法正确的选项是（）①▱AEBF的面积先由小变大，再由大变小②▱AEBF的面积始终不变③线段EF最小值为4A．①B．②C．①③D．②③二．填空题11．如图，BD是▱ABCD的对角线，点E、F在BD上，要使四边形AECF是平行四边形，还需增加的一个条件是．12．如图，在▱ABCD中，AB＝2cm，AD＝4cm，AC⊥BC，则△DBC比△ABC的周长长cm．13．如图，在四边形ABCD中，若AB＝CD，则添加一个条件，能得到平行四边形ABCD．（不添加辅助线，任意添加一个符合题意的条件即可）14．在平面直角坐标系中，A（﹣1，1），B（2，3），C（3m，4m+1），D在x轴上，若以A，B，C，D四点为顶点的四边形是平行四边形，求点D的坐标．15．如图，四边形ABCD中，AD∥BC，AD＝12cm，BC＝15cm，点P自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，直线PQ截原四边形为两个新四边形．则当P，Q同时出发秒后其中一个新四边形为平行四边形．16．如图，在平面直角坐标系中，有一Rt△ABC，∠C＝90°且A（﹣1，3）、B（﹣3，﹣1）、C（﹣3，3），已知△A1AC1是由△ABC旋转得到的．若点Q在x轴上，点P在直线AB上，要使以Q、P、A1、C1为顶点的四边形是平行四边形，满足条件的点Q的坐标为．17．在平面直角坐标系里，A（1，0），B（0，2），C（﹣4，2），若以A、B、C、D为顶点的四边形是平行四边形，则点D的坐标为．18．如图，在平面直角坐标系中，点A的坐标为（1，0），点B的坐标为（4，0），点C在y的正半轴上，且OB＝2OC，在直角坐标平面内确定点D，使得以点D、A、B、C为顶点的四边形是平行四边形，请写出点D的坐标为．三．解答题19．如图，点B，E，C，F在一条直线上，AB＝DE，AB∥DE，BE＝CF．（1）求证：△ABC≌△DEF；（2）连接AD，求证：四边形ACFD是平行四边形．20．E，F是四边形ABCD对角线AC上的两点，AD∥BC，DF∥BE，AE＝CF．（1）根据题意，画出图形；（2）求证：①△AFD≌△CEB；②四边形ABCD是平行四边形．21．已知，如图所示，AB∥CD，AB＝CD，点E、F在BD上．∠BAE＝∠DCF，连接AF、EC，求证：（1）AE＝FC；（2）四边形AECF是平行四边形．22．如图，四边形ABCD中AC、BD相交于点O，延长AD至点E，连接EO并延长交CB的延长线于点F，∠E＝∠F，AD＝BC．（1）求证：O是线段AC的中点：（2）连接AF、EC，证明四边形AFCE是平行四边形．23．如图，AB＝CD，E，F分别为AB、CD上的点，连接BC，分别与AF、ED相交于点G，H．∠B＝∠C，BH＝CG．（1）求证：AG＝DH；（2）求证：四边形AFDE是平行四边形．24．已知，如图，在平行四边形ABCD中，延长DA到点E，延长BC到点F，使得AE＝CF，连接EF，分别交AB，CD于点M，N，连接DM，BN．（1）求证：△AEM≌△CFN；（2）求证：四边形BMDN是平行四边形．参考答案一．选择题1．解：∵AD∥BC∴∠A+∠B＝180°，∠D+∠C＝180°∴A．∠A+∠C＝180°，可得∠B＝∠C，这样的四边形是等腰梯形，不是平行四边形，故此选项错误；B．∠A+∠B从题目已知条件即可得出，无法证明四边形为平行四边形，此选项错误；C．同理A，这样的四边形是等腰梯形，故此选项错误；D．∠B＝∠D，可得∠A+∠D＝180°，则BA∥CD，故四边形ABCD是平行四边形，此选项正确；故选：D．2．解：∵AB∥DC，AD∥BC∴四边形ABCD是平行四边形，故选项A不合题意；∵AB＝CD，AD＝BC∴四边形ABCD是平行四边形，故选项B不合题意；∵AO＝CO，BO＝DO∴四边形ABCD是平行四边形，故选项C不合题意；∵AB＝CD，AD∥BC∴四边形ABCD不一定是平行四边形，故选项D符合题意；故选：D．3．解：A、∵AD∥BC∴∠ABC+∠BAD＝180°∵∠ABC＝∠ADC∴∠ADC+∠BAD＝180°∴AB∥CD∴四边形ABCD是平行四边形，故此选项不合题意；B、∵∠ABD＝∠BDC，∠BAD＝∠DCB∴∠ADB＝∠CBD∴AD∥CB∵∠ABD＝∠BDC∴AB∥CD∴四边形ABCD是平行四边形，故此选项不合题意；C、∵∠ABD＝∠BDC，OA＝OC又∠AOB＝∠COD∴△AOB≌△COD（AAS）∴四边形ABCD是平行四边形，故此选项不合题意；D、∠ABC＝∠ADC，AB＝CD不能判断四边形ABCD是平行四边形，故此选项符合题意；故选：D．4．解：A、∵两组对边分别平行的四边形是平行四边形∴选项A不符合题意；B、∵一组对边平行，另一组对边相等的四边形不一定是平行四边形∴选项B符合题意；C、∵一组对边平行且相等的四边形是平行四边形∴选项C不符合题意；D、∵一组对边平行，一组对角相等的四边形是平行四边形∴选项D不符合题意；故选：B．5．解：∵四边形ABCD是平行四边形∴AB∥CD，AD＝BC＝8，CD＝AB＝6∴∠F＝∠DCF∵CF平分∠BCD∴∠FCB＝∠DCF∴∠F＝∠FCB∴BF＝BC＝8同理：DE＝CD＝6∴AF＝BF﹣AB＝2，AE＝AD﹣DE＝2∴AE+AF＝4；故选：C．6．解：∵四边形ABCD是平行四边形∴AB∥CD∴∠ACD＝∠BAC由折叠的性质得：∠BAC＝∠B′AC∴∠BAC＝∠ACD＝∠B′AC＝∠1＝22°∴∠B＝180°﹣∠2﹣∠BAC＝180°﹣44°﹣22°＝114°；7．解：①与⑤根据两组对边分别平行的四边形是平行四边形，能推出四边形ABCD为平行四边形；①与③根据一组对边平行且相等的四边形是平行四边形，能推出四边形ABCD为平行四边形；①与④，⑤与④根据两组对角分别相等的四边形是平行四边形，能推出四边形ABCD为平行四边形；①与②，②与⑤根据对角线互相平分的四边形是平行四边形，能推出四边形ABCD为平行四边形．所以能推出四边形ABCD为平行四边形的有6组．故选：C．8．解：如图，连接AC与BD相交于O在▱ABCD中，OA＝OC，OB＝OD要使四边形AECF为平行四边形，只需证明得到OE＝OF即可；A、若BE＝DF，则OB﹣BE＝OD﹣DF，即OE＝OF，故本选项不符合题意；B、若AE＝CF，则无法判断OE＝OE，故本选项符合题意；C、AF∥CE能够利用“角角边”证明△AOF和△COE全等，从而得到OE＝OF，故本选项不符合题意；D、由∠BAE＝∠DCF，从而推出△DFC≌△BEA，然后得出∠DFC＝∠BEA，∴∠CFE＝∠AEF，∴FC∥AE，由全等可知FC＝AE，所以四边形AECF是平行四边形；故本选项不符合题意；故选：B．9．解：①正确，理由如下：∵四边形ABCD平行四边形∴AD＝BC，AD∥BC又∵BE＝DF∴AF＝EC．又∵AF∥EC∴四边形AECF是平行四边形．②正确，理由如下：∵AF∥EC，AE∥CF∴四边形AECF是平行四边形；④正确；理由如下：∵四边形ABCD是平行四边形∴∠B＝∠D∵∠BAE＝∠DCF∴∠AEB＝∠CFD．∵AD∥BC∴∠AEB＝∠EAD．∴∠CFD＝∠EAD．∴AE∥CF．∵AF∥CE∴四边形AECF是平行四边形．∵AE＝CF不能得出四边形AECF是平行四边形∴③不正确；能使四边形AECF是平行四边形的条件有3个．故选：C．10．解：过点C作CG⊥AB于点G则∵AB与CG的值始终不变化∴△ABF的面积始终不变化∵▱AEBF的面积＝2×△ABF的面积∴▱AEBF的面积始终不变∴①错误，②正确；连接EF，与AB交于点H∵四边形AEBF是平行四边形∴AH＝BH，EH＝FH当FH⊥AB时，FH的值最小，EF＝2FH的值也最小此时，FH＝CG∵∠ABC＝45°，CG⊥AB∴BG＝CG∵BG2+CG2＝BC2＝16∴∴FH＝∴线段EF最小值为EF＝2FH＝4．∴③正确故选：D．二．填空题（共8小题）11．解：如图，连接AC交BD于点O∵四边形ABCD为平行四边形∴AO＝CO，BO＝DO∴当BE＝DF时，可得OE＝OF，则四边形AECF为平行四边形∴可增加BE＝DF故答案为：BE＝DF（答案不唯一）．12．解：在▱ABCD中，∵AB＝CD＝2cm，AD＝BC＝4cm，AO＝CO，BO＝DO ∵AC⊥BC∴AC＝＝6cm∴OC＝3cm∴BO＝＝5cm∴BD＝10cm∴△DBC的周长﹣△ABC的周长＝BC+CD+BD﹣（AB+BC+AC）＝BD﹣AC＝10﹣6＝4cm 故答案为：4．13．解：根据平行四边形的判定，可再添加一个条件：AD＝BC．故答案为：AD＝BC（答案不唯一）．14．解：由点C的坐标可以判断出点C在直线y＝上已知A、B两点，所以以AB为边和对角线分类讨论当AB为边时，AB∥CD，AB＝CD，如图可证得△ABE≌△CDF∴FC＝BE＝2，AE＝DF＝3若点D在x轴正半轴时∴点C坐标为（，﹣2）∴点D坐标为（，0）若点D在x轴负半轴时点C坐标为（，2）点D坐标为（﹣，0）当AB为对角线时AB与CD相交于AB的中点（，2）设点D（m，0）可得点C坐标为（1﹣m，4）将点C坐标代入解析式可得m＝点D坐标为（，0）故点D的坐标为（，0）或（，0）或（﹣，0）．15．解：根据题意有AP＝tcm，CQ＝2tcm，PD＝（12﹣t）cm，BQ＝（15﹣2t）cm．①∵AD∥BC∴当AP＝BQ时，四边形APQB是平行四边形．∴t＝15﹣2t解得t＝5．∴t＝5s时四边形APQB是平行四边形；②AP＝tcm，CQ＝2tcm∵AD＝12cm，BC＝15cm∴PD＝AD﹣AP＝（12﹣t）cm∵AD∥BC∴当PD＝QC时，四边形PDCQ是平行四边形．即：12﹣t＝2t解得t＝4s∴当t＝4s时，四边形PDCQ是平行四边形．综上所述，当P，Q同时出发4或5秒后其中一个新四边形为平行四边形．故答案是：4或5．16．解：∵点Q在x轴上，点P在直线AB上，以Q、P、A1、C1为顶点的四边形是平行四边形当A1C1为平行四边形的边时∴PQ＝A1C1＝2∵P点在直线y＝2x+5上∴令y＝2时，2x+5＝2，解得x＝﹣1.5令y＝﹣2时，2x+5＝﹣2，解得x＝﹣3.5∴点Q的坐标为（﹣1.5，0），（﹣3.5，0）当A1C1为平行四边形的对角线时∵A1C1的中点坐标为（3，2）∴P的纵坐标为4代入y＝2x+5得，4＝2x+5解得x＝﹣0.5∴P（﹣0.5，4）∵A1C1的中点坐标为：（3，2）∴直线PQ的解析式为：y＝﹣x+当y＝0时，即0＝﹣x+解得：x＝6.5故Q为（﹣1.5，0）或（﹣3.5，0）或（6.5，0）．故答案为（﹣1.5，0）或（﹣3.5，0）或（6.5，0）．17．解：如图有三种情况：①平行四边形AD1CB∵A（1，0），B（0，2），C（﹣4，2）∴AD1＝BC＝4，OD1＝3则D的坐标是（﹣3，0）；②平行四边形AD2BC∵A（1，0），B（0，2），C（﹣4，2）∴AD2＝BC＝4，OD2＝1+4＝5则D的坐标是（5，0）；③平行四边形ACD3B∵A（1，0），B（0，2），C（﹣4，2）∴D3的纵坐标是2+2＝4，横坐标是﹣（4+1）＝﹣5则D的坐标是（﹣5，4）故答案为：（﹣3，0）或（5，0）或（﹣5，4）．18．解：如图，①当BC为对角线时，易求M1（3，2）；②当AC为对角线时，CM∥AB，且CM＝AB．所以M2（﹣3，2）；③当AB为对角线时，AC∥BM，且AC＝BM．则|M y|＝OC＝2，|M x|＝OB+OA＝5，所以M3（5，﹣2）．综上所述，符合条件的点D的坐标是M1（3，2），M2（﹣3，2），M3（5，﹣2）．故答案为：（3，2）（﹣3，2）（5，﹣2）．三．解答题19．证明：（1）∵AB∥DE∴∠B＝∠DEF∵BE＝CF∴BE+CE＝CF+CE即BC＝EF在△ABC和△DEF中∴△ABC≌△DEF（SAS）；（2）由（1）得：△ABC≌△DEF∴AC＝DF，∠ACB＝∠F∴AC∥DF∴四边形ACFD是平行四边形．20．（1）解：如图，即为所画的图形；（2）证明：①如图，∵AD∥BC，DF∥BE∴∠DAF＝∠BCE，∠DF A＝∠BEC又AE＝CF∴AE+EF＝CF+EF即AF＝CE在△AFD与△CEB中∴△AFD≌△CEB（ASA）；②由①知，△AFD≌△CEB则AD＝CB又∵AD∥BC∴四边形ABCD是平行四边形．21．证明：（1）∵AB∥CD∴∠B＝∠D．在△ABE和△CDF中∴△ABE≌△CDF（ASA）．∴AE＝CF．（2）由（1）△ABE≌△CDF得AE＝CF，∠AEB＝∠CFD ∴180°﹣∠AEB＝180°﹣∠CFD即∠AEF＝∠CFE．∴AE∥CF．∵AE＝CF∴四边形AECF是平行四边形．22．证明：（1）∵∠E＝∠F∴AD∥BC∵AD＝BC∴四边形ABCD是平行四边形∴AC，BD互相平分；即O是线段AC的中点．（2）∵AD∥BC∴∠EAC＝∠FCA在△OAE和△OCF中∴△OAE≌△OCF（ASA）．∴OE＝OF又∵OA＝OC∴四边形AFCE是平行四边形．23．证明：（1）∵BH＝CG∴BH+HG＝CG+HG∴BG＝CH在△ABG与△CDH中∴△ABG≌△CDH（SAS）∴AG＝DH；（2）∵△ABG≌△CDH∴∠AGB＝∠CHD∴AF∥DE∵∠B＝∠C∴AB∥CD∴四边形AFDE是平行四边形．24．证明：（1）四边形ABCD是平行四边形∴∠DAB＝∠BCD∴∠EAM＝∠FCN又∵AD∥BC∴∠E＝∠F．∵在△AEM与△CFN中∴△AEM≌△CFN（ASA）；（2）∵四边形ABCD是平行四边形∴AB＝CD，AB∥CD又由（1）得AM＝CN∴BM＝DN，BM∥DN∴四边形BMDN是平行四边形．。

平行四边形判定专项练习30题

平行四边形的判定专项练习30题（有答案）1．如图，四边形ABCD中，AD∥BC，ED∥BF，AF=CE，求证：ABCD是平行四边形．2．如图，四边形ABCD中，∠BAC=90°，AB=11﹣x，BC=5，CD=x﹣5，AD=x﹣3，AC=4．求证：四边形ABCD为平行四边形．3．已知四边形ABCD的对角线AC与BD交于点O，现给出四个条件：①OA=OC；②AB=CD；③∠BAD=∠DCB；④AD∥BC．请你从中选择两个，推出四边形ABCD为平行四边形，并写出你的推理过程．（1）从以上4个条件中任意选取2个条件，能推出四边形ABCD是平行四边形的有（用序号表示）_________ ．（2）从（1）中选出一种情况，写出你的推理过程．4．如图，已知：点B、E、F、D在一条直线上，DF=BE，AE=CF．请从下列三个条件中选择一个合适的条件，添加到已知条件中，使四边形ABCD是平行四边形，并说明理由，供选择的三个条件（请从其中选择一个）：①AB=DC；②BC=AD；③∠AED=∠CFB．5．如图，在▱ABCD中，AC交BD于点O，点E，点F分别是OA，OC的中点，请判断线段BE，DF的位置关系和数量关系，并说明你的结论．6．如图所示，以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF，猜想：四边形ADEF 是什么四边形，试证明你的结论．7．如图，已知BE⊥AD，CF⊥AD，且BE=CF．求证：（1）AD是△ABC的中线；（2）请连接BF、CE，试判断四边形BECF是何种特殊四边形，并说明理由．8．如图，矩形ABCD的两条对角线AC和BD相交于点O，E、F是BD上的两点，且∠AEB=∠CFD．求证：四边形AECF 是平行四边形．9．如图：在四边形ABCD中，AD∥BC，AB=CD，E是BC上一点，DE=AB．求证：四边形ABED是平行四边形．10．如图，已知 AB∥DC，E是BC的中点，AE，DC的延长线交于点F；（1）求证：△ABE≌△FCE；（2）连接AC，BF．则四边形ABFC是什么特殊的四边形？请说明理由．11．等边△ABC中，点D在BC上，点E在AB上，且CD=BE，以AD为边作等边△ADF，如图．求证：四边形CDFE是平行四边形．12．如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE．若∠BAC=30°，EF⊥AB，垂足为F，连结DF．求证：（1）△ABC≌△EAF；（2）四边形ADFE是平行四边形．13．已知：如图，在△ABC中，中线BE，CD交于点O，F，G分别是OB，OC的中点．求证：四边形DFGE是平行四边形．14．如图所示：在四边形ABCD中，AD∥BC、BC=18cm，CD=15cm，AD=10cm，AB=12cm，动点P、Q分别从A、C同时出发，点P以2cm/秒的速度由A向D运动，点Q以3cm/秒的速度由C向B运动．（1）几秒钟后，四边形ABQP为平行四边形？并求出此时四边形ABQP的周长（2）几秒钟后，四边形PDCQ为平行四边形？并求出此时四边形PDCQ的周长．15．求证：顺次连接四边形各边中点所得的四边形是平行四边形．16．△ABC中，中线BE、CF相交于O，M是BO的中点，N是CO的中点，求证：四边形MNEF是平行四边形．17．如图，AD=DB，AE=EC，FG∥AB，AG∥BC．（1）证明：△AGE≌△CFE；（2）说明四边形ABFG是平行四边形；（3）研究图中的线段DE，BF，FC之间有怎样的位置关系和数量关系．18．如图，△ABC和△ADE都是等边三角形，点D在BC边上，AB边上有一点F，且BF=DC，连接EF、EB．（1）求证：△ABE≌△ACD；（2）求证：四边形EFCD是平行四边形．19．已知在△ABC中，D、E分别是AB、AC的中点，点F在DE的延长线上，且EF=DE，图中有几个平行四边形？请说明你的理由．20．如图，在△ABC中，AD是中线，点E是AD的中点，过A点作BC的平行线交CE的延长线于点F，连接BF．求证：四边形AFBD是平行四边形．21．如图：在四边形ABCD中，AD∥BC，E是BC的中点，BC=2AD．找出图中所有的平行四边形，并选择一个说明它是平行四边形的理由．22．求证：两组对角分别相等的四边形是平行四边形．23．已知：如图，A、B、C、D在同一条直线上，且AB=CD，AE∥DF，AE=DF．求证：四边形EBFC是平行四边形．24．如图，在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，CE∥BF，连接BE、CF．图中的四边形BFCE 是平行四边形吗？为什么？25．已知点E、F、G、H分别为四边形ABCD四边的中点，试问四边形EFGH的形状并说明理由．26．如图，已知四边形ABCD中AD=BC，点A、B、E在同一条直线上，且∠B=∠EAD，试说明四边形ABCD是平行四边形．27．如图，AD∥BC，ED∥BF，且AE=CF，求证：四边形ABCD是平行四边形．28．已知：△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点．求证：四边形DEFG是平行四边形．29．如图，△ACD、△ABE、△BCF均为直线BC同侧的等边三角形．当AB≠AC时，求证：四边形ADFE为平行四边形．30．已知：在四边形ABCD中，AD∥BC，且AB=DC=5，AC=4，BC=3．求证：四边形ABCD为平行四边形．平行四边形的判定30题参考答案：1．∵AD∥BC，∴∠DAE=∠BCF，∵ED∥BF，∴∠DEF=∠BFE，∴∠AED=∠CFB，又∵AF=CE，∴AE=CF，在△ADE和△CBF中：∵∠DAE=∠BCF，∠AED=∠CFB，AE=CF，∴△ADE≌△CBF（AAS），∴AD=CB，即：AD∥CB，AD=CB，∴四边形ABCD是平行四边形，2．∵∠BAC=90°，AB=11﹣x，BC=5，AC=4．∴（11﹣x）2+42=52，解得：x1=8，x2=14＞11（舍去），当x=8时，BC=AD=5，AB=CD=3，∴四边形ABCD为平行四边形．3．（1）解：能推出四边形ABCD是平行四边形的有①④、③④；故答案是：①④、③④；（2）以①④为例进行证明．如图，在四边形ABCD中，OA=OC，AD∥BC．证明：∵AD∥BC，∴∠DAO=∠BCO．∴在△AOD与△COB中，，∴△AOD≌△COB（ASA），∴AD=BC，∴在四边形ABCD中，AD BC，∴四边形ABCD为平行四边形．4．选择①，∵DF=BE，AE=CF，AB=CD，∴△ABE≌△CDF（sss），∴∠ABE=∠CDF，∴四边形ABCD是平行四边形．5. BE=DF，BE∥DF因为ABCD是平行四边形，所以OA=OC，OB=OD，因为E，F分别是OA，OC的中点，所以OE=OF，所以BFDE是平行四边形，所以BE=DF，BE∥DF 6．四边形ADEF是平行四边形．连接ED、EF，∵△ABD、△BCE、△ACF分别是等边三角形，∴AB=BD，BC=BE，∠DBA=∠EBC=60°．∴∠DBE=∠ABC．∴△ABC≌△DBE．同理可证△ABC≌△FEC，∴AB=EF，AC=DE．∵AB=AD，AC=AF，∴AD=EF，DE=AF．∴四边形ADEF是平行四边形7．（1）∵BE⊥AD，CF⊥AD，∴∠BED=∠CFD．∵∠BDE=∠CDF，BE=CF，∴△BED≌△CFD．∴BD=CD．∴AD是△ABC的中线．（2）四边形BECF是平行四边形，由（1）得：BD=CD，ED=FD．∴四边形BECF是平行四边形8．∵四边形ABCD是矩形∴AB∥CD，AB=CD，∴∠ABE=∠CDF，又∵∠AEB=∠CFD，∴△ABE≌△CDF，∴BE=DF，又∵四边形ABCD是矩形，∴OA=OC，OB=OD，∴OB﹣BE=OD﹣DF，∴OE=OF，∴四边形AECF是平行四边形9．∵AD∥BC，AB=CD，∴四边形ABCD是等腰梯形，∴∠B=∠C，∵DE=AB，∴∠DEC=∠B，∴AB∥DE，∴四边形ABED是平行四边形．10．（1）证明：∵AB∥DC，∴∠1=∠2，∠FCE=∠EBA，∵E为BC中点，∴CE=BE，∵在△ABE和△FCE中，∠1=∠2，∠FCE=∠EBA，CE=BE，∴△ABE≌△FCE；（2）四边形ABFC是平行四边形；理由：由（1）知：△ABE≌△FCE，∴EF=AE，∵CE=BE，∴四边形ABFC是平行四边形11．连接BF，∵△ADF和△ABC是等边三角形，∴AF=AD=DF，AB=AC=BC，∠ABC=∠ACD=∠CAB=∠FAD=60°，∴∠FAD﹣∠EAD=∠CAB﹣∠EAD，∴∠FAB=∠CAD，在△FAB和△DAC中，∴△FAB≌△DAC（SAS），∴BF=DC，∠ABF=∠ACD=60°，∵BE=CD，∴BF=BE，∴△BFE是等边三角形，∴EF=BE=CD，在△ACD和△CBE中∵，∴△ACD≌△CBE（SAS），∴AD=CE=DF，∵EF=CD，∴四边形CDFE是平行四边形．12．（1）∵△ABE为等边三角形，EF⊥AB，∴EF为∠BEA的平分线，∠AEB=60°，AE=AB，在△ABC和△EAF中，，∴△ABC≌△EAF（AAS）；（2）∵∠BAC=30°，∠DAC=60°，∴∠DAB=90°，即DA⊥AB，∵EF⊥AB，∴AD∥EF，∵△ABC≌△EAF，∴EF=AC=AD，∴四边形ADFE是平行四边形13．在△ABC中，∵AD=BD，AE=CE，∴DE∥BC且DE=BC．在△OBC中，∵OF=FB，OG=GC，∴FG∥BC且FG=BC．∴DE∥FG，DE=FG．∴四边形DFGE为平行四边形14．（1）x秒后，四边形ABQP为平行四边形．则2x=18﹣3x，解得x=3.6．3.6秒钟后，四边形ABQP为平行四边形，此时四边形ABQP的周长是3.6×2×2+12×2=38.4cm．（2）y秒后，四边形PDCQ为平行四边形．10﹣2y=3y，解得y=2.2秒钟后，四边形PDCQ为平行四边形，此时四边形PDCQ的周长是3.6×2×2+15×2=43.2cm．15．：连接BD，∵E、F为AD，AB中点，∴FE BD．又∵G、H为BC，CD中点，∴GH BD，故GH FE．同理可证，EH FG．∴四边形FGHE是平行四边形16．∵BE，CF是△ABC的中线，∴EF∥BC且EF=BC，∵M是BO的中点，N是CO的中点，∴EF∥MN且EF=MN，∴四边形MNEF是平行四边形．17．（1）证明：∵AG∥BC（已知）∴∠G=∠EFC（两直线平行，内错角相等）∵∠AEG=∠FEC（对顶角相等），又AE=EC（已知）∴△AGE≌△CFE（AAS）；（2）说明：∵FG∥AB，AG∥BC（已知）∴四边形ABFG是平行四边形（平行四边形的定义）；（3）解：线段DE，BF，FC之间的位置关系是DE∥BF，DE∥FC，数量关系是DE=BF=FC，理由：由（1）可知△AGE≌△CFE∴AG=FC，FE=EG（全等三角形的对应边相等），∴E是FG的中点，又∵AD=DB（已知）∴DE为三角形ABC的中位线，∴DE=BC，DE∥BC，即DE∥BF，DE∥FC，由（2）可知四边形ABFG是平行四边形∴AG=BF，∴BF=FC=BC，∴DE=BF=FC，即线段DE，BF，FC之间的位置关系是DE∥BF，DE∥FC，数量关系是DE=BF=FC．18．（1）∵△ABC和△ADE都是等边三角形，∴AE=AD，AB=AC，∠EAD=∠BAC=60°，∴∠EAD﹣∠BAD=∠BAC﹣∠BAD，即：∠EAB=∠DAC，∴△ABE≌△ACD（SAS）；（2）证明：∵△ABE≌△ACD，∴BE=DC，∠EBA=∠DCA，又∵BF=DC，∴BE=BF．∵△ABC是等边三角形，∴∠DCA=60°，∴△BEF为等边三角形．∴∠EFB=60°，EF=BF∵△ABC是等边三角形，∴∠ABC=60°，∴∠ABC=∠EFB，∴EF∥BC，即EF∥DC，∴四边形EFCD是平行四边形19．平行四边形ADCF和平行四边形DBCF．理由：（1）∵D、E分别是AB、AC边的中点，∴DE∥BC ，．又∵EF=DE，∴DF=BC，∴四边形DBCF是平行四边形；（2）在四边形ADCF中，∵EF=DE，又∵E是AC边的中点，∴EA=EC，∴四边形ADCF是平行四边形20．∵E为AD中点，∴AE=DE，∵AF∥BC，∴∠AFE=∠DCE，在△AEF和△CED中∵，∴△AEF≌△CED（AAS），∴AF=DC，∵AD是△ABC的中线，∴BD=DC，∴AF=BD，即AF∥BD，AF=BD，故四边形AFBD是平行四边形21．图中有两个平行四边形：▱ABED、▱AECD．∵，∴AD=BE，∵AD∥BC，∴四边形ABED是平行四边形．22．已知：四边形ABCD，∠A=∠C，∠B=∠D，求证：四边形ABCD是平行四边形，证明：∵∠A=∠C，∠B=∠D，∠A+∠B+∠C+∠D=360°，∴2∠A+2∠B=360°，∴∠A+∠B=180°，∴AD∥BC，同理AB∥CD，∴四边形ABCD是平行四边形．在△ABE和△DCF中∴△ABE≌△DCF（SAS），∴EB=FC，∠ABE=∠DCF，∵∠ABE+∠EBC=180°，∠DCF+∠FCB=180°，∴∠EBC=∠FCB，∴BE∥FC，∵BE=FC，∴四边形EBFC是平行四边形24．∵CE∥BF，BD=CD，∴△BDF≌△CDE，∴BF=CE，∴四边形BFCE是平行四边形．25．四边形EFGH是平行四边形证明：连接AC、BD∵E、F、G、H分别为四边形ABCD四边的中点∴EH=BD，FG=BD，HG=AC，EF=AC∴EH=FG，EF=HG∴四边形EFGH是平行四边形．26．∵∠B=∠EAD，∴AD∥BC，∵AD=BC，∴四边形ABCD是平行四边形．27．∵AD∥BC，∴∠EAD=∠FCB，又ED∥BF，∴∠FED=∠EFB，∠AED=180°﹣∠FED，∠CFB=180°﹣∠EFB，∴∠AED=∠CFB，又已知AE=CF，∴△AED≌△CFB，∴AD=BC，∴四边形ABCD是平行四边形．28．∵AD∥BC，∴∠EAD=∠FCB，又ED∥BF，∴∠FED=∠EFB，∠AED=180°﹣∠FED，∠CFB=180°﹣∠EFB，∴∠AED=∠CFB，又已知AE=CF，∴△AED≌△CFB，∴AD=BC，∴四边形ABCD是平行四边形．29．∵△ABE、△BCF为等边三角形，∴AB=BE=AE，BC=CF=FB，∠ABE=∠CBF=60°．∴∠FBE=∠CBA，在△FBE和△CBA中，，∴△FBE≌△CBA（SAS）．∴EF=AC．又∵△ADC为等边三角形，∴CD=AD=AC．∴EF=AD．同理可得AE=DF．∴四边形AEFD是平行四边形30．∵AB=5，AC=4，BC=3∴AB2=AC2+BC2∴∠BCA=90°∵AD∥BC∴∠DAC=∠BCA=90°∵DC=5，AC=4，∴AD2=DC2﹣AC2=9∴AD=BC=3∴四边形ABCD为平行四边形．。

(完整版)平行四边形的判定练习及答案

诘你添加一个适当的条 A.1： 2 ：B.2 ： 2 ：C.2 ： 3 ：平行四边形的判定二、课中强化（10分钟训练）1•如图3,在匚ABCD 中，对角线F 满足F 列哪个条件时，四边形AC 、BD 相交于点0,E 、F 是对角线AC 上的两点，当E 、 DEBF 不一定是平行四边形（ A.AE=CFC.Z ADE=/CBFB.DE=BF D. / AED= / CFB 2•如图 4,AB\|DC, DC=EF=10 , DE=CF=8，则图中的平行四边形有由分别是 ___________________3.如图5,E 、F 是平行四边形ABCD 对角线BD 上的两点,'使四边形AECF 是平行四边形.4.如图6,AD=BC,要使四边形ABCD 是平行四边形，还需补充的一个条件是： __________三、课后巩固（30分钟训练）1 •以不在同一直线上的三个点为顶点作平行四边形最多能作（） A.4个 B.3个 C.2个 D.1个2. 下面给出了四边形ABCD 中/A 、/ B 、/ C 、/ D 的度数之比，其中能判定四边形ABCD 是平行四边形的是（）3. 九根火柴棒排成如右图形状，图中 __个平行四边形，你判断的根据是 __________________4. 已知四边形ABCD 的对角线AC 、BD 相交于点O,给出下列5个条件：①AB // CD ； OA=OC ; ③AB=CD :④/ BAD= / DCB ; ® AD // BC.（1）从以上5个条件中任意选取2个条件，能推出四边形ABCD 是平行四边形的有（用序图4图5 图6⑵对由以上5个条件中任意选取2个条件，不能推出四边形ABCD 是平行匹边形的，请选取一种情形举出反例说明 •5•若三条线段的长分别为平行四边形？20 cm,14 cm,16 cm,以其中两条为对角线，另一条为一边，是否可以画 6•如图，E 、F 是四边形ABCD 的对角线AC 上的两点，AF=CE , DF=BE , DF// BE.求证：(】)△AFD ©A CEB;(2)四边形ABCD 是平行四边形.17•如图，已知DC // AB ，且DC= —AB, E 为AB 的中点• 2⑴求证：△ AED EBC ;(2)观察图形，在不添加辅助线的情况下，除厶 EBC 夕卜，请再写出两个与厶AED 的面积相等的三角形(直接写出结果，不要求证明)： __________________________________8•如图，已知二1ABCD中DE丄AC,BF丄AC,证明四边形DEBF为平行四边形9•如图，已知■ ABCD中,E、F分别是AB、CD的中点•求证:(1) △ AFD ©A CEB;⑵四边形AECF是平行四边形•二、课中强化（10分钟训练）1懈析：当E、F满足AE=CF时，由平行四边形的对角线相等知OB=OD,OA=OC ,故OE=OF.可知四边形DEBF是平行四边形•当E、F满足/ ADE= / CBF 时，因为AD // BC,所以/ DAE= / BCF.又AD=BC，可证出厶ADE OA CBF，所以DE=BF，/ DEA= / BFC.故/ DEF= / BFE.因此DE// BF，可知四边形DEBF是平行四边形•类似地可说明D也可以•答案:B2•解析：因为ABWDC，根据一组对边平行且相等的四边形是平行四边形可判定四边形ABCD是平行四边形；DC=EF , DE=CF,根据两组对边分别相等的四边形是平行四边形可判定四边形CDEF是平行四边形•答案：四边形ABCD，四边形CDEF —组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形3•解析：根据平行四边形的定义和判定方法可填BE=DF ; Z BAE= / CDF^-答案：BE=DF或ZBAE=ZCDF等任何一个均可4•解析：根据平行四边形的判定定理，知可填（DAD// BC,② AB=CD,③ ZA+ZB=180。

中考数学总复习《平行四边形的判定与性质》练习题及答案

中考数学总复习《平行四边形的判定与性质》练习题及答案班级:___________姓名：___________考号：_____________一、单选题1．如图在四边形ABCD中AB=CD，对角线AC、BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连接AF、CE，若DE=BF，则下列结论不一定正确的是（）A．CF=AE B．OE=OFC．△CDE为直角三角形D．四边形ABCD是平行四边形2．如图四边形ABCD中AB∥CD，∥B＝∥D点E为BC延长线上一点，连接AE，AE交CD于点H，∥DCE的平分线交AE于点G．若AB＝2AD＝10，点H为CD的中点，HE＝6，则AC的值为（）A．9B．√97C．10D．3 √103．如图在Rt∥ABC中∥ACB=90°，分别以AB、AC为腰向外作等腰直角三角形∥ABD和∥ACE，连结DE，CA的延长线交DE于点F,则与线段AF相等的是()A．AC B．AB C．BC D．AB4．如图在菱形ΑΒCD中∠Α=60∘，AD=8，F是ΑΒ的中点．过点F作FΕ⊥ΑD，垂足为Ε．将ΔΑΕF沿点Α到点Β的方向平移，得到ΔΑ′Ε′F ′．设Ρ、Ρ′分别是ΕF、Ε′F ′的中点，当点Α′与点Β重合时，四边形ΡΡ′CD的面积为（）A．28√3B．24√3C．32√3D．32√3−85．下列说法中错误的是()A．平行四边形的对角线互相平分B．对角线互相垂直的四边形是菱形C．菱形的对角线互相垂直D．对角线互相平分的四边形是平行四边形6．如图．若要使平行四边形ABCD成为菱形．则需要添加的条件是（）A．AB=CD B．AD=BC C．AB=BC D．AC=BD7．如图点A是直线l外一点，在l上取两点B，C，分别以A，C为圆心，BC，AB的长为半径作弧，两弧交于点D，分别连接AB，AD，CD，若∥ABC+∥ADC=120°，则∥A的度数是（）A．100°B．110°C．120°D．125°8．如图在∥ABC中AB＝AC＝10，BC＝12，点D是BC上一点，DE∥AC，DF∥AB，则∥BED与∥DFC的周长的和为（）A．34B．32C．22D．209．如图在平面直角坐标系中点A(1,5),B(4,1),C(m,−m),D(m−3,−m+4)，当四边形ABCD 的周长最小时，则m 的值为（）.A．√2B．32C．2D．310．如图分别在四边形ABCD的各边上取中点E，F，G，H，连接EG，在EG上取一点M，连接HM，过F作FN∥HM，交EG于N，将四边形ABCD中的四边形①和②移动后按图中方式摆放，得到四边形AHM′G′和AF′N′E，延长M′G′，N′F′相交于点K，得到四边形MM′KN′．下列说法中错误的是（）A．S四边形MM′KN′=S四边形ABCD B．HM=NFC．四边形MM′KN′是平行四边形D．∠K=∠AHM′11．如图,已知∥ABC与∥CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD 是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤∥AOE与∥COF成中心对称.其中正确的个数为（）A．2B．3C．4D．512．如图P为平行四边形ABCD内一点，过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点，若S四边形AHPE＝3，S四边形PFCG＝5，则S∥PBD为（）A．0.5B．1C．1.5D．2二、填空题13．如图在平行四边形ABCD中点E，F分别在BC，AD上，请添加一个条件，使四边形AECF是平行四边形（只填一个即可）．14．如图在Rt△ABC中AC=2√3，BC=2，点P是斜边AB上任意一点，D是AC的中点，连接PD并延长，使DE=PD.以PE，PC为边构造平行四边形PCQE，则对角线PQ的最小值为.15．如图▱ABCD中∥BAD=120°，E、F分别在CD和BC的延长线上，AE∥BD，EF∥BC，EF=5√3，则AB的长是16．如图在∥ABC中∥ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD= 13BD，连接DM、DN、MN．若AB=6，则DN=．17．若AC＝10，BD＝8，那么当AO＝DO＝时，四边形ABCD是平行四边形。

平行四边形的判定基础练习

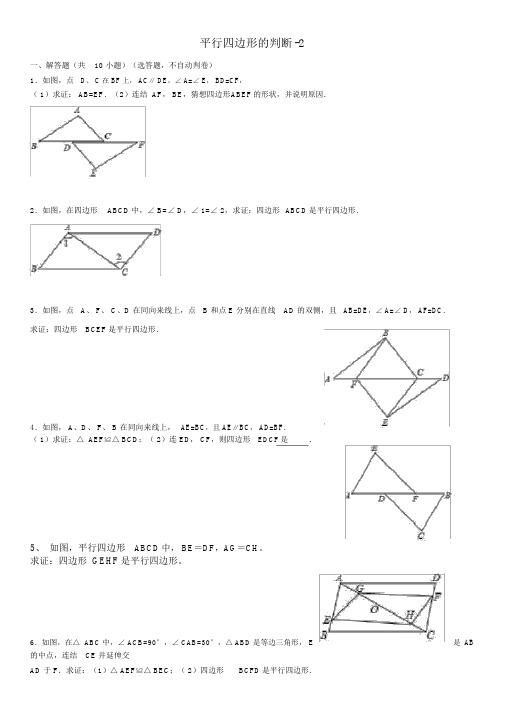
平行四边形的判断 -2一、解答题（共10 小题）（选答题，不自动判卷）1．如图，点D、 C 在 BF 上， AC∥ DE，∠ A=∠ E， BD=CF，（ 1）求证： AB=EF．（2）连结 AF， BE，猜想四边形A BEF的形状，并说明原因．2．如图，在四边形ABCD中，∠ B=∠ D，∠ 1=∠ 2，求证：四边形ABCD是平行四边形．3．如图，点A、 F、 C、D 在同向来线上，点 B 和点 E 分别在直线AD 的双侧，且AB=DE，∠ A=∠ D， AF=DC．求证：四边形BCEF是平行四边形．4．如图， A、D、 F、 B 在同向来线上，AE=BC，且 AE∥BC， AD=BF．（ 1）求证：△ AEF≌△ BCD；（ 2）连 ED， CF，则四边形EDCF是．5、如图，平行四边形ABCD中， BE＝DF，AG＝CH。

求证：四边形 GEHF是平行四边形。

6．如图，在△ ABC 中，∠ ACB=90°，∠ CAB=30°，△ ABD 是等边三角形，E是AB 的中点，连结CE并延伸交AD 于 F．求证：（1）△ AEF≌△ BEC；（ 2）四边形BCFD是平行四边形．7．已知：如图，在四边形ABCD中， AB∥ CD，E， F 为对角线AC 上两点，且AE=CF， DF∥ BE．求证：四边形ABCD为平行四边形．8．如图， AB∥ CD， AB=CD，点 E、F 在 BC 上，且 BE=CF．（ 1）求证：△ ABE≌△ DCF；（ 2）试证明：以A、F、 D、 E 为极点的四边形是平行四边形．9．如图，已知BE∥ DF，∠ ADF=∠ CBE， AF=CE，求证：四边形DEBF是平行四边形．10．如图，已知： AB∥CD， BE⊥ AD，垂足为点 E， CF⊥AD，垂足为点 F，而且 AE=DF．求证：四边形 BECF是平行四边形．【考点训练】平行四边形的判断-2参照答案与试题分析一、解答题（共10 小题）（选答题，不自动判卷）1．如图，点D、 C 在 BF 上， AC∥ DE，∠ A=∠ E， BD=CF，（1）求证： AB=EF．（2）连结 AF， BE，猜想四边形 ABEF的形状，并说明原因．【剖析】（1）利用AAS证明△ ABC≌△ EFD，再依据全等三角形的性质可得AB=EF；（ 2）第一依据全等三角形的性质可得∠B=∠ F，再依据内错角相等两直线平行可获得AB∥ EF，又AB=EF，可证出四边形 ABEF为平行四边形．【解答】（1）证明：∵ AC∥DE，∴∠ ACD=∠EDF，∵BD=CF，∴BD+DC=CF+DC，即BC=DF，又∵∠ A=∠E，∴△ ABC≌△ EFD（AAS），∴ AB=EF；（2）猜想：四边形 ABEF为平行四边形，原因以下：由（ 1）知△ ABC≌△ EFD，∴∠ B=∠ F，∴ AB∥ EF，又∵ AB=EF，∴四边形 ABEF为平行四边形．【评论】本题主要考察了全等三角形的判断与性质，平行四边形的判断，解决问题的重点是证明△ ABC ≌△ EFD．2．如图，在四边形ABCD中，∠ B=∠D，∠ 1=∠2，求证：四边形 ABCD是平行四边形．【剖析】依据三角形内角和定理求出∠ DAC=∠ACB，依据平行线的判断推出 AD∥ BC，AB∥CD，依据平行四边形的判断推出即可．【解答】证明：∵∠ 1+∠B+∠ACB=180°，∠ 2+∠D+∠ CAD=180°，∠ B=∠D，∠1=∠ 2，∴∠ DAC=∠ACB，∴AD∥ BC，∵∠ 1=∠ 2，∴AB∥ CD，∴四边形 ABCD是平行四边形．【评论】本题考察了平行线的判断和平行四边形的判断的应用，主要考察学生的推理能力．3．如图，点 A、F、C、D 在同向来线上，点 B 和点 E 分别在直线 AD 的双侧，且 AB=DE，∠ A=∠D，AF=DC．求证：四边形 BCEF是平行四边形．【剖析】第一证明△ AFB≌△ DCE（SAS），从而得出 FB=CE，FB∥CE，从而得出答案．【解答】证明：在△ AFB和△ DCE中，，∴△ AFB≌△ DCE（SAS），∴FB=CE，∴∠ AFB=∠DCE，∴FB∥CE，∴四边形 BCEF是平行四边形．【评论】本题主要考察了平行四边形的判断以及全等三角形的判断与性质，得出△ AFB≌△ DCE 是解题重点．4．如图， A、D、F、B 在同向来线上， AE=BC，且 AE∥ BC， AD=BF．（1）求证：△ AEF≌△ BCD；（2）连 ED，CF，则四边形 EDCF是．（从平行四边形，矩形，菱形，正方形中选填）．【剖析】（1）依据 AE∥BC 可得∠ A=∠ B，再由 AD=BF可得 AF=BD，再加上条件 AE=CB，可依据SAS 定理证明△ AEF≌△ BCD；（2）依据△ AEF≌△ BCD，可得 EF=CD，∠ EFA=∠ CDB，从而证明出 EF∥ DC，再依据一组对边平行且相等的四边形 EDCF是平行四边形．【解答】解：（1）证明：∵AE∥BC，∴∠ A=∠ B，∵AD=BF，∴AF=DB，∵ AE=BC，在△ AEF和△ BCD中，∴△ AEF≌△ BCD（SAS）；（2）平行四边形．∵△AEF≌△BCD，∴ EF=CD，∠ EFA=∠CDB，∴ EF∥DC，∴四边形 EDCF是平行四边形．【评论】本题主要考察了全等三角形的判断与性质，以及平行四边形的判断，重点是掌握一组对边平行且相等的四边形是平行四边形．5．如图，在 ABCD中， AC 交 BD 于点 O，点 E，点 F 分别是 OA， OC的中点，请判断线段BE，DF 的地点关系和数目关系，并说明你的结论．【剖析】依据平行四边形的性质对角线相互均分得出OA=OC，OB=OD，利用中点的意义得出OE=OF，从而利用平行四边形的判断定理“对角线相互均分的四边形是平行四边形”判断BFDE是平行四边形，从而得出 BE=DF， BE∥DF．【解答】解： BE=DF，BE∥ DF由于 ABCD是平行四边形，因此OA=OC，OB=OD，由于 E，F 分别是 OA，OC的中点，因此OE=OF，因此 BFDE是平行四边形，因此BE=DF，BE∥DF【评论】主要考察了平行四边形的基天性质和判断定理的运用．性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线相互均分．判断：①两组对边分别平行的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；③两组对角分别相等的四边形是平行四边形；④对角线相互均分的四边形是平行四边形；⑤一组对边平行且相等的四边形是平行四边形．6．如图，在△ ABC中，∠ ACB=90°，∠ CAB=30°，△ ABD 是等边三角形， E 是 AB 的中点，连结CE并延伸交 AD 于 F．求证：（1）△ AEF≌△ BEC；（2）四边形 BCFD是平行四边形．【剖析】（1）利用等边三角形的性质得出∠DAB=60°，即可得出∠ ABC=60°，从而求出△ AEF≌△ BEC （ASA）；（2）利用平行线的判断方法以及直角三角形的性质得出 CF∥BD，从而求出答案．【解答】证明（1）∵ E 是 AB 中点，∴ AE=BE，∵△ABD 是等边三角形，∴∠ DAB=60°，∵∠CAB=30°，∠ACB=90°，∴∠ ABC=60°，在△ AEF和△ BEC中，∴△ AEF≌△ BEC（ASA）；（2）∵∠ DAC=∠DAB+∠ BAC，∠ DAB=60°，∠ CAB=30°，∴∠ DAC=90°，∴AD∥ BC，∵E 是 AB 的中点，∠ACB=90°，∴ EC=AE=BE，∴∠ ECA=30°，∠ FEA=60°，∴∠ EFA=∠BDA=60°，∴CF∥BD，∴四边形 BCFD是平行四边形．【评论】本题主要考察了平行四边形的判断以及全等三角形的判断方法，得出∠ ABC=60°是解题重点．7．已知：如图，在四边形ABCD中， AB∥ CD，E，F 为对角线 AC上两点，且 AE=CF，DF∥BE．求证：四边形 ABCD为平行四边形．【剖析】第一证明△ AEB≌△ CFD可得 AB=CD，再由条件 AB∥CD 可利用一组对边平行且相等的四边形是平行四边形证明四边形 ABCD为平行四边形．【解答】证明：∵ AB∥ CD，∴∠ DCA=∠BAC，∵DF∥BE，∴∠DFA=∠BEC，∴∠AEB=∠DFC，在△ AEB和△ CFD中，∴△ AEB≌△ CFD（ASA），∴AB=CD，∵ AB∥ CD，∴四边形 ABCD为平行四边形．【评论】本题主要考察了平行四边形的判断，重点是掌握一组对边平行且相等的四边形是平行四边形．8．如图， AB∥CD，AB=CD，点 E、F 在 BC上，且 BE=CF．（1）求证：△ ABE≌△ DCF；（2）试证明：以 A、 F、 D、 E 为极点的四边形是平行四边形．【剖析】（1）由全等三角形的判断定理SAS证得△ ABE≌△ DCF；（ 2）利用（ 1）中的全等三角形的对应角相等证得∠AEB=∠DFC，则∠ AEF=∠DFE，因此依据平行线的判断能够证得AE∥ DF．由全等三角形的对应边相等证得AE=DF，则易证得结论．【解答】证明：（1）如图，∵ AB∥CD，∴∠ B=∠ C．∵在△ ABE与△ DCF中，，∴△ ABE≌△ DCF（SAS）；（2）如图，连结 AF、DE．由（ 1）知，△ ABE≌△ DCF，∴ AE=DF，∠ AEB=∠DFC，∴∠ AEF=∠DFE，∴ AE∥DF，∴以 A、F、D、E 为极点的四边形是平行四边形．【评论】本题考察了平行四边形的判断、全等三角形的判断与性质．在证明（2）题时，利用了“一组对边平行且相等的四边形是平行四边形”的判断定理．9．如图，已知 BE∥DF，∠ ADF=∠CBE，AF=CE，求证：四边形D EBF是平行四边形．【剖析】第一依据平行线的性质可得∠ BEC=∠ DFA，再加上条件∠ ADF=∠CBE，AF=CE，可证明△ADF ≌△ CBE，再依据全等三角形的性质可得 BE=DF，依据一组对边平行且相等的四边形是平行四边形进行判断即可．【解答】证明：∵ BE∥ DF，∴∠ BEC=∠DFA，在△ ADF和△ CBE中，∴△ ADF≌△ CBE（AAS），∴BE=DF，又∵ BE∥ DF，∴四边形 DEBF是平行四边形．【评论】本题主要考察了平行四边形的判断，重点是掌握一组对边平行且相等的四边形是平行四边形．10．如图，已知： AB∥ CD， BE⊥AD，垂足为点 E， CF⊥AD，垂足为点 F，而且 AE=DF．求证：四边形 BECF是平行四边形．【剖析】经过全等三角形（△ AEB≌△ DFC）的对应边相等证得 BE=CF，由“在同一平面内，同垂直于同一条直线的两条直线相互平行”证得 BE∥CF．则四边形 BECF是平行四边形．【解答】证明：∵BE⊥ AD，CF⊥AD，∴∠ AEB=∠DFC=90°，∵AB∥ CD，∴∠ A=∠ D，在△ AEB与△ DFC中，，∴△ AEB≌△ DFC（ASA），∴BE=CF．∵BE⊥AD，CF⊥AD，∴ BE∥CF．∴四边形 BECF是平行四边形．【评论】本题考察了平行四边形的判断、全等三角形的判断与性质．一组对边平行且相等的四边形是平行四边形．。

(完整版)平行四边形的性质及判定典型例题

平行四边形的性质及判定（典型例题）1.平行四边形及其性质例1如图，O 是卜二・ABCD 对角线的交点.△ OBC 的周长为59, BD=38 , AC=24，贝卩AD= __ 若厶OBC 与厶OAB 的周长之差为 15，贝y AB=QABCD 的周长= _____ .AC ,可得BC ,再由平行四边形对边相等知 AD=BC ，由平行四边形的对角线互相平分，可知△ OBC 与厶OAB 的周长之差就为BC 与AB 之差，可得AB ，进而可得」ABCD 的周长.解 EBCD 中0A 二= OB = OD = |E D （平行四边形的对角线互相平分）•••△ OBC 的周长=0B + 0C +EC分析: 根据平行四边形对角线互相平先所OC =1=19 + 12 + BC=59••• BC=28—ABCD 中，•BC=AD(平行四边形对边相等)•AD=28△ OBC的周长-△ OAB的周长=(OB + OC + BC)-(OB + OA+AB)=BC-AB=15•AB=13•••二ABCD的周长=AB + BC + CD + AD=2(AB + BC)=2(13 + 28)=82说明：本题条件中的△ OBC占厶OAB的周长之差为15”，用符号语言表示出来后，便容易发现其实质，即BC与AB之差是15 .例2判断题(1) 两条对边平行的四边形叫做平行四边形. ()(2) 平行四边形的两角相等.()(3) 平行四边形的两条对角线相等.()(4) 平行四边形的两条对角线互相平分. ()(5) 两条平行线中，一条直线上任一点到另一条直线的垂线段叫做两条平行线的距离.()(6) 平行四边形的邻角互补.()分析：根据平行四边形的定义和性质判断.解：(1) 错两组对边分别平行的四边形叫做平行四边形”是两组对边，而不是两条对边.如图四边形ABCD，两条对边AD // BC .显然四边形ABCD 不是平行四边形．(2) 错平行四边形的性定理1，“平行四边形的对角相等．”对角是指四边形中设有公共边的两个角，也就是相对的两个角．(3) 错平行四边形的性质定理3，“平行四边形的对角线互相平分．”一般地不相等．(矩形的两条对角线相等)．(4) 对根据平行四边形的性质定理 3 可判断是正确的．(5) 错线段图形，而距离是指线段的长度，是正值正确的说法是：两条平行线中，一条直线上任一点到另一条直线的垂线段的长度叫做这两条平行线的距离．(6) 对由定义知道，平行四边形的对边平行，根据平行线的性质可知．平行四边形的邻角互补．例3 .如图1,在二ABCD中，E、F是AC上的两点.且AE=CF .求证：ED // BF .分析：欲址DE // BF，只需/ DEC二/ AFB,转证=/ ABF CDF, 因卜二，ABCD，则有AB丄CD，从而有/ BAC= / CDA .再由AF=CF 得AF=CE .满足了三角形全等的条件.证明：v AE=CFAE+EF二CF+EF••• AF=CE在二ABCD中AB // CD（平行四边形的对边平行）• / BAC= / DCA（两直线平行内错角相等）AB=CD（平行四边形的对边也相等）•••△ ABF刍乂 CDE（SAS）•••/ AFB= / DCE• ED // BF（内错角相等两直线平行）说明：解决平行四边形问题的基本思想是化为三角形问题不处理.例4如图已知在△ ABC中DE // BC // FG，若BD=AF、求证; DE + FG=BC .分析1:要证DE + FG=DC由于它们是平行线，由平行四边形定义和性质.考虑将DE平移列BC上为此，过E（或D）作EH // AB（或DM // AC）,得至U DE=BH、只需证HC=FG ,因AF=BD=EH , / CEH=/ A. / AGF = Z C所以△ AFG幻/ EHC .此方法称为截长法.分析2:过C点作CK // AB交DE的延长线于K，只需证FG=EK , 转证△ AFG CKE .过E作EH // AB交于Hv DE // BC•••四边形DBHE是平行四边形（平行四边形定义）••• DB=EHDE=BH（平行四边形对边也相等）又BD=AF• AF=EHv BC // FGAGF= / C（两直线平行同位角相等）同理 / A= / CEH• △ AFG EHC(AAS)••• FG=HC••• BC二BH+HC二DE二FG.过C作CK // AB交DE的延长线于K.v DE // BC•四边形DBCK是平行四边形（平行四边形定义）•CK=BD DK=BC（平行四边形对边相等）又BD=AF•AF=CKv CK // AB• / A= / ECK（两直线平行内错角相等）v BC // FG•••/ AGF二/ AED（两直线平行同位角相等）又/ CEK二/ AED（对顶角相等）•••/ AGF= / CEK•••△ AFG S' CKE（AAS）FG=EKDE+EK=BC• DE+FG=BC例 5 如图I—ABCD 中，/ ABC=3 /A，点 E 在CD 上,CE=1 , EF丄CD交CB延长线于F，若AD=1，求BF的长.u --- ---------- r分析：根据平行四边形对角相等，邻角互补，可得/ C= / F=45°进而由勾股定理求出CF ,再根据平行四边形对边相等，得BF的长.解：在二ABCD 中，AD // BC•••/ A +/ ABC=180 （两直线平行同旁内角互补）vZ ABC=3 / A•••/ A=45 ,Z ABC=135•••Z C= Z A=45 （平行四边形的对角相等）•EF 丄CD•Z F=45°（直角三角形两锐角互余）•EF=CE=1在RtAOEF中,CF = JCE之》EF金=（勾股定理）v AD=BC=1二BF = CF”EC = Q[例6如图1，‘ ■ ABCD中，对角线AC长为10cm , Z CAB=30 , AB长为6cm，求一ABCD的面积.解：过点C作CH丄AB，交AB的延长线于点H .(图2)vZ CAB=30-■.CH 二丄= 1 X10=52 2••• S—ABCD = AB-CH = 6X5=30(cm2)答：二ABCD的面积为30cm2 .说明：由于二=底＞高，题设中已知AB的长，须求出与底AB 相应的高，由于本题条件的制约，不便于求出过点D的高，故选择过点C 作高.例7如图，E、F分别在’・ABCD的边CD、BC上，且EF //求证：S△ ACE二S △ ABF分析：运用平行四形的性质，利用三角形全等，将其转化为等底同高的三角形.证明：将EF向两边延长分别交AD、AB的延长线于G、H.二ABCD DE // AB•••/ DEG= / BHF（两直线平行同位角相等）/ GDE= / DAB（同上）AD // BC•••/ DAB= / FBH（同上）:丄 GDE= / FBHv DE // BH , DB // EH•四边形BHED是平行四边形V DE二BH（平行四边形对边相等）GDE 刍乂 FBH（ASA）••• S△ GDE=S △ FBH（全等三角形面积相等）.GE=FH（全等三角形对应边相等）.S△ ACE=S △ AFH（等底同高的三角形面积相等）.S △ ADE = S △ ABF说明：平行四边形的面积等于它的底和高的积.即S二二a・ha .a 可以是平行四边形的任何一边，h必须是a边与其对边的距离.即对应的高，为了区别，可以把高记成ha，表明它所对应的底是a.例8如图，在二ABCD中，BE平分/ B交CD于点E, DF 平分/ D交AB于点F,求证BF=DE .分析EF二DE （目标）十BEDP 为口DF"d叫西3 ]1=Z 3 r Z 1=Z 2f t"S亠彩姑皤彩B口ABCD证明：T四边形ABCD是平行四边形二DE // FB，/ ABC= / ADC（平行四边形的对边也平行对角相等）•••/仁/ 3（两直线平行内错角相等）而Z]=^Z ADC,Z2=|ZABC•••/ 2= / 3• DF // BE（同位角相等两条直线平行）•四边形BEDF为平行四边形（平行四边形定义）• BF=DE .（平行四边形的对边相等）说明：此例也可通过△ ADF CBE来证明，但不如上面的方法简捷.例9如图，CD的Rt△ ABC斜边AB上的高，AE平分/ BAC 交CD于E, EF // AB，交BC于点F,求证CE=BF .分析作EG // BC,交AB于G,易得EG=BF .再由基本图, 可得EG=EC ,从而得出结论.过E点作EG // BC交AB于G点.v EF // AB••• EG=BFv CD为Rt△ ABC斜边AB上的高•/ BAC + / B=90°.Z BAC + / ACD = 90°•/ B= Z ACD•Z ACD=Z EGAv AE 平分Z BAC•Z 1= Z 2又AE=AE•△ AGE ACE(AAS)•CE=EG•CE=BF .说明：(1)在上述证法中，“平移”起着把条件集中的作用.(2)本题也可以设法平移AE .(连F点作FG // AE，交AB于G)例10如图，已知I —ABCD的周长为32cm , AB : BC=5 : 3, AE 丄BC 于E, AF 丄DC 于F，/ EAF=2 / C,求AE 和AF 的长.分析：从化简条件开始①由二ABCD的周长及两邻边的比，不难得到平行四边形的边长.口虹CD 的周长=321 fAB=10AB : BC-5 : 3 p |BC=6②/ EAF=2 / C告诉我们什么？AF i FC1 ZFAE^ZC=180°] oAE 1 EAF-2 Z C j討c=6°这样，立即可以看ADF、△ AEB都是有一个锐角为30°的直角三角形.于是有= = = 3再由勾股定理求出解：——ABCD的周长为32cm即AB+BC+CD+DA=32v AB=CD BC=DA（平行四边形的对边相等）/.AB + BC = - X32 = 16 2又AB : BC=5 : 35+3BC= —X3 = 65+3/ EAF+ / AFC+ / C+ / CEA=360 （四边形内角和等于360°v AE 丄BC / AEC=90AF 丄DC / AFC=90•••/ EAF+ / C=180/ EAF=2 / CT AB // CD(平行四边形的对边平行)•••/ ABE二/ C=60 (两直线平行同位角相等)同理/ ADF=60SRiAABE 中，ZBAE = 30* BE = |AB = 5£—■Al = ja =E^ = 5^3 (cm)在RtAADF中，ZDAF = 30° DF= ^AP = |B C=3■f-j d—iAF - 7A D3 -I>F a = M Ccm)说明：化简条件，化简结论，总之，题目中哪一部分最复杂就从化简那一部分开始，这是一种常用的解题策略，我们把这种解题策略称为：从最复杂的地方开始.它虽简单，却很有效.2 .平行四边形的判定例1填空题(1)如图1,四边形ABCD与四边形BEFC都是平行四边形，则四边形AEFD是—，理由是（2）如图2, D、E分别在△ ABC的边AB、AC上，DE=EF , AE=EC , DE // BC贝卩四边形ADCF是__,理由是__ ,四边形BCFD 是—，理由是—分析：判定一个四边形是平行四边形的方法较多，要从已知条件出发，具体问题具体分析：（1）根据平行四边形的性质可得AD平行且等于BC，BC平行且等于EF，从而得AD平行且等于EF，由判定定理4可得.（2）由AE=EC , DE=EF，由判定定理3可得四边形ADCF是平行四边形，从而得AD // CF即BD // CF，再由条件，可得四边形BCFD是平行四边形.解：（1）平行四边形，一组对边平行且相等的四边形是平行四边形（2）平行四边形，对角线互相平分的四边形是平行四边形，平行四边形，两组对边分别平行的四边形是平行四边形.说明：平行四边形的定义（两组对边分别平行的四边形叫做平行四边形，既是平行四边形的一个性质，又是平行四边形的一个判定方法.例 2 女口图，四边形 ABCD 中，AB=CD . / ADB 二 /CBD=90 .求证：四边形ABCD 是平行四边形.分析：判定一个四边形是平行四边形，有三类五个判定方法, 这三类也是按边、角和对角线分类，具体的五个方法如下表：CIID 从对角钱看一（5 ）对角线互相平分因此必须根据已知条件与图形结构特点，选择判定方法.证法一:v AB=CD . Z ADB= / CBD=90 , BD=DB .••• Rt △ ABD 坐 Rt △ CDB .「（ 1）两组对边分别平存C I ）从边看 —（2）两组对边分别相等_（3）-组对边平行且相尊（1）从边看（II ）从角看（4）两组对角分别相等的四边形绘平行四边形•••/ ABD= / CDB，/ A= / C.•/ ABD+ / CBD= / CDB+ / ADB即 / ABC= / CDA .•四边形ABCD 是平行四边形（两组对角分别相等的四边形是平行四边形）．证法二：vZ ADB= / CBD=90 , AB=CD、BD=DB .•Rt△ ABD 坐Rt△ CDB .•Z ABD=Z CDB．•AB //CD.（内错角相等两直线平行）•四边形ABCD 是平行四边形（一组对边平行且相等的四边形是平行四边形）．证法三：由证法一知，Rt △ ABD幻Rt △ CDB .••• DA=BC又T AB二CD•四边形ABCD是平行四边形（两组对边分别相等的四边形是平行四边形）说明：证明一个四边形是平行四边形，往往有多种证题思路，我们必须注意分析，通过比较，选择最简捷的证题思路.本题三种证法中，证法二与证法三比较简捷，本题还可用定义来证明.例3如图，‘「ABCD中，E、G、F、H分别是四条边上的点, 且AE=CF , BG=DH，求证：EF与GH互相平分.分析：只须证明EGFH为平行四边形.证明：连结EG 、GF、FH 、HE．T四边形ABCD是平行四边形•••/ A= / C, AD=CB .T BG=DH•AH=CG又AE=CF•△ AEH CFG（SAS）•HE=GF同理可得EG=FH•四边形EGFH 是平行四边形（两组对边分别相等的四边形是平行四边形）•EF 与GH 互相平分（平行四边形的对角线互相平分）．说明：平行四边形的性质，判定的综合运用是解决有关线段和角问题基本方法．例4如图，二ABCD中，AE丄BD于E, CF丄BD于F.求证：四边形AECF是平行四边形.分析：由平行四边形的性质，可得△ ABE CDF••• AE= CF进而可得四边形AECF是平行四边形.证明：口ABCD中，AB屯CD（平行四边形的对边平行，对边相等）•/ ABD= / CDB（两直线平行内错角相等）AE 丄BD、CF 丄BD•AE // CF / AEB= / CFD=90•△ ABE CDF（AAS）•AE=CF•四边形AECF是平行四边形（一组对边平行且相等的四边形是平行四边形）说明：平行四边形的定义，既是平行四边形的一个性质，又是平行四边形的一个判定方法.例5如图，二ABCD中，E、F分别在AD、BC上，且AE=CF , AF、BE相交于G, CE、DF相交于H求证：EF与GH互相平分分析：欲证EF与GH互相平分，只需四边形EGFH为平行四边形，利用已知条件可知四边形AFCE、四边形EBFD都为平行四边形，所以可得AF // EC , BE // DF，从而四边形GEHF为平行四边形.证明：」ABCD中，AD丄BC（平行四边形对边平行且相等）v AE=CF /. DE=BFT四边形AFCE、四边形BFDE是平行四边形（一组对边平行且相等的四边形是平形四边形）二AF // CE , BE // DF（平行四边形对边平行）•••四边形EGFH是平行四边形（两组对边分别平行的四边形是平行四边形）••• GH与EF互相平分（平行四边形的对角线互相平分）说明：平行四边形问题，并不都是以求证某一个四边形为平行四边形的形式出现的.往往更多的是求证线段的相等、角的相等、直线的平行、线段的互相平分等等.要灵活地根据题中已知条件，以及定义、定理等.先判定某一四边形为平行四边形，然后再应用平行四边形的性质加以证明.例6如图，已知—ABCD中，EF在BD上，且BE=DF ,点G、H 在AD、CB上，且有AG=CH , GH与BD交于点0,求证EG丄HF分析：证EF 、GH 互相平分二GEHF 为平行四边形.证明:连 BG 、DH 、GF 、EHT ABCD 为平行四边形.••• AD 垒 BC又 AG=HC• DG 丄 BH•四边形BGDH 为平行四边形（一组对边平行且相等的四边形是平行四边形）• HO = GO , DO=BO （平行四边形的对角线互相平分）又 BE=DF•OE=OF•四边形GEHF为平行四边形（对角线互相平分的四边形是平行四边形）••• EG丄HF.（平行四边形的对边平行相等）说明：由于条件BE=DF涉及到对角线BD，所以考虑用对角线互相平分来证明例7如图，——ABCD中，AE丄BD于E, CF丄BD于F, G、H分别为AD、BC的中点，求证：EF和GH互相平分.分析：连结EH , HF、FG、GE，只须证明EHFG为平行四边证法一:连结EH , HF、FG、GEv AE丄BD , G是AD中点.-■.GE=C J D =^AD2/ GED二 / GDE同理可得HF =HB =^EC,Z HFE =Z HEFV四边形ABCD是平行四边形••• AD 岂BC,/ GDE= / HBF••• GE=HF，/ GED= / HFB•GE // HF•四边形GEHF为平行四边形（一组对边平行且相等的四边形是平行四边形）•EF和GH互相平分.（平行四边形对角线互相平分）证法二：容易证明厶ABE CDF• BE=DFT四边形ABCD为平行四边形••• AD 些BCT G、H分别为AD、BC的中点•DG 丄BH•四边形BHDG为平行四边形（一组对边平行且相等的四边形是平行四边形）•BD和GH互相平分（平行四边形对角线互相平分）•OG=OH , OB=OD又BE=DF•OE=OF•EF和GH互相平分.例8如图，已知线段a、b与/ a,求作：—ABCD ,使/ ABC二/ a, AB=a , BC=b ,分析：已知两边与夹角，可先确定△ ABC，根据判定定理2(两组对边分别相等的四边形是平行四边形)，再确定点D，从而平行四边形可作出.作法:(1) 作/ EBF二/ a,⑵在BE、BF上分别截取BA=a , BC=b ,⑶分别为A、C为圆心，b, a为半径作弧，两弧交于点D, 二四边形ABCD为所求.*证明：由作法可知AB=CD = aBC=AD=b二四边形ABCD 为平行四边形(两组对边分别相等的四边形为平行四边形)且/ ABC 二 / a, AB=a , BC=b- ABCD 为所求说明：常见的平行四边形作图有以下几种：(1) 已知两邻边(AB 、BC)和夹角(/ B).(2) 已知一边(BC)和两条对角线(AC , BD).(3) 已知一边(BC)和这条边与两条对角线的夹角 (如/ DBC ,Z ACB).⑷已知一边(CD)和一个内角(/ ABC)以及过这个角的顶点的一条对角线(BD ，且BD > CD)求作平行四边形(如图)完成这些作图的关键点，都在于先作出一个三角形，然后再完成平行四边形的作图，体现了把平行四边形的问题化归为三角形问题的思想方法.。

平行四边形的判定练习题(含(答案))

平行四边形的判定及中位线知能点1 平行四边形的判定方法1．能够判定四边形ABCD是平行四边形的题设是（）．A．AB∥CD，AD=BC B．∠A=∠B，∠C=∠DC．AB=CD，AD=BC D．AB=AD，CB=CD2．具备下列条件的四边形中，不能确定是平行四边形的为（）．A．相邻的角互补 B．两组对角分别相等C．一组对边平行，另一组对边相等 D．对角线交点是两对角线中点3．如下左图所示，四边形ABCD的对角线AC和BD相交于点O，下列判断正确的是（）．A．若AO=OC，则ABCD是平行四边形;B．若AC=BD，则ABCD是平行四边形;C．若AO=BO，CO=DO，则ABCD是平行四边形;D．若AO=OC，BO=OD，则ABCD是平行四边形4．如上右图所示，对四边形ABCD是平行四边形的下列判断，正确的打“∨”，错误的打“×”．（1）因为AD∥BC，AB=CD，所以ABCD是平行四边形．（）（2）因为AB∥CD，AD=BC，所以ABCD是平行四边形．（）（3）因为AD∥BC，AD=BC，所以ABCD是平行四边形．（）（4）因为AB∥CD，AD∥BC，所以ABCD是平行四边形．（）（5）因为AB=CD，AD=BC，所以ABCD是平行四边形．（）（6）因为AD=CD，AB=AC，所以ABCD是平行四边形．（）5．已知AD∥BC，要使四边形ABCD为平行四边形，需要增加条件________．6．如图所示，∠1=∠2，∠3=∠4，问四边形ABCD是不是平行四边形．7．如图所示，在四边形ABCD中，AB=CD，BC=AD，E，F为对角线AC上的点，且AE=CF，求证：BE=DF．8．如图所示，D为△ABC的边AB上一点，DF交AC于点E，且AE=CE，FC∥AB．求证：CD=AF．9．如图所示，已知四边形ABCD是平行四边形，在AB的延长线上截取BE=•AB，BF=BD，连接CE，DF，相交于点M．求证：CD=CM．10．如图所示，在四边形ABCD中，DC∥AB，以AD，AC为边作□ACED，延长DC•交EB于F，求证：EF=FB．知能点2 三角形的中位□线11．如图所示，已知E 为□ABCD 中DC 边的延长线上的一点，且CE=DC ，连接AE ，分别交BC ，BD 于点F ，G ，连接AC 交BD 于点O ，连接OF ，求证：AB=2OF ．12．如图所示，在ABCD 中，EF ∥AB 且交BC 于点E ，交AD 于点F ，连接AE ，BF•交于点M ，连接CF ，DE 交于点N ，求证：MN ∥AD 且MN=12AD ．13．如图所示，DE 是△ABC 的中位线，BC=8，则DE=_______．14．如图所示，在□ABCD 中，对角线AC ，BD 交于点O ，OE ∥BC 交CD•于E ，•若OE=3cm ，则AD 的长为（）． A ．3cm B ．6cm C ．9cm D ．12cm15．如图所示，在四边形ABCD 中，E ，F ，G ，H 分别是AB ，BC ，CD ，AD 的中点，•则四边形EFGH 是平行四边形吗？为什么？16．如图所示，在△ABC 中，AC=6cm ，BC=8cm ，AB=10cm ，D ，E ，F 分别是AB ，BC ，CA 的中点，求△DEF 的面积．规律方法应用17．如图所示，A ，B 两点被池塘隔开，在A ，B 外选一点C ，连接AC 和BC ，•并分别找出AC 和BC 的中点M ，N ，如果测得MN=20m ，那么A ，B 两点间的距离是多少？18．如图所示，在□ABCD 中，AB=2AD ，∠A=60°，E ，F 分别为AB ，CD 的中点，EF=1cm ，那么对角线BD 的长度是多少？你是怎样得到的？19．如图所示，在△ABC 中，E 为AB 的中点，CD 平分∠ACB ，AD ⊥CD 于点D ．• 试说明：（1）DE ∥BC ．（2）DE=12（BC-AC ）．开放探索创新20．如图所示，在△ABC中，∠BAC=90°，AD⊥BC于D，BE平分∠ABC交AD•于E，EF∥BC交AC于F，那么AE与CF相等吗？请验证你的结论．中考真题实战21．（长沙）如下左图所示，在四边形ABCD中，AB∥CD，要使四边形ABCD•为平行四边形，则应添加的条件是________．（添加一个即可）22．（呼和浩特）如上右图所示，已知E，F，G，H是四边形ABCD各边的中点，•则S四边形EFGH：S四边形ABCD的值是_________．23．（南京）已知如图19-1-55所示，在ABCD中，E，F分别是AB，CD的中点.求证：（1）•△AFD≌△CEB．（2）四边形AECF是平行四边形．答案:1．C 2．C 3．D4．（1）×（2）×（3）∨（4）∨（5）∨（6）× 5．AD=BC或AB∥CD6．解：∵∠1=∠2，∴AD∥BC．又∵∠3=∠4，∴AB∥CD．∴四边形ABCD是平行四边形．7．证明：∵AB=CD，BC=AD，∴四边形ABCD是平行四边形．∴AB∥CD，∴∠BAE=∠DCF．又∵AE=CE，∴△ABE≌△CDF（SAS），∴BE=EF．8．证明：∵FC∥AB，∴∠DAC=∠ACF，∠ADF=∠DFC．又∵AE=CE，∴△ADE≌△CFE（AAS），∴DE=EF．∵AE=CE，∴四边形ADCF为平行四边形．∴CD=AF．9．证明：∵四边形ABCD是平行四边形．∴AB//DC．又∵BE=AB，∴BE//DC，∴四边形BDCE是平行四边形．∵DC∥BF，∴∠CDF=∠F．同理，∠BDM=∠DMC．∵BD=BF，∴∠BDF=∠F．∴∠CDF=∠CMD，∴CD=CM．10．证明：过点B作BG∥AD，交DC的延长线于G，连接EG．∵DC∥AB，∴ABGD是平行四边形，∴BG// AD．在□ACED中，AD//CE，∴CE//BG．∴四边形BCEG为平行四边形，∴EF=FB．11．证明：∵四边形ABCD是平行四边形，∴AB//CD，AD=BC．∵CE=CD，∴AB//CE，∴四边形ABEC为平行四边形．∴BF=FC，∴OF//12AB，即AB=2OF．12．证明：∵四边形ABCD是平行四边形，∴AB ∥CD ，AD ∥BC ．又∵EF ∥AB ，∴EF ∥CD ．∴四边形ABEF ，ECDF 均为平行四边形．又∵M ，N 分别为ABEF 和ECDF 对角线的交点． ∴M 为AE 的中点，N 为DE 的中点，即MN 为△AED 的中位线． ∴MN ∥AD 且MN=12AD ． 13．4 14．B15．解：EFGH 是平行四边形，连接AC ，在△ABC 中，∵EF 是中位线，∴EF //12AC ．同理，GH //12AC ． ∴EF //GH ，∴四边形EFGH 为平行四边形． 16．解：∵EF ，DE ，DF 是△ABC 的中位线， ∴EF=12AB ，DE=12AC ，DF=12BC ．又∵AB=10cm ，BC=8cm ，AC=6cm ，∴EF=5cm ，DE=3cm ，DF=4cm ，而32+42=25=52，即DE 2+DF 2=EF 2． ∴△EDF 为直角三角形． ∴S △EDF =12DE ·DF=12×3×4=6（cm 2）． 17．解：∵M ，N 分别是AC ，BC 的中点． ∴MN 是△ABC 的中位线，∴MN=12AB ． ∴AB=2MN=2×20=40（m ）．故A ，B 两点间的距离是40m ． 18．解：连接DE ．∵四边形ABCD 是平行四边形， ∴AB //CD ． ∵DF=12CD ，AE=12AB ， ∴DF //AE ．∴四边形ADFE 是平行四边形．∴EF=AD=1cm ．∵AB=2AD ，∴AB=2cm ．∵AB=2AD ，∴AB=2AE ，∴AD=AE ． ∴∠1=∠4．∵∠A=60°，∠1+∠4+∠A=180°， ∴∠1=∠A=∠4=60°．∴△ADE 是等边三角形，∴DE=AE ． ∵AE=BE ，∴DE=BE ，∴∠2=∠3．∵∠1=∠2+∠3，∠1=60°，∴∠2=∠3=30°． ∴∠ADB=∠3+∠4=90°． ∴BD=222221AB AD -=-=3（cm ）．19．解：延长AD 交BC 于F ．（1）∵AD ⊥CD ，∴∠ADC=∠FDC=90°．∵CD 平分∠ACB ，∴∠ACD=∠FCD ．在△ACD 与△FCD 中，∠ADC=∠FDC ，DC=DC ，∠ACD=∠FCD ． ∴△ACD ≌△FCD ，∴AC=FC ，AD=DF ．又∵E 为AB 的中点，∴DE ∥BF ，即DE ∥BC ．（2）由（1）知AC=FC ，DE=12BF ． ∴DE=12（BC-FC ）=12（BC-AC ）． 20．解：AE=CF ．理由：过E 作EG ∥CF 交BC 于G ， ∴∠3=∠C ．∵∠BAC=90°，AD ⊥BC ，∴∠ABC+∠C=90°，∠ABD+∠BAD=90°． ∴∠C=∠BAD ，∴∠3=∠BAD ．又∵∠1=∠2，BE=BE ， ∴△ABE ≌△GBE （AAS ），∴AE=GE ． ∵EF ∥BC ，EG ∥CF ，∴四边形EGCF 是平行四边形，∴GE=CF ， ∴AE=CF ．21．答案不唯一，如AB=CD 或AD ∥BC ． 22．1223．解：（1）在□ABCD 中，AD=CB ，AB=CD ，∠D=∠B ． ∵E ，F 分别为AB ，CD 的中点， ∴DF=12CD ，BE=12AB ，∴DF=BE ， ∴△AFD ≌△CEB ．（2）在□ABCD 中，AB=CD ，AB ∥CD ．由（1）得BE=DF ，∴AE=CE ，∴四边形AECF 是平行四边形．。

重点突围：专题05 平行四边形的判定与性质(原卷版)-人教八下期中综合复习

八年级数学下册期中期末综合复习专题提优训练（人教版）专题05平行四边形的判定与性质【典型例题】1．（2022·黑龙江肇源·八年级期末）如图，在△ABC中，点D，E分别是AC，AB的中点，点F是CB延长线上的一点，且CF＝3BF，连接DB，EF．（1）求证：四边形DEFB是平行四边形；（2）若△ACB＝90°，AC＝12cm，DE＝4cm，求四边形DEFB的周长．【专题训练】一、选择题1．（2022·山东安丘·八年级期末）如图所示，四边形ABCD是平行四边形，点E在线段BC 的延长线上，若△DCE＝128°，则△A＝（）A．32°B．42°C．52°D．62°2．（2022·山东龙口·八年级期末）如图，平行四边形ABCD中，两对角线交于点O，AB△AC，AD=5cm，OC=2cm，则对角线BD的长为（）A B．8cm C．3cm D．3．（2021·山东·宁津县教育和体育局教育科学研究所二模）如图，直线EF 过平行四边形ABCD 对角线的交点O ，分别交AB 、CD 于E 、F ，那么阴影部分的面积是平行四边形ABCD 面积的（）A ．15B ．14C ．13D ．12 4．（2022·江苏·八年级专题练习）如图，在▱ABCD 中，对角线AC 、BD 相交于点O ，过点O 作OE △AC ，交AD 于点E ，连接CE ，若△CDE 的周长为8，则▱ABCD 的周长为（）A ．8B ．10C ．16D ．205．（2022·福建泉港·八年级期末）如图，点E 、F 分别是▱ABCD 边AD 、BC 的中点，G 、H 是对角线BD 上的两点，且BG =DH ．则下列结论中不正确的是（）A ．GF EH =B ．四边形EGFH 是平行四边形C ．EG FH =D ．EH BD ⊥6．（2022·安徽庐江·九年级期末）如图①，在▱ABCD 中，动点P 从点B 出发，沿折线B →C →D →B 运动，设点P 经过的路程为x ，△ABP 的面积为y ，y 是x 的函数，函数的图象如图②所示，则图②中的a 值为（）A ．B ．C ．14D ．18二、填空题7．（2022·江苏·八年级专题练习）如图，四边形ABCD是平行四边形，BE平分△ABC，与AD 交于点E，BC＝5，DE＝2，则AB的长为___．8．（2022·全国·八年级课前预习）四边形ABCD中，AD△BC，要使它平行四边形，需要增加条件________（只需填一个条件即可）．9．（2022·山东莱芜·八年级期末）如图，已知▱ABCD的周长为38，对角线AC、BD相交于点O，点E是CD的中点，△DOE的周长为16，则BD的长为_____．10．（2021·广东阳东·一模）在探索数学名题“尺规三等分角”的过程中，有下面的问题：如图，AC是▱ABCD的对角线，AD＝AE＝BE，△D＝108°，则△BAC＝___．11．（2021·山东任城·七年级期中）如图，四边形ABCD中，AB△CD，AD△BC，且△BAD、△ADC 的角平分线AE、DF分别交BC于点E、F．若EF＝2，AB＝5，则AD的长为_______．12．（2022·山东·济宁学院附属中学八年级期末）在四边形ABCD中，AD△BC，BC△CD，BC ＝10cm，M是BC上一点，且BM=4cm，点E从A出发以1cm/s的速度向D运动，点F从点B出发以2cm/s的速度向点C运动，当其中一点到达终点，而另一点也随之停止，设运动时间为t，当t的值为_____时，以A、M、E、F为顶点的四边形是平行四边形．三、解答题13．（2022·江苏·八年级专题练习）如图，四边形ABCD 为平行四边形，△BAD 的角平分线AE 交CD 于点F ，交BC 的延长线于点E ．(1)求证：BE ＝CD ；(2)连接BF ，若BF ⊥AE ，△BEA ＝60°，AB ＝2，求平行四边形ABCD 的面积．14．（2022·江苏·八年级专题练习）如图，平行四边形ABCD 的对角线AC ，BD 相交于О点，DE AC ⊥于E 点，BF AC ⊥于F ．(1)求证：四边形DEBF 为平行四边形；(2)若20AB =，13AD =，21AC =，求DOE △的面积．15．（2022·全国·八年级）已知，在ABCD中，E是AD边的中点，连接BE．（1）如图①，若BC=2，求AE的长；（2）如图②，延长BE交CD的延长线于点F，求证：FD=AB．16．（2022·黑龙江·哈尔滨工业大学附属中学校九年级期末）如图，四边形ABCD是平行四边形，BE DF∥，且分别交对角线于点E、F，连接ED、BF．（1）求证：四边形BEDF是平行四边形；（2）若AE＝EF，请直接写出图2中面积等于四边形ABCD的面积的13的所有三角形．17．（2021·全国·八年级课时练习）如图，ABCD的对角线AC与BD相交于点O，E，F是BD 上的两点．BE DF满足什么条件时，四边形AECF是平行四边形？请说明理由；（1）当,∠满足什么条件时，四边形AECF是平行四边形？请说明理由．（2）当AEB∠与CFD18．（2021·江苏射阳·九年级阶段练习）如图，在四边形ABCD中，△ACB＝△CAD＝90°，点E在BC上，AE△DC，EF△AB，垂足为F．（1）求证：四边形AECD是平行四边形；（2）若AE平分△BAC，BE＝5，BF：BE＝4：5，求AD长．19．（2022·湖南·长沙市湘一立信实验学校八年级期末）如图，△ABC中，D是AB边上任意一点，F是AC中点，过点C作CE//AB交DF的延长线于点E，连接AE，CD．(1)求证：四边形ADCE是平行四边形；(2)若△B＝30°，△CAB＝45°，AC=，求AB的长．20．（2022·山东莱芜·八年级期末）点E 是▱ABCD 的边CD 上的一点，连接EA 并延长，使EA ＝AM ，连接EB 并延长，使EB ＝BN ，连接MN ，F 为MN 的中点，连接CF ，DM ．(1)求证：四边形DMFC 是平行四边形；(2)连接EF ，交AB 于点O ，若OF ＝2，求EF 的长．21．（2021·浙江拱墅·八年级期末）如图，在平行四边形ABCD 中，△ABC ，△BCD 的平分线分别交AD 于点E ，F ，线段BE ，CF 相交于点G ．（1）问：线段BE 与CF 的位置关系，并说明理由；（2）若AB ＝3，CF ＝4，求BE 的长．22．（2022·黑龙江·大庆市第四十四中学校八年级期末）如图，ABCD 的对角线AC 与BD 相交于点O ，点E ，F 分别在OB 和OD 上，且AEB CFD ∠=∠．（1）求证：四边形AECF 是平行四边形；（2）若90AEB =︒∠，4AE =．且45EAF ∠=︒，求线段AC 的长．23．（2021·浙江下城·八年级期末）在四边形ABCD中，已知AD△BC，△B＝△D，AE△BC于点E，AF△CD于点F．（1）求证：四边形ABCD是平行四边形；（2）若AF＝2AE，BC＝6，求CD的长．24．（2022·江苏·八年级专题练习）已知如图，在▱ABCD中，点F是▱ABCD内一点，AB△BF，AB＝BF，过点F作FE△AD，垂足为点E．(1)如图1，若BF＝3EF＝6，求四边形ABFE的面积；(2)如图2，连接BE、CE，若BE＝CE，求证：AE+EF＝BC．。

平行四边形性质和判定习题(答案详细)

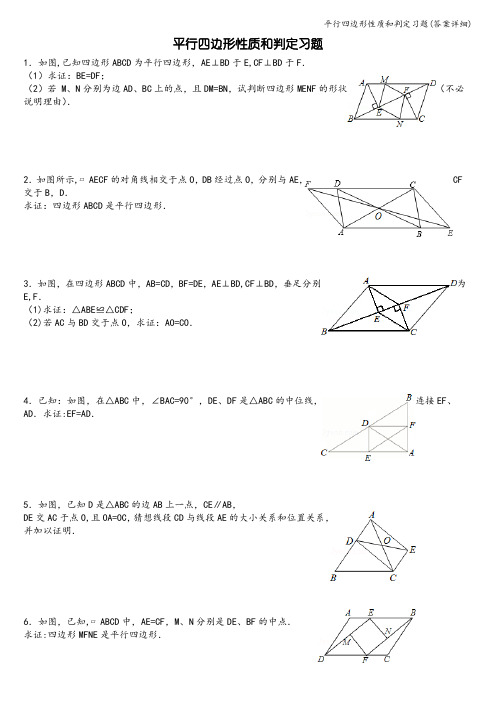
平行四边形性质和判定习题1．如图,已知四边形ABCD为平行四边形，AE⊥BD于E,CF⊥BD于F．（1）求证：BE=DF；（2）若 M、N分别为边AD、BC上的点，且DM=BN，试判断四边形MENF的形状（不必说明理由）．2．如图所示,▱AECF的对角线相交于点O，DB经过点O，分别与AE，CF 交于B，D．求证：四边形ABCD是平行四边形．3．如图，在四边形ABCD中，AB=CD，BF=DE，AE⊥BD,CF⊥BD，垂足分别为E,F．（1)求证：△ABE≌△CDF；（2)若AC与BD交于点O，求证：AO=CO．4．已知：如图，在△ABC中，∠BAC=90°，DE、DF是△ABC的中位线，连接EF、AD．求证:EF=AD．5．如图，已知D是△ABC的边AB上一点，CE∥AB，DE交AC于点O,且OA=OC，猜想线段CD与线段AE的大小关系和位置关系，并加以证明．6．如图，已知,▱ABCD中，AE=CF，M、N分别是DE、BF的中点．求证:四边形MFNE是平行四边形．7．如图，平行四边形ABCD，E、F两点在对角线BD上，且BE=DF，连接AE，EC，CF，FA．求证:四边形AECF是平行四边形．8．在▱ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF．求证:四边形BEDF是平行四边形．9．如图所示，DB∥AC，且DB=AC，E是AC的中点，求证：BC=DE．10．已知：如图，在梯形ABCD中，AD∥BC，AD=24cm,BC=30cm，点P自点A向D以1cm/s的速度运动,到D 点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，直线PQ截梯形为两个四边形．问当P，Q 同时出发,几秒后其中一个四边形为平行四边形？11．如图：已知D、E、F分别是△ABC各边的中点,求证：AE与DF互相平分．12．已知:如图，在▱ABCD中，对角线AC交BD于点O，四边形AODE是平行四边形．求证：四边形ABOE、四边形DCOE都是平行四边形．13．如图,已知四边形ABCD中，点E，F，G，H分别是AB、CD、AC、BD的中点，并且点E、F、G、H有在同一条直线上．求证：EF和GH互相平分．14．如图：▱ABCD中，MN∥AC，试说明MQ=NP．15．已知：如图所示，平行四边形ABCD的对角线AC，BD相交于点O,EF经过点O并且分别和AB，CD相交于点E，F，点G,H分别为OA,OC的中点．求证：四边形EHFG是平行四边形．16．如图，已知在▱ABCD中，E、F是对角线BD上的两点,BE=DF，点G、H分别在BA和DC的延长线上,且AG=CH，连接GE、EH、HF、FG．（1）求证：四边形GEHF是平行四边形；（2)若点G、H分别在线段BA和DC上,其余条件不变，则（1）中的结论是否成立？（不用说明理由）17．如图，在△ABC中，D是AC的中点，E是线段BC延长线一点，过点A作BE的平行线与线段ED的延长线交于点F，连接AE、CF．（1)求证:AF=CE；（2）如果AC=EF，且∠ACB=135°，试判断四边形AFCE是什么样的四边形，并证明你的结论．18．如图平行四边形ABCD中，∠ABC=60°，点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF，垂足为点F，DF=2（1)求证:D是EC中点；(2）求FC的长．19．如图,已知△ABC是等边三角形，点D、F分别在线段BC、AB上，∠EFB=60°，DC=EF．（1）求证：四边形EFCD是平行四边形；（2）若BF=EF，求证：AE=AD．20．如图,四边形ABCD，E、F、G、H分别是AB、BC、CD、DA的中点．（1）请判断四边形EFGH的形状？并说明为什么；（2）若使四边形EFGH为正方形，那么四边形ABCD的对角线应具有怎样的性质？21．如图，△ACD、△ABE、△BCF均为直线BC同侧的等边三角形．(1）当AB≠AC时，证明：四边形ADFE为平行四边形；（2）当AB=AC时，顺次连接A、D、F、E四点所构成的图形有哪几类?直接写出构成图形的类型和相应的条件．22．如图，以△ABC的三边为边，在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF，那么，四边形AFED是否为平行四边形?如果是，请证明之,如果不是，请说明理由．23．在△ABC中，AB=AC，点P为△ABC所在平面内一点，过点P分别作PE∥AC交AB于点E，PF∥AB交BC 于点D，交AC于点F．若点P在BC边上（如图1），此时PD=0，可得结论：PD+PE+PF=AB．请直接应用上述信息解决下列问题:当点P分别在△ABC内(如图2)，△ABC外（如图3）时，上述结论是否成立？若成立，请给予证明；若不成立，PD，PE，PF与AB之间又有怎样的数量关系，请写出你的猜想，不需要证明．24．如图1,P为Rt△ABC所在平面内任意一点（不在直线AC上），∠ACB=90°，M为AB边中点．操作：以PA、PC为邻边作平行四边形PADC，连续PM并延长到点E，使ME=PM,连接DE．探究:(1)请猜想与线段DE有关的三个结论;(2）请你利用图2,图3选择不同位置的点P按上述方法操作;（3）经历（2）之后,如果你认为你写的结论是正确的，请加以证明；如果你认为你写的结论是错误的,请用图2或图3加以说明；（注意:错误的结论，只要你用反例给予说明也得分）（4）若将“Rt△ABC”改为“任意△ABC"，其他条件不变，利用图4操作，并写出与线段DE有关的结论（直接写答案）．。

平行四边形的性质与判定

平行四边形的性质与判定【典型例题】利用平行四边形的性质求解边和角例1 如图，□ABCD 中，AD ⊥BD ，垂足为D ，OA=10，OB=6，求BC 、AB 的长。

# 灵活运用平行四边形性质进行边长、周长计算例2—1 如图，四边形ABCD 为平行四形，∠A+∠C=80°，□ABCD 的周长为40cm ，且AB －BC=2cm ，求□ABCD 各边长和各内角的度数。

例2—2 如图，四边形ABCD 是平行四边形，∠DAB:∠ABC=1:3，AB=4，BD 与AC 相交于O ，且BD ⊥AB ，求AD ，BC 和AC 的长。

# 利用平行四边形中对角线与边长的关系求取值范围例3—1 如图，□ABCD 中，对角线AC 和BD 相交于O 点，若AC=8，BD=6，则边AB 长的取值范围为（） A ．1﹤AB ﹤7 B ．2﹤AB ﹤14 C ．6﹤AB ﹤8D ．3﹤AB14例3—2 平行四边形的一边长为10，那么它的对角线长度可以是（） A ．8和12B ．20和30C ．6和8D ．4和6# 灵活运用平行四边形的面积公式计算例4 已知□ABCD 中周长是36cm ，且AB=10cm ，AD 与BC 间的距离为6cm ，求：AB 与CD 之间的距离。

ABCDOA BCDA BCDOABCDO DCBA h2* 例5 如图所示，□ABCD 中，∠ABC=75°，AF ⊥BC ，垂足为F ，AF 交BD 于E 。

若DE=2AB ，求∠AED 的度数。

* 例6 如图，在平行四边形ABCD 中，点E 、F 分别在边BC 、CD 上，且EF ∥BD ，求证：S △ABE =S △ADF 。

例7.A 、B 、C 、D 在同一平面内，从①AB ∥CD ；②AB=CD ；③BC ∥AD ；④BC=AD ，这四个条件中选两个，能使四边形ABCD 是平行四边形的选法有多少种（） A ．3 B ．4C ．5D ．6# 例8、如图，四边形ABCD 为平行四边形，E 、F 分别为AB 、DC 的中点，AF 、DE 交于G ，BF 、CE 交于H ，试说明：EHFG 为平行四边形。