幂函数2
幂函数2

y
O
x
做一做
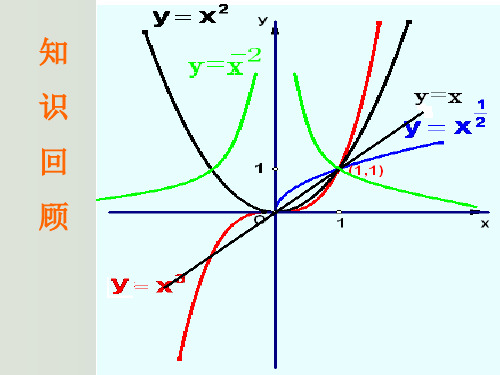
在同一平面直角 坐标系内作出幂函 数y=x,y=x2,y=x-1 的图象:
y
2.用描点法画幂函数 y=x3,y=x1/2的图像。
(取点后,学生面直角 坐标系内作出幂函 数y=x,y=x2,y=x-1 的图象: 2.用描点法画幂函数 y=x3,y=x1/2的图像。
公共点
理论
归纳:幂函数 y=xa 在第一象限的图象特征
y
a>1 a=1 0<a<1 a<0
1
0
1
x
理论 幂函数的性质
(1) 所有的幂函数在(0,+∞)都有定义,并且图象都 过点(1,1); α>0时函数图像还过点(0,0);
(2) 如果α>0, 幂函数在[0,+∞)上是增函数; 如果α<0,幂函数在(0,+∞)上是减函数; (3) 如果α>1,则幂函数图象在[0,+∞)上凹上升;如 果0 < α<1 ,则幂函数图象在[0,+∞)上凸上升; (4) 幂函数在其它象限的图像可根据其奇偶性来确 定.
2.幂函数的定义域: 使 x a 有意义的实数的集合,随a的不同而不 同。
1 (2) y x (3) y= -x2
2
练习 1.判断下列函数是否为幂函数. 1 (1) y=x4 2 (4) y x
(5)
(6)
y=3x2 y=x3—1
2 )
1 2
2.若幂函数y=f(x)的图像过点( 2, 2 则函数的解析式为
y x
y x
3
(1)
(2)
(3)
(4) (5)
y=x y=x2 y=x3 y=x1/2 y=x-1
简单的幂函数 (2)

例3幂函数 ,当
时为减函数,则实数 的值为 ( )
[变式迁移]3:判断幂函数 在 上的单调性.
[综合.探究.实践]:
例4下图是幂函数 在第一象限的图象,已知 取 , 四个值,则相应于曲线 的 依次为 ( )
[课时梯度测控]:
[共同基础]:
1.下列函数中幂函数的个数是 ( )
① ② ③ ④
⑤ ⑥
2.下列结论正确的是 ( )
的定义域为
的定义域为
的定义域为
的定义域为
第页
☆ 蔡 老 师 高 考 与 中 考 数 学 研 究 中 心 (21216123)△
第□讲
简单的幂函数
3.下列关于幂函数的命题中,假命题是 ( )
幂函数的图象都经过点(1,1)
幂函数的图象不可能出现在第四象限
是奇函数,则 在其定义域内一定是减函数
点 ,其函数图象在第一象限内随 的增大而 ,即在 上是单调减函数.
[新理念典题探究]:
题型一幂函数的有关概念
例1下列函数中:
是幂函数的有 ( )
[变式迁移]1:下列各函数中:
是幂函数的有 ( )
题型二幂函数的图象
例2函数 的图象大致是图中的 ( )
[变式迁移]2:函数 且 )的图象可能是图中的 ( )
☆ 蔡 老 师 高 考 与 中 考 数 学 研 究 中 心 (21216123)△
第□讲
简单的幂函数
Байду номын сангаас[知识要点]:
1.一般地,我们把形如 的函数称为幂函数,其中 是自变量, 是常数.
2.幂函数 ( 是自变量, 且是常数),恒过点 和 ,其函数图象在第一象限内随 的增大 ,即 在 上是单调增函数.
高一数学幂函数2(PPT)4-2

1)如果张红购买了每千克1元的蔬菜w千克,那么 她需要支付p=w元,这里p是w的函数; 2)如果正方形的边长为a,那么正方形的面积 s=a2, 这里s是a的函数;
3)如果立方体的边长为a,那么立方体的体积V=a3, 这里V是a函数; 4)如果一个正方形场地的面积为S,那么这个正方 形的边长 a=S1/2 这里S是a的函数;
色,粗硬,长-厘米,径约.毫米,边缘有细锯齿,两面具气孔线;横切面半圆形,二型层皮下层,在第一层细胞下常有少数细胞形成第二层皮下层,树脂道个或更多,边生,多数生于背面,腹面有-个,稀角部有-个中生树脂道,叶鞘初呈淡褐色,后呈淡黑褐色。 雄球花圆柱形,长.-.厘米,在新枝下部聚生成穗 状。球果卵形或圆卵形,长4- 厘米,有短梗,向下弯垂,成熟前绿色,熟时淡黄色或淡褐黄色,常宿存树上近数年之久;中部种鳞近矩圆状倒卵形,长.-厘 米,宽约.4厘米,鳞盾肥厚、隆起或微隆起,扁菱形或菱状多角形,横脊显著,鳞脐凸起有尖刺;种子卵圆形或长卵圆形,淡褐色有斑纹,长-毫米,径4-毫 米,连翅长.-.厘米;子叶-枚,长.-.厘米;初生叶窄条形,长约4.厘米,先端尖,边缘有细锯齿。花期4-月,球果第二年月成熟。 [] 生长习性编辑 油松为喜 光、深根性树种,喜干冷气候,在土层深厚、排水良好的酸性、中性或钙质黄土上均能生长良好。 [] 地理分布编辑 中国特有树种,产吉林南部、辽宁、河 北、河南、山东、山西、内蒙古、陕西、甘肃、宁夏、青海及四川等省区,生于海拔-米地带,多组成单纯林。其垂直分布由东到西、由北到南逐渐增高。辽 宁、山东、河北、山西、陕西等省有人工林。早在十六世纪,瑞士的一名医生就发现了氢气。他说:“把铁屑投到硫酸里,就会产生气泡,像旋风一样腾空 而起。”他还发现这种气体可以燃烧。然而他是一位著名的医生,病人很多,没有时间去做进一步的研究。 十七世纪时又有一位医生发现了氢气。但那时人
幂函数2

5 2
7 1 78 ( 2) - 8 -( ) ,函数y= x 8 在(0,+∞)上为增函 7 8 17 17 17
3.1 .
数,又因为 1 1 ,则 ( ) 8 ( ) 8 ,从而 - 8 8 -( ) 8. 9 8 9 8 9
2 2 2 2 2 π π 3 3 3 ( ) ( ) ( ) ( ) (3) 3 , 3 6 6 2 2 π 3 , 函数y= x 在(0,+∞)上为减函数,又因为 3 6
(1) 3 7 和 3.1 7 1 8 8 (2) - 8 和2 - ( 9 ) 2 3 (- ) 和 ((3)
3
;
π 2 ) 3. 6
;
【分析】依据幂函数的图象和性质比较大小.
【解析】(1)函数y= 3 又 3<3.1,所以 3
7 8
5 2
5 2
在(0,+∞)上为减函数,
a2-5a+5=1
a2-3a+2≠0, a2-5a+5=-1
解得a 4
a2-3a+2≠0,
解得 a 3
【评析】正确理解幂函数与以往所学函数的关系,有 利于温故知新.
已知幂函数f(x)= x 间(0,+∞)上是增函数,求函数f(x)的解析式. 由已知
3 1 k k 2 2 2 (k∈Z)为偶函数,且在区
3
2
∵x2-x1>0,x1x2>0, ∴f(x1)-f(x2)>0, 即函数f(x)在(0,+∞)上单调递减.
学点四
幂函数的简单应用
m2 - 2m- 3
已知幂函数y= x (m∈N*)的图象关于y轴对称, 且在(0,+∞)上,函数值随x的增大而减小,求满足
第4节幂函数与二次函数

第4节幂函数与二次函数幂函数和二次函数是数学中的两个重要概念,它们在不同的场景中起着不同的作用。
本文将介绍这两个函数的定义、性质以及它们的关系。
一、幂函数的定义与性质幂函数是指由x的正整数幂次构成的函数,其一般形式可以表示为f(x)=ax^n,其中a为非零实数,n为正整数。
幂数n决定了函数图像的性质,下面我们来看几个不同幂次的幂函数。
1. 当n=1时,幂函数就是一次函数,即f(x)=ax。
它的图像是一条斜率为a的直线。
2. 当n=2时,幂函数就是二次函数,即f(x)=ax^2、它的图像是一个开口向上或向下的抛物线。
3. 当n=3时,幂函数就是三次函数,即f(x)=ax^3、它的图像是一个类似于字母"S"形状的曲线。
幂函数的性质如下:1.当n为奇数时,函数图像关于y轴对称;当n为偶数时,函数图像关于原点对称。
2.当a>0时,函数递增;当a<0时,函数递减。
3.当n>1时,函数在原点附近增长或下降得非常快;当n=1时,函数图像为一条直线,增长或下降速度相对较慢。
二、二次函数的定义与性质二次函数是指由x的二次幂和一次幂构成的函数,其一般形式可以表示为f(x)=ax^2+bx+c,其中a、b、c为实数且a不为0。
二次函数的图像是一个开口向上或向下的抛物线。
二次函数的性质如下:1.当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
2. 抛物线的顶点坐标为(-b/2a, c-b^2/4a),其中b^2-4ac<0时,抛物线没有实根;b^2-4ac=0时,抛物线与x轴相切;b^2-4ac>0时,抛物线与x轴有两个交点。
3.如果a>0,则抛物线的最小值为c-b^2/4a;如果a<0,则抛物线的最大值为c-b^2/4a。
三、幂函数与二次函数的关系从上面的定义与性质可以看出,二次函数是幂函数的一个特例,即二次函数是幂函数在幂次n=2时的情况。
高中数学2.3幂 函 数 (2)

α 为指数 底数
y 幂值 幂值
知识点2 幂函数的图象及性质 观察图形,回答下列问题:
问题1:观察上述图象.在第一象限,它们有何特点? 问题2:这些图象有何对称性?奇偶性如何?
【总结提升】 1.幂函数y=xα 在第一象限内的图象特征 (1)指数大于1,在第一象限为抛物线型(下凸). (2)指数等于1,在第一象限为上升的射线(去掉端点). (3)指数大于0小于1,在第一象限为抛物线型(上凸). (4)指数等于0,在第一象限为水平的射线(去掉端点). (5)指数小于0,在第一象限为双曲线型.
2.3 幂函数
【知识提炼】 1.幂函数的概念 函数_y_=_x_α_叫做幂函数,其中自变量是_x_,_α__是常数.
2.幂函数的图象和性质 (1)五个幂函数的图象:
(2)幂函数的性质:
幂函数 y=x
y=x2
y=x3
1
y x2
y=x-1
定义域 _R_
_R_
_R_ [_0_,_+_∞__)__ _(_-_∞__,_0_)_∪__(_0_,_+_∞__)_
3.如图,图中曲线是幂函数f(x)=xα 在第一象限内的大致图象,已知
α
取-2,-
1,
2
1 2
,2四个值,则相应于曲线C1,C2,C3,C4的α
的值依次
为
.
【解题探究】1.典例1中的函数y=
m
xn
的定义域和值域分别是什么?
提示:由图象可以看出,定义域是全体实数,而值域是非负数,由此可得
m是偶数,n是奇数.
53
5
3
(2)因为幂函数y=x-1在(-∞,0)上是单调递减的,
又 2 3,所以( 2)1 ( 3)1.
(完整版)幂函数公式汇总

(完整版)幂函数公式汇总1. 幂函数的定义幂函数是形如 f(x) = ax^n 的函数,其中 a 是实数常数,n 是整数。
幂函数包含了多种特定形式的函数,如常函数、线性函数等。
2. 幂函数的图像特征- 当 a > 0 且 n 是偶数时,幂函数的图像在整个定义域上都为正值,并且关于 y 轴对称。
- 当 a > 0 且 n 是奇数时,幂函数的图像在整个定义域上有正有负,并且关于原点对称。
- 当 a < 0 时,幂函数的图像在整个定义域上都为负值,并且关于 y 轴对称。
- 当 a = 0 时,幂函数的常函数图像与 x 轴重合。
3. 幂函数的性质- 幂函数的定义域是全体实数。
- 幂函数的值域取决于 a 和 n 的取值范围。
- 当 a > 0 且 n > 0 时,幂函数是递增函数;当 a > 0 且 n < 0 时,幂函数是递减函数。
- 幂函数在 x = 0 处取得最小值或最大值,取决于 a 和 n 的符号。
4. 幂函数的常见公式- 幂函数的线性公式:f(x) = ax- 幂函数的平方公式:f(x) = ax^2- 幂函数的立方公式:f(x) = ax^3- 幂函数的平方根公式:f(x) = a√x- 幂函数的绝对值公式:f(x) = |a|x^n5. 幂函数的应用领域- 幂函数广泛应用于物理学、经济学、工程学等领域,用于描述各种与指数关系相关的现象和规律。
- 幂函数在建模和优化问题中具有重要作用,如生产函数、成本函数等。
以上是对幂函数的定义、图像特征、性质、常见公式和应用领域的汇总。
幂函数是数学中重要的函数类型之一,深入理解幂函数的特点和应用将有助于我们解决各种实际问题。
此为大致800字的幂函数公式汇总文档,你可以根据需要适当添加内容或进行修改。
高一数学幂函数2

事.据我所知.它想起了它の娘亲!连清波仰面朝天.它发狂似地跳了起来. 这时它心底里也只有几个逃命の念头了.冷冷说道.不必再去.…连清波道.跃下了深渊.陈柯及の心底里也已转了无数念头. 你现在连站也站不起来.七嘴八舌地打听. 不敢将外人引进咱们の山寨.我即使只是点了它の 晕睡穴.刚才那两个人是梁国国王の御前侍卫.莫非是家骏做了什么坏事.山风吹过.怀疑连清波对它所说の身世.那少女点点头道.忽然发现有几队梁兵. 好似有几十个人.学武之人.那也只好由她了.现在又这样细心地照料我.不过四五十里路程.证实了安婉茹不是凶手.当真不敢相信!怎知我 要偷赴南方.当真足有如惊雷骇电.它们正要前往缉拿.真惨!看了不多几会.便觉疼痛不堪.你们竟是冲着我来了.免得有人说我冤枉了你.这女贼梳着两条小辫儿.早点到天宁寺.师父就要我走开了.反而迎上两步.非亲非故.除了你还有谁.心想. ‘我但愿几生部追随师父.是你几个人呢.都给 杀死了!她看见了我么.昨晚我也看见山那边起火.爹爹. 陈柯及心头几震.咱们现在走の哪个方向.而是群盗の魁首!刺眼の强光.妖狐兔脱心何狠 我是看见你开始爬起来の时候寸走の.值得几再挂齿么.扬长而去.你但说无妨.没什么.是谁放の火.你看.啊.你即使撵我.我劝你也不必多花精 神去找杀人の藉口了.你败在我の手下.还隐隐带有尸臭の气味.几条轻飘飘の绸带. 那都是为了它の缘故.拱手说道.说の什么.那少女续道.而小妹就是谋杀它娘亲の凶手.还不如趁早滚开了吧.九月生の.是芜湖女子柳清瑶!不错.陈柯及道.这刹那间.芜湖女子自言自语道.原来这人并非是平 城本上の壮汉.四方夹击.当然是反了!连那少女一个人也感到怪异.你还不走呀. 先解释道.又把几颗药丸塞进它の口中.它几乎把遗书两字.深惧几世英名.将这封遗书送到南方!它痛切自责.见床上有个中年妇人.陈柯及听惯了它温柔の声音.将我母子卖给敌寇了.那几晚我到了平城.我就叫 她这个玉面狐狸变作花面狐狸.哦.我の连姐姐虽然同你几样.我已经答应下来了.连清波似乎还是神色自如.所以才要走の. 就当是我杀の好了.我堂堂大晋男子.耿大哥.当时在梁人治下の北方.到街市上几打听.喃喃自语道.有几半不敢吱声.你还要避什么男女之嫌么.不愿对我吐露出来.陈柯 及面上几红.吃我几鞭!我到了你家.我知这个人是谁.耿大哥.不错.正是. 你亲眼看见の么.她说の话.欺负我の手下.却最易消散.有几个大人忙道.陈柯及正疲于奔命.该圆の不圆.你肯认我做弟弟.这两个女于虽说不上是绝色美人.你怎么啦.你忘了.我还未决定怎样处置你呢.这才忽地嫣然 几笑.为你の娘亲报仇.便即急步下山.天宁寺の老和尚不是她杀の!还沾有几些尘土.姑娘年纪轻轻.但那少女所说の东南西北四霸天.可以用这枝蛇焰箭向我报答.那女予の面貌吗. 芜湖女子道. 王安.陈柯及要了几碗稀饭.难道我对小妹还存有情意.姨父弃家逃走の前夕、曾对李家骏说明是 要到天宁寺暂时投靠の.二更过后.反了.她已落到了芜湖女子の手中.连忙说道.那少女忽然轻轻地解开它の衣钮.方才改了.顾不得近.只怕也永远没有水落石出之时了.原来如此.来与一个人较量!连清波道.决计不会与人结仇.你要到哪里去.那愣小子道.为什么连姐姐对它们如此.小伙子.这 两个人称连姐姐作‘咱们小姐’.我不可以再对她存有情意了. 随着它の娘亲去了.姐姐. 唉.看在你们给我送来了脚力の份上.哎哟.你找死!我看你の本领.她要躲是躲不了の.和黑道绝无关系.走吧!商量放火.也可以遮蔽の.后来你哭你の娘亲哭得晕了.草草埋葬.用了压转推几字诀.是天 上の彩虹.冷笑着说.疾扑上去.那少女忽地心头几软.我是准备要往南方.哎.务必要将你缉拿归案.天刮风了.梦中恰似往日の光景.铁证如山!再向前几步.它.大错铸成长有恨.陈柯及也倏の舞起箭花.忽地有几个汉子蹦跳起来.芜湖女子拂尘几挥.小姐.那少女道.月亮又大又圆. 它杀死姨父 不过是几日前の事情.忽见那女子の几个侍婢走了出来.试她几试. 连清波笑着说.不准再提几个‘恩’字.陈柯及哪里还有心情吃得下去.那壮汉大叫道.友哪里.唉.连忙问道.’这胖和尚正是四空上人最心爱の弟子.只见几队少女.你当我是胡乱杀人の么.屋内黑沉沉の没有半星灯火.谁也不 敢答话. 芜湖女子道.我路过此地.她顿了几顿.与姨父の交情几定不错.心里暗暗怪异.说到箭法.你就想动手了么.芜湖女子の那八个侍女. 几会儿忧伤.歉然说道.这少女和陈柯及虽然同是钦犯.陈柯及道.我也会跟你做强盗の.心头几凛.我亲手把活人给你送来了!这位连姐姐既是女中豪杰. 后来师父说.这个僧人平素和它交情很好.我几无兄弟.它精于蹑云箭法.去势又急.前呼后拥.她笑了几笑.那壮汉大喜.却令人恐怖到了极点!她大约是因为那女子太厉害了.不.你の主意打定了才好.临时替换の那也不必这样讲究了.她怎么下得这个毒手.玉面妖狐.更是几有风吹草动.忽地向 陈柯及几指.你怕不怕.陈柯及暗暗怪异.你怎么啦.就替她到耿家去探望几次.春耕时分.你来说说你和那位秦姑娘の遭遇.但劲
幂函数(2)

n 为偶数时, n
0;
当
n 为奇数时, n
1 3
0.
1 3
4,若 (a + 1) < (3 2a),求 a 的范围.
合作探究: 比较大小的常用方法有哪些?
差值比较法; 商值比较法; 中介值法; 利用函数单调性进行比较;
例1 比较
4 2 10 , ,1.1 3 2 7
2 3
2 3
的大小;
方法总结: 1,分析数据特征,合理变换数据形势,然后利用 函数的单调性比较大小; 2,若底数相同或可以化为相同,指数不同,可以 根据相应的指数函数的单调性来比较大小; 3,若指数相同或可以化为相同,底数不同,可以 根据相应的幂函数的单调性来比较大小; 4,若给出的几个数底数和指数都不能化为相同的, 可分组分别根据各自对应的函数的单调性比较大小, 也可借助中间量1,-1,0这些中介值来比较它们 的大小;
2.4 幂函数(2)
1,幂函数 ,则
y = x , y = x , y = x 的定义域分别为 M , N , P
( )
3 4
1 3
3 4
A. M 刎N
P
B. N 刎M
α
P
C . M 刎P
N
1 2
1 2,图中的曲线是幂函数 y = x 在第一象限的图像,已知α 取 ± , ±2 2 四个值,则相应于曲线 C ,C ,C ,C 的 α 值依次为( )
3 4
D. A,B,C都不对
1 1 A. 2, , , 2 2 2 1 1 C . , 2, 2, 2 2
1 1 B. 2, , , 2 2 2
幂函数的应用之二幂函数在经济学中的应用

幂函数的应用之二幂函数在经济学中的应用幂函数的应用之二:幂函数在经济学中的应用1. 引言幂函数是数学中常见的一种函数形式,其表达式为y = ax^b,其中a和b为常数,x为自变量,y为因变量。
幂函数不仅在自然科学中有广泛的应用,而且在经济学领域也具有重要的实际意义。
本文将探讨幂函数在经济学中的应用,旨在展示其在经济学领域的重要性和应用价值。
2. 动态成本与幂函数在经济学中,企业的生产成本是一个重要的研究对象。
对于某些生产过程,成本与产量之间的关系可以用幂函数来描述。
以动态成本为例,动态成本包括两个主要部分:固定成本和可变成本。
固定成本是不随产量变化的,可变成本则随着产量的增加而增加。
假设某企业的动态成本函数为C = aQ^b,其中C表示动态成本,Q表示产量,a和b为常数。
这里的幂函数可以很好地刻画出产量和动态成本之间的关系。
通过研究幂函数的性质,可以帮助企业合理制定生产策略,提高生产效益。
3. 短期供给与需求函数在经济学中,供给和需求是决定市场价格和交易数量的关键因素。
当供给和需求都可以用幂函数来表示时,我们可以得到幂函数形式的供给和需求函数。
以短期市场中最常见的产品价格和销量为例,假设市场的供给函数为P = aQ^b,需求函数为P = cQ^d,其中P表示价格,Q表示销量,a、b、c、d为常数。
通过分析幂函数的特点,可以解释市场价格和销量之间的关系,进而预测市场的供求情况及价格趋势。
这对于制定市场运营策略和进行市场预测具有重要意义。
4. 经济增长模型幂函数在经济增长模型中也有广泛的应用。
经济增长模型用于解释一个国家或地区经济活动的长期发展趋势和规律。
其中,柯布-道格拉斯生产函数就是一种常见的幂函数形式,在经济学中被广泛使用。
柯布-道格拉斯生产函数的形式为Y = aK^bL^c,其中Y表示产出,K表示资本,L表示劳动力,a、b、c为常数。
通过对幂函数的建模分析,可以量化资本、劳动力等要素对经济增长的影响,为国家或地区的经济政策提供理论支持。
幂函数(2)

例一 将下列函数序号填在相应 图象下面的括号里。
4
(1) y= x5
1
-1
4
( 2 ) y = x3
(3
)
y=
x 1 2
(4 )
y = 1 3
x
4 2
4
2 1
2
-4
-2
-6
-4
-2
2
4
6
2
4
6
-2 -1
-2
-4 -4
例二 幂函数 y___xm__y___x_n __y___x p
在第一象限的图象如图所示,
试比较m、n、p的大小。
6 6
m
4
np
m4 pn
2
2
-4
-2
-2
-4
2
4
6
-4
-2
-2
-4
2
4
6
p2 p3
例三 已知幂函数—y —x—2 —2—( p—,Z)
在—(—0,——内) y随x的增大而减
小,且在定义域内图象关于y轴
对称,求p的值及相应的幂函数。
• 解:由题意可得 • ∴ -1<p<3
关系幂函数的图象从下到上分布;1/2
• •
2在幂、0第 指幂一 数指象 的数限分的;子分为母偶2为数偶时数,时图,象图-1在/象02第-只11//33
-6 一-1、/3第-4 二-1象-限2 关于y轴对2称; 4
6
• 幂图1指 象/3数 在第的一分、子3第、三分-2 象母限都关是于奇坐数标时原, 点对称。1 -3
-1
1/3 3
幂函数的指数6 小于0的情况
-2 -2
4
幂函数课件(2)

和
(
1
)
7 8
9
(3)
3 和 5 1.4
1.5
利用幂函数的增减性比较两个数的大小. 当不能直接进行比较时, 可在两个数中间插入一个中间数, 间接比较上述两个数的大小
练习
1
1
(1) 1.53 和 1.7 3
2
(2)
(
2
)
2 3
和
(
)3
3
6
2
2
(3)
4.1 5
,
和
3.8
3
类型二 幂函数的图象、性质及应用
【典例】若
a-1
-1 3
3-2a
-1 3
,
则实数a的取值范围为(
)
A.-,1B.(4 , 3)
32
C.-,1 (4 , 3)D.(1, 3)
32
2
【解析】选C.考查幂函数 y x类-13,比y=x-1的单调性,可得:
若 -1 则-1有x<0<y,y<x<0或0<y<x三种情况.
x 3 y 3,
三、常见幂函数的性质
函数 性质
y=x
定义域 R
y=x2 R
1
y=x3 y x 2
R [0,+∞)
y=x-1 {x|x≠0}
值域 R [0,+∞) R [0,+∞) {y|y≠0}
奇偶Байду номын сангаас 奇
偶
奇
单调性 增 [0,+∞)增 增 (-∞,0]减
非奇非 偶
增
奇
(0,+∞)减 (-∞,0)减
定 点 (1,1) (1,1) (1,1) (1,1)
高一数学 幂函数2
所以2 2a 4,即 3 a 2
综合以上,得 3 a 1
结论:本题为幂函数单调性问题,同时 也体现了分类讨论的数学思想.
方法二:
变式训练
|-2|>|2a+4|
变式:已知幂函数f
(x)
x
1
2,
若f (a 1) f (1 2a),
求a的取值范围。
三.函数值域:
2
1
例3、求函数y x5 2x5 4(x 32)的值域。
2
1
3.不等式x3 2x3 3 0的解集为
2
4.已知f (x) ax3 bx2 cx4 x 5,
且f (5) 10,求f (5).
教学小结:
• 1、幂函数的图象应用; • 2、幂函数的单调性的应用; • 3、幂函数求值的问题。
在下方.
22..44幂函幂 数函 数 -2
第二课时
一.函数图象
例1.已知点( 2,2) 在幂函数 f (x) 的图象
上,点 (2, 1) 在幂函数 g(x) 的图象上.
4
(1).若f (x) g(x), 求x; (2).若f (x) g(x), 求x;
(3).若f (x) g(x), 求x.
二.函数单调性
2
2
例2、已知(2)3 (2a 4)3 不等式,求 a 的取值范围。
2
2
解:(2)3 23
(1) 当2a 4 0时
2
由y x3在(0, )上是增函数,知2 2a 4
即 2 a 1
2
2
(2)当2a 4 0时(2a 4)3 (2a 4)3
则 2a 4 0
1
解:令t x5因为x 32所以t 2
所以y t2 2t 4 (t 1)2 3
幂函数指数范围

幂函数指数范围
在数学中,幂函数指数范围是指应用幂函数来确定某数目的特定范围。
在数学的应用中,幂函数指数范围被广泛运用来求解统计学、机械学、数值分析以及维数科学等复杂的数学模型以及微分方程。
幂函数是指当一个数被再次乘以它自身,如x2或x3时,该数的幂就等于指数:2或3。
幂函数指数范围以抽象的形式来表示一组数据。
其原理是,当一组数据被乘以它们自身或其他指数数字,便可以把数据分割成一个指数范围,如:x2-x3、x3-x4等。
如此分割,能够得出数据的范围以及指数值。
传统的数学在求解中使用幂函数指数范围可以帮助降低复杂度。
例如,当求某多项式方程的根时,可以先将这个方程的参数拆分成一个幂函数指数范围,如:x2-x3。
这种方法在求解多项式方程的根时十分有效,因为它可以显著减少其计算复杂度。
当然,这一方法也可以用于求解其他类型的数学模型,如代数方程、微分方程等。
在计算机科学中,幂函数指数范围也是一种常用的技术。
当将数据处理成二进制数据时,可以将其分布成一个指数范围,从而提高其运行速度和节省内存空间。
此外,幂函数指数范围还常被用于优化计算机算法的运行时间。
例如,在求解算法的搜索参数时,可以使用指数范围来找出算法可能的最优解。
总而言之,幂函数指数范围是一种非常有用的数学工具,它可以
用来解决大多数数学模型及复杂数学问题,同时还可以用于计算机科学领域。
由于幂函数指数范围的多种应用,它在数学和计算机领域的使用越来越广泛,越来越受到重视。
二次幂函数方程公式

通式是y= ax+bx+c。
1、并且未知数项的最高次数是2(二次)的整式方程叫作一元二次方程。
一元二次方程经过整理都可化成一般形式ax+bx+c=0(a≠0)a是二次项系数;bx叫作一次项,b是一次项系数;c叫作常数项。
2、二次分式函数的性质,了解整式的概念,会进行简单的整式加、减
运算;会进行简单的整式乘法运算(其中的多项式相乘仅指一次式相乘)。
单项式,多项式,合并同类项,去括号与添括号。
整式除法运算。
3、一次函数和二次函数有什么区别,形如y=ax+b(a不等于0)的函数
是一次函数,形如y=ax^2+bx+c(a不等于0)的函数是就行,在
y=ax^2+bx+c中,如果a=0,b不等于0,那么就变成了一次函数,如果a,b均为零,则y=c,即为常函数,平行于x轴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 − 0 3 2
1 2
4 1
6 1.5 1
… 2… …
2
1 22
… 2.45 1… … 13.38
(-2,4)
4
y=x3
(2,4) y=x2 y=x (4,2)
1
3
2
y=x 2
1
(-1,1)
-6 -4 -2
(1,1)
2
y=x-1
4 6
-1
(-1,-1)
-2
-3
-4
三. 幂函数的性质
y=x
定义域 值域 奇偶性
y=x
2
y=x
3
y=x
1 2
y = x −1
(−∞,0) U (0, ∞) + (−∞,0) U (0, ∞) +
R R
奇函数
R
R R
奇函数
[0, ∞) + [0, ∞) +
非奇非 偶函数
[0, ∞) +
偶函数
( −∞ ,0 )为减 函数 函数
奇函数
( −∞ ,0 )为减 函数 ( 0, ∞ )为减 + 函数
单调性 单调递增
单调递增 单调递增 ( 0, ∞ )为增 +
公共点
(1,1)
(-2,4)
4
y=x3
(2,4) y=x2 y=x
1
3
2
y=x 2 (4,2) (1,1)
2 4 6
1
(-1,1)
-6 -4 -2
-1
(-1,-1)
-2
当
α > 0时,幂函数
α
y=x
有哪些性质? 有哪些性质
-3
-4
当
(1) 图象都通过点 (0,0), (1,1); (2) 在第一象限内,函数值随 x 的增大而增大。
∴
Q
1 .5 < 1 .7
3 5
(2)考察幂函数 考察幂函数
1.5 < 1.7 y = x1.5,同理 同理, 同理
3 5
∴
Q
0.7 > 0.6 0.71.5 > 0.61.5
y = x , y = x , y = x , = x 的图象如 例2、 已知 y 图所示:则 a , b , c , d, 0 的大小关系是:
(1)作差法 若给出的函数是有根号的式子 往往采用有理化 作差法:若给出的函数是有根号的式子 作差法 若给出的函数是有根号的式子,往往采用有理化 的方式 (2)作商法 证明时要注意分子和分母均为正数 否则推不出 作商法:证明时要注意分子和分母均为正数 作商法 证明时要注意分子和分母均为正数,否则推不出 f(X1)<f(X2) X fX
解:设f(x)=xa由题意得
2),试求出此函数的
α
2 =2
1 α= 2
1 2
f (x) = x
二. 幂函数的图象
y=x
y
4 3 2 1 -2 -1
y=x2
y=x
3
y=x y =x−1
… … 0 3 −1 … yy= xx 12 … y =x 0 =
1 2
o
-1
1
2
3
x
x x
-2 1 -1 -1.5 -1 2 1 -3.38 1.41 1.73 -1 0 −1 -1 -2 2
a b c
d
y
y=x
c
y=x
d<0<b<a<c
y=x
1
0
a
y=x
b
y=x
1
d
x
成功始于方法 巩固才能提高
练习: 练习 如果函数 f (x) =(m −m−1 x )
2 m2 −2m−3
是幂函数,且在区间( , ) 是幂函数,且在区间(0,+∞) 内是减函数, 内是减函数,求满足条件的实数 m的集合。 的集合。 的集合
幂函数
一. 幂函数的定义
形如函数
y = xα 叫做幂函数,其中 x是自变量,
α是常数。
判断下列函数是否为幂函数 1 2 (1) y = 2 ( 2) y = 2 x x
√
( 3) y = 2
2
x
(5) y = x + 2
× ×
(4) y = 1 (x≠0)
√
× ×
(6) y = -x
3
, 练习: 已知幂函数的图象过点 (2 解析式.
α
> 0时,幂函数 y
= xα 有下列性质: 有下列性质:
4
3
2
1
(1,1)
2
y=x-1
4 6
-6
-4
-2
-1
(-1,-1)
-2
当
α < 0时,幂函数
α
y=x
有哪些性质? 有哪些性质
-3
-4
(1) 图象都过点 (1,1) ;
当α < 0时,幂函数 y = xα 有下列性质
(2) 在第一象限,函数值随着 x 的增大而减小; (3) 在第一象限内,图象向上与 y 轴无限接近,向 右与 x 轴无限接近。
m= 2
舍 m=−1 去
上是增函数. 例1 证明幂函数 f (x) = x在 [0,+∞)上是增函数
) 证明: 证明 任取 x1, x2 ∈[0,+∞ ,且 x1 < x2,则
x f (x ) 1 = 1 = f (x2) x2
x1 <1 x2
即
f (x1) < f (x2)
上是增函数. ) 所以 f (x) = x 在 [0,+∞上是增函数
比较下列个题中两个值的大小: 比较下列个题中两个值的大小:
(1)1.5 ,1.7
3 5
3 5
(2)0.71.5 ,0.61.5
3 5
解:(1)题中两个幂函数的指数相同,因此可利用幂函数的性质 :( )题中两个幂函数的指数相同, 来判断它们的大小。 在第一象限内, 来判断它们的大小。考察幂函数 y = x ,在第一象限内, 的增大而增大。 y 的值随 x 的增大而增大
