2020年中考数学一轮复习之二次函数动点问题(面积、长度最值与定长)(解析版)
初三复习二次函数动点问题(含答案)

二次函数的动态问题(动点)1.如图①,正方形ABCD 的顶点A B ,的坐标分别为()()01084,,,,顶点C D ,在第一象限.点P 从点A 出发,沿正方形按逆时针方向匀速运动,同时,点Q 从点()40E ,出发,沿x 轴正方向以相同速度运动.当点P 到达点C 时,P Q ,两点同时停止运动,设运动的时间为t 秒. (1)求正方形ABCD 的边长.(2)当点P 在AB 边上运动时,OPQ △的面积S (平方单位)与时间t (秒)之间的函数图象为抛物线的一部分(如图②所示),求P Q ,两点的运动速度.(3)求(2)中面积S (平方单位)与时间t (秒)的函数关系式及面积S 取最大值时点P 的坐标. (4)若点P Q ,保持(2)中的速度不变,则点P 沿着AB 边运动时,OPQ ∠的大小随着时间t 的增大而增大;沿着BC 边运动时,OPQ ∠的大小随着时间t 的增大而减小.当点P 沿着这两边运动时,使90OPQ =∠的点P 有 个.(抛物线()20y ax bx c a =++≠的顶点坐标是2424b ac b aa ⎛⎫-- ⎪⎝⎭,.[解] (1)作BF y ⊥轴于F .()()01084A B ,,,,86FB FA ∴==,.10AB ∴=.(2)由图②可知,点P 从点A 运动到点B 用了10秒. 又1010101AB =÷=,.P Q ∴,两点的运动速度均为每秒1个单位.(3)方法一:作PG y ⊥轴于G ,则PG BF ∥.图①图②GA AP FA AB ∴=,即610GA t=.35GA t ∴=.3105OG t ∴=-.4OQ t =+,()113410225S OQ OG t t ⎛⎫∴=⨯⨯=+- ⎪⎝⎭.即231920105S t t =-++. 19195323210b a -=-=⎛⎫⨯- ⎪⎝⎭,且190103≤≤, ∴当193t =时,S 有最大值. 此时4763311051555GP t OG t ===-=,,∴点P 的坐标为7631155⎛⎫⎪⎝⎭,.(8分)方法二:当5t =时,1637922OG OQ S OG OQ ====,,. 设所求函数关系式为220S at bt =++.抛物线过点()63102852⎛⎫ ⎪⎝⎭,,,,1001020286325520.2a b a b ++=⎧⎪∴⎨++=⎪⎩,31019.5a b ⎧=-⎪⎪∴⎨⎪=⎪⎩,231920105S t t ∴=-++.19195323210b a -=-=⎛⎫⨯- ⎪⎝⎭,且190103≤≤, ∴当193t =时,S 有最大值. 此时7631155GP OG ==,,∴点P 的坐标为7631155⎛⎫⎪⎝⎭,.(4)2.[点评]本题主要考查函数性质的简单运用和几何知识,是近年来较为流行的试题,解题的关键在于结合题目的要求动中取静,相信解决这种问题不会非常难。
2020年中考数学二轮复习压轴专题:二次函数(解析版)

2020 年中考数学二轮复习压轴专题:《二次函数》1.如图,平面直角坐标系中,点 A、点B 在 x 轴上(点A在点B 的左边),点 C在第一象限,知足∠ ACB为直角,且恰使△OCA∽△ OBC,抛物线y=ax2﹣8ax+12a( a<0)经过A、 B、C三点.(1)求线段OB、OC的长.(2)求点C的坐标及该抛物线的函数关系式;( 3)在x 轴上能否存在点,使△为等腰三角形?若存在,求出全部切合条件的P P BCP点的坐标:若不存在,请说明原因.解:( 1)y=ax2﹣ 8ax+12a=a(x﹣ 6)(x﹣ 2),故 OA=2, OB=6,△ OCA∽△ OBC,则2,即: OC= OA?OB,解得: CO=2;( 2)过点C作CD⊥x轴于点D,△ OCA∽△ OBC,则,设 AC=2x,则BC=2x,而AB=4,故 16=( 2x)2+( 2x)2,解得:x=1,故 AC=2, BC=2,S△ABC=AB× CD=AC× BC,解得: CD=,故 OD=3,故点 C(3,);将点 C的坐标代入抛物线表达式并解得:a=﹣,故抛物线的表达式为:y=﹣x2+x﹣4;( 3)设点P( m,0),而点B、 C的坐标分别为:(6,0)、(3,);2222则 BC=12,PB =( m﹣6), PC=( m﹣3)2+3,当BC=PB时,12=(m﹣6)2,解得:m=6;当 BC=PC时,同理可得: m=6(舍去)或0;当 PB=PC时,同理可得: m=4,综上点 P 的坐标为:(6, 0)或( 0, 0)或( 4, 0).2.直线y=﹣x+2与 x 轴交于点A,与 y 轴交于点 B,抛物线y=﹣ x2+bx+c 经过 A、 B 两点.(1)求这个二次函数的表达式;(2)若P是直线AB上方抛物线上一点;①当△ PBA的面积最大时,求点 P 的坐标;②在①的条件下,点 P 对于抛物线对称轴的对称点为Q,在直线 AB上能否存在点 M,使得直线QM与直线BA的夹角是∠QAB的两倍?若存在,直接写出点M的坐标;若不存在,请说明原因.解:( 1)直线y=﹣x+2与 x 轴交于点 A,与 y 轴交于点B,则点 A、 B 的坐标分别为:( 4, 0)、( 0, 2),将点、B 的坐标代入抛物线表达式得:,解得:,A故抛物线的表达式为:y=﹣ x2+x+2;2( 2)①过点P作y轴的平行线交BC于点 N,设 P(m,﹣ m+ m+2),点 N( m,﹣m+2),则:△ PBA的面积 S=2m+2+2PN× OA=×4×(﹣ m+m﹣2)=﹣ m+4m,当 m=2时, S 最大,此时,点 P(2,5);②点 P(2,5),则点 Q(, 5),设点M(a,﹣a+2);(Ⅰ)若:∠QMB QAM QM AM 1=2∠1,则1=1,则( a﹣)2+(a﹣3)2=( a﹣4)2+(﹣a+2)2,解得: a=,M,);故点1((Ⅱ)若∠QMB QAM2= 2∠ 1 ,则∠ QM2B=∠ QM1B, QM1= QM2,作 QH⊥AB于 H,BQ的延伸线交x 轴于点 N,则 tan ∠BAO==,则tan∠QNA=2,故直线QH表达式中的k 为2,设直线QH的表达式为:y=2x+b,将点Q的坐标代入上式并解得:b=2,故直线QH的表达式为:y=2x+2,故H(0,2)与 B 重合,M、M对于21B 对称,∴ M(﹣2,);综上,点M的坐标为:(,)或(﹣,).3.如图已知直线y=x+与抛物线y= ax2+bx+c 订交于 A(﹣1,0), B(4, m)两点,抛物线 y= ax2+bx+c 交 y 轴于点 C(0,﹣),交x轴正半轴于D点,抛物线的极点为M.(1)求抛物线的分析式;(2)设点P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求△PAB的面积及点 P的坐标;( 3)若点Q为x轴上一动点,点N 在抛物线上且位于其对称轴右边,当△QMN与△ MAD 相像时,求N点的坐标.解:( 1)将点B( 4,m)代入y=x+,∴ m=,将点 A(﹣1,0), B(4,),C(0,﹣)代入y=ax2+bx+c,解得 a=,b=﹣1,c=﹣,∴函数分析式为 y= x2﹣ x﹣;( 2)设P(n,n2﹣n﹣),则经过点 P 且与直线 y= x+垂直的直线分析式为y=﹣2x+n2+n﹣,直线 y=x+与其垂线的交点G(n2+ n﹣,n 2+ n+),∴ GP=(﹣ n2+3n+4),当 n=时, GP最大,此时△ PAB的面积最大,∴P(,),∵AB=,PG=,∴△ PAB的面积=××=;(3)∵M( 1,﹣ 2),A(﹣ 1, 0),D( 3,0),∴ AM=2, AB=4, MD=2,∴△ MAD是等腰直角三角形,∵△ QMN与△ MAD相像,∴△ QMN是等腰直角三角形,设 N(t ,t 2﹣ t ﹣)①如图 1,当MQ⊥QN时,N( 3, 0);②如图 2,当QN⊥MN时,过点N作 NR⊥ x 轴,过点 M作 MS⊥ RN交于点 S,∵QN=MN,∠ QNM=90°,∴△ MNS≌△ NMS( AAS)∴﹣ 1=﹣t 2+ + ,t t ∴ t =±,∴ t >1,∴ t =,∴N(,1﹣);③如图 3,当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点N作NR∥x轴,与过 M点的垂线分别交于点S、 R;∵QN=MQ,∠MQN=90°,∴△ MQR≌△ QNS( AAS),∴ SQ=QR=2,∴ t +2=1+t 2﹣ t ﹣,∴t =5,∴N(5,6);④如图 4,当MN⊥NQ时,过点M作 MR⊥ x 轴,过点 Q作 QS⊥ x 轴,过点N 作x轴的平行线,与两垂线交于点、;R S∵QN=MN,∠MNQ=90°,∴△ MNR≌△ NQS( AAS),∴ SQ=RN,∴ t 2﹣ t ﹣= t ﹣1,∴ t =2±,∵ t >1,∴ t =2+,∴N(2+, 1+);综上所述: N(3,0)或 N(2+, 1+)或 N(5,6)或 N(,1﹣).4.如图,在平面直角坐标系中,已知矩形ABCD的三个极点B(4,0)、C(8,0)、D(8,8).抛物线的分析式为y= ax2+bx.( 1)如图 1,若抛物线经过A,D两点,直接写出 A 点的坐标(4,8);抛物线的对称轴为直线6;( 2)如图 2:①若抛物线经过A、C两点,求抛物线的表达式.②若点 P 为线段 AB上一动点,过点P 作 PE⊥ AB交 AC于点 E,过点 E 作 EF⊥AD于点 F交抛物线于点G.当线段 EG最长时,求点E的坐标;( 3)若a =﹣ 1,且抛物线与矩形没有公共点,直接写出b的取值范围.ABCD解:( 1)点A的坐标为:( 4, 8);函数的对称轴为:x=(4+8)=6;故答案为:( 4,8); 6;( 2)①将点A、C的坐标代入抛物线表达式并解得:a=﹣,b=4,故抛物线的表达式为:y=﹣x2+4x;②由点 A、 C的坐标得,直线AC的表达式为: y=﹣2x+16;设点 E( x,﹣2x+16),则点 G( x,﹣x2+4x),EG=﹣x2+4x﹣(﹣2x+16)=﹣x2+6x﹣16,当 x=6时, EG由最大值为:2,此时点 E(2,4);( 3)若a=﹣ 1,则抛物线的表达式为:y=﹣ x2+bx,当抛物线过点B和点 D时,抛物线与矩形有一个交点,将点 B的坐标代入抛物线表达式得:0=﹣ 16+4b,解得:b= 4,将点 D的坐标代入抛物线表达式并解得:b=9,故 b 的取值范围为:b<4或 b>9.5.如图,直线y =﹣1 与抛物线y=﹣x2+6 ﹣5 订交于、D两点.抛物线的极点为,连x x A C结 AC.( 1)求A,D两点的坐标;( 2)点P为该抛物线上一动点(与点A、 D不重合),连结 PA、PD.①当点 P 的横坐标为 2 时,求△PAD的面积;②当∠ PDA=∠ CAD时,直接写出点P的坐标.解:( 1)联立方程组,解得,,,∴(1,0),(4,3),A D( 2)①过P 作⊥轴,与订交于点,PE x AD E∵点 P的横坐标为2,∴P(2,3), E(2,1),∴PE=3﹣1=2,∴=3;②过点 D作 DP∥AC,与抛物线交于点P,则∠ PDA=∠ CAD,∵y=﹣ x2+6x﹣5=﹣( x﹣3)2+4,∴ C(3,4),设 AC的分析式为: y= kx+b( k≠0),∵A(1,0),∴,∴,∴AC的分析式为: y =2x﹣2,设 DE的分析式为: y=2x+n,把D(4,3)代入,得3=8+n,∴n=﹣5,∴DE的分析式为: y=2x﹣5,联立方程组,解得,,,∴此时 P(0,﹣5),当 P 点在直线 AD上方时,延伸 DP,与 y 轴交于点 F,过 F 作 FG∥AC ,FG与 AD交于点 G,则∠ FGD=∠ CAD=∠ PDA,∴FG=FD,设 F(0, m),∵ AC的分析式为: y=2x﹣2,∴FG的分析式为: y=2x+m,联立方程组,解得,,∴ G(﹣ m﹣1,﹣ m﹣2),∴FG=,FD=,∵ FG=FD,∴=,∴ m=﹣5或1,∵ F 在 AD上方,∴ m>﹣1,∴ m=1,∴ F(0,1),设 DF的分析式为: y= qx+1( q≠0),把 D(4,3)代入,得4q+1=3,∴ q=,∴DF的分析式为: y= x+1,联立方程组∴,,∴此时P 点的坐标为,综上, P 点的坐标为(0,﹣ 5)或.6.综合与研究如图,抛物线y= ax2+bx+c( a≠0)经过点 A、 B、C,已知点 C(0,4),△ AOC∽△ COB,且,点 P 为抛物线上一点(异于A, B)(1)求抛物线和直线AC的表达式(2)若点P是直线AC上方抛物线上的点,过点P作PF⊥AB,与AC交于点E,垂足为F.当PE= EF时,求点 P 的坐标( 3)若点为x 轴上一动点,能否存在点,使得由,,,四点构成的四边形为平M P B C P M行四边形?若存在,直接写出点P 的坐标;若不存在,请说明原因解:( 1),则OA=4OC=8,故点A(﹣8,0);△ AOC∽△ COB,则△ ABC为直角三角形,2则 CO= OA?OB,解得: OB=2,故点 B(2,0);则抛物线的表达式为:y=a( x﹣2)( x+8),将点 C的坐标代入上式并解得:a=﹣,故抛物线的表达式为:y=﹣x2﹣x+4;精选文档666AC的表达式为:y=x+4;由点A、 C的坐标可得直线( 2)设点P( x,﹣x2﹣x+4),则点E( x,x +4),PE= EF,即﹣x2﹣x+4﹣x﹣4=x+4;解得: x=﹣8(舍去)或﹣2,故点 P(﹣2,6);2( 3)设点P(m,n),n=﹣m﹣m+4,点 M(s,0),而点 B、C的坐标分别为:(2,0)、( 0, 4);①当 BC是边时,点 B 向左平移2个单位向上平移 4 个单位获得C,相同点 P( M)向左平移 2 个单位向上平移 4 个单位获得M( P),即 m﹣2= s, n+4=0或 m+2= s, n﹣4=0,解得: m=﹣6或﹣ 3,故点P的坐标为:(﹣6,4)或(﹣ 3,﹣ 4)或(﹣﹣3,﹣ 4);②当BC是对角线时,由中点公式得:2=m+s,n= 4,故点 P(﹣6,4);综上,点 P 的坐标为:(﹣6,4)或(﹣3,﹣4)或(﹣﹣3,﹣4).7.如图 1,抛物线y=x2+mx+4m与 x 轴交于点 A( x1,0)和点 B( x2,0),与 y 轴交于点C,且 x1, x2知足 x12+x22=20,若对称轴在y 轴的右边.(1)求抛物线的分析式.(2)如图 2,若点P为线段AB上的一动点(不与A、B重合),分别以AP、BP为斜边,在直线 AB的同侧作等腰直角三角形△ APM和△ BPN,试确立△ MPN最大时 P 点的坐标.( 3)若P(x1,y1),Q(x2,y2)是抛物线上的两点,当a≤ x1≤ a+2,x2≥时,均有y1≤ y2,求 a 的取值范围.解:( 1)x1+x2=﹣ 2m,x1x2=8m,则 x12+x22=( x1+x2)2﹣2x1x2=20,即(﹣ 2m)2﹣ 16m= 20,解得: m=5(舍去)或﹣1;故抛物线的表达式为:y=x2﹣ x﹣4;(2)令y=0,则x=﹣ 2 或 4,故点A、B的坐标分别为:(﹣ 2,0)、( 4,0),则AB=6;设: AP= a,则 PN=6﹣ a,∠ MPN=180°﹣∠ MPA﹣∠ NPB=90°;S△=×PN× PMMPN=a××(6﹣a)=a(6﹣ a)=﹣( a﹣3)2+;∴当a=3时, S最大,此时△MPNOP=1,故点P(1,0);( 3)函数的对称轴为x=1,如图,x=﹣2.5和 x=对于函数对称轴对称,纵坐标均为,由图象看, a≥﹣且a+2≤,解得:﹣≤ a≤.8.如图,在平面直角坐标系中,矩形ABCD的极点B, C, D 的坐标分别(1,0),(3,0),( 3, 4),以A为极点的抛物线y= ax2+bx+c 过点 C.动点 P 从点 A出发,以每秒个单位的速度沿线段AD向点D 匀速运动,过点P 作PE⊥ x 轴,交对角线AC于点N.设点P运动的时间为t (秒).( 1)求抛物线的分析式;( 2)若PN分△ ACD的面积为1: 2 的两部分,求t的值;( 3)若动点P 从A 出发的同时,点Q 从 C出发,以每秒1 个单位的速度沿线段CD向点D匀速运动,点H为线段PE上一点.若以C,Q,N,H为极点的四边形为菱形,求 t的值.解:( 1)∵四边形ABCD为矩形,且B(1,0), C(3,0), D(3,4),∴ A(1,4),设抛物线的分析式为y=a( x﹣1)2+4,将 C(3,0)代入 y= a(x﹣1)2+4,得 0=4a+4,解得 a=﹣1,∴抛物线的分析式为 y=﹣( x﹣1)2+4=﹣ x2+2x+3;(2)∵PE⊥x轴,DC⊥x轴,∴ PE∥DC,∴△ APN∽△ ADC,∵ PN分△ ACD的面积为1:2的两部分,∴=或,当=时,==,∵AD=2,∴ AP=,∴ t 的值为× 2=;当=时,==,∵ AD=2,∴ AP=,∴ t 的值为× 2=,综上所述,t 的值为或;( 3)如图 2﹣ 1,当CN为菱形的对角线时,点 P,N的横坐标均为,设直线的分析式为y =+ ,AC kx b将 A(1,4), C(3,0)代入 y= kx+b,得,解得,∴直线 AC的表达式为y=﹣2x+6,将点 N的横坐标代入y=﹣2x+6,得,即 EN=4﹣ t ,由菱形 CQNH可得, CQ= NH= t = CH,可得 EH=(4﹣ t )﹣ t =4﹣2t ,∵∴,,在 Rt △CHE中,222∵ CE+EH= CH,∴,解得, t 1=,t2=4(舍);如图 2﹣ 2,当CN为菱形的边时,由菱形 CQHN可得, CQ= CN= t ,在 Rt △CNE中,222∵ NE+CE= CN,∴( 4﹣t)2+( 2﹣t )2= t 2,解得, t 1=20﹣8, t 2=20+8(舍);综上所述,t的值为或.9.如图1,过原点的抛物线与x 轴交于另一点A,抛物线极点 C 的坐标为,其对称轴交 x 轴于点 B.( 1)求抛物线的分析式;( 2)如图2,点D为抛物线上位于第一象限内且在对称轴右边的一个动点,求使△ACD 面积最大时点D的坐标;( 3)在对称轴上能否存在点P,使得点 A对于直线OP的对称点 A'知足以点 O、A、C、A'为极点的四边形为菱形.若存在,恳求出点P的坐标;若不存在,请说明原因.解:( 1)设抛物线分析式为y= a( x﹣ h)2+k,( a≠0)∵极点,∴,又∵图象过原点,∴,解出:,∴,即;( 2)令y= 0,即,解得: x1=0, x2=4,∴ A(4,0),设直线 AC的分析式为y=kx+b,将点 A(4,0),代入,得,精选文档666解得,∴直线AC的分析式为y=﹣x+4,过点D作DF∥ y 轴交AC于点F,设,则,∴,∴=,∴当m=3时, S△ACD有最大值,当 m=3时,,∴;( 3)∵∠CBO=∠CBA= 90°,OB=AB= 2,∴,,∴OA=OC= AC=4,∴△ AOC为等边三角形,①如图 3﹣ 1,当点P在C时,OA=AC=CA'=OA' ,∴四边形 ACA'O是菱形,∴;②作点 C对于 x 轴的对称点 C',当点 A'与点 C'重合时, OC= AC=AA'= OA',∴四边形 OCAA'是菱形,∴点 P是∠ AOA'的角均分线与对称轴的交点,记为P2,∴,∵∠2= 90°,=2,OBP OB22∴ OP=2BP,∵∠2= 90°,=2,OBP OB∴OP2=2BP2,设 BP= x,2∴ OP=2x,2又∵,∴( 2x)2=22 +x2,解得或,∴;综上所述,点P的坐标为或.10.已知二次函数与x轴交于A、B(A在B的左边)与y 轴交于点 C,连接 AC、BC.( 1)如图 1,点P是直线BC上方抛物线上一点,当△ PBC面积最大时,点M、N分别为x、y 轴上的动点,连结PM、PN、 MN,求△ PMN的周长最小值;( 2)如图 2,点C对于x轴的对称点为点E,将抛物线沿射线AE的方向平移获得新的拋物线 y',使得 y'交 x 轴于点 H、B( H在 B 的左边).将△ CHB绕点 H 顺时针旋转90°至△C' HB'.抛物线 y'的对称轴上有一动点 S,坐标系内能否存在一点 K,使得以 O、C'、K、S 为极点的四边形是菱形,若存在,请直接写出点K 的坐标;若不存在,请说明原因.解:( 1)如图 1,A(﹣ 2, 0),B( 8, 0),C( 0, 4),∴直线的分析式为,BC过点 P作 y 轴平行线,交线段BC于点 Q,设,∴=,∵ 0<m< 8,∴ P(4,6).作 P 点对于 y 轴的对称点P1,P 点对于 x 轴的对称点 P2,连结 P1P 2交 x 轴、y 轴分别为 M,,N此时△的周长最小,其周长等于线段P1P2的长;PMN∵ P1(﹣4,6), P2(4,﹣6),∴.( 2)如图 2 中,∵ ( 0,﹣ 4),平移后的抛物线经过,,E E B∴抛物线的分析式为y =﹣x2+bx﹣ 4,把( 8, 0)代入获得b=4,B∴平移后的抛物线的分析式为y=﹣x+4x﹣4=﹣(x﹣2)(x﹣8),令 y=0,获得 x=2或8,∴ H(2,0),∵△ CHB绕点 H顺时针旋转90°至△ C′ HB′,∴C′(6,2),当 OC′= C′ S时,可得菱形 OC′S1 K1,菱形 OC′ S2K2,∵ ′=′==2,OC CS∴可得 S1(5,2﹣), S2(5,2+),∵点 C′向左平移一个单位,向下平移获得 S1,∴点 O向左平移一个单位,向下平移个单位获得K1,∴K1(﹣1,﹣),同法可得K2(﹣1,),当′=时,可得菱形′,菱形′,OC OS OC K3S3OC K4S4同法可得 K3(11,2﹣),K4(11,2+),当 OC′是菱形的对角线时,设2222,S5(5, m),则有 5 +m=1 +(2﹣ m)解得 m=﹣5,∴ S5(5,﹣5),∵点O向右平移5 个单位,向下平移 5 个单位获得S5,∴ C′向上平移 5 个单位,向左平移 5 个单位获得K5,∴ K5(1,7),综上所述,知足条件的点K的坐标为(﹣1,﹣)或(﹣ 1,)或( 11,2﹣)或( 11, 2+)或( 1,7).11.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+2( a≠0)与 x 轴交于 A(﹣1,0),B(3,0)两点,与y 轴交于点 C.(1)求该抛物线的分析式;(2)如图①,若点D是抛物线上一个动点,设点D的横坐标为 m(0< m<3),连结 CD、BD、 BC、 AC,当△ BCD的面积等于△ AOC面积的2倍时,求 m的值;( 3)若点N为抛物线对称轴上一点,请在图②中研究抛物线上能否存在点M,使得以 B,C,M,N为极点的四边形是平行四边形?若存在,请直接写出全部知足条件的点M的坐标;若不存在,请说明原因.解:( 1)把(﹣ 1,0),( 3,0)代入y =ax2+bx+2 中,得:,解得:,A B∴抛物线分析式为;( 2)过点D作y轴平行线交BC于点 E,把 x=0代入中,得:y=2,∴ C点坐标是(0,2),又 B(3,0)∴直线的分析式为,BC∵∴∴=,由S =2S 得:△BCD△AOC∴,2整理得: m ﹣ 3m +2= 0解得: m = 1, m = 212∵ 0< m < 3∴ m 的值为 1 或 2;( 3)存在,原因:设:点的坐标为:( , ), =﹣2+x +2,点 ( 1, ),点 ( 3, 0)、 ( 0, 2),M m nnxNsBC①当是平行四边形的边时,BC当点 C 向右平移 3 个单位,向下平移 2 个单位获得 ,B相同点 M ( N )向右平移 3 个单位,向下平移 2 个单位 N ( M ),故: m +3= 1, n ﹣ 2= s 或 m ﹣ 3= 1, n +2= s ,解得: m =﹣ 2 或 4,故点M 坐标为:(﹣ 2,﹣)或(4,﹣);②当BC 为对角线时,由中点公式得:m +1= 3,n +3= 2,解得: m = 2,故点M ( 2,2);综上, M 的坐标为:( 2,2)或(﹣2,)或( 4,).12.已知抛物线 y =ax 2﹣ 2ax +3 与 x 轴交于点 A 、 B ( A 左 B 右),且 AB =4,与 y 轴交于 C 点.( 1)求抛物线的分析式;( 2)如图,证明:对于随意给定的一点 P (0, b )( b > 3),存在过点 P 的一条直线交抛物线于 M 、 N 两点,使得 PM = MN 建立;( 3)将该抛物线在 0≤ x ≤ 4 间的部分记为图象 G ,将图象 G 在直线 y = t 上方的部分沿 y= t 翻折,其他部分保持不变,获得一个新的函数的图象,记这个函数的最大值为,最m小值为 n ,若 m ﹣ n ≤ 6,求 t 的取值范围.解:( 1)抛物线y=ax2﹣ 2ax+3 的对称轴为x=1,又AB=4,由对称性得A(﹣ 1,0)、B ( 3, 0).把 A(﹣1,0)代入 y= ax2﹣2ax+3,得 a+2a+3=0,∴ a=﹣1.∴抛物线的分析式为 y=﹣ x2+2x+3.(2)如图,过M作GH⊥x轴,PG∥x轴,NH∥x轴,由 PM=MN,则△ PMG≌△ NMH( AAS),∴PG=NH, MG=MH.22设 M(m,﹣ m+2m+3),则 N(2m,﹣4m+4m+3),∵ P(0, b), GM= MH,∴y G+y H=2y M,222即 b+(﹣4m+4m+3)=2(﹣ m+2m+3),∴2m= b﹣3,∵ b>3,∴对于 m的方程总有两个不相等的实数根,此即说了然点M、 N存在,并使得PM=MN.证毕;( 3)图象翻折前后如右图所示,其极点分别为D(1,4)、 D′(1,2t ﹣4).①当 D′在点 H(4,﹣5)上方时,2t﹣ 4≥﹣ 5,∴t≥﹣,此时, m= t , n=﹣5,∵ m﹣ n≤6,∴ t +5≤6,∴ t ≤1,∴﹣≤ t ≤1;②当点 D′在点 H(4,﹣5)下方时,同理可得: t <﹣,m=t,n=2t﹣4,由 m﹣n≤6,得 t ﹣(2t ﹣4)≤6,∴ t ≥﹣2,∴﹣2≤t<﹣.综上所述,t的取值范围为:﹣2≤t≤ 1.y 轴交于13.如图,抛物线y= ax2+bx﹣2的对称轴是直线x=1,与x 轴交于A,B两点,与点 C,点A 的坐标为(﹣2,0),点P 为抛物线上的一个动点,过点P 作PD⊥ x 轴于点D,E.交直线BC于点(1)求抛物线分析式;(2)若点P在第一象限内,当OD= 4PE时:①求点 D、 P、 E的坐标;②求四边形 POBE的面积.(3)在( 2)的条件下,若点M为直线BC上一点,点N为平面直角坐标系内一点,能否存在这样的点 M和点 N,使得以点 B, D, M,N为极点的四边形是菱形?若存在,直接写出点 N的坐标;若不存在,请说明原因.解:( 1)∵抛物线y= ax2+bx﹣2的对称轴是直线x=1, A(﹣2,0)在抛物线上,∴x =﹣= 1,解得:a=,b=﹣,抛物线分析式为y=x2﹣x﹣2;( 2)令y=x2﹣x﹣2=0,( x﹣4)( x+2)=0,解得: x1=﹣2, x2=4,当 x=0时, y=﹣2,由 B(4,0), C(0,﹣2),得,直线BC的表达式为: y=x﹣2设 D(m,0),∵ DP∥ y 轴,∴ E( m,m﹣2), P( m,m2﹣ m﹣2),∵ OD=4PE,2m﹣2﹣ m+2),∴ m=4( m﹣∴ m=5, m=0(舍去),∴ D(5,0), P(5,),E(5,),∴四边形 POBE的面积= S△OPD﹣ S△EBD=× 5×﹣× 1×=;( 3)存在,设M( n,n ﹣2),①以 BD为对角线,如图1,∵四边形 BNDM是菱形,∴MN垂直均分 BD,∴n=4+,∴M(,),∵M,N对于 x 轴对称,∴N(,﹣);②以BD为边,如图2,∵四边形 BDMN是菱形,∴MN∥BD, MN=BD= MD=1,过 M作 MH⊥ x 轴于 H,222∴ MH+DH= DM,即(n﹣2)2+( n﹣5)2=12,∴n1=4(不合题意), n2=5.6,∴N(4.6,),同理(n ﹣ 2)2+(4﹣)2= 1,n∴ n1=4+(不合题意,舍去),n2=4﹣,∴N(5﹣,﹣),③以 BD为边,如图3,过 M作 MH⊥ x 轴于 H,∴2+2=2,MH BH BM即(n﹣2)2+( n﹣4)2=12,∴ n1=4+, n2=4﹣(不合题意,舍去),∴N(5+,),综上所述,点 N坐标为:()或(,)或( 5﹣,)或(5+,).14.如图,矩形中,为原点,点A 在y轴上,点C在x轴上,点B的坐标为( 4,3),OABC O抛物线y =﹣x2+ +与y轴交于点,与直线AB交于点,与x轴交于,两点.bx c A D C E( 1)求抛物线的表达式;( 2)点P 从点C出发,在线段上以每秒 1 个单位长度的速度向点B运动,与此同时,CB点Q 从点A出发,在线段上以每秒个单位长度的速度向点C运动,当此中一点抵达AC终点时,另一点也停止运动.连结、、,设运动时间为t (秒).DP DQ PQ①当 t 为什么值时,△ DPQ的面积最小?②能否存在某一时辰t ,使△ DPQ为直角三角形?若存在,直接写出t 的值;若不存在,请说明原因.解:( 1)点A( 0, 3),点C( 4, 0),将点 A、 C的坐标代入抛物线表达式,解得:b=,c=3,故抛物线的表达式为:y=﹣x2+x+3;( 2)y=﹣x2+x+3=﹣(x﹣4)(x+2),故点E(﹣2,0);抛物线的对称轴为:x=1,则点 D(2,3),由题意得:点Q(t ,3﹣ t ),点 P(4, t ),①△ DPQ的面积= S△ABC﹣( S△ADQ+S△PQC+S△BPD)=3×4﹣ [2 ×t +2( 3﹣t)+( 5﹣)× t ×]= t 2﹣2t .∵> 0,故△的面积有最小值,此时,t =;DPQ②点( 2, 3),点(t , 3﹣),点(4,),D Q t P t (Ⅰ)当是斜边时,如图1,PQ过点作⊥于点,则=,=2﹣t ,= 4﹣ 2=2,=3﹣,Q QM ABMMQ t MD BD PBt则 tan ∠MQD= tan ∠BDP,即,解得:t=(舍去);(Ⅱ)当 PD为斜边时,过点 Q作 y 轴的平行线交AB于点 N,交过点 P 于 x 轴的平行线于点M,则 ND=2﹣t , QN= t ,MP=4﹣t , QM=3﹣ t ﹣ t =3﹣2t ,同理可得:,解得: t =或;(Ⅲ)当 QD为斜边时,同理可得:故t =;综上, t =或或或.15.如图,已知抛物线y= ax2+bx+3经过点 A(﹣1,0)、B(3,0),且与 y 轴交于点 C,抛物线的极点为D,连结 BD,点 P 是线段 BD上的一个动点(不与B、 D)重合.( 1)求抛物线的分析式,并写出极点D的坐标;( 2)过点P 作⊥轴于点,求△面积的最大值及获得最大值时P点的坐标;PE y E PBE(3)在( 2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断能否存在这样的点 M,使得以点 B, P, M, N为极点的四边形是平行四边若存在,请直接写出点 M 的坐标:若不存在,请说明原因.解:( 1)∵二次函数y= ax2+bx+3经过点 A(﹣1,0)、B(3,0)∴因此二次函数的分析式为:y=﹣ x2+2x+3∵ y=﹣ x2+2x+3=﹣( x﹣1)2+4∴ D的坐标为(1,4);( 2)设BD的分析式为y= kx+b∵过点 B(3,0), D(1,4)∴解得BD的分析式为y=﹣2x+6设 P(m,﹣2m+6),∵ PE⊥y 轴于点 E,∴ PE=m,△ BPE的 PE边上的高 h=﹣2m+6,∴ S =×PE× h= m(﹣2m+6)△BPE2=﹣ m+3m=,∵ a=﹣1<0,∴当 m=时△ BPE的面积获得最大值为,当 m=时, y=﹣2×+6=3,∴ P 的坐标是(,3);2( 3)设点M(s, 0),点N(m,n),n=﹣m+2m+3,①当 BP是边时,点 P 向右平移个单位向下平移 3 个单位获得B,同理点 M( N)向右平移个单位向下平移 3 个单位获得N( M),即 s=m,0± 3=n,解得: s=﹣或或;②当 PB为对角线时,m+s=3+,n=3,解得: s=或,故: M点的坐标为:;;;;;.。
2020年九年级数学中考复习:二次函数压轴动点问题

二次函数动点问题以不变应万变 一题多问 多题归一类型一 定点问题类型二 抛物线动点存在性问题 ———线段和差问题类型三 抛物线动点存在性问题———等腰三角形存在性问题 类型四 抛物线动点存在性问题———三角形面积最大值类型五 抛物线动点存在性问题 ——— 四边形面积最大值 类型六 抛物线动点存在性问题——— 特殊角度问题类型七 抛物线动点存在性问题———直角三角形存在性问题 类型八 抛物线动点存在性问题——— 相似三角形存在性问题 类型九 抛物线动点存在性问题———平行四边形存在性问题 类型十 抛物线动点存在性问题———梯形存在性问题题干:抛物线32-x y 2-=x 与y 轴交于点B ,与x 轴交于C,D (C 在D 点的左侧),点A 为顶点 。
类型一定点问题(直接三角形判定,两点之间距离公式,勾股定理的运用)(1)判定三角形ABD的形状?并说明理由。
【通法:运用两点间的距离公式,求出该三角形各边的长】(两点之间距离公式,相似三角形的判定)(2)三角形ABD与三角形BOD是否相似?说明理由。
【通法:用两点间的距离公式分别两个三角形的各边之长,再用相似的判定方法】类型二抛物线动点存在性问题———线段和差问题(3)在x轴上是否存在点P,使PB+PA最短?若存在求出点P的坐标,并求出最小值。
若不存在,请说明理由。
【通法:在两定点中任选一个点(为了简单起见,常常取轴上的点),求出该点关于题中的动点运动所经过的那条直线的对称点的坐标,再把此对称点与余下定点相连】(4)在y轴上是否存在点P,使三角形PAD的周长最小?若存在,求出点P的坐标,并求出周长的最小值;若不存在,请说明理由。
【通法:注意到AD是定线段,其长度是个定值,因此只需PA+PD最小】(5)在直线BC上是否存在点P,使三角形PAD的周长最小?若存在,求出点P的坐标,并求出周长的最小值;若不存在,请说明理由。
(6)在y轴上是否存在点P,使PAPD-最大?若存在,求出点P的坐标,并求出PAPD-的最大值;若不存在,请说明理由。
二次函数与几何的动点及最值、存在性问题(解析版)

二次函数与几何的动点及最值、存在性问题目录题型01平行y轴动线段最大值与最小值问题题型02抛物线上的点到某一直线的距离问题题型03已知点关于直线对称点问题题型04特殊角度存在性问题题型05将军饮马模型解决存在性问题题型06二次函数中面积存在性问题题型07二次函数中等腰三角形存在性问题题型08二次函数中直角三角形存在性问题题型09二次函数中全等三角形存在性问题题型10二次函数中相似三角形存在性问题题型11二次函数中平行四边形存在性问题题型12二次函数中矩形存在性问题题型13二次函数中菱形存在性问题题型14二次函数中正方形存在性问题二次函数常见存在性问题:(1)等线段问题:将动点坐标用函数解析式以“一母式”的结构表示出来,再利用点到点或点到直线的距离公式列出方程或方程组,然后解出参数的值,即可以将线段表示出来.【说明】在平面直角坐标系中该点在某一函数图像上,设该点的横坐标为m,则可用含m字母的函数解析式来表示该点的纵坐标,简称“设横表纵”或“一母式”.(2)平行y轴动线段最大值与最小值问题:将动点坐标用函数解析式以“一母式”的结构表示出来,再用纵坐标的较大值减去较小值,再利用二次函数的性质求出动线段的最大值或最小值.(3)求已知点关于直线对称点问题:先求出直线解析式,再利用两直线垂直的性质(两直线垂直,斜率之积等于-1)求出已知点所在直线的斜率及解析式,最后用中点坐标公式即可求出对称点的坐标.(4)“抛物线上是否存在一点,使其到某一直线的距离为最值”的问题:常常利用直线方程与二次函数解析式联立方程组,求出切点坐标,运用点到直线的距离公式进行求解.(5)二次函数与一次函数、特殊图形、旋转及特殊角度综合:图形或一次函数与x 轴的角度特殊化,利用与角度有关知识点求解函数图像上的点,结合动点的活动范围,求已知点与动点是否构成新的特殊图形.2.二次函数与三角形综合(1)将军饮马问题:本考点主要分为两类:①在定直线上是否存在点到两定点的距离之和最小;②三角形周长最小或最大的问题,主要运用的就是二次函数具有对称性.(2)不规则三角形面积最大或最小值问题:利用割补法将不规则三角形分割成两个或以上的三角形或四边形,在利用“一母式”将动点坐标表示出来,作线段差,用线段差来表示三角形的底或高,用面积公式求出各部分面积,各部分面积之和就是所求三角形的面积.将三角形的面积用二次函数的结构表示出来,再利用二次函数的性质求出面积的最值及动点坐标.(3)与等腰三角形、直角三角形的综合问题:对于此类问题,我们可以利用两圆一线或两线一圆的基本模型来进行计算.问题分情况找点画图解法等腰三角形已知点A ,B 和直线l ,在l 上求点P ,使△PAB 为等腰三角形以AB为腰分别以点A ,B 为圆心,以AB 长为半径画圆,与已知直线的交点P 1,P 2,P 4,P 5即为所求分别表示出点A ,B ,P 的坐标,再表示出线段AB ,BP ,AP 的长度,由①AB =AP ;②AB =BP ;③BP =AP 列方程解出坐标以AB 为底作线段AB 的垂直平分线,与已知直线的交点P 3即为所求分别表示出点A ,B ,P 的坐标,再表示出线段AB ,BP ,AP 的长度,由①AB =AP ;②AB =BP ;③BP =AP 列方程解出坐标问题分情况找点画图解法直角三角形已知点A ,B 和直线l ,在l 上求点P ,使△PAB 为直角三角形以AB为直角边分别过点A ,B 作AB 的垂线,与已知直线的交点P 1,P 4即为所求分别表示出点A ,B ,P 的坐标,再表示出线段AB ,BP ,AP 的长度,由①AB 2=BP 2+AP 2;②BP 2=AB 2+AP 2;③AP 2=AB 2+BP 2列方程解出坐标以AB 为斜边以AB 的中点Q 为圆心,QA 为半径作圆,与已知直线的交点P 2,P 3即为所求注:其他常见解题思路有:①作垂直,构造“三垂直”模型,利用相似列比例关系得方程求解;②平移垂线法:若以AB 为直角边,且AB 的一条垂线的解析式易求(通常为过原点O 与AB 垂直的直线),可将这条直线分别平移至过点A 或点B 得到相应解析式,再联立方程求解.(4)与全等三角形、相似三角形的综合问题:在没有指定对应点的情况下,理论上有六种情况需要讨论,但在实际情况中,通常不会超过四种,要注意边角关系,积极分类讨论来进行计算.情况一探究三角形相似的存在性问题的一般思路:解答三角形相似的存在性问题时,要具备分类讨论思想及数形结合思想,要先找出三角形相似的分类标准,一般涉及动态问题要以静制动,动中求静,具体如下:①假设结论成立,分情况讨论.探究三角形相似时,往往没有明确指出两个三角形的对应点(尤其是以文字形式出现求证两个三角形相似的题目),或者涉及动点问题,因动点问题中点的位置的不确定,此时应考虑不同的对应关系,分情况讨论;②确定分类标准.在分类时,先要找出分类的标准,看两个相似三角形是否有对应相等的角,若有,找出对应相等的角后,再根据其他角进行分类讨论来确定相似三角形成立的条件;若没有,则分别按三种角对应来分类讨论;③建立关系式,并计算.由相似三角形列出相应的比例式,将比例式中的线段用所设点的坐标表示出来(其长度多借助勾股定理运算),整理可得一元一次方程或者一元二次方程,解方程可得字母的值,再通过计算得出相应的点的坐标.情况二探究全等三角形的存在性问题的思路与探究相似三角形的存在性问题类似,但是除了要找角相等外,还至少要找一组对应边相等.3.二次函数与四边形的综合问题特殊四边形的探究问题解题步骤如下:①先假设结论成立;②设出点坐标,求边长;③建立关系式,并计算.若四边形的四个顶点位置已确定,则直接利用四边形边的性质进行计算;若四边形的四个顶点位置不确定,需分情况讨论:a.探究平行四边形:①以已知边为平行四边形的某条边,画出所有的符合条件的图形后,利用平行四边形的对边相等进行计算;②以已知边为平行四边形的对角线,画出所有的符合条件的图形后,利用平行四边形对角线互相平分的性质进行计算;③若平行四边形的各顶点位置不确定,需分情况讨论,常以已知的一边作为一边或对角线分情况讨论.b.探究菱形:①已知三个定点去求未知点坐标;②已知两个定点去求未知点坐标,一般会用到菱形的对角线互相垂直平分、四边相等的性质列关系式.c.探究正方形:利用正方形对角线互相垂直平分且相等的性质进行计算,一般是分别计算出两条对角线的长度,令其相等,得到方程再求解.d.探究矩形:利用矩形对边相等、对角线相等列等量关系式求解;或根据邻边垂直,利用勾股定理列关系式求解.题型01平行y轴动线段最大值与最小值问题1(2023·广东东莞·一模)如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,OA=OC =3,顶点为D.(1)求此函数的关系式;(2)在AC 下方的抛物线上有一点N ,过点N 作直线l ∥y 轴,交AC 与点M ,当点N 坐标为多少时,线段MN 的长度最大?最大是多少?(3)在对称轴上有一点K ,在抛物线上有一点L ,若使A ,B ,K ,L 为顶点形成平行四边形,求出K ,L 点的坐标.(4)在y 轴上是否存在一点E ,使△ADE 为直角三角形,若存在,直接写出点E 的坐标;若不存在,说明理由.【答案】(1)y =x 2+2x -3(2)当N 的坐标为-32,-154 ,MN 有最大值94(3)K -1,4 ,L -1,-4 或K -1,12 ,L -5,12 或K -1,12 ,L 3,12(4)存在,点E 的坐标为0,32 或0,-72或0,-1 或0,-3【分析】(1)由OA =OC =3求得A -3,0 ,C 0,-3 ,再分别代入抛物线解析式y =x 2+bx +c ,得到以b ,c 为未知数的二元一次方程组,求出b ,c 的值即可;(2)求出直线AC 的解析式,再设出M 、N 的坐标,把MN 表示成二次函数,配方即可;(3)根据平行四边形的性质,以AB 为边,以AB 为对角线,分类讨论即可;(4)设出E 的坐标,分别表示出△ADE 的平分,再分每一条都可能为斜边,分类讨论即可.【详解】(1)∵抛物线y =x 2+bx +c 经过点A ,点C ,且OA =OC =3,∴A -3,0 ,C 0,-3 ,∴将其分别代入抛物线解析式,得c =-39-3b +c =0,解得b =2c =-3 .故此抛物线的函数表达式为:y =x 2+2x -3;(2)设直线AC 的解析式为y =kx +t ,将A -3,0 ,C 0,-3 代入,得t =-3-3k +t =0 ,解得k =-1t =-3 ,∴直线AC 的解析式为y =-x -3,设N 的坐标为n ,n 2+2n -3 ,则M n ,-n -3 ,∴MN =-n -3-n 2+2n -3 =-n 2-3n =-n +32 +94,∵-1<0,∴当n =-32时,MN 有最大值,为94,把n =-32代入抛物线得,N 的坐标为-32,-154,当N 的坐标为-32,-154 ,MN 有最大值94;(3)①当以AB 为对角线时,根据平行四边形对角线互相平分,∴KL 必过-1,0 ,∴L 必在抛物线上的顶点D 处,∵y =x 2+2x -3=x +1 2-4,∴K -1,4 ,L -1,-4②当以AB 为边时,AB =KL =4,∵K 在对称轴上x =-1,∴L 的横坐标为3或-5,代入抛物线得L -5,12 或L 3,12 ,此时K 都为-1,12 ,综上,K -1,4 ,L -1,-4 或K -1,12 ,L -5,12 或K -1,12 ,L 3,12 ;(4)存在,由y =x 2+2x -3=x +1 2-4,得抛物线顶点坐标为D -1,-4 ∵A -3,0 ,∴AD 2=-3+1 2+0+4 2=20,设E 0,m ,则AE 2=-3-0 2+0-m 2=9+m 2,DE 2=-1-0 2+-4-m 2=17+m 2+8m ,①AE 为斜边,由AE 2=AD 2+DE 2得:9+m 2=20+17+m 2+8m ,解得:m =-72,②DE 为斜边,由DE 2=AD 2+AE 2得:9+m 2+20=17+m 2+8m ,解得:m =32,③AD 为斜边,由AD 2=ED 2+AE 2得:20=17+m 2+8m +9+m 2,解得:m =-1或-3,∴点E 的坐标为0,32 或0,-72或0,-1 或0,-3 .【点睛】本题主要考查待定系数法求二次函数解析式,二次函数图象与性质,平行四边形的判定与性质以及勾股定理等知识,会运用待定系数法列方程组,两点间距离公式求MN 的长,由平行四边形的性质判定边相等,运用勾股定理列方程.2(2023·河南南阳·统考一模)如图,抛物线与x 轴相交于点A 、B (点A 在点B 的左侧),与y 轴的交于点C 0,-4 ,点P 是第三象限内抛物线上的一个动点,设点P 的横坐标为m ,过点P 作直线PD ⊥x 轴于点D ,作直线AC 交PD 于点E .已知抛物线的顶点P 坐标为-3,-254.(1)求抛物线的解析式;(2)求点A 、B 的坐标和直线AC 的解析式;(3)求当线段CP =CE 时m 的值;(4)连接BC ,过点P 作直线l ∥BC 交y 轴于点F ,试探究:在点P 运动过程中是否存在m ,使得CE =DF ,若存在直接写出m 的值;若不存在,请说明理由.【答案】(1)y =14x 2+32x -4(2)A -8,0 ,B 2,0 ,y =-12x -4(3)-4(4)存在,m =2-25或m =-4【分析】(1)运用待定系数法即可求得抛物线的解析式;(2)令y =0,解方程即可求得点A 、B 的坐标,再运用待定系数法即可求得直线AC 的解析式;(3)过点C 作CF ⊥PE 于点F ,根据等腰三角形的性质可得点F 是PE 的中点,设P m ,14m 2+32m -4 ,则E m ,-12m -4 ,可得F m ,18m 2+12m -4 ,再由点F 与点C 的纵坐标相同建立方程求解即可;(4)过C 作CH ⊥PD 于H ,设P m ,14m 2+32m -4 ,由PF ∥BC ,可得直线PF 解析式为y =2x +14m 2-12m -4,进而可得OF =14m 2-12m -4 ,再证得Rt △CHE ≅Rt △DOF HL ,得出∠HCE =∠FDO ,进而推出∠FDO =∠CAO ,即tan ∠FDO =tan ∠CAO ,据此建立方程求解即可.【详解】(1)解:∵抛物线的顶点坐标为-3,-254∴设抛物线的解析式为y =a x +3 2-254,把点C 0,-4 代入,得:-4=9a -254,解得:a =14,∴y =14x +3 2-254=14x 2+32x -4,∴该抛物线的解析式为y =14x 2+32x -4.(2)解:令y =0,得14x 2+32x -4=0,解得:x 1=-8,x 2=2,∴A -8,0 ,B 2,0 ,,设直线AC 的解析式为y =kx +b ,则-8k +b =0b =-4 ,解得:k =-12b =-4 ,∴直线AC 的解析式为y =-12x -4.(3)解:如图,过点C 作CF ⊥PE 于点F ,∵CP =CE ,∴EF =PF ,即点F 是PE 的中点,设P m ,14m 2+32m -4 ,则E m ,-12m -4 ,∴F m ,18m 2+12m -4 ,∵PE ∥y 轴,CF ⊥PE ,∴CF ∥x 轴,∴18m 2+12m -4=-4,解得:m =-4或m =0(不符合题意,舍去),∴m =-4.(4)解:存在m ,使得CE =DF ,理由如下:如图:过C 作CH ⊥PD 于H ,设P m,14m2+32m-4,由B2,0,C0,-4,由待定系数法可得直线BC解析式为y=2x-4,根据PF∥BC,设直线PF解析式为y=2x+c,将P m,14m2+32m-4代入得:1 4m2+32m-4=2m+c,∴c=14m2-12m-4,∴直线PF解析式为y=2x+14m2-12m-4,令x=0得y=14m2-12m-4,∴F0,14m2-12m-4,∴OF=14m2-12m-4,∵∠CHD=∠PDO=∠COD=90°,∴四边形CODH是矩形,∴CH=OD,∵CE=DF,∴Rt△CHE≅Rt△DOF HL,∴∠HCE=∠FDO,∵∠HCE=∠CAO,∴∠FDO=∠CAO,∴tan∠FDO=tan∠CAO,∴OF OD =OCOA,即14m2-12m-4-m=48=12,∴1 4m2-12m-4=-12m或14m2-12m-4=12m,解得:m=-4或m=4或m=2-25或m=2+25,∵P在第三象限,∴m=2-25或m=-4.【点睛】本题属于二次函数综合题,主要考查了待定系数法求函数解析式、二次函数综合应用、等腰三角形性质、矩形判定及性质、相似三角形判定及性质、解直角三角形等知识点,解题的关键是用含m的代数式表示相关点坐标和相关线段的长度.3(2023·山东聊城·统考三模)抛物线y=-x2+bx+c与x轴交于点A3,0,与y轴交于点C0,3,点P 为抛物线上的动点.(2)若P 为直线AC 上方抛物线上的动点,作PH ∥x 轴交直线AC 于点H ,求PH 的最大值;(3)点N 为抛物线对称轴上的动点,是否存在点N ,使直线AC 垂直平分线段PN ?若存在,请直接写出点N 的纵坐标;若不存在,请说明理由.【答案】(1)b =2,c =3(2)PH 取得最大值为94(3)存在,2-2或2+2【分析】(1)将坐标代入解析式,构建方程求解;(2)设PH 交y 轴于点M ,P m ,-m 2+2m +3 ,则PM =m ;待定系数法确定直线AC 的解析式为y =-x +3,从而确定PH =m -m 2-2m =-m 2+3m =-m -32 2+94,解得PH 最大值为94;(3)如图,设PN 与AC 交于点G ,可设直线PN 的解析式为y =x +p ,设点N (1,n ),求得y =x +(n -1);联立y =-x +3y =x +(n -1) ,解得x =-n 2+2y =n 2+1,所以点P 的横坐标为2×-n 2+2 -1=-n +3,纵坐标为2×n2+1 -n =2,由二次函数解析式构建方程-(-n +3)2+2(-n +3)+3=2,解得n =2±2;【详解】(1)∵抛物线y =-x 2+bx +c 与x 轴交于点A 3,0 ,与y 轴交于点C 0,3 ,∴-9+3b +c =0c =3,解得:b =2c =3 ,∴b =2,c =3;(2)设PH 交y 轴于点M ,P m ,-m 2+2m +3 ,∴PM =m ,∵PH ∥x 轴,∴点H 的纵坐标为-m 2+2m +3,设直线AC 的解析式为y =kx +n ,∴3k +n =0n =3 ,解得:k =-1n =3 ,∴直线AC 的解析式为y =-x +3.∴-m 2+2m +3=-x +3,∴x =m 2-2m ,∴H m 2-2m ,-m 2+2m +3 ,∴PH =m -m 2-2m =-m 2+3m =-m -322+94,∴当m =32时,PH 取得最大值为94(3)存在点N ,使直线AC 垂直平分线段PN ,点N 的纵坐标为2-2或2+2如图,设PN 与AC 交于点G ,∵AC 垂直平分PN ,直线AC 的解析式为y =-x +3∴可设直线PN 的解析式为y =x +p 设点N (1,n ),则n =1+p ∴p =n -1,∴y =x +(n -1)联立y =-x +3y =x +(n -1) ,解得x =-n 2+2y =n 2+1∴点P 的横坐标为2×-n 2+2 -1=-n +3,纵坐标为2×n 2+1 -n =2∴-(-n +3)2+2(-n +3)+3=2,解得n =2±2∴点N 的纵坐标为2-2或2+2.【点睛】本题考查利用二次函数解析式及点坐标求待定参数、待定系数法确定函数解析式、二次函数极值及其它二次函数综合问题,利用直线间的位置关系、点线间的位置关系,融合方程的知识求解坐标是解题的关键.题型02抛物线上的点到某一直线的距离问题1(2023·广东梅州·统考二模)探究求新:已知抛物线G 1:y =14x 2+3x -2,将抛物线G 1平移可得到抛物线G 2:y =14x 2.(1)求抛物线G 1平移得到抛物线G 2的平移路径;(2)设T 0,t ,直线l :y =-t ,是否存在这样的t ,使得抛物线G 2上任意一点到T 的距离等于到直线l 的距离?若存在,求出t 的值;若不存在,试说明理由;(3)设H 0,1 ,Q 1,8 ,M 为抛物线G 2上一动点,试求QM +MH 的最小值.参考公式:若点M x 1,y 1 ,N x 2,y 2 为平面上两点,则有MN =x 1-x 22+y 1-y 2 2.【答案】(1)将G 1向左平移-6个单位,向上平移11个单位(2)存在,1(3)9【分析】(1)设G 1向左平移a 个单位,向上平移b 个单位得到函数G 2,列方程组即可求解;(2)设P x 0,x 204为抛物线G 2上的一点,根据题意列方程即可;(3)点H 坐标与(2)中t =1时的T 点重合,过点M 作MA ⊥l ,垂足为A ,如图所示,则有MH =MA ,当且仅当Q ,M ,A 三点共线时QM +MA 取得最小值.【详解】(1).解:设G 1向左平移a 个单位,向上平移b 个单位得到函数G 2,由平移法则可知14(x +a )2+3(x +a )-2+b =14x 2,整理可得14x 2+3+12a x +14a 2+3a -2+b =14x 2,可得方程组3+12a =014a 2+3a -2+b =0,解得a =-6b =11 ;∴平移路径为将G 1向左平移-6个单位,向上平移11个单位;(2)解:存在这样的t ,且t =1时满足条件,设P x 0,x 204为抛物线G 2上的一点,则点P 到直线l 的距离为x 204+t ,点P 到点T 距离为(x 0-0)2+x 204-t2,联立可得:x 204+t =(x 0-0)2+x 204-t2,两边同时平方合并同类项后可得x 20-x 20t =0解得:t =1;(3)解:点H 坐标与(2)中t =1时的T 点重合,作直线l :y =-1,过点M 作MA ⊥直线l ,垂足为A ,如图所示,则有MH =MA ,此时QM +MH =QM +MA ,当且仅当Q ,M ,A 三点共线时QM +MA 取得最小值即QM +MA =QA =8-(-1)=9∴QM +MH 的最小值为9;【点睛】本题考查二次函数综合题,涉及到线段最小值、平移性质等,灵活运用所学知识是关键.2(2023·湖北宜昌·统考一模)如图,已知:点P 是直线l :y =x -2上的一动点,其横坐标为m (m 是常数),点M 是抛物线C :y =x 2+2mx -2m +2的顶点.(1)求点M 的坐标;(用含m 的式子表示)(2)当点P 在直线l 运动时,抛物线C 始终经过一个定点N ,求点N 的坐标,并判断点N 是否是点M 的最高位置?(3)当点P 在直线l 运动时,点M 也随之运动,此时直线l 与抛物线C 有两个交点A ,B (A ,B 可以重合),A ,B 两点到y 轴的距离之和为d .①求m 的取值范围;②求d 的最小值.【答案】(1)M -m ,-m 2-2m +2(2)N (1,3),点N 是点M 的最高位置(3)①m ≤-52或m ≥32;②d 取得最小值为2【分析】(1)将抛物线解析式写成顶点式即可求解;(2)根据解析式含有m 项的系数为0,得出当x =1时,y =3,即N (1,3),根据二次函数的性质得出-m 2-2m +2=-m +1 2+3的最大值为3,即可得出点N 是点M 的最高位置;(3)①根据直线与抛物线有交点,联立方程,根据一元二次方程根的判别式大于等于0,求得m 的范围,即可求解;②设A ,B 的坐标分别为x 1,y 1 ,x 2,y 2 ,其中x 1<x 2,由①可知x 1,x 2是方程x 2+2mx -x -2m +4=0的两根,根据x 1+x 2=-2m +1,分情况讨论,求得d 是m 的一次函数,进而根据一次函数的性质即可求解.【详解】(1)解:y =x 2+2mx -2m +2=x +m 2-m 2-2m +2,∴顶点M -m ,-m 2-2m +2 ,(2)解:∵y =x 2+2mx -2m +2=x 2+2+2m x -1 ,∴当x =1时,y =3,抛物线C 始终经过一个定点1,3 ,即N (1,3);∵M -m ,-m 2-2m +2 ,-m 2-2m +2=-m +1 2+3,∴M 的纵坐标最大值为3,∴点N 是点M 的最高位置;(3)解:①联立y =x -2y =x 2+2mx -2m +2 ,得x 2+2mx -x -2m +4=0,∵直线l 与抛物线C 有两个交点A ,B (A ,B 可以重合),∴Δ=b 2-4ac =2m -1 2-4-2m +4 ,=4m 2+4m -15≥0,∵4m 2+4m -15=0,解得m 1=-52,m 2=32,∴当4m 2+4m -15≥0时,m ≤-52或m ≥32,②设A ,B 的坐标分别为x 1,y 1 ,x 2,y 2 ,其中x 1<x 2,由①可知x 1,x 2是方程x 2+2mx -x -2m +4=0的两根,∴x1+x 2=-2m +1,当m =-3时,如图所示,y A =0,当-3≤m ≤-52时,y 1≥0,y 2≥0,则d =x 1+x 2 =-2m +1 ,∵-2<0,∴当m =-52时,d 取得最小值为-2×-52 +1=5+1=6,当m ≥32时,d =-x 1+x 2 =--2m +1 =2m -1,∴当m =32时,d 取得最小值为2×32-1=2,综上所述,d 取得最小值为2.【点睛】本题考查了二次函数的性质,一元二次方程与二次函数的关系,熟练掌握二次函数的性质是解题的关键.3(2023·云南楚雄·统考一模)抛物线y =x 2-2x -3交x 轴于A ,B 两点(A 在B 的左边),C 是第一象限抛物线上一点,直线AC 交y 轴于点P .(1)直接写出A ,B 两点的坐标;(2)如图①,当OP =OA 时,在抛物线上存在点D (异于点B ),使B ,D 两点到AC 的距离相等,求出所有满足条件的点D 的横坐标;(3)如图②,直线BP 交抛物线于另一点E ,连接CE 交y 轴于点F ,点C 的横坐标为m ,求FP OP 的值(用含m 的式子表示).【答案】(1)A (-1,0),B (3,0)(2)0或3-41或3+41(3)13m 【分析】(1)令y =0,解方程可得结论;(2)分两种情形:①若点D 在AC 的下方时,过点B 作AC 的平行线与抛物线交点即为D 1.②若点D 在AC 的上方时,点D 1关于点P 的对称点G (0,5),过点G 作AC 的平行线交抛物线于点D 2,D 3,D 2,D 3符合条件.构建方程组分别求解即可;(3)设E 点的横坐标为n ,过点P 的直线的解析式为y =kx +b ,由y =kx +b y =x 2-2x -3 ,可得x 2-(2+k )x -3-b =0,设x 1,x 2是方程x 2-(2+k )x -3-b =0的两根,则x 1x 2=-3-b ,推出x A ⋅x C =x B ⋅x E =-3-b 可得n =-1-b 3,设直线CE 的解析式为y =px +q ,同法可得mn =-3-q 推出q =-mn -3,推出q =-(3+b )-1-b 3 -3=13b 2+2b ,推出OF =13b 2+b ,可得结论.【详解】(1)解:令y =0,得x 2-2x -3=0,解得:x =3或-1,∴A (-1,0),B (3,0);(2)∵OP =OA =1,∴P (0,1),∴直线AC 的解析式为y =x +1.①若点D 在AC 的下方时,过点B 作AC 的平行线与抛物线交点即为D 1.∵B (3,0),BD 1∥AC ,∴直线BD 1的解析式为y =x -3,由y =x -3y =x 2-2x -3,解得x =3y =0 或x =0y =-3 ,∴D 1(0,-3),∴D 1的横坐标为0.②若点D 在AC 的上方时,点D 1关于点P 的对称点G (0,5),过点G 作AC 的平行线l 交抛物线于点D 2,D 3,D 2,D 3符合条件.直线l 的解析式为y =x +5,由y =x +5y =x 2-2x -3 ,可得x 2-3x -8=0,解得:x =3-412或3+412,∴D 2,D 3的横坐标为3-412,3+412,综上所述,满足条件的点D 的横坐标为0,3-412,3+412.(3)设E 点的横坐标为n ,过点P 的直线的解析式为y =kx +b ,由y =kx +b y =x 2-2x -3,可得x 2-(2+k )x -3-b =0,设x 1,x 2是方程x 2-(2+k )x -3-b =0的两根,则x 1x 2=-3-b ,∴x A ⋅x C =x B ⋅x E =-3-b∵x A =-1,∴x C =3+b ,∴m =3+b ,∵x B =3,∴x E =-1-b 3,∴n =-1-b 3,设直线CE 的解析式为y =px +q ,同法可得mn =-3-q∴q =-mn -3,∴q =-(3+b )-1-b 3 -3=13b 2+2b ,∴OF =13b 2+2b ,∴FP OP=13b +1=13(m -3)+1=13m .【点睛】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质,一元二次方程的根与系数的关系等知识,解题的关键是学会构建一次函数,构建方程组确定交点坐标,学会利用参数解决问题,属于中考压轴题.题型03已知点关于直线对称点问题1(2023·辽宁阜新·统考中考真题)如图,在平面直角坐标系中,二次函数y =-x 2+bx -c 的图象与x 轴交于点A (-3,0)和点B (1,0),与y 轴交于点C .(1)求这个二次函数的表达式.(2)如图1,二次函数图象的对称轴与直线AC :y =x +3交于点D ,若点M 是直线AC 上方抛物线上的一个动点,求△MCD 面积的最大值.(3)如图2,点P 是直线AC 上的一个动点,过点P 的直线l 与BC 平行,则在直线l 上是否存在点Q ,使点B 与点P 关于直线CQ 对称?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.【答案】(1)y =-x 2-2x +3;(2)S △MCD 最大=98;(3)Q 1-5,-5 或1+5,5 .【分析】(1)根据抛物线的交点式直接得出结果;(2)作MQ ⊥AC 于Q ,作ME ⊥AB 于F ,交AC 于E ,先求出抛物线的对称轴,进而求得C ,D 坐标及CD 的长,从而得出过M 的直线y =x +m 与抛物线相切时,△MCD 的面积最大,根据x +m =-x 2-2x +3的△=0求得m 的值,进而求得M 的坐标,进一步求得CD 上的高MQ 的值,进一步得出结果;(3)分两种情形:当点P 在线段AC 上时,连接BP ,交CQ 于R ,设P (t ,t +3),根据CP =CB 求得t 的值,可推出四边形BCPQ 是平行四边形,进而求得Q 点坐标;当点P 在AC 的延长线上时,同样方法得出结果.【详解】(1)解:由题意得,y =-(x +3)(x -1)=-x 2-2x +3;(2)解:如图1,作MQ ⊥AC 于Q ,作ME ⊥AB 于F ,交AC 于E ,∵OA =OC =3,∠AOC =90°,∴∠CAO =∠ACO =45°,∴∠MEQ =∠AEF =90°-∠CAO =45°,抛物线的对称轴是直线:x =-3+12=-1,∴y =x +3=-1+3=2,∴D (1,2),∵C (0,3),∴CD =2,故只需△MCD 的边CD 上的高最大时,△MCD 的面积最大,设过点M 与AC 平行的直线的解析式为:y =x +m ,当直线y =x +m 与抛物线相切时,△MCD 的面积最大,由x +m =-x 2-2x +3得,x 2+3x +(m -3)=0,由△=0得,32-4(m -3)=0得,m -3=94,∴x 2+3x +94=0,∴x 1=x 2=-32,∴y =--32 2-2×-32 +3=154,y =x +3=-32+3=32,∴ME =154-32=94,∴MQ =ME ⋅sin ∠MEQ =ME ⋅sin45°=94×22=928,∴S △MCD 最大=12×2×928=98;(3)解:如图2,当点P 在线段AC 上时,连接BP ,交CQ 于R ,∵点B 和点Q 关于CQ 对称,∴CP =CB ,设P (t ,t +3),由CP 2=CB 2得,2t 2=10,∴t 1=-5,t 2=5(舍去),∴P -5,3-5 ,∵PQ ∥BC ,∴CR =BR =1,∴CR =QR ,∴四边形BCPQ 是平行四边形,∵1+(-5)-0=1-5,0+(3-5)-3=-5,∴Q 1-5,-5 ;如图3,当点P 在AC 的延长线上时,由上可知:P 5,3+5 ,同理可得:Q 1+5,5 ,综上所述:Q 1-5,-5 或1+5,5 .【点睛】本题考查了二次函数及其图象的性质,一元二次方程的解法,平行四边形的判定和性质,轴对称的性质等知识,解决问题的关键是分类讨论.2(2023·四川甘孜·统考中考真题)已知抛物线y =x 2+bx +c 与x 轴相交于A -1,0 ,B 两点,与y 轴相交于点C 0,-3 .(1)求b ,c 的值;(2)P 为第一象限抛物线上一点,△PBC 的面积与△ABC 的面积相等,求直线AP 的解析式;(3)在(2)的条件下,设E 是直线BC 上一点,点P 关于AE 的对称点为点P ,试探究,是否存在满足条件的点E ,使得点P 恰好落在直线BC 上,如果存在,求出点P 的坐标;如果不存在,请说明理由.【答案】(1)b =-2,c =-3.(2)y =x +1(3)存在,点P 的坐标为1+21,-2+21 或1-21,-2-21【分析】(1)由待定系数法即可求解;(2)S △PBC =S △ABC 得到AP ∥BC ,即可求解;(3)由题意的:∠AEP =∠AEP ,P E =PE ,即可求解.【详解】(1)由题意,得1-b +c =0,c =-3.∴b =-2,c =-3.(2)由(1)得抛物线的解析式为y =x 2-2x -3.令y =0,则x 2-2x -3=0,得x 1=-1,x 2=3.∴B 点的坐标为3,0 .∵S △PBC =S △ABC ,∴AP ∥BC .∵B 3,0,C 0,-3 ,∵AP∥BC,∴可设直线AP的解析式为y=x+m.∵A(-1,0)在直线AP上,∴0=-1+m.∴m=1.∴直线AP的解析式为y=x+1.(3)设P点坐标为m,n.∵点P在直线y=x+1和抛物线y=x2-2x-3上,∴n=m+1,n=m2-2m-3.∴m+1=m2-2m-3.解得m1=4,m2=-1(舍去).∴点P的坐标为4,5.由翻折,得∠AEP=∠AEP ,P E=PE.∵AP∥BC,∴∠PAE=∠AEP '.∴∠PAE=∠PEA.∴PE=PA=4+12=52.2+5-0设点E的坐标为t,t-3,则PE2=t-42.2+t-3-52=52∴t=6±21.当t=6+21时,点E的坐标为6+21,3+21.设P (s,s-3),由P E=AP,P E=PE=52得:s-6-212,2=522+s-3-3-21解得:s=1+21,则点P 的坐标为1+21,-2+21.当t=6-21时,同理可得,点P 的坐标为1-21,-2-21.综上所述,点P 的坐标为1+21,-2+21.或1-21,-2-21【点睛】本题是二次函数的综合题,主要考查了用待定系数法求一次函数、二次函数的解析式,二次函数的性质,此题题型较好,综合性比较强,用的数学思想是分类讨论和数形结合的思想.3(2023·江苏连云港·连云港市新海实验中学校考二模)如图,“爱心”图案是由抛物线y=-x2+m的一部分及其关于直线y=-x的对称图形组成,点E、F是“爱心”图案与其对称轴的两个交点,点A、B、C、D是该图案与坐标轴的交点,且点D的坐标为6,0.(1)求m 的值及AC 的长;(2)求EF 的长;(3)若点P 是该图案上的一动点,点P 、点Q 关于直线y =-x 对称,连接PQ ,求PQ 的最大值及此时Q 点的坐标.【答案】(1)m =6,AC =6+6(2)52(3)2542,Q -234,-12【分析】(1)用待定系数法求得m 与抛物线的解析式,再求出抛物线与坐标轴的交点坐标,进而求得A 的坐标,根据对称性质求得B ,C 的坐标,即可求得结果;(2)将抛物线的解析式与直线EF 的解析式联立方程组进行求解,得到E ,F 的坐标,即可求得结果;(3)设P (m ,-m 2+6),则Q (m 2-6,-m ),可得PQ =2×m -12 2-252 ,即求m -12 2-252的最值,根据二次函数的最值,即可得到m 的值,即可求得.【详解】(1)把D 6,0 代入y =-x 2+m 得0=-6+m解得m =6∴抛物线的解析式为:y =-x 2+6∴A 0,6根据对称性可得B -6,0 ,C 0,-6∴AC =AO +OC =6+6(2)联立y =-x y =-x 2+6解得x =3y =-3 或x =-2y =2 ∴E -2,2 ,F 3,-3∴EF =-2-3 2+2+3 2=52(3)设P (m ,-m 2+6),则Q (m 2-6,-m )∴PQ =m -m 2-6 2+-m 2+6--m 2整理得PQ =2×m -12 2-254 ∵m -12 2≥0∴当m -12 2=0时,即m =12时,m -12 2-254 有最大值为254∴PQ 的最大值为2542∴12 2-6=-234故Q -234,-12【点睛】本题考查二次函数综合应用,涉及待定系数法求函数解析式,两点间的距离公式,求抛物线与一次函数的交点坐标,二次函数的最值等知识,解题的关键是掌握关于直线y =-x 对称的点坐标的关系.题型04特殊角度存在性问题1(2023·山西忻州·统考模拟预测)如图,抛物线y =18x 2+34x -2与x 轴交于A ,B 两点,与y 轴交于点C .P 是直线AC 下方抛物线上一个动点,过点P 作直线l ∥BC ,交AC 于点D ,过点P 作PE ⊥x 轴,垂足为E ,PE 交AC 于点F .(1)直接写出A ,B ,C 三点的坐标,并求出直线AC 的函数表达式;(2)当线段PF 取最大值时,求△DPF 的面积;(3)试探究在拋物线的对称轴上是否存在点Q ,使得∠CAQ =45°?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.【答案】(1)A -8,0 ,B 2,0 ,C 0,-2 .y =-14x -2(2)85(3)存在,-3,3 或-3,-253【分析】(1)对于直线y =18x 2+34x -2,当x =0时,y =-2,即点C 0,-2 ,令18x 2+34x -2=0,则x =2或-8,则点A ,B 的坐标分别为-8,0 ,2,0 即求出三个点的坐标,设直线AC 的表达式为y =kx +b ,利用待定系数法求解即可;(2)设点P 的横坐标为m ,则P m ,18m 2+34m -2 ,F m ,-14m -2 ,表示出PF =-18m 2-m ,求出PF max =2,再表示出点D 到直线PF 的距离d =85,利用S △DPF =12⋅PF ⋅d 进行求解即可;(3)由抛物线的表达式知,其对称轴为x =-3,当点Q 在x 轴上方时,设抛物线的对称轴交x 轴于点N ,交AC 于H ,故点Q 作QT ⊥AC 于点T ,在△AQH 中,∠CAQ =45°,tan ∠QHA =4,用解直角三角形的方法求出QH =174,即可求出Q 点坐标,当点Q Q 在x 轴上方时,直线AQ 的表达式为y =35x +8 ,当∠CAQ =45°时,AQ ⊥AQ ,即可求解.【详解】(1)解:对于抛物线y =18x 2+34x -2,当x =0时,y =-2,即点C 0,-2 ,令18x 2+34x -2=0,则x =2或-8,则点A ,B 的坐标分别为-8,0 ,2,0 ,即点A ,B ,C 三点的坐标分别为-8,0 ,2,0 ,0,-2 ,设直线AC 的表达式为y =kx +b ,则-8k +b =0b =-2 ,解得k =-14b =-2 ,∴直线AC 的函数表达式为y =-14x -2;(2)设点P 的横坐标为m ,则P m ,18m 2+34m -2 ,F m ,-14m -2 ,PF =-14m -2 -18m 2+34m -2 =-18m 2-m ,当m =--12×-18 =-4时,PF 最大,PF max =-18×(-4)2--4 =2,此时,P -4,-3 ,由B 2,0 ,C 0,-2 ,可得直线BC 的函数表达式为y =x -2,设直线l 的函数表达式为y =x +p ,将P -4,-3 代入可得p =1,∴直线l 的函数表达式为y =x +1,由y =-14x -2y =x +1 ,解得x =-125y =-75,∴D -125,-75 ,点D 到直线PF 的距离d =-125--4 =85,∴S △DPF =12⋅PF ⋅d =12×2×85=85.(3)存在,理由:由抛物线的表达式知,其对称轴为x =-3,当点Q 在x 轴上方时,如下图:设抛物线的对称轴交x 轴于点N ,交AC 于H ,故点Q 作QT ⊥AC 于点T ,则∠ACO =∠QHA ,则tan ∠ACO =tan ∠QHA =4,当x =3时,y =-14x -2=-54,则点H -3,-54 ,由点A ,H 的坐标得,AH =5174,在△AQH 中,∠CAQ =45°,tan ∠QHA =4,设TH =x ,则QT =4x ,则QH =17x ,则AH =AT +TH =5x =5174,则x =174,则QH =17x =174,则174-54=3,则点Q -3,3 ;当点Q Q 在x 轴上方时,直线AQ 的表达式为y =35x +8 ,当∠CAQ =45°时,AQ ⊥AQ ,则直线AQ 的表达式为y =-53x +8 ,当x =-3时,y =-5x +8 =-25,。
2020中考数学考点22二次函数解析版

2201二次函数的定义〖案例分析〗二次函数y=2x2﹣3的二次项系数、一次项系数和常数项分別是()A.2、0、﹣3B.2、﹣3、0C.2、3、0D.2、0、3【分析】根据二次函数的定义:一般地,形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数,叫做二次函数.其中x、y是变量,a、b、c是常量,a是二次项系数,b是一次项系数,c是常数项可得二次项系数是2,一次项系数是0,常数项是﹣〖课后巩固〗【解答】解:二次函数y=2x2﹣3的二次项系数是2,一次项系数是0,常数项是﹣3,故选:A.【点评】此题主要考查了二次函数的定义,关键是注意在找二次项系数,一次项系数和常数项时,不要漏掉符号.〖课堂练习〗若y=(m﹣1)是关于x的二次函数,则m的值为()A.﹣2B.1C.﹣2或1D.2或1【分析】直接利用二次函数的定义分析得出答案.【解答】解:∵y=(m﹣1)x+m是关于x的二次函数,∴m2+m=2,且m﹣1≠0,解得:m=﹣2故选:A.【点评】此题主要考查了二次函数的定义,正确把握二次函数的定义是解题关键.〖课后巩固〗若函数y=(3﹣m)x﹣x+1是二次函数,则m的值为()A.3B.﹣3C.±3D.9【分析】直接利用二次函数的定义分析得出答案.【解答】解:∵函数y=(3﹣m)x﹣x+1是二次函数,∴m2﹣7=2,且3﹣m≠0,解得:m=﹣〖课后巩固〗故选:B.【点评】此题主要考查了二次函数的定义,正确把握二次函数次数与系数的值是解题关键.〖考前再练〗若y=(a+3)x|a|﹣1﹣3x+2是二次函数,则a的值为3.【分析】根据二次函数的定义,令|a|﹣1=2且a+3≠0即可解答.【解答】解:当|a|﹣1=2且a+3≠0时,为二次函数,∴a=﹣3(舍去),a=3故答案为3【点评】本题考查了二次函数的定义,令最高次项为2,最高次项系数不为0即可.2202二次函数与一次函数图像综合信息〖案例分析〗在同一平面直角坐标系中,函数y=2x2+kx与y=kx+k(k≠0)的图象大致是()A.B.C.D.【分析】分两种情况进行讨论:k>0与k<0进行讨论即可.【解答】解:当k>0时,函数y=kx+k的图象经过一、二、三象限;函数y=2x2+kx的开口向上,对称轴在y轴的左侧;当k<0时,函数y=kx+k的图象经过二、三、四象限;函数y=2x2+kx的开口向上,对称轴在y轴的右侧,故C正确.故选:C.【点评】本题考查了二次函数的图象和系数的关系以及一次函数的图象,是基础知识要熟练掌握.〖课堂练习〗二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是()A.B.C.D.【分析】由一次函数y=ax+a可知,一次函数的图象与x轴交于点(﹣1,0),即可排除A、B,然后根据二次函数的开口方向,与y轴的交点;一次函数经过的象限,与y轴的交点可得相关图象进行判断.【解答】解:由一次函数y=ax+a可知,一次函数的图象与x轴交于点(﹣1,0),排除A、B;当a>0时,二次函数y=ax2开口向上,一次函数y=ax+a经过一、二、三象限,当a<0时,二次函数开口向下,一次函数经过二、三、四象限,排除C;故选:D.【点评】本题主要考查一次函数和二次函数的图象,解题的关键是熟练掌握二次函数的图象和一次函数的图象与系数之间的关系.〖课后巩固〗已知a,b是非零实数,|a|>|b|,在同一平面直角坐标系中,二次函数y1=ax2+bx 与一次函数y2=ax+b的大致图象不可能是()A.B.C.D.【分析】根据二次函数y=ax2+bx与一次函数y=ax+b(a≠0)可以求得它们的交点坐标,然后根据一次函数的性质和二次函数的性质,由函数图象可以判断a、b的正负情况,从而可以解答本题.【解答】解:解得或.故二次函数y=ax2+bx与一次函数y=ax+b(a≠0)在同一平面直角坐标系中的交点在x 轴上为(﹣,0)或点(1,a+b).在A中,由一次函数图象可知a>0,b>0,二次函数图象可知,a>0,b>0,﹣<0,a+b>0,故选项A有可能;在B中,由一次函数图象可知a>0,b<0,二次函数图象可知,a>0,b<0,由|a|>|b|,则a+b>0,故选项B有可能;在C中,由一次函数图象可知a<0,b<0,二次函数图象可知,a<0,b<0,a+b<0,故选项C有可能;在D中,由一次函数图象可知a<0,b>0,二次函数图象可知,a<0,b>0,由|a|>|b|,则a+b<0,故选项D不可能;故选:D.【点评】本题考查二次函数的图象、一次函数的图象,解题的关键是明确二次函数与一次函数图象的特点.〖考前再练〗在同一坐标系中,二次函数y=ax2+bx与一次函数y=bx﹣a的图象可能是()A.B.C.D.【分析】直线与抛物线联立解方程组,若有解,则图象由交点,若无解,则图象无交点;根据二次函数的对称轴在y左侧,a,b同号,对称轴在y轴右侧a,b异号,以及当a 大于0时开口向上,当a小于0时开口向下,来分析二次函数;同时在假定二次函数图象正确的前提下,根据一次函数的一次项系数为正,图象从左向右逐渐上升,一次项系数为负,图象从左向右逐渐下降;一次函数的常数项为正,交y轴于正半轴,常数项为负,交y轴于负半轴.如此分析下来,二次函数与一次函数无矛盾者为正确答案.【解答】解:由方程组得ax2=﹣a,∵a≠0∴x2=﹣1,该方程无实数根,故二次函数与一次函数图象无交点,排除B.A:二次函数开口向上,说明a>0,对称轴在y轴右侧,则b<0;但是一次函数b为一次项系数,图象显示从左向右上升,b>0,两者矛盾,故A错;C:二次函数开口向上,说明a>0,对称轴在y轴右侧,则b<0;b为一次函数的一次项系数,图象显示从左向右下降,b<0,两者相符,故C正确;D:二次函数的图象应过原点,此选项不符,故D错.故选:C.【点评】本题考查的是同一坐标系中二次函数与一次函数的图象问题,必须明确二次函数的开口方向与a的正负的关系,a,b的符号与对称轴的位置关系,并结合一次函数图象得相关性质进行分析,本题中等难度偏上.2203二次函数与反比例函数图像综合信息处理〖案例分析〗函数y1=ax2+b,y2=(ab<0)的图象在下列四个示意图中,可能正确的是()A.B.C.D.【解答】解:A、函数y2=(ab<0)可知,ab>0,故本选项错误;B、函数y2=(ab<0)可知,ab>0,故本选项错误;C、由抛物线可知,a>0,b<0,由直线可知,函数y1=ax2+b,y2=(ab<0)的图象可知ab<0,故本选项正确;D、由抛物线可知,a<0,b<0,则ab>0,故本选项错误.故选:C.〖课堂练习〗二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y=在同一坐标系内的图象大致为()A.B.C.D.【解答】解:由抛物线的图象可知,横坐标为1的点,即(1,a+b+c)在第四象限,因此a+b+c<0;∴双曲线的图象在第二、四象限;由于抛物线开口向上,所以a>0;对称轴x=>0,所以b<0;抛物线与x轴有两个交点,故b2﹣4ac>0;∴直线y=bx+b2﹣4ac经过第一、二、四象限.故选:D.〖课后巩固〗抛物线y=ax2+bx+c图象如图所示,则一次函数y=﹣bx﹣4ac+b2与反比例函数y=在同一坐标系内的图象大致为()A.B.C.D.【解答】解:如图所示,抛物线y=ax2+bx+c的开口方向向下,则a<0.对此轴在y轴的右侧,则a、b异号,即b>0,所以﹣b<0.抛物线与x轴有2个不同的交点,则b2﹣4ac>0,所以一次函数y=﹣bx﹣4ac+b2经过第一、二、四象限.又当x=﹣1时,y<0,即a﹣b+c<0,所以反比例函数y=经过第二、四象限.综上所述,一次函数y=﹣bx﹣4ac+b2经过第一、二、四象限.反比例函数y=经过第二、四象限.故选:C.〖考前再练〗已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y =mx+n与反比例函数y=的图象可能是()A.B.C.D.【解答】解:由图可知,m<﹣1,n=1,所以,m+n<0,所以,一次函数y=mx+n经过第二四象限,且与y轴相交于点(0,1),反比例函数y=的图象位于第二四象限,纵观各选项,只有C选项图形符合.故选C.2204二次函数过原点的特点〖案例分析〗若二次函数y=x2+3x+a﹣1的图象经过原点,则a的值为()A.0B.1C.﹣1D.1或﹣1【分析】根据二次函数图象上点的坐标特征,把原点坐标代入解析式求出a=1【解答】解:把(0,0)代入y=x2+3x+a﹣1得a﹣1=0,解得a=1,所以a的值为1故选:B.【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.〖课堂练习〗已知二次函数y=ax2+x+a(a﹣2)的图象经过原点,则a的值为()A.0或2B.0C.2D.无法确定【分析】根据二次函数y=ax2+x+a(a﹣2)的图象经过原点,可以求得a的值,本题得以解决.【解答】解:∵二次函数y=ax2+x+a(a﹣2)的图象经过原点,∴0=a×02+0+a(a﹣2)且a≠0,解得,a=2,故选:C.【点评】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.〖课后巩固〗抛物线y=ax2+(a﹣1)(a≠0)经过原点,那么该抛物线在对称轴左侧的部分是下降的.(填“上升”或“下降”)【分析】根据抛物线y=ax2+(a﹣1)(a≠0)经过原点,从而可以求得a的值,进而得到该抛物线在对称轴左侧的部分是上升还是下降,本题得以解决.【解答】解:∵抛物线y=ax2+(a﹣1)(a≠0)经过原点,∴0=a×02+(a﹣1),得a=1,∴y=x2,∴该函数的顶点坐标为(0,0),函数图象的开口向上,∴该抛物线在对称轴左侧的部分是下降的,故答案为:下降.【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.〖考前再练〗如果开口向下的抛物线y=ax2+5x+4﹣a2(a≠0)过原点,那么a的值是﹣2.【分析】由抛物线开口向下及过原点,即可得出关于a的一元一次不等式及一元二次方程,解之即可得出a的值.【解答】解:∵抛物线y=ax2+5x+4﹣a2(a≠0)过原点,且开口向下,∴,解得:a=﹣2故答案为:﹣2【点评】本题考查了二次函数的性质以及二次函数图象上点的坐标特征,利用二次函数的性质及二次函数图象上点的坐标特征,找出关于a的一元一次不等式及一元二次方程是解题的关键.2205二次函数开口方向的确定〖案例分析〗抛物线y=﹣(x﹣2)2+3,下列说法正确的是()A.开口向下,顶点坐标(2,3)B.开口向上,顶点坐标(2,﹣3)C.开口向下,顶点坐标(﹣2,3)D.开口向上,顶点坐标(2,﹣3)【分析】根据二次函数的性质对各小题分析判断即可得解.【解答】解:∵抛物线y=﹣(x﹣2)2+3中a=﹣1<0,∴抛物线的开口向下,顶点为(2,3)故选:A.【点评】本题考查了二次函数的性质,主要利用了抛物线的开口方向、对称轴、顶点坐标.〖课堂练习〗对于二次函数y=2(x+1)(x﹣3),下列说法正确的是()A.图象开口向下B.当x>1时,y随x的增大而减小C.图象的对称轴是直线x=﹣1D.当x<1时,y随x的增大而减小【分析】先把二次函数化为顶点式的形式,再根据二次函数的性质进行解答.【解答】解:二次函数y=2(x+1)(x﹣3)可化为y=2(x﹣1)2﹣8的形式,∵此二次函数中a=2>0,∴抛物线开口向上,对称轴为x=1,∴当x>1时,y随x的增大而增大,当x<1时,y随x的增大而减小,故选:D.【点评】本题考查的是二次函数的性质,根据题意把二次函数化为顶点式的形式是解答此题的关键.〖课后巩固〗若+2x﹣3是二次函数,且开口向下,则m的值为﹣3.【分析】根据二次函数定义可得m2﹣7=2,计算出m=±3,再根据二次函数的性质可得1+m<0,再根据m的取值范围确定m的值.【解答】解:由题意得:m2﹣7=2,解得:m=±3,∵开口向下,∴1+m<0,∴m<﹣1,∴m=﹣3,故答案为:﹣3【点评】此题主要考查了二次函数定义,关键是掌握形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数,叫做二次函数.〖考前再练〗若函数y=(m﹣1)x是二次函数,且开口向下,则m=﹣2.【分析】根据二次函数的定义得到m2﹣2=2,且m﹣1<0.【解答】解:∵函数y=(m﹣1)x是二次函数,其函数的开口向下,∴m2﹣2=2,且m﹣1<0.解得m=﹣2故答案是:﹣2【点评】本题考查了二次函数的定义.注意:此题中的抛物线开口方向向下,所以m﹣1是负数.2206二次函数的最值〖案例分析〗抛物线y=﹣(x+1)2+3有()A.当x=1,y有最大值3B.当x=1,y有最小值3C.当x=﹣1,y有最大值3D.当x=﹣1,y有最小值3【分析】根据题目中的函数解析式和二次函数的性质,可以得到当x取何值时,函数取得最大值,本题得以解决.【解答】解:∵抛物线y=﹣(x+1)2+3,∴当x=﹣1时,该抛物线有最大值,此时y=3,故选:C.【点评】本题考查二次函数的性质、二次函数的最值,解答本题的关键是明确题意,利用二次函数的性质解答.〖课堂练习〗对于函数y=(x+2)2﹣9,下列结论错误的是()A.图象顶点是(﹣2,﹣9)B.图象开口向上C.图象关于直线x=﹣2对称D.函数最大值为﹣9【分析】根据函数解析式和二次函数的性质可以判断各个选项中的说法是否正确,本题得以解决.【解答】解:∵函数y=(x+2)2﹣9=x2+4x﹣5,∴该函数图象的顶点坐标是(﹣2,﹣9),故选项A正确;a=1>0,该函数图象开口向上,故选项B正确;该函数图象关于直线x=﹣2对称,故选项C正确;当x=﹣2时,该函数取得最小值y=﹣9,故选项D错误;故选:D.【点评】本题考查二次函数的性质、二次函数的最值,解答本题的关键是明确题意,利用二次函数的性质解答.〖课后巩固〗对于抛物线y=﹣(x+2)2﹣1,下列说法错误的是()A.开口向下B.对称轴是直线x=﹣2C.x>﹣2时,y随x的增大而增大D.x=﹣2,函数有最大值y=﹣1【分析】根据二次函数的性质可以判断各个选项中的结论是否正确,从而可以解答本题.【解答】解:∵y=﹣(x+2)2﹣1,∴该抛物线的开口向下,顶点坐标是(﹣2,﹣1),对称轴为直线x=﹣2,当x=﹣2时,函数有最大值y=﹣1,当x>﹣2时,y随x的增大而减小,故选项C的说法错误,故选:C.【点评】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.〖考前再练〗对于二次函数y=﹣(x﹣1)2+2的图象与性质,下列说法正确的是()A.对称轴是直线x=1,最大值是2B.对称轴是直线x=1,最小值是2C.对称轴是直线x=﹣1,最大值是2D.对称轴是直线x=﹣1,最小值是2【分析】根据抛物线的图象与性质即可判断.【解答】解:由抛物线的解析式:y=﹣(x﹣1)2+2,可知:对称轴x=1,开口方向向下,所以有最大值y=2,故选:A.【点评】本题考查二次函数的性质,解题的关键是正确理解抛物线的图象与性质,本题属于基础题型.2207二次函数顶点坐标〖案例分析〗抛物线y=x2﹣6x+11的顶点为()A.(﹣3,2)B.(3,2)C.(6,﹣2)D.(3,12)【分析】将题目中的函数解析式化为顶点式,即可得到抛物线的顶点坐标,本题得以解决.【解答】解:∵抛物线y=x2﹣6x+11=(x﹣3)2+2,∴该抛物线的顶点坐标为(3,2),故选:B.【点评】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.〖课堂练习〗抛物线y=﹣(x﹣)2﹣2的顶点坐标是()A.(,2)B.(﹣,2)C.(﹣,﹣2)D.(,﹣2)【分析】直接利用顶点式的特点可求顶点坐标.【解答】解:因为y=﹣(x﹣)2﹣2是抛物线的顶点式,根据顶点式的坐标特点可知,顶点坐标为(,﹣2).故选:D.【点评】本题主要考查了二次函数的性质,用到的知识点:二次函数y=a=(x﹣h)2+k 的顶点坐标是(h,k).〖课后巩固〗抛物线y=1﹣3x2的顶点是()A.(1,﹣3)B.(﹣3,1)C.(1,0)D.(0,1)【分析】根据题目中的抛物线解析式可以直接写出该抛物线的顶点坐标,本题得以解决.【解答】解:∵抛物线y=1﹣3x2=﹣3x2+1,∴该抛物线的顶点坐标为(0,1),故选:D.【点评】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.〖考前再练〗抛物线y=﹣(x﹣3)2+1的顶点坐标为()A.(3,1)B.(﹣3,1)C.(1,3)D.(1,﹣3)【分析】根据二次函数顶点式解析式写出顶点坐标即可.【解答】解:抛物线y=﹣(x﹣3)2+1的顶点坐标为(3,1).故选:A.【点评】本题考查了二次函数的性质,熟练掌握利用二次函数顶点式解析式求顶点的方法是解题的关键.2208函数值〖案例分析〗二次函数y=﹣x2+2x﹣4,当﹣1<x<2时,y的取值范围是()A.﹣7<y<﹣4B.﹣7<y≤﹣3C.﹣7≤y<﹣3D.﹣4<y≤﹣3【分析】先求出二次函数的对称轴,再根据二次函数的增减性求出最小值和最大值即可.【解答】解:∵y=﹣x2+2x﹣4,=﹣(x2﹣2x+4)=﹣(x﹣1)2﹣3,∴二次函数的对称轴为直线x=1,∴﹣1<x<2时,x=1取得最大值为﹣3,x=﹣1时取得最小值为﹣(﹣1)2+2×(﹣1)﹣4=﹣7,∴y的取值范围是﹣7<y≤﹣3故选:B.【点评】本题考查了二次函数与不等式,主要利用了二次函数的增减性和对称性,确定出对称轴从而判断出取得最大值和最小值的情况是解题的关键.〖课堂练习〗已知点P(x,y)在抛物线y=(x﹣1)2+2的图象上,若﹣1<x<2,则y的取值范围是2≤y<6.【分析】根据题目中的函数解析式和二次函数的性质,可以求得﹣1<x<2时,y的取值范围.【解答】解:∵抛物线y=(x﹣1)2+2,∴该函数开口向上,当x>1时,y随x的增大而增大,当x<1时,y随x的增大而减小,∵点P(x,y)在抛物线y=(x﹣1)2+2的图象上,﹣1<x<2,1﹣(﹣1)=2,2﹣1=1,∴当x=1时,y取得最小值,此时y=2,当x=﹣1时,y取得最大值,此时y=(﹣1﹣1)2+2=6,∴﹣1<x<2,则y的取值范围是2≤y<6,故答案为:2≤y<6.【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.〖课后巩固〗已知y=﹣x2﹣3x+4(﹣10≤x≤0),则函数y的取值范围是4≤y≤13.【分析】根据题目中的函数解析式、二次函数的性质和x的取值范围,可以求得函数值的取值范围.【解答】解:∵y=﹣x2﹣3x+4=﹣(x+6)2+13,∴该函数的开口向下,对称轴是直线x=﹣6,当x<﹣6时,y随x的增大而增大,当x >﹣6时,y随x的增大而减小,∵﹣10≤x≤0,当x=0时,y=4,∴函数y的取值范围是4≤y≤13,故答案为:4≤y≤1〖课后巩固〗【点评】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.〖考前再练〗抛物线y=2x2﹣4x﹣3,当﹣1≤x≤4时,y的取值范围是﹣5≤y≤13.【分析】首先利用配方法求出二次函数的最值,进而利用x的取值范围得出y的取值范围.【解答】解:∵y=2x2﹣4x﹣3=2(x2﹣2x)﹣3,=2(x2﹣2x+1﹣1)﹣3,=2(x﹣1)2﹣5,=﹣5,∴当x=1时,y最小值∵﹣1≤x≤4,且|4﹣1>|﹣1﹣1|,∴x=4时,y=13,最大∴当﹣1≤x≤4时,y的取值范围是:﹣5≤y≤13故答案为﹣5≤y≤13【点评】此题主要考查了二次函数的性质以及配方法的应用,根据已知得出顶点坐标是解题关键.2209对称轴〖案例分析〗二次函数y=a(x+1)(x﹣4)的对称轴是x=.【分析】首先求得方程与x轴的两个交点坐标,然后根据交点坐标求得对称轴方程即可.【解答】解:令y=a(x+1)(x﹣4)=0,解得:x=﹣1或x=4,∴y=a(x+1)(x﹣4)与x轴交与点(﹣1,0),(4,0)∴对称轴为:x==.故答案为:x=.【点评】此题考查了二次函数点的对称性.解题的关键是注意审题,理解题意,根据函数的对称性解题.〖课堂练习〗二次函数y=x2﹣4x+3的对称轴为直线x=2,顶点坐标为(2,﹣1).【分析】将函数解析式配方成顶点式后即可得出答案.【解答】解:y=x2﹣4x+3=x2﹣4x+4﹣4+3=(x﹣2)2﹣1,∴顶点坐标是(2,﹣1),对称轴是直线x=2故答案为直线x=2,(2,﹣1).【点评】本题考查了二次函数的性质,把解析式化成顶点式是解题的关键.〖课后巩固〗抛物线y=﹣2x2﹣4x+8的开口向下,对称轴直线x=﹣1,顶点坐标是(﹣1,10).【分析】根据抛物线y=﹣2x2﹣4x+8,可将函数解析式化为顶点式,即可解答本题.【解答】解:∵抛物线y=﹣2x2﹣4x+8=﹣2(x+1)2+10,∴该抛物线的开口向下,对称轴是直线x=﹣1,顶点坐标是(﹣1,10),故答案为:向下,直线x=﹣1,(﹣1,10).【点评】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.〖考前再练〗抛物线y=﹣x2的开口向下,对称轴是直线x=0,顶点坐标(0,0).【分析】根据二次函数的性质和函数的解析式得出答案即可.【解答】解:抛物线y=﹣x2中a=﹣<0,∴抛物线的开口向下,对称轴是直线x=0,顶点坐标是(0,0),故答案为:下,直线x=0,(0,0).【点评】本题考查了二次函数的性质,能熟记二次函数的性质的内容是解此题的关键.2210二次函数的增减性〖案例分析〗如图,已知二次函数y=﹣x2+2x,当x<a时,y随x的增大而增大,则实数a 的取值范围是a≤1.【分析】由函数图象可得函数的增减性,即可得答案.【解答】解:∵由函数图象可知,当x<1时,y随x的增大而增大,∴a≤1,故答案为:a≤1【点评】本题主要考查二次函数的图象与系数的关系,熟练掌握二次函数的性质是解题的关键.〖课堂练习〗已知二次函数y=4x2﹣mx+5,当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,则当x=1时,y的值为25.【分析】因为当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,那么可知对称轴就是x=﹣2,结合顶点公式法可求出m的值,从而得出函数的解析式,再把x=1,可求出y的值.【解答】解:∵当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,∴对称轴x=﹣=﹣=﹣2,解得m=﹣16,∴y=4x2+16x+5,那么当x=1时,函数y的值为25.故答案为25.【点评】本题考查了函数的性质,利用二次函数的增减性得出对称轴,从对称轴入手进行求解是关键.〖课后巩固〗抛物线y=x2﹣2x,当y随x的增大而减小时x的取值范围为x<1.【分析】根据题目中的函数解析式和二次函数的性质,可以写出x的取值范围.【解答】解:∵抛物线y=x2﹣2x=(x﹣1)2﹣1,∴当y随x的增大而减小时x的取值范围为x<1,故答案为:x<1【点评】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.〖考前再练〗已知抛物线y=a(x+)2+k(a>0),点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)是图象上的三个点,则y1、y2、y3的大小关系是y2<y3<y1(用“<”连接).【分析】根据题目中的抛物线的解析式可以得到该抛物线的对称轴、开口方向,从而可以判断出y1、y2、y3的大小关系,本题得以解决.【解答】解:∵抛物线y=a(x+)2+k(a>0),苏一该函数开口向上,对称轴是直线x=﹣,当x>﹣时,y随x的增大而增大,当x<﹣时,y随x的增大而减小,∵|﹣4﹣(﹣)|=3.5,|﹣2﹣(﹣)|=1.5,|2﹣(﹣)|=2.5,点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)是图象上的三个点,∴y2<y3<y1,故答案为:y2<y3<y1【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.2211二次函数对称性的运用〖案例分析〗抛物线y=ax2+bx+c(a≠0)过(﹣1,2)和(7,2)两点,其对称轴是直线x=3.【分析】由点(﹣1,2)和(7,2)的纵坐标相等可得出点(﹣1,2)和(7,2)关于抛物线的对称轴对称,再由点(﹣1,2)和(7,2)的横坐标即可求出抛物线的对称轴,此题得解.【解答】解:∵点(﹣1,2)和(7,2)的纵坐标相等,∴点(﹣1,2)和(7,2)关于抛物线对称轴对称,∴抛物线的对称轴为直线x==3故答案为:x=3【点评】本题考查了二次函数的性质,牢记二次函数的性质是解题的关键.〖课堂练习〗某二次函数的图象过点(﹣3,m)和(7,m),则此二次函数的图象的对称轴为直线x=2.【分析】根据二次函数的图象过点(﹣3,m)和(7,m),可以求得该函数的对称轴,本题得以解决.【解答】解:∵二次函数的图象过点(﹣3,m)和(7,m),∴此二次函数的图象的对称轴为直线x==2,故答案为:直线x=2【点评】本题考查二次函数的性质、二次函数的图象、二次函数图象上的点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.〖课后巩固〗抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(m,n),且对称轴为直线l,则点C关于直线l的对称点C′的坐标为(2﹣m,n)(用含m,n的代数式表示)【分析】首先根据A和B点的坐标确定对称轴,然后确定点C到直线l的距离,从而确定点C关于直线l的对称的点的坐标即可.【解答】解:∵抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),∴对称轴l为:x==1,∴点C(m,n)到x=1的距离为m﹣1,∴点C关于直线l的对称点C′的坐标为(2﹣m,n),故答案为:(2﹣m,n).【点评】本题考查了二次函数的性质,解题的关键是能够确定二次函数的对称轴,难度不大.〖考前再练〗如图,已知二次函数y=ax2+bx+c的图象经过点A(3,0),对称轴为直线x =1,则点B的坐标是(﹣1,0).【分析】利用点B与点A关于直线x=1对称确定B点坐标.【解答】解:∵二次函数y=ax2+bx+c的图象与x轴交于A,B两点,∴点A与点B关于直线x=﹣1对称,而对称轴是直线x=1,点A的坐标为(3,0),∴点B的坐标是(﹣1,0).故答案为(﹣1,0).【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.2212双根式的运用〖案例分析〗二次函数y=a(x+1)(x﹣4)的对称轴是x=.【分析】首先求得方程与x轴的两个交点坐标,然后根据交点坐标求得对称轴方程即可.【解答】解:令y=a(x+1)(x﹣4)=0,解得:x=﹣1或x=4,∴y=a(x+1)(x﹣4)与x轴交与点(﹣1,0),(4,0)∴对称轴为:x==.故答案为:x=.【点评】此题考查了二次函数点的对称性.解题的关键是注意审题,理解题意,根据函数的对称性解题.〖课堂练习〗抛物线与x轴交于点(1,0),(﹣3,0),则该抛物线可设为:y=a(x﹣1)(x+3)(a≠0).【分析】已知抛物线与x轴的两个交点,可以设该解析式为交点式.【解答】解:∵抛物线与x轴交于点(1,0),(﹣3,0),∴设该抛物线解析式为:y=a(x﹣1)(x+3)(a≠0).故答案是:y=a(x﹣1)(x+3)(a≠0).【点评】本题考查了抛物线的三种形式.交点式:y=a(x﹣x1)(x﹣x2)(a是常数,a ≠0),该形式的优势是能直接根据解析式得到抛物线与x轴的两个交点坐标(x1,0),(x2,0).〖课后巩固〗已知抛物线y=ax2﹣3ax﹣4a(a≠0).(1)直接写出该抛物线的对称轴.(2)试说明无论a为何值,该抛物线一定经过两个定点,并求出这两个定点的坐标.【分析】(1)直接利用抛物线对称轴方程求得对称轴即可;(2)化简抛物线解析式,即可求得两个定点的横坐标,即可解题;【解答】解:(1)抛物线的对称轴方程为x=﹣=;(2)y=ax2﹣3ax﹣4a=a(x+1)(x﹣4),当(x+1)(x﹣4)=0,即x=﹣1或4时y=0,∴抛物线一定经过(﹣1,0),(4,0);【点评】考查了二次函数的性质,解题的关键时了解抛物线的对称轴方程,难度不大.〖考前再练〗已知二次函数y=a(x+a)(x+a﹣1).(1)当a=2时,求该二次函数图象的对称轴.(2)当a<0时,判断该二次函数图象的顶点所在的象限,并说明理由.(3)当0<x<3时,y随着x增大而增大,求a的取值范围.【分析】(1)当a=2时,y=2(x+2)(x+1),根据与x轴的交点坐标可知其对称轴为直线x=.;(2)求出二次函数与x轴的交点坐标为(﹣a,0),(1﹣a,0),画出二次函数的大致图象即可判断顶点的位置.(3)分析可知当a=0时,明显不符合题意;然后讨论a>0和a<0两种情况,根据二次函数的性质可求解.【解答】解:(1)当a=2时,y=2(x+2)(x+1),∴二次函数的对称轴为x=.(2)由题知二次函数与x轴的交点坐标为(﹣a,0),(1﹣a,0);∵a<0,∴二次函数的开口方向向下;又﹣a>0,1﹣a>0,所以对称轴所在直线为x==>0,当x=时,y=﹣>0,所以顶点坐标(,﹣)在第一象限.(3)当a=0时,明显不符合题意;∴a≠0;由(2)知,二次函数的对称轴为直线x=,∵当0<x<3时,y随着x增大而增大,∴当a>0时,≤0,解得a≥;当a<0,≥3,解得a≤﹣.∴a的取值范围为a≥或a≤﹣.【点评】本题主要考查二次函数性质、与x轴的交点的坐标,解题关键是要熟练掌握二次函数的图象和性质,能快速画出简图分析问题,同时也要多方面考虑问题,避免漏解.2213二次函数图像与系数的信息处理〖案例分析〗如图,函数y=ax2+bx+c的图象过点(﹣1,0)和(m,0),请思考下列判断,正确的个数是()①abc<0;②4a+c<b;③=1﹣;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=A.2个B.3个C.4个D.5个【分析】①利用图象信息即可判断;②根据x=﹣1时,y=0得到b=a+c,由a<0得到2a+c<a+c,即2a+c<b,即可判断;③根据m是方程ax2+bx+c=0的根,结合两根之积﹣m=,即可判断;④根据两根之和﹣1+m=﹣,可得ma=a﹣b,可得am2+(2a+b)m+a+b+c=am2+bm+c+2am+a+b=2a﹣2b+a+b=3a﹣b<0,⑤根据抛物线与x 轴的两个交点之间的距离,列出关系式即可判断;【解答】解:∵抛物线开口向下,∴a<0,∵抛物线交y轴于正半轴,。
初中数学一轮复习《二次函数专题--动点最值问题》

2 0 19
引例: 某种中性笔的进价为1元,在某时段若 以每支x元出售,可卖(5-x)支,应如何 定价才能使利润最大? 解:设利润为y元.
知识点1:二次函数的解析式. 1.二次函数的图象交x轴于A、B点,交y轴于点D, 点B的坐标(5,0),顶点C的坐标为(3 , 4) 求二次函数的解析式________________
(1)若每件衬衫降低 x 元(x 取整数),商场平均 每天盈利 y 元, 试写出 y 与 x 之间的函数关系式,并写 出自变量 x 的取值范围.
y =((20+2x)(0≤x≤12).
2.练习,巩固所学二次函数内容
(2)每件衬衫降低多少元时,商场每天(平均) 盈利最多?
y =-2(x - 15)2 +1 250(0≤x≤12). 当 x = 12 时,盈利最多,为 1 232 元.
知识点3:二次函数综合应用
知识点4:二次函数综合应用
知识点4:二次函数综合应用
3.小结
(1)我们是如何研究二次函数的动点最值问题? (2)二次函数在动点最值问题应用中需要注意什么?
4.布置作业
学有余力:巩固所学二次函数内容
问题 某商场销售一批名牌衬衫,平均每天可售出 20 件,
进价是每件 80 元,售价是每件 120 元,为了扩大销售, 增加盈利, 减少库存, 商场决定采取适当的降价措施, 经调查发现,如果每件衬衫降低 1 元, 商场平均每天可 多售出 2 件,但每件最低价不得低于 108 元.
中考数学专题之二次函数与图形面积的最值及定值压轴问题

2020年中考数学必考经典专题2二次函数与图形面积的最值及定值压轴问题【方法指导】面积是平面几何中一个重要的概念,关联着平面图形中的重要元素边与角,由动点而生成的面积问题,是抛物线与直线形结合的觉形式,常见的面积问题有规则的图形的面积(如直角三角形、平行四边形、菱形、矩形的面积计算问题)以及不规则的图形的面积计算,解决不规则的图形的面积问题是中考压轴题常考的题型,此类问题计算量较大。
有时也要根据题目的动点问题产生解的不确定性或多样性。
解决动点产生的面积问题,常用到的知识和方法有:(1)如果三角形的某一条边与坐标轴平行,计算这样“规则”的三角形的面积,直接用面积公式.(2)三角形的三条边没有与坐标轴平行的,计算这样“不规则”的三角形的面积,用“割”或“补”的方法.(3)同底等高三角形的面积相等.平行线间的距离处处相等.(4)同底三角形的面积比等于高的比.(5)同高三角形的面积比等于底的比.【题型剖析】【类型1】二次函数与面积最值问题【例1】如图,抛物线2(1)y x k =-+与x 轴相交于A ,B 两点(点A 在点B 的左侧),与y 轴相交于点(0,3)C -.P 为抛物线上一点,横坐标为m ,且0m >.(1)求此抛物线的解析式;(2)当点P 位于x 轴下方时,求ABP ∆面积的最大值;(3)设此抛物线在点C 与点P 之间部分(含点C 和点)P 最高点与最低点的纵坐标之差为h .①求h 关于m 的函数解析式,并写出自变量m 的取值范围;②当9h =时,直接写出BCP ∆的面积.【变式训练】如图,抛物线22(0)y ax ax c a =-+≠与y 轴交于点(0,4)C ,与x 轴交于点A 、B ,点A 坐标为(4,0).(1)求该抛物线的解析式;(2)抛物线的顶点为N ,在x 轴上找一点K ,使CK KN +最小,并求出点K 的坐标;(3)点Q 是线段AB 上的动点,过点Q 作//QE AC ,交BC 于点E ,连接CQ .当CQE ∆的面积最大时,求点Q 的坐标;【类型2】二次函数与面积定值问题【例2】抛物线229y x bx c =-++与x 轴交于(1,0)A -,(5,0)B 两点,顶点为C ,对称轴交x 轴于点D ,点P 为抛物线对称轴CD 上的一动点(点P 不与C ,D 重合).过点C 作直线PB 的垂线交PB 于点E ,交x 轴于点F .(1)求抛物线的解析式;(2)当PCF ∆的面积为5时,求点P 的坐标;(3)当PCF ∆为等腰三角形时,请直接写出点P 的坐标.【变式训练】已知抛物线23y ax bx =++经过点(1,0)A 和点(3,0)B -,与y 轴交于点C ,点P 为第二象限内抛物线上的动点.(1)抛物线的解析式为____,抛物线的顶点坐标为____;(2)如图1,连接OP 交BC 于点D ,当:1:2CPD BPD S S ∆∆=时,请求出点D 的坐标;(3)如图2,点E 的坐标为(0,1)-,点G 为x 轴负半轴上的一点,15OGE ∠=︒,连接PE ,若2PEG OGE ∠=∠,请求出点P 的坐标;(4)如图3,是否存在点P ,使四边形BOCP 的面积为8?若存在,请求出点P 的坐标;若不存在,请说明理由.【类型3】二次函数与等面积问题【例3】如图,二次函数23y x bx =-++的图象与x 轴交于点A 、B ,与y 轴交于点C ,点A 的坐标为(1,0)-,点D 为OC 的中点,点P 在抛物线上.(1)b =______;(2)若点P 在第一象限,过点P 作PH x ⊥轴,垂足为H ,PH 与BC 、BD 分别交于点M 、N .是否存在这样的点P ,使得PM MN NH ==?若存在,求出点P 的坐标;若不存在,请说明理由;(3)若点P 的横坐标小于3,过点P 作PQ BD ⊥,垂足为Q ,直线PQ 与x 轴交于点R ,且2PQB QRB S S ∆∆=,求点P 的坐标.【变式训练】如图,抛物线2y ax bx c =++的图象过点(1,0)A -、(3,0)B 、(0,3)C .(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在一点P ,使得PAC ∆的周长最小,若存在,请求出点P 的坐标及PAC ∆的周长;若不存在,请说明理由;(3)在(2)的条件下,在x 轴上方的抛物线上是否存在点M (不与C 点重合),使得PAM PAC S S ∆∆=?若存在,请求出点M 的坐标;若不存在,请说明理由.【类型4】二次函数与面积数量关系【例4】如图,已知二次函数的图象与x 轴交于A 、B 两点,D 为顶点,其中点B 的坐标为(5,0),点D 的坐标为(1,3).(1)求该二次函数的表达式;(2)点E 是线段BD 上的一点,过点E 作x 轴的垂线,垂足为F ,且ED EF =,求点E 的坐标.(3)试问在该二次函数图象上是否存在点G ,使得ADG ∆的面积是BDG ∆的面积的35?若存在,求出点G 的坐标;若不存在,请说明理由.【变式训练】如图抛物线2y ax bx c =++经过点(1,0)A -,点(0,3)C ,且OB OC =.(1)求抛物线的解析式及其对称轴;(2)点D 、E 在直线1x =上的两个动点,且1DE =,点D 在点E 的上方,求四边形ACDE 的周长的最小值.(3)点P 为抛物线上一点,连接CP ,直线CP 把四边形CBPA 的面积分为3:5两部分,求点P 的坐标.【达标检测】1.如图,已知抛物线23y ax bx =+-与x 轴交于点(3,0)A -和点(1,0)B ,交y 轴于点C ,过点C 作//CD x 轴,交抛物线于点D .(1)求抛物线的解析式;(2)若直线(30)y m m =-<<与线段AD 、BD 分别交于G 、H 两点,过G 点作EG x ⊥轴于点E ,过点H 作HF x ⊥轴于点F ,求矩形GEFH 的最大面积;(3)若直线1y kx =+将四边形ABCD 分成左、右两个部分,面积分别为1S ,2S ,且12:4:5S S =,求k 的值.2.如图,抛物线2(0)y ax bx a =+<过点(10,0)E ,矩形ABCD 的边AB 在线段OE 上(点A 在点B 的左边),点C ,D 在抛物线上.设(,0)A t ,当2t =时,4AD =.(1)求抛物线的函数表达式.(2)当t 为何值时,矩形ABCD 的周长有最大值?最大值是多少?(3)保持2t =时的矩形ABCD 不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G ,H ,且直线GH 平分矩形的面积时,求抛物线平移的距离.3.已知:如图,抛物线223y x x =--与x 轴交于A 、B 两点,与y 轴交于点C ,该抛物线的顶点为M .(1)求点A 、B 、C 的坐标.(2)求直线BM 的函数解析式.(3)试说明:90CBM CMB ∠+∠=︒.(4)在抛物线上是否存在点P ,使直线CP 把BCM ∆分成面积相等的两部分?若存在,请求出点P 的坐标;若不存在,请说明理由.4.如图1,抛物线21:C y x ax =+与22:C y x bx =-+相交于点O 、C ,1C 与2C 分别交x 轴于点B 、A ,且B 为线段AO 的中点.(1)求a b的值;(2)若OC AC ⊥,求OAC ∆的面积;(3)抛物线2C 的对称轴为l ,顶点为M ,在(2)的条件下:①点P 为抛物线2C 对称轴l 上一动点,当PAC ∆的周长最小时,求点P 的坐标;②如图2,点E 在抛物线2C 上点O 与点M 之间运动,四边形OBCE 的面积是否存在最大值?若存在,求出面积的最大值和点E 的坐标;若不存在,请说明理由.5.如图,在平面直角坐标系中,已知抛物线232y x bx c =++与x 轴交于(1,0)A -,(2,0)B 两点,与y 轴交于点C .(1)求该抛物线的解析式;(2)直线y x n =-+与该抛物线在第四象限内交于点D ,与线段BC 交于点E ,与x 轴交于点F ,且4BE EC =.①求n 的值;②连接AC ,CD ,线段AC 与线段DF 交于点G ,AGF ∆与CGD ∆是否全等?请说明理由;(3)直线(0)y m m =>与该抛物线的交点为M ,N (点M 在点N 的左侧),点M 关于y 轴的对称点为点M ',点H 的坐标为(1,0).若四边形OM NH '的面积为53.求点H 到OM '的距离d 的值.6.如图,已知二次函数23(2)34y ax a x =--+的图象经过点(4,0)A ,与y 轴交于点B .在x 轴上有一动点(C m ,0)(04)m <<,过点C 作x 轴的垂线交直线AB 于点E ,交该二次函数图象于点D .(1)求a 的值和直线AB 的解析式;(2)过点D 作DF AB ⊥于点F ,设ACE ∆,DEF ∆的面积分别为1S ,2S ,若124S S =,求m 的值;(3)点H 是该二次函数图象上位于第一象限的动点,点G 是线段AB 上的动点,当四边形DEGH 是平行四边形,且DEGH 周长取最大值时,求点G 的坐标.7.如图①,在平面直角坐标系xOy 中,抛物线23y ax bx =++经过点(1,0)A -、(3,0)B 两点,且与y 轴交于点C .(1)求抛物线的表达式;(2)如图②,用宽为4个单位长度的直尺垂直于x 轴,并沿x 轴左右平移,直尺的左右两边所在的直线与抛物线相交于P 、Q 两点(点P 在点Q 的左侧),连接PQ ,在线段PQ 上方抛物线上有一动点D ,连接DP 、DQ .(Ⅰ)若点P 的横坐标为12-,求DPQ ∆面积的最大值,并求此时点D 的坐标;(Ⅱ)直尺在平移过程中,DPQ ∆面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.8.已知抛物线2(1)y a x =-过点(3,1),D 为抛物线的顶点.(1)求抛物线的解析式;(2)若点B 、C 均在抛物线上,其中点1(0,)4B ,且90BDC ∠=︒,求点C 的坐标;(3)如图,直线4y kx k =+-与抛物线交于P 、Q 两点.①求证:90PDQ ∠=︒;②求PDQ ∆面积的最小值.9.如图,在平面直角坐标系中,抛物线222433y x x =--与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C .(1)求点A ,B ,C 的坐标;(2)点P 从A 点出发,在线段AB 上以每秒2个单位长度的速度向B 点运动,同时,点Q 从B 点出发,在线段BC 上以每秒1个单位长度的速度向C 点运动,当其中一个点到达终点时,另一个点也停止运动.设运动时间为t 秒,求运动时间t 为多少秒时,PBQ ∆的面积S 最大,并求出其最大面积;(3)在(2)的条件下,当PBQ ∆面积最大时,在BC 下方的抛物线上是否存在点M ,使BMC ∆的面积是PBQ ∆面积的1.6倍?若存在,求点M 的坐标;若不存在,请说明理由.10.如图,已知抛物线2342y ax x =++的对称轴是直线3x =,且与x 轴相交于A ,B 两点(B 点在A 点右侧)与y 轴交于C 点.(1)求抛物线的解析式和A 、B 两点的坐标;(2)若点P 是抛物线上B 、C 两点之间的一个动点(不与B 、C 重合),则是否存在一点P ,使PBC ∆的面积最大.若存在,请求出PBC ∆的最大面积;若不存在,试说明理由;(3)若M 是抛物线上任意一点,过点M 作y 轴的平行线,交直线BC 于点N ,当3MN =时,求M 点的坐标.。
2020年中考数学考点一遍过考点11二次函数(含解析)

3.抛物线的移动主要看顶点的移动, y=ax2 的顶点是( 0,0), y=a( x–h)2 的顶点是( h,0), y=a
(x–
h) 2+k 的顶点是( h, k).
4.抛物线的平移口诀:自变量加减左右移,函数值加减上下移.
典例 7 如果将抛物线 y=–x2–2 向右平移 3 个单位长度,那么所得到的新抛物线的表达式是
左侧 y 随 x 的增大而增大,在对称轴右侧 y 随 x 的增大而减小
6.( 2019 ·南通市启秀中学初三期中)关于下列说法:(
1)反比例函数 y 1 ,在每个象限内 y
3mx
随 x 的增大而减小; ( 2)函数 y
1 x , y 随 x 的增大减小; ( 3)函数 y
3
12 x ,当 x 0 时,
A . –1 【答案】 A
B.2
C. –1 或 2
【解析】依题意
m2 m 2
,解得 m=–1,故选 A.
m20
【名师点睛】此题主要考察二次函数的定义,需要注意
a 0.
典例 2 ( 2019·河北初三期中)下列函数是二次函数的是
D. m 不存在
A . y=2x+2 【答案】 C
B . y=﹣ 2x
【解析】直接根据二次函数的定义判定即可.
二次函数的图象是一条关于某条直线对称的曲线,叫做抛物线,该直线叫做抛物线的对称轴,对称 轴与抛物线的交点叫做抛物线的顶点 .
典例 3 函数 y=ax2+bx+a+b( a≠0)的图象可能是
A.
B.
C.
D.
【答案】 C
【解析】 A ,由图象可知,开口向下,则 a<0 ,又因为顶点在 y 轴左侧,则 b<0 ,则 a+b<0,而图象 与 y 轴交点为( 0, a+b)在 y 轴正半轴,与 a+b<0 矛盾,故此选项错误; B,由图象可知,开口向下,则 a<0,又因为顶点在 y 轴左侧,则 b<0,则 a+b<0,而图象与 y 轴交 点为( 0, 1)在 y 轴正半轴,可知 a+b=1 与 a+b<0 矛盾,故此选项错误; C,由图象可知,开口向上,则 a>0,顶点在 y 轴右侧,则 b<0, a+b=1 可能成立,故此选项正确; D,由图象可知,开口向上,则 a>0,顶点在 y 轴右侧,则 b<0 ,与 y 轴交于正半轴,则 a+b>0,而 图象与 x 轴的交点为 (1,0),则 a+b+a+b=0,显然 a+b=0 与 a+b>0 矛盾, 故此选项错误. 故选 C. 典例 4 如果二次函数 y=ax2+bx+c( a≠0)的图象如图所示,那么下列不等式成立的是
二次函数背景下的动点问题探究(解析版)

备战2020年中考数学压轴题之二次函数专题09 二次函数背景下的动点问题探究【方法综述】动点是常见的综合问题中的构成要件,通过点的运动命题者可以构造各种问题情景。
动点的呈现方式从动点个数往往有单动点或双动点,从运动呈现方式分为无速度动点和有速度动点,从动点的引起的变化分为单个动点变化和以动点驱动的图形运动。
【典例示范】类型一常规单动点问题例1:如图,抛物线y=x2+bx+c与直线y=12x﹣3交于,B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.(1)求抛物线对应的函数解析式;(2)以O,A,P,D为顶点的平行四边形是否存在若存在,求点P的坐标;若不存在,说明理由.【答案】(1) y=x2+92x﹣3;(2)见解析.【思路引导】(1)将点A、B的坐标代入抛物线表达式,即可求解;(2)PD=|m²+4m|,∵PD∥AO,则当PD=OA=3时,存在以O,A,P,D为顶点的平行四边形,即PD=|m²+4m|=3,即可求解.【解析】解:(1)将点A、B的坐标代入抛物线表达式得:16453b cc-+=-⎧⎨=-⎩,解得:923bc⎧=⎪⎨⎪=-⎩,故抛物线的表达式为:y=x2+92x﹣3;(2)存在,理由:同理直线AB 的表达式为:y =12x ﹣3, 设点P (m ,m 2+92m ﹣3),点D (m ,12 m ﹣3)(m <0),则PD =|m 2+4m|, ∵PD ∥AO ,则当PD =OA =3时,存在以O ,A ,P ,D 为顶点的平行四边形,即PD =|m 2+4m|=3,①当m 2+4m =3时,解得:m =﹣(舍去正值),即m 2+92m ﹣3=1﹣2,故点P (﹣2,﹣1﹣2), ②当m 2+4m =﹣3时,解得:m =﹣1或﹣3,同理可得:点P (﹣1,﹣132)或(﹣3,﹣152);综上,点P (﹣2,﹣1﹣2)或(﹣1,﹣132)或(﹣3,﹣152). 【方法总结】本题考查的是二次函数综合运用,涉及到待定系数法求函数解析式、平行四边形性质等,要注意分类讨论思想的运用.例2:在平面直角坐标系中,点O 为坐标原点,抛物线y=ax 2+bx+c 与x 轴交于点A (-1,0),B (3,0),与y 轴交于点C (0,3),顶点为G .(1)求抛物线和直线AC 的解析式;(2)如图1,设E (m ,0)为x 正半轴上的一个动点,若△CGE 和△CGO 的面积满足S △CGE =43S △CGO ,求点E 的坐标;(3)如图2,设点P 从点A 出发,以每秒1个单位长度的速度沿x 轴向右运动,运动时间为ts ,点M 为射线AC 上一动点,过点M 作MN ∥x 轴交抛物线对称轴右侧部分于点N .试探究点P 在运动过程中,是否存在以P ,M ,N 为顶点的三角形为等腰直角三角形,若存在,求出t 的值;若不存在,请说明理由.【答案】(1)2y x 2x 3=-++;y=3x+3;(2)点E 的坐标为:(1,0)或(-7,0);(3)存在,t 的值为10049或1316或134. 【思路引导】(1)用待定系数法即能求出抛物线和直线AC 解析式.(2)△CGE 与△CGO 虽然有公共底边CG ,但高不好求,故把△CGE 构造在比较好求的三角形内计算.延长GC 交x 轴于点F ,则△FGE 与△FCE 的差即为△CGE .(3)设M 的坐标(e ,3e +3),分别以M 、N 、P 为直角顶点作分类讨论,利用等腰直角三角形的特殊线段长度关系,用e 表示相关线段并列方程求解,再根据e 与AP 的关系求t 的值.【解析】解:(1)将点A (-1,0),B (3,0),点C (0,3)代入抛物线y=ax 2+bx+c 得,09303a b c a b c c -+=⎧⎪++=⎨⎪=⎩,解得123a b c =-⎧⎪=-⎨⎪=⎩,∴2y x 2x 3=-++,设直线AC 的解析式为y=kx+n ,将点A (-1,0),点C (0,3)代入得:03k n n -+=⎧⎨=⎩,解得:k=3,n=3 ∴直线AC 的解析式为:y=3x+3(2)延长GC 交x 轴于点F ,过点G 作GH ⊥x 轴于点H ,∵2(1)4y x =--+∴G (1,4),GH=4, ∴11331222CGO G SOC x =⨯=⨯⨯=, 若S △CGE =43S △CGO , 则S △CGE =43S △CGO =43232⨯=,①若点E 在x 轴的正半轴,设直线CG 为13y k x =+,将G (1,4)代入得134k +=∴11k =,∴直线CG 的解析式为y=x+3,∴当y=0时,x=-3,即F(-3,0)∵E (m,0)∴EF=m -(-3)=m+3∴CGE FGE FCE SS S =- =1122EF GH EF OC ⋅-⋅ = 1()2EF GH OC ⋅- =1(3)(43)2m +⋅- =1(3)2m + ∴1(3)22m +=,解得:m=1 ∴E 的坐标为(1,0)②若点E 在x 轴的负半轴上,则点E 到直线CG 的距离与点(1,0)到直线CG 的距离相等,即点E 到点F 的距离等于点(1,0)到点F 的距离,∴EF=-3-m=1-(-3)=4∴m=-7,即E (-7,0)综上所述,点E 的坐标为:(1,0)或(-7,0)(3)存在以P ,M ,N 为顶点的三角形为等腰直角三角形,设M (e,3e+3),e >-1,则33N M y y e ==+,①如图2,若∠MPN=90°,PM=PN ,过点M 作MQ ⊥x 轴于点Q ,过N 作NR ⊥x 轴于点R ,∵MN ∥x 轴∴MQ =NR =3e +3∴Rt △MQP ≌Rt △NRP (HL )∴PQ =PR ,∠MPQ =∠NPR =45°∴MQ =PQ =PR =NR =3e +3∴x N =x M +3e +3+3e +3=7e +6,即N (7e +6,3e +3)∵N 在抛物线上∴−(7e +6)2+2(7e +6)+3=3e +3,解得:11e =-(舍去),22449e =- ∵AP =t ,OP =t−1,OP +OQ =PQ∴t −1−e =3e +3∴t =4e +4=10049,②如图3,若∠PMN =90°,PM =MN ,∴MN =PM =3e +3∴x N =x M +3e +3=4e +3,即N (4e +3,3e +3)∴−(4e +3)2+2(4e +3)+3=3e +3解得:e 1=−1(舍去),e 2=316-,∴t=AP=e−(−1)=31311616 -+=,③如图4,若∠PNM=90°,PN=MN,∴MN=PN=3e+3,N(4e+3,3e+3)解得:e=3 16 -∴t=AP=OA+OP=1+4e+3=13 4综上所述,存在以P,M,N为顶点的三角形为等腰直角三角形,t的值为10049或1316或134.【方法总结】本题考查了待定系数法求函数解析式,坐标系中三角形面积计算,等腰直角三角形的性质,解一元二次方程,考查了分类讨论和方程思想.第(3)题根据等腰直角三角形的性质找到相关线段长的关系是解题关键,灵活运用因式分解法解一元二次方程能简便运算.针对训练1.如图①,已知抛物线y=ax2﹣4amx+3am2(a、m为参数,且a>0,m>0)与x轴交于A、B两点(A 在B的左边),与y轴交于点C.(1)求点B的坐标(结果可以含参数m);(2)连接CA 、CB ,若C (0,3m ),求tan ∠ACB 的值;(3)如图②,在(2)的条件下,抛物线的对称轴为直线l :x =2,点P 是抛物线上的一个动点,F 是抛物线的对称轴l 上的一点,在抛物线上是否存在点P ,使△POF 成为以点P 为直角顶点的的等腰直角三角形.若存在,求出所有符合条件的点P 的坐标,若不存在,请说明理由.【答案】(1)B (3m ,0);(2)tan ∠ACB =12;(3)点P 的坐标是:(5122+)或(5122-)或(3122+)或(3122). 【解析】 解:(1)令y =0,则有ax 2﹣4amx +3am 2=0,解得:x 1=m ,x 2=3m ,∵m >0,A 在B 的左边,∴B (3m ,0);(2)如图1,过点A 作AD ⊥BC ,垂足为点D ,由(1)可知B (3m ,0),则△BOC 为等腰直角三角形,∵OC =OB =3m ,∴BC =m ,又∵∠ABC =45°,∴∠DAB =45°,∴AD =BD ,∵AB =2m ,∴AD =,CD =m ,∴tan ∠ACB =AD 1CD 2==; (3)∵由题意知x =2为对称轴,∴2m =2,即m =1,∵在(2)的条件下有(0,3m ),∴3m =3am 2,解得m =1a,即a =1, ∴抛物线的解析式为y =x 2﹣4x +3,①当P 在对称轴的左边,如图2,过P 作MN ⊥y 轴,交y 轴于M ,交l 于N ,∵△OPF 是等腰直角三角形,且OP =PF ,易得△OMP ≌△PNF ,∴OM =PN ,∵P (m ,m 2﹣4m +3),则﹣m 2+4m ﹣3=2﹣m ,解得:m∴P);②当P在对称轴的右边,如图3,过P作MN⊥x轴于N,过F作FM⊥MN于M,同理得△ONP≌△PMF,∴PN=FM,则﹣m2+4m﹣3=m﹣2,解得:x 35;P的坐标为(31522-)或(3122+);综上所述,点P)或)或)或).2.如图1,在平面直角坐标系xOy中,抛物线y=−(x−a)(x−4)(a<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.(1)若D点坐标为(32,254),求抛物线的解析式和点C的坐标;(2)若点M为抛物线对称轴上一点,且点M的纵坐标为a,点N为抛物线在x轴上方一点,若以C、B、M、N 为顶点的四边形为平行四边形时,求a的值;(3)直线y=2x+b与(1)中的抛物线交于点D、E(如图2),将(1)中的抛物线沿着该直线方向进行平移,平移后抛物线的顶点为D′,与直线的另一个交点为E,与x轴的交点为B′,在平移的过程中,求D′E′的长度;当∠E′D′B′=90°时,求点B′的坐标.【答案】(1)y =−x 2+3x +4;C (0,4);(2)a =−2±2√13; a 1=−2−2√13,a 2=6−2√213;(3)B ′(−1,0) 【解析】(1)依题意得:254=−(32−a)(32−4)解得a =−1,∴抛物线的解析式为:y=-(x+1)(x -4)或y =−x 2+3x +4∴C (0,4)(2)由题意可知A (a,0)、B (4,0)、C (0,−4a )对称轴为直线x =a+42,则M (a+42,a)①MN//BC ,且MN =BC ,根据点的平移特征可知N (a−42,−3a) 则−3a =−(a−42−a)⋅(a−42−4),解得:a =−2±2√13(舍去正值);②当BC 为对角线时,设N (x,y ),根据平行四边形的对角线互相平分可得 {a+42+x =4a +y =−4a , 解得{x =4−a 2y =−5a ,则−5a =−(4−a 2−a)⋅(4−a 2−4) 解得:a =6±2√213∴a 1=−2−2√13,a 2=6−2√213 (3)联立{y =2x +134y =−x 2+3x +4解得:{x 1=32y 1=254 (舍去),{x 2=−12y 2=94则DE =2√5,根据抛物线的平移规律,则平移后的线段D ′E ′始终等于2√5设平移后的D ′(m,2m +134),则E ′(m −2,2m −34) 平移后的抛物线解析式为:y =−(x −m )2+2m +134 则D ′B ′:y =−12x +n 过(m,2m +134), ∴y =−12x +52m +134,则B ′(5m +132,0)抛物线y =−(x −m )2+2m +134过B ′(5m +132,0) 解得m 1=−32,m 2=−138∴B 1′(−1,0),B 2′(−138,0)(与D ′重合,舍去)∴B ′(−1,0) 3.如图,已知直线AB 与抛物线C :y =ax 2+2x+c 相交于点A(﹣1,0)和点B(2,3)两点.(1)求抛物线C 函数表达式;(2)若点M 是位于直线AB 上方抛物线上的一动点,当MAB △的面积最大时,求此时MAB △的面积S 及点M 的坐标.【答案】(1) y =﹣x 2+2x+3;(2) △MAB 的面积最大值是278,M(12,154) 【解析】(1)由题意把点(﹣1,0)、(2,3)代入y =ax 2+2x+c , 得20443a c a c -+=⎧⎨++=⎩,解得1,3,a c =-⎧⎨=⎩, ∴此抛物线C 函数表达式为:y =﹣x 2+2x+3;(2)如图,过点M 作MH ⊥x 轴于H ,交直线AB 于K ,将点(﹣1,0)、(2,3)代入y =kx+b 中,得023k b k b -+=⎧⎨+=⎩,解得1,1,k b =⎧⎨=⎩, ∴y AB =x+1,设点M(x ,﹣x 2+2x+3),则K(x ,x+1),则MK =﹣x 2+2x+3﹣(x+1)=﹣x 2+x+2,∴S △MAB=S △AMK +S △BMK =12MK•(x M ﹣x A )+ 12MK•(x B ﹣x M ) =12MK•(x B ﹣x A ) =12×(-x 2+x+2)×3 =23127()228x --+, ∵302-<,当x =12时,S △MAB 最大=278,此时21115()23224M y =-+⨯+=, ∴△MAB 的面积最大值是278,M(12,154).4.如图,直线y =34x +a 与x 轴交于点A (4,0),与y 轴交于点B ,抛物线y =34x 2+bx +c 经过点A ,B .点M (m ,0)为x 轴上一动点,过点M 且垂直于x 轴的直线分别交直线AB 及抛物线于点P ,N .(1)填空:点B 的坐标为 ,抛物线的解析式为 ;(2)当点M 在线段OA 上运动时(不与点O ,A 重合),①当m 为何值时,线段PN 最大值,并求出PN 的最大值;②求出使△BPN 为直角三角形时m 的值;(3)若抛物线上有且只有三个点N 到直线AB 的距离是h ,请直接写出此时由点O ,B ,N ,P 构成的四边形的面积.【答案】(1)(0,﹣3),y =34x2﹣94x ﹣3;(2)①是3,②3或119;(3)6或6+6√2或6√2﹣6.【解析】解:(1)把点A 坐标代入直线表达式y =34x+a ,解得:a =﹣3,则:直线表达式为:y═34x ﹣3,令x =0,则:y =﹣3,则点B 坐标为(0,﹣3),将点B 的坐标代入二次函数表达式得:c =﹣3,把点A 的坐标代入二次函数表达式得:34×16+4b ﹣3=0, 解得:b =﹣94, 故抛物线的解析式为:y =34x2﹣94x ﹣3,(2)①∵M (m ,0)在线段OA 上,且MN ⊥x 轴,∴点P (m ,34m ﹣3),N (m ,34m2﹣94m ﹣3), ∴PN =34m ﹣3﹣(34m2﹣94m ﹣3)=﹣34(m ﹣2)2+3,∵a =﹣34<0, ∴抛物线开口向下,∴当m =2时,PN 有最大值是3,②当∠BNP =90°时,点N 的纵坐标为﹣3,把y =﹣3代入抛物线的表达式得:﹣3=34m2﹣94m ﹣3,解得:m =3或0(舍去m =0),∴m =3;当∠NBP =90°时,∵BN ⊥AB ,两直线垂直,其k 值相乘为﹣1,设:直线BN 的表达式为:y =﹣43x+n , 把点B 的坐标代入上式,解得:n =﹣3,则:直线BN 的表达式为:y =﹣43x ﹣3,将上式与抛物线的表达式联立并解得:m =119或0(舍去m =0), 当∠BPN =90°时,不合题意舍去,故:使△BPN 为直角三角形时m 的值为3或43;(3)∵OA =4,OB =3,在Rt △AOB 中,tanα=43,则:cosα=35,sinα=45, ∵PM ∥y 轴,∴∠BPN =∠ABO =α,若抛物线上有且只有三个点N 到直线AB 的距离是h ,则只能出现:在AB 直线下方抛物线与过点N 的直线与抛物线有一个交点N ,在直线AB 上方的交点有两个.当过点N 的直线与抛物线有一个交点N ,点M 的坐标为(m ,0),设:点N 坐标为:(m ,n ),则:n =34m2﹣94m ﹣3,过点N 作AB 的平行线,则点N 所在的直线表达式为:y =34x+b ,将点N 坐标代入,解得:过N 点直线表达式为:y =34x+(n ﹣34m ),将抛物线的表达式与上式联立并整理得:3x 2﹣12x ﹣12+3m ﹣4n =0,△=144﹣3×4×(﹣12+3m ﹣4n )=0,将n =34m 2﹣94m ﹣3代入上式并整理得:m 2﹣4m+4=0, 解得:m =2,则点N 的坐标为(2,﹣92),则:点P 坐标为(2,﹣32), 则:PN =3,∵OB =3,PN ∥OB ,∴四边形OBNP 为平行四边形,则点O 到直线AB 的距离等于点N 到直线AB 的距离,即:过点O 与AB 平行的直线与抛物线的交点为另外两个N 点,即:N′、N″,直线ON 的表达式为:y =34x ,将该表达式与二次函数表达式联立并整理得:x 2﹣4x ﹣4=0,解得:x =2±2√2,则点N′、N″的横坐标分别为2+2√2,2﹣2√2,作NH ⊥AB 交直线AB 于点H ,则h =NH =NPsinα=125, 作N′P′⊥x 轴,交x 轴于点P′,则:∠ON′P′=α,ON′=OP ′sinα=54(2+2√2),S 四边形OBPN =BP•h =52×125=6,则:S 四边形OBP′N′=S △OP′N′+S △OBP′=6+6√2,同理:S 四边形OBN″P″=6√2﹣6,故:点O ,B ,N ,P 构成的四边形的面积为:6或6+6√2或6√2﹣6.5.在平面直角坐标系xOy 中,直线1(0)y kx k =+≠经过点23A (,),与y 轴交于点B ,与抛物线2y ax bx a =++的对称轴交于点C m 2(,).(1)求m 的值;(2)求抛物线的顶点坐标;(3)11N x y (,)是线段AB 上一动点,过点N 作垂直于y 轴的直线与抛物线交于点22P x y (,),33Q x y (,)(点P 在点Q 的左侧).若213x x x <<恒成立,结合函数的图象,求a 的取值范围.【答案】(1)1;(2)()10,.(3)01a <<.【解析】解:(1)∵()10y kx k =+≠ 经过点23A (,), ∴将点A 的坐标代入1y kx =+ ,即321k =+ ,得1k =.∵直线1y x =+ 与抛物线2y ax bx a =++ 的对称轴交于点(,2)C m ,∴将点(,2)C m 代入1y x =+,得1m = .(2)∵抛物线2y ax bx a =++ 的对称轴为1x =, ∴12b a-= ,即2b a =-. ∴22y ax ax a =-+()21a x =- . ∴抛物线的顶点坐标为()10, . (3)当0a >时,如图,若拋物线过点01B (,),则1a = . 结合函数图象可得01a << .当0a <时,不符合题意.综上所述,a 的取值范围是01a <<.类型二 双动点问题例3.如图①,在平面直角坐标系中,二次函数y =13-x 2+bx+c 的图象与坐标轴交于A ,B ,C 三点,其中点A 的坐标为(﹣3,0),点B 的坐标为(4,0),连接AC ,BC .动点P 从点A 出发,在线段AC 上以每秒1个单位长度的速度向点C 作匀速运动;同时,动点Q 从点O 出发,在线段OB 上以每秒1个单位长度的速度向点B 作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t 秒.连接PQ .(1)填空:b = ,c = ;(2)在点P ,Q 运动过程中,△APQ 可能是直角三角形吗?请说明理由;(3)点M 在抛物线上,且△AOM 的面积与△AOC 的面积相等,求出点M 的坐标。
2020年初三数学下册中考专题复习 二次函数面积最值问题(含答案)

2020年初三数学下册中考专题复习二次函数面积最值问题1.如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N 从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.2.如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=﹣x2+2x+3经过点A、C、A′三点.(1)求A、A′、C三点的坐标;(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积;(3)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并写出此时M的坐标.3.如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.(1)求抛物线的解析式及顶点坐标;(2)在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;(3)在直线AB的下方抛物线上找一点P,连接P A,PB使得△P AB的面积最大,并求出这个最大值.4.如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.(1)求抛物线C2的解析式;(2)在抛物线C2的对称轴上是否存在点P,使P A+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.5.如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.(1)求这个二次函数的解析式;(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.6.如图,二次函数y=﹣x2+3x+m的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点(1)求m的值及C点坐标;(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由(3)P为抛物线上一点,它关于直线BC的对称点为Q①当四边形PBQC为菱形时,求点P的坐标;②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.7.如图,抛物线y=ax2+bx+与直线AB交于点A(﹣1,0),B(4,),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.(1)求抛物线的表达式;(2)设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出当S 取最大值时的点C的坐标.8.如图A(0,3),B(3,0),C(1,0)分别是抛物线:y=ax2+bx+c(a≠0)上的三点,点P为抛物线上一动点.(1)求此抛物线的解析式.(2)当△P AB是以AB为一直角边的直角三角形时,求此时点P的坐标.(3)若点P在抛物线上A、B两点之间移动时,是否存在一个位置,使△P AB的面积最大?若存在,请求此时点P的坐标.若不存在,请说明理由.9.如图,抛物线y=ax2+bx+c经过A(0,3)、B(﹣1,0)、D(2,3),抛物线与x轴的另一交点为E.点P为直线AE上方抛物线上一动点,设点P的横坐标为t.(1)求抛物线的表达式;(2)当t为何值时,△P AE的面积最大?并求出最大面积;(3)是否存在点P使△P AE为直角三角形?若存在,求出t的值;若不存在,说明理由.10.如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C (0,﹣3)(1)求出该抛物线的函数关系式及对称轴(2)点P是抛物线上的一个动点,设点P的横坐标为t(0<t<3).当△PCB的面积的最大值时,求点P的坐标(3)在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B、C、P、Q为顶点的四边形是平行四边形时,求P点的坐标.11.如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B,与y轴交于C(0,3),直线y=+m经过点C,与抛物线的另一交点为点D,点P是直线CD上方抛物线上的一个动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.(1)求抛物线解析式并求出点D的坐标;(2)连接PD,△CDP的面积是否存在最大值?若存在,请求出面积的最大值;若不存在,请说明理由;(3)当△CPE是等腰三角形时,请直接写出m的值.12.如图1,在平面直角坐标系中,直线y=x﹣与抛物线y=﹣x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣8.点P是直线AB上方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线,垂足为E,交直线AB于点C,作PD⊥AB于点D,交x轴于点F.(1)求该抛物线的解析式;(2)求sin∠ACE的值;(3)连接P A、PB(如图2所示),设△P AB的面积为S,点P的横坐标为x,求S关于x的函数关系式,并求出S的最大值.13.如图,⊙M的圆心M(﹣1,2),⊙M经过坐标原点O,与y轴交于点A.经过点A的一条直线l解析式为:y=﹣x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(﹣4,0).(1)求抛物线的解析式;(2)求证:直线l是⊙M的切线;(3)点P为抛物线上一动点,且PE与直线l垂直,垂足为E;PF∥y轴,交直线l于点F,是否存在这样的点P,使△PEF的面积最小.若存在,请求出此时点P的坐标及△PEF面积的最小值;若不存在,请说明理由.14.如图,已知抛物线y=ax2﹣x+c与x轴相交于A、B两点,并与直线y=x﹣2交于B、C两点,其中点C是直线y=x﹣2与y轴的交点,连接AC.(1)求抛物线的解析式;(2)证明:△ABC为直角三角形;(3)△ABC内部能否截出面积最大的矩形DEFG?(顶点D、E、F、G在△ABC各边上)若能,求出最大面积;若不能,请说明理由.15.如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E (0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.(1)填空:点A坐标为;抛物线的解析式为.(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?16.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1,P为抛物线上的一个动点.(1)求抛物线的解析式并写出其顶点坐标;(2)当点P的纵坐标为2时,求点P的横坐标;(3)当点P在运动过程中,求四边形P ABC面积最大时的值及此时点P的坐标.17.如图,在平面直角坐标系中,顶点为(4,﹣1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).(1)求此抛物线的解析式;(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△P AC的面积最大?并求出此时P点的坐标和△P AC的最大面积.18.如图,已知抛物线y=﹣+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).(1)求抛物线的解析式及其对称轴方程.(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由.(3)在抛物线上BC之间是否存在一点D,使得△DBC的面积最大?若存在请求出点D 的坐标和△DBC的面积;若不存在,请说明理由.19.如图1,抛物线y=﹣x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:(1)求出抛物线的解析式,并写出C点的坐标;(2)试求出当n为何值时,△ANC恰能构成是等腰三角形.(3)如图2,过N作NF∥BC,与AC相交于D点,连结CN,请问在N点的运动过程中,△CDN的面积是否存在最大值;若存在,试求出该最大面积,若不存在,请说明理由.20.抛物线y=ax2+bx+c与x轴交于点A(1,0)和点B(5,0),与y轴交于点C(0,3).该抛物线与直线相交于C,D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M,N.(1)求该抛物线所对应的函数解析式;(2)连结PC,PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;(3)连结PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ 与△PBM相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.详细答案一.解答题(共20小题)1.【解答】解:(1)把A(1,0)和C(0,3)代入y=x2+bx+c,解得:b=﹣4,c=3,∴二次函数的表达式为:y=x2﹣4x+3;(2)令y=0,则x2﹣4x+3=0,解得:x=1或x=3,∴B(3,0),∴BC=3,点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图1,①当CP=CB时,PC=3,∴OP=OC+PC=3+3或OP=PC﹣OC=3﹣3∴P1(0,3+3),P2(0,3﹣3);②当BP=BC时,OP=OB=3,∴P3(0,﹣3);③当PB=PC时,∵OC=OB=3∴此时P与O重合,∴P4(0,0);综上所述,点P的坐标为:(0,3+3)或(0,3﹣3)或(0,﹣3)或(0,0);(3)如图2,设A运动时间为t,由AB=2,得BM=2﹣t,则DN=2t,∴S△MNB=×(2﹣t)×2t=﹣t2+2t=﹣(t﹣1)2+1,即当M(2,0)、N(2,2)或(2,﹣2)时△MNB面积最大,最大面积是1.2.【解答】解:(1)当y=0时,﹣x2+2x+3=0,解得x1=3,x2=﹣1,则C(﹣1,0),A′(3,0);当x=0时,y=3,则A(0,3);(2)∵四边形ABOC为平行四边形,∴AB∥OC,AB=OC,而C(﹣1,0),A(0,3),∴B(1,3)∴OB==,S△AOB=×3×1=,又∵平行四边形ABOC旋转90°得平行四边形A′B′OC′,∴∠ACO=∠OC′D,OC′=OC=1,又∵∠ACO=∠ABO,∴∠ABO=∠OC′D.又∵∠C′OD=∠AOB,∴△C′OD∽△BOA,∴=()2=()2=,∴S△C′OD=×=;(3)设M点的坐标为(m,﹣m2+2m+3),0<m<3,作MN∥y轴交直线AA′于N,易得直线AA′的解析式为y=﹣x+3,则N(m,﹣m+3),∵MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,∴S△AMA′=S△ANM+S△MNA′=MN•3=(﹣m2+3m)=﹣m2+m=﹣(m﹣)2+,∴当m=时,S△AMA'的值最大,最大值为,此时M点坐标为().3.【解答】解:(1)抛物线的顶点D的横坐标是2,则x=﹣=2…①,抛物线过是A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,把B点坐标代入上式得:9=25a+5b﹣3…②,联立①、②解得:a=,b=﹣,c=﹣3,∴抛物线的解析式为:y=x2﹣x﹣3,当x=2时,y=﹣,即顶点D的坐标为(2,﹣);(2)A(0,﹣3),B(5,9),则AB=13,①当AB=AC时,设点C坐标(m,0),则:(m)2+(﹣3)2=132,解得:m=±4,即点C坐标为:(4,0)或(﹣4,0);②当AB=BC时,设点C坐标(m,0),则:(5﹣m)2+92=132,解得:m=5,即:点C坐标为(5,0)或(5﹣2,0),③当AC=BC时,设点C坐标(m,0),则:点C为AB的垂直平分线于x轴的交点,则点C坐标为(,0),故:存在,点C的坐标为:(4,0)或(﹣4,0)或(5,0)或(5﹣2,0)或(,0);(3)过点P作y轴的平行线交AB于点H,设:AB所在的直线过点A(0,﹣3),则设直线AB的表达式为y=kx﹣3,把点B坐标代入上式,9=5k﹣3,则k=,故函数的表达式为:y=x﹣3,设:点P坐标为(m,m2﹣m﹣3),则点H坐标为(m,m﹣3),S△P AB=•PH•x B=(﹣m2+12m),当m=2.5时,S△P AB取得最大值为:,答:△P AB的面积最大值为.4.【解答】解:(1)令:y=x2﹣2x=0,则x=0或2,即点B(2,0),∵C1、C2:y=ax2+bx开口大小相同、方向相反,则a=﹣1,则点A(4,0),将点A的坐标代入C2的表达式得:0=﹣16+4b,解得:b=4,故抛物线C2的解析式为:y=﹣x2+4x;(2)联立C1、C2表达式并解得:x=0或3,故点C(3,3),作点C关于C2对称轴的对称点C′(1,3),连接AC′交函数C2的对称轴与点P,此时P A+PC的值最小为:线段AC′的长度=3,此时点P(2,2);(3)直线OC的表达式为:y=x,过点M作y轴的平行线交OC于点H,设点M(x,﹣x2+4x),则点H(x,x),则S△MOC=MH×x C=(﹣x2+4x﹣x)=﹣x2+x,∵﹣<0,故x=,故当点M(,)时,S△MOC最大值为.5.【解答】解:(1)设抛物线解析式为y=ax2+bx+c,把A、B、C三点坐标代入可得,解得,∴抛物线解析式为y=x2﹣3x﹣4;(2)作OC的垂直平分线DP,交OC于点D,交BC下方抛物线于点P,如图1,∴PO=PC,此时P点即为满足条件的点,∵C(0,﹣4),∴D(0,﹣2),∴P点纵坐标为﹣2,代入抛物线解析式可得x2﹣3x﹣4=﹣2,解得x=(小于0,舍去)或x=,∴存在满足条件的P点,其坐标为(,﹣2);(3)∵点P在抛物线上,∴可设P(t,t2﹣3t﹣4),过P作PE⊥x轴于点E,交直线BC于点F,如图2,∵B(4,0),C(0,﹣4),∴直线BC解析式为y=x﹣4,∴F(t,t﹣4),∴PF=(t﹣4)﹣(t2﹣3t﹣4)=﹣t2+4t,∴S△PBC=S△PFC+S△PFB=PF•OE+PF•BE=PF•(OE+BE)=PF•OB=(﹣t2+4t)×4=﹣2(t﹣2)2+8,∴当t=2时,S△PBC最大值为8,此时t2﹣3t﹣4=﹣6,∴当P点坐标为(2,﹣6)时,△PBC的最大面积为8.6.【解答】解:(1)将B(4,0)代入y=﹣x2+3x+m,解得,m=4,∴二次函数解析式为y=﹣x2+3x+4,令x=0,得y=4,∴C(0,4),(2)存在,理由:∵B(4,0),C(0,4),∴直线BC解析式为y=﹣x+4,当直线BC向上平移b单位后和抛物线只有一个公共点时,△MBC面积最大,∴,∴x2﹣4x+b=0,∴△=16﹣4b=0,∴b=4,∴,∴M(2,6),(3)①如图,∵点P在抛物线上,∴设P(m,﹣m2+3m+4),当四边形PBQC是菱形时,点P在线段BC的垂直平分线上,∵B(4,0),C(0,4)∴线段BC的垂直平分线的解析式为y=x,∴m=﹣m2+3m+4,∴m=1±,∴P(1+,1+)或P(1﹣,1﹣),②如图,设点P(t,﹣t2+3t+4),过点P作y轴的平行线l,过点C作l的垂线,∵点D在直线BC上,∴D(t,﹣t+4),∵PD=﹣t2+3t+4﹣(﹣t+4)=﹣t2+4t,BE+CF=4,∴S四边形PBQC=2S△PCB=2(S△PCD+S△PBD)=2(PD×CF+PD×BE)=4PD=﹣4t2+16t,∵0<t<4,∴当t=2时,S四边形PBQC最大=167.【解答】解:(1)∵由题意得解得:,∴y=﹣x2+2x+.(2)设直线AB为:y=kx+b.则,解得直线AB的解析式为y=+.如图所示:记CD与x轴的交点坐标为E.过点B作BF⊥DC,垂足为F.设D(m,﹣m2+2m+)则C(m,m+).∵CD=(﹣m2+2m+)﹣(m+)=m2+m+2,∴S=AE•DC+CD•BF=CD(AE+BF)=DC=m2+m+5.∴S=m2+m+5.∵﹣<0,∴当m=时,S有最大值.∴当m=时,m+=×+=.∴点C(,).8.【解答】解:(1)将A(0,3),B(3,0),C(1,0)代入y=ax2+bx+c,得:,解得:,∴抛物线的解析式为y=x2﹣4x+3.(2)设点P的坐标为(m,m2﹣4m+3).∵点A的坐标为(0,3),点B的坐标为(3,0),∴AP2=(m﹣0)2+(m2﹣4m+3﹣3)2=m4﹣8m3+17m2,BP2=(m﹣3)2+(m2﹣4m+3)2=m4﹣8m3+23m2﹣30m+18,AB2=(3﹣0)2+(0﹣3)2=18.分两种情况考虑:①当∠BAP=90°时,AB2+AP2=BP2,即18+m4﹣8m3+17m2=m4﹣8m3+23m2﹣30m+18,整理,得:m2﹣5m=0,解得:m1=0(舍去),m2=5,∴点P的坐标为(5,8);②当∠ABP=90°时,AB2+BP2=AP2,即18+m4﹣8m3+23m2﹣30m+18=m4﹣8m3+17m2,整理,得:m2﹣5m+6=0,解得:m3=2,m3=3(舍去),∴点P的坐标为(2,﹣1).综上所述:当△P AB是以AB为一直角边的直角三角形时,点P的坐标为(5,8)或(2,﹣1).(3)存在,如图过点P作PD∥y轴交直线AB于点D.设直线AB的解析式为y=kx+d(k≠0),将A(0,3),B(3,0)代入y=kx+d,得:,解得:,∴直线AB的解析式为y=﹣x+3.设点P的坐标为(n,n2﹣4n+3)(0<n<3),则点D的坐标为(n,﹣n+3),∴PD=(﹣n+3)﹣(n2﹣4n+3)=﹣n2+3n,∴S△P AB=OB•PD=﹣n2+n=﹣(n﹣)2+.∵﹣<0,∴当n=时,S△P AB取得最大值,此时最大值为,∴当△P AB的面积取最大值时,点P的坐标为(,﹣).9.【解答】解:(1)由题意得:,解得:,∴抛物线解析式为y=﹣x2+2x+3;(2)∵A(0,3),D(2,3),∴抛物线对称轴为x=1,∴E(3,0),设直线AE的解析式为y=kx+3,∴3k+3=0,解得,k=﹣1,∴直线AE的解析式为y=﹣x+3,如图1,作PM∥y轴,交直线AE于点M,设P(t,﹣t2+2t+3),M(t,﹣t+3),∴PM=﹣t2+2t+3+t﹣3=﹣t2+3t,∴==,∴t=时,△P AE的面积最大,最大值是.(3)由图可知∠PEA≠90°,∴只能有∠P AE=90°或∠APE=90°,①当∠P AE=90°时,如图2,作PG⊥y轴,∵OA=OE,∴∠OAE=∠OEA=45°,∴∠P AG=∠APG=45°,∴PG=AG,∴t=﹣t2+2t+3﹣3,即﹣t2+t=0,解得t=1或t=0(舍去),②当∠APE=90°时,如图3,作PK⊥x轴,AQ⊥PK,则PK=﹣t2+2t+3,AQ=t,KE=3﹣t,PQ=﹣t2+2t+3﹣3=﹣t2+2t,∵∠APQ+∠KPE=∠APQ+∠P AQ=90°,∴∠P AQ=∠KPE,且∠PKE=∠PQA,∴△PKE∽△AQP,∴,∴,即t2﹣t﹣1=0,解得:t=或t=<0(舍去),综上可知存在满足条件的点P,t的值为1或.10.【解答】解:(1)设抛物线解析式为y=a(x+1)(x﹣3),∵抛物线与y轴交于点C(0,﹣3),∴﹣3=a(0+1)(0﹣3),∴a=1∴设抛物线解析式为y=(x+1)(x﹣3)=x2﹣2x﹣3,对称轴为直线x=1;(2)设P(t,t2﹣2t﹣3),S△PCB=S△POC+S△POB﹣S△BOC=×3t+×3×|t2﹣2t﹣3|﹣=∵a=<0,∴函数有最大值,当t=时,面积最大,∴P()(3)设Q(1,n)),①当PQ、PC为平行四边形的对角线时,P(4,n+3),∴42﹣2×4﹣3=n+3,n=2,∴P(4,5);②当CQ、BP为平行四边形的对角线时,P(﹣2,n﹣3),∴(﹣2)2﹣2×(﹣2)﹣3=n﹣3,n=8,∴P(﹣2,5);综上所述,以BC为边,以点B、C、P、Q为顶点的四边形是平行四边形时,P点的坐标(4,5),(﹣2,5).11.【解答】解:(1)把A(﹣1,0),C(0,3)分别代入y=﹣x2+bx+c得,解得,∴抛物线的解析式为y=﹣x2+2x+3;把C(0,3)代入y=﹣x+m,解得m=3,∴直线CD的解析式为y=﹣x+3,解方程组,解得或,∴D点坐标为(,);(2)存在.设P(m,﹣m2+2m+3),则E(m,﹣m+3),∴PE=﹣m2+2m+3﹣(﹣m+3)=﹣m2+m,∴S△PCD=••(﹣m2+m)=﹣m2+m=﹣(m﹣)2+,当m=时,△CDP的面积存在最大值,最大值为;(3)当PC=PE时,m2+(﹣m2+2m+3﹣3)2=(﹣m2+m)2,解得m=0(舍去)或m=;当CP=CE时,m2+(﹣m2+2m+3﹣3)2=m2+(﹣m+3﹣3)2,解得m=0(舍去)或m=(舍去)或m=;当EC=EP时,m2+(﹣m+3﹣3)2=(﹣m2+m)2,解得m=(舍去)或m =,综上所述,m的值为或或.12.【解答】解:(1)当x=﹣8时,y=x﹣=﹣,则B(﹣8,﹣),当y=0时,x﹣=0,解得x=2,则A(2,0),把B(﹣8,﹣),A(2,0)代入y=﹣x2+bx+c得,解得,∴抛物线的解析式y=﹣x2﹣x+;(2)当x=0时,y=x﹣=﹣,则G(0,﹣),在Rt△AOG中,∵OG=,OA=2,∴AG==,∴sin∠AGO===,∵PC⊥x轴,∴PC∥OG,∴∠ACE=∠AGO,∴sin∠ACE=;(3)设P(x,﹣x2﹣x+),则C(x,x﹣),∴PC=﹣x2﹣x+﹣(x﹣)=﹣x2﹣x+4,∴S=•(2+8)•(﹣x2﹣x+4)=﹣x2﹣x+20=﹣(x+3)2+,当x=﹣3时,S的最大值为.13.【解答】解:(1)设抛物线的解析式为y=a(x﹣2)(x+4),将点M的坐标代入得:﹣9a=2,解得:a=﹣.∴抛物线的解析式为y=﹣x2﹣x+.(2)连接AM,过点M作MG⊥AD,垂足为G.把x=0代入y=﹣x+4得:y=4,∴A(0,4).将y=0代入得:0=﹣x+4,解得x=8,∴B(8,0).∴OA=4,OB=8.∵M(﹣1,2),A(0,4),∴MG=1,AG=2.∴tan∠MAG=tan∠ABO=.∴∠MAG=∠ABO.∵∠OAB+∠ABO=90°,∴∠MAG+∠OAB=90°,即∠MAB=90°.∴l是⊙M的切线.(3)∵∠PFE+∠FPE=90°,∠FBD+∠PFE=90°,∴∠FPE=∠FBD.∴tan∠FPE=.∴PF:PE:EF=:2:1.∴△PEF的面积=PE•EF=×PF•PF=PF2.∴当PF最小时,△PEF的面积最小.设点P的坐标为(x,﹣x2﹣x+),则F(x,﹣x+4).∴PF=(﹣x+4)﹣(﹣x2﹣x+)=﹣x+4+x2+x﹣=x2﹣x+=(x﹣)2+.∴当x=时,PF有最小值,PF的最小值为.∴P(,).∴△PEF的面积的最小值为=×()2=.14.【解答】(1)解:∵直线y=x﹣2交x轴、y轴于B、C两点,∴B(4,0),C(0,﹣2),∵y=ax2﹣x+c过B、C两点,∴,解得,∴y=x2﹣x﹣2.(2)证明:如图1,连接AC,∵y=x2﹣x﹣2与x负半轴交于A点,∴A(﹣1,0),在Rt△AOC中,∵AO=1,OC=2,∴AC=,在Rt△BOC中,∵BO=4,OC=2,∴BC=2,∵AB=AO+BO=1+4=5,∴AB2=AC2+BC2,∴△ABC为直角三角形.(3)解:△ABC内部可截出面积最大的矩形DEFG,面积为,理由如下:①一点为C,AB、AC、BC边上各有一点,如图2,此时△AGF∽△ACB∽△FEB.设GC=x,AG=﹣x,∵,∴,∴GF=2﹣2x,∴S=GC•GF=x•(2)=﹣2x2+2x=﹣2[(x﹣)2﹣]=﹣2(x﹣)2+,即当x=时,S最大,为.②AB边上有两点,AC、BC边上各有一点,如图3,此时△CDE∽△CAB∽△GAD,设GD=x,∵,∴,∴AD=x,∴CD=CA﹣AD=﹣x,∵,∴,∴DE=5﹣x,∴S=GD•DE=x•(5﹣x)=﹣x2+5x=﹣[(x﹣1)2﹣1]=﹣(x﹣1)2+,即x=1时,S最大,为.综上所述,△ABC内部可截出面积最大的矩形DEFG,面积为.15.【解答】解:(1)∵抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上,∴点A坐标为(1,4),设抛物线的解析式为y=a(x﹣1)2+4,把C(3,0)代入抛物线的解析式,可得a(3﹣1)2+4=0,解得a=﹣1.故抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;(2)依题意有:OC=3,OE=4,∴CE===5,当∠QPC=90°时,∵cos∠QCP==,∴=,解得t=;当∠PQC=90°时,∵cos∠QCP==,∴=,解得t=.∴当t=或t=时,△PCQ为直角三角形;(3)∵A(1,4),C(3,0),设直线AC的解析式为y=kx+b,则,解得.故直线AC的解析式为y=﹣2x+6.∵P(1,4﹣t),将y=4﹣t代入y=﹣2x+6中,得x=1+,∴Q点的横坐标为1+,将x=1+代入y=﹣(x﹣1)2+4中,得y=4﹣.∴Q点的纵坐标为4﹣,∴QF=(4﹣)﹣(4﹣t)=t﹣,∴S△ACQ=S△AFQ+S△CFQ=FQ•AG+FQ•DG=FQ(AG+DG)=FQ•AD=×2(t﹣)=﹣+t=﹣(t2+4﹣4t﹣4)=﹣(t﹣2)2+1,∴当t=2时,△ACQ的面积最大,最大值是1.16.【解答】解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A和点B(1,0),与y 轴交于点C(0,3),其对称轴l为x=﹣1,∴A(﹣3,0),∴解得:,∴二次函数的解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,∴顶点坐标为(﹣1,4).(2)设点P(x,2)即y=﹣x2﹣2x+3=2,解得x1=﹣1或x2=﹣﹣1,∴点P(﹣1,2)或(﹣﹣1,2).(3)设点P(x,y),则y=﹣x2﹣2x+3,∵S四边形BCP A=S△OBC+S△OAP+S△OPC,∴=,∵﹣<0,∴当x=﹣时,四边形P ABC的面积有最大值,所以点P(﹣,).17.【解答】解:(1)设抛物线为y=a(x﹣4)2﹣1,∵抛物线经过点A(0,3),∴3=a(0﹣4)2﹣1,;∴抛物线为;(2)相交.证明:连接CE,则CE⊥BD,当时,x1=2,x2=6.A(0,3),B(2,0),C(6,0),对称轴x=4,∴OB=2,AB==,BC=4,∵AB⊥BD,∴∠OAB+∠OBA=90°,∠OBA+∠EBC=90°,∴△AOB∽△BEC,∴=,即=,解得CE=,∵>2,故抛物线的对称轴l与⊙C相交.(3)如图,过点P作平行于y轴的直线交AC于点Q;可求出AC的解析式为;设P点的坐标为(m,),则Q点的坐标为(m,);∴PQ=﹣m+3﹣(m2﹣2m+3)=﹣m2+m.∵S△P AC=S△P AQ+S△PCQ=×(﹣m2+m)×6=﹣(m﹣3)2+;∴当m=3时,△P AC的面积最大为;此时,P点的坐标为(3,).18.【解答】解:(1)∵B点的坐标为B(8,0),∴﹣16+8b+4=0,解得b=,∴抛物线的解析式为y═﹣+x+4,对称轴方程为x=﹣=3;(2)∵由(1)知,抛物线的对称轴方程为x=3,B(8,0)∴A(﹣2,0),C(0,4),∴OA=2,OC=4,OB=8,∴tan∠ACO=tan∠CBO=,∴∠ACO=∠CBO.∵∠AOC=∠COB=90°,∴△AOC∽△COB.(3)设BC解析式为y=kx+b,把(8,0),(0,4)分别代入解析式得,,解得,解得y=﹣x+4,作DH⊥x轴,交BC于H.设D(t,﹣t2+t+4),H(t,﹣t+4),S△BCD=DH•OB=×(﹣t2+t+4+t﹣4)×8=﹣t2+8t=﹣(t2﹣8t+42﹣16)=﹣(t﹣4)2+16,当t=4时,△DBC的最大面积为16,此时D点坐标为(4,6).19.【解答】解:(1)∵抛物线y=﹣x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,不妨设抛物线的解析式为y=﹣(x+4)(x﹣1),即y=﹣x2﹣x+2.∴C(0,2).(2)分两种情形:①当AN=AC时,如图1中,∵AC==2,∴n﹣(﹣4)=2,∴n=2﹣4.②当NA=NC时,如图2中,在Rt△NOC中,OC=2,∵NC=NA=n﹣(﹣4)=n+4,ON=n,∴n2+22=(n+)2,解得n=﹣.综上所述,当n=2﹣4或﹣时,△ANC是等腰三角形.(3)如图3中,由题意可知:直线BC的解析式为y=﹣2x+2,直线AC的解析式为y=x+2,设N(n,0),易知N在线段OB上时,△CDN的面积较小,不妨设n<0,∵ND∥BC,设ND的解析式为y=﹣2x+b,代入(n,0)可得b=2n,∴ND的解析式为y=﹣2x+2n,由,可得点D的纵坐标:y D=(8+2n),∴S△CDN=S△AOC﹣S△ADN﹣S△CON=[2×4﹣2|n|﹣(8+2n)(n+4)=﹣(n+)2+,∵﹣<0,∴当n=﹣时,△DCN的面积最大,最大值为.20.【解答】解:(1)∵抛物线y=ax2+bx+c经过点A(1,0)、点B(5,0)和点C(0,3),因为与y轴相较于点C,所以c=3.∴,解得,∴该抛物线对应的函数解析式为y=x2﹣x+3;(2)∵点P是抛物线上的动点且位于x轴下方,∴可设P(t,t2﹣t+3)(1<t<5),∵直线PM∥y轴,分别与x轴和直线CD交于点M、N,∴M(t,0),N(t,t+3),∴PN=t+3﹣(t2﹣t+3)=﹣(t﹣)2+直线CD与抛物线解析式可得,解得或,∴C(0,3),D(7,),分别过C、D作直线PN的垂线,垂足分别为E、F,如图1,则CE=t,DF=7﹣t,∴S△PCD=S△PCN+S△PDN=PN•CE+PN•DF=PN=[﹣(t﹣)2+]=﹣(t﹣)2+,∴当t=时,△PCD的面积有最大值,最大值为;(3)存在.∵∠CQN=∠PMB=90°,∴当△CNQ与△PBM相似时,有或两种情况,∵CQ⊥PM,垂足为Q,∴Q(t,3),且C(0,3),N(t,t+3),∴CQ=t,NQ=t+3﹣3=t,∴,∵P(t,t2﹣t+3),M(t,0),B(5,0),∴BM=5﹣t,PM=0﹣(t2﹣t+3)=﹣t2+t﹣3,当时,则PM=BM,即﹣t2+t﹣3=(5﹣t),解得t=2或t=5(舍去),此时P(2,﹣);当时,则BM=PM,即5﹣t=(﹣t2+t﹣3),解得t=或t=5(舍去),此时P(,﹣);综上可知存在满足条件的点P,其坐标为(2,﹣)或(,﹣).。
二次函数中求线段,线段和,面积等最值问题—备战2024年中考数学(全国通用)(解析版)

二次函数中求线段,线段和,面积等最值问题(压轴通关) 目录【中考预测】预测考向,总结常考点及应对的策略【误区点拨】点拨常见的易错点【抢分通关】精选名校模拟题,讲解通关策略(含新考法、新情境等)二次函数中求线段,线段和,面积等最值问题是全国中考的热点内容,更是全国中考的必考内容。
每年都有一些考生因为知识残缺、基础不牢、技能不熟、答欠规范等原因导致失分。
1.从考点频率看,二次函数的图象和性质是考查的基础,也是高频考点、必考点。
2.从题型角度看,以解答题的最后一题或最后第二题为主,分值12分左右,着实不少!题型一 二次函数中求线段的最值问题【例1】(2024·安徽滁州·一模)已知抛物线()22131y x n x n =−++++交x 轴于点()10A −,和点B ,交y 轴于点C .(1)求抛物线的函数解析式;(2)如图1,已知点P 是位于BC 上方的抛物线上的一点,作PM BC ⊥,垂足为M ,求线段PM 长度的最大值;(3)如图2,已知点Q 是第四象限抛物线上一点,45ACQ ∠=︒,求点Q 的坐标.【答案】(1)234y x x =−++;(2)PM 的最大值为(3)点Q 的坐标为143439⎛⎫− ⎪⎝⎭,.【分析】(1)将点()10A −,代入()22131y x n x n =−++++,求得1n =,即可得解;(2)求得点B 和C 的坐标,推出45OAB OBC ∠=∠=︒,作PF x ⊥轴于点F ,交BC 于点E ,得到PEM △是等腰直角三角形,2PM PE =,设()234P m m m −++,,求得PM 关于m 的二次函数,利用二次函数的性质求解即可;(3)作BG CQ ⊥轴于点G ,作GH x ⊥轴于点H ,求得BC =ACO GCB ∠=∠,利用正切函数的定义求得BG ,证明HBG 是等腰直角三角形,求得()31G −,,再求得直线CG 的解析式,据此求解即可.【详解】(1)解:∵抛物线()22131y x n x n =−++++交x 轴于点()10A −,, ∴()121310n n −−+++=,解得1n =,∴抛物线的函数解析式为234y x x =−++; (2)解:当0x =时,4y =;当0y =时,2340x x −++=,解得4x =或=1x −;∴()40B ,,()04C ,,∴4OA OB ==,∴45OCB OBC ∠=∠=︒,作PF x ⊥轴于点F ,交BC 于点E ,∴9045PEM BEF OBC ∠=∠=︒−∠=︒,∴PEM △是等腰直角三角形,∴PM =,设直线BC 的解析式为4y kx =+,把()40B ,代入得044k =+,解得1k =−,∴直线BC 的解析式为4y x =−+,设()234P m m m −++,,则()4E m m −+,,∴))223442PM PE m m m m ==−+++−=−+∵0>,∴PM 有最大值,最大值为(3)解:作BG CQ ⊥轴于点G ,作GH x ⊥轴于点H ,∵()10A −,,()40B ,,()04C ,,∴1OA =,4OB OC ==,BC =∵45ACQ ∠=︒,45OCB ∠=︒,∴ACO GCB ∠=∠,∴tan tan ACO GCB ∠=∠,即OA BG OC BC =,∴14=∴BG ,∵45OBC ∠=︒,∴45HBG ∠=︒,∴HBG 是等腰直角三角形,∴1BH GH ==,∴413OH =−=,∴()31G −,,同理直线CG 的解析式为543y x =−+, 联立得235434x x x =−+++−,解得0x =或143x =; 当143x =时,514344339y =−⨯+=−, ∴点Q 的坐标为143439⎛⎫− ⎪⎝⎭,.【例2】(2024·江苏淮安·二模)如图,在平而直角坐标系中,二次函数2y =+的图象与x 轴分别交于点,O A ,顶点为B .连接,OB AB ,将线段AB 绕点A 按顺时针方向旋转60︒得到线段AC ,连接BC .点,D E 分别在线段,OB BC 上,连接,,,AD DE EA DE 与AB 交于点,60F DEA ∠=︒.(1)求点A ,B 的坐标;(2)随着点E 在线段BC 上运动.①EDA ∠的大小是否发生变化?请说明理由;②线段BF 的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.【答案】(1)()20A ,,(B ;(2)①EDA ∠的大小不变,理由见解析;②线段BF 的长度存在最大值为12【分析】(1)0y =得20+=,解方程即可求得A 的坐标,把2y =+化为顶点式即可求得点B 的坐标;(2)①在AB 上取点M ,使得BM BE =,连接EM ,证明AED △是等边三角形即可得出结论;②证BDF OAD ∽,利用相似三角形的性质得BD BF OA OD =即22x BF x −=,解得()211122BF x =−−+进而利用二次函数的性质即可得解.【详解】(1)解:∵)221y x =+=−+∴顶点为(B ,令0y =,20+=,解得0x =或2x =,∴()20A ,;(2)解:①EDA ∠的大小不变,理由如下:在AB 上取点M ,使得BM BE =,连接EM ,∵)21y x =−∴抛物线对称轴为1x =,即1ON =,∵将线段AB 绕点A 按顺时针方向旋转60︒得到线段AC ,∴60BAC ∠=︒,AB AC =,∴BAC 是等边三角形,∴AB AC BC ==,60C ∠=︒,∵()20A ,,(B ,()00O ,,1ON =,∴2OA =,OB =2,AB =2=,∴OA OB AB ==,∴OAB 是等边三角形,2OA OB AC BC ====,∴60∠=∠=∠=︒OAB OBA AOB ,∵60MBE ∠=︒,BM BE =,∴BME 是等边三角形,∴60BME ABE ∠∠=︒=,ME BE BM ==,∴180120AME BME ∠∠=︒−=︒,BD EM ∥,∵120DBE ABO ABC ∠∠∠=+=︒,∴DBE AME ∠∠=,∵BD EM ∥,∴18012060FEM BED AEF MEA FEM ∠∠∠∠∠+=︒−︒=︒==+,∴BED MEA ∠∠=,∴BED MEA ≌,∴DE EA =,又60AED ∠=︒,∴AED △是等边三角形,∴60ADE ∠=︒,即ADE ∠的大小不变;②设OD x =,则2BD x =−,∵OAB 是等边三角形,60ADE ∠=︒,∴60DOA FBD ADE ∠∠∠===︒,∵BDA BDF ADE DOA OAD ∠∠∠∠∠=+=+,∴BDF OAD ∠∠=,∴BDF OAD ∽,∴BD BF OA OD =即22x BF x −=, ∴()211122BF x =−−+,∴当1x =时,BF 有最大值为12.【点睛】本题主要考查了二次函数的图像及性质,全等三角形的判定及性质,相似三角形的判定及性质以及等边三角形的判定及性质,题目综合性较强,熟练掌握各知识点是解题的关键.1.(2024·四川南充·一模)如图,已知抛物线2y x bx c =++与x 轴交于0()1,A -,B 两点,与y 轴交于点C (0,3)−.(1)求抛物线的解析式;(2)如图1,点P 是抛物线上位于第四象限内一动点,PD BC ⊥于点D ,求PD 的最大值及此时点P 的坐标;(3)如图2,点E 是抛物线的顶点,点M 是线段BE 上的动点(点M 不与B 重合),过点M 作MN x ⊥轴于N ,是否存在点M ,使CMN 为直角三角形?若存在,求出点M 的坐标;若不存在,请说明理由.【答案】(1)223y x x =−−(2)当32m =时,PD取得最大值为.此时315,24P ⎛⎫− ⎪⎝⎭ (3)CMN 为直角三角形时,点M 的坐标为:3,32⎛⎫− ⎪⎝⎭或()12【分析】(1)把点,A C 坐标代入函数的解析式,利用待定系数法求解即可;(2)先求线BC 的解析式,设点p 的横坐标为m ,再用m 的代数式表示PD 的长度建立二次函数求解即可;(3)先求直线BE 的解析式,再分三种情况,根据相似三角形的判定和性质求解即可.【详解】(1)由题意得103b c c −+=⎧⎨=−⎩,解得:23b c =−⎧⎨=−⎩.则抛物线的解析式为:223y x x =−−;(2)过点P 作PH x ⊥轴于点H ,交BC 于点G当0y =时,2230x x −−=,解得=1x −或3,∴(3,0)B设直线BC 的解析式为:1y kx b =+,则11303k b b +=⎧⎨=−⎩,解得:113k b =⎧⎨=−⎩∴3y x =−设点()2,23P m m m −−(03m <<),则3G m m −(,), ∴()()223233PG m m m m m =−−−−=−, ∵OB OC =,∴45OBC OCB ∠=∠=︒,∴45BGH ∠=︒∴45PGD BGH ∠=∠=︒,∴PD =.)22332228PD m m m ⎫=−+=−−+⎪⎝⎭ ∴当32m =时,PD取得最大值为8.此时315,24P ⎛⎫− ⎪⎝⎭. (3)在EB 上存在点M ,使CMN 为直角三角形.抛物线顶点(1,4)E −,设直线BE 的解析式为:22y k x b =+,则2222430k b k b +=−⎧⎨+=⎩,解得:2226k b =⎧⎨=−⎩,∴26y x =−.设26M n n −(,)13n ≤<(),①∵90CNM ONC ∠=︒−∠,∴90CNM ∠<︒,不可能为直角;②当90CMN ∠=︒时,则90CMN MNB ∠=∠=︒ ∴//MC x 轴,则263n −=−,∴32n =,∴3,32M ⎛⎫− ⎪⎝⎭. ③当90MCN ∠=︒时,过点M 作MF y ⊥轴于点F .∵90MCF NCO ∠+∠=︒,90CNO NCO ∠+∠=︒,∴MCF CNO ∠=∠,又90MFC CON ∠=∠=︒,∴MFC CON ∽, ∴CF MF NO CO =, ∴()3263n nn −−−=,∴2690n n +−=,解得:123,3n n ==−.∵13n ≤<,∴23n =−不合题意,应舍去,∴3n =∴()12M综上所述,CMN 为直角三角形时,点M 的坐标为:3,32⎛⎫− ⎪⎝⎭或()12.【点睛】本题考查用待定系数法求二次函数的解析式,构造二次函数求线段的最值,二次函数与直角三角形的存在性问题,相似三角形的判定和性质,难度较大,是中考的压轴题,解题的关键是数形结合,提高综合运用的能力.2.(23-24九年级下·江苏宿迁·阶段练习)如图,在平面直角坐标系中抛物线214y x bx c =++与x 轴交于点A ,B ,与y 轴交于点C ,其中()3,0B ,()0,3C −.(1)求该抛物线的表达式;(2)点P 是直线AC 下方抛物线上一动点,过点P 作PD AC ⊥于点D ,求PD 的最大值及此时点P 的坐标;(3)在(2)的条件下,将该抛物线向右平移5个单位,点E 为点P 的对应点,平移后的抛物线与y 轴交于点F ,Q 为平移后的抛物线的对称轴上任意一点.求出所有使得以QF 为腰的QEF △是等腰三角形的点Q 的坐标.【答案】(1)211344y x x =+−;(2)PD 的最大值为45,此时点52,2P ⎛⎫−− ⎪⎝⎭; (3)Q 点的坐标为9,12⎛⎫− ⎪⎝⎭或9,52⎛⎫ ⎪⎝⎭或97,24⎛⎫ ⎪⎝⎭.【分析】(1)待定系数法求二次函数解析式即可求解;(2)直线AC 的解析式为334y x =−−,过点P 作PE x ⊥轴于点E ,交AC 于点Q ,设211,344P t t t ⎛⎫+− ⎪⎝⎭,则3,34Q t t ⎛⎫−− ⎪⎝⎭,则45PD PQ =,进而根据二次函数的性质即可求解;(3)根据平移的性质得出219494216y x ⎛⎫=−− ⎪⎝⎭,对称轴为直线92x =,点52,2P ⎛⎫−− ⎪⎝⎭向右平移5个单位得到53,2E ⎛⎫− ⎪⎝⎭,()0,2F ,勾股定理分别表示出2EF ,2QE ,2QF 进而分类讨论即可求解. 【详解】(1)解:将点()3,0B ,()0,3C −,代入214y x bx c =++得,2133043b c c ⎧⨯++=⎪⎨⎪=−⎩,解得:143b c ⎧=⎪⎨⎪=−⎩,∴抛物线解析式为:211344y x x =+−; (2)∵211344y x x =+−与x 轴交于点A ,B ,当0y =时,2113044x x +−=,解得:124,3x x =−=, ∴()4,0A −, ∵()0,3C −, 设直线AC 的解析式为3y kx =−,∴430k −−=, 解得:34k =−,∴直线AC 的解析式为334y x =−−,如图所示,过点P 作PE x ⊥轴于点E ,交AC 于点Q ,设211,344P t t t ⎛⎫+− ⎪⎝⎭,则3,34Q t t ⎛⎫−− ⎪⎝⎭, ∴223111334444PQ t t t t t ⎛⎫=−−−+−=−− ⎪⎝⎭,∵AQE PQD ∠=∠,90AEQ QDP ∠=∠=︒,∴OAC QPD ∠=∠,∵4,3OA OC ==,∴5AC =, ∴4cos cos =5PD AO QPD OAC PQ AC ∠==∠=, ∴()222441141425545555PD PQ t t t t t ⎛⎫==−−=−−=−++ ⎪⎝⎭, ∴当2t =−时,PD 取得最大值为45,()()2211115322344442t t +−=⨯−+⨯−−=−, ∴52,2P ⎛⎫−− ⎪⎝⎭; (3)∵抛物线211344y x x =+−211494216x ⎛⎫=+− ⎪⎝⎭, 将该抛物线向右平移5个单位,得到219494216y x ⎛⎫=−− ⎪⎝⎭,对称轴为直线92x =, 点52,2P ⎛⎫−− ⎪⎝⎭向右平移5个单位得到53,2E ⎛⎫− ⎪⎝⎭, ∵平移后的抛物线与y 轴交于点F ,令0x =,则2194924216y ⎛⎫=⨯−= ⎪⎝⎭, ∴()0,2F , ∴22251173224EF ⎛⎫=++= ⎪⎝⎭, ∵Q 为平移后的抛物线的对称轴上任意一点,则Q 点的横坐标为92, 设9,2Q m ⎛⎫ ⎪⎝⎭,∴22295322QE m ⎛⎫⎛⎫=−++ ⎪ ⎪⎝⎭⎝⎭,()222922QF m ⎛⎫=+− ⎪⎝⎭, 当QF EF =时,()229117224m ⎛⎫+−= ⎪⎝⎭, 解得:1m =−或5m =,当QE QF =时,()222295932222m m ⎛⎫⎛⎫⎛⎫−++=+− ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 解得:74m =, 综上所述,Q 点的坐标为9,12⎛⎫− ⎪⎝⎭或9,52⎛⎫ ⎪⎝⎭或97,24⎛⎫ ⎪⎝⎭. 【点睛】本题考查了二次函数综合问题,解直角三角形,待定系数法求解析式,二次函数的平移,线段周长问题,特殊三角形问题,熟练掌握二次函数的性质是解题的关键.3.(2024·山西阳泉·一模)综合与探究 如图,二次函数213442y x x =−−的图象与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,对称轴与x 轴交于点D ,连接AC ,作直线BC .(1)求A ,B ,C 三点的坐标,并直接写出直线BC 的表达式;(2)如图1,若点P 是第四象限内二次函数图象上的一个动点,其横坐标为m ,过点P 分别作x 轴、y 轴的垂线,交直线BC 于点M ,N ,试探究线段MN 长的最大值;(3)如图2,若点Q 是二次函数图象上的一个动点,直线BQ 与y 轴交于点H ,连接CD ,在点Q 运动的过程中,是否存在点H ,使以H ,C ,B 为顶点的三角形与ACD 相似?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.【答案】(1)()20A −,,()80B ,,()04C −,,直线BC 的表达式为1y x 42=−;(2)线段MN长的最大值为(3)点Q 的坐标为3954⎛⎫− ⎪⎝⎭,或()46−,.【分析】(1)令0y =,求得x 的值,令0x =,求得y 的值,可求得A ,B ,C 三点的坐标,利用待定系数法即可求得直线BC 的表达式;(2)设213442P m m m ⎛⎫−− ⎪⎝⎭,,则142M m m ⎛⎫− ⎪⎝⎭,,证明PNM OBC ∠=∠,利用正切函数的定义推出2PN PM =,求得MN ,得到MN 关于m 的二次函数,利用二次函数的性质求解即可;(3)利用勾股定理求得AC =,5AD OC ==,作DG AC ⊥于点G ,用正切函数的定义推出OCA BCH ∠=∠,分BC BH =和BH CH =两种情况讨论,分别求得点H 的坐标,求得直线BH 的表达式,与二次函数的表达式联立求解即可.【详解】(1)解:令0y =,则2134042x x −−=,解得12x =−,28x =,令0x =,则4y =−,∴()20A −,,()80B ,,()04C −,,设直线BC 的表达式为4y kx =−,代入()80B ,得084k =−,解得12k =, ∴直线BC 的表达式为1y x 42=−; (2)解:∵()20A −,,()80B ,,()04C −,,∴2OA =,8OB =,4OC =, 设213442P m m m ⎛⎫−− ⎪⎝⎭,,则142M m m ⎛⎫− ⎪⎝⎭,,2211314422424PM m m m m m ⎛⎫=−−−−=−+ ⎪⎝⎭,∵PN OB ∥,PM OC ∥,∴PNM OBC ∠=∠, ∴41tan tan 82OC PNM OBC OB ∠=∠===,∴2PN PM =,MN ,∴)221244MN m m m ⎫=−+=−+⎪⎭∵0<,∴当4m =时,线段MN 长的最大值为 (3)解:∵()20A −,,()80B ,,()04C −,, ∴对称轴为直线2832x −+==, ∴()30D ,,∴()325AD =−−=,5CD ==,AC == ∴5AD DC ==,作DG AC ⊥于点G ,∴12AG CG AC ===∴DG == ∴tan 2DG DCA CG ∠==, ∵tan 2OB BCO OC ∠==,∴DCA BCH ∠=∠,以H ,C ,B 为顶点的三角形与ACD 相似,则分BC BH =和BH CH =两种情况讨论,①当BC BH =时,∵BO CH ⊥,∴OH OC =,∴()04H ,,同理求得直线BH 的表达式为142y x =−+, 联立得241234412x x x −−−+=,解得14x =−,28x =(舍去),()14462y =−⨯−+=,∴点Q 的坐标为()46−,;①当BH CH =时,设()0H t ,,则2264BH t =+,()2224816CH t t t =+=++,∴2264816t t t +=++,解得6t =,∴()06H ,,同理求得直线BH 的表达式为364y x =−+, 联立得261434432x x x −−−+=,解得15x =−,28x =(舍去),()3395644y =−⨯−+=,∴点Q 的坐标为3954⎛⎫− ⎪⎝⎭,; 综上,点Q 的坐标为3954⎛⎫− ⎪⎝⎭,或()46−,.【点睛】本题是二次函数的综合题,考查了待定系数法求一次函数的解析式,点的坐标表示三角形的面积,勾股定理,正切函数,解方程,熟练掌握待定系数法,勾股定理,正切函数是解题的关键.题型二 将军饮马河求二次函数中线段和最值问题【例1】(2024·天津津南·一模)综合与探究:如图,抛物线2y x bx c =−++上的点A ,C 坐标分别为()0,2,()4,0,抛物线与x 轴负半轴交于点B ,且2OM =,连接AC ,CM .(1)求点M 的坐标及抛物线的解析式;(2)点P 是抛物线位于第一象限图象上的动点,连接AP ,CP ,当PAC ACM S S =△△时,求点P 的坐标;(3)将抛物线沿x 轴的负方向平移得到新抛物线,点A 的对应点为点A ',点C 的对应点为点C ',当MA MC ''+的值最小时,新抛物线的顶点坐标为 ,MA MC ''+的最小值为 .【答案】(1)()0,2M −,2722y x x =−++ (2)()2,5P(3)1181,1216⎛⎫− ⎪⎝⎭,【分析】(1)根据点M 在y 轴负半轴且2OM =可得点M 的坐标为()0,2M −,利用待定系数法可得抛物线的解析式为2722y x x =−++;(2)过点P 作PF x ⊥轴于点F ,交线段AC 于点E ,用待定系数法求得直线AC 的解析式为122y x =−+,设点P 的横坐标为()04p p <<,则27,22P p p p ⎛⎫−++ ⎪⎝⎭,1,22E p p ⎛⎫−+ ⎪⎝⎭,故24(04)PE p p p =−+<<,先求得8ACM S =△,从而得到212882PAC S PE OC p p =⋅=−+=△,解出p 的值,从而得出点P 的坐标;(3)设抛物线沿x 轴的负方向平移m 个单位长度得到新抛物线,将点M 右平移m 个单位长度得到点M ',由平移的性质可知,,MA M A MC M C ''''==,MA MC ''+的值最小就是M A M C ''+最小值,作出点C 关于直线=2y −对称的对称点C '',连接AC ''交直线=2y −于点M ',连接M C '则此时M A M C ''+取得最小值,即为AC ''的长度,利用两点间的距离公式求这个长度,用待定系数法求出直线AC ''的解析式,从而确定M '的坐标,继而确定平移距离,将原抛物线的解析式化为顶点式,从而得到其顶点,继而确定新抛物线的顶点.【详解】(1)解:∵点M 在y 轴负半轴且2OM =,∴()0,2M −将()0,2A ,()4,0C 代入2y x bx c =−++,得:21640c b c =⎧⎨−++=⎩,解得722b c ⎧=⎪⎨⎪=⎩∴抛物线的解析式为2722y x x =−++(2)解:过点P 作PF x ⊥轴于点F ,交线段AC 于点E ,设直线AC 的解析式为()0y kx m k =+≠,将()0,2A ,()4,0C 代入y kx m =+,得:240m k m =⎧⎨+=⎩,解得122k m ⎧=−⎪⎨⎪=⎩,∴直线AC 的解析式为122y x =−+ 设点P 的横坐标为()04p p << 则27,22P p p p ⎛⎫−++ ⎪⎝⎭,1,22E p p ⎛⎫−+ ⎪⎝⎭, ∴2271224(04)22PE p p p p p p ⎛⎫=−++−−+=−+<< ⎪⎝⎭∵8ACM S =△,∴212882PAC S PE OC p p =⋅=−+=△,解得122p p ==, ∴()2,5P ;(3)1181,1216⎛⎫− ⎪⎝⎭,补充求解过程如下:设抛物线沿x 轴的负方向平移m 个单位长度得到新抛物线,将点M 向右平移m 个单位长度得到点M ',作出图形如下:由平移的性质可知,,MA M A MC M C ''''==,∴MA MC ''+的值最小就是M A M C ''+最小值, 显然点M '在直线=2y −上运用,作出点C 关于直线=2y −对称的对称点C '',连接AC ''交直线=2y −于点M ',连接M C '则此时M A M C ''+取得最小值,即为AC ''的长度,∵点C 关于直线=2y −C '',()4,0C ∴()4,4C ''−,∴()()min min MA MC M A M C AC ''''''+=+== 设直线AC ''的解析式是:11y k x b =+将点()0,2A ,()4,4C ''−代入得:111244b k b =⎧⎨+=−⎩,解得:11322k b ⎧=−⎪⎨⎪=⎩直线AC ''的解析式是:322y x =−+令3222y x =−+=−,解得:83x =, ∴8,23M ⎛⎫'− ⎪⎝⎭,∴平移的距离是83m = 又∵22778122416y x x x ⎛⎫=−++=−−+ ⎪⎝⎭, ∴平移前的抛物线的坐标是781416,⎛⎫ ⎪⎝⎭∴新抛物线的顶点坐标为7881,4316⎛⎫− ⎪⎝⎭即1181,1216⎛⎫− ⎪⎝⎭ 故答案是:1181,1216⎛⎫− ⎪⎝⎭,【例2】(2024·江苏宿迁·模拟预测)如图1,抛物线2y x bx =−+与x 轴交于点A ,与直线y x =−交于点()4,4B −,点()0,4C −在y 轴上.点P 从点B 出发,沿线段BO 方向匀速运动,运动到点O 时停止.(1)求抛物线2y x bx =−+的表达式;(2)当BP =1中过点P 作PD OA ⊥交抛物线于点D ,连接PC OD ,,判断四边形OCPD 的形状,并说明理由;(3)如图2,点P 从点B 开始运动时,点Q 从点O 同时出发,以与点P 相同的速度沿x 轴正方向匀速运动,点P 停止运动时点Q 也停止运动.连接BQ PC ,,求CP BQ +的最小值.【答案】(1)抛物线的表达式为23y x x =−+ (2)平行四边形,见解析(3)【分析】(1)利用待定系数法将B 点坐标代入抛物线2y x bx =−+中,即可求解.(2)作辅助线,根据题意,求出PD 的长,PD OC =,PD OC ∥,利用一组对边平行且相等的四边形是平行四边形即可得证.(3)作出图,证明()SAS CBP MOQ ≌,CP BQ +的最小值为MB ,根据勾股定理求出MB 即可解答. 【详解】(1)解: 抛物线2y x bx =−+过点(4,4)B −,1644b ∴−+=−,3b ∴=,23y x x ∴=−+.即抛物线的表达式为23y x x =−+. (2)解:四边形OCPD 是平行四边形,理由如下:如图1,作PD OA ⊥交x 轴于点H ,连接PC 、OD ,点P 在y x =−上,OH PH ∴=,45POH ∠=︒,连接BC ,4OC BC ==,OB ∴= 2BP =OP OB BP ∴=−=2OH PH ∴===,当2D x =时,4322D DH y ==−+⨯=,224PD DH PH ∴=+=+=, (0,4)C −,4OC ∴=,PD OC ∴=,OC x ⊥Q 轴,PD x ⊥轴,PD OC ∴∥,∴四边形OCPD 是平行四边形.(3)如图2,由题意得,BP OQ =,连接BC ,在OA 上方作OMQ ,使得45MOQ ∠=︒,OM BC =,4OC BC ==,BC OC ⊥,45CBP ∴∠=︒,CBP MOQ ∴∠=∠,BP OQ =,CBP MOQ ∠=∠,BC OM ,(SAS)CBP MOQ ∴△≌△,CP MQ ∴=,CP BQ MQ BQ MB ∴+=+≥(当M ,Q ,B 三点共线时最短),CP BQ ∴+的最小值为MB ,454590MOB MOQ BOQ ∠=∠+∠=︒+︒=︒,MB ∴即CP BQ +的最小值为答:CP BQ +的最小值为【点睛】本题主要考查待定系数法,二次函数图象与性质,平等四边形的判定,全等三角形的判定与性质以及勾股定理等知识,正确作出辅助线是解答醒的关键.1.(2024·宁夏银川·一模)如图,已经抛物线经过点()00O ,,()55A ,,且它的对称轴为2x =.(1)求此抛物线的解析式;(2)若点B 是抛物线对称轴上的一点,且点B 在第一象限,当OAB 的面积为15时;求点B 的坐标.(3)在(2)的条件下,P 是抛物线上的动点,求P 的坐标以及PA PB −的最大值.【答案】(1)24.y x x =- (2)()2,8B (3)()2,12,P - PA PB −的最大值为【分析】(1)根据题意可设抛物线为2,y ax bx =+再利用待定系数法求解抛物线的解析式即可; (2)设()2,,B y 且0,y > 记OA 与对称轴的交点为Q ,设直线OA 为:,y kx = 解得:1,k = 可得直线OA 为:,y x = 则()2,2,Q 利用()12OAB BOQ ABQ A O S S S BQ x x =+=⨯⨯−列方程,再解方程即可;(3)如图,连接AB ,延长AB 交抛物线于P ,则此时PA PB AB −=最大,由勾股定理可得最小值,再利用待定系数法求解AB 的解析式,联立一次函数与二次函数的解析式,解方程组可得P 的坐标.【详解】(1)解: 抛物线经过点(0,0)O ,∴设抛物线为:2,y ax bx =+抛物线过(5,5)A ,且它的对称轴为2x =.2555,22a b b a +=⎧⎪∴⎨−=⎪⎩ 解得:1,4a b =⎧⎨=−⎩∴抛物线为:24.y x x =-(2)解:如图,点B 是抛物线对称轴上的一点,且点B 在第一象限,设()2,,B y 且0,y > 记OA 与对称轴的交点为Q ,设直线OA 为:,y kx =55,k \= 解得:1,k =∴ 直线OA 为:,y x =()2,2,Q ∴ ()12OAB BOQ ABQ A O SS S BQ x x ∴=+=⨯⨯− 12515,2y =−⨯=解得:8y =或4,y =−∵0,y > 则8,y =()2,8.B ∴(3)如图,连接AB ,延长AB 交抛物线于P ,则此时PA PB AB −=最大,()()5,5,2,8,A BAB ∴=设AB 为:,y k x b ''=+ 代入A 、B 两点坐标,55,28k b k b '''+=⎧∴⎨+=⎩' ,解得:1,10k b =−⎧⎨='⎩'∴AB 为:10,y x =-+210,4y x y x x =−+⎧∴⎨=−⎩ 解得:52,,512x x y y ==−⎧⎧⎨⎨==⎩⎩()2,12.P ∴−【点睛】本题考查的是利用待定系数法求解二次函数的解析式,坐标与图形面积,三角形三边关系的应用,勾股定理的应用,确定PA PB −最大时P 的位置是解本题的关键.2.(2024·湖南怀化·一模)如图1,在平面直角坐标系中,抛物线2y x bx c =−++与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,5OB OC ==,顶点为D ,对称轴交x 轴于点E .图1 图2 图3(1)求抛物线的解析式、对称轴及顶点D 的坐标;(2)如图2,点Q 为抛物线对称轴上一动点,当Q 在什么位置时QA QC +最小,求出Q 点的坐标,并求出此时QAC △的周长;(3)如图3,在对称轴左侧的抛物线上有一点M ,在对称轴右侧的抛物线上有一点N ,满足90MDN ∠=︒.求证:直线MN 恒过定点,并求出定点坐标.【答案】(1)245y x x =−++,对称轴为直线2x =,顶点D 的坐标为()29,;(2)QAC △(3)直线MN 恒过定点,定点坐标为()28,.【分析】(1)求得点B 的坐标为()50,,点C 的坐标为()05,,利用待定系数法求解,再配成顶点式,即可得解;(2)先求得直线BC 的解析式,再求直线BC 与对称轴交点Q ,将AQ CQ +转化为BC ,在Rt AOC 中求AC ,在Rt BOC 中求BC 即可求解;(3)如图,过点D 作直线l 垂直y 轴,再过点M ,N 分别作直线l 的垂线,设点M 的坐标为()245m m m −++,,点N 的坐标为()245n n n −++,,证明MDH DNG ∽△△,求得()250mn m n −++=,再利用待定系数法求得直线MN 的解析式为()45y m n x mn =−−+++,据此求解即可. 【详解】(1)解:∵5OB OC ==,∴点B 的坐标为()50,,点C 的坐标为()05,,∴25505b c c −++=⎧⎨=⎩,解得4b =,∴抛物线的解析式为245y x x =−++, ∵()224529y x x x =−++=−−+,∴对称轴为直线2x =,顶点D 的坐标为()29,; (2)解:∵点A 与点()50B ,关于直线2x =对称,∴直线BC 与对称轴的交点为Q ,则Q 为QA QC +最小时位置,设直线BC 的解析式为5y kx =+,代入点()50B ,得055k =+,解得1k =−,∴直线BC 的解析式为5y x =−+,当2x =,253y =−+=,∴()23Q ,,∵点()10A −,,∵ACAQ CQ CB +===∴QAC △(3)解:如图,过点D 作直线l 垂直y 轴,再过点M ,N 分别作直线l 的垂线,垂足分别为H ,G ,设点M 的坐标为()245m m m −++,,点N 的坐标为()245n n n −++,,∵顶点D 的坐标为()29,, ∴()()222945442MH m m m m m =−−++=−+=−,2DH m =−,()()222945442GN n n n n n =−−++=−+=−,2DG n =−,由题意得90H G MDN ∠=∠=∠=︒,∴90MDH NDG DNG ∠=︒−∠=∠, ∴MDH DNG ∽△△, ∴MH HD DG NG =,即()()222222m mn n −−=−−,∴()()221m n −−=−, ∴()250mn m n −++=,∵点M 的坐标为()245m m m −++,,点N 的坐标为()245n n n −++,,设直线MN 的解析式为11y k x b =+,∴2112114545mk b m m nk b n n ⎧+=−++⎨+=−++⎩①②,−①②得()()()2214m n k m n m n −=−−+−, ∵m n ≠,∴14k m n =−−+,将14k m n =−−+代入①得()21445m m n b m m −−++=−++,求得15b mn =+;∴直线MN 的解析式为()45y m n x mn =−−+++, ∵()250mn m n −++=,即()25m n mn +=+, ∴()()428y m n x =−−+−+, ∴当20x −=即2x =时,8y =,∴无论m n 、为何值,直线MN 总会经过定点()28,, ∴直线MN 恒过定点,定点坐标为()28,.【点睛】本题考查了二次函数的综合运用.考查了待定系数法求函数解析式,相似三角形的判定和性质,熟练掌握二次函数的图象与性质、轴对称的性质,添加适当的辅助线,是解题的关键.3.(2024·安徽池州·二模)如图,抛物线2Ly ax bx c =++∶与x 正半轴交于点(3,0)A ,与y 轴交于点(0,3)B ,对称轴为直线1x =.(1)求直线AB 的解析式及抛物线的解析式;(2)如图①,点P 为第一象限抛物线上一动点,过点P 作PC x ⊥轴,垂足为C ,PC 交AB 于点D ,求当点P 的横坐标为多少时,PD AD +最大;(3)如图②,将抛物线2Ly ax bx c =++∶向左平移得到抛物线L ',直线AB 与抛物线L '交于M 、N 两点,若点B 是线段MN 的中点,求抛物线'L 的解析式.【答案】(1)3y x =−+,223y x x =−++;(2)点P 的横坐标为时,PD AD +有最大值; (3)2154y x x =−−+.【分析】(1)利用待定系数法解答即可求解;(2)设点P 的横坐标为t ,则()2,23P t t t −++,(,0)C t ,(,3)D t t −+,先证明ACD 为等腰直角三角形,得到)AD t =−,进而得到2PD AD t ⎛+=−+ ⎝⎭,根据二次函数的性质即可求解;(3)设平移后抛物线L '的解析式2()4y x m =−−+,联立函数解析式得23()4x x m −+=−−+,整理得,22(21)10x m x m −++−=,设()11,M x y ,()22,N x y ,则1x ,2x 是方程22(21)10x m x m −++−=的两根,由B 为MN 的中点可得210m +=,求出m 即可求解;本题考查了二次函数与一次函数的交点问题,待定系数法求函数解析式,二次函数的性质,二次函数图象的平移,掌握二次函数的图象和性质是解题的关键.【详解】(1)解:抛物线2L y ax bx c =++∶与x 正半轴交于点(3,0)A ,与y 轴交于点(0,3)B ,对称轴为直线1x =,930312a b c c b a ⎧⎪++=⎪∴=⎨⎪⎪−=⎩,解得123a b c =−⎧⎪=⎨⎪=⎩,∴抛物线L 的解析式为223y x x =−++;设直线AB 的解析式为3(0)y kx k =+≠,把(3,0)A 代入得,330k +=,解得1k =−,∴直线AB 的解析式为3y x =−+;(2)解:设点P 的横坐标为t ,则()2,23P t t t −++,(,0)C t ,(,3)D t t −+, 3AC t ∴=−,23PD t t =−+,(3,0)A ,(0,3)B −,3OA OB ∴==,AOB ∴为等腰直角三角形,45OAB ∴∠=︒,PC x ⊥轴, ACD ∴为等腰直角三角形,)AD t ∴==−,∴223PD AD t t t ⎛+=−++=− ⎝⎭,∴当t =时,PD AD +有最大值,即点P的横坐标为32时,PD AD +有最大值;(3)解:由(1)可知,直线AB 的解析式为3y x =−+,抛物线L 为:2223(1)4y x x x =−++=−−+,∴设平移后抛物线L '的解析式2()4y x m =−−+,联立函数解析式得,()234y x y x m =−+⎧⎪⎨=−−+⎪⎩,23()4x x m ∴−+=−−+,整理得,22(21)10x m x m −++−=, 设()11,M x y ,()22,N x y ,则1x ,2x 是方程22(21)10x m x m −++−=的两根,1221x x m ∴+=+,∵B 为MN 的中点,∴120x x +=,∴210m +=, 解得12m =−,∴抛物线L '的解析式22115424y x x x ⎛⎫=−++=−−+ ⎪⎝⎭.题型三 胡不归求二次函数中线段和最值问题【例1】(新考法,拓视野)(2024·陕西西安·三模)已知抛物线2(,,y ax bx c a b c =++为常数,0)a ≠与x 轴交于点()A −、点B 两点,与y 轴交于点()0,2C,对称轴为x =(1)求抛物线的表达式;(2)M 是抛物线上的点且在第二象限,过M 作MN AC ⊥于点N,求AN 的最大值.【答案】(1)22y x =−+(2)496【分析】(1)用待定系数法求解即可;(2)过点M 作MF y ∥轴,交AC 于点E ,先求出一次函数AC 的解析式,用解直角三角形的方法求出30OAC ∠=︒,表示出MN =,设2,2M m m ⎛⎫−+ ⎪⎝⎭,2E m ⎛⎫+ ⎪ ⎪⎝⎭,分别表示出EF ME AE MN ,,,,最后得到249=26AN m ⎛−+ ⎝⎭,求出最后结果即可.【详解】(1)解:点()A −,对称轴为x =(2a c ∴−−+=,2c =,2b a −=解得:1a =−,b = ∴抛物线的表达式为:22y x =−+;(2)如图,过点M 作MF y ∥轴,交AC 于点E ,设AC 的解析式为y kx b =+,02b b ⎧−+=⎪∴⎨=⎪⎩,2k b ⎧=⎪⎨⎪=⎩,∴AC的解析式为2y =+,2AO =2CO =,tan CO OAC AO ∴∠==,30OAC ∴∠=︒,90AFE MNE ∠=︒=∠,AEF MEN ∠=∠, 30M OAC ∴∠=∠=︒,2AE EF ∴=,12EN ME =,sin MN ME ACO ∴=⋅∠=,设2,2M m m ⎛⎫−+ ⎪⎝⎭,2E m ⎛⎫+ ⎪ ⎪⎝⎭,2EF ∴=+,2222ME m m ∴=−+−=−−,24AE EF ∴==+,21122EN ME m ==−,23MN m==−,AN ∴,AE EN=+2213422m m =+−−−224m =−+24926m ⎛=−++ ⎝⎭,20−<,∴当m =时,AN 的最大值为496.【例2】(2024·浙江·一模)如图,在平面直角坐标系中,抛物线24y ax bx =++交y 轴于点A ,交x 轴于点()6,0B −和点()2,0C ,连接AB 、AQ 、BQ ,BQ 与y 轴交于点N .(1)求抛物线表达式;(2)点713Q ⎛⎫⎪⎝⎭,,点M 在x 轴上,点E 在平面内,BME AOM ≌,且四边形ANEM 是平行四边形.①求点E 的坐标;②设射线AM 与BN 相交于点P ,交BE 于点H ,将BPH 绕点B 旋转一周,旋转后的三角形记为11BPH △,求11BP 的最小值. 【答案】(1)214433y x x =−−+(2)①()2,2E −−;②【分析】(1)将点B 、C 的坐标代入抛物线,利用待定系数法求得解析式;(2)①由Q 坐标求出BQ 解析式,然后根据四边形ANEM 是平行四边形和BME AOM ≌得出4BM OA ==,再分类讨论求得M 和E 的坐标;②求出AM 解析式,交点为P ,再求出H 坐标,然后由两点间距离公式求出BP 和BH 长度,因为旋转不改变长度,所以1BP长度不变,当H 旋转到x 轴上时,此时1OH 最短,所以此时1OH 等于BO BH −,然后代入计算即可.【详解】(1)解:①抛物线24y ax bx =++交y 轴于点A ,交x 轴于点()6,0B −和点()2,0C , ∴366404240a b a b −+=⎧⎨++=⎩,解得:1343a b ⎧=−⎪⎪⎨⎪=−⎪⎩ ∴214433y x x =−−+;(2)解:214433y x x =−−+4∴=OA ,设直线BQ 的解析式为1y kx b =+, ()6,0B −,713Q ⎛⎫ ⎪⎝⎭,∴117360k b k b ⎧+=⎪⎨⎪−+=⎩,解得1132k b ⎧=⎪⎨⎪=⎩,∴直线BQ 的解析式为123=+y x ,N Q 为BQ 与y 轴交点, ()0,2N ∴,2AN ∴=,四边形ANEM 是平行四边形,∴AN EM ∥且2EM AN ==,且点E 在点M 下方, 点M 在x 轴上,点E 在平面内,BME AOM ≌,4BM OA ∴==, ()6,0B −, ()2,0M ∴−或()10,0−,若M 为()2,0−,90BME AOM ∠=∠=︒,故()2,2E −−, 若M 为()10,0−,2OM ME ==,此时10OM =,(矛盾,舍去),综上,点E 的坐标为()2,2−−;②如图,设AM 的解析式为,y kx b =+抛物线24y ax bx =++交y 轴于点A ,∴点A 的坐标为(0,4),将点()0,4A 、()2,0M −的坐标代入y kx b =+得:420b k b =⎧⎨−+=⎩,解得24k b =⎧⎨=⎩,AM ∴的解析式为24y x =+,AM 与BQ 相交于点P ,∴24123y x y x =+⎧⎪⎨=+⎪⎩,解得6585x y ⎧=−⎪⎪⎨⎪=⎪⎩, 所以点P 的坐标为68,55⎛⎫− ⎪⎝⎭,设直线BE 的解析式为y mx n =+,将点B 、E 的坐标代入直线BE 的解析式得:2260m n m n −+=−⎧⎨−+=⎩,解得123m n ⎧=−⎪⎨⎪=−⎩, 所以直线BE 的解析式为132y x =−−,BE 与AM 相交于点H ,∴24132y x y x =+⎧⎪⎨=−−⎪⎩,解得14585x y ⎧=−⎪⎪⎨⎪=−⎪⎩, ∴点H 的坐标为148,55⎛⎫−− ⎪⎝⎭,BP ∴==BH ==1BP ∴当H 旋转到x 轴上时,此时1OH 最短,∴16OH BO BH =−=116BP ∴==⎭∴11BP的最小值为1.(2024·河南洛阳·一模)在平面直角坐标系中,抛物线212y x bx c =−++交x 轴于()4,0A 、B 两点,交y 轴于点()0,4C .(1)求抛物线表达式中的b 、c ;(2)点P 是直数AC 上方抛物线上的一动点,过点F 作PF y 轴交AC 于点E ,作PE AC ∥交x 轴于点F ,求PE 的最大值及此时点P 的坐标; (3)将该抛物线沿射线CA方向平移1y ,请直接写出新抛物线1y 的表达式______.【答案】(1)1b =,4c =(2)PE 取得最大值为254,此时335,28P ⎛⎫ ⎪⎝⎭.(3)()2115322y x =−−+【分析】本题考查了二次函数的综合,待定系数法求函数解析式: (1)利用待定系数法即可求解;(2)延长PE 交x 轴于H ,根据题意求得直线AC 的解析式为4y x =−+,OC OA =,设点()21,4042P p p p p ⎛⎫−++<< ⎪⎝⎭,则(),4E p p −+,(),0H p ,证得PHF是等腰直角三角形,从而求得232524PE PE PH p ⎛⎫=+=−−+⎪⎝⎭,即可求解; (3)先求得CA =,根据1y 由抛物线()2211941222y x x x =−++=−−+,向右和向下分别平移2个单位长度得到,进而可求解;掌握待定系数法求函数解析式及利用数学结合是解题的关键.【详解】(1)解:抛物线212y x bx c =−++交于()4,0A 和()0,4C ,8404b c c −++=⎧∴⎨=⎩,解得:14b c =⎧⎨=⎩. (2)延长PE 交x 轴于H()4,0A ,()0,4C ,∴直线AC 的解析式为4y x =−+,OC OA =, PE y ∥Q 轴,PE x ∴⊥轴, 90AOC ∴∠=︒,45OAC ∴∠=︒,PFAC ,45OFP ∴∠=︒,2PH PF ∴=,PE PE PH ∴+=+,设点()21,4042P p p p p ⎛⎫−++<< ⎪⎝⎭,则(),4E p p −+,(),0H p , ()221144222PE p p p p p ∴=−++−−+=−+,2142PH p p =−++,222211325243422224PE PF PE PH p p p p p p p ⎛⎫∴+=+=−+−++=−++=−−+⎪⎝⎭,PE ∴+的最大值为254,此时点P 的坐标为325,24⎛⎫ ⎪⎝⎭.(3)()4,0A ,()0,4C ,CA ∴=将抛物线y 沿射线CA 方向平移1y ,∴1y 由抛物线()2211941222y x x x =−++=−−+,向右和向下分别平移2个单位长度得到, ()2115322y x ∴=−−+,故答案为:()2115322y x =−−+.2.(2024·海南海口·一模)如图,抛物线2y ax bx c =++过点()1,0A −,()3,0B ,()0,3C .(1)求抛物线的解析式;(2)设点P 是第一象限内的抛物线上的一个动点, ①当P 为抛物线的顶点时,求证:PBC 直角三角形; ②求出PBC 的最大面积及此时点P 的坐标;③过点P 作PN x ⊥轴,垂足为N ,PN 与BC 交于点E.当PE 的值最大时,求点P 的坐标.【答案】(1)223y x x =−++(2)①PBC 是直角三角形;②315,24P ⎛⎫ ⎪⎝⎭;③57,24P ⎛⎫ ⎪⎝⎭【分析】(1)把A 、B 、C 三点坐标代入2y ax bx c =++求解即可; (2)①作PH y ⊥轴于点H ,易证PCH △和BOC 是等腰直角三角形,即可求出90PCB ∠=︒; ②先求出直线BC 的解析式,过点P 作PD x ⊥轴于点D ,交BC 于点E ,设点()2,23P x x x −++,则(),3E x x −+,故23PE x x =−+,23922PBC S x x ∆=−+,然后根据二次函数的性质求解即可; ③过点P 作PN x ⊥轴于点N ,交BC 于点E ,设点()2,23P x x x −++,则(),3E x x −+,故23PE x x =−+,判断BEN是等腰直角三角形得出BE =,即可求出25PE x x =−+,然后根据二次函数的性质求解即可. 【详解】(1)解:将点()1,0A −,()3,0B ,()0,3C 代入解析式得:09303a b c a b c c −+=⎧⎪++=⎨⎪=⎩,解得:123a b c =−⎧⎪=⎨⎪=⎩,∵抛物线的解析式为223y x x =−++;(2)解:①配方得()222314y x x x =−++−−+∴点P 的坐标为()1,4,作PH y ⊥轴于点H ,则1PH CH ==,∴45HCP ∠=︒又∵在Rt BOC 中,3OB OC ==, ∴45OCB ∠=︒, ∴90PCB ∠=︒∴PCB 是直角三角形②设直线BC 的解析式为y kx b =+,将点B 、C 代入得:303k b b +=⎧⎨=⎩,解得:13k b =−⎧⎨=⎩, ∴直线BC 的解析式为3y x =−+, ∵()3,0B ,∴3OB =, 设点()2,23P x x x −++(03x <<),过点P 作PD x ⊥轴于点D ,交BC 于点E ,如图所示:∴(),3E x x −+,∴()222333PE x x x x x=−++−−+=−+,∴()22211393327332222228PBCSPE OB x x x x x ⎛⎫=⨯⨯=⨯−+⨯=−+=−−+ ⎪⎝⎭,当32x =时,PBC 的最大面积为278,2915233344x x −++=−++=,∴315,24P ⎛⎫⎪⎝⎭③设点()2,23P x x x −++(03x <<),过点P 作PN x ⊥轴于点N ,交BC 于点E ,如图所示:∴(),3E x x −+,∴()222333PE x x x x x =−++−−+=−+, ∵()0,3C ,()3,0B ,∴3OC OB ==,3BN x =−,∴45OBC OCB ∠=∠=︒,∴45NEB OBC ∠=∠=︒,∴BE ==,∴()CE BC BE =−==,∴22525524PE x x x ⎛⎫=−+=−−+ ⎪⎝⎭, ∴当52x =时,PE 有最大值,此时57,24P ⎛⎫ ⎪⎝⎭. 【点睛】本题考查了二次函数综合问题,面积问题,线段问题,掌握二次函数的性质是解题的关键.3.(2023·山东济南·一模)抛物线()21122y x a x a =−+−+与x 轴交于(),0A b ,()4,0B 两点,与y 轴交于点()0,C c ,点P 是抛物线在第一象限内的一个动点,且在对称轴右侧.(1)求a ,b ,c 的值;(2)如图1,连接BC 、AP ,交点为M ,连接PB ,若14PMB AMB S S =V V ,求点P 的坐标; (3)如图2,在(2)的条件下,过点P 作x 轴的垂线交x 轴于点E ,将线段OE 绕点O 逆时针旋转得到OE ',旋转角为9(0)0αα︒<<︒,连接E B ',E C ',求34E B E C ''+的最小值. 【答案】(1)2a =,2b =−,4c = (2)53,2P ⎛⎫ ⎪⎝⎭(3)【分析】(1)利用待定系数法求解即可;(2)过点P 作PD x ⊥轴,交BC 于点D ,过点A 作y 轴的平行线交BC 的延长线于H ,求得BC l 的解析式,设21,42P m m m ⎛⎫−++ ⎪⎝⎭,则(),4D m m −+,利用相似三角形的判定与性质可得答案; (3)在y 轴上取一点F ,使得94OF =,连接BF ,由相似三角形的判定与性质可得34FE CE ''=,可得34E B E C BE E F '''+'+=,即可解答.【详解】(1)解:将()4,0B 代入()21122y x a x a =−+−+,得()84120a a −+−+=,2a ∴=,∴抛物线的解析式为2142y x x =−++,令0x =,则4y =,4c ∴=,令0y =,则21042x x =−++,14x ∴=,22x =−,()2,0A ∴−,即2b =−; ∴2a =,2b =−,4c =(2)过点P 作PD x ⊥轴,交BC 于点D ,过点A 作y 轴的平行线交BC 的延长线于H ,设BC l :y kx b =+,将()0,4,()4,0代入得440b k b =⎧⎨+=⎩解得:4b =,1k =−,BC l ∴:4y x =−+, 设21,42P m m m ⎛⎫−++ ⎪⎝⎭,则(),4D m m −+, ()221144222P D PD y y m m m m m =−=−++−−+=−+,PD HA ∥,AMH PMD ∴∽,PM PD MA HA ∴=,将2x =−代入4y x =−+,6HA ∴=,112142PMB AMBPM h S PM S AM AM h ⋅===⋅, 164PD PD HA ∴==,32PD ∴=, 231222m m ∴=−+,11(m ∴=舍),23m =,53,2P ⎛⎫∴ ⎪⎝⎭;(3)在y 轴上取一点F ,使得94OF =,连接BF ,根据旋转得性质得出:3OE OE '==,∵9494OF OC ⋅=⨯=, 2OE OFOC '∴=⋅,∴OE OC OF OE '=',COE FOE ''∠=∠,∴FOE E OC ''∽,。
2020年中考数学一轮复习基础考点专题13二次函数(含解析)

专题13 二次函数考点总结【思维导图】【知识要点】知识点一二次函数的概念概念:一般地,形如y=ax^2+bx+c(a , b , c是常数,a≠0)的函数,叫做二次函数。
注意:二次项系数a≠0,而b , c可以为零.二次函数y=ax^2+bx+c的结构特征:等号左边是函数,右边是关于自变量x的二次式,x的最高次数是2.a ,b ,c是常数,a是二次项系数,b是一次项系数,c是常数项.1.(2017·甘肃中考模拟)下列函数中,是二次函数的有()①y=1-√2 x^2②y=1/x^2 ③y=x(1-x)④y=(1-2x)(1+2x)A.1个 B.2个 C.3个 D.4个【答案】C【详解】①y=1−√2×2=−√2×2+1,是二次函数;②y=1/x^2 ,分母中含有自变量,不是二次函数;③y=x(1−x)=−x2+x,是二次函数;④y=(1−2x)(1+2x)=−4×2+1,是二次函数.二次函数共三个,故答案选C.2.(2013·湖南中考真题)下列函数是二次函数的是()A.”y”=2″x”+1 B.”y”=-2″x”+1 C.”y”=”x” ^2+2 D.”y”=1/2 “x”-2【答案】C【详解】根据二次函数的定义,形如”y”=〖”ax” 〗^”2″ +”bx”+”c” (其中a,b,c是常数,a≠0)的函数叫做二次函数,所给函数中是二次函数的是”y”=”x” ^2+2。
故选C。
3.(2018·安徽中考模拟)下列函数不属于二次函数的是()A.y=(x-1)(x+2) B.C.y=1-√3 x^2 D.【答案】D【详解】把每一个函数式整理为一般形式,A、y=(x-1)(x+2)=x2+x-2,是二次函数,正确;B、 =1/2×2+x+1/2,是二次函数,正确;C、y=1-√3 x^2,是二次函数,正确;D、 =2×2+12x+18-2×2=12x+18,这是一个一次函数,不是二次函数,故选D.4.(2018·上海中考模拟)下列函数中是二次函数的是()A.y=2(x﹣1) B.y=(x﹣1)2﹣x2 C.y=a(x﹣1)2 D.y=2×2﹣1【答案】D【详解】A、y=2x﹣2,是一次函数,B、y=(x﹣1)2﹣x2=﹣2x+1,是一次函数,C、当a=0时,y=a(x﹣1)2不是二次函数,D、y=2×2﹣1是二次函数.故选D.考查题型一待定系数法求二次函数解析式1.(2018·广东中考模拟)二次函数y=ax2+bx+c的自变量x与函数y的对应值如下表:x …-5 -4 -3 -2 -1 0 …y … 4 0 -2 -2 0 4 …下列说法正确的是( )A.抛物线的开口向下 B.当x>-3时,y随x的增大而增大C.二次函数的最小值是-2 D.抛物线的对称轴是直线x=-5/2【答案】D【详解】将点(−4,0)、(−1,0)、(0,4)代入到二次函数y=ax2+bx+c中,得:{■(0=16a-4b+c@0=a-b+c@4=c)┤,解得:{■(a=1@b=5@c=4)┤,∴二次函数的解析式为y=x ²+5x+4.A. a=1>0,抛物线开口向上,A不正确;B. −b/2a=−5/2,当x⩾−5/2时,y随x的增大而增大,B不正确;C. y=x²+5x+4=(x+5/2) ²−9/4,二次函数的最小值是−9/4,C不正确;D. −b/2a=−5/2,抛物线的对称轴是x=−5/2,D正确.故选D.2.(2018·上海中考模拟)已知二次函数y=ax2+bx+c的图象上部分点的横坐标x与纵坐标y的对应值如下表:x …-1 0 1 2 …y … 0 3 4 3 …那么关于它的图象,下列判断正确的是( )A.开口向上B.与x轴的另一个交点是(3,0)C.与y轴交于负半轴D.在直线x=1的左侧部分是下降的【答案】B【详解】A、由表格知,抛物线的顶点坐标是(1,4).故设抛物线解析式为y=a(x﹣1)2+4.将(﹣1,0)代入,得a(﹣1﹣1)2+4=0,解得a=﹣2.∵a=﹣2<0,∴抛物线的开口方向向下,故本选项错误;B、抛物线与x轴的一个交点为(﹣1,0),对称轴是x=1,则抛物线与x轴的另一个交点是(3,0),故本选项正确;C、由表格知,抛物线与y轴的交点坐标是(0,3),即与y轴交于正半轴,故本选项错误;D、抛物线开口方向向下,对称轴为x=1,则在直线x=1的左侧部分是上升的,故本选项错误;故选:B.考查题型二根据二次函数的定义求参数值1.(2012·山东中考真题)抛物线”y”=〖”ax” 〗^2+”bx”-3经过点(2,4),则代数式8″a”+4″b”+1的值为()A.3 B.9 C.15 D.-15【答案】C【详解】∵抛物线”y”=〖”ax” 〗^2+”bx”-3经过点(2,4),∴”4″=4″a”+2″b”-3,即4″a”+2″b”=7。
2020年中考数学二次函数专题复习(含答案解析)
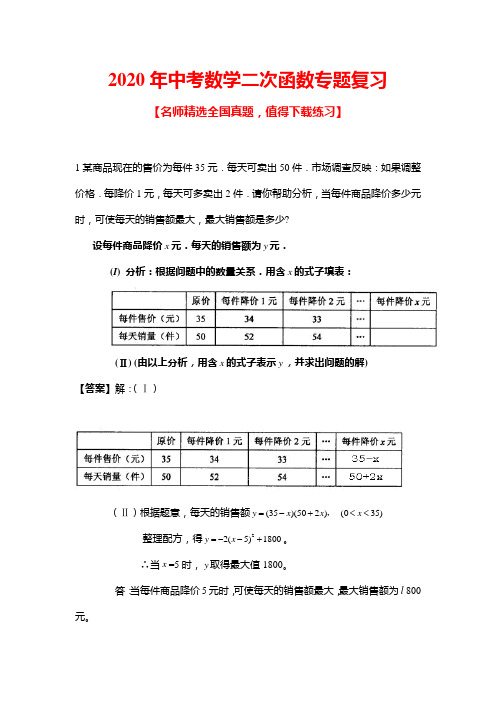
2020年中考数学二次函数专题复习【名师精选全国真题,值得下载练习】1某商品现在的售价为每件35元.每天可卖出50件.市场调查反映:如果调整价格.每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,最大销售额是多少?设每件商品降价x元.每天的销售额为y元.(I) 分析:根据问题中的数量关系.用含x的式子填表:(Ⅱ) (由以上分析,用含x的式子表示y,并求出问题的解)【答案】解:(Ⅰ)(Ⅱ)根据题意,每天的销售额(35)(502)(035),=-+<<y x x x整理配方,得2=--+。
2(5)1800y x∴当x=5时,y取得最大值1800。
答:当每件商品降价5元时,可使每天的销售额最大,最大销售额为l 800元。
【考点】列函数关系式,二次函数的应用。
【分析】(Ⅰ)根据题意,可分析出结果。
(Ⅱ)列函数关系式是找出等量关系:每天的销售额=每件售价×每天销量y x x=-⋅+(35)(502)求每件商品降价多少元时的每天的销售额最大和最大销售额是多少,只要把二次函数变形为顶点式()2=-+的形式即可求出。
y a x m n(Ⅱ)列函数关系式是找出等量关系:每天的销售额=每件售价×每天销量=-⋅+y x x(35)(502)求每件商品降价多少元时的每天的销售额最大和最大销售额是多少,只要把二次函数变形为顶点式()2=-+的形式即可求出。
y a x m n2.如图,抛物线y=ax2﹣4ax+c(a≠0)经过A(0,﹣1),B(5,0)两点,点P 是抛物线上的一个动点,且位于直线AB的下方(不与A,B重合),过点P作直线PQ⊥x轴,交AB于点Q,设点P的横坐标为m.(1)求a,c的值;(2)设PQ的长为S,求S与m的函数关系式,写出m的取值范围;(3)以PQ为直径的圆与抛物线的对称轴l有哪些位置关系?并写出对应的m 取值范围.(不必写过程)【答案】解:(1)∵抛物线y=ax2-4ax+c过A(0,-1),B(5,0),∴⎩⎪⎨⎪⎧c =-125a -20a +c =0 ,解得:⎩⎪⎨⎪⎧a =15c =-1。
二次函数动点问题解答方法技巧(含例解答案)

函数解题思路方法总结:⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;⑶ 根据图象的位置判断二次函数ax ²+bx+c=0中a,b,c 的符号,或由二次函数中a,b,c 的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标.⑸ 与二次函数有关的还有二次三项式,二次三项式ax ²+bx+c ﹙a ≠0﹚本身就是所含字母x 的二次函数;下面以a >0时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:动点问题题型方法归纳总结动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
) 动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、 相似三角形、平行四边形、梯形、特殊角或 其三角函数、线段或面积的最值。
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
二、 抛物线上动点5、(湖北十堰市)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C .(1) 求抛物线的解析式;(2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.(3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.注意:第(2)问按等腰三角形顶点位置分类讨论画图再由图形性质求点P坐标----①C为顶点时,以C为圆心CM 为半径画弧,与对称轴交点即为所求点P,②M为顶点时,以M为圆心MC为半径画弧,与对称轴交点即为所求点P,③P为顶点时,线段MC的垂直平分线与对称轴交点即为所求点P。
2020年中考数学必考专题12 二次函数(解析版)

专题12 二次函数1.二次函数的概念:一般地,自变量x 和因变量y 之间存在如下关系: y=ax 2+bx+c(a≠0,a 、b 、c 为常数),则称y 为x 的二次函数。
抛物线)0,,(2≠++=a c b a c bx ax y 是常数,叫做二次函数的一般式。
2.二次函数y=ax 2+bx+c(a ≠0)的图像与性质(1)对称轴:2bx a=-(2)顶点坐标:24(,)24b ac b a a-- (3)与y 轴交点坐标(0,c ) (4)增减性:当a>0时,对称轴左边,y 随x 增大而减小;对称轴右边,y 随x 增大而增大; 当a<0时,对称轴左边,y 随x 增大而增大;对称轴右边,y 随x 增大而减小。
3.二次函数的解析式三种形式。
(1)一般式 y=ax 2+bx+c(a ≠0).已知图像上三点或三对x 、y 的值,通常选择一般式. (2)顶点式 2()y a x h k =-+224()24b ac b y a x a a-=-+ 已知图像的顶点或对称轴,通常选择顶点式。
(3)交点式 12()()y a x x x x =--专题知识回顾yx O已知图像与x 轴的交点坐标1x 、2x ,通常选用交点式。
4.根据图像判断a,b,c 的符号(1)a 确定开口方向 :当a>0时,抛物线的开口向上;当a<0时,抛物线的开口向下。
(2)b ——对称轴与a 左同右异。
(3)抛物线与y 轴交点坐标(0,c ) 5.二次函数与一元二次方程的关系抛物线y=ax 2 +bx+c 与x 轴交点的横坐标x 1, x 2 是一元二次方程ax 2 +bx+c=0(a ≠0)的根。
抛物线y=ax 2 +bx+c ,当y=0时,抛物线便转化为一元二次方程ax 2 +bx+c=024b ac ->0时,一元二次方程有两个不相等的实根,二次函数图像与x 轴有两个交点; 24b ac -=0时,一元二次方程有两个相等的实根,二次函数图像与x 轴有一个交点;24b ac -<0时,一元二次方程有不等的实根,二次函数图像与x 轴没有交点。
2020届中考数学压轴题专题:17 二次函数的面积问题【含解析】

2020届中考数学压轴题专题专题17二次函数的面积问题【考点1】二次函数的线段最值问题【例1】如图,抛物线y=ax2+bx+c经过A(﹣1,0)、B(4,0)、C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于点E.(1)求抛物线的函数表达式;(2)求线段DE长度的最大值.【答案】(1)y=﹣34x2+94x+3;(2)最大值是125.【解析】【分析】(1)根据待定系数法,可得函数解析式;(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得DM,根据相似三角形的判定与性质,可得DE的长,根据二次函数的性质,可得答案.【详解】解:(1)由题意得,0 16403a b ca b cc===-+⎧⎪++⎨⎪⎩,解得,3 4 9 43abc===⎧-⎪⎪⎪⎨⎪⎪⎪⎩,抛物线的函数表达式为y=﹣34x2+94x+3;(2)过点D作DM⊥x轴交BC于M点,由勾股定理得,BC22OC OB+5,设直线BC的解析是为y=kx+b,则403k bb+⎧⎨⎩==,解得343kb⎧=-⎪⎨⎪=⎩,∴直线BC的解析是为y=﹣34x+3,设点M的坐标为(a,﹣34a+3),DM=(﹣34a2+94a+3)﹣(﹣34a+3)=﹣34a2+3a,∵∠DME=∠OCB,∠DEM=∠BOC,∴△DEM∽△BOC,∴DE BODM BC,即DEDM=45,解得,DE=45 DM∴DE=﹣35a2+125a=﹣35(a﹣2)2+125,当a=2时,DE取最大值,最大值是125.【点睛】本题考查的是二次函数、一次函数的性质,相似三角形的判定和性质,掌握待定系数法求二次函数解析式、一次函数解析式的一般步骤是解题的关键.【变式1-1】.已知抛物线y=mx2+2mx+m-1和直线y=mx+m-1,且m≠0.(1)求抛物线的顶点坐标;(2)试说明抛物线与直线有两个交点;(3)已知点T(t,0),且-1≤t≤1,过点T作x轴的垂线,与抛物线交于点P,与直线交于点Q,当0<m≤3时,求线段PQ长的最大值.【答案】(1)(-1,-1);(2)见解析;(3)PQ的最大值为6.【解析】【分析】(1)化为顶点式即可求顶点坐标;(2)由y=mx2+2mx+m-1和y=mx+m-1可得:mx2+2mx+m-1=mx+m-1,整理得,mx(x+1)=0,即可知抛物线与直线有两个交点;(3)由(2)可得:抛物线与直线交于(-1,-1)和(0,m-1)两点,点P的坐标为(t,mt2+2mt+m-1),点Q的坐标为(t,mt+m-1).故分两种情况进行讨论:①如图1,当-1≤t≤0时;②如图2,当0<t≤1时,求出对应的最大值即可.【详解】解:(1)∵y=mx2+2mx+m-1=m(x+1)2-1,∴抛物线的顶点坐标为(-1,-1).(2)由y=mx2+2mx+m-1和y=mx+m-1可得:mx2+2mx+m-1=mx+m-1,mx2+mx=0,mx(x+1)=0,∵m≠0,∴x1=0,x2=-1.∴抛物线与直线有两个交点.(3)由(2)可得:抛物线与直线交于(-1,-1)和(0,m -1)两点,点P 的坐标为(t ,mt 2+2mt +m -1),点Q 的坐标为(t ,mt +m -1).①如图1,当-1≤t ≤0时,PQ =2Q P y y mt mt -=--=211()24m t m -++. ∵m >0,当12t =-时,PQ 有最大值,且最大值为14m . ∵0<m ≤3,∴14m ≤34,即PQ 的最大值为34.②如图2,当0<t ≤1时,PQ =2P Q y y mt mt -=+=211()24m t m +-. ∵m >0,∴当t =1时,PQ 有最大值,且最大值为2m . ∵0<m ≤3,∴0<2m ≤6,即PQ 的最大值为6. 综上所述,PQ 的最大值为6. 【点睛】此题主要考查二次函数的应用,(1)(2)题相对简单,(3)题要分情况进行讨论方右解答,因此做此类题型,在进行分类讨论时,尽量通过大致图象数型结合进行解答.【变式1-2】如图1,已知抛物线y=﹣x 2+mx+m ﹣2的顶点为A ,且经过点B (3,﹣3). (1)求顶点A 的坐标(2)若P 是抛物线上且位于直线OB 上方的一个动点,求△OPB 的面积的最大值及比时点P 的坐标; (3)如图2,将原抛物线沿射线OA 方向进行平移得到新的抛物线,新抛物线与射线OA 交于C ,D 两点,请问:在抛物线平移的过程中,线段CD 的长度是否为定值?若是,请求出这个定值;若不是,请说明理由.【答案】(1)(﹣1,1);(2)P(,);(3).【解析】【分析】(1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;(2)过点P作y轴的平行线交OB与点Q,求出直线BP的解析式,表示出点Q的坐标,根据三角形的面积公式列出函数关系式,利用二次函数的最值可得P点坐标;(3)根据平移规律,可得新抛物线,根据联立抛物线与OA的解析式,可得C、D点的横坐标,根据勾股定理,可得答案.【详解】解:(1)把B(3,﹣3)代入y=﹣x2+mx+m2得:﹣3=﹣32+3m+m2,解得m=2,∴y=﹣x2+2x=﹣(x+1)2+1,∴顶点A的坐标是(﹣1,1);(2)过点P作y轴的平行线交OB与点Q.∵直线OB的解析式为y=﹣x,故设P(n,﹣n2+2n),Q(n,﹣n),∴PQ=﹣n2+2n﹣(﹣n)=﹣n2+3n,∴S△OPB=(﹣n2+3n)=﹣(n﹣)+,当n=时,S△OPB的最大值为.此时y=﹣n2+2n=,∴P(,);(3)∵直线OA 的解析式为y=x ,∴可设新的抛物线解析式为y=﹣(x ﹣a )2+a , 联立,∴﹣(x ﹣a )2+a=x , ∴x 1=a ,x 2=a ﹣1,即C 、D 两点间的横坐标的差为1, ∴CD=.【点睛】本题考查了待定系数法求函数解析式,三角形的面积公式,利用二次函数求最值,勾股定理二次函数与一次函数的交点问题,难度适中,是常见题型. 【考点2】二次函数的面积定值问题【例2】已知二次函数2248y x mx m =-+-.(1)图象经过点1,1()时,则m =_________;(2)当2x ≤时,函数值y 随x 的增大而减小,求m 的取值范围;(3)以抛物线2248y x mx m =-+-的顶点A 为一个顶点作该抛物线的内接正三角形AMN (M ,N 两点在抛物线上),请问:AMN ∆的面积是与m 无关的定值吗?若是,请求出这个定值;若不是,请说明理由.【答案】(1)4;(2)m≥2;(3)AMN ∆的面积是与m 无关的定值,S △AMN =33【解析】 【分析】(1)将点1,1()代入二次函数解析式即可求出m ;(2)求出二次函数的对称轴为x =m ,由抛物线的开口向上,在对称轴的左边y 随x 的增大而减小,可求出m 的取值范围;(3)在抛物线内作出正三角形,求出正三角形的边长,然后计算三角形的面积,可得到△AMN 的面积是与m 无关的定值. 【详解】解:(1)将点1,1()代入2248y x mx m =-+-可得:11248m m =-+-,解得:m=4;(2)二次函数2248y x mx m =-+-的对称轴是:x =m , ∵当x≤2时,函数值y 随x 的增大而减小, ∴m≥2;(3)AMN ∆的面积是与m 无关的定值;如图:顶点A 的坐标为(m ,−m 2+4m −8),△AMN 是抛物线的内接正三角形,MN 交对称轴于点B , ∵tan∠AMB=tan60°=3ABBM,3BM 3, 设BM =BN =a ,则AB 3,∴点M 的坐标为(m +a 3a −m 2+4m −8),∵点M在抛物线上,∴3a−m2+4m−8=(m+a)2−2m(m+a)+4m−8,整理得:230a a,解得:a=3或a=0(舍去),∴△AMN是边长为23的正三角形,∴AB=3,S△AMN=1233332⨯⨯=,与m无关.【点睛】本题是二次函数综合题,考查了二次函数的图象和性质、等边三角形的性质以及特殊角三角函数的应用,其中(3)问有一定难度,根据点M在抛物线上,求出正三角形的边长是解题关键.【变式2-1】如图,已知抛物线交x轴于A、B两点,交y轴于C点,A点坐标为(﹣1,0),OC=2,OB=3,点D为抛物线的顶点.(1)求抛物线的解析式;(2)P为坐标平面内一点,以B、C、D、P为顶点的四边形是平行四边形,求P点坐标;(3)若抛物线上有且仅有三个点M1、M2、M3使得△M1BC、△M2BC、△M3BC的面积均为定值S,求出定值S及M1、M2、M3这三个点的坐标.【答案】(1)y=﹣23x2+43x+2;(2)见解析;(3)见解析.【解析】【详解】分析:(1)由OC与OB的长,确定出B与C的坐标,再由A坐标,利用待定系数法确定出抛物线解析式即可;(2)分三种情况讨论:当四边形CBPD是平行四边形;当四边形BCPD是平行四边形;四边形BDCP是平行四边形时,利用平移规律确定出P坐标即可;(3)由B与C坐标确定出直线BC解析式,求出与直线BC平行且与抛物线只有一个交点时交点坐标,确定出交点与直线BC解析式,进而确定出另一条与直线BC平行且与BC距离相等的直线解析式,确定出所求M 坐标,且求出定值S的值即可.详解:(1)由OC=2,OB=3,得到B(3,0),C(0,2),设抛物线解析式为y=a(x+1)(x﹣3),把C(0,2)代入得:2=﹣3a,即a=﹣23,则抛物线解析式为y=﹣23(x+1)(x﹣3)=﹣23x2+43x+2;(2)抛物线y=﹣23(x+1)(x﹣3)=﹣23x2+43x+2=﹣23(x﹣1)2+83,∴D(1,83),当四边形CBPD是平行四边形时,由B(3,0),C(0,2),得到P(4,23);当四边形CDBP是平行四边形时,由B(3,0),C(0,2),得到P(2,﹣23);当四边形BCPD是平行四边形时,由B(3,0),C(0,2),得到P(﹣2,143);(3)设直线BC解析式为y=kx+b,把B(3,0),C(0,2)代入得:302k bb+=⎧⎨=⎩,解得:232kb⎧=-⎪⎨⎪=⎩,∴y=﹣23x+2,设与直线BC 平行的解析式为y=﹣23x+b , 联立得:22324233yx b y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩,消去y 得:2x 2﹣6x+3b ﹣6=0,当直线与抛物线只有一个公共点时,△=36﹣8(3b ﹣6)=0,解得:b=72,即y=﹣23x+72, 此时交点M 1坐标为(32,52);可得出两平行线间的距离为913, 同理可得另一条与BC 平行且平行线间的距离为91326的直线方程为y=﹣23x+12,联立解得:M 2(332-,122-),M 3(3+32,122--),此时S=1.点睛:此题属于二次函数综合题,涉及的知识有:待定系数法求函数解析式,一次函数的性质,利用了分类讨论的思想,熟练掌握待定系数法是解本题的关键. 【变式2-2】如图:已知抛物线()()13(0)2y x m x m m m=-+->与x 轴交于A 、B 两点(点A 在点B 左侧),与y 交于点C ,抛物线对称轴与x 轴交于点D ,932E ⎛⎫⎪ ⎪⎝⎭为x 轴上一点.(1)写出点A 、B 、C 的坐标(用m 表示);(2)若以DE 为直径的圆经过点C 且与抛物线交于另一点F , ①求抛物线解析式;②P 为线段DE 上一动(不与D 、E 重合),过P 作PQ EC ⊥作PH DF ⊥,判断PQ PHDC EF+是否为定值,若是,请求出定值,若不是,请说明理由;(3)如图②,将线段AB 绕点A 顺时针旋转30°,与y 相交于点M ,连接BM .点S 是线段AM 的中点,连接OS .若点N 是线段BM 上一个动点,连接SN ,将△SMN 绕点S 逆时针旋转60得到△SOT ,延长TO 交BM 于点K .若△KTN 的面积等于△ABM 的面积的112,求线段MN 的长.【答案】(1)A(-3m ,0),B(m ,0),C(0,32m )(2)①2333y x x =-++1PQ PH DC EF =,理由见解析; (3)线段MN 的长为2或5【解析】(1)A (-3m ,0),B (m ,0),C (0,32m ) (2)△DCE 为直角三角形. ①OC 2=OD ·OE ,m =32333y x x =-+②∵DE 为直径,∴∠DCE =∠DFE =90°,∵PQ ⊥EC ,PH⊥DF ,∴PQ ∥DC ,PH∥EF PQ PE DC DE ∴=,,PH DPEF DE=,∴+1PQ PH PE DP DEDC EF DE DE+===(3)A (63-0),B (30),又∠OAM =60° ,∴cos30°=OMOA,∴OM =6,M (0,6) 又tan∠ABM =OMOB3OBM =60° ,∠AMB =90° , S 是线段AM 的中点,∴∠OSM =60° ,∴∠AOS =30° ,又∠SOT =90° ,∠AOT =60° ,∴直线TK :y 3x ;BM :y 3x -6,联立两个方程,解得:K 3-3)设MN =a ,TK =TO +OK =a 3KTN 的高h =TK 33+ NK =23a ,∵S △KTN =112S △ABM 1232NK h ⋅⋅=, ∴13233232a ()⨯+= a =2或a =5点睛:本题考查二次函数综合题、旋转变换、解直角三角形等知识,平行线的性质,解题的关键是学会转化,属于中考压轴题.【考点3】二次函数的面积最值问题 【例3】已知抛物线22y x x m m =---. (1)求证:抛物线与x 轴必定有公共点;(2)若P (a ,y 1),Q (-2,y 2)是抛物线上的两点,且y 1>y 2,求a 的取值范围;(3)设抛物线与x 轴交于点()1,0A x 、()2,0B x ,点A 在点B 的左侧,与y 轴负半轴交于点C ,且123x x +=,若点D 是直线BC 下方抛物线上一点,连接AD 交BC 于点E ,记△ACE 的面积为S 1,△DCE 的面积为S 2,求21S S 是否有最值?若有,求出该最值;若没有,请说明理由. 【答案】(1)见解析;(2)2a <-或3a >,(3)21S S 没有最小值;21S S 有最大值是13【解析】分析:(1)本题需先根据判别式解出无论m 为任何实数都大于零,再判断出物线与x 轴总有交点. (2)分两种情况:当点P 在对称轴的左侧时,y 随x 的增大而减小,得2a <-;当点P 在对称轴的右侧时,y 随x 的增大而增大,3a >,故得解.详解:(1)令0y = 得220x x m m ---=∴224441b ac m m ∆=-=++ ∴()221m ∆=+无论m 取何值,()2210m ∆=+≥ ∴ 抛物线与x 轴必定有公共点(2)∵22y x x m m =---,抛物线的对称轴是12x = 当点P 在对称轴的左侧时,y 随x 的增大而减小, ∵y 1>y 2, 2a <-当点P 在对称轴的右侧时,y 随x 的增大而增大, Q (-2,y 2)关于对称轴的对称点是(3,y 2) ∵y 1>y 2, 3a > 综上所述:2a <-或3a > (3)11x m =+,2x m =-∵123x x += 、∴ 13m m ++-=,解得1m =或2m =- ∴ 22y x x =--∴ ()1,0A -、()2,0B ,()0,2C - ∴ 直线BC 的解析式是2y x =-设点A 到直线BC 的距离是1h ,点D 到直线BC 的距离是2h , △ACE 的面积S 1112CE h =⨯,△DCE 的面积S 2212CE h =⨯ ∴ 1322h =,2221123S h h S h == ∴ 求21S S 的最值转化为求2h 的最值 设过点D 与直线BC 平行的直线解析式为y x b =+当点D 在直线BC 下方的抛物线上运动时,2h 无最小值,仅当直线y x b =+与抛物线22y x x =--只有一个公共点时,2h 有最大值即方程组22y x x y x b⎧=--⎨=+⎩有两个相等的实数根∴2220x x b ---=, 4840b ∆=++=, ∴3b =-,此时222h =∴21S S 没有最小值;21S S 有最大值是13∴()1,0A -、()2,0B点睛:本题主要考查了二次函数的综合问题,在解题时要注意找出各点的坐标问题,再把各点代入解析式是解题的关键.【变式3-1】如图,直线334x y =-+与x 轴交于点C ,与y 轴交于点B ,抛物线234y ax x c =++经过B 、C 两点.①求点C 的坐标; ②求抛物线的解析式;③如图,点E 是直线BC 上方抛物线上的一动点,当BEC ∆面积最大时,请求出点E 的坐标和BEC ∆面积的最大值.【答案】①()4,0C ;②233384y x x =-++;③点E 的坐标是()2,3时,BEC ∆的面积最大,最大面积是3.【解析】 【分析】①利用利用x 轴上点的坐标特点代入一次函数即可.②根据抛物线234y ax x c =++经过B 、C 两点,先求出B 点坐标,再用待定系数法求解析式即可. ③根据“铅垂高,水平宽”方法求面积.过点E 作y 轴的平行线EF 交直线BC 于点M ,EF 交x 轴于点F ,利用E 、M 横坐标相等及所在函数关系式设出坐标,求出EM 的长,再利用BEC BEM MEC S S S ∆∆∆=+,把EM 看作△BEM 和△MEC 的底,求出面积写出关系式,最后利用二次函数求最值即可. 【详解】解:①∵直线334xy =-+与x 轴交于点C , ∴当y=0时,解得x=4 ∴C 点坐标为:()4,0 ②直线334y x =-+与x 轴交于点C ,与y 轴交于点B ,∴当x=0时,解得y=3∴点B 的坐标是()0,3,点C 的坐标是()4,0, 抛物线234y ax x c =++经过B 、C 两点, 3164043a c c ⎧+⨯+=⎪∴⎨⎪=⎩ 解得383a c ⎧=-⎪⎨⎪=⎩,∴抛物线的解析式为233384y x x =-++.③如图,过点E 作y 轴的平行线EF 交直线BC 于点M ,EF 交x 轴于点F ,已知点E 是直线BC 上方抛物线上的一动点,则可设点E 的坐标是233,384x x x ⎛⎫-++ ⎪⎝⎭, ∴点M 的坐标是3,34x x ⎛⎫-+ ⎪⎝⎭,22333333384482EM x x x x x ⎛⎫∴=-++--+=-+ ⎪⎝⎭.BEC BEM MEC S S S ∆∆∆=+,22113334(2)322824BEC S ME OC x x x ∆⎛⎫∴=⋅=⨯-+⨯=--+ ⎪⎝⎭. 即当2x =时,即点E 的坐标是()2,3时,BEC ∆的面积最大,最大面积是3. 【点睛】此题考查的是①一次函数的与坐标轴的交点坐标;②待定系数法求二次函数解析式;③用“铅垂高,水平宽”求面积最值问题.【变式3-2】如图,抛物线22y ax bx =++交x 轴于点()30A -,和点()10B ,,交y 轴于点C .(1)求这个抛物线的函数表达式;(2)若点D 的坐标为()1,0-,点P 为第二象限内抛物线上的一个动点,求四边形ADCP 面积的最大值.【答案】(1)224233y x x =--+;(2)S 的最大值为174.【解析】 【分析】(1)根据A,B 两点坐标可得出函数表达式; (2)设点224,233P x x x ⎛⎫--+ ⎪⎝⎭,根据+APO CPO ODC ADCP S S S S S ==-△△△四边形列出S 关于x 的二次函数表达式,再根据二次函数的性质求最值. 【详解】解:(1)将A,B 两点的坐标代入解析式得,9320,20,a b a b -+=⎧⎨++=⎩解得2,34.3a b ⎧=-⎪⎪⎨⎪=-⎪⎩故抛物线的表达式为:224233y x x =--+; (2)连接OP ,设点224,233P x x x ⎛⎫--+ ⎪⎝⎭, 由(1)中表达式可得点()0,2C , 则 +APO CPO ODC ADCP S S S S S ==-△△△四边形111222p P AO y OC x CO OD =⨯⨯+⨯⨯-⨯⨯ 222411221()213=3323222x x x x x ⎛⎫--++⨯⨯--⨯⨯=--+ ⎪⎝⎭⨯⨯, ∵10-<,故S 有最大值,当32x =-时,S 的最大值为174.【点睛】本题主要考查二次函数表达式的求法以及二次函数的图像与性质,有一定的综合性.对于二次函数中的面积问题,常需用到“割补法”. 【考点4】二次函数面积的其它问题【例4】如图,在平面直角坐标系中,直线55y x =-+与x 轴、y 轴分别交于,A C 两点,抛物线2y x bx c =++经过,A C 两点,与x 轴交于另一点B .(1)求抛物线解析式及B 点坐标; (2)连接BC ,求ABC ∆的面积;(3)若点M 为抛物线上一动点,连接,MA MB ,当点M 运动到某一位置时,ABM ∆面积为ABC ∆的面积的45倍,求此时点M 的坐标.【答案】(1)265y x x =-+,()5,0B ;(2)10ABC S ∆=;(3)M 点的坐标为1M ,2M 3-22(,),3M ,见解析. 【解析】 【分析】(1)利用,A C 两点是一次函数上的点求出,A C 两点,再代入二次函数求解即可. (2)根据()1,0A ,()5,0B ,求出4AB =,求出△ABC. (3)根据ABM ∆面积为ABC ∆的面积的45倍,求出4410855ABM ABC S S ∆∆==⨯=,得出1644M y =÷=,求出此时M 的坐标即可. 【详解】(1)解:∵直线55y x =-+∴令0y =,则055x =-+,解得1x = ∴()1,0A令0x =,则5y =,∴()0,5C将点()1,0A ,()0,5C 代入2y x bx c =++中得,105b c c ++=⎧⎨=⎩,解得65b c =-⎧⎨=⎩ ∴抛物线的解析式为:265y x x =-+; 令0y =,则2650x x -+=,解得121,5x x == ∴()5,0B .(2)解:∵()1,0A ,()5,0B ∴4AB = ∴11451022ABC S AB OC ∆=⨯=⨯⨯=(3)∵ABM ∆面积为ABC ∆的面积的45倍, ∴4410855ABM ABC S S ∆∆==⨯= ∵AB=4 ,∴1644M y =÷=, ∵()226534y x x x =-+=--∴抛物线的顶点坐标为()13,4M -符合条件,当4M y =时,2654x x -+=,解的,x 1=3-22,x 2=322+,∴M 点的坐标为1M (3,-4),2M ()3-224,,3M ()3224+,. 【点睛】本题考查的是二次函数,熟练掌握二次函数是解题的关键.【变式4-1】如图,抛物线y =ax 2+bx +c 经过原点O ,与x 轴交于另一点N ,直线y =kx +4与两坐标轴分别交于A 、D 两点,与抛物线交于点B(1,m)、C(2,2).1. 求直线与抛物线的解析式.2.若抛物线在x 轴上方的部分有一动点P(x ,y),设∠PON=,求当△PON 的面积最大时tan的值.3. 若动点P 保持(2)中的运动线路,问是否存在点P ,使得△POA 的面积等于△PON 的面积的?若存在,请求出点P 的坐标;若不存在,请说明理由 【答案】(1) 所求的抛物线为. (2)(3) 存在点,其坐标为(1,3)【解析】 【分析】(1)根据C 点的坐标可确定直线AD 的解析式,进而可求出B 点坐标,将B 、C 、O 三点坐标代入抛物线中,即可求得此二次函数的解析式;(2)此题的关键是求出P 点的坐标;△PON 中,ON 的长为定值,若△PON 的面积最大,那么P 点离ON 的距离最远,即P 点为抛物线的顶点,根据(1)所得的抛物线解析式即可求得P 点的坐标,进而可求出α的正切值;(3)设出点P 的横坐标,根据抛物线的解析式可表示出P 点的纵坐标;根据直线AD 和抛物线的解析式可求出A 、N 的坐标;以ON 为底,P 点纵坐标为高可得到△OPN 的面积,以OA 为底,P 点横坐标为高可得到△OAP 的面积,根据题目给出的△POA 和△PON 的面积关系即可求出P 点的横坐标,进而可求出P 点的坐标.【详解】(1)将点C(2,2)代入直线y=kx+4,可得k=-1所以直线的解析式为y=-x+4当x=1时,y=3,所以B点的坐标为(1,3)将B、C、O三点的坐标分别代入抛物线y=ax2+bx+c,可得解得,所以所求的抛物线为y=-2x2+5x.(2)因为ON的长是一定值,所以当点P为抛物线的顶点时,△PON的面积最大,又该抛物线的顶点坐标为(,此时tan∠α=(3)存在;把x=0代入直线y=-x+4得y=4,所以点A(0,4)把y=0代入抛物线y=-2x2+5x得x=0或x=,所以点N(,0)设动点P坐标为(x,y),其中y=-2x2+5x (0<x<)则得:S△OAP=|OA|•x=2xS△ONP=|ON|•y=ו(-2x2+5x)=(-2x2+5x)由S△OAP=S△ONP,即2x=•(-2x2+5x)解得x=0(舍去)或x=1,得x=1,由此得y=3所以得点P存在,其坐标为(1,3).【点睛】此题考查了一次函数与二次函数解析式的确定、函数图象与坐标轴交点坐标的求法、图形面积的求法等知识,主要考查学生数形结合的数学思想方法.【变式4-2】如图1,抛物线23y x x =--与直线22y x =--交于A 、B 两点,过A 作//AC x 轴交抛物线于点C ,直线AB 交x 轴于点D .()1求A 、B 、C 三点的坐标;()2若点H 是线段BD 上的一个动点,过H 作//HE y 轴交抛物线于E 点,连接OE 、OH ,当310HE AC =时,求OEHS的值;()3如图2,连接BO ,CO 及BC ,设点F 是BC 的中点,点P 是线段CO 上任意一点,将BFP 沿边PF翻折得到GPF ,求当PC 为何值时,GPF 与CFP 重叠部分的面积是BCP 面积的14.【答案】(1)点A 坐标()1,4-,点B 坐标()2,2-,点C 坐标()4,4--;(2)333OEHS+=;(3)当2PC =10时,GPF 与CFO 重叠部分的面积是BCP 面积的14. 【解析】 【分析】(1)列方程组可知A 、B 两点坐标,根据点C 的纵坐标与点A 的纵坐标相同,列方程可求得点C 坐标. (2)如图1中,设(),22H m m --,(21)m -<<-,则()2,3E m m m --,根据310HE AC =, 列出方程求出点H 的横坐标,根据三角形的面积公式计算即可解决问题.(3)分两种情形①若翻折后,点G 在直线OC 下方时,连接CG .如图2,可证四边形PFCG 是平行四边形,得10PB PG CF ===Rt△PBO 中,根据22OP PB BO -,即可解决问题.②若翻折后,点G在直线OC 上方时,连接CG .如图3,可证四边形PFGC 是平行四边形,得12PC FG BF BC ===即可解决问题. 【详解】解:()1由2322y x x y x ⎧=--⎨=--⎩解得22x y =-⎧⎨=⎩或14x y =⎧⎨=-⎩,∴点A 坐标()1,4-,点B 坐标()2,2-, ∵//AC x 轴, ∴点C 纵坐标为4-,由234x x --=-,解得4x =-或1, ∴点C 坐标()4,4--.()2如图1中,设(),22H m m --,(21)m -<<-,则()2,3E m m m --,由题意()23322510m m m -----=⨯, 解得13m --=13-+(舍弃), ∴131333322OEHS++=⨯=. ()3∵()2,2B -,()4,4C --,∴2226210BC =+=,2OB =2OC = ∵222OB OC BC +=, ∴90BOC ∠=.①若翻折后,点G 在直线OC 下方时,连接CG .如图2,∵111422PFLPBCPFCPFGS S S S ===,∴PFLFCLPLGSSS==,∴FL LG =.CL LP =, ∴四边形PFCG 是平行四边形, ∴10PB PG CF ===, 在Rt PBO 中,222OP PB BO =-=,∴42232PC OC OP =-=-=.②若翻折后,点G 在直线OC 上方时,连接CG .如图3,∵111422PFLPBCPFCPFGS S S S ===,∴PFLFCLPLGSSS==,∴FL LG =.CL LP =, ∴四边形PFGC 是平行四边形, ∴1102PC FG BF BC ==== 综上所述:当2PC =10时,GPF 与CFO 重叠部分的面积是BCP 面积的14.【点睛】属于二次函数综合题,考查二次函数与一次函数的交点问题,平行四边形的判定与性质,勾股定理,综合性比较强,难度较大.一、解答题1.如图,抛物线2y x bx c =++交x 轴于A 、B 两点,其中点A 坐标为()1,0,与y 轴交于点()0,3C-.(1)求抛物线的函数表达式;(2)如图①,连接AC ,点P 在抛物线上,且满足2PAB ACO ∠=∠.求点P 的坐标;(3)如图②,点Q 为x 轴下方抛物线上任意一点,点D 是抛物线对称轴与x 轴的交点,直线AQ 、BQ 分别交抛物线的对称轴于点M 、N .请问DM DN +是否为定值?如果是,请求出这个定值;如果不是,请说明理由.【答案】(1)223y x x =+-(2)939,416⎛⎫-- ⎪⎝⎭或1557,416⎛⎫- ⎪⎝⎭(3)DM DN +为定值 【解析】 【分析】(1)把点A 、C 坐标代入抛物线解析式即求得b 、c 的值.(2)点P 可以在x 轴上方或下方,需分类讨论.①若点P 在x 轴下方,延长AP 到H ,使AHAB =构造等腰ABH ∆,作BH 中点G ,即有22PAB BAG ACO ∠=∠=∠,利用ACO ∠的三角函数值,求BG 、BH 的长,进而求得H 的坐标,求得直线AH 的解析式后与抛物线解析式联立,即求出点P 坐标.②若点P 在x 轴上方,根据对称性,AP 一定经过点H 关于x 轴的对称点'H ,求得直线'AH 的解析式后与抛物线解析式联立,即求出点P 坐标.(3)设点Q 横坐标为t ,用t 表示直线AQ 、BN 的解析式,把1x =-分别代入即求得点M 、N 的纵坐标,再求DM 、DN 的长,即得到DM DN +为定值. 【详解】(1)∵抛物线2y x bx c =++经过点1,0A ,()0,3C-.∴10003b c c ++=⎧⎨++=-⎩,解得:23b c =⎧⎨=-⎩.∴抛物线的函数表达式为223y x x =+-. (2)①若点P 在x 轴下方,如图1, 延长AP 到H ,使AH AB =,过点B 作BI x ⊥轴,连接BH ,作BH 中点G ,连接并延长AG 交BI 于点F ,过点H 作HIBI ⊥于点I .∵当2230x x +-=,解得:13x =-,21x =. ∴()3,0B -. ∵1,0A ,()0,3C-,∴1OA =,3OC =,221310AC =+4AB =,∴Rt AOC ∆中,10sin OA ACO AC ∠==310cos OC ACO AC ∠==, ∵AB AH =,G 为BH 中点, ∴AG BH ⊥,BG GH =,∴BAG HAG ∠=∠,即2PAB BAG ∠=∠, ∵2PAB ACO ∠=∠, ∴BAG ACO ∠=∠,∴Rt ABG ∆中,90AGB ∠=︒,10sin BG BAG AB ∠==, ∴10210105BG AB ==, ∴4102BH BG ==. ∵90HBI ABG ABG BAG ∠+∠=∠+∠=︒,∴HBI BAG ACO ∠=∠=∠,∴Rt BHI ∆中,90BIH ∠=︒,10sin HI HBI BH ∠==310cos BI HBI BH ∠==∴104105HI BH ==,31012105BI BH ==, ∴411355H x =-+=-,125H y =-,即1112,55H ⎛⎫-- ⎪⎝⎭,设直线AH 解析式为y kx a =+,∴0111255k a k a +=⎧⎪⎨-+=-⎪⎩,解得:3434k a ⎧=⎪⎪⎨⎪=-⎪⎩, ∴直线AH :33y x 44=-. ∵2334423y x y x x ⎧=-⎪⎨⎪=+-⎩,解得:1110x y =⎧⎨=⎩(即点A ),22943916x y ⎧=-⎪⎪⎨⎪=-⎪⎩, ∴939,416P ⎛⎫-- ⎪⎝⎭. ②若点P 在x 轴上方,如图2,在AP 上截取'AH AH =,则'H 与H 关于x 轴对称, ∴1112',55H ⎛⎫-⎪⎝⎭, 设直线'AH 解析式为''y k x a =+,∴''01112''55k a k a +=⎧⎪⎨-+=⎪⎩,解得:3'43'4k a ⎧=-⎪⎪⎨⎪=⎪⎩, ∴直线'AH :3344y x =-+.∵2334423y x y x x ⎧=-+⎪⎨⎪=+-⎩,解得:1110x y =⎧⎨=⎩(即点A ),221545716x y ⎧=-⎪⎪⎨⎪=⎪⎩, ∴1557,416P ⎛⎫-⎪⎝⎭. 综上所述,点P 的坐标为939,416⎛⎫-- ⎪⎝⎭或1557,416⎛⎫- ⎪⎝⎭. (3)DM DN +为定值.∵抛物线223y x x =+-的对称轴为:直线1x =-, ∴()1,0D -,1M N x x ==-, 设()()2,2331Q t t t t +--<<,设直线AQ 解析式为y dx e =+,∴2023d e dt e t t +=⎧⎨+=+-⎩,解得:33d t e t =+⎧⎨=--⎩, ∴直线AQ :()33y t x t =+--,当1x =-时,3326M y t t t =----=--, ∴()02626DM t t =---=+, 设直线BQ 解析式为y mx n =+,∴23023m n mt n t t -+=⎧⎨+=+-⎩,解得:133m t n t =-⎧⎨=-⎩, ∴直线BQ :()133y t x t =-+-, 当1x =-时,13322N y t t t =-++-=-, ∴()02222DN t t =--=-+,∴()26228DM DN t t +=++-+=,为定值.【点睛】本题考查了求二次函数解析式、求一次函数解析式,解一元二次方程、二元一次方程组,等腰三角形的性质,三角函数的应用.解题关键在于第(2)题由于不确定点P位置需分类讨论;(2)(3)计算量较大,应认真理清线段之间的关系再进行计算.2.如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PF⊥BC于点F,点D、E的坐标分别为(0,6),(﹣4,0),连接PD,PE,DE.(1)求抛物线的解析式;(2)小明探究点P的位置是发现:当点P与点A或点C重合时,PD与PF的差为定值,进而猜想:对于任意一点P,PD与PF的差为定值,请你判定该猜想是否正确,并说明理由;(3)请直接写出△PDE周长的最大值和最小值.【答案】(1)y=﹣18x2+8;(2)正确,d=|PD﹣PF|为定值2;理由见解析;(3)△PDE周长的最大值是13,最小值是213+10.【解析】【分析】(1)利用待定系数法求出抛物线解析式即可;(2)首先表示出P,F点坐标,再利用两点之间距离公式得出PD,PF的长,进而求出即可;(3)过E作EF⊥x轴,交抛物线于点P,求得C△PDE=ED+PE+PD=ED+PE+PF+2=ED+2+(PE+PF),当P、E、F三点共线时,PE+PF最小;当P与A重合时,PE+PF最大;即可解答.【详解】(1)∵边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,∴C(0,8),A(﹣8,0),设抛物线解析式为:y=ax2+c,则8640 ca c=⎧⎨+=⎩,解得:188ac⎧=-⎪⎨⎪=⎩.∴抛物线解析式为y=﹣18x2+8.(2)设P(x,﹣18x2+8),则F(x,8),则PF=8﹣(﹣18x2+8)=18x2.PD2=x2+[6﹣(﹣18x2+8)]2=164x4+12x2+4=(18x2+2)2∴PD=18x2+2,∴d=|PD﹣PF|=|18x2+2﹣18x2|=2∴d=|PD﹣PF|为定值2;(3)如图,过点E作EF⊥x轴,交抛物线于点P,由d=|PD﹣PF|为定值2,得C△PDE=ED+PE+PD=ED+PE+PF+2=ED+2+(PE+PF),又∵D(0,6),E(﹣4,0)∴DE=22+==.6452213∴C△PDE=213+2+(PE+PF),当PE和PF在同一直线时PE+PF最小,得C△PDE最小值=213+2+8=2 13+10.设P为抛物线AC上异于点A的任意一点,过P作PM∥x轴,交AB于点M,连接ME,如图2.由于E是AO的中点,易证得ME≥PE(当点P接近点A时,在△PME中,显然∠MPE是钝角,故ME≥PE,与A重合时,等号成立),而ME≤AE+AM,所以PE≤AE+AM.所以当P与A重合时,PE+PF最大,AE=8﹣4=4,PD2222++10.86AO DO得C△PDE最大值=13=13.综上所述,△PDE周长的最大值是13,最小值是13.【点睛】此题主要考查了二次函数综合以及两点距离公式以及配方法求二次函数最值等知识,利用数形结合得出符合题意的答案是解题关键.3.如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA="16" cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒2cm的速度匀速运动,Q在线段CO上沿CO 方向以每秒1 cm的速度匀速运动.设运动时间为t秒.(1)用含t的式子表示△OPQ的面积S;(2)判断四边形OPBQ的面积是否是一个定值,如果是,请求出这个定值;如果不是,请说明理由;(3)当△OPQ∽△ABP时,抛物线y=x2+bx+c经过B、P两点,求抛物线的解析式;(4)在(3)的条件下,过线段BP上一动点M作轴的平行线交抛物线于N,求线段MN的最大值.【答案】(1);(2)是;(3);(4)9【解析】试题分析:(1)根据速度与时间的关系分别表示出CQ、OP、OQ的长度,然后利用三角形的面积公式列列式整理即可得解;(2)用矩形OABC的面积减去△ABP与△BCQ的面积,根据面积公式分别列式进行整理即可得解;(3)根据相似三角形对应边成比例列出比例式,然后代入数据求解即可得到t值,从而得到点P的坐标;(4)先求出直线BP的解析式,然后根据直线解析式与抛物线解析式设出点M、N的坐标,再根据两点间的距离表示出MN的长度,根据二次函数的最值问题解答.(1)∵CQ=t,OP=2t,CO=8,∴OQ=8-t,=128-64+8t-8t=64,∴四边形OPBQ 的面积为一个定值,且等于64; (3)当△OPQ ∽△ABP 时,./解得:t 1=2,t 2=8(舍去), 此时P (4,0), ∵B (16,8),∴抛物线解析式是;(4)设直线BP 的解析式为y=kx+b∴直线BP 的解析式是∵M 在BP 上运动, ∴4≤m≤16,∴当时,MN 有最大值是9.考点:二次函数的综合题点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型. 4.如图1所示,抛物线2y ax bx c =++交x 轴于点()A 4,0-和点()B 1,0,交y 轴于点()C 0,4.()1求抛物线的函数表达式;()2如图2所示,若点M 是抛物线上一动点,且AOM S BOC S 3=,求点M 的坐标;()3如图3所示,设点N 是线段AC 上的一动点,作PN x ⊥轴,交抛物线于点P ,求线段PN 长度的最大值.【答案】(1)2y x 3x 4=--+;(2)点P 坐标为3372⎛⎫- ⎪ ⎪⎝⎭或337,32⎛⎫- ⎪ ⎪⎝⎭或313,32⎛⎫-+- ⎪ ⎪⎝⎭或3133⎫---⎪⎪⎝⎭;()3 线段PN 长度最大值为4. 【解析】 【分析】(1)把函数设为交点式,代入C 点坐标,进而求出a 的值即可; (2)设M 点坐标为(x ,-x 2-3x+4),根据S △AOM =3S △BOC列出关于x 的方程,解方程求出x 的值,进而得到点P 的坐标;(3)先运用待定系数法求出直线AC 的解析式为y=x+4,再设N 点坐标为(x ,x+4),则P 点坐标为(x ,-x 2-3x+4),然后用含x 的代数式表示PN ,根据二次函数的性质即可求出线段PN 长度的最大值. 【详解】解:(1)把函数设为交点式()()12y a x x x x =--,由()A 4,0-,()B 1,0得()()y a x 4x 1=+-,把()C 0,4代入,得a 1=-, 故抛物线的解析式为2y x 3x 4=--+; (2)设M 点坐标为()2x,x 3x 4--+,AOMSBOCS3=,2114x 3x 431422∴⨯⨯--+=⨯⨯⨯,整理得2x 3x 43+-=或2x 3x 43+-=-, 解得337x -±=或313x -±=,则符合条件的点P 坐标为337,3⎛⎫-+ ⎪⎪⎝⎭或337,3⎛⎫-- ⎪ ⎪⎝⎭或313,3⎛⎫-+- ⎪ ⎪⎝⎭或313,3⎛⎫--- ⎪ ⎪⎝⎭; (3)设直线AC 的解析式为y kx b =+,将()A 4,0-,()C 0,4代入,4k b 0b 4-+=⎧⎨=⎩, 解得k 1b 4=⎧⎨=⎩,即直线AC 的解析式为y x 4=+,设点N 坐标为()x,x 4+,()4x 0-≤≤,则P 点坐标为()2x,x 3x 4--+,设PN y =,则()()222y x 3x 4x 4x 4x (x 2)4=--+-+=--=-++,即当x 2=-时,y 有最大值4, 故线段PN 长度最大值为4. 【点睛】本题考查二次函数的综合问题,涉及待定系数法求函数解析式,面积问题以及线段最值问题,熟练掌握二次函数的图像与性质是解题的关键.5.如图,在直角坐标系中,抛物线经过点A (0,4),B (1,0),C (5,0) (1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P ,使△PAB 的周长最小?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)该抛物线有一点D (x ,y ),使得S △ABC =S △DBC ,求点D 的坐标.【答案】(1)y =2424455x x -+,x =3;(2)P (3,85);(3)D 的坐标为(6,4). 【解析】 【分析】(1)因为抛物线经过点B (1,0),C (5,0),可以假设抛物解析式为y=a (x-1)(x-5),把A (0,4)代入即可解决问题,对称轴根据图象即可解决.(2)连接AC 与对称轴的交点即为点P ,此时△PAB 周长最小.求出直线AC 的解析式即可解决问题; (3)根据面积相等且底边相等的三角形的高也应该相等得出D 的纵坐标为±4,代入抛物线的解析式即可求得. 【详解】(1)∵抛物线经过点B (1,0),C (5,0),∴可以假设抛物解析式为y =a (x ﹣1)(x ﹣5),把A (0,4)代入得4=5a , ∴a =45, ∴抛物线解析式为y =45(x ﹣1)(x ﹣5)=45x 2﹣245x +4. 抛物线对称轴x =1+52=3. (2)连接AC 与对称轴的交点即为点P ,此时△PAB 周长最小.设直线AC 的解析式为y =kx +b , ∵A (0,4),C (5,0), ∴450b k b =⎧⎨+=⎩,解得454k b ⎧=-⎪⎨⎪=⎩,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年中考数学一轮复习之二次函数动点问题(面积、长度最值与定长)1.如图1,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴分别交于A(﹣3,0),B两点,与y轴交于点C,抛物线的顶点E(﹣1,4),对称轴交x轴于点F.(1)请直接写出这条抛物线和直线AE、直线AC的解析式;(2)连接AC、AE、CE,判断△ACE的形状,并说明理由;(3)如图2,点D是抛物线上一动点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK⊥x轴于点K,DK分别交线段AE、AC于点G、H.在点D的运动过程中,①DG、GH、HK这三条线段能否相等?若相等,请求出点D的坐标;若不相等,请说明理由;②在①的条件下,判断CG与AE的数量关系,并直接写出结论.解:(1)抛物线的表达式为:y=a(x+1)2+4=a(x2+2x+1)+4,故a+4=3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2﹣2x+3;将点A、E的坐标代入一次函数表达式并解得:直线AE的表达式为:y=2x+6;同理可得:直线AC的表达式为:y=x+3;(2)点A、C、E的坐标分别为:(﹣3,0)、(0,3)、(﹣1,4),则AC2=18,CE2=2,AE2=20,故AC2+CE2=AE2,则△ACE为直角三角形;(3)①设点D、G、H的坐标分别为:(x,﹣x2﹣2x+3)、(x,2x+6)、(x,x+3),DG=﹣x2﹣2x+3﹣2x﹣6=﹣x2﹣4x﹣3;HK=x+3;GH=2x+6﹣x﹣3=x+3;当DG=HK时,﹣x2﹣4x﹣3=x+3,解得:x=﹣2或﹣3(舍去﹣3),故x=﹣2,当x=﹣2时,DG=HK=GH=1,故DG、GH、HK这三条线段相等时,点D的坐标为:(﹣2,3);②CG==;AE==2,故AE=2CG.2.如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.(1)求该抛物线的函数表达式;(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.写出点M′的坐标.解:(1)直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,则点A、B的坐标分别为:(1,0)、(0,3),抛物线y=ax2﹣2ax+a+4(a<0)经过点B(0,3),则a+4=3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2+2x+3;(2)过点M作MH⊥x轴于点H,设点M(m,﹣m2+2m+3),则S=S梯形BOHM﹣S△OAB﹣S△AMH=(﹣m2+2m+3+3)×m﹣[3×1+(m﹣1)(﹣m2+2m+3)]=﹣m2+m,∵0,故S有最大值,当m=时,S的最大值为:;(3)当S取得最大值时,此时,m=,则y=﹣m2+2m+3=,故点M′的坐标为:(,).3.已知抛物线y=ax2+bx﹣4经过点M(﹣4,6)和点N(2,﹣6).(1)试确定该抛物线的函数表达式;(2)若该抛物线与x轴交于点A,B(点A在点B的左侧),与y轴交于点C①试判断△ABC的形状,并说明理由;②在该抛物线的对称轴上是否存在点P,使PM+PC的值最小?若存在,求出它的最小值;若不存在,请说明理由.解:(1)将点M、N的坐标代入抛物线表达式得:,解得:,故抛物线的表达式为:y=x2﹣x﹣4;(2)①y=x2﹣x﹣4,令y=0,则x=﹣2或8,x=0,则y=﹣4,故点A、B、C的坐标分别为:(﹣2,0)、(8,0)、(0,﹣4),则函数的对称轴为:x=3,则AB=10,BC=,AC=,则AB2=BC2+AC2,故△ABC为直角三角形;②作点M关于函数对称轴的对称点D(10,6),连接CD交函数对称轴于点P,则点P为所求,将点CD的坐标代入一次函数表达式:y=kx+b并解得:直线CD的表达式为:y=x﹣4,当x=3时,y=﹣1,故点P(3,﹣1),此时PM+PC的值最小为CD=10.4.如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C,顶点是D,对称轴交x轴于点E.(1)求抛物线的解析式;(2)点P是抛物线在第四象限内的一点,过点P作PQ∥y轴,交直线AC于点Q,设点P的横坐标是m.①求线段PQ的长度n关于m的函数关系式;②连接AP,CP,求当△ACP面积为时点P的坐标;(3)若点N是抛物线对称轴上一点,则抛物线上是否存在点M,使得以点B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出线段BN的长度;若不存在,请说明理由.解:(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),故﹣3a=﹣3,解得:a=1,故抛物线的表达式为:y=x2﹣2x﹣3;(2)设点P(m,m2﹣2m﹣3),①将点A、C的坐标代入一次函数表达式并解得:直线AC的表达式为:y=﹣3x﹣3,则点Q(m,﹣3m﹣3),n=PQ=m2﹣2m﹣3+3m+3=m2+m;②连接AP交y轴于点H,同理可得:直线AP的表达式为:y=(m﹣3)x+m﹣3,则OH=3﹣m,则CH=m,△ACP面积=×CH×(xP﹣xA)=m(m+1)=,解得:m=(不合题意的值已舍去),故点P(,﹣);(3)点C(0,﹣3),点B(3,0),设点M(m,n),n=m2﹣2m﹣3,点N(1,s),①当BC是边时,点C向右平移3个单位向上平移3个单位得到B,同样点M(N)向右平移3个单位向上平移3个单位得到N(M),即m±3=1,n±3=s,解得:m=﹣2或4,s=8或2,故点N(1,2)或(1,8),则BN=2或2;②当BC是对角线时,由中点公式得:3=m+1,﹣3=s+n,解得:s=0,故点N(1,0),则BN=2,综上,BN=2或2或2.5.如图直角坐标系中,△ABO,O为坐标原点,A(0,3),B(6,3),二次函数y=﹣x2+bx+c的图象经过点A,B,点P为抛物线上AB上方的一个点,连结PA,作PQ⊥AB垂足为H,交OB于点Q.(1)求b,c的值;(2)当∠APQ=∠B时,求点P的坐标;(3)当△APH面积是四边形AOQH面积的2倍时,求点P的坐标.解:(1)把A(0,3),B(6,3)代入y=﹣x2+bx+c并解得:;(2)设P(m,﹣m2+6m+3)∵∠P=∠B,∠AHP=∠OAB=90°,∴△ABO~△HPA,∴,∴,解得m=4.∴P(4,11)(3)当△APH的面积是四边形AOQH的面积的2倍时,则2(AO+HQ)=PH∴,得:m1=4,m2=3,∴P(4,11)或P(3,12)6.在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B,C,已知A(﹣1,0),C (0,3).(1)求抛物线的解析式;(2)如图1,P为线段BC上一动点,过点P作y轴的平行线,交抛物线于点D,是否存在这样的P点,使线段PD的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是直线EF上一动点,M(m,0)是x轴一个动点,请直接写出CN+MN+MB的最小值以及此时点M、N的坐标,直接写出结果不必说明理由.解:(1)y=﹣x2+bx+c经过点C,则c=3,将点A的坐标代入抛物线表达式:y=﹣x2+bx+3并解得:b=2,抛物线的表达式为:y=﹣x2+2x+3;(2)存在,理由:令y=0,则x=﹣1或3,故点B(3,0),将点B、C的坐标代入一次函数表达式并解得:直线BC的表达式为:y=﹣x+3,设点D(x,﹣x2+2x+3),则点P(x,﹣x+3),则PD=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x,当x=时,PD最大值为:;(3)过点B作倾斜角为30°的直线BH,过点C作CH⊥BH交于点H,CH交对称轴于点N,交x轴于点M,则点M、N为所求,直线BH表达式中的k值为,则直线CH的表达式为:y=﹣x+3,当x=1时,y=3﹣,当y=0时,x=,故点N、M的坐标分别为:(1,3﹣)、(,0),CN+MN+MB的最小值=CH=CM+FH=.7.如图,抛物线y=(x+2)(x﹣2k)交x轴于点A、B,(A左B右),与y轴交于点C,把射线BC沿x轴翻折交抛物线于点D,交y轴于点F,点D纵坐标为6.(1)求抛物线的解析式;(2)点P为第四象限抛物线上一点,连接PB、PC,设点P横坐标为m,△PBC的面积为S,求S与m的函数解析式(不要求写出自变量取值范围);(3)在(2)的条件下,PD交y轴于点E,交BC于点M,过点P作y轴平行线交BD、BC于点G、H,若△MEF与△MGH面积的和为6,求△PBC的面积.解:(1)过点D作DS⊥x轴于S.令y=0,即(x+2)(x﹣2k)=0解得x=﹣2或x=2k∴OA=2,OB=2k令x=0,则y=﹣k,∴OC=k∴tan∠OBC=tan∠OBD=,∵点D纵坐标为6,∴DS=6,BS=12,∴OS=12﹣2k∴点D坐标为(2k﹣12,6),代入解析式得:6=(2k﹣12+2)(2k﹣12﹣2k)解得k=4∴抛物线解析式为y=(x+2)(x﹣8)或y=x2﹣x﹣4;(2)过点P作PN⊥BC于N,PR⊥x轴于R,PR交BC于K 令x=0,y=﹣4,∴OC=4C(0,﹣4),由(1)得B(8,0)先求出直线BC解析式y=x﹣4,PK=PR﹣RK点P(m,m2﹣m﹣4)PR=m2﹣m﹣4),K(m,m﹣4)RK=m+4PK=﹣(m2﹣m﹣4)﹣(m+4)=﹣,∠NPK=∠OBC∴cos∠OBC=cos∠NPK=PN=PK cos∠NPK=﹣m2+m BC =4S=BC×PN=(﹣m2+m)S=﹣m2+8m;(3)在(1)图基础上,过点P作PQ⊥DS,设PQ交y轴于点L,tan∠DPQ===,即∴EL=可知点F(0,4)EF=FL﹣EL=4﹣()﹣EF=8﹣m,求出直线BF解析式为y=﹣x+4,点G纵坐标为﹣m+4,点H纵坐标为m﹣4,GH=(﹣m+4,)﹣(m﹣4,)=8﹣m,∵△MEF面积与△MGH面积和为6∴(8﹣m)m=6解得m=2或m=6∵S=﹣m2+8m∴S=12.8.如图,抛物线y=﹣x﹣1与y轴交于点A,点B是抛物线上的一点,过点B 作BC⊥x轴于点C,且点C的坐标为(9,0).(1)求直线AB的表达式;(2)若直线MN∥y轴,分别与抛物线,直线AB,x轴交于点M、N、Q,且点Q位于线段OC之间,求线段MN长度的最大值;(3)当四边形MNCB是平行四边形时,求点Q的坐标.解:(1)令x=0,则y=﹣1,即A(0,﹣1).∵B为抛物线上的一点,BC⊥x轴,C(9,0),∴B点的横坐标为9,纵坐标为,即B(9,2).设直线AB的函数解析式为y=kx+b,将A(0,﹣1),B(9,2)代入上式并解得:直线AB的函数解析式为;(2)设线段MN的长为L,由抛物线和直线AB的解析式,得:==.故线段MN长度的最大值为;(3)若四边形MNCB是平行四边形,则需要MN=BC,由点B、C的坐标可知BC=2,∴,解得:x=1或x=8.故当点Q的坐标为(1,0)或(8,0)时,四边形MNCB是平行四边形.9.如图,在平面直角坐标系中,已知点B的坐标为(﹣1,0),且OA=OC=4OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点.(1)求A,C两点的坐标;(2)求抛物线的解析式;(3)若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P的坐标及PD的最大值.解:(1)OA=OC=4OB=4,故点A、C的坐标分别为(4,0)、(0,﹣4);(2)抛物线的表达式为:y=a(x+1)(x﹣4)=a(x2﹣3x﹣4),即﹣4a=﹣4,解得:a=1,故抛物线的表达式为:y=x2﹣3x﹣4;(3)直线CA过点C,设其函数表达式为:y=kx﹣4,将点A坐标代入上式并解得:k=1,故直线CA的表达式为:y=x﹣4,过点P作y轴的平行线交AC于点H,∵OA=OC=4,∴∠OAC=∠OCA=45°,∵PH∥y轴,∴∠PHD=∠OCA=45°,设点P(x,x2﹣3x﹣4),则点H(x,x﹣4),PD=HP sin∠PFD=(x﹣4﹣x2+3x+4)=﹣x2+2x,∵<0,∴PD有最大值,当x=2时,其最大值为2,此时点P(2,﹣6).10.在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.(1)求这个二次函数的关系解析式,x满足什么值时y<0?(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP面积最大?若存在,求出点P的坐标;若不存在,说明理由;(3)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.解:(1)函数表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),﹣3a=2,解得:a=﹣,抛物线的表达式为:y=﹣x2﹣x+2,当x<﹣3或x>1时,y<0;(2)存在,理由:过点P作平行于y轴的直线交AC于点H,将点A(﹣3,0)、C(0,2)的坐标代入一次函数表达式:y=kx+b得:,解得:,故直线AC的表达式为:y=x+2,设点P(x,﹣x2﹣x+2),则点H(x,x+2),△ACP面积S=×PH×OA=×3(﹣x2﹣x+2﹣x﹣2)=﹣x2﹣3x,∵<0,故当x=﹣时,S有最大值,此时点P(﹣,);(3)设点M的坐标为:(m,n),则n=﹣m2﹣m+2,点Q(s,0),点A、C的坐标分别为:(﹣3,0)、(0,2),①当AC是平行四边形的一条边时,点A向右平移3个单位、向上平移2个单位得到C,同样点M(Q)向右平移3个单位、向上平移2个单位得到Q(M),即:m+3=s,n+2=0或m﹣3=s,n﹣2=0,且n=﹣m2﹣m+2,解得:s=2或﹣5;②当AC是平行四边形的对角线时,则m+s=﹣3,n+0=2,且n=﹣m2﹣m+2,解得:s=﹣1,故点Q的坐标为:(﹣1,0)或(﹣5,0)或(2,0)或(2﹣,0).11.如图,抛物线y=x2+bx+c与轴交于点A和点B,与y轴交于点C,作直线BC,点B的坐标为(6,0),点C的坐标为(0,﹣6).(1)求抛物线的解析式并写出其对称轴;(2)D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求D点坐标;(3)若E为y轴上且位于点C下方的一点,P为直线BC上的一点,在第四象限的抛物线上是否存在一点Q.使以C,E,P,Q为顶点的四边形是菱形?若存在,请求出Q点的横坐标;若不存在,请说明理由.解:(1)将点B、C的坐标代入二次函数表达式得:,解得:,故抛物线的表达式为:y=x2﹣2x﹣6,令y=0,则x=﹣2或6,则点A(﹣2,0),则函数的对称性x=2;(2)①当∠BCD=90°时,将点B、C的坐标代入一次函数表达式得:直线BC的表达式为:y=x﹣6,则直线CD的表达式为:y=﹣x﹣6,当x=2时,y=﹣8,故点D(2,﹣8);②当∠DBC=90°时,同理可得点D(2,4),故点D(2,﹣8)或(2,4);(3)①当CE为菱形的一条边时,则PQ∥CE,设点P(m,m﹣6),则点Q(m,n),则n=m2﹣2m﹣6…①,由题意得:CP=PQ,即m=m﹣6﹣n…②,联立①②并解得:m=6﹣2,n=4﹣8,则点Q(6﹣2,4﹣8);②当CE为菱形的对角线时,则PQ⊥CE,即PQ∥x轴,设点P(m,m﹣6),则点Q(s,m﹣6),其中m﹣6=s2﹣2s﹣6…③,则PC=﹣m,CQ2=s2+m2,由题意得:CQ=CP,即:(﹣m)2=s2+m2…④,联立③④并解得:m=6或﹣2(舍去6),故点(2,﹣8);综上,点Q(6﹣2,4﹣8)或(2,﹣8).12.如图,直线AB经过x轴上一点A(3,0),且与抛物线y=ax2+1相交于B、C两点,点B的坐标为(1,2).(1)求抛物线和直线AB的解析式;(2)若点D是抛物线上一点,且D在直线BC下方,若S△BCD=3,求点D的坐标;(3)设抛物线顶点为M,问在抛物线上是否存在点P使△PMC是以MC为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.解:(1)将点A、B的坐标代入一次函数表达式:y=kx+b得:,解得:,故直线AB的表达式为:y=﹣x+3…②,同理将点B的坐标代入抛物线表达式并解得:抛物线的表达式为:y=x2+1…②;(2)联立①②并解得:x=1或﹣2,故点C(﹣2,5),如图1,过点D作y轴的平行线交BC于点H,设点D(x,x2+1),则点H(x,﹣x+3),则S△BCD=3=DH×(x B﹣x C)=(x2+1﹣x+3)×(1+2),解得:x=0或﹣1,故点D(﹣1,2)或(0,1);(3)如图2,点M的坐标为:(0,1),点C(﹣2,5),则直线CM函数表达式中的k值为:﹣2,①当∠PCM=90°时,则直线CP的函数表达式为:y=x+m,将点C的坐标代入上式并解得:m=6,故直线PC的表达式为:y=x+6…③,联立②③并解得:x=﹣2或(舍去﹣2),故点P的坐标为:(,);②当∠CMP(P′)=90°时,同理可得:点P(P′)(,),综上,点P的坐标为:(,)或(,).13.如图,已知抛物线y=﹣x2+4x+5与x轴交于A、B两点(点A在点B的左侧),与y 轴交于点C.(1)直接写出点A、B、C的坐标;(2)在抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;(3)点D是第一象限内抛物线上的一个动点(与点C、B不重合)过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,直线BC把△BDF的面积分成两部分,使S△BDE:S△BEF=2:3,请求出点D的坐标;(4)若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请直接写出点M的坐标.解:(1)令y=0,则x=﹣1或5,令x=0,则y=5,故点A、B、C的坐标分别为:(﹣1,0)、(5,0)、(0,5);(2)抛物线的对称轴为:x=2,点B是点A关于函数对称轴的对称点,连接BC交抛物线对称轴于点P,则点P为所求,直线BC的表达式为:y=﹣x+5,当x=2时,y=3,故点P(2,3);(3)设点D(x,﹣x2+4x+5),则点E(x,﹣x+5),S△BDE:S△BEF=2:3,则,即:=,解得:m=或5(舍去5),故点D(,);(4)设点M(2,m),而点B、C的坐标分别为:(5,0)、(0,5),则MB2=9+m2,MC2=4+(m﹣5)2,BC2=50,①当MB为斜边时,则9+m2=4+(m﹣5)2+50,解得:m=7;②当MC为斜边时,同理可得:m=﹣3;③当BC为斜边时,同理可得:m=6或﹣1;综上点M的坐标为:(2,7)或(2,﹣3)或(2,6)或(2,﹣1).14.如图,抛物线y=ax2+bx﹣4a(a≠0)经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B,连接AC,BC.(1)求抛物线的解析式;(2)过点C作x轴的平行线交抛物线于另一点D,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标;(3)在抛物线的对称轴上是否存在点M,使得由点M,A,C构成的△MAC是直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.解:(1)﹣4a=4,解得:a=﹣1,则抛物线的表达式为:y=﹣x2+bx+4,将点A的坐标代入上式并解得:b=3,故抛物线的表达式为:y=﹣x2+3x+4…①;(2)抛物线的对称轴为:x=,点D(3,4),过点D作x轴的垂线交BP于点H,交x轴于点G,过点H作HR⊥BD与点R,则BG=1,GD=4,tan∠BDG=,∠DBP=45°,设:HR=BR=x,则DR=4x,BD =5x==,x=,BH=x,BG=1,则GH==,故点H(3,),而点B(4,0),同理可得直线HB的表达式为:y=﹣x+…②,联立①②并解得:x=4或﹣(舍去4),故点P(﹣,);(3)设点M(,m),而点A(﹣1,0)、点C(0,4),则AM2=+m2,CM2=+(m﹣4)2,AC2=17,①当AM是斜边时,+m2=+(m﹣4)2+17,解得:m=;②当CM是斜边时,同理可得:m=﹣;③当AC是斜边时,同理可得:m=或;综上,点M的坐标为:(,)或(,﹣)或(,)或(,).15.如图,已知在平面直角坐标系xOy中,直线y=x+与x轴交于点A,与y轴交于点B,点F是点B关于x轴的对称点,抛物线y=x2+bx+c经过点A和点F,与直线AB交于点C.(1)求b和c的值;(2)点P是直线AC下方的抛物线上的一动点,连结PA,PB.求△PAB的最大面积及点P到直线AC的最大距离;(3)点Q是抛物线上一点,点D在坐标轴上,在(2)的条件下,是否存在以A,P,D,Q为顶点且AP为边的平行四边形,若存在,直接写出点Q的坐标;若不存在,说明理由.解:(1)直线y=x+与x轴交于点A,与y轴交于点B,则点A、B的坐标分别为:(﹣3,0)、(0,),则点F(0,﹣),抛物线y=x2+bx+c经过点A和点F,则c=﹣,将点A的坐标代入抛物线表达式并解得:b=,故抛物线的表达式为:y=x2+x﹣,b=,c=﹣;(2)过点P作y轴的平行线交AB于点H,设点P(x,x2+x﹣),则点H(x,x+),则△PAB的面积S=×PH×OA=(x+﹣x2﹣x+)=(﹣x2﹣x+2),当x=﹣时,S的最大值为,此时点P(﹣,﹣),设:P到直线AC的最大距离为d,AB=2S=AB×d=,解得:d=;(3)存在,理由:点A(﹣3,0),点P(﹣,﹣),设点Q(m,n),n=m2+m﹣,①当点D在x轴上时,若存在以A,P,D,Q为顶点且AP为边的平行四边形时,则n=±,即m2+m﹣=±,解得:m=﹣(舍去)或﹣或﹣1;②当点D在y轴上时,同理可得:0±=m,故点P(,)或(﹣,﹣);故点Q的坐标为:(﹣1﹣,)或(,﹣)或(﹣1+,)或(,)或(﹣,﹣).。
