模式识别习题参考1-齐敏教材第6章分析解析
模式识别课后习题答案

• 2.16 证明M ahalanobis距离r符合距离定义三定理,即 – (1) r(a, b) = r(b, a) – (2) 当且仅当a = b时,r(a, b) = 0 – (3) r(a, c) ≤ r(a, b) + r(b, c) 证明: (1) r(a, b) = (a − b)T Σ−1 (a − b) = (b − a)T Σ−1 (b − a) = r(b, a) (2) Σ为半正定矩阵所以r(a, b) = (a − b)T Σ−1 (a − b) ≥ 0,只有当a = b时,才有r(a, b) = 0。 (3) Σ−1 可对角化,Σ−1 = P ΛP T • 2.17 若将Σ−1 矩阵写为:Σ−1 h1d h2d ,证明M ahalanobis距离平方为 . . . hdd
• 2.13 把连续情况的最小错误率贝叶斯决策推广到离散情况,并写出其判别函数。 • 2.14 写出离散情况条件风险R(ai |x)的定义,并指出其决策规则。 解: R(ai |x) = = R(ak |x) = min
c ∑ j =1 c ∑ j =1
λij P (wj |x) λij pቤተ መጻሕፍቲ ባይዱx|wj )P (wj )////omit the same part p(x)
j =1,...,c j =1,...,c
考虑两类问题的分类决策面为:P (w1 |x) = P (w2 |x),与p(x|w1 )P (w1 ) = p(x|w2 )P (w2 ) 是相同的。 • 2.9 写出两类和多类情况下最小风险贝叶斯决策判别函数和决策面方程。 • 2.10 随机变量l(x)定义为l(x) = p(x|w1 ) ,l(x)又称为似然比,试证明 p(x|w2 )
1
模式识别(山东联盟)智慧树知到课后章节答案2023年下青岛大学

模式识别(山东联盟)智慧树知到课后章节答案2023年下青岛大学青岛大学第一章测试1.关于监督模式识别与非监督模式识别的描述正确的是答案:非监督模式识别对样本的分类结果是唯一的2.基于数据的方法适用于特征和类别关系不明确的情况答案:对3.下列关于模式识别的说法中,正确的是答案:模式可以看作对象的组成成分或影响因素间存在的规律性关系4.在模式识别中,样本的特征构成特征空间,特征数量越多越有利于分类答案:错5.在监督模式识别中,分类器的形式越复杂,对未知样本的分类精度就越高答案:错第二章测试1.下列关于最小风险的贝叶斯决策的说法中正确的有答案:条件风险反映了对于一个样本x采用某种决策时所带来的损失;最小风险的贝叶斯决策考虑到了不同的错误率所造成的不同损失;最小错误率的贝叶斯决策是最小风险的贝叶斯决策的特例2.我们在对某一模式x进行分类判别决策时,只需要算出它属于各类的条件风险就可以进行决策了。
答案:对3.下面关于贝叶斯分类器的说法中错误的是答案:贝叶斯分类器中的判别函数的形式是唯一的4.当各类的协方差矩阵相等时,分类面为超平面,并且与两类的中心连线垂直。
答案:错5.当各类的协方差矩阵不等时,决策面是超二次曲面。
答案:对第三章测试1.概率密度函数的估计的本质是根据训练数据来估计概率密度函数的形式和参数。
答案:对2.参数估计是已知概率密度的形式,而参数未知。
答案:对3.概率密度函数的参数估计需要一定数量的训练样本,样本越多,参数估计的结果越准确。
答案:对4.下面关于最大似然估计的说法中正确的是答案:在最大似然函数估计中,要估计的参数是一个确定的量。
;在最大似然估计中要求各个样本必须是独立抽取的。
;最大似然估计是在已知概率密度函数的形式,但是参数未知的情况下,利用训练样本来估计未知参数。
5.贝叶斯估计中是将未知的参数本身也看作一个随机变量,要做的是根据观测数据对参数的分布进行估计。
答案:对第四章测试1.多类问题的贝叶斯分类器中判别函数的数量与类别数量是有直接关系的。
模式识别复习要点和参考习题

复习要点绪论1、举出日常生活或技术、学术领域中应用模式识别理论解决问题的实例。
答:我的本科毕设内容和以后的研究方向为重症监护病人的状态监测与预诊断,其中的第一步就是进行ICU病人的死亡率预测,与模式识别理论密切相关。
主要的任务是分析数据库的8000名ICU病人,统计分析死亡与非死亡的生理特征,用于分析预测新进ICU病人的病情状态。
按照模式识别的方法步骤,首先从数据库中采集数据,包括病人的固有信息,生理信息,事件信息等并分为死亡组和非死亡组,然后分别进行数据的预处理,剔除不正常数据,对数据进行插值并取中值进行第一次特征提取,然后利用非监督学习的方法即聚类分析进行第二次特征提取,得到训练样本集和测试样本集。
分别利用判别分析,人工神经网络,支持向量机的方法进行训练,测试,得到分类器,实验效果比传统ICU 中采用的评价预测系统好一些。
由于两组数据具有较大重叠,特征提取,即提取模式特征就变得尤为重要。
语音识别,图像识别,车牌识别,文字识别,人脸识别,通信中的信号识别;① 文字识别汉字已有数千年的历史,也是世界上使用人数最多的文字,对于中华民族灿烂文化的形成和发展有着不可磨灭的功勋。
所以在信息技术及计算机技术日益普及的今天,如何将文字方便、快速地输入到计算机中已成为影响人机接口效率的一个重要瓶颈,也关系到计算机能否真正在我过得到普及的应用。
目前,汉字输入主要分为人工键盘输入和机器自动识别输入两种。
其中人工键入速度慢而且劳动强度大;自动输入又分为汉字识别输入及语音识别输入。
从识别技术的难度来说,手写体识别的难度高于印刷体识别,而在手写体识别中,脱机手写体的难度又远远超过了联机手写体识别。
到目前为止,除了脱机手写体数字的识别已有实际应用外,汉字等文字的脱机手写体识别还处在实验室阶段。
②语音识别语音识别技术技术所涉及的领域包括:信号处理、模式识别、概率论和信息论、发声机理和听觉机理、人工智能等等。
近年来,在生物识别技术领域中,声纹识别技术以其独特的方便性、经济性和准确性等优势受到世人瞩目,并日益成为人们日常生活和工作中重要且普及的安验证方式。
模式识别习题参考1-齐敏教材第6章
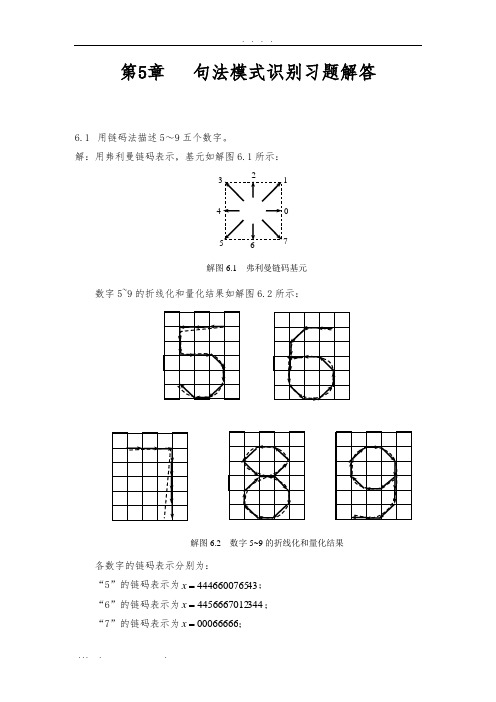
第5章 句法模式识别习题解答6.1 用链码法描述5~9五个数字。
解:用弗利曼链码表示,基元如解图6.1所示:数字5~9的折线化和量化结果如解图6.2所示:各数字的链码表示分别为:“5”的链码表示为434446600765=x ; “6”的链码表示为3444456667012=x ; “7”的链码表示为00066666=x ;0 17解图6.1 弗利曼链码基元解图6.2 数字5~9的折线化和量化结果“8”的链码表示为21013457076543=x ; “9”的链码表示为5445432107666=x 。
6.2 定义所需基本基元,用PDL 法描述印刷体英文大写斜体字母“H ”、“K ”和“Z ”。
解:设基元为:用PDL 法得到“H ”的链描述为)))))(~((((d d c d d x H ⨯+⨯+=;“K ”的链描述为))((b a d d x K ⨯⨯+=; “Z ”的链描述为))((c c g x Z ⨯-=。
6.3 设有文法),,,(S P V V G T N =,N V ,T V 和P 分别为},,{B A S V N =,},{b a V T =:P ①aB S →,②bA S →,③a A →,④aS A →⑤bAA A →,⑥b B →,⑦bS B →,⑧aBB B → 写出三个属于)(G L 的句子。
解:以上句子ab ,abba ,abab ,ba ,baab ,baba 均属于)(G L 。
bcadeabba abbA abS aB S ⇒⇒⇒⇒ ① ⑦ ② ③ab aB S ⇒⇒ ① ⑥ ba bA S ⇒⇒② ③ abab abaB abS aB S ⇒⇒⇒⇒ ① ⑦ ① ⑥baab baaB baS bA S ⇒⇒⇒⇒ ② ④ ① ⑥baba babA baS bA S ⇒⇒⇒⇒② ④ ② ③6.4 设有文法),,,(S P V V G T N =,其中},,,{C B A S V N =,}1,0{=T V ,P 的各生成式为①A S 0→,②B S 1→,③C S 1→ ④A A 0→,⑤B A 1→,⑥1→A ⑦0→B ,⑧B B 0→,⑨C C 0→,⑩1→C问00100=x 是否属于语言)(G L ? 解:由可知00100=x 属于语言)(G L 。
模式识别习题集答案解析

PCA是一种无监督的映射方法,LDA是一种有监督的映射方法。
PCA只是将整组数据映射到最方便表示这组数据的坐标轴上,映射时没有利用任何数据部的分类信息。
因此,虽然做了PCA后,整组数据在表示上更加方便(降低了维数并将信息损失降到了最低),但在分类上也许会变得更加困难;LDA在增加了分类信息之后,将输入映射到了另外一个坐标轴上,有了这样一个映射,数据之间就变得更易区分了(在低纬上就可以区分,减少了很大的运算量),它的目标是使得类别的点距离越近越好,类别间的点越远越好。
2、最大似然估计和贝叶斯方法的区别?p(x|X)是概率密度函数,X是给定的训练样本的集合,在哪种情况下,贝叶斯估计接近最大似然估计?最大似然估计把待估的参数看做是确定性的量,只是其取值未知。
利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值(模型已知,参数未知)。
贝叶斯估计则是把待估计的参数看成是符合某种先验概率分布的随机变量。
对样本进行观测的过程,把先验概率密度转化为后验概率密度,利用样本的信息修正了对参数的初始估计值。
当训练样本数量趋于无穷的时候,贝叶斯方法将接近最大似然估计。
如果有非常多的训练样本,使得p (x|X)形成一个非常显著的尖峰,而先验概率p(x)又是均匀分布,此时两者的本质是相同的。
3、为什么模拟退火能够逃脱局部极小值?在解空间随机搜索,遇到较优解就接受,遇到较差解就按一定的概率决定是否接受,这个概率随时间的变化而降低。
实际上模拟退火算法也是贪心算法,只不过它在这个基础上增加了随机因素。
这个随机因素就是:以一定的概率来接受一个比单前解要差的解。
通过这个随机因素使得算法有可能跳出这个局部最优解。
4、最小错误率和最小贝叶斯风险之间的关系?基于最小风险的贝叶斯决策就是基于最小错误率的贝叶斯决策,换言之,可以把基于最小错误率决策看做是基于最小风险决策的一个特例,基于最小风险决策本质上就是对基于最小错误率公式的加权处理。
模式识别习题及答案

模式识别习题及答案模式识别习题及答案模式识别是人类智能的重要组成部分,也是机器学习和人工智能领域的核心内容。
通过模式识别,我们可以从大量的数据中发现规律和趋势,进而做出预测和判断。
本文将介绍一些模式识别的习题,并给出相应的答案,帮助读者更好地理解和应用模式识别。
习题一:给定一组数字序列,如何判断其中的模式?答案:判断数字序列中的模式可以通过观察数字之间的关系和规律来实现。
首先,我们可以计算相邻数字之间的差值或比值,看是否存在一定的规律。
其次,我们可以将数字序列进行分组,观察每组数字之间的关系,看是否存在某种模式。
最后,我们还可以利用统计学方法,如频率分析、自相关分析等,来发现数字序列中的模式。
习题二:如何利用模式识别进行图像分类?答案:图像分类是模式识别的一个重要应用领域。
在图像分类中,我们需要将输入的图像分为不同的类别。
为了实现图像分类,我们可以采用以下步骤:首先,将图像转换为数字表示,如灰度图像或彩色图像的像素矩阵。
然后,利用特征提取算法,提取图像中的关键特征。
接下来,选择合适的分类算法,如支持向量机、神经网络等,训练模型并进行分类。
最后,评估分类结果的准确性和性能。
习题三:如何利用模式识别进行语音识别?答案:语音识别是模式识别在语音信号处理中的应用。
为了实现语音识别,我们可以采用以下步骤:首先,将语音信号进行预处理,包括去除噪声、降低维度等。
然后,利用特征提取算法,提取语音信号中的关键特征,如梅尔频率倒谱系数(MFCC)。
接下来,选择合适的分类算法,如隐马尔可夫模型(HMM)、深度神经网络(DNN)等,训练模型并进行语音识别。
最后,评估识别结果的准确性和性能。
习题四:如何利用模式识别进行时间序列预测?答案:时间序列预测是模式识别在时间序列分析中的应用。
为了实现时间序列预测,我们可以采用以下步骤:首先,对时间序列进行平稳性检验,确保序列的均值和方差不随时间变化。
然后,利用滑动窗口或滚动平均等方法,将时间序列划分为训练集和测试集。
模式识别试题答案最终版【范本模板】

模式识别非学位课考试试题考试科目:模式识别考试时间考生姓名: 考生学号任课教师考试成绩一、简答题(每题6分,12题共72分):1、监督学习和非监督学习有什么区别?参考答案:监督学习与非监督学习的区别:监督学习方法用来对数据实现分类,分类规则通过训练获得。
该训练集由带分类号的数据集组成,因此监督学习方法的训练过程是离线的.非监督学习方法不需要单独的离线训练过程,也没有带分类号(标号)的训练数据集,一般用来对数据集进行分析,如聚类,确定其分布的主分量等.2、你如何理解特征空间?表示样本有哪些常见方法?参考答案:由利用某些特征描述的所有样本组成的集合称为特征空间或者样本空间,特征空间的维数是描述样本的特征数量。
描述样本的常见方法:矢量、矩阵、列表等。
3、什么是分类器?有哪些常见的分类器?参考答案:将特征空中的样本以某种方式区分开来的算法、结构等。
例如:贝叶斯分类器、神经网络等。
4、进行模式识别在选择特征时应该注意哪些问题?参考答案:特征要能反映样本的本质;特征不能太少,也不能太多;要注意量纲。
5、聚类分析中,有哪些常见的表示样本相似性的方法?参考答案:距离测度、相似测度和匹配测度。
距离测度例如欧氏距离、绝对值距离、明氏距离、马氏距离等。
相似测度有角度相似系数、相关系数、指数相似系数等。
6、SVM的主要思想可以概括为两点:(1)它是针对线性可分情况进行分析,对于线性不可分的情况,通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分,从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能;(2)它基于结构风险最小化理论之上在特征空间中建构最优分割超平面,使得学习器得到全局最优化,并且在整个样本空间的期望风险以某个概率满足一定上界。
7、请论述模式识别系统的主要组成部分及其设计流程,并简述各组成部分中常用方法的主要思想。
特征空间信息获取:通过测量、采样和量化,可以用矩阵或向量表示二维图像或以为波形。
(完整word版)模式识别题目及答案(word文档良心出品)

一、(15分)设有两类正态分布的样本集,第一类均值为T1μ=(2,0),方差11⎡⎤∑=⎢⎥⎣⎦11/21/2,第二类均值为T2μ=(2,2),方差21⎡⎤∑=⎢⎥⎣⎦1-1/2-1/2,先验概率12()()p p ωω=,试求基于最小错误率的贝叶斯决策分界面。
解 根据后验概率公式()()()()i i i p x p p x p x ωωω=, (2’)及正态密度函数11/21()exp[()()/2]2T i i i i nip x x x ωμμπ-=--∑-∑ ,1,2i =。
(2’) 基于最小错误率的分界面为1122()()()()p x p p x p ωωωω=, (2’) 两边去对数,并代入密度函数,得1111112222()()/2ln ()()/2ln T T x x x x μμμμ----∑--∑=--∑--∑ (1) (2’)由已知条件可得12∑=∑,114/3-⎡⎤∑=⎢⎥⎣⎦4/3-2/3-2/3,214/3-⎡⎤∑=⎢⎥⎣⎦4/32/32/3,(2’)设12(,)Tx x x =,把已知条件代入式(1),经整理得1221440x x x x --+=, (5’)二、(15分)设两类样本的类内离散矩阵分别为11S ⎡⎤=⎢⎥⎣⎦11/21/2, 21S ⎡⎤=⎢⎥⎣⎦1-1/2-1/2,各类样本均值分别为T 1μ=(1,0),T2μ=(3,2),试用fisher 准则求其决策面方程,并判断样本Tx =(2,2)的类别。
解:122S S S ⎡⎤=+=⎢⎥⎣⎦200 (2’) 投影方向为*112-2-1()211/2w S μμ-⎡⎤⎡⎤⎡⎤=-==⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦1/200 (6’)阈值为[]*0122()/2-1-131T y w μμ⎡⎤=+==-⎢⎥⎣⎦(4’)给定样本的投影为[]*0-12241T y w x y ⎡⎤===-<⎢⎥-⎣⎦, 属于第二类 (3’)三、 (15分)给定如下的训练样例实例 x0 x1 x2 t(真实输出) 1 1 1 1 1 2 1 2 0 1 3 1 0 1 -1 4 1 1 2 -1用感知器训练法则求感知器的权值,设初始化权值为0120w w w ===;1 第1次迭代(4’)2 第2次迭代(2’)3 第3和4次迭代四、 (15分)i. 推导正态分布下的最大似然估计;ii. 根据上步的结论,假设给出如下正态分布下的样本{}1,1.1,1.01,0.9,0.99,估计该部分的均值和方差两个参数。
(完整word版)模式识别试题及总结

一、填空与选择填空(本题答案写在此试卷上,30分)1、模式识别系统的基本构成单元包括:模式采集、特征提取与选择和模式分类。
2、统计模式识别中描述模式的方法一般使用特真矢量;句法模式识别中模式描述方法一般有串、树、网。
3、聚类分析算法属于(1) ;判别域代数界面方程法属于(3) 。
(1)无监督分类(2)有监督分类(3)统计模式识别方法(4)句法模式识别方法4、若描述模式的特征量为0-1二值特征量,则一般采用(4)进行相似性度量。
(1)距离测度(2)模糊测度(3)相似测度(4)匹配测度5、下列函数可以作为聚类分析中的准则函数的有(1)(3)(4)。
(1)(2)(3)(4)6、Fisher线性判别函数的求解过程是将N维特征矢量投影在(2) 中进行。
(1)二维空间(2)一维空间(3)N-1维空间7、下列判别域界面方程法中只适用于线性可分情况的算法有(1);线性可分、不可分都适用的有(3)。
(1)感知器算法(2)H—K算法(3)积累位势函数法8、下列四元组中满足文法定义的有(1)(2)(4) 。
(1)({A, B}, {0,1}, {A®01, A® 0A1 ,A® 1A0 ,B®BA , B® 0}, A)(2)({A}, {0,1},{A®0, A® 0A},A)(3)({S},{a, b},{S ® 00S,S ® 11S, S ® 00,S ® 11},S)(4)({A},{0,1}, {A®01,A® 0A1, A® 1A0},A)9、影响层次聚类算法结果的主要因素有(计算模式距离的测度、(聚类准则、类间距离门限、预定的类别数目))。
10、欧式距离具有( 1、2 );马式距离具有( 1、2、3、4 )。
(1)平移不变性(2)旋转不变性(3)尺度缩放不变性(4)不受量纲影响的特性11、线性判别函数的正负和数值大小的几何意义是(正(负)表示样本点位于判别界面法向量指向的正(负)半空间中;绝对值正比于样本点到判别界面的距离。
模式识别习题及答案

第一章 绪论1.什么是模式?具体事物所具有的信息。
模式所指的不是事物本身,而是我们从事物中获得的___信息__。
2.模式识别的定义?让计算机来判断事物。
3.模式识别系统主要由哪些部分组成?数据获取—预处理—特征提取与选择—分类器设计/ 分类决策。
第二章 贝叶斯决策理论1.最小错误率贝叶斯决策过程? 答:已知先验概率,类条件概率。
利用贝叶斯公式得到后验概率。
根据后验概率大小进行决策分析。
2.最小错误率贝叶斯分类器设计过程?答:根据训练数据求出先验概率类条件概率分布 利用贝叶斯公式得到后验概率如果输入待测样本X ,计算X 的后验概率根据后验概率大小进行分类决策分析。
3.最小错误率贝叶斯决策规则有哪几种常用的表示形式? 答:4.贝叶斯决策为什么称为最小错误率贝叶斯决策?答:最小错误率Bayes 决策使得每个观测值下的条件错误率最小因而保证了(平均)错误率 最小。
Bayes 决策是最优决策:即,能使决策错误率最小。
5.贝叶斯决策是由先验概率和(类条件概率)概率,推导(后验概率)概率,然后利用这个概率进行决策。
6.利用乘法法则和全概率公式证明贝叶斯公式答:∑====mj Aj p Aj B p B p A p A B p B p B A p AB p 1)()|()()()|()()|()(所以推出贝叶斯公式7.朴素贝叶斯方法的条件独立假设是(P(x| ωi) =P(x1, x2, …, xn | ωi)⎩⎨⎧∈>=<211221_,)(/)(_)|()|()(w w x w p w p w x p w x p x l 则如果∑==21)()|()()|()|(j j j i i i w P w x P w P w x P x w P 2,1),(=i w P i 2,1),|(=i w x p i ∑==21)()|()()|()|(j j j i i i w P w x P w P w x P x w P ∑===Mj j j i i i i i A P A B P A P A B P B P A P A B P B A P 1)()|()()|()()()|()|(= P(x1| ωi) P(x2| ωi)… P(xn| ωi))8.怎样利用朴素贝叶斯方法获得各个属性的类条件概率分布?答:假设各属性独立,P(x| ωi) =P(x1, x2, …, xn | ωi) = P(x1| ωi) P(x2| ωi)… P(xn| ωi) 后验概率:P(ωi|x) = P(ωi) P(x1| ωi) P(x2| ωi)… P(xn| ωi)类别清晰的直接分类算,如果是数据连续的,假设属性服从正态分布,算出每个类的均值方差,最后得到类条件概率分布。
模式识别课后习题答案

– (1) E{ln(x)|w1} = E{ln+1(x)|w2} – (2) E{l(x)|w2} = 1 – (3) E{l(x)|w1} − E2{l(x)|w2} = var{l(x)|w2}(教材中题目有问题) 证∫ 明ln+:1p对(x于|w(12)),dxE={ln∫(x()∫p(|wp(x(1x|}w|w=1)2))∫n)+nl1nd(xx)所p(x以|w∫,1)Ed{xln=(x∫)|w(1p(}p(x(=x|w|Ew1)2{))ln)n+n+11d(xx)又|wE2}{ln+1(x)|w2} = 对于(2),E{l(x)|w2} = l(x)p(x|w2)dx = p(x|w1)dx = 1
对于(3),E{l(x)|w1} − E2{l(x)|w2} = E{l2(x)|w2} − E2{l(x)|w2} = var{l(x)|w2}
• 2.11 xj(j = 1, 2, ..., n)为n个独立随机变量,有E[xj|wi] = ijη,var[xj|wi] = i2j2σ2,计 算在λ11 = λ22 = 0 及λ12 = λ21 = 1的情况下,由贝叶斯决策引起的错误率。(中心极限 定理)
R2
R1
容易得到
∫
∫
p(x|w2)dx = p(x|w1)dx
R1
R2
所以此时最小最大决策面使得P1(e) = P2(e)
• 2.8 对于同一个决策规则判别函数可定义成不同形式,从而有不同的决策面方程,指出 决策区域是不变的。
3
模式识别(第二版)习题解答
模式识别课件(第六章 NO1)(最近邻法)

二. 剪辑近邻法
此类方法的基本思想是:剪掉(清理)两类间的边界,取 掉类别混杂的样本,使两类边界更清晰。
1. 两分剪辑近邻法(亦称剪辑最近邻法) 基本过程为: 设N个样本分成c类
æ
N
N , N ,……, = { æ1 æ2 æcN }
1
2
c
(N1+N2+……,+Nc= N)
N
step1:剪辑。利用已知样本集æ 中的样本进行预分 类,并剪辑掉被错分类的样本,留下的样本构成 NE æ 剪辑样本集 step2:分类。利用 æ
6.3 近邻法的改进算法
共同特点是如何尽快地找出最近邻可能存在的小的空间, 减少搜索的范围,从而达到减少近邻法中的计算量和存储量的 问题。 一. 快速近邻算法 该算法对最近邻法和k-近邻法都适用。下面以最近邻法为 例来讨论。 1. 基本思想 将全部已知样本按级分成一些不相交的子集,并在子集的 基础上进行搜索。也就是说,该算法由两个阶段组成: 第一阶段:将样本集按级分解,形成树状结构。
二. 最近邻法的决策规则 设有c类模式样本, ω1, ω2,……, ωc 每类有Ni个样本(i=1,2,……,c),则最近邻法的(ωi类)判别 函数为:
gi ( X ) min X X ik
k
(k 1,2,...... , Ni )
式中X ik 表示ωi类中的第k个样本。
对应的决策规则为: 如果 则决策
X i 。
具体就是:设k1,k2,......,kc分别为X的k个最近邻样本中属于
1 , 2 ,......, c
类的样本数,
则定义 i (i 1,2,......,c) 类的判别函数为:
g i ( X ) ki
模式识别练习题及答案.docx

1=填空题1、模式识别系统的基本构成单元包括:模式采集、特征选择与提取和模式分类。
2、统计模式识别中描述模式的方法一般使用特征矢量;句法模式识别中模式描述方法一般有串、树、网。
3、影响层次聚类算法结果的主要因素有计算模式距离的测度、聚类准则、类间距离门限、预定的类别数目。
4、线性判别函数的正负和数值大小的几何意义是正(负)表示样本点位于判别界面法向量指向的正(负)半空间中;绝对值正比于样本点到判别界面的距离。
5、感知器算法丄。
(1 )只适用于线性可分的情况;(2)线性可分、不可分都适用。
6、在统计模式分类问题中,聂曼-皮尔逊判决准则主要用于某一种判决错误较另一种判决错误更为重愛情况;最小最大判别准则主要用于先验概率未知的情况。
7、“特征个数越多越有利于分类”这种说法正确吗?错误。
特征选择的主要目的是从n个特征中选出最有利于分类的的m个特征(m<n),以降低特征维数。
一般在可分性判据对特征个数具有单调性和(C n m»n )的条件下,可以使用分支定界法以减少计算量。
& 散度Jij越大,说明。
类模式与3j类模式的分布差别越大;当3类模式与(Oj类模式的分布相同时,Jij=_O_.选择题1、影响聚类算法结果的主要因素有(BCD ).A.已知类别的样本质量B.分类准则C.特征选取D.模式相似性测度2、模式识别中,马式距离较之于欧式距离的优点是(CD )。
A.平移不变性B.旋转不变性C.尺度不变性D.考虑了模式的分布3、影响基本K-均值算法的主要因素有(DAB )。
A.样本输入顺序B.模式相似性测度C.聚类准则D.初始类中心的选取4、在统计模式分类问题中,当先验概率未知时,可以使用(BD )。
A.最小损失准则B.最小最大损失准则C.最小误判概率准则D.N-P判决5、散度环是根据(C )构造的可分性判据。
A.先验概率B.后验概率C.类概率密度D.信息燔E.几何距离6、如果以特征向量的相关系数作为模式相似性测度,则影响聚类算法结果的主要因素有(B C )。
模式识别试题及总结

模式识别试题及总结一、填空与选择填空(本题答案写在此试卷上,30分)1、模式识别系统的基本构成单元包括:模式采集、特征提取与选择和模式分类。
2、统计模式识别中描述模式的方法一般使用特真矢量;句法模式识别中模式描述方法一般有串、树、网。
3、聚类分析算法属于(1);判别域代数界面方程法属于(3)。
(1)无监督分类 (2)有监督分类(3)统计模式识别方法(4)句法模式识别方法4、若描述模式的特征量为0-1二值特征量,则一般采用(4)进行相似性度量。
(1)距离测度(2)模糊测度(3)相似测度(4)匹配测度5、下列函数可以作为聚类分析中的准则函数的有(1)(3)(4)。
(1)(2) (3) (4)6、Fisher线性判别函数的求解过程是将N维特征矢量投影在(2)中进行。
(1)二维空间(2)一维空间(3)N-1维空间7、下列判别域界面方程法中只适用于线性可分情况的算法有(1);线性可分、不可分都适用的有(3)。
(1)感知器算法(2)H-K算法(3)积累位势函数法8、下列四元组中满足文法定义的有(1)(2)(4)。
(1)({A, B}, {0, 1}, {A?01, A ? 0A1 , A ? 1A0 , B ? BA , B ? 0}, A) (2)({A}, {0, 1}, {A?0, A ? 0A}, A)(3)({S}, {a, b}, {S ? 00S, S ? 11S, S ? 00, S ? 11}, S)(4)({A}, {0, 1}, {A?01, A ? 0A1, A ? 1A0}, A)9、影响层次聚类算法结果的主要因素有(计算模式距离的测度、(聚类准则、类间距离门限、预定的类别数目))。
10、欧式距离具有( 1、2 );马式距离具有(1、2、3、4 )。
(1)平移不变性(2)旋转不变性(3)尺度缩放不变性(4)不受量纲影响的特性11、线性判别函数的正负和数值大小的几何意义是(正(负)表示样本点位于判别界面法向量指向的正(负)半空间中;绝对值正比于样本点到判别界面的距离。
模式识别试题及总结

模式识别试题及总结一、填空与选择填空(本题答案写在此试卷上,30分)1、模式识别系统的基本构成单元包括:模式采集、特征提取与选择和模式分类。
2、统计模式识别中描述模式的方法一般使用特真矢量;句法模式识别中模式描述方法一般有串、树、网。
3、聚类分析算法属于(1);判别域代数界面方程法属于(3)。
(1)无监督分类 (2)有监督分类(3)统计模式识别方法(4)句法模式识别方法4、若描述模式的特征量为0-1二值特征量,则一般采用(4)进行相似性度量。
(1)距离测度(2)模糊测度(3)相似测度(4)匹配测度5、下列函数可以作为聚类分析中的准则函数的有(1)(3)(4)。
(1)(2) (3) (4)6、Fisher线性判别函数的求解过程是将N维特征矢量投影在(2)中进行。
(1)二维空间(2)一维空间(3)N-1维空间7、下列判别域界面方程法中只适用于线性可分情况的算法有(1);线性可分、不可分都适用的有(3)。
(1)感知器算法(2)H-K算法(3)积累位势函数法8、下列四元组中满足文法定义的有(1)(2)(4)。
(1)({A, B}, {0, 1}, {A?01, A ? 0A1 , A ? 1A0 , B ? BA , B ? 0}, A) (2)({A}, {0, 1}, {A?0, A ? 0A}, A)(3)({S}, {a, b}, {S ? 00S, S ? 11S, S ? 00, S ? 11}, S)(4)({A}, {0, 1}, {A?01, A ? 0A1, A ? 1A0}, A)9、影响层次聚类算法结果的主要因素有(计算模式距离的测度、(聚类准则、类间距离门限、预定的类别数目))。
10、欧式距离具有( 1、2 );马式距离具有(1、2、3、4 )。
(1)平移不变性(2)旋转不变性(3)尺度缩放不变性(4)不受量纲影响的特性11、线性判别函数的正负和数值大小的几何意义是(正(负)表示样本点位于判别界面法向量指向的正(负)半空间中;绝对值正比于样本点到判别界面的距离。
模式识别导论习题参考答案-齐敏
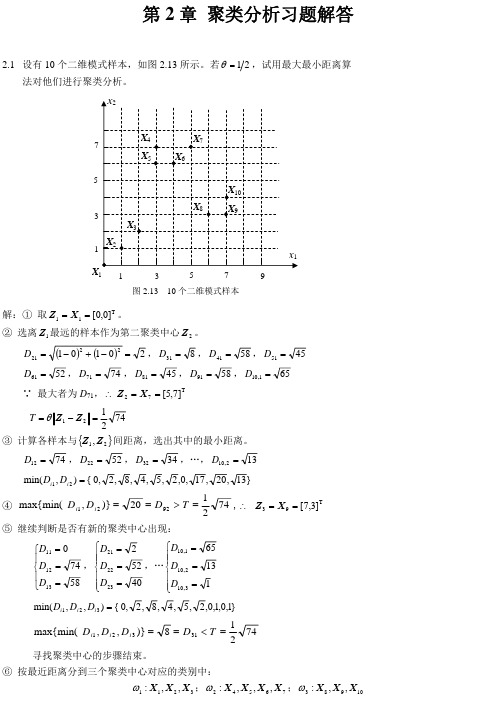
D1 || X 4 Z1 (1) || 4 2 D2 D1 X 4 S 2 (1) D2 || X 4 Z 2 (1) || 5
D21
1 02 1 02
2 , D31 8 , D41 58 , D51 45
D61 52 , D71 74 , D81 45 , D91 58 , D10,1 65
∵ 最大者为 D71, Z 2 X 7 [5,7]T
1 74 2 ③ 计算各样本与 Z 1 , Z 2 间距离,选出其中的最小距离。 T Z1 Z 2 D12 74 , D22 52 , D32 34 ,…, D10, 2 13
2.2 设有 5 个二维模式样本如下:
X 1 [ 0 , 0 ]T , X 2 [ 0 ,1]T , X 3 2 , 0 , X 4 [ 3 ,3 ] T , X 5 4, 4
T T
定义类间距离为最短距离,且不得小于 3。利用层次聚类法对 5 个样本进行 分类。 解:(1) 将每一样本看作单独一类,得
X4:
… 可得到: S1 (1) { X 1},
N1 1
S 2 (1) { X 2 , X 3 , X 4 , X 5 , X 6 }, N 2 5
③ 计算新的聚类中心:
Z 1 (2) X 1 0, 0
T
Z2 (2)
1 N2
X S 2 1
(X X 5
1
G1 (0) X 1 , G2 (0) X 2 , G3 (0) X 3 , G4 (0) X 4 , G5 (0) X 5
模式识别第二版答案完整版

1. 对c类情况推广最小错误率率贝叶斯决策规则; 2. 指出此时使错误率最小等价于后验概率最大,即P (wi|x) > P (wj|x) 对一切j ̸= i
成立时,x ∈ wi。
2
模式识别(第二版)习题解答
解:对于c类情况,最小错误率贝叶斯决策规则为: 如果 P (wi|x) = max P (wj|x),则x ∈ wi。利用贝叶斯定理可以将其写成先验概率和
(2) Σ为半正定矩阵所以r(a, b) = (a − b)T Σ−1(a − b) ≥ 0,只有当a = b时,才有r(a, b) = 0。
(3) Σ−1可对角化,Σ−1 = P ΛP T
h11 h12 · · · h1d
• 2.17 若将Σ−1矩阵写为:Σ−1 = h...12
h22 ...
P (w1) P (w2)
= 0。所以判别规则为当(x−u1)T (x−u1) > (x−u2)T (x−u2)则x ∈ w1,反
之则s ∈ w2。即将x判给离它最近的ui的那个类。
[
• 2.24 在习题2.23中若Σ1 ̸= Σ2,Σ1 =
1
1
2
策规则。
1]
2
1
,Σ2
=
[ 1
−
1 2
−
1 2
] ,写出负对数似然比决
1
6
模式识别(第二版)习题解答
解:
h(x) = − ln [l(x)]
= − ln p(x|w1) + ln p(x|w2)
=
1 2 (x1
−
u1)T
Σ−1 1(x1
−
u1)
−
1 2 (x2
模式识别练习题

模式识别练习题模式识别练习题模式识别是一种认知能力,是人类大脑的重要功能之一。
通过模式识别,我们能够从复杂的信息中抽取出有用的模式,并进行分类、归纳和推理。
模式识别在日常生活中无处不在,无论是辨认人脸、理解语言还是解读图像,都离不开模式识别的帮助。
在这里,我将给大家提供一些模式识别练习题,帮助大家锻炼和提高自己的模式识别能力。
这些题目涵盖了不同的领域,包括数字、形状和图案等,旨在让大家在娱乐中提升自己的认知水平。
1. 数字序列请观察以下数字序列:2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, ...请问下一个数字是多少?答案:2048解析:观察数字序列,可以发现每个数字都是前一个数字的2倍。
因此,下一个数字是1024的2倍,即2048。
2. 形状序列请观察以下形状序列:▲, □, ○, △, ▢, ◇, ...请问下一个形状是什么?答案:□解析:观察形状序列,可以发现每个形状都是按照一定的规律交替出现。
▲和○是封闭的形状,□和▢是开放的形状,△和◇是封闭的形状。
因此,下一个形状应该是开放的形状,即□。
3. 图案序列请观察以下图案序列:A, AB, ABA, ABAC, ABACA, ...请问下一个图案是什么?答案:ABACABAC解析:观察图案序列,可以发现每个图案都是在前一个图案的基础上添加一个新的元素。
第一个图案是A,第二个图案是在A的基础上添加B,第三个图案是在ABA的基础上添加C,依此类推。
因此,下一个图案是在ABACABAC的基础上添加ABAC,即ABACABAC。
通过这些练习题,我们可以锻炼自己的观察力和逻辑思维能力。
模式识别不仅仅是一种认知能力,也是一种解决问题的思维方式。
通过不断地练习和思考,我们可以提高自己的模式识别能力,更好地应对各种复杂的情境和挑战。
除了以上的练习题,我们还可以通过观察自然界、阅读文学作品和解决日常问题等方式来锻炼模式识别能力。
模式识别试题及总结

一、填空与选择填空(本题答案写在此试卷上,30分)1、模式识别系统的基本构成单元包括:模式采集、特征提取与选择和模式分类。
2、统计模式识别中描述模式的方法一般使用特真矢量;句法模式识别中模式描述方法一般有串、树、网。
3、聚类分析算法属于(1);判别域代数界面方程法属于(3)。
(1)无监督分类(2)有监督分类(3)统计模式识别方法(4)句法模式识别方法4、若描述模式的特征量为0-1二值特征量,则一般采用(4)进行相似性度量。
(1)距离测度(2)模糊测度(3)相似测度(4)匹配测度5、下列函数可以作为聚类分析中的准则函数的有(1)(3)(4)。
(1)(2)(3)(4)6、Fisher线性判别函数的求解过程是将N维特征矢量投影在(2)中进行。
(1)二维空间(2)一维空间(3)N-1维空间7、下列判别域界面方程法中只适用于线性可分情况的算法有(1);线性可分、不可分都适用的有(3)。
(1)感知器算法(2)H-K算法(3)积累位势函数法8、下列四元组中满足文法定义的有(1)(2)(4)。
(1)({A,B},{0,1},{A®01,A®0A1,A®1A0,B®BA,B®0},A)(2)({A},{0,1},{A®0,A®0A},A)(3)({S},{a,b},{S®00S,S®11S,S®00,S®11},S)(4)({A},{0,1},{A®01,A®0A1,A®1A0},A)9、影响层次聚类算法结果的主要因素有(计算模式距离的测度、(聚类准则、类间距离门限、预定的类别数目))。
10、欧式距离具有(1、2);马式距离具有(1、2、3、4)。
(1)平移不变性(2)旋转不变性(3)尺度缩放不变性(4)不受量纲影响的特性11、线性判别函数的正负和数值大小的几何意义是(正(负)表示样本点位于判别界面法向量指向的正(负)半空间中;绝对值正比于样本点到判别界面的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章 句法模式识别习题解答6.1 用链码法描述5~9五个数字。
解:用弗利曼链码表示,基元如解图6.1所示:数字5~9的折线化和量化结果如解图6.2所示:各数字的链码表示分别为:“5”的链码表示为434446600765=x ; “6”的链码表示为3444456667012=x ; “7”的链码表示为00066666=x ; “8”的链码表示为21013457076543=x ; “9”的链码表示为5445432107666=x 。
17解图6.1 弗利曼链码基元 解图6.2 数字5~9的折线化和量化结果6.2 定义所需基本基元,用PDL 法描述印刷体英文大写斜体字母“H ”、“K ”和“Z ”。
解:设基元为:用PDL 法得到“H ”的链描述为)))))(~((((d d c d d x H ⨯+⨯+=;“K ”的链描述为))((b a d d x K ⨯⨯+=; “Z ”的链描述为))((c c g x Z ⨯-=。
6.3 设有文法),,,(S P V V G T N =,N V ,T V 和P 分别为},,{B A S V N =,},{b a V T =:P ①aB S →,②bA S →,③a A →,④aS A →⑤bAA A →,⑥b B →,⑦bS B →,⑧aBB B → 写出三个属于)(G L 的句子。
解:以上句子ab ,abba ,abab ,ba ,baab ,baba 均属于)(G L 。
6.4 设有文法),,,(S P V V G T N =,其中},,,{C B A S V N =,}1,0{=T V ,P 的各生成式为①A S 0→,②B S 1→,③C S 1→bcadeabba abbA abS aB S ⇒⇒⇒⇒ ① ⑦ ② ③ab aB S ⇒⇒ ① ⑥ba bA S ⇒⇒② ③ abab abaB abS aB S ⇒⇒⇒⇒ ① ⑦ ① ⑥baab baaB baS bA S ⇒⇒⇒⇒ ② ④ ① ⑥baba babA baS bA S ⇒⇒⇒⇒② ④ ② ③④A A 0→,⑤B A 1→,⑥1→A ⑦0→B ,⑧B B 0→,⑨C C 0→,⑩1→C问00100=x 是否属于语言)(G L ? 解:由可知00100=x 属于语言)(G L 。
6.5 写出能产生图示树的扩展树文法,设基元a ,b 分别为“→”和“↓”,它所描述的模式是什么?解:1. 写出生成树的扩展树文法生成式集:2. 检查非终止符的等价性。
a$babbab001000010001000⇒⇒⇒⇒⇒B B A A S① ④ ⑤ ⑧ ⑦⑴$A →14A 2A 3⑵a A →2⑶a A →3⑸b A →59A 6A 5⑷b A →4⑿a A →12(6)a A →6A 7A 8⑺a A →7⑻a A →8⑼b A →9A 10⑽b A →10A 11⑾a A →11A 12查得1172A A A ≡≡。
删除7A 和11A 及其后代生成式,其余生成式中的7A 和11A 用2A 代替,合并后得到3. 建立起始产生式。
将⑴中的1A 用S 代替得到:设推断的扩展树文法为),,,(S P r V G t =',由以上推断得:T N V V V =,},,,,,,,{10965432A A A A A A A S V N =,},,{b a $V T =2)(=$r ,}0,1{)(=a r ,}1,2{)(=b rP 的各生成式为当基元a ,b 分别为“→”和“↓”时, 它所描述的模式如解图6.3所示:a ab b b ba aa aa$ $S → 4A 2⑸b A →59A 6A 5⑷b A →4(6)a A →6A 2⑼b A →9A 10⑽b A →10A 2⑴$A →14A 2A 3⑵a A →2⑶a A →3⑸b A →59A 6A 5⑷b A →4(6)a A →6A 2⑼b A →9A 10⑽b A →10A 2⑴$S →4A 2A 3⑵a A →2⑶a A →3解图6.3 描述的模式6.6 已知)(G L 的正样本集}0010,111,100,01{=+R ,试推断出余码文法c G 。
解:设余码文法为),,,(S P V V G T N c =。
(1) 由+R 得c G 的终止符集}1,0{=T V 。
(2) 求+R 的全部余码,组成非终止符集N V 。
+R 的全部余码为}0010,111,100,01{=+R D λ,}010,1{0=+R D ,}11,00{1=+R D}{01λ=+R D ,}0{10=+R D ,}1{11=+R D ,}10{00=+R D }{100λ=+R D ,}{111λ=+R D , }0{001=+R D ,}{0010λ=+R D等号右边相同的合并,非空余码标以符号组成非终止符集N V :}0010,111,100,01{==+R D S λ,}010,1{01==+R D U ,}11,00{12==+R D U}0{103==+R D U ,}1{114==+R D U ,}10{005==+R D U所以},,,,,{54321U U U U U S V N =。
(3) 建立生成式集P 。
由10}010,1{U S D ==,有生成式10U S →; 由510}10{U U D ==,有生成式510U U →; 由320}0{U U D ==,有生成式320U U →; 由λ=30U D ,有生成式03→U ;由21}11,00{U S D ==,有生成式21U S →; 由λ=11U D ,有生成式11→U ;由421}1{U U D ==,有生成式421U U →; 由λ=41U D ,有生成式14→U ; 由351}0{U U D ==,有生成式351U U →; 所以余码文法),,,(S P V V G T N c =为},,,,,{54321U U U U U S V N =,}1,0{=T V P :10U S →,510U U →,320U U →,03→U 21U S →,11→U ,421U U →,14→U ,351U U →6.7 设文法),,,(S P V V G T N =,其中},,{B A S V N =,}1,0{=T V ,P 的各生成式为①1→S ,②1B S →,③B S →④A B 1→,⑤A B B 1→,⑥0→A ,⑦0A A →设待识别链1000=x ,试用填充树图法的顶下法分析x 是否属于)(G L ? 解:(1) 从S 开始考察P 中的①、②、③式:若选①,则结果为x =1,排除;若选②,导出的x 末位必为1,与题不符,排除; 选③式,如解图6.4(a)所示。
(2) 填充目标为B ,考察④、⑤均可填充,先试④,如解图6.4(b)所示。
若不行,再返回用⑤式。
(3) 此时填充目标为A ,考察⑥、⑦。
若选⑥,导出的x 为 2位,与题不符,排除。
选⑦式,如解图6.4(c)所示。
(4) 类似地,得到图6.4所示各步结果,树叶为1000。
故x 属于)(G L 。
6.8 设上下文无关文法),,,(S P V V G T N =,},{C S V N =,}1,0{=T V ,P 中生成式的乔姆斯基范式为CC S →,CS S →,1→S ,SC C →,CS C →,0→C用CYK 分析法分析链01001=x 是否为该文法的合法句子。
解图6.4 填充树图过程 S1BAAS1BAAS1BAAS1BAS B (a) (b) (c) (d) (e)解:待识别链为5位,构造5行5列的三角形分析表,如解图6.5所示。
求表中元素ij t 的值:(1) 令1=j ,求1i t ,51≤≤i 。
各子链为0,1,0,0,1。
对于01=a ,C t =11; 对于12=a ,S t =21; 对于03=a ,C t =31; 对于04=a ,C t =41。
对于15=a ,S t =41。
(2) 令2=j ,求2i t ,41≤≤i 。
各子链为01,10,00,01。
对于0121=a a ,因有CS S →和CS C →,0→C ,1→S ,故S C t ,12=; 对于1032=a a ,有SC C →,1→S ,0→C ,故C t =22。
对于0043=a a ,有CC S →,0→C ,0→C ,故S t =32。
对于0154=a a ,有CS S →和CS C →,0→C ,1→S ,故S C t ,42=; (3) 令3=j ,求3i t ,31≤≤i 。
各子链为010,100,001。
对于010321=a a a ,因有CC S →,0→C ,10*⇒C ;和SC C →,01*⇒S , 0→C 。
故S C t ,13=。
类似地有S t =23,S C t ,33=,S C t ,14=,S C t ,24=,S C t ,15=。
填表结果如解图6.6所示。
解图6.5 分析表t 14 t 13 t 12 t 11t 23 t 22 t 21t 32 t 31t 41t 15 t 51t 42 t 33 t 24因为S 在15t 中,所以)(G L x ∈。
6.9 已知正则文法),,,(S P V V G T N =,其中},{B S V N =,},{b a V T =,P 的各生成式为aB S →,aB B →,bS B →,a B →构成对应的有限态自动机,画出自动机的状态转换图。
解:设有限态自动机),,,,(0∑=F q Q A δ,由A 与G 的对应关系得∑==},{b a VT},,{F B S F V Q N ==S q =0δ:由aB S →,有B a S =),(δ;由aB B →,a B →有},{),(F B a B =δ;由bS B →,有S b B =),(δ。
故有限态自动机),,,,(0∑=F q Q A δ为∑=},{b a ,},,{F B S Q =,S q=0δ:B a S =),(δ,},{),(F B a B =δ,S b B =),(δ解图6.6 CYK 分析表填表结果 C,S C,S CS C SS CCC,S SC,S C,S C,S C,S 解图 6.7 自动机的状态转换图6.10 已知有限态自动机),,,,(0∑=F q Q A δ,其中∑=}1,0{,},,,{321q q q q Q =,}{3q F =A 的状态转换图如图6.15所示,求A 对应的正则文法G 。
解:设正则文法为),,,(S P V V G T N =,由G 与A 的对应关系得:},,,{3210q q q q Q V N ==;∑==}1,0{T V ; 0q S =;根据状态转换图有:P :因}{)0,(20q q =δ,有200q q →; 因}{)1,(10q q =δ,有101q q →;因}{)0,(31q q =δ,有310q q →;而F q ∈3,故01→q ; 因}{)1,(01q q =δ,有011q q →; 因}{)0,(02q q =δ,有020q q →;因}{)1,(32q q =δ,有321q q →;而F q ∈3,故12→q ; 因}{)0,(13q q =δ,有130q q →; 因}{)1,(23q q =δ,有231q q →。
