热力学基础第4讲——热力学小结与习题课
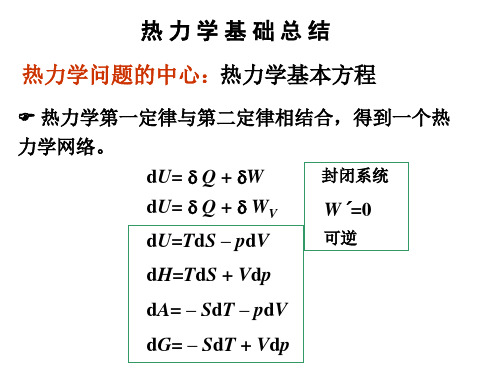
热 力 学 基 础 总 结
(CB)
;
(
A nB
)T
,v,nc
(CB)
;
(
G nB
)T
,V
,nc
; (CB)
(
U nB
)
S ,V
,nc
V
(CB)
;
( nB
)T , p,nc
H
(CB)
;
( nB
) S , p,nc
; (CB)
A ( nB )T , p,nc (CB) ;
解: 偏摩尔量:
; ; ; H
( nB )T , p,nc (CB)
• 热力学量变换法(变量变换法)就是将不能用实 验直接测量的量转换为用实验量或状态方程表 示的关系的基本方法。
变量变换法
从研究工作需要来看:
变量变换法是在学科发展中形成的科学方法。 通常在研究工作中会提出许多科学命题,为 寻求解决问题的思路或设计实验,总要想法 进行命题的转换,以利用已有信息或通过实 验进行分析,其间变量变换就是一个有效的 方法,今以实例说明。
解:在水的正常沸点时 1= 2;
在温度为 373.15K 及 202 650 Pa 下
因为 所以
故
(
Gm* p
)T
Vm
>0
3> 1
4> 2
4> 3> 2= 1。
4> 3。
计算题
1 一定量纯理想气体由同一始态,分别经绝热可逆 膨胀至(T2,p2, V2)和经绝热不可逆膨胀至(T2',p2',V2')
=
nCV,m dT T
p dV T V
dG= – SdT + Vdp dGT= Vdp
变量变换法
热力学习题课超经典 共24页PPT资料
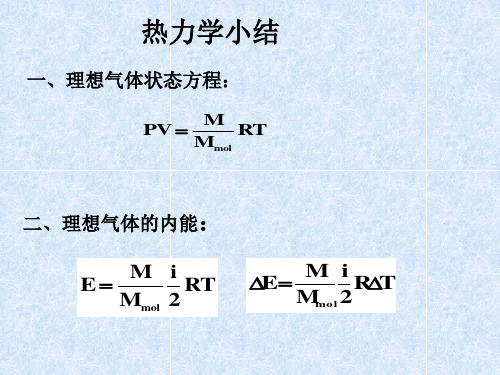
1、求Ta、Tb、Tc。 2、求气体在ab和bc 过程中吸收的热量, 气体内能的变化各如 何? 3、气体在abc过程中 最高温度如何?
P(105Pa)
1.5 b
1a
0.5
c
0 1 2 3 V(10-3m3)
P(105Pa)
1.5 b
1、由 PV M RT 1 a
Mmol
0.5
求出求Ta、Tb、Tc。 0 1
T
Skn (玻氏熵公式)
热力学第二定律的实质:一切与热现象有 关的实际宏观过程都是不可逆的。
无摩擦的准静态过程才是可逆的
熵增加原理:孤立系统内部所发生的过程 总是向着状态几率增大的方向进行
= 可逆过程
孤立系统 dS0 > 不可逆过程
例:0.1mol的单原子理想气体,经历一准 静态过程abc,ab、bc均为直线。
(A) (1)过程中吸热,(2) 过程中放热.
√(B) (1)过程中放热,(2) 过程p中吸热.
(C) 两种过程中都吸热. (D) 两种过程中都放热.
a
(2)
分析: 作一循环a(1)ba, 这是逆循环.
(1)
b
W<0, △E=0, Q<0,
O
V
(1)过程中放热;
同理可得(2) 过程中吸热。
练习13 第四题 容积为10L的盒子以速度 v=200m/s匀速运动,容器中充有质量为50g 温度为18C的氢气,设盒子突然停止,气体 的全部定向运动动能都变为气体分子热运动 动能,容器与外界没有热交换,则达到热平 衡后,氢气的温度将增加——K;氢气的压强将 增加 —— Pa
c
2 3 V(10-3m3)
2、a
b,
M QabMmoC lV(TbTa) E
第4章 热学 习题参考答案

Q1 W1 E1 950 J
B 到 C:
W2 0 E2 vCV ,m (TC TB ) 3( p CVC pBVB ) / 2 600 J Q2 W2 E2 600 J
C 到 A:
W3 p A (VA VC ) 100 J E3 vCV ,m (TA TC ) 3( p AVA pCVC ) / 2 150 J Q3 W3 E3 250 J
ca QT vRTc ln ca WTca QT
Va 3456 J Vb
(2) W WPab WVbc WTca 963J (3)
W 963 13.4% Q吸 3739.5 3456
W ( pa pc )(Vc Va ) 1.013 102 J
(4)
Pa Pd Ta Td
Pa Pb , Pc Pd ,Vb Vc
v RT v RT b c Ta Td
PbVb PcVc Ta Td
又 PV vRT
TaTc TbTd来自4-10 a 到 b 绝热
Q1 0
W1 E vCv,m (Ta Tb )
第 4 章 热力学基础 4-1(1) dW pdV (a 2 / V 2 )dV
W dW (a 2 / V 2 )dV a 2 (1 / V1 1 / V2 )
V1
V2
(2) p1V1 / T1 p2V2 / T2
T1 / T2 p1V1 / p2V2 V2 / V1
4-6(1)等体过程,V=常量,W=0
Q E W E M C p ,m (T2 T1 ) 623J M mol
热力学小结与习题课

10、 当体系向环境放热时,体系的内能一定减少。
11、 自发过程一定是不可逆过程。
12、 不可逆过程一定是自发过程。
13、 体系经过一个可逆循环过程熵变ΔS=0。
14、 体系经过一个不可逆循环过程熵变ΔS>0。
15、 体系经过一个可逆过程熵变ΔS=0。
16、 体系经过一个不可逆过程熵变ΔS>0。
17、 孤立体系中发生的可逆过程熵变ΔS=0。
8、液态水在 100℃及 101325Pa 下汽化,则过程
(
)
A)ΔH=0
B)ΔS=0
C)ΔF=0
D)ΔG=0
9、关于吉布斯能判据,下列说法中正确的有
(
)
A)当ΔG<0 时体系有自发过程 B)等温等压下,当 -ΔG>W/ 时体系有不可逆过程
C)等温等压下,当ΔG<0 时体系有自发过程
D)等温等压下且只做体积功,当 -ΔG>0 时体系有自发过程
∫ 6、 1mol 水在 101325Pa 下由 25℃升温至 120℃其
ΔH =
T2 T1
C p,m dT
。
7、 卡诺循环是可逆循环,当体系经过一个卡诺循环后,不仅体系复原了,而且环境也复原了。
8、 若一个过程中每一步都无限接近平衡态,则此过程一定是可逆过程。
9、 若一个过程是可逆过程,则该过程中的每一步都是可逆的。
kJ ⋅ mol −1 。
6、已知
H2O(l)的
Δ
f
H
0 m
(298K
)
=
−285.84kJ
⋅
mol
−1
,则
H(2 g)的
ΔC
H
0 m
热力学基础知识讲解共37页文档

谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律,就难以成功。
3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体,养 成儿童 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
第4章热力学基础.ppt

第四章 气体动理论
一、基本概念
热学
气体
动
理论(微观)
:
微观量
统计 力学
宏
观
量
热力学(宏观) : 宏观量实验宏观量
宏观量:表征大量分子集体特征的量、系统温度、压强、热容可测量出。
微观量:表征个别分子的物理量分子质量、速度、大小、能量.在现代实
验条件下是不能直接测得的量。
二、统计规律
统计规律:大量偶然事件整体遵从的规律。投掷骰子例子中,总次数N无 限增加时,任一面出现的概率均为1/6
Cv Cp 比热容比
35
1.67
57
1.4
68
1.3
(三)等温过程
1、特征: 系统的温度在状态变化过程 中始终保持不变。
T = 衡量 dT = 0 → d E = 0
P
P1 1
2、等温线:由
PV m RT 得 PV 恒量 M
3、做功: 由 PV m RT 得 P m R T
M
MV
气可看作理想气体。)
解: 本题只需考虑空气的初状态和末状态,并且把空气作为理想气 体。我们有
p1V1 p2V2
T1
T2
已知 p1=8.5104Pa , p2=4.2106Pa,T1=273K+47K=320K
V2 1 ,所以 V1` 17
T2
p2V2 p1V1
T1
930K
这一温度已超过柴油的燃点,所以柴油喷入气缸时就会立即 燃烧,发生爆炸推动活塞作功。
微观 : 分子大小忽略不计(质点) 除碰撞外, 分子间无作用力
分子与器壁, 分子间为完全弹性碰
2.理想气体状态方程
第4章 热力学基础 [2]PPT课件
![第4章 热力学基础 [2]PPT课件](https://img.taocdn.com/s3/m/6f6458e5bceb19e8b9f6ba13.png)
热一律可得能量关系:
E 2E 1A
即外界对系统所做的功等于系统内能的增量
对于微小过程有
d E d A 0
2. 绝热过程的过程方程
绝热条件:dQ dE dA 0 C V ,m d T pd0 V
状态方程: pVRT pdVVdpνRdT
比热比:
(C V ,m R )pd C V V ,m V d 0p
Cp, m1d dQ Tp2 i 1R
:摩尔数 i:自由度数
三、迈耶公式及比热容比 摩尔定体热容 CV,m 摩尔定压热容 Cp,m
CV,m
i 2
R
i2 Cp,m 2 R
迈耶公式 Cp,mCV,m R
比热容比
c p C p ,m CV ,m R 1 R
cV
C V ,m
CV ,m
CV ,m
kT
(P1,V1,T1) 等温线 (P2,V2,T1)
二、热容、摩尔热容
系统和外界之间的热传递,会引起系统温度的变化,温
度每升高 1 度 (K) 所吸收的热量,称为系统的热容,
用 C 表示。 C dQ dT
单位:J / K
系统物质量为 1 mol 时,它的热容叫摩尔热容,用
Cm 表示。
Cm
dQm dT
单位:J/mol ·K
系统质量为 1 kg 时,它的热容叫比热容(比热),用
过程 方程
内能
V 恒量 T
dE iRdT
2
E 2 E 1 C v ,m T 2 T 1
功
dA pdV
A pV2 V1
热量
dQdEdA
Qp Cp,mT2T1
二、定压热容量 Cp 定压热容 Cp:系统的压强不变的过程中的热容。
热力学与统计物理第四章知识总结

§6.1粒子运动状态的经典描述一、μ空间1、μ空间的建立在经典力学中,我们经常利用物体的坐标和动量描述物体的力学运动状态。
当然这种方法也可以用于描述遵守经典力学规律的近独立粒子。
如果粒子的自由度为r,则粒子在任一时刻的力学运动状态由粒子的r个坐标q,q,…,q和相应的r个广义动量P,P,…,P在该时刻的数值确定。
粒子的能量ε是广义坐标和广义动量的函数,即ε=ε(q,q,…,q; P,P,…,P)当存在外场时,ε还是描述外场参量的函数。
为了形象地描述粒子的力学运动状态,我们用q,q,…,q;P,P,…,P共2r个变量为直角坐标,构成一个2r维空间,称为粒子的相空间或者μ空间。
粒子在某一时刻的力学运动状态 (q,q,…,q; P,P,…,P)可以用μ空间中的一个点表示,称为粒子运动状态的代表点。
当粒子的运动状态随时间改变时,代表点相应地在μ空间中移动,描绘出一种轨迹,称为相轨迹。
由N个粒子组成的系统在某一时刻的一个特定的微观状态,在μ空间中用N个代表点表示。
随着时间的变化,系统运动状态的变化由N个代表点在μ空间中的N条运动轨迹,即N条线代表。
2、性质i) μ空间是人为想象出来的超越空间,是个相空间。
引进它的目的在于使运动状态的描述几何化、形象化,以便于进行统计。
μ空间中的一个代表点是一个粒子的微观运动状态而不是一个粒子。
ii) 在经典力学范围,在无相互作用的独立粒子系统中,任何粒子总可找到和它相应的μ空间来形象地描述它的运动状态,但不是所有的粒子的运动状态可以在同一μ空间中描述。
如一个自由度数为3的粒子,它需在一个6维的μ空间中描述;一个自由度数为5的粒子,它的μ空间是10维的,即需在10维的μ空间中描述它的运动状态。
二、自由粒子所谓自由粒子,指的是不受外力作用可以自由运动的粒子。
在通常情况下,我们还经常把可以忽略外力作用的粒子看作自由粒子。
例如,当不存在力场时,理想气体的分子或金属中的自由电子都可以被看作自由粒子。
热力学基础知识点总结

热力学基础知识点总结热力学是研究热现象中能量转化规律的科学,它为我们理解和分析许多自然现象和工程过程提供了重要的理论基础。
以下是对热力学基础知识点的总结。
一、热力学系统与状态热力学系统是我们研究的对象,可以是一个封闭的容器中的气体,也可以是整个地球的大气。
根据系统与外界的物质和能量交换情况,可分为孤立系统、封闭系统和开放系统。
系统的状态由一些宏观物理量来描述,比如压强、温度、体积等,这些被称为状态参量。
状态参量的数值确定,系统的状态就确定了。
二、热力学第一定律热力学第一定律其实就是能量守恒定律在热力学中的表现形式。
它指出,一个热力学系统从外界吸收的热量,等于系统内能的增加与系统对外做功之和。
数学表达式为:$Q =\Delta U + W$ ,其中$Q$ 表示系统从外界吸收的热量,$\Delta U$ 表示系统内能的增量,$W$ 表示系统对外界所做的功。
如果系统从外界吸热,$Q$ 为正值;系统向外界放热,$Q$ 为负值。
系统对外做功,$W$ 为正值;外界对系统做功,$W$ 为负值。
例如,在一个热机的工作循环中,燃料燃烧产生的热量一部分转化为机械能对外做功,另一部分用来增加系统的内能。
三、热力学第二定律热力学第二定律有多种表述方式,常见的有克劳修斯表述和开尔文表述。
克劳修斯表述:热量不能自发地从低温物体传向高温物体。
开尔文表述:不可能从单一热源吸取热量,使之完全变为有用功而不产生其他影响。
热力学第二定律揭示了热现象的方向性,也就是说,在自然条件下,热传递和热功转换过程都是不可逆的。
比如,冰箱能够将内部的热量传递到外部,但这需要消耗电能,并且这个过程不是自发进行的。
四、热力学温标热力学温标是一种与测温物质的性质无关的温标,单位是开尔文(K)。
热力学温度与摄氏温度的关系为:$T = t + 27315$ ,其中$T$ 是热力学温度,$t$ 是摄氏温度。
绝对零度(0 K)是理论上能达到的最低温度,但实际上无法达到。
大学物理热力学基础习题课

答案:B 9、下列说法中,哪些是正确的
1、可逆过程一定是准静态过程;2、准静态过程一定是可逆的 4、不可逆过程一定是非准静态过程;4、非准静态过程一定是 不可逆的。
A、(1,4);B、(2,3);C、(1,3);D、(1,2,3,4)
答案:A
10、根据热力学第二定律,下列那种说法正确
A.功可一全部转换成热,但热不可以全部转换成功 B.热可以从高温物体传递到低温物体,反之则不行
Q QBC QAB 14.9 105 J 由图得, TA TC 全过程:
E 0
W Q E 14.9 105 J
3. 图所示,有一定量的理想气体,从初状态 a (P1,V1)开始,经过一个等容过程达到压强为 P1/4 的 b 态,再经过一个等压过程达到状态 c , 最后经过等温过程而完成一个循环。求该循环 过程中系统对外做的功 A 和吸收的热量 Q .
a
T2 300 1 1 25% T1 400
c
d
300 400
T(K)
8. 一卡诺热机在每次循环中都要从温度为 400 K 的高温热源吸热 418 J ,向低温热源放 热 334.4 J ,低温热源的温度为 320 K 。如 果将上述卡诺热机的每次循环都逆向地进行, 从原则上说,它就成了一部致冷机,则该逆向 4 卡诺循环的致冷系数为 。
解:设状态 c 的体积为V2 , 由于a , c 两状态的温度相同
故
p1 p1V1 V2 4 V2 4V1
循环过程 E 0 , Q W
而在 a b 等容过程中功 W1 0 在 b c 等压过程中功
p1 p1 3 W2 V2 V1 4V1 V1 p1V1 4 4 4
热力学与统计物理第四章知识总结

§6.1粒子运动状态的经典描述一、μ空间1、μ空间的建立在经典力学中,我们经常利用物体的坐标和动量描述物体的力学运动状态。
当然这种方法也可以用于描述遵守经典力学规律的近独立粒子。
如果粒子的自由度为r,则粒子在任一时刻的力学运动状态由粒子的r个坐标q,q,…,q和相应的r个广义动量P,P,…,P在该时刻的数值确定。
粒子的能量ε是广义坐标和广义动量的函数,即ε=ε(q,q,…,q; P,P,…,P)当存在外场时,ε还是描述外场参量的函数。
为了形象地描述粒子的力学运动状态,我们用q,q,…,q;P,P,…,P共2r个变量为直角坐标,构成一个2r维空间,称为粒子的相空间或者μ空间。
粒子在某一时刻的力学运动状态 (q,q,…,q; P,P,…,P)可以用μ空间中的一个点表示,称为粒子运动状态的代表点。
当粒子的运动状态随时间改变时,代表点相应地在μ空间中移动,描绘出一种轨迹,称为相轨迹。
由N个粒子组成的系统在某一时刻的一个特定的微观状态,在μ空间中用N个代表点表示。
随着时间的变化,系统运动状态的变化由N个代表点在μ空间中的N条运动轨迹,即N条线代表。
2、性质i) μ空间是人为想象出来的超越空间,是个相空间。
引进它的目的在于使运动状态的描述几何化、形象化,以便于进行统计。
μ空间中的一个代表点是一个粒子的微观运动状态而不是一个粒子。
ii) 在经典力学范围,在无相互作用的独立粒子系统中,任何粒子总可找到和它相应的μ空间来形象地描述它的运动状态,但不是所有的粒子的运动状态可以在同一μ空间中描述。
如一个自由度数为3的粒子,它需在一个6维的μ空间中描述;一个自由度数为5的粒子,它的μ空间是10维的,即需在10维的μ空间中描述它的运动状态。
二、自由粒子所谓自由粒子,指的是不受外力作用可以自由运动的粒子。
在通常情况下,我们还经常把可以忽略外力作用的粒子看作自由粒子。
例如,当不存在力场时,理想气体的分子或金属中的自由电子都可以被看作自由粒子。
第4课热力学第二定律及极值原理

环境的熵变化为: dS surr 联合上二式: Q re T 0 dS
Qsurr
T0
Qre
T0
∴ Wu max dU p 0 dV T0 dS
从任意状态到环境状态积分,得到
Wu ,max (U p 0V T0 S ) (U 0 p 0V0 T0 S )
O
SA
SC
S
ABCDA的面积 循环热机的效率 ABC曲线下的面积
T-S图 及其应用 图中ABCD表示任一 循环过程。 ABCD的面积表示循环 所吸的热和所做的功 EG线是高温(T1)等温线 LH是低温( T2)等温线 EGHL代表Carnot 循环 任意循环的热机效率不可能大于EGHL所代 表的Carnot热机的效率
无质量交换
孤立系统
无热量交换 无功量交换
dS f 0
dS iso S g 0
=:可逆过程 >:不可逆过程
热二律表达式之一 结论:孤立系统的熵只能增大,或者不变, 绝不能减小,这一规律称为孤立系统 熵增原理。
孤立系熵增原理举例
取热源T1和T2为孤立系
Q Q 1 1 Siso ST1 ST2 Q T1 T2 T2 T1 T 1 当T1>T2 Siso 0 可自发传热
能量的贬值原理——任何自发的热过程,都 只向着能量品质降低的方向发展,理想情况 下,品质不变。 • 火用(exergy)概念可以说就是根据上述能量 的贬值原理引进的。下面章节着重讨论 exergy.
火用与火无的定义
火用 ——理论上可以无限转换为任何其它形式 能量的那部分能量,称为火用(exergy), Ex. 火无 ——在给定环境下,能量中不可能转换为 功的那部分能量,称为能量的火无(anergy), An. 或:火用 ——在周围环境条件,任一形式的能 量中能够最大限度地转变为有用功的那部分能量。
热力学基础知识点总结

热力学基础知识点总结热力学是研究能量转化和传递的物理学分支,它研究了热量、温度和能量之间的关系。
在热力学中,有一些基础知识点是我们必须要了解的。
本文将对热力学的一些基础知识点进行总结和介绍。
一、热力学系统和热力学过程热力学系统是指我们要研究的对象,可以是一个物体、一组物体或者一个系统。
热力学过程是系统从一个状态到另一个状态的变化过程,可以是恒温过程、绝热过程等。
在热力学中,我们通常通过观察系统的性质变化来研究热力学过程。
二、热力学函数热力学函数是描述热力学系统性质的函数,常见的热力学函数有内能、焓、自由能和吉布斯自由能等。
内能是系统热力学性质的基本函数,它是系统的微观状态和能量之间的函数关系。
焓是在恒压条件下的热力学函数,它对应于系统对外做功的能力。
自由能是系统的可用能量,它对应于系统在恒温恒容条件下对外做功的能力。
吉布斯自由能是系统在恒温恒压条件下的可用能量,它对应于系统在外界条件不变的情况下能够发生的最大非体积功。
三、热力学定律热力学定律是热力学研究的基本规律,包括零th定律、第一定律、第二定律和第三定律。
零th定律指出当两个物体与第三个物体处于热平衡时,它们之间也处于热平衡。
第一定律是能量守恒定律,它指出能量可以转化形式,但不能被创造或破坏。
第二定律是热力学不可逆性定律,它指出任何一个孤立系统的熵都不会减少,即系统总是趋于混乱。
第三定律是关于绝对零度的定律,它指出在0K时,系统的熵为零。
四、热力学平衡和热力学态热力学平衡是指系统内各部分之间不存在宏观差异,不再发生宏观的变化。
热力学态是指系统所处的状态,它可以通过温度、压力等宏观性质来描述。
在热力学中,我们通常通过热力学函数的变化来研究系统的平衡和态的变化。
五、热力学的应用热力学是一门广泛应用于工程和科学领域的学科,它在能源转换、化学反应、材料科学等方面有着重要的应用。
热力学的应用可以帮助我们理解和优化能量转化和传递的过程,提高能源利用效率。
第四热力学

M
CV ( T2
- T1) 1248
(J)
(2)2→3 等温过程
P
P2
2
V3
P2 P3
V2
3V2
7.38 10 -3( m3 )
Q23
A23
M
RT2 ln
V3 V2
822 (J)
P1
1
4
O
V1 V4
3
V V3
(3)3→4 等压过程
T4
V4 V3
T3
1 2
900
450
K
A34
P3(V4
- V3)
P—V图:平行于V 轴的直线,等压线。 P
过程方程:V/T=恒量
热一律应用:(有限过程Ⅰ→Ⅱ)
O
Ⅰ
Ⅱ
A
V1
V2 V
Q p
E
V2 V1
pdV
M
CV
(T2
- T1 )
p(V2
- V1 )
pV M RT
M
CV (T2
- T1 )
M
R(T2
-
T1
)
M
(CV
R)(T2
- T1 )
等压过程
M
Q p (CV R)(T2 - T1 )
因i=5,所以CV= iR/2=20.8J/(molK),可得:
A
M
CV
T2
- T1
1 4
20.8 181J
941J
如氧气作等温膨胀,气体所作的功为
A
M
RT1
ln
V2 V1
=1 4
8.31 300 ln 10J
1.44 103 J
热力学第四次课(2011上课).ppt

Q Q T 2 2 w 2 A Q Q T 1 2 T 1 2
二. 卡诺定理
1. 在温度分别为T1 与T2 的两个给定热源之间工作的一切可 逆热机,其效率 相同,都等于理想气体可逆卡诺热机的 效率,即
Q T 2 1 1 2 Q T 1 1
2. 在相同的高、低温热源之间工作的一切不可逆热机,其 效率都不可能大于可逆热机的效率。 说明 (1) 要尽可能地减少热机循环的不可逆性,(减少摩擦、 漏气、散热等耗散因素 )以提高热机效率。
14
1. 热力学第二定律的开尔文表述 不可能只从单一热源吸收热量,使之完全转化为功而不引 起其它变化。
说明 (1) 热力学第二定律开尔文表述 的另一叙述形式:第二类永动 机不可能制成
(2) 热力学第二定律的开尔文表述 实际上表明了
A Q 1 2 1 Q Q 1 1
而实质上说明了自发过程中功热转换过程具有一定的方向性
(2) 热力学第二定律只适用于大量分子的集体,而不适用于只 有少量分子的系统。
§11.11 卡诺循环
一. 卡诺循环
卡诺定理
卡诺循环是由两个等温过程和两个绝热过程组成 1. 卡诺热机的效率 气体从高温热源吸收 的热量为 p p1 p2
a
V 2 Q RT ln 1 1 V 1
气体向低温热源放出 的热量为
2 2
在黑夜欲保持室内温度高,卡诺机工作于致冷机状态,从室 外吸取热量Q2, 放入室内热量Q1
Q T 2 w 1 A T T 2 1
T 1 Q A 2 T2 T 1
每秒钟放入室内的热量为通过起居室墙壁导进的热量,即
Q Q A C ( T T ) 1 2 2 1
T T 1 A A 2 A T T T T 2 1 2 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22.4 44.8V (l )
A Pc (V b V c) 2269.7 ( J ) Q CV ,m (T c T a) C P,m (T b T c) R (T b T c)
A 2269.7 ( J )
作
业
题:
习题9.4 、9.11 、9.22 复习内容: 第 9 章
理想气体的典型过程
过 程 过程方程 系统对外做功 系统从外界吸热 摩尔热容
等 体 等 压
等 温
V 常量
0
CV (T 2 T 1)
i CV R 2
P 常量
T 常量
绝 热
多 方
PV 常量
PV 常量
n
P ( V 2 V 1 ) C P (T 2 T 1) C P CV R V2 V2 RT ln RT ln V1 V1 P2 V 2 P1V 1 0 0 1 n P2 V 2 P1V 1 C (T 2 T 1) C n 1 CV 1 n
令 dT / dV
4 P0 V 0
4 P0 V 4 P0 V T nR nRV0
2
0, 2 d T 2 P0 0 得 V 2V 0 , 且 2 dV nRV0 所以,在 V 2V 0 处,温度为极大值。
极大值只有一点,最小值一定在端点处。
T max
4 P0 V 0 , 3P 0 V 0 T min nR nR
热力学基础第4讲
——热力学小结与习题课
热力学基础
小结与习题课
热力学第一定律
微小过程: 有限过程:
dQ dA dE ; Q A E .
V2
准静态过程中系统对外做功
dA PdV , A
PdV .
V1
过程中系统吸收的热量和摩尔热容
d Qx C x dT , Qx
例3: n 摩尔的理想气体,经历如 有 图所示的准静态过程,图中 P0 、V 0
P
a (3P0 , V 0 )
是已知量,ab 是直线,求: b (1) 气体在该过程中所做的功和吸 ( P0 , 3V 0 ) (2) 在该过程中,温度的 收的热量; 最高和最低值是什么? O V (1) 利用定义和第一定律求; 分析: T (2) 找出 和 V 或 P 的关系,后加以判断 解:(1) 由图知, a V a P
PV RT P0 V 0 RT 0
P P0 gH .
P0 V 0 PdT TdP , dV 2 T0 P
P0 V 0 T V T0 P
dP gdH , a dT dH , T T 0 aH / h h 0 aP / h gT P0 V 0 0 0 dA dH A T 0 h P0 gH P0 gh P0 V 0 aP0 T 0 ln gh T0 P0 5 P0 V 0 E CV T a , 2 T0 P0 gh 5 P0 V 0 aP0 Q A E a gh T 0 ln 2 T 0 P0
例4: 一空气泡自深为 h 的海底浮至海面,若海水温 度 T 与深度 H 的关系为:T T 0 aH / h . 已知在海
, 面上的气体体积为 V 0 , 压强为P 0 海水密度为 . 求气泡上浮过程中对外做的功和吸收的热量。 解: 设气泡内空气 摩尔,视为刚性双原子分子理 想气体。 分析:由 dA PdV , P 和 V 都与H 有关,可 知找出这样的关系是问题的关键。
VA
d
循环过程
E 0
逆循环和制冷系数: 工质经历一个逆循环,从某 些低温热源吸收热量 Q2 (Q2 0) , 向一些高温 热源放热 Q1 (Q1 0) , 对环境做负功 A ( A 0) . 定义制冷机的制冷系数: 高温热源
Q2 Q2 . A A
Q1
致冷机
A
Q2
低温热源
熵和熵增加原理
dQ 0 克劳修斯不等式: T b dQ dQ , Sb Sa . 熵变:dS a T T
熵是状态的函数而与过程无关, 所以,无论什么过 程的熵变,均可通过在始、末态间设想一个可逆过 程找出 dQ与 T 的关系后积分求出。 熵增加原理: 当系统从一个平衡态经过绝热过程到 达另一个平衡态时,系统的熵永不减少 — 如果是 可逆过程,熵不变;如果是不可逆过程,熵增加。
Vb
E 0 , A PdV
1
c
b
22.4 44.8V (l )
3146.4 ( J ) ;
(2) a
A 0, Q E CV ,m (T c T a) ,
c b:
c:
P(atm)
2 a
1
0
c
b
A Pc (V b V c) , Q C P,m (T b T c) .
循环过程
E 0
正循环和热机效率: 工质经历一个正循环,从某 些高温热源吸收热量 Q1 (Q1 0) ,部分用来对外 做功 A( A 0) , 另一部分则向一些低温热源放出
Q2 (Q2 0) .
定义热机的循环效率:
p
A
Q1
A
c
B
VB V
Q2 A 1 . Q1 Q1
o
Q2
过程中理想气体的内能增量
T2
T1
C x dT .
i dE RdT , 式 ΔE CV ΔT (式中 CV 为定体摩尔热 容量,视为常量,ν为气体摩尔数)计算理想气 体内能增量时,此式 [ D ] (A)只适用于准静态的等体过程. (B) 只适用于一切等体过程. (C) 只适用于一切准静态过程. (D) 适用于一切始末态为平衡态的过程. 无论经历什么过程,只要系统温度的改变是 ΔT , 则内能的增量均表达为 ΔE CVΔT
卡若循环
讨 论
T2 , T2 . 卡 1 卡 T1 T 2 T1
p
图中两卡诺循环 吗 ?
1 2
p
T1
A1 A2
T2
A2
T3
A1 A2
A2
V
T1
A1
A1
T2
o
1 2
V
o
1 2
2、一定质量的理想气体完成一循环过程.此过程在V-T 图中用图线1→2→3→1描写.该气体在循环过程中吸热、 放热的情况是 [ ] C (A) 在1→2,3→1过程吸热;在2→3过程放热. (B) 在2→3过程吸热;在1→2,3→1过程放热. (C) 在1→2过程吸热;在2→3,3→1过程放热. (D) 在2→3,3→1过程吸热;在1→2过程放热.
即初、末态内能相等:E 由功的定义,看图得:
Pb V b ,
0.
Ta Tb ,
1 A ( P0 3P0)( 3V 0 V 0) 4 P0 V 0 2
应用热力学第一定律,有:
Q A E A
P0 V P (2) 由图读出: 4 P0 V0 克拉珀龙方程: PV nRT
V 3 2
1 O T
热力学第二定律
开尔文表述: 克劳修斯表述: 统计意义:孤立系统内部发生的过程总是由包含 微观状态数目少的宏观态,向包含微观状态数目 多的宏观态进行。
卡诺定理: 在温度为 T 1 的高温热源和温度为 T 2
的低温热源之间工作的一切可逆热机的效率均为 1 T 2 / T 1 , 与工作物质无关; 而一切不可逆热机 的效率均不可能大于这个值。
P P0 gH
使 例5: 1 mol 氧气由 a 等温地变到 b; a 等体 由 地变到 c 再等压地变到 b .分别 计算系统所做的功和吸收的热量。 P(atm) a 2 解:(1) a b:
0 dV RT a ln 2 , RT a V a V Q A RT a ln 2 Pa V a ln 2
