3-HSS并联机床整机静刚度预估
并联机器人机构研究概述

基金项目:河南理工大学青年基金资助项目(133111)并联机器人机构研究概述张跃敏,谢刚(河南理工大学机械与动力工程学院,河南焦作454003)工业机器人自1960年代初问世以来,得到十分迅速的发展,已广泛应用于各个工业领域以及服务行业、医疗卫生等方面。
在工业(串联)机器人方兴未艾时,又出现了一种全新的并联机器人种类。
并联机器人与串联机器人相比具有结构刚度大、承载能力强、运动精度高以及位置反解简单和力反馈控制方便等诸多优点[1,2],近年来,被广泛应用到航天器对接装置、雷达定向装置以及虚拟轴高速并联机床。
由于其卓越的运动学和动力学性能以及潜在的工业应用前景,吸引了世界范围内的众多学者对它的研究与开发。
本文对其中并联机器人机构的研究现状与成果进行概述。
1并联机器人机构的研究现状并联机器人的研究大致分为两类:一类是并联机器人机构分析,包括对已经存在的并联机器人进行机构学、运动学、动力学、运动控制、路径规划,智能设计等的研究。
其应用领域主要有:并连机床、飞行模拟器、空间飞行对接机构、装配生产线、卫星天线换向装置、海军舰艇观测台、天文望远镜跟踪定位系统、动感娱乐平台以及医疗设备。
并联机构学与运动学分析主要研究并联机器人的运动学、奇异位形、工作空间等方面,是并联机器人控制和应用研究的基础。
并联机器人动力学分析的方法很多,主要有:拉格朗日法、牛顿-欧拉法、高斯法、凯恩法等。
由于并联机构的复杂性,目前有关对并联机器人的研究大都集中在机构学方面,而对于动力学的研究相对较少。
另一类即是并联机器人机构综合,也就是寻找作为机械承载本体的新机构类型。
本质上,机构综合是最具原始创新的工作[2]。
最初,这一研究课题严重依赖设计者的经验,直觉和灵感。
因此,在研究的过程中没有可靠的方法和科学的步骤来遵循。
综合出的机构不具备完整的系统性和规律性,导致了机构综合困难很大且成果不多。
因此,许多学者在致力于寻找一种具有普遍意义的机构综合方法。
并联机器人刚度与静力学研究现状与进展_艾青林

第42卷第5期力学进展Vol.42No.5 2012年9月25日ADVANCES IN MECHANICS Sep.25,2012并联机器人刚度与静力学研究现状与进展∗艾青林†黄伟锋张洪涛张立彬浙江工业大学特种装备制造与先进加工技术教育部重点实验室,浙江省特种装备制造与先进加工技术重点实验室,杭州310014摘要并联机器人的刚度与静力学分析,对于机构力学性能研究具有重要的理论价值和意义.本文围绕杆支撑、绳牵引和钢带传动3种结构形式,详细阐述了国内外并联机构刚度和静力学分析的研究现状.着重从有限元、解析模型和性能分析3方面分析了杆支撑并联机构的刚度研究进展.讨论了有关绳牵引并联机构中绳拉力、动载荷频率、绳牵引预紧力与刚度、静力学之间关系的研究成果.根据钢带并联机器人结构的特殊性,对钢带并联机构的刚度与静力学分析中可能遇到的失稳与振动问题进行了探讨.最后,对并联机器人技术发展情况进行总结与展望,指出随着刚度分析与静力学分析的不断深入,并联机器人的力学理论将会日趋成熟和完善,为并联机器人机构优化设计提供更深入、系统的理论依据.关键词并联机器人,刚度,静力学分析,杆支撑,绳牵引1引言并联机构与串联机构相比,具有刚度大、结构稳定、承载能力强、精度高、运动惯性小、运动学反解简单、实时控制性强等特点.从连接上下平台的运动链结构形式看,可把并联机构分为杆支撑并联机构与绳牵引并联机构.杆支撑并联机构的支撑及传动部件主要是液压缸、普通刚性杆、滚珠丝杠,以及其他的一些组合的刚性结构件.而绳牵引并联机器人是一种以柔性绳为传动和牵引机构的并联机构,绳只能承受拉力,受力具有单向性.最近出现一种新型的钢带并联机构[1],其运动链是横截面具有一定圆弧形状的钢带.与杆支撑并联机构相比,钢带并联机器人的工作空间比同体积的杆支撑并联机构要大得多.由于钢带质量轻,钢带并联机器人的运动速度比杆支撑并联机构快得多;与绳牵引并联机构相比,钢带并联机器人由于不用冗余约束控制,钢带并联机器人运动学分析和动力学分析及控制较绳牵引并联机构更简单.要掌握并联机构的性能,必须先对该机构的力学特性进行彻底深入的分析.人们早已将刚度作为并联机构研究中必须分析的一项指标.而在分析刚度之前,往往先进行并联机构的静力学分析,为后续研究作准备.本文按照杆支撑、绳牵引和钢带并联机器人这3种机构形式,对国内外关于这3种并联机构的刚度分析和静力学分析的研究现状进行了详细阐述,之后对并联机器人的未来发展趋势进行了展望.2刚度分析刚度包括了静刚度和动刚度.作为一项重要的性能评价指标,刚度不仅与机器人机构的拓扑结构有关,还与机构的尺度参数和截面参数密切相关.显而易见,一种由细杆组成的并联机构不一定比粗杆构成的串联机构刚度高.于是,为设计出大刚度的并联机器人,基于刚度性能分析和设计的参数优化设计研究至关重要[2].2.1杆支撑并联机构杆支撑并联机构一般具有结构刚性好、承载能力强等特点,运用较为广泛,较之绳牵引和钢带收稿日期:2011-05-20,修回日期:2012-03-04doi:10.6052/1000-0992-11-073∗国家自然科学基金项目(50805129,51275470)资助,浙江省自然科学基金项目(LY12E07004),浙江省教育厅重点项目(Z201121137)和浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室开放基金项目(2010EM003)资助†E-mail:aiql@584力学进展2012年第42卷并联机构,其最大特点就是刚度大.而关于并联机构刚度分析的文献大部分是针对杆支撑并联机构的.2.1.1静刚度从对杆支撑并联机构的静刚度分析总结中发现,现有的静刚度分析方法包括有限元分析法、静刚度解析模型法、静刚度性能分析法等.2.1.1.1有限元分析法随着计算机技术的发展,有限元分析法成为了并联机构设计和静刚度性能预估的重要手段.该方法主要是借助如ANSYS等有限元分析软件对所设计的虚拟样机进行应力应变分析,从而对样机的尺寸结构参数等进行改进.静刚度是金属切削机床重要的性能指标之一,提高机床的静刚度有利于提高机床的效率、加工精度和表面加工质量.在计算新型3-TPS并联机床的静刚度时,罗继曼等[3]应用有限元分析软件ANSYS仿真了不同位姿下的静刚度,得到沿主刚度方向的刚度比其他方向大,以及远离极限位置可以提高刚度的结果.为研究新型四自由度并联机床的刚度,Cor-radini等[4]和Company等[5]采用一种用多梁表达模型的有限单元分析方法.对于典型机构6-UPS 并联机床的静刚度问题,李育文等[6]是基于该机床的有限元模型,通过过渡点并利用Matrix27单元来定义铰链本身的刚度,以表现铰链本身的变形情况.在研究并联刨床时,刘红军等[7]采用有限元软件对其床身框架及平面约束机构进行刚度分析,并以仿真和实验方式进行刚度特性研究的验证.陈光伟等[8]建立了新型龙门式并联机床平面并联机构整机静刚度的有限元模型,得到动平台在广义工作空间下的刚度分布规律.另外,吴镇等[9]在子结构和结构对称的基础上,采用有限单元数值仿真,对Isoglide3-T3并联机构进行刚度分析.Li等[10]先建立改进型3-PRC全柔性并联微操作机构的模型,之后利用有限元软件ANSYS分析了该模型的刚度和静力学,从中获得了该机构相关结构参数的刚度变化趋势.而Xu等[11]对新型XYZ柔性并联微操作机构建立了工作空间内的刚度模型,并用有限元分析软件ANSYS的非线性静力分析功能测试了其刚度模型.从分析过程与结果中发现,利用有限元软件计算分析机构刚度虽然精确度较高,但其耗时多,工作量大.于是,为便于对并联机构多参数变量进行优化设计,可以建立静刚度的解析或半解析模型.2.1.1.2静刚度解析模型静刚度解析模型就是建立机构操作力与末端器变形之间映射关系.早在20世纪90年代,Cho 等[12]就根据运动影响系数,给出了一种通用运动并联系统的完整解析模型和反驱动系统的刚度公式解析方法,解决了混联操作器系统的系统化建模问题.通过几何关系Lee等[13]推导出了并联机器人静刚度模型的计算公式.另外,Gosselin[14]根据虚功原理,给出了空间机构操作力与末端变形之间的映射关系.近几年来,Chakarov[15]建立了冗余并联机构的刚度解析模型,并得出了该机构的刚度控制图谱.而对于柔性机构,Dong等[16]通过组合单个柔性铰链的刚度模型和公式化约束方程,建立了整个柔性机构的系统刚度解析模型,并提出了刚度的图形分析方法.Pham等[17]将柔性部件以串联或并联的方式连接起来,建立刚度解析模型.该模型允许建立刚度与尺寸之间的函数关系,但排除了在设计过程中柔性并联机构的自由变形.通过采用螺旋理论方法求出4-RUC 四自由度并联机构的雅可比矩阵,韩书葵等[18]推导了四自由度并联机器人的刚度计算公式.而对于Stewart平台[19],El-Khasawneh等[20]计算了其在不同方向上变化的解析刚度,给出了在给定姿态下寻找机构最小最大刚度及其方向的方法,并得出Stewart平台最小最大任意方向和单尺度刚度图.为研究并联机构在机床领域的运用,陈俊等[21]建立了四自由度混联机床并联部分的支链子系统、机架子系统和整机的刚度解析模型,并分析评价了该混联机床并联部分的刚度.吕亚楠等[22]利用刚度矩阵组集方法和考虑轴承导轨系统,建立了XNZ2010型冗余驱动混联机床并联机构的可变整机刚度解析模型.Lu等[23]还得到了对称四自由度4SPS+SP并联运动机床的总刚度解析矩阵.注意到并联机构静刚度映射和雅可比矩阵的必然联系这一特性.Han等[24]建立了3-RPS 并联机床包括力雅可比矩阵变化的瞬时刚度模型,并用例子证明了雅可比矩阵变化对3-RPS并联机床瞬时刚度模型的影响.王友渔等[25]对含有恰约束支链的Tricept机械手三自由度球坐标型并联机构提出了完备静刚度映射解析模型的简单建模方法.汪满新等[26]基于全变形雅可比矩阵,建立一种新型混联机器人模块Bicept的静刚度半解析模型.该方法首先将末端执行器位姿变形分解为无约束主动支链的拉压变形、恰约束支链的弯曲变形及其扭转变形3个部分,之后利用虚功原理和第5期艾青林等:并联机器人刚度与静力学研究现状与进展585结构矩阵法建立各子结构系统的静柔度模型,最后用线性叠加原理组装整机末端静柔度模型.另外,对一些特殊并联机构运用简单的方法会对刚度的提高起到很大作用.例如,利用静力学弹性变形概念与轴承方法,Yoon等[27]通过分析修正Delta并联连杆定位机构的解析结构刚度,从而改进设计出了具有更好平衡刚度的Delta机构.在微动器的研究中,张建军等[28]建立了6-PSS并联微动平台的静刚度模型,并求解出了其刚度矩阵.通过坐标变换和虚功原理,荣伟彬等[29]得到了3-PPSR构型六自由度并联微动机器人的静刚度矩阵模型,并从中获得各参数对该并联微动机器人静刚度的影响规律.Liu等[30]将一般宏动并联机器人的力和刚度的分析方法用于并联微动机器人,分析了雅可比矩阵的重要依据数、刚度指数与微动机器人运动链长度之间的关系,得到了所设计的运动空间中各相关指数曲线图集.最近出现的大行程柔性铰链并联机器人,在微操作、微装配、精密定位,甚至大型光学设备的大范围精密位姿调整等方面具有广泛的应用.对于6-PSS大行程柔性并联机构,孙立宁等[31-32]基于刚度方程提出其弹性模型.通过利用刚度组集加入协调方程,构建得到整机系统的刚度模型,并绘制出系统刚度影响图谱来进行系统刚度性能分析.此外,白志富等[33]利用有限元分析方法将球铰链刚度抽象成一个特征参数,加入到机构的解析模型中.从以上研究可知,在每次建立机构的静刚度解析模型时,其建立过程都较繁琐,且建模方法缺乏通用性.因此,非常有必要创建通用的静刚度建模方法,为今后研究并联机器人静刚度提供便利.2.1.1.3静刚度性能分析静刚度性能分析主要是基于静刚度解析模型来评价并联机构在整个工作空间内的静刚度性能,同时为参数设计提供参考.Carbone等[34]通过将串并混联机构的刚度性能指标公式化,来求解出刚度矩阵.在仅考虑主动关节弹性的基础上,Tsai 等[35]对比分析了4种三自由度平动机构的刚度特性.通过采用小变形叠加原理,周玉林等[36-38]分别对2-RRR+RRS球面并联机构、3-RRR三自由度球面并联机构和3-RRS三自由度球面并联机构进行分析,并以机构静力学分析结果为基础,建立整体静刚柔度矩阵并分析在整个工作空间内其静刚度性能和6个主刚度指标及所在主方向.对上述3种机构的研究表明,它们的主刚度在3个主方向上较大、另3个方向较小,而零点附近刚度较小,离零点越远刚度越大.Wu等[39]分析了带有驱动冗余度的三自由度平面并联机构的刚度和灵巧性,依据刚度指标的最小特征值指标,证实驱动冗余性能改善并联机构的刚度.魏轩等[40]对3-RRR 并联机构运动学模型推导了其雅可比矩阵,提出了一种评价并联机构刚度的评价指标.在对机床的研究中,张华等[41]对龙门式混联机床中平面三自由度并联机构的静刚度性能,提出了一种新的分析方法.此方法依据微分误差模型建立机床刚度矩阵,可计算出机床位置刚度和转动刚度的分布情况.Huang等[42]准确预估了Tripod并联机床的静刚度性能,并得到实验验证.而研究微动器时,Li等[10]在刚度解析模型的基础上评价3-PRC 并联微操作机构的静刚度性能,得到了该机构结构参数对刚度的变化趋势.Bashar等[43]通过分析Stewart平台的静刚度特性,确定了系统最大最小刚度的边界,为参数设计奠定了基础.另外,通过定义和计算平面二自由度驱动冗余并联机器人的全域性能指标,包括雅可比矩阵条件数、承载能力及刚度等,张立杰等[44]绘制出了空间模型内相应的性能图谱.从上述研究可知,静刚度性能评价指标的物理含义及使用范围各不相同,缺少统一的标准.因此制定统一的静刚度性能评价指标,能极大地推动并联机构刚度性能分析研究的发展.2.1.2动刚度动刚度反映了机构在动载荷作用下抵抗变形的能力,是衡量结构抵抗预定动态激扰能力的特性.目前国内外有关这方面研究的文献报道很少.在机床应用中,动刚度最受关注,这是由于其决定了零部件加工质量的稳定性.动刚度检测有助于我们了解在整个机械系统中力是如何产生和传递的.一般来说动刚度是一个频率的函数,它可同时测定瞬时冲击力和采样系统响应信号.在讨论了冲击试验和测量中要考虑的因素后,Xu等[45]提出了两种方案来研究机床主轴冲击试验.结果表明动刚度检测可以有效地解决机床应用上的振动问题,且发生最低动刚度处的频率比所测动刚度处的幅值更加一致.陈吉清等[46]利用螺旋矢量法,建立了机床动态加工过程中6-6Stewart并联机构的动刚度数学模型,计算了动态瞬时刚度和刀具的偏移误差,并对6-6Stewart并联机床的多种不同参数变化条件进行了数值模拟.针对典型的并联机构,敖银辉等[47]分析了在外力输入时机构的静刚度和动刚度.而梁辉等[48]采用能量法推586力学进展2012年第42卷导了3PRS/UPS冗余并联机床的动刚度模型,并对具有内力的该并联机床刚度进行分析,并给出特定位姿下的刚度计算实例.Pashkevich等[49]对三轴快速机床的一类过约束Delta并联运动机构(Orthoglide)提出一种分析机构动刚度的新方法,并依据其几何性分析了工作空间的占用率、刚度准则、转动刚度和移动刚度等.2.2绳牵引并联机构相比杆支撑并联机构而言,绳牵引并联机构中绳具有单方向受力性[50],即只能承受拉力,不能承受压力的特性.因此绳牵引并联机构的刚度分析大多是绳在受拉情况下进行的.理论分析认为,绳牵引并联机构的静刚度矩阵可分为动平台位姿变化产生的静刚度和绳位形变化产生的静刚度两项[51].目前绳牵引并联机构在飞行器风洞试验和大型望远镜领域应用广泛.在对低速风洞绳牵引并联支撑系统WDPSS-8进行静刚度分析与仿真时,胡龙等[52]认为在飞行器模型的主位置处进行准静态姿态变化时,支撑系统处于力位可控范围内,且其静刚度值满足静导数试验的要求,并以此为基础对缩比模型进行低速风洞测量试验.因并联机构的动平台位置在其工作空间内处于连续不断的变化中,使得静刚度分析需要根据位姿的变化不断进行重复分析,耗时费力.于是构造一种简易且能揭示其刚度变化趋势的解析分析模型就显得十分必要.刘欣等[53]就针对一种应用于低速风洞试验的六自由度绳牵引冗余并联机构,运用微分变换推导出了其刚度解析表达式.他们还基于微分变换和线几何理论,建立了包含关节弹性变形以及绳拉力等因素在内的绳牵引并联机器人刚度模型,并推导出其刚度矩阵数学表达式[54].汤奥斐等[55]也运用微分变换原理推导出了大型射电望远镜馈源柔索支撑系统的完整刚度的解析表达式,还对LT500m原型馈源支撑系统验证了该刚度分析方法的可行性.而对大型无线望远镜,他们把其绳支撑系统看作是绳驱动并联机器人,并以该系统的非线性模型证实了绳驱动并联机器人可达到工作空间受绳拉力、球面节点和绳长度的限制.还利用有限单元法与矩阵最小特征值估计刚度特性,建立起绳驱动并联机器人的静态刚度矩阵[56].王克义等[57]针对平面1R2T绳索牵引机构,建立系统静力螺旋平衡方程,并通过微分变换推导出动平台静刚度表达式,得出影响系统静刚度的因素为绳索拉伸刚度和绳索拉力,且两者的影响是相互耦合的.Sui等[58]研究了一种利用绳弹性与冗余驱动的刚度可变三自由度并联绳驱动机构.以静力和刚度分析为基础,根据微分变换理论推导出了节点刚度矩阵和机构总刚度矩阵,并用数值模拟证实,刚度不仅与绳刚度有关,还与绳拉力有关,且刚度变化受绳拉力控制.对于绳牵引并联机器人,动刚度也是一项基本指标,其随动载荷频率变化而变化.一般频率越高动刚度越大且趋于平坦,而在低频时动刚度变化较大.另外动刚度与振动的幅值也有关系,同一频率下振动幅值越大动刚度反而越小.但当动载荷频率与结构的固有频率相近时,有可能出现共振现象,此时动刚度最小,变形最大,应避开该共振点.为了克服绳低刚度引起的振动问题,Won 等[59]有效运用绳间的内力开发了一种基于并联绳机构的六自由度超高速机器人机构FALCON-7.通过分析该绳机器人的内部刚度,发现一些自由度的刚度不能有效地随着内力增加而增大,从而导致了预期振动问题的产生.他们还通过改进运动机构的约束,来降低由绳的弹性产生的振动,并通过实验对其进行验证.2.3钢带并联机构关于钢带并联机器人及其机构的研究在国内外仍未见报道.浙江工业大学提出了一种新型的钢带并联机器人结构,如图1所示.䕈䩶⬉ ㄦ㺙㕂Ⲃ 䕂⧗䫄图1钢带并联机器人三维模型该机构中连接上下平台的中间部件是钢带运动副装置.其中钢带横截面具有一定的圆弧弯曲第5期艾青林等:并联机器人刚度与静力学研究现状与进展587形状,能够承受一定的压力.但当该压力超过了临界失稳压力值时,机构就会产生失稳.苏先义[60]采用有限元方法对六自由度钢带并联机器人进行了失稳分析.他们介绍了钢带并联机器人的工作原理,给出了弯曲截面钢带开口薄壁类型杆件的失稳临界力计算方法,并利用有限元ANSYS软件分析了在钢带厚度、长度、姿态等因素不同的条件下,单根异形或圆弧形截面钢带、两根异形或圆弧形截面钢带联接体与6根异形或圆弧形截面钢带组成的钢带并联机构,为进一步研究钢带并联机器人的性能提供了理论依据.不同于杆支撑与绳牵引并联机构,钢带并联机构既能够承受很大的拉力,又能够承受一定的压力,且承压能力取决于钢带厚度材料及其形状.如果机构承受的压力超过了临界失稳压力值就会产生失稳.而钢带并联机器人在高速运动中,也会因为钢带质量轻且薄而发生振动.故非常有必要对钢带并联机器人静刚度及动刚度进行研究.基于以上分析,钢带并联机构的静刚度应以是否失稳作为评价的标准和依据.其动刚度应该和振动频率与幅值相关,可以通过模态识别方法对其进行研究.钢带并联机器人发生失稳和振动时其机构的刚度瞬时变为最差,因此钢带并联机器人在运动时应尽量避免失稳与振动发生.但是目前没有文献对钢带并联机构的刚度特性进行系统地研究.3静力学分析目前关于并联机构静力学研究方面的文献相对较少.但是静力学分析是机构分析的必要环节,是机构刚度分析和动力学分析的基础.文献中提到的静力学分析方法有螺旋理论法[61]、有限元法、矢量法、坐标变换、影响系数法[62]等,其中以螺旋理论法、影响因数法与有限元法的运用最广.3.1杆支撑并联机构对于杆支撑并联机构来说,静力学分析是对其进行其他力学分析的基础,一般少自由度机构静力学分析相对较简单,而多自由度机构静力学分析较复杂.静力学分析方法以螺旋理论法、影响因数法、虚功原理与有限元法居多,也不乏有矢量法、柔性摩擦圆法和虚位移法等.对于少自由度并联机构,很多学者运用不同的方法对其静力学分析进行过研究.像吴培栋等[63]对3/6-SPS并联机构应用螺旋理论,建立了静力学平衡方程并求出了该并联机构的雅可比矩阵J.在研究并联机床过程中,基于螺旋理论,Han等[64]对3-RPS 并联机床进行静力学分析,并得到一种等价于广义外力下6条链并联机床的变形协调方程.运用虚功原理也是静力学分析的一种方法,Li等[65]利用微分迭代理论和虚功原理,合成了3-UPU低移动并联机构末端器在广义力空间内的机构输入输出力间的广义力综合图.之后,他们[66]又利用虚功原理,建立少自由度并联机构输入端和末端广义力间的静力映射关系.朱春霞等[67]利用有限元软件ANSYS对特定位姿不同受力下的3-TPT并联机床整机进行静力分析,得出了在不同位姿下机床的应力应变图.另外,静力关系与速度传递关系的对偶性可通过力雅可比矩阵联系在一起.于是,静力分析中对雅可比矩阵的求解成为了重要步骤.在对3-UPS/S并联机构动平台进行静力学分析过程中,赵云峰等[68]得到了该机构的静力学雅可比矩阵和动平台静力平衡方程.Hu等[69-70]建立了3-RPS并联移动机构的6×6雅可比矩阵,并运用虚功原理建立静力学模型.他们[71]还基于观测RPS脚的约束力和虚功原理,得到2SPS+ 2RPS并联机构6×6雅可比矩阵和带有约束力的6×6刚度矩阵.Gosselin等[72]推导了六自由度空间并联机构雅可比矩阵的通用公式,从而确定了带有6个输入角度的Pluker向量.而于凌涛等[73]通过对单个杆件在铰链约束及重力作用下的受力情况进行分析,推导出3-RPS机构处于任意位姿时的连杆与动平台负载间完整静力学模型.除此之外,还可利用柔性摩擦圆法等其他方法分析.在研究微操作器时,杨启志等[74]利用伪刚体模型和柔性摩擦圆法,对三平移全柔性微动并联机构各支路与动平台进行详细的静力分析. Russo等[75-76]运用矢量法将六自由度并联机构中球质心的位置矢量表述为平台与6个驱动柱面节点方向和位置的函数,从而得到静力平衡条件表达式.Xu等[11]在考虑刚度与自然频率时,对一种新设计的XY Z柔性并联微机构,进行了静力学和动力学方面的性能评估.周玉林等[77]通过拆杆法建立机构静力学平衡方程,又利用小变形叠加原理建立起变形协调补充方程,完成对三自由度球面并联机构的静力学分析.孟祥志等[78]运用虚位移原理求解了3-TPS(RRR)并联机床各构件和末端执行器上受到各种广义外力时的静力学正逆解. Li等[79]对球面三自由度机构进行了静力学分析,。
一种运动副优化布置的3-SPR并联机床的运动静力学分析

一
种运动副优化布置的 3 - S P R并联机床的运动静力学分析
石岩 ,李 国芹 ,张鹏程 ,郭联合
( 1 .河北工程技术高等专科学校电力工程 系,河北沧州 0 6 1 0 0 1 ; 2 . 燕山大学机械工程学院 ,
河 北秦皇 岛 0 6 6 0 0 4 ;3 .空军 9 5 9 2 7部 队 ,河 北沧 州 0 6 1 7 3 6 )
2 0 1 3年 8月
机床与液压
MAC HI NE T00L & HYDRAULI CS
Au g . 2 01 3 V0 1 . 41 No . 1 5
第4 1 卷 第1 5期
D O I : 1 0 . 3 9 6 9 / j . i s s n . 1 0 0 1— 3 8 8 1 . 2 0 1 3 . 1 5 . 0 4 5
3 . A i r F o r c e N o . 9 5 9 2 7,C a n g z h o u He b e i 0 6 1 7 3 6 ,C h i n a )
A b s t r a c t :T h e k i n e t o s t a t i c s o f a n o p t i m u m j o i n t d i s t i r b u t i o n 3 - S P R p a r a l l e l ma c h i n e t o o l w a s a n a l y z e d .T h e s t r u c t u r e a n d t h e j o i n t d i s t i r b u t i o n o f t h e 3 - S P R p a r a l l e l ma c h i n e t o o l w e r e i n t r o d u c e d b i r e l f y ,a n d t h e s i mu l a t i o n m a n i p u l a t o r w a s b u i l t i n a t h r e e d i m e n —
厂校合作的新成果3—HSS并联杆机床的研制及探索

厂校合作的新成果3—HSS并联杆机床的研制及探索
林汉元;黄田
【期刊名称】《世界制造技术与装备市场》
【年(卷),期】2000(000)003
【总页数】2页(P68-69)
【作者】林汉元;黄田
【作者单位】天津第一机床总厂;天津大学
【正文语种】中文
【中图分类】TG659.021
【相关文献】
1.3-HSS 并联机床运动学设计 [J], 黄田;林汉元;倪雁冰
2.3-HSS并联机床运动学分析及运动仿真 [J], 刘素明;赵强;李军
3.3-HSS并联机床装配工艺及其关键技术研究 [J], 赵学满;倪雁冰;李立贤
4.3-HSS型并联机床数控系统的开放式设计 [J], 李亚;王洋;倪雁冰
5.3-HSS并联机床动力学建模及鲁棒轨迹跟踪控制 [J], 杨志永;黄田;倪雁冰
因版权原因,仅展示原文概要,查看原文内容请购买。
3-(2SPS)并联机构静刚度分析

2 刚度 模 型
B55/ b 。 6 /B66机构 的平 行 杆 与上 下 平 台 的边 组 成
—
个 平行 四边形 , 这个 平 行 四边形 的短 边 , 即为 上
Ii b+ - l b i
一
平台( 平台) 下 两铰链 点 间的距 离 , 其为 d, 设 则
—
【 I
l
响规律 ; 于靖军 等 采用 了结构分析 中的柔 度矩 2 阵法递推出 3自由度柔性微机器人的静刚度矩阵; 张建 军 ] 义 了微 动平 台的 刚 度 ,通 过 静 刚度 等定
径为 R2取每个 平 行 四边形 下 平 台短 边 的 中点 为 , C( i= 12 3 , 到下 平 台 的 中心 为 R , , ,) 其他 的 0, , 为相关 角度 参数 。上平 台也 有 与之 对 应 2 2 2 的参 数 。此 时 便 可 以 得 出 b, i , , ) fB ( =1 … 6 和
0 一XY 图 中 Bl l/3b , 3 3/3b , Z。 6 / 1 2 B b / t4 4 2
究有如下 2 :1对应不同机构构型 , 类 () 推导出其刚 度矩阵。如荣伟彬… 等运用虚功原理 推导 出 3 1 一
PS P R构 型 6自由度 并联 微 动机 器人 静 刚度 矩 阵 , 进 而通过仿 真分 析 获 得 支杆 两端 铰 接 点 半径 及 直 角 弹性 平板 和支 杆 两 端柔 性 铰 链 尺 寸对 刚度 的影
作者简介 : 乐林林 (9 5一)男 , 18 , 湖北黄冈人 , 南京理工大学硕士研究生, 主要研究方 向为机械制造。
21 00年 7月 中国制 造业 信息 化
第3 9卷
第 1 3期
式() 2 为机 构 位 置 反解 方 程 , 将 该方 程 进 行 如
并联机床的设计理论与关键技术

详解并联机床的设计理论与关键技术1 概述为了提高对生产环境的适应性,满足快速多变的市场需求,近年来全球机床制造业都在积极探索和研制新型多功能的制造装备与系统,其中在机床结构技术上的突破性进展当属90年代中期问世的并联机床(Parallel Machine Tool),又称虚(拟)轴机床(Virtual Axis Machine Tool) 或并联运动学机器(Parallel Kinem atics Machine)。
并联机床实质上是机器人技术与机床结构技术结合的产物,其原型是并联机器人操作机。
与实现等同功能的传统五坐标数控机床相比,并联机床具有如下优点:刚度重量比大:因采用并联闭环静定或非静定杆系结构,且在准静态情况下,传动构件理论上为仅受拉压载荷的二力杆,故传动机构的单位重量具有很高的承载能力。
响应速度快:运动部件惯性的大幅度降低有效地改善了伺服控制器的动态品质,允许动平台获得很高的进给速度和加速度,因而特别适于各种高速数控作业。
环境适应性强:便于可重组和模块化设计,且可构成形式多样的布局和自由度组合。
在动平台上安装刀具可进行多坐标铣、钻、磨、抛光,以及异型刀具刃磨等加工。
装备机械手腕、高能束源或CCD摄像机等末端执行器,还可完成精密装配、特种加工与测量等作业。
技术附加值高:并联机床具有“硬件”简单,“软件”复杂的特点,是一种技术附加值很高的机电一体化产品,因此可望获得高额的经济回报。
目前,国际学术界和工程界对研究与开发并联机床非常重视,并于90年代中期相继推出结构形式各异的产品化样机。
1994年在芝加哥国际机床博览会上,美国Ingersoll铣床公司、Giddings & Lewis公司和Hexal公司首次展出了称为“六足虫”(Hexapod)和“变异型”(VARIAX)的数控机床与加工中心,引起轰动。
此后,英国Geodetic公司,俄罗斯Lapik公司,挪威Multicraft公司,日本丰田、日立、三菱等公司, 瑞士ETZH和IFW研究所,瑞典Neos Robotics公司,丹麦Braunschweig公司,德国亚琛工业大学、汉诺威大学和斯图加特大学等单位也研制出不同结构形式的数控铣床、激光加工和水射流机床、坐标测量机和加工中心。
机床静刚度测定实验报告

机床静刚度测定实验报告1.了解机床静刚度的概念和特征。
2.学习测定机床静刚度的方法。
3.运用实验数据对机床静刚度进行分析和评估。
仪器设备1.回路式测量仪。
2.单柱式万能试验机。
3.直线轴承和滑动轴承。
实验原理机床静刚度是指机床在静力作用下,从位置改变所需的力量和形变的量的比值。
机床静刚度包括了机床的刚性、变形和振动特性。
虽然静刚度的定义是一个比值,但为方便起见,通常使用力学刚度和形变刚度来表述。
力学刚度是机床在单位力作用下,床身产生的刚度变化量。
形变刚度是机床在单位刚度变化下的力量变化量。
测量机床静刚度的方法主要有自激振动法、悬臂梁法、回路法等。
其中回路法是目前最常用的一种测量机床静刚度的方法。
回路法是将测力仪和测压仪组成一个回路,以测量机床的变形量。
该方法适用于测量处于静止状态的机床并精度比较高。
实验步骤1.安装直线轴承和滑动轴承,分别测量机床的力学刚度和形变刚度。
2.根据机床的变形规律和受力情况,选择合适的位置安装测量器。
3.拧紧测量仪和测量器,调整它们的相对位置,并进行初步调整。
4.开始测量,记录数据并分析。
实验结果通过对机床静刚度的测量,得出了机床的力学刚度和形变刚度,数据如下:力学刚度:1000 N/m形变刚度:0.1 mm/N然后,根据实验数据计算出机床的回路法静刚度为1300 N/m。
这表明机床处于静态稳态,并具有良好的刚度、变形和振动特性。
结论1.机床静刚度是机床在静止状态下,从位置改变所需的力量和形变量的比值。
2.回路法是测量机床静刚度的一种常用方法。
3.机床静刚度包括了机床的刚性、变形和振动特性。
4.实验结果表明机床具有较高的静刚度,能够满足使用要求。
3-PRS并联机构空间动态精度检测与误差补偿的研究

Absr c :Th s tx ic s e he e a n to i a t ro h ta t i e td s u s s t x mi a in ma n f co ft e NC a h n o ld na i t t c u a y,a c r m c i e t o y m c sae a c r c c o d—
v l e a d a p y f r g o n fto o g x a so fd na i r cso x mi a in tc n lg . a u n p l o e r u d o h r u h e p n in o y m c p e ii n e a n t e h o o y o K e wor y ds:Dy a c Pr c so n mi e ii n;Bln n i d Zo e;3-PRS P r le e h n s ;Co a a llM c a im mpe a in ns to
c mp n a in f r PRS p r l l o e s t o o 3- a a l c a im e me h ns
Z A GY n Z A G Zi n H N u , H N hj u
3HSS并联机床运动学设计

要指标, 可用动平台三维笛卡尔速度到滑鞍移动速度 的映射矩阵——雅可比矩阵的条件数来表征。 条件数 越小, 则说明机床理论伺服精度越高, 因此可作为结构 参数的设计准则[ 6, 8 ]。 对式 ( 1) 关于时间求导, 得到点 o′ 的速度为 α ( 4) v = q i e3 + L Ξ i × w i α 式中, qi 为滑鞍 i 的移动速度, Ξ i 为支链 i 的角速度矢 量。 对上式两端点积 w i 并写成矩阵形式有 1 α q = diag T [w 1 w 2 w 3 ] T v = J v
0 ) 为点 B i 和 A i 在系 o- x y z 和 o′ - x′ 的位置矢 y′ z′
T
3
det Κ E3 -
∑ (w w
பைடு நூலகம்i i = 1
T i
2 ) (w T = 0 i e3 )
( 6)
即可解出 J 的条件数
W = m ax
Κ i
m in
Κ i
( 7)
量; ra、 静平台半径; Βi 为点 B i 和 A i 在 o- x y z rb 为动、 和 o′ - x′ ′ ′ 下位置角 , 且有 y z Π 2Π Β1 = + ( i - 1) 6 3 w i 为支链 i 的单位矢量; L 为支链杆长; q i 为滑鞍 i 相 对参考点 B i 的位移; e3 = ( 0 0 1) T 。对式 ( 1) 两端取 模方并整理得
机械工程, 1999, 10 (10)
3 H uang T , W ang J S, W h itehouse D J. C lo sed fo rm so lution to the w o rk space of hexapod based parallel m ach ine too ls, A SM E J. of M echan ical D esign, 1999, 121 (1) 4 H uang T , W ang J S, W h itehouse D J. T heo ry and m ethodo logy fo r k inem atic design of Gough 2Stew art parallel m an ipulato rs, Science in
机床静刚度测定实验报告
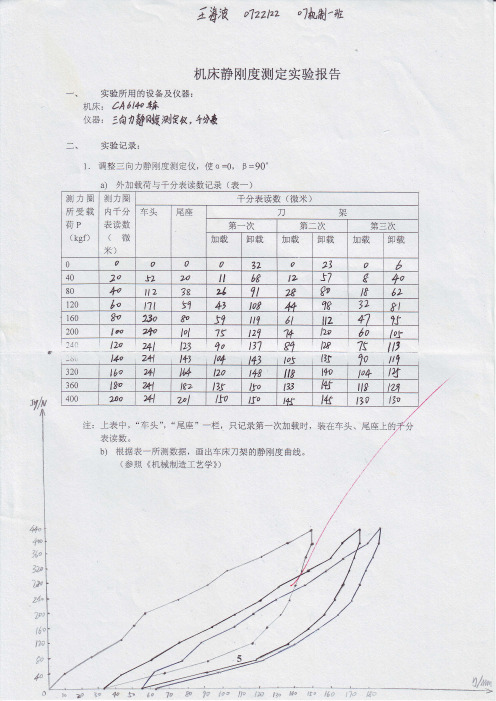
纠
驯」 捌 ^圳 ˉ 岁ˉ 驷 舻 胛 钾 靼 δ
刿
各、 铲1 螂
驷 沁 扌 f铲 /F。 /刀 9 庐 f卜 脬 9 碴 p /磅 氵 f?' '诬 r ∷
∶ ∷
∶ˉ
ˉ △ ∵
灬 :
卩
四 、思考 问答题 : (1) 据 所 画得 车床 刀架 的静 刚度 曲线 ,说 明为什 么加 载 曲线与卸载 曲 一 线不重合 ?并 且每个 实验 小组所测得 的 同 台机床 的静 刚度 曲线
测力圈 所受载 荷P (kgf) 测力 圈 内千 分 表读数 (微 冫:) 长
0
口 口
千分表读数 (微 米 )
车头 尾座
刀
力 爿
第一次
力磷 日戋
口 ' `
第二 次
加载
卸载
第 三次
加载 卸载
卸载
32
田
彡‘
口
莎
4口
多 犭 P∫
40
80
`口
Ω ″2
莎 ‘
`多
120 160 200
40
-♂ 0
F J。 o 彡
为什么不完全相 同 ? (2) 试 推导本 实验机床 、床 头 、尾架 、刀架 之 间的刚度关系式 : ∷ ;斋 T=-;亍 咭 ) (了 +丁 菖 佶 :丁 ∷
0,β 司 测 力圈承受 200公 斤力 时 ,被 加 上试棒 的 并计算 : α 〓 最大直径误差为多少 ? (假 定被加 工 试棒 是刚体 ,本 身不变形 )
, 彩 彻 :碰 g矽 喃纠蒜每 存在
″
溯劳 底 锡 溷 蛀 件 滋 朕 扣 蚓 荐 霪 纟 豸 侈圣
伪 龆 ‰∷ 饧 切 ‰ % 彻 护' 珊 ' ι一‰ 饧 烤 伪工 豇
三自由度并联机床动态有限元分析

a d d s lc m e tf r k y c m p n n s u h a o i g p af r , s hei a i g s a d sie s d e n ip a e n o e o o e t s c s m v n l to m p rc l h n e n l a dl wa d s g ie an d. Th e u t ho t tt e m o ti fu n ilfe u nce ft e d na i e f r a c r h e o d e r s ls s w ha h s n l e ta q e i so h y m c p ro m n e a e t e s c n r
第 6期
21 0 2年 6月
组 合 机 床 与 自 动 化 加 工 技 术
M o l a hi e To l& Aut m a i a du ar M c n o o tc M nuf c urng Te h q a t i c ni ue
NO. 6
J n 02 u .2 1
动 态性 能 影响 最大 。球铰 结合 部 为机 床 结 构 中薄 弱 环 节 , 由此 提 出 了机 床 结 构优 化 设 计 建议 , 球 将
形 铰 链 更 换 为 虎 克 铰 链 , 而 提 高 了机 床 的 动 态性 能 。 从
关键词 : 并联 机床 ; 限元 ; 态分析 ; 响应 有 模 谐
三自由度精密定位机构静刚度分析

三自由度精密定位机构静刚度分析对3-SPR柔性并联精密定位机构静刚度进行分析。
建立了该柔性并联定位机构的静刚度矩阵,利用建模软件SolidWorks建立机构的实体模型并基于软件ANSYS Workbench进行实例分析。
结果表明:所建立的机构理论模型具有良好的静力学性能。
标签:柔性并联机构;刚度;分析引言基于柔性并联定位机构能够对亚微米以及纳米级空间进行操作,因此在现代科学研究的多个领域都得到了越来越多的应用。
定位机构各项性能指标的优劣已经在很大程度上影响着各国微纳技术发展水平的高低。
柔性机器人要求具有很高的定位精度,而机构的静刚度在很大程度上决定着这一指标。
目前对柔性并联定位机构静刚度问题的研究还很少,微动机器人在终端受载的情况下会发生变形,在很大程度上是取决于它的刚度。
刚度在本质上反映的是力与变形的映射关系,它的大小决定了终端的精度,它决定了机器人是否具备正常工作的能力,因此刚度是分析微动机器人的一个重要过程。
一般来说动载荷对柔性并联机构的终端影响是非常小的,其主要承受的还是静载荷,因此柔性并联定位机构的静刚度就成为关键问题。
1 机构描述如图1所示为3-SPR柔性并联定位机构的模型。
该机构由动平台、定平台以及三条与二者相连SPR支链组成,并由压电陶瓷驱动器驱动。
建立3-SPR并联机构的机构简图,如图2所示,建立笛卡尔参考直角坐标系B-XYZ,以定平台中心点为坐标系原点B,X轴平行于且方向向右,Y轴沿BB2方向,Z轴垂直于面B1B2B3且方向向上。
以动平台的中心点a建立动坐标系a-xyz,x轴方向平行于A3A1且方向向右,y轴沿ay方向,z轴垂直于面A1A2A3且方向向上。
对于3-SPR机构阶数λ=6,构件数n=8,运动副数g=9,转动副的度为1,移动副的自由度为1,球铰的自由度为3,将以上的数据代入公式中可以得出机构自由度F=3。
2 静刚度矩阵建立与实例分析2.1 建立机构静刚度矩阵通过已知的动平台运动情况,可得各分支中铰链的运动表达式:?椎i为第i个分支中所包含运动副的六个广义微位移列失,Di矩阵为转换矩阵,?驻p为并联机构动平台运动微位移的列失量。
3-RPS并联机构静刚度建模方法

3-RPS并联机构静刚度建模方法落海伟;张俊;王辉;黄田【摘要】以三自由度并联动力头A3(3-RPS)为研究对象,提出了一种基于子结构综合和静态凝聚技术的静刚度建模和自重变形求解方法.建模过程中,将机构划分为动平台和RPS伸缩支链子结构,并综合考虑了铰链和支链弹性对静刚度的贡献.其中,球铰和转动副处理为具有等效刚度的集中质量虚拟弹簧;伸缩支链借助有限元软件和静态凝聚技术,建立了支链子结构质量矩阵和刚度矩阵;动平台处理为刚性质量块.通过引入变形协调条件,建立系统的整体刚度矩阵.研究结果表明,整机主刚度随机构位姿的变化而变化;在动平台连体坐标系下,3 个方向线刚度呈对称分布且 w 向刚度最大;运动部件自重会导致动平台末端产生较大弹性变形.该方法所得静刚度变化规律通过实测结果进行了验证.%A static stiffness modeling and weight deformation solving method for a three degree of freedom(3-DOF)parallel kinematic manipulator(PKM)A3 was proposed using the substructure synthesis and static condensation technique. During the modeling process,the whole system was divided into moving platform subsystem and three identical RPS limb subsystems,in which the contributions of the joint and limb compliances to the static stiffness were considered. In the stiffness model,the sphere joint and the revolute joint were treated as lumped virtual springs with equal stiffness,the platform was treated as a rigid body,and the structural mass matrix and the stiffnessmatrix of the RPS limbs were established using finite element software and static condensation technique. With the compati-bility conditions at interface between the limbs and the platform,an analytical governing dynamicequation of the system was then proposed. The simulation results show that the system stiffness vary with the changes of the configu-ration. In the coordinate system fixed to the moving platform,the distribution of the stiffness is axially symmetrical and the linear stiffness inw direction is the highest. The tip of the spindle claims a large elastic deformation due to gravity. The static stiffness simulation results are further validated by the experimental data.【期刊名称】《天津大学学报》【年(卷),期】2015(048)009【总页数】7页(P797-803)【关键词】静刚度;并联机构;子结构综合;静态凝聚【作者】落海伟;张俊;王辉;黄田【作者单位】天津大学机构理论与装备设计教育部重点实验室,天津 300072;安徽工业大学机械工程学院,马鞍山 243032;天津大学机构理论与装备设计教育部重点实验室,天津 300072;天津大学机构理论与装备设计教育部重点实验室,天津300072【正文语种】中文【中图分类】TH112.5并联机床具有结构稳定、承载能力强和运动学逆解简单等特点,正逐渐成为高速机床领域备受关注的热点,如已成功应用于航空领域高速切削的Tricept[1]系列和Z3头[2]等即是该类型机床的典型范例.基于此,有学者基于拓扑结构3-RPS(R为转动副,P,为移动副,S为球铰),发明了一种具有1平2转(1T2R)3个自由度的并联动力头——A3头[3-4],配以x、y两个平动自由度,即可形成一种新型结构的五坐标高速加工中心.并联机构的静刚度是影响机床定位精度的重要因素.在静刚度预估方法中,最常用的为有限元分析法.虽然有限元软件预估精度高,但如果要预估整个工作空间中静刚度随位型的变化规律,需要反复修改有限元模型并重新划分网格[5],耗时多,工作量大,且需要占用大量计算机资源.为便于进一步进行参数优化,一些学者提出了静刚度解析或半解析方法.Gosselin[6]基于雅可比矩阵,借助虚功原理建立了仅考虑支链驱动刚度的并联机构静刚度模型.Majou等[7]在此方法基础上引入了铰链刚度,建立了三平动并联机构Orthoglide刚度模型.Xu等[8]在进一步引入螺旋理论的基础上建立了3-P RC的静刚度模型.Wang等[9]利用同样方法建立了6-P SS的静刚度模型,并通过特征值对末端静刚度在整个工作空间下的分布特性进行了分析.Li等[3]利用虚功原理和全雅可比矩阵建立了3-RPS并联动力头的静刚度半解析模型,并基于等刚度原则对结构尺度参数进行了优化.上述方法的基本原理是建立机构关节空间到机构末端的刚度映射,进而得到机构末端刚度值,但该方法只能获得机构末端的六自由度刚度矩阵,无法建立可以反映系统各节点静刚度特性的总体刚度矩阵.通过建立系统总体刚度矩阵可以实现末端载荷与整机各节点变形的映射关系.Deblaise等[10]利用子结构综合法建立了Delta的总体刚度矩阵,并对负载作用下整机变形规律进行了分析,但该模型将支链简化为简单的空间梁单元.Goncalves等[11]利用同样方法建立了6-RSS总体刚度矩阵.Wu等[12]在利用子结构综合并考虑铰链刚度的基础上,建立了带冗余驱动的混联机床总体刚度矩阵,并通过实验进行了验证,但在该模型中,支链同样被简化为空间梁单元.由此可见,已有文献在总体刚度矩阵建模过程中,均对复杂支链体进行了简化处理,将支链处理为简单截面(矩形、圆型、圆环和中空矩形等)的空间梁单元[5,12],导致其建模精度不足.本文以3自由度并联动力头A3为对象,首先借助有限元软件和静态凝聚技术,建立支链子结构的刚度矩阵;其次在引入铰链变形协调条件的基础上,利用子结构综合构造系统总体刚度矩阵;然后对整机静刚度在工作空间中随位姿的变化规律和受重力影响的变形规律进行了分析;最后通过实测结果对静刚度的变化规律进行了验证.本文研究的目的旨在为A3头的进一步设计、改进以及实际应用提供重要的理论基础.1.1 3-RPS结构简介图1所示为A3头CAD模型结构.该机构由动平台、静平台和3条结构相同的RP S支链构成,其中,每条支链采用伺服电机通过丝杠螺母进行驱动,实现沿z 向的平动和绕x、y轴转动3个自由度(1T2R).1.2 3-RPS运动学分析图2为A3头的结构示意.其中,Ai、Bi、Ci(i=1,2,3)分别为第i条支链中球铰中心、转动副中心和支链电机.动平台△A1A2A3与静平台△B1B2B3为正三角形,点A与B分别为其几何中心.在B点建立静平台连体坐标系BxByBzB,各轴方向如图2所示;在A点建立动平台连体坐标系Auvw,初始状态下各轴方向与BxByBzB平行;At为刀尖点,相对于坐标系Auvw为wt;在Bi(i=1,2,3)点建立支链参考坐标系Bixiyizi,各轴方向如图2所示;s2i(i=1,2,3)为A3头第i支链中移动副的单位方向矢量;qi(i=1,2,3)为第i条支链球铰与转动副之间的长度.动平台连体坐标系Auvw相对于固定参考坐标系BxByBzB的姿态矩阵利用z- x- z 欧拉角表示为式中:ψ、θ、φ分别为进动角、章动角和自旋角;Rot为旋转矩阵.通过构造矢量封闭方程r,可得支链逆解为式中:rA为点A在坐标系BxByBzB的位置矢量;ai为球铰中心Ai相对于坐标系Auvw的位置矢量;bi为转动副中心Bi相对于坐标系BxByBzB的位置矢量,具体推导过程可参考文献[3].2.1 RPS支链子结构模型因伸缩支链为复杂的几何体,支链内部为带筋的中空结构,为同时满足计算效率和求解精度,采用静态凝聚技术建立支链的刚度矩阵和质量矩阵.通过有限元软件ANSYS对支链进行前处理后,将质量矩阵和刚度矩阵导入MATLAB环境中进行自由度凝聚;节点iB(转动副中心)为虚拟凝聚点[13],通过多点差值约束方程与支链在封闭框范围内的节点自由度uE连接,如图3所示.根据有限元方法可写出支链的n自由度动力学方程为式中:m、k分别为质量矩阵和刚度矩阵;u、f分别为支链的广义坐标列阵和外载荷列阵.将结构系统节点坐标划分为保留坐标au和凝聚掉的坐标bu,经排序和分块处理后得式中:aam和aak分别为与保留坐标au对应的质量矩阵和刚度矩阵;bbm和bbk分别为与凝聚坐标bu对应的质量矩阵和刚度矩阵;abm、bam、abk和bak分别为分块后的交叉质量矩阵和刚度矩阵;af和bf分别为保留外载荷列阵和凝聚掉的外载荷列阵.根据静态凝聚技术基本思想,可得根据结构系统凝聚前后动能与势能相等的原则,可得凝聚后的刚度矩阵、质量矩阵分别为式中rm和rk分别为经静态凝聚后获得的质量矩阵和刚度矩阵.因支链长度iq随机构位姿变化,在子结构综合时,随iq变化的对接节点无法满足相容条件[3,14].为实现不相容条件下的子结构综合,在对接界面中心建立虚拟凝聚点iB,Eu为au中的界面对接自由度,则式中:矩阵CT为界面节点自由度与凝聚节点自由度之间的传递矩阵,通过多点差值约束方程获取;B=u为界面自由度相对于支链广义坐标列阵的变换矩阵.根据文献[13]可建立多点差值约束方程,则式中:Bε和Bξ分别为凝聚节点的3个平动自由度和3个转动自由度;Eku为Eu中第k个节点坐标;kw为权重系数,与对应界面节点所代表的接触区域成正比,具体选取过程可参考文献[14];Ckr为虚拟节点到相应第k个界面节点的位置矢量;传递矩阵CT通过式(7)和式(8)确定.根据支链的受力情况,整条支链可以看成是由两组弹簧支撑的空间梁结构[15],其节点受力如图4所示,图中下标s和r分别代表球铰和转动副.根据式(3),可得第i条支链在支链坐标系下的静力学方程,为便于推导,各矩阵变量引入支链编号i(1,2,3),忽略其他下标,则式中ik为经自由度缩聚后第i条支链的刚度矩阵.式中分别为节点iA、iB和iC的节点坐标相对坐标系下iu的变换矩阵,可由运动学关系推知.因iB为等效虚拟节点,其坐标变换矩阵为2.2 动平台子结构模型动平台受力示意如图5所示.结合图5受力情况可写出动平台的动力学方程为式中:FPLi为动平台与第i条支链间的作用力;rAi为动平台球铰链中心向量;FP、τP分别为动平台所受到的外部力和力矩;Ri为支链坐标系Bixiyizi到系统坐标系BxByBzB的变换矩阵.3.1 变形协调条件动平台和支链间的位移关系如图6所示,图中,AiM、AiL分别表示连接界面上动平台和支链上的点;∇Ai、εAi分别为AiM、AiL在支链坐标系Bixiyizi下的位移.动平台位移与支链上球铰链中心Ai的位移之间存在关系式中rAix、rAiy和rAiz分别为Ai点在坐标系BxByBzB下向量iAr的坐标.于是,动平台和支链之间的作用力可表示成式中ksi为球铰链在支链坐标系Bixiyizi下相应方向上的刚度矩阵,ksi=diag(ksxi,ksyi,kszi),详细推导过程可参考文献[3].将式(11)代入式(15),并将ui转换为系统坐标系BxByBzB下可得同理,可推得第i条支链上转动副连接界面的作用力可表示为式中r1k和r2k分别为转动副的线刚度和角刚度.转动副的各向刚度主要由转动副轴承组件、封闭框、导轨滑块组件和丝杠组件组成,具体转动副组件受力分析可参考文献[3].3.2 系统总体矩阵将弹性变形协调方程式(16)、(17)代入各子系统动力学方程式(13),经组装并整理后可得系统静力学方程式中:K为系统的总体刚度矩阵;U和F分别为系统的广义位移列阵和广义力列阵,分别为式中:4M为动平台质量矩阵;1M、2M和3M分别为伸缩支链质量矩阵,通过式(6)中rm获得.A3头结构参数如表1所示,其中Pz=s+d为动平台与静平台中心距离,s=0~200 mm 为A3头全姿态沿zB向行程,θmax为动平台最大摆角.提取式(18)刚度矩阵K,通过矢量wt将其转换到动平台末端连体坐标系Atuvw进行度量.图7为Pz=550 mm、分别沿动平台连体坐标系u、v和w方向的线刚度变化趋势.从图7(a)和(b)可以看出:当动平台沿Bx轴摆动时,u方向刚度减小,v方向刚度增大;沿By轴摆动时,u方向刚度增大,v方向刚度减小,而且沿By轴摆动时,uv、两个方向的刚度呈典型的面对称分布.图7(c)显示,沿w方向的线刚度为三对称分布,在摆角较小的情况下,沿w轴方向的线刚度远大于其他两个方向.引入质量矩阵M,在重力Fg(g=9.8 m/s2)的作用下,整机弹性变形Δ为图8为动平台和静平台中心距分别为550mm和750mm位型时,整机在运动副自重作用下产生的弹性变形示意(变形量放大1,200倍).当机构从位型1P运动到位型2P时,在重力作用下,整机沿By轴负方向产生弹性变形,表2中yΔ为动平台受重力作用沿By轴的弹性变形量,xθΔ为变形过程中动平台沿Bx轴的转动量.表2中数据显示,动平台沿Bz轴伸长过程中,从Pz=550 mm 位型时的57μ m增加到Pz=750 mm位型时的133 mμ,在200 mm的行程范围内变形量增幅达76 mμ.在该行程范围内,绕自身的转动变化量为0.15°.从图8可以看出,在重力作用下,支链自身的变形量相对较小,球铰链和转动副的弹性变形量相对较大.因转动副的弱刚性,在负载作用下,支链绕转动副的约束轴产生弹性变形,使得机构在BBx z平面内产生平行四边形效应,进而导致动平台在伸缩过程中产生近似平行的下垂现象.因此,在进一步设计和改进过程中,应该重点加强R副的刚度并降低动平台的自身质量.图9为样机刚度实测图.本次实验选用螺旋千斤顶给动平台末端施加固定载荷,加载力测量装置为BK-2B压力测力仪,用来显示加载量,千分表①~⑤用来显示各测量点的变形量(μm),其中,千分表①用来测量机构末端对应加载方向上的变形量,千分表②~⑤用来测量因基座弹性变形所引入的测试误差,在后续静刚度分析时用以消除测量误差,提高测试精度.每个位型下分别记录u方向的加载力和各测试点静态变形量,以0.5,kN为加载量,从0加载到4,kN,提取测量结果线性度较好的数据,通过直线拟合来求解整机静刚度,为消除误差,每组数据测试3次,最后取平均.表3和表4分别为动平台沿zB轴伸出和绕yB轴转动时,沿动平台连体坐标系u方向的理论与实测刚度值.数据显示,当动平台和静平台中心距Pz增大时,沿u方向的线刚度逐渐降低.在Pz=550 mm 、θx=0°时,当θy从0°增大到30°时,u向线刚度从初始状态的7.88 N/μm增大到10.68 N/μm.其中,在摆角小于20°范围之内,仿真误差较小,当θy=30°时,误差相对较大.可以看出,静刚度理论计算值与实测结果存在一定误差,首先是由于并联机构静刚度的变化是一个非线性过程,与机构位型有极强的相关性,导致理论计算值在姿态角较大的情况下模拟值与实测值误差较大;其次,并联机构的铰链刚度对整机静刚度影响较大,在理论计算时,各关键铰链刚度都是按理想状态处理的,3条支链所对应的铰链装配精度都一样,每条支链对应轴承和导轨的预紧力一致,所以3条RPS支链上对应的3组铰链等效刚度在理论仿真过程中均按照同样的方式等效而来,但是在原型样机中,由于制造和安装原因,各关键零部件的预紧力和装配误差均存在一定差异,而且某些部件还存在预紧力不足、铰链内部存在间隙等现象,进而导致理论计算结果与实测值存在一定误差.但从总体来看,实测静刚度变化规律与理论仿真的变化规律一致,且仿真误差处于合理范围之内.其他方向刚度也可通过类似方法获取,本文不再一一赘述.(1) 整机的主刚度随机构位姿的变化而变化,且在动平台连体坐标系下u、v方向的线刚度呈面对称分布,w方向的线刚度呈三对称分布.(2) 在工作空间下,沿w方向的线刚度较高,远大于u、v方向的线刚度,尤其是在摆角为零的位姿下,沿w方向线刚度达到最大.(3) 该方法可以求出整机在重力作用下的变形规律,为整机的薄弱环节分析提供新的理论依据.(4) 本文方法求解的静刚度与实测结果相比,误差处于合理范围之内.本文方法既可以快速预估整个工作空间中静刚度随位型的变化规律,也可以求解不同位型下运动部件自重引起的弹性变形对末端定位精度的影响;而且,在末端负载或自重作用下,本文方法不仅可以求解末端执行机构的变形量,还可以获得RPS 伸缩支链各节点和铰链之间的变形量,有助于对整机各环节的柔度特性进行深入分析,为该类型机构的工程设计、改进和实际应用提供理论基础.【相关文献】[1] Caccavale F,Siciliano B,Villani L. The Tricept robot:Dynamics and impedance control[J]. IEEE/ ASME Transactions on Mechatronics,2003,8(2):263-268.[2] Hennes N,Staimer D. Application of PKM in aerospace manufacturing high performance machining centers ECOSPEED,ECOSPEED-F and ECOLINER [C]// Proceedings of the 4th Chemnitz Parallel Kinematics Seminar. Chemnitz,Germany,2004:557-568.[3] Li Yonggang,Liu Haitao,Zhao Xueman,et al. Design of a 3-DOF PKM module for large structural component machining[J]. Mechanism and Machine Theory,2010,45(6):941-954.[4]陈闯,王辉,庄嘉兴. 一种新型并联动力头的前馈控制策略与实验[J]. 天津大学学报:自然科学与工程技术版,2014,47(8):672-676. Chen Chuang,Wang Hui,Zhuang Jiaxing. Feedforward control strategy and experiment on a novel parallel spindle[J]. Journal of Tianjin University: Science and Technology,2014,47(8):672-676(in Chinese).[5] Law M,Ihlenfeldt S,Wabner M,et al. Positiondependent dynamics and stabilityof serial-parallel kinematic machines [J]. CIRP Annals:Manufacturing Technology,2013,62(1):375-378.[6] Gosselin C. Stiffness mapping for parallel manipulators [J]. IEEE Transactions on Robotics and Automation,1990,6(3):377-382.[7] Majou F,Gosselin C,Wenger P,et al. Parametric stiffness analysis of the Orthoglide[J]. Mechanism and Machine Theory,2007,42(3):296-311.[8] Xu Qingsong,Li Yangmin. An investigation on mobility and stiffness of a 3-DOF translational parallel manipulator via screw theory[J]. Robotics and Computer-Integrated Manufacturing,2008,24(3):402-414.[9] Wang Dan,Fan Rui,Chen Wuyi. Stiffness analysis of a hexaglide parallel loading mechanism[J]. Mechanism and Machine Theory,2013,70:454-473.[10] Deblaise D,Hernot X,Maurine P. A systematic analytical method for PKM stiffness matrix calculation[C]//Proceedings 2006 IEEE International Conference on Robotics and Automation. Florida,USA,2006:4213-4219.[11]Gonçalves R S,Carvalho J C M. Stiffness analysis of parallel manipulator using matrix structural analysis[C]//Proceedings of EUCOMES 08. Germany:Springer,2009:255-262.[12] Wu Jun,Wang Jinsong,Wang Liping,et al. Study on the stiffness of a 5-DOF hybrid machine tool with actuation redundancy[J]. Mechanism and Machine Theory,2009,44(2):289-305.[13] Heirman G,Desmet W. Interface reduction of flexible bodies for efficientmodeling of body flexibility in multibody dynamics[J]. Multibody System Dynamics,2010,24(2):219-234.[14] Law M,Srikantha Phani A,Altintas Y. Positiondependent multibody dynamic modeling of machine tools based on improved reduced ordermodels[J]. ASME Journal of Manufacturing Science and Engineering,2013,135(2):021008-1-021008-11.[15]宋轶民,程航,孙涛,等. 并联机构转动副滚动轴承静刚度参数辨识[J]. 天津大学学报:自然科学与工程技术版,2014,47(12):1101-1108. Song Yimin,Cheng Hang,Sun Tao,et al. Static stiffness parameter identification of rolling bearings in parallel mechanisms with revolute joints[J]. Journal of Tianjin University: Science and Technology, 2014, 47(12):1101-1108(in Chinese).。
机床静刚度的测定

实验一机床静刚度的测定一实验目的通过实验理解和掌握:1. 机床(包括夹具)——工件——刀具所组成的工艺系统是一弹性系统;2. 力和变形的关系不是直线关系,不符合虎克定律;3. 当载荷去除后,变形恢复不到起点,加载曲线与卸载曲线不重合;4. 部件的实际刚度远比我们想象要小;5.通过测量计算机床的静刚度。
二设备与仪器1.C616,CF6140 车床;2.单向静刚度仪、三向静刚度仪。
机床单向静刚度的测定一实验原理如图1--1所是:在 C616 车床的顶尖间装上一根刚度很大的光轴Ⅰ,其受力后变形可忽略不计,螺旋加力器 5 固定在刀架上,在加力器 6 与光轴间装一测力环 7 ,在该环之内孔中固定安装一千分表 3 ,当对如图所安装的测力环加力时,千分表 3 的指针就会转动,其转动量与外载荷的对应关系可在材料实验机上预先测出。
本实验中测力环的变形与外载荷( 0 - 1500N时)的对应关系见表 1 - 1 。
实验时,将测力环抵在刚性轴的中点处,在刚性轴靠近主轴端装有千分表 1 ,在刚性轴靠近尾架端装有千分表 2 ,在刀架处装有千分表 4 ,用扳手转动带有方头的加力螺杆 5 施一外载荷(F y),加载大小由千分表 3 的指针转动量所指示,千分表 3 的指针转动量与加载关系如表 1 — 1 所示,每次加载和卸载时,分别记录下千分表 1,2,4 的读数。
为了说明机床的静刚度与尾座套筒的伸出长度有关,实验时,可将套筒分别伸出 5mm 和 10mm 后各进行一次实验,可对实验结果进行比较。
二 实验步骤1.按图 1 — 1 把单向静刚度仪装在车床上,同时装好千分表。
2.把测力环抵在刚性轴的中点处,使千分表 3 的指针指零,转动加力螺杆 5 预加载荷 500N 后卸载(即千分表 3 的指针旋转 35 微米),然后,重新调整千分表 1,2,4 ,使其指针指零。
3.安照表 1 — 1 所给出的测力环所受载荷与千分表指示数之间的对应关系,千分表 3 的指针每转动 7 微米,等于测力环每次加载 100N ,顺次加至 1500N ,把每次加载后千分表 1,2,4 的位移数值记录到表 1 — 3 中。
并联机器人机构静刚度研究现状与展望

并联机器人机构静刚度研究现状与展望*李永刚1,2,宋轶民2,冯志友3(1.天津工程师范学院机械工程学院,天津300222;2.天津大学机械工程学院,天津300072;3.天津工业大学机械工程学院,天津300160)摘要:静刚度是并联机器人机构的一项重要性能评价指标,是并联机器人研究的热点领域之一。
从有限元分析、静刚度解析模型、静刚度分析和静刚度设计等4个领域对并联机器人机构的静刚度研究现状进行了总结回顾,并对其未来发展趋势进行了分析。
关键词:并联机构;静刚度;有限元;建模中图分类号:T H122文献标识码:A文章编号:1001-2354(2010)03-0001-04与串联机器人机构相比,并联机器人机构具有刚度大、结构稳定、承载能力强、累积误差小、运动惯性小、运动学反解易求和便于实时控制等互补性优点,具有广阔的应用前景。
因此,近30年来,并联机器人机构理论研究一直是机构学领域的研究热点之一。
然而,作为一项重要性能评价指标,静刚度不仅与机器人机构的拓扑结构有关,而且与机构的尺度参数和截面参数密切相关。
显而易见,一个由细杆组成的并联机器人不一定比粗杆构成的串联机器人静刚度高。
因此,为设计出大刚度的并联机器人,基于静刚度性能分析和设计的参数优化设计研究至关重要。
许多学者在此领域做了大量卓有成效的工作。
文中主要从有限元分析、静刚度解析模型、静刚度性能分析、静刚度设计4个方面对并联机器人机构静刚度研究现状进行了分析,并对其未来发展趋势进行了展望。
1国内外研究现状1.1有限元分析有限元分析是并联装备设计和静刚度性能预估的重要手段,主要是借助有限元分析软件如A NSYS等,对设计的虚拟并联装备样机进行受力分析,根据变形和应力分布情况,从而对样机的尺度参数和截面参数进行改进。
朱春霞等[1-3]利用ANSYS软件对3-TPT并联机床进行了静刚度有限元分析,得到机床在不同姿态下的静刚度和静力特性,并调查了平行四边形结构对机床性能的影响。
3-TPT并联机构静刚度特性分析与仿真

3-TPT并联机构静刚度特性分析与仿真朱春霞;刘威;赵志宇【摘要】以3-TPT并联机构为研究对象,从静力学分析入手,利用逆运动学雅可比矩阵获得机构的力雅可比矩阵,基于新刚度守恒矩阵,对机构的静刚度矩阵进行分析和求解分析机构的工作空间以避免无关数据对分析结果的影响,以静刚度性能商为评价指标,利用Matlab软件对该机构静刚度进行仿真.通过机构静刚度仿真结果,可以清楚地观察刚度的分布情况,并获得刚度薄弱区域与最大刚度区域的位置,进而分析机构静刚度的变化趋势.这一研究对并联机构的静刚度性能评价指标的建立具有重要意义,其结论也可以用于并联机构尺寸设计及其结构优化.【期刊名称】《机械设计与制造》【年(卷),期】2016(000)007【总页数】4页(P138-141)【关键词】静力学;雅可比矩阵;静刚度矩阵;静刚度性能商;工作空间;静刚度特性【作者】朱春霞;刘威;赵志宇【作者单位】沈阳建筑大学机械工程学院,辽宁沈阳110168;沈阳建筑大学机械工程学院,辽宁沈阳110168;沈阳建筑大学机械工程学院,辽宁沈阳110168【正文语种】中文【中图分类】TH16;TH122;TP242经过长期的研究,我们已经得知并联机构因其具备的各种优点,被逐步应用于工业、医疗等各个领域。
并联机构的刚度是评价并联机构性能的重要指标,是保证机构加载后定位精度的重要因素之一。
由于并联机构的刚度随位姿变化的性质,在机器人设计中若要获得期望刚度,必须了解机构位姿与刚度的关系[1]。
在早期,有学者提出一种建立并联机构刚度矩阵的方法[2],而后,以其研究为基础,又有学者提出了新的刚度守恒矩阵[3],添加了作为主动刚度,以考虑外力对于机构刚度的影响,该理论矩阵通过并联绳驱测试系统的实验得到验证[4]。
科研人员对并联机构刚度分析方法的探索从未停止,文献[5]对6-PSS并联机构的刚度特性进行了分析,并绘制了该机构的刚度映射曲线。
文献[6]通过使用螺旋理论的反螺旋解法,建立了EXECHON并联机构的静刚度模型。
3-SP S+SP并联机构的静刚度分析

3-SP S+SP并联机构的静刚度分析李晓丹;王晓磊;陈雪叶;王闯【期刊名称】《机床与液压》【年(卷),期】2016(044)015【摘要】The constraint reaction is existed in a patallel mechanism with fewer degrees of freedom ( DOF) , which leads to its de-formation.The whole Jacobian matrix containing drive and constraint was set up by 3-SPS+SP parallel mechanism .By considering the structure model of constraint reaction influence on the mechanism , the mapping relationship between input driving force and binding re-action and external load was derived .The whole of stiffness model was established , and the relationship between moving platform linear translation and angle rotation deformation with the external load was obtained .The stiffness evaluation indexes were defined .The chan-ging rule between main structural parameters and the global stiffness evaluation index are analyzed , which laid the groundwork for the structural parameters of mechanic optimization .%少自由度并联机构中存在约束反力,该力会使机构产生变形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Han X. College of Mechanical & Vehicle Engineering, Hunan University, Changsha 410082, China
e-mail:hanxu@
83mm
8mm
83mm
18mm
Abstract: In this paper, a neural network procedure is suggested to inversely determine the variable binder force in U-shaped forming from the deforming shape of the part.
Acknowledgements This work is supported by the national 973 program under the grant number 2004CB719402 and the program for New Century Excellent Talents in University, 2004 (NCET).
3.3.1 NN model
Mathematically, the NN model represents a non-linear
mapping between inputs X xi ,i 1, , Nand outputs
References 1. Cao J., Kinsey B., Solla S.A., Consistent and minimal
20mm
Proceedings of the 9th International Conference on Frontiers of Design and Manufacturing July 17~19, 2010, Changsha, China
18mm
An Inversion Procedure for Determination of Variable Binder Force in U-Shaped Forming
springback using a stepped binder force trajectory and neural network control. J. of Engineering Materials and Technology, 122, 113-118,2000 2. Schmocket D., Beth M., Springback reduction in draw bending process of sheet metals. Annals of CIRP, 42 (1):339-342,1993 3. Cho S., Cho Y., Yoon S., Reliable roll force prediction in cold mill using multiple neural networks. IEEE Trans. on Neural Networks, 8(4), 874-882,1997 4. Liu G.R., Han X., Computational inverse techniques in nondestructive evaluation, CRC Press, Florida,2003 5. Liu G.R., Han X., Xu Y.G., Lam K.Y., Material characterization of functionally graded material by means of elastic waves and a progressive-learning neural network, Composites Science and Technology, 61(10), 1401-1411, 2001
Y yi ,i 1, , Mvia the following equation:
Y g(W, X )
(1)
where W wikj ,i 1, , Ni , j 1, , N j , k 1, 2,3 is a
matrix of weights corresponding to the connections
Figure 1 The pattern of the stepped variable binder force
3 The Inverse Procedure 3.1 Teacher The FEM is employed as a teacher for the NN model. Two-dimensional degenerated shell element and elasto-plastic material model are used.
பைடு நூலகம்
between the layers, and Ni and N j are the numbers of
neurons for the ith and jth layers respectively [5].
4 Conclusions In this paper, an NN procedure is given to inversely determine the variable binder force based on the desired deformation shape in the U-shaped part forming. A method is suggested to obtain the desired deformation shape based on the CBF simulation for the designers short of the engineering experiences. The computation example indicates that the present procedure can seek the appropriate variable binder force curve according to the designer’s expectation.
2 Statement of the Problem As shown in Fig. 1, the stepped variable binder force curve is different from the constant binder force (CBF) as its binder force is not a constant in the forming process.
3.2 Progressive neural network (NN) An NN model is referred to as a type of computational model. It is made up of three parts: input layer, output layer and hidden layers.
Keywords: Springback, U-Shaped Part, Inverse Problem
1 Introduction The accuracy of the products has become the key issue of the manufacturing process. Springback is a very complex mechanical phenomenon that involves the material property and the processing parameters such as friction coefficient, thickness of the metal plate and temperature, etc. In recent years, many works have been reported for the investigation of the springback [1~4].
