浙教版数学九年级上册第4章 相似三角形达标测试卷(含答案)
【浙教版】九年级数学上册 第4章《相似三角形》过关自测卷(含答案)
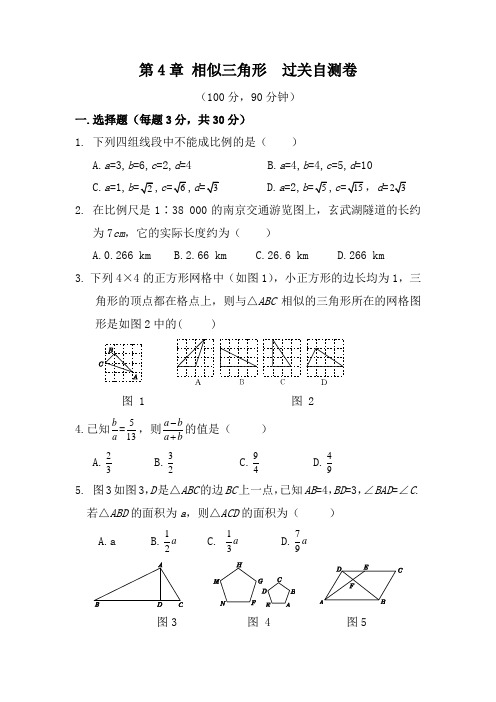
第4章相似三角形过关自测卷(100分,90分钟)一.选择题(每题3分,共30分)1. 下列四组线段中不能成比例的是()A.a=3,b=6,c=2,d=4B.a=4,b=4,c=5,d=10C.a=1,bc,d a=2,b c d=2. 在比例尺是1∶38 000的南京交通游览图上,玄武湖隧道的长约为7cm,它的实际长度约为()A.0.266 kmB.2.66 kmC.26.6 kmD.266 km3.下列4×4的正方形网格中(如图1),小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是如图2中的( )图 1 图 24.已知ba=513,则a ba b-+的值是()A.23B.32C.94D.495. 图3如图3,D是△ABC的边BC上一点,已知AB=4,BD=3,∠BAD=∠C. 若△ABD的面积为a,则△ACD的面积为()A.aB.12a C.13a D.79a图3 图 4 图56.如图4所示,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB∶FG=2∶3,则下列结论正确的是()A.2DE=3MNB.3DE=2MNC.3∠A=2∠FD.2∠A=3∠F7.如图5,在□ABCD中,E为CD上一点,连结AE.BD,且AE.BD交于点F,S△DEF∶S△ABF=4∶25,则DE∶EC=( )A. 2∶5B. 2∶3C. 3∶5D.3∶28.(2013,山东淄博)如图6,直角梯形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是( )A.2b=acB.2b=ceC.be=acD.bd=ae图6 图7 图89.如图7,等边三角形ABC的边长为3;P为BC上一点,且BP=1,D 为AC上一点,若∠APD=60°,则CD的长为( )A.32B.23C.12D.3410.图8是小明设计用平面镜来测量某古城墙高度的示意图,点P处放一水平的平面镜,小明站在点B处恰好能从镜子里看到古城墙CD的顶端C,已知小明的眼睛距离地面的高度AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是()A.6米B.8米C.18米D.24米二.填空题(每题3分,共18分)11.(2013,湖南长沙)如图9,在△ABC中,点D,点E分别是边AB,AC的中点,则△ADE与△ABC的周长之比等于___________.图9 图10 图11等于12. 如图10所示,△ABC的中线AD和BE相交于点G,则GDAG__________.13.如图11,P为平行四边形ABCD边AD上一点,E,F分别是PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,1S,2S,若S=2,则1S+2S=_________.14. 如图12,小明在A时测得某树的影长为2 m,在B时又测得该树的影长为8 m,若两次日照的光线互相垂直,则树的高度为m___________.图12 图13 图1415. 如图13,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,…,以此类推,第2 015个三角形的周长为__________. 16.如图14所示,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于点Q,CE时,EP+BP=___________.当CQ=13三.解答题(22~24题每题9分,其余每题5分,共52分)17.如图15所示,点D在△ABC的AB边上,AD=1,BD=2,AC求证:△ACD∽△ABC.图1518.(2013,湖南益阳)如图16,在△ABC中,AB=AC,BD=CD,CE⊥AB 于E,求证:△ABD∽△CBE.图1619.已知:△ABC三边的长分别是3,15,14,△A′B′C′的两边长分别为 1.5,7.5,如果△ABC∽△A′B′C′,求△A′B′C′的第三条边的长.20. 如图17所示,在平面直角坐标系中,四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1的位似图形.2图1721. 如图18,左.右并排的两棵大树的高分别是AB=8 m和CD=12 m,两树根部的距离BD=5 m,一个身高为1.6 m的人沿着正对这两棵树的一条水平直路l从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?图1822.如图19所示,已知AB为⊙O的直径,点E是OA上任意一点,过E作弦CD⊥AB,点F是BC上一点,连结AF交CE于点H,连结AC,CF,BD,OD.(1)求证:△ACH∽△AFC;(2)猜想:AH·AF与AE·AB的数量关系,并说明你的猜想;(3)当AE=AB时,S△AEC∶S△BOD=1∶4.(直接在空格处填上正确答案,不需要说明理由)图19 23. 如图20,点C为线段AB上任意一点(不与点A,B重合),分别以AC,BC为一腰在AB的同侧作等腰三角形ACD和等腰三角形BCE,使CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连结AE交CD于点M,连结BD交CE于点N,AE与BD交于点P,连结PC. (1)求证:△ACE≌△DCB;(2)请你判断△AMC与△DMP的形状有何关系并说明理由;(3)求证:∠APC =∠BPC.图2024.如图21,在Rt△ABC中,∠C=90°,AC=4 cm,BC=5 cm,点D在BC上,且CD=3 cm, 现有两个动点P,Q分别从点A和点B同时出发,其中点P以1 cm/s的速度沿AC向终点C运动;点Q以1. 25 cm/s的速度沿BC向终点C运动.过点P作PE∥BC交AD于点E,连结EQ.设动点运动的时间为t s(t>0).(1) 连结DP,经过1 s后,四边形EQDP能够成为平行四边形吗?请说明理由;(2) 连结PQ,在运动的过程中,不论t取何值时,总有线段PQ与线段AB平行,为什么?(3) 当t为何值时,△EDQ为直角三角形?图 21参考答案及点拨一.1.B 2.B3. B 点拨:方法一:由勾股定理得BC,AB=AC选项A 中三角形的三边长是2B 中三角形的三边长是2,4,C 中三角形的三边长是2,3项D4.其中对应边的比相等的只有2=4,∴与△ABC 相似的三角形是选项B 中的三角形.方法二:易知△ABC 是两直角边长之比为1∶2的直角三角形,从而可快速找出正确选项B .4. D 点拨:可利用特殊值法或比例的性质解题,也可用参数法解答,即先设出b =5k ,得出a =13k ,再把a ,b 的值代入即可求出答案.5.C 点拨:∵∠BAD =∠C ,∠ABD =∠CBA ,∴△BAD ∽△BCA ,∴BAD BCA S S =2BD AB ⎛⎫ ⎪⎝⎭=916,即BCA S =169BAD S ,∴BAD S =97ACD S ,∴ACD S =7a 9.本题考查的是相似三角形的判定与性质.根据两角对应相等判断两三角形相似,然后根据相似三角形面积的比等于相似比(即对应边的比)的平方列比例式,从而可知三角形的面积之间的关系.6.B 点拨:根据相似三角形对应边的比等于相似比可得答案.7.B 点拨:先根据平行四边形的性质及相似三角形的判定定理得出△DEF ∽△BAF ,再根据DEF S ∶ABF S =4∶25即可得出其相似比,由相似三角形的性质即可求出 DE ∶EC 的值.8.A 点拨:∵AB ∥CD ,∴∠CDB =∠DBA ,又∵∠C =∠BDA =90°,∴可判定△CDB ∽△DBA ,利用相似三角形的对应边成比例,即可判断各选项的正误.9.B 10.B二.11. 1∶2 点拨:∵点D ,点E 分别是边AB ,AC 的中点,∴DE 是△ABC 的中位线,∴DE ∥BC ,且DE ∶BC = 1∶2,故△ADE 和△ABC 的周长之比为1∶2. 12. 1213.8点拨:由平行四边形的性质及面积公式和三角形的面积公式可得:BPC S =12ABCD S 平行四边形,∴1S +2S =12ABCD S 平行四边形.由三角形的中位线定理及相似三角形的性质等可得BPC S =4S =8,∴1S +2S =8.14.4 点拨:本题考查相似三角形的判定和性质,易忽略隐含条件树和地面垂直,而判断不出三角形相似,从而无法求解. 15.201412 点拨:用从一般到特殊法解题,因为连结各边的中点所得到的三角形都与原三角形相似,所以周长比等于相似比.又因为第一个三角形的周长为1,所以第二个三角形的周长是12,第三个三角形的周长是212⎛⎫ ⎪⎝⎭,…,以此类推,第n 个三角形的周长是n 112-⎛⎫ ⎪⎝⎭,所以第2 015个三角形的周长为201412.答图1 16.12 点拨:如答图1所示,延长BQ 交射线EF 于M ,根据三角形的中位线平行于第三边可得EF ∥BC ,则△MEQ ∽△BCQ ,根据两直线平行,内错角相等可得∠M =∠CBM ,再根据角平分线的定义可得∠PBM =∠CBM ,从而得到∠M =∠PBM ,根据等角对等边可得BP =PM ,求出EP +BP =EM ,再根据CQ = 13CE 求出EQ =2CQ ,然后根据△MEQ 和△BCQ 相似,利用相似三角形的对应边成比例列式求解即可.三.17.证明:因为AD =1,BD =2,AC,所以AB =3.所以ADAC =3,AC AB AD AC =AC AB.又因为∠A =∠A ,所以△ACD ∽△ABC . 18.证明:在△ABC 中,AB =AC ,BD =CD ,∴AD ⊥BC .又∵CE ⊥AB ,∴∠ADB =∠CEB =90°,又∵∠B =∠B ,∴△ABD ∽△CBE .点拨:本题主要考查等腰三角形的性质及三角形相似的判定,要判定有一对角对应相等的两个三角形相似,只需再证得另一对角对应相等即可.19.解:由已知得31.5=157.5,即3与1.5,15与7.5对应成比例.由△ABC ∽△A ′B ′C ′,可得它们的相似比为 2.设△A ′B ′C ′的第三边的长为x ,由相似三角形的对应边成比例,得14∶x =3∶1.5,所以x =7,即△A ′B ′C ′的第三条边的长为7.20.解:如答图2所示,四边形A ′B ′C ′D ′即为所求.答图2 21.解:由题图,观察者从左向右走到点E 时,他的眼睛的位置点F 与两棵树的顶端点A .C 恰好在一条直线上.∵AB ⊥l ,CD ⊥l ,∴AB ∥CD ,∴△AFH ∽△CFK ,∴FH ∶FK =AH ∶CK ,即5FH FH +=8 1.612 1.6-+=6.410.4,解得FH =8(m ).∴当他与左边较低的树的距离小于8 m时,就不能看到右边较高的树的顶端点C.22.(1)证明:∵直径AB⊥CD,∴AD=AC,∴∠ACH=∠F.又∵∠HAC=∠CAF,∴△ACH∽△AFC.(2)解:AH·AF=AE·AB.连结FB.∵AB是⊙O的直径,CD⊥AB,∴∠AFB=∠AEH=90°.又∵∠EAH=∠FAB,∴△AEH∽△AFB,∴AEAF =AHAB,即AH·AF=AE·AB.(3)18点拨:本题利用了相似三角形的判定和性质,考查了同学们综合运用知识的能力.23.(1)证明:∵∠ACD =∠BCE,∴∠ACE =∠DCB.在△ACE和△DCB中,,,,AC DCACE DCBCE CB=⎧⎪∠=∠⎨⎪=⎩∴△ACE≌△DCB.(2)解:△AMC∽△DMP.理由如下:由(1)知△ACE≌△DCB,∴∠CAE =∠CDB.又∵∠AMC =∠DMP,∴△AMC∽△DMP.答图3(3)证明:在DB上截取DF=AP,连结CF,如答图3.由(1)知△ACE≌△DCB,∴∠CAE =∠CDB.又∵CA = CD,AP=DF,∴△ACP≌△DCF,∴∠APC=∠DFC,CP=CF,∴∠BPC =∠DFC,∴∠APC =∠BPC .24.解:(1)能.理由:当t =1时,AP =1 cm ,BQ =1.25 cm .∴QD =BD -BQ =2-1.25=0.75 cm .∵PE ∥BC ,∴△APE ∽△ACD ,∴PE CD =AP AC ,即3PE =14,∴PE =0.75 cm .∴PE =QD ,∴四边形EQDP 是平行四边形. (2)AP =t cm ,CP =(4-t ) cm ,BQ =1.25t cm ,CQ =(5-1.25t ) cm .∵CQ CB =5 1.25t 5-=4t 4-,CP AC =4t 4-,∴CQ CB =CP AC,∴PQ ∥AB .(3)当∠EQD =90°时,△EDQ ∽△ADC ,∴DQ DC =EQ AC ,∴1.25t 23-=4t 4-,解得t =2.5.当∠DEQ =90°时,△DEQ ∽△DCA ,∴DE DC =DQ DA .∵PE ∥BC ,∴△APE ∽△ACD ,∴AE AD =AP AC ,即5AE =t 4,∴AE =1.25t cm ,DE =AD -AE =(5-1.25t )cm ,∴5 1.25t 3-=1.25t 25-,解得t =3.1.∴当t 为2.5或3.1时,△EDQ 为直角三角形.。
浙教版九年级上册第4章《相似三角形》测试卷(含答案)

九年级上册第4章《相似三角形》测试卷满分100分,考试时间90分钟一、选择题(每小题3分,共30分)1.已知四条线段错误!未找到引用源。
是成比例线段,即dcb a =,下列说法错误的是( ) A .错误!未找到引用源。
B .b a d bc a =++ C .dbc bd a -=-D .2222dc b a =2.若875cb a ==,且3a -2b +c =3,则2a +4b -3c 的值是( ) A .14B .42C .7D .314 3.若如图所示的两个四边形相似,则∠α的度数是( ) A .75° B .60° C .87°D .120°第3题图4.已知两个相似多边形的面积比是9︰16,其中较小多边形的周长为36 cm ,则较大多边形的周长为( ) A .48 cm B .54 cm C .56 cm D .64 cm 5.如图,在△ABC 中,∠BAC =90°,D 是BC 中点,AE ⊥AD 交CB 延长线于点E ,则结论正确的是( ) A .△AED ∽△ACB B .△AEB ∽△ACD C .△BAE ∽△ACE D .△AEC ∽△DAC第5题图6.如图,若∠1=∠2=∠3,则图中相似三角形有( ) A .2 对 B .3 对 C .4 对D .5 对第6题图7.如图,在平行四边形ABCD 中,EF //AB ,DE : EA =2 : 3,EF =4,则CD 的长为( ) A .163B .8C .10D .16第7题图8.“标准对数视力表”对我们来说并不陌生,如图是视力表的一部分,其中最上面较大的“E”与下面四个较小“E”中的哪一个是位似图形()A.左上B.左下C.右上D.右下第8题图9.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,则△BCD与△ABC的周长之比为()A.1︰2 B.1︰3 C.1︰4 D.1︰5第9题图10.已知:如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP·AB;④AB·CP=AP·CB.能满足△APC和△ACB相似的条件是()A.①②④B.①③④C.②③④D.①②③二、填空题(每小题3分,共30分)11.在比例尺为1:2000的地图上测得A、B两地间的图上距离为5cm,则A、B两地间的实际距离为m.12.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边为39,那么较大的三角形的周长为.13.若582=+bba,则baba-+= .14.己知:线段MN的长为20cm,点P是线段MN的黄金分割点,则较长线段MP的长是cm.15.已知两个正五边形的边长之比为1:2,如果较小的正五边形的面积是4cm2,那么较大的正五边形的面积是cm2.16.如图,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长为.第10题图第16题图17.如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度h 为 .第17题图18.如图,已知AD ∥BE ∥CF ,它们依次交直线l 1、l 2于点A 、B 、C 和点D 、E 、F ,如果DE :EF =3:5,AC =24,则BC = .第18题图19.在△ABC 和△A ′B ′C ′中,有下列条件:①;AB BC A B B C =''''②BC ACB C A C ='''';③∠A =∠A ′;④∠B =∠B ′;如果从中任取两个条件组成一组,那么能判断△ABC 的△A 'B 'C '的共有 组.20.如图,正方形ABCD 和正方形OEFG 中,点A 和点F 的坐标分别为(3,2),(-1,-1),则两个正方形的位似中心的坐标是 .第20题图三、解答题(共40分) 21.(6分)如图,在6×8网格图中,每个小正方形边长均为1,点O 和△ABC 的顶点均在小正方形的顶点.(1)以O 为位似中心,在网格图中作△A′B′C′和△ABC 位似,且位似比为12; (2)连接(1)中的AA′,求四边形AA′C′C 的周长(结果保留根号).22.(6分)网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.23.(6分)阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.24.(6分)如图,等腰三角形ABC中,若∠A=∠B=∠DPE.(1)求证:△APD∽△BEP;(2)若31,2,2AP PB BE===,试求出AD的长.25.(8分)如图,在正△ABC 中,点D 是AC 的中点,点E 在BC 上,且CE BC =13. (1)求证:△ABE ∽△DCE ; (2)263DCE S cm ∆=,求ABC S ∆.26.(8分)如图,已知一次函数22y x =+的图象与y 轴交于点B ,与反比例函数1k y x=的图象的一个交点为A (1,m ),过点B 作AB 的垂线BD ,与y 轴交于点B ,与反比例函数2k y x=的图象交于点D (n ,-2). (1)求k 1,k 2的值;(2)若直线AB ,BD 分别交x 轴于点C ,E ,试问在y 轴上是否存在一点F ,使得ΔBDF ∽ΔACE .若存在,求出点F 的坐标;若不存在,请说明理由.九年级上册第4章《相似三角形》答案解析1.C 2.D 3.C 4.D 5.C 6.C 7.C 8.C 9.A 10.D 11.100 12.90 13.37-14.-1015.16 16.7 17.1.5米 18.15 19.3 20.(1,0),(-5,-2) 21.(1)图略;(2)四边形错误!未找到引用源。
浙教版九年级上册数学第4章 相似三角形含答案(配有卷)

浙教版九年级上册数学第4章相似三角形含答案一、单选题(共15题,共计45分)1、如图,在矩形ABCD中,,,将其折叠使AB落在对角线AC 上,得到折痕AE,那么BE的长度为()A. B. C. D.2、如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连结BD交 CE于点G,连结BE. 下列结论中:① CE=BD;② △ADC是等腰直角三角形;③ ∠ADB=∠AEB;④ CD·AE=EF·CG;一定正确的结论有( )A.1个B.2个C.3个D.4个3、如图,在正方形中,的顶点,分别在,边上,高与正方形的边长相等,连接分别交,于点,,下列说法:① ;②连接,,则为直角三角形;③ ;④若,,则的长为,其中正确结论的个数是()A.4B.3C.2D.14、如图,在中,,则DF的长为()A.4B.C.D.35、如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG 分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?()A. B. C. D.6、如图,l1∥l2∥l3,直线a,b与l1, l2, l3分别相交于点A、B、C和点D、E、F,若,DE=4,则DF的长是()A. B. C.10 D.67、如图,已知l1∥l2∥l3,直线AC分别交l1、l2、l3于点A,B,C,直线DF分别交l1、l2、l3于D,E,F,DE=4,EF=6,AB=5,则BC的长为()A. B. C. D.8、如图,直线l1∥l2∥l3 ,直线AC分别交l1 , l2 , l3于点A,B,C;直线DF分别交l1 , l2 , l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则的值为()A. B.2 C. D.9、如图,在菱形ABCD中,AC=8,BD=6,DE⊥AB,垂足为E,DE与AC交于点F,则sin∠DFC的值为()A. B. C. D.10、两相似三角形的周长之比为1:4,那么他们的对应边上的高的比为()A.1∶4B.1∶2C.2∶1D. ∶211、如图,在△ABC中,∠C=90°,过重心G作AC、BC的垂线,垂足分别为D、E,则四边形GDCE的面积与△ABC的面积之比为( )A. B. C. D.12、如图,在正方形ABCD的外侧,作等边△ADE,BE、CE分别交AD于G、H,设△CDH、△GHE的面积分别为S1、S2,则()A.3S1=2S2B.2S1=3S2C.2S1= S2D. S1=2S213、如图,一组互相平行的直线a,b,c分别与直线l1, 12交于点A,B,C,D,E,F,直线11, l2交于点O,则下列各式不正确的是()A. B. C. D.14、如图,在平面直角坐标系中,矩形OABC的顶点A,B在反比例函数的图像上,纵坐标分别为1和3,则k的值为()A. B. C.2 D.315、如图,⊙O的直径为6,在⊙O上位于直径AB的异侧有定点C和动点P.已知BC:CA=4:3,P在半圆上运动,CP⊥CD交PB的延长线于D点.当点P运动到什么位置时,△PCD的面积最大为()A.36B.24C.18D.12二、填空题(共10题,共计30分)16、如图,在正方形ABCD中,E是边BC的中点,连接AE,作EF⊥AE交正方形的外角平分线于点F,连接AF,交CD于点H,连接EH.若AB=4,则EH的长为________.17、如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为2,则平行四边形ABCD的面积是________.18、如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF=________.19、如图所示,已知点E,F分别是△ABC的边AC,AB的中点,BE,CF相交于点G,FG=1,则CF的长为________.20、若a:b:c=3:2:5,则=________.21、如图,在平面直角坐标系中,△OAB与△OCD是以原点O为位似中心的位似图形,且位似比为1:3,已知点A的坐标为(1,2),则点C的坐标是________.22、如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O 为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C 的坐标为________ .23、我国古代数学著作《九章算术》中记载:“今有方不知大小,各开中门,出北门四十步有木,出西门八百一十步见木,问:邑方几何?”译文:如图,一座正方形城池北、西边正中A、C处各开一道门,从点A往正北方向走40步刚好有一棵树位于点B处,若从点C往正西方向走810步到达点D处时正好看到此树,则正方形城池的边长为________步。
浙教版数学九年级上册 第四章 相似三角形 单元练习(含答案)

浙教版数学九年级上册第四章相似三角形一、选择题1.如果2a =5b ,那么下列比例式中正确的是( )A .a b =25B .a 5=2b C .a 2=b 5D .a 5=b 22.如图,直线l 1∥l 2∥l 3,AC =6,DE =3,EF =2,则AB 的长为( )A .3B .125C .165D .1853.如图,点P 是线段AB 的黄金分割点,且PA >PB ,若AB =2,则PA 的长度是( )A .5−1B .3−5C .25−4D .14.如图, 在▱ABCD 中, E 是边AB 上一点, 连结AC ,DE 相交于点F . 若AE EB =23,则 AF CF 等于( )A .13B .23C .25D .355.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC 相似的是( )A .B .C.D.6.△ABC和△DEF是两个等边三角形,AB=2,DE=4,则△ABC与△DEF的面积比是( ) A.1:2B.1:4C.1:8D.1:27.如图,在△ABC中,BC=6,AC=8,∠C=90°,以B为圆心,BC长为半径画弧,与AB交于点D,再分别以点A,D为圆心,大于12AD的长为半径画弧,两弧交于点M,N,作直线MN,分别交AC,AB于点E,F,则AE的长度为( )A.52B.103C.3D.228.如图,△ABC和△A1B1C1是以点O为位似中心的位似图形,点A在线段O A1上,若OA:A A1=1:2,则△ABC和△A1B1C1的周长之比为( )A.1:2B.2:1C.1:3D.3:19.如图,在△ABC中,D为线段AC上一点,点E在AC的延长线上,过点D作DF∥AB交BC于点F,连结BE,EF,若A C2+D E2=A E2,则△BEF与△DCF的面积比为( )A.1:2B.1:3C.2:3D.2:510.如图,矩形ABCD中,AB=4,AD=2,E为边AD上一个动点,连接BE,取BE的中点G,点G绕点E逆时针旋转90°得到点F,连接CF,则△CEF面积的最小值是( )A .4B .154C .3D .114二、填空题11.如图,AC 、BD 交于点O ,连接AB 、CD ,若要使△AOB ∽△COD ,可以添加条件 .(只需写出一个条件即可)12.已知△ABC ∽△DEF ,且AB:DE =1:3,△ABC 与△DEF 的周长比是 .13.如图,在这架小提琴中,点C 是线段AB 的黄金分割点(BC >AC ).若AB =60cm ,则BC = cm .14.如图,在Rt △ABC 中,∠ABC =90°,AB =4,AC =5,AE 平分∠BAC ,点D 是AC 的中点,AE 与BD交于点O ,则的值AOOE .15.如图,矩形ABCD 中,AB =3 6 ,BC =12,E 为AD 中点,F 为AB 上一点,将△AEF 沿EF 折叠后,点A 恰好落到CF 上的点G 处,则折痕EF 的长是 .16.如图,正方形ABCD 中,BF =FG =CG ,BE =2AE ,CE 交DF 、DG 于M 、N 两点,有下列结论:①DF ⊥EC ;②S △MFC =59S 四边形MFBE ;③DM :MF =2:1;④MN NC =913.其中,正确的有 .三、解答题17.(1)已知线段a =2,b =6,求线段a ,b 的比例中项线段c 的长.(2)已知x :y =3:2,求2x−yx的值.18.如图,已知D 、E 分别是△ABC 的边AB 、AC 上的点,DE ∥BC ,AD BD =32,求DE BC 的值.19.如图,AD 、BC 相交于点P ,连接AC 、BD ,且∠1=∠2,AC =6,CP =4,DP =2,求BD 的长.20. 如图,在平行四边形ABCD 中,E 为DC 边上一点,∠EAB =∠EBC .(1)求证:△ABE∽△BEC ;(2)若AB=4,DE=3,求BE的长.21.如图,在四边形ABCD中,OA=OC,OB=OD,AB=BC,AC=12,BD=16.(1)求证:四边形ABCD时菱形;(2)延长BC至点M,连接OM交CD于点N,若∠M=12∠BAC,求MNOM.22.如图,AB∥CD,且AB=2CD,E是AB的中点,F是边BC上的动点(F不与B,C重合),EF与BD相交于点M.(1)求证:△FDM∽△FBM;(2)若F是BC的中点,BD=18,求BM的长;(3)若AD=BC,BD平分∠ABC,点P是线段BD上的动点,是否存在点P使DP⋅BP=BF⋅CD,若存在,求出∠CPF的度数;若不存在,请说明理由.23.如图,在平面直角坐标系中,已知抛物线y=12x2+bx+c与x轴交于A、B两点,与y轴交于C点,且OB=OC=4.(1)求抛物线的解析式;(2)在抛物线上是否存在点M,使∠ABC=∠BCM,如果存在,求M点的坐标,如果不存在,说明理由;(3)若D是抛物线第二象限上一动点,过点D作DF⊥x轴于点F,过点A、B、D的圆与DF交于E点,求△ABE的面积.答案解析部分1.【答案】D2.【答案】D3.【答案】A4.【答案】C5.【答案】B6.【答案】B7.【答案】A8.【答案】C9.【答案】A10.【答案】B11.【答案】∠A=∠C(答案不唯一)12.【答案】1:313.【答案】(305−30)14.【答案】9415.【答案】21516.【答案】①④17.【答案】(1)解:∵线段a=2,b=6,线段c是线段a、b的比例中项,∴c2=ab=12,∴c=23(负值舍去);(2)解:∵x:y=3:2,∴可设x=3k,y=2k(k≠0),∴2x−yx=6k−2k3k=43.18.【答案】3519.【答案】BD=320.【答案】(1)证明:∵平行四边形ABCD,∴AB//CD,∴∠EBA=∠BEC,又∵∠EAB=∠EBC,∴△ABE∽△BEC.(2)解:∵四边形ABCD 平行四边形,∴AB =DC =4,∵DE =3,∴CE =1,∵△ABE∽△BEC ,∴AB EB =EBEC,∴AB ⋅CE =B E 2=4×1=4,∴BE =2.21.【答案】(1)证明:∵ 在四边形ABCD 中,OA=OC ,OB=OD∴ 四边形ABCD 是平行四边形 ∵ AB=BC∴ 平行四边形ABCD 是菱形。
【九年级】九年级上册第4章相似三角形单元试题(浙教版带答案)

【九年级】九年级上册第4章相似三角形单元试题(浙教版带答案)m第4章相似三角形检测(本试卷满分120分,时间:120分钟)一、(每题3分,共30分)1.已知四条线段是成比例线段,即,下列说法错误的是()答。
b.Cd.2.如果和的值为()a.14b.42c.7d.3.在以下四组数字中,不相似的是()4.已知两个相似多边形的面积比是9?16,其中较小多边形的周长为36cm,则较大多边形的周长为()a、 48cmb。
54cmc。
56cmd。
64厘米5.如图,在△中,点分别是的中点,则下列结论:①;②△∽△;③. 正确的是()a.3个b.2个c.1个d.0个6.如图所示,如果//和//已知且分别在点处相交,则图中有类似的三角形()a.4对b.5对c.6对d.7对7.如图所示,在△ 垂直平分线穿过的延长线∠ 在点上,那么的长度是()a.b.c.d.8.如果△ 如图所示,以下四个三角形中△ 是()9.(2021四川中考)如图,在rt△abc中,∠acb=90°,∠a=30°,cd⊥ab于点d.则△bcd与△abc的周长之比为()a、 1号?2b。
1.三c.1?4d.1?510.在手工课上,萧红用一些花布的边角料来切割和装裱手工画。
以下四种图案是她切割的中空等边三角形、等边三角形、方形和矩形蕾丝。
每个图案花边的宽度相同,因此每个图案中由花边内外边缘包围的几何图形不同二、题(每小题3分,共24分)11.如果三角形的三条边的长度分别为5、12和13,而类似三角形的最长边为39,则较大三角形的周长为____,面积为____12.已知,且,则_______.13.折叠三角纸(△ ABC)以图中所示的方式,使点B落在边AC上,边AC记录为点B',折痕为EF。
已知ab=AC=3,BC=4。
如果以点B',F和C为顶点的三角形与△ ABC,BF的长度是14.若,则.15.图为小明用手电筒测量古城墙高度的设计示意图。
浙教版数学九年级上册第四章相似三角形 单元测试(含答案)

浙教版数学九年级上册第四章相似三角形一、选择题1.已知c 是a 和b 的比例中项,a =2,b =18,则c =( )A .±6B .6C .4D .±32.如图,DE ∥BC ,在下列比例式中,不能成立的是()A .AD DB =AEECB .DE BC =AEEC C .AB AD =AC AED .DB EC =ABAC3.如果两个相似三角形的周长之比为5:7,那么这两个三角形的面积之比为( )A .5:7B .7:5C .25:49D .49:254.如图,已知AB ∥CD ∥EF ,AE =9,AC =6,BD =4,则BF 的长是( )A .5B .6C .7D .85.小明在测量楼高时,先测出楼房落在地面上的影长BA 为15米(如图),然后在A 处树立一根高2米的标杆,测得标杆的影长AC 为3米,则楼高为( )A .10米B .12米C .15米D .22.5米6.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC 相似的是( )A .B .C.D.7.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( ).A.1:2B.1:3C.1:4D.1:58.如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为5,则下列结论中正确的是( )A.m=5B.m=45C.m=35D.m=109.如图,已知AB=AC,∠B<30°,BC上一点D满足∠BAD=120°,BDCD =73,则ADAC的值为( )A.12B.33C.13D.3210.如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O,点P是BD上的一个动点,过点P作EF∥AC,分别交正方形的两条边于点E,F,连接OE,OF,设BP=x,△OEF的面积为y,则能大致反映y与x之间的函数关系的图像为( )A .B .C .D .二、填空题11.如图,线段AC 、BD 交于点O ,请你添加一个条件: ,使△AOB ∽△COD .12.如图,点G 为△ABC 的重心,GE ∥AC ,若DE =2,则DC = .13.在某市建设规划图上,城区南北长为120cm ,该市城区南北实际长为36km ,则该规划图的比例尺是 .14.如图,在Rt △ABC 中,∠ABC =90°,AB =4,AC =5,AE 平分∠BAC ,点D 是AC 的中点,AE 与BD交于点O ,则的值AOOE .15.如图, EB 为驾驶员的盲区,驾驶员的眼睛点 P 处与地面 BE 的距离为1.6米,车头 FACD 近似看成一个矩形,且满足 3FD =2FA ,若盲区 EB 的长度是6米,则车宽 FA 的长度为 米.16.如图,在△ABC中,点D是AC边上一点,将△ABD沿BD翻折得到△EBD,BE与AC交于点F,设AF=x,EF=y.(1)当BE⊥AC,x=9,y=3时,AD的长是 ;(2)当BD=BF,2x=7y时,△DEF与△ABD的面积之比是 .三、解答题17.如图,已知D、E分别是△ABC的边AB、AC上的点,DE∥BC,ADBD =32,求DEBC的值.18.如图,在△ABC中,D为BC上一点,∠BAD=∠C.(1)求证:△ABD∽△CBA;(2)若AB=6,BD=3,求CD的长.19.在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部的(全身)的高度比,可以增加视觉美感,按比例,如果雕像的高为2m,那么它的下部设计为多高?(结果保留小数点后两位)参考数据:2=1.414,3=1.732,5=2.23620.如图,在矩形ABCD中,AB=6,BC=4,E是边BC上的一点(不与B、C重合),DF⊥AE,垂足为F.(1)求证:△ABE∽△DFA;S△ABE,求BE的长.(2)若S△DFA=1321.如图,在△ABC中,AD是BC上的高,且BC=3,AD=2,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB、AC上.(1)设EF=x(0<x<2),矩形EFGH的周长为y,求y关于x的函数解析式;(2)当EFGH为正方形时,求正方形EFGH的面积.22.如图,矩形ABCD中,点M在对角线BD上,过点A、B、M的圆与BC交于点E.(1)若AM=4,EB=EM=3,求BM.(2)若AB=6,BC=8,①求AM:ME.②若BM=7,求BE.23.如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O.点P从点A出发,沿AD方向匀速运动速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长交BC于点E,过点Q作QF//AC,交BD于点F,设运动时间为t(s)(0<t<6),解答下列问题:(1)当t为何值时,△AOP是等腰三角形;(2)设五边形OECQF的面积为S(c m2),试确定S与t的函数关系式;(3)在运动过程中,当S五边形OECQF:S△ACD=9:16时.直接写出t的值.答案解析部分1.【答案】A2.【答案】B3.【答案】C4.【答案】B5.【答案】A6.【答案】A7.【答案】C8.【答案】B9.【答案】A10.【答案】C11.【答案】AB∥CD(答案不唯一)12.【答案】6.13.【答案】1:3000014.【答案】9415.【答案】12716.【答案】5;1417.【答案】3518.【答案】(1)证明:∵∠BAD=∠C,∠B=∠B,∴△ABD∽△CBA(2)解:设DC=x,∵△ABD∽△CBA,∴ABBD=BCAB,∴63=2+x6,解得,x=9;即CD=719.【答案】1.24米.20.【答案】(1)证明:∵四边形ABCD是矩形,AB=6,BC=4,∴∠B=90°,AD∥BC,AD=BC=4,∴∠AEB=∠DAF,∵DF⊥AE,∴∠DFA=90°,∴∠B=∠DFA,∴△ABE∽△DFA;(2)解:∵△ABE∽△DFA,S△DFA=13S△ABE,∴(AEAD )2=S△ABES△DFA=3,∴AEAD=3或AEAD=−3(负数不符合题意,舍去),∴AE=3AD=43,∴BE=AE2−AB2=(43)2−62=12=23,∴BE的长为23.21.【答案】(1)解:设AD,EH交于点M,∵矩形EFGH,∴EH∥BC,AM⊥EH,∴△ABC∼△AEH,∴EHBC=AMAD∵EF=DM=x,AD=2∴AM=2−x∴EH3=2−x2∴EH=32(2−x)∴y=2(EH+EF)=2(3−32x+x)=−x+6(0<x<2)∴y关于x的函数解析式为∴y=−x+6(0<x<2)(2)解:当EFGH为正方形时,∴EF=EH,由(1)得:EF =x ,EH =32(2−x),∵EF =EH ,∴x =3(2−x)2,∴x =65,即EF =65.正方形EFGH 的面积=65×65=3625.22.【答案】(1)245(2)①43,②17423.【答案】(1)解:在矩形ABCD 中,AB =6cm ,BC =8cm ,∴AC =10,①当AP =PO =t ,如图1,过P 作PM ⊥AO 于点M ,∴AM =12AO =52,∵∠PMA =∠ADC =90°,∠PAM =∠CAD ,∴△APM∽△ACD ,∴AP AC =AM AD,∴AP =t =258,②当AP =AO =t =5,∴当t 为258或5时,△AOP 是等腰三角形;(2)解:如图2,过点O 作OH ⊥BC 交BC 于点H ,则OH =12CD =12AB =3cm ,由矩形的性质可知∠PDO =∠EBO ,DO =BO ,又得∠DOP =∠BOE ,∴△DOP≌BOE(ASA),∴BE =PD =8−t ,则S △BOE =12BE ⋅OH =12×3(8−t)=12−32t.∵FQ//AC ,∴△DFQ∽△DOC ,相似比为DQ DC =t6,∴S △DFQ S △DOC =t 236,∵S △DOC =14S 矩形ABCD =14×6×8=12c m 2,∴S △DFQ =12×t 236=t 23,∴S 五边形OECQF =S △DBC −S △BOE −S △DFQ =12×6×8−(12−32t)−t 23=−13t 2+32t +12;∴S 与t 的函数关系式为S =−13t 2+32t +12;(3)t =3或32。
2020年浙教版初三数学上册第4章 相似三角形测试题(含答案)

第4章 相似三角形测试卷一、选择题(每题3分,共30分) 1.若m +n n =52,则m n等于( )A .52B .23C .25D .322.若两个相似多边形的面积之比为1:4,则它们的周长之比为( )A .1:4B .1:2C .2:1D .4:13.如图,l 1∥l 2∥l 3,直线a ,b 与l 1,l 2,l 3分别相交于点A ,B ,C 和点D ,E ,F .若AB =3,DE =2,BC =6,则EF =( ) A .2 B .3 C .4 D .54.已知△ABC ∽△A ′B ′C ′,AB =8,A ′B ′=6,则BCB ′C ′=( )A .2B .43C .3D .1695.如图,以点O 为位似中心,把△ABC 放大为原图形的2倍得到△A ′B ′C ′,以下说法中错误的是( )A .△ABC ∽△A ′B ′C ′ B .点C 、点O 、点C ′在同一直线上 C .AO :AA ′=1:2D .AB ∥A ′B ′6.如图,为估算某河的宽度(河两岸平行),在河对岸选定一个目标点A ,在近岸取点B ,C ,D ,使得AB ⊥BC ,CD ⊥BC ,点E 在BC 上,并且点A ,E ,D 在同一条直线上,若测得BE =20 m ,CE =10 m ,CD =20 m ,则河的宽度AB 等于( ) A .60 m B .40 m C .30 m D .20 m7.如图,小正方形的边长均为1,则下列选项中的三角形与△ABC 相似的是( )8.如图,在矩形ABCD 中,AB =2,BC =3,点E 是AD 的中点,CF ⊥BE 于点F ,则CF等于( ) A .2 B .2.4 C .2.5 D .2.259.如图,在△ABC 中,AB =AC =18,BC =12,正方形DEFG 的顶点E ,F 在△ABC 内,顶点D ,G 分别在AB ,AC 上,AD =AG ,DG =6,则点F 到BC 的距离为( ) A .1 B .2 C .122-6 D .62-610.如图,在钝角三角形ABC 中,分别以AB 和AC 为斜边向△ABC 的外侧作等腰直角三角形ABE 和等腰直角三角形ACF ,EM 平分 ∠AEB 交AB 于点M ,取BC 的中点D ,AC 的中点N ,连结DN ,DE ,DF .下列结论:①EM =DN ;②S △CND =13S四边形ABDN;③DE =DF ;④DE ⊥DF .其中正确结论的个数为( ) A .1 B .2 C .3 D .4 二、填空题(每题3分,共24分) 11.已知b a =713,则aa +b=________.12.如图,在△ABC 中,若DE ∥BC ,AD =2,BD =4,DE =1.5,则BC 的长为__________.13.如图,已知点C 是线段AB 的黄金分割点,且BC >AC .若S 1表示以BC 为边的正方形的面积,S 2表示长为AD (AD =AB )、宽为AC 的矩形的面积,则S 1与S 2的大小关系为________.14.如图,在平面直角坐标系中,有点A (6,3),B (6,0),以原点O 为位似中心,位似比为13,在第一象限内把线段AB 缩小后得到CD ,则点C 的坐标为________.15.如图,在△ABC中,∠BAC=90°,∠B=45°,在△ACD中,∠ACD=90°,∠D=30°,则BEEC的值是________.16.如图,身高为1.7 m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD 的高度,CD在水中的倒影为C′D,A,E,C′在一条直线上.已知河BD的宽度为12 m,BE=3 m,则树CD的高度为________.17.如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,则BM的长为________.18.如图,正三角形ABC的边长为2,以BC边上的高AB1为边作正三角形AB1C1,△ABC 与△AB1C1公共部分的面积记为S1,再以正三角形AB1C1边B1C1上的高AB2为边作正三角形AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2……以此类推,则S n=____________.(用含n的式子表示)三、解答题(19,21题每题8分,24题14分,其余每题12分,共66分)19.如图,四边形ABCD∽四边形EFGH,试求出x及α的大小.20.如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(-2,4),B(-2,1),C(-5,2).(1)请画出△ABC关于x轴对称的△A1B1C1;(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;(3)求△A1B1C1与△A2B2C2的面积比.(不写解答过程,直接写出结果)21.如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.(1)求证:△ADE≌△CFE;(2)若GB=2,BC=4,BD=1,求AB的长.22.如图,一条河的两岸BC与DE互相平行,两岸各有一排景观灯(图中黑点代表景观灯),每排相邻两个景观灯的间隔都是10 m,在与河岸DE的距离为16 m的A处(AD⊥DE)看对岸BC,看到对岸BC上的两个景观灯的灯杆恰好被河岸DE上两个景观灯的灯杆遮住.河岸DE上的这两个景观灯之间有1个景观灯,河岸BC上被遮住的两个景观灯之间有4个景观灯,求这条河的宽度.23.如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以每秒2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.请解答下列问题:(1)当t为何值时,△CEF是等腰直角三角形?(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?24.如图,E,F分别是正方形ABCD的边DC,CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连结DF.(1)求证:△ADE≌△DCF.(2)若E是CD的中点,求证:Q为CF的中点.(3)连结AQ,设S△CEQ=S1,S△AED=S2,S△EAQ=S3,在(2)的条件下,判断S1+S2=S3是否成立?并说明理由.答案一、1.D 2.B 3.C 4.B 5.C 6.B 点拨:∵AB ⊥BC ,CD ⊥BC , ∴∠ABC =∠DCE =90°. 又∵∠AEB =∠DEC , ∴△ABE ∽△DCE . ∴AB DC =BE CE ,即AB 20=2010.∴AB =40 m. 7.A 8.B9.D 点拨:如图,过点A 作AM ⊥BC 于点M ,交DG 于点N ,延长GF 交BC 于点H .∵AB =AC ,AD =AG , ∴AD ∶AB =AG ∶AC .又∵∠BAC =∠DAG ,∴△ADG ∽△ABC . ∴∠ADG =∠B .∴DG ∥BC . ∴AN ⊥DG .∵四边形DEFG 是正方形, ∴FG ⊥DG .∴FH ⊥BC . ∵AB =AC =18,BC =12, ∴BM =12BC =6.∴AM =AB 2-BM 2=12 2. ∵AN AM =DG BC ,即AN 122=612, ∴AN =6 2.∴MN =AM -AN =6 2. 易得四边形GHMN 为矩形, ∴GH =MN =6 2.∴FH =GH -GF =6 2-6.故选D .10.D 点拨:∵△ABE 是等腰直角三角形,EM 平分∠AEB ,∴EM 是AB 边上的中线.∴EM =12AB .∵点D ,点N 分别是BC ,AC 的中点,∴DN 是△ABC 的中位线.∴DN =12AB ,DN ∥AB .∴EM =DN .①正确.∵DN ∥AB ,∴△CDN ∽△CBA . ∴S △CND S △CAB =⎝⎛⎭⎫DN AB 2=14. ∴S △CND =13S 四边形ABDN .②正确.如图,连结DM ,FN ,则DM 是△ABC 的中位线,∴DM =12AC ,DM ∥AC .∴四边形AMDN 是平行四边形. ∴∠AMD =∠AND .易知∠ANF =90°,∠AME =90°, ∴∠EMD =∠DNF . ∵FN 是AC 边上的中线, ∴FN =12AC .∴DM =FN .又∵EM =DN , ∴△DEM ≌△FDN .∴DE =DF ,∠FDN =∠DEM .③正确. ∵∠MDN +∠AMD =180°,∴∠EDF =∠MDN -(∠EDM +∠FDN )=180°-∠AMD -(∠EDM +∠DEM )=180°-(∠AMD +∠EDM +∠DEM )=180°-(180°-∠AME )=180°-(180°-90°)=90°. ∴DE ⊥DF .④正确.故选D . 二、11.1320 点拨:∵b a =713,∴设a =13x ,b =7x , 则a a +b =13x 13x +7x =1320. 12.4.5 13.S 1=S 2 14.(2,1) 15.3316.5.1 m 17.163或318.32×⎝⎛⎭⎫34n点拨:在正三角形ABC 中,AB 1⊥BC ,∴BB 1=12BC =1.在Rt △ABB 1中,AB 1=AB 2-BB 21=22-12=3, 根据题意可得△AB 2B 1∽△AB 1B , 记△AB 1B 的面积为S , ∴S 1S =⎝⎛⎭⎫322. ∴S 1=34S .同理可得S 2=34S 1,S 3=34S 2,S 4=34S 3,….又∵S =12×1×3=32,∴S 1=34S =32×34,S 2=34S 1=32×⎝⎛⎭⎫342,S 3=34S 2=32×⎝⎛⎭⎫343,S 4=34S 3=32×⎝⎛⎭⎫344,…,S n =32×⎝⎛⎭⎫34n. 三、19.解:因为四边形ABCD ∽四边形EFGH ,所以∠H =∠D =95°,则α=360°-95°-118°-67°=80°.再由x ∶7=12∶6,解得x =14. 20.解:(1)如图,△A 1B 1C 1即为所求.(2)如图,△A 2B 2C 2即为所求. (3)S △A 1B 1C 1∶S △A 2B 2C 2=1∶4.21.(1)证明:∵AB ∥FC ,∴∠A =∠ECF .又∵∠AED =∠CEF ,且DE =FE , ∴△ADE ≌△CFE .(2)解:方法一:∵AB ∥FC , ∴△GBD ∽△GCF .∴GB GC =BDCF .∴22+4=1CF.∴CF =3. 由(1)得△ADE ≌△CFE , ∴AD =CF =3,∴AB =AD +BD =3+1=4.方法二:如图,取BC 的中点H ,连结EH .∵△ADE ≌△CFE ,∴AE =CE .∴EH 是△ABC 的中位线. ∴EH ∥AB ,且EH =12AB .∴△GBD ∽△GHE . ∴DB EH =GB GH .∴1EH =22+2. ∴EH =2.∴AB =2EH =4.22.解:由题意可得DE ∥BC ,所以△ADE ∽△ABC .所以AD AB =DE BC ,即AD AD +DB =DE BC.因为AD =16 m ,BC =50 m ,DE =20 m , 所以1616+DB =2050.所以DB =24 m.所以这条河的宽度为24 m.23.解:(1)由题意可知BE =2t ,CF =4t ,CE =12-2t .因为△CEF 是等腰直角三角形,∠ECF 是直角,所以CE =CF . 所以12-2t =4t ,解得t =2.所以当t =2时,△CEF 是等腰直角三角形. (2)根据题意,可分为两种情况: ①若△EFC ∽△ACD ,则EC AD =FCCD,所以12-2t 12=4t 24,解得t =3, 即当t =3时,△EFC ∽△ACD .②若△FEC ∽△ACD ,则FC AD =EC CD, 所以4t 12=12-2t 24,解得t =1.2, 即当t =1.2时,△FEC ∽△ACD .因此,当t 为3或1.2时,以点E ,C ,F 为顶点的三角形与△ACD 相似.24.(1)证明:因为AD =DC ,∠ADE =∠DCF =90°,DE =CF ,所以△ADE ≌△DCF .(2)证明:因为四边形AEHG 是正方形,所以∠AEH =90°.所以∠QEC +∠AED =90°.又因为∠AED +∠EAD =90°,所以∠QEC =∠EAD .因为∠C =∠ADE =90°,所以△ECQ ∽△ADE .所以CQ DE =EC AD. 因为E 是CD 的中点,所以EC =DE =12CD =12AD .所以EC AD =12. 因为DE =CF ,所以CQ DE =CQ CF =12. 即Q 是CF 的中点.(3)解:S 1+S 2=S 3成立.理由如下:因为△ECQ ∽△ADE ,所以CQ DE =QE AE .所以CQ CE =QE AE. 因为∠C =∠AEQ =90°,所以△ECQ ∽△AEQ .所以△AEQ ∽△ECQ ∽△ADE .所以S 1S 3=⎝⎛⎭⎫EQ AQ 2,S 2S 3=⎝⎛⎭⎫AE AQ 2. 所以S 1S 3+S 2S 3=⎝⎛⎭⎫EQ AQ 2+⎝⎛⎭⎫AE AQ 2=EQ 2+AE 2AQ 2. 在Rt △AEQ 中,由勾股定理,得EQ 2+AE 2=AQ 2,所以S 1S 3+S 2S 3=1,即S 1+S 2=S 3.1、只要朝着一个方向努力,一切都会变得得心应手。
浙教版数学九年级上册 第四章 相似三角形 综合测试卷(原卷+答案)

第四章综合测试卷 相似三角形班级 学号 得分 姓名一、选择题(本大题有10小题,每小题3分,共30分)1.己知 ab =25,则a +b b的值为( )A 25B 35C 75D 232.如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )A.BC DF=12 B.∠A 的度数∠D 的度数=12C.△ABC的面积△def 的面积= 12 D. △ABC 的周长△def 的周长= 123.如图,在直角坐标系中,△OAB 的顶点为O(0,0),A(4,3),B(3,0).以点O 为位似中心,在第三象限内作与△OAB 的位似比 13的位似图形△OCD,则点C 坐标为( )A. (-1,-1)B.(−43,−1)C.(−1,−43) D. (-2,-1)4. 如图,四边形ABCD 是正方形,E 是CD 的中点,P 是BC 边上的一点,下列条件中,不能推出 △ABP 与△ECP 相似的是( )A.∠APB=∠EPCB. ∠APE=90°C. 点 P 是BC 的中点D. BP: BC=2:35.如图,在△ABC 中,点D 在BC 边上,连结AD,点E 在AC 边上,过点E 作EF∥BC,交 AD 于点F,过点E 作EG∥AB,交BC 于点G,则下列式子一定正确的是( ) A.AE EC=EF CDB.EF CD=EG ABC.AFFD=BG GCD.CG BC=AF AD6. 如图,小明为了测量一凉亭的高度AB(顶端A 到水平地面BD 的距离),在凉亭的旁边放置一个与凉亭台阶BC 等高的台阶DE(DE=BC=0.5m ,A ,B ,C 三点共线),把一面镜子水平放置在平台上的点 G 处,测得CG=15m ,然后沿直线CG 后退到点E 处,这时恰好在镜子里看到凉亭的顶端A ,测得 EG=3m ,小明身高EF=1.6m,则凉亭的高度AB 约为( )A. 8.5mB. 9mC. 9.5mD. 10m7. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似( )A. ①处B. ②处C. ③处D. ④处8. 如图,在△ABC 中,AD 平分∠BAC,按如下步骤作图:第一步,分别以点A ,D 为圆心,以大 12AD 的长为半径在AD 两侧作弧,交于两点M ,N第二步,连结MN 分别交AB,AC 于点E,F;第三步,连结DE,DF.若BD=6,AF=4,CD=3,则BE 的长是( )A. 2B. 4C. 6D. 89. 如图,在△ABC 中,点 D 为BC 边上的一点,且AD=AB=2,AD⊥AB,过点 D 作DE⊥AD,DE 交AC 于点E,若DE=1,则△ABC 的面积为( )A. 2B. 4C.25D. 810. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分 AC,点 H 为垂足.设AB=x ,AD=y ,则y 关于x 的函数关系用图象大致可以表示为( )二、填空题(本大题有6小题,每小题4分,共24分)11. 如图所示,点 E 是平行四边形ABCD 的边BC 延长线上一点,连结AE ,交 CD 于点F ,连结BF.写出图中任意一对相似三角形: .12. 已知 a6=b5=c4,且a+b-2c=6,则a 的值为 .13. 如图,在平行四边形ABCD 中,AB=10,AD=6,点E 是AD 的中点,在AB 上取一点F,使△CBF∽△CDE,则 BF 的长是 .14. 如图,在一块斜边长为30cm 的直角三角形木板(Rt△ACB)上截取一个正方形CDEF ,点D 在边BC 上,点E 在斜边AB 上,点F 在边AC 上,若AF :AC=1:3,则这块木板截取正方形 CDEF 后,剩余部分的面积为 .15.如图①,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图②是此时的示意图,则图②中水面高度为16. 如图所示,在直角坐标系中有两点A(4,0),B(0,2).如果点C 在x 轴上,且点 C 与点O 及点A 不重合,当点 C 的坐标为 时,使得由点B ,O ,C 构成的三角形与△AOB 相似(至少找出两个符合条件的点).三、解答题(本大题有8小题,共66分)17.(6分)如图,在△ABC中,DE‖BC,EF‖AB,求证:△ADEO△EFC.18. (6分)如图,一块材料的形状是锐角三角形 ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是多少?19.(6分)如图,点 P 是⊙O的直径AB 延长线上一点,且AB=4,点 M为A AB上一个动点(不与A,B重合),射线 PM与⊙O交于点 N(不与M重合).(1)当M在什么位置时,△MAB的面积最大? 并求出这个最大值;(2)求证:△PAN∽△PMB.20. (8 分)如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.21. (8分)如图,在△ABC中,点 D,E分别在边AB,AC上,且∠ABE=∠ACD,BE,CD交于点G,连结DE.(1)求证:△AEDO△ABC;(2)如果BE平分∠ABC,求证:DE=CE.22.(10分)如图,在 △ABC 中,点D,E,F 分别在AB,BC,AC 边上, DE‖AC,EF‖AB.(1)求证: △BDEO △EFC.(2)设AF FC=12,①若. BC =12,,求线段BE 的长;②若△EFC 的面积是20,求△ABC 的面积.23.(10分)在矩形ABCD 中,AE⊥BD 于点E,点 P 是边AD 上一点.(1)若BP 平分∠ABD,交 AE 于点G,PF⊥BD 于点F,如图①,证明四边形 AGFP 是菱形;(2)如图②,若PE⊥EC,求证:AE·AB=DE·AP;(3)在(2)的条件下,若AB=1,BC=2,求AP 的长.24.(12分)如图,已知 △ABC 是边长为6cm 的等边三角形,动点P ,Q 同时从A ,B 两点出发,分别沿AB,BC 匀速运动,其中点 P 运动的速度是 1cm/s,点 Q 运动的速度是2cm/s,当点 Q 到达点C 时,P ,Q 两点都停止运动.设运动时间为t(s),解答下列问题:(1) 当 t =2时,判断 △BPQ 的形状,并说明理由;(2)设 △BPQ 的面积为 S (cm²),求S 与t 的函数表达式;(3)如图,作 QR//BA 交AC 于点R,连结PR,当t 为何值时,△APR∽△PRQ?第四章综合测试卷 相似三角形1. C2. D3. B4. C5. C6. A7. B8. D9. B 10. D 11. △ADF∽△ECF(答案不唯一)12. 12 13. 1.8 14. 100cm² 15.24516. (-1,0)或(1,0)或(-4,0)(答案不唯一)17. 证明:∵DE∥BC,∴△ADE∽△ABC,∵EF∥AB,∴△EFC∽△ABC,∴△ADE∽△EFC.18. 解:设这个正方形零件的边长为 xmm ,则△AEF 的边EF 上的高AK=(80-x) mm.∵四边形EF-HG是正方形,∴EF∥GH,即 EF∥BC.∴△AEF CABC.∴EF BC=AK AD,即 x 120=80−x 80⋅∴x =48.∴这个正方形零件的边长是48mm.19. (1)解:当点 M 在 AB 的中点处时,△MAB 的面积最大,此时( OM⟂AB,∵OM =12AB =12×4=2,∴S ABM =12AB ⋅OM =12×4×2=4. (2)证明:∵∠PMB=∠PAN,∠P=∠P,∴△PAN∽△PMB.20. 解: ∵BD 为∠ABC 的平分线,∴∠ABD =∠CBD,∵AB∥CD,∴∠D=∠ABD,∴∠D=∠CBD,∴BC=CD.∵BC=4,∴CD=4.∵AB∥ CD,∴ABECDE,∴AB CD=AE CE,∴84=AE CE,∴AE=2CE,∵AC=6=AE+CE,∴AE=4.21. 证明:(1)∵∠ABE=∠ACD,且∠A 是公共角, ∴ABEACD.∴AE AD=AB AC,即AEAB =ADAC ,又∵∠A 是公共角,∴△AED∽△ABC. (2)∵∠ABE=∠ACD,∠BGD=∠CGE,∴△BGD∽ CGE.:DG EG=BG CG,即DG BG=EG CG.又∵∠DGE=∠BGC,∴△DGE∽△BGC.∴∠GBC=∠GDE,∵BE 平分∠ABC,∴∠GBC=∠ABE,∵∠ABE=∠ACD,∴∠GDE=∠ACD.∴DE=CE.22. (1)证明:∵DE∥AC,∴∠BED=∠C.∵EF∥AB,∴∠B=∠FEC,∴△BDE∽△EFC.(2)解:①∵EF//AB,∴BE EC=AF FC=12.∵BC = 12,∴BE12−BE =12,∴BE =4.②∵EF∥AB,∴△EFC∽△BAC,∴S△BC= (EC BC)2⋅∴BE EC=12,∴EC BC=23.又∵△EFC 的面积是20, ∴20SABC=(23)2,∴SABC=45,即△ABC 的面积是45.23. (1)证明:∵四边形 ABCD 是矩形,∴∠BAD=90°,∵AE⊥BD,∴∠AED=90°,∴∠BAE+∠EAD=90°,∠EAD+∠ADE=90°,∴∠BAE=∠ADE,∵BP 平分∠ABD,∴∠ABG=∠PBD.∵∠AGP=∠BAG+∠ABG,∠APB =∠ADE+∠PBD,∠ABG=∠PBD,∴∠AGP=∠APG,∴AP=AG,∵PA⊥AB,PF⊥BD,BP 平分∠ABD,∴PA=PF,∴PF=AG,∵AE⊥BD,PF⊥BD,∴PF∥AG,∴四边形AGFP 是平行四边形,∵PA=PF,∴四边形AGFP 是菱形.(2)证明:∵AE⊥BD,PE⊥EC,∴∠AED=∠PEC=90°,∴∠AEP=∠DEC,∵∠EAD+∠ADE=90°,∠ADE+∠CDE=90°,∴∠EAP=∠EDC,∴△AEP∽△DEC,∴DE·AP.(3)解:∵四边形 ABCD 是矩形,∴AD=BC=2,∠BAD=90°,∴BD=√AB²+AD² =5,∵AE ⊥BD,∴S ABD =12⋅BD ⋅AE = 12⋅AB ⋅AD,∴AE =255,∴DE =AD 2−AE 2=455,∵AE ⋅AB =DE ⋅AP,∴ AP =255×1455=12.24. 解:(1)△BPQ 是等边三角形.当t=2时,AP=21 =2( cm),BQ=2×2=4( cm),∴BP=AB-AP=6-2=4( cm),∴BQ=BP,又∵∠B = 60°,∴△BPQ 是等边三角形.(2)如图,过点 Q 作QE⊥AB,垂足为 E,由 QB=2tcm,∠B=60°,∠BEQ=90°,得 QE =3tcm,由AP= tcm,得 PB =(6−t )cm,∴S =12BP ⋅QE = 12×(6−t )×3t =−32t 2+33t.(3)∵QR‖BA,∴∠QRC=∠A=60°,∠RQC=∠B=60°,∴△QRC是等边三角形,∴QR=RC=QC=(6-2t)cm⋅:BE=12BQ=12×2t=t(cm),∴EP=AB−AP−BE=6−t−t=6−2t(cm),∵EP‖QR,EP=QR,∴四边形 EPRQ是平行四边形,∴PR=EQ3tcm.又∵∠PEQ=90°,∴∠APR∠PRQ=90°,∴△APR∽△PRQ,∴∠QPR=∠A=60∘,QRPR=6−2t3t=3,解得t=65.∴当t=65时,△APR∽△PRQ.。
浙教版九年级上册数学第4章 相似三角形 含答案

浙教版九年级上册数学第4章相似三角形含答案一、单选题(共15题,共计45分)1、过△ABC的重心G作GE∥BC交AC于点E,线段BC=12,线段GE长为( )A.4B.4.5C.6D.82、如图,在△ABC中,D,E分别为AB,AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是()A. B. C. D.3、如图,已知,和是位似图形,点是位似中心,若的面积为2,则的面积为()A.4B.8C.12D.184、已知:如图,在△ABC中,∠AED=∠B,则下列等式成立的是()A. B. C. D.5、如图,在平行四边形ABCD中,E是BC上一点,BE:EC=1:2,AE与BD相交于点F,若S△BEF =2,则S△ABD=()A.24B.25C.26D.236、如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )A. B. C. D.7、如图,已知AB,CD,EF都与BD垂直,垂足分别是B,D,F,且AB=1,CD=3,则EF的长是( )A. B. C. D.8、如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为()A.5B.6C.7D.89、如图,在正方形中,的顶点,分别在,边上,高与正方形的边长相等,连接分别交,于点,,下列说法:①;②连接,,则为直角三角形;③;④若,,则的长为,其中正确结论的个数是()A.4B.3C.2D.110、在△ABC和△A′B′C′中,如果AB=9,BC=8,AC=5,A′B′=, B′C′=,A′C′=4,那么()A.∠A=∠A′B.∠B=∠A′C.∠A=∠C′D.不能确定11、如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',以下说法中错误的是( )A.△ABC∽△A'B'C'B.点C,点O,点C'三点在同一直线上C.AO:AA'=1∶2D.AB∥A'B'12、如图,AB//CD//MN,点M,N分别在线段AD,BC上,AC与MN交于点E,则()A. B. C. D.13、如图,函数的图象经过斜边的中点,与直角边相交于,连结.若,则的周长为()A.12B.C.D.14、两个相似多边形的面积之比是1:4,则这两个相似多边形的周长之比是()A.1:2B.1:4C.1:8D.1:1615、如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE=,则△ABC的面积为()A. B.15 C. D.二、填空题(共10题,共计30分)16、把一个矩形剪去一个正方形,若剩下的矩形与原矩形相似,则原矩形的长边与短边之比为________.17、有一张矩形风景画,长为90cm,宽为60cm,现对该风景画进行装裱,得到一个新的矩形,要求其长、宽之比与原风景画的长、宽之比相同,且面积比原风景画的面积大44%.若装裱后的矩形的上、下边衬的宽都为acm,左、右边衬的宽都为bcm,那么ab=________ cm218、如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具.移动竹竿使竹竿,旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为________ m.19、如图,等边△ABC的边长为5,D在BC延长线上,CD=3,点E在线段AD 上,且AE=AB,连接BE交AC于F,则CF的长为________。
浙教版九年级数学上册 第四章 相似三角形基础能力测试卷(含答案)

第四章相似三角形基础能力测试卷班级姓名学号一、选择题(共10小题,每小题3分,满分30分)1、如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥A B、若AD=2BD,则的值为()A、B、C、D、(第1题) (第2题)(第5题)2、如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB=()A、1:4B、2:3C、1:3D、1:23、如果两个相似三角形的面积比是1:2,那么它们的周长比是()A、1:4B、1:C、:1D、4:14、某块面积为4000m2的多边形草坪,在嘉兴市政建设规划设计图纸上的面积为250cm2,这块草坪某条边的长度是40m,则它在设计图纸上的长度是( )A、4cmB、5cmC、10cmD、40cm5、如图,若P为△ABC的边AB上一点(AB>AC),则下列条件不一定能保证△ACP∽△ABC的有( )A、∠ACP=∠BB、∠APC=∠ACBC、=D、=6、如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为()A、(3,3)B、(4,3)C、(3,1)D、(4,1)(第6题) (第7题)7、如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=()A、1:16B、1:18C、1:20D、1:248、如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,则DC的长等于()A、B、C、D、(第8题)(第9题)9、已知△ABC中,G是三角形的重心,AB=,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为()A、3B、4C、D、510、某小区现有一块等腰直角三角形形状的绿地,腰长为100米,直角顶点为A、小区物业管委会准备把它分割成面积相等的两块,有如下的分割方法:方法一:在腰AB上找一点D,作DE∥BC,交AC于点E,DE作为分割线;方法二:以点A为圆心,AD为半径作弧,交AB于点D,交AC于点E,弧DE作为分割线;方法四:在腰AC上找一点D,连接BD作为分割线、这些分割方法中分割线最短的是()A、方法一B、方法二C、方法三D、方法四二、填空题(共6小题,每小题4分,满分24分)11、如图,△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,则CD的长为、第11题图第12题图12、如图,A、B两地被一座小山阻隔,为了测量A、B两地之间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E,测得DE的长度为360米,则A、B两地之间的距离是米、13、已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DE的面积比为、14、如图,已知BE平分∠ABC,DE∥BC,AD=3,DE=2,AC=4,则AE= 、第14题图第15题图15、如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1、如果△BEC的面积为2,那么四边形ABED的面积是_______、16、如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为、(第16题)(第17题)三、解答题(本题有7个小题,共66分)解答应写出证明过程或推演步骤、17、(6分)如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长、18、(8分)已知:如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D、(1)求证:△ABC∽△BCD;(2)若BC=2,求AB的长、19、(8分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B、(1)求证:△ADF∽△DEC;(2)若AB=4,AD=33,AE=3,求AF的长、20、(10分)已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度)、(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是;(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是;(3)△A2B2C2的面积是平方单位、PAB DC21、(10分)如图所示,梯形ABCD 中,AD ∥BC ,∠A =90°,AB =7,AD =2,BC =3,试在腰AB 上确定点P 的位置,使得以P ,A ,D 为顶点的三角形与以P ,B ,C 为顶点的三角形相似、22、(12分)如图,四边形ABCD 中,AC 平分∠DAB ,∠ADC =∠ACB =90°,E 为AB 的中点,(1)求证:AC 2=AB •AD ; (2)求证:CE ∥AD ; (3)若AD =4,AB =6,求的值、23、(12分)如图,四边形ABCD 内接于⊙O ,AB 是⊙O 的直径,AC 和BD 相交于点E ,且DC 2=CE •C A 、 (1)求证:BC =CD ;(2)分别延长AB ,DC 交于点P ,过点A 作AF ⊥CD 交CD 的延长线于点F ,若PB =OB ,CD =22,求DF 的长、答案详解一、选择题(共10小题,每小题3分,满分30分)2、如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB=()A、1:4B、2:3C、1:3D、1:2【解答】解:∵BE和CD是△ABC的中线,∴DE=BC,DE∥BC,∴=,△DOE∞△COB,∴=()2=()2=,故选A、A、1:4B、1:C、:1D、4:1【解答】解:∵两个相似三角形的面积比是1:2,∴这两个相似三角形的相似比是1:,∴它们的周长比是1:、故选B、4、某块面积为4000m2的多边形草坪,在嘉兴市政建设规划设计图纸上的面积为250cm2,这块草坪某条边的长度是40m,则它在设计图纸上的长度是( )A、4cmB、5cmC、10cmD、40cm【解答】解:设这块草坪在设计图纸上的长度是xcm,4000m2=40000000m2,40m=4000cm,根据题意得:=()2,解得:x=10,即这块草坪在设计图纸上的长度是10cm、故选C、5、如图,若P为△ABC的边AB上一点(AB>AC),则下列条件不一定能保证△ACP∽△ABC 的有( )A、∠ACP=∠BB、∠APC=∠ACBC、=D、=【解答】解:∵∠A=∠A,∴当∠APC=∠ACB或∠ACP=∠B或AC:AB=AP:AC或AC2=AB•AP时,△ACP∽△AB C、故选D、6、如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为()A、(3,3)B、(4,3)C、(3,1)D、(4,1)【解答】解:∵线段AB的两个端点坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,∴端点C的横坐标和纵坐标都变为A点的一半,∴端点C的坐标为:(3,3)、故选:A、7、如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=()A、1:16B、1:18C、1:20D、1:24【解答】解:∵S△BDE:S△CDE=1:4,∴设△BDE的面积为a,则△CDE的面积为4a,∵△BDE和△CDE的点D到BC的距离相等,1∴=41∴=5∵DE∥AC,∴△DBE∽△ABC,∴S△DBE:S△ABC=1:25,∴S△ACD=25a﹣a﹣4a=20a,∴S△BDE:S△ACD=a:20a=1:20、故选C、8、如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,则DCA、B、C、D、【解答】解:∵∠C=∠E,∠ADC=∠BDE,∴△ADC∽△BDE,∴=,又∵AD:DE=3:5,AE=8,∴AD=3,DE=5,∵BD=4,∴=,∴DC=,故应选:A、9、已知△ABC中,G是三角形的重心,AB=,过点G的直线MN∥AB,交AC于M,BC 于N,则MN的长为()A、3B、4C、D、5【解答】解:如图所示,连接CD,∵MN∥AB,∴∠CMN=∠A,∠CNM=∠B,∴△CMN∽△CAB,同理可证△CMG∽△CAD,∴,又∵G是三角形的重心,∴,∴===,∴MN=AB=×=5、故选:D、10、某小区现有一块等腰直角三角形形状的绿地,腰长为100米,直角顶点为A、小区物业管委会准备把它分割成面积相等的两块,有如下的分割方法:方法一:在腰AB上找一点D,作DE∥BC,交AC于点E,DE作为分割线;方法二:以点A为圆心,AD为半径作弧,交AB于点D,交AC于点E,弧DE作为分割线;方法三:在底边BC上找一点D,连接AD作为分割线;方法四:在腰AC上找一点D,连接BD作为分割线、这些分割方法中分割线最短的是()A、方法一B、方法二C、方法三D、方法四【解答】解:根据等腰直角三角形的性质,方法一中,△ADE∽△ABC,有DE2:BC2=S△ADE:S△ABC=1:2,∵腰长为100米,∴BC=100m,∴DE=100m;方法二中,S△ABC=×100×100=5000,故扇形的面积==2500=×AD2π,则AD=,故==50(m )、 方法三中,AD ==50(m ); 方法四中,BD ==50(m );则方法三中的分割线最短、 故选:C 、二、填空题(共6小题,每小题4分,满分24分)11、如图,△ABC 中,D 为BC 上一点,∠BAD =∠C ,AB =6,BD =4,则CD 的长为 、【解答】 解:∵∠BAD =∠C ,∠B =∠B ,∴ABD CBA ∆∆∽、∴BD AB BA CB =、 ∵AB =6,BD =4,∴4664DC =+,解得5DC =、12、如图,A 、B 两地被一座小山阻隔,为了测量A 、B 两地之间的距离,在地面上选一点C ,连接CA 、CB ,分别取CA 、CB 的中点D 、E ,测得DE 的长度为360米,则A 、B 两地之间的距离是 米、【解答】 解:根据三角形中位线求出AB =2DE ,代入求出即可:∵D 、E 分别是AC 、BC 的中点,DE =360米, ∴AB =2DE =720米、13、已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积比为9:16、【解答】解:∵△ABC∽△DEF,△ABC与△DEF的相似比为3:4,∴△ABC与△DEF的面积比为9:16、故答案为:9:16、14、如图,已知BE平分∠ABC,DE∥BC,AD=3,DE=2,AC=4,则AE=2、4、【解答】解:如图,∵BE平分∠ABC,DE∥BC,∴∠DBE=∠CBE,∠DEB=∠CBE,∴∠DBE=∠DEB,∴DB=DE=2,AB=AD+DB=5;∵DE∥BC,∴△ADE∽△ABC,∴,而AC=4,AD=3,∴AE=2、4,故答案为2、4、15、如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1、如果△BEC的面积为2,那么四边形ABED的面积是_______、【解答】解:延长BA,CD交于点F,∵BE平分∠ABC,∴∠EBF=∠EBC,∵BE⊥CD,∴∠BEF =∠BEC =90°, 在△BEF 和△BEC 中,,∴△BEF ≌△BEC (ASA ),∴EC =EF ,S △BEF =S △BEC =2, ∴S △BCF =S △BEF +S △BEC =4,∵CE :ED =2:1 ∴DF :FC =1:4, ∵AD ∥BC , ∴△ADF ∽△BCF ,∴161CF DF S S 2BCF ADF =⎪⎭⎫ ⎝⎛=∆ ∴411614S ADF =⨯=∆ ∴S 四边形ABED =S △BEF ﹣S △ADF =2﹣41=47、 故答案为:47、 16、如图,在直角三角形ABC 中(∠C =90°),放置边长分别3,4,x 的三个正方形,则x 的值为7 、【解答】 解:如图∵在Rt △ABC 中∠C =90°,放置边长分别3,4,x 的三个正方形, ∴△CEF ∽△OME ∽△PFN , ∴OE :PN =OM :PF , ∵EF =x ,MO =3,PN =4, ∴OE =x ﹣3,PF =x ﹣4, ∴(x ﹣3):4=3:(x ﹣4),∴(x ﹣3)(x ﹣4)=12,∴x 1=0(不符合题意,舍去),x 2=7、 故答案为:7、三、解答题(本题有7个小题,共66分)解答应写出证明过程或推演步骤、17、(6分)如图,D 是△ABC 的边AC 上的一点,连接BD ,已知∠ABD =∠C ,AB =6,AD =4,求线段CD 的长、【解答】 解: 在△ABD 和△ACB 中, ∠ABD =∠C ,∠A =∠A ,∴△ABD ∽△ACB ,ABADAC AB =∴ ∵AB =6,AD =4,94362===∴AD AB AC则CD =AC ﹣AD =9﹣4=5、18、(8分)已知:如图,在△ABC 中,AB =AC ,∠A =36°,∠ABC 的平分线交AC 于D 、 (1)求证:△ABC ∽△BCD ; (2)若BC =2,求AB 的长、【解答】 解:证明:(1)∵AB =AC ,∠A =36°, ∴∠ABC =∠C =72°、 ∵BD 平分∠ABC , ∴∠ABD =∠DBC =36°、 ∴∠DBC =∠A =36°、又∵∠ABC =∠C , ∴△ABC ∽△BC D 、 (2)∵∠ABD =∠A =36°, ∴AD =BD ,∠BDC =∠C =72°、 ∴BD =BC =A D 、 ∵△ABC ∽△BCD , ∴、即、 解得:AB =1+或1﹣(不符合题意)、∴AB =1+、 19、(8分)如图,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为E ,连接DE ,F 为线段DE 上一点,且∠AFE =∠B 、 (1)求证:△ADF ∽△DEC ;(2)若AB =4,AD =33,AE =3,求AF 的长、 【解答】 解:证明:∵四边形ABCD 是平行四边形∴AD ∥BC AB ∥CD∴∠ADF =∠CED ∠B +∠C =180° ∵∠AFE +∠AFD =180 ∠AFE =∠B ∴∠AFD =∠C ∴△ADF ∽△DEC(2)解:∵四边形ABCD 是平行四边形 ∴AD ∥BC CD =AB =4又∵AE ⊥BC ∴ AE ⊥AD 在Rt △ADE 中,DE =63)33(2222=+=+AE AD∵△ADF ∽△DEC ∴CD AF DE AD = ∴4633AF= AF =32P A B DC20、(10分)已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度)、(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是;(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是;(3)△A2B2C2的面积是平方单位、【解答】解:(1)如图所示:C1(2,﹣2);故答案为:(2,﹣2);(2)如图所示:C2(1,0);故答案为:(1,0);(3)∵A2C22=20,B2C=20,A2B 2=40,∴△A2B2C2是等腰直角三角形,∴△A2B2C2的面积是:××20=10平方单位、故答案为:10、21、(10分)如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似、【解答】解:(1)若点A,P,D分别与点B,C,P对应,即△APD∽△BCP,∴AD AP BP BC=,∴273APAP=-,∴AP2-7AP+6=0,∴AP=1或AP=6,检测:当AP=1时,由BC=3,AD=2,BP=6,∴AP AD BC BP=,又∵∠A=∠B= 90°,∴△APD∽△BCP、当AP=6时,由BC=3,AD=2,BP=1,又∵∠A=∠B=90°,∴△APD∽△BCP、(2)若点A,P,D分别与点B,P,C对应,即△APD∽△BPC、∴AP ADBP BC=,∴273APAP=-, ∴AP=145、检验:当AP=145时,由BP=215,AD=2,BC=3,∴AP AD BP BC=,又∵∠A=∠B=90°,∴△APD∽△BPC、因此,点P的位置有三处,即在线段AB距离点A1、145、6 处、22、(12分)如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,(1)求证:AC2=AB•AD;(2)求证:CE∥AD;(3)若AD=4,AB=6,求的值、【解答】解:(1)证明:∵AC平分∠DAB,∴∠DAC =∠CAB , ∵∠ADC =∠ACB =90°, ∴△ADC ∽△ACB , ∴AD :AC =AC :AB , ∴AC 2=AB •AD ;(2)证明:∵E 为AB 的中点, ∴CE =AB =AE , ∴∠EAC =∠ECA , ∵∠DAC =∠CAB , ∴∠DAC =∠ECA , ∴CE ∥AD ;(3)解:∵CE ∥AD , ∴△AFD ∽△CFE , ∴AD :CE =AF :CF , ∵CE =AB , ∴CE =×6=3, ∵AD =4, ∴, ∴、23、(12分)如图,四边形ABCD 内接于⊙O ,AB 是⊙O 的直径,AC 和BD 相交于点E ,且DC 2=CE •C A 、 (1)求证:BC =CD ;(2)分别延长AB ,DC 交于点P ,过点A 作AF ⊥CD 交CD 的延长线于点F ,若PB =OB ,CD =22,求DF 的长、【解答】 解:(1)证明:∵DC 2=CE •CA ,∴DCCACE DC△CDE∽△CAD,∴∠CDB=∠DBC,∵四边形ABCD内接于⊙O,∴BC=CD;(2)解:如图,连接OC,∵BC=CD,∴∠DAC=∠CAB,又∵AO=CO,∴∠CAB=∠ACO,∴∠DAC=∠ACO,∴AD∥OC,∴=,2,∵PB=OB,CD=2∴=4∴PC=2又∵PC•PD=PB•P A∴P A=4也就是半径OB=4,在RT△ACB中,2,AC===14∵AB是直径,∴∠ADB=∠ACB=90°∴∠FDA+∠BDC=90°∠CBA+∠CAB=90°∵∠BDC=∠CAB∴∠FDA=∠CBA又∵∠AFD=∠ACB=90°∴△AFD∽△ACB∴722142CB C ===A FD AF 在Rt △AFP 中,设FD =x ,则AF =x 7,∴在RT △APF 中有,,求得DF =223、 http ://www 、czsx 、com 、cn。
浙教版九年级上册数学第4章 相似三角形含答案

浙教版九年级上册数学第4章相似三角形含答案一、单选题(共15题,共计45分)1、如图,若BC∥DE,则下面比例式不能成立的是()A. B. C. D.2、如图,在△ABC中,点D、E分AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于()A.3B.4C.6D.83、如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论错误的是()A.△ADC∽△CFBB.AD=DFC. =D. =4、如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则()A. B. C. D.5、已知2x=3y,则下列比例式成立的是()A. B. C. D.6、如图,直线,若,,,则的长为()A. B.10C.3D.7、如图所示,不能判定△ABC∽△DAC的条件是( )A.∠B=∠DACB.∠BAC=∠ADCC. AC2=DC·BCD. AD2=BD·BC8、如图,边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连接AH、FH,FH与AC交于点M,以下结论:①FH=2BH;②AC⊥FH;③S=1;④CE= AF;⑤=FG•DG,其中正确结论△ACF的个数为()A.2B.3C.4D.59、如图,在中,点D,E,F分别在AB,AC,BC上,,,则下列式子一定正确的是()A. B. C. D.10、在▱ABCD中,E为BD上一点,在连结AE并延长交BC于F点,且BD=4BE,△BEF的面积为1,则▱ABCD的面积为()A.12B.24C.13D.2611、两个相似三角形的最短边分别是5cm和3cm,它们的周长之差为12cm,那么小三角形的周长为()A.14cmB.16cmC.18cmD.30cm12、如图,在正方形ABCD中,点O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE≌△DOF;②△OGE∽△FGC;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=OG·OC。
浙教版九年级上册数学第4章 相似三角形 含答案

浙教版九年级上册数学第4章相似三角形含答案一、单选题(共15题,共计45分)1、如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′,B′,A′,B′均在图中格点上,若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为()A.(, n)B.(m,n)C.(,)D.(m,)2、如图,已知BC∥DE,则下列说法中不正确的是()A.两个三角形是位似图形B.点A是两个三角形的位似中心C.AE︰AD是位似比D. 点B与点E、点C与点D是对应位似点3、在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判定DE∥BC的是()A. B. C. D.4、如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE的是( )A.∠B=∠DB.∠C=∠AEDC. =D. =5、如图,在Rt△ABC中,AC⊥BC,过C作CD⊥AB,垂足为D,若AD=3,BC=2,则△ABC的内切圆的面积为()A.πB.(4﹣2 )πC.()πD.2π6、如图,在中,点,点为边的三等分点,与交于点,则下列比例式正确的是()A. B. C. D.7、在平面直角坐标系中,△ABC顶点A(2,3).若以原点O为位似中心,画三角形ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为,则A′的坐标为()A. B. C. D.8、如图,比例规是伽利略发明的一种画图工具,使用它可以把线段按一定比例伸长或缩短,它是由长度相等的两脚和交叉构成的.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使,),然后张开两脚,使A、B两个尖端分别在线段I的两个端点上.若,则的长是()A. B. C. D.9、如图,射线OC分别交反比例函数,的图象于点A,B,若OA:OB=1:2,则k的值为()A.2B.3C.4D.610、如图,点F是口ABCD的边CD上一点,直线BF交AD的延长线与点E ,则下列结论错误的是().A. B. C. D.11、一个矩形按如图1的方式分割成三个直角三角形,把较大两个直角三角形纸片按图2中①、②两种方式放置,设①中的阴影部分面积为,②中的阴影部分面积为,当时,则矩形的两边之比为()A. B. C. D.12、如图,△ABC 中,DE // AB 交AC 于D,交BC 于E,若AD=2,CD=3,DE=4,则AB =()A. B. C. D.613、“差之毫厘,失之千里”是一句描述开始时虽然相差很微小,结果会造成很大的误差或错误的成语.现实中就有这样的实例,如步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,眼睛距离目标为200m,步枪上准星宽度AB为2mm,若射击时,由于抖动导致视线偏离了准星1mm,则目标偏离的距离为()cm.A.25B.50C.75D.10014、如图,在中,,以上一点O为圆心作与、都相切,与的另一个交点为D,则线段的长为()A. B. C. D.115、若,则的值是()A. B. C.-16 D.二、填空题(共10题,共计30分)16、如图,在△ABC中,P,Q分别为AB,AC的中点.若S△APQ=1,则S四边形=________.PBCQ17、如图,正方形的边长是,除和四点外,图形的其他顶点均为所在的一条线段的中点,则从正方形中挖掉阴影部分后,所剩下部分面积等于________.18、如图,点G是正六边形ABCDEF的CD边的中点,AG与CF交于H点.则∠AHF+∠HGC=________度,若AB=a,则FH=________(用含a的代数式表示).19、如果,那么=________.20、已知:在平行四边形ABCD中,点E在DA的延长线上,AE= AD,连接CE 交BD于点F,则的值是________.21、已知反比例函数y= 在第二象限内的图象如图,经过图象上两点A、E分别引y轴与x轴的垂线,交于点C,且与y轴与x轴分别交于点M、B.连接OC 交反比例函数图象于点D,且,连接OA,OE,如果△AOC的面积是15,则△ADC与△BOE的面积和为________.22、如图,∠BAC=80°,∠B=40°,∠E=60°,若将图中的△ADE旋转(平移),则所得到的新三角形与△ABC________,与△ADE________23、如图,AB,CD相交于O点,△AOC∽△BOD,OC:OD=1:2,AC=5,则BD的长为________.24、两个相似三角形一组对应角平分线的长分别是2 cm和5 cm,那么这两个三角形的相似比是________,如果在这两个三角形的一组对应中线中,较短的中线是3 cm,那么较长的中线是________cm.25、如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,AC=10m,则建筑物CD的高是________m.三、解答题(共5题,共计25分)26、如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,求DF的长度.27、为了测量学校操场上旗杆的高度,小明请同学帮忙,测量了同一时刻自己的影长EC和旗杆的影长BC分别为0.6m和3.6m,如图,如果小身高CD为1.5m,请计算旗杆AB的高度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章达标测试卷一、选择题(每题3分,共30分)1.若m +n n =52,则mn 等于( )A .52B .23C .25D .322.若两个相似多边形的面积之比为1:4,则它们的周长之比为( )A .1:4B .1:2C .2:1D .4:13.如图,l 1∥l 2∥l 3,直线a ,b 与l 1,l 2,l 3分别相交于点A ,B ,C 和点D ,E ,F .若AB =3,DE =2,BC =6,则EF =( ) A .2 B .3 C .4 D .54.已知△ABC ∽△A ′B ′C ′,AB =8,A ′B ′=6,则BCB ′C ′=( )A .2B .43C .3D .1695.如图,以点O 为位似中心,把△ABC 放大为原图形的2倍得到△A ′B ′C ′,以下说法中错误的是( )A .△ABC ∽△A ′B ′C ′ B .点C 、点O 、点C ′在同一直线上 C .AO :AA ′=1:2D .AB ∥A ′B ′6.如图,为估算某河的宽度(河两岸平行),在河对岸选定一个目标点A ,在近岸取点B ,C ,D ,使得AB ⊥BC ,CD ⊥BC ,点E 在BC 上,并且点A ,E ,D 在同一条直线上,若测得BE =20 m ,CE =10 m ,CD =20 m ,则河的宽度AB 等于( )A .60 mB .40 mC .30 mD .20 m7.如图,小正方形的边长均为1,则下列选项中的三角形与△ABC 相似的是( )8.如图,在矩形ABCD 中,AB =2,BC =3,点E 是AD 的中点,CF ⊥BE 于点F ,则CF 等于( ) A .2 B .2.4 C .2.5 D .2.259.如图,在△ABC 中,AB =AC =18,BC =12,正方形DEFG 的顶点E ,F 在△ABC内,顶点D ,G 分别在AB ,AC 上,AD =AG ,DG =6,则点F 到BC 的距离为( )A .1B .2C .122-6D .62-610.如图,在钝角三角形ABC 中,分别以AB 和AC 为斜边向△ABC 的外侧作等腰直角三角形ABE 和等腰直角三角形ACF ,EM 平分 ∠AEB 交AB 于点M ,取BC 的中点D ,AC 的中点N ,连结DN ,DE ,DF .下列结论:①EM =DN ;②S △CND =13S 四边形ABDN ;③DE =DF ;④DE ⊥DF .其中正确结论的个数为( ) A .1 B .2 C .3 D .4 二、填空题(每题3分,共24分) 11.已知b a =713,则a a +b=________.12.如图,在△ABC 中,若DE ∥BC ,AD =2,BD =4,DE =1.5,则BC 的长为__________.13.如图,已知点C 是线段AB 的黄金分割点,且BC >AC .若S 1表示以BC 为边的正方形的面积,S 2表示长为AD (AD =AB )、宽为AC 的矩形的面积,则S 1与S 2的大小关系为________.14.如图,在平面直角坐标系中,有点A(6,3),B(6,0),以原点O为位似中心,位似比为13,在第一象限内把线段AB缩小后得到CD,则点C的坐标为________.15.如图,在△ABC中,∠BAC=90°,∠B=45°,在△ACD中,∠ACD=90°,∠D=30°,则BEEC的值是________.16.如图,身高为1.7 m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条直线上.已知河BD的宽度为12 m,BE=3 m,则树CD的高度为________.17.如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP 相似,则BM的长为________.18.如图,正三角形ABC的边长为2,以BC边上的高AB1为边作正三角形AB1C1,△ABC与△AB1C1公共部分的面积记为S1,再以正三角形AB1C1边B1C1上的高AB2为边作正三角形AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2……以此类推,则S n=____________.(用含n的式子表示)三、解答题(19,21题每题8分,24题14分,其余每题12分,共66分) 19.如图,四边形ABCD∽四边形EFGH,试求出x及α的大小.20.如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(-2,4),B(-2,1),C(-5,2).(1)请画出△ABC关于x轴对称的△A1B1C1;(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;(3)求△A1B1C1与△A2B2C2的面积比.(不写解答过程,直接写出结果)21.如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.(1)求证:△ADE≌△CFE;(2)若GB=2,BC=4,BD=1,求AB的长.22.如图,一条河的两岸BC与DE互相平行,两岸各有一排景观灯(图中黑点代表景观灯),每排相邻两个景观灯的间隔都是10 m,在与河岸DE的距离为16 m的A处(AD⊥DE)看对岸BC,看到对岸BC上的两个景观灯的灯杆恰好被河岸DE上两个景观灯的灯杆遮住.河岸DE上的这两个景观灯之间有1个景观灯,河岸BC上被遮住的两个景观灯之间有4个景观灯,求这条河的宽度.23.如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以每秒2个单位长度的速度运动;点F沿CD边从点C开始向点D 以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.请解答下列问题:(1)当t为何值时,△CEF是等腰直角三角形?(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?24.如图,E,F分别是正方形ABCD的边DC,CB上的点,且DE=CF,以AE 为边作正方形AEHG,HE与BC交于点Q,连结DF.(1)求证:△ADE≌△DCF.(2)若E是CD的中点,求证:Q为CF的中点.(3)连结AQ,设S△CEQ=S1,S△AED=S2,S△EAQ=S3,在(2)的条件下,判断S1+S2=S3是否成立?并说明理由.答案一、1.D2.B3.C4.B5.C 6.B点拨:∵AB⊥BC,CD⊥BC,∴∠ABC=∠DCE=90°.又∵∠AEB=∠DEC,∴△ABE∽△DCE.∴ABDC=BECE,即AB20=2010.∴AB=40 m.7.A8.B9.D点拨:如图,过点A作AM⊥BC于点M,交DG于点N,延长GF交BC 于点H.∵AB=AC,AD=AG,∴AD∶AB=AG∶AC.又∵∠BAC=∠DAG,∴△ADG∽△ABC.∴∠ADG=∠B.∴DG∥BC.∴AN⊥DG.∵四边形DEFG是正方形,∴FG⊥DG.∴FH⊥BC.∵AB=AC=18,BC=12,∴BM=12BC=6.∴AM=AB2-BM2=12 2.∵ANAM=DGBC,即AN122=612,∴AN=6 2.∴MN=AM-AN=6 2. 易得四边形GHMN为矩形,∴GH=MN=6 2.∴FH=GH-GF=6 2-6.故选D.10.D 点拨:∵△ABE 是等腰直角三角形,EM 平分∠AEB ,∴EM 是AB 边上的中线.∴EM =12AB .∵点D ,点N 分别是BC ,AC 的中点,∴DN 是△ABC 的中位线.∴DN =12AB ,DN ∥AB .∴EM =DN .①正确. ∵DN ∥AB ,∴△CDN ∽△CBA . ∴S △CND S △CAB =⎝ ⎛⎭⎪⎫DN AB 2=14. ∴S △CND =13S 四边形ABDN .②正确.如图,连结DM ,FN ,则DM 是△ABC 的中位线,∴DM =12AC ,DM ∥AC . ∴四边形AMDN 是平行四边形. ∴∠AMD =∠AND .易知∠ANF =90°,∠AME =90°, ∴∠EMD =∠DNF . ∵FN 是AC 边上的中线, ∴FN =12AC .∴DM =FN . 又∵EM =DN , ∴△DEM ≌△FDN .∴DE =DF ,∠FDN =∠DEM .③正确. ∵∠MDN +∠AMD =180°,∴∠EDF =∠MDN -(∠EDM +∠FDN )=180°-∠AMD -(∠EDM +∠DEM )=180°-(∠AMD +∠EDM +∠DEM )=180°-(180°-∠AME )=180°-(180°-90°)=90°.∴DE ⊥DF .④正确.故选D . 二、11.1320 点拨:∵b a =713,∴设a =13x ,b =7x , 则a a +b =13x 13x +7x=1320.12.4.5 13.S1=S2 14.(2,1)15.3 316.5.1 m17.163或318.32×⎝⎛⎭⎪⎫34n点拨:在正三角形ABC中,AB1⊥BC,∴BB1=12BC=1.在Rt△ABB1中,AB1=AB2-BB21=22-12=3,根据题意可得△AB2B1∽△AB1B,记△AB1B的面积为S,∴S1S=⎝⎛⎭⎪⎫322.∴S1=34S.同理可得S2=34S1,S3=34S2,S4=34S3,….又∵S=12×1×3=32,∴S1=34S=32×34,S2=34S1=32×⎝⎛⎭⎪⎫342,S3=34S2=32×⎝⎛⎭⎪⎫343,S4=34S3=32×⎝⎛⎭⎪⎫344,…,S n=32×⎝⎛⎭⎪⎫34n.三、19.解:因为四边形ABCD∽四边形EFGH,所以∠H=∠D=95°,则α=360°-95°-118°-67°=80°.再由x∶7=12∶6,解得x=14.20.解:(1)如图,△A1B1C1即为所求.(2)如图,△A2B2C2即为所求.(3)S△A1B1C1∶S△A2B2C2=1∶4.21.(1)证明:∵AB∥FC,∴∠A=∠ECF.又∵∠AED=∠CEF,且DE=FE,∴△ADE≌△CFE.(2)解:方法一:∵AB∥FC,∴△GBD∽△GCF.∴GBGC=BDCF.∴22+4=1CF.∴CF=3.由(1)得△ADE≌△CFE,∴AD=CF=3,∴AB=AD+BD=3+1=4.方法二:如图,取BC的中点H,连结EH.∵△ADE≌△CFE,∴AE=CE.∴EH是△ABC的中位线.∴EH∥AB,且EH=12AB.∴△GBD∽△GHE.∴DBEH=GBGH.∴1EH=22+2.∴EH=2.∴AB=2EH=4.22.解:由题意可得DE ∥BC ,所以△ADE ∽△ABC .所以AD AB =DE BC ,即AD AD +DB=DE BC . 因为AD =16 m ,BC =50 m ,DE =20 m ,所以1616+DB=2050. 所以DB =24 m.所以这条河的宽度为24 m.23.解:(1)由题意可知BE =2t ,CF =4t ,CE =12-2t .因为△CEF 是等腰直角三角形,∠ECF 是直角,所以CE =CF . 所以12-2t =4t ,解得t =2.所以当t =2时,△CEF 是等腰直角三角形.(2)根据题意,可分为两种情况:①若△EFC ∽△ACD ,则EC AD =FC CD ,所以12-2t 12=4t 24,解得t =3,即当t =3时,△EFC ∽△ACD .②若△FEC ∽△ACD ,则FC AD =EC CD ,所以4t 12=12-2t 24,解得t =1.2,即当t =1.2时,△FEC ∽△ACD .因此,当t 为3或1.2时,以点E ,C ,F 为顶点的三角形与△ACD 相似.24.(1)证明:因为AD =DC ,∠ADE =∠DCF =90°,DE =CF ,所以△ADE ≌△DCF .(2)证明:因为四边形AEHG 是正方形,所以∠AEH =90°.所以∠QEC +∠AED =90°.又因为∠AED +∠EAD =90°,所以∠QEC =∠EAD .因为∠C =∠ADE =90°,所以△ECQ ∽△ADE .所以CQ DE =EC AD .因为E 是CD 的中点,所以EC =DE =12CD =12AD .所以EC AD =12.因为DE =CF ,所以CQ DE =CQ CF =12.即Q 是CF 的中点.(3)解:S 1+S 2=S 3成立.理由如下:因为△ECQ ∽△ADE ,所以CQ DE =QE AE .所以CQ CE =QE AE .因为∠C =∠AEQ =90°,所以△ECQ ∽△AEQ .所以△AEQ ∽△ECQ ∽△ADE .所以S 1S 3=⎝ ⎛⎭⎪⎫EQ AQ 2,S 2S 3=⎝⎛⎭⎪⎫AE AQ 2. 所以S 1S 3+S 2S 3=⎝ ⎛⎭⎪⎫EQ AQ 2+⎝ ⎛⎭⎪⎫AE AQ 2=EQ 2+AE 2AQ 2. 在Rt △AEQ 中,由勾股定理,得EQ 2+AE 2=AQ 2,所以S 1S 3+S 2S 3=1,即S 1+S 2=S 3.。
