辐射度学与光度学基础
第六章-辐射度学和光度学基础

dΦ' dΦ EdS 对朗伯体 dΦ' LdS EdS 1 全扩散表面的光亮度公式 L E
dΦ dS
E
§6-6 全扩散表面的光亮度
常见物体表面的漫反射系统
照明表面
氧化镁 石灰
漫反射系统/%
96 91
照明表面
黏土 月亮
漫反射系统/%
16 10-20
雪
白纸 白砂
78
70-80 25
A的辐射强度应该是辐射体B强度的一半。
§6-4 光度学中的基本量
一、发光强度和光通量 光度学中的光通量与辐射度学中的辐射通量相对应。假定有一单色 光,其辐射通量为 Φ ,其中能够引起视觉的部分为光通量--------用 人眼视觉强度来度量的辐射通量。 对某一立体角 d
Φ C V ( ) Φe
第六章 辐射度学和光度学基础
概述
▲
光学系统是一个传输辐射能量的系统
▲ 能量传输能力的强弱,影响像的亮暗 ▲辐射度学:研究电磁波辐射的测试、计量、 计算的学科 ▲光度学:在人眼视觉的基础上,研究可见 光的测试、计量、计算的学科
§6-1
立体角的意义和它在光度学中的应用
一、立体角的意义和单位
平面上的角: A
全光谱光通量与辐射通量之间的关系
Φ dΦ
0
0
K ( )dΦe
0
K ( )Φe d
定义:光视效能
Φ K Φe
光视效能的单位为:lm/W
0
K ( )Φe d
0
Φe d
§6-4 光度学中的基本量
V ( ) 表示人眼对不同波长光辐射的敏感度差别,
第一章辐射度与光度基础教材

图1 电磁辐射波谱
8
2. 光辐射
以电磁波形式或粒子(光子)形式传播的能量,它们可
以用光学元件反射、成像或色散,这种能量及其传播过程 称为光辐射。 一 般 认 为 其 波 长 在 10nm~1mm , 或 频 率 在 31016Hz~31011Hz范围内。 一般按辐射波长及人眼的生理视觉效应将光辐射分成三 部分:紫外辐射、可见光和红外辐射。
单位:瓦特/球面度米2(W/sr m2)。
d
d
dS S
图2 辐射亮度示意图
22
⑹ 辐射照度:在辐射接收面上的辐照度定义为照射在面元dA 上的辐射通量与该面元的面积之比。即
Ee
de dA
单位:(W/m2)。
(1.2-9)
⑺ 单色辐射度量:对于单色光辐射,同样可以采用上述物 理量表示,只不过均定义为单位波长间隔内对应的辐射度量, 并且对所有辐射量X来说单色辐射度量与辐射度量之间均满 足
Iθ=I0cosθ θ=90°时,Iθ=0
35
二、距离平方反比定律: 描述点辐射源产生的照度的规律。
设:点辐射源的辐射强度为I;源到被照表面P点的距离为d (P点为小面 元dA);小面元dA的法线与到辐射源之间的夹角为θ, 求:点辐射源在P点产生的照度
X e 0 X e, d
(1.2-10)
23
§ 1-2. 光度的基本物理量
由于人眼的视觉细胞对不同频率的辐射有不同响应,故用辐射 度单位描述的光辐射不能正确反应人的亮暗感觉。
光度单位体系是一套反映视觉亮暗特性的光辐射计量单位,在 光频区域,光度学的物理量可以用与辐度学的基本物理量对应的 来表示,其定义完全一一对应。
9
辐射度学和光度学基础

第二节 辐射度学中的基本量
三、辐出射度、辐照度 辐出射度、
假定dS微面辐射出的辐射通量为d 假定dS微面辐射出的辐射通量为d Φ e ,如图a所示:则A点的辐出射度 dS微面辐射出的辐射通量为 如图a所示:
M 为: e =
d Φe dS
把微面dS接受的d dS接受的 dS的比值称为辐照度 的比值称为辐照度。 表示。 把微面dS接受的d Φ e与dS的比值称为辐照度。用 Ee 表示。Ee =
视见函数曲线 有了视见函数就可以比较两个不同波长的辐射体对人眼产生视觉的强 弱
上一页 下一页 返回
第四节 光度学中的基本量
一、发光强度和光通量
根据视见函数的定义, 根据视见函数的定义,人眼产生的视觉强度应与辐射通量和视见函数 成正比,因此, 成正比,因此,我们用
d Φ = C V (λ ) d Φ e
第七节 光学系统中光束的光亮度
二、折射情形: 折射情形:
如图所示,有关系: 如图所示,有关系:
L2 L1 = 2 2 n2 n1
上一页
下一页
返回
第七节 光学系统中光束的光亮度
三、反射情形: 反射情形:
反射可以看成是n2=-n1的折射 反射可以看成是n2=-n1的折射,即L2=L1 的折射, 普遍关系式: 普遍关系式:
上一页 下一页 返回
第二节 辐射度学中的基本量
d Φe Ie = dΦ dΦ
Ie 二、辐射强度:如图所示 辐射强度:
定义:给定方向上的立体角dΩ,在dΩ范围内的辐射通量为:d Φ e dΩ, dΩ范围内的辐射通量为: 定义:给定方向上的立体角dΩ 范围内的辐射通量为 单位: 单位:瓦每球面度
上一页 下一页 返回
如图所示,光亮度用下式表示: 如图所示,光亮度用下式表示:
1辐射度与光度学基础知识

1.4 黑体辐射
2.黑体辐射的三个基本定律 (1)普朗克辐射定律
式中,λ— 波长,m ; T — 黑体温度,K ;
Eb
c15 ec
2
( T )
1
c1 — 第一辐射常数,3.742×10-16 Wm2; c2 — 第二辐射常数,1.4388×10-2 WK;
1
d T 4
式中,σ= 5.67×10-12 w/(cm2K4),是Stefan-Boltzmann常数。
黑体辐射函数 黑体在波长λ1和λ2区 段内所发射的辐射度, 如图1-5所示。
图1-5 特定波长区段内的黑体辐射
1.4 黑体辐射
(3)维恩位移定律
峰值光谱辐射出度Me,s, λm所对应的波长λm与绝对温
Φe(λ)
Φe(λ)=d Φe / d λ
图1-2 光谱辐射通量与波长关系 0
λ λ +d λ
基本辐射度量的名称、符号和定义方程
1.3 光度量的基本物理量
发光强度Iv 发出波长为555nm的单色辐射,在给定方向上的辐 射强度为1/683(Wsr-1)时,在该方向上的发光强度 规定为1cd。单位:坎德拉(Candela)[cd],它是 国际单位制中七个基本单位之一。 光通量Φv 光强度为1cd的均匀点光源在1sr内发出的光通量。 单位:流明[lm]。 光照度Ev 单位面积所接受入射光的量 ,单位:勒克斯 lx,相 当于 1平方米面积上接受到1个流明的光通量。
1.3 光度量的基本物理量
结论
光度量和辐射度量的定义及表达式是一一对应的。
辐射度量下标为e,例如Qe,Φe,Ie,Me,Ee,光 度量下标为v,Qv,Φv,Iv,Lv,Mv,Ev。 光度量只在可见光区(380-780nm)才有意 义。
红外物理(第二版)课件:辐射度学和光度学基础

辐射度学和光度学基础 2.2.3 辐射功率
辐射功率就是发射、传输或接收辐射能的时间速率,用 P 表示,单位是 W,其定义 式为
其中,t为时间,单位为s。
辐射度学和光度学基础
辐射功率主要描述辐射能的时间特性,如许多辐射源的 发射特性,以及辐射探测器的 响应值不取决于辐射能的时间 积累,而取决于辐射功率的大小。
辐射度学和光度学基础 因此,在θ方向观测到的辐射源表面上位置x 处的辐亮度,
就是 Δ2P与 ΔAθ及 ΔΩ 之比的极限值,即
辐亮度的单位是 W/(m2·sr)。
辐射度学和光度学基础
图2-5 辐亮度的定义
辐射度学和光度学基础
由(2-7)式可知,源面上的小面源dA在θ方向的小立体角元 dΩ 内发射的辐射功率为d2P=LcosθdΩdA,所以,dA 向半球空 间发射的辐射功率可以通过对立体角积分得到,即
辐射度学和光度学基础
辐射度学主要是建立在几何光学的基础上,作两个假设: 第一,辐射按直线传播,因 此,辐射的波动性不会使辐射能的空 间分布偏离一条几何光线所规定的光路;第二,辐射 能是不相 干的,所以辐射度学不考虑干涉效应。
与其他物理量的测量相比较,辐射能的测量误差是很大 的,百分之一的误差就认为是 很精确的了。这也只能是在操 作非常小心,所采用的元件、技术、测试标准与上述误差十 分匹配的条件下才能达到的。
辐射度学和光度学基础 对于上述所测量的小面源 ΔA,有
由上式可得
辐射度学和光度学基础 如果小面源的辐亮度L 不随位置变化(由于小面源 ΔA
面积较小,通常可以不考虑L 随 ΔA 上位置的变化),则
即小面源在空间某一方向上的辐射强度等于该面源的辐 亮度乘以小面源在该方向上的 投影面积(或表观面积)。
1.辐射学和光度量学基本概念

辐[射]亮度(或称辐射度) Le 对于小面积的面辐射源,以辐亮度Le来表示其表面不同位置
在不同方向上的辐射特性。
一小平面辐射源的面积为dS,与dS的法线夹角的方向θ上有 一面元dA。若dA所对应的立体角dΩ内的辐通量为dΦe ,
则面源在此方向上的辐亮度为:
式中是面辐射源正对dA的有效面积。辐亮度Le就是该面源在
壳层容纳一定数量的电子。每个电子具有确定的分立能量值, 也就是电子按能级分布。 固体中大量原子紧密结合在一起,而且原子间距很小,以致 使原子的各个壳层之间有不同程度的交叠。最外面的电子壳 层交叠最多,内层交叠较少,如图1-5 所示。壳层的交叠使 外层的电子不再局限于某个原子上,它可能转移到相邻原子 的相似壳层上去,例如电子可以从某个原子的2P壳层转移到 相邻原子的2P壳层,也可能从相邻原子运动到更远的原子的 相近壳层上去。这样电子有可能在整个晶体中运动。晶体中 电子的这种运动称为电子的共有化。外层电子的共有化较为 显著,而内壳层因交叠少而共有化不十分显著。 电子的共有化使本来处于同一能级的电子能量发生微小的差 异。例如,组成固体的N个原子在某一能级上的电子来都具 有相同的能量,由于共有化运动使它们在固体中不仅仅受本 身原子核的作用,而且还受到周围其它原子的作用而具有各 自不同的能量。于是,一个电子能级因受N个原子核的作用 而分裂成N个新的靠得很近的能级。N新能级之间能量差异 极小,而N值很大,于是这N个能级几乎连成一片而形成具 有一定宽度的能带。
其它基本概念 ▪ 点源:照度与距离之间的平方反比定律 ▪ 扩展源:朗伯源的辐出度与辐亮度间的关系 ▪ 漫反射面:漫反射体的视亮度与照度间的关系 ▪ 定向辐射体
d
dA cos
l2
第二章辐射度光度基础
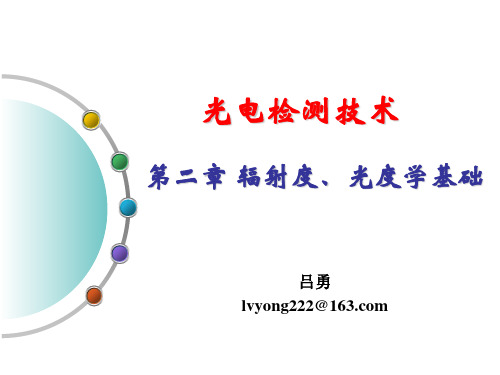
朗伯(J. H. Lambert)定律——余弦定律
• 按照cos 规律发射光通量的规 律,叫朗伯定律; • 余弦辐射体可以是自发光面, 也可以是透射或反射体; • 黑体,太阳和平面灯丝钨丝等 可视为余弦辐射体; • 一个均匀的球形余弦发射体, 从远处的观察者看来,与同样 半径同样亮度的圆盘无疑。
XV Km
780
380
X e ( )V( )d
人眼的光视效能K (lm/W)
V K m 0 V ( ) e ( ) d K K mV e ( ) d
0
e
V ( )视效率
常见光源的光视效能
• 光通量:光源在单位时间内,向周围空间辐射出的、使人 光视效能 光视效能 光源类型 光源类型 眼产生光感觉的能量,称为光通量,用符号Φv表示,单 (lm/W) (lm/W) 位为流明 (lm)。 钨丝灯 (真空) 8~9.2 1W电功率所发出的流明数 日光灯 27~41 • 人们通常以电光源消耗 (lm/W) 钨丝灯 (充气) 9.2~21 高压水银灯 34~45 来表征电光源的特性,称为发光效率,简称光效。电光源 的光效越高越好。 石英卤钨灯 30 超高压水银灯 40~47.5
的余弦变化。
朗伯余弦辐射体
发光强度的空间分布满足 的发光表面叫做余弦辐射体。
I0为发光面在法线方向的发光强度, Iθ为和法线成任意 角度θ方向的发光强度。发光强度向量Iθ端点的轨迹是一个与 发光面相切的球面,球心在法线上,球的直径为I0。
上图为用向量表示的余弦辐射体在通过法线的任意截面 内的光强度分布。
朗伯辐射体的辐射出射度与亮度的关系
dΦ L cos dSd LdS cos d LdS d 2 sin cos d
辐射度学与光度学的基础知识

• 辐射度学基础 • 光度学基础 • 辐射度学与光度学的关系 • 实际应用中的辐射度和光度问题 • 总结与展望
01
辐射度学基础
辐射度学的定义与概念
总结词
辐射度学是研究电磁辐射的发射、传 播、吸收、散射和转换等过程的科学。
详细描述
辐射度学主要关注电磁辐射的能量、 功率、辐射通量、辐射强度等物理量 的测量和计算,以及这些物理量在不 同介质和环境中的变化规律。
02
光度学基础
光度学的定义与概念
总结词
光度学是研究光辐射的度量、测量和应用的学科,它涉及到光辐射的定量描述和测量。
详细描述
光度学主要研究光辐射的属性、度量单位、测量方法和应用。它关注的是光辐射的能量、 功率和辐射通量等物理量的度量,以及这些物理量在不同媒介中的传播、散射和吸收等
行为。
光度量
1. 光通量
光度定律
总结词
光度定律是描述光辐射在不同媒介中传播时遵循的规律, 包括斯涅尔定律、反射定律和折射定律等。
1. 斯涅尔定律
也称为反射定律,它描述了光线在两种不同媒介的交界面 上的反射和折射行为,即入射角等于反射角,折射角与入 射角成正比。
2. 折射定律
当光线从一种媒介进入另一种媒介时,其传播方向会发生 变化,这个变化与两种媒介的折射率有关。折射定律描述 了折射光线与入射光线之间的关系。
光源的辐射度和光度性能
光谱分布
不同光源的光谱分布不同,这决定了它们在颜色 表现、显色指数等方面的性能。
光效
光效是衡量光源效率的指标,光效高的光源在相 同亮度下消耗的电能更少。
寿命与稳定性
光源的寿命和稳定性也是重要的性能指标,它们 决定了光源的使用和维护成本。
辐射度与光度学的基础知识

Xνλ——光度量;Xeλ——辐射量; Km是常数;V(λ)光谱光视效率。 5. 明视觉和暗视觉:人眼在环境亮度不同时对 颜色的视觉效率不同。 明视觉:光亮度大于几个cd/m2 暗视觉:光亮度小于0.01cd/m2
二、光度的基本物理量
1. 光通量
单位时间内光源发出的光能量(功率)
780nm
K m
注:
1. 光度量的定义和辐射度量的定义只一字之差,‚
2. 3. 4. 5. 辐射‛——“光‛。 下角标有e、λ、ν,辐射量在与其它量同用时 标e。 从表达式可直接说出定义及物理意义 从表达式可直接说出单位 出射度和照度的表达式相同、单位也相同,注 意一个是发射,一个是接收。
三个发射量的区别和关系
是辐射量对人眼视觉的刺激值。是主观的,不管辐射量大小 ,以看到为准。光谱光视效率是评定该刺激值的参数。 基本物理量是发光强度,单位坎德拉。一个光源发出频率 为540*1012Hz的单色辐射,若在一给定方向上的辐射强度
为1/683W/sr,则该光源在该方向上的发光强度为1cd。
一、光谱光视效能和光谱光视效率
光谱光视效能(K) ,描述某一波长的单色光辐射 通量产生多少相应的单色光通量。即光视效能K定 义为同一波长下测得的光通量与辐射通量的比值, 即
Φ ——在波长λ处的光通量 Φeλ ——在波长λ处的辐射通量 单位:流明/瓦特(lm/W)。
νλ
通过对标准光度观察者的实验测定,在辐射频率
5401012Hz(波长555nm)处,K有最大值,其
黑体 在物理学中,所谓黑体,是指这样 一种物体,在任何温度下,它将入射的任 何波长的电磁波全部吸收,没有一点反射, 而在相同温度下,它所发射出的热辐射比 任何其他物体都强。 光有多种颜色组成, 黑色吸收所有颜色,不反射任何颜色,即没 有光线进入眼睛时,称之为黑色。如果一个 物体能够全部吸收而不反射投射于其上的 辐射,就称它为绝对黑体,简称为黑体。
辐射度学与光度学基本知识

光照度Ev:单位面积所接受的入射光的量 ,单位:勒 克斯[lx],相当于 1平方米面积上接受到1个流明的 光通量。
光度的基本物理量总结
光度量和辐射度量的定义、定义方程是一一对应的
– 辐射度量下标为e,例如Qe,Φe,Ie,Me,Ee – 光度量下标为v,Qv,Φv,Iv,Lv,Mv,Ev
– 有时为了充分利用光源,常在光源上附加一个反射装置, 使得某些方向能够得到比较多的光通量,以增加这一被照 面上的照度。例如汽车前灯、手电筒、摄影灯等。
– 黑夜:0.001—0.02;月夜:0.02—0.3; 阴天室内:5—50;阴天室外:50—500; 晴天室内:100—1000; 夏季中午太阳光下的照度:约为109; 阅读书刊时所需的照度:50—60; 家用摄像机标准照度:1400
• 当光通量到达一个表面时,我们用辐照度E (irradiance) 这一 词。
• 当光通量离开一个表面时,我们用辐出度M(radiance exitance)这一词,辐出度有时也称辐射度(Radiosity)。
立体角
• 在计算机图形学中,光源和视点常被看成点。用面积来度 量不太适合,而是用立体角(solid angle)来描述。立体角的 度量单位为球面度sr(steradians) 。
• 等价于每焦耳的光子数目为5.034×1015乘以光子的波长。 例如,在波长为550nm的波段处,每焦耳的光子数目大约 为2.77×109个。
光通量密度
• 光源的光通量Φ为每秒钟发射出的焦耳数(dΦ/dt)。也可用瓦特 W来度量(1W=1J/s)
• 在光子离开光源后,下一步为如何度量它们到达表面。光通量 密度为单位面积接收的光通量,用瓦特/米2来度量。光通量密 度的概念可以应用于任何表面,无论是真实的或虚拟的。
大学物理下_第12章_辐射度学和光度学基础

d内的光通量
dv
Ivd
IvdS cos
r2
de
n
dS dS
dS面上的光照度
Ev
dv dS
Iv cos
r2
它描述了点辐射源产生的照度的规律,是 来自均匀点光源向空间发射球面波的特性。
24
大学物理
例12-1 一氦氖激光器发出10mW的波长为632.8nm的激 光束,发散角为1mrad,发散角与立体角的关系 为 2 ,若波长632.8nm光波的光谱光效率 V=0.24, 试求: (1)此激光束的光通量和发光强度; (2)若此激光输出光束的截面的直径为1mm,求其光亮度; (3)以这样的激光束照射在10m处的白色屏幕上的光照度.
同一波长下测得的光通量与辐射通量的比之,即
K
v e
单位:流明/瓦特(lm/W)
通过对标准光度观察者的实验测定,在辐射频率 5401012Hz(波长555nm)处,K有最大值,其数值为 Km=683lm/W。
单色光视效率是K用Km归一化的结果,定义为
V
K Km
1 Km
v e
大学物理
例12-1 一氦氖激光器发出10mW的波长为632.8nm的激 光束,发散角为1mrad,发散角与立体角的关系 为 2 ,若波长632.8nm光波的光谱光效率 V=0.24, 试求: (1)此激光束的光通量和发光强度; (2)若此激光输出光束的截面的直径为1mm,求其光亮度; (3)以这样的激光束照射在10m处的白色屏幕上的光照度.
解:(3)激光在屏幕上照射的面积
S r 2 102 3.14 106 3.14 104 m2
辐射度与光度学的基础知识

辐射度与光度学的基础知识目录一、辐射度学基础知识 (3)1. 辐射度概念及原理 (4)1.1 辐射度的定义 (5)1.2 辐射度的物理量及其单位 (5)1.3 辐射源的类型与特点 (6)2. 辐射的传播与转换 (7)2.1 辐射的传播方式 (8)2.2 辐射能的转换与传输 (10)2.3 辐射强度的衰减规律 (11)二、光度学基础知识 (12)1. 光度学概述 (13)1.1 光度学的定义与目的 (14)1.2 光学系统的基本组成 (15)1.3 光度学与辐射度学的关系 (16)2. 光学量的测量与计算 (17)2.1 光照度及其测量 (18)2.2 亮度及其计算 (19)2.3 色温与显色指数 (20)三、辐射度与光度在照明设计中的应用 (21)1. 照明设计基本原理 (22)1.1 照明设计的基本要求 (23)1.2 照明设计的步骤与方法 (24)1.3 照明设计的注意事项 (25)2. 辐射度与光度在照明设计中的应用实例 (26)2.1 室内照明设计 (27)2.2 室外照明设计 (28)2.3 特殊场合照明设计 (30)四、辐射安全与防护 (32)1. 辐射安全基础知识 (33)1.1 辐射的种类与特点 (35)1.2 辐射对人体的影响 (36)1.3 辐射安全标准与规范 (37)2. 辐射防护措施及方法 (38)2.1 时间防护 (39)2.2 距离防护 (40)2.3 屏蔽防护 (41)2.4 个人剂量监测与健康管理 (42)五、实验及案例分析 (43)1. 实验教程 (45)1.1 实验一 (46)1.2 实验二 (47)1.3 实验三 (48)2. 案例分析 (49)2.1 案例一 (50)2.2 案例二 (51)一、辐射度学基础知识辐射源与辐射类型:辐射源是发出辐射能量的物体或点。
辐射可以是电磁辐射,如可见光、红外线和紫外线等;也可以是粒子辐射,如电子和光子等。
在光度学中,主要关注的是电磁辐射。
第1章 光电检测技术中的基础知识

(2)空穴扩散电流密度
J
pD
qD
d ( p )
p
dx
Dn和Dp是电子和空穴的扩散系数,式中负号表示空穴扩 散方向由高浓度向低浓度运动。
2、漂移运动
漂移运动是在电场作用下,除了热运动之外获得的 附加运动。 如在外加电场的作用下,电子的电流密度:
(2) 发光强度Iv:点光源单位立体角内所发出的光 通量,称为光源在该方向上的发光强度。
I v d v / d
单位:cd ,是国际单位制中七个基本单位之一。 1cd是指光源在给定方向上发出波长为555nm的单 色辐射,且其辐射强度是1/683W/sr。
意义:描述光源发出的光通量在空间一定范围内的分布 值。
cd,lm/sr
nt, cd/m2 lx,lm/m2 lx,lm/m2
I d / d
L d / d dA cos
2
= dI / dA cos
辐射出射度 Wm-2 辐射照度 Wm-2
M d / dA
E d / dA
辐射度学与光度学的比较 1、两者的相同点: ①光度量和辐射度量的定义、定义方程是
3、非平衡载流子的产生 产生非平衡载流子的方式:光照、电注入或其他能 量传递方式。 如:光照产生非平衡载流子的过程,如图所示:
n
光照
p
在一般情况下,注入的非平衡载流子浓度比平衡时的多数载流子浓度 小很多,如n型材料,△n≤n0, △p≤n0,满足这个条件称小注入。
4、非平衡少数载流子寿命
有光等外界影响发生时,载流子产生率大于复合率,并最 终平衡;光等外界因素消除时,复合率大于产生率,并最后 趋于平衡。 当给半导体材料去掉外界条件(停止光照)时,由于净复 合的作用,非平衡载流子会逐渐衰减以致消失,最后载流子 浓度恢复到平衡状态时的值。但非平衡载流子不是立刻消失, 而是有一个过程,即他们在导带和价带上有一定的生存时间。 这些非平衡少数载流子在半导体内平均存在的时间称为非平 衡载流子的寿命,简称少子寿命, 用τ 表示。非平衡少数 载流子寿命的衰减规律成指数衰减
12辐射度学与光度学基本知识
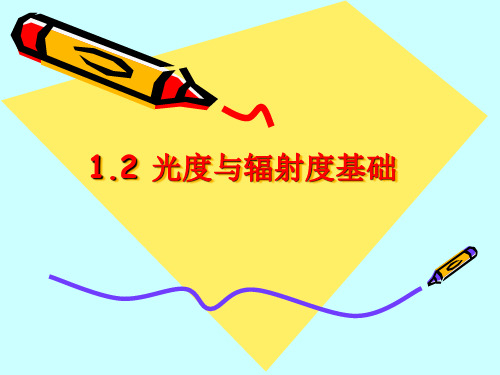
三个发射量的区别和关系
源特点
辐射强度I 点源
辐射出射度 M
面源
辐射亮度L 面源
辐射特点 立体角内 2π空间 立体角内
§2-4 朗伯余弦定律和漫辐射源的辐射特性
一、漫辐射源: 辐射亮度L与方向无关的辐射源。(太阳、 荧光屏等) 漫辐射:漫辐射源发出的辐射 漫反射:与漫辐射具有相同特性的反射。 (电影屏幕等)
所对应的立体角称为一个单位立体角,或一球面 度。
• 对于一个给定顶点O 和一个随意方向的微小面积 dS ,它们对应的立体角为
d
dS cos
R2
• 其中θ为dS 与投影面积 dA的夹角,R为O 到dS中 心的距离。
[例] • 1、球面所对应的立体角:根据定义
S R2
• 全球所对应的立体角
4R2 4
• 数学描述:若辐射源的微小面积△A向半球空间 的辐射功率为△Φ,则△Φ与△A之比的极限值定 义为辐射出射度.
lim M
A0 A A
单位:w/㎡
• 物理描述:扩展源单位面积向半球空间发射的功 率(或辐射通量)。
扩展源总的辐射通量,等于辐射出射度对辐射表 面积的积分:
M dA
A
A为扩展源面积。
IP
P
LP
2P
Acos
光子辐射度 光子照度
MP
P A
LPcosd
EP
P A
§2.3光度量
• 光度量:辐射量对人眼视觉的刺激值。 是主观的,不管辐射量大小,以看到为 准。 光谱光视效能是评定该刺激值的参数。
1.光谱光视效能和光谱光视效率
• 即光人视眼效对能不同K波 长的eΦ辐ν—射—产光生通光量感觉Φ的e—效—率辐。射通量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
吸收系数通常用α表示,它在数值上等于光波强度因吸收而减弱 到1/e时透过的物质厚度的倒数,它的单位用cm-1表示。 吸收系数与材料的特性有关,各种物质的吸收系数差别很大, 一般对可见光而言,金属的吸收系数为α≈106cm-1, 玻璃的吸收系数为α≈10-2cm-1, 一个大气压下空气的吸收系数为α≈10-5cm-1, 这就表示空气的吸收最小,玻璃次之,而金属的吸收较大, 故极薄的金属片就能够吸收掉入射的全部光能,因此金属一般并 不透明,而空气和玻璃则是透明的。 光学玻璃的光吸收系数分为六类,最小为0.001,最大为 0.03,故多数无色透明光学玻璃对白光的平均吸收系数取均 值,即α≈0.015cm-1,而1-α则表示透明系数。
光在透明介质中传播所产生的能量损失不仅与介质的吸收系数有 关,还与光学零件的厚度有关,一般来说光学零件越厚其能量吸
收也就越多,损失也就越大。若系统中所使用材料的吸收系数相
同,且所有元件中心厚度之和为d(单位为cm),考虑到介质 吸收而造成的能量损失,其透过的光通量为
d (1 )
上述计算与比较表明,在照明系统中加入聚光镜后,可使被照明 平面上的照度得到显著提高(本例照度增强近40倍),因而体现 了照明系统中聚光镜的重要作用。
余弦辐射体
6.7光学系统中光通量与光亮度的传递
1、在介绍光度学基本概念的基础上,研究光学系统中光能的传递
与变化规律。 2、光学系统可以视为光能的传递系统,我们除关心最终像面处
(或接收器处)的光能情况外,还常常关心光学系统中间过程光
能的传递规律。 3、光能在光学系统中的传递与变化规律,可以通过两个量来表征,
即光通量与光亮度。
4、光通量的传递规律比较简单。如果不存在传递过程中的拦光、 吸收、反射等损失,则由能量守恒定律可知,从系统出射的光
通量应等于进入系统的光通量,即在传递过程中,光通量 应保持不变;
由于光传递过程中能量是守恒的,故dΦ1=dΦ2,相应得到
2.不同介质分界面上光亮度的传递 一束光射向两个不同透明介质n、n′分界面上时将同时发生反 射和折射,各参量如下图所示,若不考虑介质吸收及散射,则 入射光能dΦ= 反射光能dΦ″+折射光能dΦ′ 投射在介质分界面上的微面元 之上。
以入射角i投射在介质分界面上的微面元dS之上,反射角、折射
*
而系统总的透过率τ为
*
例:如图所示,该系统由两个透镜组Ⅰ、Ⅱ及一个镀银的反射面 构成。透镜组Ⅰ的有关数据如表所示,透镜组Ⅱ的透过率 τ2=0.66,求整个系统的透过率τ。
解 各元件中心厚度之和为 d=8.257cm,故
整个系统的透过率为
由于胶合面的光能损失很小故可 忽略不计,
8) 由于透过率τ可表示为透射的光通量Φ′与入射的光通量Φ之比,
即
则单个折射面的透过率为 τ=1-ρ 9)若系统由k个折射面构成,则当光射入系统时将在每一个不同 透明介质分界面上都存在一定程度的反射损失,射出系统的光通 量
式中,ρ1,ρ2,…,ρk分别表示第一个折射面,第二个折
射面,…,第k个折射面的反射率。整个系统的透过率则为
4.光学系统的总透射率 由于光学系统中往往既有折射元件又有反射元件,为计算光经过 整个光学系统的光能损失,就需要同时考虑透明介质分界面的反 射损失、反射面的光能损失和透明介质材料的吸收损失。若系统 由k个折射面、m个反射面构成,且存在n种介质材料,相应材 料制成元件的中心厚度之和分别为Σd1,Σd2,…,Σdn, 各种介质材料的吸收率分别为α1,α2,…,αn,各折射面 的反射率分别为ρ1,ρ2,…,ρk,各反射面的反射率分别为 ρ′1,ρ′2,…,ρ′m,射入系统的光通量为Φ,则射出系 统的光通量Φ′为
由高斯公式
1 1 1 在空气中 l l f h h h h 乘h : tgu tgu l l f f h tgu tgu f
由上述光束变换分析,可求得灯泡A的位置:
(2)求光源经聚光镜成像前后的照明立体角由孔径角与立体角
之间的转换式,可求光源A对聚光镜构成的立体角为
Φ″=ρ′Φ 而且反射面越多,由此所造成的光能量损失就越大。若系统中存在
m个反射面,则反射后的能量为
式中,ρ′1,ρ′2,…,ρ′m分别代表第一个,第二个,…, 第m个反射面的反射率。 3.透明介质材料的吸收损失 光在透明介质中传播时也存在一定程度的能量吸收,只不过吸 收比较小而已,所以在前面探讨中没有过多考虑它的吸收效应。但 实际上光在介质中传播时的吸收损失也是不可忽略的,其吸收能量 的大小与介质的吸收系数密切相关。
这意味着在系统传递过程中不可避免地存在一定的光能损失。
造成光能损失的因素是多方面的,主要体现在透明介质分界面的 反射损失、反射面的光能损失和透明介质材料的吸收损失。
1.透明介质分界面的反射损失
1)按照折射定律和反射定律,当光照射到两个透明介质分界面上
(折射率分别为n、n′)时将同时发生反射及折射,
故由于反射造成的光能损失约为1-τ4≈0.1。
② 若两透镜不用树胶黏合,而仅是留有一空气薄隙时,则同理 可得
由于反射造成的光能损失约为1-τ4≈0.18。
此外,从例可见,在每一个空气玻璃介质分界面上都将产生4% ~6%的光能损失,若光学系统由多个折射面构成,则仅由于反 射所产生的光能损失就相当可观。 一般情况下可认为未镀增透膜表面的冕牌玻璃透过率τ≈ 0.96,火石玻璃透过率τ≈0.95,镀增透膜表面的透 过率τ≈0.98。 2.反射面的光能损失 1)光系统中存在大量的反射元件,反射元件将涂镀不同的金属材料 (或介质材料)以提高其反射性能。 2)由于金属层(或介质层)反射面也不同程度上存在一定的光能 吸收,不能将入射其上的光通量全部反射,因此反射面的吸收 损失也是必须要考虑的一个主要因素。 3)以金属反射面为例,由于其反射率与所使用的材料、波长及所 使用的工艺方法有关,在可见光区范围内多使用银(化学镀银 后镀铜,再涂保护漆,反射率ρ′≈0.95)和铝(真空镀 铝后氧化加固,反射率ρ′≈0.85)作为反射材料,但是 毕竟存光能损失。设入射的光通量为Φ,则反射的光通量为
6)实际上,光束经光学系统传播时光线在每一个面上的入射角很少
会超过45°,因此光学系统的反射率可以近似用垂直入射时反射
率的相关公式进行计算,即
7)从式可见,反射率仅取决于介质分界面两侧的折射率大小,n′
、n的差值越大,反射率就越大。若不考虑吸收及散射,则反射
光通量Φ″、透射光通量Φ′与入射光通量Φ是守恒的,即
dΩ=dΩ″,则
ρ为n、n′介质分界面上的反射率,故有
即反射光光亮度等于入射光光亮度与介质分界面的反射率之积。
2)折射光的光亮度传递
对折射定律公式两边进行微分有
n sin i n sin i
将折射定律nsini=n′sini′与微分式相乘,有
进一步整理得到
又由于dΦ′=dΦ-dΦ″, 则透射率
借助于元光管概念来研究。
1.单一无损介质中光束光亮度的传递) 如图:
1)假设任意两个微面元dS1、dS2,两面元之间的距离为r, 2)面元各自法线方向与r之间的夹角分别为i1、i2, 3)dS1 上的光亮度为L1,dS2 上的光亮度为L2, 4)dS2 对dS1 所张的立体角为dΩ1,dS1 对dS2 所 张的立体角为dΩ2。
5)若光能量在传递过程中没有光能损失(不考虑介质吸收、散
射等因素),即dS1 发出的光能量全部传递到dS2 上
(或dS2 发出的光能量全部传递到dS1 上), 6)则由dS1 辐射出的到达dS2 上的所有光通量为
由 L
d ds cos id
得
相应地由dS2 辐射出的到达dS1 上的所有光通量为
计算表明,光源经聚光镜后,虽光通量未变,但由于ω′大大减 小,光能重新分配,故 I′大大增强。
(4)计算被照圆屏上的平均照度 被照明的圆面积为:
圆面积上的平均光照度为
(5)对比光源直接照明圆屏(不加聚光镜)的效果: 光源对圆屏所构成的光锥角α为
对应的立体角为
被照圆屏上所接受的光通量为
圆屏上的平均照度为:
角分别用i″、i′表示,
设入射光、反射光、折射光的光亮度分别为L、L″、L′,各自 所对应的立体角分别为dΩ、dΩ″、dΩ′,则根据立体角公 式有
入射光、反射光及折 射光的光通量分别为
1)反射光的光亮度传递) 根据反射定律i=i″,故sini=sini″, cosi=cosi″,di=di″,由上边式子可得
d d d 1 d d
表明,折射光束的光亮度与介质分界面的透射率及两边介质的折
射率有关。
若折射前后光能没有损失即ρ=0,τ=1,则式又可以转化为
即折射前后光亮度虽然发生改变,
L 但是 2 值保持不变。 n
6.8光学系统的光能损失
任何一个实际的光学系统都不可能完全透明, 射入系统的光能量Φ永远要大于射出系统的光能量Φ′, 即光学系统的透过率τ=Φ′/Φ<1,
τk=Φk’/Φ=(1-ρ1)(1-ρ2)…(1-ρk) 光学系统的透过率实际上反映了经过系统之后光通量的损失 程度,透过率值越小说明光通量损失越大。 例 一胶合物镜由两片透镜组成,其折射率分别为n1= 1.52,n2=1.60,这两片透镜用n=1.54的树胶
黏在一起,设光在透镜上的入射角都很小,①试求光在透过此物 镜时由于反射而造成的光能损失;②若两透镜不用树胶黏合,而 仅是留有一空气薄隙,由于反射而造成的光能损失又是多少? 不考虑介质吸收及散射。
光源像A′对圆屏所构成的立体角为u′
(3)计算光源在聚光镜前后的发光强度
卤钨灯发出的总光通量为
假定卤钨灯可近似视为各向均匀发光的点光源,它在通过聚光镜的部分为
忽略经聚光镜的光能损失,即经聚光镜后光束的立体角变为ω′, 但光通量不变,应有
因而可求出经聚光镜后的发光强度为
