圆锥曲线的原理最详细图解(平面与圆锥面的截线)
圆锥曲线的原理最详细图解(平面与圆锥面的截线).

平面与圆锥面的截线一、直观感受:观察平面截圆锥面的图形,截线是什么图形?改变平面的位置,可得到三种曲线,它们统称为圆锥曲线(下图由软件《立几画板》制作):二、分类探究:从平面图形入手,开始讨论一条直线与等腰三角形的位置关系:将等腰三角形拓广为圆锥,直线拓广为平面。
如果用一平面去截一个正圆锥,而且这个平面不通过圆锥的顶点,会出现哪些情况呢?如下图:归纳提升:定理在空间中,取直线l为轴,直线l'与l相交于O点,其夹角为α,l'围绕l旋转得到以O为顶点,l'为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行,记作β=0),则:(1)β>α,平面π与圆锥的交线为椭圆;(2)β=α,平面π与圆锥的交线为抛物线;(3)β<α,平面π与圆锥的交线为双曲线。
三、证明结论:利用Dandelin双球(这两个球位于圆锥的内部,一个位于平面的上方,一个位于平面的下方,并且与平面及圆锥均相切)证明:β>α,平面与圆锥的交线为椭圆.如图,利用切线长相等,容易证明PF1+PF2=PQ1+PQ2=Q1Q2=定值.下面证明:β=α时,平面与圆锥面的交线为抛物线。
下面讨论当平面与圆锥面的交线为双曲线时准线的及离心率:换个角度看图:容易知道:截得的圆锥曲线的离心率等于截面和圆锥轴的夹角的余弦与圆锥顶角一半的余弦之比.四、知识运用用图霸制作三维直观图:解答参看下图:五、图形制作三种曲线的丹迪林Dandelin双球图可以在《几何图霸》中统一到一幅图中,主要制作步骤如下:1.作全自由点O,过点O作平行于z轴上的点B,过B作平行于x轴上的点C,作点B、C 关于O的对称点B’、C'.2.选取点O、B、C,作圆锥,选取点O、B’、C’,作圆锥.3.在圆B上任取点D,作D关于B对称点,连接OD,OD’,在OD上任取一点E,以E 为圆心画过点D’、D的心点圆,在圆E上任取点F,连EF,它表示截面的位置,可以绕点E转动.4.作角OEF的平分线,与轴BB’交于O1;作角DEF的平分线,与轴BB’交于O2,它们就是双球的球心.5.过球心O1、O2分别作边EF的垂线,垂足分别为F1、F2,它们就是焦点.6.选取点O1、F1,作球O1(图中显示大圆,光照后显示为球),同法作球O2.7.取线EF上的点G、H,作GDO垂线上的伸缩点I,作点I关于点G的对称点I’,按向量GH平称点I、I’,得点I2、I".添加面II2I"I’,连接四边,表示截面.它的长宽可以用点G、H、I控制;点F控制其转动.8.添加下底圆上的点J,连结OJ交截面于点K,选取点J、K,添加轨迹,它就是截线,如上图中的椭圆.9.点E按向量OD’平移得点E’,EE’交圆于点G1,EG1平行于母线OD’,添加点F到点G1的动画,名为“抛物线”.10.参看前面各图添加其它图元.下载图霸文件后在“对象浏览器”中查看各对象.课件下载:共享文件下载中心相关文章:1 利用丹迪林Dandelin双球证明平面与圆锥面的截线定理2平面与圆柱面的截线更多文章:《几何图霸》文章列表几何图霸网站:。
圆锥曲线的基本概念与图像

确定圆锥曲线的类型和参数
绘制圆锥曲线的常用方法
极坐标法:将圆锥曲线转换为极坐标形式,然后绘制出曲线的图像。
数值法:通过数值计算的方法,近似地绘制出圆锥曲线的图像。
直接法:根据圆锥曲线的定义和性质,直接绘制出曲线的图像。
参数法:通过引入参数方程,将圆锥曲线表示为参数方程,然后绘制出曲线的图像。
绘制圆锥曲线的注意事项
圆锥曲线的焦点与准线
焦点:圆锥曲线上的点到曲线的两个焦点的距离之和等于常数
准线:与圆锥曲线的母线平行的直线,与曲线相交于焦点
圆锥曲线的离心率
定义:圆锥曲线的离心率是用来描述圆锥曲线形状的一个重要参数,定义为焦距与轴线长度之比。
单击此处添加标题
单击此处添加标题
计算方法:离心率可以通过圆锥曲线的标准方程进行计算,也可以通过图形直观地测量得出。
圆锥曲线在三维空间中的形态和性质
圆锥曲线在解决实际问题中的应用
圆锥曲线在解决几何问题中的优势和局限性
05
圆锥曲线在物理中的应用
圆锥曲线在光学中的应用
椭圆和抛物线的光学性质
双曲线的光学性质
圆锥曲线在光学仪器中的应用
圆锥曲线在光波导中的应用
圆锥曲线在力学中的应用
抛物线在射程运动中的应用
圆锥曲线在碰撞与动量守恒定律中的应用
特性:渐近线的斜率等于圆锥曲线在顶点处的切线斜锥曲线的类型,渐近线可分为水平渐近线、竖直渐近线、斜渐近线等
03
圆锥曲线的图像绘制
绘制圆锥曲线的基本步骤
使用绘图软件或手动画图,连接点形成曲线
根据参数方程计算曲线上点的坐标
建立坐标系,确定坐标轴
抛物线在几何问题中的应用:抛物线的性质,如所有从焦点出发的线段都与抛物线相切,使得它在解决与焦点、准线和切线相关的问题中非常有用。
“高中数学课件-圆锥曲线”

抛物线
抛物线是另一种圆锥曲线形式,其特点是离焦点和准线的距离相等。它在物理学和工程学中常用于描述抛体的轨迹。
双曲线
双曲线是圆锥曲线的第三种形式,其特点是离焦点和准线的距离之差固定。它在物理、电子学和天文学中有广泛的 应用。
圆锥曲线的性质
对称性
圆锥曲线通常具有对称性,可 以通过某种轴或中心进行对称。
焦距与半径
焦距与半径是圆锥曲线的重要 性质,它们决定了曲线的形状 和特性。
离心率
离心率是描述曲线形状的重要 参数,在椭圆、抛物线和双曲 线中有不同的取值。
判定圆锥曲线的方法
1 焦点和准线
2 轨迹类型
根据给定的焦点和准线坐标, 可以确定圆锥曲线的形状和 方程。
圆锥曲线的轨迹类型(椭圆、 抛物线、双曲线)可以通过 经验判断或图形分析得出。
极坐标方程的抛物线
同样,抛物线也可以用极坐标方程来描述。通过极径和极角,我们可以方便地表示抛物线的形状和位置。
双曲线的性质
双曲线具有独特的性质,如焦点与准线的距离之差、离心率的关系、边缘的特点等。它在物理学和工程学中有广泛 的应用。
双曲线的方程
双曲线的方程可以通过焦点和准线的坐标来表示。这是描述双曲线形状和位 置的重要工具。
孤点椭圆
孤点椭圆是一种特殊的椭圆形状,它只有一个焦点,没有准线。它在天文学 和轨道动力学中有重要的应用。
抛物线的性质
抛物线具有许多有趣的性质,如焦点与准线的距离相等、对称性、方程的特 点等。
抛物线的方程
抛物线的方程可以通过焦点和准线的坐标,或者通过经验公式来表示。这是 描述抛物线形状和位置的重要工具。
高中数学课件——圆锥曲 线
让我们一起探索圆锥曲线吧!从基本形式到各种性质,以及判定方法和方程。 让数学变得有趣和令人着迷!
圆锥曲线 课件

利用线性代数知识求解圆锥曲线问题
线性方程组
线性方程组是线性代数中的基础内容, 它可以用来求解与圆锥曲线相关的问题 。例如,通过解线性方程组,可以找到 满足特定条件的点的坐标。
VS
特征值与特征向量
特征值和特征向量在解析几何中也有广泛 应用。通过计算圆锥曲线的特征值和特征 向量,可以深入了解曲线的性质,从而更 好地解决相关问题。
椭圆离心率的范围是0<e<1,双曲线的离心率范围是e>1。
圆锥曲线的光学性质
01
光线经过圆锥曲线上的点时,其 方向会发生改变,这种现象叫做 圆锥曲线的光学性质。
02
光线经过椭圆时,会沿着椭圆的 主轴方向折射;经过双曲线时, 会沿着双曲线的副轴方向折射。
圆锥曲线的对称性
圆锥曲线具有对称性,即如果将圆锥 曲线沿其对称轴旋转180度,它仍然 与原来的曲线重合。
02 圆锥曲线的性质
焦点与准线
焦点
圆锥曲线上的点到曲线的两个焦 点的距离之和等于常数,这个常 数等于椭圆的长轴长,等于双曲 线的实轴长。
准线
与圆锥的母线平行的线,在平面 内与准线相交的直线与圆锥相切 于一点,这个点叫做切点。
离心率
离心率:是描述圆锥曲线形状的一个重要参数,它等于圆锥顶点到曲线的距离与 圆锥的半径之比。离心率越大,圆锥曲线越扁平,反之则越接近于球形。
双曲线的极坐标 方程
$frac{rho^2}{a^2} frac{rho^2}{b^2} = 1$
圆锥曲线在极坐 标下的表…
将圆锥曲线问题转化为极 坐标形式,便于理解和求 解。
利用极坐标求解圆锥曲线问题
利用极坐标求解圆锥曲线问题的步骤
首先将问题转化为极坐标形式,然后利用极坐标的性质和公式进行求解。
圆锥曲线定义(适合公开课) PPT

第三章Biblioteka 2019/09/301 圆锥曲线 前世今生
•圆锥面
•定义
两直线相交,其中一条直线
以另外一条直线为旋转轴进
行旋转所形成的曲面,称为
圆锥面。
也可以理解为两个全等的圆 锥顶点重合,高线重合,相 对放置时,两个侧面所形成 的的整体。
母线和圆锥的夹角为半顶角α。
•圆锥曲线
平面截圆锥面所得到的曲线,叫做圆锥曲线。 根据平面与圆锥轴线所成的角θ不同,所截圆锥曲线也不同。
•圆
•椭圆
大家应该也有点累了,稍作休息
大家有疑问的,可以询问和交流
•抛物线
•双曲线
2 圆锥曲线 平面定义
•圆锥曲线
•圆
平面内,到一个定点的距离为定长的点构成的集
合.
椭圆 平面内,到两个定点的距离之和为定长(大于两 定点之间的距离)的点构成的集合.
抛物线 平面内,到一个定点的距离与到一条定直线(不 过定点)的距离相等的点构成的集合.
双曲线 平面内,到两个定点的距离之差为定长(小于两 定点之间的距离)的点构成的集合.
•椭圆
•抛物线
•双曲线
3 圆锥曲线 光学性质
•椭圆
一个焦点处出发的 光,经反射后汇聚 到另一个焦点。
•抛物线
焦点处出发的光, 经反射后变成平 行光。
•双曲线
一个焦点处出发的光, 经反射后看上去就好像 是从另一个焦点处出发 的光。
其实,这哪里是什么悲伤的双曲线? •悲伤的双曲线 渐近线,越走越近,又给了彼此空间!
词、曲、唱:王渊超 如果我是双曲线,恩~你就是那渐近线 如果我是反比例函数,你就是那坐标轴 虽然我们有缘,能够生在同一个平面 然而我们又无缘,恩~慢慢长路无交点 为何看不见,等式成立要条件 难到正如书上说的,无限接近不能达到 如果我是双曲线,恩~你就是那渐近线
圆锥曲线知识图表

6.共渐近线的双曲线系方程.
二、抛物线的标准方程、类型及其几何性质:
图形
焦点
准线
范围
对称轴
轴
轴
顶点
(0,0)
离心率
焦点
注:① 顶点 .
② 则焦点半径 ; 则焦点半径为 .
③通径为2p,这是过焦点的所有弦中最短的.
④ (或 )的参数方程为 (或 )( 为参数).
2.与定点和直线的距离之比为定值e的点的轨迹.(e>1)
与定点和直线的距离相等的点的轨迹.
图形
方
程
标准方程
( >0)
(a>0,b>0)
y2=2pxb
|x|a,yR
x0
中心
原点O(0,0)
原点O(0,0)
顶点
(a,0), (─a,0), (0,b) , (0,─b)
(a,0), (─a,0)
(0,0)
对称轴
x轴,y轴;
长轴长2a,短轴长2b
x轴,y轴;
实轴长2a,虚轴长2b.
x轴
焦点
F1(c,0), F2(─c,0)
F1(c,0), F2(─c,0)
焦距
2c(c= )
2c(c= )
离心率
e=1
准线
x=
x=
渐近线
y=± x
焦半径
通径
2p
焦参数
P
1.椭圆、双曲线、抛物线的标准方程的其他形式及相应性质.
高中数学圆锥曲线知识图表
一、椭圆、双曲线、抛物线的标准方程与几何性质
椭圆
双曲线
抛物线
圆锥曲线的截法

圆锥曲线的截法
圆锥曲线的截法是指将一个圆锥曲线与一直线相交所得的交点。
不同的圆锥曲线有不同的截法。
1. 椭圆的截法:椭圆与一直线的截点是椭圆上的两个点,除非直线与椭圆相切于唯一一点或者不与椭圆相交。
2. 双曲线的截法:双曲线与一直线的截点是双曲线上的两个点,除非直线与双曲线相切于唯一一点或者不与双曲线相交。
3. 抛物线的截法:抛物线与一直线的截点是抛物线上的一个点,除非直线与抛物线相切于该点或者不与抛物线相交。
在实际应用中,可以根据截法确定圆锥曲线的方程和特征。
圆锥曲线知识点图像

圆锥曲线一:椭圆【1】第必定义: PF 1 PF 2 2a第二定义:PF 2ePP注意:当2a 1 2 时表示椭圆;1 2 时表示线段F 1F 2 ;2a 1 2 ,没有轨迹 .F F 2a F FF F【2】标准方程:x 2y 21 (a b 0) x a cos ,为参数 )参数方程:( a 2b 2y b sin .【3】焦点三角形 PF 1F 2 的性质b 2 ①【定义推出周长】周长 l 2a 2c;②| PF 1 || PF 2 |21 cos③【 S 1 底 高1PF 1 PF 2 sin余弦定理】 S c y pb 2 tan (F 1 PF 2 )222④ PQ 为 F 1PF 2 的角均分线, I 为 F 1PF 2 的心里,依据SS1 F 1Q h 高1 F 1P PQ sinF 1QF 1P则有以下结论:F 1 PQ222 ,即F 2 PQ1 F 2Q h 高 1 F2 P PQ sin F 2Q F 2 P2 22F 1Q F 2QF 1Q F 2Q F 1 F 2 sin 2c QI F 1P F 2 P F 1 P F 2PF 1P F 2 P sinsin2aeIP【4】 P ( x , y ) 为椭圆上随意一点,则过点P 的切线 PT 方程为:x 0 x y 0 y 1 . 剖析 :可理解为切线是一次的方程,点 P (x 0 , y 0 )的 a 2b 2坐标既要知足椭圆又要知足切线,相当于把椭圆里面的此中一对( x, y) 换成 (x 0 , y 0 ) .此外切线 PT 也是 F 1 PF 2 的外角角均分线 .扩展:① 焦点 F 1, F 2 在直线 PT 上的射影 H 点的轨迹是以长轴为直径的圆, 除掉长轴的两个端点,即 x 2y 2 a 2 .② 若 0在椭圆x 2 y 2 1 外 ,则过 P 作椭圆的两条切线切点为P 1 , P 2 ,则a2b2P ( x , y )切点弦 P P 的直线方程是x 0xy 0 y 1 . 1 2a 2b 2③ 椭圆 x2y 2 1 ( a > b > 0)的两个极点为 A 1 ( a,0) , A 2 ( a,0) ,与 y 轴平行的直线 a 2b 2交椭圆于 P 1, P 2 时 , A P 与 A P 交点的轨迹方程是双曲线 x 2 y 2 1 .a 2b 21 12 2④ 设A 1, A 2 是椭圆 x 2y 21的长轴的两个端点,QQ 是与 A 1 A 2 垂直的弦,则直线22abx 2y 2A Q 与 A Q 的交点 P 的轨迹是双曲线1.2212ab【5】“点差法”或许“中点弦性质”直线 AB 与椭圆交于 A(x , y ), B( x 2 , y ) 两点, M (x , y ) 为 AB 的中点 ,则有:1120 0x 12y 12 1222y 222b 2( y 1 y 2 )( y 1y 2 ) b 2b 2a 2b 2作差x 1x 2y 12整理y 1 y 2x 22 y 221a2b2x 12x 22a 2( x 1x 2 )( x 1 x 2 )a2k AB k OMa 2a2 b 2【总结】 当题目中出现弦的中点时或许提到直线的斜率了, 那我们就能够试试看看是否是符合点差法的基础图形或许结论了. 拓展 :点差法的变形第 2 页【6】设A, B为椭圆x2 y2k(k 0, k 1)上两点,其直线x2 y2 a2 b2订交于 P,Q ,则 AP BQ .(两个椭圆AB 与椭圆b2 1a2离心率相等,即圆扁程度同样)【7】过椭圆一个焦点 F 的直线与椭圆交于P, Q 两点,A , A1 2为椭圆长轴上的极点,A1P 和 A2 Q 交于点 M , A2 P 和 A1Q 交于点 N ,则 MF NF【8】比较小众化的解决一些线段取值范围问题的思路题目背景: P 为椭圆上任一点, E 为椭圆内一点,求 | PE | | PF | 这类形式的取值范围.2思路:|PE | |PF2 | | PE | ( 2a | PF1 |) 2a (| PE | | PF1 |) ,而后利用 P, E, F1三点共线来解决取值范围.(用定义变换此中一个和定义相关的线段,再利用三点共线办理)圆锥曲线二:双曲线【1】第必定义:PF1 PF2 2a 第二定义:PF2e PP注意:当 1 2 时表示双曲线; 1 2 时表示线段F1F2 ;2a 1 2,没有轨迹.2a F F 2a F F F F注:焦点 F 往渐近线y bx 做垂线,垂直距离恒为 b ,垂足在准线 x a2 上 .a c【2】标准方程:x 2y2 x a , 为参数 )1 (a b 0) cos参数方程:(a2 b2 y b tan .【3】焦点PF1F2的性质:①| PF1 || PF2 |2b2;1 cos【S 1 底高1 PF1 PF2 sin 余弦定理】S c y p b2 ( F1 PF2 )2 2 tan22 2②设双曲线 x2y 2 1(a > 0,b > 0)的两个焦点为 F 1, F 2 , P (异于长轴端点)为双曲线上 a b任 意 一 点 , 在 PF 1F 2 中 , 记F 1 PF 2 , PF 1 F 2 , F 1F 2P , 则 有sinc e .(sinsin)a③ P(x , y ) 为双曲线上随意一点,则过点P 的切线 PT 方程为: x 0 xy 0 y1. 此外切线a 2 b2PT 也是 F 1PF 2 的外角角均分线(拜见椭圆的切线性质) .焦点 F 1 , F 2 在直线 PT 上的射影H 点的轨迹是以实轴为直径的圆,除掉实轴的两个端点,即x 2 y 2 a 2 .④若) 在双曲线x 2y 21 外 ,则过 P 作双曲线的两条切线,切点为P 1 , P 2 ,则a 2b 2P (x , y切点弦 P P 的直线方程是 x 0 x y 0 y 1 .1 2 a 2 b 2⑤双曲线x 2y 21 ( a > 0,b > 0)的两个极点为 A 1 ( a,0) ,A 2 (a,0) ,与 y 轴平行的直线a 2b 2交双曲线于 P , P 时 , A P 与 A P 交点的轨迹方程是椭圆x 2 y 2 1.22121 122a b是双曲线x 2y 2⑥设A 1, A 2 1的实轴的两个端点,QQ 是与 A A 垂直的弦,则直线 A Qa 2b 21 21与 A Q 的交点 P 的轨迹是椭圆x 2y 2 1 .2a 22b【4】焦点三角形内切圆(或许说是和角均分线相关)①如下图, I 为F PF 2 的心里, S,T , Q 为切点,利用双曲线的定义,可得T 的地点恒为1双曲线的极点 A 2 ,即 F 1 PF 2 内切圆的圆心横坐标恒为 a ,即 IA 1, IA 2x轴 ;② PI 为角均分线,过F 2 做 PI 的垂线,垂足为 D ,利用双曲线的定义可得 OD a ,即垂足的轨迹方程为:x 2 y 2 a 2 (卡在双曲线中间的一个半径为 a 的圆)【5】设 A, B 为双曲线x2y 2 k ( a >0,b >0, k 0, k 1 )上两点,其直线 AB 与双曲线 x2y 2a 2b 21 订交于 P, Q ,则 AP BQ .(两个双曲线离心率相等,即张口程度同样)a 2b 2【6】过双曲线一个焦点F 的直线与双曲线交于P, Q两点,A 1 , A 2 为双曲线实轴上的极点,A P 和 A Q 交于点 M , A P 和 A Q 交于点 N ,则 MF NF .1221【7】“点差法”或许“中点弦性质”直线 AB 与双曲线交于 A ( x , y ), B (x , y )两点, M (x 0, y ) 为 AB 的中点,则有:1122x 12 y 12 1 222222b 2( y 1 y 2 )( y 1 y 2 ) b 2b 22 2a b作差 x 1x 2y 1y 2整理 y 1y 2a 2b 2x 22a 2(x 1 x 2 )( x 1 x 2 )a 2k AB k OMa 2x 22 y 221x 12a2b2注:点差法的变形拜见椭圆的变形图形.【8】比较小众化的解决一些线段取值范围问题的思路题目背景: P 为双曲线上一点, E 为双曲线内一点,求 | PE | | PF 2 | 这类形式的取值范围 .思路: | PE | | PF 2 | | PE | (| PF 1 | 2a)(| PF 1 | | PE |) 2a ,而后利用 P, E, F 1 三点共线来解决取值范围 .(用定义变换此中一个和定义相关的线段,再利用三点共线办理)圆锥曲线三:抛物线【1】定义:PF PP抛物线上任一点到焦点的距离等于到准线的距离.【2】标准方程:右:y2 2 px ( p 0)一共四种方程:左: y 2 2 px 上: x2 2 py 下: x2 2 py【3】焦点弦性质过焦点 F 倾斜角为的直线 PQ :y k( x p) 交抛物线于 P, Q 两点,2P( x1 , y1 ), Q ( x2 , y2 ) , P , Q 为 P, Q 在准线的投影, MN 是过焦点与直线PQ 垂直的直线,准线与 x 轴交于点 T ,则有:y k(x p 1 x1 x2 k2 p 2 p2 2 2 2 2 2 2)x p 2 p) x p 0 k y1 y2p2 k ( k ky 2 2 px 4 x1 x2 1 2p4PFxpQF x2 p122PQ x 1 x 2 p2 pPF p 1 121 112cossin1cosPF QFQFpPFQF pPQMN 2pPF QFcos1 特别地当60时,PF3QF1注: 通径为 2 p ,三角形 POQ 的面积 S POQ1PQ dp 22 sin2如下图:①点 P, O,Q ,P , O,Q 三点必定共线,充任直角梯形的对角线,交点为 O .②以 PQ 为直径的圆必与准线相切,圆心与切点连线充任半径和中位线.③ x 轴为PTQ 的角均分线.【4】随意一条直线与抛物线交于A, B 两点,则有:①点差法: k AB y 0p ②若 OA OB , 则直线 AB 必过点 (2 p,0)【5】比较小众化的解决一些线段取值范围问题的思路题目背景: P 为抛物线上一点,E 为抛物线内一点,求 | PE | | PF | 这类形式的取值范围 .思路: | PE | | PF | | PE |PP ,而后利用 P, E, P 三点共线来解决取值范围.(用定义转换此中一个和定义相关的线段,再利用三点共线办理)【6】对于抛物线切线问题,由于抛物线是一个二次和一次的联合,在求一些对于切线的问题时能够适合的利用求导来解决.D 为准线上任一点,DA, DB 为抛物线的两条切线,以下三个结论和DA, DB 切线为等价结论,知一求三:① A, F , B 三点共线;② DA DB ; ③ DF AB。
圆锥曲线统一定义动画演示

焦点之间的距离叫做焦距.
它们分别给我们什么印象?
双曲线的定义 : 可以用数学表达式来体现:
平面内两个定点F1,F2的距离的差的绝对值等于常数(小于
距离)的点的轨迹叫做双曲线,两个定点F1,F2叫做双曲线的叫焦点
,两焦点间的距离叫做双曲线的焦距
平面内与两定点F1、F2的距离的差的绝对 当a = c>0时,动点M的轨迹是两条射线;
直线L的距离)
当a = c>0时,动点M的轨迹是两条射线; 关于椭圆、双曲线、抛物线你了解多少?
平面内与两定点F1、F2的距离的差的绝对值是常数(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点F1、F2叫做双曲线的焦点,两个 焦点之间的距离叫做焦距.
当 0 < c < a时,动点M无轨迹 平面内到两定点F1 ,F2的距离之和为常数(大于F1 F2距离)的点的轨迹叫椭圆,两个定点叫椭圆的焦点,两焦点的距离叫做椭圆的焦
直线l(F不在l上)的距离相等
的点的轨迹叫做抛物线.
· N M
ห้องสมุดไป่ตู้
定点F叫做抛物线的焦点.
·F
定直线l 叫做抛物线的准线.
即: 若︳M ︳MNF︳︳1,则点M的轨迹是抛物线
椭圆的定义:
平面内到两定点F1、F2的距离之和等于 常数(大于|F1F2|)的点的轨迹叫做椭圆. 这两个定点叫做椭圆的焦点,两焦点 间的距离叫做焦距.
距. 常数(大于|F1F2|)的点的轨迹叫做椭圆.
它们分别给我们什么印象?
绝对值为2a ,| F1 F2| = 2c
抛物线的定义 :
平面内到一个定点F和一条定直线L(F不在L 上)的距离相等的点轨迹叫做抛物线,定点F叫做 抛物线的焦点,定直线L叫做抛物线的准线.
圆锥曲线图解

标准方程
a>b>0
a>b>0
a>0,b>0
a>0,b>0
p>0
p>0
p>0
p>0
标准方程图形
abc关系
a -b =c
a -b =c
a +b =c
a +b =c
离心率e=
0<e<1
0<e<1
e>1
e>1
e=1
e=1
e=1
e=1
离心率是圆锥曲线的一个重要参数,是圆锥曲线的本质属性之一,它的变化将导致曲线形状的变化,甚至影响曲线的类型,是圆锥曲线统一定义中的三要素(定点、定线、定比)之一,当离心率在0—1间变化时,离心率越大(即越接近于1)椭圆越扁,反之越圆;当离心率在1—∞间变化时,离心率越大,双曲线开口越宽阔,反之越窄;离心率从0 的变化过程反映了圆锥曲线:圆 椭圆 抛物线 双曲线的变化过程
几何条件
针对于焦点在x轴上的曲线来说第二定义
在平面内到定点F(c,0)(或F(-c,0))与到定直线 (或 )的距离之比为常数 (a>c>0)的点M的轨迹
在平面内到定点F(c,0)(或F(-c,0))与到定直线 (或 )的距离之比为常数 (c>a>,则
顶点坐标
(a,0),(-a,0),
(0,b)(0,-b)
(0,a), (0, -a)
(b,0),(-b,0)
(a,0), (-a,0)
虚点(0,b),(0,-b)
(0,a), (0, -a)
虚点(b,0),(-b,0)
(0,0)
所有圆锥曲线图表总结
针对于焦点在x轴上的曲线来说第二定义
在平面内到定点F(c,0)(或F(-c,0))与到定直线 (或 )的距离之比为常数 (a>c>0)的点M的轨迹
在平面内到定点F(c,0)(或F(-c,0))与到定直线 (或 )的距离之比为常数 (c>a>0)的点M的轨迹
注:设椭圆或双曲线的轨迹为集合p,则
即 (或 )其中a>0,c>0
标准方程
a>b>0
a>b>0
a>0,b>0
a>0,b>0
p>0
p>0
p>0
p>0
标准方程图形
a、b、c关系
a -b =c
a -b =c
a +b =c
a +b =c
离心率e=
0<e<1
0<e<1
e>1
e>1
e=1
e=1
e=1
e=1
离心率是圆锥曲线的一个重要参数,是圆锥曲线的本质属性之一,它的变化将导致曲线形状的变化,甚至影响曲线的类型,是圆锥曲线统一定义中的三要素(定点、定线、定比)之一,当离心率在0—1间变化时,离心率越大(即越接近于1)椭圆越扁,反之越圆;当离心率在1—∞间变化时,离心率越大,双曲线开口越宽阔,反之越窄;离心率从0 的变化过程反映了圆锥曲线:圆 椭圆 抛物线 双曲线的变化过程;
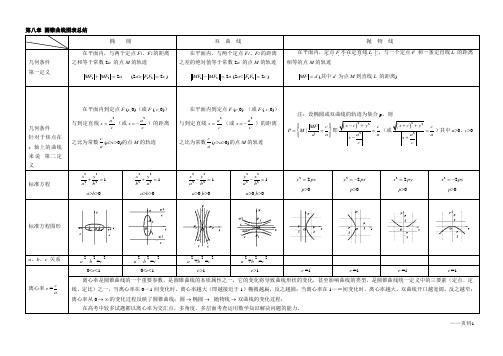
第八章圆锥曲线图表总结
椭圆
双曲线
抛物线
几何条件
第一定义
在平面内,与两个定点F1、F2的距离之和等于常数2a的点M的轨迹
(2a> )
在平面内,与两个定点F1、F2的距离之差的绝对值等于常数2a的点M的轨迹
高中数学思维导图:圆锥曲线

位置关系
点 在抛物线外 点 在抛物线外上 点 在抛物线内
焦点弦
双曲线
第一
第二 定义
的点 轨迹 的点 轨迹;
的轨迹
弦长公式
同椭圆
焦点三角形
点 在
点 在双曲线内
等轴
两渐近线互相垂直 与
共轭 四个焦点共圆; M为线段AB中点
常用结论 斜率
共轭
解析关系(直线与双曲线)
直线AB方程
第一
1
第二
1
同椭圆
定义 弦长公式
焦点三角形
1
位置关系
3
等轴
2
共轭
2
M为线段AB中点
双 曲 线
常
解析关系(直线与双曲线)
用
6
结
论
圆锥 曲线 (一)
(
2
焦半径公式
定义
4
椭圆
弦长公式
2
焦半径公式
4
焦点三角形
2
M为线段AB中点
常用结论
解析关系(直线与椭圆)
6
位置关系
3
定义
1
解析关系
2
位置关系
3
抛物线
焦点弦
4
(
2
定义一
定义
定义二
的点 的轨迹
或
的点 的轨迹, 为离心率
弦长公式
椭圆
焦点在x轴 焦半径公式
焦点在y轴
焦点三角形
常用结论
M为线段AB中点
斜率
解析关系(直线与椭圆)
直线AB方程
AB垂直平分线方程
位置关系
点 在椭圆外 点 在椭圆上 点 在椭圆内
抛物线
的点 的轨迹;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面与圆锥面的截线一、直观感受:
观察平面截圆锥面的图形,截线是什么图形?
改变平面的位置,可得到三种曲线,它们统称为圆锥曲线(下图由软件《立几画板》制作):
二、分类探究:
从平面图形入手,开始讨论一条直线与等腰三角形的位置关系:
将等腰三角形拓广为圆锥,直线拓广为平面。
如果用一平面去截一个正圆锥,而且这个平面不通过圆锥的顶点,会出现哪些情况呢?如下图:
归纳提升:
定理在空间中,取直线l为轴,直线l'与l相交于O点,其夹角为α,l'围绕l旋转得到以O为顶点,l'为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行,记作β=0),
则:
(1)β>α,平面π与圆锥的交线为椭圆;
(2)β=α,平面π与圆锥的交线为抛物线;
(3)β<α,平面π与圆锥的交线为双曲线。
三、证明结论:
利用Dandelin双球(这两个球位于圆锥的内部,一个位于平面的上方,一个位于平面的下方,并且与平面及圆锥均相切)证明:β>α,平面与圆锥的交线为椭圆.
如图,利用切线长相等,容易证明PF1+PF2=PQ1+PQ2=Q1Q2=定值.
下面证明:β=α时,平面与圆锥面的交线为抛物线。
下面讨论当平面与圆锥面的交线为双曲线时准线的及离心率:
换个角度看图:
容易知道:截得的圆锥曲线的离心率等于截面和圆锥轴的夹角的余弦与圆锥顶角一半的余弦之比.
四、知识运用
用图霸制作三维直观图:
解答参看下图:
五、图形制作
三种曲线的丹迪林Dandelin双球图可以在《几何图霸》中统一到一幅图中,主要制作步骤如下:
1.作全自由点O,过点O作平行于z轴上的点B,过B作平行于x轴上的点C,作点B、C 关于O的对称点B’、C'.
2.选取点O、B、C,作圆锥,选取点O、B’、C’,作圆锥.
3.在圆B上任取点D,作D关于B对称点,连接OD,OD’,在OD上任取一点E,以E 为圆心画过点D’、D的心点圆,在圆E上任取点F,连EF,它表示截面的位置,可以绕点E转动.
4.作角OEF的平分线,与轴BB’交于O1;作角DEF的平分线,与轴BB’交于O2,它们就是双球的球心.
5.过球心O1、O2分别作边EF的垂线,垂足分别为F1、F2,它们就是焦点.
6.选取点O1、F1,作球O1(图中显示大圆,光照后显示为球),同法作球O2.
7.取线EF上的点G、H,作GDO垂线上的伸缩点I,作点I关于点G的对称点I’,按向量GH平称点I、I’,得点I2、I".添加面II2I"I’,连接四边,表示截面.它的长宽可以用点G、H、I控制;点F控制其转动.
8.添加下底圆上的点J,连结OJ交截面于点K,选取点J、K,添加轨迹,它就是截线,如上图中的椭圆.
9.点E按向量OD’平移得点E’,EE’交圆于点G1,EG1平行于母线OD’,添加点F到点G1的动画,名为“抛物线”.
10.参看前面各图添加其它图元.下载图霸文件后在“对象浏览器”中查看各对象.
课件下载:
共享文件下载中心
相关文章:
1 利用丹迪林Dandelin双球证明平面与圆锥面的截线定理
2平面与圆柱面的截线
更多文章:
《几何图霸》文章列表
几何图霸网站:。
