2012年陕西省普通高等教育专升本招生

合集下载

普通高校专升本招生考试大学英语考试中词汇和语法结构考试特点及复习对策

普通高校专升本招生考试大学英语考试中词汇和语法结构考试特点及复习对策作者：吕芳亢宇来源：《考试周刊》2013年第28期摘要：作者通过对普通高校专升本招生考试大学英语科考试说明及2009至2012年考试真题的分析，结合多年的专升本考前辅导经验，总结出大学英语的专升本考试中词汇和语法结构部分具有词汇量大、语法点多等特点，并提出了相应的复习策略，期望使广大考生和教师在备考专升本英语考试词汇和语法结构时获得良好效果。

关键词：普通高校专升本大学英语词汇语法结构复习对策多年来很多高职学生通过参加普通高校专升本考试（以下简称“专升本”）提高学历，获得更高层次的就业机会与更顺畅的未来职业发展，提高就业后的工资待遇，更好地准备考研或职称评定。

专升本考试也成为各高职院校的另一种“就业”模式。

按照国家教育部规定，专升本考试在高职学生毕业前（大三第二学期）举行。

应届毕业生只有一次参加普通高校专升本考试的机会。

而公共课程的考查不论是理科还是文科，大学英语都是必考科目。

因此有针对性地复习可以帮助考生获得较好的考试成绩。

笔者结合考试说明、历年真题和多年的考前辅导经验总结出词汇和语法结构部分的特点，并提出相应策略。

1.词汇特点：词汇及短语考查量大。

《陕西省普通高等教育专升本招生考试说明》中对词汇的要求为“领会式掌握词汇4200个（其中复用式掌握的单词为2500个），以及500个常用短语和词组”。

相对于高考考试大纲要求的“2000左右词汇和相关词组”，英语应用能力考试B级要求的2500个单词和大学英语四级考试要求的领会式掌握4200个、复用式掌握2500个词汇和由这些词组成的常用词组1600个，专升本英语考试的词汇仅次于四级。

随着近几年高职生源质量的不断下降，学生在词汇方面能达到B级考试要求并不容易。

因此，学生备考专升本大学英语时，词汇成了最大的障碍。

第一大题的40个单项选择题中，2009年有28道题考查词汇和短语的用法，2010年有23道题考查词汇和短语的用法，2011年有14道题考查词汇和短语的用法，2012年有21道题考查词汇和短语的用法。

陕西专升本专业对照表

陕西省专升本专业对照表如下：
1.电气工程及其自动化：可以报考的本科专业有通信工程、计算机科学与技术
等。

2.会计学：可以报考的本科专业有财务管理、金融学、工商管理等。

3.土木工程：可以报考的本科专业有建筑环境与能源应用工程、给排水科学与
工程、土木工程等。

4.物流管理：可以报考的本科专业有物流管理、交通运输等。

5.英语：可以报考的本科专业有英语、商务英语等。

6.化学工程与工艺：可以报考的本科专业有化学工程与工艺、制药工程等。

7.计算机科学与技术：可以报考的本科专业有计算机科学与技术、软件工程等。

8.机械设计制造及其自动化：可以报考的本科专业有机械设计制造及其自动化、
机械电子工程等。

9.药学：可以报考的本科专业有药学、中药学等。

10.临床医学：可以报考的本科专业有临床医学、医学影像学等。

陕西统招专升本政策

陕西统招专升本政策
陕西省为加强我省经济社会发展，促进普通高校和中等职业学校毕业生就业，引导参加高等教育有条件的普通高中毕业生走进高校，根据国务院、教育部关于解决高校招生政策以及省委、省政府部署，就实行普通高中毕业生参加普通高等学校统招专升本政策，制定本政策：
一、招生范围：除招生表规定招收本省外省（区）普通高校高三适龄学生以外，陕西省本科批次及以下招生普通高校招收2010年陕西省普通高中毕业生参加统招专升本，实行以专升本为招生导向的招生制度。

二、报考和考试：报考普通高等学校统招专升本的普通高校学生，报考时要求提交本科入学考试报名表，以及本地普通高校成绩通知书等文件资料；报考的学生应按本省招生表所述要求参加本省普通高等学校本科入学考试開考范围内有关学科的考试。

三、资格审核：审核学生报考资格时，参照普通高等学校高中毕业生报考本科阶段专业和总分线以及预定最低分数线。

四、录取：按报考考生的总分线分类录取，以录取学生本地普通高等学校的总分排名线代替本科入学总分线实行录取。

五、其他：普通高等学校应在招生表中注明有关学校招收普通高中毕业生参加本科统考文体专业名称以及专业、考试学位要求，按本省招生计划实施统考。

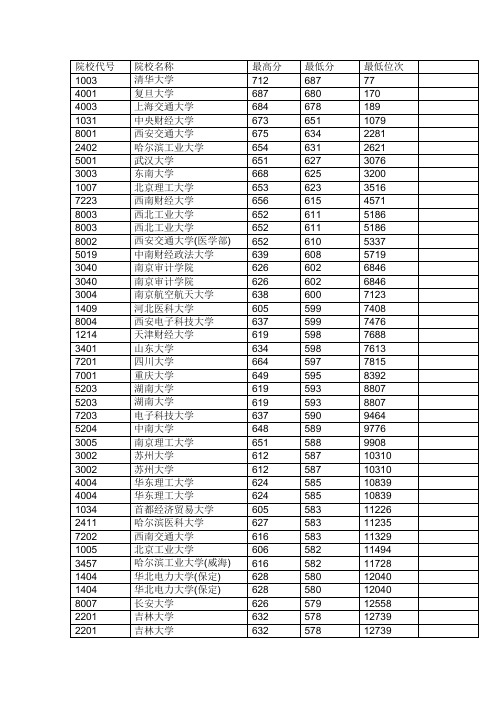
2012年陕西省高考各学校录取分数线

624
568
16317
1020
北京林业大学
640
566
17050
3456
山东大学威海分校
589
565
17263
3456
山东大学威海分校
589
565
17263
4007
东华大学
608
565
17108
5402
郑州大学
598
565
17327
3012
江南大学
583
564
17629
1050
中国矿业大学(北京)
601
4004
华东理工大学
624
585
10839
4004
华东理工大学
624
585
10839
1034
首都经济贸易大学
605
583
11226
2411
哈尔滨医科大学
627
583
11235
7202
西南交通大学
616
583
11329
1005
北京工业大学
606
582
11494
3457
578
541
28631
1421
石家庄铁道大学
592
537
30557
5201
湘潭大学
566
536
31175
5011
华中农业大学
566
534
32634
8401
宁夏大学
558
534
32354
5014
湖北大学
561
533
32918
8023

2012年陕西省专升本(高等数学)真题试卷(题后含答案及解析)

2012年陕西省专升本（高等数学）真题试卷(题后含答案及解析) 题型有：1. 选择题 2. 填空题 5. 综合题 6. 证明题选择题在每小题给出的四个选项中，只有一项是符合要求的。

1．x=0是函数的A．可去问断点B．连续点C．无穷间断点D．跳跃间断点正确答案：A解析：因为即f(x)在x=0处极限存在但f(x)在x=0处无定义，所以x=0为可去间断点，所以选A。

2．设∫f(x)dx=ex+C，则不定积分∫f(x)exdx=A．2ex+CB．C．D．2e2x+C正确答案：C解析：由∫(x)dx=ex+C两边同时对x求导得f(x)=ex，把f(x)=ex代入∫f(x)exdx有，所以选C。

3．函数在点x=1处A．可导且f’(1)=2B．不可导C．不连续D．不能判定是否可导正确答案：A解析：由原式可得由此可知在x=1处f’(1)=2，所以选A。

4．设级数收敛于S，则级数收敛于A．SB．2SC．2S+u1D．2S一u1正确答案：D解析：设的前n项和为Tn，则Tn=(u1+u2)+(u2+u3)+…+(un+un+1)=2(u1+u2+u3+…+un)一u1+un+1=2Sn一u1+un+15．微分方程的通解为A．ey+ex=CB．ey一ex=CC．e-y+ex=CD．e-y一ex=C正确答案：B解析：即ey 一ex=c，所以选B。

填空题6．设函数在x=0处连续，则a的值为_________．正确答案：一1解析：由连续充要条件得．即有；0=1+a 解得a=一17．设函数f(x)在点x0处可导，且f’(x0)=2，则的值为__________.正确答案：4解析：8．设函数f(x，y，z)=x2+y2+z2，则函数f(x，y，z)在点(1，1，一1)处的梯度gradf(1，1，一1)为___________．正确答案：2(i+j一k)解析：gradf(1，1，一1)={fx’(1，1，一1),fy’(1，1，一1)，fz’(1，1，一1)}={2，2，一2}或写成2(i+j一k)．9．设方程∫0xsintdt+∫0ye-tdt=xy确定函数y=y(x)，则=_________．正确答案：解析：公式法求：10．曲面z=x2+2y2一1在点(1，1，2)处的切平面方程为__________．正确答案：2x+4y—z一4=0解析：由题知法向量为n={zx’(1，1，2)，zy’(1，1，2)，一1)，即n={2，4，一1)，故在点(1，1，2)处法平面方程为：2(x一1)+4(y一1)一(2—2)=0，即2x+4y —z一4=0．综合题11．求极限正确答案：12．设参数方程正确答案：13．求函的单调区间和极值．正确答案：当时，f’(x)＞0，故函数f(x)在(一∞，0]和内单调增加，在内单调减少,函数f(x)在x=0取得极大值f(0)=0，在处取得极小值14．设函数，其中f具有二阶连续偏导数，求正确答案：15．计算定积分正确答案：16．计算二重积分，其中D是由圆与直线y=x及y轴所围成第一象限的区域．正确答案：17．将函数展开为(x一1)的幂级数，指出展开式成立的区间，并求级数正确答案：18．设函数，求函数f(x，y，z)的偏导数及在点(1,1，1)处的全微分df(1，1,1)正确答案：19．设L为取正向的圆周x2+y2=4，计算曲线积分正确答案：20．求微分方程y’’一y=3e2x满足初始条件y｜x=0=1，y’｜x=04的特解?正确答案：特征方程r2一1=0，r1,2=±1对应齐次方程的通解为y=C1ex+C2e-x，求出其一个特解为y*=e2x其通解为：y=C1ex+C2e-x+e2x解出C1=1，C2=一1满足初始条件的特解为y=ex一e-x+e2x证明题21．设曲线方程为y=1一x2，(1)求该曲线及其在点(1，0)和点(-1，0)处的法线所围成的平面图形的面积；(2)求上述平面图形绕y轴旋转一周所得旋转体的体积．正确答案：y’=一2x由线在点(1，0)处的法线方程为曲线在点(一1，0)处的法线方程为(1)所求面积为(2)所求体积为22．设函数f(x)在[0，1]上连续，且∫01f(x)dx=0，证明：在(0，1)内至少存在点ξ，使得正确答案：令F(x)=x∫0xf(t)dt，则F(x)在[0，1]上连续，在(0，1)内可导，且F(0)=F(1)=0由Rolle定理知，至少存在一点ξ∈(0，1)，使得F’(ξ)=ξf(ξ)+∫0tf(t)dt=0即ξf(ξ)+｜f(x)dx=0。

2012年陕西高考试卷(理综)有答案

2012年普通高等学校招生全国统一考试理科综合能力测试本试卷分第I卷（选择题）和第II卷（非选择题）两部分。

第I卷1至8页，第II卷9至16页，共300分。

考生注意：1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2.第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

第II卷用黑色墨水签字笔在答题卡上书写作答，在试题卷上作答，答案无效。

3.考试结束，监考员将试题卷、答题卡一并收回。

第I卷一、选择题：1.同一物种的两类细胞各产生一种分泌蛋白，组成这两种蛋白质的各种氨基酸含量相同，但排列顺序不同。

其原因是参与这两种蛋白质合成的是（B）A. tRNA 种类不同 B. mRNA碱基序列不同C.核糖体成分不同D.同一密码子所决定的氨基酸不同2.下列关于细胞癌变的叙述，错误的是（D）A.癌细胞在条件不适宜时可无限增殖B.癌变前后，细胞的形态和结构有明显差别C.病毒癌基因可整合到宿主基因组诱发癌变D.原癌基因的主要功能是阻止细胞发生异常增殖3.哺乳动物因长时间未饮水导致机体脱水时，会发生的生理现象是（B）A.血浆渗透压降低B.抗利尿激素分泌增加C.下丘脑渗透压感受器受到的刺激减弱D.肾小管和集合管对水的重吸收作用减弱4.当人看到酸梅时唾液分泌会大量增加，对此现象的分析，错误的是（C）A.这一反射过程需要大脑皮层的参与B.这是一种反射活动，其效应器是唾液腺C.酸梅色泽直接刺激神经中枢引起唾液分泌D.这一过程中有“电—化学—电”信号的转化5.取生长状态一致的燕麦胚芽鞘，分为a、b、c、d四组。

将a、b两组胚芽鞘尖端下方的一段切除，再从c、d两组胚芽鞘中的相应位置分别切取等长的一段，并按图中所示分别接入a、b两组胚芽鞘被切除的位置，得到a′、b′两组胚芽鞘。

陕西专升本对应院校表

年陕西专升本对应院校表————————————————————————————————作者：————————————————————————————————日期：文史类专业代码专业名称院校代码院校名称01 电子商务(文) 021 渭南师范学院033 西安培华学院041 西安欧亚学院043 西安翻译学院044 西京学院02 工程管理(文) 041 西安欧亚学院043 西安翻译学院050 西安思源学院085 西安建筑科技大学华清学院093 西安科技大学高新学院03 工程造价(文) 033 西安培华学院043 西安翻译学院050 西安思源学院093 西安科技大学高新学院04 人力资源管理(文) 033 西安培华学院042 西安外事学院052 陕西国际商贸学院087 西安工业大学北方信息工程学院089 西安财经学院行知学院05 新闻学(文) 041 西安欧亚学院044 西京学院06 英语(文) 018 陕西理工大学019 宝鸡文理学院020 咸阳师范学院021 渭南师范学院029 西安文理学院030 榆林学院031 商洛学院032 安康学院033 西安培华学院041 西安欧亚学院042 西安外事学院043 西安翻译学院044 西京学院050 西安思源学院085 西安建筑科技大学华清学院092 西北工业大学明德学院097 延安大学西安创新学院098 西安交通大学城市学院103 陕西学前师范学院07 汉语言文学(文) 018 陕西理工大学019 宝鸡文理学院020 咸阳师范学院021 渭南师范学院029 西安文理学院030 榆林学院031 商洛学院032 安康学院033 西安培华学院042 西安外事学院043 西安翻译学院050 西安思源学院085 西安建筑科技大学华清学院087 西安工业大学北方信息工程学院097 延安大学西安创新学院103 陕西学前师范学院08 法学(文) 023 西北政法大学033 西安培华学院09 工商管理(文) 041 西安欧亚学院042 西安外事学院089 西安财经学院行知学院098 西安交通大学城市学院10 金融学(文) 041 西安欧亚学院089 西安财经学院行知学院092 西北工业大学明德学院098 西安交通大学城市学院11 旅游管理(文) 019 宝鸡文理学院020 咸阳师范学院021 渭南师范学院031 商洛学院032 安康学院041 西安欧亚学院042 西安外事学院043 西安翻译学院089 西安财经学院行知学院12 思想政治教育(文) 021 渭南师范学院029 西安文理学院031 商洛学院103 陕西学前师范学院14 学前教育(文) 032 安康学院019 宝鸡文理学院020 咸阳师范学院021 渭南师范学院030 榆林学院031 商洛学院043 西安翻译学院050 西安思源学院103 陕西学前师范学院15 应用心理学(文) 031 商洛学院16 会计学(文) 019 宝鸡文理学院021 渭南师范学院029 西安文理学院030 榆林学院031 商洛学院032 安康学院033 西安培华学院041 西安欧亚学院042 西安外事学院044 西京学院064 陕西服装工程学院085 西安建筑科技大学华清学院087 西安工业大学北方信息工程学院089 西安财经学院行知学院092 西北工业大学明德学院097 延安大学西安创新学院098 西安交通大学城市学院17 国际经济与贸易(文) 023 西北政法大学033 西安培华学院041 西安欧亚学院042 西安外事学院043 西安翻译学院044 西京学院050 西安思源学院052 陕西国际商贸学院087 西安工业大学北方信息工程学院092 西北工业大学明德学院098 西安交通大学城市学院18 市场营销(文) 019 宝鸡文理学院021 渭南师范学院023 西北政法大学033 西安培华学院041 西安欧亚学院042 西安外事学院044 西京学院050 西安思源学院052 陕西国际商贸学院064 陕西服装工程学院087 西安工业大学北方信息工程学院092 西北工业大学明德学院098 西安交通大学城市学院19 财务管理(文) 020 咸阳师范学院021 渭南师范学院030 榆林学院031 商洛学院032 安康学院033 西安培华学院041 西安欧亚学院042 西安外事学院043 西安翻译学院044 西京学院050 西安思源学院052 陕西国际商贸学院087 西安工业大学北方信息工程学院089 西安财经学院行知学院093 西安科技大学高新学院098 西安交通大学城市学院20 物流管理(文) 035 西安邮电大学041 西安欧亚学院042 西安外事学院043 西安翻译学院044 西京学院098 西安交通大学城市学院21 心理学(文) 021 渭南师范学院103 陕西学前师范学院22 德语(文) 043 西安翻译学院23 法语(文) 043 西安翻译学院24 汉语国际教育(文) 043 西安翻译学院044 西京学院25 教育学(文) 021 渭南师范学院050 西安思源学院26 小学教育(文) 031 商洛学院032 安康学院103 陕西学前师范学院艺术类专业代码专业名称院校代码院校名称28 视觉传达设计(艺) 020 咸阳师范学院021 渭南师范学院031 商洛学院032 安康学院041 西安欧亚学院042 西安外事学院043 西安翻译学院044 西京学院064 陕西服装工程学院085 西安建筑科技大学华清学院092 西北工业大学明德学院098 西安交通大学城市学院29 服装与服饰设计(艺) 012 西安工程大学052 陕西国际商贸学院064 陕西服装工程学院30 美术学(艺) 103 陕西学前师范学院31 播音与主持艺术(艺) 092 西北工业大学明德学院32 动画(艺) 021 渭南师范学院044 西京学院052 陕西国际商贸学院33 环境设计(艺) 041 西安欧亚学院043 西安翻译学院064 陕西服装工程学院085 西安建筑科技大学华清学院34 音乐学(艺) 103 陕西学前师范学院理工类专业代码专业名称院校代码院校名称35 国际经济与贸易（理）041 西安欧亚学院050 西安思源学院36 机械电子工程(理) 007 西安工业大学37 教育学(理) 050 西安思源学院38 数字媒体技术(理) 103 陕西学前师范学院39 学前教育(理) 050 西安思源学院40 应用化学(理) 029 西安文理学院41 工程造价(理) 050 西安思源学院064 陕西服装工程学院093 西安科技大学高新学院42 财务管理(理) 021 渭南师范学院031 商洛学院032 安康学院033 西安培华学院041 西安欧亚学院042 西安外事学院050 西安思源学院052 陕西国际商贸学院089 西安财经学院行知学院093 西安科技大学高新学院098 西安交通大学城市学院43 电子商务（理）041 西安欧亚学院042 西安外事学院44 电子信息工程(理) 007 西安工业大学031 商洛学院050 西安思源学院098 西安交通大学城市学院45 园艺(理) 029 西安文理学院46 制药工程(理) 064 陕西服装工程学院47 工商管理(理) 041 西安欧亚学院089 西安财经学院行知学院48 化学(理) 021 渭南师范学院029 西安文理学院031 商洛学院103 陕西学前师范学院49 市场营销(理) 050 西安思源学院50 土木工程(理) 030 榆林学院031 商洛学院033 西安培华学院041 西安欧亚学院050 西安思源学院085 西安建筑科技大学华清学院098 西安交通大学城市学院51 物流管理(理) 041 西安欧亚学院043 西安翻译学院52 信息管理与信息系统(理) 052 陕西国际商贸学院53 通信工程(理) 035 西安邮电大学041 西安欧亚学院085 西安建筑科技大学华清学院092 西北工业大学明德学院54 计算机科学与技术(理) 007 西安工业大学012 西安工程大学018 陕西理工大学019 宝鸡文理学院020 咸阳师范学院021 渭南师范学院031 商洛学院032 安康学院033 西安培华学院037 西安航空学院042 西安外事学院044 西京学院050 西安思源学院085 西安建筑科技大学华清学院092 西北工业大学明德学院093 西安科技大学高新学院097 延安大学西安创新学院098 西安交通大学城市学院55 工程管理(理) 018 陕西理工大学031 商洛学院032 安康学院041 西安欧亚学院044 西京学院050 西安思源学院085 西安建筑科技大学华清学院56 机械设计制造及其自动化(理)012 西安工程大学018 陕西理工大学030 榆林学院037 西安航空学院044 西京学院050 西安思源学院064 陕西服装工程学院085 西安建筑科技大学华清学院092 西北工业大学明德学院098 西安交通大学城市学院57 电气工程及其自动化(理) 007 西安工业大学012 西安工程大学019 宝鸡文理学院021 渭南师范学院031 商洛学院037 西安航空学院042 西安外事学院050 西安思源学院092 西北工业大学明德学院093 西安科技大学高新学院098 西安交通大学城市学院58 电子信息科学与技术(理) 021 渭南师范学院031 商洛学院043 西安翻译学院59 数学与应用数学(理) 021 渭南师范学院029 西安文理学院031 商洛学院032 安康学院103 陕西学前师范学院60 化学工程与工艺(理) 029 西安文理学院030 榆林学院61 生物科学(理) 030 榆林学院103 陕西学前师范学院62 药学(理) 033 西安培华学院052 陕西国际商贸学院63 园林(理) 031 商洛学院032 安康学院64 会计学(理) 021 渭南师范学院029 西安文理学院031 商洛学院032 安康学院033 西安培华学院041 西安欧亚学院042 西安外事学院044 西京学院064 陕西服装工程学院085 西安建筑科技大学华清学院089 西安财经学院行知学院092 西北工业大学明德学院098 西安交通大学城市学院65 宝石及材料工艺学(理) 052 陕西国际商贸学院66 食品科学与工程(理) 103 陕西学前师范学院医学类专业代码专业名称院校代码院校名称67 中药学(医) 052 陕西国际商贸学院68 护理学(医)033 西安培华学院042 西安外事学院043 西安翻译学院044 西京学院097 延安大学西安创新学院098 西安交通大学城市学院69 临床医学(医)（学制3年） 039 西安医学院70 口腔医学(医)（学制3年） 039 西安医学院11。

2012年陕西省公务员考试职位表(全)

2012年陕西公务员考试信息公告报名入口职位表下载准考证打印入口历年真题复习备考资料等国家公务员考试信息详情点击：/1cyUM2012年陕西省公务员考试职位表陕西省2012年统一考试录用公务员（选调生）和参照公务员法管理单位工作人员工作已启动，面向社会，公开考试录用公务员（选调生）和参照公务员法管理单位工作人员3299名。

其中担任主任科员以下及其他相当职务层次非领导职务公务员2873名（含选调生183名，人民警察901名），参照公务员法管理单位工作人员426名。

国家公务员考试网（/）第一时间发布了2012年陕西省公务员考试职位表，为方便考生查看更多考试相关信息，建议将本站添加收藏。

·2012年考试录用公务员党群系统各市职位表·2012年考试录用公务员党群系统省直部门职位表·2012年陕西省委组织部统一考试录用选调生职位表·2012年考试录用公务员行政系统市区职位表·2012年考试录用公务员行政系统省直部门职位表·2012年考试录用公务员省级垂直管理系统职位表为进一步加强全省公务员队伍建设，满足全省各级机关和参照公务员法管理单位补充公务员和工作人员的需要，根据《公务员法》、《公务员录用规定(试行)》和《陕西省考试录用公务员办法(试行)》规定，经省考试录用公务员工作领导小组会议研究决定，由省委组织部、省人力资源和社会保障厅、省公务员局组织实施全省2012年统一考试录用公务员(选调生)和参照公务员法管理单位工作人员工作。

面向社会，公开考试录用公务员(选调生)和参照公务员法管理单位工作人员3299名。

其中担任主任科员以下及其他相当职务层次非领导职务公务员2873名(含选调生183名，人民警察901名)，参照公务员法管理单位工作人员426名。

现将有关事项公告如下：一、报考条件(一)报考的基本条件1.具有中华人民共和国国籍;2.年龄为18周岁以上，35周岁以下(1976年3月27日至1994年3月27日期间出生);3.拥护中华人民共和国宪法;4.具有良好的品行;5.具有正常履行职责的身体条件。

2012年普通高校“专升本”招生学校及专业

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
专业测试专业测试
专业测试专业测试
专业测试
专业测试
2 2 2 2 2 2 2 3 3 2 2 2 2 3 2 3 3 2 3 2 3 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
专业测试
专业测试专业测试专业测试专业测试与应用数学英语音乐学应用化学汉语言文学(文秘方向)
附件1：
2012年普通高校“专升本”招生学校及专业
招生专业电气工程及其自动化山西大学工程热能与动力工程学院土木工程计算机科学与技术会计学太原理工大学金融学财经学院市场营销机械设计制造及其自动化法学采矿工程土木工程太原理工大学会计学阳泉学院计算机科学与技术测绘工程国际经济与贸易电气工程及其自动化太原理工大学轻纺工程与美艺术设计术学院园林园艺山西农业大学动物医学农林经济管理临床医学山西医科大学护理学汾阳学院医学检验医学影像学山西医科大学护理学护理学院社会体育山西师范大学编辑出版学广播电视编导中北大学山西法学（侦查方向）警官高等专科安全工程（民爆公共安全管理方学校办学点向）化学工程与工艺太原科技大学化学与生物工过程装备与控制工程程学院市场营销学校类别非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范非师范学制 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 3 2 2 2 2 2 2 2 2 2 专业测试备注

2015年陕西省普通高等教育专升本招生考试大学语文试题及答案

2015年陕西省普通高等教育专升本招生考试大学语文试题及答案注意事项：1．考生领到试题后，须按规定在试题上填写行姓名、准考证号和座位号，并在答题卡上填涂对应的试卷类型信息点。

2．所有答案必须按照答题号在答题卡上对应的答题卡区域内作答，超出各题答题区域的答案无效。

在草稿纸、试题上作答无效。

考试结束后，将试题和答题卡一并交回。

3．满分为150分，考试时间为150分钟。

一、单项选择题：本大题共20小题，每小题1分，共20分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．《诗经》收录的诗歌总篇数是（）。

A．160篇B．40篇C．105篇D．305篇【答案】D。

【解析】本题考查《诗经》的构成数量。

《诗经》共305篇，也被称为“诗三百”。

其中《风》包含160篇，《雅》包含105篇，《颂》包含40篇。

2．先秦诸子中，倡导“民为贵，社稷次之，君为轻”思想的是（）。

A．孔子B．孟子C．庄子D．墨子【答案】B【解析】本题考查先秦诸子的思想主张。

孟子主张“仁政、王道、民贵君轻”。

A项孔子的思想是“仁”和“礼”，C项庄子的思想是“无为而治”，D项墨子的思想是“兼爱”“非攻”。

3．《左传》的体例是（）。

A．编年体B．国别体C．纪传体D．语录体【答案】A【解析】本题考查作品体例。

《左传》是编年体，B项国别体的著作有《国语》和《战国策》，C项纪传体的著作有《史记》和《汉书》，D项语录体的著作有《论语》。

4．《战国策》的整理编订者是（）。

A．李斯B．左丘明C．刘向D．司马迁【答案】C【解析】本题考查作品与作者的对应关系。

《战国策》是西汉刘向整理编订的。

A项李斯的作品是《谏逐客书》，B项左丘明整理编订的是《左传》，D项司马迁的作品是《史记》。

5．被称为“汉之飞将军”的是（）。

A．李广B．李蔡C．项羽D．程不识【答案】A【解析】本题考察人物的评价，出自《李将军列传》。

李广骁勇善战，被称为“汉之飞将军”。

6．下列作家中领导古文运动的是（）。

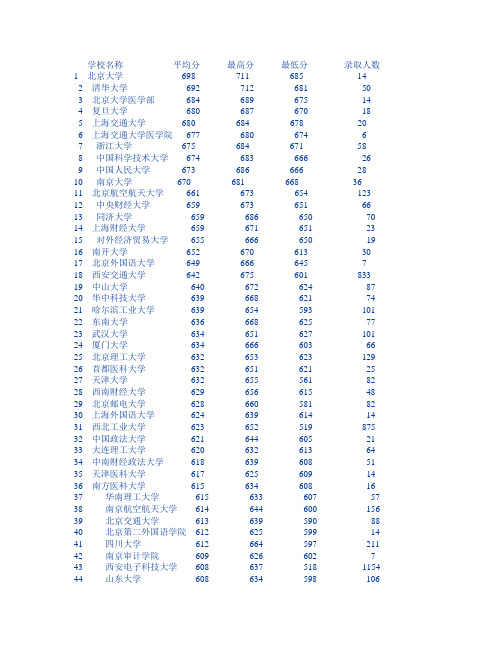
陕西理科2012年高校投档排序

学校名称平均分最高分最低分录取人数1 北京大学698 711 685 142 清华大学692 712 681 503 北京大学医学部684 689 675 144 复旦大学680 687 670 185 上海交通大学680 684 678 206 上海交通大学医学院677 680 674 67 浙江大学675 684 671 588 中国科学技术大学674 683 666 269 中国人民大学673 686 666 2810 南京大学670 681 668 3611 北京航空航天大学661 673 654 12312 中央财经大学659 673 651 6613 同济大学659 686 650 7014 上海财经大学659 671 651 2315 对外经济贸易大学655 666 650 1916 南开大学652 670 613 3017 北京外国语大学649 666 645 718 西安交通大学642 675 601 83319 中山大学640 672 624 8720 华中科技大学639 668 621 7421 哈尔滨工业大学639 654 593 10122 东南大学636 668 625 7723 武汉大学634 651 627 10124 厦门大学634 666 603 6625 北京理工大学632 653 623 12926 首都医科大学632 651 621 2527 天津大学632 655 561 8228 西南财经大学629 656 615 4829 北京邮电大学628 660 581 8230 上海外国语大学624 639 614 1431 西北工业大学623 652 519 87532 中国政法大学621 644 605 2133 大连理工大学620 632 613 6434 中南财经政法大学618 639 608 5135 天津医科大学617 625 609 1436 南方医科大学615 634 608 1637 华南理工大学615 633 607 5738 南京航空航天大学614 644 600 15639 北京交通大学613 639 590 8840 北京第二外国语学院612 625 599 1441 四川大学612 664 597 21142 南京审计学院609 626 602 743 西安电子科技大学608 637 518 115444 山东大学608 634 598 10645 电子科技大学607 637 590 14946 天津财经大学605 619 598 2747 重庆大学605 649 595 13748 重庆医科大学603 621 596 4549 北京科技大学602 620 591 11150 河北医科大学602 605 599 451 中国农业大学601 664 588 8152 中南大学601 648 589 19953 华北电力大学(北京) 600 648 517 7554 湖南大学600 619 593 11255 中国传媒大学599 620 583 2156 中国石油大学(北京) 599 642 520 9457 华北电力大学(保定) 598 628 580 7458 北京中医药大学597 629 579 2859 南京理工大学597 651 588 13860 山西医科大学597 607 592 361 中国医科大学596 619 561 3262 苏州大学596 612 587 2863 华东理工大学596 624 585 9564 首都经济贸易大学593 605 583 865 哈尔滨医科大学593 627 583 3066 大连医科大学593 610 586 2967 西南交通大学592 616 583 19368 吉林大学591 632 578 21369 哈尔滨工业大学(威海) 590 616 572 6670 中国海洋大学589 623 578 7171 长安大学589 626 519 138272 北京工业大学587 606 582 2273 广州中医药大学587 588 586 274 广东外语外贸大学586 624 568 1775 兰州大学586 611 554 12176 武汉理工大学585 605 578 14177 东北大学585 626 574 10778 东北财经大学585 628 525 1179 河海大学584 614 577 11080 广西医科大学584 595 574 881 中国药科大学584 618 574 5382 哈尔滨工程大学584 615 572 8583 上海大学584 616 577 3384 北京化工大学582 609 571 11285 深圳大学581 602 569 2286 中国石油大学(华东) 580 634 517 12587 江西财经大学579 599 569 1988 合肥工业大学579 595 573 9589 中国地质大学(北京) 579 608 521 8590 中国民航大学578 624 562 12691 电子科技大学(沙河校区) 578 599 566 2892 西北大学578 620 519 108093 北京林业大学577 640 566 7094 中国矿业大学(北京) 577 601 562 7195 南京邮电大学576 586 566 1896 中国地质大学(武汉) 575 594 567 8897 福州大学575 580 569 898 北京邮电大学(宏福校区) 575 610 554 1099 东华大学574 608 565 58 100 上海理工大学574 590 568 35 101 大连海事大学574 616 565 51 102 南京信息工程大学573 620 558 29 103 中央民族大学572 607 561 32 104 郑州大学572 598 565 128 105 成都中医药大学572 575 570 6 106 中国矿业大学571 607 561 256 107 河北工业大学571 585 565 40 108 山东大学威海分校571 589 565 45 109 江南大学570 583 564 53 110 华东政法大学569 614 538 16 111 陕西师范大学568 618 524 652 112 燕山大学567 586 557 70 113 南昌大学566 611 558 210 114 西南大学565 583 560 96 115 江苏大学564 599 554 37 116 西安建筑科技大学563 634 518 2943 117 西南政法大学562 611 545 20 118 华南师范大学562 585 554 5 119 北京工商大学562 576 555 36 120 太原理工大学561 596 553 290 121 暨南大学560 596 517 17 122 青岛大学559 585 548 56 123 宁波诺丁汉大学559 633 532 12 124 沈阳药科大学559 578 542 38 125 浙江理工大学558 580 551 30 126 南京工业大学558 578 551 40 127 西北农林科技大学556 607 544 1353 128 西交利物浦大学555 632 520 170 129 东北大学秦皇岛分校555 579 547 60 130 安徽大学554 568 532 42 131 南京师范大学554 600 542 32 132 西安理工大学554 597 518 2974 133 北京建筑大学554 583 538 13 134 天津中医药大学553 573 543 5135 沈阳建筑大学552 572 539 40 136 湖南师范大学551 566 545 30 137 河南大学551 583 518 24 138 宁波大学551 577 543 34 139 石家庄铁道大学550 592 537 124 140 云南大学550 576 541 113 141 湖南中医药大学549 590 532 30 142 黑龙江中医药大学549 558 542 6 143 西安邮电大学548 578 520 412 144 中南林业科技大学548 576 517 58 145 东北石油大学548 577 523 43 146 华侨大学547 585 537 72 147 东北师范大学546 571 519 13 148 北方工业大学546 567 528 20 149 辽宁大学546 567 535 12 150 青岛科技大学546 567 537 60 151 湘潭大学546 606 536 209 152 延安大学545 583 521 304 153 宁夏医学院544 574 533 80 154 西安外国语大学544 605 528 375 155 东北农业大学544 580 519 32 156 南京农业大学544 572 535 77 157 合肥工业大学(宣城校区)543 586 517 87 158 海南大学543 577 534 180 159 长春理工大学542 586 531 79 160 天津外国语大学542 565 518 10 161 南华大学542 589 517 101 162 湖北大学541 561 533 37 163 重庆邮电大学541 595 528 81 164 宁夏大学541 583 530 65 165 西安石油大学541 604 517 2664 166 广西大学540 574 531 106 167 浙江工业大学540 570 531 40 168 华中农业大学540 566 534 67 169 贵州大学539 554 533 62 170 湖南农业大学539 567 518 67 171 西安科技大学538 616 532 751 172 延边大学538 556 528 34 173 长沙理工大学537 553 530 61 174 青海大学536 577 521 162 175 山西大学535 570 526 45 176 内蒙古大学535 622 525 114 177 北京体育大学534 599 518 19 178 四川外语学院534 557 527 7 179 武汉科技大学533 565 526 94180 北京机械工业学院533 554 526 40 181 辽宁工程技术大学533 554 524 35 182 陕西科技大学532 578 519 3436 183 天津工业大学532 557 522 91 184 天津理工大学530 615 520 84 185 江苏科技大学530 564 520 61 186 四川农业大学529 543 524 60 187 山东科技大学528 536 523 40 188 东北林业大学528 574 520 79 189北京师范大学-香港浸会大学联合国际学院528 571 517 9 190 新疆大学527 557 521 72 191 西安工业大学525 599 517 3662 192 沈阳农业大学524 533 517 12。

陕西省2000年至2010年专升本高等数学真题及部分样题(呕心沥血地珍藏)

2001年陕西普通高校专生本招生高等数学试题一. 填空题 (每小题3分,共计30分)1. 函数)2ln(3-+-=x x y 的定义域是_______.2. =-∞→3)21(lim xx x________.3. =-+∞→)2(lim n n n n ________.4. 设函数⎩⎨⎧-≥+-<-=+1,1,1,1)(x x x e x f a x 在),(+∞-∞连续,则.______=a5. 设)(x f 为[-1,1]上可导的偶函数,则=')0(f _______.6. 函数)()2)(1()(n x x x x f ---= 的导数有______个实根.7. 函数109323+--=x x x y 拐点坐标为_______.8. 函数x x a x f 3cos 33sin )(+=在6π=x 处有极值,则.______=a9.=+-⎰dx x x 2223________.10. 设域D:,322x y x ≤+则=+⎰⎰dxdy y x D22_______.二. 单项选择题 (每小题3分,共计30分) 1. 设⎩⎨⎧≥<+=0,2,0,2)(x x x x f ,则))((x f f 等于( ) A. 2+x B. 2 C. ⎩⎨⎧-≥-<+2224x ,,x ,x D. ⎩⎨⎧-≥+-<2,4,2,2x x x2. 函数)1ln(+=x y 在)0,1(-内( )A. 严格单调增加且有界B. 严格单调增加且无界C. 严格单调减少且有界D. 严格单调减少且无界3. )(lim 0x f x x -→存在是)(lim 0x f x x →存在的( ) A. 充分条件 B. 必要条件 C. 充分必要条件 D. 既非充分又非必要条件 4. 当0→x 时,)sin(3x x +与x 3比较是( )A. 高阶无穷小量B. 低阶无穷小量C. 同阶无穷小量D. 等价无穷小量 5. 直线95-=x y 与曲线3732+-=x x y 相切,则切点坐标为( )A. (2,1)B. (-2,1)C. (2,-1)D. (-2,-1) 6. 设)(x f 的一个原函数为23+-x e ,则=')(x f ( )A. 233+--x eB. 2331+--x eC. 239+-x e D. 239+--x e7. 设级数∑∞=1n nU收敛,则必收敛的级数为( )A.∑∞=12n nUB.)(2112n n n U U-∑∞=- C. ∑∞=1n n U D. )(11+∞=+∑n n n U U8. 函数1),(22--+++=y x y xy x y x f 的极值为（） A. 1- B. 2- C. 1 D. 2 9. 设⎰⎰=Ddxdy y x g I ),(,其中D 是由曲线x y 42=与x y =所围成的闭区域,则I=( ) A.⎰⎰402),(xxdy y x g dx B.⎰⎰404),(x xdy y x g dx C.⎰⎰4402),(y dx y x g dy D.⎰⎰442),(y ydx y x g dy10. 平面632=++z y x 与三个坐标平面围城的四面体的为( ) A. 1 B. 2 C. 3 D. 6 三. 计算题 (每小题8分,共计40分) 1. 求极限xx xx x sin tan lim20-→.2. 计算不定积分dx x⎰+11.3. 求函数9824)(23+--=x x x x f 在区间 ]2,2[-上的最大值和最小值.4. 设x y z u arctan =,化简 222222zuy u x u ∂∂+∂∂+∂∂.5. 求幂级数∑∞=+01n nn x 的收敛区间及和函数.四. (10分) 证明当0>x 时有不等式 ).1ln(21x xxx +>++ 五. (10分) 过点M(2,1)作抛物线1-=x y 的切线,求由切线, 抛物线及x 轴所围平面图形的面积.六. (10分) 求微分方程165+=+'-''xe y y y 的通解. 七. (10分) 证明曲面x +)0(>=+a a z y 上任一点的切平面在三个坐标轴上的截距之和为一常数.八. (10分) 设L 表示自点A(2a ,0)到点B(0,0)的上半圆周)0(222>=+a ax y x , 计算曲线积分dy y x y x dx yx x L)12()11(2222+++++++⎰.2001年陕西普通高校专升本招生高等数学试题答案一. 填空题 1. 32≤<x 2. 32-e3. 14. 15. 06. 1-n7. )1,1(-8. 29. 1 10. 12二. 单项选择题1. C2. B3. B4. C5. A6. C.7. D8. B9. A 10. D 三. 计算题1. 312. c x x ++-+14)1(34233. 最大值17)2(=f ,最小值15)2(-=-f4. 05. )1,1[,)1ln(-∈--x x x 四. 证设),1ln(21)(x x x x x f +-++=因,0)111()(2>+-='xx f 所以当0>x 时)(x f 单增,又0)0(=f ,所以得证. 五.31六. 61213221+++=x x xe e c ec y七. 证设,),,(a z y x z y x F -++=则.21,21,21zF yF xF z y x ===设),,(000z y x 为曲面上任一点,则该点处的切平面方程为1000=++az zay y ax x , 于是截距之和为a a az ay ax ==++2000)(为常量.八. ).41ln(21222a a a +--π 2002年陕西高校专升本招生高等数学试题一. 填空题 (每小题3分,共计30分) 1. 函数)1012ln(512++++=x x x y 的定义域是_________. 2. 极限=+++∞→2)21(lim x x x x __________.3. =++++++∞→)12111(lim 222nn nnn _________.4. 设函数⎪⎩⎪⎨⎧=≠=0,20,sin )(x x x ax x f 在(),-∞∞+上连续,则=a ________.5. )23sin(+x 是)(x f 的一个原函数,则=')(x f _________.6.=+-⎰dx x x 3234_________.7.∑∞=+1)2(1n n n 的和为_______. 8. 设,ln 222z y x u ++=则=∂∂+∂∂+∂∂zuz y u y x u x________. 9. 设,182222π=+⎰⎰≤+dxdy y x r y x 则=r ________.10. 级数∑∞=+13n nnn x 的收敛区间是________.二. 单项选择题(每小题3分,共计30分)1. 设)1ln()(2x x x f ++=在(+),-∞∞上是( )A. 偶函数B. 奇函数C. 单调减少函数D. 有界函数. 2. 0→x 时x x x sin )6sin(2++较x 7sin 是( )A. 高阶无穷小量B. 低阶无穷小量C. 同阶无穷小量D. 等价无穷小量 3. )(lim 0x f x x →存在是0)0()(limx x x f x f x x --→存在的（）A. 必要条件B.充分条件C. 充分必要条件D. 既非充分又非必要条件. 4. 函数x x a y 3cos sin +=在6π=x 取极值, 则=a ( )A. 3B.32C. 33D.435. 设点(1,1)为曲线1123++=bx ax y 的拐点,则=),(b a ( ) A. (1,-15) B. (5,1) C. (-5,15) D.(5.-15) 6. 曲面1=xyz 在(1,1,1)处的切平面方程是( )A. 3=++z y xB. 2=++z y xC.1=++z y xD.0=++z y x7. 级数∑∞=1n nU收敛是∑∞=12n nU收敛的( )A. 必要条件B.充分条件C. 充要条件D. 既非充分又非必要条件. 8. 设⎰⎰=D dxdy y x f I ),(,其中D 是由曲线24xy =与x y =所围成的闭区域,则I=( )A.⎰⎰41042),(xx dy y x f dx B. ⎰⎰442),(x x dy y x f dxC.⎰⎰4102),(y y dx y x f dy D. ⎰⎰42),(y ydy y x f dx9. 曲线32,,t z t y t x ===在1=t 处的切线方程是( )A. 213111-=-=-z y x B. 312111-=-=-z y xC. 112131-=-=-z y x D.211131-=-=-z y x10.),(lim 00y x f y y x x →→存在是),(lim )(),(0,0y x f y x y x →存在的( )A. 必要条件B. 充分条件C. 充要条件D. 既非充分又非必要条件三.计算题(每小题8分,共计40分) 1. 求极限)111(lim 0--→x x e x ; 2. 求不定积分dx x x x⎰+)1(arctan ;3. 求定积分⎰exdx 13ln .4. 求函数)0()(>=x x x f x的极值,并判断是极大值还是极小值. 5. 求三重积分dxdydz y x)(22+⎰⎰⎰Ω.其中Ω由抛物面z y x 222=+与平面2=z 所围.四. (10分) 设),0(2,110≥==+n x x x n n 证明数列{}n x 收敛,并求n n x ∞→lim .五.(10分) 证明:若,0b a ≤<则aab a b b a b -≤≤-ln . 六.(10分) 判定方程)0(ln >=a ax x 有几个根? 七.(10分) 求微分方程x e y y y x+=+'+''245的通解.八.(10分) 计算⎰⎰∑++-+,)2()(2322dxdy z y dzdx z y x dydz xz 其中∑为上半球面 224y x z --=外侧.2002年陕西普通高校专升本招生高等数学试题答案一. 填空题 1. 626->x 2. 1-e 3. 1 4. 2 5. )23sin(9+-x6.38 7. 438. 1 9. 3 10. )3,3(- 二. 单项选择题1. B2. D3. A4. B5. D6. A7. D8. A9. B 10. C 三. 计算题1. 212. c x +2)(arctan3. e 26-4. 极小值e ef 1)1()21(= 5. π316四. 证因,210<=x 设2<n x 成立，则22221=⋅<=+n n x x ，所以,20<<n x 即数列{}n x 有界, 又02)2(21>+-=-=-+nn n n n n n n x x x x x x x x ,则{}n x 单调递增,即数列{}n x 收敛.设,lim a x n n =∞→ 对n n x x 2=两边取极限,得2=a .五. 证设x x f ln )(=,则)(x f 在],[b a 上连续,在),(b a 内可导,有ab a ba b a b f -=--=='lnln ln 1)(ξξ，因,b a ≤≤ξ 得,111a b ≤≤ξ即aa b a b b 1ln1≤-≤. 六. 设 ,ln )(ax x x f -= )0(>x ,则由a x x f -='1)(得)1(af 为极大值,且,)0(-∞=f -∞=+∞)(f ,则当0)1(<a f 即e a 1>时,方程无实根.当0)1(=a f 即e a 1=时,方程仅有一个实根.当0)1(>a f 即ea 10<<时,方程有两个实根.七. 16541012241-+++=--x e e c ec y x x x. 八. .332π2003年陕西高校专升本招生高等数学试题一. 单选题 (每题5分,共25 分)1. 当0→x 时，x x a --+=11是无穷小量，则( ) A. a 是比x 2 高阶的无穷小量 B. a 是比x 2 低阶的无穷小量C. a 与x 2是同阶的无穷小量,但不是等价无穷小量D. a 与x 2是等价无穷小量 2. )(x y y =是由方程22ln arctany x x y +=确定的隐函数,则=dxdy ( ) A.x y x y +- B. x y x y -+ C. y x y x +- D. yx yx -+ 3. 函数x xe y -=在]2,1[-上的最大值或最小值正确的是( )A. 最大值为 1-e B. 最小值为 1-e C. 最小值为0 D. 最小值为12-e 4. 设曲线L 的方程是),20,0(sin ,cos π≤≤>==t a t a y t a x 则曲线积分=+⎰Ln ds y x )(22( )A. n a 22πB. 122+n a πC. n a π-D. n a π 5. 下列级数中,条件收敛的级数是( ) A.∑∞=11011n nB.∑∞=-1)1(n nn C. ∑∞=+-1221)1(n n n n D. ∑∞=-12)1(n nn 二. 填空题 (每题5分,共25 分) 6. 已知函数)],([)(,1)(x f f x g xxx f =+=则_______)(='x g . 7. 极限=+→xx x 20)21(lim __________.8. 过点（-1，2，0）并且与平面32=++z y x 垂直的直线方程为._________9. 设D 是第一象限中由曲线02,2=-+=y x x y 和0=y 所围成的区域，则.________⎰⎰=Dxdxdy 10.),0(ln 3>=x x x y 则.___________)4(=y三. 计算题 (每题9分.共81分)11. 求极限：)1cos )1(3sin 8(lim 70xe x e e x x x x -+--→12. 求函数y x xy x z 1215323--+=的极值 . 13. 求不定积分⎰.arctan xdx x14. 设,0,10,411)(2⎪⎪⎩⎪⎪⎨⎧<+≥+=x e e x x x f xx求定积分.)(211dx x f ⎰- 15. 已知)(x f 为可导函数,并且,0)(>x f 满足方程dt ttt f x f x⎰++=02cos 1sin )(9)(,求).(x f16. 设),3()tan(221arcsin3y yf y x xy e z xx-+++=-其中f 为可导函数，求.x z ∂∂ 17. 求曲面3632222=++z y x 在点)3,2,1(P 处的切平面. 18. 将函数)1ln()(2x x x f +=展开为麦克劳林级数. 19. 求微分方程x e y y y 232232+=-'-''的通解. 四. 应用与证明题 (20题11分,21题8分)20. 求曲线1)2(22=-+y x 所围图形绕X 轴旋转一周所得旋转体的体积. 21. 设)(),(x g x f 都是可导函数,且),()(x g x f '<'证明: 当a x >时,).()()()(a g x g a f x f -<-2003年陕西高校专升本招生高等数学试题答案一. 单选题1. C2. D3. A4. B5. B 二. 填空题6.2)21(1x + 7. 4e 8. 201211-=-=+z y x 9. 1211 10. x 6 三. 计算题11.3112. 极大值为,28)1,2(=--z 极小值为28)1,2(-=z 13. C x x x x +--)arctan (21arctan 212 14. 8)1ln(2ln 1π++--e15. 2ln 213)cos 1ln(21)(+++-=x x f16. )3(3ln 3)()tan(2)(sec )(1322222221arcsin3y f y y x xy x xy y x y x x e x z xx x-'⋅⋅++-++-=∂∂- 17. 3694=++z y x18. +-++-+-=++1219753)1(413121)(n n x nx x x x x f 1≤x 19. 通解x x xe e C eC x y 32221731)(+-+=-四. 应用题与证明题 20. 24π=x V21. 证已知)()(x g x f '<',故有)()()(x g x f x g '<'<'-.令)()()(x g x f x F -=, 则 )(,0)()()(x F x g x f x F <'-'='单减, 所以 a x >时, 有)()(a F x F <,即)()()()(a g x g a f x f -<-.2005年陕西高校专升本招生高等数学试题一. 单选题 (每题5分,共25 分)1. 设函数⎪⎩⎪⎨⎧=≠=0,00,1sin )(x x xx x f ,则0=x 是( ) A. 可去间断点 B. 跳跃间断点 C. 第二类间断点 D. 连续点 2.⎰='dx x f )3(( )A. c x f +)3(B.c x f +)3(31 C. c x f +)(3 D.c x f +)(313. 设由方程0),(=++bz y az x F 确定隐函数),(y x z z =,则yzb x z a ∂∂+∂∂= ( ) A. a B. b C. 1- D. 1 4. 下列级数为绝对收敛的是( ) A.n n n1)1(1∑∞=- B. ∑∞=-12)1(n n n C. ∑∞=-12)1(n nn D. nn n )23()1(0∑∞=-5. =⎰⎰-dx edy yx 1012( )A.)11(21e - B. )11(21-e C. )11(2e - D. )11(2-e二. 填空题 (每题5分,共25 分)6. 已知)(x f 的定义域为[0,2], 则)21()21(-++x f x f 的定义域为__________. 7. 设e xm xx =+∞→3)1(lim ,则=m __________. 8. 设23)(23+-=x x x f ,则曲线)(x f y =的拐点是__________.9. dx x x x )1sin (1122⎰--+=___________.10. 设)cos(y x e z xy -+=,则=)1,1(|dz __________. 三. 计算题 (每题9分.共81分)11. 计算.sin )1ln(lim2202xx dtt x x ⎰+→12. 已知参数方程 ⎩⎨⎧+-==)1ln(1arctan 2t y t x ,求.,|221dx yd dx dy t = 13. 求不定积分.1arctan 22dx xxx ⎰+ 14. 已知)(x f 是可导函数,且0)1(=f ,,311)(=⎰dx ex f 求dx x f xe x f )(1)('⎰.15. 已知xy v y x u v u f z =+==,),,(,f 具有二阶连续的偏导数,求.2yx z∂∂∂16. 已知曲线方程⎩⎨⎧==21xy xyz ,求在点(1,1,1)处曲线的切线方程和法平面方程.17. 求曲线积分,22⎰+-Lyx xdy ydx 其中L 为)0(222>=+a a y x 取逆时针方向. 18. 将函数24x xy +=展开为麦克劳林级数,并确定其定义域.19. 求微分方程xxe y y y 244=+'-''的通解.四. 应用与证明题 (20题11分,21题8分)20. 设抛物线,2bx ax y +=当0,10≥≤≤y x 时，已知它与直线1,0==x y 所围成的图形的面积为31.求b a ,的值,使此图形绕X 轴旋转一周而成的旋转体的体积最小. 21. 证明:若)(),(x g x f 在],[b a 上连续,在),(b a 内可导,,0)(,0)()(≠==x g b f a f 则至少存在一点),(b a ∈ξ,使.0)()(2)()(='+'ξξξξf g g f2005年陕西高校专升本招生高等数学试题答案一. 单选题1. D2. B3. C4. B5. A 二. 填空题6. ]23,21[ 7. 31 8. )0,1( 9. 2π10. )(dy dx e + 三. 计算题11. 21 12. 2|)2(|11-=-===t t t dx dy . )1(2112)2()(2222t t dt dx t dt ddx dy dx d dxy d +-=+-=-==13. C x x x x +++-22)(arctan 21)1ln(21arctan14. dx x f xex f )(1)('⎰=32311|)(1)(1)(1)(=-=-=⎰⎰dx e xeexd x f x f x f 15. 2222112112)(f y x f f x f f yx z +⋅++⋅+=∂∂∂16. ⎪⎪⎩⎪⎪⎨⎧+-==⇒⎪⎪⎩⎪⎪⎨⎧=-=+⇒⎪⎩⎪⎨⎧==y x xz dxdz x dx dyx dx dy x dx dz y dx dy z x y x yz 222122211,在(1,1,1)处 3,2)1,1,1()1,1,1(-==dx dzdx dy , 切向量)3,2,1(-=T 切线为312111--=-=-z y x 法平面为0)1(3)1(2)1(1=---+-⋅z y x 即032=-+z y x 17. 不能用格林公式. L:π20,sin ,cos ≤≤==t t a y t a x 有.2cos sin 202222222⎰⎰-=--=+-Ldt a ta t a yx xdyydx ππ18. )2,2(,2)1()2()1(4)2(1144112022-∈-=-⋅=+⋅=+=+∞=+∞=∑∑x x x x x xxx y n n n n n nn 19. 特征根221==r r ，齐次方程通解为x x xe C e C Y 2221+=.设非齐次方程的特解形式为x e b ax x y 22)(+=*，代入非齐次方程比较系数得：0,61==b a .故非齐次方程的通解为x xxe x xeC e C y 2322216++= 四. 应用题与证明题20. 有3123)(102=+=+⎰b a dx bx ax ，)325()(22122b ab a dx bx ax V ++=+=⎰ππ 因)1(32a b -=，故)94954514(2+-=a a V π，令0='V ，得2825=a ，又 04528)2825(>=''V ，于是141,2825==b a 时旋转体的体积最小.21. 令)()()(2x g x f x F =,则)(x F 在],[b a 上连续,在),(b a 内可导.0)()(==b F a F ,由罗尔定理知,至少存在),(b a ∈ξ使0)(='ξF , 0)()()(2)()(2='+'ξξξξξf g g g f 即.0)()(2)()(='+'ξξξξf g g f2005年陕西高校招生高等数学(样)题一. 单选题 (每题5分,共25 分)1. 设函数)2(8log )(2≥+=x x x f ,则其反函数的定义域是( ) A. ),(+∞-∞ B. ),2[+∞ C. ]2,0( D. ),9[+∞2. 设,sin )(x x f = 则=)()21(x f( )A. x sinB. x cosC. x sin -D. x cos - 3. 函数1)(+-=xe x xf ,在),0(+∞内 ( )A. 是单调增加函数B. 是单调减少函数C. 有极大值D. 有极小值 4. 过点),3,1,2-且与直线⎩⎨⎧=+-=--+0807232z x z y x 垂直的平面方程为 ( )A. 019343=-+-z y xB. 01343=---z y xC. 05=-+z xD. 01=+-z x5. 微分方程x xe y y y 223=+'-''利用待定系数法求其特解*y 时, 下列特解设法正确的是 ( )A. x e b ax x y 2)(+=*B. x e b ax y 2)(+=*C. x axe y 2=*D. x e b ax x y 22)(+=* 二. 填空题 (每题5分,共25 分) 6. 设=+-++∞→1)11(lim x x x x __________. 7. 设函数xy 1sin 22-=,则.___________=dy8. 已知)(x f 满足⎰-=12)()(dx x f x x f ,则)(x f _____________.9. 二重积分dy yydx x ⎰⎰11sin =___________. 10. 幂级数nn nx nn ∑∞=1!的收敛半径=R __________. 三. 计算题 (每题9分.共81分) 11. 计算 ).)1(tan sin 1sin(lim 20--+→x x e x x x x x 12. 设参数方程 ⎪⎩⎪⎨⎧-=+=2211ty tx 确定了)(x y y =,求.,22dx y d dx dy 13. 求不定积分.122dx xx ⎰+14. 求曲线xe y =及该曲线过原点的切线与y 轴所围成的平面图形的面积和该平面图形绕x 轴旋转所得的旋转体体积.15. 已知)),ln(,(y x e f z xy+=其中),(v u f 具有二阶连续的偏导数,求.,22yzx z ∂∂∂∂16. 计算曲线积分),1(22>⎰+a ds aL y x 其中L 为曲线x y y x 3,162=-=及x 轴所围区域的边界. 17. 设⎰-=xt f dt t f x t x F 0)(,)()2()(为可导函数且0)(>'x f ,确定曲线)(x F y =的凹凸区间及拐点. 18. 将函数2312++=x x y 展开成)1(+x 的幂级数,并确定其收敛区间.19. 已知曲线)(x f y =在其上任意点),(y x 处的切线斜率为y x +3,并且过原点,求曲线)(x f y =.四. 应用与证明题 (20题11分,21题8分)20. 假设由曲线),10(1:21≤≤-=x x y L x 轴和y 轴所围成区域被曲线22:ax y L =分成面积相等的两部分,其中a 是大于零的常数, 试确定a 的值.21. 设)(x f 在],[b a 上连续,在),(b a 内可导,,0)()(==b f a f 证明则在),(b a 内至少存在一点ξ,使)()(ξξf f ='.2005年陕西高校专升本招生高等数学(样)题答案一. 单选题1. D2. B3. B4. C5. A 二. 填空题6. 2-e 7. 21sin 2sin2ln 22xx x⋅⋅- 8. 612-x 9. 1cos 1- 10. e三. 计算题11. 21- 12. 2211tt dx dy -+-=， 23222)1(2t dx y d --=13.C x x x x +++-+|1|ln 2112122 14. 所求切线方程为 ex y =. 面积121)(10-=-=⎰e dx ex e s x . 体积.26)()(2102210ππππ-=-=⎰⎰e dx ex dx e v x15.211f y x f ye x z xy ++=∂∂， 211f yx f xe y z xy ++=∂∂ )1(1)(1)1(22212212111222f y x f xe y x f y x f y x f xe xe f e x y z xy xy xy xy +++++-+++=∂∂ 16. +=⎰⎰++ds ads aL y x Ly x 12222ds ads aL y x L y x ⎰⎰+++322222=.34ln )1(23144440223a a a ds a dx a dx aL xxπ+-=+++⎰⎰⎰17. ⎰⎰-=xxdt t f x dt t f t x F 0)()(2)(，⎰--='xx xf dx x f x xf x F 0)()()(2)()()(x f x x F '='', 当0>x 时0)(>''x F ，当0<x 时0)(<''x F ，曲线)(x F y =的上凹区间为),0[+∞，上凸区间为]0,(-∞，拐点为)0,0(. 18. 231121)3(112111)2)(1(1)(+-⋅-+-=+-+=++=x x x x x x x f 1|3|)3)(211()23(21)3(0100<++-=+-+=∑∑∑∞=+∞=∞=x x x x nn n nn n n.收敛区间为)2,4(--.19.y x dxdy += 通解为 ]3[)()1()1(C dx xe e x y dx dx +⎰⎰=⎰---)1(3+-=x Ce x由 0)0(=y 得2=C ,故所求曲线为)1(33+-=x e y x . 四. 应用题与证明题20. 设点M 的坐标为),(00y x ,由⎰⎰-=--12022)1(])1[(2dx x dx ax x x 得3131300=+-x a x , 又20201x ax -=, 即1)1(20=+x a , 解得3=a . 21. 令)()(x f e x F x -=,则)(x F 在],[b a 上连续,在),(b a 内可导.0)()(==b F a F ,由罗尔定理知,至少存在),(b a ∈ξ使0)(='ξF , 0)()(=-'--ξξξξf e f e ,即).()(ξξf f ='2010年陕西省普通高等教育专升本招生考试（样题）一、单项选择题：本大题共5小题，每小题5分，共25分。

大学本科专业目录(2012年教育部)

80101 80102 802 80201 80202 80203 80204 80205 80206 80207 80208 803 80301 804 80401 80402 80403 80404 80405 80406 80407 80408 805 80501 806 80601 807 80701 80702 80703 80704 80705 80706 808 80801 809 80901 80902 80903 080904K 80905 80906 810 81001 81002 81003
阿尔巴尼亚语保加利亚语波兰语捷克语斯洛伐克语罗马尼亚语葡萄牙语瑞典语塞尔维亚语土耳其语希腊语匈牙利语意大利语泰米尔语普什图语世界语孟加拉语尼泊尔语克罗地亚语荷兰语芬兰语乌克兰语挪威语丹麦语冰岛语爱尔兰语拉脱维亚语立陶宛语斯洛文尼亚语爱沙尼亚语马耳他语哈萨克语乌兹别克语祖鲁语拉丁语翻译商务英语新闻传播学类新闻学广播电视学广告学传播学编辑出版学学科门类：历史学历史学类历史学
100801 100802 1009 100901K 1010 101001 101002 101003 101004 101005 101006 101007 1011 101101 12 1201 120101 120102 120103 120104 120105 1202 120201K 120202 120203K 120204 120205 120206 120207 120208 120209 120210 1203 120301 120302 1204 120401 120402 120403 120404 120405 1205 120501 120502 120503 1206

陕西统招专升本高等数学真题10年真题(2011-2019)

2011年陕西省普通高等教育专升本招生考试一、单项选择题：（本大题共5小题,每小题5分,共25分.在每小题给出的四个选项中,只有一项是符合题目要求的） 1、下列极限存在的是（） A 、11lim0-→x x e B 、x x 1sin lim 0→ C 、xx x 1sinlim 0→ D 、跳跃间断点 2、设曲线22-+=x x y 在点M 处的切线斜率为3，则点M 的坐标是（）A 、()0,2-B 、()0,1C 、()20-，D 、()4,2xxe x f =，则()()=x f11（）()e x 10+ ）C 、∞=n )+⎪⎭⎫ ⎝⎛1321nn的值为（）C 、22e π ,每小题5⎰21=y 8、过点并且与平面32=-+z y x ______ 9、设函数()233,xy x y x f +=，则函数()y x f ,在点()1,1处的梯度为_______10、已知函数()x f 在[]1,0上有连续的二阶导数，且()()()31,21,10='==f f f ，则定积分()_______1=''⎰dx x f x三、计算题（本大题共10小题,每小题8分,共80分.计算题要有计算过程）11、求极限()xdt t x x 4sin 1ln lim2⎰+→12、设参数方程⎪⎩⎪⎨⎧==+te y ex tt cos 212确定了函数()x y y =，求22dx y d13、设函数()3129223-+-=x x x x f ，求()x f 的单调区间和极值14、设函数()y x x f z ln ,=，其中()v u f ,具有二阶连续偏导数，求xy z∂∂∂215、计算不定积分()⎰+x x dx 116、设函数()x f 在()+∞∞-,内具有二阶导数，且()()000='=f f ，试求函数()()⎪⎩⎪⎨⎧=≠=0,00,x x x x fx g 的导数.dxdy y -+122(){,22+y x y x (⎰+=Ly xI 2L 是圆周()[]⎰-Lxx f exoy ()x f2小题,9 22、设函数()x f 在[]3,1上连续，在()3,1内可导，并且()()⎰=321dx x xf f ，证明：在()3,1内至少存在一点c ，使得()()c f c c f '-=2012年陕西省普通高等教育专升本招生考试一、单项选择题：（本大题共5小题,每小题5分,共25分.在每小题给出的四个选项中,只有一项是符合题目要求的） 1、0=x 是函数()2cos 1x xx f -=的（） B 、可去间断点 B 、连续点 C 、无穷间断点 D 、跳跃间断点 2、设()C e dx x f x +=⎰，则不定积分()⎰=dx e x f x （）B 、C e x+2 B 、C e x +21 C 、C e x +221D 、C e x +22 3、函数()⎨⎧≥=11,22x x x f 在点1=x 处（）C 、不连续D 、不能判断是否可导 ()∑∞=++11n n nu u收敛于（）1u S + D 、12u S - ） C e x=- C 、C e ex y=+- D 、C e e x y =--,每小题5分,共25分） <≥0,0x x 在0=x 处连续，则____=a7、设函数()x f 在点0x 处可导，且()20='x f ，则()()___lim000=∆∆--∆+→∆xx x f x x f x8、设函数()222,,z y x z y x f ++=，则函数()z y x f ,,在点()1,1,1-处的梯度()1,1,1-gradf 为_____ 9、设方程⎰⎰=+-yt xxy dt e tdt 0sin 确定函数()x y y =，则____=dxdy10、曲面1222-+=y x z 在点()2,1,1处的切平面方程为_____三、计算题（本大题共10小题,每小题8分,共80分.计算题要有计算过程） 11、求极限()xexx x x sin 1sin lim2--→12、设参数方程()⎪⎩⎪⎨⎧+==⎰-tt du u y e x 02123确定函数()x y y =，求0=t dx dy 13、求函数()()322x x x f -=的单调区间和极值14、设函数),(yxx f z =，其中f 具有二阶连续偏导数，求y x z x z ∂∂∂∂∂2, 15、计算不定积分⎰+exx dx1ln 116、计算二重积分+=dxdy y x I 22sin，其中D 是由圆222π=+y x 与直线x y =及y()1-x z1⎫，求函数(f 422=+y x22小题,21、设曲线方程21x y -=（1）求该曲线及其在点()0,1和点()0,1-处的法线所围成的平面图形的面积（2）求上述平面图形绕y 轴旋转一周所得旋转体体积22、设函数()x f 在点[]1,0上连续，且()⎰=100dx x f ，证明：在()1,0内至少存在一点ξ，使得()()⎰=+ξξξ00dx x f f2013年陕西省普通高等教育专升本招生考试一、单项选择题：（本大题共5小题,每小题5分,共25分.在每小题给出的四个选项中,只有一项是符合题目要求的）1、0=x 是函数()21x e x f x -=的（）A 、可去间断点B 、振荡间断点C 、无穷间断点D 、跳跃间断点 2、不定积分⎰=dx x xsin （）A 、C x +-cos 2B 、C x +cos C 、C x +cos 2D 、C x +-cos)3,2B 、2+x D 、2-x 0=ydy 、y x +22ln ln C y = D ）、∑∞=131n n D 、∑∞=1n ,每小题56、设函数()xx f +=1，则()()=x f f 7、设函数()x f 满足()()20,00='=f f ，则极限()____lim 0=→xx f x 8、函数xxey -=的极大值为_______9、交换积分次序()⎰⎰=11______,xdy y x f dx10、设L 为连接点()0,1和点()1,0的直线段，则对弧长的曲线积分为()⎰=+Lds y x _____三、计算题（本大题共10小题,每小题8分,共80分.计算题要有计算过程）11、求极限()xx x e x x 220sin cos 11lim 2---→12、已知椭圆的参数方程⎩⎨⎧==tb y t a x sin cos 确定了函数()x y y =，求22dx yd dx dy ， 13、求不定积分⎰+dx e x 1114、计算定积分⎰-=π42sin sin dx x x I15、设函数⎪⎪⎭⎫ ⎝⎛=y x xyf z ，其中()u f 可导，求y zy x z x ∂∂+∂∂16、求函数()xyz z xy z y x f -+=32,,在点()2,1,10-P 处沿方向{}1,1,1--=l 的方向导数17、计算二重积分()⎰⎰+++=Dy x dxdy exy I 221，其中积分区域(){}1,22≤+=y xy x D(⎰+=Ly x I L 是曲线x y sin =上由142+xe的通解2小题,应用题的计算要有计算过程,在(1,0()=0dx x f ，证明：在()1,0()()0=-'ξξf （1）求该曲线在点()1,1处的切线方程（2）求该曲线和该切线及直线0=y 所围成的平面图形的面积（3）求上述平面图形绕x 轴旋转一周所得旋转体体积2013年陕西省普通高等教育专升本招生考试试题解析1、因为()∞===-=→→→→x x x x e x f x x x x x 1lim lim 1limlim 020200，则为无穷间断点，故选C. 2、原式⎰+-==C x x d x cos 2sin 2，故选A.3、令()()()()1|,2|,22|,2,,3,2,13,2,13,2,122-=-====-+=---z y x F y F x F z y x z y x F ，则法向量{}1,2,2--=n ，通过点法式得平面方程为()()()032212=--+--z y x ，即0322=---z y x ，故选D.4、分离变量得xxdxy ydy ln ln -=，两边同时积分得，得通解为C y x =+22ln ln ，故选B.5、A 选项用逆否命题可知发散，B 选项为调和级数发散，C 选项用比较判别法可知发散，Dx0=，得1=x ，代入原方程9、由题可知⎩⎨⎧≤≤≤≤110y x x ，通过图形可知⎩⎨⎧≤≤≤≤y x y 010，故原式为()⎰⎰y dx y x f dy 010,10、L的直线方程为()1,01∈+-=x x y ，，则曲线积分为()()⎰⎰=='++-10122211dx dx y x x11、解：原式1lim 1lim 222lim 211lim 22020*******22==-=-=--=→→→→x x x e x x xe xx x e x x x x x x x 12、解：，t b dtdxt a dt dy cos ,sin =-= 则t a b t a t a b dtdx dx dy dt d dx y d t a b dt dx dt dy dx dy 32222sin 1sin 1csc 1,cot -=-⋅=⋅⎪⎭⎫ ⎝⎛=-== 13、解：原式()⎰⎰⎰⎰++-=++-=+-=+-+=C e x e d e x dx e e dx dx ee e xx x x x x x x 1ln 111111 14、解：原式=()⎰⎰⎰⎰-=-==-ππππππ2220202222|sin 21cos sin cos sin cos sinsin1sinx xdx x xdx x dx x x dx x x=⎪⎪⎭⎫⎝⎛'yf y x f y 1⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛'y x y x f x 2 cos ,31=β)xy z y -=2,,)(,,0|0=z p x f z ()31013⋅+-⋅⎪⎭⎫⎝17、解：令,sin ,cos θθr y r x ==而⎩⎨⎧≤≤≤≤πθ2010r ，则()e e edr re d rdrd e I r r Dr -=⋅===+++⎰⎰⎰⎰2101101201|212222ππθθπ 18、解：()()1,,1,+-=-+=y x y x Q y x y x P ，1,1=∂∂=∂∂y Px Q ，由格林公式知，积分与路径无关，则()()⎰⎰+=+-+-=21221811ππdy y dx x I19、解：，则收敛半径为当时，原函数为()∑∞=-111n n n 收敛；当时，原函数为发散；故收敛域为，令，则()[)1,1,11 (1121)1-∈-=+++++=='-∞=-∑x xx x x x X S n n n ，则()()()⎰⎰--=-='=x t dx X S X S x1ln 110，而当21=x 时，2ln 21ln 21211=-=⎪⎭⎫⎝⎛=∑∞=S n n n20、解：特征方程为042=-r ，解得特征值为，又因为2=λ，为特征单根，所以1=k ，则齐次线性微分方程的通解为x xe C e C y 222-11+=，设非齐次微分方程的一个特解为xAxe y 21*=，另一个特解为B y=2*，代入原方程中解得411-==B A ，,解为1*=y ，故微分412-+x xec ⎰212()(f c f =令()()x f ex F x-=，又因为在[]c ，0上连续，在()c ，0内可导，且()()c F F =0,由罗尔定理得至少存在一点()()1,00⊂∈c ，ξ，使得()0='ξF ，即()()0=-'ξξf f . 22、解：（1）因为切线斜率2|1='==x y k ，则切线方程为()121-=-x y ，即12-=x y（2）⎰=⎪⎪⎭⎫ ⎝⎛-+=⎪⎭⎫⎝⎛-+=1010232121|32214121y y y dy y y A （3）()()ππ30112210121244=⎥⎦⎤⎢⎣⎡--+=⎰⎰dx x x dx x V x2014年陕西省普通高等教育专升本招生考试一、单项选择题：（本大题共5小题,每小题5分,共25分.在每小题给出的四个选项中,只有一项是符合题目要求的） 1、当0=x 时，是()()xx x f +=1ln 的（）A 、可去间断点B 、跳跃间断点C 、无穷间断点D 、振荡间断点2、若()20='x f ，则极限()()=--+→hh x f h x f h 000lim（） A 、2- B 、2 C 、4- D 、43、若不定积分()⎰+=C x dx x f 1，则()='x f （）x 1 132x42=)=+ds 1 ∞=n B 、∞=1n D 38、不定积分_____)ln 1(2013=+⎰dx xx 9、过点()3,2,1且与直线11232+==-z y x 垂直的平面方程是_________ 10、微分方程yx ey +='的通解是_________三、计算题（本大题共10小题,每小题8分,共80分.计算题要有计算过程）11、求极限)1(sin lim2240-⎰→x x x e x tdtt12、设函数()x y y =由参数方程()⎩⎨⎧+==21ln arctan t y t x 所确定，求22,dx yd dx dy13、求不定积分⎰-dx x x 21ln14、计算定积分求函数dx x x I ⎰+-=2212的全微分15、设函数()2,y x xy f z +=，其中()v u f ,具有二阶连续偏导数，求y x z x z ∂∂∂∂∂2,16、求函数z xy u 2=在点()1,1,1-P 处的梯度，并求该函数在P 点处沿梯度方向的方向导17、交换二次积分⎰⎰10122yx dx edy 的次序，并计算其值18、计算曲线积分()⎰++=Lxdy dx y I 22，其中L 为从点()0,1A 沿上半圆周122=+y x 到xey 2-=的通解2小题,每小题10分,共20分.应用题的计算要有计算过程, ()()010<⋅f f ，证明在()1,0内至少存在一点ξ，使得)1≤上一点处的切线，使该切线与直线1,0==x y 和曲线2xy =2015年陕西省普通高等教育专升本招生考试一、单项选择题：（本大题共5小题,每小题5分,共25分.在每小题给出的四个选项中,只有一项是符合题目要求的） 1、点0=x 是函数()xx x f =的（）A 、连续点B 、可去间断点C 、跳跃间断点D 、无穷间断点 3、设极限()()()12lim2000-=--→x x x f x f x x ，则点0x x =是函数()x f 的（） B 、极大值点 B 、极小值点 C 、驻点，但非极值点 D 、非驻点）C C y =>→7、已知当0→x 时，⎰22cos x dt t 与a x 是等价无穷小，则____=a8、设方程e xy e y=+2确定了隐函数()x y y =，则___0==x dxdy9、不定积分⎰=+____2sin 12cos dx x x10、设曲线4:222π=+y x L ，则对弧长的曲线积分()⎰=++Lds y x x ____sin22三、计算题（本大题共10小题,每小题8分,共80分.计算题要有计算过程）11、求极限()xx x x e x x 30sin 1sin lim +-→ 12、设函数()x y y =由参数方程⎪⎩⎪⎨⎧=+=tey tx 331所确定，求22,dx y d dx dy 13、求不定积分dx e x⎰14、计算定积分()⎰--+=442cos arctan ππdx x x I15、设函数()xy y x f z ,2+=，其中f 具有二阶连续偏导数，求y x zx z ∂∂∂∂∂2, )z xy +2在点()1,1,1的方向导数)+22dy y x++dy y x x )sin sin 11(22，其中L 是从点)0≥到点(B xxe y -=122小题,应用题的计算要有计算过程,21、设曲线C 的方程xe y =，（1）在曲线C 上求切点P ，使P 点处曲线C 的切线过坐标原点（2）求P 点处法线L 的方程（3）求由曲线C 、法线L 及y 轴所围成图形的面积A22、设函数()x f 在闭区间[]π,0上连续，在开区间()π,0内可导，证明在开区间()π,0内至少存在一点ξ，使得()()ξξξξcos sin f f -='2016年陕西省普通高等教育专升本招生考试一、单项选择题：（本大题共5小题,每小题5分,共25分.在每小题给出的四个选项中,只有一项是符合题目要求的）1、点0=x 是函数21()x e f x x-=的（）A 、连续点B 、可去间断点C 、跳跃间断点D 、无穷间断点2、设在闭区间[]b a ,上, ()0f x >,()()0,0<''>'x f x f ，令1()baS f x dx =⎰,2()()S f a b a =-,3[()()]2b aS f a f b -=+,则必有（）312S S S << C 、213S S S <<D 、132S S S <<)0,1,1(处的切平面方程为（）B 、4480x y z ++-=D 、4480x y z +++=）CC 、C y x =-D. C y x =+22在2=x 处发散,则该幂级数在1-=x 处（）C 、发散D 、敛散性不确定,每小题5分,共25分） 6、极限0sin 2limln(1arcsin )x xx →+=7、已知当0x →时,sin 20xt dt ⎰与a x 是同阶无穷小,则常数=a8、定积分33(cos x x dx -+⎰=9、二元函数y z x = ()0,1x x >≠的全微分=dz 10、设曲线L 为圆周122=+y x ,则弧长的曲线积分⎰=+Lds y x 22_______三、计算题（本大题共10小题,每小题8分,共80分.计算题要有计算过程）11、已知函数⎩⎨⎧<≥+=0,0,)(x e x b ax x f x,在0=x 处可导,试确定常数a 和b12、设函数()y y x =由参数方程2,21t x y t⎧=⎪⎨⎪=-⎩所确定,求dy dx ,22d y dx13、求函数3()31f x x x =-+的极值点及其图形的拐点 14、求不定积分arctan xdx ⎰),其中f ,22zx ∂∂)1,1,1( 2dy xy++x dx y ()2)0,0(经过点)0,1(A 到点xe x y )1(+=2.应用题的计算要有计算21、设0a b >>,1n >,证明：11()()n n n n nb a b a b na a b ---<-<-22、求曲线2y x =和y =S ,并求次图形绕x 轴旋转一周所形成的旋转体的体积V2017年陕西省普通高等教育专升本招生考试一、单项选择题：本大题共5小题，每小题5分，共25分。

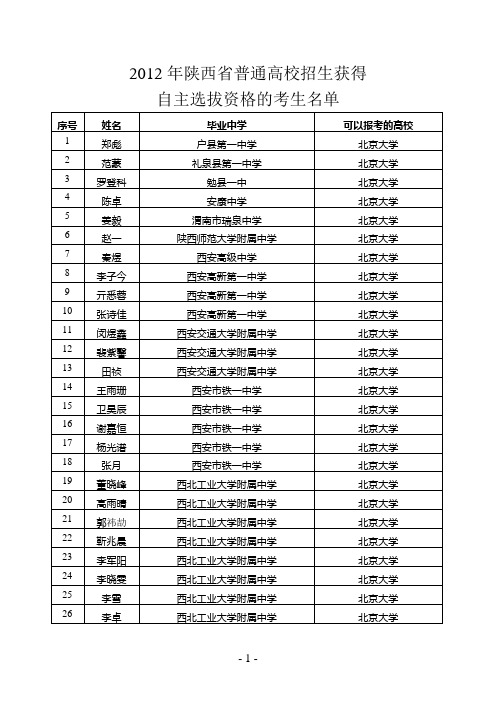
2012年陕西省普通高校招生获得

-8-
同济大学同济大学同济大学同济大学上海交通大学上海交通大学上海交通大学上海交通大学上海交通大学上海交通大学上海交通大学上海财经大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学浙江大学
140 刘道洲
141 肖武心
142 刘晗之
143 任白帆
144
谭笑
145 杨栋栋
146 王昊辰
西安高新第一中学西安建筑科技大学附中西安市第八十三中学西安市第八十三中学西安市铁一中国际合作学校
西安市铁一中学西安市铁一中学西北工业大学附属中学
山阳中学商洛中学高新一中西安交通大学附属中学西北工业大学附属中学西北工业大学附属中学岐山高级中学西安交通大学附属中学三原县南郊中学西安市高新一中西安交通大学附属中学西北工业大学附属中学西北工业大学附属中学西北工业大学附属中学西安市铁一中学山阳中学西安高级中学西北工业大学附属中学西北工业大学附属中学西北工业大学附属中学榆林中学汉江机床厂子弟学校
-2-
北京大学北京大学北京大学北京大学北京大学北京大学北京大学北京大学北京大学北京大学中国人民大学中国人民大学中国人民大学中国人民大学中国人民大学中国人民大学中国人民大学中国人民大学中国人民大学中国人民大学中国人民大学中国人民大学中国人民大学清华大学清华大学清华大学清华大学清华大学清华大学清华大学
87
张宇
88
张子扬
89
周万锋
90
肖玉婷
91
华彦裴

陕西省普通高等教育专升本分专业及学校

07电子商务（文）
西安科技大学
08工商管理（文）
宝鸡文理学院\西安财经学院
09市场营销（文）
渭南师范学院\西北政法大学\西安财经学院\西安邮电学院
10会计学（文）
西安工业大学\西安石油大学\西安财经学院
11财务管理（文）
安康学院
12旅游管理（文）
宝鸡文理学院
13广播电视新闻学（文）
陕西省普通高等教育专升本分专业及学校是：
普通高等教育专升本按文史、外语、艺术、理工、医学五个类别编排（每年的专业和计划有所差别，具体可查陕西省专升本网）。
(一)、文史类
01国际经济与贸易（文）
西安工程大学\西北政法大学\西安财经学院
02金融学（文）
西安财经学院
03法学（文）
西安财经学院
14学前教育（文）咸来自师范学院（二）、外语类
15英语（外）
西安科技大学\陕西理工学院\宝鸡文理学院\咸阳师范学院\渭南师范学院\西安外国语大学\榆林学院\商洛学院\安康学院
(三)、艺术类
16艺术教育（艺）
宝鸡文理学院
17音乐学（艺）
宝鸡文理学院
18
美术学（艺）
宝鸡文理学院
商洛学院
19艺术设计（艺）
西安工程大学\西安美术学院
西北政法大学\榆林学院
04思想政治教育（文)
咸阳师范学院\渭南师范学院\榆林学院\商洛学院\安康学院
05汉语言文学（文）
延安大学\陕西理工学院\宝鸡文理学院\咸阳师范学院\渭南师范学院\榆林学院\商洛学院\安康学院
06历史学（文）
咸阳师范学院\渭南师范学院\西安文理学院\榆林学院\商洛学院

2012年普通高等学校招生全国统一考试(陕西卷)英语试题含答案

2012年普通高等学校招生全国统一考试（陕西卷）英语试题含答案第一部分：英语知识运用（共四节，满分55分）第一节语音知识（共5小题；每小题1分，满分5分）从每小题的A、B、C、D四个选项中，找出其划线部分与所给单词的划线部分读音相同的选项，并在答题卡上将该选项涂黑。

1. regardA. designB. gentleC. collegeD.forget2. refuseA. discussB. rudeC. focusD.excuse3. chargeA. toothacheB. machineC. searchD.Christian4. fieldA. quietB. pieceC. friendD.experience5. tapesA. potatoesB. speechesC. cakesD.bridges第二节情景对话（共5小题；每小题1分，满分5分）根据对话情境和内容，从对话后所给的选项中选出能填入每一空白处的最佳选项，并在答题卡上将该选项涂黑。

选项中有两个为多余选项。

Repairman：Good afternoon. 6Customer: Hello. My mobile phone isn’t working. Could you repair it, please?Repairman: 7Customer: It worked well yesterday, but I simply couldn’t turn it on this morning. Repairman: 8Customer: Here you are.Repairman: Well, I think we’ll be able to fix it. You can pick it up this Friday.Customer: Oh, no. That’s too long. 9 I need it as soon as possible. Repairman: Let me see. How about Wednesday afternoon?Customer: 10 What time?Repairman: After five o’clock.Customer: Ok. Thank you.A. That’s great.B. I beg your pardon?C. Let me have a look.D. What’s the problem?E. I’m sorry to hear that.F. What can I do for you?G. I wonder if you could fix it earlier.第三节语法和词汇知识（共15小题；每小题1分，满分15分）从每小题的A、B、C、D四个选项中，选出可以填入空白处的最佳选项，并在答题卡上将该选项涂黑。