Stata基本操作和数据分析入门直线回归
STATA软件操作相关与回归分析

STATA软件操作相关与回归分析一、相关分析相关分析用于研究两个变量之间的相关性。
在STATA中,可以使用命令"correlate"进行相关分析。
语法:correlate 变量列表例子:我们以一个示例数据集"auto"为例,研究汽车价格与里程数和马力之间的相关性。
```sysuse autocorrelate price mpg turn```上述命令将计算汽车价格(price)与里程数(mpg)和轮胎转向(turn)之间的相关系数。
输出结果将显示相关系数矩阵,其中包括Pearson相关系数、Spearman相关系数和Kendall相关系数。
二、简单线性回归简单线性回归分析用于研究一个因变量和一个自变量之间的关系。
在STATA中,可以使用命令“regress”进行简单线性回归分析。
语法:regress 因变量自变量例子:我们继续使用上述示例数据集"auto",研究汽车价格与里程数之间的关系。
```sysuse autoregress price mpg```上述命令将进行汽车价格(price)与里程数(mpg)之间的简单线性回归分析。
输出结果将包括回归系数估计值、拟合优度、标准误差、t值、P值等。
另外,使用命令“predict”可以进行预测。
例子:我们可以使用上述回归模型,对新数据进行价格的预测。
```predict new_price, x```上述命令将对新数据集中的里程数进行预测,并将结果保存在新的变量new_price中。
三、多元回归分析多元回归分析用于研究一个因变量和多个自变量之间的关系。
在STATA中,可以使用命令“regress”进行多元回归分析。
语法:regress 因变量自变量1 自变量2 ...例子:我们使用示例数据集"auto",研究汽车价格与里程数、马力和重量之间的关系。
```sysuse autoregress price mpg displacement weight```上述命令将进行汽车价格(price)与里程数(mpg)、马力(displacement)和重量(weight)之间的多元线性回归分析。
Stata软件基本操作和数据分析入门(完整版讲义)

Stata软件基本操作和数据分析入门(完整版讲义)Stata软件基本操作和数据分析入门第一讲Stata操作入门张文彤赵耐青第一节概况Stata最初由美国计算机资源中心(Computer Resource Center)研制,现在为Stata公司的产品,其最新版本为7.0版。
它操作灵活、简单、易学易用,是一个非常有特色的统计分析软件,现在已越来越受到人们的重视和欢迎,并且和SAS、SPSS一起,被称为新的三大权威统计软件。
Stata最为突出的特点是短小精悍、功能强大,其最新的7.0版整个系统只有10M左右,但已经包含了全部的统计分析、数据管理和绘图等功能,尤其是他的统计分析功能极为全面,比起1G以上大小的SAS 系统也毫不逊色。
另外,由于Stata在分析时是将数据全部读入内存,在计算全部完成后才和磁盘交换数据,因此运算速度极快。
由于Stata的用户群始终定位于专业统计分析人员,因此他的操作方式也别具一格,在Windows席卷天下的时代,他一直坚持使用命令行/程序操作方式,拒不推出菜单操作系统。
但是,Stata的命令语句极为简洁明快,而且在统计分析命令的设置上又非常有条理,它将相同类型的统计模型均归在同一个命令族下,而不同命令族又可以使用相同功能的选项,这使得用户学习时极易上手。
更为令人叹服的是,Stata 语句在简洁的同时又拥有着极高的灵活性,用户可以充分发挥自己的聪明才智,熟练应用各种技巧,真正做到随心所欲。
除了操作方式简洁外,Stata的用户接口在其他方面也做得非常简洁,数据格式简单,分析结果输出简洁明快,易于阅读,这一切都使得Stata成为非常适合于进行统计教学的统计软件。
Stata的另一个特点是他的许多高级统计模块均是编程人员用其宏语言写成的程序文件(ADO文件),这些文件可以自行修改、添加和下载。
用户可随时到Stata网站寻找并下载最新的升级文件。
事实上,Stata 的这一特点使得他始终处于统计分析方法发展的最前沿,用户几乎总是能很快找到最新统计算法的Stata 程序版本,而这也使得Stata自身成了几大统计软件中升级最多、最频繁的一个。
stata 拟合方程

stata拟合方程
在Stata中,进行回归分析(拟合方程)是一种常见的统计分析方法。
它可以帮助探索变量之间的关系,并进行预测和推断。
下面介绍如何在Stata中进行回归分析:
1.数据准备:
首先,确保数据已经被加载到Stata中,并且了解想要探索的变量。
2.简单线性回归:
假设想要进行简单线性回归,即一个自变量和一个因变量的关系。
以下是一个示例:
使用regress命令进行简单线性回归
regress y x
这里的y是因变量,x是自变量。
regress命令将拟合一个简单线性回归模型,并输出回归系数、拟合优度、残差等统计信息。
3.多元回归:
如果有多个自变量,可以进行多元回归分析:
使用regress命令进行多元回归
regress y x1 x2 x3
这里x1、x2和x3是多个自变量。
regress命令将拟合一个多元线性回归模型,并输出相关的统计信息。
4.分析结果:
在回归分析完成后,Stata会输出回归系数、拟合优度、标准误差、t值、p 值等统计信息。
这些信息可以帮助理解变量之间的关系、各自的影响力、统计显著性等。
5.可选项和进阶:
●可以使用robust选项来计算鲁棒标准误差。
●可以使用predict命令获取回归结果的预测值、残差等。
●还可以执行其他类型的回归分析,如Logistic回归、Poisson回归等。
Stata提供丰富的选项和功能来进行回归分析,并生成详细的统计摘要。
这些步骤和命令是简单示例,可以根据具体需求和数据特点进行更多的分析和探索。
Stata基本操作和数据分析入门直线回归

进行假设检验。回归系数的假设检验一般要求资料满足独立性、正态性 和等方差。
直线回归对资料的要求小结
❖ 独立性(independent):指任意两条记录互相独立,一个个体 的取值不受其它个体的影响。通常可以利用专业知识或经验来判断 这项假定是否成立。
直线回归系数的估计
❖ 用最小二乘法拟合直线,选择a和b使其残差(样 本点到直线的垂直距离)平方和达到最小。即:使 下列的SSE达到最小值。
SSE ( yi yˆi )2 ( yi a bxi )2
由此得到
b
( yi y)( xi (xi x)2
x)
,a
y
bx
回归系数的意义
❖由总体回归方程可知 Y|X X ❖回归系数表示:x增加一个单位,总体均数 Y X
❖ 正态 (normal):假定线性模型的误差项服从正态分布(等价于 当为定值时的值也呈正态分布)。由于残差是误差项的估计值,所 以一般只需检验残差是否服从正态分布,可以直接对残差作正态性 检验或正态概率图来考察这一条件是否成立。样本量较大时,可以 忽略残差的正态性要求。
❖ 等方差(equal variance):是指在自变量取值范围内,不论取 什么值,都具有相同的方差,等价于残差的方差齐性。 通常可采 用散点图或残差的散点图判断该假设。
增加个单位
❖由于 Yˆ a bX 是 Y|X X
的估计表达式 ,所以(样本)回归系数b表示x增加 一个单位,样本观察值y平均增加b个单位。
回归系数假设检验的必要性
❖由于 =0时, Y|X ,Y与x之间不存在直
线回归关系,因此是否为0,涉及到所建立的回归 方程是否有意义的重大问题,然而即使 =0,样 本回归系数b一般不为0(原因?),因此需要对回归
stata软件基本操作和简单的一元线性回归

16
回归结果的提供和分析
Page 17
回归结果提供的两种格式
ˆ 3.805 0.4845 X Y (1.79) (14.96) ˆ 3.805 0.4845 X Y
se: (2.12) (0.03)
R 2 0.9655 注:括号内数字为t检验值 R 2 0.9655 注:括号内数字为标准误(se)
(2)拟合优度检验、t检验和F检验
P值为0.000,在任何显著性水平下,斜率项和截距项显然不为 零,拒绝两系数为零的假设。另外,拟合优度R方表明,食品 支出的97.5%的变化也以由收入X的变化来解释,因此拟合情 况较好。 如果需要查看残差值e,输入scatter e即可,list e可以列出所 有ei值,scatter e X可以看ei残差图
Stata基本操作及 简单的线性回归 邬龙
一、 Stata软件介绍
Stata是世界著名的统计分析软件之一。 Stata 是一套提供其使用者数据分析、数据管理以 及绘制专业图表的完整及整合性统计软件。它提供 许许多多功能,包含线性混合模型、均衡重复反复 及多项式普罗比模式。用Stata绘制的统计图形相当 精美。 Stata的统计功能很强,除了传统的统计分析方法外, 还收集了近20 年发展起来的新方法,如 Cox 比例风 险回归,指数与Weibull回归,多类结果与有序结果 的logistic回归,Poisson回归,负二项回归及广义负 二项回归,随机效应模型等。
分析命令在这里输入
4
查看历史命令
数据读入和保存(从Excel)
1. 点击data editor(edit)图标进入数据编辑器 2. 复制数据(连同第一行表头),在数据编辑器里 粘贴 3. 弹出提示,询问第一行是否要当成变量名称(表 头),选左边为是,选第二个为否 4. 点击保存,存为xxx.dta文件,便于以后使用
第十章直线回归和相关Stata实现
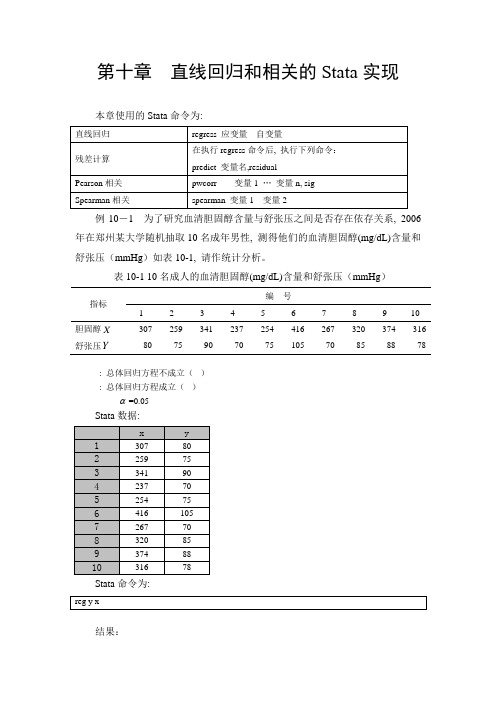
第十章直线回归和相关的Stata实现本章使用的Stata命令为:例10-1 为了研究血清胆固醇含量与舒张压之间是否存在依存关系, 2006年在郑州某大学随机抽取10名成年男性, 测得他们的血清胆固醇(mg/dL)含量和舒张压(mmHg)如表10-1, 请作统计分析。
表10-1 10名成人的血清胆固醇(mg/dL)含量和舒张压(mmHg)指标编号1 2 3 4 5 6 7 8 9 10胆固醇X307 259 341 237 254 416 267 320 374 316 舒张压Y80 75 90 70 75 105 70 85 88 78: 总体回归方程不成立(): 总体回归方程成立()=0.05Stata数据:Stata命令为:结果:t=8.07 ,P 值<0.001(Stata 输出值0.000),构建直线回归方程 将 和 代入式(10-2), 可知,X Y178.062.26ˆ+= 本例中, 的统计学意义为:血清胆固醇含量每增加1mg/dL, 总体中舒张压平均增加0.178mmHg 。
总体均数 的区间估计 给定 时, 的总体均数的点估计, 例10-1中, 当自变量 取值为307 mg/dL 时。
个体 值的容许区间估计 给定 值时, 估计总体中个体 值的波动范围, 以例10-1中第一个样本点的数据(307,80)为例。
Stata 命令:结果:x y yhat stdp stdf clm1 clm2 clp1 clp2 307 80 81.23 1.19 3.96 78.4 84.05 71.86 90.59259 75 72.69 1.63 4.11 68.84 76.53 62.97 82.41341 90 87.27 1.39 4.02 84 90.55 77.76 96.78237 70 68.78 1.99 4.27 64.08 73.48 58.69 78.87254 75 71.8 1.7 4.14 67.77 75.83 62 81.59416 105 100.61 2.64 4.61 94.37 106.86 89.72 111.51267 70 74.11 1.51 4.07 70.54 77.69 64.49 83.73320 85 83.54 1.22 3.97 80.66 86.42 74.16 92.92374 88 93.14 1.86 4.21 88.74 97.55 83.19 103.1316 78 82.83 1.2 3.96 79.98 85.67 73.46 92.2例10-2 某发热门诊医生根据患者就诊顺序随机抽取12名20~40岁发热患者, 试探讨体温与脉搏之间的伴随关系, 数据见表10-4。
stata操作介绍之基础部分(一)讲述

3.1 变量与变量值
• Stata变量的命名原则:
. 变量名中字符的组成部分为A~Z,a~z、0~9与下划线“ _ ” ,这些字符以外的其他符号不能出现在变量名当中; . 变量名不能以数字作为开始符号; . 变量名区分大小写字母,而且不能识别汉字;
• 变量的取值类型: 1、字符型变量:由特定的字符串构成,用来分辨不同的类型; 2、数值型变量:数值变量的取值由数字构成,参与数字运算; 3、日期型变量:在Stata中,1960 年1 月1 日被认为是第0 天, 因此1959 年12 月31 日为第-1天,表示形式为:jan/10/2001或者 10jan2001; 4、缺失值:STATA 默认的缺失值用“.”来表示;
• 网络帮助: 如 . net from (连接stata官网)
二、Stata使用基础
2.1 Stata命令结构
• Stata的通用命令结构如下:
[ prefix : ] command [ varlist ] [= exp.] [ if exp. ] [ using filename ] [ in range ] [ weight = ] [ , options ]
术语 prefix command 含义 命令前缀 命令 术语 using filename in range 含义 使用的文件 观察个案范围
varlist
= exp.
变量串
表达式 条件表达式
weight
权重
选项
options
if exp.
• Stata常用命令及其缩写
命令或选项 list describe display summarize tabulate lable li des di, dis sum ta, tab lab 缩写 含义 列出变量 描述分析 展示变量 统计摘要 列表显示 标签 命令或选项 rename generate graph regress variable column ren gen, g gr reg var col 缩写 含义 重命名 新建变量 绘图 回归 变量 列
stata软件基本操作和简单的一元线性回归

数据读入和保存(从Excel)
Page 5
1. 点击data editor(edit)图标进入数据编辑器 2. 复制数据(连同第一行表头),在数据编辑器里
粘贴 3. 弹出提示,询问第一行是否要当成变量名称(表
头),选左边为是,选第二个为否 4. 点击保存,存为xxx.dta文件,便于以后使用
16
回归结果的提供和分析
Page 17
回归结果提供的两种格式
Y ˆ 3 .8 0 5 0 .4 8 4 5 X R 2 0 .9 6 5 5 (1 .7 9 ) (1 4 .9 6 ) 注 : 括 号 内 数 字 为 t检 验 值
Y ˆ 3 .8 0 5 0 .4 8 4 5 X R 2 0 .9 6 5 5 se: (2 .1 2 )(0 .0 3 ) 注 : 括 号 内 数 字 为 标 准 误 ( se模型的命令为:regress Y X,简写reg Y X 即可
若想做无常数项回归则为:reg Y X, noconstant
15
第四步 模型检验
(1)经济意义检验
Page 16
斜率 为边际消费倾向,表明人均可支配收入每增加1元时,食 品消费平均增加0.135元。从经济意义上是合理的。
4. 点击variables manager按钮,更改变量名为英文,消费 为Y,收入为X
11
第二步描述统计/画散点图
(1)描述统计
Page 12
按钮操作方法1:在data editor数据表窗口中,点击Data— Describe data—Summary statistics,如图所示选择第二个
这两种方式都要自己查表找ta/2(n-2)临界值对比 当然,除了这些基本信息以外,一般还会列出样本区间、 DW值等重要信息。这会在后面的课程中说明。
STATA 第一章 回归分析讲解学习

S T A T A第一章回归分析在此处利用两个简单的回归分析案例让初学者学会使用STATA进行回归分析。
STATA版本:11.0案例1:某实验得到如下数据x 1 2 3 4 5y 4 5.5 6.2 7.7 8.5对x y 进行回归分析。
第一步:输入数据(原始方法)1.在命令窗口输入 input x y /有空格2.回车得到:3.再输入:1 42 5.53 6.24 7.75 8.5end4.输入list 得到5.输入 reg y x 得到回归结果回归结果:=+3.02 1.12y xT= (15.15) (12.32) R2=0.98解释一下:SS是平方和,它所在列的三个数值分别为回归误差平方和(SSE)、残差平方和(SSR)及总体平方和(SST),即分别为Model、Residual和Total相对应的数值。
df(degree of freedom)为自由度。
MS为SS与df的比值,与SS对应,SS是平方和,MS是均方,是指单位自由度的平方和。
coef.表明系数的,因为该因素t检验的P值是0.001,所以表明有很强的正效应,认为所检验的变量对模型是有显著影响的。
_cons表示常数项6.作图可以通过Graphics——>twoway—twoway graphs——>plots——>Create 案例2:加大一点难度1.首先将excel另存为CSV格式文件2. 将csv文件导入STATA, File——>import——>选第一个3.输入 list4.进行回归reg inc emp inv pow5.回归结果=-+++395741.718.18 4.3530.22inc emp inv pow。
stata操作介绍之基础部分(一)

精选ppt课件
33
•Stata常用命令及其缩写
精选ppt课件
34
2.2 输入、输出与存储
•数据的输入包括三种方法: 1.直接从键盘输入 2.打开已有数据文件 3.拷贝、粘贴方式交互数据
精选ppt课件
35
1.直接键盘输入 在Stata中可以使用命令行方式直接建立数据集,首先使用input命令制定相 应的变量名称,然后一次录入数据,最后使用end语句表明数据录入结束。
方法二:导入的方式
先做好excel数据文件,并以“xml 表格(*.xml)”的形式保存,注意不能以“xml 数据(*.xml)”的形
式保存。而且注意,保存时不能在第一行中输入变量名,只能全部为数据。
精选ppt课件
40
精选ppt课件
41
•数据的输出可通过命令直接输出和使用菜单栏输出:
1、命令输出格式
精选ppt课件
39
3.拷贝、粘贴方式交互数据
Stata的数据编辑窗口是一个简单的电子表格,可以使用拷贝、粘贴方式直接和EXCEL等软件交互数据, 在数据量不大时,这种方式操作极为方便。
把excel数据导入stata
方法一:拷贝和粘贴方式
先做好excel数据文件, 在stata数据编辑器粘贴,变量名也可以复制过来,应该是最容易的方法。只 有点stata数据编辑器第一格即可复制全部数据。复制会问你是否把第一行作为变量。
1.7 Stata安装
1、首先下载文件然后解压。解压完成后双击 “SetupStata14.exe”进行安装。点击“Next”继续。如下图:
精选ppt课件
11
2、选中“I accept the....”然后点击“Next”
精选ppt课件
第四讲 stata线性回归

r 0.3:变量之间的相关程度极弱,可视为不相关
但这种解释必须建立在对相关系数进行显著性检 验的基础之上。
相关系数:其它特征
(a) r 不区分 DV 和 IV;相关关系不一定就是因果关系 (b) r 的计算以数值型变量为主,不适用于类别变量 (c) r 的计算使用 Z 值,与各数值型变量的度量单位无关 (d) r 仅能衡量变量的线性关系,无法衡量曲线关系强度 i. ii. iii.
0 是回归系数在 y 轴上的截距,是当 x 为 0 时 y 的取值
1 是直线的斜率,表示当 x 每变动一个单位时,y 的变化值
总体回归方程(II)
等式(9.4)从平均意义上表达了变量 y 与 x 的统计规律性 如果回归方程中的参数 0 和 1 是已知的,对于一个给定的 x 值,利 用等式(9.4)就能计算出 y 的期望值
第九章 线性回归
(Linear Regression)
导论
统计分析:根据统计数据提供的资料,揭示变量之间的关 系,并由此推演为事物之间内在联系的规律性
为什么学习回归分析
回归分析探讨客观事物之间的联系,表现为变量之间的统计关系 建立在对客观事物进行大量实验和观察的基础上,用来寻找隐藏在看 起来不确定的现象中的统计规律的统计方法 因因变量衡量方式的不同,回归分析可分为线性回归和非线性回归 线性回归适用于因变量为连续衡量的场合 非线性回归多适用于因变量为虚拟变量、多分类变量、计数变量 等场合 即便在这两大类中,分析方法又可区分为许多不同的类型 根据处理的变量多少来看,回归分析又分为: 简单相关和一元回归:研究的是两个变量之间的关系 多元相关或多元回归:研究的是多个变量之间的关系
第二讲stata画图和线性回归基础共25页文档

回归结果解读
MSS:回归平方和 df1 自由度
RSS:残差平方和 df2
TSS:总平方和
df3
MMS=MSS/df1 RMS=RSS/df2 TMS=TSS/df3
F值 R2=MSS/TSS 调整的R2 Root MSE=sqrt(RMS)
Coef:回归系数 Std.Err:标准误差 方差协方差矩阵的对角线元素的开方(vce) 95%下限=估计值-t临界值下限*标准误差 95%下限=估计值+t临界值上限*标准误差
+b3*exper^2+ u
例二:利用phillips的数据拟合预期增强的菲 利普斯曲线为
in ft in fte1 (u n e m t0 ) u t
其中,unemt表示第t期的失业率(%), inft 表示第t期的通货膨胀率(%),infte表 示预期通货膨胀率,μ0表示自然失业率 (%)。
Stata 画图和回归基础
Stata作图
stata 提供各种曲线类型,包括点 (scatter)、线(line)、面(area),直 方图(histogram)、
条形图(bar)、饼图(pie)、函数曲线 (function)以及矩阵图(matrix)等。
同时,对时间序列数据有以ts 开头的一系列 特殊命令,如tsline。还有一类是对双变量 的回归拟合图(lfit、qfit 、lowess)等。
模型常用的其他形式:
对数 半对数 平方项 n次方 指数 交乘项
虽然对函数形式和自变量的选取有选择和检 验的方法,但最好还是从“经济意义”角度 确定。
例如:考察消费受收入影响的方程,即使参 数项不显著,也不能把它删除掉。
例题
例一:利用wage2的数据检验明瑟(mincer) 工资方程的简单形式: Ln(wage)=b0+b1*educ+b2*exper
stata画图和线性回归基础

test exper 或者 test exper =0 3。检验 educ和 tenure的联合显著性
test educ tenure 或者 test (educ=0) (tenure=0)
a
21
例三:生产函数production use production,clear reg lny lnl lnk
a
10
1。要求方程省略常数项
reg price mpg weight foreign, nocons 2。稳健性估计(一般用于大样本OLS)
reg price mpg weight foreign, vce(robust) 或者:reg price mpg weight foreign, r
3。设置置信区间(默认95%)
a
2
作图时命令方式比较复杂,建议多用菜单方式。 一起来做下列图形: 打开wage2.dta 1。 男性和女性工资均值的条形图 2。 白人和其他人的工资的冰饼图 3。 wage的直方图,并检验是否服从正态分布。
a
3
组合图形:
画出price与weight的散点图,并画出其拟 合线。
图形界面设计:
图形标题,X轴标志,Y轴标志,样式选择, 图例,分组标志。
Coef:回归系数 Std.Err:标准误差 方差协方差矩阵的对角线元素的开方(vce) 95%下限=估计值-t临界值下限*标准误差 95%下限=估计值+t临界值上限*标准误差
a
14
模型常用的其他形式:
对数 半对数 平方项 n次方 指数 交乘项
虽然对函数形式和自变量的选取有选择和检 验的方法,但最好还是从“经济意义”角度 确定。
stata基础回归命令

stata基础回归命令Stata基础回归命令回归分析是统计学中常用的一种分析方法,用于研究变量之间的关系。
Stata是一种流行的统计软件,提供了丰富的回归分析功能。
本文将介绍Stata中的基础回归命令,并以实例演示其使用方法。
一、简单线性回归命令简单线性回归是回归分析中最简单的一种形式,用于研究两个变量之间的线性关系。
在Stata中,可以使用regress命令进行简单线性回归分析。
例如,我们有一个数据集,包含了变量Y和变量X,我们想要研究Y和X之间的关系。
我们可以使用以下命令进行简单线性回归分析:regress Y X其中,Y是因变量,X是自变量。
执行该命令后,Stata会输出回归结果,包括回归系数、标准误差、t值、p值等信息。
二、多元线性回归命令多元线性回归是回归分析中常用的一种形式,用于研究多个自变量对因变量的影响。
在Stata中,可以使用regress命令进行多元线性回归分析。
例如,我们有一个数据集,包含了因变量Y和自变量X1、X2、X3,我们想要研究这些自变量对Y的影响。
我们可以使用以下命令进行多元线性回归分析:regress Y X1 X2 X3执行该命令后,Stata会输出回归结果,包括各个自变量的回归系数、标准误差、t值、p值等信息。
三、加入控制变量的回归命令在实际研究中,我们常常需要控制其他变量的影响,以准确评估自变量对因变量的影响。
在Stata中,可以使用regress命令加入控制变量。
例如,我们有一个数据集,包含了因变量Y、自变量X和控制变量Z,我们想要研究X对Y的影响,并控制Z的影响。
我们可以使用以下命令进行回归分析:regress Y X Z执行该命令后,Stata会输出回归结果,包括X的回归系数、标准误差、t值、p值等信息。
四、回归诊断命令回归分析不仅包括了回归系数的估计,还需要对回归模型进行诊断,以评估模型的拟合优度和假设的满足程度。
在Stata中,可以使用一系列命令进行回归诊断。
Stata面板数据回归分析的步骤和方法

Stata面板数据回归分析的步骤和方法面板数据回归分析是一种用于分析面板数据的统计方法,可以通过观察个体和时间上的变化来研究变量之间的关系。
Stata软件是进行面板数据回归分析的常用工具之一,下面将介绍Stata中进行面板数据回归分析的步骤和方法。
一、数据准备在进行面板数据回归分析前,首先需要准备好相关的数据。
面板数据通常由个体和时间两个维度构成,个体维度可以是不同的个体、公司或国家,时间维度可以是不同的年、季度或月份。
将数据按照面板结构整理好,并确保数据的一致性和准确性,可以直接在Stata中导入数据进行处理。
二、面板数据回归模型选择在进行面板数据回归分析时,需要选择适合的回归模型来研究变量之间的关系。
常见的面板数据回归模型包括固定效应模型(Fixed Effects Model)和随机效应模型(Random Effects Model)。
固定效应模型通过控制个体固定效应来分析变量间的关系,而随机效应模型则假设个体固定效应与解释变量无关。
三、面板数据回归分析步骤1. 导入数据在Stata中,可以使用"import"命令导入面板数据。
例如:`import excel "data.xlsx", firstrow`可以导入Excel文件,并指定首行为变量名。
2. 设定面板数据结构在Stata中,需要将数据设置为面板数据结构,采用"xtset"命令即可完成设置。
例如:`xtset id year`将数据的个体维度设定为"id",时间维度设定为"year"。
3. 估计面板数据回归模型在Stata中,可以使用"xtreg"命令来估计面板数据回归模型。
例如:`xtreg dependent_var independent_var1 independent_var2, fe`可以用固定效应模型进行回归分析。
Stata面板数据回归分析的步骤和方法

Stata面板数据回归分析的步骤和方法哎哟,说起Stata面板数据回归分析,我这心里就直发痒。
我这人就是喜欢琢磨这些个数字,特别是这面板数据,看着就亲切。
来来来,咱们就坐在这,我给你掰扯掰扯这回归分析的步骤和方法。
首先啊,你得准备数据。
这数据啊,得是面板数据,就是横着竖着都是数据。
你得把数据导进Stata里头,看着那一排排数字,心里就得有谱,知道这数据从哪儿来,将来要干啥用。
然后啊,咱们先得把数据整理一下。
Stata里有那么多命令,咱们得用上“xtset”这个命令,告诉Stata这是面板数据。
然后呢,就得看看数据有没有问题,比如有没有缺失值啊,有没有异常值啊。
这就像咱们做人,也得讲究个整洁,别邋里邋遢的。
接下来啊,咱们得确定模型。
面板数据回归模型有好几种,比如说固定效应模型、随机效应模型,还有混合效应模型。
你得根据实际情况来选择。
就像做菜,得看你要做什么菜,是做炒菜还是炖菜。
选好了模型,那就得建模型了。
Stata里有“xtreg”这个命令,专门干这个活。
你把数据输入进去,再指定你的模型,Stata就帮你算出来了。
就像咱们孩子写作业,咱们给他点拨点拨,他就写得有模有样了。
算完模型,就得检验。
这就像咱们看完电影,得聊聊感想。
检验模型,就是看这个模型有没有问题,比如有没有多重共线性啊,残差有没有自相关啊。
这就像咱们吃饭,得看看吃得饱不饱,营养均衡不均衡。
最后啊,你得解释结果。
这结果啊,得结合实际情况来说。
就像咱们买衣服,得看合不合身。
解释结果,就是要看这些数字背后的故事,看看这些数据能告诉我们什么。
哎呀,说起来这Stata面板数据回归分析,真是门学问。
得有耐心,得有细心,还得有恒心。
就像咱们种地,得用心浇灌,才能收获满满。
好啦,我这就唠叨这么多了。
你要是想学这玩意儿,得多看多练。
就像咱们学说话,得多说多练,才能说得溜。
来来来,咱们下次再聊聊其他的话题。
stata估计回归方程

stata估计回归方程使用Stata软件进行回归分析引言:回归分析是一种常用的统计分析方法,用于研究两个或多个变量之间的关系。
在实际应用中,我们常常需要利用已知数据来建立回归方程,并利用该方程对未知数据进行预测或分析。
本文将介绍如何使用Stata软件进行回归分析,并通过一个实例来说明具体操作步骤。
数据收集和准备:我们需要收集相关数据,并将其整理成适合进行回归分析的格式。
在这个例子中,我们将使用一个虚构的数据集,其中包含了一个自变量X和一个因变量Y。
我们假设X对Y具有线性影响。
数据导入和描述性统计:在使用Stata进行回归分析之前,我们需要先导入数据并进行描述性统计。
首先,我们可以使用Stata的"import"命令将数据导入软件。
然后,我们可以使用Stata的"summarize"命令对数据进行描述性统计,包括均值、标准差等。
回归方程建立:在进行回归分析之前,我们需要先建立回归方程。
在Stata中,我们可以使用"regress"命令进行回归分析。
具体地,我们可以输入"regress Y X"来建立一个简单线性回归方程,其中Y是因变量,X 是自变量。
Stata将自动为我们计算回归系数、标准误差、t值和p 值等统计量。
回归结果解读:通过回归分析,我们可以得到回归方程的系数和显著性检验结果。
系数表示自变量对因变量的影响程度,显著性检验结果则用于判断该影响是否显著。
在Stata的回归结果中,我们可以查看系数的估计值、标准误差、t值和p值。
一般来说,如果p值小于0.05,则我们可以认为该系数是显著的。
回归诊断:在得到回归结果后,我们还需要对回归模型进行诊断,以确保模型的准确性和有效性。
在Stata中,我们可以使用多种方法进行回归诊断,如残差分析、异常值检测等。
通过这些诊断方法,我们可以判断回归模型是否满足线性关系、正态分布、同方差性等假设。
stata中回归知识点总结

stata中回归知识点总结简单线性回归简单线性回归是回归分析中最基本的形式。
它用于研究一个自变量对一个因变量的影响。
在Stata中进行简单线性回归可以使用reg命令。
比如,我们有一个数据集包含了两个变量x和y,我们想知道x对y的影响,可以使用如下命令进行简单线性回归:```reg y x```这条命令将会输出回归方程的拟合结果,包括截距项和自变量系数。
多元线性回归多元线性回归是回归分析中更常见的形式。
它用于研究多个自变量对一个因变量的影响。
在Stata中进行多元线性回归同样可以使用reg命令。
比如,我们有一个数据集包含了三个变量x1、x2和y,我们想知道x1和x2对y的影响,可以使用如下命令进行多元线性回归:```reg y x1 x2```逻辑回归逻辑回归是用来处理因变量为二值变量的回归分析方法。
在Stata中进行逻辑回归可以使用logit命令。
比如,我们有一个数据集包含了两个变量x和y,其中y是一个二值变量(比如0和1),我们想知道x对y的影响,可以使用如下命令进行逻辑回归:```logit y x```高级回归技巧除了上述的基本回归分析方法,Stata还提供了许多高级的回归技巧,比如假设检验、多重共线性检验、残差分析等。
其中,假设检验是用来检验回归模型的显著性,通常使用命令test。
多重共线性检验是用来检验自变量之间的相关性,通常使用命令collin。
残差分析是用来检验模型的拟合情况,通常使用命令predict和rvfplot。
总结回归分析是统计学中常用的一种分析方法,它用于研究自变量和因变量之间的关系。
在Stata中,回归分析是一种非常常见的数据分析方法,包括简单线性回归、多元线性回归、逻辑回归和一些高级回归技巧。
希望本文对Stata用户们有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
年龄X 3
334 4
4555
身高Y 92.5 97 96 100 96.5 101 106 104 107
年龄X 6
667 7
7888
身高Y 115.5 116 110 126 118 118 122 129 124
本例的研究目的和实现方法
1. 研究目的:了解年龄与儿童人群的平均身高对 应关系。
2. 方法1:可以做普查,得到每个年龄组所有儿童 的身高,并且计算每个年龄组的儿童人群的平 均身高。
正态分布性质简述
性质1:设Y 服从某个正态分布,则Y的总体均数
和总体方差2唯一决定了Y的确切分布。
性质2:设 Y ~ N (, 2 ) 则: Z ~ N (0, 2 )
,令 Z Y
回归模型
根据上述性质,应用到本例的实际问题:
1. 固定年龄X,身高Y服从总体均数为 Y X ,方差
为2的正态分布 Y ~ N(Y X , 2 ) 。 2. 由散点图可以假定总体均数 Y|X X 3. 故 Y ~ N ( x, 2 )
直线回归系数的估计
❖ 用最小二乘法拟合直线,选择a和b使其残差(样 本点到直线的垂直距离)平方和达到最小。即:使 下列的SSE达到最小值。
SSE ( yi yˆi )2 ( yi a bxi )2
由此得到
b
( yi y)( xi (xi x)2
x)
,a
y
bx
回归系数的意义
❖由总体回归方程可知 Y|X X ❖回归系数表示:x增加一个单位,总体均数 Y X
增加个单位
❖由于 Yˆ a bX 是 Y|X X
的估计表达式 ,所以(样本)回归系数b表示x增加 一个单位,样本观察值y平均增加b个单位。
回归系数假设检验的必要性
❖由于 =0时, Y|X ,Y与x之间不存在直
线回归关系,因此是否为0,涉及到所建立的回归 方程是否有意义的重大问题,然而即使 =0,样 本回归系数b一般不为0(原因?),因此需要对回归
系数是否等于0进行假设检验。
回归系数的假设检验
❖H0:=0 vs H1: 0
❖=0.05 ❖回归系数的标准误为
Sb
SY ,X
n
(Xi X )2
i1
❖ 其中s为残差的标准差
n
(Yˆi Yi )2
SY ,X
i1
n2
❖则回归系数的检验统计量为
t b0 n2
Sb
回归系数的假设检验
可以证明:H0:=0 成立时,检验统计量tb服
实例的回归系数的假设检验
❖ H0:=0 vs H1: 0 ❖ =0.05
s
( yi y)2 b2
(xi x )2
2186.11 6.2572 52.5 2.857
n2
18 2
se(b)
(xi x)2 52.2
(yi y)2 2186.111
故 (yi y)(xi x) 328.5 x 5.5, y=109.78
b
( xi
x)( yi (xi x )2
y)
328.5 52.5
6.257
a y bx 109.78 6.2575.5 75.363
Y|X X
并且称上述直线方程为(总体)回归方程。 Y称为应变量或反应变量,X为自变量, 为回归直线的截
距参数。 为回归直线的斜率
回归方程
❖ 回归方程中,为未知参数,需要用样本资料通 过拟合曲线后得到其估计值,并分别记为a和b, 相应得到样本估计的回归方程
Yˆ a bX
❖通常称 Yˆ 为Y的预测值,其意义为固定x,Y的
3. 身高的总体均数 Y|X 是年龄x的一个函数
画散点图考查身高与年龄的分布关系
y
130
120
110
100
90
3
4
5
6
7
8
x
Y的离散程度与X没有关系,并且散点呈直线带
画散点图考查身高总体均数与年龄的关系
年龄组的身高样本均数与年龄的散点图
由散点图确定身高总体均数与年龄 可能是直线关系
❖可以假定固定年龄的身高总体均数 Y|X 与年龄x的关系可能是直线关系,即假定:
从自由度为n-2的t分布。即:当出现
| t | t0.05/ 2,n2 , =0 而言这是小概率事
件,故可以拒绝H0 :=0,认为 0 。
回归系数检验统计量t的分布示意图
பைடு நூலகம் 0
0
当|t|>t0.05,1,n-2时,对=0而言是小概率事件, 对>0而言并非是小概率事件。
实例计算
年龄X 3 3 3 4 4 4 5 5 5 身高Y 92.5 97 96 100 96.5 101 106 104 107 年龄X 6 6 6 7 7 7 8 8 8 身高Y 115.5 116 110 126 118 118 122 129 124
直线回归
直线回归
❖直线回归的基本概念 ❖直线回归方程的建立 ❖关于回归系数的估计和假设检验 ❖直线回归的统计应用
举例
❖例 为了研究3岁至8岁男孩人群平均身高(cm) 与年龄(year)的规律,在某地区在3岁至8岁男 孩中随机抽样,共分6个年龄层抽样:3岁,4 岁,…,8岁,每个层抽3名男孩,共抽18名男 孩。资料如下:
4. 令 Y Y|X , ~ N (0, 2 )
5. 即: Y X ,并称为直线回归模型。
误差与残差
Y Y|X
Y
Y
称为随机误差 称为残差(residual)
根据上述,直线回归分析要求资料满足固定X,Y服
从正态分布等价于残差服从正态分布。
直线回归原理示意图
所以如果固定x,Y服从正态分布,其散点图呈直线带分布
总体均数 Y X 的估计值。
Y与x的直线回归关系
❖由总体回归方程 Y|X X
可知:当=0时, Y|X 。即:对于x的任
何值,总体均数 Y X 没有任何改变,因此建
立Y与x的直线回归方程就没有任何意义了,所 以称 0时, Y与x 之间存在直线回归关系, 反之 =0 Y与x 之间称不存在直线回归关系。
3. 方法2:作抽样调查,本例就是通过按年龄组分 层抽样调查,获得样本后用回归分析的方法得 到每个年龄组儿童人群的平均身高估计值和并 作相应的统计推断。
儿童身高的分布特征
一般而言,儿童身高满足 1. 同一年龄x的儿童身高y近似服从正态分布,因
此对于每个年龄x,均有一个身高y的总体均 数 Y|X 。 2. 不同年龄x的儿童身高分别近似服从对应不同 身高总体均数 Y|X 的正态分布。
