数字移相
第4章-数字式移相信号发生器的设计

第4章
2. DDS DDS技术将输出波形的一个完整周期的幅度值都顺 序地存放在波形存储器中, 通过控制相位增量产生频 率、相位可控制的波形。DDS电路一般包括基准时钟、 相位增量寄存器、相位累加器、波形存储器、D/A转换 器和低通滤波器(LPF)等模块, 如图4.4所示。
第4章
相位 增量
相位
地址
K
m
ax
128 359 45
1021.55
则相位控制字K的位数取10 bit就能满足设计任务关于
移相的要求(分辨率为1°, 移相范围是0~359°)。
若“相位加法器”采用24 bit加法器实现, 则上述10 bit的相位控制字应扩展成24 bit, 具体扩展方法是在上述 10 bit相位控制字后面(右边)添加14个逻辑0就可以了。
基于DDS技术的数字式移相信号发生器的主 要模块框图如图4.5所示。
第4章
频率 控制 字 寄 存 器
相位 控制 字 寄 存 器
相位 累加 器
相位 加法 器
寄 存
Address1
器
寄 存
Address2
器
图4.5 基于DDS技术的数字式移相信号发生器主要模块框图
第4章
3. 1)确定系统时钟频率fcp 不妨设输出信号最高频率为fmax 、最高频率 fmax下的最少采样点数为Smin , 则有
第4章
4.3 系统硬件设计
4.3.1 DDS 1. DDS 1971年, 美国学者J.Tierncy、C.M.Rader和B.Gold提出了以全数
字技术从相位概念出发直接合成所需波形的一种新的频率合成原理。 随着电子技术的发展和水平的提高, 一种新的频率合成技术——直接数 字频率合成(DDS, Direct Digital Synthesis)技术得到了飞速发展。 DDS技术是一种把一系列数字形式的信号通过D/A转换而成模拟形式的 信号合成技术, 目前使用最广泛的一种DDS方式是利用高速存储器作查 找表, 然后通过高速D/A转换输出已经用数字形式存入存储器的正弦波。
一种精度可调的数字控制移相原理.

一种精度可调的数字控制移相原理1 引言移相2基本原理本系统是基于数字倍频器进行延时操作而实现的移相。
实现原理是把输入模拟波形(如正弦信号)的周期Tin转化为原来的1/data,Tin/data即为移相精度,data值通过精度控制输入信号赋值。
当data为360时,精度为1°;当data为720时,精度为0.5°;若要更小的精度,可依此类推。
本文中为便于显示移相波形,把精度设置为1°。
则精度为Tin/360,所用的倍频器倍频因子即为360。
这样经n个Tin/360延时(n为移相的具体数值,由记时控制输入信号D赋值),再输出波形。
和原波形相比就形成了移相。
从实现的电路方面来讲,要把输入波形周期变为原来的1/360,或者说把输入波形的频率变为原来的360倍,最直接的办法就是采用倍频器。
而数字倍频器的输入是数字信号,则应先把模拟量转化为数字量,这就需要一个模拟比较器。
在得到倍频输出信号后,为了要得到希望的n值,还应在倍频器后添加数字定时输出计数器,以输出延时控制信号。
最后把模拟信号输入A/D电路,通过ROM存储,再在延时控制信号的作用下延时输出数字量,再经过D/A电路还原为模拟量,最终实现移相操作。
其中倍频器具有360倍倍频能力。
输入模拟信号(如正弦波)经过信号比较器,波形电压与零伏比较后,高于零伏的电压段转化为高电平,低于的转化为低电平,这样输入信号就转化为周期相同的数字信号。
A/D,ROM,D/A和一些控制电路构成移相输出控制模块。
其中移相控制部分的倍频器,定时输出计数器构成可编程数字控制部分,都可以通过硬件语言编译实现。
2.1数字倍频器这里使用的数字倍频器(电路如图2所示)的算法是基于采样的原理来实现[4],理论上能够实现任意倍倍频,这里为方便说明和显示波形,设置为360倍,即倍频因子为360,精度为1°。
当信号A经过比较器后,A转化为具有相同周期的数字信号DA,他们的周期均为Tclk_in。
数字式三相移相器基本原理和使用方法
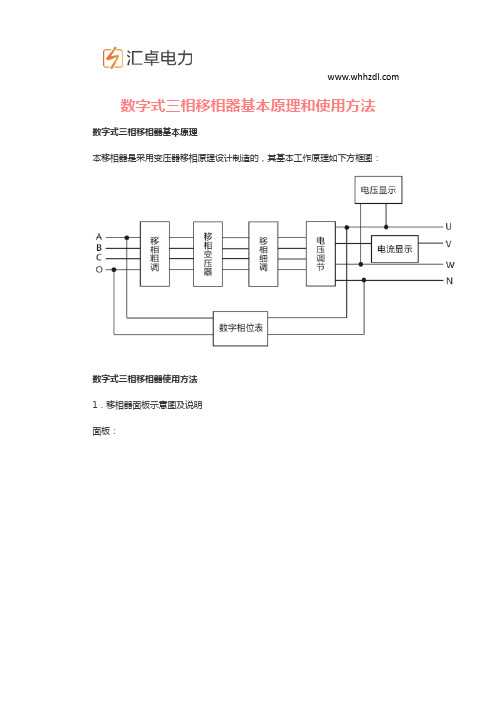
数字式三相移相器基本原理和使用方法数字式三相移相器基本原理本移相器是采用变压器移相原理设计制造的,其基本工作原理如下方框图:数字式三相移相器使用方法1.移相器面板示意图及说明面板:A1、移相显示表头,四位数字显示00~3600相角。
A2、输出V相负载电流显示表头,3位半数字显示。
A3、输出间U、W电压显示表头,3位半数字显示。
A4、移相粗调旋钮,依面极刻度旋转移相。
A5、相位表头复位键。
按此键后可显示移相角度。
A6、相位表头锁存键。
调好移相角度不需变化时,按此键可锁表头数字。
A7、电源开关,此键可切断或接通整机内部电源。
A8、输出功能选择开关,开关拨向电压输出则输出三相电压U﹑V﹑W对应输入A、B、C电源移相;开关拨向电流输出则可输出AC 0~20A电流,对应B相输入移相。
A9、移相细调选择按钮,根据标记可选择-30~180,120~330细调范围。
A10、输出电压调节旋钮、输出U﹑V﹑W三相由此旋钮一起同步调节,其中U、W之间电压由表头显示0V~380V。
A11、移相细调旋钮,此旋钮配合A9可实现30º范围移相调节。
B1、输入三相四线接线柱。
B2、机壳接地柱。
B3、F1、F2、F3是分别对应输入C、B、A三相的保险座。
B4、输出三相四线接线柱。
B5、F4、F5、F6是分别对应输出W、V、U三相的保险座。
B6、电流输出接线柱2. 使用方法1)检查面板B3、B5各保险管是否完好。
2)关断本机电源开关A7,将电压调节旋钮A10调至最低位,再接上面板B1三相四线A、B、C、O输入电源。
3)接上面板B3电压输出U、V、W、N所需加负载,但负载功率不能超出本机最大输出功率。
4)合上外部闸刀,打开本机电源开关A7,A1、A2、A3三表头也均应点亮。
5)通电预热约半分钟后调节电压输出旋钮A10至所需值,三相移相电压输出U、V、W、N,其中U、W间电压由A3表头显示,V相负载电流由A2表头显示。
6)调节移相粗调旋钮A4至所需移相角度大致档位,再调节移相细调旋钮A11,配合细调选择开关A9(开关拨向上方,移相细调旋钮A11顺时针调节1圈移相150,开关拨向下方,移相细调旋钮A11逆时针调节1圈移相150),每当调节移相粗调旋钮A4后,要将细调选择开关A9拨向上方,移相细调旋钮A11顺时针调节相位表头显示相位增加。
数字移相技术的分析与实现
式 的 实质 是 将 数 据 地 址 的 偏 移 量 映 射 为 信 号 的
相 位 值
进 行 移 相 , 如 : 容移 相 、 压 器 移 相 等 方 式 例 阻 变 采 用 上 述 方 式 设 ’ 的 移 相 器 存 在 许 多 不 足 之 计 外 : 相 精 确 度 不 高 , 出波 形受 到 输 人 波 形 的 移 输
维普资讯
《 铁 科 技 ) 0 2年 第 1期 西  ̄ 0 2
数 字 移 相 技 术 的 分 析 与 实 现
郑 州铁 路 局 西 安 科研 所 何 志 坚
摘
要
本 文 介 绍 了 目前 兴 起 的 数 字 移 相 技 术 , 且 时 两 种 数 字 移 相 方 式 的 工 作 原 理 并
4
阍 l
维普资讯
数 字 移 相 技 术 的 分析 与 实 现 据 , 储 在数 据存储 器 中, 存 即模 拟 信号 的 一 个时
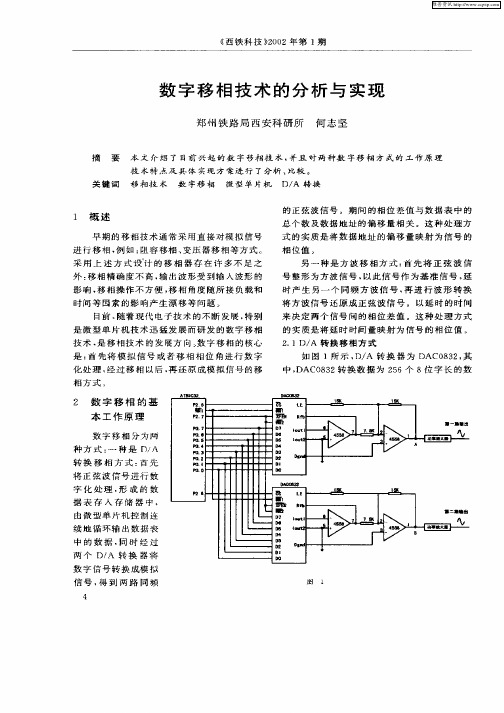
钟 周 期 对 应 于 2 6个 转 换 值 DAC 8 2是 电 流 5 03 型 输 出 , 们 采 用 双 极 型 运 算 放 大 器 IM 4 5 我 58
将 电 流 型 信 号 转 换 为 电压 型 信 号 。 T8 C 2为 A 95
微 型单 片 机 。
在 模 拟 信 号 进 行 数 字 化 转 换 后 , 据 表 中 数
得 到 的 波 形 数 字 转 化 数 据 共 有 2 6个 , A 转 5 D/ 换 器 数 据 表 中 2 6个 数 据 还 原 模 拟 信 号 。 由 5 模 拟 信 号 电 压 表 达 式 : u i o + : , 一 “一 s a n( t ) 2 u i o m@ ) 以得 知 , 个 数 据 之 间 的 相 位 差 s J n( t 可 每
一种数字精密移相方法及移相器[发明专利]
![一种数字精密移相方法及移相器[发明专利]](https://img.taocdn.com/s3/m/01c0c3cf4b35eefdc8d333fe.png)
专利名称:一种数字精密移相方法及移相器
专利类型:发明专利
发明人:余钫,陈智勇,鲁道邦,王艳,裘晓俊,金鑫,李超,陈云起,管妮娜,朱熙文,盛荣武
申请号:CN200610020040.8
申请日:20060824
公开号:CN1913349A
公开日:
20070214
专利内容由知识产权出版社提供
摘要:本发明公开了一种数字精密移相方法及移相器,首先是将高频输入信号接入计数器,计数器输出待移相的低频方波信号;其次是计数器输出待移相信号的二倍频方波信号;第三是将高频输入信号和二倍频方波信号接入可预置计数器,可预置计数器根据预置数输出移相标志方波;第四是移相标志方波与待移相的低频方波信号接入触发器,触发器输出经移相的低频方波信号,完成移相。
实现该方法的装置包括计数器、可预置计数器和触发器。
本发明方法易行,结构简单,成本低廉,既能够用可编程逻辑器件实现,又可用分立器件实现,移相范围覆盖0~360度且移相精度极高,移相值修改方便且相移稳定,输出信号与输入信号同步。
申请人:中国科学院武汉物理与数学研究所
地址:430071 湖北省武汉市武昌小洪山
国籍:CN
代理机构:武汉宇晨专利事务所
代理人:王敏锋
更多信息请下载全文后查看。
一种精度可调的数字控制移相原理.

种精度可调的数字控制移相原理1 引言移相2 基本原理本系统是基于数字倍频器进行延时操作而实现的移相。
实现原理是把输入 模拟波形 (如正弦信号 ) 的周期 Tin 转化为原来的 1/data ,Tin/data 即为移相 精度, data 值通过精度控制输入信号赋值。
当 data 为 360 时,精度为 1°; 当 data 为 720 时,精度为 0.5 °;若要更小的精度,可依此类推。
本文中为便 于显示移相波形,把精度设置为 1°。
则精度为 Tin/360 ,所用的倍频器倍频因 子即为360。
这样经n 个Tin/360延时(n 为移相的具体数值,由记时控制输 入信号 D 赋值) ,再输出波形。
和原波形相比就形成了移相。
从实现的电路方 面来讲,要把输入波形周期变为原来的 1/360 ,或者说把输入波形的频率变为 原来的 360 倍,最直接的办法就是采用倍频器。
而数字倍频器的输入是数字信 号,则应先把模拟量转化为数字量,这就需要一个模拟比较器。
在得到倍频输 出信号后,为了要得到希望的 n 值,还应在倍频器后添加数字定时输出计数 器,以输出延时控制信号。
最后把模拟信号输入 A/D 电路,通过 ROM 存储, 再在延时控制信号的作用下延时输出数字量,再经过 D/A 电路还原为模拟量, 最终实现移相操作。
其中倍频器具有 360 倍倍频能力。
输入模拟信号 (如正弦波 ) 经过信号比较器,波形电压与零伏比较后,高于 零伏的电压段转化为高电平,低于的转化为低电平,这样输入信号就转化为周 期相同的数字信号。
A/D ,ROM ,D/A 和一些控制电路构成移相输出控制模 块。
其中移相控制部分的倍频器,定时输出计数器构成可编程数字控制部分, 都可以通过硬件语言编译实现。
这里使用的数字倍频器 (电路如图 2 所示)的算法是基于采样的原理来实现 ,理论上能够实现任意倍倍频,这里为方便说明和显示波形,设置为 360 即倍频因子为 360 ,精度为 1°。
中频及微波数字移相器

h
20
平衡式移相器
ej11jjBB1B12B22jB
21
移相器基本原理
★高通/低通滤波器型移相器
-jBn
-jBn -jXn
-jXn
-jBn -jXn
Input
jBn
jXn jBn
Output Input
jXn
jXn
jBn
(a)
(b)
◆适用于频率低端 ◆适于宽频带应用
Output
h
22
各种移相器的特点比较
h
5
引言
★中频宽带五位数字移相器的电路设计指标如下:
◆工作频率:60±10MHz ◆输入信号:-10~10dBm ◆插入损耗:≤5dB ◆相位误差:≤±3.5度 ◆输入、输出端电压驻波
比小于2 ◆移相范围:360度 ◆幅度不平衡:≤±1dB
◆工作电压:±5V ◆电流:≤0.1A ◆控制电压:TTL电平 ◆外形尺寸:
h
25
★中频宽带五位数字移相器设计方案
h
23
中频宽带五位数字移相器研究
★中频宽带五位数字移相器设计方案 ★π型结构的高通/低通滤波器型移相器理论相位误
差分析 ★中频宽带五位数字移相器的电路设计 ★中频宽带五位数字移相器的实现 ★中频宽带五位数字移相器的测试及结果分析
h
24
★中频宽带五位数字移相器设计方案
◆设计要求(难点) 1、相对带宽超过33% 2、超小的实物外形→40mm×30mm×20mm ◆高通/低通滤波器型移相器
h
3
引言
★移相器发展动态
◆国内 与国外相比,国内对MMIC的研究起步较晚,工艺还不
成熟,但也进行了各类MMIC的研制,包括MMIC移相器, 并取得了一定的成果.
一文看懂移相器的发展历程

一文看懂移相器的发展历程移相器是雷达和通信系统中的重要器件,它是通过改变微波组件的相位一致性,来提高微波组件输出功率合成效率或回波信号的合成效率,提高雷达或通信系统监视能力。
移相器发展大致可以分为四个阶段微带式移相器、数控式移相器、数字式移相器、直接数字合成(DDS)芯片,移相器的每次进步都给终端设备功能带来跳跃式的发展。
1、引言移相器是微波组件中一个重要的器件,它是通过改变微波组件的相位一致性,来提高微波组件功率合成效率或回波信号的合成效率,提高雷达或通信系统监视能力,,移相器发展大致可以分为四个阶段:微带式移相器、数控式移相器、数字式移相器、直接数字合成(DDS)芯片,,四个阶段都实现了移相器技术及设计理念的巨大进步,移相器的每次进步都给终端设备功能带来跳跃式的发展,2、移相器的分类本文分别从微带式移相器、数控式移相器、数字式移相器、直接数字合成(DDS)芯片四个阶段介绍移相器的发展历程和工作原理。
2.1、微带式移相器微带式移相器是最早的移相器,它是通过改变微波信号通过路径的长短来改变微波组件的相位。
它是主动改变相位无法实现被动控制,也就是常说的模拟移相器。
工作原理:在使用过程中要测试出被测组件(DUT)与相位基准的相位差O中,所以,L 既是需要更改微带线的长度(单位厘米/毫米),入微波组件工作频率对应波长(单位厘米/毫米)。
在实际的操作过程中,需要测试出组件与基准相位相位差,换算出要移相的长度,在组件输入端增加或减少相应的微带线长度(增加微带线的长度相位值减少、减少微带线长度相位值增加),即完成组件的配相工序,2.2、数控式移器数控式移相器是实现数字电平控制相位,它是通过改变控制信号,来控制微波二极管的通断,改变微波信号路径的长短,从而达到控制组件的相位。
图1是典型的6位数控式移相器原理电路图。
数字移相器的工作原理

数字移相器的工作原理
数字移相器是一种基于相位控制的电路,在射频和微波电路中广泛应用。
它的主要作用是移动电路中的信号相位,实现相位偏移,相移调节和
频率合成等功能。
数字移相器通常由相位锁定环(PLL)和电子开关(ESW)构成。
数字移相器的工作原理是通过电子开关控制射频信号经过不同的时延
路径,从而改变信号的相位。
当输入的信号经过锁相环(PLL)时,PLL
会将输入信号的频率锁定到一个精准的参考频率上。
然后,电子开关根据
外部控制信号选择一个时延路径,将信号从同一时刻延迟到不同的时刻,
并控制相位的变化。
如果相移器希望按照一定的步进调整相位,可以通过ESW控制第二级信号,机械式的开关是ESW的代表形式,另一种电容向地
分支的芯片也叫做ESW。
一般来说,数字移相器可以实现相位变化步进的
精度可以达到几度甚至更小,且可靠性高和频率节约。
应用方面,数字移相器被广泛应用于相位调制、相位移位键控(PSK)通信、频率合成、成像雷达、数字信号处理等领域。
在通信系统中,它通
常用于频率和相位调制技术,以获得更高的信号传输速率和更好的信号质量。
在雷达中,数字移相器通常用于成像雷达中,以获得更好的成像分辨
率和空间分辨率。
总的来说,数字移相器是一种功能强大的电路,可以实现相位调节、
相位偏移、频率合成和成像雷达等应用。
它的优点是精度高、可靠性好和
使用方便,因此在许多电子领域得到广泛应用。
数字移相芯片

数字移相芯片数字移相芯片是一种集成电路,其主要功能是对输入的数字信号进行移相处理。
移相是指改变信号的相位,即将信号波形在时间轴上向前或向后移动一定的时间。
数字移相芯片通过数字信号处理技术,实现对信号相位的精确控制和调整。
数字移相芯片广泛应用于通信系统、雷达系统、无线电系统、声音处理等领域。
在通信系统中,数字移相芯片可以用于同步信号的生成和调整,提高信号的传输质量和可靠性。
在雷达系统中,数字移相芯片可以用于目标探测和跟踪,提高雷达系统的性能和精度。
在无线电系统中,数字移相芯片可以用于信号的调制和解调,实现无线通信。
在声音处理领域,数字移相芯片可以用于音频信号的调整和均衡,提高音质和音效。
数字移相芯片的工作原理是将输入的数字信号转换成模拟信号,通过模拟电路对信号进行相位调整,再将调整后的模拟信号转换成数字信号输出。
在数字信号处理过程中,数字移相芯片可以实现相位的连续调整和高精度控制,具有灵活性和可靠性。
数字移相芯片的设计和制造需要考虑到电路的稳定性、抗干扰能力、功耗和成本等因素,以满足不同应用的需求。
数字移相芯片的应用还涉及到信号处理算法和系统设计。
在信号处理算法方面,数字移相芯片可以通过数字滤波、相位调整和时域/频域分析等技术,对信号进行处理和优化。
在系统设计方面,数字移相芯片需要与其他电路和器件配合工作,实现整个系统的协调和稳定运行。
随着科技的发展和应用的广泛,数字移相芯片的性能和功能不断提升。
现代数字移相芯片已经实现了多通道、高速率和多功能的特点,能够适应复杂的信号处理和控制需求。
数字移相芯片的发展也推动了通信、雷达、无线电和音频等领域的技术进步和创新。
未来,数字移相芯片有望在人工智能、物联网和虚拟现实等领域得到更广泛的应用和发展。
数字移相芯片作为一种重要的集成电路,具有广泛的应用前景和技术挑战。
通过对数字信号的处理和控制,数字移相芯片可以实现信号的精确移相和调整,提高系统的性能和可靠性。
随着科技的不断发展,数字移相芯片的功能和性能将不断提升,为各个领域的应用提供更好的解决方案。
基于ISP芯片的可编程数字移相器设计

基于ISP芯片的可编程数字移相器设计移相常用于同步检测器的数据处理系统中。
传统移相器的实现办法有多种,大致可分为模拟式和数字式两类。
模拟式移相器电路复杂、线性差、精度低;而数字式移相器大多以标准规律器件(如中小规模TTL系列、系列)按传统数字系统设计办法设计而成,其主要缺点是规律规模小、功耗大、牢靠性低。
本文介绍一种基于在系统可编程规律器件实现的新型可编程数字移相器的设计计划,该移相器移相范围为0~360°,辨别率为1°,它可以便利地和微处理机及其它设备联接,以构成同步检测器数据处理系统。
1 新型数字式移相器的工作原理图1为数字移相器的工作原理框图,其工作原理如下:输入信号的频率为fi,数字锁相环被设置在360倍输入信号频率上,即锁相环输出频率为360fi。
90分频器由8421BCD码计数器构成的模90计数器组成,对锁相环输出信号举行计数分频,并将计数器的输出以8421BCD码的形式输入数值,该信号将和来自锁存器的相角码举行比较。
相角码为两位8421BCD码,它的值为所需相移角度数对于90求余运算所得的结果。
象限码为所需相移角度数整除90所得的结果,用两位二进制码表示。
象限码表示相移角所在的象限,其第一到第四象限的象限码分离表示为00、01、01、11。
例如,所需相移角度数为295°,则295-3X90=25,所以对应的相角码为00100101,因为相移角位于第四象限,其象码为11。
当计数器计到和相角码相等时,比较器输出"="为"1"电平。
因为锁相环的输出频率是360fi,计数器工作的每一循环为除以90,因而在输入信号的每个周期内,数值比较器输出"="为"1"电平的状态就浮现四次。
这样,通过移相输出控制电路,在象限码的作用下,就可获得精确的移信任号输出。
图1中,移相输出控制电路除形成移信任号外,还产生计数器复位信号、锁相环鉴相器输入信号,通过锁相环的自动调整功能,以保证信号和输入信号的循环周期相全都,并和计数器复位信号同相。
数字相移测量中的高精度相位误差补偿

数字相移测量中的高精度相位误差补偿数字相移测量技术已经成为了一种越来越重要的测量方法。
在许多应用领域中,数字相移测量能够提供高精度、高分辨率、高可靠性的测量结果。
然而,在数字相移测量中,相位误差往往是一个需要特别注意的问题。
相位误差是指在数字相移测量中由于各种因素引起的相位偏差。
这些因素包括时钟漂移、温度变化、幅度变化等,这些都可能导致相位误差的出现。
相位误差的出现会导致系统的测量精度受到严重影响,从而降低数字相移测量的可靠性。
为了解决数字相移测量中的相位误差问题,一个有效的方法是使用高精度相位误差补偿技术。
高精度相位误差补偿技术可以对数字相移测量中的相位误差进行有效的校正,从而提高测量精度和可靠性。
高精度相位误差补偿技术通常采用数字信号处理算法进行实现。
这些算法可以通过对信号进行数字滤波、相位补偿、补偿系数优化等技术手段,来达到相位误差补偿的效果。
其中,数字滤波是高精度相位误差补偿技术的核心之一。
数字滤波通常采用FIR数字滤波器或IIR数字滤波器实现。
FIR数字滤波器与IIR数字滤波器相比具有更好的响应特性和更高的灵活性,因此在数字相移测量中经常采用FIR数字滤波器进行相位误差补偿。
除了数字滤波以外,相位补偿也是另一个重要的补偿技术。
相位补偿可以根据数字信号处理的方法,动态计算相位误差,并对测量值进行相应的补偿。
相位补偿可以通过用FIR数字滤波器对信号进行相位旋转实现。
这样做的好处是可以对相位误差进行校正,同时不会对信号的原始数据造成任何影响。
补偿系数优化是另一个高精度相位误差补偿技术。
补偿系数通过对数字信号处理算法进行数值优化,可以实现对相位误差的更为精确的补偿。
当补偿系数优化算法适当应用时,可以提高数字相移测量的精度和可靠性。
总之,在数字相移测量中,相位误差是一个需要解决的关键问题。
采用高精度相位误差补偿技术可以有效地对相位误差进行校正,从而提高数字相移测量的精度和可靠性。
同时,我们需要根据实际情况选择适合于应用场景的滤波器、相位补偿和补偿系数优化方法。
第八章微波控制电路(2.数字移相器)

s
in
2
2 22
tan 2
tan( 2
) 2
tan tan
1
2 tan
2 tan
22
1
Y02
Z
2 01
sin
2
Y0 Z 01 sin
微波电子线路
由上式可以求出 则
Y01
Y0
s in
sec
2
B
Y0
(s
ec
2
c os
tan ) 2
B
Y0
(s
ec
2
c os
180度对应长度 98.6842mm
(39.0395mm)
90度对应长度 49.3421mm
(19.5197mm)
45度对应长度 24.6711mm
(9.7599mm)
高边频率 1665MHz 波长180.1800mm
(35.6396mm)
tan
) 2
按照上述方程设计移相器,虽然在中心频率上驻波系数等于1,相移误差 为零,单偏离中心频率时,因 B 和 B 都是频率的函数,相移量和驻波系数将
随频率变化而变化。所以,当移相精度和驻波系数规定时,移相器的带宽就
受到限制。进一步分析表明移相器的带宽与 有关。当驻波系数小于1.2,相
位误差小于2度时,对于45度移相器来说, =90度时,相对带宽为20%, 而 =80度时,相对带宽为15%。所以 值要根据实际的需求来选择或计算 。
2 l g
上式表明,用一般均匀传输线组成的开关线移相器是窄带的,因为 与频 率成正比。
微波电子线路
我们设计一个中心频率为1592.5MHz开关线型三位数字移相器。如下图所示;
南京理工大学科技成果——6-18GHz单片五位数字移相器

南京理工大学科技成果——6-18GHz单片五位数字移相器成果简介:
在通信、相控阵雷达、电子对抗、制导和仪器等电子系统设备中的宽带微波毫米波的控制电路中,数字模拟移相器集成电路是微波毫米波主要控制电路之一。
现有的微波毫米波宽带数字模拟兼容移相器集成电路的同类产品,由于设计采用的实现移相电路方案的缺陷,通常电性能指标均较差。
本设计的目的在于提供一种电路拓扑结构简单、大幅度减小电路插入损耗、展宽工作频率带宽、减小芯片面积、提高成品率、降低成本并具有数字和模拟控制兼容的微波毫米波移相器。
相关技术均已申请国家专利,可根据客户要求设计各种MMIC移相器。
技术指标:
1、移相态:0、11.25°22.5°、45°、90°、180°
2、插损:最大12,.最小7
3、驻波:最大2.5
4、芯片尺寸:3555mm×4.055mm×0.1mm
项目水平:国际先进,成熟程度:小试
合作方式:合作开发、专利许可、技术转让、技术入股。
0到360度移相电路 -回复

0到360度移相电路-回复什么是0到360度移相电路?0到360度移相电路是一种电子电路,它可以将输入信号的相位进行改变,从而在输出端产生相位差。
这种电路常用于频率调制、天线阵列、声波阵列等应用场合,可以帮助实现信号的定向传输、波束形成等功能。
为了更好地理解0到360度移相电路,我们需要首先了解相位和相位差的概念。
在信号处理中,相位描述了一个信号的位置和时间关系,通常以角度(度)或弧度来表示。
相位差是用来比较两个信号之间的相位差异,可以描述信号之间的延迟或提前情况。
0到360度移相电路基于一个重要原理,即改变电路中的电感或电容元件,可以引起输入信号的相位改变。
在电路中,电感和电容分别具有导致信号提前和延迟的能力。
通过合理地设计电路结构和参数,我们可以实现对输入信号相位的精确控制和调整。
在实践中,有多种方法可以实现0到360度移相电路。
下面,我将介绍其中一种常用的方法。
首先,我们考虑一个简单的电容移相电路。
该电路包含一个电容和一个电阻,并且输入信号通过电容元件,输出信号经过电阻元件。
电容的特点是导致信号延迟,而电阻的作用则是将信号传递给输出端。
接下来,我们将讨论电路的工作原理。
当输入信号通过电容时,由于电容的性质,会导致输入信号的相位发生变化。
具体来说,对于低频信号,电容会导致输入信号的相位延迟;而对于高频信号,电容则会导致输入信号的相位提前。
因此,我们可以通过合理选择电路参数,例如电容和电阻的数值,来实现对输入信号相位的精确控制。
在设计0到360度移相电路时,我们需要根据应用需求来确定电路参数。
例如,如果需要改变输入信号的相位差为180度,我们可以选择合适的电容和电阻数值,以实现这一目标。
需要注意的是,随着相位差增加,电路的稳定性和频率特性也会发生变化,因此我们需要综合考虑这些因素来进行电路设计。
除了电容移相电路,我们还可以利用电感进行相位移动。
电感移相电路的原理与电容移相电路相似,只是使用了电感元件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.两个同频信号之间的移相与实现方式所谓移相是指两路同频的信号,以其中的一路为参考,另一路相对于该参考作超前或滞后的移动,即称为是相位的移动。
两路信号的相位不同,便存在相位差,简称相差。
若我们将一个信号周期看作是3600,则相差的范围就在00∽3600之间。
例如在图1中,以A信号为参考,B信号相对于A信号作滞后移相φ0,则称A超前Bφ0,或称B滞后Aφ0。
图1 移相示意要实现B信号对A信号的移相,通常有两个途径:一是直接对模拟信号进行移相,如阻容移相,变压器移相等,早期的移相通常采用这种方式。
采用这种方式制造的移相器有许多不足之处,如:输出波形受输入波形的影响,移相操作不方便,移相角度随所接负载和时间等因素的影响而产生漂移等.在此不予讨论.另一个是随电子技术的发展,特别是单片机技术的发展而发展起来的数字移相技术,是目前移相技术的潮流。
数字移相技术的核心是:先将模拟信号或移相角数字化,经移相后再还原成模拟信号。
数字移相主要有两种形式:一种是先将正弦波信号数字化,并形成一张数据表存入ROM芯片中,此后可通过两片D/A转换芯片在单片机的控制下连续地循环输出该数据表,就可获得两路正弦波信号,当两片D/A转换芯片所获得的数据序列完全相同时,则转换所得到的两路正弦波信号无相位差,称为同相。
当两片D/A转换芯片所获得的数据序列不同时,则转换所得到的两路正弦波信号就存在着相位差。
相位差的值与数据表中数据的总个数及数据地址的偏移量有关。
这种处理方式的实质是将数据地址的偏移量映射为信号间的相位值。
另一种是先将参考信号整形为方波信号,并以此信号为基准,延时产生另一个同频的方波信号,再通过波形变换电路将方波信号还原成正弦波信号。
以延时的长短来决定两信号间的相位值。
这种处理方式的实质是将延时的时间映射为信号间的相位值。
二.利用D/A转换实现移相图2给出了一个设计实例。
单片机为8031,D/A转换芯片采用两片8位字长的DAC0832,由于DAC0832的输出信号为电流型,故需加运算放大器将电流型信号转换成电压型信号。
该设计中运算放大器采用双极型双运放4558。
转换所用的数据为256个8位字长的数据,随程序一起存入ROM存储器中,即一个信号周期有256个转换值。
图2 D/A转换移相框图进行D/A转换的程序段及正弦波的数值表如下:程序清单:MOV R5,#00H;第一路正弦波起点地址的偏移量送R5 MOV R1,#08H;第二路正弦波起点地址的偏移量送R1 LOOP:MOV A, R5MOV DPTR,#TAB;取数据表首地址MOVC A,@DPTR;取第一路数据MOV DPTR,#0DFFFH;选通第一路DAC0832MOVX @DPTR,A;数据送第一路DAC0832INC R5;修改第一路地址的偏移量MOV A,R1;MOV DPTR,#TAB:MOVC A,@DPTR;取第二路数据MOV DPTR,#0BFFFH:选通第二路DAC0832 MOVX @DPTR,A;数据送第二路DAc0832INC R1:修改第二路地址的偏移量MOV DPTR,#7FFFH;选通两片DAC0832的转换端MOVX @DPIR,A;同时转换两路数据AJMP LOOPTAB:DB 80,83,86,89,90,93,96DB 99,9C,9F,A2,A5,A8,AB,AEDB B1,B4,B7,BA,BC,BF,C2,C5DB C7,CA,CC,CP,D1,D4,D6,D8DB DA,DD,DF,E1,E3,E5,E7,E9DB EA,EC,EE,EF,F1,F2,F4,F5DB F6,F7,F8,F9,FA,FB,FC,FDDB FD,FE,FF,FF,FF,FF,FF,FFDB FF,FF,FF,FF,FF,FF,FE,FDDB FD,FC,FB,FA,F9,F8,F7,F6DB F5,F4,F2,F1,EF,EE,EC,EADB E9,E7,E5,E3,E1,DF,DD,DADB D8,D6f D4,D1,CF,CC,CA,C7DB C5,C2,BF,BC,BA,B7,B4,B1DB AE,AB,A8,A5,A2,9F,9C,99DB 96,93,90,8D,89,86,83,8ODB 80,7C,79,76,72,6F,6C,69DB 66,63,60,5D,5A,57,55,51DB 4E,4C,48,45,43,40,3D,3ADB 38,35,33,30,2E,2B,29,27DB 25,22,20,1E,1C,1A,18,16DB 15,13,11,10,0E,0D,0B,0ADB 09,08,07,06,05,04,03,02DB 02,01,00,00,00,00,00,00DB 00,00,00,00,00,00,01,02DB 02,03,04,05,06,07,08,09DB 0A,0B,0D,0E,10,11,13,15DB 16,18,1A,1C,1E,20,22,25DB 27,29,2B,2E,30,33,35,38DB 3A,3D,40,43,45,48,4C,4EDB 51,55,57,5A,5D,60,63,66DB 69,6C,6F,72,76,79,7C,80此例中,数据表中数据共有256个,每两个相邻数据之间的相位差为3600÷256=1.40。
我们只需改变R1中的值就可改变两路正弦波的相位差。
程序中R1=8,故第一路正弦波滞后第二路正弦波1.40×8=11.20。
现将以这种方式实现移相的几个技术指标作如下分析:1.波形失真度;正弦波的转换精度若不加其它的处理,则取决于D/A转换芯片的位数和数据表中数据的准确度。
8位的D/A转换芯片其输入数据的范围是0-255,也就是说最多可将模拟量分为256级。
在双级型的转换中,正、负半波被分为128级。
2.正弦波的周期;正弦波的周期由对数据表作一遍完整的转换所需要的时间决定。
显然,单片机的速度、数据表中数据的个数以及程序的算法等因素都将影响正弦波的周期。
上例中设8031的晶振频率为6MHz,则程序完成一个数据的转换所需要的时间是52us,故正弦波的周期为K×52 us×256=K×13312 us。
K为转换下一个数据前等待的时间系数,当K=l时,为连续转换,此时正弦波的周期最短。
3.移相细度;移相细度(最小移动步长)取决于数据表中数据的个数,数据越多则移相细度越细。
上例中数据表中数据的个数为256个,所以移相细度为3600÷256=1.40。
若数据表中数据的个数为360个,则移相细度为3600÷360=10。
表面上看,只要增加数据的个数,就可提高移相细度,但在不增加D/A芯片的位数的情况,单纯增加数据的个数,会使正弦波波形的失真度增加,并使正弦波的周期变长。
在正弦波周期一定的情况下,数据表中数据的个数是有限制的。
三.利用单片机进行方波信号的移相利用单片机进行方波信号的移相则是数字移相的另一个途经,已有多种成功之作,有些偏重硬件,有些偏重软件,总体说来,偏重硬件的精度较高,但制造及调试较复杂。
偏重软件的结构简单,成本较低,但往往精度受影响。
本文介绍一种己获得较为理想效果的设计。
设计的原理框图如图3所示。
upload/article/2005122581313.gif[/IMG]图3 方波移相框图工作原理:作为参考信号的A,经整形后得到方波信号a,再利用锁相技术对a作3600倍频,并将此倍频信号作为单片机中CTC的计数脉冲,以此来产生相移和测量移相的实际值。
由于计数脉冲是通过锁相环产生的,在锁相环允许的频率范围内,计数脉冲始终是a信号的3600倍,因此,可以看成是将a信号的一个信号周期分为了3600份,且允许a的频率可在一个小的范围内波动。
若一个信号周期为3600,那么在一个信号周期内每个计数脉冲即代表0.10。
我们只需以a信号为参考,延时若干个计数脉冲的时间来产生c信号即可做到移相,改变延时计数脉冲的个数即可改变移相值,亦可记录两个信号的上沿(或下沿)间的脉冲个数来获得两信号的相位差。
正是由于锁相环的存在,才使得移相信号B与参考信号A的频率完全相同。
比起由软件测得A信号的周期后再来产生B信号的方式来,其精度要高得多。
锁相环倍频的频率愈高则移相的最小单位愈小,若作7200倍频,那么在一个信号周期内每个计数脉冲即代表0.050。
图4 移相时序图4是以上述方式进行移相的时序图,设计数脉冲的频率是a信号的3600倍,那么从a信号的上沿开始经N个计数脉冲后产生c信号的上沿,则有a信号超前c信号N×0.10。
但我们需要的是A信号与B信号之间的移相。
A信号与a信号的相位是相同的,但c信号与B信号的相位,由于波形转换电路的存在而不相同,其相位差视波形转换电路的参数而定。
故A信号与B 信号之间的实际移相值无法由N×0.10来计算。
要获得A信号与B信号之间的实际移相值,可将B信号整形成b信号(两信号相位相同)后反馈给单片机,由单片机测量出a信号与b信号之间的计数脉冲个数n即可,实际移相值为n×0.10。
改变N的值即可改变移相值。
要实现上述设计,除需要用锁相环产生计数脉冲外,还需要三个16位的计数器,分别用来计N,n及1800的值。
笔者将8032中的计数器作如下分配:T0计N的值、T1计n的值、T2计1800的值。
T0、T1及T2的启停全部由中断服务程序控制。
接线如图3所示。
具体是:①a信号的上沿产生INT0中断,其中断服务程序分别将-N及0赋给TH0TL0和TH1TL1;然后使T0、T1开始计数。
②T0归零,其中断服务程序关闭T0;置P3.0;-1800赋TH2TL2;使T2开始计数。
③T2归零,其中断服务程序清P3.0;关闭T2。
④b信号的上沿产生INT0中断,其中断服务程序关闭T1;读取TH1TL1的计数值n.。
四.两种移相方式的性能比较通过以上介绍,我们可以看到:以D/A转换方式实现的移相,虽然所用元件少,但输出信号的频率难以细调,特别是移相的最小单位太大(1.40/步)。
在50Hz频率下,要达到0.10/步移相细度难以办到。
因此,该方式只适合于对频率要求不高,且移相角度固定的场合。
以延时输出方波的方式实现的移相,其硬件电路比较复杂(锁相及波形变换电路)。
输出信号的频率以参考信号的频率为准,而参考信号的频率则可以精确给定。
移相的最小单位可小于0.10/步,这就为无级移相提供了基础。
因此,该方式可用于对频率要求高,且需3600无级移相的场合。
参考资料1.王秉时,移相技术的发展与移相器产品的进步,《电测与仪表》1998。
