微积分公式大全

合集下载

微积分基本公式16个

微积分基本公式16个1. 微分：微分是数学中最重要的概念之一，它指的是在一定时间内几何形状的变化率。

可以理解为小步长地移动拟合函数，接近曲线本身。

可以表示为\frac{dy}{dx} 或f'(x) 。

2. 泰勒公式：泰勒公式是一个重要的微积分工具，它可以在某一特定点附近对任意连续函数进行展开，也就是说任意设定一个位置x0，可以根据它附近的数值向量求出函数在该位置的平均值。

可以用公式表示为：f(x) = f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)(x-x_0)^2}{2!} + \frac{f^{n}(x_0)(x-x_0)^n}{n!} + ...3. 高斯积分公式：高斯积分是指将函数抽象为一次多项式曲线，采用指数型或线性型积分方法求解积分。

它可以用公式f(x)=\sum_{i=0}^n a_i x^i 表示，其中a_i为积分下限、上限和积分点x_i处函数值相乘所得到的系数。

4. 黎曼积分：黎曼积分是一种常用的积分方法，它通过对连续函数求和，来确定函数在给定区间上的定积分。

可以用公式表示为：\int_{a}^{b}f(x)dx=\sum_{i=1}^{n}f(x_i)\Delta x_i ,其中n为梯形的节点数。

5. Stokes公式：Stokes公式是一种将多变量函数投影到多方向进行积分的方法，可以用公式表示为：\int_{\Omega}\nabla\times{\bf F} dA =\int_{\partial\Omega}{\bf F}\cdot{\bf n}dS，其中\nabla\times{\bf F} 为梯度矢量场，\partial\Omega 为边界，{\bfn}dS 为单位向量与边界面积的乘积。

6. Γ函数：Γ函数是一种重要的数学函数，通常用来表示非负整数的排列组合，也可以表示实数的阶乘，可以用公式表示为：\Gamma(x)=\int_0^{\infty}t^{x-1}e^{-t}dt7. 方阵的行列式：方阵的行列式是指一个n阶矩阵的行列式，可以用公式表示为：D= |a_{i,j}| = \begin{vmatrix} a_{1,1} & a_{1,2} & ... & a_{1,n} \\ a_{2,1} & a_{2,2} & ... & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n,2} & ... & a_{n,n} \end{vmatrix} ，其中a_{i,j} 为矩阵中的元素。

微积分的公式大全

微积分的公式大全微积分（Calculus）是数学中的一个分支，研究函数的变化率以及与函数相关的一些重要概念，如极限、导数、积分等。

本文将为你介绍微积分中的一些重要公式。

在开始之前，我们先定义一些符号：-f(x)表示一个函数-a表示一个常数- dx 表示自变量的微增量，通常取极小值- dy 表示函数的微增量，即f(x+dx)-f(x)下面是一些微积分中常用的公式：1.极限- 极限定义：lim(x->a) f(x) = L，表示当自变量 x 接近 a 时，函数 f(x) 的值接近 L。

-基本极限：a. lim(x->a) = a，表示当 x 接近 a 时，常数 a 的值保持不变b. lim(x->a) x^n = a^n，表示当 x 接近 a 时，幂函数的值保持不变c. lim(x->a) sinx = sin a，表示当 x 接近 a 时，正弦函数的值保持不变d. lim(x->a) cosx = cos a，表示当 x 接近 a 时，余弦函数的值保持不变e. lim(x->a) ex = e^a，表示当 x 接近 a 时，指数函数的值保持不变2.导数- 导数定义：f'(x) = lim(dx->0) dy/dx = lim(dx->0) [f(x+dx)-f(x)]/dx，表示函数 f(x) 在 x 处的变化率。

-基本导数：a.(c)'=0，表示一个常数c的导数为0b. (x^n)' = nx^(n-1)，表示一个幂函数 x^n 的导数c. (sinx)' = cosx，表示正弦函数的导数d. (cosx)' = -sinx，表示余弦函数的导数e.(e^x)'=e^x，表示指数函数的导数f. (lnx)' = 1/x，表示自然对数函数的导数g. (a^x)' = ln(a) * a^x，表示以 a 为底的指数函数的导数3.积分- 积分定义：∫[a, b] f(x) dx = lim(n->∞) Σ f(xi)Δx，表示在区间 [a, b] 上函数 f(x) 的累积增量。

微积分公式大全范文

微积分公式大全范文一、导数公式：1.基本导数公式：(1)常数导数公式：若f(x)=C，其中C为常数，则f'(x)=0。

(2)乘幂函数导数公式：若f(x) = x^n，其中n为常数，则f'(x) = nx^(n-1)。

(3)指数函数(e)导数公式：若f(x)=e^x，则f'(x)=e^x。

(4)对数函数导数公式：若f(x) = ln(x)，则f'(x) = 1/x。

(5)三角函数导数公式：若f(x) = sin(x)，则f'(x) = cos(x)；若f(x) = cos(x)，则f'(x) = -sin(x)；若f(x) = tan(x)，则f'(x) = sec^2(x)。

(6)反三角函数导数公式：若f(x) = arcsin(x)，则f'(x) = 1/√(1-x^2)；若f(x) = arccos(x)，则f'(x) = -1/√(1-x^2)；若f(x) = arctan(x)，则f'(x) = 1/(1+x^2)。

2.基本运算法则：(1)和差法则：设f(x)和g(x)可导，则(f+g)'(x)=f'(x)+g'(x)；若f(x)和g(x)可导，则(f-g)'(x)=f'(x)-g'(x)。

(2)积法则：设f(x)和g(x)可导，则(fg)'(x) = f'(x)g(x) + f(x)g'(x)。

(3)商法则：设f(x)和g(x)可导，且g(x)≠0，则(f/g)'(x)=(f'(x)g(x)-f(x)g'(x))/[g(x)]^23.链式法则：设y=f(u)，u=g(x)，其中u是中间变量，则y=f(g(x))，且y'=f'(g(x))g'(x)。

二、积分公式：1.基本积分公式：(1)幂函数积分公式：若f(x) = x^n，其中n≠-1，则∫f(x)dx = (x^(n+1))/(n+1) + C，其中C为常数。

常用微积分公式大全

常用微积分公式大全1. 导数公式1.1 基本导数公式•常数规则: 如果c是一个实数, 那么导数f(x)=c相对于x是f′(x)= 0。

•幂函数规则: 如果f(x)=x n, 其中n是常数, 那么导数f′(x)=nx n−1。

•指数函数规则: 如果f(x)=e x, 那么导数f′(x)=e x。

•对数函数规则: 如果 $f(x) = \\log_a(x)$, 那么导数 $f'(x) = \\frac{1}{x\\ln(a)}$。

•乘法法则: 如果f(x)=g(x)ℎ(x), 那么导数f′(x)=g′(x)ℎ(x)+g(x)ℎ′(x)。

•除法法则: 如果 $f(x) = \\frac{{g(x)}}{{h(x)}}$, 那么导数 $f'(x) =\\frac{{g'(x)h(x) - g(x)h'(x)}}{{(h(x))^2}}$。

1.2 常见函数导数表•常数函数: f(x)=c, 导数f′(x)=0。

•幂函数: f(x)=x n, 导数f′(x)=nx n−1。

•指数函数: f(x)=e x, 导数f′(x)=e x。

•对数函数: $f(x) = \\log_a(x)$, 导数 $f'(x) = \\frac{1}{x \\ln(a)}$。

•三角函数:–正弦函数: $f(x) = \\sin(x)$, 导数 $f'(x) = \\cos(x)$。

–余弦函数: $f(x) = \\cos(x)$, 导数 $f'(x) = -\\sin(x)$。

–正切函数: $f(x) = \\tan(x)$, 导数 $f'(x) = \\sec^2(x)$。

2. 积分公式2.1 基本积分公式•幂函数积分: 如果f(x)=x n, 其中n不等于−1, 那么积分 $\\intf(x)\\,dx = \\frac{1}{n+1}x^{n+1} + C$。

•指数函数积分: 如果f(x)=e x, 那么积分 $\\int f(x)\\,dx = e^x + C$。

微积分公式大全

微积分公式2 cos α sin β = sin (α+β) - sin (α-β) 2 cos α cos β = cos (α-β) + cos (α+β) 2 sin α sin β = cos (α-β) - cos (α+β)cos α - cos β = -2 sin ?(α+β) sin ?(α-β)tan (α±β)=βαβαtan tan tan tan μ±, cot (α±β)=βαβαcot cot cot cot ±μe x =1+x+!22x +!33x+…+!n x n + …sin x = x-!33x +!55x -!77x +…+)!12()1(12+-+n x n n + …cos x = 1-!22x +!44x -!66x +…+)!2()1(2n x nn -+ …ln (1+x) = x-22x +33x -44x +…+)!1()1(1+-+n x n n + …tan -1x = x-33x +55x -77x +…+)12()1(12+-+n x n n + …(1+x)r =1+r x+!2)1(-r r x 2+!3)2)(1(--r r r x 3+… -1<x<1 ∑=ni 11= n∑=ni i 1= ?n (n +1)∑=ni i 12=61n (n +1)(2n +1) ∑=ni i13= [?n (n +1)]2Γ(x) =⎰∞tx-1e -td t = 2⎰∞t2x-12t e -d t =⎰∞)1(ln tx-1 d t β(m , n ) =⎰10x m -1(1-x)n -1 d x =2⎰20sin π2m -1x cos 2n -1x d x=⎰∞+-+01)1(nm m x x d x希腊字母 (Greek Alphabets)大写小写读音大写小写读音大写小写读音 Α α alpha Ι ι iota Ρ ρrhoΒ β beta Κ κ kappa Σ σ, ? sigmaΓ γ gamma Λ λ lambda Τ τtau Δ δ delta Μ μ mu Υ υ upsilonΕ ε epsilon Ν ν nu Φ φphi Ζ ζ zeta Ξ ξ xi Χ χkhi Η η eta Ο ο omicron Ψ ψpsi ΘθthetaΠπpiΩω omega倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; ? 顺位高d 顺位低 ;0*? =∞1 *? = ∞∞ = 0*01 = 0000 = )(0-∞e ; 0∞ = ∞⋅0e ; ∞1 = ∞⋅0e顺位一: 对数; 反三角(反双曲)顺位二: 多项函数; 幂函数顺位三: 指数; 三角(双曲)算术平均数(Arithmetic mean)中位数(Median) 取排序后中间的那位数字众数(Mode)次数出现最多的数值几何平均数(Geometric mean) 调和平均数(Harmonic mean) 平均差(Average Deviatoin)1 000 000 000 000 000 000 000 000 10 yotta Y 1 000 000 000 000 000 000 000 1021 zetta Z1 000 000 000 000 000 000 1018 exa E1 000 000 000 000 000 1015 peta P1 000 000 000 000 1012 tera T 兆1 000 000 000 109 giga G 十亿1 000 000 106 mega M 百万1 000 103 kilo K 千100 102 hecto H 百10 101 deca D 十0.1 10-1 deci d 分，十分之一0.01 10-2 centi c 厘（或写作「厘」），百分之一0.001 10-3 milli m 毫，千分之一0.000 001 10-6 micro ? 微，百万分之一0.000 000 001 10-9 nano n 奈，十亿分之一0.000 000 000 001 10-12 pico p 皮，兆分之一0.000 000 000 000 001 10-15 femto f 飞（或作「费」），千兆分之一0.000 000 000 000 000 001 10-18 atto a 阿0.000 000 000 000 000 000 001 10-21 zepto z0.000 000 000 000 000 000 000 001 10-24 yocto y。

微积分公式大全

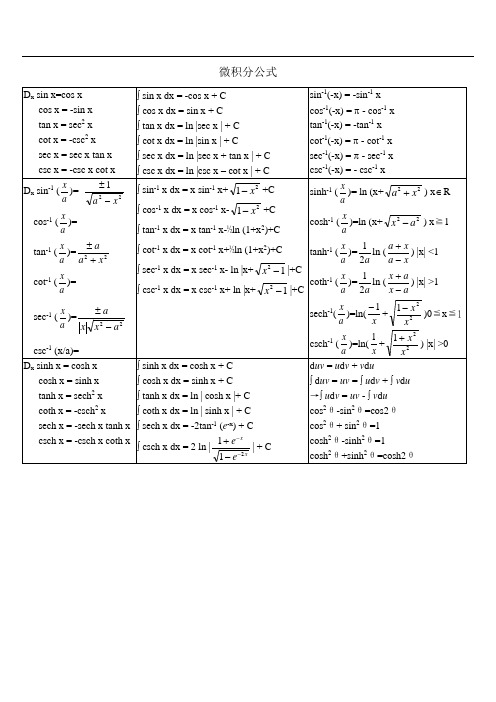
微积分公式D x sinh -1(ax)=221x a + cosh -1(ax)=221ax - tanh -1(ax)= 22x a a -± coth -1(a x)=sech -1(a x )= 22x a x a -- csch -1(x/a)=22xa x a +-⎰ sinh -1 x dx = x sinh -1 x-21x ++ C⎰ cosh -1 x dx = x cosh -1 x-12-x + C⎰ tanh -1 x dx = x tanh -1 x+ ½ ln | 1-x 2|+ C ⎰ coth -1 x dx = x coth -1 x- ½ ln | 1-x 2|+ C⎰ sech -1 x dx = x sech -1 x- sin -1 x + C ⎰ csch -1 x dx = x csch -1 x+ sinh -1 x + Csin 3θ=3sin θ-4sin 3θ cos3θ=4cos 3θ-3cos θ →sin 3θ= ¼ (3sin θ-sin3θ) →cos 3θ=¼(3cos θ+cos3θ)sin x = j e e jx jx 2-- cos x = 2jxjx e e -+ sinh x = 2x x e e -- cosh x = 2x x e e -+正弦定理:αsin a= βsin b =γsin c =2R余弦定理: a 2=b 2+c 2-2bc cos αb 2=a 2+c 2-2ac cos βc 2=a 2+b 2-2ab cos γsin (α±β)=sin α cos β ± cos α sin β cos (α±β)=cos α cos β μsin α sin β 2 sin α cos β = sin (α+β) + sin (α-β) 2 cos α sin β = sin (α+β) - sin (α-β) 2 cos α cos β = cos (α-β) + cos (α+β) 2 sin α sin β = cos (α-β) - cos (α+β)sin α + sin β = 2 sin ½(α+β) cos ½(α-β) sin α - sin β = 2 cos ½(α+β) sin ½(α-β) cos α + cos β = 2 cos ½(α+β) cos ½(α-β) cos α - cos β = -2 sin ½(α+β) sin ½(α-β)tan (α±β)=βαβαtan tan tan tan μ±, cot (α±β)=βαβαcot cot cot cot ±μe x=1+x+!22x +!33x +…+!n x n+ …sin x = x-!33x +!55x -!77x +…+)!12()1(12+-+n x n n + …cos x = 1-!22x +!44x -!66x +…+)!2()1(2n x n n -+ …ln (1+x) = x-22x +33x -44x +…+)!1()1(1+-+n x n n + …tan -1x = x-33x +55x -77x +…+)12()1(12+-+n x n n + …(1+x)r =1+r x+!2)1(-r r x 2+!3)2)(1(--r r r x 3+… -1<x<1 ∑=ni 11= n∑=ni i 1= ½n (n +1)∑=ni i 12=61n (n +1)(2n +1) ∑=ni i13= [½n (n +1)]2Γ(x) =⎰∞tx-1e -td t = 2⎰∞t2x-12te -d t =⎰∞)1(ln tx-1 d t β(m , n ) =⎰10x m -1(1-x)n -1 d x =2⎰20sin π2m -1x cos 2n -1x d x=⎰∞+-+01)1(nm m x x d x希腊字母 (Greek Alphabets)大写小写读音大写小写读音大写小写读音 Α αalpha Ιιiota Ρρrhoa b cαβγ R倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; ⎰ 顺位高d 顺位低;=212222)(221χχ--⎪⎭⎫⎝⎛ΓennnWeibullαβα--xe1⎪⎭⎫⎝⎛+Γ+111λαβλ⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛+Γ-⎪⎭⎫⎝⎛+Γ111222λλαλ1 000 000 000 000 000 000 000 000 10 yotta Y1 000 000 000 000 000 000 000 1021 zetta Z1 000 000 000 000 000 000 1018 exa E1 000 000 000 000 000 1015 peta P1 000 000 000 000 1012 tera T 兆1 000 000 000 109 giga G 十亿1 000 000 106 mega M 百万1 000 103 kilo K 千100 102 hecto H 百10 101 deca D 十0.1 10-1 deci d 分，十分之一0.01 10-2 centi c 厘（或写作「厘」），百分之一0.001 10-3 milli m 毫，千分之一0.000 001 10-6 micro ? 微，百万分之一0.000 000 001 10-9 nano n 奈，十亿分之一0.000 000 000 001 10-12 pico p 皮，兆分之一0.000 000 000 000 001 10-15 femto f 飞（或作「费」），千兆分之一0.000 000 000 000 000 001 10-18 atto a 阿0.000 000 000 000 000 000 001 10-21 zepto z0.000 000 000 000 000 000 000 001 10-24 yoctoy。

微积分的公式大全

微积分的公式大全微积分是数学的一个重要分支，应用广泛，内容繁多。

在这里，我将为您介绍一些微积分中的基本公式和定理。

请注意，这里只是列举一些常用的公式，若要深入学习微积分，请参考相关教材和课程。

1.导数的基本公式：- 常数导数法则：对于常数c，其导数为0，即d/dx(c) = 0。

- 幂函数导数法则：对于幂函数f(x) = x^n ，其中n是常数，则其导数为d/dx(x^n) = nx^(n-1)。

-和差导数法则：若f(x)和g(x)都可导，则(f(x)±g(x))'=f'(x)±g'(x)。

-积法则：若f(x)和g(x)都可导，则(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)。

-商法则：若f(x)和g(x)都可导，且g(x)≠0，则(f(x)/g(x))'=(f'(x)g(x)-f(x)g'(x))/(g(x))^22.基本积分公式：- 反微分法则：若F(x)是f(x)的一个原函数，则∫f(x)dx = F(x) + C，其中C为常数。

- 平方差公式：∫(a^2 - x^2)^(1/2) dx = (1/2)(x√(a^2 - x^2) + a^2sin^(-1)(x/a)) + C。

- 指数函数积分：∫e^x dx = e^x + C，其中e是自然对数的底数。

- 三角函数积分：∫cos(x) dx = sin(x) + C，∫sin(x) dx = -cos(x) + C。

3.特殊函数和公式：-泰勒级数展开：函数f(x)在点a处的泰勒展开式为f(x)=f(a)+f'(a)(x-a)/1!+f''(a)(x-a)^2/2!+f'''(a)(x-a)^3/3!+...。

- 自然对数函数和指数函数的微分法则：d/dx(ln(x)) = 1/x，d/dx(e^x) = e^x。

微积分公式大全

微积分公式cos (α±β)=cos α cos β μsin α sin β 2 sin α cos β = sin (α+β) + sin (α-β) 2 cos α sin β = sin (α+β) - sin (α-β) 2 cos α cos β = cos (α-β) + cos (α+β) 2 sin α sin β = cos (α-β) - cos (α+β)sin α - sin β = 2 cos ?(α+β) sin ?(α-β)cos α + cos β = 2 cos ?(α+β) cos ?(α-β)cos α - cos β = -2 sin ?(α+β) sin ?(α-β)tan (α±β)=βαβαtan tan tan tan μ±, cot (α±β)=βαβαcot cot cot cot ±μe x=1+x+!22x +!33x +…+!n x n+ …sin x = x-!33x +!55x -!77x +…+)!12()1(12+-+n x n n + …cos x = 1-!22x +!44x -!66x +…+)!2()1(2n x n n -+ …ln (1+x) = x-22x +33x -44x +…+)!1()1(1+-+n x n n + …tan -1x = x-33x +55x -77x +…+)12()1(12+-+n x n n + …(1+x)r =1+r x+!2)1(-r r x 2+!3)2)(1(--r r r x 3+… -1<x<1 ∑=ni 11= n∑=ni i 1= ?n (n +1)∑=ni i12=61n (n +1)(2n +1) ∑=ni i13= [?n (n +1)]2Γ(x) =⎰∞tx-1e -td t = 2⎰∞t2x-12t e -d t =⎰∞)1(ln tx-1 d t β(m , n ) =⎰10x m -1(1-x)n -1 d x =2⎰20sin π2m -1x cos 2n -1x d x=⎰∞+-+01)1(nm m x x d x希腊字母 (Greek Alphabets)大写小写读音大写小写读音大写小写读音 Α α alpha Ι ι iota Ρ ρrhoΒ β beta Κ κ kappa Σ σ, ? sigmaΓ γ gamma Λ λ lambda Τ τtau Δ δ delta Μ μ mu Υ υ upsilonΕ ε epsilon Ν ν nu Φ φphi Ζ ζ zeta Ξ ξ xi Χ χkhi Η η eta Ο ο omicron Ψ ψpsi ΘθthetaΠπpiΩω omega倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; ? 顺位高d 顺位低 ;0*? =∞1 *? = ∞∞= 0*01 = 0000 = )(0-∞e ; 0∞ = ∞⋅0e ; ∞1 = ∞⋅0e顺位一: 对数; 反三角(反双曲)顺位二: 多项函数; 幂函数顺位三: 指数; 三角(双曲)算术平均数(Arithmetic mean)中位数(Median) 取排序后中间的那位数字1 000 000 000 000 000 000 000 000 10 yotta Y1 000 000 000 000 000 000 000 1021 zetta Z1 000 000 000 000 000 000 1018 exa E1 000 000 000 000 000 1015 peta P1 000 000 000 000 1012 tera T 兆1 000 000 000 109 giga G 十亿1 000 000 106 mega M 百万1 000 103 kilo K 千100 102 hecto H 百10 101 deca D 十0.1 10-1 deci d 分，十分之一0.01 10-2 centi c 厘（或写作「厘」），百分之一0.001 10-3 milli m 毫，千分之一0.000 001 10-6 micro ? 微，百万分之一0.000 000 001 10-9 nano n 奈，十亿分之一0.000 000 000 001 10-12 pico p 皮，兆分之一0.000 000 000 000 001 10-15 femto f 飞（或作「费」），千兆分之一0.000 000 000 000 000 001 10-18 atto a 阿0.000 000 000 000 000 000 001 10-21 zepto z0.000 000 000 000 000 000 000 001 10-24 yocto y。

微积分公式大全

sin x dx = -cos x + C cos x dx = sin x + C tan x dx = ln |sec x | + C cot x dx = ln |sin x | + Csec x dx = ln |sec x + tan x | + Ccsc x dx = ln |csc x – cot x | +Csin -1(-x) = -sin -1 x cos -1(-x) =- cos -1 xtan -1(-x) = -tan -1 x cot -1(-x) =- cot -1 x sec -1(-x) =- sec -1 xcsc -1(-x) = - csc -1 xsin -1 x dx = x sin -1 x+21x -+C cos -1 x dx = x cos -1 x-21x -+Ctan -1 x dx = x tan -1 x-½ln (1+x 2)+C cot -1 x dx = x cot -1 x+½ln (1+x 2)+Csec -1 x dx = x sec -1x- ln|x+12-x |+C csc -1 x dx = x csc -1x+ ln |x+12-x |+C tanh coth sinh x dx = cosh x + C cosh x dx = sinh x + C tanh x dx = ln | cosh x |+ C coth x dx = ln | sinh x | + Csech x dx = -2tan -1 (e -x ) + C csch x dx = 2 ln |xx e e 211---+| + C d uv = u d v + v d u d uv = uv = u d v + v d u →u d v = uv -v d ucos 2θ-sin 2θ=cos2θ cos 2θ+ sin 2θ=1cosh 2θ-sinh 2θ=1cosh 2θ+sinh 2θ=cosh2θsinh -1x dx = x sinh -1x-21x ++ Ccosh -1 x dx = x cosh -1 x-12-x + C tanh -1 x dx = x tanh -1 x+ ½ ln | 1-x 2|+ Ccoth -1 x dx = x coth -1 x- ½ ln |1-x 2|+ Csech -1x dx = x sech -1 x- sin -1x + Ccsch -1 x dx = x csch -1 x+ sinh -1 x + CabcαβγRln (1+x) = x-22x +33x -44x +…+)!1()1(1+-+n x n n + …tan -1x = x-33x +55x -77x +…+)12()1(12+-+n x n n + …(1+x)r=1+r x+!2)1(-r r x 2+!3)2)(1(--r r r x 3+… -1<x<1 ∑=ni i 13= [½n (n +1)]2 Γ(x) = ⎰∞0t x-1e -t d t = 2⎰∞0t 2x-12t e -d t = ⎰∞0)1(ln tx-1 d tβ(m , n ) =⎰10x m -1(1-x)n -1d x =2⎰20sin π2m -1x cos 2n -1x d x= ⎰∞+-+01)1(nm m x x d x 希腊字母大写小写读音大写小写读音大写小写读音 Α α alpha Ι ι iota Ρ ρ rho Β β beta Κ κ kappa Σ σ, ς sigma Γ γ gamma Λ λ lambda Τ τ tau Δ δ delta Μ μ mu Υ υ upsilon Ε ε epsilon Ν ν nu Φ φ phi Ζ ζ zeta Ξ ξ xi Χ χ khi Η η eta Ο ο omicron Ψ ψ psi Θ θthetaΠπpiΩωomega倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高;顺位高d 顺位低 ; 0*=∞1* =∞∞ = 0*01 = 0000 = )(0-∞e ; 0∞ = ∞⋅0e ; ∞1 = ∞⋅0e顺位一:对数; 反三角(反双曲) 顺位二: 多项函数; 幂函数顺位三: 指数; 三角(双曲)。

微积分公式大全

β
x a tanh ( )= 2 a a x2 x coth ( )= a
-1
e jx e jx e jx e jx sin x = cos x = 2 2j coth-1 x dx = x coth-1 x- ½ ln | 1-x2|+ C e x ex e x ex cosh x = 2 2 a b c 正弦定理: = = =2R sin sin sin
名师推荐
精心整理
学习必备
微积分公式
Dx sin x=cos x cos x = -sin x tan x = sec2 x cot x = -csc2 x sec x = sec x tan x csc x = -csc x cot x x 1 Dx sin-1 ( )= 2 a a x2
x cos ( )= a
-1
-1
2
x a tan-1 ( )= 2 a a x2 x cot ( )= a
-1
x 1 xa coth-1 ( )= ln ( ) |x| >1 a 2a xa csc x dx = x csc x+ ln |x+ x 1 |+C
x a sec ( )= a x x2 a2
1 x2 a2
cosh-1 x dx = x cosh-1 x- x 2 1 + C tanh-1 x dx = x tanh-1 x+ ½ ln | 1-x2|+ C sech-1 x dx = x sech-1 x- sin-1 x + C csch-1 x dx = x csch-1 x+ sinh-1 x + C R
x2 x3 xn + +…+ +… 2! 3! n!

微积分公式大全

读书之法,在循序而渐进,熟读而精思
微积分公式
Dx sin x=cos x cos x = -sin x tan x = sec2 x cot x = -csc2 x sec x = sec x tan x csc x = -csc x cot x x 1 Dx sin-1 ( )= 2 a a x2
-1 -1
2
sin-1(-x) = -sin-1 x cos-1(-x) = - cos-1 x tan-1(-x) = -tan-1 x cot-1(-x) = - cot-1 x sec-1(-x) = - sec-1 x csc-1(-x) = - csc-1 x
x sinh-1 ( )= ln (x+ a 2 x 2 ) x R a x cosh-1 ( )=ln (x+ x 2 a 2 ) x≧1 a x 1 ax tanh-1 ( )= lபைடு நூலகம் ( ) |x| <1 a 2a ax
x cosh-1( )= a
-1
duv = uv = udv + vdu → udv = uv - vdu cos2θ -sin2θ =cos2θ cos2θ + sin2θ =1 cosh2θ -sinh2θ =1 cosh2θ +sinh2θ =cosh2θ sin 3θ =3sinθ -4sin3θ cos3θ =4cos3θ -3cosθ →sin3θ = ¼ (3sinθ -sin3θ ) →cos3θ =¼(3cosθ +cos3θ )
1 x2 a2
cosh-1 x dx = x cosh-1 x- x 2 1 + C tanh-1 x dx = x tanh-1 x+ ½ ln | 1-x2|+ C sech-1 x dx = x sech-1 x- sin-1 x + C csch-1 x dx = x csch-1 x+ sinh-1 x + C R

微积分公式大全

sinh x c
γ α
b
csch-1(x/a)=
a x a2 x2
餘弦定理: a2=b2+c2-2bc cosα b2=a2+c2-2ac cosβ c2=a2+b2-2ab cosγ
名师精编
优秀资料
sin (α±β)=sin α cos β ± cos α sin β cos (α±β)=cos α cos β sin α sin β 2 sin α cos β = sin (α+β) + sin (α-β) 2 cos α sin β = sin (α+β) - sin (α-β) 2 cos α cos β = cos (α-β) + cos (α+β) 2 sin α sin β = cos (α-β) - cos (α+β) ex=1+x+
-1
-1
2
x a tan-1 ( )= 2 a a x2 x cot ( )= a
-1
x 1 xa coth-1 ( )= ln ( ) |x| >1 a 2a xa csc x dx = x csc x+ ln |x+ x 1 |+C
x a sec ( )= a x x2 a2
x2 x3 xn + +…+ +… 2! 3! n!
sin α + sin β = 2 sin ½(α+β) cos ½(α-β) sin α - sin β = 2 cos ½(α+β) sin ½(α-β) cos α + cos β = 2 cos ½(α+β) cos ½(α-β) cos α - cos β = -2 sin ½(α+β) sin ½(α-β) tan (α±β)=