用Matlab实现简易图片中的星星计数及位置标记--陈宗华
MATLAB坐标图形标注指令

三、图形的修饰与标注MATLAB提供了一些特殊的函数修饰画出的图形,这些函数如下:1)坐标轴的标题:title函数其调用格式为:title('字符串')------字符串可以写中文如:title('My own plot')2)坐标轴的说明:xlabel和ylabel函数格式:xlabel('字符串')ylabel('字符串')如:xlabel('This is my X axis')ylabel('My Y axis')3)图形说明文字:text和gtext函数A.text函数:按指定位置在坐标系中写出说明文字.格式为:text(x1, y1, '字符串', '选项')x1,y1为指定点的坐标;'字符串'为要标注的文字;'选项'决定x1,y1的坐标单位,如没有选项,则x1,y1的坐标单位和图中一致;如选项为'sc',则x1,y1表示规范化窗口的相对坐标,其范围为0到1.(1,1)规范化窗口(0,0)如:text(1,2, '正弦曲线')B.gtext函数:按照鼠标点按位置写出说明文字.格式为:gtext('字符串')当调用这个函数时,在图形窗口中出现一个随鼠标移动的大十字交叉线,移动鼠标将十字线的交叉点移动到适当的位置,点击鼠标左键,gtext参数中的字符串就标注在该位置上.4)给图形加网格:grid函数在调用时直接写grid即可. 上面的函数的应用实例:例:在图形中加注坐标轴标识和标题及在图形中的任意位置加入文本.t=0:pi/100:2*pi;y=sin(t);plot(t,y),grid,axis([0 2*pi -1 1])xlabel('0 leq itt rm leq pi','FontSize',16)ylabel('sin(t)','FontSize',20)title('正弦函数图形','FontName','隶书' ,'FontSize',20)text(pi,sin(pi),'leftarrowsin(t)=0','FontSize',16)text(3*pi/4,sin(3*pi/4),'leftarrowsin(t)=0.707', 'FontSize',16)text(5*pi/4,sin(5*pi/4),' sin(t)=-0.707rightarrow',...'FontSize',16,'HorizontalAlignment','right')5)在图形中添加图例框:legend函数其调用格式为:A.legend('字符串1', '字符串2', ……)------以字符串1,字符串2…… 作为图形标注的图例.B.legend('字符串1', '字符串2', ……, pos)------pos指定图例框显示的位置.图例框被预定了6个显示位置:0------取最佳位置;1------右上角(缺省值);2------左上角;3------左下角;4------右下角;-1------图的右侧.例:在图形中添加图例.x=0:pi/10:2*pi;y1=sin(x);y2=0.6*sin(x);y3=0.3*sin(x);plot(x,y1,x,y2,'-o',x,y3,'-*')legend('曲线1','曲线2','曲线3')6)用鼠标点选屏幕上的点:ginput函数格式为:[x, y, button]=ginput(n)其中:n为所选择点的个数;x,y均为向量,x为所选n个点的横坐标;y为所选n个点的纵坐标.button为n维向量,是所选n个点所对应的鼠标键的标号:1------左键;2------中键;3------右键.可用不同的鼠标键来选点,以区别所选的点.此语句可以放在绘图语句之后,它可在绘出的图形上操作,选择你所感兴趣的点,如峰值点,达到稳态值的点等,给出点的坐标,可求出系统的性能指标.四、MATLAB下图形对象的修改MATLAB图形对象是指图形系统中最基本,最底层的单元,这些对象包括:屏幕(Root),图形窗口(Figures),坐标轴(Axes),控件(Uicontrol),菜单(Uimenu),线(Lines),块(Patches),面(Surface),图像(Images),文本(Text)等等. 根据各对象的相互关系,可以构成如下所示的树状层次:RootFiguresAxes Uicontrol Uimenu Uicontextmenu (对象菜单)Images Line Patch Surface Text对各种图形对象进行修改和控制,要使用MA TLAB的图形对象句柄(Handle).在MATLAB中,每个图形对象创立时,就被赋予了唯一的标识,这个标识就是该对象的句柄. 句柄的值可以是一个数,也可以是一个矢量.如每个计算机的根对象只有一个,它的句柄总是0,图形窗口的句柄总是正整数,它标识了图形窗口的序号等.利用句柄可以操纵一个已经存在的图形对象的属性,特别是对指定图形对象句柄的操作不会影响同时存在的其它图形对象,这一点是非常重要的.[1].对图形对象的修改可以用下面函数:1)set函数:用于设置句柄所指的图形对象的属性.Set函数的格式为:set(句柄, 属性名1, 属性值1, 属性名2, 属性值2, ……)例:h=plot(x,y)set(h, 'Color', [1,0,0])------将句柄所指曲线的颜色设为红色.2)get函数:获取指定句柄的图形对象指定属性的当前值.格式为:get(句柄, '属性名')如: get(gca, 'Xcolor')------获得X轴的当前颜色属性值.执行后可返回X轴的当前颜色属性值[0,0,0](黑色).3)如果没有设置句柄,则可以使用下列函数获得:gcf:获得当前图形窗口的句柄;gca:获得当前坐标轴对象的句柄;gco:获得当前对象的句柄.如:A.要对图形窗口的底色进行修改,可用:set(gcf, 'Color', [1,1,1])------将图形窗口底色设为白色B.要把当前X轴的颜色改为绿色,可用:set(gca, 'Xcolor', [0,1,0])C.还可对坐标轴的显示刻度进行定义:t=-pi:pi/20:pi;y=sin(t);plot(t,y)set(gca,'xtick',[-pi:pi/2:pi],'xticklabel',['-pi','-pi/2','0','pi/2','pi'])本例中用'xtick'属性设置x轴刻度的位置(从-pi~pi,间隔pi/2,共设置5个点),用'xticklabel'来指定刻度的值,由于通常习惯于用角度度量三角函数,因此重新设置['-pi','-pi/2','0','pi/2','pi']5个刻度值.[2].一些常用的属性如下:1)Box属性:决定图形坐标轴是否为方框形式,选项为'on'(有方框),'off'(无方框);2)'ColorOrder'属性:设置多条曲线的颜色顺序,默认值为:[1 1 0;1 0 1;0 1 1;1 0 0;0 1 0;0 0 1]黄色粉色天蓝红色绿色兰色颜色向量还有:[1 1 1]------白色;[0 0 0]------黑色.3)坐标轴方向属性:'Xdir','Ydir','Zdir',其选项为:'normal'------正常'reverse'------反向4)坐标轴颜色和线型属性:'Xcolor','Ycolor','Zcolor'------ 轴颜色, 值为颜色向量'LineWidth'------ 轴的线宽,值为数字'Xgrid','Ygrid','Zgrid'------坐标轴上是否加网格,值为'on'和'off'.5)坐标轴的标尺属性:'Xtick','Ytick','Ztick'------ 标度的位置,值为向量'Xticklabel','Yticklabel','Zticklabel'------ 轴上标度的符号,它的值为与标度位置向量同样大小(向量个数相同)的向量.5)字体设置属性:'FontAngle'------ 设置字体角度,选项为:'normal'------ 正常;'italic'------ 斜体;'oblique'------ 倾斜;'FontName'------ 字体名称;'FontSize'------ 字号大小'FontWeight'------ 字体的轻重,选项为:'light', 'normal','bold'我们可能需要改变某个参量,画多条类似的曲线,这时的“标注”老要手动是很麻烦的。
用Matlab实现简易图片中的星星计数及位置标记--陈宗华

用Matlab实现简易图片中的星星计数及位置标记By C.Z.H --814484233@在天文观测中,统计出星星的数量以及标记出位置对于研究不同时刻同一角度观测有着重要的意义,可以用来分析不同时刻行星的位移变化而从推测行星的运动趋势。
而Matlab 有着强大的矩阵处理功能,而图片则由数据矩阵记录图片像素信息。
利用Maltab结合图像处理和识别技术可自动化实现星星计数和标记等简单功能。
Matlab中支持真彩色图像、索引图像、灰度图像、二值图像4种不同的图像类型,不同类型的图像在Matlab中存储形式不同,部分图像间是可以进行转化的。
一、在灰度图中利用极大值方法计数和标记目前用数码相机获取图像格式为BMP或JPG的真彩图,真彩图像是既含亮度信息又含色彩信息的图像,一幅 m*n大小的真彩图像要由 m*n*3元素类型为字节的矩阵表示,其中数字3指的是像素中的RGB三层分量。
而灰度图像是只含亮度信息不含色彩信息的图像,一副灰度图像可以由m*n矩阵来表示。
将真彩色图像转换为灰度图像,一方面可以去掉一些无用的信息;另一方面大幅度减少图像的数据量,减轻后期处理的工作量,因此灰度处化处理是图像处理中很重要的一步。
把真彩图转化成灰度图后,进行滤波降噪。
我们近似的认为每一个星星的亮度都可以看成高斯波包或者类似高斯形状的波包。
此时,就可以利用寻找极大值法,标记和统计出星星的位置和数量。
其原理为:一维的情况很容易找出一数列的极大值,对于二维情况,我们只要使二维图片的x方向和y方向同时满足极大值的情况就是我们要找的二维极大值,也就是我们要找的星星,图1通过程序计算,统计出72颗星。
范例Matlab 程序见附录1。
图1 小尺度星星图图2 采用查找极大值的方法对小尺度星星进行标记及统计通过寻找极大值的方法数出并标识行星的位置存在着缺陷,因为这种方法要求星星的亮度中间必须是极大值,如果不是极大值,亮度中间是平的或者是凹陷的情况就未被识别出来。
Matlab标定工具箱的使用

1
内存使用方式后,弹出标定工具箱操作面板。图 2 是选择“Standard”后弹出的标定工具箱 操作面板。
图 2 标定工具箱操作面板 图 2 所示的标定工具箱操作面板具有 16 个操作命令键,其功能如下: (1) “Image names”键:指定图像的基本名(Basename)和图像格式,并将相应的图像读 入内存。 (2) “Read names”键:将指定基本名和格式的图像读入内存。 (3) “Extract grid corners”键:提取网格角点。 (4) “Calibration”键:内参数标定。 (5) “Show Extrinsic”键:以图形方式显示摄像机与标定靶标之间的关系。 (6) “Project on images”键:按照摄像机的内参数以及摄像机的外参数(即靶标坐标系 相对于摄像机坐标系的变换关系),根据网格点的笛卡尔空间坐标,将网格角点反投影到图 像空间。 (7) “Analyse error”键:图像空间的误差分析 (8) “Recomp. corners”键:重新提取网格角点。 (9) “Add/Suppress images”键:增加/删除图像。 (10) “Save”键:保存标定结果。将内参数标定结果以及摄像机与靶标之间的外参数 保存为 m 文件 Calib_results.m,存放于 toolbox_calib 目录中。 (11) “ Load ”键: 读入标定 结果。从 存放于 toolbox_calib 目录 中的标定 结果文件 Calib_results.mat 读入。 (12) “Exit”键:退出标定。 (13) “Comp. Extrinsic”键:计算外参数。 (14) “Undistort image”键:生成消除畸变后的图像并保存。 (15) “Export calib data”键:输出标定数据。分别以靶标坐标系中的平面坐标和图像中 的图像坐标,将每一幅靶标图像的角点保存为两个 tex 文件。 (16) “Show calib results”键:显示标定结果。
matlab编程定位方法

matlab编程定位方法
在MATLAB中,可以使用多种方法进行定位,这取决于你想要解决的具体
问题。
下面是一些基本的定位方法:
1. 二维图像定位:对于在二维图像中的目标定位,可以使用边缘检测、特征提取、模板匹配等技术。
例如,使用 `edge` 函数进行边缘检测,使用
`regionprops` 函数提取区域属性,使用 `immatch` 函数进行模板匹配等。
2. 三维空间定位:对于三维空间中的目标定位,可能需要结合多个传感器(如GPS、IMU、轮速传感器等)的数据。
这通常涉及到数据融合和卡尔曼滤波等技术。
3. 声音定位:对于声音定位,可以使用声波传播模型和阵列处理技术。
例如,使用 `audioread` 函数读取声音信号,使用 `beamform` 函数进行波束形成等。
4. 机器人定位:在机器人定位中,可以使用 SLAM(Simultaneous Localization and Mapping)技术。
MATLAB 提供了一些工具箱,如Robotics System Toolbox,可以帮助实现这一目标。
5. 雷达/激光雷达定位:对于雷达或激光雷达数据,可以使用点云处理技术。
MATLAB 的Point Cloud Processing Toolbox 可以提供一些基本的工具。
以上只是一些基本的定位方法,具体的实现会根据你的具体需求和数据类型有所不同。
如果你能提供更具体的信息(如数据类型、目标特性、应用场景等),我可以给出更详细的建议。
MATLAB计算出图像中多个物体的个数及重心

MATLAB计算出图像中多个物体的个数及重心计算出原始图像中物体的个数及每个物体的中心,并显示出来I=imread('keshe17.bmp'); //主函数figure(1),imshow(I);title('原始图像');I2 = rgb2gray(I);I4 = im2bw(I2, 0.7) ;figure(2),imshow(I4);I4=~I4;bai=double(I4);figure(3),imshow(I4);title('二值图像');%像素为1的二值图像geshu=count(bai);for i=1:geshua=fenge(bai);bai=bai-a;f=centre(a);I4(f(1),f(2))=0;I(f(1),f(2))=255;endfigure(4),imshow(I4);figure(5),imshow(I);function f=fenge(D) %对像素为255的白色的物体二值图像进行分割[m,n]=size(D);H=zeros(m,n);for i=1:mfor j=1:nif D(i,j)~=0;H(i,j)=1;a=i;b=j;break;endendif D(i,j)~=0;break;endendfor i=2:(m-1)for j=2:(n-1)if (D(i,j)~=0 )if(H(i,j-1)~=0 | H(i-1,j-1)~=0 | H(i-1,j)~=0 | H(i-1,j+1)~=0)H(i,j)=1;endendendenda=m-1;while i>1i=a;a=a-1;j=n-1;while(j>1)j=j-1;if (D(i,j)~=0)if(H(i,j+1)~=0 | H(i+1,j+1)~=0 | H(i+1,j)~=0 | H(i+1,j-1)~=0 |H(i,j-1)~=0 | H(i-1,j-1)~=0 | H(i-1,j)~=0 | H(i-1,j+1)~=0) H(i,j)=1;endendendf=H;function f=count(D) %对白色的二值图像的物体进行数数[m,n]=size(D);D=double(D);a=0;while 1B=zeros(m,n);B=fenge(D);a=a+1;D=D-B;if D==0break;endendf=a;function f=centre(H) %求白色物体的中心。
使用matlab绘制满天星

在上述示例中,首先使用rand函数生成100个随机的x坐标和y坐标,然后使用scatter函数绘制这些点。 9;MarkerFaceColor', 'k'用于设置点的填充颜色为黑色。 接下来,使用xlim和ylim函数设置坐标轴的范围为[0, 1],这样点就只会在这个范围内显示。 最后,使 用axis off函数隐藏坐标轴,只显示满天星效果。 执行上述代码,就可以在MATLAB中绘制出满天星效 果。你可以根据需要调整生成的点的数量和坐标轴的范围。
使用matlab绘制满天星
在MATLAB中,可以使用scatter函数绘制满天星效果,即绘制多个随机分布的点。 下面是一个示例代码:
% 生成随机坐标 x = rand(100,1); y = rand(100,1); % 绘制满天星 scatter(x, y, 'filled', 'MarkerFaceColor', 'k'); % 设置坐标轴范围 xlim([0, 1]); ylim([0, 1]); % 隐藏坐标轴 axis off;
基于MATLAB的相机标定及图片中人物目标定位

• 79•在相机标定中,人物目标定位是相当重要的应用领域。
人物识别的准确性与快速性决定了系统的可靠性。
本实验使用单目相机,基于MATLAB 软件对所拍摄的照片进行标定,并获得镜头参数。
进而配合Yolo v3图像识别技术,对图片中的人物进行识别而后获取相应的目标定位。
实验结果表明,本实验设计能取得良好的人物目标识别并定位的结果。
三维世界的物体标定在当今的生活中起到的作用越来越明显,在实际运用中,精准快速地识别一片区域内的人数,统计瞬时人流作为参考数据,也可以协助分散大量人流,避免人员的大量聚集带来的危险。
监控设备也可以通过该技术来自动提示敏感区域的人员出入信息,保护用户自身的利益安全。
精确,快速的识别与定位是人们所一直追求的,而基于不同算法的标定,三维识别本领各有千秋。
本实验使用单目相机来获得三维世界目标,以MATLAB 及Yolo v3作为工具。
在三维物体转换为二维图像时,相机自身引起的相机畸变会引来图像失真,影响识别精确度。
本实验使用MATLAB 的相机标定功能技术成熟,其采用的张正友方法精度高,公式理论成熟,且通过MATLAB 操作便捷。
而在图像识别技术上,通过Yolo v3识别物体轮廓,找到二维图像中的物体坐标,最后使用张正友方法的反向思维,实现物体的三维定位。
使用工具便捷,步骤简洁,趣味性强,适合相机标定初学者。
2 目标检测与相机标定的结合应用2.1 坐标系转换相机标定主要用于进行像素坐标到三维世界坐标的转换。
在本次实验中,主要通过两个步骤进行,第一步,是像素坐标到标定板坐标的转换,第二步,是标定板坐标到世界坐标的转换。
其转换公式如下:Step1:像素坐标转换为标定板坐标(1)其中,所代表的为标定板坐标系,R 表示的是在某张照片中相机的旋转矩阵,M 为相机的内参矩阵,s 为关于某张照片的扭转因子,t 为平移向量。
关于扭转因子的求解:在像素坐标到世界坐标的过程中根据公式(1),并且在获得了图片中相关已知的点坐标之后可以求得。
matlab坐标科学计数法

matlab坐标科学计数法Matlab坐标科学计数法是一种用于表示极大或极小数值的方法。
在科学计算和数据分析领域,经常会遇到极大或极小的数值,例如天文学中的星距、生物学中的分子量等。
为了方便表示这些数值,Matlab提供了科学计数法来简化数值的表达。
科学计数法的表示形式为:a x 10^b,其中a为尾数,b为指数。
尾数a是一个小于10的数,而指数b是一个整数。
通过这种表示方式,可以用较短的字符串来表示极大或极小的数值,提高了数值的可读性和可视化效果。
在Matlab中,可以使用sprintf函数将数值转换为科学计数法的形式。
例如,将一个较大的数值1.2345e+6转换为科学计数法,可以使用以下代码:```matlabnum = 1.2345e+6;str = sprintf('%.4e', num);disp(str);```运行以上代码,输出结果为1.2345e+06。
可以看到,原始的数值被转换为科学计数法的形式,并且保留了指定的小数位数。
科学计数法在科学计算和数据分析中有着广泛的应用。
例如,在天文学中,使用科学计数法可以表示宇宙中的星距,这些数值通常非常庞大,使用科学计数法可以简化表示。
在生物学中,使用科学计数法可以表示分子量,这些数值通常非常小,同样可以通过科学计数法简化表示。
除了数值的表示,Matlab还提供了一些函数来进行科学计数法的运算和转换。
例如,可以使用log10函数来计算一个数值的对数,并将结果表示为科学计数法的形式。
以下是一个示例代码:```matlabnum = 1.2345e+6;log_num = log10(num);str = sprintf('%.4e', log_num);disp(str);```运行以上代码,输出结果为6.0913e+00。
可以看到,原始数值的对数被计算出来,并以科学计数法的形式进行了表示。
在Matlab中,科学计数法不仅用于数值的表示,还可以用于格式化输出。
MATLAB星历计算绘制源代码

MA TLAB星历计算绘制源代码题目:A broadcast ephemeris file for Jan 16, 2002 is given below. All of the GPS satellites are given. For at least the set of PRN’s 4, 7, 11, 26, 27, 28 compute(1) A 3-D plot of the trajectories of the motions of the satellites in(a) Inertial space. Produce plots for 4 orbits of the satellites. Comment on the how closely the satellite tracks overlap.(b) Earth fixed frame. Plots for 2 orbits of the satellites.(2) A ground track plot (i.e., the track of the satellite position radially projected to the surface of the sphere). OPTIONAL: Extra credit for also showing projection on an ellipsoid (Projection of ground normal to the satellite).(3) A sky map for geocentric location 244.5 deg Long, 35.8 deg latitude. A sky map shows azimuth and elevation as a radial plot with zenith distance scaled to a convenient distance unit.截图如下啦:部分代码首先Matlab里画个地球function Plot3GPS(A, titlename) cla reset;load topo;[x y z] = sphere(50);s = surface(6e6*x,6e6*y,6e6*z,'FaceColor','texturemap','CData',topo); colormap(topomap1);% Brighten the colormap for better annotation visibility:brighten(.6)% Create and arrange the camera and lighting for better visibility:%campos([1.3239 -14.4250 9.4954]);camlight;lighting gouraud;axis off vis3d;这就搞定一个地球了,简单吧。
matlab浪漫星空代码

matlab浪漫星空代码(实用版)目录1.MATLAB 简介2.浪漫星空效果的实现原理3.浪漫星空代码的编写步骤4.浪漫星空效果的展示5.总结正文一、MATLAB 简介MATLAB(Matrix Laboratory)是一款广泛应用于科学计算、数据分析、可视化等领域的编程软件。
它基于矩阵计算,提供了丰富的函数库和大量的工具箱,使得用户可以方便地完成各种复杂的计算和分析任务。
同时,MATLAB 也具有较强的可视化功能,能够将数据以直观的图形形式展现出来。
二、浪漫星空效果的实现原理浪漫星空效果主要是通过模拟星空的亮度、颜色和分布等特征,以及运动效果来实现的。
在 MATLAB 中,我们可以使用自定义的函数和相应的工具箱来生成星空图像。
其中,用到的主要原理和技术包括:1.随机数生成:用于模拟星空中恒星的随机分布。
2.插值:用于计算某个位置上的亮度值。
3.颜色映射:用于将亮度值映射到相应的颜色。
4.动画制作:用于实现星空的运动效果。
三、浪漫星空代码的编写步骤1.导入所需的工具箱和函数库,如 Image Processing Toolbox、Statistics and Machine Learning Toolbox 等。
2.创建一个函数,用于生成随机数。
3.创建一个函数,用于计算插值后的亮度值。
4.创建一个函数,用于将亮度值映射到颜色。
5.创建一个函数,用于绘制星空图像。
6.创建一个函数,用于制作动画。
7.运行动画函数,生成浪漫星空效果。
四、浪漫星空效果的展示在完成代码编写后,我们可以通过运行动画函数来展示浪漫星空效果。
在 MATLAB 的 Current Folder 窗口中输入动画函数的名称并回车,即可观看到浪漫星空效果的动画。
五、总结通过本篇文章,我们了解了 MATLAB 的基本概念和浪漫星空效果的实现原理,并学会了如何编写浪漫星空代码。
在实际应用中,我们可以根据自己的需求和喜好,对代码进行调整和优化,从而创作出更加美丽的星空效果。
Matalb提取图片中点的信息并画出相关曲线的程序
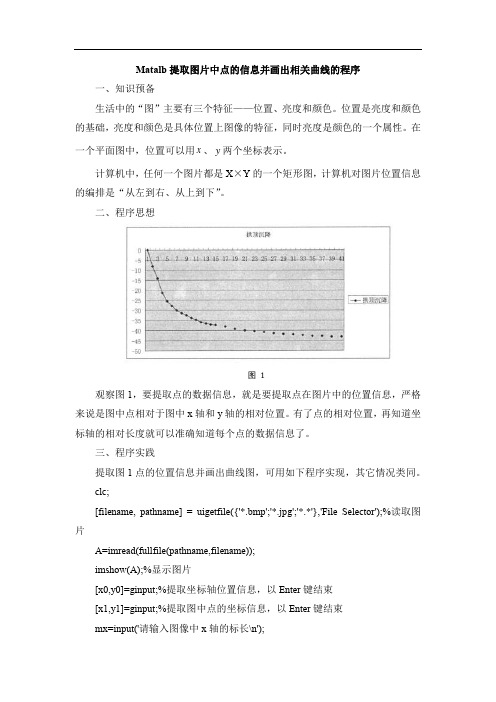
Matalb提取图片中点的信息并画出相关曲线的程序一、知识预备生活中的“图”主要有三个特征——位置、亮度和颜色。
位置是亮度和颜色的基础,亮度和颜色是具体位置上图像的特征,同时亮度是颜色的一个属性。
在一个平面图中,位置可以用x、y两个坐标表示。
计算机中,任何一个图片都是X×Y的一个矩形图,计算机对图片位置信息的编排是“从左到右、从上到下”。
二、程序思想图1观察图1,要提取点的数据信息,就是要提取点在图片中的位置信息,严格来说是图中点相对于图中x轴和y轴的相对位置。
有了点的相对位置,再知道坐标轴的相对长度就可以准确知道每个点的数据信息了。
三、程序实践提取图1点的位置信息并画出曲线图,可用如下程序实现,其它情况类同。
clc;[filename, pathname] = uigetfile({'*.bmp';'*.jpg';'*.*'},'File Selector');%读取图片A=imread(fullfile(pathname,filename));imshow(A);%显示图片[x0,y0]=ginput;%提取坐标轴位置信息,以Enter键结束[x1,y1]=ginput;%提取图中点的坐标信息,以Enter键结束mx=input('请输入图像中x轴的标长\n');my=input('请输入图像中y轴的标长\n');nx=input('请输入图像中x轴的起点坐标\n');ny=input('请输入图像中x轴的起点坐标\n');%x轴向左,y轴向下时,坐标转换关系如下,其它以此类推x11=(x1-min(x0))*mx/(max(x0)-min(x0))+nx;%转换x轴换坐标y11=(y1-min(y0))*my/(max(y0)-min(y0))+ny;%转换y轴坐标plot(x11,y11,'k.-','linewidth',2,'markersize',20);%画图set(gca,'xaxislocation','top');%将x轴上移if my>ny;axis([nx,mx,ny,my]);%设置坐标轴显示范围elseaxis([nx,mx,my,ny]);enda1=1:2:mx;%设置x轴标度set(gca,'xtick',a1);legend('\fontsize{12}拱顶下沉');%显示线条标签title('\fontsize{12}拱顶下沉')%xlabel('x轴');%ylabel('y轴');grid on;。
matlab中fig坐标轴科学计数法

在MATLAB中,经常会遇到需要对图形的坐标轴进行科学计数法的显示。
科学计数法是一种用于表示非常大或非常小的数字的简洁方式,它使用10的幂来表示数字。
在MATLAB中,通过对图形的坐标轴进行适当的设置,可以很容易地实现科学计数法的显示。
让我们来了解一下MATLAB中图形的坐标轴的基本设置。
图形的坐标轴包括x轴和y轴,它们用来表示图形中的水平和垂直方向的数值。
在MATLAB中,我们可以通过一些属性来设置坐标轴的显示格式,包括刻度的范围、刻度的间隔、刻度标签的格式等。
接下来,让我们看一下在MATLAB中如何对图形的坐标轴进行科学计数法的显示。
我们需要使用MATLAB中的plot函数或者其他绘图函数来绘制图形。
我们可以使用MATLAB中的gca函数来获取当前图形的坐标轴对象,进而通过设置坐标轴对象的属性来实现科学计数法的显示。
在MATLAB中,默认情况下,当坐标轴的数值非常大或非常小时,MATLAB会自动使用科学计数法来显示坐标轴的刻度标签。
但是,有时候我们可能希望手动地控制坐标轴的科学计数法的显示格式,这时就需要使用MATLAB中的一些函数来实现。
在MATLAB中,可以使用set函数来设置坐标轴对象的属性。
可以通过设置坐标轴对象的XAxis或者YAxis的属性来控制坐标轴的科学计数法的显示格式。
其中,可以使用Exponent属性来设置科学计数法的指数部分的显示格式,使用TickLabelFormat属性来设置刻度标签的显示格式等。
除了使用set函数来设置坐标轴对象的属性之外,还可以使用MATLAB中的一些其他函数来实现科学计数法的显示。
可以使用xticks函数和yticks函数来设置坐标轴的刻度位置,使用xticklabels函数和yticklabels函数来设置坐标轴的刻度标签等。
在实际的使用中,需要根据具体的情况来选择合适的方法来实现科学计数法的显示。
有时候,可能需要结合使用多种方法来达到最佳的显示效果。
matplotlib星形符号

文章标题:探索matplotlib中的星形符号:美丽的视觉效果背后的技术原理和应用1. 引言在数据可视化领域,matplotlib作为Python中最流行的绘图库之一,提供了丰富的图形绘制功能。
其中,星形符号作为一种特殊的符号类型,常常被应用于不同类型的图表中,既具有美丽的视觉效果,又能凸显数据的特殊意义。
本文将深入探讨matplotlib中星形符号的技术原理和应用,帮助读者更深入地理解这一特殊的数据可视化方式。
2. 星形符号的概念和特点在数据可视化中,星形符号是一种常见的绘制形状,通常用于标记散点图或者柱状图中的数据点。
与普通的圆形或方形符号不同,星形符号多以多边形的形式呈现,具有尖锐的边角和对称的外观。
其特点在于视觉上更加突出,更容易引起观者的注意,同时也能够传达出特殊的含义和数据间的差异关系。
3. 技术原理:如何在matplotlib中绘制星形符号在matplotlib中,绘制星形符号可以通过定制绘图样式来实现。
我们需要指定符号的外观(如大小、颜色、边框等),然后利用特定的绘图函数和参数来渲染数据点。
通常情况下,可以使用scatter函数来绘制散点图并指定marker为“*”,这样就能够得到星形符号的效果。
还可以通过调整marker的大小和边角数来实现不同样式的星形符号,满足不同的需求和视觉效果。
4. 应用案例:星形符号在数据可视化中的实际应用从实际应用的角度来看,星形符号在数据可视化中起到了重要的作用。
在地图绘制中,我们常常使用星形符号来标记特定的地理位置或者重要的地点,以便于用户快速识别和定位;在科学研究中,星形符号也常被用于标记实验数据中的异常值或特殊事件,以突出这些数据点的重要性和特殊性。
在商业领域,星形符号也被广泛应用于图表中,用于展示产品的特点、优势或者不足之处,提供直观的数据对比和分析结果。
可见,星形符号在各个领域都有着广泛的应用场景。
5. 个人观点和总结从个人的角度来看,我认为星形符号作为一种特殊的数据可视化方式,具有独特的魅力和功能。
matlab中用bwlabel标记

在MATLAB中,我们经常会遇到需要对二值图像进行标记的情况。
这时,可以使用MATLAB中的bwlabel函数来实现对二值图像进行标记。
bwlabel函数能够对连通区域进行分析,并给出每个连通区域的标记,方便我们进行后续的处理和分析。
下面我们将详细介绍在MATLAB中使用bwlabel函数对二值图像进行标记的方法。
一、导入二值图像在使用bwlabel函数进行标记之前,首先需要导入需要标记的二值图像。
我们可以使用imread函数将图像导入到MATLAB中,并使用imshow函数查看图像的内容和质量。
```matlabbinary_img = imread('binary_image.png');imshow(binary_img)```二、使用bwlabel进行标记接下来,我们可以使用bwlabel函数对二值图像进行标记。
bwlabel函数的语法格式为:```matlab[L, num] = bwlabel(BW, conn);```其中,BW为输入的二值图像,conn为图像的连通性,L为输出的标记后的图像,num为连通区域的数量。
bwlabel函数会将输入的二值图像BW进行标记,并将标记后的图像保存在L中。
它还会返回图像中连通区域的数量,并保存在num中。
三、显示标记后的图像标记结束后,我们可以使用imshow函数查看标记后的图像。
这可以帮助我们直观地了解图像的标记情况。
```matlabimshow(L)```四、进一步分析在标记结束后,我们可以对标记后的图像进行进一步分析和处理。
可以使用regionprops函数获取每个连通区域的属性,或者使用imfill函数对空洞进行填充等。
```matlabstats = regionprops(L, 'Area', 'Centroid');```通过以上步骤,我们可以在MATLAB中使用bwlabel函数对二值图像进行标记,并对标记后的图像进行进一步处理和分析。
matlab写的计算行星位置程序

function a=Getposition(time,n)%n=1表示地球n=2 表示火星n=3表示ceres%Ceres轨道参数ac= 2.7654089;ec=0.21432115;Mc=80.39176*0.01745329 ;ic=10.58663*0.01745329;CapitalOmegac= 0.0790083*0.01745329;Omegac=10.58663*0.01745329;Tc=1679.667171431635;%地球参数ae = 1;ee = 0.01671022;Me = -2.48074*0.01745329;ie = 0;CapitalOmegae = 0;Omegae = 102.94719*0.01745329;Te = 365.2564;%火星参数am = 1.52366231;em = 0.09341233;Mm = -4.55343205*0.01745329;im = 1.85061*0.01745329;CapitalOmegam = 49.57854*0.01745329;Omegam = 286.4623*0.01745329;Tm = 686.98;% a=5.20336301;% e=0.04839266;% M=19.65053*0.01745329;% i=1.30530*0.01745329;% w=100.55615*0.01745329;% q=274.1977*0.01745329;jD=JD(time(1),time(2),time(3));orbitparam=[am,em,Mm,im,CapitalOmegam,Omegam,Tm]; orbitparae=[ae,ee,Me,ie,CapitalOmegae,Omegae,Te]; orbitparac=[ac,ec,Mc,ic,CapitalOmegac,Omegac,Tc];if n==1a=ElipCartHelioCent(jD,orbitparae);elseif n==2a=ElipCartHelioCent(jD,orbitparam);elseif n==3a=ElipCartHelioCent(jD,orbitparac);elsea=[];endendfunction time=ElipCartHelioCent(jd1,orbitpara)% 轨道参数等a半长轴,e椭率,M平近点角,i倾角,\[CapitalOmega]升交点黄经,% \[Omega]\近日点幅角,后面加1表示角度制,不加1表示弧度制,填入参数历元year0、month0、day0% 以及你所需要的日期year1、month1、\day1、hour1% a=5.20336301;% e=0.04839266;% M1=19.65053;% i1=1.30530;% CapitalOmega1=100.55615;% Omega1=274.1977;a=orbitpara(1);e=orbitpara(2);M=orbitpara(3);i=orbitpara(4);CapitalOmega=orbitpara(5);Omega=orbitpara(6);T1=orbitpara(7);year0=2000;month0=1;day0=1;% T1=4.6*365.2564;mass=1898.6;massS = 1988910;if T1 > 0T=T1;elseT= 2*pi*(massS/(massS + mass))^0.5*a^1.5/0.0172021;endjd0 = JD(year0, month0, day0);ETinverse = ET(i, CapitalOmega, Omega);t = jd1 - jd0 + M/2/pi*T;t1 = t - T*floor(t/T + 0.5);%*计算位置角\[CurlyPhi]的值,得到行星运动平面坐标系下坐标,%经欧拉矩阵变换后,变换到日心黄道坐标系的坐标,并求出日心黄经黄纬*)CurlyPhi= fzero(@(x) F(x),[-pi,pi]);r = a*(1 - e^2)/(1 + e*cos(CurlyPhi));Coordinate1 = [r*cos(CurlyPhi), r*sin(CurlyPhi), 0];time= (ETinverse*Coordinate1')';function f=F(fai)f=atan(sqrt((1 - e)/(1 + e))*tan(fai/2))/pi - e*(1 - e^2)^0.5*sin(fai)/(1 + e*cos(fai))/2/pi - t1/T; endfunction et=ET(ii, CapitalOmega2, Omega2)E11 = cos(CapitalOmega2)*cos(Omega2)- cos(ii)*sin(CapitalOmega2)*sin(Omega2);E12 = -cos(CapitalOmega2)*sin(Omega2)-cos(ii)*sin(CapitalOmega2)*cos(Omega2);E13 = sin(ii)*cos(CapitalOmega2);E21 = sin(CapitalOmega2)*cos(Omega2) + cos(ii)*cos(CapitalOmega2)*sin(Omega2);E22 = -sin(CapitalOmega2)*sin(Omega2) +cos(ii)*cos(CapitalOmega2)*cos(Omega2);E23 = -sin(ii)*cos(CapitalOmega2);E31= sin(ii)*sin(Omega2);E32 = sin(ii)*cos(Omega2);E33 = cos(ii);et=[E11, E12, E13; E21, E22, E23; E31, E32, E33];endend%Ceres轨道参数ac= 2.7654089;ec=0.21432115;Mc=80.39176*0.01745329 ;ic=10.58663*0.01745329;CapitalOmegac= 0.0790083*0.01745329;Omegac=10.58663*0.01745329;Tc=1679.667171431635;%地球参数ae = 1;ee = 0.01671022;Me = -2.48074*0.01745329;ie = 0;CapitalOmegae = 0;Omegae = 102.94719*0.01745329;Te = 365.2564;yeare = 2000;monthe = 1;daye = 1;%火星参数am = 1.52366231;em = 0.09341233;Mm = -4.55343205*0.01745329;im = 1.85061*0.01745329;CapitalOmegam = 49.57854*0.01745329;Omegam = 286.4623*0.01745329;yearm = 2000;monthm = 1;daym = 1;Tm = 686.98;massm = 0.64185;a=5.20336301;e=0.04839266;M=19.65053*0.01745329;i=1.30530*0.01745329;w=100.55615*0.01745329;q=274.1977*0.01745329;orbitparam=[am,em,Mm,im,CapitalOmegam,Omegam,Tm]; orbitparae=[ae,ee,Me,ie,CapitalOmegae,Omegae,Te]; orbitparac=[ac,ec,Mc,ic,CapitalOmegac,Omegac,Tc];for jD=2450000:2450009ElipCartHelioCent(jD,orbitparac)endfunction jd=JD(yeaR, montH, daY)%日期转化为儒略日a1 = floor((14 - montH)/12);y = yeaR + 4800 - a1;m = montH + 12*a1 - 3;jd=daY + floor((153*m + 2)/5) + 365*y + floor(y/4) - 32083; end。
matlab图形数据点标记说明
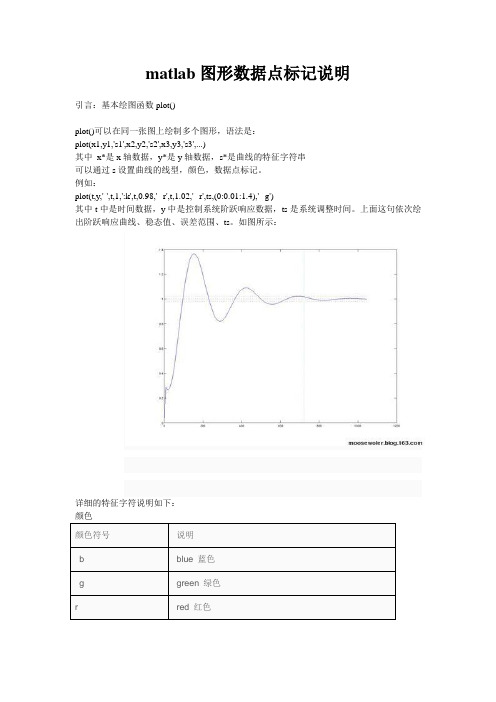
颜色颜色符号说明blue蓝色green绿色red红色cayn青色magenta品红yellow黄色black黑色white白色线型线型符号说明双划线数据点标记数据点符号说明square方块diamond菱形pentagram五角星hexagram六角星
matlab 图形数据点标记说明
引言:基本绘图函数 plot()
详细的特征字符说明如下: 颜色
颜色符号
说明
b
blue 蓝色
g
green 绿色
r
red 红色
c m y k w 线型 线型符号 : -. -数据点标记 数据点符号 . o x + * s d v ^ < > p
cayn 青色 magenta 品红 yellow 黄色 black 黑色 white 白色
说明 实线 虚线 点划线 双划线
说明 实心点 空心圆圈 叉子 十字符号 米字符号 square 方块 diamond 菱形 下三角 上三角 左三角 右三角 pentagram 五角星
基于MATLAB 的GPS 选星分析及实验研究

2. 1 星座仿真 通常 , GPS 卫星星座由 24 颗导航卫星构成 。卫星位于 6
个地心轨道平面内 ,每个轨道 4 颗卫星 。GPS 卫星的轨道周 期是半个恒星日 (即 11 小时 58 分钟) ,各轨道接近于圆形 , 而且沿赤道以 60°间隔均匀分布 ,相对于赤道面的倾斜角为 55°。GPS 卫星轨道的物理模型如图 1 所示 。
利用 MATLAB 的仿真功能 ,可以实现对 GPS 全星座运行 的实时解算并建立三维动态仿真系统 。仿真流程为图 2 所 示。
— 51 —
ห้องสมุดไป่ตู้
图 1 GPS 卫星轨道
图 2 GPS 星座仿真的流程图
卫星轨道的数学建模所需参数来自于 GPS 接收机给出 的星历数据 ;地球的数学建模所需参数来自于 WGS - 84 坐 标系指定参数 。在 MATLAB 中 ,利用三维绘图建立了 GPS 系 统的仿真模型 。
ABSTRACT :Based on the dynamic simulation function of MATLAB , the real - time calculating and analysis of the GPS satellite constellation play a crucial role in reducing the space where the best satellite constellation is selected and in de2 creasing the time of constellation - selecting , which makes the quality of real - time selecting satellites better. Combined with the method of pseudo - range positioning ,the experiments of the vehicle navigation prove its availability and precision can meet the requirements of the projects. This method of simulation also contributes to the prediction of the GPS constella2 tion. KEYWORDS :GPS ;Simulation ;Constellation - selecting ;Vehicle navigation
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用Matlab实现简易图片中的星星计数及位置标记
By C.Z.H --814484233@
在天文观测中,统计出星星的数量以及标记出位置对于研究不同时刻同一角度观测有着重要的意义,可以用来分析不同时刻行星的位移变化而从推测行星的运动趋势。
而Matlab 有着强大的矩阵处理功能,而图片则由数据矩阵记录图片像素信息。
利用Maltab结合图像处理和识别技术可自动化实现星星计数和标记等简单功能。
Matlab中支持真彩色图像、索引图像、灰度图像、二值图像4种不同的图像类型,不同类型的图像在Matlab中存储形式不同,部分图像间是可以进行转化的。
一、在灰度图中利用极大值方法计数和标记
目前用数码相机获取图像格式为BMP或JPG的真彩图,真彩图像是既含亮度信息又含色彩信息的图像,一幅 m*n大小的真彩图像要由 m*n*3元素类型为字节的矩阵表示,其中数字3指的是像素中的RGB三层分量。
而灰度图像是只含亮度信息不含色彩信息的图像,一副灰度图像可以由m*n矩阵来表示。
将真彩色图像转换为灰度图像,一方面可以去掉一些无用的信息;另一方面大幅度减少图像的数据量,减轻后期处理的工作量,因此灰度处化处理是图像处理中很重要的一步。
把真彩图转化成灰度图后,进行滤波降噪。
我们近似的认为每一个星星的亮度都可以看成高斯波包或者类似高斯形状的波包。
此时,就可以利用寻找极大值法,标记和统计出星星的位置和数量。
其原理为:一维的情况很容易找出一数列的极大值,对于二维情况,我们只要使二维图片的x方向和y方向同时满足极大值的情况就是我们要找的二维极大值,也就是我们要找的星星,图1通过程序计算,统计出72颗星。
范例Matlab 程序见附录1。
图1 小尺度星星图
图2 采用查找极大值的方法对小尺度星星进行标记及统计通过寻找极大值的方法数出并标识行星的位置存在着缺陷,因为这种方法要求星星的亮度中间必须是极大值,如果不是极大值,亮度中间是平的或者是凹陷的情况就未被识别出来。
有的峰值四周高中间低,这就出现了多个极大值点,对统计产生干扰。
二、在二值图中利用形态学进行计数和标记
对于大目标大形状的星体,可能不满足高斯包分布的情况下,还可以通过Matlab形态学工具箱功能实现星星的识别和计数。
形态学是建立在二值图像的基础上,而二值化处理是利用图像中要提取的目标物与其背景在灰度特性上的差异,把图像视为具有不同灰度级的两类区域(目标1白色和背景0黑色)的组合,其关键是选择合理的分割阈值。
当一个像素的灰度值超过这个阈值,就可以说这个像素变成1,反之则变成0。
为了增强星星和背景的区分度,便于后续的特征处理,要对图像二值化操作,为此要进行阈值分割,阈值的选取决定了最终图像效果的好坏,选取一个合适的阈值,将会得到较好的图像效果。
形态学处理是针对二值图像依据数学形态学的集合论方法发展起来的图像处理方法。
包括腐蚀、膨胀、区域填充等处理操作。
下面就看一个大尺度星星的统计与标识范例,通过对图3的计算,算出有85个星状物。
范例程序见附录2。
图3 大尺度星星图
图4 形态学操作处理
图5 通过形态学操作对大尺度星星进行标记及统计
三、总结
利用Matlab可以很方便的实现了对星星的计数及标识。
虽然算法简单粗略,但给出了简单的判断和估算,而且可做多次复杂结合处理,以便得到预期结果。
附录1 寻找极大值方法进行标记和统计
%% 通过找出极大值数出星星的个数,以及标志出来
clear;
clc;
[f,map]=imread('E:\search star\stars1.jpg');
f=rgb2gray(f);
fy=double(f);
fy(fy<100)=0;%滤波,把低于某一值的变为0
f1=(fy(:,:,1));
% f1=flipud(fy(:,:,1));%flipud使矩阵上下翻转
f2=f1';
[m,n]=size(f1);
f01=zeros(m,n);
f02=zeros(m,n);
f03=zeros(m,n);
a1=diff(f1);
b1=sign(a1);
c1=diff(b1);
[x1,y1]=find(c1==-2);
x1=x1+1;
for i=1:size(x1);
f01(x1(i),y1(i))=f1(x1(i),y1(i));
end
a2=diff(f2);
b2=sign(a2);
c2=diff(b2);
[x2,y2]=find(c2==-2);
x2=x2+1;
for i=1:size(x2);
f02(y2(i),x2(i))=f1(y2(i),x2(i));
end
[x,y]=find(f01==f02 & f01~=0);%找出极大值的位置,也即是星星的位置,星星的个数=size(x)=size(y)
for i=1:size(x);
f03(x(i),y(i))=f1(x(i),y(i));
end
figure(1)
% contour(f1)
imshow(f)
hold on
for i=1:size(x);
plot(y(i),x(i),'marker','*','markeredgecolor','r','markersize',10);
end
附录2 形态学操作进行标记及统计
clear all
close all
clc
% 载入图片
RGB = imread('E:\search star\stars2.jpg');
I = rgb2gray(RGB);%真彩图转成灰度图
figure(1);imshow(I)
% 灰度图像二值化,全局阈值分割最大化类间方差
level = graythresh(I);
BW = im2bw(I,level);
figure(2);imshow(BW)
% 孔洞填充和形态学开运算
BW1 = imfill(BW,'holes');
figure(3);imshow(BW1)
se1 = strel('disk',3);
BW2 = imdilate(BW1,se1);%膨胀操作
figure(4);imshow(BW2)
se2 = strel('disk',5);
BW3 = imopen(BW2,se2);%开运算
figure(5);imshow(BW3)
[L,N] = bwlabel(BW3,4); % N即为目标个数,4连通区域,L为位置矩阵% 标记目标物
figure(6);imshow(RGB)
hold on
for k = 1:N
[r,c] = find(L == k);
rbar = mean(r);%取r的平均值
cbar = mean(c);%取c的平均值
plot(cbar,rbar,'marker','*','markeredgecolor','b','markersize',10); end。
