华师大版八下20.5《等腰梯形的判定2》ppt课件之二
合集下载
等腰梯形课件

图形定义
总结词
通过图形展示等腰梯形的特点。
详细描述
在PPT中插入一个等腰梯形的图形,并标注出它的两腰、底边和两个底角,以便 学生更好地理解等腰梯形的定义。
性质和定理
总结词
介绍等腰梯形的一些重要性质和定理 。
详细描述
在PPT中列出等腰梯形的一些重要性 质和定理,如“等腰梯形的两腰相等 ”、“等腰梯形的两底角相等”等, 并给出相应的证明过程。
步骤四
连接底边的两个端点,完成等 腰梯形的作图。
等腰梯形和其他图形的联系
与平行四边形的联系
等腰梯形可以看作是一个平行四边形 去掉一个直角三角形后形成的。
与三角形的联系
等腰梯形可以看作是由两个三角形组 成的,其中一个是直角三角形,另一 个是等腰三角形。
THANKS 感谢观看
在建筑设计中的应用
建筑设计中的等腰梯形元素
在建筑设计中,等腰梯形经常被用作窗户、门洞或其他装饰 元素的形状,以增加建筑的美观性和设计感。
等腰梯形在结构设计中的应用
在某些建筑结构中,等腰梯形的设计可以使结构更加稳定和 安全,例如桥梁的斜拉索或高层建筑的支撑结构。
在日常生活中的应用
日常生活中的等腰梯形物品
等腰梯形的面积和周长之间没有直接的关系,它们分别由不同的公式计
算得出。
02
面积与周长的独立性
在等腰梯形中,改变上底、下底和高的长度会影响面积,同时的,改变一个不会影响另一个。
03
实际应用
在解决几何问题时,需要综合考虑面积和周长的关系,以得出正确的结
论。
04 等腰梯形的实际应用
在几何图形中的应用
等腰梯形在几何证明中的应用
等腰梯形是几何图形中的一种,它在解决几何问题,特别是关于角度、边长和面 积的问题时非常有用。例如,利用等腰梯形的性质证明某些角度相等或边长相等 。
等腰梯形的判定PPT精品课件

求证:梯形 ABCD 是等腰梯形 . 证明:过 A 作AE∥CD ,交 BC 于 E . 则∠1 = ∠C .
∵∠B = ∠C. ∴∠B = ∠1 ∴AB = AE.
∵AD∥EC , AE ∥DC. ∴AE = DC.
A
D
1
B
C
E
等腰梯形判定理:
在同一底上的两个
∴AB = DC.
角相等的梯形是等
∴梯形 ABCD 是等腰梯形. 腰梯形.
性质:(1)在同一个圆中,同弧所对的圆周角等于它所对的圆心角的一半.
A O
C
∠BAC=
1 ∠BOC
2
B
圆周角的性质(2)
在同圆或等圆中,同弧或等弧所对的所有的圆周角相等.相等的圆周角所对的弧 相等.
D
E
∵∠ADB与∠AEB 、∠ACB 是同弧所对的圆周角
C
O
∴∠ADB=∠AEB =∠ACB
A B
圆周角的性质: 性质 3:半圆或直径所对的圆周角都相等,都等于900(直角).
︵ ︵ D ∵ ∠COD =∠AOB
O
∴ AB = CD
C ∴AB=CD
A
B
3.垂径定理:
垂直于弦的直径平分这条弦,并且 平分弦所对的两条弧.
C
∵CD是圆O的直
径,CD⊥AB
. ︵ ∴AP=BP, ︵
P A
︵ ︵ B AD = BD
AC = BC
D
4.圆周角:
定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.
A
D
AB=BE=AE
EC=AD=5cm
B
E
C AB=BC=BC-CE=9-5=4cm
已知:等腰梯形的锐角等于60°,它的上底为
等腰梯形的判定PPT课件2
D
求证:AB=DC.
B
C
如图,已知:在梯形ABCD中, A
AD∥BC,∠B= ∠C .
求证:AB=DC.
B
E
D C
方法二:分别延长BA、CD,它们
相交于点E. 在⊿EBC中, ∠B=∠C ∴EB=EC A
E D
∵AD//BC
∴∠EAD=∠B=∠C=∠EDA B
C
∴EA=ED
∵AB=EB—EA DC=EC—ED
(1)有两个角相等的梯形一定是等腰梯形.
(2)两条对角线相等的梯形一定是等腰梯形.
(3)如果一个梯形是轴对称图形,则它一定是 等腰梯形. (4) 一组对边平行,另一组对边相等的四边形一定 是等腰梯形. (5)对角互补的梯形一定是等腰梯形.
2.有两个内角是70度的梯形一定是等腰
梯形. (
)
3、下列说法中,错误的是( C )
记住:这些是等腰梯形 的判定方法哦!
②若∠B= ∠ C 或∠A= ∠ D
梯形ABCD是等腰梯形 ③ 若AC = BD
梯形ABCD是等腰梯形
A B
如图,在梯形ABCD中, AD∥BC, D
给出条件:∠A与∠C互补
C
梯形ABCD是等腰梯形吗?
结论:一组对角互补的梯形是等腰梯形
达标训练:
1、抢答题 判断正误:
A
F
E
B
GD C
梯形中常需要作的辅助线有哪些?
. .
本节课你有哪些收获?
等腰梯形的判定方法
两条腰相等的梯形是等腰梯形 同一底上的两个内角相等的梯形是等腰梯形 对角线相等的梯形是等腰梯形
四边形
一组对边平行 另一组对边不平行
一组对边平行 且不相等
梯形的性质ppt2 华东师大版

图中有哪些相等的线段?
有哪些相等的角?
A
O
D
演示
B
C
1、等腰梯形的性质1:等腰梯形在同一底上的两个内角相等 A D
已知:如图5,在梯形ABCD中, AD∥BC,AB=DC。
求证:∠B=∠C 。
B
E
图5
证明:过点D作DE∥AB,交BC于点E, C 得到△DEC。
∵ AD∥BC,DE∥AB ∴四边形ABED是平行四边形 ∴ AB=DE ∵ AB=DC
梯形的性质
八年级 数学
第十九章 四边形
四边形再认识
上面的几幅图中有你熟悉的图形吗?
梯形定义
形叫做梯形.
第十九章 四边形
一组对边平行而另一组对边不平行的四边 如图,平行的两边叫做梯形的底,其中较短的底叫
做上底,较长的底叫做下底.不平行的两边叫做腰。
夹在两底之间的垂线段叫做梯形的高。
上底
腰 高 下底 腰
1、聪明的人有长的耳朵和短的舌头。 ——弗莱格 2、重复是学习之母。 ——狄慈根 3、当你还不能对自己说今天学到了什么东西时,你就不要去睡觉。 ——利希顿堡 4、人天天都学到一点东西,而往往所学到的是发现昨日学到的是错的。 ——B.V 5、学到很多东西的诀窍,就是一下子不要学很多。 ——洛 克 6、学问是异常珍贵的东西,从任何源泉吸收都不可耻。 ——阿卜· 日· 法拉兹 7、学习是劳动,是充满思想的劳动。 ——乌申斯基 8、聪明出于勤奋,天才在于积累 --华罗庚 9、好学而不勤问非真好学者。 10、书山有路勤为径,学海无涯苦作舟。 11、人的大脑和肢体一样,多用则灵,不用则废 -茅以升 12、你想成为幸福的人吗?但愿你首先学会吃得起苦 --屠格涅夫 13、成功=艰苦劳动+正确方法+少说空话 --爱因斯坦 14、不经历风雨,怎能见彩虹 -《真心英雄》 15、只有登上山顶,才能看到那边的风光。 16只会幻想而不行动的人,永远也体会不到收获果实时的喜悦。 17、勤奋是你生命的密码,能译出你一部壮丽的史诗。 1 8.成功,往往住在失败的隔壁! 1 9 生命不是要超越别人,而是要超越自己. 2 0.命运是那些懦弱和认命的人发明的! 21.人生最大的喜悦是每个人都说你做不到,你却完成它了! 22.世界上大部分的事情,都是觉得不太舒服的人做出来的. 23.昨天是失效的支票,明天是未兑现的支票,今天才是现金. 24.一直割舍不下一件事,永远成不了! 25.扫地,要连心地一起扫! 26.不为模糊不清的未来担忧,只为清清楚楚的现在努力. 27.当你停止尝试时,就是失败的时候. 28.心灵激情不在,就可能被打败. 29.凡事不要说"我不会"或"不可能",因为你根本还没有去做! 30.成功不是靠梦想和希望,而是靠努力和实践. 31.只有在天空最暗的时候,才可以看到天上的星星. 32.上帝说:你要什么便取什么,但是要付出相当的代价. 33.现在站在什么地方不重要,重要的是你往什么方向移动。 34.宁可辛苦一阵子,不要苦一辈子. 35.为成功找方法,不为失败找借口. 36.不断反思自己的弱点,是让自己获得更好成功的优良习惯。 37.垃圾桶哲学:别人不要做的事,我拣来做! 38.不一定要做最大的,但要做最好的. 39.死的方式由上帝决定,活的方式由自己决定! 40.成功是动词,不是名词! 20、不要只会吃奶,要学会吃干粮,尤其是粗茶淡饭。
(2)等腰梯形的判定课件八年级数学下册

等腰梯形判定方法: 1.两腰相等+梯形 2.在同一底边上的两个内角相等+梯形. 3.对角线相等+梯形
例题1:已知梯形ABCD中,BC//AD,DE//AB,
DE=DC,∠A=110°,求梯形其他三个内角的度数
A
D
B
EC
等腰梯形判定方法: 1.两腰相等+梯形 2.在同一底边上的两个内角相等+梯形. 3.对角线相等+梯形
A
D
B
C
等腰梯形判定方法: 1.两腰相等+梯形 2.在同一底边上的两个内角相等+ 梯形. 3.对角线相等+梯形
例2.已知梯形的两底和两腰,求作梯形. 已知:线段a,b,c,d中,a>b 求作:梯形ABCD,使AB//DC,BA=a,DC=b,DA=c,BC=d
a b
c d
课后练习3: 画一个等腰梯形,使得它的上、下底分别是5cm,13cm,高为3cm, 并求出它的周长。
等腰梯形判定方法: 1.两腰相等的梯形叫做等腰梯形 2.在同一底边上的两个内角相等的梯形是等腰梯形. 3.对角线相等的梯形是等腰梯形
A
D
B
C
首先得 是梯形!
辨析:以下图形中( )是梯形 (A)对角线相等的四边形是等腰梯形; (B)一组对边平行,另一组对边相等的四边形是等腰梯形; (C)有一组对角互补的梯形是等腰梯形; (D)有两组对角分别相等的四边形是等腰梯形.
A
D
B
C
判定方法: 1.两腰相等的梯形叫做等腰梯形
等腰梯形的判定定理: 在同一底边上的两个内角相等的梯形是等腰梯形(方法2)
A
符号语言:
∵四边形ABCD是梯形,______, ______
例题1:已知梯形ABCD中,BC//AD,DE//AB,
DE=DC,∠A=110°,求梯形其他三个内角的度数
A
D
B
EC
等腰梯形判定方法: 1.两腰相等+梯形 2.在同一底边上的两个内角相等+梯形. 3.对角线相等+梯形
A
D
B
C
等腰梯形判定方法: 1.两腰相等+梯形 2.在同一底边上的两个内角相等+ 梯形. 3.对角线相等+梯形
例2.已知梯形的两底和两腰,求作梯形. 已知:线段a,b,c,d中,a>b 求作:梯形ABCD,使AB//DC,BA=a,DC=b,DA=c,BC=d
a b
c d
课后练习3: 画一个等腰梯形,使得它的上、下底分别是5cm,13cm,高为3cm, 并求出它的周长。
等腰梯形判定方法: 1.两腰相等的梯形叫做等腰梯形 2.在同一底边上的两个内角相等的梯形是等腰梯形. 3.对角线相等的梯形是等腰梯形
A
D
B
C
首先得 是梯形!
辨析:以下图形中( )是梯形 (A)对角线相等的四边形是等腰梯形; (B)一组对边平行,另一组对边相等的四边形是等腰梯形; (C)有一组对角互补的梯形是等腰梯形; (D)有两组对角分别相等的四边形是等腰梯形.
A
D
B
C
判定方法: 1.两腰相等的梯形叫做等腰梯形
等腰梯形的判定定理: 在同一底边上的两个内角相等的梯形是等腰梯形(方法2)
A
符号语言:
∵四边形ABCD是梯形,______, ______
八年级数学下册 第行四边形的判定 等腰梯形的判定习题课件 华东师大华东师大级下册数学课件

12/12/2021
第十九页,共三十七页。
【规律总结(zǒngjié)】
等腰三角形和等腰梯形的关系
平行线截等腰三角形,四边形一定是等腰梯形, 等腰梯形两腰交一点,等腰三角形一定会出现.
12/12/2021
第二十一页,共三十七页。
【跟踪训练】
4.下列命题正确的是( )
(A)梯形的对角线相等 (B)等腰梯形的对角线相等且互相平分(píngfēn) (C)同一底上的两个角相等的梯形是等腰梯形 (D)只有两个角相等的梯形是等腰梯形
第二十八页,共三十七页。
2.在梯形中,若有两个角相等(xiāngděng),那么它一定为( )
(A)等腰梯形
(B)直角梯形
(C)一般梯形
(D)直角或等腰梯形
【解析】选D.两个角是底角时,梯形为等腰梯形;两个角是同一腰上的
角时,梯形为直角梯形.
12/12/2021
第二十九页,共三十七页。
3.有一梯形(tīxíng)的一个底角为60°,两底之差为一腰长,则这个梯形为 ______梯形.
∴∠DBC=∠ECB.
又∵BC=BC, ∴△EBC≌△DCB.
∴BE=CD.
12/12/2021
第三十五页,共三十七页。
∴AB-BE=AC-CD,即AE=AD.
∴∠AED=∠ADE.
∴∠ABC=∠AED= 180- A .
∴ED∥BC.
2
又∵BE与CD交于点A.
∴BE与CD不平行(píngxíng).
∴四边形EBCD是等腰梯形.
12/12/2021
第三十六页,共三十七页。
内容(nèiróng)总结
§20.5 等腰梯形的判定。提示:不一定.还可以是直角梯形.。(A)有一组对边平行,另一组对边相等的四 边形是等腰梯形。【证明】∵在□ABCD中,AD∥BC,AB=CD,。等腰△ABC中,点D,E分别是两腰AC,BC上的。
等腰梯形的判定PPT课件

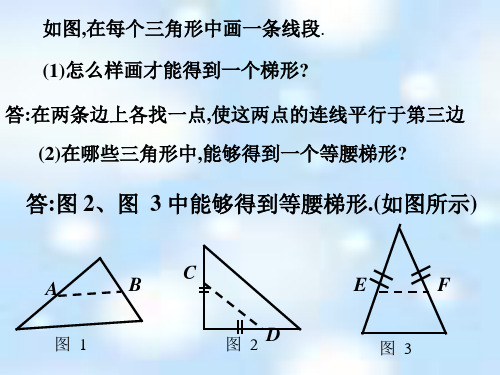
如图,在每个三角形中画一条线段. (1)怎么样画才能得到一个梯形? 答:在两条边上各找一点,使这两点的连线平行于第三边 (2)在哪些三角形中,能够得到一个等腰梯形?
答:图 2、图 3 中能够得到等腰梯形.(如图所示)
A
BC
图1
图2D
E
F
图3
回顾检测
1、定义: 两腰相等的梯形 叫做等腰梯形.
2.等腰梯形的性质
自学检测
1、判断正误:
(1)有两个角相等的梯形一定是等腰梯形. (2)两条对角线相等的梯形一定是等腰梯形.
(3)如果一个梯形是轴对称图形,则它一定是
等腰梯形. (4) 一组对边平行,另一组对边相等的四边形
一定是等腰梯形. (5)对角互补的梯形一定是等腰梯形.
(6)有两个内角是70度的梯形一定是等腰梯形 .
自学指导
• 认真看课本(P94---P95例4上面)
想一想:(1)P94“思考”和“云图” 中的问题,理解加减消元法;
(2)等腰梯形还有哪些判定?你 能证明它们吗?
A B
如图,在梯形ABCD中, AD∥BC, D
给出条件:∠A与∠C互补
C
梯形ABCD是等腰梯形吗?
结论:一组对角互补的梯形是等腰梯形
A
D
边 等腰梯形两底平行,两腰相等
B
C
角 等腰梯形同一底上的两个角相等
对角线 等腰梯形的对角线相等
对称性 轴对称图形
思维展现
思路1:转化方向——等腰三角形
思路2:转化方向——平行四边形
A
D
E
A
D
B
C B
思路3:转化方向——全等三角形
CE
9.3.2 等腰梯形的判定
答:图 2、图 3 中能够得到等腰梯形.(如图所示)
A
BC
图1
图2D
E
F
图3
回顾检测
1、定义: 两腰相等的梯形 叫做等腰梯形.
2.等腰梯形的性质
自学检测
1、判断正误:
(1)有两个角相等的梯形一定是等腰梯形. (2)两条对角线相等的梯形一定是等腰梯形.
(3)如果一个梯形是轴对称图形,则它一定是
等腰梯形. (4) 一组对边平行,另一组对边相等的四边形
一定是等腰梯形. (5)对角互补的梯形一定是等腰梯形.
(6)有两个内角是70度的梯形一定是等腰梯形 .
自学指导
• 认真看课本(P94---P95例4上面)
想一想:(1)P94“思考”和“云图” 中的问题,理解加减消元法;
(2)等腰梯形还有哪些判定?你 能证明它们吗?
A B
如图,在梯形ABCD中, AD∥BC, D
给出条件:∠A与∠C互补
C
梯形ABCD是等腰梯形吗?
结论:一组对角互补的梯形是等腰梯形
A
D
边 等腰梯形两底平行,两腰相等
B
C
角 等腰梯形同一底上的两个角相等
对角线 等腰梯形的对角线相等
对称性 轴对称图形
思维展现
思路1:转化方向——等腰三角形
思路2:转化方向——平行四边形
A
D
E
A
D
B
C B
思路3:转化方向——全等三角形
CE
9.3.2 等腰梯形的判定
等腰梯形的识别--华师大版

A D
答案①∠A= ∠ D =100°. ∠B= ∠ C = 80°. 答案② : 是等腰梯形
C
B
E
能力提升
5、在等腰梯形ABCD中, AD ∥BC , AB = DC ,∠B=60°, AD=15 , BC = 45 , 求它的周
周长为120
小结:
1、两腰相等的梯形是等腰梯形.
归纳总结: 等腰梯形的识别方法一:定义
两腰相等的梯形是等腰梯形
1、已知梯形ABCD中, AD∥BC , ∠ B = ∠ C。 四边形ABCD为等腰梯形吗?
A D
B
E
C
归纳总结: 等腰梯形识别方法二
同一底上两个内角相等的梯形 是等腰梯形
2、已知梯形ABCD中, AD∥BC,
BD =AC;四边形ABCD为等腰梯 形吗?
A D
o
B C
归纳总结:
等腰梯形识别方法三
两个对角线相等的梯形是等腰梯形
巩固提高
3、已知梯形ABCD中, ∠A∶∠B∶∠ C∶∠ D = 3∶2∶2∶3
试判断四边形ABCD 的形状。
A D
B C
4、梯形ABCD中, AD∥BC, DE∥AB , DE=DC,∠A=100°. ①求梯形ABCD的其它内角的度数. ②请问此时ABCD为等腰梯形吗?说 说你的理由.
2、同一底上两个内角相等的梯形
是等腰梯形.
3、两对角线相等的梯形是等腰梯
形.
快 1、判断: ①、有两边相等的梯形是等 速 腰梯形。 (× ) 检 ②、有两角相等的梯形是等 测 腰梯形。 (×)
2、在梯形ABCD中, AD∥BC , 添加条件____________________, 它就变成等腰梯形。
答案①∠A= ∠ D =100°. ∠B= ∠ C = 80°. 答案② : 是等腰梯形
C
B
E
能力提升
5、在等腰梯形ABCD中, AD ∥BC , AB = DC ,∠B=60°, AD=15 , BC = 45 , 求它的周
周长为120
小结:
1、两腰相等的梯形是等腰梯形.
归纳总结: 等腰梯形的识别方法一:定义
两腰相等的梯形是等腰梯形
1、已知梯形ABCD中, AD∥BC , ∠ B = ∠ C。 四边形ABCD为等腰梯形吗?
A D
B
E
C
归纳总结: 等腰梯形识别方法二
同一底上两个内角相等的梯形 是等腰梯形
2、已知梯形ABCD中, AD∥BC,
BD =AC;四边形ABCD为等腰梯 形吗?
A D
o
B C
归纳总结:
等腰梯形识别方法三
两个对角线相等的梯形是等腰梯形
巩固提高
3、已知梯形ABCD中, ∠A∶∠B∶∠ C∶∠ D = 3∶2∶2∶3
试判断四边形ABCD 的形状。
A D
B C
4、梯形ABCD中, AD∥BC, DE∥AB , DE=DC,∠A=100°. ①求梯形ABCD的其它内角的度数. ②请问此时ABCD为等腰梯形吗?说 说你的理由.
2、同一底上两个内角相等的梯形
是等腰梯形.
3、两对角线相等的梯形是等腰梯
形.
快 1、判断: ①、有两边相等的梯形是等 速 腰梯形。 (× ) 检 ②、有两角相等的梯形是等 测 腰梯形。 (×)
2、在梯形ABCD中, AD∥BC , 添加条件____________________, 它就变成等腰梯形。
等腰梯形的判定数学课件PPT

求证:梯形 ABCD 是等腰梯形 .
证明:过 A 作AE∥CD ,交 BC 于 E . 得∠AEB = ∠C .
∵∠B = ∠C.
∴∠B = ∠AEB.
∴AB = AE.
A
D
∵AD∥EC , AE ∥CD.
∴AE = DC. ∴AB = DC.
B
C
E
∴梯形 ABCD 是等腰梯形.
返回
等腰梯形判定定理:在同一底上的两个角相等的梯形是等腰梯形.
作者:大庆二十七中学牛淑文
复习提问
本
等腰梯形
判定定理
课
内
例题分析
容
练习
小结
回忆
梯形的定义和分类:
四边形
一组对边平行 另一组对边不平行
梯形
等腰梯形 直角梯形
返回
复习提问
本
等腰梯形
判定定理
课
内
例题分析
容
练习
小结
在同一底上的两个角相等的梯形是等腰梯形,这个命题成立
吗?能否加以证明?
已知:梯形 ABCD 中,AD∥BC ,∠B = ∠C .
画法:⑴画Rt△ABC ,使∠AEB = 90°,AE = 3cm , BE = 4cm . ⑵延长 BE 到 C 使 BC = 12cm . ⑶过 A 作 AM∥BC ,与 BC 在 AB 的同旁,在 AM 上截
取AD = 4cm. ⑷连结 DC ,则梯形 ABCD 就是所要画的等腰梯形.
A
DM
B
E
C
例 3 已知:如图,在直角梯形 ABCD 中,AD ∥BC ,BC – AD = 3 cm ,∠B = 90°, ∠C = 45 °,梯形面积是 19.5 cm 2 , 求梯形两底的长.
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∠ ,或 ∠ADC=∠BCD,或 或
, 梯形 梯形ABCD为等腰梯形 为等腰梯形. 为等腰梯形 A B D
C
慧眼识真
1、有两边相等的 、 梯形是等腰梯形. 梯形是等腰梯形 2、有两个角相等的梯形 、 是等腰梯形. 是等腰梯形 3、对角互补的梯形是 、 等腰梯形. 等腰梯形
4、一组对边平行,另一组对 、一组对边平行 另一组对 边相等的四边形是等腰梯形. 边相等的四边形是等腰梯形
A D
B C
2、如图:梯形ABCD中AD∥BC,AD<BC,E、F 如图:梯形ABCD中AD∥BC,AD<BC, ABCD 分别为AD BC的中点 AD、 的中点, 分别为AD、BC的中点,且EF⊥BC 求证:梯形ABCD是等腰梯形。 ABCD是等腰梯形 求证:梯形ABCD是等腰梯形。 E E
A
D
5、对角线相等的四边 、 形是等腰梯形. 形是等腰梯形
1.在四边形 在四边形ABCD(AB≠DC)中,给出下列论断: 在四边形 中 给出下列论断: ① AB∥CD ② AD=BC ③∠D =∠C, 以其 ∥ ∠ 中两个作为题设, 中两个作为题设,另外一个作为结论 , 用 如果…那么 的形式,写成一个真命题 那么…”的形式 写成一个真命题. 的形式, “如果 那么
A
D
B
M
F
N
CB
M
F
N
C
如图,在梯形 如图,在梯形ABCD中, AD∥BC, 中 C互补 与 互补
B C
梯形ABCD是等腰梯形吗? 是等腰梯形吗? 梯形 是等腰梯形吗
结论:一组对角互补的梯形是等腰梯形
如果梯形的对角线交点与 同一底的两个端点的距离相 那么它是等腰梯形吗? 等,那么它是等腰梯形吗? 为什么? 为什么?
2、等腰梯形的判定方法:
1. 两腰相等的梯形是等腰梯形; 2. 同一底上的两个底角相等的梯形是等腰梯形; 3 . 两条对角线相等的梯形是等腰梯形.
请你写出等腰梯形具有而一般梯形 不具有的三个特征: 不具有的三个特征: 两腰相等 ,
同一底上的角相等 , 对角线相等
.
梯形ABCD中AB∥CD,若添加条件 中 ∥ 梯形 若添加条件 AD=BC AC=BD
D
1 2
C O
A
B
对角线交点与同 一底的两个端点 的距离相等的梯 形是等腰梯形. 形是等腰梯形
已知等腰梯形上、下底长分别为5cm、11cm, 4cm, 已知等腰梯形上、下底长分别为5cm、11cm,高为 4cm, 5cm 计算这个等腰梯形的周长和面积. 计算这个等腰梯形的周长和面积.
D A 5
? B ? E
20.5 等腰梯形的判定(2) 等腰梯形的判定( )
梯形中辅助线有哪些作法?
1、等腰梯形的性质:
1.等腰梯形在同一底上的两个角相等. 等腰梯形在同一底上的两个角相等. 等腰梯形在同一底上的两个角相等 2.等腰梯形的对角线相等 3. 等腰梯形是轴对称图形,过两底中点的直线是 等腰梯形是轴对称图形, 它的对称轴. 它的对称轴.
4 F 11
AD + BC 面积S 面积S = 2 (5 + 11) × 4 = = 32(cm 2 ) 2 C BC− EF 11− 5 BE=CF= = = 3(cm) 2 2 在Rt△ABE中
AB = AE 2 + BE 2 = 4 2 + 32 = 5(cm)
周长L 周长L = AB+BC+CD+AD=5 + 11 + 5 +5 = 26(cm).
感悟与收获
通过以上的学习,你对等腰梯 形又有了哪些新的认识?
作业:
习题20.5 第2题
再 见
, 梯形 梯形ABCD为等腰梯形 为等腰梯形. 为等腰梯形 A B D
C
慧眼识真
1、有两边相等的 、 梯形是等腰梯形. 梯形是等腰梯形 2、有两个角相等的梯形 、 是等腰梯形. 是等腰梯形 3、对角互补的梯形是 、 等腰梯形. 等腰梯形
4、一组对边平行,另一组对 、一组对边平行 另一组对 边相等的四边形是等腰梯形. 边相等的四边形是等腰梯形
A D
B C
2、如图:梯形ABCD中AD∥BC,AD<BC,E、F 如图:梯形ABCD中AD∥BC,AD<BC, ABCD 分别为AD BC的中点 AD、 的中点, 分别为AD、BC的中点,且EF⊥BC 求证:梯形ABCD是等腰梯形。 ABCD是等腰梯形 求证:梯形ABCD是等腰梯形。 E E
A
D
5、对角线相等的四边 、 形是等腰梯形. 形是等腰梯形
1.在四边形 在四边形ABCD(AB≠DC)中,给出下列论断: 在四边形 中 给出下列论断: ① AB∥CD ② AD=BC ③∠D =∠C, 以其 ∥ ∠ 中两个作为题设, 中两个作为题设,另外一个作为结论 , 用 如果…那么 的形式,写成一个真命题 那么…”的形式 写成一个真命题. 的形式, “如果 那么
A
D
B
M
F
N
CB
M
F
N
C
如图,在梯形 如图,在梯形ABCD中, AD∥BC, 中 C互补 与 互补
B C
梯形ABCD是等腰梯形吗? 是等腰梯形吗? 梯形 是等腰梯形吗
结论:一组对角互补的梯形是等腰梯形
如果梯形的对角线交点与 同一底的两个端点的距离相 那么它是等腰梯形吗? 等,那么它是等腰梯形吗? 为什么? 为什么?
2、等腰梯形的判定方法:
1. 两腰相等的梯形是等腰梯形; 2. 同一底上的两个底角相等的梯形是等腰梯形; 3 . 两条对角线相等的梯形是等腰梯形.
请你写出等腰梯形具有而一般梯形 不具有的三个特征: 不具有的三个特征: 两腰相等 ,
同一底上的角相等 , 对角线相等
.
梯形ABCD中AB∥CD,若添加条件 中 ∥ 梯形 若添加条件 AD=BC AC=BD
D
1 2
C O
A
B
对角线交点与同 一底的两个端点 的距离相等的梯 形是等腰梯形. 形是等腰梯形
已知等腰梯形上、下底长分别为5cm、11cm, 4cm, 已知等腰梯形上、下底长分别为5cm、11cm,高为 4cm, 5cm 计算这个等腰梯形的周长和面积. 计算这个等腰梯形的周长和面积.
D A 5
? B ? E
20.5 等腰梯形的判定(2) 等腰梯形的判定( )
梯形中辅助线有哪些作法?
1、等腰梯形的性质:
1.等腰梯形在同一底上的两个角相等. 等腰梯形在同一底上的两个角相等. 等腰梯形在同一底上的两个角相等 2.等腰梯形的对角线相等 3. 等腰梯形是轴对称图形,过两底中点的直线是 等腰梯形是轴对称图形, 它的对称轴. 它的对称轴.
4 F 11
AD + BC 面积S 面积S = 2 (5 + 11) × 4 = = 32(cm 2 ) 2 C BC− EF 11− 5 BE=CF= = = 3(cm) 2 2 在Rt△ABE中
AB = AE 2 + BE 2 = 4 2 + 32 = 5(cm)
周长L 周长L = AB+BC+CD+AD=5 + 11 + 5 +5 = 26(cm).
感悟与收获
通过以上的学习,你对等腰梯 形又有了哪些新的认识?
作业:
习题20.5 第2题
再 见
