恒定电流的磁场(一[1][1]..
初中九年级(初三)物理 第五章 恒定电流的磁场 上一章说明了磁力是运动电荷之间的一种相互作用,这种相互作

第五章恒定电流的磁场上一章说明了磁力是运动电荷之间的一种相互作用,这种相互作用是通过磁场进行的。
此外还讲述了磁场对运动电荷(包括电流)的作用。
本章将介绍这种相互作用的另一个侧面,即磁场的源,如运动电荷(包括电流)产生磁场的规律。
先介绍这一规律的宏观基本形式,即描述电流元磁场的毕奥-萨伐尔定律(相当于静电场中的库仑定律),由这一定律原则上可以利用积分运算求出任意电流分布的磁场。
再在毕-萨定律的基础上导出关于恒定磁场的两条基本定理:磁通连续定理和安培环路定理,然后利用这两个定理求出有一定对称性的电流分布的磁场(类似于利用静电场黄栌定理和高斯定律来求有一定对称性的电荷分布的静电场分布)。
本章还介绍变化的电场产生磁场方面的规律。
静止电荷的周围存在着电场,电场的特征是对引入电场的电荷施加作用力。
如果电荷在运动,则在其周围不仅产生电场,而且还会产生磁场。
磁场也是物质的一种形态,它只对运动电荷施加作用,对静止电荷则毫无影响。
因此通过实验分别测定电荷静止时和运动时所受到的力,就可以把磁场从电磁场中区分出来。
由于运动和静止的相对性,本章最后还简单介绍电场和磁场有相对论性联系的内容。
Thankful good luck§1 磁现象及其与电现象的联系磁现象的研究与应用(即磁学)是一门古老而又年轻的学科,说她古老是因为关于磁现象的发现和应用的历史悠久,说她年轻是因为磁的应用目前越来越广泛已形成了许多与磁学有关的边缘学科。
磁现象是一种普遍现象即一切物质都具有磁性。
任何空间都存在磁场,所以我们可以毫不夸张地说磁学犹如一棵根深叶茂的参天大树。
尽管人们对物质磁性的认识已有两千多年,但直至19世纪20年代才出现采用经典电磁理论解释物质磁性的代表――安培分子环流假说,而真正符合实际的物质磁性理论却是在19世纪末发现电子、20世纪初有了正确的原子结构模型和建立了量子力学以后才出现。
因此在经典电磁学范围研究物质的磁性时,我们虽然采用传统的观念即安培分子环流假说和等效磁荷两种观点,但必须强调我们要在原子结构模型和量子力学的基础上建立一个正确的概念即物质的磁性来源于电子的轨道磁矩和自旋磁矩。
大学物理 磁学习题课

( I 1 I 2 ) ln 2
第11章 恒定电流的磁场
17
MN上电流元I3dx所受磁力:
0 I1
a M
dx N
c I2
d F I 3 B d x I 3 [ 2(r x) 2(2r x) ] d x
r
0 I1
I3 r Or b
r d
x
F I3 [
0
0 I1
2(r x)
0I2
2(2r x)
]d x
0I3
S
B
圆面
Φm
2 B S BR cos
1 B d S B R 2 2
n
60°
R
B
任意曲面
S
S
很多漏掉负号 类似本页二.1(1)磁通量
12
第11章 恒定电流的磁场
P42 一选择1.
H dl 2 I L1
H dl I L2
1
第11章 恒定电流的磁场
16
P44 二1、如图所示,载有电流I1和I2的长直导线ab和cd相互平行,相距为
3r,今有载有电流I3的导线MN = r,水平放置,且其两端MN分别与I1、I2 的距离都是r,ab、cd和MN共面,求导线MN所受的磁力大小和方向.
载流导线MN上任一点处的磁 感强度大小为: I 0 I 2 0 1 I1 B 2( r x ) 2( 2r x )
1
B
•直导线延长线上
a
第11章 恒定电流的磁场
P
6
2.
圆电流轴线上某点的磁场
B
大小:
恒定磁场ppt

恒定磁场研究的前沿进展
01
恒定磁场作为一种独特的物理场,具有无辐射、无污染、易于调控等优势,在 基础科学、应用科学和工程技术等领域具有广泛的应用前景。
02
近年来,研究者们在恒定磁场相关的物理、材料、生物医学等领域取得了许多 前沿进展,如在磁性材料研究方面,发现了多种新型磁性材料,提高了磁性材 料的性能和稳定性。
光学性质
恒定磁场可以影响物质的光学性质,如折射率、吸收光谱等。
恒定磁场对物质化学性质的影响
电子结构
恒定磁场可以影响物质的电子结构,从而影响化学键的形成 和断裂。
反应速率
恒定磁场可以影响化学反应速率,从而影响化学反应的能量 转换和物质转化。
04
恒定磁场的应用实例
恒定磁场在医学领域的应用
核磁共振成像(MRI)
恒定磁场的基本特征
恒定磁场是一种非均匀场,其 强度和方向随空间位置的变化
而变化。
恒定磁场具有旋度,因此不会 产生电场。
恒定磁场与电场不同,其强度 不与电流密度成正比,而是与 电流密度和磁导率成正比。
恒定磁场的应用场景
ቤተ መጻሕፍቲ ባይዱ磁性材料制备
磁记录
利用恒定磁场可以控制磁性材料的磁性能参 数,如磁化强度、磁晶各向异性等,从而制 备高性能的磁性材料。
利用恒定磁场将人体中的氢原子磁化,通过检测这些原子核产生的信号,生 成人体内部的高分辨率图像。
磁分离技术
恒定磁场可用于分离血液中的肿瘤细胞、细菌等有害物质,提高疾病诊断和 治疗的准确性。
恒定磁场在材料科学领域的应用
磁性材料制造
恒定磁场可以用于制造高性能的磁性材料,如稀土永磁材料、铁氧体材料等。
磁记录
未来,恒定磁场的研究和应用将会有更多的创新和发 展,为人类的生产和生活带来更多的便利和效益。
第5章 恒定电流的电场和磁场

dl '×R ∫C ' R 3 ⋅ dl −R ∫C ' R 3 ⋅ (−dl × dl ' )
假设回路C′对P点的立体角为 ,同时P点位移dl引起的立体角增量 为d ,那么P点固定而回路C′位移dl所引起的立体角增量也为d ′。 -dl×dl′是dl′位移-dl所形成的有向面积。注意到R=r-r′,这个立体 角为
z ' = z − r tan α , dz ' = r sec 2 α dl ' = ez dz ' = −ez r sec 2 α R = r sec α
dl '×R = ez dz '×[rer + ( z − z ' )ez ]
所以
= −eφ rdz ' = −eφ r 2 sec 2 α
∆P = ∆U∆I = E∆l∆I = EJ∆l∆S = EJ∆V
当∆V→0,取∆P/∆V的极限,就得出导体内任一点的热功 热功 率密度,表示为 率密度
∆P p = lim = EJ = σE 2 ∆V →0 ∆V
或
p = J ⋅E
此式就是焦耳定律 焦耳定律的微分形式。 焦耳定律 应该指出,焦耳定律不适应于运流电流 不 运流电流。因为对于运流电 运流电流 流而言,电场力对电荷所作的功转变为电荷的动能,而不 是转变为电荷 晶格碰撞 电荷与晶格碰撞 电荷 晶格碰撞的热能。
对于无限长直导线(l→∞),α1=π/2, α2=-π/2,其产生的磁场为
µ0 I B = eφ 2πr
5.3 恒定磁场的基本方程
5.3.1 磁通连续性原理 磁感应强度在有向曲面上的通量简称为磁通量 磁通量(或磁通),单 磁感应强度 磁通量 位是Wb(韦伯),用Φ表示:
恒定电流的电场和磁场课件

目录
• 恒定电流的基本概念 • 电场与电场力 • 磁场与磁场力 • 恒定电流的磁场效应 • 恒定电流的应用 • 实验与实践
01
恒定电流的基本概念
电流的定义与性质
电流
电荷在导体中定向移动形成电流 ,单位时间内通过导体横截面的 电荷量称为电流强度,简称电流 。
电流的性质
电荷的定向移动形成电流,其方 向由正电荷定向移动的方向决定 ,而与导体内自由电荷的运动方 向无关。
电场力是电荷在电场中受到的力,其大小与电荷的电量成正比,与电场强度成正比 。
电场强度是描述电场强弱和方向的物理量,等于单位正电荷在电场中受到的力。
电场强度具有方向性,规定正电荷受力方向为电场强度的方向。
电势与电场能量
电势是描述电场能的物理量,等于单 位正电荷在电场中具有的电势能。
电场能量是电场中储存的能量,与电 势能密切相关。
电阻
导体对电流的阻碍作用,由导体的材 料、长度、横截面积和温度等因素决 定。
02
电场与电场力
电场的概念与性质
电场是由电荷产生的 ,对放入其中的电荷 有力的作用。
电场的性质包括对放 入其中的电荷有力的 作用、静电感应现象 等。
电场具有物质性,是 传递电荷间相互作用 的一种特殊物质形态 。
电场力与电场强度
详细描述
电磁感应现象是当导体在磁场中发生相对运动时,会在导体中产生电动势或电流的现象。这个现象由英国物理学 家迈克尔·法拉第于19世纪30年代发现,是电磁化的电场和磁场相互激发,形成电磁波并传播出去。
详细描述
电磁波是由变化的电场和磁场相互激发而形成的。当电场或磁场发生变化时,就会产生电磁波,并传 播出去。电磁波的传播速度等于光速,在真空中传播不受影响,但在介质中传播速度会减慢。
1第十一章 恒定电流的磁场(一)作业答案

2 ∶4
2 ∶1 2 ∶8
a2 a1 O1 O2 I
2 2 0 I Bo1 , Bo2 4 cos 450 cos1350 , a2 2a1 a 2 4 2 a 2 由Bo1 Bo2 , 得 1 a2 8
0 I
0 I
I
[ B ] 2、 (基础训练 3)有一无限长通电流的扁平铜片,宽度为 a,厚度不计,电 流 I 在铜片上均匀分布,在铜片外与铜片共面,离铜片右边缘为 b 处的 P 点(如图)的
B B
0 Ir 2 a 2
0 I 2 r
, B
I B 2 r 0 I (r 2 b 2 ) 2 2 (c b )
B 2 r 0 0 0, B 0
2 r c 2 b 2
0 I c 2 r 2
I a b
磁感强度 B 的大小为 0 I (A) . 2(a b) 0 I a b (C) . ln 2b b
其电流为 dI
P
(B) (D)
0 I
2a
ln
ab . b
.
0 I
(a 2b)
【答】在距离 P 点为 r 处选取一个宽度为 dr 的电流(相当于一根无限长的直导线) ,
dI I dr ,它在 P 处产生的磁感应强度为 dB 0 ,方向垂直纸面朝内; a 2 r 根据 B dB 得: B 的方向垂直纸面朝内, B 的大小为
B
0 dI 0 I b a dr 0 I a b . ln 2 r 2 a r 2 a b b
b b a
图 11-51
5、 (自测提高 11)在一根通有电流 I 的长直导线旁,与之共面地放着一个长、 宽各为 a 和 b 的矩形线框,线框的长边与载流长直导线平行,且二者相距为 b, 如图 11-51 所示.在此情形中,线框内的磁通量 =
高中物理竞赛《磁场》内容讲解

磁 场一、恒定电流的磁场1、直线电流的磁场通有电流强度为I 的无限长直导线,距导线为R 处的磁感应强度为:RIB πμ20=;如下图距通有电流强度为I 的有限长直导线为R 处的P 点的磁感应强度为:)cos (cos 40βαπμ+=RIB ----------------------------------①若P 点在通电直导线的延长线上,则R=0 α=0 β=π 无法直接应用上述式子计算,可进行如下变换lR d d 21)sin(2121=+βα 上式中1d 、2d 分别为P 点到A 、B 的距离,l 为直导线的长度所以:l d d R )sin(21βα+=代入①式得:)sin(cos cos 4210βαβαπμ++=d d Il B令2sin2cos2cos 2sin 22cos2cos2)sin(cos cos βαβαβαβαβαβαβαβα+-=++-+=++=y将α=0 β=π代入上式得0=y所以:在通电直导线的延长线上任意一点的磁感应强度为0=B2、微小电流元产生的磁场微小电流元的磁场,根据直线电流的磁场公式)cos (cos 40βαπμ+=rIB得:Ⅰ若α、β都是锐角,如左图,有:)cos (cos 40βαπμ+=r I B =)sin (sin 4210θθπμ∆+∆rI因1θ∆、2θ∆0→,所以≈∆+∆=)sin (sin 4210θθπμr I B )(4210θθπμ∆+∆rI所以:θπμ∆=rIB 40Ⅱ若α、β中有一个是钝角,如β(右图),则:]sin )[sin(cos 4)cos (cos 400000θθθθπμβαπμ-+∆=+=r Id I B -------------①00000sin sin cos cos sin sin )sin(θθθθθθθθ-∆+∆=-+∆因0→∆θ,所以:0000cos cos sin sin )sin(θθθθθθθ∆≈∆≈-+∆--------------------------------②②式代入①式得:θπμ∆=rIB40总上所述,电流元I 在空间某点产生的磁场为:θπμ∆=rIB 40,式中r 为电流元到该点的距离,θ∆为电流元端点与该点连线张开的角度。
大学物理之恒定电流的磁场

磁场能量传
磁场能量传输原理
利用磁场可以实现能量的无线传输。
磁场能量传输方式
包括磁耦合、磁感应等。
磁场能量传输特点
具有高效、安全、环保等优点,是未来能源传输的重要方向之一。
THANKS FOR WATCHING
感谢您的观看
磁场与电流的关系
总结词
磁场与电流之间存在相互作用,变化的磁场可以产生 电场,而变化的电场也可以产生磁场。
详细描述
磁场与电流之间的相互作用是电磁场理论的核心内容之 一。根据法拉第电磁感应定律,变化的磁场可以产生电 场;而根据麦克斯韦方程组,变化的电场也可以产生磁 场。这种相互作用导致电磁波的传播,形成了我们现在 所知的电磁波谱。在恒定电流的磁场中,虽然磁场不随 时间变化,但电流在空间中的分布可以是不均匀的,因 此磁场与电流之间仍然存在相互作用。这种相互作用表 现为电流在磁场中受到洛伦兹力,使得电荷在空间中移 动形成电流。
洛伦兹力
洛伦兹力是磁场对运动电荷的作 用力,其大小与电荷的电量、速
度以及磁场强度有关。
洛伦兹力的方向与电荷运动方向 和磁场方向有关,遵循右手定则。
洛伦兹力在粒子加速器、回旋加 速器等领域有广泛应用,是研究
带电粒子运动规律的基础。
磁场中的运动电荷
1
在磁场中运动的电荷会受到洛伦兹力的作用,这 个力会使电荷发生偏转,改变其运动轨迹。
磁场的描述
磁感应线
用磁感应线描述磁场,磁感应线的疏密程度表示磁场强度的 大小。
磁感应强度
描述磁场强弱的物理量,其方向与磁场中某点的磁感应线垂 直。
磁场的应用
电磁感应
当导体在磁场中运动时,会产生电动 势,进而产生电流。这一现象在发电 机、变压器等设备中有广泛应用。
大学物理第八章恒定电流的磁场

Fe 2.磁性: 磁铁能吸引含有 Co 物质的性质。
Ni
3.磁极:磁铁上磁性最强的两端,分为
N S
北同 极,指向 方,
南异
斥 性相 。
吸
三.磁场
1.概念: 运动qυ电荷或电I流周围存在的物质,称为磁场。
2.对外表现
① qυ或 I 在磁场中受到力的作用。
②载流导线在磁场中移动,磁场力作功。
力的表现 功的表现
极。
然而,磁和电有很多相似之处。例如,同种电荷
互相推斥,异种电荷互相吸引;同名磁极也互相推
斥,异名磁极也互相吸引。用摩擦的方法能使物体带
上电;如果用磁铁的一极在一根钢棒上沿同一方向摩
擦几次,也能使钢棒磁化。但是,为什么正、负电荷 能够单独存在,而单个磁极却不能单独存在呢?多年 来,人们百思而不得其解。
dN B
dS
一些典型磁场的磁感线:
2.性质
①磁感线是无始无终的闭合曲线。
B
A
②任二条磁感线不相交。
B
③磁感线与电流是套合的,它们之间可用右手螺旋法 则来确定。
B
I
I
B
四.磁通量
1.定义:通过一给定曲面的磁感线的条数,称为通过该 曲面的磁通量。
电场强度通量:e S E dS
通过面元 dS的磁感线数: dN BdS BdS cos
3.电荷之间的磁相互作用与库仑相互作用的不同 ①电荷无论是静止还是运动的,它们之间都存在库仑 作用; ②只有运动的电荷之间才有磁相互作用。
四.磁感强度
电场 E 磁场 B
1.实验 在垂于电流的平面内放若干枚小磁针,发现:
①小磁针距电流远近不同,
N
受磁力大小不同。
②距电流等远处,小磁针受
恒定电流中的磁场

恒定电流中的磁场磁场是物质围绕着电流所产生的一种现象。
磁场具有方向和强度,可以对周围的物质产生作用。
在恒定电流中,磁场的特性和分布呈现出一定的规律性。
本文将探讨恒定电流中磁场的产生原理、磁场的特性以及磁场与电流之间的关系。
一、恒定电流中的磁场产生原理当电流通过导线时,周围就会形成一个闭合的磁场。
根据安培定理,恒定电流所产生的磁场的大小和方向与电流强度、距离和导线形状都有关系。
导线周围的磁场将呈现出环绕导线的形态,强度随着距离导线的远近而减弱。
二、恒定电流中磁场的特性1. 磁场强度:磁场强度是衡量磁场的大小的物理量。
在恒定电流中,磁场的强度与电流的大小成正比,即电流越大,磁场强度越大。
2. 磁场方向:根据右手定则,我们可以确定恒定电流所产生的磁场方向。
当右手握住电流方向,拇指指向电流方向时,四指弯曲的方向就是磁场的方向。
3. 磁场分布:恒定电流所产生的磁场呈现出环绕导线的形状。
随着离导线距离的增加,磁场强度逐渐减小,并形成一个闭合的磁场线圈。
三、磁场与电流的关系恒定电流所产生的磁场与电流之间存在着密切的关系。
根据安培定理和法拉第电磁感应定律,我们可以得到以下结论:1. 磁场与电流强度成正比,即电流越大,磁场强度越大。
2. 磁场与距离成反比,即离导线越近,磁场越强。
3. 磁场与导线形状有关,导线越弯曲,磁场越复杂。
4. 磁场会对周围的物质产生作用,如可以使磁性物质受力或改变电流的方向。
四、应用领域与意义恒定电流产生的磁场在很多领域有着广泛的应用。
例如,电动机、电磁铁、变压器等电磁设备的工作原理都与磁场和电流的相互作用相关。
同时,磁场在地理勘探、医学成像等领域也有重要的应用价值。
总结:恒定电流中的磁场是通过电流通过导线所产生的一种现象。
磁场具有方向和强度,其特性与电流大小和周围距离密切相关。
磁场与电流强度成正比,与距离成反比,同时与导线的形状有关。
磁场在科学研究和工程领域中有着广泛的应用,对于我们理解电磁学原理以及应用于实践中具有重要的意义。
稳恒电流的磁场

在一根载流直线上任意取一无限小 的直线,做一个矢量 I d l
Idl
大小:该小直线的长度乘以I
方向:该点直线上电流的方向
r
P
对空间任意点P,从 为 r 产生的磁场为
IddB,l到方P向的满位足置右矢手量
螺旋。
2020/4/1
21
引入电流元矢量 I d l 的物理意义
任意载流回路可设想为是由无限多个首 尾相接的电流元构成,
2020/4/1
结
计算场强的方法
1、点电荷场的场强及叠加
原理
E
EiQi r Nhomakorabea4
0
ri3
(分立)
rdQ (连续)
Q 4 0r 3
2、可有
UUEE
U x
Ex
44
典型磁场的磁感应强度
典型电场的场强
电流元
dB
0
4
I
d
l
r
r3
载流长直导线
B
0I 4r
cos1
cos2
无限长载流 长直导线
34
用B-S Low求 B 的两种思路
1.从电流产生磁场的观点 求B
dB
u0
4
Idl r
r3
B dB
r:
从电流元指向场点 (视电流元为一个点)
:视电流元有一定长度
2.从电荷运动产生磁场的 观点求B
Br: 从4u运0 q动vr电3 r荷指向场点
2020/4/1
35
例2.求:直线电流I 的磁场分布。
安培力 磁力矩
2020/4/1
7
本章学习方法
对比
与静电场的研究方法类似 与静电场的研究结论对比
第4章 恒定电流的磁场1

B 0 ( J J m )
令 H ( B
(
B
0
M) J
0
M)
H J
介质中,安培环路定理:
真空中,安培环路定理:
H B ( A / m)
§4.1 安培定律 磁感应强度
一、安培定律:描述电流回路间的相互作用力的大小。 安培定律指出:在真空中载有 R 电流I1的回路C1对另一载有电P ( r ) dV 流I2的回路C2的作用力为:
0 F12 4
C 2 C1
Байду номын сангаас
I 2 d2 I 1 dl 1 r R l r' R3 O
线元电流段: dqv
0 A 4
l
Id l ' C R
磁矢位微元 dA 与元电流 Id l ' K dS ' J dV ' 具有相同方向。
磁矢量位参考点选择原则:
电流有限分布,参考点选在无限远处 电流无限分布,参考点选在有限远处 参考点处: A 0
例4.3 计算一通过电流为I,半径为a的小圆环在远离圆环处的B。
2 1
e
若导线无限长,则 1 0, 2
0 I B e 2
§4.2 矢量磁位
1、磁矢量位的导出 回顾电位的推导: 静电场是无旋场: 根据矢量恒等式:
E 0
( ) 0
E
恒定磁场是无散场: B 0 根据矢量恒等式:
第4章 恒定电流的磁场
恒稳磁场的矢势和磁多极矩

恒稳磁场的矢势和磁多极距Part 1. 矢势及其微分方程我们考察恒定电流分布所激发的静磁场。
在给定的传导电流附近可能存在一些磁性物质,在电流的磁场作用下,物质磁化而出现磁化电流,它反过来又激发附加的磁场。
磁化电流和磁场是互相制约的。
因此解决这类问题的方法也象解静电学问题一样,即求微分方程边值问题的解。
下面我们先引入磁场的矢势,然后导出矢势所满足的微分方程。
1. 矢势恒定电流磁场的基本方程是(1.1)(1.2)式是J是自由电流密度.(1.1)和(1.2)式结合物质的电磁性质方程是解磁场问题的基础。
磁场的特点和电场不同。
静电场是有源无旋场,电场线从正电荷出发而止于负电荷,静电场线永不闭合。
静磁场则是有旋无源场,磁感应线总是闭合曲线。
由于特性上的显著差异,描述磁场和电场的方法就有所不同。
静电场由于其无旋性,可以引入标势来描述。
磁场由于其有旋性,一般不能引入一个标势来描述,但是由于磁场的无源性,我们可以引入,另一个矢量来描述它。
根据矢量分析的定理(附录Ⅰ.17式),若则 B 可表为另一矢量的旋度(1.3)A称为磁场的矢势。
为了看出矢势A的意义,我们考察(1.3)的积分形式。
把B对任一个以回路L为边界的曲面S积分,得(1.4)式中左边是通过曲面S的磁通量。
由上式,通过一个曲面的磁通量只和这曲面的边界L有关,而和曲面的具体形状无关。
如图3-1,设S1和S2矢量个共同边界L的曲面,则这正是B的无源性的表示,因为B是无源的,在S1和S2所包围的区域内没有磁感应线发出,也没有磁感应线终止,B线连续地通过该区域,因而通过曲面S1的磁通量必须等于通过曲面S2的磁通量。
这磁通量由矢势A对S1或S2的边界L的环量表示。
因此,矢势A的物理意义是它沿任一闭合回路的环量代表通过以该回路为界的任意曲面的磁通量。
只有A的环量才有物理意义,而每点上的A(x)至没有直接的物理意义。
由矢势A可以确定磁场B,但是由磁场B并不能唯一确定矢势A。
恒定电流和磁场知识点总结

磁场一、磁场:1、磁场的基本性质:磁场对放入其中的磁极、电流有磁场力的作用;2、磁铁、电流都能能产生磁场;3、磁极和磁极之间,磁极和电流之间,电流和电流之间都通过磁场发生相互作用;4、磁场的方向:磁场中小磁针北极的指向就是该点磁场的方向;二、磁感线:在磁场中画一条有向的曲线,在这些曲线中每点的切线方向就是该点的磁场方向;1、磁感线是人们为了描述磁场而人为假设的线;2、磁铁的磁感线,在外部从北极到南极,内部从南极到北极;3、磁感线是封闭曲线;三、安培定则:1、通电直导线的磁感线:用右手握住通电导线,让伸直的大拇指所指方向跟电流方向一致,弯曲的四指所指的方向就是磁感线的环绕方向;2、环形电流的磁感线:让右手弯曲的四指和环形电流方向一致,伸直的大拇指所指的方向就是环形导线中心轴上磁感线的方向;3、通电螺旋管的磁场:用右手握住螺旋管,让弯曲的四指方向和电流方向一致,大拇指所指的方向就是螺旋管内部磁感线的方向;四、地磁场:地球本身产生的磁场;从地磁北极(地理南极)到地磁南极(地理北极);五、磁感应强度:磁感应强度是描述磁场强弱的物理量。
1、磁感应强度的大小:在磁场中垂直于磁场方向的通电导线,所受的安培力F跟电流I和导线长度L的乘积的比值,叫磁感应强度。
B=F/IL2、磁感应强度的方向就是该点磁场的方向(放在该点的小磁针北极的指向)3、磁感应强度的国际单位:特斯拉T,1T=1N/A·m六、安培力:磁场对电流的作用力;1、大小:在匀强磁场中,当通电导线与磁场垂直时,电流所受安培力F等于磁感应强度B、电流I和导线长度L三者的乘积。
2、定义式F=BIL(适用于匀强电场、导线很短时)3、安培力的方向:左手定则:伸开左手,使大拇指根其余四个手指垂直,并且跟手掌在同一个平面内,把手放入磁场中,让磁感线垂直穿过手心,并使伸开四指指向电流的方向,那么大拇指所指的方向就是通电导线所受安培力的方向。
七、磁铁和电流都可产生磁场;八、磁场对电流有力的作用;九、电流和电流之间亦有力的作用:(1)同向电流产生引力;(2)异向电流产生斥力;十、分子电流假说:所有磁场都是由电流产生的;十一、磁性材料:能够被强烈磁化的物质叫磁性材料:(1)软磁材料:磁化后容易去磁的材料;例:软铁;硅钢;应用:制造电磁铁、变压器、(2)硬磁材料:磁化后不容易去磁的材料;例:碳钢、钨钢、制造:永久磁铁;十二、磁场对运动电荷的作用力,叫做洛伦兹力1、洛仑兹力的方向由左手定则判断:伸开左手让大拇指和其余四指共面且垂直,把左手放入磁场中,让磁感线垂直穿过手心,四指为正电荷运动方向(与负电荷运动方向相反)大拇指所指方向就是洛仑兹力的方向;(1)洛仑兹力F一定和B、V决定的平面垂直。
大学物理第8章《恒定电流的磁场》复习思考题

第8章《恒定电流的磁场》复习思考题一 填空题:1. 一根长直载流导线,通过的电流为2A ,在距离其2mm 处的磁感应强度为 。
(70104-⨯=πμTm/A )答:4102-⨯T2. 一根直载流导线,导线长度为100mm ,通过的电流为5A ,在与导线垂直、距离其中点的50mm 处的磁感应强度为 。
(70104-⨯=πμTm/A ) 答:5102-⨯T3. 一根载流圆弧导线,半径1m ,弧所对圆心角6π,通过的电流为10A ,在圆心处的磁感应强度为 。
(70104-⨯=πμTm/A ) 答:6106-⨯πT4. 两平行载流导线,导线上的电流为I ,方向相反,两导线之间的距离a ,则在与两导线同平面且与两导线距离相等的点上的磁感应强度大小为 。
答:aI πμ02 5. 两平行载流导线,导线上的电流为I ,方向相反,两导线之间的距离a ,则在与两导线同平面且与其中一导线距离为b 的、两导线之间的点上的磁感应强度大小为 。
答:)(2200b a I b I -+πμπμ 6.在真空中有一根半径为R 的半圆形细导线,流过的电流为I ,则圆心处的磁感应强度大小为 。
答案:R I40μ7. 一磁场的磁感应强度为k c j b i a B ++=,则通过一半径为R ,开口向Z 方向的半球壳,表面的磁通量大小为 Wb答案:c R 2π8. 一根很长的圆形螺线管,沿圆周方向的面电流密度为i ,在线圈内部的磁感应强度为 。
答案:i 0μ8. 半径为R 的闭合球面包围一个条形磁铁的一端,此条形磁铁端部的磁感应强度B ,则通过此球面的磁通量 。
答案:09. 一无限长直圆筒,半径为R ,表面带有一层均匀电荷,面密度为σ,以匀角速度ω绕轴转动,在圆筒内的磁感应强度大小为 。
答案: σωμR 010. 一根很长的螺线管,总电阻20欧姆,两端连接在12V 的电源上,线圈半径2cm ,线圈匝数200匝/厘米,在线圈内部距离轴线0.01m 处的磁场强度为 。
第11 章 恒定电流的磁场
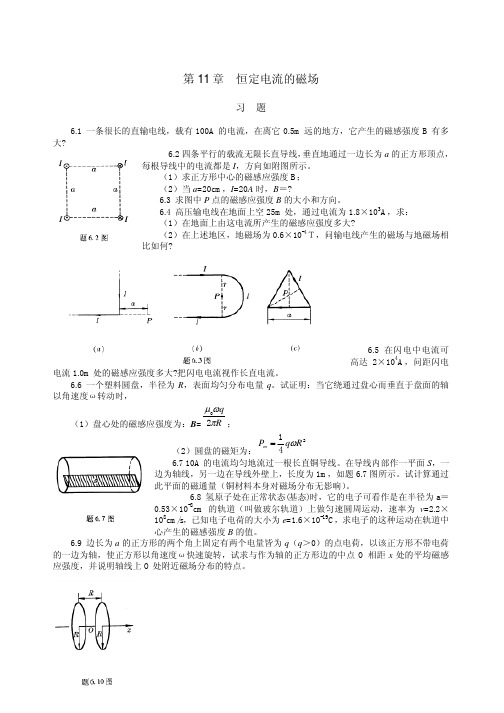
第11章 恒定电流的磁场习 题6.1 一条很长的直输电线,载有100A 的电流,在离它0.5m 远的地方,它产生的磁感强度B 有多大?6.2四条平行的载流无限长直导线,垂直地通过一边长为a 的正方形顶点,每根导线中的电流都是I ,方向如附图所示。
(1)求正方形中心的磁感应强度B ; (2)当a =20cm ,I =20A 时,B =?6.3 求图中P 点的磁感应强度B 的大小和方向。
6.4 高压输电线在地面上空25m 处,通过电流为1.8×103A ,求: (1)在地面上由这电流所产生的磁感应强度多大?(2)在上述地区,地磁场为0.6×10-4T,问输电线产生的磁场与地磁场相比如何?6.5 在闪电中电流可高达2×104A ,问距闪电电流1.0m 处的磁感应强度多大?把闪电电流视作长直电流。
6.6 一个塑料圆盘,半径为R ,表面均匀分布电量q 。
试证明:当它绕通过盘心而垂直于盘面的轴以角速度ω转动时,(1)盘心处的磁感应强度为:B =R qπωµ20;(2)圆盘的磁矩为:241R q P m ω=6.7 10A 的电流均匀地流过一根长直铜导线。
在导线内部作一平面S ,一边为轴线,另一边在导线外壁上,长度为1m ,如题6.7图所示。
试计算通过此平面的磁通量(铜材料本身对磁场分布无影响)。
6.8 氢原子处在正常状态(基态)时,它的电子可看作是在半径为a =0.53×10-8cm 的轨道(叫做玻尔轨道)上做匀速圆周运动,速率为v =2.2×108cm/s ,已知电子电荷的大小为e =1.6×10-19C ,求电子的这种运动在轨道中心产生的磁感强度B 的值。
6.9 边长为a 的正方形的两个角上固定有两个电量皆为q (q >0)的点电荷,以该正方形不带电荷的一边为轴,使正方形以角速度ω快速旋转,试求与作为轴的正方形边的中点O 相距x 处的平均磁感应强度,并说明轴线上O 处附近磁场分布的特点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一. 选择题: 1.(基础训练1)[ D ]载流的圆形线圈(半径a 1 )与正方形线圈(边长a 2 )通有相同电流I .若两个线圈的中心O 1 、O 2处的磁感强度大小相同,则半径a 1与边长a 2之比a 1∶a 2为 (A) 1∶1 (B)π2∶1(C)π2∶4 (D)π2∶8 提示()82,,22135cos 45cos 244,221200020102121ππμπμμ===-⨯⨯⨯==a a B B a Ia I B a I B o o o o 得由2.(基础训练3)[B ].有一无限长通电流的扁平铜片,宽度为a ,厚度不计,电流I 在铜片上均匀分布,在铜片外与铜片共面,离铜片右边缘为b 处的P 点(如图)的磁感强度B的大小为 (A) )(20b a I+πμ. (B) b b a a I +πln 20μ. (C)bb a bI+πln20μ. (D))2(0b a I+πμ.提示:bb a aI rdr aI rr dI dB dr a I dI ab b+======⎰⎰⎰+ln222dI B B B ,B d B ,2P ,)(dr r P 0000πμπμπμπμ的大小为:,的方向也垂直纸面向内据方向垂直纸面向内;根处产生的它在,电流为导线相当于一根无限长的直的电流元处选取一个宽度为点为在距离3.(基础训练5)[B ]无限长载流空心圆柱导体的内外半径分别为a 、b ,电流在导体截面上均匀分布,则空间各处的B的大小与场点到圆柱中心轴线的距离r 的关系定性地如图所示.正确的图是 ( )提示:根据安培环路定理: 当 a r < 时 0=B当a r b >>时 222202ab a r rI B --⋅=πμ当b r >时rIB πμ20=且a r =时0=B 和a r b >>时,曲线斜率随着r 增大。
4自测提高2[D ]通有电流I 的无限长直导线有如图所示的三种形状,则P ,Q ,O 各点磁感应强度的大小B P ,B Q ,B O 间的关系为:(A) B P > B Q > B O . (B) B Q > B P > B O . (C) B Q > B O > B P . (D) B O > B Q > B P . 提示:根据直线电流的磁场公式)cos (cos 4210θθπμ-=aIB 和圆弧电流产生磁场公式πθμ220⋅=aIB 可得aIB P πμ20=)221(2)221(4200+=+⨯=a Ia IB Q πμπμ)21(2442000ππμμπμ+=+⨯=a I a Ia IB O5、自测提高7[C ]如图,正方形的四个角上固定有四个电荷量均为q 的点电荷.此正方形以角速度ω 绕AC 轴旋转时,在中心O 点产生的磁感应强度大小为B 1;此正方形同样以角速度ω 绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感应强度的大小为B 2,则B 1与B 2间的关系为(A) B 1 = B 2. (B) B 1 = 2B 2.(C) B 1 =21B 2. (D) B 1 = B 2 /4.提示: 设正方形边长为a ,)22(a b b OC AO ===式中,两种情况下正方形旋转时的角速度ω 相同,所以每个点电荷随着正方形旋转时形成的等效电流相同, 为 πω2q I =当正方形绕AC 轴旋转时,一个点电荷在O 点产生的磁感应强度的大小为bIB 20μ=,实际上有两个点电荷同时绕AC 旋转产生电流,在O 点产生的总磁感应强度的大小为bIb I B B 001222μμ=⨯==同理,当正方形绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感应强度的大小为bIb I B B 0022244μμ=⨯==故有122B B =A Cq二. 填空题6.(基础训练11)均匀磁场的磁感强度B与半径为r 的圆形平面的法线n的夹角为α ,今以圆周为边界,作一个半球面S ,S 与圆形平面组成封闭面如所示.则通过S 面的磁通量Φ = απcos 2B r -。
提示:根据磁场的高斯定理,通过S 面的磁通量数值上等于通过圆平面的通量。
当题中涉及的是封闭曲面时,面的法向方向指向凸的一面,因此通过S 面的磁通量为负值。
7(基础训练12)一长直载流导线,沿空间直角坐标Oy 轴放置,电流沿y 正向.在原点O 处取一电流元l Id ,则该电流元在(a ,0,0)点处的磁感强度的大小为 204aI d lπμ 方向为Z 轴负方向提示: 根据毕奥-萨伐尔定律 k aIdl a i j Idl r e l Id B r202020444πμπμπμ-=⨯=⨯= 8.(基础训练18)将半径为R 的无限长导体薄壁管(厚度忽略)沿轴向割去一宽度为h ( h << R )的无限长狭缝后,再沿轴向流有在管壁上均匀分布的电流,其面电流密度(垂直于电流的单位长度截线上的电流)为i ,则管轴线磁感强度的大小是Rihπμ20.提示:Rihπμ20 利用9.(自测提高13)、一半径为a 的无限长直载流导线,沿轴向均匀地流有电流I .若作一个半径为R = 5a 、高为l 的柱形曲面,已知此柱形曲面的轴与载流导线的轴平行且相距3a (如图所示).则B在圆柱侧面S 上的积分=⎰⎰⋅SS Bd ______0______.提示:根据无限长直载流导线产生磁场的对称性,其产生磁场的磁感应线穿入侧面的根数(磁通量为负)与穿出的根数(磁通量为正)相同,代数和为零。
)(220R r r RIB ≤=πμ)(20R r rIB ≥=πμ2ln 220202πμπμφIl dr l rI S d B RR==⋅=⎰⎰→→πμπμφ82ln 200IlIl+=10.(自测提高16)如图所示.电荷q (>0)均匀地分布在一个半径为R 的薄球壳外表面上,若球壳以恒角速度ω 0绕z 轴转动,则沿着z 轴从-∞到+∞磁感应强度的线积分等于πωμ200q提示: 由安培环路定理⎰⋅⎰⋅+∞∞-=l B l Bd d I 0μ=而 π=20ωq I , 故⎰⋅+∞∞-l Bd =π200q ωμ三.计算题11. (基础训练22)一无限长圆柱形铜导体(磁导率μ0),半径为R ,通有均匀分布的电流I .今取一矩形平面S (长为l ,宽为R 2),位置如图中画斜线部分所示,求通过该矩形平面的磁通量.解:根据安培环路定理,在圆柱体内部与导体中心轴线相距为r 处的磁感应强度的大小为:因此,穿过导体内矩形截面的磁通量为πμπμ82034011Ildr r RIld R==Φ=Φ⎰⎰(详见同步辅导与复习自测例题12-3)在导体外穿过导体外矩形截面的磁通量为故总的磁通量为12.(基础训练23). 如图所示,半径为R ,线电荷密度为λ (>0)的均匀带电的圆线圈,绕过圆心与圆平面垂直的轴以角速度ω 转动,求轴线上任一点的B的大小及其方向.解: 圆线圈的总电荷 λπR q 2= ,转动时等效的电流为1 mλωωπλπR R Tq I ===/22,代入环形电流在轴线上产生磁场的公式得2/32230)(2y R R B B y +==ωλμ 方向沿y 轴正向。
13.(基础训练25). 一无限长的电缆,由一半径为a 的圆柱形导线和一共轴的半径分别为b 、c 的圆筒状导线组成,如图所示。
在两导线中有等值反向的电流I 通过,求: (1)内导体中任一点(r<a)的磁感应强度; (2)两导体间任一点(a<r<b)的磁感应强度;(3)外导体中任一点(b<r<c)的磁感应强度; (4)外导体外任一点(r>c)的磁感应强度。
解:用安培环路定理⎰∑=⋅LL l d B 内求解I 0μ。
磁感应强度的方向与内导线的电流成右手螺旋关系。
其大小满足:∑=内L r B I 20μπ (r 为场点到轴线的距离)(1)20222,2 :aIrB r aIr B a r πμππμπ=∴=⋅<(2)I r B b r a 02 :μπ=<<, rIB πμ20=∴(3)⎪⎪⎭⎫ ⎝⎛---=<<I b c b r I r B c r b )()(2 :22220ππμπ ()()222202b c r r c I B --=∴πμ (4)0B 02 :=∴=⋅>,r B c r π14. (自测提高19)将通有电流I 的导线在同一平面内弯成如图所示的形状,求D 点的磁感强度B的大小.解:其中3/4圆环在D 处的场 )8/(301a I B μ=AB 段在D 处的磁感强度 )221()]4/([02⋅π=b I B μ BC 段在D 处的磁感强度 )221()]4/([03⋅π=b I B μ1B 、2B、3B 方向相同,可知D 处总的B 为)223(40baI B +ππ=μ15(自测提高24)在氢原子中,电子沿着某一圆轨道绕核运动.求等效圆电流的磁矩m p与电子轨道运动的动量矩L 大小之比,并指出和L方向间的关系.(电子电荷为e ,电子质量为m )解:设电子绕核运动的轨道半径为R ,匀速圆周运动的速率为v 。
核外电子绕核运动等效的圆电流为 RevvR e I ππ22== 电流的磁矩 222e v R RRevIS P m =⋅==ππ电子轨道运动的动量矩 m v R L =可见 me LP m 2= 两者的方向相反[选作题] 16.(基础训练26)均匀带电刚性细杆AB ,线电荷密度为λ,绕垂直于直线的轴O 以ω 角速度匀速转动(O 点在细杆AB 延长线上).求: (1) O 点的磁感强度0B;(2) 系统的磁矩m p; (3) 若a >> b ,求B 0及p m .解:(1)将带电细杆分割为许多电荷元。
在距离o 点r 处选取长为dr 的电荷元,其带电 dr dq λ=该电荷元随细杆转动时等效为圆电流为:dr dq T dq dI πωλωπ2/2===它在O 点产生的磁感应强度为方向垂直于纸面向内。
,42000dr rrdIdB πωλμμ==根据⎰=00B d B,0B 的方向也是垂直于纸面向内,0B 的大小为ab a dr rB ba ao +==∴⎰+ln4400πωλμπωλμ(2) dq 所等效的圆电流dI 的磁矩为dr r SdI dp m πλωπ22==,方向垂直于纸面向内;根据⎰=mm p d p,m p 的方向也是垂直于纸面朝内,m p 的大小为()[]33262ab a dr rp ba am -+==∴⎰+ωλπλωπ(3)a>>b 时,AB 杆可近似看作点电荷:电量为b λ,等效的圆电流:πωλ2b I =在o 点产生的磁感应强度为abaIB πωλμμ4200==∴系统的磁矩 2222b a a b IS p m ωλππωλ===∴17. (自测提高28)用安培环路定理证明,图中所表示的那种不带边缘效应的均匀磁场不可能存在.证明:用反证法.假设存在图中那样不带边缘效应的均匀磁场,并设磁感强度的大小为B .作矩形有向闭合环路如图所示,其ab 边在磁场内,其上各点的磁感强度为B ,cd 边在磁场外,其上各点的磁感强度为零.由于环路所围的面积没有任何电流穿过,因而根据安培环路定理有:0d ==⎰⋅ab B l B L因 0≠ab .所以 B = 0,这不符合原来的假设.故这样的磁场不可能存在.。
