30°,45°,60°角的三角函数值

合集下载

1.2 30°、45°、60°角的三角函数值

2 0 0 0 3 sin 45 sin 60 2 cos45 . 2
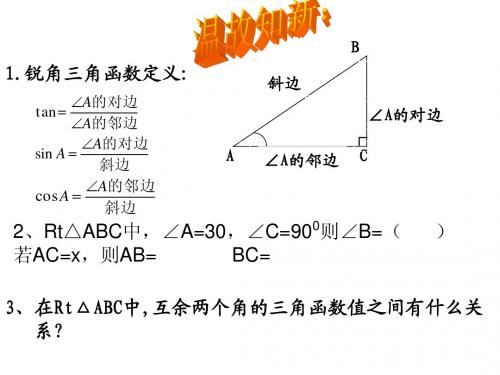
2 2 0 4 sin 30 cos2 600 2 cos2 450. 2
反思：此类题的计算步骤是什么？应该注意什么问题？
看图说话: 1、直角三角形三边的关系.
B c a
2、直角三角形两锐角的关系.
3、直角三角形边与角之间的关系.
3x
┌ x
600
2x
3、 sin45°、 cos45°、 tan45°等于多少呢?你是怎样得到的?与同伴交流.
450
450
┌
x
x
三角函数 300 锐角α
正弦sinα
余弦cosα
正切tanα
2x
600
3x
┌ x
300 450
1 2
3 2
3 3
2 2
3 2
2 2
1
3
2xxΒιβλιοθήκη 450600x
1 2
450 ┌
(2) sin2600+cos2600-tan450
反思：(1)含有特殊角的三角函数 3 1 2 1 2 2 值的计算步骤；
3 1 1 0. 4 4
2
(2)对于任意的锐角A， sin2A+cos2A=?
计算: (1)sin600-cos450; (2)cos600+tan600;
A
b
┌
C
4、特殊角300,450,600角的三角函数值. 5、互余两角之间的三角函数关系.
450
300 450
┌
600
┌
6、同角之间的三角函数关系
1、填写下表：

2.2_30度_45度_60度角的三角函数值

特殊角的三角函数值表三角函数锐角α 300 450 600 正弦 sinα 余弦 cosα
驶向胜利的彼岸
正切 tanα
驶向胜利的彼岸
特殊角的三角函数值表
三角函数正弦sinα 余弦cosα 正切tanα 锐角α
300
要能记住有多好
450 600
1 2 2 2 3 2
3 2 2 2 1 2
1．计算： (1)sin60°－tan45°； (2)cos60°＋tan60°； (3)sin45°＋sin60°－2cos45°．
达标测试

2.求下列各式中锐角A的值; 1 CosA= tanA= 3 sinA＝ 2
3 2
3 3
1
3
这张表还可以看出许多知识之间的内在联系?
例1 计算:
(1)sin300+cos450;(2) sin2600+cos2600-tan450. 解: (1)sin300+cos450 老师提示: 1 2 1 2 . 2600表示 Sin 2 2 2 0 2 (2) sin2600+cos2600-tan450 (sin60 ) ,
A
B c
a
b ┌ C
课内探究

（一）探索45°角的三角函数值．结合图2-5 sin45°=------- cos45°=-----tan45°=-------可以和同伴交流你是怎样想的？
课内探究

（二）探索30°，60°角的三角函数值．结合图2-6 Sin30°=------- cos30°=-----tan30°=-------Sin60°=------- cos60°=-----tan60°=--------

1.2 30°,45°,60°角的三角函数值

┌
┌
做一做
⑴ 60°角的三角函数值分别是多少?你是怎样得到的? ⑵ 45°角的三角函数值分别是多少?你是怎样得到的? ⑶ 完成下表:
三角函数值三角函数
sinα cosα tanα
1 2
2 2 3 2
角α
30° 45° 60°
3 2
2 2
3 3
1
1 2
3
例1 计算 ⑴ sin30°＋cos45°; ⑵ sin260°＋cos260°－tan45°. 解: 1 ⑴ sin30°＋cos45°＝ 2 ＋
1.2
30°，45°，60°角的三角函数值
⒈经历探索30°,45°,60°角的三角函数值的过程. ⒉能够进行含有30°,45°,60°角的三角函数值的计算. ⒊能够根据30°,45°,60°角的三角函数值说出相应的锐角的大小.
观察一副三角尺,其中有几个锐角?它们分别等于多少度? ⑴ sin30°等于多少? 你是怎样得到的?与同伴进行交流. ⑵ cos30°等于多少? tan30°呢?
C．△ABC是等腰直角三角形
D．△ABC是锐角三角形
5.计算2sin30°-sin245°+tan30°的结果是（ B ）
1 A． 3 3 2
C．
ቤተ መጻሕፍቲ ባይዱ
1 3 B． 2 3
D．1 -
3 2
3 2
2
3 3-2 1 1 2 3 解：（ 1 ）原式 -1 （2）原式 3 2 2 2 2
（3）原式 2 2 3 2 - 2 2 2 2 2
1 3 - 2 2 2 1 3 - 2 2 2
⒉某商场有一自动扶梯,其倾斜角为30°, 高为7m.扶梯的长度是多少?

30°,45°,60°角的三角函数值

1.2 30°，45°，60°角的三角函数值学习目标：1.运用三角函数的概念，自主探索，求出30°、 45°、60°角的三角函数值；（重点）2.熟记三个特殊锐角的三角函数值，并能准确地加以运用.(难点)学习方法：自主探索法学习过程：一、复习导入锐角三角函数的定义：sinA= .cosA= .tanA= .那么我们非常熟悉的30°，45°，60°角的三角函数值你会算吗？二、新课1.探究30°，60°角的三角函数值。

如图1，在Rt△ABC 中，△C=90°，△A=30°，若设BC=a.(1)则AB= ，AC= △B= 。

(2)根据三角函数定义，sinA=sin30°= ，cosA=cos30°= ，tanA=tan30°= . (3) 根据三角函数定义，sinB=sin60°= ，cosB=cos60°= ，tanB=tan60°= .2.探究45°角的三角函数值。

如图2，在Rt△ABC 中，△C=90°，△A=45°，若设BC=a. (1)AC= ,AB= ,△B= 。

(2)分别求出sin45°，cos45° ，tan45°的值。

sin45°= ，cos45°= ，tan45°= .(3)完成下列表格[例1]计算：(1)sin30°+cos45°； (2)sin 260°+cos 260°-tan45°.[例2] 如图3，在Rt△ABC 中，△C ＝90°，3,6==BC AB ，求△A 的度数．角度三角函数值30° 45° 60° sin cos tanAB Cc abA BC图1B C A 图2BCA例3：如图4，在鱼塘两侧有两棵树A ，B ，小华要测量此两树之间的距离，他在距A30m 的C 处测得△ACB=30°，又在B 处测得△ABC=120°.求A,B 两棵树之间的距离。

九年级上册数学 30°、45°、60°角的三角函数值

§1.2 30°、45°、60°角的三角函数值学习目标：1.经历探索30°、45°、60°角的三角函数值的过程，能够进行有关的推理.进一步体会三角函数的意义.2.能够进行30°、45°、60°角的三角函数值的计算.3.能够根据30°、45°、60°的三角函数值说明相应的锐角的大小.学习重点：1.探索30°、45°、60°角的三角函数值.2.能够进行含30°、45°、60°角的三角函数值的计算.3.比较锐角三角函数值的大小.学习难点：进一步体会三角函数的意义.学习方法：自主探索法学习过程：一、问题引入[问题]为了测量一棵大树的高度，准备了如下测量工具：①含30°和60°两个锐角的三角尺；②皮尺.请你设计一个测量方案，能测出一棵大树的高度.二、新课[问题] 1、观察一副三角尺，其中有几个锐角?它们分别等于多少度?[问题] 2、sin30°等于多少呢?你是怎样得到的?与同伴交流.[问题] 3、cos30°等于多少?tan30°呢?[问题] 4、我们求出了30°角的三个三角函数值，还有两个特殊角——45°、60°，它们的三角函数值分别是多少?你是如何得到的?(1)sin30°+cos45°； (2)sin260°+cos260°-tan45°.[例2]一个小孩荡秋千，秋千链子的长度为2.5 m，当秋千向两边摆动时，摆角恰好为60°，且两边的摆动角度相同，求它摆至最高位置时与其摆至最低位置时的高度之差.(结果精确到0.01 m)三、随堂练习 1.计算：(1)sin60°-tan45°； (2)cos60°+tan60°；(3) 22sin45°+sin60°-2cos45°； ⑷13230sin 1+-︒；⑸(2+1)-1+2sin30°-8； ⑹(1+2)0-｜1-sin30°｜1+(21)-1；⑺sin60°+︒-60tan 11； ⑻2-3-(0032+π)0-cos60°-211-.2.某商场有一自动扶梯，其倾斜角为30°.高为7 m ，扶梯的长度是多少?3．如图为住宅区内的两幢楼，它们的高AB ＝CD=30 m ，两楼问的距离AC=24 m ，现需了解甲楼对乙楼的采光影响情况.当太阳光与水平线的夹角为30°时，求甲楼的影子在乙楼上有多高?(精确到0.1 m ，2≈1.41，3≈1.73)四、课后练习：1、Rt △ABC 中，8,60=︒=∠c A ，则__________,==b a ； 2、在△ABC 中，若2,32==b c ,，则____tan =B ，面积S ＝； 3、在△ABC 中，AC ：BC ＝1：3，AB ＝6，∠B ＝，AC ＝ BC ＝ 4、等腰三角形底边与底边上的高的比是3:2，则顶角为（）（A ）600（B ）900（C ）1200（D ）1505、有一个角是︒30的直角三角形，斜边为cm 1，则斜边上的高为（）（A ）cm 41 （B ）cm 21 （C ）cm 43 （D ）cm 23 6、在ABC ∆中，︒=∠90C ，若A B ∠=∠2，则tanA 等于（）．（A ）3 （B ）33（C ）23 （D ）217、如果∠a 是等边三角形的一个内角，那么cos a 的值等于（）．（A ）21 （B ）22（C ）23 （D ）1 8、某市在“旧城改造”中计划内一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米a元，则购买这种草皮至少要（）．（A ）450a 元（B ）225a 元（C ）150a 元（D ）300a 元9、计算：︒15020米30米⑴、︒+︒60cos 60sin 22 ⑵、︒︒-︒30cos 30sin 260sin⑶、︒-︒45cos 30sin 2⑷、3245cos 2-+︒⑸、045cos 360sin 2+ ⑹、 130sin 560cos 300-⑺、︒30sin 22·︒+︒60cos 30tan tan60° ⑻、︒-︒30tan 45sin 2210、请设计一种方案计算tan15°的值。

2 30°,45°,60°角的三角函数值

B c 直角三角形三边的关系. 直角三角形三边的关系. 直角三角形两锐角的关系. 直角三角形两锐角的关系. 直角三角形边与角之间的关系. 直角三角形边与角之间的关系. 特殊角30°,45°,60°角的三角函数值. 特殊角30°,45°,60°角的三角函数值. 30 互余两角之间的三角函数关系. 互余两角之间的三角函数关系. 同角之间的三角函数关系
B
┌C D A
1.计算: 1.计算: 计算 (1)sin60° cos45° (1)sin60°-cos45°; (2)cos60°+tan60°; (2)cos60°+tan60°
( 3)
2 sin45°+sin60°− 2cos45°. 2
2 2 ( 4) sin 30°+ cos2 60°− 2cos2 45°. 2
a sin A= , c b sin B = , c
sinA=cosB, cosA=sinB
b cos A= , c a cos B = , c
A
B c a b ┌ C
3.sinA和 cosA和sinB有什么关系有什么关系? 3.sinA和cosB, cosA和sinB有什么关系?
如图,观察一副三角板: 如图,观察一副三角板: 它们其中有几个锐角?分别是多少度? 它们其中有几个锐角?分别是多少度?
sin45°的结果等于（ 2．（2010·荆门中考）计算 2 sin45°的结果等于（）．（2010·荆门中考） 2010·荆门中考 A． 2 B．1
1 C． 2
2 D． 2
【答案】选B. 答案】
3．（2010·眉山中考）如图，已知在梯形ABCD中，．（2010·眉山中考）如图，已知在梯形ABCD中 2010·眉山中考 ABCD AD∥BC， B=30° C=60° AD=4， AD∥BC，∠B=30°，∠C=60°，AD=4，AB= 3 3 ，则下底BC的长为 __________．则下底BC的长为 __________． BC

30度60度45度的正弦余弦正切值

深入探讨30度、60度和45度的正弦、余弦和正切值，需要从简单的数学概念开始逐步展开，让读者能够全面地理解这些三角函数的概念和性质。

一、简介在数学中，三角函数是研究角和角的变化关系的重要工具。

其中，正弦、余弦和正切是最常见的三角函数。

它们描述了角度和直角三角形边之间的关系。

在本文中，我们将着重讨论特定角度下的正弦、余弦和正切值，即30度、60度和45度，探究它们在数学和实际问题中的应用。

二、30度的正弦、余弦和正切值1. 正弦值：在直角三角形中，30度角的正弦值可以表示为对边与斜边的比值。

即sin(30°) = 1/2。

2. 余弦值：30度角的余弦值可以表示为邻边与斜边的比值。

即cos(30°) = √3/2。

3. 正切值：30度角的正切值可以表示为对边与邻边的比值。

即tan(30°) = 1/√3。

三、60度的正弦、余弦和正切值1. 正弦值：在直角三角形中，60度角的正弦值可以表示为对边与斜边的比值。

即sin(60°) = √3/2。

2. 余弦值：60度角的余弦值可以表示为邻边与斜边的比值。

即cos(60°) = 1/2。

3. 正切值：60度角的正切值可以表示为对边与邻边的比值。

即tan(60°) = √3。

四、45度的正弦、余弦和正切值1. 正弦值：在直角三角形中，45度角的正弦值可以表示为对边与斜边的比值。

即sin(45°) = 1/√2。

2. 余弦值：45度角的余弦值可以表示为邻边与斜边的比值。

即cos(45°) = 1/√2。

3. 正切值：45度角的正切值可以表示为对边与邻边的比值。

即tan(45°) = 1。

五、总结与回顾通过对30度、60度和45度的正弦、余弦和正切值的深入探讨，我们可以发现它们之间的关系和特点。

正弦值描述了角度对应的三角形的竖直分量，余弦值描述了水平分量，而正切值则描述了这两个分量之间的比例关系。

30°、45°、60°角的三角函数值

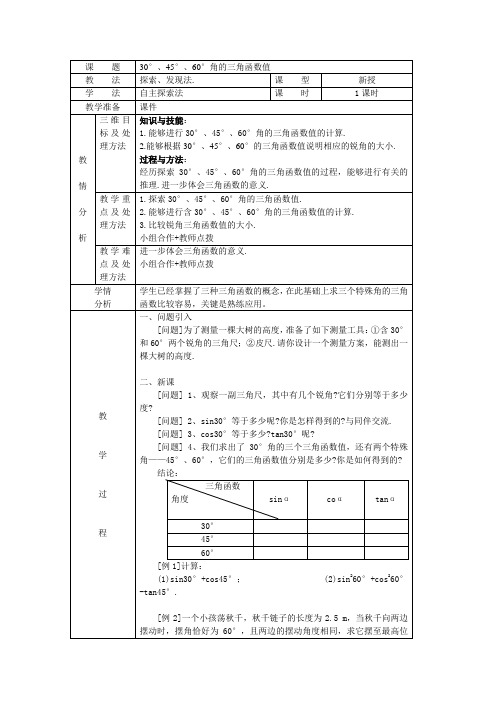
置时与其摆至最低位置时的高度之差.(结果精确到0.01 m)
三、随堂练习 1.计算：
(1)sin60°-tan45°； (2)cos60°+tan60°；
(3) 22sin45°+sin60°-2cos45°； ⑷1
3230sin 1+-
︒；
⑸(
2+1)-1+2sin30°-8； ⑹(1+2)0-｜
1-sin30°｜1+(2
1)-1
；
⑺sin60°+
︒
-60tan 11； ⑻2-3
-(
0032+
π)0
-cos60°-
2
11
-.
2.某商场有一自动扶梯，其倾斜角为30°.高为7 m ，扶梯的长度是多少?
3．如图为住宅区内的两幢楼，它们的高AB ＝CD=30 m ，两楼问的距离AC=24 m ，现需了解甲楼对乙楼的采光影响情况.当太阳光与水平线的夹角为30°时，求甲楼的影子在乙楼上有多高?(精确到0.1 m ，2≈1.41，3≈1.73)
四、课后练习：
1、Rt △ABC 中，8,60=︒=∠c A ，则__________,
==b a ； 2、在△ABC 中，若2,32==b c ,，则____tan =B ，面积S ＝；
3、在△ABC 中，AC ：BC ＝1：3，AB ＝6，∠B ＝，AC ＝ BC ＝
4、等腰三角形底边与底边上的高的比是3:2，则顶角为（）（A ）600
（B ）900
（C ）1200
（D ）150
5、有一个角是︒30的直角三角形，斜边为cm 1，则斜边上的高为（）。

§. 30°,45°,60°角的三角函数值

§1.2 30°，45°，60°角的三角函数值教学目标（一）知识与技能 1．经历探索 30°、45°、60°角的三角函数值的过程，能够实行相关的推理，进一步体会三角函数的意义． 2．能够实行 30°、45°、60°角的三角函数值的计算． 3．能够根据 30°、45°、60°的三角函数值说明相对应的锐角的大小． 1．经历探索 30°、45°、60°角的三角函数值的过程，培养学生观察、分析、发现的水平． 2．培养学生把实际问题转化为数学问题的水平．（三）情感与价值观 1．积极参与数学活动，对数学产生好奇心，培养学生独立思考问题的习惯． 2．在数学活动中获得成功的体验，锻炼克服困难的意志，建立自信心．教学重点 1．探索 30°、45°、60°角的三角函数值． 2．能够实行含 30°、45°、60°角的三角函数值的计算． 3．比较锐角三角函数值的大小．教学难点进一步体会三角函数的意义．教学方法自主探索法教学过程一．创设问题情境，引入新课 [问题]为了测量一棵大树的高度，准备了如下测量工具：① 含 30°和 60°两个锐角的三角尺；②皮尺．请你设计一个测量方案，能测出一棵大树的高度． [生]我们组设计的方案如下：让一位同学拿着三角尺站在一个适当的位置 B 处，使这位同学拿起三角尺，她的视线恰好和斜边重合且过树梢 C 点，30°的邻边和水平方向平行，用卷尺测出 AB 的长度，BE 的长度，因为 DE＝AB，所以只需在 Rt△CDA 中求出 CD 的长度即可．[生]在 Rt△ACD 中，∠CAD＝30°，AD＝BE，BE 是已知的，设 BE＝a 米，则 AD＝a 米，如何求 CD 呢？[生]含 30°角的直角三角形有一个非常重要的性质：30°的角所对的边等于斜边的一半，即 AC＝2CD，根据勾股定理，(2CD)2 ＝CD2＋a2，CD＝ 3 a．3则树的高度即可求出． [师]我们前面学习了三角函数的定义，如果一个角的大小确定，那么它的正切、正弦、余弦值也随之确定，如果能求出 30° 的正切值，在上图中，tan30°＝ CD CD ，则 CD＝atan30°，岂AD a不简单．你能求出 30°角的三个三角函数值吗？二．讲授新课 1．探索 30°、45°、60°角的三角函数值． [师]观察一副三角尺，其中有几个锐角？它们分别等于多少度？ [生]一副三角尺中有四个锐角，它们分别是 30°、60°、45°、45°． [师]sin30°等于多少呢？你是怎样得到的？与同伴交流． [生]sin30°＝ 1 ．sin30°表示在直角三角形中，30°角的对2边与斜边的比值，与直角三角形的大小无关．我们不妨设 30°角所对的边为 a(如图所示)，根据“直角三角形中 30°角所对的边等于斜边的一半”的性质，则斜边等于 2a．根据勾股定理，可知 30°角的邻边为 3 a，所以 sin30°＝ a 1 ．2a 2[师]cos30°等于多少？tan30°呢？[生]cos30°＝ 3a 3 ．2a 2tan30°＝ a 1 3 ．3a 3 3[师]我们求出了 30°角的三个三角函数值，还有两个特殊角— —45°、60°，它们的三角函数值分别是多少？你是如何得到的？[生]求 60°的三角函数值能够利用求 30°角三角函数值的三角形．因为 30°角的对边和邻边分别是 60°角的邻边和对边．利用上图，很容易求得sin60°＝ 3a 3 ，2a 2cos60°＝ a 1 ，2a 2tan60°＝ 3a 3 ．a[生]也能够利用上节课我们得出的结论：一锐角的正弦等于它余角的余弦，一锐角的余弦等于它余角的正弦．可知sin60°＝cos(90°－60°)＝cos30°＝ 3 ，2cos60°＝sin(90°－60°)＝sin30°＝ 1 ．2[师生共析]我们一同来求 45°角的三角函数值．含 45°角的直角三角形是等腰直角三角形．(如图)设其中一条直角边为 a，则另一条直角边也为 a，斜边为 2 a．由此可求得sin45°＝ a 1 2 ，2a 2 2cos45°＝ a 1 2 ，2a 2 2tan45°＝ a ＝1．a[师]下面请同学们完成下表(用多媒体演示)30°、45°、60°角的三角函数值三角函数角sctinosanααα130°2245°21360°2这个表格中的 30°、45°、60°角的三角函数值需熟记，另一方面，要能够根据 30°、45°、60°角的三角函数值，说出相应的锐角的大小．为了帮助大家记忆，我们观察表格中函数值的特点．先看第一列 30°、45°、60°角的正弦值，你能发现什么规律呢？[生]30°、45°、60°角的正弦值分母都为 2，分子从小到大分别为 1， 2 ， 3 随着角度的增大，正弦值在逐渐增大．[师]再来看第二列函数值，有何特点呢？ [生]第二列是 30°、45°、60°角的余弦值，它们的分母也都是 2，而分子从大到小分别为 3 ， 2 ，1，余弦值随角度的增大而减小． [师]第三列呢？ [生]第三列是 30°、45°、60°角的正切值，首先 45°角是等腰直角三角形中的一个锐角，所以 tan45°＝1 比较特殊． [师]很好，掌握了上述规律，记忆就方便多了．下面同桌之间可互相检查一下对 30°、45°、60°角的三角函数值的记忆情况．相信同学们一定做得很棒． 2．例题讲解(多媒体演示) [例 1]计算： (1)sin30°＋cos45°； (2)sin260°＋cos260°－tan45°．分析：本题旨在帮助学生巩固特殊角的三角函数值，今后若无特别说明，用特殊角三角函数值进行计算时，一般不取近似值，另外 sin260°表示(sin60°)2，cos260°表示(cos60°)2．解：(1)sin30°＋cos45°＝ 1 2 1 2 ；222(2)sin260°＋cos260°－tan45°＝( 3 )2＋( 1 )2－122＝ 3 1 －144＝0．[例 2]一个小孩荡秋千，秋千链子的长度为 2.5m，当秋千向两边摆动时，摆角恰好为 60°，且两边的摆动角度相同，求它摆至最高位置时与其摆至最低位置时的高度之差．(结果精确到0.01m) 分析：引导学生根据题意画出示意图，培养学生把实际问题转化为数学问题的能力．解：根据题意(如图)可知，∠BOD＝60°，OB＝OA＝OD＝2.5m，∠AOD＝ 1 ×60°＝30°，∴OC＝OD·cos30°＝2.5× 322≈2.165(m)．∴AC＝2.5－2.165≈0.34(m)．所以，最高位置与最低位置的高度约为 0.34m．三．随堂练习多媒体演示 1．计算： (1)sin60°－tan45°； (2)cos60°＋tan60°；(3) 2 sin45°＋sin60°－2cos45°．2解：(1)原式＝ 3 －1＝ 3 2 ；22(2)原式＝ 1 3 1 2 3 ；22(3)原式＝ 2 2 3 2 2 ；22 22＝1 3 2 2 ．22．某商场有一自动扶梯，其倾斜角为 30°，高为 7m，扶梯的长度是多少？解：扶梯的长度为 7 7 ＝14(m)，sin 30 1 2所以扶梯的长度为 14m．四．课堂小结本节课总结如下：(1)探索 30°、45°、60°角的三角函数值．sin30°＝ 1 ，sin45°＝ 2 ，sin60°＝ 3 ；222cos30°＝ 3 ，cos45°＝ 2 ，cos60°＝ 1 ；222tan30°＝ 3 ，tan45°＝1，tan60°＝ 3 ．3(2)能进行含 30°、45°、60°角的三角函数值的计算． (3)能根据 30°、45°、60°角的三角函数值，说出相应锐角的大小．五．课后作业习题 1．3 第 1、2 题课后反思。

30_°_45°_60°角的三角函数值

1.2. 30 °,45°,60°角的三角函数值姓名______________准备知识：1.在直角三角形中，30°角所对的直角边等于 .2. 在Rt△ABC中，∠C=90°，∠A＝30°,如果AC＝2,则BC＝ .AB＝ .3.在Rt△ABC中，∠C=90°，∠A＝45°,如果AC＝2,则AB＝ .如果AB＝4,则BC＝ .如果AB＝a,则BC= .自学提示：[问题] 1、观察一副三角尺，其中有几个锐角?它们分别等于多少度?[问题] 2、 sin30°等于多少呢?[问题] 3、 cos30°等于多少? tan30°呢?[问题] 4、我们求出了30°角的三个三角函数值，还有两个特殊角——45°、60°，它们的三角函数值分别是多少?你是如何得到的?结论：问题5对应练习：对于锐角A：若sin A=1/2，则∠A= ；若tanA=1,则cos A= 。

计算：温馨提示：sin260°即（sin60°）2(1)sin30°+cos45°； (2)sin260°+cos260°-tan45°.问题6．一个小孩荡秋千，秋千链子的长度为4 m，当秋千向两边摆动时，摆角恰好为60°，且两边的摆动角度相同，求它摆至最高位置时与其摆至最低位置时的高度之差.(结果精确到0.01 m)基础训练：1．已知△ABC 中，∠C =90°，∠B =30°，则cos A 等于_______________．2 cos A =23（A 为锐角），则∠A 的度数为______________3．若cos B =22，则∠B =__________度．（为锐角）4．在△ABC 中，∠C =90°，若cos A =21，则sin A =__________．5．在△ABC 中，∠C =90°，3a =3b ，则sin A __________．6．在△ABC 中，若｜sin A -1｜+0)cos 23(2=-B ，则∠C 的度数是_______．．设等腰三角形的腰长为2cm ，底边长为32cm ，则顶角为_______度．．在△ABC 中，已知∠A =60°，∠B =75°，AB =6，则BC =______．．如图：△ABC 中，∠C =90°，AB =310，cos B =21，D 为AC 上一点，且∠DBC =30°，AD 的长为___________．（10）22cos45°-21cos60°+sin60°cos30°．（11） ︒︒-︒+︒45tan 45cot 60sin 30sin 22（12）． 3245cos 2-+︒ （ 13）cos30°︒+︒⋅30sin 130cos14. 如上图所示，已知：在△ABC 中，∠A=60°，∠B=45°，AB=8.求：△ABC 的面积(结果可保留根号).。