高考数学出题人预测专题08 立体几何中线段与面积等求解问题(第三篇)(解析版)

合集下载

2020年高考数学(理)重难点专练03 空间向量与立体几何(解析版)

2020年高考数学（理）重难点03 空间向量与立体几何【高考考试趋势】立体几何在高考数学是一个必考知识点，一直在高中数学中占有很大的分值，未来的高考中立体几何也会持续成为高考的一个热点，理科高考中立体几何主要考查三视图的相关性质利用，简单几何体的体积，表面积以及外接圆问题.另外选择部分主要考查在点线面位置关系，简单几何体三视图.选择题主要还是以几何体的基本性质为主，解答题部分主要考查平行，垂直关系以及二面角问题.前面的重点专题已经对立体几何进行了一系列详细的说明，本专题继续加强对高考中立体几何出现的习题以及对应的题目类型进行必要的加强.本专题包含了高考中几乎所有题型，学完本专题以后，对以后所有的立体几何你将有一个更加清晰的认识.【知识点分析以及满分技巧】基础知识点考查：一般来说遵循三短一长选最长.要学会抽象问题具体会，将题目中的直线转化成显示中的具体事务，例如立体坐标系可以看做是一个教室的墙角有关外接圆问题：一般图形可以采用补形法，将几何体补成正方体或者是长方体，再利用不在同一个平面的四点确定一个立体平面原理，从而去求.内切圆问题：转化成正方体的内切圆去求.求点到平面的距离问题：采用等体积法.求几何体的表面积体积问题：应注意巧妙选取底面积与高.对于二面角问题应采用建立立体坐标系去求.但是坐标系要注意采用左手系务必要标记准确对应点以及法向量对应的坐标.【常见题型限时检测】（建议用时：35分钟）一、单选题1．（2019·遵义航天高级中学高考模拟（理））一个几何体的三视图如图所示，则该几何体的体积为（）A．83B．163C．203D．8【答案】B 【解析】由图可知该几何体底面积为8，高为2的四棱锥，如图所示：∴该几何体的体积1168233V =⨯⨯= 故选B【点睛】：思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽. 2．（2019·天津高考模拟（理））已知四面体ABCD 的四个面都为直角三角形，且AB ⊥平面BCD ，2AB BD CD ===，若该四面体的四个顶点都在球O 的表面上，则球O 的表面积为（）A ．3πB ．C ．D ．12π【答案】D 【解析】【分析】由已知中的垂直关系可将四面体放入正方体中，求解正方体的外接球表面积即为所求的四面体外接球的表面积；利用正方体外接球半径为其体对角线的一半，求得半径，代入面积公式求得结果. 【详解】2BD CD ==Q 且BCD ∆为直角三角形 BD CD ∴⊥又AB ⊥平面BCD ，CD ⊂平面BCD CD AB ∴⊥CD \^平面ABD由此可将四面体ABCD 放入边长为2的正方体中，如下图所示：∴正方体的外接球即为该四面体的外接球O正方体外接球半径为体对角线的一半，即12R == ∴球O 的表面积：2412S R ππ==本题正确选项：D 【点睛】本题考查多面体的外接球表面积的求解问题，关键是能够通过线面之间的位置关系，将所求四面体放入正方体中，通过求解正方体外接球来求得结果.3．（2019·河南高考模拟（理））如图，点P 在正方体1111ABCD A B C D -的面对角线1BC 上运动，则下列四个结论：①三棱锥1A D PC -的体积不变；1//A P ②平面1ACD ； 1DP BC ⊥③；④平面1PDB ⊥平面1ACD ．其中正确的结论的个数是( )A ．1个B ．2个C ．3个D ．4个【答案】C 【解析】【分析】利用空间中线线、线面、面面间的位置关系求解．【详解】对于①，由题意知11//AD BC ，从而1//BC 平面1AD C ，故BC 1上任意一点到平面1AD C 的距离均相等，所以以P 为顶点，平面1AD C 为底面，则三棱锥1A D PC -的体积不变，故①正确；对于②，连接1A B ，11A C ，111//AC AD 且相等，由于①知：11//AD BC ，所以11//BA C 面1ACD ，从而由线面平行的定义可得，故②正确；对于③，由于DC ⊥平面11BCB C ，所以1DC BC ⊥，若1DP BC ⊥，则1BC ⊥平面DCP ，1BC PC ⊥，则P 为中点，与P 为动点矛盾，故③错误；对于④，连接1DB ，由1DB AC ⊥且11DB AD ⊥，可得1DB ⊥面1ACD ，从而由面面垂直的判定知，故④正确．故选：C ．【点睛】本题考查命题真假的判断，解题时要注意三棱锥体积求法中的等体积法、线面平行、垂直的判定，要注意使用转化的思想．4．（2019·贵州高考模拟（理））设,m n 是两条不同的直线，,αβ是两个不同的平面，有下列四个命题：∴若m α⊂，αβ⊥，则m β⊥； ∴若//a β，m β⊂，则//m α； ∴若m α⊥，//m n ，//αβ，则n β⊥； ∴若//m α，//n β，//m n ，则//αβ其中正确命题的序号是（） A ．∴∴ B ．∴∴C ．∴∴D ．∴∴【答案】C 【解析】∴两个面垂直，推不出面中任意直线和另一个面垂直，错误；故排除A 、B 选项，对于∴，两个平行平面，其中一个平面内的任意直线都和另一个平面平行，故正确，所以选C.5．（2019·福建高考模拟（理））在三棱锥P ABC -中，3PA PB ==，BC =8AC =，AB BC ⊥，平面PAB ⊥平面ABC ，若球O 是三棱锥P ABC -的外接球，则球O 的半径为（）．A B C D ．2【答案】A 【解析】【分析】取AB 中点D ，AC 中点E ，连PD ，ED ，得E 为∴ABC 外接圆的圆心，且OE∴平面PAB ，然后求出∴PAB 的外接圆半径r 和球心O 到平面PAB 的距离等于d ，由勾股定理得R .【详解】解：取AB 中点D ，AC 中点E ，连PD ，ED 因为AB BC ⊥，所以E 为∴ABC 外接圆的圆心因为OE∴PD ，OE 不包含于平面PAB ，所以OE∴平面PAB 因为平面PAB ⊥平面ABC ，3PA PB ==，得PD ⊥AB ，ED ⊥AB 所以PD ⊥平面ABC ，ED ⊥平面PAB且AB ==PD 1=所以球心O 到平面PAB 的距离等于ED d ==在∴PAB 中，3PA PB ==，AB =1sin 3PAB ∠=，所以∴PAB 得外接圆半径2r 9sin PB PAB ∠==，即9r 2=由勾股定理可得球O 的半径R ==故选：A. 【点睛】本题考查了三棱锥的外接球问题，经常用球中勾股定理R =R 是外接球半径，d 是球心到截面距离，r 是截面外接圆半径.二、解答题6．（2019·山东高考模拟（理））如图，在四棱锥P ABCD -中，PC ⊥底面ABCD ，底面ABCD 是直角梯形,//AB AD AB CD ⊥，224AB AD CD ===，4PC =.（1）证明：当点E 在PB 上运动时，始终有平面EAC ⊥平面PBC ；（2）求锐二而角A PB C --的余弦值.【答案】（1）证明见解析；（2）5. 【解析】【分析】（1）由PC ⊥底面ABCD ，证得AC PC ⊥，又由勾股定理，得AC CB ⊥，利用线面垂直的判定定理，得到AC ⊥平面PBC ，再由面面垂直的判定定理，可得平面EAC ⊥平面PBC ，即可得到结论；（2）分别以CD ，CF ，CP 所在直线为x ，y ，z 轴建立空间直角坐标系，求得平面PBC 和平面PAB 的法向量，利用向量的夹角公式，即可求解．【详解】（1）由题意，因为PC ⊥底面ABCD ，AC ⊂平面ABCD ，所以AC PC ⊥，又因为224AB AD CD ===，所以4AB =，2AD CD ==，所以AC BC ==，所以222AC BC AB +=，从而得到AC CB ⊥．又BC ⊂Q 平面PBC ，PC ⊂平面PBC ，BC PC C ⋂=，所以AC ⊥平面PBC ，又AC ⊂Q 平面ACE ，所以平面EAC ⊥平面PBC ，所以当点E 在PB 上运动时，始终有平面EAC ⊥平面PBC. （2）由条件知PC ⊥底面ABCD ，且AB AD ⊥， AB C D ∥所以过点C 作CF CD ⊥交AB 于点F ，分别以CD ，CF ，CP 所在直线为x ，y ，z 轴建立空间直角坐标系（如图所示），所以(0,0,0)C ，(2,2,0)A ，(2,2,0)B -，(0,0,4)P .由（1）知CA u u u r为平面PBC 的一个法向量，因为(2,2,0)CA =u u u r，(2,2,4)PA =-u u u r (2,2,4)PB =--u u u r ，设平面P AB 的一个法向量为(,,)n=x y z r，则(,,)(2,2,4)00(,,)(2,2,4)00x y z n PA x y z n PB ⎧⋅-=⎧⋅=⇒⎨⎨⋅--=⋅=⎩⎩u uu v r u u u v r ，即02x y z=⎧⎨=⎩，令1z =，则2y =，所以(0,2,1)n =r，所以|||cos ,|5||||CA n CA n CA n ⋅〈〉===uu r ruu r r uu r r ，故锐二面角A PB C --的余弦值5．【点睛】本题考查了线面垂直与面面垂直的判定与证明，以及空间角的求解问题，意在考查学生的空间想象能力和逻辑推理能力，解答中熟记线面位置关系的判定定理和性质定理，通过严密推理是线面位置关系判定的关键，同时对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.7（2017·广东高考模拟（理））如图，在四棱锥P ABCD -中，90,60ABC ACD BAC CAD ∠=∠=︒∠=∠=︒， PA ⊥平面ABCD ，2,1PA AB ==.(1)设点E 为PD 的中点，求证： //CE 平面PAB ；(2)线段PD 上是否存在一点N ，使得直线CN 与平面PAC 所成的角θ的正弦值为5？若存在，试确定点N 的位置；若不存在，请说明理由. 8．（2019·天津市新华中学高考模拟（理））如图所示的几何体中，PD 垂直于梯形ABCD所在的平面，,2ADC BAD F π∠=∠=为PA 的中点，112PD AB AD CD ====，四边形PDCE 为矩形，线段PC 交DE 于点N .（1）求证：AC P 平面DEF ；（2）求二面角A PB C --的正弦值；（3）在线段EF 上是否存在一点Q ，使得BQ 与平面BCP 所成角的大小为π6？若存在，求出FQ 的长；若不存在，请说明理由.【答案】（1）见解析（23）在线段EF 上存在一点Q 满足题意，且FQ =【解析】【分析】(1)由题意结合线面平行的判定定理即可证得题中的结论；(2)建立空间直角坐标系，利用两个半平面的法向量可得二面角的余弦值，然后利用同角三角函数基本关系可得二面角的正弦值；(3)假设点Q 存在，利用直线的方向向量和平面的法向量计算可得点Q 的存在性和位置. 【详解】（1）因为四边形PDCE 为矩形，所以N 为PC 的中点.连接FN ，在PAC V 中，,F N 分别为,PA PC 的中点，所以FN AC ∥，因为FN ⊂平面DEF ，AC ⊄平面DEF ，所以AC P 平面DEF .（2）易知,,DA DC DP 两两垂直，如图以D 为原点，分别以,,DA DC DP 所在直线为,,x y z 轴，建立空间直角坐标系.则(1,0,0),(1,1,0),(0,2,0)P A B C，所以(1,1,,(1,1,0)PB BC ==-u u u r u u u r.设平面PBC 的法向量为(,,)m x y z =r，则(,,)(1,1,0(,,)(1,1,0)0m PB x y z m BC x y z ⎧⋅=⋅=⎪⎨⋅=⋅-=⎪⎩u u u v r u u u v r即0,0,x y x y ⎧+=⎪⎨-+=⎪⎩解得,,y x z =⎧⎪⎨=⎪⎩令1x =，得1,y z =⎧⎪⎨=⎪⎩所以平面PBC的一个法向量为m =r. 设平面ABP 的法向量为(,,)n x y z =r，(,,)(0,1,0)0(,,)(1,1,0n AB x y z n PB x y z ⎧⋅=⋅=⎪⎨⋅=⋅-=⎪⎩u u uv r u u uv r ，据此可得01x y z ⎧=⎪=⎨⎪=⎩，则平面ABP的一个法向量为)n =r，cos ,3m n <>==u r r，于是sin ,3m n 〈〉=r r. 故二面角A PB C --（3）设存在点Q 满足条件.由1,0,,(0,22F E ⎛⎫ ⎪ ⎪⎝⎭，设(01)FQ FE λλ=u u u r u u u r &剟，整理得1),2,22Q λλλ⎛⎫-+ ⎪ ⎪⎝⎭，则1,22BQ λλ⎛+=-- ⎝⎭u u u r . 因为直线BQ 与平面BCP 所成角的大小为6π，所以1sin |cos ,|||62||||BQ m BQ m BQ m π⋅====⋅u u u r u ru u u r u r u u ur u r 解得21λ=，由知1λ=，即点Q 与E 重合.故在线段EF 上存在一点Q，且FQ EF ==. 【点睛】本题的核心在考查空间向量的应用，需要注意以下问题：(1)求解本题要注意两点：一是两平面的法向量的夹角不一定是所求的二面角，二是利用方程思想进行向量运算，要认真细心，准确计算．(2)设,m n u r r 分别为平面α，β的法向量，则二面角θ与,m n <>u r r互补或相等.求解时一定要注意结合实际图形判断所求角是锐角还是钝角．9．（2019·山东高考模拟（理））如图，在四棱锥P ABCD -中，已知PA ⊥平面ABCD ，ABC ∆为等边三角形，22PA AB ==，AC CD ⊥，PD 与平面PAC 所成角的正切值为5.(∴)证明：//BC 平面PAD ；(∴)若M 是BP 的中点，求二面角P CD M --的余弦值.【答案】（∴）见解析.（∴ 【解析】【分析】(∴)先证明DPC ∠为PD 与平面PAC 所成的角，于是可得CD =60CAD ∠=︒．又由题意得到60BCA ∠=︒，故得//BC AD ，再根据线面平行的性质可得所证结论． (∴) 取BC 的中点N ，连接AN ，可证得AN AD ⊥．建立空间直角坐标系，分别求出平面PCD 和平面CDM 的法向量，根据两个法向量夹角的余弦值得到二面角的余弦值．【详解】(∴)证明：因为PA ⊥平面ABCD ，CD ⊂平面ABCD ，所以PA CD ⊥又AC CD ⊥,CA PA A =I , 所以CD ⊥平面PAC ，所以DPC ∠为PD 与平面PAC 所成的角．在Rt PCD V中，PC ==所以CD =所以在Rt PCD V 中，2AD =,60CAD ∠=︒. 又60BCA ∠=︒，所以在底面ABCD 中，//BC AD , 又AD ⊂平面PAD ，BC ⊄平面PAD ，所以//BC 平面PAD ．(∴)解：取BC 的中点N ，连接AN ，则AN BC ⊥,由(∴)知//BC AD ，所以AN AD ⊥，分别以AN ，AD ，AP 为x ，y ，z 轴建立空间直角坐标系Axyz .则(0,0,2)P，1,02C ⎫⎪⎪⎝⎭，(0,2,0)D，1,14M ⎫-⎪⎪⎝⎭所以3,,022CD ⎛⎫=- ⎪ ⎪⎝⎭uu u r ，(0,2,2)PD =-u u ur，9,,144DM ⎛⎫=- ⎪ ⎪⎝⎭uuu u r设平面PCD 的一个法向量为()1111,,n x y z =u r，由1100n CD n PD ⎧⋅=⎪⎨⋅=⎪⎩u u u vu u u v，即111130220y y z ⎧+=⎪⎨-=⎪⎩，得1111x z y ⎧=⎪⎨=⎪⎩，令11y =，则1,1)n =u r．设平面CDM 的一个法向量为()2222,,n x y z =u ur，由2200n CD n MD ⎧⋅=⎪⎨⋅=⎪⎩u u v u u u v u u v u u u u v，即2222230940y y z ⎧+=⎪-+=，得222232x y z ⎧=⎪⎨=⎪⎩，令21y =，则232n ⎫=⎪⎭u u r ．所以121212331cos ,||||n n n n n n ++⋅<>===⋅u r u u ru r u u r u r u u r 由图形可得二面角P CD M --为锐角，所以二面角P CD M --【点睛】空间向量是求解空间角的有利工具，根据平面的法向量、直线的方向向量的夹角可求得线面角、二面角等，解题时把几何问题转化为向量的运算的问题来求解，体现了转化思想方法的利用，不过解题中要注意向量的夹角和空间角之间的关系，特别是求二面角时，在求得法向量的夹角后，还要通过图形判断出二面角是锐角还是钝角，然后才能得到结论． 10．（2018·吉林高考模拟（理））如图，在棱长为2的正方体1111ABCD A B C D -中，E ，F ， M ， N 分别是棱AB ， AD ， 11A B ， 11A D 的中点，点P ， Q 分别在棱1DD ， 1BB 上移动，且(02)DP BQ λλ==<<.（1）当1λ=时，证明：直线1//BC 平面EFPQ ；（2）是否存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角？若存在，求出λ的值；若不存在，说明理由.【答案】（1）见解析；（2）12λ=±.【解析】以D 为原点，射线DA ， DC ， 1DD 分别为x ， y ， z 轴的正半轴建立如图所示的空间直角坐标系D xyz -.由已知得()2,2,0B ， ()10,2,2C ，()2,1,0E ，()1,0,0F ， ()0,0,P λ， ()1,0,2N ， ()2,1,2M ，则()12,0,2BC =-u u u u r， ()1,0,FP λ=-u u u r ， ()1,1,0FE =u u u r ， ()1,1,0NM =u u u u r ， ()1,0,2NP λ=--u u u r.（1）当1λ=时， ()1,0,1FP =-u u u r ，因为()12,0,2BC =-u u u u r ，所以12BC FP =u u u u r u u u r，即1//BC FP ，又FP ⊂平面EFPQ ，且1BC ⊄平面EFPQ ，故直线1//BC 平面EFPQ . （2）设平面EFPQ 的一个法向量为(),,n x y z =r，则由0{0FE n FP n ⋅=⋅=u u u r ru u u r r，得0{0.x y x z λ+=-+=，于是可取(),,1n λλ=-r . 设平面MNPQ 的一个法向量为()',','m x y z =r，由0{0NM m NP m ⋅=⋅=u u u u r ru u u r r，得()''0{'2'0x y x z λ+=-+-=，于是可取()2,2,1m λλ=--r. 若存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角，则()()2,2,1,,10m n λλλλ⋅=--⋅-=r r，即()()2210λλλλ---+=，解得1λ=±，显然满足02λ<<.故存在1λ=±，使面EFPQ 与面PQMN 所成的二面角为直二面角.点睛：立体几何的有关证明题，首先要熟悉各种证明的判定定理，然后在进行证明，要多总结题型，对于二面角问题一般直接建立空间直角坐标系，求出法向量然后根据向量夹角公式求解二面角，要注意每一个坐标的准确性。

高考数学核心考点必备专题8-2 立体几何截面问题的十种题型-(解析版)-2023年高考数学

专题8-2立体几何截面问题的十种题型目录一、热点题型归纳 (1)【题型一】做截面基本功：补全截面方法 .................................................................................................... 1 【题型二】截面形状的判断 ............................................................................................................................ 4 【题型三】平行关系确定截面 ........................................................................................................................ 8 【题型四】垂直关系确定的截面 .................................................................................................................. 10 【题型五】求截面周长 .................................................................................................................................. 13 【题型六】求截面面积 .................................................................................................................................. 17 【题型七】球截面 .......................................................................................................................................... 19 【题型八】截面分体积 .................................................................................................................................. 22 【题型九】不规则截面（曲线型截面） ...................................................................................................... 24 【题型十】截面最值 ...................................................................................................................................... 27 二、最新模考题组练 (30)【题型一】做截面的基本功：补全截面方法【典例分析】在长方体ABCD -A 1B 1C 1D 1中，AB=AA 1=2,AD=3,点E 、F 分别是AB 、AA 1的中点，点E 、F 、C 1∈平面α，直线A 1D 1⋂平面α=P ，则直线BP 与直线CD 1所成角的余弦值是3378 A 22 C B 3 D 3 99、、、、答案：B解析：如图，计算可得余弦值是223【提分秘籍】基本规律截面训练基础：模型：如下图E 、F 是几等分点，不影响作图。

【高考数学专题复习】第八章立体几何初步测试(解析版)

第八章立体几何初步测试一．单选题（每题5分，共12题，共60分）1．在四面体ABCD 中，3AB BD AD CD ====，4AC BC ==，用平行于AB ，CD 的平面截此四面体，得到截面四边形EFGH ，则四边形EFGH 面积的最大值为（）A ．43B ．94 C ．92 D ．3【答案】B【解析】设截面分别与棱,,,AD BD BC AC 交于点,,,E F G H .由直线//AB 平面EFGH ，且平面ABC I 平面EFGH GH =，平面ABD ⋂平面EFGH EF =得//GH AB ，//EF AB ，所以//GH EF ，同理可证//EH FG ，所以四边形EFGH 为平行四边形，又3AB BD AD CD ====，4AC BC ==，可证得AB CD ⊥，四边形EFGH 为矩形.设:::BF BD BG BC FG CD x ===，01x <<，则3FG x =，()31HG x =-，于是2199(1)9,0124EFGH S FG HG x x x x ⎛⎫=⋅=-=--+<< ⎪⎝⎭ 当12x =时，四边形EFGH 的面积有最大值94.故选：B.2．如图，四边形ABCD 是边长为1的正方形，MD ⊥ABCD ，NB ⊥ABCD ．且MD ＝NB ＝1．则下列结论中：①MC ⊥AN②DB ∥平面AMN③平面CMN ⊥平面AMN④平面DCM ∥平面ABN所有假命题的个数是（）A ．0B ．1C ．2D ．3【答案】B【解析】由题画出该几何体外接的正方体.对①,因为//MC EB ,AN EB ⊥,故MC ⊥AN 成立.故①正确.对②,因为//,DB MN MN ⊂平面AMN,故DB ∥平面AMN 成立.故②正确.对③,连接AC 易得A MNC -为正四面体.故平面CMN ⊥平面AMN 不成立.故③错误.对④,正方体中平面DCM 与平面ABN 分别为前后两面,故④正确.故选：B3．已知互相垂直的平面αβ，交于直线l.若直线m ，n 满足m ∥α，n ⊥β，则A ．m ∥lB ．m ∥nC ．n ⊥lD ．m ⊥n【答案】C【解析】由题意知,l l αββ⋂=∴⊂，,n n l β⊥∴⊥Q ．故选C ．4．设,αβ是两个不同的平面，l 是一条直线，以下命题正确的是（）A ．若,l ααβ⊥⊥，则l β⊂B ．若//,//l ααβ，则l β⊂C ．若,//l ααβ⊥，则l β⊥D ．若//,l ααβ⊥，则l β⊥【答案】C【解析】对于A 、B 、D 均可能出现//l β，而对于C 是正确的．5．已知正四棱柱中，，则CD 与平面所成角的正弦值等于（）A ．B ．C ．D ．【答案】A【解析】设，面积为6．在Rt ABC V 中，90ABC ∠=o ，P 为V ABC 所在平面外一点，PA ⊥平面ABC ，则四面体P ABC -中直角三角形的个数为（）A ．4B ．3C ．2D ．1【答案】A【解析】由题意，知PA ⊥平面ABC 可得PAC PAB ∆∆，都是直角三角形，且PA BC ⊥，又90ABC ∠=o ，所以V ABC 是直角三角形，且BC ⊥平面PAB ，所以BC PB ⊥，即PBC △为直角三角形.故四面体P ABC -中共有4个直角三角形.7．已知直线//l α，直线a α⊂，则l 与α必定（）A ．平行B ．异面C ．相交D ．无公共点【答案】D【解析】已知直线//l α，所以直线l 与平面α无公共点，又由a α⊂，所以直线l 与平面a 无公共点，故选D ．8．如图,各棱长均为a 的正三棱柱111ABC A B C -，M 、N 分别为线段1A B 、1B C 上的动点,且MN //平面11ACC A ,则这样的MN 有 ( )A ．1条B ．2条C ．3条D ．无数条【答案】D 【解析】由题意得112A B CB a==．在11,BA CB 上分别取,M N ，使1BM B N =，过,M N 作11,MM AB NN BC ⊥⊥，垂足分别为11,M N ，则1111,MM AA NN BB P P ，故11111,BM B N BN BM BA BA B C BC==．由于111B N BM BA B C =，故11BM BN BA BC=，从而11M N AC P ，可得11M N P 平面11ACC A ．又1MM P 平面11ACC A ，可得平面11MM N N P 平面11ACC A ．由于MN ⊂平面11MM N N ，所以//MN 平面11ACC A ，从而满足条件的MN 有无数条．选D ．9．正方体1111ABCD A B C D -中，直线AD 与平面11A BC 所成角正弦值为（）A ．12B ．32C ．33D ．63【答案】C【解析】如图所示，正方体1111ABCD A B C D -中，直线AD 与11B C 平行，则直线AD 与平面11A BC 所成角正弦值即为11B C 与平面11A BC 所成角正弦值.因为11A BC ∆为等边三角形，则1B 在平面11A BC 即为11A BC ∆的中心，则11B C O ∠为11B C 与平面11A BC 所成角.可设正方体边长为1，显然36=2=BO ⨯，因此2163=1()=3B O -，则1111103sin B B C O B C ∠==，故答案选C.10．如图所示，在正方体ABCD —A 1B 1C 1D 1中，若E 是A 1C 1的中点，则直线CE 垂直于( )A ．ACB ．BDC ．A 1D D ．A 1D 1【答案】B 【解析】以A 为原点，1AB AD AA ，，所在直线分别为x y z ，，轴建立空间直角坐标系，设正方体棱长为1，则()000A ，，，()110C ，，，()100B ，，，()010D ，，， ()1001A ，，，11122E ⎛⎫ ⎪⎝⎭，， 11122CE ⎛⎫∴=-- ⎪⎝⎭u u u v ，， ()110AC =u u u v ，，，()110BD =-u u u v ，，，()1011A D =-u u u u v ，，，()1001AA =-u u u v ，，110022CE BD ∴=-+=u u u v u u u v n 则CE BD ⊥u u u v u u u v 即CE BD ⊥故选B11．已知三棱锥S ABC -的所有顶点都在球O 的求面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =，则此棱锥的体积为（）A ．26B 3C ．23D ．22【答案】A【解析】根据题意作出图形：设球心为O ，过ABC 三点的小圆的圆心为O 1，则OO 1⊥平面ABC ，延长CO 1交球于点D ，则SD ⊥平面ABC ．∵CO 1=2333=，∴116133OO =-=， ∴高SD=2OO 1=263，∵△ABC 是边长为1的正三角形，∴S △ABC =34， ∴132623436S ABC V -=⨯⨯=三棱锥．12．已知正方体1111ABCD A B C D -的棱长为2，P 是底面ABCD 上的动点,1PA PC ≥，则满足条件的点P 构成的图形的面积等于（）A ．12B ．4πC ．44π- D ．72【答案】A【解析】如图，以,AB AD 为,x y 轴在平面ABCD 内建立平面直角坐标系，设(,)P x y ，由1PA PC ≥得22222(2)(2)2x y x y +-+-+30x y +-≥，设直线:30l x y +-=与正方形ABCD 的边交于点,M N ，则P 点在CMN ∆内部（含边界），易知(1,2)M ，(2,1)N ，∴1CM CN ==，111122CMN S ∆=⨯⨯=．故选A ．二．填空题（每题5分，共20分）13．已知在直角梯形ABCD 中，AB AD ⊥，CD AD ⊥，224AB AD CD ===，将直角梯形ABCD 沿AC 折叠，使平面BAC ⊥平面DAC ，则三棱锥D ABC -外接球的体积为__________．【答案】323π 【解析】结合题意画出折叠后得到的三棱锥D ABC -如图所示，由条件可得在底面ACB ∆中，90,22ACB AC BC ∠=︒==。

专题08 立体几何解答题常考全归类(精讲精练)(原卷版)

专题08 立体几何解答题常考全归类【命题规律】空间向量是将空间几何问题坐标化的工具，是常考的重点，立体几何解答题的基本模式是论证推理与计算相结合，以某个空间几何体为依托，分步设问，逐层加深．解决这类题目的原则是建系求点、坐标运算、几何结论．作为求解空间角的有力工具，通常在解答题中进行考查，属于中等难度．【核心考点目录】核心考点一：非常规空间几何体为载体核心考点二：立体几何探索性问题核心考点三：立体几何折叠问题核心考点四：立体几何作图问题核心考点五：立体几何建系繁琐问题核心考点六：两角相等（构造全等）的立体几何问题核心考点七：利用传统方法找几何关系建系核心考点八：空间中的点不好求核心考点九：创新定义【真题回归】1．（2022·天津·统考高考真题）直三棱柱111ABC A B C 中，112,,AA AB AC AA AB AC AB ===⊥⊥，D 为11A B 的中点，E 为1AA 的中点，F 为CD 的中点．(1)求证：//EF 平面ABC ；(2)求直线BE 与平面1CC D 所成角的正弦值；(3)求平面1ACD 与平面1CC D 所成二面角的余弦值．2．（2022·全国·统考高考真题）如图，四面体ABCD 中，,,AD CD AD CD ADB BDC ⊥=∠=∠，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设2,60AB BD ACB ==∠=︒，点F 在BD 上，当AFC △的面积最小时，求CF 与平面ABD 所成的角的正弦值．3．（2022·浙江·统考高考真题）如图，已知ABCD 和CDEF 都是直角梯形，//AB DC ，//DC EF ，5AB =，3DC =，1EF =，60BAD CDE ∠=∠=︒，二面角F DC B --的平面角为60︒．设M ，N 分别为,AE BC 的中点．(1)证明：FN AD ⊥；(2)求直线BM 与平面ADE 所成角的正弦值．4．（2022·全国·统考高考真题）如图，PO 是三棱锥-P ABC 的高，PA PB =，AB AC ⊥，E 是PB 的中点．(1)证明：//OE 平面PAC ；(2)若30ABO CBO ∠=∠=︒，3PO =，5PA =，求二面角C AE B --的正弦值．5．（2022·全国·统考高考真题）如图，四面体ABCD 中，,,AD CD AD CD ADB BDC ⊥=∠=∠，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设2,60AB BD ACB ==∠=︒，点F 在BD 上，当AFC △的面积最小时，求三棱锥F ABC -的体积．6．（2022·全国·统考高考真题）在四棱锥P ABCD -中，PD ⊥底面,,1,2,ABCD CD AB AD DC CB AB DP =====∥(1)证明：BD PA ⊥；(2)求PD 与平面PAB 所成的角的正弦值．7．（2022·北京·统考高考真题）如图，在三棱柱111ABC A B C 中，侧面11BCC B 为正方形，平面11BCC B ⊥平面11ABB A ，2AB BC ==，M ，N 分别为11A B ，AC 的中点．(1)求证：MN ∥平面11BCC B ；(2)再从条件①、条件②这两个条件中选择一个作为已知，求直线AB 与平面BMN 所成角的正弦值．条件①：AB MN ⊥；条件②：BM MN =．注：如果选择条件①和条件②分别解答，按第一个解答计分．8．（2022·全国·统考高考真题）如图，直三棱柱111ABC A B C 的体积为4，1A BC 的面积为(1)求A 到平面1A BC 的距离；(2)设D 为1A C 的中点，1AA AB =，平面1A BC ⊥平面11ABB A ，求二面角A BD C --的正弦值．【方法技巧与总结】1、用综合法求空间角的基本数学思想主要是转化与化归，即把空间角转化为平面角，进而转化为三角形的内角，然后通过解三角形求得．求解的一般步骤为：（1）作图：作出空间角的平面角．（2）证明：证明所给图形是符合题设要求的．（3）计算：在证明的基础上计算得出结果．简称：一作、二证、三算．2、用定义作异面直线所成角的方法是“平移转化法”，可固定一条，平移另一条；或两条同时平移到某个特殊的位置，顶点选在特殊的位置上．3、求直线与平面所成角的常见方法（1）作角法：作出斜线、垂线、斜线在平面上的射影组成的直角三角形，根据条件求出斜线与射影所成的角即为所求．（2）等积法：公式θ=sin h l，其中θ是斜线与平面所成的角，h 是垂线段的长，是斜线段的长，其中求出垂线段的长（即斜线上的点到面的距离）既是关键又是难点，为此可构造三棱锥，利用等体积法来求垂线段的长．（3）证垂法：通过证明线面垂直得到线面角为90°．4、作二面角的平面角常有三种方法（1）棱上一点双垂线法：在棱上任取一点，过这点分别在两个面内作垂直于棱的射线，这两条射线所成的角，就是二面角的平面角．（2）面上一点三垂线法：自二面角的一个面上一点向另一面引垂线，再由垂足向棱作垂线得到棱上的点（即垂足），斜足与面上一点连线和斜足与垂足连线所夹的角，即为二面角的平面角．（3）空间一点垂面法：自空间一点作与棱垂直的平面，截二面角得两条射线，这两条射线所成的角就是二面角的平面角．【核心考点】核心考点一：非常规空间几何体为载体【规律方法】关键找出三条两两互相垂直的直线建立空间直角坐标系．【典型例题】例1．（2022·陕西安康·统考一模）如图，已知AB 为圆锥SO 底面的直径，点C 在圆锥底面的圆周上，2BS AB ==，6BAC π∠=，BE 平分SBA ∠，D 是SC 上一点，且平面DBE ⊥平面SAB .(1)求证：SA BD ⊥；(2)求二面角E BD C --的正弦值.例2．（2022·安徽·校联考二模）如图，将长方形11OAAO （及其内部）绕1OO 旋转一周形成圆柱，其中11,2OA O O ==，劣弧11A B 的长为,6AB π为圆O 的直径.(1)在弧AB 上是否存在点C （1,C B 在平面11OAAO 的同侧），使1BC AB ⊥，若存在，确定其位置，若不存在，说明理由；(2)求平面11A O B 与平面11B O B 夹角的余弦值.例3．（2022·山东东营·胜利一中校考模拟预测）如图，,AB CD 分别是圆台上､下底面的直径，且AB CD ，点E 是下底面圆周上一点，AB =(1)证明：不存在点E 使平面AEC ⊥平面ADE ；(2)若4DE CE ==，求二面角D AE B --的余泫值.例4．（2022·河北·统考模拟预测）如图，在圆台1OO 中，上底面圆1O 的半径为2，下底面圆O 的半径为4，过1OO 的平面截圆台得截面为11ABB A ，M 是弧AB 的中点，MN 为母线，cos NMB ∠=(1)证明：1AB ⊥平面1AOM ； (2)求二面角M NB A --的正弦值.核心考点二：立体几何探索性问题【规律方法】与空间向量有关的探究性问题主要有两类：一类是探究线面的位置关系；另一类是探究线面角或二面角满足特定要求时的存在性问题．处理原则：先建立空间直角坐标系，引入参数（有些是题中已给出），设出关键点的坐标，然后探究这样的点是否存在，或参数是否满足要求，从而作出判断．【典型例题】例5．（2022·上海虹口·统考一模）如图，在三棱柱111ABC A B C 中，底面ABC 是以AC 为斜边的等腰直角三角形，侧面11AAC C 为菱形，点1A 在底面上的投影为AC 的中点D ，且2AB =．(1)求证：1BD CC ⊥；(2)求点C 到侧面11AA B B 的距离；(3)在线段11A B 上是否存在点E ，使得直线DE 与侧面11AA B B 请求出1A E 的长；若不存在，请说明理由．例6．（2022春·山东·高三山东省实验中学校考阶段练习）如图，在三棱柱111ABC A B C 中，1AB C 为等边三角形，四边形11AA B B 为菱形，AC BC ⊥，4AC =，3BC =.(1)求证：11AB AC ⊥；(2)线段1CC 上是否存在一点E ，使得平面1AB E 与平面ABC 的夹角的余弦值为14？若存在，求出点E 的位置；若不存在，请说明理由.例7．（2022春·黑龙江绥化·高三海伦市第一中学校考期中）如图1，在矩形ABCD 中，AB ＝2，BC ＝1，E 是DC 的中点，将DAE 沿AE 折起，使得点D 到达点P 的位置，且PB ＝PC ，如图2所示．F 是棱PB 上的一点．(1)若F 是棱PB 的中点，求证：//CF 平面P AE ；(2)是否存在点F ，使得二面角F AE C --？若存在，则求出PF FB 的值；若不存在，请说明理由．例8．（2022·广东韶关·统考一模）已知矩形ABCD 中，4AB =，2BC =，E 是CD 的中点，如图所示，沿BE 将BCE 翻折至BFE △，使得平面BFE ⊥平面ABCD .(1)证明：BF AE ⊥；(2)若(01)DP DB λλ=<<是否存在λ，使得PF 与平面DEF 求出λ的值；若不存在，请说明理由.核心考点三：立体几何折叠问题【规律方法】1、处理图形翻折问题的关键是理清翻折前后长度和角度哪些发生改变，哪些保持不变．2、把空间几何问题转化为平面几何问题，把握图形之间的关系，感悟数学本质．【典型例题】例9．（2022春·江苏南通·高三期中）已知梯形ABCD 中，//AD BC ，π2∠=∠=ABC BAD ，24AB BC AD ===，E ，F 分别是AB ，CD 上的点，//EF BC ，AE x =，G 是BC 的中点，沿EF 将梯形ABCD 翻折，使平面AEFD ⊥平面EBCF ．(1)当2x =时①求证：BD EG ⊥；②求二面角D BF C --的余弦值；(2)三棱锥D FBC -的体积是否可能等于几何体ABE FDC -体积的一半？并说明理由．例10．（2022春·辽宁·高三辽宁实验中学校考期中）如图1，在平面四边形ABCD 中，已知ABDC ，AB DC ∥，142AD DC CB AB ====，E 是AB 的中点．将△BCE 沿CE 翻折至△PCE ，使得2DP =，如图2所示．(1)证明：DP CE ⊥；(2)求直线DE 与平面P AD 所成角的正弦值．例11．（2022春·湖南长沙·高三宁乡一中校考期中）如图，平面五边形P ABCD 中，PAD 是边长为2的等边三角形，//AD BC ，AB ＝2BC ＝2，AB BC ⊥，将PAD 沿AD 翻折成四棱锥P －ABCD ，E 是棱PD 上的动点（端点除外），F ，M 分别是AB ，CE 的中点，且PC =(1)证明：AB FM ⊥；(2)当直线EF 与平面P AD 所成的角最大时，求平面ACE 与平面P AD 夹角的余弦值．例12．（2022·四川雅安·统考模拟预测）如图①，ABC 为边长为6的等边三角形，E ，F 分别为AB ，AC 上靠近A 的三等分点，现将AEF △沿EF 折起，使点A 翻折至点P 的位置，且二面角P EF C --的大小为120°（如图②）．(1)在PC 上是否存在点H ，使得直线//FH 平面PBE ？若存在，确定点H 的位置；若不存在，说明理由． (2)求直线PC 与平面PBE 所成角的正弦值．核心考点四：立体几何作图问题【规律方法】（1）利用公理和定理作截面图（2）利用直线与平面平行的性质定理作平行线（3）利用平面与平面垂直作平面的垂线【典型例题】例13．（2022·贵州·校联考模拟预测）如图，已知平行六面体1111ABCD A B C D -的底面ABCD 是菱形，112CD CC AC ===，3DCB π∠=且113cos cos 4C CD C CB ∠=∠=.(1)试在平面ABCD 内过点C 作直线l ，使得直线//l 平面1C BD ，说明作图方法，并证明：直线11//l B D ； (2)求点C 到平面1A BD 的距离.例14．（2022秋·河北石家庄·高一石家庄市第十五中学校考期中）如图为一块直四棱柱木料，其底面ABCD 满足：AB AD ⊥，AD BC ∥．(1)要经过平面11CC D D 内的一点P 和棱1BB 将木料锯开，在木料表面应该怎样画线？（借助尺规作图，并写出作图说明，无需证明）(2)若2AD AB ==，11BC AA ==，当点P 是矩形11CDD C 的中心时，求点1D 到平面1APB 的距离．例15．（2022·全国·高三专题练习）如图多面体ABCDEF 中，面FAB ⊥面ABCD ，FAB 为等边三角形，四边形ABCD 为正方形，//EF BC ，且332EF BC ==，H ，G 分别为CE ，CD 的中点.（1）求二面角C FH G --的余弦值；（2）作平面FHG 与平面ABCD 的交线，记该交线与直线AB 交点为P ，写出APAB的值（不需要说明理由，保留作图痕迹）.例16．（2022·全国·高三专题练习）四棱锥P ABCD -中，底面ABCD 是边长为2的菱形，23DAB π∠=.ACBD O =,且PO ⊥平面ABCD ，PO =点,F G 分别是线段.PB PD 上的中点，E 在PA 上.且3PA PE =.（Ⅰ）求证：//BD 平面EFG ；（Ⅰ）求直线AB 与平面EFG 的成角的正弦值；（Ⅰ）请画出平面EFG 与四棱锥的表面的交线，并写出作图的步骤.核心考点五：立体几何建系繁琐问题【规律方法】利用传统方法解决【典型例题】例17．如图，已知三棱柱-111ABC A B C 的底面是正三角形，侧面11BB C C 是矩形，M ，N 分别为BC ，11B C 的中点，P 为AM 上一点．过11B C 和P 的平面交AB 于E ，交AC 于F ．（1）证明：1//AA MN ，且平面⊥1A AMN 平面11EB C F ；（2）设O 为△111A B C 的中心．若//AO 平面11EB C F ，且=AO AB ，求直线1B E 与平面1A AMN 所成角的正弦值．例18．如图，在锥体-P ABCD 中，ABCD 是边长为1的菱形，且∠=︒60DAB ，==PA PD ，=2PB ，E ，F 分别是BC ，PC 的中点（1）证明：⊥AD 平面DEF （2）求二面角--P AD B 的余弦值．例19．（2022春·福建南平·高三校考期中）在三棱柱111ABC A B C 中，AB AC ⊥，1B C ⊥平面ABC ，E 、F 分别是棱AC 、11A B 的中点.(1)设G 为11B C 的中点，求证：//EF 平面11BCC B ；(2)若2AB AC ==，直线1BB 与平面1ACB 所成角的正切值为2，求多面体1B EFGC -的体积V .核心考点六：两角相等（构造全等）的立体几何问题【规律方法】构造垂直的全等关系【典型例题】例20．如图，已知三棱柱-111ABC A B C 的底面是正三角形，侧面11BB C C 是矩形，M ，N 分别为BC ，11B C 的中点，P 为AM 上一点．过11B C 和P 的平面交AB 于E ，交AC 于F ．（1）证明：1//AA MN ，且平面⊥1A AMN 平面11EB C F ；（2）设O 为△111A B C 的中心．若//AO 平面11EB C F ，且=AO AB ，求直线1B E 与平面1A AMN 所成角的正弦值．例21．如图，在锥体-P ABCD 中，ABCD 是边长为1的菱形，且∠=︒60DAB ，==PA PD ，=2PB ，E ，F 分别是BC ，PC 的中点（1）证明：⊥AD 平面DEF （2）求二面角--P AD B 的余弦值．核心考点七：利用传统方法找几何关系建系【规律方法】利用传统方法证明关系，然后通过几何关系建坐标系．【典型例题】例22．如图：长为3的线段PQ 与边长为2的正方形ABCD 垂直相交于其中心()O PO OQ >．（1）若二面角P AB Q --的正切值为3-，试确定O 在线段PQ 的位置；（2）在（1）的前提下，以P ，A ，B ，C ，D ，Q 为顶点的几何体PABCDQ 是否存在内切球？若存在，试确定其内切球心的具体位置；若不存在，请说明理由．例23．在四棱锥P ABCD -中，E 为棱AD 的中点，PE ⊥平面ABCD ，//AD BC ，90ADC ∠=︒，2ED BC ==，3EB =，F 为棱PC 的中点．（Ⅰ）求证：//PA 平面BEF ；（Ⅰ）若二面角F BE C --为60︒，求直线PB 与平面ABCD 所成角的正切值．例24．三棱柱111ABC A B C -中，AB AC ⊥，2AB AC ==，侧面11BCC B 为矩形，123A AB π∠=，二面角1A BC A --的正切值为12．（Ⅰ）求侧棱1AA 的长；（Ⅰ）侧棱1CC 上是否存在点D ，使得直线AD 与平面1A BC ，若存在，判断点的位置并证明；若不存在，说明理由．核心考点八：空间中的点不好求【规律方法】方程组思想【典型例题】例25．（2022·江苏南京·模拟预测）已知三棱台111ABC A B C 的体积为143，且π2ABC ∠=，1A C ⊥平面11BB C C . (1)证明：平面11A B C ⊥平面111A B C ；(2)若11AC B C =，11112A B B C ==，求二面角1B AA C --的正弦值.例26．（2022春·浙江·高三浙江省新昌中学校联考期中）如图，在四棱台1111ABCD A B C D -中，底面ABCD 是边长为2的菱形，3DAB π∠=，平面11BDD B ⊥平面ABCD ，点1,O O 分别为11,B D BD 的中点，1111,,O B A AB O BO ∠∠=均为锐角.(1)求证：1AC BB ⊥；(2)若异面直线CD 与1AA ，四棱锥1A ABCD -的体积为1，求二面角1B AA C --的平面角的余弦值.例27．（2022春·辽宁沈阳·高三沈阳市第一二〇中学校考期中）如图，在几何体ABCDE 中，底面ABC 为以AC为斜边的等腰直角三角形.已知平面ABC ⊥平面ACD ，平面ABC ⊥平面,//BCE DE 平面,ABC AD DE ⊥.(1)证明；DE ⊥平面ACD ；(2)若22AC CD ==，设M 为棱BE 的中点，求当几何体ABCDE 的体积取最大值时,AM 与CD 所成角的余弦值.核心考点九：创新定义【规律方法】以立体几何为载体的情境题都跟图形有关，涉及在具体情境下的图形阅读，需要通过数形结合来解决问题．图形怎么阅读一是要读特征，即从图形中读出图形的基本特征；二是要读本质，即要善于将所读出的信息进行提升，实现“图形→文字→符号”的转化；三是要有问题意识，带着问题阅读图形，将研究图形的本身特征和关注题目要解决的问题有机地融合在一起；四是要有运动观点，要“动手”去操作，动态地去阅读图形．【典型例题】例28．（2022·安徽合肥·合肥一六八中学校考模拟预测）已知顶点为S 的圆锥面（以下简称圆锥S ）与不经过顶点S 的平面α相交，记交线为C ，圆锥S 的轴线l 与平面α所成角θ是圆锥S 顶角（圆S 轴截面上两条母线所成角θ的一半，为探究曲线C 的形状，我们构建球T ，使球T 与圆锥S 和平面α都相切，记球T 与平面α的切点为F ，直线l 与平面α交点为A ，直线AF 与圆锥S 交点为O ，圆锥S 的母线OS 与球T 的切点为M ，OM a =，MS b =．(1)求证：平面SOA ⊥平面α，并指出a ，b ，θ关系式； (2)求证：曲线C 是抛物线．例29．（2022·全国·高三专题练习）类比于二维平面中的余弦定理，有三维空间中的三面角余弦定理；如图1，由射线PA ，PB ，PC 构成的三面角-P ABC ，APC α∠=，BPC β∠=，APB γ∠=，二面角A PC B --的大小为θ，则cos cos cos sin sin cos γαβαβθ=+．（1）当α、π0,2β⎛⎫∈ ⎪⎝⎭时，证明以上三面角余弦定理；（2）如图2，四棱柱1111ABCD A B C D -中，平面11AA C C ⊥平面ABCD ，160A AC ∠=︒，45BAC ∠=︒， ①求1A AB ∠的余弦值；②在直线1CC 上是否存在点P ，使//BP 平面11DA C ？若存在，求出点P 的位置；若不存在，说明理由．例30．（2022·全国·校联考模拟预测）蜂房是自然界最神奇的“建筑”之一，如图1所示．蜂房结构是由正六棱柱截去三个相等的三棱锥H ABC -，J CDE -，K EFA -，再分别以AC ，CE ，EA 为轴将ACH ∆，CEJ ∆，EAK ∆分别向上翻转180︒，使H ，J ，K 三点重合为点S 所围成的曲顶多面体（下底面开口），如图2所示．蜂房曲顶空间的弯曲度可用曲率来刻画，定义其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和，而每一顶点的曲率规定等于2π减去蜂房多面体在该点的各个面角之和（多面体的面角是多面体的面的内角，用弧度制表示）．（1）求蜂房曲顶空间的弯曲度；（2）若正六棱柱的侧面积一定，当蜂房表面积最小时，求其顶点S 的曲率的余弦值．【新题速递】1．（2022·重庆沙坪坝·重庆八中校考模拟预测）如图，在三棱柱111ABC A B C 中，1BC CC =，1AC AB =.(1)证明：平面1ABC ⊥平面11BCC B ；(2)若BC =，1AB B C =，160CBB ∠=︒，求直线1BA 与平面111A B C 所成角的正弦值.2．（2022·四川达州·统考一模）如图，三棱柱111ABC A B C -中，底面ABC 为等腰直角三角形，112AB AC BB ===，，160ABB ∠=.(1)证明: 1AB B C ⊥；(2)若12B C =，求1AC 与平面1BCB 所成角的正弦值.3．（2022·陕西宝鸡·统考一模）如图在四棱锥P ABCD -中，PA ⊥底面ABCD ，且底面ABCD 是平行四边形.已知2,1,PA AB AD AC E ====是PB 中点.(1)求证：平面PBC ⊥平面ACE ；(2)求平面PAD 与平面ACE 所成锐二面角的余弦值.4．（2022·广东广州·统考一模）如图，已知四棱锥P ABCD -的底面ABCD 是菱形，平面PBC ⊥平面ABCD ，30,ACD E ∠=为AD 的中点，点F 在PA 上，3AP AF =.(1)证明：PC //平面BEF ；(2)若PDC PDB ∠∠=，且PD 与平面ABCD 所成的角为45，求平面AEF 与平面BEF 夹角的余弦值.5．（2022·上海奉贤·统考一模）如图，在四面体ABCD 中，已知BA BD CA CD ===.点E 是AD 中点.(1)求证：AD ⊥平面BEC ；(2)已知95,arccos,625AB BDC AD ∠===，作出二面角D BC E --的平面角，并求它的正弦值.6．（2022·上海浦东新·统考一模）如图，三棱锥-P ABC 中，侧面P AB 垂直于底面ABC ，PA PB =，底面ABC 是斜边为AB 的直角三角形，且30ABC ∠=︒，记O 为AB 的中点，E 为OC 的中点.(1)求证：PC AE ⊥；(2)若2AB =，直线PC 与底面ABC 所成角的大小为60°，求四面体P AOC 的体积.7．（2022·四川成都·石室中学校考模拟预测）如图，在四棱锥P ABCD -中，AB BD BP ===PA PD ==90APD ∠=︒，E 是棱PA 的中点，且BE 平面PCD(1)证明：CD ⊥平面PAD ；(2)若1CD =，求二面角A PB C --的正弦值.8．（2022春·江苏徐州·高三期末）如图，四棱锥P ABCD -中，PA ⊥底面ABCD ，AD ∥BC ，N 为PB 的中点.(1)若点M 在AD 上，2AM MD =，34AD BC =，证明：MN 平面PCD ； (2)若3PA AB AC AD ====，4BC =，求二面角D AC N --的余弦值.9．（2022·陕西汉中·统考一模）如图，多面体ABCDEF 中，四边形ABCD 为菱形，60,ABC FA ∠=⊥平面,ABCD ED FA ∥，且22AB FA ED ===.(1)求证：BD FC ⊥；(2)求二面角F AC E --的大小.10．（2022·陕西汉中·统考一模）如图，多面体ABCDEF 中，四边形ABCD 为菱形，60,ABC FA ∠=⊥平面,ABCD FA ED ∥，且22AB FA ED ===.(1)求证：BD FC ⊥；(2)求点A 到平面FBD 的距离.11．（2022·四川广安·广安二中校考模拟预测）APD △是等腰直角三角形，AP PD ⊥且AD =ABCD 是直角梯形，AB BC ⊥，DC BC ⊥，且222AB BC CD ===，平面APD ⊥平面ABCD .(1)求证：AP ⊥平面BPD ；(2)若点E 是线段PB 上的一个动点，问点E 在何位置时三棱锥D APE -.12．（2022·四川南充·统考一模）在平面五边形ABCDE 中（如图1），ABCD 是梯形，//AD BC ，2AD BC ==AB =90ABC ∠=︒，ADE 是等边三角形．现将ADE 沿AD 折起，连接EB ，EC 得四棱锥E ABCD -（如图2）且CE =(1)求证：平面EAD ⊥平面ABCD ；(2)在棱EB 上有点F ，满足13EF EB =，求二面角E AD F --的余弦值．13．（2022·贵州贵阳·贵阳六中校考一模）如图，在四棱锥P ABCD -中，DA AB ⊥，PD PC ⊥，PB PC ⊥，1AB AD PD PB ====，4cos 5DCB ∠=.(1)求证：BD ⊥平面PAC .(2)设E 为BC 的中点，求PE 与平面ABCD 所成角的正弦值.14．（2022春·广东广州·高三校考期中）如图所示，在四棱锥P ABCD -中，PC ⊥底面ABCD ，四边形ABCD 是直角梯形，AB AD ⊥，//,222AB CD PC AB AD CD ====，点E 在侧棱PB 上.(1)求证：平面EAC ⊥平面PBC ；(2)若平面PAC 与平面ACE PE BE 的值.。

专题08 等腰三角形中的分类讨论模型(解析版)

专题08等腰三角形中的分类讨论模型模型1、等腰三角形中的分类讨论：【知识储备】凡是涉及等腰三角形边、角、周长、面积等问题，优先考虑分类讨论，再利用等腰三角形的性质与三角形三边关系解题即可。

1）无图需分类讨论①已知边长度无法确定是底边还是腰时要分类讨论；②已知角度数无法确定是顶角还是底角时要分类讨论；③遇高线需分高在△内和△外两类讨论；④中线把等腰△周长分成两部分需分类讨论。

2）“两定一动”等腰三角形存在性问题：即：如图：已知A ，B 两点是定点，找一点C 构成等腰ABC △方法：两圆一线具体图解：①当AC AB =时，以点A 为圆心，AB 长为半径作⊙A ，点C 在⊙A 上（B ，C 除外）②当BC AB =时，以点B 为圆心，AB 长为半径作⊙B ，点C 在⊙B 上（A ，E 除外）③当BC AC =时，作AB 的中垂线，点C 在该中垂线上（D 除外）例1．（2023秋·河北张家口·八年级统考期末）ABC 是等腰三角形，5,7AB AC ==，则ABC 的周长为（）A ．12B ．12或17C ．14或19D ．17或19【答案】D【分析】根据等腰三角形的定义分两种情况：当腰为5与腰为7时，即可得到答案．【详解】解：当ABC 的腰为5时，ABC 的周长55717++=；当ABC 的腰为7时，ABC 的周长57719++=．故选：D ．【点睛】本题主要考查等腰三角形的定义，掌握等腰三角形的定义是解题的关键．例2．（2023春·四川巴中·七年级统考期末）等腰三角形的周长为32cm ，一边长为8cm ，则其它两边长是（）∴150∠=︒，即顶角为150︒；故答案为：30︒或150︒．BAC【点睛】本题考查等腰三角形的性质，注意掌握分类讨论思想和数形结合思想的应用是解题的关键．例5．（2023秋·江苏·八年级专题练习）在如图所示的网格中，在格点上找一点P，使ABP为等腰三角形，则点P有（）A．6个B．7个C．8个D．9个【答案】C【分析】分三种情况讨论：以AB为腰，点A为顶角顶点；以AB为腰，点B为顶角顶点；以AB为底．【详解】解：如图：如图，以AB为腰，点A为顶角顶点的等腰三角形有5个；以AB为腰，点B为顶角顶点的等腰三角形有3个；不存在以AB为底的等腰ABP，所以合计8个．故选：C．【点睛】本题考查等腰三角形的定义，网格图中确定线段长度；在等腰三角形腰、底边待定的情况下，分类讨论是解题的关键．例6．（2023·重庆市八年级期中）如图1，一副直角三角板△ABC和△DEF，∠BAC=∠EDF=90°，∠B=45°，∠F=30°，点B、D、C、F在同一直线上，点A在DE上．如图2，△ABC固定不动，将△EDF绕点D逆时针旋转α（0°＜α＜135°）得△E′DF'，当直线E′F′与直线AC、BC所围成的三角形为等腰三角形时，α的大小为___．【答案】7.5°或75°或97.5°或120°【分析】设直线E′F′与直线AC、BC分别交于点P、Q，根据△CPQ为等腰三角形，分三种情况：①当∠PCQ 为顶角时，∠CPQ=∠CQP，如图1，可求得α=7.5°；如图2，△CPQ为等腰三角形中，∠PCQ为顶角，可求得α=∠EDE′=90°+7.5°=97.5°；②当∠CPQ为顶角时，∠CQP=∠PCQ=45°，可得∠CPQ=90°，如图3，进而求得α=90°-15°=75°；③如图4，当∠CQP为顶角时，∠CPQ=∠PCQ=45°，可得∠CQP=90°，进而求得α=∠EDE′=∠EDQ+∠QDE′=90°+30°=120°．【详解】解：设直线E′F′与直线AC、BC分别交于点P、Q，∵△CPQ为等腰三角形，∴∠PCQ为顶角或∠CPQ为顶角或∠CQP为顶角，①当∠PCQ为顶角时，∠CPQ=∠CQP，如图1，∵∠BAC=∠EDF=90°，∠B=45°，∠F=30°，∴∠E′DF′=90°，∠ACB=45°，∠E′F′D=30°，∵∠CPQ+∠CQP=∠ACB=45°，∴∠CQP=22.5°，∵∠E′F′D=∠CQP+∠F′DQ，∴∠F′DQ=∠E′F′D-∠CQP=30°-22.5°=7.5°，∴α=7.5°；如图2，∵△CPQ为等腰三角形中，∠PCQ为顶角，∴∠CPQ=∠CQP=67.5°，∵∠E′DF′=90°，∠F′=30°，∴∠E′=60°，∴∠E′DQ=∠CQP-∠E′=67.5°-60°=7.5°，∴α=∠EDE′=90°+7.5°=97.5°；②当∠CPQ为顶角时，∠CQP=∠PCQ=45°，∴∠CPQ=90°，如图3，∵∠DE ′F ′=∠CQP +∠QDE ′，∴∠QDE ′=∠DE ′F ′-∠CQP =60°-45°=15°，∴α=90°-15°=75°；③如图4，当∠CQP 为顶角时，∠CPQ =∠PCQ =45°，∴∠CQP =90°，∴∠QDF ′=90°-∠DF ′E ′=60°，∴∠QDE ′=∠E ′DF ′-∠QDF ′=30°，∴α=∠EDE ′=∠EDQ +∠QDE ′=90°+30°=120°；综上所述，α的大小为7.5°或75°或97.5°或120°．故答案为：7.5°或75°或97.5°或120°．【点睛】本题考查了等腰三角形性质，直角三角形性质，旋转的性质，三角形内角和定理等，解题关键是运用数形结合思想和分类讨论思想思考解决问题．例7．（2022秋·江苏徐州·八年级校考期中）如图，70AOB ∠=︒，点C 是边OB 上的一个定点，点P 在角的另一边OA 上运动，当COP 是等腰三角形，OCP ∠=°．【答案】40或70或55【分析】分三种情况讨论：①当OC PC =，②当PO PC =，③当OP OC =，根据等腰三角形的性质以及三角形内角和定理即可得到结论．【详解】解：如图，(1)若点P在BC上，且满足PA PB=，求此时(3)在运动过程中，当t为何值时，ACP△【答案】(1)6516(2)316或52(3)54或32或90ACB∠=︒，5cmAB=在Rt ACP中，由勾股定理得()22234x x∴+-=，解得BP 平分ABC ∠，C ∠在BCP 与BDP △中，∵A B ∠∠=︒+90，90ACP BCP ∠+∠=︒，B BCP ∴∠=∠，CP BP AP ∴==，P ∴是AB 的中点，即15cm 22AP AB ==，524AP t ∴=．②如图，当P 在AB 上且3cm AP CA ==时，∴322AP t ==．③如图，当P 在AB 上且(1)求直线AB 的表达式和点D 的坐标；(2)横坐标为m 的点P 在线段AB 上（不与点A x 轴的平行线交AD 于点E ，设PE 的长为()0y y ≠，求y 与m 之间的函数关系式并直接写出相应的范围；(3)在（2）的条件下，在x 轴上是否存在点F ，使PEF !为等腰直角三角形？若存在求出点若不存在，请说明理由．【答案】(1)()450y x D =-+-，，(2)()33242y m m =+-<<，的运用，解答本题时求出函数的解析式是关键．课后专项训练A．120︒B．75︒【答案】C【答案】D【分析】分为AB AC =、BC BA =，CB CA =三种情况画图判断即可．【详解】解：如图所示：当AB AC =时，符合条件的点有2个；当BC BA =时，符合条件的点有1个；当CB CA =，即当点C 在AB 的垂直平分线上时，符合条件的点有一个．故符合条件的点C 共有4个．故选：D ．【点睛】本题考查了等腰三角形的定义，线段垂直平分线的性质，熟练掌握线段垂直平分线的性质是解题的关键．4．（2023·江苏八年级期中）如图，在正方形网格中，每个小正方形的边长都为1，点A 、B 都是格点（小正方形的顶点叫做格点），若△ABC 为等腰三角形，且△ABC 的面积为1，则满足条件的格点C 有()A ．0个B ．2个C ．4个D ．8个【答案】C 【分析】根据等腰三角形的性质和三角形的面积解答即可．【详解】解：如图所示：∵△ABC 为等腰三角形，且△ABC 的面积为1，∴满足条件的格点C 有4个，故选C ．【点睛】本题考查了等腰三角形的判定；熟练掌握等腰三角形的性质和三角形的面积是解决问题的关键A．3【答案】D故选：满足条件的点M 的个数为2．故选A ．【点睛】本题考查了坐标与图形的性质及等腰三角形的判定；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．7．（2022·安徽淮北·九年级阶段练习）如图，在ABC 中，90C ∠=︒，8BC =，6AC =．若点P 为直线BC 上一点，且ABP △为等腰三角形，则符合条件的点P 有（）．A ．1个B ．2个C ．3个D ．4个【点睛】本题考查了等腰三角形的判定和勾股定理的应用，关键要用分类讨论的思想．8．（2022·黑龙江·哈尔滨八年级阶段练习）如图，在平面直角坐标系中，点A 的坐标为()1,1，在x 轴上确定点P ，使AOP 为等腰三角形，则符合条件的点P 有（）A．2个B．3个C．4个D．5个【答案】C【分析】先计算OA的长，再以OA为腰或底分别讨论，进而得出答案．【详解】解：如图，22112OA=+=，当AO＝OP1，AO＝OP3时，P1（﹣2，0），P3（2，0），当AP2＝OP2时，P2（1，0），当AO＝AP4时，P4（2，0），故符合条件的点有4个．故选：C．【点睛】本题以平面直角坐标系为载体，主要考查了勾股定理和等腰三角形的定义，属于常考题型，全面分类、掌握解答的方法是关键．9．（2022·四川广元·八年级期末）如图，在Rt△ABC中，∠ACB＝90°，∠CAB=36°，以C为原点，C所在直线为y轴，BC所在直线为x轴建立平面直角坐标系，在坐标轴上取一点M使△MAB为等腰三角形，符合条件的M点有（）A．6个B．7个C．8个D．9个∵BD AC ⊥，∴90ADB ∠=︒，∵∵BD AC ⊥，∴90ADB ∠=︒，∵ABD ∠11【分析】根据等腰三角形一腰上的中线将其周长分别为12和9两部分得到底和要的差是1293-=，再根据周长列式求解即可得到答案；【详解】解：∵等腰三角形一腰上的中线将其周长分别为12和9两部分，∴腰与底的差为：1293-=，①当底边比腰长时，设腰为x ，则底为3x +，由题意可得，32129x x ++=+，解得：6x =，3639x +=+=，②当腰比底边长时，设腰为x ，则底为3x -，由题意可得，32129x x -+=+，解得：8x =，3835x -=-=，故答案为：6，9或8，5．【点睛】本题主要考查三角形中线有关计算，解题的关键是得到腰长与底边之差再分类讨论．14．（2022·黑龙江哈尔滨·八年级期末）在平面直角坐标系xOy 中，已知A （1，2），在y 轴确定点P ，使△AOP 为等腰三角形，则符合条件的点P 有____个．【答案】4．【分析】根据等腰三角形的判定得出可能OA 为底，可能OA 为腰两种情况，依此即可得出答案．【详解】①以A 为圆心，以OA 为半径作圆，此时交y 轴于1个点（O 除外）；②以O 为圆心，以OA 为半径作圆，此时交y 轴于2个点；③作线段AO 的垂直平分线，此时交y 轴于1个点；共1+2+1=4．故答案为：4．【点睛】本题考查了等腰三角形的判定的应用，有两边相等的三角形是等腰三角形，注意要进行分类讨论．15．（2022秋·江苏盐城·八年级校考阶段练习）如图，ABC 中，90ACB ∠=︒，10cm AB =，8cm AC =，若点P 从点A 出发，以每秒1cm 的速度沿折线A C B A ---运动，设运动时间为t 秒()0t >，当点P 在边AB 上，【答案】19或20或21.2【分析】利用等腰三角形的性质，依次画图，分类讨论即可．【详解】∵90ACB ∠=当P 在BA 上时，①②当6cm BC CP ==时，过CD PB ⊥于点D ，如图，∴12BD DP BP ==，∵12ABC S AC BC CD ==V g g ，∴ 4.8AC BC CD AB == ，在Rt CBD △中，由勾股定理得：()2226 4.8 3.6cm BD BC CD =--=，∴)22 3.6cm BP BD ==⨯=，∴(()867.221.2s t =++，【答案】5或8【分析】ABP 是以AB 为腰的等腰三角形时，分两种情况：出BP 的长度，继而可求得t 值．【详解】解：在Rt ABC △中，∠②当AB AP =时，28cm 8BP BC t ===，故答案为：5或8．【点睛】本题考查了勾股定理以及等腰三角形的知识，解答本题的关键是掌握等腰三角形的性质，以及分情况讨论，注意不要漏解．15．（2022·河南平顶山·八年级期末）如图，ABC 中，90C ∠=︒，6BC =，ABC ∠的平分线与线段AC 交于点D ，且有AD BD =，点E 是线段AB 上的动点（与A 、B 不重合），连接DE ，当BDE 是等腰三角形时，则BE 的长为___________．【答案】4或4【分析】现根据已知条件得出30CBD ABD BAD ∠=∠=∠=︒，再根据BC =6，分别求出AB 、AC 、BD 、AD 、（2）当BE =DE ，如图：∵BE =DE ∠EDB =∠ABD =30°，∴∠AED =∠EDB ∴∠ADE =180°-∠AED -∠A =180°-60°-30°=90°，∴ ADE 为直角三角形，又∵30A ∠=︒且AD =43，∴DE ，∴BE =4；（3）当BD =DE ，时，点E 与A 重合，不符合题意；综上所述，BE 为4或43．故答案为：4或43．【点睛】本题考查了等腰三角形的性质，直角三角形的性质和判定，勾股定理的应用，16．（2023·上虞市初二月考）在如图所示的三角形中，∠A ＝30°，点P 和点Q 分别是边AC 和BC 上的两个动点，分别连接BP 和PQ ，把△ABC 分割成三个三角形△ABP ，△BPQ ，△PQC ，若分割成的这三个三角形都是等腰三角形，则∠C 有可能的值有________个．【答案】7【分析】①当AB=AP ，BQ=PQ ，CP=CQ 时；②当AB=AP ，BP=BQ ，PQ=QC 时；③当APB ，PB=BQ ，PQ=CQ 时；④AP=PB，PB=PQ，PQ=QC时；根据等腰三角形的性质和三角形的内角和即可得到结论．【解析】解：如图所示，共有9种情况，∠C的度数有7个，分别为80°，40°，35°，20°，25°，100°，50°．①当AB=AP，BQ=PQ，CP=CQ时；②当AB=AP，BP=BQ，PQ=QC时，③当AP=AB，PQ=CQ，PB=PQ时．④当AP=AB，PQ=PC，BQ=PQ时，⑤当AP=BP，CP=CQ，QB=PQ时，⑥当AP=PB，PB=BQ，PQ=CQ时；⑦AP=PB，PB=PQ，PQ=QC时．⑧AP=PB，QB=PQ，PQ=CC时．⑨BP=AB，PQ=BQ，PQ=PC时．【点睛】本题考查了等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键．17．（2022·浙江·八年级专题练习）已知：如图，线段AC和射线AB有公共端点A．求作：点P，使点P在射线AB上，且ACP为等腰三角形．（利用无刻度的直尺和圆规作出所有符合条件的点P，不写作法，保留作图痕迹）【答案】见解析．【分析】分别作出①AP=CP；②AP=AC；③AC=CP即可．【详解】如图所示，点1P、2P、3P即为所求．△是等腰三角形的三种情况，避免漏答案．【点睛】本题考查尺规作图-作等腰三角形．特别注意ACP18．（2022·山东·周村二中八年级期中）在同一平面内，若点P与△ABC三个顶点中的任意两个顶点连接形成的三角形都是等腰三角形，则称点P是△ABC的巧妙点．（1）如图，求作△ABC的巧妙点P（尺规作图，不写作法，保留作图痕迹）．（2）如图，在△ABC中，∠A＝80°，AB＝AC，若点P是△ABC的巧妙点，则符合条件的点P一共有几个？请直接写出每种情况下∠BPC的度数．（3）等边三角形的巧妙点的个数有（）A．2个B．6个C．10个D．12个【答案】（1）见解析；（2）6个；∠BPC的度数为40°或160°或140°或80°；（3）C．综上所述：∠BPC的度数40°或80°或140°或160°．（3）如图所示，分别以等边三角形的三条边作其对应边的垂直平分线，再分别以等边三角形的三个顶点为圆心，等边三角形的边长为半径画圆，分别与三条边的垂直平分线的交点和三条垂直平分线的交点即为等边三角形的巧妙点，共有10个，故选：C．【点睛】本题主要考查垂直平分线的性质、等腰三角形的性质，构建等腰三角形的作法：定顶点，定圆心；定腰，定半径；以及等边三角形的性质等．熟练掌握相关性质是解题关键．19．（2022·黑龙江密山·八年级期末）如图，直线MN与x轴、y轴分别相交于B、A两点，()2-+-=．(1)求A，B两点的坐标；(2)若点O到AB的距离为24OA OB6805，求线段AB的长；(3)在（2）的条件下，x轴上是否存在点P，使△ABP是以AB为腰的等腰三角形，若存在请直接写出满足条件的点P的坐标．【答案】(1)A （0，6），B （8，0）；(2)AB =10；(3)存在，（-8，0）、（-2，0）、（18，0）．【分析】（1）由非负数的性质知OA =6，OB =8，据此可得点A 和点B 的坐标；（2）根据1122OAB S AB d OA OB == △求解可得；（3）先设点P （a ，0），根据A （0，6），B （8，0）得()22222226810100PA a PB a AB =+=-==，，，再分PA =AB 和AB =PB 两种情况分别求解可得．(1)()2680OA OB -+-= ∴O −6=0O −8=068OA OB ∴==则A 点的坐标为A （0，6），B 点的坐标为（8，0）(2)1122OAB S AB d OA OB == △，245d =6810245OA OB AB d ⨯∴=== (3)存在点P ，使△ABP 是以AB 为腰的等腰三角形设点P （a ，0），根据A （0，6），B （8，0）得()22222226810100PA a PB a AB =+=-==，，①若PA =AB ，则22PA AB =，即226100a +=，解得a =8(舍)或a =−8，此时点P (−8，0)；②若AB =PB ，即22AB PB =，即()21008a =-解得a =18或a =−2，此时点P (18，0)或(−2，0)；综上，存在点P ，使△ABP 使以AB 为腰的等腰三角形，其坐标为(−8，0)或(18，0)或(−2，0)．【点睛】本题考察了非负数的性质、直角三角形的面积求法、勾股定理及等腰三角形的性质，分类讨论思想的运用是解决第3问的关键20．（2022秋·四川成都·八年级校考期中）如图，四边形OABC 是一张长方形纸片，将其放在平面直角坐标系中，使得点O 与坐标原点重合，点A 、C 分别在x 轴、y 轴的正半轴上，点B 的坐标为()3,4，D 的坐标为()2,4，现将纸片沿过D 点的直线折叠，使顶点C 落在线段AB 上的点F 处，折痕与y 轴的交点记为E ．。

专题08 立体几何中的计算(原卷版)

衡水中学内部资料群：591993305，高中各科学霸资料群：680662798，专题08 立体几何中的计算1、【2019年江苏数】.如图，长方体1111ABCD A B C D 的体积是120，E 为1CC 的中点，则三棱锥E -BCD 的体积是_____.2、【2018年高考江苏数】.如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________．3、【2019年高考全国Ⅰ卷文数】已知∠ACB=90°，P 为平面ABC 外一点，PC =2，点P 到∠ACB 两边AC ，BCP 到平面ABC 的距离为___________．4、【2019年高考全国Ⅱ卷文数】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图2是一个棱数为48衡水中学内部资料群：591993305，高中各科学霸资料群：680662798，的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．（本题第一空2分，第二空3分．）5、【2019年高考全国Ⅲ卷文数】学生到工厂劳动实践，利用3D 打印技术制作模型．如图，该模型为长方体1111ABCD A B C D -挖去四棱锥O −EFGH 后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H 分别为所在棱的中点，16cm 4cm AB =BC =AA =，，3D 打印所用原料密度为0.9 g/cm 3，不考虑打印损耗，制作该模型所需原料的质量为___________g.6、【2019年高考北京卷文数】已知l ，m 是平面α外的两条不同直线．给出下列三个论断：①l ⊥m ；②m ∥α；③l ⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．7、【2019.若圆柱的一个底衡水中学内部资料群：591993305，高中各科学霸资料群：680662798，面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为__________.8、【2018年高考全国II 卷文数】已知圆锥的顶点为S ，母线SA ，SB 互相垂直，SA 与圆锥底面所成角为30 ，若SAB △的面积为8，则该圆锥的体积为__________．一、柱、锥、台和球的侧面积和体积注意：(1)分的处理.(2)圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展为平面图形计算，而表面积是侧面积与底面圆的面积之和.衡水中学内部资料群：591993305，高中各科学霸资料群：680662798，二、在求解一些不规则的几何体的体积以及两个几何体的体积之比时，常常需要用到分割法.在求一个几何体被分成两部分的体积之比时，若有一部分为不规则几何体，则可用整个几何体的体积减去规则几何体的体积求出其体积.(1)解决空间几何体表面上的最值问题的根本思路是“展开”，即将空间几何体的“面”展开后铺在一个平面上，将问题转化为平面上的最值问题.(2)如果已知的空间几何体是多面体，则根据问题的具体情况可以将这个多面体沿多面体中某条棱或者两个面的交线展开，把不在一个平面上的问题转化到一个平面上.如果是圆柱、圆锥则可沿母线展开，把曲面上的问题转化为平面上的问题. 三、方法与技巧(1)棱柱、棱锥要掌握各部分的结构特征，计算问题往往转化到一个三角形中进行解决.旋转体要抓住“旋转”特点，弄清底面、侧面及展开图形状. (2)要注意将空间问题转化为平面问题.(3)求几何体的体积，要注意分割与补形.将不规则的几何体通过分割或补形将其转化为规则的几何体求解. (4)一些几何体表面上的最短距离问题，常常利用几何体的展开图解决. 四、失误与防范（1）几何体展开、折叠问题，要抓住前后两个图形间的联系，找出其中的量的关系.（2）与球有关的组合体问题，一种是内切，一种是外接.解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.题型一多面体的表面积与体积求多面体的表面积与体积常用方法：1、公式法：可以运用规则的几何体；2、割补法：把不规则的图衡水中学内部资料群：591993305，高中各科学霸资料群：680662798，形分割成规则的图形，或者把几何体补成熟悉的几何体。

立体几何中的推理证明问题(解析版)

专题07 立体几何中的推理证明问题——立体几何是高考考查逻辑推理的重要知识点数学抽象要求能够掌握常用逻辑推理方法的规则，理解其中所蕴含的思想.对于新的数学问题，能够提出不同的假设前提，推断结论，形成数学命题.对于较复杂的数学问题，通过构建过渡性命题，探索论证的途径，解决问题，并会用严谨的数学语言表达论证过程.能够理解建构数学体系的公理化思想.立体几何是高中数学考查逻辑推理的重要载体,高考通常通过立体几何中的线面位置关系的证明来考查逻辑推理.1．【2019全国Ⅰ理18】如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求二面角A-MA1-N的正弦值．【解析】（1）连结B1C，ME．因为M，E分别为BB1，BC的中点，所以ME∥B1C，且ME=12B1C．又因为N为A1D的中点，所以ND=12A1D．由题设知A1B1=P DC，可得B1C=P A1D，故ME=P ND，因此四边形MNDE 为平行四边形，MN ∥ED ．又MN ⊄平面EDC 1，所以MN ∥平面C 1DE ．（2）由已知可得DE ⊥DA ．以D 为坐标原点，DA uu u r的方向为x 轴正方向，建立如图所示的空间直角坐标系D -xyz ，则(2,0,0)A ，A 1(2,0,4)，2)M ，(1,0,2)N ，1(0,0,4)A A =-uuu r，1(12)A M =--uuuu r，1(1,0,2)A N =--uuu r ，1(1,0,2)A N =--uuu r．设(,,)x y z =m 为平面A 1MA 的法向量，则110A M A A ⎧⋅=⎪⎨⋅=⎪⎩uuuu r uuu rm m ，所以2040x z z ⎧-+-=⎪⎨-=⎪⎩，．可取=m ．设(,,)p q r =n 为平面A 1MN 的法向量，则100MN A N ⎧⋅=⎪⎨⋅=⎪⎩uuu r uuu r，．n n所以020p r ⎧=⎪⎨--=⎪⎩，．可取(2,0,1)=-n ．于是cos ,||⋅〈〉===‖m n m n m n ，所以二面角1A MA N --【素养解读】本题考查线面平行的证明及二面角的计算，线面平行的证明的关键是借助平面几何知识证明平行，二面角则借助空间向量来求，体现了逻辑推理及数学运算核心素养。

考点08 空间角的求解问题(解析版)

考点08 空间角的求解问题立体几何是历年高考的必考题，其考查形式主要为空间几何体的有关计算（主要是体积计算），空间线面的位置关系以及空间角和距离的求解。

例如：2022年全国乙卷（理）[18]，2022年全国甲卷（理）[18]，2022年浙江高考[19]，2022年新高考Ⅰ卷[19]，2022年新高考Ⅱ卷[20]，2022年天津高考[17]，2022年北京高考[17]等都对空间几何体的体积进行了考查。

〔1〕平移法求异面直线所成的角求异面直线所成的角的方法为平移法，平移法一般有3种 (1)利用图形中已有的平行线平移；(2)利用特殊点(线段的端点或中点)作平行线平移； (3)补形平移.〔2〕线面角、二面角1.线面角的求法：找出斜线在平面上的射影，关键是作垂线，找垂足，把线面角转化到一个三角形中求解.2.二面角的求法：二面角的大小用它的平面角来度量. 平面角的作法常见的有①定义法；①垂面法。

〔3〕利用空间向量求空间中的角与距离 1.异面直线所成角若异面直线1l ，2l 所成的角为θ，则|||||cos |cos b a b a b a ==θ(注意：两异面直线所成的角为锐角或直角，而不共线的两向量的夹角的取值范围为(0，π)，所以公式中要加绝对值)，其中a ，b 分别是直线1l ，2l 的方向向量。

2.直线与平面所成角已知直线l 与平面α，A l =α ，a 为l 的方向向量，n 为平面α的法向量，θ为l 与α所成的角，则|||||cos |sin n a n a n a ==θ。

(注意:直线与平面所成角的范围为⎥⎦⎤⎢⎣⎡2,0π，而向量的夹角的取值范围为[]π,0，所以公式中要加绝对值)。

3.二面角设1n 为平面α的法向量，2n 为平面β的法向量，1n ，2n 的夹角为θ，l =βα ，则二面角βα--l 的大小为θ或θπ-。

设二面角βα--l 的大小为ϕ，则|||||cos ||cos |2121n n ==θϕ①①所示。

专题08内力作用-备战2023年高考地理专题复习新题典题精练(解析版)

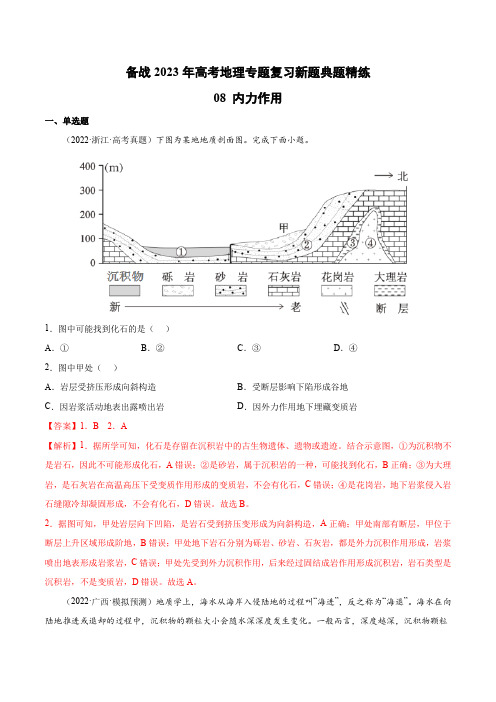
备战2023年高考地理专题复习新题典题精练08 内力作用一、单选题（2022·浙江·高考真题）下图为某地地质剖面图。

完成下面小题。

1．图中可能找到化石的是（）A．①B．②C．③D．④2．图中甲处（）A．岩层受挤压形成向斜构造B．受断层影响下陷形成谷地C．因岩浆活动地表出露喷出岩D．因外力作用地下埋藏变质岩【答案】1．B 2．A【解析】1．据所学可知，化石是存留在沉积岩中的古生物遗体、遗物或遗迹。

结合示意图，①为沉积物不是岩石，因此不可能形成化石，A错误；②是砂岩，属于沉积岩的一种，可能找到化石，B正确；③为大理岩，是石灰岩在高温高压下受变质作用形成的变质岩，不会有化石，C错误；④是花岗岩，地下岩浆侵入岩石缝隙冷却凝固形成，不会有化石，D错误。

故选B。

2．据图可知，甲处岩层向下凹陷，是岩石受到挤压变形成为向斜构造，A正确；甲处南部有断层，甲位于断层上升区域形成阶地，B错误；甲处地下岩石分别为砾岩、砂岩、石灰岩，都是外力沉积作用形成，岩浆喷出地表形成岩浆岩，C错误；甲处先受到外力沉积作用，后来经过固结成岩作用形成沉积岩，岩石类型是沉积岩，不是变质岩，D错误。

故选A。

（2022·广西·模拟预测）地质学上，海水从海岸入侵陆地的过程叫“海进”，反之称为“海退”。

海水在向陆地推进或退却的过程中，沉积物的颗粒大小会随水深深度发生变化。

一般而言，深度越深，沉积物颗粒越小。

下图示意海进或海退时形成的沉积序列，图中aa'、bb'表示垂直剖面，1.2、3、4表示海面位置的时间变化顺序。

据此完成下面小题。

3．根据材料图文信息可判断（）A．图a表示海进过程，图b表示海退过程B．形成图a沉积序列过程中海平面下降C．图a陆地面积缩小，图b陆地面积扩大D．形成图b沉积序列过程中地壳上升4．关于海退沉积序列的特点，下列说法正确的是（）①沉积物颗粒自下而上变粗②新岩层面积大于老岩层③沉积物颗粒自下而上变细④新岩层面积小于老岩层A．①③B．①④C．②③D．②④5．海退序列常常不如海进序列保存完整，是因为海退序列（）A．不易被海水淹没B．形成时间较短C．易受外力侵蚀D．沉积物数量少【答案】3．B 4．B 5．C【解析】3．根据材料中“图中1、2、3、4表示海面位置的时间变化顺序”，可推知图a从1到4表示海平面下降，陆地面积扩大，为海退过程，B正确，AC错误。

专题8.8 立体几何综合问题(精练)-2021年新高考数学一轮复习学与练(解析版)

专题8.8 立体几何综合问题一、选择题1.（2020·浙江高三月考）“直线l与平面α内无数条直线垂直”是“直线l与平面α垂直”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不必要也不充分条件【答案】B【解析】设命题p：直线l与平面α内无数条直线垂直，命题q：直线l与平面α垂直，⇒，所以p是q的必要不充分条件.则p q，但q p故选：B、是空间两个不同的平面，则“平面α上存在不共线的三点到2．（2020·上海市建平中学月考）已知αβαβ”的（）平面β的距离相等”是“//A．充分非必要条件B．必要非充分条件C．充要条件D．非充分非必要条件【答案】B【解析】、是空间两个不同的平面，若平面α内存在不共线的三点到平面β的距离相等，已知αβαβ或相交，可得//αβ，则平面α上存在不共线的三点到平面β的距离相等；反之，若//αβ”的必要不充分条件．所以“平面α上存在不共线的三点到平面β的距离相等”是“//故选：B.3.（2020·浙江高三月考）设m，n是空间两条不同直线，α，β是空间两个不同平面，则下列选项中不正确的是（）A．当n⊥α时，“n⊥β”是“α∥β”成立的充要条件⊥”的充分不必要条件B．当时，“m⊥β”是“αβC．当时，“n//α”是“”必要不充分条件D ．当时，“”是“”的充分不必要条件【答案】C 【解析】A,B,D 正确；C 错误．,////m n m n m n αα⊂⇒或与异面；,////;m n m n n ααα⊂⇒⊂或所以当m α⊂时，//n α是//m n 的既不充分又不必要条件.故选C3．（2020·河北新华·石家庄二中高三月考（理））如图，正方体1111ABCD A BC D -中，P 为底面ABCD 上的动点，1PE A C ⊥于E ，且,PA PE =则点P 的轨迹是（）A ．线段B ．圆C ．椭圆的一部分D ．抛物线的一部分【答案】A【解析】连结1AP ，可证11A AP A EP ≌，即11A A A E =，即点E 是体对角线1AC 上的定点，直线AE 也是定直线．PA PE =，∴动点P 必定在线段AE 的中垂面α上，则中垂面α与底面ABCD 的交线就是动点P 的轨迹，所以动点P 的轨迹是线段．故选：A5．（2020·河南月考（理））3D 打印属于快速成形技术的一种，它是一种以数字模型文件为基础，运用粉末状金属或塑料等可粘合材料，通过逐层堆叠累积的方式来构造物体的技术（即“积层造型法”）．过去常在模具制造、工业设计等领域被用于制造模型，现正用于一些产品的直接制造，特别是一些高价值应用（比如髋关节、牙齿或一些飞机零部件等）．已知利用3D 打印技术制作如图所示的模型．该模型为在圆锥底内挖去一个正方体后的剩余部分（正方体四个顶点在圆锥母线上，四个顶点在圆锥底面上），圆锥底面直径为31 g/cm，不考虑打印损耗，制作该模型所需原料的质量约为（）（取π 3.14=，精确到0.1）A．609.4g B．447.3g C．398.3g D．357.3g【答案】C【解析】如图，是几何体的轴截面，因为圆锥底面直径为，所以半径为OB=．因为母线与底面所成角的正切值为tan B，所以圆锥的高为10cmPO=．设正方体的棱长为a，DE=1010a-=，解得5a=．所以该模型的体积为(()2331500ππ105125cm33V=⨯⨯-=-．所以制作该模型所需原料的质量为()500π500π1251125398.3g33⎛⎫-⨯=-≈⎪⎝⎭．故选：C．6．（2020·上海浦东新·华师大二附中月考）运用祖暅原理计算球的体积时，夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意一个平面所截，若截面面积都相等，则这两个几何体的体积相等.构造一个底面半径和高都与球的半径相等的圆柱，与半球（如图①）放置在同一平面上，然后在圆柱内挖去一个以圆柱下底面圆心为顶点，圆柱上底面为底面的圆锥后得到一新几何体（如图②），用任何一个平行于底面的平面去截它们时，可证得所截得的两个截面面积相等，由此可证明新几何体与半球体积相等.现将椭圆221916x y +=绕y 轴旋转一周后得一橄榄状的几何体（如图③），类比上述方法，运用祖暅原理可求得其体积等于（）A ．64πB ．48πC ．16πD ．32π【答案】B【解析】构造一个底面半径为3，高为4的圆柱，在圆柱中挖去一个以圆柱下底面圆心为顶点的圆锥，则当截面与顶点距离为(04)h h 时，小圆锥的底面半径为r ，则43h r =， 34r h ∴=，故截面面积为26991h ππ-，把y h =代入椭圆221916x y +=可得x =， ∴橄榄球形几何体的截面面积为221699h x πππ=-，由祖暅原理可得橄榄球形几何体的体积()1229494483V V V πππ⎛⎫=-=⨯-⨯⨯= ⎪⎝⎭圆柱圆锥．故选：B ．7．（2018·浙江高考真题）已知四棱锥S ABCD -的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为1θ，SE 与平面ABCD 所成的角为2θ，二面角S AB C --的平面角为3θ，则（）A ．123θθθ≤≤B ．321θθθ≤≤C ．132θθθ≤≤D ．231θθθ≤≤【答案】D【解析】设O 为正方形ABCD 的中心，M 为AB 中点，过E 作BC 的平行线EF ，交CD 于F ，过O 作ON 垂直EF 于N ，连接SO 、SN 、OM ，则SO 垂直于底面ABCD ，OM 垂直于AB ，因此123,,,SEN SEO SMO θθθ∠=∠=∠= 从而123tan ,tan ,tan ,SN SN SO SO EN OM EO OMθθθ==== 因为SN SO EO OM ≥≥，，所以132tan tan tan ,θθθ≥≥即132θθθ≥≥，选D.8．（2019·山西高二期中（理））如图，在Rt ABC ∆中，D ，E 分别为AB ，AC 边上的中点，且4AB =，2BC =.现将ABC ∆沿DE 折起，使得A 到达1A 的位置，且二面角1A DE B --为60︒，则1AC =（）A ．B ．3CD ．【答案】A【解析】 ,D E 分别为,AB AC 中点 //DE BC ∴ DE BD ∴⊥，1DE A D ⊥又1,BD A D ⊂平面1A BD ，1BD A D D = DE ∴⊥平面1A BD二面角1A DE B --的平面角为1A DB ∠ 160A DB ∴∠=12A D BD == 12A B ∴=//BC DE BC ∴⊥平面1A BD ，又1A B ⊂平面1A BD 1BC A B ∴⊥1AC ∴===故选：A9．（2020·浙江诸暨·）正方体1111ABCD A BC D -中，在111A B D ∆内部（不含边界）存在点P ，满足点P 到平面11ACC A 的距离等于点P 到棱1BB 的距离.分别记二面角P AD B --为α，P AC B --为β，P BC A --为γ，则下列说法正确的是（）A ．αβγ>>B ．αγβ<<C ．αβγ<<D ．以上说法均不正确【答案】C【解析】如图所示，作PQ ⊥面ABCD 于Q ，作QE AD ⊥于E ，QF BC ⊥于F ，QG AC ⊥于G ，连PE ，PF ，PG ，则PEQ α=∠，PGQ β=∠，PFQ γ=∠. 因此tan PQ QE α=，tan PQ QG β=，tan PQ QFγ=，作111PE A D ⊥于1E ，111PF B C ⊥于1F ，111PG AC ⊥于1G ，1PG 即点P 到平面11ACC A 的距离，1PB 即点P 到棱1BB 的距离，因此11PB PG =，因为111QF PF PB PG QG =<==，因此tan tan βγ<，因为11QG PG PE QE =<=，因此tan tan αβ<综上有：tan tan tan αβγ<<，即αβγ<<，故选:C10．（2020·安徽合肥·高三三模（理））在长方体1111ABCD A B C D -中，6AB AD ==，12AA =，M 为棱BC 的中点，动点P 满足APD CPM ∠=∠，则点P 的轨迹与长方体的面11DCC D 的交线长等于（）A ．23πB ．πC ．43πD【答案】A【解析】如下图所示：当P 在面11DCC D 内时，AD ⊥面11DCC D ，CM ⊥面11DCC D ；又APD MPC ∠=∠，在Rt PDA △与Rt PCM 中，∵6AD =，则3MC =， ∴tan tan AD MC APD MPC PD PC ∠==∠=，则63PD PC =，即2PD PC =．在平面11DCC D 中，以DC 所在直线为x 轴，以DC 的垂直平分线为y 轴建立平面直角坐标系，则()3,0D -，()3,0C ，设(),P x y ，由2PD PC ==整理得：221090x x y -++=，即()22516x y -+=．∴点P 的轨迹是以()5,0F 为圆心，半径为4的圆．设圆F 与面11DCC D 的交点为E 、M ，作EK 垂直x 轴于点K ，则21sin 42EK EFK EF ∠===； ∴6EFK π∠=；故点P 的轨迹与长方体的面11DCC D 的交线为劣弧ME ，所以劣弧ME 的长为2463ππ⨯=. 故选：A ．二、多选题 11．（2020·广东宝安·高三开学考试）如图，正方体1111ABCD A BC D -的棱长为1，线段11B D 上有两个动点E 、F ，且12EF =，则下列结论中正确的是（）A ．AC BE ⊥B ．//EF 平面ABCDC ．AEF 的面积与BEF 的面积相等D ．三棱锥A BEF -的体积为定值【答案】ABD【解析】可证AC ⊥平面11D DBB ，从而AC BE ⊥，故A 正确；由11//B D 平面ABCD ，可知//EF 平面ABCD ，B 也正确；连结BD 交AC 于O ，则AO 为三棱锥A BEF -的高，1111224BEF S =⨯⨯=△，三棱锥A BEF -的体积为1134224⨯⨯=为定值，D 正确；很显然，点A 和点B 到的EF 距离是不相等的，C 错误. 故选：ABD 12．（2020·江苏赣榆一中高一月考）已知在矩形ABCD 中，4AB =，3BC =，将矩形ABCD 沿对角线AC 折成大小为θ的二面角B AC D --，若折成的四面体ABCD 内接于球O ，则下列说法正确的是（） A ．四面体ABCD 的体积的最大值是245 B ．球的体积随θ的变化而变化C ．球心O 为原矩形的两条对角线的交点D ．球O 的表面积为定值25π 【答案】ACD【解析】如图，（1）当面ACD ⊥面ABC 时，四面体ABCD 的体积最大，此时，如图，过点D 作AC 的垂线，交AC 于点E ，则DE 即为四面体ABCD 的高，由等面积法得：AC DE AD DC ⨯=⨯,∴ 125DE = , ∴四面体ABCD 的最大值为11112243433255ABC V S h =⋅=⨯⨯⨯⨯=，故A 选项正确；（2）在四面体ABCD 内，AC 的中点O 到点,,,A B C D 的距离相等，∴点O 为外接球的球心，此时球的半径522AC R ==，球的体积242533V R ππ== ，为定值，球的表面积2425S R ππ== ，为定制，故B 选项错误，,C D 正确，故选,,A C D 13．（2020·湖北江岸·期末）向体积为1的正方体密闭容器内注入体积为x （01x <<）的液体，旋转容器，下列说法正确的是（）A ．当12x =时，容器被液面分割而成的两个几何体完全相同 B ．不管注入多少液体，液面都可以成正三角形形状CD 【答案】AC【解析】对于A ，当12x =时，题目等价于过正方体中心的平面截正方体为两部分，根据对称性知两部分完全相同，所以A 正确；对于B ，取12x =，此时液面过正方体中心，截面不可能为三角形，所以B 错误；对于C ，当液面与正方体的体对角线垂直时，液面为如图所示正六边形时面积最大，其中正六边形的顶点均为对应棱的中点，所以液面面积的最大值为162S ==，C 正确；对于D ，当液面过1DB 时，截面为1B NDG ，将1111D C B A 绕11C D 旋转2π，如图所示；则111DN B N DN B N DB ''+=+≥= 当D 、N 、1B '三点共线时等号成立，所以液面周长最小值为D 错误. 故选：AC.14．（2020·广东深圳·高二月考）（多选题）如图，在直三棱柱111ABC A B C -中，1223AA AC AB ===，AB AC ⊥，点D ，E 分别是线段BC ，1BC 上的动点（不含端点），且1EC DC B C BC=．则下列说法正确的是（）A ．//ED 平面1ACCB ．该三棱柱的外接球的表面积为68πC ．异面直线1BC 与1AA 所成角的正切值为32 D ．二面角A EC D --的余弦值为413【答案】AD【解析】在直三棱柱111ABC A B C -中，四边形11BCC B 是矩形，因为1EC DC B C BC=，所以11////ED BB AA ，ED 不在平面1ACC 内，1AA ⊂平面1ACC ，所以//ED 平面1ACC ，A 项正确；因为1223AA AC AB ===，所以3AB =，因为AB AC ⊥，所以BC ==1BC 易知1BC 是三棱柱外接球的直径，所以三棱柱外接球的表面积为22417πππ=⨯=⎝⎭，所以B 项错误；因为11//AA BB ，所以异面直线1BC 与1AA 所成角为1BB C ∠．在1Rt B BC 中，12BB =，BC =，所以11tan BC BB C BB ∠==C 项错误；二面角A EC D --即二面角1A B C B --，以A 为坐标原点，以AB ，AC ，1AA 的方向分别为x ，y ，z 轴的正方向，建立空间直角坐标系，如图则1(0,0,0),(3,0,0),(0,2,0),(3,0,2)A B C B ，1(3,0,2)AB ∴=，(3,2,0)BC =-，1(3,2,2)BC =--，设平面1ABC 的法向量(,,)n x y z =，则1100n AB n B C ⎧⋅=⎪∴⎨⋅=⎪⎩，即3203220x z x y z +=⎧⎨-+-=⎩，令2x =可得(2,0,3)n =-，设平面1BB C 的一个法向量为(,,)m x y z =，则100m BC m B C ⎧⋅=⎪⎨⋅=⎪⎩，即3203220x y x y z -+=⎧⎨-+-=⎩，令2x =可得(2,3,0)m = 故二面角A EC D --413=，所以D 项正确．故选：AD.三、填空题15．（2020·浙江高三月考）在2000多年前，古希腊数学家阿波罗尼斯采用平面切割圆锥的方法来研究圆锥曲线：用垂直于锥轴的平面去截圆锥，得到的是圆；把平面渐渐倾斜，得到椭圆；当平面倾斜到“和且仅和”圆锥的一条母线平行时，得到抛物线；当平面再倾斜一些就可以得到双曲线.已知一个圆锥的高和底面半径都为2，则用与底面呈45的平面截这个圆锥，得到的曲线是___________.【答案】抛物线【解析】因为圆锥的高和底面半径都为2，因此有, ︒tan 145OS SAO SAO AO︒∠==⇒∠=所以母线SA 与底面所成的角为45，因为用与底面呈45的平面截这个圆锥，所以该平面一定会与圆锥的某条母线(如SA )平行，由题中所给的结论可知：用与底面呈45的平面截这个圆锥，得到的曲线是抛物线.故答案为：抛物线16．（2020·江西其他（文））《九章算术》是我国古代著名数学经典，其中对勾股定理的论述，比西方早一千多年，其中有这样一个问题：“今有圆材埋在壁中，不知大小；以锯锯之，深一寸，锯道长一尺，问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该材料，锯口深1寸，锯道长1尺，问这块圆柱形木料的直径是多少？长为0.5丈的圆柱形木材部分镶嵌在墙体中，截面图如图所示（阴影部分为镶嵌在墙体内的部分）.己知弦尺，弓形高寸，估算该木材镶嵌墙内部分的体积约为______立方寸.（注：一丈=10尺=100寸，，答案四舍五入，只取整数．．．．．．．．．．．）【答案】317 【解析】如图，设圆半径为寸（下面长度单位都是寸），连接，已知，，在中，，即，解得， ︒︒︒1AB =1CD =53.14,sin 22.513π≈≈r ,OA OD 152AD AB ==1OD OC CD r =-=-Rt ADO 222AD OD OA 2225(1)r r +-=13r =由得，所以，图中阴影部分面积为扇形（平方寸），镶嵌在墙体中木材是以阴影部分为底面，以锯刀长为高的柱体，所以其体积为（立方寸）故答案为：317．17．（2020·河北新华·石家庄二中高二月考）如图，在四棱锥中，四边形为菱形，且是等边三角形，点是侧面内的一个动点，且满足，则点所形成的轨迹长度是_______.【解析】根据题意，连接AC ，BD ，记其交点为O ，取PC 上一点为M ，连接MB ，MD ，作图如下：5sin 13AD AOD AO ∠==22.5AOD ∠=︒45AOB ∠=︒S S =214131012 6.332522AOB S πππ-=⨯⨯-⨯⨯≈△6.332550317V Sh =≈⨯≈P ABCD -ABCD 2,60,AB DAB PAD =∠=∆PB Q =PBC DQ AC ⊥Q若满足题意，又，故平面DBQ ，则点Q 只要在平面DBQ 与平面PBC 的交线上即可.假设如图所示：平面DBM 与平面DBQ 是同一个平面，则Q 点的轨迹就是线段BM.根据假设，此时直线平面DBM ，则.故三角形MOC 为直角三角形.因为三角形PAD 是等边三角形，三角形BAD 也是等边三角形，故AD ，又因为BC //AD ，故BC PB ，故三角形PBC 为直角三角形，故故在三角形PAC 中，由余弦定理可得：故在直角三角形MOC 中，在直角三角形PBC 中，在三角形BCM 中：故可得：. DQ AC ⊥AC BD ⊥AC ⊥AC ⊥AC MO ⊥PB ⊥⊥2210PC PB BC +2,23,10PA AC PC ===33021023cos PCA ∠==⨯210OC MC cos PCA ==∠BC cos PCB PC ∠=1010=2222829BM BC CM BC CM cos PCB =+-⨯⨯⨯∠=27BM =故答案为. 18．（2021·福建其他）《九章算术》中，将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的鳖臑中，平面，，，，为中点，为内的动点（含边界），且.①当在上时，______；②点的轨迹的长度为______.【答案】【解析】 (1)当在上时,因为平面,故,又,故平面.故.又,为中点,故所以为中点.故. (2)取中点则由(1)有平面,故,又,设平面则有平面.故点的轨迹为.又此时,,故. 所以3P ABC -PA ⊥ABC 90ACB ∠=︒4CA =2PA =D AB E PAC ∆PC DE ⊥E AC AE =E E AC PA ⊥ABC PA DE ⊥PC DE ⊥DE ⊥PAC DE AC ⊥90ACB ∠=︒D AB //DE BC E AC 122AE AC ==AC F DF ⊥PAC PC DF ⊥PC DE ⊥DEF PC G ⋂=PC ⊥DGF E FG 2CF =1tan 2PA PCA AC ∠==sin PCA ∠==sin 5FG CF PCA =⋅∠==故答案为：19．（2020·全国高三专题练习（文））现代足球运动是世上开展得最广泛、影响最大的运动项目，有人称它为“世界第一运动”．早在2000多年前的春秋战国时代，就有了一种球类游戏“蹴鞠”，后来经过阿拉伯人传到欧洲，发展成现代足球．1863年10月26日，英国人在伦敦成立了世界上第一个足球运动组织——英国足球协会，并统一了足球规则．人们称这一天是现代足球的诞生日．如图所示，足球表面是由若干黑色正五边形和白色正六边形皮围成的，我们把这些正五边形和正六边形都称为足球的面，任何相邻两个面的公共边叫做足球的棱．已知足球表面中的正六边形的面为20个，则该足球表面中的正五边形的面为______个，该足球表面的棱为______条．【答案】12 90【解析】足球每块黑色皮子的5条边分别与5块白色皮子的边缝在一起；每块白色皮子的6条边中，有3条边与黑色皮子的边缝在一起，另3条边则与其他白色皮子的边缝在一起.所以设这个足球有x 块正五边形，一共有5x 条边，其中白皮三条边和黑皮相连，又足球表面中的正六边形的面为20个，根据题意可得方程：，解得，该足球表面中的正五边形的面为12个；因为任何相邻两个面的公共边叫做足球的棱，所以每条棱由两条边组成，该足球表面的棱为：条.故答案为：12；90.20．如图在三棱锥S ABC -中，SA SB SC ==，且2ASB BSC CSA π∠=∠=∠=，M N 、分别是AB 和SC 的中点．则异面直线SM 与BN 所成的角的余弦值为______，直线SM 与面SAC 所成角大小为5203x =⨯12x =()125+206290⨯⨯÷=_________.4π 【解析】因为2ASB BSC CSA π∠=∠=∠=，所以以S 为坐标原点，SA,SB,SC 为x,y,z 轴建立空间直角坐标系.设2SA SB SC ===，则(1,1,0),(0,2,0),(0,0,1),(2,0,0),(0,0,2).M B N A C因为2(1,1,0),(0,2,1),cos ,2SM BNSM BN -==-==，所以异面直线SM 与BN 所成的角的余弦值为5，面SAC 一个法向量为(0,2,0),SB =则由2cos ,22SM SB ==得π,4SM SB =，即直线SM 与面SAC 所成角大小为π4. 21.（2020·包头市第九中学高一期末）设三棱锥的底面和侧面都是全等的正三角形，是棱的中点.记直线与直线所成角为，直线与平面所成角为，二面角的平面角为，则，，中最大的是_________，最小的是________.【答案】【解析】S ABC -P SA PB AC αPB ABC βP AC B --γαβγαβ作交于，由于，，所以为正三棱锥，由对称性知，取中点，连接，作平面，交平面于，连接，作平面，交平面于，连接，作，交于，连接，所以，由于，所以，由于平面，所以，由于，平面，所以，，因为，在上，平面于，平面于，所以.所以.所以，由于都是锐角，所以，由于在上，由对称性，而，则，由于也是锐角，所以，由,，所以综上所述，三个角中的最小角是，最大角是.故答案为：①；②.四、解答题//PD CA SC D AB BC CA ==SA SB SC ==S ABC -BD PB =PD E BE EH ⊥ABC ABC H BH PF ⊥ABC ABC F BF PG AC ⊥AC G GF BE PD ⊥//PD AC BPD α=∠PF ⊥ABC PBF β=∠PG AC ⊥PF ⊥ABC PGF γ=∠sin BE EH BP BP BP BPα==>=//PD CA E PD EH ⊥ABC H PF ⊥ABC F EH PF =sin PF EH BP BPβ==sin sin αβ>,αβαβ>P SA PB CP =CP PG >sin sin PF PF PF PG CP BP γβ=>==γγβ>PB BG<sin BE EH PF BP BP BP α==>==sin PF PGγ>=αγβααβ22．（2019·北京西城·高三三模）如图，在正四棱柱1111ABCD A BC D -中，1AB =，13AA =，过顶点A ，1C 的平面与棱1BB ，1DD 分别交于M ，N 两点（不在棱的端点处）.（1）求证：四边形1AMC N 是平行四边形；（2）求证：AM 与AN 不垂直；（3）若平面1AMC N 与棱BC 所在直线交于点P ，当四边形1AMC N 为菱形时，求PC 长.【答案】（1）证明见解析；（2）证明见解析；（3）=2PC .【解析】（1）依题意1AM C N ，，，都在平面1AC 上，因此AM ⊆平面1AC ，1NC ⊆平面1AC ，又AM ⊆平面11ABB A ，1NC ⊆平面11DCC D ，平面11ABB A 与平面11DCC D 平行，即两个平面没有交点，则AM 与1NC 不相交，又AM 与1NC 共面，所以//AM 1NC ，同理可证//AN 1MC ，所以四边形1AMC N 是平行四边形；（2）因为M ，N 两点不在棱的端点处，所以11MN BD AC <=，又四边形1AMC N 是平行四边形，1MN AC ≠，则1AMC N 不可能是矩形，所以AM 与AN 不垂直；（3）如图，延长1C M 交CB 的延长线于点P ，若四边形1AMC N 为菱形，则1AM MC =，易证11Rt ABM Rt C B M ≅，所以1BM B M =，即M 为1BB 的中点，因此112BM CC =，且1//BM CC ，所以BM 是1PCC 的中位线，则B 是PC 的中点，所以22PC BC ==.23．（2019·全国高三专题练习）如图，正△ABC 的边长为4，CD 为AB 边上的高，E ，F 分别是AC 和BC 边的中点，现将△ABC 沿CD 翻折成直二面角A －DC －B .(1)试判断直线AB 与平面DEF 的位置关系，并说明理由；(2)在线段BC 上是否存在一点P ，使AP DE ⊥？如果存在，求出BP BC 的值；如果不存在，请说明理由．【答案】（1）//AB 平面DEF ，理由见解析；（2）13. 【解析】(1)AB∥平面DEF ，理由如下：在△ABC 中，由E ，F 分别是AC ，BC 的中点，得EF∥AB.又因为AB ⊄平面DEF ，EF ⊂平面DEF ，所以AB∥平面DEF.(2)以点D 为坐标原点，直线DB ，DC ，DA 分别为x 轴，y 轴，z 轴，建立空间直角坐标系(如图所示)，则A(0，0，2)，B(2，0，0)，C(0，0)，E(01)，故DE ＝(01)．假设存在点P(x ，y ，0)满足条件，则AP ＝(x ，y ，－2)，AP ·DE 20-=，所以y =.又BP ＝(x 2-，y ，0)，PC ＝(－x ，y ，0)，BP ∥PC ，所以(x 2-)(y )＝xy -y +=把y =代入上式得4x 3=，所以BP ＝1BC 3，所以在线段BC 上存在点P 使AP⊥DE，此时BP 1BC 3=. 24．（2019·上海市金山中学高二月考）几何特征与圆柱类似，底面为椭圆面的几何体叫做“椭圆柱”，如图所示的“椭圆柱”中，A B ''、AB 和O '、O 分别是上下底面两椭圆的长轴和中心，1F 、2F 是下底面椭圆的焦点，其中长轴的长度为2，两中心O '、O M 、N 分别是上、下底面椭圆的短轴端点，且位于平面AA B B ''的两侧.（1）求证：OM ∥平面A B N ''；（2）求点M 到平面A B N ''的距离；（3）若点Q 是下底面椭圆上的动点，Q '是点Q 在上底面的投影，且1Q F '、2Q F '与下底面所成的角分别为α、β，试求出tan()αβ+的取值范围.【答案】（1）证明见解析；（2（3）tan()[5αβ+∈-. 【解析】（1）连接,,O M O N ON '',M N 分别为上下椭圆的短轴端点 //O M ON '∴∴四边形O MPN '为平行四边形 //OM O N '∴O N '⊂平面A B N ''，OM ⊄平面A B N '' //OM ∴平面A B N ''（2）连接OO '由“椭圆柱”定义可知OO '⊥平面12F NFON ⊂平面12F NF OO ON '∴⊥ O N '∴==由对称性可知：A N B N ''= O N A B '''∴⊥1122A B N S A B O N ''∆'''∴=⋅=⨯=又12A B M S A B O M ''∆'''=⨯⋅=，OO '1133N A B M A B M V S OO ''''-∆'∴=⋅==设点M 到平面A B N ''的距离为d ，则13M A B N N A B M A B N V V S d ''''''--∆==⋅==解得：7d =，即点M 到平面A B N ''的距离为7（3）连接12,QF QF由题意知：QQ '⊥平面12F F Q，QQ '=1Q FQ '∴∠即为1Q F'与下底面所成角；2Q F Q '∠即为2Q F '与下底面所成角即1Q FQ α'∠=，2Q F Q β'∠= 设1QF m =，由椭圆定义知：2QF m =1tan QQ QF α'∴==，2tan QQ QF β'== ()tan tan tan 1tan tan 1αβαβαβ+∴+===-21m ⎡⎤∈⎣⎦[]265,4m∴-+-∈-- ()tan 5αβ⎡∴+∈-⎢⎣⎦25.（2016·天津高考真题（理））如图，正方形ABCD 的中心为O ，四边形OBEF 为矩形，平面OBEF⊥平面ABCD ，点G 为AB 的中点，AB=BE=2.（Ⅰ）求证：EG∥平面ADF ；（Ⅱ）求二面角O −EF −C 的正弦值；（Ⅲ）设H 为线段AF 上的点，且AH=23HF ，求直线BH 和平面CEF 所成角的正弦值. 【答案】（Ⅰ）详见解析；（Ⅱ）√33；（Ⅲ）√721.【解析】依题意，OF ⊥平面ABCD ，如图，以O 为点，分别以AD ⃗⃗⃗⃗⃗ ,BA⃗⃗⃗⃗⃗ ,OF ⃗⃗⃗⃗⃗ 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，依题意可得O(0,0,0)，A(−1,1,0),B(−1,−1,0),C(1,−1,0),D(1，1,0),E(−1,−1,2),F(0,0,2),G(−1,0,0).（Ⅰ）证明：依题意，AD ⃗⃗⃗⃗⃗ =(2,0,0),AF⃗⃗⃗⃗⃗ =(1,−1,2). 设n 1=(x,y,z)为平面ADF 的法向量，则{n 1⋅AD ⃗⃗⃗⃗⃗ =0n 1⋅AF⃗⃗⃗⃗⃗ =0 ，即{2x =0x −y +2z =0 . 不妨设z =1，可得n 1=(0,2,1)，又EG ⃗⃗⃗⃗⃗ =(0,1,−2)，可得EG⃗⃗⃗⃗⃗ ⋅n 1=0，又因为直线EG ⊄平面ADF ，所以EG//平面ADF .（Ⅱ）解：易证，OA⃗⃗⃗⃗⃗ =(−1,1,0)为平面OEF 的一个法向量. 依题意，EF⃗⃗⃗⃗⃗ =(1,1,0),CF ⃗⃗⃗⃗⃗ =(−1,1,2).设n 2=(x,y,z)为平面CEF 的法向量，则{n 2⋅EF ⃗⃗⃗⃗⃗ =0n 2⋅CF⃗⃗⃗⃗⃗ =0 ，即{x +y =0−x +y +2z =0 . 不妨设x =1，可得n 2=(1,−1,1).因此有cos <OA ⃗⃗⃗⃗⃗ ,n 2>=OA⃗⃗⃗⃗⃗⃗ ⋅n 2|OA ⃗⃗⃗⃗⃗⃗ |⋅|n 2|=−√63，于是sin <OA ⃗⃗⃗⃗⃗ ,n 2>=√33，所以，二面角O −EF −C 的正弦值为√33.（Ⅲ）解：由AH =23HF ，得AH =25AF .因为，所以AH ⃗⃗⃗⃗⃗⃗ =25AF ⃗⃗⃗⃗⃗ =(25,−25,45)，进而有H(−35,35,45)，从而BH⃗⃗⃗⃗⃗⃗=(25,85,45)，因此cos <BH ⃗⃗⃗⃗⃗⃗ ,n 2>=BH⃗⃗⃗⃗⃗⃗ ⋅n 2|BH ⃗⃗⃗⃗⃗⃗ |⋅|n 2|=−√721. 所以，直线BH 和平面CEF 所成角的正弦值为√721.26．（2018·天津高考真题（理））如图，且AD =2BC ，,且EG =AD ，且CD =2FG ，，DA =DC =DG =2.（I ）若M 为CF 的中点，N 为EG 的中点，求证：；（II ）求二面角的正弦值；（III ）若点P 在线段DG 上，且直线BP 与平面ADGE 所成的角为60°，求线段DP 的长.【答案】(Ⅰ)证明见解析；(Ⅱ)；(Ⅲ). 【解析】依题意，可以建立以D 为原点，分别以，，的方向为x 轴，y 轴，z 轴的正方向的空间直角坐标系（如图），可得D （0，0，0），A （2，0，0），B （1，2，0），C （0，2，0），//AD BC AD CD ⊥//EG AD //CD FG DG ABCD ⊥平面MN CDE 平面E BC F --103DA DC DGE （2，0，2），F （0，1，2），G （0，0，2），M （0，，1），N （1，0，2）．（Ⅰ）依题意=（0，2，0），=（2，0，2）．设n 0=(x ，y ，z )为平面CDE 的法向量，则即不妨令z =–1，可得n 0=（1，0，–1）．又=（1，，1），可得，又因为直线MN 平面CDE ，所以MN ∥平面CDE ．（Ⅱ）依题意，可得=（–1，0，0），，=（0，–1，2）．设n =（x ，y ，z ）为平面BCE 的法向量，则即不妨令z =1，可得n =（0，1，1）．设m =（x ，y ，z ）为平面BCF 的法向量，则即不妨令z =1，可得m =（0，2，1）．因此有cos <m ，n>=，于是sin <m ，n．所以，二面角E –BC–F ． 32DC DE 0000DC DE ⎧⋅=⎪⎨⋅=⎪⎩，，n n 20220y x z ，，=⎧⎨+=⎩MN 32-00MN n ⋅=⊄BC ()122BE =-，，CF 00n BC n BE ，，⎧⋅=⎨⋅=⎩0220x x y z -=⎧⎨-+=⎩，，00m BC m CF ⎧⋅=⎨⋅=⎩，，020x y z -=⎧⎨-+=⎩，，10⋅=m nm n（Ⅲ）设线段DP 的长为h （h ∈［0，2］），则点P 的坐标为（0，0，h ），可得．易知，=（0，2，0）为平面ADGE 的一个法向量，故=sinh0，2］．所以线段27．（2020届浙江省宁波市余姚中学高考模拟）如图，ABC 为正三角形，且2BC CD ==，CD BC ⊥，将ABC 沿BC 翻折.（1）若点A 的射影在BD 上，求AD 的长；（2）若点A 的射影在BCD 中，且直线AB 与平面ACD ，求AD 的长. 【答案】（1）2 （2【解析】（1）过A 作AE BD ⊥交BD 于E ，则AE ⊥平面BCD .取BC 中点O ，连接AO ，OE ，∵AE ⊥平面BCD ，BC ⊂平面BCD ，∴AE BC ⊥，又ABC 是正三角形，∴BC AO ⊥，又AE AO A =，AE ，AO ⊂平面AOE ，∴BC ⊥平面AOE ，∴BC OE ⊥.又BC CD ⊥，O 为BC 的中点，∴E 为BD 的中点.()12BP h =--，，DC BP DCcos BP DC BP DC h ⋅⋅==DP∵2BC CD ==，∴112OE CD ==，AO =BD =∴DE =AE =∴2AD =；（2）取BC 中点为,O 过点A 作平面BCD 的垂线，垂足为E ,连接AO ,因为,AB AC OE BC =∴⊥.以O 为原点，以BC 为x 轴，以OE 为y 轴，以平面BCD 的过O 的垂线为z 轴建立空间直角坐标系，如图所示：设二面角D BC A --为θ，因为AE ⊥平面BCD ，与（1）同理可证BC ⊥平面AOE ，OE BC ⊥，AOE θ∴∠=，AO则)A θθ，(1,0,0)B -，(1,0,0)C ，(1,2,0)D .∴(1,)BA θθ=，(0,2,0)CD =，(1)CA θθ=-，设平面ACD 的法向量为(,,)n x yz =，则200n CD y n CA x y z θθ⎧⋅==⎪⎨⋅=-⋅+⋅=⎪⎩，令1z =，得(3sin ,0,1)n θ=.∴cos ,n BA <>==解得sin 6θ=. ∴1(0,,22A ，又(1,2,0)D ，∴AD ==。

2023高一下学期备战期末立体几何专题期末专题08 立体几何大题综合解析版

期末专题08 立体几何大题综合1．（2021春·江苏南京·高一校联考期末）如图，在五面体ABCDEF 中，已知DE ⊥平面ABCD ，//AD BC ，60BAD ∠=°，2AB =，1DE EF ==．（1）求证：//BC EF ；（2）求三棱锥B DEF −的体积．2．（2022春·江苏南京·高一南京市中华中学校考期末）如图，在四棱锥P ABCD −中，平面PAD ⊥平面ABCD ，//AD BC ，6ABAD AC ===，8PA BC ==，10PD =，M 为棱AD 上一点，且2AM MD =，N 为棱PC 的中点．(1)证明：平面PAB ⊥平面ABCD ；(2)求四棱锥N BCDM −的体积．3．（2021·江苏·高一期末）如图在四棱锥P - ABCD 中，底面ABCD 是矩形，点E ，F 分别是棱PC 和PD 的中点.（1）求证：EF ∥平面P AB；2023高一下学期备战期末立体几何专题（2）若AP =AD ，且平面P AD ⊥平面ABCD ，证明AF ⊥平面PCD .4．（2022春·江苏南京·高一江苏省江浦高级中学校联考期末）如图，四棱锥P ABCD −中，PA ⊥底面ABCD ，底面ABCD 为菱形，点F 为侧棱PC 上一点．(1)若PF FC =，求证：//PA 平面BDF ； (2)若BF PC ⊥，求证：平面⊥BDF 平面PBC ．5．（2021春·江苏常州·高一校联考期末）如图，在四棱锥P ABCD −中，底面ABCD 为直角梯形，//AD BC ，90ADC ∠=°，平面PAD ⊥底面ABCD ，E 为AD 的中点，M 是棱PC 的中点，2PA PD ==，112BC AD ==，CD =（1）若平面PBC 与平面PAD 的交线为l ，求证：//l BC ；（2）求直线BM 与平面ABCD 所成角的正切值；（3）求直线BM 与CD 所成角的余弦值．6．（2022春·江苏扬州·高一统考期末）如图，四棱锥P ABCD −中，底面ABCD 为平行四边形，6810PAAD PD AB PB =====，，，平面PAD ⊥平面ABCD ，平面PAB ∩平面PCD l =．(1)求四棱锥P ABCD −的体积； (2)求二面角A l D −−的余弦值．7．（2022春·江苏常州·高一统考期末）刍（ch ú）甍（m éng ）是几何体中的一种特殊的五面体.中国古代数学名著《九章算术》中记载：“刍甍者，下有袤有广，而上有袤无广.刍，草也.甍，屋盖也.求积术日：倍下表，上袤从之，以广乘之，又以高乘之，六而一.”翻译为“底面有长有宽为矩形，顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶 ”现有一个刍甍如图所示，四边形ABCD 为长方形，//EF 平面ABCD ，ADE 和BCF △是全等的等边三角形.(1)求证：//EF DC ；(2)若已知224AB BC EF ===， ①求二面角A EF C −−的余弦值； ②求该五面体ABCDEF 的体积.8．（2022春·江苏盐城·高一统考期末）如图，四棱锥P -ABCD 的底面是平行四边形，P A ⊥平面ABCD ，1,AB BC==4ABC π∠=.(1)求证：平面PCD ⊥平面P AC ； (2)若PD 与平面P AC 所成的角为6π，求PC 与平面P AD 所成的角的正弦值. 9．（2022春·江苏盐城·高一统考期末）如图，在四棱锥P -ABCD 中，112ABBC CD AD ====，//AD BC ，P 在以AD 为直径的圆O 上，平面ABCD ⊥平面P AD .(1)设点Q 是AP 的中点，求证：BQ //平面PCD ；(2)若二面角C PD A −−的平面角的正切值为2，求三棱锥A -PCD 的体积.10．（2022春·江苏宿迁·高一统考期末）在斜三棱柱111ABC A B C 中，底面是边长为4的正三角形，1=A B 1160A AB A AC ∠=∠=°．(1)证明：11//A C 平面1AB C ； (2)证明：1BC AA ⊥；(3)求直线BC 与平面11ABB A 所成角的正弦值．11．（2022春·江苏无锡·高一统考期末）如图，在四棱锥P ABCD −中，底面ABCD 为正方形，PA ⊥底面ABCD ，2PA AB ==，E 为PB 中点，M 为AD 中点，F 为线段BC 上一点.(1)若F 为BC 中点，求证：//PM 平面AEF ；(2)设直线EF 与底面ABCD 所成角的大小为α，二面角E AF B −−的大小为β，若tan =βα，求BF 的长度.12．（2021春·江苏南京·高一南京师大附中校考期末）如图，在三棱柱111ABC A B C -中，1B C AB ⊥，侧面11BCC B 为菱形.（1）求证：1B C ⊥平面1ABC .（2）如果点D ，E 分别为11A C ，1BB 的中点，求证：//DE 平面1ABC .13．（2021春·江苏南京·高一校联考期末）如图，在直三棱柱111ABC A B C -中，点D 是线段AB 上的动点.（1）线段AB 上是否存在点D ，使得1//AC 平面1B CD ？若存在，请写出ADDB值，并证明此时，1//AC 平面1B CD ；若不存在，请说明理由；（2）已知平面11ABB A ⊥平面1CDB ，求证：CD AB ⊥.14．（2021·江苏·高一期末）如图，在四棱锥P ABCD −中，平面ABCD ⊥平面PAB ，PAB 为等边三角形，四边形ABCD 为矩形，E 为PB 的中点.（1）证明：平面ADE ⊥平面PBC .（2）平面ADE 分此棱锥为两部分，若2AB AD =，求大的部分体积与小的部分体积之比.15．（2021·江苏·高一期末）已知在六面体PABCDE 中，PA ⊥平面ABCD ，ED ⊥平面ABCD ，且2PA ED =，底面ABCD 为菱形，且60ABC ∠=°.（1）求证：平面PAC ⊥平面PBD ；（2）若2AB =，1DE =，且M 为PB 的中点，求三棱锥E PAM −的体积.16．（2021春·江苏常州·高一校联考期末）如图，三棱锥−P ABC 的底面是等腰直角三角形，其中2ABAC ==，PA PB =，平面PAB ⊥平面ABC ，点E ，F ，M ，N 分别是AB ，AC ，PC ，BC 的中点．（1）证明：平面EMN ⊥平面PAB ；（2）当PF 与平面ABC 所成的角为3π时，求四棱锥A PMNB −的体积． 17．（2021春·江苏南京·高一南京师大附中校考期末）如图，圆锥顶点为P ，底面圆心为O ，其母线与底面所成的角为22.5°，AB 和CD 是底面圆O 上的两条平行的弦，轴OP 与平面PCD 所成的角为60°.（1）证明：平面P AB 与平面PCD 的交线平行于底面；（2）求二面角C OP D −−的余弦值.18．（2021春·江苏南京·高一南京市第二十九中学校考期末）如图在三棱柱111ABC A B C -中，侧面11BCC B 为菱形，平面11BCC B ⊥平面ABC ，直线1BB 与平面ABC 所成线面角为60°，且8BC =，10AC =，3cos 5CAB ∠=.（1）求证：平面1AB C ⊥平面1ABC ；（2）设P 为线段11A B 上一点，求三棱锥A PBC −的体积.19．（2021春·江苏苏州·高一统考期末）如图1，在矩形ABCD 中，已知2AB BC =，E 为AB 的中点.将ADE 沿DE 向上翻折，进而得到多面体1A BCDE −（如图2）.（1）求证：1DE A C ⊥；（2）在翻折过程中，求二面角1A DC B −−的最大值.20．（2021春·江苏南京·高一校联考期末）如图，在三棱柱111ABC A B C -中，侧面11ACC A 是矩形，侧面11BCC B 是菱形，M 、N 分别是1AB 、1BC 的中点，1AC BC ⊥（1）求证：//MN 平面111A B C ；（2）求证：11BC AB ⊥；（3）若2AC =，1BCC 是边长为4的正三角形，求三棱锥1B AB C −的体积． 21．（2021春·江苏徐州·高一统考期末）如图①，在正方体ABCD -A 1B 1C 1D 1中，E ，F ，G 分别为AB ，BC ，BB 1，的中点．（1）求证：平面EFG ⊥平面BB 1D 1D ；（2）将该正方体截去八个与四面体B -EFG 相同的四面体得到一个多面体(如图②)，若该多面体的体积是1603，求该正方体的棱长． 22．（2021春·江苏南京·高一校考期末）如图，A 是以BD 为直径的半圆O 上一点，BC 垂直于圆O 所在的平面．（1）求证：AD ⊥平面ABC ；（2）若22BD BC ==， AD AB =，求二面角A CD B −−的余弦值．23．（2021春·江苏南京·高一南京市第一中学校考期末）如图，在四棱锥P ﹣ABCD 中，底面ABCD 为直角梯形，AD ∥BC ，∠ADC ＝90°，AD ＝2BC ＝2，CD ．平面P AD ⊥平面ABCD ，∠PDA ＝90°．(1)若平面P AD ∩平面PBC ＝l ，求证：l ∥BC ；(2)求证：平面P AC ⊥平面PBD ；(3)若二面角B ﹣P A ﹣D 的正切值为，求四棱锥P ﹣ABCD 的体积．24．（2022春·江苏常州·高一校联考期末）如图，在三棱锥A BCD −中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点.（1）证明：OA CD ⊥；（2）若OCD 是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D −−的大小为45°，求三棱锥A BCD −的体积.25．（2022春·江苏南京·高一统考期末）如图，三棱锥A BCD −中，ABC 为等边三角形，且面ABC ⊥面BCD ，CD ⊥．(1)求证：CD AB ⊥；(2)当AD 与平面BCD 所成角为45°时，求二面角C AD B −−的余弦值．26．（2022春·江苏苏州·高一江苏省昆山中学校考期末）已知一圆形纸片的圆心为O ，直径2AB =，圆周上有C 、D 两点.如图，OC AB ⊥，6AOD π∠=，点P 是 BD 上的动点.沿AB 将纸片折为直二面角，并连结PO ，PD ，PC ，CD .(1)当//AB 平面PCD 时，求PD 的长；(2)当三棱锥P COD −的体积最大时，求二面角O PD C −−的余弦值.27．（2022春·江苏连云港·高一连云港高中校考期末）在四棱锥P ABCD −中，平面ABCD⊥平面PCD ，底面ABCD 为梯形，//AB CD ，AD DC ⊥，且1AB =，2AD DC DP ===，120PDC ∠=°．(1)求证：AD PC ⊥； (2)求二面角______的余弦值；从① P AB C ，② P BD C −−，③ P BC D −−这三个条件中任选一个，补充在上面问题中并作答．(3)若M 是棱PA 的中点，求证：对于棱BC 上任意一点F ，MF 与PC 都不平行． 28．（2022春·江苏南通·高一金沙中学校考期末）如图，在四棱锥P ABCD −中，底面ABCD 为直角梯形，//CD AB ，90ABC ∠= ，2AB BC ==2CD ，侧面PAD ⊥平面ABCD ．(1)求证：BD PA ⊥；(2)设平面PAD 与平面PBC 的交线为l ，PA 、PB 的中点分别为E 、F ，证明：//l 平面DEF ．29．（2022春·江苏苏州·高一江苏省昆山中学校考期末）如图，在四棱锥P ABCD −中，底面ABCD 是矩形，4PA AD ==，2AB =，PA ⊥平面ABCD ，且M 是PD 的中点.(1)求证：AM ⊥平面PCD ；(2)求异面直线CD 与BM 所成角的正切值；(3)求直线CD 与平面ACM 所成角的正弦值.30．（2022春·江苏扬州·高一期末）如图，在斜三棱柱111ABC A B C 中，AC BC =，D 为AB 的中点，1D 为11A B 的中点，平面111A B C ⊥平面11ABB A ，异面直线1BC 与1AB 互相垂直.（1）求证：平面1//A DC 平面11BD C ；（2）若1CC 与平面11ABB A 的距离为x ，116AC AB ==，三棱锥1A ACD −的体积为y ，试写出y 关于x 的函数关系式；（3）在（2）的条件下，当1CC 与平面11ABB A 的距离为多少时，三棱锥1A ACD −的体积取得最大值？并求出最大值.期末专题08 立体几何大题综合1．（2021春·江苏南京·高一校联考期末）如图，在五面体ABCDEF 中，已知DE ⊥平面ABCD ，//AD BC ，60BAD ∠=°，2AB =，1DE EF ==．（1）求证：//BC EF ；（2）求三棱锥B DEF −的体积．【答案】（1）证明见解析；（2【分析】（1）先证明//BC 平面ADEF ，再利用线面平行的性质，证明//BC EF ；（2）在平面ABCD 内作BH AD ⊥于点H ，证明BH 是三棱锥B DEF −的高，即可求三棱锥B DEF −的体积．【详解】（1）因为//AD BC ，AD ⊂平面ADEF ，BC ⊄平面ADEF ，所以//BC 平面ADEF ，又BC ⊂平面BCEF ，平面BCEF 平面ADEF EF =，所以//BC EF ．（2）如图，在平面ABCD 内过点B 作BH AD ⊥于点H ．因为DE ⊥平面ABCD ，BH ⊂平面ABCD ，所以DE BH ⊥．又AD ，DE ⊂平面ADEF ，AD DE D ∩=，所以BH ⊥平面ADEF ，所以BH 是三棱锥B DEF −的高．在直角三角形ABH 中，o 60BAD ∠=，2AB =，所以BH =因为DE ⊥平面ABCD ，AD ⊂平面ABCD ，所以DE AD ⊥．又由（1）知，//BC EF ，且//AD BC ，所以//AD EF ，所以DE EF ⊥，所以三棱锥B DEF −的体积11111332DEF V S BH ∆=××=×××= 2．（2022春·江苏南京·高一南京市中华中学校考期末）如图，在四棱锥P ABCD −中，平面PAD ⊥平面ABCD ，//AD BC ，6ABAD AC ===，8PA BC ==，10PD =，M 为棱AD 上一点，且2AM MD =，N 为棱PC 的中点．(1)证明：平面PAB ⊥平面ABCD ；(2)求四棱锥N BCDM −的体积．【答案】(1)证明见解析【分析】（1）依题意可得PA AD ⊥，由面面垂直的性质得到PA ⊥平面ABCD ，即可证明平面PAB ⊥平面ABCD ；（2）根据图中的几何关系，求出四边形BCDM 的面积，根据N 是PC 的中点，即可求解．【详解】（1）证明：由题意，222PA AD PD +=，PA AD ∴⊥，平面PAD ⊥平面ABCD ，PA ⊂平面PAD ，平面PAD ∩平面ABCD AD =， PA ∴⊥平面ABCD ，又PA ⊂ 平面PAB ，∴平面PAB ⊥平面ABCD ；（2）解：设BC 的中点为H ，连接AH ，AB AC = ，所以ABC 是等腰三角形，AH BC ∴⊥，即AH 是梯形底边上的高，AH ==由题意知，2MD =，所以()12822BCDM S DM BC AH ++⋅× N 是PC 的中点，N ∴到底面的距离为142PA =，四棱锥N BCDM −的体积为143××；综上，四棱锥N BCDM − 3．（2021·江苏·高一期末）如图在四棱锥P - ABCD 中，底面ABCD 是矩形，点E ，F 分别是棱PC 和PD 的中点.（1）求证：EF ∥平面P AB ；（2）若AP =AD ，且平面P AD ⊥平面ABCD ，证明AF ⊥平面PCD .【答案】（1）证明见解析；（2）证明见解析．【分析】（1）由中位线定理得//EF CD ，从而可得//EF AB ，得线面平行；（2）由等腰三角形得AF PD ⊥，再由面面垂直的性质定理得CD 与平面PAD 垂直，从而得CD AF ⊥，再由线面垂直的判定定理得证线面垂直．【详解】证明：（1）因为点E ，F 分别是棱PC 和PD 的中点.，所以//EF CD ，又//CD AB ，所以//EF AB ，而EF ⊄平面PAB ，AB ⊂平面PAB ，所以//EF 平面PAB ；（2）AP AD =，F 是PD 的中点，所以AF PD ⊥，又平面P AD ⊥平面ABCD ，平面P AD 平面ABCD AD =，CD AD ⊥，CD ⊂平面ABCD ，所以CD ⊥平面PAD ，AF ⊂平面PAD ，所以CD AF ⊥，CD PD D = ，,CD PD ⊂平面PCD ，所以AF ⊥平面PCD ．4．（2022春·江苏南京·高一江苏省江浦高级中学校联考期末）如图，四棱锥P ABCD −中，PA ⊥底面ABCD ，底面ABCD 为菱形，点F 为侧棱PC 上一点．(1)若PF FC =，求证：//PA 平面BDF ；(2)若BF PC ⊥，求证：平面⊥BDF 平面PBC ．【答案】(1)证明见解析；(2)证明见解析.【分析】（1）AC ，BD 的交点为O ，连接OF ，由菱形及中位线性质有//PA OF ，再由线面平行的判定可证结论；（2）由题意及线面垂直的性质有BD AC ⊥、BD PA ⊥，再由线面垂直的判定和性质得BD PC ⊥，最后根据线面垂直、面面垂直的判定证结论.（1）设AC ，BD 的交点为O ，连接OF ，因为底面ABCD 为菱形，且O 为AC 中点，PF FC =，所以//PA OF ，又PA ⊄平面BDF ，OF ⊂平面BDF ，故//PA 平面BDF ．（2）因为底面ABCD 为菱形，所以BD AC ⊥，因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD PA ⊥，又AC PA A ∩=，AC 、PA ⊂平面PAC ，所以BD ⊥平面PAC ，又PC ⊂平面PAC ，所以BD PC ⊥，又BF PC ⊥，BD BF B = ，BD ，BF ⊂平面BDF ，所以PC ⊥平面BDF ，又PC ⊂平面PBC ，故平面⊥BDF 平面PBC .5．（2021春·江苏常州·高一校联考期末）如图，在四棱锥P ABCD −中，底面ABCD 为直角梯形，//AD BC ，90ADC ∠=°，平面PAD ⊥底面ABCD ，E 为AD 的中点，M 是棱PC 的中点，2PA PD ==，112BC AD ==，CD =（1）若平面PBC 与平面PAD 的交线为l ，求证：//l BC ；（2）求直线BM 与平面ABCD 所成角的正切值；（3）求直线BM 与CD 所成角的余弦值．【答案】（1）证明见解析；（2（3．【分析】（1）利用线面平行的判定定理和性质定理进行证明即可；（2）根据面面垂直的性质，结合线面角定义进行求解即可；（3）根据平行线的性质，结合异面直线所成角的定义和余弦定理进行求解即可.【详解】证明：（1）∵//AD BC 、AD ⊂面PAD 、BC ⊄面PAD ，∴//BC 面PAD ,BC ⊂面PBC ，又∵面PAD ∩面PBC l =，∴//BC l ．（2）解：连结EC ，取EC 中点H ，连结MH ，HB ，∵M 是PC 的中点，H 是EC 的中点，∴//MH PE ，∵PA PD =，E 为AD 的中点，∴PE AD ⊥，又∵平面PAD ⊥平面ABCD ，且平面PAD ∩平面ABCD AD =，∴PE ⊥平面ABCD ，∴MH ⊥平面ABCD ，∴HB 是BM 在平面ABCD 内的射影，∴MBH ∠为BM 与平面ABCD 所成的角，∵//AD BC ，12BC AD =，E 为AD 的中点，90ADC ∠=°， ∴四边形BCDE 为矩形，∴EC =112HB EC ==，又∵12MH PE ==∴MHB 中，tan MH MBH HB ∠=，∴直线BM 与平面ABCD （3）解：由（2）知//CD BE ， ∴直线BM 与CD 所成角即为直线BM 与BE 所成角，连接ME ，Rt MHE △中，ME =Rt MHB △中，BM又BE CD ==∴MEB中，222cos 2BM BE ME MBE BM BE +−∠==⋅ ∴直线BM 与CD6．（2022春·江苏扬州·高一统考期末）如图，四棱锥P ABCD −中，底面ABCD 为平行四边形，6810PA AD PD AB PB =====，，，平面PAD ⊥平面ABCD ，平面PAB ∩平面PCD l =．(1)求四棱锥P ABCD −的体积；(2)求二面角A l D −−的余弦值．【答案】(2)23【分析】（1）作PM AD ⊥，垂足为M ，显然PM ，P A 不重合，作AN PD ⊥，垂足为N ，由平面PAD ⊥平面ABCD ，得到PM ⊥平面ABCD ，再由平行四边形ABCD 为矩形，且面积为48，利用锥体的体积公式求解；（2）由AB ∥平面PCD ，平面PAB ∩平面PCD l =，得到AB l ∥，结合（1）得到l ⊥平面P AD ，则APD ∠二面角A l D −−的平面角求解．(1)解：如图所示：作PM AD ⊥，垂足为M ，显然PM ，P A 不重合，作AN PD ⊥，垂足为N ．在PAD 中，68PAAD PD ===，，所以N 为PD 中点，且AN =所以118622PAD S PM =××=××△，解得：PM = 因为6,8,10PA AB PB ===，所以222PA AB PB +=，则PA AB ⊥；因为平面PAD ⊥平面ABCD ，平面PAD ∩平面,,ABCD AD PM AD PM =⊥⊂平面P AD ，所以PM ⊥平面ABCD ，又AB ⊂平面ABCD ，所以PM AB ⊥，又,,PA PM P PA PM =⊂ 平面P AD ，则AB ⊥平面P AD ，又AD ⊂平面P AD ，所以AB AD ⊥，则平行四边形ABCD 为矩形，且面积为48；所以四棱锥P ABCD −的体积为1483× (2)因为底面ABCD 为平行四边形，所以AB CD ∥，又因为CD ⊂平面PCD ，AB ⊄位平面PCD ，所以AB ∥平面PCD ．又因为AB ⊂平面P AB ，平面PAB ∩平面PCD l =，所以AB l ∥．由（1）知AB ⊥平面P AD ，所以l ⊥平面P AD ，又因为PA PD ⊂，平面P AD ，所以PA l ⊥且PD l ⊥，所以二面角A l D −−的平面角即APD ∠．在PAD 中，68PAAD PD ===，，由余弦定理得2222226862cos 22683AP PD AD APD AP PD +−+−∠===⋅××．所以二面角A l D −−的余弦值为23．7．（2022春·江苏常州·高一统考期末）刍（ch ú）甍（m éng ）是几何体中的一种特殊的五面体.中国古代数学名著《九章算术》中记载：“刍甍者，下有袤有广，而上有袤无广.刍，草也.甍，屋盖也.求积术日：倍下表，上袤从之，以广乘之，又以高乘之，六而一.”翻译为“底面有长有宽为矩形，顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶 ”现有一个刍甍如图所示，四边形ABCD 为长方形，//EF 平面ABCD ，ADE 和BCF △是全等的等边三角形.(1)求证：//EF DC ；(2)若已知224AB BC EF ===， ①求二面角A EF C −−的余弦值； ②求该五面体ABCDEF 的体积. 【答案】(1)证明见解析；(2)①13【分析】（1）利用线面平行的性质定理即得；（2）过点E 作EG DC ⊥，作EH AB ⊥，过点F 作FM DC ⊥，作FN AB ⊥，由题可得HEG ∠即为二面角A EF C −−的平面角，结合条件利用余弦定理可得；利用割补法可把该五面体分为两个四棱锥和一个三棱柱，然后利用锥体及柱体的体积公式即得. 【详解】（1）五面体ABCDEF 中，因为//EF 平面ABCD ， EF ⊂平面CDEF ，平面CDEF 平面ABCD CD =，所以//EF CD .（2）过点E 作EG DC ⊥，作EH AB ⊥，垂足分别为G ，H ，过点F 作FM DC ⊥，作FN AB ⊥，垂足分别为M ，N ，连结GH ，MN ，如图，①由（1）及四边形ABCD 为长方形知，AB CD EF ∥∥，所以EG EF ⊥，EH EF ⊥，所以HEG ∠即为二面角A EF C −−的平面角，因为224AB BC EF ===，且ADE 和BCF △是全等的等边三角形，所以222GMDG MC ===，2ED EA FC FB ====，因此，在EGH 中，EG EH ==2GH =，由余弦定理，得2221cos 23EH EG GH HEGEG EH +−∠==⋅，故二面角A EF C −−的余弦值为13.②取GH 中点O ，连结EO ，由EG EH =知，EO GH ⊥，因为DC EG ⊥，DC GH ⊥，且EG ，GH 是平面EGH 内两相交直线，所以DC ⊥平面EGH ，因为EO ⊂平面EGH ，所以EO DC ⊥，又GH ，DC 是平面ABCD 内两相交直线，所以EO ⊥平面ABCD ，在EGH 中，EG EH ==2GH =，可得EO =所以，四棱锥E ADGH −和F BCMN −的体积均为111(12)33ADGH V S EO =⋅=××=三棱柱EGH FMN −的体积21222FGH V S EF =⋅=××= △所以，该五面体ABCDEF 的体积为122V V +8．（2022春·江苏盐城·高一统考期末）如图，四棱锥P -ABCD 的底面是平行四边形，P A ⊥平面ABCD ，1,AB BC==4ABC π∠=.(1)求证：平面PCD ⊥平面P AC ； (2)若PD 与平面P AC 所成的角为6π，求PC 与平面P AD 所成的角的正弦值.【答案】(1)证明见解析；【分析】（1）由余弦定理、勾股定理知AC CD ⊥，根据线面垂直的性质得PA CD ⊥，再根据线面垂直、面面垂直的判定证结论.（2）由（1）知PD 与平面P AC 所成角的平面角为6CPD π∠=求得PC =，再通过线面垂直证面面垂直并找到在面PAD 上C 的射影位置，即可求C 到面PAD 的距离，即可求PC 与平面P AD 所成的角的正弦值.【详解】（1）由题意BC AD ==，1ABCD ==，又4ABC ADC π∠=∠=，在△ADC 中1AC =，故222AC CD AD +=，所以AC CD ⊥，又P A ⊥平面ABCD ，CD ⊂面ABCD ，则PA CD ⊥，而PA AC A = ，,PA AC ⊂面PAC ，则CD ⊥面PAC ，由CD ⊂面PCD ，故面PCD ⊥面PAC .（2）由（1）知：CD ⊥面PAC ，则PD 与平面P AC 所成角的平面角为6CPD π∠=，而1CD =，易知：PC =，又P A ⊥平面ABCD ，PA ⊂面PAD ，则面ABCD ⊥面PAD ，而C ∈面ABCD ，面ABCD ∩面PAD AD =，则在面PAD 上C 的射影在AD 上，又△ADC 为等腰直角三角形，故C 在AD 上射影为AD 中点，所以C 到面PAD 的距离为2ADh==故PC 与平面P AD 所成的角的正弦值为h PC =. 9．（2022春·江苏盐城·高一统考期末）如图，在四棱锥P -ABCD 中，112AB BC CD AD ====，//AD BC ，P 在以AD 为直径的圆O 上，平面ABCD ⊥平面P AD .(1)设点Q 是AP 的中点，求证：BQ //平面PCD ；(2)若二面角C PD A −−的平面角的正切值为2，求三棱锥A -PCD 的体积. 【答案】(1)证明见解析；(2)14.【分析】（1）E 为PD 中点，连接,QE CE ，中位线性质得//QE AD 且12QE AD =，结合已知有BCEQ 为平行四边形，再由线面平行的判定证明结论.（2）找到C 在面PAD 上射影F ，过F 作//FG AP 交PD 于G ，进而求出CF 、PA 、PD ，根据A PCD C ADP V V −−=及棱锥的体积公式求体积即可.【详解】（1）若E 为PD 中点，连接,QE CE ，又Q 是AP 的中点，即//QE AD 且12QE AD =，又12BC AD =，//AD BC ，故BC QE =且//BC QE ，所以BCEQ 为平行四边形，故//BQ CE ，由⊄BQ 面PCD ，CE ⊂面PCD ，则//BQ 面PCD .（2）面ABCD ⊥面P AD ，面ABCD ∩面PAD AD =，C ∈面ABCD ，则C 在面PAD 上射影F 在AD 上，即CF ⊥面PAD ，PD ⊂面PAD ，所以CF PD ⊥，又112ABBC CD AD ====，//AD BC ，故12DF =，CF 过F 作//FG AP 交PD 于G ，则14DF FG DG AD PA PD ===，由P 在以AD 为直径的圆O 上，即AP PD ⊥，所以FG PD ⊥，又CF FG F = ，,CF FG ⊂面CFG ，故PD ⊥面CFG ，而CG ⊂面CFG ，所以PD CG ⊥由FG ⊂面PAD ，CG ⊂面CDP ，面PAD ∩面CDP PD =，所以二面角C PD A −−对应平面角为CGF ∠，即tan 2CFCGF FG∠==，故FG =PA =，则1PD =，所以111324A PCD C ADP V V CF PA PD −−==××××=.10．（2022春·江苏宿迁·高一统考期末）在斜三棱柱111ABC A B C 中，底面是边长为4的正三角形，1=A B 1160A AB A AC ∠=∠=°．(1)证明：11//A C 平面1AB C ； (2)证明：1BC AA ⊥；(3)求直线BC 与平面11ABB A 所成角的正弦值．【答案】(1)证明见解析 (2)证明见解析【分析】（1）由线线平行证明线面平行；（2）作出辅助线，得到11A AB A AC ≌△△，即有11=AC A B ，证明出1BC A M ⊥，再有BC AM ⊥，证明出BC ⊥平面1AA M ，从而得到1BC AA ⊥；（3）法一：由余弦定理得到16AA =，得到1AM A M ⊥，求出11123−=×⋅△B AA C AA M V S BM ，由等体积法求出C 到平面11ABB A 的距离d ，设直线BC 与平面11ABB A 所成角为θ，从而得到sin ==dBC θ，法二：作出辅助线，找到线面角，求出各边长，从而得到BC 与平面11ABB A 所成角的正弦值. （1）证明：在三棱柱111ABC A B C 中有11//A C AC 又因为11A C ⊄平面1AB C ，AC ⊂平面1AB C 即有11//A C 平面1AB C（2）取BC 中点M ，连接1,AM A M因为ABC 为正三角形，AC AB =，M 为BC 中点所以BC AM ⊥，因为111160,∠=∠=°=A AB A AC AA AA 所以11A AB A AC ≌△△，即有11=AC A B所以1BC A M ⊥又因为1,=⊂ AM A M M AM 平面11,⊂AA M A M 平面1AA M 所以BC ⊥平面1AA M ，又1AA ⊂平面1AA M ，即有1BC AA ⊥ （3）法一：在1A AB △中，由余弦定理得：2221111cos 2+−∠=⋅AA AB A B A AB AA AB 得21111628224+−=⋅AA AA 解得：16AA =或2−（舍去） 1A M BC ⊥，由勾股定理得：1A M ==因为AM =22211AM A M A A +=，由勾股定理逆定理得：1AM A M ⊥，所以111122A AM S A M AM =⋅=× 由BC ⊥平面1AA M得11123−=×⋅△B AA C AA M V S BM ，记C 到平面11ABB A 的距离为d因为11113C A AB B AA C A AB V V S d −−==⋅=，11111sin 46sin 6022ABA S AB AA BAA =⋅∠=××°=所以d =，又因为4BC = 记直线BC 与平面11ABB A 所成角为θ，则sin ==dBC θ法二：过点B 作1BE AA ⊥于点E ，连接EC ，又因为1,,,⊥=⊂ BC AA BC BE B BC BE 平面BEC ，所以1AA ⊥平面BEC 过C 作CH BE ⊥于H由CH ⊂平面CBE ，则1CH AA ⊥因为11,,=⊂ BE AA E AA BE 平面11ABB A 所以CH ⊥平面11ABB A ，则sin 604BE CE AB ==°=则2221cos23BE CE BC BEC BE CE +−∠==⋅，则sin BEC ∠所以1sin 2BEC S BE CE BEC =⋅∠= CH记直线BC 与平面11ABB A 所成角为θ，则sin ==CH BC θ11．（2022春·江苏无锡·高一统考期末）如图，在四棱锥P ABCD −中，底面ABCD 为正方形，PA ⊥底面ABCD ，2PA AB ==，E 为PB 中点，M 为AD 中点，F 为线段BC 上一点.(1)若F 为BC 中点，求证：//PM 平面AEF ；(2)设直线EF 与底面ABCD 所成角的大小为α，二面角E AF B −−的大小为β，若tan =βα，求BF 的长度.【答案】(1)证明见解析； (2)2或1.【分析】（1）连接BM 交AF 于点O ，连接OE ，易得ABFM 为平行四边形，即O 为BM 中点，可得//EO PM ，再由线面平行的判定证结论.（2）取AB 中点H ，连接FH ，由中点及线面垂直的性质得EH ⊥底面ABCD ，则EFH ∠为直线EF 与底面ABCD 所成角，过H 作⊥HN AF 于N ，连接EH ，EN ，利用线面垂直的判定及性质得AF EN ⊥，则ENH ∠为二面角E AF B −−的平面角，用线段表示出tan ,tan βα，结合222AF AB BF =+求BF 的长度.(1)连接BM 交AF 于点O ，连接OE ，底面ABCD 为正方形，F 为BC 中点，//AM BF ∴且AM BF =，∴四边形ABFM 为平行四边形.O ∴为BM 中点，又E 为PB 中点，//EO PM ∴，又PM ⊄平面AEF ，EO ⊂平面AEF ，//PM ∴平面AEF . (2)取AB 中点H ，连接FH . E 为线段PB 中点，//EH PA ∴且112EH PA ==，又PA ⊥底面ABCD ， EH ∴⊥底面ABCD ，HF ∴为斜线EF 在平面ABCD 内的射影，则EFH ∠为直线EF 与底面ABCD 所成角，即∠=EFH α，1tan ==EH HF HFα. 过H 作⊥HN AF 于N ，连接EH ，EN .⊥ EH 底面ABCD ，AF ⊂底面ABCD ，∴⊥EH AF ，又⊥HN AF ，= HN EH H ，,HN EH ⊂面EHN ， AF ∴⊥平面EHN ，EN ⊂平面EHN ，∴⊥AF EN ，综上，ENH ∠为二面角E AF B −−的平面角，即∠=ENH β，1tan ==EH NH NHβ.由tan =βα，知1=NH =HF .设0 =≤≤ NH t t ，=HF ，则=AN 3=NF t ，=BF由222AF AB BF =+得：)22232+=+t，化简得4210710−+=t t ，解得212t =或15，则2BF =或1.12．（2021春·江苏南京·高一南京师大附中校考期末）如图，在三棱柱111ABC A B C -中，1B C AB ⊥，侧面11BCC B 为菱形.（1）求证：1B C ⊥平面1ABC .（2）如果点D ，E 分别为11A C ，1BB 的中点，求证：//DE 平面1ABC . 【答案】（1）证明见解析.（2）证明见解析【分析】（1）根据侧面11BCC B 为菱形，则11B C BC ⊥，进而可得结论；（2）取1AA 的中点F ，连DF ，FE ，可得//DF 面1ABC ，同理可得//EF 面1ABC ，进而可得//DE 面1ABC .【详解】（1）因三棱柱111ABC A B C -的侧面11BCC B 为菱形，则11B C BC ⊥. 又1B C AB ⊥，且AB ，1BC 为平面1ABC 内的两条相交直线，故1B C ⊥平面1ABC（2）如图，取1AA 的中点F ，连DF ，FE .因D 为11A C 的中点，则1//DF AC ，//EF AB 而DF ⊄平面1ABC ，1AC ⊂平面1ABC ，故//DF 面1ABC . 同理，//EF 面1ABC .因DF ，EF 为平面DEF 内的两条相交直线，故平面//DEF 面1ABC . 因DE ⊂平面DEF ，故//DE 面1ABC .【点睛】本题考查线面垂直，线面平行的证明，属于基础题.13．（2021春·江苏南京·高一校联考期末）如图，在直三棱柱111ABC A B C 中，点D 是线段AB 上的动点.（1）线段AB 上是否存在点D ，使得1//AC 平面1B CD ？若存在，请写出ADDB值，并证明此时，1//AC 平面1B CD ；若不存在，请说明理由；（2）已知平面11ABB A ⊥平面1CDB ，求证：CD AB ⊥. 【答案】（1）存在，1=ADDB，证明见解析；（2）证明见解析. 【分析】（1）在线段AB 上存在点D ，当1=ADDB时，1//AC 平面1B CD ，连接1BC ，交1B C 于点E ，连接DE ，则点E 是1BC 的中点，证明1//DE AC 即可；（2）过B 作1⊥BP DB 并交1DB 于点P ，由平面11ABB A ⊥平面1CDB 可得BP ⊥平面1CDB ，从而得到CD BP ⊥，然后再证明1CD BB ⊥，然后可得CD ⊥平面11ABB A ，可得CD AB ⊥.【详解】（1）在线段AB 上存在点D ，当1=ADDB时，1//AC 平面1B CD . 证明如下：连接1BC ，交1B C 于点E ，连接DE ，则点E 是1BC 的中点，又当1=ADDB，即点D 是AB 的中点，由中位线定理得1//DE AC ， ∵DE ⊂平面1B CD ，1AC ⊄平面1B CD ， ∴1//AC 平面1B CD .（2）证明：过B 作1⊥BP DB 并交1DB 于点P ，又∵平面11ABB A ⊥平面1CDB ，BP ⊂平面11ABB A ，平面11ABB A 平面11=CDB DB ， ∴BP ⊥平面1CDB ，又∵CD ⊂平面1CDB ，∴CD BP ⊥.在直三棱柱111ABC A B C 中，1BB ⊥平面ABC ，CD ⊂平面ABC ， ∴1CD BB ⊥，又∵1BB ⊂平面11ABB A ，BP ⊂平面11ABB A ，1= BB BP B ， ∴CD ⊥平面11ABB A .又∵AB ⊂平面11ABB A ，∴CD AB ⊥.【点睛】本题主要考查的是立体几何中的平行和垂直关系，考查了学生的空间想象能力，属于中档题.14．（2021·江苏·高一期末）如图，在四棱锥P ABCD −中，平面ABCD ⊥平面PAB ，PAB 为等边三角形，四边形ABCD 为矩形，E 为PB 的中点.（1）证明：平面ADE ⊥平面PBC .（2）平面ADE 分此棱锥为两部分，若2AB AD =，求大的部分体积与小的部分体积之比. 【答案】（1）证明见解析；（2）53.【分析】（1）先证明AE PB ⊥，AD PB ⊥，可得PB ⊥平面ADE ，再利用面面垂直的判定定理可得结论.（2）求得P ABCD V −=F 为PC 的中点，连接DF ，EF ，则3322P ADFEP ADE D AEP V V V −−−===. 【详解】（1）证明：因为PAB 为等边三角形，E 为PB 的中点，所以AE PB ⊥. 因为平面ABCD ⊥平面PAB 且相交于AB ，AD AB ⊥，所以AD ⊥平面PAB ，则AD PB ⊥. 又AD AE A ∩=，所以PB ⊥平面ADE .因为PB ⊂平面PBC ，所以平面ADE ⊥平面PBC .（2）设F 为PC 的中点，连接DF ，EF ，所以//EF DA ，12EF DA =令1AD =，则2AB =，AE =所以1213P ABCD V −=××=33311122232P ADFE P ADE D AEP V V V −−−===×××=所以大的部分体积与小的部分体积之比为53=.【点睛】方法点睛：空间几何体体积问题的常见类型及解题策略：（1）求简单几何体的体积时若所给的几何体为柱体锥体或台体，则可直接利用公式求解(2)求组合体的体积时若所给定的几何体是组合体，不能直接利用公式求解，则常用转换法、分割法、补形法等进行求解.15．（2021·江苏·高一期末）已知在六面体PABCDE 中，PA ⊥平面ABCD ，ED ⊥平面ABCD ，且2PA ED =，底面ABCD 为菱形，且60ABC ∠=°.（1）求证：平面PAC ⊥平面PBD ；（2）若2AB =，1DE =，且M 为PB 的中点，求三棱锥E PAM −的体积.【答案】（1）证明见解析；（2【分析】（1）连接BD 交AC 于O ，易知BD AC ⊥，由PA ⊥平面ABCD 得PA BD ⊥，进而得BD ⊥平面PAC ，由于BD ⊂平面PBD ，故即可证得；（2）根据题意易得//DE 平面PAC ，//BC 平面ADEP ，故根据等体积法得11112222E PAM M PAEB PAEC PAE E PACD PAC V V V V V V −−−−−−=====，再根据几何关系求解即可. 【详解】解：（1）证明：连接BD 交AC 于O ，∵ 底面ABCD 为菱形，∴BD AC ⊥，O 为,BD AC 中点， ∵ PA ⊥平面ABCD ，BD ⊂平面ABCD ， ∴ PA BD ⊥，∵ AC PA A ∩=， ∴ BD ⊥平面PAC ， ∵ BD ⊂平面PBD ， ∴ 平面PAC ⊥平面PBD .（2）∵ PA ⊥平面ABCD ，ED ⊥平面ABCD ， ∴//PA DE ，∵ DE ⊄平面PAC ，PA ⊂平面PAC ， ∴//DE 平面PAC ，∵ 底面ABCD 为菱形，∴ //BC AD ∵BC ⊄平面ADEP ，AD ⊂平面ADEP ∴//BC 平面ADEP ， ∵ M 为PB 的中点，∴ 三棱锥E PAM −的体积11112222E PAM M PAEB PAEC PAE E PACD PAC V V V V V V −−−−−−=====，由（1）知得BD ⊥平面PAC ，2AB =，1DE =，60ABC ∠=°，2PA ED =，∴ 12222PAC S =××= ，12OD BD ==所以11233D PAC PAC V S OD −=⋅=×=△所以12E PAM D PAC V V −−=【点睛】本题考查面面垂直的证明，等体积法求几何体的体积，考查空间想象能力，逻辑推理能力，运算求解能力，是中档题.本题第二问解题的关键在于根据已知条件，利用等体积转化法得11112222E PAM M PAEB PAEC PAE E PACD PAC V V V V V V −−−−−−=====. 16．（2021春·江苏常州·高一校联考期末）如图，三棱锥−P ABC 的底面是等腰直角三角形，其中2ABAC ==，PA PB =，平面PAB ⊥平面ABC ，点E ，F ，M ，N 分别是AB ，AC ，PC ，BC 的中点．（1）证明：平面EMN ⊥平面PAB ；（2）当PF 与平面ABC 所成的角为3π时，求四棱锥A PMNB −的体积．【答案】（1）证明见解析；（2 【分析】（1）先由平面PAB ⊥平面ABC ，得到EN ⊥平面PAB ，利用面面垂直的判定定理证明平面EMN ⊥平面PAB ；（2）连结PE ，证明PFE ∠就是直线PF 与平面ABC 所成的角，于是PE = 用切割法把四棱锥A PMNB −看出三棱锥−P ABC 切去三棱锥M ANC −,直接求体积即可.【详解】解：（1）证明：由题意可得，AB AC ⊥，点E ，N 分别是AB ，BC 的中点，故EN ∥AC ，故EN AB ⊥，平面PAB ⊥平面ABC ，交线为AB 故EN ⊥平面PAB EN 在平面EMN 内，故平面EMN ⊥平面PAB ；（2）连结PE ，由PA PB =，点E 是AB 的中点，可知PE AB ⊥，再由平面PAB ⊥平面ABC ，可知PE ⊥平面ABC ，连结EF ，可知PFE ∠就是直线PF 与平面ABC 所成的角，于是tan PEPFE EF=∠PE 因为PA PB =，E 是AB 中点，故PE AB ⊥，又平面PAB ⊥平面ABC ，故PE ⊥平面ABC ，即点P 到平面ABC 的距离为PE点M 是PC 中点，故点M 到平面ABC 的距离为d =1133A PMNB P ABC M ANC ABC ANC V V V PE S d S −−−∆∆=−=⋅−⋅111122213232=××−××即四棱锥A PMNB − 【点睛】立体几何解答题的基本结构：(1)第一问一般是几何关系的证明，用判定定理；(2)第二问是计算，求角或求距离（求体积通常需要先求距离）.如果求体积（距离），常用的方法有：（1）直接法；（2）等体积法；（3）补形法；（4）向量法.17．（2021春·江苏南京·高一南京师大附中校考期末）如图，圆锥顶点为P ，底面圆心为O ，其母线与底面所成的角为22.5°，AB 和CD 是底面圆O 上的两条平行的弦，轴OP 与平面PCD 所成的角为60°.（1）证明：平面P AB 与平面PCD 的交线平行于底面；（2）求二面角C OP D −−的余弦值.【答案】（1）证明见解析；（2）17−【分析】（1）设平面P AB 与平面PCD 的交线为l .由题意可证明//AB 平面PCD ，从而可得//AB l ，从而可证明结论.（2）由题意可得COD ∠为二面角C OP D −−的平面角. 可证平面OPF ⊥平面PCD ，直线OP 在平面PCD 上的射影为直线PF OPF 为OP 与平面PCD 所成的角，通过解三角形可得答案.【详解】（1）证明：设平面P AB 与平面PCD 的交线为l . ∵//AB CD ，AB ⊄平面PCD ，∴//AB 平面PCD∵AB ⊂面P AB ，平面P AB 与平面PCD 的交线为l ，∴//AB l ∵AB 在底面上，l 在底面外 ∴l 与底面平行；（2）因为OP OD ⊥，OP OC ⊥，所以COD ∠为二面角C OP D −−的平面角. 设CD 的中点为F ，连接OF ，PF ,由圆的性质，2COD COF ∠=∠，OF CD ⊥ ∵OP ⊥底面，CD ⊂底面，∴OP CD ⊥ ∵OP OF O ∩=,∴CD ⊥平面OPF ∵CD ⊂平面PCD ，∴平面OPF ⊥平面PCD ∴直线OP 在平面PCD 上的射影为直线PF ∴OPF ∠为OP 与平面PCD 所成的角。

几何图形中求线段,线段和,面积等最值问题(4题型)—2024年中考数学压轴题(全国通用)(解析版)

几何图形中求线段，线段和，面积等最值问题（压轴通关）目录【中考预测】预测考向，总结常考点及应对的策略【误区点拨】点拨常见的易错点【抢分通关】精选名校模拟题，讲解通关策略（含新考法、新情境等）几何图形中求线段、线段和、面积最值题是全国中考的热点内容，更是全国中考的必考内容。

每年都有一些考生因为知识残缺、基础不牢、技能不熟、答欠规范等原因导致失分。

1．从考点频率看，几何图形中的性质综合问题，是高频考点、也是必考点。

2．从题型角度看，以解答题的最后一题或最后二题为主，分值12分左右，着实不少！题型一线段最值问题【例1】（2024·四川成都·一模）如图1，在四边形ABFE 中，90F ∠=︒，点C 为线段EF 上一点，使得AC BC ⊥，24AC BC ==，此时BF CF =，连接BE ，BE AE ⊥，且AE BE =．(1)求CE 的长度；(2)如图2，点D 为线段AC 上一动点（点D 不与A ，C 重合），连接BD ，以BD 为斜边向右侧作等腰直角三角形BGD ．①当DG AB ∥时，试求AD 的长度；②如图3，点H 为AB 的中点，连接H G ，试问H G 是否存在最小值，如果存在，请求出最小值；如果不存在，请说明理由．【答案】(2)①103；②2【分析】（1）取AB 的中点H ，连接,EH HC ，证明FEB CAB ∠=∠，得出1tan tan 2FB FEB CAB EF ∠==∠=则12BF EF =，进而根据CE EF CF =−（2）①如图所示，过点D 作DM EF ⊥于点M ，过点D 作DN AB ⊥于点N ，证明DBC GBF ∽得出DC ，即可得出DM GF =，证明DMG GFB ≌，进而证明G 在EF 上，根据已知条件证明D 在EB上，然后解直角三角形，即可求解；②如图所示，过点H 作HP EF ⊥于点P ，连接EH ，由①可得G 在EF 上运动，当HG EF ⊥时，H G 取得最小值，即,G P 重合时，HP 的长即为HG 的最小值，由①可得103AT =，求得sin ETA ∠=45HEF ETA α∠=+︒=∠，即可求解．【详解】（1）解：如图所示，取AB 的中点H ，连接,EH HC ，∵BF CF =，90F ∠=︒，∴45BCF ∠=︒，BC ，又∵AC BC ⊥ ∴45ECA ∠=︒ ∵AE BE =，BE AE ⊥ ∴45EBA ∠=︒ ∴45ECA ABE ∠=∠=︒ ∴FEB CAB ∠=∠ ∵24AC BC ==， ∴2BC =∴BF CF = ∴1tan 2CB CAB AC ∠== ∴1tan tan 2FB FEB CAB EF ∠==∠= ∴12BF EF =∴EF =∴CE EF CF =−（2）①如图所示，过点D 作DM EF ⊥于点M ，过点D 作DN AB ⊥于点N ，由（1）可得45ACE ABE ∠=∠=︒ ∴CDM V 是等腰直角三角形，∴CD ，∵,CBF DBG 都是等腰直角三角形，∴CB DBBF BG==∴BD BGBC BF= 又∵DBG CBF ∠=∠ ∴DBC GBF ∠=∠ ∴DBC GBF ∽∴DC DBGF GB==∴DC ∴DM GF = 在,DMG GFB 中，DM GF DMG F DG BG =⎧⎪∠=∠⎨⎪=⎩∴DMG GFB ≌ ∴MGD FBG ∠=∠ ∵90FBG FGB ∠+∠=︒∴90MGD FGB ∠+∠=︒ 又∵90DGB ∠=︒ ∴180MGF ∠=︒ ∴G 在EF 上，∵DG AB ∥，90DGB ∠=︒ ∴90GBA ∠=︒∵45,45ABE DBG ABD ∠=︒∠=︒=∠ ∴D 在EB 上， ∵1tan 2CAB ∠=，∴12DN AN =，则AD ∵,45DN AB ABE ⊥∠=︒ ∴DN DB = ∴3AB DN =， ∵4AC =，2CB =∴AB ==∴13DN AB ==∴103AD ==， ②如图所示，过点H 作HP EF ⊥于点P ，连接EH ，由①可得G 在EF 上运动，∴当HG EF ⊥时，HG 取得最小值，即,G P 重合时，HP 的长即为H G 的最小值，设,AC EB 交于点T ，即与①中点D 重合，由①可得103AT =∵AB =∴AE 12EH AB ==∴sin 3AE ETA AT ∠=== 设FEB CAB α∠=∠= 则45HEF ETA α∠=+︒=∠，在Rt PEH △中，sin sin 102PH HEF EH ETA EH =∠⨯=∠⨯= 【点睛】证明G 点在EF 上是解题的关键．【例2】（2024·天津红桥·一模）在平面直角坐标系中，点()0,0O ，()2,0A ， (2,B )，C ，D 分别为OA ，OB 的中点．以点O 为中心，逆时针旋转OCD ，得OC D ''，点C ，D 的对应点分别为点C '，D ¢．(1)填空∶如图①，当点D ¢落在y 轴上时，点D ¢的坐标为_____，点C '的坐标为______； (2)如图②，当点C '落在OB 上时，求点D ¢的坐标和 BD '的长； (3)若M 为C D ''的中点，求BM 的最大值和最小值(直接写出结果即可)．逆时针旋转OCD ，得OC D ''，知为中心，逆时针旋转OCD，得OC D''，可得(2,23B为中心，逆时针旋转OCD，得OC D''，()A，2,0()A2,0,(2,23 B是AOB的中位线，为中心，逆时针旋转OCD，得OC D''，'==，D CD3M是C'(2,23B1．（2024·山东济宁·模拟预测）已知，四边形ABCD 是正方形，DEF 绕点D 旋转（DE AB <），90EDF ∠=︒，DE DF =，连接AE CF ，．(1)如图1，求证：ADE CDF ≅； (2)直线AE 与CF 相交于点G ．①如图2，BM AG ⊥于点M ，⊥BN CF 于点N ，求证：四边形BMGN 是正方形；②如图3，连接BG ，若6AB =，3DE =，直接写出在DEF 旋转的过程中，线段BG 长度的最小值为．再证明AMB CNB ≅可得MB ，证明BGM 是等腰直角三角形，然后求出【详解】（1）证明：四边形ABCD 是正方形，AD DC ∴=，90ADC ∠=︒，DE DF =，90EDF ∠=︒，ADC EDF ∴∠=∠，ADE CDF \Ð=Ð，在ADE V 和CDF 中，DA DC ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩， SAS ADE CDF ∴（）≌．（2）解：①证明：如图2中，设AG 与CD 相交于点P ，90ADP ∠=︒， 90DAP DPA ∴∠+∠=︒，ADE CDF ≅，DAE DCF ∴∠=∠，DPA GPC ∠∠=，90DAE DPA GPC GCP ∠∠∠∠∴+=+=︒， 90PGN ∠∴=︒，BM AG ⊥，BN GN ⊥，∴四边形BMGN 是矩形，90MBN ∴∠=︒，四边形ABCD 是正方形，AB BC ∴=，90ABC MBN∠∠==︒，ABM CBN ∴∠=∠，又90AMB BNC ∠∠==︒，AMB CNB ∴≅，MB NB ∴=，∴矩形BMGN 是正方形；∵DAH BAM ABM ∠+∠=∠∴DAH ABM ∠=∠，又∵AD BA =，DHA ∠∴AMB DHA ≌△△， BM AH ∴=，2AH AD =DH ∴最大时，可知，BGM 是等腰直角三角形，23⨯=(1)若AC AB AD BC >⊥，，当点E 在线段AC 上时，AD BE ，交于点F ，点F 为BE 中点．①如图1，若37BF BD AD ===，，求AE 的长度；②如图2，点G 为线段AF 上一点，连接GE 并延长交BC 的延长线于点H ．若点E 为GH 中点，602BAC DAC EBC ∠=︒∠=∠，，求证：12AG DF AB +=． (2)如图3，若360AC AB BAC ︒==∠=，．当点E 在线段AC 的延长线上时，连接DE ，将DCE △沿DC 所在直线翻折至ABC 所在平面内得到DCM △，连接AM ，当AM 取得最小值时，ABC 内存在点K ，使得ABK CAK ∠=∠，当KE 取得最小值时，请直接写出2AK 的值．的长，证明(AAS)FDB FGE ≌AD BC EG AD ⊥⊥，， 90BDF ∴∠=︒，EGF ∠=BDF EGF ∴∠=∠，在Rt BDF △中，90BDF ∠=点(AAS)FDB FGE ∴≌3BD GE ∴==DFAD=，7∴=AG ADRt AGE中，2⊥，AD BC90∴∠=︒，ADC点E为GH的中点，∴=，GE HE在AGE和KHE△中，=AE KE∴≌(SAS) AGE KHE∴∠=∠34∠=DAC∴设EBC∠点和KEF中，(SAS)AFB KEF ∴≌89AB FK ∴=∠=∠，BAC ∠=Rt FDM 中，1由题意可知：160∠=︒，AC 30CAM ∴∠=︒，1322CM AC ∴==， ABK ∠=ABK ∴∠+∠EKQ EOA ∴∽，KE KQ QE（1）如图①，在ABC 中，点M ，N 分别是AB ，AC 的中点，若BC =MN 的长为__________．问题探究：（2）如图②，在正方形ABCD 中，6AD =，点E 为AD 上的靠近点A 的三等分点，点F 为AB 上的动点，将AEF △折叠，点A 的对应点为点G ，求CG 的最小值．问题解决：（3）如图③，某地要规划一个五边形艺术中心ABCDE ，已知120ABC ∠=︒，60BCD ∠=︒，40m AB AE ==，80m BC CD ==，点C 处为参观入口，DE 的中点P 处规划为“优秀”作品展台，求点C 与点P 之间的最小距离．是ABC 的中位线，由中位线的性质，即可求解，Rt EDC 中，根据勾股定理，求出∵点E为AD上的靠近点∴11633AE AD==⨯=在Rt EDC中，EC 根据折叠的性质，【问题提出】（1）如图1，点D 为ABC 的边BC 上一点，连接2,,3BD AD BDA BAC AB ∠=∠=，若ABD △的面积为4，则ACD 的面积为______；【问题探究】（2）如图2，在矩形ABCD 中，6,5AB BC ==，在射线BC 和射线CD 上分别取点E F 、，使得65BE CF =，连接AE BF 、相交于点P ，连接CP ，求CP 的最小值；【问题解决】（3）如图3，菱形ABCD 是某社区的一块空地，经测量，120AB =米，60ABC ∠=︒．社区管委会计划对该空地进行重新规划利用，在射线AD 上取一点E ，沿BE CE 、修两条小路，并在小路BE 上取点H ，将CH 段铺设成某种具有较高观赏价值的休闲通道（通道宽度忽略不计），根据设计要求，BHC BCE ∠=∠，为了节省铺设成本，要求休闲通道CH 的长度尽可能小，问CH 的长度是否存在最小值？若存在，求出CH 长度的最小值；若不存在，请说明理由．994CBAABDSS ==，即可得到ACD 的面积；为直径的O 上交O 于点P ）证明,CBH EBC ∽得到，再证明,ABH EBA ∽得到在O 的劣弧与O 相交于点ABDCBAS S=994CBAABDSS ==，∴ACD 的面积为9CBAABDS S−=故答案为：为直径的O 上运动，交O 于点P，作ABH 的外接圆O ，连接∴,CBH EBC ∽ BC BH∴,ABH EBA ∽ 120AHB EAB ∠=∠=在O 的劣弧120=︒在AOB 中，则1602BM AM AB ===米，与O 相交于点题型二线段和的最小值问题【例1】（2024·四川达州·模拟预测）【问题发现】（1）如图1，在OAB 中，3OB =，若将OAB 绕点O 逆时针旋转120︒得OA B ''，连接BB '，则BB '=________．【问题探究】（2）如图2，已知ABC 是边长为BC 为边向外作等边BCD △，P 为ABC 内一点，连接AP BP CP ，，，将BPC △绕点C 逆时针旋转60︒，得DQC △，求PA PB PC ++的最小值；【实际应用】（3）如图3，在长方形ABCD 中，边1020AB AD ==，，P 是BC 边上一动点，Q 为ADP △内的任意一点，是否存在一点P 和一点Q ，使得AQ DQ PQ ++有最小值？若存在，请求出此时PQ 的长，若不存在，请说明理由．将AQD 绕点BC ⊥在OAB 中，3OB =，将OAB 绕点120BOB '∴∠=︒，3OB OB '==，OBB OB B ''∴∠=∠，OBB '∠+OC BB ⊥OCB '∴∠将∴++=+PA PB PC PA∴当点D、Q、P、A⊥连接AD，作DE AC∠=，ABC边长为DCBDCE BCA∴∠=∠=60）如图所示，将AQD绕点，90EA︒=【例2】（2024·贵州毕节·一模）在学习了《图形的平移与旋转》后，数学兴趣小组用一个等边三角形继续进行探究．已知ABC 是边长为2的等边三角形．(1)【动手操作】如图1，若D 为线段BC 上靠近点B 的三等分点，将线段AD 绕点A 逆时针旋转60︒得到线段AE ，连接CE ，则CE 的长为________；(2)【探究应用】如图2,D 为ABC 内一点，将线段AD 绕点A 逆时针旋转60︒得到线段AE ，连接CE ，若,,B D E本题主要考查了等边三角形的性质与判定，矩形的性质与判定，旋转的性质，勾股定理，含度角的直角三角形的性质，解题的关键在于利用旋转构造等边三角形，从而把三条不在一条直线的线段之和的问题，转换成几点共线求线段的最值问题是解题的关键．三点共线，求证：EB 平分AEC ∠；(3)【拓展提升】如图3，若D 是线段BC 上的动点，将线段AD 绕点D 顺时针旋转60︒得到线段DE ，连接CE ．请求出点D 在运动过程中，DEC 的周长的最小值．证明BAD CAE ≌，的三等分点和ABC 是边长为ADB AEC =∠60BEC ∠=︒EB（3）由ABD ACE ≌△△，得CE BD =，可得DEC 的周长BC DE =+，而DE AD =，知AD 的最小时，DEC的周长最小，此时AD BC ⊥，即可求得答案．∵ABC 是等边三角形，AB AC =，∴SAS ABD ACE ≌（）BD CE =；的三等分点，且ABC 是边长为∵ABC 是等边三角形，AB AC =，∴SAS ABD ACE≌（），120ADB AEC ∠=∠=上时，DEC 的周长存在最小值，如图：∵ABD ACE ≌△△， ∴CE BD =，∴DEC 的周长DE CE =++∴当点D 在线段BC 上时，DEC 的周长∵DEC 为等边三角形，DE AD =，的最小时，DEC 的周长最小，此时∴DEC 的周长的最小值为【点睛】本题考查几何变换综合应用，旋转性质、涉及等边三角形的性质，全等三角形的判定和性质，垂1．（2024·陕西·二模）在平面直角坐标系中，A 为y 轴正半轴上一点，B 为x 轴正半轴上一点，且4OA OB ==，连接AB ．(1)如图1，C 为线段AB 上一点，连接OC ，将OC 绕点O 逆时针旋转90︒得到OD ，连接AD ，求AC AD +的值．(2)如图2，当点C 在x 轴上，点D 位于第二象限时，90ADC ∠=︒，且AD CD =，E 为AB 的中点，连接DE ，试探究线段AD DE +是否存在最小值？若存在，求出AD DE +的最小值；若不存在，请说明理由．≌，可得出点，证明AND CMDAOC的平分线对称，由∴AND CMD≌，DN DM=，P大值和最小值分别是______和______；（2）如图2，在矩形ABCD中，4AB=，6AD=，点P在AD上，点Q在BC上，且AP CQ=，连接CP、QD，求PC QD+最小时AP的长；（3）如图3，在ABCDY中，10AB=，20AD=，点D到AB的距离为动点E、F在AD边上运动，始终保持3EF=，在BC边上有一个直径为BM的半圆O，连接AM与半圆O交于点N，连接CE、FN，求CE EF FN++的最小值．()SASABP CDQ≌=的O 外有一点在O 上，如图，当点P 在AO 的延长线上时，此时PA 的最大值为：PO OA +故答案为：11；3；（2）延长BA 至点B '，使AB ∵在矩形ABCD 中，4AB =，∴DAB BAP CBA DCQ '∠=∠=∠=∠在ABP 和CDQ 中，AB CD =∴()SAS ABP CDQ ≌Rt B BC '中，AB P BB ''=∠ （3）如图，过点F 作FG EC ∥，交BC OG '，NO ，∵在ABCD Y 中，10AB =，20AD =，点∴AD BC ∥，即EF CG ∥，BC AD =EFGC【点睛】本题考查圆的基本性质，全等三角形的判定和性质，相似三角形的判定和性质，矩形的性质，平行四边形的判定和性质，对称的性质，勾股定理，三角形三边关系定理，两点之间线段最短等知识点．灵活运用所学知识、弄清题意并作出适当辅助线是解题的关键．3．（2024·陕西西安·三模）【问题提出】（1）如图①，AB 为半圆O 的直径，点P 为半圆O 的AB 上一点，BC 切半圆O 于点B ，若10AB =，12BC =，则CP 的最小值为；【问题探究】（2）如图②，在矩形ABCD 中，3AB =，5BC =，点P 为矩形ABCD 内一点，连接PB 、PC ，若矩形ABCD 的面积是PBC 面积的3倍，求PB PC +的最小值；【问题解决】（3）如图③，平面图形ABCDEF 为某校园内的一片空地，经测量，AB BC ==米，=60B ∠︒，150BAF BCD ∠=∠=︒，DE DC ⊥，20CD =米，劣弧E F 所对的圆心角为90︒，E F 所在圆的圆心在AF 的延长线上，10AF =米．某天活动课上，九（1）班的同学准备在这块空地上玩游戏，每位同学在游戏开始前，在BC 上选取一点P ，在弧E F 上选取一点Q ，并在点P 和点Q 处各插上一面小旗，从点A 出发，先到点P 处拔下小旗，再到点Q 处拔下小旗，用时最短者获胜．已知晓雯和晓静的跑步速度相同，要使用时最短，则所跑的总路程()AP PQ +应最短，问AP PQ +是否存在最小值？若存在，请你求出AP PQ +的最小值；若不存在，请说明理由．交O于点P⊥PH BC交O于点P点P为半圆O的AB上一点，∴当点P与点P不重合时，1当点P与点P重合时，BC切半圆∴∠=ABC=OB OP矩形ABCD 的面积是PBC 面积的13553PBCS∴=⨯⨯=CF PH =又5BC =，60ABC ∠=︒，AB BC ==ABC ∴是等边三角形， 60BAC BCA ∴∠=∠=︒，150BAF BCD ∠=∠=︒，DE AA M '∴和CMN ∴∠=点'A Q OQ+∴的最小值为A Q'ABC为等边三角形，点∴点为BC△,E G分别作,,⊥⊥与EF交于点F，连接CF．EF AD FG AB FG特例感知（1）以下结论中正确的序号有______；ED CF BG为边围成的三角形不是直①四边形AGFE是矩形；②矩形ABCD与四边形AGFE位似；③以,,角三角形；类比发现（2）如图2，将图1中的四边形AGFE绕着点A旋转，连接BG，观察CF与BG之间的数量关系和位置关系，并证明你的发现；拓展应用（3）连接CE ，当CE 的长度最大时， ①求BG 的长度；②连接,,AC AF CF ，若在ACF △内存在一点P ，使CP AP ++的值最小，求CP AP ++的最小值．先证明APF AKL ∽，得到∴HF DE =，CH BG =，∴CHF 是直角三角形，∵四边形ABCD 是矩形，∴43AB CD ==，AD =∴228AC AB BC =+=，则由（2）知，90CEF ∠=︒，∵2247CF CE EF =+=，根据旋转，可得30PAF KAL ∠=∠=，根据两边对应成比例且夹角相等可得APF AKL ∽， ∴3KL PF =，过P 作PS AK ⊥于S ，则12PS AP =题型三面积的最小值问题【例1】（新考法，拓视野）（2024·陕西西安·一模）【问题提出】（1）如图1，已知在边长为5的等边ABC 中，点D 在边BC 上，3BD =，连接AD ，则ACD 的面积为；【问题探究】（2）如图2，已知在边长为6的正方形ABCD 中，点E 在边BC 上，点F 在边CD 上，且45EAF ∠=︒，若5EF =，求AEF △的面积；【问题解决】（3）如图3是某座城市廷康大道的一部分，因自来水抢修在4AB =米，AD =ABCD 区域内开挖一个AEF △的工作面，其中B 、F 分别在BC CD 、边上（不与B 、C 、D 重合），且60EAF ∠=︒，为了减少对该路段的拥堵影响，要求AEF △面积最小，那么是否存在一个面积最小的AEF △？若存在，请求出AEF △面积的最小值；若不存在，请说明理由．，证明()SAS ABG ADF ≌，再证明()SAS AEF AEG ≌，得到ABG ，则)()33AEF AEG SS==最小值最小值∵ABC 是边长为 ∴()SAS ABG ADF ≌∴()SAS AEF AEG ≌，得到ABG ， )()33AEF AEG SS==最小值最小值【例2】（2024·陕西西安·二模）图形旋转是解决几何问题的一种重要方法．如图1，正方形ABCD 中，E F 、分别在边AB BC 、上，且45EDF ∠=︒，连接EF ，试探究AE CF EF 、、之间的数量关系．解决这个问题可将ADE V 绕点D 逆时针旋转90︒到CDH △的位置（易得出点H 在BC 的延长线上），进一步证明DEF 与DHF △全等，即可解决问题．(1)如图1，正方形ABCD 中，45,3,2EDF AE CF ∠=︒==，则EF =______；(2)如图2，正方形ABCD 中，若30EDF ∠=︒，过点E 作EM BC ∥交DF 于M 点，请计算AE CF +与EM 的比值，写出解答过程；(3)如图3，若60EDF ∠=︒，正方形ABCD 的边长8AB =，试探究DEF 面积的最小值．进一步证明DEF,,,D F H G 四点共圆；进而可得30FHG ∠=，根据1tan 30AE CF CH CF FH EM GH GH ++====︒（3）过点E 作EK CD ⊥于K ，交DF 于M ，作FT EK ⊥于T ，得出 4DEFS EM =，进而根据（2）的方法得出EM GH =，根据FC AE CH ==时，面积最小，得出32OF =− 【详解】（1）解：∵将ADE V 绕点D 逆时针旋转90︒， ∴90DCH A DCB ∠=∠=︒=∠，DH DE HDC EDA =∠=∠， ∴点H 在BC 的延长线上， ∵四边形ABCD 是正方形 ∴90ADC ∠=︒， ∵45EDF ∠=︒，∴45HDF CDH FDC ADE FDC EDF ∠=∠+∠=∠+∠=︒=∠ 又∵DF DF =，∴DEF ()SAS DHF ≌，∴235EF FH FC CH FC AE ==+=+=+=，故答案为：5．（2）解：将ADE V ，DEM △绕点D 逆时针旋转90︒，得,DCH DHG∴,AED CHD DEM DHG ∠=∠∠=∠， ∵EM BC ∥，则EM AB ⊥， ∴90AEM ∠=︒，∴90CHG CHD DHG AED DEM AEM ∠=∠+∠=∠+∠=∠=︒， ∵30EDF ∠=︒，EM BC ∥则EM AD ∥， ∴ADE CDH ∠=∠，30GDH MDE ∠=∠=︒， ∵EM BC ∥， ∴EMF DFC ∠=∠，∴180EMD EMF EMD DFC ∠+∠=∠+∠=︒，即180DFC DGH ∠+∠=︒， ∴,,,D F H G 四点共圆； ∴30GFH GDH ∠=∠=︒，又30FHG ∠=︒∴1tan 30AE CF CH CF FH EM GH GH ++====︒（3）如图，过点E 作EK CD ⊥于K ，交DF 于M ，作FT EK ⊥于T ，90FTK TKC BCD ∠=∠=∠=︒∴四边形CFTK 是矩形， FT CK ∴=8DK CK DK FT ∴+=+= 111()4222DEFEMDEMFSSSEM DK EM FT EM DK FH EM ∴=+=⋅+⋅=+=同（2）将ADE V ，DEM △绕点D 逆时针旋转90︒，得,DCH DHG ，可得60GFH EDM ∠=∠=︒，EM GH = 取得最小值时，DEF 的面积最小，∵2220−=≥，∴FH x y =+≥ 当且仅当x y =时取得等于号，此时FC AE CH ==，设,,,D F H G 的圆心为O ， ∵DC FH ⊥，FC CH =， ∴DC 经过点O ，∴OF OD =，sin 602OC OF =︒= ∵8OD OC +=8OF +=解得：32OF =−∴232FH FC OF ===−∴48GH =，∴()44448192DEFSEM GH ====，即DEF 面积的最小为192．【点睛】本题考查了旋转的性质，正方形的性质、全等三角形的判定与性质、四点共圆等知识，解直角三角形，熟练掌握旋转的性质是解题的关键．1．（2023·陕西西安·一模）问题发现（1）在ABC 中，2AB =，60C ∠=︒，则ABC 面积的最大值为；（2）如图1，在四边形ABCD 中，6AB AD ==，90BCD BAD ∠=∠=︒，8AC =，求BC CD +的值．问题解决（3）有一个直径为60cm 的圆形配件O ，如图2所示．现需在该配件上切割出一个四边形孔洞OABC ，要求60O B ∠=∠=︒，OA OC =OABC 的面积尽可能小．试问，是否存在符合要求的面积最小的四边形OABC ？若存在，请求出四边形OABC 面积的最小值及此时OA 的长；若不存在，请说明理由．为弦的确定的圆上，作ABC 的外接圆，可得当点时，ABC 的面积最大，求出，再根据三角形的面积公式计算即可；将ABC 绕点A 逆时针旋转、D 、E 在同一条直线上，求出BCES，可得要使四边形面积最小，就要使BCE 的面积最大，然后由（时，BCE 的面积最）的方法求出BCE 面积的最大值，可得四边形，根据OA 如图，作ABC 的外接圆，∴当点C 在C '的位置，即时，ABC 的面积最大，∴C A C B ''=，BD =∴ABC '△是等边三角形，∴ABC 面积的最大值为）如图，将ABC 绕点∴B ADE ∠=∠，BAC ∠∵6AB AD ==，BCD ∠∴180B ADC ∠+∠=︒，∵60AOC ∠=︒，OA OC =∴将AOB 绕O 点顺时针旋转至COE ，连接∴60BOE ∠=︒，OE OB =∴BOE △是等边三角形，AOBBCOSS+COEBCOSS+ BOE BCES S− BCESBCES，的面积最小，就要使BCE 的面积最大，作BCE 的外接圆I ，点F 是I 上一点，CF 交由（1）可知，当CF 是直径，且CF BE ⊥时，BCE 的面积最大，∴BCE 面积的最大值为150BCES=（1）如图①，已知ABC 是面积为AD 是BAC ∠的平分线，则AB 的长为______．问题探究：（2）如图②，在ABC 中，90C ∠=︒，AC BC =，4AB =，点D 为AB 的中点，点E ，F 分别在边AC ，BC 上，且90EDF ∠=︒．证明：DE DF =．问题解决：（3）如图③，李叔叔准备在一块空地上修建一个矩形花园ABCD ，然后将其分割种植三种不同的花卉．按照他的分割方案，点P ，Q 分别在AD ，BC 上，连接PQ 、PB 、PC ，60BPC ∠=︒，E 、F 分别在PB 、PC 上，连接QE 、QF ，QE QF =，120EQF ∠=︒，其中四边形PEQF 种植玫瑰，ABP 和PCD 种植郁金香，剩下的区域种植康乃馨，根据实际需要，要求种植玫瑰的四边形PEQF 的面积为2，为了节约成本，矩形花园ABCD 的面积是否存在最小值？若存在，请求出矩形ABCD 的最小面积，若不存在，请说明理由．）设ABC 的边长为EQG ，根据四边形则当PQ BC ⊥时，矩形ABCD 的面积最小，根据2ABCD PEQF S S =四边形四边形，即可求解．【详解】解：（1）∵ABC 是面积为AD 是BAC ∠的平分线， ∴12BD CD AB ==设ABC 的边长为a∴AD ==∴2112224ABCS BC AD a =´=´´=∴24a =解得：4a =，故答案为：4．（2）如图所示，连接CD ，∵在ABC 中，90C ∠=︒，AC BC =，4AB =，点D 为AB 的中点， ∴CD AD =，90ADC ∠=︒，45A DCF ∠=∠=︒ 又∵90EDF ∠=︒∴ADE ADC CDE EDF EDC CDF ∠=∠−∠=∠−∠=∠ 在,ADE CDF △△中，45A DCF ADE CDF AD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴ADE CDF V V ≌ ∴DE DF =；（3）如图所示，∵60BPC ∠=︒，120EQF ∠=︒， ∴36060120180PFQ PEQ ∠+∠=︒−︒−︒=︒ 将QFP △绕点Q 逆时针旋转120︒，得到EQG ， ∴,,P E G 三点共线，∴四边形PEQF 的面积等于PQG ，又∵120,PQG PQ GQ ∠=︒=，∴30QPG QGP ∠=∠=︒过点Q 作QN PG ⊥于点N ，则12QN PQ =设PQ b =，则1,22NQ b PN ==∴2PG PN ==∴2111222PQGSPG NQ b =⨯=⨯=∵四边形PEQF 的面积为 ∴16b =，即16PQ =,如图所示，作QM PM ⊥于点M ，∵30EPQ FPQ ∠=∠=︒，QM PM ⊥，QN PG ⊥，则QN QM =，在,ENQ FMQ 中，QN QM EQ FQ =⎧⎨=⎩∴()HL ENQ FMQ ≌，同理可得PNQ PMQ ≌ 则2PNQPEQF S S=四边形∴PEQF PNQM S S =四边形四边形，作点Q 关于PE 的对称点T ，连接PT ，则PTQ 是等边三角形，则PTQS=如图所示，依题意，当PQ BC ⊥时，矩形ABCD 的面积最小，此时,E F 与,N M 重合，，∴22ABCD PEQF S S ==⨯四边形四边形∴矩形ABCD 的最小面积为2【点睛】本题考查了全等三角形的性质与判定，等边三角形的性质与判定，等腰三角形的性质与判定，勾股定理，旋转的性质，综合运用以上知识是解题的关键．3．（2024·陕西榆林·二模）（1）如图1，AB CD ∥，1,2AB CD ==，AD ，BC 交于点E ，若4=AD ，则AE = ；（2）如图2，矩形ABCD 内接于O ， 2,AB BC ==点 P 在AD 上运动，求 PBC 的面积的最大值；（3）为了提高居民的生活品质，市政部门计划把一块边长为 120米的正方形荒地 ABCD (如图3)改造成一个户外休闲区，计划在边AD ，BC 上分别取点P ，Q ，修建一条笔直的通道PQ ，要求 2CQ AP =，过点 B 作 BE PQ ⊥于点E ，在点E 处修建一个应急处理中心，再修建三条笔直的道路BE CE DE ，，，并计划在 CDE 内种植花卉， DEP 内修建老年活动区， BCE 内修建休息区，在四边形ABEP 内修建儿童游乐园．问种植花卉的 CDE 的面积是否存在最小值？若存在，求出最小值；若不存在，请说明理由．得ABE DCE ∽，得对应成比例的线段，于是得到结论；时，PBC 的面积有最大值，解直角三角形求出PBC 的高即可得到结论；于点M ，作BME 的外接圆O ，过点OF DC ⊥₂E CD ₂的面积最小．（）∥AB CD DCE ，是O的直径．₂的面积最大．P BC上任意另取一点P₁PBC的面积最大．Rt OBE中，．S=PBC。

高考数学 6年高考母题精解精析专题08 立体几何03 文

备战2013高考数学（文）6年高考母题精解精析专题08 立体几何03 36.【2102高考北京文16】（本小题共14分）如图1，在Rt△ABC中，∠C=90°，D，E分别为AC，AB的中点，点F为线段CD上的一点，将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD，如图2。

(I)求证：DE∥平面A1CB；(II)求证：A1F⊥BE；(III)线段A1B上是否存在点Q，使A1C⊥平面DEQ？说明理由。

【答案】37.【2012高考浙江文20】（本题满分15分）如图，在侧棱锥垂直底面的四棱锥ABCD-A1B1C1D1中，AD∥BC，AD⊥AB，AB=AD=2，BC=4,AA1=2，E是DD1的中点，F是平面B1C1E与直线AA1的交点。

（1）证明：（i）EF∥A1D1；（ii）BA1⊥平面B1C1EF；（2）求BC1与平面B1C1EF所成的角的正弦值。

38.【2012高考陕西文18】（本小题满分12分）直三棱柱ABC- A 1B 1C 1中，AB=A A 1 ，C A B∠=2π（Ⅰ）证明11B A C B ⊥;（Ⅱ）已知AB=2，11C A AB - 的体积【答案】39.【2012高考辽宁文18】(本小题满分12分)如图，直三棱柱///ABC A B C -，90BAC ∠= ，AB AC ==AA ′=1，点M ，N 分别为/A B和//B C 的中点。

(Ⅰ)证明：M N ∥平面//A ACC ; (Ⅱ)求三棱锥/A MNC -的体积。

（椎体体积公式V=13Sh,其中S 为地面面积，h 为高）【答案】【解析】本题以三棱柱为载体主要考查空间中的线面平行的判定、棱锥体积的计算，考查空间想象能力、推理论证能力、运算求解能力，难度适中。

第一小题可以通过线线平行来证明线面平行，也可通过面面平行来证明；第二小题求体积根据条件选择合适的底面是关键，也可以采用割补发来球体积。

40.【2012高考江苏16】（14分）如图，在直三棱柱111ABC A B C -中，1111A B A C =，D E ，分别是棱1BC CC ，上的点（点D 不同于点C ），且AD DE F ⊥，为11B C 的中点．求证：（1）平面AD E ⊥平面11BCC B ；（2）直线1//A F 平面ADE ．41.【2102高考福建文19】（本小题满分12分）如图，在长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，M为棱DD1上的一点。

全国通用2020_2022三年高考数学真题分项汇编专题08平面解析几何解答题

08 平面解析几何（解答题）1．【2022年全国甲卷】设抛物线C:y 2=2px(p >0)的焦点为F ，点D (p,0)，过F 的直线交C 于M ，N 两点．当直线MD 垂直于x 轴时，|MF |=3．(1)求C 的方程；(2)设直线MD,ND 与C 的另一个交点分别为A ，B ，记直线MN,AB 的倾斜角分别为α,β．当α−β取得最大值时，求直线AB 的方程．【答案】(1)y 2=4x ； (2)AB:x =√2y +4. 【解析】【分析】（1）由抛物线的定义可得|MF|=p +p2，即可得解；（2）设点的坐标及直线MN:x =my +1，由韦达定理及斜率公式可得k MN =2k AB ，再由差角的正切公式及基本不等式可得k AB =√22，设直线AB:x =√2y +n ，结合韦达定理可解.(1)抛物线的准线为x =−p2，当MD 与x 轴垂直时，点M 的横坐标为p ，此时|MF|=p +p2=3，所以p =2，所以抛物线C 的方程为y 2=4x ； (2)设M(y 124,y 1),N(y 224,y 2),A(y 324,y 3),B(y 424,y 4)，直线MN:x =my +1，由{x =my +1y 2=4x 可得y 2−4my −4=0，Δ>0,y 1y 2=−4，由斜率公式可得k MN =y 1−y 2y 124−y 224=4y 1+y 2，k AB=y 3−y 4y 324−y 424=4y 3+y 4，直线MD:x =x 1−2y 1⋅y +2，代入抛物线方程可得y 2−4(x 1−2)y 1⋅y −8=0，Δ>0,y 1y 3=−8，所以y 3=2y 2，同理可得y 4=2y 1，所以k AB =4y3+y 4=42(y1+y 2)=k MN 2又因为直线MN 、AB 的倾斜角分别为α,β，所以k AB =tanβ=k MN 2=tanα2，若要使α−β最大，则β∈(0,π2)，设k MN =2k AB=2k >0，则tan(α−β)=tanα−tanβ1+tanαtanβ=k 1+2k 2=11k+2k ≤2√1k⋅2k=√24，当且仅当1k =2k 即k =√22时，等号成立，所以当α−β最大时，k AB =√22，设直线AB:x =√2y +n ，代入抛物线方程可得y 2−4√2y −4n =0， Δ>0,y 3y 4=−4n =4y 1y 2=−16，所以n =4，所以直线AB:x =√2y +4. 【点睛】关键点点睛：解决本题的关键是利用抛物线方程对斜率进行化简，利用韦达定理得出坐标间的关系.2．【2022年全国乙卷】已知椭圆E 的中心为坐标原点，对称轴为x 轴、y 轴，且过A (0,−2),B (32,−1)两点． (1)求E 的方程；(2)设过点P (1,−2)的直线交E 于M ，N 两点，过M 且平行于x 轴的直线与线段AB 交于点T ，点H 满足MT ⃑⃑⃑⃑⃑⃑ =TH ⃑⃑⃑⃑⃑ ．证明：直线HN 过定点．【答案】(1)y 24+x 23=1(2)(0,−2) 【解析】【分析】（1）将给定点代入设出的方程求解即可；（2）设出直线方程，与椭圆C 的方程联立，分情况讨论斜率是否存在，即可得解. (1)解：设椭圆E 的方程为mx 2+ny 2=1，过A (0,−2),B (32,−1)，则{4n =194m +n =1 ，解得m =13，n =14，所以椭圆E 的方程为：y 24+x 23=1.(2)A(0,−2),B(32,−1)，所以AB:y +2=23x ，①若过点P(1,−2)的直线斜率不存在，直线x =1.代入x 23+y 24=1，可得M(1,2√63)，N(1,−2√63)，代入AB 方程y =23x −2，可得T(√6+3,2√63)，由MT⃑⃑⃑⃑⃑⃑ =TH ⃑⃑⃑⃑⃑ 得到H(2√6+5,2√63).求得HN 方程： y =(2−2√63)x −2，过点(0,−2).②若过点P(1,−2)的直线斜率存在，设kx −y −(k +2)=0,M(x 1,y 1),N(x 2,y 2).联立{kx −y −(k +2)=0x 23+y 24=1,得(3k 2+4)x 2−6k(2+k)x +3k(k +4)=0，可得{x 1+x 2=6k(2+k)3k 2+4x 1x 2=3k(4+k)3k 2+4，{y 1+y 2=−8(2+k)3k 2+4y 2y 2=4(4+4k−2k 2)3k 2+4，且x 1y 2+x 2y 1=−24k3k 2+4(∗) 联立{y =y 1y =23x −2 ,可得T(3y 12+3,y 1),H(3y 1+6−x 1,y 1).可求得此时HN:y −y 2=y 1−y 23y1+6−x 1−x 2(x −x 2)，将(0,−2)，代入整理得2(x 1+x 2)−6(y 1+y 2)+x 1y 2+x 2y 1−3y 1y 2−12=0，将(∗)代入，得24k +12k 2+96+48k −24k −48−48k +24k 2−36k 2−48=0, 显然成立，综上，可得直线HN 过定点(0,−2). 【点睛】求定点、定值问题常见的方法有两种：①从特殊入手，求出定值，再证明这个值与变量无关；②直接推理、计算，并在计算推理的过程中消去变量，从而得到定值. 3．【2022年新高考1卷】已知点A(2,1)在双曲线C:x 2a 2−y 2a 2−1=1(a >1)上，直线l 交C 于P ，Q 两点，直线AP,AQ 的斜率之和为0．(1)求l 的斜率；(2)若tan ∠PAQ =2√2，求△PAQ 的面积．【答案】(1)−1； (2)16√29．【解析】【分析】（1）由点A(2,1)在双曲线上可求出a ，易知直线l 的斜率存在，设l:y =kx +m ，P (x 1,y 1),Q (x 2,y 2)，再根据k AP +k BP =0，即可解出l 的斜率；（2）根据直线AP,AQ 的斜率之和为0可知直线AP,AQ 的倾斜角互补，再根据tan ∠PAQ =2√2即可求出直线AP,AQ 的斜率，再分别联立直线AP,AQ 与双曲线方程求出点P,Q 的坐标，即可得到直线PQ 的方程以及PQ 的长，由点到直线的距离公式求出点A 到直线PQ 的距离，即可得出△PAQ 的面积． (1)因为点A(2,1)在双曲线C:x 2a 2−y 2a 2−1=1(a >1)上，所以4a 2−1a 2−1=1，解得a 2=2，即双曲线C:x 22−y 2=1易知直线l 的斜率存在，设l:y =kx +m ，P (x 1,y 1),Q (x 2,y 2)，联立{y =kx +m x 22−y 2=1可得，(1−2k 2)x 2−4mkx −2m 2−2=0，所以，x 1+x 2=−4mk 2k 2−1,x 1x 2=2m 2+22k 2−1，Δ=16m 2k 2+4(2m 2+2)(2k 2−1)>0⇒m 2−1+2k 2>0．所以由k AP +k BP =0可得，y 2−1x2−2+y 1−1x 1−2=0，即(x 1−2)(kx 2+m −1)+(x 2−2)(kx 1+m −1)=0，即2kx 1x 2+(m −1−2k )(x 1+x 2)−4(m −1)=0，所以2k ×2m 2+22k 2−1+(m −1−2k )(−4mk2k 2−1)−4(m −1)=0，化简得，8k 2+4k −4+4m (k +1)=0，即(k +1)(2k −1+m )=0，所以k =−1或m =1−2k ，当m =1−2k 时，直线l:y =kx +m =k (x −2)+1过点A (2,1)，与题意不符，舍去，故k =−1． (2)不妨设直线PA,PB 的倾斜角为α,β(α<β)，因为k AP +k BP =0，所以α+β=π，因为tan ∠PAQ =2√2，所以tan (β−α)=2√2，即tan2α=−2√2，即√2tan 2α−tanα−√2=0，解得tanα=√2，于是，直线PA:y =√2(x −2)+1，直线PB:y =−√2(x −2)+1，联立{y =√2(x −2)+1x 22−y 2=1可得，32x 2+2(1−2√2)x +10−4√2=0，因为方程有一个根为2，所以x P =10−4√23，y P =4√2−53，同理可得，x Q =10+4√23，y Q = −4√2−53．所以PQ:x +y −53=0，|PQ |=163，点A 到直线PQ 的距离d =|2+1−53|√2=2√23，故△PAQ 的面积为12×163×2√23=16√29．4．【2022年新高考2卷】已知双曲线C:x 2a2−y 2b 2=1(a >0,b >0)的右焦点为F(2,0)，渐近线方程为y =±√3x ． (1)求C 的方程；(2)过F 的直线与C 的两条渐近线分别交于A ，B 两点，点P (x 1,y 1),Q (x 2,y 2)在C 上，且x 1>x 2>0,y 1>0．过P 且斜率为−√3的直线与过Q 且斜率为√3的直线交于点M .从下面①②③中选取两个作为条件，证明另外一个成立：①M在AB上；②PQ∥AB；③|MA|=|MB|．注：若选择不同的组合分别解答，则按第一个解答计分.【答案】(1)x2−y23=1(2)见解析【解析】【分析】（1）利用焦点坐标求得c的值，利用渐近线方程求得a,b的关系，进而利用a,b,c的平方关系求得a,b的值，得到双曲线的方程；（2）先分析得到直线AB的斜率存在且不为零，设直线AB的斜率为k, M(x0,y0),由③|AM|=|BM|等价分析得到x0+ky0=8k2k2−3；由直线PM和QM的斜率得到直线方程，结合双曲线的方程，两点间距离公式得到直线PQ的斜率m=3x0y，由②PQ//AB等价转化为ky0=3x0，由①M在直线AB上等价于ky0=k2(x0−2)，然后选择两个作为已知条件一个作为结论，进行证明即可.(1)右焦点为F(2,0)，∴c=2,∵渐近线方程为y=±√3x，∴ba=√3，∴b=√3a，∴c2=a2+ b2=4a2=4，∴a=1，∴b=√3．∴C的方程为：x2−y23=1；(2)由已知得直线PQ的斜率存在且不为零，直线AB的斜率不为零，若选由①②推③或选由②③推①：由②成立可知直线AB的斜率存在且不为零；若选①③推②，则M为线段AB的中点，假若直线AB的斜率不存在，则由双曲线的对称性可知M在x轴上，即为焦点F,此时由对称性可知P、Q关于x轴对称，与从而x1=x2，已知不符；总之，直线AB的斜率存在且不为零.设直线AB的斜率为k,直线AB方程为y=k(x−2),则条件①M在AB上，等价于y0=k(x0−2)⇔ky0=k2(x0−2)；两渐近线的方程合并为3x2−y2=0,联立消去y并化简整理得：(k2−3)x2−4k2x+4k2=0设A(x3,y3),B(x3,y4),线段中点为N(x N,y N),则x N=x3+x42=2k2k2−3,y N=k(x N−2)=6kk2−3,设M(x0,y0),则条件③|AM|=|BM|等价于(x0−x3)2+(y0−y3)2=(x0−x4)2+(y0−y4)2, 移项并利用平方差公式整理得：(x 3−x 4)[2x 0−(x 3+x 4)]+(y 3−y 4)[2y 0−(y 3+y 4)]=0， [2x 0−(x 3+x 4)]+y 3−y 4x 3−x 4[2y 0−(y 3+y 4)]=0,即x 0−x N +k (y 0−y N )=0,即x 0+ky 0=8k 2k 2−3；由题意知直线PM 的斜率为−√3, 直线QM 的斜率为√3, ∴由y 1−y 0=−√3(x 1−x 0),y 2−y 0=√3(x 2−x 0), ∴y 1−y 2=−√3(x 1+x 2−2x 0), 所以直线PQ 的斜率m =y 1−y2x 1−x 2=−√3(x 1+x 2−2x 0)x 1−x 2, 直线PM:y =−√3(x −x 0)+y 0,即y =y 0+√3x 0−√3x ,代入双曲线的方程3x 2−y 2−3=0,即(√3x +y)(√3x −y)=3中，得：(y 0+√3x 0)[2√3x −(y 0+√3x 0)]=3, 解得P 的横坐标：x 1=2√3(y +√3x +y 0+√3x 0),同理：x 2=2√3(y−√3x y 0−√3x 0)，∴x 1−x 2=√3(3y0y 02−3x 02+y 0),x 1+x 2−2x 0=−3xy 02−3x 02−x 0,∴m =3x 0y 0,∴条件②PQ//AB 等价于m =k ⇔ky 0=3x 0，综上所述：条件①M 在AB 上，等价于ky 0=k 2(x 0−2)；条件②PQ//AB 等价于ky 0=3x 0；条件③|AM|=|BM|等价于x 0+ky 0=8k 2k 2−3；选①②推③:由①②解得：x 0=2k 2k 2−3,∴x 0+ky 0=4x 0=8k 2k 2−3,∴③成立；选①③推②：由①③解得：x 0=2k 2k 2−3，ky 0=6k 2k 2−3， ∴ky 0=3x 0，∴②成立；选②③推①：由②③解得：x 0=2k 2k 2−3，ky 0=6k 2k 2−3，∴x 0−2=6k 2−3， ∴ky 0=k 2(x 0−2)，∴①成立.5．【2021年甲卷文科】抛物线C 的顶点为坐标原点O ．焦点在x 轴上，直线l ：1x =交C 于P ，Q 两点，且OP OQ ⊥．已知点()2,0M ，且M 与l 相切．（1）求C ，M 的方程；（2）设123,,A A A 是C 上的三个点，直线12A A ，13A A 均与M 相切．判断直线23A A 与M 的位置关系，并说明理由．【答案】（1）抛物线2:C y x =，M 方程为22(2)1x y -+=；（2）相切，理由见解析【解析】【分析】（1）根据已知抛物线与1x =相交，可得出抛物线开口向右，设出标准方程，再利用对称性设出,P Q 坐标，由OP OQ ⊥，即可求出p ；由圆M 与直线1x =相切，求出半径，即可得出结论；（2）方法一：先考虑12A A 斜率不存在，根据对称性，即可得出结论；若121323,,A A A A A A 斜率存在，由123,,A A A 三点在抛物线上，将直线121223,,A A A A A A 斜率分别用纵坐标表示，再由1212,A A A A 与圆M 相切，得出2323,y y y y +⋅与1y 的关系，最后求出M 点到直线23A A 的距离，即可得出结论. 【详解】（1）依题意设抛物线200:2(0),(1,),(1,)C y px p P y Q y =>-， 20,1120,21OP OQ OP OQ y p p ⊥∴⋅=-=-=∴=，所以抛物线C 的方程为2y x =，()2,0,M M 与1x =相切，所以半径为1，所以M 的方程为22(2)1x y -+=；（2）[方法一]：设111222333(),(,),(,)A x y A x y A x y 若12A A 斜率不存在，则12A A 方程为1x =或3x =，若12A A 方程为1x =，根据对称性不妨设1(1,1)A ，则过1A 与圆M 相切的另一条直线方程为1y =，此时该直线与抛物线只有一个交点，即不存在3A ，不合题意；若12A A 方程为3x =，根据对称性不妨设12(3,A A 则过1A 与圆M 相切的直线13A A为3)y x -=-，又131********A A y y k y x x y y -==∴=-+， 330,(0,0)x A =，此时直线1323,A A A A 关于x 轴对称，所以直线23A A 与圆M 相切；若直线121323,,A A A A A A 斜率均存在，则121323121323111,,A A A A A A k k k y y y y y y ===+++，所以直线12A A 方程为()11121y y x x y y -=-+，整理得1212()0x y y y y y -++=，同理直线13A A 的方程为1313()0x y y y y y -++=，直线23A A 的方程为2323()0x y y y y y -++=， 12A A 与圆M相切，1=整理得22212121(1)230y y y y y -++-=，13A A 与圆M 相切，同理22213131(1)230y y y y y -++-= 所以23,y y 为方程222111(1)230y y y y y -++-=的两根，2112323221123,11y y y y y y y y -+=-⋅=--，M 到直线23A A 的距离为：2123|2|y -+=22121111y y +===+，所以直线23A A 与圆M 相切；综上若直线1213,A A A A 与圆M 相切，则直线23A A 与圆M 相切.[方法二]【最优解】：设()()()222111113333322222,,,,,,,,A x y y x A x y y x A x y y x ===．当12x x =时，同解法1．当12x x ≠时，直线12A A 的方程为()211121y y y y x x x x --=--，即121212y y x y y y y y =+++．由直线12A A 与M1=，化简得()121212130y y x x x +--+=，同理，由直线13A A 与M 相切得()131312130y y x x x +--+=．因为方程()1112130y y x x x +--+=同时经过点23,A A ，所以23A A 的直线方程为()1112130y y x x x +--+=，点M 到直线23A A1==．所以直线23A A 与M 相切．综上所述，若直线1213,A A A A 与M 相切，则直线23A A 与M 相切．【整体点评】第二问关键点：过抛物线上的两点直线斜率只需用其纵坐标（或横坐标）表示，将问题转化为只与纵坐标（或横坐标）有关；法一是要充分利用1213,A A A A 的对称性，抽象出2323,y y y y +⋅与1y 关系，把23,y y 的关系转化为用1y 表示，法二是利用相切等条件得到23A A 的直线方程为()1112130y y x x x +--+=，利用点到直线距离进行证明，方法二更为简单，开拓学生思路6．【2021年乙卷文科】已知抛物线2:2(0)C y px p =>的焦点F 到准线的距离为2．（1）求C 的方程;（2）已知O 为坐标原点，点P 在C 上，点Q 满足9PQ QF =，求直线OQ 斜率的最大值. 【答案】（1）24y x =；（2）最大值为13.【解析】【分析】（1）由抛物线焦点与准线的距离即可得解；（2）设()00,Q x y ，由平面向量的知识可得()00109,10P x y -，进而可得20025910y x +=，再由斜率公式及基本不等式即可得解. 【详解】（1）抛物线2:2(0)C y px p =>的焦点,02p F ⎛⎫⎪⎝⎭，准线方程为2p x =-，由题意，该抛物线焦点到准线的距离为222p p p ⎛⎫--== ⎪⎝⎭，所以该抛物线的方程为24y x =；（2）[方法一]：轨迹方程+基本不等式法设()00,Q x y ，则()00999,9PQ QF x y ==--，所以()00109,10P x y -，由P 在抛物线上可得()()200104109y x =-，即20025910y x +=，据此整理可得点Q 的轨迹方程为229525=-y x ，所以直线OQ 的斜率000220001025925910OQ y y y k y x y ===++，当00y =时，0OQ k =；当00y ≠时，0010925OQ k y y =+，当00y >时，因为0092530y y +≥=，此时103OQ k <≤，当且仅当00925y y =，即035y =时，等号成立；当00y <时，0OQ k <；综上，直线OQ 的斜率的最大值为13.[方法二]：【最优解】轨迹方程+数形结合法同方法一得到点Q 的轨迹方程为229525=-y x ．设直线OQ 的方程为y kx =，则当直线OQ 与抛物线229525=-y x 相切时，其斜率k 取到最值．联立2,29,525y kx y x =⎧⎪⎨=-⎪⎩得22290525k x x -+=，其判别式222940525⎛⎫∆=--⨯= ⎪⎝⎭k ，解得13k =±，所以直线OQ 斜率的最大值为13．[方法三]：轨迹方程+换元求最值法同方法一得点Q 的轨迹方程为229525=-y x ．设直线OQ 的斜率为k ，则22229525⎛⎫==- ⎪⎝⎭y k x x x．令11009⎛⎫=<≤ ⎪⎝⎭t t x ，则2292255=-+k t t 的对称轴为59t =，所以21110,933≤≤-≤≤k k ．故直线OQ 斜率的最大值为13．[方法四]：参数+基本不等式法由题可设()24,4(0),(,)>P t t t Q x y ．因为(1,0),9=F PQ QF ，所以()24,49(1,)--=--x t y t x y ．于是249(1)49x t x y t y ⎧-=-⎨-=-⎩，所以21049104x t y t ⎧=+⎨=⎩则直线OQ的斜率为244194934==≤=++y t x t t t ．当且仅当94t t=，即32t =时等号成立，所以直线OQ 斜率的最大值为13．【整体点评】方法一根据向量关系，利用代点法求得Q 的轨迹方程，得到直线OQ 的斜率关于y 的表达式，然后利用分类讨论，结合基本不等式求得最大值；方法二同方法一得到点Q 的轨迹方程，然后利用数形结合法，利用判别式求得直线OQ 的斜率的最大值，为最优解；方法三同方法一求得Q 的轨迹方程，得到直线OQ 的斜率k 的平方关于x 的表达式，利用换元方法转化为二次函数求得最大值，进而得到直线OQ 斜率的最大值；方法四利用参数法，由题可设()24,4(0),(,)>P t t t Q x y ，求得x,y 关于t 的参数表达式，得到直线OQ 的斜率关于t 的表达式，结合使用基本不等式，求得直线OQ 斜率的最大值.7．【2021年乙卷理科】已知抛物线()2:20C x py p =>的焦点为F ，且F 与圆22:(4)1M x y ++=上点的距离的最小值为4．（1）求p ；（2）若点P 在M 上，,PA PB 是C 的两条切线，,A B 是切点，求PAB △面积的最大值．【答案】（1）2p =；（2）【解析】【分析】（1）根据圆的几何性质可得出关于p 的等式，即可解出p 的值；（2）设点()11,A x y 、()22,B x y 、()00,P x y ，利用导数求出直线PA 、PB ，进一步可求得直线AB 的方程，将直线AB 的方程与抛物线的方程联立，求出AB 以及点P 到直线AB 的距离，利用三角形的面积公式结合二次函数的基本性质可求得PAB △面积的最大值. 【详解】（1）[方法一]：利用二次函数性质求最小值由题意知，0,2p F ⎛⎫ ⎪⎝⎭，设圆M 上的点()00,N x y ，则()22041++=x y ．所以()()22001453=-+-≤≤-x y y ．从而有||==FN=因为053y -≤≤-，所以当03y=-时，min ||4FN ．又0p >，解之得2p =，因此2p =．[方法二]【最优解】：利用圆的几何意义求最小值抛物线C 的焦点为0,2p F ⎛⎫ ⎪⎝⎭，42pFM =+，所以，F 与圆22:(4)1M x y ++=上点的距离的最小值为4142p+-=，解得2p =；（2）[方法一]：切点弦方程+韦达定义判别式求弦长求面积法抛物线C 的方程为24x y =，即24x y =，对该函数求导得=2xy '，设点()11,A x y 、()22,B x y 、()00,P x y ，直线PA 的方程为()1112x y y x x -=-，即112x xy y =-，即11220x x y y --=，同理可知，直线PB 的方程为22220x x y y --=，由于点P 为这两条直线的公共点，则10102020220220x x y y x x y y --=⎧⎨--=⎩，所以，点A 、B 的坐标满足方程00220x x y y --=，所以，直线AB 的方程为00220x x y y --=，联立0022204x x y y x y --=⎧⎪⎨=⎪⎩，可得200240x x x y -+=，由韦达定理可得1202x x x +=，1204x x y =，所以，AB ==点P 到直线AB的距离为d =所以，()3220011422PABS AB d x y =⋅==-△， ()()2222000000041441215621x y y y y y y -=-+-=---=-++，由已知可得053y -≤≤-，所以，当05y =-时，PAB △的面积取最大值321202⨯=[方法二]【最优解】：切点弦法+分割转化求面积+三角换元求最值同方法一得到1201202,4+==x x x x x y ．过P 作y 轴的平行线交AB 于Q ，则2000,2⎛⎫- ⎪⎝⎭x Q x y ．()32221200001111||242222⎛⎫=⋅-=-- ⎪⎝⎭PABSPQ x x x y x y ． P 点在圆M 上，则00cos ,4sin ,x y αα=⎧⎨=-+⎩()()333222222001114cos 4sin 16(sin 2)21222ααα⎡⎤=-=-+=-++⎣⎦PABSx y ．故当sin 1α=-时PAB △的面积最大，最大值为 [方法三]：直接设直线AB 方程法设切点A ，B 的坐标分别为211,4x A x ⎛⎫⎪⎝⎭，222,4x B x ⎛⎫ ⎪⎝⎭．设:AB l y kx b =+，联立AB l 和抛物线C 的方程得2,4,y kx b x y =+⎧⎨=⎩整理得2440x kx b --=．判别式2Δ16160=+>k b ，即20k b +>，且12124,4x x k x x b +==-．抛物线C 的方程为24x y =，即24x y =，有2x y '=．则()2111:42-=-PA x x l y x x ，整理得21124x x y x =⋅-，同理可得222:24=⋅-PB x x l y x ．联立方程211222,24,24x x y x x x y x ⎧=⋅-⎪⎪⎨⎪=⋅-⎪⎩可得点P 的坐标为1212,24x x x x P +⎛⎫ ⎪⎝⎭，即(2,)P k b -．将点P 的坐标代入圆M 的方程，得22(2)(4)1+-+=k b ，整理得221(4)4b k --=．由弦长公式得12||=-=AB x=点P 到直线AB的距离为d =所以21||222==+=PABSAB d k b= 其中[5,3]=-∈--P y b ，即[3,5]∈b ．当5b =时，()max=PAB S【整体点评】（1）方法一利用两点间距离公式求得FN 关于圆M 上的点()00,N x y 的坐标的表达式，进一步转化为关于0y 的表达式，利用二次函数的性质得到最小值，进而求得p 的值；方法二，利用圆的性质，F 与圆22:(4)1M x y ++=上点的距离的最小值，简洁明快，为最优解；（2）方法一设点()11,A x y 、()22,B x y 、()00,P x y ，利用导数求得两切线方程，由切点弦方程思想得到直线AB 的坐标满足方程00220x x y y --=，然手与抛物线方程联立，由韦达定理可得1202x x x +=，1204x x y =，利用弦长公式求得AB 的长，进而得到面积关于()00,P x y 坐标的表达式，利用圆的方程转化得到关于0y 的二次函数最值问题；方法二，同方法一得到1202x x x +=，1204x x y =，过P 作y 轴的平行线交AB 于Q ，则2000,2⎛⎫- ⎪⎝⎭x Q x y ．由121||2PABSPQ x x =⋅-求得面积关于()00,P x y 坐标的表达式，并利用三角函数换元求得面积最大值，方法灵活，计算简洁，为最优解；方法三直接设直线:AB l y kx b =+，联立直线AB 和抛物线方程，利用韦达定理判别式得到20k b +>，且12124,4x x k x x b +==-．利用点P 在圆M 上，求得,k b 的关系，然后利用导数求得两切线方程，解方程组求得P 的坐标(2,)P k b -，进而利用弦长公式和点到直线距离公式求得面积关于b 的函数表达式，然后利用二次函数的性质求得最大值；8．【2021年新高考1卷】在平面直角坐标系xOy 中，已知点()1F 、)2122F MF MF -=，，点M 的轨迹为C .（1）求C 的方程；（2）设点T 在直线12x =上，过T 的两条直线分别交C 于A 、B 两点和P ，Q 两点，且TA TB TP TQ ⋅=⋅，求直线AB 的斜率与直线PQ 的斜率之和.【答案】（1）()221116y x x -=≥；（2）0. 【解析】【分析】(1) 利用双曲线的定义可知轨迹C 是以点1F 、2F 为左、右焦点双曲线的右支，求出a 、b 的值，即可得出轨迹C 的方程；(2)方法一：设出点的坐标和直线方程，联立直线方程与曲线C 的方程，结合韦达定理求得直线的斜率，最后化简计算可得12k k +的值.【详解】(1)因为12122MF MF F F -=<=所以，轨迹C 是以点1F 、2F 为左、右焦点的双曲线的右支，设轨迹C 的方程为()222210,0x y a b a b-=>>，则22a =，可得1a =，4b =，所以，轨迹C 的方程为()221116y x x -=≥.（2）[方法一] 【最优解】：直线方程与双曲线方程联立如图所示，设1(,)2T n ,设直线AB 的方程为112211(),,(2,(),)y n k x A x y B x y -=-．联立1221()2116y n k x y x ⎧-=-⎪⎪⎨⎪-=⎪⎩, 化简得22221111211(16)(2)1604k x k k n x k n k n -+---+-=.则22211112122211111624,1616k n k n k k n x x x x k k +-+-+==--．故12,11||)||)22TA x TB x -=-．则222111221(12)(1)11||||(1)()()2216n k TA TB k x x k ++⋅=+--=-．设PQ 的方程为21()2y n k x -=-，同理22222(12)(1)||||16n k TP TQ k ++⋅=-．因为TA TB TP TQ ⋅=⋅，所以22122212111616k k k k ++=--，化简得22121717111616k k +=+--，所以22121616k k -=-，即2212k k =．因为11k k ≠，所以120k k +=． [方法二] ：参数方程法设1(,)2T m ．设直线AB 的倾斜角为1θ，则其参数方程为111cos 2sin x t y m t θθ⎧=+⎪⎨⎪=+⎩，联立直线方程与曲线C 的方程2216160(1)x y x --≥=，可得222221111cos 116(cos )(sin 2sin )1604t m t t mt θθθθ+-++-=+，整理得22221111(16cos sin )(16cos 2sin )(12)0t m t m θθθθ-+--+=．设12,TA t TB t ==，由根与系数的关系得2212222111(12)12||||16cos sin 117cos t m m TA TB t θθθ-++⋅===--⋅．设直线PQ 的倾斜角为2θ，34,TP t TQ t ==，同理可得2342212||||117cos m T T t P Q t θ+⋅==-⋅由||||||||TA TB TP TQ ⋅=⋅，得2212cos cos θθ=．因为12θθ≠，所以12s o o s c c θθ=-．由题意分析知12θθπ+=．所以12tan tan 0θθ+=，故直线AB 的斜率与直线PQ 的斜率之和为0． [方法三]：利用圆幂定理因为TA TB TP TQ ⋅=⋅，由圆幂定理知A ，B ，P ，Q 四点共圆．设1(,)2T t ,直线AB 的方程为11()2y t k x -=-，直线PQ 的方程为21()2y t k x -=-,则二次曲线1212()()022k kk x y t k x y t --+--+=．又由22116y x -=，得过A ，B ，P ，Q 四点的二次曲线系方程为： 221212()()(1)0(0)2216k k y k x y t k x y t x λμλ--+--++--=≠，整理可得： []2212121212()()()()16k x y k k xy t k k k k k x μμλλλλ++--+++-12(2)02y k k t m λ++-+=，其中21212()42k k t m t k k λμ⎡⎤=+-+-⎢⎥⎣⎦．由于A ，B ，P ，Q 四点共圆，则xy 项的系数为0，即120k k +=. 【整体点评】(2)方法一：直线方程与二次曲线的方程联立，结合韦达定理处理圆锥曲线问题是最经典的方法，它体现了解析几何的特征，是该题的通性通法，也是最优解；方法二：参数方程的使用充分利用了参数的几何意义，要求解题过程中对参数有深刻的理解，并能够灵活的应用到题目中.方法三：圆幂定理的应用更多的提现了几何的思想，二次曲线系的应用使得计算更为简单.9．【2021年新高考2卷】已知椭圆C 的方程为22221(0)x y a b a b +=>>，右焦点为F ，且．（1）求椭圆C 的方程；（2）设M ，N 是椭圆C 上的两点，直线MN 与曲线222(0)x y b x +=>相切．证明：M ，N ，F三点共线的充要条件是||MN =【答案】（1）2213x y +=；（2）证明见解析.【解析】【分析】（1）由离心率公式可得a =2b ，即可得解；（2）必要性：由三点共线及直线与圆相切可得直线方程，联立直线与椭圆方程可证MN 充分性：设直线():,0MN y kx b kb =+<，由直线与圆相切得221b k =+，联立直线与椭圆方=1k =±，即可得解. 【详解】（1）由题意，椭圆半焦距c =c e a ==a = 又2221b a c =-=，所以椭圆方程为2213x y +=；（2）由（1）得，曲线为221(0)x y x +=>，当直线MN 的斜率不存在时，直线:1MN x =，不合题意；当直线MN 的斜率存在时，设()()1122,,,M x y N x y ，必要性：若M ，N ，F三点共线，可设直线(:MN y k x =即0kx y -=，由直线MN 与曲线221(0)x y x +=>1=，解得1k =±，联立(2213y x x y ⎧=±⎪⎨⎪+=⎩可得2430x -+=，所以121234x x x x +=⋅=，所以MN 所以必要性成立；充分性：设直线():,0MN y kx b kb =+<即0kx y b -+=，由直线MN 与曲线221(0)x y x +=>1=，所以221b k =+，联立2213y kx b x y =+⎧⎪⎨+=⎪⎩可得()222136330k x kbx b +++-=，所以2121222633,1313kb b x x x x k k -+=-⋅=++，所以MN ==化简得()22310k -=，所以1k =±，所以1k b =⎧⎪⎨=⎪⎩1k b =-⎧⎪⎨=⎪⎩:MN y x =y x =-所以直线MN 过点F ，M ，N ，F 三点共线，充分性成立；所以M ，N，F 三点共线的充要条件是||MN = 【点睛】关键点点睛：解决本题的关键是直线方程与椭圆方程联立及韦达定理的应用，注意运算的准确性是解题的重中之重.10．【2020年新课标1卷理科】已知A 、B 分别为椭圆E ：2221x y a+=（a >1）的左、右顶点，G 为E 的上顶点，8AG GB ⋅=，P 为直线x =6上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ．（1）求E 的方程；（2）证明：直线CD 过定点.【答案】（1）2219x y +=；（2）证明详见解析.【解析】【分析】（1）由已知可得：(),0A a -， (),0B a ，()0,1G ，即可求得21AG GB a ⋅=-，结合已知即可求得：29a =，问题得解.（2）方法一：设()06,P y ，可得直线AP 的方程为：()039y y x =+，联立直线AP 的方程与椭圆方程即可求得点C 的坐标为20022003276,99y y y y ⎛⎫-+ ⎪++⎝⎭，同理可得点D 的坐标为2002200332,11y y y y ⎛⎫-- ⎪++⎝⎭，当203y ≠时，可表示出直线CD 的方程，整理直线CD 的方程可得：()02043233y y x y ⎛⎫=- ⎪-⎝⎭即可知直线过定点3,02⎛⎫ ⎪⎝⎭，当203y =时，直线CD ：32x =，直线过点3,02⎛⎫⎪⎝⎭，命题得证. 【详解】（1）依据题意作出如下图象：由椭圆方程222:1(1)x E y a a +=>可得：(),0A a -， (),0B a ，()0,1G∴(),1AG a =，(),1GB a =- ∴218AG GB a ⋅=-=，∴29a =∴椭圆方程为：2219x y +=（2）[方法一]：设而求点法证明：设()06,P y ，则直线AP 的方程为：()()00363y y x -=+--，即：()039y y x =+联立直线AP 的方程与椭圆方程可得：()2201939x y y y x ⎧+=⎪⎪⎨⎪=+⎪⎩，整理得：()2222000969810y x y x y +++-=，解得：3x =-或20203279y x y -+=+将20203279y x y -+=+代入直线()039y y x =+可得：02069y y y =+所以点C 的坐标为20022003276,99y y y y ⎛⎫-+ ⎪++⎝⎭. 同理可得：点D 的坐标为2002200332,11y y y y ⎛⎫-- ⎪++⎝⎭ 当203y ≠时，∴直线CD 的方程为：0022200002222000022006291233327331191y y y y y y y x y y y y y y ⎛⎫-- ⎪++⎛⎫⎛⎫--⎝⎭-=-⎪ ⎪-+-++⎝⎭⎝⎭-++，整理可得：()()()2220000002224200000832338331116963y y y y y y y x x y y y y y +⎛⎫⎛⎫--+=-=- ⎪ ⎪+++--⎝⎭⎝⎭ 整理得：()()0002220004243323333y y y y x x y y y ⎛⎫=+=- ⎪---⎝⎭所以直线CD 过定点3,02⎛⎫⎪⎝⎭．当203y =时，直线CD ：32x =，直线过点3,02⎛⎫ ⎪⎝⎭．故直线CD 过定点3,02⎛⎫⎪⎝⎭．[方法二]【最优解】：数形结合设(6,)P t ，则直线PA 的方程为(3)9ty x =+，即930-+=tx y t ．同理，可求直线PB 的方程为330--=tx y t ．则经过直线PA 和直线PB 的方程可写为(93)(33)0-+--=tx y t tx y t ．可化为()22292712180-+-+=txy txy ty ．④易知A ，B ，C ，D 四个点满足上述方程，同时A ，B ，C ，D 又在椭圆上，则有2299x y -=-，代入④式可得()2227912180--+=tytxy ty ．故()227912180⎡⎤--+=⎣⎦y t y tx t ，可得0y =或()227912180--+=t y tx t ．其中0y =表示直线AB ，则()227912180--+=t y tx t 表示直线CD ．令0y =，得32x =，即直线CD 恒过点3,02⎛⎫⎪⎝⎭．【整体点评】本题主要考查了椭圆的简单性质及方程思想，还考查了计算能力及转化思想、推理论证能力，属于难题.第二问的方法一最直接，但对运算能力要求严格；方法二曲线系的应用更多的体现了几何与代数结合的思想，二次曲线系的应用使得计算更为简单.11．【2020年新课标2卷理科】已知椭圆C 1：22221x y a b +=(a >b >0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD |=43|AB |.（1）求C 1的离心率；（2）设M 是C 1与C 2的公共点，若|MF |=5，求C 1与C 2的标准方程.【答案】（1）12；（2）221:13627x y C +=，22:12C y x =.【解析】【分析】（1）求出AB 、CD ，利用43CD AB =可得出关于a 、c 的齐次等式，可解得椭圆1C 的离心率的值；（2）[方法四]由（1）可得出1C 的方程为2222143x y c c+=，联立曲线1C 与2C 的方程，求出点M 的坐标，利用抛物线的定义结合5MF =可求得c 的值，进而可得出1C 与2C 的标准方程. 【详解】（1）(),0F c ，AB x ⊥轴且与椭圆1C 相交于A 、B 两点，则直线AB 的方程为x c =，联立22222221x cx y a b a b c =⎧⎪⎪+=⎨⎪=+⎪⎩，解得2x c b y a =⎧⎪⎨=±⎪⎩，则22b AB a =，抛物线2C 的方程为24y cx =，联立24x cy cx =⎧⎨=⎩，解得2x cy c =⎧⎨=±⎩，4CD c ∴=，43CD AB =，即2843b c a=，223b ac =，即222320c ac a +-=，即22320e e +-=，01e <<，解得12e =，因此，椭圆1C 的离心率为12；（2）[方法一]：椭圆的第二定义由椭圆的第二定义知20||=-MF e a x c，则有200||⎛⎫=-=- ⎪⎝⎭a MF e x a ex c ，所以0152-=a x ，即0210=-x a ．又由0||5=+=MF x c ，得052=-a x ．从而21052-=-aa ，解得6a=．所以3,6,6====c a b p ．故椭圆1C 与抛物线2C 的标准方程分别是2221,123627+==x y y x ．[方法二]：圆锥曲线统一的极坐标公式以(c,0)F 为极点，x 轴的正半轴为极轴，建立极坐标系．由（Ⅰ）知2a c =，又由圆锥曲线统一的极坐标公式2||1cos θ=-cMF ，得255cos θ=-c ，由132||11cos 2θ⨯=+c MF ，得3105cos θ=+c ，两式联立解得3c =．故1C 的标准方程为2213627x y+=，2C 的标准方程为212y x =．[方法三]：参数方程由（1）知2,a c b ==，椭圆1C 的方程为2222143x yc c+=，所以1C 的参数方程为{x =2c ⋅cosθ,y =√3c ⋅sinθ（θ为参数），将它代入抛物线22:4C y cx =的方程并化简得23cos 8cos 30θθ+-=，解得1cos 3θ=或cos 3θ=-（舍去），所以sin θ=M的坐标为23⎛ ⎝⎭c ．又||5MF =，所以由抛物线焦半径公式有5+=M x c ，即253+=cc ，解得3c =．故1C 的标准方程为2213627x y+=，2C 的标准方程为212y x =．[方法四]【最优解】：利用韦达定理由（1）知2a c =，b =，椭圆1C 的方程为2222143x yc c+=，联立222224143y cx x y c c ⎧=⎪⎨+=⎪⎩，消去y 并整理得22316120x cx c +-=，解得23x c =或6x c =-（舍去），由抛物线的定义可得25533cMF c c =+==，解得3c =. 因此，曲线1C 的标准方程为2213627x y+=，曲线2C 的标准方程为212y x =. 【整体点评】(2)方法一：椭圆的第二定义是联系准线与离心率的重要工具，涉及离心率的问题不妨考虑使用第二定义，很多时候会使得问题简单明了.方法二：圆锥曲线统一的极坐标公式充分体现了圆锥曲线的统一特征，同时它也是解决圆锥曲线问题的一个不错的思考方向.方法三：参数方程是一种重要的数学工具，它将圆锥曲线的问题转化为三角函数的问题，使得原来抽象的问题更加具体化.方法四：韦达定理是最常用的处理直线与圆锥曲线位置关系的方法，联立方程之后充分利用韦达定理可以达到设而不求的效果.12．【2020年新课标2卷文科】已知椭圆C 1：22221x y a b +=(a >b >0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合．过F 且与x 轴垂直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD |=43|AB |．（1）求C 1的离心率；（2）若C 1的四个顶点到C 2的准线距离之和为12，求C 1与C 2的标准方程．【答案】（1）12；（2）1C ：2211612x y +=，2C ： 28y x =. 【解析】【分析】（1）根据题意求出2C 的方程，结合椭圆和抛物线的对称性不妨设,A C 在第一象限，运用代入法求出,,,A B C D 点的纵坐标，根据4||||3CD AB =，结合椭圆离心率的公式进行求解即可；（2）由（1）可以得到椭圆的标准方程，确定椭圆的四个顶点坐标，再确定抛物线的准线方程，最后结合已知进行求解即可；【详解】解：（1）因为椭圆1C 的右焦点坐标为：(c,0)F ,所以抛物线2C 的方程为24y cx =，其中c 不妨设,A C 在第一象限，因为椭圆1C 的方程为：22221x ya b+=，所以当x c =时，有222221c y b y a b a +=⇒=±，因此,A B 的纵坐标分别为2b a ，2b a-；又因为抛物线2C 的方程为24y cx =，所以当x c =时，有242y c c y c =⋅⇒=±，所以,C D 的纵坐标分别为2c ，2c -，故22||bAB a=，||4CD c =.由4||||3CD AB =得2843b c a=，即2322()c c a a ⋅=-，解得2c a =-（舍去），12c a =.所以1C 的离心率为12.（2）由（1）知2a c =，b =，故22122:143x y C c c+=，所以1C 的四个顶点坐标分别为(2,0)c ，(2,0)c -，)，(0,)，2C 的准线为x c =-. 由已知得312c c c c +++=，即2c =.所以1C 的标准方程为2211612x y+=，2C 的标准方程为28y x =.【点睛】本题考查了求椭圆的离心率，考查了求椭圆和抛物线的标准方程，考查了椭圆的四个顶点的坐标以及抛物线的准线方程，考查了数学运算能力.13．【2020年新课标3卷理科】已知椭圆222:1(05)25x y C m m +=<<，A ，B 分别为C 的左、右顶点．（1）求C 的方程；（2）若点P 在C 上，点Q 在直线6x =上，且||||BP BQ =，BP BQ ⊥，求APQ 的面积．【答案】（1）221612525x y +=；（2）52. 【解析】【分析】（1）因为222:1(05)25x y C m m+=<<，可得5a =，b m =，根据离心率公式，结合已知，即可求得答案；（2）方法一：过点P 作x 轴垂线，垂足为M ，设6x =与x 轴交点为N ，可得 PMB BNQ ≅△△，可求得P 点坐标，从而求出直线AQ 的直线方程，根据点到直线距离公式和两点距离公式，即可求得APQ 的面积. 【详解】（1）222:1(05)25x y C m m +=<<∴5a =，b m =，根据离心率c e a ===，解得54m =或54m =-(舍)，∴C 的方程为：22214255x y ⎛⎫ ⎪⎝⎭+=，即221612525x y +=．（2）［方法一］：通性通法不妨设P ,Q 在x 轴上方，过点P 作x 轴垂线，垂足为M ，设直线6x =与x 轴交点为N 根据题意画出图形，如图||||BP BQ =，BP BQ ⊥， 90PMB QNB ∠=∠=︒，又90PBM QBN ∠+∠=︒， 90BQN QBN ∠+∠=︒，∴PBM BQN ∠=∠，根据三角形全等条件“AAS ”，可得：PMB BNQ ≅△△，221612525x y +=，∴(5,0)B ，∴651PM BN ==-=，设P 点为(,)P P x y ，可得P 点纵坐标为1P y =，将其代入221612525x y +=，可得：21612525P x +=，解得：3P x =或3P x =-，∴P 点为(3,1)或(3,1)-，①当P 点为(3,1)时，故532MB =-=，PMB BNQ ≅△△，∴||||2MB NQ ==，可得：Q 点为(6,2)，画出图象，如图(5,0)A -, (6,2)Q ，可求得直线AQ 的直线方程为：211100x y -+=，根据点到直线距离公式可得P 到直线AQ 的距离为d ===，根据两点间距离公式可得：AQ ==，∴APQ 面积为：1522⨯=； ②当P 点为(3,1)-时，故5+38MB ==，PMB BNQ ≅△△，∴||||8MB NQ ==，可得：Q 点为(6,8)，画出图象，如图(5,0)A -, (6,8)Q ，可求得直线AQ 的直线方程为：811400x y -+=，根据点到直线距离公式可得P 到直线AQ 的距离为d ==根据两点间距离公式可得：AQ =∴APQ 面积为： 1522=，综上所述，APQ 面积为：52. ［方法二］【最优解】：由对称性，不妨设P ，Q 在x 轴上方，过P 作PE x ⊥轴，垂足为E ．设(6,0)D ，由题知，PEB BDQ ≌．故131p BP PE PEPE x QB BD ==⇒=⇒=±， ①因为(3,1),(5,0),(6,2)P A Q -，如图，所以，52APQAQDPEDQ PEAS SS S=--=．②因为(3,1),(5,0),(6,8)P A Q --，如图，所以52APQAQDPEDQ PEASSS S=--=．综上有52APQ S =△ ［方法三］：由已知可得()5,0B ，直线,BP BQ 的斜率一定存在，设直线BP 的方程为()5y k x =-，由对称性可设0k <，联立方程22(5),161,2525y k x x y =-⎧⎪⎨+=⎪⎩消去y 得()22221161601625250k x k x k +-+⨯-=，由韦达定理得221625255116P k x k ⨯-=+，所以22805116P k x k -=+，将其代入直线BP 的方程得210116P ky k -=+，所以22280510,116116k k P k k ⎛⎫-- ⎪++⎝⎭，则||BP = 因为BP BQ ⊥，则直线BQ 的方程为1(5)y x k=--，则16,,||Q BQ k ⎛⎫-== ⎪⎝⎭ 因为||||BP BQ ==422566810k k -+=，即()()22641410k k --=，故2164k =或214k =，即18k =-或12k =-．当18k =-时，点P ，Q的坐标分别为(3,1),(6,8),||P Q PQ -=直线PQ 的方程为71093y x =+，点A 到直线PQ故APQ 的面积为1522=．当12k =-时，点P ，Q 的坐标分别为(3,1),(6,2),||P Q PQ =直线PQ 的方程为13y x =，点(5,0)A -到直线PQ故APQ 的面积为1522．综上所述，APQ 的面积为52．［方法四］：由（1）知椭圆的方程为221612525x y +=，(5,0),(5,0)A B -．不妨设()00,P x y 在x 轴上方，如图．设直线:(5)(0)AP y k x k =+>．因为||||,BP BQ BP BQ =⊥，所以00||1,||5Q y BN y BM x ====-．由点P 在椭圆上得201612525x +=，所以209x =．由点P 在直线AP 上得()015k x =+，所以015k x k -=．所以2159k k -⎛⎫= ⎪⎝⎭，化简得216101k k =-．所以0110155516k x k k k -⎛⎫-=--== ⎪⎝⎭，即(6,16)Q k ．所以，点Q 到直线AP 的距离d ==又)0||5AP x ==+=．故115222APQSAP d =⋅==．即APQ 的面积为52．［方法五］：由对称性，不妨设P ，Q 在x 轴上方，过P 作PC x ⊥轴，垂足为C ，设(6,0)D ，由题知PCB BDQ ≌，所以131p BP PC PCPC x QB BD ==⇒=⇒=±．（1）(3,1),(5,0),(6,2)P A Q -．则221221115(||||)(||||)|82111|222APQSAP AQ AP AQ x y x y =⋅-⋅=-=⨯-⨯=．（其中()()1122,,,AP x y AQ x y ==）．（2）(3,1),(5,0),(6,8)P A Q --．同理，221221115(||||)()|28111|222APQSAP AQ AP AQ x y x y =-⋅=-=⨯-⨯=．（其中()()1122,,,AP x y AQ x y ==）综上，APQ 的面积为52．【整体点评】（2）方法一：根据平面几何知识可求得点P 的坐标，从而得出点Q 的坐标以及直线AQ 的方程，再根据距离公式即可求出三角形的面积，是通性通法；方法二：同方法一，最后通过面积分割法求APQ 的面积，计算上有简化，是本题的最优解；方法三：通过设直线BP 的方程()5y k x =-与椭圆的方程联立，求出点P 的坐标，再根据题目等量关系求出k 的值，从而得出点Q 的坐标以及直线AQ 的方程，最后根据距离公式即可求出三角形的面积，思想简单，但运算较繁琐；方法四：与法三相似，设直线AP 的方程:(5)(0)AP y k x k =+>，通过平面知识求出点P 的坐标，表示出点Q ，再根据距离公式即可求出三角形的面积；方法五：同法一，只是在三角形面积公式的选择上，利用三角形面积的正弦形式结合平面向量的数量积算出．14．【2020年新高考1卷（山东卷）】已知椭圆C ：22221(0)x y a b a b +=>>过点()2,1A ．（1）求C 的方程：（2）点M ，N 在C 上，且AM AN ⊥，AD MN ⊥，D 为垂足．证明：存在定点Q ，使得DQ 为定值．【答案】（1）22163x y +=；（2）详见解析.【解析】【分析】（1）由题意得到关于,,a b c 的方程组，求解方程组即可确定椭圆方程.（2）方法一：设出点M ，N 的坐标，在斜率存在时设方程为y kx m =+, 联立直线方程与椭。

立体几何中线段与面积等求解问题

立体几何中线段与面积等求解问题【典例1】【2021·湖南衡阳市·高三一模】如图，直四棱柱1111ABCD A BC D -，底面ABCD 是边长为2的菱形，12AA =，23ADC ∠=π，点E 在平面11AC D 上，且BE ⊥平面11AC D .（1）求BE 的长；（2）若F 为1A A 的中点，求BE 与平面1FC B 所成角的正弦值.【思路引导】（1）建立空间直角坐标系，利用点到平面的距离的向量公式求解；（2）利用向量法求线面角的正弦即可.【典例2】【湖南省衡阳市高三第一次模拟考试】如图所示，在四棱锥P ABCD -中，90ABC ACD ∠=∠=，60BAC CAD ∠=∠=，PA ⊥平面ABCD ，2PA =，1AB =，设M 、N 分别为PD 、AD 的中点.（1）求证：平面//CMN 平面PAB ；（2）求三棱锥A CMN -的侧面积.【思路引导】（1）要证明面面平行，需根据判断定理证明平面内的两条相交直线与另一个平面平行，根据平行关系，证明//MN 平面PAB ，//CN 平面PAB ；（2）根据边长和三角形面积公式，分别求三棱锥A CMN -的三个侧面的面积.【典例3】【2021·甘肃高三高三年级第二次模拟考试】如图，在直四棱柱1111ABCD A BC D -中，底面ABCD 是边长为2的菱形，且13AA =，E 、F 分别为1CC 、1BD 的中点．（1）证明：EF ⊥平面11BB D D ；（2）若60DAB ∠=，求点1D 到BED 的距离．【思路引导】（1）连接AC 交BD 于O 点，连接OF ，证明四边形OCEF 为平行四边形，可得出//EF OC ，再证明出OC ⊥平面11BB D D ，由此可得出EF ⊥平面11BB D D ；（2）计算出三棱锥1B DD E -的体积，并计算出BDE 的面积，利用等体积法可计算出点1D 到BED 的距离.【针对训练】1. 【2021上海虹口区·高三三模】如图，在直四棱柱1111ABCD A BC D -中，底面ABCD 为菱形，4,2,AC BD ==且侧棱1 3.AA = 其中1O 为11AC 的11B D 交点.（1）求点1B 到平面1D AC 的距离；（2）在线段1BO 上，是否存在一个点P ，使得直线AP 与1CD 垂直？若存在，求出线段BP 的长；若不存在，请说明理由.【思路引导】（1）由于菱形的对角线互相垂直平分，故以AC 与BD 的交点O 为原点，以射线OA 、OB 、1OO分别为x y z 、、轴，建立空间直角坐标系.由向量法求点到平面的距离．（2）1,BPBO λ由向量的数量积为0求得λ，从而求得线段长．2．【2021·云南高三二模质量调研】如图，在三棱柱111ABC A B C -中，四边形11B BCC 是菱形，160B BC ∠=，AB BC ⊥，1AB BB ⊥，D 为棱BC 的中点.（1）求证：平面1AB D ⊥平面ABC ；（2）若2AB BC ==，求点C 到平面1AB D 的距离.【思路引导】（1）设2BC a =，利用余弦定理结合勾股定理可证得1B D BC ⊥，证明AB ⊥平面11BB C C ，可得出1B D AB ⊥，再利用线面垂直和面面垂直的判定定理可证得结论成立；（2）分析得出三棱锥1B ACD -的高为1B D ，计算出ACD △、1A BD 的面积，利用等体积法可求得点C 到平面1AB D 的距离.3．【天津市蓟州等部分区2019届高三上学期期末联考】如图，三棱柱111ABC A B C -,1A A ⊥平面ABC ,BC AC ⊥,1BC AC ==,D 为AC 的中点．（1）求证：1AB ∥平面1BDC ；（2）若12AA =，求二面角1C BD C --的余弦值；（3）若点P 在线段1AB 上，且⊥CP 平面1BDC ,确定点P 的位置并求线段1AA 的长．【思路引导】（1）连接1B C ，交1BC 于点O ，点O 为1B C 的中点，D 为AC 的中点，求得OD ∥1AB ，利用线面平行的判定定理，即可得到1AB ∥平面1BDC .（2）以C 为原点，分别以1,,CA CB CC 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，求得平面1C BD H 和平面BDC 的法向量，利用向量的夹角公式，即可求解.（3）设11=,AA a AP AB λ=，根据CP ⊥平面1BDC ，列出方程组，即可求解.4．【2021·吉林吉林市·高三三模】如图，已知图1中△ABC 是等腰三角形，AC ＝BC ，D ，E 分别是AC ，BC 的中点，沿着DE 把△CDE 折起到△C ′DE ，使得平面C ′DE ⊥平面BADE ，图2中AD ＝2，AB ＝4，F 为BC ′的中点，连接EF ．（1）求证：EF //平面AC ′D ；（2）求四棱锥C ′﹣ABED 的侧面积．【思路引导】（1）由三角形中位线，证得四边形DEFG 是平行四边形，进而得到DG ∥EF ，结合线面平行判定定理，即可证得EF //平面AC ′D ；（2）分别取DE 、AB 的中点H 、Ⅰ，连接C ′H ，H Ⅰ，C ′Ⅰ，证得C ′H ⊥DE ，得到C ′H ⊥平面BADE ，得出C ′H ⊥H Ⅰ，根据图形的翻折，以及面积公式，即可求解.5．【2019年全国统一高考数学试卷（文科)（新课标Ⅲ)】图1是由矩形,ADEB Rt ABC ∆和菱形BFGC 组成的一个平面图形，其中1,2AB BE BF ===， 60FBC ∠=，将其沿,AB BC 折起使得BE 与BF 重合，连结DG ，如图2.（1）证明图2中的,,,A C G D 四点共面，且平面ABC ⊥平面BCGE ；（2）求图2中的四边形ACGD 的面积.【思路引导】(1)因为折纸和粘合不改变矩形ABED ，Rt ABC 和菱形BFGC 内部的夹角，所以//AD BE ，//BF CG 依然成立，又因E 和F 粘在一起，所以得证.因为AB 是平面BCGE 垂线，所以易证.(2) 欲求四边形ACGD 的面积，需求出CG 所对应的高，然后乘以CG 即可．参考答案【典例1】【2021·湖南衡阳市·高三一模】如图，直四棱柱1111ABCD A BC D -，底面ABCD 是边长为2的菱形，12AA =，23ADC ∠=π，点E 在平面11AC D 上，且BE ⊥平面11AC D .（1）求BE 的长；（2）若F 为1A A 的中点，求BE 与平面1FC B 所成角的正弦值. 【思路引导】（1）建立空间直角坐标系，利用点到平面的距离的向量公式求解；（2）利用向量法求线面角的正弦即可.【解析】如图建立空间直角坐标系，则1(0,0,0),(3,1,0),(0,2,0),(3,1,0)(3,1,2)D B C A A --,1(0,2,2)C 1(0,0,2),(3,1,1)D F -. （1）设平面11D AC 的法向量为(),,m x y z =，1(0,2,2)DC →=, 1(3,1,2)DA →=-,则1122003200y z m DA x y z m DC ⎧+=⎧⋅=⎪⎪⇒⎨⎨-+=⋅=⎪⎪⎩⎩，取1y =，1z =-，3x =∴m 可为)3,1,1-455m BD BE m ⋅===. （2）由（1）知平面11D AC 的法向量为()3,1,1m =-，且m BE ∥，设平面1FC B 的法向量为(),,n x y z =, 1(3,3,1),(0,2,1)FC FB →→=-=-，112003300y z n FC x y z n FC ⎧-=⎧⋅=⎪⎪∴⇒⎨⎨-++=⋅=⎪⎪⎩⎩，取1y =，2z =，53x =， ∴53(,1,2)3n →=， 6sin cos ,52003m n θ∴=<>==. 【典例2】【湖南省衡阳市高三第一次模拟考试】如图所示，在四棱锥P ABCD -中，90ABC ACD ∠=∠=，60BAC CAD ∠=∠=，PA ⊥平面ABCD ，2PA =，1AB =，设M 、N 分别为PD 、AD 的中点.（1）求证：平面//CMN 平面PAB ；（2）求三棱锥A CMN -的侧面积.【思路引导】（1）要证明面面平行，需根据判断定理证明平面内的两条相交直线与另一个平面平行，根据平行关系，证明//MN 平面PAB ，//CN 平面PAB ；（2）根据边长和三角形面积公式，分别求三棱锥A CMN -的三个侧面的面积.【解析】（1）∵M 、N 分别为PD 、AD 的中点，∴//MN PA ，又MN ⊄平面PAB ，PA ⊂平面PAB ，∴//MN 平面PAB ，在Rt ACD ∆中，60CAD ∠=，CN AN =，∴60ACN ∠=，又60BAC ∠=，∴//CN AB ，∵CN ⊄平面PAB ，AB平面PAB ，∴//CN 平面PAB ，又CN MN N =，∴平面//CMN 平面PAB ，（2）∵PA ⊥平面ABCD ，AN ⊂平面ABCD ，CN ⊂平面ABCD ，由（1）可知//MN PA ，∴MN AN ⊥、MN CN ⊥，∵90ABC ACD ∠=∠=，60BAC CAD ∠=∠=，2PA =，1AB =，∴22AC AB ==，24AD AC ==，112MN PA ==，由（1）可知122CN AN AD ===，在Rt CMN 中，AM CM ==∴11sin 602222ACN SAN CN =⋅⋅=⨯⨯= 又1121122AMNS AN MN =⋅=⨯⨯=，在ACM △中，AM CM =，∴AC 边上的高2h ===， ∴1122222ACM S AC h =⋅=⨯⨯=，∴三棱锥A CMN -的侧面积3ACN AMN ACM S S S S =++=【典例3】【2021·甘肃高三高三年级第二次模拟考试】如图，在直四棱柱1111ABCD A BC D -中，底面ABCD 是边长为2的菱形，且13AA =，E 、F 分别为1CC 、1BD 的中点．（1）证明：EF ⊥平面11BB D D ；（2）若60DAB ∠=，求点1D 到BED 的距离．【思路引导】（1）连接AC 交BD 于O 点，连接OF ，证明四边形OCEF 为平行四边形，可得出//EF OC ，再证明出OC ⊥平面11BB D D ，由此可得出EF ⊥平面11BB D D ；（2）计算出三棱锥1B DD E -的体积，并计算出BDE 的面积，利用等体积法可计算出点1D 到BED 的距离.【解析】（1）证明：连接AC 交BD 于O 点，连接OF ，因为四边形ABCD 为菱形，且AC BD O =，O ∴为BD 的中点，因为F 为1BD 的中点，所以，1//OF DD 且112OF DD =，在直四棱柱1111ABCD A BC D -中，11//CC DD 且11CC DD=， E 为1CC 的中点，则1//CE DD 且112CE DD =，//OF CE ∴且OF CE =，所以，四边形OCEF 为平行四边形，所以，//EF OC ，（2）解：若60DAB ∠=，则ABD △和CBD 为等边三角形，2BD BC CD ===，1CC ⊥平面ABCD ，BC ⊂平面ABCD ，1CC BC ∴⊥，113CC AA ==，则32CE =，由勾股定理可得2252BE BC CE =+=，同理52DE =，连接OE ，则OE BD ⊥，所以，22212OE BE OB =-=，所以，12122BDE S BD OE =⋅=△，而11132BDD S BD DD =⋅=△ 设点1D 到面BED 的距离为h ，则由（1）知3EF CO ==及11E D DB D EDB V V --=得112133332h ⨯⨯=⨯⋅，解得677h =，所以点1D 到面BED 的距离677．【针对训练】1. 【2021上海虹口区·高三三模】如图，在直四棱柱1111ABCD A BC D -中，底面ABCD 为菱形，4,2,AC BD ==且侧棱1 3.AA = 其中1O 为11AC 的11B D 交点.（1）求点1B 到平面1D AC 的距离；（2）在线段1BO 上，是否存在一个点P ，使得直线AP 与1CD 垂直？若存在，求出线段BP 的长；若不存在，请说明理由.【思路引导】（1）由于菱形的对角线互相垂直平分，故以AC 与BD 的交点O 为原点，以射线OA 、OB 、1OO 分别为x y z 、、轴，建立空间直角坐标系.由向量法求点到平面的距离．（2）1,BP BO λ由向量的数量积为0求得λ，从而求得线段长．【解析】(1) 由于菱形的对角线互相垂直平分，故以AC 与BD 的交点O 为原点，以射线OA 、OB 、1OO 分别为x y z 、、轴，建立空间直角坐标系.由已知条件，相关点的坐标为(2,0,0),(0,1,0)A B ，111(2,0,0),(0,0,3),(0,1,3),(0,1,3).C O B D设平面1D AC 的法向量为(,,),n x y z =由(4,0,0),AC =-1(2,1,3),AD =--得10,403.230x n AC x y z n AD x y z ⎧=⎧⋅=-=⇒⎨⎨=⋅=--+=⎩⎩令1z =，则(0,3,1)n =. 因11(0,2,0),D B 故点1B 到平面1D AC 的距离为 11(0,2,0)(0,3,1)310(0,3,1)5D B nd n；(2) 设1,BP BO λ 则由(2,1,0),AB =-1(0,1,3),BO =-得 (2,1,3).AP AB BP λλ 又1(2,1,3),CD =-故当1AP CD ⊥时，11(2,1,3)(2,1,3)1050.2AP CD λλλλ⋅=--⋅-=-=⇒=于是，在线段1BO 上存在点P ，使得1;AP CD ⊥此时11102BP BO ==2．【2021·云南高三二模质量调研】如图，在三棱柱111ABC A B C -中，四边形11B BCC 是菱形，160B BC ∠=，AB BC ⊥，1AB BB ⊥，D 为棱BC 的中点.（1）求证：平面1AB D ⊥平面ABC ；（2）若2AB BC ==，求点C 到平面1AB D 的距离.【思路引导】（1）设2BC a =，利用余弦定理结合勾股定理可证得1B D BC ⊥，证明AB ⊥平面11BB C C ，可得出1B D AB ⊥，再利用线面垂直和面面垂直的判定定理可证得结论成立；（2）分析得出三棱锥1B ACD -的高为1B D ，计算出ACD △、1A BD 的面积，利用等体积法可求得点C 到平面1AB D 的距离.【解析】（1）证明：设2BC a =.四边形11B BCC 是菱形，D 为棱BC 的中点，12BC BB a ∴==，12BD BC a ==. 在1BB D △中，1160B BD B BC ∠=∠=，由余弦定理得22211112cos B D BD BB BD BB B BD =+-⋅∠，解得13B D a =. 22211BD B D BB ∴+=，190BDB ∴∠=，即1B D BC ⊥.AB BC ⊥，1AB BB ⊥，且1BC BB B =，AB ∴⊥平面1BDB .1B D ⊂平面1BDB ，1AB B D ∴⊥.1AB B D ⊥，1B D BC ⊥，且AB BC B ⋂=，1B D ∴⊥平面ABC .1B D ⊂平面1AB D ，∴平面1AB D ⊥平面ABC ；（2）由2AB BC ==和（1）知13B D =，1B D ⊥平面ABC ，1B D ∴是点1B 到平面ABC 的距离.AD ⊂平面ABC ，1B D AD ∴⊥，则1AB D △是以1AB 为斜边的直角三角形，AB BC ⊥，2AB BC ==，点D 为棱BC 的中点，225AD BD AB ∴=+=，ACD △的面积12ACD CD AB S ⨯==△，1AB D △的面积111522AB D AD DB S ⨯==△. 设点C 到平面1AB D 的距离为h ，则11C AB D B ACD V V --=.111133AB D ACD S h S B D ∴⨯⨯=⨯⨯△△，解得25h =. ∴点C 到平面1AB D 的距离为25. 3．【天津市蓟州等部分区2019届高三上学期期末联考】如图，三棱柱111ABC A B C -,1A A ⊥平面ABC ,BC AC ⊥,1BC AC ==,D 为AC 的中点．（1）求证：1AB ∥平面1BDC ；（2）若12AA =，求二面角1C BD C --的余弦值；（3）若点P 在线段1AB 上，且⊥CP 平面1BDC ,确定点P 的位置并求线段1AA 的长．【思路引导】（1）连接1B C ，交1BC 于点O ，点O 为1B C 的中点，D 为AC 的中点，求得OD ∥1AB ，利用线面平行的判定定理，即可得到1AB ∥平面1BDC .（2）以C 为原点，分别以1,,CA CB CC 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，求得平面1C BD H 和平面BDC 的法向量，利用向量的夹角公式，即可求解.（3）设11=,AA a AP AB λ=，根据CP ⊥平面1BDC ，列出方程组，即可求解. 【详解】（1）连接1B C ，交1BC 于点O ，则点O 为1B C 的中点，因为D 为AC 的中点，所以OD ∥1AB .又1AB ⊄平面1BDC ，OD ⊂平面1BDC ，所以1AB ∥平面1BDC .（2）因为1AA ⊥平面ABC ，1AA ∥1CC ，所以1CC ⊥平面ABC ，又BC AC ⊥故以C 为原点，分别以1,,CA CB CC 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，则()()110,0,2,0,1,0,,0,02C B D ⎛⎫ ⎪⎝⎭，所以111(,0,2),(0,1,2)2C D C B =-=-设平面1C BD 的法向量为(,,)n x y z =，则有1100n C D n C B ⎧⋅=⎪⎨⋅=⎪⎩ 即120220z x z y ⎧-+=⎪⎨⎪-+=⎩ 令1z =，则得()4,2,1n =.又平面BDC 的法向量为()1=0,0,2CC ，且二面角1C BD C --为锐角，故二面角1C BD C --的余弦值为111||21|cos,|21||421CC n CC n CC n ⋅〈〉===⋅⨯ （3）设11=,,AA a AP AB λ=因为()()1100,01,A B a ，，，，所以(),,AP a λλλ=-， ()1,,CP CA AP a λλλ=+=-.又1C D (),0,=-,(),1,0BD =-,平面1BDC ，所以()()2111021102CP C D a CP BD λλλλ⎧⋅=-+-=⎪⎪⎨⎪⋅=--=⎪⎩解得11,3a λ== 所以11AA =，且点P 在线段1AB 的三等分点处，即1AP AB =4．【2021·吉林吉林市·高三三模】如图，已知图1中△ABC 是等腰三角形，AC ＝BC ，D ，E 分别是AC ，BC 的中点，沿着DE 把△CDE 折起到△C ′DE ，使得平面C ′DE ⊥平面BADE ，图2中AD ＝2，AB ＝4，F 为BC ′的中点，连接EF ．（1）求证：EF //平面AC ′D ；（2）求四棱锥C ′﹣ABED 的侧面积．【思路引导】（1）由三角形中位线，证得四边形DEFG 是平行四边形，进而得到DG ∥EF ，结合线面平行判定定理，即可证得EF //平面AC ′D ；（2）分别取DE 、AB 的中点H 、Ⅰ，连接C ′H ，H Ⅰ，C ′Ⅰ，证得C ′H ⊥DE ，得到C ′H ⊥平面BADE ，得出C ′H ⊥H Ⅰ，根据图形的翻折，以及面积公式，即可求解.【解析】（1）取AC ′中点G ，连接DG ，FG ，由点F 、G 分别是BC ′，AC ′的中点，可得GF ∥AB ，GF 12=AB ，又由DE ∥AB ，DE 12=AB ，所以四边形DEFG 是平行四边形，所以DG ∥EF ，且EF ⊄平面AC ′D ，DG ⊂平面AC ′D ，所以EF ∥平面AC ′D ；（2）因为△ABC 是等腰三角形，AC ＝BC ，AD ＝2，AB ＝4，所以∠ACB ＝90°，所以△ABC 是等腰直角三角形，且AC ＝BC 22=．分别取DE 、AB 的中点H 、Ⅰ，连接C ′H ，H Ⅰ，C ′Ⅰ，从而有C ′H ⊥DE ．又因为平面C ′DE ⊥平面BADE ，平面C ′DE ∩平面BADE ＝DE ，所以C ′H ⊥平面BADE ，又H Ⅰ⊂平面BADE ，所以C ′H ⊥H Ⅰ，在△C ′H Ⅰ中，C ′H ＝H Ⅰ＝1，所以2C I '=，又翻折后，C ′A ＝C ′B ，在△C ′ⅠA 中，6C A '=，所以四棱锥C ′﹣ABED 的侧面积为：221161212(2)()64213222222S =⨯⨯+⨯⨯-⨯+⨯⨯=++.5．【2019年全国统一高考数学试卷（文科)（新课标Ⅲ)】图1是由矩形,ADEB Rt ABC ∆和菱形BFGC 组成的一个平面图形，其中1,2AB BE BF ===， 60FBC ∠=，将其沿,AB BC 折起使得BE 与BF 重合，连结DG ，如图2.（1）证明图2中的,,,A C G D 四点共面，且平面ABC ⊥平面BCGE ；（2）求图2中的四边形ACGD 的面积.【思路引导】(1)因为折纸和粘合不改变矩形ABED ，Rt ABC 和菱形BFGC 内部的夹角，所以//AD BE ，//BF CG 依然成立，又因E 和F 粘在一起，所以得证.因为AB 是平面BCGE 垂线，所以易证.(2) 欲求四边形ACGD 的面积，需求出CG 所对应的高，然后乘以CG 即可．【详解】(1)证：//AD BE ，//BF CG ，又因为E 和F 粘在一起.∴//AD CG ，A ，C ，G ，D 四点共面.又,AB BE AB BC ⊥⊥.AB ∴⊥平面BCGE ，AB ⊂平面ABC ，∴平面ABC ⊥平面BCGE ，得证.(2)取CG 的中点M ，连结,EM DM .因为//AB DE ，AB ⊥平面BCGE ，所以DE ⊥平面BCGE ，故DE CG ⊥，由已知，四边形BCGE 是菱形，且60EBC ∠=得EM CG ⊥，故CG ⊥平面DEM ．因此DM CG ⊥．在Rt DEM △中，DE=1，3EM =，故2DM =．所以四边形ACGD 的面积为4.。

高中数学第八章立体几何初步知识总结例题(带答案)

高中数学第八章立体几何初步知识总结例题单选题1、如图，点N为正方形ABCD的中心，ΔECD为正三角形，平面ECD⊥平面ABCD,M是线段ED的中点，则A．BM=EN，且直线BM,EN是相交直线B．BM≠EN，且直线BM,EN是相交直线C．BM=EN，且直线BM,EN是异面直线D．BM≠EN，且直线BM,EN是异面直线答案：B解析：利用垂直关系，再结合勾股定理进而解决问题．如图所示，作EO⊥CD于O，连接ON，过M作MF⊥OD于F．连BF，∵平面平面ABCD．EO⊥CD,EO⊂平面CDE，∴EO⊥平面ABCD，MF⊥平面ABCD，∴ΔMFB与ΔEON均为直角三角形．设正方形边长为2，易知EO=√3,ON =EN=2，MF=√32,BF=52,∴BM=√7．∴BM≠EN，故选B．CDE小提示：本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形．2、如图直角△O′A′B′是一个平面图形的直观图，斜边O′B′=4，则原平面图形的面积是（）A．8√2B．4√2C．4D．√2答案：A解析：根据斜二测画法规则可求原平面图形三角形的两条直角边长度，利用三角形的面积公式即可求解. 由题意可知△O′A′B′为等腰直角三角形，O′B′=4，则OʹAʹ=2√2，所以原图形中，OB=4，OA=4√2，故原平面图形的面积为1×4×4√2=8√2.2故选：A3、如图，用斜二测画法作水平放置的正三角形A1B1C1的直观图，则正确的图形是（）A．B．C．D．分析：由斜二侧画法的规则分析判断即可先作出一个正三角形A1B1C1，然后以B1C1所在直线为x轴，以B1C1边上的高所在的直线为y轴建立平面直角坐标系，画对应的x′,y′轴，使夹角为45°，画直观图时与x轴平行的直线的线段长度保持不变，与y轴平行的线段长度变为原来的一半，得到的图形如图，然后去掉辅助线即可得到正三角形的直观图如图，故选：A4、下列空间图形画法错误的是（）A．B．C．D．分析：根据空间图形画法：看得见的线画实线，看不见的线画虚线.即可判断出答案.D选项：遮挡部分应画成虚线．故选:D.5、如图，已知正方体的棱长为a，沿图1中对角面将它分割成两个部分，拼成如图2的四棱柱，则该四棱柱的全面积为（）A．(8+2√2)a2B．(2+4√2)a2C．(4+2√2)a2D．(6−4√2)a2答案：C分析：拼成的几何体比原正方体的表面增加了两个截面，减少了原来两个正方形面，据此变化，进行求解. 由题意，拼成的几何体比原正方体的表面增加了两个截面，减少了原来两个正方形面，由于截面为矩形，长为√2a，宽为a，所以面积为√2a2，所以拼成的几何体的表面积为4a2+2√2a2=(4+2√2)a2.故选：C.6、已知三棱锥A−BCD的所有顶点都在球O的球面上，且AB⊥平面BCD，AB=2√3，AC=AD=4，CD= 2√2，则球O的表面积为（）A．20πB．18πC．36πD．24π答案：A分析：根据AB⊥平面BCD，得到AB⊥BC，AB⊥BD，再由AB=2√3，AC=AD=4，CD=2√2，得到BC⊥BD，则三棱锥A−BCD截取于一个长方体，然后由长方体的外接球即为三棱锥的外接球求解.因为AB⊥平面BCD，所以AB⊥BC，AB⊥BD，∴BC=BD=√42−(2√3)2=2，在△BCD中，CD=2√2，∴CD2=BC2+BD2，∴BC⊥BD.如图所示：三棱锥A−BCD的外接球即为长方体AGFH-BCED的外接球，设球O的半径为R，则2R=√BA2+BC2+BD2=√(2√3)2+22+22=2√5，解得R=√5，所以球O的表面积为20π，故选：A.7、下列条件中，能得出直线m与平面α平行的是（）A．直线m与平面α内的所有直线平行B．直线m与平面α内的无数条直线平行C．直线m与平面α没有公共点D．直线m与平面α内的一条直线平行答案：C分析：根据线面平行的判定，线面平行的性质逐个辨析即可.对A ，直线m 与平面α内的所有直线平行不可能，故A 错误；对B ，当直线m 在平面α内时，满足直线m 与平面α内的无数条直线平行，但m 与α不平行；对C ，能推出m 与α平行；对D ，当直线m 在平面α内时，m 与α不平行.故选：C.8、如图是长方体被一平面所截得到的几何体，四边形EFGH 为截面，长方形ABCD 为底面，则四边形EFGH 的形状为（）A ．梯形B ．平行四边形C ．可能是梯形也可能是平行四边形D ．矩形答案：B解析：利用面面平行的性质判断EF 与的平行、EH 与FG 平行.因为平面ABFE //平面CGHD ,且平面EFGH ∩平面ABFE =EF ,平面EFGH ∩平面CGHD =GH ,根据面面平行的性质可知EF //,同理可证明EH //FG .所以四边形EFGH 为平行四边形.故选：B.小提示：本题考查长方体截面形状判断，考查面面平行的性质应用，较简单.多选题9、（多选）一个几何体有6个顶点，则这个几何体可能是（）A ．三棱柱B ．三棱台C ．五棱锥D ．四面体答案：ABCGH GH分析：根据棱柱、棱台、棱锥及四面体的图形分析，即可得答案.对于A ，三棱柱是上下两个三角形，有6个顶点，满足题意；对于B ，三棱台是上下两个三角形，有6个顶点，满足题意；对于C ，五棱锥是底面为五边形及一个顶点，有6个顶点，满足题意；对于D ，四面体的顶点个数为4个，不满足题意.故选：ABC.10、我国古代数学名著《九章算术》中将正四棱锥称为方锥．已知半球内有一个方锥，方锥的底面内接于半球的底面，方锥的顶点在半球的球面上，若方锥的体积为18，则半球的说法正确的是（）A ．半径是3B ．体积为18πC ．表面积为27πD ．表面积为18π答案：ABC分析：作出正四棱锥的对角面，为半球的半个大圆的内接三角形，由图形可用球的半径表示出棱锥底面边长，高，由棱锥体积求得半球半径．然后计算半球体积，表面积，判断各选项．如图，是正四棱锥的对角面，设球半径为r ，AC 是半圆的直径，则正四棱锥底面边长为√2r ，棱锥体积为V =13×(√2r)2×r =23r 3=18，r =3，半球体积为V =23πr 3=23π×33=18π，表面积为S =2π×32+π×32=27π，故选：ABC ．11、如图，正方体ABCD −A 1B 1C 1D 1的棱长为1，则下列四个命题正确的是（）PAC △PAC△A．两条异面直线D1C和BC1所成的角为π4B．直线BC与平面ABC1D1所成的角等于π4C．点D到面ACD1的距离为√33D．三棱柱AA1D1−BB1C1外接球半径为√32答案：BCD分析：对于A：根据异面直线的求法易得：异面直线D1C和BC1所成的角为∠AD1C；对于B：可证B1C⊥平面ABC1D1，则直线BC与平面ABC1D1所成的角为∠CBC1；对于C：根据等体积转换V D−ACD1=V D1−ACD，求点D到面ACD1的距离；对于D：三棱柱AA1D1−BB1C1的外接球即为正方体ABCD−A1B1C1D1的外接球，直接求正方体外接球的半径即可．连接AC、AD1∵AB∥C1D1且AB=C1D1，则四边形ABC1D1为平行四边形，∴异面直线D1C和BC1所成的角为∠AD1C∵AC=AD1=D1C，则△ACD1为正三角形，即∠AD1C=π3A不正确；连接B1C在正方形BB1C1C中，BC1⊥B1C∵AB⊥平面BB1C1C，B1C⊂平面BB1C1C∴AB⊥B1CAB∩BC1=B，则B1C⊥平面ABC1D1∴直线BC与平面ABC1D1所成的角为∠CBC1=π4 B正确；根据等体积转换可知：V D−ACD1=V D1−ACD即13×ℎ×12×√2×√2×√32=13×1×12×1×1，则ℎ=√33C正确；三棱柱AA1D1−BB1C1的外接球即为正方体ABCD−A1B1C1D1的外接球则外接球的半径即为正方体ABCD−A1B1C1D1体对角线的一半，即R=√32D正确；故选：BCD．12、如图，四边形ABCD为正方形，ED⊥平面ABCD，FB∥ED,AB=ED=2FB，记三棱锥E−ACD，F−ABC，F−ACE的体积分别为V1,V2,V3，则（）A．V3=2V2B．V3=V1C．V3=V1+V2D．2V3=3V1答案：CD分析：直接由体积公式计算V1,V2，连接BD交AC于点M，连接EM,FM，由V3=V A−EFM+V C−EFM计算出V3，依次判断选项即可.设AB=ED=2FB=2a，因为ED⊥平面ABCD，FB∥ED，则V1=13⋅ED⋅S△ACD=13⋅2a⋅12⋅(2a)2=43a3，V2=13⋅FB⋅S△ABC=13⋅a⋅12⋅(2a)2=23a3，连接BD交AC于点M，连接EM,FM，易得BD⊥AC，又ED⊥平面ABCD，AC⊂平面ABCD，则ED⊥AC，又ED∩BD=D，ED,BD⊂平面BDEF，则AC⊥平面BDEF，又BM=DM=12BD=√2a，过F作FG⊥DE于G，易得四边形BDGF为矩形，则FG=BD=2√2a,EG=a，则EM=√(2a)2+(√2a)2=√6a,FM=√a2+(√2a)2=√3a，EF=√a2+(2√2a)2=3a，EM2+FM2=EF2，则EM⊥FM，S△EFM=12EM⋅FM=3√22a2，AC=2√2a，则V3=V A−EFM+V C−EFM=13AC⋅S△EFM=2a3，则2V3=3V1，V3=3V2，V3=V1+V2，故A、B错误；C、D正确.故选：CD.13、正三棱锥底面边长为3，侧棱长为2√3，则下列叙述正确的是（）A．正三棱锥高为3B．正三棱锥的斜高为√392C．正三棱锥的体积为27√34D．正三棱锥的侧面积为9√394答案：ABD分析：先求出正三棱锥的高和斜高，从而可判断AB的正误，再计算出体积和侧面积，从而可判断CD的正误.设E为等边三角形ADC的中心，F为CD的中点，连接PF,EF,PE，则PE为正三棱锥的高，PF为斜高，又PF=√12−94=√392，EF=32×√33=√32，故PE=√394−34=3,故AB正确.而正三棱锥的体积为13×3×√34×9=9√34，侧面积为3×12×3×√392=9√394，故C错误，D正确.故选：ABD.填空题14、如图，在棱长为2的正方体ABCD−A1B1C1D1中，P为线段A1B上的动点（不含端点），则下列结论正确的是____．①平面A 1D 1P ⊥平面BB 1P ；②DC 1⊥PC ；③∠APD 1的取值范围是[π2,π)； ④三棱锥C 1−D 1PC 的体积为定值43．答案：①②④分析：由正方体的特征知A 1D 1⊥平面AA 1B 1B ，DC 1⊥对角面A 1BCD 1，由面面垂直的判定和线面垂直的性质可知①②正确；当点P 为线段A 1B 的一个四等分点且靠近点B 时，由长度关系可求得cos∠APD 1>0，知③错误；由体积桥和三棱锥体积公式可确定④正确.对于①，∵几何体是正方体，∴A 1D 1⊥平面AA 1B 1B ，又A 1D 1⊂平面A 1D 1P ，∴平面A 1D 1P ⊥平面BB 1P ，①正确；对于②，在正方体ABCD −A 1B 1C 1D 1中，DC 1⊥对角面A 1BCD 1，对角面A 1BCD 1，∴DC 1⊥PC ，②正确；对于③，当点P 为线段A 1B 的一个四等分点且靠近点B 时，可得：AP =√102，D 1P =√342，AD 1=2√2，由余弦定理得：cos∠APD 1=AP 2+D 1P 2−AD 122AP⋅D 1P =52+172−82×√102×√342=√85>0，此时∠APD 1<π2，③错误；对于④，∵△D 1C 1C 的面积是定值S =12×2×2=2，点P 到面D 1C 1C 的距离为BC =2，∴三棱锥C 1−D 1PC的体积V =13×2×2=43，④正确． PC所以答案是：①②④．15、如图，在正方体中，A 、B 、C 、D 分别是顶点或所在棱的中点，则A 、B 、C 、D 四点共面的图形______（填上所有正确答案的序号）．答案：①③④分析：四点共面主要通过证明两线平行说明，本题利用中位线、平行四边形的性质结合平行线的传递性进行说明，证明平行时绝不能凭直观感觉或无理论依据．图①：证明AB ∥EF ，CD ∥EF ，可得AB ∥CD ；图③：证明BD ∥EF ，AC ∥EF ，可得BD ∥AC ；图④：证明GH ∥EF ，AC ∥EF ， BD ∥GH ，可得BD ∥AC ．图①：取GD 的中点F ，连结BF 、EF ，∵B 、F 均为相应边的中点，则：BF ∥HG又∵HG ∥，则BF ∥即ABFE 为平行四边形∴AB ∥EF同理: CD ∥EF则AB ∥CD 即A 、B 、C 、D 四点共面，图①正确；图②：显然AB 与CD 异面，图②不正确；AEAE图③：连结AC,BD,EF,∵BE∥DF即BDFE为平行四边形∴BD∥EF又∵A、C分别为相应边的中点，则AC∥EF∴BD∥AC即A、B、C、D四点共面，图③正确；图④：连结AC,BD,EF,GH,∵GE∥HF即GEFH为平行四边形，则GH∥EF又∵A、C分别为相应边的中点，则AC∥EF同理：BD∥GH∴BD∥AC即A、B、C、D四点共面，图④正确．所以答案是：①③④．16、一个正四棱柱的底面边长为2，高为4，则该正四棱柱的体积为________．答案：16分析：根据棱柱的体积公式直接计算即可.由题可得该正四棱柱的体积为2×2×4=16.所以答案是：16.解答题17、在正方体ABCD—A1B1C1D1中，E是棱BB1的中点．(1)求证：B1D∥平面ACE．(2)若F是棱CC1的中点，求证：平面B1DF∥平面ACE．答案：(1)证明见解析(2)证明见解析分析：（1）连BD，使BD∩AC＝G，连EG，由中位线定理以及线面平行判定定理证明即可；（2）证明B1F∥平面ACE，结合B1D∥平面ACE，利用面面平行判定定理证明即可.（1）连BD，使BD∩AC＝G，连EG．∵ABCD是正方形，BD∩AC＝G，∴DG＝BG．又∵E是BB1中点，∴B1E＝BE，∴DB1∥GE，又DB1⊄平面ACE，GE⊂平面ACE，∴B1D∥平面ACE．（2）∵E是棱BB1的中点，F是棱CC1的中点．∴B1E∥CF且B1E＝CF，∴四边形B1ECF是平行四边形，∴B1F∥CE，又∴B1F⊄平面ACE，CE⊂平面ACE，∴B1F∥平面ACE，由（1）B1D∥平面ACE，又∵DB1∩B1F＝B1，∴平面B1DF∥平面ACE．18、用符号表示下列语句，并画出图形.（1）平面α与β相交于直线l，直线a与α，β分别相交于点A，B；（2）点A，B在平面α内，直线a与平面α交于点C，点C不在直线AB上.答案：（1）α∩β＝l，a∩α＝A，a∩β＝B；图象见解析；（2）A∈α，B∈α，a∩α＝C，C∉AB；图象见解析分析：由题意将自然语言转化为符号语言,根据点线面的关系,借用集合符号,表示即可.（1）用符号表示：α∩β＝l,a∩α＝A,a∩β＝B，如图.（2）用符号表示：A∈α,B∈α,a∩α＝C,C∉AB，如图.小提示：本题主要考查点、线、面的关系的符号表达,属于基础题.。

高中数学必修二第八章立体几何初步考点题型与解题方法(带答案)

高中数学必修二第八章立体几何初步考点题型与解题方法单选题1、下列说法中正确的是（）A．如果一条直线与一个平面平行，那么这条直线与平面内的任意一条直线平行B．平面α内△ABC的三个顶点到平面β的距离相等，则α与β平行C．α//β，a//α，则a//βD．a//b，a//α，b⊄α，则b//α答案：D分析：根据线面关系，逐一判断每个选项即可.解：对于A选项，如果一条直线与一个平面平行，那么这条直线与平面内的无数条直线平行，而不是任意的直线平行，故错误；对于B选项，如图1，D，E，F，G分别为正方体中所在棱的中点，平面DEFG设为平面β，易知正方体的三个顶点A，B，C到平面β的距离相等，但△ABC所在平面α与β相交，故错误；对于选项C，a可能在平面β内，故错误；对于选项D，正确.故选：D.2、已知直三棱柱ABC−A1B1C1的各顶点都在同一球面上，且该棱柱的体积为√3，AB=2，AC=1，∠BAC=60°，则该球的表面积为（）A．4πB．4√2πC．8πD．32π答案：C解析：利用三棱柱ABC −A 1B 1C 1的侧棱垂直于底面，棱柱的体积为√3，AB =2，AC =1，∠BAC =60°，求出AA 1，再求出ΔABC 外接圆的半径，即可求得球的半径，从而可求球的表面积. ∵三棱柱ABC −A 1B 1C 1的侧棱垂直于底面，棱柱的体积为√3，AB =2，AC =1，∠BAC =60°， ∴12×2×1×sin60°×AA 1=√3，∴AA 1=2∵BC 2=AB 2+AC 2−2AB ⋅ACcos60°=4+1−2=3，∴BC =√3. 设ΔABC 外接圆的半径为R ，则BCsin60°=2R ，∴R =1.∴外接球的半径为√1+1=√2，∴球的表面积等于4π×(√2)2=8π. 故选：C.小提示：本小题主要考查根据柱体体积求棱长，考查几何体外接球有关计算，属于基础题.3、牟合方盖是由我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法，该方法不直接给出球体的体积，而是先计算牟合方盖的体积.刘徽通过计算，“牟合方盖”的体积与球的体积关系为V 牟V 球=4π，并且推理出了“牟合方盖”的八分之一的体积计算公式，即V 牟8=r 3−V 方盖差，从而计算出V 球=43πr 3.如果记所有棱长都为r 的正四棱锥的体积为V ，则V 方差盖:V =（） A ．√22B ．1C ．√2D ．2√2 答案：C分析：计算出V 方盖差，V ，即可得出结论.由题意，V 方盖差=r 3−18V 牟=r 3−18×4π×43×π×r 3=13r 3，所有棱长都为r 的正四棱锥的体积为V 正=13×r ×r ×r 2−(√2r 2)2=√26r 3， ∴V 方盖差V 正=13r 3√2r 36=√2，故选：C ．4、已知圆锥的底面半径为R ，高为3R ，在它的所有内接圆柱中，全面积的最大值是（） A ．2πR 2B ．94πR 2C ．83πR 2D ．πR 2答案：B分析：根据圆柱的表面积公式以及二次函数的性质即可解出．设圆柱的底面半径为r，圆柱的高为ℎ，所以在轴截面三角形中，如图所示：由相似可得，rR =3R−ℎ3R，所以，ℎ=3R−3r，即圆柱的全面积为S=2πr2+2πrℎ=2πr2+2πr(3R−3r)=2π(−2r2+3rR)=2π[−2(r−34R)2+98R2]≤9π4R2，当且仅当r=34R时取等号．故选：B．5、如图所示的是平行四边形ABCD所在的平面，有下列表示方法：①平面ABCD；②平面BD；③平面AD；④平面ABC；⑤AC；⑥平面α.其中不正确的是（）A．④⑤B．③④⑤C．②③④⑤D．③⑤答案：D解析：根据平面的表示方法判断．③中AD不为对角线，故错误；⑤中漏掉“平面”两字，故错误.故选：D.6、如图，矩形BDEF所在平面与正方形ABCD所在平面互相垂直，BD=2，DE=1，点P在线段EF上.给出下列命题：①存在点P，使得直线DP//平面ACF；②存在点P，使得直线DP⊥平面ACF；,1]；③直线DP与平面ABCD所成角的正弦值的取值范围是[√55④三棱锥A−CDE的外接球被平面ACF所截得的截面面积是9π.8其中所有真命题的序号（）A．①③B．①④C．①②④D．①③④答案：D分析：当点P是线段EF中点时判断①；假定存在点P，使得直线DP⊥平面ACF，推理导出矛盾判断②；利用线面角的定义转化列式计算判断③；求出△ACF外接圆面积判断④作答.取EF中点G，连DG，令AC∩BD=O，连FO，如图，在正方形ABCD中，O为BD中点，而BDEF是矩形，则DO//GF且DO=GF，即四边形DGFO是平行四边形，即有DG//FO，而FO⊂平面ACF，DG⊄平面ACF，于是得DG//平面ACF，当点P与G重合时，直线DP//平面ACF，①正确；假定存在点P，使得直线DP⊥平面ACF，而FO⊂平面ACF，则DP⊥FO，又DG//FO，从而有DP⊥DG，在Rt△DEF中，∠DEF=90∘，DG是直角边EF上的中线，显然在线段EF上不存在点与D连线垂直于DG，因此，假设是错的，即②不正确；因平面BDEF⊥平面ABCD，平面BDEF∩平面ABCD=BD，则线段EF上的动点P在平面ABCD上的射影在直线BD上，于是得∠PDB是直线DP与平面ABCD所成角的，在矩形BDEF中，当P与E不重合时，∠PDB=∠DPE，sin∠PDB=sin∠DPE=DEDP =√DE2+EP2=√1+EP2，而0<EP≤2，则√55≤sin∠PDB<1，当P与E重合时，∠PDB=π2，sin∠PDB=1，因此，√55≤sin∠PDB≤1，③正确；因平面BDEF⊥平面ABCD，平面BDEF∩平面ABCD=BD，BF⊥BD，BF⊂平面BDEF，则BF⊥平面ABCD，BC=√2，在△ACF中，AF=CF=√BC2+BF2=√3，显然有FO⊥AC，sin∠FAC=FOAF =√BO2+BF2AF=√2√3，由正弦定理得△ACF外接圆直径2R=CFsin∠FAC =√2，R=2√2，三棱锥A−CDE的外接球被平面ACF所截得的截面是△ACF的外接圆，其面积为πR2=9π8，④正确，所以所给命题中正确命题的序号是①③④.故选：D小提示：名师点评两个平面互相垂直，则一个平面内任意一点在另一个平面上的射影都在这两个平面的交线上.7、边长为5 cm的正方形EFGH是圆柱的轴截面，则从E点沿圆柱的侧面到相对顶点G的最短距离是（）A．10cm B．5√2cmC．5√π2+1cm D．52√π2+4cm答案：D分析：将圆柱展开，根据题意即可求出答案.圆柱的侧面展开图如图所示，展开后E′F=12×2π×52=52π(cm)，∴E′G=√52+(5π2)2=52√π2+4(cm)，即为所求最短距离．8、下面四个选项中一定能得出平面α/⁄平面β的是（）A．存在一条直线a，a//α，a//βB．存在一条直线a，a⊂α，a//βC．存在两条平行直线a，b，a⊂α，b⊂β，a//β，b//αD．存在两条异面直线a，b，a⊂α，b⊂β，a//β，b//α答案：D分析：对于A，B，C，举出符合条件的特例即可判断；对于D，过直线a作平面γ∩β=c，再证c//α即可. 如图，ABCD−A1B1C1D1是长方体，平面ABCD为平面α，平面ABB1A1为平面β，对于A，直线C1D1为直线a，显然a//α，a//β，而α与β相交，A不正确；对于B，直线CD为直线a，显然a⊂α，a//β，而α与β相交，B不正确；对于C，直线CD为直线a，直线A1B1为直线b，显然a⊂α，b⊂β，a//β，b//α，而α与β相交，C不正确；对于D，因a，b是异面直线，且a⊂α，b⊂β，过直线a作平面γ∩β=c，如图，则c//a，并且直线c与b必相交，而c⊄α，于是得c//α，又b//α，即β内有两条相交直线都平行于平面α，⁄平面β.因此，平面α/多选题9、(多选题)下列说法中，正确的结论有（）A．如果一个角的两边与另一个角的两边分别平行，那么这两个角相等B．如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角(或直角)相等C．如果一个角的两边和另一个角的两边分别垂直，那么这两个角相等或互补D．如果两条直线同时平行于第三条直线，那么这两条直线互相平行答案：BD分析：由等角定理可判断A的真假；根据直线夹角的定义可判断B的真假；举反例可判断C的真假；由平行公理可判断D的真假.对于选项A：如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补，故选项A错误；对于选项B：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角或直角相等，故选项B正确；对于选项C：如果一个角的两边和另一个角的两边分别垂直，这两个角的关系不确定，既可能相等也可能互补，也可能既不相等，也不互补.反例如图，在立方体中，∠A1D1C1与∠A1BC1满足A1D1⊥A1B，C1D1⊥C1B，但是∠A1D1C1=π2，∠A1BC1=π3，二者不相等也不互补.故选项C错误；对于选项D：如果两条直线同时平行于第三条直线，那么这两条直线平行，故选项D正确.故选：BD.10、矩形ABCD中，AB=2，BC=1，将此矩形沿着对角线BD折成一个三棱锥C−BDA，则以下说法正确的有（）A．三棱锥C−BDA的体积最大值为2√515B．当二面角C−BD−A为直二面角时，三棱锥C−BDA的体积为2√515C．当二面角C−BD−A为直二面角时，三棱锥C−BDA的外接球的表面积为5πD．当二面角C−BD−A不是直二面角时，三棱锥C−BDA的外接球的表面积小于5π答案：ABC分析：求出点C到平面ABD的最大距离即可计算棱锥的最大体积判断选项A，B；求出三棱锥C−BDA的外接球的半径即可判断选项C，D作答.过C作CE⊥BD于E，在平面DBA内过E作BD的垂线EG，则∠CEG为二面角C−BD−A的平面角，如图，平面CEG⊥平面DBA，过C作CF⊥EG于F，则CF⊥平面DBA，在直角△BCD中，∠BCD=90∘，BC=1,CD=2,CE=BC⋅CDBD =2√55，显然CF≤CE，当且仅当点E与F重合时取“=”，即点C到平面ABD距离的最大值为CE=2√55，而S△DBA=12AB⋅AD=1，则三棱锥C−BDA的体积最大值为13CE⋅S△DBA=2√515，A正确；当CF取最大值2√55时，CF⊂平面BCD，又CF⊥平面DBA，则平面BCD⊥平面DBA，即二面角C−BD−A为直二面角，三棱锥C−BDA的体积为2√515，B正确；取BD中点O，连接AO，CO，显然有AO=CO=12BD=BO=DO，于是得点A，B，C，D在以O为球心，AO=√52为半径的球面上，显然，无论二面角C−BD−A如何变化，点A，B，C，D都在上述的球O上，其表面积为5π，C正确，D不正确.故选：ABC11、如图，正方体ABCD−A1B1C1D1的棱长为1，则下列四个命题正确的是（）A．两条异面直线D1C和BC1所成的角为π4B．直线BC与平面ABC1D1所成的角等于π4C．点D到面ACD1的距离为√33D．三棱柱AA1D1−BB1C1外接球半径为√32答案：BCD分析：对于A：根据异面直线的求法易得：异面直线D1C和BC1所成的角为∠AD1C；对于B：可证B1C⊥平面ABC1D1，则直线BC与平面ABC1D1所成的角为∠CBC1；对于C：根据等体积转换V D−ACD1=V D1−ACD，求点D到面ACD1的距离；对于D：三棱柱AA1D1−BB1C1的外接球即为正方体ABCD−A1B1C1D1的外接球，直接求正方体外接球的半径即可．连接AC、AD1∵AB∥C1D1且AB=C1D1，则四边形ABC1D1为平行四边形，∴异面直线D1C和BC1所成的角为∠AD1C∵AC=AD1=D1C，则△ACD1为正三角形，即∠AD1C=π3A不正确；连接B1C在正方形BB1C1C中，BC1⊥B1C∵AB⊥平面BB1C1C，B1C⊂平面BB1C1C∴AB⊥B1CAB∩BC1=B，则B1C⊥平面ABC1D1∴直线BC与平面ABC1D1所成的角为∠CBC1=π4 B正确；根据等体积转换可知：V D−ACD1=V D1−ACD即13×ℎ×12×√2×√2×√32=13×1×12×1×1，则ℎ=√33C正确；三棱柱AA1D1−BB1C1的外接球即为正方体ABCD−A1B1C1D1的外接球则外接球的半径即为正方体ABCD−A1B1C1D1体对角线的一半，即R=√32 D正确；故选：BCD．填空题12、一个圆锥的母线长为20，母线与轴的夹角为60∘，则圆锥的高为________．答案：10分析：利用圆锥的几何性质可求得该圆锥的高.由题意可知，该圆锥的高为ℎ=20cos60∘=10.所以答案是：10.13、若将两个半径为1的铁球熔化后铸成一个球，则该球的半径为______．答案：√23分析：根据球的体积等于两个半径为1的球的体积之和即可求其半径．设大球的半径为r，则根据体积相同，可知43π+43π=43πr3，则r3=2，解得r=√23.所以答案是：√23．14、已知一三角形ABC用斜二测画法画出的直观图是面积为√3的正三角形A′B′C′(如图)，则三角形ABC中边长与正三角形A′B′C′的边长相等的边上的高为______．答案：2√6分析：根据面积公式求出三角形的边长，以及高，利用斜二测画法的原理还原出原三角形的高，并求出答案. 设正三角形A′B′C′的边长为a，∵S△A′B′C′=√34a2=√3∴a=2，DC′=√3O′C′=√6∴O′C=2√6所以答案是：2√6.解答题15、如图，在正方体ABCD−A1B1C1D1中，A1C1与B1D1交于点O1，求证：(1)直线A1B∥平面ACD1；(2)直线BO1∥平面ACD1．答案：(1)证明见解析(2)证明见解析分析：(1)根据题意，先证得四边形A1D1CB是平行四边形，从而证得A1B∥D1C，即可证得线面垂直；(2)连接BD，交AC于O，连接D1O，只需证明O1B∥D1O，即可证得线面垂直；（1）证明：直线A1B在平面ACD1外，因为A1D1∥BC，A1D1=BC，所以四边形A1D1CB是平行四边形，所以A1B∥D1C，而D1C是平面ACD1内的直线，根据判定定理可知，直线A1B∥平面ACD1．（2）证明：如图，连接BD，交AC于O，连接D1O，易知D1O1∥OB，D1O1=OB，则四边形D1O1BO是平行四边形，所以O1B∥D1O，所以D1O在平面ACD1上，根据判定定理可知，O1B∥平面ACD1．。

(精选试题附答案)高中数学第八章立体几何初步解题方法技巧

(名师选题)（精选试题附答案）高中数学第八章立体几何初步解题方法技巧单选题1、球面上两点之间的最短连线的长度，就是经过这两个点的大圆在这两点间的一段劣弧的长度（大圆就是经过球心的平面截球面所得的圆），我们把这个弧长叫做两点的球面距离.已知正△ABC 的项点都在半径为2的球面上，球心到△ABC 所在平面距离为2√63，则A 、B 两点间的球面距离为（） A ．πB ．π2C ．2π3D ．3π4答案：C分析：设球心为点O ，计算出∠AOB ，利用扇形弧长公式可求得结果.设球心为点O ，平面ABC 截球O 所得截面圆的半径为r =√22−(2√63)2=2√33，由正弦定理可得4√33=AB sin∠ACB ，∴AB =4√33sin π3=2，又∵OA =OB =2，所以，△AOB 为等边三角形，则∠AOB =π3，因此，A 、B 两点间的球面距离为2×π3=2π3.故选：C.小提示：思路点睛：求球面距离，关键就是要求出球面上两点与球心所形成的角，结合扇形的弧长公式求解，同时在计算球的截面圆半径时，利用公式r =√R 2−d 2（其中r 为截面圆的半径，R 为球的半径，d 为球心到截面的距离）来计算.2、如图，用斜二测画法作水平放置的正三角形A 1B 1C 1的直观图，则正确的图形是（）A．B．C．D．答案：A分析：由斜二侧画法的规则分析判断即可先作出一个正三角形A1B1C1，然后以B1C1所在直线为x轴，以B1C1边上的高所在的直线为y轴建立平面直角坐标系，画对应的x′,y′轴，使夹角为45°，画直观图时与x轴平行的直线的线段长度保持不变，与y轴平行的线段长度变为原来的一半，得到的图形如图，然后去掉辅助线即可得到正三角形的直观图如图，故选：A3、如图直角△O′A′B′是一个平面图形的直观图，斜边O′B′=4，则原平面图形的面积是（）A．8√2B．4√2C．4D．√2答案：A解析：根据斜二测画法规则可求原平面图形三角形的两条直角边长度，利用三角形的面积公式即可求解.由题意可知△O′A′B′为等腰直角三角形，O′B′=4，则O′A′=2√2，所以原图形中，OB=4，OA=4√2，×4×4√2=8√2.故原平面图形的面积为12故选：A4、如图1，已知PABC是直角梯形，AB∥PC，AB⊥BC，D在线段PC上，AD⊥PC．将△PAD沿AD折起，使平面PAD⊥平面ABCD，连接PB，PC，设PB的中点为N，如图2．对于图2，下列选项错误的是（）A．平面PAB⊥平面PBC B．BC⊥平面PDCC．PD⊥AC D．PB＝2AN答案：A分析：由已知利用平面与平面垂直的性质得到PD⊥平面ABCD，判定C正确；进一步得到平面PCD⊥平面ABCD，结合BC⊥CD判定B正确；再证明AB⊥平面PAD，得到△PAB为直角三角形，判定D正确；可证明平面PBC⊥平面PDC，若平面PAB⊥平面PBC，则平面PAB与平面PDC的交线⊥平面PBC，矛盾，可判断A 图1中AD⊥PC，则图2中PD⊥AD，又∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，∴PD⊥平面ABCD，则PD⊥AC，故选项C正确；由PD⊥平面ABCD，PD⊂平面PDC，得平面PDC⊥平面ABCD，而平面PDC∩平面ABCD＝CD，BC⊂平面ABCD，BC⊥CD，∴BC⊥平面PDC，故选项B正确；∵AB⊥AD，平面PAD⊥平面ABCD，且平面PAD∩平面ABCD＝AD，∴AB⊥平面PAD，则AB⊥PA，即△PAB是以PB为斜边的直角三角形，而N为PB的中点，则PB＝2AN，故选项D正确．由于BC⊥平面PDC，又BC⊂平面PBC∴平面PBC⊥平面PDC若平面PAB⊥平面PBC，则平面PAB与平面PDC的交线⊥平面PBC由于AB//平面PDC，则平面PAB与平面PDC的交线//AB显然AB不与平面PBC垂直，故A错误故选：A5、已知圆锥的母线长为3，其侧面展开图是一个圆心角为2π3的扇形，则该圆锥的体积为（）A．√23πB．2√23πC．πD．√2π答案：B分析：根据弧长计算公式，求得底面圆半径以及圆锥的高，即可求得圆锥的体积.设圆锥的底面圆半径为r，故可得2πr=2π3×3，解得r=1，设圆锥的高为ℎ，则ℎ=√32−12=2√2，则圆锥的体积V=13×πr2×ℎ=13×π×2√2=2√23π.故选：B.6、已知一个圆锥的体积为3π，其侧面积是底面积的2倍，则其底面半径为（）A．2√3B．3C．√3D．√33答案：C分析：根据圆锥的侧面展开图和圆锥体积公式以及侧面积公式，即可求出结果. 设底面半径为r，高为ℎ，母线为l，如图所示：则圆锥的体积V=13πr2ℎ=3π，所以r2ℎ=9，即ℎ=9r2，S 侧=12⋅2πrl=2πr2，则l=2r，又ℎ=√l2−r2=√3r，所以√3r3=9，故r=√3．故选：C．7、如图是四边形ABCD的水平放置的直观图A′B′C′D′，则原四边形ABCD的面积是（）A．14B．10√2C．28D．14√2答案：C分析：根据斜二测画法的定义，还原该四边形得到梯形，根据梯形的面积公式即可计算求解. ∵A′D′∥y′轴，A′B′∥C′D′，A′B′≠C′D′，∴原图形是一个直角梯形．又A′D′＝4，∴原直角梯形的上、下底及高分别是2，5，8，故其面积为S=12×(2+5)×8=28.故选：C8、下列命题中①空间中三个点可以确定一个平面.②直线和直线外的一点，可以确定一个平面.③如果三条直线两两相交，那么这三条直线可以确定一个平面.④如果三条直线两两平行，那么这三条直线可以确定一个平面.⑤如果两个平面有无数个公共点，那么这两个平面重合.真命题的个数为（）A．1个B．2个C．3个D．4个答案：A分析：根据空间位置关系可直接判断各命题.命题①：空间中不共线三个点可以确定一个平面，错误；命题②：直线和直线外的一点，可以确定一个平面，正确；命题③：三条直线两两相交，若三条直线相交于一点，则无法确定一个平面，所以命题③错误；命题④：如果三条直线两两平行，那么这三条直线不能确定一个平面，所以命题④错误；命题⑤：两个平面有无数个公共点，则两平面可能相交，所以命题⑤错误；故选：A.9、正方体中，点P，O，R，S是其所在棱的中点，则PQ与RS是异面直线的图形是（）A．B．C．D．答案：C分析：对于A，B，D，利用两平行线确定一个平面可以证明直线PQ与RS共面，对于C，利用异面直线的定义推理判断作答．对于A，在正方体ABCD−A1B1C1D1中，连接AC，A1C1，则AC//A1C1，如图，因为点P，Q，R，S是其所在棱的中点，则有PQ//AC，RS//A1C1，因此PQ//RS，则直线PQ与RS共面，A错误；对于B，在正方体ABCD−A1B1C1D1中，连接AC，QS，PR，如图，因为点P，Q，R，S是其所在棱的中点，有AP//CR且AP=CR，则四边形APRC为平行四边形，即有AC//PR，又QS//AC，因此QS//PR，直线PQ与RS共面，B错误；对于C，在正方体ABCD−A1B1C1D1中，如图，因为点P，Q，R，S是其所在棱的中点，有RS//BB1，而BB1⊂平面ABB1A1，RS⊄平面ABB1A1，则RS//平面ABB1A1，PQ⊂平面ABB1A1，则直线PQ与RS无公共点，又直线PQ与直线BB1相交，于是得直线PQ与RS不平行，则直线PQ与RS是异面直线，C正确；对于D，在正方体ABCD−A1B1C1D1中，连接A1B，D1C，PS，QR，如图，因为A1D1//BC且A1D1=BC，则四边形A1D1CB为平行四边形，有A1B//D1C，因为点P，Q，R，S是其所在棱的中点，有PS//A1B，QR//D1C，则PS//QR，直线PQ与RS共面，D错误.故选：C10、南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148．5m时，相应水面的面积为140．0km2；水位为海拔157．5m时，相应水面的面积为180．0km2，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148．5m上升到157．5m时，增加的水量约为（√7≈2.65）（）A．1.0×109m3B．1.2×109m3C．1.4×109m3D．1.6×109m3答案：C分析：根据题意只要求出棱台的高，即可利用棱台的体积公式求出．依题意可知棱台的高为MN=157.5−148.5=9(m)，所以增加的水量即为棱台的体积V．棱台上底面积S=140.0km2=140×106m2，下底面积S′=180.0km2=180×106m2，∴V=13ℎ(S+S′+√SS′)=13×9×(140×106+180×106+√140×180×1012)=3×(320+60√7)×106≈(96+18×2.65)×107=1.437×109≈1.4×109(m3)．故选：C．填空题11、如图，在棱长为2的正方体ABCD−A1B1C1D1中，P为线段A1B上的动点（不含端点），则下列结论正确的是____．①平面A1D1P⊥平面BB1P；②DC1⊥PC；③∠APD1的取值范围是[π2,π)；④三棱锥C1−D1PC的体积为定值43．答案：①②④分析：由正方体的特征知A1D1⊥平面AA1B1B，DC1⊥对角面A1BCD1，由面面垂直的判定和线面垂直的性质可知①②正确；当点P为线段A1B的一个四等分点且靠近点B时，由长度关系可求得cos∠APD1>0，知③错误；由体积桥和三棱锥体积公式可确定④正确.对于①，∵几何体是正方体，∴A1D1⊥平面AA1B1B，又A1D1⊂平面A1D1P，∴平面A1D1P⊥平面BB1P，①正确；对于②，在正方体ABCD−A1B1C1D1中，DC1⊥对角面A1BCD1，PC⊂对角面A1BCD1，∴DC1⊥PC，②正确；对于③，当点P为线段A1B的一个四等分点且靠近点B时，可得：AP=√102，D1P=√342，AD1=2√2，由余弦定理得：cos∠APD1=AP2+D1P2−AD122AP⋅D1P =52+172−82×√102×√342=√85>0，此时∠APD1<π2，③错误；对于④，∵△D1C1C的面积是定值S=12×2×2=2，点P到面D1C1C的距离为BC=2，∴三棱锥C1−D1PC的体积V=13×2×2=43，④正确．所以答案是：①②④．12、如图，OABC是边长为1的正方形，AC⌢是四分之一圆弧，则图中阴影部分绕轴OC旋转一周得到的旋转体的表面积为________________.答案：5π分析：几何体是一个圆柱挖去一个半球后剩余的部分，结合几何特征，可得几何体的表面积.几何体是一个圆柱挖去一个半球后剩余的部分，且圆柱的底面半径是1，高是1，球的半径是1，所以该几何体的表面积为π×12+2π×1×1+12×4π×12=5π.所以答案是：5π.13、已知P，Q，R，S是相应长方体或空间四边形的边或对角线的中点，则这四点必定共面的是______．（写序号）答案：①③④分析：利用平面的基本性质及推论，逐一检验即可．①中，∵PR//QS，∴P，Q，R，S四点共面；②中，PR和QS是异面直线，故四点不共面；③中，∵PS//QR，∴P，Q，R，S四点共面；④中，∵PQ//RS//BC，∴P，Q，R，S四点共面；所以答案是：①③④14、设∠A和∠B的两边分别平行，若∠A=45°，则∠B的大小为___________.答案：45°或135°##135°或45°分析：根据等角定理即可得到答案.根据等角定理：一个角的两边平行于另外一个角的两边，则这两个角相等或互补. 所以答案是：45°或135°.15、已知圆锥的母线长等于2，侧面积等于2π，则该圆锥的体积等于________．答案：√3π3##√33π分析：根据圆锥的侧面积公式S侧=πrl，代入可得r=1，根据图形结合勾股定理可得ℎ=√3，再代入锥体体积公式V=13Sℎ．设圆锥的母线长为l，底面半径为r，高为ℎ根据题意可得：l=2,πrl=2π，则r=1∴ℎ=√l2−r2=√3则该圆锥的体积V=13πr2×ℎ=√3π3所以答案是：√3π3．解答题16、如图所示，在正方体ABCD−A1B1C1D1中，E，F，G，H分别是BC，CC1，C1D1，A1A的中点．求证：（1）BF//HD1；（2）EG//平面BB1D1D：（3）平面BDF//平面B1D1H．答案：（1）证明见解析；（2）证明见解析；（3）证明见解析.分析：（1）取DD1中点M，连接AM,FM，先证明四边形ABFM为平行四边形，再证明四边形AMD1H为平行四边形可得；（2）连接AC，交BD于O，连接OE，OD1，通过证明四边形D1GEO为平行四边形得出EG//D1O可证；（3）通过BF//HD1得BF//平面B1D1H，通过BD//B1D1得BD//平面B1D1H可证明.（1）取DD1中点M，连接AM,FM，∵F是CC1中点，∴MF//CD且MF=CD，∵AB//CD,AB=CD，∴AB//MF,AB=MF，则四边形ABFM为平行四边形，∴BF//AM，∵H是AA1中点，∴AH//D1M,AH=D1M，则四边形AMD1H为平行四边形，∴AM//HD1，∴BF//HD1；（2）连接AC，交BD于O，连接OE，OD1，CD，∵O,E为BD,BC中点，∴OE//CD,OE=12CD，∵G为C1D1中点，∴D1G//CD,D1G=12∴D1G//OE,D1G=OE，∴四边形D1GEO为平行四边形，∴EG//D1O，∵D1O⊂平面BB1D1D，EG⊄平面BB1D1D，∴EG//平面BB1D1D；（3）由（1）BF//HD1，∵HD1⊂平面B1D1H，BF⊄平面B1D1H，∴BF//平面B1D1H，又正方体中，BB1//DD1,BB1=DD1，则四边形BB1D1D为平行四边形，∴BD//B1D1，∵B1D1⊂平面B1D1H，BD⊄平面B1D1H，∴BD//平面B1D1H，∵BD∩BF=B，∴平面BDF//平面B1D1H.小提示：关键点睛：解决本题的关键是正确理解线面平行、面面平行的判定定理.17、如图，已知三棱柱ABC−A1B1C1，平面AA1C1C⊥平面ABC,∠ABC=90°，∠BAC=30°,A1A=A1C= AC,E,F分别是AC,A1B1的中点.（1）证明：EF⊥BC；（2）求直线EF与平面A1BC所成角的余弦值.答案：（1）证明见解析；（2）3.5分析：(1)由题意首先证得线面垂直，然后利用线面垂直的定义即可证得线线垂直；(2)建立空间直角坐标系，分别求得直线的方向向量和平面的法向量，然后结合线面角的正弦值和同角三角函数基本关系可得线面角的余弦值.(1)如图所示，连结A1E,B1E，等边△AA 1C 中，AE =EC ，则A 1E ⊥AC ，平面ABC ⊥平面A 1ACC 1，且平面ABC ∩平面A 1ACC 1=AC ，由面面垂直的性质定理可得：A 1E ⊥平面ABC ，故A 1E ⊥BC ，由三棱柱的性质可知A 1B 1∥AB ，而AB ⊥BC ，故A 1B 1⊥BC ，且A 1B 1∩A 1E =A 1，由线面垂直的判定定理可得：BC ⊥平面A 1B 1E ，结合EF⊆平面A 1B 1E ，故EF ⊥BC .(2)在底面ABC 内作EH ⊥AC ，以点E 为坐标原点，EH ,EC ,EA 1方向分别为x ,y ,z 轴正方向建立空间直角坐标系E −xyz .设EH =1，则AE =EC =√3，AA 1=CA 1=2√3,BC =√3,AB =3，据此可得：A(0,−√3,0),B (32,√32,0),A 1(0,0,3),C(0,√3,0)，由AB ⃑⃑⃑⃑⃑ =A 1B 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ 可得点B 1的坐标为B 1(32,32√3,3)，利用中点坐标公式可得：F (34,34√3,3)，由于E (0,0,0)，故直线EF 的方向向量为：EF ⃑⃑⃑⃑⃑ =(34,34√3,3) 设平面A 1BC 的法向量为m ⃑⃑ =(x,y,z )，则：{m ⃑⃑ ⋅A 1B ⃑⃑⃑⃑⃑⃑⃑ =(x,y,z )⋅(32,√32,−3)=32x +√32y −3z =0m ⃑⃑ ⋅BC ⃑⃑⃑⃑⃑ =(x,y,z )⋅(−32,√32,0)=−32x +√32y =0 ，据此可得平面A 1BC 的一个法向量为m ⃑⃑ =(1,√3,1)，EF ⃑⃑⃑⃑⃑ =(34,34√3,3) 此时cos⟨EF ⃑⃑⃑⃑⃑ ,m ⃑⃑ ⟩=EF ⃑⃑⃑⃑⃑ ⋅m ⃑⃑⃑ |EF ⃑⃑⃑⃑⃑ |×|m ⃑⃑⃑ |=√5×3√52=45，设直线EF 与平面A 1BC 所成角为θ，则sinθ=cos⟨EF ⃑⃑⃑⃑⃑ ,m ⃑⃑ ⟩=45,cosθ=35.小提示：本题考查了立体几何中的线线垂直的判定和线面角的求解问题，意在考查学生的空间想象能力和逻辑推理能力；解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化，通过严密推理，同时对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.18、如图，已知矩形CDEF 和直角梯形ABCD ，AB ∥CD ，∠ADC ＝90°，DE ＝DA ，M 为AE 的中点.（1）求证：AC ∥平面DMF ；（2）求证：BE ⊥DM .答案：（1）证明见解析；（2）证明见解析.分析：（1）根据三角形中位线定理，结合线面平行的判定定理进行证明即可；（2）根据矩形的性质，结合线面垂直的性质和判定定理进行证明即可.（1）如图，连结EC 交DF 于点N ，连结MN .因为CDEF为矩形，所以EC，DF相互平分，所以N为EC的中点.又因为M为EA的中点，所以MN∥AC.又因为AC⊄平面DMF，且MN⊂平面DMF.所以AC∥平面DMF.（2）因为矩形CDEF，所以CD⊥DE.又因为∠ADC＝90°，所以CD⊥AD.因为DE∩AD＝D，DE，AD⊂平面ADE，所以CD⊥平面ADE.又因为DM⊂平面ADE，所以CD⊥DM.又因为AB∥CD，所以AB⊥DM.因为AD＝DE，M为AE的中点，所以AE⊥DM.又因为AB∩AE＝A，AB，AE⊂平面ABE，所以MD⊥平面ABE.因为BE⊂平面ABE，所以BE⊥MD.19、如图，在三棱柱ABC−A1B1C1中，BB1⊥平面ABC，AB⊥BC，AA1=AB=BC=2．（1）求证：BC1⊥平面A1B1C；（2）求异面直线B1C与A1B所成角的大小；（3）点M 在线段B 1C 上，且B 1MB 1C =13，点N 在线段A 1B 上，若MN//平面A 1ACC 1，求A 1N A 1B 的值．答案：（1）证明见解析；（2）60°；（3）23.分析：（1）推导出BC 1⊥B 1C ，BB 1⊥A 1B 1，A 1B 1⊥B 1C 1，从而A 1B 1⊥平面BCC 1B 1，进而A 1B 1⊥BC 1，由此能证明BC 1⊥平面A 1B 1C ．（2）以B 为原点，BC 为x 轴，BA 为y 轴，BB 1为z 轴，建立空间直角坐标系，利用向量法能求出异面直线B 1C 与A 1B 所成角的大小为60°．（3）求出平面ACC 1A 1的法向量，由MN//平面A 1ACC 1，利用向量法能求出A 1NA 1B 的值．（1）证明：∵在三棱柱ABC −A 1B 1C 1中，BB 1⊥平面ABC ，AB ⊥BC ，AA 1=AB =BC =2．∴BC 1⊥B 1C ，BB 1⊥A 1B 1，A 1B 1⊥B 1C 1，∵BB 1∩B 1C 1=B 1，∴A 1B 1⊥平面BCC 1B 1，∵BC 1⊂平面BCC 1B 1，∴A 1B 1⊥BC 1，∵A 1B 1∩B 1C =B 1，∴BC 1⊥平面A 1B 1C ．（2）以B 为原点，BC 为x 轴，BA 为y 轴，BB 1为z 轴，建立空间直角坐标系， B 1(0，0，2)，C(2，0，0)，A 1(0，2，2)，B(0，0，0)，B 1C ⃑⃑⃑⃑⃑⃑⃑ =(2，0，−2)，A 1B ⃑⃑⃑⃑⃑⃑⃑ =(0，−2，−2)，设异面直线B 1C 与A 1B 所成角为θ，则cosθ=|B 1C ⃑⃑⃑⃑⃑⃑⃑⃑ ·A 1B ⃑⃑⃑⃑⃑⃑⃑⃑ ||B 1C ⃑⃑⃑⃑⃑⃑⃑⃑ |·|A 1B ⃑⃑⃑⃑⃑⃑⃑⃑ |=√8·√8=12，∴θ=60°． ∴异面直线B 1C 与A 1B 所成角的大小为60°．（3）解：A(0,2,0)，C(2,0,0)，C 1(2,0,2)，B(0,0,0)，B 1(0,0,2)，A 1(0,2,2)， CA ⃑⃑⃑⃑⃑ =(−2,2,0)，CC 1⃑⃑⃑⃑⃑⃑⃑ =(0,0,2)，设平面ACC 1A 1的法向量n ⃑ =(x ，y ，z)，则{n ⃑ ·CA ⃑⃑⃑⃑⃑ =−2x +2y =0n ⃑ ·CC 1⃑⃑⃑⃑⃑⃑⃑ =2z =0，取x =1，得n ⃑ =(1,1,0)，点M 在线段B 1C 上，且B 1MB 1C =13，点N 在线段A 1B 上，设M(a ，b ，c)，N(x ，y ，z)，A 1NA 1B =λ，则BC 1⃑⃑⃑⃑⃑⃑⃑ =3B 1M ⃑⃑⃑⃑⃑⃑⃑⃑ ，A 1N ⃑⃑⃑⃑⃑⃑⃑⃑ =λA 1B ⃑⃑⃑⃑⃑⃑⃑ ，0⩽λ⩽1，即(2,0,−2)=3(a,b,c −2),(x,y −2,z −2)=λ(0,−2,−2)，解得M (23,0,43),N(0,2−2λ, 2−2λ),MN ⃑⃑⃑⃑⃑⃑⃑ =(−23, 2−2λ,23−2λ)， ∵MN//平面A 1ACC 1，∴ n ⃑ ·MN ⃑⃑⃑⃑⃑⃑⃑ =−23+2−2λ=0，解得λ=23． ∴ A 1N A 1B 的值为23．小提示：本题考查线面垂直的证明，考查异面直线所成角的求法，考查满足线面平行的两线段的比值的求法，考查空间中线线、线面、面面间的位置关系，考查化归与转化思想，是中档题．。