全国高中数学青年教师展评课直线与平面垂直教学设计

合集下载

全国高中数学青年教师展评课直线与平面垂直的判定教学设计(吉林吉林一中) (2)

2.3.1直线与平面垂直的判定(第1课时)Ⅰ．教学内容解析《直线与平面垂直的判定》共2课时，本课是第1课时，本节课的内容包括直线与平面垂直的定义和判定定理两部分，均为概念性知识．本节内容以“垂直”的判定为主线展开，“垂直”在定义和描述直线和平面位置关系中起着重要的作用，集中体现在：空间中垂直关系的相互转化．教学重点是直线与平面垂直的判定定理的探究及简单应用．尽管新课标在必修课程中不要求证明，但通过定理的探索过程，培养和发展学生的几何直觉以及运用图形语言进行交流的能力，并体会“平面化”以及“降维”的转化思想，是本节课的重要任务．空间直线与平面的垂直关系是学生在已有“直线与平面位置关系，直线与直线垂直定义与判定”的基础上，又一次接触空间位置关系，是对垂直关系的再认识，是学生认知在维度和深度上的又一次拓展．本节课采用直观感知、操作确认、推理论证、度量计算等研究几何问题的方法，学习了直线与平面垂直的定义、判定定理及其初步运用．其中，线面垂直的定义是线面垂直最基本的判定方法和性质，它是探究线面垂直判定定理的基础；线面垂直的判定定理充分体现了线线垂直与线面垂直之间的转化，它既是后面学习面面垂直的基础，又是连接线线垂直和面面垂直的纽带．学好这部分内容，对于学生建立空间观念，实现从认识平面图形到认识立体图形的飞跃，是非常重要的．Ⅱ．教学目标设置1．学生能从生活中的具体实例感知概括线面垂直的特征，解释“直线与平面垂直”的含义．2．学生通过参与折纸试验，归纳和确认直线与平面垂直的判定定理，并尝试用数学语言（文字、符号、图形语言）对定义、定理进行准确表述．3．学生在探究活动中会用直线与平面垂直的定义和判定定理进行简单的推理论证，并体会线线垂直与线面垂直相互转化的数学思想，从而更好地发展学生的合情推理能力和演绎推理能力，培养其空间想象能力．4．在探究活动中，学生亲历从“感性认识”到“理性认识”获取新知的过程，体验探索的乐趣，通过独立思考和合作交流，发展思维，养成良好思维习惯，提升自主学习能力．Ⅲ．学生学情分析1．学生已有认知基础（1）学生在初中已经掌握了平面内证明线线垂直的方法，学习本课前，学生又通过直观感知、操作确认的方法，学习了直线、平面平行的判定定理，对空间概念建立有一定基础，同时，获得了研究线面位置关系时，从定义到判定，再到性质的经验，因而会比较轻松地融入对本课的探究．（2）虽然学生对空间几何体的学习有了一段时间，已经具备了基本的图形语言能力,但对问题的说理和论证只是刚刚接触，没有形成一种熟练运用文字语言和符号语言的能力，存在对问题的推理和论证还有些望而却步,难以把理论和实践结合到一起．2．达成目标所需要的认知基础学生需要对研究的目标、方法和途径有初步的认识，需要具备较好的归纳、猜想和推理能力．3．难点及突破策略难点：对直线与平面垂直的定义的理解和对判定定理的探究．突破策略：1．理解直线与平面垂直的定义，让学生认识到线面垂直是用线线垂直来刻画的，逐步形成概念体系，体会其中的转化思想，这对于高一的学生来讲是比较困难的．所以在设计教学时，首先通过一组图片让学生直观感知直线与平面垂直的具体形象，然后将其抽象为几何图形，再用数学语言对几何图形进行精确的描述，让学生在此过程中体会直线与平面垂直定义的合理性．2．用定义去判定直线与平面垂直是不方便的，如何在较短的时间内，让多数学生找到判定直线与平面垂直的简便方法，这需要一个较好的载体，去引导学生探究直线与平面垂直的判定定理，同时完成对定理条件的确认．所以，在教学过程中，通过折纸试验，精心设置问题，引导学生归纳出直线与平面垂直的判定定理．并且引导学生通过操作、摆出反例模型，对定理的两个关键条件“双垂直”和“相交”进行理解和确认．Ⅳ．教学策略设计为提升学生的学习能力，本节课的教学，采用启发探究式与自主学习相结合的教学方式，通过教师引领学生经历研究直线与平面垂直的判定过程，认识研究的目标与策略，在研究的过程中逐渐完善研究的方法与手段．学生的自主学习，具体落实在三个环节：（1）建构直线与平面垂直的概念时，学生自主举例，归纳特征，数学语言（文字、符号、图形语言）对定义、定理进行准确表述，完善概念．（2）探究直线与平面垂直的判定定理时，根据学生已有学习基础，通过观察、感知、实践、对比，开展自主研究，并通过汇报交流相互提升．（3）定理应用阶段，学生自主研讨发现垂直关系的转化，初步体验定理的应用．本节课立足教材，重视对具体实例的观察、分析，并且给学生提供动手操作的机会，引导学生通过自己的观察、操作等活动获得数学结论，把合情推理作为一个重要的推理方式融入到学生的学习过程中．Ⅴ．教学过程设计一、创设情境引入新课复习空间直线与平面的位置关系，在此基础上提出本节课将重点研究线面的垂直关系．师：前几节课我们已经对直线与平面平行的概念、判定、性质进行了研究，对于直线与平面90相交存在着一种特殊位置关系——垂直．前面我们已经学习了通过两条异面直线所成角为来判断两条直线垂直，那么直线与平面的垂直关系如何从理论上认识呢？【设计意图】直接从已有知识中引出新的学习问题，使学生意识到直线与平面垂直是直线与平面相交中的一种特殊情况并明确本节课学习的内容．另外这样设计也吸引了学生的注意力，激发了学生的好奇心，使其主动参与到本节课的学习中来．二、联系实际感知定义师：同学们能否举出一些日常生活中直线与平面垂直的例子吗？生甲：教室的墙角看成一条直线，它与地面垂直；生乙：教室内的竖直的暖气管与地面垂直；生丙：操场上的旗杆与地面垂直．师：引导学生动手操作身边实例：将书打开直立于桌面．（出示情境问题）[情境问题1]将一本书打开直立在桌面上，观察书脊（想象成一条直线）与桌面的位置关系呈什么状态？此时书脊与每页书和桌面的交线的位置关系如何？[情境问题2]地面上竖立的旗杆与地面的位置关系给人以什么感觉？【设计意图】从实际背景出发，直观感知直线和平面垂直的位置关系，从而建立初步印象，为下一步的教学做准备．[情境问题3]在阳光下观察直立于地面的旗杆及它在地面的影子，随着时间的变化，影子BC 的位置在移动，在各时刻旗杆AB 所在直线与影子BC 所在直线的位置关系如何？使其发现：旗杆所在直线l 与地面所在平面α内经过点B 的直线都是垂直的．进而提出问题：那么直线l 与平面α内不经过点B 的直线垂直吗？为什么？师生活动：学生思考作答, 教师用多媒体课件演示旗杆在地面上的影子随着时间的变化而移动的过程，再引导学生根据异面直线所成角的概念得出旗杆所在直线与地面内的任意一条直线都垂直．【设计意图】第（1）问旨在让学生发现旗杆AB 所在直线始终与地面上任意一条过点B 的直线垂直，第（2）问进一步让学生发现旗杆AB 所在直线始终与地面上任意一条不过点B 的直线也垂直，在这里，主要引导学生通过观察直立于地面的旗杆与它在地面的影子的位置关系来分析、归纳直线与平面垂直这一概念．三、实验探索互动交流1．总结定义——形成概念师生活动：学生回答，教师补充完善，指出定义中的“任意一条直线”与“所有直线”是同意词，同时给出直线与平面垂直的记法与画法．定义：如果直线l 与平面α内的任意一条直线都垂直，我们就说直线 l 与平面α互相垂直，记作： l ⊥α．直线l 叫做平面α的垂线，平面α叫做直线l 的垂面．直线与平面垂直时，它们唯一的公共点P 叫做垂足．画法：画直线与平面垂直时，通常把直线画成与表示平面的平行四边形的一边垂直．【设计意图】示范演示，突出定义的文字、图形、符号这三种语言的相互转化．2．实践对比理解定义练习1：已知下列命题：①如果直线 l 与平面α内的一条直线垂直，则 l ⊥α；②如果直线 l 与平面α内的两条直线垂直，则 l ⊥α；③如果直线 l 与平面α内的无数条直线垂直，则 l ⊥α；④如果直线 l ⊥α ，则直线 l 与平面α内的任意一条直线都垂直．其中正确命题的序号是P l α生：辨析讨论，借助身边的笔、尺进行实践活动，亲身感知、体会线面垂直的定义．师：由命题④给出下列常用命题：【设计意图】通过学生动手操作，突出定义中的“任意”，加深学生对定义的准确理解，层层设问，注重知识的发生发现过程，充分发挥学生的主观能动性，并为进一步推导判定定理做好了铺垫．3．动手实验归纳定理师：如果用定义判断一条直线与一个平面是否垂直，需要寻求平面内的任意一条直线都与该直线垂直，显然不好操作．能否在平面内寻求有限条直线与该直线存在某种位置关系，从而，推断出直线与平面垂直呢？【设计意图】由定义中线线垂直的特征，将线面关系转化为线线关系，由无限问题向有限问题转化．师：继续引导练习1中命题①若只寻求一条直线显然不能得到线面垂直；命题②若寻求两条直线呢？刚才同学们已举出反例：两条直线平行不能得到l ⊥α．追问：那么平面内两条直线除了平行还有什么位置关系？生：沿着教师的启发思路，在平面内寻求两条相交直线操作确认．师生活动：实验：请同学们拿出准备好的一块（任意）三角形的纸片，我们一起来做一个试验：过△ABC 的顶点A 翻折纸片，得到折痕AD ，将翻折后的纸片竖起放置在桌面上，（BD 、DC 与桌面接触）．（如图1）问题1：（1）折痕AD 与桌面垂直吗？（2）如何翻折才能使折痕AD 与桌面所在的平面垂直？【设计意图】通过观察试验，分析折痕AD 与桌面不垂直的原因，探究发现折痕AD 与桌面垂直的条件．师生活动：在折纸试验中，学生会出现“垂直”与“不垂直”两种情况，引导学生进行交流，根据直线与平面垂直的定义分析“不垂直”的原因．学生再次折纸，经过讨论交流，发现当且仅当折痕AD 是BC 边上的高，即AD ⊥BC ，翻折后折痕AD问题2: 由折痕AD ⊥BC ，翻折之后垂直关系，即AD ⊥CD ，AD ⊥BD 发生变化吗？由此你能得到什么结论？（如图2）【设计意图】引导学生发现折痕AD 与桌面垂直的条件：AD 垂直桌面内两条相交直线．A CB D （图1） b a b a ⊥⇒⎭⎬⎫⊂⊥αα师生活动：师生共同分析折痕AD 是BC 边上的高时，翻折之后垂直关系不变，即AD ⊥CD ，AD ⊥BD ．这就是说，当AD 垂直于桌面内的两条两条相交直线CD 、BD 时，它就垂直于桌面．问题3：（1）（如图3）把AD 、BD 、CD 抽象为直线l 、m 、n ，把桌面抽象为平面α，直线 l 与平面α垂直的条件是什么？（2）（如图4）若α内两条相交直线m 、n 与l 无公共点且l ⊥m 、l ⊥n ，直线l 还垂直平面α吗？由此你能给出判定直线与平面垂直的方法吗？【设计意图】让学生归纳出直线与平面垂直的判定定理，并能用符号语言准确表示，使学生明白要判断一条直线与一个平面是否垂直,取决于在这个平面内能否找到两条相交直线和已知直线垂直，至于这两条相交直线是否和已知直线有公共点是无关紧要的．师生活动：学生叙述结论，不完善的地方教师引导、补充完整，并结合“两条相交直线确定一个平面”的事实作简要说明．然后让学生用图形语言与符号语言来表示定理．指出定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．符号语言：.,,,,ααα⊥⇒=⊂⊂⊥⊥l A n m n m n l m l I四、新知应用巩固深化1．例题剖析例1 已知：.,//α⊥a b a 求证：.α⊥b分析过程：证明：在平面α内作两条相交直线n m ,．因为直线α⊥a ，根据直线与平面垂直的定义知n a m a ⊥⊥,；α l n m O （图4）l α n m O （图3） m α na b αα⊥⇒⎩⎨⎧⊥⊥⇒⎪⎩⎪⎨⎧⊥⊥⇒⊥b n b m b b a n a m a a //又因为b a //，所以n b m b ⊥⊥,；又因为α⊂m ，，α⊂n ，n m ,是两条相交直线，所以α⊥b ．师生活动：请学生用文字语言将例1表示出来：如果两条平行线中的一条直线与一个平面垂直，那么另外一条直线也与此平面垂直．【设计意图】不仅让学生学会使用判定定理，而且要让他们掌握分析此类问题的方法和步骤，进一步体会空间中平行关系与垂直关系的转化与联系．２．随堂练习练习2 如图，在三棱锥V-ABC 中，VA=VC ，AB=BC ．求证：VB ⊥AC ．生：学生小组讨论，代表发言，不完善之处，通过合作交流完善补充．师：巡视，必要时参与讨论，关注部分探究意识与能力都薄弱的学生的表现，鼓励他们大胆发言．配合发言学生利用多媒体课件进行展示证明过程．证明：取AC 中点O ，连接VO 和BO∵VA=VC ，BA=BC∴VO ⊥AC,BO ⊥AC,即AC ⊥OV,AC ⊥OB又OV ⊂平面VOB,OB ⊂平面VOB ，且0V ∩OB=O∴AC ⊥平面VOB又VB ⊂平面VOB∴AC ⊥VB ，即VB ⊥AC【设计意图】激励他们主动参与活动，让全体学生成为真正的学习主体．自主探究活动能充分激发学生的相互学习能力．练习3 在三棱锥P-ABC 中，PA ⊥平面ABC ，AB ⊥BC ，PA=AB ，D 为PB 的中点，求证：AD ⊥PC ．生：线面垂直关系的相互转化过程．【设计意图】用投影仪展示部分学生的解题过程，督促学生规范化做题，同时增强学生的应用意识．3．深化认识，提升能力探究题：侧棱与底面垂直的棱柱称为直棱柱.在直四棱柱1111D C B A ABCD -中，当底面四边形ABCD 满足什么条件时，有111D B C A ⊥，说明你的理由.V A BC O师生活动：学生小组合作分析：要证线线垂直，只需满足线面垂直，而要满足线面垂直，还需线线垂直，体会数学中线线垂直与线面垂直相互转化的思想．教师适当加以点拨．【设计意图】扩大知识迁移，在推理论证中感悟、体会联想、归纳、概括的思想方法，达到对新知巩固记忆，加深理解．五、总结提炼概括提升（1）本节课我们学习了哪些知识？你有什么收获?（2）上述判断直线与平面垂直的方法体现了什么数学思想？师生活动：学生发言，互相补充，教师点评完善，归纳出判断直线与平面垂直的三种方法：利用定义，利用判定定理，利用例1的结论．这些方法体现了转化的数学思想．同时强调“平面化”是解决立体几何问题的一般思路．无限问题⇒有限问题【设计意图】以问题讨论的方式进行小结，通过知识和方法两个层面上的总结提炼，增强学生学会归纳的意识，培养总结归纳的能力培养学生反思的习惯．六、课后作业1．理解运用：P74 习题2．3 ； B 组：2，4．2．课后思考：（1）已知一个平面α和一个定点A ，则过A 点可作多少条直线与平面α垂直？（2）已知一条直线 l 和一个定点A ，则过A 点可作多少个平面与直线 l 垂直？（3）在正方体1AC 中，与直线1AC 垂直的棱和对角线有哪些？【设计意图】“理解运用”面向全体学生，旨在掌握并初步运用定理．“思考运用”为学生提供探究的空间，并为下一节三垂线定理的引入做了铺垫．C 1 A A 1 B CD B 1 D 1Ⅵ．教后反思回顾一．关于教学设计的反思本节课的教学设计，力图体现因材施教原则，通过“你是怎么想的？”“你认为这种说法对吗？为什么”等问话形式，促使学生暴露思维过程．在学生已经直观感知直线与平面垂直的基础上让学生亲自动手试验、探究、体验，使其经历知识的形成过程．练习1的引入，起到了承上启下的作用，既加深了学生对线面垂直定义的理解，又为判定定理的推导做好了铺垫．由定义中线线垂直的特征，顺利完成将线面关系转化为线线关系，由无限问题向有限问题转化．二．关于教学过程的反思本节课基本上达到了预期目标，通过发现、概括判定定理的过程，使学生的推理论证能力得到全方位的发展．在认知水平上的升维和在研究方法上的降维，在这“一升一降”的过程中体会转化化归的思想．在直观感知得到直线与平面垂直判定定理的过程中，试验—归纳—猜想--检验的方法为感知获得结论提供了有力的帮助．自我感到不足之处是：1．引导学生归纳出直线与平面垂直的判定定理后，应向学生指出这样归纳得出的定理是需要证明的，只是教材对这一定理的证明不作要求，因此本节课没有给出严格的证明，在后续选修系列2中我们将用向量方法加以论证．2．探究题的研讨没有达到预设的效果．本题思路跳跃性较大，直接让学生去做有一部分学生产生了畏难情绪，导致学生在研讨过程中没有完全放开．如果在探究之前先搭建两个台阶：试判断直线BD 与平面11AC A 是否垂直？直线BD 与C A 1是否垂直？这样学生思维活动就会比较平缓，大部分学生都能顺利探究出问题答案，可以更好地调动更多同学的学习积极性．3.由于本人目前正在高三任教，只能用高一学生进行授课，导致师生间缺少熟知的沟通与交流，因而课堂上学生气氛没有预设的活跃，教师的讲授略多．由于学校条件有限录课的全部过程都是在学生教室完成，学生声音偏小，没有达到预设效果．。

高中数学_直线与平面垂直教学设计学情分析教材分析课后反思

直线与平面垂直一、教学目标1. 知识与技能目标：掌握直线与直线、直线与平面垂直的定义以及直线与平面垂直的判定定理。

2. 过程与方法目标：在教学过程中体现的主要数学能力及数学思想方法。

（1）空间想象能力：认识空间图形的位置关系，遵循从较简单的位置关系认识较复杂的位置关系的原则，从空间的线线垂直过渡到线面垂直，逐步培养和发展学生的几何直观和空间想象能力。

（2）转化的思想方法：在三维与二维空间的转化以及线面关系与线线的转化过程中，体现出转化的思想方法。

（3）逻辑思维能力：通过对判定定理和其推论的证明以及应用，加强学生逻辑思维能力和推理论证能力的培养。

3. 情感、态度与价值观目标：体验线面垂直的判定定理的发现过程和线面垂直的概念在实际问题中的应用，培养创新意识和数学应用意识，提高学生学习数学的兴趣。

并注意在小组合作学习中培养学生的协作精神。

二、教学重点与难点教学重点：直线与平面垂直的概念，直线平面垂直的判定定理及应用。

教学难点：直线平面垂直的判定定理证明思路的理解。

直线与直线垂直的证明思路的理解。

三、教学方法“问题探究式”教学法，通过学生发现问题、分析问题和解决问题的过程，让学生主动参与到教学和学习活动中来，并且始终处于积极地动手操作、问题探究和辨析思考的学习气氛之中，形成以学生为中心的探究性学习活动。

四、教学过程复习回顾：新课认知： 1.直线与直线垂直思考：（1）正方体1111D C B A ABCD -中棱AB 与BC 是什么关系？棱AB 与1AA 呢？（2）正方体1111D C B A ABCD -中与棱1BB 垂直的棱有哪些？直线与直线垂直的定义：2.直线与平面垂直的定义（1）请同学们观察图片，说出旗杆与地面、电视塔与地面的位置有什么关系？（2）思考：一条直线与平面垂直时，这条直线与平面内的直线有什么样的位置关系？定义：图示：用符号语言表示为：思想：3.直线与平面垂直的性质定理：图示：用符号语言表示为：思想：4. 直线与平面垂直的判定定理如图，请同学们拿出准备好的一块（任意）三角形的纸片，我们一起来做一个实验：过△ABC的顶点A翻折纸片，得到折痕AD，将翻折后的纸片竖起放置在桌面上，（BD、DC与桌面接触）.观察并思考：①折痕AD与桌面垂直吗？②如何翻折才能使折痕AD与桌面所在的平面垂直？AA定理：图示：用符号语言表示为：思想：例.如图，已知l∥m，l⊥α，求证：m⊥α。

直线与平面垂直的教案

8.6.2 直线与平面垂直——直线与平面垂直的判定一、教学目标1.探索直线与平面垂直的判定定理，能应用判定定理证明直线和平面垂直的简单问题2.在探索直线与平面垂直判定定理的过程中发展合情推理能力、感悟和体验“空间问题转化为平面问题”“线面垂直转化为线线垂直”，进一步感悟数学中以“化繁为简”的转化思想.二、教学重难点重点：直线与平面垂直的判定定理的理解难点：直线和平面垂直的判定定理及其应用三、教学过程1.复习回顾直线与平面垂直的定义：一般地，如果直线 l 与平面α内的任意一条直线都垂直，我们就说直线l 与平面α互相垂直，记作l ⊥α．直线l 叫做平面α的垂线，平面α 叫做直线l 的垂面．直线与平面垂直时，它们唯一的公共点P 叫做垂足．注：通过解读直线与平面垂直的定义，得出下面这个结论：,.l a l a αα⊥⊂⇒⊥简记为：线面垂直，则线线垂直.2.探究新知下面我们来研究直线与平面垂直的判定，即探究直线与平面垂直的充分条件．根据定义可以进行判断，但无法验证一条直线与一个平面内的所有直线都垂直．那么，有没有可行的方法？【探究活动】引导学生动手操作；如图准备一块三角形纸片ABC，过顶点A翻折纸片，得到折痕AD，将翻折后的纸片竖起放置在桌面上，并请学生思考;（1）折痕AD与桌面垂直吗？不一定（2）如何翻折才能得到使折痕AD与桌面垂直？为什么？折痕AD是BC边上的高根据基本事实推论2可知：两条相交直线可以确定一个平面，两条平行直线也可以确定一个平面。

猜想：如果一条直线和一个平面内的两条相交直线都垂直，这条直线就和这个平面垂直.直线与平面垂直的判定定理：如果一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直．图形语言：符号语言：简记为：线线垂直⇒线面垂直思考两条相交直线可以确定一个平面，两条平行直线也可以确定一个平面，那么定理中的“两条相交直线”可以改为“两条平行直线”吗？你能从向量的角度解释原因吗？如果改为“无数条直线”呢？平面内的两条相交直线代表两个不共线向量，而平面内的任意向量都可以以它们为基底进行线性表示，从而平面内的两条相交直线可以“代表”这个平面上的任意一条直线；而两条平行直线所表示的向量是共线的，它们不能作为平面内的任意向量的基底，用它们不能“代表”这个平面上的任意一条直线．如果将上述问题中的“”两条相交直线“”改为“无数条直线”的话，答案也是否定的。

直线与平面垂直教案

直线与平面垂直教案
一、教学目标
1.借助对图片、实例的观察，抽象概括出直线与平面垂直的定义，并能正确理解直线与平面垂直的定义。

2.通过直观感知，操作确认，归纳直线与平面垂直判定的定理，并能运用判定定理证明一些空间位置关系的简单命题，进一步培养学生的空间观念。

3.让学生亲身经历数学研究的过程，体验探索的乐趣，增强学习数学的兴趣。

二、教学重点、难点
1.教学重点：操作确认并概括出直线与平面垂直的定义和判定定理。

2.教学难点：操作确认并概括出直线与平面垂直的判定定理及初步运用。

三、课前准备
1.教师准备：
教学课件。

2.学生自备：
三角形纸片、铁丝（代表直线）、纸板（代表平面）、三角板。

四、教学过程设计
1.直线与平面垂直定义的建构：
（1）创设情境：
①请同学们观察图片，说出旗杆与地面、高楼的侧棱与地面的位置有什么关系？
②请把自己的数学书打开直立在桌面上，观察书脊与桌面的位置有什么关系？
③请将①中旗杆与地面的位置关系画出相应的几何图形。

（2）观察归纳：
①思考：一条直线与平面垂直时，这条直线与平面内的直线有什么样的位置关系？
②多媒体演示：旗杆与它在地面上影子的位置变化。

③归纳出直线与平面垂直的定义及相关概念。

定义：如果直线l与平面α内的任意一条直线都垂直，我们就说直线l与平面α互相垂直，记作：l⊥α。

直线l叫做平面α的垂线，平面α叫做直线l的垂面．直线与平面垂直时，它们唯一的公共点P叫做垂足。

全国高中数学青年教师展评课直线与平面垂直教学设计

课题：1.2.3 直线与平面垂直教材：苏教版高中数学·必修 2江苏省扬中市第二高级中学宫建红【教学内容解析】本节课是苏教版教材必修2中第一章第二节的内容，属于新授概念原理课.其中直线与平面垂直的概念、判定定理的形成是教学重点.这是直线与平面垂直在本节中的位置.线面垂直是在学生掌握了线在面内，线面平行之后紧接着研究的线面相交位置关系中的特例.线面平行研究了定义、判定定理以及性质定理，为本节课提供了研究内容和研究方法上的范式.线面垂直是线线垂直的拓展，又是面面垂直的基础，且后续内容如：空间的角和距离等又都使用它来定义，在本章中起着承上启下的作用.通过本节课的学习研究，可进一步完善学生的知识结构，更好地培养学生观察发现、空间想象、推理能力，体会由特殊到一般、类比、归纳、猜想、化归等数学思想方法．因此，学习这部分知识有着非常重要的意义．【教学目标设置】1.学生通过对实例、模型的观察、抽象,概括出直线与平面垂直的定义，发现、猜想、归纳直线与平面垂直的判定定理．2.在定义、定理的探究活动中，学生通过独立思考和合作交流，发展类比、归纳等合情推理能力、逻辑思维能力和空间想象能力．3.学生运用特殊化、类比、化归等数学思想，体验了研究空间关系的一般方法.4.在探究线面垂直的定义和判定的过程中，体会数学的严谨、简洁之美，体验探究发现的乐趣，培养善于观察、勇于探索的良好习惯.【学生学情分析】1.学生已有的认知基础学生能够感知生活中有大量的线面垂直关系，已经掌握了线线垂直、线面平行的相关知识，从而具备了研究空间位置关系的经验，也体会了立体几何中化归的数学思想方法.2.达成标所需要的认知基础要达成本节课的目标，这些已有的知识和经验基础不可或缺，还需要整体上把握本节课的研究内容、方法和途径，能运用类比、化归等数学思想，同时具备较好地观察发现、空间想象、合情推理、抽象概括等能力，以及独立思考、合作交流、反思质疑等良好的数学学习习惯.我校为普通高中，招收的学生大部分基础薄弱，自主学习能力差.进入高一，虽然能领悟一些基本的数学思想与方法，但还没有形成完整、严谨的数学思维习惯，对问题的探究能力也有待培养.3.难点及突破策略难点：1.运用类比、化归等数学思想方法来研究直线与平面垂直的定义，突破“任意”的生成和理解.3.探究、归纳、理解直线与平面垂直判定定理，突破“无限”与“有限”的转化.突破策略：1.启发学生明确研究的内容与方法，从总体上认识研究的目标与手段．2.引导学生经过直观感知、操作确认、思辨论证的过程形成线面垂直的定义和判定定理.3.发动学生通过问题串交流、汇报、展示思维过程，相互启发.【教学策略分析】根据学生已有学习基础，为提升学生的学习能力，本节课的教学，采用教法和学法如下：1.教师创设情境，学生列举实例，形成关于线面垂直的直观感知.2.教师启发引导，学生明确按照“定义——判定——性质”的研究程序，强化空间位置关系的常用研究策略——降维化归.3.教师以问题串为载体，驱动学生主动参与知识建构、合作探究.4.教师分层设计知识应用，引导反思，学生深化理解，形成知识体系.【教学过程】一、创设情境、建构定义1.回顾旧知引入课题[问题1]直线和平面有几种位置关系？[问题2] 已经掌握了直线和平面平行的哪些内容？[问题3]直线与平面相交中最特殊的一种位置关系是什么？[问题4]研究关于“直线与平面垂直”的什么内容？[问题5]怎样研究“直线与平面垂直”呢？师生活动：通过问题让学生复习了已经学过的知识，让学生利用手中的工具摆出“线面相交”的情形，并指出其中最特殊的情况，并进行命名.学生能说出研究“线面垂直”的哪些内容和怎样去进行研究.设计意图：简单回顾直线与平面的三种位置关系和线面平行的研究内容、研究方法，引出直线与平面相交时的特殊情况——“直线与平面垂直”及其研究内容.2.创设情境启发定义情境1“直线与平面垂直”在我们的生活中有许多直观的感知，请举例.几何体中“直线与平面垂直”形象吗？请举例.情境2有没有与地面不垂直的建筑物呢？请举例.[问题6]为什么感觉斜塔与地面不垂直？[问题7]关于“垂直”我们已知的是什么？[问题8]能不能用已知的“线与线的垂直关系”来刻画未知的“线与面的垂直关系”呢？师生活动：学生能够从直观感知入手，通过教师的追问，引起学生思考，何刻画出斜塔与地面不垂直的原因，进而抓住线面“垂直”就是平面内找不到与它不垂直的直线.设计意图：旨在让学生直观感知“线面垂直”.学生自由举例，列举生活中，几何体中“线面垂直”的例子.大量丰富的正面例子有助于学生观察不同的例子所具有的共同特征，形成关于线面垂直的直观感知.再从反例——“比萨斜塔”，借助“比萨斜塔”的“斜”启发定义.正反例的对比中更容易抓住事物的本质与核心.3.验证猜想建构定义[问题9]一条直线真的能与一个平面内的所有直线都垂直吗？有这样的实际模型吗？师生活动：通过教师提问：“圆锥的轴所在的直线与底面内所有的直线都垂直吗？”学生独立思考，小组交流，汇报.教师再用几何画板演示，进行说明猜想的合理性.设计意图：对于定义合理性的解释、猜想正确性的检验，直观演示能起到不可替代的效果.因此通过圆锥的实例，说明一条直线与平面内的所有直线都垂直的状态是存在的，也让学生的认知结构中拥有了关于概念的实际模型.4.认识定义巩固深化[问题10]你能给“直线与平面垂直”下个定义吗？师生活动：通过辨析定义——“‘任意’的含义是什么？等价于‘所有’吗？等价于‘无数’吗？”；通过三种语言表示定义；通用利用定义证明例题1——“求证：如果两条平行线中的一条垂直于一个平面，那么另一条也垂直与这个平面.”等多个环节进一步认识定义，体会定义中“双向叙述”的功能.并在作图的同时介绍垂线，垂面，垂足等概念.设计意图：对定义进行多角度和深入理解，对数学思维方法的渗透和对研究问题的方法的指导能在教学中达到事半功倍的效果.例题1的教学，在学生独立思考后，让学生板演展示和相互评价，让学生得到充分的训练和表达，同时对证明格式提出规范性要求.证明之后，再对此题重新深刻理解，从直观的判断变为理性的思考，符合学生的认知规律.定义的认识和例题的证明中多次使用三种语言转换，也有助于学生空间想象能力的培养.二、简化定义获得猜想[问题11]工人怎样检验旗杆是否与地面垂直呢？师生活动：通过检验“旗杆与地面是否垂直”的问题激发学生寻求判定线面垂直的新方法.学生有要简化定义中的“任意一条直线”为“有限条直线”的想法.教师进而追问:简化成“一条直线”行吗？“两条直线”呢？学生进行思考，辩证.学生能够猜想到：一条直线垂直于平面内的两条相交直线就可以得到一条直线垂直于这个平面.设计意图：通过询问学生工人如何检验旗杆是否与地面垂直的？让学生感受到了寻求判断线面垂直新方法的必要性，又开启了他们简化定义中“任意一条”的想法，于此同时对每一种想法进行辨析，培养了学生的空间想象能力，而后获得关于线面垂直判定定理的猜想.三、汇报交流形成定理1.直观感知师生活动：学生带着猜想，寻找辅证的实例.2.操作试验师生活动：学生带着猜想，通过实验：“（1）怎样将一本书立在桌面上，使得书脊能与桌面垂直？这样的书至少需要几页呢？（2）将手中的练习纸折叠，折痕满足什么条件，折痕与桌面垂直？”进行动手操作，确认猜想.3.直观演示师生活动：教师通过几何画板演示进一步说明猜想的合理性,学生进一步增加直观体验.4.形成判定师生活动：学生叙述线面垂直的判定定理，并用图形语言和符号语言表示“直线与平面垂直”的判定定理.教师进行点评与总结.am n a mnA ,,a m a n m n A a m n aa a ü^^???轣y ?烫?t 师：如图，哪一幅作图更具有一般性？说明理由.师：判定定理也是由线“线”垂直推出线“面”垂直.这里的“线”较之定义发生了怎样的变化？生：已经简化为了“面”内两条相交直线.师：“线不在多，相交则行”.现在去判断线面垂直有哪些方法？生：可以用定义，也可以用判定定理.师：这样，除了定以外，我们就又增加了一个判定“线面垂直”的方法.在这里，我们把“线面垂直的问题转化为线线垂直”来解决，充分体现了“降维转化”的思想.我们解决问题时也要选择最佳方法.设计意图：获得猜想是合情推理的第一步，如何让学生在不加证明的情况下，心悦诚服的接受“判定定理”呢？于是引导学生带着猜想，寻找实例验证，再通过折纸试验和几何画板演示双重操作确认，进一步增强学生的直观感受的同时进行理性思考，最终形成定理.接着同样要求学生用三种语言表示它，认识定理.四、数学应用巩固深化[问题11]现在你是工人，怎样检验旗杆是否与地面垂直呢？例2：在正方体ABCD-A1B1C1D1中，求证：（1）AC ⊥平面BDD1（2）求证：AC ⊥BD1师生活动：学生分析条件以及要证明的结论，合理选择方法，独立求解，教师板书示范解题过程,并引导学生进行归纳：线线垂直线面垂直.设计意图：判定定理的应用分为三个层次进行：第一层次让学生理解、记忆定理并进行简单运用；第二层次通过空间简单位置关系的证明，培养学生逻辑推理能力，重视对学生思考策略的引导和启发，通过教师示范、学生互评规范证明题的书写；第三层次是训练学生灵活应用判定定理和定义，能适当的进行线线和线面位置关系之间的转化.五、概括总结分层作业[问题12]本节课我们学习了哪些知识？掌握了哪些方法？体会了哪些思想？今后我们还要学习什么呢？师生活动：学生思考、回答，教师适当点拨、补充.设计意图：开放式小结，使得不同的学生有不同的学习体验和收获. 引导学生主动建构，形成知识体系；预测未来的学习内容，旨在进一步感悟数学思想；规范立几学习，提出能力要求.课后作业必做题：第34页第1（1）（2），3题；第36页第6,7题选做题：第37页第10题拓展题：运用今天的研究方法，你还能进行其它位置关系的探究吗？设计意图：分层布置作业，满足不同学生的学习能力要求.。

直线与平面垂直教学设计

直线与平面垂直一、新知导学：1、两直线垂直：如果两条直线相交于一点或经过平移后,并且交角为，则称这两条直线O2、线面垂直：如果一条直线（AB）和一个平面α相交于点0,并且和这个平面内过交点（0）的任何直线都,我们就说.若直线I与平面α垂直记作o画直线和平面垂直时，通常要__________________________________________ 3、线面垂直的判定定理：如果一条直线与一个平面内的两条____ 直线都垂直，则该直线与这个平面_________ . ______ 1用符号语言表示为：∕⅛⅜推论1：如果在两条平行直线中，有一条垂直于平面，那么另一条直线也_________ .推论2：如果两条直线垂直于同一个平面，那么4、线面垂直的性质：如果一条直线垂直于一个平面，那么它就和平面内的任意一条直线O用符号语言表示为：___________________________二、典例分析例1、有一根旗杆高8阳，它的顶端A挂一条长IOm的绳子，拉紧绳子并把它的下端放在地面上的两点（和旗杆脚不在同一直线上）GO ,如果这两点都和旗杆脚8的距离是6小，那么旗杆就和地面垂直，为什么？变式：如图，点P是平行四边形ABCD所在平面外一点，。

是对角线AC与BD的交点，且PA=PC, PB=PD. 求证：PO_L平面ABCD例2过一点和已知平面垂直的直线只有一条已知：平面α和一点P求证：过点P与α垂直的直线只有一条例3、已知：空间四边形ABCO, AB = AC f求证：BC-LAD0变式：已知：点。

是ΔABC的垂心，PO_L平面ABC,垂足为。

, 求证：PAYBC.三、课堂小结：证明线面垂直的方法:。

《直线与平面垂直的性质》教学设计、导学案、同步练习

《8.6.2 直线与平面垂直》教学设计第2课时直线与平面垂直的性质【教材分析】本节课选自《普通高中课程标准数学教科书-必修第二册》（人教A版）第八章《立体几何初步》，本节课主要直线与平面垂直的性质及其应用，直线到平面的距离、两平行平面间的距离。

课本从长方体的侧棱垂直与底面，考虑侧棱之间的关系入手，通过用反证法证明垂直与一个平面的两直线平行，引入直线与平面垂直的性质定理，通过例题引入直线到平面的距离的定义以及两平行平面之间的距离定义。

直线与平面垂直的性质定理是判断两直线平行的一种方法。

【教学目标与核心素养】【教学重点】：直线与平面平行的性质定理，直线到平面的距离，两平行平面的距离；【教学难点】：用直线与平面平行的性质定理解决相关问题。

【教学过程】2.直线与平面垂直的判定定理【答案】一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。

二、探索新知观察：如图，长方体ABCD —A 1B 1C 1D 1中，棱AA 1，BB 1，CC 1，DD 1所在直线与底面ABCD 的位置关系如何？它们彼此之间具有什么位置关系？【答案】平行思考：如图，已知直线a ,b 和平面α，如果a ⊥α,b ⊥α，则那么直线a ,b 一定平行吗？已知：a ⊥α， b ⊥α 求证：a ∥b ．证明：假设b 不平行于a,是经过点O 与直线a 平行的直线。

因为。

即经过同一个点O 的两条直线b,c 都垂直于平面，这是不可能的。

因此，a//b.1.直线和平面垂直的性质定理：垂直于同一个平面的两条直线平行. 符号语言：图形语言：作用：证线线平行。

例1.如图，直线平行于平面，求证：直线上各点到平面的距通过观察与思考，得到直线与平面平行性质定理，的提高学生的解决问题、分析问题的能力。

通过符号语言与图形语言，让学生进一步理解直线与平面垂直的性质定理，提高学生的概括能力。

c O b ,=α αα⊥⊥c a c a 所以,,//αb a b a //,⇒⊥⊥ααl αl α离相等。

高中数学必修二《直线与平面垂直的性质》优秀教学设计

三、即时练习：
判断下面命题的真假：
①平行于同一条直线的两条直线互相平行;
②垂直于同一条直线的两条直线互相平行;
③平行于同一个平面的两条直线互相平行；
④垂直于同一个平面的两条直线互相平行.
四、命题的变式探究
1：直线与平面垂直的性质2反映了多线垂直于一面
，则线线平行。那么请大家思考一下多面垂直于一线
则面面之间有何关系呢？
你是怎么样得到这些线之间的关系的呢？你能证明吗？
（图1）
由于我们很难判断两直线是否在一个平面中，因此我们很难判定与是否平行，那么我们用下面的方法试试！（直线与只有两种位置关系，① ,② ,如果否定②，那么①成立）
已知求证
（图2）
●线面垂直的性质2：
垂直于同一平面的两条直线互相平行
图形语言表示：符号语言表示：
2：交换“平行”与“垂直”
，
，
3：变“直线”为“平面”
，
，。
4交换“条件”与“结论”
,ห้องสมุดไป่ตู้
, .
五、理论迁移：
例1：如图3，已知，于点 , 于点 , ，．求证： ∥ ．
（图3）
●解题反思
本题证明的思路是什么？其关键步骤是什么？体现了什么思想方法？
六、课堂小结
1.本节课学习了什么知识？
2.本节课涉及到了什么数学思想与方法？
一条直线与一个平面内的直线都垂直，则该直线与此平面。
二、学习探究
直线与平面垂直的判定定理，解决了直线与平面垂直的条件问题；反之，在直线与平面垂直的条件下，能得到什么结论呢？
首先由线面垂直的定义可以得到:
●即线面垂直的性质1：。
生活中有很多线面垂直的例子，你能举出在教室中有哪些线面垂直的例子？

高中数学《直线和平面垂直》三篇教学设计的评析之一

高中数学《直线和平面垂直》三篇教学设计的评析之一Title: Analysis of Three Lesson Designs on "Perpendicular Lines and Planes" in High School MathematicsIntroduction:In this article, we will analyze and evaluate three different lesson designs on the topic of "Perpendicular Lines and Planes" in high school mathematics education. Each lesson design aims to provide students with a thorough understanding of the concepts and applications related to perpendicular lines and planes. By examining the strengths and weaknesses of each lesson design, we will gain insights into effective teaching strategies for this topic.Lesson Design 1: Understanding the Concept of PerpendicularityIn this lesson, the teacher introduces the concept of perpendicular lines and planes through real-life examples. The lesson starts with a brief discussion on the characteristics of perpendicular lines and planes, focusing on their 90-degree angle formation. To facilitate understanding, visual aids such as geometrical drawings and interactive diagrams are employed.After the introduction, students are given the opportunity to explore various scenarios involving perpendicular lines and planes. They are encouraged to identify perpendicular relationships in different objects, ranging from common household items to architectural structures. By actively engaging with the materials, students develop a deeperunderstanding of the concept of perpendicularity and its relevance in everyday life.To consolidate their learning, students are then provided with practical exercises and problem-solving tasks. These activities challenge students to apply their knowledge of perpendicular lines and planes to solve mathematical problems accurately. The teacher also ensures that students receive immediate, constructive feedback during this process to enhance their understanding.Strengths:- Real-life examples and visual aids make the concept more relatable and engaging.- Active learning through exploration and problem-solving fosters deeper comprehension.- Immediate feedback helps students rectify misconceptions promptly.Weaknesses:- The lesson may lack a formal introduction to mathematical definitions and notations.- The focus on real-life examples could lead to difficulty in transferring knowledge to abstract mathematical problems.Lesson Design 2: Analyzing Geometrical Properties of Perpendicular LinesThis lesson design employs a more deductive approach to understanding perpendicular lines and planes. The teacher begins by presenting the basicdefinitions and properties of perpendicular lines using abstract mathematical language. Clear explanations and illustrative examples are provided to ensure students grasp key concepts.Following the introduction, students are given a set of geometric figures and shapes. They are required to identify and analyze properties that are directly related to perpendicular lines and planes. Through guided practice and independent exploration, students uncover the geometric principles governing perpendicularity.To reinforce their understanding, students engage in collaborative activities, such as group discussions and peer teaching. This encourages active participation and fosters a supportive learning environment. The teacher also encourages students to apply the acquired knowledge to solve practical problems and examine its applications in various fields.Strengths:- Deductive approach provides a solid foundation in mathematical definitions and properties.- Collaborative activities promote peer learning and increase student engagement.- Practical problem-solving tasks enhance the application of knowledge.Weaknesses:- The abstract nature of the lesson may lead to difficulties in connecting with real-life applications.- Limited emphasis on concrete examples may hinder some students' comprehension.Lesson Design 3: Enhancing Visualization through Interactive TechnologyThis lesson design utilizes interactive technology to enhance students' visualization skills in understanding perpendicular lines and planes. Students are introduced to geometric software or virtual manipulatives, which allow them to dynamically interact with 3D representations of lines and planes.The teacher guides students through a series of interactive activities and simulations. Students manipulate virtual objects and observe the resulting changes in the relationships between lines and planes. The teacher encourages students to make connections between their observations and the mathematical concepts of perpendicularity.To consolidate their understanding, students engage in hands-on activities involving physical manipulatives, such as wooden blocks or rulers. This tactile experience further strengthens their visualization skills and solidifies their understanding of perpendicular lines and planes.Strengths:- Interactive technology provides a dynamic and engaging learning experience.- Visualization skills are developed and reinforced through hands-on activities.- Connections between concrete manipulatives and abstract concepts are facilitated.Weaknesses:- Limited access to technology or resources may hinder the implementation of this lesson design.- The heavy reliance on visual aids may overshadow the importance of formal mathematical notation.Conclusion:Each of these lesson designs offers unique approaches to teaching "Perpendicular Lines and Planes" in high school mathematics. While the first design prioritizes real-life examples, the second focuses on deductive thinking, and the third emphasizes visualization and interactive technology. Consideration of students' diverse learning styles and preferences is crucial in selecting an effective lesson design. By incorporating elements from each design and adapting them to individual teaching contexts, educators can create engaging and comprehensive learning experiences for their students.。

《直线与平面垂直判定定理》教学设计

A．①②B．②③④
C．①②④D．①②③
通过例1的铺垫，进一步感受如何运用直线与平面垂直的判定定理证明线面垂直，体会转化思想的应用。
进一步深化理解概念。
【教师设计4】
教学环节
教学过程
设计意图
四．总结回顾，布置作业
（六）总结反思——提高认识
（1）通过本节课的学习，你学会了哪些判断直线与平面垂直的方法？
（2）上述判断直线与平面垂直的方法体现了什么数学思想？
生：折痕AD是BC边上的高的时候，折痕AD所在的直线与桌面所在的平面垂直。
师：由折痕AD⊥BC，翻折之后垂直关系AD⊥CD，AD⊥BD发生变化了么？
问题2：在你翻折纸片的过程中，纸片的形状发生了变化，这是变的一面，那么不变的一面是什么呢？（可从线与线的关系考虑）如果我们把折痕抽象为直线，把BD、CD抽象为直线，把桌面抽象为平面 (如图3)，那么你认为保证直线与平面垂直的条件是什么？
2.动手操作——确认定理
（学生实验）请同学们拿出一块三角形纸片，我们一起做一个试验：过三角形的顶点A翻折纸片，得到折痕AD（如图1），将翻折后的纸片竖起放置在桌面上（BD、DC与桌面接触）
问题1：（1）折痕AD与桌面垂直吗？
(2)如何翻折才能使折痕AD与桌面所在的平面垂直?
师：请同学到台前来演示一下你的实验
思考：如图6，已知，则吗？请说明理由．
师生活动：学生思考讨论，教师适时引导，最后教师给出详细的证明过程，给学生以示范。
（五）练习巩固与升华
1、下列命题正确的是（）
①如果直线l与平面α内的无数条直线垂直,则l⊥α ;
②如果直线l与平面α内的一条直线垂直,则l⊥α;
③如果直线不垂直于α,则α内没有直线与l垂直;

高中数学优秀课评比教案直线与平面垂直的判定教案

课题：直线与平面垂直的判定（一）授课教师：江苏省宿迁中学张明星教材：苏教版·必修二教学目标1.通过对图片、实例的观察，抽象概括出直线与平面垂直的定义，能正确理解直线与平面垂直的定义，并能简单的运用定义。

2.通过类比联想，直观感知，操作确认，归纳出直线与平面垂直判定的定理，并能运用判定定理证明一些的简单命题。

3.让学生亲身经历数学研究的过程，体验探索的乐趣，增强学习数学的兴趣，培养主动探究的习惯，并渗透事物间相互转化和理论联系实际的辨证唯物主义观点.教学重点、难点教学重点：操作确认并概括出直线与平面垂直的定义和判定定理。

教学难点：操作确认并概括出直线与平面垂直的判定定理及初步运用。

教学方法与教学手段教学方法：启发式与实验探究式相结合教学手段：计算机、多媒体课件、三角形卡纸教学过程一、直线与平面垂直定义的构建1、创设情境——感知概念复习直线与平面的三种位置关系，指出已经系统学习过直线与平面平行的定义、判定定理和性质定理后，进一步提出问题：你认为直线与平面相交中哪种情况最特殊？最值得研究？展示几幅生活中常见的图片，让学生指出其中给人以“直线与平面垂直”形象的部分，从中抽取出直线与平面垂直的几何图形，进而引出课题：直线与平面垂直.设计意图：从数学知识内部发展和生活应用两个角度让学生认识到研究“直线与平面垂直”的必要性.并通过抽象的三部曲：实物模型空间直观图，抽象出直线与平面垂直的几何图形，让学生直观感知直线与平面垂直的位置关系，使学生头脑中产生直线与平面垂直的初步印象．2、观察归纳——形成概念从陀螺中抽象出圆锥模型，学生通过旋转纸片，感受圆锥的形成过程，并思考：问题1：旋转轴与底面内哪些直线垂直？（教师播放动画）并追问为什么？进而归纳出直线与平面垂直的定义.设计意图：在具体的情境中，让学生感知直线与平面垂直的本质属性，体会到定义的合理性．3、讨论辨析——深化概念引导学生用数学符号将定义表示出来，接着提出问题：（1）如果将定义中的“任意一条直线”改成“无数条直线”，结论还成立吗？（2）若l⊥α,m α，则l⊥m成立吗？设计意图：通过对两个问题的讨论辨析，让学生加深对概念的理解,并让学生体会到通过定义可以实现“线线垂直”与“线面垂直”的相互转化.二、直线与平面垂直判定定理的构建1、类比联想——提出问题根据线面平行的判定定理进行类比，通过不断的猜想和分析，最终提出问题：如果一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直吗？设计意图：从学生的已有知识出发，类比联想，符合学生的认知规律，使学生的思维顺畅，并激发学生进一步探究的欲望．2、动手实验——提出猜想演示实验过程：先将三角形纸片折叠一次，再将纸片略打开放置于桌面上，A使折痕与桌面相交．思考：（1）折痕与桌面一定垂直吗？（2）如何折叠才能使折痕与桌面所在的平面垂直？学生解释，并给出不同的折法.问题2：这两种不同的折法有何共同特点？你有何猜想？猜想：若一条直线和平面内的两条相交直线垂直，那么这条直线垂直于这个平面设计意图：一方面让学生从另一个角度来理解定义——只要直线l 与平面α内有一条直线不垂直，那么直线l 就与平面α不垂直；另一方面让学生通过讨论不同折法的共同特点，直观感知并归纳猜想出直线与平面垂直的判定定理.3、合作探究——形成定理问题3：为什么折痕能与桌面所在的平面垂直？学生讨论探究，以折痕AD 为轴转动纸片，来说明AD 与平面α内过D 点的所有直线都垂直，平面α内不过D 点的直线，可以通过平移经过D 点，说明它们与AD 都垂直，符合直线与平面垂直的定义，验证了猜想的正确性（辅以动画演示），得出直线与平面垂直的判定定理.直线与平面垂直的判定定理：一条直线与一个平面内的两条相交直线垂直，则该直线与此平面垂直．让学生用图形语言表示判定定理并辨析：直线l 是否必须经过经过直线m 与直线n 的交点O ？符号语言：m l ⊥，n l ⊥，α⊂m ，α⊂n ，m n O =⇒l α⊥．设计意图：让学生通过动手操作，经历观察、归纳、猜想及验证的探究过程，增强学生的学习兴趣，提高学生的抽象概括能力，培养学生严谨细致的作风在理解直线与平面垂直的判定定理时，强调“两条”、“相交”缺一不可.指出要判断一条直线与一个平面是否垂直,取决于在这个平面内能否找到两条相交直线与已知直线垂直.三、初步应用——深化认识1. 图形感知——提出命题从图中可以看出边AB 与折痕平行，边AB 是否也与平面α垂直？本题可以使用直线与平面垂直的定义来证明，也可以使用直线与平面垂直的判定定理来证明，让学生展现其解决问题的思路，并通过学生的交流，完善并规范解题过程的书写.设计意图：一方面让学生学会使用定义和判定定理，让他们掌握分析此类问题的方法和步骤，另一方面让学生学会思考，增强其逻辑推理能力，并给学生更多的发展机会.问题4：判定直线与平面垂直有哪些方法？学生总结出利用定义和定理两种方法.设计意图：让学生在头脑中初步形成将线面垂直转化为线线垂直的意识，为下面的应用打下铺垫.请学生用文字语言将例题表述出来——如果两条平行线中的一条直线与一个平面垂直，那么另外一条直线也与此平面垂直．2. 命题变式——探究证明将命题的题设和结论交换，得出变式例题.例2.已知：AB α⊥，DE α⊥．求证：AB //DE ．本题证明有一定困难，需要适当的引导，师生共同探究，完成证明，进而总结出直线与平面的性质定理．性质定理：如果两条直线垂直于同一个平面，那么这两条直线平行符号语言：a ⊥α,b ⊥αa//b 图形语言：设计意图：“授人以鱼，不如授人以渔”，在共同探究的过程中，不仅体现了知识的运用，更重要的是展示了思维的过程，增强学生分析问题、解决问题的能力.四、回顾总结，反思升华问题5：这节课，我们有哪些收获？知识方面：线面垂直的定义、线面垂直的判定定理、线面垂直的性质定理．方法方面：掌握了立体几何中研究线面位置关系思路与方法．数学思想：转化思想（空间平面、无限有限、线面垂直线线垂直、平行垂直）五、布置作业，巩固理解（1）阅读课本相关内容进行复习；（2）课本第41-42页习题1.2（2）的“感受·理解”部分的第7题和第9题；（3）课本第42页习题1.2（2）的“思考·运用”部分的第12题.ba α 线线平行性质定理 a//b,a ⊥b b ⊥α a//b a ⊥α,b ⊥α 判定定理（两相交直线）定义法（任一直线）线线垂直线线平行线面垂直。

全国高中数学青年教师展评课直线与平面垂直的判定教学设计(江西抚州一中)

直线与平面垂直的判定（第1课时）【教材】高中数学教材必修2（北师大版），第一章“立体几何初步”，第6节“垂直关系的判定”（第1课时）. 1．教学内容解析本节教学内容主要有：直线与平面垂直的定义、直线与平面垂直的判定及其应用.边BC，而另一直角边AC图1是通过让学生观察长方体内线面位置关系来感悟的：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直.该定理把原来定义中要求与任意一条（无限）直线垂直转化为只要与两条（有限）相交直线垂直就行了，从而使直线与平面垂直的判定具有可操作性.直线与平面垂直是直线和平面相交的一种特殊情况，它是空间中线线垂直的拓展，又是面面垂直的基础，是空间中垂直关系之间转化的轴心，同时它也是直线与平面所成的角等内容的基础.因而它是空间点、线、面位置关系中的核心概念之一.2．教学目标设置●知识与技能理解直线与平面垂直的定义和判定定理，并能运用直线与平面垂直的定义和判定定理解决一些简单的问题.●过程与方法体验直线与平面垂直概念的形成过程，培养观察与抽象概括能力；体验直线与平面垂直判定定理产生的过程，体会知识产生的必要性与合理性，培养空间观念，发展合情推理能力；在知识的运用过程中体会转化的思想方法.●情感、态度与价值观通过不断地提出问题、解决问题，培养学习热情，体验探索乐趣，培育“数学源于实践又服务于实践”的辩证观.3．学生学情分析学生已学过了两直线垂直关系的判定，以及线面平行关系的判定和性质，有了“通过观察、操作，然后抽象概括出数学结论”的经验与体会，有一定的空间想象能力、推理论证能力以及运用图形符号进行交流的能力，具备学习本节知识的基础.存在的认知困难之一是如何从直线和平面垂直的直观形象中抽象概括出直线和平面垂直的定义.因为学生直观感知中的形象与定义中“直线与平面内任意一条直线都垂直”的内涵有一定的潜在距离.存在的认知困难之二是在探究直线与平面垂直的判定定理过程中，对为什么要且只要“两条相交直线”的理解.因为定义中“任意一条直线”指的是“所有直线”，这种有“有限”代替“无限”的过程在一定程度上会使学生产生思维障碍.4．教学策略分析数学教学是数学思维活动的教学，而思维又是从问题开始的，所以本节课在总体上采用“问题引导”策略.通过精心设计一个个问题，激发学生的求知欲，并通过观察、分析、实验、说理、自主探究、合作交流等活动，领悟定义与判定定理的本质内涵，体会解决问题过程中思路的形成过程，感悟蕴涵其中的数学思想方法.同时借助多媒体辅助教学，增加教学的直观性，提高课堂教学效率.针对学生的第一个认知困难，教学中首先通过实例让学生直观感知直线与平面垂直的形象，然后利用“圆锥或圆柱形成”的情境，从中抽象概括出定义，体会其合理性.针对学生的第二个认知困难，教学中利用“折纸”实验，引导学生操作、观察、思考与说理，挖掘实验的数学内涵，对定理中的两个关键条件“双垂直”和相交进行确认.5．教学过程设计（一）提出问题问1：直线与平面的位置关系有哪几种？（预设：在平面内、平行与相交三种）直线在平面内、直线与平面平行这两种情形我们已经系统研究过了，接下来我们研究直线与平面相交的情形.观察以下图片：图2问2：如果将图片中的旗杆、比萨斜塔和电线杆抽象为直线，地面抽象为平面，如上图，请问这三个图形中的直线与平面的位置关系分别是怎样的？反馈：它们的位置关系均为相交，但旗杆给我们的印象是垂直，而比萨斜塔和被大风吹歪了的电线杆则给人以不垂直的印象. 问题：假如我们要将被大风吹歪了的电线杆扶直，请问：怎样才能知道电线杆被扶直了？从数学角度来说，也就是怎样判定直线与平面垂直？（板书课题）（二）分析问题、解决问题点拨：要解决上述问题，必须首先弄清什么叫做直线与平面垂直，也就是直线与平面垂直的定义.找一找：（1）在教室里找直线与平面垂直的例子；（2）在已学过的几何体中找直线与平面垂直的例子.（1讨论1讨论2：从圆锥与圆柱的形成过程中，你们看到了直线与平面垂直有什么特征吗？预设：直线与平面垂直的特点是直线垂直平面内过交点的所有直线.点拨：当旗杆或电线杆垂直地面内过交点的所有直线时，旗杆或电线杆就不会发生倾斜，此时旗杆或电线杆也是最稳定的.A 图3问1：你认为应当怎样定义直线与平面垂直？合作交流，然后提问.（预设：从回答“直线垂直平面内过交点的所有直线”过渡到回答“直线垂直平面内任何一条直线”.）（板书）定义：则称这条直线与这个平面垂直.图4 垂直，如图4所示.符号：lα⊥.说明：直线l叫做平面α的垂线，平面α叫做直线l的垂面，直线与平面的交点叫做垂足.问2：定义中“任何一条直线”可改为“任意一条直线”“所有直线”或“无数条直线”吗？问3：回到前面的问题上来，用直线与平面垂直的定义可以判定电线杆与地面垂直吗？为什么？反馈：利用定义来判定电线杆与地面是否垂直，需要作无限次验证，这在实际操作中是难于做到的。

高中数学第四届全国高中青年数学教师优秀课观摩大赛《直线与平面垂直的判定》教案

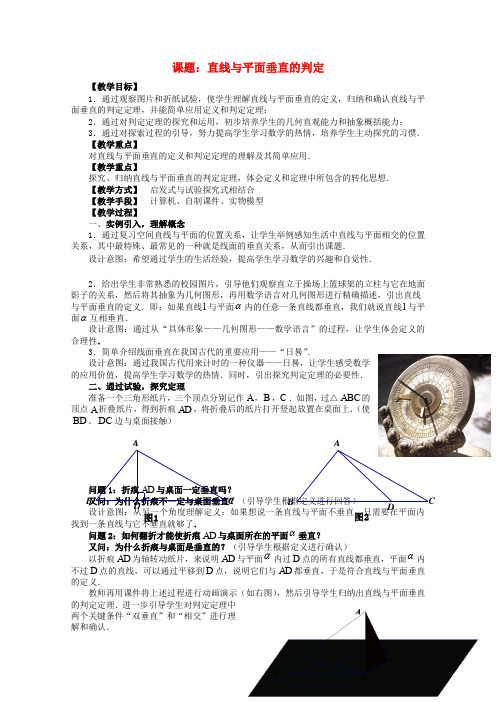
课题：直线与平面垂直的判定【教学目标】1．通过观察图片和折纸试验，使学生理解直线与平面垂直的定义，归纳和确认直线与平面垂直的判定定理，并能简单应用定义和判定定理；2．通过对判定定理的探究和运用，初步培养学生的几何直观能力和抽象概括能力；3．通过对探索过程的引导，努力提高学生学习数学的热情，培养学生主动探究的习惯．【教学重点】对直线与平面垂直的定义和判定定理的理解及其简单应用．【教学重点】探究、归纳直线与平面垂直的判定定理，体会定义和定理中所包含的转化思想．【教学方式】启发式与试验探究式相结合【教学手段】计算机、自制课件、实物模型【教学过程】一、实例引入，理解概念1．通过复习空间直线与平面的位置关系，让学生举例感知生活中直线与平面相交的位置关系，其中最特殊、最常见的一种就是线面的垂直关系，从而引出课题．设计意图：希望通过学生的生活经验，提高学生学习数学的兴趣和自觉性．2．给出学生非常熟悉的校园图片，引导他们观察直立于操场上篮球架的立柱与它在地面影子的关系，然后将其抽象为几何图形，再用数学语言对几何图形进行精确描述，引出直线与平面垂直的定义．即：如果直线l 与平面α内的任意一条直线都垂直，我们就说直线l 与平面α互相垂直．设计意图：通过从“具体形象——几何图形——数学语言”的过程，让学生体会定义的合理性．3．简单介绍线面垂直在我国古代的重要应用——“日晷”．设计意图：通过我国古代用来计时的一种仪器——日晷，让学生感受数学的应用价值，提高学生学习数学的热情．同时，引出探究判定定理的必要性．二、通过试验，探究定理准备一个三角形纸片，三个顶点分别记作A ，B ，C ．如图，过△ABC 的顶点A 折叠纸片，得到折痕AD ，将折叠后的纸片打开竖起放置在桌面上．（使BD 、DC 边与桌面接触）问题1：折痕AD 与桌面一定垂直吗？又问：为什么折痕不一定与桌面垂直？（引导学生根据定义进行回答）设计意图：从另一个角度理解定义：如果想说一条直线与平面不垂直，只需要在平面内找到一条直线与它不垂直就够了．问题2：如何翻折才能使折痕AD 与桌面所在的平面α垂直？又问：为什么折痕与桌面是垂直的？（引导学生根据定义进行确认）以折痕AD 为轴转动纸片，来说明AD 与平面α内过D 点的所有直线都垂直，平面α内不过D 点的直线，可以通过平移到D 点，说明它们与AD 都垂直，于是符合直线与平面垂直的定义．教师再用课件将上述过程进行动画演示（如右图），然后引导学生归纳出直线与平面垂直的判定定理．进一步引导学生对判定定理中两个关键条件“双垂直”和“相交”进行理解和确认．图1D C A B 图2D B A C问题3：(1)如果一条直线与平面内的一条直线垂直，能判断此直线和平面垂直吗？(2)定理条件中的两条直线必须相交吗？要求学生摆出反例模型进行说明，让学生在操作过程中，确认并理解判定定理的条件．设计意图：通过折纸试验，让学生在发现定理的过程中，不仅有直观上的感知，提高了几何直观能力，而且通过理性的说理，增加了逻辑思维的成分．最后，引导学生从文字语言、符号语言、图形语言三个方面归纳直线和平面垂直的判定定理．文字语言：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．符号语言：a l ⊥，b l ⊥，α⊂a ，α⊂b ，A b a = ⇒l α⊥．图形语言：例1 （1）正方体ABCD A - （2）正三棱锥P ABC -中，M 为棱BC 的中点，则棱BC 和平面PAM 垂直．例2 求证：如果两条平行线中的一条与一个平面垂直，则另一条也与该平面垂直．分析：首先需要把文字语言叙述的命题分别用符号语言和图形语言叙述出来．欲证线面垂直，需证线与面内两条相交直线垂直；而已知线面垂直，可得线线垂直，所以，在平面内两条相交直线n m ,作为辅助线，命题可证．已知：b a //，α⊥a , 求证：α⊥b ．证明：在平面α内作两条相交直线,m n ．因为直线a α⊥，根据直线与平面垂直的定义知,a m a n ⊥⊥．又因为 //a b ，所以 m b ⊥，n b ⊥．又因为α⊂m ，α⊂n ，m ，n 是两条相交直线，所以 α⊥b ．养学生的逻辑推理能力；同时规范证明题的书写．例3 如图，AC 是Rt △ABC 的斜边，过A 点作△ABC 所在平面的垂线PA ，连PB 、 PC ．问：图中有多少个直角三角形？分析：说明PAB ∠、PAC ∠为直角是比较容易的．证明PBC ∠是直角有两种方法：一是通过线线与线面之间垂直关系的相互转化得出PBC ∠是直角；二是依据勾股定理的逆定理，通过C P AB C计算证明△PBC是直角三角形．设计意图：通过对△PBC是直角三角形进行证明，意在培养学生熟练进行线线和线面之间垂直关系的转化，从而准确和灵活地应用判定定理和定义．四、归纳小结，提高认识1．学习小结：从知识和方法两个方面进行．知识方面：线面垂直的定义、线面垂直的判定定理．方法方面：转化思想．2．布置作业：（1）阅读课本相关内容进行复习；（2）做课本79页复习参考题A组第10题，B组第1题；（3）完成课本66页课后探究题．。

第五届全国高中数学青年教师观摩与评比活动《直线与平面垂直的判定》说课稿

诚西郊市崇武区沿街学校直线与平面垂直的断定〔一〕教材：普通高中课程标准实验书·数学必修②一、教材分析直线与平面垂直是直线与平面相交中的一种特殊情况．它既是线线垂直的拓展，也是学习面面垂直的根底，同时它也为研究线面角、二面角、点到平面的间隔、直线到平面的间隔、两个平行平面间的间隔等内容进展了必要的知识准备．因此它不仅是连接线线垂直和面面垂直的纽带，也是空间中点、线、面位置关系的核心内容．本节课主要研究了直线与平面垂直的定义、断定定理以及它们初步应用，并在此过程中浸透了类比、猜想、归纳等方法，让学生从中体会将空间问题转化为平面问题，将无限转化为有限，将线面垂直转化为线线垂直的化归思想．二、教学目的分析根据新课标的教学要求和学生的认知程度，确定如下的教学目的：在知识与技能方面：通过本节课的学习，使学生理解直线与平面垂直的定义和断定定理，并能对它们进展简单的应用；在过程与方法方面：通过对定义总结和对断定定理的探究，不断进步学生的抽象概括和逻辑思维才能；在情感态度与价值观方面：通过学习，使学生在认识到数学源于生活的同时，体会到数学中的严谨细致之美，简洁朴实之美，和谐自然之美，从而使学生更加热爱数学，热爱生活．三、教学问题诊断及相应教学策略分析1、学生对直线与平面垂直的现象是很容易有“感觉〞的，但是假设你要问他们什么是直线与平面垂直，他们却往往不知道怎么答复．所以如何让学生对线面垂直的认识由感性上升到理性是本节课的一个教学难点．这里我没有直接告诉学生定义的内容，而是把它放到了详细的情境中让学生自己去感受和体会．按说定义是不需要这样的分析和探究的，但是通过对旗杆和它在地面内影子的位置关系的观察，通过对旗杆所在直线l和地面所在平面α内不经过点B﹙点B是直线l和平面α的交点﹚的直线的位置关系的考虑，让学生亲自参与定义的构建，就使本来干巴巴的定义在学生心中变得详细生动，有血有肉．再通过对定义中的“任意一条直线〞能否换成“无数条直线〞问题的讨论，使学生对定义的认识经一步深化．考虑到学生的空间想象才能和语言表达才能的参差不齐，这里可以根据学生在课堂上的反响进展适当的启发引导，也对到讲台上进展演示讲解同学之答案进展补充和完善．2、虽然在新课程中对断定定理是通过试验确认并不需要严格证明的，但如何将线面垂直转化成线线垂直，如何提出“假设一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面是否垂直的问题〞是本节课的另一个教学难点．不少老师在这里都进展了有益的尝试．但是考虑到学生的认知程度，我并没有采取通过引导观察现实生活中的实例，进展猜想，从而提出问题的方法．因为一百个人心中就有一百个哈姆雷特，不同的人看同一幅图的感受可能是千差万别的，采用这种方法可能更多的时候是老师在进展引导，对学生认知的帮助不大．所以这里我仍然采用了类比猜想的方法，从学生已有的知识出发，通过合情推理最终提出上面的问题．然后通过试验探究总结出线面垂直的断定定理．其实通过试验并不能直接得出直线与平面垂直的断定定理，这里我会引导学生对“假设直线l与平面α内的两条相交直线m、n都垂直，但不经过它们的交点，那么直线l还与平面α垂直吗？〞这个问题进展探究．一方面是因为这个问题难度并不大，与新课程中的降低断定定理部分的难度并不违犯，另一方面通过对这个问题的研究也培养了学生严谨细致的作风，进步了学生的抽象概括才能和逻辑思维才能．3、在直线与平面垂直的断定这部分的题目中往往要进展屡次线面垂直和线线垂直之间的转化而且有时还需要添加辅助线，而这些都是学生感觉比较棘手的问题．所以本节课中我会对例1进展透彻的分析，从而让学生掌握分析此类问题的方法和步骤，然后通过几道有梯度的练习题让学生逐步对定义和断定定理可以进展灵敏运用，并不断增强学生的空间感．四、教学方法分析法无定法，本节并没有简单的只使用某一种教学方法，而是根据学生情况和教材特点同时进展了多方面的尝试．在定义的构建中通过创设情景，使学生对定义的总结水到渠成．在断定定理的构建中，通过小组增强了数学学习的气氛，也使学生在交流中互相学习一一共同进步．对直线与平面垂直的画法这样会用就行的问题直接传授，而对折纸试验中提出的问题却给学生留出充足的时间是是进展讨论，并根据情况进展适时的启发引导．总之一句话，所有的教学活动都要以学生的可持续开展为根本出发点，以学生在知识、才能和情感的进步和进步为根本出发点．。

直线与平面垂直的判定教案(教学设计) 【第九届全国高中青年数学教师优秀课展示与培训活动】

直线与平面垂直的判定铜陵市第三中学曹君一、教学内容解析：本节课选自人教A版教材必修2中第二章第三节第一小节《直线与平面垂直的判定》，共2课时，本节为第一课时。

本节课的内容主要包括直线与平面垂直的定义和判定定理两部分，均为概念性知识．线面垂直是在学生掌握了线在面内，线面平行之后，紧接着研究的线面相交位置关系中的特例.线面平行研究了定义、判定定理、相关结论以及性质定理，为本节课提供了研究内容和研究方法上的范例.线面垂直是线线垂直的拓展，又是面面垂直的基础，且后续内容如：空间的角和距离等又都使用它来定义，在本章中起着承上启下的作用.教学重点是操作确认并概括出直线与平面垂直的定义，对直线与平面垂直的判定定理的探究及简单应用．判定定理的教学，尽管新课程在必修课程中不要求证明，但通过定理的探索过程，培养和发展学生的几何直觉以及运用图形语言进行交流的能力，并体会“空间问题转化为平面问题”，“无限问题转化为有限问题”，“线线垂直与线面垂直互相转化”等数学思想，是本节课的重要任务．通过本节课的学习研究，可进一步完善学生的知识结构，更好地培养学生观察发现、空间想象、推理能力，体会由特殊到一般、类比、归纳、猜想、化归等数学思想方法．因此，学习这部分知识有着非常重要的意义．二、教学目标设置：课程和单元目标：教材淡化了对定理的证明，侧重于对几何体的直观感知，这就要在教学过程中多设置学生的自主观察环节及动手体会的过程.通过学生亲身经历观察、发现、猜想、直观感知、操作确认、思辨论证等定理形成与应用的全过程，使学生真正地逐步具备空间想象能力，以及体会等价转化思想在解决问题中的运用.最终达到，学会数学知识，更学会数学方法.课堂教学目标：（1）、学生通过对实例、模型的观察、抽象,概括出直线与平面垂直的定义，并对定义进行应用.让学生分组探究、猜想、归纳直线与平面垂直的判定定理，能对定义与判定定理进行简单应用，初步培养学生的几何直观能力和抽象概括能力；（2）、学生通过参与折纸试验，归纳和确认直线与平面垂直的判定定理，并尝试用数学语言（文字、符号、图形语言）对定义、定理进行准确表述．在活动中，学生通过独立思考和合作交流，发展类比、归纳等合情推理能力、逻辑思维能力和空间想象能力；（3）、在探究线面垂直的定义和判定的过程中，体会数学的严谨、简洁之美，体验探究发现的乐趣，培养善于观察、勇于探索的良好习惯.三、学生学情分析：学生已学过了两直线垂直关系的判定，以及线面平行关系的判定和性质，有了“通过观察、操作，然后抽象概括出数学结论”的经验与体会，有一定的空间想象能力、推理论证能力以及运用图形符号进行交流的能力，具备学习本节知识的基础.要达成本节课的目标，这些已有的知识和经验基础不可或缺，还需要整体上把握本节课的研究内容、方法和途径，能运用类比、化归等数学思想，同时具备较好地观察发现、空间想象、合情推理、抽象概括等能力，以及独立思考、合作交流、反思质疑等良好的数学学习习惯.存在的认知困难：一是如何从直线和平面垂直的直观形象中抽象概括出直线和平面垂直的定义.因为学生直观感知中的形象与定义中“直线与平面内任意一条直线都垂直”的内涵有一定的潜在距离；二是在探究直线与平面垂直的判定定理过程中，对为什么要且只要“两条相交直线”的理解.因为定义中“任意一条直线”指的是“所有直线”，这种有“有限”代替“无限”的过程在一定程度上会使学生产生思维障碍.教学难点：①从直线和平面垂直的直观形象中抽象概括出直线和平面垂直的定义；②探究、归纳、理解直线与平面垂直判定定理，突破“无限”与“有限”的转化.四、教学策略分析：（1）、启发引导学生类比探究线面平行的研究过程，按照“定义——判定定理——有关结论——性质定理”的研究程序，强化空间位置关系的常用研究策略——降维化归；（2）、如何从直线与平面垂直的直观形象中提炼出直线与平面垂直的定义，让学生认识到线面垂直是由线线垂直来刻画的，逐步形成概念体系，体会其中的转化思想，这对学生来讲还比较困难.因此，在设计教学时，首先通过照片让学生直观感知直线与平面垂直的具体形象，然后将模型抽象为几何图形，再用数学语言对几何图形进行精确的描述，让学生在观察演示过程中体会直线与平面垂直定义的合理性.总言之，创设情境，让学生形成关于线面垂直的直观感知，归纳定义；（3）、用定义去判定直线与平面垂直往往是不方便的，如何在较短的时间内，让学生找到判定直线与平面垂直的简便方法，这对于学生来说又是一个难题.因此，在教学过程中，先通过小组成员合作探究，类比之前探究其他判定定理的过程和方法，大胆猜想，反复验证，得出可能的线面垂直的判定定理；再通过折纸试验，精心设置问题，并且引导学生通过动手操作、摆出模型，然后借助动画加深对定理的两个关键词“双垂直”和“相交”的理解和确认.五、教学过程设计：（一）、引入：1、先看天安门广场五星红旗的照片，激发学生的爱国热情.引导学生思考如果三中操场上立一面新的旗杆，将旗杆抽象成一条直线，地面抽象成一个平面，“怎样检验旗杆与地面是不是垂直”.这个问题就是“如何判定直线与平面是否垂直”的问题，也就是今天我们要研究的课题，从而引出新课.【设计意图】借助学生观察生活中的数学问题引出课题，自然生动，既提高了学生学习数学的兴趣，又体现了数学来源于生活.观察图片，将图片中的实物抽象为几何图形，直观感知直线与平面的垂直.同时，也激发学生的爱国热情.【师生互动】观察图片，将图片中的实物抽象为几何图形，直观感知直线与平面的垂直.2、复习空间中点、直线、平面的位置关系中学习过的直线与平面的位置关系中平行的探究过程，类比出研究直线与平面垂直的探究思路.直线和平面有几种位置关系？已经掌握了直线和平面平行的哪些内容？怎样研究“直线与平面垂直”呢？研究关于“直线与平面垂直”的什么内容？【设计意图】启发引导学生类比探究线面平行的研究过程，明确按照“定义——判定定理——有关结论——性质定理”的研究程序，强化空间位置关系的常用研究策略——降维化归.【师生互动】观察图片，将图片中的实物抽象为几何图形，直观感知直线与平面的垂直.发挥想象，构思意境，进一步体会直线与平面的垂直.（二）、探索新知：从路由器模型中判断哪些直线与平面垂直，哪些不垂直？找出直观感受的原因，“在平面内找出一条和已知直线不垂直，则线面不垂直”，即“已知直线与所有直线都垂直才可以达到线面垂直的目的”.“所有直线”不能换为“无数条直线”，归纳出直线与平面垂直的准确定义.1、定义：如果直线与平面内的任意一条直线都垂直，我们就说直线与平面l αl 互相垂直，记作：．直线叫做平面的垂线，平面叫做直线的垂αα⊥l l ααl 面．直线与平面垂直时，它们唯一的公共点P画法：平面的平行四边形的一边垂直．【设计意图】借助模型的演示过程构建直线与平面垂直的定义，可以帮助学生建立对定义的直观感受，既真实又有效. 并引导学生用“正难则反”的思想来思考问题，进一步概括直线与平面垂直的定义.【师生互动】学生思考作答，教师补充完善，指出定义中的“任意一条直线”与“所有直线”是同义词，定义是说这条直线和平面内所有直线垂直．引导学生主动思考辨析，利用现有工具摆出反例模型，提高学生动手能力，同时给出线面垂直的记法与画法．2、定义应用：小实验：拿一块教学用的直角三角板，验证旗杆与地面的垂直. αα⇔⊥垂直于内的任何一条直线l l。

全国高中数学 青年教师展评课 直线与平面垂直教学设计

全国高中数学 青年教师展评课 直线与平面垂直的判定教学设计(吉林吉林一中) (2)

高中数学_直线与平面垂直教学设计学情分析教材分析课后反思

直线与平面垂直的教案

直线与平面垂直教案

全国高中数学青年教师展评课直线与平面垂直教学设计

直线与平面垂直 教学设计

《直线与平面垂直的性质》教学设计、导学案、同步练习

高中数学必修二《直线与平面垂直的性质》优秀教学设计

高中数学《直线和平面垂直》三篇教学设计的评析之一

《直线与平面垂直判定定理》教学设计

高中数学优秀课评比教案直线与平面垂直的判定教案

全国高中数学 青年教师展评课 直线与平面垂直的判定教学设计(江西抚州一中)

高中数学第四届全国高中青年数学教师优秀课观摩大赛《直线与平面垂直的判定》教案

第五届全国高中数学青年教师观摩与评比活动《直线与平面垂直的判定》说课稿

直线与平面垂直的判定 教案(教学设计) 【第九届全国高中青年数学教师优秀课展示与培训活动】

全国高中数学青年教师展评课直线与平面垂直教学设计

全国高中数学青年教师展评课直线与平面垂直的判定教学设计(吉林吉林一中) (2)

直线与平面垂直教学设计

全国高中数学青年教师展评课直线与平面垂直的判定教学设计(江西抚州一中)

直线与平面垂直的判定教案(教学设计) 【第九届全国高中青年数学教师优秀课展示与培训活动】