汤姆孙和瑞利散射-天文学导论
历年诺贝尔奖成果

1901年诺贝尔物理学奖——X 射线的发现 伦琴1901年,首届诺贝尔物理学奖授予德国物理学家伦琴(Willhelm Konrad Ro tgen, 1845---1923), 以表彰他在1895年发现的X 射线。
1895年,物理学已经有了相当的发展,它的几个主要部门--牛顿力学、热 力学和分子运动论、电磁学和光学,都已经建立了完整的理论,在应用上也取得 了巨大成果。
这时物理学家普遍认为,物理学已经发展到顶了,以后的任务无非 是在细节上作些补充和修正而已,没有太多的事情好做了。
正是由于X 射线的发现唤醒了沉睡的物理学界。
它像一声春雷,引发了一系列重 大的发现,把人们的注意力引向更深入、更广阔的天地,从而揭开了现代物理学 的序幕。
1902年诺贝尔物理学奖——塞曼效应的发现和研究洛伦兹 塞曼1902年诺贝尔物理学奖授予荷兰莱顿大学的洛伦兹(Hendrik Antoon Lorentz, 1853 ---1928)和荷兰阿姆斯特丹大学塞曼(Pieter Zeeman , 1865---1943),以表彰他们在研究磁性对辐射现象的影响所作的特殊贡献。
磁性对辐射现象的影响也叫塞曼效应,是塞曼在1896年发现的。
它是继法拉第效应和克尔效应之后又一项反映光的电磁特性的效应。
塞曼效应更进一步涉及了光的辐射机理,因此人们把它看成是继X 射线之后物理学最重要的发现之一。
洛伦兹是荷兰物理学家,他的主要贡献是创立了经典电子论,这一理论能解释物质中一系列的电磁现象,以及物质在电磁场中运动的一些效应。
由于塞曼效应发现时及时地从洛伦兹理论得到了解释,由此所确定的电子荷质比与J.J.汤姆孙用阴极射线所得数量级相同,相互间得到验证,因此1902年洛伦兹与塞曼共享诺贝尔物理学奖。
塞曼也是荷兰人,1885年进入莱顿大学后,与洛伦兹多年共事,并当过洛伦兹的助教。
塞曼对洛伦兹的电磁理论很熟悉,实验技术也很精湛,1892年曾因仔细测量克尔效应而获金质奖章,并于1893年获博士学位。
第5章 紫外灾难

第5章紫外灾难(1)纵使天空再深,看不见裂痕。
在云没有罅隙的时候,紫外线也能踩着猫步从天外爬下来。
街上的丽人在脸上涂满防晒霜,喜欢在夏天打着遮阳伞走来走去。
紫外线对皮肤具有很强的杀伤力。
对于做伞的公司来说,一把遮阳伞最重要的技术指标就是伞对UVA(长波紫外线)和UVB(中波紫外线)两个波段的透过率。
人的眼睛,是一台傅里叶变换的仪器,在眼睛里,世界是五颜六色。
一般人的眼睛,能看到的最短波长是380nm,波长比380nm短的光,统称为“紫外”。
但在物理学的意义上,一般把频率很大的时候,泛称为紫外(UV)。
因为光子的能量是正比于频率的,所以紫外光比红外光具有更高的能量,因为这个原因,物理学家一般把高能量区域叫做紫外区域。
这种术语是物理学家们喜欢的,正好象在经济学家那里,他们喜欢把钱叫做“流动性”是一个道理。
最近物理学的前沿,是所谓强弱对偶,也就是紫外与红外是对偶的,人们可以从低能量区域(也就是红外区域)的物理规律,推出高能量区域的物理规律。
比如说,质谱仪器只需要10个电子伏特的能量,属于低能量仪器,而北京正负电子对撞机则需要1个亿的电子伏特的能量。
街上的美女自然不知道"紫外"的深刻含义,长得越美,越不明白紫外的背后曾经有很严重的“灾难”。
不过这个灾难倒不是与皮肤有关,而是与量子力学的源起有关。
(2)对于宏观物体,它们会产生的辐射形式非常多变,比如你无法计算一个家里用来照明的那个钨灯的发射光谱,因为这些光谱具有很多复杂的参数,与电压有关,与供电频率有关,有灯泡里的气体压强有关。
最简单的辐射是黑体辐射和激光,前者系统处于热平衡态,唯一可调节参数是温度。
后者系统处于非热平衡态,也就是说系统并不处于玻尔兹曼分布,处于高能量态的原子数远远多于处于基态的原子数,打个比方,在激光产生的系统中,这个原子组成的社会中,富人远远多于穷人。
在发出的激光里,光子的频率全是一样的,因为是玻色子,很多光子能处于同一个状态,因此激光往往只具有一个颜色,是非常纯洁的单色光。
瑞利散射和米氏散射的主要差异-概述说明以及解释

瑞利散射和米氏散射的主要差异-概述说明以及解释1.引言文章1.1 概述散射是指当电磁波或粒子经过介质或粒子时,由于与介质或粒子的相互作用而改变传播方向或路径的现象。
在散射现象中,两种主要类型是瑞利散射和米氏散射。
瑞利散射和米氏散射在物理特性和应用方面存在一些显著的差异。
首先,瑞利散射是一种针对小尺寸颗粒或分子的散射现象。
当入射波的波长远大于颗粒或分子的尺寸时,瑞利散射发生。
这种散射主要由分子或小颗粒的碰撞所引起,导致入射波在所有方向上均匀地散射。
相比之下,米氏散射则是指入射波与中等尺寸颗粒相互作用的散射现象。
当入射波的波长与颗粒尺寸相当时,米氏散射发生。
米氏散射会引起入射波在特定方向上的增强或衰减,形成明显的散射模式。
其次,瑞利散射和米氏散射的特点也有所不同。
瑞利散射的强度与波长的四次方成反比,这意味着较短波长的入射波会更容易产生强烈的瑞利散射。
而米氏散射的强度与波长的平方成反比,这使得较长波长的入射波更容易产生强烈的米氏散射。
此外,瑞利散射和米氏散射对入射波的偏振状态也有不同的响应。
瑞利散射不会改变入射波的偏振状态,而米氏散射会导致入射波的偏振发生改变。
最后,散射现象在许多领域中具有重要的应用和意义。
瑞利散射和米氏散射的差异在遥感、气候研究、大气科学、通信技术等领域中都有广泛的应用。
通过研究和理解散射现象的特点和行为,科学家和工程师能够利用散射现象来获取关于颗粒尺寸、成分、分布等信息,从而推动相关领域的研究和发展。
总之,瑞利散射和米氏散射是两种不同类型的散射现象,它们在物理特性和应用方面存在显著的差异。
深入了解和研究这些差异,对于我们理解和应用散射现象具有重要的意义。
1.2 文章结构文章结构的主要内容如下:本文主要分为三大部分:引言、正文和结论。
在引言部分,我们将对瑞利散射和米氏散射进行概述,介绍它们的背景和特点,并明确本文的目的。
接下来,在正文部分,我们将详细探讨瑞利散射和米氏散射。
首先,我们将介绍瑞利散射的背景和特点,包括其产生机制和物理原理。
天文学导论复习资料

第一讲天文学导论●古希腊天文学:毕达哥拉斯,亚里斯多德(地球中心学说),托勒密的地球中心学说天文学的发展期:哥白尼、第谷、开普勒和伽利略牛顿的万有引力定律爱因斯坦的相对论●开普勒第一定律:(轨道形状)所有行星皆以椭圆轨道环绕太阳运行,而太阳位于椭圆的一个焦点上●开普勒第二定律:(行星速度)行星和太阳的(假想)连线在相同的时间内扫过相等的面积。
行星越接近太阳则运行速度越快近日点,运动最快远日点,运动最慢●开普勒第三定律:(轨道周期)行星公转周期的平方和其到太阳的平均距离的立方成正比(公转周期)2 = (常数) x (平均距离)3第二讲天体的视运动●月相与食无关天体的视运动月全食时月亮变为黄铜色或血红色,这是由于地球大气中的尘埃颗粒折射阳光中的红光并到达月球所致●内行星:水星,金星外行星:火星、木星、土星、天王星和海王星●头顶的星空取决于你在地球表面上的位置和当地时间●北京时间正午12点(东经120度)时,北京地方时(东经116.5度)即太阳时为11点46分,所以此时北京的太阳在子午线以东约3.5度,再过约14分钟北京“真”正午●南北天极:不变的参考点北天极:北极星南天极:南十字座●天赤道:不变的参考点所有恒星沿与天赤道平行的路径由东向西运动(圆弧轨迹在地球两极,天赤道=地平线●天顶、地平线和子午线:本地参考系天顶和子午线的位置不随观测者的地平线移动相对于星星来讲,天顶和子午线的位置在变天体的运行(圆弧)轨迹与地平面的夹角为:90 度-观测者所在地理位置的纬度(=天赤道与地面夹角)●在北极:所有星星沿与地平面平行的圆轨迹运行,从不下落赤道上:所有星垂直于地平面升起和下落“可见所有星”●太阳在天球上的视运动轨迹称为黄道●太阳日=24小时:太阳连续两次到达子午线的时间恒星日=23小时56分:恒星连续两次到达子午线的时间恒星日是地球真实的自转周期,不随其绕太阳公转而变化,均为23小时56分●月球回到原处(相对于恒星)的周期约为27.323 天,此为恒星周期●两个天体之间的距离常用它们与观测者之间的夹角表示,即角距●北京:东经116度22分;北纬39度58分本初子午线:格林尼治天文台●把地球的经度、纬度投影到天球上便成为天球的赤道坐标系赤纬:从天赤道开始至两极Dec [–90,90] 度赤经:用小时、分和秒的时间单位来表示,并由西向东由0增加到24小时赤经的计算起点为春分点,在天赤道上由西向东分为24小时地球“24小时”自转一周360度赤经1小时对应地球自转15度▪对于赤经相差1小时的两颗恒星,例如,RA2-RA1= +1小时:•恒星1比恒星2早1小时通过你的子午线(上中天)•如果不是拱极星,恒星1比恒星2早1小时从东方升起●某地某时刻的恒星时等于此时此刻位于子午线上的恒星的赤经(天球上与子午线重合的赤经)赤经小于地方恒星时的恒星位于子午线以西赤经大于地方恒星时的恒星位于子午线以东●一颗恒星的时角τ、赤经α和当地的恒星时θ之间的关系为τ= θ−ατ< 0, 在子午线以东(α> θ)τ> 0, 在子午线以西(α< θ)第三讲辐射与天文望远镜●黑体谱:连续谱的形状只与物体(恒星)的表面温度有关•其峰值波长(颜色)由其表面温度决定温度降低,黑体谱的峰值向长波方向移动•冷物体产生长波(低频)辐射•热物体产生短波(高频)辐射●辐射的平方反比定律:强度x 距离2 = 常数(恒星辐射能力)●关于天文望远镜的常见误解(wrong) 放大作用:大型望远镜把天体放得更大(Right) 聚光作用:使(暗弱)天体的图像更亮更清晰(wrong) 望远镜究竟可以看到多远的天体?只要一个物体足够亮,无论多远都可以看到(right) 望远镜可以看到多暗的天体?或望远镜可以看到几等星?只要一个物体足够暗,无论多近都看●光学望远镜的类型:折射式望远镜反射式望远镜第四讲太阳系(1) 行星●行星是一个具有如下性质的天体:(a)位于围绕太阳的轨道上,(b)有足够大的质量来克服固体应力以达到流体静力平衡的形状(近于球形),以及(c)已经清空了其轨道附近的区域。
什么是瑞利散射

瑞利散射是一种光学现象。
当光线(如太阳光)进入介质(如地球大气层)时,光线会与介质中的微粒(像大气中的气体分子,它们的尺寸远小于光的波长)相互作用。
对于微粒尺寸小于光波长的情况,光的散射强度与光波长的四次方成反比。
简单来说,蓝光波长较短,根据这个反比关系,蓝光就更容易被散射。
这就好比有一群小颗粒,短波长的光更容易被这些小颗粒弹向各个方向。
这种散射现象是以英国物理学家瑞利男爵(Lord Rayleigh)的名字命名的,他在19世纪末首先对这种散射行为进行了详细的理论研究,这一发现很好地解释了天空为什么是蓝色等诸多自然现象。
Born近似解与Mie散射解的分析比较

Born 近似解与Mie 散射解的分析比较Ξ马丽珍,李新虎,史 鹏(中国海洋大学物理系,山东青岛266100)摘 要: 在遥感研究中,微分散射截面是1个重要的参数。
针对相对折射率趋近于1的均匀球形粒子,在Born 近似条件下求解出粒子的散射振幅函数和微分散射截面,通过与Mie 散射理论结果的比较,对Born 近似的适用范围进行了讨论,提出相对折射率处于[1.01,1.09]之间的散射粒子近似解适用的范围。
关键词: Born 近似;Mie 散射;微分散射截面;相对折射率;尺度参数中图法分类号: P412.25 文献标识码: A 文章编号: 167225174(2009)0621275203 电磁散射是指当电磁波通过不均匀介质时偏离原传播方向的现象。
严格的电磁散射理论,是在一定颗粒的形状和尺寸所决定的边界条件下,对粒子内部和外部区域的Maxwell 方程组求解,得到散射振幅函数和散射截面函数。
1908年,米氏(G.Mie )借助Maxwell 的电磁场方程解出了关于均匀球形粒子散射的严格解,这就是著名的Mie 散射理论[1]。
Mie 散射理论虽严格,但解的形式复杂,且计算过程繁琐。
因此,在实际应用中,人们用一些近似解来描述散射规律,如Rayleigh 近似[2];Born 近似[3];W K B 近似;MRD 近似等。
其中Born 近似已成功地应用于许多问题的研究中[425],但对于Born 近似的条件没有给出具体的判据,本文针对相对折射率处于[1.01,1.09]的均匀球形粒子,在Born 近似条件下利用Maxwell 方程求解出粒子的散射振幅函数和微分散射截面,通过与Mie 散射理论结果的比较,对Born 近似的适用范围进行了讨论,提出该近似解适用范围。
1 Mie 散射理论设有一单色平面偏振波沿z 轴方向传播,其电矢量方向沿x 轴方向振动(见图1),则入射波函数为E i =e x E 0exp [-i (kz -ωt )](1)其中,e x 为x 轴正向单位矢量,k =2πλ为波数。
瑞利散射和米氏散射的主要差异

瑞利散射和米氏散射的主要差异全文共四篇示例,供读者参考第一篇示例:瑞利散射和米氏散射是大气中两种常见的光学现象,它们都是光线在大气中与颗粒发生散射而产生的效应,但其机制和特点有很大的不同。
本文将从几个方面对瑞利散射和米氏散射进行比较,以便更好地理解它们之间的区别。
瑞利散射和米氏散射在物理机制上有着明显的不同。
瑞利散射是由于大气分子对光线的散射而产生的,这种散射主要发生在波长比较短的光线(如紫外线、蓝光等)。
而米氏散射则是由于大气中的大颗粒(如水滴、冰晶等)对光线的散射而产生的,这种散射主要发生在波长较长的光线(如红光、红外线等)。
瑞利散射和米氏散射在大气中的发生机制有着明显的不同。
在散射光线的强度上,瑞利散射和米氏散射也有着明显的差异。
瑞利散射的强度与波长的四次方成反比,即短波长的光线散射强度更大。
瑞利散射主要造成天空呈现蓝色,并且太阳在日出和日落时呈现红色。
而米氏散射的强度与波长的四次方无关,因此在日出和日落时,太阳会呈现出更加深红色的现象。
瑞利散射和米氏散射对于气候和环境的影响也有所不同。
由于瑞利散射主要散射波长较短的光线,因此它对大气层的温度有所影响,会导致大气层中的气温呈现上升趋势。
而米氏散射主要散射波长较长的光线,因此对气温的变化影响较小,但其对于大气中颗粒物的传播和扩散有一定的影响。
从观测技术和应用上来看,瑞利散射和米氏散射也有着不同的特点。
由于瑞利散射的波长较短,因此它可以被用于遥感观测大气中的温度和湿度等参数。
而米氏散射的波长较长,主要可以用于遥感观测大气中的颗粒物质浓度和分布等参数。
瑞利散射和米氏散射在物理机制、散射光线强度、气候环境影响以及观测技术等方面都存在着明显的差异。
通过对二者的比较分析,我们可以更好地理解它们在大气光学中的作用和特点,为相关研究提供一定的参考依据。
希望本文能够对读者有所帮助,同时也能够促进人们对大气光学现象的深入研究和探讨。
【以上文字均为创作,仅供参考。
瑞利散射
反应液 白
自然光源
屏
瑞利散射
Rayleigh scattering
ห้องสมุดไป่ตู้文迪许实验室主任 发现了第一个惰性气体——氩 1904年诺贝尔物理学奖 瑞利散射
John William Strutt 瑞 利
&拉姆塞
瑞利散射:入射光在线度小于光波长的微粒
上散射后散射光和入射光波长相同的现象。
散射光强与入射光波长的4次方成反比 自然光入射时,散射光强随观察方向而变化 自然光入射时,散射光具有一定程度的偏振性, 且偏振性随θ 而变化
瑞利散射的应用
摄影 共振光散射法------DNA的定量分析进展 瑞利光散射光谱法研究牛血红蛋白与镝(Ⅲ) 的相互作用 基于瑞利散射的分布式光纤传感技术 其他
原创教科版原子的核式结构模型
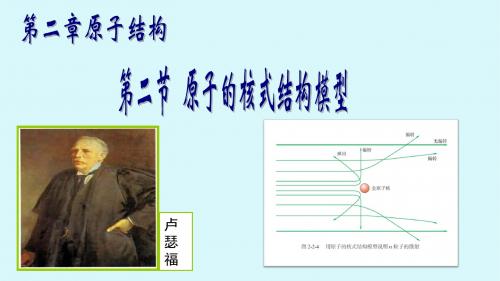
荧光屏
放射α粒子
注意:1.实验在真空中进行 2.金箔必须很薄(厚度方向上金 原子的个数很少,单个原子对α粒 子的散射基本上不受到其他原子 二次散射的干扰就可以直接被探 测器探测到)。
二. α粒子散射实验
汤姆逊枣糕原子模型能否解释实验现象?
(1)粒子出现大角度散射有没有可能是 与电子碰撞后造成的? 没有可能
卢 瑟 福
一.汤姆孙的原子模型
汤姆孙原子模型:汤姆孙于1898年
提出了原子模型,他认为
球体 ,________ 正电荷 弥漫 原子是一个______
电子 性地均匀分布在整个球内,______
镶嵌在球中.
汤姆生提出的枣糕原子模 型是否正确呢?
正电荷
电子
枣糕模型
二. α粒子散射实验(散射:是 分子或原子相互接近时,由于 双方具有很强的相互斥力,迫 使它们在接触前就偏离了原来 的运动方向而分开,这通常称 为“散射”。)
由于电子质量远小于α粒 子质量(6.64X10-27kg), 所以电子不可能使α粒子 发生大角度偏转. 正电荷在原子内是均匀分布 的,α粒子穿过原子时,受 到的两侧斥力大部分抵消, 最多能使α粒子偏转0.03°。 不可能使α粒子发生大角度 偏转,更不可能被反向弹回。
这与α粒子的散 (2)按照枣糕模型,粒子在原子附近或 射实验相矛盾 穿越原子内部后有没有可能发生大角度 没有可能 偏转?
三. 卢瑟福的核式结构
1内容: 1911年由卢瑟福提出,在原子 原子核 它集 中心有一个很小的核,叫_______. 中了原子全部的________ 正电荷 和几乎全部的 质量 ,_______ 电子 在核外空间运动. ______
三. 卢瑟福的核式结构
4.原子核的尺度
汤姆孙

3
物理学
第五版
诺贝尔奖获得者介绍
选为卡文迪许实验室教授,接替瑞利的主 任职位.1911─1913年任英国皇家学会副 会长,1915─1920年任会长. 1918年起 担任三一学院院长,1919年他辞去卡文迪 许实验室教授的职位,推荐他的学生 E.卢瑟福继任,而自己在实验室继续进 行研究工作,长达21年,1940年8月30日 在剑桥逝世.
2
物理学
第五版
诺贝尔奖获得者介绍
汤姆孙,(Joseph John Thomson, 1856─1940) 英国物理学家1856年12月8 日生于曼彻斯特郊区齐山姆的一个书商家 庭.14岁进欧文学院学习,1884年春被选 为英国皇家学会会员,随后转入卡文迪许 实验室工作.1884年12月他完成精确测定 电荷量的静电单位与电磁单位两数值之比 等实验研究,即被剑桥大学评选委员会评
物理学
第五版
诺贝尔奖获得者介绍
汤 姆 孙
1
物理学
第五版
诺贝尔奖获得者介绍
1906年诺贝尔物理学奖授予英国剑桥 大学的J.J.汤姆孙爵士(S电理论和实验所作的贡献.J.J.汤姆孙 对气体导电理论和实验研究最重要的结果 是发现了电子,这是继X射线和放射性之 后又一重大的发现.人们把这三件事称为 世纪之交的三大发现.
汤姆孙电子衍射试验

经典粒子 不被分割的整体,有确定位置和运动 轨道 ;经典的波 某种实际的物理量的空间分布作周 期性的变化,波具有相干叠加性 . 二象性 要求将 波和粒子两种对立的属性统一到同一物体上 .
1926 年玻恩提出 德布罗意波是概率波 .
统计解释:在某处德布罗意波的强度是与粒子在 该处邻近出现的概率成正比的 .
镍晶体
d 2.151010 m
d sin 1.651010 m
电子波的波长
h h 1.671010 m
mev 2meEk
第一章 质点运动学
简明物理学 教程
8-6 波粒二象性
d sin kh 1
2emU
sin kh 1
d 2emU
sin 0.777k
简明物理学 教程
8-6 波粒二象性
光的波动性
光的粒子性
电磁波
光子
有波动参量 如:
有粒子参量 如:
波长
动量
频率 波速
光的波粒二象动能质量性量
有波的行为特性 如:
波的干涉 波的衍射 横波偏振
有粒子的行为特性 如:
黑体辐射 光电效应 康普顿效应
光 既 又具具有有波粒动子性性,光的这种双重特性,称为光的波粒二象性。
方均根速率为: v2 =
3kT Mmol = vs
则 = h
p
代入数据:
=
h mv s
=
h M mol NA
vs
=
hN A 3Mmol kT
氧分子的德布罗意波长: λ=0.026nm
与X射线同数量级, 因此穿过晶片可产生衍射图样.
第一章 质点运动学
简明物理学 教程
*四 德布罗意波的统计解释
汤姆孙散射:等离子体参数诊断的强大工具.

汤姆孙散射:等离子体参数诊断的强大工具汤姆孙散射:等离子体参数诊断的强大工具2009-2-12 11:40:29摘要:汤姆孙散射是低能光子与自由电子之间的弹性散射.因为汤姆孙散射光谱携带着等离子体涨落的信息,通过测量汤姆孙散射光谱可以高精度地测量等离子体的多种参数,如电子温度、电子密度、等离子体流速等等.经过多年的发展,汤姆孙散射已经成为等离子体物理研究中最重要的一种诊断工具.关键词:等离子体物理,汤姆孙散射,动力学形状因子,等离子体参数Thomson scattering: a powerful diagnostic tool of plasma physicsZHENG Jian YU Chang\|Xuan(Key Laboratory of Basic Plasma Physics, Chinese Academy of Sciences, Department of Modern Physics, University of Science andTechnology of China,Hefei 230026, China)AbstractThomson scattering is the process in which a low\|energy photon scatters from a free electron. When a laser pulse propagates through a plasma, the spectrum of the scattered light due to the Thomson scattering is proportional to the power spectrum of the electron density fluctuations, i.e., dynamic form factor, from which various plasma parameters can be inferred, such as electron temperature and plasma flow velocity. After years of development, Thomson scattering has now become a powerful diagnostic tool of plasma physics.Keywordsplasma physics, Thomson scattering, dynamic form factor,plasma diagnostics1 引言精确测量等离子体的状态参数是深入研究等离子体物理过程的基本前提之一.对于高温高密度的等离子体,由于受到可接近性的限制,实验室常用的主动诊断手段(如探针)是无法接近需要探测的等离子体的.当然也有其他被动诊断方式可以提供众多等离子体参数的测量手段,如X射线能谱测量.相对被动诊断手段,汤姆孙散射作为一种主动诊断手段有其独特的一面:它可以高时空分辨地测量等离子体参数,且实验结果的解释相对简单,即散射光谱以比较直接的方式与等离子体参数有关.后者特别重要,因为有些诊断方法严重依赖于对实验数据的解释和处理,导致获得的等离子体参数的置信度较低.经过多年的发展,特别是由于激光技术以及高速高灵敏度探测器的进步,汤姆孙散射已经逐渐演化成为惯性约束聚变等离子体的标准诊断手段,成为精确研究等离子体行为的强大工具.2 汤姆孙散射的基本原理汤姆孙散射是低能光子(光子能量远远小于0.511MeV)与低能自由电子之间的弹性散射.该过程的经典物理图像是,在入射电磁波场中振荡的电子发射电磁波——散射电磁波.若电子有一运动速度v,散射电磁波的频率将不同于入射电磁波的频率,其差别为汤姆孙散射:等离子体参数诊断的强大工具2009-2-12 11:40:29这里k=ks-k0是散射波的波矢与入射电磁波的波矢之差,称为散射差矢.由这个简单的公式可以看到,散射电磁波携带了电子的运动信息,这就是汤姆孙散射可以用来诊断等离子体的基本原因.当然,当我们采用汤姆孙散射诊断等离子体时,我们测量到的散射光谱来自许多电子产生的散射电磁波的相干叠加.叠加的结果是,散射光谱与电子密度涨落功率谱成正比,ωdΩ=NeI0r2esin2θS(k,ω这里S(k,ω)就是所谓的动力学形状因子,它是电子密度涨落自相关函数的谱密度;I0是入射电磁波的功率密度;Ne是发生汤姆孙散射的电子数;re 是经典电子半径;θ是入射电磁波的极化方向与散射波矢之间的夹角.若电子彼此之间是完全无关的,那么散射光谱就是各个电子散射光谱的简单相加,此时散射光谱反映了电子在散射差矢方向上的速度分布.若等离子体中存在集体运动,电子之间不是彼此完全相互无关的,干涉效应会导致散射光谱在相应于等离子体集体运动模式的频率和波矢处出现尖锐的极大值.对于无磁化的等离子体,我们知道等离子体中的集体运动模式有两个:高频的电子等离子体波和低频的离子声波.这两种集体运动模式的色散关系为ω2epw=ω2pe(1+3k2λω2ia=11+k2λ这里ωpe是朗谬尔振荡频率,λDe是电子德拜长度,Te,i是电子/离子温度,Z是离子电荷数,mi是离子温度.经过适当的实验安排,以满足k2λ,那么我们就能够从散射光谱中获得电子密度ne以及电子密度与离化态乘积ZTe的信息.此外,散射光谱的宽度与集体运动模式的阻尼有关,而阻尼也取决于等离子体的状态参数,因此通过散射光谱的宽度,原则上也可以推断出等离子体的参数.例如,通过电子等离子体波的散射光谱的宽度,可以测量电子温度3 汤姆孙散射实验结果。
天文学导论习题答案

(50)
该行星的密度与木星的密度比为:
ρp = Mp · ρJ MJ
Dp DJ
−3
= 0.69 ×
2.1 × 105 1.42 × 105
−3
= 0.21
(51)
11
12
第五章 望远镜的基本原理
1. 暗7个星等需要的放大倍数为:
A = 2.5127 = 631
(52)
由A = (D/d)2,其中D为望远镜的口径,d为人眼在夜间瞳孔的直径,
Npp
=
F ∗A ∆mc2
=
1300 × 1 4.6 × 10−29 × (3 × 108)2
=
3.14 × 1014
(30)
每个质子-质子链产生两个电子型的中微子,因此单位面积上照射的中微
子数目为:
Nν = 2Npp = 6.28 × 1014
(31)
7
在 北 纬620处 , 中 午 太 阳 照 射 的 角 度 与 地 面 的 法 线 方 向 的 夹 角 为θ = 620 − 23.50 = 38.50, 因此,照射到A = 1m2上的中微子数目为:
rperi = a(1 − e) = 3.844 × 108 × (1 − 0.056) = 3.629 × 108m
(25)
远地点为:
rap = a(1 + e) = 3.844 × 108 × (1 + 0.056) = 4.059 × 108m (26)
在地球上看来太阳的角直径为:
θ
d =
= 1.39 × 109 = 0.927 × 10−2
40其中5710278k4110如果t278100000773au4230101712142010181043转动周期p为121018102110066years44第第第四四四章章章太太太阳阳阳系系系外外外行行行星星星38101145由恒星的视向速度v3012610601046根据质心的定义得到行星的质量m6010381011157101au6010272010331510113010451048太阳的视向速度v为
原子核式结构

α粒子散射实验的结果是: 粒子散射实验的结果是:
绝大多数 α粒子穿过金箔后几乎仍沿原 来的方向前进, 来的方向前进, 少数 α粒子发生了较大
的偏转, 的偏转, 极少数 α粒子偏转角超过了 90° 90°, 有的甚至 几乎达到180°。 几乎达到180° 180
结果分析:
电子能否使α粒子大角度偏转? ① 电子能否使α粒子大角度偏转? 少数α ② 少数α粒子的大角度偏转甚至反 弹是怎么造成的? 弹是怎么造成的?
原子的核式结构模型
电子的发现之旅
阴极射线 汤姆孙发现电子
原子可以分割。 无论哪种材料作为阴极产生的粒子质量 电荷相同,说明它们是原子的组成部分。 粒子质量小于氢原子的千分之一。
汤姆孙的原子模型: 汤姆孙的原子模型:
原子是一个球体,正电荷均匀分布在 原子是一个球体,正电荷均匀分布在 均匀分布 整个球体内,电子镶嵌其中。 镶嵌其中 整个球体内,电子镶嵌其中。
卢瑟福α粒子散射实验的解释 卢瑟福 粒子散射实验的解释
原子的核式结构的提出
在原子的中心有一个很小的核,叫做原子核. 在原子的中心有一个很小的核,叫做原子核. 原子的全部正电荷和几乎全部质量都集中在原 子核里. 子核里. 带负电的电子在核外空间绕着核旋转. 带负电的电子在核外空间绕着核旋转.
原子核的核式结构 根据卢瑟福的原子结构模型, 根据卢瑟福的原子结构模型,原子内 部是十分“空旷” 举一个简单的例子: 部是十分“空旷”的,举一个简单的例子: •
答案:B 答案:
2、卢瑟福α粒子散射实验的结果 、卢瑟福 粒子散射实验的结果 A、证明了质子的存在 、 B、证明了原子核是由质子和中子组成的 、 C、说明原子的全部正电荷和几乎全部质量都 、 集中在一个很小的核上 D、说明原子的电子只能在某些不连续的轨道 、 上运动
wangdongmei

荧光屏
高速
α粒子
放射源——放射性元素钋(Po)放出α粒子,α粒子 是氦核, 带2e正电荷,质量是氢原子的4倍,具有较大的动能。 金箔——作为靶子,厚度1μm, 重叠了3000层左右的 金原子。
荧光屏——α粒子打在上面发出闪光。
显微镜——通过显微镜观察闪光,且可360°转动观察不同角
度α粒子的到达情况。
第十二页,编辑于星期六:六点 二十九分。
课堂练习
2、卢瑟福α粒子散射实验的结果( )C A、证明了质子的存在
B、证明了原子核是由质子和中子组成的
C、说明原子的全部正电荷和几乎全部质量都集中在一个 很小的核上
D、说明原子的电子只能在某些不连续的轨道上运动
第十三页,编辑星期六:六点 二十九分。
课堂练习
第十一页,编辑于星期六:六点 二十九分。
课堂练习
1、在用α粒子轰击金箔的实验中,卢瑟福观察 到的α粒子的运动情况是( B ) A、全部α粒子穿过金属箔后仍按原来的方向前 进 B、绝大多数α粒子穿过金属箔后仍按原来的方 向前进,少数发生较大偏转,极少数甚至被弹回 C、少数α粒子穿过金属箔后仍按原来的方向前 进,绝大多数发生较大偏转,甚至被弹回 D、全部α粒子都发生很大偏转
22.1 《原子的核式结构 原子核》
第一页,编辑于星期六:六点 二十九分。
一.汤姆孙的原子模型 电子
正电荷
原子是一个球体,里面充满了均匀
分布的带正电的流体,电子镶嵌在正 电荷液体中,就象枣点缀在一块蛋糕 里一样,所以又被人们称为“枣糕模 型”。
电子等间隔地排列在与正电球同 心的圆周上,并以一定的速度做 圆周运动从而发出电磁辐射,原 子光谱所反映的就是这些电子的 辐射频率。
撞,其原因是( ) B
第四章 章末素养提升

章末素养提升物理观念电子的发现阴极射线:物理学家汤姆孙发现了电子,使人们认识到原子是可分的。
在此基础上提出了“枣糕模型”电子的电荷量:科学家密立根采用“油滴实验”测出电子的电荷量e=1.6×10-19 C元电荷:电子所带的电荷就是元电荷,任何带电体的电荷量都是元电荷电荷量的整数倍原子的核式结构模型α粒子散射实验现象:绝大多数α粒子仍沿原来的方向前进或只发生很小的偏转,少数α粒子发生了较大的偏转,极少数α粒子甚至被“弹”回来实验意义:否定了汤姆孙的原子模型,建立了核式结构模型卢瑟福的核式结构模型:原子中间有一个体积很小、带正电荷的核,而电子在核外绕核运动光谱光谱分为发射光谱和吸收光谱,发射光谱包含连续光谱和明线光谱明线光谱中的明线和吸收光谱中的暗线位置相同,称为原子光谱光谱分析:利用原子光谱的特征谱线。
优点:极为灵敏,精确度远高于化学分析和其他分析手段氢原子光谱氢原子光谱的实验规律玻尔的原子模型玻尔理论的三个基本假设:(1)轨道量子化:核外电子围绕原子核运动的轨道是一系列分立的、特定的轨道,即轨道是量子化的(2)能量量子化:不同的轨道对应着原子的不同的能量,原子的能量也是量子化的(3)辐射或吸收光子的能量满足频率条件:hν=E n-E m(m<n)玻尔原子结构理论对氢原子光谱的解释科学思维1.能用玻尔原子结构理论解释氢原子能级图及光谱2.能够用玻尔原子结构理论解释与解决有关问题科学态度与责任1.认识玻尔的原子结构理论和卢瑟福的原子核式结构模型之间的继承和发展关系2.了解玻尔模型的不足之处及其原因例1 (多选)(2022·成都市高二月考)物理学家通过实验及科学推理,从而获得了对自然现象的科学认识,推动了物理学的发展。
下列说法符合事实的是( )A .汤姆孙通过对阴极射线的研究发现了电子,并测量了电子的比荷B .密立根通过“油滴实验”直接测出了电子的电荷量C .卢瑟福通过分析α粒子散射实验现象,提出了原子内部有一个原子核D .在α粒子散射实验中,正对原子核入射的粒子,离核越近速度越小,电势能也越小 答案 AC解析 汤姆孙通过对阴极射线的研究发现了电子,并测量了电子的比荷,选项A 正确;密立根通过“油滴实验”间接测出了电子的电荷量,选项B 错误;卢瑟福通过分析α粒子散射实验现象,提出了原子内部有一个原子核,选项C 正确;在α粒子散射实验中,正对原子核入射的粒子,粒子克服电场力做功,离核越近速度越小,则电势能越大,选项D 错误。
激光原理及应用课件—陈鹤鸣第12章 激光与物质的相互作用

增加。
激光原理及应用 陈鹤鸣 赵新彦
20
12.4.3 液体、固体的光化学反应
一般而言,液体中的反应效率比气体中的要小(这里 额效率是指量子吸收量,用单个光子的反应比例表 示)。这是因为能量迁移造成了驰豫,产生了再复合 的逆反应。
光子的能量一部分用于光解离,一部分转变为热能。 一旦产生解离,周围的溶质争相返回形成再复合,称 为“回笼效应”,这也是溶液等物质的量子吸收量变 小的另一个原因
热反应是正向反应; 激光引起的光化学反应通过有效地进行分子(原子)选 择、反应场或空间的选择以及微粒子操作等方式,即使 在不升高温度的情况下也可以发生
激光原理及应用 陈鹤鸣 赵新彦
15
12.4.1 激光切断分子
切断分子的第一步是使分子吸收光,称之为激励光子。 切断分子的首要条件使分子具备的能量要大于解离能, 因此激光切断分子的过程也称为光解离反应。
激光原理及应用 陈鹤鸣 赵新彦
16
1. 直接解离
由于处于分子结合间的电子偏离位置不同,从而 形成结合和反结合轨道的电子状态。在结合轨道存 在极小的能量值。相反,反结合轨道对于分离态来 说是比较稳定的轨道。在激光作用下,分子一旦被 激励到反结合轨道,分子结合键便会瞬间断裂,这 就是直接解离。
在解离过程中,光激励时间非常短,只有飞秒级, 因此,电子在接收能量的过程中,相对较重的原子 核处于近似静止的状态。切断结合键的激光光子能 量必须大于分离能。
使材料处于松散状态,致使材料蒸发。 光化学效应蒸发的必要条件:光子的能量 > 分子的结合能。
激光原理及应用 陈鹤鸣 赵新彦
14
12.4 激光诱导化学过程
半导体芯片是经过了许多的薄膜加工过程制作而成的。在 热分解、等离子体、离子束等能源作用下,分子首先被分 解,然后再重新组合制成薄膜,这一过程分别称为热过程、 等离子体过程等。如果使用激光,薄膜可以做得更微细、 杂质含量更少。而这一过程是从化学反应开始的,称为激 光诱导化学过程。
J.J.汤姆孙及其对科学的贡献

汤姆逊及其对科学的贡献约翰·约瑟夫·汤姆逊(Jhon Joseph Thornson,1856—1940)是英国著名物理学家、电子的发现者,汤姆逊不仅是一位杰出的科学家,而且是一位卓越的科学研究组织者和领导者,还是一位伟大的教师和科学教育家。
他一生取得了举世瞩目的科学成就,同时也培养了一批优秀科学人才,为科学的发展作出了重大贡献。
本文就汤姆逊一生的科学活动及其对科学发展所作的贡献予以介绍。
1、汤姆逊的科学生涯汤姆逊1856年12月18日出生于英国曼彻斯特郊区的契特海姆山村,他的父亲是一位图书商。
汤姆逊14岁时,就进入曼彻斯特的欧文斯学院即现在曼彻斯特大学学习。
当时的欧文斯学院不但拥有一批优秀的科学人才,而且与同时代的其他大学相比,开设了一些实验掺理学方面的课程。
这就使汤姆逊在此不仅接触到了物理学,而且做了一些物理实验。
汤姆逊的父亲希望他的儿子成为一名工程师,让汤姆逊在欧文斯学院学习工程。
汤姆逊在学习期间,其父不幸去世。
之后,家庭没有能力负担他的经济费用,依靠奖学金的支持,汤姆逊在欧文斯学院继续工程学学位学习。
1876年,汤姆逊获得剑桥大学三一学院的奖学金,进入三一学院学习数学。
1880年,汤姆逊分获数学优等生学位考试第二名。
取得数学学土学位后,由于进行实验研究,使他有机会到卡文迪什实验室去。
1881年,三一学院给予汤姆逊研究员职位,1883年晋升为该校讲师。
1884年,汤姆逊当选为伦敦皇家学会会员。
同年,瑞利勋爵辞去卡文迪什实验物理学教授兼指导,经过选举委员会投票表决,汤姆逊当选为第三任卡文迪什教授兼指导。
他的这一职务直到1919年由他的学生卢瑟福继承。
在此期间,他领导卡文迪什实验室不仅在科学研究上取得举世瞩目的成就,而且为科学的发展培养了一大批优秀人才,把卡文迪什实验室建成了世界科学研究中心。
1905年,汤姆逊被任命为英国皇家研究所的自然哲学教授,1906年获得诺贝尔物理学奖,1908年被封为爵士。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.282 汤姆孙散射和瑞利散射
假设在y=0处有一个自由电子,一束频率为ω的电磁波经过,电场强度为E 0:
其中()()ky t E t y E Z −=ωsin ,0。
电子的运动方程为:
t eE z m ωsin 0−=
≡22dt z d z
其中m 为电子的质量,e 为电子的电荷。
瞬时加速度为:
t m
eE z
a ωsin 0
−==
由于带电粒子的加速而产生的瞬时能量辐射由下式(在8.03导出—有希望的话)给出,
3
2232c a e P = [cgs 单位]
用震荡电子的加速度来估计这个表达式:
t c
m E e P ω23
2204sin 32=.
就如同讲稿中定义的一样,散射截面项σ为,
σ 散射的能量
=
入射流量
.
然而,平面电磁波的能流很容易从坡印廷矢量得到(见8.03):
t E c flux ωπ
2
20sin 4=
因此,我们求得:
电子经典半径≡2
2mc
e (2.8×10-13
cm)
瑞利散射
考虑一个简单的原子经典模型
电子的运动方程和上面自由电子给出的一样,只是增加一个“恢复力”项,-k z :
t eE kz z
m ωsin 0−−=
试一下t A Z ωsin =的解,其中A 是个待确定的常数。
20sin sin sin ,m A t kA t eE t ωωωω−=−−
于是得到,
()()
m k t m eE A /sin /2
0−=
ω
ω.
瞬时加速度(t A z
ωωsin 2
−= )为: ()()
m k t m eE z a /sin /2
02−−==ωωω 截面为:
22
3
22
023sin 4e a c
c E t σωπ
=(散射的能量)(入射流量) , 和之前的情形一样。
()
⇒−= /382
24244m k c m e ωωπ
σ
()
4
hom 2
2
/Rayleigh T son
k m ωσσω
=−
在这种表达里,量k/m 是电子在弹簧系统的固有频率的平方,也就是我们说的ω0。
当入射的辐射频率和系统的固有频率接近时,截面就会变得非常大!对于入射辐射的频率在激发原子所需的激发频率之下,比如,ω<<ω0,则截面为:。
