第八 假设检验与SPSS软件入门
统计分析软件spss使用指南

03
参数估计的应用场 景
适用于需要对总体参数进行推断 的情况,如市场调研、医学研究 等。
假设检验原理及步骤
原假设和备择假设
明确研究问题的原假设和备择假设,确 定检验方向。
P值和决策规则
计算P值并与显著性水平进行比较, 根据决策规则得出假设检验的结论。
检验统计量和拒绝域
选择合适的检验统计量,并根据显著 性水平确绩分析、教育评估、课程设计等。
医学领域应用案例
临床医学研究
SPSS可用于医学实验设计、临床试验数据分析、疾 病预测等。
公共卫生研究
SPSS可用于流行病学调查、健康相关行为研究、健 康影响因素分析等。
生物医学研究
SPSS可用于生物医学实验数据分析、基因表达分析、 药物研发等。
或属性。
变量定义
03
在SPSS中,每个变量都需要定义名称、类型、宽度
、小数位数等属性,以确保数据的准确性和一致性。
数据录入与编辑
数据录入
可以通过手动输入或导入外部数据文 件的方式将数据录入到SPSS中。
数据编辑
提供数据编辑功能,可以对数据进行 增加、删除、修改等操作,确保数据 的完整性和准确性。
数据整理与转换
ABCD
医学
医学研究中经常需要用到统计分析,SPSS软件 提供了丰富的医学统计方法。
其他领域
如金融、经济、管理等领域也经常使用SPSS软 件进行数据分析。
02
数据输入与整理
数据类型及变量定义
数值型数据
01
包括整数和浮点数,可用于进行各种数学运算和统计
分析。
分类型数据
02 包括有序分类和无序分类两种,用于表示不同的类别
描述统计量
参数估计与假设检验SPSS

3
区别
参数估计更侧重于总体参数的估计和推断,而假 设检验更侧重于对总体参数的假设进行验证和决 策。
02
SPSS软件介绍
SPSS软件的特点与优势
强大的统计分析功能
SPSS提供了广泛的统计分析方法,包括描述性统计、推论性统计、 多元统计分析等,能够满足各种数据分析和科学研究的需求。
易用性
SPSS的用户界面友好,操作简单,使得用户可以快速上手,减少了 学习成本。
参数估计与假设检验的应用场景与注 意事项
参数估计与假设检验的应用场景
社会科学研究 在社会科学研究中,参数估计与 假设检验是常用的统计方法,用 于检验理论模型和假设,评估变 量之间的关系。
心理学研究 在心理学研究中,参数估计与假 设检验用于研究人类行为、认知 和情感等方面的规律和特点。
医学研究 在医学研究中,参数估计与假设 检验常用于临床试验和流行病学 研究中,以评估治疗效果、疾病 发病率和风险因素等。
04
05
根据输出结果判断假设是否 成立。
假设检验的实例分析
以一个实际研究问题为例,如比较两组人群的平均身高是否存在显著差异。
在SPSS中实现该实例分析,包括数据导入、选择统计方法、设置参数、运 行统计方法和结果解读等步骤。
根据SPSS的输出结果,判断提出的假设是否成立,并解释结果的实际意义。
05
数据处理技术,提高分析效率和准确性。
多变量分析方法
03
多变量分析方法的发展将促进参数估计与假设检验的进一步应
用,能够更全面地揭示变量之间的关系。
THANKS
感谢观看
使用SPSS进行参数估计,例如使用逻辑回归分 析来估计吸烟与肺癌之间的关系。
04
假设检验在SPSS中的实现
spss假设检验

SPSS假设检验1. 简介SPSS(Statistical Package for the Social Sciences)是一种非常常用的统计软件,被广泛应用于社会科学研究中。
其中,假设检验是SPSS中常用的统计方法之一,用于验证研究者对总体或样本的某种假设。
2. 假设检验的概念假设检验是统计学中的一种重要方法,用于判断一个统计推断是否与样本数据一致。
在假设检验中,通常会提出一个原假设(H0)和一个备择假设(H1),然后根据样本数据对两个假设进行检验,以确定是否拒绝原假设,从而对总体进行推断。
3. SPSS中的假设检验SPSS中提供了丰富的假设检验方法,涵盖了多种统计推断的情况。
下面将介绍几种常见的假设检验方法。
3.1 单样本 t 检验单样本 t 检验用于判断一个样本的均值是否与一个已知的常数有显著性差异。
在SPSS中,进行单样本 t 检验的步骤如下:1.导入数据:在SPSS中打开或导入数据文件。
2.选择变量:选择要进行 t 检验的变量。
3.进行检验:选择菜单栏上的“分析”-“比较均值”-“单样本 t 检验”。
4.设置参数:选择相关的变量和检验参数,点击“确定”进行分析。
5.查看结果:SPSS将显示 t 检验的结果,包括均值、标准差、t 值、自由度和显著性等。
3.2 独立样本 t 检验独立样本 t 检验用于判断两个独立样本的均值是否存在显著性差异。
在SPSS中,进行独立样本 t 检验的步骤如下:1.导入数据:在SPSS中打开或导入数据文件。
2.选择变量:选择需要进行对比的两个变量。
3.进行检验:选择菜单栏上的“分析”-“比较均值”-“独立样本 t 检验”。
4.设置参数:选择相关的变量和检验参数,点击“确定”进行分析。
5.查看结果:SPSS将显示独立样本 t 检验的结果,包括均值、标准差、t 值、自由度和显著性等。
3.3 配对样本 t 检验配对样本 t 检验用于判断同一组个体在两个不同时间点或条件下的均值是否存在显著性差异。
如何在spss上进行假设检验
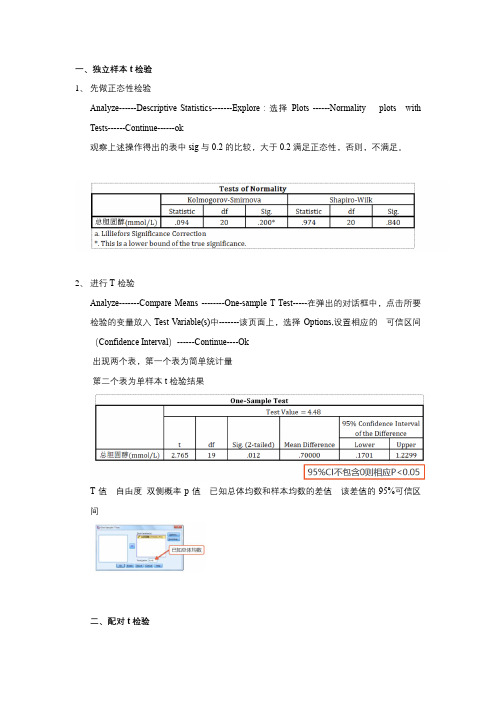
当两样本的方差齐时,看第一行。不齐,看第二行。Sig与0.1?
四、完全随机设计方差分析
1、检验是否满足正正态性、方差齐性
Analyze------desctiptive statistic -------explore-------plots-------none normality plots with tests (正态性)、untransformed(组间方差齐性检验)(选择相应的dependent list、factor list)----ok
一、独立样本t检验
1、先做正态性检验
Analyze------DescriptiveStatistics-------Explore:选择Plots------Normality plots with Tests------Continue------ok
观察上述操作得出的表中sig与0.2的比较,大于0.2满足正态性,否则,不满足。
3、两组间多重比较
Analyze-----Nonparametric Tests----Legacy Dialogs----2 Independent Samples----选入相应的Test Variable List(应变量)和Grouping Variable选好要比较的两组放在前后相应的位置,两两依次比较---- Mann-Whitney U检验----OK
4、多重比较
Analyze----General Linear Model---- Univariate----Post Hoc----block(区组)----group(处理)------ Bonferroni---- Continue------OK
刘红云-SPSS基础与应用-第八章

第八章非参数检验OUTLINE计数数据的检验01独立样本的非参数检验02相关样本的非参数检验03计数数据的检验配合度的卡方检验操作过程打开数据文件“fit_test.sav”,在SPSS中选择“Data→Weight Cases…”;选择“Weight cases by”,在“Frequency Variable”下选择“freq”,点击“OK”;选择“Analyze→NonparametricTests→Legacy Dialogs→Chi-square…”;将“major”选入“Test Variable List”框中,在“Expected Values”框中选择“Values”,并将国家统计比例依次“Add”;这里我们选择“Add”选项,并依次输入各类别的比例。
如果假设各类别比例相同,则可以选择默认的“All categories equal”选项。
在“Exact…”选项框中选择“Asymptotic only”选项,点击“Continue→OK”配合度的卡方检验操作过程打开数据文件“fit_test.sav”,在SPSS中选择“Data→Weight Cases…”;选择“Weight cases by”,在“Frequency Variable”下选择“freq”,点击“OK”;选择“Analyze→NonparametricTests→Legacy Dialogs→Chi-square…”;将“major”选入“Test Variable List”框中,在“Expected Values”框中选择“Values”,并将国家统计比例依次“Add”;这里我们选择“Add”选项,并依次输入各类别的比例。
如果假设各类别比例相同,则可以选择默认的“All categories equal”选项。
在“Exact…”选项框中选择“Asymptotic only”选项,点击“Continue→OK”配合度的卡方检验操作过程打开数据文件“fit_test.sav”,在SPSS中选择“Data→Weight Cases…”;选择“Weight cases by”,在“Frequency Variable”下选择“freq”,点击“OK”;选择“Analyze→NonparametricTests→Legacy Dialogs→Chi-square…”;将“major”选入“Test Variable List”框中,在“Expected Values”框中选择“Values”,并将国家统计比例依次“Add”;这里我们选择“Add”选项,并依次输入各类别的比例。
管理定量分析课程第8章:假设检验

判决
无罪 有罪
陪审团审判
真实的情况
无罪
有罪
判决正确
判决错误
判决错误
判决正确
结论
未拒绝原假设 拒绝原假设
假设检验 总体参数的实际情况
原假设为真 备择假设为真 结论正确 第二类错误 第一类错误 结论正确
11
假设检验中犯Ⅰ型错误的概率,称为显著性水平(level of significance),即指当零假设实际上是正确时,检验统计量落
7
又如:教育部要检验2012年录取的大学新生平均身高是否 达到了170cm标准,这样需要提出原假设(H0):2012
年大学新生(总体)的平均身高(µ )是170cm。为了检
验这个假设是否正确,需要根据随机取样的原则,从2012 年的大学新生总体中选取样本并计算样本的平均高度,以 此来检验原假设的正确性。
8
假设检验一般分为参数假设检验和非参数假设检验两种类型。参 数假设检验对变量的要求较为严格,适合于等距变量和比率变量 ,非参数假设检验对变量的要求较为自由,既适合于等距变量和 比率变量,也适用于类别变量和顺序变量。
变量测量层次
分类(nominal)变 量
数学性(interval)变量
4
一、假设与假设检验
假设是科学研究中广泛应用的方法,它是根据已知理 论与事实对研究对象所作的假定性说明。统计学中的 假设一般专指用统计学术语对总体参数所做的假定性 说明。在进行任何一项研究时,都需要根据已有的理 论和经验事先对研究结果作出一种预想的假设。这种 假设叫科学假设,在统计学上称为研究假设。对这种 研究假设进行证实或证伪的过程叫假设检验。
非参数检验是一种与总体分布状况无关的检验方法,它不 依赖于总体分布的形式。
SPSS假设检验

SPSS假设检验实验⽬的::实验⽬的1、学会使⽤SPSS的简单操作。
2、掌握假设检验。
:实验内容:实验内容1.⼀个总体均值的检验(⼩样本);2.两个总体均值之差的检验;3.绘制正态概率图;4.S—W检验。
实验步骤: 1.⼀个总体均值的检验(⼩样本):单总体的Z检验和t检验。
设是取⾃正态总体的⼀个样本,要检验。
其中为已知的常数。
为了说明如何构造检验统计量和拒绝域,先看⼀个简单的情形。
设总体⽅差是已知的,记为,设为样本均值,则。
设为真,即,对作标准化,得到上述的Z就是要构造的检验统计量。
设定显著性⽔平为0.05,因为,的概率为0.05,所以检验的拒绝域是。
如果由样本计算得到,与⼩概率原理⽭盾,从⽽拒绝原假设。
在实际应⽤中,总体的⽅差是未知的。
因⽽需要样本⽅差代替总体⽅差,相应地,检验统计量编程了t统计量。
设与分别为样本的均值和样本⽅差,当为真时,可知统计量对于给定的显著性⽔平,检验的拒绝域是。
其中临界值满⾜条件。
它就是⾃由度为(N-1)的t分布的双侧分为点。
如果由样本观测值代⼊,计算得到的t值满⾜,则拒绝原假设。
SPSS检验结果不给出临界值,⽽是在给出t值的同时给出它的显著性概率(也成为p值或相伴概率,记为p或Sig)。
计算⼀个双侧检验问题,SPSS操作如下:“分析”→“⽐较均值”→“单样本T检验”,在打开的对话框中填好“检验变量”列表框和“检验值”⽂本框。
单击“确定”。
输出结果中的Sig.(双侧)就是p值。
⽐较p值与检验⽔准。
1 T-TEST2 /TESTVAL=803 /MISSING=ANALYSIS4 /VARIABLES=score5 /CRITERIA=CI(.95).⼀个总体的均值检验 差齐性检验:Sig=0.397>0.05,⽅差不显著,可以认为两个独⽴样本的⽅差⼀致。
均值之差t检验:在⽅差相等的条件下,Sig=0.004<0.05,均值之差显著,可以认为两个独⽴样本均值有显著差异。
SPSS统计分析详细操作指南

SPSS统计分析详细操作指南在当今的数据驱动时代,掌握有效的数据分析工具对于研究人员、学生、企业决策者等来说至关重要。
SPSS(Statistical Package for the Social Sciences)作为一款功能强大且广泛应用的统计分析软件,能够帮助我们从海量的数据中提取有价值的信息。
接下来,将为您详细介绍 SPSS 的操作指南。
一、软件安装与界面认识首先,您需要获取 SPSS 软件的安装包,可以从官方网站或其他可靠渠道下载。
安装过程相对简单,按照提示逐步进行即可。
成功安装后打开 SPSS,您会看到一个简洁直观的界面。
主要包括菜单栏、工具栏、数据视图窗口和变量视图窗口。
数据视图窗口用于输入和编辑数据,每一行代表一个观测值,每一列代表一个变量。
变量视图窗口则用于定义变量的属性,如名称、类型、标签等。
二、数据输入与导入SPSS 支持手动输入数据和导入外部数据文件。
如果数据量较小,您可以直接在数据视图窗口中逐行逐列输入数据。
对于已有数据文件,SPSS 可以导入多种格式,如 Excel 文件(xls 或xlsx)、文本文件(txt 或csv)等。
通过菜单栏中的“文件”“打开”“数据”选择相应的文件类型,并按照向导进行操作即可完成数据导入。
三、数据预处理在进行正式的统计分析之前,通常需要对数据进行预处理,以确保数据的质量和适用性。
1、缺失值处理检查数据中是否存在缺失值。
SPSS 提供了多种处理缺失值的方法,如删除包含缺失值的观测、用均值或中位数等替代缺失值等。
2、数据标准化为了消除不同变量量纲的影响,可以对数据进行标准化处理。
SPSS 中有相应的功能可以实现这一操作。
3、变量重新编码有时需要对变量进行重新编码,例如将连续变量转换为分类变量,或者对分类变量的类别进行重新定义。
四、描述性统计分析描述性统计分析可以帮助我们了解数据的基本特征,如均值、中位数、标准差、最小值、最大值等。
在菜单栏中选择“分析”“描述统计”“描述”,将需要分析的变量选入变量框,点击“确定”即可得到描述性统计结果。
SPSS入门软件操作资料

SPSS入门软件操作资料SPSS是一款常用的统计分析软件,可以用来进行数据清理、数据处理和数据分析。
以下是SPSS入门软件操作资料,帮助您快速入门和使用SPSS。
第一部分:数据准备和导入1.打开SPSS软件,选择“新建”创建一个新的数据文件。
2.在新建的数据文件中,点击菜单栏上的“变量视图”,在表格中输入变量名称和变量类型。
3.在输入变量名称和变量类型后,点击菜单栏上的“数据视图”,在表格中输入实际数据。
第二部分:数据清理和检查1.缺失值处理:在数据视图中,选中需要处理的变量,点击菜单栏上的“转换”,选择“缺失值”,然后选择相应的处理方法。
2.异常值处理:在数据视图中,选中需要处理的变量,点击菜单栏上的“转换”,选择“异常值”,然后选择相应的处理方法。
3.数据检查:在数据视图中,点击菜单栏上的“分析”,选择“描述性统计”,选择需要进行统计描述的变量。
第三部分:数据分析1.描述统计:在数据视图中,点击菜单栏上的“分析”,选择“描述性统计”,然后选择需要进行统计描述的变量。
2.相关分析:在数据视图中,点击菜单栏上的“分析”,选择“相关”,然后选择需要进行相关分析的变量。
3.t检验:在数据视图中,点击菜单栏上的“分析”,选择“比较手段”,然后选择“独立样本t检验”或“配对样本t检验”,根据需要选择相关变量。
4.方差分析:在数据视图中,点击菜单栏上的“分析”,选择“方差”,然后选择“单因素方差分析”或“多因素方差分析”,根据需要选择相关变量。
5.回归分析:在数据视图中,点击菜单栏上的“分析”,选择“回归”,然后选择需要进行回归分析的自变量和因变量。
第四部分:结果输出1.结果输出:在分析结果窗口中,可以查看分析结果的表格、图表和统计描述。
2.结果保存:在分析结果窗口中,点击菜单栏上的“文件”,选择“另存为”,选择保存的文件格式和保存的位置。
第五部分:其他操作1.数据转换:在数据视图中,点击菜单栏上的“转换”,选择需要进行的数据转换方法,例如计算新变量、变量转化等。
假设检验的基本原理spss课件知识介绍

SPSS中各类假设检验的函数介绍
Student's t-test
Understand how to use the t-test function in SPSS for comparing two means.
Chi-Square Test
Learn how to perform a chi-square test in SPSS for analyzing categorical data.
假设检验的结果与解读
1
Statistical Significance
Understand how to interpret the
Effect Size
2
p-value and determine the statistical significance of your
Learn about effect size measures
ANOVA
Explore the ANOVA function in SPSS for comparing means across more than two groups.
Correlation Analysis
Discover the correlation analysis function in SPSS for examining relationships between variables.
hypothesis testing.
testing methods
commonly used in
statistical analysis.
S PS S 软件中假设检验的操作步骤
1
数据导入
Learn how to import data into SPSS for hypothesis testing.
如何在SPSS数据分析报告中进行假设检验?

如何在SPSS数据分析报告中进行假设检验?关键信息项:1、假设检验的类型独立样本 t 检验配对样本 t 检验单因素方差分析多因素方差分析卡方检验2、数据准备要求数据的完整性数据的准确性数据的正态性异常值处理3、假设的设定原假设和备择假设的明确表述假设的合理性和基于的理论或经验基础4、检验步骤选择合适的检验方法在 SPSS 中输入数据和执行检验操作解读检验结果5、结果报告内容检验统计量的值自由度p 值效应量(如适用)6、结果的解释和结论根据 p 值做出决策对效应大小的解释结果在研究背景下的意义11 假设检验的类型在 SPSS 数据分析报告中,常见的假设检验类型包括但不限于以下几种:111 独立样本 t 检验用于比较两个独立样本的均值是否存在显著差异。
例如,比较两组不同治疗方法下患者的康复时间。
112 配对样本 t 检验适用于配对数据,即同一组对象在不同条件下或不同时间点的测量值。
比如,比较同一批患者治疗前后的体重变化。
113 单因素方差分析用于检验一个因素的不同水平对因变量的均值是否有显著影响。
例如,研究不同教育程度对收入的影响。
114 多因素方差分析当存在多个因素同时影响因变量时,使用多因素方差分析。
比如,研究教育程度和工作经验对收入的共同影响。
115 卡方检验主要用于检验两个分类变量之间是否存在关联。
例如,分析性别与某种疾病的患病率是否有关。
12 数据准备要求在进行假设检验之前,确保数据满足以下要求:121 数据的完整性数据应包含所需的所有变量和观测值,不允许有缺失值。
若存在缺失值,需要采取适当的方法进行处理,如删除含缺失值的观测、均值插补或多重插补等。
122 数据的准确性对数据进行仔细检查,确保其没有录入错误或异常值。
异常值可能会对假设检验的结果产生较大影响,需要谨慎处理。
123 数据的正态性对于一些基于正态分布假设的检验方法(如 t 检验和方差分析),需要检查数据是否近似服从正态分布。
可以通过绘制直方图、正态概率图或进行正态性检验(如 ShapiroWilk 检验)来判断。
假设检验及SPSS实现

单样本的T检验 One Sample T Test
独立样本的T检验Independent Samples T Test
配对样本的T检验Paired- Samples T Test 注:t检验要求总体来自正态分布,因此一般事先都要检验样本数据是否来自正态分布。
2、独立样本的T检验Independent Samples T Test 该过程主要用于两个独立样本原始资料对两个总体均值的假设检验. 双样本均值共有3种类型: 双尾检验(two-tailed test): H0:μ1=μ2 , H1:μ1≠μ2 单尾检验(one-tailed test) : H0:μ1≥μ2 , H1:μ1<μ2 H0:μ1≤μ2 , H1:μ1>μ2
配对样本的T检验 Paired- Samples T Test
该过程主要用于配对样本资料对两个总体均值之差的假设检验.
配对样本与独立样本的差异在于: 配对样本的抽样不是相互独立的,而是相互关联的。
配对样本可以是同一个变量在“前与后”、“新与旧”等
两种状态下的两组抽样数据, 也可以是对某一问题两个不同侧面的表述。
04
假设检验问题的基本步骤:
假设检验的方法-P值法
所谓P值是指H0视为真时,检验统计量在以其观察值为端点的某区域内取值的概率。
计算方法:
在 已知时,检验统计量为Z= ,其样本观测值为Z0= ,表示样本均值的观察值。 在左侧检验中,P值=P(Z≤Z0); 在右侧检验中,P值=P(Z≥Z0); 在双侧检验中,P值=2 P(Z≥| Z0|);
正常饲料组 3550 2000 3000 3950 3800 3750 3450 3050
SPSS检验步骤总结

SPSS检验步骤总结SPSS(Statistical Package for the Social Sciences)是一种常用的统计分析软件,广泛应用于社科、医学、生物、市场调研等领域。
SPSS 提供了众多的统计分析方法和功能,可以用来处理和分析数据,进行假设检验、回归分析等统计操作。
在使用SPSS进行假设检验时,通常有以下几个步骤:1. 数据导入:首先需要将待分析的数据导入SPSS软件。
SPSS支持导入各种格式的数据,包括Excel、CSV、文本文件等。
导入数据后,可以查看数据的基本信息和属性。
2.数据清理:数据清理是数据分析的重要步骤。
在数据清理过程中,需要检查数据的完整性和准确性,删除缺失值、异常值等不符合要求的数据。
SPSS提供了丰富的数据处理和清理工具,可以帮助用户轻松完成数据清理操作。
3.描述性统计分析:在进行假设检验之前,可以先对数据进行描述性统计分析。
描述性统计分析可以提供数据的基本统计信息,包括均值、标准差、频数分布等。
SPSS提供了简单和直观的功能来生成这些统计结果。
4. 建立假设:在进行假设检验之前,需要先建立研究假设。
研究假设通常包括原假设(null hypothesis)和备择假设(alternative hypothesis)。
原假设是指对现象或关系的默认假设,备择假设则是指要证明的假设。
5.选择合适的统计检验方法:根据研究问题的性质和变量类型,选择合适的统计检验方法。
SPSS提供了多种常见的假设检验方法,如t检验、方差分析(ANOVA)、卡方检验等。
不同的检验方法适用于不同类型的数据和研究设计。
6.进行假设检验:一旦选定了合适的统计检验方法,就可以进行假设检验了。
SPSS提供了简便的功能来执行各种假设检验操作。
用户需要输入所需参数和所需样本,之后SPSS将生成检验结果,包括显著性水平(P 值)和置信区间等。
7.结果解释:假设检验完成后,需要对结果进行解释。
如果P值小于设定显著性水平(通常为0.05),则可以拒绝原假设,接受备择假设。
统计软件spss操作3_常用假设检验与相关分析

三、无序分类变量的统计推断:卡方检验
三)检验某两个分类变量是否相互独立 例2:考察2004年CCSS调查样本中不同级别 收入家庭(变量Ts9)轿车拥有率比较。 (两样本) 操作: “分析变量的统计推断:卡方检验
三)检验某两个分类变量是否相互独立 例3:考察阶级认知样本中父代不同级别职业 子代收入的比较。 操作: “分析”—“描述统计”—“交叉表” (“统计量”—“卡方”)
一、分布类型检验
四)用K-S图检验数据分布形态 原理:
Kolmogorov-Sminov单样本检验是一种分布拟合优 度的检验,其方法是将一个变量的累积分布与特定 理论分布相比较:
K=lim|Ai-Oi|
如果频数绝对差太大,就不符合特定分布。 检验CCSS的总指数是否符合正态分布。
例4: “分析”—“非参数检验”—“单样本”
二、连续变量的统计推断:t-检验
问题: 做“比较均值—独立样本 t 检验“之前是否要 检查数据的正态性?方差齐性?独立性?
练习: 试检验CCSS数据中2007年4月样本的不同收 入组别(变量Ts9)的信心指数index1的均值 是否相等。
二、连续变量的统计推断:t-检验
3、 “比较均值”—配对样本 t 检验
例5:在轿车拥有率案例中,控制城市影响条 件下,更准确研究收入与轿车拥有率的关系。
三、无序分类变量的统计推断:卡方检验
五)分层卡方检验 (控制某些分类因素) 操作: “分析”—“描述统计”—“交叉表” (“层”框中选入城市变量S0) (“统计量”选中“风险”、 “Cochran‟s…”)
三、无序分类变量的统计推断:卡方检验
spss假设检验

8.3 利用SPSS实现独立样本t检验
第8章 简单统计 推断:假设检验
例8-3 利用“1991年美国综合社会调查数据”,分析美国 男女的受教育年数是否有显著差异。 假设检验问题为(双尾检验) :
H0 : 男 女 H1 : 男 女
菜单:“分析”->“比较均值”->“独立样本T检验”
Xiang Ye School of Information, Renmin University of China
8.1 假设检验的基本原理
第8章 简单统计 推断:假设检验
假设检验是一种方法,目的是为了决 定一个关于总体特征的定量的断言( 比如一个假设)是否真实。 通过计算从总体中抽出的随机样本的 适当的统计量来检验一个假设。 如果得到的统计量的实现值在假设为 真时应该是罕见的(小概率事件), 将有理由拒绝这个假设。
Xiang Ye School of Information, Renmin University of China
8.1 假设检验的基本原理
第8章 简单统计 推断:假设检验
如果一个人说他从来没有骂过人。他能够证明吗? 如果非要证明他没有骂过人,他必须出示他从小到 大每一时刻的录音录像,所有书写的东西等,还要 证明这些物证是完全的、真实的、没有间断的。这 简直是不可能的。即使他找到一些证人,比如他的 同学、家人和同事来证明,那也只能够证明在那些 证人在场的某些片刻,他没有被听到骂人。 但是,反过来,如果要证明这个人骂过人很容易, 只要有一次被抓住就足够了。 看来,企图肯定什么事物很难,而否定却要相对容 易得多。物理学以及其他科学都是在否定中发展的 ,这也是假设检验背后的哲学。
单尾检验Biblioteka H0 : 500 H1 : 500
假设检验及SPSS实现31页PPT

45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ,而不 是为了 束缚他 的才能 。—— 罗伯斯 庇尔
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
假设检验及SPSS实现
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
SPSS 软件入门教程

SPSS软件入门教程1、关于SPSS软件SPSS是“社会科学统计软件包”(Statistical Package for the Social Science)的简称,是一种集成化的计算机数据处理应用软件。
1968年,美国斯坦福大学H.Nie等三位大学生开发了最早的SPSS统计软件,并于1975年在芝加哥成立了SPSS公司,已有30余年的成长历史,全球约有25万家产品用户,广泛分布于通讯、医疗、银行、证券、保险、制造、商业、市场研究、科研、教育等多个领域和行业。
SPSS是世界上公认的三大数据分析软件之一(SAS、SPSS和SYSTAT)。
1994至1998年间,SPSS公司陆续购并了SYSTAT公司、BMDP公司等,由原来单一统计产品开发转向企业、教育科研及政府机构提供全面信息统计决策支持服务。
伴随SPSS服务领域的扩大和深度的增加,SPSS公司已决定将其全称更改为Statistical Product and Service solutions(统计产品与服务解决方案)。
目前,世界上最著名的数据分析软件是SAS和SPSS。
SAS由于是为专业统计分析人员设计的,具有功能强大,灵活多样的特点,为专业人士所喜爱。
而SPSS是为广大的非专业人士设计,它操作简便,好学易懂,简单实用,因而很受非专业人士的青睐。
此外,比起SAS软件来,SPSS主要针对着社会科学研究领域开发,因而更适合应用于教育科学研究,是国外教育科研人员必备的科研工具。
1988年,中国高教学会首次推广了这种软件,从此成为国内教育科研人员最常用的工具。
2、SPSS软件的特点①集数据录入、资料编辑、数据管理、统计分析、报表制作、图形绘制为一体。
从理论上说,只要计算机硬盘和内存足够大,SPSS可以处理任意大小的数据文件,无论文件中包含多少个变量,也不论数据中包含多少个案例。
②统计功能囊括了《教育统计学》中所有的项目,包括常规的集中量数和差异量数、相关分析、回归分析、方差分析、卡方检验、t检验和非参数检验;也包括近期发展的多元统计技术,如多元回归分析、聚类分析、判别分析、主成分分析和因子分析等方法,并能在屏幕(或打印机)上显示(打印)如正态分布图、直方图、散点图等各种统计图表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当然,在两个假设中用哪一个作为原假设,哪 一个作为备择假设,视具体问题的题设和要求而定。 在许多问题中,当总体分布的类型已知时,只对其中 一个或几个未知参数作出假设,这类问题通常称之为 参数假设检验,如例1。而在有些问题中,当总体的 分布完全不知或不确切知道,就需要对总体分布作出 某种假设,这种问题称为分布假设检验,如例2。
在本讲中,我们将讨论不同于参数估计 的另一类重要的统计推断问题. 这就是根据 样本的信息检验关于总体的某个假设是否 正确. 这类问题称作假设检验问题 . 假设检验
参数假设检验 非参数假设检验
总体分布已知, 检验关于未知参数 的某个假设
总体分布未知时的 假设检验问题
一、 假设检验问题的提出
统计推断的另一个重要问题是假设检验问题。在总体 的分布函数未知或只知其形式,但不知其参数的情况 下,为了推断总体的某些性质,提出某些关于总体的 假设。例如,提出总体服从泊松分布的假设,又如, 对于正态总体提出数学期望μ0的假设等。 假设检验就是根据样本对所提出的假设作出 判断:是接受,还是拒绝。 这里,先结合例子来说明假设检验的基本思 想和做法。
以上两例都是科技领域中常见的假设检验问题。 我们把问题中涉及到的假设称为零假设或称原假 设,一般用H0表示。零假设是对一种没有差异、没有 影响的状态的表述。 把与原假设对立的断言称为备择假设,备选稼穑 就是存在一些差异或影响的状态。记为H1。 如例1,若原假设为H0:= 0=4.55,则备择假设 为H1:≠4.55。 若例2的原假设为H0:X服从正态分布,则备 择假设为H1:X不服从正态分布。
假设检验的步骤:
Fig. 15.3 建立假设
选择适当的检验方法
选择显著性水平 收集数据
决定概率
决定检验统计量的临界值
与显著水平比较 拒绝或不拒绝 H0 得出市场营销研究结论
决定临界值是否位于 拒绝假设的区域
思考题1:
• 某工厂生产10欧姆的电阻.根据以往生产的 电阻实际情况,可以认为其电阻值X~N( , 2),标准差σ=0.1.现在随机抽取10个电阻, 测得它们的电阻值为: • 9.9, 10.1, 10.2, 9.7, 9.9, 9.9, 10, 10.5, 10.1, 10.2. • 试问:从这些样本,我们能否认为该厂生产 的电阻的平均值为10欧姆?
接下来我们要做的事是:给出一个合理的法则,根 据这一法则,利用巳知样本做出判断是接受假设H0 ,还是拒绝假设H0。
二、 假设检验的基本思想
假设检验的一般提法是:在给定备择假设H1下, 利用样本对原假设H0作出判断,若拒绝原假设H0,那 就意味着接受备择假设H1,否则,就接受原假设H0。 换句话说,假设检验就是要在原假设H0和备择假 设H1中作出拒绝哪一个和接受哪一个的判断。究竟如 何作出判断呢?对一个统计假设进行检验的依据是 所谓小概率原理,即 概率很小的事件在一次试验中是几乎不可能发 生
将上述检验思想归纳起来,可得参数的假设检 验的一般步骤: (1)根据所讨论的实际问题建立原假设H0及备择假设H1; (2)选择合适的检验统计量Z,并明确其分布; (3)对预先给定的小概率>0,由确定临界值; (4)由样本值具体计算统计量Z的观察值z,并作出判 断,若|z|≥z/2 ,则拒绝H0,接受H1;若|z|< z/2 , 则接受H0。
例2 某自动车床生产了一批铁钉,现从该批铁钉 中随机抽取了11根,测得长度(单位:mm)数据为: 10.41,10.32,10.62,40.18,10.77,10.64, 10.82, 10.49,10.38,10.59,10.54。 试问铁钉的长度X是否服从正态分布? 而在本例中,我们关心的问题是总体X是否服从 正态分布。如同例1那样,选择是或否作为假设,然 后利用样本对假设的真伪作出判断。
第九章 假设检验
本章内容介绍
本章将讨论统计推断的另一个重要方面——统计 假设检验。出于某种需要,对未知的或不完全明 确的总体给出某些假设,用以说明总体可能具备 的某种性质,这种假设称为统计假设。如正态分 布的假设,总体均值的假设等。这个假设是否成 立出判断,是接受假设还是拒绝假设。 本章主要介绍假设检验的基本思想和常用的检验 方法,重点解决正态总体参数的假设检验 。
例如,在100件产品中,有一件次品,随机地从中 取出一个产品是次品的事件就是小概率事件。 因为此事件发生的概率=0.01很小,因此, 从中任意抽一件产品恰好是次品的事件可认为几乎不 可能发生的,如果确实出现了次品,我们就有理由怀 疑这“100件产品中只有一件次品”的真实性。 那么取值多少才算是小概率呢?这就要视实 际问题的需要而定,一般取0.1,0.05,0.01等。 以例1为例:首先建立假设 : H0:=0=4.55,H1:≠4.55。 其次,从总体中作一随机抽样得到一样本观察 值(x1,x2,…,xn)。
自然,我们希望一个假设检验所作的判断犯这 两类错误的概率都很小。事实上,在样本容量n固 定的情况下,这一点是办不到的。因为当减小时, 就增大;反之,当减小时,就增大。
那么,如何处理这一问题呢? 事实上,在处理实际问题中,对原假设H0, 我们都是经过充分考虑的情况下建立的,或者认 为犯弃真错误会造成严重的后果。
检验统计量的分布特征(续)
• H0和H1的不同分布图以及Z>1.64的概率
X 0 统计量 Z 称为检验统计量。 / n 当检验统计量取某个区域C中的值时,就拒绝H0, 则称C为H0的拒绝域,拒绝域的边界点称为临界值。如
例1中拒绝域为|
z | z / 2,临界值为 z z / 2和z z / 2
显然,这里需要解决的问题是,如何根据样本判 断现在冶炼的铁水的含碳量是服从≠4.55的正态分 布呢?还是与过去一样仍然服从 =4.55的正态分布 呢?若是前者,可以认为新工艺对铁水的含碳量有显 著的影响;若是后者,则认为新工艺对铁水的含碳量 没有显著影响。通常,选择其中之一作为假设后,再 利用样本检验假设的真伪。
故Z的观察值 x 0 4.364 4.55 z 3.9 / n 0.108/ 5 因为| z|=3.9>1.96,所以拒绝H0,接受H1,即认为 新工艺改变了铁水的平均含碳量。
三、假设检验中两类错误
第Ⅰ类错误,当原假设H0为真时,却作出拒绝 H0的判断,通常称之为弃真错误,由于样本的随机 性,犯这类错误的可能性是不可避免的。若将犯这 一类错误的概率记为,则有P{拒绝H0|H0为真}=。 第Ⅱ类错误,当原假设H0不成立时,却作出接 受H0的决定,这类错误称之为取伪错误,这类错误 同样是不可避免的。若将犯这类错误的概率记为, 则有P{接受H0|H0为假}= 。
具体设想是,对给定的小正数,由于事件
| X 0 | z / 2 / n 是概率为的小概率事件,即 | X 0 | P z / 2 / n X 0 因此,当用样本值代入统计量 Z 具体 / n | x 0 | | z | 计算得到其观察值 时,若 | z | z / 2 ,即 / n 说明在一次抽样中,小概率事件居然发生了。因此 依据小概率原理,有理由拒绝H0,接受H1; 若| z | z / 2 ,则没有理由拒绝H0,只能接受H0。
例如,原假设是前人工作的结晶,具有稳定性, 从经验看,没有条件发生变化,是不会轻易被否定的, 如果因犯第Ⅰ类错误而被否定,往往会造成很大的损 失。 因此,在H0与H1之间,我们主观上往往倾向于 保护H0,即H0确实成立时,作出拒绝H0的概率应是 一个很小的正数,也就是将犯弃真错误的概率限制在 事先给定的范围内,这类假设检验通常称为显著性假 设检验,小正数称为检验水平或称显著性水平。
例1 已知某炼铁厂的铁水含碳量X在某种工艺条 件下服从正态分布N(4.55,0.1082)。现改变了工艺条 件,又测了五炉铁水,其含碳量分别为: 4.28,4.40,4.42,4.35,4.37。 根据以往的经验,总体的方差2= 0.1082一般不会改 变。试问工艺改变后,铁水含碳量的均值有无改变?
现在,我们来解决例1提出的问题: (1)假设H0:= 0=4.55,H1:≠4.55;
X 0 (2)选择检验用统计量 Z ~ N (0 , 1) ; / n
(3)对于给定小正数,如=0.05,查标准正态分表得 到临界值z/2 =z0.025 =1.96;
x 4.364 , 2 0.1082 , (4)具体计算:这里n=5,
1 n 是的无偏估计量。因此,若H 正 注意到 X X i 0 n i 1 确,
1 n 则 x n xi 与0的偏差一般不应太大,即 | x 0 | 不 i 1
应太大,若过分大,我们有理由怀疑H0的正确性而拒
X 0 绝H0。由于 Z ~ N (0 , 1) ,因此,考察 / n | x 0 | | x 0 | 的大小等价于考察 的大小,哪么如 / n | x 0 | 何判断 是否偏大呢? / n
互联网使用数据
Table 15.1
Respondent Number 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 Sex 1.00 2.00 2.00 2.00 1.00 2.00 2.00 2.00 2.00 1.00 2.00 2.00 1.00 1.00 1.00 2.00 1.00 1.00 1.00 2.00 1.00 1.00 2.00 1.00 2.00 1.00 2.00 2.00 1.00 1.00 Familiarity 7.00 2.00 3.00 3.00 7.00 4.00 2.00 3.00 3.00 9.00 4.00 5.00 6.00 6.00 6.00 4.00 6.00 4.00 7.00 6.00 6.00 5.00 3.00 7.00 6.00 6.00 5.00 4.00 4.00 3.00 Internet Usage 14.00 2.00 3.00 3.00 13.00 6.00 2.00 6.00 6.00 15.00 3.00 4.00 9.00 8.00 5.00 3.00 9.00 4.00 14.00 6.00 9.00 5.00 2.00 15.00 6.00 13.00 4.00 2.00 4.00 3.00 Attitude Toward Internet Technology 7.00 6.00 3.00 3.00 4.00 3.00 7.00 5.00 7.00 7.00 5.00 4.00 4.00 5.00 5.00 4.00 6.00 4.00 7.00 6.00 4.00 3.00 6.00 4.00 6.00 5.00 3.00 2.00 5.00 4.00 4.00 3.00 5.00 3.00 5.00 4.00 6.00 6.00 6.00 4.00 4.00 2.00 5.00 4.00 4.00 2.00 6.00 6.00 5.00 3.00 6.00 6.00 5.00 5.00 3.00 2.00 5.00 3.00 7.00 5.00 Usage of Internet Shopping Banking 1.00 1.00 2.00 2.00 1.00 2.00 1.00 2.00 1.00 1.00 1.00 2.00 2.00 2.00 2.00 2.00 1.00 2.00 1.00 2.00 2.00 2.00 2.00 2.00 2.00 1.00 2.00 2.00 1.00 2.00 2.00 2.00 1.00 1.00 1.00 2.00 1.00 1.00 2.00 2.00 2.00 2.00 2.00 1.00 2.00 2.00 1.00 1.00 1.00 2.00 1.00 1.00 1.00 1.00 2.00 2.00 1.00 2.00 1.00 2.00
