中央财经大学MATLAB第2讲课余作业

合集下载

matlab课后习题解答第二章doc

tao=sym('tao','positive');
f=A*((1+t/tao)*(heaviside(t+tao)-heaviside(t))+(1-t/tao)*(heaviside(t)-heaviside(t-tao)));
（2）数值计算复验
xx=-10*pi:pi/100:1.7*pi;
sn=trapz(exp(-abs(xx)).*abs(sin(xx)))*pi/100
sn =
1.0877
110
〖目的〗
变上限二重积分的符号计算法。
〖解答〗
syms x y
f=x^2+y^2;
r=int(int(f,y,1,x^2),x,1,2)
d =
1/(a11*a22*a33 - a11*a23*a32 - a12*a21*a33 + a12*a23*a31 + a13*a21*a32 - a13*a22*a31)
16
〖目的〗
symsum, subs的应用。
从实例中，感受指令所给出的关于符号解的含义。
〖解答〗
symsx k
f=x^(k);
y3d =
1.2935547796148951782413405453553
113
〖目的〗
符号离散卷积直接法和变换法。
〖解答〗
（1）直接法
syms a b kn
x=a^k;
h=b^k;
w=symsum(subs(h,k,n)*subs(x,k,k-n),n,0,k)%据定义
y1=simple(w)
w =
〖解答〗
syms x
syms n positive

MATLAB课程作业

注意：11月15日是交作业的最后期限。

（交word和MATLAB程序清单，word以“班级-学号-姓名”命名，每个MATLAB程序以”zuoye_题号”命名后，放在一个文件夹下（文件夹命名为“作业程序”），如zuoye_1_1.m），将word和“作业程序”文件夹放在一个文件夹（文件夹以“班级-学号-姓名”）交到班长处，班长统一交到教学办公室。

第一部分程序设计1.1、用MA TLAB可以识别的格式输入下面两个矩阵：(1) 矩阵A的维数；(2) 矩阵A中的元素a41的值；(3) 修改矩阵A的元素，使a41 =3.0；(4) 矩阵A中最后2行和最后3列交汇形成的子矩阵的值。

(5)求出A和B的乘积矩阵C，并将C矩阵的右下角2X 3子矩阵赋给D矩阵。

1.2、已知111121111,131,111214A B⎡⎤⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求(1)AB-2A，(2)A*B，(3)A﹒*B，(4) AB-BA 1.3、解线性方程：1.4、解方程组：1.5、用MA TLAB语言实现下面的分段函数：1.6、已知x=[1 2 3 ],y=[4 5 6 ]，试计算z=x.*y 、x.\y 和x./y.1.7、分别用for 和while 循环语句编写程序，求出1.8、已知在平面坐标中两点(x 1, y 1)和(x 2, y 2)之间的距离计算公式为 ()()222121y y x x L -+-=(1) 利用命令文件的形式，编写求解该距离的M 文件dis1.m ；(2) 利用函数文件的形式，编写求解该距离的M 文件dis2.m ；(3) 给定两点坐标的值(2,3)和(8, －5)，试分别调用命令文件dis1.m 和函数文件dis2.m 求解该两点间距离的值。

1.9、求解方程x 5+6x 3一3x 2＝10的5个根，并将其位置用五角星符号标记在复平面上，要求横纵坐标袖的刻度等长，注明虚轴和实轴，在title 位置上写㈩方程。

学生实验作业matlab

实验报告（MATLAB课后作业练习题）学院电子信息学院班级学号姓名任课教师目录实验作业1 (3)第一题、一阶电路 (3)实验作业2 (7)第一题Waterfall Scope（瀑布显示图） (7)Chirp Signal扫频信号源 (7)Uniform Random Number信号源下 (8)Band-Limited White Noise信号源 (8)第二题：设计一个编程开关仿真系统框图 (9)仿真实验作业3 (10)第一题 (10)第二题 (13)仿真实验作业4 (14)第一题 (14)第二题 (16)仿真实验作业5 (19)仿真实验作业6 (21)仿真实验作业7 (23)仿真实验作业8 (26)实验作业1第一题、一阶电路(1)、电路图如下，R=1.4欧，L=2亨，C=0.32法，初始状态：电感电流为零，电容电压为0.5V ，t=0时刻接入1V 的电压，求0<t<15s 时，i (t)，v o (t)的值，并且用Simulink 仿真画出R=1.4、R=5和 R=9的电流与电容电压的关系曲线。

还可以进一步修改信号源参数，使用三角波、正弦波等作为激励信号，观察输出信号的情况。

function xdot=funcforexl23(t,x,~,R,L,C)xdot=zeros(2,1); %矩阵初始化 xdot(1)=-R/L*x(1)-1/L*x(2)+1/L* f(t); %方程1 xdot(2)=1/C * x(1); %方程2 function in=f(t) %输入信号 in=(t>0)*1; %阶跃信号%filename ex123.mL=2; %电感值 C=0.32; %电容值for R=[1.4 5 9] %仿真电阻值分别为1.5, 3, 5欧姆的情况[t,x]=ode45('funcforexl23',[0,15],[0;0.5],[],R,L,C); %也可采用ode23, ode15s 等求解figure(1);plot(t,x(:,1));hold on ; xlabel('time sec'); text(2,0.07,'\leftarrow i_L(t)');grid;figure(2);plot(t,x(:,2));hold on ;xlabel('time sec'); text(2.1,0.75,'\leftarrow u_C(t)');grid; End输入输出的传递函数：11)()()(2++==RCs LCs s F s U s H c① R=1.4时：1448.064.01)(2++=s s s H ±Vs=1Vt=0R L C +-)(t i )(t v o② R=5时：16.164.01)(2++=s s s H③ R=9时：188.264.01)(2++=s s s H连续系统的传递函数如下：借助多项式乘法函数conv 来处理：两个向量分别用num 和den 表示。

matelab作业2参考答案

matelab作业2参考答案Matlab作业2参考答案Matlab作业2是一项综合性的任务，要求学生运用Matlab编程语言解决一系列数学问题。

本文将为大家提供一份参考答案，帮助学生更好地理解和完成这项作业。

首先，我们将讨论作业的第一个问题，即给定一个矩阵A，求解其特征值和特征向量。

在Matlab中，可以使用eig函数来实现这一功能。

例如，假设我们有一个3×3的矩阵A，可以按照以下方式计算其特征值和特征向量：```A = [1 2 3; 4 5 6; 7 8 9];[eigenvectors, eigenvalues] = eig(A);```在上述代码中，变量eigenvectors将存储A的特征向量，而变量eigenvalues 将存储A的特征值。

通过打印这两个变量的值，我们可以得到矩阵A的特征值和特征向量。

接下来，我们将探讨作业的第二个问题，即求解线性方程组。

假设我们有一个3×3的系数矩阵A和一个3×1的常数向量b，我们需要求解方程组Ax=b。

在Matlab中，可以使用backslash运算符来求解线性方程组。

例如，假设我们有以下方程组：```A = [1 2 3; 4 5 6; 7 8 9];b = [10; 20; 30];x = A \ b;```在上述代码中，变量x将存储方程组的解。

通过打印变量x的值，我们可以得到方程组的解。

此外，作业的第三个问题要求学生使用Matlab绘制函数图像。

在Matlab中，可以使用plot函数来实现这一功能。

例如，假设我们要绘制函数y=sin(x)，其中x的取值范围为0到2π，可以按照以下方式绘制函数图像：```x = 0:0.1:2*pi;y = sin(x);plot(x, y);```在上述代码中，变量x将存储x的取值范围，变量y将存储对应的函数值。

通过调用plot函数，我们可以将函数y=sin(x)的图像绘制出来。

中央财经大学matlab复习总结

第一章基础准备及入门1、指令提示符：〉〉2、默认变量名ans3、续行三个或以上连续黑点4、变量名函数名对字母大小写敏感5、变量名第一个字符是英文字母，可包含英文、数字、下连符，不可包含空格、标点、运算符。

6、左除和右除：对标量而言结果相同，对矩阵结果不同7、不用事先对数组维数及大小做任何说明，内存自动配置8、二维数组输入的三大要素：数组标识符 [ ]；元素分隔符空格或逗号；数组行间分隔符分号或回车9、常用符号：，指令之间分隔，输入量之间，数组元素之间. 小数点，数组运算符；抑制计算结果显示，不显示计算结果指令与其后指令的分隔，数组行间分隔符{ }胞元数组记述符：用以生成一维数值数组% 由其开头的所有物理行部分被看成是非执行的注释10、常用指令ans 最新计算结果默认变量名clf 清除图形窗clc 清除指令窗显示内容（历史命令里，工作空间中仍然存在）clear 清除工作空间中保存的变量which 后面输入要找的文件名，显示所在目录课后习题【2】只有包含英文字母、数字和下划线的合法，第二个和第五个【6】（1）不正确，显示的精度可以调整（2）内存的数据总是保持精确的，但显示的可以调整。

【例】用format函数>> format long……………..显示全部>> a=2.3334343434a =2.333434343400000>> format short………………默认的，就显示四位>> a=3.444434343442a =3.4444用vpa>> a=2.54234345a =2.5423>> vpa(a,10)ans =2.54234345【7】只有第二个，注意中文状态下输入没有用第二章符号计算符号计算：计算时，不是在离散的数值点上进行，是根据恒等式和数学定理，通过演绎推理得到，数值完全准确1、创建符号数字：sym(‘Num’)，符号常数sc=sym(‘Num’)【例】>> a=sin(1/10)a =0.0998>> b=sym('sin(1/10)')b =sin(1/10)>> vpa(a-b,40)ans =0.000000000000000002443367540153074826826593858808322656667Tips：Num是整数，有理数，预定义常数（比如pi）时，创建的才完全精准，也就是说，上题若用sin0.1，误差就大了2、a、b、x等都被称为基本符号变量，x默认为自由符号变量，而其他的被当成符号参数3、sym和syms（1）只有sym可以创建符号数字和符号常数（2）均可以创建单个符号变量，多个符号变量只能syms（3）都能撤销单变量限定假设，多变量限定假设职能syms>> sym x real>> sym('x','clear')或者sym x clearTips：reset（symengine）重启MuPAD4、自由符号变量symvar(expression) 列出所有基本符号变量symvar（expression，n）列出认定的n个自由符号变量比如：定义了一个符号表达式Eqsymvar（Eq）就是按照字母表顺序列出基本符号变量symvar（Eq，100）按离x的距离列出前100个自由符号变量，其实这个值只要大于等于真实的自由变量数即可5、whos可以给出所有内存变量的属性6、符号变量的限定性默认x=sym(‘x’) 复数符号变量x=sym（’x’，’real’）实数‘positive’正数若是多个变量syms x y z positive7、clear x 清除内存中的x，不清除关于x的假设，当以后运算又出现x符号变量，原有假设将继续约束新出现的x变量8、双精度数字向符号数字转换双精度数字：8字节，64位2进制，提供16位有效数字，也就是说跟符号数字相比，它是一个有误差的数sym(Num,’real’) 数值类数字Num的有理分数表达的符号数字（’r’可以省略），Num输入的是双精度数字例如：>> s=sin(1)s =0.8415>> sym(0.8451)ans =8451/100009、符号向双精度转换double(Num_sym)…………………. Num_sym是符号数字例如：>> double(1/2)ans =0.500010、符号数字的任意精度表达形式（1）digits 当前环境下符号数字的有效数字位数例如：>> double(1/2)ans =0.5000>> digitsDigits = 32（2）xs=vpa(x) 根据表达式x得到digits指定精度下符号数字xsxs=vpa(x,n) 得到n位有效数字的符号数字xs，只在运行当时有用【例】>> xs=vpa(log(34),10)……………………..log后面的数字加括号xs =3.52636052511、subs函数：RES=subs（f，旧的，新的）【2.2-4】（1）>> syms a b x>> f=a*sin(x)+bf =b + a*sin(x)（2）>> f1=subs(f,sin(x),'log(y)')………….输入的第三个量可以是字符串，加引号f1 =b + a*log(y)(3)>> f2=subs(f,a,3.11)f2 =b + (311*sin(x))/100>> class(f2)………………………………观察结果的类型ans =sym（4）所有变量被数字置换（至少一个符号数字），结果是符号对象（5）所有被双精度置换，结果双精度>> f2=subs(f,a,3.11)f2 =b + (311*sin(x))/100>> class(f2)ans =sym>> f4=subs(f,{a,b,x},{2,5,pi/3})f4 =6.7321>> class(f4)ans =double（6）（7）略（8）通过两次置换把三个变量都变成双精度数，得到双精度数组12、极限和导数右极限limit(f,v,a,’right’) v→a+左极限limit(f,v,a,’left’) v→a-求n阶导数dfdvn=diff(f,v,n)Jacobian矩阵fjac=jacobian(f,v)【书2.3-1】研究两个重要极限>> clear>> syms t x k>> s=sin(k*t)/(k*t)s =sin(k*t)/(k*t)>> f=(1-1/x)^(k*x)f =(1 - 1/x)^(k*x)>> Lsk=limit(s,t,0)Lsk =1>> Lf=limit(f,x,inf)Lf =exp(-k)>> Ls1=subs(Lsk,k,1)Ls1 =1>> Lf1=vpa(subs(Lf,k,1),48)Lf1 =0.367879441171442334024277442949824035167694091797 【书2.3-2】求导数>> syms a t x>> f=[a,t^3;t*cos(x),log(x)]f =[ a, t^3][ t*cos(x), log(x)]（1）求一阶的>> df=diff(f)df =[ 0, 0][ -t*sin(x), 1/x]（2）二阶的>> dfdt2=diff(f,t,2)dfdt2 =[ 0, 6*t][ 0, 0]（3）混合的>> dfdxdt=diff(diff(f,x),t)dfdxdt =[ 0, 0][ -sin(x), 0]13、符号积分intf=int(f,v) 不定积分intf=int(f,v,a,b)定积分14、符号矩阵diag(A) 取对角元构成向量，或根据向量构成对角阵[V,D]=eig(A) 特征值分解，使A V=VDinv(A) 求矩阵逆rank（A）求矩阵秩15、求解指令solve不存在符号解，又无其他自由参数时，solve将给出数值解【例】S=solve(eq1,eq2,x,y) 含义是解方程一方程二关于x和y的解16、可视化plot 不可用于符号运算中的绘图ezplot 符号运算中，画二维曲线ezplot3 画三维曲线【例】>> syms t>> ezplot3(sin(t),cos(t),t)课后习题【3】解方程>> reset(symengine)>> syms x a positive>> f1=x^3+(4-a)*x^2+(3-4*a)*x-3*af1 =x^3 + (4 - a)*x^2 + (3 - 4*a)*x - 3*a>> f2=x^2-a*x+a^2f2 =a^2 - a*x + x^2>> solve(f1)……………………默认是对x解ans =a>> sym x clear……………………….清除关于x的假设ans =x>> solve(f2)ans =a/2 + (3^(1/2)*a*i)/2a/2 - (3^(1/2)*a*i)/2>> assumptions……………………………显示对所有变量做的假设ans =0 < a【7】求和>> syms x k positive……………….别忘了k（k也可以另用syms定义为无限定假设）>> f=2/(2*k+1)*[(x-1)/(x+1)]^(2*k+1)f =(2*((x - 1)/(x + 1))^(2*k + 1))/(2*k + 1)>> a=symsum(f,k,0,inf)…………………symsum，不是sum>>a=simple(a)a =piecewise([abs(x - 1) < x + 1, log(x)])【8】求导数>> syms t>> y=abs(sin(t))abs(sin(t))>> dydt=diff(y)dydt =sign(sin(t))*cos(t)>> a=limit(y,t,0,'left')a =>> b=limit(y,t,0,'right')b =【10】算二重积分（连续用两次int）>> syms x y>> f=x^2+y^2f =x^2 + y^2>> a=int(int(f,y,1,x^2),x,1,2)a =1006/105【20】解方程>> syms x y>> [x,y]=solve('x^2+y^2=1','x*y=2','x','y')结果显示略第三章数值列阵及向量化运算1、矩阵运算规则A+B，b+A，B=A’，inv（A）或C=A\eye(N)求方阵逆，C=A^m 2、数组维度1为行维，2为列维，3为页维。

matlab课程设计大作业

matlab课程设计大作业一、教学目标本课程的教学目标是使学生掌握MATLAB基本语法、编程技巧以及MATLAB 在工程计算和数据分析中的应用。

通过本课程的学习，学生将能够熟练使用MATLAB进行简单数学计算、线性方程组求解、函数图像绘制等。

1.掌握MATLAB基本语法和编程结构。

2.了解MATLAB在工程计算和数据分析中的应用。

3.熟悉MATLAB的函数库和工具箱。

4.能够使用MATLAB进行简单数学计算。

5.能够使用MATLAB求解线性方程组。

6.能够使用MATLAB绘制函数图像。

7.能够利用MATLAB进行数据分析和处理。

情感态度价值观目标：1.培养学生对计算机辅助设计的兴趣和认识。

2.培养学生团队合作和自主学习的能力。

二、教学内容本课程的教学内容主要包括MATLAB基本语法、编程技巧以及MATLAB在工程计算和数据分析中的应用。

1.MATLAB基本语法：介绍MATLAB的工作环境、基本数据类型、运算符、编程结构等。

2.MATLAB编程技巧：讲解MATLAB的函数调用、脚本编写、函数文件编写等编程技巧。

3.MATLAB在工程计算中的应用：介绍MATLAB在数值计算、线性方程组求解、图像处理等方面的应用。

4.MATLAB在数据分析中的应用：讲解MATLAB在数据采集、数据分析、数据可视化等方面的应用。

三、教学方法本课程采用讲授法、案例分析法、实验法等多种教学方法相结合的方式进行教学。

1.讲授法：通过讲解MATLAB的基本语法、编程技巧以及应用案例，使学生掌握MATLAB的基本知识和技能。

2.案例分析法：通过分析实际工程案例，使学生了解MATLAB在工程计算和数据分析中的应用。

3.实验法：安排上机实验，使学生在实际操作中巩固所学知识，提高实际编程能力。

四、教学资源本课程的教学资源包括教材、实验设备、多媒体资料等。

1.教材：选用《MATLAB教程》作为主要教材，辅助以相关参考书籍。

2.实验设备：为学生提供计算机实验室，配备有MATLAB软件的计算机。

matlab章课后作业

matlab章课后作业MATLAB基础教程1~8章作业Matlab第⼀章1.阐述Matlab的功能Matlab作为⼀种⾼级计算软件，是进⾏算法开发、数据可视化、数据分析以及数值计算的交互式应⽤开发环境，已被⼴泛应⽤于不同领域。

Matlab的基本功能包括：数学计算功能、图形化显⽰功能、M 语⾔编程功能、编译功能、图形⽤户界⾯开发功能、Simulink建模仿真功能、⾃动代码⽣成功能。

Matlab第⼆章1．创建double的变量，并进⾏计算。

(1)a=87，b=190，计算a+b、a-b、a*b。

(2)创建uint8 类型的变量，数值与(1)中相同，进⾏相同的计算。

>> a=87,b=190a =87b =190>> a+bans =277>> a-bans =-103>> a*bans =16530>> c=uint8(87), d=uint8(190)c =87d =190>> c+dans =255>> c-dans =>> c*dans =2552.计算(1)sin(60)(2)e^3(3)cos(3π/4)>> sind(60)ans =0.8660>> exp(3)ans =20.0855>> cos(3*pi/4)ans =-0.70713.设u=2，v=3，计算：(1)(2)(3)>> u=2;>> v=3;>> 4*u*v/log(v)ans =21.8457>> (exp(u)+v)^2/(v^2-u) ans = 15.4189>> sqrt(u-3*v)/(u*v) ans =0 + 0.4410i 4.计算如下表达式：(1)(2)>> (3-5*i)*(4+2*i)ans =22.0000 -14.0000i >> sin(2-8*i) 1.3553e+003 +6.2026e+002i5.判断下⾯语句的运算结果。

MATLAB程序设计及应用(第二版)课后实验答案

Matlab 课后实验题答案实验一 MATLAB 运算基础1. 先求下列表达式的值，然后显示MATLAB 工作空间的使用情况并保存全部变量。

(1) 0122sin851z e=+(2) 21ln(2z x =，其中2120.455i x +⎡⎤=⎢⎥-⎣⎦(3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩，其中t =0:: 解：2. 已知：1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值：(1) A+6*B和A-B+I（其中I为单位矩阵）(2) A*B和A.*B(3) A^3和A.^3(4) A/B及B\A(5) [A,B]和[A([1,3],:);B^2]解：3. 设有矩阵A 和B1234530166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ (1) 求它们的乘积C 。

(2) 将矩阵C 的右下角3×2子矩阵赋给D 。

(3) 查看MATLAB 工作空间的使用情况。

解：. 运算结果：4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。

(2) 建立一个字符串向量，删除其中的大写字母。

解：(1) 结果：(2). 建立一个字符串向量例如：ch='ABC123d4e56Fg9';则要求结果是：实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵，试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。

MATLAB-第二次实验课课堂作业

M A T L A B-第二次实验课课堂作业(4学时)(共4页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--MATLAB 第二次实验课课堂作业（4学时）注：1）此课堂作业作为本课程结业成绩的重要依据，请同学们认真、独立完成，不得抄袭。

2）请在授课教师规定的时间内完成；3）完成作业后，请以word格式保存，文件名为：学号+姓名1.请完成如下4小题：1) 在区间[0,1]s上生成均匀分布的长度为20的向量A。

2) 请生成均值为、方差为的5阶正态分布随机矩阵B。

2) 生成长度为100的单位阶跃序列，阶跃点n0＝25。

用离散信号图示。

3）幅度为1V，频率为5Hz的正弦信号和（0，）的白噪声信号的叠加。

信号长1秒。

设采样频率为100Hz。

将正弦信号和白噪声信号表示在一张图形框，不同坐标系内。

另起一个图形框对叠加信号作图。

要求: 1. 给出1和2 小题的矩阵A 和B2. 给出3和4小题中的2组图形3. 给出你的程序内容2. 已知y=conv(x,h)能够完成输入信号x（n）与系统单位样值响应h（n）的卷积操作，得到输出信号y（n）。

请通过调用子函数y=conv(x,h)，编制一个程序 [y ny ]=conv1(x,h,nx,nh)，其中ny是y （n）第一个样值的n值， nx是x（n）第一个样值的n值， nh是h（n）第一个样值的n值.完成: 1）若 x（n）=[3 1 21 5 2 ] ,nx =-1; h（n）=[1 1 3 ] ,nh=-2 ,则y（n）和ny为多少？请用你编制的函数conv1完成。

2）给出conv1的程序内容解1）程序clc;clear;closeA=linspace(0,1,20)A=Columns 1 through 11Columns 12 through 202）程序clc;clear;close allB=+sqrt*randn(5)B =c3)程序内容Clc;clear;close all N=100;n0=25;u=ones(1,N);u(1,1:n0)=0;stem(0:N-1,u) 4)00.51-1-0.8-0.6-0.4-0.20.20.40.60.8100.51-0.25-0.2-0.15-0.1-0.050.050.10.150.200.10.20.30.40.50.60.70.80.91-1.5-1-0.50.511.5程序 clc;clear;close allts=0;te=1;fs=100 ;f1=5;t=ts:1/fs:te;y1=sin(2*pi*f1*t);y2=sqrt*randn(size(t));subplot(1,2,1);plot(t,y1);subplot(1,2,2);plot(t,y2);figure(2)plot(t,y1+y2)2.1)y =3 4 31 29 70 17 6ny =-32) function [y,ny]=conv1(x,nx,h,nh)y =conv(x,h);ny=nx+nh;。

MATLAB实验报告第二章

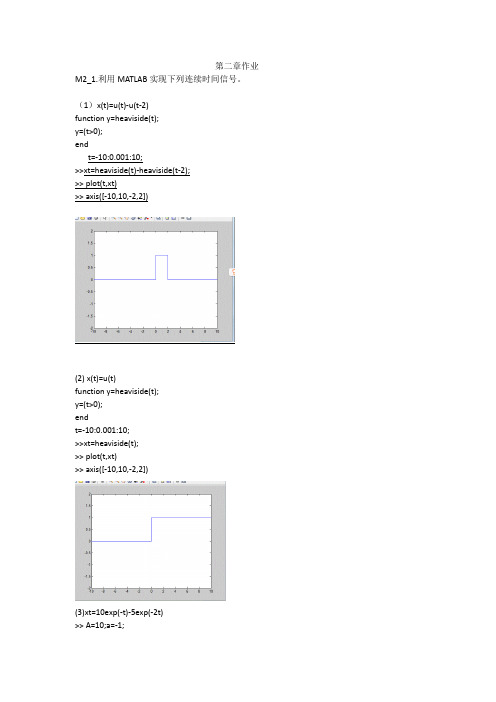
第二章作业M2_1.利用MATLAB实现下列连续时间信号。

（1）x(t)=u(t)-u(t-2)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t)-heaviside(t-2);>>plot(t,xt)>>axis([-10,10,-2,2])(2) x(t)=u(t)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t);>>plot(t,xt)>>axis([-10,10,-2,2])(3)xt=10exp(-t)-5exp(-2t)>> A=10;a=-1;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=5;a=-2;>> t=0:0.001:10;>> x2t=A*exp(a*t);>>xt=x1t-x2t;>>plot(t,xt)(4)xt=tu(t)>> t=-10:0.001:10;>>xt=t.*heaviside(t);>>plot(t,xt)（5）xt=2|sin（10pit+pi/3）| >> A=2;w0=10*pi;phi=pi/3; >> t=0:0.001:1;>>xt=A*abs(sin(w0*t+phi)); >>plot(t,xt)>>axis([0,1,-4,4])Xt=cost+sin(2pit)>> A=1;w0=1;phi=0; >> t=0:0.002:10;>> x1t=A*cos(w0*t+phi); >> A=2;w0=2*pi;phi=0; >> t=0:0.002:10;>> x2t=A*sin(w0*t+phi); >>xt=x1t+x2t;>>plot(t,xt)(7)xt=4exp(-0.5t)cos(2pit) >> A=5;a=-0.5;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=1;w0=2*pi;phi=0; >> t=0:0.001:10;>> x2t=A*cos(w0*t+phi); >>xt=x1t.*x2t;>>plot(t,xt)(8)Sa(pit)cos(30t)A=1;w0=30;phi=0;>> t=0:0.001:3;>> x1t=A*cos(w0*t+phi);>> t=0:0.001:3;>> x2t=sinc(t);>>xt=x1t.*x2t;>>plot(t,xt)M2-3，写出书中图示波形函数，并画出xt，x0.5t,x(2-0.5t)的图像function yt=x2_3(t)yt=t.*(t>=0&t<2)+2*(t>=2&t<3)+(-1)*(t>=3&t<=5); end>> t=0:0.001:5;>>xt=x2_3(t);>>title('x(t)');>>plot(t,xt)>>axis([0,6,-2,3])>> t=0:0.001:10;xt=x2_3(0.5*t); >>plot(t,xt)>>title('x(0.5t)')>>axis([0,10,-2,3])x(0.5t)>> t=-10:0.001:10;>>xt=x2_3(2-0.5*t);>>plot(t,xt)>>title('x(2-0.5t)')>>axis([-10,10,-2,3])M2-4画出图示的奇分量和偶分量。

matlab作业

Matlab 小学期作业土木工程2012-3班李然2012212218 尽管在大二上学期我们已经在王教授的指导和引领下对matlab已经有了一个比较感性的认识，自己也对matlab 最基本的操作和应用略知一二，但是总归是冰山一角，九牛一毛。

在小学期中，我们荣幸的再次接受王教授的教导，对matlab在解决实际问题的领域有了更深层次的理解。

在课程上，我们在王教授精彩讲授下，学会了许多实用的编程方法，学会了求解一些简单的matlab问题，并且可以求解线性和非线性方程组，以及常微分方程。

在敬业的教授认真负责下，我们还学习了一些课外知识，如门德卡洛法解决工程问题和最小二乘法求解最优解的问题。

在讲解每一问题时，老师都将问题的编程脚本文件仔细工整的写在黑板上，这极大地帮助了我们课下再去理解和消化这些问题。

也对我们解决此次作业起了很大的借鉴和引导作用。

此次作业共有六道题，分别是1.迭代法编写函数文件2.rand与randn应用区别3.Montecarlo法求解概率问题4.最小二乘法解决荷载变形问题5.1116.ode45解决常微分方程在重新认真翻阅书籍和上网查阅资料后，我对这六道题目有了一个大概的了解；在经过反复调试和修改的过程中，我终于编写出了这些m文件也弄懂了相关知识。

我的作业包括一份word版的matlab习题解答（即本文档，主要包括每个题目的m文件拷屏以及运行拷屏）还有各个题目的m文件，望老师能够抽空修改并给出点建议。

通过这次作业，增强了自己的自主学习能力，充分认识到了matlab的强大，增进了自己的学习兴趣。

在这个过程中巩固和提高了自己对所学知识的掌握和理解，感受到自身能力的提高，自己还认识到了持之以恒的重要性，只要全身心的投入一项工作，每件事都可以做到自己心中的完美。

总之，业精之法在于专，读书贵在有常，只有坚定的决心，不懈的努力，顽强的斗志才能做好每一件事，成为一个对社会有用的人。

以下就是作业的具体内容：第1题（1）m文件拷屏（2）运行显示拷屏，令fab（4）（1）x服从-8～12的正态分布，y服从0～5的随机分布（2）x的均值为10，标准差为2y的均值为2.5，标准差为1.44以下是运行结果（1）M文件拷屏（2）程序运行拷屏（1）m文件拷屏（2）运行程序拷屏（1）M文件拷屏（2）程序运行拷屏。

MATLAB作业2参考答案（2018年）

MA TLAB 作业二参考答案1、试求下面线性代数方程的解析解与数值解，并检验解的正确性。

2932114010110503848246303356684953X -----⎡⎤⎡⎤⎢⎥⎢⎥----⎢⎥⎢⎥=⎢⎥⎢⎥---⎢⎥⎢⎥------⎣⎦⎣⎦【求解】求出A , [A;B ] 两个矩阵的秩，可见二者相同，所以方程不是矛盾方程，应该有无穷多解。

>> A=[2,-9,3,-2,-1; 10,-1,10,5,0; 8,-2,-4,-6,3; -5,-6,-6,-8,-4]; B=[-1,-4,0; -3,-8,-4; 0,3,3; 9,-5,3]; [rank(A), rank([A B])] ans =4 4用下面的语句可以求出方程的解析解，并可以验证该解没有误差。

>> x0=null(sym(A));x_analytical=sym(A)\B; syms a; x=a*[x0 x0 x0]+x_analyticalx =[ a+967/1535, a-943/1535, a-159/1535][ -1535/1524*a, -1535/1524*a, -1535/1524*a][ -3659/1524*a-1807/1535,-3659/1524*a-257/1535,-3659/1524*a-141/1535] [ 1321/508*a+759/1535, 1321/508*a-56/1535, 1321/508*a-628/1535] [ -170/127*a-694/307, -170/127*a+719/307, -170/127*a+103/307] >> A*x-B ans = [ 0, 0, 0][ 0, 0, 0] [ 0, 0, 0] [ 0, 0, 0]用数值解方法也可以求出方程的解，但会存在误差，且与任意常数a 的值有关。

>> x0=null(A); x_numerical=A\B; syms a; x=a*[x0 x0 x0]+x_numerical; vpa(x,10)ans =[ .2474402553*a+.1396556436, .2474402553*a-.6840666849, .2474402553*a-.1418420333][-.2492262414*a+.4938507789,-.2492262414*a+.7023776988e-1,-.2492262414*a+.3853511888e-1][ -.5940839201*a, -.5940839201*a, -.5940839201*a][ .6434420813*a-.7805411315, .6434420813*a-.2178190763,.6434420813*a-.5086089095][-.3312192394*a-1.604263460, -.3312192394*a+2.435364854, -.3312192394*a+.3867176824] >> A*x-B[ 1/18014398509481984*a, 1/18014398509481984*a, 1/18014398509481984*a] [ -5/4503599627370496*a, -5/4503599627370496*a, -5/4503599627370496*a][ -25/18014398509481984*a, -25/18014398509481984*a, -25/18014398509481984*a] [ 13/18014398509481984*a, 13/18014398509481984*a, 13/18014398509481984*a]2、求解下面的联立方程，并检验得出的高精度数值解（准解析解）的精度。

MATLAB大作业

M A T L A B大作业(总15页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--MATLAB大作业作业要求：（1）编写程序并上机实现，提交作业文档，包括打印稿（不含源程序）和电子稿（包含源程序），以班为单位交，作业提交截止时间6月24日。

（2）作业文档内容：问题描述、问题求解算法（方案）、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。

打印稿不要求MATLAB程序，但电子稿要包含MATLAB程序。

（3）作业文档字数不限，但要求写实，写出自己的理解、收获和体会，有话则长，无话则短。

不要抄袭复制，可以参考网上、文献资料的内容，但要理解，要变成自己的语言，按自己的思路组织内容。

（4）从给出的问题中至少选择一题(多做不限，但必须独立完成，严禁抄袭)。

（5）大作业占过程考核的20%，从完成情况、工作量、作业文档方面评分。

第一类：绘制图形。

（B级）问题一：斐波那契（Fibonacci）螺旋线，也称黄金螺旋线（Golden spiral），是根据斐波那契数列画出来的螺旋曲线，自然界中存在许多斐波那契螺旋线的图案，是自然界最完美的经典黄金比例。

斐波那契螺旋线，以斐波那契数为边的正方形拼成的长方形，然后在正方形里面画一个90度的扇形，连起来的弧线就是斐波那契螺旋线，如图所示。

问题二：绘制谢尔宾斯基三角形（Sierpinskitriangle）是一种分形，由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。

其生成过程为：取一个实心的三角形（通常使用等边三角形），沿三边中点的连线，将它分成四个小三角形，然后去掉中间的那一个小三角形。

接下来对其余三个小三角形重复上述操作，如图所示。

问题三：其他分形曲线或图形。

分形曲线还有很多，教材介绍了科赫曲线，其他还有皮亚诺曲线、分形树、康托（G. Cantor）三分集、Julia集、曼德布罗集合（Mandelbrot set），等等。

matlab软件培训讲稿2_优化计算13页

第二篇优化计算篇用最优化方法解决最优化问题的技术称为最优化技术，它包含两个方面的内容：（1）建立数学模型，即用数学语言来描述最优化问题。

模型中的数学关系式反映了最优化问题所表要达到的目标和各种约束条件。

（2）数学求解，即数学模型建好以后，选择合理的最优化方法进行求解。

最优化方法的发展很快，现在已经包含有多个分支，如线性规划、整数规划、非线性规划、动态规划、多目标规划等。

利用Matlab 的优化工具箱，可以求解线性规划、非线性规划和多目标规划问题。

具体而言，包括线性、非线性最小化，最大最小化，二次规划，半无限问题，线性、非线性方程（组）的求解，线性、非线性的最小二乘问题。

另外，该工具箱还提供了线性、非线性最小化，方程求解，曲线拟合，二次规划等问题中大型课题的求解方法。

1. 优化工具箱中的函数优化工具箱中的函数包含下面几类：2. 优化函数的变量下面两个表描述工具箱中优化函数的输入输出变量：3. 参数设置利用optimset 函数，可以创建和编辑参数结构；利用optimget 函数，可以获得options 优化参数。

3.1 optimget函数利用该函数获得options 优化参数，其语法结构如下：●val=optimget(options,’param’)返回优化参数options 中指定的参数的值。

●val=optimget(options,’param’，default)若options 结构参数中没有定义指定参数，则返回默认值。

3.2 optimset函数利用该函数创建或编辑优化选项参数结构，其语法结构如下： ● options=optimset(‘param1’,values1,’param2’,value2,…) 创建一个称为 options 的优化选项参数，其中指定的参数具有指定值。

● options=optimset()创建一个选项结构，其中所有的元素被设置为 []（默认值）。

● options=optimset(potimfun)创建一个含有所有参数名和与优化函数 optimfun 相关的默认值的选项结构 options 。

MATLAB上机内容及作业

MATLAB上机内容及作业无约束优化求解函数fminsearch和fminunc求解无约束非线性优化问题的函数包括fminsearch函数和fminunc函数。

fminsearch和fminunc的函数相同，但fminunc函数可以在最优解处获得目标函数的梯度和Hessian矩阵值。

无约束优化数学模型为：minf(x)x∈rn求解无约束非线性优化问题的步骤为：第一步：先写目标函数的m文件；第二步是在命令窗口中调用相应的优化函数。

1.Fminsearch函数调用格式为[x,fval]=fminsearch(@myfun,x0)输出参数的含义：x：返回最优解的设计变量值；fval：在最优设计变量值时，目标函数的最小值；Exitflag：返回算法的终止标志。

在下列情况下，>0表示算法收敛到最优解；=0表示算法已达到最大迭代次数；＜0表示算法不收敛。

output：返回优化算法信息的一个数据结构，有以下信息：输出Iteration表示迭代次数output Algorithm表示算法output Funccount表示函数求值的次数输入参数的含义：@Myfun：目标函数的m文件，前面加“@”或表示为“Myfun”，可以任意命名；X0：调用优化函数时，需要先给设计变量赋值；2、fminunc函数的调用格式[x，fval]=fminunc（@myfun，x0）grad：返回目标函数在最优解处的梯度信息；hessian：返回目标函数在最优解处的hessian矩阵信息。

其余含义同上。

3、实例已知某一优化问题的数学模型为：Minf（x）=3x12+2x1x2+x22x∈ r n由MATLAB程序编写的代码为：第一步：首先编写目标函数的.m文件，并保存为examplefsearch.m文件（先单击file菜单，后点击new命令中的m―file，即可打开m文件编辑窗口进行代码的编辑，在英文状态下输入程序代码），代码为：函数f=examplefsearch（x）f=3*x（1）^2+2*x（1）*x（2）+x（2）^2；1.0e-0.08*-0.79140.2260%分别为x1和x2的最优点的值（近似为0）Fval=1.5722e-016%，对应于最佳优势的最佳目标函数值（约为0）4。