基于小波包的图像压缩及Matlab实现
基于MATLAB的小波变换在图象压缩中的应用

基于MATLAB的⼩波变换在图象压缩中的应⽤毕业论⽂设计题⽬:基于MATLAB的⼩波变换在图象压缩中的应⽤姓名:学号:院(系):信息⼯程学院专业:通信⼯程指导教师:职称:教授评阅⼈:职称:年⽉本科⽣毕业论⽂(设计)原创性声明本⼈以信誉声明:所呈交的毕业论⽂(设计)是在导师指导下进⾏的研究⼯作及取得的研究成果,论⽂中引⽤他⼈的⽂献、数据、图件、资料均已明确标注出,论⽂中的结论和结果为本⼈独⽴完成,不包含他⼈成果及为获得中国地质⼤学或其他教育机构的学位或证书⽽使⽤过的材料。
与我⼀同⼯作的同志对本研究所做的任何贡献均已在论⽂中作了明确的说明并表⽰了谢意。
毕业论⽂作者(签字):签字⽇期:年⽉⽇⽬录摘要 (3)Abstract (4)第⼀章绪论 (5)课题研究背景 (5)1.2 国内外研究现状 (6)1.3 本⽂主要⼯作 (6)第⼆章⼩波变换 (7)2.1 ⼩波变换的诞⽣ (7)2.2 ⼩波变换的原理 (9)第三章⼩波变换在图象压缩中的应⽤ (12)3.1基于⼩波变换的图象压缩流程 (12)3.2利⽤⼩波压缩函数进⾏图像压缩 (13)3.2.1使⽤全局阈值 (14)3.2.2在⽔平,垂直,对⾓三个⽅向使⽤层相关阈值 (15)3.3 利⽤⼩波分解去掉图像的⾼频部分⽽只保留低频部分 (16)第四章实验结果及分析 (18)4.1 实验结果及分析 (18)第五章结论 (19)5.1 结论 (19)致谢辞 (20)参考⽂献 (21)附录:部分程序代码 (22)摘要⼩波分析在图像处理中有⾮常重要的应⽤,包括图像压缩,图像去噪,图像融合,图像分解,图像增强等。
⼩波分析是傅⽴叶分析思想⽅法的发展与延拓。
针对暂态电能质量扰动现象的内在特征,提出了⼩波变换和模糊逻辑相结合的暂态电能质量扰动分类⽅法。
该⽅法使⽤⼩波变换提取扰动的时间特征,将扰动持续时间、扰动幅度、扰动频率、电压变化率绝对值作为暂态电能质量扰动的特征向量,输⼊到4输⼊2输出的模糊逻辑推理系统,⾃动判别暂态电能质量的扰动类型及扰动强度。
小波包变换matlab程序

小波包变换matlab程序小波包变换是一种信号分析的方法,可以对信号进行多尺度的分解与重构。
在Matlab中,我们可以使用Wavelet Toolbox来实现小波包变换。
本文将介绍小波包变换的原理以及如何在Matlab中进行实现。
我们来了解一下小波包变换的原理。
小波包变换是基于小波变换的一种扩展方法,它在小波变换的基础上进一步增加了尺度的变化。
小波包变换通过不断地分解和重构信号,可以得到信号的不同频率成分。
在小波包变换中,我们可以选择不同的小波基函数和分解层数,以得到适合信号特征的频率分解结果。
在Matlab中,我们可以使用Wavelet Toolbox中的函数实现小波包变换。
首先,我们需要通过调用`wavedec`函数对信号进行小波分解。
该函数的输入参数包括信号、小波基函数、分解层数等。
通过调用该函数,我们可以得到信号在不同频率尺度上的系数。
接下来,我们可以选择一些感兴趣的频率尺度,对系数进行进一步的分解。
在Matlab中,我们可以使用`wprcoef`函数对系数进行小波包分解。
该函数的输入参数包括小波包分析对象、系数所在的频率尺度等。
通过调用该函数,我们可以得到信号在指定频率尺度上的小波包系数。
除了分解,小波包变换还可以进行重构。
在Matlab中,我们可以使用`waverec`函数对系数进行小波重构。
该函数的输入参数包括小波包系数、小波基函数等。
通过调用该函数,我们可以得到信号的重构结果。
在实际应用中,小波包变换可以用于信号的特征提取、信号去噪等。
通过分解信号,我们可以得到不同频率尺度上的信号成分,从而对信号进行分析和处理。
在Matlab中,我们可以通过可视化小波包系数的方法,对信号进行频谱分析。
通过观察小波包系数的幅值和相位信息,我们可以了解信号的频率成分及其变化规律。
总结一下,在Matlab中实现小波包变换的步骤如下:1. 调用`wavedec`函数对信号进行小波分解,得到信号在不同频率尺度上的系数。
基于小波分析的图像压缩处理

基金项目:西安石油大学科技创新基金项目,项目编号为2004-35.基于小波分析的图像压缩处理娄 莉(西安石油大学计算机学院西安710065)【摘 要】 介绍了应用MA TL AB 小波分析软件包的低频信息保留压缩和小波包最佳基方法进行图像压缩处理的原理,并通过实验说明其实现过程。
【关键词】 MA TL AB ;小波;小波包;图像压缩1 引言随着信息技术的发展,要求大量存储和传输图像,如何能够在保证质量的前提下以较小的空间存储图像和较少的比特率传输图像,这就需要采用各种图像压缩技术来实现。
而将小波分析引入图像压缩的范畴是一个重要的手段。
小波分析有它独特的特点。
它的压缩比高、压缩速度快,压缩后能保持信号与图像的特征基本不变,且在传递过程中可以抗干扰。
可以克服传统方法产生的缺陷,因此获得了较好的压缩效果。
随着MA TLAB 软件的出现,小波分析及其应用变得更加广泛和简单。
MA TLAB 中的小波工具箱(Wavelet tool box )是许多基于MA TLAB 技术计算环境的函数包的集合。
它应用MA TLAB 体系下的小波和小波包,提供了分解及重构图像的多种工具。
工具箱中包含的各种小波分析函数,可用于对信号与图像的压缩处理。
2 小波变换原理小波变换是一种同时具有时-频二维分辨率的变换。
其优于传统变换之处在于它具有时域和频域“变焦距”特性,十分有利于信号的精细分析。
第一个正交小波基是Harr 于1910年构造的;但Harr 小波基是不连续的。
到80年代,Meyer ,Daubechies 等人从尺度函数的角度出发构造出了连续正交小波基。
1989年,Mallat 等人在前人大量工作的基础上提出多尺度分析的概念和基于多尺度分析的小波基构造方法,将小波正交基的构造纳入统一的框架之中,使小波分析成为一种实用的信号分析工具。
以一维情况为例,信号的多尺度分析算法可表示如下: S m (n )∑kh (k -2n )S m -1(k ) (1) C m (n )∑kg (k -2n )S m -1(k ) (2)其中h (n )和g (n )分别是低通和高通滤波器,m 是多尺度分解的层数,Sm (n )是S m -1(n )在2-m 上的近似,C m (n )是信号S 从2-m +1到2-m 的尺度近似时丢失的信息。
基于小波变换的图像压缩

个新 方向 。作为 数 学工 具 , 波被 迅速 应 用 到 图 小
率 高的编程工 具 … 。本 研究采 用 maa tb编程 。 l
1 原理 与方法
像和语音分析等众多领域。小波变换是一种信号的
时 间一 尺度分 析方法 , 具有 多分辨率 分析 的特点 , 而
且在时频两域都具有表征信号局部特征的能力 , 是
种 窗 口大小 固定 不 变但 其形 状 可 变 , 间窗 和频 时
率窗都可变的时频局部化分析方法 。 即在低频部分 具有较高的频率分辨率和时间分辨率, 在高频部分
具 有较 高 的时间分 辨 率 和较低 的频 率分 辨 率 , 很适
合探测正常信号 中夹带的瞬态反常现象并展示其成 分, 所以被誉为信号分析的显微镜。
W N i n , I eg, H N u— i , H i X a Z A G Y fi Z A u n A Gj 一 g L n S A G Y l n a — i, H N u-e, H OX e一 P a
(T i a dcl oee T i 70 0 hn ) as nMei U g , aa 2 0 .C ia h aC n 1
l w T e c mp e so ai f l s c n i a i h r a d t e i g eq ai sg o o . h o r s in r t o e e o d t o f i me w sh g e , n h ma u l ywa o d.Co cu in: e meh i t n lso T t o i sm- h d s pe,rl b e a d e e t e i g o r s in i e i l n f ci n i e c mp e so . a v ma
小波分析在基于Matlab的图像压缩中的实现

④X=waverec2(‘type’,C,S,Lo—R,Hi—R,N)
5 图像压缩结果分析
用bior3.7小波对图像进行单尺度二维离散小 波分解,重构低频和高频部分,由小波逆变换恢复信 号,再对其进行多尺度二维分解,重构低频和高频部 分‘2一引。
收稿日期:2008—10—28 作者简介:董文汇(1983一),女,中国地质大学(北京)地球物理与信
息技术学院在读硕士,研究方向为信息与通信工程、地 球物理信息技术。
小波分解后,平滑板块系数和所有的细节板块系数 之和等于原始图像灰度系数个数,总数据量未变…。
生成的小波图像具有原图像不同的特性,能量 主要集中在其中的低频部分的平滑板块,而细节所 对应的水平、垂直和对角线的能量较少,它们表征了 一些原图像的水平、垂直和对角线的边缘信息,具有 的是方向特性。对于所得图像,根据人眼的敏感度 不同,进行不同的量化和编码处理以达到对原图像 的高压缩比,对于平滑板块大部分或者完全保留,对 于高频信息根据压缩的倍数和效果要求来保留。
如果s(菇)是一光滑的连续时间信号,对较大的
-『系数,则有: (s,垆似)一2一胆s(2Jk) 如果s(x)是一个d级的多项式,d≤N—l则有 (s,纺.^)=2一胆s(2Jk)
(5)BiorSplines小波:其主要应用在信号与图像 的重构中,具有线性相位的特性。通常的用法是采 用两个小波,即小波对一个函数进行分解,另一个函 数用于进行重构。分别是:
Realization of image compression with wavelet
analysis based on Matlab
基于小波包的图像压缩及matlab实现

基于小波包的图像压缩及matlab实现摘要:小波包分析理论作为新的时频分析工具,在信号分析和处理中得到了很好的应用,它在信号处理、模式识别、图像分析、数据压缩、语音识别与合成等等许多方面都取得了很有意义的研究成果。
平面图像可以看成是二维信号,因此,小波包分析很自然地应用到了图像处理领域,如在图像的压缩编码、图像消噪、图像增强以及图像融合等方面都很好的应用。
本文将对小波包分析在图像处理中的应用作以简单介绍。
关键词:小波包图像处理消噪1.小波包基本理论1.1 小波包用于图像消噪图像在采集、传输等过程中,经常受到一些外部环境的影响,从而产生噪声使得图像发生降质,图像消噪的目的就是从所得到的降质图像中去除噪声还原原始图像。
图像降噪是图像预处理中一项应用比较广泛的技术,其作用是为了提高图像的信噪比突出图像的期望特征。
图像降噪方法有时域和频域两种方法。
频率域方法主要是根据图像像素噪声频率范围,选取适当的频域带通过滤波器进行滤波处理,比如采用Fourier变换(快速算法FFT)分析或小波变换(快速算法Mallat 算法)分析。
空间域方法主要采用各种平滑函数对图像进行卷积处理,以达到去除噪声的目的,如邻域平均、中值(Median)滤波等都属于这一类方法。
还有建立在统计基础上的lee滤波、Kuan滤波等。
但是归根到底都是利用噪声和信号在频域上分布不同进行的:信号主要分布在低频区域。
而噪声主要分布在高频区域,但同时图像的细节也分布在高频区域。
所以,图像降噪的一个两难问题就是如何在降低图像噪声和保留图像细节上保持平衡,传统的低通滤波方法将图像的高频部分滤除,虽然能够达到降低噪声的效果,但破坏了图像细节。
如何构造一种既能够降低图像噪声,又能保持图像细节的降噪方法成为此项研究的主题。
在小波变换这种有力工具出现之后,这一目标已经成为可能。
基于小波包变换消噪方法的主要思想就是利用小波分析的多尺度特性,首先对含有噪声的图像进行小波变换,然后对得到的小波系数进行阈值化处理,得到新的小波系数,对其进行反变换,这样我们就得到了消噪之后的图像,从而实现了对图像的恢复。
基于Matlab的小波变换在图像压缩中的应用

、 H } l 、 H
图3 2次小波变换后的频 率分布
用子带 结构 实现离散 小波变换 的计算 , 以迭代的方式使用 双 子带编码并 且 自底向上地建立小波变换 , 即分别用低通滤 波 器 和高通滤波器对 fX y 滤波 , 间隔抽样 产生两个 高 、 ( ,) 再 低 半带信号 , 然后对低半带 信号再 一次实施 双子带 编码 , 连续
输 。小波编码方法是 近年来发 展起来 新型编 码方法 。因其
图 2 图像 小 波 重 建 过 程
其 中 h() 0x 是低 通滤波器 , 1x 是 高通滤波器 , 表示 h()
间隔采样 , 即只剩下采样数的一半 , 十表示加倍采样 , 即每 隔
一
具有压缩 比高 , 压缩 速度快 , 压缩 后能保持 信号与 图像 的特
量大 , 且受通 信带 宽、 储 容量 和计 算机 处理 速度 限 制 , 存 因
此, 为满 足实际应 用需 要 , 有必要对图像数据进 行压缩处理 ,
图 1 图像小波分解过程
,
)
以提高图像传 输和存储 的效率。
小波分析 是傅里叶分析 和调和分 析发展史 上 的一个 里
程碑 , 被誉 为“ 数学 显微 镜” …。作 为一种 多 分辨 率分 析 方 法, 小波分析 具有很 好 的时频局部 化特性 , 特别适 合按 照人 眼视觉特性设计编码方法 , 也非常有 利于图像信 号的渐进传
维普资讯
山
图像的细节变化。
西
电
Hale Waihona Puke 子技术 20 0 7年
方法 是一种最 简单 的压缩方法 , 它不需要经过其它处理 即可
2 小波 变换用 于 图像 压缩
如何在Matlab中进行图像压缩和图像加密

如何在Matlab中进行图像压缩和图像加密图像压缩和图像加密是图像处理中的两个重要方面。
图像压缩可以将图像的数据量减小,从而方便存储和传输;而图像加密可以保护图像的机密性,防止未授权的访问和篡改。
Matlab作为一种强大的数学软件,也提供了丰富的功能来实现图像压缩和图像加密。
本文将介绍如何在Matlab中进行图像压缩和图像加密的方法和技巧。
一、图像压缩图像压缩可以分为有损压缩和无损压缩两种方式。
有损压缩可以在保留人眼感知的主要信息的前提下,通过抛弃一些不重要的细节来减小图像的数据量。
无损压缩则可以完全恢复原始图像的每个像素点的数值,但通常会导致较大的压缩比。
在Matlab中,有许多算法可以用于图像压缩。
其中最常用的算法之一是离散余弦变换(DCT)。
DCT可以将图像转换为一组频域系数,通过保留部分重要的低频系数来实现压缩。
在Matlab中,可以使用dct2函数进行二维离散余弦变换,使用idct2函数进行反变换。
除了DCT,小波变换也是常用的图像压缩算法。
小波变换基于信号在时频域的分析,可以将图像划分为不同的尺度和方向,并通过保留部分重要的小波系数来实现压缩。
Matlab提供了多个小波变换的函数,如wavedec2和waverec2。
另外,还有一些其他的图像压缩算法,如JPEG、JPEG2000、PNG等。
这些算法可以在压缩比和图像质量之间做出不同的权衡。
Matlab中可以使用imwrite函数来实现这些压缩算法,你可以指定压缩比、图像质量等参数。
二、图像加密图像加密是保护图像的机密性和完整性的一种方法。
常见的图像加密算法包括DES、AES、RSA等。
这些算法使用不同的加密密钥和算法来对图像数据进行加密和解密。
在Matlab中,可以使用一些函数和工具箱来实现图像加密。
例如,可以使用.ftp.FTP这个类来实现对图像文件的加密上传和解密下载。
你可以使用ftp函数来连接FTP服务器,并使用put和get函数来上传和下载加密的图像文件。
同步压缩小波变换matlab程序

同步压缩小波变换matlab程序英文回答:Wavelet transform is a powerful tool in signal processing and data compression. It is widely used in various fields such as image and audio compression, denoising, and feature extraction. In MATLAB, there are built-in functions and toolboxes that can be used to perform wavelet transform and compression.To perform synchronous wavelet compression in MATLAB, we can follow these steps:1. Load the signal or image data: We first need to load the signal or image data that we want to compress. This can be done using the appropriate MATLAB functions, such as`audioread` for audio signals or `imread` for images.2. Choose a wavelet: Next, we need to choose a suitable wavelet for the compression. MATLAB provides a variety ofwavelets, such as Daubechies, Coiflets, and Symlets. We can use the `wfilters` function to obtain the coefficients of a specific wavelet.3. Perform wavelet decomposition: We can use the`wavedec` function to decompose the signal or image into different frequency subbands using the chosen wavelet. This will result in a set of approximation and detail coefficients.4. Set a compression threshold: In order to reduce the amount of data to be stored or transmitted, we can set a compression threshold to discard or truncate the detail coefficients with small magnitudes. This can be done by comparing the magnitude of each coefficient with the threshold value.5. Reconstruct the compressed signal or image: After discarding or truncating the detail coefficients, we can use the `waverec` function to reconstruct the compressed signal or image using the remaining approximation anddetail coefficients.6. Evaluate the compression performance: Finally, wecan evaluate the compression performance by comparing the quality of the reconstructed signal or image with the original data. This can be done using various metrics such as peak signal-to-noise ratio (PSNR) or mean squared error (MSE).中文回答:小波变换是信号处理和数据压缩中的一种强大工具。
MATLAB小波变换在图像压缩中的应用

小波变换在图像压缩中的应用1 引言小波分析诞生于20世纪80年代, 被认为是调和分析即现代Fourier分析发展的一个崭新阶段。
众多高新技术以数学为基础,而小波分析被誉为“数学显微镜”,这就决定了它在高科技研究领域重要的地位。
目前, 它在模式识别、图像处理、语音处理、故障诊断、地球物理勘探、分形理论、空气动力学与流体力学上的应用都得到了广泛深入的研究,甚至在金融、证券、股票等社会科学方面都有小波分析的应用研究。
在传统的傅立叶分析中,信号完全是在频域展开的,不包含任何时频的信息,这对于某些应用来说是很恰当的,因为信号的频率的信息对其是非常重要的。
但其丢弃的时域信息可能对某些应用同样非常重要,所以人们对傅立叶分析进行了推广,提出了很多能表征时域和频域信息的信号分析方法,如短时傅立叶变换,Gabor变换,时频分析,小波变换等。
其中短时傅立叶变换是在傅立叶分析基础上引入时域信息的最初尝试,其基本假定在于在一定的时间窗内信号是平稳的,那么通过分割时间窗,在每个时间窗内把信号展开到频域就可以获得局部的频域信息,但是它的时域区分度只能依赖于大小不变的时间窗,对某些瞬态信号来说还是粒度太大。
换言之,短时傅立叶分析只能在一个分辨率上进行。
所以对很多应用来说不够精确,存在很大的缺陷。
而小波分析则克服了短时傅立叶变换在单分辨率上的缺陷,具有多分辨率分析的特点,在时域和频域都有表征信号局部信息的能力,时间窗和频率窗都可以根据信号的具体形态动态调整,在一般情况下,在低频部分(信号较平稳)可以采用较低的时间分辨率,而提高频率的分辨率,在高频情况下(频率变化不大)可以用较低的频率分辨率来换取精确的时间定位。
2 设计原理2.1 小波变换的分解和重构算法2.1.1 小波变换的分解算法构成了信号),(y x f 的二维正交小波分解系数(如图2.3所示),图2.3 二维正交小波分解系数Z Z j j j j j j m n f W m n f W m n f W m n f S m n ⨯∈--=})},(),,(),,(){,(1,...,),(它们每一个都可被看做一幅图像,),(1m n f W j 给出了),(y x f 垂直方向的高频分量的小波分解系数,),(3m n f W j 给出了),(y x f 水平方向的高频分量的小波分解系数,),(2m n f W j 给出了),(y x f 对角方向高频分量的小波分解系数,f S J 给出了),(y x f 的低频分量的小波分解系数。
一种基于小波变换的图像压缩方法与实现

一种基于小波变换的图像压缩方法与实现谭艳梅【摘要】Tiffs paper discusses an algorithm based on wavelet transformation, which is realized by programming in Matlab. The .riginal image is de-noised by using the functions of wavelet toolbox at first. The simulation results show that the algorithm has excellent effects in the image reconstruction, and the study shows valuable in image compression.%提出了一种先去噪再利用小波变换的图像压缩方法,用Matlab软件编程实现算法。
实验仿真结果显示,图像在具有高压缩比的同时,重构图像的质量也较优;使用不同的小波基函数,效果不同。
【期刊名称】《微型机与应用》【年(卷),期】2011(030)017【总页数】3页(P44-45,48)【关键词】小波变换;图像压缩;图像去噪;重构图像【作者】谭艳梅【作者单位】广西机电职业技术学院,广西南宁530007【正文语种】中文【中图分类】TN919.81随着计算机、通信、电子信息技术的快速发展,人们的生活与图像紧密相连,如数字电视图像、3G通信、彩信、导航系统图像、视频图像防盗系统等。
然而图像信息包含的信息量巨大,这给储存、处理和传输带来了很多困难,这也是相关技术发展的瓶颈。
不断地增加信道带宽和储存容量并不能解决根本问题,而现有技术已经显得力不从心。
解决问题的根本就是必须要对图像信息进行压缩处理,在保证一定图像质量的基础上,能用尽可能少的信息量表示重构的原始图像,即用最少的信息还原出最近似原始图像的重构图像。
基于小波变换的彩色图像压缩编码算法的MATLAB实现.

(2009届)本科毕业设计(论文)资料湖南工业大学教务处2009届本科毕业设计(论文)资料第一部分毕业论文(2009届)本科毕业设计(论文)基于小波变换的彩色图像压缩编码算法的MATLAB实现2009年6月湖南工业大学本科毕业设计(论文)摘要随着信息技术的发展,图像以其信息量丰富的特点,成为通信和计算机系统中信息传输的重要载体,而图像信息占据了大量的存储容量,因而图像压缩编码是图像存贮的一个重要课题。
图像压缩是用最少的数据量来表示尽可能多的原图像信息的一个过程。
小波变换是当前数学中一个迅速发展的新领域,在MATLAB中,图像压缩是其应用领域中的一个方面。
论文首先介绍了图像压缩编码的研究背景和论文的研究内容及结构安排,然后详细地从理论上介绍了图像压缩,并讲解了小波变换的由来、定义和特点,以及在分析中所涉及到的连续小波变换、离散小波变换、二维小波变换,同时说明了当前小波变换在图像方面的各个应用领域和研究的意义。
接着介绍了其研究工具MATLAB的组成和特点。
通过小波变换的理论研究,应用MATLAB来实现了一般彩色图像的压缩,最后利用小波分析的工具箱来实现相关小波变换的应用。
论文对程序中用到的主要函数给予了说明, 较直观的探讨了小波变换在图像压缩中的应用。
由于小波变换在图像中有许多的优点,因此小波变换在各个应用领域也越来越广。
关键词:图像压缩,小波变换, MATLAB,彩色图像I湖南工业大学本科毕业设计(论文)ABSTRACTWith the development of information technology, image,rich features of its information, has become in an important carrier of information transmission in the communications and computer systems. And as the image information occupy a large amount of storage capacity, the image compression is an important issue of the image storage.Image compression is a process using the amount of data at least as much as possible to show that the original image information. Wavelet Transform is a new field rapidly developing in present mathematics. In MATLAB, the image compression is a respect of its application.The research background of image coding and the research content and structure of this paper are introduced firstly. Then in terms of theory, we elaborate upon the image compression, the origin of the wavelet transform, the definition and the characteristics, and explain the wavelet continuous transform, the discrete wavelet transform, the two dimensional wavelet, which are involved in analyzing. At the same time, the application fields of Wavelet Transform in the aspect of image are described in detail, and the meaning of its research has got cleared. This text has introduced its research toolMATLAB and relevant composition and characteristics. Through the theoretical research of the Wavelet Transform, this paper use MATLAB to implement the compression, and this can implement something about the Wavelet Transform of application and realize the anticipated purpose basically.And more intuitively explore the application of wavelet transform in image compression by giving a description of the procedures for the main function that were used. Because there are a lot of advantages in wavelet image, Wavelet Transform will be applied much wider in each field.Keywords: Wavelet Transform , Image Compression, MATLAB, Color ImageII湖南工业大学本科毕业设计(论文)目录第1章前言 (1)1.1 研究背景 (1)1.2 研究内容 (2)1.3 文章结构安排 (2)第2章系统理论基础 (3)2.1 图像压缩 (3)2.2 小波变换 (3)2.2.1 小波变换的由来 (4)2.2.2 小波变换的基本思想 (5)2.2.3 小波变换的特点 (6)2.2.4 常用的小波变换 (7)2.2.5小波变换在图像压缩中的应用 (10)2.2.6小波变换在图像处理中的其他应用 (11)2.3 离散余弦变换 (12)2.3.1离散余弦变换的定义 (12)2.3.2离散余弦变换应用于图像压缩 (13)2.4 其他重要理论 (14)第3章系统设计 (15)3.1 设计思想 (15)3.2 MATLAB简介 (15)3.2.1 MATLAB小波工具箱 (15)3.2.2 MATLAB用户图形界面 (17)3.3 系统功能模块 (18)第4章系统实现 (20)III湖南工业大学本科毕业设计(论文)4.1 系统的使用方法 (20)4.2 重要代码的实现 (20)4.2.1打开图像 (20)4.2.2变换为灰度图像 (22)4.2.3小波压缩——低频信息保留压缩方法 (23)4.2.4二维小波压缩 (25)4.2.5小波包压缩变换 (30)4.2.6 DCT压缩 (32)4.2.7小波消噪 (34)第5章总结体会 (37)5.1 小波图像压缩总结 (37)5.2 小波图像分析展望 (38)参考文献 (39)致谢 (40)IV湖南工业大学本科毕业设计(论文)过程管理资料第1章前言1.1 研究背景图像压缩是计算机应用领域中一个重要的问题。
基于小波变换及Matlab的遥感图像压缩效果分析

基于小波变换及Matlab的遥感图像压缩效果分析袁蔚林;马燕;刘圣伟;许玉斌;孙华波【期刊名称】《地理信息世界》【年(卷),期】2013(000)003【摘要】主要对小波变换在遥感图像压缩中的应用进行了研究。
首先对小波变换理论及其实现进行了简要的介绍。
然后,重点分析了小波变换分解层次、阈值选择对图像压缩效果的影响。
利用MATLAB小波工具箱提供的小波变换函数,采用haar小波、db小波、sym小波、coif小波、bior小波进行遥感图像压缩,并对压缩效果进行了分析比较。
结果表明,随着压缩倍数的增加,所需小波变换的分解层次也相应增加;但当压缩倍数选定后,对于大小一定的遥感图像,小波变换分解层次达到某一定级次时,再增加变换的分解层次,对压缩效果的作用甚微。
因此,当图像大小一定时,压缩倍数和小波变换的分解层次之间存在一个较佳匹配问题。
同时,通过实验数据,说明了在小波压缩过程中,阈值对压缩图像的压缩比和能量保持比的定量影响,表明将小波变换用于遥感图像压缩具有压缩比大,压缩效率高的优点。
实验结果为小波变换在遥感图像压缩中的实际应用提供了理论参考。
% In this paper, the basic principle of wavelet transform is briefly described, focusing on the influence of decomposition level and threshold of wavelet transform on emulate compression effect of RS images. The RS images are compressed by haar wavelet, db wavelet, sym wavelet, coif wavelet as well as bior wavelet which are provided by MATLAB Wavelet Toolbox. According to the analyzed and compared results, the necessary decomposition level of wavelet transform is supposed to be increased withthe multiple of compression. But for the RS images with a certain size besides the chosen compression multiple, when it is increased to a certain level, the effect of compression will keep steadiness. The matching between compression multiple and the decomposition level of wavelet transform is also discussed in detail. On the other hand, the effect of the threshold to the image compression ratio and energy-keeping is studied at the same time. The experimental results and analysis indicate that high compression ratio and high efficiency satisfy the requirement on RS images compression. The result of research provides the theoretical reference of RS images compression using wavelet transform.【总页数】6页(P39-44)【作者】袁蔚林;马燕;刘圣伟;许玉斌;孙华波【作者单位】中国国土资源航空遥感中心,北京 100083;北京大学遥感与地理信息系统研究所,北京 100871; 中国民航科学技术研究院,北京 100082;中国国土资源航空遥感中心,北京 100083;北京大学遥感与地理信息系统研究所,北京100871;中国民航科学技术研究院,北京 100082【正文语种】中文【中图分类】TP7【相关文献】1.基于Matlab的小波变换在图像压缩中的应用 [J], 王洪涛;沈有建;李满枝2.基于MATLAB的小波变换在图像压缩中的应用 [J], 马涛;葛卫平3.基于DFT、DCT和小波变换图像压缩与Matlab实现 [J], 张雅琪;才华4.小波变换在遥感图像压缩中的应用及Matlab实现 [J], 易美华;朱自强;黄国祥;邹声杰5.基于Matlab的小波变换图像压缩算法研究 [J], 关雪梅因版权原因,仅展示原文概要,查看原文内容请购买。
基于MATLAB的图像压缩处理及其实现

基于MATLAB 的图像压缩处理及其实现一.图像压缩的概念从实质上来说,图像压缩就是通过一定的规则及方法对数字图像的原始数据进行组合和变换,以达到用最少的数据传输最大的信息。
二.图像压缩的基本原理图像数据之所以能被压缩,就是因为数据中存在着大量冗余信息,另外还有相当数量的不相干信息,这为数据压缩技术提供了可能。
数据压缩技术就是利用数据固有的冗余性和不相干性,将一个大的数据文件转化成较小的文件,图像技术压缩就是要去掉数据的冗余性。
图像数据的冗余主要表现为:图像中相邻像素间的相关性引起的空间冗余;图像序列中不同帧之间存在相关性引起的时间冗余;不同彩色平面或频谱带的相关性引起的频谱冗余。
由于图像数据量的庞大,在存储、传输、处理时非常困难,因此图像数据的压缩就显得非常重要。
三.图像的编码质量评价在图像编码中,编码质量是一个非常重要的概念,怎么样以尽可能少的比特数来存储或传输一幅图像,同时又让接收者感到满意,这是图像编码的目标。
对于有失真的压缩算法,应该有一个评价准则,用来对压缩后解码图像质量进行评价。
常用的评价准则有两种:一种是客观评价准则;另一种是主观评价准则。
主观质量评价是指由一批观察者对编码图像进行观察并打分,然后综合所有人的评价结果,给出图像的质量评价。
而对于客观质量评价,传统的编码方法是基于最小均方误差(MSE)和峰值信燥比(PSNR)准则的编码方法,其定义如下MSE=1NxNyi=0Nij=0Nj[fi,j-fi,j]2 (1)PSNR=101g(255×255MSE)(2)式中:Nx,Nr图像在x方向和Y方向的像素数,f(i,j)——原图像像素的灰度值,f(i,j)--处理后图像像素的灰度值。
对于主观质量,客观质量评价能够快速有效地评价编码图像的质量,但符合客观质量评价标准的图像不一定具有较好的主观质量,原因是均方误差只是从总体上反映原始图像和压缩图像的差别,但对图像中的所有像点同等对待,因此并不能反映局部和人眼的视觉特性。
基于小波包的图像压缩及Matlab实现

基于小波包的图像压缩及Matlab实现
张波;周文娟;杨晓;熊丽
【期刊名称】《电脑知识与技术》
【年(卷),期】2009(005)028
【摘要】小波包是近年来的一个研究热点,在图像处理方面有着很广泛的应用.文中提出了基于小波包的图像压缩及Matlab实现方法,加快了图像压缩的进程,取得了很好的实验效果.将图像在小渡包最优基下展开,利用小波包最优基极好的空间、尺度定位性,使得图像的小波包变换系数在小波变换域极可能的集中从而使在不降低压缩信号的视频质量情况下,提高了图像的压缩比.
【总页数】3页(P8050-8052)
【作者】张波;周文娟;杨晓;熊丽
【作者单位】贵州大学,计算机科学与信息学院,贵州,贵阳,550025;贵州大学,计算机科学与信息学院,贵州,贵阳,550025;贵州大学,计算机科学与信息学院,贵州,贵阳,550025;贵州大学,计算机科学与信息学院,贵州,贵阳,550025
【正文语种】中文
【中图分类】TP317
【相关文献】
1.基于变换域的图像压缩及Matlab实现 [J], 王静
2.基于DCT变换的图像压缩编码的MATLAB实现 [J], 彭干涛;禹峰;林嘉居
3.基于DFT、DCT和小波变换图像压缩与Matlab实现 [J], 张雅琪;才华
4.基于MatLab的JPEG图像压缩标准的仿真实现 [J], 王文娟;陶杰;刑娜
5.基于小波包的图像压缩及Matlab实现 [J], 张波;周文娟;杨晓;熊丽
因版权原因,仅展示原文概要,查看原文内容请购买。
Matlab工具箱做小波音频图像压缩去噪
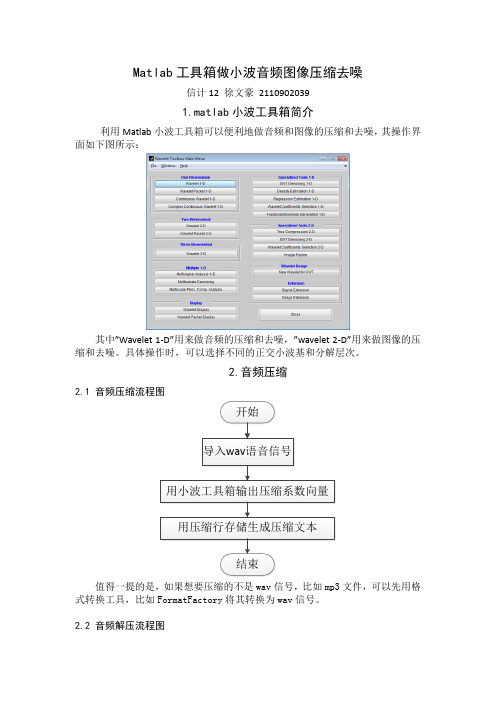
Matlab工具箱做小波音频图像压缩去噪信计12 徐文豪21109020391.matlab小波工具箱简介利用Matlab小波工具箱可以便利地做音频和图像的压缩和去噪,其操作界面如下图所示:其中”Wavelet 1-D”用来做音频的压缩和去噪,”wavelet 2-D”用来做图像的压缩和去噪。
具体操作时,可以选择不同的正交小波基和分解层次。
2.音频压缩2.1 音频压缩流程图值得一提的是,如果想要压缩的不是wav信号,比如mp3文件,可以先用格式转换工具,比如FormatFactory将其转换为wav信号。
2.2 音频解压流程图2.3 音频压缩效果比较考虑到正交小波基种类繁多,因而只比较较常用的haar、db和sym。
(1)量化音频压缩效果为了比较用不同正交小波基在不同分解层次下的压缩效果,有必要做一些量化处理。
考虑到,对同一音频信号,在取0率相同的情况下,压缩效果越好的正交小波基,其能量保留的应该越多。
因而,可先固定取0率,然后以能量保留百分比作为压缩效果的衡量指标。
(2)不同分解层次音频压缩效果比较不失一般性,考虑db4在取0率为95%的情况下在不同分解层次下的压缩效果,结果如下图:从图中可以看出,压缩效果随着分解层次的增加而增大,且增大速度先快后慢,最终压缩效果趋于稳定。
从理论上看,分解层次越多,出现小系数比率就越大,因而实验所得结果是与理论相符的。
可惜的是,在分解层次小于5时,可能是因为压缩效果已经太差,小波工具箱没给出其取0率为95%的情况,不然图像可以更加细致。
然而,也不能说分解层次越多越好,因为随着分解层次的增加,用于压缩和解压的时间会明显增加,因而这需要有一个折中。
(3)不同连续等级音频压缩效果比较对同种正交小波基,在分解层次固定时,可以比较不同连续等级对压缩效果的影响,考虑分解层次为5,取0率为95%,连续等级从1到7的db小波,结果如下图所示:从图中可以看出,随着小波基越来越连续,压缩效果是逐渐变大的,但增长速度也是先快后慢,且最终趋于平稳。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本栏目责任编辑:唐一东
多媒体技术及其应用 8051
Computer Knowledge and Technology 电脑知识与技术
第 5 卷第 28 期 (2009 年 10 月)
利用小波包最优基进行图像压缩的算法框图如图 1 所示。
4 MATLAB 下图像压缩实验
本 文 实 验 中 ,利 用 MATLAB 小 波 工 具 箱 ,以 Shannon 为 代 价 函 数 , 采用全局阈值处理方法,基于小波包的图像压缩效果如图 2 所示。 相同 阈值下,基于小波变换的图像压缩效果如图 3 所示。
1)图像的小波包分解,选择一个小波并确定所需分解的层次,然后对图像进行小波包分解。 2)确定最优小波包分解,对于一个给定的熵标准,计算最优树。 3)小波包分解系数的阈值量化,对于每一个小波包分解系数,选择一个恰当的阈值并对系数进行阈值量化。 4)图像的小波包重构,根据最低层的小波包分解系数和经过量化处理系数,进行小波包重构。 关键是如何选取阈值和如何进行 阈值量化。
3 图像的小波包压缩
小波包分析中,压缩的算法思想和 An,k 小波分析中基本相同,不同的是小波包提供了一种更为复杂、更为灵活的分析手段。 因为 小波包分析对上一层的低频部分和高频部分同时进行分解,具有更加精确的局部分析能力。 对图像进行小波分解时,可以采用多种 小波包基。 根据分析要求,从中选择最好的一种小波包基,即最优基。 其选择的标准是熵标准。 应用小波包分析对图像进行压缩处 理是它的一个最基本功能。 如下为图像小波包压缩的步骤。
在分布式网络多媒体应用中,为了达到令人满意的画面和听觉效果,需要对视频信号和音频信号进行实时处理,因此对数据实 现高保真,大压缩比的压缩是非常必要。 数据压缩主要包含无失真压缩和有失真压缩两大类,无失真压缩是指图像数据经压缩后可 以完全地得到恢复,复原后的图像和原始图像一致。 而有失真压缩是指经过压缩后的图像数据在保持原图特征的前提下,不可避免 地要丢失一部分不重要的图像原始信息。 目前基于小波变换的图像压缩方法已经逐步取代了基于离散余弦或者其他子代编码技 术,而成为新的图像压缩国际标准的首选方法。 在小波包分析中,其信号压缩的算法思想和在小波分析中的基本相同,所不同的就 是小波包提供了一种更为复杂,也更为灵活的分析手段。 因为小波包分析对上一层的低频部分和高频部分同时进行分解,具有更加 精确的局部分析能力。
称此正交基库是一个二叉树结构。 如果库是一个二叉树,可以通过对 K 的归纳找到最优基。 记 Bnk 对应于 Ink 向量基,An,k 是 X 受限于最优基。 实际应用中,对 VN 做有限次分解。由小波包算法可以算出信号函数 f(x)在各个子空间的系数,然后由 M(x)可以计算出各层上系 数的代价函数值。
ISSN 1009-3044
CCoommppuutteerr KKnnoowwlleeddggee aanndd TTeecchhnnoollooggyy 电电脑脑知知识识与与技技术术
Vol.5,No.28, October 2009, pp.8050-8052
E-mail: eduf@ 第 5 卷第 28h期ttp://(w2w0w0.9dn年zs.1n0et.月cn) Tel:+86-551-5690963 5690964
在图 2 中,其中左图是原始图像,右图是基于小波包最优基,经过 全局阈值压缩过的图像
压缩效率: 小波分解系数中置 0 的系数个数百分比: perf0 = 37.4352 压缩后图像剩余能量百分比: perfl2 = 99.9703 在图 3 中,其中左图是原始图像,右图是基于小波经过全局阈值压 缩过的图像 结果如下: 小波分解系数中置 0 的系数个数百分比: perf0 = 40.1967 压缩后图像剩余能量百分比: perfl2 = 99.9616 在实验中,将小波包压缩效果与基于相同的小波压缩相比较,从图 中和数据显示,我们可以看出小波包压缩优于小波压缩
Image Compression based on Wavelet Packet and Realization with Matlab ZHANG Bo,ZHOU Wen-juan,YANG Xiao, XIONG Li (School of Computer Science and Information,GuiZhou University,Guiyang 550025,China) Abstract: Wavelet packet is becoming the focus of research.This paper gives image noise reduction based on wavelet packet and realization with Matlab.It quickens the process of image compression and gets a very good experiment result.The image is expressed as a linear combination of the best bases of wavelet packet.The energy of expansion coefficients is concentrated in a small number of coefficients because of the location properties of wavelet packet best bases.So it achieves high compression without any losses of visual information of the compressed image. Key words:wavelet;wavelet packet;best basis;image compression;matlab
8050 多媒体技术及其应用
本栏目责任编辑:唐一东
第 5 卷第 28 期 (2009 年 10 月)
式中,hok、h1k 是多分辨率分析中的滤波器系数。 当 n=0 时,W0(t)=准(t),W1(t)=ψ(t)。 以上义的函数集合{Wn(t)},n∈Z 为 W0(t)=准(t)所定 的小波包,由此,小波包{Wn(t)},n=Z 是包括度函数 W0(t)和小波母函数 W1(t)在内的一个具一定联系的函数集合。 2.2 小波包的正交性质
1 图像压缩简述
图像压缩是一个具有很大实际应用价值的问题。 压缩中一个极其重要的方面就是变换压缩。 所谓变换压缩,就是将原来信号进 行变换(这种变换一般要求是可逆的,以保证变换后能进行恢复),希望变换后的信号具有比较特殊的结构,比如大量的信号数据非 常接近零,这样,在量化数据时就会连续出现大量的零值,从而使必须记忆的非零数据个数很少,最终达到以极少的存储空间储存 大量信息的目的。 在变换压缩中,正交变换是其中重要得一大类方法。 其基本思想是,在高维向量空间中选择恰当的正交基,使变换 后的数据出现两个极端,要么非常小要么非常大,达到集中信息的目的。 通常应用的变换方法有:傅立叶变换,余弦变换,小波变换 等。 小波包理论是小波变换的极其精彩的延伸,尤其是正交小波包。 它(通过选择再分割的级别)为向量空间提供了大量的正交基,充 分发挥了正交多分辨分析的思想,成功地解决了小波变换固有的“高频低分辨”问题,从而为图像的压缩提供了新的途径。
2 小波包的基本理论
2.1 小波包 给定正交尺度函数 准(t)和小波函数 ψ(t),其尺度关系是
式中,hok、h1k 是多分辨率分析中的滤波器系数。 二尺度方程的进一步推广,递推关系为
收 稿 日 期 :2009-08-04 基 金 项 目 :贵 州 大 学 研 究 生 创 新 基 金 项 目 ,校 研 理 工 (2009008) 作 者 简 介 :张 波 (1984-),男 ,四 川 人 ,硕 士 生 ,研 究 方 向 :嵌 入 式 系 统 。
基于小波包的图像压缩及 Matlab 实现
张波,周文娟,杨晓,熊丽
(贵州大学 计算机科学与信息学院,贵州 贵阳 550025)
摘要:小波包是近年来的一个研究热点,在图像处理方面有着很广泛的应用。 文中提出了基于小波包的 图 像 压 缩 及 Matlab 实 现 方 法,加快了图像压缩的进程,取得了很好的实验效果。 将图像在小波包最优基下展开, 利用小波包最优基极好的空间、尺度定位性, 使得图像的小波包变换系数在小波变换域极可能的集中从而使在不降低压缩信号的视频质量情况下, 提高了图像的压缩比。 关 键 词 :小 波 ;小 波 包 ;最 优 基 ;图 像 压 缩 ;;Matlab 中图分类号:TP317 文献标识码:A 文章编号:1009-3044(2009)28-8050-03
小波包基上,获得一系列系数,要用一系列系数刻画信号特征。 首先要定义一个序列代价函数,然后在小波库的所有小波包基中找
使代价最小的基。 该基就是最优基。 代价函数定义为关于序列的实函数 M,可加性指如果满足 M(0)=0 和
,则称 M 为
可加性的信息代价函数。
若代价函数 M 已经选定,最优基概念如下:
图 1 利用小波包最优基进行图形压缩 图 2 基于小波包最优基的图像ቤተ መጻሕፍቲ ባይዱ缩效果
5 结论
小波包对图像的分解确实是一种有效的视频分析工具, 对图像采
图 3 基于小波的图像压缩效果
用多分辨率的分解方式,与人眼由粗到细,由全貌到细节的观察习惯相
一致,同时编码的量化失真随机地分布在整幅图像中,人眼不易察觉,重建图像主观效果比较好,达到了压缩比高而失真度减少的
1)平移正交性 设函数族{Wn(t)},n∈Z 为标准正交小波基尺度函数 W0(t)=准(t)所生成的小波包,也具有正交性,即有正交性,即
2)W2n(t)和 W2n+1(t)的正交关系 W2n(t)和 W2n+1(t)之间有类似与 准 和小波函数 ψ 之间的正交关系。 设函数族{Wn(t)},n∈Z 为标正交小波基的尺度函数 W0(t)=准(t)所 生成的小波包,它们之间的正交关系如下:
