微观经济学第四章 生产论
微观经济学 第四章 生产论知识点

第四章生产论成本理论和生产理论是企业经营管理的关键所在,把生产函数和成本结合起来,就可以分析作为“经济人”的企业或厂商的利润函数。
本章讨论的企业或厂商,其生产的唯一目的就是使得其利润最大化,具体体现为利润最大化。
本章分析生产者行为,通过这种分析可以加深对供给定理的理解,本章只分析生产要素投入量和产出量之间的物质技术关系,不涉及货币因素,因而是一种实物关系。
难点在于各种产量的变化规律、一种要素的合理投入、多种要素的合理投入。
第一部分考查重点1、生产和生产函数2、短期生产函数3、长期生产函数4、等成本线和最优生产要素组合5、生产的经济区域6、规模报酬7、齐次生产函数与欧拉定理8、规模经济与范围经济第二部分主要内容解析一、生产和生产函数1、生产(1)厂商在微观经济分析中,生产者亦称厂商,是指能够做出统一的生产决策的单个经济单位,包括个人、合伙和公司性质的经营组织形式。
厂商被假定为合乎理性的经济人,其生产目的是为了追求最大化的利润。
(2)生产要素生产中的投入程总生产要素。
厂商进行生产的过程就是从生产要素的投入到产品产出的过程。
生产要素一般分为四类:①劳动(L):指人类在生产过程中提供的体力和智力的总和。
②土地(N):包括土地和地上、底下的一球自然资源。
③资本(K):包括资本品(实物形态)和货币资本(货币形态)。
④企业家才能(E):指企业家组织建立和经营管理企业的才能。
2、生产函数的概念生产函数表示在一定时间内,在技术水平不变的情况下,生产中所使用的各种生产要素的投入数量与所能生产的最大产量之间的关系。
一般地,如果1x ,2x ,…,n x 表示生产过程中投入的各种要素数量,Q 表示所能生产的最大产量,则生产函数可以表示为:),...,,(21n x x x f Q =假定生产者只投入劳动和资本这两种要素,则生产函数可表示为),(K L f Q =3、常见的生产函数(1)固定投入比例生产函数(也称为里昂惕夫生产函数)①概念固定投入比例生产函数:是指在每一产量水平上任何一对要素投入量之间的比例都是固定的生产函数的。
微观经济学第四章生产理论

目录
• 生产理论概述 • 生产函数 • 成本最小化与产出最大化 • 生产要素的最优组合 • 扩展生产理论
01 生产理论概述
生产、生产函数与生产可能性边界
01
02
03
生产
生产是指企业使用一定数 量的生产要素,经过一定 的加工或组合,创造新的 使用价值或效用的过程。
生产函数
生产函数描述了在一定技 术条件下,一定数量的投 入与最大产出之间的关系。
生产可能性边界
生产可能性边界描述了在 一定资源和技术条件下, 一个经济能够生产的商品 的最大数量组合。
短期与长期生产函数
短期生产函数
短期生产函数描述了在固定生产 规模下,一定数量的可变投入与 最大产出之间的关系。
长期生产函数
长期生产函数描述了在可变规模 下,一定数量的可变投入与最大 产出之间的关系。
详细描述
固定投入比例生产函数形式为 Y=min{aX,bK},其中Y表示产出,X和 K分别表示劳动和资本两种投入要素,a 和b为常数。这种生产函数形式强调各 投入要素之间的比例关系固定不变。
柯布-道格拉斯生产函数
总结词
柯布-道格拉斯生产函数是一种常用的生产函数形式,用于描述现实生产过程中投入和产出的关系。
最优的生产要素组合应当满足边际技术替代率和边际替代率相等,即等产量线和等 成本线相切的条件。
05 扩展生产理论
要素可替代性
要素替代性
在生产过程中,如果两种或多种生产要 素可以互相替代使用,则它们被称为可 替代要素。可替代要素之间存在一定的 替代关系,当一种要素价格上涨时,生 产者可能会选择使用更多的另一种要素 来代替它,以保持生产成本不变或降低 生产成本。
规模收益对于企业的竞争策略具有重要影响 。企业可以通过扩大生产规模来降低成本和 提高市场份额,从而在竞争中获得优势。同 时,企业也需要根据市场需求和自身条件, 合理地选择生产规模和经营策略,以实现最
姚磊微观经济学-第四章生产者理论

技术水平给定。
例如:1 、
用L表示劳动投入量 用K表示资本投入量 用M表示原材料投入量 Q=f(L,K,M)表示给定生产技术和投入量
最多可生产Q台电视
〔三〕投入
固定投入 可变投入 长时期 短时期
〔四〕技术系数
生产要素之间的配合比例
〔五〕产出〔量〕
总产量〔TP〕 平均产量(AP) 边际产量(MP) 例如:
A0
劳动L价格上升使等成本线 以顺时针方向旋转,斜率变大
O B2
B0
B1
L
练习:按表列式作图
注意:等本钱线斜率绝对值的涵义 ——反映了两要素在购置中的替代比率
价格
在要素市场上,放弃一单位的劳动节约下来 的 厂本 商钱 总,的可生用产于本购钱置支出wr不单变位的资本,此时
在要素市场上,放弃一单位的资本节约下来 的 厂本 商钱 总,的可生用产于本购钱置支出wr不单变位的劳动,此时
上的边际产量相等。 〔每一元本钱 都很有效〕
三、产量既定,本钱最小
1、图示分析
K
A”
A’
A
E
K1
Q
0
L1 B
B’ B” L
2、条件:
在E点,两线斜率相等:
四、公式
PK--- K的价格 PL--- L的价格
QK--- K的数量 QL--- L的数量
MPK--- K的边际产量 MPL--- L的边际产量
L2
TP
L
L3
AP
L3
MP
〔五〕短期生产的三个阶段
平均产量递增
平均产量递减 边际产量为正
AP
MP I II III
边际产量为负
MP
O
AP
微观经济学第四章

•成本理论
C L rK C K L r r
K
isocost line
r
注意:1.一条等成本线 对应某一给定的成本;2. 一条等成本线上不同的 点对应不同的(L,K) 组合,但成本支出相同; 3.等成本线的斜率 K/L=-/r 表示由市场 确定的两要素的替代比 例。如=10, r =5,则 K/L=-/r =-2,表示 企业可以用两个单位的 资本来替代一个单位的 劳动而总成本保持不变。
- - - -由于K减少带来的产出变化 A B的变化是在同一条等量 曲线上
K
A
C
B
MPL L MPK K 0 MPL K L MPK
MRTS LK
MPL
MPK
L
生产的基本规律
也可以用数学方法得到上面的结论
Q f ( L, K ) f f dQ dL dK 0 L K dK f L dL f K
生产理论
成本理论
pi yi j x j
i 1 j 1
n
m
收益
生产ቤተ መጻሕፍቲ ባይዱ基本规律
利润
生产的基本规律
二、生产函数的概念(production
function) (一). 生产的概念 生产是对各种生产要素进行组合以制成 产品的行为。也可以将生产理解为将投入 转化为产出的过程。
Input
AP L
L L
生产的基本规律
MPL
AP L
• AP和MP的关系 MP>AP , 则AP增加 MP<AP , 则AP减少 MP=AP , 则AP最大
L L
生产的基本规律
二、边际报酬(收益)递减规律
对外经贸--微观经济学--第四章生产理论(第六七章)资料

第四章
第6页
厂商
厂商的组织形式.
合伙制企业
➢ 两个人以上合资经营的厂商组织
1)资金相对较多,规模较大,比较易于管理。 2)分工和专业化得到加强。 3)多人所有并管理企业,不利于协调和统一。 4)资金和规模仍有限,不利于企业发展。 5)合伙人之间的契约关系欠稳定。
第四章
第7页
厂商
厂商的组织形式.
生产要素的种类 ➢ 劳动 ➢ 土地 ➢ 资本 ➢ 企业家才能
第四章
第21页
生产函数
生产函数
生产要素的种类 ➢ 劳动
人类在生产过程中提供的体力和智力的总和
第四章
第22页
生产函数
生产函数
生产要素的种类 ➢ 土地
不仅指土地本身,还包括地上和地下的 一切自然资源。
第四章
第23页
生产函数
生产函数
公司制企业 ➢ 按公司法建立和经营的具有法人资 格的厂商组织 ➢ 这是一种重要的现代企业组织形式
第四章
第8页
厂商
厂商的组织形式.
公司制企业
➢ 特点
1)公司为股东所有,但控制权掌握在董事 会监督下的总经理手中。
2)公司主要利用发行债券和股票来筹集资 金。
3)资金雄厚,利于规模生产,也进一步强 化了分工和专业化。
第四章
第18页
厂商
厂商的目标
结论 ➢ 实现利润最大化是一个企业竞争生存的基本 准则 ➢ 这也是今后讨论中始终坚持的一个基本假设
第四章
第19页
生产函数
生产函数
生产过程 ➢ 把生产要素(投入)结合起来获得产出 的过程
➢ 产出最终以实物产品和无形服务形态为 结果
第四章
第20页
微观经济学-第四章:生产理论

第三节:多种投入要素的合理利用
二、边际技术替代率
1、边际技术替代率 △边际技术替代率:在产量不变的条件下,一种要素增加的投 入量与另一种要素减少的投入量之比。 MRTSLK=﹣△K/△L 产量一定时,用L去替K代,增加一单位L放弃K的数量。 例:计算边际技术替代率(见表2) 2、边际技术替代率递减规律 △在产量不变时,当一种要素投入量不断增加时,每一单位 这种要素能够替代另一种要素的数量是递减的。 3、最小成本组合(产量一定时,成本最小) Px:要素x的价格,Py:要素y的价格
第二节:单一可变投入要素的合理利用(短期分析)
因为: R(x) = Q(x) P , 所以:E(x)= R(x) ﹣ C(x)= Q(x) P ﹣ C(x) 要利润最大,利润函数一阶导数应为零, 有:E′(x)= R′(x) ﹣ C′(x)= Q′(x) P ﹣ C′(x)=0 即: Q′(x) P = C′(x), 或:MRP=p Q′(x) P:叫边际产量收入(边际收益产品,MRP), C′(x):叫边际要素成本(投入要素的边际成本)即要素价格p 有: MRP=p时, 利润最大,达到最优投入量。 MRP﹤p时,减少投入量。(例1:见表1) MRP﹥p时,增加投入量。
例:原来,要素x的价格是每单位5元,要素y的价格是每单位 10元。Px=5、Py=10,总成本(支出)30元。 等成本线为:5Px+10Py=30,生产均衡点为A点。 现在,要素x的价格变动为每单位10元,要素y的价格变动为每 单位5元。P′x=10、P′y=5,总成本不变仍为30元。 等成本线为:10P′x+5P′y=30,生产均衡点为B点。 生产均衡点发生效应变动(图示见黑板)
第二节:单一可变投入要素的合理利用(短期分析)
微观经济学答案解析第四章生产论
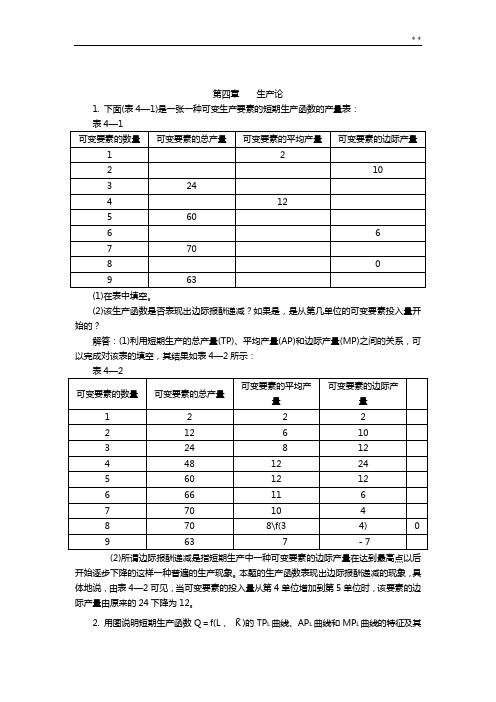
第四章生产论1. 下面(表4—1)是一张一种可变生产要素的短期生产函数的产量表:(2)该生产函数是否表现出边际报酬递减?如果是,是从第几单位的可变要素投入量开始的?解答:(1)利用短期生产的总产量(TP)、平均产量(AP)和边际产量(MP)之间的关系,可以完成对该表的填空,其结果如表4—2所示:开始逐步下降的这样一种普遍的生产现象。
本题的生产函数表现出边际报酬递减的现象,具体地说,由表4—2可见,当可变要素的投入量从第4单位增加到第5单位时,该要素的边际产量由原来的24下降为12。
2. 用图说明短期生产函数Q=f(L,K-)的TP L曲线、AP L曲线和MP L曲线的特征及其相互之间的关系。
解答:短期生产函数的TP L 曲线、AP L 曲线和MP L 曲线的综合图如图4—1所示。
图4—1由图4—1可见,在短期生产的边际报酬递减规律的作用下,MP L 曲线呈现出先上升达到最高点A 以后又下降的趋势。
从边际报酬递减规律决定的MP L 曲线出发,可以方便地推导出TP L 曲线和AP L 曲线,并掌握它们各自的特征及相互之间的关系。
关于TP L 曲线。
由于MP L =d TP L d L,所以,当MP L >0时,TP L 曲线是上升的;当MP L<0时,TP L 曲线是下降的;而当MP L =0时,TP L 曲线达最高点。
换言之,在L =L 3时,MP L 曲线达到零值的B 点与TP L 曲线达到最大值的B ′点是相互对应的。
此外,在L <L 3即MP L >0的范围内,当MP ′L >0时,TP L 曲线的斜率递增,即TP L 曲线以递增的速率上升;当MP ′L <0时,TP L 曲线的斜率递减,即TP L 曲线以递减的速率上升;而当MP ′=0时,TP L 曲线存在一个拐点,换言之,在L =L 1时,MP L 曲线斜率为零的A 点与TP L 曲线的拐点A ′是相互对应的。
关于AP L 曲线。
由于AP L =TP LL ,所以,在L =L 2时,TP L 曲线有一条由原点出发的切线,其切点为C 。
微观经济学.ch04.生产理论

2.固定投入比例的生产函数
固定投入比例的生产函数:表示在每一个产量水平上任何一对要 素投入量的比例都是固定不变的。用函数式表示: Q=min(
一、一种可变生产要素的生产函数
Q=f(L, K )
我们现在来考察一下,当资本固定不变,而劳动投入可变的情 况下,厂商如何通过增加劳动投入来提高产量。
二、总产量、平均产量和边际产量
总产量:使用一定量的某种要素投入所获得的产量总和。即 TPL=Q=f(L)=APL•L 平均产量:平均每单位变动要素投入所能生产的产量。即 APL=TPL/L= f(L)/L 边际产量:每增加一单位变动要素投入所增加的总产量。即 MPL=TPL/L或MPL = dTPL/dL
MPL MPK 即: w r MPK r
MPL w
5. 生产要素的最优组合
2)既定产量条件下成本最小化
MPL MPK 即:
w r MPK r
MPL w5. Leabharlann 产要素的最优组合当 MP w
L
MP r
K
时,说明一单位成本的 支出,用
来购买劳动所得的边际 产量大于用来购买资本 获得的边际产量,因此 ,厂商会扩大劳动投入 量,减少资本投入量, 直到 MP w
例如:农业生产中劳动量、水 或者肥料等要素的投入。 原因:任何一种产品的生产技 术都要求各个要素投入之间有 适当的比例,这意味着要素之 间的替代是有限制的。
K
5 4 3
2
微观经济学 第四章 生产函数——厂商(生产者)行为理论之一

二、短期生产与长期生产
经济学中的短期与长期
短期:生产者来不及调整全部生产要素的数量, 至少有一种生产要素的数量固定不变的时间周 期。 长期:生产者可以调整全部生产要素的数量的 时间周期。
划分的标准是,生产者能否变动全部要素投入 量的数量。
第三节
短期生产函数
举例:连续投入劳动L
劳动量L 总产量TP 边际产量MP 平均产量AP
是固定的。
Q=aL+bK
2.2固定投入比例生产函数(里昂惕夫生产函数)
指在每一产量水平上任何要素投入量之间的比例都是固定的
生产函数。
假定只用L和K,则固定比例生产函数的通常形式为: Q=Minimum(L/u,K/v) u为固定的劳动生产系数(单位产量配备的劳动数) v为固定的资本生产系数(单位产量配备的资本数)
厂商的目标:利润最大化。
条件要求:完全信息 。
长期的目标:销售收入最大化或市场销售份额最大化。 原因:信息是不完全的,厂商面临的需求可能是不确
定的。
今后讨论中始终坚持的一个基本假设:实现利润最大
化是一个企业竞争生存的基本准则 。
第二节
生产
一、生产函数
1、生产函数 产量Q与生产要素L、K、N、E等投入存在着一定依存关
在固定比例生产函数下,产量取决于较小比值的那一
要素。 产量的增加,必须有L、K按规定比例同时增加,若其 中之一数量不变,单独增加另一要素量,则产量不变。
2.3、柯布-道格拉斯生产函数
(C-D生产函数),由美国数学家柯布和经济学家道格
拉斯于1982年根据历史统计资料提出的。
Q AL K
西方经济学(微观部分)第四章生产论

[资料] 罗纳德·H·科斯
[资料] 罗纳德·H·科斯
❖ 1910年生于伦敦威尔斯登。 ❖ 1929年在伦敦经济学院习。 ❖ “普兰特不仅影响他的思想,
还改变了他的一生。”
❖ 依靠塞尔旅行奖金,他来 美国度过了1931~1932年。
第一节 厂商 二、企业的本质
第一节 厂商
二 企业的本质
❖ 科斯通俗地以“走失的牛群损害庄稼”为例加 以说明: “牧场主和农场主对自己行为的调整, 其结果都使自己占有的资源得到当时条件下最 有利的使用。”
❖ 新制度经济学主要创新在这些方面,其中心问 题是通过个人之间的共同协议而进行经济交易 的协调问题,有关合约被用来解释在一个预见 不到的世界中个人之间的合作问题。
[资料] 生产的三个特性
[资料] 生产的三个特性
❖ 首先,生产不仅是创造 了物质,更是生产效用 (或者说是价值);
❖ 其次,生产不等同于劳 动,生产往往要靠多种 因素同时发生作用;
❖ 最后,生产的结果是创 造出新的价值,经过生 产提高了对人的效用。
[案例] 鲁宾逊的生产函数
[案例] 鲁宾逊的生产函数
西方经济学
(微观部分)
第四章 生产论
主讲人:韩松
*自我介绍*
* 自嘲*
一介学究,惶惶似狗。 东拼西凑,闲来插柳。 或存疏漏,等着挨揍。 钱财无有,知识半斗。 交流携手,相逢美酒。 余望何求?潮起云收。
第一节
厂商
第四章 生产论 目录
目录
厂商的含义; 企业的本质
第二节
生产函数
生产函数的定义; 两种类型的生产函数
[视频] 企业与社会
复旦冯剑亮-微观经济学-4

Microeconomics
复旦大学经济学院 冯剑亮
微观经济学 Microeconomics
第四章
生产理论
© Copyright by Jianliang Feng 2003 All rights reserved. Fudan University
第四章 生产理论
本章从生产函数出发,分别研究短期生 产和长期生产中的投入量与产出量之 间的关系及其有关规律。其目标
第二节 生产过程与生产函数 第三节 短期生产函数与生产决策 第五节 规模报酬
第四节 长期生产函数与生产决策 • 问/答
24
© copyrights by Jianliang Feng 2003. Fudan University.
等产量曲线
定义 等产量曲线(isoquants)表示在一定技术条件下,生 产既定产品产量所需投入的生产要素的各种可能组 合点的轨迹。
4
5
65
75
85
90
100
105
110
115
115
120
13
© copyrights by Jianliang Feng 2003. Fudan University.
生产与生产函数
• 生产函数(production function)(续2) – 表述方法 图像法:三维产量山,生产面(production surface) Q K A0 K0 A0’ (L0,K0) L0 L
当MPL=APL,则dAPL/dL=0,APL极大。
20
© copyrights by Jianliang Feng 2003. Fudan University.
边际报酬递减规律
精选微观经济学第4章生产者行为理论

一、等产量曲线
等产量曲线[Isoquanta Curve]——表示能生产出相等产量的两种要素投入量的全部组合方式的曲线。 TP = f(L , K) L—劳动;K—资本;TP—总产量
1
2
3
5
1
2
3
4
K
L
0
A
B
C
4
5
产量为15单位的等产量线
Q[15]
1
2
3
5
1
2
3
4
K
L
0
1
2
3
5
1
2
3
4
K
L
0
A
B
C
4
5
总成本为100元的等成本线
D
E
●
●
●
●
●
C[100]
C[75]
C[125]
教材P114图4-7
三、生产要素的最佳投入组合
假定技术条件和两种要素的价格都不变: 如果总产量已定,成本最低的组合方式利润最大; 如果总成本已定,产量最高的组合方式利润最大。 要素最佳投入组合点就是等产量曲线与等成本线相切的切点。
思考题: (1)什么是边际报酬递减规律?其发生作用的条件如何? (2)人类历史为什么没有按照马尔萨斯的预言发展? (3)既然马尔萨斯的预言失败,你认为边际报酬递减规律还起作用吗? (4)请你谈谈“中国人口太多,将来需要世界来养活中国”或“谁来养活中国?”的观点。
9、静夜四无邻,荒居旧业贫。。10、雨中黄叶树,灯下白头人。。11、以我独沈久,愧君相见频。。12、故人江海别,几度隔山川。。13、乍见翻疑梦,相悲各问年。。14、他乡生白发,旧国见青山。。15、比不了得就不比,得不到的就不要。。。16、行动出成果,工作出财富。。17、做前,能够环视四周;做时,你只能或者最好沿着以脚为起点的射线向前。。9、没有失败,只有暂时停止成功!。10、很多事情努力了未必有结果,但是不努力却什么改变也没有。。11、成功就是日复一日那一点点小小努力的积累。。12、世间成事,不求其绝对圆满,留一份不足,可得无限完美。。13、不知香积寺,数里入云峰。。14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。15、楚塞三湘接,荆门九派通。。。16、少年十五二十时,步行夺得胡马骑。。17、空山新雨后,天气晚来秋。。9、杨柳散和风,青山澹吾虑。。10、阅读一切好书如同和过去最杰出的人谈话。11、越是没有本领的就越加自命不凡。12、越是无能的人,越喜欢挑剔别人的错儿。13、知人者智,自知者明。胜人者有力,自胜者强。14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。15、最具挑战性的挑战莫过于提升自我。。16、业余生活要有意义,不要越轨。17、一个人即使已登上顶峰,也仍要自强不息。
【微观经济学】生产理论(教学课件)

4、等产量曲线的两种特例
1、固定技术系数的等产量曲线
2、生产要素完全可替代条件下的等产量曲线
K Q1 Q2 Q3
K Q3
Q2 Q1
3210 10 8 6 4 2 0
123
L
123
L
5、脊线和生产区域
脊线:是把所有等产量线上斜率为零和斜率无穷 大的点与原点一起联结起来,形成的两条线。
脊线内表明生产要素替代的有效范围。
10 8 6 4 2 0
K
E3 E1E2
生产扩展线
C1 C2 C3 L
已知生产函数,求扩展线
10题:Q=KL2 依据均衡条件:
MPK MPL PK PL
L2
PK
2KL PL
MPK L2 K LPL
2PK
MPL 2KL
第四节 规模报酬 returns to scale
一、规模报酬的含义:生产规模扩大,各种生产要素同时 增加,产量增加的情况。
E1
Q2=200 C2
C1 Q1=100 123456 L
规模报酬递减
规模报酬递减的原因:。生产要素投入量增加一倍,生产 规模扩大一倍,产量增加小于一倍,是因为规模过大往往造 成管理混乱,权责不分,效率低下。
二、规模报酬的三种情况:
1、规模报酬Q 递 增f 。( L 生, 产K ) 要素如 投入量f ( 增L 加, 倍K ,) 产 果 量f 将( L 增, K 加) 一倍以上。
2加、一规倍模。报酬Q 不 变f 。( L 生, K 产) 要素如 投入量f 增( 加L , 一K 倍) , 产果 量f ( 将L , 增K )
(1)边际技术替代率:在维持产量不变的条件下,增加一单 位生产要素投入量与所需减少的另一种生产要素投入量的比 率。是等产量曲线上各点切线的斜率值。
西方经济学微观部分-第四章_生产论

4.边际报酬递减规律的3阶段
总产量要经历一个逐渐上升加快 增长趋缓 最大不变绝对下降的 过程。
一种生产要素增加所引起的边 际产量变动三阶段:
第一阶段:边际产量递增 总产量增加
第二阶段:边际产量递减 总产量增加
第三阶段:边际产量为负 总产量开始减少
Q
G
B
TP
Ⅰ
O
ⅡⅢ
A E
F AP
L1 L2 L3 MP L
来的全部产量。 TPL f (L, K )
平均产量AP(average product ) :平均每单位要素所生产出来的产
量。 (如劳动力L)
AP = TP/L
APL
f (L, K ) TPL
L
L
边际产量MP(marginal product) :增加一单位要素所增加的产量。
(如劳动力L) MP = TP/ L
技术水平
如果生产技术发生了变化……
“足蒸暑土气,背灼炎天光,力尽不知热,但惜夏日
长”VS“联合收割机伴随音乐,倘佯在诗情画意的田
野上”
一、技术变革 生产过程改进、旧产品革新、新产品发明
二、作用——生产函数发生移动 使用相同数量的投入获得更多的产出 用更少的投入获得相同数量的产出
1.生产函数
在一定时期、一定的生产技术水平下,生产要素投入量与最大 产出量之间的物质数量关系。
金字塔
(1)企业家:顶层 冒着一定风险,在变幻莫测的市场风云中抓 住机会成就事业的人。“四有”+高等教育
(2)管理者:中层 落实企业家的意志和决策。“上传下达”
(3)工人:底层 把原料变成产品的执行者
2.厂商(企业)的本质
(一)大规模生产的经济性 在自己家地下室生产自己所需产品,经济吗?
4第四章 生产论 微观经济学
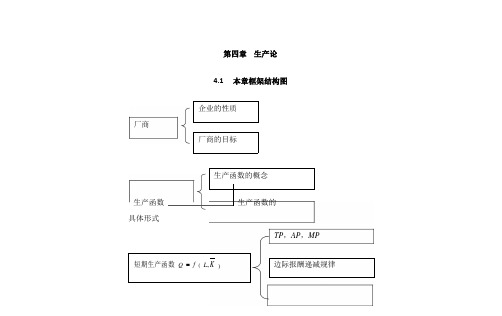
四、长期生产函数:两种可变生产要素的生产函 数1.长期生产函数的形式 在生产理论中,为了简化分析,通常以两种可变生产要素的生产函数来考察长期生产问题。假定生产者使用劳 动和资本两种可变生产要素来生产一种产品,则两种可变生产要素的长期生产函数可以写为:
Q f L,K 2.等产量曲线 等产量曲线(Equal-Product Curves)是在技术水平不变的条件下生产同一产量的两种生产要素投入量的所有不 同组合的轨迹,每一条等产量曲线对应的是特定的产出水平。等产量曲线如图4-2所示。
点的线段的斜率,就是相应的 APL 值。(3)边际产量和平均产量之间 的关系
就平均产量 APL 和边际产量 MPL来说,当 MPL APL 时, APL 曲线是上升的;当MPL APL 时,APL曲
线是下降的;当 MPL APL 时,APL 曲线达极大值。数学证明如下:
dTPL L −TP
d APL d TPL dL
二、生产函数 1.生产函数的概念
劳动、土地、资本和企业家才能
生产函数表示在一定时期内,在技术水平不变的情况下,生产中所使用的各种生产要素的数量与所能生产的最
大产量之间的关系(The production function specifies the maximum output that can be produced with a given quantity of
劳动的平均产量 APL 指平均每一单位可变要素劳动的投入量所生产的产量,即 APL = TPL L,K 。
L
劳动的边际产量 MPL 指增加一单位可变要素劳动投入量所增加的产量,即:
TPL L,K
MP
lim
TP dTPL L,K
L
L
微观经济学第四章生产理论

3. 总产量与平均产量的关系
根据平均产量的定义,总产量曲线上任一点与原点连 线的斜率就是平均产量。从图4-1可以看出,总产量曲线 上的B点和原点的连线的斜率最大,所以此时平均产量达 到最大,相应的劳动投入量为L2。
4. 平均产量与边际产量的关系
当边际产量大于平均产量时,平均产量是递增的;当 边际产量小于平均产量时,平均产量是递减的;而在边际 产量等于平均产量时,平均产量达到最大值。边际产量和 平均产量之间的这种关系对任何函数都存在。在图4-1中, 可以看出,总产量曲线上的B点与原点的连线正好是B点处 的切线,即在劳动投入量为L2时,边际产量等于平均产量, 平均产量达到最大值。
二、 等成本线
等成本线也称厂商预算线,是指在既定成本及既定生 产要素价格条件下,生产者可以购买到的最大数量的两 种生产要素的各种不同数量组合的轨迹。等成本线表示 厂商对两种生产要素的购买不能超出其总成本的限制。
设厂商给定的总成本为C,劳动的价格或工资率为w ,资本的价格为r,那么厂商购买的劳动L和资本K两种生 产要素的数量满足下面的方程:
在对生产者行为进行分析时,假定所有厂商都知道相 应产品的生产函数,因此他们总能达到技术上高效率的产 量。这是因为,一方面以盈利为目的的厂商总在寻求达到 最大产量的途径;另一方面,做不到这点的厂商难免会在 竞争中被淘汰。
三、 几种常见的生产函数
1. 固定投入比例的生产函数
任何生产过程中的各种生产要素投入数量之间都存 在一定的比例关系。固定投入比例生产函数也被称为里 昂惕夫生产函数,是指在每一个产量水平上任何一对要 素投入量之间的比例都是固定的生产函数。假定生产过 程中只使用劳动和资本两种要素,则固定投入比例生产 函数的通常形式为
在理解边际报酬递减规律时应注意以下几点: (1) 边际报酬递减是以技术水平不变和其他 要素投入量不变为前提的。 (2) 边际报酬递减是以可变要素投入量超过 一定限度为前提的。 (3) 边际报酬递减规律假定所增加的生产要 素是同质的,不存在技术性与非技术性要素的区别。
微观经济学 生产理论

二、生产函数(production function)
1、生产四要素: 劳动 L、 资本 K、 土地 N 、 企业家才能 E 2、产量Q与生产要素L、K、N、E的投入存在着一定 的依存关系。 Q = f(L、K、N、E)--- 生产函数 其中N是固定的,E难以估算,所以一般的简化为, Q = f(L、K) (便于分析问题)
劳动的平均产量为: AP = TP/L = 9+3L-L² 劳动的边际产量为: MP = d(TP)/dL =9+6L-3L²
8/1/2013
10
例如连续投入劳动L
劳动量L 0 1 2 3 4 5 6 7 8 总产量TP 0 6 13 21 28.5 34.5 39 39 37
Q f L, K
K
Q1Q2 Q3 Q4
L
同一条曲线代表相同的 产量水平; 不同的曲线代表不同的 产量水平。 离原点越远代表产量水 平越高 高位等产量线的生产要 素组合量大。
边际产量MP(marginal product) :增加一单位某种要素
所增加的产量。(如劳动力L) MP = TP/ L
8/1/2013
劳动的平均产量、边际产量记为AP L、 MP L , 资本的平均产量、边际产量记为AP K、 MP K 。
9
若生产函数为:
TP = 9L +3L² ³ -L
8/1/2013 20
特写:三季稻不如两季稻
1958年“大跃进”是一个不讲理性的年代,时髦的口 号是“人有多大胆,地有多高产”。于是一些地方把传统 的两季稻改为三季稻。结果总产量反而减少了。从经济学 的角度看,这是因为违背了一个最基本的经济规律:边际 产量递减规律。 两季稻是农民长期生产经验的总结,它行之有效,说 明在传统农业技术下,固定生产要素已经得到了充分利用。 改为三季稻之后,土地过度利用引起肥力下降,设备、肥 料、水利资源等由两次使用改为三次使用,每次使用的数 量不足。这样,三季稻的总产量就低于两季稻了。群众总 结的经验是“三三见九,不如二五一十”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等成本线的方程:c=wL+rK
c r
K
w c k L r r
c w
等成本线斜率为 与 w r 预算线类似。
O
L
第四章 生产论
第五节
素最优组合
生产者均衡——生产要素最优组合
K C B N E
一、既定成本下最大产量的要
等成本线与等产量线相切 于一点,在切点实现要素 最优组合。
在E点,两线斜率相等:
Q
TP
Ⅰ
A E
Ⅱ
F
Ⅲ
AP
O
L1 L2
L3
MP
L
第四章 生产论
练习:错误的一种说法是:()
( 1)
A.只要总产量减少,边际产量一定是负
数 B.只要边际产量减少,总产量也一定是 减少 × C.边际产量曲线一定在平均产量曲线的 最高点与之相交
第四章 生产论
( 2) A.劳动的边际产量曲线、总产量曲线、 平均产量曲线均呈先增后递减的趋势 B.劳动的边际产量为负值时,总产量会 下降 C.边际产量为0时,总产量最大 D.平均产量曲线与边际产量曲线交于平 均产量曲线的最大值点上 E.平均产量曲线与边际产量曲线交于边 际产量曲线的最大值点上 ×
Q f ( x1, x 2,, xn)
又可简写成:Q=f(L,K)
第四章 生产论
二、常见的生产函数 1、固定投入比例生产函数 也称里昂惕夫生产函数,表示各种 要素投入数量之间存在着固定的配合比 例,即每单位劳动必须有相应单位的资 本配合使用,多了少了都不能达到最优 产量。
K/L=常数
每一产量水平上
K3 O
Q2=200 C Q1=100
L1
L2
L3
C. 等产量线凸向原点。
第四章 生产论
三、边际技术替代率 MRTSLK
1.边际技术替代率(marginal rate of
technical substitution ,缩写为MRTS), 是指在维持产量水平不变的条件下,增加一 单位的某种要素投入量所减少的另一种要素 的投入数量。
长期生产函数
(两种可变生产要素的生产函数)
一、长期生产函数 长期中,所有的要素都是可变的。 通常以两种可变要素的生产函数来研究长期生产问 题。
Q f ( X 1 , X 2 ,, X n ) Q f ( L, K )
第四章 生产论
二、等产量线 Isoquante
1.等产量线:在技术水平不 变的条件下,可以带来相等 产量的两种生产要素L、K 的投入数量的所有不同组合 对应点的轨迹。
意味着:产量增加。 直到两种要素的边际技术 替代率(生产中的替代率)
等于两要素价格之比(市场 购买中的替代率)时,便获 得最大产量。
第四章 生产论
二、既定产量下成本最小的 要素最佳组合 w MRTSLK K r
A
A'
A'' K0
C
表明厂商应该选择最优的生产要素组合,使 两要素的边际技术替代率等于两要素价格之 比,从而实现既定产量条件下的成本最小。
第四章 生产论
2、柯布—道格拉斯生产函数 柯布—道格拉斯生产函数是经济学中 使用最为普遍的简单生产函数,一般形式 为: 劳动的产出弹性
Q A L K
技术系数
资本的产出弹性
1 : 规模报酬递减 1 : 规模报酬不变 1 : 规模报酬递增
第四章 生产论
AP是TP曲线上的点与原点连线的斜率,当连 线与TP曲线相切时,AP达到最大;
2、TP与MP的关系:
MP是TP曲线的斜率, MP的最高点是TP曲 线的拐点,当MP=0时,TP最大;
3、AP与MP的关系:
当MP>AP时,AP曲线上升,当MP<AP时, AP曲线 下降,MP自上而下穿过AP曲线的最高点。
Curve
K 线上任何一点,L、K组 合不同,但产量却相同。 与无差异曲线的比较?
O
Q
f L, K Q
Q
0
L
第四章 生产论
2.等产量线的特征
A. 在同一个平面上可以
K H
有无数条等产量线。离原 点越远的表示产量水平越 高。
A K1
R
B. 同一平面坐标图上的等
K2 B
Q3=300
产量线不会相交。
第四章 生产论
三、总产量曲线、平均产量曲线和边际产量曲线 每月产量 II I III D
Q2
C
Q1
总产量
B
L3
0
L 11
L2
每月投入劳动
每月产量
Q﹡ Q〞 Q′ 0 L1 A
E
平均产量
边际产量
L2 L3
每月投入劳动
第四章 生产论
四、总产量、平均产量、边际产量之间的关系 返回 1、TP与AP的关系:
MP
L
总产出绝对下降。 (需减员增效)
第四章 生产论
进 一 步 图 示
MP=0 TP最大
Q MP>AP AP
G
B MP<AP AP Ⅱ
A
MP=AP E AP最大
TP
MP<0 TP
Ⅰ
Ⅲ
F AP O L1 L2 L3 L MP
第四章 生产论
例1:短期生产函数为
Q L 24L 240L
E D
MPL MPK w r
B L
0
L0
B''
B'
第四章 生产论
三、追求利润最大化的厂商能够实现最优的生产组合
( L, K ) P f ( L, K ) (w L r K )
f P w0 L L
f P r 0 K K
f / L MPL w f / K MPK r
第四章 生产论
练习:
已知某企业的生产函数Q=L2/3K1/3,劳动的价格w=2, 资本的价格r=1, (1)当成本C=3000时,企业实现最大产量时的L、K 和Q的均衡值。 (2)当产量Q=800时,企业实现最小成本时的L、 K和C 的均衡值。
第四章 生产论
第六节 扩展线( Expansion path )
动所生产出来的全部产量。
TP f(L)
平均产量AP(average product ) :平均每单位可变要
素劳动的投入所生产出来的产量。 AP = f(L)/L
边际产量MP(marginal product) :增加一单位可变要
素劳动的投入量所增加的产量。
df ( L ) MP dL
1.等斜线 等斜线是一组等产量线上边际技术 替代率相等的点的轨迹。
脊线就是等斜线
在一个平面坐标图形中有无数条等斜线。
第四章 生产论
二、厂商的目标
遵循微观经济学中理性人的 假定,我们一般认为厂商的目标 就是追求利润最大化.
第四章 生产论
第二节 生产函数
一、生产函数(product function) 生产函数表示在一定的时期内,在一 定的生产技术水平不变的条件下,生产中 所使用的各种生产要素的投入量与所能产 生的最大产量之间的关系。通常可写成:
第四章 生产论
对均衡条件的进一步说明:
If: MRTS LK
dk 4 w 1 dl 1 r 1
说明:生产者在成本不变 的条件下,减少一单位资
这样:理性生产者 就会调整这两种要素 的投入量: 减少资本的投入 增加劳动的投入 (C点向E点移动)
本的投入,增加一单位劳 动的投入,可以使产量增 加。
w MRTSLK r
Q1 L O A M 既定成本下最大产量 的要素最佳组合
D
Q3 Q2
MPL MPK w r
为了实现既定成本条件下的最大产量,厂商可 以通过对两要素投入量的不断调整,使得最后 一单位货币成本无论用来购买哪一种生产要素 所带来的边际产量相等时,生产者便实现了既 定成本条件下的最大产量。
脊线:所有等产量线上斜率为零的点和斜率为无穷大的点与原 点连接起来而形成的两条线。 F K 上脊线(0F):所 E 有等产量曲线上斜 率为无穷大的点的 连线。或者说是资 本的边际产量为零 的点的连线。
K H A REEE K1 K2 Q3=300 B Q2=200 K3 C Q1=100 O
下脊线(0E):所 有等产量曲线上斜 率为零的点的连线 或者说是劳动的边 际产量为零的点的 连线。
L1
L2
L3
L
0
L
第四章 生产论
五、 等成本线(企业预算线)
等成本线是在既定的成本和 既定的生产要素的价格下, 生产者可以购买到的两种生 产要素的各种不同数量组合 对应点的轨迹。
c=600,w=20,r=10 组合方式 L 30 20 10 0 K 0 20 40 60
K
●B
A B C
●A
D
O
L
第四章 生产论
第四章 生产论
3、边际技术替代率递减规律 在维持产量水平不变的前提下, 随着一种生产要素投入数量的增加, K 每一单位的这种生产要素所能替代的 另一种生产要素的数量是递减的。
K1
等产量线某一点的边际技术替代率等 于该点的斜率的绝对值,决定了等产 量线凸向原ቤተ መጻሕፍቲ ባይዱ。
K2
O
L
L
L
第四章 生产论
四、生产的经济区域
一、短期生产函数
假定在一定的技术条件下,生产某产品的 各投入要素中只有一种(通常是劳动)是可变 的,分析这种可变要素(劳动)投入量的变化 对产量的影响就是短期生产函数。可写成:
Q f ( L)
或
