最新-2018届高考数学解答题编拟(3)理科番禺区大岗中学李奎光 精品
2018年高考广东卷理科数学试题及答案解析版 精品

2018年普通高等学校招生全国统一考试(广东卷)A数学(理科)一 、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的 1 设i 为虚数单位,则复数56ii-= A 6+5i B 6-5i C -6+5i D -6-5i2 设集合U={1,2,3,4,5,6}, M={1,2,4 } 则CuM= A .U B {1,3,5} C {3,5,6} D {2,4,6}3 若向量BA=(2,3),CA =(4,7),则BC =A (-2,-4)B (3,4)C (6,10)D (-6,-10)4.下列函数中,在区间(0,+∞)上为增函数的是 A.y=ln (x+2) B.y=-1x + C.y=(12)x D.y=x+1x5.已知变量x ,y 满足约束条件⎪⎩⎪⎨⎧≤-≥+≤112y x y x y ,则z=3x+y 的最大值为A.12B.11C.3D.-16,某几何体的三视图如图1所示,它的体积为A .12π B.45π C.57π D.81π7.从个位数与十位数之和为奇数的两位数种任取一个,其个位数为0的概率是 A.49 B. 13 C. 29D. 198.对任意两个非零的平面向量α和β,定义βββαβα∙∙=∙。
若平面向量a ,b 满足|a|≥|b|>0,a 与b 的夹角⎪⎭⎫⎝⎛0,∈4πθ,且a ·b 和b ·a 都在集合⎭⎬⎫⎩⎨⎧∈Z n 2中,则b a ∙= A .12 B.1 C. 32 D. 52二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分。
(一)必做题(9-13题)9.不等式|x+2|-|x|≤1的解集为_____。
10. 621⎪⎭⎫ ⎝⎛+x x 的展开式中x ³的系数为______。
(用数字作答)11.已知递增的等差数列{a n }满足a 1=1,423-=a a ,则a n =____。
2018高考天津卷理科数学真题与答案解析

2021年普通高等学校招生全国统一考试〔天津卷〕数学〔理工类〕本试卷分为第一卷〔选择题〕和第二卷〔非选择题〕两局部,共150 分,考试用时 120 分钟。
第一卷 1 至 2 页,第二卷 3 至 5 页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试完毕后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第I 卷考前须知:1.每题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共 8 小题,每题 5 分,共 40 分。
参考公式:如果事件 A,B互斥,那么P( AB) P( A) P(B) .如果事件 A,B 相互独立,那么P( AB)P( A) P(B) .棱柱的体积公式V Sh ,其中 S 表示棱柱的底面面积,h 表示棱柱的高 .1棱锥的体积公式 VSh,其中S表示棱锥的底面面积,h 表示棱3锥的高 .一.选择题:在每题给出的四个选项中,只有一项为哪一项符合题目要求word 版本整理分享的.(1) 设全集为 R,集合A { x 0x 2} , B{ x x1} ,那么A I (e R B)(A){ x 0x1}(B){ x 0x1}(C){ x 1x2}(D) { x 0x2}x y5,(2) 设变量x,y满足约束条件2x y4,那么目标函数z3x 5y 的最大x y1,y0,值为(A)6(B)19(C) 21(D)45(3)阅读如图的程序框图,运行相应的程序,假设输入 N的值为20,那么输出 T 的值为(A) 1(B) 2(C) 3(D) 4word 版本整理分享(4) 设x R ,那么“| x1 | 1〞是“x31〞的2 2(A)充分而不必要条件(B)必要而不充分条件(C)充要条件(D)既不充分也不必要条件(5) a log 2 e , b ln 2 , c log 11,那么 a,b,c 的大小关系为23(A) a b c(B) b a c(C) c b a(D) c a b(6) 将函数ysin(2x) 的图象向右平移个单位长度,所得图象对应510的函数word 版本整理分享(A) 在区间[3, 5] 上单调递增 (B) 在区间[3, ]上单调4 44递减(C) 在区间[5, 3] 上单调递增 (D) 在区间[3, 2]上单4 22调递减(7) 双曲线x 2y 21( a0, b0) 的离心率为2 ,过右焦点且垂直于a 2b 2x 轴的直线与双曲线交于A ,B 两点.设 A ,B 到双曲线同一条渐近线的距离分别为 d 1和 d 2,且 d 1 d 2 6 ,那么双曲线的方程为(A)x 2y 2 1 (B) x 2y 214 12124(C)x 2 y 2 1(D) x 2y 2 13 993(8) 如图,在平面四边形ABCD 中,ABBC ,AD CD , BAD120,AB AD 1 .uuur uur假设点 E 为边 CD 上的动点,那么AE BE 的最小值为(A)21 (B)3(C)25(D) 316216第二卷考前须知:1. 用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2018年高考广东卷理科数学试题及答案解析版 精品

2018年普通高等学校招生全国统一考试(广东卷)数学(理科)本试题共4页,21小题,满分150分,考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:柱体的体积公式V Sh =,其中S 为柱体的底面积,h 为柱体的高.线性回归方程 y bx a =+ 中系数计算公式121()()()niii nii x x y y bx x ==--=-∑∑ , a y bx =- ,其中x ,y 表示样本均值.n 是正整数,则1221()()n n n n n n a b a b a a b ab b -----=-++++ .一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数z 满足(1)2i z +=,其中i 为虚数单位,则z =A .1i +B .1i -C .22i +D .22i -1.(B ).22(1)11(1)(1)iz i i i i -===-++-2.已知集合{(,)|,A x y x y =为实数,且221}x y +=,{(,)|,B x y x y =为实数,且}y x =,则A B ⋂的元素个数为A .0B .1C .2D .32.(C ).A B ⋂的元素个数等价于圆221x y +=与直线y x =的交点个数,显然有2个交点 3.若向量,,a b c 满足a ∥b 且⊥a c ,则(2)⋅+=c a bA .4B .3C .2D .0 3.(D ).依题意得⊥c a ,⊥c b ,则(2)20⋅+=⋅+⋅=c a b c a c b正视图 图1 侧视图 图24.设函数()f x 和()g x 分别是R 上的偶函数和奇函数,则下列结论恒成立的是 A .()()f x g x +是偶函数 B .()()f x g x -是奇函数 C .()()f xg x +是偶函数 D .()()f xg x -是奇函数4.(A ).由()f x 是偶函数、()g x 是奇函数,得()f x 和()g x 都是偶函数,所以()()f xg x +与()()f xg x -都是偶函数,()()f xg x +与()()f xg x -的奇偶性不能确定5.已知平面直角坐标系xOy 上的区域D 由不等式组02x y x ⎧⎪⎨⎪⎩≤≤给定.若(,)M x y 为D 上的动点,点A的坐标为,则z OM OA=⋅的最大值为A. B . C .4D .3 5.(C ).zy =+,即y z=+,画出不等式组表示的平面区域,易知当直线y z =+经过点时,z 取得最大值,max24z == 6.甲、乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢两局才能得冠军. 若两队胜每局的概率相同,则甲队获得冠军的概率为A .12B .35C .23D .346.(D ).乙获得冠军的概率为111224⨯=,则甲队获得冠军的概率为13144-=7.如图1 ~ 3,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为A. B. C. D.7.(B ).该几何体是一个底面为平行四边形,高为3则33V Sh ===8.设S 是整数集Z 的非空子集,如果,a b S ∀∈,有ab S ∈,则称S 关于数的乘法是封闭的.若,T V 是Z 的两个不相交的非空子集,T V Z ⋃=,且,,a b c T ∀∈,有abc T ∈;,,x y z V ∀∈,有xyz V ∈,则下列结论恒成立的是A .,T V 中至少有一个关于乘法是封闭的B .,T V 中至多有一个关于乘法是封闭的C .,T V 中有且只有一个关于乘法是封闭的D .,T V 中每一个关于乘法都是封闭的 8.(A ).若T 为奇数集,V 为偶数集,满足题意,此时T 与V 关于乘法都是封闭的,排除B 、C 若T 为负整数集,V 为非负整数集,也满足题意,此时只有V 关于乘法是封闭的,排除D二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9 ~ 13题) 9.不等式13x x +--≥0的解集是 .9.[1,)+∞.13x x +--≥0 ⇒1x +≥3x -⇒2(1)x +≥2(3)x -⇒x ≥110.72()x x x -的展开式中,4x 的系数是 (用数字作答) 10.84.72()x x x -的通项7821772()(2)r r r r r r r T xC x C x x --+=-=-,由824r -=得2r =,则227(2)84C -= 11.等差数列{}n a 前9项的和等于前4项的和.若11a =,40k a a +=,则k = .11.10.方法1:由94S S =得93646d d +=+,求得16d =-,则4111(1)()13()066k a a k +=+-⨯-++⨯-=,解得10k =方法2:由94S S =得567890a a a a a ++++=,即750a =,70a =,即104720a a a +==,即10k =12.函数32()31f x x x =-+在x = 处取得极小值. 12.2.2()363(2)f x x x x x '=-=-,令()0f x '=得0x =或2x =,显然当0x <时()0f x '>;当02x <<时()0f x '<;当2x >时()0f x '>,函数32()31f x x x =-+在2x =处取得极小值 13.某数学老师身高176cm ,他爷爷、父亲和儿子的身高分别是173cm 、170cm 和182cm .因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为 cm . 13.185.设父亲的身高为x cm ,儿子的身高为y cm ,则根据上述数据可得到如下表格:上表中的最后一组(182,?)是预测数据,173,176x y ==12221()()00361033()niii nii x x y y bx x ==--++⨯===++-∑∑ , 3a y bx =-=线性回归方程3y x =+,所以当182x =时,185y =,即他孙子的预测身高为185 cm .(二)选做题(14 ~ 15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)已知两曲线参数方程分别为sin xy θθ⎧=⎪⎨=⎪⎩(0)θπ<≤和254x t y t ⎧=⎪⎨⎪=⎩ (t ∈)R ,它们的交点坐标为___________.14.(1,5.sin x y θθ⎧=⎪⎨=⎪⎩表示椭圆2215x y +=(01)x y <≤≤,254x t y t ⎧=⎪⎨⎪=⎩表示抛物线245y x =图4COPBA22221(01)5450145x y x y x x x y x ⎧+=≤≤≤⎪⎪⇒+-=⇒=⎨⎪=⎪⎩或5x =-(舍去),又因为01y ≤≤,所以它们的交点坐标为15.(几何证明选讲选做题)如图4,过圆O 外一点P 分别作 圆的切线和割线交圆于,A B ,且7PB =,C 是圆上一点使得5BC =,BAC APB ∠=∠,则AB =___________.15由弦切角定理得PAB ACB ∠=∠,又BAC APB ∠=∠,则△PAB ∽△ACB ,则PB ABAB BC =,235AB PB BC =⋅=,即AB =三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数1()2sin()36f x x π=-,x ∈R . (1)求5()4f π的值;(2)设,0,2παβ⎡⎤∈⎢⎥⎣⎦,10(3)213f πα+=,6(32)5f βπ+=,求cos()αβ+的值.16.解:(1)515()2sin()2sin 43464f ππππ=⨯-==(2)110(3)2sin[(3)]2sin 232613f πππααα+=+-==,即5sin 13α=16(32)2sin[(32)]2sin()3625f ππβπβπβ+=+-=+=,即3cos 5β=∵,0,2παβ⎡⎤∈⎢⎥⎣⎦,∴12cos 13α==,4sin 5β==∴1235416cos()cos cos sin sin 13513565αβαβαβ+=-=⨯-⨯=17.(本小题满分13分)为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中微量元素,x y 的含量(单位:毫克).下表是乙厂的5件产品的测量数据:(1)已知甲厂生产的产品共有98件,求乙厂生产的产品数量; (2)当产品中的微量元素,x y 满足175x ≥且75y ≥时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数ξ的分布列及其均值(即数学期望).17.解:(1)设乙厂生产的产品数量为a 件,则98145a =,解得35a =图5CDPAEFPF所以乙厂生产的产品数量为35件(2)从乙厂抽取的5件产品中,编号为2、5的产品是优等品,即5件产品中有2件是优等品由此可以估算出乙厂生产的优等品的数量为235145⨯=(件)(3)ξ可能的取值为0,1,223253(0),10C P C ξ=== 1123256(1),10C C P C ξ=== 22251(2),10C P C ξ===∴ξ的分布列为:∴3614012.1010105E ξ=⨯+⨯+⨯=18.(本小题满分13分)如图5,在锥体P ABCD -中,ABCD 是边长为1的 菱形,且60DAB ∠=,PA PD ==2PB =,,E F分别是BC ,PC 的中点. (1)证明:AD ⊥平面DEF ; (2)求二面角P AD B --的余弦值.18.(1)证明:取AD 的中点H ,连接,,PH BH BD ∵PA PD =,∴AD PH ⊥∵在边长为1的菱形ABCD 中,60DAB ∠=∴△ABD 是等边三角形 ∴AD HB ⊥,PH HB H = ∴AD ⊥平面PHB ∴AD PB ⊥∵,E F 分别是BC ,PC 的中点 ∴EF ∥PB ,HB ∥DE∴AD DE ⊥,AD EF ⊥,DE EF E = ∴AD ⊥平面DEF(2)解:由(1)知PH AD ⊥,HB AD ⊥ ∴PHB ∠是二面角P AD B --的平面角易求得PH BH ==∴2227334cos 27PH HB PB PHB PH HB +--+-∠====-⋅∴二面角P AD B --的余弦值为7-19.(本小题满分14分)设圆C与两圆22(4x y +=,22(4x y +=中的一个内切,另一个外切. (1)求C 的圆心轨迹L 的方程;(2)已知点M,F ,且P 为L 上动点,求MP FP - 的最大值及此时点P 的坐标.19.解:(1)设(F F ',圆C 的半径为r ,则(2)(2)4CF CF r r '-=+--=< ∴C 的圆心轨迹L 是以,F F '为焦点的双曲线,2a =,c =1b =∴C 的圆心轨迹L 的方程为2214x y -=(2)2MP FP MF -≤== ∴MP FP - 的最大值为2如图所示,P 必在L 直线MF 的斜率2k =-:2MF y x =-+22142x y y x ⎧-=⎪⎨⎪=-+⎩215280x -+=6)0--=12x x ==∵P x >P x =,P y =∴MP FP - 的最大值为2,此时P 为(55-20.(本小题满分14分)设0b >,数列{}n a 满足1a b =,1122n n n nba a a n --=+-(2)n ≥.(1)求数列{}n a 的通项公式;(2)证明:对于一切正整数n ,1112n n n b a ++≤+.20.(1)解:∵1122n n n nba a a n --=+-∴1122n n n a ba n a n --=+- ∴1211nn n n a b a b --=⋅+ ① 当2b =时,1112nn n n a a ---=,则{}n n a 是以12为首项,12为公差的等差数列∴11(1)22nn n a =+-⨯,即2n a = ② 当0b >且2b ≠时,11211()22n n n n a b b a b --+=+-- 当1n =时,122(2)nn a b b b +=--∴1{}2nn a b +-是以2(2)b b -为首项,2b 为公比的等比数列 ∴112()22n nn a b b b +=⋅-- ∴212(2)2(2)n n nn n n n b a b b b b b -=-=---∴(2)2n n nn n b b a b -=- 综上所述(2),02222nn nn n b b b b a b b ⎧->≠⎪=-⎨⎪=⎩ 且, (2)方法一:证明:① 当2b =时,11122n n n b a ++=+=;② 当0b >且2b ≠时,12212(2)(222)nnn n n n b b b b b -----=-++++1221222n nnn n n n n n b a b b b ----⋅=≤=++++111211112222222n n n n n n n n b b b b+++---++=====<=⋅1112n n b +++∴对于一切正整数n ,1112n n n b a ++≤+.方法二:证明:① 当2b =时,11122n n n b a ++=+=;② 当0b >且2b ≠时,要证1112n n n b a ++≤+,只需证11(2)122n n n nn nb b b b ++-≤+-, 即证1(2)122n nn n n b b bb +-≤+- 即证1221112222n n n n n n n b b b bb ----+≤+++++ 即证122111()(222)2n n n n n n b b b b n b ----++++++≥即证2112231122221()()2222n n n n n n n n b b b b nb b b b ---+-+++++++++≥ ∵2112231122221()()2222n n n n n n n n b b b b b b b b ---+-+++++++++ 2121232111222()()()()2222n n n n n n n n b b b b b b b b ----+=++++++++n≥+= ,∴原不等式成立∴对于一切正整数n ,1112n n n b a ++≤+.21.(本小题满分14分)在平面直角坐标系xOy 上,给定抛物线L :214y x =.实数,p q 满足24p q -≥0,12,x x 是方程20x px q -+=的两根,记12(,)max{,}p q x x ϕ=.(1)过点2001(,)4A p p 0(0)p ≠作L 的切线交y 轴于点B .证明:对线段AB 上的任一点(,)Q p q ,有0(,)2p p q ϕ=;(2)设(,)M a b 是定点,其中,a b 满足240a b ->,0a ≠.过(,)M a b 作L 的两条切线12,l l ,切点分别为2111(,)4E p p ,2221(,)4E p p ',12,l l 与y 轴分别交于,F F '.线段EF 上异于两端点的点集记为X .证明:112(,)(,)2p M a b X p p a b ϕ∈⇔>⇔=;(3)设{(,)|D x y y =≤1x -,y ≥215(1)}44x +-.当点(,)p q 取遍D 时,求(,)p q ϕ的最小值 (记为min ϕ)和最大值(记为max ϕ)21.解:(1)2001(,)4A p p 是抛物线L 上的点,12y x '=,则切线的斜率012k p = 过点A 的抛物线L 的切线方程为AB :200011()42y p p x p -=-,即2001124y p x p =-∵(,)Q p q 在线段AB 上,∴2001124q p p p =-,∴22220001144()()24p q p p p p p p -=--=-≥0不妨设方程20x px q -+=的两根为1x =,2x =则12p p p x --=,22p p p x +-=① 当00p >时,00p p ≤≤,001222p p p x p -==-,022px =∵00122p p x -<≤,∴12x x ≤,∴122(,)max{,}p q x x x ϕ==02p =② 当00p <时,00p p ≤≤,012p x =,002222p p px p -==-∵00222p px ≤<-,∴12x x ≥,∴121(,)max{,}p q x x x ϕ==02p =综上所述,对线段AB 上的任一点(,)Q p q ,有(,)2p p q ϕ=(2)由(1)知抛物线L 在2001(,)4p p 处的切线方程为2001124y p x p =-,即200240p p x y -+=∵切线恒过点(,)M a b ,则200240p ap b -+=,∴1,2p a =① 当0a >时,(,)M a b X ∈⇔10a p <<⇔1p a =+2p a =⇔12p p >② 当0a <时,(,)M a b X ∈⇔10p a <<⇔1p a =-2p a =⇔12p p >综合①②可得(,)M a b X ∈⇔12p p >∵由(1)可知,若2111(,)4E p p ,点(,)M a b 在线段EF 上,有1(,)2p a b ϕ=∴(,)M a b X ∈⇒1(,)2p a b ϕ=③由(1)可知,方程20x ax b -+=的两根11,22p x =或12p a -,21,22p x =或22pa -若1(,)2p a b ϕ=,即112max{,}2px x =则1122p a p -≥、 2122p p ≥、 2122p a p -≥∴12p p >∴1(,)2p a b ϕ=⇒12||||p p >⇒(,)M a b X ∈ ④综合③④可得(,)M a b X ∈⇔1(,)2p a b ϕ=综上所述112(,)(,)2p M a b X p p a b ϕ∈⇔>⇔=;(3)由2115(1)44y x y x =-⎧⎪⎨=+-⎪⎩,求得两个交点(0,1),(2,1)- 则02p ≤≤,过点(,)G p q 作抛物线L 的切线,设切点为N2001(,)4x x ,切线与y 轴的交点为H由(2)知200240x px q -+=,解得0x p =,①若0x p =,则点(,)G p q 在线段NH 上由1y x ≤-,得1q p ≤-,∴022x p p p p =+≥=+-=,∴m min in )12(x ϕ==.由215(1)44y x ≥+-,得221511(1)14442q p p p ≥+-=+-∴2442p q p -≤-,∴0x p p =++t =,则2122p t =-+,02t ≤≤∴22011552(1)2222x t t t ≤-++=--+≤∴0max max 5)24(x ϕ==②若0x p =,则点(,)G p q 在线段NH 的延长线上方程20x px q -+=的两根为12p p x x --=,22p p x x +-=即01,22x x =或02xp -∵0x p ≤∴00012(,)max{,}max{,}222x x xp q x x p p ϕ==-=-p ==,同理可得51(,)4p q ϕ≤≤综上所述min 1ϕ=,max 54ϕ=。
高考最新-2018广东理数 精品
2018年普通高等学校招生全国统一考试 数学(广东理科卷)编辑:广东省连南民族高级中学 绿梦飘渺一.选择题:各5分,共40分。
1.已知函数f (x )=x11-的定义域为M ,g (x )=ln (1+x )的定义域为N ,则M ∩N =A.{x |x >-1} B.{x |x <1} C.{x |-1<x <1} D.φ[解]要确保f (x )有意义,需要1-x >0⇒x <1;要确保g (x )有意义,需要1+x >0⇒x >-1。
所以答案是C。
2.若复数(1+bi )(2+i )是纯虚数(i 是虚数单位,b 是实数),则b = A.2 B.21 C.-21D.-2 [解](1+bi )(2+i )=2-b +(2b +1)i ,因为是纯虚数,所以2-b =0,得b =2。
答案是A。
3.若函数f (x )=sin 2x -21(x ∈R ),则f (x )是: A.最小正周期为2π的奇函数 B.最小正周期为π的奇函数 C.最小正周期为2π的偶函数 D.最小正周期为π的偶函数 [解]f (x )=sin 2x -21=-21(1-2 sin 2x )=-21cos2x =-21cos (2x +2π)=-21cos2(x +π) 所以函数的最小正周期是π。
又f (-x )=sin 2(-x )-21=(-sinx )2-21=sin 2x -21=f (x ),所以函数是偶函数。
综上所述,得出答案是D。
4.客车从甲地以60km /h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km /h 的速度匀速行驶1小时到达丙地。
下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图象中,正确的是:[解]客车在中途停留的半小时里,经过的路程保持在60km 不变,所以排除了C;客车行驶的总路程是140km ,所以排除了A;客车从甲地到丙地所用的总时间是2.5h ,所以排除了D,从而得出答案是B。
2018年数学真题及解析_2018年全国统一高考数学试卷(理科)(全国新课标ⅲ)

2018年云南省高考数学试卷(理科)(全国新课标Ⅲ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5.00分)已知集合A={x|x﹣1≥0},B={0,1,2},则A∩B=()A.{0}B.{1}C.{1,2}D.{0,1,2}2.(5.00分)(1+i)(2﹣i)=()A.﹣3﹣i B.﹣3+i C.3﹣i D.3+i3.(5.00分)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()A. B. C. D.4.(5.00分)若sinα=,则cos2α=()A.B.C.﹣ D.﹣5.(5.00分)(x2+)5的展开式中x4的系数为()A.10 B.20 C.40 D.806.(5.00分)直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x﹣2)2+y2=2上,则△ABP面积的取值范围是()A.[2,6]B.[4,8]C.[,3]D.[2,3]7.(5.00分)函数y=﹣x4+x2+2的图象大致为()A.B.C.D.8.(5.00分)某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数,DX=2.4,P(x=4)<P(X=6),则p=()A.0.7 B.0.6 C.0.4 D.0.39.(5.00分)△ABC的内角A,B,C的对边分别为a,b,c.若△ABC的面积为,则C=()A.B.C.D.10.(5.00分)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且面积为9,则三棱锥D﹣ABC体积的最大值为()A.12B.18C.24D.5411.(5.00分)设F1,F2是双曲线C:﹣=1(a>0.b>0)的左,右焦点,O是坐标原点.过F2作C的一条渐近线的垂线,垂足为P,若|PF1|=|OP|,则C的离心率为()A.B.2 C.D.12.(5.00分)设a=log0.20.3,b=log20.3,则()A.a+b<ab<0 B.ab<a+b<0 C.a+b<0<ab D.ab<0<a+b二、填空题:本题共4小题,每小题5分,共20分。
最新-2018年普通高等学校招生全国统一考试数学理试题广东卷 精品002

2018年普通高等学校招生全国统一考试数学理试题(广东卷,解析版)本试卷共4页,21小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时.请先用2B 铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、错涂、多涂的.答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式V =13sh ,其中S 是锥体的底面积,h 是锥体的高.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={x|-2<x <1},B=A={x|0<x <2},则集合A ∩B=A.{x|-1<x <1}B.{x|-2<x <1}C.{x|-2<x <2}D.{x|0<x <1} 1. 答案:D【命题意图】本题考查了集合的运算,考查了学生的计算能力。
【解析】本题考查了集合的运算。
结合数轴易得}10|{<<=x x B A .2.若复数z 1=1+i,z 2=3-i,则z1`z1= A.4+2i B.2+i C.2+2i D.3+i 2.答案:A【命题意图】本题考查复数的乘法运算,考查了学生的计算能力。
【解析】本题考查复数的乘法运算,考查了学生的计算能力。
计算得212(1)(3)3342z z i i i i i i ∙=+∙-=-+-=+.3.若函数f(x)=3x+3x -与g(x)=33x x--的定义域均为R ,则 A .f(x)与g(x)均为偶函数 B .f(x)为奇函数,g(x)为偶函数 C .f(x)与g(x)均为奇函数 D .f(x)为偶函数.g(x)为奇函数3.答案:B4.已知数列{n a }为等比数列,n s 5是它的前n 项和,若2a *3a =2a .,且4a 与27a 的等差中项为54,则5s = A .35 B .33 C .3l D .29 4.答案:C5. “14m <”是“一元二次方程20x x m ++=有实数解”的 A.充分非必要条件 B.充分必要条件 C.必要非充分条件 D.非充分非必要条件 5.答案:A 【命题意图】本题是在知识的文汇处命题,考查了充要条件的相关知识及一元二次方程有解的条件【解析】本题考查充要条件的相关知识及一元二次方程有解的条件。
广东理科高考数学试题及答案

2018年普通高等学校招生全国统一考试(广东卷)A数学(理科)本试卷共4页,21题,满分150分。
考试用时120分钟。
ShShV?为柱体的高。
为柱体的底面积,,其中参考公式:柱体的体积公式1ShShV?为锥体的高。
为锥体的底面积,锥体的体积公式为,其中3一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
5?6i i= 设为虚数单位,则复数1.i6?5i6?5i?6?5i?6?5i..AD.C.B【答案】D CM1,2,3,4,5,6}U?{1,2,4}M?{=,2.设集合,则U U{1,3,5}{3,5,6}{2,4,6}.B..DA .C【答案】CBC(4,7)?(2,3)CABA?,,则3.若向量(?2,?4)(3,4)(6,10)(?6,?10)B.DCA...【答案】A4.下列函数中,在区间(0,+∞)上为增函数的是11x??x)y?(y2)?y?ln(x1?y??x B CA...D.x2【答案】Ay?2??z?3x?y y,x1x?y?的最大值为5.已知变量,则满足约束条件??1??yx?1 3 D.-12 B.11 C.A.B【答案】所示,它的体积为某几何体的三视图如图16..81π57πD45πC12πBA...C【答案】 1 / 8从个位数与十位数之和为奇数的两位数种任取一个,其个位数万恶哦0的概率是7.1124D.C B.A..9399D【答案】?????a b?0|a|?|b|?ba,的。
若平面向量,与满足α8.对任意两个非零的平面向量和β,定义????n?babbaa(0,}?n{)|?Z夹角都在集合,且中,则= 和42513B.1C.D. A.222|bb?a|2|a?b|a?????b1?cosa?cos??ab?cos??cos,【解读】:因为|a?a|a2bb?|b|nabba}n?{|Z中和且都在集合2|a|1|1|b|b|2????b?2cos?2acos?ba??cos,,所以所以,?||b2cos|||a|2a2ab?12?ab?,故有所以2【答案】B二、填空题:本大题共7小题,考生答6小题,每小题5分,满分30分。
2018年高考广东省理科数学真题答案

2018 年一般高等学校招生全国一致考试理科数学答案123456789101112C B A BD A B D C A B A13.614.6315.1616.33217. ( 12分)解:( 1)在△ABD中,由正弦定理得BD AB.sin A sin ADB由题设知,52,所以 sin ADB 2 .sin 45sin ADB5由题设知,ADB90,所以 cos ADB1223 .255(2)由题设及(1)知,cos BDC sin ADB 2 .5在△ BCD 中,由余弦定理得BC 2BD 2DC 2 2 BD DC cos BDC2582522 2525.所以 BC 5.18.(12 分)解:( 1)由已知可得,BF⊥PF,BF⊥EF,所以 BF⊥平面 PEF.又 BF 平面ABFD,所以平面PEF⊥平面ABFD.(2)作PH⊥EF,垂足为H.由( 1)得,PH⊥平面ABFD.以 H 为坐标原点,HF的方向为 y 轴正方向,| BF |为单位长,成立如下图的空间直角坐标系 H- xyz.由( 1)可得,DE⊥PE.又DP=2,DE=1,所以PE= 3 .又PF=1,EF=2,故 PE⊥PF.可得 PH3,EH 3 . 22则 H (0,0,0),P(0,0,3), D( 1,3,0), DP(1,3,3), HP(0,0,3) 为平面ABFD的22222法向量 .HP DP 33 .设 DP 与平面 ABFD 所成角为,则 sin||4|HP| |DP|34所以 DP 与平面 ABFD 所成角的正弦值为 3 .419. ( 12 分)解:( 1)由已知得F (1,0) ,l的方程为x=1.由已知可得,点 A 的坐标为(1,2)或 (1,2) . 22所以 AM 的方程为y 2 x2或 y 2 x 2 .22(2)当l与x轴重合时,OMA OMB0 .当 l 与 x 轴垂直时, OM 为 AB 的垂直均分线,所以OMA OMB .当 l 与 x 轴不重合也不垂直时,设l 的方程为y k(x 1)(k0),A(x1, y1 ), B( x2 , y2 ) ,则 x12, x2 2 ,直线MA,MB的斜率之和为k MA k MB y1y 2.x12x2 2由 y1kx1k, y2kx2k得kMA kMB2kx1 x23k( x1x2)4k .( x12)( x22)将 y k( x1) 代入x2y21得2(2k21)x24k 2 x2k 220 .所以, x1x24k 2, x1x22k 22. 2k22k211则 2kx1 x2 3k( x1x2 )4k34k12k 38k 34k0. 4k2k21进而 k MA kMB0,故MA,MB的倾斜角互补,所以OMA OMB .综上,OMA OMB .20.(12 分)解:( 1) 20 件产品中恰有 2 件不合格品的概率为 f ( p) C220 p2 (1p)18.所以f ( p) C220 [2 p(1 p)1818 p2 (1 p)17 ] 2C220 p(1p)17 (1 10 p) .令 f ( p) 0 ,得 p 0.1.当 p (0,0.1) 时, f ( p) 0 ;当 p (0.1,1) 时, f ( p)0 .所以 f ( p) 的最大值点为p00.1 .(2)由( 1)知,p 0.1.(i)令Y表示余下的 180 件产品中的不合格品件数,依题意知Y : B(180,0.1) , X 20225Y ,即 X 40 25Y .所以 EX E(40 25Y )4025EY 490 .( ii)假如对余下的产品作查验,则这一箱产品所需要的查验费为400元 .因为 EX 400 ,故应当对余下的产品作查验.21.(12 分)解:( 1)f (x)的定义域为(0,) , f ( x)11a x2ax1. x2x x2(i)若a 2 ,则 f ()x 0,当且仅当 a 2 ,x 1时 f(x)0 ,所以 f ( x) 在 (0,)单一递减 .(ii)若a 2 ,令 f (x)0 得,x a a24或 x a a2 4 .22当 x(0, aa24) U (aa2 4 ,) 时,f( x) 0;22当x ( aa2 4 , a a 2 4 )时, f ( x).所以f ( x)在22(0, aa24),(aa24,) 单一递减,在 (aa24,aa24)单一递加.2222(2)由( 1)知,f ( x)存在两个极值点当且仅当a 2 .因为 f ( x) 的两个极值点x1, x2知足 x2ax 1 0 ,所以x1x2 1 ,不如设 x1x2,则 x21.因为f (x1) f (x2 )1 1 a ln x1ln x2 2 aln x1ln x2x1x2x1x2x1x2x1x2所以f ( x1)f ( x2 )a2等价于1x2 2ln x2 0 .x1x2x2设函数 g(x)1x2ln x ,由(1)知, g (x) 在 (0,x 2a2ln x2,1x2x2) 单一递减,又 g(1)0 ,进而当 x(1,) 时, g( x)0 .所以1x2 2ln x20,即 f ( x1 ) f ( x2 )a2. x2x1x222 . [选修 4-4 :坐标系与参数方程]( 10分)【分析】( 1)由xsoc,ysin得C2 的直角坐标方程为( x1)2y2 4 .(2)由( 1)知C2是圆心为A(1,0),半径为 2 的圆.由题设知,C1 是过点B(0, 2)且对于y轴对称的两条射线.记y轴右侧的射线为l1 ,y轴左侧的射线为l2.因为B在圆C2的外面,故C1与C2有且仅有三个公共点等价于l1 与C2 只有一个公共点且l2 与C2有两个公共点,或l2 与C2 只有一个公共点且l1与C2有两个公共点.当l1 与C2 只有一个公共点时,A到l1 所在直线的距离为2 ,所以| k 2 |4或k0 .k 22,故 k3 1经查验,当k4时,l1与C2只有一个0 时,l1与C2没有公共点;当k3公共点,l2 与C2 有两个公共点.当l2 与C2 只有一个公共点时,A到l2 所在直线的距离为 2 ,所以| k 2 |,故k4.k 220 或 k13经查验,当 k0 时, l 1 与C2没有公共点;当k4时, l 2 与C2没有公共3点.综上,所求C1的方程为y4| x | 2 .323 . [选修 4-5 :不等式选讲 ]( 10 分)2, x 1, 【分析】( 1)当 a 1 时,f (x)| x1| | x 1| ,即 f ( x)2x, 1 x 1,2, x1.故不等式f (x)1的解集为 { x | x1} .2(2)当 x (0,1) 时 | x 1| | ax 1|x 成立等价于当 x (0,1) 时 | ax 1| 1成立.若 a 0 ,则当 x(0,1) 时 | ax 1| 1 ;若 a 0 , | ax 1| 1 的解集为 0x 2 ,所以 2 1,故 0 a 2 . a a综上, a的取值范围为(0, 2].。
2018届广州市高三年级调研测试(理科数学)答案

4.只给整数分数.选择题不给中间分.
•选择题题号1源自2345
6
7
8
9
10
11
12
答案
A
C
B
B
A
A
D
D
B
A
C
C
.填空题
13.10
14.4
15.4
16.11
三、解答题
17.(1)解法1:由已知,得acosB bcosA 2c cos A.
由正弦定理,得si n AcosB si n BcosA 2si n Ceos A ,1分
即sin (A B) 2si nCcosA.
因为sin (A B) sin( C) si nC,
所以si nC 2si nCcosA.
因为si nC 0,所以cos A丄
2
因为0 A,所以A -.
3
2 2 2 2 2 2
解法2:由已知根据余弦定理,得aa c——2c bb c―—.
2ac2bc
即b2c2a2bc
因为BD P EF,所以EF平面PAC.5分
因为FE平面PCE,所以平面PAC平面PCE.6分
(2)解法1:因为直线PC与平面ABCD所成角为45°,
所以PCA45,所以AC PA2.7分
所以AC AB,故△ABC为等边三角形.
2018
理科数学试题答案及评分参考
评分说明:
1•本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内 容比照评分参考制订相应的评分细则.
2•对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度, 可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答 有较严重的错误,就不再给分.
2018年高考理科数学选考内容100题(含答案解析)

2018年高考理科数学选考内容精编100题(含答案解析)1.极坐标方程cos ρθ=和参数方程123x ty t =--⎧⎨=+⎩(t 为参数)所表示的图形分别是( ).A .直线、直线B .圆、圆C .直线、圆D .圆、直线2.极坐标方程2cos ρθ=表示的圆的半径是( ). A .12B .14C .2D .13.在极坐标系中,点(1,4π)与点(1,43π)的距离为( ) A .1 B .2 C .3 D . 5 4.在极坐标系中,圆ρ=sinθ的圆心的极坐标是( ) A .(1,2π)B .(1,0) C .(21,2π) D .(21,0)5.在极坐标系中,点π2,6⎛⎫⎪⎝⎭到直线(cos 3sin )3ρθθ+=的距离为__________.6.极坐标系下,方程πcos 24ρθ⎛⎫-= ⎪⎝⎭与方程2ρ=表示的曲线的公共点个数为__________.7.已知x ,y ∈R ,满足x 2+2xy+4y 2=6,则z=x 2+4y 2的取值范围为 . 8.已知C 1在直角坐标系下的参数方程为,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,有曲线C 2:ρ=2cosθ﹣4sinθ. (Ⅰ)将C 1的方程化为普通方程,并求出C 2的直角坐标方程; (Ⅱ)求曲线C 1和C 2两交点之间的距离. 9.已知函数3)(--=x m x f ,不等式2)(>x f 的解集为(2,4). (1)求实数m 的值;(2)若关于x 的不等式)(x f a x ≥-恒成立,求实数a 的取值范围. 10.在直角坐标系xoy 中,设倾斜角为α的直线l 的参数方程为3cos sin x t y t αα=+⎧⎨=⎩(t 为参数)与曲线1:cos tan x C y θθ⎧=⎪⎨⎪=⎩(θ为参数)相交于不同的两点A 、B .(I )若3πα=,求线段AB 的中点的直角坐标;(II )若直线l 的斜率为2,且过已知点(3,0)P ,求||||PA PB ⋅的值. 11.已知函数()|1|(1)f x ax a x =---.(Ⅰ)当2a =时,满足不等式()0f x >的x 的取值范围为__________.(Ⅱ)若函数()f x 的图象与x 轴没有交点,则实数a 的取值范围为__________. 12.已知圆O 1和圆O 2的极坐标方程分别为ρ=2,ρ2﹣2ρcos(θ﹣)=2.(1)把圆O 1和圆O 2的极坐标方程化为直角坐标方程;(2)设两圆交点分别为A 、B ,求直线AB 的参数方程,并利用直线AB 的参数方程求两圆的公共弦长|AB|. 13.设函数f (x )=|x ﹣a|.(1)当a=2时,解不等式f (x )≥7﹣|x ﹣1|; (2)若f (x )≤1的解集为[0,2], +=a (m >0,n >0),求证:m+4n ≥2+3.14.在平面直角坐标系中,椭圆C 的参数方程为(θ为参数),已知以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,射线l 的极坐标方程为θ=α(ρ≥0)(注:本题限定:ρ≥0,θ∈[0,2π)) (1)把椭圆C 的参数方程化为极坐标方程;(2)设射线l 与椭圆C 相交于点A ,然后再把射线l 逆时针90°,得到射线OB 与椭圆C 相交于点B ,试确定是否为定值,若为定值求出此定值,若不为定值请说明理由. 15.设函数f (x )=|x+2|﹣|x ﹣1| (I )画出函数y=f (x )的图象;(II )若关于x 的不等式f (x )+4≥|1﹣2m|有解,求实数m 的取值范围. 16.已知直线的极坐标方程为,圆M 的参数方程为(其中θ为参数).(Ⅰ)将直线的极坐标方程化为直角坐标方程; (Ⅱ)求圆M 上的点到直线的距离的最小值. 17.已知曲线C 1的参数方程为⎪⎩⎪⎨⎧θ=θ=sin 3y cos 2x (θ为参数),以原点O 为极点,以x 轴的非负半轴为极轴建立极坐标系,曲线C 2的极坐标方程为msinθ﹣cosθ=ρ1. (1)求C 1,C 2的直角坐标方程;(2)若曲线C2与C1交于M,N两点,与x轴交于P点,若MP=2PN,求m的值.18.已知函数f(x)=m﹣|x﹣1|﹣2|x+1|.(Ⅰ)当m=5时,求不等式f(x)>2的解集;(Ⅱ)若二次函数y=x2+2x+3与函数y=f(x)的图象恒有公共点,求实数m的取值范围.19.在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2sin(θ﹣),直线l的参数方程为,直线l和圆C交于A,B两点,P是圆C上不同于A,B的任意一点(1)求圆C的直角坐标方程;(2)求△PAB面积的最大值.20.已知函数f(x)=的定义域为R.(Ⅰ)求实数m的取值范围;(Ⅱ)若m=4,解不等式f(x)>2.21.在平面直角坐标系中,以O为极点,x轴为正半轴建立极坐标系,取相同的长度单位,若曲线C1的极坐标方程为ρsin(θ﹣)=3,曲线C2的参数方程为(θ为参数).(1)将曲线C1的极坐标方程化为直角方程,C2的参数方程化为普通方程;(2)设P是曲线C1上任一点,Q是曲线C2上任一点,求|PQ|的最小值.22.已知函数f(x)=|x+1|+|x﹣2|,f(x)﹣m≥0恒成立.(1)求实数m的取值范围;(2)m的最大值为n,解不等式|x﹣3|﹣2x≤n+1.23.已知曲线C1的参数方程为(t为参数),以坐标项点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣2sinθ.(1)把C1的参数方程化为极坐标系方程;(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).24.如图所示,AC 为⊙O 的直径,D 为的中点,E 为BC 的中点.(Ⅰ)求证:DE ∥AB ; (Ⅱ)求证:AC•BC=2AD•CD.25.已知关于x 的不等式(其中a >0).(1)当a=3时,求不等式的解集; (2)若不等式有解,求实数a 的取值范围. 26.在直角坐标系中,直线l 的参数方程为(t 为参数),在极坐标系(与直角坐标系xoy 取相同的单位长度,且以原点为极点,x 轴的正半轴为极轴)中,圆C 的极坐标方程为ρ=4cosθ.(1)若直l 线与圆C 相切,求实数a 的值;(2)若点M 的直角坐标为(1,1),求过点M 且与直线l 垂直的直线m 的极坐标方程. 27.在矩阵A 的变换下,坐标平面上的点的横坐标伸长到原来的3倍,纵坐标不变. (1)求矩阵A 及A ﹣1;(2)求圆x 2+y 2=4在矩阵A ﹣1的变换下得到的曲线方程. 28.[选修4-2:矩阵与变换] 已知变换T 将平面上的点(1,21),(0,1)分别变换为点 (49,﹣2),(﹣23,4).设变换T 对应的矩阵为M . (1)求矩阵M ;(2)求矩阵M 的特征值. 29.[选修4-4:坐标系与参数方程]设极坐标系的极点为直角坐标系的原点,极轴为x 轴的正半轴.已知曲线C 的极坐标方程为ρ=8sinθ(1)求曲线C 的直角坐标方程;(2)设直线⎩⎨⎧+==2t y tx (t 为参数)与曲线C 交于A ,B 两点,求AB 的长.30.金鱼草的花色由一对等位基因控制,科研小组进行杂交实验的结果如下表所示,下列相关叙述错误的是A. 红花植株与红花植株杂交,后代均为红花植株B. 白花植株与白花植株杂交,后代均为白花植株C. 红花植株与白花植株杂交,后代均为粉红花植株D. 红花植株为显性纯合子,粉红花植株为杂合子31.已知某精原细胞分裂过程中染色体数目与DNA 分子数目相同,此时该细胞中不可能 A. 发生基因重组 B. 存在等位基因C. 含有两个Y 染色体D. 与体细胞含有相同的染色体数32.下列各句中,没有语病的一项是(3分)( )A .别里科夫的悲剧,不仅是19世纪末沙皇统治下的众多的保守的知识分子的悲剧,更是他个人的悲剧。
2018年高三数学(理)各地优质金卷分项解析专题13 选讲部分Word版含答案

【2018高三数学各地优质一模试题分项精品】一、解答题1.【2018为极点,(1的极坐标方程和的平面直角坐标系方程;(2的交点为面积.【答案】(1)见解析2.【2018(1(2.【答案】【解析】试题分析:(1)对分三种情况讨论,取掉绝对值符号,分别求解不等式组,然后求并集即可求得(2等式求解即可.试题解析:(1,得,无解;,得,即时,,综上,的解集为3. 【2018山西省高三一模】在平面直角坐标系中,曲线的参数方程为:(为参数,),将曲线经过伸缩变换:得到曲线.(1)以原点为极点,轴的正半轴为极轴建立坐标系,求的极坐标方程;(2)若直线(为参数)与相交于两点,且,求的值.【答案】(1) (2) 或【解析】【试题分析】(1)先将的参数方程消参变为直销坐标方程, 把代入上述方程可得到的方程,代入极坐标和直角坐标转化公式可求得的极坐标方程.(2)写出直线的极坐标方程,分别代入的极坐标方程,求得对应,结合可求得的值.【试题解析】(1)的普通方程为,把代入上述方程得,,∴的方程为,令,所以的极坐标方程为;4. 【2018山西省高三一模】已知函数.(1)若的最小值不小于3,求的最大值;(2)若的最小值为3,求的值.【答案】(1) (2) 或-4【解析】【试题分析】(1)由,求得的取值范围和最大值.(2)对分成和三类,去绝对值,将变为分段函数,利用最小值为求得的值.【试题解析】(1)因为,所以,解得,即;(2),当时,,所以不符合题意,当时,,即,所以,解得,当时,同法可知,解得,综上,或-4.5. 【2018安徽芜湖高三一模】已知函数.(1)解不等式;(2)已知,若恒成立,求实数的取值范围.【答案】(1);(2).试题解析:(1)不等式可化为:①当时,①式为,解得;当时,①式为,解得;当时,①式为,无解.综上所述,不等式的解集为.(2)解:令∴,要使不等式恒成立,只需,即∴实数取值范围是.点睛:含绝对值不等式的解法有两个基本方法,一是运用零点分区间讨论,二是利用绝对值的几何意义求解.法一是运用分类讨论思想,法二是运用数形结合思想,将绝对值不等式与函数以及不等式恒成立交汇、渗透,解题时强化函数、数形结合与转化化归思想方法的灵活应用,这是命题的新动向.6. 【2018,其参数方程为为极点,轴非负半轴为极轴建立极坐标系,曲线的极坐标方程为(1(2)求已知曲线交于两点,且【答案】(1(2【解析】试题分析:(1)先根据加减消元法得曲线将曲(2)将直线参数方程代入曲线的直角坐标方程,由7. 【2018(1(2【答案】(1(2)【解析】试题分析:(1)根据绝对值定义将不等式转化为三个不等式组,分别求解,最后求并集,(2)根据试题解析:解:(1,解得时,,解得综合①②③可知,原不等式的解集为(2上恒成立,当,从而可得,因此8. 【2018山东济南高三一模】在直角坐标系中,过点的直线的参数方程为(为参数).以原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)求直线的普通方程和曲线的直角坐标方程;(2)若直线与曲线相交于,两点,求的值.【答案】(1) (2)试题解析:(1)由已知得:,消去得,∴化为一般方程为:,即::.曲线:得,,即,整理得,即::.9. 【2018福建南平高三一模】在直角坐标系中,圆的参数方程为(为参数).以坐标原点为极点,轴的正半轴为极轴建立极坐标系,直线的极坐标方程为.(1)求圆的极坐标方程和直线的直角坐标方程;(2)设|与的交点为,求的面积.【答案】(1)的极坐标方程为;(2)的面积为.【解析】试题分析:(1)圆消去参数得普通方程,由得圆的极坐标方程,直线为过原点的直线,且斜率为1,从而得方程;(2)将代入圆的极坐标方程得,,,从而得的面积.试题解析:(Ⅰ)直线的直角坐标方程为圆的普通方程为因为,所以的极坐标方程为(Ⅱ)将代入,得,解得,故,即.由于圆的半径为,所以的面积为10. 【2018广东江门高三一模】.的参数方程化为普通方程;与曲线交点的极坐标.【答案】 (2)【解析】【试题分析】(I)利用加减消元法消去参数.(II)由(I)求得曲线坐标方程,,可求得交点的极坐标.,对应点的极坐标为同理可得对应点的极坐标为,所求交点的极坐标为11.【2018广东江门高三一模】【答案】【解析】【试题分析】(I)利用单个绝对值不等式的解法求解出不等式的解集.(2)先求得,.,,求出对应的值域,.12. 【2018贵州黔东南高三一模】设.(Ⅰ)求不等式的解集;(Ⅱ),,求实数的取值范围.【答案】(1)解集为;(2)实数的取值范围是.【解析】试题分析:(Ⅰ)去掉绝对值,得到分段函数,由,即可取得不等式的解集;(Ⅱ) 由(Ⅰ)及一次函数的性质,求得区间上,的值,进而求得实数的取值范围.试题解析:(Ⅰ),由解得,故不等式的解集为.(Ⅱ) 由(Ⅰ)及一次函数的性质知:在区间为减函数,在区间上为增函数,而,故在区间上,,.由.所以且,于是且,故实数的取值范围是.13. 【2018河北唐山高三一模】在直角坐标系中,圆:,圆:.以坐标原点为极点,轴的正半轴为极轴建立极坐标系.(1)求,的极坐标方程;(2)设曲线:(为参数且),与圆,分别交于,,求的最大值.【答案】(1)ρ=2cosθ;ρ=6cosθ(2) 当α=±时,S△ABC2取得最大值314. 【2018河北唐山高三一模】设函数的最大值为.(1)求的值;(2)若正实数,满足,求的最小值.【答案】(1) m=1 (2)【解析】试题分析:(1)零点分区间去掉绝对值,得到分段函数的表达式,根据图像即可得到函数最值;(2)将要求的式子两边乘以(b+1)+(a+1),再利用均值不等式求解即可.解析:(Ⅰ)f(x)=|x+1|-|x|=由f(x)的单调性可知,当x≥1时,f(x)有最大值1.所以m=1.15. 【2018江西南昌高三一模】在平面直角坐标系中,曲线的参数方程为(为参数),以坐标原点为极点,轴非负半轴为极轴建立极坐标系.(1)求的极坐标方程;(2)若直线的极坐标方程分别为,,设直线与曲线的交点为,,,求的面积.【答案】(1);(2).【解析】试题分析:(1)由题意可得C的普通方程,极坐标方程为.(2)由题意可得,,△OMN为直角三角形,则.试题解析:(1)由参数方程,得普通方程,所以极坐标方程,即.(2)直线与曲线的交点为,得,又直线与曲线的交点为,得,且,所以.16. 【2018江西南昌高三一模】已知.(1)当时,求不等式的解集;(2)对于任意实数,不等式成立,求实数的取值范围.【答案】(1);(2).试题解析:(1)当时,,得;得;得,所以的解集为.(2)对于任意实数,不等式成立,即恒成立,又因为,要使原不等式恒成立,则只需,当时,无解;当时,,解得;当时,,解得.所以实数的取值范围是.17. 【2018辽宁抚顺高三3,以平面直角坐标系的极坐标方程为上的动点的距离的最大值;两点,且与【答案】(1(2【解析】【试题分析】(I)方程展开后化为直角坐标方程,值.(II)求出直线的参数方程,代入椭圆方程,.……8分18. 【2018辽宁抚顺高三3月模拟】已知函数【答案】(1)M=4(2)见解析【解析】【试题分析】(I),,对原不等式左边,转化为基19. 【2018四川德阳高三二诊】在平面直角坐标系中,直线:(为参数),以坐标原点为极点,轴正半轴为极轴,建立极坐标系,曲线:.(1)求直线的极坐标方程及曲线的直角坐标方程;(2)记射线与直线和曲线的交点分别为点和点(异于点),求的最大值.【答案】(1). .(2).【解析】试题分析:(1)根据极坐标方程、参数方程与普通方程的对应关系即可得出答案;(2)由(1),,所以,即可得到的最大值.试题解析:(1)由题意得直线的普通方程为:,所以其极坐标方程为:.由得:,所以,所以曲线的直角坐标方程为:.(2)由题意,,所以,由于,所以当时,取得最大值:.20. 【2018四川德阳高三二诊】已知函数.(1)解关于的不等式;(2)若关于的不等式的解集非空,求实数的取值范围.【答案】(1).(2).【解析】试题分析:(1)由题意或,由此可解不等式;(2)由于关于的不等式的解集非空,函数的最小值为-1,由此解得的范围.【点睛】本题主要考查绝对值的意义,绝对值不等式的解法,21. 【2018辽宁瓦房店高三一模】选修4-4:坐标系与参数方程在直角坐标系中,圆的参数方程为(为参数),圆的参数方程(为参数),以为极点,轴的正半轴为极轴建立极坐标系.(Ⅰ)求和的极坐标方程;(Ⅱ)和交于两点,求点的一个极坐标.【答案】(1) (2)【解析】试题分析:(1)把圆,的参数方程转化为普通方程,进而转化为极坐标方程;(2)设,则有,解得,,所以点的极坐标为试题解析:(Ⅰ)圆的普通方程为:,则的极坐标方程为:圆的普通方程为:,则的极坐标方程为:(Ⅱ)设,则有,解得,,所以点的极坐标为。
2018年广东高考理科数学试题和答案解析

2018年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、设i iiz 211++-=,则|z|= A 、0B 、21 C 、1D 、22、已知集合{}022>--=x x x A ,则A C R = A 、{}21<<-x x C 、{}{}21>⋃-<x x x xB 、{}21≤≤-x xD 、{}{}21≥⋃-≤x x x x3、某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是:A 、新农村建设后,种植收入减少。
B 、新农村建设后,其他收入增加了一倍以上。
C 、新农村建设后,养殖收入增加了一倍。
D 、新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半。
4、记n S 为等差数列{}n a 的前n 项和,若4233S S S +=,21=a ,则5a = A 、-12B 、-10C 、10D 、125、设函数ax x a x x f +-+=231)()(,若)(x f 为奇函数,则曲线)(x f y =在点(0,0)处的切线方程为: A 、x y 2-=B 、x y -=C 、x y 2=D 、x y =6、在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB =A 、4143- C 、AC AB 4143+B 、4341- D 、AC AB 4341+7、某圆柱的高为2,底面周长为16,其三视图如右图,圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为 A 、172 B 、52 C 、3 D 、28.设抛物线x y C 42=:的焦点为F ,过点),(02-且斜率为32的直线与C 交于M ,N 两点,则FN FM ⋅= A.5B.6C.7D.89.已知函数⎩⎨⎧>≤=,,,,)(0ln 0x x x e x f x a x x f x g ++=)()(,若)(x g 存在2个零点,则a 的取值范围是A. [)01,-B. [)∞+,0C. [)∞+-,1D. [)∞+,1 10.下图来自古希腊数学家希波克拉底所研究的几何图形。
高三数学-【数学】广东省广州市番禺高级中学2018届高
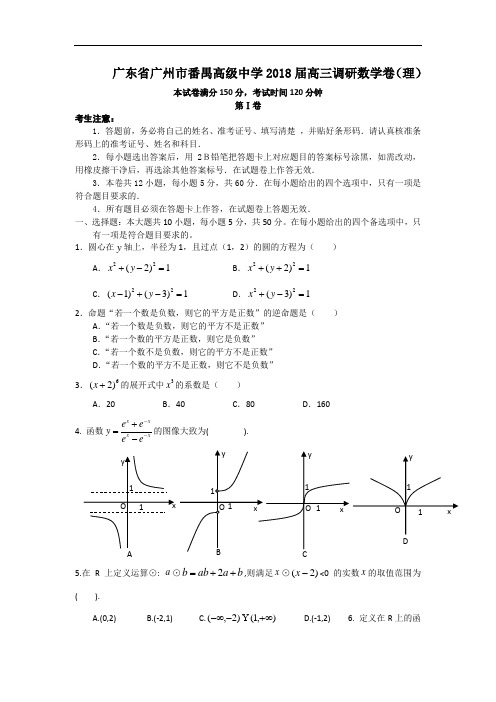
广东省广州市番禺高级中学2018届高三调研数学卷(理)本试卷满分150分,考试时间120分钟第Ⅰ卷考生注意: 1.答题前,务必将自己的姓名、准考证号、填写清楚 ,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效.3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.4.所有题目必须在答题卡上作答,在试题卷上答题无效.一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个备选项中,只有一项是符合题目要求的。
1.圆心在y 轴上,半径为1,且过点(1,2)的圆的方程为( )A .22(2)1x y +-=B .22(2)1x y ++=C .22(1)(3)1x y -+-=D .22(3)1x y +-=2.命题“若一个数是负数,则它的平方是正数”的逆命题是( )A .“若一个数是负数,则它的平方不是正数”B .“若一个数的平方是正数,则它是负数”C .“若一个数不是负数,则它的平方不是正数”D .“若一个数的平方不是正数,则它不是负数” 3.6(2)x +的展开式中3x 的系数是( )A .20B .40C .80D .1604. 函数x xx xe e y e e --+=-的图像大致为( ).5.在R 上定义运算⊙: a ⊙b a ab b ++=2,则满足x ⊙)2(-x <0的实数x 的取值范围为( ).A.(0,2)B.(-2,1)C.),1()2,(+∞--∞D.(-1,2) 6. 定义在R 上的函1xy 1OAxyO 11BxyO 1 1 Cx y 1 1 DO数f(x )满足f(x)= ⎩⎨⎧>---≤-0),2()1(0),4(log 2x x f x f x x ,则f (3)的值为( )A.-1B. -2C.1D. 27.一个棱锥的三视图如图,则该棱锥的全面积(单位:c 2m )为(A )48+122 (B )48+242 (C )36+122 (D )36+2428已知O ,N ,P 在ABC ∆所在平面内,且,0OA OB OC NA NB NC ==++=,且PA PB PB PC PC PA∙=∙=∙,则点O ,N ,P 依次是ABC ∆的 (A )重心 外心 垂心 (B )重心 外心 内心(C )外心 重心 垂心 (D )外心 重心 内心 9.若函数()y f x =的导函数...在区间[,]a b 上是增函数, 则函数()y f x =在区间[,]a b 上的图象可能是A .B .C .D .10.设函数()y f x =在(,)-∞+∞内有定义,对于给定的正数K ,定义函数(),(),(),().K f x f x K f x K f x K ≤⎧=⎨>⎩ 取函数()2xf x -=。
高三数学-2018学年高三年级数学科第三次段考试题答案

番禺中学2018学年高三年级数学科第三次段考试题答案第I 卷(选择题,共50分)一、选择题:本题共有10个小题,每小题5分,共50分. 在每小题给出的四个选项中,1.双曲线19422=-y x 的渐近线方程是( A )A .x y 23±=B .x y 32±=C .x y 49±=D .x y 94±=2.已知函数()fx 的定义域是[0,2],则函数)21()21()(--+=x f x f x g 的定义域是 (D )A .[0,2]B .]23,21[-C .]25,21[D .]23,21[3.设)4tan(,41)4tan(,52)tan(παπββα+=-=+则的值是 ( B )A .61B . 223C .1813D .22134.已知向量a 和b 不共线,且|a |=3,|b |=4,又向量a +k b 与a -k b 互相垂直,则实数k 的值为 ( C )A .43-B .43C .43±D .34±5.已知集合=≤=<--=P M a x x P x x x M 若},|{},02|{2∅,则实数a 的取值范围是 ( D ) A .}1|{-<a a B .}2|{≥a a C .}21|{<<-a a D .}1|{-≤a a 6.下面四个命题中正确是( B )A “直线a ∥直线b ”的充要条件是“a 平行于b 所在的平面”;B “直线l ⊥平面α内所有直线”的充要条件是“l ⊥平面α”;C “直线a 、b 为异面直线”的充分不必要条件是“直线a 、b 相交”;D “平面α∥平面β”的充要条件是“α内存在不共线三点到β的距离相等”; 7.等于则且满足数列n nn n n x n x x x x x x ),2(211,32,1}{1121≥=+==+- (A) 2n 2D. )32( C. )32( B. 1n 2.A 1++-n n 8.M (),00y x 为圆)0(222>=+a a y x 内异于圆心的一点,则直线200a y y x x =+与该圆的位置关系为( C ) A .相切 B .相交 C .相离 D .相切或相交9.已知p :关于x 的方程x 2-ax +4=0有实根,q :二次函数y =2x 2+ax +4在[3,+∞)上是增函数,若“p 或q ”是真命题,而“p 且q 是假命题”,则a 的取值范围是 (C) A .(-12,-4]∪[4,+∞) B .[-12,-4]∪[4,+∞) C .(-∞,-12)∪(-4,4) D .[-12,+∞)10.设),(y x P 是曲线192522=+y x 上的点C ,F 1(-4,0),F 2(4,0),则( C )A .10||||21<+P F P FB .10||||21>+P F P FC .10||||21≤+P F P FD .10||||21≥+P F P F第II 卷(非选择题,共100分)二.填空题(本大题共有4个小题,每小题5分,共20分,请把答案填在答卷的横线上) 11.若等差数列{}n a 的公差0d ≠,且137,,a a a 成等比数列,则1324a a a a ++= 34 12.拟定从甲地到乙地通话m 分钟的电话费由[]() 1.06(0.51)f m m =⋅⋅+(元)决定,其中[]0,m m >是大于或等于m 的最小整数(如[][][]33,3.84,3.14===),则从甲地到乙地通话时间为5.5分钟的电话费为 4.24元13.在正方体ABCD —A 1B 1C 1D 1中,E 是AD 的中点,则异面直线 C 1E 与BC 所成角的余弦值是13 14. 圆x 2+y 2-4x +2y +c=0与y 轴交于A 、B 两点,圆心为P ,若∠APB =90°,则c 的值是- 3 三、解答题:(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤) 15.(本题满分13分)已知函数a x f x +=2)((a 为常数). (1)求反函数)(1x f -与它的定义域; (2)如果)()2,(),1,(1x fy a x Q a x P -=-+是上不同两点,求PQ 中点R 的坐标.解:(1)由)(log 222a y x a y a y x x-=-=+=)(log )(21a x x f -=∴-……5分 定义域为}|{a x x >…………………7分 (2)由已知得1=)2(log 2)(log 22a x a a x -=-+且即{{{1242272)2(log 1log 22-==∴=-==-=a x a x x a x x 即分…10分 ∴P (1,1)、Q (3,2).则PQ 中点Q 坐标是)23,2(………………13分16.(本小题满分13分)在一次人才招聘会上,有A ,B 两家公司分别开出他们的工资标准:A 公司允诺第一年月工资为1500元,以后每年月工资比上一年月工资增加230元:B 公司允诺第一年月工资为2000元,以后每年月工资在上一年的月工资基础上递增5%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018届高考数学解答题编拟(理科)(番禺区大岗中学 李奎光)题目 1. 已知函数22s (in c o s s 1)2c o f x x x x ωωω++=(,0x R ω∈>)的最小值正周期是2π.(Ⅰ)求ω的值;(Ⅱ)求函数()f x 的最大值,并且求使()f x 取得最大值的x 的集合. 解:(Ⅰ)()242sin 224sin 2cos 4cos 2sin 222cos 2sin 12sin 22cos 12+⎪⎭⎫ ⎝⎛+=+⎪⎭⎫ ⎝⎛+=++=+++⋅=πωπωπωωωωωx x x x x x xx f 由题设,函数()x f 的最小正周期是2π,可得222πωπ=,所以2=ω.(Ⅱ)由(Ⅰ)知,()244sin 2+⎪⎭⎫ ⎝⎛+=πx x f .当πππk x 2244+=+,即()Z kk x ∈+=216ππ时,⎪⎭⎫ ⎝⎛+44sin πx 取得最大值1,所以函数()x f 的最大值是22+,此时x 的集合为⎭⎬⎫⎩⎨⎧∈+=Z k k x x ,216|ππ 命题意图:本小题主要考查特殊角三角函数值、两角和的正弦、二倍角的正弦与余弦、函数sin ()y A x ωϕ=+的性质等基础知识,考查基本运算能力.题目2. 在直角坐标系x O y 中,点P到两点(0-,,(0的距离之和等于4,设点P 的轨迹为C ,直线1y kx =+与C 交于A ,B 两点. (Ⅰ)写出C 的方程;(Ⅱ)若OA ⊥OB ,求k 的值;解:(Ⅰ)设P (x ,y ),由椭圆定义可知,点P 的轨迹C是以(0(0-,,为焦点,长半轴为2的椭圆.它的短半轴1b ==,故曲线C 的方程为2214yx +=.(Ⅱ)设1122()()A x y B x y ,,,,其坐标满足2214 1.yx y k x ⎧+=⎪⎨⎪=+⎩, 消去y 并整理得22(4)230k x k x ++-=, 故1212222344k x x x x kk+=-=-++,.若O A O B⊥,即12120x x y y +=.而2121212()1y y k x x k x x =+++,于是22121222233210444k k x x y y kkk+=---+=+++,化简得2410k -+=,所以12k =±.命题意图:本小题主要考查平面向量,椭圆的定义、标准方程及直线与椭圆位置关系等基础知识,考查综合运用解析几何知识解决问题的能力.题目3. 在数列{}n a 中,11a =,22a =,且11(1)n n n a q a q a +-=+-(2,0n q ≥≠).(Ⅰ)设1n n n b a a +=-(*n N ∈),证明{}n b 是等比数列;(Ⅱ)求数列{}n a 的通项公式;(Ⅰ)证明:由题设11(1)n n n a q a q a +-=+-(2n ≥),得11()n n n n a a q a a +--=-,即1n n b q b -=,2n ≥.又1211b a a =-=,0q ≠,所以{}n b 是首项为1,公比为q 的等比数列. (Ⅱ)解:由(Ⅰ)211a a -=, 32a a q -=, ……21n n a a q --=,(2n ≥).将以上各式相加,得211n n a a q q--+++=(2n ≥).所以当2n ≥时,11,,.1,111n nq q q a n q -≠=⎧-+⎪=-⎨⎪⎩上式对1n =显然成立.命题意图:本小题主要考查等差数列、等比数列的概念、等比数列的通项公式及前n 项和公式,考查运算能力和推理论证能力.题目4. 已知26列货车以相同速度 v 由 A 地驶向400千米处的 B 地,每两列货车间距离为 d 千米,现知 d 与速度 v 的平方成正比,且当 v =20(千米/时)时,d =1(千米).(1)写出d 关于v 的函数关系式;(2)若不计货车的长度,则26列货车都到达 B 地最少需要多少小时?此时货车速度为多少?解:(1)由题意可设d =kv 2,其中k 为比例系数,k >0.∵当v =20时,d =1,∴1=k ·202,即k =4001. ∴d =4001 v 2(v >0).(2)∵ 每两列货车间距离是d (千米), ∴ 最后一列货车出发时已等待的时间为 vd 25(小时),于是全部货车到达B 地的时间为 vd vt 25400+=.由(1)可知d =4001 v 2,代入上式整理得16400v vt +=,(v >0).惯于 105216400216400=⨯=⋅≥+=v vv vt .当且仅当16400v v=,即v =80(千米/时)时,等号成立.∴26列货车都到达B 地最少用10小时,此时货车速度为80千米/时.命题意图:本题考查学生的建模能力,考查基本不等式的知识的应用,及基本的计算能力。
本题的取材背景很公平,每个人都接触到这样的运输问题,实际中也是这样,比如100辆运输车辆若起程,不可能同时出发,最后一辆车,要等待多久?每两辆车之间要保持多大的车距?这是读者要弄清的问题.另外,整批货物运到目的地,需要从第一辆车出发开始记时,到最后一辆车到达为止.题目5.如图底面是菱形的四棱锥P —ABCD 中,,2,,60a PD PB a AC PA ABC ====︒=∠点E在PD 上,且PE:ED= 2: 1. (Ⅰ)证明 PA ⊥平面ABCD;(Ⅱ)求以AC 为棱,EAC 与DAC 为面的二面角θ的大小:(Ⅲ)在棱PC 上是否存在一点F, 使BF ∥平面AEC?证明你的结论.(Ⅰ)证明: 因为底面ABCD 是菱形, ∠ABC=60º, 所以AB=AD=AC=a.在△PAB 中,由22222PBaABPA==+知PA ⊥AB.同理, PA ⊥AD,所以PA ⊥平面ABCD.(Ⅱ)解:作EG ∥PA 交AD 于G,由PA ⊥平面ABCD 知EG ⊥平面ABCD.作GH ⊥AC 于H,连结EH,则EH ⊥AC. ∠EHG 为二面角θ的平面角. 又PE:ED=2:1 所以,3360sin ,32,31a AG GHa AG a EG =︒===从而.30,33tan ︒===θθGHEG(Ⅲ)当F 是棱PC 的中点时,BF ∥平面AEC.证明如下. 取PE 的中点M,连结FM,则FM ∥CE. ① 由,21ED PE EM ==知E 是MD 的中点.连接BM 、BD,设BD AC=O ,则O 为BD 的中点。
所以BM ∥OE 。
②由①、②知,平面BFM ∥平面AEC.命题意图:本小题主要考查直线和平面垂直,二面角等基础知识,考查空间想象能力,运算能力和探索、推理论证能力.题目6. 甲、乙、丙三人分别独立的进行某项技能测试,已知甲能通过测试的概率是25,甲、乙、丙三人都能通过测试的概率是320,甲、乙、丙三人都不能通过测试的概率是340,且乙通过测试的概率比丙大.(Ⅰ)求乙、丙两人各自通过测试的概率分别是多少; (Ⅱ)求测试结束后通过的人数ξ的数学期望E ξ.解(Ⅰ)设乙、丙两人各自通过测试的概率分别是x 、y 依题意得:23,52033(1)(1),540x y x y ⎧=⎪⎪⎨⎪--=⎪⎩ 即3,41.2x y ⎧=⎪⎪⎨⎪=⎪⎩或1,23.4x y ⎧=⎪⎪⎨⎪=⎪⎩(舍去)┅┅┅┅┅┅┅4分所以乙、丙两人各自通过测试的概率分别是34、12. ┅┅┅┅┅┅┅6分 (Ⅱ)因为3(0)40P ξ==3(3)20P ξ==2312312317(1)(1)(1)(1)(1)(1)(1)54254254220P ξ==--+--+--=01317(2)1()40P P P P ξ==-++=所以E ξ=371733301234020402020⋅+⋅+⋅+⋅= ┅┅┅┅┅┅┅12分命题意图:本小题主要考查随机事件、互斥事件、相互独立事件等概率的基础知识,考查运用概率知识解决实际问题的能力.题目7. 已知向量(c o s ,s in )a αα=,(c o s ,s in )b ββ=,255a b -=.(Ⅰ)求c o s()αβ-的值;(Ⅱ)若02πα<<,02πβ-<<,且5s in 13β=-,求sin α的值.解(Ⅰ)()()co s sin co s sin a b ααββ==,,,,()co s co s sin sin a b αβαβ∴-=--,.255a b -=,5∴=,即 ()422c o s 5αβ--=. ()3c o s 5αβ∴-=.(Ⅱ)0,0,0.22ππαβαβπ<<-<<∴<-<()3c o s 5αβ-=,()4sin .5αβ∴-=5s i n 13β=-,12c o s .13β∴=()()()s i n s i n s i n c o s c o s s i nααββαββαββ∴=-+⎡⎤⎣⎦=-+-412353351351365⎛⎫=⋅+⋅-= ⎪⎝⎭. 命题意图:本题考查三角函数知识,平面向量基础知识的综合运用,以及计算能力。
