matlab仿真作业
MATLAB与控制系统仿真练习题及答案 (2)

MATLAB与控制系统仿真练习题1、在同一坐标系内,画出一条正弦曲线和一条余弦曲线,要求正弦曲线用红色实线、数据点用“+”号显示;余弦曲线用黑色点线、数据点用“*”显示。
x=0:1 /10:2*pi;y=sin(x);plot(x,y,'r--+')hold ont=cos(x);plot(x,t,'k-.*')>>2、绘制单位圆。
a=0:1/10:2*pi;x=cos(a);y=sin(a);plot(x,y)axis squaregrid on3、使用极坐标函数绘制)3/ρ=的曲线。
8θsin10(t=0:0.01:2*pi;>> y=8*sin((10*t)/3);>> polar(t,y)4、绘制方程⎪⎩⎪⎨⎧===)cos()sin(t z t y t x 在[]π20,=t 区间的三维曲线。
t=0:pi/50:2*pi;x=t;y=sin(t);z=cos(t);plot3(x,y,z)5、用不同的线型和颜色在同一坐标内绘制曲线x 5.0e 21y -=、)2sin(2y x π=的图形。
x=0:1/10:10;y1=2*exp(-0.5*x);y2=sin(2*pi*x);plot(x,y1,'r');>> hold onplot(x,y2,'b')6、绘制二维正态分布密度函数)(212221),(y x e y x f +-=π的三维图形。
syms x yz=(1/(2*pi))*exp(-0.5*(x.^2+y.^2));ezsurf(x,y,z)7、选择合适的步长绘制下列函数的图形。
(1)x y cos =,⎥⎦⎤⎢⎣⎡-∈2,2ππx (2)x xe y = x=-2/pi:1/20:2/pi; >> y=sqrt(cos(x)); >> plot(x,y)>> hold on>> y=x.*exp(x);>> plot(x,y)>>8、在同一坐标下绘制函数x 、2x 、3x -、)sin(x x 在()π,0的曲线。
Matlab电气仿真实验作业

Matlab电气仿真实验指导老师:学生姓名:爸爸专业班级:电气工程及其自动化1班学号:222012!!!!本课程设计的目的:1、掌握Matlab/Simulink中SimPowerSystems 工具箱的基本建模方法;2、掌握Matlab/Simulink 电气仿真的基本步骤;3、利用Matlab/Simulink 在基本电路与磁路、电力电子技术、电气传动等方面的仿真设计。
实验一设计任务:单相桥式整流加LC滤波电路,电源为220V,50Hz,整流电路输入为24V,负载为10Ω阻性负载,滤波电感L=100mH,滤波电容C=200uF。
实验步骤:在matlab/simulink中选取相应的器件,如图连接运行。
注意事项:将全部示波器scope中的“limit data point to the last”选项应该去掉。
参数设置:交流电压源幅值:220*sqrt(2),频率:50HZ。
变压器参数,容量S=200V A,变比k=220V/24V。
电感:100mH;电容:200uF;电阻:10欧。
实验结果:二极管Diode3电流电压曲线第一个图显示的为二极管电流I ,第二个图显示为二极管电压U 。
当diode3导通时其电压接近为0V (管压降为0.7V ),其电流有值;当diode3关断时,其电流值为0A ,此时功率二极管承受反向电压,承受的最大反向电压幅值为24*sqrt (2)=33.94V 。
而电流图像上出现波动是因为电感L 的值不是无穷大,会受频率电压幅值的影响,所以如图所示。
二极管Diode4电压电流曲线结论分析:第一个图显示的为二极管电流I ,第二个图显示为二极管电压U 。
当diode3导通时其电压接近为0V (管压降为0.7V ),其电流有值;当diode3关断时,其电流值为0A ,此时功率二极管承受反向电压,承受的最大反向电压幅值为24*sqrt (2)=33.94V 。
而电流图像上出现波动是因为电感L 的值不是无穷大,会受频率电压幅值的影响,所以如图所示。
MATlab 仿真部分习题答案
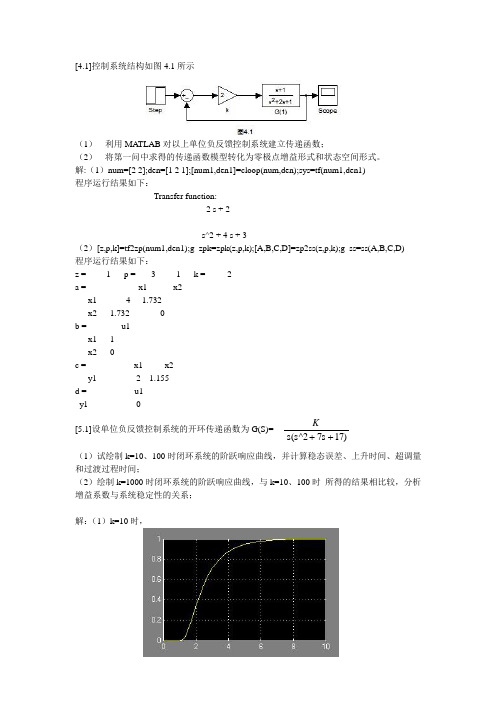
[4.1]控制系统结构如图4.1所示(1)利用MATLAB对以上单位负反馈控制系统建立传递函数;(2)将第一问中求得的传递函数模型转化为零极点增益形式和状态空间形式。
解:(1)num=[2 2];den=[1 2 1];[num1,den1]=cloop(num,den);sys=tf(num1,den1)程序运行结果如下:Transfer function:2 s + 2-------------s^2 + 4 s + 3(2)[z,p,k]=tf2zp(num1,den1);g_zpk=zpk(z,p,k);[A,B,C,D]=zp2ss(z,p,k);g_ss=ss(A,B,C,D)程序运行结果如下:z = -1 p = -3 -1 k = 2a = x1 x2x1 -4 -1.732x2 1.732 0b = u1x1 1x2 0c = x1 x2y1 2 1.155d = u1y1 0K[5.1]设单位负反馈控制系统的开环传递函数为G(S)=+s(s^2+7s17)(1)试绘制k=10、100时闭环系统的阶跃响应曲线,并计算稳态误差、上升时间、超调量和过渡过程时间;(2)绘制k=1000时闭环系统的阶跃响应曲线,与k=10、100时所得的结果相比较,分析增益系数与系统稳定性的关系;解:(1)k=10时,K=100时,K=10时,利用MA TLAB工作区输入程序:num=[10];den=[1,7,17,0];[z,p,k]=tf2zp( num,den);运行得z,p,k的值p= -3.5+2.1794*i -3.5-2.1794*i k=10G=zpk([ ],[-3.5+2.1794*i,-3.5-2.1794*i],10);c=dcgain(G);[y,t]=step(G);plot(t,y)[Y,K]=max(y);timetopeak=t(k);percentovershoot=100*(y-c)/cn=1;while y(n)<c n=n+1;end risetime=t(n) i=length(t);while(y(i)>0.98*c&y(i)<1.02*c) i=i-1;End setllingtime=t(i) 运行程序结果为:稳定值c=0.5882,响应时间setllingtime=1.0096s,上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555% 同理得k=100时,稳定值c=5.882,响应时间setllingtime=1.0096s, 上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555%(3)k=1000时,由其响应曲线可知,增益系数越大,其稳定性越差。
matlab电磁场仿真作业

matlab电磁场仿真作业一、介绍本文将介绍matlab电磁场仿真作业的相关知识和技巧。
电磁场仿真是指利用计算机模拟电磁场的分布和变化规律,以实现对电磁场问题的分析和解决。
matlab是一种强大的数学软件,可以用于各种科学计算、数据分析和图形处理等工作。
在电磁场仿真中,matlab具有良好的适用性和灵活性,可以方便地进行数据处理、可视化和模拟等操作。
二、基本概念1. 电磁场电磁场是指由带电粒子或导体所产生的物理现象,包括静电场、磁场和电磁波等。
在空间中,任何带有电荷或运动电荷的物体都会产生相应的电磁场。
2. 仿真仿真是指利用计算机模拟某个系统或过程的行为方式和结果。
在电磁场仿真中,可以通过建立数学模型来描述物理系统,并利用计算机进行计算和可视化。
3. 离散化离散化是指将连续变量转换为离散变量的过程。
在matlab中进行离散化操作可以将连续的电磁场分布转换为离散的数据点,以便进行计算和可视化。
三、matlab电磁场仿真的步骤1. 建立模型在进行电磁场仿真前,需要建立合适的模型来描述物理系统。
模型应该包括几何形状、物理特性和边界条件等信息。
可以使用matlab中的几何建模工具来创建三维模型,并定义相应的物理参数。
2. 离散化将连续的电磁场分布离散化为数据点。
可以使用matlab中的网格生成工具来生成离散化网格,并对网格进行调整以满足精度和计算效率要求。
3. 求解方程根据物理特性和边界条件,建立相应的方程组并求解。
常用的求解方法包括有限元法、有限差分法和边界元法等。
在matlab中,可以利用数值计算工具箱提供的函数来求解方程组。
4. 可视化将结果可视化以便于分析和展示。
可以使用matlab中强大的图形处理工具来生成二维或三维图像,并添加必要的标注和注释。
四、实例演示以下是一个简单的电磁场仿真实例,演示了如何在matlab中进行电磁场仿真。
1. 建立模型假设有一个长方体导体,其底面和侧面都被接地,导体顶部施加了一个电势差为V的电源。
MATLAB与控制系统仿真大作业

>> G1=tf(num,den);
>> G1=zpk(G1)
G1 =
5 (s+0.6) ----------------(s+3) (s+2) (s+1)
>> num=[2 1]; den=[1 2.9 1]; G2=tf(num,den); >> G2=zpk(G2)
G2 =
2 (s+0.5)
>> xlabel('x') ylabel('exp(-2.*x)')
三、simulink 建模(每题 10 分,共 20 分)
1、已知单位负反馈的开环传递函数为 G(s) =
2 s2 + 4s
,试利用
simulink
建立系在单位阶跃输入作用下的模型。
要求答案包括:(1)simulink 建模结构图;
(2)在同一个坐标中的阶跃信号和响应曲线图。
2、已知系统的开环传递函数为
G1(s)
=
2s2 + 5s + 6 s2 + 2s + 3
、G2 (s)
=
s2
s+6 + 7s +1
,H
(s)
=
5(s + 2) s +10
求:建立 Simulink 仿真模型,并求出其系统在单位阶跃响应;
要求答案包括:(1)simulink 建模结构图;
x=
-2.9709
0.5491
3.6000
0.0509
2. 已知下列矩阵
2 3 1
−1 3 5
A
=
MATLAB语言与控制系统仿真_参考题答案_第3章

3.5 MATLAB 绘图实训3.5.1 实训目的1.学会MATLAB 绘图的基本知识;2.掌握MATLAB 子图绘制、图形注释、图形编辑等基本方法;3.学会通过MATLAB 绘图解决一些实际问题;4.练习二维、三维绘图的多种绘图方式,了解图形的修饰方法;5.学会制作简单的MATLAB 动画。
图3-46 炮弹发射示意图3.5.2 实训内容1. 炮弹发射问题〔1炮弹发射的基础知识炮弹以角度α射出的行程是时间的函数,可以分解为水平距离)(t x 和垂直距离)(t y 。
)cos()(0αtv t x = %水平方向的行程; 205.0)sin()(gt tv t y -=α %垂直方向的行程;其中,0v 是初速度;g 是重力加速度,为9.82m/s ;t 是时间。
〔2炮弹发射程序举例:分析以下程序以及图3-47各个图形的实际意义。
a=pi/4; v0=300; g=9.8;t=0:0.01:50; x=t*v0*cos<a>;y=t*v0*sin<a>-0.5*g*t.^2;subplot<221>;plot<t,x>;grid;title<‘时间-水平位移曲线'>; subplot<222>;plot<t,y>;grid;title<‘时间-垂直位移曲线'>; subplot<223>;plot<x,y>;grid;title<‘水平位移-垂直位移曲线'>; subplot<224>;plot<y,x>;grid;title<‘垂直位移-水平位移曲线'>; 图3-4745角发射曲线 〔3编程解决炮弹发射问题①假设在水平地面上以垂直于水平面的角度向上发射炮弹,即发射角90=α,假设初速度分别为[310,290,270]m/s,试绘制时间-垂直位移曲线,编程求取最高射程;绘图要求:◆ 标题设为"炮弹垂直发射问题";◆ 在图上通过添加文本的方式表明初速度; ◆ 在x 轴标注"时间";◆ 在y 轴上标注"垂直距离"; ◆ 添加网格线;◆ 将310m/s 的曲线改为线粗为2的红色实线; ◆ 将290m/s 的曲线改为线粗为3的绿色点划线;◆ 将270m/s 的曲线改为线粗为2的蓝色长点划线;a=pi/2; v1=310; g=9.8;t=0:0.01:50; x1=t*v1*cos<a>;y1=t*v1*sin<a>-0.5*g*t.^2;plot<t,y1>;grid; title<'炮弹垂直发射问题'>; xlabel<'时间'>; ylabel<'垂直距离'>; hold on; v2=290;x2=t*v2*cos<a>;y2=t*v2*sin<a>-0.5*g*t.^2; plot<t,y2>; v3=270;x3=t*v3*cos<a>;y3=t*v3*sin<a>-0.5*g*t.^2; plot<t,y3>;zgsc=[max<y1>; max<y2>; max<y3>] %三次发射的最高射程 运行结果如下: zgsc =1.0e+003 * 4.9031 4.29083.7194最高射程分别为:4903.1米,4290.8米,3719.4米。
MATLAB仿真作业

1、用信号发生器发生幅值为1,频率为2Hz 的正弦波信号,分别按1倍和5倍送入两个示波器。
9.59.559.69.659.79.759.89.859.99.9510-1-0.8-0.6-0.4-0.200.20.40.60.81t9.59.559.69.659.79.759.89.859.99.9510-5-4-3-2-112345t2、直流电动机双闭环调速系统如图所示0.210.15s+1Transfer Fcn80.10.01s+1Transfer Fcn70.15s+10.051s Transfer Fcn6700.0067s+1Transfer Fcn50.00440.01s+1Transfer Fcn4130s Transfer Fcn30.10.01s+1Transfer Fcn21.5s+10.085s Transfer Fcn10.10.01s+1Transfer FcnStepScope-K-Gain1、(1)建立系统的Simulink 的模型,并进行仿真,用示波器观察系统的阶跃响应曲线。
(2)调整转速调节器的参数,观察其系统的阶跃响应曲线并进行比较0.17α=12345678910510152025303540t直接控制效果0.5α=012345678910510152025303540ta 等于1的调整参数控制效果1.0α=012345678910510152025303540ta 等于1的调整效果1.5α=12345678910510152025303540ta 等于1.5的调整效果3、分别用m 文件和Simulink 求解VanderPol 方程:2(1)0x x x x ⋅⋅+-+=取状态变量12x x x x ==,自己设置初始条件和仿真时间,打印状态响应曲线和相平面图-2.5-2-1.5-1-0.500.51 1.52 2.5-3-2-1123x1x 2相平面图(编程实现)02468101214161820-3-2-1123tx响应曲线(编程实现)M 文件function xdot=vdpol(t,x) xdot(1,1)=x(2);xdot(2,1)=x(2)*(1-x(1)^2)-x(1); EndCommand Window>> [t,x]=ode45('vdpol',0,20,[0 0.25],1e-6); >> plot(x(:,1),x(:,2))>> plot(t,x(:,1),'b-',t,x(:,2),'r-')XY GraphScopeProduct1Product1s Integrator11sIntegrator02468101214161820-3-2-1123tx响应曲线(simulink 仿真)-2.5-2-1.5-1-0.500.51 1.52 2.5-3-2-1123x1x 2相平面图(simulink 仿真)1、考虑如下系统:()221002011401111x x u y x--⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭=-试判断系统的能控能观性。
MATLAB与控制系统仿真练习题(含图)及答案
MATLAB 与控制系统仿真练习题(含图)1、已知函数x x e x f x sin cos )(-=,作出函数的大致图像。
>> syms x>> y=exp(x)*cos(x)-sin(x); >> ezplot(y)2、求下列极限:(1)30sin lim xx x x -→ >> syms x>> y=(x-sin(x))/(x^3);>> limit(y,x,0)ans =1/6(2) xx x ⎪⎭⎫ ⎝⎛+∞→11lim >> y=(1+1/x)^x;>> limit(y,x,inf)ans =exp(1)3、求下列函数的导数:(1)x e y x sin =>> syms x>> y=exp(x)*sin(x);>> diff(y,x)ans =exp(x)*sin(x)+exp(x)*cos(x)(2) x e x x y 22sin +=>> syms x>> y=sin(x)+x^2*exp(2*x);>> diff(y,x)ans =cos(x)+2*x*exp(2*x)+2*x^2*exp(2*x)4、求.)1(532⎰-dx x x 和.sin ⎰xdx e x(1).)1(532⎰-dx x xsyms x>> int(x^2*(1-x^3)^5)ans =-1/18*x^18+1/3*x^15-5/6*x^12+10/9*x^9-5/6*x^6+1/3*x^3(2).sin ⎰xdx e x>> int(exp(x)*sin(x))ans =-1/2*exp(x)*cos(x)+1/2*exp(x)*sin(x)5、求.)(102⎰-dx x x 和.1102⎰-dx x x (1) .)(102⎰-dx x x>> syms x>> int(x-x^2,0,1)ans =1/6(2) .1102⎰-dx x x>> syms x>> int(x*(1-x^2)^0.5,0,1)ans =1/36、已知二元函数),(cos )sin(2xy xy z +=试求y x z x z y z x z ∂∂∂∂∂∂∂∂∂222,,,。
matlab仿真实例100题

matlab仿真实例100题Matlab是一种强大的数学软件,广泛应用于科学计算、数据分析和工程仿真等领域。
在学习和使用Matlab的过程中,通过实例的方式进行仿真练习是一种非常有效的学习方法。
下面将给出100个Matlab仿真实例题目,帮助读者更好地掌握Matlab的使用。
1. 编写一个程序,计算并输出1到100之间所有奇数的和。
2. 编写一个程序,计算并输出1到100之间所有偶数的乘积。
3. 编写一个程序,计算并输出1到100之间所有素数的个数。
4. 编写一个程序,计算并输出1到100之间所有整数的平方和。
5. 编写一个程序,计算并输出1到100之间所有整数的立方和。
6. 编写一个程序,计算并输出1到100之间所有整数的阶乘和。
7. 编写一个程序,计算并输出1到100之间所有整数的倒数和。
8. 编写一个程序,计算并输出1到100之间所有整数的平均值。
9. 编写一个程序,计算并输出1到100之间所有整数的中位数。
10. 编写一个程序,计算并输出1到100之间所有整数的标准差。
11. 编写一个程序,计算并输出1到100之间所有整数的方差。
12. 编写一个程序,计算并输出1到100之间所有整数的最大值。
13. 编写一个程序,计算并输出1到100之间所有整数的最小值。
15. 编写一个程序,计算并输出1到100之间所有整数的平方根和。
16. 编写一个程序,计算并输出1到100之间所有整数的立方根和。
17. 编写一个程序,计算并输出1到100之间所有整数的对数和。
18. 编写一个程序,计算并输出1到100之间所有整数的指数和。
19. 编写一个程序,计算并输出1到100之间所有整数的正弦和。
20. 编写一个程序,计算并输出1到100之间所有整数的余弦和。
21. 编写一个程序,计算并输出1到100之间所有整数的正切和。
22. 编写一个程序,计算并输出1到100之间所有整数的双曲正弦和。
23. 编写一个程序,计算并输出1到100之间所有整数的双曲余弦和。
MATLAB仿真课后习题答案

MATLAB仿真课后习题答案MATLAB仿真课后习题答案第一章1.要求在闭区间[0,2Π]上产生具有10个等间距采样点的一维数组。
试用两种不同的指令实现。
解答:方法1:a=0:2*pi/9:2*pi方法2:a1=linspace(0,2*pi,10)4.任意建立矩阵A,然后找出在[10,20]区间的元素的位置。
解答:A=[4,15,-45,10,6;56,0,17,-45,0]A =4 15 -45 10 656 0 17 -45 0>> find(A>=10&A<=20)ans =367第二章M文件的2种形式:命令文件和函数文件。
命令文件没有输入输出参数,执行时只需在命令窗口中键入文件名回车即可;而函数文件是一条以function语句作为引导。
即文件的第一行为function[返回参数1,返回参数2,…]=函数名(输入参数1,输入参数2,…)。
这一行的有无是区分命令文件与函数文件的重要标志。
函数文件可以接受输入变量,还可以返回输出变量,执行时需在命令窗口中以固定格式调用函数方可。
习题22-1.编写程序,建立向量N=[1,2,3,4,5],然后利用向量N产生下列向量:(1) 2,4,6,8,10(2) 1/2, 1, 3/2, 2, 5/2(3) 1, 1/2, 1/3, 1/4, 1/5(4) 1, 1/4, 1/9, 1/16, 1/25解答:>> N1=2*N >> N2=N/2 >> N3=1./N >> N4=1./N.^2 2-2从键盘输入一个3位数的整数,将它反向输出。
如输入639,输出936。
输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
控制系统MATLAB仿真作业学习资料

Ce 0.132V /(r • min 1 ) ,允许过载倍数λ=1.5;
2.晶闸管装置放大系数: K s 40 ;
3.电枢回路总电阻:R=0.5Ω;
4.时间常数:Tl=0.05s,Tm=0.3s;
5.电流反馈系数:
U
* im
Байду номын сангаас
10
0.05V / A ;
1.5I N 1.5136
6.转速反馈系数:
(3)按小时间常数近似处理,取 Tn =0.0074+0.02=0.00274。
2.转速调节器的结构选择:PI 型,其传递函数为:WASR
s
Kn
ns ns
1
。
3.选择转速调节器参数
取 h=5,则 ASR 超前时间常数:τn=h*Tn =5*0.00274=0.137s
转速开环增益:KN =h + 1/2 h2 T2Σn2=159.84s- 1; 于是ASR的比例系数为:Kn =( h + 1)βCe Tm/2 hαRT Σn=12.388
直流电动机双闭环控制系统的仿真结构图
转速环空载高速起动波形图
收集于网络,如有侵权请联系管理员删除
精品文档
转速环满载高速起动波形图
转速环抗扰波形图
4 分析
一般来说,我们总希望在最大电流受限制的情况下,尽量发挥直流电动机的过载能力,使电力拖动控制系 统以尽可能大的加速度起动,达到稳态转速后,电流应快速下降,保证输出转矩与负载转矩平衡,进入稳 定运行状态。为实现在约束条件快速起动,关键是要有一 个使电流保持在最大值的恒流过程。根据反馈 控制规律,要控制某个量,就要引入这个量的负反馈。因此很自然地想到要采用电流负反馈控制过程。这 里实际提到了两个控制阶段。起动过程中,电动机转速快速上升,而要保持电流恒定,只需电流负反馈; 稳定运行过程中,要求转矩保持平衡,需使转速保持恒定,应以转速负反馈为主。
MATLAB仿真课后习题

第一章习题3.请指出以下的变量名(函数名、M文件名)中,哪些是合法的?Abc 2004x lil-1 wu_2004 a&b qst.u _xyz 解:合法的变量名有:Abc wu_20044.指令窗操作(1)求[12+2×(7-4)]÷32的运算结果解:>> [12+2*(7-4)]/3^2ans =2(2)输入矩阵A=[1,2,3;4,5,6;7,8,9],观察输出。
解:>> A=[1,2,3;4,5,6;7,8,9]A =1 2 34 5 67 8 9(3)输入以下指令,观察运算结果;clear;x=-8:0.5:8;y=x';X=ones(size(y))*x;Y=y*ones(size(x));R=sqrt(X.^2+Y.^2)+eps;Z=sin(R)./R;mesh(X,Y,Z);colormap(hot)xlabel('x'),ylabel('y'),zlabel('z')解:7.指令行编辑(1)依次键入以下字符并运行:y1=2*sin(0.3*pi)/(1+sqrt(5))解:>>y1=2*sin(0.3*pi)/(1+sqrt(5))y1 =0.5000(2)通过反复按键盘的箭头键,实现指令回调和编辑,进行新的计算;y2=2*cos(0.3*pi)/(1+sqrt(5))解:>>y2=2*cos(0.3*pi)/(1+sqrt(5))y2 =0.363311.编写题4中(3)的M脚本文件,并运行之。
解:第二章习题1.在指令窗中键入x=1:0.2:2和y=2:0.2:1,观察所生成的数组。
解:>> x=1:0.2:2 x =1.0000 1.2000 1.4000 1.6000 1.80002.0000 >> y=2:0.2:1 y =Empty matrix: 1-by-02.要求在[0,2π]上产生50个等距采样数据的一维数组,试用两种不同的指令实现。
matlab仿真实例

峰值时间tp=32s 上升时间tr=10.3s 调整时间ts=3.9e+003s
超调量σ%=96.7%
图一
图二
图三
4)修改参数,分别实现ξ=1和ξ=2的响应曲线,并记录:
ξ=1:
程序: >> zeta=1;
>> wn=sqrtm(10)
wn =
3.1623
>> sys=tf(10,[1,2*wn*zeta,10]);
>> step(sys)
>> title('ξ=1响应曲线' )
(图见下页)
ξ=2:
程序:
>> zeta=2;
程序:
>> sys=tf(10,[1,2,10]);step(sys)
>> sys=tf(10,[1,2,10]);
>>step(sys)
>>hold on
>>sys=tf([1,0.5,10],[1,2,10]);
>>step(sys)
>>gtext('\leftarrow G(s)');
>>gtext('\leftarrow G2(s)');
G(s)=0.01/(s^2+0.002*s+0.01)的峰值时间tp上升时间tr调整时间ts超调量
σ%。
G(s)=120/(s^2+12*s+120):
程序:
>> sys=tf(120,[1,12,120]);
>> step(sys)
利用matlab进行仿真的案例

利用matlab进行仿真的案例利用Matlab进行仿真可以涉及多个领域的案例,下面列举10个案例:1. 汽车碰撞仿真:利用Matlab中的物理仿真库,可以模拟汽车碰撞的过程,分析碰撞时车辆的变形、撞击力等参数。
可以根据不同的碰撞角度和速度,评估不同碰撞条件下的安全性能。
2. 电力系统仿真:利用Matlab中的电力系统仿真工具,可以模拟电力系统的运行情况,包括电压、电流、功率等参数的变化。
可以用于分析电力系统的稳定性、短路故障等问题,并进行相应的优化设计。
3. 通信系统仿真:利用Matlab中的通信系统仿真工具箱,可以模拟无线通信系统的传输过程,包括信号的发送、接收、调制解调等环节。
可以用于评估不同调制方式、编码方式等对通信系统性能的影响。
4. 智能控制仿真:利用Matlab中的控制系统仿真工具,可以模拟各种控制系统的运行情况,包括PID控制、模糊控制、神经网络控制等。
可以用于设计、优化和评估各种控制算法的性能。
5. 雷达系统仿真:利用Matlab中的雷达仿真工具,可以模拟雷达系统的工作原理和性能,包括发射、接收、信号处理等过程。
可以用于评估雷达系统的探测能力、跟踪精度等指标,并进行系统参数的优化设计。
6. 气候变化模拟:利用Matlab中的气候模型,可以模拟气候系统的变化过程,包括温度、降水、风速等参数的变化。
可以用于研究气候变化对生态环境、农业生产等方面的影响,以及制定相应的应对策略。
7. 人体生理仿真:利用Matlab中的生理仿真工具箱,可以模拟人体的生理过程,包括心血管系统、呼吸系统、神经系统等。
可以用于研究不同疾病、药物对人体的影响,以及评估各种治疗方案的效果。
8. 金融市场仿真:利用Matlab中的金融工具箱,可以模拟金融市场的价格变化过程,包括股票、期货、汇率等。
可以用于研究不同投资策略、风险管理方法等对投资收益的影响,并进行相应的决策分析。
9. 电子器件仿真:利用Matlab中的电子器件仿真工具,可以模拟各种电子器件的工作原理和性能,包括二极管、晶体管、集成电路等。
MATLAB系统级仿真分析作业-Read
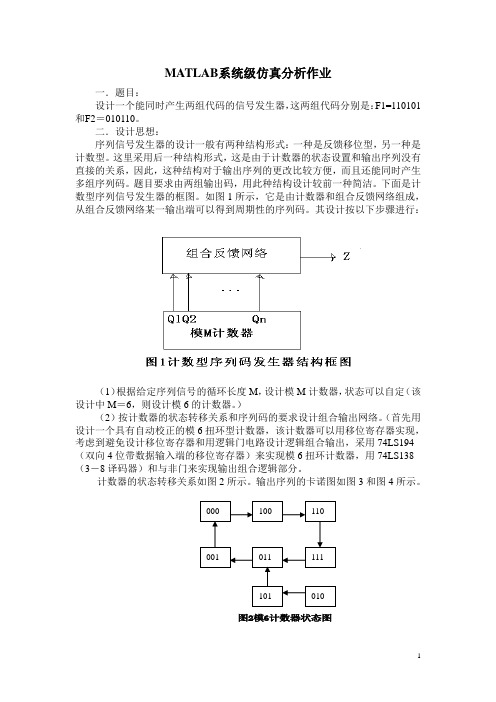
MATLAB系统级仿真分析作业一.题目:设计一个能同时产生两组代码的信号发生器,这两组代码分别是:F1=110101和F2=010110。
二.设计思想:序列信号发生器的设计一般有两种结构形式:一种是反馈移位型,另一种是计数型。
这里采用后一种结构形式,这是由于计数器的状态设置和输出序列没有直接的关系,因此,这种结构对于输出序列的更改比较方便,而且还能同时产生多组序列码。
题目要求由两组输出码,用此种结构设计较前一种简洁。
下面是计数型序列信号发生器的框图。
如图1所示,它是由计数器和组合反馈网络组成,从组合反馈网络某一输出端可以得到周期性的序列码。
其设计按以下步骤进行:(1)根据给定序列信号的循环长度M,设计模M计数器,状态可以自定(该设计中M=6,则设计模6的计数器。
)(2)按计数器的状态转移关系和序列码的要求设计组合输出网络。
(首先用设计一个具有自动校正的模6扭环型计数器,该计数器可以用移位寄存器实现,考虑到避免设计移位寄存器和用逻辑门电路设计逻辑组合输出,采用74LS194(双向4位带数据输入端的移位寄存器)来实现模6扭环计数器,用74LS138(3-8译码器)和与非门来实现输出组合逻辑部分。
计数器的状态转移关系如图2所示。
输出序列的卡诺图如图3和图4所示。
图2模6计数器状态图3 F1图4 F2系统的MATLAB分析与仿真:根据设计思想,对系统进行建模和仿真,首先建立74LS138和74LS194的模型,然后依据上面的设计结果建立系统模型并且仿真和验证结果。
具体步骤如下:1.子系统系统的建模与仿真(1)74LS138子系统的建模与仿真由上面的分析和设计结果,74LS138是系统实现组合逻辑输出网络主体部分,在MATLAB建模和仿真中,把74LS138做为子系统进行建模与仿真,最后进行封装做为一个通用模块在系统中使用。
这样降低系统建模与仿真的复杂程度。
下面在MATLAB中进行74LS138的建模与仿真。
matlab仿真作业

matlab仿真作业实验报告(MATLAB课后作业练习题)学院电⼦信息学院班级学号姓名任课教师⽬录实验作业1 (3)第⼀题、⼀阶电路 (3)实验作业2 (7)第⼀题Waterfall Scope(瀑布显⽰图) (7)Chirp Signal扫频信号源 (7)Uniform Random Number信号源下 (8)Band-Limited White Noise信号源 (8)第⼆题:设计⼀个编程开关仿真系统框图 (9)仿真实验作业3 (10)第⼀题 (10)第⼆题 (13)仿真实验作业4 (14)第⼀题 (14)第⼆题 (16)仿真实验作业5 (19)仿真实验作业6 (21)仿真实验作业7 (23)仿真实验作业8 (26)实验作业1第⼀题、⼀阶电路(1)、电路图如下,R=1.4欧,L=2亨,C=0.32法,初始状态:电感电流为零,电容电压为0.5V ,t=0时刻接⼊1V 的电压,求0 function xdot=funcforexl23(t,x,~,R,L,C)xdot=zeros(2,1); %矩阵初始化 xdot(1)=-R/L*x(1)-1/L*x(2)+1/L* f(t); %⽅程1 xdot(2)=1/C * x(1); %⽅程2 function in=f(t) %输⼊信号 in=(t>0)*1; %阶跃信号%filename ex123.mL=2; %电感值 C=0.32; %电容值for R=[1.4 5 9] %仿真电阻值分别为1.5, 3, 5欧姆的情况[t,x]=ode45('funcforexl23',[0,15],[0;0.5],[],R,L,C); %也可采⽤ode23, ode15s 等求解figure(1);plot(t,x(:,1));hold on ; xlabel('time sec'); text(2,0.07,'\leftarrow i_L(t)');grid;figure(2);plot(t,x(:,2));hold on ;xlabel('time sec'); text(2.1,0.75,'\leftarrow u_C(t)');grid; End输⼊输出的传递函数:11)()()(2++==RCs LCss F s U s H c±Vs=1V t=0R L C +-)(t i )(t v o① R=1.4时:1448.064.01)(2++=s s s H② R=5时:16.164.01)(2++=s s s H ③ R=9时:188.264.01)(2++=s s sH连续系统的传递函数如下:借助多项式乘法函数conv 来处理:两个向量分别⽤num 和den 表⽰。
MATLAB控制系统各种仿真例题(包括simulink解法)

一、 控制系统的模型与转换1. 请将下面的传递函数模型输入到matlab 环境。
]52)1)[(2(24)(32233++++++=s s s s s s s G )99.02.0)(1(568.0)(22+--+=z z z z z H ,T=0.1s >> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5));GTransfer function:s^3 + 4 s + 2------------------------------------------------------s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3>> num=[1 0 0.56];den=conv([1 -1],[1 -0.2 0.99]);H=tf(num,den,'Ts',0.1)Transfer function:z^2 + 0.56-----------------------------z^3 - 1.2 z^2 + 1.19 z - 0.992. 请将下面的零极点模型输入到matlab 环境。
请求出上述模型的零极点,并绘制其位置。
)1)(6)(5()1)(1(8)(22+++-+++=s s s s j s j s s G )2.8()6.2)(2.3()(1511-++=----z z z z z H ,T=0.05s>>z=[-1-j -1+j];p=[0 0 -5 -6 -j j];G=zpk(z,p,8)Zero/pole/gain:8 (s^2 + 2s + 2)--------------------------s^2 (s+5) (s+6) (s^2 + 1)>>pzmap(G)>> z=[0 0 0 0 0 -1/3.2 -1/2.6];p=[1/8.2];H=zpk(z,p,1,'Ts',0.05)Zero/pole/gain:z^5 (z+0.3125) (z+0.3846)-------------------------(z-0.122)Sampling time: 0.05>>pzmap (H )num=[0,7.1570,-6.4875 ];den=[1,-2.2326,1.7641,-0.4966];sysd=tf(num,den,0.05,'variable','z^-1')Transfer function:7.157 z^-1 - 6.487 z^-2-----------------------------------------1 - 2.233 z^-1 + 1.764 z^-2 - 0.4966 z^-3Sampling time: 0.05二、 线性系统分析1. 请分析下面传递函数模型的稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB仿真院(系)专业班级姓名学号时间Matlab作业1、一个50Hz的简单电力系统如下图所示,试在Simulink中建立仿真模型研究该系统性能。
k1系统建模要求如下:(1)发电机G采用“Synchronous Machine pu Fundamental”模型,变压器T采用“Three-Phase Transformer (Two Windings)”模型,输电线路L采用“Three-Phase Series RLC Branch”模型,负荷LD1、LD2采用“Three-Phase Parelell RLC Load”模型。
(2)发电机模型参数:采用预设模型,其中学号末位数字为1的同学使用编号为01的模型参数,学号末位数字为2的同学使用编号为02的模型参数,……,学号末位数字为0的同学使用编号为10的模型参数。
(3)变压器模型采用默认参数,副边电压10kV,但需要注意与发电机模型相匹配参数的设置(原边电压、频率等),变压器容量设置为发电机额定功率的1.2倍;(4)线路参数的设置原则:忽略电容,X/R=3,线路通过发电机额定功率时首末端压降约为0.05p.u.;(5)负荷模型采用默认参数,但需要注意与整个系统模型相匹配参数的设置(电压、频率等),负荷LD1容量设置为发电机额定功率的5%,LD2容量为发电机额定功率的30%,功率因数0.95。
(6)其他模块(如短路模拟、测量、示波、powergui等)的使用根据研究要求自行确定。
性能研究要求:(1)利用powergui计算该系统的稳态潮流情况;(2)利用powergui将系统设置为零初始状态,仿真系统达到稳态的过程;(3)利用powergui将系统设置为稳态,仿真k点发生三相短路、持续0.15秒后切除的系统过渡过程,要求输出短路电流的波形。
作业形式要求:(1)根据题目要求进行理论分析,计算出发电机稳态时转速,短路电流周期分量以及冲击电流的大小。
(2)进行上机建模、仿真,完成后将发电机、变压器、线路、负荷的参数,以及模型图、稳态潮流结果、仿真过程曲线等结果抓图打印粘贴在大作业报告中。
仿真结果必须同理论分析结果基本保持一致。
(3)对自己在建模和仿真过程中遇到的关键问题和收获、结论等进行阐述。
(4)对抄袭作业者,不论原创者还是山寨盗版者,成绩一律判为零分!!!!解:1、参数计算及截图(1)模型的搭建(2)选取06号p.u.基本同步电机(细图)其余参数去默认值。
(3)变压器参数计算容量)(10285*2.1KVA S n ==;原边电压V U N 4001=,副边电压KV U N 102=; 其余参数皆取默认值。
(细图)(细图)(4)线路参数计算利用线路通过发电机额定功率时首末端压降约为0.05p.u.可以得到: V U 50010000*05.0==∆线路上的电压降为 (式1)额定电流为A I 5.81000085000==,Ω=∆=823.58IUZ 那么。
又由已知得到: 3=RX(式2)由(式1)和(式2)解得Ω=6.18R ,Ω===8.556.18*33R X .注意此时参数设置上是要求电感值,不是电抗值。
电容是无穷大,即为inf 。
(5)负荷参数计算(默认负荷为感性负荷) 负荷load1:WW S P G 404095.0*85000*%595.0**%595.0===,由于功率因素为 Var Q L 1327=,Var Q C 0取。
(细图)负荷load2:W W S P G 2420095.0*85000*%3095.0**%30===, Var Var P Q L 796032868.0*24200tan *===ϕ,Var Q C 0取。
(细图)(6)三相故障模块时间设置设置如下:0.1S开始故障,0.25S故障切除,故障持续0.15S。
其余参数采用默认值。
(细图)2、仿真、理论分析及对比(1)利用powergui计算该系统的稳态潮流情况(细图)根据powergui 计算得发电机潮流情况:W P G 27394=实际发出,Var Q G 03941=实际发出。
理论分析的整个系统消耗:W W W P P P LD LD 2824024200404021=+=+=理论消耗(忽略变压器和线路的有功损耗), Var Var Var Var Q Q Q Q Q LD T L LD 16.101587960)10*10210*10086.18*3(*100007960242001327)(3222221=++++=+++=理论消耗 两者相比较得: 理论消耗实际发出P P G <,理论消耗实际发出和Q Q G 基本平衡。
分析其原因可能是:1、理论消耗实际发出和P P G 不平衡,分析其原因主要是由于发电机的转速下降的问题,通过转速的波形图可以看到:发电机的转速从理论的额定值min /1500min /250*60*60r r P f n N ===极对数逐渐下降,最终稳定在1450r/min 左右。
而根据电力系统的有功功率—频率静态特性可以看出:当频率降低时,发电机会多发出有功,而负荷吸收的有功会减少。
最终二者在一个低于额定频率值下的频率平衡,而此时理论消耗实际消耗实际发出P P P G <=2、理论消耗实际发出和Q Q G 基本平衡,是因为在仿真发电机潮流时是将发电机设为平衡节点,发电机端电压的大小和相位保持不变,发电机不能通过降低电压来少发无功,负荷也不能通过降低电压来少要无功。
故发电机会自励磁保持机端电压且平衡系统无功。
(2)利用powergui 将系统设置为零初始状态,仿真系统达到稳态的过程 利用powergui 将系统设置为零初始状态:Scope3系统电流仿真模拟:系统电流有个逐渐衰减至稳定的过程,产生这种情况的原因是由于发电机频率的下降,使得系统的有功在零初始状态至稳态的过程中随着频率的下降而下降,最终平衡,故系统电流曲线也在此过程中逐渐衰减并最终稳定。
Scope2系统电压仿真模拟:系统电压基本保持不变,产生这种情况的原因是由于设置发电机为平衡节点,发电机机端电压大小、相位保持不变,且系统无功基本平衡,故系统电压曲线基本保持稳定。
(3)利用powergui 将系统设置为稳态,仿真k 点发生三相短路、持续0.15秒后切除的系统过渡过程,要求输出短路电流的波形。
利用powergui 将系统设置为稳态a 、Scope3系统电流仿真模拟:从系统电流波形上得出:在短路设置的时间上0.1到0.25秒内系统电流瞬间扩大为冲击电流,大小为A i imp 4.27=实际,而在0.25秒后故障切除,因而电流恢复到原来的水平。
b 、短路电流周期分量及冲击电流大小的理论分析 设置统一的基准值KVA S B 85=,av B V V =则A A I B 674.45.10*385==,0667.010285*1008*1008.===T B pu T S S X , 04302.010*5.1085*8.5510**6.18*33232.===--avB pu L V S X ,01434.0304302.03..===pu L pu T X R 所以短路电流周期分量:AA I X X R IB pu T pu L pu L pm 4889.34674.4*)0667.0043024.0(01434.0*32*)(*31*2222..2.=++=++=理论冲击电流:AA A I X X R i pm T L L imp 8.564889.34*47.6014889.34)10*10210*10088.556.18*14.3*100*01.0exp 1(*)**100*01.0exp1(32=+=+-+=+-+=)(理论π c 、理论分析与实际仿真结果对比、分析、验证由上可见,实际理论与imp imp i i 相差较大。
分析原因是:短路后发电机的机端电压有了个较大的降低。
又短路冲击电流是取短路后2T周期时的电流幅值,此时所对应的实际电压幅值要比理论分析时所用的电压幅值小很多,故使得实际理论与imp imp i 相差较大。
这一点可从下图中看出。
发电机端电压仿真模拟:由Scope1发电机端电压仿真模拟图可以看出,在短路后2T周期时,发电机端电压有较大的下降,具体根据该图知:4.0400100.==pu G U 则用pu G U .再次理论分析得: 短路电流周期分量:AA I X X R U IB pu T pu L pu L puG pm 90.16674.4*)0667.004302.0(01434.04.0*)(222..2..=++=++=理论冲击电流:A A i imp 83.279.16*47.601=+=)(理论将新得到的理论分析冲击电流与实际仿真冲击电流A i imp 4.27=实际对比,发现1理论imp i 和实际imp i 基本一致。
3、心得体会通过本次Matlab 的仿真作业,我对Matlab 有了新的认识及了解,过程中我掌握了一些平时课程中未掌握的知识点,加上运用平日里所学的知识,完整的进行了电力系统的分析。
当然这次作业也遇到过一些问题,比如参数设置比较繁琐,容易设置错误,但在我认真的核实之后,完满解决了这一问题。
这次锻炼了我熟练使用Matlab 在电力系统方面的建模,并且温故而知新了电力系统的相关知识,让我受益匪浅!。
