16第十六讲伯德图分析-稳定性-及幅值和相角裕度
合集下载
16 第十六讲 伯德图分析-稳定性-及幅值和相角裕度
作业： P339 P339 16.1 a. 16.3 e.
当 k > k1时， 系统是稳定的
Im
ω =0
-1
ω=∞
Re
图.16.14
稳定系统的奈奎斯特图
例题 16.1
问题: 如图所示的系统， 画出当K=45时 的伯德图， 并确定增益裕度和相位裕度。 计算使系统稳定的最大K值， 并用劳斯阵 列验证其结果。
R +
⊕
-
C
K
1 ( s + 2)( s + 3)3
Mdb
log10 ω
GM
0db
φ
−1800
PM
log10 ω
图.16.3 增益裕度和相位裕度
系统的型和从伯德图得到 稳态误差
一般开环传递函数
Kb (1+ s / z1 )(1+ s / z2 )L(1+ s / zm ) GH(s) = n s (1+ s / p1 )(1+ s / p2 )L(1+ s / pk )
GM 1 = K1db GM 2 = K 2 db
图.16.11 系统的根轨迹图
单一频率穿越点: 增加相位 考虑下面的例子
(1+ s / 2) GH(s) =
s3
2
相位裕度是负的，表明系统是不稳定的。 增益裕度是正的，表明系统是稳定的。 考虑相位裕度，系统是稳定的。
0.1 40
1
10
100
ω
M db
伯德图中的相位裕度： - 相位裕度是使相角曲线向下移动 直到 增益和相角穿越点发生在同一频率时 的纯相角滞后量 。 - 在图16.1中
PM = 54
伯德图分析-稳定性-及幅值和相角裕度
-270
0.01
0.1
1.0
10
增益穿 越点
相位穿
图16.1 例子系统的伯德图
越点
增加K 将使幅值曲线向上平移动，从 而使幅值穿越点向右移。但是相角穿越点 保持不变。 系统最终处在临界不稳定点上。
▽ 计算临界不稳定时系统的幅值。
20 lg NK 20 lg K 20 lg N
20 lg NK KdB NdB
渐近线的延长线求出。
M db
20 log10 Kv
-
20d
b/d
log10
eca1
图.16.6 1 型系统的另一种伯德图
2型系统
GHs
Kb s2
GH
j
Ka
j 2
如果 ka=1。对数幅频特性在当ω =1时，其低频段或它的延长线会以– 40db/decade 的斜率穿过 零分贝线 。
Ka 的值可以通过测量ω = 1 处的 增益值来获得。
PM 54
▽ 在伯德图中获得增益裕度和相位裕 度:
增益裕度是通过相角穿越频率得出的。 它是该频率处的幅值分贝值与0dB线之间
的差值(用分贝表示) 。 相角裕度是通过增益穿越频率得出的， 它是此频率处的相角与-180o线之间的差值。
M db
0 d b
1800
log10
G M
P
log10
M
图.16.3 增益裕度和相位裕度
线性控制系统工程
第16章
伯德图分析，稳 定性，
及幅值和相角 裕度
第16章 伯德图分析,稳定性 及幅值和相角裕度
伯德图中的增益裕度和相角裕度
g c
(g c)
(g c)
GM Kc
0.01
0.1
1.0
10
增益穿 越点
相位穿
图16.1 例子系统的伯德图
越点
增加K 将使幅值曲线向上平移动，从 而使幅值穿越点向右移。但是相角穿越点 保持不变。 系统最终处在临界不稳定点上。
▽ 计算临界不稳定时系统的幅值。
20 lg NK 20 lg K 20 lg N
20 lg NK KdB NdB
渐近线的延长线求出。
M db
20 log10 Kv
-
20d
b/d
log10
eca1
图.16.6 1 型系统的另一种伯德图
2型系统
GHs
Kb s2
GH
j
Ka
j 2
如果 ka=1。对数幅频特性在当ω =1时，其低频段或它的延长线会以– 40db/decade 的斜率穿过 零分贝线 。
Ka 的值可以通过测量ω = 1 处的 增益值来获得。
PM 54
▽ 在伯德图中获得增益裕度和相位裕 度:
增益裕度是通过相角穿越频率得出的。 它是该频率处的幅值分贝值与0dB线之间
的差值(用分贝表示) 。 相角裕度是通过增益穿越频率得出的， 它是此频率处的相角与-180o线之间的差值。
M db
0 d b
1800
log10
G M
P
log10
M
图.16.3 增益裕度和相位裕度
线性控制系统工程
第16章
伯德图分析，稳 定性，
及幅值和相角 裕度
第16章 伯德图分析,稳定性 及幅值和相角裕度
伯德图中的增益裕度和相角裕度
g c
(g c)
(g c)
GM Kc
系统的稳定性分析Bode稳定判据PPT优选版
严格地讲，应当同时给出相角裕度和增益裕度，才能确定系统的相对稳定性。
虚线，该虚线通过的相位为ν·90°，计算正负穿越时， 反之，称为负穿越（相角减少）。
在相频特性等于－180°的频率ωg （穿越频率）处，开环幅频特性A(ωg)的倒数，称为增益裕度，记做Kg 。 反之，称为负穿越（相角减少）。
应将补画的虚线看成对数相频特性曲线的一部分。 Nyquist图上的负实轴 Bode图上的相频特性的
稳定裕度可以定量地确定一个系统的稳定程度。 它包括相位裕度和幅值裕度。
7.7 控制系统的相对稳定性
➢相对稳定性：若系统开环传递函数没有右半平面的 极点，且闭环系统是稳定的，那么乃氏曲线 G(jω)H(jω)离(－1, j0)点越远，则闭环系统的稳定程 度越高；反之，G(jω)H(jω)离(－1, j0)点越近，则闭 环系统的稳定程度越低；如果G(jω)H(jω)穿过(－1, j0)点，则闭环系统处于临界稳定状态。 ➢稳定裕度：衡量闭环稳定系统稳定程度的指标，常 用的有相角裕度γ和幅值裕度 Kg。
频特性(ω)不穿越－180°线，故闭环系统必
然稳定。
例2. 判定下列图的稳定性
下图(a)表示的具有正相角裕度的系统不仅稳定，而且还有相当的稳定储备，它可以在ωc的频率下，允许相角再增加（迟后）γ度才达 到临界稳定状态。 在相频特性等于－180°的频率ωg （穿越频率）处，开环幅频特性A(ωg)的倒数，称为增益裕度，记做Kg 。 解：相角裕度可通过对数幅频特性用图解法求出。 根据稳定性判据可以判别一个系统是否稳定。 严格地讲，应当同时给出相角裕度和增益裕度，才能确定系统的相对稳定性。 相对稳定性：若系统开环传递函数没有右半平面的极点，且闭环系统是稳定的，那么乃氏曲线G(jω)H(jω)离(－1, j0)点越远，则闭环系 统的稳定程度越高； 显然，对于稳定系统，1/Kg＜1，如图(a) 所示； 在Bode图上，增益裕度改以分贝(dB)表示 在频率特性上对应于幅值A(ω)＝1(即L(ω)=0)的角频率称为剪切频率(截止频率)，以ωc表示，在剪切频率处，相频特性距－180°线的 相位差γ叫做相角裕度。 由伯德图判断系统的稳定性 一、 乃奎斯特图与伯德图的对应关系 显然，对于稳定系统，1/Kg＜1，如图(a) 所示；
虚线，该虚线通过的相位为ν·90°，计算正负穿越时， 反之，称为负穿越（相角减少）。
在相频特性等于－180°的频率ωg （穿越频率）处，开环幅频特性A(ωg)的倒数，称为增益裕度，记做Kg 。 反之，称为负穿越（相角减少）。
应将补画的虚线看成对数相频特性曲线的一部分。 Nyquist图上的负实轴 Bode图上的相频特性的
稳定裕度可以定量地确定一个系统的稳定程度。 它包括相位裕度和幅值裕度。
7.7 控制系统的相对稳定性
➢相对稳定性：若系统开环传递函数没有右半平面的 极点，且闭环系统是稳定的，那么乃氏曲线 G(jω)H(jω)离(－1, j0)点越远，则闭环系统的稳定程 度越高；反之，G(jω)H(jω)离(－1, j0)点越近，则闭 环系统的稳定程度越低；如果G(jω)H(jω)穿过(－1, j0)点，则闭环系统处于临界稳定状态。 ➢稳定裕度：衡量闭环稳定系统稳定程度的指标，常 用的有相角裕度γ和幅值裕度 Kg。
频特性(ω)不穿越－180°线，故闭环系统必
然稳定。
例2. 判定下列图的稳定性
下图(a)表示的具有正相角裕度的系统不仅稳定，而且还有相当的稳定储备，它可以在ωc的频率下，允许相角再增加（迟后）γ度才达 到临界稳定状态。 在相频特性等于－180°的频率ωg （穿越频率）处，开环幅频特性A(ωg)的倒数，称为增益裕度，记做Kg 。 解：相角裕度可通过对数幅频特性用图解法求出。 根据稳定性判据可以判别一个系统是否稳定。 严格地讲，应当同时给出相角裕度和增益裕度，才能确定系统的相对稳定性。 相对稳定性：若系统开环传递函数没有右半平面的极点，且闭环系统是稳定的，那么乃氏曲线G(jω)H(jω)离(－1, j0)点越远，则闭环系 统的稳定程度越高； 显然，对于稳定系统，1/Kg＜1，如图(a) 所示； 在Bode图上，增益裕度改以分贝(dB)表示 在频率特性上对应于幅值A(ω)＝1(即L(ω)=0)的角频率称为剪切频率(截止频率)，以ωc表示，在剪切频率处，相频特性距－180°线的 相位差γ叫做相角裕度。 由伯德图判断系统的稳定性 一、 乃奎斯特图与伯德图的对应关系 显然，对于稳定系统，1/Kg＜1，如图(a) 所示；
自动控制原理之稳定性裕量分析.ppt
4.4 稳定性裕量
G平面
Im
对于大的K值，系统是不稳定的。 当增益减小到一定值时，G( j) K大时 的轨迹通过(-1,j0)点。
对于小的K值，系统是稳定的。
1
0 Re
K小时
G( j) 的极坐标图
G( j) 的轨迹对(-1,j0)
点的靠近程度，可以用来
度量稳定裕量。在实际系
统中常用相位裕量和增益
裕量表示。
c2 n2 ( (4 4 1 2 2 ) c n (4 4 1 2 2
() 90 arctg 2 n
根据相位裕度的定义
180 (c ) 180 90 arctg
c 2 n
90 arctg
4 4 1 2 2 2
arctg
2 4 4 1 2 2
上式说明相位裕度仅仅与阻尼比有关。
对于稳定的最小相位系统，增益裕度指出了系统在不稳定之前， 增益能够增大多少。对于不稳定系统，增益裕度指出了为使系 统稳定，增益应当减少多少。
一阶或二阶系统的增益裕度为多少？
一阶或二阶系统的增益裕度为无穷大，因为这类系统的 极坐标图与负实轴不相交。因此，理论上一阶或二阶系统 不可能是不稳定的。当然，一阶或二阶系统在一定意义上 说只能是近似的，因为在推导系统方程时，忽略了一些小 的时间滞后，因此它们不是真正的一阶或二阶系统。如果 计及这些小的滞后，则所谓的一阶或二阶系统可能是不稳 定的。
G(s) 10(1 10s) s(1 100 s)(1 0.2s)
由于是最小相位系统，因而可通过计算相位裕度
是否大于零来判断系统的稳定性。由图可知 c 1
在 c 处
(c
)
90
arctg
1 0.1
arctg
G平面
Im
对于大的K值，系统是不稳定的。 当增益减小到一定值时，G( j) K大时 的轨迹通过(-1,j0)点。
对于小的K值，系统是稳定的。
1
0 Re
K小时
G( j) 的极坐标图
G( j) 的轨迹对(-1,j0)
点的靠近程度，可以用来
度量稳定裕量。在实际系
统中常用相位裕量和增益
裕量表示。
c2 n2 ( (4 4 1 2 2 ) c n (4 4 1 2 2
() 90 arctg 2 n
根据相位裕度的定义
180 (c ) 180 90 arctg
c 2 n
90 arctg
4 4 1 2 2 2
arctg
2 4 4 1 2 2
上式说明相位裕度仅仅与阻尼比有关。
对于稳定的最小相位系统，增益裕度指出了系统在不稳定之前， 增益能够增大多少。对于不稳定系统，增益裕度指出了为使系 统稳定，增益应当减少多少。
一阶或二阶系统的增益裕度为多少？
一阶或二阶系统的增益裕度为无穷大，因为这类系统的 极坐标图与负实轴不相交。因此，理论上一阶或二阶系统 不可能是不稳定的。当然，一阶或二阶系统在一定意义上 说只能是近似的，因为在推导系统方程时，忽略了一些小 的时间滞后，因此它们不是真正的一阶或二阶系统。如果 计及这些小的滞后，则所谓的一阶或二阶系统可能是不稳 定的。
G(s) 10(1 10s) s(1 100 s)(1 0.2s)
由于是最小相位系统，因而可通过计算相位裕度
是否大于零来判断系统的稳定性。由图可知 c 1
在 c 处
(c
)
90
arctg
1 0.1
arctg
自动控制原理：第六章频域分析法——伯特图及稳定性分析
• 当阻尼系数接近1时，振荡环节具有低通滤波的作用； • 而随着减小，=n=1/T处的幅值迅速增大，表明其对输
入信号中该频率附近分量的放大作用逐渐加强，此时，振
荡环节具有选频作用。
6.4 系统开环频率特性-典型环节的伯德图
40
Bode Diagram
二阶微分环节:
30
20
转折频率 渐近线
L() /(dB)
10 /T
1) 将乘除运算转化为加减运算，因而可通过简单的图像叠加 快速绘制高阶系统的伯德图 ；如 G( j) A1()e j1() A2 ()e , j2 () 则20lgA1()A2()=20lgA1()+20lgA2()
2) 伯德图还可通过实验方法绘制，经分段直线近似整理后， 很容易得到实验对象的频率特性表达式或传递函数.
i 1
i m1 1
v n1
v n1 nv n1 2
( jTl 1)
(1 Tl2 2 2 j lTl )
l v 1
l v n1 1
(6 - 17)
其 中 ，K ,0 i 1,0 l 1, i 0,Tl 0都 为 常 数 。
除此外，也存在某个Tl<0,开环不稳定，但闭环可能仍然 稳定的情况。
1
A(ω)
1 ωT 2 2 2ζωT 2
L() /(dB)
10
0
-10 -20
(1 T 22
j2T)1
0.05 0.1 0.3
-30
0.7
1 -40
180
转折频率 渐近线
135
(ω)
arctan
1
2ζωT
ωT
2
90 45
0
() /()
稳定裕度的定义
5.5 稳定裕度5.5.1 稳定裕度的定义控制系统稳定与否是绝对稳定性的概念。
而对一个稳定的系统而言，还有一个稳定的程度，即相对稳定性的概念。
相对稳定性与系统的动态性能指标有着密切的关系。
在设计一个控制系统时，不仅要求它必须是绝对稳定的，而且还应保证系统具有一定的稳定程度。
只有这样，才能不致因系统参数的小范围漂移而导致系统性能变差甚至不稳定。
对于一个最小相角系统而言，)(ωj G 曲线越靠近点（0,1j −），系统阶跃响应的振荡就越强烈，系统的相对稳定性就越差。
因此，可用)(ωj G 曲线对点（）的接近程度来表示系统的相对稳定性。
通常，这种接近程度是以相角裕度和幅值裕度来表的。
0,1j −相角裕度和幅值裕度是系统开环频率指标，它们与闭环系统的动态性能密切相关。
1．相角裕度相角裕度是指开环幅相频率特性)(ωj G 的幅值1)()(==ωωj G A 时的向量与负实轴的夹角，常用希腊字母γ表示。
图5-47 相角裕度和幅值裕度的定义 图 5-48 稳定裕度在Bode 图上的表示在G 平面上画出以原点为圆心的单位圆，见图5-47。
)(ωj G 曲线与单位圆相交，交点处的频率c ω称为截止频率，此时有1)(=c A ω。
按相角裕度的定义180()c γϕω=+o （5-69）由于01lg 20)(lg 20)(===c c A L ωω，故在伯德图中，相角裕度表现为dB L 0)(=ω处的相角)(c ωϕ与水平线之间的角度差，如图5-48所示。
上述两图中的o 180−γ均为正值。
2．幅值裕度)(ωj G 曲线与负实轴交点处的频率g ω称为相角交界频率，此时幅相特性曲线的幅值为)(g A ω，如图5-47所示。
幅值裕度是)(ωj G 与负实轴交点至虚轴距离的倒数，即1()g A ω，常用h 表示，即)(1g A h ω=（5-70）在对数坐标图上20lg 20lg ()()g g h A L =−ω=−ω （5-71）即的分贝值等于h )(g L ω与之间的距离（下为正）。
伯德图分析稳定性及幅值和相角裕度共52页
16、业余生活要有意义，不要越轨。——华盛顿 17、一个人即使已登上顶峰，也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人，而用人最大的突破在于信任人。——马云 19、自己活着，就是为了使别人过得更美好。——雷锋 20、要掌握书，莫被书掌握；要为生而读，莫为读而生。——布尔沃
1、不要轻言放弃，否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意 去做，并愿意去冒险的人。“稳妥”之船，从未能从岸边走远。-戴尔．卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡，喝起来是苦涩的，回味起来却有 久久不会退去的余香。
伯德图分析稳定性及幅值和相角裕度 4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失 去今生对你的记忆，我不求天长地久的美景，我只要生生世世的轮 回
控制系统的伯德图分析——自动控制原理
() 0
伯德图
c
GMb>0
g
PM>0 Kg>1
PM -180
稳定闭环系统的GM和PM
奈氏图 jIm
L()
伯德图
c 1
0 GMb<0
c
ReΒιβλιοθήκη PM()0g
1
PM<0 Kg
-180
PM
Kg<1
不稳定闭环系统的GM和PM
GM，PM常作为控制系统的频域设计指标。
GM，PM大表明相对稳定性好,但响应速度低。 GM，PM小表明相对稳定性差,但响应速度高。 过大或过小都不好，较好的经验值为：
0时有低频渐近线方程
L( ) 20 lg K 20 lg K p
1
斜率=0， 与实轴无交点。
T
(2) N=1 (1型系统)
G( j)H ( j) K j (Tj 1)
L( ) 20 lg K 20 lg 20 lg T 2 2 1
0时有低频渐近线方程
L( ) 20 lg K 20 lg 20 lg K v 20 lg
斜率=-40 db/dec，交点: K a
L ()
1 T
Ka
-40db/dec
1
T Ka
L ()
1 T
Ka
-40db/dec
1
Ka
T
三、 伯德图与稳态误差的关系
表5-2 系统类型和低频渐近线特征
系统类型 斜率
0
0
1 -20
2 -40
L(=1) 与L=0的交点
20 lg K无p 交点
20 lg Kv
Kv
20 lg K a
Ka
斜率=-20 db/dec，交点: =Kv
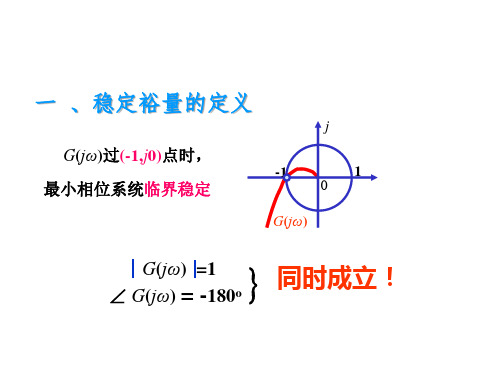
伯德图
c
GMb>0
g
PM>0 Kg>1
PM -180
稳定闭环系统的GM和PM
奈氏图 jIm
L()
伯德图
c 1
0 GMb<0
c
ReΒιβλιοθήκη PM()0g
1
PM<0 Kg
-180
PM
Kg<1
不稳定闭环系统的GM和PM
GM，PM常作为控制系统的频域设计指标。
GM，PM大表明相对稳定性好,但响应速度低。 GM，PM小表明相对稳定性差,但响应速度高。 过大或过小都不好，较好的经验值为：
0时有低频渐近线方程
L( ) 20 lg K 20 lg K p
1
斜率=0， 与实轴无交点。
T
(2) N=1 (1型系统)
G( j)H ( j) K j (Tj 1)
L( ) 20 lg K 20 lg 20 lg T 2 2 1
0时有低频渐近线方程
L( ) 20 lg K 20 lg 20 lg K v 20 lg
斜率=-40 db/dec，交点: K a
L ()
1 T
Ka
-40db/dec
1
T Ka
L ()
1 T
Ka
-40db/dec
1
Ka
T
三、 伯德图与稳态误差的关系
表5-2 系统类型和低频渐近线特征
系统类型 斜率
0
0
1 -20
2 -40
L(=1) 与L=0的交点
20 lg K无p 交点
20 lg Kv
Kv
20 lg K a
Ka
斜率=-20 db/dec，交点: =Kv
16第十六讲伯德图分析-稳定性-及幅值和相角裕度
转折频率: ω =1( 两次), ω =5 (零), ωn=2 (二 阶系统的转折频率).
1 n 4 2
0.25
将在以下频率范围内画出伯德图：
0.1 100
1.25K 0 dB
画出每一个环节的增益和相位曲线
0.01 40
0.1
1.0
10
M db
20
0
-20
伯德图中的增益裕度和相角裕度伯德图中的增益裕度和相角裕度dblg20lg20相位裕度是使相角曲线向下移动直到增益和相角穿越点发生在同一频率时的纯相角滞后量
线性控制系统工程
第16章 伯德图分析，稳定性， 及幅值和相角裕度
第16章 伯德图分析,稳定性 及幅值和相角裕度
伯德图中的增益裕度和相角裕度
M ( pc)
6 20 lg 2 K 20 lg 2 20 lg K K dB 6 20 lg 0.5K 20 lg 0.5 20 lg K K dB
• 考虑下面的例子： K GH s s1 2s 1 3s K=0.1
转折频率为 1, 0.5, 0.34
g c
(g c)
(g c)
GM
PM 180 gc GM db 20 lg 1
Kc 1 K M pc 20 lg M pc
M pc
条件稳定
• 改变增益的作用是使幅值曲线上下平 移，而相角曲线不变。 如果 20 lg K K dB 那么
画出当 K=0.8时系统的伯德图， 并确定 增益裕度和相位裕度。 使系统的相位裕 度约为 60º 的K为何值? 解:
5K 1 s / 5 1.25K 1 s / 5 GH s 2 4s1 s 1 s / 4 s / 4 s1 s 1 s / 4 s 2 / 4 2
稳定裕度专题知识讲座
G( j0) = K j0
G( j) = 0 j0
Imag Axis
1.5
1
0.5
0
-0.5
-1
-1.5
-1
-0.5
T1 = 1,T2 = 2,T3 = 3, K = 2
0
0.5
1
1.5
2
Real Axis
Imag Axis
1.5
1
0.5
0
-0.5
-1
-1.5
-1
-0.5
T1 = 1,T2 = 2,T3 = 3, K = 2
0
0.5
1
1.5
2
Real Axis
G( jw) =
K
[T1T2 ( jw)2 T2 jw 1](T3 jw 1)
展开
？与负实
轴旳交点
=
K
T1T2T3 ( jw)3 (T1T2 T2T3 )( jw)2 (T2 T3 ) jw 1
=
K
1 T2 (T1 T3 )w 2 (T2 T3 T1T2T3w 2 ) jw
为了得到满意旳性能，相位裕度应该在 30与60 之间，
增益裕度应该不小于6分贝。
【例5-5-1】研究经典二阶系统旳相角裕度。
（1）写出开环频率特征
G( jw) =
w
2 n
=
jw( jw 2wn ) w
w
2 n
w 2 4
w2 2 n
arctg
w 2w n
90
（2）根据定义拟定截止频率
G( jwc ) = 1
在 GH 平面旳映象若穿过( -1, 0 ) ，意味着闭环有极点在虚轴上。若某–s 线穿过( -1, 0 ) 点，则意味着闭环有极点在–s 线上。用一样措施，也能够
相位裕度 增益裕度
相位裕度增益裕度
相位裕度和增益裕度是电路稳定性分析中非常重要的指标。
它们分别
表示了电路输出信号的相位和增益与输入信号之间的差异，也就是说，它们衡量了电路对输入信号变化的响应能力。
一、相位裕度
相位裕度是指系统在增益等于1时，输出信号的相位与输入信号之间
的差异。
在Bode图中，相位裕度可以通过从幅频曲线上找到交点并
测量其左侧位置来计算。
具体来说，如果系统的幅频曲线在增益等于1时与负实轴之间有90度的距离，则该系统具有45度的相位裕度。
相位裕度越大，系统越稳定。
这是因为当系统受到外部扰动时，它需
要能够快速响应并保持输出信号与输入信号之间的相对位置。
如果相
位裕度不足，则可能会发生震荡或不稳定现象。
二、增益裕度
增益裕度是指系统在输出信号达到最大值前可承受多少衰减。
在Bode 图中，增益裕度可以通过从幅频曲线上找到交点并测量其右侧位置来
计算。
具体来说，如果系统的幅频曲线在相位裕度为45度时与-20dB
的水平线相交，则该系统具有20dB的增益裕度。
增益裕度越大，系统越稳定。
这是因为当系统受到外部扰动时，它需要能够快速响应并保持输出信号与输入信号之间的比例关系。
如果增益裕度不足，则可能会发生失真或不稳定现象。
综上所述，相位裕度和增益裕度都是电路稳定性分析中非常重要的指标。
它们可以用来衡量电路对输入信号变化的响应能力，并帮助工程师设计更加稳定和可靠的电路。
在实际应用中，工程师可以通过调整电路参数或使用反馈控制等技术来改善相位裕度和增益裕度，从而提高电路的性能和可靠性。
相角裕度幅值裕度PPT课件
(x ) 9 0 a 0r x a c0 r t . 1 x a c 1 t n 0 8 a x 3 0 . 1 n r s a 6
5
5
5
h 2 l0 g x1 x 21 0 .0 1 •x 2 2 l0 g x0 x 2 2 l3 0 g .1 2 6 6 .0 d 2
低低低
3
100 200
4
400 1000
lg rad
s
-40
低 低 低 -60
-
17
5-5 从开环频率特性研究闭环系统性能
▪低频段
低频段取决于开环增益和开环积分环节的数目; 开环对数幅频特性在第一个转折频率以前的频段; 低频段决定了系统的稳态精度。
▪中频段
指开环幅相特性曲线在截止频率 c 附近的频段。
G(j) =1
-1
∠ G(j) = -180o G(j)
0
同时成立！
此时，截止频率等于穿越频率
=0+
G(j)j(jT 1K 1)(jT 21)
1 =0
幅值裕度: hdB=－20lgG(jx)
c
0dB
20lg G(jx )
c
x
∠ G(jc)
-180o
相角裕度: =1800+ ∠ G(jc)
稳定裕度的定义续2
计算K=20：由图读出相位裕量和幅值裕量 辅助计算
20 20 20
A ()
1 ,
1 21 0 .02 11 2 0 2
c2
1 0 8 9 0 a 0 0 r 2 a c 0 0 . r 1 • t 2 c a 9 0 t 0 n 7 a . 0 4 0 n 2 7 . 1 0 4 1 . 5 0
伯徳图的画法和在判稳中的应用
例：开环特征方程有两个右根，P=2，试判定闭环系统的稳定性。 解：
P=2
正负穿越数之差（N+-N-）为1
Z=P-2N=2-2=0 系统闭环稳定
例：开环特征方程无右根，P=0，试判定闭环系统的稳定性。 解：
P=0
正负穿越数之差为0
系统闭环稳定
§ 5.4 稳定裕度
♣ ♣ ♣
K值较小时，系统稳定； K值较大时，系统不稳定的； K取某个值时，Nyquist曲线通过 (-1,j0)点，系统处于临界稳定状态。
c ——Nyquist曲线与单位圆交点处(此处幅值为1）的 称为 截止频率(又称剪切频率)，记为 c 。
G( jωc ) H ( jωc ) 1
相角裕度 180 G( jc ) H ( jc ) 含义：如果系统对频率为截止频率的信 号的相角滞后再增大 度，则系统处于临界 稳定状态。稳定系统的 > 0 , 越大,系统相 对稳定性越高。
(5) 系统开环对数相频特性表达式为
( ) arctan0.5 900 arctan arctan0.05
逐点计算结果
系统开环相频特性数据
－20dB/dec
20
－20dB/dec －40dB/dec －40dB/dec
例：
L(1) 20lg 7.5 17.5
2. Bode图上的稳定判据
闭环系统稳定的充要条件是：当ω 由0变到 +∞ 时，在开环 对数幅频特性 L(ω)≥0 的频段内，相频特性φ(ω) 穿越-π线的次 数（正穿越与负穿越次数之差）为p/2，p为s平面右半部的开 环极点数。 若开环传递函数无极点分布在S右半平面，即 P 0 ， 则闭环系统稳定的充要条件是：在L(ω)≥0 的频段内，相频 特性φ(ω) 在-π线上正负穿越次数代数和为零，或者不穿越 -π线 。 Nyquist图 Bode图
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
M db
0db GM
1800
PM
图.16.3 增益裕度和相位裕度
log10 log10
系统的型和从伯德图得到 稳态误差
一般开环传递函数
G s H s K n b 1 1 s s // p z 1 1 1 1 s s / /p z 2 2 1 1 s s / /z p m k
GM Kc K
GdM B 2l0 g K c2l0 g K
伯德图中的相位裕度： - 相位裕度是使相角曲线向下移动 直到 增益和相角穿越点发生在同一频率时 的纯相角滞后量 。 - 在图16.1中
PM54
▽ 在伯德图中获得增益裕度和相位裕 度:
增益裕度是通过相角穿越频率得出的。 它是该频率处的幅值分贝值与0dB线之间 的差值(用分贝表示) 。 相角裕度是通过增益穿越频率得出的， 它是此频率处的相角与-180o线之间的差值。
获得最大值 Kmax=NK
1 1 2 0 l o g 1 0 N N 3 . 5 5 K 4 5 3 . 5 5 1 6 0
用劳斯阵列来验证结果： 特征方程为
( s 2 ) ( s 3 ) 2 K s 3 8 s 2 2 1 s 1 8 K 0
20lg M pc
条件稳定
• 改变增益的作用是使幅值曲线上下平 移，而相角曲线不变。
如果 那么
20lgKKd B
20lg 2K 20lg 2 20lg K KdB 6
20lg 0.5K 20lg 0.5 20lg K KdB 6
• 考虑下面的例子：
但相位裕度判断系统的确是不稳定的。
40
M db
0 -40
-80
0
-90 -180 -270
0.01
0.1
-60
GM1=K (db)
-40
1.0
10
K=1 GM2=K(db)
-20 -40
PM
图16.10 具有两个相位穿越点的系统
MATLAB 仿真
GH ss31 1s /1 s1 0 1s0 /1 s/1 0000
当 k > k1时， 系统是稳定的
Im
0
-1 Re
图.16.14 稳定系统的奈奎斯特图
例题 16.1
问题: 如图所示的系统， 画出当K=45时 的伯德图， 并确定增益裕度和相位裕度。 计算使系统稳定的最大K值， 并用劳斯阵 列验证其结果。
R
+
C
K
-
1 (s 2)(s 3)3
20lgNKKdBNdB
M db
－90 －180 －270
K3
Kc K2
log10
K1
Im
Kc
K2 K1
K3
Re
Im
－1 K1
Kc K2 K3
Re
图.16.2 具有变化K的系统伯德图、奈奎斯特图和根轨迹
在相位-180°时， K dB 幅值约为 – 18dB， 如果系统不稳定：
K=0.1
GH ss12sK13s
转折频率为 1, 0.5, 0.34
• 奈奎斯特稳定性判据：
当相角为-180o时，如果系统幅值小于或等 于1，那么这个系统是稳定的。
在伯德图中， 单位幅值对应于 MdB=0。 例子中: 相位为-180°时， 幅值约为 – 18dB ，因此系统是稳定的。
线性控制系统工程
第16章
伯德图分析，稳定性， 及幅值和相角裕度
第16章 伯德图分析,稳定性 及幅值和相角裕度
伯德图中的增益裕度和相角裕度
M ( pc)
g c
(g c)
(g c)
GM Kc
1
KM pcຫໍສະໝຸດ PM 180 gc
1
GMdb 20lg M pc
2 1 0.25 n 4
将在以下频率范围内画出伯德图：
0.1100
1.2K 50dB
画出每一个环节的增益和相位曲线
0.01
0.1
1.0
10
40
M db
20
0
-20 -40
0
-90
-180
-270
图16.2.1
0.01
0.1
1.0
10
40
M db
20
0
3db
GM=3db
-20 -40
0
-180
-360
PM=60
图16.2.2
二阶环节
频率比=ω/ ωn 频率比=ω/ ωn
增益裕度为 3 dB，相位裕度约为35º。 为了给系统提供一个 60º的相位裕度，幅 值曲线需要下平移约3dB
20 lg NK K dB N dB 3 20 lg N N 0.7 K 0.7 0.8 0.56
Mdb= 0dB线。
M db
-20db/decade
20log10 Kv
1800
图.16.5
1
1型系统的伯德图
log10
Kv的值可以通过测量在ω =1处的增益 来获得。如果其他环节在频率ω =1之前作 用于对数幅频特性， 那么应该用低频渐近 线的延长线求出。
M db
-20db/decade
20
M db
0 -20
-40
0.1
1
10
100
GM
0
-90
-180
-270
PM
图.SP16.1.2
MATLAB 仿真
GH ss24 s53211s2 .5 11s2
2 3
sys=tf([45],[1 8 21 18]); bode(sys) pause
sys=tf([0.1 1.1 1],[0.00001 0.011 1 0 0 0]); bode(sys) pause
用根轨迹来验证：
在k<k1时， 系统是不稳定的； 在 k1<k<k2时， 系统是稳定的； 在 k>k2时， 系统再次不稳定。
GM 1 K1db GM 2 K 2db
K=K2 Im
解:
G s H 4 s 1 5 s K 1 1 s s /4 /5 s 2 /4 s 1 1 s .2 1 K s 1 / 5 4 s / s 5 2 /4 2
转折频率: ω =1( 两次), ω =5 (零), ωn=2 (二 阶系统的转折频率).
K=K1
-1000
-100
-10
-1
K=1 Re
3 poles
图.16.11 系统的根轨迹图
单一频率穿越点: 增加相位 考虑下面的例子
GHs1ss3/22
相位裕度是负的，表明系统是不稳定的。 增益裕度是正的，表明系统是稳定的。 考虑相位裕度，系统是稳定的。
40
M db
0 -40
-40
0.01
0.1
1.0
10
40
M db
20
增益穿越点
0
-20 -40
0
-90
-180
-270
相位穿越点
图16.1 例子系统的伯德图
增加K 将使幅值曲线向上平移动，从 而使幅值穿越点向右移。但是相角穿越点 保持不变。 系统最终处在临界不稳定点上。 ▽ 计算临界不稳定时系统的幅值。
20lgNK20lgK20lgN
0.01
0.1
1.0
10
40
M db
20
0
K=1
-20
-40
0
-90
-180
-270
图16.8 无相位穿越点的伯德图
MATLAB 仿真
GH ss211ss/10
sys=tf([1 1],[0.2 1 0 0]); bode(sys) pause
用根轨迹来验证： Im
Re
0 18 N dB K c NK 0 .794
NdB20lgN18 N7.94
这个结果接近于先前分析的结果 K=0.832. 误差是由伯德图的相角曲线 用直线近似引起的。
伯德图中的增益裕度和相角裕度
伯德图中的增益裕度
增益裕度 (用分贝表示)为 Kc 的分贝值 与增益K的分贝值之差。
M db
-40db/decade
20log10 Ka
1
图.16.7 2 型系统的伯德图
log10
进一步讨论增益裕度和相位裕度
相角裕度是确定系统稳定性的唯一可靠 的参数。
无频率穿越点： - 考虑下面的例子 GH ss2K 11 s/s10
- 相角绝不会穿过 -180º线。 但是相位裕 度可以从增益穿越点 PM=45º处获得， 系统是稳定的。
20log10 Kv
log10
1
图.16.6 1 型系统的另一种伯德图
2型系统
GHs
Kb s2
GH
j
Ka
j2
如果 ka=1。对数幅频特性在当ω =1时，其低频段或它的延长线会以– 40db/decade 的斜率穿过 零分贝线 。
Ka 的值可以通过测量ω = 1 处的 增益值来获得。
作业： P339 16.1 a. P339 16.3 e.
Im K=K1
K=1
Re -2 2 zeroes 3 poles
图.16.13 系统的根轨迹图
通过伯德图判断稳定性的可靠方法是: - 如果系统有正的相角裕度，那么系统是