2013-2014南京市鼓楼区初一期中考试
2013-1014学年苏科版七年级上期中考试数学试题(含答案)

2013-2014学年度第一学期期中测试七年级数学试题一、用心选一选,将你认为正确的答案填入下表中。
(每题2分,共16分)1. 5的绝对值是( ) A. 51 B. 5- C. 5D. 5± 2.南京市某天最高气温8°C ,最低气温1-°C ,那么这天的日温差是( )A .7℃B .9℃C .9-℃D .7-℃3.下列等式不.成立..的是 ( )A.()55-=-+B.()5.05.0=--C. 33=--D. 632-=⨯-4.下列各组整式中,不属于...同类项的是 ( ) A .233m n 和232m n - B .xy 21-和2yx C .32和22 D .2x 和23 5.下列运算中,正确的是 ( )A .3a+2b=5abB .325=-y yC .222426xy xy xy =- D .-(a+b )+(c-d )=-a-b-c+d6.一天有86400秒,86400秒用科学计数法表示为 ( )A.41064.8⨯秒B.510864.0⨯秒C. 51064.8⨯秒D. 3104.86⨯ 秒7. 下面关于式子()43-的几个说法中,正确的是 ( ) A .(—3)是底数,4是幂 B .3是底数,4是幂C .3是底数,4是指数D .(—3)是底数,4是指数8.若A=x 2-5x +2,B=x 2-5x-6,则A 与B 的大小关系是 ( )(A )A>B (B )A=B (C )A<B (D )无法确定二、细心填一填:(每题2分,共20分) 9. 135-的相反数是________. 10. 某工厂5月生产机床n 台,6月比5月增产10%,则6月生产机床 台,11. 在数轴上,与表示-3的点相距6个单位长度的点所表示的数是_________12. ()()______2132009=-⨯- 13.若24b a m 与222--n b a 是同类项,则______3=-n m .14.一个两位数的个位数字为a ,十位数字比个位数字大2,这个两位数为_ _ .15. 已知5=x ,3=y 且0>xy ,则y x +=____ ____.16.观察:1234111111113355779a a a a =-=-=-=-,,,,…, 则n a = (n 为正整数).17. 如图,在宽为m 30,长为m 40的矩形地面上修建两条宽 (17题图)都是m 1的道路,余下部分种植花草.那么,种植花草的面积为 2m .18. 有一个运算程序,可以使:x y n ⊕=(n 为常数)时,(1)1x y n +⊕=+,(1)2x y n ⊕+=-.现在已知112⊕=,那么20102010______⊕=.三、耐心做一做(共84分)19.计算:(每小题3分,共12分)(1)7149)7(35⨯--÷- (2) []34)1(4511--⨯+- (3)(21—95+127)×(—36) (4) ()22121(2)73233⎡⎤---÷⨯--⎣⎦23. (本题6分) 已知一个多项式A 减去22xy x +-的3倍得到24x -,(1)求这个多项式A.(2)若21(2)0x y-++=,求A的值.24.(本题6分)谭维维、老狼等明星在今年的瓜洲国际音乐节上进行表演,市文化局策划本次活动,在与单位协商团购票时推出两种方案.方案一:若单位赞助广告费6000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)方案二:直接购买门票若不超过100张,票价为120/张;如果超过100张,则票价为100/张.设购买门票数为x(张),总费用为y(元).(1)方案一中,总费用y= ;方案二中,当0≤x≤100时,总费用y= ;当x>100时,总费用y= .(2)如果某单位购买本次音乐节门票200张,那么选择哪一种方案可使总费用最省?请说明理由.25.(本题8分)有理数a、b、c在数轴上的位置如图(1)判断正负,用“>”或“<”填空: b-c 0; b-a 0; a+c 0.(2)化简: |b-c|+|b-a|+|a+c|26.(本题8分)要建一个如下图所示的长方形养鸡场(分为两个区域),养鸡场的一边靠着一面墙,另几条边用总长为a m的竹篱笆围成,每块区域的前面各开一个宽1m的门.(1)如果a=26,AB=CD=5,那么AD= m.(2)如果AB=CD=b m,求AD的长,并用字母表示这个长方形养鸡场的面积. (要求:列式后,再化简)27.(本题10分) A 、B 两个果园分别有苹果30吨和20吨,C 、D 两城市分别需要苹果35吨和15吨;已知从A 、B 到C 、D 的运价如下表:(1)若从A 果园运到C 城的苹果为x 吨,则从A 果园运到D 城的苹果为____ 吨,从A 果园将苹果运往D 的运输费用为____ 元.(2)用含x 的式子表示出总运输费.(要求:列式后,再化简)28. (本题10分)根据下面的材料解答问题:已知点A 、B 在数轴上分别表示有理数a 、b ,则数轴上A 、B 两点之间的距离b a AB -=.(1)如果a>b,那么b a AB -== ;如果a<b,那么b a AB -== .(2)如果a=5, b=-2, 则AB= ;(3)数轴上从左到右...等距排列着点A 1、A 2、A 3、…、A 2010等共2010个整数点,它们表示的整数分别记作a 1、a 2、a 3、…、a 2010,且a 1、a 2、a 3、…、a 2010为连续整数.①求点A 2010到点的距离A 1;②已知a 13=-8,求a 1、a 2008的值;2013-2014 学年度第一学期期中质量检测七年级数学试题答案= -1+1 =0 ………………4分(3)解:原式=21×(-36)-95 ×(-36)+127×(-36)………2分 =-18+20-21=-19………………4分 (4)解:原式=4-61×3×(7-9)………3分 =4+1=5………………4分20、(1)解:原式=x-3x+7 +8x-28 ………………3分=6x-21 ………………5分(2)解:原式=2ax+6x 2 -14-6x 2+3ax-9 …………3分=5ax-23 ……………5分21、解:原式= x 2 -x 2+3xy+2y 2-2x 2+2xy-4y 2 …………2分=-2x 2+ 5xy -2y 2 …………4分当x=-1 y=2时 原式=-2+15-18=-5 …………6分22、 (1) 保洁结束时回到学校东大门.-1+0.8+3+1-0.6-1.2-2 …………2分=0 …………3分(2)4; …………5分(3) (|-1|+|0.8|+|3|+|1|+|-0.6|+|-1.2|+|-2|) ×0.5 …………7分=4.8(h) ………………8分23、解:A=x 2-4+3(2+xy- x 2)……………2分=x 2-4+6+3xy-3 x 2………………4分=2+3xy-2x 2………………6分当x=1 y=-2时 原式=2-6-2=-6 ………………8分24、(1)6000+5x ;120x;100x. …………6分(2)方案一:y=6000+50×200=16000………8分方案二:y=100×200=20000所以,方案一费用最省。
2013年鼓楼区七年级期中考试(数学) (1)

▲
23 (用“>” “<” “=”连接) . 7
9.用代数式表示“ m 与 n 积的平方” : 10.计算: a 2b ( ▲ ) a 2b .
▲
.
11.用字母表示初中阶段学过的 1 个数学公式、运算法则或运算律:
▲
.
12.已知代数式 x 2 y 的值是 3,则代数式 2 x 4 y 1 的值是 13.写出一个解为 x 4 的一元一次方程: ▲ . 14.按图中程序计算,若输入-3,则最后输出的结果是 ▲
② AC C 1
C 1 3 c 5
CB C 5
零点分段 c 1 和 c 5 当 C 1 时 (C 1) 3[(c 5)] ∴ C 1 3 C 5 C 1 3C 15 ∴ 2C 16 无解. 当 1≤ C ≤ 5 时 C 1 3(C 5)
20. (6 分)有 20 筐白菜,以每筐 25 千克为标准质量,超过标准质量的千克数记为正数,不足标准质 量的千克数记为负数,记录如下: 偏差/千克 筐数 -3 1 -2 4 -1.5 2 0 3 1 2 2.5 8
(1)这 20 筐白菜中ห้องสมุดไป่ตู้最重的一筐比最轻的一筐要重多少千克? (2)与标准质量比较,这 20 筐白菜总计超过或不足多少千克? (3)若白菜每千克售价 2.6 元,则出售这 20 筐白菜可卖多少元?
▲ .
.
输入
×3
-(-4) 否 <-5 是 输出
15.某市出租车的收费标准是:起步价为 8 元,起步里程为 3 千米(3 千米以内按起步价付费) ,3 千 米后每千米收 2 元.某人乘出租车从甲地到乙地共付费 16 元.求甲、乙两地的路程.若设甲、乙两地 的路程为 x 千米,则列方程 为 ▲ . ... 16.同样大小的黑色棋子按下图的方式摆放,第( n )个图需棋子 ▲ 枚.
鼓楼区2013-2014学年度第一学期期中七年级(上)期中试卷数学参考答案

原式=-3(-a2+4ab-2b2)
=3a2-12ab+6b2……………………………4分
19.(7分)
(1)………………………2分
(2)解:去分母,得3(5x+1)=4(2x-1)-4…………………………………3分
去括号,得15x+3=8x-4-24………………………………………4分
移项,得15x-8x=-3-4-24…………………………………………5分
10.-2a2b11.答案不唯一12.-713.答案不唯一
14.− 1115.8+2(x-3)=1616.3n+3
三、解答题(本大题共12小题,共68分)
17.(12分)
(1)解:-6+(-) +9-(-0.75);
=-6-+9+0.7……………………………………………3分
(2)解:(-2)3-32
=-8-9………………………………………………………………2分
=-17………………………………………………………………3分
(3)解:(+-)×(-36);
=-18-30+21………………………………………………………………2分
=-37………………………………………………………………3分
(2)当m=4,n=3,a=1,b=2时,
mn-πa2-bm+2ab
=12-3-8+2×2……………………………………………………5分
=5.……………………………………………………6分
22.(8分)
(1)原点…………………………………………………………1分
(2)①它本身;它的相反数;……………………………………………………………3分
南京鼓楼实验学校七年级上册历史期中试卷及答案

南京鼓楼实验学校七年级上册历史期中试卷及答案一、选择题1.下列有关我国夏、商、周三代兴亡的叙述不正确的是()A.启建立了夏朝B.汤灭夏建立商朝C.周平王迁都洛邑,建立东周D.周武王建立周朝,史称西周2.佛教西汉末年传入我国后,很快受到封建统治者的积极提倡和扶植。
其根本原因是A.一些封建贵族信奉佛教B.对我国文化的发展有深远影响C.虔诚地信佛来世就可以得到幸福D.有利于统治人民3.以下关于秦汉时期领先世界的科学技术和文化的叙述,错误的是A.东汉时期,蔡伦发明了造纸术,推动了人类文明的进步B.汉代,华佗发明了全身麻醉药剂“麻沸散”,这是世界医学史上的创举C.东汉时期的张仲景被后人尊为“医圣”D.佛教通过丝绸之路传入中国,在东汉明帝时得到上层统治阶级的扶持。
4.东汉后期,政治统治的突出特点是()A.皇帝专权B.宦官专权C.外戚专权D.外戚和宦官交替专权5.春秋战国时期社会急剧变化,主要指()A.诸侯争霸B.生产力飞跃C.社会制度更替D.思想大解放6.距今约170万年,生活在我国云南的远古人类是A.元谋人B.北京人C.半坡人D.河姆渡人7.周平王东迁后,直接管辖的地区仅在洛邑一带。
诸侯国各自为政,不再听从王命,不再定期向天子纳贡,周王室甚至要依赖诸侯国的经济支持。
这主要反映出A.诸侯国“尊王攘夷”的策略B.周王室衰微的政治局面C.春秋时期大规模的兼并战争D.春秋时期社会动荡局面8.下图是船型彩陶壶。
下列表述与图片无关(错误)的是 ( )A.当时已有较高的制陶技术B.当时人们已经掌握了造船技术C.印证了当时的文明程度D.证明了船就是黄帝的发明9.以下早期人类中,最早懂得人工取火的远古人类是()A.元谋人B.北京人C.蓝田人D.山顶洞人10.这是迄今所知世界上内涵最丰富,材料最齐全的直立人遗址,这个遗址是()。
A.山顶洞人遗址B.元谋人遗址C.半坡人遗址D.北京人遗址11.战国时期,百家争鸣有力地促进了当时思想文化和社会的发展。
南京市鼓楼区年七年级下期中数学试卷及答案
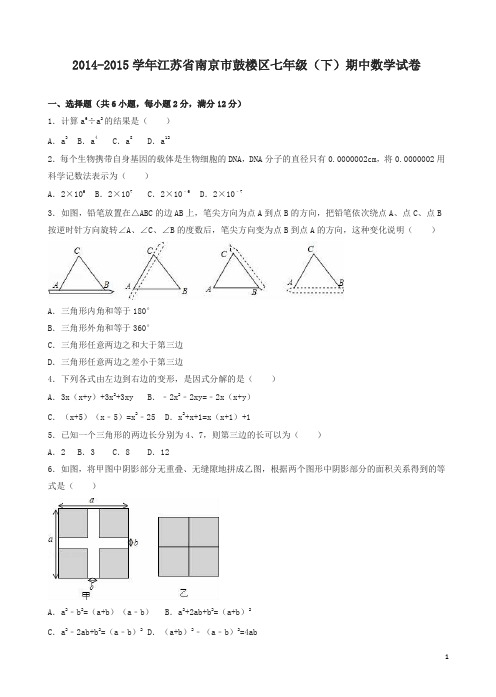
2014-2015学年江苏省南京市鼓楼区七年级(下)期中数学试卷一、选择题(共6小题,每小题2分,满分12分)1.计算a6÷a2的结果是()A.a3B.a4C.a8D.a122.每个生物携带自身基因的载体是生物细胞的DNA,DNA分子的直径只有0.0000002cm,将0.0000002用科学记数法表示为()A.2×106B.2×107C.2×10﹣6D.2×10﹣73.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B 按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明()A.三角形内角和等于180°B.三角形外角和等于360°C.三角形任意两边之和大于第三边D.三角形任意两边之差小于第三边4.下列各式由左边到右边的变形,是因式分解的是()A.3x(x+y)+3x2+3xy B.﹣2x2﹣2xy=﹣2x(x+y)C.(x+5)(x﹣5)=x2﹣25 D.x2+x+1=x(x+1)+15.已知一个三角形的两边长分别为4、7,则第三边的长可以为()A.2 B.3 C.8 D.126.如图,将甲图中阴影部分无重叠、无缝隙地拼成乙图,根据两个图形中阴影部分的面积关系得到的等式是()A.a2﹣b2=(a+b)(a﹣b)B.a2+2ab+b2=(a+b)2C.a2﹣2ab+b2=(a﹣b)2 D.(a+b)2﹣(a﹣b)2=4ab二、填空题(共10小题,每小题2分,满分20分)7.计算3﹣2的结果是 .8.计算:(﹣2xy 2)3= .9.已知a m =4,a n =5,则a m+n 的值是 .10.多边形的每个外角的度数都等于45°,则这个多边形的边数为 .11.把方程4x ﹣y=3写成用含x 的代数式表示y 的形式为y= .12.如图,把等腰直角三角尺的直角顶点放在直尺的一边上,则∠1+∠2= .13.二元一次方程的一个解是,这个二元一次方程可以是 .14.已知x+y=5,xy=3,则(x ﹣y )2= .15.如图,∠1=70°,∠2=130°,直线m 平移后得到直线n ,则∠3= .16.前n (n >3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x 1,x 2,x 3,…,x n ,将卡片上的数先平方再求和,得x 12+x 22+x 32+…+x n 2=28,将卡片上的数先立方再求和,得x 13+x 23+x 33+…+x n 3=4,则x 14+x 24+x 34+…+x n 4的值是 .三、解答题(共10小题,满分68分)17.计算:(1)(5﹣3)0﹣()﹣3(2)﹣a 2•(﹣6ab )(3)x (y+5)+y (3﹣x )(4)(2a+b )(2a ﹣b )﹣(a ﹣3b )2.18.把下列各式因式分解:(1)4x2﹣6xy(2)a2(x+y)﹣b2(x+y)(3)(a2+1)2﹣4a2.19.解方程组.20.已知△ABC.(1)平移△ABC,使点A移到点A1的位置,画出平移后得到的△A1B1C1;(2)根据平移的性质,写出两条不同类型的正确结论.21.如图,∠A=∠F,∠C=∠D,判断BD与CE的位置关系,并说明理由.22.根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等).(1)如图①,测量△ABC的面积;(2)如图②,平分△DEF的面积.23.如图,△ABC的角平分线BP、CP相交于点P,∠P=140°,求∠A的度数.24.当abc≠0时,要说明(a+b+c)2≠a2+b2+c2不成立,下面三位同学提供了三种不同的思路(1)小明说,“不妨设a=1,b=2,c=3,通过计算能发现式子不成立”,请你完成他的说理过程;(2)小刚说,“根据整式乘法的运算法则,通过计算能发现式子不成立”,请你完成他的说理过程;(3)小丽说,“构造正方形,通过计算面积能发现式子不成立”.请你帮她画出图形,并完成说理过程.25.如图,在一张长方形纸片ABCD中,AB=3,AD=m,边AB的中垂线分别交于AB、CD于点E、F;在边BC上取一点H(即AH为折痕),使得△ABH沿AH折叠后点B恰好落在线段EF上,设为点G.(1)按上述描述画出图形(要求尺规作图,不写作法,保留画图痕迹);(2)求证:△ABG是等边三角形;(3)若要使图形折叠后点A、G、C在一直线上,试求m的值.26.数与形都是数学研究的对象,它们有着密切的联系,我们可以利用图形对整式乘法和因式分解进行研究(1)计算(a+b)(a+2b).小丽的操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C型纸片是边长为b的正方形;②用①中的纸片拼成两边长分别为a+b、a+2b的长方形③数出用了A型纸片1张,B型纸片3张,C型纸片2张,得(a+b)(a+2b)=(2)分解因式a2+5ab+6b2小明的操作步骤如下:①准备若干块(1)中的A、B、C型纸片②用1块A型纸片,5块B型纸片和6块纸片拼成一个长方形③分别计算出长方形相邻两边的长,得a2+5ab+6b2=(3)计算(a+b)3请你仿照小丽的探究过程,写出操作步骤(4)分解因式a3+6a2b+12ab2+8b3请你仿照小明的探究过程,直接写出因式分解的结果.2014-2015学年江苏省南京市鼓楼区七年级(下)期中数学试卷参考答案与试题解析一、选择题(共6小题,每小题2分,满分12分)1.计算a6÷a2的结果是()A.a3B.a4C.a8D.a12【考点】同底数幂的除法.【分析】根据同底数幂的除法法则,同底数幂相除,底数不变,指数相减计算即可.【解答】解:a6÷a2=a6﹣2=a4.故选B.【点评】本题主要考查同底数幂的除法,熟练掌握运算性质是解题的关键.2.每个生物携带自身基因的载体是生物细胞的DNA,DNA分子的直径只有0.0000002cm,将0.0000002用科学记数法表示为()A.2×106B.2×107C.2×10﹣6D.2×10﹣7【考点】科学记数法—表示较小的数.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.000 0002=2×10﹣7,故选:D.【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.3.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B 按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明()A.三角形内角和等于180°B.三角形外角和等于360°C.三角形任意两边之和大于第三边D.三角形任意两边之差小于第三边【考点】三角形内角和定理.【分析】根据三角形的内角和定理解答即可.【解答】解:这种变化说明三角形的内角和是180°,故选A.【点评】此题考查三角形的内角和定理,关键是根据三角形的内角和定理是180°.4.下列各式由左边到右边的变形,是因式分解的是()A.3x(x+y)+3x2+3xy B.﹣2x2﹣2xy=﹣2x(x+y)C.(x+5)(x﹣5)=x2﹣25 D.x2+x+1=x(x+1)+1【考点】因式分解的意义.【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.【解答】解:A、是整式的乘法,故A错误;B、是把一个多项式转化成几个整式积的形式,故B正确;C、是整式的乘法,故C错误;D、没是把一个多项式转化成几个整式积的形式,故D错误;故选:B.【点评】本题考查了因式分解的意义,因式分解是把一个多项式转化成几个整式积的形式,注意因式分解与整式乘法的区别.5.已知一个三角形的两边长分别为4、7,则第三边的长可以为()A.2 B.3 C.8 D.12【考点】三角形三边关系.【分析】根据三角形的三边关系定理可得7﹣4<x<7+4,计算出不等式的解集,再确定x的值即可.【解答】解:设第三边长为x,则7﹣4<x<7+4,3<x<11,故选:C.【点评】此题主要考查了三角形的三边关系,关键是掌握第三边的范围是:大于已知的两边的差,而小于两边的和.6.如图,将甲图中阴影部分无重叠、无缝隙地拼成乙图,根据两个图形中阴影部分的面积关系得到的等式是()A.a2﹣b2=(a+b)(a﹣b)B.a2+2ab+b2=(a+b)2C.a2﹣2ab+b2=(a﹣b)2 D.(a+b)2﹣(a﹣b)2=4ab【考点】完全平方公式的几何背景.【分析】分别计算出甲、乙两图中阴影部分的面积,根据面积相等,即可解答.【解答】解:甲图中阴影部分的面积为:a2﹣2ab+b2,图乙中阴影部分的面积为:(a﹣b)2,所以a2﹣2ab+b2=(a﹣b)2,故选:C.【点评】本题考查了完全平方公式,解决本题的关键是分别计算出甲、乙两图中阴影部分的面积.二、填空题(共10小题,每小题2分,满分20分)7.计算3﹣2的结果是.【考点】负整数指数幂.【专题】计算题.【分析】此题考查的是负整数指数幂的计算方法,按照负指数为正指数的倒数进行计算即可.【解答】解:3﹣2==.故答案为.【点评】此题主要考查的是负整数指数幂,幂的负整数指数运算,先把底数化成其倒数,然后将负整数指数幂当成正的进行计算.8.计算:(﹣2xy2)3= ﹣8x3y6.【考点】幂的乘方与积的乘方.【分析】根据积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘;幂的乘方,底数不变指数相乘计算.【解答】解:(﹣2xy2)3,=(﹣2)3x3(y2)3,=﹣8x3y6.故填﹣8x3y6.【点评】本题考查积的乘方的性质,幂的乘方的性质,熟练掌握运算性质是解题的关键.9.已知a m=4,a n=5,则a m+n的值是20 .【考点】同底数幂的乘法.【分析】根据同底数幂的乘法,底数不变指数相加,可得答案.【解答】解:a m+n=m•a n=4×5=20,故答案为:20.【点评】本题考查了同底数幂的乘法,同底数幂的乘法底数不变指数相加.10.多边形的每个外角的度数都等于45°,则这个多边形的边数为8 .【考点】多边形内角与外角.【分析】多边形的外角和是360°,又有多边形的每个外角都等于45°,所以可以求出多边形外角的个数,进而得到多边形的边数.【解答】解:这个多边形的边数是: =8,故答案为:8.【点评】本题考查多边形的外角和,以及多边形外角的个数与其边数之间的相等关系.11.把方程4x﹣y=3写成用含x的代数式表示y的形式为y= 4x﹣3 .【考点】解二元一次方程.【专题】计算题;一次方程(组)及应用.【分析】把x看做已知数求出y即可.【解答】解:方程4x﹣y=3,解得:y=4x﹣3.故答案为:4x﹣3.【点评】此题考查了解二元一次方程,解题的关键是将x看做已知数求出y.12.如图,把等腰直角三角尺的直角顶点放在直尺的一边上,则∠1+∠2= 135°.【考点】平行线的性质.【分析】根据等腰直角三角形得出∠ACB=90°,∠A=∠B=45°,根据平行线性质求出∠1=∠ACM,根据三角形外角性质求出∠2=∠B+∠BCM,求出∠1+∠2=∠ACB+∠B即可.【解答】解:如图:∵△ACB是等腰直角三角形,∴∠ACB=90°,∠A=∠B=45°,∵EF∥MN,∴∠1=∠ACM,∵∠2=∠B+∠BCM,∴∠1+∠2=∠ACM+∠B+∠BCM=∠ACB+∠B=90°+45°=135°,故答案为:135°.【点评】本题考查了平行线的性质,等腰直角三角形,三角形的外角性质的应用,能求出∠1+∠2=∠ACB+∠B是解此题的关键,题目比较典型,难度适中.13.二元一次方程的一个解是,这个二元一次方程可以是2x+3y=13 .【考点】二元一次方程的解.【专题】开放型;一次方程(组)及应用.【分析】以2与3列出算式,即可确定出所求方程.【解答】解:根据题意得:2x+3y=13,故答案为:2x+3y=13.【点评】此题考查了二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.14.已知x+y=5,xy=3,则(x﹣y)2= 13 .【考点】完全平方公式.【专题】计算题;整式.【分析】原式利用完全平方公式化简,将已知等式代入计算即可求出值.【解答】解:∵x+y=5,xy=3,∴(x ﹣y )2=x 2﹣2xy+y 2=x 2+2xy+y 2﹣4xy=(x+y )2﹣4xy=25﹣12=13,故答案为:13【点评】此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.15.如图,∠1=70°,∠2=130°,直线m 平移后得到直线n ,则∠3= 20° .【考点】平移的性质;平行线的性质.【专题】计算题.【分析】如图,根据平移的性质得m ∥n ,则利用平行线的性质得∠DAB=180°﹣∠1=110°,再根据三角形外角性质可计算出∠ABC=130°﹣∠CAB=20°,然后根据对顶角的性质求解.【解答】解:如图,∵直线m 平移后得到直线n ,∴m ∥n ,∴∠1+∠DAB=180°,∴∠DAB=180°﹣70°=110°,∵∠2=∠CAB+∠ABC ,∴∠ABC=130°﹣110°=20°,∴∠3=∠ABC=20°.故答案为20°.【点评】本题考查了平移的性质把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.16.前n (n >3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x 1,x 2,x 3,…,x n ,将卡片上的数先平方再求和,得x 12+x 22+x 32+…+x n 2=28,将卡片上的数先立方再求和,得x 13+x 23+x 33+…+x n 3=4,则x 14+x 24+x 34+…+x n 4的值是 52 .【考点】有理数的混合运算. 【专题】探究型.【分析】根据题意可以设n 个数中含有a 个﹣2,b 个1,然后根据x 12+x 22+x 32+…+x n 2=28,x 13+x 23+x 33+…+x n 3=4,可以求得a 、b 的值,从而可以求得x 14+x 24+x 34+…+x n 4的值.【解答】解:∵前n (n >3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x 1,x 2,x 3,…,x n ,∴设这n 个数中,含有a 个﹣2,b 个1, ∵x 12+x 22+x 32+…+x n 2=28,x 13+x 23+x 33+…+x n 3=4,∴解得,∴x 14+x 24+x 34+…+x n 4=(﹣2)4×2+14×20=16×2+1×20=32+20=52. 故答案为:52.【点评】本题考查有理数的混合运算,解题的关键是明确题意,求出n 个数中﹣2和1的个数.三、解答题(共10小题,满分68分) 17.计算:(1)(5﹣3)0﹣()﹣3(2)﹣a 2•(﹣6ab ) (3)x (y+5)+y (3﹣x )(4)(2a+b )(2a ﹣b )﹣(a ﹣3b )2.【考点】整式的混合运算;零指数幂;负整数指数幂. 【分析】(1)根据零指数和负整数指数的意义运算; (2)根据同底数幂的乘法法则运算; (3)先去括号,然后合并即可;(4)先利用平方差公式和完全平方公式展开,然后合并即可. 【解答】解:(1)原式=1﹣27 =﹣26;(2)原式=2a 3b ; (3)原式=xy+5x+3y ﹣xy =5x+3y ;(4)原式=4a2﹣b2﹣(a2﹣6ab+9b2)=4a2﹣b2﹣a2+6ab﹣9b2=3a2﹣10b2+6ab.【点评】本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.18.把下列各式因式分解:(1)4x2﹣6xy(2)a2(x+y)﹣b2(x+y)(3)(a2+1)2﹣4a2.【考点】提公因式法与公式法的综合运用.【分析】(1)直接提取公因式2x,进而分解因式得出答案;(2)首先提取公因式(x+y),进而利用平方差公式分解因式得出即可;(3)直接利用平方差公式分解因式进而结合完全平方公式的应用分解因式即可.【解答】解:(1)4x2﹣6xy=2x(2x﹣3y);(2)a2(x+y)﹣b2(x+y)=(x+y)(a2﹣b2)=(x+y)(a+b)(a﹣b);(3)(a2+1)2﹣4a2=(a2+1+2a)(a2+1﹣2a)=(a+1)2(a﹣1)2.【点评】此题主要考查了提取公因式法以及公式法分解因式,正确应用乘法公式是解题关键.19.解方程组.【考点】解二元一次方程组.【专题】计算题;一次方程(组)及应用.【分析】方程组利用加减消元法求出解即可.【解答】解:,①+②得:4x=8,即x=2,把x=2代入①得:y=2,则方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.20.已知△ABC.(1)平移△ABC,使点A移到点A1的位置,画出平移后得到的△A1B1C1;(2)根据平移的性质,写出两条不同类型的正确结论.【考点】作图-平移变换.【分析】(1)根据图形平移的性质画出图形即可;(2)根据图形平移的性质可直接得出结论.【解答】解:(1)如图所示;(2)△ABC≌△△A1B1C1,AA1=BB1=CC1.【点评】本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.21.如图,∠A=∠F,∠C=∠D,判断BD与CE的位置关系,并说明理由.【考点】平行线的判定与性质.【分析】根据平行线的判定得出AC∥DF,根据平行线的性质求出∠C=∠CEF,求出∠D=∠CEF,根据平行线的判定得出即可.【解答】解:BD∥CE,理由是:∵∠A=∠F,∴AC∥DF,∴∠C=∠CEF,∵∠C=∠D,∴∠D=∠CEF,∴BD∥CE.【点评】本题考查了平行线的性质和判定的应用,能正确运用定理进行推理是解此题的关键,题目比较好,难度适中.22.根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等).(1)如图①,测量△ABC的面积;(2)如图②,平分△DEF的面积.【考点】作图—应用与设计作图.【分析】(1)计算三角形的面积需要知道三角形的底边长和高长,需要作出AB边上的高线,(2)三角形的中线平分三角形的面积,需要找出三角形,一边上的中点,故此可作出一边的垂直平分线得到一边的中点,然后作出中线即可.【解答】解:(1)如图①所示:过点C作AB的垂线.需要测量:AB和DC的长,.(2)如图②所示:作ED的垂直平分线,交ED于点G,连接GF.GF平分△DEF的面积.【点评】本题主要考查的是作图应用与设计,掌握五种基本作图以及三角形的中线平分三角形的面积是解题的关键.23.如图,△ABC的角平分线BP、CP相交于点P,∠P=140°,求∠A的度数.【考点】三角形内角和定理.【分析】根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形的内角和等于180°列式计算即可得解.【解答】解:∵△ABC,∴∠ABC+∠ACB=180°﹣∠A,∵∠ABC与∠ACB的角平分线相交于P,∴∠PBC+∠PCB=(∠ABC+∠ACB)=,在△PBC中,∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣=140°,∴∠A=100°.【点评】此题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.24.当abc≠0时,要说明(a+b+c)2≠a2+b2+c2不成立,下面三位同学提供了三种不同的思路(1)小明说,“不妨设a=1,b=2,c=3,通过计算能发现式子不成立”,请你完成他的说理过程;(2)小刚说,“根据整式乘法的运算法则,通过计算能发现式子不成立”,请你完成他的说理过程;(3)小丽说,“构造正方形,通过计算面积能发现式子不成立”.请你帮她画出图形,并完成说理过程.【考点】整式的混合运算.【分析】(1)把a、b、c的值代入,求出两边的值,即可得出答案;(2)根据多项式乘以多项式法则求出后,再判断即可;(3)化成边长为a+b+c的正方形,即可得出答案.【解答】解:(1)∵当a=1,b=2,c=3时,(a+b+c)2=(1+2+3)2=36a2+b2+c2=12+22+32=14,∴(a+b+c)2≠a2+b2+c2;(2)∵(a+b+c)2=(a+b+c)(a+b+c)=a2+ab+ac+ab+b2+bc+ac+bc+c2=a2+b2+c2+2ab+2bc+2ac,∴(a+b+c)2≠a2+b2+c2;(3)如图所示:(a+b+c)2=a2+b2+c2+ab+ac+bc+ab+ac+bc,即(a+b+c)2≠a2+b2+c2.【点评】本题考查了整式的运算法则的应用,能正确根据整式的运算法则进行化简是解此题的关键,也培养了学生的动手操作能力.25.如图,在一张长方形纸片ABCD中,AB=3,AD=m,边AB的中垂线分别交于AB、CD于点E、F;在边BC上取一点H(即AH为折痕),使得△ABH沿AH折叠后点B恰好落在线段EF上,设为点G.(1)按上述描述画出图形(要求尺规作图,不写作法,保留画图痕迹);(2)求证:△ABG是等边三角形;(3)若要使图形折叠后点A、G、C在一直线上,试求m的值.【考点】四边形综合题.【分析】(1)先根据基本作图的方法作出线段AB的垂直平分线EF,在EF上取一点G,使AG=AB,连结GH,则△AGH与△ABH关于AH成轴对称;(2)连接GB,由中垂线的性质就可以得出AG=BG,由轴对称的性质就可以得出AG=AB而得出结论;(3)由(2)的结论就可以得出∠CAB=60°,由勾股定理就可以求出BC的值,得出结论.【解答】解:(1)由题意作出图形,如图1.(2)如图2,连接GB,∵EF垂直平分AB,点G在EF上,∴AG=GB.∵△AGH与△ABH关于AH对称,∴△AGH≌△ABH,∴AG=AB,∴AG=AB=GB,∴△ABG是等边三角形;(3)如图2,∵△ABG是等边三角形,∴∠CAB=60°.∵四边形ABCD是矩形,∴∠ABC=90°.AD=BC=m,∴∠ACB=30°,∴AC=2AB.∵AB=3,∴AC=6.在Rt△ABC中,由勾股定理,得BC=9,∴m=9.【点评】本题考查了矩形的性质的运用,尺规作图的运用,垂直平分线的性质的运用,等边三角形的判定及性质的运用,轴对称的性质的运用,勾股定理的性质的运用,解答时证明三角形ABG是等边三角形是关键.26.数与形都是数学研究的对象,它们有着密切的联系,我们可以利用图形对整式乘法和因式分解进行研究(1)计算(a+b)(a+2b).小丽的操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C型纸片是边长为b的正方形;②用①中的纸片拼成两边长分别为a+b、a+2b的长方形③数出用了A型纸片1张,B型纸片3张,C型纸片2张,得(a+b)(a+2b)= a2+3ab+2b2(2)分解因式a2+5ab+6b2小明的操作步骤如下:①准备若干块(1)中的A、B、C型纸片②用1块A型纸片,5块B型纸片和6块纸片拼成一个长方形③分别计算出长方形相邻两边的长,得a2+5ab+6b2= (a+2b)(a+3b)(3)计算(a+b)3请你仿照小丽的探究过程,写出操作步骤(4)分解因式a3+6a2b+12ab2+8b3请你仿照小明的探究过程,直接写出因式分解的结果.【考点】因式分解的应用.【专题】阅读型.【分析】(1)根据小丽的操作步骤可以得到问题的答案;(2)根据小明的操作步骤可以得到问题的答案;(3)根据第一问中小丽的操作步骤可以设计出相应的方案;(4)根据小明的操作步骤可以得到问题的答案.【解答】解:(1)根据题意可得,A型纸片1张,B型纸片3张,C型纸片2张,∴(a+b)(a+2b)=a2+3ab+2b2.故答案为:a2+3ab+2b2.(2)根据题意可得,a2+5ab+6b2=(a+2b)(a+3b).故答案为:(a+2b)(a+3b).(3)计算(a+b)3操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C型纸片是边长为b的正方形;②用①中的纸片拼成棱长为a+b的正方体;③数出以a为棱长的正方体一个,以a为边长的正方形做底面,高为b的长方体三个,以b为边长的正方形做底面,高为a的长方体三个,以b为棱长的正方体一个,得(a+b)3=a3+3a2b+3ab2+b3.(4)分解因式a3+6a2b+12ab2+8b3根据小明的操作步骤可得,a3+6a2b+12ab2+8b3=(a+2b)3.【点评】本题考查解因式分解的应用,解题的关键是能看懂小丽和小明的操作步骤,在(3)和(4)中可以与长方体和正方体联系在一起.。
鼓楼2013-1024期中卷

图1
图2
图3
24. (8 分)设 a ≠ 0 , x 、 y 是正整数,定义新运算 a x a x (如果有括号,规定先算括号里面的)如
2 2 2 4 , 4 m 1 4m1 .
(1)若 10 n 100 ,则 n
;
(2)请说明 a x a y a x y 成立的理由; (3)若 2 x 2 2 y 8 且 3 x 3 y 9 ,请运用(2)中的结论求 x 、 y 的值. 25. (9 分)已知,直线 AB ∥CD ,点 E 在直线 AB 上,点 F 、 G 在直线 CD 上, EFC 、 EGD 的平分线 FM 、 GN 分别交直线 AB 于点 M 、 N . (1)如果 △EFG 为等边三角形(如图 1) ,那么 1 2 ; 如果 △EFG 为等腰三角形(如图 2)且顶角 FEG 36 ,那么 1 2 ; (2)如果 △EFG 为任意三角形(如图 3) ,那么 1 2 与 FEG 有什么关系?试说明理由;
5
1
A
E F B D C
14. 已知, 正方形 BDEF 的边长为 2 厘米,△ABC 是等腰直角三角形, 其直角边长为小正方形边长的 2 倍, 点 D 、 B 、 C 在同一条直线上,正方形 BDEF 以 1 厘米/秒的速度沿直线 BC 向右平移,起始状态如图 两个图形重叠部分的面积为 S 平方厘米, 当 t 3 秒时, 平 所示, 设平移的时间为 t 秒, S为 方厘米.
鼓楼区 卷满分 100 分.考试时间为 100 分钟.考生答题全部答在答题卷上,答在本试卷上无效. 一、选择题(本大题共 6 小题,每小题 2 分,共 12 分) 1.计算 22 的结果是( ) 1 1 B. A. 4 4 2.下列各式中,正确的是( A. a a a
南京市鼓楼区七年级上学期语文期中考试试卷

南京市鼓楼区七年级上学期语文期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共3题;共6分)1. (2分) (2018八上·深圳月考) 下列说法不正确的一项是()A . 新闻特写与消息的差异在于,消息往往要报道新闻事件的全过程,新闻特写则主要描绘新闻事件中的片段。
B . “从高速飞行的舰载战斗机上往下看,航母就像汪洋中的一片树叶,在海上起伏行进,飞机每次着舰都面临着生与死的考验。
”这是一个比喻句,写出了飞机着舰的难度和危险性。
C . 消息正文的结构通常是按照重要性递增的原则安排的,即所谓“倒金字塔结构”。
D . 《藤野先生》选自鲁迅的《朝花夕拾》。
2. (2分) (2017七上·怀柔期末) 下列词语中没有错别字的一项是()A . 竭然不同喜出旺外踉踉跄跄人迹罕至B . 惊慌失措废寝忘食疲倦不堪各得其所C . 翻来复去小心翼翼混为一谈惶然大悟D . 油然而生呼朋引伴漠不关心美不盛收3. (2分)(2012·丹东) 选出下列划线的词语使用正确的一项。
()A . 一般人都有很隐秘的“心理缺陷”——害怕见大人物。
见了大人物就手足无措,张牙舞爪,甚至还要浑身发抖。
B . 家长对孩子们的关心真是处心积虑、无微不至。
C . 她小心翼翼地撕开信封,将里面的百元大钞捏取出来,塞到衣服布袋里,然后将信件递给他。
D . 他是日常生活里一个声名显赫的小人物,在他身上,却拥有着许多熠熠生辉的可贵品质。
二、书写 (共1题;共5分)4. (5分)根据提示,将对应的汉字按顺序写在下面的横线上。
A.狡xiá:有诡诈,狡猾之意。
B.心无旁wù:心中没有另外的杂念。
形容心思集中,专心致志。
C.吹毛求cī:比喻故意挑剔别人的缺点,寻找差错。
也指细致到繁琐,挑剔的地步。
D.一póu黄土:一捧黄土。
借指坟墓,现多比喻不多的土地或没落、渺小的反动势力。
南京市鼓楼区2014-2015学年七年级下期中数学试卷含答案解析

2014-2015学年江苏省南京市鼓楼区七年级(下)期中数学试卷一、选择题(共6小题,每小题2分,满分12分)1.计算a6÷a2的结果是()A.a3B.a4C.a8D.a122.每个生物携带自身基因的载体是生物细胞的DNA,DNA分子的直径只有0.0000002cm,将0.0000002用科学记数法表示为()A.2×106B.2×107C.2×10﹣6D.2×10﹣73.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明()A.三角形内角和等于180°B.三角形外角和等于360°C.三角形任意两边之和大于第三边D.三角形任意两边之差小于第三边4.下列各式由左边到右边的变形,是因式分解的是()A.3x(x+y)+3x2+3xy B.﹣2x2﹣2xy=﹣2x(x+y)C.(x+5)(x﹣5)=x2﹣25 D.x2+x+1=x(x+1)+15.已知一个三角形的两边长分别为4、7,则第三边的长可以为()A.2 B.3 C.8 D.126.如图,将甲图中阴影部分无重叠、无缝隙地拼成乙图,根据两个图形中阴影部分的面积关系得到的等式是()A.a2﹣b2=(a+b)(a﹣b)B.a2+2ab+b2=(a+b)2C.a2﹣2ab+b2=(a﹣b)2D.(a+b)2﹣(a﹣b)2=4ab二、填空题(共10小题,每小题2分,满分20分)7.计算3﹣2的结果是.8.计算:(﹣2xy2)3=.9.已知a m=4,a n=5,则a m+n的值是.10.多边形的每个外角的度数都等于45°,则这个多边形的边数为.11.把方程4x﹣y=3写成用含x的代数式表示y的形式为y=.12.如图,把等腰直角三角尺的直角顶点放在直尺的一边上,则∠1+∠2=.13.二元一次方程的一个解是,这个二元一次方程可以是.14.已知x+y=5,xy=3,则(x﹣y)2=.15.如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3=.16.前n(n>3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x1,x2,x3,…,x n,将卡片上的数先平方再求和,得x12+x22+x32+…+x n2=28,将卡片上的数先立方再求和,得x13+x23+x33+…+x n3=4,则x14+x24+x34+…+x n4的值是.三、解答题(共10小题,满分68分)17.计算:(1)(5﹣3)0﹣()﹣3(2)﹣a2•(﹣6ab)(3)x(y+5)+y(3﹣x)(4)(2a+b)(2a﹣b)﹣(a﹣3b)2.18.把下列各式因式分解:(1)4x2﹣6xy(2)a2(x+y)﹣b2(x+y)(3)(a2+1)2﹣4a2.19.解方程组.20.已知△ABC.(1)平移△ABC,使点A移到点A1的位置,画出平移后得到的△A1B1C1;(2)根据平移的性质,写出两条不同类型的正确结论.21.如图,∠A=∠F,∠C=∠D,判断BD与CE的位置关系,并说明理由.22.根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等).(1)如图①,测量△ABC的面积;(2)如图②,平分△DEF的面积.23.如图,△ABC的角平分线BP、CP相交于点P,∠P=140°,求∠A的度数.24.当abc≠0时,要说明(a+b+c)2≠a2+b2+c2不成立,下面三位同学提供了三种不同的思路(1)小明说,“不妨设a=1,b=2,c=3,通过计算能发现式子不成立”,请你完成他的说理过程;(2)小刚说,“根据整式乘法的运算法则,通过计算能发现式子不成立”,请你完成他的说理过程;(3)小丽说,“构造正方形,通过计算面积能发现式子不成立”.请你帮她画出图形,并完成说理过程.25.如图,在一张长方形纸片ABCD中,AB=3,AD=m,边AB的中垂线分别交于AB、CD于点E、F;在边BC上取一点H(即AH为折痕),使得△ABH沿AH折叠后点B恰好落在线段EF上,设为点G.(1)按上述描述画出图形(要求尺规作图,不写作法,保留画图痕迹);(2)求证:△ABG是等边三角形;(3)若要使图形折叠后点A、G、C在一直线上,试求m的值.26.数与形都是数学研究的对象,它们有着密切的联系,我们可以利用图形对整式乘法和因式分解进行研究(1)计算(a+b)(a+2b).小丽的操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C 型纸片是边长为b的正方形;②用①中的纸片拼成两边长分别为a+b、a+2b的长方形③数出用了A型纸片1张,B型纸片3张,C型纸片2张,得(a+b)(a+2b)=(2)分解因式a2+5ab+6b2小明的操作步骤如下:①准备若干块(1)中的A、B、C型纸片②用1块A型纸片,5块B型纸片和6块纸片拼成一个长方形③分别计算出长方形相邻两边的长,得a2+5ab+6b2=(3)计算(a+b)3请你仿照小丽的探究过程,写出操作步骤(4)分解因式a3+6a2b+12ab2+8b3请你仿照小明的探究过程,直接写出因式分解的结果.2014-2015学年江苏省南京市鼓楼区七年级(下)期中数学试卷参考答案与试题解析一、选择题(共6小题,每小题2分,满分12分)1.计算a6÷a2的结果是()A.a3B.a4C.a8D.a12【考点】同底数幂的除法.【分析】根据同底数幂的除法法则,同底数幂相除,底数不变,指数相减计算即可.【解答】解:a6÷a2=a6﹣2=a4.故选B.【点评】本题主要考查同底数幂的除法,熟练掌握运算性质是解题的关键.2.每个生物携带自身基因的载体是生物细胞的DNA,DNA分子的直径只有0.0000002cm,将0.0000002用科学记数法表示为()A.2×106B.2×107C.2×10﹣6D.2×10﹣7【考点】科学记数法—表示较小的数.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.000 0002=2×10﹣7,故选:D.【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.3.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明()A.三角形内角和等于180°B.三角形外角和等于360°C.三角形任意两边之和大于第三边D.三角形任意两边之差小于第三边【考点】三角形内角和定理.【分析】根据三角形的内角和定理解答即可.【解答】解:这种变化说明三角形的内角和是180°,故选A.【点评】此题考查三角形的内角和定理,关键是根据三角形的内角和定理是180°.4.下列各式由左边到右边的变形,是因式分解的是()A.3x(x+y)+3x2+3xy B.﹣2x2﹣2xy=﹣2x(x+y)C.(x+5)(x﹣5)=x2﹣25 D.x2+x+1=x(x+1)+1【考点】因式分解的意义.【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.【解答】解:A、是整式的乘法,故A错误;B、是把一个多项式转化成几个整式积的形式,故B正确;C、是整式的乘法,故C错误;D、没是把一个多项式转化成几个整式积的形式,故D错误;故选:B.【点评】本题考查了因式分解的意义,因式分解是把一个多项式转化成几个整式积的形式,注意因式分解与整式乘法的区别.5.已知一个三角形的两边长分别为4、7,则第三边的长可以为()A.2 B.3 C.8 D.12【考点】三角形三边关系.【分析】根据三角形的三边关系定理可得7﹣4<x<7+4,计算出不等式的解集,再确定x的值即可.【解答】解:设第三边长为x,则7﹣4<x<7+4,3<x<11,故选:C.【点评】此题主要考查了三角形的三边关系,关键是掌握第三边的范围是:大于已知的两边的差,而小于两边的和.6.如图,将甲图中阴影部分无重叠、无缝隙地拼成乙图,根据两个图形中阴影部分的面积关系得到的等式是()A.a2﹣b2=(a+b)(a﹣b)B.a2+2ab+b2=(a+b)2C.a2﹣2ab+b2=(a﹣b)2D.(a+b)2﹣(a﹣b)2=4ab【考点】完全平方公式的几何背景.【分析】分别计算出甲、乙两图中阴影部分的面积,根据面积相等,即可解答.【解答】解:甲图中阴影部分的面积为:a2﹣2ab+b2,图乙中阴影部分的面积为:(a﹣b)2,所以a2﹣2ab+b2=(a﹣b)2,故选:C.【点评】本题考查了完全平方公式,解决本题的关键是分别计算出甲、乙两图中阴影部分的面积.二、填空题(共10小题,每小题2分,满分20分)7.计算3﹣2的结果是.【考点】负整数指数幂.【专题】计算题.【分析】此题考查的是负整数指数幂的计算方法,按照负指数为正指数的倒数进行计算即可.【解答】解:3﹣2==.故答案为.【点评】此题主要考查的是负整数指数幂,幂的负整数指数运算,先把底数化成其倒数,然后将负整数指数幂当成正的进行计算.8.计算:(﹣2xy2)3=﹣8x3y6.【考点】幂的乘方与积的乘方.【分析】根据积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘;幂的乘方,底数不变指数相乘计算.【解答】解:(﹣2xy2)3,=(﹣2)3x3(y2)3,=﹣8x3y6.故填﹣8x3y6.【点评】本题考查积的乘方的性质,幂的乘方的性质,熟练掌握运算性质是解题的关键.9.已知a m=4,a n=5,则a m+n的值是20.【考点】同底数幂的乘法.【分析】根据同底数幂的乘法,底数不变指数相加,可得答案.【解答】解:a m+n=m•a n=4×5=20,故答案为:20.【点评】本题考查了同底数幂的乘法,同底数幂的乘法底数不变指数相加.10.多边形的每个外角的度数都等于45°,则这个多边形的边数为8.【考点】多边形内角与外角.【分析】多边形的外角和是360°,又有多边形的每个外角都等于45°,所以可以求出多边形外角的个数,进而得到多边形的边数.【解答】解:这个多边形的边数是:=8,故答案为:8.【点评】本题考查多边形的外角和,以及多边形外角的个数与其边数之间的相等关系.11.把方程4x﹣y=3写成用含x的代数式表示y的形式为y=4x﹣3.【考点】解二元一次方程.【专题】计算题;一次方程(组)及应用.【分析】把x看做已知数求出y即可.【解答】解:方程4x﹣y=3,解得:y=4x﹣3.故答案为:4x﹣3.【点评】此题考查了解二元一次方程,解题的关键是将x看做已知数求出y.12.如图,把等腰直角三角尺的直角顶点放在直尺的一边上,则∠1+∠2=135°.【考点】平行线的性质.【分析】根据等腰直角三角形得出∠ACB=90°,∠A=∠B=45°,根据平行线性质求出∠1=∠ACM,根据三角形外角性质求出∠2=∠B+∠BCM,求出∠1+∠2=∠ACB+∠B即可.【解答】解:如图:∵△ACB是等腰直角三角形,∴∠ACB=90°,∠A=∠B=45°,∵EF∥MN,∴∠1=∠ACM,∵∠2=∠B+∠BCM,∴∠1+∠2=∠ACM+∠B+∠BCM=∠ACB+∠B=90°+45°=135°,故答案为:135°.【点评】本题考查了平行线的性质,等腰直角三角形,三角形的外角性质的应用,能求出∠1+∠2=∠ACB+∠B 是解此题的关键,题目比较典型,难度适中.13.二元一次方程的一个解是,这个二元一次方程可以是2x+3y=13.【考点】二元一次方程的解.【专题】开放型;一次方程(组)及应用.【分析】以2与3列出算式,即可确定出所求方程.【解答】解:根据题意得:2x+3y=13,故答案为:2x+3y=13.【点评】此题考查了二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.14.已知x+y=5,xy=3,则(x﹣y)2=13.【考点】完全平方公式.【专题】计算题;整式.【分析】原式利用完全平方公式化简,将已知等式代入计算即可求出值.【解答】解:∵x+y=5,xy=3,∴(x﹣y)2=x2﹣2xy+y2=x2+2xy+y2﹣4xy=(x+y)2﹣4xy=25﹣12=13,故答案为:13【点评】此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.15.如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3=20°.【考点】平移的性质;平行线的性质.【专题】计算题.【分析】如图,根据平移的性质得m∥n,则利用平行线的性质得∠DAB=180°﹣∠1=110°,再根据三角形外角性质可计算出∠ABC=130°﹣∠CAB=20°,然后根据对顶角的性质求解.【解答】解:如图,∵直线m平移后得到直线n,∴m∥n,∴∠1+∠DAB=180°,∴∠DAB=180°﹣70°=110°,∵∠2=∠CAB+∠ABC,∴∠ABC=130°﹣110°=20°,∴∠3=∠ABC=20°.故答案为20°.【点评】本题考查了平移的性质把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.16.前n(n>3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x1,x2,x3,…,x n,将卡片上的数先平方再求和,得x12+x22+x32+…+x n2=28,将卡片上的数先立方再求和,得x13+x23+x33+…+x n3=4,则x14+x24+x34+…+x n4的值是52.【考点】有理数的混合运算.【专题】探究型.【分析】根据题意可以设n个数中含有a个﹣2,b个1,然后根据x12+x22+x32+…+x n2=28,x13+x23+x33+…+x n3=4,可以求得a、b的值,从而可以求得x14+x24+x34+…+x n4的值.【解答】解:∵前n(n>3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x1,x2,x3,…,x n,∴设这n个数中,含有a个﹣2,b个1,∵x12+x22+x32+…+x n2=28,x13+x23+x33+…+x n3=4,∴解得,∴x14+x24+x34+…+x n4=(﹣2)4×2+14×20=16×2+1×20=32+20=52.故答案为:52.【点评】本题考查有理数的混合运算,解题的关键是明确题意,求出n个数中﹣2和1的个数.三、解答题(共10小题,满分68分)17.计算:(1)(5﹣3)0﹣()﹣3(2)﹣a2•(﹣6ab)(3)x(y+5)+y(3﹣x)(4)(2a+b)(2a﹣b)﹣(a﹣3b)2.【考点】整式的混合运算;零指数幂;负整数指数幂.【分析】(1)根据零指数和负整数指数的意义运算;(2)根据同底数幂的乘法法则运算;(3)先去括号,然后合并即可;(4)先利用平方差公式和完全平方公式展开,然后合并即可.【解答】解:(1)原式=1﹣27=﹣26;(2)原式=2a3b;(3)原式=xy+5x+3y﹣xy=5x+3y;(4)原式=4a2﹣b2﹣(a2﹣6ab+9b2)=4a2﹣b2﹣a2+6ab﹣9b2=3a2﹣10b2+6ab.【点评】本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.18.把下列各式因式分解:(1)4x2﹣6xy(2)a2(x+y)﹣b2(x+y)(3)(a2+1)2﹣4a2.【考点】提公因式法与公式法的综合运用.【分析】(1)直接提取公因式2x,进而分解因式得出答案;(2)首先提取公因式(x+y),进而利用平方差公式分解因式得出即可;(3)直接利用平方差公式分解因式进而结合完全平方公式的应用分解因式即可.【解答】解:(1)4x2﹣6xy=2x(2x﹣3y);(2)a2(x+y)﹣b2(x+y)=(x+y)(a2﹣b2)=(x+y)(a+b)(a﹣b);(3)(a2+1)2﹣4a2=(a2+1+2a)(a2+1﹣2a)=(a+1)2(a﹣1)2.【点评】此题主要考查了提取公因式法以及公式法分解因式,正确应用乘法公式是解题关键.19.解方程组.【考点】解二元一次方程组.【专题】计算题;一次方程(组)及应用.【分析】方程组利用加减消元法求出解即可.【解答】解:,①+②得:4x=8,即x=2,把x=2代入①得:y=2,则方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.20.已知△ABC.(1)平移△ABC,使点A移到点A1的位置,画出平移后得到的△A1B1C1;(2)根据平移的性质,写出两条不同类型的正确结论.【考点】作图-平移变换.【分析】(1)根据图形平移的性质画出图形即可;(2)根据图形平移的性质可直接得出结论.【解答】解:(1)如图所示;(2)△ABC≌△△A1B1C1,AA1=BB1=CC1.【点评】本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.21.如图,∠A=∠F,∠C=∠D,判断BD与CE的位置关系,并说明理由.【考点】平行线的判定与性质.【分析】根据平行线的判定得出AC∥DF,根据平行线的性质求出∠C=∠CEF,求出∠D=∠CEF,根据平行线的判定得出即可.【解答】解:BD∥CE,理由是:∵∠A=∠F,∴AC∥DF,∴∠C=∠CEF,∵∠C=∠D,∴∠D=∠CEF,∴BD∥CE.【点评】本题考查了平行线的性质和判定的应用,能正确运用定理进行推理是解此题的关键,题目比较好,难度适中.22.根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等).(1)如图①,测量△ABC的面积;(2)如图②,平分△DEF的面积.【考点】作图—应用与设计作图.【分析】(1)计算三角形的面积需要知道三角形的底边长和高长,需要作出AB边上的高线,(2)三角形的中线平分三角形的面积,需要找出三角形,一边上的中点,故此可作出一边的垂直平分线得到一边的中点,然后作出中线即可.【解答】解:(1)如图①所示:过点C作AB的垂线.需要测量:AB和DC的长,.(2)如图②所示:作ED的垂直平分线,交ED于点G,连接GF.GF平分△DEF的面积.【点评】本题主要考查的是作图应用与设计,掌握五种基本作图以及三角形的中线平分三角形的面积是解题的关键.23.如图,△ABC的角平分线BP、CP相交于点P,∠P=140°,求∠A的度数.【考点】三角形内角和定理.【分析】根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形的内角和等于180°列式计算即可得解.【解答】解:∵△ABC,∴∠ABC+∠ACB=180°﹣∠A,∵∠ABC与∠ACB的角平分线相交于P,∴∠PBC+∠PCB=(∠ABC+∠ACB)=,在△PBC中,∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣=140°,∴∠A=100°.【点评】此题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.24.当abc≠0时,要说明(a+b+c)2≠a2+b2+c2不成立,下面三位同学提供了三种不同的思路(1)小明说,“不妨设a=1,b=2,c=3,通过计算能发现式子不成立”,请你完成他的说理过程;(2)小刚说,“根据整式乘法的运算法则,通过计算能发现式子不成立”,请你完成他的说理过程;(3)小丽说,“构造正方形,通过计算面积能发现式子不成立”.请你帮她画出图形,并完成说理过程.【考点】整式的混合运算.【分析】(1)把a、b、c的值代入,求出两边的值,即可得出答案;(2)根据多项式乘以多项式法则求出后,再判断即可;(3)化成边长为a+b+c的正方形,即可得出答案.【解答】解:(1)∵当a=1,b=2,c=3时,(a+b+c)2=(1+2+3)2=36a2+b2+c2=12+22+32=14,∴(a+b+c)2≠a2+b2+c2;(2)∵(a+b+c)2=(a+b+c)(a+b+c)=a2+ab+ac+ab+b2+bc+ac+bc+c2=a2+b2+c2+2ab+2bc+2ac,∴(a+b+c)2≠a2+b2+c2;(3)如图所示:(a+b+c)2=a2+b2+c2+ab+ac+bc+ab+ac+bc,即(a+b+c)2≠a2+b2+c2.【点评】本题考查了整式的运算法则的应用,能正确根据整式的运算法则进行化简是解此题的关键,也培养了学生的动手操作能力.25.如图,在一张长方形纸片ABCD中,AB=3,AD=m,边AB的中垂线分别交于AB、CD于点E、F;在边BC上取一点H(即AH为折痕),使得△ABH沿AH折叠后点B恰好落在线段EF上,设为点G.(1)按上述描述画出图形(要求尺规作图,不写作法,保留画图痕迹);(2)求证:△ABG是等边三角形;(3)若要使图形折叠后点A、G、C在一直线上,试求m的值.【考点】四边形综合题.【分析】(1)先根据基本作图的方法作出线段AB的垂直平分线EF,在EF上取一点G,使AG=AB,连结GH,则△AGH与△ABH关于AH成轴对称;(2)连接GB,由中垂线的性质就可以得出AG=BG,由轴对称的性质就可以得出AG=AB而得出结论;(3)由(2)的结论就可以得出∠CAB=60°,由勾股定理就可以求出BC的值,得出结论.【解答】解:(1)由题意作出图形,如图1.(2)如图2,连接GB,∵EF垂直平分AB,点G在EF上,∴AG=GB.∵△AGH与△ABH关于AH对称,∴△AGH≌△ABH,∴AG=AB,∴AG=AB=GB,∴△ABG是等边三角形;(3)如图2,∵△ABG是等边三角形,∴∠CAB=60°.∵四边形ABCD是矩形,∴∠ABC=90°.AD=BC=m,∴∠ACB=30°,∴AC=2AB.∵AB=3,∴AC=6.在Rt△ABC中,由勾股定理,得BC=9,∴m=9.【点评】本题考查了矩形的性质的运用,尺规作图的运用,垂直平分线的性质的运用,等边三角形的判定及性质的运用,轴对称的性质的运用,勾股定理的性质的运用,解答时证明三角形ABG是等边三角形是关键.26.数与形都是数学研究的对象,它们有着密切的联系,我们可以利用图形对整式乘法和因式分解进行研究(1)计算(a+b)(a+2b).小丽的操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C 型纸片是边长为b的正方形;②用①中的纸片拼成两边长分别为a+b、a+2b的长方形③数出用了A型纸片1张,B型纸片3张,C型纸片2张,得(a+b)(a+2b)=a2+3ab+2b2(2)分解因式a2+5ab+6b2小明的操作步骤如下:①准备若干块(1)中的A、B、C型纸片②用1块A型纸片,5块B型纸片和6块纸片拼成一个长方形③分别计算出长方形相邻两边的长,得a2+5ab+6b2=(a+2b)(a+3b)(3)计算(a+b)3请你仿照小丽的探究过程,写出操作步骤(4)分解因式a3+6a2b+12ab2+8b3请你仿照小明的探究过程,直接写出因式分解的结果.【考点】因式分解的应用.【专题】阅读型.【分析】(1)根据小丽的操作步骤可以得到问题的答案;(2)根据小明的操作步骤可以得到问题的答案;(3)根据第一问中小丽的操作步骤可以设计出相应的方案;(4)根据小明的操作步骤可以得到问题的答案.【解答】解:(1)根据题意可得,A型纸片1张,B型纸片3张,C型纸片2张,∴(a+b)(a+2b)=a2+3ab+2b2.故答案为:a2+3ab+2b2.(2)根据题意可得,a2+5ab+6b2=(a+2b)(a+3b).故答案为:(a+2b)(a+3b).(3)计算(a+b)3操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C 型纸片是边长为b的正方形;②用①中的纸片拼成棱长为a+b的正方体;③数出以a为棱长的正方体一个,以a为边长的正方形做底面,高为b的长方体三个,以b为边长的正方形做底面,高为a的长方体三个,以b为棱长的正方体一个,得(a+b)3=a3+3a2b+3ab2+b3.(4)分解因式a3+6a2b+12ab2+8b3根据小明的操作步骤可得,a3+6a2b+12ab2+8b3=(a+2b)3.【点评】本题考查解因式分解的应用,解题的关键是能看懂小丽和小明的操作步骤,在(3)和(4)中可以与长方体和正方体联系在一起.。
2013-2014第二学期南京联合体七年级期中数学试卷

(3)(y-2x)( x+2y);
(4)
(-3a+2b)(3a+2b)
1 20. (5 分)先化简,再求值:(2a+1)2-2(2a+1)+3,其中 a=- . 2
21. (6 分)将下列各式因式分解: (1)x3-x (2)4a2x2-12ax+9
22. (5 分)解方程组
2x+y=4, x+2y=5.
D C M A 图② (第 27 题) B P Q
②直接运用(2)中的结论,试说明:PM⊥QM.
七年级数学试卷 第 6 页(共 10 页)
2013/2014 学年度第二学期期中测试试卷七年级数学试题 参考答案及评分标准
一、选择题(本大题共 8 小题,每小题 2 分,共 16 分) 1.C 2.A 3.D 4.B 5.C 6.D 7.B 8.A
2013/2014 学年度第二学期期中测试试卷 七年级数学
(满分:100 分 注意: 1.选择题答案请用 2B 铅笔填涂在答题 纸 相应位置 上. .. . .... 2.非选择题答案必须用 0.5 毫米黑色墨水签字笔写在答题卷上的指定位置,在其他位置答 题一律无效. 一、选择题(本大题共 8 小题,每小题 2 分,共 16 分.在每小题所给出的四个选项中, 恰有一项是符合题目要求的,请将正确选项前的字母代号涂在答题 卡 相应位置上 ) .. . ..... 1.计算 5–1 的结果是( A.5 ) B.-5 1 C. 5 ) C.2x2+3y-5=0 1 D. 2x+ =2 y D.(x3)2=x6 1 D.- 5 考试时间:100 分钟)
七年级数学试卷 第 4 页(共 10 页)
25. (7 分)如图,把一副三角板如图放置,其中∠ACB=∠DEC=90° ,∠A=45° , ∠D=30° ,斜边 AB、CD 相交于 O 点.求∠AOC 的度数.
南京市鼓楼区年七年级下期中数学试卷及答案-超值

2014-2015学年江苏省南京市鼓楼区七年级(下)期中数学试卷一、选择题(共6小题,每小题2分,满分12分)1.计算a6÷a2的结果是()A.a3B.a4C.a8D.a122.每个生物携带自身基因的载体是生物细胞的DNA,DNA分子的直径只有0.0000002cm,将0.0000002用科学记数法表示为()A.2×106B.2×107C.2×10﹣6D.2×10﹣73.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明()A.三角形内角和等于180°B.三角形外角和等于360°C.三角形任意两边之和大于第三边D.三角形任意两边之差小于第三边4.下列各式由左边到右边的变形,是因式分解的是()A.3x(x+y)+3x2+3xy B.﹣2x2﹣2xy=﹣2x(x+y)C.(x+5)(x﹣5)=x2﹣25 D.x2+x+1=x(x+1)+15.已知一个三角形的两边长分别为4、7,则第三边的长可以为()A.2 B.3 C.8 D.126.如图,将甲图中阴影部分无重叠、无缝隙地拼成乙图,根据两个图形中阴影部分的面积关系得到的等式是()A.a2﹣b2=(a+b)(a﹣b)B.a2+2ab+b2=(a+b)2C.a2﹣2ab+b2=(a﹣b)2D.(a+b)2﹣(a﹣b)2=4ab二、填空题(共10小题,每小题2分,满分20分)7.计算3﹣2的结果是.8.计算:(﹣2xy2)3= .9.已知a m=4,a n=5,则a m+n的值是.10.多边形的每个外角的度数都等于45°,则这个多边形的边数为.11.把方程4x﹣y=3写成用含x的代数式表示y的形式为y= .12.如图,把等腰直角三角尺的直角顶点放在直尺的一边上,则∠1+∠2= .13.二元一次方程的一个解是,这个二元一次方程可以是.14.已知x+y=5,xy=3,则(x﹣y)2= .15.如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3= .16.前n(n>3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x1,x2,x3,…,xn,将卡片上的数先平方再求和,得x12+x22+x32+…+xn2=28,将卡片上的数先立方再求和,得x13+x23+x33+…+xn3=4,则x 14+x24+x34+…+xn4的值是.三、解答题(共10小题,满分68分)17.计算:(1)(5﹣3)0﹣()﹣3(2)﹣a2•(﹣6ab)(3)x(y+5)+y(3﹣x)(4)(2a+b)(2a﹣b)﹣(a﹣3b)2.18.把下列各式因式分解:(1)4x2﹣6xy(2)a2(x+y)﹣b2(x+y)(3)(a2+1)2﹣4a2.19.解方程组.20.已知△ABC.(1)平移△ABC,使点A移到点A1的位置,画出平移后得到的△A1B1C1;(2)根据平移的性质,写出两条不同类型的正确结论.21.如图,∠A=∠F,∠C=∠D,判断BD与CE的位置关系,并说明理由.22.根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等).(1)如图①,测量△ABC的面积;(2)如图②,平分△DEF的面积.23.如图,△ABC的角平分线BP、CP相交于点P,∠P=140°,求∠A的度数.24.当abc≠0时,要说明(a+b+c)2≠a2+b2+c2不成立,下面三位同学提供了三种不同的思路(1)小明说,“不妨设a=1,b=2,c=3,通过计算能发现式子不成立”,请你完成他的说理过程;(2)小刚说,“根据整式乘法的运算法则,通过计算能发现式子不成立”,请你完成他的说理过程;(3)小丽说,“构造正方形,通过计算面积能发现式子不成立”.请你帮她画出图形,并完成说理过程.25.如图,在一张长方形纸片ABCD中,AB=3,AD=m,边AB的中垂线分别交于AB、CD于点E、F;在边BC上取一点H(即AH为折痕),使得△ABH沿AH折叠后点B恰好落在线段EF上,设为点G.(1)按上述描述画出图形(要求尺规作图,不写作法,保留画图痕迹);(2)求证:△ABG是等边三角形;(3)若要使图形折叠后点A、G、C在一直线上,试求m的值.26.数与形都是数学研究的对象,它们有着密切的联系,我们可以利用图形对整式乘法和因式分解进行研究(1)计算(a+b)(a+2b).小丽的操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C型纸片是边长为b的正方形;②用①中的纸片拼成两边长分别为a+b、a+2b的长方形③数出用了A型纸片1张,B型纸片3张,C型纸片2张,得(a+b)(a+2b)=(2)分解因式a2+5ab+6b2小明的操作步骤如下:①准备若干块(1)中的A、B、C型纸片②用1块A型纸片,5块B型纸片和6块纸片拼成一个长方形③分别计算出长方形相邻两边的长,得a2+5ab+6b2=(3)计算(a+b)3请你仿照小丽的探究过程,写出操作步骤(4)分解因式a3+6a2b+12ab2+8b3请你仿照小明的探究过程,直接写出因式分解的结果.2014-2015学年江苏省南京市鼓楼区七年级(下)期中数学试卷参考答案与试题解析一、选择题(共6小题,每小题2分,满分12分)1.计算a6÷a2的结果是()A.a3B.a4C.a8D.a12【考点】同底数幂的除法.【分析】根据同底数幂的除法法则,同底数幂相除,底数不变,指数相减计算即可.【解答】解:a6÷a2=a6﹣2=a4.故选B.【点评】本题主要考查同底数幂的除法,熟练掌握运算性质是解题的关键.2.每个生物携带自身基因的载体是生物细胞的DNA,DNA分子的直径只有0.0000002cm,将0.0000002用科学记数法表示为()A.2×106B.2×107C.2×10﹣6D.2×10﹣7【考点】科学记数法—表示较小的数.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.000 0002=2×10﹣7,故选:D.【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.3.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明()A.三角形内角和等于180°B.三角形外角和等于360°C.三角形任意两边之和大于第三边D.三角形任意两边之差小于第三边【考点】三角形内角和定理.【分析】根据三角形的内角和定理解答即可.【解答】解:这种变化说明三角形的内角和是180°,故选A.【点评】此题考查三角形的内角和定理,关键是根据三角形的内角和定理是180°.4.下列各式由左边到右边的变形,是因式分解的是()A.3x(x+y)+3x2+3xy B.﹣2x2﹣2xy=﹣2x(x+y)C.(x+5)(x﹣5)=x2﹣25 D.x2+x+1=x(x+1)+1【考点】因式分解的意义.【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.【解答】解:A、是整式的乘法,故A错误;B、是把一个多项式转化成几个整式积的形式,故B正确;C、是整式的乘法,故C错误;D、没是把一个多项式转化成几个整式积的形式,故D错误;故选:B.【点评】本题考查了因式分解的意义,因式分解是把一个多项式转化成几个整式积的形式,注意因式分解与整式乘法的区别.5.已知一个三角形的两边长分别为4、7,则第三边的长可以为()A.2 B.3 C.8 D.12【考点】三角形三边关系.【分析】根据三角形的三边关系定理可得7﹣4<x<7+4,计算出不等式的解集,再确定x的值即可.【解答】解:设第三边长为x,则7﹣4<x<7+4,3<x<11,故选:C.【点评】此题主要考查了三角形的三边关系,关键是掌握第三边的范围是:大于已知的两边的差,而小于两边的和.6.如图,将甲图中阴影部分无重叠、无缝隙地拼成乙图,根据两个图形中阴影部分的面积关系得到的等式是()A.a2﹣b2=(a+b)(a﹣b)B.a2+2ab+b2=(a+b)2C.a2﹣2ab+b2=(a﹣b)2D.(a+b)2﹣(a﹣b)2=4ab【考点】完全平方公式的几何背景.【分析】分别计算出甲、乙两图中阴影部分的面积,根据面积相等,即可解答.【解答】解:甲图中阴影部分的面积为:a2﹣2ab+b2,图乙中阴影部分的面积为:(a﹣b)2,所以a2﹣2ab+b2=(a﹣b)2,故选:C.【点评】本题考查了完全平方公式,解决本题的关键是分别计算出甲、乙两图中阴影部分的面积.二、填空题(共10小题,每小题2分,满分20分)7.计算3﹣2的结果是.【考点】负整数指数幂.【专题】计算题.【分析】此题考查的是负整数指数幂的计算方法,按照负指数为正指数的倒数进行计算即可.【解答】解:3﹣2==.故答案为.【点评】此题主要考查的是负整数指数幂,幂的负整数指数运算,先把底数化成其倒数,然后将负整数指数幂当成正的进行计算.8.计算:(﹣2xy2)3= ﹣8x3y6.【考点】幂的乘方与积的乘方.【分析】根据积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘;幂的乘方,底数不变指数相乘计算.【解答】解:(﹣2xy2)3,=(﹣2)3x3(y2)3,=﹣8x3y6.故填﹣8x3y6.【点评】本题考查积的乘方的性质,幂的乘方的性质,熟练掌握运算性质是解题的关键.9.已知a m=4,a n=5,则a m+n的值是20 .【考点】同底数幂的乘法.【分析】根据同底数幂的乘法,底数不变指数相加,可得答案.【解答】解:a m+n=m•a n=4×5=20,故答案为:20.【点评】本题考查了同底数幂的乘法,同底数幂的乘法底数不变指数相加.10.多边形的每个外角的度数都等于45°,则这个多边形的边数为8 .【考点】多边形内角与外角.【分析】多边形的外角和是360°,又有多边形的每个外角都等于45°,所以可以求出多边形外角的个数,进而得到多边形的边数.【解答】解:这个多边形的边数是: =8,故答案为:8.【点评】本题考查多边形的外角和,以及多边形外角的个数与其边数之间的相等关系.11.把方程4x﹣y=3写成用含x的代数式表示y的形式为y= 4x﹣3 .【考点】解二元一次方程.【专题】计算题;一次方程(组)及应用.【分析】把x看做已知数求出y即可.【解答】解:方程4x﹣y=3,解得:y=4x﹣3.故答案为:4x﹣3.【点评】此题考查了解二元一次方程,解题的关键是将x看做已知数求出y.12.如图,把等腰直角三角尺的直角顶点放在直尺的一边上,则∠1+∠2= 135°.【考点】平行线的性质.【分析】根据等腰直角三角形得出∠ACB=90°,∠A=∠B=45°,根据平行线性质求出∠1=∠ACM,根据三角形外角性质求出∠2=∠B+∠BCM,求出∠1+∠2=∠ACB+∠B即可.【解答】解:如图:∵△ACB是等腰直角三角形,∴∠ACB=90°,∠A=∠B=45°,∵EF∥MN,∴∠1=∠ACM,∵∠2=∠B+∠BCM,∴∠1+∠2=∠ACM+∠B+∠BCM=∠ACB+∠B=90°+45°=135°,故答案为:135°.【点评】本题考查了平行线的性质,等腰直角三角形,三角形的外角性质的应用,能求出∠1+∠2=∠ACB+∠B是解此题的关键,题目比较典型,难度适中.13.二元一次方程的一个解是,这个二元一次方程可以是2x+3y=13 .【考点】二元一次方程的解.【专题】开放型;一次方程(组)及应用.【分析】以2与3列出算式,即可确定出所求方程.【解答】解:根据题意得:2x+3y=13,故答案为:2x+3y=13.【点评】此题考查了二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.14.已知x+y=5,xy=3,则(x﹣y)2= 13 .【考点】完全平方公式.【专题】计算题;整式.【分析】原式利用完全平方公式化简,将已知等式代入计算即可求出值.【解答】解:∵x+y=5,xy=3,∴(x﹣y)2=x2﹣2xy+y2=x2+2xy+y2﹣4xy=(x+y)2﹣4xy=25﹣12=13,故答案为:13【点评】此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.15.如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3= 20°.【考点】平移的性质;平行线的性质.【专题】计算题.【分析】如图,根据平移的性质得m∥n,则利用平行线的性质得∠DAB=180°﹣∠1=110°,再根据三角形外角性质可计算出∠ABC=130°﹣∠CAB=20°,然后根据对顶角的性质求解.【解答】解:如图,∵直线m平移后得到直线n,∴m∥n,∴∠1+∠DAB=180°,∴∠DAB=180°﹣70°=110°,∵∠2=∠CAB+∠ABC,∴∠ABC=130°﹣110°=20°,∴∠3=∠ABC=20°.故答案为20°.【点评】本题考查了平移的性质把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.16.前n (n >3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x 1,x 2,x 3,…,x n ,将卡片上的数先平方再求和,得x 12+x 22+x 32+…+x n 2=28,将卡片上的数先立方再求和,得x 13+x 23+x 33+…+x n 3=4,则x 14+x 24+x 34+…+x n 4的值是 52 . 【考点】有理数的混合运算. 【专题】探究型. 【分析】根据题意可以设n 个数中含有a 个﹣2,b 个1,然后根据x 12+x 22+x 32+…+x n 2=28,x 13+x 23+x 33+…+x n 3=4,可以求得a 、b 的值,从而可以求得x 14+x 24+x 34+…+x n 4的值.【解答】解:∵前n (n >3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x 1,x 2,x 3,…,x n ,∴设这n 个数中,含有a 个﹣2,b 个1,∵x 12+x 22+x 32+…+x n 2=28,x 13+x 23+x 33+…+x n 3=4,∴解得,∴x 14+x 24+x 34+…+x n 4=(﹣2)4×2+14×20=16×2+1×20=32+20=52. 故答案为:52.【点评】本题考查有理数的混合运算,解题的关键是明确题意,求出n 个数中﹣2和1的个数.三、解答题(共10小题,满分68分) 17.计算:(1)(5﹣3)0﹣()﹣3 (2)﹣a 2•(﹣6ab )(3)x (y+5)+y (3﹣x )(4)(2a+b )(2a ﹣b )﹣(a ﹣3b )2.【考点】整式的混合运算;零指数幂;负整数指数幂. 【分析】(1)根据零指数和负整数指数的意义运算; (2)根据同底数幂的乘法法则运算; (3)先去括号,然后合并即可;(4)先利用平方差公式和完全平方公式展开,然后合并即可. 【解答】解:(1)原式=1﹣27 =﹣26;(2)原式=2a 3b ;(3)原式=xy+5x+3y ﹣xy =5x+3y ;(4)原式=4a 2﹣b 2﹣(a 2﹣6ab+9b 2) =4a 2﹣b 2﹣a 2+6ab ﹣9b 2 =3a 2﹣10b 2+6ab .【点评】本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.18.把下列各式因式分解: (1)4x 2﹣6xy(2)a 2(x+y )﹣b 2(x+y ) (3)(a 2+1)2﹣4a 2.【考点】提公因式法与公式法的综合运用.【分析】(1)直接提取公因式2x ,进而分解因式得出答案;(2)首先提取公因式(x+y),进而利用平方差公式分解因式得出即可;(3)直接利用平方差公式分解因式进而结合完全平方公式的应用分解因式即可.【解答】解:(1)4x2﹣6xy=2x(2x﹣3y);(2)a2(x+y)﹣b2(x+y)=(x+y)(a2﹣b2)=(x+y)(a+b)(a﹣b);(3)(a2+1)2﹣4a2=(a2+1+2a)(a2+1﹣2a)=(a+1)2(a﹣1)2.【点评】此题主要考查了提取公因式法以及公式法分解因式,正确应用乘法公式是解题关键.19.解方程组.【考点】解二元一次方程组.【专题】计算题;一次方程(组)及应用.【分析】方程组利用加减消元法求出解即可.【解答】解:,①+②得:4x=8,即x=2,把x=2代入①得:y=2,则方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.20.已知△ABC.(1)平移△ABC,使点A移到点A1的位置,画出平移后得到的△A1B1C1;(2)根据平移的性质,写出两条不同类型的正确结论.【考点】作图-平移变换.【分析】(1)根据图形平移的性质画出图形即可;(2)根据图形平移的性质可直接得出结论.【解答】解:(1)如图所示;(2)△ABC≌△△A1B1C1,AA1=BB1=CC1.【点评】本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.21.如图,∠A=∠F,∠C=∠D,判断BD与CE的位置关系,并说明理由.【考点】平行线的判定与性质.【分析】根据平行线的判定得出AC∥DF,根据平行线的性质求出∠C=∠CEF,求出∠D=∠CEF,根据平行线的判定得出即可.【解答】解:BD∥CE,理由是:∵∠A=∠F,∴AC∥DF,∴∠C=∠CEF,∵∠C=∠D,∴∠D=∠CEF,∴BD∥CE.【点评】本题考查了平行线的性质和判定的应用,能正确运用定理进行推理是解此题的关键,题目比较好,难度适中.22.根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等).(1)如图①,测量△ABC的面积;(2)如图②,平分△DEF的面积.【考点】作图—应用与设计作图.【分析】(1)计算三角形的面积需要知道三角形的底边长和高长,需要作出AB边上的高线,(2)三角形的中线平分三角形的面积,需要找出三角形,一边上的中点,故此可作出一边的垂直平分线得到一边的中点,然后作出中线即可.【解答】解:(1)如图①所示:过点C作AB的垂线.需要测量:AB和DC的长,.(2)如图②所示:作ED的垂直平分线,交ED于点G,连接GF.GF平分△DEF的面积.【点评】本题主要考查的是作图应用与设计,掌握五种基本作图以及三角形的中线平分三角形的面积是解题的关键.23.如图,△ABC的角平分线BP、CP相交于点P,∠P=140°,求∠A的度数.【考点】三角形内角和定理.【分析】根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形的内角和等于180°列式计算即可得解.【解答】解:∵△ABC,∴∠ABC+∠ACB=180°﹣∠A,∵∠ABC与∠ACB的角平分线相交于P,∴∠PBC+∠PCB=(∠ABC+∠ACB)=,在△PBC中,∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣=140°,∴∠A=100°.【点评】此题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.24.当abc≠0时,要说明(a+b+c)2≠a2+b2+c2不成立,下面三位同学提供了三种不同的思路(1)小明说,“不妨设a=1,b=2,c=3,通过计算能发现式子不成立”,请你完成他的说理过程;(2)小刚说,“根据整式乘法的运算法则,通过计算能发现式子不成立”,请你完成他的说理过程;(3)小丽说,“构造正方形,通过计算面积能发现式子不成立”.请你帮她画出图形,并完成说理过程.【考点】整式的混合运算.【分析】(1)把a、b、c的值代入,求出两边的值,即可得出答案;(2)根据多项式乘以多项式法则求出后,再判断即可;(3)化成边长为a+b+c的正方形,即可得出答案.【解答】解:(1)∵当a=1,b=2,c=3时,(a+b+c)2=(1+2+3)2=36a2+b2+c2=12+22+32=14,∴(a+b+c)2≠a2+b2+c2;(2)∵(a+b+c)2=(a+b+c)(a+b+c)=a2+ab+ac+ab+b2+bc+ac+bc+c2=a2+b2+c2+2ab+2bc+2ac,∴(a+b+c)2≠a2+b2+c2;(3)如图所示:(a+b+c)2=a2+b2+c2+ab+ac+bc+ab+ac+bc,即(a+b+c)2≠a2+b2+c2.【点评】本题考查了整式的运算法则的应用,能正确根据整式的运算法则进行化简是解此题的关键,也培养了学生的动手操作能力.25.如图,在一张长方形纸片ABCD中,AB=3,AD=m,边AB的中垂线分别交于AB、CD于点E、F;在边BC上取一点H(即AH为折痕),使得△ABH沿AH折叠后点B恰好落在线段EF上,设为点G.(1)按上述描述画出图形(要求尺规作图,不写作法,保留画图痕迹);(2)求证:△ABG是等边三角形;(3)若要使图形折叠后点A、G、C在一直线上,试求m的值.【考点】四边形综合题.【分析】(1)先根据基本作图的方法作出线段AB的垂直平分线EF,在EF上取一点G,使AG=AB,连结GH,则△AGH与△ABH关于AH成轴对称;(2)连接GB,由中垂线的性质就可以得出AG=BG,由轴对称的性质就可以得出AG=AB而得出结论;(3)由(2)的结论就可以得出∠CAB=60°,由勾股定理就可以求出BC的值,得出结论.【解答】解:(1)由题意作出图形,如图1.(2)如图2,连接GB,∵EF垂直平分AB,点G在EF上,∴AG=GB.∵△AGH与△ABH关于AH对称,∴△AGH≌△ABH,∴AG=AB,∴AG=AB=GB,∴△ABG是等边三角形;(3)如图2,∵△ABG是等边三角形,∴∠CAB=60°.∵四边形ABCD是矩形,∴∠ABC=90°.AD=BC=m,∴∠ACB=30°,∴AC=2AB.∵AB=3,∴AC=6.在Rt△ABC中,由勾股定理,得BC=9,∴m=9.【点评】本题考查了矩形的性质的运用,尺规作图的运用,垂直平分线的性质的运用,等边三角形的判定及性质的运用,轴对称的性质的运用,勾股定理的性质的运用,解答时证明三角形ABG是等边三角形是关键.26.数与形都是数学研究的对象,它们有着密切的联系,我们可以利用图形对整式乘法和因式分解进行研究(1)计算(a+b)(a+2b).小丽的操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C型纸片是边长为b的正方形;②用①中的纸片拼成两边长分别为a+b、a+2b的长方形③数出用了A型纸片1张,B型纸片3张,C型纸片2张,得(a+b)(a+2b)= a2+3ab+2b2(2)分解因式a2+5ab+6b2小明的操作步骤如下:①准备若干块(1)中的A、B、C型纸片②用1块A型纸片,5块B型纸片和6块纸片拼成一个长方形③分别计算出长方形相邻两边的长,得a2+5ab+6b2= (a+2b)(a+3b)(3)计算(a+b)3请你仿照小丽的探究过程,写出操作步骤(4)分解因式a3+6a2b+12ab2+8b3请你仿照小明的探究过程,直接写出因式分解的结果.【考点】因式分解的应用.【专题】阅读型.【分析】(1)根据小丽的操作步骤可以得到问题的答案;(2)根据小明的操作步骤可以得到问题的答案;(3)根据第一问中小丽的操作步骤可以设计出相应的方案;(4)根据小明的操作步骤可以得到问题的答案.【解答】解:(1)根据题意可得,A型纸片1张,B型纸片3张,C型纸片2张,∴(a+b)(a+2b)=a2+3ab+2b2.故答案为:a2+3ab+2b2.(2)根据题意可得,a2+5ab+6b2=(a+2b)(a+3b).故答案为:(a+2b)(a+3b).(3)计算(a+b)3操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C型纸片是边长为b的正方形;②用①中的纸片拼成棱长为a+b的正方体;③数出以a为棱长的正方体一个,以a为边长的正方形做底面,高为b的长方体三个,以b为边长的正方形做底面,高为a的长方体三个,以b为棱长的正方体一个,得(a+b)3=a3+3a2b+3ab2+b3.(4)分解因式a3+6a2b+12ab2+8b3根据小明的操作步骤可得,a3+6a2b+12ab2+8b3=(a+2b)3.【点评】本题考查解因式分解的应用,解题的关键是能看懂小丽和小明的操作步骤,在(3)和(4)中可以与长方体和正方体联系在一起.。
南京市鼓楼区七年级上学期语文期中考试试卷

南京市鼓楼区七年级上学期语文期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共5题;共10分)1. (2分)下列划线字注音完全正确的一项是()A . 应和(hè)抖擞(sǒu)酝酿(yùn liàng)B . 着落(zhuó)贮蓄(zhù)吝啬(lìn sè)C . 莅临(lì)粗犷(kuàng)静谧(mì)D . 薄雪(báo)发髻(jǐ)高邈(miǎo)2. (2分)(2014·云南) 下列词语中没有错别字的一项是()A . 装钉针砭厉行节约歪风斜气B . 缭草急躁一愁莫展出类拔萃C . 禁锢狼藉人才倍出冥思遇想D . 苍茫斑斓陈词滥调漫不经心3. (2分) (2017九上·抚宁期中) 下列句子中划线成语使用错误的一项是()A . 我们感谢他光临做客,惋惜他即将离去,两种情感都溢于言表,这实在是一次完美的送别了。
B . 一个从不阅读文学作品的人,纵然他有“硕士”“博士”或者更高的学位,他也只能是一个“高智商的野蛮人”,这不是危言耸听。
C . 伟大的革命先驱孙中山先生的雕像,端坐平视,神态安详,栩栩如生。
D . 几十年来,作者多次想把心里话向这位知心朋友倾诉,可是都失之交臂。
4. (2分)选出下列没有语病的一句()A . 我校开展了向雷锋同志学习的活动。
B . 屋子里放着各式各样的鲁迅过去所使用过的东西和书籍。
C . 读了这篇文章之后,对我的教育太大了。
D . 谁也不会否认提高学习成绩不是勤奋学习的结果。
5. (2分)给下列句子排序,最恰当的一项是()①它们都贴有特殊的绿色食品标志,象征着产品是无污染的、充满健康和活力的产品。
②我国绿色食品行业民展也很快,日前已有203家企业开发了389种绿色食品。
③最先闻名于世的绿色产品是各种绿色食品。
南京市鼓楼区年七年级下期中数学试卷及答案-精编

2014-2015学年江苏省南京市鼓楼区七年级(下)期中数学试卷一、选择题(共6小题,每小题2分,满分12分)1.计算a6÷a2的结果是()A.a3B.a4C.a8D.a122.每个生物携带自身基因的载体是生物细胞的DNA,DNA分子的直径只有0.0000002cm,将0.0000002用科学记数法表示为()A.2×106B.2×107C.2×10﹣6D.2×10﹣73.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明()A.三角形内角和等于180°B.三角形外角和等于360°C.三角形任意两边之和大于第三边D.三角形任意两边之差小于第三边4.下列各式由左边到右边的变形,是因式分解的是()A.3x(x+y)+3x2+3xy B.﹣2x2﹣2xy=﹣2x(x+y)C.(x+5)(x﹣5)=x2﹣25 D.x2+x+1=x(x+1)+15.已知一个三角形的两边长分别为4、7,则第三边的长可以为()A.2 B.3 C.8 D.126.如图,将甲图中阴影部分无重叠、无缝隙地拼成乙图,根据两个图形中阴影部分的面积关系得到的等式是()A.a2﹣b2=(a+b)(a﹣b)B.a2+2ab+b2=(a+b)2C.a2﹣2ab+b2=(a﹣b)2D.(a+b)2﹣(a﹣b)2=4ab二、填空题(共10小题,每小题2分,满分20分)7.计算3﹣2的结果是.8.计算:(﹣2xy2)3= .9.已知a m=4,a n=5,则a m+n的值是.10.多边形的每个外角的度数都等于45°,则这个多边形的边数为.11.把方程4x﹣y=3写成用含x的代数式表示y的形式为y= .12.如图,把等腰直角三角尺的直角顶点放在直尺的一边上,则∠1+∠2= .13.二元一次方程的一个解是,这个二元一次方程可以是.14.已知x+y=5,xy=3,则(x﹣y)2= .15.如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3= .16.前n(n>3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x1,x2,x3,…,xn,将卡片上的数先平方再求和,得x12+x22+x32+…+xn2=28,将卡片上的数先立方再求和,得x13+x23+x33+…+xn3=4,则x 14+x24+x34+…+xn4的值是.三、解答题(共10小题,满分68分)17.计算:(1)(5﹣3)0﹣()﹣3(2)﹣a2•(﹣6ab)(3)x(y+5)+y(3﹣x)(4)(2a+b)(2a﹣b)﹣(a﹣3b)2.18.把下列各式因式分解:(1)4x2﹣6xy(2)a2(x+y)﹣b2(x+y)(3)(a2+1)2﹣4a2.19.解方程组.20.已知△ABC.(1)平移△ABC,使点A移到点A1的位置,画出平移后得到的△A1B1C1;(2)根据平移的性质,写出两条不同类型的正确结论.21.如图,∠A=∠F,∠C=∠D,判断BD与CE的位置关系,并说明理由.22.根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等).(1)如图①,测量△ABC的面积;(2)如图②,平分△DEF的面积.23.如图,△ABC的角平分线BP、CP相交于点P,∠P=140°,求∠A的度数.24.当abc≠0时,要说明(a+b+c)2≠a2+b2+c2不成立,下面三位同学提供了三种不同的思路(1)小明说,“不妨设a=1,b=2,c=3,通过计算能发现式子不成立”,请你完成他的说理过程;(2)小刚说,“根据整式乘法的运算法则,通过计算能发现式子不成立”,请你完成他的说理过程;(3)小丽说,“构造正方形,通过计算面积能发现式子不成立”.请你帮她画出图形,并完成说理过程.25.如图,在一张长方形纸片ABCD中,AB=3,AD=m,边AB的中垂线分别交于AB、CD于点E、F;在边BC上取一点H(即AH为折痕),使得△ABH沿AH折叠后点B恰好落在线段EF上,设为点G.(1)按上述描述画出图形(要求尺规作图,不写作法,保留画图痕迹);(2)求证:△ABG是等边三角形;(3)若要使图形折叠后点A、G、C在一直线上,试求m的值.26.数与形都是数学研究的对象,它们有着密切的联系,我们可以利用图形对整式乘法和因式分解进行研究(1)计算(a+b)(a+2b).小丽的操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C型纸片是边长为b的正方形;②用①中的纸片拼成两边长分别为a+b、a+2b的长方形③数出用了A型纸片1张,B型纸片3张,C型纸片2张,得(a+b)(a+2b)=(2)分解因式a2+5ab+6b2小明的操作步骤如下:①准备若干块(1)中的A、B、C型纸片②用1块A型纸片,5块B型纸片和6块纸片拼成一个长方形③分别计算出长方形相邻两边的长,得a2+5ab+6b2=(3)计算(a+b)3请你仿照小丽的探究过程,写出操作步骤(4)分解因式a3+6a2b+12ab2+8b3请你仿照小明的探究过程,直接写出因式分解的结果.2014-2015学年江苏省南京市鼓楼区七年级(下)期中数学试卷参考答案与试题解析一、选择题(共6小题,每小题2分,满分12分)1.计算a6÷a2的结果是()A.a3B.a4C.a8D.a12【考点】同底数幂的除法.【分析】根据同底数幂的除法法则,同底数幂相除,底数不变,指数相减计算即可.【解答】解:a6÷a2=a6﹣2=a4.故选B.【点评】本题主要考查同底数幂的除法,熟练掌握运算性质是解题的关键.2.每个生物携带自身基因的载体是生物细胞的DNA,DNA分子的直径只有0.0000002cm,将0.0000002用科学记数法表示为()A.2×106B.2×107C.2×10﹣6D.2×10﹣7【考点】科学记数法—表示较小的数.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.000 0002=2×10﹣7,故选:D.【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.3.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明()A.三角形内角和等于180°B.三角形外角和等于360°C.三角形任意两边之和大于第三边D.三角形任意两边之差小于第三边【考点】三角形内角和定理.【分析】根据三角形的内角和定理解答即可.【解答】解:这种变化说明三角形的内角和是180°,故选A.【点评】此题考查三角形的内角和定理,关键是根据三角形的内角和定理是180°.4.下列各式由左边到右边的变形,是因式分解的是()A.3x(x+y)+3x2+3xy B.﹣2x2﹣2xy=﹣2x(x+y)C.(x+5)(x﹣5)=x2﹣25 D.x2+x+1=x(x+1)+1【考点】因式分解的意义.【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.【解答】解:A、是整式的乘法,故A错误;B、是把一个多项式转化成几个整式积的形式,故B正确;C、是整式的乘法,故C错误;D、没是把一个多项式转化成几个整式积的形式,故D错误;故选:B.【点评】本题考查了因式分解的意义,因式分解是把一个多项式转化成几个整式积的形式,注意因式分解与整式乘法的区别.5.已知一个三角形的两边长分别为4、7,则第三边的长可以为()A.2 B.3 C.8 D.12【考点】三角形三边关系.【分析】根据三角形的三边关系定理可得7﹣4<x<7+4,计算出不等式的解集,再确定x的值即可.【解答】解:设第三边长为x,则7﹣4<x<7+4,3<x<11,故选:C.【点评】此题主要考查了三角形的三边关系,关键是掌握第三边的范围是:大于已知的两边的差,而小于两边的和.6.如图,将甲图中阴影部分无重叠、无缝隙地拼成乙图,根据两个图形中阴影部分的面积关系得到的等式是()A.a2﹣b2=(a+b)(a﹣b)B.a2+2ab+b2=(a+b)2C.a2﹣2ab+b2=(a﹣b)2D.(a+b)2﹣(a﹣b)2=4ab【考点】完全平方公式的几何背景.【分析】分别计算出甲、乙两图中阴影部分的面积,根据面积相等,即可解答.【解答】解:甲图中阴影部分的面积为:a2﹣2ab+b2,图乙中阴影部分的面积为:(a﹣b)2,所以a2﹣2ab+b2=(a﹣b)2,故选:C.【点评】本题考查了完全平方公式,解决本题的关键是分别计算出甲、乙两图中阴影部分的面积.二、填空题(共10小题,每小题2分,满分20分)7.计算3﹣2的结果是.【考点】负整数指数幂.【专题】计算题.【分析】此题考查的是负整数指数幂的计算方法,按照负指数为正指数的倒数进行计算即可.【解答】解:3﹣2==.故答案为.【点评】此题主要考查的是负整数指数幂,幂的负整数指数运算,先把底数化成其倒数,然后将负整数指数幂当成正的进行计算.8.计算:(﹣2xy2)3= ﹣8x3y6.【考点】幂的乘方与积的乘方.【分析】根据积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘;幂的乘方,底数不变指数相乘计算.【解答】解:(﹣2xy2)3,=(﹣2)3x3(y2)3,=﹣8x3y6.故填﹣8x3y6.【点评】本题考查积的乘方的性质,幂的乘方的性质,熟练掌握运算性质是解题的关键.9.已知a m=4,a n=5,则a m+n的值是20 .【考点】同底数幂的乘法.【分析】根据同底数幂的乘法,底数不变指数相加,可得答案.【解答】解:a m+n=m•a n=4×5=20,故答案为:20.【点评】本题考查了同底数幂的乘法,同底数幂的乘法底数不变指数相加.10.多边形的每个外角的度数都等于45°,则这个多边形的边数为8 .【考点】多边形内角与外角.【分析】多边形的外角和是360°,又有多边形的每个外角都等于45°,所以可以求出多边形外角的个数,进而得到多边形的边数.【解答】解:这个多边形的边数是: =8,故答案为:8.【点评】本题考查多边形的外角和,以及多边形外角的个数与其边数之间的相等关系.11.把方程4x﹣y=3写成用含x的代数式表示y的形式为y= 4x﹣3 .【考点】解二元一次方程.【专题】计算题;一次方程(组)及应用.【分析】把x看做已知数求出y即可.【解答】解:方程4x﹣y=3,解得:y=4x﹣3.故答案为:4x﹣3.【点评】此题考查了解二元一次方程,解题的关键是将x看做已知数求出y.12.如图,把等腰直角三角尺的直角顶点放在直尺的一边上,则∠1+∠2= 135°.【考点】平行线的性质.【分析】根据等腰直角三角形得出∠ACB=90°,∠A=∠B=45°,根据平行线性质求出∠1=∠ACM,根据三角形外角性质求出∠2=∠B+∠BCM,求出∠1+∠2=∠ACB+∠B即可.【解答】解:如图:∵△ACB是等腰直角三角形,∴∠ACB=90°,∠A=∠B=45°,∵EF∥MN,∴∠1=∠ACM,∵∠2=∠B+∠BCM,∴∠1+∠2=∠ACM+∠B+∠BCM=∠ACB+∠B=90°+45°=135°,故答案为:135°.【点评】本题考查了平行线的性质,等腰直角三角形,三角形的外角性质的应用,能求出∠1+∠2=∠ACB+∠B是解此题的关键,题目比较典型,难度适中.13.二元一次方程的一个解是,这个二元一次方程可以是2x+3y=13 .【考点】二元一次方程的解.【专题】开放型;一次方程(组)及应用.【分析】以2与3列出算式,即可确定出所求方程.【解答】解:根据题意得:2x+3y=13,故答案为:2x+3y=13.【点评】此题考查了二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.14.已知x+y=5,xy=3,则(x﹣y)2= 13 .【考点】完全平方公式.【专题】计算题;整式.【分析】原式利用完全平方公式化简,将已知等式代入计算即可求出值.【解答】解:∵x+y=5,xy=3,∴(x﹣y)2=x2﹣2xy+y2=x2+2xy+y2﹣4xy=(x+y)2﹣4xy=25﹣12=13,故答案为:13【点评】此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.15.如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3= 20°.【考点】平移的性质;平行线的性质.【专题】计算题.【分析】如图,根据平移的性质得m∥n,则利用平行线的性质得∠DAB=180°﹣∠1=110°,再根据三角形外角性质可计算出∠ABC=130°﹣∠CAB=20°,然后根据对顶角的性质求解.【解答】解:如图,∵直线m平移后得到直线n,∴m∥n,∴∠1+∠DAB=180°,∴∠DAB=180°﹣70°=110°,∵∠2=∠CAB+∠ABC,∴∠ABC=130°﹣110°=20°,∴∠3=∠ABC=20°.故答案为20°.【点评】本题考查了平移的性质把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.16.前n (n >3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x 1,x 2,x 3,…,x n ,将卡片上的数先平方再求和,得x 12+x 22+x 32+…+x n 2=28,将卡片上的数先立方再求和,得x 13+x 23+x 33+…+x n 3=4,则x 14+x 24+x 34+…+x n 4的值是 52 . 【考点】有理数的混合运算. 【专题】探究型. 【分析】根据题意可以设n 个数中含有a 个﹣2,b 个1,然后根据x 12+x 22+x 32+…+x n 2=28,x 13+x 23+x 33+…+x n 3=4,可以求得a 、b 的值,从而可以求得x 14+x 24+x 34+…+x n 4的值.【解答】解:∵前n (n >3)张卡片,在卡片上分别写上﹣2、0、1中的任意一个数,记为x 1,x 2,x 3,…,x n ,∴设这n 个数中,含有a 个﹣2,b 个1,∵x 12+x 22+x 32+…+x n 2=28,x 13+x 23+x 33+…+x n 3=4,∴解得,∴x 14+x 24+x 34+…+x n 4=(﹣2)4×2+14×20=16×2+1×20=32+20=52. 故答案为:52.【点评】本题考查有理数的混合运算,解题的关键是明确题意,求出n 个数中﹣2和1的个数.三、解答题(共10小题,满分68分) 17.计算:(1)(5﹣3)0﹣()﹣3 (2)﹣a 2•(﹣6ab )(3)x (y+5)+y (3﹣x )(4)(2a+b )(2a ﹣b )﹣(a ﹣3b )2.【考点】整式的混合运算;零指数幂;负整数指数幂. 【分析】(1)根据零指数和负整数指数的意义运算; (2)根据同底数幂的乘法法则运算; (3)先去括号,然后合并即可;(4)先利用平方差公式和完全平方公式展开,然后合并即可. 【解答】解:(1)原式=1﹣27 =﹣26;(2)原式=2a 3b ;(3)原式=xy+5x+3y ﹣xy =5x+3y ;(4)原式=4a2﹣b2﹣(a2﹣6ab+9b2)=4a2﹣b2﹣a2+6ab﹣9b2=3a2﹣10b2+6ab.【点评】本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.18.把下列各式因式分解:(1)4x2﹣6xy(2)a2(x+y)﹣b2(x+y)(3)(a2+1)2﹣4a2.【考点】提公因式法与公式法的综合运用.【分析】(1)直接提取公因式2x,进而分解因式得出答案;(2)首先提取公因式(x+y),进而利用平方差公式分解因式得出即可;(3)直接利用平方差公式分解因式进而结合完全平方公式的应用分解因式即可.【解答】解:(1)4x2﹣6xy=2x(2x﹣3y);(2)a2(x+y)﹣b2(x+y)=(x+y)(a2﹣b2)=(x+y)(a+b)(a﹣b);(3)(a2+1)2﹣4a2=(a2+1+2a)(a2+1﹣2a)=(a+1)2(a﹣1)2.【点评】此题主要考查了提取公因式法以及公式法分解因式,正确应用乘法公式是解题关键.19.解方程组.【考点】解二元一次方程组.【专题】计算题;一次方程(组)及应用.【分析】方程组利用加减消元法求出解即可.【解答】解:,①+②得:4x=8,即x=2,把x=2代入①得:y=2,则方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.20.已知△ABC.(1)平移△ABC,使点A移到点A1的位置,画出平移后得到的△A1B1C1;(2)根据平移的性质,写出两条不同类型的正确结论.【考点】作图-平移变换.【分析】(1)根据图形平移的性质画出图形即可;(2)根据图形平移的性质可直接得出结论.【解答】解:(1)如图所示;(2)△ABC≌△△A1B1C1,AA1=BB1=CC1.【点评】本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.21.如图,∠A=∠F,∠C=∠D,判断BD与CE的位置关系,并说明理由.【考点】平行线的判定与性质.【分析】根据平行线的判定得出AC∥DF,根据平行线的性质求出∠C=∠CEF,求出∠D=∠CEF,根据平行线的判定得出即可.【解答】解:BD∥CE,理由是:∵∠A=∠F,∴AC∥DF,∴∠C=∠CEF,∵∠C=∠D,∴∠D=∠CEF,∴BD∥CE.【点评】本题考查了平行线的性质和判定的应用,能正确运用定理进行推理是解此题的关键,题目比较好,难度适中.22.根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等).(1)如图①,测量△ABC的面积;(2)如图②,平分△DEF的面积.【考点】作图—应用与设计作图.【分析】(1)计算三角形的面积需要知道三角形的底边长和高长,需要作出AB边上的高线,(2)三角形的中线平分三角形的面积,需要找出三角形,一边上的中点,故此可作出一边的垂直平分线得到一边的中点,然后作出中线即可.【解答】解:(1)如图①所示:过点C作AB的垂线.需要测量:AB和DC的长,.(2)如图②所示:作ED的垂直平分线,交ED于点G,连接GF.GF平分△DEF的面积.【点评】本题主要考查的是作图应用与设计,掌握五种基本作图以及三角形的中线平分三角形的面积是解题的关键.23.如图,△ABC的角平分线BP、CP相交于点P,∠P=140°,求∠A的度数.【考点】三角形内角和定理.【分析】根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形的内角和等于180°列式计算即可得解.【解答】解:∵△ABC,∴∠ABC+∠ACB=180°﹣∠A,∵∠ABC与∠ACB的角平分线相交于P,∴∠PBC+∠PCB=(∠ABC+∠ACB)=,在△PBC中,∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣=140°,∴∠A=100°.【点评】此题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.24.当abc≠0时,要说明(a+b+c)2≠a2+b2+c2不成立,下面三位同学提供了三种不同的思路(1)小明说,“不妨设a=1,b=2,c=3,通过计算能发现式子不成立”,请你完成他的说理过程;(2)小刚说,“根据整式乘法的运算法则,通过计算能发现式子不成立”,请你完成他的说理过程;(3)小丽说,“构造正方形,通过计算面积能发现式子不成立”.请你帮她画出图形,并完成说理过程.【考点】整式的混合运算.【分析】(1)把a、b、c的值代入,求出两边的值,即可得出答案;(2)根据多项式乘以多项式法则求出后,再判断即可;(3)化成边长为a+b+c的正方形,即可得出答案.【解答】解:(1)∵当a=1,b=2,c=3时,(a+b+c)2=(1+2+3)2=36a2+b2+c2=12+22+32=14,∴(a+b+c)2≠a2+b2+c2;(2)∵(a+b+c)2=(a+b+c)(a+b+c)=a2+ab+ac+ab+b2+bc+ac+bc+c2=a2+b2+c2+2ab+2bc+2ac,∴(a+b+c)2≠a2+b2+c2;(3)如图所示:(a+b+c)2=a2+b2+c2+ab+ac+bc+ab+ac+bc,即(a+b+c)2≠a2+b2+c2.【点评】本题考查了整式的运算法则的应用,能正确根据整式的运算法则进行化简是解此题的关键,也培养了学生的动手操作能力.25.如图,在一张长方形纸片ABCD中,AB=3,AD=m,边AB的中垂线分别交于AB、CD于点E、F;在边BC上取一点H(即AH为折痕),使得△ABH沿AH折叠后点B恰好落在线段EF上,设为点G.(1)按上述描述画出图形(要求尺规作图,不写作法,保留画图痕迹);(2)求证:△ABG是等边三角形;(3)若要使图形折叠后点A、G、C在一直线上,试求m的值.【考点】四边形综合题.【分析】(1)先根据基本作图的方法作出线段AB的垂直平分线EF,在EF上取一点G,使AG=AB,连结GH,则△AGH与△ABH关于AH成轴对称;(2)连接GB,由中垂线的性质就可以得出AG=BG,由轴对称的性质就可以得出AG=AB而得出结论;(3)由(2)的结论就可以得出∠CAB=60°,由勾股定理就可以求出BC的值,得出结论.【解答】解:(1)由题意作出图形,如图1.(2)如图2,连接GB,∵EF垂直平分AB,点G在EF上,∴AG=GB.∵△AGH与△ABH关于AH对称,∴△AGH≌△ABH,∴AG=AB,∴AG=AB=GB,∴△ABG是等边三角形;(3)如图2,∵△ABG是等边三角形,∴∠CAB=60°.∵四边形ABCD是矩形,∴∠ABC=90°.AD=BC=m,∴∠ACB=30°,∴AC=2AB.∵AB=3,∴AC=6.在Rt△ABC中,由勾股定理,得BC=9,∴m=9.【点评】本题考查了矩形的性质的运用,尺规作图的运用,垂直平分线的性质的运用,等边三角形的判定及性质的运用,轴对称的性质的运用,勾股定理的性质的运用,解答时证明三角形ABG是等边三角形是关键.26.数与形都是数学研究的对象,它们有着密切的联系,我们可以利用图形对整式乘法和因式分解进行研究(1)计算(a+b)(a+2b).小丽的操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C型纸片是边长为b的正方形;②用①中的纸片拼成两边长分别为a+b、a+2b的长方形③数出用了A型纸片1张,B型纸片3张,C型纸片2张,得(a+b)(a+2b)= a2+3ab+2b2(2)分解因式a2+5ab+6b2小明的操作步骤如下:①准备若干块(1)中的A、B、C型纸片②用1块A型纸片,5块B型纸片和6块纸片拼成一个长方形③分别计算出长方形相邻两边的长,得a2+5ab+6b2= (a+2b)(a+3b)(3)计算(a+b)3请你仿照小丽的探究过程,写出操作步骤(4)分解因式a3+6a2b+12ab2+8b3请你仿照小明的探究过程,直接写出因式分解的结果.【考点】因式分解的应用.【专题】阅读型.【分析】(1)根据小丽的操作步骤可以得到问题的答案;(2)根据小明的操作步骤可以得到问题的答案;(3)根据第一问中小丽的操作步骤可以设计出相应的方案;(4)根据小明的操作步骤可以得到问题的答案.【解答】解:(1)根据题意可得,A型纸片1张,B型纸片3张,C型纸片2张,∴(a+b)(a+2b)=a2+3ab+2b2.故答案为:a2+3ab+2b2.(2)根据题意可得,a2+5ab+6b2=(a+2b)(a+3b).故答案为:(a+2b)(a+3b).(3)计算(a+b)3操作步骤如下:①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C型纸片是边长为b的正方形;②用①中的纸片拼成棱长为a+b的正方体;③数出以a为棱长的正方体一个,以a为边长的正方形做底面,高为b的长方体三个,以b为边长的正方形做底面,高为a的长方体三个,以b为棱长的正方体一个,得(a+b)3=a3+3a2b+3ab2+b3.(4)分解因式a3+6a2b+12ab2+8b3根据小明的操作步骤可得,a3+6a2b+12ab2+8b3=(a+2b)3.【点评】本题考查解因式分解的应用,解题的关键是能看懂小丽和小明的操作步骤,在(3)和(4)中可以与长方体和正方体联系在一起.。
2014秋南京鼓楼区初一英语试卷分析

鼓楼区期中统考七年级(上)英语试卷分析一.题量&题型语言知识点②连词but表示转折,前后意思相反;③频度(率)副词never, sometimes, often, always 的含义用法区别。
题目的意思是“Millie家住的离学校很远,但是她______迟到”,通过题意可知此处为never。
做此类选择题时,要注意综合考虑句义与逻辑关系,不可只关注一点。
21.- ______ does Daniel look?A.WhatB. WhyC. WhichD. How解析:D本题是现阶段学习中最常考查的一类题型(问外貌),How does sb. look (like)问的是外貌,look 在这里是系动词,后跟形容词作表语(主语补足语),like在这里是介词,要注意区分like 做动词(“喜欢”)与做介词(像……)时的用法区别。
22.-Would you like to visit Rubber Duck in Mochou Lake with me?- ______, but I should ask my mum first.A.Yes, I wouldB. Yes, I doC. I’d like toD. Sorry, I don’t解析:C本题考查建议句型Would you like...的回答方式,回答包括了Yes, please. / Sure. / Certainly / Of course. / OK. / All right./ Yes, I'd love to. / Yes, I'd like to.等,否定回答时也要注意委婉,一般会使用“I’d like/ love to, but...”这样的形式来回答,而很少直截了当的拒绝。
(三)阅读理解【题型分析】本试卷阅读题有三篇文章,第一篇为表格文章,另两篇均为记叙文。
考查题型集中在细节事实题和细节判断题。
难度不大。
江苏省南京市鼓楼区七年级上学期期中考试(语文)

(满分:100分,时间:120南京市鼓楼区七年级(上)期中试卷分钟)一(26分)1.请用诗文原句填空,第(3)题还需填写作者。
(10分)(1)水何澹澹,。
(曹操《观沧海》)(2),闻道龙标过五溪。
(李白《闻王昌龄左迁龙标遥有此寄》)(3)正是江南好风景,。
(《江南逢李龟年》)(4),受降城外月如霜。
(李益《夜上受降城闻笛》)(5)接天莲叶无穷碧,。
(杨万里《晓出净慈寺送林子方》)(6)四时之景不仅传情,也蕴含哲理。
王湾《次北固山下》中“,”一联就是通过冬春交替之景道出了新事物必将代替旧事物的哲理。
(7)我们如果想在任何领域获得成功,都需要发自内心地喜爱,并乐在其中。
用《论语》中的话来说,就是“,”。
班级开展“青春路飞天梦”为主题的语文综合性学习活动,请你积极参与。
2.小语写了一段开场白,请阅读后完成题目。
(9分)2021年10月16日,神舟十三号载人飞船发射圆满成功!翟志刚、王亚平和叶光富三名航天员带着国人“飞天”强国的q ǐ()盼,再次开启求索宇宙奥秘.()的征程。
自2003年杨利伟成为浩瀚太空的第一位中国访客以来,目前已经有十二名中国航天员zào f ǎng ()太空。
我国的航天事业取得了令世人信.()服的成绩!每每看到这样的消息,中华儿女的自豪感油然而生!(1)临写下面这幅字。
(3分)青春路飞天梦(2)给加点字注音,根据拼音写汉字。
(4分)①q ǐ()盼②奥秘.()③zào f ǎng ()④信.()服(3)文中画线词语使用不当,应将“求索”修改为下列选项中的“()”。
(2分)A.摸索 B.探索 C.搜索 D.思索3.班级拟邀请航天专家刘教授给同学们开设关于“飞天梦”的讲座,小文写了一份邀请函。
请阅读后完成题目。
(3分)邀请函尊敬的刘教授:您好!久仰您的大名!为了让同学们更好地了解中国人追寻“飞天梦”的历程,激发同学们的文化自信和民族自豪感,特邀请您来我班开设关于“飞天梦”的讲座。
