2013-2014年第一学期期末理科试题答案
北京市丰台区2014学年度高三年级第一学期期末考试理科数学

丰台区2013-2014学年度第一学期期末练习高 三 数 学(理科) 2014.1第一部分 (选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的4个选项中,选出符合题目要求的一项。
1. 在复平面内,复数1i i-对应的点位于 (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限2. 函数11(0)=++>y x x x的最小值为 (A )1 (B )2 (C )3 (D )43. 已知命题p: ∀21x x >,22x >12x ,则p ⌝是(A )∀21x x >,22x ≤12x (B )∃21x x >,22x ≤12x(C )∀21x x >,22x <12x (D )∃21x x >,22x <12x4. 过双曲线221916x y -=的右焦点,且平行其渐近线的直线方程是 (A ) 3(5)4y x =±- (B ) 4(5)3y x =±- (C ) 3(5)4y x =±+ (D ) 3(5)4y x =±+5.如图,已知曲边梯形ABCD 的曲边DC 所在的曲线方程 为1(0)y x x=>,e 是自然对数的底,则曲边梯形的面积是 (A )1 (B )e (C )1e (D )126. 已知平行四边形ABCD 中,AB=1,AD=2,∠DAB=60o,则且⋅AC AB uu u r uu u r 等于(A )1 (B (C )2 (D )7.已知函数()2sin()f x x ωϕ=+(0,||)ωϕπ><的部分图象如图所示,那么()f x 的表达式为(A )5()2sin(2)6π=+f x x (B )5()2sin(2)6π=-f x x (C )()2sin(2)6f x x π=+(D )()2sin(2)6f x x π=-8. 如图,一个底面半径为R 的圆柱被与其底面所成角为θ(00090θ<<)的平面所截,截面是一个椭圆.当θ为30o 时,这个椭圆的离心率为 (A )12 (B(C(D )23第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
北京市西城区2013—2014学年度高三年级第一学期期末数学理科
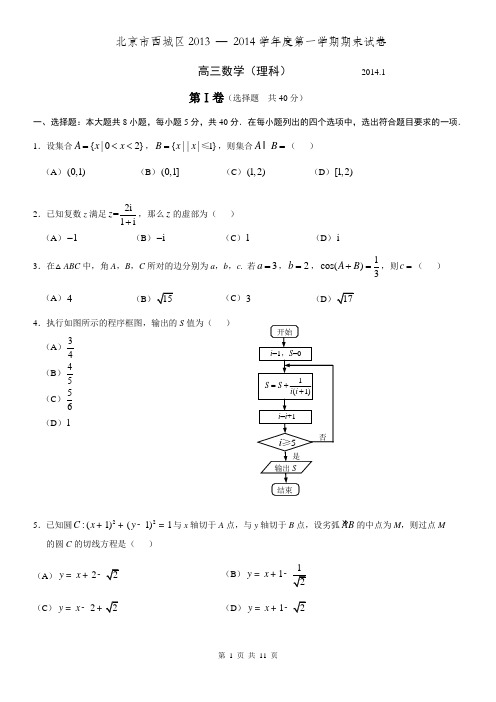
北京市西城区2013 — 2014学年度第一学期期末试卷高三数学(理科)2014.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.设集合{|02}A x x =<<,1{|||}B x x =≤,则集合A B = ( ) (A )(0,1)(B )(0,1](C )(1,2)(D )[1,2)3.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若3a =,2b =,1cos()3A B +=,则c =( ) (A )4(B(C )3(D4.执行如图所示的程序框图,输出的S 值为( ) (A )34 (B )45(C )56(D )12.已知复数z 满足2i=1iz +,那么z 的虚部为( ) (A )1-(B )i -(C )1(D )i5.已知圆22:(1)(1)1C x y ++-=与x 轴切于A 点,与y 轴切于B 点,设劣弧»AB 的中点为M ,则过点M 的圆C 的切线方程是( ) (A)2y x =+-(B)1y x =+-(C)2y x =-+(D)1y x =+-6. 若曲线221ax by +=为焦点在x 轴上的椭圆,则实数a ,b 满足( ) (A )22a b > (B )11a b< (C )0a b <<(D )0b a <<7.定义域为R 的函数()f x 满足(1)2()f x f x +=,且当(0,1]x ∈时,2()f x x x =-,则当[2,1]x ∈--时,()f x 的最小值为( ) (A )116-(B ) 18-(C ) 14-(D ) 08. 如图,正方体1111ABCD A B C D -的棱长为P 在对角线1BD 上,过点P 作垂直于1BD 的平面α,记这样得到的截面多边形(含三角形)的周长为y ,设BP =x , 则当[1,5]x ∈时,函数()y f x =的值域为( )(A) (B) (C) (D)第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9. 在平面直角坐标系xOy 中,点(1,3)A ,(2,)B k -,若向量OA AB ⊥,则实数k = ____. 10.若等差数列{}n a 满足112a =,465a a +=,则公差d =______;24620a a a a ++++= ______.11.已知一个正三棱柱的所有棱长均相等,其侧(左)视图如图所示,那么此三棱柱正(主)视图的面积为______.12.甲、乙两名大学生从4个公司中各选2个作为实习单位,则两人所选的实习单位中恰有1个相同的选法种数是______. (用数字作答)13. 如图,,B C 为圆O 上的两个点,P 为CB 延长线上一点,PA 为圆O 的切线,A 为切点. 若2PA =,3BC =,则PB =______;ACAB=______.1侧(左)视图14.在平面直角坐标系xOy 中,记不等式组220,0,2x y x y x y +⎧⎪-⎨⎪+⎩≥≤≤所表示的平面区域为D .在映射,:u x y T v x y =+⎧⎨=-⎩的作用下,区域D 内的点(,)x y 对应的象为点(,)u v . (1)在映射T 的作用下,点(2,0)的原象是 ; (2)由点(,)u v 所形成的平面区域的面积为______.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数()f x x ω=,π()sin()(0)3g x x ωω=->,且()g x 的最小正周期为π.(Ⅰ)若()2f α=[π,π]α∈-,求α的值; (Ⅱ)求函数()()y f x g x =+的单调增区间.16.(本小题满分13分)以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a 表示.(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求a 的值; (Ⅱ)求乙组平均成绩超过甲组平均成绩的概率;(Ⅲ)当2a =时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为X ,求随机变量X 的分布列和数学期望.17.(本小题满分14分)如图,在多面体ABCDEF 中,底面ABCD 是边长为2的菱形, 60=∠BAD ,四边形BDEF 是矩形,平面BDEF ⊥平面ABCD ,BF =3, H 是CF 的中点.(Ⅰ)求证:AC ⊥平面BDEF ;(Ⅱ)求直线DH 与平面BDEF 所成角的正弦值; (Ⅲ)求二面角H BD C --的大小.甲组 乙组 891 a822 F CEHD18.(本小题满分13分)已知函数()()e xf x x a =+,其中e 是自然对数的底数,a ∈R . (Ⅰ)求函数)(x f 的单调区间;(Ⅱ)当1a <时,试确定函数2()()g x f x a x =--的零点个数,并说明理由.19.(本小题满分14分)已知,A B 是抛物线2:W y x =上的两个点,点A 的坐标为(1,1),直线AB 的斜率为k , O 为坐标原点. (Ⅰ)若抛物线W 的焦点在直线AB 的下方,求k 的取值范围;(Ⅱ)设C 为W 上一点,且AB AC ⊥,过,B C 两点分别作W 的切线,记两切线的交点为D ,求OD 的最小值.20.(本小题满分13分)设无穷等比数列{}n a 的公比为q ,且*0()n a n >∈N ,[]n a 表示不超过实数n a 的最大整数(如[2.5]2=),记[]n n b a =,数列{}n a 的前n 项和为n S ,数列{}n b 的前n 项和为n T . (Ⅰ)若114,2a q ==,求n T ; (Ⅱ)若对于任意不超过2014的正整数n ,都有21n T n =+,证明:120122()13q <<. (Ⅲ)证明:n n S T =(1,2,3,n =L )的充分必要条件为1,a q N N **挝.北京市西城区2013 — 2014学年度第一学期期末高三数学(理科)参考答案及评分标准2014.1一、选择题:本大题共8小题,每小题5分,共40分.1.B 2.C 3.D 4.B 5.A 6.C 7.A 8.D 二、填空题:本大题共6小题,每小题5分,共30分. 9.4 10.125511. 12.24 13.1 214.(1,1) π注:第10、13、14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:因为π()sin()(0)3g x x ωω=->的最小正周期为π, 所以2||ωπ=π,解得2ω=. ……………… 3分由 ()2f α=22α=, 即 cos 22α=, ……… 4分 所以 π22π4k α=±,k ∈Z . 因为 [π,π]α∈-, 所以7πππ7π{,,,}8888α∈--. ……………… 6分(Ⅱ)解:函数 π()()2sin(2)3y f x g x x x =+=+-ππ2sin 2cos cos 2sin 33x x x =+- ……………… 8分1sin 222x x =πsin(2)3x =+, ……………10分 由 2πππ2π2π232k k x -++≤≤, ………………11分 解得 5ππππ1212k k x -+≤≤. ………………12分所以函数()()y f x g x =+的单调增区间为5ππ[ππ]()1212k k k -+∈Z ,.…………13分16.(本小题满分13分)(Ⅰ)解:依题意,得 11(889292)[9091(90)]33a ++=+++, ……………… 2分解得 1a =. ……………… 3分 (Ⅱ)解:设“乙组平均成绩超过甲组平均成绩”为事件A , ……………… 4分依题意 0,1,2,,9a = ,共有10种可能. ……………… 5分 由(Ⅰ)可知,当1a =时甲、乙两个小组的数学平均成绩相同,所以当2,3,4,,9a = 时,乙组平均成绩超过甲组平均成绩,共有8种可能.… 6分 所以乙组平均成绩超过甲组平均成绩的概率84()105P A ==. ……………… 7分 (Ⅲ)解:当2a =时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有339⨯=种, 它们是:(88,90),(88,91),(88,92),(92,90),(92,91),(92,92),(92,90),(92,91),(92,92), ……………… 9分则这两名同学成绩之差的绝对值X 的所有取值为0,1,2,3,4. ……………… 10分 因此2(0)9P X ==,2(1)9P X ==,1(2)3P X ==,1(3)9P X ==,1(4)9P X ==. ……………… 11分所以随机变量X 的分布列为:………………12分所以X 的数学期望221115()01234993993E X =⨯+⨯+⨯+⨯+⨯=.……………13分 17.(本小题满分14分)(Ⅰ)证明:因为四边形ABCD 是菱形,所以 AC BD ⊥. ……… 1分因为平面BDEF ⊥平面ABCD ,且四边形BDEF 是矩形,所以 ED ⊥平面ABCD , ……………… 2分 又因为 AC ⊂平面ABCD ,所以 ED AC ⊥. …………… 3分 因为 ED BD D = ,所以 AC ⊥平面BDEF . …………… 4分 (Ⅱ)解:设AC BD O = ,取EF 的中点N ,连接ON ,因为四边形BDEF 是矩形,,O N 分别为,BD EF 的中点,所以 //ON ED ,又因为 ED ⊥平面ABCD ,所以 ON ⊥平面ABCD ,由AC BD ⊥,得,,OB OC ON 两两垂直.所以以O 为原点,,,OB OC ON 所在直线分别为x 轴,y 轴,z 轴,如图建立空间直角坐标系. ……… 5分 因为底面ABCD 是边长为2的菱形,60BAD ∠= ,3BF =, 所以(0,A ,(1,0,0)B ,(1,0,0)D -,(1,0,3)E -,(1,0,3)F,C,13()22H . ………………6分因为 AC ⊥平面BDEF ,所以平面BDEF的法向量AC =. …………7分设直线DH 与平面BDEF 所成角为α,由33(,)222DH = , 得sin |cos ,|DH AC DH AC DH ACα⋅=<>=== ,所以直线DH 与平面BDEF. ………………9分 (Ⅲ)解:由(Ⅱ),得13()222BH =- ,(2,0,0)DB = .设平面BDH 的法向量为111(,,)x y z =n ,所以0,0,BH DB ⎧⋅=⎪⎨⋅=⎪⎩ n n ………………10分即111130,20,x z x ⎧-++=⎪⎨=⎪⎩ 令11z =,得(0,=n . ………………11分由ED ⊥平面ABCD ,得平面BCD 的法向量为(0,0,3)ED =-,则00(01(3)1cos ,232ED ED ED⋅⨯+⨯+⨯-<>===-⨯n n n . ………………13分 由图可知二面角H BD C --为锐角,所以二面角H BD C --的大小为60 . ………………14分18.(本小题满分13分)(Ⅰ)解:因为()()e xf x x a =+,x ∈R ,所以()(1)e x f x x a '=++. ……………… 2分 令()0f x '=,得1x a =--. ……………… 3分 当x 变化时,()f x 和()f x '的变化情况如下:……………… 5分故()f x 的单调减区间为(,1)a -∞--;单调增区间为(1,)a --+∞.………… 6分 (Ⅱ)解:结论:函数()g x 有且仅有一个零点. ……………… 7分理由如下:由2()()0g x f x a x =--=,得方程2e x ax x -=,显然0x =为此方程的一个实数解.所以0x =是函数()g x 的一个零点. ……………… 9分 当0x ≠时,方程可化简为e x ax -=.设函数()ex aF x x -=-,则()e 1x a F x -'=-,令()0F x '=,得x a =.当x 变化时,()F x 和()F x '的变化情况如下:即()F x 的单调增区间为(,)a +∞;单调减区间为(,)a -∞.所以()F x 的最小值min ()()1F x F a a ==-. ………………11分 因为 1a <,所以min ()()10F x F a a ==->, 所以对于任意x ∈R ,()0F x >, 因此方程e x a x -=无实数解.所以当0x ≠时,函数()g x 不存在零点.综上,函数()g x 有且仅有一个零点. ………………13分19.(本小题满分14分)(Ⅰ)解:抛物线2y x =的焦点为1(0,)4. ……………… 1分由题意,得直线AB 的方程为1(1)y k x -=-, ……………… 2分 令 0x =,得1y k =-,即直线AB 与y 轴相交于点(0,1)k -. ……………… 3分 因为抛物线W 的焦点在直线AB 的下方, 所以 114k ->, 解得 34k <. ……………… 5分 (Ⅱ)解:由题意,设211(,)B x x ,222(,)C x x ,33(,)D x y ,联立方程21(1),,y k x y x -=-⎧⎨=⎩ 消去y ,得210x kx k -+-=,由韦达定理,得11x k +=,所以 11x k =-. ……………… 7分 同理,得AC 的方程为11(1)y x k-=--,211x k =--. ……………… 8分对函数2y x =求导,得2y x '=,所以抛物线2y x =在点B 处的切线斜率为12x ,所以切线BD 的方程为21112()y x x x x -=-, 即2112y x x x =-. ……………… 9分 同理,抛物线2y x =在点C 处的切线CD 的方程为2222y x x x =-.………………10分联立两条切线的方程2112222,2,y x x x y x x x ⎧=-⎪⎨=-⎪⎩ 解得12311(2)22x x x k k +==--,3121y x x k k==-,所以点D 的坐标为111((2),)2k k k k---. ………………11分 因此点D 在定直线220x y ++=上. ………………12分因为点O 到直线220x y ++=的距离d ==所以5OD ≥,当且仅当点42(,)55D --时等号成立. ………………13分 由3125y k k =-=-,得k =.所以当k =OD………………14分20.(本小题满分13分)(Ⅰ)解:由等比数列{}n a 的14a =,12q =, 得14a =,22a =,31a =,且当3n >时,01n a <<. ……………… 1分所以14b =,22b =,31b =,且当3n >时,[]0n n b a ==. ……………… 2分即 ,6, 2,4, 17, 3.n n n T n ==⎧⎪=⎨⎪⎩≥ ……………… 3分(Ⅱ)证明:因为 201421()n T n n =+≤,所以 113b T ==,120142(2)n n n b T T n -=-=≤≤. ……………… 4分 因为 []n n b a =,所以 1[3,4)a ∈,2014[2,3)(2)n a n ∈≤≤. ……………… 5分 由 21a q a =,得 1q <. ……………… 6分 因为 201220142[2,3)a a q =∈,所以 20122223qa >≥,第 11 页 共 11 页 所以 2012213q <<,即 120122()13q <<. ……………… 8分 (Ⅲ)证明:(充分性)因为 1a N *Î,q N *Î, 所以 11n n a a q N -*= ,所以 []n n n b a a == 对一切正整数n 都成立.因为 12n n S a a a =+++L ,12n n T b b b =+++L ,所以 n n S T =. ……………… 9分 (必要性)因为对于任意的n N *Î,n n S T =,当1n =时,由1111,a S b T ==,得11a b =;当2n ≥时,由1n n n a S S -=-,1n n n b T T -=-,得n n a b =.所以对一切正整数n 都有n n a b =.由 n b Z Î,0n a >,得对一切正整数n 都有n a N *Î, ………………10分 所以公比21a q a =为正有理数. ………………11分 假设 q N *Ï,令p q r=,其中,,1p r r N *?,且p 与r 的最大公约数为1. 因为1a 是一个有限整数,所以必然存在一个整数()k k N Î,使得1a 能被k r 整除,而不能被1k r+整除. 又因为111211k k k k a p a a q r++++==,且p 与r 的最大公约数为1. 所以2k a Z +Ï,这与n a N *Î(n N *Î)矛盾.所以q *∈N .因此1a N *Î,q *∈N . ……………13分。
昌平区2013-2014学年第一学期高三年级期末理科数学

昌平区2013-2014学年第一学期高三年级期末质量抽测数 学 试 卷(理 科)(满分150分,考试时间120分钟) 2014.1考生须知:1. 本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分。
2. 答题前考生务必将答题卡上的学校、班级、姓名、考试编号用黑色字迹的签字笔填写。
3.答题卡上第I 卷(选择题)必须用2B 铅笔作答,第II 卷(非选择题)必须用黑色字迹的签字笔作答,作图时可以使用2B 铅笔。
请按照题号顺序在各题目的答题区内作答,未在对应的答题区域内作答或超出答题区域作答的均不得分。
4.修改时,选择题部分用塑料橡皮擦涂干净,不得使用涂改液。
保持答题卡整洁,不要折叠、折皱、破损。
不得在答题卡上做任何标记。
5.考试结束后,考生务必将答题卡交监考老师收回,试卷自己妥善保存。
第Ⅰ卷(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项.)(1) 已知全集=R U ,集合{1,0,1}=-A ,2{20}=-<B x x x , 则=I ðU A B(A) {1,0}- (B) {1,0,2}- (C) {0} (D) {1,1}- (2) “1cos 2α=”是“3πα=”的(A )充分而不必要条件 (B )必要而不充分条件(C )充要条件(D )既不充分也不必要条件(3) 给定函数①21y x =+,②12log y x =,③12y x =,④1()2xy =,其中在区间(0,1)上单调递增的函数的序号是(A )② ③(B )① ③ (C )① ④(D )② ④w(4) 执行如图所示的程序框图,输出的k 值是 (A)1 (B)2 (C)3 (D)4俯视图左视图主视图(5) 若实数,x y 满足10,2,3,+-≥⎧⎪≤⎨⎪≤⎩x y x y 则z y x =-的最小值是(A) 1 (B) 5 (C) 3- (D) 5- (6) 一个几何体的三视图如图所示,则这个几何体的体积是 (A) 1 (B) 2(C)23 (D)13(7) 连掷两次骰子得到的点数分别为m 和n ,若记向量()m n ,a =与向量(12)=-,b 的夹角为θ,则θ为锐角的概率是 (A)536 (B) 16 (C) 736(D) 29(8)已知函数21, 0,(),40⎧+>⎪=-≤≤x x f x a x 在点(1,2)处的切线与()f x 的图象有三个公共点,则a 的取值范围是(A)[8,4--+ (B)(44---+ (C)(48]-+ (D)(48]---第二卷(非选择题 共110分)二、填空题(本大题共6小题,每小题5分,共30分.)(9) 已知θ是第二象限的角,3sin 5θ=,则tan θ的值为___________ .(10) 如图,在复平面内,复数z 对应的向量为OA uu r,则复数i ⋅z =_______ .(11) 已知等差数列{}n a 的前n 项和为n S ,若2461a a a -+=,则4a =_____ ,7S = _____.(12)曲线11,2,,0====x x y y x所围成的图形的面积等于___________ . (13) 在ABC ∆中,4,5,2==⋅=AB BC BA AC uu r uuu r,则AC =________ .(14) 将含有3n 个正整数的集合M 分成元素个数相等且两两没有公共元素的三个集合A B C 、、,其中12{,,,}n A a a a =L ,12{,,,}n B b b b =L ,12{,,,}n C c c c =L ,若A B C 、、中的元素满足条件:12n c c c <<<L ,k k k a b c +=,(1,2,3,,)k n =,则称M 为“完并集合”.①若{1,,3,4,5,6}M x =为“完并集合”,则x 的一个可能值为 .(写出一个即可)②对于“完并集合”{1,2,3,4,5,6,7,8,9,10,11,12}M =,在所有符合条件的集合C 中,其元素乘积最小的集合是 .D CBAP三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)(15)(本小题满分13分)已知函数2()cos 2sin 1f x x x x =+-. (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)当5[,]126x ππ∈-时,求函数()f x 的取值范围.(16)(本小题满分13分)为了调研某校高一新生的身高(单位:厘米)数据,按10%的比例对700名高一新生按性别分别进行“身高”抽样检查,测得“身高”的频数分布表如下表1、表2.(Ⅰ)求高一的男生人数并完成下面的频率分布直方图; (Ⅱ)估计该校学生“身高”在[165,180)之间的概率;(Ⅲ)从样本中“身高”在[180,190)的男生中任选2人,求至少有1人“身高”在[185,190)之间的概率.(17)(本小题满分14分)在四棱锥P ABCD -中,PD ⊥平面ABCD ,2PD CD BC AD ===,//,90AD BC BCD ∠=︒.(Ⅰ)求证:BC PC ⊥;(Ⅱ)求PA 与平面PBC 所成角的正弦值;(Ⅲ)线段PB 上是否存在点E ,使AE ⊥平面PBC ?说明理由.(18)(本小题满分13分)在平面直角坐标系x y O 中,已知点(,0)(0)≠A a a ,圆C 的圆心在直线4y x =-上,并且与直线:10l x y +-=相切于点(3,2)P -.(Ⅰ)求圆C 的方程;(Ⅱ)若动点M 满足2MA MO =,求点M 的轨迹方程;(Ⅲ)在(Ⅱ)的条件下,是否存在实数a ,使得CM 的取值范围是[1,9],说明理由.(19)(本小题满分13分)已知函数2(2)()m xf x x m-=+. (Ⅰ)当1m =时,求曲线()f x 在点11(,())22f 处的切线方程; (Ⅱ)求函数()f x 的单调区间.(20)(本小题满分14分)设满足以下两个条件的有穷数列123,,,,n a a a a L 为(2,3,4,)=L n n 阶“期待数列”: ①1230++++=L n a a a a ,②1231++++=L n a a a a . (Ⅰ)若等比数列{}n a 为2()∈N*k k 阶“期待数列”,求公比q ;(Ⅱ)若一个等差数列{}n a 既是2()∈N*k k 阶“期待数列”又是递增数列,求该数列的通项公式; (Ⅲ)记n 阶“期待数列”{}i a 的前k 项和为(1,2,3,,)=L k S k n .(1)求证: 12≤k S ; (2)若存在{1,2,3,,}∈L m n ,使12=m S ,试问数列{}(1,2,3,,)=L i S i n 能否为n 阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.昌平区2013-2014学年第一学期高三年级期末质量抽测数学试卷(理科)参考答案及评分标准 2014.1一、选择题共10小题,每小题5分,共50分。
揭阳第一中学2013—2014学年度第一学期物理期末试题(含答案,题目难度中等)很好的

揭阳第一中学2013—2014学年度第一学期高一级学期末考试物理科试题一、单项选择题(本题共4小题,每小题4分,共16分)1、在国际单位制中,力学的三个基本单位是( )A .㎏、N 、mB .㎏、N 、sC .㎏、m 、sD .N 、m 、s2、某航母跑道长200m.飞机在航母上滑行的最大加速度为6m/s 2,起飞需要的最低速度为50m/s.那么,飞机在滑行前,需要借助弹射系统获得的最小初速度为( )A.5m/sB.10m/sC.15m/sD.20m/s3、如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ。
若此人所受重力为G ,则椅子各部分对他的作用力的合力大小为( )A .GB .GsinθC .GcosθD .Gtanθ4、物体A 在外力F 作用下静止在水平面上,关于物体的受力存在几对作用力与反作用力( )A.1对B.2对C.3对D.4对二、双项选择题(本题共5小题,每小题6分,共30分)5、关于速度、加速度、合外力之间的关系,正确的是( )A .物体的速度越大,则加速度越大,所受的合外力也越大B .物体的速度为零,则加速度为零,所受的合外力也为零C .物体的速度为零,但加速度可能很大,所受的合外力也可能很大D .物体的速度很大,但加速度可能为零,所受的合外力也可能为零6、如图所示,在光滑水平地面上,水平外力F 拉动小车和木块一起做无相对滑动的加速运动.小车质量为M ,木块质量为m ,加速度大小为a ,木块和小车之间的动摩擦因数为μ,则在这个过程中,木块受到的摩擦力大小是 ( ).A .μmg B.M +m mF C .μ(M +m)g D .ma7、将地面上静止的货物竖直向上吊起,货物由地面运动至最高点的v -t 图象如下图所示. 以下判断正确的是ks5uA .前3 s 内货物处于超重状态B .3 s 末货物运动至最高点C .第3 s 末至第5 s 末的过程中,货物静止D.前3 s内与最后2 s内货物的平均速度相同8、为了测出楼房的高度,让一石块从楼顶自由落下(不计空气阻力),测出下列哪个物理量就可以算出楼房的高度()A.物体的质量B.物体的密度C.石块下落到地面的总时间D.物体落地时的速度9、如图所示,在匀速前进的磁悬浮列车里,小明将一小球放在水平桌面上,且小球相对桌面静止.关于小球与列车的运动,下列说法正确的是( ).A.若小球向前滚动,则磁悬浮列车在加速前进B.若小球向后滚动,则磁悬浮列车在加速前进C.磁悬浮列车急刹车时,小球向前滚动D.磁悬浮列车急刹车时,小球向后滚动三、实验题(本题共6个空,每空3分,共18分)10、图为“验证牛顿第二定律”的实验装置示意图.砂和砂桶的总质量为m,小车和砝码的总质量为M.实验中用砂和砂桶总重力的大小作为细线对小车拉力的大小.(1)实验中,为了使细线对小车的拉力等于小车所受的合外力,先调节长木板一端滑轮的高度,使细线与长木板平行.接下来还需要进行的一项操作是( ).A.将长木板水平放置,让小车连着已经穿过打点计时器的纸带,给打点计时器通电,调节m的大小,使小车在砂和砂桶的牵引下运动,从打出的纸带判断小车是否做匀速运动B.将长木板的一端垫起适当的高度,让小车连着已经穿过打点计时器的纸带,撤去砂和砂桶,给打点计时器通电,轻推小车,从打出的纸带判断小车是否做匀速运动C.将长木板的一端垫起适当的高度,撤去纸带以及砂和砂桶,轻推小车,观察判断小车是否做匀速运动D. 将长木板的一端垫起适当的高度,撤去纸带以及砂和砂桶,释放小车,观察判断小车是否能自由滑动(2)实验中要进行质量m和M的选取,以下最合理的一组是 ( )A.M=200g,m=10g、15g、20g、25g、30g、40gB.M=200g,m=20g、40g、60g、80g、100g、120gC.M=400g,m=10g、15g、20g、25g、30g、40gD.M=400g,m=20g、40g、60g、80g、100g、120g(3)右图是实验中得到的一条纸带,相邻计数点间的时间间隔是t. 测出纸带各相邻计数点之间的距离分别为、、、,为使由实验数据计算的结果更精确一些,计算加速度平均值的公式应为a=____ _ _。
2013-2014学年惠州市高二数学上学期期末考试试题(理科)

惠州市2013-2014学年第一学期期末考试高二数学(理科)试题说明:1、全卷满分150分,时间120分钟。
2、答卷前,考生将自己的学校、班级、姓名、试室号、座位号,填写在答题卷上。
3、考试结束后,考生将答题卷交回。
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一个是符合题目要求的)1、椭圆13610022=+y x 的焦距等于( ) A 、20 B 、16 C 、12 D 、82、某企业为了监控产品质量,从产品流转均匀的生产线上每间隔10分钟抽取一个样本进行检测,这种抽样方法是( )A 、抽签法B 、随机数表法C 、系统抽样法D 、分层抽样法 3、空间中,与向量(3,0,4)a =同向共线的单位向量e 为( ) A 、(1,0,1)e = B 、(1,0,1)e = 或(1,0,1)e =--C 、34(,0,55e = D 、34(,0,55e =或34(,0,)55e =-- 4、已知点F 是抛物线24y x =的焦点,点P 在该抛物线上,且点P 的横坐标是2,则||PF =( ).A 、2B 、3C 、4D 、5 5、已知事件A 与事件B 发生的概率分别为()P A 、()P B ,有下列命题:①若A 为必然事件,则()1P A =. ②若A 与B 互斥,则()()1P A P B +=. ③若A 与B 互斥,则()()()P A B P A P B ⋃=+. 其中真命题有( )个A 、0B 、1C 、2D 、36、“0a >”是“方程2y ax =表示的曲线为抛物线”的( )条件。
A 、充分不必要B 、必要不充分C 、充要D 、既不充分也不必要7、执行右边的程序框图,如果输入5a =,那么输出=n ( ).A 、2B 、3C 、4D 、5A 1C 8、已知椭圆22219x y b+=(03)b <<,左右焦点分别为1F ,2F ,过1F 的直线交椭圆于,A B 两点,若22||||AF BF +的最大值为8,则b 的值是()A 、BC D二、填空题:(本大题共6题,每小题5分,共30分.请将答案填写在答卷相应位置上.)9的渐近线方程为 .10、样本2-,1-,0,1,2的方差为 .11、已知(1,5,2)a =-,(,2,2)b m m =+,若a b ⊥,则m 的值为 .12、命题“2,210x R x ∀∈+>”的否定是 .13、某城市近10年居民的年收入x 与支出y 之间的关系大致符合0.90.2y x =+(单位:亿元),预计今年该城市居民年收入为20亿元,则年支出估计是 亿元.14、如图,在棱长为2的正方体1111D C B A ABCD -内(含正方体表面) 任取一点M ,则11≥⋅AM AA 的概率=p .三、解答题:(本大题共6题,满分80.解答应写出文字说明,证明过程或演算步骤.) 15、(本小题满分12分)某社团组织20名志愿者利用周末和节假日参加社会公益活动,志愿者中,年龄在20至40岁的有12人,年龄大于40岁的有8人.(1)在志愿者中用分层抽样方法随机抽取5名,年龄大于40岁的应该抽取几名?(2)上述抽取的5名志愿者中任取2名,求取出的2人中恰有1人年龄大于40岁的概率.16、(本小题满分12分)已知22x -≤≤,22y -≤≤,点P 的坐标为(,)x y .(1)求当,x y R ∈时,点P 满足22(2)(2)4x y -+-≤的概率; (2)求当,x y Z ∈时,点P 满足22(2)(2)4x y -+-≤的概率.17、(本小题满分14分)设命题p :实数x 满足22430x ax a -+<,其中0a >;命题q :实数x 满足2560x x -+≤;(1)若1a =,且p q ∧为真,求实数x 的取值范围; (2)若p 是q 成立的必要不充分条件,求实数a 的取值范围.ABCD1A 1B 1C 1D EFG 18、(本小题满分14分)已知椭圆2222:1x y C a b +=(0)a b >>的离心率为3,直线:2l y x =+与圆222x y b +=相切.(1)求椭圆C 的方程;(2)设直线l 与椭圆C 的交点为,A B ,求弦长||AB .19、(本小题满分14分)如图,已知正方体1AC 棱长为2,E 、F 、G 分别是1CC 、BC 和CD 的中点. (1)证明:1AG ⊥面EFD ; (2)求二面角E DF C --的余弦值.20、(本小题满分14分)已知动直线l 与椭圆C :22132x y +=交于P ()11,x y 、Q ()22,x y 两不同点,且△OPQ 的面积OPQ S ∆O 为坐标原点. (1)证明2212x x +和2212y y +均为定值;(2)设线段PQ 的中点为M ,求||||OM PQ ⋅的最大值;(3)椭圆C 上是否存在点D E G 、、,使得ODE ODG OEG S S S ∆∆∆===?若存在,判断△DEG 的形状;若不存在,请说明理由.惠州市2013-2014学年第一学期期末考试高二数学(理科)试题答案一、选择题(本大题共8小题,每小题5分,共40分)1、【解析】由8c ==,所以焦距为16.∴选B .2、【解析】因为间隔相同,所以是系统抽样法,∴选C .3、【解析】2||305a =+=,∴134(3,0,4)(,0,)555||a e a ==⋅=,∴选C .4、【解析】抛物线24y x =知12p =,||2132P pPF x =+=+=,∴选B . 5、【解析】由概率的性质知①③为真命题,∴选C .6、【解析】当且仅当0a ≠时,方程2y ax =表示的曲线为抛物线,∴选A .7、【解析】5a =,进入循环后各参数对应值变化如下表:∴选B .8、【解析】∵|AF 1|+|AF 2|=6,|BF 1|+|BF 2|=6,∴△AF 2B 的周长为|AB|+|AF 2|+|BF 2|=12;若|AB|最小时,|BF 2|+|AF 2|的最大,又当AB ⊥x 轴时,|AB|最小,此时|AB|=22223b b a =,故221283b b -=⇒=D . 二、填空题:(本大题共6题,每小题5分,共30分.) 9、23y x =±10、2 11、6 12、200,210.x R x ∃∈+≤ 13、18.2 14、34;9、 10、【解析】222222(20)(10)(00)(10)(20)25s --+--+-+-+-==. 11、【解析】a b ⊥(1,5,2)⇒-⋅(,2,2)0m m +=102406m m m ⇒+--=⇒=. 12、【解析】全称命题的否定为特称命题.13、【解析】0.9200.218.2y =⋅+=.14、【解析】以A 为原点AB 为x 轴建立空间直角坐标系,则()10,0,2AA =,设(),,M x y z ,则(),,AM x y z =,则111212AA AM z z ⋅≥⇒⋅≥⇒≥,从而12-2232==2224M V p V ⎛⎫⋅⋅ ⎪⎝⎭=⋅⋅正. 三、解答题:(本大题共6题,满分80.解答应写出文字说明,证明过程或演算步骤.) 15、(本小题满分12分)解:(1)若在志愿者中随机抽取5名,则抽取比例为51204=………………………2分 ∴年龄大于40岁的应该抽取1824⨯=人. ……………………………4分 (2)上述抽取的5名志愿者中,年龄在20至40岁的有3人,记为1,2,3年龄大于40岁的有2人,记为4,5,……………………………………………6分 从中任取2名,所有可能的基本事件为:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5)(3,4),(3,5),(4,5),共10种,…8分其中恰有1人年龄大于40岁的事件有(1,4),(1,5),(2,4),(2,5)(3,4),(3,5),共6种,………………………………10分∴恰有1人年龄大于40岁的概率63105P ==.…………………………………12分 16、(本小题满分12分)解:(1)点P 所在的区域为正方形ABCD 的内部(含边界),……………(1分)满足22(2)(2)4x y -+-≤的点的区域为以(2,2)为圆心,2为半径的圆面(含边界). ……………………(3分)∴所求的概率211244416P ππ⨯==⨯. …………………………(5分) (2)满足,x y ∈Z ,且22x -≤≤,22y -≤≤的整点有25个 …………(8分)满足,x y ∈Z ,且22(2)(2)4x y -+-≤的整点有6个,……………(11分)∴所求的概率2625P =. ………………………………(12分) 17、(本小题满分14分)解 (1)由22430x ax a -+<得(3)()0x a x a -⋅-<.……………………………1分 又0a >,所以3a x a <<,………2分当1a =时,13x <<,即p 为真命题时,实数x 的取值范围是13x <<……4分 由2560x x -+≤得23x ≤≤.所以q 为真时实数x 的取值范围是23x ≤≤.…………………………………6分 若p q ∧为真,则23x ≤<,所以实数x 的取值范围是[)2,3.……………8分 (2) 设{}|3A x a x a =<<,{}|23B x x =≤≤…………………………………10分q 是p 的充分不必要条件,则B A ⊂…………………………………………12分所以021233a a a <<⎧⇒<<⎨>⎩,所以实数a 的取值范围是()1,2.………14分18、(本小题满分12分)解:(1)又由直线:2l y x =+与圆222x y b +=相切得b==2分由e =3a == 4分 ∴椭圆方程为22132x y +=…………………………………………………6分 (2)2222123(2)60322x y x x y x ⎧+=⎪⇒++-=⎨⎪=+⎩251260x x ⇒++=…………8分 21245624∆=-⋅⋅=,设交点,A B 坐标分别为()()1122,,,x y xy ………9分则1212126,,55x x x x +=-⋅=…………………………………………………11分从而||AB =所以弦长||5AB =14分 19、(本小题满分14分)解:以D 为原点建立如图空间直角坐标系,正方体棱长为2, 则D (0,0,0)、E (0,2,1)、F (1,2,0) 、G (0,1,0) 、A 1 (2,0,2) 、C (0,2,0),…… 2分 (1)则1(2,1,2)AG =--,(0,2,1)DE =, (1,2,0)DF =………………………… 3分∵1(2,1,2)AG DE ⋅=--(0,2,1)0⋅=, ∴1AG DE ⊥ ………………………… 4分 ∵1(2,1,2)AG DF ⋅=--(1,2,0)0⋅=, ∴1AG DF ⊥ ………………………… 5分 又DE DF D ⋂=,DE DEF ⊂面,DF DEF ⊂面……………… 6分 ∴1AG ⊥面EFD …………………………………………………………7分 (2)由(1)知1(2,1,2)AG =--为面EFD 的法向量,………………………… 8分 ∵CE ⊥面CFD ,(0,0,1)CE =为面CFD 的法向量,……………… 9分 设1AG 与CE 夹角为θ,则11cos AG CE AG CE θ⋅==⋅231-⋅23=-……… 12分 由图可知二面角E DF C --的平面角为πθ-, ∴二面角E DF C --的余弦值为23.…………………………………… 14分 20、(本小题满分14分)解:(1)当直线l 的斜率不存在时,P ,Q 两点关于x 轴对称,所以2121,.x x y y ==-因为11(,)P x y 在椭圆上,因此2211132x y += ①又因为OPQ S ∆=所以11||||x y ⋅= ②由①、②得11||| 1.2x y ==此时222212123,2,x x y y +=+=…………… 2分 当直线l 的斜率存在时,设直线l 的方程为,y kx m =+由题意知0m ≠,将其代入22132x y +=,得222(23)63(2)0k x kmx m +++-=, 其中22223612(23)(2)0,k m k m ∆=-+->即2232k m +>…(*)又212122263(2),,2323km m x x x x k k-+=-=++所以2||23PQ k==+因为点O 到直线l的距离为d =所以1||2OPQS PQ d ∆=⋅==又OPQ S ∆=整理得22322,k m +=且符合(*)式, 此时222221212122263(2)()2()23,2323km m x x x x x x k k-+=+-=--⨯=++ 222222121212222(3)(3)4() 2.333y y x x x x +=-+-=-+=综上所述,222212123;2,x x y y +=+=结论成立。
2013-2014学年度第一学期期末统一考试高三数学试卷(理科)

曲靖市2013—2014学年度第一学期期末统一考试高三数学试卷(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试用时120分钟. 注意事项:1、答第I 卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上.2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上.3、不可以使用计算器.4、考试结束,将答题卡交回,试卷不用上交.第Ⅰ卷(选择题共40分)一、选择题:(本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设全集{}1,2,3,4,5,6,7,8U =,集合{1,2,3,5}A =,{2,4,6}B =,则图中的阴影部分表示的集合为 ( ) A .{}2 B .{}4,6C .{}1,3,5D .{}4,6,7,82.等差数列}{n a 的前n 项和为n S ,若301272=++a a a ,则13S 的值是( ) A .130 B .65 C .70 D .753.“22ab >”是 “22log log a b >”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.若△ABC 的三个内角满足sin :sin :sin 5:11:13A B C =,则△ABC ( ) A .一定是锐角三角形 B .一定是直角三角形C .一定是钝角三角形D .可能是锐角三角形,也可能是钝角三角形5.直线2(1)10x a y +++=的倾斜角的取值范围是( ) A .[0,]4πB .3,4ππ⎡⎫⎪⎢⎣⎭C .[0,](,)42πππD .3,,424ππππ⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭6.有编号分别为1,2,3,4,5的5个红球和5个黑球,从中取出4个,则取出的编号互不相同的概率为( )A .521B .27C .13D .8217.若右边的程序框图输出的S 是126,则条件①可为( ) A .n ≤5B .n ≤6C .n ≤7D .n ≤88.如图,在透明塑料制成的长方体1111D C B A ABCD -容器内灌进一些水,将容器底面一边BC 固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法: ①水的部分始终呈棱柱状;②水面四边形EFGH 的面积不改变; ③棱11D A 始终与水面EFGH 平行; ④当1AA E ∈时,BF AE +是定值.其中所有正确的命题的序号是( )A .①②③B .①③C .②④D .①③④第Ⅱ卷(非选择题共110分)二、填空题:(本大题共6小题,每小题5分,共30分.)9.在二项式()62+x 的展开式中,含3x 的项的系数是__________10.曲线2:x y C =、直线2:=x l 与x 轴所围成的图形面积为_________11.已知函数()x f 的导数()()()()1,f x a x x a f x x a '=+-=若在处取得极大值,则a 的取值范围为__________12.若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积...等于 13.已知直线0=++c by ax 与圆1:22=+y x O 相交于,A B 两点,且,3=AB 则OB OA ⋅的值是14.如下图,对大于或等于2的自然数m 的n 次幂进行如下方式的“分裂”:C1BA 241357341315171944616365672213323542792313533791143252729仿此,26的“分裂”中最大的数是 ;32013 的“分裂”中最大的数是 ; 三、解答题:(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.) 15.(本小题满分12分)函数()2sin()ωϕ=+f x x (0,0)2ωϕπ><<的部分图象如下图所示,该图象与y 轴交于点(0,1)F ,与x 轴交于点,B C ,M 为最高点,且三角形MBC 的面积为π.(Ⅰ)求函数()f x 的解析式;(Ⅱ)若((0,)62f ααππ-=∈,求cos(2)4απ+的值.16.(本小题满分12分)已知等差数列{}n a 的公差大于0,且53,a a 是方程045142=+-x x 的两根,数列{}n b 的前n 项的和为n S ,且n n b S 211-= (*n N ∈). (1) 求数列{}n a ,{}n b 的通项公式; (2) 记n n n b a c ⋅=,求证:n n c c ≤+1.17.(本小题满分14分) 如图,三棱柱111ABC A B C -中,1AA ⊥平面ABC ,D 、E 分别为11A B 、1AA 的中点,点F 在棱AB 上,且14AF AB =. (Ⅰ)求证://EF 平面1BDC ;(Ⅱ)在棱AC 上是否存在一个点G ,使得平面EFG 将三棱柱分割成的两部分体积之比为1:15,若存在, 指出点G 的位置;若不存在,说明理由.18.(本小题满分14分)某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:(Ⅰ)该同学为了求出y 关于x 的线性回归方程ˆˆˆybx a =+,根据表中数据已经正确计算出ˆ0.6b=,试求出ˆa 的值,并估计该厂6月份生产的甲胶囊产量数; (Ⅱ)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊,后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为ξ,求ξ的分布列和数学期望.19.(本小题满分14分) 已知函数()b ax x x f +-=331,其中实数b a ,是常数. (Ⅰ)已知{}2,1,0∈a ,{}2,1,0∈b ,求事件A :“()01≥f ”发生的概率;(Ⅱ)若()x f 是R 上的奇函数,()a g 是()x f 在区间[]1,1-上的最小值,求当1≥a 时A 1x()a g 的解析式;(Ⅲ)记()x f y =的导函数为()x f ',则当1=a 时,对任意[]2,01∈x ,总存在[]2,02∈x 使得12()()f x f x '=,求实数b 的取值范围.20.(本小题满分14分) 已知函数()2ln bf x ax x x=--,(1)0f =. (Ⅰ)若函数()f x 在其定义域内为单调函数,求实数a 的取值范围; (Ⅱ)若函数()f x 的图象在1x =处的切线的斜率为0,且211()11n n a f n a n +'=-+-+,已知14a =,求证:22n a n ≥+;(Ⅲ)在(Ⅱ)的条件下,试比较1231111...1111n a a a a ++++++++与25的大小,并说明你的理由.中山市高三级2012—2013学年度第一学期期末统一考试数学试卷(理科)答案一、选择题二、填空题9.160; 10.83; 11.01<<-a ; 12.326+; 13.12-;14.11(本空2分);3m (m 为奇数)的“分拆”的最大数是21m m +-,所以2201320124054181+=(本空3分,写成“220132012+”或“4054181”都给3分)三、解答题15.(本小题满分12分)解:(I )∵122MBC S BC BC ∆=⨯⨯==π, ∴周期2,1T ωω2π=π== ……….2分由(0)2sin 1f ϕ==,得1sin 2ϕ=, ……………………………………3分∵02ϕπ<<,∴6ϕπ=,∴()2sin()6f x x π=+. …………………………………………….6分 (Ⅱ)由()2sin 6f ααπ-=sin α=, ∵(0,2απ∈,∴cos α=, ∴234cos 22cos 1,sin 22sin cos 55ααααα=-===,∴cos(2)cos2cos sin 2sin 444αααπππ+=-3455==. …………………….12分16.(本小题满分12分)解:(Ⅰ)∵53,a a 是方程045142=+-x x 的两根,且数列}{n a 的公差0d >,∴355,9a a ==,公差.23535=--=a a d∴.12)5(5-=-+=n d n a a n ( *n N ∈)………………4分又当n=1时,有b 1=S 1=1-.32,2111=∴b b 当).2(31),(21,2111≥=∴-=-=≥---n b b b b S S b n n n n n n n n 有时 ∴数列{b n }是等比数列,.31,321==q b ∴.3211nn n q b b ==- ( *n N ∈) …………8分 (Ⅱ)由(Ⅰ)知,3)12(2,3)12(211+++=-==n n n n n n n c n b a c …………10分∴.03)1(83)12(23)12(2111≤-=--+=-+++n n n n n n n n c c ∴.1n n c c ≤+ …………………………12分在三棱柱111ABC A B C -中,,D M 分别为11,A B AB 的中点,11//,A D BM A D BM ∴=,1A DBM ∴为平行四边形,1//A M BD ∴ //,EF BD ∴BD ⊆ 平面1BC D ,EF ⊄平面1BC D//EF ∴平面1BC D…………………….7分(II )设AC 上存在一点G ,使得平面EFG 将三棱柱分割成两 部分的体积之比为1︰15,则111:1:16E AFG ABC A B C V V --=111111sin 321sin 2E AFG ABC A B C AF AG GAF AEV V AB AC CAB A A --⨯⋅∠⋅=⋅⋅∠⋅ 111134224AG AG AC AC =⨯⨯⨯=⋅112416AG AC ∴⋅=, 32AG AC ∴=, 32AG AC AC ∴=> 所以符合要求的点G 不存在 ……………………….14分18.(本小题满分14分)解:(Ⅰ)11(12345)3,(44566)555x y =++++==++++=,因线性回归方程ˆ=+ybx a 过点(,)x y , ∴50.66 3.2a y bx =-=-⨯=,∴6月份的生产甲胶囊的产量数:ˆ0.66 3.2 6.8y=⨯+=…………….6分(Ⅱ)0,1,2,3,ξ=31254533991054010(0),(1),84428421C C C P P C C ξξ======== 213454339930541(2),(3).84148421C C C P P C C ξξ======== …………………….10分5105140123 422114213E ξ∴=⨯+⨯+⨯+⨯= …………………….14分19.(本小题满分14分)解:(Ⅰ)当{}{}0,1,2,0,1,2a b ∈∈时,等可能发生的基本事件(,)a b 共有9个: (00)(01)(02),(10)(11)(12)(20)(21)(22).,,,,,,,,,,,,,,,, 其中事件A : “1(1)03f a b =-+≥”,包含6个基本事件: (00)(01)(02)(11)(12)(22).,,,,,,,,,,,故62()93P A ==. 即事件“(1)0f ≥”发生的概率23…………………….4分 (Ⅱ)31(),3f x x ax b =-+是R 上的奇函数,得(0)0,0.f b ==(5分)∴31(),3f x x ax =- 2()f x x a '=-,① 当1a ≥时,因为11x -≤≤,所以()0f x '≤,()f x 在区间[]1,1-上单调递减,从而1()(1)3g a f a ==-; ② 当1a ≤-时,因为11x -≤≤,所以()0f x '>,()f x 在区间[]1,1-上单调递增,从而1()(1)3g a f a =-=-+, 综上,知1,13().1,13a a g a a a ⎧-≤-⎪⎪=⎨⎪-+≥⎪⎩…………………….9分(Ⅲ)当1=a 时,()()1,3123-='∴+-=x x f b x x x f当()()()()02,1,01,0>'∈<'∈x f x x f x 时当时()()()上递增上递减,在在2,11,0x f ∴,即()()b f x f +-==321m in 又()()()0322,0f b f b f >+== ,[]()⎥⎦⎤⎢⎣⎡++-∈∈∴b b x f x 32,3220时,,当 而()[]210,2f x x x '=-∈在上递增,()[1,3]f x '∈-对任意[]2,01∈x ,总存在[]2,02∈x 使得)()(21x f x f '=()()f x f x '∴⊆的值域的值域,[]22-,1,333b b ⎡⎤++⊆-⎢⎥⎣⎦即∴ 2-13b +≥-且233b +≤,解得13-73b ≤≤.…………………….14分20.(本小题满分14分)解(Ⅰ) (1)0f a b a b =-=⇒= ,()2ln a f x ax x x ∴=--, 22 ()a f x a x x'∴=+-. 要使函数()f x 在其定义域内为单调函数,则在定义域(0,)+∞内, ① 当0a =时,2()0f x x'=-<在定义域(0,)+∞内恒成立, 此时函数()f x 在其定义内为单调递减函数,满足题意; ②当0a >时,要使222111 ()()0a f x a a a x x x a a '=+-=-+-≥恒成立,则10a a-≥,解得1a ≥;此时函数()f x 在其定义内为单调递增函数,满足题意;③ 当0a <时,22()0a f x a x x'=+-<恒成立;此时函数()f x 在其定义内为单调递减函数,满足题意;综上所述,实数a 的取值范围是(,0][1,)-∞⋃+∞;…………………….4分(注: 本问也可采用“分离变量”的方法,酌情给分)(Ⅱ)由题意知(1)0f '=,可得20a a +-=,解得1a =,所以21()(1)f x x'=-于是/2211(1211n n n n a f n a na a n +=-+=-+-+,下面用数学归纳法证明22n a n ≥+成立,数学归纳法证明如下:(i )当1n =时,14212a =≥⨯+,不等式成立;(ii )假设当n k =时,不等式22k a k ≥+成立,即22k a k -≥成立,则当1n k =+时,1(2)1(22)21452(1)2k k k a a a k k k k +=-+≥+⨯+=+>++, 所以当1n k =+时,不等式也成立,由(i )(ii )知*n N ∀∈时都有22n a n ≥+成立. …………………….8分(Ⅲ) 由(Ⅱ)得1111(22)1[2(1)222]121n n n n n a a a n a n n a ----=-++≥-+-++=+,(*,2n N n ∀∈≥)于是112(1)n n a a -+≥+, (*,2n N n ∀∈≥)成立,所以2112(1)a a +≥+,3212(1),...a a +≥+,112(1)n n a a -+≥+成立 累乘可得:1112(1)n n a a -+≥+,则1111112(1)n n a a -≤++成立,(*,2n N n ∀∈≥) 所以1231111...1111n a a a a ++++++++2111111212(1...)(1)1222525n n a -≤++++=-<+.。
上海第期高三名校数学理试题分省分项汇编 专题 数列数学归纳法与极限解析含解析

一.基础题组1. 【上海市黄浦区2014届高三上学期期末考试(即一模)数学(理)试题】已知数列{}n a 是公差为2的等差数列,若6a 是7a 和8a 的等比中项,则n a =________.2. 【上海市嘉定区2014届高三上学期期末质量调研(一模)数学(理)试卷】已知数列}{n a 的前n 项和2n S n =(*N ∈n ),则8a 的值是__________.3. 【上海市嘉定区2014届高三上学期期末质量调研(一模)数学(理)试卷】若nn r r ⎪⎭⎫ ⎝⎛+∞→12lim 存在,则实数r 的取值范围是_____________.4. 【虹口区2013学年度第一学期高三年级数学学科期终教学质量监控测试题】在n n n C B A ∆中,记角n A 、n B 、n C 所对的边分别为n a 、n b 、n c ,且这三角形的三边长是公差为1的等差数列,若最小边1+=n a n ,则=∞→n n C lim ( )..A 2π .B 3π .C 4π .D 6π5. 【上海市浦东新区2013—2014学年度第一学期期末质量抽测高三数学试卷(理卷)】221lim 2n n n n→∞+=-___________.6. 【上海市普陀区2014届高三上学期12月质量调研数学(理)试题】若圆1)1(22=-+y x 的圆心到直线:n l 0=+ny x (*N n ∈)的距离为n d ,则=∞→n n d lim .【答案】1 【解析】试题分析:圆心为(0,1),21nd n =+,22limlim1111n n n n→∞→∞==++. 考点:点到直线距离公式,极限.7.【2013学年第一学期十二校联考高三数学(理)考试试卷】计算:2(1)(13)lim(2)(1)n n n n n n →∞+-=-++________.8. 【上海市浦东新区2013—2014学年度第一学期期末质量抽测高三数学试卷(理卷)】已知数列{}n a 中,11a =,*13,(2,)n n a a n n N -=+≥∈,则n a =___________.9. 【2013学年第一学期十二校联考高三数学(理)考试试卷】设正项数列}{n a 的前n 项和是n S ,若}{n a 和}{n S 都是等差数列,且公差相等,则1a =_______________. 【答案】14【解析】试题分析:等差数列}{n a 的公差为d ,则21()22n d dS n a n =+-,21()22n d dS n a n =+-,数列}{n S 是等差数列,则n S 是关于n 的一次函数(或者是常函数),则102da -=,2n d S n =,从而数列}{n S 的公差是2d ,那么有2d d =,0d =(舍去)或12d =,114a =. 考点:等差数列的通项公式.10. 【上海市十三校2013年高三调研考数学试卷(理科)】计算:2211lim[()]12n n n n n →+∞--++=_________.11. 【上海市十三校2013年高三调研考数学试卷(理科)】设正数数列{}n a 的前n 项和是n S ,若{}n a 和{n S }都是等差数列,且公差相等,则=+d a 1__ _.12. 【2013学年第一学期徐汇区学习能力诊断卷高三年级数学学科(理科)】计算:210lim323xnn→∞++=.【答案】23【解析】试题分析:这属于“∞∞”型极限问题,求极限的方法是分子分母同时除以n(n的最高次幂),化为一般可求极限型,即210lim323xnn→∞++1022lim2333nnn→∞+==+.考点:“∞∞”型极限13.【2013学年第一学期徐汇区学习能力诊断卷高三年级数学学科(理科)】如果()1111112312nf nn n=++++++++L L(*n N∈)那么()()1f k f k+-共有项.14.【上海市杨浦区2013—2014学年度第一学期高三年级学业质量调研数学试卷(理科)】计算:=+∞→133limnnn.15.【上海市长宁区2013—2014第一学期高三教学质量检测数学试卷(理科)】已知数列{}{}n n b a ,都是公差为1的等差数列,其首项分别为11,b a ,且,511=+b a,,11N b a ∈设),(N n a c n b n ∈=则数列{}n c 的前10项和等于______.【答案】85 【解析】试题分析:数列{}n c 到底是什么暂时不知,因此我们试着把其前10项的和10S 表示出来,1210b b S a a =++L10b a +11121[(1)][(1)][(1)]n a b a b a b =+-++-+++-L 1121010()10a b b b =++++-L =111091010102a b ⨯++-1110()451085a b =++-=. 考点:等差数列的通项公式与前n 和公式.二.能力题组1. 【上海市黄浦区2014届高三上学期期末考试(即一模)数学(理)试题】已知数列{}na 满足()()*+∈=-+N n n a a n nn ,11,则数列{}na 的前2016项的和2016S 的值是___________.可行,由此我们可得2016S =12344342414()()k k k k a a a a a a a a ---+++++++++L L 20132014(a a ++2015a + 2016)a +(222)(226)(22(42))(222014)k =+⨯++⨯+++⨯-+++⨯L L 25044(13=⨯+⨯++5+L 1007)+=1017072.考点:分组求和.2. 【上海市嘉定区2014届高三上学期期末质量调研(一模)数学(理)试卷】某种平面分形图如下图所示,一级分形图是一个边长为1的等边三角形(图(1));二级分形图是将一级分形图的每条线段三等分,并以中间的那一条线段为一底边向形外作等边三角形,然后去掉底边(图(2));将二级分形图的每条线段三等边,重复上述的作图方法,得到三级分形图(图(3));…;重复上述作图方法,依次得到四级、五级、…、n 级分形图.则n 级分形图的周长为__________.3. 【虹口区2013学年度第一学期高三年级数学学科期终教学质量监控测试题】已知函数2sin)(2πn n n f =,且)1()(++=n f n f a n ,则=++++2014321a a a a Λ . 【答案】4032- 【解析】试题分析:考虑到sin2n π是呈周期性的数列,依次取值1,0,1,0,-L ,故在122014a a a +++L 时要分组求和,又由n a 的定义,知1352013a a a a ++++L (1)(2)(3)(4)(2013)(2014)f f f f f f =++++++L2222221357200920112013=-+-++-+L 1(53)(53)(97)(97)=+-++-++L (20132011)+-⋅(20132011)+12(357920112013)=+++++++L 110062016=+⨯,242014a a a +++L(2)(3)(4)f f f =+++(5)(2014)(2015)f f f +++L 22223520132015=-+++-L 22(352013)2015=+++-L 2100620062015=⨯-,从而122014a a a +++L 1210062016=+⨯⨯图(1)图(2)图(3)……22015-4032=-.考点:周期数列,分组求和.4. 【虹口区2013学年度第一学期高三年级数学学科期终教学质量监控测试题】已知{}n a 是各项均为正数的等比数列,且1a 与5a 的等比中项为2,则42a a +的最小值等于 .5. 【上海市长宁区2013—2014第一学期高三教学质量检测数学试卷(理科)】数列{}n a 满足*,5221...2121221N n n a a a n n ∈+=+++,则=n a .6. 【上海市浦东新区2013—2014学年度第一学期期末质量抽测高三数学试卷(理卷)】已知函数,1)(22+=x x x f 则 ()()()111112(2013)20142320132014f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫+++++++++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭K L ( )(A) 201021 (B) 201121 (C) 201221 (D) 2013217. 【上海市普陀区2014届高三上学期12月质量调研数学(理)试题】数列}{n a 中,若11=a ,n n n a a 211=++(*N n ∈),则=+++∞→)(lim 221n n a a a Λ .8. 【上海市普陀区2014届高三上学期12月质量调研数学(理)试题】数列}{n a 的前n 项和为n S ,若2cos 1πn n a n +=(*N n ∈),则=2014S . 【答案】1006 【解析】试题分析:组成本题数列的通项公式中,有式子cos2n π,它是呈周期性的,周期为4,因此在求和2014S 时,想象应该分组,依次4个为一组,12341(12)1(14)a a a a +++=+-+++6=,56781(16)1(18)6a a a a +++=+-+++=,43424141[1(42)]1(14)k k k k a a a a k k ---+++=+--+++6=,最后还剩下20131a =,2014120142013a =-=-,所以20146503120131006S =⨯+-=.考点:分组求和.9. 【2013学年第一学期十二校联考高三数学(理)考试试卷】若数列{}n a 满足:111,2()n n a a a n N *+==∈,则前6项的和6S= .(用数字作答)10. 【上海市十三校2013年高三调研考数学试卷(理科)】等差数列{}n a 中,1102,15a S ==,记2482n n B a a a a =++++L ,则当n =____时,n B 取得最大值.11. 【上海市十三校2013年高三调研考数学试卷(理科)】已知函数()(2318,3133,3x tx x f x t x x ⎧-+≤⎪=⎨-->⎪⎩,记()()*n a f n n N =∈,若{}n a 是递减数列,则实数t 的取值范围是______________.12. 【上海市十三校2013年高三调研考数学试卷(理科)】已知无穷数列{}n a 具有如下性质:①1a 为正整数;②对于任意的正整数n ,当n a 为偶数时,12nn a a +=;当n a 为奇数时,112n n a a ++=.在数列{}n a 中,若当n k ≥时,1n a =,当1n k ≤<时,1n a >(2k ≥,*k N ∈),则首项1a 可取数值的个数为 (用k 表示)三.拔高题组1. 【虹口区2013学年度第一学期高三年级数学学科期终教学质量监控测试题】数列{}n a 是递增的等差数列,且661-=+a a ,843=⋅a a . (1)求数列{}n a 的通项公式;(2)求数列{}n a 的前n 项和n S 的最小值; (3)求数列{}n a 的前n 项和n T .【答案】(1) 210n a n =-;(2)20-;(3)229,15,*,940,6,*,n n n n n N T n n n n N ⎧-+≤≤∈⎪=⎨-+≥∈⎪⎩.【解析】2.【上海市普陀区2014届高三上学期12月质量调研数学(理)试题】已知数列{}a中,n13a =,132n n n a a ++=⋅,*n N ∈.(1)证明数列{}2n n a -是等比数列,并求数列{}n a 的通项公式;(2)在数列{}n a 中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;(3)若1r s <<且r ,*s N ∈,求证:使得1a ,r a ,s a 成等差数列的点列(),r s 在某一直线上.(2)假设在数列{}n a 中存在连续三项成等差数列,不妨设连续的三项依次为1k a -,k a ,1k a +(2k ≥,*k N ∈),由题意得,112+-+=k k k a a a ,将1)1(2--+=k k k a ,211)1(2----+=k k k a ,kk k a )1(211-+=++代入上式得……7分])1(2[])1(2[])1(2[21211k k k k k k -++-+=-++---………………8分化简得,21)1(42---⋅=-k k ,即11)1(42---⋅=k k ,得4)2(1=--k ,解得3=k所以,存在满足条件的连续三项为2a ,3a ,4a 成等比数列。
油田高中2013-2014学年第一学期期末考试 高二(理科)-总分-成绩榜

105 108 108 108 111 111 111 114 115 115 117 117 119 120 120 120 120 124 124 124 127 127 127 130 131 131 133 134 134 136 137 137 139 140 140 142 143 143 145 146 147 148 149 150 151 151 153 154 154 154 157 158 158 158 158
卓1 卓3 卓3 卓1 2A 卓1 1B 卓2 卓3 卓1 卓3 卓2 1B 卓3 卓3 卓2 3A 卓3 卓3 1B 卓2 卓1 卓1 卓3 卓2 1B 1B 2B 1B 卓2 卓2 卓2 2A 2A 卓3 1A 卓1 卓3 1A 卓2 1B 卓3 卓2 1B 卓1 3A 卓3 卓3 卓1 卓3 卓1 卓1 2A 卓3 卓1
ቤተ መጻሕፍቲ ባይዱ
22013012980301311128 22021112980301311159 22023512980301311161 22041912980301311106 22014612980301310118 22021212980301311109 22024712980301311285 22020212980301311246 22024812980301311271 22053512980301311175 22013812980301311135 22022512980301311213 22053712980301311331 22012812980301311181 22013912980301311258 22033812980301311201 22040312980301310213 22021712980301311255 22022412980301311266 22031012980301311306 22032712980301310068 22024412980301311102 22063312980301311156 22020112980301311261 22031812980301311186 22033912980301311350 22034512980301311355 22052612980301311361 22020512980301311309 22032112980301311253 22034112980301311227 22040112980301311231 22041212980301310103 22062012980301310153 22033112980301311165 22012212980301310026 22031312980301311136 22023412980301311200 22031212980301310030 22033312980301311235 220303 20121888 22012312980301311168 22030912980301311206 22033612980301311347 22050512980301311149 22050812980301310196 22021512980301310139 22022912980301311119 22054712980301311108 22012712980301311166 22022112980301311133 22044112980301311114 22041412980301310096 22012112980301311153 22022612980301311127
石景山区2013—2014学年第一学期期末高三数学理科

石景山区2013—2014学年第一学期期末考试试卷高三数学(理科)本试卷共6页,满分为150分,考试时间为120分钟.请务必将答案答在答题卡上,在试卷上作答无效,考试结束后上交答题卡.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.已知集合{}2230M x x x =∈+-≤R ,{}10N x x =∈+<R ,那么M N = ( )A .{101}-,,B .{321}---,,C .{11}x x -≤≤D .{31}x x -≤<-2.复数1ii =-( ) A .122i + B .122i -C .122i-+ D .122i -- 3.已知向量(1)x =,a ,(4)x =,b ,则“2x =”是“a ∥b ”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.已知数列}{n a 为等差数列,4724a a ==-,,那么数列}{n a 通项公式为( ) A .210n a n =-+ B .25n a n =-+ C .1102n a n =-+ D .152n a n =-+5.执行如图所示的程序框图,若输入的x 的值为2,则输出的x 的值为( )A .3B .126C .127D .1286. 在边长为1的正方形OABC 中任取一点P ,则点P 恰好落在正方形与曲线y x =围成的区域内(阴影部分)的概率为( )A .12B .23 C .34D .45是 输入x21x x =-126x ≥输出x 开始 结束否OCxyy x =AB7.用0到9这10个数字,可以组成没有重复数字的三位偶数的个数为( )A .324B .328C .360D .6488.已知函数()f x 满足1()1(1)f x f x +=+,当[01]x ∈,时,()f x x =,若在区间(11]-,上方程()0f x mx m --=有两个不同的实根,则实数m 的取值范围是( )A .1[0)2,B .1[)2+∞,C .1[0)3,D .1(0]2,第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分.9.已知圆C 的参数方程为12cos 2sin x y θθ+⎧⎨=⎩,,=(θ为参数),则圆C 的直角坐标方程为_______________,圆心C 到直线:10l x y ++=的距离为______.10.在ABC ∆中,角A B C ,,的对边分别为a b c ,,,若=6a ,4c =,1cos =3B ,则b =______. 11. 若x ,y 满足约束条件1020x y x y ≤⎧⎪≥⎨⎪-+≥⎩,,,则z x y =+的最大值为 .12.如图,已知在ABC ∆中,o 90B ∠=,O 是AB 上一点,以O 为圆心,OB 为半径的圆与AB 交于点E ,与AC 切 于点D ,2AD =,1AE =,则AB 的长为 ,CD 的长为 .13.已知抛物线24y x =的焦点为F ,准线为直线l ,过抛物线上一点P 作PE l ⊥于E ,若直线EF 的倾斜角为o150,则||PF =______.14. 已知四边形ABCD 是边长为1的正方形,且1A A ⊥平面ABCD ,P 为1A A 上动点,过BD 且垂直于PC 的平面交PC 于E ,那么异面直线PC 与BD 所成的角的度数为 ,当三棱锥E BCD -的体积取得最大值时, 四棱锥P ABCD -的高PA 的长为 .A DCBE.OA 1ABDCPE三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)已知函数()23sin cos cos 21f x x x x =++()x ∈R . (Ⅰ)求函数)(x f 的单调递增区间; (Ⅱ)求函数()f x 在44ππ⎡⎤-⎢⎥⎣⎦,上的最小值,并写出()f x 取最小值时相应的x 值.16.(本小题满分13分)北京市各级各类中小学每年都要进行“学生体质健康测试”,测试总成绩满分为100分,规定测试成绩在[85100],之间为体质优秀;在[7585),之间为体质良好;在[6075),之间为体质合格;在[060),之间为体质不合格.现从某校高三年级的300名学生中随机抽取30名学生体质健康测试成绩,其茎叶图如下:9 1 3 5 68 0 1 1 2 2 3 3 3 4 4 5 6 6 7 7 9 7 0 5 6 6 7 9 6 4 5 8 5 6(Ⅰ)试估计该校高三年级体质为优秀的学生人数;(Ⅱ)根据以上30名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取5名学生,再从这5名学生中选出3人.(ⅰ)求在选出的3名学生中至少有1名体质为优秀的概率;(ⅱ)记X 为在选出的3名学生中体质为良好的人数,求X 的分布列及数学期望.17.(本小题满分14分)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是直角梯形,o 90ABC ∠=,AD ∥BC ,且2PA AD ==,1AB BC ==,E 为PD 的中点.(Ⅰ)求证:CD ⊥平面PAC ; (Ⅱ)求二面角E AC D --的余弦值;(Ⅲ)在线段AB 上是否存在一点F (不与A B ,两点重合),使得AE ∥平面PCF ?若存在,求出AF 的长;若不存在,请说明理由.A PEBDC18.(本小题满分13分)已知函数()xf x e ax =-(e 为自然对数的底数).(Ⅰ)当2a =时,求曲线()f x 在点(0(0))f ,处的切线方程; (Ⅱ)求函数()f x 的单调区间;(Ⅲ)已知函数()f x 在0x =处取得极小值,不等式()f x mx <的解集为P ,若1{|2}2M x x =≤≤,且M P ≠∅ ,求实数m 的取值范围.19.(本小题满分14分)已知椭圆C :22221x y a b +=(0a b >>)过点(20),,且椭圆C 的离心率为12.(Ⅰ)求椭圆C 的方程;(Ⅱ)若动点P 在直线1x =-上,过P 作直线交椭圆C 于M N ,两点,且MP PN =,再过P 作直线l MN ⊥.证明:直线l 恒过定点,并求出该定点的坐标.20.(本小题满分13分)已知集合{101}A =-,,,对于数列{}n a 中(123)i a A i n ∈= ,,,,. (Ⅰ)若50项数列{}n a 满足5019ii a==-∑,5021(1)107i i a =-=∑,则数列{}n a 中有多少项取值为零?(121nin i aa a a n *==+++∈∑N ,)(Ⅱ)若各项非零数列{}n a 和新数列{}n b 满足11i i i b b a ---=(23i n = ,,,). (ⅰ)若首项10b =,末项1n b n =-,求证数列{}n b 是等差数列;(ⅱ)若首项10b =,末项0n b =,记数列{}n b 的前n 项和为n S ,求n S 的最大值和最小值.石景山区2013—2014学年第一学期期末考试高三数学(理科)参考答案一、选择题共8小题,每小题5分,共40分.题号 1 2 3 4 5 6 7 8 答案DCAA CBBD二、填空题共6小题,每小题5分,共30分.(两空的题目第一空2分,第二空3分) 三、解答题共6小题,共80分. 15.(本小题共13分)解:(Ⅰ)()f x 3sin 2cos 2+1x x =+ …………2分 2sin 2+16x π=+(), ……………4分222262k x k πππππ-≤+≤+,k ∈Z , 36k x k ππππ-≤≤+,k ∈Z ,……6分所以函数)(x f 的单调递增区间为[]36k k ππππ-+,()k ∈Z . ……………7分(Ⅱ)因为44x ππ-≤≤,22363x πππ-≤+≤, ……………9分3sin(2)126x π-≤+≤,312sin 2+136x π-+≤+≤(), ……11分 所以当2=63x ππ+-,即=4x π-时,函数)(x f 取得最小值31-+.…………13分16.(本小题共13分)解:(Ⅰ)根据抽样,估计该校高三学生中体质为优秀的学生人数有10300=10030⨯人.…………3分 (Ⅱ)依题意,体质为良好和优秀的学生人数之比为 15:103:2=.所以,从体质为良好的学生中抽取的人数为3535⨯=,从体质为优秀的学生中抽取的人数为2525⨯=.…6分 (ⅰ)设“在选出的3名学生中至少有1名体质为优秀”为事件A ,则 3335C 9()1C 10P A =-=. 故在选出的3名学生中至少有1名体质为优秀的概率为910.…9分 (ⅱ)解:随机变量X 的所有取值为123,,.123235C C 3(1)C 10P X ⋅===,213235C C 6(2)C 10P X ⋅===,3335C 1(3)C 10P X ===.…………12分 题号 9 1011 12 13 14答案 22(1)4x y -+=,2 64 4,34390 ,2所以,随机变量X 的分布列为:X 123 P31061011036191231010105EX =⨯+⨯+⨯=. ……………13分 17.(本小题共14分) (Ⅰ)证明:因为PA ⊥平面ABCD ,CD ⊂平面ABCD ,所以PA CD ⊥. ……………1分 取AD 的中点G ,连结GC ,因为底面ABCD 为直角梯形,AD ∥BC ,o90ABC ∠=,且1AB BC ==, 所以四边形ABCG 为正方形,所以CG AD ⊥,且1=2CG AD , 所以o=90ACD ∠,即AC CD ⊥. ……………3分 又PA AC A = , 所以CD ⊥平面PAC . ……………4分(Ⅱ)解:如图,以A 为坐标原点,AB AD AP ,,所在直线分别为x y z ,,轴建立空间直角坐标系xyz A -.…5分则(000)A ,,,(110)C ,,,(011)E ,,,(002)P ,,,所以(002)AP = ,,,(110)AC = ,,,(011)AE =,,. 因为PA ⊥平面ABCD ,所以(002)AP =,,为平面ACD 的一个法向量. ………6分 设平面EAC 的法向量为1()n x y z = ,,,由10n AC ⋅= ,10n AE ⋅= 得00x y y z +=⎧⎨+=⎩,,令1x =,则1y =-,1z =,所以1(111)n =-,,是平面EAC 的一个法向量. ……………8分 所以12221(1)0123cos 31(1)12n AP ⨯+-⨯+⨯<>==+-+⋅ 0, 因为二面角E AC D --为锐角,A PEBDCG DA PBCzyxE所以二面角E AC D --的余弦值为33. ……………9分 (Ⅲ)解:假设在线段AB 上存在点F (不与A B ,两点重合),使得AE ∥平面PCF .设(00)F a ,,,则(110)CF a =-- ,,,(112)CP =--,,. 设平面PCF 的法向量为2()n x y z =,,, 由20n CF ⋅= ,20n CP ⋅= 得(1)020a x y x y z --=⎧⎨--+=⎩,,令1x =,则1y a =-,2az =, 所以2(11)2a n a =- ,,是平面PCF 的一个法向量.………12分因为AE ∥平面PCF ,所以20AE n ⋅= ,即(1)02aa -+=, ……………13分解得23a =,所以在线段AB 上存在一点F (不与A B ,两点重合),使得AE ∥平面PCF ,且2=3AF . ……14分 18.(本小题共13分)解:(Ⅰ)当2a =时,()2x f x e x =-,(0)1f =, ()2xf x e '=-,得(0)1f '=-, ……2分所以曲线()f x 在点(0(0))f ,处的切线方程为1y x =-+. ……………3分 (Ⅱ)()xf x e a '=-.当0a ≤时,()0f x '>恒成立,此时()f x 的单调递增区间为()-∞+∞,,无单调递减区间;………5分 当0a >时,(ln )x a ∈-∞,时,()0f x '<,(ln )x a ∈+∞,时,()0f x '>, 此时()f x 的单调递增区间为(ln )a +∞,,单调递减区间为(ln )a -∞,.………7分 (Ⅲ)由题意知(0)0f '=得1a =,经检验此时()f x 在0x =处取得极小值. ………8分因为M P ≠∅ ,所以()f x mx <在1[2]2,上有解,即1[2]2x ∃∈,使()f x mx <成立,………9分即1[2]2x ∃∈,使x e x m x ->成立, …………10分 所以min ()x e x m x ->. 令()1x e g x x =-,2(1)()xx e g x x -'=, DA PB C zyx EF所以()g x 在1[1]2,上单调递减,在[12],上单调递增, 则min ()(1)1g x g e ==-, ……………12分 所以(1)m e ∈-∞,+. ……………13分 19.(本小题共14分)解:(Ⅰ)因为点(20),在椭圆C 上,所以22401a b+=, 所以24a =, …………1分 因为椭圆C 的离心率为12, 所以12c a =,即22214a b a -= ,…………2分 解得23b =, ……………4分所以椭圆C 的方程为22143x y +=. ……………5分 (Ⅱ)设0(1)P y -,,033()22y ∈-,, ①当直线MN 的斜率存在时,设直线MN 的方程为0(1)y y k x -=+,11()M x y ,,22()N x y ,, 由2203412(1)x y y y k x ⎧+=⎨-=+⎩,,得22222000(34)(88)(48412)0k x ky k x y ky k ++++++-=, ………7分所以2012288+34ky k x x k +=-+, ……………8分 因为MP PN = ,即P 为MN 中点,所以12=12x x +-,即20288=234ky k k +--+. 所以003(0)4MN k y y =≠, ……………9分 因为直线l MN ⊥, 所以043l y k =-,所以直线l 的方程为004(1)3yy y x -=-+, 即041()34y y x =-+ ,显然直线l 恒过定点1(0)4-,. ………11分②当直线MN 的斜率不存在时,直线MN 的方程为1x =-, 此时直线l 为x 轴,也过点1(0)4-,. ……………13分 综上所述直线l 恒过定点1(0)4-,. ……………14分 20.(本小题共13分)解:(Ⅰ)设数列{}n a 中项为110-,,分别有x y z ,,项.由题意知5094107x y z x y z y ++=⎧⎪-=-⎨⎪+=⎩,,,解得11z =.所以数列{}n a 中有11项取值为零. ……………3分 (Ⅱ)(ⅰ){11}i a ∈-,且11i i i b b a ---=,得到121(23)i i b a a a i n -=+++= ,,,, 若1(121)i a i n ==- ,,,,则满足1n b n =-. 此时11i i b b --=,数列{}n b 是等差数列;若121n a a a - ,,,中有*(0)p p p >∈,N 个1-,则121n b n p n =--≠-不满足题意; 所以数列{}n b 是等差数列. ……………7分 (ⅱ)因为数列{}n b 满足11i i i b b a ---=,所以121(23)i i b a a a i n -=+++= ,,,, 根据题意有末项0n b =,所以1210n a a a -+++= .而{11}i a ∈-,,于是n 为正奇数,且121n a a a - ,,,中有12n -个1和12n -个1-. 12112121()()n n n S b b b a a a a a a -=+++=+++++++121(1)(2)n n a n a a -=-+-++要求n S 的最大值,则只需121n a a a - ,,,前12n -项取1,后12n -项取1-, 所以2max(1)()(2)(4)14n n S n n -=-+-++=(n 为正奇数). 要求n S 的最小值,则只需121n a a a - ,,,前12n -项取1-,后12n -项取1, 则2min(1)()(2)(4)14n n S n n -=------=-(n 为正奇数). …………13分【注:若有其它解法,请酌情给分.】。
陕西省西安市第一中学2013届高三上学期期末考试理科综合试题

1. 本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分300 分。
考试时间150 分钟。
2.可能用到的相对原子质量H 1 N 14 O 16 Na 23 Al 27 Cu第I卷一、选择题:本题共13小题,每小题6分,在每小题给出的4个选项中,只有一项是符合题目要求的。
1.有关下图所示四种不同生物的叙述正确的是( )A.甲、乙两种细胞的细胞壁都可用纤维素酶完全分解B.乙为低等植物细胞,细胞中的核糖体和叶绿体均含RNAC.丙的遗传物质是单链RNA,其突变率远高于DNA病毒D.丁细胞的有氧呼吸被抑制会影响脂溶性小分子物质的运输2.下列哪项组合与图示结构的功能特性....有直接关系( )①神经纤维上动作电位的形成②效应B细胞分泌抗体③植物生长素由形态学上端→形态学下端④吞噬细胞吞噬病菌⑤抗利尿激素促进肾小管的重吸收作用⑥植物体细胞杂交中,原生质体的融合A.①②⑤B.②④⑥C.①④⑥D.①③⑤3.人类的肤色由A/a、B/b、E/e三对等位基因共同控制,A/a、B/b、E/e位于三对同源染色体上。
AABBEE为黑色,aabbee为白色,其他性状与基因型的关系如下图所示,即肤色深浅与显性基因个数有关,如基因型为AaBbEe、AABbee与aaBbEE等与含任何三个显性基因的肤色一样。
若双方均含3个显性基因的杂合体婚配(AaBbEe×AaBbEe),则子代肤色的基因型和表现型分别有多少种( )A.27,7 B.16,9 C. 27,9 D.16,74.某池塘中,早期藻类大量繁殖,食藻浮游动物水蚤大量繁殖,藻类减少,接着又引起水蚤减少。
后期排入污水,引起部分水蚤死亡,加重了污染,导致更多水蚤死亡。
关于上述过程的叙述,正确的是( )A.早期不属于负反馈,后期属于负反馈B.早期属于负反馈,后期不属于负反馈C.早期、后期均属于负反馈D.早期、后期均不属于负反馈5.将甲、乙、丙三株大小相近的同种植物,分别进行如下表的处理,实验结果如图所示。
北京市海淀区2013届高三第一学期期末考试数学(理科)

北京市海淀区2013届高三第一学期期末考试数学(理)试题一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 复数21i-化简的结果为 A.1i + B.1i -+ C. 1i - D.1i --2.已知直线2,:2x t l y t =+⎧⎨=--⎩(t 为参数)与圆2cos 1,:2sin x C y θθ=+⎧⎨=⎩(θ为参数),则直线l 的倾斜角及圆心C 的直角坐标分别是A.π,(1,0)4B.π,(1,0)4-C.3π,(1,0)4D.3π,(1,0)4-3.向量(3,4),(,2)x ==a b , 若||⋅=a b a ,则实数x 的值为A.1-B.12-C.13- D.14.某程序的框图如图所示, 执行该程序,若输入的p 为24,则输出 的,n S 的值分别为A.4,30n S ==B.5,30n S ==C.4,45n S ==D.5,45n S ==5.如图,PC 与圆O 相切于点C ,直线PO 交圆O 于,A B 两点,弦CD 垂直AB 于E . 则下面结论中,错误..的结论是 A.BEC ∆∽DEA ∆ B.ACE ACP ∠=∠ C.2DE OE EP =⋅ D.2PC PA AB =⋅6.数列{}n a 满足111,n n a a r a r +==⋅+(*,n r ∈∈N R 且0r ≠),则“1r =”是“数列{}n a 成等差数列”的A.充分不必要条件B. 必要不充分条件C.充分必要条件D. 既不充分也不必要条件7. 用数字0,1,2,3组成数字可以重复的四位数, 其中有且只有一个数字出现两次的四位数的个数为 A. 144 B.120 C. 108 D.728. 椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ,若椭圆C 上恰好有6个不同的点P ,使得12F F P∆为等腰三角形,则椭圆C 的离心率的取值范围是A.12(,)33B.1(,1)2C. 2(,1)3D.111(,)(,1)322二、填空题:本大题共6小题,每小题5分,共30分.9. 以y x =±为渐近线且经过点(2,0)的双曲线方程为______.10.数列{}n a 满足12,a =且对任意的*,N m n ∈,都有n mn ma a a +=,则3_____;a ={}n a 的前n 项和n S =_____.BP11. 在261(3)x x+的展开式中,常数项为______.(用数字作答)12. 三棱锥D ABC -及其三视图中的主视图和左视图如图所示,则棱BD 的长为_________.13. 点(,)P x y 在不等式组 0,3,1x x y y x ≥⎧⎪+≤⎨⎪≥+⎩表示的平面区域内,若点(,)P x y 到直线1y kx =-的最大距离为则___.k =14. 已知正方体1111ABCD A B C D -的棱长为1,动点P 在正方体1111ABCD A B C D -表面上运动,且PA r =(0r <<,记点P 的轨迹的长度为()f r ,则1()2f =____;关于r 的方程()f r k =的解的个数可以为_.(填上所有可能的值).三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15. (本小题满分13分)已知函数21()cos cos 2222x x x f x =+-,ABC ∆三个内角,,A B C 的对边分别为,,a b c .(I )求()f x 的单调递增区间;(Ⅱ)若()1,f B C +=1a b =,求角C 的大小. 16.(本小题满分13分)汽车租赁公司为了调查A,B 两种车型的出租情况,现随机抽取了这两种车型各100辆汽车,分别统计了每辆车某个星期内的出租天数,统计数据如下表:A 型车(I )从出租天数为3天的汽车(仅限A,B 两种车型)中随机抽取一辆,估计这辆汽车恰好是A 型车的概率; (Ⅱ)根据这个星期的统计数据,估计该公司一辆A 型车,一辆B 型车一周内合计出租天数恰好为4天的概率;(Ⅲ)如果两种车型每辆车每天出租获得的利润相同,该公司需要从A ,B 两种车型中购买一辆,请你根据所学的统计知识,给出建议应该购买哪一种车型,并说明你的理由.DABC左视图17. (本小题满分14分)如图,在直三棱柱111ABC A B C -中,90BAC ∠=︒,12,AB AC AA ===E 是BC 中点. (I )求证:1//A B 平面1AEC ;(II )若棱1AA 上存在一点M ,满足11B M C E ⊥,求AM 的长; (Ⅲ)求平面1AEC 与平面11ABB A 所成锐二面角的余弦值.18. (本小题满分13分)已知函数e ().1axf x x =- (I ) 当1a =时,求曲线()f x 在(0,(0))f 处的切线方程; (Ⅱ)求函数()f x 的单调区间.19. (本小题满分14分)已知()2,2E 是抛物线2:2C y px =上一点,经过点(2,0)的直线l 与抛物线C 交于,A B 两点(不同于点E ),直线,EA EB 分别交直线2x =-于点,M N . (Ⅰ)求抛物线方程及其焦点坐标;(Ⅱ)已知O 为原点,求证:MON ∠为定值. 20. (本小题满分13分)已知函数()f x 的定义域为(0,)+∞,若()f x y x=在(0,)+∞上为增函数,则称()f x 为“一阶比增函数”;若2()f x y x =在(0,)+∞上为增函数,则称()f x 为“二阶比增函数”. 我们把所有“一阶比增函数”组成的集合记为1Ω,所有“二阶比增函数”组成的集合记为2Ω. (Ⅰ)已知函数32()2f x x hx hx =--,若1(),f x ∈Ω且2()f x ∉Ω,求实数h 的取值范围; (Ⅱ)已知0a b c <<<,1()f x ∈Ω且()f x 的部分函数值由下表给出,求证:(24)0d d t +->;(Ⅲ)定义集合{}2()|(),,(0,)(),f x f x k x f x k ψ=∈Ω∈+∞<且存在常数使得任取,请问:是否存在常数M ,使得()f x ∀∈ψ,(0,)x ∀∈+∞,有()f x M <成立?若存在,求出M 的最小值;若不存在,说明理由.EC 1B 1A 1CBA海淀区高三年级第一学期期末练习数 学 (理)参考答案及评分标准 2013.1说明: 合理答案均可酌情给分,但不得超过原题分数. 一、选择题(本大题共8小题,每小题5分,共40分)二、填空题(本大题共6小题,每小题5分, 有两空的小题,第一空3分,第二空2分,共30分)三、解答题(本大题共6小题,共80分)15.(本小题满分13分)解:(I )因为21()cos cos 2222x x x f x =+-cos 122cos 121x x x x =+-=++ πsin()6x =+ ………6分又sin y x =的单调递增区间为ππ2π,2π 22k k -+(),()Z k ∈ 所以令πππ2π2π262k x k -<+<+ 解得2ππ2π2π 33k x k -<<+ 所以函数()f x 的单调增区间为2ππ(2π,2π) 33k k -+,()Z k ∈ ………………8分 (Ⅱ) 因为()1,f B C +=所以πsin()16B C ++=,又(0,π)B C +∈,ππ7π(,)666B C ++∈所以πππ,623B C B C ++=+=,所以2π3A = ……10分 由正弦定理sin sin B A b a= 把1a b =代入,得到1sin 2B = …………12分 又,b a <B A <,所以π6B =,所以π6C = …………13分16.(本小题满分13分) 解:(I )这辆汽车是A 型车的概率约为3A 3A,B =出租天数为天的型车辆数出租天数为天的型车辆数总和300.63020=+这辆汽车是A 型车的概率为0.6 …………3分 (II )设“事件i A 表示一辆A型车在一周内出租天数恰好为i 天”,“事件j B 表示一辆B型车在一周内出租天数恰好为j 天”,其中,1,2,3,...,7i j = 则该公司一辆A 型车,一辆B 型车一周内合计出租天数恰好为4天的概率为132231132231()()()()P A B A B A B P A B P A B P A B ++=++ ………………5分132231()()()()()()P A P B P A P B P A P B =++ ………………7分520102030141001001001001001009125=⋅+⋅+⋅=该公司一辆A 型车,一辆B 型车一周内合计出租天数恰好为4天的概率为9125………………9分(Ⅲ)设设Y 为B 型车出租的天数,则Y 的分布列为()10.0520.1030.3040.3550.1560.0370.02=3.62E X =⨯+⨯+⨯+⨯+⨯+⨯+⨯()10.1420.2030.2040.1650.1560.1070.05E Y =⨯+⨯+⨯+⨯+⨯+⨯+⨯=3.48………………12分 一辆A 类型的出租车一个星期出租天数的平均值为3.62天,B 类车型一个星期出租天数的平均值为3.48天. 从出租天数的数据来看,A 型车出租天数的方差小于B 型车出租天数的方差,综合分析,选择A 类型的出租车更加合理 . ………………13分17.(本小题满分14分)(I) 连接A C 1交AC 1于点O ,连接EO因为1ACC A 1为正方形,所以O 为A C 1中点,又E 为CB 中点,所以EO 为1A BC ∆的中位线, 所以1//EO A B ………………2分又EO ⊂平面1AEC ,1A B ⊄平面1AEC 所以1//A B 平面1AEC…4分(Ⅱ)以A 为原点,AB 为x 轴,AC 为y 轴,1AA 为z 轴建立空间直角坐标系 所以111(0,0,0),(0,0,2),(2,0,0),(2,0,2),(0,2,0),(0,2,2),(1,1,0),A A B B C C E 设(0,0,)(02)M m m ≤≤,所以11(2,0,2),(1,1,2)B M m C E =--=--,因为11B M C E ⊥,所以 110B M C E ⋅=,解得1m =,所以1AM = ………………8分 (Ⅲ)因为1(1,1,0),(0,2,2)AE AC ==,设平面1AEC 的法向量为(,,)n x y z =, 则有100AE n AC n ⎧⋅=⎪⎨⋅=⎪⎩ ,得00x y y z +=⎧⎨+=⎩,令1,y =-则1,1x z ==,所以可以取(1,1,1)n =-, ………10分因为AC ⊥平面1ABB A 1,取平面1ABB A 1的法向量为 (0,2,0)AC =………11分所以cos ,||||AC n AC n AC n ⋅<>==………………13分平面1AEC 与平面1ABB A 1………………14分 18. (本小题满分13分)解:当1a =时,e ()1axf x x =-,2e (2)'()(1)x xf x x -=- ………………2分 又(0)1f =-,'(0)2f =-,所以()f x 在(0,(0))f 处的切线方程为21y x =-- ………4分(II )2e [(1)]'()(1)ax ax a f x x -+=- 当0a =时,21'()0(1)f x x -=<- 又函数的定义域为{|1}x x ≠ 所以 ()f x 的单调递减区间为(,1),(1,)-∞+∞ ………6分 当 0a ≠时,令'()0f x =,即(1)0ax a -+=,解得1a x a+=………………7分 当0a >时,11a x a+=>,所以()f x ',()f x 随x 的变化情况如下表:所以()f x 的单调递减区间为(,1)-∞,1(1,)a a +, 单调递增区间为1(,)a a++∞ ……10分 当0a <时,11a x a+=< 所以()f x ',()f x 随x 的变化情况如下表:所以()f x 的单调递增区间为1(,)a a+-∞,单调递减区间为1(,1)a a +,(1,)+∞ ………13分19. (本小题满分14分)解:(Ⅰ)将()2,2E 代入22y px =,得1p = 所以抛物线方程为22y x =,焦点坐标为1(,0)2…3分(Ⅱ)设211(,)2y A y ,222(,)2y B y ,(,),(,)M M N N M x y N x y ,法一:因为直线l 不经过点E ,所以直线l 一定有斜率 设直线l 方程为(2)y k x =-与抛物线方程联立得到 2(2)2y k x y x=-⎧⎨=⎩,消去x ,得:2240ky y k --=则由韦达定理得:121224,y y y y k=-+= …6分 直线AE 的方程为:()12122222y y x y --=--,即()12222y x y =-++,令2x =-,得11242M y y y -=+ …………9分 同理可得:22242N y y y -=+ …10分又 4(2,),(2,)m m OM y ON y -=-=- ,所以121224244422M N y y OM ON y y y y --⋅=+=+⋅++ 121212124[2()4]4[2()4]y y y y y y y y -++=++++ 44(44)444(44)k k--+=+-++ 0= …13分所以OM ON ⊥,即MON ∠为定值π2…………14分 法二:设直线l 方程为2x my =+ 与抛物线方程联立得到 222x my y x=+⎧⎨=⎩,消去x ,得:2240y my --= 则由韦达定理得:12124,2y y y y m =-+= ……6分直线AE 的方程为:()12122222y y x y --=--,即()12222y x y =-++, 令2x =-,得11242M y y y -=+ ………………9分 同理可得:22242N y y y -=+ …10分又 4(2,),(2,)m m OM y ON y -=-=- ,12124(2)(2)44(2)(2)M N y y OM ON y y y y --⋅=+=+++ 121212124[2()4]4[2()4]y y y y y y y y -++=++++ 4(424)44(424)m m --+=+-++ 0= ……12分所以OM ON ⊥,即MON ∠为定值π2………………13分 20. (本小题满分14分)解:(I )因为1(),f x ∈Ω且2()f x ∉Ω, 即2()()2f x g x x hx h x==--在(0,)+∞是增函数,所以0h ≤ ………………1分而2()()2f x h h x x h x x ==--在(0,)+∞不是增函数,而2'()1hh x x =+ 当()h x 是增函数时,有0h ≥,所以当()h x 不是增函数时,0h < 综上,得0h < …4分(Ⅱ) 因为1()f x ∈Ω,且0a b c a b c <<<<++ 所以()()4=f a f a b c a a b c a b c++<++++, 所以4()a f a d a b c =<++,同理可证4()b f b d a b c =<++,4()cf c t a b c=<++三式相加得4()()()()24,a b c f a f b f c d t a b c++++=+<=++ 所以240d t +-< ……6分因为,d d a b <所以()0,b a d ab-<而0a b <<, 所以0d < 所以(24)0d d t +-> ……8分 (Ⅲ) 因为集合{}2()|(),,(0,)(),f x f x k x f x k ψ=∈Ω∈+∞<且存在常数使得任取, 所以()f x ∀∈ψ,存在常数k ,使得 ()f x k < 对(0,)x ∈+∞成立我们先证明()0f x ≤对(0,)x ∈+∞成立 假设0(0,),x ∃∈+∞使得0()0f x >, 记020()0f x m x => 因为()f x 是二阶比增函数,即2()f x x是增函数. 所以当0x x >时,0220()()f x f x m x x >=,所以2()f x mx > 所以一定可以找到一个10x x >,使得211()f x mx k >> 这与()f x k < 对(0,)x ∈+∞成立矛盾……11分()0f x ≤对(0,)x ∈+∞成立 所以()f x ∀∈ψ,()0f x ≤对(0,)x ∈+∞成立下面我们证明()0f x =在(0,)+∞上无解假设存在20x >,使得2()0f x =,则因为()f x 是二阶增函数,即2()f x x 是增函数 一定存在320x x >>,322232()()0f x f x x x >=,这与上面证明的结果矛盾 所以()0f x =在(0,)+∞上无解 综上,我们得到()f x ∀∈ψ,()0f x <对(0,)x ∈+∞成立 所以存在常数0M ≥,使得()f x ∀∈ψ,(0,)x ∀∈+∞,有()f x M <成立又令1()(0)f x x x=->,则()0f x <对(0,)x ∈+∞成立,又有23()1f x x x-=在(0,)+∞上是增函数 ,所以()f x ∈ψ,而任取常数0k <,总可以找到一个00x >,使得0x x >时,有()f x k >所以M 的最小值 为0 ……13分。
2014年高三数学上学期期末测试题理科(答案)

2014年高三上学期期末测试题理科(答案)一、选择题:本大题共 12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求.1、已知全集U R =,集合{}{}()3021,log 0,xU A x B x x A C B =<<=>⋂=则( )A.{}1x x >B.{}0x x >C.{}01x x <<D.{}0x x <2、若{}n a 为等差数列,n S 是其前n 项和,且32211π=S ,则6tan a 的值为( ) A.3B.3-C.3±D.33-3、设i 是虚数单位,若复数iai --310是实数,则a 的值为( ) A.3- B.1- C.3 D.14、已知某几何体的俯视图是如图所示的边长为的正方形,主视图与左视图是 边长为的正三角形,则其全面积是( )A.8B.12C.4(1+3)D.43 5、已知函数()sin()(,0)4f x x x R πωω=+∈>的最小正周期为π,为了得到函数()sin g x x ω=的图象,只要将()y f x =的图象( )A.向右平移4π B.向左平移4π C.向右平移8π D.向左平移8π 6、下列函数中,在其定义域中,既是奇函数又是减函数的是( ) A.x x f -=)( B.x x x f 22)(-=- C.x x f tan )(-= D.xx f 1)(=7、已知)(x f 满足1)2()4(=-=f f ,)(x f '为导函数,且导函数)(x f y '=的图象如右图所示.则1)(<x f 的解集是( )A.)0,2(- B .)4,2(- C.(0,4) D.),4()2,(+∞⋃--∞A.1313 B.53C.54D.13392 9、已知函数y =f (x )为偶函数,满足条件f (x +1)=f (x -1),且当x ∈[-1,0]时,f (x )=3x +49,则)5(log 31f 的值等于( ) A.-1 B.5029 C.45101 D.1 10、等差数列{}n a 前n 项和n S , 15890,0S a a >+<,则使0nn S a n+<的最小的n 为( )A .10B . 11 C. 12 D . 1311、椭圆)0(122>=+m m y x 的离心率大于21的充分必要条件是( ) A.41<m B.3443<<m C.43>m D.430<<m 或34>m12、已知双曲线)0,0(12222>>=-b a by a x 的离心率为2,一个焦点与抛物线x y 162=的焦点相同,则双曲线的渐近线方程为( )A .x y 23±=B .x y 23±=C .x y 33±=D .x y 3±=第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题, 每小题4分,共16分13、若圆22(2)2x y -+=与双曲线22221(0,0)x y a b a b-=>>的渐近线相切,则双曲线的离心率是 .14、向量,满足||=2 , ||=3,|2+|=37,则, 的夹角为________15、已知实数x,y 满足010240y y x y x ≥⎧⎪-+≤⎨⎪-+≥⎩若z y ax =-取得最大值时的最优解(x,y )有无数个,则a 的值为________ 16、若直线y ax =与函数ln y x =的图象相切于点P , 则切点P 的坐标为________三、解答题:本大题共6小题,共74分 17、(本小题满分12分)已知函数2cos 4)62sin(2)(2+-+=x x x f π(1)求函数)(x f 的单调减区间; (2)若[,]42x ππ∈求函数)(x f 的值域。
海淀区第一学期期末练习答案2013.1高二理科数学

海淀区高二年级第一学期期末练习数 学(理科)参考答案及评分标准2013.1一. 选择题:本大题共8小题, 每小题4分,共32分.二.填空题:本大题共6小题, 每小题4分,共24分. 9. x y 21±= 10.∈∃b a ,R ,ab b a 222<+ 11. 012. 1 13. ①④ 14. 5-;()152n n b -=--(第一空3分,第二空2分)三.解答题:本大题共4小题,共44分. 15. (本小题满分10分)解: (I )因为点()2,1A 在抛物线px y 22=上,所以p 222=, -------------2分 解得2=p , -------------3分 故抛物线C 的方程为x y 42=. -------------4分 (II )设点B 的坐标为()00,y x ,由题意可知00≠x ,直线OA 的斜率2=OA k ,直线OB 的斜率00x y k OB =,因为90A O B ∠=︒,所以1200-==⋅x y k k OB OA , -------------6分又因为点()00,y x B 在抛物线x y 42=上,所以0204x y = , -------------7分联立200004,2,y x y x ⎧=⎨=-⎩ 解得⎩⎨⎧-==81600y x 或 ⎩⎨⎧==0000y x (舍), -------------9分所以点B 的坐标为()8,16-.-------------10分16.(本小题满分12分)解: (I )当1=n 时,911011=-==S a ; -------------1分 当2≥n 时,()()22110[1011]211n n n a S S n n n n n -=-=-----=-+.-----3分 综上可知,数列{}n a 的通项公式为112+-=n a n . -------------4分 (II )解法1:()2551022+--=-=n n n S n , -------------6分所以,当5=n 时,n S 取得最大值25. -------------7分 解法2:令0112≥+-=n a n ,得211≤n ,即此等差数列前5项为正数,从第6项起开始为负数,所以,5S 最大, -------------6分 故255510)(25max =-⨯==S S n . -------------7分 (III) 令0112≥+-=n a n ,得211≤n . -------------8分n n n a a a a b b b b T ++++=++++= 321321,当5≤n 时,210n n S T n n -==. -------------9分当5>n 时,56543212S S a a a a a a a T n n n +-=---++++=21050n n +-=. -------------11分综上可知,数列{}n b 的前n 项和⎪⎩⎪⎨⎧>+-≤-=5,10505,1022n n n n n n T n . -------12分17.(本小题满分10分)解: (I )令,0)1)(2(=---a x a x 得,1,221+==a x a x -------------1分()11221-=+-=-a a a x x ,因为1>a ,所以01>-a ,即12+>a a , -------------2分 由()()()012≤---=a x a x x f ,解得a x a 21≤≤+ . -------------4分(II )解法1:当1=a 时,12+=a a , ()()22-=x x f ,不符合题意. -----5分当1>a 时,12+>a a ,若(5,7)x ∀∈,不等式0)(≤x f 恒成立,则有15,27,a a +≤⎧⎨≥⎩解得427≤≤a . -------------7分当1<a 时,12+<a a ,若(5,7)x ∀∈,不等式0)(≤x f 恒成立,则有25,17,a a ≤⎧⎨+≥⎩a 无解. ------------9分综上,实数a 的取值范围是427≤≤a . -------------10分解法2:()()()21f x x a x a =---的图像是开口向上的抛物线, --------5分 若(5,7)x ∀∈,不等式0)(≤x f 恒成立,需且仅需(5)0,(7)0,f f ≤⎧⎨≤⎩-------------7分解得54,276,2a a ⎧≤≤⎪⎪⎨⎪≤≤⎪⎩ 所以.427≤≤a故实数a 的取值范围是427≤≤a . -------------10分18.(本小题满分12分)解: (I )由题意,可设椭圆C 的方程为()012222>>=+b a by ax ,则3=c ,23=ac ,所以2=a ,1222=-=c a b , -------------2分所以椭圆C 的方程为1422=+yx. -------------3分(II )由椭圆C 的方程可知,点1A 的坐标为()0,2-,点2A 的坐标为()0,2,设动点M 的坐标为()00,y x ,由题意可知200<<x , 直线1MA 的斜率01002y k x =>+,直线2MA 的斜率02002y k x =>-,所以420221-=⋅x y k k , -------------4分因为点()00,y x M 在椭圆1422=+yx上,所以142020=+y x ,即412020x y -=, -------------5分所以.4144120221-=--=⋅x x k k-------------6分 (III )设直线1MA 的方程为()12y k x =+,令0=x ,得12y k =,所以点P 的坐标为()10,2k , --------7分 设直线2MA 的方程为()22y k x =-,令0=x ,得22y k =-,所以点Q 的坐标为()20,2k -, ---------8分 由椭圆方程可知,点B 的坐标为()1,0, 由BQ PB 21=,得121|12||21|2k k -=--,由题意,可得12112(21)2k k -=--整理得12423k k -=, ---------9分与1214k k =-联立,消1k 可得2222310k k ++=,解得21k =-或212k =-, ---------10分所以直线2MA 的直线方程为)2(--=x y 或1(2)2y x =--,因为1(2)2y x =--与椭圆交于上顶点,不符合题意.把(2)y x =--代入椭圆方程,得2516120x x -+=, 解得65x =或2,---------11分因为002x <<,所以点M 的坐标为⎪⎭⎫⎝⎛54,56. ---------12分 说明:解答题有其它正确解法的请酌情给分.。
2013-2014学年度第一学期期末高二年级化学(选修4)(理科)试题(含答案)

2013-2014学年度第一学期期末高二年级化学(选修4)(理科)试题可能用到的相对原子质量:H-1 C-12 O-16 Fe-56 Cu-64 Ag-108 一、选择题(本题包括25小题,每小题2分,共50分。
每小题只有一个选项符合题意)1、全球变暖给我们敲响了警钟,地球正面临巨大的挑战.下列说法不.正确的是A.推进小火力发电站的兴建,缓解地方用电困难,促进地方经济的快速发展B.推广“低碳经济”,减少温室气体的排放C.推广“绿色自由”计划,吸收空气中的CO2并利用廉价能源合成汽油D.利用晶体硅制作的太阳能电池可将太阳能直接转化为电能2、在25 OC,1.01×105Pa条件下,反应2N2O5(g)===4NO2(g)+O2(g)△H=+56.7kJ/mol能自发进行的合理解释是A.该反应是熵减反应 B.该反应是分解反应C.该反应的焓变效应大于熵变效应 D.该反应的熵变效应大于焓变效应3、已知下面三个数据:7.2×10-4、4.6×10-4、4.9×10-10分别是下列有关的三种酸的电离常数,若已知下列反应可以发生:NaCN+HNO2HCN+NaNO2NaCN+HF HCN+NaF NaNO2+HF HNO2+NaF由此可判断下列叙述不正确的是A.K(HF)=7.2×10-4 B.K(HNO2)=4.9×10-10C.根据两个反应即可得出结论D.K(HCN)<K(HNO2)<K(HF)4、25℃时,水的电离达到平衡:H2O H++OH-ΔH>0,下列叙述正确的是A.向水中加入稀氨水,平衡逆向移动,c(OH-)降低B.向水中加入少量固体硫酸氢钠,c(H+)增大,KW不变C.向水中加入少量固体CH3COONa,平衡逆向移动,c(H+)降低D.将水加热,KW增大,pH不变5、要除去MgCl2酸性溶液中少量的FeCl3,不宜选用的试剂是A.MgO B.MgCO3 C.NaOH D.Mg(OH)26、用石墨作电极,电解1 mol/L下列物质的溶液,溶液的pH保持不变的是A.Na2SO4B.NaOH C.HCl D.NaCl7、某学生的实验报告所列出的下列数据中合理的是A.用10mL量筒量取7.13mL稀盐酸B.用25mL滴定管做中和滴定实验时,用去某浓度的碱溶液21.70mLC.用广泛pH试纸测得某溶液的pH为2.3D.用托盘天平称量25.20g NaCl8、下列溶液加热蒸干后,能析出溶质固体的是A. Al Cl3 B. KHCO3C.Fe2(SO4)3D.NH4HCO39、将各0.05 mol的下列物质置于500 mL水中充分搅拌后,溶液中阴离子数目最多的是A.NH4Br B.K2SO4C.Mg(OH)2D.Na2S10、在一密闭容器中,mA(g)+bB(g)pC(g)反应平衡时,测得c(A)为0.5mol·L-1,在温度不变的情况下,将容器体积增大一倍,当达到新的平衡时,测得c(A)为0.3 mol·L-1,则下列判断中正确的是A.平衡向正反应方向移动了 B.物质B的转化率减小了C.化学计量数:m+n<p D.物质C的质量分数增加了11、下列各组离子在指定条件下,一定能大量共存的是A.使石蕊试液变红色的溶液中:K+、Na+、CO32-、NO3-B.在酸性高锰酸钾溶液中:Na+、NH4+、I-、Br-C.c(H+)=10-1 mol/L的溶液中:Cu2+、Al3+、SO42-、、、NO3-D.水电离出的c(H+)=10-12 mol/L的溶液中:Na+、Mg2+、Cl-、SO42-12、若pH=3的酸溶液和pH=11的碱溶液等体积混合后溶液呈酸性,其原因可能是A.生成了一种强酸弱碱盐 B.弱酸溶液与强碱溶液反应C.强酸溶液与强碱溶液反应 D.一元强酸溶液和一元强碱溶液反应13、化学用语是学习化学的重要工具,下列用来表示物质变化的化学用语中,正.确.的是A.电解饱和食盐水时,阳极的电极反应式为:2Cl--2e-==Cl2↑B.氢氧燃料电池的负极反应式:O2 + 2H2O+ 4e-== 4OH-C.粗铜精炼时,与电源正极相连的是纯铜,电极反应式为:Cu-2e-== Cu2+ D.钢铁发生电化学腐蚀的正极反应式:Fe-2e- == Fe2+14、25℃时,有浓度均为1 mol/L的(NH4)2SO4、(NH4)2CO3、(NH4)2Fe(SO4)2三种溶液,若测得其中c(NH4)分别为 a、b、c(单位为mol/L),则下列判断正确的是A.a=b=c B.c>a>b C.b>a>c D.a>c>b 15、下列各现象不能用平衡移动原理解释的是A.FeS不溶于水,但能溶于稀盐酸中B.CaCO3难溶于稀硫酸中,却能溶于醋酸中C.分别用等体积的蒸馏水和稀硫酸洗涤BaSO4沉淀,用水洗涤造成BaSO4的损失量大于用稀硫酸造成的损失量D.Cl2与Na2S溶液反应生成单质S沉淀16、下列依据热化学方程式得出的结论正确的是A.已知C(石墨, s)=C(金刚石, s); ΔH>0,则金刚石比石墨稳定[]B.已知C(s)+O2(g)=CO2(g);ΔH1C(s)+1/2O2(g)=CO(g);ΔH2,则ΔH2>ΔH1C.已知2H2(g)+O2(g)=2H2O(g);ΔH=-483.6kJ/mol,则氢气的燃烧热为241.8kJ/molD.已知NaOH(aq)+HCl(aq)=NaCl(aq)+H2O(l)ΔH=-57.3kJ/mol,则含20gNaOH 的稀溶液与稀盐酸完全中和,中和热为28.65kJ/mol17、在一定温度下的定容密闭容器中,当下列物理量不再改变时,不能表明反应A(s)+2B(g)C(g)+D(g)已达平衡的是A.混合气体的压强 B.混合气体的密度C.混合气体的相对分子质量 D.C的物质的量18、现有X(g)+Y(g) 2Z(g);正反应放热。
2013-2014学年上学期期末考试理科数学答案

2013-2014学年上学期期末调研考试高二理科数学答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个备选项中,只有一项是符合题目要求的.1. D 2.C 3.B 4.C 5.C 6.D 7.C 8.B 9.A 10.A 11.C 12.D 二、填空题:本大题共4小题,每小题5分,共20分.13.32π; 14. 1+n n ; 15.34; 16. ①③④ 三、解答题:本大题6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)过抛物线)0(22>=p px y 的焦点F 的直线交抛物线于B A ,两点,通过点A 和抛物线顶点O 的直线交抛物线的准线于点D ,求证:直线DB 平行于抛物线的对称轴.证明:设),,2(020y pyA 则直线OA 的方程为)0(200≠=y x y py ①……………2分 准线方程为2p x -=② 联立①②可得点D 的纵坐标为02y p y -=③……………4分因为)0,2(p F ,所以可得直线AF 的方程为)2(22200px py py y --=,④ 其中.220p y ≠将④与)0(22>=p px y 联立可得点B 的纵坐标为02y p y -=⑤…………7分由③⑤可知,DB ∥x 轴.……………8分 当220p y =时,结论显然成立.……………9分所以,直线DB 平行于抛物线的对称轴.……………10分 18.(本小题满分12分)已知命题[]0,2,1:2≥-∈∀a x x p ;命题,:0R x q ∈∃使得01)1(020<+-+x a x .若“p 或q ”为真,“p 且q ”为假,求实数a 的取值范围.解:p 真,则1≤a ,q 真,则,04)1(2>--=∆a 即3>a 或1-<a .………3分 因为“p 或q ”为真,“p 且q ”为假,所以p ,q 中必有一个为真,另一个为假,……………7分当p 真q 假时,有⎩⎨⎧≤≤-≤311a a 得11≤≤-a ,……………9分当p 假q 真时,有⎩⎨⎧-<>>131a a a 或得3>a ,……………11分综上,实数a 的取值范围为11≤≤-a 或3>a .……………12分 19.(本小题满分12分)如图,已知四棱锥ABCD P -的底面为等腰梯形,AB ∥BD AC CD ⊥,,H 为垂足,PH 是四棱锥的高,,E 为AD 中点.请建立合适的空间直角坐标系,在坐标系下分别解答下列问题.(1)证明:BC PE ⊥;(2)若,60=∠=∠ADB APB 求直线PA 与平面PEH 所成角的正弦值.BA解:以H 为原点,HP HB HA ,,所在直线分别为x 轴,y 轴,z 轴,线段HA 的长为单位长,建立空间直角坐标系如图,则).0,1,0(),0,0,1(B A ………1分(1)证明:设),0,0)(,0,0(),0,0,(><n m n P m C 则).0,2,21(),0,,0(mE m D 可得).0,1,(),,2,21(-=-=→-→-m BC n mPE因为,0022=+-=⋅→-→-mm BC PE 所以BC PE ⊥.………4分 (2)由已知条件可得,1,33=-=n m 故).1,0,0(),0,63,21(),0,33,0(),0,0,33(P E D C ---………5分 设),,(z y x n =→为平面PEH 的法向量,则,00⎪⎩⎪⎨⎧=⋅=⋅→-→→-→HP n HE n 即⎪⎩⎪⎨⎧==--,0,06321z z y x ……………8分 因此可以取).0,3,1(=→n ……………9分 由),1,0,1(-=→-PA 可得,42,cos =><→→-n PA ……………11分 所以直线PA 与平面PEH 所成角的正弦值为.42……………12分 20.(本小题满分12分)如图,一个结晶体的形状为平行六面体.(1)如果其中,以顶点A 为端点的三条棱长都相等,且它们彼此的夹角都是60,求以这个顶点A 为端点的晶体的对角线的长与棱长的关系;(2)如果已知,1d AC =,,b AD a AB ==,1c AA =,并且以A 为端点的各棱间的夹角都相等为θ,试用d c b a ,,,表示θcos 的值;(3)如果已知该平行六面体的各棱长都等于a ,并且以某一顶点为端点的各棱间的夹角都等于θ,求这个平行六面体相邻两个面夹角α的余弦值.解:(1)设.60,1111=∠=∠=∠===DAA BAA BAD AD AA AB2121)(→-→-→-→-++=AA AD AB AC)(2112122→-→-→-→-→-→-→-→-→-⋅+⋅+⋅+++=AA AD AA AB AD AB AA AD AB,6)60cos 60cos 60(cos 2111=+++++= ……………2分所以,61=→-AC 即A 为端点的晶体的对角线的长是棱长的6倍.……………3分(2)21212)(→-→-→-→-++==AA AD AB AC d,cos )(2222θca bc ab c b a +++++=解得)(2cos 2222ca bc ab c b a d ++---=θ.……………6分(3)在平面1AB 内作E AB E A ,1⊥为垂足,在平面AC 内作F AB CF ,⊥为垂足..cos ,sin 1θθa BF AE a CF E A ====……………9分θα22111sin )()(cos a BF CB AE A A CFE A CF E A →-→-→-→-→-→-→-→-+⋅+=⋅⋅=θθθπθθπθθ2222222sin cos )cos(cos )cos(cos cos a a a a a +-+-+=.cos 1cos θθ+=……………12分11D CA21.(本小题满分12分)两个数列{}n a 和 {}n b ,满足)(2132*321N n nna a a a b nn ∈+⋅⋅⋅+++⋅⋅⋅+++=,6)12)(1(3212222++=+⋅⋅⋅+++n n n n .求证:{}n b 为等差数列的充要条件是{}n a 为等差数列. 证明:(必要性)由已知,得,2)1(32321n n b n n na a a a +=+⋅⋅⋅+++① …………………1分于是有,2)1()1(3211321--+=-+⋅⋅⋅+++n n b n n a n a a a ②……………2分 由①-②,得1)1(21)1(21---+=n n n b n b n a .………………3分 设等差数列{}n b 的公差为d ,由已知,得,11b a =则d n a b n )1(1-+=, 所以[]d n a d n a a n 23)1()1(322111∙-+=-+=.……………5分 所以数列{}n a 是以1a 为首项,以d 23为公差的等差数列.…………6分 (充分性)由已知,得,322)1(321n n na a a a b n n +⋅⋅⋅+++=+③ 设等差数列{}n a 的公差为/d ,则[]/1/1/11321)1()2(3)(232d n a n d a d a a na a a a n -++⋅⋅⋅+++++=+⋅⋅⋅+++)-3-32-2)321(222/1n n d n a +⋅⋅⋅++++⋅⋅⋅+++=(⎥⎦⎤⎢⎣⎡+-++∙++=2)1(6)12)(1(2)1(/1n n n n n d n n a ),1(322)1(2)1(/1-∙+∙++=n n n d n n a 由③,得),1(32/1-+=n d a b n …………………10分 所以数列{}n b 是以1a 为首项,以/32d 为公差的等差数列.……………11分综上,{}n b 为等差数列的充要条件是{}n a 为等差数列.…………………12分 22.(本小题满分12分)已知椭圆)0(1:22221>>=+b a by a x C 的右焦点与抛物线x y C 4:22=的焦点重合,椭圆1C 与抛物线2C 在第一象限的交点为P ,.35=PF 过点)0,1(-A 作直线交椭圆与M 、N 两点.(1)求椭圆1C 的方程; (2)求MN 的最大值;(3)求线段MN 的中点R 的轨迹方程. 解:(1)易得),0,1(F 因为35=PF ,根据抛物线定义知,351=+p x 所以32=p x , 将),32(p y P 代入x y C 4:22=解得38=p y , 所以)38,32(P ,将点P 坐标代入)0(1:22221>>=+b a by a x C 得1389422=+b a ①……………3分 又在椭圆中有1222==-c b a ② 联立①②解得,3,422==b a所以椭圆1C 的方程为13422=+y x .……………4分 (2)当直线MN 垂直x 轴时,方程为,1-=x 此时线段MN 为通径MN =322=ab ; 当直线MN 不垂直x 轴时,设直线MN 的斜率为k ,方程为)1(+=x k y ,………5分与13422=+y x 联立消去y 得,01248)43(2222=-+++k x k x k 设),(),,(2211y x N y x M ,由韦达定理得2221222143124,438k k x x k k x x +-=+=+根据弦长公式得)43()124(4)43(641242242k k k k kMN +-⨯-++= 2243)1(12k k ++=……………6分设m k k =++22431,所以)041(41132≠---=m m m k 因为,02≥k 所以04113≥--m m ,解得,3141≤<m ……………7分所以,4123≤<m由前面知MN =322=ab 所以43≤≤MN ,故MN 的最小值为3(此时为通径长),最大值为4(此时为实轴长).……………8分 (3)设),,(y x R ),(),,(2211y x N y x M ,则21212,2y y y x x x +=+=,③………9分将),(),,(2211y x N y x M 分别代入13422=+y x 得 ,134,13422222121=+=+yx y x 两式相减得 ,4321212121-=++⨯--x x y y x x y y ④因为M 、N 、R 、A 四点共线,所以有12121+=--x yx x y y ⑤ 将③、⑤代入④化简得034322=++x y x ,……………11分因为点R 在椭圆1C 的内部,所以13422<+y x , 因此R 的轨迹方程为034322=++x y x (13422<+y x ).……………12分。
响水中学2013-2014学年高二上学期期末考试数学(理)试题

命题人:沈爱华 考生注意:1.本试题分第I 卷和第II 卷,共4页。
2.考试时间为120分钟,试卷总分为160分。
3.请将答案认真填写在答题纸上,答在试卷上无效。
第I 卷 填空题(共70分)一、填空题(每题5分,计70分)1.某县中学高二年级文科班共有学生350人,其中,男生70人,女生280人,为了调查男女生数学成绩性别差异,现要从350名学生中抽取50人,则男生应抽取 人.2.“2x >-”是“24x >”的 条件(填:“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”).3.根据《环境空气质量指数AQI 技术规定》,AQI共分为六级:(0,50]为优,(50,100]为良,(100,150] 为轻度污染,(150,200]为中度污染,(200, 300]为重度污染,300以上为严重污染.右图是根 据盐城市2013年12月份中20天的AQI 统计数据 绘制的频率分布直方图.由图中的信息可以得出这4.现有4根竹竿,他们的长度(单位:m )分别为1,2,3,4,若从中一次随机抽取两根竹竿,则他们的长度恰好相差2m 的概率 .5.如图2所示的框图,若输入值n =8,则输出s 的值为 .6. 若双曲线22214x y b-=的右焦点与抛物线y 2=12x 的焦点重合,则该双曲线的渐近线方程为 .7.空间三点)2,5,1(-A ,)1,4,2(B ,(,2,2)+C p q ,若A 、B 、C 三点共线,则p q += .8.椭圆2212516+=x y 上一点P 到左焦点的距离为3,则P 到右准线的距离为 .9.点(3,2,4)--A ,它关于原点的对称点为B ,关于平面yOz 的对称点为C ,则BC = .10. 已知P 是椭圆22221(0)+=>>x y a b a b上一点,且满足1212=PF PF ,则椭圆的离心率的取值范围是 .11.已知数据x 1,x 2,……,x 10的方差为2,且(x 1-2)2+(x 2-2)2+……+(x 10-2)2=110,则数据x 1,x 2,……,x 10的平均数是 .12.已知实数,x y 满足线性约束条件20403->⎧⎪+->⎨⎪≤⎩x y x y x ,则22+x y xy 的取值范围是 .13.若抛物线28=y x 的顶点是抛物线上到点M (a ,0)距离最近的点,则实数a 的取值范围是 .14.若关于x 的不等式22(2)->x ax 的解集中的整数恰有两个,则实数a 的取值范围是 .第II 卷 解答题(共90分)二、解答题(第15、16、17题每题14分,第18、19、20题每题16分,计90分)15. 命题p :“对x R ∀∈,220x x m -+≥恒成立”,命题q :“方程22146x y m m+=--表示双曲线”.(1)若p 为假命题,求实数m 的取值范围; (2)若p ∧q 是假命题,p ∨q 是真命题,求实数m 的取值范围.16.已知关于x 的一元二次函数f (x )=ax 2-2bx +1.(1)设集合P={1,2,3},Q={-1,1,2,3,4},从集合P 中随机取一个数作为a ,从集合Q 中随机取一个数作为b ,求方程0)(=x f 有两相等实根的概率;(2)设点(a ,b )是区域⎪⎩⎪⎨⎧>>≤-+0008y x y x 内的随机点,求函数),1[)(+∞=在区间x f y 上是增函数的概率.17.已知Q 是椭圆22143+=x y 上一点,P (1,1)-,F 1、F 2分别是椭圆的左、右焦点.(1)若22124-=QF QF ,求cos ∠F 1QF 2的值; (2)求2+QP QF 的最大值,并求出此时Q 点坐标.18.为响应党的十八大提出的文化强国建设的号召,某县政府计划建立一个文化产业园区,计划在等腰三角形OAB 的空地上修建一个占地面积为S 的矩形CDEF 文化园展厅,如图点C 、D 在底边AB 上,E 、F 分别在腰OB 、OA 上,已知OA=OB=30米,AB=米,OE= x 米,1420[,]x ∈. (1)试用x 表示S ,并求S 的取值范围; (2)若矩形CDEF,绿化 (图中阴影部分)k 为正常数),并求当OE 为何值时总造价W 最低.19.在如图所示的几何体中,四边形ABCD 为矩形,直线//⊥AF ABCD EF AB 平面,,2,21,====AD AB AF EF 点P 在棱DF 上。
深圳市南山区2013届高三上学期期末考试理科数学试题及答案

高三数学(文)第 1 页 共 11 页深圳市南山区2013届高三上学期期末考试数 学 (理科) 2013.01.16本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.注意事项:1、答卷前,考生首先检查答题卡是否整洁无缺损. 之后务必用黑色签字笔在答题卡指定位置填写自己的学校、班级、姓名及座位号,在右上角的信息栏填写自己的考号,并用2B 铅笔填涂相应的信息点.2013-1-262、选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上. 不按要求填涂的,答案无效.3、非选择题必须用黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,请注意每题答题空间,预先合理安排. 如需改动,先划掉原来的答案,然后再写上新的答案.不准使用铅笔和涂改液. 不按以上要求作答的答案无效.4、考生必须保持答题卡的整洁,不折叠,不破损.考试结束后,将答题卡交回.5、考试不可以使用计算器.第Ⅰ卷(选择题共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中, 只有一项是符合题目要求的,请将正确答案的编号用铅笔涂在答题卡上................... 1、已知全集 U={x ∈N*|x<6},A={1,3},B={3,5},则∁U (A ∪B)等于A. {1,4}B. {1,5}C.{2,4} D.{2,5}2、复数41(1)i--的值是A. 4B.-4iC.4iD.-43是边长为1那么这个几何体的全面积为 A.4π B. 2π C.3πD.32π4、如右图所示为函数f(x)=2sin(ωx+Φ) (ω>0,π<<π2φ)的部分图像,其中A ,B两点之间的距离为5,那么f(-1)= A.2 B.C. D.-25、阅读右侧程序框图,为使输出的数据为 31,则处应填写的数字为A.5B.4C.6D.7 6、点P(2,-1)为圆(x -1)2+y 2=25的弦AB A. x+y -1=0 B. 2x+y -3=0 C.2x -y -5=0 D. x -y -3=0主视图 左视图高三数学(文)第 2 页 共 11 页7、将一枚骰子抛掷两次,所得向上点数分别为m 和m ,则函数32y =m x nx +13-在[1,+∞)上为增函数的概率是 A.12B.23C.34D.568、定义运算a b =⊕a b =⊗2x f(x)=(x 2)2⊕⊗-为A.奇函数B.偶函数C.常函数D.非奇非偶函数第Ⅱ卷(非选择题共110分)二、填空题:本大题共7小题,第14、15小题任选一题作答,多选的按第14小题给分,每小题5分,共30分.请把答案填在答题卡上.......... 9、251(x )x-展开式中x 4的系数是 (用数字作答).10、已知等差数列{a n }的公差d≠0,它的第1、5、17项顺次成等比数列,则这个等比 数列的公比是 . 11、已知双曲线2222x y 1ab-= (a>0,b>0)的一条渐近线方程为x+2y=0,则双曲线的离心率e 的值为_____.则f[g(1)]的值为;满足的f[g(x)]>g[f(x)]的值是____.13、若实数x ,y 满足约束条件x 2y 32x y 3+≥⎧⎨+≤⎩,且x ≥0,则x -y 的最大值是_______.14、(坐标系与参数方程选讲选做题)已知曲线C 的极坐标方程是ρ=6sinθ,以极点为平面直角坐标系的原点,极轴为x 的正半轴,建立平面直角坐标系,直线l 的参数方程是x 1y t 2⎧=-⎪⎨=⎪⎩(t 为参数)上,则直线l 与曲线C 相交所得的弦的弦长为_______.15、(几何证明选讲选做题)如右图,O 是半圆的圆心,直径AB =PB 是圆的一条切线,割线PA 与半圆交于点C ,AC=4,则PB=____. 三、解答题:本大题共6小题,共80分,解答应写出文字说明或演算步骤.16、(本小题满分12分)第15题图已知函数2xf(x)=sinx+acos2,a为常数,a∈R,且x=2π是方程f(x)=0的解.(1)求函数f(x)的最小正周期;(2)当x∈[0,π],求函数f(x)的值域.17、(本小题满分12分)(1)求该运动员两次都命中7环的概率;(2)求ξ的分布列;(3)求的数学期望Eξ.18、(本小题满分14分)如图,已知四棱柱P-ABCD中,底面ABCD是直角梯形,AB//CD,∠ABC=450,DC=1,A B=2,PA⊥平面ABCD,PA=1.(1) 求证:AB//平面PCD;(2)求证:BC⊥平面PAC;(3)求二面角A-PC-D的平面角α的正弦值.19、(本小题满分14分)设函数1f(x)=x lnx⋅(x>0且x≠1).ACP高三数学(文)第 3 页共11 页高三数学(文)第 4 页 共 11 页(1)若f′(x 0)=0,求x 0的值; (2)求函数f(x)的单调区间;(3)已知1αx 2x >对任意x ∈(0,1)成立,求实数x 的取值范围.20、(本小题满分14分) 已知椭圆C :2222xy1a b+= (a>b>0)3.(1)求椭圆C 的方程;(2)设直线l 与椭圆C 交于A ,B 两点,坐标原点O 到直线l2,求△AOB 面积的最大值.21、(本小题满分14分)数列{a n }中,a 1=1,a n+1=2a n -n 2+3n ,(n ∈N*). (1)求a 2,a 3的值;(2)试求λ,μ的值,使得数列{a n +λn 2+μn}为等比数列; (3)设数列{b n }满足:n n 1n 1b =a n 2-+-,S n 为数列{b n }的前n 项和, 证明:n≥2时,n 6n 5<S <(n +1)(2n +1)3.高三数学(理)参考答案及评分标准2013.01.16一、选择题:(10×5′=50′)高三数学(文)第 5 页 共 11 页则A ∪B={1,3,5},所以∁U (A ∪B)= {2,4},故选择B. 2、解:复数4421(1)(1i)(2i)4i --=-+=-=,故选择A.3、解:一个空间几何体的主视图和左视图都是边长为1的正方形, 俯视图是一个直径为1的圆,那么这个几何体是底面直径为1, 高为1的圆柱,其全面积为132(1222⨯)π+π⨯=π,故选择D.4、解:如右图所示为函数f(x)=2sin(ωx+Φ) (ω>0,π<<π2φ)的部分图像,其中|AB|=5,|AC|=4,则|BC|=3,所以A(-1,2),f(x)的最小正周期为6, 则2ππ63ω==,所以πf(x)=2sin(x )3+φ, 把点A(-1,2)代入上式,得πsin()13-+φ=,ππ32-+φ=(π<<π2φ),5π6φ=,所以π5πf(x)=sin(x )36+, 那么π5ππf(1)=2sin()2sin2362--+==,故选择C.5、解:阅读右侧程序框图,S=1,i=1→S=3,i=2→S=7,i=3→S=15,i=4→S=31,i=5.为使输出的数据为31,则①处应填写的数字为5,故选择C.6、解:由题意知,点P (2,-1),圆心C(1,0),则k PC =-1,所以k AB =1, 故直线AB 的方程为y ―(―1)=1×(x -2),即x -y -3=0,故选择C.7、解:函数32y =m x nx +13-,则y ′=2mx 2-n ,而函数32y =m x nx +13-在[1,+∞)上为增函数,等价于在[1,+∞)上y ′=2mx 2-n≥0恒成立,等价于2m≥n(1≤m ,n≤6,m ,n ∈N*). 将一枚骰子抛掷两次,所有事件的基本情况(m ,n):(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4), (2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2), (4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共有36种.其中2m≥n 有:(1,1),(1,2),(2,1),(2,2),(2,3),(2,4), (3,1),(3,2), (3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6), (5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4), (6,5),(6,6),共有30种,第4题图高三数学(文)第 6设事件“函数32y =m x n x +13-在[1,+∞)上为增函数”为M ,则满足条件的概率是305P (M )366==,故选择D.8、解:由题意知,则f(x)=f(x)的定义域为24x 02⎧-≥⎪≠,2x 2x 04-≤≤⎧⎨≠⎩,, 所以{x|-2≤x ≤2且x ≠0},即定义域关于原点成中心对称. 而f(x)==|x 2|22x 2x==-----,所以f(x)f(x)(x)x-==-=----,所以f(x)为奇函数,故选择A.二、填空题:(4×5′=20′) 9、解:251(x )x-展开式中的通项公式:5rr 2r 5r 5r r 3r 5r +1551T (1)C (x )()(1)C x x----=-⋅⋅=-⋅,令3r -5=4,则r=3,所以251(x )x-展开式中x 4的系数是(-1)2C 53=10.10、解:已知等差数列{a n }的公差d≠0,它的第1、5、17项顺次成等比数列,则a 52=a 1·a 16,即(a 1+4d)2=a 1·(a 1+16d),整理得a 1=2d , 而这个等比数列的公比是5111a a 4d 2d 4d q 3a a 2d++====.11、解:由题意知,双曲线的一条渐近线方程为x+2y=0,即b 1a2=,则双曲线的离心率为:e 2===.当x=1时,f[g(1)]=3,g[f(1)]=3,f[g(x)]>g[f(x)]不成立; 当x=2时,f[g(2)]=3,g[f(2)]=1,f[g(x)]>g[f(x)]成立; 当x=3时,f[g(3)]=1,g[f(3)]=1,f[g(x)]>g[f(x)]不成立. 故f[g(1)]的值为1;满足的f[g(x)]>g[f(x)]的值是13、解:实数x ,y 满足约束条件x 2y 32x y 3+≥⎧⎨+≤⎩,且x ≥0,其平面区域如图所示, 设目标函数z=x -y ,当目标函数线经过点A(1,1)时,高三数学(文)第 7 页 共 11 页则x -y 的最大值是1-1=0.14、解:把曲线C 的极坐标方程ρ=6sinθ,化为普通方程为:x 2+ y 2=6y ,即x 2+ (y -3)2=9,其圆心为(0,3),半径r=3. 直线l 的参数方程是x 1y t 2⎧=-⎪⎨=⎪⎩(t 为参数)化为普通方程为:x -2y+1=0, 圆心(0,3)到直线l 的距离为d -⨯+==,则直线l 与曲线C 相交所得的弦的弦长为4=. 15、解:连结BC ,在Rt △ABC 中,AB = AC=4,由勾股定理得,BC =由射影定理BC 2=AC·CP ,得CP=2,再由切割线定理PB 2=PC·PA=2×6=12,即PB =. 三、解答题:(80′) 16、解:(1) 2f()sin+acos0224πππ==,则11+a 02=,解得a=-2. ……3分所以2x f(x)=sinx 2cossinx cosx 12-=--,则f(x)=(x )14π--, ……5分所以函数f(x)的最小正周期为2π. ……6分 (2)由x ∈[0,π],得x []444ππ3π-∈-,,则sin (x )[1]42π-∈-, ……10分(x )[14π-∈-(x )1[21]4π--∈-,则函数f(x)的值域为[21]-. ……12分 (2)ξ可能取值为7,8,9,10, ……4分 P(ξ=7)= 0.04;P(ξ=8)= 2×0.2×0.3+0.32= 0.21; ……5分 P(ξ=9)= 2×0.2×0.3+ 2×0.3×0.3+0.32= 0.39; ……7分 P(ξ=10)= 2×0.2×0.2+ 2×0.3×0.2+ 2×0.3×0.2+0.22= 0.36; ……9分 10分(3)ξ的数学期望E ξ=7×0.04+8×0.21+9×0.39+10×0.36=9.07. ……12分18、解:(1)证明:∵AB//CD ,CD ⊂平面PDC ,AB ⊄平面PDC ,∴AB//平面PDC.第15题图APE高三数学(文)第 8 页 共 11 页……3分(2)证明:在是直角梯形ABCD 中,过点C 作CE ⊥AB 于点E , 则四边形ADCE 为矩形,∴AE=DC=1,又AB=2,∴BE=1, 在Rt △BEC 中,∠ABC=450,∴CE=BE=1,CB =,……4分∴AD=CE=1,则AC ==,∴AC 2+BC 2=AB 2,∴BC ⊥AC. ……6分又PA ⊥平面ABCD ,BC ⊂平面ABCD ,∴BC ⊥PA , ……7分而PA ∩AC=A ,∴BC ⊥平面PAC ; ……8分 (3)方法1 PA ⊥平面ABCD , CD ⊂平面ABCD ,∴CD ⊥PA ,又CD ⊥AD ,而PA ∩AD=A ,∴CD ⊥平面PAD ,PD ⊂平面PAD ,∴CD ⊥PD. 又PA=AD=1,AC =PC =,PD = ……10分∴点D 到PC的距离PC D S h'1PC2==V ……11分在三棱锥P-ACD 中,A D C 11S C D A D 22=⋅⋅=V,PAC 1S AC PA 22=⋅⋅=V ,V P-ACD =V D-PAC ,∴点D 到PAC的距离AD C P AC D PACPAC1S PA V 3h 11S S 33-⋅===V V V ……13分∴h sin h'2α==. ……14分方法2如图,分别以AD ,AB ,AP 为x 轴,y 轴, z 轴建立空间直角坐标系,则由题设可知,A(0,0,0),P(0,0,1),C(1,1,0),D(1,0,0),……9分∴AP (001)=uur ,,,PC (111)=-uu r ,,, 设m (a b c)=u r ,,为平面PAC 的一个法向量,则m AP 0m PC 0⎧⋅=⎪⎨⋅=⎪⎩u r uur u r uu r,即c 0a b c 0=⎧⎨+-=⎩, 设a=1,则b=-1,∴m (110)=-u r,,, ……10分 同理设n (x y z)=r ,,为平面PCD 的一个法向量,求得∴n (101)=r,,,……11分高三数学(文)第 9 页 共 11 页∴m n 1cos =2|m ||n |⋅α==⋅u r r u r u u r -, ……13分∴sin 2α= ……14分19、解:(1)函数1f(x)=x lnx ⋅(x>0且x≠1),则22ln x 1f'(x)=x ln x+-⋅, ……2分若f′(x 0)=0,可求得01x =e. ……4分故单调递增区间是1(0)e,,单调递减区间是1(1)e,和(1,+∞). (3)在1αx 2x >两边取对数,得1ln 2alnx x>, ……10分由于0<x<1,所以a 1ln 2xlnx>(*),……11分由(*)的结果可知,当x ∈(0,1)时,1f(x)f()=e e ≤-, ……13分 为使(1)式对所有x ∈(0,1)成立,当且仅当ae ln 2>-,即a>-eln2. ……14分20、解:(1)设椭圆的半焦距为c ,依题意22b 1())a 3a ⎧-=⎪⎨⎪=⎩, ……2分 解得a =b=1, ……3分 ∴c = ……4分∴所求椭圆C 的方程为:22xy 13+=.……5分(2)设A(x 1,y 1),B(x 2,y 2),①当AB ⊥x 轴时,|AB |=; ……6分②当AB 与x 轴不垂直时,设直线AB 的方程为y=kx+m , ……7分 =2223m =(k +1)4, ……8分把y=kx+m 代入椭圆方程,整理得(3k 2+1)x 2+6kmx+3m 2-3=0,高三数学(文)第 10 页 共 11 页∴1226km x +x =3k +1-,21223(m 1)x x =3k +1-⋅, ……9分22222221222236k m12(m 1)|AB |(1+k )(x x )(1+k )[](3k +1)3k +1-=--22222222224212(k 1)(3k +1m )3(k 1)(9k 1)12k3(3k +1)(3k +1)9k +6k 1+-++===++2212319k 6k=+++(k ≠0) 1234236≤+=⨯+, ……11分当且仅当2219k k=,即k 3=±时等号成立. ……12分当k=0时,|AB |=,综上可知,|AB|max =2, ……13分∴当|AB|最大时,△AOB面积的最大值为max 1S |AB |222=⨯=.21、解:(1)数列{a n }中,a 1=1,a n+1=2a n -n 2+3n ,(n ∈N*),所以a 2=2a 1-12+3×1=4,a 3=2a 2-22+3×2=10. ……2分(2)若数列{a n +λn 2+μn}为等比数列,则存在q ≠0,使a n+1+λ(n+1)2+μ(n+1)=q(a n +λn 2+μn ) 对∀n ∈N*成立. ……3分由已知a n+1=2a n -n 2+3n ,代入上式得,2a n -n 2+3n +λ(n+1)2+μ(n+1)= q(a n +λn 2+μn ),整理得 (q -2)a n +(λq -λ+1) n 2+(μq -2λ-μ-3)n -λ-μ=0,① ……5分因为①式对∀n ∈N*成立,所以q 20q 10q 2300-=⎧⎪λ-λ+=⎪⎨μ-λ-μ-=⎪⎪-λ-μ=⎩,解得q=2,λ=-1,μ=1,此时,a n +λn 2+μn = a n -n 2+ n , ……7分当λ=-1,μ=1时,数列{a n +λn 2+μn}是公比为2的等比数列. ……8分(3)证明:由(2)得,a n -n 2+ n=(a 1-12+ 1)2n-1=2n-1,即a n =n 2-n+2n-1, 所以n n 12n 11b =a n 2n-=+-, ……9分因为n 2221111b 111nn n n 422=<=---+, ……10分当n ≥2时,S n = b 1+ b 2+ b 3+…+ b n1111112151()()...()1355711133n n n 2222222<+-+-++-=+-<-++, ……11分现证n 6n S >(n 2)(n +1)(2n +1)≥.证法1:当n=2时,21215S =b b 144+=+=,高三数学(文)第 11 页 共 11 页而6n 62124(n +1)(2n +1)(2+1)(22+1)355⨯===⨯⨯,5445>,当n=2时成立,……12分当n≥3时,由n 21111b =nn (n 1)nn 1>=-++,S n = b 1+ b 2+ b 3+…+ b n 11111111n (1)()()...()122334n n 1n 1n 1>-+-+-++-=-=+++,且2n+1>6得,612n 1>+,∴n n6n S >n 1(n +1)(2n +1)>+. ……14分证法2:当n≥2时,2222n 222211111n (n 1)(2n 1)S (123...n )(...)6123n++=++++++++>(1+1+1+…+1)2=n 2,∴n 6n S >(n +1)(2n +1). ……14分证法3:(数学归纳法)①当n=2时,21215S =b b 144+=+=,而6n62124(n +1)(2n +1)(2+1)(22+1)355⨯===⨯⨯,5445>,故当n=2时不等式成立, ……12分②假设n=k(n ≤k)时不等式成立,即k 6kS >(k +1)(2k +1)成立,则当n=k+1时,2k 1k k 1226k 16k 8k 1S =S b >(k +1)(2k +1)(k +1)(k +1)(2k +1)++++++=,因为226k 8k 16(k +1)(k +1)(2k +1)(k +2)(2k +3)++-222(6k 8k 1)(k +2)(2k +3)6(k +1)(2k +1)(k +1)(2k +1)(k +2)(2k +3)++-=32216k 40k 25k 0(k +1)(2k +1)(k +2)(2k +3)++=>,所以k +16(k +1)S >(k +2)(2k +3)成立, 根据①②可知,n 6nS >(n +1)(2n +1)对于n≥2,n ∈N*都成立. ……14分。
唐山市2013到2014期末理科成绩

KSH XM KDDM KDMC ZKZH JDZXDM 11401012181830韩璐0101唐山市第一中学0101117300101 11401012171701刘泽群0101唐山市第一中学0101116220101 11401012171729孙子轩0101唐山市第一中学0101102360101 11401012151501李明月0101唐山市第一中学0101115160101 11401012171730熊天宇0101唐山市第一中学0101104110101 11401012141437王伟昊0101唐山市第一中学0101102380101 11401012161602贾云琪0101唐山市第一中学0101103170101 11401012161639刘新宇0101唐山市第一中学0101102070101 11401012181831王堃宇0101唐山市第一中学0101123070101 11401012131305武哲宇0101唐山市第一中学0101101200101 11401012171705张艾琳0101唐山市第一中学0101115180101 11401012181804来鑫0101唐山市第一中学0101113050101 11401012181838郭玉峰0101唐山市第一中学0101119340101 11401012060631张真溥0101唐山市第一中学0101120030101 11401012151510刘瑶佳0101唐山市第一中学0101122270101 11401012171703黄楚芸0101唐山市第一中学0101102300101 11401012171736陈雷0101唐山市第一中学0101106200101 11401012171710郑雨婷0101唐山市第一中学0101115200101 11401012181801姚尧0101唐山市第一中学0101115250101 11401012181820付冰纯0101唐山市第一中学0101119300101 11401012131301白如水0101唐山市第一中学0101108260101 11401012161640高可名0101唐山市第一中学0101110380101 11401012181802夏鹤铭0101唐山市第一中学0101114240101 11401012131306魏佳丽0101唐山市第一中学0101109080101 11401012181833张宏图0101唐山市第一中学0101111220101 11401012151537艾禹名0101唐山市第一中学0101105190101 11401012080829孟新元0101唐山市第一中学0101101290101 11401012181844李堃0101唐山市第一中学0101116080101 11401012171744李思远0101唐山市第一中学0101105400101 11401012080832施宇轩0101唐山市第一中学0101122250101 11401012131304郑欢0101唐山市第一中学0101117290101 11401012181817褚润聪0101唐山市第一中学0101106150101 11401012131308张安0101唐山市第一中学0101110080101 11401012151536赵维嘉0101唐山市第一中学0101101090101 11401012171711曹天意0101唐山市第一中学0101102020101 11401012151512郑凯月0101唐山市第一中学0101109290101 11304012011001李赤0401唐山市开滦第二中学0401107260401 11401012131309王逸嘉0101唐山市第一中学0101114270101 11401012181807张琪0101唐山市第一中学0101113310101 11401012181845杨佳禾0101唐山市第一中学0101101350101 11401012151517刘蓝忆0101唐山市第一中学0101106260101 11401012131343张朔川0101唐山市第一中学0101120210101 11401012181811周伯宇0101唐山市第一中学0101122070101 11401012171707杨璐铭0101唐山市第一中学0101102140101 11401012080831李克0101唐山市第一中学0101106030101 11401012161646史旭东0101唐山市第一中学010110635010111401012171719苏天晴0101唐山市第一中学0101119270101 11401012171737杨佳澄0101唐山市第一中学0101103110101 11401012181837庞珞0101唐山市第一中学0101104270101 11401012161601杨雨欣0101唐山市第一中学0101107020101 11401012181803陈沛瑾0101唐山市第一中学0101116130101 11401012111135李皓天0101唐山市第一中学0101115390101 11401012161650井浩然0101唐山市第一中学0101104060101 11401022102922罗瑞丰0102唐山市第二中学0102119280102 11401012131313李皓晴0101唐山市第一中学0101111240101 11401022110122剧小萌0102唐山市第二中学0102111320102 11401012151513王佳炜0101唐山市第一中学0101122030101 11401012151516张路鸣0101唐山市第一中学0101121280101 11401012171713王珊0101唐山市第一中学0101115300101 11401012131302周梦园0101唐山市第一中学0101120150101 11401012161652刘致君0101唐山市第一中学0101104280101 11304012011002王旋0401唐山市开滦第二中学0401106170401 11401012171708牟鹳冰0101唐山市第一中学0101123340101 11401012171745支元祺0101唐山市第一中学0101122090101 11202012010001付傲0201唐山市开滦第一中学0201103220201 11401012070701王张安平0101唐山市第一中学0101101130101 11401012141408马红磊0101唐山市第一中学0101113280101 11401012181836李见哲0101唐山市第一中学0101117350101 11401012121232徐志锟0101唐山市第一中学0101115260101 11401012141440王雨舟0101唐山市第一中学0101108020101 11401012161638张宇博0101唐山市第一中学0101121180101 11401012171717侯欣语0101唐山市第一中学0101111140101 11401012151506吴桐0101唐山市第一中学0101112270101 11401012171702张心怡0101唐山市第一中学0101112110101 11401012050538刘霖0101唐山市第一中学0101120070101 11401012121202王伟0101唐山市第一中学0101113190101 11401012171742董丞育0101唐山市第一中学0101119330101 11401012141401刘可欣0101唐山市第一中学0101108290101 11401012171733仝义0101唐山市第一中学0101116360101 11401022202322高睿杰0102唐山市第二中学0102117260102 11401012131303张圆0101唐山市第一中学0101112190101 11401012131340李承霖0101唐山市第一中学0101115020101 11401012151539孟庆远0101唐山市第一中学0101111330101 11401012171731周逊0101唐山市第一中学0101121320101 11401012161611马梦皎0101唐山市第一中学0101114050101 11401012050534佟佳弘0101唐山市第一中学0101107400101 11401012161663冯天昊0101唐山市第一中学0101115040101 11401012181843赵梓皓0101唐山市第一中学0101112060101 11401012131311张文馨0101唐山市第一中学0101111070101 11401012151520孟凡颖0101唐山市第一中学0101123330101 11401012171714王洋0101唐山市第一中学0101103060101 11401012171716吕行0101唐山市第一中学0101104250101 11401012181808黄佳淇0101唐山市第一中学010110436010111401022102822史东旭0102唐山市第二中学0102111060102 11401012161645晏阳0101唐山市第一中学0101102370101 11401012171734迟嘉琦0101唐山市第一中学0101107330101 11401012181825张诗培0101唐山市第一中学0101123270101 11401022102522赵康诣0102唐山市第二中学0102116120102 11401022172522马畅0102唐山市第二中学0102110200102 11401022182122彭毅0102唐山市第二中学0102105320102 11401012131345刘帅0101唐山市第一中学0101123140101 11401012161603卢宇峥0101唐山市第一中学0101121160101 11401022112422闫富宸0102唐山市第二中学0102119090102 11401012090931付茁林0101唐山市第一中学0101106020101 11401012171718康伟祺0101唐山市第一中学0101101340101 11401012171738马旭0101唐山市第一中学0101119290101 11401022100122张雅琢0102唐山市第二中学0102121240102 11401012151541邵沛涵0101唐山市第一中学0101115280101 11401012111132王亚群0101唐山市第一中学0101123050101 11401012141439王旭辉0101唐山市第一中学0101113160101 11401012080830刘笑尘0101唐山市第一中学0101107130101 11401012131342徐昭若0101唐山市第一中学0101104350101 11401012171715边梦葳0101唐山市第一中学0101114090101 11401012121231周鹤川0101唐山市第一中学0101124020101 11401012171722赵方舟0101唐山市第一中学0101116200101 11401012171732邹昊孚0101唐山市第一中学0101103090101 11401012171741陈潇雨0101唐山市第一中学0101107240101 11401012151528王宇晴0101唐山市第一中学0101109280101 11401012161613许晴0101唐山市第一中学0101115050101 11401022130722侯晨悦0102唐山市第二中学0102121280102 11401012151504刘雨宁0101唐山市第一中学0101121310101 11401012101049孙博伟0101唐山市第一中学0101122080101 11401012050533李佳蔚0101唐山市第一中学0101117030101 11401012131325于兰0101唐山市第一中学0101120300101 11401012141416郑之杰0101唐山市第一中学0101108280101 11401012161630王晴0101唐山市第一中学0101122050101 11401012181812刘哲绮0101唐山市第一中学0101121010101 11401012060603张琬乔0101唐山市第一中学0101109250101 11401012131327宋梦雅0101唐山市第一中学0101111200101 11401012161617王卓妍0101唐山市第一中学0101109370101 11401012171706赵钊然0101唐山市第一中学0101114060101 11401012060636杨蓄0101唐山市第一中学0101105300101 11401012070703魏潇扬0101唐山市第一中学0101110300101 11401012181860王瑶0101唐山市第一中学0101105070101 11401022202422刘冉0102唐山市第二中学0102106040102 11401012151540李悦0101唐山市第一中学0101112340101 11401012070732刘鑫玺0101唐山市第一中学0101108200101 11401012141406王潆0101唐山市第一中学0101108380101 11401012181806周雪霁0101唐山市第一中学0101117310101 11401012181832桑宇辰0101唐山市第一中学010111139010111401012060635刘雨蒙0101唐山市第一中学0101116090101 11401012131312马一凡0101唐山市第一中学0101109260101 11401012131317曹原0101唐山市第一中学0101121100101 11401012181810苏蕊0101唐山市第一中学0101107030101 11401012181816王竹青0101唐山市第一中学0101101110101 11401022082122张津川0102唐山市第二中学0102112020102 11401012090901魏思遥0101唐山市第一中学0101115240101 11401012111131孟令涵0101唐山市第一中学0101119110101 11401012141442夏一平0101唐山市第一中学0101110150101 11401012151552韩刘众极0101唐山市第一中学0101105380101 11401012171724张晨曦0101唐山市第一中学0101105120101 11401012121201周雪晴0101唐山市第一中学0101123320101 11401012151507赵亦奇0101唐山市第一中学0101121040101 11401012181834高越0101唐山市第一中学0101121370101 11202012010012郑文更0201唐山市开滦第一中学0201105250201 11401012101002牛轶梦0101唐山市第一中学0101119020101 11401012131307马宇航0101唐山市第一中学0101107210101 11401012141443张致皓0101唐山市第一中学0101115380101 11401022123122韩雷0102唐山市第二中学0102104100102 11401012131324陈祉娴0101唐山市第一中学0101122310101 11401012171723张浩艾0101唐山市第一中学0101104260101 11401012171746吴尚泽0101唐山市第一中学0101121020101 11401012181813李金原0101唐山市第一中学0101104130101 11401012181815戚婧晨0101唐山市第一中学0101121070101 11401022192822吴易明0102唐山市第二中学0102108130102 11401012161604徐艺玮0101唐山市第一中学0101123370101 11401012161610尹悦0101唐山市第一中学0101105320101 11401012151502杨丝雨0101唐山市第一中学0101104220101 11401012151566柴新港0101唐山市第一中学0101110090101 11401012161616刘章心怡0101唐山市第一中学0101112200101 11401012161644高铭序0101唐山市第一中学0101117170101 11202012010002王艺0201唐山市开滦第一中学0201113280201 11202012010010吕奕霏0201唐山市开滦第一中学0201101310201 11401022163222付欣然0102唐山市第二中学0102111300102 11401012131339郭津铭0101唐山市第一中学0101123120101 11401022102322曹雨宸0102唐山市第二中学0102112370102 11401012181809孙咏文0101唐山市第一中学0101108220101 11401012181818王月琛0101唐山市第一中学0101123300101 11401022065022薄盛0102唐山市第二中学0102110340102 11401022074622高晗0102唐山市第二中学0102106010102 11401022100222魏漪0102唐山市第二中学0102102090102 11401012070705李子茹0101唐山市第一中学0101116140101 11401012131337张宸瑞0101唐山市第一中学0101113020101 11401012161605周羲佳0101唐山市第一中学0101102010101 11401012161642陈方远0101唐山市第一中学0101115060101 11401012080802刘洁铮0101唐山市第一中学0101107060101 11401012111101蒋欣宇0101唐山市第一中学010112302010111401012171752杨一凡0101唐山市第一中学0101117160101 11401012181846徐兰天0101唐山市第一中学0101124030101 11401012151544高齐鸿0101唐山市第一中学0101112250101 11401012171709李昀彤0101唐山市第一中学0101118120101 11402022020044张艺竞0202唐山市第八中学0202116160202 11401012070716李玥0101唐山市第一中学0101123080101 11401012141414赵思琪0101唐山市第一中学0101123100101 11401012151538徐迟0101唐山市第一中学0101123060101 11401012171758熊承尧0101唐山市第一中学0101114170101 11401022092522王朝阳0102唐山市第二中学0102112210102 11401022182022马明宇0102唐山市第二中学0102104190102 11401022115522王兴业0102唐山市第二中学0102115040102 11401012141438张军培0101唐山市第一中学0101108130101 11401012171749范恩明0101唐山市第一中学0101102110101 11304012012041高敬媛0401唐山市开滦第二中学0401104070401 11401022103022马天翼0102唐山市第二中学0102114020102 11401022172422张壮0102唐山市第二中学0102104160102 11401012171739杨宇涵0101唐山市第一中学0101106390101 11401022062422王庆睿0102唐山市第二中学0102122310102 11401022092922王融0102唐山市第二中学0102108310102 11401012131318周欣蕊0101唐山市第一中学0101116170101 11401012101001李怡然0101唐山市第一中学0101113350101 11401012131310刘羽蕉0101唐山市第一中学0101122360101 11401012141407李奕璇0101唐山市第一中学0101121230101 11401012161618刘珺伊0101唐山市第一中学0101111060101 11401022070222毕毓琳0102唐山市第二中学0102118290102 11401022200122佟如艺0102唐山市第二中学0102122110102 11401012050540段伟健0101唐山市第一中学0101108080101 11401012060633李晓峰0101唐山市第一中学0101116020101 11401012171712刘若瀛0101唐山市第一中学0101106400101 11401012181847张昊宸0101唐山市第一中学0101101240101 11304012012036杜静伟0401唐山市开滦第二中学0401110010401 11401022060222王嘉漉0102唐山市第二中学0102116370102 11401012101008范丽爽0101唐山市第一中学0101121380101 11202012010015吴昊学0201唐山市开滦第一中学0201113370201 11401012121239于志伟0101唐山市第一中学0101104210101 11401012151515王雅明0101唐山市第一中学0101117150101 11401012171720李欣洋0101唐山市第一中学0101119140101 11304012011003梁春栋0401唐山市开滦第二中学0401108310401 11202012010013刘禹彤0201唐山市开滦第一中学0201105350201 11202012010020姚赤云0201唐山市开滦第一中学0201101360201 11401022070322李美佳0102唐山市第二中学0102111130102 11401012090906刘艺0101唐山市第一中学0101110190101 11401012131338徐畅0101唐山市第一中学0101102170101 11401012151543邢淳0101唐山市第一中学0101114020101 11401022062522张柯瑞0102唐山市第二中学0102121250102 11401022130322刘学0102唐山市第二中学010210518010211401012121207金扶摇0101唐山市第一中学0101110030101 11401022074722杨雨萌0102唐山市第二中学0102104090102 11401022100522张熠爽0102唐山市第二中学0102119290102 11401022120222陈钰0102唐山市第二中学0102121070102 11401012080836张子祎0101唐山市第一中学0101116040101 11401022160122王岚婷0102唐山市第二中学0102115120102 11401012090930齐政锡0101唐山市第一中学0101120050101 11401012141402高婧雅0101唐山市第一中学0101123380101 11401012141419韩悦0101唐山市第一中学0101114070101 11401012171725么知为0101唐山市第一中学0101103270101 11401012111115刘倩0101唐山市第一中学0101114290101 11401012151545张海威0101唐山市第一中学0101106250101 11401012161641杜佳男0101唐山市第一中学0101119280101 11401012161649王伟懿0101唐山市第一中学0101119380101 11401012181840杨晨0101唐山市第一中学0101118240101 11401012111136杨家祺0101唐山市第一中学0101103330101 11401012090911张冬雪0101唐山市第一中学0101114230101 11401012111103刘雨欣0101唐山市第一中学0101102040101 11401012141441纪宏豫0101唐山市第一中学0101101250101 11202012010003李懋0201唐山市开滦第一中学0201102070201 11401012080806孙爱博0101唐山市第一中学0101114190101 11401012121208高川琪0101唐山市第一中学0101106170101 11401012141422张婉瑶0101唐山市第一中学0101102080101 11401012161614田颖楠0101唐山市第一中学0101108240101 11401012161654王子曌0101唐山市第一中学0101108070101 11401022061122刘雨桐0102唐山市第二中学0102102250102 11401012090929郑一凡0101唐山市第一中学0101107080101 11401012090935孙朴诚0101唐山市第一中学0101107110101 11401012131362李众0101唐山市第一中学0101105110101 11401012161619尚昱昊0101唐山市第一中学0101105250101 11401012171727刘佳溪0101唐山市第一中学0101117210101 11401022082222吴靖轩0102唐山市第二中学0102111210102 11401012151542么学华0101唐山市第一中学0101106270101 11304012011011刘德祥0401唐山市开滦第二中学0401108290401 11304012011021张鸿羽0401唐山市开滦第二中学0401108160401 11202012010011赵莹莹0201唐山市开滦第一中学0201104140201 11402022020048葛畅0202唐山市第八中学0202116070202 11401022060322孙冉0102唐山市第二中学0102122050102 11401012090904李薇0101唐山市第一中学0101111280101 11401012101009廖悦言0101唐山市第一中学0101121140101 11401012101042陈虹圻0101唐山市第一中学0101102350101 11401012121210董雅娴0101唐山市第一中学0101123210101 11202012010009王子琪0201唐山市开滦第一中学0201108350201 11401012131346朱凯新0101唐山市第一中学0101110340101 11401012141403刘思爱0101唐山市第一中学0101118090101 11401012161615李素璇0101唐山市第一中学0101117100101 11202012010007纪昌浩0201唐山市开滦第一中学020111314020111401012131368曹建昊0101唐山市第一中学0101112170101 11401012070734杜雄梓0101唐山市第一中学0101104180101 11401012080809么一诺0101唐山市第一中学0101114210101 11401012101038姜占0101唐山市第一中学0101120200101 11401022140222邢丹0102唐山市第二中学0102105280102 11401012050504孙洋0101唐山市第一中学0101116010101 11401012060634张宽0101唐山市第一中学0101109210101 11401012101021姜迪0101唐山市第一中学0101114120101 11401012111134刘晨昕0101唐山市第一中学0101106190101 11401012131347王鹏0101唐山市第一中学0101106310101 11401012141455赵简平0101唐山市第一中学0101112040101 11401012181849张紫强0101唐山市第一中学0101117360101 11401012181853李朝阳0101唐山市第一中学0101115190101 11401022062722杨迪青0102唐山市第二中学0102119100102 11401022102422信淇梵0102唐山市第二中学0102110370102 11401022130822李瑛钰0102唐山市第二中学0102122030102 11401022132822张家瑞0102唐山市第二中学0102118200102 11401022145122侯瑛0102唐山市第二中学0102105220102 11401022200822刘嘉琦0102唐山市第二中学0102104150102 11401012131357李双木0101唐山市第一中学0101114380101 11401022074822李晨溪0102唐山市第二中学0102102190102 11401012060611韩莉钧0101唐山市第一中学0101113320101 11401012161664张璐阳0101唐山市第一中学0101105060101 11304012011014冯烁0401唐山市开滦第二中学0401103150401 11401012171726杜佳0101唐山市第一中学0101117140101 11401022075422李伟健0102唐山市第二中学0102121290102 11401022130122刘渊晨0102唐山市第二中学0102109030102 11401022140122刘卉0102唐山市第二中学0102106140102 11401012101036王晗0101唐山市第一中学0101121170101 11401012131354张智博0101唐山市第一中学0101109150101 11401012161623齐伊蒙0101唐山市第一中学0101115010101 11401012181839闫铮0101唐山市第一中学0101102330101 11401012181850么航0101唐山市第一中学0101108120101 11401022072522王嘉琦0102唐山市第二中学0102102340102 11401012090903王琨0101唐山市第一中学0101116110101 11402022010003于海彤0202唐山市第八中学0202116010202 11401022072722刘敬文0102唐山市第二中学0102114280102 11401012050535尚天行0101唐山市第一中学0101112160101 11401012181805姜雨辰0101唐山市第一中学0101118150101 11202012010016信欣0201唐山市开滦第一中学0201107250201 11401012050503安琪0101唐山市第一中学0101104320101 11401012090933张天造0101唐山市第一中学0101109330101 11401012111145马天宇0101唐山市第一中学0101113390101 11401012141412张怡婧0101唐山市第一中学0101113030101 11401012161637朱胤0101唐山市第一中学0101112210101 11401022082722胡英杰0102唐山市第二中学010211105010211401012141404徐小汐0101唐山市第一中学0101111020101 11401012181842柳子朝0101唐山市第一中学0101119230101 11401012050539赵晨臣0101唐山市第一中学0101103390101 11401012131344黄家辉0101唐山市第一中学0101117120101 11304012012035张子慧0401唐山市开滦第二中学0401105210401 11202012010006周桐0201唐山市开滦第一中学0201110060201 11401022062922窦启明0102唐山市第二中学0102106360102 11401022112522王颢0102唐山市第二中学0102120380102 11401022133022王鸣展0102唐山市第二中学0102115140102 11401022180522何世宜0102唐山市第二中学0102110380102 11401012050520魏博0101唐山市第一中学0101103130101 11401012101003郝岱麒0101唐山市第一中学0101122300101 11401012131330桑园0101唐山市第一中学0101120350101 11401012161609王子卓0101唐山市第一中学0101111360101 11304012012039杨雪0401唐山市开滦第二中学0401101110401 11401012060632张天航0101唐山市第一中学0101113080101 11401012151529李嘉慧0101唐山市第一中学0101111040101 11401012161628李姝洁0101唐山市第一中学0101121270101 11401022104822何翔宇0102唐山市第二中学0102101020102 11401022154922宋逸玮0102唐山市第二中学0102114010102 11401012060606王子晗0101唐山市第一中学0101105280101 11401012151546王宇翔0101唐山市第一中学0101105330101 11401022130422侯玉冰0102唐山市第二中学0102106380102 11401012050521张琪0101唐山市第一中学0101107150101 11401012101039张鑫宇0101唐山市第一中学0101113300101 11401012121204杜郁坤0101唐山市第一中学0101122150101 11401012141445杨啸宇0101唐山市第一中学0101111090101 11401012141460王靖凯0101唐山市第一中学0101121050101 11401012050505王佳明0101唐山市第一中学0101116310101 11401012141452魏佳兴0101唐山市第一中学0101119180101 11401012171704冉庚鑫0101唐山市第一中学0101116280101 11401012181835李牧狄0101唐山市第一中学0101105020101 11202012010021李一石0201唐山市开滦第一中学0201112290201 11401012070715李尧0101唐山市第一中学0101111120101 11401012151508郭映辉0101唐山市第一中学0101104070101 11304012011006杨佳宇0401唐山市开滦第二中学0401102240401 11401022122522于硕0102唐山市第二中学0102108300102 11401012060643杨诚0101唐山市第一中学0101101020101 11401012131316刘忆珂0101唐山市第一中学0101116390101 11401012131322高炅0101唐山市第一中学0101106180101 11401012141444马铎0101唐山市第一中学0101104230101 11401012161620董丹阳0101唐山市第一中学0101117050101 11401022115422陈祎航0102唐山市第二中学0102109090102 11401012070708史秋羽0101唐山市第一中学0101111250101 11401012080810王丹彤0101唐山市第一中学0101108050101 11401012131331张馨予0101唐山市第一中学010111029010111401012151550刘义杰0101唐山市第一中学0101120270101 11202012010034罗睿0201唐山市开滦第一中学0201102170201 11401022112722徐思远0102唐山市第二中学0102110400102 11401022182922蒋子栋0102唐山市第二中学0102114370102 11401012111104高浩浙0101唐山市第一中学0101122190101 11401012111139江程舟0101唐山市第一中学0101116050101 11401012121236宿文杰0101唐山市第一中学0101105160101 11401022113322于克松0102唐山市第二中学0102111240102 11401012131349檀敬波0101唐山市第一中学0101107350101 11401012141450李昊宇0101唐山市第一中学0101107050101 11304012011010毛建宇0401唐山市开滦第二中学0401101180401 11401012161655张树斌0101唐山市第一中学0101120360101 11401012181852刘芮0101唐山市第一中学0101119150101 11401022072922赵子明0102唐山市第二中学0102101050102 11401022082022张天昊0102唐山市第二中学0102118210102 11401022200522孟繁妍0102唐山市第二中学0102117380102 11401012101045胡少康0101唐山市第一中学0101115150101 11401012131351张晟0101唐山市第一中学0101117370101 11401012161658姜礼0101唐山市第一中学0101101380101 11401022203022卞霖丰0102唐山市第二中学0102114310102 11401012060601吕征阳0101唐山市第一中学0101109090101 11304012012034刘莹0401唐山市开滦第二中学0401101310401 11401022162922孙钰茗0102唐山市第二中学0102123090102 11401012070704于惠雯0101唐山市第一中学0101120290101 11401012070711韩雨彤0101唐山市第一中学0101105340101 11401012070713朱怡迪0101唐山市第一中学0101111030101 11401012101011李婷0101唐山市第一中学0101119240101 11401022083022王硕峰0102唐山市第二中学0102114290102 11401022133422杨学尧0102唐山市第二中学0102103400102 11401022140922张蕊0102唐山市第二中学0102114140102 11401012060642李方驰0101唐山市第一中学0101106340101 11401012151521于冰0101唐山市第一中学0101102160101 11401012151557张硕潇0101唐山市第一中学0101113230101 11401022112822王子康0102唐山市第二中学0102114080102 11401022142922时智昊0102唐山市第二中学0102116140102 11401012111108王萱0101唐山市第一中学0101102050101 11401012141423石丽0101唐山市第一中学0101123260101 11202012010046郑凯中0201唐山市开滦第一中学0201105040201 11401022095522刘品源0102唐山市第二中学0102109070102 11401012050548李泓江0101唐山市第一中学0101110110101 11401012060605卞金瑶0101唐山市第一中学0101120280101 11401012080840王嗣晨0101唐山市第一中学0101110120101 11401012121206董楠0101唐山市第一中学0101112240101 11401012131350朱铭宇0101唐山市第一中学0101120010101 11401012151526胡琨0101唐山市第一中学0101108150101 11401012151527翟慧0101唐山市第一中学010111535010111202012010027张韵秋0201唐山市开滦第一中学0201105370201 11401022070122谷懿寰0102唐山市第二中学0102104340102 11401022103222董世杰0102唐山市第二中学0102109320102 11401022192622王焕宇0102唐山市第二中学0102114350102 11401012070737窦展思0101唐山市第一中学0101120080101 11401012080801郑皓月0101唐山市第一中学0101108390101 11401012131314李享0101唐山市第一中学0101118050101 11401012141411王佳琦0101唐山市第一中学0101117270101 11304012012040李柠菡0401唐山市开滦第二中学0401108200401 11402022020047丁浩峰0202唐山市第八中学0202114320202 11401022074122卢琦0102唐山市第二中学0102104070102 11401012101046侯占斌0101唐山市第一中学0101123040101 11401012131320孙韶阳0101唐山市第一中学0101104370101 11401012181822赵子琦0101唐山市第一中学0101107200101 11202012010019尹领0201唐山市开滦第一中学0201103100201 11402022020046周航0202唐山市第八中学0202115290202 11401022132722刘睿0102唐山市第二中学0102119190102 11401012141410韩玉婷0101唐山市第一中学0101123350101 11401012181854朱志海0101唐山市第一中学0101116030101 11304012011031张璐0401唐山市开滦第二中学0401101260401 11202012010023曹原0201唐山市开滦第一中学0201112370201 11401022060122李思扬0102唐山市第二中学0102116040102 11401012151518赵元媛0101唐山市第一中学0101119130101 11401012161606张笑祎0101唐山市第一中学0101123200101 11401012171753刘嘉伟0101唐山市第一中学0101112230101 11401022113122金博栋0102唐山市第二中学0102102290102 11401022130222葛安0102唐山市第二中学0102117080102 11401022204922赵子莹0102唐山市第二中学0102118180102 11401012111138于涛0101唐山市第一中学0101119160101 11401012181848赵翰宇0101唐山市第一中学0101114340101 11401012070702谭伊笑0101唐山市第一中学0101120100101 11401012080835李鑫冰0101唐山市第一中学0101121190101 11401012111102吴佳玉0101唐山市第一中学0101120400101 11304012012042王迪0401唐山市开滦第二中学0401109390401 11401022080422杨明月0102唐山市第二中学0102105030102 11401022180222吉悦0102唐山市第二中学0102112060102 11401012101015赵文青0101唐山市第一中学0101107320101 11401012111106边妍0101唐山市第一中学0101112290101 11401022115622霍谊0102唐山市第二中学0102118400102 11401012070709杨磊0101唐山市第一中学0101103150101 11202012010018汪鹭宁0201唐山市开滦第一中学0201104210201 11402022010010陈杰雄0202唐山市第八中学0202115080202 11401022073022孟令伟0102唐山市第二中学0102114170102 11401022142522王紫阳0102唐山市第二中学0102103340102 11401012070721郭雨竹0101唐山市第一中学0101116350101 11401012161648初晓0101唐山市第一中学010110836010111401022110422丁凡彧0102唐山市第二中学0102107180102 11401022150322李希源0102唐山市第二中学0102104180102 11401012050545杜哲民0101唐山市第一中学0101121330101 11304012011007贺云飞0401唐山市开滦第二中学0401105070401 11401022105022徐诗童0102唐山市第二中学0102104050102 11401022172222赵琦0102唐山市第二中学0102116030102 11401022182322项晨0102唐山市第二中学0102106270102 11401012101048王岩0101唐山市第一中学0101123280101 11202012040002王天宇0201唐山市开滦第一中学0201108040201 11401012111148史浩磊0101唐山市第一中学0101121030101 11401012121233高天宇0101唐山市第一中学0101111300101 11401012141425叶琦0101唐山市第一中学0101121260101 11401012141458张天0101唐山市第一中学0101110280101 11202012010004程颖0201唐山市开滦第一中学0201107370201 11401022084822孟悦0102唐山市第二中学0102108170102 11401022090222孙一博0102唐山市第二中学0102115270102 11401022113522董润泽0102唐山市第二中学0102111110102 11401022122722王泽铭0102唐山市第二中学0102112380102 11401022171422张巧双0102唐山市第二中学0102121350102 11401012050501陈茹0101唐山市第一中学0101115340101 11401012060639李卓一0101唐山市第一中学0101110250101 11401012070733张子梦0101唐山市第一中学0101102260101 11401012121234王则陈0101唐山市第一中学0101122280101 11401012121237李文杰0101唐山市第一中学0101106230101 11304012011018刘子健0401唐山市开滦第二中学0401102220401 11202012010045王志安0201唐山市开滦第一中学0201109230201 11401012060602艾舫0101唐山市第一中学0101111130101 11401012111110安楚薇0101唐山市第一中学0101116070101 11401012111149李文亮0101唐山市第一中学0101109010101 11401012131353王泽铭0101唐山市第一中学0101117180101 11202012010029孟佳成0201唐山市开滦第一中学0201111120201 11202012010039高婧昕0201唐山市开滦第一中学0201102300201 11401022170322孙博0102唐山市第二中学0102111360102 11401022193222焦阳0102唐山市第二中学0102107110102 11401012050542石勇刚0101唐山市第一中学0101115090101 11401012060604王佳楠0101唐山市第一中学0101102180101 11401012090942王双星0101唐山市第一中学0101101010101 11401022080222赵淼0102唐山市第二中学0102116280102 11401022160322王晨0102唐山市第二中学0102109170102 11401012050536尚帅0101唐山市第一中学0101116190101 11401012090905杨帆0101唐山市第一中学0101111190101 11401012141446阳宇皓0101唐山市第一中学0101103030101 11401022102722韩潇昱0102唐山市第二中学0102119230102 11401022131122曹煜祺0102唐山市第二中学0102105240102 11401022141022张雨萌0102唐山市第二中学0102110170102 11401022150622赵一锦0102唐山市第二中学010211220010211401012101034王弘毅0101唐山市第一中学0101109400101 11401012141417崔予芃0101唐山市第一中学0101113170101 11401012171747曹一荻0101唐山市第一中学0101111160101 11401022073122高家琛0102唐山市第二中学0102114070102 11401022075522周也扉0102唐山市第二中学0102106250102 11401022113222李文浩0102唐山市第二中学0102111280102 11401022135922玄立伟0102唐山市第二中学0102106120102 11401022153422王韩0102唐山市第二中学0102107160102 11401012080805王昭0101唐山市第一中学0101112360101 11401012181857王欣楚0101唐山市第一中学0101123030101 11202012010014王雅娇0201唐山市开滦第一中学0201106070201 11401022130622白楠0102唐山市第二中学0102117110102 11401022140522李壬华0102唐山市第二中学0102115220102 11401022152122赵国璇0102唐山市第二中学0102120130102 11401012080813张雅坤0101唐山市第一中学0101112180101 11401012141415杜宪0101唐山市第一中学0101108030101 11401012161647陆则奕0101唐山市第一中学0101121200101 11401012181841王俊儒0101唐山市第一中学0101112310101 11401022080122李璐琦0102唐山市第二中学0102109300102 11401012070743姜湛宽0101唐山市第一中学0101122240101 11401012101017王一帆0101唐山市第一中学0101115070101 11401012101024温子璇0101唐山市第一中学0101115030101 11401012101035王业0101唐山市第一中学0101105180101 11401012111141张天昉0101唐山市第一中学0101110260101 11401012131319王潆萱0101唐山市第一中学0101122120101 11401012151511谷瑶0101唐山市第一中学0101117020101 11304012012033罗丽娜0401唐山市开滦第二中学0401105050401 11402022010001贺莞婷0202唐山市第八中学0202114170202 11402022030080高万爱0202唐山市第八中学0202115170202 11401022072822张喆鉴0102唐山市第二中学0102105070102 11401022122822刘超0102唐山市第二中学0102122300102 11401012161627吴宇亭0101唐山市第一中学0101101160101 11401012161667纪雲桐0101唐山市第一中学0101120380101 11401012171740马碧原0101唐山市第一中学0101118280101 11401012181821邓琪0101唐山市第一中学0101119190101 11402022010006王欣悦0202唐山市第八中学0202115390202 11402022010011甘佳惠0202唐山市第八中学0202115330202 11401022065222孙渝0102唐山市第二中学0102101320102 11401012070718王佳楠0101唐山市第一中学0101105260101 11401012151505董晗曦0101唐山市第一中学0101101320101 11401012151564武春韬0101唐山市第一中学0101103100101 11401012181814吴佳澳0101唐山市第一中学0101114250101 11401022112622吴启昀0102唐山市第二中学0102110120102 11401022152422刘瀛0102唐山市第二中学0102121080102 11401022152522刘宇昊0102唐山市第二中学0102107090102 11401022163022戚子羿0102唐山市第二中学010211937010211401022182222曹琦0102唐山市第二中学0102119340102 11401012141409姚馨0101唐山市第一中学0101101140101 11401012141447朱文正0101唐山市第一中学0101115220101 11202012010017李易0201唐山市开滦第一中学0201107400201 11402022020052刘思恩0202唐山市第八中学0202115090202 11401022062622高帆0102唐山市第二中学0102105360102 11401022070422庞陈旭0102唐山市第二中学0102103280102 11401022091122王霄0102唐山市第二中学0102105100102 11401022113922王权超0102唐山市第二中学0102120180102 11401022182622孙卓0102唐山市第二中学0102119150102 11401012060618刘思媛0101唐山市第一中学0101104200101 11401012070717张梦溪0101唐山市第一中学0101123240101 11401012131348孔淳0101唐山市第一中学0101107160101 11401012141405董羽佳0101唐山市第一中学0101105130101 11401012171759孙冀川0101唐山市第一中学0101111150101 11304012011012吴焕巍0401唐山市开滦第二中学0401101080401 11304012011013李林青0401唐山市开滦第二中学0401109090401 11402022020049蒋松辰0202唐山市第八中学0202115180202 11401022080322单诗琦0102唐山市第二中学0102119020102 11401022133222刘帅齐0102唐山市第二中学0102101070102 11401022150222张名轩0102唐山市第二中学0102112280102 11401012101006刘斐然0101唐山市第一中学0101122140101 11401012141418尹飞天0101唐山市第一中学0101110170101 11401012151523赵婧0101唐山市第一中学0101108040101 11304012011005李瀚翔0401唐山市开滦第二中学0401108060401 11202012010008张晨0201唐山市开滦第一中学0201106290201 11202012030002裴行智0201唐山市开滦第一中学0201102340201 11401022100922李玥0102唐山市第二中学0102116240102 11401022105222阚迪0102唐山市第二中学0102118250102 11401022185222刘一凡0102唐山市第二中学0102106330102 11401012161629曹爱0101唐山市第一中学0101119210101 11401022093222侯健0102唐山市第二中学0102111390102 11401022110322闫丹0102唐山市第二中学0102117360102 11401022123022夏童0102唐山市第二中学0102117180102 11401022152822裴梓言0102唐山市第二中学0102118140102 11401022160222佟薇0102唐山市第二中学0102121060102 11401022174822史静雨0102唐山市第二中学0102104370102 11401012050502张美琪0101唐山市第一中学0101120130101 11401012050509谭嵘0101唐山市第一中学0101110100101 11401012141424段妍0101唐山市第一中学0101101050101 11401022100722郭麟坤0102唐山市第二中学0102101370102 11401022131022邹童0102唐山市第二中学0102103130102 11202012030006费俊源0201唐山市开滦第一中学0201104010201 11401022082522张靖宗0102唐山市第二中学0102120240102 11401022103322史义夫0102唐山市第二中学0102116070102 11401022110522陈阳0102唐山市第二中学0102105270102 11401012121238路敬一0101唐山市第一中学010110906010111401012151533王思纯0101唐山市第一中学0101102340101 11401012171756李佳伟0101唐山市第一中学0101113110101 11401022075322鲍佳明0102唐山市第二中学0102116110102 11401022105322孟浩东0102唐山市第二中学0102117330102 11401022145822傅丹秋0102唐山市第二中学0102117200102 11401022152222张铠霖0102唐山市第二中学0102103230102 11401022200222王珊0102唐山市第二中学0102111180102 11401012090917桑巧稚0101唐山市第一中学0101111170101 11401012141454赵子章0101唐山市第一中学0101117090101 11401012101037高宇轩0101唐山市第一中学0101110130101 11401012151560钱檑0101唐山市第一中学0101113180101 11202012020007芦伟0201唐山市开滦第一中学0201110180201 11401022070922高诗雨0102唐山市第二中学0102106210102 11401022092722王旭阳0102唐山市第二中学0102114040102 11401022190322陈珂轩0102唐山市第二中学0102103310102 11401012111107鞠萌0101唐山市第一中学0101103360101 11401012111140黄昱0101唐山市第一中学0101107280101 11401012151525夏江艳0101唐山市第一中学0101123170101 11401022130922王佳佳0102唐山市第二中学0102102040102 11401012080804刘利卓0101唐山市第一中学0101120250101 11401012151509马茹钰0101唐山市第一中学0101113290101 11401012151519曹瑾薇0101唐山市第一中学0101122340101 11401012151551张果晨0101唐山市第一中学0101119260101 11401012161626肖依可0101唐山市第一中学0101118220101 11401012161657杨波0101唐山市第一中学0101116060101 11304012110030李健伟0401唐山市开滦第二中学0401117040401 11401022060522张濛0102唐山市第二中学0102110030102 11401022140422张无双0102唐山市第二中学0102119140102 11401022142722张磊0102唐山市第二中学0102107370102 11401022160422付琳0102唐山市第二中学0102102030102 11401022180822王瑶0102唐山市第二中学0102109330102 11401012161643李凌涵0101唐山市第一中学0101118400101 11401012161653韩光辉0101唐山市第一中学0101101360101 11401022101122赵梦南0102唐山市第二中学0102117400102 11401022163422董胜钰0102唐山市第二中学0102117390102 11401012050550马广原0101唐山市第一中学0101101270101 11401012080838武立超0101唐山市第一中学0101113270101 11401012101010石静延0101唐山市第一中学0101112320101 11401012141462兰添贺0101唐山市第一中学0101108310101 11401012171721毕月薇0101唐山市第一中学0101109070101 11304012011026赵靖轩0401唐山市开滦第二中学0401107230401 11304012012037王可心0401唐山市开滦第二中学0401108270401 11304012012047张文怡0401唐山市开滦第二中学0401103060401 11401022180322张雪飞0102唐山市第二中学0102121190102 11401012101054张新天0101唐山市第一中学0101120320101 11401012151562胡东杰0101唐山市第一中学0101103240101 11401022113022隗轶伦0102唐山市第二中学010212014010211401012070706陈靖0101唐山市第一中学0101121350101 11401012111105黄晨0101唐山市第一中学0101106100101 11401012151549赵健宇0101唐山市第一中学0101101330101 11202012050005侯景荣0201唐山市开滦第一中学0201109080201 11401022150522余泽楠0102唐山市第二中学0102107300102 11401012121244彭子懿0101唐山市第一中学0101107180101 11401012151563刘博凡0101唐山市第一中学0101120160101 11401022080722韩静怡0102唐山市第二中学0102106050102 11401022200322王可欣0102唐山市第二中学0102108370102 11401012050554吴栋0101唐山市第一中学0101112380101 11401012101051李铭轩0101唐山市第一中学0101115370101 11401012161631徐冰0101唐山市第一中学0101115330101 11401012181823董宇梦0101唐山市第一中学0101108270101 11401022082322吴彦达0102唐山市第二中学0102108120102 11401022103122刘澄林0102唐山市第二中学0102110130102 11401022131522李梅娜0102唐山市第二中学0102119300102 11401022160622赵宇0102唐山市第二中学0102115100102 11401012070739周凯歌0101唐山市第一中学0101109350101 11401012101044周靖峥0101唐山市第一中学0101121060101 11401012121215王一淼0101唐山市第一中学0101108250101 11401012161622高轶博0101唐山市第一中学0101102280101 11304012011019李坤屿0401唐山市开滦第二中学0401102270401 11401022083722高福洋0102唐山市第二中学0102122160102 11401022104222蔡艺0102唐山市第二中学0102113070102 11401022143122王洛书0102唐山市第二中学0102107100102 11401012121203李玲珊0101唐山市第一中学0101104300101 11401022070722王靖雅0102唐山市第二中学0102111010102 11401022072422张鑫0102唐山市第二中学0102116010102 11401022093622王展帆0102唐山市第二中学0102106060102 11401012080812裴曾薇0101唐山市第一中学0101113340101 11401012111146王贺锋0101唐山市第一中学0101103080101 11304012011017陈亮0401唐山市开滦第二中学0401109100401 11304012011032王艺锦0401唐山市开滦第二中学0401105360401 11202012080001石莹0201唐山市开滦第一中学0201108310201 11401022193022田硕琛0102唐山市第二中学0102105350102 11401012070710魏心语0101唐山市第一中学0101120340101 11401012131323吴瑞欣0101唐山市第一中学0101112220101 11202012010026彭成0201唐山市开滦第一中学0201104080201 11401022094222许之恒0102唐山市第二中学0102114180102 11401022103522朱宏宇0102唐山市第二中学0102112170102 11401022110822柳睿0102唐山市第二中学0102107400102 11401022152922王思凡0102唐山市第二中学0102121270102 11401022191022温馨0102唐山市第二中学0102117020102 11401012161656于弘宸0101唐山市第一中学0101122320101 11304012011029房玉龙0401唐山市开滦第二中学0401106110401 11202012010036孙诚祥0201唐山市开滦第一中学0201103180201。
北京市东城区2014届九年级上期末考试物理试题及答案

东城区2013-2014学年第一学期期末统一测试初 三 物 理学校 班级 姓名 考号一、单项选择题(下列各小题均有四个选项,其中只有一个选项符合题意。
共28分,每小题2分)1.在国际单位制中,电流的单位是A .安培B .伏特C .焦耳D .瓦特 2.下列物体中,通常情况下属于导体的是A .玻璃B .塑料C .铁丝D .橡胶3.下列用电器中,利用电流热效应工作的是A .手机B .电脑C .照相机D .电饭锅4.图1中,在书房里学习的小明闻到了一股烟味后,走出房间对正在客厅里抽烟的爸爸说:“吸烟有害健康,我和妈妈都跟着吸二手烟了”。
小明在书房里就能闻到客厅烟味的原因是 A .分子间有空隙B .分子之间存在相互作用力C .一切物体都是由分子组成的D .分子在不停地做无规则的运动5.生活中掌握一些安全用电常识很有必要,下列做法中正确的是A .更换灯泡时要先切断电源B .用湿布擦拭插座或用电器的开关C .发现有人触电时直接用手将触电者拉开D .用电器失火时,先用水灭火,再切断电源6.图2所示的滑动变阻器中,当滑片P 向左滑动时,连入电路的电阻变小的是7. 图3所示的四个电路中,开关S 闭合后,电源被短路的电路是图1 图8.一个标有“12V 6W ”的灯泡接入某电路中,测得通过它的电流是0.4A ,则它的实际功率 A .等于6WB.小于6W C .大于6WD .无法判断9. 图4所示的事例中,通过热传递的方式改变物体内能的是10.已知水的比热容为4.2×103J/(kg·℃),则质量为0.2kg 的水,温度从10°C 升高到25°C 吸收的热量是A .4.2×103JB .4.2×104JC .2.1×103JD .2.1×104J11. 图5中,当开关S 闭合时,小灯泡L 1和L 2均不亮。
某同学用一根导线去查找电路故障,他先用导线把L 1短接,发现L 2亮,L 1不亮;再用该导线把L 2短接,发现两灯均不亮。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
18.解:(Ⅰ)函数f(x)的定义域为 .
当 =0时, , .-----------------------1分
令 得 .------------------------------------------2分
-
0
+
递减
极小值
递增
.
------------5分
∴ 的最小值为 .--------------------------------6分
令 ,解得 ,则 =8,点M(8,0)为直线AB过的定点.
----------------------------------------------------------12分
下面证明直线AB过M点
∵ ,
由 可知向量 与 共线.
∴直线AB过定点M.----------------------------------------13分
∴排序数列为n,n-1,n-2,…,1.
∴排序数列为等差数列.
综上,数列 为单调数列时,排序数列为等差数列.---------5分
必要性:
∵排序数列为等差数列
∴排序数列为1,2,3,…,n或n,n-1,n-2,…,1.--------------7分
∴ … 或 …
∴数列 为单调数列.-------------------------------------8分
(Ⅲ)∵数列 的排序数列仍为
∴数列 是1,2,3,…,n的某一个排序,----------------9分
假设不存在一项 ,即 ,
则在各项从小到大排列后 排在第 位--------------------11分
∴排序数列 中 ,∴n为偶数12分.
∴当n为奇数时,一定存在一项 ,
当n为偶数时,不一定存在一项 .-------------------13分
设 为平面VBC的法向量,则 ,
所以 令 ,解得 .----------------------12分
同理,求得平面VOE的法向量为 .--------------------13分
= ,
所以 .----------------------------------------------14分
17.解:
方法二:设 .
(1)若直线AB斜率存在,设其方程为 .---------------4分
即 .----------------------7分
∴ , .----------------------------------9分
∵直线OA、OB的斜率之积为 ,即 ,
∴ ,即 ,带入直线方程,得直线AB方程为 .
2013-2014学年度丰台区高三第一学期期末
数学(理科)试题答案
一、选择题
ACBB ACDA
二、填空题
9. 2n-1 10.乙11. 160 12. 13.40 14.①②③分
注:14题给出一个正确得1分,给出两个正确得3分,给出三个正确得5分.若给出④均不得分.
三、解答题
15.解:(Ⅰ)在△ABC中 ,∴ .--------------------------2分
(Ⅰ)设甲、乙、丙三个家庭能住在同一单元为事件A.---------------------1分
则
答:甲、乙、丙三个家庭能住在同一单元的概率为 .-------------------6分
(没有答,不扣分)
(Ⅱ)设甲、乙、丙三个家庭中恰有两个家庭能住在同一单元为事件B.----家庭能住在同一单元的概率为 .--------13分
19.解:(Ⅰ)∵焦点为F(1,0),∴ ,∴抛物线方程为 .-----3分
(Ⅱ)方法一:∵直线OA、OB的斜率之积为
∴设直线OA的方程为 ;直线OB的方程为 .------5分
联立 得 ,同理 .-----------------9分
由抛物线关于x轴对称可知定点在x轴上,那么当A,B横坐标相同时的横坐标即为定点的横坐标.-------------------------------11分
∵ ,∴ ,-----------------------------------2分
∴ ,--------------------------------------------------------5分
∴c=4.---------------------------------------------------6分
又 O为AB中点,∴VO⊥AB;--------------------------------------5分
在△VOA和△VOC中,OA =OC,VO=VO,VA=VC,△VOA≌△VOC;-----------6分
∴∠V0A=∠VOC=90o.∴VO⊥OC;--------------------------------------7分
(2)当 时,在 内, ;在 内, .
∴ 递减区间, 递增区间.---------------------------13分
综上所述,当 时, 单调递增区间为 ,递减区
间为 ;当 时, 单调递增区间为 ,减区间
为 .-----------------------------------------------------14分
AB∩OC=O,AB 平面ABC,OC 平面ABC,---------------------8分
∴VO⊥平面ABC. ---------------------------------------------------9分
(Ⅲ)解:在圆O内,OA=OC,∠CAO=45o,所以CO⊥AO.
由(Ⅱ)VO⊥平面ABC,如图,
16.(Ⅰ)证明:
O,E分别是AB和AC的中点, OE∥BC.--------------2分
又 面VBC, 面VBC.----------------------------3分
面VBC.-----------------------------------------4分
(Ⅱ)证明:
VA=VB,∵△ABC为等腰三角形,
(Ⅱ)在△ABC中, ,--------------------------------8分
∵ ,∴ .-------------------------------10分
∵ ,∴ .-------------------------------12分
∴ .-------------------------------------------------------13分
建立空间直角坐标系.-------------------------10分
OA=OB=OC=OV=1,
∴C(1,0,0),A(0,1,0),B(0,-1,0),V(0,0,1),E( ,0).
-------------------------------------------11分
=(-1,-1,0), =(-1,0,1)
20.解:(Ⅰ)排序数列为4,1,3,2.--------------------------------3分
(Ⅱ)证明:充分性:
当数列 单调增时,∵ … ,
∴排序数列为1,2,3,…,n.
∴排序数列为等差数列.----------------------------------4分
当数列 单调减时,∵ … ,
∴即直线AB过定点(8,0).-------------------------------11分
(2)若直线AB斜率不存在,则 ,
由 可得 ,
∴直线AB方程为 ,过定点(8,0).-------------------12分
综上,直线AB过定点.---------------------------------13分
(Ⅱ)
∵
∴ .-----------------------------7分
,--------------------------------------8分
,
.------------------------------------9分
(1)当 时,在 , 内 ;在 内 .
∴ 为递减区间, 递增区间.----------------11分
