风荷载内力计算
风荷载计算书

七、水平荷载(风荷载)计算1、设计资料基本风压:2/35.0m KN =ωο,地面粗糙度类别为C 类。
房屋高度H=21.9m 。
2、荷载计算风荷载近似按阶梯形分布,首先应将其简化为作用在框架节点上的节点荷载。
作用在屋面梁和楼面梁节点处的集中风荷载标准值:0k z s z ωβμμω=式中 K W ——风荷载标准值(KN/m ²);z β——高度z 处的风振系数,结构高度H=21.9m <30m ,故取βZ=1.0;s μ——风荷载体型系数,对于矩形截面s μ=1.3; z μ——风压高度变化系数(地面粗糙度类别为C 类);0w ——基本风压(KN/m ²);风压高度变化系数z μ可查荷载规范取得。
将风荷载换算成作用与框架每层节点上的集中荷载,计算过程如下表所示。
表中z 为框架节点至室外地面的高度,A 为一榀框架各层节点的受风面积表4.1层次 z β s μ0wZ μk z s z ωβμμω=A(m 2) P K (kN)=A ×k ω 6 1.0 1.3 0.35 1.00 0.46 5.85 2.69 5 1.0 1.3 0.35 0.84 0.38 14.63 5.56 4 1.0 1.3 0.35 0.84 0.38 16.88 6.41 3 1.0 1.3 0.35 0.74 0.34 16.2 5.51 2 1.0 1.3 0.35 0.74 0.34 16.2 5.51 11.01.30.35 0.740.3424.38.26213.245.4)2/6.36.3(m A =⨯+= 222.165.46.3mA =⨯= 232.165.46.3mA =⨯=2488.165.4)2/6.32/9.3(m A =⨯+=2563.145.4)2/6.22/9.3(m A =⨯+=2685.55.4)2/6.2(m A =⨯= 故风荷载下的计算简图为:图4.13 风荷载计算简图 3. 风荷载下的横向框架内力计算—反弯点法 3.1各柱剪力按刚度分配法计算公式为:1ijij pi sijj D V V D==∑式中,pi V ——为该平面框架i 层总剪力; ij V ——为i 层第j 根柱分配到的剪力;ij D ——为i 层第j 根柱的抗侧刚度; 1sij j D =∑——为i 层s 根柱的抗侧刚度之和。
风荷载
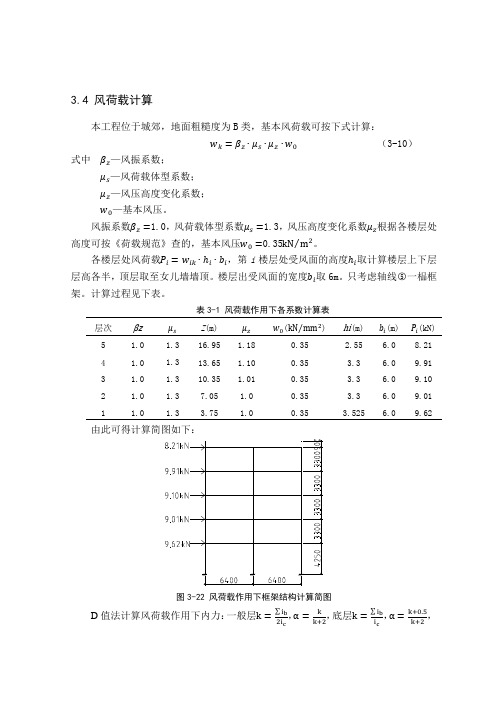
3.4 风荷载计算本工程位于城郊,地面粗糙度为B类,基本风荷载可按下式计算:w k=βz∙μs∙μz∙w0(3-10)式中βz—风振系数;μs—风荷载体型系数;μz—风压高度变化系数;w0—基本风压。
风振系数βz=1.0,风荷载体型系数μs=1.3,风压高度变化系数μz根据各楼层处高度可按《荷载规范》查的,基本风压w0=0.35kN m2⁄。
各楼层处风荷载P i=w ik∙ℎi∙b i,第i楼层处受风面的高度ℎi取计算楼层上下层层高各半,顶层取至女儿墙墙顶。
楼层出受风面的宽度b i取6m。
只考虑轴线○5一榀框架。
计算过程见下表。
表3-1 风荷载作用下各系数计算表层次βzμs Z(m) μz w0(kN mm2⁄) hi(m) b i(m) P i(kN)5 1.0 1.316.95 1.18 0.35 2.55 6.0 8.21图3-22 风荷载作用下框架结构计算简图D值法计算风荷载作用下内力:一般层k=∑i b2i c ,α=kk+2,底层k=∑i bi c,α=k+0.5k+2,柱子的抗侧移刚度D =α12i c h j2,计算结果如下表:表3-2 框架柱抗侧移刚度计算表层次 柱的类型 kα D (kN m ⁄)2~5层 中柱 (1根) 2.44 0.550 1.884×104 边柱(2根) 1.22 0.379 1.298×104 底层中柱(1根) 3.15 0.709 1.138×104 边柱(2根)1.570.5800.931×104注:∑i b 指框架梁线刚度之和,i c 指柱子的线刚度,k 指框架梁柱线刚度比,α指柱侧向线刚度降低系数。
3.4.1 各楼层风荷载剪力计算风荷载作用下各层剪力可按公式3-11计算: V jk =D jk∑D jk mk=1V j (3-11) 式中 V jk —第j 层第k 柱所分配到的剪力; D jk —第j 层第k 柱的侧向刚度D 值; m —第j 层框架柱数;V j —第j 层框架柱所承受的层间总剪力。
抗风柱计算(2012年版规范)

us= uz=
Wo
B= q=
地面粗糙度可分为A、B、C、D四类:A类指近海海面和海岛、海岸、湖岸及沙漠地区; B类指田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇;C类指有密集建筑群的城市市区; D类指有密集建筑群且房屋较高的城市市区。(GB50009-2012,8.2.1)
二:柱几何参数(按“构造手册”第四版208页注6取) Hc= Hl= H= b= h1= h2= 三:求柱顶反力系数 2100 9000 11100 277.50 360 350 mm mm mm 400 600 mm 上柱高 (下柱高,至基础顶面) (柱全高,至基础顶面) mm mm (柱截面宽) (下柱截面高) (上柱截面高)
mm4 mm
4
下柱惯性矩 上柱惯性矩
无单位 根据09SG117-1,122页,附录二表,第6栏,R= q*H*C6,C6=3/8*[1+λ ^4*(1/n-1)]/S,n=I上/I下, 无单位 λ =H上/H,S=1+λ ^3*(1/n-1),公式的来历见该 图集93页;梁兴文、史庆轩主编的《混凝 无单位 土结构设计(2009年4月第一版)》138~139 无单位 页有推导过程 无单位 无单位
I1=b.(h1)^3/12= I2=b.(h2)^3/12= n=I2/I1= λ =HC/H= S1=1/n-1= S2=1+λ ^4*S1= S3=1+λ^3*S1= C6=0.375*S2/S3=
四:求内力(标准值) 1.柱顶反力: R=C6*q*H=
7200000000 1429166667 0.19849537 0.189189189 4.037900875 1.005172981 1.027342902 0.366907551
风荷载作用下框架内力计算
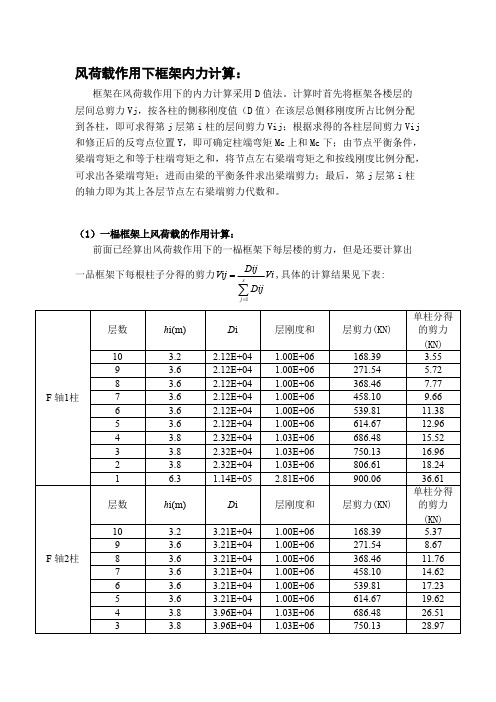
风荷载作用下框架内力计算:框架在风荷载作用下的内力计算采用D 值法。
计算时首先将框架各楼层的层间总剪力Vj ,按各柱的侧移刚度值(D 值)在该层总侧移刚度所占比例分配到各柱,即可求得第j 层第i 柱的层间剪力Vij ;根据求得的各柱层间剪力Vij和修正后的反弯点位置Y ,即可确定柱端弯矩Mc 上和Mc 下;由节点平衡条件,梁端弯矩之和等于柱端弯矩之和,将节点左右梁端弯矩之和按线刚度比例分配,可求出各梁端弯矩;进而由梁的平衡条件求出梁端剪力;最后,第j 层第i 柱的轴力即为其上各层节点左右梁端剪力代数和。
(1)一榀框架上风荷载的作用计算:前面已经算出风荷载作用下的一榀框架下每层楼的剪力,但是还要计算出一品框架下每根柱子分得的剪力,具体的计算结果见下表:Vi DijDijVij sj ∑==1层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 2.12E+04 1.00E+06168.39 3.55 9 3.6 2.12E+04 1.00E+06271.54 5.72 8 3.6 2.12E+04 1.00E+06368.46 7.77 7 3.6 2.12E+04 1.00E+06458.10 9.66 6 3.6 2.12E+04 1.00E+06539.81 11.38 5 3.6 2.12E+04 1.00E+06614.67 12.96 4 3.8 2.32E+04 1.03E+06686.48 15.52 3 3.8 2.32E+04 1.03E+06750.13 16.96 2 3.8 2.32E+04 1.03E+06806.61 18.24 F 轴1柱1 6.31.14E+052.81E+06900.06 36.61 层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 3.21E+04 1.00E+06168.39 5.37 9 3.6 3.21E+04 1.00E+06271.54 8.67 8 3.6 3.21E+04 1.00E+06368.46 11.76 7 3.6 3.21E+04 1.00E+06458.10 14.62 6 3.6 3.21E+04 1.00E+06539.81 17.23 5 3.6 3.21E+04 1.00E+06614.67 19.62 4 3.8 3.96E+04 1.03E+06686.48 26.51 F 轴2柱33.83.96E+041.03E+06750.1328.972 3.8 3.96E+04 1.03E+06806.61 31.15 1 6.3 1.31E+05 2.81E+06900.06 41.86层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 3.21E+04 1.00E+06168.39 5.379 3.6 3.21E+04 1.00E+06271.54 8.678 3.6 3.21E+04 1.00E+06368.46 11.767 3.6 3.21E+04 1.00E+06458.10 14.626 3.6 3.21E+04 1.00E+06539.81 17.235 3.6 3.21E+04 1.00E+06614.67 19.624 3.8 3.96E+04 1.03E+06686.48 26.513 3.8 3.96E+04 1.03E+06750.13 28.972 3.8 3.96E+04 1.03E+06806.61 31.15 F轴3柱1 6.3 1.31E+05 2.81E+06900.06 41.86层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 2.12E+04 1.00E+06168.39 3.559 3.6 2.12E+04 1.00E+06271.54 5.728 3.6 2.12E+04 1.00E+06368.46 7.777 3.6 2.12E+04 1.00E+06458.10 9.666 3.6 2.12E+04 1.00E+06539.81 11.385 3.6 2.12E+04 1.00E+06614.67 12.964 3.8 2.32E+04 1.03E+06686.48 15.523 3.8 2.32E+04 1.03E+06750.13 16.962 3.8 2.32E+04 1.03E+06806.61 18.24 F轴4柱1 6.3 1.14E+05 2.81E+06900.06 36.61(2)风荷载作用下反弯点高度的计算:反弯点高度比即: V=V0+V1+V2+V3式中:V0 ——标准层反弯点高度比;注:本框架风荷载采用分段式均布荷载,故可查《高层建筑结构设计》表5.8a。
建筑风荷载计算

风荷载标准值计算风荷载标准值计算公式为:0k z s z w w βμμ=,作用在屋面梁和楼面梁节点处的集中风荷载标准值计算公式为:0W z s z P w A βμμ= 式中:W P -作用于框架节点的集中风荷载标准值(KN) z β-风振系数s μ-风荷载体型系数 z μ-风压高度变化系数0w -基本风压(KN/㎡)A -一榀框架各层节点受风面积(㎡)本建筑基本风压为:200.3/w KN m =,由《荷载规范》得,地面粗糙为C 类。
s μ风荷载体系系数,根据建筑物体型查得 1.3s μ=。
z β风振系数,因结构总高度H=21.128m<30m ,故 1.0z β=。
风压高度变化系数z μ查《荷载规范》表7.2.1。
一榀框架各层节点受风面积A 计算,B 为3.3 3.9() 3.622m +=, h 取上层的一半和下层的一半之和,屋面层取到女儿墙顶,底层取底层的一半。
底层的计算高度从室外地面取()mm 45003004200=+。
一层: 24.5 3.9() 3.615.1222A m =+⨯= 二层: 23.9 3.9() 3.614.0422A m =+⨯=三层: 23.9 3.9() 3.614.0422A m =+⨯=四层: 23.9 3.9() 3.614.0422A m =+⨯=五层:23.9(1.50) 3.612.422A m =+⨯=计算过程见表所示:欠左风、右风荷载受荷简图框架梁柱线刚度计算框架梁柱线刚度计算见表表7-1 纵梁线刚度计算表表7-2 柱线刚度Ic 计算表7.2.2 侧移刚度D 值计算 考虑梁柱的线刚度比,用D 值法计算柱的侧位移刚度,表7-4 柱侧移刚度计算表2~5层柱D 值计算2~5层柱D 值合计:D ∑=1.572+1.572=3.144KN/m底层柱D 值计算低层柱D 值合计:D ∑=1.612+1.612=3.224KN/m 7.2.3 风荷载作用下框架位移的计算风荷载作用下框架的层间侧移可按下式计算,即jj ijV u D∆=∑式中:j V -第j 层的总剪力;ij D ∑-第j 层所有柱的抗侧刚度之和;j u ∆-第j 层的层间位移。
风力计算

风力计算台风按热带气旋中心附近最大风力的大小进行分级。
过去中国气象部门将8级至11级风称为台风,12级和12级以上的称为强台风。
1989年1月1日起,采用国际统一分级方法,近中心最大风力在8级~9级时称为热带风暴,近中心最大风力在l0级~11级时称为强热带风暴,近中心最大风力在12级或12级以上时称为台风。
为了叙述简单,以下仍统称为台风。
热带气旋按中心附近地面最大风速划分为四个等级:台风(Typhoon)最大风速出现>32.6米/秒,也即12级以上(64海里/小时或以上)强热带风暴(Severe tropical storm)最大风速出现24.5-32.6米/秒,也即风力10-11级(48-63海里/小时)热带风暴(Tropical storm)最大风速出现17.2-24.4米/秒,也即风力8-9级(34-47海里/小时)热带低压(Tropical depression)最大风速出现<17.2米/秒,也即风力为6-7级(22-33海里/小时)风力等级表风力等级陆地地面物体征象相当风速0静,烟直上小于1公里/时0~ 0.2米/秒1烟能表示风向1-5 公里/时0.3~1.5米/秒2人面感觉有风,树叶微动6~11公里/时1.6~3.3米/秒3树叶及微技摇动不息,旌旗展开12~19公里/时3.4~5.4米/秒4能吹起地面灰尘和纸张,树的小枝摇动。
20~28 公里/时5.5~7.9米/秒5能吹起地面灰尘和纸张,树的小枝摇动20~28 公里/时5.5~7.9米/秒6有叶的小树摇摆,内陆的水面有小波29~38公里/时8.0一10.7米/秒7大树枝摇动,电线呼呼有声,举伞困难39~49 公里/时10.8~13.8米/秒8微枝折毁,人向前行感觉阻力甚大62~74公里/时17.2~20.7米/秒9草房遭受破坏,大树枝可折断75~88公里/时20.8~24.4米/秒10树木可被吹倒,,一般建筑物遭破坏89~102公里/时24.5~28.4 米/秒11陆上少见,大树可被吹倒,一般建筑物遭严重破坏103~117公里/时28.5~32.6米/秒12陆上绝少,其催毁力极大118~133公里/时32.7~36.9米/秒13级134~149公里/时37.0~41.4 米/秒14级150一166公里/时41.5~46.1米/秒15级167~183公里/时46.2——50.9米/秒16级184~201公里/时51.0~56.0米/秒17级202~220公里/时56.1——61.2米/秒1、根据伯努力公式进行计算,例如垂直于被吹物体的风速为10m/s时,作用在1平方米面积上的垂直风压为:p=1/2*rho*v**2 = 0.5*1.225*100 = 61.25 (N/m^2)F=p*s=61.25*1.0= 61.25 N2、是要进行内力组合,来具体进行计算,还有地震力,恒荷载,活荷载,综合起来考虑。
计算书 4 内力

第四章 内力计算4.1 恒荷载作用下的内力计算恒荷载(竖向荷载)作用下的内力计算采用分层法,并进行以下修正:①除底层外其它层柱的线刚度均乘以0.9的折减系数;②底层柱传递系数取为1/2,其他各层取为1/3。
对各层用弯矩分配法进行计算,并可利用结构对称性取二分之一结构计算。
远端固定,传递系数为0.5;远端滑动支承,传递系数为-1。
4.1.1固端弯矩计算(1)第5层恒荷载作用下的内力计算梯形荷载等效系数2.0624.21=÷=α 25312115'AB 5)21(g AB AB g g αα+-+==4.84+(1-0.08+0.008)×9.94=14.06kN/mg 5BC =2.2kN/mM AB =121×14.06×62=42.18kN •mM BC =31×2.2×1.22=1.06kN •mM CB =61×2.2×1.22=0.53kN •m(2)第4层恒荷载作用下的内力计算'A 4g B =18.48+(1-0.08+0.008)×7.78=25.70kN/m g 4BC =2.2kN/mM AB =121×25.70×62=77.1kN •mM BC =31×2.2×1.22=1.06kN •mM CB =61×2.2×1.22=0.53kN •m(3)第1~3层恒荷载作用下的内力计算'A g B =4.84+(1-0.08+0.008)×7.78=12.06kN/mg BC =2.2kN/mM AB =121×12.06×62=36.18kN •mM BC =31×2.2×1.22=1.06kN •mM CB =61×2.2×1.22=0.53kN •m4.1.2 弯矩分配法计算内力4底层柱线刚度为2.16×1010N ·mm ,其他各层柱线刚度为3.2×0.9=2.88×1010N ·mm 。
地震作用内力及风荷载作用内力计算表
D柱梁端弯矩 和
0.9 0.9 0.9 0.9 0.9 0.9
1.97 1.97 1.97 1.97 1.97 1.97
18.36380711 44.00795939
64.521 79.90781726 90.16515228 90.34764975
表5-30结 构变形验
算
层间剪力 层间刚度
层次 6 5
n
Gj
ji
2029.4 3138.7 3154.8
3 3 3 3 3 3
Fi H i
0.00 0.00 0.00 0.00 0.00 0.00 3063.43 3564.52 2281.29 1283.23 570.32 143.50
5447261.55
(kN)
D轴
F轴
11.27080234 11.27080234
2
381000 0.0038
1 1499.82 285000 0.0053
备注:层 间相对弹 性转角均 满足
3
0.001266667
3
0.001766667
表5-4各楼层 的刚重比和
剪重比
层号 6 5 4 3 2 1
层号 6 5 4 3 2 1
)
3
192375 3
3
192375 3
3
192375 3
h (m)
轴号 A轴
D轴 F轴
楼层 6 5
4 3 2 1 6 5
(kN)
6.988 16.745
24.551 30.405 34.308 43.606 11.27 27.008
(m)
1.125 1.35
1.425 1.5 1.5 1.8 1.35 1.5
风荷载标准值

风荷载标准值关于风荷载计算风荷载是高层建筑主要侧向荷载之一,结构抗风分析(包括荷载,内力,位移,加速度等)是高层建筑设计计算的重要因素。
脉动风和稳定风风荷载在建筑物表面是不均匀的,它具有静力作用(长周期哦部分)和动力作用(短周期部分)的双重特点,静力作用成为稳定风,动力部分就是我们经常接触的脉动风。
脉动风的作用就是引起高层建筑的振动(简称风振)。
以顺风向这一单一角度来分析风载,我们又常常称静力稳定风为平均风,称动力脉动风为阵风。
平均风对结构的作用相当于静力,只要知道平均风的数值,就可以按结构力学的方法来计算构件内力。
阵风对结构的作用是动力的,结构在脉动风的作用下将产生风振。
注意:不管在何种风向下,只要是在结构计算风荷载的理论当中,脉动风一定是一种随机荷载,所以分析脉动风对结构的动力作用,不能采用一般确定性的结构动力分析方法,而应以随机振动理论和概率统计法为依据。
从风振的性质看顺风向和横风向风力顺风向风力分为平均风和阵风。
平均风相当于静力,不引起振动。
阵风相当于动力,引起振动但是引起的是一种随机振动。
也就是说顺风向风力除了静风就是脉动风,根本就没有周期性风力会引起周期性风振,绝对没有,起码从结构计算风载的理论上顺风向的风力不存在周期性风力。
横风向,既有周期性振动又有随机振动。
换句话说就是既有周期性风力又有脉动风。
反映在荷载上,它可能是周期性荷载,也可能是随机性荷载,随着雷诺数的大小而定。
有的计算方法根据现有的研究成果,风对结构作用的计算,分为以下三个不同的方面:(1)对于顺风向的平均风,采用静力计算方法(2)对于顺风向的脉动风,或横风向脉动风,则应按随机振动理论计算(3)对于横风向的周期性风力,或引起扭转振动的外扭矩,通常作为稳定性荷载,对结构进行动力计算风荷载标准值的表达可有两种形式,其一为平均风压加上由脉动风引起导致结构风振的等效风压;另一种为平均风压乘以风振系数。
由于在结构的风振计算中,一般往往是第1振型起主要作用,因而我国与大多数国家相同,采用后一种表达形式,即采用风振系数βz,它综合考虑了结构在风荷载作用下的动力响应,其中包括风速随时间、空间的变异性和结构的阻尼特性等因素。
内力计算方式

内力计算为简化计算,考虑下面5种受荷情况:①恒载作用②恒载满跨布置③与地震作用相组合的重力荷载代表值计算④风荷载作用(从左到右,或从右到左)⑤横向水平地震作用(从左到右,或从右到左)。
对于①②③三种情况,采用迭代法计算,④⑤两种情况,采用D 值法计算。
6.1 恒荷载标准值作用下的内力计算(1)恒载引起的屋面梁的固端弯矩和不平衡弯矩g ww B A M ,=(-3×62/92×177.3-3×62/92×177.3-(1/12)×1.39×92)kN ·m=-482.2kN ·m=g w w A B M ,g w w B C M ,=g w w C B M ,=482.2kN ·m(2)标准层楼面的固端弯矩:gAb M =(-3×62 /92×140.1-3×62 /92×140.1-(1/12)×7.27×92)kN · m=-422.7kN · m g w w B C M ,=g w w C B M ,=422.7kN ·m(3)恒载引起的节点不平衡弯矩gAbM =-482.2kN ·m Bw M =0Cw M =482.2kN ·mb A M =-422.7kN ·m b B M =0b C M =422.7kN ·m叠加过程与内力结构图略。
6.2活荷载标准值作用下的内力计算活荷载与恒载的比值小于1,故可采取满跨布置,求得的内力在支座处与按最不利荷载位移法求得的内力很相近。
可直接进行内力组合,梁的跨中弯矩应乘以1.2的系数予以增大。
(1)屋面梁处gw w B A M ,=-(3×62/92)×60-(32×6/92)×60 =-120kN ·m=gw w A B M ,g w w C B M ,=g w w B C M ,=120kN ·m标准层楼面梁处;gAbM =-120kN ·m g w w C B M ,=gw w B C M ,=120kN ·m活荷载引起的固端不平衡弯矩w A M =-120kN ·mw B M =0b A M =-120kN ·m Bb M =0 Cb M =120kN ·m叠加过程与内力结构图略。
5-风荷载计算

5 风荷载计算5.1 风荷载标准值主体结构计算时,为了简化计算,作用在外墙面上的风荷载可近似作用在屋面梁和楼面梁处的等效集中荷载替代,垂直于建筑物表面的风荷载标注值按公式5-1计算。
0k z s z ωβμμω⋅⋅⋅= (5-1)式中:k ω——风荷载标准值;s μ——风荷载体型系数;z μ——风压高度变化系数;0ω——基本风压值,本设计中的基本风压取30.00=ω; z β——高度z 处的风振系数;根据《建筑结构荷载规范》(GB50009—2012)第8.2.1条规定:地面粗糙度可分为四类:A 类指近海海面和海岛、海岸、湖岸及沙漠地区;B 类指田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇;C 类指有密集建筑群的城市市区;D 类指有密集建筑群且房屋较高的城市市区。
本设计中地面粗糙度取C 类。
高度z 处的风振系数z β的计算式见公式5-2。
1zz z ξνϕβμ=+(5-2)ξ——脉动增大系数;ν——脉动影响系数;z ϕ——振型系数;z μ——风压高度变化系数。
根据《建筑结构荷载规范》(GB50009—2012)第8.3节可知:对于框架结构的基本自振周期可以近似按照()10.08~0.10T n n =(n 为建筑层数)估算,应考虑风压脉动对结构发生顺风向风振的影响,本设计中自振周期取10.090.0960.54T n s ==⨯=,经过计算,21200.300.54=0.087T ω=⨯。
风载体型系数由《建筑结构荷载规范》(GB50009—2012)第8.3节续表8.3.1可以查得:8.0=s μ(迎风面)和5.0-=s μ(背风面)。
根据《建筑结构荷载规范》(GB50009—2012)第8.4.1条规定:当结构基本自振周期s T 25.0≥时,以及对于高度超过30m 且高宽比大于1. 5 的高柔房屋,由风引起的结构振动比较明显,而且随着结构自振周期的增长,风振也随之增强。
因此在设计中应考虑风振的影响,而且原则上还应考虑多个振型的影响。
风荷载标准值

风荷载标准值文件排版存档编号:[UYTR-OUPT28-KBNTL98-UYNN208]风荷载标准值关于风荷载计算风荷载是高层建筑主要侧向荷载之一,结构抗风分析(包括荷载,内力,位移,加速度等)是高层建筑设计计算的重要因素。
脉动风和稳定风风荷载在建筑物表面是不均匀的,它具有静力作用(长周期哦部分)和动力作用(短周期部分)的双重特点,静力作用成为稳定风,动力部分就是我们经常接触的脉动风。
脉动风的作用就是引起高层建筑的振动(简称风振)。
以顺风向这一单一角度来分析风载,我们又常常称静力稳定风为平均风,称动力脉动风为阵风。
平均风对结构的作用相当于静力,只要知道平均风的数值,就可以按结构力学的方法来计算构件内力。
阵风对结构的作用是动力的,结构在脉动风的作用下将产生风振。
注意:不管在何种风向下,只要是在结构计算风荷载的理论当中,脉动风一定是一种随机荷载,所以分析脉动风对结构的动力作用,不能采用一般确定性的结构动力分析方法,而应以随机振动理论和概率统计法为依据。
从风振的性质看顺风向和横风向风力顺风向风力分为平均风和阵风。
平均风相当于静力,不引起振动。
阵风相当于动力,引起振动但是引起的是一种随机振动。
也就是说顺风向风力除了静风就是脉动风,根本就没有周期性风力会引起周期性风振,绝对没有,起码从结构计算风载的理论上顺风向的风力不存在周期性风力。
横风向,既有周期性振动又有随机振动。
换句话说就是既有周期性风力又有脉动风。
反映在荷载上,它可能是周期性荷载,也可能是随机性荷载,随着雷诺数的大小而定。
有的计算方法根据现有的研究成果,风对结构作用的计算,分为以下三个不同的方面:(1)对于顺风向的平均风,采用静力计算方法(2)对于顺风向的脉动风,或横风向脉动风,则应按随机振动理论计算(3)对于横风向的周期性风力,或引起扭转振动的外扭矩,通常作为稳定性荷载,对结构进行动力计算风荷载标准值的表达可有两种形式,其一为平均风压加上由脉动风引起导致结构风振的等效风压;另一种为平均风压乘以风振系数。
风荷载标准值

风荷载标准值关于风荷载计算风荷载是高层建筑主要侧向荷载之一,结构抗风分析(包括荷载,内力,位移,加速度等)是高层建筑设计计算的重要因素。
脉动风和稳定风风荷载在建筑物表面是不均匀的,它具有静力作用(长周期哦部分)和动力作用(短周期部分)的双重特点,静力作用成为稳定风,动力部分就是我们经常接触的脉动风。
脉动风的作用就是引起高层建筑的振动(简称风振)。
以顺风向这一单一角度来分析风载,我们又常常称静力稳定风为平均风,称动力脉动风为阵风。
平均风对结构的作用相当于静力,只要知道平均风的数值,就可以按结构力学的方法来计算构件内力。
阵风对结构的作用是动力的,结构在脉动风的作用下将产生风振。
注意:不管在何种风向下,只要是在结构计算风荷载的理论当中,脉动风一定是一种随机荷载,所以分析脉动风对结构的动力作用,不能采用一般确定性的结构动力分析方法,而应以随机振动理论和概率统计法为依据。
从风振的性质看顺风向和横风向风力顺风向风力分为平均风和阵风。
平均风相当于静力,不引起振动。
阵风相当于动力,引起振动但是引起的是一种随机振动。
也就是说顺风向风力除了静风就是脉动风,根本就没有周期性风力会引起周期性风振,绝对没有,起码从结构计算风载的理论上顺风向的风力不存在周期性风力。
横风向,既有周期性振动又有随机振动。
换句话说就是既有周期性风力又有脉动风。
反映在荷载上,它可能是周期性荷载,也可能是随机性荷载,随着雷诺数的大小而定。
有的计算方法根据现有的研究成果,风对结构作用的计算,分为以下三个不同的方面:(1)对于顺风向的平均风,采用静力计算方法(2)对于顺风向的脉动风,或横风向脉动风,则应按随机振动理论计算(3)对于横风向的周期性风力,或引起扭转振动的外扭矩,通常作为稳定性荷载,对结构进行动力计算风荷载标准值的表达可有两种形式,其一为平均风压加上由脉动风引起导致结构风振的等效风压;另一种为平均风压乘以风振系数。
由于在结构的风振计算中,一般往往是第1振型起主要作用,因而我国与大多数国家相同,采用后一种表达形式,即采用风振系数βz,它综合考虑了结构在风荷载作用下的动力响应,其中包括风速随时间、空间的变异性和结构的阻尼特性等因素。
风荷载作用下的内力和位移计算

第7章 风荷载作用下的内力和位移计算由设计任务资料知,该建筑为五层钢筋混凝土框架结构体系,室内外高差为基本风压20m /4.0KN =ω,地面粗糙度为C 类,结构总高度+=(基础顶面至室内地面1m )。
计算主要承重结构时,垂直于建筑物表面上的风荷载标准值,应按下式计算,即o z s z k w w μμβ=1、因结构高度H=<30m,高宽比÷=<,故可取0.1z =β;2、s μ为风荷载体型系数,本设计按《建筑结构荷载规范》(GB50009--2012)中规定,迎风面取,背风面取,合计s μ=。
3、z μ为风压高度变化系数,本设计的地面粗糙度类别为C 类,按下表选取风压高度变化系数。
横向框架在风荷载作用下的计算简图6轴线框架的负荷宽度B=(+)/2=。
各层楼面处集中风荷载标准值计算如表:表根据表,画出6轴框架在风荷载作用下的计算简图,如图所示:图 框架在风荷载作用下的计算简图位移计算框架梁柱线刚度计算考虑现浇楼板对梁刚度的加强作用,故对6轴线框架(中框架梁)的惯性矩乘以,框架梁的线刚度计算: 跨度为的梁(b ×h=250mm ×600mm ):)(109126.0250.0212bh 24333m I -⨯=⨯⨯=⨯= m KN L I E c b /105.33.7109108.2i 437b ⨯=⨯⨯⨯==- 跨度为的梁 (b ×h=200mm ×400mm ):)(43-33m 101.2124.02.0212bh 2⨯=⨯⨯=⨯=I m KN L I E c b /109.13.31013.2108.2i 437b ⨯=⨯⨯⨯==- 框架柱的线刚度 1、底层柱: A 、D 轴柱:)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.32.51021.5100.3i 437⨯=⨯⨯⨯==- B 、C 轴柱:)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.32.51021.5100.3i 437⨯=⨯⨯⨯==- 2、上层柱: A 、D 轴柱:)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.49.31021.5100.3i 437⨯=⨯⨯⨯==- B 、C 轴柱:)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.49.31021.5100.3i 437⨯=⨯⨯⨯==- 侧移刚度D 计算框架柱刚度修正系数计算公式见表: 表表 各层柱侧向刚度计算风荷载作用下框架的层间侧移可按下式计算,即有:∑=∆ijjj DV u式中 jV ------第j 层的总剪力标准;∑ijD --------第j 层所有柱的抗侧刚度之和;ju ∆--------第j 层的层间侧移。
3.3.3 风荷载内力计算风荷载内力计算

三、在风荷载作用下内力计算对于作用在屋面的风荷载可以分解为水平方向的分力xq 和竖向分力yq 。
(1)在迎风面横梁上风荷载竖向分力2yqω作用下(见图)0206 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.125911=85=850.167=0.13381616 4.12591.8920kN 4.73kN 88( 1.8910 4.73)kN 14.17kN (4E A A E l H f h k h s k ql qlV V H H λμμλ===ψ=======++ψ+ψ=++⨯+=Φ+ψ⨯+⨯⨯-⨯===-=-⨯+=-==Φ=()()221.8920 3.3330.13384)kN 4.21kN 1.89200.1338kN=25.29kN 44BD ql MM-⨯⨯⨯=-⨯==Φ=⨯ 22[(1)]4C ql M α=-+ψΦ221.8920[0.5(10.167)0.1338]17.74kN =-⨯⨯-+=-17.74k N ·m在迎风面横梁上风荷载竖向分力作用的M 图(2) 在背风面横梁上风荷载竖向分力4yqω作用下(见图)4 1.23/q k N m ω=-0206 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.125911=85=850.167=0.13381616 4.12591.2320kN 3.08kN 88( 1.2310 3.08)kN 9.22kN 4A E A E l H f h k h s k ql qlV V H H λμμλ===ψ=======++ψ+ψ=++⨯+=Φ+ψ⨯+⨯⨯-⨯===-=-⨯+=-=-=-Φ=()()222222( 1.2320 3.3330.13384)kN 2.74kN 1.23200.1338kN=16.46kN 44[(1)] 1.2320[0.5(10.167)0.1338]411.54kN 4BDC ql ql MMM α--⨯⨯⨯=⨯==Φ=⨯=-+ψΦ=-⨯⨯-+=--11.54kN ·m在背风面横梁上风荷载竖向分力作用下M 图(3) 在迎风面柱上风荷载1q ω作用下(见图)A E020 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.12591l H f h k h s k λμα===ψ=======++ψ+ψ=++⨯+==222222211=[65]=[620.16750.597]=0.968744 4.12590.476kN 0.42kN22200.476(2)(20.9687)kN=4.36kN m4411(0.47 4.36)kN 2.1kN 62(0.476 2.1)kN 0.7kN[1(14A E B D A E C k qh l qh qh V V M M H H M μααΦ+ψ+++⨯⨯⨯=-==-=-⨯⨯==-Φ=-=⨯-==⨯-==-+ (2)()220.4761)][1(10.167)0.9687]0.55kN m 4⨯⨯ψΦ=-+⨯=-(4) 在背风面柱上风荷载竖向分力3q ω作用下(见图)A E0206 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.12591l H f h k h s k λμα===ψ=======++ψ+ψ=++⨯+==22211=[65]=[620.16750.597]=0.968744 4.12591.046kN 0.94kN22201.04611(2)(20.9687)kN 4.73kN 2222(1.046 4.73) 1.51kN(4.736 1.0462)kN=9.66kN 1.516kN=9A E EA D Bk qh l qh V V H H M MμααΦ+ψ+++⨯⨯⨯=-==-=-⨯⨯⨯=--Φ=-⨯==⨯-==⨯-⨯=⨯(2)()2222.06kN1.0461[1(1)][1(10.167)0.9687] 1.22kN 44C qh M α⨯⨯=-+ψΦ=-+⨯=-(5) 在迎风面横梁上风荷载水平分力2xq ω作用下(见图)160.167610.04990.5973(3)30.5970.167(30.167) 4.12591f h k h s k μαψ=======++ψ+ψ=++⨯+== 0.167=3=430.167=0.045588 4.12591.89161kN 0.61kN 22201.89110.0455kN 0.98kN 22(1.8910.98)0.91kN[0.5(1)]21.8916[0.50.167(10.167)2A E A E C qf h f l qf qfhV V H H M μψΦ+ψ+⨯⨯⨯=-=-+=-⨯+=⨯⨯=+Φ=+==⨯-==ψ-+ψΦ⨯⨯=⨯-+(4)()(2)(2)()(1)0.0455]0.17kN m0.986 5.88kN m0.916 5.46kN mB DM M⨯==⨯==⨯=C·m(6) 在背风面横梁上风荷载水平分力4xq ω作用下(见图)1.89k N/mA E160.167610.04990.5973(3)30.5970.167(30.167) 4.12591f h k h s k μαψ=======++ψ+ψ=++⨯+== 0.167=3=430.167=0.045588 4.12591.23161kN 0.40kN 22201.23110.0455kN 0.64kN 22(1.2310.64)0.59kN[0.5(1)]21.2316[0.50.167(10.167)2A E E A C qf h f l qf qfhV V H H M μψΦ+ψ+⨯⨯⨯=-=-+=-⨯+=⨯⨯=+Φ=+==⨯-==ψ-+ψΦ⨯⨯=⨯-+(4)()(2)(2)()(1)0.0455]0.11kN m0.596 3.54kN m0.646 3.84kN mB DM M⨯==⨯==⨯=A(7) 用叠加法绘制在风荷载作用下刚加的组合内力。
风荷载作用下的内力和位移计算

风荷载作用下的内力和位移计算
风荷载作用下的内力和位移计算通常涉及以下步骤:
1.确定建筑物的风荷载标准以及建筑物的几何形状和尺寸参数;
2.计算建筑物的风荷载大小和方向,可采用建筑物结构设计规
范或专业软件进行计算;
3.将风荷载作用下的内力和位移分解为平面内力和垂直于平面
的剪力与弯矩,根据不同的加载条件,可以采用不同的计算方法进行计算;
4.通过应力-strain关系计算元件的应力和应变,然后对于剪切
应力和弯曲应力进行的评估。
对于抗弯性能较弱的构件,需要考虑稳定性及挠度分析;
5.通过数值算法,考虑各种边界条件下的结构位移情况,可以
计算出风荷载作用下的建筑物结构的整体变形情况,以评估结构的稳定性和安全性。
需要注意的是,针对不同的建筑物结构类型和工作条件,风荷载作用下的内力和位移计算方法可能会有所不同,需要设计师按照相关规范和标准进行具体的计算。
第七章风荷载作用下的内力和位移计算

第七章风荷载作⽤下的内⼒和位移计算第7章风荷载作⽤下的内⼒和位移计算由设计任务资料知,该建筑为五层钢筋混凝⼟框架结构体系,室内外⾼差为0.45m 基本风压20m /4.0KN =ω,地⾯粗糙度为C 类,结构总⾼度19.8+0.45=20.25m (基础顶⾯⾄室内地⾯1m )。
计算主要承重结构时,垂直于建筑物表⾯上的风荷载标准值,应按下式计算,即oz s z k w w µµβ=1、因结构⾼度H=20.25m<30m,⾼宽⽐20.25÷18.2=1.11<1.5,故可取0.1z =β;2、s µ为风荷载体型系数,本设计按《建筑结构荷载规范》(GB50009--2012)中规定,迎风⾯取0.8,背风⾯取0.5,合计sµ=1.3。
3、z µ为风压⾼度变化系数,本设计的地⾯粗糙度类别为C 类,按下表选取风压⾼度变化系数。
7.1 横向框架在风荷载作⽤下的计算简图6轴线框架的负荷宽度B=(6.6+6.6)/2=6.6m。
各层楼⾯处集中风荷载标准值计算如表7.1:表7.1根据表7.1,画出6轴框架在风荷载作⽤下的计算简图,如图7.2所⽰:图7.2框架在风荷载作⽤下的计算简图7.2 位移计算7.2.1框架梁柱线刚度计算考虑现浇楼板对梁刚度的加强作⽤,故对6轴线框架(中框架梁)的惯性矩乘以2.0,框架梁的线刚度计算:跨度为7.3m 的梁(b ×h=250mm ×600mm ):)(109126.0250.0212bh 24333m I -?=??=?=m KN L I E c b /105.33.7109108.2i 437b ?===-跨度为3.3m 的梁 (b ×h=200mm ×400mm ):)(43-33m 101.2124.02.0212bh 2?=??=?=Im KN L I E c b /109.13.31013.2108.2i 437b ?===-7.2.1.1 框架柱的线刚度 1、底层柱: A 、D 轴柱:)(1021.512500500433c m I -?=?=m KN h I E c c c /100.32.51021.5100.3i 437?===-B 、C 轴柱:)(1021.512500500433c m I -?=?=m KN h I E c c c /100.32.51021.5100.3i 437?===-2、上层柱: A 、D 轴柱:)(1021.512500500433c m I -?=?=m KN h I E c c c /100.49.31021.5100.3i 437?===-B 、C 轴柱:)(1021.512500500433c m I -?=?=m KN h I E c c c /100.49.31021.5100.3i 437?===-7.2.1.2 侧移刚度D 计算框架柱刚度修正系数a 计算公式见表7.3: 表7.3表7.4 各层柱侧向刚度计算风荷载作⽤下框架的层间侧移可按下式计算,即有:∑= ijjj DV u式中jV ------第j 层的总剪⼒标准;D--------第j 层所有柱的抗侧刚度之和;ju ?--------第j 层的层间侧移。
