八年级数学图形的证明测试题3
2020年北师大版八年级数学下册第一章 三角形的证明单元测试题及答案

北师大版八年级数学下册第一章三角形的证明单元测试题一.选择题(共10小题,每小题3分,共30分)1.等腰三角形的对称轴是()A.底边上的高所在的直线B.底边上的高C.底边上的中线D.顶角平分线2.如图在3×3的网格中,点A、B在格点处:以AB为一边,点P在格点处,则使△ABP为等腰三角形的点P有()个.A.2个B.3个C.4个D.5个3.如图,在△ABC中,∠B与∠C的角平分线相交于点I,过点I作BC的平行线,分别交AB、AC于点D、E.若AB=9,AC=6,BC=8,则△ADE的周长是()A.14 B.15 C.174.如图所示,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE等于()A.10°B.15°C.20°D.25°5.在△ABC中,AB=AC,∠A=60°,BC=6,则AB的值是()A.12 B.8 C.6 D.36.用反证法证明“a≥b”,对于第一步的假设,下列正确的是()A.a≤b B.a≠b C.a<b D.a=b7.下列说法:①一个底角和一条边分别相等的两个等腰三角形全等;②底边及底边上的高分别相等的两个等腰三角形全等;③两边分别相等的两个直角三角形全等;④一个锐角和一条边分别相等的两个直角三角形全等,其中正确的个数是()A.1 B.2 C.3 D.48.如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E,则下列结论正确的是()A.AE=3CE B.AE=2CE C.AE=BD D.BC=2CE9.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是边AB的中点,AB=10,DE =4,则S△AEC=()A.8 B.7.5 C.7 D.610.如图,在△ABC中,CD⊥AB于点D,BE平分∠ABC,交CD于点E,若S△BCE=10,BC=5,则DE等于()A.10 B.7 C.5 D.4二.填空题(共8小题,每小题3分,共24分)11.等腰三角形的周长为12cm,其中一边长为3cm,则该等腰三角形的腰长为.12.如图:已知∠B=20°,AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,以此类推∠A的度数是.13.如图,在△ABC中,AB=AC=10,AD平分∠BAC,点E为AC中点,则DE=.14.在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分AC,交AC于点E,交AB于点D,连接CD,若BD=2,则AD的长是.15.如图,DE是△ABC的边AC上的垂直平分线,AB=5cm,BC=8cm,则△ABD的周长为cm.16.如图,点D,P在△ABC的边BC上,DE,PF分别垂直平分AB,AC,连接AD、AP,若∠DAP=20°,则∠BAC=.17.如图,AB∥CD,∠BAC与∠ACD的平分线交于点P,过P作PE⊥AB于E,交CD于F,EF=10,则点P到AC的距离为.18.如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=40,DE=4,AC=12,则AB长是.三.解答题(共7小题,共66分)19.如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,求∠DBA的度数.20.如图,已知AB∥CD,∠BCF=180°,BD平分∠ABC,CE平分∠DCF,∠ACE=90°.求证:AC⊥BD.21.已知:如图,在△ABC中,∠ACB=90°,CD是高,AE是△ABC内部的一条线段,AE交CD于点F,交CB于点E,且∠CFE=∠CEF.求证:AE平分∠CAB.22.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD于点F,交CB于点E,且∠EAB=∠DCB.(1)求∠B的度数:(2)求证:BC=3CE.23.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB,BC于点D 和点E.(1)若AB=10,则△CDE的周长是多少?为什么?(2)若∠ACB=125°,求∠DCE的度数.24.如图,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D.(1)求∠DBC的度数;(2)若△DBC的周长为14cm,BC=5cm,求AB的长.25.如图,已知AC∥BD,AE,BE分别平分∠CAB和∠DBA,点E在线段CD上.(1)求∠AEB的度数;(2)求证:CE=DE.参考答案一.选择题1.解:等腰三角形的对称轴是底边的垂直平分线,故选:A.2.解:如图所示,以AB为腰的等腰三角形的点P有2个,以AB为底边的等腰三角形的点P有3个,∴△ABP为等腰三角形的点P有5个;故选:D.3.解:∵BI平分∠DBC,∴∠DBI=∠CBI,又∵DE∥BC,∴∠DIB=∠IBC,∴∠DIB=∠DBI,∴BD=DI.同理CE=EI.∴△ADE的周长=AD+DI+IE+EA=AB+AC=15,故选:B.4.解:∵在等边三角形ABC中,AD⊥BC,∴AD是BC的线段垂直平分线,∵E是AD上一点,∴EB=EC,∴∠EBD=∠ECD,∵∠CED=50°,∴∠ECD=40°,又∵∠ABC=60°,∠ECD=40°,∴∠ABE=60°﹣40°=20°,故选:C.5.解:∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴AB=BC=6,故选:C.6.解:反证法证明“a≥b”,第一步是假设,a<b,故选:C.7.解:①一个底角和一条边分别相等的两个等腰三角形不一定全等;②底边及底边上的高分别相等的两个等腰三角形全等,正确;③两边分别相等的两个直角三角形不一定全等;④如果在两个直角三角形中,例如:两个30°角的直角三角形,一个三角形的直角边与另一个三角形的斜边相等,这两个直角三角形肯定不全等,错误;故选:A.8.解:连接BE,∵DE是AB的垂直平分线,∴AE=BE,∴∠ABE=∠A=30°,∴∠CBE=∠ABC﹣∠ABE=30°,在Rt△BCE中,BE=2CE,∴AE=2CE,故选:B.9.解:∵在△ABC中,∠ACB=90°,C点E是边AB的中点,∴AE=BE=CE=AB=5,∵CD⊥AB,DE=4,∴CD==3,∴S△AEC=S△BEC=BE•CD=3=7.5,故选:B.10.解:作EF⊥BC于F,∵S△BCE=10,∴×BC×EF=10,即×5×EF=10,解得,EF=4,∵BE平分∠ABC,CD⊥AB,EF⊥BC,∴DE=EF=4,故选:D.二.填空题11.解:由题意知,应分两种情况:(1)当腰长为3cm时,则另一腰也为3cm,底边为12﹣2×3=7cm,∵3+3<7,∴边长分别为3,3,7不能构成三角形;(2)当底边长为3cm时,腰的长=(12﹣3)÷2=4.5cm,∵0<3<4.5+4.5=9,∴边长为3,4.5,4.5,能构成三角形,则该等腰三角形的一腰长是4.5cm.故答案为:4.5cm.12.解:∵∠B=20°,AB=A1B,∴∠A=(180°﹣∠B)=80°,故答案为:80°.13.解:∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴∠ADC=90°,又点E为AC中点,∴DE=AC=5,故答案为:5.14.解:∵DE垂直平分AC,∴CD=AD,∴∠ACD=∠A=30°,∵在Rt△ABC中,∠B=90°,∠A=30°,∴∠ACB=90°﹣∠A=60°,∴∠BCD=∠ACB﹣∠ACD=30°,∴CD=2BD=2×2=4,∴AD=CD=4.故答案为:4.15.解:∵DE是△ABC中的边AC上的垂直平分线,∴AD=CD,∵AB=5cm,BC=8cm,∴△ABD的周长为:AB+BD+AD=AB+BD+CD=AB+BC=13(cm).故答案是:13.16.解:∵DE,PF分别垂直平分AB,AC,∴∠B=∠BAD,∠C=∠CAP,又∵∠DAP=20°,∴∠B+∠C=(180°﹣20°)=80°,∴∠BAC=180°﹣80°=100°,故答案为:100°.17.解:作PH⊥AC于H,∵AP平分∠BAC,PE⊥AB,PH⊥AC,∴PE=PH,∵AB∥CD,PE⊥AB,∴PF⊥CD,∵CP平分∠ACD,PF⊥CD,PH⊥AC,∴PF=PH,∴PH=PE=PF=EF=5,即点P到AC的距离为5,故答案为:5.18.解:作DF⊥AC于F,如图,∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DF=DE=4,∵S△ABD+S△ADC=S△ABC,∴•4•AB+•12•4=40,∴AB=8.故答案为8.三.解答题19.解:∵在△ABC中,AB=BC,∠ABC=110°,∴∠A=∠C=35°,∵AB的垂直平分线DE交AC于点D,∴AD=BD,∴∠DBA=∠A=35°20.证明:∵AB∥CD,∴∠ABC=∠DCF.(两直线平行,同位角相等)∵BD平分∠ABC,CE平分∠DCF,∴∠2=∠ABC,∠4=∠DCF.(角平分线的定义)∴∠2=∠4.∴BD∥CE.(同位角相等,两直线平行)∴∠BGC=∠ACE.(两直线平行,内错角相等)∵∠ACE=90°,∴∠BGC=90°,即AC⊥BD.(垂直的定义)21.证明:∵CD⊥AB,∴在△ADF中,∠DAF=90°﹣∠AFD=90°﹣∠CFE.∵∠ACE=90°,∴在△AEC中,∠CAE=90°﹣∠CEF.∵∠CFE=∠CEF,∴∠DAF=∠CAE,即AE平分∠CAB.22.解:(1)∵AE⊥CD,∴∠AFC=∠ACB=90°,∴∠CAF+∠ACF=∠ACF+∠ECF=90°,∴∠ECF=∠CAF,∵∠EAD=∠DCB,∴∠CAD=2∠DCB,∵CD是斜边AB上的中线,∴CD=BD,∴∠B=∠DCB,∴∠CAB=2∠B,∵∠B+∠CAB=90°,∴∠B=30°;(2)∵∠B=∠BAE=∠CAE=30°,∴AE=BE,CE=AE,∴BC=3CE.23.解:(1)△CDE的周长为10.∵直线l与m分别是△ABC边AC和BC的垂直平分线,∴AD=CD,BE=CE,∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10;(2)∵直线l与m分别是△ABC边AC和BC的垂直平分线,∴AD=CD,BE=CE,∴∠A=∠ACD,∠B=∠BCE,又∵∠ACB=125°,∴∠A+∠B=180°﹣125°=55°,∴∠ACD+∠BCE=55°,∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°.24.解:(1)∵AB=AC,∴∠ABC=∠ACB,∵∠A=40°,∴∠ABC=∠ACB=70°,∵MN是AB的垂直平分线,∴DA=DB,∴∠A=∠ABD=40°,∴∠DBC=∠ABC﹣∠ABD=70﹣40°=30°;(2)∵MN是AB的垂直平分线,∴BD=AD,∵△DBC的周长为14cm,∴BD+BC+CD=14cm,∵BC=5cm,∴BD+CD=AD+CD=AC=9cm,∵AB=AC,∴AB=9cm.25.解:(1)∵AC∥BD,∴∠CAB+∠ABD=180°.∵AE平分∠CAB,∴∠EAB=∠CAB.同理可得∠EBA=∠ABD.∴∠EAB+∠EBA=90°,∴∠AEB=90°;(2)如图,在AB上截取AF=AC,连接EF,在△ACE和△AFE中,∴△ACE≌△AFE(SAS).∴CE=FE,∠CEA=∠FEA.∵∠CEA+∠DEB=90°,∠FEA+∠FEB=90°,∴∠DEB=∠FEB.在△DEB和△FEB中∴△DEB≌△FEB(ASA).∴ED=EF.∴ED=CE.。
(典型题)初中数学八年级数学下册第一单元《三角形的证明》检测题(含答案解析)
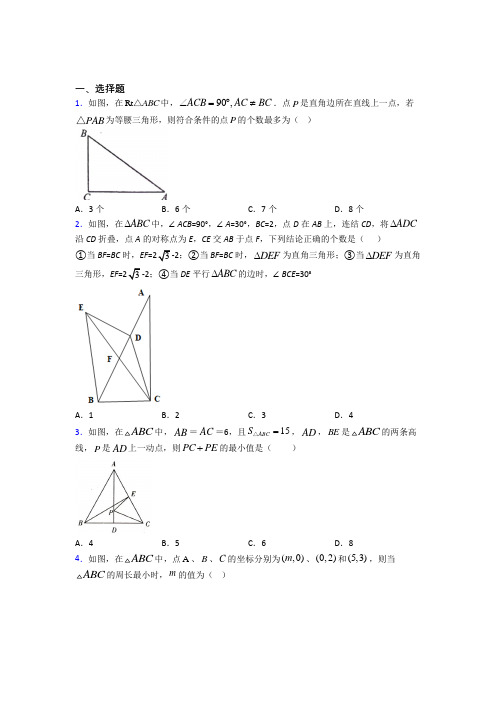
一、选择题1.如图,在Rt ABC △中,90,ACB AC BC ∠=︒≠.点P 是直角边所在直线上一点,若PAB △为等腰三角形,则符合条件的点P 的个数最多为( )A .3个B .6个C .7个D .8个2.如图,在ABC ∆中,∠ACB =90°,∠A =30°,BC =2,点D 在AB 上,连结CD ,将ADC ∆沿CD 折叠,点A 的对称点为E ,CE 交AB 于点F ,下列结论正确的个数是( ) ①当BF =BC 时,EF =23-2;②当BF =BC 时,DEF ∆为直角三角形;③当DEF ∆为直角三角形,EF =23-2;④当DE 平行ABC ∆的边时,∠BCE =30°A .1B .2C .3D .43.如图,在ABC 中,AB =AC =6,且15ABC S =△,AD ,BE 是ABC 的两条高线,P 是AD 上一动点,则PC PE +的最小值是( )A .4B .5C .6D .84.如图,在ABC 中,点A 、B 、C 的坐标分别为(,0)m 、(0,2)和(5,3),则当ABC 的周长最小时,m 的值为( )A.0 B.1 C.2 D.35.下列各组线段a、b、c中不能组成直角三角形的是()A.a=7,b=24,c=25 B.a=4,b=5,c=6C.a=3,b=4,c=5 D.a=9,b=12,c=156.如图,△ABC中,DC=2BD=2,连接AD,∠ADC=60°.E为AD上一点,若△BDE和△BEC都是等腰三角形,且AD=31,则∠ACB=()A.60°B.70°C.55°D.75°7.如图,直线AB,CD交于点O,若AB,CD是等边△MNP的两条对称轴,且点P在直线CD上(不与点O重合),则点M,N中必有一个在()A.∠AOD的内部B.∠BOD的内部C.∠BOC的内部D.直线AB上8.如图,在平面直角坐标系中,点A1在x轴的正半轴上,B1在第一象限,且△OA1B1是等边三角形.在射线OB1上取点B2,B3,…,分别以B1B2,B2B3,…为边作等边三角形△B1A2B2,△B2A3B3,…使得A1,A2,A3,…在同一直线上,该直线交y轴于点C.若OA1=1,∠OA1C=30°,则点B9的横坐标是()A .2552B .5112C .256D .51329.如图,点B 是线段AC 上任意一点(点B 与点A ,C 不重合),分别以AB 、BC 为边在直线AC 的同侧作等边三角形ABD 和等边三角形BCE ,AE 与BD 相交于点G 、CD 与BE 相交于点F ,AE 与CD 相交于点H ,连HB ,则下列结论:①AE CD =;②120AHC ∠=︒;③HB 平分AHC ∠;④CH EH BH =+.其中正确的结论有( )A .4个B .3个C .2个D .1个10.如图所示,在ABC 中,90BAC ∠=︒,30ACB ∠=︒,AD BC ⊥于D ,BE 是ABC ∠的平分线,且交AD 于P ,如果1AP =,则AC 的长为( )A .1B .2C .3D .411.如图,在平面直角坐标系中,点A 的坐标为()1,0,以线段OA 为边在第四象限内作等边ABO ,点C 为x 轴正半轴上一动点(1OC >),设点C 的坐标为(),0x ,连结BC ,以线段BC 为边的第四象限内作等边CBD ,直线DA 交y 轴于点E ,点E 的坐标是( )A .()0,3B .0,2x ⎛⎫ ⎪⎝⎭C .()0,3D .30,x ⎛⎫ ⎪ ⎪⎝⎭ 12.等腰三角形一腰的垂直平分线与另一腰所在直线的夹角是40°,则这一等腰三角形的底角为( )A .65°B .25°C .50°D .65°或25°二、填空题13.如图,在△ABC 中,∠C =90°,以A 为圆心,任意长为半径画弧,分别交AC ,AB 于点M ,N ,再分别以M ,N 为圆心,大于12MN 长为半径画弧,两弧交于点O ,作射线AO ,交BC 于点E .已知CB =8,BE =5,则点E 到AB 的距离为_____.14.如图,等腰三角形ABC 的面积为80,底边10BC =,腰AC 的垂直平分线EF 交,AC AB 于点E ,F ,若D 为BC 边中点,M 为线段EF 上一动点,则CDM 的周长最小值为________.15.如图,DE ∥BC ,AE =DE =1,BC =3,则线段CE 的长为_____.16.如图,在Rt △ABC 中,∠ACB =90°,AC =BC =6,D 为BC 上一点,连接AD ,过点A作AE ⊥AD ,取AE =AD ,连接BE 交AC 于F .当△AEF 为等腰三角形时,CD =_____.17.如图,D 是等边三角形ABC 外一点,3AD =,2CD =,则BD 的最大值是________________.18.如图,80AOB ∠=︒,OC 平分AOB ∠,如果射线OA 上的点E 满足OCE △是等腰三角形,那么OEC ∠的度数为________.19.如图,在ABC 中,AB BC =,30C ∠=︒,过点B 作BD BC ⊥,交AC 于点D ,若2CD =,则AD 的长为__________.20.如图,△ABC 中,∠ABC 与∠ACB 的平分线交于点D ,过点D 作EF ∥BC ,分别交AB 、AC 于点E 、F .那么下列结论:①BD=DC ;②△BED 和△CFD 都是等腰三角形;③点D 是EF 的中点;④△AEF 的周长等于AB 与AC 的和.其中正确的有______.(只填序号)三、解答题21.如图1,直线AB :y=43x +4分别与x 轴、y 轴交于A 、B 两点,过点B 的直线交x 轴负半轴于点C ,将△BOC 沿BC 折叠,使点O 落在BA 上的点M 处.(1)求A 、B 两点的坐标;(2)求线段BC 的长;(3)点P 为x 轴上的动点,当∠PBA=45°时,求点P 的坐标.22.如图,在ABC 中,AB BC =,90ABC ∠=︒,点E 在BC 上,点F 在AB 的延长线上,且AE CF =.(1)求证:ABE CBF △≌△;(2)若75ACF ∠=︒,求EAC ∠的度数.23.阅读下列材料,完成相应任务.三角形中边与角之间的不等关系学习了等腰三角形,我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.那么,不相等的边所对的角之间的大小关系怎样呢?大边所对的角也大吗?下面是奋进小组的证明过程.如图1,在△ABC中,已知AB>AC>BC.求证:∠C>∠B>∠A.证明:如图2,将△ABC折叠,使边AC落在AB上,点C落在AB上的点C′处,折痕AD交BC于点D.则∠A C′D=∠C.∵∠A C′D=∠B+∠BDC′(依据1)∴∠A C′D>∠B∴∠C>∠B(依据2)如图3,将△ABC折叠,使边CB落在CA上,点B落在CA上的点B′处,折痕CE交AB于点E.则∠CB′E=∠B.∵∠CB′E=∠A+∠AEB′∴∠CB′E>∠A∴∠B>∠A∴∠C>∠B>∠A.归纳总结:利用轴对称的性质可以把研究边与角之间的不等问题,转化为较大量的一部分与较小量相等的问题,这是几何中研究不等问题是常用的方法.类似地,应用这种方法可以证明“在一个三角形中,大角对大边,小角对小边”的问题.如图1,已知△ABC中,∠C>∠B>∠A.求证:AB>AC>BC.下面是智慧小组的证明过程(不完整).证明:如图2,在∠BCA的内部,作∠BCF=∠B,CF交AB于点F.则CF=BF(依据3)在△ACF中,AF+CF>AC,∴AF+BF>AC,∴AB>AC;…任务一:①上述材料中依据1,依据2,依据3分别指什么?依据1:;依据2:;依据3:.②上述材料中不论是由边的不等关系,推出角的不等关系,还是由角的不等关系推出边的不等关系,都是转化为较大量的一部分与较小量相等的问题,再用三角形外角的性质或三边关系进而解决,这里主要体现的数学思想是_____________;(填正确选项的代码) A . 转化思想 B . 方程思想 C . 数形结合思想任务二:请将智慧小组的证明过程补充完整,并在备用图中作出辅助线.任务三:根据上述材料得出的结论,判断下列说法,正确的有__________(将正确的代码填在横线处).①在△ABC 中,AB >BC ,则∠A >∠B ;②在△ABC 中,AB >BC >AC ,∠C =89°,则△ABC 是锐角三角形;③Rt △ABC 中,∠B =90°,则最长边是AC ;④在△ABC 中,∠A =55°,∠B =70°,则AB =BC .24.如图,已知点D 、E 是△ABC 内两点,且∠BAE =∠CAD ,AB =AC ,AD =AE .(1)求证:ABD ACE △≌△.(2)延长BD 、CE 交于点F ,若86BAC ∠=︒,20ABD ∠=︒,求BFC ∠的度数. 25.如图,在ABC 中,AB AC =,100BAC ∠=︒,AD 是BC 边上的中线,且BD BE =,CD 的垂直平分线FM 交AC 于点F ,交BC 于点M .(1)求ADE ∠的度数;(2)ADF 是什么三角形?说明理由.(3)若将题目中“100BAC ∠=︒”改为“∠BAC =120°”,且FM =4,其他条件不变,求AB 的长.26.如图,射线,ON OE OS OW 、、分别表示从点O 出发北、东、南、西四个方向,将直角三角尺的直角顶点与点O 重合.(1)图中与∠BOE 互余的角是____________或____________;(2)①用直尺和量角器作AOE ∠的平分线OP ;②在①所做的图形中,如果132AOE ∠=︒,那么点P 在点O 北偏东____________°的方向上(请说明理由).【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】分为三种情况:①BP=AB,②AP=AB,③AP=BP,再求出答案即可.【详解】解:作BC、AC所在直线,然后分别以B、A点为圆心,以AB为半径作圆分别交BC、AC 所在直线于6点,再作AB的垂直平分线与BC所在直线交于2点,总共符合条件的点P的个数最多有8个,故选:B.【点睛】本题考查了等腰三角形的判定,线段垂直平分线的性质.能求出符合的所有情况是解此题的关键.2.C解析:C【分析】由勾股定理可求A C 的长,利用折叠的性质和等腰三角形的性质依次计算可得①②正确.利用直角三角形分类讨论可知EF 有两种情况,③不正确,由平行内错角角相等可知④正确;【详解】解:①∵BF =BC ,且∠ABC =60°,∴BCF ∆为等边三角形,BF =CF =BC =2,ACAB =4,∵ADC ∆沿CD 折叠,∴CE =ACEF =CE -CF ,故①正确;②当BF =BC 时,∠EFD =∠BFC =60°,∴∠DEF =∠A =30°,∠EDF =90°,∴EDF ∆为直角三角形,故②正确;③当DEF ∆为直角三角形时,此处要分情况讨论,当∠EDF =90°时,∵∠DEF =∠A =30°,∴∠EFD =60°=∠BFC ,EF =EC -CF-2,当∠EFD =90°时,∵∠ABC =60°,∠BCF =30°,∴FCEF =EC -FC ,综上所述,EF ,故③错误;④当DE 平行于ABC ∆的边时,∵DE ∥BC ,∴∠EDF =∠ABC =60°,∵∠DEC =30°,∴∠BCF =∠DEC =30°,故④正确,故选C【点睛】本题考查了翻折变换,等腰三角形的判定和性质,勾股定理等知识;熟练掌握翻折变换的性质,由直角三角形的性质和勾股定理求出CA ,学会运用分类讨论是解题的关键. 3.B解析:B【分析】连接PB ,根据等腰三角形的性质和垂直平分线的性质计算即可;【详解】连接PB ,∵AB AC =,BD CD =,∴AD 是等腰△ABC 底边BC 边的中垂线,∴PB PC =,∴PC PE PB PE +=+,又PB PE BE +≥,∴B ,P ,E 三点共线时,PB PE +最小,即等于BE 的长,又∵△1152ABC S AC BE ==,6AC =, ∴5BE =;故答案选B .【点睛】本题主要考查了等腰三角形的性质、垂直平分线的性质,结合轴对称的性质计算是解题的关键. 4.C解析:C【分析】做出B 关于x 轴对称点为B′,连接B′C ,交x 轴于点A',此时ABC 的周长最小,由等腰直角三角形的性质可求∠OB'A'=∠OA'B'=45°,可求OB'=OA'=1,即可求解.【详解】解:如图所示,做出B 关于x 轴对称点为B′,连接B′C ,交x 轴于点A',此时△ABC 周长最小过点C作CH⊥x轴,过点B'作B'H⊥y轴,交CH于H,∵B(0,2),∴B′(0,-2),∵C(5,3),∴CH= B′H=5,∴∠CB'H=45°,∴∠BB' A'=45°,∴∠OB'A'=∠OA'B'=45°,∴OB'=OA'=2,则此时A'坐标为(2,0).m的值为2.故选:C.【点睛】此题考查了轴对称-最短路径问题,考查了轴对称的性质,等腰直角三角形的性质等知识,根据已知得出A点位置是解题关键.5.B解析:B【分析】根据判断三条线段是否能构成直角三角形的三边,需验证两小边的和的平方是否等于最长边的平方,分别对每一项进行分析,即可得出答案;【详解】A、222724=25+,能构成直角三角形;B、222+≠,不能构成直角三角形;45=416C、222+,能构成直角三角形;34=5D、222912=225=15+,能构成直角三角形;故选:B.【点睛】本题考查了勾股定理的逆定理,用到的知识点是已知△ABC 的三边满足222+=a b c ,则△ABC 是直角三角形;6.D解析:D【分析】根据等腰三角形的性质求解即可;【详解】∵60EDC ∠=︒,∴60EBD BED ∠+∠=︒,∵△BDE 是等腰三角形,∴30EBD BED ∠=∠=︒,1BD DE ==,∵△BEC 是等腰三角形,∴30EBD ECD ∠=∠=︒,∵60EDC ∠=︒,∴90DEC ∠=︒,在Rt △DEC 中,∵30ECD ∠=︒,1DE =,∴tan 30DEEC ==︒又∵AD 1, ∴AE AD DE EC =-==,∴△AEC 为等腰三角形,又∵90DEC AEC ∠=∠=︒,∴45ECA EAC ∠=∠=︒,∴453075ACB ACE ECD ∠=∠+∠=︒+︒=︒;故答案选D .【点睛】本题主要考查了等腰三角形的性质应用,准确计算是解题的关键.7.D解析:D【分析】根据等边三角形是轴对称图形,利用轴对称图形的性质解决问题即可.【详解】解:如图,∵△PMN 是等边三角形,等边三角形的对称轴一定经过三角形的顶点,又∵直线CD ,AB 是△PMN 的对称轴,直线CD 经过点P ,∴直线AB 一定经过点M 或N ,故选:D .【点睛】本题考查轴对称,等边三角形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.8.B解析:B【分析】利用待定系数法求得两条直线的解析式,根据等边三角形的性质,点的坐标规律,即可求解.【详解】解:∵OA 1=1,∠OA 1C=30︒,∴3 ∴点C 的坐标为(0,33-), ∵A 1、A 2、A 3所在直线过点A 1(1,0),C (0,33-, 设直线A 1A 2的解析式为3y kx =-∴30k =, ∴3k = ∴直线A 1A 2的解析式为3333y x =-, ∵△OA 1B 1为等边三角形,∴点B 1的坐标为(123, ∵B 1、B 2、B 3所在直线过点O(0,0),B 1 (12,32),同理可求得直线O B 1的解析式为y =,∵△OA 1B 1和△B 1A 2B 2为等边三角形,∴∠B 1OA 1=∠B 2 B 1A 2=60︒,∴B 1A 2∥OA 1,∵B 1 (12,∴A 2的纵坐标为2x = 解得:52x =,∴点A 2的坐标为(52, ∴B 1A 2=2,同理点B 2的坐标为(32,点B 3的坐标为(72,点B 4的坐标为(152, ,总结规律: B 1的横坐标为12, B 2的横坐标为13122+=, B 3的横坐标为171222++=, B 4的横坐标为11512422+++=, ,∴B 9的横坐标为1511124816326422+++++++=, 故选:B【点睛】本题考查了待定系数法求一次函数的解析式,点的坐标规律,等边三角形的性质,解决本题的关键是寻找点的坐标规律. 9.A解析:A【分析】利用等边三角形,ABD BCE 的性质,证明 ,ABE DBC ≌ 从而可判断①,由,ABE DBC ≌可得,EAB CDB ∠=∠ 再利用三角形的内角和定理可判断②,如图,过B 作BM AE ⊥交AE 于,M 过B 作BN DC ⊥交DC 于,N 利用全等三角形的对于高相等证明,BM BN = 从而可判断③,如图,在CH 上截取,HK HE = 连接,EK 证明EHK 为等边三角形,再证明,EHB EKC ≌ 可得,HB KC = 从而可判断④.【详解】解:,ABD BCE 为等边三角形, ,60,60BA BD ABD BC BE CE CBE ∴=∠=︒==∠=︒,,,ABD DBE CBE DBE ∴∠+∠=∠+∠ 即,ABE DBC ∠=∠(),ABE DBC SAS ∴≌,AE DC ∴= 故①符合题意;,ABE DBC ≌,EAB CDB ∴∠=∠,DGH AGB ∠=∠180,180,DHG CDB DGH ABD EAB AGB ∠=︒-∠-∠∠=︒-∠-∠60DHG ABD ∴∠=∠=︒,120AHC ∴∠=︒,故②符合题意; 如图,过B 作BM AE ⊥交AE 于,M 过B 作BN DC ⊥交DC 于,N,ABE DBC ≌,AE DC 为对应边,,BM BN ∴=HB ∴平分,AHC ∠ 故③符合题意;如图,在CH 上截取,HK HE = 连接,EK60,EHK AHD ∠=∠=︒EHK ∴为等边三角形,,60,EK EH HEK ∴=∠=︒60,60,HEK HEB FEK BEC FEK KEC ∠=︒=∠+∠∠=︒=∠+∠,HEB KEC ∴∠=∠,BE CE =(),EHB EKC SAS ∴≌,HB KC ∴=.CH CK HK BH EH ∴=+=+ 故④符合题意;综上:①②③④都符合题意,故选:.A【点睛】本题考查的是三角形的内角和定理的应用,全等三角形的判定与性质,等边三角形的判定与性质,角平分线的判定,掌握以上知识是解题的关键.10.C解析:C【分析】由三角形的内角和定理和等腰三角形的性质,得到AP=BP=AE=PE=1,CE=BE=2,即可求出AC 的长度.【详解】解:∵在ABC 中,90BAC ∠=︒,30ACB ∠=︒,∴60ABC ∠=︒,∵AD BC ⊥于D ,BE 是ABC ∠的角平分线,∴30ABP DBP BAP ∠=∠=∠=︒,∴1AP BP ==,∵90BAC ∠=︒,30ACB ∠=︒,∴60EAP AEP ∠=∠=︒,∴△APE 是等边三角形,∴AP=BP=AE=PE=1,∵30DBP C ∠=∠=︒,∴CE=BE=1+1=2,∴213AC CE AE =+=+=;故选:C .【点睛】本题考查了等边三角形的判定和性质,等腰三角形的性质,三角形的内角和定理,解题的关键是熟练掌握所学的知识,正确的进行解题.11.A解析:A【分析】由等边三角形的性质可得AO =OB =AB =1,BC =BD =CD ,∠OBA =∠CBD =60°,可证△OBC ≌△ABD ,可得∠BAD =∠BOC =60°,可求∠EAO =60°,即可求OE 3点E 坐标.【详解】解:∵△AOB ,△BCD 是等边三角形,∴AO =OB =AB =1,BC =BD =CD ,∠OBA =∠CBD =60°,∴∠OBC =∠ABD ,且OB =AB ,BC =BD ,∴△OBC ≌△ABD (SAS ),∴∠BAD =∠BOC =60°,∴∠EAO =180°−∠OAB−∠BAD =60°,在Rt △AOE 中,AO =1,∠EAO =60°,∠OEA=30°,∴AE=2 AO=2,∴OE=2221-=3,∴点E 坐标(0,3),故选A .【点睛】本题考查了全等三角形的判定和性质,等边三角形的性质,坐标与图形性质,灵活运用全等三角形的判定和性质是本题的关键.12.D解析:D【分析】由题意可知其为锐角等腰三角形或钝角等腰三角形,不可能是等腰直角三角形,所以应分开来讨论.【详解】解:①当为锐角等腰三角形时,如图:∵∠ADE =40°,∠AED =90°,∴∠A =50°,∴∠B=∠C=180502︒-︒ =65°; ②当为钝角等腰三角形时,如图:∵∠ADE =40°,∠AED =90°,∴∠BAC =∠ADE+∠AED =40°+90°=130°,∴∠B=∠C=1801302︒-︒ =25°. 故选:D .【点睛】本题考查了等腰三角形的性质、三角形内角和定理以及三角形外角性质,分类讨论是正确解答本题的关键. 二、填空题13.【分析】根据作图过程可知AE 平分∠CAB 根据角平分线的性质即可得出结论【详解】解:根据作图过程可知:AE 平分∠CAB ∵CB =8BE =5∴CE =BC ﹣BE =8﹣5=3∵∠C =90°∴EC ⊥AC ∴点E 到解析:【分析】根据作图过程可知AE 平分∠CAB ,根据角平分线的性质即可得出结论.【详解】解:根据作图过程可知:AE 平分∠CAB ,∵CB =8,BE =5,∴CE =BC ﹣BE =8﹣5=3,∵∠C =90°,∴EC ⊥AC ,∴点E 到AB 的距离为3.故答案为:3.【点睛】本题考查了作图-基本做图,解决本题的关键是掌握基本的作图方法和理解角平分线的性质.14.21【分析】连接ADAM 由于△ABC 是等腰三角形点D 是BC 边的中点故AD ⊥BC 再根据三角形的面积公式求出AD 的长再根据EF 是线段AC 的垂直平分线可知点A 关于直线EF 的对称点为点CMA =MC 推出MC +解析:21【分析】连接AD ,AM ,由于△ABC 是等腰三角形,点D 是BC 边的中点,故AD ⊥BC ,再根据三角形的面积公式求出AD 的长,再根据EF 是线段AC 的垂直平分线可知,点A 关于直线EF 的对称点为点C ,MA =MC ,推出MC +DM =MA +DM≥AD ,故AD 的长为BM +MD 的最小值,由此即可得出结论.【详解】解:连接AD ,MA .∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S△ABC=12BC•AD=12×10×AD=80,解得:AD=16,∵EF是线段AC的垂直平分线,∴点A关于直线EF的对称点为点C,MA=MC,∴MC+DM=MA+DM≥AD,∴AD的长为CM+MD的最小值,∴△CDM的周长最短=(CM+MD)+CD=AD+12BC=16+12×10=21.故答案是:21.【点睛】本题考查的是轴对称−最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.15.【分析】由平行线的性质可得∠ADE=∠B由AE=DE=1可得∠ADE=∠DAE易得∠DAE=∠B可得AC=BC易得结果【详解】解:∵DE∥BC∴∠ADE=∠B∵AE =DE=1∴∠ADE=∠DAE∴∠解析:【分析】由平行线的性质可得∠ADE=∠B,由AE=DE=1,可得∠ADE=∠DAE,易得∠DAE=∠B,可得AC=BC,易得结果.【详解】解:∵DE∥BC,∴∠ADE=∠B,∵AE=DE=1,∴∠ADE=∠DAE,∴∠DAE=∠B,BC=3,∴AC=BC=3,∴CE=AC﹣AE=3﹣1=2,故答案为:2.【点睛】本题主要考查了平行线的性质和等腰三角形的性质等,关键是运用性质定理得出AC=BC=3.16.2或6【分析】分两种情形:当AE=AF时如图1中过点E作EH⊥AC于H证明AH=FH=CF=CD可得结论如图2中当AF=EF时点D与D重合此时CD=BC =6【详解】解:①当AE=EF时如图1中过点E解析:2或6【分析】分两种情形:当AE=AF 时,如图1中,过点E 作EH ⊥AC 于H .证明AH =FH =CF =CD ,可得结论,如图2中,当AF =EF 时,点D 与D 重合,此时CD =BC =6【详解】解:①当AE=EF 时,如图1中,过点E 作EH ⊥AC 于H .∵EA =EF ,EH ⊥AF ,∴AH =HF ,∵EA ⊥AD ,∴∠EAD =∠EHA =∠C =90°,∴∠EAH +∠CAD =90°,∠CAD +∠ADC =90°,∴∠EAH =∠ADC ,在△EHA 和△ACD ,EAH ADC EHA C AE DA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EHA ≌△ACD (AAS ),∴AH =CD ,EH =AC =CB .在△EHF 和△BCF 中,EFH BFC EHF C EH BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EHF ≌△BCF (AAS ),∴FH =CF ,∴AH =FH =CF =CD ,∴CD =13AC =2, ②如图2中,当AF =EF 时,点B 与点D 重合,此时CD =BC =6综上所述,满足条件的CD的长度为2或6故答案为:2或6【点睛】本题考查等腰直角三角形的性质,全等三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.17.5【分析】将AD顺时针旋转60°得连结可得AD=DD′=AD′可证△ABD′≌△ACD(SAS)可得BD′=CD由BD′+DD′≥BD当BD′D三点在一线时BD最大BD最大=BD′+DD′=5【详解解析:5【分析】将AD顺时针旋转60°,得AD',连结BD',可得AD=DD′=AD′,可证△ABD′≌△ACD (SAS),可得BD′=CD,由BD′+DD′≥BD,当B、D′、D三点在一线时,BD最大,BD最大=BD′+DD′=5.【详解】解:∵将AD顺时针旋转60°,得AD',连结BD',则AD=DD′=AD′,∴△ADD′是等边三角形,又∵等边三角形ABC,∴∠BAC=∠D AD',∴∠BAD′+∠D′AC=∠CAD+∠D′AC=60°,∴AB=AC,AD′=AD,∴△ABD′≌△ACD(SAS),∴BD′=CD,∴BD′+DD′≥BD,当B、D′、D三点在一线时,BD最大,BD最大=BD′+DD′=CD+AD=2+3=5.故答案为:5..【点睛】本题考查三角形旋转变换,等边三角形判定与性质,掌握三角形旋转变换的性质,等边三角形判定与性质,用三角形三边关系确定B、D′、D共线是解题关键.18.40°或70°或100°【分析】求出∠AOC根据等腰得出三种情况OE=CEOC=OEOC=CE根据等腰三角形性质和三角形内角和定理求出即可【详解】解:∵∠AOB=80°OC平分∠AOB∴∠AOC=4解析:40°或70°或100°【分析】求出∠AOC,根据等腰得出三种情况,OE=CE,OC=OE,OC=CE,根据等腰三角形性质和三角形内角和定理求出即可.【详解】解:∵∠AOB=80°,OC平分∠AOB,∴∠AOC=40°,①当E在E1时,OE=CE,∵∠AOC=∠OCE=40°,∴∠OEC=180°﹣40°﹣40°=100°;②当E在E2点时,OC=OE,则∠OCE=∠OEC=12(180°﹣40°)=70°;③当E在E3时,OC=CE,则∠OEC=∠AOC=40°;故答案为:100°或70°或40°.【点睛】本题考查了角平分线定义,等腰三角形性质,三角形的内角和定理的应用,用了分类讨论思想.19.【分析】利用等腰三角形的性质判定证明BD=AD 利用直角三角形中30°角的性质计算BD 即可得解【详解】∵∴∠A=30°∠ABC=120°∵∴∠CBD=90°BD=1∴∠DBA=30°∴∠DBA=∠A ∴ 解析:1.【分析】利用等腰三角形的性质,判定,证明BD=AD ,利用直角三角形中30°角的性质计算BD 即可得解.【详解】∵AB BC =,30C ∠=︒,∴∠A=30°,∠ABC=120°,∵BD BC ⊥,2CD =,∴∠CBD=90°,BD=1,∴∠DBA=30°,∴∠DBA=∠A ,∴BD=AD ,∴AD=1.【点睛】本题考查了等腰三角形的判定和性质,直角三角形的性质,熟练掌握性质,并灵活运用性质是解题的关键.20.②④【分析】由平行线得到角相等由角平分线得角相等根据平行线的性质及等腰三角形的判定和性质逐一判断即得答案【详解】解:∵EF ∥BC ∴∠EDB=∠DBC ∠FDC=∠DCB ∵∠ABC 与∠ACB 的平分线交于 解析:②④【分析】由平行线得到角相等,由角平分线得角相等,根据平行线的性质及等腰三角形的判定和性质逐一判断即得答案.【详解】解:∵EF ∥BC ,∴∠EDB=∠DBC ,∠FDC=∠DCB ,∵∠ABC 与∠ACB 的平分线交于点D ,∴∠EBD=∠DBC ,∠FCD=∠DCB ,∴∠EDB =∠EBD ,∠FCD=∠FDC ,∴ED=EB ,FD=FC ,即△BED 和△CFD 都是等腰三角形;故②正确;∴△AEF 的周长为:AE+EF+AF=AE+ED+DF+AF=AB+AC ;故④正确;∵∠ABC 不一定等于∠ACB ,∴∠DBC 不一定等于∠DCB ,∴BD 与CD 不一定相等,故①错误.∵BE 与CF 无法判定相等,∴ED 与DF 无法判定相等,故③错误;综上,正确的有②④.故答案为:②④.【点睛】本题考查了等腰三角形的性质及角平分线的性质及平行线的性质;题目利用了两直线平行,内错角相等,及等角对等边来判定等腰三角形;等量代换的利用是解答本题的关键.三、解答题21.(1)A (-3,0),B (0,4);(2)BC ;(3)P (-28,0)或(47,0)【分析】(1)令0x =,求得y ,令0y =,求得x ,即可求解;(2)设OC=a ,在Rt △ACM 中,利用勾股定理列式计算可求得43a =,即可求解; (3)分点P 在点A 的右边和左边两种情况讨论,分别作出辅助线,构造直角三角形,利用勾股定理求解即可.【详解】(1)令0x =,4443y x =+=, 令0y =,4043x =+,则3x =-, ∴点A 的坐标为(-3,0),点B 的坐标为(0,4);(2)设OC=a ,由折叠的性质可知:CM ⊥AB ,OC=CM=a ,OB=BM=4,由勾股定理得:5==,∴AM=1,在Rt △ACM 中,222AM MC AC +=,∴2221(3)a a +=-, ∴43a =, ∴222244()03341BC BO CO =+=+=; (3)如图,点P 在点A 的右边时,过P 作PG ⊥AB 于G , ∵点A 的坐标为(-3,0),点B 的坐标为(0,4),∴OA<OB ,∴点P 在点O 的右边,设PO= m ,则AP=3m +,∵APB 1122S AB PG AP OB =⨯=⨯, ∴()435PG m =+, ()()()22224333355AG AP PG m m m ⎡⎤=-=+-+=+⎢⎥⎣⎦, ∵∠PBA=45°,∴△BPG 是等腰直角三角形,∴()435BG PG m ==+, ∵ AG BG AB +=,∴()()3433555m m +++=, 解得:47m =, 此时点P 的坐标为(47,0); 如图,点P 在点A 的左边时,过P 作PH ⊥AB 于H ,设PO= n ,则AP=n 3-, ∵APB 1122S AB PH AP OB =⨯=⨯, ∴()4n 35PH =-, ()()()22224333355AH AP PH n n n ⎡⎤=-=---=-⎢⎥⎣⎦, ∵∠PBA=45°,∴△BPH 是等腰直角三角形,∴()435BH PH n ==-, ∵BH AH AB -=, ∴()()4333555n n ---=, 解得:28n =,此时点P 的坐标为(28-,0);综上,点P 的坐标为(28-,0)或(47,0) . 【点睛】本题考查了坐标与图形,一次函数的性质,以及等腰直角三角形的判定和性质,解题的关键是作出合适的辅助线,构造直角三角形,利用勾股定理求解.22.(1)见详解;(2)15°【分析】(1)由AB =CB ,∠ABC =90°,AE =CF ,即可利用HL 证得Rt △ABE ≌Rt △CBF ;(2)由AB =CB ,∠ABC =90°,即可求得∠CAB 与∠ACB 的度数,即可得∠FCB 的度数,又由Rt △ABE ≌Rt △CBF ,即可求得∠EAB 的度数,再得出∠EAC 的度数即可.【详解】(1)证明:∵∠ABC =90°,∴△ABE 与△CBF 为直角三角形.∵在Rt △ABE 与Rt △BCF 中,AB BC AE CF⎧⎨⎩==, ∴Rt △ABE ≌Rt △CBF (HL );(2)∵AB =BC ,∠ABC =90°,∴∠BAC =∠ACB =45°,∵∠ACF =75°,∴∠FCB =30°,∵Rt △ABE ≌Rt △CBF ,∴∠EAB =∠FCB =30°,∴∠EAC =45°-30°=15°.【点睛】此题考查了直角三角形全等的判定与性质,等腰直角三角形的性质,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.23.任务一:①依据1:三角形的外角等于与它不相邻的两个内角的和; 依据2:等量代换;依据3:如果一个三角形有两个角相等,那么这两个角所对的边也相等(或等角对等边); ②A ;任务二:见解析;任务三:②③④【分析】任务一:①根据三角形的外角性质、等量代换以及三角形中等角对等边性质即可写出依据;②根据分析过程渗透的思想为转化的思想方法;任务二:仿照推导AB >AC 的方法证明AC >BC 即可证明结论正确;任务三:根据结论“在一个三角形中,大角对大边,小角对小边,等边对等角”进行判断即可解答.【详解】解:任务一:①根据推导过程可知:依据1:三角形的外角等于与它不相邻的两个内角的和;依据2:等量代换;依据3:如果一个三角形有两个角相等,那么这两个角所对的边也相等(或等角对等边);故答案为:三角形的外角等于与它不相邻的两个内角的和;等量代换;如果一个三角形有两个角相等,那么这两个角所对的边也相等(或等角对等边);②根据推导过程体现了转化的数学思想方法,故选:A ;任务二:智慧小组的证明过程补充如下:证明:如图2,在∠BCA 的内部,作∠BCF=∠B ,CF 交AB 于点F .则CF=BF ,(等边对等角)在△ACF 中,AF+CF >AC ,∴AF+BF >AC ,∴AB >AC ;同理,如图,在∠ABC 的内部,作∠ABG=∠A ,BG 交AC 于点G ,如图,则AG=BG在△BCG 中,BG+CG >BC ,∴BG+CG >BC ,∴AC >BC∴AB >AC >BC .任务三:①∵AB >BC ,∴∠C >∠A ,错误;②∵在△ABC 中,AB >BC >AC ,∠C=89°,∴∠C >∠A >∠B ,又∠C=89°<90°,∴△ABC 是锐角三角形,正确;③∵Rt △ABC 中,∠B=90°,则最长边是斜边AC ,正确;④∵在△ABC 中,∠A=55°,∠B=70°,∴∠C=180°﹣∠A ﹣∠B=180°﹣55°﹣70°=55°,∴∠A=∠C∴AB=BC ,正确,故答案为:②③④.【点睛】本题考查三角形的边与角之间的不关系的推导及其应用,涉及三角形的外角性质、等腰三角形的等角对等边性质、三角形的内角和定理、判断三角形的形状、命题的证明等知识,掌握在一个三角形中,大角对大边,小角对小边这一性质的推导过程,会利用转化的思想进行命题的证明是解答的关键.24.(1)见解析;(2)126BFC ∠=︒.【分析】(1)由SAS 证明ABD ACE △≌△即可;(2)先由全等三角形的性质的20ACE ABD ∠=∠=︒再由等腰三角形的性质和三角形内角和定理得47ABC ACB ∠=∠=︒,则27FBC FCB ∠=∠=︒,即可得出答案.【详解】(1)证明∵BAE CAD ∠=∠∴BAD CAE ∠=∠,在ABD △和ACE △中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴ABD ACE SAS △≌△();(2)解:∵ABD ACE △≌△,∴20ACE ABD ∠=∠=︒,∵AB =AC , ∴1(18086)472ABC ACB ∠=∠=︒-︒=︒, ∴472027FBC FCB ∠=∠=︒-︒=︒,∴1802727126BFC ∠=︒-︒-︒=︒.【点睛】本题主要考查全等三角形的性质及判定、等腰三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.25.(1)∠ADE =20°;(2)△ADF 是等腰三角形,证明见解析;(3)AB=16.【分析】(1)根据等腰三角形的性质和三角形内角和定理求出∠B 和∠C ,求出∠BDE ,即可求出答案;(2)根据垂直平分线的性质定理和等边对等角可求得∠FDC ,再根据三线合一和直角三角形两锐角互余可求得∠DAF 和∠ADF 得出它们相等即可得出△ADF 为等腰三角形;(3)可求得∠C=30°根据30°角所对直角边是斜边的一般可得FC ,可证明△ADF 为等边三角形即可求得AF ,从而求得AC ,继而求得AB .【详解】解:(1)∵在△ABC 中,AB=AC ,∠BAC=100°,∴∠B=∠C=12×(180°-∠BAC )=40°, ∵BD=BE ,∴∠BDE=∠BED=12×(180°-∠B )=70°, ∵在△ABC 中,AB=AC ,AD 是BC 边上的中线,∴AD ⊥BC ,∴∠ADB=90°,∴∠ADE=∠ADB-∠BDE=20°;(2)△ADF 是等腰三角形,理由是:∵CD 的垂直平分线MF 交AC 于F ,交BC 于M ,∴DF=CF ,∵∠C=40°,∴∠FDC=∠C=40°,∵AD ⊥BC ,∴∠ADC=90°,∴∠DAF=90°-∠C=50°,∴∠ADF=50°,∴∠DAF=∠ADF ,∴AF=DF ,∴△ADF 是等腰三角形;(3)∵∠BAC =120°,AB=AC ,∴∠B=∠C=12×(180°-∠BAC )=30°, 又∵AD 是BC 边上的中线,∴AD ⊥BC ,∴∠DAC=90°-∠C=60°,∵CD 的垂直平分线MF ,∴∠FMC=90°,DF=FC ,∴∠FDC=∠C=30°,∴∠ADF=∠ADC-∠FDC=60°,∠AFD=∠C+∠FDC=60°,∴△ADF 为等边三角形,AF=DF=FC ,∵MF=4,∴FC=2MF=8,∴AF= 8,∵AC=AF+CF=8+8=16,∵AB=AC ,∴AB=16.【点睛】本题考查了线段垂直平分线性质,等边三角形的性质和判定,含30°角的直角三角形的性质,等腰三角形的性质等知识点,能综合运用定理进行推理是解此题的关键.26.(1)BON ∠;AOW ∠;(2)①见解析;②24︒,见解析【分析】(1)根据互余,平角的定义判断即可;(2)①作出角平分线即可;②利用角平分线的定义求出∠POE ,再求出∠NOP 即可解决问题;【详解】(1)90180AOB WOE ︒∠=∠=︒,,90AOW BOE ∴∠+∠=︒,90NOB BOE ∠+∠=︒, ∴图中与∠BOE 互余的角是BON ∠和AOW ∠;故答案为:BON ∠和AOW ∠;(2)①如图所示:②132AOE ∠=︒,OP 平分AOE ∠,1132662POE ∴∠=⨯︒=︒, 90NOE ∠=︒,906624NOB ∴∠=︒-︒=︒,∴点P 在点O 北偏东24︒的方向上;【点睛】本题考查了作图-应用与设计,角平分线的定义,方向角等知识解题的关键是理解题意,灵活运用所学知识解决问题;。
初中数学北师大版八年级下册第六章 平行四边形3.三角形的中位线-章节测试习题(3)

章节测试题1.【答题】如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是()A. 2B. 3C. 4D. 5【答案】B【分析】本题考查三角形的中位线.【解答】∵点D,E分别是边AB,AC的中点,∴DE是△ABC的中位线,∵BC=14,∴DE BC=7,∵∠AFB=90°,AB=8,∴DF AB=4,∴EF=DE﹣DF=7﹣4=3,选B.2.【答题】如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD 的中点,AD=BC,∠EPF=140°,则∠EFP的度数是()A. 50°B. 40°C. 30°D. 20°【答案】D【分析】本题考查三角形的中位线.【解答】∵P是BD的中点,E是AB的中点,∴PE是△ABD的中位线,∴PE AD,同理,PF BC,∵AD=BC,∴PE=PF,∴∠EFP(180°﹣∠EPF)(180°﹣140°)=20°,选D.3.【答题】如图,在△ABF中,点C在中位线DE上,且CE CD,连接AC,BC,∠ACB=90°,若BF=20,则AB的长为()A. 10B. 12C. 14D. 16【答案】D【分析】本题考查三角形的中位线.【解答】∵DE是△ABC的中位线,BF=20,∴DE BF=10,∵CE CD,∴CD DE=8,∵∠ACB=90°,∴AB=2CD=16,选D.4.【答题】如图,△ABC中,N是BC边上的中点,AM平分∠BAC,BM⊥AM于点M,若AB=8,MN=2.则AC的长为()A. 10B. 11C. 12D. 13【答案】C【分析】本题考查三角形的中位线.【解答】延长BM交AC于D,如图所示:∵BM⊥AM于点M,∴∠AMB=∠AMD=90°,∵AM平分∠BAC,∴∠BAM=∠DAM,在△BAM和△DAM中,,∴△BAM≌△DAM(ASA).∴AD=AB=8,BM=MD,∵N是BC边上的中点,∴MN为△BCD的中位线,∴DC=2MN=4,∴AC=AD+DC=8+4=12.选C.5.【答题】如图,在△ABC中,∠A=90°,D是AB的中点,过点D作BC的平行线交AC于点E,作BC的垂线交BC于点F,若AB=CE,且△DFE的面积为1,则BC的长为()A. 2B. 5C. 4D. 10【答案】A【分析】本题考查三角形的中位线.【解答】如图,过A作AH⊥BC于H.∵D是AB的中点,∴AD=BD,∵DE∥BC,∴AE=CE,∴DE BC,∵DF⊥BC,∴DF∥AH,DF⊥DE,∴BF=HF,∴DF AH,∵△DFE的面积为1,∴DE•DF=1,∴DE•DF=2,∴BC•AH=2DE•2DF=4×2=8,∴AB•AC=8,∵AB=CE,∴AB=AE=CE AC,∴AB•2AB=8,∴AB=2(负值舍去),∴AC=4,∴BC.选A.6.【答题】如图,∠MAN=90°,点C在边AM上,AC=2,点B为边AN上一动点,连接BC,△A'BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A'B于点F,连接A'E.当△A'EF为直角三角形时,AB的长为______.【答案】或2【分析】本题考查三角形的中位线.【解答】当△A'EF为直角三角形时,存在两种情况:①当∠A'EF=90°时,如图,∵△A'BC与△ABC关于BC所在直线对称,∴A'C=AC=2,∠ACB=∠A'CB,∵点D,E分别为AC,BC的中点,∴DE是△ABC的中位线,∴DE∥AB,∴∠CDE=∠MAN=90°,∴∠CDE=∠A'EF,∴∠ACB=∠A'EC,∴∠A'CB=∠A'EC,∴A'C=A'E=2,在Rt△A'CB中,E是斜边BC的中点,∴BC=2AE'=4,由勾股定理可得AB2=BC2﹣AC2,∴AB;②当∠A'FE=90°时,如图,∵∠ADF=∠A=∠DFB=90°,∴∠ABF=90°,∵△A'BC与△ABC关于BC所在直线对称,∴∠ABC=∠CBA'=45°,∴△ABC为等腰直角三角形,∴AB=AC=2.综上,AB的长为或2.故答案为或2.7.【答题】如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为______.【答案】2【分析】本题考查三角形的中位线.【解答】∵M,N分别是AB和AC的中点,∴MN是△ABC的中位线,∴MN BC=2,MN∥BC,∴∠NME=∠D,∠MNE=∠DCE,∵点E是CN的中点,∴NE=CE,∴△MNE≌△DCE(AAS),∴CD=MN=2.故答案为2.8.【答题】如图,△ABC的周长为16,D,E,F分别为AB,BC,AC的中点,M,N,P分别为DE,EF,DF的中点,则△MNP的周长为______.如果△ABC,△DEF,△MNP分别为第1个,第2个,第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是______.【答案】4;【分析】本题考查三角形的中位线.【解答】∵△ABC的周长为16,D、F、E分别为AB、AC、BC的中点,∴EF、DF、DE为三角形中位线,∴EF AB,DE AC,DF BC,∴EF+DE+DF(AB+AC+BC),即△DEF的周长是△ABC周长的一半,同理,△MNP的周长是△DEF的周长的一半,即△MNP的周长=△ABC的周长的16=4,以此类推,第n个小三角形的周长是第一个三角形周长的16=,故答案为4;.9.【题文】如图,在△ABC中,AB=AC,点D是边AB的点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.(1)求证:FG=FH;(2)当∠A为多少度时,FG⊥FH?并说明理由.【答案】(1)见解答;(2)当∠A=90°时,FG⊥FH.理由见解答. 【分析】本题考查三角形的中位线.【解答】(1)证明:∵AB=AC.∴∠ABC=∠ACB,∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,∴∠ADE=∠AED,∴AD=AE,∴DB=EC,∵点F、G、H分别为BE、DE、BC的中点,∴FG是△EDB的中位线,FH是△BCE的中位线,∴FG BD,FH CE,∴FG=FH;(2)解:如图,延长FG交AC于N,∵FG是△EDB的中位线,FH是△BCE的中位线,∴FH∥AC,FN∥AB,∵FG⊥FH,∴∠A=90°,∴当∠A=90°时,FG⊥FH.10.【题文】如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.(1)如图1,BE的延长线与AC边相交于点D,求证:EF(AC﹣AB);(2)如图2,△ABC中,AB=9,AC=5,求线段EF的长.【答案】(1)见解答;(2)2.【分析】本题考查三角形的中位线.【解答】(1)证明:在△AEB和△AED中,,∴△AEB≌△AED(ASA),∴BE=ED,AD=AB,∵BE=ED,BF=FC,∴EF CD(AC﹣AD)(AC﹣AB);(2)解:如图,分别延长BE、AC交于点H,在△AEB和△AEH中,,∴△AEB≌△AED(ASA),∴BE=EH,AH=AB=9,∵BE=EH,BF=FC,∴EF CH(AH﹣AC)=2.11.【答题】如图,在中,,分别是,的中点,,是上一点,连接,,.若,则的长度为()A. B. C. D.【答案】B【分析】本题考查的是三角形中位线定理和直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.根据直角三角形的性质求出FE,根据三角形中位线定理计算即可.【解答】,,,;,分别是,的中点,为的中位线,,选B.12.【答题】如图,的周长为,点,都在边上,的平分线垂直于,垂足为,的平分线垂直于,垂足为,若,则的长为()A. B. C. D.【答案】C【分析】本题考查了三角形的中位线定理,解答本题的关键是判断出△BAE、△CAD是等腰三角形,利用等腰三角形的性质确定PQ是△ADE的中位线.首先判断△BAE、△CAD是等腰三角形,从而得出BA=BE,CA=CD,由△ABC的周长为32,及BC=12,可得DE=8,利用中位线定理可求出PQ.【解答】平分,,.,,,,同理,点是的中点,点是中点(三线合一),是的中位线,,,.选C.13.【答题】如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为()A. 50°B. 25°C. 15°D. 20°【答案】B【分析】本题考查了三角形中位线定理及等腰三角形的判定和性质,解题时要善于根据已知信息,确定应用的知识.根据中位线定理和已知,易证明△PMN是等腰三角形,根据等腰三角形的性质和已知条件即可求出∠PMN的度数.【解答】在四边形ABCD中,∵M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM AB,PN DC,PM∥AB,PN∥DC.∵AB=CD,∴PM=PN,∴△PMN是等腰三角形,∴∠PMN=∠PNM.∵PM∥AB,PN∥DC,∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,∴∠MPN=∠MPD+∠NPD=20°+(180﹣70)°=130°,∴∠PMN25°.选B.14.【答题】已知,四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是()A. 1<MN<5B. 1<MN≤5C. <MN<D. <MN≤【答案】D【分析】本题考查了三角形的中位线,解答此题的关键是根据题意作出辅助线,利用三角形的中位线定理和三角形的三边关系求解.当AB∥CD时,MN最短,利用中位线定理可得MN的最长值,作出辅助线,利用三角形中位线及三边关系可得MN的其他取值范围.【解答】连接BD,过M作MG∥AB,连接NG.∵M是边AD的中点,AB=2,MG∥AB,∴MG是△ABD的中位线,BG=GD,MG=AB=×2=1;∵N是BC的中点,BG=GD,CD=3,∴NG是△BCD的中位线,NG=CD=×3=,在△MNG中,由三角形三边关系可知MG-NG<MN<MG+NG,即-1<MN<+1,∴<MN<,当MN=MG+NG,即MN=时,四边形ABCD是梯形,故线段MN长的取值范围是<MN≤.选D.15.【答题】如图,点、、分别是的边、、的中点,连接、、得,如果的周长是,那么的周长是()A. B. C. D.【答案】B【分析】本题考查了三角形中位线定理.解题的关键是根据中位线定理得出边之间的数量关系.由于D、E分别是AB、BC中点,则DE是△ABC的中位线,那么DE=AC,同理有EF=AB,DF=BC,于是易求△DEF的周长.【解答】、分别是的边、的中点,,同理,,.选B.16.【答题】如图,中,是的中点,平分,于点,若,,则等于()A. B. C. D.【答案】C【分析】本题考查的是三角形中位线定理、全等三角形的判定和性质,三角形的中位线平行于第三边,且等于第三边的一半.延长BD交AC于H,证明△ADB≌△ADH,根据全等三角形的性质得到AH=AB=12,BD=DH,求出HC,根据三角形中位线定理计算即可.【解答】延长交于,平分,,,,,是中点,,,选C.17.【答题】如图,在四边形中,,,,分别是,,的中点,若,,则等于()A. B. C. D.【答案】A【分析】本题考查了三角形中位线定理和等腰三角形的判定与性质.中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.根据三角形中位线定理和等腰三角形等边对等角的性质求解即可.【解答】,,,分别是,,中点,是的中位线,是的中位线,,,,.又,,,,,,.选A.18.【答题】已知△ABC的周长为1,连接其三边中点构成第二个三角形,再连接第二个三角形的中点构成第三个三角形,以此类推,则第2012个三角形的周长为()A. B. C. D.【答案】C【分析】本题考查相似三角形的性质.【解答】∵连接△ABC三边中点构成第二个三角形,∴新三角形的三边与原三角形的三边的比值为1:2,∴它们相似,且相似比为1:2,同理:第三个三角形与第二个三角形的相似比为1:2,即第三个三角形与第一个三角形的相似比为1:22,以此类推:第2012个三角形与原三角形的相似比为1:22011,∵周长为1,∴第2012个三角形的周长为1:22011.选C.19.【答题】如图,▱ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为()A. 3cmB. 6cmC. 9cmD. 12cm【答案】B【分析】本题考查三角形的中位线.【解答】∵四边形ABCD是平行四边形,∴OA=OC;又∵点E是BC的中点,∴BE=CE,∴AB=2OE=2×3=6(cm),选B.20.【答题】如图,在中,,分别是,的中点,是线段上一点,连接,,若,,,则的长为______.【答案】18【分析】本题考查是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.根据直角三角形的性质得到DF=8,根据EF=1,得到DE=9,根据三角形中位线定理解答即可.【解答】,点是的中点,,,,、分别是,的中点,,故答案为.。
北师大版八年级数学下册第一章三角形的证明单元测试题(答案及解析)
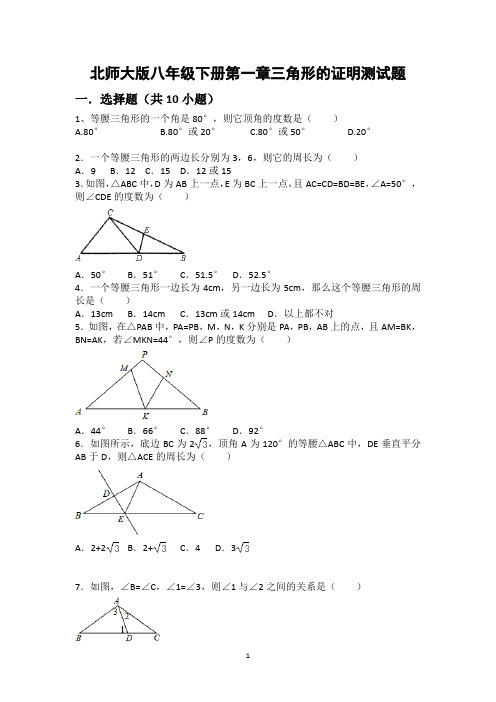
北师大版八年级下册第一章三角形的证明测试题一.选择题(共10小题)1、等腰三角形的一个角是80°,则它顶角的度数是()A.80°B.80°或20°C.80°或50°D.20°2.一个等腰三角形的两边长分别为3,6,则它的周长为()A.9 B.12 C.15 D.12或153.如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为()A.50°B.51°C.51.5°D.52.5°4.一个等腰三角形一边长为4cm,另一边长为5cm,那么这个等腰三角形的周长是()A.13cm B.14cm C.13cm或14cm D.以上都不对5.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为()A.44°B.66°C.88°D.92°6.如图所示,底边BC为2,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为()A.2+2B.2+C.4 D.37.如图,∠B=∠C,∠1=∠3,则∠1与∠2之间的关系是()A.∠1=2∠2 B.3∠1﹣∠2=180°C.∠1+3∠2=180° D.2∠1+∠2=180°8.如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于()A.110°B.120°C.130°D.140°9.如图,在△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF=()A.55°B.60°C.65°D.70°10.如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm²,则S阴影等于()A.2cm²B.1cm²C.cm²D.cm²二.填空题(共5小题)11.等边三角形是一个轴对称图形,它有______条对称轴.12.等腰三角形一腰上的高与另一腰的夹角为48°,则该等腰三角形的底角的度数为______.13.在等腰△ABC中,AB=AC,AC腰上的中线BD将三角形周长分为15和21两部分,则这个三角形的底边长为______.14.等腰三角形的一个内角为70°,它一腰上的高与底边所夹的度数为______.15.如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为______.三.解答题(共8小题)16.如图,在△ABC中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,且BE=.求证:AB平分∠EAD.17.如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:△OAB是等腰三角形.18.如图,已知△ABC中,AB=BD=DC,∠ABC=105°,求∠A,∠C度数.19.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.(1)求∠NMB的度数;(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;(3)你发现∠A与∠NMB有什么关系,试证明之.20.如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E.求证:△BDE是等腰三角形.21.如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DE⊥AB于点E,DF ⊥AC于点F.求证:△ABC是等腰三角形.22.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.23.如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.(1)当D点在BC的什么位置时,DE=DF?并证明.(2)DE,DF,CG的长之间存在着怎样的等量关系?并加以证明:(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?北师大版八年级下册第一章三角形的证明测试题参考答案与试题解析一.选择题(共10小题)1、等腰三角形的一个角是80°,则它顶角的度数是()【解答】解:①80°角是顶角时,三角形的顶角为80°,②80°角是底角时,顶角为180°﹣80°×2=20°,综上所述,该等腰三角形顶角的度数为80°或20°.故选B.2.一个等腰三角形的两边长分别为4,8,则它的周长为()A.12 B.16 C.20 D.16或20【解答】解:①当4为腰时,4+4=8,故此种情况不存在;②当8为腰时,8﹣4<8<8+4,符合题意.故此三角形的周长=8+8+4=20.故选C.3.如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为()A.50°B.51°C.51.5°D.52.5°【解答】解:∵AC=CD=BD=BE,∠A=50°,∴∠A=∠CDA=50°,∠B=∠DCB,∠BDE=∠BED,∵∠B+∠DCB=∠CDA=50°,∴∠B=25°,∵∠B+∠EDB+∠DEB=180°,∴∠BDE=∠BED=(180°﹣25°)=77.5°,∴∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°,故选D.4.一个等腰三角形一边长为4cm,另一边长为5cm,那么这个等腰三角形的周长是()A.13cm B.14cm C.13cm或14cm D.以上都不对【解答】解:当4cm为等腰三角形的腰时,三角形的三边分别是4cm,4cm,5cm符合三角形的三边关系,∴周长为13cm;当5cm为等腰三角形的腰时,三边分别是,5cm,5cm,4cm,符合三角形的三边关系,∴周长为14cm,故选C5.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为()A.44°B.66°C.88°D.92°【解答】解:∵PA=PB,∴∠A=∠B,在△AMK和△BKN中,∴△AMK≌△BKN,∴∠AMK=∠BKN,∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,∴∠A=∠MKN=44°,∴∠P=180°﹣∠A﹣∠B=92°,故选:D.6.如图所示,底边BC为2,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为()A.2+2B.2+C.4 D.3【解答】解:过A作AF⊥BC于F,∵AB=AC,∠A=120°,∴∠B=∠C=30°,∴AB=AC=2,∵DE垂直平分AB,∴BE=AE,∴AE+CE=BC=2,∴△ACE的周长=AC+AE+CE=AC+BC=2+2,故选:A.7.如图,∠B=∠C,∠1=∠3,则∠1与∠2之间的关系是()A.∠1=2∠2 B.3∠1﹣∠2=180°C.∠1+3∠2=180° D.2∠1+∠2=180°【解答】解:∵∠1=∠3,∠B=∠C,∠1+∠B+∠3=180°,∴2∠1+∠C=180°,∴2∠1+∠1﹣∠2=180°,∴3∠1﹣∠2=180°.故选B.8.如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于()A.110°B.120°C.130°D.140°【解答】解:∵∠A=40°,∴∠ACB+∠ABC=180°﹣40°=140°,又∵∠ABC=∠ACB,∠1=∠2,∴∠PBA=∠PCB,∴∠1+∠ABP=∠PCB+∠2=140°×=70°,∴∠BPC=180°﹣70°=110°.故选A.9.如图,在△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF=()A.55°B.60°C.65°D.70°【解答】解:∵AB=AC,∴∠B=∠C,在△DBE和△ECF中,∴△DBE≌△ECF(SAS),∴∠EFC=∠DEB,∵∠A=50°,∴∠C=(180°﹣50°)÷2=65°,∴∠CFE+∠FEC=180°﹣65°=115°,∴∠DEB+∠FEC=115°,∴∠DEF=180°﹣115°=65°.故选:C.10.如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm2,则S阴影等于()A.2cm2 B.1cm2 C.cm2 D.cm2【解答】解:根据三角形的面积公式,知:等底等高的两个三角形的面积相等.即有:S阴影=S△BCE=S△ABC=1cm2.故选:B.二.填空题(共10小题)11.等边三角形是一个轴对称图形,它有 3 条对称轴【解答】解:等边三角形是轴对称图像,它有三个顶点,所以对应3条对称轴故答案为:312.等腰三角形一腰上的高与另一腰的夹角为48°,则该等腰三角形的底角的度数为69°或21°.【解答】解:分两种情况讨论:①若∠A<90°,如图1所示:∵BD⊥AC,∴∠A+∠ABD=90°,∵∠ABD=48°,∴∠A=90°﹣48°=42°,∵AB=AC,∴∠ABC=∠C=(180°﹣42°)=69°;②若∠A>90°,如图2所示:同①可得:∠DAB=90°﹣48°=42°,∴∠BAC=180°﹣42°=138°,∵AB=AC,∴∠ABC=∠C=(180°﹣138°)=21°;综上所述:等腰三角形底角的度数为69°或21°.故答案为:69°或21°.13.在等腰△ABC中,AB=AC,AC腰上的中线BD将三角形周长分为15和21两部分,则这个三角形的底边长为16或8.【解答】解:∵BD是等腰△ABC的中线,可设AD=CD=x,则AB=AC=2x,又知BD将三角形周长分为15和21两部分,∴可知分为两种情况①AB+AD=15,即3x=15,解得x=5,此时BC=21﹣x=21﹣5=16;②AB+AD=21,即3x=21,解得x=7;此时等腰△ABC的三边分别为14,14,8.经验证,这两种情况都是成立的.∴这个三角形的底边长为8或16.故答案为:16或8.14.等腰三角形的一个内角为70°,它一腰上的高与底边所夹的度数为35°或20°.【解答】解:在△ABC中,AB=AC,①当∠A=70°时,则∠ABC=∠C=55°,∵BD⊥AC,∴∠DBC=90°﹣55°=35°;②当∠C=70°时,∵BD⊥AC,∴∠DBC=90°﹣70°=20°;故答案为:35°或20°.15.如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为32a .【解答】解:∵△A1B1A2是等边三角形∴∠B1A1A2=60°,A1B1=B1A2=A1A2∵∠MON=30°∴∠OB1A1=30°(三角形的一个外角等于和它不相邻的两个外角和∠OB1A1=∠B1A1A2-∠MON)∴OA1=A1B1(等边对等角)∴OA1=A1A2=a同理,根据∠MON=∠OB2A2,可得:A2A3=A2B2=OA1+A1A2=2A1A2=2a同理,可推出:A3A4=2A2A3=4a同理,可推出:A4A5=2A3A4=8a同理,可推出:A5A6=2A4A5=16a同理,可推出:A6A7=2A5A6=32a 即题目所求另外我们不难发现,第n个(△A1B1A2为第一个)等边三角形的边长为AnAn+1=(2^n-1)a 注:2的n-1次方倍的a三.解答题(共8小题)16.如图,在△ABC中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,且BE=.求证:AB平分∠EAD.【解答】证明:∵AB=AC,AD是BC边上的中线,∴BD=BC,AD⊥BC,∵BE=BC,∴BD=BE,∵AE⊥BE,∴AB平分∠EAD.17.如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:△OAB是等腰三角形.【解答】证明:∵AC⊥BC,BD⊥AD∴∠D=∠C=90°,在Rt△ABD和Rt△BAC中,,∴Rt△ABD≌Rt△BAC(HL),∴∠DBA=∠CAB,∴OA=OB,即△OAB是等腰三角形.另外一种证法:证明:∵AC⊥BC,BD⊥AD∴∠D=∠C=90°在Rt△ABD和Rt△BAC中∴Rt△ABD≌Rt△BAC(HL)∴AD=BC,在△AOD和△BOC中,∴△AOD≌△BOC(AAS),∴OA=OB,即△OAB是等腰三角形.18.如图,已知△ABC中,AB=BD=DC,∠ABC=105°,求∠A,∠C度数.【解答】解:∵AB=BD,∴∠BDA=∠A,∵BD=DC,∴∠C=∠CBD,设∠C=∠CBD=x,则∠BDA=∠A=2x,∴∠ABD=180°﹣4x,∴∠ABC=∠ABD+∠CDB=180°﹣4x+x=105°,解得:x=25°,所以2x=50°,即∠A=50°,∠C=25°.19.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.(1)求∠NMB的度数;(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;(3)你发现∠A与∠NMB有什么关系,试证明之.【解答】解:(1)∵在△ABC中,AB=AC,∠A=40°,∴∠ABC=∠ACB=70°,∵AB的垂直平分线交AB于点N,交BC的延长线于点M,∴MN⊥AB,∴∠NMB=90°﹣∠ABC=20°;(2)∵在△ABC中,AB=AC,∠A=70°,∴∠ABC=∠ACB=55°,∵AB的垂直平分线交AB于点N,交BC的延长线于点M,∴MN⊥AB,∴∠NMB=90°﹣∠ABC=35°;(3)∠NMB=∠A.理由:∵在△ABC中,AB=AC,∴∠ABC=∠ACB=,∵AB的垂直平分线交AB于点N,交BC的延长线于点M,∴MN⊥AB,∴∠NMB=90°﹣∠ABC=∠A.20.如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E.求证:△BDE是等腰三角形.【解答】解:(1)∵AD平分∠BAC,DE∥AC,∴∠EAD=∠CAD,∠EDA=∠CAD,∴∠EAD=∠EDA,∵BD⊥AD,∴∠EBD+∠EAD=∠BDE+∠EDA∴∠EBD=∠BDE,∴DE=BE,∴△BDE是等腰三角形.21.如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DE⊥AB于点E,DF ⊥AC于点F.求证:△ABC是等腰三角形.【解答】证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,∴DE=DF,在Rt△BDE和Rt△CDF中,,∴Rt△BDE≌Rt△CDF(HF),∴∠B=∠C,∴△ABC为等腰三角形.22.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.【解答】证明:∵AB=AC,AD是BC边上的中线,BE⊥AC,∴∠CBE+∠C=∠CAD+∠C=90°,∠CAD=∠BAD,∴∠CBE=∠BAD.23.如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.(1)当D点在BC的什么位置时,DE=DF?并证明.(2)DE,DF,CG的长之间存在着怎样的等量关系?并加以证明:(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?【解答】解:(1)当点D在BC的中点时,DE=DF,理由如下:∵D为BC中点,∴BD=CD,∵AB=AC,∴∠B=∠C,∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°,在△BED和△CFD中,∴△BED≌△CFD(AAS),∴DE=DF.(2)DE+DF=CG.证明:连接AD,则S△ABC=S△ABD+S△ACD,即AB•CG=AB•DE+AC•DF,∵AB=AC,∴CG=DE+DF.(3)当点D在BC延长线上时,(1)中的结论不成立,但有DE﹣DF=CG.理由:连接AD,则S△ABD=S△ABC+S△ACD,即AB•DE=AB•CG+AC•DF∵AB=AC,∴DE=CG+DF,即DE﹣DF=CG.同理当D点在CB的延长线上时,则有DE﹣DF=CG,说明方法同上.。
2019年秋浙教版初中数学八年级下册《图形与证明》单元测试(含答案) (145)

八年级数学下册《图形与证明》测试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)下面四个语句:①内错角相等;②OC是∠AOB的角平分线吗?③π不是有理数.其中是真命题的个数为()A.1个B.2个C.3个D.4个2.(2分)如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,若BF=AC,则∠ABC的大小是()A.40°B.45°C.50°D.60°3.(2分)对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的例子是()A.∠1=50°,∠2=40°B.∠1=50°,∠2=50°C.∠1=∠2=45°D.∠1=40°,∠2=40°4.(2分)下列语句是命题的有()①若两个角都等于50o,则这两个角是对顶角;②直角三角形一定不是轴对称图形;③画线段AB=2㎝;④在同一平面内的两条直线,若不相交,则平行A.1个B.2个C.3个D.4个5.(2分)如图,在△ABC中,∠B和∠C的平分线相交于点F,过点F作DE∥BC,交AB 于点D,交AC于点E.若 BD+CE=9,则线段DE的长为()A.9 B.8 C.7 D.66.(2分)已知a,b,C是同一平面内三条直线,下列命题中,属于假命题的是()A.若a⊥c,b⊥c,则a⊥bB.若a∥b,b⊥c,则a⊥cC.若a⊥c,b⊥c,则a∥bD.若a⊥c,b∥a,则b⊥c7.(2分)“a,b,c三数中至少有一个正数”的反面是()A.a,b,c三个都是正数B.a,b,c至少有一个负数C.a,b,c有两个或三个是负数D.a,b,c全都是非正数8.(2分)如图,如果AB∥CD,那么角α,β,γ之间的关系式为()A.α+β+γ=360° B.α-β+γ=180°C.α+β+γ=180° D.α+β-γ=180°9.(2分)如图所示,能使BF∥EG的条件是()A.∠l=∠3 B.∠2=∠4 C.∠2=∠3 D.∠l=∠410.(2分)如图,在Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,则下列结论中不正确的是()A.∠ACD=∠B B. CH=CE=EF C.AC=AF D.CH=HD11.(2分)等腰三角形的一个外角是80°,则其底角是()A.40°B.100°或40°C.100°D.80°12.(2分)如图所示是人字形屋架的设计图,由AB、AC、AD、BC四根钢条焊接而成,其中A、B、C、D均为焊接点,现在焊接所需要的四根钢条已截好,且已标出BC的中点D,如果焊接工身边只有检验直角的角尺,那么为了准确快速度地焊接,他首先应取的两根钢条及焊接点是()A.AB和BC,焊接点B B.AB和AC,焊接点AC.AD和BC,焊接点D D.AB和AD,焊接点A13.(2分)下列命题中,假命题的个数为()①若线段AC,BC满足AC=BC,则点C是线段AB的中点;②若b>0,则a+b>a;③如果一个角的两条边分别平行于另一个角的两条边,那么这丽个角相等;④如果两个数中有一个数是负数,那么这两个数之积是负数.A.4个B.3个C.2个D.1个14.(2分)下列命题中,是假命题的为()A.两条直线相交,只有一个交点B.全等三角形对应边上的中线相等C.全等三角形对应边上的高相等D.三角形一边上的中线把这个三角形分成两个全等的小三角形评卷人得分二、填空题15.(3分)在△ABC和△DEF中,①AB=DE;②BC=EF;③AC=DF;④∠A=∠D.从这四个条件中选取三个条件能判定△ABC≌△DEF的方法共有种.解答题16.(3分)如图,在△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数= .17.(3分)如图,点B,D在AN上,点C,E在AG上,且AB=BC=CD,EC=ED=EF,∠A=20°,则∠EG= .18.(3分)天河宾馆在重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯宽2 m,其侧面图如图所示,则购买地毯至少需要元.19.(3分)已知:如图所示,直线A8,CD相交.求证:AB,CD只有一个交点.证明:假设AB,CD相交有两个交点0与0′,那么过0,0′两点就有条直线.这与矛盾,所以假设不成立.所以.20.(3分)如图,点A,C在EF上,AD=BC,AD∥BC,AE=CF.求证:BF=DE.分析:要证BF=DE,只要证△≌△,已有条件AD=BC,AE=CF,只需证∠ =∠,只需证∠ =∠,而这可由证得.21.(3分)如图,把△ABC绕点C顺时针旋转35°到△A′B′C的位置,交AC于点D,若∠A′DC=90°,则∠A= .22.(3分)判断线段相等的定理(写出2个);.23.(3分)下面的判断是否正确:(1)我从书架上取出了5本书,5本书都是数学书.因此书架上的书都是数学书. ( )(2)有一条线段AB长3 cm.另一条线段BC长2 cm,那么AC长5cm ( )(3)直线AB,CD相交于O,∠AOC=30°,那么∠BOD=30°. ( )评卷人得分三、解答题24.(6分)判断命题“等腰三角形的角平分线平分对边”的真假,并给出证明.25.(6分)判断命题“两边及第三边上的高分别对应相等的两个三角形全等”的真假,并给出证明.26.(6分)如图,△ABC 中,AC ⊥BC ,CE ⊥AB 于点E ,AF 平分∠CAB 交CE 于点F ,过点F 作FD ∥BC 交AB 于点D ,求证:AC=AD .27.(6分)一个零件的形状如图所示,按规定∠A 应等于90°,∠B 和∠C 分别是32°和21°,检验工人量得∠BDC =148°,就断定这个零件不合格,你能否运用三角形的有关知识说明这个零件不合格的理由?28.(6分)阅读理解题:(1)如图,在△ABC 中,AD 是BC 边上的中线,且AD=21BC . 求证:∠BAC=90°. 证明:∵AD=12BC ,BD=CD=12BC ,∴AD=BD=DC , ∴∠B=∠BAD ,∠C=∠CAD , ∵∠B+∠BAD+∠CAD+∠C=180°,∴∠BAD+∠CAD=90°,即∠BAC=90°.(2)此题实际上是直角三角形的另一个判定定理,请你用文字语言叙述出来.(3)直线运用这个结论解答题目:一个三角形一边长为2,这边上的中线长为1,另两边之和为3,求这个三角形的面积.AB CD29.(6分)下列语句中,哪些是命题,哪些不是命题?若是命题,指出它的题设和结论.(1)立方等于本身的数是0或1;(2)画线段AB=3 cm.30.(6分)观察如图所示的四个图形,找出它们的共同特征并给以名称,再作出定义.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.A2.B3.A4.C5.A6.A7.D8.D9.A10.D11.A12.C13.B14.D二、填空题15.216.36°17.100°18.480°19.两;两点确定一条直线;AB,CD只有一个交点20.DEA,BFC,EAD,FCB,DAF,BCE,AD∥BC21.55°22.全等三角形的对应边相等;在一个三角形中,等角对等边23.(1)× (2)× (3)√三、解答题24.假命题.若这条角平分线是底角的平分线,则不一定平分对边25.假命题,证明略26.利用“ASA”证△ACF≌△ADF,得AC=AD27.连结BC,则∠DBC+∠DCB=180°-148°=32°,∴∠ABC+∠ACB=32°+32°+21°=85°,∴∠A=95°>90°所以这个零件不合格.28.如果三角形一边上的中线等于这边的一半,则这个三角形是直角三角形,S=3 2.29.(1)是;题设:一个数的立方等于它本身;结论:这个数是0或1;(2)不是30.轴对称图形:把一个图形沿着一条直线对折,直线两旁的部分能够互相重合,这样的图形叫做轴对称图形.。
(必考题)初中数学八年级数学下册第一单元《三角形的证明》检测卷(含答案解析)(3)
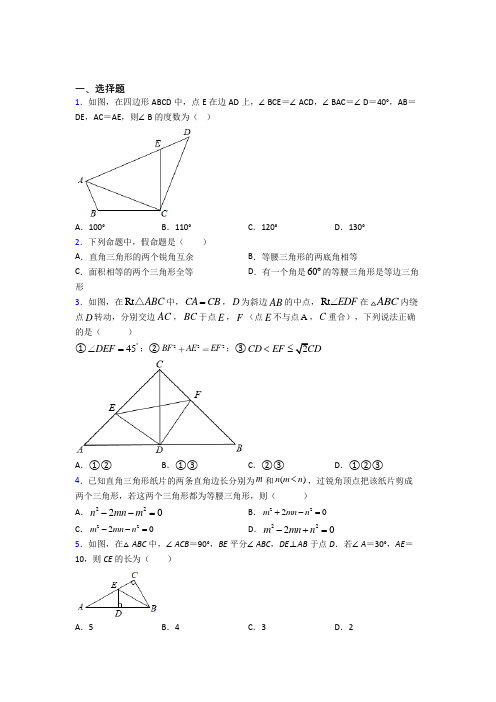
一、选择题1.如图,在四边形ABCD 中,点E 在边AD 上,∠BCE =∠ACD ,∠BAC =∠D =40°,AB =DE ,AC =AE ,则∠B 的度数为( )A .100°B .110°C .120°D .130°2.下列命题中,假命题是( )A .直角三角形的两个锐角互余B .等腰三角形的两底角相等C .面积相等的两个三角形全等D .有一个角是60︒的等腰三角形是等边三角形3.如图,在Rt ABC △中,CA CB =,D 为斜边AB 的中点,Rt EDF ∠在ABC 内绕点D 转动,分别交边AC ,BC 于点E ,F (点E 不与点A ,C 重合),下列说法正确的是( )①45DEF ︒∠=;②222BF AE EF ;③2CD EF CD <≤A .①②B .①③C .②③D .①②③ 4.已知直角三角形纸片的两条直角边长分别为m 和()n m n <,过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则( )A .2220n mn m --=B .2220m mn n +-=C .2220m mn n --=D .2220m mn n -+= 5.如图,在△ABC 中,∠ACB =90°,BE 平分∠ABC ,DE ⊥AB 于点D .若∠A =30°,AE =10,则CE 的长为( )A .5B .4C .3D .26.如图,直线AB ,CD 交于点O ,若AB ,CD 是等边△MNP 的两条对称轴,且点P 在直线CD 上(不与点O 重合),则点M ,N 中必有一个在( )A .∠AOD 的内部B .∠BOD 的内部C .∠BOC 的内部D .直线AB 上 7.如图,在△ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,若∠A =30°,BD =1,则AD 的长为( )A .3B .2C .3D .23 8.如图,在ABC 中,AB AC =,以点C 为圆心,CB 长为半径 画弧,交AB 于点B 和点D ,再分别以点,B D 为圆心,大于12BD 长为半径画弧,两弧相交于点M ,作射线CM 交AB 于点E .若4,1AE BE ==,则EC 的长度是( )A .3B .5C 5D 79.如图,在ABC 中,以点A 为圆心,AC 的长为半径作弧,与BC 交于点E ,分别以点E 和点C 为圆心、大于12EC 的长为半径作弧,两弧相交于点P ,作射线AP 交BC 于点D .若45B ∠=︒,2C CAD ∠=∠,则BAE ∠的度数为( )A .15︒B .25︒C .30D .35︒10.如图,ABC 中,AB 的垂直平分线分别交AB 、BC 于点D 、E ,AC 的垂直平分线分别交AC 、BC 于点F 、G ,若100BAC ∠=︒,则EAG ∠的度数是( )A .10°B .20°C .30°D .40°11.如图,在ABC 中,∠C =90°,∠B =30°,以点A 为圆心,任意长为半径画弧分别交AB ,AC 于点M 和N ,再分别以M ,N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,连接AP 并延长交BC 于点D ,则下列结论不正确的是( )A .AD 平分∠BACB .∠ADC =60° C .点D 在AB 的垂直平分线上 D .:DAC ABC S S =1:212.如图,A ,B 两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C 也在格点上,且ABC 为等腰三角形,在图中所有符合条件的点C 的个数为( )A .7B .8C .9D .10二、填空题13.如图,△ACD 是等边三角形,若AB =DE ,BC =AE ,∠E =115°,则∠BAE =_____°.14.如图,在Rt △ABC 中,∠ACB =90°,AC =BC =6,D 为BC 上一点,连接AD ,过点A 作AE ⊥AD ,取AE =AD ,连接BE 交AC 于F .当△AEF 为等腰三角形时,CD =_____.15.如图,已知△ABC 的周长是18,OB 、OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,且OD =1,△ABC 的面积是_____.16.如图,∠MON =33°,点P 在∠MON 的边ON 上,以点P 为圆心,PO 为半径画弧,角OM 于点A ,连接AP ,则∠APN =____.17.如图,在ABC 中,6,,BC AD DC =分别平分,BAC ACB ∠∠,点E 为BC 上一点,若105ADC ︒∠=,则CD DE +的最小值为________.18.如图,∠AOB =30°,点P 在∠AOB 的内部,OP =6cm ,点E 、F 分别为OA 、OB 上的动点,则△PEF 周长的最小值为________cm .19.在锐角ABC 中,AB AC =,CE 是高,且36ECA ∠=︒,平面内有一异于点A ,B ,C ,E 的点D ,若ABC CDA △△≌,则DAE ∠的度数为______.20.如图,AD 平分BAC ∠,DE AC ⊥,垂足为E ,//BF AC 交ED 的延长线于点F ,若BC 恰好平分ABF ∠.则下列结论中:①AD 是ABC ∆的高;②ABC ∆是等边三角形;③ED FD =;④AB AE BF =+.其中正确的是______________(填写序号)三、解答题21.数学课上,老师出示了如下的题目.在等边三角形ABC 中,点E 在边AB 上,点D 在CB 的延长线上,且ED EC =,如图,试确定线段AE 与DB 的大小关系,并说明理由.第一学习小组讨论后,进行了如下解答:(1)特殊情况,探索结论:当点E 为边AB 的中点时,如图2,确定线段AE 与DB 的大小关系,请你直接写出结论:AE ______DB (填“>”,“<”或“=”).(2)一般情况,启发解答:当点E 为边AB 上任意一点时,如图1,试确定线段AE 与DB 的大小关系,并说明理由.22.已知:如图,ABC 是等腰三角形,AB AC =,36A ∠=︒(1)利用尺规作B 平分线BD ,交AC 于点D ;(保留作图痕迹,不写作法) (2)判断ABD △是否为等腰三角形,并说明理由.23.如图,在等边△ABC 的AC ,BC 上各取一点D ,E ,使AD =CE ,AE ,BD 相交于点M ,过点B 作直线AE 的垂线BH ,垂足为H .(1)求证:△ACE ≌△BAD ;(2)若BE =2EC =4.①求△ABC 的面积;②求MH 的长.24.已知,如图,在△ABC 中,AD 是BC 边上的高线,CE 是AB 边上的中线(1)若∠B=30°,∠ACD=45°,AB=2,求BC 的长.(2)若点G是线段CE的中点,连接DG,当DG⊥EC时,求证: AB=2CD.(3)在(2)的条件下,试判断∠AEC与∠B之间的数量关系,并说明理由.25.如图,∠BAC=∠DAE=90°,AB=AC,AD=AE,BE、CD交于F.(1)求证:BE=CD;(2)连接CE,若BE=CE,求证:从“①DE⊥AC”、“②DE∥AB”中选择一个填入(2)中,并完成证明26.在△ABC中,AB=AC,∠BAC=90,BD平分∠AB C交AC于点D.(1)如图1,点F为BC上一点,连接AF交BD于点E.若AB=BF,求证:BD垂直平分AF.(2)如图2,CE⊥BD,垂足E在BD的延长线上.试判断线段CE和BD的数量关系,并说明理由.(3)如图3,点F为BC上一点,∠EFC=12∠ABC,CE⊥EF,垂足为E,EF与AC交于点M.直接写出线段CE与线段FM的数量关系.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】先ASA证明△BAC≌△EDC,再利用全等三角形的性质,等腰三角形的两底角相等即可求解.【详解】解:∵∠BCE=∠ACD,又∵∠BCE=∠BCA+∠ACE,∠ACD=∠DCE+∠ACE,∴∠BCA=∠DCE,∵∠BAC=∠D=40°,AB=DE,∴△BAC≌△EDC(ASA),∴AC=CD,∴∠CAE=∠D=40°,∵AC=AE,∴∠AEC=∠ACE=1(180°﹣∠CAE)=70°,2∵∠AEC=∠D+∠DCE,∴∠DCE=30°,∴∠ACB=30°,∴∠B=180°﹣∠ACB﹣∠BAC=110°.故选:B.【点睛】考查了全等三角形的判定与性质,等腰三角形的性质,关键是根据ASA证明△BAC≌△EDC.2.C解析:C【分析】根据直角三角形的性质、等腰三角形的性质、全等三角形的概念、等边三角形的判定定理判断即可.【详解】解:A、直角三角形的两个锐角互余,本选项说法是真命题;B、等腰三角形的两底角相等,本选项说法是真命题;C、面积相等的两个三角形不一定全等,本选项说法是假命题;D、有一个角是60°的等腰三角形是等边三角形,本选项说法是真命题;故选:C.【点睛】本题考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.3.A解析:A【分析】①证明∠A=∠DCB ,AD=CD ,∠ADE=∠CDF ,根据ASA 证明△ADE CDF ≅∆得ED=FD ,从而可判断①;②运用SAS 证明△EDC FDB ≅∆,得到CE BF =,再由222CE CF EF +=即可判断②;③当DE AC ⊥时,DE最短,从而可得DE CD ≤<,整理后代换即可判断③. 【详解】解:①∵,90CA CB ACB =∠=︒,∴△ABC 是等腰直角三角形∴∠45A B =∠=︒∵点D 是AB 的中点,∴,DA DB DC CD AB ==⊥,∠45DCB DCA =∠=︒∵∠EDF ADC =∠∴∠EDF EDC ADC EDC -∠=∠-∠∴∠ADE CDF =∠在△ADE 和△CDF 中A DCB AD CDADE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADE CDF ≅∆∴,DE DF AE CF ==∴△DEF 是等腰直角三角形∴∠45DEF =︒,故①正确;②∵∠90EDF CDB ︒=∠=∴∠EDF CDF CDB CDF -∠=∠-∠∴∠EDC FDB =∠在△EDC 与△FDB 中DE DF EDC FDB DC DB =⎧⎪∠=∠⎨⎪=⎩∴△EDC FDB ≅∆∴CE BF =∵222CE CF EF +=∴222BF AE EF ,故②正确; ③∵△DEF 是等腰直角三角形,∴EF =∵当DE AC ⊥时,22DE CD ==最短, ∴22CD DE CD ≤< ∴22CD DE CD ≤<即2CD EF CD ≤<,故③错误;∴综上,正确的是①②,故选:A .【点睛】 此题考查了全等三角形的判定与性质以及等腰直角三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.4.B解析:B【分析】根据等腰三角形的性质和勾股定理可得m 2+m 2=(n−m )2,整理即可求解【详解】解:如图,ABD 是等腰三角形,ACD 是等腰直角三角形,∴AD=BD=n-m ,根据勾股定理得:m 2+m 2=(n−m )2,∴2m 2=n 2−2mn +m 2,m 2+2mn−n 2=0.故选:B .【点睛】本题主要考查等腰三角形的性质,勾股定理,关键是熟练掌握等腰三角形的性质,根据勾股定理得到等量关系.5.A解析:A【分析】先根据含30°角的直角三角形的性质求出DE =5,再根据角平分线的性质求出CE =DE =5即可.【详解】解:∵DE⊥AB,∴∠ADE=90°,在Rt△ADE中,∠A=30°,AE=10,∴DE=1AE=5,2∵BE平分∠ABC,DE⊥AB,∠ACB=90°,∴CE=DE=5,故选:A.【点睛】本题考查的是角平分线的性质、含30°角的直角三角形的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.6.D解析:D【分析】根据等边三角形是轴对称图形,利用轴对称图形的性质解决问题即可.【详解】解:如图,∵△PMN是等边三角形,等边三角形的对称轴一定经过三角形的顶点,又∵直线CD,AB是△PMN的对称轴,直线CD经过点P,∴直线AB一定经过点M或N,故选:D.【点睛】本题考查轴对称,等边三角形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.7.C解析:C【分析】求出∠BCD=30°,根据含30°角的直角三角形的性质求出BC=2,求出AB=4,即可得出答案.【详解】解:∵△ABC中,∠ACB=90°,∠A=30°,∴∠B=60°,∵CD是高,∴∠CDB=90°,∴∠BCD=30°,∵BD=1,∴BC=2BD=2,∵在△ACB 中,∠ACB=90°,∠A=30°,∴AB=2BC=4,∴AD=AB-BD=4-1=3,故选:C .【点睛】本题考查了三角形的内角和定理,含30度角的直角三角形的性质的应用,解题的关键是得出BC=2BD 和AB=2BC ,难度适中.8.A解析:A【分析】利用基本作图得到CE AB ⊥,再根据等腰三角形的性质得到5AC =,然后利用勾股定理计算即可;【详解】由做法得CE AB ⊥,则90AEC ∠=︒,145AC AB BE AE ==+=+=,在Rt △ACE 中,3CE ===; 故答案选A .【点睛】 本题主要考查了等腰三角形的性质,准确计算是解题的关键.9.A解析:A【分析】 根据作图过程可得,AP 是EC 的垂直平分线,可得AE =AC ,∠ADB =∠ADC =90°,再根据∠B =45°,∠C =2∠CAD ,即可求出∠CAD 的度数,进而即可求解.【详解】解:由作图过程可知:AP 是EC 的垂直平分线,也是∠CAE 的角平分线,∴AE =AC ,∠ADB =∠ADC =90°,∵∠B =45°,∴∠BAD =45°,∵∠C =2∠CAD ,∴3∠CAD =90°,∴∠CAD =30°,∴∠EAD =30°,∴BAE ∠=45°-30°=15°.故选:A .【点睛】本题考查了作图−基本作图,直角三角形的性质,解决本题的关键是掌握基本作图方法. 10.B解析:B【分析】根据三角形内角和定理求出∠C +∠B ,根据线段的垂直平分线的性质得到EA =EB ,根据等腰三角形的性质得到∠EAB =∠B ,同理,∠GAC =∠C ,计算即可.【详解】解:∵∠BAC =100°,∴∠C +∠B =180°−100°=80°,∵DE 是AB 的垂直平分线,∴EA =EB ,∴∠EAB =∠B ,同理:∠GAC =∠C ,∴∠EAB +∠GAC =∠C +∠B =80°,∴∠EAG =100°−80°=20°,故选B .【点睛】本题考查的是线段的垂直平分线的性质和等腰三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.11.D解析:D【分析】由作图可得:AD 平分,BAC ∠ 可判断A ,再求解1302DAC DAB BAC ∠=∠=∠=︒, 可得60,ADC ∠=︒ 可判断B ,再证明,DA DB = 可判断C ,过D 作DF AB ⊥于,F 再证明,DC DF = 再利用 ACD ACD ABC ACD ABD S S S S S =+ ,可判断,D 从而可得答案. 【详解】解:90,30,C B ∠=︒∠=︒903060,BAC ∴∠=︒-︒=︒由作图可得:AD 平分,BAC ∠ 故A 不符合题意;1302DAC DAB BAC ∴∠=∠=∠=︒, 903060,ADC ∴∠=︒-︒=︒ 故B 不符合题意;30,DAB B ∠=∠=︒,DA DB ∴=D ∴在AB 的垂直平分线上,故C 不符合题意;过D 作DF AB ⊥于,F90,C AD ∠=︒平分,BAC ∠,DC DF ∴=30B ∠=︒,2,AB AC ∴= 11,,22ACD ABD S AC CD SAB DF ∴== 121122ACDACD ABC ACD ABD AC CD SS S S S AC CD AB DF ∴==++ 1.233AC AC AC AC AB AC AC AC ====++ 故D 符合题意; 故选:.D【点睛】 本题考查的是三角形的内角和定理,角平分线的作图,角平分线的性质,线段垂直平分线的判定,等腰三角形的判定,掌握以上知识是解题的关键.12.B解析:B【分析】分两种情况:①AB 为等腰三角形的底边;②AB 为等腰三角形的一条腰;画出图形,即可得出结论.【详解】解:如图所示:①AB 为等腰三角形的底边,符合条件的点C 的有5个;②AB 为等腰三角形的一条腰,符合条件的点C 的有3个.所以符合条件的点C 共有8个.故选:B .【点睛】此题考查了等腰三角形的判定,熟练掌握等腰三角形的判定是解题的关键,注意数形结合的解题思想.二、填空题13.125【分析】先证明得到再根据三角形内角和得到所求角中两角的和最后与等边三角形内角相加就得到结果【详解】解:是等边三角形在与中故答案为125【点睛】这道题考察的是等边三角形的性质全等三角形的判定和性 解析:125【分析】先证明ABC DEA ≌,得到BAC ADE ∠∠=,再根据三角形内角和得到所求角中两角的和BAC DAE ∠+∠,最后与等边三角形内角CAD ∠相加就得到结果.【详解】解:ACD 是等边三角形,AC AD ∴=,60CAD ∠︒=在ABC 与DEA 中, =⎧⎪=⎨⎪=⎩AB DE BC AE AC AD ABC DEA SSS ∴≌()BAC ADE ∴∠∠=18011565BAC DAE ADE DAE ∴∠+∠∠+∠︒-︒︒===6560125BAE BAC DAE CAD ∴∠∠+∠+∠︒+︒︒===故答案为125.【点睛】这道题考察的是等边三角形的性质,全等三角形的判定和性质,三角形内角和的概念.解题的关键在于熟练掌握这些相关知识点.14.2或6【分析】分两种情形:当AE=AF 时如图1中过点E 作EH ⊥AC 于H 证明AH =FH =CF =CD 可得结论如图2中当AF =EF 时点D 与D 重合此时CD =BC =6【详解】解:①当AE=EF 时如图1中过点E解析:2或6【分析】分两种情形:当AE=AF 时,如图1中,过点E 作EH ⊥AC 于H .证明AH =FH =CF =CD ,可得结论,如图2中,当AF =EF 时,点D 与D 重合,此时CD =BC =6【详解】解:①当AE=EF 时,如图1中,过点E 作EH ⊥AC 于H .∵EA =EF ,EH ⊥AF ,∴AH =HF ,∵EA ⊥AD ,∴∠EAD =∠EHA =∠C =90°,∴∠EAH +∠CAD =90°,∠CAD +∠ADC =90°,∴∠EAH =∠ADC ,在△EHA 和△ACD ,EAH ADC EHA C AE DA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EHA ≌△ACD (AAS ),∴AH =CD ,EH =AC =CB .在△EHF 和△BCF 中,EFH BFC EHF C EH BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EHF ≌△BCF (AAS ),∴FH =CF ,∴AH =FH =CF =CD ,∴CD=13AC =2, ②如图2中,当AF =EF 时,点B 与点D 重合,此时CD =BC =6综上所述,满足条件的CD的长度为2或6故答案为:2或6【点睛】本题考查等腰直角三角形的性质,全等三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.15.9【分析】过点O作OE⊥AB于EOF⊥AC与F连接OA根据角平分线的性质求出OEOF根据三角形面积公式计算得到答案【详解】解:过点O作OE⊥AB 于EOF⊥AC于F连接OA∵OB平分∠ABCOD⊥BC解析:9【分析】过点O作OE⊥AB于E,OF⊥AC与F,连接OA,根据角平分线的性质求出OE、OF,根据三角形面积公式计算,得到答案.【详解】解:过点O作OE⊥AB于E,OF⊥AC于F,连接OA,∵OB平分∠ABC,OD⊥BC,OE⊥AB,∴OE=OD=1,同理可知,OF=OD=1,∴△ABC的面积=△OAB的面积+△OAC的面积+△OBC的面积,=12×AB×OE+12×AC×OF+12×BC×OD,=12×18×1,=9,故答案为:9.【点睛】本题主要考查了角平分线的性质,准确计算是解题的关键.16.66°【分析】根据等腰三角形的性质可知∠MON=∠PAO再用外角的性质求解即可【详解】解:由作图可知PO=PA∴∠MON=∠PAO=33°∠APN=∠MON+∠PAO=66°故答案为:66°【点睛】解析:66°【分析】根据等腰三角形的性质可知∠MON=∠PAO,再用外角的性质求解即可.【详解】解:由作图可知,PO=PA,∴∠MON=∠PAO=33°,∠APN =∠MON+∠PAO=66°,故答案为:66°.【点睛】本题考查了等腰三角形的性质和外角的性质,解题关键是通过作图得到等腰三角形,依据等腰三角形的性质熟练计算.17.3【分析】如图过作于连接先说明平分当时可得可得所以当三点共线时此时最短再求解结合从而可得答案【详解】解:如图过作于连接分别平分平分当时则所以当三点共线时此时最短分别平分即的最小值是故答案为:【点睛】 解析:3【分析】如图,过D 作DP AB ⊥于,P 连接,BD 先说明BD 平分,ABC ∠ 当DE BC ⊥时,可得,DP DE = 可得,CD DE CD DP +=+ 所以当,,C D P 三点共线时,,CD DP CP += 此时最短,再求解30ABC ∠=︒,结合,CP AB ⊥ 从而可得答案. 【详解】解:如图,过D 作DP AB ⊥于,P 连接,BD,AD DC 分别平分,BAC ACB ∠∠,BD ∴平分,ABC ∠当DE BC ⊥时,则,DP DE =,CD DE CD DP ∴+=+所以当,,C D P 三点共线时,,CD DP CP += 此时最短,105ADC ∠=︒,18010575DAC DCA ∴∠+∠=︒-︒=︒,,AD DC 分别平分,BAC ACB ∠∠,()2150,BAC BCA DAC DCA ∴∠+∠=∠+∠=︒18015030ABC ∴∠=︒-︒=︒,,CP AB ⊥116322CP BC ∴==⨯=, 即CD DE +的最小值是3,故答案为:3.【点睛】本题考查的是三角形的内角和定理,三角形的角平分线的性质,含30的直角三角形的性质,垂线段最短,掌握以上知识是解题的关键.18.6【分析】作点P 关于OA 对称的点作点P 关于OB 对称的点连接与OA 交于点E 与OB 交于点F 此时△PEF 的周长最小然后根据∠AOB=30°结合轴对称的性质证明△是等边三角形从而可得答案【详解】解:如图作点解析:6【分析】作点P 关于OA 对称的点1P ,作点P 关于OB 对称的点2P ,连接1122,,,OP PP OP 12PP 与OA 交于点E ,与OB 交于点F ,此时△PEF 的周长最小,然后根据∠AOB=30°,结合轴对称的性质证明△12OPP 是等边三角形,从而可得答案.【详解】解:如图,作点P 关于OA 对称的点1P ,作点P 关于OB 对称的点2P ,连接1122,,,OP PP OP 12PP 与OA 交于点E ,与OB 交于点F ,此时△PEF 的周长最小.此时△PEF 的周长就是12PP 的长,由轴对称的性质可得:12,,POE POE P OF POF ∠=∠∠=∠12OP OP OP ==()122222,POP POE POF POE POF AOB ∴∠=∠+∠=∠+∠=∠∵∠AOB=30°,∴1260POP ∠=︒,∴△12OPP 是等边三角形.6OP =,∴121 6.PP OP OP ===∴△PEF 周长的最小值是6.故答案为:6.【点睛】本题考查轴对称最短路径问题,关键是确定E ,F 的位置,本题的突破点是证明△12OPP 是等边三角形.19.117°或9°【分析】根据等腰三角形的性质和全等三角形的性质解答即可【详解】如图所示∵在△ABC中AB=ACCE是高且∠ECA=36°∴∠BAC=90°-36°=54°∠ACB=∠ABC=63°∵△解析:117°或9°【分析】根据等腰三角形的性质和全等三角形的性质解答即可.【详解】如图所示,∵在△ABC中,AB=AC,CE是高,且∠ECA=36°,∴∠BAC=90°-36°=54°,∠ACB=∠ABC=63°,∵△ABC≌△CDA,∴∠CAD=∠ACB=63°,∴∠DAE=∠CAD+∠BAC=63°+54°=117°,同理,∠D1AE=∠CAD1-∠BAC=63°-54°=9°,故答案为:117°或9°【点睛】本题考查了全等三角形的性质及等腰三角形的性质,熟练掌握等腰三角形的性质,正确找出对应角是解题关键.20.①③④【分析】利用平行线的性质∠C=∠FBD则可证明∠C=∠ABC于是可根据等腰三角形的性质对①②进行判断;过D点作DH⊥AB如图利用角平分线的性质得到DE=DHDH=DF则可对③进行判断;证明△A解析:①③④【分析】利用平行线的性质∠C=∠FBD,则可证明∠C=∠ABC,于是可根据等腰三角形的性质对①②进行判断;过D点作DH⊥AB,如图,利用角平分线的性质得到DE=DH,DH=DF,则可对③进行判断;证明△ADE≌△ADH得到AH=AE,同理可得BH=BF,则可对④进行判断.【详解】解:∵BC恰好平分∠ABF,∴∠ABC=∠FBD,∵AC ∥BF ,∴∠C=∠FBD ,∴∠C=∠ABC ,∴△ABC 为等腰三角形,∵AD 平分∠BAC ,∴AD ⊥BC ,CD=BD ,∴AD 是ABC ∆的高;ABC ∆是等腰三角形;所以①正确;②错误;过D 点作DH ⊥AB 于H ,如图,∵AD 平分∠BAC ,DE ⊥AC ,DH ⊥AB ,∴DE=DH ,∵AC ∥BF ,DE ⊥AC ,∴DF ⊥BF ,∵BD 平分∠ABF ,DH ⊥AB ,∴DH=DF ,∴DE=DF ,所以③正确;在△ADE 和△ADH 中,AD AD DE DH =⎧⎨=⎩, ∴△ADE ≌△ADH (HL ),∴AH=AE ,同理可得BH=BF ,∴AB=AH+BH=AE+BF ,所以④正确.故答案为:①③④.【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了平行线的性质和等腰三角形的性质.三、解答题21.(1)AE BD =;(2)AE BD =,见解析【分析】(1)根据等边三角形性质可得∠ECB=30°=∠D=∠DEB ,从而DB=BE=AE ;(2)作EF ∥BC ,交AC 于点F .则△AEF 为等边三角形.根据“SAS”证明△BDE ≌△FEC ,得BD=EF=AE .【详解】解:(1)E 为AB 的中点时,AE 与DB 的大小关系是:AE=DB .理由如下:∵△ABC 是等边三角形,点E 是AB 的中点,∴AE=BE ;∠BCE=30°.∵ED=EC ,∴∠ECD=∠D=30°.又∵∠ABC=60°,∴∠DEB=30°.∴DB=BE=AE ;故答案为:=.(2)证明:如图,过点E 作//EF BC 交AC 于F ,∵ABC 是等边三角形∴60ABC ACB BAC ∠=∠=∠=︒,AB BC AC ==∵//EF BC∴AFE ACB ,AEF ABC ∠=∠∴AFE AEF BAC ∠=∠=∠∴AEF 是等边三角形∴AE AF EF ==,∴BE CF =∵ED EC =∴ECB EDB ∠=∠又∵60EBC BED EDB ∠=∠+∠=︒ 60ACB ECB FCE ∠=∠+∠=︒∴BED FCE ∠=∠∵BE CF =,DE EC =∴BDE FEC ≌ ∴DB EF =,∵AE EF =,∴AE BD =.【点睛】本题考查了全等三角形的性质和判定,三角形的内角和定理,等边三角形的性质和判定的理解和运用,能综合运用性质进行推理是解此题的关键.22.(1)见详解;(2)是等腰三角形,证明见详解.【分析】(1)以B为圆心,以任意长为半径画弧交AB、AC于两点,再以这两点为圆心,以大于这两点的距离的一半为半径画弧,交于一点,过点B和这点作射线交AC与点D即可;(2)由∠A=36°,求出∠ABC=72°,进而求出∠ABD,根据等角对等边即可证明结论.【详解】解:(1)如图所示:BD即为所求;(2)ABD△是等腰三角形.∵AB=AC,∴∠ABC=∠C,∵∠A=36°,∴∠ABC=∠ACB=(180°﹣36°)÷2=72°,∵BD平分∠ABC,∴∠ABD=∠DBC=36°,∴∠ABD=∠A,∴AD=BD,∴ABD△是等腰三角形.【点睛】本题主要考查了等腰三角形的性质和判定,三角形的内角和定理,角平分线的性质,尺规作图-作已知角的平分线等知识点,解此题的关键是能正确画图和求出∠ABD的度数.23.(1)见解析;(2)①367【分析】(1)根据等边三角形的性质,直接运用SAS证明即可;(2)①作AF⊥BC于F点,利用“三线合一”的性质结合已知条件先求出AF的长度,从而根据12·ABCS BC AF即可求解;②先在Rt△AFE中求解出AE的长度,再求出△ABE的面积,结合等面积法即可求出BH的长度,然后根据(1)的结论进一步证明∠BMH=60°,则在Rt△BMH中即可求解MH的长度.【详解】(1)∵△ABC为等边三角形,∴AB=CA ,∠BAD=∠ACE=60°,在△BAD 和△ACE 中,AD CE BAD ACE AB CA =⎧⎪∠=∠⎨⎪=⎩∴△ACE ≌△BAD (SAS );(2)如图所示,作AF ⊥BC 于F 点,①由“三线合一”知,∠BAF=30°,∵BC=BE+EC=4+2=6,∴AB=6,BF=3, 由勾股定理可得:33AF =,∴116339322ABC S BC AF ==⨯⨯=△; ②由①可知,33AF =,FE=1,∴根据勾股定理可得,2227AE AF FE =+=, ∵114336322ABE S BE AF ==⨯⨯=△, ∴226362127ABE S BH AE ⨯===△, 由(1)可得,∠ABD=∠CAE ,∴∠ABD+∠BAM=∠CAE+∠BAM=60°,即:∠BMH=∠ABD+∠BAM=60°,则在Rt △BHM 中,∠MBH=30°,∴3BH MH =, ∴6773MH ==.【点睛】本题主要考查等边三角形的性质以及全等三角形的判定与性质综合运用,灵活运用全等三角形的性质以及等面积法求高是解题关键.24.(1)31+;(2)见解析;(3)32AEC B =∠∠,理由见解析. 【分析】(1)由直角三角形中,30°角所对的直角边等于斜边的一半解得AD=DC=1,再结合勾股定理解题即可;(2)由三线合一性质证明DC=DE ,由直角三角形斜边中线等于斜边的一半得到12DE AB =,据此利用等量代换解题即可; (3)由直角三角形斜边中线性质可证BE=ED ,再结合等边对等角解得∠DEC=∠DCE ,最后根据角的和差解题即可.【详解】解:(1)∵AD 是BC 边上的高线∴∠ADC=∠ADB=90°∵∠ACD=45°,∠B=30°∴∠ACD=∠CAD=45°,∠BAD=60°∴AD=DC ,12AD AB =又∵AB=2∴AD=DC=1在Rt △ABD 中,22BD AB AD =-=3∴BC=BD+CD=31+;(2)证明:∵G 是线段CE 的中点,DG ⊥EC∴DC=DE∵CE 是AB 边上的中线,AD ⊥BC ∴12DE AB =∴12DC AB =即AB=2CD ;(3)32AEC B =∠∠,理由如下, ∵12DE AB =,AE=BE ∴BE=ED∴∠B=∠EDB∵DE=DC∴∠DEC=∠DCE∴∠B=∠EDB=2∠DCE又∵∠AEC=∠B+∠DCE∴∠AEC=3∠DCE ∴32AEC B =∠∠. 【点睛】本题考查含30°的直角三角形的性质、直角三角形斜边的中线、三线合一性质、勾股定理、等边对等角等知识,是重要考点,难度一般,掌握相关知识是解题关键.25.(1)见解析;(2)见解析【分析】(1)根据“SAS”证明△BAE ≌△CAD ,然后根据全等三角形的性质解答即可;(2)根据线段垂直平分线的判定可知CA 垂直平分DE ,进而可证明结论成立.【详解】证明:(1)∵∠BAC =∠DAE =90°,∴∠DAE +∠DAB =∠BAC +∠DAB ,即∠BAE =∠CAD ,在△BAE 与△CAD 中,AD AE CAD BAE AB AC =⎧⎪∠=∠⎨⎪=⎩,∴△BAE ≌△CAD (SAS ),∴BE =CD ;(2)∵BE =CD ,BE =CE ,∴CE =CD ,又∵AD =AE ,∴CA 垂直平分DE ,∴DE ⊥AC (可得①),又∵∠BAC =90°,∴DE//AB (可得②).【点睛】本题主要考查了全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.也考查了线段垂直平分线的判定、平行线的判定等知识.26.(1)见解析;(2)BD=2CE,理由见解析;(3)FM=2CE.【分析】(1)由BD平分∠AB C,可得∠ABE=∠FBE,可证△ABE≌△FBE(SAS),可得AE=FE,∠AEB=∠FEB=12×180°=90°即可;(2)延长CE,交BA的延长线于G,由CE⊥BD,∠ABE=∠FBE,可得GE=2CE=2GE,可证△BAD≌△CAG(ASA),可得BD=CG=2CE;(3)作FM的中垂线NH交CF于N,交FM于H,由FN=MN,MH=FH=12FM,可得∠NMH=∠NBH,由∠EFC=12∠ABC=22.5°,可求∠ABC=∠ACB=∠MNC=45°,可得NM=CM=FN,由外角∠EMC=∠MFC+∠MCF=22.5°+45°=67.5°,可求∠ECM=90°-∠EMC=22.5°,可证△FNH≌△CME(AAS),可得FH=CE即可.【详解】证明(1)∵BD平分∠AB C,∴∠ABE=∠FBE,∵BA=BF,BE=BE,∴△ABE≌△FBE(SAS),∴AE=FE,∠AEB=∠FEB=12× 180°=90°,∴BD垂直平分AF.(2)BD=2CE,理由如下:延长CE,交BA的延长线于G,∵CE⊥BD,∠ABE=∠FBE,∴GE=2CE=2GE,∵∠CED=90°=∠BAD,∠ADB=∠EDC,∴∠ABD=∠GCA,又AB=AC,∠BAD=∠CAG,,∴△BAD≌△CAG(ASA),∴BD=CG=2CE,(3)FM=2 CE,理由如下:作FM的中垂线NH交CF于N,交FM于H,∴FN=MN,MH=FH=1FM,2∴∠NMH=∠NBH,∵∠EFC=1∠ABC=22.5°,2∠ABC=∠ABC,∴∠MNC=2∠NFH=2×12∵AB=AC,∠BAC=90,∴∠ABC=∠ACB=∠MNC=45°,∴NM=CM=FN,∵∠EMC=∠MFC+∠MCF=22.5°+45°=67.5°,∴∠ECM=90°-∠EMC=22.5°,∴∠NFH=∠MCE,又∵∠FHN=∠E=90°,∴△FNH≌△CME(AAS),∴FH=CE,∴FM=2FH=2CE.【点睛】本题考查角平分线性质,三角形全等判定与性质,直角三角形两锐角互余,线段垂直平分线,三角形外角性质,掌握角平分线性质,三角形全等判定与性质,直角三角形两锐角互余,线段垂直平分线是解题关键.。
八年级数学上册试题 第13章《三角形中的边角关系、命题与证明》章节测试卷-沪科版(含解析)

第13章《三角形中的边角关系、命题与证明》章节测试卷一.选择题(共10小题,满分30分,每小题3分)1.下列实际情景运用了三角形稳定性的是()A.人能直立在地面上B.校门口的自动伸缩栅栏门C.古建筑中的三角形屋架D.三轮车能在地面上运动而不会倒2.如图,△ABC的三边长均为整数,且周长为22,AM是边BC上的中线,△ABM的周长比△ACM的周长大2,则AC长的可能值有()个.A.3B.4C.5D.63.下列命题是假命题的是( )A.如果∠1=∠2,∠2=∠3,那么∠1=∠3B.对顶角相等C.如果一个数能被6整除,那么它肯定也能被3整除D.内错角相等4.如图所示,∠F=90°,CE⊥AB,C是BF的中点,D是BE上的一点,下列说法正确的是( )A.CD是△ABC的中线B.AF是△ABC的高C.CE是△ABF的中位线D.AC是△ABF的角平分线5.如图,在△ABC中,AD是△ABC的角平分线,DE⊥AC,若∠B=40°,∠C=60°,则∠ADE的度数为()A.30°B.40°C.50°D.60°6.如图,在△ABC中,G是边BC上任意一点,D、E、F分别是AG、BD、CE的中点,S△ABC 的值为()=48,则SΔDEFA.2B.4C.6D.87.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为3、4、5、7,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值是( )A.7B.8C.9D.108.如图,△ABC中,∠ABC=3∠C,E分别在边BC,AC上,∠EDC=24°,∠ADE=3∠AED,∠ABC的平分线与∠ADE的平分线交于点F,则∠F的度数是( )A.54°B.60°C.66°D.72°9.如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D.∠ABD的角平分线BF所在直线与射线AE 相交于点G,若∠ABC=3∠C,且∠G=20°,则∠DFB的度数为()A.50°B.55°C.60°D.65°10.如图,∠ABC=∠ACB,BD、CD、BE分别平分∠ABC,外角∠ACP,外角∠MBC,以下结论:①AD∥BC,②BD⊥BE,③∠BDC+∠ABC=90°,④∠BAC+2∠BEC=180°,其中正确的结论有()A.1个B.2个C.3个D.4个二.填空题(共6小题,满分18分,每小题3分)11.如图,有一张三角形纸片ABC,∠B=32°,∠A=100°,点D是AB边上的固定点(BD<1AB),2在BC上找一点E,将纸片沿DE折叠(DE为折痕),点B落在点F处,当EF与AC边平行时,∠BDE的度数为.12.如图,AD为△ABC的中线,DE,DF分别为△ABD,△ACD的一条高,若AB=6,DE=4,则AC=.,DF=8313.已知△ABC的边长a,b,c满足(a−2)2+|b−4|=0,则a、b的值分别是,若c为偶数,则△ABC的周长为.14.如图,在△ABC中,点D是AC边上一点,CD:AD=1:2,连接BD,点E是线段BD上一点,BE:ED=1:3,连接AE,点F是线段AE的中点,连接CF交线段BD于点G,若△ABC的面积是12,则△EFG的面积是.15.如图△AOB和△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=70°,点D在边OA上,将△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中当CD∥AB时,旋转时间秒.16.如果三角形中任意两个内角∠α与∠β满足2α−β=60°,那么我们称这样的三角形为“斜等边三角形”.在锐角三角形ABC中,BD⊥AC于点D,若△ABC、△ABD、△BCD都是“斜等边三角形”,则∠ABC=.三.解答题(共7小题,满分52分)17.(6分)(1)一个多边形的内角和是外角和的3倍,这个多边形是几边形?(2)小明求得一个多边形的内角和为1280°,小强很快发现小明所得的度数有误,后来小明复查时发现他重复加了一个内角,求出这个多边形的边数以及他重复加的那个角的度数.18.(6分)如图所示,D是△ABC的边AC上任意一点(不含端点),连结BD,请判断AB+BC+AC 与2BD的大小关系,并说明理由.19.(8分)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.将△ABC平移,使点C平移至点D,点A、B的对应点分别是点E、F.(1)在图中请画出△ABC平移后得到的△DEF;(2)在图中画出△ABC的AB边上的高CH;(3)若连接CD、AE,则这两条线段之间的关系是 ;(4)△DEF的面积为 .20.(8分)如图所示,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10 cm,∠CAB=90°.(1)求AD的长;(2)求△ACE和△ABE周长的差.21.(8分)在△ABC中,∠B,∠C均为锐角且不相等,线段AD是△ABC中BC边上的高,AE是△ABC的角平分线.(1)如图1,∠B=70°,∠C=30°,求∠DAE的度数;(2)若∠B=x°,∠DAE=10°,则∠C=______;(3)F是射线AE上一动点,C、H分别为线段A B,BC上的点(不与端点重合),将△BGH沿着GH 折叠,使点B落到点F处,如图2所示,请直接写出∠1,∠2与∠B的数量关系.22.(8分)已知,在△ABC中,∠BAC=∠ABC,点D在AB上,过点D的一条直线与直线AC、BC分别交于点E、F.(1)如图1,∠BAC=70°,则∠CFE+∠FEC=______°.(2)如图2,猜想∠BAC、∠FEC、∠CFE之间的数量关系,并加以证明;(3)如图3,直接写出∠BAC、∠FEC、∠CFE之间的数量关系______.23.(8分)将含30°角的三角板ABC(∠B=30°)和含45°角的三角板FDE及一把直尺按图方式摆放在起.使两块三角板的直角顶点A,F重合.点A,F,C,E始终落在直尺的PQ边所在直线上.将含45°角的三角板FDE沿直线PQ向右平移.(1)当点F与点C重合,请在备用图中补全图形,并求平移后DC与CB形成的夹角∠DCB的度数;(2)如图,点F在线段AC上移动,M是边AB上的动点,满足∠DFM被FB平分,∠EFM的平分线FN与边BC交于点N,请证明在移动过程中,∠NFB的大小保持不变;(3)仿照(2)的探究,点F在射线CQ上移动,M是边AB上的动点,满足∠DFM被FB平分,∠EFM的平分线F N'所在直线与直线BC交于点N,请写出一个与平移过程有关的合理猜想.(不用证明)答案一.选择题1.C【分析】根据三角形的稳定性进行判断即可求解.【详解】解:古建筑中的三角形屋架是利用了三角形的稳定性,故选C2.B【分析】依据ΔABC的周长为22,ΔABM的周长比ΔACM的周长大2,可得2<BC<11,再根据ΔABC的三边长均为整数,即可得到BC=4,6,8,10.【详解】解:∵ΔABC的周长为22,ΔABM的周长比ΔACM的周长大2,∴2<BC<22−BC,解得2<BC<11,又∵ΔABC的三边长均为整数,ΔABM的周长比ΔACM的周长大2,∴AC=22−BC−22=10−12BC为整数,∴BC边长为偶数,∴BC=4,6,8,10,即AC的长可能值有4个,故选:B.3.D【分析】利用对顶角的性质、实数的性质、平行线的性质分别判断后即可确定正确的选项.【详解】解:A、如果∠1=∠2,∠2=∠3,那么∠1=∠3,正确,是真命题,故本选项不符合题意;B、对顶角相等,正确,是真命题,故本选项不符合题意;C、如果一个数能被6整除,那么它肯定也能被3整除,正确,是真命题,故本选项不符合题意;D、两直线平行,内错角相等,原命题是假命题,故本选项符合题意.故选:D.4.B【分析】根据三角形中位线的定义,三角形角平分线、中线和高的定义作答.【详解】解:A、AC是△ABC的中线,故本选项不符合题意.B 、由∠F =90°知,AF 是△ABC 的高,故本选项符合题意.C 、CE 是△ABC 的高,故本选项不符合题意.D 、AC 是△ABF 的中线,故本选项不符合题意.故选:B .5.C【分析】根据三角形内角和定理求出∠BAC ,再根据角平分线的定义可得∠BAD=∠DAC =40°,最后利用垂线的定义可得∠AED=90°,进而解答即可.【详解】解:∵∠B =40°,∠C =60°,∴∠BAC=180°−40°−60°=80°.∵AD 平分∠BAC ,∴∠BAD=∠DAC =40°.∵DE ⊥AC ,∴∠AED =90°,∴∠ADE =90°−∠DAE =50°.故选C .6.C【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答.【详解】解:连接CD ,如图所示:∵点D 是AG 的中点,∴S △ABD =12S △ABG ,S △ACD =12S △AGC ,∴S △ABD +S △ACD =12S △ABC =24,∴S △BCD =12S △ABC =24,∵点E 是BD 的中点,∴S△CDE =12S△BCD=12,∵点F是CE的中点,∴S△DEF =12S△CDE=6.故选:C.7.C【分析】若两螺丝的距离最大,则此时这个木框的形状为三角形,根据三角形任意两边之和大于第三边,进行求解即可.【详解】解:①当3、4在一条直线上时,三边长为:5、7、7,此时最大距离为7;②∵4+5<3+7,∴3、7不可能在一条直线上;③当4、5在一条直线上时,三边长为:3、7、9,此时最大距离为9;④∵4+3<5+7,∴5、7不可能在一条直线上;综上所述:最大距离为9.故选:C.8.B【分析】根据题意可知∠FBC=32∠C,设∠C=x,表示出∠ADE,根据角平分线的定义,可得∠EDF的度数,根据∠FDC=∠F+∠FBC列方程,即可求出∠F的度数.【详解】解:∵BF平分∠ABC,∴∠FBC=12∠ABC,∵∠ABC=3∠C,∴∠FBC=32∠C,设∠C=x,则∠FBC=32x,∵∠EDC=24°,∴∠AED=x+24°,∵∠ADE=3∠AED,∴∠ADE=3x+72°,∵DF平分∠ADE,∴∠EDF=32x+36°,∵∠FDC=∠F+∠FBC,∴32x+36°+24°=∠F+32x,∴∠F=60°.故选:B.9.C【分析】由角平分线的定义可以得到∠CAE=∠BAE,∠ABF=∠DBF,设∠CAE=∠BAE=x,假设∠C=y,∠ABC=3y,通过角的等量代换可得到∠DFB=3∠G,代入∠G的值即可.【详解】∵AE平分∠BAC,BF平分∠ABD∴∠CAE=∠BAE,∠ABF=∠DBF设∠CAE=∠BAE=x∵∠ABC=3∠C∴可以假设∠C=y,∠ABC=3y∴∠ABF=∠DBF=∠CBG=12(180°−3y)=90°−32y∵AD⊥CD∴∠D=90°∴∠DFB=90°−∠DBF=32y设∠ABF=∠DBF=∠CBG=z,则{z=x+∠Gz+∠G=x+y∴∠G=12y∴∠DFB=3∠G∵∠G=20°∴∠DFB=60°故答案选:C10.D【分析】根据角平分线的定义、三角形的内角和定理、三角形的外角性质、平行线的判定一一判定即可.【详解】解:①设点A、B在直线MF上,∵BD、CD分别平分△ABC的内角∠ABC,外角∠ACP,∴AD平分△ABC的外角∠FAC,∴∠FAD=∠DAC,∵∠FAC=∠ACB+∠ABC,且∠ABC=∠ACB,∴∠FAD=∠ABC,∴AD∥BC,故①正确.②∵BD、BE分别平分△ABC的内角∠ABC、外角∠MBC,∴∠DBE=∠DBC+∠EBC=12∠ABC+12∠MBC=12×180°=90°,∴EB⊥BD,故②正确.③∵∠DCP=∠BDC+∠CBD,2∠DCP=∠BAC+2∠DBC,∴2(∠BDC+∠CBD)=∠BAC+2∠DBC,∴∠BDC=12∠BAC,∵∠BAC+2∠ACB=180°,∴12∠BAC+∠ACB=90°,∴∠BDC+∠ACB=90°,故③正确.④∵∠BEC=180°−12(∠MBC+∠NCB)=180°−12(∠BAC+∠ACB+∠BAC+∠ABC)=180°−12(180°+∠BAC)∴∠BEC=90°−12∠BAC,∴∠BAC+2∠BEC=180°,故④正确.故选:D.二.填空题11.124°【分析】根据已知、折叠和平行线,得∠BEF=∠C,再计算∠BED的度数,最后根据三角形内角和为180°计算∠BDE的度数即可.【详解】∵EF∥AC,∠B=32°,∠A=100°,∴∠BEF=∠C=180°−∠A−∠B=180°−100°−32°=48°(两直线平行,同位角相等),∵纸片沿DE折叠(DE为折痕),点B落在点F处,∴∠BED=12∠BEF=12×48°=24°,∴∠BDE=180°−∠B−∠BED=180°−32°−24°=124°(三角形内角和为180°),故答案为:124°.12.9【分析】由AD为△ABC的中线得S△ABD =S△ACD,从而得到12⋅AB⋅DE=12⋅AC⋅DF,代入进行计算即可得到答案.【详解】解:∵AD为△ABC的中线,∴BD=CD,∴S△ABD =S△ACD,∵DE,DF分别为△ABD,△ACD的一条高,∴12⋅AB⋅DE=12⋅AC⋅DF,∵AB=6,DE=4,DF=83,∴AC=9,故答案为:9.13. 2、4 10【分析】由(a −2)2+|b −4|=0,可得a −2=0,b −4=0,解得a =2,b =4,由三角形三边关系可得,b −a <c <a +b ,即2<c <6,由c 为偶数,可得c =4,然后求周长即可.【详解】解:∵(a −2)2+|b −4|=0,∴a −2=0,b −4=0,解得a =2,b =4,由三角形三边关系可得,b −a <c <a +b ,即2<c <6,∵c 为偶数,∴c =4,∴△ABC 的周长为2+4+4=10,故答案为:2、4,10.14.94【分析】连接DF ,CE .由题意中的线段的比和S △ABC =12,可推出S △ABD =23S △ABC =8,S △CBD=13S △ABC =4,从而可求出S △ABE =14S △ABD =2,S △ADE =34S △ABD =6.结合中点的性质即得出S △ADF =S △EDF =12S △ADE =3,从而可求出S △CDF =12S △ADF =32,进而得出S △ECF =S △ACF=S △ADF +S △CDF =92,最后即得出DGEG =S △CDF S △ECF=13,最后即可求出S △EFG =34S △EDF =94.【详解】解:如图,连接DF ,CE .∵CD:AD=1:2,S △ABC =12,∴S △ABD =23S △ABC =8,S △CBD =13S △ABC =4.又∵BE:ED =1:3,∴S△ABE =14S△ABD=2,S△ADE=34S△ABD=6.∵点F是线段AE的中点,∴S△ADF =S△EDF=12S△ADE=3.∵CD:AD=1:2,∴S△CDF =12S△ADF=32,∴S△ACF =S△ADF+S△CDF=92,∴S△ECF =S△ACF=92,∴S△CDFS△ECF =3292=13,即S△DEF+S△DGCS△EFG+S△EGC=13,∴DGEG =13,∴S△EFG =34S△EDF=94.故答案为:94.15.11或29【分析】根据题意,画出图形,进行分类讨论,①当点C在△AOB内时,根据三角形的内角和定理可得∠D=20°,根据平行线的性质得出∠1=∠B=40°,再根据三角形的外角定理求出∠2,进而得出∠AOD=∠AOB+∠2,即可求解;②当点C在△AOB外时,延长BO交CD 于一点,根据平行线的性质得出∠3=∠B=40°,再根据三角形的外角定理求出∠4=20°,即可得出∠AOD,即可求解.【详解】解:①当点C在△AOB内时,如图,在Rt△OCD中,∠C=70°,∴∠D=180°−90°−70°=20°,∵CD∥AB,∠B=40°,∴∠1=∠B=40°,∵∠D+∠2=∠1,∴∠2=40°−20°=20°,∴∠AOD=∠AOB+∠2=90°+20°=110°,∴旋转时间=110÷10=11(秒),②当点C在△AOB外时,延长BO交CD于一点,如图,∵CD∥AB,∠B=40°,∴∠3=∠B=40°,由①可得,∠D=20°,∴∠4=∠3−∠D=40°−20°=20°,∴∠AOD=90°−∠4=70°,∴△COD绕点O沿顺时针方向旋转了360°−70°=290°,∴旋转时间=290÷10=29(秒),故答案为:11或29.16.55°【分析】根据新定义的“斜等边三角形”的特点分情况分析,然后利用三角形内角和定理求解即可.【详解】解:△ABD是“斜等边三角形”,BD⊥AC,∴∠ADB=90°(1)2∠A−∠ABD=60°,∵∠A+∠ABD=90°,∴解得:∠A=50°,∠ABD=40°;(2)2∠A−∠ADB=60°,∴解得:∠A=75°,∠ABD=15°;(3)2∠ABD−∠A=60°,∵∠A+∠ABD=90°,∴解得:∠A=40°,∠ABD=50°;(4)2∠ABD−∠ADB=60°,∴解得:∠ABD=75°,∠A=15°;△BCD是“斜等边三角形”,①2∠C−∠CBD=60°,∵∠C+∠CBD=90°,∴解得:∠C=50°,∠CBD=40°;②2∠C−∠CDB=60°,∴解得:∠C=75°,∠CBD=15°;③2∠CBD−∠C=60°,∵∠C+∠CBD=90°,∴解得:∠C=40°,∠CBD=50°;④2∠CBD−∠CDB=60°,∴解得:∠CBD=75°,∠C=15°;当(1)①成立时,∠A=50°,∠ABD=40°,∠C=50°,∠CBD=40°,∴∠CBA=40°+40°=80°,∴三个角中不满足“斜等边三角形”的定义,不符合题意;当(1)②成立时,∠A=50°,∠ABD=40°,∠C=75°,∠CBD=15°,∴∠CBA=40°+15°=55°,∵2∠CBA−∠A=60°,∴△ABC是“斜等边三角形”,符合题意;同理得:符合题意的只有∠ABC=55°,故答案为:55°三.解答题17.解:(1)设这个多边形的边数是n,由题意得:(n−2)×180=360×3,∴n=8,∴这个多边形是八边形;(2)设这个多边形的边数是m,由题意得:(m−2)×180<1280<(m−2)×180+180,解得:819<m<919,∵m为整数∴m=9,∴重复加的那个角的度数是:1280°−(9−2)×180°=20°答:这个多边形的边数是9,重复加的那个角的度数是20°.18.解:AB+BC+AC>2BD.理由如下:在△ABD中,AB+AD>BD,在△BCD中,BC+CD>BD,∴AB+AD+BC+CD>2BD,即AB+BC+AC>2BD.19.(1)如图所示,△DEF即为所求;(2)如图所示,CH即为所求;(3)如图所示,∵△ABC平移后得到的△DEF∴若连接CD、AE,CD∥AE,CD=AE∴这两条线段之间的关系是平行且相等;(4)如图所示,△DEF的面积=4×6−12×4×3−12×1×3−12×3×6=152.20.(1)解:∵∠BAC=90°,AD是边BC上的高,∴12AB⋅AC=12BC⋅AD,∴AD=AB⋅ACBC =6×810= 4.8(cm),即AD的长度为4.8cm;(2)∵AE为BC边上的中线,∴BE=CE,∴△ACE的周长−△ABE的周长=(AC+AE+CE)−(AB+BE+AE)=AC−AB=8−6=2(cm),即△ACE和△ABE的周长的差是2cm.21.(1)解:在△ABC中,∠B=70°,∠C=30°,∴∠BAC=180°−∠B−∠C=180°−70°−30°=80°,∵AE是△ABC的角平分线.∴∠BAE=12∠BAC=12×80°=40°,∵线段AD是△ABC中BC边上的高,∴∠ADB=90°,∴∠BAD=180°−∠B−∠ADB=180°−70°−90°=20°,∴∠DAE=∠BAE−∠BAD=40°−20°=20°,(2)解:∵∠B=x°,线段AD是△ABC中BC边上的高,∴∠BAD=90°−∠B=90°−x°,∵∠DAE=10°,∴∠BAE=∠BAD+∠DAE=90°−x°+10°=100°−x°,∵AE是△ABC的角平分线,∴∠BAC=2∠BAE=200°−2x°,∴∠C=180°−∠B−∠BAC=180°−x°−(200°−2x°)=(x−20°),故答案为:(x−20)°;(3)解:连接BF,∵∠1=∠GBF+∠GFB,∠2=∠HBF+∠HFB,∴∠1+∠2=∠GBF+∠GFB+∠HBF+∠HFB=∠B+∠GFH,∵△GFH由△GBH折叠所得,∴∠B=∠GFH,∴∠1+∠2=2∠B.22.(1)解:∵∠ACB+∠ABC+∠BAC=180°,∠BAC=∠ABC,∴∠ACB=180°−2∠BAC,∵∠CFE+∠FEC=180°−∠ACB,∴∠CFE+∠FEC=180°−(180°−2∠BAC)=2∠BAC,∵∠BAC=70°,∴∠CFE+∠FEC=140°;(2)∠FEC+∠CFE=2∠BAC,证明:在△CEF中∵∠C+∠CEF+∠CFE=180°,∴∠CEF+∠CFE=180°−∠C,在△ABC中,∵∠C+∠BAC+∠ABC=180°,∴∠BAC+∠ABC=180°−∠C,∴∠CEF+∠CFE=∠BAC+∠ABC,∵∠BAC=∠ABC,∴∠CEF+∠CFE=2∠BAC;(3)解:∵∠ACB=∠FEC+∠CFE,∠ACB+∠ABC+∠BAC=180°,∠BAC=∠ABC,∴180°−2∠BAC=∠FEC+∠CFE,∴∠FEC+∠CFE=180°−2∠BAC.23.(1)解:如图所示,∵DC∥AB∴∠DCB=∠B=30°,(2)证明:∵AB∥FD∴∠DFB=∠MBF,设∠DFB=∠MBF=α∵∠DFM被FB平分∴∠DFB=∠MFB,则∠DFB=∠MFB=α,∴∠AMF=∠MBF+∠MFB=2α,∵∠BAC=90°∴∠MFA=90°−2α,∵FN平分∠EFM∴∠EFN=∠MFN=12(180°−∠MFA)=12(180°−90°+2α)=45°+α∴∠NFB=∠NFM−∠BFM=45°+α−α=45°,即∠NFB的大小保持不变;(3)解:在移动过程中,∠NFB的大小保持不变;如图所示,证明:∵AB∥FD∴∠DFB=∠MBF,设∠DFB=∠MBF=α∵∠DFM被FB平分∴∠DFB=∠MFB,则∠DFB=∠MFB=α,∴∠AMF=∠MBF+∠MFB=2α,∵∠BAC=90°∴∠MFA=90°−2α,∵F N'平分∠EFM∴∠EF N'=∠MF N'=12(180°−∠MFA)=12(180°−90°+2α)=45°+α∴∠N'FB=∠N'FM−∠BFM=45°+α−α=45°,∴∠NFB=135°,即∠NFB的大小保持不变;。
北师大版八年级下册数学第一章三角形的证明单元测试题(含详细解析)
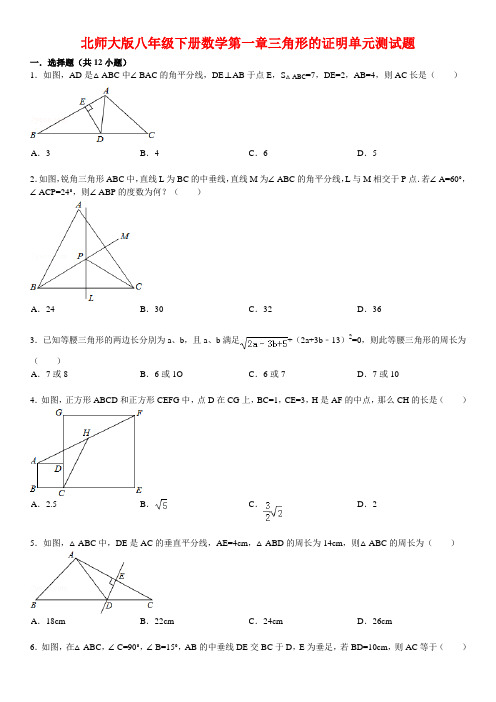
北师大版八年级下册数学第一章三角形的证明单元测试题一.选择题(共12小题)1.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是()A.3B.4C.6D.52.如图,锐角三角形ABC中,直线L为BC的中垂线,直线M为∠ABC的角平分线,L与M相交于P点.若∠A=60°,∠ACP=24°,则∠ABP的度数为何?()A.24 B.30 C.32 D.363.已知等腰三角形的两边长分別为a、b,且a、b满足+(2a+3b﹣13)2=0,则此等腰三角形的周长为()A.7或8 B.6或1O C.6或7 D.7或104.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是()A.2.5 B.C.D.25.如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为()A.18cm B.22cm C.24cm D.26cm6.如图,在△ABC,∠C=90°,∠B=15°,AB的中垂线DE交BC于D,E为垂足,若BD=10cm,则AC等于()A.10cm B.8cm C.5cm D.2.5cm7.如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是()A.2B.C.D.8.如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB:∠CAE=3:1,则∠C等于()A.28°B.25°C.22.5°D.20°9.若一个等腰三角形至少有一个内角是88°,则它的顶角是()A.88°或2°B.4°或86°C.88°或4°D.4°或46°10.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为()A.3B.3.5 C.2.5 D.2.811.如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是()A.1B.2C.D.12.如图,在△ABC中,∠ACB=100°,AC=AE,BC=BD,则∠DCE的度数为()A.20°B.25°C.30°D.40°二.填空题(共6小题)13.如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为_________.14.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是_________.15.如图,△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E,若∠BAC=70°,则∠CAE=_________.16.如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO= _________.17.在△ABC中,已知AB=AC,DE垂直平分AC,∠A=50°,则∠DCB的度数是_________.18.如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB= _________度.三.解答题(共12小题)19.如图,已知DE是AC的垂直平分线,AB=10cm,BC=11cm,求△ABD的周长.20.如图,D为△ABC边BC延长线上一点,且CD=CA,E是AD的中点,CF平分∠ACB交AB于点F.求证:CE⊥CF.21.如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,BC=4,CD=3,求AB的长.22.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.(1)求DE的长;(2)求△ADB的面积.23.如图,已知△ABC和△ABD均为直角三角形,其中∠ACB=∠ADB=90°,E为AB的中点,求证:CE=DE.24.如图所示,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F.点E是AB的中点,连接EF.(1)求证:EF∥BC;(2)若△ABD的面积是6,求四边形BDFE的面积.25.如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于点E.求证:AD=BE.26.已知;如图,在△ABC中,AB=BC,∠ABC=90度.F为AB延长线上一点,点E在BC上,BE=BF,连接AE、EF和CF.(1)求证:AE=CF;(2)若∠CAE=30°,求∠EFC的度数.27.如图,在△ABC中,AB≠AC,∠BAC的外角平分线交直线BC于D,过D作DE⊥AB,DF⊥AC分别交直线AB,AC于E,F,连接EF.(1)求证:EF⊥AD;(2)若DE∥AC,且DE=1,求AD的长.28.如图,Rt△ABC中,∠C=90°,AC=6,∠A=30°,BD平分∠ABC交AC于点D,求点D到斜边AB的距离.29.如图,在△ABC中,∠CAB=90°,AB=3,AC=4,AD是∠CAB的平分线,AD交BC于D,求BD的长.30.如图,四边形ABCD中,AB=BC,AB∥CD,∠D=90°,AE⊥BC于点E,求证:CD=CE.参考答案与试题解析一.选择题(共12小题)1.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是()A.3B.4C.6D.5考点:角平分线的性质.专题:几何图形问题.分析:过点D作DF⊥AC于F,根据角平分线上的点到角的两边距离相等可得DE=DF,再根据S△ABC=S△ABD+S△ACD列出方程求解即可.解答:解:如图,过点D作DF⊥AC于F,∵AD是△ABC中∠BAC的角平分线,DE⊥AB,∴DE=DF,由图可知,S△ABC=S△ABD+S△ACD,∴×4×2+×AC×2=7,解得AC=3.故选:A.点评:本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键.2.如图,锐角三角形ABC中,直线L为BC的中垂线,直线M为∠ABC的角平分线,L与M相交于P点.若∠A=60°,∠ACP=24°,则∠ABP的度数为何?()A.24 B.30 C.32 D.36考点:线段垂直平分线的性质.分析:根据角平分线的定义可得∠ABP=∠CBP,根据线段垂直平分线上的点到两端点的距离相等可得BP=CP,再根据等边对等角可得∠CBP=∠BCP,然后利用三角形的内角和等于180°列出方程求解即可.解答:解:∵直线M为∠ABC的角平分线,∴∠ABP=∠CBP.∵直线L为BC的中垂线,∴BP=CP,∴∠CBP=∠BCP,∴∠ABP=∠CBP=∠BCP,在△ABC中,3∠ABP+∠A+∠ACP=180°,即3∠ABP+60°+24°=180°,解得∠ABP=32°.故选:C.点评:本题考查了线段垂直平分线上的点到两端点的距离相等的性质,角平分线的定义,三角形的内角和定理,熟记各性质并列出关于∠ABP的方程是解题的关键.3.已知等腰三角形的两边长分別为a、b,且a、b满足+(2a+3b﹣13)2=0,则此等腰三角形的周长为()A.7或8 B.6或1O C.6或7 D.7或10考点:等腰三角形的性质;非负数的性质:偶次方;非负数的性质:算术平方根;解二元一次方程组;三角形三边关系.分析:先根据非负数的性质求出a,b的值,再分两种情况确定第三边的长,从而得出三角形的周长.解答:解:∵|2a﹣3b+5|+(2a+3b﹣13)2=0,∴,解得,当a为底时,三角形的三边长为2,3,3,则周长为8;当b为底时,三角形的三边长为2,2,3,则周长为7;综上所述此等腰三角形的周长为7或8.故选:A.点评:本题考查了非负数的性质、等腰三角形的性质以及解二元一次方程组,是基础知识要熟练掌握.4.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是()A.2.5 B.C.D.2考点:直角三角形斜边上的中线;勾股定理;勾股定理的逆定理.专题:几何图形问题.分析:连接AC、CF,根据正方形性质求出AC、CF,∠ACD=∠GCF=45°,再求出∠ACF=90°,然后利用勾股定理列式求出AF,再根据直角三角形斜边上的中线等于斜边的一半解答即可.解答:解:如图,连接AC、CF,∵正方形ABCD和正方形CEFG中,BC=1,CE=3,∴AC=,CF=3,∠ACD=∠GCF=45°,∴∠ACF=90°,由勾股定理得,AF===2,∵H是AF的中点,∴CH=AF=×2=.故选:B.点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,正方形的性质,勾股定理,熟记各性质并作辅助线构造出直角三角形是解题的关键.5.如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为()A.18cm B.22cm C.24cm D.26cm考点:线段垂直平分线的性质.分析:根据线段垂直平分线上的点到线段两端点的距离相等可得AD=CD,然后求出△ABD的周长=AB+BC,再求出AC的长,然后根据三角形的周长公式列式计算即可得解.解答:解:∵DE是AC的垂直平分线,∴AD=CD,∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC,∵AE=4cm,∴AC=2AE=2×4=8cm,∴△ABC的周长=AB+BC+AC=14+8=22cm.故选B.点评:本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,求出△ABD的周长=AB+BC是解题的关键.6.如图,在△ABC,∠C=90°,∠B=15°,AB的中垂线DE交BC于D,E为垂足,若BD=10cm,则AC等于()A.10cm B.8cm C.5cm D.2.5cm考点:线段垂直平分线的性质;勾股定理.专题:探究型.分析:连接AD,先由三角形内角和定理求出∠BAC的度数,再由线段垂直平分线的性质可得出∠DAB的度数,根据线段垂直平分线的性质可求出AD的长及∠DAC的度数,最后由直角三角形的性质即可求出AC的长.解答:解:连接AD,∵DE是线段AB的垂直平分线,BD=15,∠B=15°,∴AD=BD=10,∴∠DAB=∠B=15°,∴∠ADC=∠B+∠DAB=15°+15°=30°,∵∠C=90°,∴AC=AD=5cm.故选C.点评:本题考查的是直角三角形的性质及线段垂直平分线的性质,熟知线段垂直平分的性质是解答此题的关键.7.如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是()A.2B.C.D.考点:角平分线的性质;含30度角的直角三角形;直角三角形斜边上的中线;勾股定理.分析:由OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,易得△OCP是等腰三角形,∠COP=30°,又由含30°角的直角三角形的性质,即可求得PE的值,继而求得OP的长,然后由直角三角形斜边上的中线等于斜边的一半,即可求得DM的长.解答:解:∵OP平分∠AOB,∠AOB=60°,∴∠AOP=∠COP=30°,∵CP∥OA,∴∠AOP=∠CPO,∴∠COP=∠CPO,∴OC=CP=2,∵∠PCE=∠AOB=60°,PE⊥OB,∴∠CPE=30°,∴CE=CP=1,∴PE==,∴OP=2PE=2,∵PD⊥OA,点M是OP的中点,∴DM=OP=.故选:C.点评:此题考查了等腰三角形的性质与判定、含30°直角三角形的性质以及直角三角形斜边的中线的性质.此题难度适中,注意掌握数形结合思想的应用.8.如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB:∠CAE=3:1,则∠C等于()A.28°B.25°C.22.5°D.20°考点:线段垂直平分线的性质.专题:计算题.分析:设∠CAE=x,则∠EAB=3x.根据线段的垂直平分线的性质,得AE=CE,再根据等边对等角,得∠C=∠CAE=x,然后根据三角形的内角和定理列方程求解.解答:解:设∠CAE=x,则∠EAB=3x.∵AC的垂直平分线交AC于D,交BC于E,∴AE=CE.∴∠C=∠CAE=x.根据三角形的内角和定理,得∠C+∠BAC=180°﹣∠B,即x+4x=140°,x=28°.则∠C=28°.故选A.点评:此题综合运用了线段垂直平分线的性质、等腰三角形的性质以及三角形的内角和定理.9.若一个等腰三角形至少有一个内角是88°,则它的顶角是()A.88°或2°B.4°或86°C.88°或4°D.4°或46°考点:等腰三角形的性质.分析:分88°内角是顶角和底角两种情况讨论求解.解答:解:88°是顶角时,等腰三角形的顶角为88°,88°是底角时,顶角为180°﹣2×88°=4°,综上所述,它的顶角是88°或4°.故选C.点评:本题考查了等腰三角形的两底角相等的性质,难点在于要分情况讨论.10.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为()A.3B.3.5 C.2.5 D.2.8考点:线段垂直平分线的性质;勾股定理;矩形的性质.专题:计算题.分析:根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AE=CE,设CE=x,表示出ED的长度,然后在Rt△CDE中,利用勾股定理列式计算即可得解.解答:解:∵EO是AC的垂直平分线,∴AE=CE,设CE=x,则ED=AD﹣AE=4﹣x,在Rt△CDE中,CE2=CD2+ED2,即x2=22+(4﹣x)2,解得x=2.5,即CE的长为2.5.故选:C.点评:本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,勾股定理的应用,把相应的边转化为同一个直角三角形的边是解题的关键.11.如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是()A.1B.2C.D.考点:角平分线的性质;含30度角的直角三角形;勾股定理.分析:根据直角三角形两锐角互余求出∠ABC=60°,再根据角平分线的定义求出∠ABD=∠DBC=30°,从而得到∠DBC=∠ACB,然后利用等角对等边的性质求出BD的长度,再根据直角三角形30°角所对的直角边等于斜边的一半求出AD,过点D作DE⊥BC于点E,然后根据角平分线上的点到角的两边的距离相等解答即可.解答:解:∵Rt△ABC中,∠ACB=30°,∴∠ABC=60°,∵BD平分∠ABC,∴∠ABD=∠DBC=30°,∴∠DBC=∠ACB,∴BD=CD=4,在Rt△ABD中,∵∠ABD=30°,∴AD=BD=×4=2,过点D作DE⊥BC于点E,则DE=AD=2.故选B.点评:本题考查了角平分线上的点到角的两边的距离相等的性质,30°角所对的直角边等于斜边的一半的性质,以及等角对等边的性质,小综合题,但难度不大,熟记各性质是解题的关键.12.如图,在△ABC中,∠ACB=100°,AC=AE,BC=BD,则∠DCE的度数为()A.20°B.25°C.30°D.40°考点:等腰三角形的性质.专题:几何图形问题.分析:根据此题的条件,找出等腰三角形,找出相等的边与角度,设出未知量,找出满足条件的方程.解答:解:∵AC=AE,BC=BD∴设∠AEC=∠ACE=x°,∠BDC=∠BCD=y°,∴∠A=180°﹣2x°,∠B=180°﹣2y°,∵∠ACB+∠A+∠B=180°,∴100+(180﹣2x)+(180﹣2y)=180,得x+y=140,∴∠DCE=180﹣(∠AEC+∠BDC)=180﹣(x+y)=40°.故选D.点评:根据题目中的等边关系,找出角的相等关系,再根据三角形内角和180°的定理,列出方程,解决此题.二.填空题(共6小题)13.如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为15.考点:角平分线的性质.专题:几何图形问题.分析:要求△ABD的面积,现有AB=7可作为三角形的底,只需求出该底上的高即可,需作DE⊥AB于E.根据角平分线的性质求得DE的长,即可求解.解答:解:作DE⊥AB于E.∵AD平分∠BAC,DE⊥AB,DC⊥AC,∴DE=CD=3.∴△ABD的面积为×3×10=15.故答案是:15.点评:此题主要考查角平分线的性质;熟练运用角平分线的性质定理,是很重要的,作出并求出三角形AB边上的高时解答本题的关键.14.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是2.考点:含30度角的直角三角形;线段垂直平分线的性质.分析:根据同角的余角相等、等腰△ABE的性质推知∠DBE=30°,则在直角△DBE中由“30度角所对的直角边是斜边的一半”即可求得线段BE的长度.解答:解:∵∠ACB=90°,FD⊥AB,∴∠ACB=∠FDB=90°,∵∠F=30°,∴∠A=∠F=30°(同角的余角相等).又∵AB的垂直平分线DE交AC于E,∴∠EBA=∠A=30°,∴直角△DBE中,BE=2DE=2.故答案是:2.点评:本题考查了线段垂直平分线的性质、含30度角的直角三角形.解题的难点是推知∠EBA=30°.15.如图,△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E,若∠BAC=70°,则∠CAE=55°.考点:角平分线的性质.分析:首先过点E作EF⊥BD于点F,作EG⊥AC于点G,作EH⊥BA于点H,由△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E,易证得AE是∠CAH的平分线,继而求得答案.解答:解:过点E作EF⊥BD于点F,作EG⊥AC于点G,作EH⊥BA于点H,∵△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E,∴EH=EF,EG=EF,∴EH=EG,∴AE是∠CAH的平分线,∵∠BAC=70°,∴∠CAH=110°,∴∠CAE=∠CAH=55°.故答案为:55°.点评:此题考查了角平分线的性质与判定.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.16.如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO= 4:5:6.考点:角平分线的性质.专题:压轴题.分析:首先过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,由OA,OB,OC是△ABC的三条角平分线,根据角平分线的性质,可得OD=OE=OF,又由△ABC的三边AB、BC、CA长分别为40、50、60,即可求得S△ABO:S△BCO:S△CAO的值.解答:解:过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,∵OA,OB,OC是△ABC的三条角平分线,∴OD=OE=OF,∵△ABC的三边AB、BC、CA长分别为40、50、60,∴S△ABO:S△BCO:S△CAO=(AB•OD):(BC•OF):(AC•OE)=AB:BC:AC=40:50:60=4:5:6.故答案为:4:5:6.点评:此题考查了角平分线的性质.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.17.在△ABC中,已知AB=AC,DE垂直平分AC,∠A=50°,则∠DCB的度数是15°.考点:线段垂直平分线的性质;等腰三角形的性质.分析:由DE垂直平分AC,∠A=50°,根据线段垂直平分线的性质,易求得∠ACD的度数,又由AB=AC,可求得∠ACB的度数,继而可求得∠DCB的度数.解答:解:∵DE垂直平分AC,∴AD=CD,∴∠ACD=∠A=50°,∵AB=AC,∠A=50°,∴∠ACB=∠B==65°,∴∠DCB=∠ACB﹣∠ACD=15°.故答案为:15°.点评:此题考查了线段垂直平分线的性质与等腰三角形的性质.此题比较简单,注意数形结合思想的应用.18.如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB= 72度.考点:线段垂直平分线的性质;菱形的性质.专题:计算题.分析:欲求∠CPB,可根据菱形、线段垂直平分线的性质、对称等方面去寻求解答方法.解答:解:先连接AP,由四边形ABCD是菱形,∠ADC=72°,可得∠BAD=180°﹣72°=108°,根据菱形对角线平分对角可得:∠ADB=∠ADC=×72°=36°,∠ABD=∠ADB=36度.EP是AD的垂直平分线,由垂直平分线的对称性可得∠DAP=∠ADB=36°,∴∠PAB=∠DAB﹣∠DAP=108°﹣36°=72度.在△BAP中,∠APB=180°﹣∠BAP﹣∠ABP=180°﹣72°﹣36°=72度.由菱形对角线的对称性可得∠CPB=∠APB=72度.点评:本题开放性较强,解法有多种,可以从菱形、线段垂直平分线的性质、对称等方面去寻求解答方法,在这些方法中,最容易理解和表达的应为对称法,这也应该是本题考查的目的.灵活应用菱形、垂直平分线的对称性,可使解题过程更为简便快捷.三.解答题(共12小题)19.如图,已知DE是AC的垂直平分线,AB=10cm,BC=11cm,求△ABD的周长.考点:线段垂直平分线的性质.分析:先根据线段垂直平分线的性质得出AD=CD,故可得出BD+AD=BD+CD=BC,进而可得出结论.解答:解:∵DE垂直平分,∴AD=CD,∴BD+AD=BD+CD=BC=11cm,又∵AB=10cm,∴△ABD的周长=AB+BC=10+11=21(cm).点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.20.如图,D为△ABC边BC延长线上一点,且CD=CA,E是AD的中点,CF平分∠ACB交AB于点F.求证:CE⊥CF.考点:等腰三角形的性质.专题:证明题.分析:根据三线合一定理证明CF平分∠ACB,然后根据CF平分∠ACB,根据邻补角的定义即可证得.解答:证明:∵CD=CA,E是AD的中点,∴∠ACE=∠DCE.∵CF平分∠ACB,∴∠ACF=∠BCF.∵∠ACE+∠DCE+∠ACF+∠BCF=180°,∴∠ACE+∠ACF=90°.即∠ECF=90°.∴CE⊥CF.点评:本题考查了等腰三角形的性质,顶角的平分线、底边上的中线和高线、三线合一.21.如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,BC=4,CD=3,求AB的长.考点:含30度角的直角三角形;相似三角形的判定与性质.专题:计算题.分析:延长DA,CB,交于点E,可得出三角形ABE与三角形CDE相似,由相似得比例,设AB=x,利用30角所对的直角边等于斜边的一半得到AE=2x,利用勾股定理表示出BE,由BC+BE表示出CE,在直角三角形DCE中,利用30度角所对的直角边等于斜边的一半得到2DC=CE,即可求出AB的长.解答:解:延长DA,CB,交于点E,∵∠E=∠E,∠ANE=∠D=90°,∴△ABE∽△CDE,∴=,在Rt△ABE中,∠E=30°,设AB=x,则有AE=2x,根据勾股定理得:BE==x,∴CE=BC+BE=4+x,在Rt△DCE中,∠E=30°,∴CD=CE,即(4+x)=3,解得:x=,则AB=.点评:此题考查了相似三角形的判定与性质,含30度直角三角形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.22.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.(1)求DE的长;(2)求△ADB的面积.考点:角平分线的性质;勾股定理.分析:(1)根据角平分线性质得出CD=DE,代入求出即可;(2)利用勾股定理求出AB的长,然后计算△ADB的面积.解答:解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=DE,∵CD=3,∴DE=3;(2)在Rt△ABC中,由勾股定理得:AB===10,∴△ADB的面积为S△ADB=AB•DE=×10×3=15.点评:本题考查了角平分线性质和勾股定理的运用,注意:角平分线上的点到角两边的距离相等.23.如图,已知△ABC和△ABD均为直角三角形,其中∠ACB=∠ADB=90°,E为AB的中点,求证:CE=DE.考点:直角三角形斜边上的中线.专题:证明题.分析:由于AB是Rt△ABC和Rt△ABD的公共斜边,因此可以AB为媒介,再根据斜边上的中线等于斜边的一半来证CE=ED.解答:证明:在Rt△ABC中,∵E为斜边AB的中点,∴CE=AB.在Rt△ABD中,∵E为斜边AB的中点,∴DE=AB.∴CE=DE.点评:本题考查的是直角三角形的性质:在直角三角形中,斜边上的中线等于斜边的一半.24.如图所示,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F.点E是AB的中点,连接EF.(1)求证:EF∥BC;(2)若△ABD的面积是6,求四边形BDFE的面积.考点:等腰三角形的性质;三角形中位线定理;相似三角形的判定与性质.专题:几何综合题.分析:(1)在等腰△ACD中,CF是顶角∠ACD的平分线,根据等腰三角形三线合一的性质知F是底边AD的中点,由此可证得EF是△ABD的中位线,即可得到EF∥BC的结论;(2)易证得△AEF∽△ABD,根据两个相似三角形的面积比(即相似比的平方),可求出△ABD的面积,而四边形BDFE的面积为△ABD和△AEF的面积差,由此得解.解答:(1)证明:∵在△ACD中,DC=AC,CF平分∠ACD;∴AF=FD,即F是AD的中点;又∵E是AB的中点,∴EF是△ABD的中位线;∴EF∥BC;(2)解:由(1)易证得:△AEF∽△ABD;∴S△AEF:S△ABD=(AE:AB)2=1:4,∴S△ABD=4S△AEF=6,∴S△AEF=1.5.∴S四边形BDFE=S△ABD﹣S△AEF=6﹣1.5=4.5.点评:此题主要考查的是等腰三角形的性质、三角形中位线定理及相似三角形的判定和性质.25.如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于点E.求证:AD=BE.考点:直角三角形全等的判定;全等三角形的性质.专题:证明题.分析:此题根据直角梯形的性质和CE⊥BD可以得到全等条件,证明△ABD≌△BCE,然后利用全等三角形的性质证明题目的结论.解答:证明:∵AD∥BC,∴∠ADB=∠DBC.∵CE⊥BD,∴∠BEC=90°.∵∠A=90°,∴∠A=∠BEC.∵BD=BC,∴△ABD≌△BCE.∴AD=BE.点评:本题考查了直角三角形全等的判定及性质;此题把全等三角形放在梯形的背景之下,利用全等三角形的性质与判定解决题目问题.26.已知;如图,在△ABC中,AB=BC,∠ABC=90度.F为AB延长线上一点,点E在BC上,BE=BF,连接AE、EF和CF.(1)求证:AE=CF;(2)若∠CAE=30°,求∠EFC的度数.考点:等腰三角形的性质;全等三角形的判定与性质.专题:计算题;证明题.分析:根据已知利用SAS判定△ABE≌△CBF,由全等三角形的对应边相等就可得到AE=CF;根据已知利用角之间的关系可求得∠EFC的度数.解答:(1)证明:在△ABE和△CBF中,∵,∴△ABE≌△CBF(SAS).∴AE=CF.(2)解:∵AB=BC,∠ABC=90°,∠CAE=30°,∴∠CAB=∠ACB=(180°﹣90°)=45°,∠EAB=45°﹣30°=15°.∵△ABE≌△CBF,∴∠EAB=∠FCB=15°.∵BE=BF,∠EBF=90°,∴∠BFE=∠FEB=45°.∴∠EFC=180°﹣90°﹣15°﹣45°=30°.点评:此题主要考查了全等三角形的判定方法及等腰三角形的性质等知识点的掌握情况;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.27.如图,在△ABC中,AB≠AC,∠BAC的外角平分线交直线BC于D,过D作DE⊥AB,DF⊥AC分别交直线AB,AC于E,F,连接EF.(1)求证:EF⊥AD;(2)若DE∥AC,且DE=1,求AD的长.考点:角平分线的性质;全等三角形的判定与性质;线段垂直平分线的性质.专题:几何综合题;压轴题.分析:(1)根据AD是∠EAF的平分线,那么DE=DF,如果证得EA=FA,那么我们就能得出AD是EF的垂直平分线,那么就证得EF⊥AD了.因此证明EA=FA是问题的关键,那么就要先证得三角形AED和AFD全等.这两个三角形中已知的条件有∠EAD=∠FAD,一条公共边,一组直角,因此两三角形全等,那么就可以得出EA=AF了.(2)要求AD的长,在直角三角形AED中,有了DE的值,如果知道了∠ADE或∠EAD的度数,那么就能求出AD了.如果DE∥AC,那么∠EAC=90°,∠EAD=45°,那么在直角三角形AED中就能求出AD的长了.解答:(1)证明:∵AD是∠EAF的平分线,∴∠EAD=∠DAF.∵DE⊥AE,DF⊥AF,∴∠DEA=∠DFA=90°又AD=AD,∴△DEA≌△DFA.∴EA=FA∵ED=FD,∴AD是EF的垂直平分线.即AD⊥EF.(2)解:∵DE∥AC,∴∠DEA=∠FAE=90°.又∠DFA=90°,∴四边形EAFD是矩形.由(1)得EA=FA,∴四边形EAFD是正方形.∵DE=1,∴AD=.点评:本题考查了全等三角形的判定,角平分线的性质,线段垂直平分线的性质等知识点.本题中利用全等三角形得出线段相等是解题的关键.。
沪科版八年级数学上册试题 第13章 三角形中的边角关系、命题与证明 单元测试卷 (含解析)

第13章《三角形中的边角关系、命题与证明》单元测试卷一、选择题(本大题共10个小题,每小题3分,共30分;在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知一个三角形的两边长分别为6和3,则这个三角形的第三边长可能是()A .3B .6C .9D .102.下列图形中具有稳定性的是( )A .B .C .D .3.如图,CE 是的外角的平分线,若,,则的度数为( ).A .95°B .90°C .85°D .80°4.下列长度的三条线段能首尾相接构成三角形的是( )A .,,B .,,C .,,D .,,5.以下命题的逆命题中,属于真命题的是( ).A .如果a>0,b>0,则a+b>0B .直角都相等C .两直线平行,同位角相等D .若a=b ,则|a|=|b|6.具备下列条件的,不是直角三角形的是( )A .B .C .D .::::7.如图,直线CE ∥DF ,∠CAB =125°,∠ABD =85°,则∠1+∠2=( )ABC ACD ∠40B ∠=︒65ACE ∠=︒A ∠1cm 2cm 3cm 3cm 4cm 5cm4cm 5cm 10cm 6cm 9cm 2cmABC A B C ∠+∠=∠1123A B C∠=∠=∠23A B C ∠=∠=∠A ∠B ∠1C ∠=34A .30°B .35°C .36°D .40°8.已知中,,求证:,下面写出运用反证法证明这个命题的四个步骤:①∴,这与三角形内角和为矛盾②因此假设不成立.∴③假设在中,④由,得,即.这四个步骤正确的顺序应是( )A .④③①②B .③④②①C .①②③④D .③④①②9.用反证法证明命题“在三角形中,至少有一个内角大于或等于60°”时,第一步应先假设( )A .三角形中有一个内角小于B .三角形中有一个内角大于C .三角形的三个内角都小于D .三角形的三个内角都大于10.如图,中,、分别是高和角平分线,点在的延长线上,,交于点,交于点;下列结论中正确的结论有( )①;②;③;④.A .①②③B .①③④C .①②④D.①②③④ABC ∆AB AC =90B ∠<︒180A B C ∠+∠+∠>︒180︒90B ∠<︒ABC ∆90B ∠≥︒AB AC =90B C ∠=∠≥︒180B C ∠+∠≥︒60︒60︒60︒60︒ABC BD BE F CA FH BE ⊥BD G BC H DBE F ∠=∠()12F BAC C ∠=∠-∠2BEF BAF C ∠=∠+∠BGH ABE C ∠=∠+∠二、填空题(本大题共6个小题,每题3分,共18分)11.命题“平行四边形的对角线互相平分”,它的逆命题是__________,逆命题是__________命题(填“真”或“假”)12.现将一把直尺和的直角三角板按如图摆放,经测量得,则___________.13.BM 是ABC 中AC 边上的中线,AB=7cm ,BC=4cm ,那么ABM 与BCM 的周长之差为_________________cm .14.用一组整数a ,b ,c 的值说明命题“若a >b >c ,则a+b >c”是错误的,这组值可以是a =__,b =__,c =__.15.如图所示,在△ABC 中,已知点D ,E ,F 分别是BC ,AD ,CE 的中点,且△ABC 的面积为4.则△BEF 的面积为_________.16.如图,射线AB 与射线CD 平行,点F 为射线AB 上的一定点,连接CF ,点P 是射线CD 上的一个动点(不包括端点C ),将沿PF 折叠,使点C 落在点E 处.若,当点E 到点A 的距离最大时,_____.三、解答题(本大题共8小题,共72分;第17-18每小题6分,第19-21每小题8分,第22小题10分,第23小题12分,第24小题14分)17.如图,在Rt △ABC 中,∠ACB =90°,∠A =40°,△ABC 的外角∠CBD 的平分线BE 交AC 的延长线于点E ,点F 为AC 延长线上的一点,连接DF.60︒1142∠=︒2∠= PFC △=62DCF ∠︒=CFP ∠(1)求∠CBE 的度数;(2)若∠F =25°,求证:.18.如图,有下列三个条件:①DE//BC ;②;③.(1)若从这三个条件中任选两个作为题设,另一个作为结论,组成一个命题,一共能组成几个命题?请你都写出来;(2)你所写出的命题都是真命题吗?若是,请你就其中的一个真命题给出推理过程;若不是,请你对其中的假命题举出一个反例(温馨提示:)BE DF ∥12∠=∠B C ∠=∠180B C BAC ∠+∠+∠=︒19.先阅读下面的内容,再解决问题,例题:若,求和的值.解:问题:(1)若,求的值.(2)已知是的三边长,满足,且是中最长的边,求的取值范围.20.如图,△ABC 中,∠ABC 与∠ACB 的外角的平分线相交于点E ,且∠A=60°.(1)①若∠ABC=40°,则∠E=________;②若∠ABC=100°,则∠E=________.(2)嘉嘉说∠E 的大小与∠B 的度数无关,你认为他说得对吗?请说明理由.2222690m mn n n ++-+=m n 2222222226902690()(3)0m mn n n m mn n n n m n n ++-+=∴+++-+=∴++-=Q 0,303,3m n n m n ∴+=-=∴=-=2222440x y xy y +-++=y x ,,a b c ABC 2210841a b a b +=+-c ABCc21.用反证法证明:两条直线被第三条直线所截.如果同旁内角互补,那么这两条直线平行.已知:如图,直线l1,l2被l3所截,∠1+∠2=180°.求证:l1 l2证明:假设l1 l2,即l1与l2交与相交于一点P.则∠1+∠2+∠P 180° 所以∠1+∠2 180°,这与 矛盾,故 不成立.所以 .22.如图,四边形ABCD中,AB∥CD,∠B=∠D,点E为BC延长线上一点,连接AE,AE交CD 于H.∠DCE的平分线交AE于G.(1)求证:AD∥BC;(2)若∠BAC=∠DAE,∠AGC=2∠CAE.求∠CAE的度数;(3)(2)中条件∠BAC=∠DAE仍然成立,若∠AGC=3∠CAE,直接写出∠CAE的度数 .23.如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.(1)求证:∠A+∠C=∠B+∠D;(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,与CD、AB分别相交于点M、N.①以线段AC为边的“8字型”有_______个,以点O为交点的“8字型”有________个:②若∠B=100°,∠C=120°,求∠P的度数;③若角平分线中角的关系改为“∠CAB=3∠CAP,∠CDB=3∠CDP”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.24.在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如图①,若∠BPC=α,则∠A= ;(用α的代数式表示,请直接写出结论)(2)如图②,作△ABC外角∠MBC、∠NCB的角平分线交于点Q,试探究∠Q与∠BPC之间的数量关系,并说明理由;(3)如图③,延长线段CP、QB交于点E,△CQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.答案一、选择题1.B【分析】组成三角形的三边的大小关系是:两边之和大于第三边,两边之差小于第三边,由此即可求出答案.【详解】解:设第三边长为x ,根据三角形的三边关系得,∴,即.故选:.2.C【分析】根据三角形具有稳定性,即可对图形进行判断.【详解】解:A 、中间竖线的两侧是四边形,不具有稳定性,故本选项错误;B 、对角线下方是四边形,不具有稳定性,故本选项错误;C 、对角线两侧是三角形,具有稳定性,故本选项正确;D 、对角线两侧是四边形,不具有稳定性,故本选项错误.故选C .3.B【分析】根据角平分线的定义,可求出∠ACD=2∠ACE ,再根据三角形的外角定理即可求出.【详解】∵CE 是的外角的平分线,,∴∠ACD=2∠ACE=130°,∵,∴∠A=130°-40°=90°,故选:B .4.B【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.【详解】解:根据三角形的三边关系,知A 、1+2=3,不能组成三角形,故选项错误,不符合题意;B 、3+4>5,能够组成三角形,故选项正确,符合题意;6363x -<<+39x <<B A ∠ABC ACD ∠65ACE ∠=︒40B ∠=︒C 、5+4<10,不能组成三角形,故选项错误,不符合题意;D 、2+6<9,不能组成三角形,故选项错误,不符合题意;故选:B .5.C【分析】首先明确各个命题的逆命题,再分别分析各逆命题的题设是否能推出结论,可以利用排除法得出答案.【详解】解:A.如果,则不一定是,,选项错误,不符合题意;B.如果角相等,但不一定是直角,选项错误,不符合题意;C.同位角相等,两直线平行,选项正确,符合题意;D.如果,可得或,选项错误,不符合题意.故选:C .6.C【分析】分别求出各个选项中,三角形的最大的内角,即可判断.【详解】解:根据三角形的内角和为180°,可知,据此逐项判断:A 、由,可以推出,本选项不符合题意;B 、由,可以推出,本选项不符合题意;C 、由,推出,是钝角三角形,本选项符合题意;D 、由,可以推出,本选项不符合题意;故选:C .7.A【分析】根据三角形的外角的性质可得,根据平行线的性质可得,进而即可求得.【详解】解:∵CE ∥DF ,∴∠CAB =125°,∠ABD =85°,0a b +>0a >0b >a b =a b =a b =-180A B C ∠+∠+∠=o A B C ∠+∠=∠90C ∠=︒1123A B C ∠=∠=∠90C ∠=︒23A B C ∠=∠=∠108011A ⎛⎫∠=︒ ⎪⎝⎭ABC ∆::1:3:4A B C ∠∠∠=90C ∠=︒1,2CAB CEA DBA DFB ∠=∠+∠∠=∠+∠180CEA DFB ∠+∠=︒12∠+∠180CEA DFB ∠+∠=︒1,2CAB CEA DBA DFB∠=∠+∠∠=∠+∠()12CAB ABD CEA DFB ∴∠+∠=∠+∠-∠+∠,故选A .8.D【分析】根据反证法的一般步骤判断即可.【详解】解:运用反证法证明这个命题的四个步骤1、假设在中,2、由,得,即3、,这与三角形内角和为矛盾4、因此假设不成立.综上所述,这四个步骤正确的顺序应是:③④①②故选:D9.C【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,可据此进行判断.【详解】解:用反证法证明命题“三角形中至少有一个角大于或等于60°”时,第一步应假设这个三角形中三个内角内角都小于60°,故选:C .10.D【分析】根据角平分线的性质、三角形的高线性质和三角形内角和定理判断即可;【详解】∵,∴,∵,∴,∵,∴,故①正确;,,∵,∴,12585180=︒+︒-︒=30︒ABC ∆90B ∠≥︒AB AC =90B C ∠=∠≥︒180B C ∠+∠≥︒180A B C ∴∠+∠+∠>︒180︒90B ∴∠<︒BD FD ⊥90FGD F ∠+∠=︒FH BE ⊥90BGO DBE ∠+∠=︒FGD BGH ∠=∠DBE F ∠=∠90ABD BAC ∠=︒-∠9090DBE ABE ABD ABE BAC CBD DBE BAC ∠=∠-∠=∠-︒+∠=∠-∠-︒+∠90CBD C ∠=︒-∠DBE BAC C DBE ∠=∠-∠-∠由①得,,∴,故②正确;∵BE 平分,∴,,∴,,∴,故③正确;∵,,∴,∵,,∴,∴,故④正确;∴正确的有①②③④;故选:D .二、填空题11. 对角线互相平分的四边形是平行四边形 真【分析】根据逆命题的要求写出逆命题,再判断即可.【详解】解:命题“平行四边形的对角线互相平分”,它的逆命题是对角线互相平分的四边形是平行四边形,此命题是真命题.故答案为:对角线互相平分的四边形是平行四边形;真.12.【分析】由直尺可得,由直角三角板可知,再利用三角形外角定理和平行线性质推角,即可得到答案.【详解】解:如图,由题可知∴∵,∴又∵∴故答案为:.DBE F ∠=∠()12F BAC C ∠=∠-∠ABC ∠ABE CBE ∠=∠BEF CBE C ∠=∠+∠22BEF ABC C ∠=∠+∠BAF ABC C ∠=∠+∠2BEF BAF C ∠=∠+∠AEB EBC C ∠=∠+∠ABE CBE ∠=∠AEB ABE C ∠=∠+∠BD FC ⊥FH BE ⊥FGD FEB ∠=∠BGH ABE C ∠=∠+∠52︒AB CD 490∠=︒AB CD 56∠=∠1142∠=︒490∠=︒5141429052∠=∠-∠=︒-︒=︒26∠=∠252∠=︒52︒13.3【分析】根据中线的定义可得,ABM 与BCM 的周长之差=AB BC ,据此即可求解.【详解】解:∵BM 是ABC 的中线,∴MA=MC ,∴=AB+BM+MA BC CM BM=AB BC=74=3(cm).答:ABM 与BCM 的周长是差是3 cm .故答案是:3.14. -2 -3 -4【分析】根据题意选择a 、b 、c 的值,即可得出答案,答案不唯一.【详解】解:当a =﹣2,b =﹣3,c =﹣4时,﹣2>﹣3>﹣4,则(﹣2)+(﹣3)<(﹣4),∴命题若a >b >c ,则a+b >c ”是错误的;故答案为:﹣2,﹣3,﹣4.15.1【分析】根据点D ,E ,F 分别是BC ,AD ,CE 的中点,可以推出,进而推出,即可得到答案.【详解】解:∵点D 是BC的中点- ΔΔABM BCM C C ------ 12S S =△BEC △ABC 14B E F A B C S S =∴∵点E 是AD 的中点∴∴又∵点F 是CE 的中点∴又∵∴故答案为:1.16.【分析】利用三角形三边关系可知:当E 落在AB 上时,AE 距离最大,利用且,得到,再根据折叠性质可知:,利用补角可知,进一步可求出.【详解】解:利用两边之和大于第三边可知:当E 落在AB 上时,AE 距离最大,如图:∵且,∴,∵折叠得到,∴,∵,∴.故答案为:三、解答题17.(1)解:∵∠ACB =90°,∠A =40°,∴∠CBD=∠A+∠ACB=130°,∵BE 平分∠CBD,ABD ADCS S = DEC S S S S ===△ABE △DBE △AEC △12S S =△BEC △ABC1124BEF BEC ABCS S S == 4ABC S = 1BEF S =△59︒AB CD =62DCF ∠︒=62CFA ∠︒EFP CFP ∠=∠118EFP CFP ∠+∠=︒59EFP CFP ∠=∠=︒AB CD =62DCF ∠︒=62CFA ∠︒PCF PEF EFP CFP ∠=∠118EFP CFP ∠+∠=︒59EFP CFP ∠=∠=︒59︒∴;(2)证明:∵∠ACB =90°,∴∠BCE=90°,∵∠CBE=65°,∴∠BEC=90°-65°=25°,∵∠F =25°,∴∠F=∠BEC ,∴.18.(1)解:一共能组成三个命题:①如果DE//BC ,,那么;②如果DE//BC ,,那么;③如果,,那么DE//BC ;(2)解:都是真命题,如果DE//BC ,,那么,理由如下:∵DE//BC ,∴,∵,∴.如果DE//BC ,,那么;理由如下:∵DE//BC ,∴,,∵,∴;如果,,那么DE//BC ;理由如下:∵,∴∠B+∠C=180°-∠BAC ,∵∠1+∠2+∠BAC=180°,∴∠1+∠2=180°-∠BAC ,1652CBE CBD ∠=∠=︒BE DF ∥12∠=∠B C ∠=∠B C ∠=∠12∠=∠12∠=∠B C ∠=∠12∠=∠B C ∠=∠1B ∠=∠2C∠=∠12∠=∠B C ∠=∠B C ∠=∠12∠=∠1B ∠=∠2C ∠=∠B C ∠=∠12∠=∠12∠=∠B C ∠=∠180B C BAC ∠+∠+∠=︒∴∠B+∠C=∠1+∠2,∵,,∴∠B=∠1,∴DE//BC .19.解:(1)∵,∴,∴,∴,∴,∴;(2)∵,∴,∴,∴,∴,∵是中最长的边,∴,即.20.(1)解:①∵BE ,CE 分别是△ABC 的内角和外角的平分线∴∠DBE=∠ABC=20°,∠DCE=∠ACD∵∠ACD=∠ABC+∠A=60°+40°=100°,∠DCE=∠DBE+∠E∴∠DCE=∠ACD=50°,∴∠E=∠DCE-∠DBE=50°-20°=30°;②∵BE ,CE 分别是△ABC 的内角和外角的平分线∴∠DBE=∠ABC=50°,∠DCE=∠ACD∵∠ACD=∠ABC+∠A=100°+60°=160°,∠DCE=∠DBE+∠E∴∠DCE=∠ACD=80°,12∠=∠B C ∠=∠2222440x y xy y +-++=2222440x xy y y y -++++=()()2220x y y -++=0,20x y y -=+=2,2x y =-=-()2124y x -=-=2210841a b a b +=+-2210258160a a b b -+++=-()()22450a b -+=-50,40a b -=-=5,4a b ==c ABC 545c ≤<+59c ≤<121212121212∴∠E=∠DCE-∠DBE=80°-50°=30°;故答案为:①30°;②30°;(2)解:嘉嘉说得对.理由如下:∵BE ,CE 分别是△ABC 的内角和外角的平分线∴∠DBE=∠ABC ,∠DCE=∠ACD∵∠DCE=∠DBE+∠E∴∠E=∠DCE -∠DBE=∠ACD -∠ABC=(∠ACD -∠ABC)又∵∠ACD=∠ABC+∠A∴∠E=(∠ABC+∠A-∠ABC )=∠A∴∠E 的大小与∠B 的度数无关.21.已知:如图,直线l 1,l 2被l 3所截,∠1+∠2=180°.求证:证明:假设l 1不平行l 2,即l 1与l 2交与相交于一点P .则∠1+∠2+∠P=180°(三角形内角和定理),所以∠1+∠2<180°,这与∠1+∠2=180°矛盾,故假设不成立.所以结论成立,l 1∥l 2.22.(1)证明:∵AB ∥CD ,∴∠B =∠DCE ,∵∠B =∠D ,∴∠D =∠DCE ,∴AD ∥BC ;1212121212121212l l //(2)解:设∠CAG =x ,∠DCG =z ,∠BAC =y ,则∠EAD =y ,∠D =∠DCE =2z ,∠AGC =2∠CAE =2x ,∵AB ∥CD ,∴∠AHD =∠BAH =x +y ,∠ACD =∠BAC =y ,△AHD 中,x +2y +2z =180°①,△ACG 中,x +2x +y +z =180°,即3x +y +z =180°,∴6x +2y +2z =360°②,②﹣①得:5x =180°,解得:x =36°,∴∠CAE =36°;(3)解:设∠CAE =x ,∠DCG =z ,∠BAC =y ,则∠EAD =y ,∠D =∠DCE =2z ,∠AGC =3∠CAE =3x ,∵AB ∥CD ,∴∠AHD =∠BAH =x +y ,∠ACD =∠BAC =y ,△AHD 中,x +2y +2z =180°①,△ACG 中,x +3x +y +z =180°,∴4x +y +z =180°,∴8x +2y +2z =360°②,②﹣①得:7x =180°,解得:x =,∴∠CAE =;故答案为:.23.(1)解:△AOC 中,∠A+∠C=180°-∠AOC ,△BOD 中,∠B+∠D=180°-∠BOD ,∵∠AOC=∠BOD ,∴∠A+∠C=∠B+∠D ;1807︒1807︒1807︒(2)解:①以线段AC 为边的“8字型”有:△ACM 和△PDM ,△ACO 和△BOD ,△ACO 和△DNO ,共3个;以点O 为交点的“8字型”有:△ACO 和△BDO ,△ACO 和△DNO ,△AMO 和△BDO ,△AMO 和△DNO ,共4个;②△AMC 和△DMP 中,∠C+∠CAM=∠P+∠PDM ,△BDN 和△PAN 中,∠B+∠BDN=∠P+∠PAN ,∴∠C+∠CAM+∠B+∠BDN =∠P+∠PDM+∠P+∠PAN ,∵PA 平分∠BAC ,PD 平分∠BDC ,∴∠CAM=∠PAN ,∠BDN=∠PDM ,∴∠C+∠B=2∠P ,∴120°+100°=2∠P ,∴∠P=110°;③∵∠CAB=3∠CAP ,∠CDB=3∠CDP ,∴∠CAM=∠CAB ,∠PAN=∠CAB ,∠BDN=∠BDC ,∠PDM=∠BDC ,△AMC 和△DMP 中,∠C+∠CAM=∠P+∠PDM ,∠C-∠P=∠PDM-∠CAM=∠BDC-∠CAB ,3(∠C-∠P )=∠BDC-∠CAB ,△BDN 和△PAN 中,∠B+∠BDN=∠P+∠PAN ,∠P-∠B=∠BDN-∠PAN=∠BDC-∠CAB ,(∠P-∠B )=∠BDC-∠CAB ,∴3(∠C-∠P )=(∠P-∠B ),2∠C-2∠P=∠P-∠B ,3∠P=∠B+2∠C ;24.(1)如图①中,13232313131323233232∵∠ABC 与∠ACB 的平分线相交于点P ,∴∠BPC=180°﹣(∠PBC+∠PCB )=180°(∠ABC+∠ACB )=180°(180°﹣∠A ),=90°∠A ,∵∠BPC=α,∴∠A=2α﹣180°.故答案为2α﹣180°.(2)结论:∠BPC+∠BQC=180°.理由:如图②中,∵外角∠MBC ,∠NCB 的角平分线交于点Q ,∴∠QBC+∠QCB (∠MBC+∠NCB )(360°﹣∠ABC ﹣∠ACB )(180°+∠A )12-12-12+12=12=12==90°∠A ,∴∠Q=180°﹣(90°∠A )=90°∠A ,∵∠BPC=90°∠A ,∴∠BPC+∠BQC=180°.(3)延长CB 至F ,∵BQ 为△ABC 的外角∠MBC 的角平分线,∴BE 是△ABC 的外角∠ABF 的角平分线,∴∠ABF=2∠EBF ,∵CE 平分∠ACB ,∴∠ACB=2∠ECB ,∵∠EBF=∠ECB+∠E ,∴2∠EBF=2∠ECB+2∠E ,即∠ABF=∠ACB+2∠E ,又∵∠ABF=∠ACB+∠A ,∴∠A=2∠E ,∵∠ECQ=∠ECB+∠BCQ∠ACB ∠NCB =90°,如果△CQE 中,存在一个内角等于另一个内角的2倍,那么分四种情况:①∠ECQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;②∠ECQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;12+12+12-12+12=12+③∠Q=2∠E,∵∠Q+∠E=90°,∴∠E=30°,则∠A=2∠E=60°;④∠E=2∠Q,∵∠Q+∠E=90°,∴∠E=60°,则∠A=2∠E=120°.综上所述,∠A的度数是90°或60°或120°.。
2020-2021学年八年级数学北师大版下册 第一章 三角形的证明 单元测试

第一章三角形的证明单元测试一.选择题1.在等腰△ABC中,∠A=70°,则∠C的度数不可能是()A.40°B.55°C.65°D.70°2.如图,在等腰三角形△ABC中,AC=BC,AC边上的垂直平分线分别交AC,BC于点D 和点E,若∠BAE=45°,DE=2,则AE的长度为()A.2B.3C.3.5D.43.如图,△ABC是等边三角形,点D是AC的中点,DE⊥BC,CE=3,则AB等于()A.11B.12C.13D.144.如图,△ABC中,BC=10,AC﹣AB=4,AD是∠BAC的角平分线,CD⊥AD,则S△BDC 的最大值为()A.40B.28C.20D.105.如图,△ABC中,∠ACB=90°,∠CAB=60°,动点P在斜边AB所在的直线m上运动,连结PC,那点P在直线m上运动时,能使图中出现等腰三角形的点P的位置有()A.6个B.5个C.4个D.3个6.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,则AB等于()A.2B.3C.4D.67.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD,CF,若∠CFE=32°,∠ADB=45°,则∠B的大小是()A.32°B.64°C.77°D.87°8.如图,DE是△ABC中AC边的垂直平分线,若BC=4cm,AB=5cm,则△EBC的周长为()A.8cm B.9cm C.10cm D.11cm9.如图,在△ABC中,∠B=15o,∠C=30o,MN是AB的中垂线,PQ是AC的中垂线,已知BC的长为,则阴影部分的面积为()A.B.C.3D.10.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是()①△ABE的面积=△BCE的面积;②∠F AG=∠FCB;③AF=AG;④BH=CH.A.①②③④B.①②③C.②④D.①③二.填空题11.如图,已知△ABC中,AB=AC,BD⊥AC于D,∠A=50°,则∠DBC的度数是.12.等腰三角形ABC中,∠A=4∠B.若∠A为底角,则∠C=°.13.如图,在△ABC中,AB=AC.AD是BC边上的中线,点E在边AB上,且BD=BE.若∠BAC=100°,则∠ADE的大小为度.14.如图,在Rt△ABC中,∠ABC=90°,CD⊥AB,垂足为点D,∠DCB=30°,BD=1,则AB的长为.15.如图,在Rt△ABC中,∠A=90°,∠B=30°,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为.16.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.若AB=5cm,BC=6cm,则AC=,DE=.17.如图所示,在△ABC中,DE、MN是边AB、AC的垂直平分线,其垂足分别为D、M,分别交BC于E、N,且DE和MN交于点F.(1)若∠B=20°,则∠BAE=;(2)若∠EAN=40°,则∠F=;(3)若AB=8,AC=9,设△AEN周长为m,则m的取值范围为.18.如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是.19.如图,AD垂直平分BC于点D,EF垂直平分AB于点F,点E在AC上,BE+CE=20cm,则AB=.20.如图,Rt△ABC中,∠C=90°,∠BAC的角平分线AE与AC的中线BD交于点F,P 为CE中点,连结PF,若CP=2,S△BFP=15,则AB的长度为.三.解答题21.如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=40°.求:(1)∠ADC的大小;(2)∠BAD的大小.22.如图,△ABC中,∠ABC=∠ACB,点D、E分别在AB、AC上,DE∥BC,BE,CD 交于点F.(1)求证:DC=EB;(2)在不添加任何辅助线的情况下,请直接写出图中所有的等腰三角形.23.如图,已知Rt△ABC中,∠ACB=90°,∠A=30°,AC边上的垂直平分线DE交AB 于点D,交AC于E.求:(1)∠BCD的度数;(2)若DE=3,求AB的长.24.如图,在Rt△ABC中,∠ACB=90°,∠CAB=2∠B,AD平分∠CAB.(1)求∠CAD的度数;(2)延长AC至E,使CE=AC,求证:DB=DE.25.如图,在△ABC中,∠ACB为直角,AB上的高CD及中线CE恰好把∠ACB三等分,若AC=20,求△ABC的两锐角及AD、DE、EB各为多少?26.(1)如图1,求证:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等;(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,若∠BAC=62°,则∠P AC是度.27.如图,已知四边形ABCD中,∠ABC与∠BCD的平分线交于点O,作OE⊥AB于点E,OF⊥CD于点F.求证:OE=OF.28.如图(1)将三角板ABC与∠DAE摆放在一起,射线AE与AC重合,射线AD在三角形ABC外部,其中∠ACB=30°,∠B=60°,∠BAC=90°,∠DAE=45°.固定三角板ABC,将∠DAE绕点A按顺时针方向旋转,如图(2),记旋转角∠CAE=α.(1)当α为60°时,在备用图(1)中画出图形,并判断AE与BC的位置关系,并说明理由;(2)在旋转过程中,当0°<α<180°,∠DAE的一边与BC平行时,求旋转角α的值;(3)在旋转过程中,当0°<α≤90°时,探究∠CAD与∠BAE之间的关系.(温馨提示:对于任意△ABC,都有∠A+∠B+∠C=180°)参考答案一.选择题1.解:当∠A=∠C时,∠C=70°;当∠A=∠B=70°时,∠C=180°﹣∠A﹣∠B=40°;当∠B=∠C时,∠C=∠B=(180°﹣∠A)=55°;即∠C的度数可以是70°或40°或55°,故选:C.2.解:设∠C=x.∵DE垂直平分线段AC,∴EA=EC,∴∠EAC=∠C=x,∴∠AEB=∠EAC+∠C=2x,∵CA=CB,∴∠B=∠CAB=45°+x,在△ABE中,∵∠BAE+∠B+∠AEB=180°,∴45°+45°+x+2x=180°,∴x=30°,∵∠EDC=90°,DE=2,∴AE=EC=2DE=4,故选:D.3.解:∵△ABC是等边三角形,∴AB=AC,∠C=60°,∵DE⊥BC,∴∠DEC=90°,∴CD=2CE=6,∵点D是AC的中点,∴AC=2CD=12,∴AB=AC=12,故选:B.4.解:如图:延长AB,CD交于点E,∵AD平分∠BAC,∴∠CAD=∠EAD,∵CD⊥AD,∴∠ADC=∠ADE=90°,在△ADE和△ADC中,,∴△ADE≌△ADC(ASA),∴AC=AE,DE=CD;∵AC﹣AB=4,∴AE﹣AB=4,即BE=4;∵DE=DC,∴S△BDC=S△BEC,∴当BE⊥BC时,S△BDC最大,即S△BDC最大=××10×4=10.故选:D.5.解:如图所示:以B为圆心,BC长为半径画弧,交直线m于点P4,P2,以A为圆心,AC长为半径画弧,交直线m于点P1,P3,边AC和BC的垂直平分线都交于点P3位置,因此出现等腰三角形的点P的位置有4个,故选:C.6.解:∵在Rt△ABC中,∠A=30°,BC=2,∴AB=2CB=4,故选:C.7.解:如图,取CF的中点T,连接DT,AT.∵∠BAC=90°,FD⊥BC,∴∠CAF=∠CDF=90°,∴AT=DT=CF,∴TD=TC=TA,∴∠TDA=∠TAD,∠TDC=∠TCD,∵∠ADB=45°,∴∠ADT+∠TDC=135°,∴∠ATC=360°﹣2×135°=90°,∴AT⊥CF,∵CT=TF,∴AC=AF,∴∠AFC=45°,∴∠BFD=45°﹣32°=13°,∵∠BDF=90°,∴∠B=90°﹣∠BFD=77°,故选:C.8.解:∵DE是△ABC中AC边的垂直平分线,∴AE=CE,∴AE+BE=CE+BE=AB=5cm,∴△EBC的周长=BC+BE+CE=5+4=9(cm).故选:B.9.解:∵MN是AB的中垂线,PQ是AC的中垂线,AN=BN,AQ=CQ,∴∠BAN=∠B=15°,∠CAQ=∠C=30°,∴∠ANQ=∠B+∠BAN=30°,∠AQN=∠C+∠CAQ=60°,∴∠NAQ=90°,∴BN=AN=NQ,AQ=CQ=NQ,∵BC=,∴NQ+NQ+NQ=3+,∴NQ=2,∴AN=,AQ=1,∴阴影部分的面积=AN•AQ==,故选:B.10.解:∵BE是AC边的中线,∴AE=CE,∵△ABE的面积=,△BCE的面积=AB,∴△ABE的面积=△BCE的面积,故①正确;∵AD是BC边上的高,∴∠ADC=90°,∵∠BAC=90°,∴∠DAC+∠ACB=90°,∠F AG+∠DAC=90°,∴∠F AG=∠ACB,∵CF是∠ACB的角平分线,∴∠ACF=∠FCB,∠ACB=2∠FCB,∴∠F AG=2∠FCB,故②错误;∵在△ACF和△DGC中,∠BAC=∠ADC=90°,∠ACF=∠FCB,∴∠AFG=180°﹣∠BAC﹣∠ACF,∠AGF=∠DGC=180°﹣∠ADC﹣∠FCB,∴∠AFG=∠AGF,∴AF=AG,故③正确;根据已知不能推出∠HBC=∠HCB,即不能推出HB=HC,故④错误;即正确的为①③,故选:D.二.填空题11.解:∵AB=AC,∴∠C=∠ABC,∵∠A=50°.∴∠C=∠ABC===65°,∵BD⊥AC,∴∠BDC=90°,∴∠DBC=90°﹣∠C=90°﹣65°=25°.故答案为:25°.12.解:设∠B=x°,当∠A是底角时,∠A=∠C=4∠B=4x°,∵∠A+∠B+∠C=180°,∴4x+x+4x=180,解得x=20,∴∠C=80°故答案为:80.13.解:∵AB=AC,∠BAC=100°,∴∠B=∠C=(180°﹣∠BAC)=40°,∵BD=BE,∴∠BDE=∠BED=(180°﹣∠B)=70°,∵AB=AC,AD⊥BC,∴∠ADB=90°,∴∠ADE=∠ADB﹣∠BDE=90°﹣70°=20°,故答案为:20.14.解:在Rt△ABC中,∠ABC=90°,∠DCB=30°,∴2BD=BC,∵CD⊥AB,∴∠A=∠DCB=30°,∴2BC=AB,∴AB=4BD,∵BD=1,∴AB=4.故答案为:4.15.解:在Rt△ABC中,∠A=90°,∠B=30°,∴∠ACB=60°,∵MN∥BC,∴∠AMN=∠B=30°,∵∠A=90°,AN=1,∴MN=2AN=2,∵MN平分∠AMC,∠AMN=30°,∴∠AMC=∠NMC=60°,∵CM平分∠ACB,∠ACB=60°,∴∠ACM=ACB=30°,∴∠ACM=∠NMC,∴MNCN=2,∴AC=AN+CN=1+2=3,∵在Rt△ABC中,∠A=90°,∠B=30°,∴BC=2AC=2×3=6,故答案为:6.16.解:∵BC=6cm,∴BD=DC=3(cm),∵AD⊥BC,BD=DC,AB=5cm,∴AC=AB=5(cm),∵点C在AE的垂直平分线上,∴EC=AC=5(cm),∴DE=DC+EC=8(cm),故答案为:5cm;8cm.17.解:(1)∵DE是线段AB的垂直平分线,∴EA=EB,∴∠BAE=∠B=20°;(2))∵DE、MN是边AB、AC的垂直平分线,∴AE=BE,AN=CN,∴∠BAE=∠B,∠CAN=∠C,∵∠EAN=40°,∠B+∠BAE+∠EAN+∠CAN+∠C=180°,∴∠BAE+∠CAN=70°,∴∠BAC=∠BAE+∠CAN+∠EAN=110°,∵∠ADF=∠AMF=90°,∴∠F=360°﹣∠ADF﹣∠AMF﹣∠BAC=360°﹣90°﹣90°﹣110°=70°;(3)∵DE、MN是边AB、AC的垂直平分线,∴AE=BE,AN=CN,∴△AEN的周长=AE+EN+AN=BE+EN+CN=BC,在△ABC中,AB=8,AC=9,∴9﹣8<BC<9+8,∴1<m<17.故答案为:(1)20°;(2)70°;(3)1<m<17.18.解:∵DE是AB的垂直平分线,∴EA=EB,∴△ACE的周长=AC+CE+EA=AC+CE+EB=AC+CB=11,故答案为:11.19.解:∵EF垂直平分AB于点F,∴AE=BE,∵BE+CE=20cm,∴AE+CE=20cm,即AC=20cm,∵AD垂直平分BC于点D,∴AB=AC=20cm,故答案为:20cm.20.解:过E作EG⊥AB于G,连接CF,∵P为CE中点,∵S△EFP=S△CFP,设S△EFP=S△CFP=y,∵BD是AC边上的中线,∴设S△CDF=S△AFD=z,∵S△BFP=15,∴S△BCD=15+y+z,∴S△ABC=2S△BCD=30+2y+2z,∵S△ACE=S△ACF+S△CEF=2y+2z,∴S△ABE=S△ABC﹣S△ACE=30+2y+2z﹣(2y+2z)=30,∵AE是∠CAB的角平分线,∴EG=CE=2CP=4,∴S△ABE=AB•EG=30,∴AB=15,故答案为:15.三.解答题21.解:(1)∵AB=AC,D是BC边上的中点,∴AD⊥BC,即∠ADC=90°;(2)∵∠B=40°,∴∠BAD=50°.22.(1)证明:∵∠ABC=∠ACB,∴AB=AC,∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,∴∠ADE=∠AED,∴AD=AE,∴AB=AD=AC=AE,即BD=CE,在△DBC和△ECB中,,∴△DBC≌△ECB(SAS),∴DC=EB;(2)解:图中所有的等腰三角形为△ABC、△ADE、△DEF、△BCF,理由如下:由(1)得:AB=AC,AD=AE,△DBC≌△ECB,∴△ABC、△ADE是等腰三角形,∠BCD=∠CBE,∴△BCF是等腰三角形,BF=CF,∵DE∥BC,∴∠FDE=∠BCD,∠FED=∠CBE,∴∠FDE=∠FED,∴△DEF是等腰三角形,FE=FD.23.解:(1)∵AC边上的垂直平分线是DE,∴CD=AD,DE⊥AC,∴∠A=∠DCA=30°,∵∠ACB=90°,∴∠BCD=∠ACB﹣∠DCA=90°﹣30°=60°,(2)∵∠B=60°∴∠BCD=∠B=60°∴BD=CD,∴BD=CD=AD=AB,∵DE=3,DE⊥AC,∠A=30°,∴AD=2DE=6,∴AB=2AD=12.24.证明:(1)∵∠ACB=90°,∴∠CAB+∠B=90°,又∵∠CAB=2∠B,∴∠B=30°,∠CAB=60°,∵AD平分∠CAB,∴∠CAD=∠DAB=30°;(2)∵∠DAB=30°=∠B,∴AD=DB,∵AC=EC,∠ACB=90°,∴AD=DE,∴DE=DB.25.解:∵△ABC中,∠C为直角,AB上的高CD及中线CE恰好把∠ACB三等分,∴∠ACD=∠DCE=∠ECB=30°,又∵CD⊥AB,AC=20,∴∠A=60°,AD=10,∵∠ACB为直角,∴∠B=30°∵AC=20,∴AB=40,∵CE是△ABC中线,∴AE=BE=20,∴DE=10.26.解:(1)已知:△ABC.求证:∠ABC、∠BCA、∠ACB三个角的平分线相交于点F,且点F到三边的距离相等.证明:如图,作∠ABC的角平分线FB,作∠BCA的角平分线FC,两条线相交于点F,作FG⊥AB于点G,FD⊥BC边于点D,FE⊥AC于点E,∵点F是∠ABC平分线上的一点,∴FG=FD,同理可得,FD=FE,∴FG=FD=FE(等量代换),∴点F在∠BAC的平分线上,∴三角形的三条角平分线相交于一点,并且这一点到三边的距离相等;(2)解:延长BA,作PN⊥BD于N,PF⊥BA于F,PM⊥AC于M,∵CP平分∠ACD,∴∠ACP=∠PCD,PM=PN,∵BP平分∠ABC,∴∠ABP=∠PBC,PF=PN,∴PF=PM,∴∠F AP=∠P AC,∴∠F AC=2∠P AC,∵∠F AC+∠BAC=180°,∴∠P AC=(180°﹣∠BAC)=(180°﹣62°)=59°.故答案为:59.27.证明:作OG⊥BC,∵∠ABC的平分线,OE⊥AB,OG⊥BC,∴OE=OG,∵∠BCD的平分线,OF⊥CD,OG⊥BC,∴OF=OG,∴OE=OF.28.解:(1)当α为60°时,AE⊥BC,如图(1),设AE与BC交于点F,∵∠CAE=α=60°,∠ACB=30°,∴∠AFC=90°,∴AE⊥BC;(2)当AD∥BC时,如图(2),∠DAC=∠C=30°,∵∠DAE=45°,∴∠CAE=α=15°;当AE∥BC时,如图(3),∠B=∠EAB=60°,∴∠CAE=α=∠BAC+∠EAB=150°,故旋转角α的值为15°或150°;(3)①如(2),当α≤45°时,α+∠BAE=90°,α+∠CAD=45°,∴∠BAE﹣∠CAD=45°;②如图(1),当45°<α<90°时,∵∠DAE+∠CAD+∠BAE=90°,∠DAE=45°,。
2020-2021学年八年级数学北师大版下册 第一章_三角形的证明 单元综合测试

第一章综合提升卷测试范围:三角形的证明时间:90分钟分值:100分第Ⅰ卷(选择题共30分)一、选择题(每小题3分,共30分)1.关于等腰三角形,有以下说法:(1)有一个角为46°的等腰三角形一定是锐角三角形;(2)等腰三角形两边的中线一定相等;(3)两个等腰三角形,若一腰以及该腰上的高对应相等,则这两个等腰三角形全等;(4)等腰三角形两底角的平分线的交点到三边距离相等.其中,正确说法的个数为()A.1B.2C.3D.42.用反证法证明命题:“如图1-Z-1,如果AB∥CD,AB∥EF,那么CD∥EF.”证明的第一步是()图1-Z-1A.假设CD∥EFB.假设CD不平行于EFC.已知AB∥EFD.假设AB不平行于EF3.已知下列命题:①若|x|=3,则x=3;②全等三角形的三组对应角相等;③直角三角形中30°角所对的直角边等于斜边的一半;④有理数与数轴上的点一一对应.其中原命题与逆命题均为真命题的个数是()A.1B.2C.3D.44.如图1-Z-2,若BD为等边三角形ABC的一条中线,延长BC至点E,使CE=CD=1,连接DE,则DE的长为()图1-Z-2A.√32B.√3C.√52D.√55.如图1-Z-3,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC,设△ABD,△BCD的面积分别为S1,S2,则S1∶S2等于()图1-Z-3A.2∶1B.√2∶1C.3∶2D.2∶√36.如图1-Z-4,在△ABC中,分别以点A和点B为圆心,大于12AB的长为半径作弧,两弧相交于M,N两点,连接MN,交AB于点H,以点H为圆心,HA的长为半径作的弧恰好经过点C,以点B 为圆心,BC的长为半径作弧交AB于点D,连接CD,若∠A=22°,则∠BDC等于()图1-Z-4A.52°B.55°C.56°D.60°7.如图1-Z-5,△ABC是等边三角形,AD,CE分别是BC,AB边上的高,且AD,CE相交于点O.若CE=1,则OD的长是()图1-Z-5A.13B.12C.√2D.√38.如图1-Z-6,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,DE⊥AB于点E,连接CE交AD 于点H,则图中的等腰三角形有()图1-Z-6A.5个B.4个C.3个D.2个9.如图1-Z-7,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论中,正确的有()图1-Z-7①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN;⑤△AFN≌△AEM.A.2个B.3个C.4个D.5个10.如图1-Z-8,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在其右侧作等边三角形ACD,连接BD,则BD所在直线与OA所在直线的位置关系是()图1-Z-8A.平行B.相交C.垂直D.平行、相交或垂直请将选择题答案填入下表:题号12345678910总分答案第Ⅱ卷(非选择题共70分)二、填空题(每小题3分,共18分)11.命题“全等三角形的面积相等”的逆命题是命题.(填“真”或“假”)12.如图1-Z-9,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为°.图1-Z-913.如图1-Z-10,有一张直角三角形纸片,两直角边AC=5 cm,BC=10 cm,将△ABC折叠,使点B 与点A重合,折痕为DE,则CD的长为.图1-Z-10 图1-Z-1114.如图1-Z-11,在△ABC中,AB=AC,∠A=120°,D是BC上任意一点,过点D分别作DE⊥AB 于点E,DF⊥AC于点F.如果BC=20 cm,那么DE+DF=cm.15.如图1-Z-12,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=3 cm,则BF=cm.图1-Z-12 图1-Z-1316.如图1-Z-13,等边三角形ABC的边AB上有一点P,作PE⊥AC于点E,Q为BC延长线上的一点,当P A=CQ时,连接PQ交AC于点D,则有下列结论:①PD=DQ;②∠Q=30°;③DE=12AC;④AE=12CQ.其中正确的结论有.(把所有正确结论的序号都写在横线上)三、解答题(共52分)17.(5分)如图1-Z-14,已知等腰三角形ABC,顶角∠A=36°.(1)在AC上作一点D,使AD=BD(要求:尺规作图,保留作图痕迹,不必写作法和证明);(2)求证:△BCD是等腰三角形.图1-Z-1418.(5分)如图1-Z-15,在△ABC中,∠C=90°,AB的垂直平分线分别交AB,AC于点D,E,且∠A=30°,DE=1 cm.求△ABC的面积.(结果保留根号)图1-Z-1519.(6分)如图1-Z-16,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E.若AB=6 cm,请求出△BDE的周长.图1-Z-1620.(6分)如图1-Z-17,点P,M,N分别在等边三角形ABC的各边上,且MP⊥AB于点P,NM⊥BC 于点M,PN⊥AC于点N.(1)求证:△PMN是等边三角形;(2)若AB=12 cm,求MC的长.图1-Z-1721.(7分)如图1-Z-18,在四边形ABCD中,AB∥CD,∠ABC的平分线交CD的延长线于点E,F 是BE的中点,连接CF并延长交AD于点G.(1)求证:CG平分∠BCD;(2)若∠ADE=110°,∠ABC=52°,求∠CGD的度数.图1-Z-1822.(7分)如图1-Z-19,在等腰三角形ABC中,AB=AC=8,∠BAC=100°,AD是△ABC的角平分线,DE∥AC交AB于点E.(1)求∠BAD的度数;(2)求∠B的度数;(3)求线段DE的长.图1-Z-1923.(8分)在△ABC中,∠BAC=120°,AB=AC,PC=√3P A,设∠APB=α,∠BPC=β.(1)如图1-Z-20①,点P在△ABC内.①若β=153°,求α的度数.小明同学通过分析已知条件发现:△ABC是顶角为120°的等腰三角形,且PC=√3P A,从而容易联想到构造一个顶角为120°的等腰三角形.于是,他过点A作∠DAP=120°,且AD=AP,连接DP,DB,发现两个不同的三角形全等:≌,再利用全等三角形及等腰三角形的相关知识可求出α的度数.请利用小明同学分析的思路,通过计算求得α的度数为;②小明在①的基础上进一步进行探索,发现α,β之间存在一种特殊的等量关系,请写出这个等量关系,并加以证明.(2)如图②,点P在△ABC外,那么a,β之间的数量关系是否改变?若改变,请直接写出它们之间的数量关系;若不变,请说明理由.图1-Z-2024.(8分)如图1-Z-21①,已知点B(0,9),点C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.(1)求证:DE=BO.(2)如图②,当点D恰好落在BC上时,①求点E的坐标.②在x轴上是否存在点P,使△PEC为等腰三角形?若存在,写出点P的坐标;若不存在,请说明理由.③如图③,点M是线段BC上的动点(不与点B,C重合),过点M作MG⊥BE于点G,MH⊥CE 于点H,当点M运动时,MH+MG的值是否发生变化?若不发生变化,直接写出MH+MG的值;若发生变化,简要说明理由.图1-Z-21详解1.B[解析] (1)(4)正确.2.B3.A4.B5.A6.C[解析] 如图,连接CH.由题意得,直线MN是线段AB的垂直平分线,∴AH=BH.又∵CH=AH,∴CH=1AB,2∴∠ACB=90°.∵∠A=22°,∴∠ACH=∠A=22°,∴∠BCH=∠B=68°.∵BC=BD,∴∠BDC=∠BCD=1(180°-68°)=56°.27.A8.B9.C[解析] ∵∠E=∠F=90°,∠B=∠C,AE=AF,∴△ABE≌△ACF(AAS),∴BE=CF,故②正确,∠BAE=∠CAF,∴∠BAE-∠BAC=∠CAF-∠BAC,即∠1=∠2,故①正确.∵△ABE≌△ACF,∴AB=AC.又∵∠BAC=∠CAB,∠B=∠C,∴△ACN≌△ABM(ASA),故③正确.不能证明CD=DN成立,故④错误.∵∠1=∠2,AF=AE,∠F=∠E,∴△AFN≌△AEM(ASA),故⑤正确.10.A[解析] ∵∠AOB=60°,OA=OB,∴△OAB是等边三角形,∴OA=AB,∠OAB=∠ABO=60°.如图①,若点C在线段OB上,∵△ACD是等边三角形,∴AC=AD,∠CAD=60°,∴∠OAC=∠BAD.在△AOC和△ABD中,∵OA=BA,∠OAC=∠BAD,AC=AD,∴△AOC≌△ABD,∴∠ABD=∠AOC=60°,∴∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,∴BD∥OA.如图②,若点C在线段OB的延长线上,∵△ACD是等边三角形,∴AC=AD,∠CAD=60°,∴∠OAC=∠BAD.在△AOC和△ABD中,∵OA=BA,∠OAC=∠BAD,AC=AD,∴△AOC≌△ABD,∴∠ABD=∠AOC=60°,∴∠DBE=180°-∠ABO-∠ABD=60°=∠AOB,∴BD∥OA.故选A.11.假12.3413.154cm [解析] 设CD=x cm,则BD=AD=(10-x )cm .在Rt △ACD 中,由勾股定理,得(10-x )2=x 2+52,解得x=154.14.10 [解析] 利用含30°角的直角三角形的性质得,DE+DF=12(BD+CD )=12BC. 15.6 [解析] 在Rt △ADB 与Rt △ADC 中,AB=AC ,AD=AD ,∴Rt △ADB ≌Rt △ADC ,∴S △ABC =2S △ABD =2×12AB ·DE=AB ·DE=3AB.∵S △ABC =12AC ·BF ,∴12AC ·BF=3AB.∵AC=AB ,∴12BF=3,∴BF=6(cm).16.①③④ [解析] ①过点P 作PF ∥BQ ,交AC 于点F .∵△ABC 是等边三角形,∴∠ACB=∠A=60°. ∵PF ∥BQ ,∴∠AFP=∠ACB=60°,∠PFD=∠QCD , ∴△AFP 是等边三角形, ∴PF=P A.∵P A=CQ ,∴PF=CQ.在△PFD 和△QCD 中,∵∠FDP=∠CDQ ,∠PFD=∠QCD ,PF=CQ , ∴△PFD ≌△QCD , ∴PD=DQ ,故①正确. ②∵△PFD ≌△QCD , ∴∠DPF=∠Q. ∵△APF 为等边三角形, ∴∠APF=60°.∵QP 与AB 不一定垂直, ∴∠Q 不一定为30°,故②不正确. ③∵△APF 是等边三角形,PE ⊥AC , ∴EF=12AF .∵△PFD ≌△QCD ,∴DF=DC ,∴DF=12FC ,∴DE=EF+DF=12AF+12FC=12AC ,故③正确. ④在Rt △AEP 中,∠A=60°,∴∠APE=30°,∴AE=12AP ,∴AE=12CQ ,故④正确.则本题正确的结论有①③④.17.解:(1)如图,点D 为所作.(2)证明:∵∠A=36°,AB=AC ,∴∠ABC=∠C=12(180°-36°)=72°.∵AD=BD ,∴∠ABD=∠A=36°,∴∠BDC=∠A+∠ABD=36°+36°=72°,∴∠BDC=∠C ,∴BD=BC ,∴△BCD 是等腰三角形.18.解:∵DE 垂直平分AB ,∠A=30°,DE=1 cm, ∴AE=2 cm,∴AD=√22-12=√3(cm),∴AB=2AD=2√3 cm .在Rt △ABC 中,∠A=30°,∴BC=12AB=√3 cm,∴AC=√(2√3)2-(√3)2=3(cm),∴S △ABC =12×√3×3=32 √3(cm 2).19.解:∵AD 平分∠CAB ,∠C=90°,DE ⊥AB , ∴DE=DC.在Rt △ADC 和Rt △ADE 中,∵DC=DE ,AD=AD ,∴Rt △ADC ≌Rt △ADE (HL),∴AC=AE.又∵AC=BC,∴AE=BC,∴△BDE的周长=DE+DB+EB=BC+EB=AE+EB=AB.∵AB=6 cm,∴△BDE的周长为6 cm.20.解:(1)证明:∵△ABC是等边三角形,∴∠A=∠B=∠C.∵MP⊥AB,NM⊥BC,PN⊥AC,∴∠MPB=∠NMC=∠PNA=90°,∴∠PMB=∠MNC=∠APN,∴∠NPM=∠PMN=∠MNP,∴△PMN是等边三角形.(2)∵△PMN是等边三角形,∴PN=PM=NM.又∵∠A=∠B=∠C,∠PNA=∠MPB=∠NMC,∴△PBM≌△MCN≌△NAP,∴P A=BM=CN,PB=MC=AN,∴BM+PB=AB=12 cm.∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,∴2PB=BM,∴2PB+PB=12 cm,∴PB=4 cm,∴MC=4 cm.21.解:(1)证明:∵BE平分∠ABC,∴∠ABF=∠CBF=1∠ABC.2∵AB∥CD,∴∠ABF=∠E,∴∠CBF=∠E,∴BC=CE,∴△BCE是等腰三角形.∵F为BE的中点,∴CF平分∠BCD,即CG 平分∠BCD.(2)∵AB ∥CD ,∴∠ABC+∠BCD=180°.∵∠ABC=52°,∴∠BCD=128°.∵CG 平分∠BCD ,∴∠GCD=12∠BCD=64°.∵∠ADE=110°,∠ADE=∠CGD+∠GCD ,∴∠CGD=46°.22.解:(1)∵∠BAC=100°,且AD 平分∠BAC , ∴∠BAD=50°.(2)在等腰三角形ABC 中,∠B=180°-100°2=40°.(3)∵AD 平分∠BAC , ∴∠EAD=∠CAD.∵DE ∥AC ,∴∠ADE=∠CAD ,∴∠EAD=∠ADE ,∴AE=DE.∵DE ∥AC ,∴∠EDB=∠C.∵AB=AC ,∴∠B=∠C ,∴∠EDB=∠B ,∴BE=DE ,∴DE=BE=AE=12AB=12×8=4.23.解:(1)①△ADB △APC 63° ②β-α=90°.证明:如图①,过点A 作AH ⊥DP 于点H.∵∠DAP=∠BAC=120°,∴∠DAB=∠P AC,且AD=AP,AB=AC,∴△ADB≌△APC(SAS),∴BD=PC=√3P A,∠ADB=∠APC.∵∠DAP=120°,AD=AP,AH⊥DP,∴∠ADP=∠APD=30°,DH=PH,∴AP=2AH,HP=√3AH,∴DP=√3AP,∴BD=DP,∴∠DBP=∠DPB=∠APB-∠APD=α-30°,∴∠BDP=180°-2(α-30°)=240°-2α,∴∠ADB=∠BDP+∠ADP=270°-2α=∠APC.∵∠APB+∠APC+∠BPC=360°,∴270°-2α+α+β=360°,∴β-α=90°.(2)α,β之间的数量关系改变了,α+β=90°.理由如下:如图②,作∠P AN=120°,且P A=NA,连接PN,BN.∵∠P AN=∠BAC=120°,∴∠BAN=∠P AC.又∵AB=AC,NA=P A,∴△ABN≌△ACP(SAS),∴∠BNA=∠APC,PC=BN=√3AP.∵∠P AN=120°,P A=NA,∴∠APN=∠ANP=30°,∴PN=√3P A=BN,∴∠BPN=∠PBN=α+30°.∵∠BPN+∠PBN+∠BNP=180°,∴2(α+30°)+β-α+30°=180°,∴α+β=90°.24.解:(1)证明:∵△ODC和△EBC都是等边三角形,∴OC=DC,BC=CE,∠OCD=∠BCE=60°,∴∠BCE+∠BCD=∠OCD+∠BCD,即∠ECD=∠BCO,∴△DEC≌△OBC(SAS),∴DE=BO.(2)①∵△ODC是等边三角形,∴∠OCB=60°.∵∠BOC=90°,∴∠OBC=30°.设OC=x,则BC=2x,∴x2+92=(2x)2,解得x=3√3,∴BC=6√3.∵△EBC是等边三角形,∴BE=BC=6√3,∠CBE=60°,∴∠OBE=∠OBC+∠CBE=90°,BE∥轴,∴E(6√3,9).②存在.当CP=CE=6√3时,△PEC是等腰三角形.∵C(3√3,0),∴点P的坐标为(-3√3,0)或(9√3,0).③MH+MG的值不发生变化.如图,连接EM.由(1)知△DEC≌△OBC,∴DE=BO=9,∠EDC=∠BOC=90°,即ED⊥BC.∵S △EBC =S △EBM +S △ECM ,MG ⊥BE ,MH ⊥EC , ∴12BC ·DE=12BE ·MG+12EC ·MH. ∵BE=BC=EC ,∴MG+MH=DE=9.。
八年级下册数学第3章 图形与坐标测试题(二)

第3章图形与坐标测试题(浙江李奇)一、选择题(每小题3分,共30分)1.根据下列表述,能确定位置的是()A. 广州白云区以北B. 万达广场3楼C. 博罗中学北偏东35°D. 东经120°,北纬30°2.在平面直角坐标系中,若点A(-m,n)在第四象限,则点B(1-n,m)在()A.第一象限B.第二象限C.第三象限D.第四象限3. 在平面直角坐标系中,下列各点在y轴上的点是()A. (2,0 )B. (-2,3 )C. (0,3)D. (1,-3 )4.小明和妈妈在家门口打车出行,借助某打车软件,他看到了当时附近的出租车分布情况.若以他现在的位置为原点,正东、正北分别为x轴、y轴的正方向,图1中点A的坐标为(1,0),那么离他最近的出租车所在位置的坐标大约是()A.(3.2,1.3)B.(-1.9,0.7)C.(0.7,-1.9)D.(3.8,-2.6)图15. 已知点A(2,-1)和点B(m-1,3),如果直线AB∥y轴,那么m的值为()A. 1B. -4C. -1D. 36.点P(m,-2)与点P1(-4,n)关于x轴对称,则m,n的值分别为()A. 4,-2B. -4,2C. -4,-2D. 4,27. 有下列说法:①点(3,2)与(2,3)是同一个点;②点(0,-2)在x轴上;③点(0,0)是坐标原点;④点(-2,-6)在第三象限内.其中正确的有()A. 0个B. 1个C. 2个D. 3个8. 已知直角坐标系中点P到y轴的距离为5,且点P到x轴的距离为3,则这样的点P的个数是()A.1B.2C.3D.49. 图2为晓莉使用微信与晓红的对话记录.根据图中两个人的对话记录,若下列有一种走法能从邮局出发走到晓莉家,此走法为()A.向北直走700米,再向西直走100米B.向北直走100米,再向东直走700米C.向北直走300米,再向西直走400米D.向北直走400米,再向东直走300米图2 图310. 如图3,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的格点上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有()A. 2个B. 3个C. 4个D. 5个二、填空题(本大题共6小题,每小题4分,共24分.请你把答案填在横线上方)11. 如果用(7,3)表示七年级三班,则(9,6)表示________.12. 在平面直角坐标系中,点P(-2,1)关于y轴对称的点P的坐标是________.13.已知点P(5a﹣7,﹣6a﹣2)在第二、四象限的角平分线上,则a=.14. 图4是北京市地铁部分线路示意图.若分别以正东、正北方向为x轴,y轴的正方向建立平面直角坐标系,表示西单的点的坐标为(-4,0),表示雍和宫的点的坐标为(4,6),则表示南锣鼓巷的点的坐标是.图 4 图515.在平面直角坐标系中,一个点的横、纵坐标都是整数,并且它们的乘积是4,满足条件的点共有个.16.如图5,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(-1,1),第2次运动到点(-2,0),第3次运动到点(-3,2),…… 按这样的运动规律,经过第2020次运动后,动点P的坐标是_______.三、解答题(共52分)17.(6分)如图6,将△ABC各顶点的横坐标都乘以-1,纵坐标不变,请在下面的平面直角坐标系中描出对应点A′,B′,C′,并依次连接这三个点,则所得△A′B′C′与△ABC有怎样的位置关系?图618.(6分)图7是某动物园的平面示意图,请按要求回答下列问题:(1)正门北偏东30°的方向上有哪些动物景点?要想确定蝴蝶馆的位置,还需要有什么数据?(2)距正门的图上距离为1个单位长度的景点有哪些?图719. (8分)图8是学校的平面示意图,已知旗杆的位置是(-2,3),实验室的位置是(1,4).(1)根据所给条件建立适当的平面直角坐标系,并用坐标表示食堂、图书馆的位置;(2)已知办公楼的位置是(-2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;(3)如果1个单位长度表示30米,求宿舍楼到教学楼的实际距离.20.(10分)如图9,平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0),B(5,0),C(3,3),D(2,4),求四边形ABCD的面积.21. (10分)在平面直角坐标系中,点P (x ,y )的横坐标x 的绝对值表示为|x|,纵坐标y 的绝对值表示为|y|,我们把点P (x ,y )的横坐标与纵坐标的绝对值之和叫做点P (x ,y )的勾股值,记为[P],即[P]=|x|+|y|(其中“+”是四则运算中的加法),例如点P (1,2)的勾股值为[P]=|1|+|2|=3.(1)求点A (-2,4),B (32+,32-)的勾股值[A],[B];(2)若点M 在x 轴的上方,其横、纵坐标均为整数,且[M]=3,请求出点M 的坐标.22.(12分)如图10,一只甲虫在5×5的方格(每个小方格的边长为1)上沿着网格线运动. 它从A 处出发去看望B ,C ,D 处的其他甲虫,规定:向上、向右走均为正,向下、向左走均为负. 如果从A 到B 记为:A→B (+1,+4),从B 到A 记为:B→A (-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.(1)图中A→D ( , ),C→B ( , ),B → (+3,-2);(2)若这只甲虫从A 处去甲虫P 处的行走路线依次为(+1,+2),(+4,-1),(-2,+3),(-1,-1),请在图中标出P 的位置;(3)若这只甲虫的行走路线为A→B →C→D ,请计算该甲虫走过的路程.(4)若图中另有两个格点M ,N ,且M→A (3-a ,b -4),M→N (5-a ,b -2),则N→A 应记为什么?图10附加题(20分,不计入总分)23. 在平面直角坐标系中,O 为坐标原点,过点A (8,6)分别作x 轴,y 轴的平行线,交y 轴于点B ,交x 轴于点C ,点P 是从点B 出发,沿B→A→C 以2个单位长度/秒的速度向终点C 运动的一个动点,运动时间为t (秒).(1)直接写出点B 和点C 的坐标:B ,C ;(2)当点P 运动时,用含t 的式子表示线段AP 的长;(不要求写出t 的取值范围)(3)点D (2,0),连接PD ,AD ,在(2)的条件下是否存在这样的t 值,使S △APD =18S 四边形ABOC ,若存在,请求出t 值;若不存在,请说明理由.图11第3章图形与坐标测试题参考答案一、1.D 2.D 3.C 4.B 5.D 6.B 7.C 8.D 9.A10.B二、11. 九年级六班12.(2,1)13.-9 14.(1,3)15.616. (-2020,0)提示:动点P第1次从原点运动到点(-1,1),第2次运动到点(-2,0),第3次运动到点(-3,2),第4次运动到点(-4,0),第5次接着运动到点(-5,1),……所以经过第2020次运动后,动点P的横坐标为-2020;纵坐标为1,0,2,0,每4个为一个循环,且2020÷4=505,所以纵坐标为0.即经过第2020次运动后,动点P的坐标是(-2020,0).三、17.解:如图1,△A′B′C′与△ABC关于y轴对称.图118. 解:(1)观察图形知,正门北偏东30°的方向上的有蝴蝶馆、大象馆.要想确定蝴蝶馆的位置,还需知道蝴蝶馆与正门的距离.(2)距正门的图上距离为1个单位长度的景点有长颈鹿馆和猴园.19. 解:(1)建立平面直角坐标系如图2所示,食堂(-5,5),图书馆(2,5).图2(2)如图2所示,办公楼和教学楼的位置即为所求.(3)由坐标系可知宿舍楼到教学楼的距离是8个单位长度,所以宿舍楼到教学楼的实际距离为:8×30= 240(米).20. 解:如图3,作CE⊥x轴于点E,DF⊥x轴于点F.图3则S △ADF =12×(2-1)×4=2,S 梯形DCEF =12×(3+4)×(3-2)=3.5,S △BCE =12×(5-3)×3=3. 所以S 四边形ABCD =2+3.5+3=8.5.答:四边形ABCD 的面积是8.5.21. 解:(1)由题意,[A]=|-2|+|4|=2+4=6,[B]=|32+|+|32-|=2332-++=23.(2)因为点M 在x 轴的上方,其横、纵坐标均为整数,且[M]=3,所以x=±1,y=2,或x=±2,y=1, x=0,y=3.所以点M 的坐标为(-1,2),(1,2),(-2,1),(2,1)或(0,3).22. 解:(1)+4 +2 -2 0 D(2)点P 的位置如图4所示.图4(3)A B 记为(1,4),B C 记为(2,0),C D 记为(1,-2),则该甲虫走过的路程为1+4+2+1+2=10.(4)由M A (3-a ,b -4),M N (5-a ,b -2),所以5-a -(3-a )=2,b -2-(b -4)=2.所以点A 向右走2格,向上走2格到N ,所以N A 记为(-2,-2).23. 解:(1)(0,6) (8,0)(2)由题意可得AB=8,AC=6.当点P 在线段BA 上时, AP=8-2t ;当点P 在线段AC 上时,AP=2t -8.(3)如图5,当点P 在线段BA 上时,AB ÷2=4,所以t <4.设点D 到AP 的距离为h ,则h=AC.因为S △APD =12AP•h=12AP•AC ,S 四边形ABOC =AB•AC ,所以12•(8-2t )×6=18×8×6,解得t=3<4;图5 图6如图6,当点P 在线段AC 上时,4<t <862+,即4<t <7.因为S△APD=12AP•CD,CD=8-2=6,S四边形ABOC=AB•AC,所以12•(2t-8)×6=18×8×6,解得t=5<7.综上所述,当t为3秒或5秒时,S△APD=18S四边形ABOC.。
北师大版八年级下学期数学第一章三角形的证明同步练习题

新北师大版八年级下学期《第一章三角形的证明》同步测试题一、选择题1、用反证法证明“若a⊥c,b⊥c,则a∥b”时,应假设【】A、a不垂直于cB、a,b都不垂直于cC、a⊥bD、a与b相交2、有下列四个命题:①等腰三角形两腰上的中线相等,②等腰三角形两腰上的高相等,③等腰三角形两底角的平分线相等,④等腰三角形底边上的中点到两腰的距离相等. 正确的命题的个数有【】 A、1个B、2个C、3个D、4个3、如图,△A BC中,∠B=∠BAD,∠ADC=∠C,BD=5,DC=m,则AC是【】A、4B、m-5C、5D、m+54、下列图形中,两个三角形一定全等的是【】A、含80°角的两个锐角三角形 B、边长为20cm的两个等边三角形 C、腰长对应相等的两个等腰三角形 D、有一个钝角对应相等的两个等腰三角形5、在证明“在△ABC中至多有一个直角或钝角”时,第一步应假设【】A、三角形中至少有一个直角或钝角B、三角形中至少有两个直角或钝角C、三角形中没有直角或钝角D、三角形中三个角都是直角或钝角6、下列命题中正确的个数是【】①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高重合;④只有两条边相等的等腰三角形是轴对称图形,对称轴有1条.A、1个B、2个 C、3个 D、4个7、等腰三角形的一个外角是120°,一边长为acm,那么它的周长是【】A、3acmB、2acmC、acmD、无法确定8、如图,在∠AOB的两边上截取AO=BO,CO=DO,连接AD,BC交于点P,则下列结论正确的是:(1)△AOD≌△BOC;(2)△APC≌△BPD;(3)点P在∠AOB的平分线上【】A、只有(1) B、只有(2)C、只有(1)(2)D、(1)(2)(3)9、如图,∠AOB和一条定长线段a,在∠AOB内找一点P,使P到OA,OB的距离都等于a,作法如下:(1)作OB的垂线NH,使NH=a,H为垂足.(2)过N作NM∥OB.(3)作∠AOB的平分线OP,与NM交于P.(4)点P即为所求.其中(3)的依据是【】A、平行线之间的距离处处相等 B、到角的两边距离相等的点在角的平分线上 C、角的平分线上的点到角的两边的距离相等 D、到线段的两个端点距离相等的点在线段的垂直平分线上10、△ABC中,若,则此三角形为【】三角形. A、等腰B、直角C、等腰直角 D、等边11、如图,已知△ABC是等边三角形,点O是BC上任意一点,OE、OF分别与两边垂直,等边三角形的高为1,则OE+OF的值为【】 A、B、1 C、2 D、不确定12、已知等边三角形的面积是,则它的高是【】A、cmB、cmC、cmD、cm13、Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:①BE+CF=BC;②;③=AD·EF;④AD≥EF;⑤AD与EF可能互相平分,其中正确结论的个数是【】A、1个B、2个C、3个D、4个14、如图所示,AD平分∠BAC,AD=BD,AC=AB,则【】A、AC⊥CDB、AC=2CDC、AC=BDD、BD=2CD15、如图,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A→B→C的方向运动,到达点C时停止.设点M运动的路程为x,,则y关于x的函数图象大致为【】A、B、C、D、二、填空题16、等边三角形的每个内角都等于______________________.17、如图,已知∠A=∠D=90°,若要依据“HL”证明△ABC≌△DCB,应添加条件_________ ___________ _____;若要依据“AAS”证明△ABC≌△DCB,应添加的条件是_________________________________.18、等腰三角形是轴对称图形,它的对称轴是__________________.19、如图,在△ABC中,AB=AC,∠B=40°,则∠A=____________.20、如图,在△ABC中,AB=AC,D、E、F分别为边BC、AB、AC上的点,且BE=CD,CF=BD.若∠A=40°,则∠EDF=______°.21、在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为50°,则∠B 等于_______________度.22、△ABC中,AB=AC,若BC=CD=DE=EF=FA,则∠A=______°.23、如图,AC平分∠BAD,CE⊥AB,且2AE=AB+AD,∠ADC=146°,则∠BCE=___________°.三、解答题24、(1)小丽同学说“每一个定理不一定都有逆定理,因为逆命题不一定正确.”你认为她的说法正确吗?如果不正确,应如何改正?25、写出命题“平行于同一条直线的两条直线互相平行”的逆命题,并判定这对互逆命题的真假.26、如下图所示,在△ABC中,∠ACB=120°,CD平分∠ACB,AE∥DC,交BC的延长线于点E,试说明△ACE是等边三角形.27、如图,△ABC中,∠A=60°,高BD、CE交于M,MD=5,ME=7. 求BD、CE的长.28、如图,△ABC中,AB=AC,∠A=100°,BD平分∠ABC交AC于D.求证:AD+BD=BC.四、证明题29、求证:在一个三角形中,如果两个角不等,那么它们所对的边也不等.30、如图所示,AB=AC,DB=DC,AD的延长线交BC于点E.求证:BE=EC.31、写出下列命题的已知、求证,并完成证明过程.命题:如果一个三角形的两个角相等,那么这两个角所对的边也相等(简称:“等角对等边”).已知:如图,____________________________________.求证:______________________________________________________.证明:32、如图所示,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB于E,DF⊥AC于F.求证:∠B=∠C.33、如图,△ABC中,从点C向∠BAC的平分线引垂线,垂足为点E,设AE交BC于点D,且AB=AD.求证:.五、应用题34、如图是某市部分街道示意图,AB=BC=AC,CD=CE=DE,A、B、C、D、E、F、G、H为“公共汽车”停靠点,“公共汽车甲”从A站出发,按照A、H、G、D、E、C、F的顺序到达F站,“公共汽车乙”从B站出发,沿F、H、E、D、C、G的顺序到达G站.如果甲、乙分别从A、B 站同时出发,在各站耽误的时间忽略不计,两车的速度一样,试问哪一辆汽车先到达指定站?为什么?35、有一块直角三角形的绿地,量得两直角边长分别为6m,8m.现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 答案 D D C B B D A D B C B C C A B题号16 17 18 19 20 21 22 23答案60AB=DC或AC=DB;∠ABC=∠DCB或∠ACB=∠DBC顶角平分线所在直线100°7070或2020 5624)、解:她的说法正确,理由如下:命题有真假命题之分,而定理是经过证明后得出的正确的命题,命题正确时逆命题不一定正确,即定理的逆命题不一定是真命题,所以虽然每个命题都有逆命题,但每个定理不一定存在逆定理,只有当原定理的逆命题是真命题时,原定理的逆命题才能称为逆定理.25)、【解答】1、逆命题:“如果两条直线互相平行,那么这两条直线都与第三条直线平行”,该命题是假命题;而原命题是真命题.26)、【解答】1、因为CD平分∠ACB,∠ACB=120°,所以∠ACE=180°-∠ACB=60°,且.因为AE∥DC,所以∠ACD=∠CAE,∠BCD=∠E.所以∠CAE=∠E=∠ACE=60°.所以△ACE是等边三角形.27)、【解答】解:∵BD⊥AC,∴∠ADB=90°.又∵∠A=60°,∴∠ABD=90°-60°=30°,同理可得∠ACE=30°,在Rt△BEM中,∠EBM=30°,∠BEM=90°,∴BM=2ME.∵ME=7,∴BM=14.同理由MD=5,得CM=2MD=10,∴BD=BM+MD=19,CE=CM+EM=10+7=17. CE取点F,使DE=DF.∵AB=AC,∠A=100°,∴∠ABC=∠C==40°.∵BD平分∠ABC,∴∠ABD=∠DBE=20°.∵在△ABD和△EBD中,AB=EB,∠ABD=∠DBE,BD=BD,∴△ABD≌△EBD,∴∠BED=∠A=100°,∴∠DEF=180°-100°=80°.∵DE=DF,∴∠DFE=∠DEF=80°,∴∠BDF=180°-80°-20°=80°,∴BD=BF,∠DFC=180°-80°=100°,∴∠FDC=180°-100°-40°=40°,∴DF=FC,∴DF=FC=DE=AD,∴BC=BF+FC=BD+AD.29)、【解答】1、证明:假设在一个三角形中,这两个不等的角所对的边相等,根据等边对等角,它们所对的两个角也相等,这与已知条件相矛盾,说明假设不成立,所以在一个三角形中,如果两个角不等,那么它们所对的边也不等.30)、【解答】1、证明:因为AB=AC,BD=DC,AD=AD,所以∠BAE=∠CAE.又因为AB=AC,所以BE=EC.31)、【解答】解:在△ABC中,∠B=∠C,求证:AB=AC.证明:过点A作AD⊥BC于D,∴∠ADB=∠ADC=90°,在△ABD和△ACD中,∴△ABD≌△ACD(AAS),∴AB=AC.32)、【解答】1、∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF.又∵BD=CD,∠DEB=∠DFC=90°,∴(Rt)△DEB≌(Rt)△DFC(HL).∴∠B=∠C.33)、【解答】1、分别延长AB,CE交于点F.∵AE平分∠FAC,∴∠FAE=∠CAE.∵∠FAE=∠CAE,∠AEF=∠AEC=90°,AE=AE,∴△AEF≌△AEC(AS A),∴AF=AC,EF=EC.又过点E作EG∥AF,交BC于点G,∴,∠ABD=∠DGE.∵AB=AD,∠ABD=∠ADB=∠GDE=∠DGE,∴DE=EG,∴AE=AD+DE=AB+EG====. 所以△ABC与△ECD均为等边三角形,且∠ACE=60°.在△ACD和△BCE中,AC=BC,∠ACD=∠BCE=120°,CD=CE,所以△ACD≌△BCE(SAS).所以AD=BE,∠1=∠2.在△BCF和△ACG中,∠1=∠2,BC=AC,∠BCF=∠ACG=60°,所以△BCF≌△ACG(ASA).所以CF=CG.又因为DE+EC=ED+CD,所以AD+DE+EC+CF=BE+ED+CD+CG.即甲、乙两车同时到达指定站.35)、【解答】1、解:在Rt△ABC中,∠ACB=90°,AC=8,BC=6,由勾股定理有AB=10.扩充部分为Rt△ACD,扩充成等腰△ABD,应分以下三种情况:①如图1,当AB=AD=10时,可求CD=CB =6.得△ABD的周长为32m.②如图2,当AB=BD=10时,可求CD=4.由勾股定理,得.得△ABD的周长为m.如图③,当AB为底时,设AD=BD=x,则CD=x-6,由勾股定理,得.得△ABD 的周长为m.====Word行业资料分享--可编辑版本--双击可删====。
(必考题)初中数学八年级数学下册第一单元《三角形的证明》测试卷(包含答案解析)(3)

一、选择题1.如图,P 为ABC 的边BC 上一点,且2PC PB =,已知45ABC ∠=︒,60APC ∠=︒,则ACB ∠的度数为( )A .75︒B .80︒C .85︒D .88︒2.已知点P 是ABC 内一点,且它到三角形的三个顶点距离之和最小,则P 点叫ABC 的费马点(Fermat point ).已经证明:在三个内角均小于120︒的ABC 中,当120APBAPC BPC 时,P 就是ABC 的费马点.若点P 是腰长为6的等腰直角三角形DEF 的费马点,则PD PE PF ++=( ) A .6 B .33+C .63D .9 3.如图,在Rt △ABC 中,∠BAC=90°,∠C=45°,AD ⊥BC 于点D ,∠ABC 的平分线分别交 AC 、AD 于E 、F 两点,M 为EF 的中点,AM 的延长线交 BC 于点N ,连接EN ,下列结论:①△AFE 为等腰三角形;②DF= DN ;③AN = BF ;④EN ⊥NC .其中正确的结论有( )A .1个B .2个C .3个D .4个4.如图,在ABC 中,4AB AC ==,ABC ∠和ACB ∠的平分线交于点E ,过点E 作//MN BC 分别交AB 、AC 于M 、N ,则AMN 的周长为( )A .12B .4C .8D .不确定 5.如图,在ABC 中,点A 、B 、C 的坐标分别为(,0)m 、(0,2)和(5,3),则当ABC 的周长最小时,m 的值为( )A.0 B.1 C.2 D.36.已知等腰三角形的腰长为5,一腰上的高线长为4,则底边长是()A.3 B.20C.3或20D.20或80 7.如图,△ABC中,DC=2BD=2,连接AD,∠ADC=60°.E为AD上一点,若△BDE和△BEC都是等腰三角形,且AD=31 ,则∠ACB=()A.60°B.70°C.55°D.75°8.如图,直线AB,CD交于点O,若AB,CD是等边△MNP的两条对称轴,且点P在直线CD上(不与点O重合),则点M,N中必有一个在()A.∠AOD的内部B.∠BOD的内部C.∠BOC的内部D.直线AB上9.如图,在△ABC中,AD平分∠BAC,过B点作BE⊥AD于E,过E作EF//AC交AB于F,则()A.不确定B.AF=BFC .AF >BFD .AF <BF 10.如图,ABC 为等边三角形,BO 为中线,延长BA 至D ,使AD AO =,则DOB∠的度数为( )A .105︒B .120︒C .135︒D .150︒11.如图,在锐角ABC 中,AB AC =,D ,E 是ABC 内的两点,AD 平分BAC ∠,60EBC E ∠=∠=,若6BE cm =,2DE cm =,则BC 的长度是( )A .6cmB .6.5cmC .7cmD .8cm12.如图,在ABC 中,ED //BC ,ABC ∠和ACB ∠的平分线分别交ED 于点F 、G ,若2FG =,6ED =,则DB EC +的值为( )A .3B .4C .5D .9二、填空题13.如图,O 是正ABC 内一点,6OA =,8OB =,10OC =,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ',下列结论:①点O 与O '的距离为6;②BO A '△可以由BOC 绕点B 逆时针旋转60°得到;③150AOB ∠=︒;④1263BOC S =+△;⑤24163AOBO S '=+四边形.其中正确的结论是________.(填序号)14.如图,OA OB OC ==且30ACB ∠=︒,则AOB ∠的大小是______度.15.小华的作业中有一道题:“如图,,AC BD 在AB 的同侧,1,4,4AC BD AB ===,点E 为AB 的中点.若120CED ∠=︒,求CD 的最大值.”哥哥看见了,提示他将ACE 和BDE 分别沿CE 、DE 翻折得到A CE '△和B DE ',连接A B ''.最后小华求解正确,得到CD 的最大值是__________.16.已知:如图,在△ABC 中CD 交AB 边于点D ,直线DE 平分BDC ∠且与直线BE 相交于点E ,2BDC A ∠=∠,3E ∠=∠.求证://CD EB证明:理由如下: DE 平分,BDC ∠(已知)_____ 2.∴=∠2,BDC A ∠=∠(已知)2,A ∴∠=∠(等量代换)____//____,______________,______________)∴(____3,______________,______________)∴=∠(又3,E ∠=∠(已知)________.∴=(等量代换)//____,______________,______________)CD ∴(17.如图,等腰三角形ABC 的面积为80,底边10BC =,腰AC 的垂直平分线EF 交,AC AB 于点E ,F ,若D 为BC 边中点,M 为线段EF 上一动点,则CDM 的周长最小值为________.18.如图,在Rt △ABC 中,∠ACB =90°,AC =BC =6,D 为BC 上一点,连接AD ,过点A 作AE ⊥AD ,取AE =AD ,连接BE 交AC 于F .当△AEF 为等腰三角形时,CD =_____.19.如图,在ABC 中,AB AC =,38A ∠=︒,AB 的垂直平分线交AC 点E ,垂足为点D ,连接BE ,则EBC ∠的度数为________.20.如图,30,AOB OC ︒∠=为AOB ∠内部一条射线,点P 为射线OC 上一点,6OP =,点,M N 分别为,OA OB 边上动点,则MNP △周长的最小值为______.三、解答题21.如图,在四边形ABCD 中,90B ∠=︒,AC 平分BAD ∠,DE AC ⊥,AB AE =.(1)求证:AC AD =.(2)若BC CD ⊥,试判断ACD △的形状,并说明理由.22.如图,已知,在△ABC中,AB =AC,AD是BC边上的中线,AM是△ABC的外角∠CAE 的平分线.(1)求证:AM∥BC;(2)若DN平分∠ADC交AM于点N,判断△ADN的形状并说明理由.23.如图1,将三角形纸片ABC,沿AE折叠,使点B落在BC上的F点处;展开后,再沿BD折叠,使点A恰好仍落在BC上的F点处(如图2),连接DF.(1)求∠ABC的度数;(2)若△CDF为直角三角形,且∠CFD=90°,求∠C的度数;(3)若△CDF为等腰三角形,求∠C的度数.24.在等腰直角三角形ABC中,∠ACB=90°,CD⊥AB于点D,点E是平面内任意一点,连接DE.(1)如图1,当点E在边BC上时,过点D作DF⊥DE交AC于点F.i)求证:CE=AF;ii)试探究线段AF,DE,BE之间满足的数量关系.(2)如图2,当点E在△BDC内部时,连接AE,CE,若DB=5,DE=2,∠AED=45°,求线段CE的长.25.在ABC 中,AB CB =,CB 垂直于AB ,E 为CB 延长线上一点,点F 在AB 上,且AE CF =.(1)求证:ABE CBF △≌△;(2)若70CAE ∠=︒,求ACF ∠的度数.26.如图,在ABC 中,D 为BC 上一点,BD CD =,AD AC ⊥于点A ,30BAD ∠=︒.(1)求证:12AC AB =; (2)当4AB =,3AD =时,求ABD S .【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】根据三角形内角和定理求出∠DCP =30°,求证PB =PD ;再根据三角形外角性质求证BD =AD ,再利用△BPD 是等腰三角形,然后可得AD =DC ,∠ACD =45°从而求出∠ACB 的度数.【详解】解:过C 作AP 的垂线CD ,垂足为点D .连接BD ;∵△PCD 中,∠APC =60°,∴∠DCP =30°,PC =2PD ,∵PC =2PB ,∴BP =PD ,∴△BPD 是等腰三角形,∠BDP =∠DBP =30°,∵∠ABP =45°,∴∠ABD =15°,∵∠BAP =∠APC -∠ABC =60°-45°=15°,∴∠ABD =∠BAD =15°,∴BD =AD ,∵∠DBP =45°-15°=30°,∠DCP =30°,∴BD =DC ,∴△BDC 是等腰三角形,∵BD =AD ,∴AD =DC ,∵∠CDA =90°,∴∠ACD =45°,∴∠ACB =∠DCP +∠ACD =75°,故选A .【点睛】此题主要考查学生三角形内角和定理,等腰三角形的判定与性质,三角形外角的性质等知识点,综合性较强,有一定的拔高难度,属于难题.2.B解析:B【分析】根据题意首先画出图形,过点D 作DM EF ⊥于点M ,在BDE ∆内部过E 、F 分别作30MEP MFP ∠=∠=︒,则120EPF FPD EPD ∠=∠=∠=︒,点P 就是费马点,求出PE ,PF ,DP 的长即可解决问题.【详解】解:如图:过点D 作DM EF ⊥于点M ,在BDE ∆内部过E 、F 分别作30MEP MFP ∠=∠=︒,则120EPF FPD EPD ∠=∠=∠=︒,点P 就是费马点,在等腰Rt DEF △中,6DE DF ==,DM EF ⊥,223EF DE ∴==,3EM DM ∴==,∵∠PEM =30°,∠PME =90°,∴EP =2PM ,则()2222PM EM PM +=,解得:1PM =,则2PE =,故31DP =-,同法可得2PF =,则312233PD PE PF ++=-++=+.故选:B .【点睛】此题主要考查了等腰三角形的性质,正确画出图形进而求出PE 的长是解题关键. 3.D解析:D【分析】利用等腰三角形的性质,直角三角形的性质,线段垂直平分线的性质,三角形的全等,角平分线的定义,逐一判断即可.【详解】∵∠BAC=90°,AD ⊥BC ,BE 平分∠ABC ,∴∠DBF+∠DFB=90°,∠ABE+∠AEF=90°,∠ABE=∠DBF ,∴∠AEF=∠DFB=∠AFE ,∴△AFE 为等腰三角形,∴结论①正确;∵△AFE 为等腰三角形,M 为EF 的中点,∴∠AMF=90°,∴∠DBF=∠DAN ,∵∠BAC=90°,∠C=45°,AD ⊥BC 于点D ,∴AD=BD ,∴△DBF≌△DAN,∴DF= DN,AN=BF,∴结论②③正确;∵∠ABM=∠NBM,∴∠BMA=∠BMN= 90°,BM=BM,∴△BMA≌△BMN,∴AM=MN,∴BE是线段AN的垂直平分线,∴EA=EN,∴∠EAN=∠ENA=∠DAN,∴AD∥EN,∵AD⊥BC∴EN⊥NC,∴结论④正确;故选D.【点睛】本题考查了等腰三角形的判定和性质,三角形的全等,线段的垂直平分线的定义和性质,平行线的判定和性质,直角三角形的性质,角平分线的定义,熟练掌握知识,灵活运用知识是解题的关键.4.C解析:C【分析】由角平分线的定义和平行线性质易证△BME和△CNE是等腰三角形,即BM=ME,CN=NE,由此可得△AMN的周长=AB+AC.【详解】解:∵∠ABC和∠ACB的平分线交于点E,∴∠ABE=∠CBE,∠ACE=∠BCE,∵MN//BC,∴∠CBE=∠BEM,∠BCE=∠CEN,∴∠ABE=∠BEM,∠ACE=∠CEN,∴BM=ME,CN=NE,∴△AMN的周长=AM+ME+AN+NE=AB+AC,∵AB=AC=4,∴△AMN的周长=4+4=8.故选C.【点睛】本题考查了等腰三角形的判定与性质,平行线的性质,熟记各性质是解题的关键.5.C解析:C【分析】做出B关于x轴对称点为B′,连接B′C,交x轴于点A',此时ABC的周长最小,由等腰直角三角形的性质可求∠OB'A'=∠OA'B'=45°,可求OB'=OA'=1,即可求解.【详解】解:如图所示,做出B关于x轴对称点为B′,连接B′C,交x轴于点A',此时△ABC周长最小过点C作CH⊥x轴,过点B'作B'H⊥y轴,交CH于H,∵B(0,2),∴B′(0,-2),∵C(5,3),∴CH= B′H=5,∴∠CB'H=45°,∴∠BB' A'=45°,∴∠OB'A'=∠OA'B'=45°,∴OB'=OA'=2,则此时A'坐标为(2,0).m的值为2.故选:C.【点睛】此题考查了轴对称-最短路径问题,考查了轴对称的性质,等腰直角三角形的性质等知识,根据已知得出A点位置是解题关键.6.D解析:D【分析】需分等腰三角形的顶角是钝角和等腰三角形的顶角是锐角两种情况解答即可.【详解】解:如图:(1)当顶角是钝角时,在Rt△ACO中,由勾股定理可得AO2=AC2-OC2=52-42=9∴AO=3,即OB=AB+AO=5+3=8在Rt △BCO 中,由勾股定理可得BC 2=OB 2+OC 2=82+42=80,则BC=80; (2)顶角是锐角时在Rt △ACD 中,由勾股定理可得AD 2=AC 2-DC 2=52-42=9,∴AD=3,DB=AB-AD=5-3-2在Rt △BCD 中,由勾股定理,得BC 2=DB 2+DC 2=22+42=20,则BC=20;综上,该等腰三角形的底的长度为20或80.故选D .【点睛】本题主要考查了勾股定理及等腰三角形的性质,灵活运用勾股定理和分情况讨论思想是解答本题的关键.7.D解析:D【分析】根据等腰三角形的性质求解即可;【详解】∵60EDC ∠=︒,∴60EBD BED ∠+∠=︒,∵△BDE 是等腰三角形,∴30EBD BED ∠=∠=︒,1BD DE ==,∵△BEC 是等腰三角形,∴30EBD ECD ∠=∠=︒,∵60EDC ∠=︒,∴90DEC ∠=︒,在Rt △DEC 中,∵30ECD ∠=︒,1DE =,∴3tan 30DEEC ==︒又∵AD 31,∴3AE AD DE EC =-==,∴△AEC 为等腰三角形,又∵90DEC AEC ∠=∠=︒,∴45ECA EAC ∠=∠=︒,∴453075ACB ACE ECD ∠=∠+∠=︒+︒=︒;故答案选D .【点睛】本题主要考查了等腰三角形的性质应用,准确计算是解题的关键.8.D解析:D【分析】根据等边三角形是轴对称图形,利用轴对称图形的性质解决问题即可.【详解】解:如图,∵△PMN 是等边三角形,等边三角形的对称轴一定经过三角形的顶点,又∵直线CD ,AB 是△PMN 的对称轴,直线CD 经过点P ,∴直线AB 一定经过点M 或N ,故选:D .【点睛】本题考查轴对称,等边三角形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.9.B解析:B【分析】根据角平分线的定义和两直线平行,内错角相等的性质得到FAE FEA ∠=∠,即可得到AF=EF ,再根据BE ⊥AD ,得到90AEB =︒∠,再根据等角的余角相等得到ABE BEF ∠=∠,根据等边对等角的性质得到BF=EF ,即可得解;【详解】∵AD 平分∠BAC ,EF //AC ,∴FAE FEA ∠=∠,∴AF=EF ,∵BE ⊥AD ,∴90FAE ABE ∠+=︒,90AEF BEF ∠+∠=︒, ∴ABE BEF ∠=∠,∴BF=EF ,∴AF=BF ;故答案选B .【点睛】本题主要考查了平行线的性质、三角形的角平分线,准确分析证明是解题的关键. 10.B解析:B【分析】由△ABC 为等边三角形,可求出∠BOA =90°,由△ADO 是等腰三角形求出∠ADO =∠AOD =30°,即可求出∠BOD 的度数.【详解】解:∵△ABC 为等边三角形,BO 为中线,∴∠BOA =90°,∠BAC =60°∴∠CAD =180°﹣∠BAC =180°﹣60°=120°,∵AD =AO ,∴∠ADO =∠AOD =30°,∴∠BOD =∠BOA +∠AOD =90°+30°=120°,故选:B .【点睛】本题主要考查了等边三角形的性质及等腰三角形的性质,解题的关键是熟记等边三角形的性质及等腰三角形的性质.11.D解析:D【分析】延长ED 交BC 于点M ,延长AD 交BC 于点N ,过点D 作//DF BC 交BE 于点F ,根据等腰三角形的性质得出AN BC ⊥,BN CN =,根据60EBC E ∠=∠=,得出EBM △是等边三角形,进而得到6EB EM BM cm ===,通过//DF BC ,证明EFD △是等边三角形,进而得到2EF FD ED cm ===,所以求出4DM cm =,根据直角三角形的性质得到MN 的长度,从而得出BN 的长度,最后求出BC 的长度.【详解】延长ED 交BC 于点M ,延长AD 交BC 于点N ,过点D 作//DF BC 交BE 于点F ,如图,AB AC =,AD 平分BAC ∠,∴AN BC ⊥,BN CN =,∴90ANB ANC ∠=∠=,60EBC E ∠=∠=,∴EBM △是等边三角形,6=,BE cm∴6===,EB EM BM cmDF BC,//∴60∠=∠=,EFD EBM∴EFD△是等边三角形,=,DE cm2∴2EF FD ED cm===,∴4=,DM cm△是等边三角形,EBM∴60∠=,EMB∴30∠=,NDM∴2=,NM cm∴4=-=,BN BM NM cm∴28BC BN cm==.故选:D.【点睛】本题考查了等腰三角形的性质和等边三角形的性质,直角三角形中30角所对的直角边是斜边长的一半,求出MN的长度是解决问题的关键.12.B解析:B【分析】根据平行线的性质和等腰三角形的判定证得EG=EB,DF=DC即可求得结果.【详解】解:∵ED∥BC,∴∠DFB=∠FBC,∠EGC=∠GCB,∵∠DBF=∠FBC,∠ECG=∠GCB,∴∠DFB=∠DBF,∠ECG=∠EGC,∴BD=DF,CE=GE,∵FG=2,ED=6,∴DB+EC=DF+GE=ED−FG=6−2=4,故选:B.【点睛】本题考查等腰三角形的判定和性质、角平分线的定义,平行线的性质等知识,解题的关键是等腰三角形的证明.二、填空题13.②③⑤【分析】由题意易得进而可证如图所示连接根据旋转的性质可知进而可求面积为等边面积为过点B作交的延长线于点E然后可得最后可排除选项【详解】解:∵是正三角形∴∵∴在和中∴∴∴可以由绕点B 逆时针旋转6 解析:②③⑤【分析】由题意易得BA BC AC ==,60BAC ABC ACB ==︒=∠∠∠,O BA OBC '∠=∠,进而可证BO A BOC '△≌△,如图所示,连接OO '根据旋转的性质,可知60ABO '∠=︒,OB O B '=,进而可求Rt AOO '面积为168242⨯⨯=,等边BOO '面积为18431632,过点B 作BE AO ⊥交AO 的延长线于点E ,然后可得146122AOB S =⨯⨯=△,最后可排除选项. 【详解】解:∵ABC 是正三角形∴BA BC AC ==,60BAC ABC ACB ==︒=∠∠∠,∵60O BA ABO O BO ABC OBC ABO ''∠+∠=∠=︒=∠=∠+∠,∴O BA OBC '∠=∠,在BO A '△和BOC 中,BO BO O BA OBC BA BC =⎧⎪∠=∠'⎨='⎪⎩,∴()BO A BOC SAS '△≌△,∴O A OC '=,∴BO A '△可以由BOC 绕点B 逆时针旋转60°得到,∴②正确;如图所示,连接OO '根据旋转的性质,可知60ABO '∠=︒,OB O B '=,∴BOO '是等边三角形,∴点O 与O '的距离为8,∴①错误;在AOO '△中,6AO =,8OO '=,10AO OC '==, ∴222AO OO AO ''=+,∴AOO '△是直角三角形,90AOO '∠=︒,∴Rt AOO '面积为168242⨯⨯=, 等边BOO '面积为18431632, ∴四边形AOBO 的面积为24+∴⑤正确;∵9060150AOB AOO BOO ''∠=∠+∠=︒+︒=︒,∴③正确;过点B 作BE AO ⊥交AO 的延长线于点E ,∵150AOB ∠=︒,∴30BOE ∠=︒,∵8OB =,∴4BE =, ∴146122AOB S =⨯⨯=△, ∴ 241631212163BOC AOB xAOBO S S S '=-=+-=+△△四边形.∴④错误;故答案为:②③⑤.【点睛】本题主要考查等边三角形的性质与判定、含30°的直角三角形的性质及勾股定理,熟练掌握等边三角形的性质与判定、含30°的直角三角形的性质及勾股定理是解题的关键. 14.【分析】设∠OAC=x ∠CAB=y 根据等腰三角形的性质则∠OCA=x ∠OBA=x+y ∠OBC=x+30°利用三角形内角和定理计算即可【详解】解:设∠OAC=x ∠CAB=y ∵OA=OC ∴∠OCA=x ∵解析:60.【分析】设∠OAC=x ,∠CAB=y ,根据等腰三角形的性质,则∠OCA=x ,∠OBA=x+y ,∠OBC=x+30°,利用三角形内角和定理计算即可.【详解】解:设∠OAC=x ,∠CAB=y ,∵OA=OC ,∴∠OCA=x ,∵OA=OB ,∴∠OBA=x+y ,∵OC=OB ,∴∠OBC=x+30°,∵30ACB ∠=︒,∴∠CAB+∠OBA+∠OBC=150°,∴y+x+y+ x+30°=150°,∴2(x+y)=120°,∵∠AOB=180°-2∠OBA=180°-2(x+y),∴∠AOB=180°-120°=60°,故答案为:60.【点睛】本题考查了等腰三角形的性质,三角形内角和定理,熟练应用性质,合理引进未知数,采用设而不求的思想计算是解题的关键.15.7【分析】根据对称的性质得到∠A′EB′=60°结合点E 是AB 中点可证明△A′EB′是等边三角形从而有CD≤CA′+A′B′+B′D=CA+AE+BD 即可求出CD 的最大值【详解】解:∵∠CED=12解析:7【分析】根据对称的性质得到∠A′EB′=60°,结合点E 是AB 中点,可证明△A′EB′是等边三角形,从而有CD≤CA′+A′B′+B′D=CA+AE+BD ,即可求出CD 的最大值.【详解】解:∵∠CED=120°,∴∠AEC+∠DEB=60°,∴∠CEA′+∠DEB′=60°,∴∠A′EB′=60°,∵点E 是AB 中点,AE=A′E ,BE=B′E ,∴A′E=B′E ,∴△A′EB′是等边三角形,∵CD≤CA′+A′B′+B′D=CA+AE+BD=1+2+4=7,∴CD 的最大值为7,故答案为:7.【点睛】本题考查了翻折的性质,等边三角形的判定和性质,熟练掌握折叠的性质是解题的关键. 16.ACDE 同位角相等两直线平行;两直线平行内错角相等;;EB 内错角相等两直线平行【分析】由平分可得由可得可推出利用平行线性质可得由利用传递性可得利用判定定理可得【详解】证明:理由如下:平分(已知)(已解析:1∠,AC ,DE ,同位角相等,两直线平行;1∠,两直线平行,内错角相等;1∠,E ∠;EB,内错角相等,两直线平行【分析】由DE 平分,BDC ∠可得1 2.∠=∠由2,BDC A ∠=∠可得2,A ∠=∠可推出AC //DE,利用平行线性质可得13,∠=∠由3,E ∠=∠利用传递性可得1 E.∠=∠利用判定定理可得//BE CD .【详解】证明:理由如下: DE 平分,BDC ∠(已知)_1 2.∴∠=∠2,BDC A ∠=∠(已知)2,A ∴∠=∠(等量代换)AC //DE,∴(同位角相等,两直线平行)13,∴∠=∠(两直线平行,内错角相等)又3,E ∠=∠(已知)1 E.∴∠=∠(等量代换)//BE CD ∴(内错角相等,两直线平行).故答案为:1∠;AC DE,,同位角相等,两直线平行;1,∠两直线平行,内错角相等;1E ∠∠,;BE,内错角相等,两直线平行.【点睛】本题考查平行线的判定与性质,角分线性质,等量代换,熟练掌握平行线的判定与性质,角平分线性质是解题关键.17.21【分析】连接ADAM由于△ABC是等腰三角形点D是BC边的中点故AD⊥BC再根据三角形的面积公式求出AD的长再根据EF是线段AC的垂直平分线可知点A关于直线EF的对称点为点CMA=MC推出MC+解析:21【分析】连接AD,AM,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AC的垂直平分线可知,点A关于直线EF的对称点为点C,MA=MC,推出MC+DM=MA+DM≥AD,故AD的长为BM+MD的最小值,由此即可得出结论.【详解】解:连接AD,MA.∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S△ABC=12BC•AD=12×10×AD=80,解得:AD=16,∵EF是线段AC的垂直平分线,∴点A关于直线EF的对称点为点C,MA=MC,∴MC+DM=MA+DM≥AD,∴AD的长为CM+MD的最小值,∴△CDM的周长最短=(CM+MD)+CD=AD+12BC=16+12×10=21.故答案是:21.【点睛】本题考查的是轴对称−最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.18.2或6【分析】分两种情形:当AE=AF时如图1中过点E作EH⊥AC于H证明AH=FH=CF=CD可得结论如图2中当AF=EF时点D与D重合此时CD=BC =6【详解】解:①当AE=EF时如图1中过点E解析:2或6【分析】分两种情形:当AE=AF时,如图1中,过点E作EH⊥AC于H.证明AH=FH=CF=CD,可得结论,如图2中,当AF=EF时,点D与D重合,此时CD=BC=6【详解】解:①当AE=EF时,如图1中,过点E作EH⊥AC于H.∵EA =EF ,EH ⊥AF ,∴AH =HF ,∵EA ⊥AD ,∴∠EAD =∠EHA =∠C =90°,∴∠EAH +∠CAD =90°,∠CAD +∠ADC =90°,∴∠EAH =∠ADC ,在△EHA 和△ACD ,EAH ADC EHA C AE DA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EHA ≌△ACD (AAS ),∴AH =CD ,EH =AC =CB .在△EHF 和△BCF 中,EFH BFC EHF C EH BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EHF ≌△BCF (AAS ),∴FH =CF ,∴AH =FH =CF =CD ,∴CD=13AC =2, ②如图2中,当AF =EF 时,点B 与点D 重合,此时CD =BC =6综上所述,满足条件的CD 的长度为2或6故答案为:2或6【点睛】本题考查等腰直角三角形的性质,全等三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.19.33°【分析】先根据等腰三角形的性质求出再根据垂直平分线的性质求解即可;【详解】∵在中∴∵的垂直平分线交点垂足为点∴AE=BE ∴∴;故答案是【点睛】本题主要考查了等腰三角形的判定与性质垂直平分线的性解析:33°【分析】先根据等腰三角形的性质求出71ABC C ∠=∠=︒,再根据垂直平分线的性质求解即可;【详解】∵在ABC 中,AB AC =,38A ∠=︒,∴71ABC C ∠=∠=︒,∵AB 的垂直平分线交AC 点E ,垂足为点D ,∴AE=BE ,∴38A ABE ∠=∠=︒,∴713833EBC ∠=︒-︒=︒;故答案是33︒.【点睛】本题主要考查了等腰三角形的判定与性质、垂直平分线的性质,准确计算是解题的关键. 20.6【分析】作点P 关于OA 的对称点P1点P 关于OB 的对称点P2连结P1P2与OA 的交点即为点M 与OB 的交点即为点N 则此时MN 符合题意求出线段P1P2的长即可【详解】解:作点P 关于OA 的对称点P1点P 关解析:6【分析】作点P 关于OA 的对称点P 1,点P 关于OB 的对称点P 2,连结P 1P 2,与OA 的交点即为点M ,与OB 的交点即为点N ,则此时M 、N 符合题意,求出线段P 1P 2的长即可.【详解】解:作点P 关于OA 的对称点P 1,点P 关于OB 的对称点P 2,连结P 1P 2与OA 的交点即为点M ,与OB 的交点即为点N ,△PMN 的最小周长为PM +MN +PN =P 1M +MN +P 2N =P 1P 2,即为线段P 1P 2的长, 连结OP 1、OP 2,则OP 1=OP 2=OP =6,又∵∠P 1OP 2=2∠AOB =60°,∴△OP 1P 2是等边三角形,∴P 1P 2=OP 1=6,即△PMN 的周长的最小值是6.故答案是:6.【点睛】本题考查了等边三角形的性质和判定,轴对称−最短路线问题的应用,关键是确定M 、N 的位置.三、解答题21.(1)见解析;(2)等边三角形,理由见解析【分析】(1)根据题意可证ABC AED ≌△△,继而得出结论; (2)根据BC CD ⊥,可知90BCD B ∠=∠=︒,即可判断//AB CD ,进而可证AD CD AC ==,从而得出结论;【详解】(1)证明:∵90B ∠=︒,DE AC ⊥,∴90B AED ∠=∠=︒,∵AC 平分BAD ∠,∴BAC EAD ∠=∠,在ABC 和AED 中,∵ABC AED AB AE BAC EAD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ABC AED ASA ≌△△,∴AC AD =;(2)解:ACD △是等边三角形,理由如下:∵BC CD ⊥,∴90BCD B ∠=∠=︒,∴//AB CD ,∴BAC ACD DAC ∠=∠=∠,∴AD CD AC ==,∴ACD △是等边三角形;【点睛】本题考查了全等三角形的性质与判定、平行线的性质与判定、等边三角形的判定,熟练掌握知识点是解题的关键;22.(1)见解析;(2)ADN △等腰直角三角形,理由见解析【分析】(1)先证明∠MAD=90°,再证明∠ADC =90°,问题得证;(2)证明∠ADN =∠NDC =∠AND ,得到AD=AN ,即可证明△ADN 是等腰直角三角形.【详解】解:证明:(1)∵AB =AC ,AD 是BC 边上的中线,∴∠BAD =∠CAD 12BAC =∠ ,AD ⊥BC , ∵AM 平分∠EAC ,∴∠EAM =∠MAC 12EAC =∠. ∴∠MAD =∠MAC +∠DAC 11118090222EAC BAC =∠+∠=⨯︒=︒. ∵AD ⊥BC ,∴∠ADC =90°,∴∠MAD +∠ADC =180°,∴AM //BC .(2)△ADN 是等腰直角三角形,理由是:∵AM //BC ,∴∠AND =∠NDC ,∵DN 平分∠ADC ,∴∠ADN =∠NDC =∠AND .∴AD =AN ,∴△ADN 是等腰直角三角形.【点睛】此题考查等腰三角形的判定与性质,熟知等腰三角形的判定定理与性质定理并灵活应用是解题关键.23.(1)60°;(2)30°;(3)20°或40°.【分析】(1)由折叠的性质可知△ABF 是等边三角形,即可得出结论;(2)根据折叠的性质及三角形内角和定理即可得出结论;(3)根据折叠的性质、三角形外角的性质及等腰三角形的性质表示出∠AFD ,根据平角的定义表示出∠DFC ,然后分三种情况讨论即可得出结论.【详解】解:(1)由折叠的性质可知:AB =AF ,BA =BF ,∴AB =BF =AF ,∴△ABF 是等边三角形,∴∠ABC =∠AFB =60°;(2)∵∠CFD =90°,∴∠BFD =90°.由折叠的性质可知:∠BAD =∠BFD ,∴∠BAC =∠BAD =90°,∴∠C =180°-∠BAC -∠ABC =180°-90°-60°=30°;(3)设∠C =x °.由折叠的性质可知,AD =DF ,∴∠FAD =∠AFD .∵∠AFB =∠FAD +∠C ,∴∠FAD =∠AFB -∠C =60°-x ,∴∠AFD =60°-x ,∴∠DFC =180°-∠AFB -∠AFD =180°-60°-(60°-x )=60°+x .∵△CDF 为等腰三角形,∴分三种情况讨论:①若CF =CD ,则∠CFD =∠CDF ,∴60°+x +60°+x +x =180°,解得:x =20°;②若DF =DC ,则∠DFC =∠C ,∴60°+x =x ,无解,∴此种情况不成立;③若DF =FC ,则∠FDC =∠C =x ,∴60°+x +x +x =180°,解得:x =40°.综上所述:∠C 的度数为20°或40°.【点睛】本题考查了等边三角形的判定与性质,等腰三角形的判定与性质,折叠的性质.分三种情况讨论是解答本题的关键.24.(1)i )证明见解析;ii )2222DE AF BE =+,证明见解析;(2) 1.CE =【分析】(1)i )由等腰直角三角形ABC ,∠ACB =90°,,CD AB ⊥ 证明,45,CD AD DCE A =∠=∠=︒ 由,,CD AB DF DE ⊥⊥ 证明,ADF CDE ∠=∠ 可得,CDE ADF ≌ 从而可得结论;ii )如图,连接,EF 由,CDE ADF ≌,DE DF = 证明,CF BE = 222,EF DE = 结合222,EF CF CE =+ 从而可得答案;(2)过点D 作DH AE ⊥于点H ,过点D 作DG DE ⊥交AE 于点G ,根据SAS 证明CDE ADG ≅△△,进而利用全等三角形的性质和勾股定理即可得出答案.【详解】证明:(1)i ) 等腰直角三角形ABC ,∠ACB =90°,,CD AB ⊥,45,,AC BC ACD BCD A B AD BD ∴=∠=∠=︒=∠=∠=,CD AD BD ∴==,,CD AB DF DE ⊥⊥90,ADF CDF CDF CDE ∴∠+∠=︒=∠+∠,ADF CDE ∴∠=∠在DAF △与DCE 中,45CDE ADF CD ADDCE A ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩(),CDE ADF ASA ∴≌.CE AF ∴=ii )2222.DE AF BE =+理由如下:如图,连接,EF,CDE ADF ≌,DE DF ∴=,,AC BC AF CE ==,CF BE ∴=,DE DF ⊥22222,EF DE DF DE ∴=+=22222,EF CF CE BE AF =+=+2222.DE AF BE ∴=+(2)如图,过点D 作DH AE ⊥于点H ,过点D 作DG DE ⊥交AE 于点G ,90ACB AC BC CD AB ∠=︒=⊥,,,45ACD BCD A ∴∠=∠=∠=︒,∴CD=AD ,,45DG DE AED ⊥∠=︒,45DGE AED ∴∠=︒=∠,∴DG=DE ,在CDE △和ADG 中AD CD ADG CDE DG DE =⎧⎪∠=∠⎨⎪=⎩CDE ADG ∴≅△△(SAS )∴CE=AG在Rt DEG △中,DE DG ==6EG ∴=DH AE ⊥3DH GH EH ∴===在Rt ADH 中,AD=54AH ∴===1CE AG AH GH ∴==-=.【点睛】本题考查的是三角形全等的判定与性质,等腰直角三角形的性质,勾股定理的应用,利用平方根解方程,方程组思想,掌握以上知识是解的关键.25.(1)证明见解析;(2) ∠ACF 的度数是20°.【分析】(1)根据HL 即可解决问题;(2)求出∠BAE 的度数,可得∠BCF 的度数,由此即可解决问题.【详解】解:(1)∵CB 垂直于AB ,∴∠ABC=∠ABE=90°,在Rt △ABE 和Rt △CBF 中,∵AE CF AB CB =⎧⎨=⎩, ∴Rt △ABE ≌Rt △CBF (HL );(2)∵在△ABC 中,AB=CB ,∠ABC=90°,∴∠ACB=∠CAB=45°,∵70CAE ∠=︒,∴∠BAE=∠CAE-∠CAB=25°.又由(1)知,Rt △ABE ≌Rt △CBF ,∴∠BAE=∠BCF=25°,∴∠ACF=∠ACB-∠BCF=20°.即∠ACF 的度数是20°.【点睛】本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是准确寻找全等三角形解决问题,属于中考常考题型.26.(1)见详解;(2)3【分析】(1)延长AD 到E ,使DE =AD ,然后利用“边角边”证明△ACD 和△EBD 全等,根据全等三角形对应边相等可得BE =AC ,全等三角形对应角相等可得∠E =∠CAD ,再根据直角三角形30°角所对的直角边等于斜边的一半证明;(2)求出BE ,然后利用三角形的面积公式列式计算即可得解.【详解】(1)证明:如图,延长AD 到E ,使DE =AD ,在△ACD 和△EBD 中,AD DE ADC EDB BD CD ⎧⎪∠∠⎨⎪⎩===, ∴△ACD ≌△EBD (SAS ),∴BE =AC ,∠E =∠CAD =90°,∵∠BAD =30°,∴BE =12AB , ∴12AC AB =; (2)解:∵AB =4,∴BE =12×4=2, ∴S △ABD =12AD•BE =1233. 【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,全等三角形的判定与性质,“遇中线,加倍延”作辅助线,构造出全等三角形是解题的关键.。
八年级数学全等三角形证明题(供参考)

第十三章 全等三角形测试卷(测试时间:90分钟 总分:100分)班级 姓名 得分一、选择题(本大题共10题;每小题2分,共20分)1. 对于△ABC 与△DEF ,已知∠A =∠D ,∠B =∠E ,则下列条件①AB=DE ;②AC=DF ;③BC=DF ;④AB=EF 中,能判定它们全等的有( )A .①②B .①③C .②③D .③④2. 下列说法正确的是( )A .面积相等的两个三角形全等B .周长相等的两个三角形全等C .三个角对应相等的两个三角形全等D .能够完全重合的两个三角形全等3. 下列数据能确定形状和大小的是( )A .AB =4,BC =5,∠C =60° B .AB =6,∠C =60°,∠B =70°C .AB =4,BC =5,CA =10D .∠C =60°,∠B =70°,∠A =50°4. 在△ABC 和△DEF 中,∠A=∠D ,AB = DE ,添加下列哪一个条件,依然不能证明△ABC ≌△DEF ( )A .AC = DFB .BC = EF C .∠B=∠ED .∠C=∠F5. OP 是∠AOB 的平分线,则下列说法正确的是( )A .射线OP 上的点与OA ,OB 上任意一点的距离相等B .射线OP 上的点与边OA ,OB 的距离相等C .射线OP 上的点与OA 上各点的距离相等D .射线OP 上的点与OB 上各点的距离相等 6. 如图,∠1=∠2,∠E=∠A ,EC=DA ,则△ABD ≌△EBC时,运用的判定定理是( ) A .SSSB .ASAC .AASD .SAS7. 如图,若线段AB ,CD 交于点O ,且AB 、CD 互相平分,则下列结论错误的是( ) A .AD=BCB .∠C=∠DC .AD ∥BCD .OB=OC8. 如图,AE ⊥BD 于E ,CF ⊥BD 于F ,AB = CD ,AE = CF , 则图中全等三角形共有( )A .1对B .2对C .3对D .4对 9. 如图,AB =AC ,CF ⊥AB 于F ,BE ⊥AC 于E ,CF 与BE 交于点D .有下列结论:①△ABE ≌△ACF ;②△BDF ≌△CDE ;③点D 在∠BAC 的平分线上.以上结论正确的( ) A .只有①(第8题) A D C B E FC EO A D CB (第7题) B AC ED (第6题) 2 1B .只有②C .只有③D .有①和②和③10.如图,DE ⊥BC ,BE=EC ,且AB =5,AC =8, 则△ABD 的周长为( ) A .21B .18C .13D .9 二、填空题(本大题共6小题;每小题2分,共12分)11.如图,除公共边AB 外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使△ABC 与△ABD 全等:(1) , (ASA);(2) ,∠3=∠4 (AAS).12.如图,AD 是△ABC 的中线,延长AD 到E ,使DE =AD ,连结BE ,则有△ACD ≌△ 。
北师大版八年级数学下册 第一章 三角形的证明 单元测试题含答案

北师大版八年级数学下册第一章三角形的证明单元测试题一.选择题(共10小题,每小题3分,共30分)1.等腰三角形的对称轴是()A.底边上的高所在的直线B.底边上的高C.底边上的中线D.顶角平分线2.如图在3×3的网格中,点A、B在格点处:以AB为一边,点P在格点处,则使△ABP为等腰三角形的点P有()个.A.2个B.3个C.4个D.5个3.如图,在△ABC中,∠B与∠C的角平分线相交于点I,过点I作BC的平行线,分别交AB、AC于点D、E.若AB=9,AC=6,BC=8,则△ADE的周长是()A.14 B.15 C.174.如图所示,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE等于()A.10°B.15°C.20°D.25°5.在△ABC中,AB=AC,∠A=60°,BC=6,则AB的值是()A.12 B.8 C.6 D.36.用反证法证明“a≥b”,对于第一步的假设,下列正确的是()A.a≤b B.a≠b C.a<b D.a=b7.下列说法:①一个底角和一条边分别相等的两个等腰三角形全等;②底边及底边上的高分别相等的两个等腰三角形全等;③两边分别相等的两个直角三角形全等;④一个锐角和一条边分别相等的两个直角三角形全等,其中正确的个数是()A.1 B.2 C.3 D.48.如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E,则下列结论正确的是()A.AE=3CE B.AE=2CE C.AE=BD D.BC=2CE9.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是边AB的中点,AB=10,DE =4,则S△AEC=()A.8 B.7.5 C.7 D.610.如图,在△ABC中,CD⊥AB于点D,BE平分∠ABC,交CD于点E,若S△BCE=10,BC=5,则DE等于()A.10 B.7 C.5 D.4二.填空题(共8小题,每小题3分,共24分)11.等腰三角形的周长为12cm,其中一边长为3cm,则该等腰三角形的腰长为.12.如图:已知∠B=20°,AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,以此类推∠A的度数是.13.如图,在△ABC中,AB=AC=10,AD平分∠BAC,点E为AC中点,则DE=.14.在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分AC,交AC于点E,交AB于点D,连接CD,若BD=2,则AD的长是.15.如图,DE是△ABC的边AC上的垂直平分线,AB=5cm,BC=8cm,则△ABD的周长为cm.16.如图,点D,P在△ABC的边BC上,DE,PF分别垂直平分AB,AC,连接AD、AP,若∠DAP=20°,则∠BAC=.17.如图,AB∥CD,∠BAC与∠ACD的平分线交于点P,过P作PE⊥AB于E,交CD于F,EF=10,则点P到AC的距离为.18.如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=40,DE=4,AC=12,则AB长是.三.解答题(共7小题,共66分)19.如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,求∠DBA的度数.20.如图,已知AB∥CD,∠BCF=180°,BD平分∠ABC,CE平分∠DCF,∠ACE=90°.求证:AC⊥BD.21.已知:如图,在△ABC中,∠ACB=90°,CD是高,AE是△ABC内部的一条线段,AE交CD于点F,交CB于点E,且∠CFE=∠CEF.求证:AE平分∠CAB.22.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD于点F,交CB于点E,且∠EAB=∠DCB.(1)求∠B的度数:(2)求证:BC=3CE.23.如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB,BC于点D 和点E.(1)若AB=10,则△CDE的周长是多少?为什么?(2)若∠ACB=125°,求∠DCE的度数.24.如图,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D.(1)求∠DBC的度数;(2)若△DBC的周长为14cm,BC=5cm,求AB的长.25.如图,已知AC∥BD,AE,BE分别平分∠CAB和∠DBA,点E在线段CD上.(1)求∠AEB的度数;(2)求证:CE=DE.参考答案一.选择题1.解:等腰三角形的对称轴是底边的垂直平分线,故选:A.2.解:如图所示,以AB为腰的等腰三角形的点P有2个,以AB为底边的等腰三角形的点P有3个,∴△ABP为等腰三角形的点P有5个;故选:D.3.解:∵BI平分∠DBC,∴∠DBI=∠CBI,又∵DE∥BC,∴∠DIB=∠IBC,∴∠DIB=∠DBI,∴BD=DI.同理CE=EI.∴△ADE的周长=AD+DI+IE+EA=AB+AC=15,故选:B.4.解:∵在等边三角形ABC中,AD⊥BC,∴AD是BC的线段垂直平分线,∵E是AD上一点,∴EB=EC,∴∠EBD=∠ECD,∵∠CED=50°,∴∠ECD=40°,又∵∠ABC=60°,∠ECD=40°,∴∠ABE=60°﹣40°=20°,故选:C.5.解:∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴AB=BC=6,故选:C.6.解:反证法证明“a≥b”,第一步是假设,a<b,故选:C.7.解:①一个底角和一条边分别相等的两个等腰三角形不一定全等;②底边及底边上的高分别相等的两个等腰三角形全等,正确;③两边分别相等的两个直角三角形不一定全等;④如果在两个直角三角形中,例如:两个30°角的直角三角形,一个三角形的直角边与另一个三角形的斜边相等,这两个直角三角形肯定不全等,错误;故选:A.8.解:连接BE,∵DE是AB的垂直平分线,∴AE=BE,∴∠ABE=∠A=30°,∴∠CBE=∠ABC﹣∠ABE=30°,在Rt△BCE中,BE=2CE,∴AE=2CE,故选:B.9.解:∵在△ABC中,∠ACB=90°,C点E是边AB的中点,∴AE=BE=CE=AB=5,∵CD⊥AB,DE=4,∴CD==3,∴S△AEC=S△BEC=BE•CD=3=7.5,故选:B.10.解:作EF⊥BC于F,∵S△BCE=10,∴×BC×EF=10,即×5×EF=10,解得,EF=4,∵BE平分∠ABC,CD⊥AB,EF⊥BC,∴DE=EF=4,故选:D.二.填空题11.解:由题意知,应分两种情况:(1)当腰长为3cm时,则另一腰也为3cm,底边为12﹣2×3=7cm,∵3+3<7,∴边长分别为3,3,7不能构成三角形;(2)当底边长为3cm时,腰的长=(12﹣3)÷2=4.5cm,∵0<3<4.5+4.5=9,∴边长为3,4.5,4.5,能构成三角形,则该等腰三角形的一腰长是4.5cm.故答案为:4.5cm.12.解:∵∠B=20°,AB=A1B,∴∠A=(180°﹣∠B)=80°,故答案为:80°.13.解:∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴∠ADC=90°,又点E为AC中点,∴DE=AC=5,故答案为:5.14.解:∵DE垂直平分AC,∴CD=AD,∴∠ACD=∠A=30°,∵在Rt△ABC中,∠B=90°,∠A=30°,∴∠ACB=90°﹣∠A=60°,∴∠BCD=∠ACB﹣∠ACD=30°,∴CD=2BD=2×2=4,∴AD=CD=4.故答案为:4.15.解:∵DE是△ABC中的边AC上的垂直平分线,∴AD=CD,∵AB=5cm,BC=8cm,∴△ABD的周长为:AB+BD+AD=AB+BD+CD=AB+BC=13(cm).故答案是:13.16.解:∵DE,PF分别垂直平分AB,AC,∴∠B=∠BAD,∠C=∠CAP,又∵∠DAP=20°,∴∠B+∠C=(180°﹣20°)=80°,∴∠BAC=180°﹣80°=100°,故答案为:100°.17.解:作PH⊥AC于H,∵AP平分∠BAC,PE⊥AB,PH⊥AC,∴PE=PH,∵AB∥CD,PE⊥AB,∴PF⊥CD,∵CP平分∠ACD,PF⊥CD,PH⊥AC,∴PF=PH,∴PH=PE=PF=EF=5,即点P到AC的距离为5,故答案为:5.18.解:作DF⊥AC于F,如图,∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DF=DE=4,∵S△ABD+S△ADC=S△ABC,∴•4•AB+•12•4=40,∴AB=8.故答案为8.三.解答题19.解:∵在△ABC中,AB=BC,∠ABC=110°,∴∠A=∠C=35°,∵AB的垂直平分线DE交AC于点D,∴AD=BD,∴∠DBA=∠A=35°20.证明:∵AB∥CD,∴∠ABC=∠DCF.(两直线平行,同位角相等)∵BD平分∠ABC,CE平分∠DCF,∴∠2=∠ABC,∠4=∠DCF.(角平分线的定义)∴∠2=∠4.∴BD∥CE.(同位角相等,两直线平行)∴∠BGC=∠ACE.(两直线平行,内错角相等)∵∠ACE=90°,∴∠BGC=90°,即AC⊥BD.(垂直的定义)21.证明:∵CD⊥AB,∴在△ADF中,∠DAF=90°﹣∠AFD=90°﹣∠CFE.∵∠ACE=90°,∴在△AEC中,∠CAE=90°﹣∠CEF.∵∠CFE=∠CEF,∴∠DAF=∠CAE,即AE平分∠CAB.22.解:(1)∵AE⊥CD,∴∠AFC=∠ACB=90°,∴∠CAF+∠ACF=∠ACF+∠ECF=90°,∴∠ECF=∠CAF,∵∠EAD=∠DCB,∴∠CAD=2∠DCB,∵CD是斜边AB上的中线,∴CD=BD,∴∠B=∠DCB,∴∠CAB=2∠B,∵∠B+∠CAB=90°,∴∠B=30°;(2)∵∠B=∠BAE=∠CAE=30°,∴AE=BE,CE=AE,∴BC=3CE.23.解:(1)△CDE的周长为10.∵直线l与m分别是△ABC边AC和BC的垂直平分线,∴AD=CD,BE=CE,∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10;(2)∵直线l与m分别是△ABC边AC和BC的垂直平分线,∴AD=CD,BE=CE,∴∠A=∠ACD,∠B=∠BCE,又∵∠ACB=125°,∴∠A+∠B=180°﹣125°=55°,∴∠ACD+∠BCE=55°,∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°.24.解:(1)∵AB=AC,∴∠ABC=∠ACB,∵∠A=40°,∴∠ABC=∠ACB=70°,∵MN是AB的垂直平分线,∴DA=DB,∴∠A=∠ABD=40°,∴∠DBC=∠ABC﹣∠ABD=70﹣40°=30°;(2)∵MN是AB的垂直平分线,∴BD=AD,∵△DBC的周长为14cm,∴BD+BC+CD=14cm,∵BC=5cm,∴BD+CD=AD+CD=AC=9cm,∵AB=AC,∴AB=9cm.25.解:(1)∵AC∥BD,∴∠CAB+∠ABD=180°.∵AE平分∠CAB,∴∠EAB=∠CAB.同理可得∠EBA=∠ABD.∴∠EAB+∠EBA=90°,∴∠AEB=90°;(2)如图,在AB上截取AF=AC,连接EF,在△ACE和△AFE中,∴△ACE≌△AFE(SAS).∴CE=FE,∠CEA=∠FEA.∵∠CEA+∠DEB=90°,∠FEA+∠FEB=90°,∴∠DEB=∠FEB.在△DEB和△FEB中∴△DEB≌△FEB(ASA).∴ED=EF.∴ED=CE.。
(最新)数学八年级下册《 三角形的证明》单元综合检测试题(含答案)

第一章三角形的证明第Ⅰ卷(选择题共30分)一、选择题(每小题3分,共30分)1.已知一个等腰三角形的一边长为5,另一边长为7,则这个等腰三角形的周长为()A.12 B.17或19C.17 D.192.用反证法证明命题:“如图1,如果AB∥CD,AB∥EF,那么CD∥EF.”证明的第一个步骤是()图1A.假定CD∥EF B.假定CD不平行于EFC.已知AB∥EF D.假定AB不平行于EF3.已知下列命题:①若|x|=3,则x=3;②全等三角形的三组对应角相等;③直角三角形中30°角所对的直角边等于斜边的一半;④有理数与数轴上的点一一对应.其中原命题与逆命题均为真命题的个数是()A.1 B.2 C.3 D.44.如图2,在Rt△ABC中,∠ACB=90°,BC的垂直平分线交斜边AB于点D,交BC于点E,AB=7.8,AC=3.9,则图中等于60°的角有()图2A.2个B.3个C.4个D.5个5.如图3,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC,设△ABD,△BCD的面积分别为S1,S2,则S1∶S2等于()图3A .2∶1 B.2∶1 C .3∶2 D .2∶ 36.如图4,在等腰三角形ABC 中,AB =AC ,ED 是AB 边的垂直平分线.若BD =BC ,则∠1的度数是( )图4A .44°B .46°C .54°D .56°7.如图5,△ABC 是等边三角形,AD ,CE 分别是BC ,AB 边上的高,且AD ,CE 相交于点O .若CE =1,则OD 的长是( )图5A.13B.12C. 2D. 3 8.如图6,在△ABC 中,AB =20 cm ,AC =12 cm ,点P 从点B 出发以每秒3 cm 的速度向点A 运动,点Q 从点A 同时出发以每秒2 cm 的速度向点C 运动,其中一个动点到达端点时,另一个动点也随之停止运动.当△APQ 是以∠A 为顶角的等腰三角形时,运动的时间是( )图6A .2.5秒B .3秒C .3.5秒D .4秒9.如图7,P 是等边三角形ABC 内的一点,且P A =3,PB =4,PC =5,以BC 为边在△ABC 外作△BQC ≌△BP A ,连接PQ ,则以下结论错误的是( )图7A.△BPQ是等边三角形B.△PCQ是直角三角形C.∠APB=150°D.∠APC=135°10.如图8,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下列四个结论:图8①AD上任意一点到点C,B的距离相等;②AD上任意一点到直线AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.其中正确的个数为()A.1 B.2 C.3 D.4第Ⅱ卷(非选择题共70分)二、填空题(每小题3分,共18分)11.命题“全等三角形的面积相等”的逆命题是________命题.(填“真”或“假”)12.如图9,P,Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠ABC的度数为________°.图913.如图10,有一张直角三角形纸片,两直角边AC=5 cm,BC=10 cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD的长为________.图1014.如图11,在△ABC中,AB=AC,∠A=120°,D是BC上任意一点,过点D分别作DE⊥AB于点E,DF⊥AC于点F.如果BC=20 cm,那么DE+DF=________ cm.图1115.如图12,在△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,可以判定△ABC是等腰三角形的两个条件是________(用序号写出一种情形即可).图1216.已知:如图13,O为平面直角坐标系中的坐标原点,四边形OABC为长方形,A(10,0),C(0,4),D是OA的中点,点P在BC上运动.若△ODP是腰长为5的等腰三角形,则点P的坐标为________________.图13三、解答题(共52分)17.(5分)如图14所示,在△ABC中,∠C=90°.(1)用圆规和直尺在AC上求作点P,使点P到点A,B的距离相等(保留作图痕迹,不写作法和证明);(2)当满足(1)的点P到AB,BC的距离相等时,求∠A的度数.图1418.(5分)如图15,在△ABC中,∠C=90°,AB的垂直平分线分别交AB,AC于点D,E,且∠A=30°,DE=1 cm.求△ABC的面积.(结果保留根号)图1519.(6分)如图16,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E.若AB=6 cm,你能求出△BDE的周长吗?若能,请求出;若不能,请说明理由.图1620.(6分)如图17,D,E分别为△ABC的边AB,AC上的点,BE与CD相交于点O.现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD.(1)请你选出两个条件作为题设,余下的两个条件作为结论,写出一个正确..的命题:命题的条件是______和______,命题的结论是______和______(均填序号);(2)证明你写出的命题.已知:求证:证明:图1721.(7分)如图18,在△ABC中,AD平分∠BAC,AD的垂直平分线交AB于点E,交AC于点F,连接DE.求证:AF=ED.图1822.(7分)如图19,在等腰三角形ABC中,AB=AC=8,∠BAC=100°,AD是∠BAC的平分线,交BC于点D,E是AB的中点,连接DE.(1)求∠BAD的度数;(2)求∠B的度数;(3)求线段DE的长.图1923.(8分)已知∠MAN,AC平分∠MAN,试解决下列问题:(1)在图20①中,若∠MAN=120°,∠ABC=∠ADC=90°.求证:AB+AD=AC.(2)在图②中,若∠MAN=120°,∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.图2024.(8分)如图21,△ABC是边长为6的等边三角形,P是AC边上一动点,由点A向点C运动(与点A,C不重合),Q是CB延长线上一点,与点P同时以相同的速度由点B向CB延长线方向运动(点Q不与点B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.(1)当∠BQD=30°时,求AP的长.(2)运动过程中线段DE的长是否发生变化?如果不变,请求出线段DE的长;如果变化,请说明理由.图211.B 2.B 3.A 4.D 5.A 6.C 7.A 8.D 9.D 10.D 11.假 12.3013.154 cm [解析] 设CD =x cm ,则易证得BD =AD =(10-x )cm.在Rt △ACD 中,由勾股定理,得(10-x )2=x 2+52,解得x =154.14.10 [解析] 利用含30°角的直角三角形的性质得,DE +DF =12(BD +CD )=12BC .15.答案不唯一,如①③16.(2,4)或(3,4)或(8,4) [解析] 当OD =PD (点P 在点D 的右边)时,根据题意画出图形, 如图①所示:过点P 作PQ ⊥x 轴于点Q .在Rt △DPQ 中,PQ =4,PD =OD =12OA =5,根据勾股定理,得DQ =3,故OQ =OD +DQ =5+3=8,则P 1(8,4);当PD =OD (点P 在点D 的左边)时,根据题意画出图形,如图②所示:过点P 作PQ ⊥x 轴于点Q .在Rt △DPQ 中,PQ =4,PD =OD =5, 根据勾股定理,得QD =3,故OQ =OD -QD =5-3=2,则P 2(2,4); 当PO =OD 时,根据题意画出图形,如图③所示:过点P 作PQ ⊥x 轴于点Q .在Rt △OPQ 中,OP =OD =5,PQ =4,根据勾股定理,得OQ =3,则P 3(3,4).综上,满足题意的点P 的坐标为(2,4)或(3,4)或(8,4).17.解:(1)图略.提示:作线段AB 的垂直平分线交AC 于点P .(2)连接BP .∵点P 到AB ,BC 的距离相等,∴BP 平分∠ABC ,∴∠ABP =∠PBC .又∵点P 在线段AB 的垂直平分线上,∴P A =PB ,∴∠A =∠ABP ,∴∠A =∠ABP =∠PBC =13×90°=30°.18.解:∵DE 垂直平分AB ,∠A =30°,DE =1 cm ,∴AE =2 cm ,∴AD =22-12=3(cm),∴AB =2AD =2 3 cm.在Rt △ABC 中,∠A =30°,∴BC =12AB = 3 cm ,∴AC =(2 3)2-(3)2=3(cm), ∴S △ABC =12×3×3=32 3(cm 2).19.解:能.∵∠C =90°,DE ⊥AB ,AD 平分∠CAB ,∴DE =DC .在Rt △ADC 和Rt △ADE 中,∵DC =DE ,AD =AD ,∴Rt △ADC ≌Rt △ADE (HL),∴AC =AE .又∵AC =BC ,∴AE =BC ,∴△BDE 的周长为DE +DB +EB =BC +EB =AE +EB =AB .∵AB =6 cm ,∴△BDE 的周长为6 cm.20.解:答案不唯一,如:(1)① ③ ② ④(2)已知:D ,E 分别为△ABC 的边AB ,AC 上的点,BE 与CD 相交于点O ,且AB =AC ,∠ABE =∠ACD .求证:OB =OC ,BE =CD .证明:在△ABE 和△ACD 中,∵∠ABE =∠ACD ,AB =AC ,∠A =∠A ,∴△ABE ≌△ACD (ASA),∴BE =CD .∵AB =AC ,∴∠ABC =∠ACB ,∴∠BCD =∠ACB -∠ACD =∠ABC -∠ABE =∠CBE ,∴OB =OC .21.证明:∵EF 是AD 的垂直平分线,∴AE =ED .∵AD 平分∠BAC ,∴∠EAO =∠F AO .∵∠AOE =∠AOF =90°,AO =AO ,∠EAO =∠F AO ,∴△AEO ≌△AFO ,∴AE =AF ,∴AF =ED .22.解:(1)∵∠BAC =100°,且AD 是∠BAC 的平分线,∴∠BAD =50°.(2)在等腰三角形ABC 中,∠B =180°-100°2=40°. (3)∵AB =AC ,AD 平分∠BAC ,∴AD 是等腰三角形ABC 底边BC 上的中线,∴D 是BC 的中点.又∵E 是AB 的中点,∴DE 是△ABC 的中位线,∴DE =12AC =4. 23.解:(1)证明:∵∠MAN =120°,AC 平分∠MAN ,∴∠CAD =∠CAB =60°.又∠ABC =∠ADC =90°,∴∠ACD =∠ACB =30°,∴AD =12AC ,AB =12AC ,∴AB +AD =12AC +12AC =AC .(2)(1)中的结论仍然成立.证明:如图,过点C 分别作CE ⊥AM 于点E ,CF ⊥AN 于点F ,则∠CED =∠CFB =90°.∵AC 平分∠MAN ,∴CE =CF .∵∠CBF +∠ADC =180°,∠ADC +∠CDE =180°,∴∠CDE =∠CBF . 在△CDE 和△CBF 中,∵∠CDE =∠CBF ,∠CED =∠CFB ,CE =CF ,∴△CDE ≌△CBF ,∴DE =BF .∵∠MAN =120°,AC 平分∠MAN ,∴∠MAC =∠NAC =60°,∴∠ECA =∠FCA =30°.在Rt △ACE 和Rt △ACF 中,AE =12AC ,AF =12AC ,∴AD +AB =AD +AF +BF =AD +AF +DE =AE +AF =12AC +12AC =AC ,即AB +AD =AC .24.解:(1)∵△ABC 是边长为6的等边三角形,∴∠ACB =60°.∵∠BQD =30°,∴∠QPC =90°.设AP =x ,则PC =6-x ,QB =x ,∴QC =QB +BC =x +6.∵在Rt △QCP 中,∠BQD =30°,∴PC =12QC ,即6-x =12(x +6),解得x =2,∴当∠BQD =30°时,AP =2.(2)线段DE 的长不会发生变化.如图,过点Q 作QF ⊥AB ,交直线AB 于点F ,连接QE ,PF . 又∵PE ⊥AB 于点E ,∴∠DFQ =∠AEP =90°.∵点P ,Q 的运动速度相同,∴AP =BQ .∵△ABC 是等边三角形,∴∠A =∠ABC =∠FBQ =60°.在△APE 和△BQF 中,∵∠AEP =∠BFQ ,∠A =∠FBQ ,AP =BQ ,∴△APE ≌△BQF (AAS),∴AE =BF ,PE =QF ,易证△QFD ≌△PED ,∴DE =DF ,∴DE =12EF .∵EF =BE +BF =BE +AE =AB ,∴DE =12AB . 又∵等边三角形ABC 的边长为6,∴DE =3.。
2022-2023学年八年级数学常考点精练(苏科版):专题03 一线三等角模型证全等(解析版)

专题03一线三等角模型证全等模型感知1.【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一,请根据以下问题,把你的感知填写出来:①如图1,ABC 是等腰直角三角形,90C ,AE =BD ,则AED ≌_______;②如图2,ABC 为正三角形,,60BD CF EDF ,则BDE ≌________;③如图3,正方形ABCD 的顶点B 在直线l 上,分别过点A 、C 作AE l 于E ,CF l 于F .若1AE ,2CF ,则EF 的长为________.【答案】①△BDF ;②△CFD ;③3;①根据等腰直角三角形的性质及和角关系,可得△AED ≌△BDF ;②根据等边三角形的性质及和角关系,可得△BDE ≌△CFD ;③根据正方形的性质及和角关系,可得△ABE≌△BCF,由全等三角形的性质即可求得EF的长;类型一一线三直角证全等2.在△ABC中,∠ACB=90°,AC=BC,且AD⊥MN于D,BE⊥MN于E.(1)直线MN绕点C旋转到图(1)的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到图(2)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系(不写证明过程);(3)当直线MN绕点C旋转到图(3)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系(不写证明过程).【答案】(1)证明见详解(2)DE+BE=AD.理由见详解(3)DE=BE-AD(或AD=BE-DE,BE=AD+DE等).理由见详解.【解析】【分析】(1)根据题意由垂直得∠ADC=∠BEC=90°,由同角的余角相等得:∠DAC=∠BCE,因此根据AAS可以证明△ADC≌△CEB,结合全等三角形的对应边相等证得结论;(2)由题意根据全等三角形的判定定理AAS推知△ACD≌△CBE,然后由全等三角形的对应边相等、图形中线段间的和差关系以及等量代换证得DE+BE=AD;(3)由题意可知DE、AD、BE具有的等量关系为:DE=BE-AD(或AD=BE-DE,BE=AD+DE等).证明的方法与(2)相同.(1)证明:如图1,∵AD⊥MN,BE⊥MN,∴∠ADC=∠BEC=90°,∴∠DAC+∠ACD=90°,∵∠ACB =90°,∴∠ACD +∠BCE =90°,∴∠DAC =∠BCE ,在△ADC 和△CEB 中,∵ADC BEC DAC BCE AC BC,∴△ADC ≌△CEB ;∴DC =BE ,AD =EC ,∵DE =DC +EC ,∴DE =BE +AD .(2)解:DE +BE =AD .理由如下:如图2,∵∠ACB =90°,∴∠ACD +∠BCE =90°.又∵AD ⊥MN 于点D ,∴∠ACD +∠CAD =90°,∴∠CAD =∠BCE .在△ACD 和△CBE 中,90ADC CEB CAD BCE AC BC,∴△ACD ≌△CBE (AAS ),∴CD =BE ,AD =CE ,∴DE +BE =DE +CD =EC =AD ,即DE +BE =AD .(3)解:DE =BE -AD (或AD =BE -DE ,BE =AD +DE 等).理由如下:如图3,易证得△ADC ≌△CEB ,∴AD =CE ,DC =BE ,∴DE =CD -CE =BE -AD ,即DE =BE -AD .【点睛】本题属于几何变换综合题,考查等腰直角三角形和全等三角形的性质和判定,熟练掌握全等三角形的四种判定方法是关键:SSS 、SAS 、AAS 、ASA ;在证明线段的和与差时,利用全等三角形将线段转化到同一条直线上得出结论.3.通过对下面数学模型的研究学习,解决下列问题:(1)如图1,点A 在直线l 上,90,BAD AB AD ,过点B 作BC l 于点C ,过点D 作DE l 交于点E .由12290D ,得1D .又90BCA AED ,可以推理得到()ABC DAE AAS ≌.进而得到结论:AC _____,BC _____.我们把这个数学模型称为“K 字”模型或“一线三直角”模型;(2)如图2,90,,,BAD MAN AB AD AM AN BM l 于点C ,NG l 于点G ,由(1)易知NG _______,ND 与直线l 交于点P ,求证:NP DP .【答案】(1)DE ,AE ;(2)AC .证明见详解.【解析】【分析】(1)根据(AAS)≌ABC DAE ,得出AC =DE ,BC =AE 即可;(2)过D 作DE ⊥直线l 于E ,先证△MCA ≌△AGN (AAS ),得出AC =NG ,由(1)知(AAS)≌ABC DAE ,得出AC =DE ,再证△NGP ≌△DEP (AAS )即可.(1)解:∵(AAS)≌ABC DAE ,∴AC =DE ,BC =AE ,故答案为DE ,AE ;(2)证明:过D 作DE ⊥直线l 于E ,∵90MAN ,∴∠CAM +∠NAG =90°,∵BM ⊥l ,∴∠MCA =90°,∴∠M +∠CAM =90°,∴∠M =∠NAG ,∵NG l ,∴∠AGN =90°,在△MCA 和△AGN 中,MCA AGN M GAN MA AN,∴△MCA ≌△AGN (AAS ),∴AC =NG ,由(1)知(AAS)≌ABC DAE ,∴AC =DE ,∴NG =DE ,在△NGP 和△DEP 中,90NGP DEP GPN EPD NG DE,∴△NGP ≌△DEP (AAS )∴NP =DP ,故答案为AC.【点睛】本题考查一线三直角全等问题,掌握余角性质,三角形全等判定与性质是解题关键.类型二一线非直角证全等4.(1)如图1,直线m经过等边三角形ABC的顶点A,在直线m上取两点D,E,使得∠ADB=60°,∠AEC =60°.求证:BD+CE=DE;(2)将(1)中的直线m绕着点A逆时针方向旋转一个角度到如图2的位置,并使∠ADB=120°,∠AEC =120°.若BD=3,CE=7,求DE的长.【答案】(1)证明见解析;(2)DE=4【解析】【分析】(1)利用等边三角形的性质和已知角的度数,证明∠ABD=∠CAE,利用AAS证明△ABD≌△CAE,推出BD=AE,AD=CE,即可证明;(2)同(1)证明△ABD≌△CAE,推出BD=AE,AD=CE,则DE=AD-AE=CE-BD.【详解】(1)证明:∵△ABC为等边三角形,∴AB=AC,∠BAC=60°,∴∠DAB+∠CAE=120°又∠ADB=∠AEC=60°,∴∠ABD+∠DAB=120°,∴∠ABD=∠CAE,∴△ABD≌△CAE(AAS),∴BD=AE,AD=CE,∴DE=AD+AE=BD+CE.(2)解:∵△ABC为等边三角形,∴AB =AC ,∠BAC =60°,∴∠BAD +∠CAE =60°又∠ADB =∠AEC =120°,∴∠ABD +∠BAD =60°,∴∠ABD =∠CAE ,∴△ABD ≌△CAE (AAS ),∴BD =AE ,AD =CE ,∴DE =AD -AE =CE -BD =4.【点睛】本题考查等边三角形的性质,全等三角形的判定和性质,读懂题意,找出图形中的全等三角形是解题的关键.5.已知:CD 是经过BCA 的顶点C 的一条直线,CA CB .E 、F 是直线CD 上两点,BEC CFA .(1)若直线CD 经过BCA 的内部,BCD ACD .①如图1,90BCA ,90 ,直接写出BE ,EF ,AF 间的等量关系:__________.②如图2, 与BCA 具有怎样的数量关系,能使①中的结论仍然成立?写出 与BCA 的数量关系,并对结论进行证明;(2)如图3,若直线CD 经过BCA 的外部,BCA ,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.【答案】(1)①EF BE AF ;②180BCA ,证明见解析;(2)不成立,EF FA BE ,理由见解析【解析】【分析】(1)①根据题意,推导得ACF CBE ,通过证明ACF CBE ≌△,得BE CF ,CE AF ,结合EF CF CE ,即可得到答案;②结合题意,根据三角形内角和性质,推导得CBE ACF ,通过证明BCE CAF ≌△△,即可完成证明;(2)根据题意,结合三角形内角和的性质,推导得CBE ACF ,通过证明BCE CAF ≌△△,得EC FA ,BE CF ;根据EF CE CF ,即可得到答案.【详解】(1)①∵90BCA ,90∴90ACF BCE ,90CBE BCE∴ACF CBE∴BEC CFAACF CBECA CB∴ACF CBE≌△∴BE CF ,CE AF∵EF CF CE∴EF BE AF ;②满足180BCA ,理由如下:∵180CBE BCE BEC ,180BCA∴CBE BCE BEC BCA∴CBE BCE BCE ACF∴CBE ACF∵BEC CFA ,CA CB ,∴BCE CAF≌△△∴BE CF ,CE AF∵EF CF CE ,∴EF BE AF(2)不成立,EF BE AF ,理由如下:∵180CBE BCE BEC ,180BCE BCA ACF ,BEC CFA BCA∴CBE BCE BCE ACF∴CBE ACF∵BEC CFA ,CA CB ,∴BCE CAF≌△△∴BE CF ,CE AF∵EF CF CE ,∴EF BE AF【点睛】本题考查了三角形内角和、余角、全等三角形的知识;解题的关键是熟练掌握三角形内角和、全等三角形的性质,从而完成求解.类型三综合运用6.(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在ABC 中,90BAC ,AB AC ,直线l 经过点A ,BD 直线l ,CE 直线l ,垂足分别为点D ,E .求证:DE BD CE .(2)组员小明想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在ABC 中,AB AC ,D ,A ,E 三点都在直线l 上,并且有BDA AEC BAC ,其中 为任意锐角或钝角.请问结论DE BD CE 是否成立?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过ABC 的边AB ,AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高.延长HA 交EG 于点I .若7AEG S △,则AEI S △______.【答案】(1)见解析;(2)结论成立,理由见解析;(3)3.5【解析】【分析】(1)由条件可证明△ABD ≌△CAE ,可得DA =CE ,AE =BD ,可得DE =BD +CE ;(2)由条件可知∠BAD +∠CAE =180°-α,且∠DBA +∠BAD =180°-α,可得∠DBA =∠CAE ,结合条件可证明△ABD ≌△CAE ,同(1)可得出结论;(3)由条件可知EM =AH =GN ,可得EM =GN ,结合条件可证明△EMI ≌△GNI ,可得出结论I 是EG 的中点.【详解】解:(1)证明:如图1中,∵BD ⊥直线l ,CE ⊥直线l ,∴∠BDA =∠CEA =90°,∵∠BAC =90°,∴∠BAD +∠CAE =90°,∵∠BAD +∠ABD =90°,∴∠CAE =∠ABD ,在△ADB 和△CEA 中,ABD CAE BDA CEA AB AC,∴△ADB ≌△CEA (AAS ),∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE .(2)解:成立.理由:如图2中,∵∠BDA =∠BAC =α,∴∠DBA +∠BAD =∠BAD +∠CAE =180°-α,∴∠DBA =∠CAE ,在△ADB 和△CEA 中,BDA AEC DBA CAE AB AC,∴△ADB ≌△CEA (AAS ),∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE .(3)如图3,过E 作EM ⊥HI 于M ,GN ⊥HI 的延长线于N .∴∠EMI =∠GNI =90°由(1)和(2)的结论可知EM =AH =GN∴EM =GN在△EMI 和△GNI 中,GIN EIM EM GN GNI EMI,∴△EMI ≌△GNI (AAS ),∴EI =GI ,∴I 是EG 的中点.∴S △AEI =12S △AEG =3.5.故答案为:3.5.【点睛】本题是四边形综合题,考查了全等三角形的判定和性质,正方形的性质,直角三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键.7.(1)如图(1),已知:在△ABC 中,∠BAC =90°,AB =AC ,直线m 经过点A ,BD ⊥直线m ,CE ⊥直线m ,垂足分别为点D 、E .证明∶DE =BD +CE .(2)如图(2),将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线m 上,并且有∠BDA =∠AEC =∠BAC = ,其中 为任意锐角或钝角.请问结论DE =BD +CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D 、E 是D 、A 、E 三点所在直线m 上的两动点(D 、A 、E 三点互不重合),点F 为∠BAC 平分线上的一点,且△ABF 和△ACF 均为等边三角形,连接BD 、CE ,若∠BDA =∠AEC =∠BAC ,试判断△DEF 的形状.【答案】(1)见解析(2)成立,证明见解析(3)△DEF为等边三角形,证明见解析【解析】【分析】(1)因为DE=DA+AE,故由AAS证△ADB≌△CEA,得出DA=EC,AE=BD,从而证得DE=BD+CE.(2)成立,仍然通过证明△ADB≌△CEA,得出BD=AE,AD=CE,所以DE=DA+AE=EC+BD.(3)由△ADB≌△CEA得BD=AE,∠DBA=∠CAE,由△ABF和△ACF均等边三角形,得∠ABF=∠CAF=60°,FB=FA,所以∠DBA+∠ABF=∠CAE+∠CAF,即∠DBF=∠FAE,所以△DBF≌△EAF,所以FD=FE,∠BFD=∠AFE,再根据∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600得到△DEF是等边三角形.【详解】解:(1)证明:∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°.∵∠BAC=90°,∴∠BAD+∠CAE=90°.∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.又AB=AC,∴△ADB≌△CEA(AAS).∴AE=BD,AD=CE.∴DE=AE+AD=BD+CE.(2)成立.证明如下:∵∠BDA=∠BAC= ,∴∠DBA+∠BAD=∠BAD+∠CAE=180°- .∴∠DBA=∠CAE.∵∠BDA=∠AEC= ,AB=AC,∴△ADB ≌△CEA (AAS ).∴AE =BD ,AD =CE .∴DE =AE +AD =BD +CE .(3)△DEF 为等边三角形.理由如下:由(2)知,△ADB ≌△CEA ,BD =AE ,∠DBA =∠CAE ,∵△ABF 和△ACF 均为等边三角形,∴∠ABF =∠CAF =60°.∴∠DBA +∠ABF =∠CAE +∠CAF .∴∠DBF =∠FAE .∵BF =AF ,∴△DBF ≌△EAF (ASA ).∴DF =EF ,∠BFD =∠AFE .∴∠DFE =∠DFA +∠AFE =∠DFA +∠BFD =60°.∴△DEF 为等边三角形.【点睛】此题考查了全等三角形的性质和判定,等边三角形的性质和判定,解题的关键是熟练掌握全等三角形的性质和判定,等边三角形的性质和判定.8.通过对下面数学模型的研究学习,解决下列问题:【模型呈现】(1)如图,90BAD ,AB AD ,过点B 作BC AC 于点C ,过点D 作DE AC 于点E .由12290D ,得1D .又90ACB AED ,可以推理得到ABC DAE ≌.进而得到AC __________,BC AE .我们把这个数学模型称为“K 字”模型或“一线三等角”模型;【模型应用】(2)如图,90BAD CAE ,AB AD ,AC AE ,连接BC ,DE ,且BC AF 于点F ,DE 与直线AF 交于点G .求证:点G 是DE 的中点;【深入探究】(3)如图,已知四边形ABCD 和DEGF 为正方形,AFD 的面积为1S ,DCE 的面积为2S ,则有1S __________2S (填“>、=、<”)(4)如图,点A 、B 、C 、D 、E 都在同一条直线上,四边形ABAH 、KCMG 、DENM 都是正方形,若该图形总面积是16,正方形KCMG 的面积是4,则HKG D 的面积是__________.【答案】(1)DE ;(2)见解析;(3)=;(42【解析】【分析】(1)根据全等三角形的性质即可得到答案;(2)分别过点D 和点E 作DM FG 于点M ,EN FG 于点N ,由(1)中结论可得到AF =DM ,AF =EN ,然后只需要证明DMG ENG △≌△即可得到答案;(3)过点D 作DO ⊥AF 交AF 于O ,过点E 错EN ⊥OD 交OD 延长线于N ,过点C 作CM ⊥OD 交OD 延长线于M ,然后同(2)中证明AOD DMC △≌△,FOD DNE △≌△,ENP CMP △≌△即可得到答案;(4)同(3)中的方法可以证明GHK KBC CMD GMN S S S S △△△△==,然后利用勾股定理得到ABKH MDEN KCMG S S S 正方形正方形正方形即可得到答案.【详解】解:(1)∵ABC DAE△≌△∴AC DE(2)分别过点D 和点E 作DM FG 于点M ,EN FG 于点N ,∴90DAM ADM ,∵90BAD ,∴90BAF DAM ,∴BAF ADM∵BC AF ,∴90BFA AMD ,在ABF 和DAM 中,BAF ADN ,BFA AMD ,BA AD ,∴ABF DAM ≌,∴AF DM同理AF EN∴DM EN ,∵DM FG ,EN FG ,∴DMG ENG ,在DMG △和ENG △中,DGM EGN ,DMG ENG ,DM EN ,∴DMG ENG△≌△∴DG EG ,即点G 是DE 的中点;(3)如图所示,过点D 作DO ⊥AF 交AF 于O ,过点E 作EN ⊥OD 交OD 延长线于N ,过点C 作CM ⊥OD 交OD 延长线于M∵四边形ABCD 与四边形DEGF 都是正方形∴∠ADC =∠90°,AD =DC ,DF =DE∵DO ⊥AF ,CM ⊥OD∴∠AOD =∠CMD =90°,∠OAD +∠ODA =90°,∠CDM +∠DCM =90°,又∵∠ODA +∠DCM =90°∴∠A DO =∠DCM∴AOD DMC△≌△∴AOD DMC S S △△,OD =MC同理可以证明FOD DNE△≌△∴FOD DNE S S △△,OD =NE∴MC =NE∵EN ⊥OD ,CM ⊥OD ,∠EPN =∠CMP∴ENP CMP△≌△∴ENP CMPS S △△=∵ADF AOD FOD S S S △△△=,DCE DCM CMP DEN ENPS S S S S △△△△△=∴=DCE DCM DEN AOD FODS S S S S △△△△△=∴DCE ADF S S △△=即12S S =;(4)同(3)中的方法可以证明GHK KBC CMD GMN S S S S △△△△==,且KBC CDM△≌△即BC DM由勾股定理得:222KB BC KC ∴222KB DM KC ∴ABKH MDEN KCMGS S S 正方形正方形正方形∵图形总面积是16,正方形KCMG 的面积是4∴=4ABKH MDEN KCMG S S S 正方形正方形正方形∴=8GHK KBC CMD GMN S S S S △△△△++∴2GHK S △=【点睛】本题主要考查了全等三角形的性质与判定,正方形的性质,解题的关键在于能够熟练掌握全等三角形的性质与判定.9.(1)【问题情境】八上《伴你学》第138页有这样一个问题:如图1,把一块三角板(,90AB BC ABC )放入一个“U ”形槽中,使三角形的三个顶点A 、B 、C 分别在槽的两壁及底边上滑动,已知90D E ,在滑动过程中,你发现线段AD 与BE 有什么关系?试说明你的结论;(2)【变式探究】小明在解决完这个问题后,将其命名为“一线三等角”模型;如图2,在ABC 中,点D 、E 、F 分别在边BC 、AC 、AB 上,若B FDE C ,则这三个相等的角之间的联系又会使图形中出现其他的一些等角.请你写出其中的一组,并加以说理;(3)【拓展应用】如图3,在ABC 中,BA BC ,45B ,点D 、F 分别是边BC 、AB 上的动点,且2AF BD .以DF 为腰向右作等腰DEF ,使得DE DF ,45EDF ,连接CE .①试判断线段DC 、BD 、BF 之间的数量关系,并说明理由;②如图4,已知2AC ,点G 是AC 的中点,连接EA 、EG ,直接写出EA EG 的最小值.【答案】【小问1】AD BE ,说明见解析【小问2】BED FDC ,EDB DFC ;说理见解析【小问3】①BD BF CD ,理由见解析;②AE EG 【解析】【分析】(1)【问题情境】证明()ABD BCE AAS ,即可求解.(2)【变式探究】利用等量代换即可求解.(3)【拓展应用】①等量代换即可求解;②在CD 上截取DM BF ,连接EM ,作点G 关于CE 的对称点N ,连接CN ,AN ,先证明()BDF MED SAS ,得到EM =CM ,在求出22.5ECM MEC ,即可确定E 点在射线CE 上运动,当A 、E 、N 三点共线时,EA +EG 的值最小,最小值为AN ,在Rt ANC 中求出AN 即可.【详解】(1)【问题情境】AD BE ,理由如下:90ABC ∵,90ABD CBE ,90BAD ABD ∵,BAD CBE ,AB BC ∵,()ABD BCE AAS ,AD BE ;(2)【变式探究】BED FDC ,EDB DFC ;理由如下:B FDEC ∵,180EDB BED EDB FDC FDC DFC EDF ,BED FDC ,EDB DFC ;(3)【拓展应用】①AB BC ∵,AF BF BD CD ,2AF BD ∵,2BD BF BD CD ,BD BF CD ;②在CD 上截取DM BF ,连接EM ,作点G 关于CE 的对称点N ,连接CN ,AN ,45B ∵,45EDF ,BFD EDM ,DF DE ∵,()BDF MED SAS ,BD EM ,EM BD ,45B DME ,CD BD BF ∵,CM BD ,EM CM ,MCE MEC ,45EMD ∵,22.5ECM MEC ,E 点在射线CE 上运动,G ∵点与N 的关于CE 对称,EG EN ,EA EG EA EN AN , 当A 、E 、N 三点共线时,EA EG 的值最小,最小值为AN ,45B ∵,AB BC ,67.5ACB ,45ACE ,由对称性可知,ACE ECN ,90ACN ,∵点G 是AC 的中点,2AC ,1CG ,1CN ,在Rt ANC 中,AN ,AE EG【点睛】本题是三角形的综合题,熟练掌握三角形全等的判定及性质,轴对称求最短距离的方法是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学(下)第十一章图形与证明(一) 提高测试
满分:100分时间:90分钟得分:_________
一、选择题(每题2分,共20分)
1.下列关于判断一个数学结论是否正确的叙述中,正确的是 ( ) A.只需观察得出 B.只需依靠经验获得
C.通过亲自实验得出 D.必须进行有根据地推理
2.如图,在一个规格为4×8的球台上,有两个小球P和Q.若击打小球P经过球台的边AB 反弹后,恰好击中小球Q.则小球P击出时,应瞄准AB边上的 ( )
A.点O1 B.点O2 C.点O3 D.点O4
3.下列句子中.不属于命题的是 ( ) A.三角形的内角和等于180度
B.对顶角相等
C.过直线外一点作已知直线的平行线
D.两点之间线段最短
4.将命题“同角的余角相等”改写成“如果……,那么……”的形式,有下列写法:①如果同角,那么余角相等;②如果两个角是同一个角的余角,那么这两个角相等:③如果两个角相等,那么这两个角是同一个角的余角,其中改写正确的有 ( )
A.3 个 B.2个 C.1个 D.0个
5.如图,直线a、b与直线c相交,给出下列条件:①∠2=∠3;②∠1=∠4;③∠1+∠4=180°,其中能判断a∥b的是 ( )
A.①②③ B.①② C.①③ D.只有①
6.如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需再有下列条件中的 ( )
A.∠1=∠2 B.∠1=∠DFE
C.∠1=∠AFD D.∠2=∠AFD
7.已知AC为矩形ABCD的对角线,则图中∠1与∠2一定不相等的是 ( )
8.给出下列四个命题:①全等三角形是相似三角形;②顶角相等的两个等腰三角形相似;③所有的等边三角形都相似;④所有的直角三角形都相似,其中真命题的个数为 ( ) A.1 B.2 C.3 D.4
9.已知下列命题:①若a>0,b>0,则a+b>0;②若a≠b,则a2≠b2;③角的平分线上的点到角的两边的距离相等;④平行四边形的对角线互相平分,其中原命题与逆命题均为真命题的个数是 ( )
A.1 B.2 C.3 D.4
10.如图,一个平面镜以与平面成45°角固定在水平桌面上,小球以l米/秒的速度沿桌面向平面镜匀速滚去,则小球在平面镜里所成的像 ( )
A.以1米/秒的速度,做竖直向上运动
B.以1米/秒的速度,做竖直向下运动
C.以2米/秒的速度,做竖直向上运动
D.以2米/秒的速度,做竖直向下运动
二、填空题(每小题2分,共20分)
11.要判断两条线段是否垂直,仅靠观察是_________的(填“行”或“不行”).
12.三角形被它一边上的中线所分成的两个三角形面积相等吗?________(填“相等”或“不相等”).
13.如图是一幅“苹果图”,第一行有一个苹果,第二行有2个,第三行有4个,第四行有8个……你是否发现苹果的排列规律?猜猜看,第十行有________个苹果.
14.下列句子:①今天的天气好吗:②作线段AB∥CD;③连接A、B两点;④正数大于负数,其中属于命题的是__________(填写正确答案的序号).
15.下列命题:①矩形是平行四边形;②相似三角形一定是全等一角形;③等腰梯形的对角线相等;④两既线平行,同位角相等,其中属于假命题的是________(填写正确答案的序号).
16.下列命题:①两个负数的差一定是负数;②两边分别平行的两个角一定相等;③全等的两个三角形一定关于某条直线对称;④对角线互相垂直、平分且相等的四边形是正方形,其中真命题有_________个.
17.命题“矩形的对角线相等”的逆命题是_____________________.
18.如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且与EF交于点O,那么与∠AOE 相等的角有__________个.
19.如图,AB∥DE,∠B=80°,∠CDE=135°,则∠C=_________.
20.在四边形ABCD中,AC是对角线,现有三个条件:①∠BAC=∠DAC;②BC=DC;
③AB=AD,请将其中的两个条件作为已知条件,另一个作为结论构成一个真命题:
现将与上述大小相同、花朵颜色分布完全一样的四个立方体,拼成一个水平放置的长方体,如图所示,那么此长方体的下底面有多少朵花?试写出你的结论并说出推理
过程.
22.(6分)写出下面命题的逆命题,并判断原命题与逆命题的真假.
(1)等角的补角相等.
(2)全等三角形的周长相等.
23.(8分)写出下面证明过程的证明理由.
已知:AB=DC,∠BAD=∠CDA.
求证:∠ABC=∠DCB.
证明:连接AC、BD交于点O.
在△ADB与△DAC中,
因为∠BAD=∠ADC,( )
AD=DA,( )
AB=DC,( )
所以△ADB≌△DAC.( )
所以BD=CA.
又在△ABC与△DCB中,
因为BD=CA,( )
AB=DC,( )
BC=BC,( )
所以△ABC≌△DCB.( )
所以∠ABC=∠DCB.
24.(6分)已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE 的平分线相交于点P.
求证:∠P=90°.
25.(7分)如图,在△ABC中,AB=AC,点D在BC上,且BD=AD,DC=AC,求∠B的度数.
26.(7分)已知命题:如图,点A、D、B、E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.
27.(10分)如图,在△ABC中,AB=AC,BE平分∠ABC,DE∥BC.
求证:DE=EC.
28.(10分)如图,在等腰梯形ABCD中,AB∥CD,AC、BD是对角线,将△ABD沿AB向下翻折到△ABE的位置,试判定四边形AEBC的形状.并证明你的结论.
参考答案
一、1.D 2.B 3.C 4.C 5.C 6.B 7.D 8.C 9.B 10.B
二、11.不行 12.相等 13.29或512 14.④ 15.② 16.1 17.对角线相等的
四边形是矩形 18.5 19.35° 20.①③②
三、21.将此长方体从右到左数记为Ⅰ、Ⅱ、Ⅲ、Ⅳ,由Ⅱ、Ⅳ可知,白色的面与红、黄两种颜色的面必相邻,又由Ⅰ知,白色的面应是蓝色的对面,恰为Ⅰ中的下底面,由Ⅲ知红与紫必相邻,再与Ⅰ相比较知,黄色的对面必为紫色了,从而红色的对面必为绿色了,通过上面的推理可以知道Ⅰ的下底面为白色,有4朵花,Ⅱ的下底面为绿色,有6朵花,Ⅲ的下底面为黄色,有2朵花,Ⅳ的下底面为紫色,有5朵花,故这个长方体的下底面有(4+6+2+5)朵花,即共17朵花 22.(1)逆命题:补角相等的两个角相等;原命题是真命题,逆命题是真命题 (2)
24.因为AB∥CD,所以∠BEF+∠DFE=180°.又因为∠BEF
于点P,所以∠PEF=1
2
∠BEF,∠PFE=
1
2
∠DFE.所以∠∠
DFE)=90°.因为∠PEF+∠PFE+∠P=180°,所以∠P=90°
25.因为AB=AC(已知),所以∠B=∠C(等边对等角).同理,∠B=
∠B=x°,则∠C=x°,∠BAD=x°.所以∠ADC=2x°,∠CAD=2x°.在△ADC中,因为∠C+∠CAD+∠ADC=180°.所以x+2x+2x=180.所以x=36.所以∠B的度数为36°26.是假命题.以下任一方法均可.①添加条件:AC=DF.证明:因为AD=BE,所以AD+BD=BE+BD,即AB=DE 在△ABC和△DEF中,AB=DE,∠A=∠FDE,AC=DF,所以△ABC∥△DEF;②添加条件:∠CBA=∠E.证明:因为AD=BE,所以AD+BD=BE+BD,即AB=DE.在△ABC和△DEF中,∠A=∠FDE,AB=DE,∠CBA=∠E,所以△ABC≌△DEF;③添加条件:∠C=∠F.证明:因为AD=BE,所以AD+BD=BE+BD,即AB=DE在△ABC和△DEF中,∠A=∠FDE,∠C=∠F,AB=DE,所以△ABC≌△DEF
27.因为AB=AC,所以∠ABC=∠C因为DE∥BC,所以∠ADE=∠ABC,∠AED=∠C所以∠ADE=∠AED.所以AD=AE因为AB=AC,所以AB-AD=AC-AE,即BD=EC因为BE平分∠ABC,所以∠ABE=∠CBE因为DE∥C,所以∠DEB=∠CBE所以∠ABE=∠DEB.所以BD=DE所以DE=EC 28.四边形AEBC是平行四边形.因为四边形ABCD是等腰梯形,AB∥CD,所以AD=BC,AC=BD.因为△ABD沿AB向下翻折得到△ABE,所以△ABD≌△ABE所以AD=AE,BE=B D.所以AC=BE,AE=BC.所以四边形AEBC是平行四边形。
