控制理论基础第5章习题解答
现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Prepared on 22 November 2020《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有相应的模拟结构图如下: 1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图 (2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P(或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P )当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为(1)⎥⎦⎤⎢⎣⎡=11b解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
自动控制理论二第5章习题

⾃动控制理论⼆第5章习题⾃动控制理论(⼆) 第五章测试题⼀、单项选择题(每⼩题2分)1、系统特征⽅程式的所有根均在根平⾯的左半部分是系统稳定的( )A.充分条件B.必要条件C.充分必要条件D.以上都不是 2、下列判别系统稳定性的⽅法中,哪⼀个是在频域⾥判别系统稳定性的判据() A.劳斯判据 B.赫尔维茨判据 C.奈奎斯特判据 D.根轨迹法 3、设单位负反馈系统的开环传函为G(s)=3)1s (22+,那么它的相位裕量γ的值为() A.15o B.60o C.30o D.45o4、系统稳定的充分必要条件是其特征⽅程式的所有根均在根平⾯的( ) A. 实轴上 B. 虚轴上 C. 左半部分 D. 右半部分5、下列频域性能指标中,反映闭环频域性能指标的是( ) A.谐振峰值M r B.相位裕量γ C.增益裕量K g D.剪切频率ωc6、在经典控制理论中,临界稳定被认为是( )A.稳定B.BIBO 稳定C.渐近稳定D.不稳定 7、奈奎斯特稳定性判据是利⽤系统的( )来判据闭环系统稳定性的⼀个判别准则。
A.开环幅值频率特性B.开环相⾓频率特性C.开环幅相频率特性D.闭环幅相频率特性 8、系统的开环传递函数由1)s(s K +变为2)1)(s s(s K++,则新系统( )。
A.稳定性变好 B.稳定性变坏C.稳定性不变D.相对稳定性变好 9、利⽤奈奎斯特图可以分析闭环控制系统的() A.稳态性能 B.动态性能C.稳态和动态性能D.抗扰性能 10、设单位负反馈控制系统的开环传递函数G o (s)=)a s (s K+,其中K>0,a>0,则闭环控制系统的稳定性与() A.K 值的⼤⼩有关 B.a 值的⼤⼩有关C.a 和K 值的⼤⼩有关D.a 和K 值的⼤⼩⽆关11、已知系统的特征⽅程为(s+1)(s+2)(s+3)=s+4,则此系统的稳定性为() A .稳定 B .临界稳定 C .不稳定 D .⽆法判断12、已知系统前向通道和反馈通道的传递函数分别为G (s )=s K 1)s (H ,)1s (s 10h +=-,当闭环临界稳定时,K h 值应为() A .-1 B .-0.1 C .0.1 D .113、闭环系统特征⽅程为G(s)H(s)=-1,其中G(s)H(s)的⽮量表⽰为() A .1/(2l+1)π B .1/±(2l+1)π C .1/(±2l π) D .1/(±l π) (各备选项中l =0,1,2……)14、若系统的特征⽅程式为 s 3+4s+1=0 ,则此系统的稳定性为 ( ) A .稳定 B .临界稳定 C .不稳定 D .⽆法判断 15、已知单位负反馈控制系统的开环传递函数为)5s )(1s (s )1s (10)s (G +-+=,该系统闭环系统是()A .稳定的B .条件稳定的C .临界稳定的D .不稳定的 16、系统的开环传递函数为)1TS (s 2)s (G k +=,当T=1s 时,系统的相位裕量为()A .30° B .45° C .60° D .90° 17、设某闭环传递函数为1s 101)s (R )s (Y +=,则其频带宽度为() A .0~10 rad/s B .0~1 rad/s C .0~0.1 rad/sD .0~0.01 rad/s18、已知某单位负反馈系统的开环传递函数为 G(s)=,则相位裕量γ的值为() A . 30° B . 45° C . 60° D . 90°19、若⼀系统的特征⽅程式为 (s+1)2(s - 2)2+3 = 0 ,则此系统是() A .稳定的 B .临界稳定的 C .不稳定的 D .条件稳定的 20、在奈⽒判据中,若F(s)在F(s)平⾯上的轨迹顺时针包围原点两次,则N 的值为()A .-2 B .-1 C .1 D .221、若劳斯阵列表中第⼀列的系数为(3,1,ε,2-ε1,12)T ,则此系统的稳定性为()A .稳定B .临界稳定C .不稳定D .⽆法判断 22、设开环系统频率特性为G (j ω)=)12)(1(1++ωωωj j j ,则其频率特性的奈⽒图与负实轴交点的频率值ω为() A .rad 22/s B .1rad /s C .2rad/s D .2rad/s 23、已知单位负反馈控制系统的开环传递函数为G (s )=1-s K,则系统稳定时K的范围为()A .K <0B .K >0C .K >1D .K >224、某单位反馈控制系统开环传递函数G (s )=21s s +α,若使相位裕量γ=45°,α的值应为多少?()A .21 B .21 C .321 D .42125、已知单位负反馈系统的开环传递函数为G (s )=12)1(223++++s as s s ,若系统以ωn =2rad/s的频率作等幅振荡,则a 的值应为()A .0.4B .0.5C .0.75D .126、设G (s )H (s )=)5)(2()10(+++s s s k ,当k 增⼤时,闭环系统()A .由稳定到不稳定B .由不稳定到稳定C .始终稳定D .始终不稳定⼆、填空题(每⼩题1分)1、已知单位反馈系统的开环传递函数为)1Ts (s K)s (G +=,若要求带宽增加a 倍,相位裕量保持不变,则K 应为,T 应为。
《现代控制理论》第三版_.习题答案

1 0 0 3 1 0 5 2 1 52 7 1 5 2 70 125 3 5 7 5 0 0 1 1 B 2 ; 2 5 5
1 0 a1 0 0 1 0 1 0 0 1 a2 3 7 5
0 B 0 1
C (b0 a0bn ) (bn1 an1bn ) 2 1 0
3 1 a 或者 2 2 1 a1 0 a0
e At I At 1 22 1 33 A t A t 2! 3! t2 t4 t6 t3 t5 1 4 16 64 , 4 16 t 2! 4! 6! 3! 5! 3 5 2 4 6 t t t t t t 4 16 64 , 1 4 16 64 3! 5! 2! 4! 6!
0 0 1 B M 1 0 0 0 0 1 M2
1 0 B 1 M1 B1 M2
1 B1 M1 B1 B2 M2
0
0 0 1 0 C 0 0 0 1
1-5. 根据微分方程, 写状态方程, 画模 拟结构图。
1 a2 a2 2 a1 3 2 a a a 1 2 2 a0
1 a2 a1
1 a2
12 b1 b0
b3 b 2 b1 1 b0
凯莱哈密顿法: 1,2 2 j
0 (t ) 1 1 e1t 1 2(e 2 jt e 2 jt ) (t ) 1 2t 4 2 jt 2 jt e j ( e e ) 2 1
自动控制理论二第5章习题

自动控制理论(二) 第五章测试题一、单项选择题(每小题2分)1、系统特征方程式的所有根均在根平面的左半部分是系统稳定的( )A.充分条件B.必要条件C.充分必要条件D.以上都不是 2、下列判别系统稳定性的方法中,哪一个是在频域里判别系统稳定性的判据( ) A.劳斯判据 B.赫尔维茨判据 C.奈奎斯特判据 D.根轨迹法 3、设单位负反馈系统的开环传函为G(s)=3)1s (22+,那么它的相位裕量γ的值为( ) A.15º B.60º C.30º D.45º4、 系统稳定的充分必要条件是其特征方程式的所有根均在根平面的( ) A. 实轴上 B. 虚轴上 C. 左半部分 D. 右半部分5、下列频域性能指标中,反映闭环频域性能指标的是( ) A.谐振峰值M r B.相位裕量γ C.增益裕量K g D.剪切频率ωc6、在经典控制理论中,临界稳定被认为是( )A.稳定B.BIBO 稳定C.渐近稳定D.不稳定 7、奈奎斯特稳定性判据是利用系统的( )来判据闭环系统稳定性的一个判别准则。
A.开环幅值频率特性B.开环相角频率特性C.开环幅相频率特性D.闭环幅相频率特性 8、系统的开环传递函数由1)s(s K +变为2)1)(s s(s K++,则新系统( )。
A.稳定性变好 B.稳定性变坏C.稳定性不变D.相对稳定性变好 9、利用奈奎斯特图可以分析闭环控制系统的( ) A.稳态性能 B.动态性能C.稳态和动态性能D.抗扰性能 10、设单位负反馈控制系统的开环传递函数G o (s)=)a s (s K+,其中K>0,a>0,则闭环控制系统的稳定性与( ) A.K 值的大小有关 B.a 值的大小有关 C.a 和K 值的大小有关 D.a 和K 值的大小无关11、已知系统的特征方程为(s+1)(s+2)(s+3)=s+4,则此系统的稳定性为( ) A .稳定 B .临界稳定 C .不稳定 D .无法判断12、已知系统前向通道和反馈通道的传递函数分别为G (s )=s K 1)s (H ,)1s (s 10h +=-,当闭环临界稳定时,K h 值应为( ) A .-1 B .-0.1 C .0.1 D .113、闭环系统特征方程为G(s)H(s)=-1,其中G(s)H(s)的矢量表示为( ) A .1/(2l+1)π B .1/±(2l+1)π C .1/(±2l π) D .1/(±l π) (各备选项中l =0,1,2……)14、若系统的特征方程式为 s 3+4s+1=0 ,则此系统的稳定性为 ( ) A .稳定 B .临界稳定 C .不稳定 D .无法判断 15、已知单位负反馈控制系统的开环传递函数为)5s )(1s (s )1s (10)s (G +-+=,该系统闭环系统是( )A .稳定的B .条件稳定的C .临界稳定的D .不稳定的 16、系统的开环传递函数为)1TS (s 2)s (G k +=,当T=1s 时,系统的相位裕量为( )A .30° B .45° C .60° D .90° 17、设某闭环传递函数为1s 101)s (R )s (Y +=,则其频带宽度为( ) A .0~10 rad/s B .0~1 rad/s C .0~0.1 rad/sD .0~0.01 rad/s18、已知某单位负反馈系统的开环传递函数为 G(s)= ,则相位裕量 γ 的值为( ) A . 30° B . 45° C . 60° D . 90°19、若一系统的特征方程式为 (s+1)2(s - 2)2+3 = 0 ,则此系统是( ) A .稳定的 B .临界稳定的 C .不稳定的 D .条件稳定的 20、在奈氏判据中,若F(s)在F(s)平面上的轨迹顺时针包围原点两次,则N 的值为( )A .-2 B .-1 C .1 D .221、若劳斯阵列表中第一列的系数为(3,1,ε,2-ε1,12)T ,则此系统的稳定性为( )A .稳定B .临界稳定C .不稳定D .无法判断 22、设开环系统频率特性为G (j ω)=)12)(1(1++ωωωj j j ,则其频率特性的奈氏图与负实轴交点的频率值ω为( ) A .rad 22/s B .1rad /s C .2rad/s D .2rad/s 23、已知单位负反馈控制系统的开环传递函数为G (s )=1-s K,则系统稳定时K的范围为( )A .K <0B .K >0C .K >1D .K >224、某单位反馈控制系统开环传递函数G (s )=21s s +α,若使相位裕量γ=45°,α的值应为多少?( )A .21 B .21 C .321 D .42125、已知单位负反馈系统的开环传递函数为G (s )=12)1(223++++s as s s ,若系统以ωn =2rad/s的频率作等幅振荡,则a 的值应为( )A .0.4B .0.5C .0.75D .126、设G (s )H (s )=)5)(2()10(+++s s s k ,当k 增大时,闭环系统( )A .由稳定到不稳定B .由不稳定到稳定C .始终稳定D .始终不稳定二、填空题(每小题1分)1、已知单位反馈系统的开环传递函数为)1Ts (s K)s (G +=,若要求带宽增加a 倍,相位裕量保持不变,则K 应为 ,T 应为 。
现代控制理论基础_周军_第五章状态反馈与状态观测器
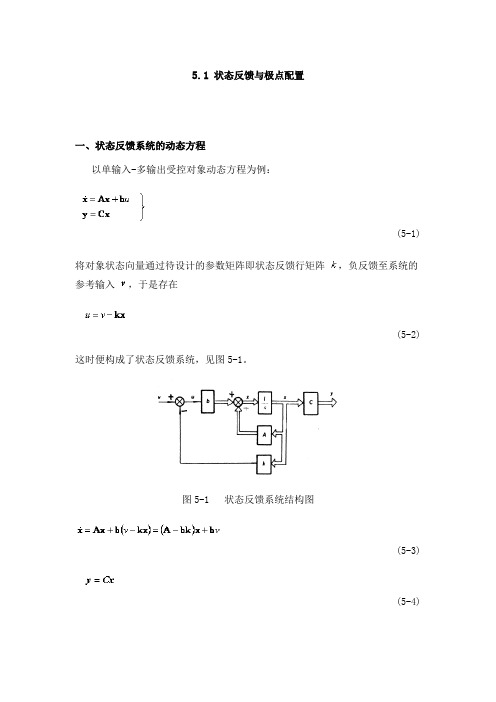
5.1状态反馈与极点配置一、状态反馈系统的动态方程以单输入-多输出受控对象动态方程为例:(5-1)将对象状态向量通过待设计的参数矩阵即状态反馈行矩阵,负反馈至系统的参考输入,于是存在(5-2)这时便构成了状态反馈系统,见图5-1。
图5-1 状态反馈系统结构图(5-3)(5-4)式中v为纯量,为维向量,为维矩阵,为维向量,为维行矩阵,为维向量,为维矩阵。
为闭环状态阵,为闭环特征多项式。
二、用状态反馈使闭环极点配置在任意位置上的充要条件是:受控对象能控证明若式(5-1)所示对象可控,定可通过变换化为能控标准形,有若在变换后的状态空间内引维状态反馈矩阵:(5-5)其中分别为由状态变量引出的反馈系数,则变换后的状态反馈系统动态方程为:(5-6)(5-7)式中(5-8)该式与仍为能控标准形,故引入状态反馈后,系统能控性不变。
特征方程为:(5-9)显见,任意选择阵的个元素,可使特征方程的个系数满足规定要求,能保证特征值(即闭环极点)任意配置。
将逆变换代入式(5-6),可求出原状态空间内的状态反馈系统状态方程:(5-10)与式(5-3)相比,式(5-10)所示对象应引入状态反馈阵为:(5-11)需指出,当受控对象可控时,若不具有能控标准形形式,并不必象如上证明那样去化为能控标准形,只要直接计算状态反馈系统闭环特征多项式,这时,其系数为的函数,与给定极点的特征多项式系数相比较,便可确定。
能控的多输入-多输出系统,经如上类似分析可知,实现闭环极点任意配置的状态反馈阵K为维。
若受控对象不稳定,只要有能控性,完全可由状态反馈配置极点使系统稳定。
状态变量受控情况下,引入状态反馈表示增加一条反馈通路,它能改变反馈所包围环节的传递特性,即通过改变局部回路的极点来改变闭环极点配置。
不能控状态变量与控制量无关,即使引入状态反馈,对闭环极点位置也不会产生任何影响,这是因为传递函数只与系统能控、能观测部分有关的缘故。
若不能控状态变量是稳定的状态变量,那么系统还是能稳定的,否则,系统不稳定。
控制理论基础第二版部分习题答案

第二章2.1 求解下列微分方程2)dd2yy ddtt2+ddyy ddtt=ee4tt,初始条件yy(0)=2, yy(0)=0.解:首先对微分方程两边进行拉氏变换,得代数方程:ss2YY(ss)−ssyy(0)−yy(0)+ssyy(ss)−yy(0)=1ss−4代入初始条件yy(0)=2, yy(0)=0.ss2YY(ss)−ssyy(ss)=1ss−4+2ss+2YY(ss)=2ss+1ss(ss−4)(ss+1)YY(ss)=2ss+AA ss+BB(ss−4)+CC(ss+1)计算得到A=-0.25,B=0.05,C=0.2;YY(ss)=47ss+15(ss−4)+120(ss+1)拉氏反变换y(t)=1.75+0.05ee4tt+0.2ee−tt(t>0)3)dd2xx ddtt2+5ddxx ddtt+6xx=6,初始条件xx(0)=2,xx(0)=2.解:首先对微分方程两边进行拉氏变换,得代数方程:ss2XX(ss)−ssxx(0)−xx(0)+5ssxx(ss)−5xx(0)+6XX(ss)=6ssXX(ss)=2ss2+12ss+6ss(ss+2)(ss+3)=AA ss+BB ss+2+CC ss+3计算得到A=1,B=5,C=-4,拉氏反变换得到,x(t)=1+5ee−2tt−4ee−3tt(t>0)2.2.一阶微分方程组为4'103'20x yx y y+=−++=,已知(0)0,'(0)0,(0)5x x y===,求解(),()x t y t。
解:首先对微分方程两边进行拉氏变换,得代数方程组:4ssXX(ss)−4xx(0)+YY(ss)=10/s−XX(ss)+(3ss+2)YY(ss)=3yy(0)XX (ss )=15ss +20ss (2ss +1)(6ss +1)YY (ss )=60ss 2+10ss (2ss +1)(6ss +1)得到:XX (ss )=20ss +6.25ss +12�+−26.25ss +16�YY (ss )=10ss +12.5ss +12�+−17.5ss +16�x(t)=20+6.25ee −12�tt-26.25ee −16�tt (t>0)y(t)=10+12.5ee −12�tt-17.5ee −16�tt(t>0)2.3解:根据基尔霍夫定律写出电路方程: 如ii 1为分电流VV =(ii 1+ii 2)RR 1+LL 1dd (ii 1+ii 2)ddtt +ii 1RR 2+1CC 1�ii 1ddtt VV =(ii 1+ii 2)RR 1+LL 1dd (ii 1+ii 2)ddtt +LL 2ddii 2ddtt +1CC 2�ii 2ddttORVV =(ii 1+ii 2)RR 1+LL 1dd (ii 1+ii 2)ddtt +ii 1RR 2+1CC 1�ii 1ddttii 1RR 2+1CC 1�ii 1ddtt =LL 2ddii 2ddtt +1CC 2�ii 2ddtt如ii 1为总电流:VV =ii 1RR 1+LL 1ddii 1ddtt +LL 2ddii 2ddtt +1CC 2�ii 2ddttLL 2ddii 2ddtt+1CC 2∫ii 2ddtt )RR 2+1CC 1∫(ii 1−ii 2)ddtt2.5将滑阀节流扣流量方程Q c x ω=Q 是阀芯位移x v 和节流口压p 的函数,c 、w 分别为流量系数和滑阀面梯度,ρ为油的密度。
自动控制理论第五章习题汇总

自动控制理论第五章习题汇总填空题1、系统的频率响应与正弦输入信号之间的关系称为频率响应2、在正弦输入信号的作用下,系统输入的稳态分量称为频率响应简答题:5-2、什么是最小相位系统及非最小相位系统?最小相位系统的主要特点是什么?答在s平面上,开环零、极点均为负实部的系统称为最小相位系统;反之,开环零点或极点中具有正实部的系统称为非最小相位系统。
最小相位系统的主要特点是:相位滞后最小,并且幅频特性与相频特性有惟一的确定关系。
如果知道最小相位系统的幅频特性,可惟一地确定系统的开环传递函数。
5-3、什么是系统的频率响应?什么是幅频特性?什么是相频特性?什么是频率特性?答对于稳定的线性系统,当输入信号为正弦信号时,系统的稳态输出仍为同频率的正弦信号,只是幅值和相位发生了改变,如图5-3所示,称这种过程为系统的频率响应。
图5-3称为系统的幅频特性,它是频率的函数;称为系统的相频特性,它是频率的函数:称为系统的频率特性。
稳定系统的频率特性可通过实验的方法确定。
计算题5-1、设某控制系统的开环传递函数为)()(s H s G =)10016()12.0(752+++s s s s 试绘制该系统的Bode 图,并确定剪切频率c ω的值。
解:Bode 图如下所示剪切频率为s rad c /75.0=ω。
5-2、某系统的结构图和Nyquist 图如图(a)和(b)所示,图中2)1(1)(+=s s s G 23)1()(+=s s s H 试判断闭环系统稳定性,并决定闭环特征方程正实部根的个数。
解:由系统方框图求得内环传递函数为:ss s s s s s H s G s G +++++=+23452474)1()()(1)( 内环的特征方程:04742345=++++s s s s s由Routh 稳定判据:1:0310:16:44:171:01234s s s s s由此可知,本系统开环传函在S 平面的右半部无开环极点,即P=0。
《现代控制理论基础》第2版 现代控制理论基础_上海交通大学_施颂椒等_PPT_第5章

① 定义 有理函数 g(s) 当s 时,
② g(假)设
常n数(s〔) d(s) g(s)〕, 就称为正那么有理函数。
③ g假( 设)那么有理函数。
④
假g(设) 〔 n(s)d(s)
g(〕s) , 就是 非正那么有理函数。
有理函数阵 G (s) 假设G() 0 ,那G (s么) 是严格正那么有理函数阵〔其每个元均为
G (s) C (sI A )1BD
那么(称A,B,C,D) 是G (s) 的一个实现。
•实现研究的问题
⑴ G (s)可实现为 (A,B,C,D) 的条件问题 ⑵ G (s) 实现的方法
〔5-1〕
•最小实现
如果 (A,B,C,D)是G (s) 的一个实现,那么其所有等价系统也都是其 实现 。 G (s) 可有不同维数的实现,其中维数最小的实现称为最小实 现。它描述了系统的既能控又能观的局部。通常要求的实现 为最小实现。
s 1 s4 s(s1) (s1)s(3) (s1)s(3)
s
1
3
s(s 1 )s( 2 ) (s 1 )s( 2 )s( 3 ) s(s 1 )s( 2 )s( 3 )
G (s) 的特征多项式为:s(s1)s(2)s(3),deG g(s)4。
⑵ G (s) 可实现为 (A,B,C,D) 的条件
③ 非正那么传递函数〔G() 〕,也存在实现,其实现具有
④ 如下形式
Ex(t)A(xt)Bu(t) y(t)Cx(t)Du(t)
〔5-9〕
式中 E为奇异阵。这种形式的系统称为广义系统,或奇异 系统。(本书不予讨论,在专门文献中研究)
5.2.2 最小实现的性质
如果将例〔5-5〕的传递函数阵写成
G ( s ) G 1 ( s )G 2 ( s )
现代控制理论课后习题答案

前言本书是为了与张嗣瀛院士等编写的教材《现代控制理论》相配套而编写的习题解答。
本书对该教材中的习题给予了详细解答,可帮助同学学习和理解教材的内容。
由于习题数量较多,难易程度不同,虽然主要对象是研究型大学自动化专业本科学生,但同时也可以作使用其它教材的专科、本科、以及研究生的学习参考书。
书中第5、6、8章习题由高立群教授组织编选和解答;第4、7 章由井元伟教授组织编选和解答,第1、2章由郑艳副教授组织编选和解答。
由于时间比较仓促,可能存在错误,请读者批评、指正。
另外有些题目解法和答案并不唯一,这里一般只给出一种解法和答案。
编者 2005年5月第2章 “控制系统的状态空间描述”习题解答2.1有电路如图P2.1所示,设输入为1u ,输出为2u ,试自选状态变量并列写出其状态空间表达式。
图P2.1解 此题可采样机理分析法,首先根据电路定律列写微分方程,再选择状态变量,求得相应的系统状态空间表达式。
也可以先由电路图求得系统传递函数,再由传递函数求得系统状态空间表达式。
这里采样机理分析法。
设1C 两端电压为1c u ,2C 两端的电压为2c u ,则212221c c c du u C R u u dt++= (1) 112121c c c du u duC C dt R dt+= (2) 选择状态变量为11c x u =,22c x u =,由式(1)和(2)得:1121121121212111c c c du R R C u u u dt R R C R C R C +=--+ 2121222222111c c c du u u u dt R C R C R C =--+ 状态空间表达式为:12111211212121212122222221111111R R C x x x u R R C R C R C x x x u R C R C R C y u u x +⎧=--+⎪⎪⎪=--+⎨⎪⎪==-⎪⎩即: 12121121211112222222211111R R C R C R R C R C x x u x x R C R C R C +⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦[]11210x y u x ⎡⎤=-+⎢⎥⎣⎦2.2 建立图P22所示系统的状态空间表达式。
《现代控制理论》第3版课后习题答案
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc ---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
现代控制理论课后答案(俞立)第五章
《现代控制理论》第5章习题解答5.1 已知系统的状态空间模型为Cx y Bu Ax x =+=, ,画出加入状态反馈后的系统结构图,写出其状态空间表达式。
答:具有状态反馈的闭环系统状态空间模型为:u Kx =−+v ()xA BK x Bv y Cx=−+=相应的闭环系统结构图为闭环系统结构图5.2画出状态反馈和输出反馈的结构图,并写出状态反馈和输出反馈的闭环系统状态空间模型。
答:具有状态反馈的闭环系统状态空间模型为u Kx =−+v ()xA BK x Bv y Cx=−+=相应的反馈控制系统结构图为具有输出反馈的闭环系统状态空间模型为u Fy =−+v ()x A BFC x Bv y Cx=−+=相应的反馈控制系统结构图为后案网 ww w.kh d5.3 状态反馈对系统的能控性和能观性有什么影响?输出反馈对系统能控性和能观性的影响如何?答:状态反馈不改变系统的能控性,但不一定能保持系统的能观性。
输出反馈不改变系统的能控性和能观性。
5.4 通过检验能控性矩阵是否满秩的方法证明定理5.1.1。
答:加入状态反馈后得到闭环系统K S ,其状态空间模型为()x A BK x Bv y Cx=−+=开环系统的能控性矩阵为0S 1[,][]n c A B BAB A B −Γ="闭环系统K S 的能控性矩阵为 1[(),][()()]n cK A BK B B A BK B A BK B −Γ−=−−"由于222()()()()(A BK B AB BKBA BKB A ABK BKA BKBK B)A B AB KB B KAB KBKB −=−−=−−+=−−−#以此类推,总可以写成的线性组合。
因此,存在一个适当非奇异的矩阵U ,使得()m A BK B −1,,,m m A B A B AB B −[(),][,]cK c A BK B A B U Γ−=Γ由此可得:若rank([,])c A B n Γ=,即有个线性无关的列向量,则n [(),]cK A BK B Γ−也有个线性无关的列向量,故n rank([(),])cK A BK B n Γ−=5.5 状态反馈和输出反馈各有什么优缺点。
自动控制理论第五章习题

第五章习题E5.2 The engine,body,and tires of a racing vehicle affect the acceleration and speed attainable.The speed control of the car is represented by the model shown in FigureE5.2.(a)Calculate the steady-state error of the car to a step command in speed.(b)Calculate overshoot of the speed to a step command.E5.3 For years,Amtrak has struggled to attract passengers on its routes in the Midwest,using technology developed decades ago.During the same time,foreign railroads were developing new passenger rail systems that could profitably compete with air travel.Two of these systems,the French TGV and the Japanese Shinkansen,reach speed of 160 mph.The Transrapid-06,a U.S. Experimental magnetic levitation train,is shown in Figure E5.3(a).The use of magnetic levitation and electromagnetic propusion to provide contactless vehicle movement makes the Transrapid-06 technolog radically different from the existing Metroliner.The underside of the TR-06 carriage(where the wheel trucks would be on a conventional car)wraps around a guideway.Magnets on the bottom of the guideway attract electromagnets on the "wraparound,"pulling it up toward the guideway.This suspends the vehicles about one centimeter above the guideway.The levitation control is represented by Figure E5.3(b).(a)usingTable 5.6 for a step input,select K so that the system provide anoptimum ITAE response.(b)Using Figure5.3 determine the expected overshoot to a step input of I(s).E5.5 A low-inertia plotter is shown in Figure E5.5(a).This system may be represented by block diagram shown in Figure E5.5(b).(a)Calculate the steady error for a ramp input.(b)Select a value of K that will result in zero overshoot to a step input.Provide the most rapid response that is attainable.Plot the poles and zeros of the system and discuss the dominance of the complex poles.What overshoot for a step input do you expect?E5.6 Effective control of insulin injection can result in better lives for diabetic persons.Automatically controlled insulin jection by means of a pump and a sensor that measures blood sugar can be very effective.A pump and injection system has a feedback control as shown in Figure E5.6.Calculate the suitable gain K,so that the overshoot of the step response due to the drug injection is approximately 7%.R(s) is the desired blood-sugar level and Y(s),is the actual blood-sugar level.Figure E5.6E5.8 A unity negative feedback control system has the plant transfer function(a)Determine the percent overshoot and setting time (using a 2% setting criterion) due to a unit step input.(b)For what range of K is the setting time less than 1 second?E5.10 A system with unity feedback is shown in Figure E5.10.Determine the steady-state error for a step and ramp input whenE5.11 We are all familiar with the Ferris wheel featured at state fairs and carnivals,George Ferris was born in Galesbueg,Illinois,in 1859;he later moved to Nevada and then graduated from Rensselaer Polytechnic Institute in 1881. By 1891,Ferris had considerable experience with iron,steel,and bridge construction.He conceived and constructed his famous wheel for the 1893 Columbian Exposition in Chicago. To avoid upsetting passegers,set a requirement that the steady-state speed must be controlled to within 5% of the desired speed for thesystem shown in Figure E5.11.(a)Determine the required gain K to achieve the steady-state requirement.(b)For the gain of the part(a),determine and plot the error e(t) for a distrbance D(s)=1/s.Does the speed change more than 5%?(set R(s)=0 for ease of computation.)E5.13 A feedback system is shown in Figure E5.13.(a)Determine the steady-state error for a unit step when K=0.4 and G p(s)=1.(b)Select an appropriate value for G p(s) so that the steady-state error is equal to zero for the unit step input.E5.16 A closed-loop control system transfer function T(s) has two dominant complex conjugate poles.Sketch the region in the left-hand s-plane where the complex poles should be located to meet the given specifications.E5.17 A system is shown in Figure E5.17(a).The response to a unit step,when K=1,is shown in Figure E5.17(b).Determine the value of K so that the steady-state error is equal to zero.P5.1 A important problem for television systems is the jumping or wobbling of the picture due to the movement of thecamera.This effect occurs when the camera is mounted in a moving truck or airplane. The Dynalens system has been designed to reduce the effect of rapid scanning motion;see Figure P5.1. A maximum scanning motion of 25% is expected.Let K g=K f=1 and assume that τg is negligible.(a)Determine the error of the system E(s).(b)Determine the necessary loop gain,K a K m Kt,when a 10/s steady-state error is allowable.(c)The motor time constant is 0.40s.Determine the necessary loop gain so that the setting time(to within 2% of the final value of v b) is less than or equal to 0.03s.P5.2 A specific closed-loop control system is to be designedfor an underramped response to a step input.The specification for the system are as follows:10%<percent overshoot<20%, Setting time<0.6s.(a)Identify the desired area for the dominant roots of the sytem(b)Determine the smallest value of a third root,r3 ,if the complex conjugate roots are to represent the dominant response.(c)The closed-loop system transfer function T(s) is third-order,and the feedback has a unity gain, Determine the forword transfer function,G(s)=Y(s)/E(s).when the setting time to within 2% of the final value is 0.6s and the percent overshoot is 20%.P5.5 A space telescope is to be launched to carry out astronamical experiments.The pointing control system is desried to achieve 0.01 minute of arc and track solar objects with apparent motion up to 0.21 minute per second. Tne system is illustrated in Figure P5.5(a).The control system is shown in Figure P5.5(b). Assume that τ1 =1second and τ2 =0(an approximation).(a)Determine the gain K=K1K2 required so that the response to a step command is as rapid as reasonable with an overshoot of less than 5%(b)Determine the steady-state error of the system for a step and ramp input(c)Determine the value of K1K2 for ITAE optimal system for (1) a step input and (2)a ramp input.P5.6 A robot is programmed to have a tool or welding torch follow a prescribed path. Consider a robot tool that is to follow a sawtooth path.as shown in Figure P5.6(a).The transferfunction of the plant isThe transfer function of the plant is for the closed-loop system shown in Figure P5.6(b).Calculate the steady-state error.P5.7 Astronaut Bruce McCandless II took the first unthethered walk in space on February 7,1984,using the gas-jet propulsion device illustrated in Figure P5.7(a).The controller can be represented by a gain K2 , shown in Figure P5.7(b).The inertia of the equipment and man with his arms at his sides is 25 Kg-m2.FIGURE P5.7 (a)Astronaut Bruce McCandless II is shown a few meters away from the earth-orbiting space shuttle, Challenger. He used a nitrogenpropelled handcontrolled device called the manned maneuvering unit.(Courtesy of National Aeronautic and space Administration) (b)Block diagram of controller(a)Determine the necessary gain K3to maintain a steady-state error equal to 1 cm when the input is a ramp r(t)=t(meters). (b)With this gain K3,determine the necessary gain K1K2 in order to restrict the percent overshoot to 10%.(c)Determine annalytically the gain K1K2 in order to minimize the ISE performance index for a step input.P5.16 Electronic pacemakers for human hearts regulate the speed of the heart pump.A proposed closed-loop system that includes a pacemaker and measurement of the heart rate is shown in Figure P5.16.The transfer function of the heart pump and the pacemake is found to be:Design the amplifier gain to yield a system with a setting time to a step disturbance of less than 1 second.The overshoot to a step in desired heart rate should be less than 10%.FIGURE P5.16 Heart pacemaker(a)Find a suitable range of K(b)If the nominal value of K is K=10,find the sensitivity of the system to a small change in K.(c)Evaluate the sensitivity of part(b) at DC(set s=0).(d)Evaluate the magnitude of the sensitivity at normal heart rate of 60 beats/minute.P5.19 A system is shown in Figure P5.19.(a)Determine the steady-state error for a unit step input in terms of K and K1,where E(s)=R(s)-Y(S).(b)Select K1 so that the steady-state error is zero.AP5.1 A closed-loop transfer function is(a)Determine the steady-state error for a unit step input R(s)=1/s(b)Assume that the complex poles dominate,and determine the overshoot and setting time to within 2% of the final value(c)Plot the actual system response,and compare it with the estimate of part(b).AP5.3 A closed-loop system is shown in Figure AP5.3.Plot the response to a unit step input for system with τp=0, 0.5, 2,and 5. Record the percent overshoot,rise time,and settling time(with a 2% criterion) as τp varies.Describe the effect of varying τp .Compare the location of the closed-loop roots.AP5.4 The speed control of a high-speed train is represented by the system shown in Figure AP5.4.Determine the equation for steady-state error for K for a unit step input r(t).Consider the three values for equal to 1, 10, 100.(a)Determine the steady-state error.(b)Determine and plot the response y(t) for (i) a unit step input r(t) and (ii) a unit step disturbance input d(t).(c)Creat a table showing overshoot,setting time (with a 2% criertion),e ss for r(t),and |y/d|max for the three values of K.Select the best comprise value.AP5.6 The block diagram model of an armature-current-controlled DC motor is shown in FigureAP5.6.(a)Determine the steady-state error for a step input r(t)=t,t>=0, in terms of K,K b,and K m .(b)Let K m=10 and K b=0.05,and select K so that steady-state error is equal to 1.(c)Plot the response to a unit step and a unit ramp input for 20 seconds,Are the responses acceptable?。
现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有相应的模拟结构图如下: 1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图 (2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P(或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P )当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为(1)⎥⎦⎤⎢⎣⎡=11b解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
现代控制理论第五章
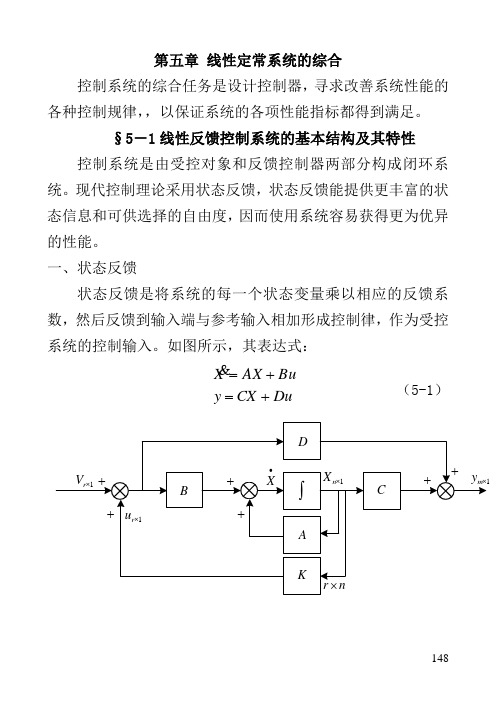
148第五章 线性定常系统的综合控制系统的综合任务是设计控制器,寻求改善系统性能的各种控制规律,,以保证系统的各项性能指标都得到满足。
§5-1线性反馈控制系统的基本结构及其特性 控制系统是由受控对象和反馈控制器两部分构成闭环系统。
现代控制理论采用状态反馈,状态反馈能提供更丰富的状态信息和可供选择的自由度,因而使用系统容易获得更为优异的性能。
一、状态反馈状态反馈是将系统的每一个状态变量乘以相应的反馈系数,然后反馈到输入端与参考输入相加形成控制律,作为受控系统的控制输入。
如图所示,其表达式:Du CX y Bu AX X+=+= (5-1)149多输入多输出系统式中:nR X ∈,TR u ∈,mRy ∈,n n A ⨯,r n B ⨯,n m C ⨯,r m D ⨯若0=D ,则受控系统X AX Buy C X ∙⎧⎪=+⎨=⎪⎩简记为:)=(C B A ,,0∑状态反馈控制规律:u kX v =+ (5-3) 其中:v -1⨯r 维参考输入;k-n r ⨯维状态反馈系数或状态反馈增益阵。
把式(5-3)代入式(5-1)得到状态反馈闭环系统表达式()()()()X AX Bu AX B kX v AX BkX Bv A Bk X Bv y C X D u C X D kX v C X D kX D v C D k X D v∙=+=++=++=++=+=++=++=++ 若=D ,()X A Bk X Bv y CX ∙⎧⎪=++⎨=⎪⎩简记为:])[(C B Bk A k ,,+=∑闭环系统的传递函数矩阵BBk A sI C s W k 1)]([)(-+-=状态反馈阵k 的引入,并不增加系统的维数,通过k 的选择自由地改变闭环系统的特征值,从而改变系统获得所要求的性能。
二、输出反馈150输出反馈是采用输出矢量y 构成线性反馈律,如图所示,受控系统)=(D C B A ,,,0∑为:X AX Bu y C X D u∙=+=+ (5-7)=D 时为X AX Bu y C X∙=+=输出线性反馈控制律为: v Hy u += (5-9)式中:H —m r ⨯维输出反馈增益阵,对单输出系统H 为1⨯r 维列矢量。
现代控制理论第版课后习题答案

现代控制理论参考答案第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式; 解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示;以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程; 解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵;解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图; 解:令..3.21y x y x y x ===,,,则有 相应的模拟结构图如下: 1-6 2已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++=1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图(2) 求系统的传递函数 解:2⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量3⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P 当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P 1-9将下列状态空间表达式化成约旦标准型并联分解2⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P 当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1s 和W 2s试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:1串联联结 2并联联结1-11 第3版教材已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解:1-11第2版教材 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b 即控制列阵为 1⎥⎦⎤⎢⎣⎡=11b 解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e ;2 A=1141⎛⎫⎪⎝⎭解:第一种方法: 令0I A λ-=则11041λλ--=-- ,即()2140λ--=;求解得到13λ=,21λ=- 当13λ=时,特征矢量11121p p p ⎡⎤=⎢⎥⎣⎦由 111Ap p λ=,得11112121311341p p p p ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即112111112121343p p p p p p +=⎧⎨+=⎩,可令112p ⎡⎤=⎢⎥⎣⎦当21λ=-时,特征矢量12222p p p ⎡⎤=⎢⎥⎣⎦由222Ap p λ=,得121222221141p p p p -⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦即1222121222224p p p p p p +=-⎧⎨+=-⎩ ,可令212p ⎡⎤=⎢⎥-⎣⎦则1122T ⎡⎤=⎢⎥-⎣⎦,111241124T -⎡⎤⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦第二种方法,即拉氏反变换法:第三种方法,即凯莱—哈密顿定理 由第一种方法可知13λ=,21λ=-2-5 下列矩阵是否满足状态转移矩阵的条件,如果满足,试求与之对应的A 阵;3()22222222t tt t ttt t e e e e t e e e e --------⎡⎤--Φ=⎢⎥--⎣⎦ 4()()()()3333112412t t t t t tt t e e e e t e e e e ----⎡⎤+-+⎢⎥Φ=⎢⎥⎢⎥-++⎢⎥⎣⎦解:3因为 ()10001I ⎡⎤Φ==⎢⎥⎣⎦,所以该矩阵满足状态转移矩阵的条件 4因为()10001I ⎡⎤Φ==⎢⎥⎣⎦,所以该矩阵满足状态转移矩阵的条件2-6 求下列状态空间表达式的解:初始状态()101x ⎡⎤=⎢⎥⎣⎦,输入()u t 时单位阶跃函数;解: 0100A ⎡⎤=⎢⎥⎣⎦ 因为 01B ⎡⎤=⎢⎥⎣⎦,()()u t I t =2-9 有系统如图所示,试求离散化的状态空间表达式;设采样周期分别为T=和1s,而1u 和2u 为分段常数; 图 系统结构图 解:将此图化成模拟结构图 列出状态方程则离散时间状态空间表达式为 由()At G T e =和()0TAt H T e dtB =⎰得:当T=1时 ()()()()11111001111k e e x k x k u k e ke ----⎡⎤-⎡⎤+=+⎢⎥⎢⎥--⎢⎥⎣⎦⎣⎦当T=时 ()()()()()0.10.10.10.11001110.90.1k e e x k x k u k e k e ----⎡⎤-⎡⎤⎢⎥+=+⎢⎥⎢⎥---⎣⎦⎣⎦第三章习题3-1判断下列系统的状态能控性和能观测性;系统中a,b,c,d 的取值对能控性和能观性是否有关,若有关,其取值条件如何 1系统如图所示: 解:由图可得: 状态空间表达式为:由于•2x 、•3x 、•4x 与u 无关,因而状态不能完全能控,为不能控系统;由于y 只与3x 有关,因而系统为不完全能观的,为不能观系统; 3系统如下式:解:如状态方程与输出方程所示,A 为约旦标准形;要使系统能控,控制矩阵b 中相对于约旦块的最后一行元素不能为0,故有0,0≠≠b a ;要使系统能观,则C 中对应于约旦块的第一列元素不全为0,故有0,0≠≠d c ; 3-2时不变系统试用两种方法判别其能控性和能观性; 解:方法一:方法二:将系统化为约旦标准形;⎥⎦⎤⎢⎣⎡=1-111T ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=21212121T 1- B T -1中有全为零的行,系统不可控;CT 中没有全为0的列,系统可观; 3-3确定使下列系统为状态完全能控和状态完全能观的待定常数i i βα和 解:构造能控阵:要使系统完全能控,则211αα≠+,即0121≠+-αα 构造能观阵:要使系统完全能观,则121αα-≠-,即0121≠+-αα 3-4设系统的传递函数是1当a 取何值时,系统将是不完全能控或不完全能观的 2当a 取上述值时,求使系统的完全能控的状态空间表达式; 3当a 取上述值时,求使系统的完全能观的状态空间表达式; 解:1 方法1 :)6)(3)(1()()()(++++==s s s as s u s y s W 系统能控且能观的条件为Ws 没有零极点对消;因此当a=1,或a=3或a=6时,系统为不能控或不能观; 方法2:系统能控且能观的条件为矩阵C 不存在全为0的列;因此当a=1,或a=3或a=6时,系统为不能控或不能观;2当a=1, a=3或a=6时,系统可化为能控标准I 型3根据对偶原理,当a=1, a=2或a=4时,系统的能观标准II 型为 3-6已知系统的微分方程为:u y y y y 66116...=+++试写出其对偶系统的状态空间表达式及其传递函数; 解:63611603210=====b a a a a ,,,,系统的状态空间表达式为 传递函数为其对偶系统的状态空间表达式为: 传递函数为61166)(23+--=s s s s W 3-9已知系统的传递函数为 试求其能控标准型和能观标准型;解:345213486)(222++++=++++=s s s s s s s s W系统的能控标准I 型为 能观标准II 型为3-10给定下列状态空间方程,试判别其是否变换为能控和能观标准型;解:[]100210311032010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=C b A ,, 3-11试将下列系统按能控性进行分解1[]111,100,340010121-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=C b A 解:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==9310004102b A Ab bM rankM=2<3,系统不是完全能控的; 构造奇异变换阵c R :⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==010*********R Ab R b R ,,,其中3R 是任意的,只要满足c R 满秩;即⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=031100010c R 得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-010*******c R 3-12 试将下列系统按能观性进行结构分解1 []111,100,340010121-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=C b A 解: 由已知得[]111,100,340010121-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=C b A 则有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=4742321112CA CA C Nrank N=2<3,该系统不能观构造非奇异变换矩阵10R -,有10111232001R --⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦ 则0311210001R --⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦3-13 试将下列系统按能控性和能观性进行结构分解1[]211,221,102322001=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=C b A 解:由已知得211121226202M A Ab Ab ⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥-⎣⎦rank M=3,则系统能控 rank N=3,则系统能观所以此系统为能控并且能观系统取211121226202c T ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,则1217344173215344c T -⎡⎤-⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦则002105014A ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,12100c B T b -⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦,[]271323c c cT == 3-14求下列传递函数阵的最小实现; 1 ()111111w s s ⎡⎤=⎢⎥+⎣⎦解: 01α=,01111B ⎡⎤=⎢⎥⎣⎦,1001c A -⎡⎤=⎢⎥-⎣⎦ 1001c B ⎡⎤=⎢⎥⎣⎦,1111c C ⎡⎤=⎢⎥⎣⎦,0000c D ⎡⎤=⎢⎥⎣⎦ 系统能控不能观取101101R -⎡⎤=⎢⎥⎣⎦,则01101R -⎡⎤=⎢⎥⎣⎦所以10010ˆ01A R AR --⎡⎤==⎢⎥-⎣⎦,1011ˆ01c B R B -⎡⎤==⎢⎥⎣⎦ 010ˆ10c C C R ⎡⎤==⎢⎥⎣⎦,00ˆ00D ⎡⎤=⎢⎥⎣⎦所以最小实现为ˆ1m A =,[]ˆ11m B =,1ˆ1m C ⎡⎤=⎢⎥⎣⎦,00ˆ00m D ⎡⎤=⎢⎥⎣⎦ 验证:()()1111ˆˆˆ111m mm C sI A B w s s -⎡⎤-==⎢⎥+⎣⎦3-15设1∑和2∑是两个能控且能观的系统1试分析由1∑和2∑所组成的串联系统的能控性和能观性,并写出其传递函数; 2试分析由1∑和2∑所组成的并联系统的能控性和能观性,并写出其传递函数; 解: 11∑和2∑串联当1∑的输出1y 是2∑的输入2u 时,331222x x x x =-++010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=--+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,[]001y x = 则rank M=2<3,所以系统不完全能控; 当2∑得输出2y 是1∑的输入1u 时011034100021x x u ⎡⎤⎡⎤⎢⎥⎢⎥=--+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,[]210y x = 因为 2001016124M bAbA b ⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥--⎣⎦rank M=3 则系统能控因为2210321654c N cA cA ⎡⎤⎡⎤⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦rank N=2<3 则系统不能观 21∑和2∑并联010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=--+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,[]211y x = 因为rank M=3,所以系统完全能控 因为rank N=3,所以系统完全能观现代控制理论第四章习题答案4-1判断下列二次型函数的符号性质:1222123122313()31122Q x x x x x x x x x x =---+-- 2222123122313()4262v x x x x x x x x x x =++--- 解:1由已知得110∆=-<,2112013-∆==>-,31111711302411112--∆=--=-<--- 因此()Q x 是负定的 2由已知得110∆=>,2113014-∆==>-,3111143160131--∆=--=-<--因此()Q x 不是正定的 4-2已知二阶系统的状态方程:试确定系统在平衡状态处大范围渐进稳定的条件;解:方法1:要使系统在平衡状态处大范围渐进稳定,则要求满足A 的特征值均具有负实部;即:有解,且解具有负实部; 即:1122112212210a a a a a a +<>且方法2:系统的原点平衡状态0e x =为大范围渐近稳定,等价于T A P PA Q +=-;取Q I =,令11121222PP P P P ⎡⎤=⎢⎥⎣⎦,则带入TA P PA Q +=-,得到 若 11211211222111221122122112222204()()0022a a a a a a a a a a a a a a +=+-≠,则此方程组有唯一解;即 其中11221221det A A a a a a ==- 要求P 正定,则要求 因此11220a a +<,且det 0A >4-3试用lyapunov 第二法确定下列系统原点的稳定性;11123x x -⎡⎤=⎢⎥-⎣⎦ 21111x x -⎡⎤=⎢⎥--⎣⎦解:1系统唯一的平衡状态是0e x =;选取Lyapunov 函数为2212()0V x x x =+>,则 ()V x •是负定的;x →∞,有()V x →∞;即系统在原点处大范围渐近稳定;2系统唯一的平衡状态是0e x =;选取Lyapunov 函数为2212()0V x x x =+>,则 ()V x •是负定的;x →∞,有()V x →∞;即系统在原点处大范围渐近稳定;4-6设非线性系统状态方程为: 试确定平衡状态的稳定性;解:若采用克拉索夫斯基法,则依题意有: 取P I =很明显,()Q x 的符号无法确定,故改用李雅普诺夫第二法;选取Lyapunov 函数为2212()0V x x x =+>,则()V x •是负定的;x →∞,有()V x →∞;即系统在原点处大范围渐近稳定;4-9设非线性方程:试用克拉索夫斯基法确定系统原点的稳定性; 解:1采用克拉索夫斯基法,依题意有:x →∞,有()V x →∞; 取P I =则2121013()132x Q x x ⎡⎤-+=⎢⎥-+⎣⎦,根据希尔维斯特判据,有: 2221121210310310132x x x -∆=∆==->-+,(),()Q x 的符号无法判断; 2李雅普诺夫方法:选取Lyapunov 函数为421233()042V x x x =+>,则 ()V x •是负定的;x →∞,有()V x →∞;即系统在原点处大范围渐近稳定;4-12试用变量梯度法构造下列系统的李雅普诺夫函数 解:假设()V x 的梯度为: 计算()V x 的导数为:选择参数,试选112212211,0a a a a ====,于是得:12x V x ⎛⎫∇= ⎪⎝⎭,显然满足旋度方程12122121,0V V x xx x x x ∂∇∂∇∂∂===∂∂∂∂即,表明上述选择的参数是允许的;则有:如果121211202x x x x -><或,则()V x •是负定的,因此,1212x x <是12x x 和的约束条件; 计算得到()V x 为:()V x 是正定的,因此在121211202x x x x -><即范围内,0e x =是渐进稳定的;现代控制理论第五章习题答案5-1已知系统状态方程为:试设计一状态反馈阵使闭环系统极点配置为-1,-2,-3; 解:依题意有:2011012112M bAbA b ⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥⎣⎦3rankM =,系统能控; 系统0(,,)A b C =∑的特征多项式为:则将系统写成能控标准I 型,则有010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦; 引入状态反馈后,系统的状态方程为:()x A bK x bu =++,其中3K ⨯为1矩阵,设[]012K k k k =,则系统(,,)K A bK C =∑的特征多项式为:根据给定的极点值,得到期望特征多项式为:比较*()()f f λλ与各对应项系数,可解得:012599k k k =-=-=-,则有:[]-5-9-9K =;5-3有系统:(1) 画出模拟结构图;(2) 若动态性能不满足要求,可否任意配置极点 (3) 若指定极点为-3,-3,求状态反馈阵; 解1系统模拟结构图如下:2系统采用状态反馈任意配置极点的充要条件是系统0(,,)A b C =∑完全能控; 对于系统0(,,)A b C =∑有: []0111M bAb ⎡⎤==⎢⎥-⎣⎦2rankM =,系统能控,故若系统动态性能不满足要求,可任意配置极点;3系统0(,,)A b C =∑的特征多项式为:则将系统写成能控标准I 型,则有010231x x u ⎡⎤⎡⎤=+⎢⎥⎢⎥--⎣⎦⎣⎦; 引入状态反馈后,系统的状态方程为:()x A bK x bu =++,设[]01K k k =,则系统(,,)KA bK C =∑的特征多项式为:根据给定的极点值,得到期望特征多项式为:比较*()()f f λλ与各对应项系数,可解得:[]017373k k K =-=-=--,; 5-4设系统传递函数为试问能否利用状态反馈将传递函数变成 若有可能,试求出状态反馈K ,并画出系统结构图;解:6522)3)(2)(1()2)(1()(232--+-+=+-++-=s s s s s s s s s s s W由于传递函数无零极点对消,因此系统为能控且能观; 能控标准I 型为 令[] 210k k k K =为状态反馈阵,则闭环系统的特征多项式为由于状态反馈不改变系统的零点,根据题意,配置极点应为-2,-2,-3,得期望特征多项式为比较 )(λf 与 )(*λf 的对应项系数,可得 即[]52118---=K 系统结构图如下:5-5使判断下列系统通过状态反馈能否镇定;11222 A 011,01011b ---⎡⎤⎡⎤⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦解:系统的能控阵为:2240010115M bAbA b -⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥-⎣⎦3rankM =,系统能控; 由定理 5.2.1可知,采用状态反馈对系统0(,,)A b C =∑任意配置极点的充要条件是(,,)A b C =∑完全能控;又由于3rankM =,系统0(,,)A b C =∑能控,可以采用状态反馈将系统的极点配置在根平面的左侧,使闭环系统镇定; 5-7设计一个前馈补偿器,使系统 解耦,且解耦后的极点为1,1,2,2----; 解:0()()() d W s W s W s = 5-10已知系统:试设计一个状态观测器,使观测器的极点为-r,-2rr>0;解:因为1001c N cA ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦满秩,系统能观,可构造观测器; 系统特征多项式为[]21det det 0I A λλλλ-⎡⎤-==⎢⎥⎣⎦,所以有10010,0,10a a L ⎡⎤===⎢⎥⎣⎦ 于是11001100x T ATx T bu x u --⎡⎤⎡⎤=+=+⎢⎥⎢⎥⎣⎦⎣⎦ 引入反馈阵12g G g ⎡⎤=⎢⎥⎣⎦,使得观测器特征多项式:根据期望极点得期望特征式:比较()f λ与()*f λ各项系数得:即223r G r ⎡⎤=⎢⎥⎣⎦,反变换到x 状态下2201321023r r G TG r r ⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 观测器方程为:。
现代控制理论第五章答案

满秩,状态反馈可实现极点的任意配置。
(3)若指定极点为-3,-3,求状态反馈矩阵。
设状态反馈矩阵为
Kk1 k2
加入状态反馈矩阵后的系统矩阵为
A b k 0 2 1 1 1 0 k 1 k2 k 1 2 1 1 k2
比较 f () 和 f * ( ) 求出反馈矩阵
2 k3 7
5
k2
16
6
k1
12
所求的状态反馈矩阵为
k3 5
k
2
21
k 1 18
K k 1k 2k 3 1 2 8 5 1
闭环系统的模拟结构图如下:
反馈矩阵K
输出矩阵C
【习题5-5】试判断下列系统通过状态反馈能否镇定
0
0
0
5
1
0 0 0 0 5
4 5 b0 7 0
【解】系统通过状态反馈能否镇定的充要条件是:不能控 子系统是渐近稳定的。
该状态空间表达式是约旦标准型,利用约旦标准型能控 性判据可知下列状态是不能控的:
第五章主要内容:
§5—1 线性反馈控制系统的基本结构及其特性 主要知识点:
1、状态反馈、输出反馈的基本概念; 2、三种反馈控制系统的基本结构和特点; 3、闭环系统的能控性和能观性。
§ 5—2 极点配置问题
主要知识点: 1、极点配置的基本概念; 2、极点任意配置的条件; 3、极点配置的设计方法。
§5—3 系统镇定问题 主要知识点:
a1 a2 1 990 1001011 11 1
10 0 0 0 10 0
0 10 10
1 0 0
Tc11 0
1
0
0 1 1
自动控制理论课后习题详细解答答案(夏德钤翁贻方版)第五章

第五章5-1 已知单位反馈系统的开环传递函数,试绘制其开环频率特性的极坐标图(1)解:幅频特性:相频特性:列表取点并计算。
0.5 1.0 1.5 2.0 5.010.01.790.7070.370.2240.0390.0095-116.6-135-146.3-153.4-168.7-174.2系统的极坐标图如下:(2)解:幅频特性:相频特性:列表取点并计算。
00.20.50.8 1.0 2.0 5.010.910.630.4140.3170.1720.01950-15.6-71.6-96.7-108.4-139.4-162.96系统的极坐标图如下:(3)解:幅频特性:相频特性:列表取点并计算。
0.20.30.51254.55 2.74 1.270.3170.0540.0039-105.6-137.6-161-198.4-229.4-253系统的极坐标图如下:(4)解:幅频特性:相频特性:列表取点并计算。
0.20.250.30.50.60.8122.7513.87.86 2.520.530.650.317-195.6-220.6-227.6-251.6-261.6-276.7-288.4系统的极坐标图如下:5-2 试绘制上题中各系统的开环对数频率特性(伯德图)。
(1)解:系统为Ⅰ型,伯德图起始斜率为-20dB/dec,在处与=20=0相交。
环节的交接频率,斜率下降20dB/dec,变为-40dB/de c。
系统的伯德图如图所示:(2)解:伯德图起始为0dB线,的交接频率,斜率下降20dB/dec,变为-20dB/de c。
的交接频率,斜率下降20dB/dec,变为-40dB/de c。
系统的伯德图如图所示。
(3)解:系统为Ⅰ型,伯德图起始斜率为-20dB/dec,其延长线在=1处与=20=0相交。
的交接频率,斜率下降20dB/dec,变为-40dB/de c。
的交接频率,斜率下降20dB/dec,变为-60dB/de c。
现代控制理论习题解答(第五章)

第五章 状态反馈和状态观测器3-5-1 已知系统结构图如图题3-5-1图所示。
(1)写出系统状态空间表达式;(2)试设计一个状态反馈矩阵,将闭环极点特征值配置在j 53±-上。
)(t y题3-5-1图【解】:方法一:根据系统结构直接设状态变量如题3-5-1图所示,写状态空间表达式:[]x y u x x 10112101=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--= 23111=⎥⎦⎤⎢⎣⎡--=c c U rank U系统能控,可以设计状态反馈阵。
设状态反馈阵为][21k k K =状态反馈控制规律为:Kx r u -= 求希望特征多项式:34625)3()(*22++=++=s s s s f求加入反馈后的系统特征多项式:)22()3()(1212k s k k s bK A sI s f ++-++=+-=依据极点配置的定义求反馈矩阵:]1316[131634)22(6)3(21112=⎩⎨⎧==⇒⎩⎨⎧=+=+-K k k k k k 方法二:[][][]1316)346(311110)(*10211=++⎥⎦⎤⎢⎣⎡--==--I A A A f U K c方法三:(若不考虑原受控对象的结构,仅从配置极点位置的角度出发)求系统传递函数写出能控标准型:2321)111()()(2++-=+-+=s s ss s s U s Y []xy u x x 10103210-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--= 求系统希望特征多项式:34625)3()(*22++=++=s s s s f求状态反馈矩阵K ~:[][][]33236234~21=--==k k K [][][][]5.05.031111010111=⎥⎦⎤⎢⎣⎡--==--Ab bP⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=105.05.011A P P P []1316~==P K K3-5-2的极点在-2,j ±-1。
【解】:依据系统传递函数写出能控标准型ss s s s s s U s Y 2310)2)(1(10)()(23++=++= []x y u x x 0010100320100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=求系统希望特征多项式:464]1)1)[(2()(*232+++=+++=s s s s s s f求状态反馈矩阵:[][][]144342604321=---==k k k K 。
大连理工大学 现代控制理论 王金城 第四、五章 答案

第四章习题参考答案4-1(1)211P 130101-⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,,123212061506132013-∆=>∆==-=>∆=--=>-∴V(x)为正定的(2)841P 421111-⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦,,12380020∆=>∆=∆-<∴V(x)为不定的4-2 ∵12x x 0==,∴e x 是系统的唯一平衡状态()3112211V x 4x x 2x x 42=⋅⋅+⋅⋅⋅ 31122x x x x =⋅+⋅ 22x =- 半负定 ∴系统在原点处的平衡状态是稳定的 ∴()421211V x x x 42=+可成为系统的李氏函数。
4-3(1)1122xx 21xx 04--⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ ,1212xx 0x 0x 0==⇒== ∴e x 是系统的平衡状态 设李氏函数为()T V x x Px =,TA P PA I +=-1112111212221222P P P P 202110P P P P 140401----⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ 得11424P 1132496⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦,()2121113100449624∆=>∆=⋅-> ∴P 是正定的,系统在原点处的平衡状态是渐进稳定的。
李氏函数为()T221253V x x Px x x 2432==+用李氏第一方法校核,21221I A 67303004λλλλλλλ+-==++⇒=-+<=-+ ∴系统在原点处的平衡状态是渐进稳定的(2)112233x200x x 010x x 101x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦设李氏函数为()T V x x Px =,T A P PA I +=-111213111213122223122223132333132333201P P P P P P 200100010P P P P P P 010010001P P P P P P 101001---⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⇒-+-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦∴110361P 00211062⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,,1235110003672∆=>∆=>∆=>∴P 阵是正定阵,系统在原点处的平衡状态是渐进稳定的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制理论基础第5章习题解答
5-1 设单位反馈系统的开环传递函数为
对系统进行串联校正,满足开环增益 及 解:
① 首先确定开环增益K,00()12
lim v s K SG S k
→===
② 未校正系统开环传函为:012()(1)
G s s s =
+
-100-50
50
100
M a g n i t u d e (d B )10
-2
10
-1
10
10
1
10
2
-180
-135
-90
P h a s e (d e g )
Bode Diagram
Gm = 70.5 dB (at 200 rad/sec) , P m = 16.5 deg (at 3.39 rad/sec)
Frequency (rad/sec)
③ 绘制未校正系统的开环对数频率特性,得到幅穿频率 3.4
c ω=,
对应相位角'0
()164,16
c G j ωγ∠=-∴=
,采用超前校正装置,最大相角
0(180())4016630
m
c G j ϕγωγ=-+∠+=-+=
④ 1
1sin
,3
1
m
αϕαα--=∴=+
0()(1)
K G s s s =
+40γ=︒
1
12K s -=
⑤ 在已绘图上找出10lg 10lg 3 4.77
α-=-=-的频率 4.4
m
ω=弧度/秒
令c m
ωω=
⑥ 1
1
0.128/,0.385/m
m
T s T s
T
ω
αααω=
⇒=
=∴=
校正装置的传函为:110.385()110.128T s s G s T s
s
α++=
=
++
校正后的开环传函为:012(10.39)()()()(1)(10.13)
c s G s G s G s s s s +==++
校正后1801374340
γ
=-=>
,满足指标要求。
-100-50
50
100
M a g n i t u d e (d B )10
-2
10
-1
10
10
1
10
2
10
3
-180
-135
-90
P h a s e (d e g )
Bode Diagram
Gm = 99.2 dB (at 1.82e+003 rad/sec) , P m = 42.4 deg (at 4.53 rad/sec)
Frequency (rad/sec)
5-2 设单位反馈系统的开环传递函数为
要求 设计串联迟后校正装置。
0()(1)(0.251)
K
G s s s s =
++141,5, 1.02/b K s rad s γω-=︒≥=
解:
由题意,取5,v K
K ==待校正系统的传函为:05
()(1)(0.251)
G s s s s =
++
① 绘制未校正系统的开环对数频率特性,得出:
-100-50
50
100
M a g n i t u d e (d B )10
-2
10
-1
10
10
1
10
2
-270
-225-180-135-90P h a s e (d e g )
Bode Diagram
Gm = 0.0388 dB (at 2 rad/sec) , P m = 0.102 deg (at 2 rad/sec)
Frequency (rad/sec)
''0'02/,180()0
c
c ra
d s G ω
γω==-∠=
,采用滞后校正装置;
② 选取''
()9,c
ϕω=-
而要求''
'
''
''
''
41,()()50c c γγωγϕω=∴=-=
选取''0.6/,c
rad s ω
=于是可测得'
''
()15.8c L dB
ω=
③ 由'
''
20lg (),0.1622
c
b L b ω
=-⇒=,令
''
10.1102.754,16.67c T bT bT
ω=⇒=⇒=
④ 串联滞后校正装置的传函为:1116.67()11102.754bT s s G s T s
s
++==
++
⑤ 校
正
后
系
统
的开
环
传
函
为:05(16.671)
()()()(1)(0.251)(102.7541)
c s G s G s G s s s s s +==+++
校正后,1801364441
γ
=-=>
,满足性能指标要求。
-150-100-50050
100M a g n i t u d e (d B )10
-4
10
-3
10
-2
10
-1
10
10
1
10
2
-270
-225-180-135-90P h a s e (d e g )
Bode Diagram
Gm = 15.2 dB (at 1.94 rad/sec) , P m = 42.4 deg (at 0.666 rad/sec)
Frequency (rad/sec)
5-3 请分别写出超前校正网络和滞后校正网络的传递函数,画出的它们的Bode 图,写出最大超前相位角和滞后相位角的关系式。
解:
超前校正网络:1(),11T s G s T s
αα+=
>+
ω
φ
ω
L
45
20dB/dec 90
1/αT
1/T
1arcsin
1
m
αϕα-=+
滞后校正网络: 1(),011bT s G s b T s
+=
<<+
φ
ωL
45
20dB/dec
90
1/αT
1/T
ω
1arcsin
1m b b
ϕ-=+
5-4 写出PID 模型,给出四种改进PID 的方法,并指出他们的主要作用。
解:
PID 模型2
()D P I
K s K s K G s s
++=
1.积分分离的PID 算法
作用:防止系统启动,结束或大幅度增加减设值时,短时间内系统输出有很大的偏差,引起系统较大的超调和振荡; 2.抗积分饱和PID 控制算法
作用:避免控制量长期停留在饱和区; 3.不完全微分PID 控制算法
作用:在控制算法中加入低通滤波器,降低高频干扰,改善系统性能;
4.微分先行控制算法
作用:适用于给定值频繁升降的场合,可以避免给定值升降时引起系统振荡,从而改善系统的动态特性。
