2010年浙江省义乌市中考数学试卷及解析

合集下载

浙江省义乌市中考数学试题.doc

浙江省初中毕业生学业考试（义乌市卷）数学试题卷考生须知：1. 全卷共4页，有3大题，24小题. 满分为1考试时间1.2. 本卷答案必须做在答题纸的对应位置上，做在试题卷上无效.3. 请考生将姓名、准考证号填写在答题纸的对应位置上，并认真核准条形码的姓名、准考证号.4. 作图时，可先使用2B 铅笔，确定后必须使用0.5毫米及以上的黑色签字笔涂黑.5. 本次考试不能使用计算器.温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！参考公式：二次函数y =ax 2+bx +c 图象的顶点坐标是)442(2ab ac a b --，．试卷 Ⅰ说明：本卷共有1大题，10小题，每小题3分，共30分．请用2B 铅笔在“答题纸”上将你认为正确的选项对应的小方框涂黑、涂满．一、选择题(请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分) 1. －3的绝对值是A ．3B ．－3C ．－D ．2．如图，DE 是△ABC 的中位线，若BC 的长是3cm ，则DE 的长是 A ．2cm B ．1.5cm C ．1.2cm D ．1cm 3．下列计算正确的是A ．246x x x += B ．235x y xy +=C ．632x x x ÷=D ．326()x x =4．如图，下列水平放置的几何体中，主视图不是．．长方形的是5．我市市场交易持续繁荣，市场成交额连续全国各大专业市场榜首. 中国小商品城成交额首次突破450亿元关口.请将数据450亿元用科学记数法表示为（单位：元）A ．B ．C ．D ．3131 E A BCDA ．4.50×102B ．0.45×103C ．4.50×1010D ．0.45×10116．下列图形中，中心对称图形有A ．4个B ．3个C ．2个D ．1个 7．不等式组⎨⎧≥->+125523x x 的解在数轴上表示为8．如图，已知AB ∥CD ，∠A =60°，∠C =25°，则∠E 等于 A. 60° B. 25° C. 35° D. 45°9．某校安排三辆车，组织九年级学生团员去敬老院参加学雷锋活动，其中小王与小菲都可以从这三辆车中任选一辆搭乘，则小王与小菲同车的概率为A ．B ．C ．D ．10．如图，△ABC 和△ADE 都是等腰直角三角形，∠BAC =∠DAE =90°，四边形ACDE 是平行四边形，连结CE 交AD 于点F ，连结BD 交CE 于点G ，连结BE . 下列结论中：① CE =BD ； ② △ADC 是等腰直角三角形； ③ ∠ADB =∠AEB ； ④ CD ·AE =EF ·CG ；一定正确的结论有 A ．1个 B ．2个C ．3个D ．4个试卷 Ⅱ说明：本卷共有2大题，14小题，共90分. 答题请用0.5毫米及以上的黑色签字笔书写在“答题纸”的对应位置上.二、填空题（本题有6小题，每小题4分，共24分）11．一次函数y =2x －1的图象经过点（a ，3），则a = ▲ ．12．如果x 1与x 2的平均数是4，那么x 1＋1与x 2＋5的平均数是 ▲ ．AB CDEFG 91312132 ABCDE60°A ．B ．C ．D ．13．已知⊙O 1与⊙O 2的半径分别为3和5，且⊙O 1与⊙O 2相切，则O 1O 2等于 ▲ ． 14．某校为了选拔学生参加我市无线电测向比赛中的装机比赛，教练对甲、乙两选手平时五次训练成绩进行统计，两选手五次训练的平均成绩均为30分钟，方差分别是251S =甲、212S =乙. 则甲、乙两选手成绩比较稳定的是 ▲ .15．右图是市民广场到解百地下通道的手扶电梯示意图．其中AB 、CD 分别表示地下通道、市民广场电梯口处地面的水平线，∠ABC =135°，BC 的长约是25m ，则乘电梯从点B 到点C 上升的高度h 是 ▲ m ．16．如图，一次函数y =－2x 的图象与二次函数y =－x 2+3x 图象的对称轴交于点B .（1）写出点B 的坐标 ▲ ；（2）已知点P 是二次函数y =－x 2+3x 图象在y 轴右侧．．部分上的一个动点，将直线y =－2x 沿y 轴向上平移，分别交x 轴、y 轴于C 、D 两点. 若以CD 为直角边的△PCD 与△OCD 相似，则点 P 的坐标为 ▲ .三、解答题（本题有8小题，第17～19题每题6分，第1题每题8分，第22、23题每题10分，第24题12分，共66分） 17．（1）计算： ο45sin 2820110-+；（2）解分式方程：2323=-+x x .18．如图，已知E 、F 是□ABCD 对角线AC 上的两点，且BE ⊥AC ，DF ⊥AC . （1）求证：△ABE ≌△CDF ；（2）请写出图中除△ABE ≌△CDF 外其余两对全等三角形（不再添加辅助线）．19．商场某种商品平均每天可销售30件，每件盈利50元. 为了尽快减少库存，商场决定采取适当的降价措施. 经调查发现，每件商品每降价1元，商场平均每天可多售出 2件．设每件商品降价x 元. 据此规律，请回答：135°A BChFEABCDOBCD（1）商场日销售量增加 ▲ 件，每件商品盈利 ▲ 元（用含x 的代数式表示）；（2）在上述条件不变、销售正常情况下，每件商品降价多少元时，商场日盈利可达到2100元？为了解某市九年级学生学业考试体育成绩，现从中随机抽取部分学生的体育成绩进行分段（A ：50分；B ：49-45分；C ：44-40分；D ：39-30分；E ：29-0分）统计如下：根据上面提供的信息，回答下列问题：（1）在统计表中，a 的值为 ▲ ，b 的值为 ▲ ，并将统计图补充完整（温馨提示：作图时别忘了用0.5毫米及以上的黑色签字笔涂黑）；（2）甲同学说：“我的体育成绩是此次抽样调查所得数据的中位数. ”请问：甲同学的体育成绩应在什么分数段内？ ▲ （填相应分数段的字母）（3）如果把成绩在40分以上（含40分）定为优秀，那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名？21．如图，已知⊙O 的直径AB 与弦CD 互相垂直，垂足为点E . ⊙O 的切线BF 与弦AD 的延长线相交于点F ，且AD =3，cos ∠BCD= . （1）求证：CD ∥BF ；（2）求⊙O 的半径；（3）求弦CD 的长.22．如图，在直角坐标系中，O 为坐标原点. 已知反比例函数y= （k>0）的图象经过点A (2，m )，过点A 作AB ⊥x 轴于点B ，且△AOB 的面积为 . （1）求k 和m 的值；分数段AB C D E学业考试体育成绩（分数段）统计表学业考试体育成绩（分数段）统计图 12243648607284人数分数段ACx k 21xk BOA43DE OC（2）点C （x ，y ）在反比例函数y= 的图象上，求当1≤x ≤3时函数值y 的取值范围；（3）过原点O 的直线l 与反比例函数y= 的图象交于P 、Q 两点，试根据图象直接写出线段PQ 长度的最小值.23．如图1，在等边△ABC 中，点D 是边AC 的中点，点P 是线段DC 上的动点(点P 与点C不重合)，连结BP . 将△ABP 绕点P 按顺时针方向旋转α角（0°＜α＜180°），得到△A 1B 1P ,连结AA 1，射线AA 1分别交射线PB 、射线B 1B 于点E 、F .（1）如图1，当0°＜α＜60°时，在α角变化过程中，△BEF 与△AEP 始终存在 ▲关系（填“相似”或“全等”），并说明理由；（2）如图2，设∠ABP =β . 当60°＜α＜180°时，在α角变化过程中，是否存在△BEF 与△AEP 全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由；（3）如图3，当α=60°时，点E 、F 与点B 重合. 已知AB =4，设DP =x ，△A 1BB 1的面积为S ，求S 关于x 的函数关系式.24．已知二次函数的图象经过A （2，0）、C (0，12) 两点，且对称轴为直线x =4. 设顶点为点P ，与x 轴的另一交点为点B .（1）求二次函数的解析式及顶点P 的坐标；（2）如图1，在直线 y=2x 上是否存在点D ，使四边形OPBD 为等腰梯形？若存在，求出点D 的坐标；若不存在，请说明理由；（3）如图2，点M 是线段OP 上的一个动点（O 、P 两点除外），以每秒2个单位长度的速度由点P 向点O 运动，过点M 作直线MN ∥x 轴，交PB 于点N. 将△PMN 沿直线MN 对折，得到△P 1MN. 在动点M 的运动过程中，设△P 1MN 与梯形OMNB 的重叠部分的面积为S ，运动时间为t 秒. 求S 关于t 的函数关系式.x k图1图2图311B 1浙江省初中毕业生学业考试（义乌市卷）数学参考答案和评分细则一、选择题(本题有10小题，每小题3分，共30分)二、填空题(本题有6小题，每小题4分，共24分)11. 2 12. 7 13. 2或8（对一个得2分） 14. 乙 15． 5 16．（1）)3-23(， (2分) （2）（2，2）、⎪⎭⎫⎝⎛4521，、⎪⎭⎫ ⎝⎛1611411，、⎪⎭⎫ ⎝⎛2526513，（注：共2分．对一个给0.5分，得2分的要全对，其余有错不倒扣分）三、解答题(本题有8小题，第17～19题每题6分，第1题每题8分，第22、23题每题10分，第24题12分，共66分)17. 解：（1）原式=1+22－2 (算对一项或两项给1分，全对2分) …………………题号 1 2 3 4 5 6 78 9 10 答案A BDBCB CCA DOPC BAxy图1图2MO AxPNCBy2分=1+2……………………………………………………………………3分（2）2（x+3）=3 (x-2) ……………………………………………………………1分解得：x=12 …………………………………………………………………2分经检验：x=12是原方程的根………………………………………………3分18.解：（1）∵四边形ABCD是平行四边形∴AB=CD AB∥CD∴∠BAE=∠FCD又∵BE⊥AC DF⊥AC∴∠AEB=∠CFD=90°∴△ABE≌△CDF （AAS）…………………………………………………4分（2）①△ABC≌△CDA②△BCE≌△DAF（每个1分）……………………6分19. 解：（1） 2x 50－x（每空1分） (2)分（2）由题意得：（50－x）（30＋2x）=2100 (4)分化简得：x2－35x+300=0解得：x1=15，x2=………………………………………………5分∵该商场为了尽快减少库存，则x=15不合题意，舍去. ∴x=：每件商品降价商场日盈利可达2100元. ……………………6分：（1） 60 ， 0.15 (图略) （每空1分，图1分）........................3分（2） C (5)分（3）0.8×10440=8352（名） (7)分答：该市九年级考生中体育成绩为优秀的学生人数约有8352名. (8)分21．解：（1）∵BF 是⊙O 的切线 ∴AB ⊥BF …………………………………………1分∵AB ⊥CD∴CD ∥BF (2)分（2）连结BD∵AB 是直径 ∴∠ADB =90° (3)分∵∠BCD =∠BAD cos ∠BCD =43…………………4分 ∴cos ∠BAD =43=AB AD又∵AD =3 ∴AB =4∴⊙O 的半径为2 ……………………………………5分（3）∵cos ∠DAE =43=AD AE AD =3∴AE =49 ………………………………6分∴ED =47349322=⎪⎭⎫⎝⎛- (7)分∴CD =2ED =273 ………………………………………………………………8分22．解：（1）∵A (2，m ) ∴OB =2 AB =m ∴S △AOB =21•OB •AB =21×2×m =21 ∴m =21………………………………2分∴点A 的坐标为（2，21）把A （2，21）代入y=x k ，得21=2k∴k =1 ……………………………………………………………………………4分A（2）∵当x =1时，y =1；当x =3时，y =31…………………………………………6分又 ∵反比例函数y =x1在x >0时，y 随x 的增大而减小…………………………7分∴当1≤x ≤3时，y 的取值范围为31≤y ≤1 …………………………………8分（3）由图象可得，线段PQ 长度的最小值为22 ……………………………10分23．解: （1）相似 …………………………………………………………………………1分由题意得：∠APA 1=∠BPB 1=α AP = A 1P BP =B 1P则 ∠PAA 1 =∠PBB 1 =2902180αα-=-οο (2)分∵∠PBB 1 =∠EBF ∴∠PAE =∠EBF又∵∠BEF =∠AEP∴△BEF ∽△AEP (3)分（2）存在，理由如下： ………………………………………………………………4分易得：△BEF ∽△AEP若要使得△BEF ≌△AEP ，只需要满足BE =AE 即可 (5)分∴∠BAE =∠ABE∵∠BAC =60° ∴∠BAE =οοο30229060-=⎪⎭⎫ ⎝⎛--αα ∵∠ABE =β ∠BAE =∠ABE ……………………………………………6分∴βα=-ο302即α=2β+60° ……………………………………………7分（3）连结BD ，交A 1B 1于点G ，过点A 1作A 1H ⊥AC 于点H . ∵∠B 1 A 1P =∠A 1PA =60° ∴A 1B 1∥AC由题意得：AP= A 1 P ∠A =60° ∴△PAA 1是等边三角形∴A 1H=)2(23x + ………………………………………………………………8分在Rt △ABD 中，BD =32∴BG =x x 233)2(2332-=+-…………………………………… 9分∴x x S BB A 33223342111-=⎪⎪⎭⎫⎝⎛-⨯⨯=∆ （0≤x ＜2）……………………10分24．解：（1）设二次函数的解析式为y =ax 2+bx +c由题意得⎪⎪⎩⎪⎪⎨⎧=++==-0241242c b a c a b 解得⎪⎩⎪⎨⎧=-==1281c b a∴二次函数的解析式为y = x 2－8x +12 ……………………………………………2分点P 的坐标为（4，－4） …………………………………………………………3分（2）存在点D ，使四边形OPBD 为等腰梯形. 理由如下：当y =0时，x 2-8x +12=0 ∴x 1=2 ， x 2=6 ∴点B 的坐标为（6，0）设直线BP 的解析式为y =kx +mCy1AD CB A 1G则⎩⎨⎧-=+=+4406m k m k 解得⎩⎨⎧-==122m k∴直线BP 的解析式为y =2x －12∴直线OD ∥BP ………………………………………4分∵顶点坐标P （4，－4） ∴ OP =42 设D (x ，2x ) 则BD 2=（2x ）2+(6－x )2当BD =OP 时，（2x ）2+(6－x )2=32解得：x 1=52，x 2=2…………………………………………………………………6分当x 2=2时，OD =BP =52，四边形OPBD 为平行四边形，舍去∴当x =52时四边形OPBD 为等腰梯形 …………………7分 ∴当D (52，54)时，四边形OPBD 为等腰梯形 ………8分（3）① 当0＜t ≤2时，∵运动速度为每秒2个单位长度，运动时间为t 秒，则MP =2t ∴PH =t ，MH =t ，HN =21t ∴MN =23t∴S =23t ·t ·21=43t 2……………………10分② 当2＜t ＜4时，P 1G =2t －4，P 1H =t∵MN ∥OB ∴ EF P 1∆∽MN P 1∆∴211)(11H P G P S S MNP EF P =∆∆ ∴22)42(431t t t S EF P -=∆ ∴ EF P S 1∆=3t 2－12t +12∴S =43t 2－(3t 2－12t +12)= －49t 2+12t －12 ∴ 当0＜t ≤2时，S=43t2当2＜t ＜4时，S =－49t 2+12t －12 ……………12分xP 1 MAO BCPNyHxP 1M A OB CPNG HE F y。

中考数学试题及解析浙江义乌

浙江省义乌市初中毕业生学业考试数学试题试卷 Ⅰ一、选择题 1. －3的绝对值是A ．3B ．－3C ．－13D ．132．如图，DE 是△ABC 的中位线，若BC 的长是3cm ，则DE 的长是 A ．2cm B ．1.5cm C ．1.2cm D ．1cm 3．下列计算正确的是A ．246x x x +=B ．235x y xy +=C ．632x x x ÷=D ．326()x x =4．如图，下列水平放置的几何体中，主视图不是．．长方形的是5．我市市场交易持续繁荣，市场成交额连续20年居全国各大专业市场榜首. 中国小商品城成交额首次突破450亿元关口.请将数据450亿元用科学记数法表示为（单位：元） A ．4.50×102B ．0.45×103C ．4.50×1010D ．0.45×10116．下列图形中，中心对称图形有A ．4个B ．3个C ．2个D ．1个7．不等式组⎩⎨⎧≥->+125523x x 的解在数轴上表示为8．如图，已知AB ∥CD ，∠A =60°，∠C =25°，则∠E 等于 A. 60° B. 25° C. 35° D. 45°9．某校安排三辆车，组织九年级学生团员去敬老院参加学雷锋活动，其中小王与小菲都可以从这三辆车中任选一辆搭乘，则小王与小菲同车的概率为 A ．13 B ．19 C ．12 D ．2310．如图，△ABC 和△ADE 都是等腰直角三角形，∠BAC =∠DAE =90°，四边形ACDE 是平行四边形，连结CE 交AD 于点F ，连结BD 交CE 于点G ，连结BE . 下列结论中：1 02 A ．1 02 B ．1 02 C ．1 02 D ． A ．B ．C ．D ．AB CDE60° E A BCD① CE =BD ； ② △ADC 是等腰直角三角形； ③ ∠ADB =∠AEB ； ④ CD ·AE =EF ·CG ；一定正确的结论有 A ．1个 B ．2个C ．3个D ．4个试卷 Ⅱ二、填空题（本题有6小题，每小题4分，共24分）11．一次函数y =2x －1的图象经过点（a ，3），则a = ▲ ． 12．如果x 1与x 2的平均数是4，那么x 1＋1与x 2＋5的平均数是 ▲ ．13．已知⊙O 1与⊙O 2的半径分别为3和5，且⊙O 1与⊙O 2相切，则O 1O 2等于 ▲ ． 14．某校为了选拔学生参加我市无线电测向比赛中的装机比赛，教练对甲、乙两选手平时五次训练成绩进行统计，两选手五次训练的平均成绩均为30分钟，方差分别是251S =甲、212S =乙. 则甲、乙两选手成绩比较稳定的是 ▲ .15．右图是市民广场到解百地下通道的手扶电梯示意图．其中AB 、CD 分别表示地下通道、市民广场电梯口处地面的水平线，∠ABC =135°，BC 的长约是25m ，则乘电梯从点B 到点C 上升的高度h 是 ▲ m ．16．如图，一次函数y =－2x 的图象与二次函数y =－x 2+3x 图象的对称轴交于点B .（1）写出点B 的坐标 ▲ ；（2）已知点P 是二次函数y =－x 2+3x 图象在y 轴右侧．．部分上的一个动点，将直线y =－2x 沿y 轴向上平移，分别交x 轴、y 轴于C 、D 两点. 若以CD 为直角边的△PCD 与△OCD 相似，则点P 的坐标为 ▲ .三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）17．（1）计算： 45sin 2820110-+；（2）解分式方程：2323=-+x x . 18．如图，已知E 、F 是□ABCD 对角线AC 上的两点，且BE ⊥AC ，DF ⊥AC .（1）求证：△ABE ≌△CDF ；（2）请写出图中除△ABE ≌△CDF 外其余两对全等三角形（不再添加辅助线）．19．商场某种商品平均每天可销售30件，每件盈利50元. 为了尽快减少库存，商场决定采取适当的降价措施. 经调查发现，每件商品每降价1元，商场平均每天可多售出 2件．设每件商品降价x 元. 据此规律，请回答：（1）商场日销售量增加 ▲ 件，每件商品盈利 ▲ 元（用含x 的代数式表示）；A BCDEF G 135° ABCDhFEABCDOBC D（2）在上述条件不变、销售正常情况下，每件商品降价多少元时，商场日盈利可达到2100元？ 20 . 为了解某市九年级学生学业考试体育成绩，现从中随机抽取部分学生的体育成绩进行分段（A ：50分；B ：49-45分；C ：44-40分；D ：39-30分；E ：29-0分）统计如下：学业考试体育成绩（分数段）统计图学业考试体育成绩（分数段）统计表根据上面提供的信息，回答下列问题：（1）在统计表中，a 的值为 ▲ ，b 的值为 ▲ ，并将统计图补充完整（温馨提示：作图时别忘了用0.5毫米及以上的黑色签字笔涂黑）；（2）甲同学说：“我的体育成绩是此次抽样调查所得数据的中位数. ”请问：甲同学的体育成绩应在什么分数段内？ ▲ （填相应分数段的字母）（3）如果把成绩在40分以上（含40分）定为优秀，那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名？21．如图，已知⊙O 的直径AB 与弦CD 互相垂直，垂足为点E . ⊙O 的切线BF 与弦AD 的延长线相交于点F ，且AD =3，cos ∠BCD=34. （1）求证：CD ∥BF ；（2）求⊙O 的半径；（3）求弦CD 的长.22．如图，在直角坐标系中，O 为坐标原点. 已知反比例函数y=k xk>0）的图象经过点A (2，m )，过点A 作AB ⊥x 轴于点B ，且△AOB 的面积为12.（1）求k 和m 的值；（2）点C （x ，y ）在反比例函数y=k x的图象上，求当1≤x ≤3时函数值y 的取值范围；（3）过原点O 的直线l 与反比例函数y=k x的图象交于P 、Q 两点，试根据图象直接写出线段PQ 长度的最小值.分数段人数（人）频率 A 48 0.2 B a 0.25 C 84 0.35 D 36 b E120.0512243648607284人数分数段ABCDEBOA FMADOECO CB23．如图1，在等边△ABC 中，点D 是边AC 的中点，点P 是线段DC 上的动点(点P 与点C 不重合)，连结BP . 将△ABP 绕点P 按顺时针方向旋转α角（0°＜α＜180°），得到△A 1B 1P ,连结AA 1，射线AA 1分别交射线PB 、射线B 1B 于点E 、F .（1）如图1，当0°＜α＜60°时，在α角变化过程中，△BE F 与△AEP 始终存在 ▲ 关系（填“相似”或“全等”），并说明理由；（2）如图2，设∠ABP =β . 当60°＜α＜180°时，在α角变化过程中，是否存在△BEF 与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由；（3）如图3，当α=60°时，点E 、F 与点B 重合. 已知AB =4，设DP =x ，△A 1BB 1的面积为S ，求S 关于x 的函数关系式.24．已知二次函数的图象经过A （2，0）、C (0，12) 两点，且对称轴为直线x =4. 设顶点为点P ，与x 轴的另一交点为点B .（1）求二次函数的解析式及顶点P 的坐标；（2）如图1，在直线 y=2x 上是否存在点D ，使四边形OPBD 为等腰梯形？若存在，求出点D的坐标；若不存在，请说明理由；（3）如图2，点M 是线段OP 上的一个动点（O 、P 两点除外），以每秒2个单位长度的速度由点P 向点O 运动，过点M 作直线MN ∥N 沿直线MN 对折，得到△P 1MN. 在动点M 的运动过程中，设△P 1MN 与梯形OMNB 的重叠部分的面积为S ，运动时间为t 秒. 求S 关于t 的函数关系式.图1图2图3P B 1FM AD E C CBA 1PB 1FMADECCBA 1 PB 1AD CB A 1O PCBAxy图1图2MOAxPNCBy参考答案和评分细则一、选择题(本题有10小题，每小题3分，共30分)二、填空题(本题有6小题，每小题4分，共24分)11. 2 12. 7 13. 2或8（对一个得2分） 14. 乙 15． 5 16．（1）)3-23(， (2分) （2）（2，2）、⎪⎭⎫⎝⎛4521，、⎪⎭⎫ ⎝⎛1611411，、⎪⎭⎫ ⎝⎛2526513，（注：共2分．对一个给0.5分，得2分的要全对，其余有错不倒扣分）三、解答题(本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分)17. 解：（1）原式=1+22－2 (算对一项或两项给1分，全对2分) ……2分=1+2 …………………………………………………3分（2）2（x +3）=3 (x -2) …………………………………1分解得：x =12 ………………………………………………2分经检验：x =12是原方程的根 ……………………………3分18. 解：（1）∵四边形ABCD 是平行四边形∴AB =CD AB ∥CD ∴∠BAE =∠FCD 又∵BE ⊥AC DF ⊥AC ∴∠AEB =∠CFD =90°∴△ABE ≌△CDF （AAS ）…………………………4分（2）①△ABC ≌△CDA ②△BCE ≌△DAF （每个1分）………………6分19. 解：（1） 2x 50－x （每空1分）………………………2分（2）由题意得：（50－x ）（30＋2x ）=2100 …………………………4分化简得：x 2－35x +300=0解得：x 1=15， x 2=20……………………………………5分∵该商场为了尽快减少库存，则x =15不合题意，舍去. ∴x =20 答：每件商品降价20元，商场日盈利可达2100元. …………6分20．解：（1） 60 ， 0.15 (图略) （每空1分，图1分） …………3分（2） C ……………………………………………………5分（3）0.8×10440=8352（名）……………………………………7分答：该市九年级考生中体育成绩为优秀的学生人数约有8352名.……8分21．解：（1）∵BF 是⊙O 的切线 ∴AB ⊥BF ………………………1分 ∵AB ⊥CD∴CD ∥BF ……………………………………………………2分（2）连结BD∵AB 是直径 ∴∠ADB =90°…………………………3分∵∠BCD =∠BAD cos ∠BCD =43…………………4分 ∴cos ∠BAD =43=AB AD 又∵AD =3 ∴AB =4∴⊙O 的半径为2 …………………………………5分（3）∵cos ∠DAE =43=AD AE AD =3∴AE =49 …………6分∴ED =47349322=⎪⎭⎫ ⎝⎛- ………………………7分∴CD =2ED =273 …………………………………8分 22．解：（1）∵A (2，m ) ∴OB =2 AB =m ∴S △AOB =21•OB •AB =21×2×m =21 ∴m =21…………………2分 ∴点A 的坐标为（2，21）把A （2，21）代入y=x k ，得21=2k∴k =1 ………………………………………………………4分（2）∵当x =1时，y =1；当x =3时，y =31…………………6分又 ∵反比例函数y =x1在x >0时，y 随x 的增大而减小……………7分 ∴当1≤x ≤3时，y 的取值范围为31≤y ≤1 ………………8分（3）由图象可得，线段PQ 长度的最小值为22 …………………10分23．解: （1）相似 …………………………………………………1分由题意得：∠APA 1=∠BPB 1=α AP = A 1P BP =B 1P则 ∠PAA 1 =∠PBB 1 =2902180αα-=- ……………………2分∵∠PBB 1 =∠EBF ∴∠PAE =∠EBF又∵∠BEF =∠AEP∴△BE F ∽△AEP ……………………………………3分（2）存在，理由如下： ………………………………………4分易得：△BE F ∽△AEP若要使得△BEF ≌△AEP ，只需要满足BE =AE 即可……………5分 ∴∠BAE =∠ABE∵∠BAC =60° ∴∠BAE =30229060-=⎪⎭⎫ ⎝⎛--αα ∵∠ABE =β ∠BAE =∠ABE ………………………6分 ∴βα=- 302即α=2β+60° ……………………7分B（3）连结BD ，交A 1B 1于点G ，过点A 1作A 1H ⊥AC 于点H . ∵∠B 1 A 1P =∠A 1PA =60° ∴A 1B 1∥AC由题意得：AP= A 1 P ∠A =60° ∴△PAA 1是等边三角形∴A 1H=)2(23x + ……………………………8分在Rt △ABD 中，BD =32∴BG =x x 233)2(2332-=+-………………… 9分 ∴x x S BB A 33223342111-=⎪⎪⎭⎫⎝⎛-⨯⨯=∆ （0≤x ＜2）………10分24．解：（1）设二次函数的解析式为y =ax 2+bx +c由题意得⎪⎪⎩⎪⎪⎨⎧=++==-0241242c b a c a b 解得⎪⎩⎪⎨⎧=-==1281c b a∴二次函数的解析式为y = x 2－8x +12 …………2分点P 的坐标为（4，－4） ……………………3分（2）存在点D ，使四边形OPBD 为等腰梯形. 理由如下：当y =0时，x 2-8x +12=0 ∴x 1=2 ，则⎩⎨⎧-=+=+4406m k m k 解得⎩⎨⎧-==122m k∴直线BP 的解析式为y =2x －12∴直线OD ∥BP ………………………4分xP 1 MAOBCPN yH DO xAOBCP yPB 1D B A 1H G∵顶点坐标P （4，－4） ∴ OP =42 设D (x ，2x ) 则BD 2=（2x ）2+(6－x )2当BD =OP 时，（2x ）2+(6－x )2=32解得：x 1=52，x 2=2…………………………6分当x 2=2时，OD =BP =52，四边形OPBD 为平行四边形，舍去∴当x =52时四边形OPBD 为等腰梯形…………7分 ∴当D (52，54)时，四边形OPBD 为等腰梯形……8分（3）① 当0＜t ≤2时，∵运动速度为每秒2个单位长度，运动时间为t 秒，则MP =2t ∴PH =t ，MH =t ，HN =21t ∴MN =23t ∴S =23t ·t ·21=43t 2 ……………………10分② 当2＜t ＜4时，P 1G =2t －4，P 1H =t ∵MN ∥OB ∴ EF P 1∆∽MN P 1∆∴211)(11H P G P S S MNP EF P =∆∆ ∴ 22)42(431t t t S EF P -=∆∴ EF P S 1∆=3t 2－12t +12∴S =43t 2－(3t 2－12t +12)= －49t 2+12t －12 ∴ 当0＜t ≤2时，S=43t 2当2＜t ＜4时，S =－49t 2+12t －12 ……12分xP 1 MA OBCPNG H E F y。

初三数学有关圆的各地中考题汇编(含答案)

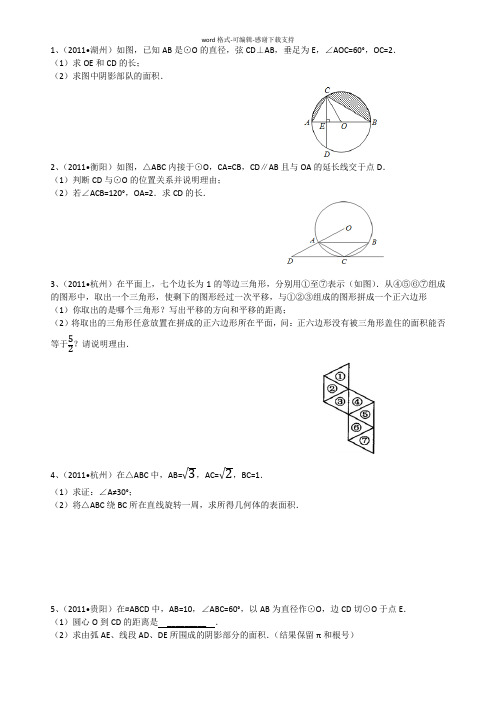
1、（2011•湖州）如图，已知AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，∠AOC=60°，OC=2．（1）求OE 和CD 的长；（2）求图中阴影部队的面积．2、（2011•衡阳）如图，△ABC 内接于⊙O ，CA=CB ，CD ∥AB 且与OA 的延长线交于点D ．（1）判断CD 与⊙O 的位置关系并说明理由；（2）若∠ACB=120°，OA=2．求CD 的长．3、（2011•杭州）在平面上，七个边长为1的等边三角形，分别用①至⑦表示（如图）．从④⑤⑥⑦组成的图形中，取出一个三角形，使剩下的图形经过一次平移，与①②③组成的图形拼成一个正六边形（1）你取出的是哪个三角形？写出平移的方向和平移的距离；（2）将取出的三角形任意放置在拼成的正六边形所在平面，问：正六边形没有被三角形盖住的面积能否等于52？请说明理由．4、（2011•杭州）在△ABC 中，AB=√3，AC=√2，BC=1．（1）求证：∠A≠30°；（2）将△ABC 绕BC 所在直线旋转一周，求所得几何体的表面积．5、（2011•贵阳）在▱ABCD 中，AB=10，∠ABC=60°，以AB 为直径作⊙O ，边CD 切⊙O 于点E ．（1）圆心O 到CD 的距离是 _________ ．（2）求由弧AE 、线段AD 、DE 所围成的阴影部分的面积．（结果保留π和根号）6、（2011•抚顺）如图，AB 为⊙O 的直径，弦CD 垂直平分OB 于点E ，点F 在AB 延长线上，∠AFC=30°．（1）求证：CF 为⊙O 的切线．（2）若半径ON ⊥AD 于点M ，CE=√3，求图中阴影部分的面积．7、（2011•北京）如图，在△ABC ，AB=AC ，以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ，点F 在AC 的延长线上，且∠CBF=12∠CAB ．（1）求证：直线BF 是⊙O 的切线；（2）若AB=5，sin ∠CBF=√55，求BC 和BF 的长．8、（2010•义乌市）如图，以线段AB 为直径的⊙O 交线段AC 于点E ，点M 是AE ̂的中点，OM 交AC 于点D ，∠BOE=60°，cosC=12，BC=2√3．（1）求∠A 的度数；（2）求证：BC 是⊙O 的切线（3）求MD 的长度．9、（2010•沈阳）如图，AB 是⊙O 的直径，点C 在BA 的延长线上，直线CD 与⊙O 相切与点D ，弦DF ⊥AB 于点E ，线段CD=10，连接BD ．（1）求证：∠CDE=2∠B ；（2）若BD ：AB=√3：2，求⊙O 的半径及DF 的长．10、（2010•绍兴）如图，已知△ABC 内接于⊙O ，AC 是⊙O 的直径，D 是AB ̂的中点，过点D 作直线BC的垂线，分别交CB 、CA 的延长线E 、F ．（1）求证：EF 是⊙O 的切线；（2）若EF=8，EC=6，求⊙O 的半径．11、（2010•丽水）如图，直线l 与⊙O 相交于A ，B 两点，且与半径OC 垂直，垂足为H ，已知AB=16cm ，．（1）求⊙O 的半径；（2）如果要将直线l 向下平移到与⊙O 相切的位置，平移的距离应是多少？请说明理由．1、（2011•湖州）如图，已知AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，∠AOC=60°，OC=2．（1）求OE 和CD 的长；（2）求图中阴影部队的面积．考点：扇形面积的计算；垂径定理。

2010浙江义乌中考数学试卷(含答案)

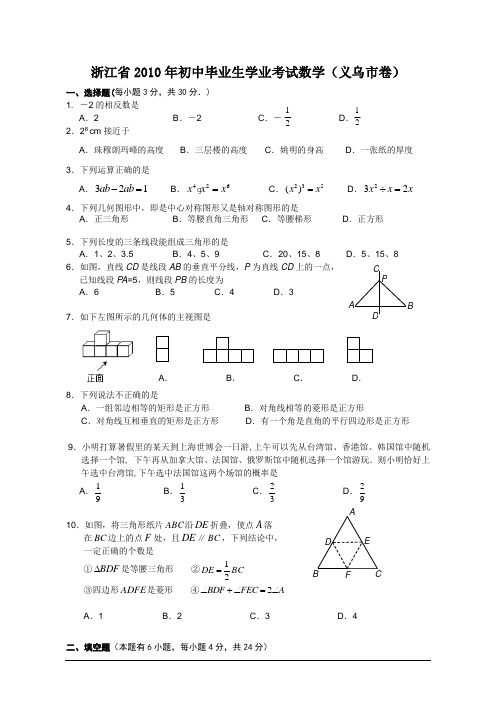
浙江省2010年初中毕业生学业考试数学（义乌市卷）一、选择题(每小题3分，共30分．) 1. －2的相反数是A ．2B ．－2C ．－D ．2．28cm 接近于A ．珠穆朗玛峰的高度B ．三层楼的高度C ．姚明的身高D ．一张纸的厚度3．下列运算正确的是A ．321ab ab -=B ．426x x x =C ．235()x x =D ．x x x 232=÷4．下列几何图形中，即是中心对称图形又是轴对称图形的是A ．正三角形B ．等腰直角三角形C ．等腰梯形D ．正方形5．下列长度的三条线段能组成三角形的是A ．1、2、3.5B ．4、5、9C ．20、15、8D ．5、15、8 6．如图，直线CD 是线段AB 的垂直平分线，P 为直线CD 上的一点，已知线段PA =5，则线段PB 的长度为A ．6B ．5C ．4D ．3 7．如下左图所示的几何体的主视图是8．下列说法不正确的是A ．一组邻边相等的矩形是正方形B ．对角线相等的菱形是正方形C ．对角线互相垂直的矩形是正方形D ．有一个角是直角的平行四边形是正方形9．小明打算暑假里的某天到上海世博会一日游,上午可以先从台湾馆、香港馆、韩国馆中随机选择一个馆, 下午再从加拿大馆、法国馆、俄罗斯馆中随机选择一个馆游玩．则小明恰好上午选中台湾馆,下午选中法国馆这两个场馆的概率是A ．19B ．13C ．23D ．2910．如图，将三角形纸片ABC 沿DE 折叠，使点A 落在BC 边上的点F 处，且DE ∥BC ，下列结论中，一定正确的个数是①BDF ∆是等腰三角形 ②BC DE 21=③四边形ADFE 是菱形 ④2BDF FEC A ∠+∠=∠A ．1B ．2C ．3D ．4A B C D E F A BCDP A ．B．C ．D ． 1212二、填空题（本题有6小题，每小题4分，共24分）11．从26个英文字母中任意选一个，是C 或D 的概率是．12．在直角三角形中，满足条件的三边长可以是．(写出一组即可)13．已知直线l 与⊙O 相切，若圆心O 到直线l 的距离是5，则⊙O 的半径是．14．改革开放后，我市农村居民人均消费水平大幅度提升．下表是2004年至2009年我市农村居民人均食品消费支出的统计表（单位：元）．则这几年我市农村居民人均食品消费支出的中位数是元，极差是元．15．课外活动小组测量学校旗杆的高度．如图，当太阳光线与地面成30°角时，测得旗杆AB 在地面上的投影BC 长为24米，则旗杆AB 的高度约是米．（结果保留3个有效数字，3≈1.732）16．（1）将抛物线y 1＝2x 2向右平移2个单位，得到抛物线y 2的图象，则y 2= ；（2）如图，P 是抛物线y 2对称轴上的一个动点，直线x ＝t 平行于y 轴，分别与直线y ＝x 、抛物线y 2交于点A 、B ．若△ABP 是以点A 或点B 为直角顶点的等腰直角三角形，求满足条件的t 的值，则t ＝．三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分） 17．（1）计算：1tan 45⎪-°（2）化简：244222x x x x x -+--- 18．（1）解不等式： 32x -≥21x +（2）解分式方程： 22122x x x +=+x19．我市举办的“义博会”是国内第三大展会，从1995年以来已成功举办了15届.（1）1995年“义博会”成交金额为1.01亿元,1999年“义博会”成交金额为35.2亿元,求1999年的成交金额比1995年的增加了几倍? (结果精确到整数)（2）2000年“义博会”的成交金额与2009年的成交金额的总和是153.99亿元,且2009年的成交金额是2000年的3倍少0.25亿元，问2009年“义博会”的成交金额是否突破了百亿元大关?20．“知识改变命运，科技繁荣祖国”．我市中小学每年都要举办一届科技运动会．下图为我市某校2009年参加科技运动会航模比赛（包括空模、海模、车模、建模四个类别）的参赛人数统计图：（1）该校参加车模、建模比赛的人数分别是人和人；（2）该校参加航模比赛的总人数是人，空模所在扇形的圆心角的度数是 °，并把条形统计图补充完整；（温馨提示：作图时别忘了用0.5毫米及以上的黑色签字笔涂黑）（3）从全市中小学参加航模比赛选手中随机抽取80人，其中有32人获奖. 今年我市中小学参加航模比赛人数共有2485人，请你估算今年参加航模比赛的获奖人数约是多少人?空模建模车模海模25% 25% 某校2009年航模比赛参赛人数扇形统计图某校2009年航模比赛参赛人数条形统计图21．如图，以线段AB 为直径的⊙O 交线段AC 于点E ，点M 是AE 的中点，OM 交AC 于点D ，60BOE ∠=°，1cos 2C =，BC = （1）求A ∠的度数；（2）求证：BC 是⊙O 的切线；（3）求MD 的长度．22．如图，一次函数2y kx =+的图象与反比例函数m y x=的图象交于点P ，点P 在第一象限．PA ⊥x 轴于点A ，PB ⊥y 轴于点B ．一次函数的图象分别交x 轴、y 轴于点C 、D ，且S △PBD =4，12OC OA =．（1）求点D 的坐标；（2）求一次函数与反比例函数的解析式；（3）根据图象写出当0x >时，一次函数的值大于反比例函数的值的x 的取值范围.23．如图1，已知∠ABC =90°，△ABE 是等边三角形，点P为射线BC 上任意一点（点P 与点B 不重合），连结AP ，将线段AP 绕点A 逆时针旋转60°得到线段AQ ，连结 QE 并延长交射线BC 于点F .（1）如图2，当BP =BA 时，∠EBF = °，猜想∠QFC = °；（2）如图1，当点P 为射线BC 上任意一点时，猜想∠QFC 的度数，并加以证明；（3）已知线段AB =32，设BP =x ，点Q 到射线BC 的距离为y ，求y 关于x 的函数关系式．图2ABEQP F 图1AEQF P OBACEM D24．如图1，已知梯形OABC ，抛物线分别过点O （0，0）、A （2，0）、B （6，3）．（1）直接写出抛物线的对称轴、解析式及顶点M 的坐标；（2）将图1中梯形OABC 的上下底边所在的直线OA 、CB 以相同的速度同时向上平移，分别交抛物线于点O 1、A 1、C 1、B 1，得到如图2的梯形O 1A 1B 1C 1．设梯形O 1A 1B 1C 1的面积为S ，A 1、 B 1的坐标分别为 (x 1，y 1)、(x 2，y 2)．用含S 的代数式表示2x －1x ，并求出当S =36时点A 1的坐标；（3）在图1中，设点D 坐标为(1，3)，动点P 从点B 出发，以每秒1个单位长度的速度沿着线段BC 运动，动点Q 从点D 出发，以与点P 相同的速度沿着线段DM 运动．P 、Q 两点同时出发，当点Q 到达点M 时，P 、Q 两点同时停止运动．设P 、Q 两点的运动时间为t ，是否存在某一时刻t ，使得直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称轴．．．围成的三角形相似？若存在，请求出t 的值；若不存在，请说明理由．图1 图2浙江省2010年初中毕业生学业考试（义乌市卷）数学参考答案和评分细则一、选择题(本题有10小题，每小题3分，共30分)二、填空题(本题有6小题，每小题4分，共24分) 11.11312. 3、4、5（满足题意的均可） 13. 5 14. 2304，1112 （每空2分） 15． 13.916．（1）2(x －2)2 或2288x x -+ (2分)（2）3、12分．对一个给0.5分，得2分的要全对，其余有错不倒扣分）三、解答题(本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分) 17. 解：（1）原式=1+2－1 (算对一项或两项给1分，全对2分) ……………2分=2…………………………………………………………………3分（2）原式=2442x x x -+-…………………………………………………1分=2(2)2x x --…………………………………………………… 2分=2x -……………………………………………………………3分18. 解：（1）32x x -≥21+…………2分得 x ≥3 ……………………3分（2）222124x x x +=+…………………………………………………1分 41x =……………………………………………………………2分14x =…………2.5分经检验14x =是原方程的根…………3分 19. 解：（1）（35.2－1.01）÷1.01≈34答：1999年的成交金额比1995年约增加了34倍…………………3分（2）设2000年成交金额为x 亿元，则2009年成交金额为（3x －0.25）亿元30.25153.99x x +-=………1分解得：x =38.56 ∴30.25115.43x -=＞100……………………………………………2分 ∴2009年“义博会”的成交金额突破了百亿元大关．………………3分20．（1） 4 ， 6 …………………………………………（每空1分，共2分）（2） 24 ， 120 ……………………………………………（每空1分，共2分）(图略)…………………………………………………………………………3分（3）32÷80=0.4……………………1分 0.4×2485=994答：今年参加航模比赛的获奖人数约是994人．………………………3分21．解：（1）∵∠BOE =60° ∴∠A ＝12∠BOE ＝ 30°……………2分（2）在△ABC 中 ∵1cos 2C =∴∠C =60°…1分又∵∠A ＝30° ∴∠ABC =90°∴AB BC ⊥……2分 ∴BC 是⊙O 的切线……3分（3）∵点M 是AE 的中点 ∴OM ⊥AE ………………………………1分在Rt △ABC 中∵BC = ∴AB=tan 60BC ︒==6……2分 ∴OA =32AB = ∴OD =12OA =32 ∴MD =32………………3分22．解：（1）在2y kx =+中，令0x =得2y = ∴点D 的坐标为（0，2）…2分（2）∵ AP ∥OD ∴Rt △PAC ∽ Rt △DOC ……………………………1分∵ 12OC OA = ∴13OD OC AP AC == ∴AP =6……………………2分又∵BD =624-= ∴由S △PBD =4可得BP =2……………………3分 ∴P (2，6) ……4分把P (2，6)分别代入2y kx =+与my x=可得一次函数解析式为：y =2x +2……………………………………………5分反比例函数解析式为：12y x=………………………………………6分（3）由图可得x ＞2…………………………2分23．解: （1）=∠EBF 30°...............................1分 QFC ∠= 60°..................................2分（2）QFC ∠=60°.....................................1分不妨设BP, 如图1所示∵∠BAP=∠BAE+∠EAP=60°+∠EAP∠EAQ=∠QAP+∠EAP=60°+∠EAP∴∠BAP=∠EAQ ..........................................2分在△ABP 和△AEQ 中 AB=AE ，∠BAP=∠EAQ ， AP=AQ∴△ABP ≌△AEQ （SAS ）.........................3分 ∴∠AEQ=∠ABP=90°...............................4分∴∠BEF 180180906030AEQ AEB =︒-∠-∠=︒-︒-︒=︒ ∴QFC ∠=EBF BEF ∠+∠=3030︒+︒=60°……………......5分 (事实上当BP 时，如图2情形，不失一般性结论仍然成立，不分类讨论不扣分） (3)在图1中，过点F 作FG ⊥BE 于点G∵△ABE 是等边三角形 ∴BE=AB=32，由（1）得=∠EBF 30° 在Rt △BGF 中，2BE BG == ∴BF=2cos30BG=︒∴EF =2.......1分图2A B E Q PF C G图1A B E Q F P H∵△ABP ≌△AEQ ∴QE=BP=x ∴QF =QE ＋EF 2x =+................2分过点Q 作QH ⊥BC ，垂足为H 在Rt △QHF 中，3sin 60(2)y QH QF x ==︒=+（x ＞0）即y 关于x 的函数关系式是：y x =分 24．解：（1）对称轴：直线1x =……………………………………………………..… 1分解析式：21184y x x =-或211(1)88y x =--……………………………….2分顶点坐标：M （1，18-）……….…………………………………………..3分（2）由题意得 213y y -=2221221111118484y y x x x x -=--+=3……………………………………..1分得：212111()[()]384x x x x -+-=①…………….………………….……2分12122(11)3()62x x s x x -+-⨯3==+-得：1223s x x +=+ ②….…………..3分把②代入①并整理得：2172x x s -=(S ＞0) (事实上，更确切为S ＞66)4分当36s =时，2121142x x x x +=⎧⎨-=⎩ 解得：1268x x =⎧⎨=⎩(注：S ＞0或S ＞66不写不扣分)把16x =代入抛物线解析式得13y =∴点A 1（6，3）…5分（3）存在…………………………………….…..……1分解法一：易知直线AB 解析式为3342y x =-，可得直线AB 与对称轴的交点E 的坐标为31,4⎛⎫- ⎪⎝⎭∴BD =5，DE =154，DP =5－t ，DQ = t当PQ ∥AB 时，DQ DP DE DB=51554t t -=得 157t =………2分下面分两种情况讨论: 设直线PQ 与直线AB 、x 轴的交点分别为点F 、G①当0<157t <时，如图1-1 ∵△FQE ∽△FAG ∴∠FGA ＝∠FEQ ∴∠DPQ ＝∠DEB 易得△DPQ ∽△DEB ∴DQ DPDB DE=图1-1∴51554t t -= 得201577t => ∴207t =(舍去)……………………3分 ② 当157<18t <3时，如图1-2∵△FQE ∽△FAG ∴∠FAG ＝∠FQE ∵∠DQP ＝∠FQE ∠FAG ＝∠EBD∴∠DQP ＝∠DBE 易得△DPQ ∽△DEB ∴DQ DP DB DE=∴51554t t -=， ∴207t = ∴当207t =秒时，使直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称轴围成的三角形相似………………4分 (注:未求出157t =能得到正确答案不扣分) 解法二：可将284x x y =-向左平移一个单位得到2188x y =-,再用解法一类似的方法可求得2172x x S ''-= , 1(5,3)A ', 207t = ∴2172x x S-= 1(6,3)A , 207t =.。

(中考数学真题复习)第7讲一元一次方程及分式方程基础例题附答案解析

中考数学复习一元一次方程及分式方程【基础演练】1．(2013·滨州)把方程12x＝1变形为x＝2，其依据是() A．等式的性质1B．等式的性质2C．分式的基本性质D．不等式的性质1解析把方程12x＝1变形为x＝2，其依据是等式的性质2.答案B2．(2013·泰安)某电子元件厂准备生产4600个电子元件，甲车间独立生产了一半后，由于要尽快投入市场，乙车间也加入该电子元件的生产，若乙车间每天生产的电子元件是甲车间的1.3倍，结果用33天完成任务，问甲车间每天生产电子元件多少个？在这个问题中设甲车间每天生产电子元件x个，根据题意可得方程为()A.2300x＋23001.3x＝33 B.2300x＋2300x＋1.3x＝33C.2300x＋4600x＋1.3x＝33 D.4600x＋2300x＋1.3x＝33解析设甲车间每天能加工x个，则乙车间每天能加工1.3x个，根据题意可得：2300 x＋2300x＋1.3x＝33.答案B3．(2013·丽水)分式方程1x－2＝0的解是________．解析方程两边同乘以x，得1－2x＝0，解得x＝12.检验：当x＝12时，x＝12≠0，所以，原方程的解为x ＝12.答案x ＝124．(2012·宁波)分式方程x －2x ＋4＝12的解是________．解析方程的两边同乘2(x ＋4)，得2(x －2)＝x ＋4，2x －4＝x ＋4，解得x ＝8.检验：把x ＝8代入x ＋4＝12≠0.故原方程的解为x ＝8.答案x ＝85．(2013·绍兴)分式方程2xx －1＝3的解是________．解析方程两边同乘以x －1，得2x ＝3(x －1)，解得x ＝3.检验：当x ＝3时，x －1＝3－1＝2≠0，所以，原方程的解为x ＝3.答案x ＝36．(2013·滨州)解方程：3x ＋52＝2x －13.解去分母得：3(3x ＋5)＝2(2x －1)，去括号得：9x ＋15＝4x －2，移项合并得：5x ＝－17，解得：x ＝－175.7．(2010·台州)解方程：3x ＝2x －1.解方程两边同乘以x (x －1)，得3(x －1)＝2x ，解得x ＝3.经检验：x ＝3是原方程的解，所以原方程的解是x ＝3.8．(2010·义乌市)解分式方程：2x2＋1x＋2＝2x.解方程的两边同乘x＋2，得2x2＋1＝2x2＋4x，∴4x＝1，∴x＝1 4 .经检验，x＝14是原方程的解．9．(2012·北京)列方程或方程组解应用题：据林业专家分析，树叶在光合作用后产生的分泌物能够吸附空气中的一些悬浮颗粒物，具有滞尘净化空气的作用．已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克，若一年滞尘1000毫克所需的银杏树叶的片数与一年滞尘550毫克所需的国槐树叶的片数相同，求一片国槐树叶一年的平均滞尘量．解设一片国槐树叶一年的平均滞尘量为x毫克，则一片银杏树叶一年的平均滞尘量为(2x－4)毫克，由题意得：10002x－4＝550x，解得：x＝22.经检验：x＝22是所列方程的解．答：一片国槐树叶一年的平均滞尘量为22毫克．【能力提升】10．(2013·台湾)附表为服饰店贩卖的服饰与原价对照表．某日服饰店举办大拍卖，外套依原价打六折出售，衬衫和裤子依原价打八折出售，服饰共卖出200件，共得24000元．若外套卖出x件，则依题意可列出下列哪一个一元一次方程式？()服饰原价(元)外套250衬衫125裤子125A．0.6×250x＋0.8×125(200＋x)＝24000B．0.6×250x＋0.8×125(200－x)＝24000C．0.8×125x＋0.6×250(200＋x)＝24000D．0.8×125x＋0.6×250(200－x)＝24000解析若外套卖出x 件，则衬衫和裤子卖出(200－x )件，由题意得：0．6×250x ＋0.8×125(200－x )＝24000，答案B11．(2012·山西)图1是边长为30cm 的正方形纸板，裁掉阴影部分后将其折叠成如图2所示的长方体盒子，已知该长方体的宽是高的2倍，则它的体积是________cm 3.解析长方体的高为x cm ，然后表示出其宽为30－4x ，根据题意得：30－4x ＝2x ，解得：x ＝5.故长方体的宽为10cm ，长为20cm 则长方体的体积为5×10×20＝1000cm 3.答案100012．(2012·攀枝花)若分式方程：2＋1－kx x －2＝12－x有增根，则k ＝________.解析∵2＋1－kx x －2＝12－x，去分母得：2(x －2)＋1－kx ＝－1，整理得：(2－k )x ＝2，当2－k ＝0时，此方程无解，不符合题意．∵分式方程2＋1－kx x －2＝12－x 有增根，∴x －2＝0，2－x ＝0，解得：x ＝2，把x ＝2代入(2－k )x ＝2得：k ＝1.答案113．(2010·嘉兴)解方程：x x ＋1＋x ＋1x＝2.解设x x ＋1＝y ，则原方程化为y ＋1y ＝2.整理得，y 2－2y ＋1＝0，解之得，y ＝1.当y ＝1时，xx ＋1＝1，此方程无解．故原方程无解．14．(2010·义乌市)我市举办的“义博会”是国内第三大展会，从1995年以来已成功举办了15届．(1)1995年“义博会”成交金额为1.01亿元，1999年“义博会”成交金额为35.2亿元，求1999年的成交金额比1995年的增加了几倍？(结果精确到整数)(2)2000年“义博会”的成交金额与2009年的成交金额的总和是153.99亿元，且2009年的成交金额是2000年的3倍少0.25亿元，问2009年“义博会”的成交金额是否突破了百亿元大关？解(1)(35.2－1.01)÷1.01≈34.答：1999年的成交金额比1995年约增加了34倍；(2)设2000年成交金额为x 亿元，则2009年成交金额为(3x －0.25)亿元．由题意得x ＋3x －0.25＝153.99，解得x ＝38.56，∴3x －0.25＝115.43＞100，∴2009年“义博会”的成交金额突破了百亿元大关．。

2010年浙江省义乌中考数学试题及答案

浙江省2010年初中毕业生学业考试（义乌市卷）数学试题卷考生须知：1. 全卷共4页，有3大题，24小题. 满分为120分.考试时间120分钟.2. 本卷答案必须做在答题纸的对应位置上，做在试题卷上无效.3. 请考生将姓名、准考证号填写在答题纸的对应位置上，并认真核准条形码的姓名、准考证号.4. 作图时，可先使用2B 铅笔，确定后必须使用0.5毫米及以上的黑色签字笔涂黑.5. 本次考试不能使用计算器.温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！参考公式：二次函数y =ax 2+bx +c 图象的顶点坐标是)44,2(2ab ac a b --．试卷 Ⅰ说明：本卷共有1大题，10小题，每小题3分，共30分．请用2B 铅笔在“答题纸”上将你认为正确的选项对应的小方框涂黑、涂满．一、选择题(请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分)1. －2的相反数是A ．2B ．－2C ．－D ．2．28cm 接近于A ．珠穆朗玛峰的高度B ．三层楼的高度C ．姚明的身高D ．一张纸的厚度3．下列运算正确的是A ．321ab ab -=B ．426x x x =C ．235()x x = D ．x x x 232=÷4．下列几何图形中，即是中心对称图形又是轴对称图形的是A ．正三角形B ．等腰直角三角形C ．等腰梯形D ．正方形 5．下列长度的三条线段能组成三角形的是A ．1、2、3.5B ．4、5、9C ．20、15、8D ．5、15、8 6．如图，直线CD 是线段AB 的垂直平分线，P 为直线CD 上的一点，已知线段PA =5，则线段PB 的长度为A ．6B ．5C ．4D ．3 7．如下左图所示的几何体的主视图是8．下列说法不正确的是A ．一组邻边相等的矩形是正方形B ．对角线相等的菱形是正方形C ．对角线互相垂直的矩形是正方形D ．有一个角是直角的平行四边形是正方形9．小明打算暑假里的某天到上海世博会一日游,上午可以先从台湾馆、香港馆、韩国馆中随机选择一个馆, 下午再从加拿大馆、法国馆、俄罗斯馆中随机选择一个馆游玩．则小明恰好上午选中台湾馆,下午选中法国馆这两个场馆的概率是ABCDP A ．B ．C ．D ． 1212A ．19B ．13C ．23D ．2910．如图，将三角形纸片ABC 沿DE 折叠，使点A 落在BC 边上的点F 处，且DE ∥BC ，下列结论中，一定正确的个数是 ①BDF ∆是等腰三角形 ②BC DE 21=③四边形ADFE 是菱形 ④2BDF FEC A ∠+∠=∠A ．1B ．2C ．3D ．4试卷 Ⅱ说明：本卷共有2大题，14小题，共90分. 答题请用0.5毫米及以上的黑色签字笔书写在“答题纸”的对应位置上.二、填空题（本题有6小题，每小题4分，共24分）11．从26个英文字母中任意选一个，是C 或D 的概率是 ▲ ．12．在直角三角形中，满足条件的三边长可以是 ▲ ．(写出一组即可)13．已知直线l 与⊙O 相切，若圆心O 到直线l 的距离是5，则⊙O 的半径是 ▲ ．14．改革开放后，我市农村居民人均消费水平大幅度提升．下表是2004年至2009年我市农村居民人均食品消费支出的统计表（单位：元）．则这几年我市农村居民人均食品消费支出的中位数是 ▲ 元，极差是 ▲ 元．15．课外活动小组测量学校旗杆的高度．如图，当太阳光线与地面成30°角时，测得旗杆AB 在地面上的投影BC 长为24米，则旗杆AB 的高度约是 ▲ 米．（结果保留3个有效数字，3≈1.732）16．（1）将抛物线y 1＝2x 2向右平移2个单位，得到抛物线y 2的图象，则y 2= ▲ ；（2）如图，P 是抛物线y 2对称轴上的一个动点，直线x ＝t 平行于y 轴，分别与直线y ＝x 、抛物线y 2交于点A 、B ．若△ABP 是以点A 或点B 为直角顶点的等腰直角三角形，求满足条件的t 的值，则t ＝ ▲ ．三、（本题有8小题，第17～19题每题6分，第20、23题每题10分，第24题12分，共66分） 17．（1）计算：1tan 45⎪-°（2）化简：244222x x x x x -+---A B C DE F x18．（1）解不等式： 32x -≥21x +（2）解分式方程： 22122x x x +=+19．我市举办的“义博会”是国内第三大展会，从1995年以来已成功举办了15届.（1）1995年“义博会”成交金额为1.01亿元,1999年“义博会”成交金额为35.2亿元,求1999年的成交金额比1995年的增加了几倍? (结果精确到整数)（2）2000年“义博会”的成交金额与2009年的成交金额的总和是153.99亿元,且2009年的成交金额是2000年的3倍少0.25亿元，问2009年“义博会”的成交金额是否突破了百亿元大关?20．“知识改变命运，科技繁荣祖国”．我市中小学每年都要举办一届科技运动会．下图为我市某校2009年参加科技运动会航模比赛（包括空模、海模、车模、建模四个类别）的参赛人数统计图：（1）该校参加车模、建模比赛的人数分别是 ▲ 人和 ▲ 人；（2）该校参加航模比赛的总人数是 ▲ 人，空模所在扇形的圆心角的度数是 ▲ °，并把条形统计图补充完整；（温馨提示：作图时别忘了用0.5毫米及以上的黑色签字笔涂黑）（3）从全市中小学参加航模比赛选手中随机抽取80人，其中有32人获奖. 今年我市中小学参加航模比赛人数共有2485人，请你估算今年参加航模比赛的获奖人数约是多少人?空模建模车模海模25% 25% 某校2009年航模比赛参赛人数扇形统计图某校2009年航模比赛参赛人数条形统计图21．如图，以线段AB 为直径的⊙O 交线段AC 于点E ，点M 是 AE 的中点，OM 交AC 于点D ，60BOE ∠=°，1cos 2C =，BC =（1）求A ∠的度数；（2）求证：BC 是⊙O 的切线；（3）求 MD的长度．22．如图，一次函数2y kx =+的图象与反比例函数my x=的图象交于点P ，点P 在第一象限．PA ⊥x 轴于点A ，PB ⊥y 轴于点B ．一次函数的图象分别交x 轴、y 轴于点C 、D ，且S △PBD =4，12OC OA =．（1）求点D 的坐标；（2）求一次函数与反比例函数的解析式；（3）根据图象写出当0x >时，一次函数的值大于反比例函数的值的x 的取值范围.OBACEM D图1 图223．如图1，已知∠ABC =90°，△ABE 是等边三角形，点P 为射线BC 上任意一点（点P 与点B 不重合），连结AP ，将线段AP 绕点A 逆时针旋转60°得到线段AQ ，连结QE 并延长交射线BC 于点F .（1）如图2，当BP =BA 时，∠EBF = ▲ °，猜想∠QFC = ▲ °；（2）如图1，当点P 为射线BC 上任意一点时，猜想∠QFC 的度数，并加以证明；（3）已知线段AB =32，设BP =x ，点Q 到射线BC 的距离为y ，求y 关于x 的函数关系式．24．如图1，已知梯形OABC ，抛物线分别过点O （0，0）、A （2，0）、B （6，3）．（1）直接写出抛物线的对称轴、解析式及顶点M 的坐标；（2）将图1中梯形OABC 的上下底边所在的直线OA 、CB 以相同的速度同时向上平移，分别交抛物线于点O 1、A 1、C 1、B 1，得到如图2的梯形O 1A 1B 1C 1．设梯形O 1A 1B 1C 1的面积为S ，A 1、B 1的坐标分别为 (x 1，y 1)、(x 2，y 2)．用含S 的代数式表示2x －1x ，并求出当S =36时点A 1的坐标；（3）在图1中，设点D 坐标为(1，3)，动点P 从点B 出发，以每秒1个单位长度的速度沿着线段BC 运动，动点Q 从点D 出发，以与点P 相同的速度沿着线段DM 运动．P 、Q 两点同时出发，当点Q 到达点M 时，P 、Q 两点同时停止运动．设P 、Q 两点的运动时间为t ，是否存在某一时刻t ，使得直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称轴．．．围成的三角形相似？若存在，请求出t 的值；若不存在，请说明理由．图2ABEQP F 图1 ACBEQ F P浙江省2010年初中毕业生学业考试（义乌市卷）数学参考答案和评分细则一、选择题(本题有10小题，每小题3分，共30分)二、填空题(本题有6小题，每小题4分，共24分)11.11312. 3、4、5（满足题意的均可） 13. 5 14. 2304，1112 （每空2分） 15． 13.916．（1）2(x －2)2 或2288x x -+ (2分)（2）3、12分．对一个给0.5分，得2分的要全对，其余有错不倒扣分）三、解答题(本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分) 17. 解：（1）原式=1+2－1 (算对一项或两项给1分，全对2分) …………………………2分=2……………………………………………………………………………3分（2）原式=2442x x x -+-……………………………………………………………1分=2(2)2x x --……………………………………………………………… 2分 =2x -……………………………………………………………………3分18. 解：（1）32x x -≥21+…………2分得 x ≥3 ………………………………3分（2）222124x x x +=+……………………………………………………………1分 41x =……………………………………………………………………2分14x =…………2.5分经检验14x =是原方程的根…………………3分 19. 解：（1）（35.2－1.01）÷1.01≈34答：1999年的成交金额比1995年约增加了34倍…………………………3分（2）设2000年成交金额为x 亿元，则2009年成交金额为（3x －0.25）亿元30.25153.99x x +-=………1分解得：x =38.56∴30.25115.43x -=＞100……………………………………………………2分 ∴2009年“义博会”的成交金额突破了百亿元大关．………………………3分20．（1） 4 ， 6 …………………………………………………（每空1分，共2分）（2） 24 ， 120 ………………………………………………（每空1分，共2分）(图略)…………………………………………………………………………………3分（3）32÷80=0.4……………………1分 0.4×2485=994答：今年参加航模比赛的获奖人数约是994人．………………………………3分21．解：（1）∵∠BOE =60° ∴∠A ＝12∠BOE ＝ 30°……………………2分（2）在△ABC 中 ∵1cos 2C =∴∠C =60°…1分又∵∠A ＝30° ∴∠ABC =90°∴AB BC ⊥……2分 ∴BC 是⊙O 的切线……………3分（3）∵点M 是 AE 的中点 ∴OM ⊥AE ………………………………………1分在Rt △ABC 中∵BC = ∴AB=tan60BC ︒== 6……2分 ∴OA =32AB = ∴OD =12OA =32 ∴MD =32………………………3分22．解：（1）在2y kx =+中，令0x =得2y = ∴点D 的坐标为（0，2）………2分（2）∵ AP ∥OD ∴Rt △PAC ∽ Rt △DOC …………………………………1分∵ 12OC OA = ∴13OD OC AP AC == ∴AP =6…………………………2分又∵BD =624-= ∴由S △PBD =4可得BP =2…………………………3分 ∴P (2，6) …………4分把P (2，6)分别代入2y kx =+与my x=可得一次函数解析式为：y =2x +2…………………………………………………5分反比例函数解析式为：12y x=………………………………………………6分（3）由图可得x ＞2…………………………2分23．解: （1）=∠EBF 30°...............................1分 QFC ∠= 60°..................................2分（2）QFC ∠=60°.....................................1分不妨设BP, 如图1所示∵∠BAP=∠BAE+∠EAP=60°+∠EAP∠EAQ=∠QAP+∠EAP=60°+∠EAP∴∠BAP=∠EAQ ..........................................2分在△ABP 和△AEQ 中 AB=AE ，∠BAP=∠EAQ ， AP=AQ∴△ABP ≌△AEQ （SAS ）.........................3分∴∠AEQ=∠ABP=90°...............................4分∴∠BEF 180180906030AEQ AEB =︒-∠-∠=︒-︒-︒=︒∴QFC ∠=EBF BEF ∠+∠=3030︒+︒=60°…………………………............5分(事实上当BP 时，如图2情形，不失一般性结论仍然成立，不分类讨论不扣分）(3)在图1中，过点F 作FG ⊥BE 于点G∵△ABE 是等边三角形 ∴BE=AB=32，由（1）得=∠EBF 30° 在Rt △BGF 中，2BE BG == ∴BF=2cos30BG=︒∴EF =2.......1分 ∵△ABP ≌△AEQ ∴QE=BP=x ∴QF =QE ＋EF 2x =+................2分图2A BEQ P F G图1A B E Q F P H过点Q 作QH ⊥BC ，垂足为H在Rt △QHF中，sin 602)y QH QF x ==︒=+ （x ＞0）即y 关于x的函数关系式是：y x =分 24．解：（1）对称轴：直线1x =……………………………………………………..… 1分解析式：21184y x x =-或211(1)88y x =--……………………………….2分顶点坐标：M （1，18-）……….…………………………………………..3分（2）由题意得 213y y -=2221221111118484y y x x x x -=--+=3……………………………………..1分得：212111()[()]384x x x x -+-=①…………….………………….……2分12122(11)3()62x x s x x -+-⨯3==+-得：1223sx x +=+ ②….………………………………………..………..3分把②代入①并整理得：2172x x s -=(S ＞0) (事实上，更确切为S ＞66)4分当36s =时，2121142x x x x +=⎧⎨-=⎩ 解得：1268x x =⎧⎨=⎩(注：S ＞0或S ＞66不写不扣分) 把16x =代入抛物线解析式得13y = ∴点A 1（6，3）………5分（3）存在………………………………………………………………….…..……1分解法一：易知直线AB 的解析式为3342y x =-，可得直线AB 与对称轴的交点E 的坐标为31,4⎛⎫- ⎪⎝⎭∴BD =5，DE =154，DP =5－t ，DQ = t当PQ ∥AB 时，DQ DP DE DB= 51554t t -=得 157t =………2分下面分两种情况讨论: 设直线PQ 与直线AB 、x 轴的交点分别为点F 、G①当0<157t <时，如图1-1 ∵△FQE ∽△FAG ∴∠FGA ＝∠FEQ ∴∠DPQ ＝∠DEB 易得△DPQ ∽△DEB ∴DQ DPDB DE=图1-1∴51554t t -= 得201577t => ∴207t =(舍去)…………………………3分 ② 当157<18t <3时，如图1-2∵△FQE ∽△FAG ∴∠FAG ＝∠FQE∵∠DQP ＝∠FQE ∠FAG ＝∠EBD ∴∠DQP ＝∠DBE 易得△DPQ ∽△DEB∴DQ DP DB DE = ∴51554t t -=， ∴207t = ∴当207t =秒时，使直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称轴围成的三角形相似………………………………4分(注:未求出157t =能得到正确答案不扣分)解法二：可将284x x y =-向左平移一个单位得到2188x y =-,再用解法一类似的方法可求得2172x x S ''-= , 1(5,3)A ', 207t =∴2172x x S -= 1(6,3)A , 207t =.。

2010年浙江省金华市初中毕业生学业考试数学试卷正卷及答案

浙江省2010年初中毕业生学业考试(金华卷)数学试题卷考生须知：1.全卷共三大题,24小题，满分为120分.考试时间为100分钟,本次考试采用开卷形式.2.全卷分为卷Ⅰ（选择题）和卷Ⅱ（非选择题）两部分，全部在答题纸上作答.卷Ⅰ的答案必须用2B 铅笔填涂；卷Ⅱ的答案必须用黑色字迹钢笔或签字笔写在答题纸相应的位置上.3.请用黑色字迹钢笔或签字笔在答题纸上先填写姓名和准考证号.4.作图时,可先使用2B 铅笔,确定后必须使用黑色字迹的钢笔或签字笔描黑.5.本次考试不得使用计算器.卷 Ⅰ说明：本卷共有1大题，10小题，共30分.请用2B 铅笔在答题纸上将你认为正确的选项对应的小方框涂黑、涂满.一、选择题(本题有10小题,每小题3分,共30分)1. 在 -3－1， 0 这四个实数中，最大的是（ ▲ ）A . -3B .C . －1D . 02. 据报道，5月28日参观2010上海世博会的人数达35.6万﹒用科学记数法表示数35.6万是（ ▲ ） A ．3.56×101 B ．3.56×104 C ．3.56×105 D ．35.6×104 3. 在平面直角坐标系中，点P （－1，3）位于（ ▲ ） A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限 4. 下图所示几何体的主视图是（ ▲ ） A . B . C . D .5. 小明的讲义夹里放了大小相同的试卷共12页，其中语文4页、数学2页、英语6页，他随机地从讲义夹中抽出1页，抽出的试卷恰好是数学试卷的概率为（ ▲ ） A .21B .31C .61D .121 6. 如图，△ABC 内接于⊙O ，∠A =40°，则∠BOC 的度数为（ ▲ ） A . 20° B . 40° C . 60° D . 80° 7. 如果33-=-b a ，那么代数式b a 35+-的值是（ ▲ ） A ．0 B ．2 C ．5 D ．88. 已知抛物线c bx ax y ++=2的开口向下,顶点坐标为（2，－3） ,那么该抛物线有（ ▲ ） A . 最小值－3B . 最大值－3C . 最小值2D . 最大值29. 如图，若A 是实数a 在数轴上对应的点，则关于a ，－a ，1的大小关系表示正确的是（ ▲ ） A ．a ＜1＜－aB ．a ＜－a ＜1(第6题图)正面1A(第9题图)(第14题图)1C ．1＜－a ＜a D ．－a ＜a ＜110. 如图，在等腰梯形ABCD 中，AB ∥CD ，对角线AC ⊥BC ，∠B ＝60º，BC ＝2cm ，则梯形ABCD 的面积为（ ▲ ） A ．33cm 2 B ．6 cm 2C ．36cm 2D ．12 cm 2卷 Ⅱ说明：本卷共有2大题，14小题，共90分.请用黑色字迹钢笔或签字笔将答案写在答题纸相应位的置上.二、填空题 (本题有6小题,每小题4分,共24分) 11. 分解因式=-92x ▲.12. 分式方程112x =-的解是 ▲ .13. 如果半径为3cm 的⊙O 1与半径为4cm 的⊙O 2内切，那么两圆的圆心距O 1O 2＝ ▲ cm . 14﹒如图，在平面直角坐标系中，若△ABC 与△A 1B 1C 1关于E 点成中心对称，则对称中心E15. 若二次函数k x x y ++-=22的部分图象如图所示，则关于x 的一元二次方程022=++-k x x 的一个解31=x ，另一个解=2x ▲ ；16. 如图在边长为2的正方形ABCD 中，E ，F ，O 分别是AB ，CD ，AD 的中点，以O 为圆心，以OE 为半径画弧EF .P 是上的一个动点，连结OP ，并延长OP 交线段BC 于点K ，过点P 作⊙O 的切线，分别交射线AB 于点M ，交直线BC 于点G . 若3=BMBG，则BK ﹦ ▲ .三、解答题 (本题有8小题, 共66分，各小题都必须写出解答过程) 17．(本题6分)计算：4cos30°．(第15题图)AODBFKE (第16题G MCACBD(第10题图)18．(本题6分)如图，在△ABC 中，D 是BC 边上的点（不与B ，C 重合），F ，E 分别是AD 及其延长线上的点，CF ∥BE . 请你添加一个条件，使△BDE ≌△CDF (不再添加其它线段，不再标注或使用其他字母)，并给出证明．（1）你添加的条件是： ▲ ；（2）证明：19．(本题6分)在一个阳光明媚、清风徐来的周末，小明和小强一起到郊外放风筝﹒他们把风筝放飞后，将两个风筝的引线一端都固定在地面上的C 处(如图).现已知风筝A 的引线（线段AC ）长20m ，风筝B 的引线（线段BC ）长24m ，在C 处测得风筝A 的仰角为60°，风筝B 的仰角为45°. （1）试通过计算，比较风筝A 与风筝B谁离地面更高？（2）求风筝A 与风筝B 的水平距离.(精确到0.01 m ；参考数据：sin45°≈0.707,cos45°≈0.70tan45°=1,sin 60°≈0.866,cos60°=0.5,tan 60°≈1.732）20．(本题8分)已知二次函数y =ax 2＋bx －3的图象经过点A （2，－3），B （－1，0）．（1）求二次函数的解析式；（2）填空：要使该二次函数的图象与x 轴只有一个交点，应把图象沿y 轴向上平移 ▲ 个单位．21．(本题8分)如图，AB 是⊙O 的直径，C 是的中点，CE ⊥AB 于 E ，BD 交CE 于点F ．（1）求证：CF ﹦BF ；（2）若CD ﹦6， AC ﹦8，则⊙O 的半径为 ▲ ，CE 的长是 ▲ ．A CBD FE(第18题B(第19题B (第21题图)22．(本题10分)一方有难，八方支援．2010年4月14日青海玉树发生7.1级强烈地震，给玉树人民造成了巨大的损失﹒灾难发生后，实验中学举行了爱心捐款活动，全校同学纷纷拿出自己的零花钱，踊跃捐款支援灾区人民﹒小慧对捐款情况进行了抽样调查，抽取了40名同学的捐款数据，把数据进行分组、列频数分布表后，绘制了频数分布直方图．图中从左到右各长方形高度之比为3∶4∶5∶7∶1（如图）．（1）捐款20元这一组的频数是▲；（2）40名同学捐款数据的中位数是▲；（3）若该校捐款金额不少于34500 元，请估算该校捐款同学的人数至少有多少名？23. (本题10分）已知点P的坐标为（m，0），在x轴上存在点Q（不与P点重合），以PQ为边作正方形PQMN，使点M落在反比例函数y =2x-的图像上.小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有．．两个，且一个正方形的顶点M在第四象限，另一个正方形的顶点M1在第二象限.（1）如图所示，若反比例函数解析式为y=2x-，P点坐标为（1，0），图中已画出一符合条件的一个正方形PQMN，请你在图中画出符合条件的另一个正方形PQ1M1N1，并写出点M1的坐标；（温馨提示：作图时，别忘了用黑色字迹的钢笔或签字笔描黑喔！）M1的坐标是▲（2）请你通过改变P点坐标，对直线M1 M的解析式y﹦kx＋b进行探究可得k﹦▲，若点P的坐标为（m，0）时，则b﹦▲；（3）依据(2)的规律，如果点P的坐标为（6，0），请你求出点M1和点M的坐标．24.(本题12分)如图，把含有30°角的三角板ABO置入平面直角坐标系中，A，B两点坐标分别为（3，0）和(0，.动点P从A点开始沿折线AO-OB-BA运动，点P在AO，OB，40名同学捐款的频数分布直(第22题(第23题BA 上运动的速度分别为12 (长度单位/秒)﹒一直尺的上边缘l 从x 轴的位置开始以33(长度单位/秒)的速度向上平行移动（即移动过程中保持l ∥x 轴），且分别与OB ， AB 交于E ，F 两点﹒设动点P 与动直线l 同时出发，运动时间为t 秒，当点P 沿折线 AO -OB -BA 运动一周时，直线l 和动点P 同时停止运动．请解答下列问题：（1）过A ，B 两点的直线解析式是 ▲ ；（2）当t ﹦4时，点P 的坐标为 ▲ ；当t ﹦ ▲ ，点P 与点E 重合；（3）① 作点P 关于直线EF 的对称点P′. 在运动过程中，若形成的四边形PEP′F 为菱形，则t 的值是多少？② 当t ﹦2时，是否存在着点Q ，使得△FEQ ∽△BEP ?若存在, 求出点Q 的坐标；若不存在，请说明理由．浙江省2010年初中毕业生学业考试(金华卷)数学卷参考答案及评分标准一、二、填空题（本题有6小题，每小题4分，共24分）11．(x -3)(x +3)； 12.x =3； 13. 1； 14.（3，-1）； 15. -1； 16. 31, 35.（每个2分）三、解答题（本题有8小题，共66分）17. (本题6分)解：原式﹦1＋33－32…………5分（三式化简对1个2分，对2个4分，对3个5分） ﹦1＋3．……………………………………………………………………………1分 18．(本题6分)解：（1）DC BD =(或点D 是线段BC 的中点)，ED FD =，BE CF =中任选一个即可﹒………………………………2分（2）以DC BD =为例进行证明：∵CF∥BE ， ∴∠FCD ﹦∠EBD ．又∵DC BD =，∠FDC ﹦∠EDB ，∴△BDE ≌△CDF ．…………………4分 19．(本题6分) 解：（1）分别过A ，B 作地面的垂线，垂足分别为D 在Rt △ADC 中，∵AC ﹦20，∠ACD ﹦60°，∴AD ﹦20×sin 60°﹦103≈17.32m在Rt △BEC 中，∵BC ﹦24，∠BEC ﹦45°，∴BE ﹦24×sin 45°﹦122≈16.97 m∵17.32>16.97∴风筝A 比风筝B 离地面更高． ………………………………………………………3分（2）在Rt △ADC 中，∵AC ﹦20，∠ACD ﹦60°， ∴DC ﹦20×cos 60°﹦10 m在Rt △BEC 中，∵BC ﹦24，∠BEC ﹦45°，∴EC ﹦BC ≈16.97 m∴EC －DC ≈16.97－10﹦6.97m即风筝A 与风筝B 的水平距离约为6.97m ．…………………………………………3分 20. (本题8分)解：(1)由已知，有⎩⎨⎧=---=-+033324b a b a ，即⎩⎨⎧=-=+3024b a b a ，解得⎩⎨⎧-==21b a∴所求的二次函数的解析式为322--=x x y . …………………………………………6分 (2) 4 …………………………………………………………………………………………2分 21. (本题8分)解：(1) 证明：∵AB 是⊙O 的直径，∴∠ACB ﹦90 又∵CE ⊥AB ， ∴∠CEB ﹦90° ∴∠2﹦90°－∠A ﹦∠1又∵C 是弧BD 的中点，∴∠1﹦∠A∴∠1﹦∠2,ACBD FEB∴ CF ﹦BF ﹒ …………………4分 (2) ⊙O 的半径为5 ， CE 的长是524﹒ ………4分（各2分） 22．(本题10分) 解：（1）14 ………3分（2）15 …………3分(3) 设该校捐款的同学有x 人由题意得 15x ≥ 34500 解得 x ≥2300答：该校捐款的同学至少有2300人． ……4分23．(本题10分)解：（1）如图；M 1 的坐标为（－1，2） ……（2）1-=k ，m b = …………………4分（各2 （3）由（2）知，直线M 1 M 的解析式为+-=x y 则M (x ，y )满足2)6(-=+-⋅x x 解得1131+=x ，1132-=x ∴ 1131-=y ，1132+=y∴M 1，M 的坐标分别为（113-，113+），（113+，113-）．……………4分 24．(本题12分)解：（1）333+-=x y ；………4分（2）（0,3），29=t ；……4分（各2分）（3）①当点P 在线段AO 上时，过F 作FG ⊥x 轴，G ∵FG OE =,FP EP =,∠=EOP ∠=FGP 90° ∴△EOP ≌△FGP ，∴PG OP =﹒又∵t FG OE 33==,∠=A 60°,∴t FG AG 3160tan 0== 而t AP =，∴t OP -=3,t AG AP PG 32=-=由t t 323=-得 59=t ；………………………………………………………………1分当点P 在线段OB 当点P 在线段BA 上时，过P 作PH ⊥EF ，PM ⊥OB ，H 、M (图1)40名同学捐款情况统计图∵t OE 33=,∴t BE 3333-=,∴3360tan 0t BE EF -== ∴6921tEF EH MP -===，又∵)6(2-=t BP 在Rt △BMP 中，MP BP =⋅060cos 即6921)6(2t t -=⋅-，解得745=t ．…………………………………………………1分 ②存在﹒理由如下：∵2=t ，∴332=OE ,2=AP ，1=OP 将△BEP 绕点E 顺时针方向旋转90°，得到 △EC B '（如图3）∵OB ⊥EF ，∴点B '在直线EF 上， C 点坐标为（332，332－1）过F 作FQ ∥C B '，交EC 于点Q ,则△FEQ ∽△EC B '由3=='=QE CE FE E B FE BE ，可得Q 的坐标为（－32，33）………………………1分根据对称性可得，Q 关于直线EF 的对称点Q '（－32，3）也符合条件．……1分。

浙江省2010年初中毕业生学业考试(义乌市卷)

浙江省2010年初中毕业生学业考试（义乌市卷）科学试题卷考生须知：1.全卷共8页，有4大题。

满分为150分，考试时间120分钟。

2.本卷答案必须做在答题纸的相应位置上，做在试题卷上无效。

3.请考生将姓名、准考证号填写在答题卡的对应位置上。

并认真核准条形码上的姓名、准考证号。

4.本卷可能用到的相对原子质量：H:1 C:12 N:14 O:16 Na:23 Cl:35.5温馨提示：请仔细审题，细心答题，相信你一定有出色的表现！试卷Ⅰ说明：本卷有1大题，20小题，共60分。

请用2B铅笔在“答题纸”上将你认为正确的选项对应的小方框涂黑、涂满。

一、选择题（本题有20小题，每小题3分，共60分。

请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）1.下列措施符合“生态义乌”理念的是①将垃圾分类处理②禁止尾气排放不达标的机动车上路③提倡使用一次性筷子④大力提倡植树造林A.①②③B.①②④C.①③④D.②③④2.下列实验操作中，正确的是3.过几天就是我们传统的端午节，根据历法成分，下列节日和端午节不同．．的是A.中秋节B.元宵节C.清明节D.重阳节4.系列过程属于物理变化的是A.蜡烛燃烧B.冰雪融化C.牛奶变质D.瓦斯爆炸5.科学知识与生活有着密切的联系。

对下列生活现象的解释正确的是A.灭蚊是防控登革热的有效措施，因为蚊子是传染源B.冬天用热水袋取暖，因为做功可以改变物体的内能C.筷子在水中看起来被“折断”了，因为发生了反射D.汽车刹车后还要滑行一段距离，因为汽车具有惯性6.下列关于宇宙的认识错误．．的是A.太阳是宇宙的中心B.宇宙是无边的、膨胀的C.地球是太阳系的行星之一D.宇宙是有大量不同层次的星系构成的7.下列有关生态系统的描述，正确的是A.生态系统中的物质流动是单向的B.生态系统是由生产者、消费者和分解者组成的C.生态系统内的能量是通过食物链和食物网来传递的D.研究生态系统中能量流动的主要目的，就是使能量尽可能地保留在生产者体内8.下列关于蒸发和沸腾的说法正确的是A.蒸发和沸腾都需要从外界吸收能量B.蒸发和沸腾都可以在任何温度下进行C.蒸发和沸腾都属于液化现象D.蒸发的快慢与温度无关，沸腾时温度保持不变9.如图，用100牛的力把一个重为10牛的物体压在竖直墙壁上，物体处于静止状态。

浙江省义乌市中考真题 2

浙江省2010年初中毕业生学业考试（义乌市卷）数学试题卷考生须知：1．全卷共4页，有3大题，24小题，满分为120分.考试时间120分钟. 2．本卷答案必须做在答题纸的对应位置上，做在试题卷上无效.3．请考生将姓名、准考证号填写在答题纸的对应位置上，并认真核准条形码的姓名、准考证号.4．作图时，可先使用2B 铅笔，确定后必须使用0.5毫米及以上的黑色签字笔涂黑. 5．本次考试不能使用计算器.温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！参考公式：二次函数y =ax 2+bx +c 图象的顶点坐标是)44,2(2ab ac a b --．试卷 Ⅰ说明：本卷共有1大题，10小题，每小题3分，共30分．请用2B 铅笔在“答题纸”上将你认为正确的选项对应的小方框涂黑、涂满．一、选择题（请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分） 1．－2的相反数是（ ▲ ）A ．2B ．－2C ．－D ． 2．28 cm 接近于（ ▲ ） A ．珠穆朗玛峰的高度B ．三层楼的高度C ．姚明的身高D ．一张纸的厚度3．下列运算正确．．的是（ ▲ ） A ．321ab ab -= B ．426x x x =C ．235()x x = D ．x x x 232=÷4．下列几何图形中，即是中心对称图形又是轴对称图形的是（ ▲ ）A ．正三角形B ．等腰直角三角形C ．等腰梯形D ．正方形 5．下列长度的三条线段能组成三角形的是（ ▲ ）A ．1、2、3.5B ．4、5、9C ．20、15、8D ．5、15、8 6．如图，直线CD 是线段AB 的垂直平分线，P 为直线CD 上的一点，已知线段P A =5，则线段PB 的长度为（ ▲ ）A ．6B ．5C ．4D ．3 7．如下左图所示的几何体的主视图是（ ▲ ）8．下列说法不正确．．．的是（ ▲ ） A ．一组邻边相等的矩形是正方形 B ．对角线相等的菱形是正方形 C ．对角线互相垂直的矩形是正方形D ．有一个角是直角的平行四边形是正方形ABCDPA ．B ．C ．D ．12129．小明打算暑假里的某天到上海世博会一日游,上午可以先从台湾馆、香港馆、韩国馆中随机选择一个馆, 下午再从加拿大馆、法国馆、俄罗斯馆中随机选择一个馆游玩．则小明恰好上午选中台湾馆,下午选中法国馆这两个场馆的概率是（ ▲ ）A ．19B ．13C ．23D ．2910．如图，将三角形纸片ABC 沿DE 折叠，使点A 落在BC 边上的点F 处，且DE ∥BC ，下列结论中，一定正确．．的个数是（ ▲ ） ①BDF ∆是等腰三角形 ②BC DE 21=③四边形ADFE 是菱形 ④2BDF FEC A ∠+∠=∠ A ．1 B ．2 C ．3 D ．4试卷 Ⅱ说明：本卷共有2大题，14小题，共90分．答题请用0.5毫米及以上的黑色签字笔书写在“答题纸”的对应位置上.二、填空题（本题有6小题，每小题4分，共24分）11．从26个英文字母中任意选一个，是C 或D 的概率是 ▲ ． 12．在直角三角形中，满足条件的三边长可以是 ▲ ．(写出一组即可)13．已知直线l 与⊙O 相切，若圆心O 到直线l 的距离是5，则⊙O 的半径是 ▲ ． 14．改革开放后，我市农村居民人均消费水平大幅度提升．下表是2004年至2009年我市农村居民人均食品消费支出的统计表（单位：元）．则这几年我市农村居民人均食品消费支出的中位数是 ▲ 元，极差是 ▲ 元．15．课外活动小组测量学校旗杆的高度．如图，当太阳光线与地面成30°角时，测得旗杆AB 在地面上的投影BC 长为24米，则旗杆AB 的高度约是 ▲ 米．（结果保留3个有效数字，3≈1.732）16．（1）将抛物线y 1＝2x 2向右平移2个单位，得到抛物线y 2的图象，则y 2= ▲ ；（2）如图，P 是抛物线y 2对称轴上的一个动点，直线x ＝t 平行于y 轴，分别与直线yA BCDEFx＝x 、抛物线y 2交于点A 、B ．若△ABP 是以点A 或点B 为直角顶点的等腰直角三角形，求满足条件的t 的值，则t ＝ ▲ ．三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分） 17．（1）计算：1tan 45⎪-°（2）化简：244222x x x x x -+--- 18．（1）解不等式： 32x -≥21x +（2）解分式方程： 22122x x x +=+19．我市举办的“义博会”是国内第三大展会，从1995年以来已成功举办了15届. （1）1995年“义博会”成交金额为1.01亿元,1999年“义博会”成交金额为35.2亿元,求1999年的成交金额比1995年的增加了几倍? (结果精确到整数)（2）2000年“义博会”的成交金额与2009年的成交金额的总和是153.99亿元,且2009年的成交金额是2000年的3倍少0.25亿元，问2009年“义博会”的成交金额是否突破了百亿元大关?20．“知识改变命运，科技繁荣祖国”．我市中小学每年都要举办一届科技运动会．下图为我市某校2009年参加科技运动会航模比赛（包括空模、海模、车模、建模四个类别）的参赛人数统计图：（1）该校参加车模、建模比赛的人数分别是 ▲ 人和 ▲ 人；（2）该校参加航模比赛的总人数是 ▲ 人，空模所在扇形的圆心角的度数是 ▲ °，并把条形统计图补充完整；（温馨提示：作图时别忘了用0.5毫米及以上的黑色签字笔涂黑）（3）从全市中小学参加航模比赛选手中随机抽取80人，其中有32人获奖. 今年我市中小学参加航模比赛人数共有2485人，请你估算今年参加航模比赛的获奖人数约是多少人?空模建模车模海模25%25% 某校2009年航模比赛参赛人数扇形统计图某校2009年航模比赛参赛人数条形统计图21．如图，以线段AB 为直径的⊙O 交线段AC 于点E ，点M 是AE 的中点，OM 交AC 于点D ，60BOE ∠=°，1cos 2C =，BC = （1）求A ∠的度数；（2）求证：BC 是⊙O 的切线；（3）求MD 的长度．22．如图，一次函数2y kx =+的图象与反比例函数my x=的图象交于点P ，点P 在第一象限．P A ⊥x 轴于点A ，PB ⊥y 轴于点B ．一次函数的图象分别交x 轴、y 轴于点C 、D ，且S △PBD =4，12OC OA=．（1）求点D 的坐标；（2）求一次函数与反比例函数的解析式；（3）根据图象写出当0x >时，一次函数的值大于反比例函数的值的x 的取值范围.23．如图1，已知∠ABC =90°，△ABE 是等边三角形，点P 为射线BC 上任意一点（点P 与点B 不重合），连结AP ，将线段AP 绕点A 逆时针旋转60°得到线段AQ ，连结QE 并延长交射线BC 于点F .（1）如图2，当BP =BA 时，∠EBF = ▲ °，猜想∠QFC = ▲ °；（2）如图1，当点P 为射线BC 上任意一点时，猜想∠QFC 的度数，并加以证明；（3）已知线段AB =32，设BP =x ，点Q 到射线BC 的距离为y ，求y 关于x 的函数关系式．图2ABE QPF 图1ACBEQF P OBACEM D24．如图1，已知梯形OABC ，抛物线分别过点O （0，0）、A （2，0）、B （6，3）．（1）直接写出抛物线的对称轴、解析式及顶点M 的坐标；（2）将图1中梯形OABC 的上下底边所在的直线OA 、CB 以相同的速度同时向上平移，分别交抛物线于点O 1、A 1、C 1、B 1，得到如图2的梯形O 1A 1B 1C 1．设梯形O 1A 1B 1C 1的面积为S ，A 1、 B 1的坐标分别为（x 1，y 1）、（x 2，y 2）．用含S 的代数式表示2x －1x ，并求出当S =36时点A 1的坐标；（3）在图1中，设点D 坐标为（1，3），动点P 从点B 出发，以每秒1个单位长度的速度沿着线段BC 运动，动点Q 从点D 出发，以与点P 相同的速度沿着线段DM 运动．P 、Q 两点同时出发，当点Q 到达点M 时，P 、Q 两点同时停止运动．设P 、Q 两点的运动时间为t ，是否存在某一时刻t ，使得直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称．．轴．围成的三角形相似？若存在，请求出t 的值；若不存在，请说明理由．浙江省2010年初中毕业生学业考试（义乌市卷）数学参考答案和评分细则一、选择题(本题有10小题，每小题3分，共30分)二、填空题(本题有6小题，每小题4分，共24分)图1图211.11312. 3、4、5（满足题意的均可） 13. 5 14. 2304，1112 （每空2分） 15． 13.9 16．（1）2(x －2)2 或2288x x -+ (2分)（2）3、12分．对一个给0.5分，得2分的要全对，其余有错不倒扣分）三、解答题(本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分) 17. 解：（1）原式=1+2－1 (算对一项或两项给1分，全对2分) …………………………2分=2……………………………………………………………………………3分（2）原式=2442x x x -+-……………………………………………………………1分=2(2)2x x --………………………………………………………………2分=2x -……………………………………………………………………3分18. 解：（1）32x x -≥21+…………2分得 x ≥3 ………………………………3分（2）222124x x x +=+ (1)分41x = (2)分14x =…………2.5分经检验14x =是原方程的根…………………3分19. 解：（1）（35.2－1.01）÷1.01≈34答：1999年的成交金额比1995年约增加了34倍 (3)分（2）设2000年成交金额为x 亿元，则2009年成交金额为（3x －0.25）亿元30.25153.99x x +-=………1分解得：x =38.56∴30.25115.43x -=＞100……………………………………………………2分∴2009年“义博会”的成交金额突破了百亿元大关．………………………3分20．（1） 4 ， 6 …………………………………………………（每空1分，共2分）（2） 24 ， 120 ………………………………………………（每空1分，共2分）(图略)…………………………………………………………………………………3分（3）32÷80=0.4……………………1分 0.4×2485=994答：今年参加航模比赛的获奖人数约是994人． (3)分21．解：（1）∵∠BOE =60° ∴∠A ＝12∠BOE ＝ 30° (2)分（2）在△ABC 中 ∵1cos 2C = ∴∠C =60°…1分又∵∠A ＝30°∴∠ABC =90°∴AB BC ⊥……2分 ∴BC 是⊙O 的切线……………3分（3）∵点M 是AE 的中点 ∴OM ⊥AE ………………………………………1分在Rt △ABC 中∵BC = ∴AB=tan 60BC ︒==6……2分 ∴OA =32AB = ∴OD =12OA =32 ∴MD =32 (3)分22．解：（1）在2y kx =+中，令0x =得2y = ∴点D 的坐标为（0，2）………2分（2）∵ AP ∥OD ∴Rt △P AC ∽ Rt △DOC …………………………………1分∵12OC OA = ∴13OD OC AP AC == ∴AP =6…………………………2分又∵BD =624-= ∴由S △PBD =4可得BP =2…………………………3分 ∴P (2，6) …………4分把P (2，6)分别代入2y kx =+与my x=可得一次函数解析式为：y =2x +2…………………………………………………5分反比例函数解析式为：12y x= (6)分（3）由图可得x ＞2…………………………2分23．解: （1）=∠EBF 30°...............................1分 QFC ∠= 60°..................................2分ACBEQ（2）QFC ∠=60°.....................................1分不妨设BP, 如图1所示∵∠BAP=∠BAE+∠EAP=60°+∠EAP ∠EAQ=∠QAP+∠EAP=60°+∠EAP∴∠BAP=∠EAQ ..........................................2分在△ABP 和△AEQ 中 AB=AE ，∠BAP=∠EAQ ， AP=AQ ∴△ABP ≌△AEQ （SAS ）.........................3分 ∴∠AEQ=∠ABP=90°...............................4分∴∠BEF 180180906030AEQ AEB =︒-∠-∠=︒-︒-︒=︒ ∴QFC ∠=EBF BEF ∠+∠=3030︒+︒=60°…………………………............5分(事实上当BP 时，如图2情形，不失一般性结论仍然成立，不分类讨论不扣分）(3)在图1中，过点F 作FG ⊥BE 于点G∵△ABE 是等边三角形 ∴BE=AB=32，由（1）得=∠EBF 30° 在Rt △BGF 中，2BE BG == ∴BF=2cos30BG=︒∴EF =2.......1分∵△ABP ≌△AEQ ∴QE=BP=x ∴QF =QE ＋EF 2x =+................2分过点Q 作QH ⊥BC ，垂足为H在Rt △QHF 中，3sin 60(2)y QH QF x ==︒=+（x ＞0）即y 关于x 的函数关系式是：2y x =分24．解：（1）对称轴：直线1x =……………………………………………………..… 1分解析式：21184y x x =-或211(1)88y x =--……………………………….2分顶点坐标：M （1，18-） (3)分（2）由题意得 213y y -=图2A BE Q PF GH2221221111118484y y x x x x -=--+=3……………………………………..1分得：212111()[()]384x x x x -+-=① (2)分12122(11)3()62x x s x x -+-⨯3==+-得：1223sx x +=+ ②….………………………………………..………..3分把②代入①并整理得：2172x x s-=(S ＞0) (事实上，更确切为S ＞66)4分当36s =时，2121142x x x x +=⎧⎨-=⎩ 解得：1268x x =⎧⎨=⎩(注：S ＞0或S ＞66不写不扣分) 把16x =代入抛物线解析式得13y = ∴点A 1（6，3） (5)分（3）存在 (1)分解法一：易知直线AB 的解析式为3342y x =-，可得直线AB 与对称轴的交点E 的坐标为31,4⎛⎫- ⎪⎝⎭∴BD =5，DE =154，DP =5－t ，DQ = t当PQ ∥AB 时，DQ DPDE DB=51554t t -=得 157t =………2分下面分两种情况讨论: 设直线PQ 与直线AB 、x 轴的交点分别为点F 、G①当0<157t <时，如图1-1 ∵△FQE ∽△F AG ∴∠FGA ＝∠FEQ图1-1∴∠DPQ ＝∠DEB 易得△DPQ ∽△DEB ∴DQ DPDB DE=∴51554t t -= 得201577t =>∴207t =(舍去)…………………………3分② 当157<18t <3时，如图1-2 ∵△FQE ∽△F AG ∴∠F AG ＝∠FQE∵∠DQP ＝∠FQE ∠F AG ＝∠EBD∴∠DQP ＝∠DBE 易得△DPQ ∽△DEB∴DQ DPDB DE =∴51554t t -=， ∴207t =∴当207t =秒时，使直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称轴围成的三角形相似………………………………4分(注:未求出157t =能得到正确答案不扣分)解法二：可将284x x y =-向左平移一个单位得到2188x y =-,再用解法一类似的方法可求得2172x x S''-= , 1(5,3)A ', 207t =∴2172x x S-= 1(6,3)A , 207t =.。

2010年浙江省义乌市中考数学试卷

2010年浙江省义乌市中考数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．（3分）﹣2的相反数是（）A．﹣ B．﹣2 C．D．2【考点】M111 相反数【难度】容易题【分析】根据相反数的定义：只有符号不同的两个数叫做互为相反数即可得到﹣2的相反数是2，故选：D．【解答】D．【点评】此题主要考查了相反数，关键是掌握相反数的定义：只有符号不同的两个数叫做互为相反数即可得到﹣2的相反数是2。

2．（3分）（2010•义乌市）28cm接近于（）A．珠穆朗玛峰的高度 B．三层楼的高度C．姚明的身高D．一张纸的厚度【考点】M115 有理数M11U 乘方M11N 整式运算【难度】容易题【分析】根据有理数的乘方运算法则，计算28=24×24=16×16=256（cm）=2.56（m）．然后根据生活实际来确定：A、珠穆朗玛峰峰的高度约8848米，错误；B、三层楼的高度20米左右，错误；C、姚明的身高是2.23米，接近2.56米，正确；D、一张纸的厚度只有几毫米，错误．故选C．【解答】C．【点评】解答这样的题目有两个要点需要注意，一是有理数的乘方运算法则要记牢；二是根据生活实际情况来做出选择．3．（3分）（2010•义乌市）下列运算正确的是（）A．3ab﹣2ab=1 B．x4•x2=x6C．（x2）3=x5D．3x2÷x=2x【考点】M11N 整式运算M11O 指数幂M11U 乘方【难度】容易题【分析】根据合并同类项法则；同底数幂相乘，底数不变指数相加；幂的乘方，底数不变指数相乘；同底数幂相除，底数不变指数相减，对各选项计算得：A、应为3ab﹣2ab=ab，故选项错误；B、x4•x2=x6，正确；C、应为（x2）3=x6，故选项错误；D、应为3x2÷x=3x，故选项错误．故选B．【解答】B．【点评】本题主要考查了同底数幂的乘法、除法运算，幂的乘方的性质，熟练掌握运算性质和法则是解题的关键．4．（3分）（2010•义乌市）下列几何图形中，即是中心对称图形又是轴对称图形的是（）A．正三角形 B．等腰直角三角形C．等腰梯形 D．正方形【考点】M326 等腰三角形性质与判定M327 等边三角形性质与判定M328 直角三角形性质与判定M335 正方形的性质与判定M337 等腰梯形的性质与判定M412 图形的对称【难度】容易题【分析】根据轴对称图形与中心对称图形的概念求解：A、是轴对称图形，不是中心对称图形，不符合题意；B、是轴对称图形，不是中心对称图形，不符合题意；C、是轴对称图形，不是中心对称图形，不符合题意；D、既是中心对称图形又是轴对称图形，符合题意．故选D．【解答】D．【点评】掌握中心对称图形与轴对称图形的概念．①如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．②如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．5．（3分）（2010•义乌市）下列长度的三条线段能组成三角形的是（）A．1、2、3.5 B．4、5、9 C．20、15、8 D．5、15、8【考点】M322 三角形三边的关系【难度】容易题【分析】根据三角形任意两边之和大于第三边，任意两边之差小于第三边，利用排除法求解．具体为：A、∵1+2=3＜3.5，∴不能组成三角形；B、∵4+5=9，∴不能组成三角形；C、20、15、8，能组成三角形；D、5+8=13＜15，不能组成三角形．故选：C．【解答】C．【点评】本题主要考查三角形的三边性质，需要熟练掌握．注意：三角形任意两边之和大于第三边，任意两边之差小于第三边。

2010年浙江省金华市中考数学试卷(全解全析)

2010年浙江省金华市中考数学试卷（全解全析）一、选择题（共10小题，每小题3分，满分30分）1、（2010•金华）在﹣3，﹣√3，﹣1，0这四个实数中，最大的是（）A、﹣3B、﹣√3C、﹣1D、0考点：实数大小比较。

分析：由于正数、0大于所有负数，根据这个法则即可比较四个数的大小．解答：解：∵|﹣3|=3，|﹣√3|=√3，|﹣1|=1，3＞√3＞1，∴﹣3＜﹣√3＜﹣1，又因为0大于一切负数，所以﹣3＜﹣√3＜﹣1＜0．故选D．点评：此题主要考查了实数的大小的比较，比较两个实数的大小，可以采用作差法、取近似值法等．实数大小比较法则：（1）正数大于0，0大于负数，正数大于负数；（2）两个负数，绝对值大的反而小．2、（2010•金华）据报道，5月28日参观2010上海世博会的人数达35.6万，用科学记数法表示数35.6万是（）A、3.56×101B、3.56×104C、3.56×105D、35.6×104考点：科学记数法—表示较大的数。

专题：应用题。

分析：应先把35.6万整理为用个表示的数，科学记数法的一般形式为：a×10n，在本题中a 为3.56，10的指数为整数数位减1．解答：解：35.6万=356 000=3.56×105．故选C．点评：将一个绝对值较大的数写成科学记数法a×10n的形式时，其中1≤|a|＜10，n为比整数位数少1的数．3、（2010•金华）在平面直角坐标系中，点P（﹣1，3）位于（）A、第一象限B、第二象限C、第三象限D、第四象限考点：点的坐标。

分析：应先判断出所求点的横纵坐标的符号，进而判断点所在的象限．解答：解：因为点P（﹣1，3）的横坐标是负数，纵坐标是正数，所以点P在平面直角坐标系的第二象限．故选B．点评：解决本题的关键是掌握好四个象限的点的坐标的符号特征：第一象限正正，第二象限负正，第三象限负负，第四象限正负．4、（2010•金华）图中几何体的主视图是（）A 、B 、C 、D 、考点：简单组合体的三视图。

2010义乌市中考数学试题及答案

浙江省2010年初中毕业生学业考试（义乌市卷）数学参考答案和评分细则一、选择题(本题有10小题，每小题3分，共30分)二、填空题(本题有6小题，每小题4分，共24分)11.11312. 3、4、5（满足题意的均可） 13. 5 14. 2304，1112 （每空2分） 15． 13.916．（1）2(x －2)2 或2288x x -+ (2分) （2）3、12分．对一个给0.5分，得2分的要全对，其余有错不倒扣分）三、解答题(本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分)17. 解：（1）原式=1+2－1 (算对一项或两项给1分，全对2分) …………………………2分=2……………………………………………………………………………3分（2）原式=2442x x x -+-……………………………………………………………1分=2(2)2x x --……………………………………………………………… 2分 =2x -……………………………………………………………………3分18. 解：（1）32x x -≥21+…………2分得 x ≥3 ………………………………3分（2）222124x x x +=+……………………………………………………………1分 41x =……………………………………………………………………2分14x =…………2.5分经检验14x =是原方程的根…………………3分 19. 解：（1）（35.2－1.01）÷1.01≈34答：1999年的成交金额比1995年约增加了34倍…………………………3分（2）设2000年成交金额为x 亿元，则2009年成交金额为（3x －0.25）亿元30.25153.99x x +-=………1分解得：x =38.56∴30.25115.43x -=＞100……………………………………………………2分 ∴2009年“义博会”的成交金额突破了百亿元大关．………………………3分20．（1） 4 ， 6 …………………………………………………（每空1分，共2分）（2） 24 ， 120 ………………………………………………（每空1分，共2分）(图略)…………………………………………………………………………………3分（3）32÷80=0.4……………………1分 0.4×2485=994答：今年参加航模比赛的获奖人数约是994人．………………………………3分21．解：（1）∵∠BOE =60° ∴∠A ＝12∠BOE ＝ 30°……………………2分（2）在△ABC 中 ∵1cos 2C =∴∠C =60°…1分又∵∠A ＝30° ∴∠ABC =90°∴AB BC ⊥……2分 ∴BC 是⊙O 的切线……………3分（3）∵点M 是AE 的中点 ∴OM ⊥AE ………………………………………1分在Rt △ABC 中∵BC = ∴AB=tan 60BC ︒==6……2分 ∴OA =32AB = ∴OD =12OA =32 ∴MD =32………………………3分22．解：（1）在2y kx =+中，令0x =得2y = ∴点D 的坐标为（0，2）………2分（2）∵ AP ∥OD ∴Rt △P AC ∽ Rt △DOC …………………………………1分∵12OC OA = ∴13OD OC AP AC == ∴AP =6…………………………2分又∵BD =624-= ∴由S △PBD =4可得BP =2…………………………3分 ∴P (2，6) …………4分把P (2，6)分别代入2y kx =+与my x=可得一次函数解析式为：y =2x +2…………………………………………………5分反比例函数解析式为：12y x=………………………………………………6分（3）由图可得x ＞2…………………………2分23．解: （1）=∠EBF 30°...............................1分 Q F C ∠= 60°..................................2分（2）QFC ∠=60°.....................................1分不妨设BP, 如图1所示∵∠BAP=∠BAE+∠EAP=60°+∠EAP ∠EAQ=∠QAP+∠EAP=60°+∠EAP∴∠BAP=∠EAQ ..........................................2分在△ABP 和△AEQ 中 AB=AE ，∠BAP=∠EAQ ， AP=AQ ∴△ABP ≌△AEQ （SAS ）.........................3分 ∴∠AEQ=∠ABP=90°...............................4分∴∠BEF 180180906030AEQ AEB =︒-∠-∠=︒-︒-︒=︒∴QFC ∠=EBF BEF ∠+∠=3030︒+︒=60°…………………………............5分图2ABEQ PF CG 图1ACB EQF P H(事实上当BP时，如图2情形，不失一般性结论仍然成立，不分类讨论不扣分）(3)在图1中，过点F 作FG ⊥BE 于点G∵△ABE 是等边三角形 ∴BE=AB=32，由（1）得=∠EBF 30° 在Rt △BGF中，2BE BG == ∴BF=2cos30BG=︒∴EF =2.......1分 ∵△ABP ≌△AEQ ∴QE=BP=x ∴QF =QE ＋EF 2x =+................2分过点Q 作QH ⊥BC ，垂足为H在Rt △QHF 中，3sin 60(2)y QH QF x ==︒=+（x ＞0）即y 关于x 的函数关系式是：y x =+.......................................................3分 24．解：（1）对称轴：直线1x =……………………………………………………..… 1分解析式：21184y x x =-或211(1)88y x =--……………………………….2分顶点坐标：M （1，18-）……….…………………………………………..3分（2）由题意得 213y y -=2221221111118484y y x x x x -=--+=3……………………………………..1分得：212111()[()]384x x x x -+-=①…………….………………….……2分12122(11)3()62x x s x x -+-⨯3==+-得：1223sx x +=+ ②….………………………………………..………..3分把②代入①并整理得：2172x x s-=(S ＞0) (事实上，更确切为S ＞66)4分当36s =时，2121142x x x x +=⎧⎨-=⎩ 解得：1268x x =⎧⎨=⎩(注：S ＞0或S ＞66不写不扣分) 把16x =代入抛物线解析式得13y = ∴点A 1（6，3）………5分（3）存在………………………………………………………………….…..……1分解法一：易知直线AB 的解析式为3342y x =-，可得直线AB 与对称轴的交点E 的坐标为31,4⎛⎫- ⎪⎝⎭∴BD =5，DE =154，DP =5－t ，DQ = t当PQ ∥AB 时，DQ DPDE DB=51554t t -=得 157t =………2分下面分两种情况讨论: 设直线PQ 与直线AB 、x 轴的交点分别为点F 、G①当0<157t <时，如图1-1 ∵△FQE ∽△F AG ∴∠FGA ＝∠FEQ ∴∠DPQ ＝∠DEB 易得△DPQ ∽△DEB ∴DQ DPDB DE=∴51554t t -= 得201577t => ∴207t =(舍去)…………………………3分 ② 当157<18t <3时，如图1-2∵△FQE ∽△F AG ∴∠F AG ＝∠FQE∵∠DQP ＝∠FQE ∠F AG ＝∠EBD∴∠DQP ＝∠DBE 易得△DPQ ∽△DEB∴DQ DPDB DE=∴51554t t -=， ∴207t =∴当207t =秒时，使直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称轴围成的三角形相似………………………………4分(注:未求出157t =能得到正确答案不扣分) 解法二：可将284x x y =-向左平移一个单位得到2188x y =-,再用解法一类似的方法可求得2172x x S ''-= , 1(5,3)A ', 207t =∴2172x x S -=1(6,3)A , 207t =.图1-1。

义乌中考数学试卷真题答案

---义乌市中考数学试卷真题答案一、选择题（每题3分，共30分）1. 若a、b、c是等差数列，且a+c=2b，则b的值为（）A. 1B. 2C. 3D. 4答案：B2. 下列函数中，定义域为全体实数的是（）A. y = √(x+1)B. y = 1/xC. y = x^2D. y = |x|答案：C3. 在△ABC中，若∠A=30°，∠B=45°，则sinC的值为（）A. √3/2B. 1/2C. √2/2D. 1答案：C4. 若函数f(x) = x^2 - 4x + 3在区间[1,3]上单调递增，则f(2)的值为（）A. 1B. 2C. 3D. 4答案：A5. 已知等比数列{an}的前三项分别为1，a，a^2，若公比q=√2，则数列的第10项an为（）A. 2^8B. 2^9C. 2^10D. 2^11答案：D6. 在平面直角坐标系中，点P(2,3)关于直线y=x的对称点为（）A. (2,3)B. (3,2)C. (3,-2)D. (-2,3)答案：B7. 若等差数列{an}的前n项和为S_n，公差为d，则S_10=（）A. 5(a_1 + a_10)B. 5(a_1 + a_9)C. 10(a_1 + a_10)D. 10(a_1 + a_9)答案：A8. 已知一元二次方程x^2 - 5x + 6 = 0的两根为x_1和x_2，则(x_1 + x_2)^2的值为（）A. 25B. 30C. 35D. 40答案：A9. 在△ABC中，若∠A=60°，∠B=45°，则△ABC的周长与面积之比为（）A. 1:√3B. 1:2C. 2:1D. 2:√3答案：C10. 若函数f(x) = ax^2 + bx + c在区间[-1,1]上恒大于0，则a、b、c的取值范围为（）A. a>0, b=0, c>0B. a>0, b=0, c<0C. a<0, b=0, c>0D. a<0, b=0, c<0答案：A二、填空题（每题5分，共20分）11. 已知等差数列{an}的第一项a_1=3，公差d=2，则第10项a_10=______。

浙江省义乌市2010年初中毕业生学业考试数学试题

浙江省义乌市2010年初中毕业生学业考试数学试题参考公式：二次函数y =ax 2+bx +c 图象的顶点坐标是)44,2(2ab ac a b --．一、选择题（10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，） 1．－2的相反数是（ ▲ ）A ．2B ．－2C ．－D ． 2．28 cm 接近于（ ▲ ） A ．珠穆朗玛峰的高度B ．三层楼的高度C ．姚明的身高D ．一张纸的厚度3．下列运算正确．．的是（ ▲ ） A ．321ab ab -= B ．426x x x =C ．235()x x = D ．x x x 232=÷4．下列几何图形中，即是中心对称图形又是轴对称图形的是（ ▲ ）A ．正三角形B ．等腰直角三角形C ．等腰梯形D ．正方形 5．下列长度的三条线段能组成三角形的是（ ▲ ）A ．1、2、3.5B ．4、5、9C ．20、15、8D ．5、15、86．如图，直线CD 是线段AB 的垂直平分线，P 为直线CD 上的一点，已知线段P A =5，则线段PB 的长度为（ ▲ ）A ．6B ．5C ．4D ．3 7．如下左图所示的几何体的主视图是（ ▲ ）8．下列说法不正确．．．的是（ ▲ ） A ．一组邻边相等的矩形是正方形 B ．对角线相等的菱形是正方形 C ．对角线互相垂直的矩形是正方形D ．有一个角是直角的平行四边形是正方形9．小明打算暑假里的某天到上海世博会一日游,上午可以先从台湾馆、香港馆、韩国馆中随机选择一个馆, 下午再从加拿大馆、法国馆、俄罗斯馆中随机选择一个馆游玩．则小明恰好上午选中台湾馆,下午选中法国馆这两个场馆的概率是（ ▲ ）A ．19B ．13C ．23 D ．2910．如图，将三角形纸片ABC 沿DE 折叠，使点A 落在BC 边上的点F 处，且DE ∥BC ，下列结论中，一定正确．．的个数是（ ▲ ） ①BDF ∆是等腰三角形 ②BC DE 21=③四边形ADFE 是菱形 ④2BDF FEC A ∠+∠=∠ A ．1 B ．2 C ．3 D ．4 二、填空题（本题有6小题，每小题4分，共24分）ABCDEFABCD PA ．B ．C ．D ．121211．从26个英文字母中任意选一个，是C 或D 的概率是 ▲ ． 12．在直角三角形中，满足条件的三边长可以是 ▲ ．(写出一组即可)13．已知直线l 与⊙O 相切，若圆心O 到直线l 的距离是5，则⊙O 的半径是 ▲ ．14．改革开放后，我市农村居民人均消费水平大幅度提升．下表是2004年至2009年我市农村居民人均食品消费支出的统计表（单位：元）．则这几年我市农村居民人均食品消费支出的中位数是 ▲ 元，极差是 ▲ 元．15．课外活动小组测量学校旗杆的高度．如图，当太阳光线与地面成30°角时，测得旗杆AB 在地面上的投影BC 长为24米，则旗杆AB 的高度约是 ▲ 米．（结果保留3个有效数字，3≈1.732）16．（1）将抛物线y 1＝2x 2向右平移222= ▲ ；（2）如图，P 是抛物线y 2对称轴上的一个动点，直线x ＝t 平行于y轴，分别与直线y ＝x 、抛物线y 2交于点A 、B ．若△ABP 是以点A 或点B 为直角顶点的等腰直角三角形，求满足条件的t 的值，则t ＝ ▲ ．三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）17．（1）计算：1tan 45⎪-°（2）化简：244222x x x x x -+--- 18．（1）解不等式： 32x -≥21x +（2）解分式方程： 22122x x x +=+19．我市举办的“义博会”是国内第三大展会，从1995年以来已成功举办了15届.（1）1995年“义博会”成交金额为1.01亿元,1999年“义博会”成交金额为35.2亿元,求1999年的成交金额比1995年的增加了几倍? (结果精确到整数)（2）2000年“义博会”的成交金额与2009年的成交金额的总和是153.99亿元,且2009年的成交金额是2000年的3倍少0.25亿元，问2009年“义博会”的成交金额是否突破了百亿元大关?20．“知识改变命运，科技繁荣祖国”．我市中小学每年都要举办一届科技运动会．下图为我市某校2009年参加科技运动会航模比赛（包括空模、海模、车模、建模四个类别）的参赛人数统计图：空模某校2009年航模比赛参赛人数扇形统计图x某校2009年航模比赛参赛人数条形统计图（1）该校参加车模、建模比赛的人数分别是 ▲ 人和 ▲ 人；（2）该校参加航模比赛的总人数是 ▲ 人，空模所在扇形的圆心角的度数是 ▲ °，并把条形统计图补充完整；（温馨提示：作图时别忘了用0.5毫米及以上的黑色签字笔涂黑）（3）从全市中小学参加航模比赛选手中随机抽取80人，其中有32人获奖. 今年我市中小学参加航模比赛人数共有2485人，请你估算今年参加航模比赛的获奖人数约是多少人?21．如图，以线段AB 为直径的⊙O 交线段AC 于点E ，点M 是AE 的中点，OM 交AC 于点D ，60BOE ∠=°，1cos 2C =，BC = （1）求A ∠的度数；（2）求证：BC 是⊙O 的切线；（3）求MD 的长度．22．如图，一次函数2y kx =+的图象与反比例函数my x=的图象交于点P ，点P 在第一象限．P A ⊥x 轴于点A ，PB ⊥y 轴于点B ．一次函数的图象分别交x 轴、y 轴于点C 、D ，且S △PBD =4，12OC OA =．（1）求点D 的坐标；（2）求一次函数与反比例函数的解析式；（3）根据图象写出当0x >时，一次函数的值大于反比例函数的值的x 的取值范围.23．如图1，已知∠ABC =90°，△ABE 是等边三角形，点P 为射线BC 上任意一点（点P 与点B 不重合），连结AP ，将线段AP 绕点A 逆时针旋转60°得到线段AQ ，连结QE 并延长交射线BC 于点F . （1）如图2，当BP =BA 时，∠EBF = ▲ °，猜想∠QFC = ▲ °；OBACEM D（2）如图1，当点P 为射线BC 上任意一点时，猜想∠QFC 的度数，并加以证明；（3）已知线段AB =32，设BP =x ，点Q 到射线BC 的距离为y ，求y 关于x 的函数关系式．24．如图1，已知梯形OABC ，抛物线分别过点O （0，0）、A （2，0）、B （6，3）．（1）直接写出抛物线的对称轴、解析式及顶点M 的坐标；（2）将图1中梯形OABC 的上下底边所在的直线OA 、CB 以相同的速度同时向上平移，分别交抛物线于点O 1、A 1、C 1、B 1，得到如图2的梯形O 1A 1B 1C 1．设梯形O 1A 1B 1C 1的面积为S ，A 1、 B 1的坐标分别为（x 1，y 1）、（x 2，y 2）．用含S 的代数式表示2x －1x ，并求出当S =36时点A 1的坐标；（3）在图1中，设点D 坐标为（1，3），动点P 从点B 出发，以每秒1个单位长度的速度沿着线段BC 运动，动点Q 从点D 出发，以与点P 相同的速度沿着线段DM 运动．P 、Q 两点同时出发，当点Q 到达点M 时，P 、Q 两点同时停止运动．设P 、Q 两点的运动时间为t ，是否存在某一时刻t ，使得直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称轴．．．围成的三角形相似？若存在，请求出t 的值；若不存在，请说明理由．浙江省2010年初中毕业生学业考试（义乌市卷）数学参考答案和评分细则一、选择题(本题有10小题，每小题3分，共30分)图1 图2ABE Q PF C图1ACE QF P 图2二、填空题(本题有6小题，每小题4分，共24分)11.11312. 3、4、5（满足题意的均可） 13. 5 14. 2304，1112 （每空2分） 15． 13.9 16．（1）2(x －2)2 或2288x x -+ (2分) （2）3、12分．对一个给0.5分，得2分的要全对，其余有错不倒扣分）三、解答题(本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分) 17. 解：（1）原式=1+2－1 (算对一项或两项给1分，全对2分) …………2分 =2………3分（2）原式=2442x x x -+-……1分 =2(2)2x x --…………2分 =2x -…………3分18. 解：（1）32x x -≥21+……2分得 x ≥3 ……3分（2）222124x x x +=+…1分41x =……2分 14x =…………2.5分经检验14x =是原方程的根…………………3分 19. 解：（1）（35.2－1.01）÷1.01≈34 答：1999年的成交金额比1995年约增加了34倍………3分（2）设2000年成交金额为x 亿元，则2009年成交金额为（3x －0.25）亿元 30.25153.9x x +-=………1分解得：x =38.56 ∴30.25115.43x -=＞100…………2分 ∴2009年“义博会”的成交金额突破了百亿元大关．………………………3分 20．（1） 4 ， 6 …………（每空1分，共2分）（2） 24 ， 120 ……（每空1分，共2分） (图略)……3分（3）32÷80=0.4………1分 0.4×2485=994答：今年参加航模比赛的获奖人数约是994人．………………………………3分21．解：（1）∵∠BOE =60° ∴∠A ＝12∠BOE ＝ 30°……………………2分（2）在△ABC 中 ∵1cos 2C = ∴∠C =60°…1分又∵∠A ＝30°∴∠ABC =90°∴AB BC ⊥……2分 ∴BC 是⊙O 的切线……………3分（3）∵点M 是AE 的中点 ∴OM ⊥AE ………………………………………1分在Rt △ABC 中∵BC = ∴AB=tan 60BC ︒=6……2分 ∴OA =32AB = ∴OD =12OA =32 ∴MD =32………………………3分22．解：（1）在2y kx =+中，令0x =得2y = ∴点D 的坐标为（0，2）………2分（2）∵ AP ∥OD ∴Rt △P AC ∽ Rt △DOC ………1分 ∵12OC OA = ∴13OD OC AP AC == ∴AP =6……………2分又∵BD =624-= ∴由S △PBD =4可得BP =2……3分∴P (2，6) …………4分把P (2，6)分别代入2y kx =+与my x=可得一次函数解析式为：y =2x +…5分反比例函数解析式为：12y x=……………6分（3）由图可得x ＞2…………2分23．解: （1）=∠EBF 30° (1)分 Q F C ∠= 60°..............2分（2）QFC ∠=60°..........1分不妨设BP , 如图1所示∵∠BAP=∠BAE+∠EAP=60°+∠EAP ∠EAQ=∠QAP+∠EAP=60°+∠EAP∴∠BAP=∠EAQ ................2分在△ABP 和△AEQ 中 AB=AE ，∠BAP=∠EAQ ， AP=AQ ∴△ABP ≌△AEQ （SAS ）.............3分 ∴∠AEQ=∠ABP=90°..............4分 ∴∠BEF 180180906030AEQ AEB =︒-∠-∠=︒-︒-︒=︒ ∴QFC ∠=EBF BEF ∠+∠=3030︒+︒=60°…......5分(事实上当BP 时，如图2情形，不失一般性结论仍然成立，不分类讨论不扣分） (3)在图1中，过点F 作FG ⊥BE 于点G ∵△ABE 是等边三角形∴BE=AB=32，由（1）得=∠EBF 30° 在Rt △BGF 中，2BEBG ==∴BF=2cos30BG=︒ ∴EF =2.......1分 ∵△ABP ≌△AEQ ∴QE=BP=x∴QF =QE ＋EF 2x =+................2分过点Q 作QH ⊥BC ，垂足为H 在Rt △QHF 中，3sin 60(2)y QH QF x ==︒=+（x ＞0）即y 关于x 的函数关系式是：2y x =+.......................................................3分 24．解：（1）对称轴：直线1x =……..… 1分解析式：21184y x x =-或211(1)88y x =--…….2分顶点坐标：M （1，18-）………..3分（2）由题意得 213y y -=2221221111118484y y x x x x -=--+=3………..1分得：212111()[()]384x x x x -+-=①………2分12122(11)3()62x x s x x -+-⨯3==+- 得：1223sx x +=+ ②….…………..3分图2 ABEQP F C G 图1 ACBEQF H把②代入①并整理得：2172x x s-=(S ＞0) (事实上，更确切为S ＞66)4分当36s =时，2121142x x x x +=⎧⎨-=⎩ 解得：1268x x =⎧⎨=⎩(注：S ＞0或S ＞66不写不扣分)把16x =代入抛物线解析式得13y = ∴点A 1（6，3）………5分（3）存在………..……1分解法一：易知直线AB 的解析式为3342y x =-，可得直线AB 与对称轴的交点E 的坐标为31,4⎛⎫- ⎪⎝⎭∴BD =5，DE =154，DP =5－t ，DQ = t当PQ ∥AB 时，DQ DPDE DB=51554t t -=得 157t =………2分下面分两种情况讨论: 设直线PQ 与直线AB 、x 轴的交点分别为点F 、G ①当0<157t <时，如图1-1 ∵△FQE ∽△F AG ∴∠FGA ＝∠∴∠DPQ ＝∠DEB 易得△DPQ ∽△DEB ∴DQ DPDB DE=∴51554t t -= 得201577t => ∴207t =(舍去)…………3分 ②当157<18t <3时，如图1-2∵△FQE ∽△F AG ∴∠F AG ＝∠FQE ∵∠DQP ＝∠FQE ∠F AG ∴∠DQP ＝∠DBE 易得△DPQ ∽△DEB ∴DQ DP DB DE =∴51554t t -=， ∴207t = ∴当207t =秒时，使直线PQ 、直线AB 、x 轴围成的三角形与直线PQ 、直线AB 、抛物线的对称轴围成的三角形相似………………………………4分 (注:未求出157t =能得到正确答案不扣分)解法二：可将284x x y =-向左平移一个单位得到2188x y =-,再用解法一类似的方法可求得 2172x x S ''-= , 1(5,3)A ', 207t = ∴2172x x S -= 1(6,3)A , 207t =.图1-1。

浙江2010年初中毕业生学业考试义乌卷

浙江省2010年初中毕业生学业考试（义乌市卷）科学试题卷考生须知：1.全卷共8页，有4大题。

满分为150分，考试时间120分钟。

2.本卷答案必须做在答题纸的相应位置上，做在试题卷上无效。

3.请考生将姓名、准考证号填写在答题卡的对应位置上。

并认真核准条形码上的姓名、准考证号。

请用2B铅笔在“答题纸”上将你认为正确的选项对应的小方框涂黑、涂满。

一、选择题（本题有20小题，每小题3分，共60分。

浙江省金华市2010年中考数学试卷及答案(word版)

浙江省2010年初中毕业生学业考试（金华卷）数学试题卷考生须知：1•全卷共三大题,24小题，满分为120分.考试时间为100分钟，本次考试采用开卷形式•2•全卷分为卷I （选择题）和卷n （非选择题）两部分，全部在答题纸上作答•卷I的答案必须用2B铅笔填涂；卷n的答案必须用黑色字迹钢笔或签字笔写在答题纸相应的位置上•3•请用黑色字迹钢笔或签字笔在答题纸上先填写姓名和准考证号4•作图时，可先使用2B铅笔，确定后必须使用黑色字迹的钢笔或签字笔描黑5•本次考试不得使用计算器•卷I说明：本卷共有1大题，10小题，共30分•请用2B铅笔在答题纸上将你认为正确的选项对应的小方框涂黑、涂满•一、选择题（本题有10小题,每小题3分，共30分）1•在-3 , - 3 , —1, 0这四个实数中，最大的是（▲）A. -3B. — 3C. —1D. 02. 据报道，5月28日参观2010上海世博会的人数达35.6万•用科学记数法表示数35.6万是（▲）1 4 5A . 3.56 氷0 B. 3.56 X0 C . 3.56 X04D. 35.6 氷03. 在平面直角坐标系中，点P （—1 , 3）位于（▲）A.第一象限B.第二象限C.第三象限D.第四象限4. 下图所示几何体的主视图是（▲）正面5.小明的讲义夹里放了大小相同的试卷共 12页，其中语文4页、数学2页、英语6页,他随ABCD说明：本卷共有2大题，14小题，共90分.请用黑色字迹钢笔或签字笔将答案写在答题纸相应位的置上.二、填空题（本题有6小题,每小题4分，共24分）11. 分解因式x 2 -9 = ▲.112. 分式方程—1的解是 ▲.x —213. 如果半径为3cm 的O O 1与半径为4cm 的O O 2内切，那么两圆的圆心距Oe ^ ▲cm. 14 •如图，在平面直角坐标系中，若A ABC 与Z\A 1B 1C 1关于E 点成中心对称，则对称中A.B. C.D. 6. 7. 机地从讲义夹中抽出 1页，抽出的试卷恰好是数学试卷的概率为（ 1 1 1 A.B.C.-236如图，△ABC 内接于O O ,/ A=40 °,则/ B0C 的度数为（A. 20 °B. 40°C. 60°如果a _3b =「3，那么代数式5 -a 3b 的值是（▲A . 0 C . 5▲)1D.—12▲)9. 已知抛物线▲）A.最小值如图，若A y =ax 2是实数 bx c 的开口向下,顶点坐标为（ —3）,那么该抛物线有B.最大值—3C.最小值D.最大值2 a 在数轴上对应的点，则关于 a , — a , 1的大小关系表示正确的是A . a v 1 v — aB . a v — a v1C .1v — a v a D .—a v a v 1A 0 1(第9题图)10.如图，在等腰梯形对角线 AC 丄BC ,/ B = 60o , BC = 2cm ,则梯形的面积为（▲）: 2A . 3\3 cm2B . 6 cm— 2C . 6. 3 cm 2D . 12 cm▲)ABCD 中，AB // CD ,心15. 若二次函数y 二「x 2，2x k 的部分图象如图所示，则关于-x 2 2x k =0 的一个解 x 1 =3，另一个解 x 2 =▲16. 如图在边长为 2的正方形 ABCD 中，E ，F , O 分别是AB ，CD ，AD 的中点,圆心，以OE 为半径画弧EF. P 是…上的一个动点，连结OP ，并延长OP 交线段BC 于点K ，过点P 作O O 的切线，分别交射线 AB 于点M ，交直线BC 于点G. 若匹=3，则BK = ▲.BM三、解答题（本题有8小题，共66分，各小题都必须写出解答过程 17. （本题6分）计算：3 .27 -4cos30 °18. （本题6分）如图，在 △KBC 中，D 是BC 边上的点（不与 B , C 重合），F , E 分别是AD 及其延长线上的点，CF // BE •请你添加一个条件，使不再标注或使用其他字母），并给出证明.（1）你添加的条件是：_▲_;X 的一元二次方程△BDE CDF （不再添加其它线段,E 点的坐标是（第15题图）以O 为BAFDCE '（第18题（2）证明:19. （本题6分）在一个阳光明媚、清风徐来的周末，小明和小强一起到郊外放风筝•他们把风筝放飞后，将两个风筝的引线一端都固定在地面上的C处（如图）.现已知风筝A的引线（线段AC）长20m，风筝B的引线（线段BC）长24m，在C处测得风筝A的仰角为60 °风筝B的仰角为45°（1）试通过计算，比较风筝A与风筝B谁离地面更高?（2）求风筝A与风筝B的水平距离.(精确到0.01 m ;参考数据:sin45 °.707,cos45 "0.707,tan45 =1,sin60 ° " 0.866s60 =0.5,tan60 ° " 1.7)220. （本题8分）已知二次函数y=ax2+ bx—3的图象经过点 A （2, - 3）, B （- 1, 0）.（1）求二次函数的解析式；（2）填空：要使该二次函数的图象与x轴只有一个交点，应把图象沿y轴向上平移▲ 个单位.21. （本题8分）如图，AB是O O的直径，C是上莒的中点，CE丄AB于E, BD交CE于点F.(1) 求证：CF = BF;(2) 若CD = 6, AC = 8,则O O的半径为CE的长是▲.22. （本题10分）一方有难，八方支援.2010年4月14日青海玉树发生7.1级强烈地震，给玉树人民造成了巨大的损失•灾难发生后，实验中学举行了爱心捐款活动，全校同学纷纷拿出自的零花钱，踊跃捐款支援灾区人民•小慧对捐款情况进行了抽样调查,的捐款数据，把数据进行分组、列频数分布表后，绘制了频数分布直方图•图中从左到右各长方形高度之比为3 ： 4 ： 5 : 7 : 1 (如图).(1)捐款20元这一组的频数是 ▲;(2)40名同学捐款数据的中位数是▲;(3) 若该校捐款金额不少于 34500元，请估算该校捐款同学的人数至少有多少名？抽取了 40名同40名同学捐款的频数分布直(第22题23. （本题10分）已知点P 的坐标为（m , 0），在x 轴上存在点Q （不与P 点重合），以PQ 为边作2正方形PQMN ，使点M 落在反比例函数y = 的图像上.小明对上述问题进行了探究，x发现不论m 取何值，符合上述条件的正方形只有两个，且一个正方形的顶点 M 在第四象限，另一个正方形的顶点M !在第二象限.（1 ）如图所示，若反比例函数解析式为 y= ， P 点坐标为（1，x出一符合条件的一个正方形 PQMN ， PQ 1M 1N 1，并写出点M !的坐标；（温馨提示：作图时，别忘了用黑色字迹的钢笔或签字笔描黑喔！）M 1的坐标是 ▲（2）请你通过改变 P 点坐标，对直线 M 1 M 的解析式y = kx + b 进行探究可得 k =▲, 若点P 的坐标为（m , 0 ）时，则b = ▲;（3）依据⑵的规律，如果点P 的坐标为（6,0）,请你求出点M 1和点M 的坐标.24.（本题12分）0），图中已画请你在图中画出符合条件的另一个正方形24. 如图，把含有30。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

数学试题
一、选择题（本大题共12小题，每小题3分，共36分）
1、下列计算正确的是（）
（A ）5322x x x =+ （B ）632x x x =⋅ （C ）623)(x x -=- （D ）336x x x =÷
2、若02|2|=+--a a ，则a 的取值范围是（）
（A ）2≤a （B ）2<a （C ）2≥a （D ）2>a
3、用换元法解方程x x x x +=
++2221，如果设y x x =+2，那么原方程可变形成的整式方程为（）
（A ）y
y 21=+ （B ）022=--y y （C ）022=+-y y （D ）022=-+y y
4、已知菱形ABCD 的两条对角线分别为8cm 和6cm ，那么菱形的一个锐角的正弦值为（）
（A ）0.60 （B ）0.96 （C ）0.80 （D ）0.28
5、在计算样本方差的公式])10()10()10[(20
1222212--+-=n x x x s 中，可得出样本的容量为（）
（A ）10 （B ）20 （C ）200 （D ）不能确定
6、将一长方形纸片按如图的方式折叠，BC 和BD
为折痕，则∠CBD 的度数为（）
（A ）6
0° （B ）75°
（C ）90° （D ）95°
7、若直线A （a ，6）、B （2，a ）、C （0，2）三点
在同一条直线上，则a 的值为（）
（A ）4或－2 （B ）4或－１（C ）－4或1 （D ）－4或2
8、已知1x 与2x 是方程012=--x x 的两根，则根为
11x 和2
1x 的一元二次方程为
( )
(A)012=+-y y (B) 012=++y y
(C) 012=-+y y (D) 0122=--y y
9、如图，A 、B 、C 、D 是⊙O 上四点，且D 是弧AB 的中点，CD
交OB 于E ，∠AOB ＝100°，∠OBC ＝75°，则∠OEC 等于（）
（A ）155° （B ）105° （C ）100° D 、80°
10、已知012=-+x x ，012=-+y y ，且y x ≠，则y x xy ++的值为（）
（A ）2 （B ）－2 （C ）－1 （D ）0
11、如图，⊙O 的弦AB 垂直于直径MN ，C 为垂足，若
OA ＝5cm ，下面四个结论中可能成立的是（）
（A ）AB ＝12cm （B ）OC ＝6cm
（C ）MN ＝8cm （D ）AC ＝2.5cm
12、如图，两个同心圆，过大圆上一点A 作小圆的割线交
小圆于B 、C 两点，且A B ·AC ＝4，则图中圆环的面积为（）
（A ）π4 （B ）3π
（C ）2π （D ）π
二、填空题（本大题共6小题，每小题4分，共24分）
13、若二次三项式142
-+-a x x 在实数范围内能够分解因
式，则a 。

14、如果把某种100元的商品先涨价10%再降价10%后售出，
那么其售价应为元。

15、如图，在△ABC 中，DE ∥BC ，EF ∥AB ，且DE ＝2cm ，
BD ＝CF ＝3cm 。

则AD ＝ cm 。

16、半径为5cm 的⊙O 中，长为8cm 的弦的中点的轨迹是：。

17、如果数据1x ，2x …n x 的平均数为x ，方差为2s 。

那么新数据b ax +1，b ax +2…b ax n +的平均数为，方差为。

18、锥角为60°,底面半径为2的圆锥的侧面积为。

三、（本大题共2小题，每小题5分，共10分）
19、计算|38|30cot 30sin 23212132
+-︒+︒+--⎪⎭
⎫ ⎝⎛-
20、解方程21
33311322=-+-+-x x x x
四、（本大题共3小题，每小题7分，共21分）
21、如图，已知∠1＝∠2，BC ＝EF 。

求证：△AB C ≌△DEF
（1）图中的有一个已知条件被墨水覆盖，请补
上：。

（2）完成此题的证明。

22、明星中学开展了“环境与人
类生
存”为主题的研讨活动，活动之一是对我们的生存环境进行社会调查，并对学生的调查报告进行评比。

初三·3班将本班50篇学生调查报告得分进行整理（成绩均为整数），
根据以上信息回答下列问题：
（1）补全频率分布表和频率分布直方图。

（2）该班90分以上（含90分）的调查报告共有篇。

（3）该班被评为优秀等级（80分及80分以上）的调查报告占%。

23、如图，自卸车车厢的一个侧面
是矩形ABCD，AB＝3米，BC＝0.5米，
车厢底部距地面1.2米，卸车时，车厢
倾斜的角度为60°，问此时车厢的最高
点A距地面多少米？（精确到1米）
五、（本大题共2小题，每小题9分，共18分）
24、如图，已知：AC切⊙O于C点，CP为⊙O直径，AB切⊙O于D，且与CP的延长线交于B点，若BD＝2BP，求证：(1)PC＝3BP；(2)AC＝PC
25、某商场销售一批名牌服装，平均每天可售出20件，每件赢利40元，为了扩大销售，增加赢利，尽快减少库存；商场决定采取适当的降价措施，经调查发现，如果每件服装每降价1元，商场平均每天可多售出2件，（1）若商场平均每天要赢利1200元，每件服装应降价多少元？（2）每件服装应降价多少元，商场平均每天赢利最多？
六、（本大题共1小题，共11分
26、如图已知，直线)0(343>+=
k k x y 与x 轴、y 轴分别交于A 、B 两点，点P 是线段AB 的中点，抛物线c bx x y ++-=28
3经过A 、P 、O 三点。

（1）求过点A 、P 、O 的抛物线解析式；
（2）在x 轴上方（1）中所得的抛物线上，是否存在一点Q ，使∠QAO ＝45°，如果有，求出Q 点的坐标，如果不存在，请说明理由。

（3）求出△PAO 的面积。