三角形五心与向量 - 360文档中心

完整版三角形的五心向量结论证明

三角形的五心向量结论证明1. O是RP2R的重心UJU uuir umr rOp OP, OP3 0(其中a,b,c 是PP2P3 三边)P2 PP3uu uur uur r证明：充分性：OR OF2 OP30 O是PP2F3的重心uuu uir uur r uur uur uur uuur uur若OR OP，OP3 0 ，则O R OP2 OR，以OR，OF2OP1P3 ' P2，设OP3与RP2交于点P3，则F3为RF2的中点，有即O,R, P,p四点共线，故PP2P3的中线，同理,uur uuuOP3 OP3 ，为邻边作平行四边形uurOP1uur uuur,OP2OP3，得PO, P2O亦为PP2P3的中线，所以，O为的重心。

2•在ABC中，给uurADuur uuuAB AC ,等于已知AD是ABC 中BC边的中线；————uur* △ ABC中AB AC 一定过BC的中点，通过△ABC的重心luuAPuuBP*PUG1 uuu(AB31 uuu-(BA31 uur -(PAuurAC),uurBC),P为VABC的重心uur uirPB PC)uuu uu uur uur uur urir uur uur uur uur uuu uuu uuu uurPG PA AG PB BG PC CG 3PG (AG BG CG) (PA PB PC)-G是厶ABC的重心uur uuu uuu r UU uur uuu r 亦uur uuu uuu uuu-GA GB GC = 0 AG BG CG : =0，即3PG PA PB PCG ABC的重心（P是平面上任意点）.证明（反之亦然（证略））uurPBuirPC).uur 1 uur 由此可得PG (PA3S*若O是ABC的重心，则BOC S AOC S AOB1SS ABC3uuu umrAPgBC 0 2. uuu uuirBPgAC 0则0是厶ABC 的垂心证明：由 OA '\BC 3 = 003 +CA J ,得 -0?)3 = OB \COC -OA )2 ,所以.■ .' ■''"。

必修4-向量-三角形的五心

设D为AB的中点 .
PA BC ( PD DA) BC
P A
DA BC
B
D
C
2 2 1 5 1 ( AC AB ) ( AC AB ) ( AB AC ) 2 2 2
问题4 : 在ABC中,已知AB 3, AC 2, 点H , P分别是ABC的垂心和外心, 求 PH BC .
三角形“五心”向量形式的充要条件设O为ABC所在平面上一点，角 A、B、C所对边长分别为a、b、c，则：
2 2 2
（ 1）O为ABC的外心 OA OB OC ；
（2）O为ABC的重心 OA OB OC 0
（3）O为ABC的垂心 OA OB OB OC OC OA;
问题2 : 点P为ABC的外心 , | AB | 3, | AC | 2, 求 AP BC的值.
P A
r 2 uuu r2 1 uuu 5 ( AC - AB ) B 2 2
D
C
问题3 : 在ABC 中, AB 3, AC 2, P是 BC中垂线上任一点, 则 PA BC ____ .
（4）O为ABC的内心 a OA b OB c OC 0
（5）O为ABC的A的旁心 a OA b OB c OC
问题1 : 在ABC中, AB 3, AC 2, P是BC中点, 则 AP BC ____ .
r 2 uuu r2 1 uuu 5 ( AC - AB ) 2 2
PH BC ( PA AH ) BC
PA BC AH BC PA BC PA ( AC AB)
A
AP AC AP AB

高考数学专题突破：三角形的五心与向量【精编版】

高考数学专题突破：三角形的五心与向量一、外心1.定义：三角形的三条边的垂直平分线交于一点,这点称为三角形的外心(外接圆圆心)．三角形的外心到三角形的三个顶点距离相等，都等于三角形的外接圆半径．AB CO2.性质：① 锐角三角形的外心在三角形内；直角三角形的外心在斜边中点；钝角三角形的外心在三角形外． ②三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合。

③OA=OB=OC=R④∠BOC=2∠BAC，∠AOB=2∠ACB，∠COA=2∠CBA⑤S△ABC=abc/4R⑥||||||==(或222O O O ==)⑦C 2sin :B 2sin :A 2sin AOB sin AOC sin BOC sin S S S A OB A OC BOC =∠∠∠=∆∆∆：：：：故0OC C 2sin OB B 2sin OA A 2sin =++二、内心1.定义：三角形的三条内角平分线交于一点,这点称为三角形的内心(内切圆圆心)．三角形的内心到三边的距离相等,都等于三角形内切圆半径．IK H E F AB C M2.性质：内切圆半径r 的计算：设三角形面积为S ，r=2S/(a+b+c)特别的，在直角三角形中,有 r =12(a +b －c )． ②∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/2③S△ABC=[(a+b+c)r]/2 (r 是内切圆半径)④O 是内心ABC ∆的充要条件是0|CB ||CA ||BC ||BA |AC |AB |=-⋅=-⋅=-⋅引进单位向量，使条件变得更简洁。

如果记CA ,BC ,AB 的单位向量为321e ,e ,e ，则刚才O 是ABC ∆内心的充要条件可以写成 0)e e (O )e e (O )e e (O 322131=+⋅=+⋅=+⋅ ⑤O 是ABC ∆内心的充要条件也可以是0OC c OB b OA a =++⑥若O 是ABC ∆的内心，则c b a S S S A OB A OC BOC ：：：：=∆∆∆ 故 0OC C sin OB B sin OA A sin 0OC c OB b OA a =++=++或;⑦||||||0AB PC BC PA CA PB P ++=⇔ ABC ∆的内心; ⑧向量()(0)||||AC AB AB AC λλ+≠ 所在直线过ABC ∆的内心(是BAC ∠的角平分线所在直线)；三、垂心2.性质：①锐角三角形的垂心在三角形内；直角三角形的垂心在直角顶点上；钝角三角形的垂心在三角形外② 垂心O 关于三边的对称点，均在△ABC 的外接圆上 ③△ABC 中，有六组四点共圆，有三组(每组四个)相似的直角三角形，且AO·OD=BO ·OE=CO ·OF④ H 、A 、B 、C 四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。

专题(3)三角形“五心”与向量相关知识

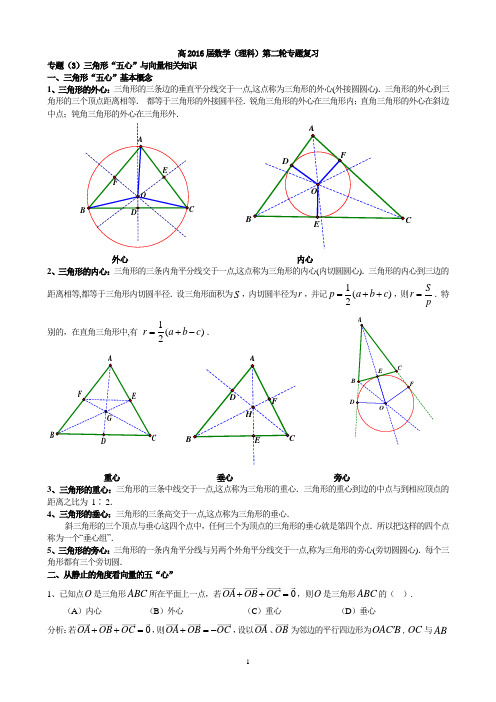
高2016届数学（理科）第二轮专题复习专题（3）三角形“五心”与向量相关知识一、三角形“五心”基本概念1、三角形的外心：三角形的三条边的垂直平分线交于一点,这点称为三角形的外心(外接圆圆心)．三角形的外心到三角形的三个顶点距离相等．都等于三角形的外接圆半径．锐角三角形的外心在三角形内；直角三角形的外心在斜边中点；钝角三角形的外心在三角形外．外心内心2、三角形的内心：三角形的三条内角平分线交于一点,这点称为三角形的内心(内切圆圆心)．三角形的内心到三边的距离相等,都等于三角形内切圆半径．设三角形面积为S ，内切圆半径为r ，并记1()2p a b c =++，则S r p =．特别的，在直角三角形中,有 1()2r a b c =+-．重心垂心旁心3、三角形的重心：三角形的三条中线交于一点,这点称为三角形的重心．三角形的重心到边的中点与到相应顶点的距离之比为 1∶ 2．4、三角形的垂心：三角形的三条高交于一点,这点称为三角形的垂心．斜三角形的三个顶点与垂心这四个点中，任何三个为顶点的三角形的垂心就是第四个点．所以把这样的四个点称为一个“垂心组”．5、三角形的旁心：三角形的一条内角平分线与另两个外角平分线交于一点,称为三角形的旁心(旁切圆圆心)．每个三角形都有三个旁切圆．二、从静止的角度看向量的五“心”1、已知点O 是三角形ABC 所在平面上一点，若0OA OB OC ++=，则O 是三角形ABC 的（）.（A ）内心（B ）外心（C ）重心（D ）垂心分析：若0OA OB OC ++=，则OA OB OC +=-，设以OA 、OB 为邻边的平行四边形为OAC B ',OC 与ABB交于点D ,则D 为AB 的中点,由OA OB OC '+=得,OC OC '=-,即C 、O 、D 、C '四点共线,故CD 为ABC ∆的中线,所以O 在边AB 的中线上,同理可证, O 在边AC 的中线上, O 在边BC 的中线上所以O 是三角形ABC 的重心.2、已知点O 是三角形所在平面上一点，若OA OB OB OC OC OA ⋅=⋅=⋅,则O 是三角形ABC 的（）.（A ）内心（B ）外心（C ）重心（D ）垂心分析:由OA OB OB OC ⋅=⋅得,()0OB OA OC ⋅-=,即0OB CA ⋅=,所以,OB CA ⊥同理可证：,OC AB OA BC ⊥⊥,所以O 是ABC ∆的垂心.3、已知点O 是三角形所在平面上一点，若0aOA bOB cOC ++=,则O 是三角形ABC 的（）.（A ）内心（B ）外心（C ）重心（D ）垂心分析::若0aOA bOB cOC ++=,又因为,,OB OA AB OC OA AC =+=+则()0a b c OA bAB cAC ++++=.所以||||bc AB AC AO a b c AB AC ⎛⎫=+ ⎪++⎝⎭,因为||AB AB 与||AC AC 分别表示AB 和AC 方向上的单位向量,设AP =||AB AB +||AC AC ,则AP 平分BAC ∠.又AO 、AP 共线，知AO 平分BAC ∠。

O向量表示三角形的五心

O向量表示三角形的五心Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】向量代表三角形的“心”向量是代数与几何的主要桥梁，这种联系不仅体现在平面直角坐标系中点的坐标与向量的坐标之间的对应关系，还体现在由向量表达式和向量的几何中意义与平面几何中三角形的“心”之间的密切联系。

一、重心例1 已知O 是△ABC 的重心，求证：0=++OC OB OA 。

解：如图，由已知，O 是△ABC 的重心。

连结AO 、BO 、CO ，使它们的延长线与BC 、CA 、AB 分别交于点D 、E 、F 。

)(3232CA DC DA OA +==，)(3232AB EA EB OB +==， )(3232BC FB FC OC +==，所以BC BC AB CA FB EA DA OC OB OA 21(32)(32=+++++=++0)2121=++=+++++BC AB CA BC AB CA AB CA 。

例2 已知A 、B 、C 是不共线的三点，O 是△ABC 内一点，若0=++OC OB OA ，则O 是△ABC 的重心。

证：∵0=++OC OB OA ，∴)(OC OB OA +-=，即OC OB +是与OA 方向相反且长度相等的向量。

以OB 、OC 为相邻的两边作平行四边形BOCD ，则OC OB OD +=，∴OA OD -=。

在平行四边形BOCD 中，设BC 与OD 相交于E ，EC BE =，则ED OE =。

∴点O 是△ABC 的重心例3 在凸六边形A 1A 2A 3A 4A 5A 6中，各边A 1A 2、A 2A 3、A 3A 4、A 4A 5、A 5A 6、A 6A 1的中点依次为M 1、M 2、M 3、M 4、M 5、M 6。

求证：△M 1M 3M 5与△M 2M 4M 6的重心重合。

证：设△M 1M 3M 5的重心为G ，则对于平面内的任一点O ，有)(31531OM OM OM OG ++=。

三角形五心的向量表达式

三角形五星的向量表达式1若P是△ABC的重心PA+PB+PC=02若P是△ABC的垂心PA•PB=PB•PC=PA•PC(内积）3若P是△ABC的内心aPA+bPB+cPC=0(abc是三边）4若P是△ABC的外心|PA|²=|PB|²=|PC|²（AP就表示AP向量|AP|就是它的模）5AP=λ（AB/|AB|+AC/|AC|),λ∈[0,+∞)则直线AP经过△ABC内心6AP=λ（AB/|AB|cosB+AC/|AC|cosC),λ∈[0,+∞)经过垂心7AP=λ（AB/|AB|sinB+AC/|AC|sinC),λ∈[0,+∞）或AP=λ(AB+AC),λ∈[0,+∞)经过重心8.若aOA=bOB+cOC,则0为∠A的旁心,∠A及∠B,C的外角平分线的交点【以下是一些结论的有关证明】1.O是三角形内心的充要条件是aOA向量+bOB向量+cOC向量=0向量充分性：已知aOA向量+bOB向量+cOC向量=0向量，延长CO交AB于D，根据向量加法得：OA=OD+DA,OB=OD+DB,代入已知得：a(OD+DA)+b(OD+DB)+cOC=0,因为OD与OC共线，所以可设OD=kOC,上式可化为(ka+kb+c)OC+(aDA+bDB)=0向量,向量DA与DB共线，向量OC与向量DA、DB不共线，所以只能有：ka+kb+c=0，aDA+bDB=0向量,由aDA+bDB=0向量可知：DA与DB的长度之比为b/a,所以CD为∠ACB的平分线，同理可证其它的两条也是角平分线。

必要性：已知O是三角形内心,设BO与AC相交于E，CO与AB相交于F，∵O是内心∴b/a=AF/BF，c/a=AE/CE过A作CO的平行线，与BO的延长线相交于N，过A作BO的平行线，与CO的延长线相交于M，所以四边形OMAN是平行四边形根据平行四边形法则，得向量OA=向量OM+向量ON=(OM/CO)*向量CO+(ON/BO)*向量BO=(AE/CE)*向量CO+(AF/BF)*向量BO=(c/a)*向量CO+(b/a)*向量BO∴a*向量OA=b*向量BO+c*向量CO∴a*向量OA+b*向量OB+c*向量OC=向量02.已知△ABC为斜三角形,且O是△ABC所在平面上的一个定点,动点P满足向量OP=OA+入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},求P点轨迹过三角形的垂心OP=OA+入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},OP-OA=入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},AP=入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},AP•BC=入{(AB•BC/|AB|＾2*sin2B)+AC•BC/(|AC|＾2*sin2C)}, AP•BC=入{|AB|•|BC|cos(180°-B)/(|AB|＾2*sin2B)+|AC|•|BC| cosC/(|AC|＾2*sin2C)},AP•BC=入{-|AB|•|BC|cos B/(|AB|＾2*2sinB cos B)+|AC|•|BC| cosC/(|AC|＾2*2sinC cosC)},AP•BC=入{-|BC|/(|AB|*2sinB)+|BC|/(|AC|*2sinC)},根据正弦定理得：|AB|/sinC=|AC|/sinB,所以|AB|*sinB=|AC|*sinC ∴-|BC|/(|AB|*2sinB)+|BC|/(|AC|*2sinC)=0，即AP•BC=0，P点轨迹过三角形的垂心3.OP=OA+λ(AB/(|AB|sinB)+AC/(|AC|sinC))OP-OA=λ(AB/(|AB|sinB)+AC/(|AC|sinC))AP=λ(AB/(|AB|sinB)+AC/(|AC|sinC))AP与AB/|AB|sinB+AC/|AC|sinC共线根据正弦定理：|AB|/sinC=|AC|/sinB,所以|AB|sinB=|AC|sinC,所以AP与AB+AC共线AB+AC过BC中点D，所以P点的轨迹也过中点D，∴点P过三角形重心。

三角形五心的向量表达式

三角形五星的向量表达式1若P是△ABC的重心PA+PB+PC=02若P是△ABC的垂心PA•PB=PB•PC=PA•PC(内积）3若P是△ABC的内心aPA+bPB+cPC=0(abc是三边）4若P是△ABC的外心|PA|²=|PB|²=|PC|²（AP就表示AP向量|AP|就是它的模）5AP=λ（AB/|AB|+AC/|AC|),λ∈[0,+∞)则直线AP经过△ABC内心6AP=λ（AB/|AB|cosB+AC/|AC|cosC),λ∈[0,+∞)经过垂心7AP=λ（AB/|AB|sinB+AC/|AC|sinC),λ∈[0,+∞）或AP=λ(AB+AC),λ∈[0,+∞)经过重心8.若aOA=bOB+cOC,则0为∠A的旁心,∠A及∠B,C的外角平分线的交点【以下是一些结论的有关证明】1.O是三角形内心的充要条件是aOA向量+bOB向量+cOC向量=0向量充分性：已知aOA向量+bOB向量+cOC向量=0向量，延长CO交AB于D，根据向量加法得：OA=OD+DA,OB=OD+DB,代入已知得：a(OD+DA)+b(OD+DB)+cOC=0,因为OD与OC共线，所以可设OD=kOC,上式可化为(ka+kb+c)OC+(aDA+bDB)=0向量,向量DA与DB共线，向量OC与向量DA、DB不共线，所以只能有：ka+kb+c=0，aDA+bDB=0向量,由aDA+bDB=0向量可知：DA与DB的长度之比为b/a,所以CD为∠ACB的平分线，同理可证其它的两条也是角平分线。

必要性：已知O是三角形内心,设BO与AC相交于E，CO与AB相交于F，∵O是内心∴b/a=AF/BF，c/a=AE/CE过A作CO的平行线，与BO的延长线相交于N，过A作BO的平行线，与CO的延长线相交于M，所以四边形OMAN是平行四边形根据平行四边形法则，得向量OA=向量OM+向量ON=(OM/CO)*向量CO+(ON/BO)*向量BO=(AE/CE)*向量CO+(AF/BF)*向量BO=(c/a)*向量CO+(b/a)*向量BO∴a*向量OA=b*向量BO+c*向量CO∴a*向量OA+b*向量OB+c*向量OC=向量02.已知△ABC为斜三角形,且O是△ABC所在平面上的一个定点,动点P满足向量OP=OA+入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},求P点轨迹过三角形的垂心OP=OA+入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},OP-OA=入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},AP=入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},AP•BC=入{(AB•BC/|AB|＾2*sin2B)+AC•BC/(|AC|＾2*sin2C)}, AP•BC=入{|AB|•|BC|cos(180°-B)/(|AB|＾2*sin2B)+|AC|•|BC| cosC/(|AC|＾2*sin2C)},AP•BC=入{-|AB|•|BC|cos B/(|AB|＾2*2sinB cos B)+|AC|•|BC| cosC/(|AC|＾2*2sinC cosC)},AP•BC=入{-|BC|/(|AB|*2sinB)+|BC|/(|AC|*2sinC)},根据正弦定理得：|AB|/sinC=|AC|/sinB,所以|AB|*sinB=|AC|*sinC ∴-|BC|/(|AB|*2sinB)+|BC|/(|AC|*2sinC)=0，即AP•BC=0，P点轨迹过三角形的垂心3.OP=OA+λ(AB/(|AB|sinB)+AC/(|AC|sinC))OP-OA=λ(AB/(|AB|sinB)+AC/(|AC|sinC))AP=λ(AB/(|AB|sinB)+AC/(|AC|sinC))AP与AB/|AB|sinB+AC/|AC|sinC共线根据正弦定理：|AB|/sinC=|AC|/sinB,所以|AB|sinB=|AC|sinC,所以AP与AB+AC共线AB+AC过BC中点D，所以P点的轨迹也过中点D，∴点P过三角形重心。

(完整版)用向量表示三角形的五心

用向量表示三角形的五心如图，ABC ∆中，E 是AC 上一点，F 是AB 上一点，且ln EC AE l m FB AF ==,（通分总可以把异分母分数化为同分母分数）.连接BE 、CF 交于点D ，确定点D 的位置. 解:设.,b AC a AB == DF CD DE BD μλ==,由定比分点的向量表达式,得b a m l m a m l m b AB ml m AC AF AC AD b n l n a AC nl n AB AE AB AD μμμμμμμμμμμλλλλλλλλ++++=++++=+⋅+++=++=++++=+⋅+++=++=11))(1())(1(11)(1111))(1(11)(1111 ⎪⎪⎩⎪⎪⎨⎧+=+=⎪⎪⎩⎪⎪⎨⎧+=++++=+∴n m l m n l n l n m l m μλμλλμμλ解得11))(1())(1(11 代入得:b nm l n a n m l m AD +++++= 设O 是平面上任意一点,则有.,,OA OC b OA OB a OA OD AD -=-=-= 上式可化为:OC nm l n OB n m l m OA n m l l OD ++++++++= (*) 由(*)式出发,可得三角形五心的向量表达式.(1).若BE 、CF 是∆ABC 两边的中线,交点D 是三角形的重心.则1,1====FBAF l m EC AE l n )(31OC OB OA OD ++=(2)若BE 、CF 是∆ABC 两内角的平分线，交点D 是三角形的内心.则ab BC AC FB AF l m ac BC AB EC AE l n ======, 代入(*)式得:.OC cb ac OB c b a b OA c b a a OD ++++++++=(3)若BE 、CF 是∆ABC 两边上的高，交点D 是三角形的垂心. A B C D E F则Aa B bFBAF l m A a C c C a A c EC AE l n cos cos ,cos cos cos cos ===⋅⋅==同理. OC Cc B b A a C cOB C c B b A a B b OA C c B b A a A a OD cos cos cos cos cos cos cos cos cos cos cos cos ++++++++=∴ (4)若BE 、CF 的交点D 是∆ABC 的外心,即三边中垂线的交点,则有:DA=DB=DC. 根据正弦定理有:A C A A C C BDC A ADBC CBE C BE EBA A BE EC AE l n 2sin 2sin cos sin cos sin )(21sin sin )(21sin sin sin sin sin sin =⋅⋅=∠-⋅∠-⋅=∠⋅∠⋅==ππ 同理AB FB AF l m 2sin 2sin == OC CB AC OB C B A B OA C B A A OD 2sin 2sin 2sin 2sin 2sin 2sin 2sin 2sin 2sin 2sin 2sin 2sin ++++++++=∴(1) 重心O:0=++OC OB OA(2) 内心O:0=++OC c OB b OA a(3) 垂心O:0cos cos cos =++OC Cc OB B b OA A a (4) 外心O:02sin 2sin 2sin =⋅+⋅+⋅OC C OB B OA A(5) A 对的旁心O:0=++-OC c OB b OA a ; B 对的旁心O:0=+-OC c OB b OA aC 对的旁心O:0=-+OC c OB b OA a . E。

向量五心终极版本(老师)

向量与三角形内心、外心、重心、垂心、旁心知识的交汇一、五心的概念介绍(1)重心——中线的交点:重心将中线长度分成2:1; (2)垂心——高线的交点:高线与对应边垂直;(3)内心——角平分线的交点(内切圆的圆心):角平分线上的任意点到角两边的距离相等; (4)外心——中垂线的交点(外接圆的圆心):外心到三角形各顶点的距离相等。

(5) 旁心——三角形两条外角平分线与一条内角平分线的交点二、 “重心”的向量风采【命题1】已知G 就是ABC △所在平面上的一点,若0GA GB GC ++=u u u r u u u r u u u r,则G 就是ABC △的重心.如图⑴、A'A【命题2】已知O 就是平面上一定点,AB C ，，就是平面上不共线的三个点,动点P 满足()OP OA AB AC λ=++u u u r u u u r u u u r u u u r,(0)λ∈+∞，,则P 的轨迹一定通过ABC △的重心、【解析】由题意()AP AB AC λ=+u u u r u u u r u u u r ,当(0)λ∈+∞，时,由于()AB AC λ+u u u r u u u r 表示BC 边上的中线所在直线的向量,所以动点P 的轨迹一定通过ABC △的重心,如图⑵、二、“垂心”的向量风采【命题3】 P 就是ABC △所在平面上一点,若⋅=⋅=⋅,则P 就是ABC △的垂心.【解析】由PA PB PB PC ⋅=⋅u u u r u u u r u u u r u u u r ,得()0PB PA PC ⋅-=u u u r u u u r u u u r ,即0PB CA ⋅=u u u r u u u r ,所以PB CA u u u r u u u r⊥.同理可证PC AB u u u r u u u r ⊥,PA BC u u u r u u u r⊥.∴P 就是ABC △的垂心.如图⑶、【命题4】已知O 就是平面上一定点,A B C ，，就是平面上不共线的三个点,动点P 满足cos cos AB AC OP OA AB B AC C λ⎛⎫ ⎪=++ ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r,(0)λ∈+∞，,则动点P 的轨迹一定通过ABC △的垂心. 【解析】由题意cos cos AB AC AP AB B AC C λ⎛⎫ ⎪=+ ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r ,由于0cos cos AB AC BC AB B AC C ⎛⎫ ⎪+⋅= ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r, 即0cos cos AB BC AC BCBC CB AB B AC C⋅⋅+=-=u u u r u u u r u u u r u u u ru u u u r u u u u r u u u r u u u r,所以AP u u u r 表示垂直于BC uuu r 的向量,即P 点在过点A 且垂直于BC 的直线上,所以动点P 的轨迹一定通过ABC △的垂心,如图⑷、三、“内心”的向量风采【命题5】已知I 为ABC △所在平面上的一点,且AB c =,AC b =,BC a = .若0aIA bIB cIC ++=u u r u u r u u r,则I 就是ABC △的内心.AB ⋅u u u r ∴bc AB AC AI a b c AB AC ⎛⎫ ⎪=+ ⎪++⎝⎭u u u r u u u r u u r u u u r u u u r .∵AB AB u u u r u u ur 与AC ACu u u r u u u r 分别为AB u u u r 与AC u u u r 方向上的单位向量, ∴AI u u r与BAC ∠平分线共线,即AI 平分BAC ∠.同理可证:BI 平分ABC ∠,CI 平分ACB ∠.从而I 就是ABC △的内心,如图⑸、【命题6】已知O 就是平面上一定点,AB C ，，就是平面上不共线的三个点,动点P 满足图⑴ 图⑵图⑶ ABO CABAB AC OP OA AB AC λ⎛⎫ ⎪=++ ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r ,(0)λ∈+∞，,则动点P 的轨迹一定通过ABC △的内心. 【解析】由题意得AB AC AP AB AC λ⎛⎫ ⎪=+ ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r ,∴当(0)λ∈+∞，时,AP u u u r 表示BAC ∠的平分线所在直线方向的向量,故动点P 的轨迹一定通过ABC △的内心,如图⑹、四、“外心”的向量风采【命题7】已知O 就是ABC △所在平面上一点,若222OA OB OC ==u u u u r u u u u r u u u u r,则O 就是ABC △的外心.【解析】若222OA OB OC ==u u u r u u u r u u u r ,则222OA OB OC ==u u u r u u u r u u u r ,∴OA OB OC ==u u u r u u u r u u u r,则O 就是ABC△的外心,如图⑺。

向量与三角形五心证明及知识运用(精华版AAA)精品资料

（B
）
Ａ外心Ｂ内心 C 重心 D 垂心
2
2
12．在三角形 ABC 中，动点 P 满足： CA CB 2AB• CP ，则 P 点轨迹一定
通过△ABC 的：
（B）
Ａ外心Ｂ内心 C 重心 D 垂心
13.已知非零向量A→B与A→C满足(|AA→→BB|
A→C +|A→C|
)·B→C=0
且|AA→→BB|
分析：如图所示 ABC， D、E 分别为边 BC、AC 的
中点.
AB AC 2AD
OP OA 2 AD
B
OP OA AP
AP 2 AD AP // AD 点 P 的轨迹一定通过 ABC 的重心，即选 C .
A E
D
C
例 2、（03 全国理 4） O 是平面上一定点， A、B、C 是平面上不共线的三
PG
1 3
(PA
PB
PC)
G
为 ABC 的重心.
2、O 是 ABC 的垂心 OA OB OB OC OC OA ; 若 O 是 ABC (非直角三角形)的垂心，则 S BOC：S AOC：S AOB tan A：tan B：tan C
故 tan AOA tan BOB tan COC 0
4运用向量等式实数互化解与三角形有关的向量问题abocacobbcoaa重心b垂心c外心d内心5运用向量等式图形化解与三角形有关的向量问题acacababoaopa重心b垂心c外心d内心练习2已知为平面内一点abc平面上不共线的三点动点bcaboaopa重心b垂心c外心d内心13coscosacacababoaopa重心b垂心c外心d内心coscosacacababocobop则动点p一定过abc的a重心b垂心c外心d内心作直线与abac分别相交于两点且ac6作业1已知o是abcocoboaa重心b垂心c外心d内心2若abc的外接圆的圆心为o半径为1且ocoboaoboa是abc所在平面上的一点abc所对的过分别是a重心b垂心c外心d内心4已知p是abc所在平面内与不重合的一点满足apacaba重心b垂心c外心d内心ocoboaocoboa求证

向量与三角形的五心

重心性质
重心将顶点与对边中点连线，且三条中线都经过重心。
重心在几何问题中的应用
010203Fra bibliotek面积分割
重心将三角形面积分为三个相等的部分。
力的平衡
在静态平衡状态下，作用于三角形上的力矩与重心位置密切相关。
三角形不等式
通过重心可以推导三角形不等式，用于解决几何问题。
重心定理
定理内容
三角形的重心将中线分为 2:1的比例。
内心定理
• 内心定理：三角形的内心将三角形的三边分别延长，与相对角的延长线相交于一点，这三个交点与内心构成的三个线段相等。
05
向量与三角形的外心
外心定义与性质
外心定义
外心是三角形三边的垂直平分线的交点。
外心性质
外心到三角形三个顶点的距离相等，即外接圆的半径。外心到三角形三边的垂直平分线的交点。
证明方法
利用向量加法的平行四边形法则和向量的共线性。
应用场景
在几何、物理和工程领域中，重心定理都有广泛的应用。
03
向量与三角形的垂心
垂心定义与性质
垂心定义
三角形垂心是三条高线的交点，也是三角形三个顶点向对边所作的高线的交点。
垂心性质
三角形的垂心具有一些特殊的性质，如垂心到三角形三边的距离相等，且等于对边上的高的长度。此外，三角形的垂心也是三角形三个内角平分线的交点。
• 三角形的内心：内心是三角形三条内角平分线的交点，向量形式上表示为$\overrightarrow{I} = \frac{\overrightarrow{a} \cdot \overrightarrow{b} \cdot \overrightarrow{c}}{|\overrightarrow{a}| |\overrightarrow{b}| |\overrightarrow{c}|}$ ，其中$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$是三角形三边的向量。

三角形各个心的有关向量结论

三角形各个心的有关向量结论三角形是初中数学的重点之一，它们在几何的许多领域都有应用。

除了三条边之外，三角形还有很多其他有趣的属性和结论。

今天，我们将重点关注与三角形各个心的有关向量结论。

首先，让我们来介绍一下三角形的“心”。

一个三角形的“心”是它的重心、外心、内心、垂心和费马点。

这五个点都具有特殊的几何意义，它们与三角形的性质密切相关。

现在，我们来看一些关于这五个“心”的向量结论。

这些结论包括：1. 重心：三角形的三条中线的交点是三角形的重心。

向量表示为$$\overrightarrow{G}=\frac{1}{3}(\overrightarrow{A}+\overrigh tarrow{B}+\overrightarrow{C})$$其中，A、B、C分别是三角形的三个顶点的向量表示。

2. 外心：三角形外接圆的圆心是三角形的外心。

向量表示为$$\overrightarrow{O}=\frac{\overrightarrow{a}\times\overright arrow{b}+\overrightarrow{a}\times\overrightarrow{c}+\overrigh tarrow{b}\times\overrightarrow{c}}{2\overrightarrow{a}\cdot\o verrightarrow{b}\times\overrightarrow{c}}$$其中，a、b、c分别是三角形的三个边的向量表示。

3. 内心：三角形内切圆的圆心是三角形的内心。

向量表示为$$\overrightarrow{I}=\frac{a\overrightarrow{A}+b\overrightarr ow{B}+c\overrightarrow{C}}{a+b+c}$$其中，a、b、c分别是三角形的三个边的长度；A、B、C分别是三角形的三个顶点的向量表示。

4. 垂心：三角形的三条高线交于垂心，它与对应的顶点相连的线段垂直。

三角形的五心在向量的结论

三角形的五心在向量的结论三角形的五心是指三角形的外心、内心、垂心、重心和旁心。

这五个特殊的点在三角形中有着重要的几何性质和向量关系。

本文将通过向量的角度来探讨这五个特殊点之间的关系。

我们先来介绍一下五个特殊点。

外心是通过三角形三个顶点的垂直平分线的交点，它到三角形三个顶点的距离都相等。

内心是通过三角形三个边的角平分线的交点，它到三角形三个边的距离都相等。

垂心是通过三角形三个顶点与对边垂直的高的交点，它到三角形三个顶点的距离满足垂心定理。

重心是通过三角形三个顶点的中线的交点，它到三角形三个顶点的距离满足重心定理。

旁心是通过三角形的一条边的垂直平分线的延长线与对边的交点，它到三角形的一条边的距离相等。

现在，我们来探讨这五个特殊点之间的向量关系。

我们可以将三角形的顶点表示为向量A、B、C，那么外心O可以表示为向量O=（A+B+C）/3，内心I可以表示为向量I=（aA+bB+cC）/（a+b+c），垂心H可以表示为向量H=A+B+C，重心G可以表示为向量G=(A+B+C)/3，旁心J可以表示为向量J=(2A+B+C)/4。

根据向量的定义，我们可以得到以下结论：1. 外心O到三个顶点的向量和为零，即AO+BO+CO=0。

这是因为外心是通过三个顶点的垂直平分线的交点，所以它到三个顶点的距离相等，即向量AO=向量BO=向量CO，因此它们的和为零。

2. 内心I到三个边的向量和为零，即aIA+bIB+cIC=0。

这是因为内心是通过三个边的角平分线的交点，所以它到三个边的距离相等，即向量IA=向量IB=向量IC，因此它们的和为零。

3. 垂心H到三个顶点的向量和为零，即AH+BH+CH=0。

这是因为垂心是通过三个顶点与对边垂直的高的交点，所以它到三个顶点的距离满足垂心定理，即向量AH=向量BH=向量CH，因此它们的和为零。

4. 重心G到三个顶点的向量和为零，即AG+BG+CG=0。

这是因为重心是通过三个顶点的中线的交点，所以它到三个顶点的距离满足重心定理，即向量AG=向量BG=向量CG，因此它们的和为零。

三角形的五心向量结论证明

三角形的五心向量结论证明I.。

是时^月的重心U>函+茂+甌=6（其中。

力,C是月三边）证明：充分性：斑+而+兢=6=>。

是MEg的重心若勇+而+死=6,则op{+op2 = -dp.,以逐，死为邻边作平行四边形OPRE，设朗与交于点球，则g 为的中点，有如+死=两，得两=一两，即月,四点共线，故gP为△*吕月的中线，同理，氏0匸。

亦为△4^4的中线，所以，。

为的重心。

）,2•在AABC AD = ^ + AC等于己知AD是中BC边的中线：* AABC中而+花一定过※的中点，通过AABC的重心AP = -（AB + AC）,< 3nP为A ABCM重心BP = ^（BA + BC）,★PG=^（PA + PB + PC） = G ABC的重心（P是平面上任意点）.证明PG = PA + AG = PB+BG = PC+CG => 3PG =（AG + BG + CG）+（PA + PB+PC）•••G是△48C的重心GA + GB + GC = O => AG + BG + CG =0 :艮卩3西=旋+ 应+ 祐由此可得PG = ^（PA + PB + PC）.（反之亦然（证略））A * I»/-1 ^ABOC = =^A AOB = T^A-XBC*若。

是MBC的重心，则3"・8C = 0 “…工、2.________ => P为△人BCK垂心BP・AC = O* 点。

是的垂心<=> OP[ OR=O E O^=O^ OP1证明：。

是月的垂心<=> 死丄密，两职二0 =两（区-死） = 00死而二两函同理勇丄感。

O^ OP^OP^OR故当且仅当0P c0R,=0R10P i = 0P.0P i*。

是△奶C所在平面内一点岡 + BC = OC + BA = OB + AQ则0是左ABC的垂心*若H是Z\ABC（非直角三角形）的垂心,AP = AAB I cos B I AC I cos C | AB \ cos B \ AC |cosC_ I BC I -1 AB I cos（刀一B） * I BC \ -1 AC | cos C故tanA・用+tanB・丽+tanC・我=63.点。