排列组合专题之染色问题3
8、排列组合问题之涂色问题(四个方面)

排列组合问题之涂色问题(四个方面)一、区域涂色问题1、根据分步计数原理,对各个区域分步涂色,这是处理区域染色问题的基本方法。
例1、用5种不同的颜色给图中标①、②、③、④的各部分涂色,每部分只涂一种颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种?解析:先给①号区域涂色有5种方法;再给②号涂色有4种方法;接着给③号涂色方法有3种方法;由于④号与①号、②号不相邻,因此④号有4种涂法。
根据分步计数原理,不同的涂色方法有5434240⨯⨯⨯=种。
2、根据共用了多少种颜色讨论,分别计算出各种情形的种数,再用分类计数原理求出不同的涂色方法种数。
例2、4种不同的颜色涂在如图所示的6个区域,且相邻两个区域不能同色。
解析:依题意只能选用4种颜色,要分四类:㈠②与⑤同色、④与⑥同色,则有44A 种;㈡③与⑤同色、④与⑥同色,则有44A 种; ㈢②与⑤同色、③与⑥同色,则有44A 种;㈣③与⑤同色、②与④同色,则有44A 种; ㈤②与④同色、③与⑥同色,则有44A 种。
根据分类计数原理得涂色方法总数为445120A =。
例3、如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色。
现有4解析:依题意至少要用3种颜色。
①若用3种颜色,区域2与4必须同色, 区域3与5必须同色,故有34A 种;②若用4种颜色,则区域2与4同色,区域3与5不同色,有44A 种;或区域3与5同色,区域2与不同色,有4种。
共有4种。
根据分类计数原理得满足题意的着色方法共有3444272A A +=。
3、根据某两个不相邻区域是否同色分类讨论。
从某两个不相邻区域同色与不同色入手,分别计算出两种情形的种数,再用分类计数原理求出不同涂色方法总数。
例4、用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一种颜色,相邻两个区域涂不同的颜色,五种颜色可以反复使用,共有多少种不同的涂色方法?解析:可把问题分为三类:①四格涂不同的颜色,有34A 种;②有且仅有两个区域颜色相同,即只有 一组对角小方格涂相同的颜色。
排列组合中的染色问题

排列组合中的染色问题作者:林维祥来源:《学校教育研究》2018年第02期引言组合计数问题是组合数学的重要内容,也是竞赛数学不可或缺的重要组成部分,而染色问题是数学竞赛中常见的一类问题,也是与实际生活联系最为直接的内容. 若能顺利解决此类问题则其他排列组合问题也就迎刃而解了.解决组合计数问题的主要方法有枚举法、利用计数原理及基本公式、递推方法、容斥原理等,其中蕴含着分类讨论、转化和化归、函数与方程等数学思想。
在平时遇到的某些计数问题(如染色问题)看似排列组合类应用题,但又复杂万分,若从元素递增的角度考虑,建立递推数列就能迎刃而解.例:如图1所示,将一个城市划分为5个行政区域,现给地图着色,要求相邻区域不得使用同一种颜色,有4种不同颜色可供选择,不同的着色方法有多少?解:(1)先给B、D着相同的颜色,有种方法,再依次给A、C、E着色,有种方法,共有种方法;(2)先给B、D着不同颜色,有种方法,再依次给A、C、E着色,有种方法,共有种方法。
所以,不同的着色方法共有 + =72(种)。
例题中的图形我们可以将其抽象为图2,即把图形分成如图的五块,则改变图形至图3,即将图形分成n+1块,有命题1 如图3所示的一个图形被分成n+1块小块,现将其染色,要求相邻的小块不得使用同一种颜色,有四种颜色可供选择,则有种方法。
分析:如图3中第O块与每个小块都相邻,则其所涂的颜色必与剩余的任何一个小块的颜色不同;因此,当O块涂了四种颜色中的一种后,就只剩下三种颜色可供剩余的小块涂色,根据此分析,我们有如下证明:证明:第O小块可以从四种颜色中任意选一种有种,设n个小块区域、、… 的涂法总数为,整个图形的涂法总数为。
不难算出、;、。
现寻找的递推关系:当、、… 区域涂色完毕后,区域的涂色有两种情况:第一种情况:与颜色一样的涂法为,区域有2种涂色方法;第二种情况:与颜色不一样的涂法为,区域只有一种涂色方法。
命题2 如图3所示的一个图形被分成n+1块小块,现将其染色,要求相邻的小块不得使用同一种颜色,有m种颜色可供选择,则有种方法。
8、排列组合问题之涂色问题(四个方面)

排列组合问题之涂色问题(四个方面)一、区域涂色问题1、根据分步计数原理,对各个区域分步涂色,这是处理区域染色问题的基本方法。
例1、用5种不同的颜色给图中标①、②、③、④的各部分涂色,每部分只涂一种颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种?解析:先给①号区域涂色有5种方法;再给②号涂色有4种方法;接着给③号涂色方法有3种方法;由于④号与①号、②号不相邻,因此④号有4种涂法。
根据分步计数原理,不⨯⨯⨯=种。
同的涂色方法有54342402、根据共用了多少种颜色讨论,分别计算出各种情形的种数,再用分类计数原理求出不同的涂色方法种数。
例2、4种不同的颜色涂在如图所示的6个区域,且相邻两个区域不能同色。
解析:依题意只能选用4种颜色,要分四类:34、根据相间区域使用颜色分类讨论。
例5、如图,6个扇形区域A 、B 、C 、D 、E 、F ,现给这6个区域着色,要求同一区域涂同一种颜色,相邻的两个区域不得使用同一种颜色,现有4种不同的颜色可以反复使用,共有多少种不同的涂色方法?解析:①当相间区域A 、C 、E 着同一种颜 色时,有4种着色方法,此时B 、D 、F 各有3 种着色方法,共有4333108⨯⨯⨯=种方法。
②当相间区域A 、C 、E 着两种不同的颜色时,有2234C A 种着色方法,此时B 、D 、F有322⨯⨯种着色方法,共有2234322432C A ⨯⨯⨯=种方法。
③当相间区域A 、C 、E 着三种不同的颜色时有34A 种着色方法,此时B 、D 、F 各有2种着色方法,共有34222192A ⨯⨯⨯=种方法。
总计有108432192732++=种不同的涂色方法。
5、用数列递推公式解决扇形区域涂色问题。
例6、把一个圆分成()2n n ≥个扇形,每个扇形用红、白、蓝、黑四色之一染色,要求相邻扇形不同色,有多少种不同的染色方法?解析:设n 个扇形分别为1A 、2A 、、n A ,分成n 个扇形时的染色方法有n a 种,则①当2n =时1A 、2A 有2412A =种染色方法,即212a =。
排列组合中染色问题(教师用)
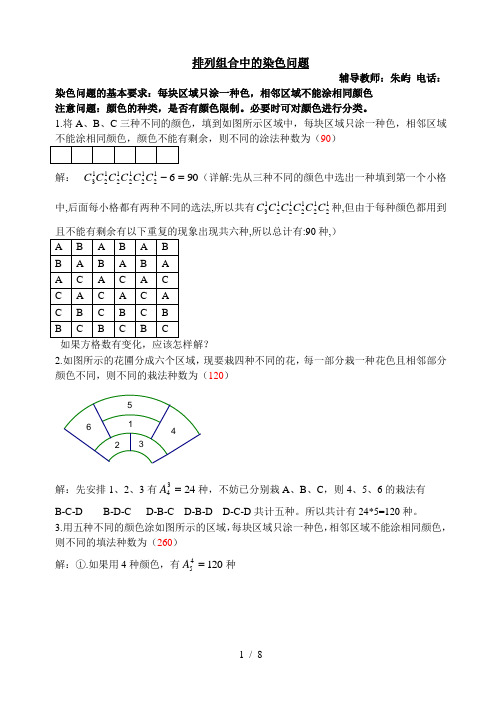
排列组合中的染色问题辅导教师:朱屿 电话:染色问题的基本要求:每块区域只涂一种色,相邻区域不能涂相同颜色 注意问题:颜色的种类,是否有颜色限制。
必要时可对颜色进行分类。
1.将A 、B 、C 三种不同的颜色,填到如图所示区域中,每块区域只涂一种色,相邻区域不能涂相同颜色,颜色不能有剩余,则不同的涂法种数为(90)解:906121212121213=-C C C C C C (详解:先从三种不同的颜色中选出一种填到第一个小格中,后面每小格都有两种不同的选法,所以共有121212121213C C C C C C 种,但由于每种颜色都用到且不能有剩余有以下重复的现象出现共六种,所以总计有:90种,)如果方格数有变化,应该怎样解? 2.如图所示的花圃分成六个区域,现要栽四种不同的花,每一部分栽一种花色且相邻部分颜色不同,则不同的栽法种数为(120)562341解:先安排1、2、3有2434=A 种,不妨已分别栽A 、B 、C ,则4、5、6的栽法有 B-C-D B-D-C D-B-C D-B-D D-C-D 共计五种。
所以共计有24*5=120种。
3.用五种不同的颜色涂如图所示的区域,每块区域只涂一种色,相邻区域不能涂相同颜色,则不同的填法种数为(260)解:①.如果用4种颜色,有12045=A 种1432②.如果用3种颜色,选色的1035=C ,填色方案有2*2*3=12种,共计10*12=120种,B BBC CCAAABC A③.用2色图,20225=⨯C ,综上共计120+120+20=260种。
4.用五种颜色涂如图所示的区域,有多少种不同的涂法?(180) 解:1432①.如果用3种颜色,603335=⨯A C ;②. .如果用4种颜色,有12045=A 种。
所以共计180种。
5.用六种广告色着色图中区域,每块区域只涂一种色,相邻区域不能涂相同颜色。
(480)1432解:4804456=⨯⨯⨯6.用n 种不同的颜色涂如图所示的区域,每块区域只涂一种色,相邻区域不能涂相同颜色,不同的图法种数为120种,则n=(120)。
高中数学《排列组合染色问题》典例讲解

排列组合染色问题的探究上饶县二中 徐 凯在任教高二数学教学时,有许多同学被排列组合题的灵活性所困惑,甚至有学生向我询问有没有公式之类的解决途径,每道题都去分析似乎很累。
其实就某些特殊的排列组合问题是可以抽象出数学模型来加以研究的,比如说下面我们所要提到的染色问题。
一、一个结论。
若把一个圆(除中间同心圆外的圆环部分)分成n 份( n > 1) , 每部分染一种颜色且相邻部分不能染同种颜色, 现有m (m > 1) 种不同颜色可供使用, 那么共有S)1()1()1(--+-=m m n n 种染色方法。
例:在一个圆形花坛种颜色花卉,现有4种颜色可供选择,要求相邻两个区域不同色,则共有多少种方法?解:从图中可以发现除同心圆部分外的圆环部分被分成了n=5份,因为有4种颜色可供选择,我们先给同心圆①染色有4种方法,那么圆环部分有3种颜色可供选择,即m=3,所以圆环部分共有S=()30232)13()1(1355=-=--+-种染色方法,从而整个圆形花坛共有120304=⨯种染色方法。
用常规方法同学们是否也能做到那么快和准确呢?二、结论的证明。
把圆(除中间同心圆部分)分成n 份( n > 1) , 每部分染一种颜色且相邻。
部分不能染同种颜色, 现有m (m > 1) 种不同颜色可供使用, 求不同的染色方法总数。
(1) 当m = 2时, n 为偶数时有2种栽种法,n 为奇数时无解。
(2) 当m > 2时设把圆分成的n 部分为n n T T T T T 、、、、1321...-。
开始时,1T 有m 种不同的染色法;1T 染好后, 2T 有m - 1 种染色法;21T T 、染好后,3T 也有m - 1种染色法; 这样依次下去, 染色的方法总数为1)1(--n m m 。
但是在这些染色方法中, 包括1-n T 与n T 染同种颜色的情况,若某种染色法使1-n T 与n T 同色, 拆去1-n T 与n T 的边界后, 就是分圆为n-1部分, 相邻部分染不同颜色的方法。
排列组合中的染色问题

排列组合中的染色问题作者:林维祥来源:《学校教育研究》2017年第14期引言组合计数问题是组合数学的重要内容,也是竞赛数学不可或缺的重要组成部分,而染色问题是数学竞赛中常见的一类问题,也是与实际生活联系最为直接的内容. 若能顺利解决此类问题则其他排列组合问题也就迎刃而解了.解决组合计数问题的主要方法有枚举法、利用计数原理及基本公式、递推方法、容斥原理等,其中蕴含着分类讨论、转化和化归、函数与方程等数学思想。
在平时遇到的某些计数问题(如染色问题)看似排列组合类应用题,但又复杂万分,若从元素递增的角度考虑,建立递推数列就能迎刃而解.例:如图1所示,将一个城市划分为5个行政区域,现给地图着色,要求相邻区域不得使用同一种颜色,有4种不同颜色可供选择,不同的着色方法有多少?解:(1)先给B、D着相同的颜色,有种方法,再依次给A、C、E着色,有种方法,共有种方法;(2)先给B、D着不同颜色,有种方法,再依次给A、C、E着色,有种方法,共有种方法。
所以,不同的着色方法共有 + =72(种)。
例题中的图形我们可以将其抽象为图2,即把图形分成如图的五块,则改变图形至图3,即将图形分成n+1块,有命题1 如图3所示的一个图形被分成n+1块小块,现将其染色,要求相邻的小块不得使用同一种颜色,有四种颜色可供选择,则有种方法。
分析:如图3中第O块与每个小块都相邻,则其所涂的颜色必与剩余的任何一个小块的颜色不同;因此,当O块涂了四种颜色中的一种后,就只剩下三种颜色可供剩余的小块涂色,根据此分析,我们有如下证明:分析:图4中的图形相对图3增加了n个外面的半圆,而外面的半圆的染色数目只与相邻的小块颜色有关(如的颜色只与有关,即与颜色不相同)。
当里面的小块已经染色完毕后,还有m-1种颜色可供选择,同理均有m-1种颜色可供选择。
所以根据乘法原理共有种方法。
从上可知,常规的方法不仅繁杂而且容易遗漏;但是若能熟练运用式(*)或(**),则问题就变得简单易解,而且在解题过程中不会出现重复或遗漏的情况。
最新高中数学《排列组合染色问题》典例讲解

排列组合染色问题的探究上饶县二中 徐 凯在任教高二数学教学时,有许多同学被排列组合题的灵活性所困惑,甚至有学生向我询问有没有公式之类的解决途径,每道题都去分析似乎很累。
其实就某些特殊的排列组合问题是可以抽象出数学模型来加以研究的,比如说下面我们所要提到的染色问题。
一、一个结论。
若把一个圆(除中间同心圆外的圆环部分)分成n 份( n > 1) , 每部分染一种颜色且相邻部分不能染同种颜色, 现有m (m > 1) 种不同颜色可供使用, 那么共有S)1()1()1(--+-=m m n n 种染色方法。
例:在一个圆形花坛种颜色花卉,现有4种颜色可供选择,要求相邻两个区域不同色,则共有多少种方法?解:从图中可以发现除同心圆部分外的圆环部分被分成了n=5份,因为有4种颜色可供选择,我们先给同心圆①染色有4种方法,那么圆环部分有3种颜色可供选择,即m=3,所以圆环部分共有S=()30232)13()1(1355=-=--+-种染色方法,从而整个圆形花坛共有120304=⨯种染色方法。
用常规方法同学们是否也能做到那么快和准确呢?二、结论的证明。
把圆(除中间同心圆部分)分成n 份( n > 1) , 每部分染一种颜色且相邻。
部分不能染同种颜色, 现有m (m > 1) 种不同颜色可供使用, 求不同的染色方法总数。
(1) 当m = 2时, n 为偶数时有2种栽种法,n 为奇数时无解。
(2) 当m > 2时设把圆分成的n 部分为n n T T T T T 、、、、1321...-。
开始时,1T 有m 种不同的染色法;1T 染好后, 2T 有m - 1 种染色法;21T T 、染好后,3T 也有m - 1种染色法; 这样依次下去, 染色的方法总数为1)1(--n m m 。
但是在这些染色方法中, 包括1-n T 与n T 染同种颜色的情况,若某种染色法使1-n T 与n T 同色, 拆去1-n T 与n T 的边界后, 就是分圆为n-1部分, 相邻部分染不同颜色的方法。
排列组合着色问题

排列组合着色问题————————————————————————————————作者:————————————————————————————————日期:排列组合专题之染色问题 【引例】引例1.在一个正六边形的6个区域栽种观赏植物,如右图,要求同一块中种同一种植物,相邻的两块种不同的植物.现有四种不同的植物可供选择,则有________种栽种方案.引例2.某城市在中心广场建造一个花圃,花圃分为6个部分(如图),现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有_____种.(以数字作答)【分析】首先栽种第1部分,有14C 种栽种方法;然后问题就转化为用余下3种颜色的花,去栽种周围的5个部分(如右图所示),此问题和引例1是同一题型,因此我们有必要对这一题型的解法做一深入探讨。
【剖析】为了深入探讨这一题型的解法,(1)让我们首先用m (m≥3)种不同的颜色(可供选择),去涂4个扇形的情形(要求每一个扇形着一种颜色,相邻扇形着不同颜色),如图所示以1和3(相间)涂色相同与否为分类标准:①1和3涂同一种颜色,有m 种涂法;2有m -1种涂法,4也有m -1种涂法,∴ 共有 (1)(1)m m m ⋅-⋅-种涂法。
②1和3涂不同种颜色,有2m A 种涂法;2有m -2种涂法,4也有m -2种涂法,∴ 共有 2(2)(2)m A m m ⋅-⋅-种涂法。
综合①和②,共有(1)(1)m m m ⋅-⋅-+2(2)(2)mA m m ⋅-⋅-432463m m m m =-+-种涂法。
(2)下面来分析引例1以A 、C 、E (相间)栽种植物情况作为分类标准:①A 、C 、E 栽种同一种植物,有4种栽法;B 、D 、F 各有3种栽法,∴ 共有 4×3×3×3=108 种栽法。
②A 、C 、E 栽种两种植物,有222432C C A 种栽法(24C 是4种植物中选出2种,23C 是A 、C 、E3个区域中选出2个区域栽种同一种植物,22A 是选出的2种植物排列),B 、D 、F 共有3×2×2 种栽法(注:若A 、C 栽种同一种植物,则B 有3 种栽法,D 、F 各有2种栽法),222432322432C C A ∴⨯⨯⨯=共有种栽法。
解决排列组合中涂色问题专题讲座(有详细答案)

解决排列组合中涂色问题的常见方法及策略专题讲座与涂色问题有关的试题新颖有趣,其中包含着丰富的数学思想。
解决涂色问题方法技巧性强且灵活多变,故这类问题的利于培养学生的创新思维能力、分析问题与观察问题的能力,有利于开发学生的智力。
本文拟总结涂色问题的常见类型及求解方法。
一、区域涂色问题1、 根据分步计数原理,对各个区域分步涂色,这是处理染色问题的基本方法。
例1、 用5种不同的颜色给图中标①、②、③、④的各部分涂色,每部分只涂一种颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种分析:先给①号区域涂色有5种方法,再给②号涂色有4种方法,接着给③号涂色方法有3种,由于④号与①、②不相邻,因此④号有4种涂法,根据分步计数原理,不同的涂色方法有5434240⨯⨯⨯=2、 根据共用了多少种颜色讨论,分别计算出各种出各种情形的种数,再用加法原理求出不同的涂色方法种数。
例2、(2003江苏卷)四种不同的颜色涂在如图所示的6个区域,且相邻两个区域不能同色。
分析:依题意只能选用4种颜色,要分四类: (1)②与⑤同色、④与⑥同色,则有44A ; (2)③与⑤同色、④与⑥同色,则有44A ; (3)②与⑤同色、③与⑥同色,则有44A ;①②③④ ⑤⑥(4)③与⑤同色、② 与④同色,则有44A ;(5)②与④同色、③与⑥同色,则有44A ; 所以根据加法原理得涂色方法总数为544A =120例3、(2003年全国高考题)如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着方法共有多少种 分析:依题意至少要用3种颜色1) 当先用三种颜色时,区域2与4必须同色, 2) 区域3与5必须同色,故有34A 种; 3) 当用四种颜色时,若区域2与4同色,4) 则区域3与5不同色,有44A 种;若区域3与5同色,则区域2与4不同色,有44A 种,故用四种颜色时共有244A 种。
排列组合中涂色问题

解决排列组合中涂色问题的常见方法及策略与涂色问题有关的试题新颖有趣,其中包含着丰富的数学思想。
解决涂色问题方法技巧性强且灵活多变,故这类问题的利于培养学生的创新思维能力、分析问题与观察问题的能力,有利于开发学生的智力。
本文拟总结涂色问题的常见类型及求解方法。
一、区域涂色问题1、 根据分步计数原理,对各个区域分步涂色,这是处理染色问题的基本方法。
例1、 用5种不同的颜色给图中标①、②、③、④的各部分涂色,每部分只涂一种颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种?分析:先给①号区域涂色有5种方法,再给②号涂色有4种方法,接着给③号涂色方法有3种,由于④号与①、②不相邻,因此④号有4种涂法,根据分步计数原理,不同的涂色方法有5434240⨯⨯⨯=2、 根据共用了多少种颜色讨论,分别计算出各种出各种情形的种数,再用加法原理求出不同的涂色方法种数。
例2、(2003卷)四种不同的颜色涂在如图所示的6个区域,且相邻两个区域不能同色。
分析:依题意只能选用4种颜色,要分四类:(1)②与⑤同色、④与⑥同色,则有44A ;(2)③与⑤同色、④与⑥同色,则有44A ;(3)②与⑤同色、③与⑥同色,则有44A ;(4)③与⑤同色、② 与④同色,则有44A ;(5)②与④同色、③与⑥同色,则有44A ;所以根据加法原理得涂色方法总数为544A =120例3、(2003年全国高考题)如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着方法共有多少种? 分析:依题意至少要用3种颜色1) 当先用三种颜色时,区域2与4必须同色, 2) 区域3与5必须同色,故有34A 种;① ②③ ④ ⑤ ⑥3) 当用四种颜色时,若区域2与4同色,4) 则区域3与5不同色,有44A 种;若区域3与5同色,则区域2与4不同色,有44A 种,故用四种颜色时共有244A 种。
由加法原理可知满足题意的着色方法共有34A +244A =24+2⨯24=723、 根据某两个不相邻区域是否同色分类讨论,从某两个不相邻区域同色与不同色入手,分别计算出两种情形的种数,再用加法原理求出不同涂色方法总数。
排列组合中的染色问题(学生版)

排列组合中的染色问题辅导教师:朱屿 电话:150********染色问题的基本要求:每块区域只涂一种色,相邻区域不能涂相同颜色;染色问题的基本方法:先选色后涂色;染色问题的注意事项;分清区域数量和可供选择的颜色种类。
必要时可以对颜色或区域进行分类。
1.将A 、B 、C 三种不同的颜色,填到如图所示区域中,每块区域只涂一种色,相邻区域不能涂相同颜色,三种颜色都用到,则不同的涂法种数为( 90种 )变式训练:1、如果方格数有变化,应该怎样解?2、如果颜色有变化呢?2.如图所示的花圃分成六个区域,现要栽四种不同的花,每一部分栽一种花色且相邻部分不种同颜色的花,则不同的栽法种数为(120种 )3.用五种不同的颜色涂如图所示的区域,每块区域只涂一种色,相邻区域不能涂相同颜色,则不同的填法种数为(260种)56234114324、2区域有3*3=9种涂法,所以总的涂法种数为A 52*(4+9)=260种。
4.用五种颜色涂如图所示的区域,每块区域只涂一种色,相邻区域不能涂相同颜色,有多少种不同的涂法?(180种)5.用六种广告色着色图中区域,每块区域只涂一种色,相邻区域不能涂相同颜色。
(480种)7.将一个四棱锥的每个顶点染上一种颜色,并且使同一条棱上的两端异色,若只有五种颜色可供选用,则不同的染色方案有多少种?(420种)14321432SCDB A8. 如图所示的花圃分成六个区域,现要栽四种不同的花,每一部分栽一种花色且相邻部分颜色不同,则不同的栽法种数为(120种 )解:同第2题。
9.一个地区有五个行政区域,现给地图着色,有4种颜色可供选用,每块区域只涂一种色,相邻区域不能涂相同颜色,则不同的涂法种数为( 72种)10. 用五种不同的颜色涂如图所示的区域,每块区域只涂一种色,相邻区域不能涂相同颜色,则不同的填法种数为(260种)11.用4种不同颜色给正方体1111D C B A ABCD 的六个面涂色,要求相邻的两个面涂不同的颜色,共有多少种不同的涂法(96种)14325614325b dc aD1C1B1A1C DB A12.1*6矩形长条中,涂红,黄,蓝三种颜色,每种颜色限涂两个格,相邻格不涂同一色,13.用六种不同的颜色涂如图所示的四个方格,要求最多使用三种颜色,相邻格不涂同一390 )14.在平面内,直线x=0,y=x ,分圆422=+y x 成四个区域,用五种不同的颜色给四个区域涂色,要求相邻的两个面涂不同的颜色,则不同的涂法种数为( 260)与第三题相类似。
排列组合中的染色问题(教师版)

排列组合中的染色问题辅导教师:朱屿 电话:150****8809染色问题的基本要求:每块区域只涂一种色,相邻区域不能涂相同颜色; 染色问题的基本方法:先选色后涂色;染色问题的注意事项;分清区域数量和可供选择的颜色种类。
必要时可以对颜色或区域进行分类。
1.将A 、B 、C 三种不同的颜色,填到如图所示区域中,每块区域只涂一种色,相邻区域不能涂相同颜色,三种颜色都用到,则不同的涂法种数为( 90种 )解:906121212121213=-C C C C C C (详解:先从三种不同的颜色中选出一种填到第一个小格中,后面每小格都有两种不同的选法,所以共有121212121213C C C C C C 种,但由于每种颜色都用到,所以总计有:(90种,) 变式训练:1、如果方格数有变化,应该怎样解?2、如果颜色有变化呢? 2.如图所示的花圃分成六个区域,现要栽四种不同的花,每一部分栽一种花色且相邻部分不种同颜色的花,则不同的栽法种数为(120种 )解:先安排六个区域的中1、2、3有2434=A 种,不妨已分别栽A 、B 、C ,则余下的区域4、5、6的栽法有B-C-D , B-D-C , D-B-C ,D-B-D ,D-C-D 共计五种。
所以共计有24*5=120种。
3.用五种不同的颜色涂如图所示的区域,每块区域只涂一种色,相邻区域不能涂相同颜色,则不同的填法种数为(260种)解法一:①.如果用4种颜色,有12045=A 种562341②.如果用3种颜色,选色有1035=C ,填色方案有2*2*3=12种,共计10*12=120种,③.用2色图,20225=⨯C ,综上共计120+120+20=260种。
解法二:从五种颜色中选出两种涂到1、3有A 52=20种,然后涂4区域,分为两种情况:不妨假设1、3涂的是A 、B ,如果4中涂B ,4、2区域有4种涂法;如果4区域不是B ,4、2区域有3*3=9种涂法,所以总的涂法种数为A 52*(4+9)=260种。
排列组合中涂色问题的常见方法及策略

排列组合中涂色问题的常见方法及策略排列组合中涂色问题的常见方法及策略与涂色问题有关的试题新颖有趣,其中包含着丰富的数学思想。
解决涂色问题方法技巧性强且灵活多变,故这类问题的利于培养学生的创新思维能力、分析问题与观察问题的能力,有利于开发学生的智力。
本专题总结涂色问题的常见类型及求解方法。
一、区域涂色问题1、根据分步计数原理,对各个区域分步涂色,这是处理染色问题的基本方法。
例1、用5种不同的颜色给图中标①、②、③、④的各部分涂色,每部分只涂一种颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种?①③④②分析:先给①号区域涂色有5种方法,再给②号涂色有4种方法,接着给③号涂色方法有 3 种,由于④号与①、②不相邻,因此④号有 4 种涂法,根据分步计数原理,不同的涂色方法有 5 4 3 4 2402、根据共用了多少种颜色讨论,分别计算出各种出各种情形的种数,再用加法原理求出不同的涂色方法种数。
例2、(2003江苏卷)四种不同的颜色涂在如图所示的 6 个区域,且相邻两个区域不能同色。
精心整理,用心做精品2分析:依题意只能选用 4 种颜色,要分四类:(1)②与⑤同色、④与⑥同色,则有(2)③与⑤同色、④与⑥同色,则有4A ;44A ;4⑥⑤①②③④(3)②与⑤同色、③与⑥同色,则有 4 A ;4(4)③与⑤同色、②与④同色,则有 4 A ;(5)②与④同色、③与⑥同4色,则有 4 A ;4所以根据加法原理得涂色方法总数为 5 4 A =1204例3、(2003年全国高考题)如图所示,一个地区分为 5 个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有 4 种颜色可供选择,则不同的着方法共有多少种?分析:依题意至少要用3种颜色21) 当先用三种颜色时,区域 2 与4必须同色,1 532) 区域3 与5必须同色,故有 3 A 种;443) 当用四种颜色时,若区域 2 与4同色,4) 则区域3 与5不同色,有 4 A 种;若区域3与5同色,则区域2与44 不同色,有 4 A 种,故用四种颜色时共有 244A 种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
排列组合专题之染色问题 【引例】
引例1.在一个正六边形的6个区域栽种观赏植物,如右图,要求同一块中种
同一种植物,相邻的两块种不同的植物.现有四种不同的植物可供选择,则有
________种栽种方案.
引例2.某城市在中心广场建造一个花圃,花圃分为6个部分(如图),现要
栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,
不同的栽种方法有_____种.(以数字作答)
【分析】首先栽种第1部分,有14C 种栽种方法;
然后问题就转化为用余下3种颜色的花,去栽种周围的5个部分(如右图所
示),
此问题和引例1是同一题型,因此我们有必要对这一题型的解法做一深入探讨。
【剖析】
为了深入探讨这一题型的解法,
(1)让我们首先用m (m ≥3)种不同的颜色(可供选择),去涂4个扇形的情形
(要求每一个扇形着一种颜色,相邻扇形着不同颜色),如图所示
以1和3(相间)涂色相同与否为分类标准:
①1和3涂同一种颜色,有m 种涂法;2有m-1种涂法,4也有m-1种涂法,
∴ 共有 (1)(1)m m m ⋅-⋅-种涂法。
②1和3涂不同种颜色,有2m A 种涂法;2有m-2种涂法,4也有m-2种涂
法,
∴ 共有 2(2)(2)m A m m ⋅-⋅-种涂法。
综合①和②,共有(1)(1)m m m ⋅-⋅-+2(2)(2)m A m m ⋅-⋅-432
463m m m m =-+-种涂法。
(2)下面来分析引例1
以A 、C 、E (相间)栽种植物情况作为分类标准:
①A 、C 、E 栽种同一种植物,有4种栽法;B 、D 、F 各有3种栽法,
∴ 共有 4×3×3×3=108 种栽法。
②A 、C 、E 栽种两种植物,有222432C C A 种栽法(24C 是4种植物中选出2
种,23C 是A 、C 、E3个区域中选出2个区域栽种同一种植物,22A 是
选出的2种植物排列),B 、D 、F 共有3×2×2 种栽法(注:若A 、C 栽种同一种植物,则B 有 3 种栽法,D 、F 各有2种栽法),
222432322432C C A ∴⨯⨯⨯=共有种栽法。
③A 、C 、E 栽种3种植物,有3
4A 种栽法;B 、D 、F 各有2种栽法,
∴ 共有 34A ×2×2×2=192 种栽法。
综合①、②、③,共有 108+432+192=732种栽法。
(3)上述(1)、(2)给出了“设一个圆分成P 1,P 2,…,Pn ,共n (n 为偶数)个扇形,用m 种不同的颜色
对这n 个扇形着色(m ≥3,n ≥3),每一个扇形着一种颜色,相邻扇形着不同颜色,共有多少种不同的着色方法”这类问题的一般解题思路:即以相间扇形区域的涂色情况作为分类标准,再计算其余相间扇形区域的涂色种数。
(4)那么,“设一个圆分成P 1,P 2,…,Pn ,共n (n 为奇数)个扇形,用m 种不同的颜色对这n 个扇形
着色(m ≥3,n ≥3),每一个扇形着一种颜色,相邻扇形着不同颜色,共有多少种不同的着色方法” 这类问题的解题思路又如何呢?
【分析】
对扇形P 1有m 种涂色方法,
扇形P 2有m -1种涂色方法,
扇形P 3也有m -1种涂色方法,
…………
扇形P n 也有m -1种涂色方法.
于是,共有1(1)n m m -⋅-种不同的涂色方法。
但是,这种涂色方法可能出现P 1与P n 着色相同的情形,这
是不符合题意的,因此,答案应从1(1)n m m -⋅-中减去这些不符合题意的涂色方法。
那么,这些不符合
题意的涂色方法,又怎样计算呢?这时,把P 1与P n 看作一个扇形,其涂色方法相当于用m 种颜色对n -1(n -1为偶数)个扇形涂色(这种转换思维相当巧妙)。
而用m 种颜色对偶数个扇形的涂色问题,已在上述的(3)中给出了解题思路。
下面,就让我们把这种解题思路应用于引例2.
【分析】
①首先栽种第1部分,有14C 种栽种方法;
②然后问题就转化为用余下3种颜色的花,去栽种周围的5个部分(如右图
所示),
对扇形2有3种栽种方法,
扇形3有2种栽种方法,
扇形4也有2种栽种方法,
扇形5也有2种栽种方法,
扇形6也有2种栽种方法.
于是,共有432⨯种不同的栽种方法。
但是,这种栽种方法可能出现区域2与6着色相同的情形,这是不符合题意的,因此,答案应从4
32⨯中减去这些不符合题意的栽种方法。
这时,把2与6看作一个扇形,其涂色方法相当于用3种颜色的花对4个扇形区域栽种(这种转换思维相当巧妙)。
而用3种颜色的花对4个扇形区域的栽种问题,已在上述的(1)中解决了。
综合①和②,共有1412433[32(2211)]4(4818)430120C C A ⋅⨯-⨯⨯+⨯⨯=⨯-=⨯=种栽法。
(当然此式中的12332211C A ⨯⨯+⨯⨯=18也可以直接用(1)中的公式算出:即 432463m m m m -+-=432343633318-⨯+⨯-⨯=).
【拓展】上面,我们分别就n 为偶数和奇数给出了“设一个圆分成P 1,P 2,…,Pn ,共n 个扇形,用m 种不同的颜色对这n 个扇形着色(m ≥3,n ≥3),每一个扇形着一种颜色,相邻扇形着不同颜色,共有多少种不同的着色方法” 这类问题的解题思路。
那么,这类问题有没有更为一般的解法(即通法)呢?(n 为不小于3的整数)
【分析】设n a 为符合要求的对n 个扇形的涂色方法。
对扇形P 1有m 种涂色方法,
扇形P 2有m -1种涂色方法,
扇形P 3也有m -1种涂色方法,
…………
扇形P n 也有m -1种涂色方法.
于是,共有1(1)n m m -⋅-种不同的涂色方法。
但是,n a ≠1(1)n m m -⋅-,因为这种涂色方法可能出现P 1
与P n 着色相同的情形,这是不符合题意的,因此,答案应从1(1)n m m -⋅-中减去这些不符合题意的涂色
方法。
那么,这些不符合题意的涂色方法,又怎样计算呢?这时,把P 1与P n 看作一个扇形,其涂色方法相当于用m 种颜色对n -1个扇形涂色(这种转换思维相当巧妙),不同的涂色方法有1n a -种,于是,有 n a =1(1)n m m -⋅--1n a -(n ≥3),①. 显然,3(1)(2)a m m m =--.
上述的式①就是数列的递推公式,由此,我们就可以推导出n a 的通项公式:
n a =(1)(1)(1)(3)n n m m n -+--≥.
至此,我们就找到了“设一个圆分成P 1,P 2,…,Pn ,共n 个扇形,用m 种不同的颜色对这n 个扇形着色(m ≥3,n ≥3),每一个扇形着一种颜色,相邻扇形着不同颜色,共有多少种不同的着色方法” 这类问题的通项公式:即n a =(1)(1)(1)(3)n n
m m n -+--≥.
【注意】上述问题中的m 种颜色是可供选择的,而不是全部都要用上的。
【迁移练习】
1.某城市在中心广场建造一个花圃,花圃分为6个部分(如图),每部分
栽种一种且相邻部分不能栽种同样颜色的花,现有5种不同颜色的花可供选
择,则不同的栽种方法有_____种; 若要求5种不同颜色的花全部栽种,则
不同的栽种方法有_____种.(以数字作答)
2.在一个正六边形的6个区域栽种观赏植物,如右图,要求同一块中种同一
种植物,相邻的两块种不同的植物.现有四种不同的植物可供选择,则有
________种栽种方案;若要求四种不同的植物全部栽种,则有________种栽种
方案.
【答案】1.1200,600; 2.732,480。
